Matematiken|Ekvationsläran II — Universums Historia

EKVATIONSLÄRA II — UNIVERSUMS HISTORIA | a production 2008XII22 | Efter sammanställningar från 1986VI | Senast uppdaterade version: 2018-12-27 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Polynomdivision | Iterationsteknik | Graflära | KALKYL_0-3 2005XII | i sammanställning för Universums Historia

andragradsekvationen

POLYNOMDIVISION

kompletterande deldokument ENLIGT RELATERAD MATEMATIK till EKVATIONSLÄRAN i DEN HÖGRE ANALYSEN

Polynomdivisionens begrepp utgår ifrån Divisionsalgoritmen (DIAL) från Grundmatematiken

TÄLJARE

————— = KVOT + Rest/Nämnaren

NÄMNARE

EKVATIONSLÄRANS GRUNDSATSER ENLIGT RELATERAD MATEMATIK

Grundbegrepp

POLYNOMDIVISION används med fördel i studiet av Den Högre analysen (integralkalkylen i vidare mening) — i samband med faktorisering och lösandet av rötterna till en ekvation. Framställningen nedan beskriver exemplifierat hur polynomdivision går till med grund i DIVISIONSALGORITMEN; den beskrivs här från grunden med enkla räkneexempel.

Två scheman för division

Det finns (främst) två olika scheman eller metoder man kan använda som hjälp för uppställningen av en division och som starkt underlättar hela förfarandet. Bägge bygger på den enda och samma princip som ovanstående grundsamband uttrycker.

Metodernas användning i gängse litteratur

Gymnasiematematiken (serie 2000 [NoK, Björk 1996], samt även ITK [Brandqvist 1961-1962]) tycks mest intresserad av positiva metoden. Matematiklexikon [W&W 1991, Se divisionsalgoritmen s91sp1ö] använder emellertid den negativa metoden.

Bägge sätten är ungefär lika krångliga att komma ihåg, och lika lätta att glömma av.

ENBART av de enkla exemplen framgår omedelbart den positiva metodens nackdel: man måste justera nämnarens placering till höger efter det utrymme som resultaten kräver. Men resultaten kan man ju inte veta på förhand! I den negativa metoden DÄREMOT löper alla resultat direkt LOGISKT (västerlandet) i nedåtgående och obegränsad utsträckning, »så långt papperet räcker»

— den negativa metoden är därmed naturligt synnerligen lämpad för längre divisioner.

Bägge metoderna ger emellertid samma resultat. Har man redan vant sig vid sitt eget sätt och finner detta det mest bekväma finns ingen anledning att införa någon ändring på den punkten. Av skälen ovan används emellertid här genomgående den negativa metoden.

Divisionen (exemplifierat)

T 100 + 50 + 15

—— = ——————— = 10 + 1 = 11

N 10 + 5

utförs förnämligt genom att arbeta på en av nämnarens termer. Vilkensom går på ett ut; Resten sköter sig själv — BLOTT vi behandlar resttermen på korrekt sätt.

Divisionen enligt negativa metoden blir i fallet ovan

KVOT .

NÄMNARE | TÄLJARE

divisor | dividend

- - - - - - - - - - - -

resultaträkning ¯

10 + 1 (1)

10 + 5 | 100 + 50 + 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)

–(100 + 50 (3)

0 + 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (4)

–( 10 + 5 (5)

0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (6). Rest 0. KLAR.

Utförlig beskrivning med förklaring

Vi ser efter hur många gånger (K) nämnarens första term (10) ryms i täljarens första (största) term (100). Svaret blir ”10 gånger”. Vi skriver in ”10” på rad 1 (kvotraden) ovanför ”100”. Vi multiplicerar sedan KN = 10(10 + 5) och skriver in resultatet på rad 3, rakt under täljartermerna på rad 2. Nu utför vi den centrala subtraktionen. Vi drar (3) från (2) och för ner summan eller resten (R) på rad 4. Denna sekvens utgör den egentliga divisionsfasen i hela uppställningen ;

T–KN = R som motsvarar (100 + 50 + 15) – (100 + 50) = 15.

Vi behandlar sedan resten (R=15) på rad 4 som en ny täljare och börjar om från början igen!

Vi utför exakt samma procedur:

Vi ser efter hur många gånger (K) nämnarens första term (10) ryms i restens första (största) term (15) [Vi kan uppfatta att resten från början är T eftersom NK då =0]. Svaret blir ”en gång”. Vi håller hela tiden koll på tecknen ± som bestäms av R/N i varje fas. Vi för in resultatet ”+1” på kvotraden (rakt ovanför motsvarande algoritmterm så blir det enklare att studera och kontrollera). Vi multiplicerar sedan på vanligt sätt (KN = 1[10+5] = 10 + 5), vi för in resultatet ”10+5” på rad 5, och utför den centrala subtraktionen T–KN med resultatet (R) på rad 6. Här gick skillnaden i noll och därmed ingen rest. Således resultatet totalt K = 10 + 1 = 11.

Prövar vi resultatet finner vi 11(10+5) = 11·15 = 165 vilket vi ser stämmer utmärkt med det givna värdet på täljarens T = 100 + 50 + 15 = 165.

exempel

polynomdivision

DIVISION MED POLYNOM utförs på samma smidiga sätt:

Exempel 1

Betrakta kvoten

T x²

—— = ———

N x² – 1

Försök sönderdela kvoten så att graden i täljaren blir lägre än graden i nämnaren.

Lösning:

Vi tillämpar negativa metoden för division och får

KVOT .

NÄMNARE | TÄLJARE

divisor | dividend

- - - - - - - - - - - -

resultaträkning ¯

1 .

x² – 1 | x²

–(x² – 1

+ 1 .................................. Rest 1 ® Vi kommer ihåg att T/N = K + R/N;

;

T x² 1

Svar : —— = ———— = 1 + ————

N x² – 1 x² – 1

Kontrollräkning via GNGEMENSAM NÄMNARE enligt

(x²–1 + 1)/(x²–1) = x²/(x²–1). Lösningen verifierad.

Förklaring

Första delen ges direkt av kvoten x²/x² = 1 [första (största) nämnarfaktorn]/[första (här enda) täljarfaktorn].

Vi för upp detta resultat 1 i kvotraden. Vi multiplicerar sedan nämnaren med kvotvärdet K vilket ger oss

KN =1·(x²–1)=(x²–1). Subtraktionen T–KN=R ger oss så resten

x²

– (x²–1)

= 1.

Stannar vi här betyder resttermen 1 en total restterm tillsammans med N via R/N enligt 1/(x²–1);

Med grundformen T/N = K + R/N har vi alltså funnit (del-)resultatet:

x²/(x²–1) = 1 + 1/(x²–1).

KOMMENTAR

Det finns ingen som helst begränsning i vad som kan åstadkommas med detta (synnerligen enkla) verktyg.

Vi har visst och sant (oftast) ingen (större) användning av DIAL numera — vid rena sifferräkningar. Kalkylatorer och datorer tar hand om det mesta av det rutinjobbet. Manuella Polynomdivisioner däremot har (ännu) inte (helt) försvunnit in i den lilla kalkylatorns rutiner och vi har därför (fortfarande, 2005 — och ännu 2008) STOR användning av divisionsalgoritmen.

Men även om den dagen kommer, är det hur som helst alltid stimulerande att kunna utföra till synes »hopplösa» divisioner med osviklig träffsäkerhet och exakthet. För att förklara matematiken på högre nivå är DIAL oundgänglig.

ORDNINGEN VID POLYNOMDIVISION och övriga

Som vi redan observerat kan man utföra divisionerna med givna termer i vilken som helst ordning, analogt med preferens på vilken som helst term, bara man kommer ihåg att behandla den viktiga resttermen på korrekt sätt.

Den mest effektiva metoden (i allmänhet) är att alltid utföra operationerna (främst) på de största värdemängderna (vilket ger det snabbaste resultatet).

Exempel 2

T Ax³ – Bx² + Cx – D

—— = —————————

N ax³ – bx² – cx – d

De bägge polynomen i täljare (T) och nämnare (N) är i ovanstående kvot helt ordnad efter fallande grad. Uppställningen utgör därmed också den mest optimala ordningen för divisionsalgoritmen.

Ställer man upp termerna efter denna inbördes fallande ordning blir det också mycket enklare att utföra de nödvändiga resultaträkningarna (varje variabelgrad får sin särskilda kolumn).

Att en division mellan två polynom kan vara en ytterst fruktbärande handling att utföra för att åstadkomma en (eventuell) förenkling i hanteringen av ett matematiskt uttryck visar följande formella exempel.

Uppgift:

[ref. ITK 4 (Algebra II), Brandqvist 1961, s9-10].

Författaren i referensen ovan använder genomgående den positiva metoden — och han har också tydliga problem med att klargöra tydligheten i de uppställningarna (han försöker förtydliga med olika pek-pilar). Här använder vi den negativa metoden som inte har några sådana begränsningar.

Utför divisionen i nedanstående kvot mellan de bägge polynomen i T och N.

T 6x² + 1 + 7x + 6x⁴ + x³

—— = ———————————

N x³ + 1 + x

Lösning

Vi ordnar först polynomen efter fallande gradtal.

T 6x⁴ + x³ + 6x² + 7x + 1

—— = ———————————

N x³ + 1 + x

Vi utför sedan divisionen enligt den negativa metoden

Vi börjar sedan divisionen med att betrakta första kvoten 6x⁴/x³ = 6x. Vi avancerar sedan till andra kvoten som ger x³/x³ = 1. Vi får

KVOT .

NÄMNARE | TÄLJARE

divisor | dividend

- - - - - - - - - - - -

resultaträkning ¯

6x + 1

x³ + x + 1 | 6x⁴ + x³ + 6x² + 7x + 1

–(6x⁴ + 6x² + 6x

x³ + x + 1

–( x³ + x + 1

0 ..................................... Rest 0. KLAR.

Kontrollräkning: (6x + 1)(x³ + x + 1) = 6x⁴ + 6x² + 6x + x³ + x + 1 = 6x⁴ + x³ + 6x² + 7x + 1.

Lösningen verifierad.

T 6x⁴ + x³ + 6x² + 7x + 1

Svar: —— = —————————— = 6x + 1

N x³ + x + 1

Iterationsteknik

ITERATIONSTEKNIK

ITERATIONSTEKNIK MED GRAFLÄRA

Hur man löser reella och imaginära rötter

Exempel: Bestäm rötterna till funktionen

y = x³ – 3x – 2

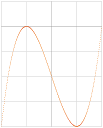
Funktionens nollställen

y = 0 = x³ – 3x – 2

definierar funktionens s.k. rötter,

analogt skärningspunkterna med x-axeln.

Här SER vi x-skärningarna DIREKT som respektive x=–1 och x=2.

Kontroll på funktionssambandet genom direkt huvudräkning, visar att observationen är korrekt.

Resultatet blir i bägge fallen y=0.

Svar: Rötterna är x=–1 (en dubbelrot, funktionens parabeldel) och x=2 (en singelrot, funktionens linjedel, se vidare nedan):

Antalet engradiga faktorer (rotparenteser) i funktionens polynom är alltid lika med högsta gradtalet, här 3. Rotvärdet för varje rotparentes (x+a) bestäms x+a=0; x=–a, –a är rotvärdet eller (x+a)-faktorns rot.

FAKTORISERINGEN av transformenen blir då:

x³ – 3x – 2 = (x+1)²(x–2) = x³ + 2x² + x – 2x² – 4x – 2.

Funktionskurvan kan alltså skrivas likvärdigt

y = (x–2)_LINJEN[(x+1)² + 0]_PARABELN.

ROTVÄRDET

betyder stället där variantens, transformens eller funktionens värde (y) tangerar/skär x-axeln, ett s.k. nollställe.

Komplexa nollställen är s.k. imaginära nollställen

x=a±iÖ|b|, a anger »kurvVändningsStällets» x-koordinat, se även illustrerat nedan, |b| anger y-koordinat

enligt

alltid +

(x – a_x)² + b_y som medför att x = a_x ± Ö –b_y = a_x ± iÖ |b_y|, absoluttecknet garanterar + i roten

a_x ................. imaginärrotens x-koordinat

b_y ................. imaginärrotens y-koordinat

vilket betyder att rotkurvan som alltid är en parabel [(x – a_x)²+ b_y] INTE skär x-axeln på något enda ställe.

—————————————————————————————————

Se även ROTKARTAN som (förenklat) visar rotfallen för polynomgrad 2.

—————————————————————————————————

Från föregående exempel kan vi enkelt generera en funktion med komplexa rötter

— helt enkelt genom att flytta upp högra avrundningen (se föregående kurvfigur) ovanför x-axeln.

Vi studerar först den enkla grafiska lösningen och sedan en mera noggrann.

Exempel: Bestäm rötterna grafiskt till funktionen

y = x³ – 3x + 3

Lösning:

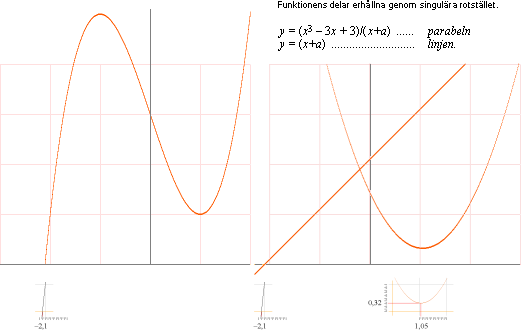
GRAFISKT från funktionskurvans uppritning vänster läser vi direkt av ett rotvärde x=–2,1 från en typfaktor (x–a) som ger

a=2,1

Vi dividerar sedan funktionen med den så erhållna linjen (x+a) som hade roten x=–a enligt y = (x³ – 3x + 3)/(x+a), se POLYNOMDIVISION; Se även efterföljande utvecklingsexempel i polynomdivision, där visas hur uppgiften löses i detta fall. Det ger den återstående parabeln där vi direkt approximerat kan avläsa det komplexa nollställets koordinater x=1,05 och y=0,32, bilden till höger ovan underst.

Funktionskurvan kan alltså skrivas likvärdigt men approximerat

y = (x+2,1)_LINJEN[(x–1,05_x)² + 0,32_y]_PARABELN = (x+a)[(x – a_x)² + b_y]

Svar: Rötterna är alltså approximativt
x=–2,1 för linjedelen och
x = a_x ± iÖ |b_y| för parabeldelen med a_x = 1,05 och b_y = 0,32.

Vi studerar hur de approximativt erhållna rötterna kan lösas mera numeriskt exakt.

ARITMETISK LÖSNING AV RÖTTERNA GENOM ITERATION

Forts. föregående exempelfunktion y = x³ – 3x + 3

ARITMETISKA ROTLÖSNINGEN FÖR x.

Om vi undersöker y-formen [x³ – 3x + 3] i fallet =0 ser vi att det finns ett antal olika sätt att skriva x på. OM en sådan skrivning x:=f(x) ligger så belägen i xy-planet att den

1. skär ITERATORN — se illustrationen nedan — y=x i P(x;y) med

2. tangenten i P inom ±45° relativt x-axeln,

DÅ är aritmetiska funktionsvärdet för y=x SJÄLVGENERERANDE med början från x=0 eller 1. Illustrationen och exemplen nedan visar principen.

Graferna nedan visar hur vi UR x³ – 3x + 3 = 0 får fram ett godtyckligt noggrant värde för den första roten ur iterationsfunktionerna respektive (vilkensom)

y = Ö 3(1 + 1/x) eller

y = [3(1 + x)]^1/3 med y = x.

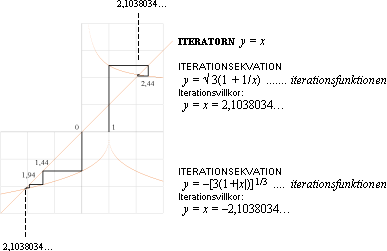
Iterationskurvorna genom den centrala ITERATORN y=x som OBS bara omfattar kvadranterna I och III. Med lämpligt preparerad funktionsform, självgenereras rotvärdet med successiva beräkningar eller ”varv” genom funktionen. Figuren ovan visar hur Iteratorn ser till att värdet ”snäpper exakt” i rotpunkten.

Som framgår i rotexemplet (ellipsfunktionerna i samband med atomvikterna) kan vi ta ut själva funktionens byggnad ur negativa rötter — som om de vore positiva. Därmed kan vi också generellt använda rötter för att beräkna negativa rotuttryck genom positiva värdeformer;

Med funktionen x³ – 3x + 3 = 0 = x³ – 3(x + 1) ges

x³ = 3(x–1);

x = [3(x–1)]^1/3

Men denna funktion (Kvadrant I) kan bara ge positiva resultatvärden (y). För att få negativa x=y måste funktionen roteras motsvarande 180° (multiplikation med i²) så att man får samma funktion i Kvadrant III på ekvationen

y = –[3(x+1)]^1/3

;

Vi frånser då minustecknet i början och utför iterationen y=x regelrätt positivt med hjälp av en enklare teknisk räknare enligt

x = [3(x+1)]^1/3 = 2,1038034 , iterera från x=0;

[3]^1/3+1)3]^1/3+1)3]^1/3+1)3]^1/3… , tills resultatet inte ändras mer enligt önskad precision;

1,44…; 1,94…; 2,06…; 2,09…; 2,10…; 2,1033…; 2,103706…; 2,103781… 2,103798…; 2,1038023…; 2,1038034… .

Resultat:

–x = –y = 2,1038034

Man måste alltså göra den till synes omständliga omvandlingen

(–y)³ = (–x)³ = 3(x+1) ;

(–x)³ = 3(x+1) = –x³ ;

–3(x+1) = x³ = – 3x – 3 ;

ALTERNATIVT kan samma rot också erhållas genom omskrivningen av grunduttrycket

x³ – 3x + 3 = 0 till

x(x² – 3) + 3 = 0

som ger

x² – 3 = –3/x ;

x² = 3–3/x = 3(1–1/x) ;

x = Ö 3(1–1/x)

med den omvända iterationsfunktionen y=x för att få positivt x i Kvandrant I enligt

y = Ö 3(1+1/x)

Iterera från x=1, börja bakifrån Ö6 och läs ledet mot början …

Ö 3(1+1/Ö 3(1+1/Ö 3(1+1/Ö6, tills resultatet inte ändras mer enligt önskad precision;

2,44…; 2,055…; 2,111…; 2,1025…; 2,1040…; 2,1037…; 2,1038087; 2,1038025; 2,1038035; 2,1038033; 2,1038034… .

Resultat:

–x = –y = 2,1038034

Man måste alltså också här göra den till synes omständliga omvandlingen

y² = x² = 3(1+1/x)

x² = (1/x)3(x+1);

x³ = 3x+3; x³ – 3x – 3 = 0

Resultat:

x = a = – 2,1038034…, singulära reella roten i y = x³ – 3x + 3.

Vi ska nu se hur vi från detta resultat också kan få fram lika noggranna värden för den återstående imaginärrotens bägge koordinater.

ARITMETISK LÖSNING AV RÖTTERNA GENOM ITERATION

Forts. föregående exempelfunktion y = x³ – 3x + 3

Från den nyssnämnda iterativa alternativfunktionen

x = Ö 3(1–1/x)

och den erhållna roten

x=a=– 2,1038034

som ger

a = Ö 3(1–1/a)

a² = 3 – 3/a

har vi ekvivalenterna

(a² – 3) = 3/a = b för vidare utveckling längre ner, referens ges hit därifrån; x(a² – 3) = xb

Ur denna ekvivalent kan lösningens två övriga rötter utvecklas.

DIVISION MED LINJEN (x–a) i y=x³–3x+3 betyder att linjen tas bort och bara parabeln kommer fram. Därmed kan koefficienterna för de två återstående imaginära rötterna bestämmas. Divisionen sker genom

POLYNOMDIVISION

se från Divisionsalgoritmen om ej redan bekant

referensexempel

enligt

T x³ – 3x + 3

—— = ——————

N x – a

a = – 2,1038034 [från föreg. iteration med negativt a i a² =3(1+1/|a|) med startvärde a=1]

Vi utför divisionen enligt den negativa metoden. Första kvoten ger x³/x = x².

Erinra den enkla lagen för divisionsalgoritmen: ta EN term ur N, summera på Resten.

KVOT .

NÄMNARE | TÄLJARE

divisor | dividend

- - - - - - - - - - - -

resultaträkning ¯

x² + ax + b

x – a | x³ – 3x + 3

–( x³ – ax²

® ax² – 3x + 3

–( ax² – a²x

® a²x – 3x + 3 .................. vi har (a²x – 3x) = x(a² – 3) = x·b

® bx + 3 .................. b = (a² – 3) = 1,4259887… (= 3/a)

–( bx – ba

® – ba + 3 .................. ska bli noll! Stämmer! Rest 0. KLAR.

Resultat

x³ – 3x + 3

————— = x² + ax + 3/a

x – a

(x³ – 3x + 3) = (x – a)(x² + ax + 3/a) = (x–a)[b_y+ (x – a_x)2] med –(a/2) = a_x = 1,0519017 …

De två återstående rötterna — Se ANDRAGRADSEKVATIONENS LÖSNING —

blir

–(a/2)±Ö–b_y med iÖ|b_y| = Ö|(a/2)²+3/a| = Ö |b_y= 0,3194386|.

— Se ANDRAGRADSEKVATIONENS LÖSNING i ROTKARTAN

Genom ett grafritande program kontrollerar vi att resultaten överensstämmer — så att inga galna felskrivningar har smugit sig in.

Den mera fullständiga lösningen kan då skrivas enligt Svar nedan:

Svar: Rötterna till funktionen y = x³ – 3x + 3 är med sju decimalers noggrannhet

x = –2,1038034 ................... för linjedelen och
x = a_x ± iÖ |b_y| ...................... för parabeldelen med

a_x = 1,0519017 och

b_y = 0,3194386
med det komplext konjugerade rotparet eller komplexa rötterna
x = 1,0519017 ± i 0,5651889

OM DET GÄLLER ENSTAKA (kritiska, avgörande) ANALYSER:

Använd med fördel ovanstående exempel som MALL för alla övriga problem som rör lösningen av polynomAtomen y=(linje)(parabel).

GRAFLÄRA OCH GRAFRITANDE PROGRAM

GRAFLÄRA

ENLIGT RELATERAD MATEMATIK

Följande refererar bara till Windows programmiljö — jag vet inte (exakt) vad som finns i andra operativsystem

— Macintosh OperativSystem (Mac OS X v10.4) har, enligt uppgift, ett extremt snyggt grafritande program (Grapher)

Ett (relativt enkelt) grafritande gratis program (men på engelska med svenska menyer)

— som inte överfaller en med ”tusentals funktioner” och därigenom bara verkar avskräckande för nybörjaren

— finns på

[http://www.padowan.dk/graph/Download.php] (2007),

Ivan Johansen

Funktionen skrivs in via tangentkommando Ins [efter vissa regler … typ sinx som sin(x) och x² som x^2], ett separat fönster öppnas och man verkställer med Enter. Presentationen är enkel och tydlig; I Hjälpen finns tydliga förteckningar över de funktioner som programmet stödjer, samt hur man skriver indata.

Använd det (eller annat som passar) för att få grundläggande uppfattning om hur en viss funktion verkligen ter sig i praktiken — eller använd ”traditionella medel”; kalkylator, rutat papper, penna, räkna ut punktvärden och skissa upp grafen manuellt.

— Programmet saknar dock RUTNÄT.

Jämför (det här är vad ett grafritande datorprogram bör kunna/innehålla minimum):

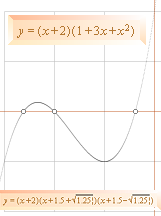
RUTNÄT (Jämför: försök rita en graf på ett papper utan rutnät: det går inte) är ytterst värdefullt vid allmän utvärdering av olika funktioners enkla (elementära) rötter (och skärningar). Man kan i många fall se direkt om det lönar sig att anställa en viss ansats på en viss funktion som rent visuellt uppvisar synbarliga enhetsskärningar (typ grafen ovan); Enkla algebraiska prövningar härifrån ger (oftast) direkta resultat.

Det grafritande program jag själv använder (Test2002),

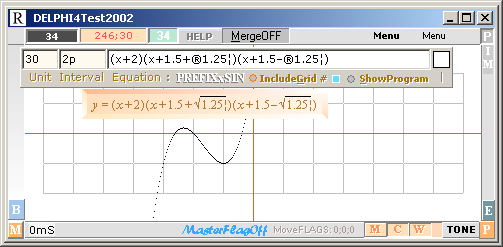
har integrerade bildbehandlingsrutiner — jämför föregående bild, det är samma kurva men gjord från ett original med enheten 200 pixel och därifrån förminskad genom elementär men avancerad bildbehandling för snygg presentation. Men det är mitt eget program — utformat under åren för att få fram det man verkligen önskar av ett grafritande program — och som jag mer och mer upptäcker på webben att de grafritande program som ändå finns (gratis), samtliga, tycks sakna: enkelheten. En ruta för funktionen, enheten, intervallet, Enter, färdigt. Tydlig display.

— Rutnätet är ett måste — finns det inte är det som att någon ”har knyckt ratten från bilen”: det GÅR att köra (med hjälp av en lånad skiftnyckel) — men det är inget vidare kul att köra den bilen.

— Men kan inte du låta oss få ta del av ditt grafritande program då?

— Oh, såå gärna. Problemet är bara att »mitt program» innehåller »alla program»; det finns dessutom inga (vanliga) menyer, knappast ens en enda verktygsknapp, allt sköts från tangentbord (höger hand) och mus (vänster hand) på rityta och genom att minnas kortkommandon från utförliga manualer i separata ordbehandlingsdokument; enklast tänkbara kortkommandon som (alltså) är enkla att komma ihåg; mest logiska tangenter och musknappar — ALLT enligt MIN uppfattning. Jag är inte säker på att DET är vad du söker. Dessutom: För att SÄKERT kunna köra programmet (och dessutom ändra i det, om du så skulle vilja) krävs att DELPHI 4 (ett gratisprogram från Borland som gavs ut av datortidningar i slutet på 1990-talet) finns installerat på datorn; Men DELPHI 4 kompilerar inte i Windows Vista, bara i Windows XP — och Windows 95 — och de finns inte längre i marknaden, det går dock att köra programmet i Vista — men då med äventyr som varken jag eller någon annan (veterligt) kan svara för. Tyvärr. Dessutom vandaliserar Vista vissa displaydelar (de fragmenteras) på grund av Vistas multiplexsystem — visserligen bara en visuell petitess, men ändock en vandalisering. Det är det tråkiga facit.

Innebörden av termen graflära visar sig PRAKTISKT FÖRST när man tecknat upp sin allra första funktionskurva — någonsin, från en given matematisk form och verkligen SER hur den ser ut; — Aha, var det SÅ den såg ut. Det är graflära. Därifrån växer kunskapen med ytterligare studier. GRAFLÄRAN är — således i den här presentationens ljus — en personlig, individuell, gren i matematiken och kan aldrig »läras ut generellt»: det finns tusentals och åter tusentals ”elementära grafer”, men var och en av oss kommer att utvecklas på sin egen väg — och därmed samla ett unikt erfarenhetsområde som knappast någon annan har.

Tillämpningar, se nedan.

Tillämpningar i graflära

FAKTORISERINGSEXEMPEL med graflärans hjälp

Exempel 1:

På @INTERNET Wikipedia Partial fraction 2009-01-02 PRESENTERAS ett polynomled i en nämnare enligt typformen

—————————

x³ – 11x² + 40x – 48

OM uppgiften gäller att uppdela bråket i partialbråk:

— Vi måste först kunna lösa uppgiften att FAKTORISERA nämnaren (x³ – 11x² + 40x – 48) i (enskilda) parentesfaktorer.

Men hur gör man det?

— Det är GARANTERAT nybörjarens allra första och största problem:

— Jag fattar inte ett dyft av hur man ska närma sig det problemet.

— Hur gör man?

Kolla:

GRAFEN y=(x³ – 11x² + 40x – 48) ser ut så här

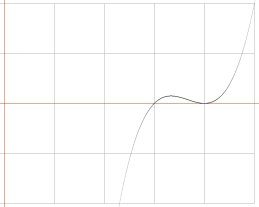
— JAHA. Var det SÅ enkelt.

— Minsann. Rötterna — ställena där kurvan skär x-axeln — är tydligen bara två: x={3, 4}.

— Och alltså skulle det gälla — om allt stämmer — att

(x–3)(x–4)² = x³ – 11x² + 40x – 48;

Vi kollar upp det:

(x–4)² = x² – 8x + 16;

(x–3)(x² – 8x + 16) = x³ – 8x² + 16x –3(x² – 8x + 16)

= x³ – 8x² + 16x –(3x² – 24x + 48)

= x³ – 8x² + 16x –3x² + 24x – 48

= x³ – 11x² + 40x – 48

Lösningen verifierad.

— Men vänta nu fröken IQ, hur visste du att den högra roten skulle var den med multipliciteten 2?

— Därför att jag redan, via grafläran, VET att kurvtypen ovan i högerdelen gömmer motsvarande parabeldel — som alltid optimerar två symmetriska rötter — och det är den som (därför) bör innehålla dubbelformen. Kontrollräkningen visade också att så är fallet. Genius, vet du väl.

Resten av problemet bör inte vara någon svårighet med kännedom om PFECD.

Exempel 2:

I samma källa som den nyssnämnda ovan (se Exempel 1) PRESENTERAS OCKSÅ UTAN HÄRLEDNING en polynomNämnarfaktor x³ – 8 via bråktypen

———

x³ – 8

På samma sätt skulle (med största sannolikhet) även här en nybörjare förtvivla och utbrista,

— Jag fattar inte.

— Hur gör man? Hjälp MIG.

GRAFEN hjälper direkt enligt

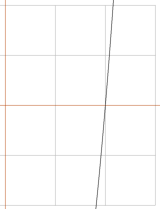
— eller direkt via ekvationen (se Potenslagarna)

x = 8^1/3

= 2 ;

Det finns bara en rot att välja på, x=2, och därmed en polynomfaktor (x–2);

Polynomfaktorn (x³ – 8) som sådan kan då sönderdelas genom en polynomdivision enligt

T/N=K=(x³ – 8)/(x – 2):

KVOT .

NÄMNARE | TÄLJARE

divisor | dividend

- - - - - - - - - - - -

resultaträkning ¯

x² + 2x + 4

x – 2 | x³ – 8

–( x³ – 2x²

® 2x² – 8

–( 2x² – 4x – 8

® 4x – 8

–( 4x – 8

® 0 ............. Rest 0. KLAR.

Resultat

x³ – 8

——— = x² + 2x + 4

x – 2

Kontrollräkning

(x – 2)(x² + 2x + 4) = (x³ + 2x² + 4x) – 2(x² + 2x + 4)

= x³ + 2x² + 4x – 2x² – 4x – 8

= x³ – 8

Lösningen verifierad.

FAKTORN (x³ – 8) har alltså ekvivalenten — faktoriseringen —

(x³ – 8) = (x – 2)(x² + 2x + 4)

Tillämpningar i graflära

Bråkets Elementära Atom

OCH DESS MOTSVARANDE reella PARTIALBRÅKSUPPDELNING

1 1

————————— ................................. Faktoriseringspolynomets Elementära Atom = ——————

(Cx+D)(Ax²+Bx+E) (linje)(parabel)

Exemplet nedan visar hur andragradsfaktorn (x²+3x+1) kan uppdelas i två reella engradiga faktorer (x+a)(x+b) med graflärans hjälp — under förutsättning att parabeln har någon gemensam del med x-axeln. I annat fall kan en sådan uppdelning inte göras med reella faktorer. Hur ett sådant bråk kan uppdelas visas i Parabelfaktorns komplexa lösning.

Exempel:

————————

(x+2)(x2+3x+1)

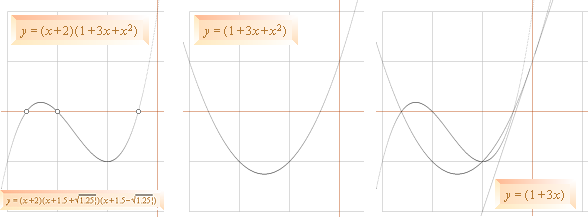
Lösning:

Frånsett möjligheten att direkt utnyttja andragradsekvationens lösning:

Vi ser direkt att första nämnarfaktorn (x+2) ger en rot x=–2, den framgår också direkt genom grafläran, funktionsgrafen ovan vänster, mittpunkten.

Vi tar tillfälligt bort (x+2) (enhetssuspension; vi sätter den tillfälligt lika med ett) och studerar återstoden, grafen ovan mitten; Vi frånser tills vidare vertikalplaceringen (+1); Funktionen (3x+x²) framställer först och främst ett tangentvillkor som här dock inte explicit är avgörande för analysen men kan vara bra att känna till ändå; parabeln x² och linjen 3x har en, och endast en, gemensam funktionsvärdespunkt (y), nämligen y=0 via x=0, vilket också är den kvalitativa definitionen för parabelns tangent.

Vi kan lösa ut parabelns nollpunkt (y-derivatan) och därmed få fram nivåskillnaden till motsvarande x-skärningar, analogt de rötter vi söker:

y’ = (1+3x+x²)’ = 0+3+2x = 0 ;

x = –3/2;

y = (1+3x+x²) = (1+3[–3/2]+[–3/2]²) = 1 – 9/2 + 9/4 = (4 –18 + 9)/4 = (4 – 9)/4 = – 5/4 = –1,25 ;

För den isolerade parabeln y=x² gäller alltså

y = x² = +1,25 som ger

x = Ö 1,25

De bägge återstående sökta rötterna ligger alltså symmetriskt ±Ö 1,25 kring y-axeln på parabeln x². Med originalgrafens förskjutning på –1,5 ges alltså

de sökta två återstående rötterna

xHÖGER = –1,5 + Ö 1,25 = –0,381966 » –0,38 = b

xVÄNSTER = –1,5 – Ö 1,25 = –2,6180339 » –2,62 = a

Motsvarande faktorer således (x+a)(x+b) enligt totalt

1 1 1

———————— = ———————— = ——————————————

(x+2)(x²+3x+1) (x+2)(x+a)(x+b) (x+2)(x+1,5+Ö 1,25)(x+1,5–Ö 1,25)

MED VIDARE FORTSÄTTNING kan sista bråket partialuppdelas på vanligt sätt enligt metoden i PFECD som

1 A B C

———————— = ———— + ———— + ————

(x + 2)(x + a)(x + b) (x + 2) (x + a) (x + b)

A = 1/(x + 2)(x + a)(x + b) ¦x=–2¦ = 1/(–2 –1,5 – Ö 1,25)(–2 –1,5 + Ö 1,25) = 1/([–3,5]² – 1,25) = 1/11

B = 1/(x + 2)(x + a)(x + b) ¦x=–a¦ = 1/(1,5 + Ö 1,25 + 2)(1,5 + Ö 1,25 – 1,5 + Ö 1,25 ) = 1/(7Ö 1,25 + 2,5)

C = 1/(x + 2)(x + a)(x + b) ¦x=–b¦ = 1/(1,5 – Ö 1,25 + 2)(1,5 – Ö 1,25 – 1,5 – Ö 1,25) = 1/(–7Ö 1,25 + 2,5)

BIHANG Partialbråksuppdelning | Parabelfaktorns komplexa lösning

Parabelfaktorns ax²+bx+c komplexa lösning

UPPDELNING AV komplexa BRÅK I PARTIELLA DELBRÅK

Se även Andragradspolynomets reducerbarhet i modern akademi.

Tillägg 2009-01-03

Se även i DEN KOMPLEXA FAKTORISERINGENS Singulära GRUNDKOMPONENT

Betrakta polynomfaktorn P(x)=N

P(x) = N = (x² + 2x + 4) = x² + 2x + 1 + 3

= (x + 1)² + 3

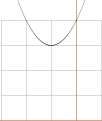
y = (x + 1)² + 3

Denna parabel saknar helt kontakt med x-axeln; N kan varken uppdelas på eller uttryckas i enkla enskilda parentesfaktorer av typen (x±a) eftersom de komplexa rötterna här har typlösningarna (x + a ± iÖb).

— Hur löser man en sådan partialbråksuppdelning?

Låt oss först se efter HUR vi säkert kan veta att en given andragradens P(x) verkligen ansluter till denna typ:

1. [P(x)]’ = 0 — polynomets nollderivata — ger parabelkurvans enda lägsta punkt

— vi huvudräknar derivatorna som vi känner från Bastablån i Formlagarna, generellt via positionsformen dy/dx=(y₀–y)/dx som i fallet y₀=y=konstant=C ger (y₀–y)/dx=0/dx=0=C’;

(x² + 2x + 4)’ = 2x + 2 = 0;

2. Vi löser ut x ; x = –1; Vi beräknar minsta y för bottenpunkten via x ;

3. y(–1) = ([–1]² + 2[–1] + 4) = 1 – 2 + 4 = 3 ....................... lägsta funktionsvärdet

Om prövningen ovan ger ett lägsta värde som är större än 0 är polynomet av den komplexa typen (se rotkartan).

I detta fall blev värdet +3 — och därmed en polynomfaktor med inre komplexa rötter.

Det finns två olika sätt att lösa en relevant partialbråksuppdelning i dessa fall, bägge med samma resultat:

1. LÖSNING GENOM LOGARITMINTEGRALENS INTEGRAND

2. LÖSNING GENOM PFECD

LÖSNINGEN GENOM LOGARITMINTEGRALENS INTEGRAND

»Partialbråksuppdelning» av den isolerat enskilda integranden

N = (ax²+bx+c)^–1

har generellt sett ingen rationell (logisk) lösning; Genom logaritmderivatan Dn ln(P) = Dn(P)/(P) ges (nämligen, se Bastablån) närmast rationella bråkform där N-typen ovan ingår enligt (P) = 1/N på formen

2ax + b

————— = Dn(P)/(P)

(ax²+bx+c)

Bråket ovan utgör alltså en (integral) grundform och har ingen ytterligare upplösning.

Integralformen för det enskilda bråket som sådant (ax²+bx+c)^–1 tillhör kategorin »mera komplicerade integraler», den ingår inte i basfunktionerna.

— Webben innehåller f.ö. flera ställen som dels visar integraltabeller, se exv

@INTERNET Wikipedia List of integrals 2009-01-04;

— och dels också visar onLineIntegrerare — man kan mata in integranden direkt [typ 1/(ax^2+bx+c)] och få ut ett svar (integralsamband i läromedel ska egentligen ha en verifierande bevisform som klargör att kopplingen integral-derivata stämmer, en sådan saknas dock i de här nämnda webbkällorna av delvis förklarliga [organisatoriska] skäl; kunskapsdelen är bortskalad, bara presentationsdelen finns kvar), se

[http://www.integrals.wolfram.com/index/jsp] 2009-01-04,

Wolfram Online Mathematica Integrator — The world’s only full-power integration solver

Artikelsidan berättar att verktyget innefattar ytterst kraftfulla metoder för att få fram resultaten (typ världens ledande integrallösare).

Förekommer — således — ytterligare, andra, nämnarfaktorer tillsammans med ovanstående andragradspolynomets nämnarfaktor (P), t.ex. av typen

————

(x±k)(P)

kan vi utnyttja ovannämnda logaritmderivatans integrandform och därmed direkt postulera en bråkekvivalent av typen

T A Bx + C

———— = ——— + —————

(x±k)(P) (x±k) (P)

Vi använder här samma exempel som i föregående del med bråket 1/(x³–8) = 1/(x – 2)(x² + 2x + 4).

Vi studerar partialbråksuppdelning av huvudbråk T/N=K med sammansatta nämnarfaktorer N av typen (x±a)(ax²+bx+c)

Uppgft:

Partialbråksuppdela

———————— = 1/(x – 2)(P)

(x – 2)(x² + 2x + 4)

med hjälp av ovanstående substitutionsbråk (Bx+C)/(P). Använd metoden med PFECD på vanlig sätt för att bestämma första koefficienten, och sedan det normala sättet för linjär ekvationslösning för de återstående koefficienterna.

Lösning:

1 A Bx + C

———————— = ———— + —————— = 1/N

(x – 2)(x² + 2x + 4) (x – 2) (x² + 2x + 4)

A = 1/(x – 2)(x² + 2x + 4) ¦x=2¦ = 1/(4 + 4 + 4) = 1/12

;

1 = (1/12)(x² + 2x + 4) + (x – 2)(Bx + C)

= (x²/12 + 2x/12 + 4/12) + (Bx² + Cx – 2Bx – 2C)

= (x²/12 + x/6 + 1/3) + Bx² + Cx – 2Bx – 2C

= x²/12 + x/6 + 1/3 + Bx² + Cx – 2Bx – 2C

= x²/12 + Bx² + x/6 + Cx – 2Bx + 1/3 – 2C

= x²(1/12 + B) + x(1/6 + C – 2B) + 1/3 – 2C

; Alla x-koefficienter = 0; återstår endast

1 = 1/3 – 2C ;

C = (1/3 – 1)/2 = (–2/3)/2 = –1/3 = –4/12

; B-koefficienten kan utlösas både ur nollkoefficienten för x och den för x², vi väljer den sista;

0 = 1/12 + B ;

B = –1/12 ;

;

Resultat:

1 1 x + 4

———————— = ———— – ——————

(x – 2)(x² + 2x + 4) 12(x – 2) 12(x² + 2x + 4)

Kontrollräkning;

(1/12)((x² + 2x + 4) – (x – 2)(x + 4))/(x – 2)(x² + 2x + 4) ;

(x² + 2x + 4) – (x – 2)(x + 4) = x² + 2x + 4 – (x² + 4x – 2x – 8)

= x² + 2x + 4 – x² – 4x + 2x + 8

= 12 ;

(1/12)(12)/(x – 2)(x² + 2x + 4) = 1/N ;

Lösningen verifierad.

LÖSNINGEN GENOM PFECD

Samma uppgift som ovan men mera direkt genom PFECD blir som följer; Vi behöver aldrig lägga några särskilda aspekter på ”komplext irreducibla faktorer” eller annat: PFECD sköter allt automatiskt.

Uppgft:

Partialbråksuppdela

———————— = 1/(x – 2)(P)

(x – 2)(x² + 2x + 4)

Använd enbart PFECD via metodidentifieraren, samt övriga grundlagar.

Lösning:

Vi söker först uttrycka andragradspolynomet (x² + 2x + 4) efter binomlagen (x+a)² med kompletteringar för att därmed förbereda metodidentifieringen i PFECD; Vi får då

1 1

———————— = ————————

(x – 2)(x² + 2x + 4) (x – 2)([1+x]² + 3)

;

mI(a) = 1+x ;

a = 1+x ; a+3, se nedan = 4+x ;

a–1 = x ;

a–3 = x–2 ;

Vi utnyttjar sedan (som vanligt subsitutioner som leder till) konjugatlagen för att om möjligt få harmoniska (likagradiga, inre) nämnarfaktorer;

1 · (a + 3) (a + 3)

———————— = ———————— ;

(a – 3)(a² + 3) · (a + 3) (a² – 9)(a² + 3)

1 A B

——————— = ———— + ————

(a² – 9)(a² + 3) (a² – 9) (a² + 3)

;

A = 1/(a² – 9)(a² + 3) ¦a²=9¦ = 1/12 = 1/12

B = 1/(a² – 9)(a² + 3) ¦a²=–3¦ = 1/–12 =–1/12

;

1 1 –1

——————— = ———— + ————

(a² – 9)(a² + 3) 12(a² – 9) 12(a² + 3)

;

1 (a + 3) (a + 3) –(a + 3) 1 (a + 3)

——————— = ——————— = ———— + ———— = ———— – ————— ;

(a – 3)(a² + 3) (a² – 9)(a² + 3) 12(a² – 9) 12(a² + 3) 12(a – 3) 12(a² + 3)

;

Återinsättning av (a – 3) · (a² + 3) = (x – 2) · (x² + 2x + 4) och (a + 3) = (x + 4) ger

Resultat:

1 1 x + 4

———————— = ———— — ——————— = 1/N

(x – 2)(x² + 2x + 4) 12(x – 2) 12(x² + 2x + 4)

;

Kontrollräkning;

(1/12)((x² + 2x + 4) – (x – 2)(x + 4))/(x – 2)(x² + 2x + 4) ;

(x² + 2x + 4) – (x – 2)(x + 4) = x² + 2x + 4 – (x² + 4x – 2x – 8)

= x² + 2x + 4 – x² – 4x + 2x + 8

= 12 ;

(1/12)(12)/(x – 2)(x² + 2x + 4) = 1/N ;

Lösningen verifierad.

SOM VI SER är lösningarna i bägge metoderna identiska.

------------------

OBSERVERA att mI(a) i PFECD

måste relateras enhetligt — utan variabel rest:

Annars hamnar vi i svåra problem

2009-01-05

OM parabelpolynomet (ax²+bx+c)=a(x²+dx+e)=aP(x) INTE matchar binomlagarna BL=(x±f)² kan P(x) skrivas som

P(x) = BL ± k ; Vi använder den ekvivalenten i andragradspolynom för att anställa en partialbråksuppdelning på mI(a) i PFECD.

OBSERVERA EMELLERTID att mI(a) i PFECD måste relateras enhetligt — utan variabel rest:

OM P(x) utvecklas så att k innefattar en restkomponent x, fungerar (naturligtvis) inte partialbråksuppdelningen via mI(a) i PFECD;

Vi studerar det.

Är k en numerisk koefficient större än 0 är P(x) komplext, men kan fortfarande lösas via mI(a) i PFECD.

Är k en x-term, samt negativ, är P(x) också komplext, men denna del kan INTE lösas via mI(a) i PFECD

— variabelsubstitutionen returnerar typoriginalet så att nettoändringen uteblir.

EXEMPEL:

y = (x+1)² + 3

Medan den komplexa parabeldelen (x² + 2x + 4)=(x+1)² + 3 i 1/(x – 2)(x² + 2x + 4) KAN anställas på mI(a)=x+1 som ger a²+3,

kan den komplexa parabeldelen (x² + x + 1)=(x+1)² – x i 1/(x – 2)(x² + x + 1) det inte; mI(a)=x+1 ger a² – a + 1 = (a–1)² + a.

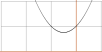
y = (x+1)² – x

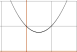
y = (a–1)² + a

Om parabelpolynomet istället skrivs ekvivalent så att ingen restfaktor för x återstår,

(x² + x + 1) = x² + x + 1/4 + 1 – 1/4 = (x+1/2)² + 3/4; a=x+1/2; a² + 3/4; x=a–1/2; x–2=a–5/2; (x – 2)(x² + x + 1) = (a – 5/2)(a² + 3/4),

då går det (se efterföljande exempel). Vilket vill säga:

— Ta parabelpolynomets ”ax²+bx” för vad det är och komplettera sedan i den numeriska koefficienten;

bryt ut a, dividera b/a med 2, (x±b/2a)² = x² ± b/a + k, och komplettera sedan i den återstående koefficienten k.

— No Problemo.

Vi studerar den fullständiga lösningen till det ovanstående exempelpolynomet nedan.

2009-01-06

Uppgft:

Partialbråksuppdela

———————— = 1/(x – 2)(P)

(x – 2)(x² + x + 1)

Använd enbart PFECD via metodidentifieraren, samt övriga grundlagar.

Lösning:

Vi söker först uttrycka andragradspolynomet (x² + x + 1) efter binomlagen (x+a)² med kompletteringar för att därmed förbereda metodidentifieringen i PFECD; Vi får då — eftersom (x² + x + 1) = (x² + x + 1/4 + 1 – 1/4) = (x + 1/2)² + 3/4) —

1 1

———————— = ——————————

(x – 2)(x² + 2x + 4) (x – 2)([x + 1/2]² + 3/4)

;

mI(a) = x+1/2 ;

a = x+1/2 ; a+5/2, se nedan = x+3 ;

a–1/2 = x ;

x–2 = a–5/2 ;

Vi utnyttjar sedan (som vanligt subsitutioner som leder till) konjugatlagen för att om möjligt få harmoniska (likagradiga, inre) nämnarfaktorer;

1 · (a + 5/2) (a + 5/2)

———————— = ———————— ;

(a – 5/2)(a² + 3/4) · (a + 5/2) (a² – 25/4)(a² + 3/4)

1 A B

———————— = ————— + ————

(a² – 25/4)(a² + 3/4) (a² – 25/4) (a² + 3/4)

;

A = 1/(a² – 25/4)(a² + 3/4) ¦a²=25/4¦ = 1/(28/4) = 1/7

B = 1/(a² – 25/4)(a² + 3/4) ¦a²=–3/4¦ = 1/(–28/4) =–1/7

;

1 1 –1

———————— = ————— + ————

(a² – 25/4)(a² + 3/4) 7(a² – 25/4) 7(a² + 3/4)

;

1 (a + 5/2) (a + 5/2) –(a + 5/2) 1 (a + 5/2)

———————— = ———————— = ————— + ————— = ———— – ————— ;

(a² – 5/2)(a² + 3/4) (a² – 25/4)(a² + 3/4) 7(a² – 25/4) 7(a² + 3/4) 7(a – 5/2) 7(a² + 3)

;

Återinsättning av (a – 5/2) · (a² + 3/4) = (x – 2) · (x² + 1x + 1) och (a + 5/2) = (x + 3) ger

Resultat:

1 1 x + 3

———————— = ———— — —————— = 1/N

(x – 2)(x² + x + 1) 7(x – 2) 7(x² + x + 1)

;

Kontrollräkning;

(1/7)((x² + x + 1) – (x – 2)(x + 3))/(x – 2)(x² + x + 1) ;

(x² + x + 1) – (x – 2)(x + 3) = x² + x + 1 – (x² + 3x – 2x – 6)

= x² + x + 1 – x² – 3x + 2x + 6

= 7 ;

(1/7)(7)/(x – 2)(x² + x + 1) = 1/N ;

Lösningen verifierad.

------------------

Vi kontrollerar att

samma resultat fås via logaritmderivatans metodform:

------------------

Uppgft:

Partialbråksuppdela

———————— = 1/(x – 2)(P)

(x – 2)(x² + x + 1)

med hjälp av substitutionsbråket (Bx+C)/(P). Använd metoden med PFECD på vanlig sätt för att bestämma första koefficienten, och sedan det normala sättet för linjär ekvationslösning för de återstående koefficienterna.

Lösning:

1 A Bx + C

———————— = ———— + —————— = 1/N

(x – 2)(x² + x + 1) (x – 2) (x² + x + 1)

A = 1/(x – 2)(x² + x + 1) ¦x=2¦ = 1/(4 + 2 + 1) = 1/7

;

1 = (1/7)(x² + x + 1) + (x – 2)(Bx + C)

= (x²/7 + x/7 + 1/7) + (Bx² + Cx – 2Bx – 2C)

= (x²/7 + x/7 + 1/7) + Bx² + Cx – 2Bx – 2C

= x²/7 + x/7 + 1/7 + Bx² + Cx – 2Bx – 2C

= x²/7 + Bx² + x/7 + Cx – 2Bx + 1/7 – 2C

= x²(1/7 + B) + x(1/7 + C – 2B) + 1/7 – 2C

; Alla x-koefficienter = 0; återstår endast

1 = 1/7 – 2C ;

C = (1/7 – 1)/2 = (–6/7)/2 = –3/7

; B-koefficienten kan utlösas både ur nollkoefficienten för x och den för x², vi väljer den sista;

0 = 1/7 + B ;

B = –1/7 ;

;

Resultat:

1 1 x + 3

———————— = ———— – ——————

(x – 2)(x² + x + 1) 7(x – 2) 7(x² + x + 1)

Kontrollräkning;

(1/7)((x² + x + 1) – (x – 2)(x + 3))/(x – 2)(x² + x + 1) ;

(x² + x + 1) – (x – 2)(x + 3) = x² + x + 1 – (x² + 3x – 2x – 6)

= x² + x + 1 – x² – 3x + 2x + 6

= 7 ;

(1/7)(7)/(x – 2)(x² + x + 1) = 1/N ;

Lösningen verifierad.

BIHANG Partialbråksuppdelning | Parabelfaktorns komplexa lösning | Andragradspolynomets reducerbarhet i modern akademi |

Andragradspolynomets reducerbarhet i modern akademi — en specialartikel om partialbråksuppdelningens spännande teori

Andragradspolynomets reducerbarhet i modern akademi

från resultatet i Bråkets elementära atom

Det finns (nämligen) i MODERN AKADEMISK LITTERATUR meningar som påstår TYP

”Polynomen ax²+bx+c, som förekommer i nämnarna i partialbråken av typ (2) [(Ax+B)/(ax²+bx+c)ⁿ] är irreducibla över R[kroppen av reella tal, s7]”,

”… varvid polynomen ax+b och ax²+bx+c i nämnarna av respektive partialbråk är de (irreducibla) delarna (faktorerna)”,

MATEMATIKLEXIKON W&W 1991 s328, allmän bibliotekslitteratur

— samtidigt som exempel visas (dock inte i källan ovan) som mera ansluter till realvillkoret.

För att (således) försöka ge korsreferenser mellan relaterad matematik och vad som går att utläsa ur den (således delvis dunkla) tillgängliga moderna akademins matematiska konventioner i den här frågan, ges ämnet här speciell belysning i särskild artikel — slutklämmen är helt enkelt den att källan ovan uttrycker sig olämpligt oklart, korrektionsexempel ges nedan med referens till andra etablerade källor.

I RELATERAD MATEMATIK, se från PFECD-lagen med ursprung i ekvationslärans huvudsats (konv. närmast motsv. algebrans fundamentalsats) gäller ekvivalenterna

k₁x ⁿ^–1 + k₂x ⁿ^–2 + k₃x ⁿ^–3 + … A B C

———————————— = ——— + ——— + ——— + … ................ PFECD-lagen

(x+a)₁(x+a)₂(x+a)₃(x+a)₄ … (x+a)₁ (x+a)₂ (x+a)₃

med den allmänna metoden i PFECD enligt

rotbestämd faktoreliminering och successiv ledöverflyttning (konv. Heaviside’s cover-up method, Heavisides övertäckningsmetod)

metodledet

N(x) A B

——————————————— = ——— + ——— + …

(x+a₁)(x+a₂)(x+a₃)(x+a₄)…(x+a_n) x+a₁ x+a₂

|_________________ _ _ _ _ ________|____________ _ _ _

Efter användning av den allmänna metodidentifieraren — som inte gör någon åtskillnad mellan ”reellt” och/eller ”komplext” utan behandlar alla lika, och som inte ingår i den moderna akademins lärosystem — återstår de slutliga möjliga icke reducerbara delbråken på de två olika typerna

(1) A/(ax+b)^m ................................. från reella rötter

(2) (Ax+B)/(ax²+bx+c)^m .................. från komplexa rötterna till (ax²+bx+c)

Vilket vill säga: Alla andragradspolynom P(x)₂ = (ax²+bx+c) = y

där

· alla y-värden ligger över x-axeln, kommer att tillhöra typ (2);

· något y-värde ligger på eller under x-axeln, kommer att tillhöra typ (1).

I MODERN AKADEMI ANVÄNDS SAMMA TYPFORMER MEN metodledet OVAN — se Modern akademi missar PFECD — INGÅR INTE; Det grundlägger (garanterat, tydligen) den moderna akademins formuleringar i ämnet som motsvarande (ytterst) ”sliriga”.

Vi studerar ett konkret citat — i samtidig koll på hur man använder matematiken praktiskt:

”partialbråk (syn. delbråk) Oftast rationella funktioner av typen

(1) A/(ax+b)ⁿ eller

(2) (Ax+B)/(ax²+bx+c)ⁿ,

där A, B, a, b, och c Î R [kroppen av reella tal, s7] samt n Î Z+ [de positiva heltalen, s7].

Polynomen ax²+bx+c, som förekommer i nämnarna i partialbråken av typ (2) är irreducibla över R. Enligt en sats tillhörande algebran kan varje rationell funktion, dvs. varje funktion av typen

R(x)=P(x)/Q(x), där P(x) och Q(x) Î R[x], skrivas som en summa

R(x) = P(x)/Q(x) = p(x) + F1(x) + F1(x) +…+ Fk(x), där p(x) Î R[x] och varje Fi (x) är ett partialbråk av typen (1) eller (2), varvid polynomen ax+b och

ax²+bx+c i nämnarna av respektive partialbråk är de (irreducibla) delarna (faktorerna) till Q(x).”

MATEMATIKLEXIKON W&W 1991 s328sp1n

JÄMFÖR MED KORREKTION — så som det används i praktiken:

”partialbråk (syn. delbråk) Oftast rationella funktioner av typen

(1) A/(ax+b)ⁿ eller

(2) (Ax+B)/(ax²+bx+c)ⁿ,

där A, B, a, b, och c Î R [kroppen av reella tal, s7] samt n Î Z+ [de positiva heltalen, s7].

DE ROTKOMPLEXA

R(x)=P(x)/Q(x), där P(x) och Q(x) Î R[x], skrivas som en summa

R(x) = P(x)/Q(x) = p(x) + F1(x) + F1(x) +…+ Fk(x), där p(x) Î R[x] och varje Fi (x) är ett partialbråk av typen (1) eller (2), varvid polynomen ax+b och

DE ROTKOMPLEXA POLYNOMEN

ax²+bx+c i nämnarna av respektive partialbråk är de (irreducibla) delarna (faktorerna) till Q(x).”

Förklaring

POLYNOMET ax²+bx+c är — se andragradsekvationens faktorisering, andragradsekvationens lösning — inte obetingat reellt irreducibelt; Endast om kurvan y=ax²+bx+c ligger ÖVER x-axeln är polynomet ax²+bx+c icke reducerbart, alltså irreducibelt, och kan inte delas upp i reella faktorer typ (x+a)(x+b).

Det rena bokcitatet (överst ovan) klargör inte detta — och boken ger heller inga P(x)₂ reducibla exempel i artikeln —

(x² + 1) ........................... engradig faktor med inre komplex rot, inversen ger arctangens integral

(x – 1)³ .......................... engradig faktor med multipliciteten 3, inversens integral tillhör basfunktionen –(x – 1)^–2/2

(x² + x + 1)² .................... parabeln ovanför x-axeln, reellt irreducibel parabelfaktor

— vilket gör att man (lätt) missförstår meningen och citatformen bara framstår som dunkel, svårfattlig och oklar — och möjligen också (därmed) motsägelsefull — och därmed läge för »felformulering» (med djupa äventyr).

@INTERNET Wikipedia Partial fraction 2009-01-04 använder samma typformalia som i MATEMATIKLEXIKON W&W 1991 ovan

— men är mera klargörande (mot slutet, General result) i det att man preciserar

”… and the terms (x_j²+b_jx+c_j) are the irreducible quadratic factors of q(x) which correspond to pairs of complex conjugate roots of q(x).”,

@INTERNET Wikipedia Partial fraction, General result 2009-01-04

Min översättning:

… och termerna (x_j²+b_jx+c_j) är de irreducibla kvadratfaktorerna i q(x) som motsvarar par av komplext konjugerade rötter i q(x).

Wikipediaartikelns författare ger också flera exempel på reducerbara andragradsfaktorer (ax²+bx+c),

(x²–3x–40) = (x–8)(x+5)

(x²+2x–3) = (x+3)(x–1)

och distanserar sig därmed (klart) från citattypen i MATEMATIKLEXIKON W&W 1991. Därmed bör ämnet inte (längre) bereda läsaren någon svårighet i fattningen på vad det är som gäller: naturligtvis är (ax²+bx+c) inte generellt omöjligt att dela upp i reella faktorer.

Wikipediaartikeln är dock (som vanligt i ”förklarande sammanhang”) något kryptisk på härledningarna till de olika uttrycken: Artikeln ställer fram en matematik som förmodligen få förstår (i stort sett de analytiska grundreferenser som man brukar se i sammanhang som rör universitets och högskolematematiken) — och som det underförstås att läsaren ska känna till »på sina högskolemeriter», eller »ta sig tid att studera särskilt» med alla regelrätta »härledningar» utspridda över enorma litterära moderna akademiska områden som tar ÅR att genomgå; Wikipediaartikeln är, tydligen som det får förstås, skriven av högeskolemeriterade för högskolemeriterade. Och inget annat är heller att vänta i den moderna akademins led, märk väl.

— Om vi söker i mera etablerade webbkällor — Wolfram Mathworld, ”the web’s most extensive mathematics resource”, webbens mest extensiva matematikkälla, Partial Fraction Decomposition — återfinner vi också här samma typformuleringar som i MATEMATIKLEXIKON W&W 1991. Wolframkällan (Januari 2009) ger dock inga exempel.

Se vidare utförliga exempel från

Parabelfaktorns komplexa lösning.

Polynomdivision | Iterationsteknik | ROTKARTAN | andragradsekvationens lösning

ROTKARTAN

ANDRAGRADSEKVATIONENS LÖSNINGSBILD

Binomlagarna — ANDRAGRADSEKVATIONENS LÖSNING

Om binomlagen skrivs generellt enligt (a+A/2)²–(A/2)²=a²+Aa=K med A/2=b från 2ab i a²+b²+2ab,

kan a lösas i alla uttryck av typen

K = a²+Aa alternativt a²+Aa – K = 0

om KA är känd. Ovanstående led ger lösningen ±(a+A/2)²=K+(A/2)², ±(a+A/2)=Ö K+(A/2)², a+A/2=±Ö K+(A/2)²;

a = –A/2 ± Ö K+(A/2)² ........................... andragradsekvationens lösning

Mera utförligt om LÖSNINGARNA TILL ANDRA GRADENS EKVATIONER

a = –A/2 ± Ö [B + (A/2)²] ................ fullständiga lösningen från …

B = a² + Aa ....................................... … det ursprungliga uttrycket

Med ekvationen för B skriven på allmän form

a = –A/2 ± Ö [B+(A/2)²] ................... fullständiga lösningen från …

a² + Aa – B = 0 ................................ … det ursprungliga uttrycket

komplexa rötter om B < (A/2)², singulär dubbelrot om B = (A/2)²

Nedanstående uppställning

visar (exemplifierat) hur reella och komplexa rötter fungerar:

Andra gradens ALLMÄNNA EKVATIONSSTRUKTUR (andra gradens polynom)

x² + ax + b = 0


reella	komplexa	reella	rötternas typ
			graf
y = x²	y = x² + 1	y = x² – 1	ekvation
x² + 0x – 0 = 0	x² + 0x + 1 = 0	x² + 0x – 1 = 0	allmänna transformen
x² = 0	x² + 1 = 0	x² – 1 = 0	ekvivalent
(x²)	(x² + 1)	(x² – 1)	faktor
B = (A/2)²	B < (A/2)²	B > (A/2)²	B
A=0, B=0	A=0, B=–1	A=0, B=1	A&B
en reell dubbel	två teckenolika i	två teckenolika reella	typ
x = 0	x = ± i	x = ± 1	rötter
	parabelskärningen y=±1	parabelskärningen x=±1

M2001_4 s13 författarens referenser

Komplexa rötter ges om parabeln ligger över x-axeln.

Exempel

Bestäm rötterna till den allmänna formens andragradspolynom x² + 4x + 3 = 0 genom mallen

a = –A/2 ± Ö [B+(A/2)²] ................... fullständiga lösningen från …

a² + Aa – B = 0 ................................ … det ursprungliga uttrycket

komplexa rötter om B < (A/2)², singulär dubbelrot om B = (A/2)²

Lösning:

x² + 4x + 3 = 0

A –B ;

A = 4 ;

B = –3 ;

x = –4/2 ± Ö [–3+(4/2)2]

= –2 ± 1 = {–1, –3}

Svar: Rötterna till x² + 4x + 3 = 0 är

x = {–1, –3}

ANDRAGRADSEKVATIONENS FAKTORER

M2001_4 s13 författarens referenser

summan av rötterna

a_P = –A/2 + Ö [B+(A/2)²]

a_N = –A/2 – Ö [B+(A/2)²]

a_P+a_N = –A

produkten av rötterna

a_Pa_N = (P+R)(P–R) = P²–R² = (A/2)² – [B+(A/2)²]

a_Pa_N = –B

tillämpat på den allmänna normalformen

a² + Aa – B = 0

ges

a² + Aa – B ;

a² + (–a_P– a_N)a + a_Pa_N ;

a² – aa_P– aa_N + a_Pa_N , = (a–a_P)(a–a_N) [andra binomlagen om P=N] ;

(a – a_P)(a – a_N) = a² + Aa – B

med en ytterligare koefficient n:

(a – a_P)(a – a_N) = a² + Aa/n – B/n = (1/n)(na² + Aa – B) ;

n(a – a_P)(a – a_N) = n(a² + Aa/n – B/n) = na² + Aa – B

¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯¯¯

För att få tvåfaktorsparentesen i VL från HL, måste vi först lösa HL-rötterna

a_P och a_N.

Andragradsekvationens fullständiga faktorisering

Den fullständigt faktoriserade formen för andra gradens ekvation blir då med ovanstående utvecklingar

n(x – x_P)(x – x_N) = nx² + ax + b

där x_Poch x_N anger respektive associerade positiva och negativa rotvärden med ovanstående suffix.

Polynomdivision | Iterationsteknik | Graflära

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Polynomdivision | Iterationsteknik

ämnesrubriker

innehåll

Polynomdivision | Iterationsteknik | Graflära

Polynomdivision

grundbegrepp

två scheman för division

Exempel

Iterationsteknik

Hur man löser reella och imaginära rötter

Rotvärdet

Graflära

GRAFLÄRA OCH GRAFRITANDE PROGRAM

Tillämpningar

Faktoriseringsexempel

Bråkets elementära atom — dess reella partialbråksuppdelning

Partialbråksuppdelning | BIHANG — huvudartikel i PFECD

Parabelfaktorns komplexa lösning

Lösningen genom logaritmintegralen

Lösningen genom PFECD

ROTKARTAN

ANDRAGRADSEKVATIONENS LÖSNINGSBILD

ANDRAGRADSEKVATIONENS FAKTORER

Andragradsekvationens fullständiga faktorisering

referenser

[ITK]. ITK 1-10 MATEMATIKBIBLIOTEK 1962 Lennart Brandqvist,

INSTITUTET FÖR TEKNISKA KURSER Stockholm, Victor Pettersons Bokindustriaktiebolag, Stockholm 1962

[M2000].

MATEMATIK 2000, Lärobok 3, Björk · Borg · Brolin · Ljungström, Natur och Kultur 1991

Innehåll och uppgifter är desamma som i den senare läroboken

MATEMATIK 2000, Kurs E, Björk · Brolin, Natur och Kultur 1996

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2018-12-27

*END.

Stavningskontrollerat 2008-12-31 | 2009-01-04.

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se