FUNKTIONSKLASSERNA — UNIVERSUMS HISTORIA | a production 2008XII22 | Efter sammanställningar från 1997IX27 | Senast uppdaterade version: 2019-01-06 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Funktionsklasserna | Korsrefererande Talnomenklatur | i sammanställning för Universums Historia

FUNKTIONSKLASSERNA I RELATERAD MATEMATIK

FUNKTIONSKLASSERNA MED FUNKTIONSTEORIN OCH FUNKTIONSBEGREPPET

NOMENKLATUR ENLIGT RELATERAD FYSIK OCH MATEMATIK

För jämförelse med grundbegreppen i modern akademi, se korsreferens

UPPRÄKNELIGHETEN |, | |, | | |, | | | |, | | | | |, … kallas för varje mängd eller kvantitet av enheter (|) ett naturligt tal N (1, 2, 3, … N) eller ett helt tal.

KLASSEN hela tal N innefattar processen med obegränsat växande N. Oändlig mängd=bestämd kvantitet finns inte.

En bestämd kvantitet N definieras som mängden N {1, 2, 3, … n}.

Alla bestämda kvantiteter definieras av matematikens fem operatorer + – × ÷ Ö.

KLASSEN rationella tal definieras som kvoten mellan två heltal y/x=N₁/N₂=Q.

KLASSEN hypomängder, som inte är lika med Q, definieras som ÖQ=H.

Klasserna Q och H bildar tillsammans klassen bestämda geometriska mängder (GM), eller funktionsklass I.

Q har bestämd aritmetisk värdemängd (AV) med avseende på Q-systemets talbas.

H saknar bestämd AV. AV(H) kan endast ges som en partiell aritmetisk värdemängd med GM(H) som gränspunkt.

Binomialteoremet (a+b)ⁿ är en talgenerator om n<1: seriens summa kan aldrig överstiga (a+b)¹=(a+b): serien är konvergent och obegränsad. Om serien inte beskriver GM, existerar heller inget bestämbart gränsvärde eller gränspunkt för ”talet” eftersom serien är obegränsad. Dessa fall definierar funktionsklass II: alla ”tal” som saknar bestämd GM och därmed bestämd AV. Det är de exponentiella, logaritmiska och trigonometriska funktionsuttrycken eller ”talen”. Utöver dessa nu nämnda finns inga ENLIGT RELATERAD MATEMATIK.

——————————

ref. MPcMatematiken.wps — Författarens ref.

Vad är en funktion?

— Allt utom det här:

Alltså allt UTOM xy-systemets egen kropp: Inte xy-axlarna, inte deras paralleller; inte konstanter; INTE verktyget.

En funktion I RELATERAD MATEMATIK är byggnaden, huset, inte verktyget som användes för att färdigställa byggnaden.

— Varför är det klart?

— Därför att xy-systemet är det enda verktyg som finns för att inte bara BESKRIVA funktionen utan även HUR funktionen skiljer sig från xy-systemet.

Se vidare utförliga exempel i EXAMINERINGSEXEMPEL.

Kort resumé av Talteorins Elementa — enligt relaterad matematik

AVSAKNADEN AV ENTYDIGHET (Mot givna relationer) i talbegreppet medför att det inte är möjligt att få en logiskt klar och sammanhängande bild av matematiken utifrån föreställningen om tal — ehuru TALEN (GM=AV) saknar entydighet mot de relationer (y/x) som bildar dem (Exv GM¹AV). Jämför enhetssystemets exakta GM=1/3=AV med tiosystemets GM(1/3)¹AV(0,333…); talbegreppet saknar entydighet. Snarare än tal framträder naturligt i relaterad matematik därför benämningen funktion. Vi studerar hur.

Alla uttryck inom matematiken som bildas genom sammanställningar (relationer) av bestämda GM — alltså bestämda kvantiteter, inget annat — kallar vi allmänt för aritmetiska uttryck. Dessa uttryck bildas alla genom matematikens fem operatorer eller relationsgeneratorer + – × ÷ Ö . Om de ingående GM representeras av bokstäver (symboler) talar vi speciellt om algebraiska uttryck (Formler, ekvationer, eller funktioner). Ett sådant, algebraiskt, uttryck är y/x = k. Det syntetiserar tillsammans med de övriga fyra relationsgeneratorerna

+ – × Ö den mest sammansatta form på vilken matematikens alla möjliga uttryck alls kan tecknas och utgör därmed grundvalen för talteorin. Vi finner dess mest utvecklade aspekt i divisionsalgoritmen (T_TÄLJARE=N_NÄMNAREK_KVOT+R_REST, »tänker»).

Genom de matematiska uttryckens allmänna klassificering med hänsyn till de skilda talsystemen och deras bildning, samt därmed i referens till grundbegreppen GM och AV, blir begreppet funktion avgörande för den allmänna klassificeringen av matematikens alla möjliga uttryck: — Alla talsystem bildas som bestämda GM ur relationsbasen y/x=k, talbas x, se TALSYSTEMEN. Snarare än benämningen tal blir därför benämningen funktionsuttryck central och vital för klassificeringen av matematikens alla möjliga uttryck. Hellre än ”talklasser” talar vi därför om funktionsklasser i den RELATERADE matematikens BESKRIVNING.

I relaterad matematik är ”talteorin” — funktionsteorin — synnerligen enkel, direkt och lättfattlig: xy-systemets fasta rambyggnad utgörs av konstanter (se Talsystemen), allt annat är funktioner; funktionerna kan antingen ha bestämda geometriska mängder — hypolinjerna eller »hypotenusorna», funktionsklass I — eller inte ha bestämda geometriska mängder — speciella sammansättningar som ansluter till oändliga serier, funktionsklass II. Utöver dessa två typer existerar inga andra; Hela matematiken med alla typer av samband och uttryck kan beskrivas enbart med hjälp av dessa två klasser. Se vidare i huvudtexten.

Funktionsklasserna indelas naturligt i två. Klass I beskriver funktionsuttryck som genererar bestämda GM (heltalskvoterna [konv. rationella tal] och hypomängderna) eller de operativa funktionsuttrycken, medan Klass II beskriver negationen: funktionsuttryck som saknar bestämda GM och därmed också saknar bestämda AV, analogt de inoperativa funktionsuttrycken.

————————

ref. IntroIntegral.wps — Författarens ref.

Funktionsklasserna i relaterad matematik

Funktionsklass I De OPERATIVA FUNKTIONSUTTRYCKEN rangterm

y₁ⁿ1^{/2^m}1

a = GM = —————— , n&m Î N , y Î GM, Î utläses ”tillhör” a

y₂ⁿ2^{/2^m}2

De Operativa funktionsuttrycken beskrivs av alla möjliga bestämda geometriska mängder a=GM i xy-planet

— analogt alla matematiska uttryck som alls kan framställas genom matematikens fem enda operatorer

+ – × ÷ Ö .

Matematikens alla möjliga bestämda aritmetiska lösningar återfaller på denna klass, lösningarnas art beror på valet av talsystem.

NOTERING med härledning till uttrycket för a=GM ovan. Heltalspotenserna framställs som produktsummor (a·a·a… n gånger = aⁿ), kvadratrötterna framställs y^{1/(2^m)} med m som heltal. Produktsummor av de senare ger motsvarande y^{n/(2^m)}. Operatorerna kan alltså inte åstadkomma godtyckliga rationella potenser av typen y^n/m med nm som godtyckliga heltal. Denna distinktion medför att det gängse begreppet algebraiskt uttryck , om det tillämpas på relaterad matematik, inte är entydigt för funktionsklass I. Klass I är dock helt entydig i avseende på vad som inom matematikens ram alls är möjligt att åstadkomma via de fem matematikens enda operatorer;

— Vilket vill säga: det blir i vilket fall enklare att läsa matematiken relaterad; den moderna akademins begrepp är primitiva i jämförelse.

Se även KORSREFERERANDE TALNOMENKLATUR, där finns de olika begreppen uppställda i tabell till jämförelse.

————————

ref. IntroIntegral.wps — Författarens ref.

Funktionsklass II De INOPERATIVA FUNKTIONSUTTRYCKEN rangterm

1. De EXPONENTIELLA funktionsuttrycken:

_n

(a±b)ⁿ = aⁿ(1+ å[[(±b/a)(n–m)]_m!/(m+1)!]) (Aⁿ, ej specificerad)

^m=0

Alla funktionsuttryck i klass II utgår ifrån ovanstående

allmänna uttryck, se binomialteoremet.

_m®¥

aⁿ = ( 1 + å [(1 – a^±1)(m–n)]_m!/(m+1)!)^±1, | a |<1 för + aⁿ

^{m=0, |n|<1}

exponentialfunktion ......................... aⁿ, funktionsuttryck som innefattar exponent, variabeln ej specificerad

exponentfunktion .............................. e^x, specialfall i gruppen exponentialfunktioner, x är variabel

2. De LOGARITMISKA funktionsuttrycken:

_m®¥

ln x = ±( – å (1 – x^±1)^m/m) , | x |<1 för +: ln x

^m=0

3. De TRIGONOMETRISKA funktionsuttrycken i PREFIXxSIN:

_{n®¥ n®¥}

sin x = å x²ⁿ(–1)ⁿ/(2n)! cos x = å x^2n–1(–1)ⁿ⁺¹/(2n–1)! sin x resp. cos x

^{n=0 n=1}

Se Härledningarna till serierna för sinus och cosinus

Sambanden för arcusfunktionerna här utelämnade

Begreppet EXPONENTIALFUNKTION i funktionsklasserna

BINOMIALTEOREMETS I SÄRKLASS MEST UTPRÄGLADE aspekt återfinner vi i positionsformen

(1+1/¥)^¥(P) ......................... (se från Härledningen till e, se även från Den mängdoberoende)

med de signifikanta ekvivalenterna

(1+1/¥)^¥(P) = (1+(P)/¥)^¥ = 1 + (P) + (P)²/2! + (P)³/3! + …

Anledningen till att denna form tas upp här, explicit, är att den och ingen annan i matematiken över huvud taget är det allra närmaste vi kan komma till ett begrepp om funktionsvariabeln som exponent. Vi studerar det.

Likheten visar (nämligen) explicit att ”variabelexponentialiseringen” resolut motas undan av binomialteoremets form — högerledet — och ersätts av en basbaserad variabel (P). Variabeln (P) som (förment) exponent, får alltså sin ekvivalenta funktion som en helt normal basfaktor.

————————————————————————————————————————————————————

Några ”exponentfunktioner” förekommer med andra ord och explicit INTE inom den praktiskt arbetande matematikens ramar.

————————————————————————————————————————————————————

Betrakta för övrigt funktionsuttrycken från Binomialteoremet se även i Härledningen till e där också en del av leden nedan omnämns

(1) (1–b)ⁿ = 1 – [bn + b²n(1–n)/2! + b³n(1–n)(2–n)/3! + … ] , | b&n | < 1

Funktionen för alla aⁿ med | n |<1 fås genom villkoren:
a>1 ger b=1–1/a, seriens slutvärde inverteras ; | a |<1 ger b=1–a .

(2) e^x = 1 + x + x²/2! + x³/3! + …

(3) n^x = 1 + (x ln n) + (x ln n)²/2! + (x ln n)³/3! + … , n = e^z, n^x = e^zx, z = ln n

Funktionsformerna i (3) och (2) innefattas i exponentialserien (1), de benämns här explicit exponentserier med hänsyftning på funktionsuttryckets karaktär.

(4) ln a = – (m + m²/2 + m³/3 + m⁴/4 + … )

Funktionen för alla ln a fås genom villkoren:
a>1 ger m=1–1/a, seriens slutvärde multipliceras med –1 ; | a |<1 ger m=1–a .
Denna funktionsform kan f.ö. härledas ur (1).

Tillsammans med de trigonometriska serierna, av samma typ som ovan, är dessa de utöver heltalskvoterna och hypomängderna i matematiken enda förekommande funktionsuttrycken. Samtliga allmänna funktionsuttryck i Klass II återfaller med andra ord på heltalspotenser och därmed på de sk rationella talen (bråkens heltalskvoter). Funktionsuttrycket (t ex e^x) saknar genom seriens obegränsade utsträckning bestämd GM och bestämd AV, men funktionsvärdet är ändå analytiskt entydigt därmed att det ges exakt motsvarande varje exakt variabelvärde (x) och endast då.

Begreppet EXPONENTIALSERIE

Alla möjliga utpräglat exponentiella funktionsuttryck inom matematiken kan beskrivas sammanfattande såsom innefattade i den elementära serieformen (1)

(1–b)ⁿ = 1 – [bn + b²n(1–n)/2! + b³n(1–n)(2–n)/3! + … ] , | b&n | < 1

Funktionen för alla aⁿ med | n |<1 fås genom villkoren:
a>1 ger b=1–1/a, seriens slutvärde inverteras ; | a |<1 ger b=1–a .

SERIEN är explicit renodlad från binomialteoremets negativa binomserie. Den är emellertid begränsad till att omfatta endast potenser med bruten exponent. För potensuttryck som innehåller heltalspotenser a^N,n avdelas funktionen med den brutna exponenten enligt a^{N,n = N+n} = a^Naⁿ. Resultatet blir därmed en produkt av produktsumman eller heltalspotensen a^N och den renodlade exponentialfunktionen aⁿ. Vi noterar rent språkligt, att en heltalspotens a^N är av formen a·a·a… N gånger. En sådan funktionstyp kan INTE varieras godtyckligt i exponenten, den tillåter endast hela tal och är alltså inte utpräglat exponentiell utan produktsummerande. Av detta skäl har det I RELATERAD MENING fallit sig naturligt att också benämna serieformen ovan som (den allmänna, generella) exponentialserien. Genom att en exponent också fungerar som logaritm, härleds också (följdriktigt) naturligt ur ovanstående serie (den allmänna, generella) logaritmserien, nr(4) ovan.

Begreppet EXPONENTSERIE

Genom att positionsformen i binomialteoremet intar sin särställning i formen av den naturliga logaritmbasen (e) ges också en speciell serie för e-potenser e^(P) enligt

e^(P) = (1+1/¥)^¥(P) = (1+(P)/¥)^¥ = 1 + (P) + (P)²/2! + (P)³/3! + …

Frånsett heltalspotenserna, ingår denna serieform i exponentialserien. Eftersom en godtycklig bas (n) i en potens kan uttryckas med hjälp av e-logaritmen enligt

n = e^z, med z = ln n som ger oss n^a = (e^z)^a = e^za = e^{a ln n} får vi en mera allmän serieform för exponentfunktionen som gäller vilka som helst fall enligt funktionsformen i föregående nr(3)

n^a = 1 + (a ln n) + (a ln n)²/2! + (a ln n)³/3! + … , n > 0

Serien är, som vi ser, en i egen form utpräglad potensserie med funktionen som en utpräglad exponentfunktion. Med hänsyftning på funktionstypen, blir det naturligt att benämna den ovanstående potensserien exponentserien och därmed se denna som en speciell utformning av den mera allmänna exponentialserien.

modern akademi

Som tidigare noterats, finns inga distinktioner eller motsvarande klassificeringar av den här beskrivna och behandlade arten i gängse nomenklatur. Man benämner [Se t.ex. MATEMATIKLEXIKON W&W 1991 s115sp2n] serien för e^a med begreppet exponentialserien. Orsaken anges/framgår INTE.

KORSREFERENS

konventionella talbegrepp belysta i relaterad matematik

begreppen refereras här (främst) till

MATEMATIKLEXIKON W&W 1991

MATHEMATICAL HANDBOOK McGraw-Hill (Biblioteksupplaga 1968)

Den moderna akademin kan NATURLIGTVIS INTE beskriva den relaterade matematiken eftersom den moderna akademin grundas på överenskommelser (imperialistiska handelssyndikat med främsta strävan att knacka ur botten på kunskapen för allmän energiutvinning). Den relaterade matematiken grundas däremot på att härleda logiken. Se explicit från Sanningsbegreppet om ej redan bekant.

exempel MAC modern akademi TNED relaterad matematik och fysik

——————— ——————————————————— ———————————————————

oändlig mängd mängden av alla hela tal (N) n®¥ är en klass (process), ingen mängd

se vidare i Den Mängdoberoende

xⁿ algebraisk funktion, variabeln i basen basfunktion, alla f(x) är algebraiska

(a + – × ÷ b)^c algebraisk operation, c är heltalsbråk alla operationer är också algebraiska

transcendent tal icke-algebraisk operation c ¹ heltalsbråk funktionsklass II, varken GM eller AV finns

periodiska tal (1/3)₁₀ rationella tal, även heltal GM=AV, beroende på val av talsystem; y_HELTAL/x_HELTAL

icke-periodiska tal (Ö2) irrationella tal GM¹AV, inkommensurabla funktioner; hypomängder

reella tal, rationella + irrationella begreppet tal saknar allmängiltighet

komplexa tal a+ib identifieras genom metod, inte tal

———————————————————————

Jämför enkelheten i relaterad matematik:

DET FINNS BARA TVÅ FUNKTIONSKLASSER ATT VÄLJA PÅ

exempel TNED relaterad matematik och fysik

————————— ——————————————————————————————————————————

a + – × ÷ Ö b = c (algebraiskt) operativa funktionsuttryck (»INtranscendenta tal»), FUNKTIONSKLASS I, bestämda GM,
y₁ⁿ1^{/2^m}1
a = GM = —————— , n&m Î N_HELTALEN , y Î GM, Î utläses ”tillhör”
y₂ⁿ2^{/2^m}2
allt som finns utläsbart i xy-systemet, motsvarande »mängderna på rutat papper»

—————————————————————————————————————————————————————

allt övrigt (algebraiskt) INoperativa funktionsuttryck (»transcendenta tal»), FUNKTIONSKLASS II, Obestämda GM,
trigonometriska, exponentiella, logaritmiska funktionsuttrycken eller ”talen”

—————————————————————————————————————————————————————

GM bestämd geometrisk mängd, samma som bestämt intervall

AV bestämd aritmetisk värdemängd beror på valet av talsystem för given GM

KORSREFERERANDE

TALNOMENKLATUR

RELATERAD MATEMATIK kontra MODERN AKADEMI

2009I20

relaterad matematik — funktionsuttryck för ”tal” — indelning med referens till det enhetsbaserade matematiska xy-planet

form	exempel	klassindivider	typ	gränssnitt eller funktionsklass	bestämning
bråk	1 — 3	RATIONELLA TAL	y —— x	OPERATIVA funktionsuttryck via operatorerna + – × ÷ Ö	AV = GM
rot	Ö 2	hypomängder — komplexa tal	Ö x^2 + y^2		AV ¹ GM
serier	p, e, 2^0,1	SERIETAL	(a+b)^n	INOPERATIVA FUNKTIONSUTTRYCK exponentiella, logaritmiska, trigonometriska SAMMANSATT OPERATIVA Oändliga Serier binomialteoremet — konvergent talbildning	AV|GM finns ej

»KOMPLEXT TAL» i relaterad matematik framkommer naturligt (se Harmoniska Trianglarna) som en metodform, inget tal, och beskrivs i särskilt avsnitt, se Den Komplexa Algebran.

De olika klasserna beskrivs|härleds utförligt i Funktionsklasserna.

I modern akademi beskrivs matematiken (företrädesvis) genom mängd|kropps|begrepp typ ”N|Q|R|C är mängden|kroppen av de |egenskap| talen”, vilket lett till ett system som i huvudsak indelas i reella tal (R) och komplexa tal (C) [nomenklaturen använder komplicerade specialtecken, konturerade bokstäver, som normalt inte kan anges här]:

modern akademi — reella tal — indelning med referens till den moderna akademins abstrakta analys

form	exempel	mängd	typ	benämning
bråk	1 — 3	RATIONELLA TAL	y —— x	ALGEBRAISKA TAL + – × ÷ x^rationella
serier	Ö 2 p, e, 2^0,1	IRRATIONELLA	Ö x^2 + y^2 (a+b)^n	ICKE-ALGEBRAISKA TAL — (transcendenta) exponentiella, logaritmiska, trigonometriska SAMMANSATT OPERATIVA Oändliga Serier binomialteoremet — konvergent talbildning

Ett algebraiskt tal kan vara både ett rationellt tal (1/3) och ett irrationellt (2^0,1);

Ett transcendent tal beskrivs entydigt som ett icke-algebraiskt tal, men distinktionen framhålls som problematisk [ML s409sp1ö, ”Att avgöra om ett tal är transcendent är alltså ett mycket komplicerat problem.”].

Begreppet ”algebraiskt tal” är i modern akademi delvis också problematiskt (beskrivningen förgrenas i abstraktioner som leder till flera olika (divergenta) strukturer — som kräver specialstudium i sig) [ML s17sp2m algebraiskt tal, Definitionen av …];

Benämningen ”irrationella algebraiska tal” förekommer explicit [ML s17sp2ö Algebraiskt tal, ”J. Liouville undersökte hur väl de irrationella algebraiska talen …”], vilket visar att »algebraiska tal» i modern akademi kan vara både av rationell och irrationell typ (den streckade delningen ovan höger). Se även nedanstående jämförande|klargörande citat;

I MATEMATIKLEXIKON W&W 1991 s408sp2m beskrivs (fetstilen bokens markering)

”transcendent Icke algebraiskt, dvs icke möjligt att uttrycka meddelst algebraiska operationer. Logaritmfunktionen, exponentialfunktionen och de trigonometriska funktionerna är exempel på transcendenta funktioner; polynomfunktionen däremot är algebraisk.”,

I MATEMATIKLEXIKON W&W 1991 s408sp2m

”algebraiska operationer I den vanliga algebran operationerna addition, subtraktion, multiplikation, division, rotutdragning och upphöjande till heltals- eller rationell potens. Icke-algebraiska eller transcendenta operationer kan exemplifieras av logaritmer, vars definition stöder sig på en gränsprocess.”,

I MATEMATIKLEXIKON W&W 1991 s15sp2n

Jämförande exempel:

Det irrationella talet 2^0,1 beskrivs alltså som en algebraisk operation i modern akademi eftersom potensen 0,1=1/10 är rationell, medan den i relaterad matematik beskrivs som ett inoperativt funktionsutttryck (sammansatt av obegränsat många operativa termer), alltså som kräver oändliga serier (vanligtvis konv. transcendena tal) för att kunna bestämmas.

modern akademi — komplexa tal

form	exempel	klass	typ	benämning
(x;y)	(–1;0)=–1=i^2	KOMPLEXA TAL	x+iy	KOMPLEXA

FUNKTIONSBEGREPPET

FUNKTIONSBEGREPPET ENLIGT RELATERAD MATEMATIK

Preferens FUNKTIONSBEGREPPET

Funktion; Den generella benämningen på varje godtyckligt bestämbar geometrisk mängd som står i ett förhållande till andra sådana mängder genom operatorerna [relationsgeneratorerna] + – × ÷ Ö.

Jämför a + – × ÷ Ö b = c.

· En konstant a (=a) är alltså ingen funktion. Heller inte a/a=1. a/b=1 är däremot en (komplex) funktion.

· En funktion kan (följaktligen) inte avbilda parallellitet med (funktions- eller) koordinataxlarna (xy) [xy-parallellerna ges av konstanter].

· Alla funktionsuttryck (tal) kan i ett eller annat avseende uttryckas på elementarformen y/x=k. Denna k-form bildar i sig fundamentet för de skilda talsystemen (talbasen är x).

· begreppet funktion är alltså meningslöst om relationsbyggnaden inte kan utsträckas från relationen (y/x) [denna detalj berör explicit funktionsbegreppet i den högre analysen (differentialer, derivator och integraler)].

————————

ref. IntroIntegral.wps

Funktionsbegreppet äger sin naturliga grund i dynamiken [Funktio´n (av lat. fu´ngi, förrätta), verksamhet, livsyttring] vilken har flödesbegreppen (analogt formerna för plus, divergens, och minus, konvergens) som fundament. Som de övriga relationsgeneratorerna ×, ÷ och Ö följer av dessa (genom utsträckningen av, och därmed analogt relationsformerna inom, xy-planet) blir funktionsbegreppet inom matematiken följaktligen analogt med den struktur av mängder och former som dessa flödesbegrepp gestaltas igenom [verbalt; den process eller aktion med ingående element varigenom en form eller gestalt beskrivs eller kommer till uttryck].

————————

ref. NOLLFORM

FUNKTION:

· allt utom konstanter;

· allt som från en godtycklig punkt P har en entydig utsträckning

En konstant kan inte gestalta en variation.

En funktion (variation) blir därför analytisk genom att den kräver positionsformen dy/dx=y’.

Funktionskriteriet i relaterad matematik ansluter också till UNIVERSALSATSEN i Den Högre Analysen. Jämför –x/x=–1: |x| är INTE en funktion utan två.

ICKE-FUNKTION definieras som ett avbrott i funktionen.

Examineringsexempel

EXAMINERINGSEXEMPEL

KALKYL_0

ENLIGT xy-SYSTEMETS PREFERENSKROPP

— xy-systemet är det enda verktyg som finns för att inte bara BESKRIVA funktionen utan även HUR funktionen skiljer sig från xy-systemet.

Exempel 1:

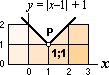
— BESKRIVER ekvationen y = |x| en funktion i xy?

— Nej. Det här är INTE en funktion i xy-systemet.

Uttrycket för y är sammansatt av TVÅ olika xy-funktioner. Den ena med en xy-skillnad på –1, och den andra med en xy-skillnad +1.

Funktionen sett totalt är BRUTEN i punkten P(0;0) för |x|-funktionen och, i illustrationsfigurens fall, i P(1;1) för |x–1| + 1. P har då två xy-differenser: det finns inget sätt att relatera P såsom tillhörande EN funktion. I respekt till den avbildningspunkten, finns inget kriterium för en singulär funktion som också saknar brytpunkter ENLIGT xy-SYSTEMETS PREFERENSKROPP.

— Vi säger att funktionen uppvisar ett avbrott i P.

Exempel 2:

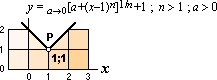
— BESKRIVER ekvationen y = [a+xⁿ]^1/n en funktion i xy?

— Ja. Det här ÄR en funktion i xy.

Med n som ett jämnt tal (2, 4, 6, …) är funktionen y-symmetrisk genom x=0 eller, som i illustrationens fall, genom x=1 i samma men längsflyttade funktion [a+(x–1)ⁿ]^1/n+1.

Förklaring:

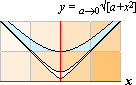
Den principiella rundheten i funktionens bottenpunkt kan studeras genom det enklare hyperboliska uttrycket

_a®0Ö[a+x²]; Genom att tillåta att a går mot noll, kommer funktionsformen att bli omöjlig att skilja från hörnet av en 45° roterad kvadrat, samma som icke-funktionen |x| i exempel 1. Subtraktion från x flyttar funktionen till höger, tillägget av en kvantitet till funktionen flyttar den vertikalt uppåt. I figuren är a skaran {1; 0,1; 0,001} med kvadraten som enhet.

Exempel 3:

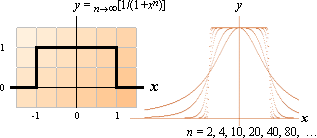
— BESKRIVER ekvationen y = (1+xⁿ)^–1 en funktion i xy?

— Ja. Det här är också en funktion i xy.

Genom att låta heltalsexponenten n växa obegränsat blir funktionens geometriska form omöjlig att skilja från en partiell rektangel.

Figurens högra del visar funktionstypen med växande n.

Exempel 4:

PREFIXxSIN

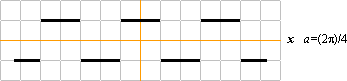
— BESKRIVER ekvationen y = (1/sinx)Ö(sinx)² en funktion i xy?

— Nej. Det här är INTE en funktion i xy. Ekvationen uttrycker en KONSTANT (är del av xy) enligt

Funktionen bryts periodiskt i PREFIXxSIN via sin(udda 90°)=0=sin(udda p/2) i alla udda enhetspunkter (med a=2p/4) enligt

P(x)={1(p/2), 3(p/2), 5(p/2), 7(p/2), …} = (2n–1)(p/2) med n som följden ±hela tal (nÎN) inkluderat noll. Brytningen får formen y=0/0. Utnyttjas positionspunkten — se differentialen — som aspekt ges y=0(1/¥)=0 vilket rent grafiskt ger 0 för brytpunkternas y-värden.

Funktionens avbildning visar x-paralleller, omväxlande över och under x-axeln för varje funktionsvärde x UTOM de angivna udda brytpunkterna.

Funktionen sett totalt är alltså dels periodiskt bruten i alla y=0 och dels för övrigt ingen funktion alls då den endast avbildar eller framhäver (processar) (fragmentariska x-) delar av xy-systemet. En raritet!

Exempel 5:

y = f_v(x)

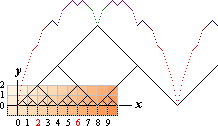
Ekvationens grafiska form indikeras av bergformationskonturen.

Den är amplitudsumman av toppsidorna på de inritade fraktala trianglarna.

Den grafiska formens motsvarande ekvation är (allmänna decimalfraktala ekvationen, här utan härledning)

_{±¥ K(n+1)}

f_v(x) = å [(x – KQ)(–1)ⁿ] .......... allmänna decimalfraktala ekvationen

^{n=0 x=nK}=2^–v/2

I figurgrafen är den angiven med Q = (2n+1 – (–1)ⁿ)/2 och K=2^–v/2.

Övre summagränsen n®¥ är här förenklad med ¥ då sammanget i vilket fall inte kan misstolkas.

— BESKRIVER ekvationen y = f_v(x) som visas ovan en funktion i xy?

Ekvationen kan skrivas förenklat

_¥

f (x) = å f_v(x)

^v=0

— Nej. Det här är INTE en funktion i xy.

Uttrycket för y är sammansatt av två principiellt olika funktioner. Den ena med xy-differensen –1, och den andra med xy-differensen +1. Funktionen totalt sett är bruten i varje punkt P(x;y) då v växer obegränsat.

Oavsett förstoring av summagrafen, nedan, innefattar den brutna delar av den ovan illustrerade bergformationskonturen. Vilket vill säga; med växande n finns inget annat att visa än K-kvantitetens systempunkter i grafformen: funktionen som sådan blir fullständigt sönderdelad eller fragmenterad i singulära fristående icke funktionssammanhängande punkter som växer obegränsat i antal.

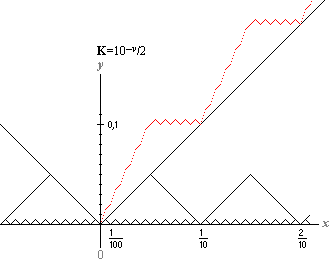
Hela byggnaden fragmenterar alltså genom den obegränsat växande mängdens minsta delar som bryter upp varje ansats till funktionsmässig kontinuitet.

I MODERN AKADEMI anses denna kurvatur innebära en kontinuerlig funktion

— som inte har derivata i någon enda punkt, enligt en demonstration år 1861 av Karl Weierstrass [ML s129sp1n fraktaler].

I ljuset av xy-SYSTEMETS PREFERENSKROPP — som Weierstrass naturligtvis inte kände till — är naturligtvis uppfattningen att ovanstående »kurva» skulle vara »kontinuerlig» en feluppfattning: Weierstrass/modern akademi utarbetade grundbegrepp som ansluter till uppfattningen att punkt och intervall är identiska (dx=Dx), därmed kommer man fram till helt andra begreppsdefinitioner: reguljära avbrott — i ljuset av xy-SYSTEMETS PREFERENSKROPP — anses som »kontinuerliga», och hela begreppsgrunden med »kontinuitet» och »definition» har därmed förlorat sin innebörd. Se även i Zenons Teorem.

I modern akademi återfaller (veterligt) begreppet kontinuitet i funktionsuttrycket på den variabla kvantiteten (x) genom ett avbildningsbegrepp

[ML s131sp1mn funktion, s234sp2n kontinuerlig funktion] — vilket i termer av relaterad matematik innebär att i modern akademi ser man alltså INTE till funktionen (= allt utom xy-systemet, enheten utan delar) för studiet av begreppet kontinuitet utan istället till verktyget (xy-systemet, uppräkneligheterna, intervallen); Eller som Karl Weierstrass (1815-1897) så träffande formulerade saken: processen är kvantiteten (gränsvärdet)

[ref. ML s22sp1n analysens aritmetisering]. Emellertid, eftersom man inte tycks vara medveten om det (heller) ändras preferenserna godtyckligt med den moderna akademins olika, löpande, uppfinningsbegrepp och som därmed ytterligare försvårar varje logiskt konsekvent beskrivning av den moderna akademins logiska lärosystem: det finns i grunden ingen sådan, förmodad, övergripande logik i modern akademi; Det finns i grunden ingen som kan förklara något.

Jämför (återigen) korsreferenserna i begreppet differential.

EXEMPLEN ENLIGT RELATERAD MATEMATIK VISAR GENOMGÅENDE att begreppet kontinuerlig funktion ENLIGT xy-SYSTEMETS PREFERENSKROPP betingas av positionsformen y’=dy/dx: en funktion i xy är kontinuerlig då, och endast då, varje funktionspunkt P(x;y) har en entydig utsträckning, och endast då.

Eftersom klassen alla möjliga funktioner förutsätter ett funktionsvärde y för varje variabelvärde x, innefattas i positionsformen y’=dy/dx därmed också alla funktioners alla möjliga funktionspunkter P(x;y) i formen av en funktionsgenerator: y’=dy/dx genererar kontinuerliga matematiska funktioner — en bestämd derivata y’ för varje P, ett bestämt funktionsvärde för varje y.

Därmed SAMLAR eller innesluter positionsformen y’=dy/dx funktionens absoluta deriverbarhet, dess absoluta integrerbarhet och dess absoluta kontinuitet I PUNKTBEGREPPET: nollformsalgebran. Den är abstrakt för intervallet. Några gränsvärdesbegrepp förekommer inte.

Se även i IdentitetsKriteriet för Integral-Funktion.

Se även i INTERVALLETS OFÖRSTÖRBARHET.

Exempel 6:

y = Y[f (x)]⁰

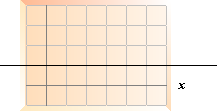
— BESKRIVER ekvationen y = Y[f(x)]⁰ en funktion i xy?

— Nej. Det här är INTE en funktion i xy. Ekvationen uttrycker en KONSTANT (är del av xy) enligt

[f(x)]⁰ = 1 som ger y = Y = konstant. Ekvationen för y avbildar xy-systemets x-paralleller med Y som avståndet från x-axeln

— Även x-axeln kan avbildas om vi sätter y = 1[f(x)]⁰ – 1.

— Vi kan säga att samtliga matematikens funktioner i xy-systemet innefattas av verktyget [f(x)]⁰=1.

Funktionsklasserna

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Funktionsklasserna

ämnesrubriker

innehåll

FUNKTIONSKLASSERNA

rationella tal

hypomängder

GM

AV

Kort resumé av Talteorins Elementa

Funktionsklasserna

Funktionsklass 1 · De operativa funktionsuttrycken

Funktionsklass 2 · De INoperativa funktionsuttrycken

Begreppet EXPONENTIALSERIE

Begreppet EXPONENTSERIE

Korsreferens

Korsrefererande Talnomenklatur

Funktionsbegreppet

FUNKTIONSBEGREPPET ENLIGT RELATERAD MATEMATIK

EXAMINERINGSEXEMPEL

Exempel 1-6

referenser

[ML]. MATEMATIKLEXIKON Wahlström&Widstrand 1991, efter The Crescent Dictionary of Mathematics, W. Karush

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2019-01-06

*END.

Stavningskontrollerat 2008-12-31.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se