UNIVERSUMS HISTORIA | AGW och
Framtiden IV — t(AGW)-integralen| 2015XI23 — a BellDHARMA production | Senast uppdaterade version: 2017-01-05 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Dokumentserie mot statens pågående
naturvandalisering från runt 2010 — Återerövringen av den naturliga biologiska
harmonin och balansen — i Sverige
BILDKÄLLA: Författarens arkiv · MONTAGE: 27Jun2012 E10 Bil22 — 20Aug2013 E25 Bild1 ·
Nikon D90 — Foto: 27Aug2014
E18 Bild146 — Den
alarmerande situationen i klartext
MainNV | MainATD
| MainBMS
| MainCAI
| MainDML
|
NV Naturen Revolterar ¦ ATD
Träddöden2015 ¦ BMS The Missing Sink ¦ CAI t(AGW)integralen ¦ DML
Mauna Loa-funktionen, Tabellvärden ¦
Tabellvärden INDUSTRIKOLET från 1751
| t(AGW)-integralen — x
= 1 till 12 med numerisk lösning | AGW-beviset förklarar IPCC-samfundets missar
|
CaseHistoryJan2016  AGWb15
AGWb15 ![]() ABCD-parametrarna
ABCD-parametrarna

CHJan2016: — CaseHistoryJan2016
ABCD-parametrarna — AGW-bevisets fem parametrar ABCDE: A/B = C/D ¦ C – D = E
AGW-beviset med Mauna Loa-funktionen förklarar:
IPCC-samfundets AGW-feluppfattning
AGW, eng. ANTHROPOGENIC GLOBAL WARMING, sv.
människoförorsakad global uppvärmning
AGW-beviset förklarar
IPCC-samfundets missar
IPCC-SAMFUNDETS AGW-FELUPPFATTNING FRAMGÅR KOMPRIMERAT I
SATSERNA NEDAN
AGWb1 ¦ AGWb2 ¦ AGWb3 ¦ AGWb4 ¦ AGWb5

AGW|S se S4; S se S2;
M se S3; I
ca 64% av M enligt resultatformen i AGW|MLF
(år2012¦1,54/2,42). I-grafens summering är rena Fossilideala Mauna Loa.
— AGW|S¦S¦I alla hyperboliska [t(AGW)-integralen], M
exponentiell p.g.a. växande [SKOGSINDUSTRIN¦Stat/Kommun,
TabellY3]
extra icke fossilt CO2.
Vad medför IPCC-samfundets feluppfattning, enligt AGW-beviset?
— SKOGSINDUSTRIN (Stat/Kommun) DUMPAR STORA mängder extra
luftkol till atmosfären
(+0,89 ppmvCO2 år2015; 38% av hela Mauna Loa-tillskottet
år2015 ¦ TabellY3:
100%=2,33 ppmvCO2),
medan IPCC-samfundet (Kyotoprotokoll, Storskalig Skogsmanipulering)
UPPMUNTRAR DEN VERKSAMHETEN: »bra för
klimatet» i feltron att »skogen kolsänker AGW». Chockerande
är inte ordet. Dementera den som kan:
— IPCC-samfundet uppträder PRIMITIVT och FARLIGT¦VÅDLIGT på
Jorden 2015: förstår inte grundfysiken.
Jämför LISTAN.
RÄKNEEXEMPLEN i BEVISET
FÖR DEN EXTRA ICKE FOSSILRELATERADE KOLDIOXIDEMISSIONENS BETYDELSE (Värmemotstånd och Trädens känslighet för LOKALA
Koldioxidvariationer)
visar att kvantitativa grunder väl finns från extra atmosfäriskt icke-fossilt
relaterat luftkol — marker
med kvarlämnad död biomassa som hindras återväxa — för att
åstadkomma den typ av negativa effekter (nekroser,
växtkvävningssymtom, tydligen hos speciellt tall över stora regionala områden
kring cykel- och gångvägar, just där stat/kommun hindrar naturlig återväxt)
av den typ som observerats i Träddöden
2015: Stat/Kommun stressar allt levande genom att kapa
levande träd, hindra återväxt och vandalisera naturlig skogsmark. Träden ropar
på hjälp. Dementera gärna.
CaseHistoryJan2016
— AGW-beviset med Mauna Loa-funktionen
Mauna
Loa-funktionen uppdagas:
|
2009 |
2011 |
2013 |
Aug2015 |
Dec2015 |
2009: AGW-beviset framställs. 2011:
Synbara brännskador noteras på en del blad bland andra helt friska efter en
period av högintensiv solgassande vårvärme. 2013: Stat och Kommun
fortsätter meja ner levande träd med hindrad naturlig återväxt: angelägenhen
växer att hitta konkreta konsekvensbevis för staten/kommunernas uppenbart
absurda naturhantering. Aug2015: Omfattande observationer kring stats-
och kommunhärjade cykel- och gångvägar speciellt av döende tall. Dec2015:
Undersökningarna leder fram till Mauna Loa-funktionen som förklarar helheten
tillsammans med AGW-beviset. AGW-beviset
ingår inte i IPCC-samfundet.
AGW-BEVISET MED MAUNA LOA-FUNKTIONEN:
—————————————————————————————————
AGW, eng. ANTHROPOGENIC GLOBAL WARMING, sv.
människoförorsakad global uppvärmning
1. Havsupptaget GER AGW. Därutöver
intet.
Bevis: NASA-CRU-kurvan → Havsperioderna
+ m/t(AGW) = 10,17094
T12 KG/°C, med m|t(AGW)-integralen
= Ideala FossilMaunaLoa (enbart fossilt CO2)
2. Extra icke-fossilt atmosfäriskt
CO2 ingen nämnvärd AGW-effekt.
Bevis:
Följdsats av 1 . [Speciellt: AGW-bevisets t/T=m/M med
fossilförbränningen T har ingen motsvarighet i icke fossilt extra CO2].
Särskilda bevis/klargöranden: Värmemotstånd och Trädens känslighet för LOKALA Koldioxidvariationer
BEVISET
FÖR DEN EXTRA ICKE FOSSILRELATERADE KOLDIOXIDEMISSIONENS BETYDELSE — ÄVEN hela (1815-2015)
116ppmvCO2 ger bara +0,001° (KalkylT¦CO2¦T2)
DÄREMOT GES STORA LOKALA EFFEKTER PÅ SMÅ JORDYTOR UNDER
KORTA TIDRYMDER: DET LILLA TILLSKOTTET BIDRAR MED EXTRA VÄDERKRAFTER SOM DRAR
OMKRING.
3. AGW-reducerande atmosfäriska
upptag finns ännu inte.
Bevis:
Följdsats av 1 & 2 . SKOGEN TAR INTE UPP NÅGONTING ALLS AV INDUSTRINS
FOSSILUTSLÄPP. Jämför IPCC|Giftlarm.
FÖRUTSÄTTNINGEN FÖR ATT AGW-REDUCERANDE ATMOSFÄRISKT UPPTAG
SKA KOMMA I FRÅGA, ÄR ATT DEN
EXTRA icke-fossila CO2-MÄNGDEN
FÖRST MÅSTE AVLÄGSNAS.
SEDAN VET VI INTE.
— DET FINNS EN TANKE SOM SÄGER ATT KEMISK JÄMVIKT HAV-LUFT
ÅSTADKOMMER AUTOMATISKA UTJÄMNINGAR. MEN VI VET INTE NÄRMARE HUR DET FUNGERAR I
AGW.
4. Trädens växtkol tas från
naturskogen (alltmer utarmad [SI]).
1: HAVSUPPTAGET STÅR FÖR AGW. DÄRUTÖVER INTET UPPTAG.
Särskilda bevis/klargöranden: TrädensVäxtkol — SÄRSKILDA RÄKNEEXEMPEL ¦ NATURSKOGEN
¦ SKOGSFÄLTET
¦
SKOGSINDUSTRINS NATURVANDALISERING ¦ NAMMNET ¦ SKOGSEXPLOATERINGEN — GRAFER ¦
5. Mauna Loa-funktionen
förklarar IPCC-samfundet | GLOBALRÄKNINGEN
Bevis: Följdsats av
1 & 2 & 3 & 4 .Kvantitativt Utförligt ÖverensStämmande Globalt KolBudgetExempel
— JÄMFÖRANDE
IPCC-BUDGET
ALLA KVANTITETER FINNS MED — MEN IPCC-SAMFUNDET HAR INTE
tAGW-INTEGRALEN, OCH DÄRMED EN MISSAD AVGÖRANDE FAKTOR FÖR EXAKT FÖRKLARING.
—————————
OVANSTÅENDE 5 PUNKTER SKA FÖRESTÄLLA GENUINA SVARPÅ/LÄNKARTILL VARJE CENTRAL AVGÖRANDE
SPECIELLT TRIXIG BEVISKRÄVANDE KLARGÖRANDE FRÅGA SOM HAR MED AGW-KOMPLEXET ATT
GÖRA.
ABCD - parametersambanden:
(D)MaunaLoaFossil =
(C)INDUSTRIÅRETSEMISSIONER 1000000000*(1,765*(1-1/(1+((år-1815)/212,7)^4))*10170,94),
se m/t(AGW)
×
(A)totaltMaunaLoaFossil (mJatm=5,28 T18 KG) · [t(AGW)INTEGRALEN]CO2ppmvSUBSTITUTIONSFUNKTIONER · t6
· 12/28,8
/
(B)INDUSTRINTOTALT(från 1815) 1000000000*INDEX(Tabell2.$A$1:$A$668;$C$7-1815+2;0) tabellvärde, årsvis trappstegssummering se S2 ¦ S4
Hur kvantiteterna beräknas sedan Mauna
Loa-funktionen bestämts (parentesvärdena i T12 KGkol, exempelår 2012):
(154)TotaltFossilAtmosfäriskt(A) (3,06)MaunaLoaFossilt(D)
—————————————— = ——————————— = 40,42% ([A/B]ÅR2012)
(381)TotaltIndustriFossilt(B) (7,61)IndustriFossilt(C)
:
RELATIONEN B/A = C/D (max2%fel) är SÅ giltig
ATT C<<B OCH D<<A med logoceptet
—————————————————————————————————————
A [CO2-skalan] kräver Mauna Loa-funktionen relativt
t(AGW)-integralen — CO2-skalans absoluta bestämning
|
|
Totalt |
|
Årligt |
|
|
- |
- |
- |
- |
- |
|
Givna |
B |
|
C |
INDUSTRIN Statistiskt |
|
|
— |
= |
— |
|
|
Beräknas |
A |
|
D |
Atmosfäriskt MAUNA LOA |
|
- |
- |
- |
- |
- |
|
|
integral |
|
derivata |
|
FossilEmissionsPreferensen
t(AGW)-integralen — Relationerna gäller Förutsatt
B >> C och A >> D (felet
är max 2%)
———————————————————————————
ALLA ABCD i KGkol ÄR HYPERBOLISKA =
slutar på raka asymptoter = ansluter till t(AGW)-integralen ¦ derivatan =
fossilenergin
—————————————————————————————————————
IPCC-samfundet har — garanterat — ingen
motsvarande uppställningen eftersom faktorn A
— t(AGW)-integralen
¦ NASA-CRU
= HavsPerioder+m|t(AGW) — inte ingår i deras.
FELET (~ max2%) är av samma typ och ordning
som i PARABELEXEMPLET
(stegvis summering kontra reguljär integrering).
— På samma sätt som i industrins statistiska årssummering
(S2 från S1) är INTE integralvärdena
explicit önskvärda, endast själva trappstegssummeringen. Tillsammans med
globala årsmedelvärden (2-5år) får vi förmodligen och i vilket fall inte göra
anspråk på mera än runt just max [100–(2-5) = (95-98)]% noggrannhet i värdena.
— Kalkylkortet
[Tabell 1 AM2015A.ods] i RESULTAT
visar för åren 1900 1950 2000 2050 A/B-värdena 44,05% 42,20% 40,47% 40,39%.
MaunaLoaFossil 40% av t(AGW) — HavsFossilUpptaget 60%
— Med relationen grovt sett (från 2000+) D/C~40% kan
vi nu på enklaste, mest översiktliga snabbaste, sättet använda t(AGW)-kurvan
reducerad till 40%, vilket direkt ger oss MaunaLoaFossilvärdena i jämförande
klartext (max 2% fel).
— Havsupptaget som ansvarar för hela
AGW blir differensen C – D.
— Se särskilt exempel i Jämförande IPCC-budget.
ABCD-parametrarna —
AGW-bevisets fem parametrar ABCDE: A/B = C/D ¦ C – D = E — fullständiga
AGW-beviset Jan2016
CaseHistory,
Översikt Jan2016 — Globalt Jämförande KolBudgetexempel nedan för år 2012 — hur
de olika parametervärdena sammanhänger.
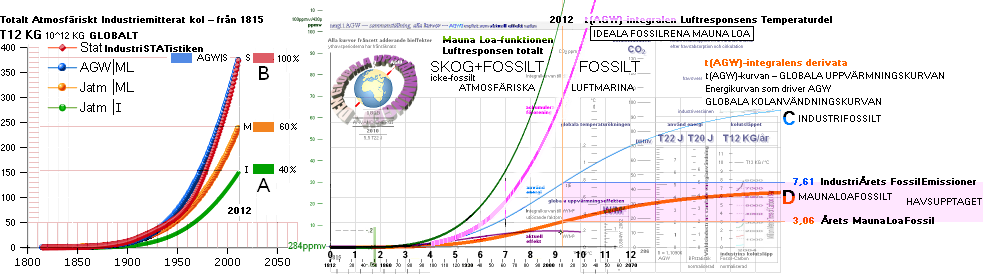
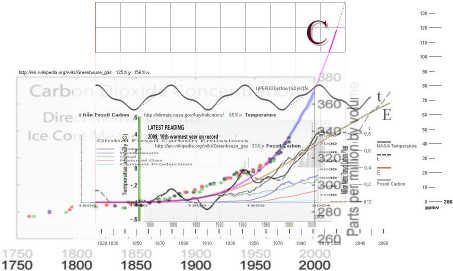
Högra
bilddelen ovan här modifierad från AGW-beviset sammanställningen [2010] EffektEnergiAGW
— med apelsingula
Mauna LoaFossil-grafen, gröna Mauna Loa-funktionen, violetta t(AGW)-integralen, sammanställning
Jan2016.
Förklaring till graferna ovan
Fullständiga AGW-beviset Jan2016 enligt AGWb15: A/B=D/C:
MAUNA
LOA-FUNKTIONEN (100,00% Mauna Loa-värden) BESTÄMMER CO2-SKALAN FÖR t(AGW)-INTEGRALEN. DÄRMED KAN TotalaMaunaLoaFossilt
A I ABCD
BESTÄMMAS, OCH DÄRMED årets Mauna LoaFossil D
DÅ (IndustrinTotalt och IndustriÅretsEmissioner) BC ÄR KÄNDA, OCH DÄRMED årets FOSSILA
HAVSUPPTAG C–D. Notera att IndustrinTotalt
B¦S2
relativt ideala trappstegssummeringen (AGW|S)¦S4 har högre värden upp mot exempelåret
2012 med större ökning än AGW|S-summeringen som har lägre värden med mindre
ökning, bägge slutar på samma summa (3,74 T14 KG år
2012 in till 99,9679% ¦ skärningen år 1936). Se vidare utförligt från GLOBALRÄKNINGEN
och RESULTAT
och JÄMFÖRANDE
IPCC-BUDGET: samma kvantiteter men i chockerande olika
tappning: väsensskilda fysikgrunder: AGW-NASA-CRU-kurvan
via havsupptaget grundas på ca 60% av industriemissionerna.
Betydelsen av Mauna
Loa-funktionen:
AGW,
eng. Anthropogentic Global Warming, sv. av människan förorsakad
global uppvärmning
—————————————————————————————————————————————
BETYDELSEN
AV DEN AVGÖRANDE MAUNA
LOA-FUNKTIONEN — DEN FASTA CO2-SKALAN
t(AGW)-integralen från 2009
t(AGW)-integralen,
FOSSILATMOSFÄRISKA CO2-KURVAN EFTER HAVSUPPTAGET, eller FossilIdeala Mauna Loa,
är given från NASA-CRU-kurvans
ekvivalenta komponenter Havsperioderna + t(AGW)-kurvan: den
sistnämndas integral:
—
Alla dessa [NasaCru¦HavsP¦tAGW)¦t(AGW)int] 1 + 2 + 1 distinkta funktionsuttryck
har automatiskt NASA-CRU-kurvans tidsskala.
—
Genom proportionaliteten mellan temperatur och energi får
t(AGW)-temperaturkurvan också betydelsen av den energikurva som styr hela
AGW-processen via fossilindustrins kolutsläpp (m), m/t-relationen.
Speciellt S4 bevisar
t(AGW)-kurvans samhörighet med fossilindustrins årssummeringar S2 i S5. Därmed 1 + 3 + 1 distinkta
funktioner.
—
FossilIdeala Mauna Loa = t(AGW)-integralen betyder särskilt att det
atmosfäriska CO2-innehållet, det (om något alls) som kvarstår efter det
AGW-nödvändiga havsupptaget, avspeglas proportionellt mot industrins
fossilanvändning, t(AGW)-kurvan: m(Cindustri)energikurvan/t(AGW)temperaturkurvan=konstant,
och därmed exakt efter t(AGW)-integralens form och utsträckning.
t(AGW)-integralen från 2009 — saknar fast CO2-skala
Emellertid,
en fast CO2-skala saknas för t(AGW)-integralen, samma som FOSSILATMOSFÄRISKA
CO2-KURVAN EFTER HAVSUPPTAGET, eller FossilIdeala Mauna Loa.
—
Vi kan veterligt bara finna en sådan bestämd CO2-skala på NASA-CRU-kurvans
givna tidsskala genom de årligt praktiskt globalt uppmätta medelvärdesbaserade
atmosfäriska Mauna Loa-CO2-värdena.
—
SOM t(AGW)-integralen, FOSSILATMOSFÄRISKA CO2-KURVAN EFTER HAVSUPPTAGET, eller
FossilIdeala Mauna Loa REDAN är grundad på ATT ett havsupptag har skett
— = själva förutsättningen för den globala
uppvärmningen enligt NASA-CRU-kurvans sammansättning i Havsperioderna +
t(AGW)-kurvan (AGWb1)
—
BÖR de verkligt årligt praktiskt globalt uppmätta medelvärdesbaserade
atmosfäriska Mauna Loa-CO2-värdena uppvisa LÄGST EXAKT PASSNING till
t(AGW)-integralen. Se alla alternativen i MLFres.
DEN FÖRUTSÄTTNINGEN MARKERAR HELA
UTGÅNGSPUNKTEN I DEN VIDARE ANALYSEN.
Mauna Loa-funktionens konturer
—
Vid UTPROVNINGEN AV EN EVENTUELLT KANDIDERANDE MAUNA LOA-FUNKTION blir alltså
grundkriteriet självskrivet: Uppgiften gäller att anställa kandidaturen PÅ — i
så nära FORM-mässig överensstämmelse följsamhet
som möjligt med — t(AGW)-integralens form. Tidsskalan är redan given.
Analysen
från 2009
FRÅN
BÖRJAN (2009) fanns inte djupsinnigheterna ovan. Föreställningen om att
praktiska Mauna Loa-CO2-värden skulle skilja sig mot t(AGW)-integralen hade
bara följande provision: naturligt marginella avvikelser (på max 2%) [TabellCO2]. Att någon egentlig,
mera systematisk skillnad skulle finnas mellan t(AGW)-integralen och verkliga
praktiska Mauna Loa-CO2-globalmedelvärden, fanns inte: »dessa är i själva
verket samma» (med mindre marginella naturliga avvikelser). Därmed
skulle ämnet ha avslutats. Kort och gott.
Men
den lilla (2%-iga) avvikelsen var envis. Den antydde att de verkligt
atmosfäriskt uppmätta Mauna Loa-CO2-värdena uppvisade en systematisk tendens
till exponentiellt växande (LavinOrange2013), medan
t(AGW)-integralen i sig slutar på en asymptotisk rät funktionslinje (atan 6).
Träddöden 2015 gav ytterligare anledning att djupdyka i
sambandsformerna, och leta i allmänt tillgänglig litteratur, för att försöka
hitta uppslag till möjliga förklaringar.
Mauna Loa-funktionen framträder Dec2015
Så
uppdagades det ena med det andra.
Mauna Loa-funktionen framkom Dec2015 med
lösningen till CO2-skalan. Enda skillnaden mot analysen från 2009 är att den
tidigare (i stort likformiga) t(AGW)-substituerade Mauna Loa-kurvformen nu ligger
vänsterdragen mot y-axeln: det tidigare antydda 2%-iga felet visade sig gömma
en mer eller mindre chockerande inte tidigare uppmärksammad detalj: De globalt
atmosfäriskt uppmätta Mauna Loa-CO2-värdena består av en del (64%)
industrifossilassocierat CO2, den aktuella del som berör själva AGW-effekten i
samband med havsupptaget, och en extra STOR (36%) del icke-fossilrelaterat CO2,
och som visar sig kunna förklaras kvantitativt på skogsindustrins verksamhet (Tabell Y2): Allmän avskogning
under 200 år, + nuvarande fortsatt inbrott i naturskogarna. Värdena stämmer med
IPCC-kvantiteterna. Men räkningen är annorlunda — tillsammans med termer och
begrepp som det verkar svårt att hitta maken till i de mest synliga delarna i
IPCC-samfundets litteratur (JordTrädet)
(SkogsFältet)
(NAMMNET) (Globalräkningen).
Se utförliga beskrivningar med exempel och
jämförelser från RESULTAT.
CO2-skalan, utvecklingarna Dec2015
Se
även utvecklingshistorien för CO2-skalan
från Okt2015.
CO2-skalans dramatiska — avgörande — historia i AGW-beviset:
2009:
t(AGW)-integralen associerades från början (2009)
med Mauna Loa-värdena (TabellCO2).
— Originaldatat med CO2-värdena (CarbonDioxideKurvan) via CO2-offset
(år1815) 286ppmv
inpassades till tidsskalan (x) för
NASA-CRU-kurvan med komponenterna Havsperioder + m|t(AGW) med koldioxidskalan|CO2-skalan
(y) justerad efter passningen till [substitutionskurvan för]
t(AGW)-integralens kurvform — med originalet i skala som ovan för passningen
nedan (Koldioxidhalten)
— enligt storleksändringen x;y: 78%;62,5%:
2011-2015:
EFTERFÖLJANDE DETALJERADE UNDERSÖKNINGAR FÖRANLEDDA
AV OBSERVATIONER
MED MISSTANKE OM SÄRSKILDA
EFFEKTER FRÅN STATEN/KOMMUNERNAS UPPENBART
NATURVANDALISERANDE VERKSAMHET (StatsFröjden)
uppdagade att Mauna Loa-värdena — relativt t(AGW)-integralens hyperboliska
slutform (atan6)
— i själva verket är exponentiella (LavinOrange):
en tydlig lavineffekt framträder, ännu ringa. Mauna Loa-värdena relativt
— t(AGW)-integralens idealt uteslutande AGW-fossilt bidragande CO2-värden —
visar otvetydigt på en liten extra ökning. Se särskilt i Globalräkningen,
ökningsformen framgår tydligt där från ca 1962.
Djupanalyserna ledde SÅ fram till Mauna
Loa-funktionen:
— Alla globalt årliga Mauna Loa-värden från
1959-2013 (sista tabelldatat Dec2015) kan med medelavvikelsen inom
100,00% anställas på en snäv samling kandidater med en exponentiell
funktionskurva för mera noggrann prövning. Med Mauna Loa-funktionens maximala
formanpassning till idealt AGW-fossila t(AGW)-integralens
nu mera noggrant framställda form, visade sig den chockerande upplösningen (GLOBALRÄKNINGEN):
Mauna Loa-värdena via Mauna Loa-funktionskurvan (gröna vänstra nedan)
uppvisar ett STORT glapp fram till t(AGW)-integralen: Mauna Loa-värdena
kamouflerar ett stort extra tillskott av icke fossilt CO2 som byggts på ända
från början från runt 1800.
CO2-skalan
i originalet ovan med Mauna Loa-funktionen får i ljuset av dessa nya
detaljer samma tidsskala som tidigare, men med en justering för ett mera
noggrant CO2-offsetvärde 284ppmvBegin1812
tillsammans med en passningsjustering i y-led, totalt från originalet x;y:
78%;102% den inlagda violetta delen nedan över den mörkgröna Mauna
Loa-funktionskurvan; högra violetta t(AGW)-integralen:
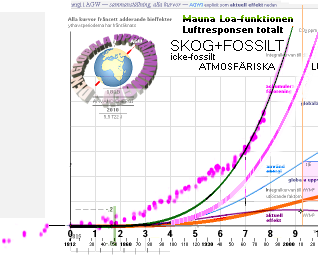
Violetta punkterna: IPCC-uppmätta CO2-värdena
insatta i AGW-beviset efter (gröna) Mauna Loa-funktionen (Dec2015). Tidsskalan
samma som NASA-CRU-kurvan. Enhetlig grafbeskrivning i ABCD-parametrarna
Originalets CO2-skala — samma tidsskala bevarad —
i bilden ovan justerad för passning till Mauna Loa-värdena via 284ppmv vid
år1812 (från IPCC-data, se 284ppmvBegin1812)
och den mera noggranna 100,00%-matchande Mauna
Loa-funktionen. Tidsskalan med början från år 1812 särskilt
anpassad efter den senare mera noggranna NASA-CRU-passningen i Alternativ4.
Den stora avvikande CO2-dataformen —Den stora
skogsavverkningsperioden 1850-1950:
— Speciellt den världsomfattande
skogsavverkningsperioden 1850-1950, den starkt avvikande raka uppgången (data
från borrkärnor), får här sin speciella förklaring via AGW-bevisets särskilda
upplysningar i
BEVISET
FÖR DEN EXTRA ICKE FOSSILRELATERADE KOLDIOXIDEMISSIONENS BETYDELSE:
— ÄVEN om man tar HELA Mauna Loa-CO2-tillskottet (116
ppmv år 2015) från 1812 (284ppmv) ger inte den delen något annat
AGW-bidrag än +0,001°C: Extra icke-fossilt CO2 har ingen nämnvärd AGW-verkan.
Den stora extra CO2-pumpen 1850-1950 syns inte i NASA-CRU-kurvan heller. Däremot
visar den enkla matematiken för Biologiska Tillväxtkonstanten (BTK) att extra atmosfäriskt
icke-fossilt CO2 kan förstås bidra katastrofalt till såväl lokala växteffekter
som lokala extra väderkrafter, se utförligt med enkla praktiska räkneexempel
från Värmemotstånd
och Trädens känslighet för LOKALA Koldioxidvariationer
.
Den egentliga exponentiella icke-fossilt relaterade
CO2-uppgången — börjar från runt år 1960, se Globalräkningen
Metoderna
för skogsavverkning perioden 1850-1950 utvecklades drastiskt från början av
1960-talet (den tvära brytningen ovan punktvioletta-grafmörkgröna) med
introduktionen av MOTORSÅGEN. Se VÄRLDSHANDELSUTVECKLINGEN FRÅN
1960-TALET. FORMEN hos Mauna Loa-funktionen visar också JUST
den avgörande tydliga EXPONENTIELLA uppgången relativt t(AGW)-integralens
slutliga hyperboliskt asymptotiska form — från omkring lägst år 1962.
Med dessa slutliga uppdaganden (Dec2015) har
AGW-beviset fått en till synes helt uttömmande totalförklaring, innefattat
klargörande jämförande exempel med IPCC-samfundets syn på sakernas tillstånd.
Se JÄMFÖRANDE
IPCC-BUDGET.
Se
totalsammanfattning CaseHistory AGW-beviset Jan2016.
AGW-beviset förklarar IPCC-samfundets missar — 6Jan2016
AGW-beviset förklarar
IPCC-samfundets första (dubbel-) miss: Miss1
¦ Miss
2 ¦ Sätt1 ¦ Sätt 2
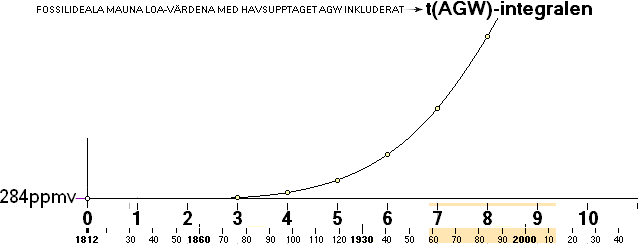
AGW-beviset: t(AGW)-integralen = Fossilideala
Mauna Loa-värden MED havsupptaget inkluderat = orsaken, grunden till AGW.
IPCC-smfunt: Det faktum att Mauna Loa-värdena är
lägre [‡]
än fossilutsläppen bevisar reducerade effekter av AGW på havsupptag.
Första missen — IndustriPreferensen till
AGW-analysen
t(AGW)-integralen ingår inte i IPCC-samfundet: Kolumn1 NASA-CRU-kurvans
ekvivalenta uppdelning i komponenterna havsperioder + t(AGW)-kurvan =
antropogena globala energianvändningen = världsindustrins kol/fossilanvändning:
dess integral, t(AGW)-integralen, avspeglar IDEALT UTAN FÖRLUSTER ELLER TILLÄGG
en motsvarande proportionell atmosfärisk CO2-ökning som ovan (»FossilIdeala
Mauna Loa»).
Andra missen — Mauna Loa-värdenas
tidssammanhängande innebörd; VÄRDEBILDENS FORM, HUR DEN VARIERAR
Utan en PREFERENSFUNKTION — t(AGW)-integralen — som grund
för en motsvarande Mauna Loa-funktion, förutsatt vi kan finna en sådan [AGW|MLF],
finns inga planer någonstans veterligt att hitta vettiga jämförande
beskrivningar på uppsamlade observerade data: Vi måste ovillkorligen VETA hur
och på vilket sätt en Mauna Loa-funktion FÖRHÅLLER SIG till ett givet globalt
industriindex: världsindustrins kol/fossilanvändning = t(AGW)-kurvan Kolumn3, samma som den
havsutjämnade versionen av fossilindustrins statistiska kurva Kolumn12.
— NÄMLIGEN — havsupptaget = AGW-orsaken — att Mauna
Loa-värden OMÖJLIGEN KAN AVSPEGLA HELA FOSSILINDUSTRINS EMISSIONER EFTERSOM AGW
BYGGER PÅ UPPVÄRMNING AV HAVET — enligt
NASA-CRU-KURVANS UPPDELNING, Kolumn1.
— Så: UTGÅNGSPUNKTEN är ATT visst havsupptag finns FÖR att
Mauna Loa-värdena ALLS ska visa något annat än noll ökning PÅ EN
FOSSILEMITTERAD grund.
IPCC-samfundet
missar det — därför att IPCC-samfundet, tydligen och uppenbarligen, inte har
någon analys som delar NASA-CRU-kurvan i ekvivalenta komponenter.
Se även i IPCC|Poängen.
ATT t(AGW)-kurvan
som sådan, som en havsutjämnad version av industristatistikens kurva, verkligen
har fog för sig visas av samhörigheten (99,9679%,
sista tillgängliga tabellåret 2011 i sammanställningen 2015) i den årsvisa
ackumulerade summeringen av totalt emitterat fossilkol, se S5: värdeformerna är (efter tid) helt
analoga.
IPCC-samfundets mening
— att havsupptaget reducerar effekterna av en annars större
AGW-effekt
— är en feluppfattning.
IPCC-samfundets mening
— att Mauna Loa-värdenas motsvarande LÄGRE S3 ackumulerade atmosfäriska
kolinnehåll relativt det som industrin faktiskt dumpar ut i luften S2, det senare överväger med runt 50% [IPCC|Poängen],
bevisar att hav/skog absorberar fossilemitterat luftkol som betyder en
reducerad AGW-verkan (”Luckily”)
— är en feluppfattning, en ren förmodan, i anledning av det
faktiska havsupptaget = AGW-beviset.
IPCC-samfundets vidare missar
Så följer konsekvenserna av den vidare analysen:
Mauna Loa-värdena visar sig kunna representeras av en snäv
skara kandidater som alla satisfierar Mauna Loa-värdena tagna genomsnittligt
MED optimal följsamhet i FORMEN in till 100,00% av typen
ppmvCO2 =
ppmvOffset + k(År–1812)^e ; Mauna
Loa-kandidater
med 100,00% matchning
e, exponetkoefficienten. Tidsskalan (År-1812) är anpassad
ekvivalent med NASA-CRU-kurvans tidsskala med justeringen 1812 på offsetvärdet
284 ppmvCO2, se ppmvBegin1812.
Därmed är x-skalan fixerad och given.
Y-skalan däremot, den aktuella ppmvCO2-skalan, är obestämd:
— Vi bestämmer den delen RELATIVT t(AGW)-integralen som
absolut industrifossil Mauna Loa-referens;
— Vi söker den förstoring eller förminskning i y-led som
MEST NÄRA MATCHAR t(AGW)‑integralens FORM — tangerande, icke skärande.
— Det betyder att vi söker vertikalkoefficienter som ändrar
vertikalformen hos den givna fortfarande giltiga x-axelsbestämda 100,00% Mauna
Loa-funktionskandidaten, så, att den så nära som alls är möjligt ansluter till
FORMEN på t(AGW)-integralen — fossilemissionernas absoluta industripreferens.
Se tillvägagångssättet utförligt redovisat i MaunaLoaFunktionen.
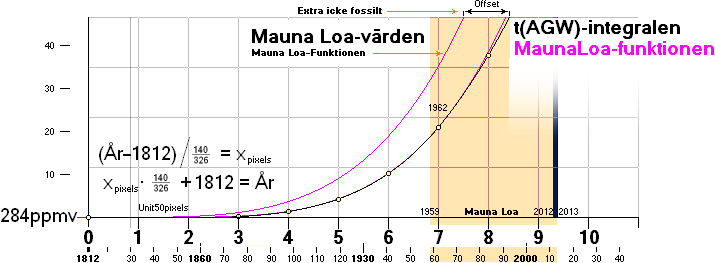
Bilden nedan visar slutresultatet med en markering
(2012-2013) i samband med jämförande IPCC-kolbudgetexempel [Resultat].
284ppmvCO2-nivån från 1812 enligt IPCC-uppgift i ppmvBegin1812.
t(AGW)-integralen beskrivs här i
separat artikel.
Högra violetta grafen visar Mauna Loa-funktionens här antagna, stadfästa,
»absoluta matchning» med den svarta t(AGW)-integralen;
Vänstra violetta grafen visar aktuella NASA-CRU-tidsanaloga placeringen av Mauna
Loa-funktionen på tidsaxeln.
— OM Mauna Loa-funktionen hade visat EXAKT följsamhet med
t(AGW)-integralen — en exponentiell avvikelse märks tydligt tidigast från ca
1962 [Se Världshandelsutvecklingen från 1960-talet]
— skulle inga extra tillskott eller reduktioner ha avspeglats i de 100,00%
matchande årligt globalt uppmätta atmosfäriska Mauna Loa-värdena.
Vi kan tills vidare helt frånse den (marginella) aspekten,
och tills vidare bara se till den möjliga slutpositionen utmed x-axeln =
tidsskalan för den aktuella 100,00% matchande Mauna Loa-funktionen.
Vi studerar de bägge möjliga upplösningarna som nedan:
Första sättet: Agenter
absorberar fossilt — utöver det redan AGW-aktiverade havsupptaget
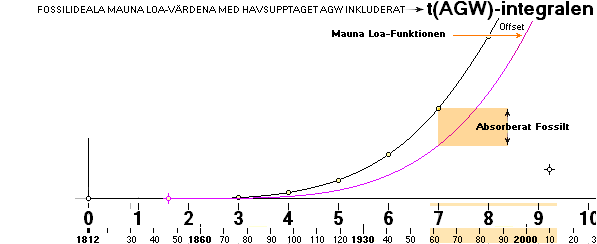
Grafen ovan, violetta Mauna Loa till höger om
t(AGW)-integralen:
— Fossilt
relaterat CO2
ingår REDUCERAT = minskat i Mauna Loa-värdena:
— Mauna Loa-värdena antyder att någon agent, utöver det
redan nödvändiga havsupptaget som grundlägger AGW Kolumn1 (Industrins emissioner
minus Mauna Loa-värdet = Havsupptaget) tar upp, absorberar EXTRA koldioxid från
fossilindustrins CO2-emssioner.
Andra sättet: Agenter
emitterar icke fossilt — NÅGON KÄLLA föranleder
att EXTRA KOLDIOXID DUMPAS UT TILL LUFTEN
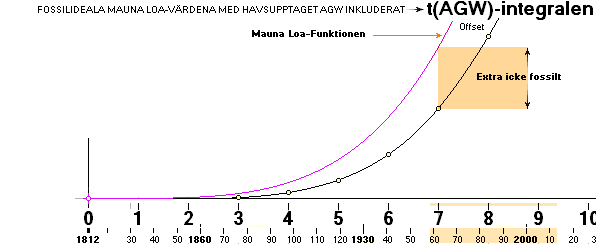
Grafen ovan, violetta Mauna Loa till vänster om
t(AGW)-integralen:
— Icke
Fossilt relaterat
CO2 adderas VÄXANDE = ökande i Mauna Loa-värdena:
— Mauna Loa-värdena antyder att någon agent ger ut, eller
föranleder utgivning av EXTRA koldioxid, UTÖVER det som redan ges ut från
fossilindustrins CO2-emssioner.
Mauna Loa-funktionen ansluter till det
andra sättet [‡] som ovan, utförligt i [Resultat].
— HUR går det ihop med AGW-effekten? Se Värmemotstånd¦INLEDNING nedan: helt
försumbar AGW för icke fossila bidrag. Däremot FRUKTANSVÄRDA EXTRA väderkrafter
om det lilla globala värme-Energi-bidraget samlas under korta tidrymder på små
lokala Jordytsplättar (som i människans lilla värld betyder omfattande
skadeverkningar).
— Vilken skulle agentkällan vara?
Det är inte vad saken handlar om: Det finns ingen egentlig
EXTRA CO2-källa;
— Det saken handlar om är, tydligen, att NATURSKOGEN
EN GÅNG I TIDEN band upp naturligt mark-luft-vatten-strömningskol(dioxid,
se Skogsfältet)
som SKOGSINDUSTRIN — vi världsmarknadsgalna profitgiriga människor — nogsamt
numera plockat sönder, bit för bit: bindningarna har upphört, och med det uppkomsten
av »EXTRAKÄLLAN». Det tidigare naturskogsbundna kolet, koldioxiden, strömmar nu
fritt ut i luften, utan naturliga regulatorer — tills dess stat och kommun på
Jorden inser vanvettet och stoppar all vidare avverkning, upphör att hindra
naturlig återväxt. Se även i ÅterväxtSuget.
AGW|MLF-resultatet
visar för år 2015 att totala differensen mot t(AGW)-integralen är +43ppmvCO2
eller totalt infört atmosfäriskt extra kol sedan början av 1800-talet:
— 94 T12 KGkol =
konv. 94 Pg = 94 PetaGram, med ett
årligt tillskott på 1,96 T12 KGkol/År2015, med tillökningstakten 4,04 T10 KGkol/år2015.
— Vilken praktisk grund finns för dessa siffror?
Från början: ingen
aning. Finns ingen sådan vettig praktisk databank, är resultatet galet.
— Tabellerna (Y2
¦ Y3)
i TabellY
ger det chockerande beskedet: detaljförklaring: skogsindustrierna
Naturen utmanar Människan: — Bygg Boendet på Höjden,
säger Naturen; Spara på JordYtsmarken och låt Skogen Växa Ifred. Fäll inte
Levande, Bioreglerande, Träd. Sluta med röjvansinnet. Vårda istället
naturväxandet som DIAMANTER. Se till att Naturskogen kommer tillbaka. Sluta
Motarbeta Naturen.
Beroende på vilka datakällor som används (här ForestWorld och FAO
prognos 2010):
— Mellan 30-50% av Naturskogarna har försvunnit från/sedan
runt 1750-1800.
— Biologiska tillväxtkonstanten BTK (Soleffekten = konstant = T/R=E/t)
utpekar en URSPRUNGLIGT VÄL BALANSERAD NATURSKOG med (perfekt) balanserad
bioreglering (BioVentilation BV)
i samspelet mark-vatten-luft-skog (SkogsFältet):
— Träden
tar sitt växtkol från marken (TrädensVäxtkol).
— Varje avlivning av ett LEVANDE bioreglerande
(syreproducerande) träd betyder ett NATURSKOGSBROTT: det trädets
bioventilation, från skogsmarken som kolkälla, förlorar sin reglerande värd,
det levande trädet som sågas ner, och därmed en extra koldioxiddump till
luften/atmosfären som inte fanns där förut (King1994).
Det är den ena
sidan av saken, den lilla delen.
Den andra sidan,
den stora delen:
Koldioxidbomben:
OREGLERAD
URSPRUNGLIGT NATURSKOGSBUNDEN KOLDIOXID VRÄKS UT:
— Med avverkningen av alla träd från runt år 1800, vad som
sparats eller lämnats, följer obevekligt en motsvarande naturlig förmultning av
hela det virkesbeståndet. Sammanställningen i Tabell Y2 redovisar globalsiffrorna.
Värdet man får (globalt 1,78 T12 KGkol perioden
från 1800-[2015], extra tillfört kol till atmosfären från förmultnande trä)
stämmer nära exakt med Mauna Loa-funktionens värden (2010: 1,76 T12 KGkol
extra; 98,8764% matchning).
— Separat undersökning av tillväxttakten (Tabell Y3)
— Mauna Loa-funktionen visar +3,69 T10 KGkol/år2009-2010 — visar att den
teoretiska tillväxttakten överensstämmer grovt (matchning 89%) med effekterna från
världsindustriernas samlade trädfällning via Globalt Årlig Timmerproduktion med
värdet (2010) 3,28 T10 KGkol/år2010. Faktorerna som tagits med i den räkningen
är här av den allra mest minimalt elementära arten (för
att inte riskera överdrivna värden: vi vet här strängt taget inte mera exakt
hur mycket som skogen släpper ut då dess naturharmonier sönderbryts):
1. trädens avskurna bioventilation (koldioxid från ORÖRD
skogsmark avges vare sig träd står där eller inte: 1,875 KGkol/årGE efter (GE) GranEkvivalentens
globalmedelvärde),
2. samma som 1 i form av (BioScience2010, NEP|NBP) trädens ännu
icke fast kolbundna ämnesomsättningsmassa (den faktorn
är här osäker: en del etablerade verk verkar mena [men det verkar också svårt
att reda ut den andemeningen] att den faktorn skulle vara MYCKET större),
3. 50% kvarlämnat avverkningsmaterial (20-40&
Grenverk+Topp, 20% Rot), halva i 1,
4. effekter från starkt uppriven vandaliserad
skogsmarksmull, (minst) samma mängd som i 1.
Där satt den. Värdena visar tydligt motsvarande väl
kvantitativt relaterbar överensstämmelse.
— Mauna Loa-funktionens tillförlitlighet är I DEN RÄKNINGENS
LJUS därmed helt säkert styrkt — med ännu viss reservation för eventuellt
försmädliga tillfälliga kvantitativa sammanträffanden utan relaterbara
sammanhang.
Se vidare i Träddöden2015.
AGW-beviset förklarar IPCC-samfundets
missar.
VärmemotståndetINLEDNING: — Aktuella Mauna Loa-funktionen
Aktuella [‡] Mauna
Loa-funktionen som visar extra tillfört CO2
OM nu verkligen så mycket som +43ppmv CO2 EXTRA har
tillkommit UTÖVER fossilemissionerna, i allt samlat från runt 1800, varför syns
då ingen extra AGW-effekt från det tillskottet?
”— Inte ens med exemplet HELA den drygt 200-åriga
fossilindustridumpen — 116ppmv perioden 1812-2015
— ges mera än en tusendels värmegrad +0,001°C i tillskott. Enbart på den
grovräkningens kredit utesluts med andra ord varje möjlighet att några som
helst nämnvärda AGW-bidrag kan komma i fråga från extra tillfört
icke-fossilrelaterad koldioxidemission till atmosfären.
— Däremot har Lokala Väderkrafterna ett och annat att
tillägga — verkligen en överraskande upplysning:”
Ovanstående i utdrag från Värmemotstånd och Trädens känslighet för LOKALA Koldioxidvariationer.
Utförliga räkneexempel ges med AGW-bevisets grundmatematik
som förklarar:
— Grundformen med relationen t/T = m/M gäller INTE med
icke-fossilt emitterat CO2:
— Förbränningsfaktorn (T) finns inte med där.
Vi beräknar istället verkan av extra icke-fossilt luftkol
via Soleffekten P=T/R=E/t=konstant i Biotermiska konstanten, eller Biologiska
tillväxtkonstanten i denna presentation, BTK.
Se utförlig förklaring med exempel från
Värmemotstånd
och Trädens känslighet för LOKALA Koldioxidvariationer.
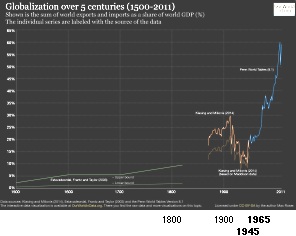
Världshandelsutvecklingen
från 1960-talet —
Mauna Loa-värdenas tydligt exponentiella tillväxt från
1960-talet
” It was in the 1960s that deforestation in the
Brazilian Amazon became more widespread, chiefly from the removal of forest
to make way for cattle ranching to raise national revenue during a period of
high world beef prices, to eliminate hunger and to pay off international debt
obligations.[5]”,
@INTERNET Wikipedia — Deforestation i
Brazil [2017-01-05]
https://en.wikipedia.org/wiki/Deforestation_in_Brazil
KÄLLA:
OUR WORLD IN DATA — International
Trade — Five hundred years of world trade to GDP ratios
http://ourworldindata.org/data/global-interconnections/international-trade/
Slarvig webbkälla — ingen upplysning om vad
förkortningar står för; GDP (Gross Domestic Production?)
Webbkällan ovan visar världshandelsutvecklingen genom fem
sekler (1500-2000). Formen ansluter helt till fossilindustrins energikurva (Kolumn12 ¦ S1), men här mera detaljerat sett ur
handelsperspektivet.
— »Lätt som en plätt» ser vi att en stark uppgång inträder i
början på 1960-talet (efter en första rush efter II:a världskrigets slut 1945):
Teknisk utveckling borgar för den nya tidens stora utbyggnad inom
verkstadsindustrin; Nya maskiner och verktyg produceras till stål-, massa- och
skogsindustrin; Skeppstonnagen byggs ut med nära enorm pace under hela
1960-talet med speciellt omfattande oljefrakter över världshaven för att förse
den exploderande världshandeln med fossilenergi. (Transistorn uppfinns 1952).
(1960-talet är en ren orgie i Ny Elektronik: Stereo).
— Där runt 1960 ligger också uppsatsen till Mauna Loa-uppgången som bryter till
exponentiellt från t(AGW)-integralens asymptotiskt fortsatt raka icke
exponentiella slutform [derivatan|gradienten] (atangens 6 = 80,537678°, se tAGW).
Vilken rationell förklaring finns till »sammanträffandet»?
— Mauna Loa-värdena som sådana (den medelmässiga
100,00%-igt matchande Mauna Loa-funktionens värden) har ingen annan
statistisk byggnad än en rent experimentellt samlad (årligt globalt
medelvärdesbildad) databild som grund. Hur kan då sammanträffandet med den
tydligt exponentiella brytningen (»motorsågseran») från 1960 förklaras
rationellt?
EN
UPPHITTAD MÖJLIG RATIONELL FÖRKLARING:
— PROFITINTRESSEN ÄR ALLTID UNDANTAGSLÖST EXPONENTIELLA.
Här speciellt markerat från början av 1960-talet med skogsindustrins
revolutionerande MotorsågsGäng. Det bildar upptakten, allt för lokal
handelsprofit.
— Men varför just den tydliga kurvbrytpunkten 1962 (AMref)?
— Till att börja med: Motorsågen kunde knappast
introduceras 1820 direkt i samband med Örstedts upptäckt av sambandet mellan
elektricitet och magnetism. Det krävs en viss teknisk utveckling.
Industrikurvan som sådan (S1)
med AGW-bevisets utjämnade havsversion som m|t|E(AGW)-kurvan (Kolumn3) är given som
mänsklighetens oundvikliga energitekniska utvecklingskurva, den går inte att
stoppa, ändra, påverka eller justera (från och med Örsteds upptäckt).
— Den
kurvans integral, samma som den rena fossilt atmosfäriska
CO2-summeringen i takt med industrins fossilanvändning, den här benämnda t(AGW)-integralen, samma som en
motsvarande rent fossilrepresenterad Mauna Loa-värdesform, är INTE exponentiell
(relativt Mauna-Loa-funktionen) efter ca 1962: t(AGW)-integralen planar ut på
en hyperbolisk asymptot (atan6) medan Mauna Loa-värdena drar iväg på en
utpräglat exponentiell avvikelse.
— Så, frågan är bara hur mänskligheten löser
problemet att hitta en bränslekälla som försörjer energibehovet:
1. Ingen nämnvärd skogsavverkning = noll extra
icke-fossilt CO2; bevarad Naturskog;
2. Ingen fossilanvändning = noll fossilt relaterat
CO2; bevarad Atmosfärisk balans, noll AGW.
Skogsavverkningen
+ Fossilanvändningen utmärker första epoken (fram till brytpunkten runt
1962, AMref);
— För Mauna Loa-funktionens del (AGW|MLF)
[Friskrivning]
är andelen icke-fossilt CO2 år 1900 61% mot fossilandelen ca 39%. Den trenden
går sedan i avtagande för icke-fossila och ökande för fossila och når ett
bottenläge omkring år 2000: icke-fossilt ca 37% mot fossilt 63%. Därefter växer
icke-fossilt igen i mera långsam takt och fossilt avtar [2050:
icke-fossilt 40%] (AGW|MLF)
— om ingen trendändring sker.
EPOKEN FRAM TILL RUNT 1960 BETINGAS AV formmässig
SAMHÖRIGHET I FUNKTION MELLAN MAUNA LOA-funktionsVÄRDEN OCH
INDUSTRIUTVECKLINGENS MOTSVARANDE IDEALT RENA FOSSILANVÄNDNING:
— Naturlig icke-profiterande
utvecklingsfysik.
— Mauna Loa-funktionens CO2-värden fram till
brytpunkten 1962, dessa värden såsom icke-exponentiella i utvecklingsformen,
uppvisar en motsvarande ICKE PROFITERANDE utvecklingsform, analogt
icke-exponentiell värdekurva: Mauna Loa-funktionens värden följer
t(AGW)-integralen som i sig slutar på en hyperbolisk rät linje = noll
profitering = noll exponentiell tendens.
— Andra epoken: Från ca 1962 AMref sker en brytning: en tydligt
profiterande värdeform visar sig med tydligt växande icke-fossilt relaterat
extra atmosfärisk Mauna Loa-CO2.
PROFITEN TAR ÖVER och ansluter till den rena
exponentkurvan (»profitkurvan»).
— Så: förklaringen skulle ligga i redan givna
(enkla) utvecklingsformer: det finns olika vägar. I vårt fall har
profiten tagit överhanden.
OM
mänsklighetens tekniska utveckling (från Örstedt 1820) ÄR rationell som sådan (strunt
samma bränslets art och typ till industriutvecklingen), har det ingen
betydelse vilka (kurvfunktionella) aspekter man vill lägga på den rent
historiska utvecklingen: den ena med den andra tekniska landvinningen är
ofrånkomlig, obönhörlig — och därmed strängt logisk: matematisk
icke-profiterande fysik styr den tekniska utvecklingen enligt
t(AGW)-integralkurvan, samma som mänsklighetens tekniska utvecklingskurva — den
är ofrånkomlig, ostoppbar, »ren i sig». Mauna Loa-kurvan skulle tydligen
också haft den formen OM ingen profit tagit över (från runt 1960).
Så: I
slutänden läser vi bara, tydligen, ur en Naturbok där alla möjligheter finns
med, där konsekvensen av alla tillval finns upptecknade, och där det enda som
bestämmer utvecklingslinjerna är våra egna VAL. Hur vi än väljer, finns i
vilket fall konsekvenser, dessa går inte att eliminera; Gott för gott; Ont för
ont. Naturharmonin är grundvalen. Acceptera den och utvecklas maximalt
positivt. Eller Mixtra, och Åk till Återvinningskrossen, och försök sedan igen.
Wikipediacitatet ovan antyder för sin del hur den stora
Brasilianska avskogningen bidrog med början från 1960-talet. Skogsindustrin
fick ny maskinpark med mera effektiva, rationella avverkningsmetoder på den nya
teknikens kredit.
PDF-källan nedan upplyser (eng. Chainsaw, sv. Motorsåg) om
motorsågens genombrott från 1950, och antyder hur effektiviteten i avverkning
och produktion sedan drastiskt ökade:
”The first chainsaws light enough to be
handled by just two persons were developed
in the USA and Sweden in the years 1916-17
(Sundberg, 1978; Silversides,
1997). In USA, a single factory was producing
chainsaws in 1938, six in 1942
and thirty in 1949 (Silversides, 1997). The definitive
breakthrough for chainsaws
occurred around 1950, when they became sufficiently
light to be handled by a single
operator (Sundberg, 1978; Drushka & Konttinen, 1997;
Silversides, 1997). In
1952, only 20% of the pulp wood
produced in eastern Canada was harvested with
chainsaws, but by 1960 this proportion
had increased to almost 100% (Silversides,
1997). Trends in the European countries were
similar, and a number of chainsaw
factories were built in Sweden and Germany. Chainsaws were still used
by full-time
professional operators at thinning operations in
Scandinavia until the beginning of
the 1990s (Lidén, 1995).”,
UMEÅ UNIVERSITET — Automation in
Forestry –
Development of Unmanned Forwarders,
Ola Ringdahl, PhD Thesis, May 2011
http://www.diva-portal.org/smash/get/diva2:412664/FULLTEXT02
Utvecklingen följer tekniken.
t(AGW)-integralen — SimpsonIntegralen | HypoSerien
| — Dec2015 — Originalförfattningen
2009 till t(AGW)-integralen, se INTEGRALKURVAN
FÖR E.
Se även i t(AGW)-integralens
substitutionskurvor och AGW-beviset
förklarar IPCC-samfundets missar
———————————————————————————————————
t(AGW)-integralens y-värden för x-värdena 1 till 12 — NASA-CRU-kurvans t-integral
Tabellen tjänar två syften — utöver ändamålet att få fram
värden till en komplicerad integral (Fossilindustrins CO2-data):
— 1. Två oberoende metoder säkrar oberoende inbördes
samhörighet:
— 2. SimpsonIntegralens ALGORITM är (oftast) överlägsen i
effektivitet: 12-13 decimalers noggrannhet uppnås redan efter 1000
delberäkningar medan samma resultat i HypoSerien kräver (minst) 1.000.000
delberäkningar.
— Överensstämmelsen markerad
orange i tabellen nedan. Programblocken beskrivs separat i länkarna
ovan.
Integrand: y/dx = 6[1 – (1+ [x/10]4)–1]
— beräkningarna
utförda i Borlands TurboPascal i DELPHI4 den 7Dec2015:
A anger antal tiopotenser utförda beräkningar, samma som antalet delintervall noll till
x; A=1=10stBer
— exeTIME mS anger tiden i millisekunder för datorprogrammet
att utföra beräkningen [Här
Borlands TurboPascal i DELPHI4]:
— 0 mS innebär att exekveringstiden ligger i området µS.
|
exeTIME mS |
A |
exeTIME mS |
||
|
x
= 1 |
|
|
x
= 1 |
|
|
0,000119993833099266 |
0 |
1 |
0,000121984936640494 |
0 |
|
0,000119993333844767 |
0 |
2 |
0,000120013329535716 |
0 |
|
0,000119993333794842 |
16 |
3 |
0,000119993533754822 |
0 |
|
0,000119993333794837 |
0 |
4 |
0,000119993335794437 |
0 |
|
0,000119993333794837 |
16 |
5 |
0,000119993333814832 |
0 |
|
0,000119993333794836 |
218 |
6 |
0,000119993333795037 |
109 |
|
0,000119993333794834 |
2219 |
7 |
0,000119993333794844 |
1047 |
|
x
= 2 |
|
|
x
= 2 |
|
|
0,00383660608889595 |
0 |
1 |
0,00390013155143439 |
0 |
|
0,00383659044453404 |
0 |
2 |
0,00383722839169685 |
0 |
|
0,00383659044296981 |
0 |
3 |
0,00383659682253806 |
0 |
|
0,00383659044296965 |
0 |
4 |
0,00383659050676535 |
0 |
|
0,00383659044296969 |
31 |
5 |
0,00383659044360762 |
16 |
|
0,00383659044296968 |
219 |
6 |
0,00383659044297608 |
109 |
|
0,00383659044296965 |
2172 |
7 |
0,00383659044296977 |
1047 |
|
x
= 3 |
|
|
x
= 3 |
|
|
0,0290296195376151 |
0 |
1 |
0,0295058419116298 |
0 |
|
0,0290295113239965 |
0 |
2 |
0,0290342934697067 |
0 |
|
0,0290295113131824 |
0 |
3 |
0,0290295591353205 |
0 |
|
0,0290295113131813 |
0 |
4 |
0,0290295117914027 |
0 |
|
0,0290295113131814 |
16 |
5 |
0,0290295113179636 |
0 |
|
0,0290295113131815 |
218 |
6 |
0,0290295113132292 |
109 |
|
0,0290295113131795 |
2203 |
7 |
0,0290295113131801 |
1047 |
|
x
= 4 |
|
|
x
= 4 |
|
|
0,12116309916898 |
0 |
1 |
0,123102258740686 |
0 |
|
0,121162752642901 |
0 |
2 |
0,121182222766149 |
0 |
|
0,121162752608322 |
0 |
3 |
0,12116294731188 |
0 |
|
0,121162752608319 |
0 |
4 |
0,121162754555355 |
0 |
|
0,121162752608319 |
16 |
5 |
0,121162752627789 |
16 |
|
0,12116275260832 |
219 |
6 |
0,121162752608516 |
109 |
|
0,121162752608318 |
2187 |
7 |
0,121162752608309 |
1047 |
|
x
= 5 |
|
|
x
= 5 |
|
|
0,362517422039095 |
0 |
1 |
0,368032573291897 |
0 |
|
0,362516935402093 |
0 |
2 |
0,362572298294524 |
0 |
|
0,362516935353723 |
0 |
3 |
0,362517488986915 |
0 |
|
0,362516935353719 |
0 |
4 |
0,362516940890051 |
0 |
|
0,362516935353718 |
32 |
5 |
0,362516935409081 |
0 |
|
0,362516935353724 |
218 |
6 |
0,362516935354277 |
109 |
|
0,362516935353717 |
2157 |
7 |
0,362516935353721 |
1078 |
|
x
= 6 |
|
|
x
= 6 |
|
|
0,871421994683344 |
0 |
1 |
0,883565988313622 |
0 |
|
0,871422499282921 |
0 |
2 |
0,871544380314034 |
0 |
|
0,871422499333544 |
0 |
3 |
0,87142371814601 |
0 |
|
0,871422499333548 |
0 |
4 |
0,871422511521673 |
0 |
|
0,871422499333549 |
15 |
5 |
0,871422499455431 |
16 |
|
0,871422499333543 |
219 |
6 |
0,871422499334768 |
94 |
|
0,871422499333491 |
2172 |
7 |
0,871422499333579 |
1047 |
|
x
= 7 |
|
|
x
= 7 |
|
|
1,78564851811469 |
0 |
1 |
1,80742536321283 |
0 |
|
1,78565249504621 |
0 |
2 |
1,78587107418243 |
0 |
|
1,78565249544159 |
0 |
3 |
1,78565468122345 |
0 |
|
1,78565249544163 |
0 |
4 |
1,78565251729945 |
0 |
|
1,78565249544163 |
15 |
5 |
1,78565249566019 |
15 |
|
1,78565249544162 |
219 |
6 |
1,78565249544382 |
110 |
|
1,78565249544162 |
2156 |
7 |
1,78565249544163 |
1047 |
|
x
= 8 |
|
|
x
= 8 |
|
|
3,23126617975036 |
0 |
1 |
3,26409957667889 |
0 |
|
3,23127562069471 |
0 |
2 |
3,23160545188868 |
0 |
|
3,23127562163137 |
0 |
3 |
3,23127891991659 |
0 |
|
3,23127562163147 |
0 |
4 |
3,23127565461432 |
0 |
|
3,23127562163148 |
16 |
5 |
3,23127562196132 |
0 |
|
3,23127562163148 |
218 |
6 |
3,23127562163471 |
109 |
|
3,23127562163126 |
2157 |
7 |
3,2312756216314 |
1047 |
|
x
= 9 |
|
|
x
= 9 |
|
|
5,28990007039869 |
0 |
1 |
5,33267260819229 |
0 |
|
5,28991353603207 |
0 |
2 |
5,29034413462111 |
0 |
|
5,28991353736991 |
0 |
3 |
5,28991784332497 |
0 |
|
5,28991353737005 |
0 |
4 |
5,28991358042958 |
0 |
|
5,28991353737003 |
31 |
5 |
5,28991353780062 |
15 |
|
5,28991353737001 |
219 |
6 |
5,28991353737428 |
110 |
|
5,28991353737015 |
2156 |
7 |
5,28991353737029 |
1047 |
|
x
= 10 |
|
|
x
= 10 |
|
|
7,98160826217935 |
0 |
1 |
8,0310708117588 |
0 |
|
7,98162075835534 |
0 |
2 |
7,98212075860534 |
0 |
|
7,98162075960521 |
0 |
3 |
7,98162575960578 |
0 |
|
7,98162075960532 |
0 |
4 |
7,98162080960537 |
0 |
|
7,98162075960535 |
31 |
5 |
7,98162076010536 |
0 |
|
7,98162075960531 |
203 |
6 |
7,98162075961053 |
109 |
|
7,98162075960501 |
2172 |
7 |
7,98162075960488 |
1047 |
|
x
= 11 |
|
|
x
= 11 |
|
|
11,2703221923795 |
0 |
1 |
11,3224362523999 |
0 |
|
11,2703284225898 |
0 |
2 |
11,2708589055839 |
0 |
|
11,270328423228 |
16 |
3 |
11,2703337281229 |
0 |
|
11,2703284232281 |
0 |
4 |
11,2703284762771 |
0 |
|
11,2703284232281 |
15 |
5 |
11,2703284237585 |
16 |
|
11,270328423228 |
219 |
6 |
11,2703284232337 |
93 |
|
11,2703284232274 |
2156 |
7 |
11,270328423228 |
1047 |
|
x
= 12 |
|
|
x
= 12 |
|
|
15,0840752675717 |
0 |
1 |
15,1352486750516 |
0 |
|
15,0840725462748 |
0 |
2 |
15,0845993249773 |
0 |
|
15,0840725460288 |
0 |
3 |
15,0840778139771 |
0 |
|
15,0840725460288 |
0 |
4 |
15,0840725987082 |
0 |
|
15,0840725460287 |
32 |
5 |
15,0840725465555 |
16 |
|
15,0840725460289 |
218 |
6 |
15,0840725460341 |
109 |
|
15,0840725460286 |
2157 |
7 |
15,0840725460295 |
1063 |
Se även motsvarande ovan i t(AGW)-integralens
substitutionskurvor.
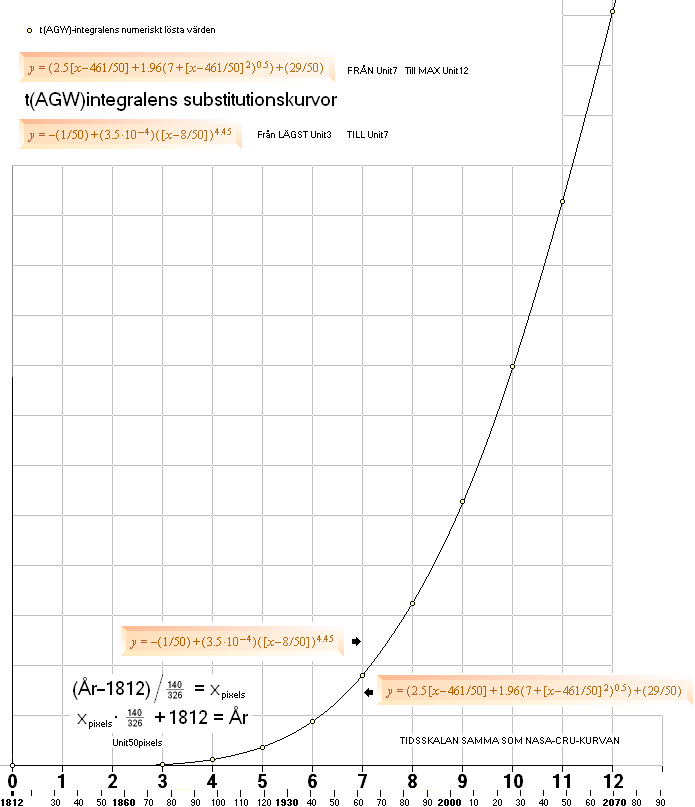
t(AGW)-integralens substitutionskurvor Dec2015 — här
längst till år 2070 — Från
t(AGW)-integralens numeriska lösningsmängder
t(AGW)-integralens substitutionskurvor
———————————————————————————————————————————————
t(AGW)-integralens ursprungliga (2009)
substitutionskurva (y = 0,74[(x/5,7)4,25]; till maxÅr2030)
— Integralkurvan
för E — AGWDerivataOchIntegral
t(AGW)subst:
15Dec2015:
t(AGW)-integralens [‡] kurv- och funktionssubstitut
— från Unit3(1876) till Unit12(2070):
lägst från Unit3:
nedre t(AGW) till Unit7: y =
–(1/50)+(3.5·10'–4)([x–8/50])'4.45
övre t(AGW) från Unit7: y =
(2.5[x–461/50]+1.96(7+[x–461/50]'2)'0.5)+(29/50)
OpenOfficeKalkyl x|t(AGW)y:
x = (År-1812)/(140/326)/50;
y = OM(x<=7; -(1/50)+(0,00035)*(x-8/50)^4,45;(2,5*(x-461/50)+1,96*(7+(x-461/50)^2)^0,5)
+ (29/50));
t(AGW)-integralens egenvärden — intervallet Unit1-12(år2070)
— finns redovisade i särskilt avsnitt via numeriska lösningar. Se t(AGW)intNum.
Grafen nedan visar t(AGW)-integralens numeriskt beräknade
punktvärden tillsammans med de bägge substitutionskurvorna.
t(AGW)-integralen Dec2015 — Numeriska lösningarnas
punktvärden Unit3-12 med motsvarande två utprovade punktskärande
substitutionskurvor
SimpsonIntegralen: Se även HypoSerien
SimpsonIntegralens härledning visas i INTEGRALEN
I NUMERISKA BERÄKNINGAR.
Numerisk lösning till
ytintegraler
Program skrivna i Borlands Turbo
Pascal DELPHI4 för Universums Historia — a BellDharma production Dec2015
SimpsonIntegralen
Programmet lagrar resultatet i en textfil zTagw.txt i exe.programmets
katalog på formen
x=värde
värde: exekveringstid [10 delintervall]
värde: exekveringstid [100 delintervall]
värde: exekveringstid [1.000 delintervall]
värde: exekveringstid [10.000 delintervall]
värde: exekveringstid [100.000 delintervall]
värde: exekveringstid [1.000.000 delintervall]
värde: exekveringstid [10.000.000 delintervall]
eller så många rader som anges av C-värdet, och så många grupper som
anges av x-intervallet ITV. Se Tabellsammanställningen.
— I min programversion är proceduren nedan inlagd i en separat Unit med
proceduren globaldeklarerad så att den (som i mitt fall) kan nås från huvudformen
(Unit1-FormClick; SimpsonIntegralBasic;) genom att
vänsterklicka på programfönstrets ram.
NYBÖRJAREN:
— Testa först med enkla integrander (typ
räta linjen y=x med integralen/ytekvationen y=x²/2) för säker
förvissning som visar hur, och att, programformen verkligen fungerar som den
ska.
Programmet i Borlands Turbo
Pascal DELPHI4:
— TS är en
globaldeklarerad TStringList som används allround:
Procedure SimpsonIntegralBasic;
var
A0,n,m,I,J,iB,C:
Integer;
xU,xJ,hU,hJ,S,a,ITV,d: Real;
{ITV övre, a undre
integrationsgränsen, d intervallet.}
W: word;
T: string;
function SimpsonTriangle(x: Real): Real;
begin
{ANPASSAT FÖR DIREKT LÖSNING AV YTINTEGRALER: Skriv in integrandens x-ekvation
på raden efter SimpsonTriangle:= nedan:}
SimpsonTriangle:=
6*(1-1/(1+power(x/10,4)))
;
end;{endFunctionST}
begin with Form1 do
begin
DecimalSeparator:= ',';
hU:= 0; hJ:= 0; xJ:= 0;
{Skriv in Startvärde = MINx:}
a:= 0;
{Skriv in Stoppvärde = MAXx:}
ITV:= 12;
{Ange Antal dekader/testvärden:}
C:= 7;
iB:= Round(ITV);
TS.Clear; {GlobalUnit1}
TS.Add('SimpsonTriangle — 7Dec2015');
TS.Add('y/dx = 6*(1-1/(1+power(x/10,4))):');
try
for J:= 1 to iB do
begin
Label1.Caption:= IntToStr(J);
Application.ProcessMessages;
ITV:= J;
T:= 'x = '+ FloatToStr(ITV) + ':';
TS.Add(T);
{A0 anges som antalet m/2=nMAX
Simpsontrianglar:}
A0:= 1;
for I:= 1 to C do
begin
A0:= 10*A0;
{Aktuella
beräkningsintervallet:}
d:= (ITV-a)/(2*A0);
W:= GetTickCount;
for n:= 1 to A0 do
begin
m:= 2*n; xU:= a+(m-1)*d;
xJ:= a+(m)*d;
hU:= hU + SimpsonTriangle(xU);
if n=A0 then
Break;
hJ:= hJ +
SimpsonTriangle(xJ);
end;
S:= SimpsonTriangle(a) + 4*hU
+ 2*hJ + SimpsonTriangle(xJ);
S:= (d/3)*S;
W:= GetTickCount-W;
T:= FloatToStr(S)+': TIME
'+IntToStr(W)+'mS';
TS.Add(T);
hU:= 0;
hJ:= 0;
end;{endForI}
end;{endForJ}
finally
TS.SaveToFile('zTagw.txt');
Label1.Caption:= 'OK';
end;{endTry}
end;{endWithForm1}
end;{endSimpsonIntegralBasic}
HypoSerien: Se även SimpsonIntegralen
Hyposerien härleds enkelt via direkt summering av intervallstaplar. Se HypoSerienAPPENDIX längre ner.
Numerisk lösning till
ytintegraler
Program skrivna i Borlands Turbo
Pascal DELPHI4 för Universums Historia — a BellDharma production Dec2015
HypoSerien
Programmet lagrar resultatet i en textfil zTagwH.txt i exe.programmets
katalog på formen
x=värde
värde: exekveringstid [10 delintervall]
värde: exekveringstid [100 delintervall]
värde: exekveringstid [1.000 delintervall]
värde: exekveringstid [10.000 delintervall]
värde: exekveringstid [100.000 delintervall]
värde: exekveringstid [1.000.000 delintervall]
värde: exekveringstid [10.000.000 delintervall]
eller så många rader som anges av C-värdet, och så många grupper som
anges av x-intervallet ITV. Se Tabellsammanställningen.
— I min programversion är proceduren nedan inlagd i en separat Unit med
proceduren globaldeklarerad så att den (som i mitt fall) kan nås från
huvudformen (Unit1-FormClick; HypoAreaSeriesBasic;) genom att vänsterklicka på programfönstrets ram.
Programmet i Borlands Turbo
Pascal DELPHI4:
— TS är en
globaldeklarerad TStringList som används allround:
Procedure HypoAreaSeriesBasic;
var
n,I,iB,J,A0,C:
Integer;
ITV,x,y,y1,y2,d: Real;
W: word;
T: string;
function HypoArea(x: Real): Real;
begin
{ANPASSAT FÖR DIREKT LÖSNING AV YTINTEGRALER: Skriv in integrandens x-ekvation
på raden efter HypoArea:= nedan:}
HypoArea:=
6*(1-1/(1+power(x/10,4)))
;
end;{endFHA}
begin with Form1 do
begin
DecimalSeparator:= ',';
TS.Clear; {GlobalUnit1}
TS.Add('HypoAreaSeries — 7Dec2015');
TS.Add('y/dx = 6*(1-1/(1+power(x/10,4))):');
try
{Skriv i Startvärde = MINx:}
x:= 0;
{Skriv in Stoppvärde = MAXx:}
ITV:= 12;
iB:= Round(ITV);
{Ange Antal dekader/testvärden:}
C:= 7;
for J:= 1 to iB do
begin
Label1.Caption:= IntToStr(J);
Application.ProcessMessages;
ITV:= J;
T:= 'x = '+ FloatToStr(ITV) + ':';
TS.Add(T);
{A0 anger antalet beräkningar i
intervallet ITV— här 10|100|1.000|10.000|.. 10^C:}
A0:= 1;
for I:= 1 to C do
begin
A0:= 10*A0;
y := 0;
{Aktuella
beräkningsintervallet:}
d := (ITV-x)/A0;
y2:= HypoArea(x);
W:= GetTickCount;
for n:= 1 to
A0-1 do begin
y1:= y2; y2:=
HypoArea((n+1)*d + x);
y:= y +
d*(y1+y2)/2;
end;
W:= GetTickCount-W;
T:=
FloatToStr(y)+': TIME '+IntToStr(W)+'mS';
TS.Add(T);
end;{endForI}
end;{endForJ}
finally
TS.SaveToFile('zTagwH.txt');
Label1.Caption:= 'OK';
end;{endTry}
end;{endWithForm1}
end;{endHypoAreaSeriesBasic}
Hyposeriens enkla härledning
Indelning av vertikala staplar mot integrandkurvan
(ytintegralens derivata), med samma delintervall, definierar
Hypo(tenusa)Serien:
— Uppgiften är att ta ut ytan (INTEGRALEN) mellan x-axeln
(horisontallinjen) och den angivna (integrandens) funktionskurva, här räta
linjen y=x.
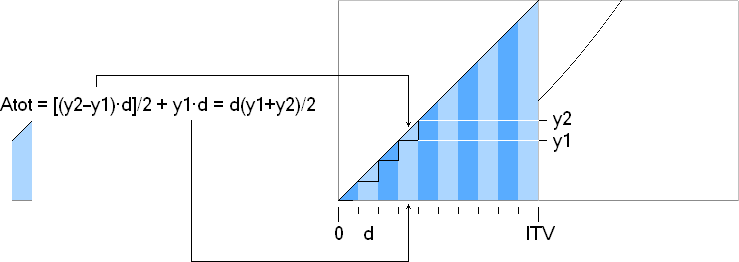
Rummet mellan funktionskurvan [INTEGRANDEN] (y=x ovan) och
x-axeln kan alltid indelas i d=ITV/N stycken lika delintervall d.
Ju mindre d, analogt ju större N, desto mera noga resultat.
— Triangelytan är alltid halva rektangelytan. Det ger
triangelytorna överst alltid som
A(T) =
(y2 — y1) · d / 2
och hela resterande ytstapeln
A(Y) =
y1 · d
som ger summan
A(tot) = (y2 — y1) ·
d / 2 + y1 · d
=
d[(y2 — y1)/2 + y1]
=
d[y2 — y1 + 2y1]/2
=
d[y2 + y1]/2
— Som summeringen avancerar, behöver man bara ersätta
föregående y1 med föregående beräknade y2, beräkna ett nytt y2, utföra A(tot)
och summera.
— Programmets kärndel (A0=N)
y := 0;
{Aktuella
beräkningsintervallet:}
d := (ITV-x)/A0;
y2:= HypoArea(x);
W:= GetTickCount;
for n:= 1 to
A0-1 do begin
y1:= y2; y2:=
HypoArea((n+1)*d + x);
y:= y +
d*(y1+y2)/2;
end;
börjar med att bestämma d ur ITV och N=A0. Efter första
y2-beräkningen tilldelas y1 det första y2-värdet, varefter första egentliga
y2-värdet bestäms i summakomplexet via HypoArea-funktionen y2:= HypoArea((n+1)*d + x). Därmed kan aktuella
d-intervallYTstapeln beräknas, den adderas till y-Summafaktorn, y1 antar
föregående y2, och proceduren upprepas genom hela antalet delintervall A0=N.
GetTickCount samplar
upp datorklockans värde i millisekunder — som kan användas i början/slutet av
en procedur för att få ett mått på exekveringstiden.
Tabellvärden, årlig global kolanvändning från 1751
ÅRLIG GLOBAL KOLANVÄNDNING
Tabellvärden — Global statistik, fossilemissioner
Årlig global kolanvändning i ekvivalenta kolmassor
med totalt globalt summerad användning från 1751
TABELLVÄRDEN
KOPIERADE FRÅN OPEN OFFICE KALKYL (Nov2015) med importerad
globalstatistik på fossilemissionerna, med jämförande värden från AGW-beviset:
———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
Se
särskild sammanställning i The
Missing Sink.
——————————
DATAKÄLLOR:
——————————
Kolumn
A: YEAR, Årtal 1751-2030.
All emission estimates are expressed in million metric tons
of carbon.
Kolumn
B: T9KGkol,
Global CO2 Emissions from Fossil-Fuel Burning, Cement Manufacture, and Gas
Flaring: 1751-2011.
http://cdiac.ornl.gov/trends/emis/meth_reg.html
http://cdiac.ornl.gov/ftp/ndp030/global.1751_2011.ems
Kolumn C: SmaT9
KGkol, Summeringen totalt av de globala kolvärdena i kolumn B.
Kolumn D: m=t(AGW)·k,
AGW-bevisets motsvarande årsvärden industriemitterat kol (motsvarande
globala industristatistiken, kolumn A) —
m = 1,765*(1-1/(1+((År-1815)/212,7)^4))*10170,94
m-kurvan beskriver den utjämnade syntesen av värdena i kolumn A, baserad på
NASA-CRU-kurvans extraherade temperaturkurva t(AGW) och den därifrån
integralbestämda, substituerade, motsvarande Mauna Loa-CO2-mätvärdeskurvan
ppmv(CO2) = 286+12,7576*((År-1815)/121,41)^4,25
syntetiserad i sammanhängande form (utvidgat från Mauna Loa 1958) med början
från år 1815.
Kolumn
E: Summeringen av årsvärdena i kolumn D, från
år 1815.
Kolumn
F: År, 1815-2030.
Årlig
global kolanvändning i ekvivalenta kolmassor med totalt globalt summerad
användning från 1751
Tabellvärdena
(282 radposter med 2 rubrikrader t.o.m. 2030 i 6 kolumner ABCDEF):
|
A |
B |
C |
D |
E |
F |
|
YEAR |
T9KGkol |
SmaT9
KGkol |
m=t(AGW)·k |
SUMMAm |
År |
|
1751 |
3 |
3 |
- |
- |
1751 |
|
1752 |
3 |
6 |
- |
- |
1752 |
|
1753 |
3 |
9 |
- |
- |
1753 |
|
1754 |
3 |
12 |
- |
- |
1754 |
|
1755 |
3 |
15 |
- |
- |
1755 |
|
1756 |
3 |
18 |
- |
- |
1756 |
|
1757 |
3 |
21 |
- |
- |
1757 |
|
1758 |
3 |
24 |
- |
- |
1758 |
|
1759 |
3 |
27 |
- |
- |
1759 |
|
1760 |
3 |
30 |
- |
- |
1760 |
|
1761 |
3 |
33 |
- |
- |
1761 |
|
1762 |
3 |
36 |
- |
- |
1762 |
|
1763 |
3 |
39 |
- |
- |
1763 |
|
1764 |
3 |
42 |
- |
- |
1764 |
|
1765 |
3 |
45 |
- |
- |
1765 |
|
1766 |
3 |
48 |
- |
- |
1766 |
|
1767 |
3 |
51 |
- |
- |
1767 |
|
1768 |
3 |
54 |
- |
- |
1768 |
|
1769 |
3 |
57 |
- |
- |
1769 |
|
1770 |
3 |
60 |
- |
- |
1770 |
|
1771 |
4 |
64 |
- |
- |
1771 |
|
1772 |
4 |
68 |
- |
- |
1772 |
|
1773 |
4 |
72 |
- |
- |
1773 |
|
1774 |
4 |
76 |
- |
- |
1774 |
|
1775 |
4 |
80 |
- |
- |
1775 |
|
1776 |
4 |
84 |
- |
- |
1776 |
|
1777 |
4 |
88 |
- |
- |
1777 |
|
1778 |
4 |
92 |
- |
- |
1778 |
|
1779 |
4 |
96 |
- |
- |
1779 |
|
1780 |
4 |
100 |
- |
- |
1780 |
|
1781 |
5 |
105 |
- |
- |
1781 |
|
1782 |
5 |
110 |
- |
- |
1782 |
|
1783 |
5 |
115 |
- |
- |
1783 |
|
1784 |
5 |
120 |
- |
- |
1784 |
|
1785 |
5 |
125 |
- |
- |
1785 |
|
1786 |
5 |
130 |
- |
- |
1786 |
|
1787 |
5 |
135 |
- |
- |
1787 |
|
1788 |
5 |
140 |
- |
- |
1788 |
|
1789 |
5 |
145 |
- |
- |
1789 |
|
1790 |
5 |
150 |
- |
- |
1790 |
|
1791 |
6 |
156 |
- |
- |
1791 |
|
1792 |
6 |
162 |
- |
- |
1792 |
|
1793 |
6 |
168 |
- |
- |
1793 |
|
1794 |
6 |
174 |
- |
- |
1794 |
|
1795 |
6 |
180 |
- |
- |
1795 |
|
1796 |
6 |
186 |
- |
- |
1796 |
|
1797 |
7 |
193 |
- |
- |
1797 |
|
1798 |
7 |
200 |
- |
- |
1798 |
|
1799 |
7 |
207 |
- |
- |
1799 |
|
1800 |
8 |
215 |
- |
- |
1800 |
|
1801 |
8 |
223 |
- |
- |
1801 |
|
1802 |
10 |
233 |
- |
- |
1802 |
|
1803 |
9 |
242 |
- |
- |
1803 |
|
1804 |
9 |
251 |
- |
- |
1804 |
|
1805 |
9 |
260 |
- |
- |
1805 |
|
1806 |
10 |
270 |
- |
- |
1806 |
|
1807 |
10 |
280 |
- |
- |
1807 |
|
1808 |
10 |
290 |
- |
- |
1808 |
|
1809 |
10 |
300 |
- |
- |
1809 |
|
1810 |
10 |
310 |
- |
- |
1810 |
|
1811 |
11 |
321 |
- |
- |
1811 |
|
1812 |
11 |
332 |
- |
- |
1812 |
|
1813 |
11 |
343 |
m=t(AGW)·k |
SUMMAm |
År |
|
1814 |
11 |
354 |
år¦T9 KG |
sma¦T9
KG |
|
|
1815 |
12 |
366 |
0 |
0 |
1815 |
|
1816 |
13 |
379 |
0 |
0 |
1816 |
|
1817 |
14 |
393 |
0 |
0 |
1817 |
|
1818 |
14 |
407 |
0 |
0 |
1818 |
|
1819 |
14 |
421 |
0 |
0 |
1819 |
|
1820 |
14 |
435 |
0 |
0 |
1820 |
|
1821 |
14 |
449 |
0 |
0 |
1821 |
|
1822 |
15 |
464 |
0 |
0 |
1822 |
|
1823 |
16 |
480 |
0 |
0 |
1823 |
|
1824 |
16 |
496 |
0 |
0 |
1824 |
|
1825 |
17 |
513 |
0 |
0 |
1825 |
|
1826 |
17 |
530 |
0 |
0 |
1826 |
|
1827 |
18 |
548 |
0 |
1 |
1827 |
|
1828 |
18 |
566 |
0 |
1 |
1828 |
|
1829 |
18 |
584 |
0 |
1 |
1829 |
|
1830 |
24 |
608 |
0 |
2 |
1830 |
|
1831 |
23 |
631 |
1 |
2 |
1831 |
|
1832 |
23 |
654 |
1 |
3 |
1832 |
|
1833 |
24 |
678 |
1 |
4 |
1833 |
|
1834 |
24 |
702 |
1 |
5 |
1834 |
|
1835 |
25 |
727 |
1 |
6 |
1835 |
|
1836 |
29 |
756 |
2 |
8 |
1836 |
|
1837 |
29 |
785 |
2 |
10 |
1837 |
|
1838 |
30 |
815 |
2 |
13 |
1838 |
|
1839 |
31 |
846 |
3 |
15 |
1839 |
|
1840 |
33 |
879 |
3 |
19 |
1840 |
|
1841 |
34 |
913 |
4 |
23 |
1841 |
|
1842 |
36 |
949 |
5 |
28 |
1842 |
|
1843 |
37 |
986 |
5 |
33 |
1843 |
|
1844 |
39 |
1025 |
6 |
39 |
1844 |
|
1845 |
43 |
1068 |
7 |
46 |
1845 |
|
1846 |
43 |
1111 |
8 |
54 |
1846 |
|
1847 |
46 |
1157 |
9 |
64 |
1847 |
|
1848 |
47 |
1204 |
10 |
74 |
1848 |
|
1849 |
50 |
1254 |
12 |
86 |
1849 |
|
1850 |
54 |
1308 |
13 |
99 |
1850 |
|
1851 |
54 |
1362 |
15 |
114 |
1851 |
|
1852 |
57 |
1419 |
16 |
130 |
1852 |
|
1853 |
59 |
1478 |
18 |
148 |
1853 |
|
1854 |
69 |
1547 |
20 |
168 |
1854 |
|
1855 |
71 |
1618 |
22 |
191 |
1855 |
|
1856 |
76 |
1694 |
25 |
216 |
1856 |
|
1857 |
77 |
1771 |
27 |
243 |
1857 |
|
1858 |
78 |
1849 |
30 |
273 |
1858 |
|
1859 |
83 |
1932 |
33 |
306 |
1859 |
|
1860 |
91 |
2023 |
36 |
342 |
1860 |
|
1861 |
95 |
2118 |
39 |
381 |
1861 |
|
1862 |
97 |
2215 |
43 |
423 |
1862 |
|
1863 |
104 |
2319 |
46 |
470 |
1863 |
|
1864 |
112 |
2431 |
50 |
520 |
1864 |
|
1865 |
119 |
2550 |
55 |
575 |
1865 |
|
1866 |
122 |
2672 |
59 |
634 |
1866 |
|
1867 |
130 |
2802 |
64 |
698 |
1867 |
|
1868 |
135 |
2937 |
69 |
767 |
1868 |
|
1869 |
142 |
3079 |
74 |
841 |
1869 |
|
1870 |
147 |
3226 |
80 |
921 |
1870 |
|
1871 |
156 |
3382 |
86 |
1007 |
1871 |
|
1872 |
173 |
3555 |
92 |
1099 |
1872 |
|
1873 |
184 |
3739 |
99 |
1198 |
1873 |
|
1874 |
174 |
3913 |
106 |
1303 |
1874 |
|
1875 |
188 |
4101 |
113 |
1416 |
1875 |
|
1876 |
191 |
4292 |
121 |
1537 |
1876 |
|
1877 |
194 |
4486 |
129 |
1666 |
1877 |
|
1878 |
196 |
4682 |
137 |
1803 |
1878 |
|
1879 |
210 |
4892 |
146 |
1949 |
1879 |
|
1880 |
236 |
5128 |
155 |
2104 |
1880 |
|
1881 |
243 |
5371 |
165 |
2269 |
1881 |
|
1882 |
256 |
5627 |
175 |
2444 |
1882 |
|
1883 |
272 |
5899 |
186 |
2629 |
1883 |
|
1884 |
275 |
6174 |
197 |
2826 |
1884 |
|
1885 |
277 |
6451 |
208 |
3034 |
1885 |
|
1886 |
281 |
6732 |
220 |
3254 |
1886 |
|
1887 |
295 |
7027 |
233 |
3487 |
1887 |
|
1888 |
327 |
7354 |
246 |
3733 |
1888 |
|
1889 |
327 |
7681 |
259 |
3992 |
1889 |
|
1890 |
356 |
8037 |
273 |
4265 |
1890 |
|
1891 |
372 |
8409 |
288 |
4553 |
1891 |
|
1892 |
374 |
8783 |
303 |
4856 |
1892 |
|
1893 |
370 |
9153 |
319 |
5175 |
1893 |
|
1894 |
383 |
9536 |
335 |
5510 |
1894 |
|
1895 |
406 |
9942 |
352 |
5862 |
1895 |
|
1896 |
419 |
10361 |
370 |
6232 |
1896 |
|
1897 |
440 |
10801 |
388 |
6620 |
1897 |
|
1898 |
465 |
11266 |
407 |
7027 |
1898 |
|
1899 |
507 |
11773 |
426 |
7453 |
1899 |
|
1900 |
534 |
12307 |
446 |
7900 |
1900 |
|
1901 |
552 |
12859 |
467 |
8367 |
1901 |
|
1902 |
566 |
13425 |
489 |
8856 |
1902 |
|
1903 |
617 |
14042 |
511 |
9367 |
1903 |
|
1904 |
624 |
14666 |
534 |
9901 |
1904 |
|
1905 |
663 |
15329 |
558 |
10458 |
1905 |
|
1906 |
707 |
16036 |
582 |
11040 |
1906 |
|
1907 |
784 |
16820 |
607 |
11647 |
1907 |
|
1908 |
750 |
17570 |
633 |
12280 |
1908 |
|
1909 |
785 |
18355 |
660 |
12940 |
1909 |
|
1910 |
819 |
19174 |
687 |
13627 |
1910 |
|
1911 |
836 |
20010 |
715 |
14342 |
1911 |
|
1912 |
879 |
20889 |
744 |
15087 |
1912 |
|
1913 |
943 |
21832 |
774 |
15861 |
1913 |
|
1914 |
850 |
22682 |
805 |
16665 |
1914 |
|
1915 |
838 |
23520 |
836 |
17502 |
1915 |
|
1916 |
901 |
24421 |
869 |
18370 |
1916 |
|
1917 |
955 |
25376 |
902 |
19272 |
1917 |
|
1918 |
936 |
26312 |
936 |
20208 |
1918 |
|
1919 |
806 |
27118 |
971 |
21178 |
1919 |
|
1920 |
932 |
28050 |
1006 |
22184 |
1920 |
|
1921 |
803 |
28853 |
1043 |
23227 |
1921 |
|
1922 |
845 |
29698 |
1080 |
24308 |
1922 |
|
1923 |
970 |
30668 |
1119 |
25427 |
1923 |
|
1924 |
963 |
31631 |
1158 |
26585 |
1924 |
|
1925 |
975 |
32606 |
1198 |
27783 |
1925 |
|
1926 |
983 |
33589 |
1240 |
29023 |
1926 |
|
1927 |
1062 |
34651 |
1282 |
30304 |
1927 |
|
1928 |
1065 |
35716 |
1325 |
31629 |
1928 |
|
1929 |
1145 |
36861 |
1368 |
32997 |
1929 |
|
1930 |
1053 |
37914 |
1413 |
34411 |
1930 |
|
1931 |
940 |
38854 |
1459 |
35870 |
1931 |
|
1932 |
847 |
39701 |
1506 |
37375 |
1932 |
|
1933 |
893 |
40594 |
1553 |
38929 |
1933 |
|
1934 |
973 |
41567 |
1602 |
40530 |
1934 |
|
1935 |
1027 |
42594 |
1651 |
42182 |
1935 |
|
1936 |
1130 |
43724 |
1702 |
43884 |
1936 |
|
1937 |
1209 |
44933 |
1753 |
45637 |
1937 |
|
1938 |
1142 |
46075 |
1806 |
47443 |
1938 |
|
1939 |
1192 |
47267 |
1859 |
49301 |
1939 |
|
1940 |
1299 |
48566 |
1913 |
51215 |
1940 |
|
1941 |
1334 |
49900 |
1968 |
53183 |
1941 |
|
1942 |
1342 |
51242 |
2024 |
55207 |
1942 |
|
1943 |
1391 |
52633 |
2081 |
57289 |
1943 |
|
1944 |
1383 |
54016 |
2139 |
59428 |
1944 |
|
1945 |
1160 |
55176 |
2198 |
61626 |
1945 |
|
1946 |
1238 |
56414 |
2258 |
63884 |
1946 |
|
1947 |
1392 |
57806 |
2319 |
66203 |
1947 |
|
1948 |
1469 |
59275 |
2380 |
68584 |
1948 |
|
1949 |
1419 |
60694 |
2443 |
71027 |
1949 |
|
1950 |
1630 |
62324 |
2506 |
73533 |
1950 |
|
1951 |
1767 |
64091 |
2571 |
76104 |
1951 |
|
1952 |
1795 |
65886 |
2636 |
78740 |
1952 |
|
1953 |
1841 |
67727 |
2702 |
81442 |
1953 |
|
1954 |
1865 |
69592 |
2769 |
84211 |
1954 |
|
1955 |
2042 |
71634 |
2837 |
87048 |
1955 |
|
1956 |
2177 |
73811 |
2906 |
89953 |
1956 |
|
1957 |
2270 |
76081 |
2975 |
92929 |
1957 |
|
1958 |
2330 |
78411 |
3045 |
95974 |
1958 |
|
1959 |
2454 |
80865 |
3117 |
99091 |
1959 |
|
1960 |
2569 |
83434 |
3188 |
102279 |
1960 |
|
1961 |
2580 |
86014 |
3261 |
105540 |
1961 |
|
1962 |
2686 |
88700 |
3335 |
108875 |
1962 |
|
1963 |
2833 |
91533 |
3409 |
112284 |
1963 |
|
1964 |
2995 |
94528 |
3484 |
115768 |
1964 |
|
1965 |
3130 |
97658 |
3560 |
119328 |
1965 |
|
1966 |
3288 |
100946 |
3636 |
122964 |
1966 |
|
1967 |
3393 |
104339 |
3713 |
126677 |
1967 |
|
1968 |
3566 |
107905 |
3791 |
130468 |
1968 |
|
1969 |
3780 |
111685 |
3870 |
134338 |
1969 |
|
1970 |
4053 |
115738 |
3949 |
138287 |
1970 |
|
1971 |
4208 |
119946 |
4029 |
142316 |
1971 |
|
1972 |
4376 |
124322 |
4109 |
146425 |
1972 |
|
1973 |
4614 |
128936 |
4190 |
150615 |
1973 |
|
1974 |
4623 |
133559 |
4272 |
154886 |
1974 |
|
1975 |
4596 |
138155 |
4354 |
159240 |
1975 |
|
1976 |
4864 |
143019 |
4437 |
163677 |
1976 |
|
1977 |
5026 |
148045 |
4520 |
168197 |
1977 |
|
1978 |
5087 |
153132 |
4604 |
172800 |
1978 |
|
1979 |
5369 |
158501 |
4688 |
177488 |
1979 |
|
1980 |
5313 |
163814 |
4773 |
182261 |
1980 |
|
1981 |
5151 |
168965 |
4858 |
187119 |
1981 |
|
1982 |
5111 |
174076 |
4943 |
192062 |
1982 |
|
1983 |
5093 |
179169 |
5029 |
197091 |
1983 |
|
1984 |
5278 |
184447 |
5116 |
202207 |
1984 |
|
1985 |
5438 |
189885 |
5202 |
207410 |
1985 |
|
1986 |
5606 |
195491 |
5290 |
212699 |
1986 |
|
1987 |
5750 |
201241 |
5377 |
218076 |
1987 |
|
1988 |
5963 |
207204 |
5465 |
223541 |
1988 |
|
1989 |
6094 |
213298 |
5553 |
229094 |
1989 |
|
1990 |
6121 |
219419 |
5641 |
234735 |
1990 |
|
1991 |
6198 |
225617 |
5730 |
240464 |
1991 |
|
1992 |
6136 |
231753 |
5818 |
246283 |
1992 |
|
1993 |
6133 |
237886 |
5907 |
252190 |
1993 |
|
1994 |
6241 |
244127 |
5997 |
258187 |
1994 |
|
1995 |
6374 |
250501 |
6086 |
264272 |
1995 |
|
1996 |
6524 |
257025 |
6175 |
270448 |
1996 |
|
1997 |
6624 |
263649 |
6265 |
276713 |
1997 |
|
1998 |
6610 |
270259 |
6355 |
283067 |
1998 |
|
1999 |
6597 |
276856 |
6444 |
289512 |
1999 |
|
2000 |
6763 |
283619 |
6534 |
296046 |
2000 |
|
2001 |
6929 |
290548 |
6624 |
302670 |
2001 |
|
2002 |
6992 |
297540 |
6714 |
309384 |
2002 |
|
2003 |
7405 |
304945 |
6804 |
316187 |
2003 |
|
2004 |
7784 |
312729 |
6894 |
323081 |
2004 |
|
2005 |
8076 |
320805 |
6984 |
330065 |
2005 |
|
2006 |
8363 |
329168 |
7073 |
337138 |
2006 |
|
2007 |
8532 |
337700 |
7163 |
344301 |
2007 |
|
2008 |
8740 |
346440 |
7253 |
351554 |
2008 |
|
2009 |
8700 |
355140 |
7342 |
358896 |
2009 |
|
2010 |
9140 |
364280 |
7432 |
366328 |
2010 |
|
2011 |
9449 |
373729 |
7521 |
373849 |
2011 |
|
2012 |
- |
- |
7610 |
381459 |
2012 |
|
2013 |
- |
- |
7699 |
389158 |
2013 |
|
2014 |
- |
- |
7788 |
396945 |
2014 |
|
2015 |
- |
- |
7876 |
404822 |
2015 |
|
2016 |
- |
- |
7964 |
412786 |
2016 |
|
2017 |
- |
- |
8053 |
420839 |
2017 |
|
2018 |
- |
- |
8140 |
428979 |
2018 |
|
2019 |
- |
- |
8228 |
437207 |
2019 |
|
2020 |
- |
- |
8315 |
445522 |
2020 |
|
2021 |
- |
- |
8402 |
453924 |
2021 |
|
2022 |
- |
- |
8489 |
462413 |
2022 |
|
2023 |
- |
- |
8575 |
470988 |
2023 |
|
2024 |
- |
- |
8661 |
479649 |
2024 |
|
2025 |
- |
- |
8747 |
488395 |
2025 |
|
2026 |
- |
- |
8832 |
497227 |
2026 |
|
2027 |
- |
- |
8917 |
506144 |
2027 |
|
2028 |
- |
- |
9001 |
515145 |
2028 |
|
2029 |
- |
- |
9085 |
524230 |
2029 |
|
2030 |
- |
- |
9169 |
533399 |
2030 |
|
A |
B |
C |
D |
E |
F |
|
YEAR |
T9KGkol |
SmaT9
KGkol |
m=t(AGW)·k |
SUMMAm |
År |
END.
AGW
Och FRAMTIDEN IV — Tabellvärden
innehåll: SÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
AGW
Och FRAMTIDEN IV
ämnesrubriker
innehåll
referenser
PREFIXEN
FÖR bråkdelar och potenser av FYSIKALISKA STORHETER
Här
används genomgående och konsekvent beteckningarna
förkortning för förenklad
potensbeteckning
d deci t1
c centi t2
m milli t3
µ mikro t6
n nano t9
p pico t12
f femto t15
Alla
Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere),
alla med stor bokstav, liksom följande successiva tusenprefix (List of
SI-prefixes, Wikipedia):
K Kilo T3
M Mega T6
G Giga T9
T Tera T12
P Peta T15
E Exa T18
Z Zetta T21
Y Yotta T24
Exempel: Medan många skriver cm för
centimeter skrivs här konsekvent cM.
t|T förenklad
exponentbeteckning: t|T för 10^ – | +; EX.: t19 = 10–19 ; T19 = 1019
Senast uppdaterade version: 2017-01-05
*END.
Stavningskontrollerat 2016-02-09.
*
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se
![]()
![]()
![]()
∫ ∫ Δ √ ω π τ ε ħ
UNICODE — ofta använda tecken i matematiska-tekniska-naturvetenskapliga
beskrivningar
— Ctrl+Shift+Q i
Microsoft WORD direkt till SYMBOL
— som INTE Firefox
vill läsa:
Firefox skriver Ö
istf. rottecknet, m.fl. Upptäcktes sent, då redan många htm-dokument skrivits.
σ
ρ ν ν υ π τ γ λ η ≠
√ ħ ω →∞ ≡
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫
≤ ≈ ≥ ˂ ˃ ← ↑ → ∞ ↓
ϑ
ζ ξ
Pilsymboler, direkt
via tangentbordet:
Alt+24
↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬
Alt+23
↨ — även Alt+18 ↕; Alt+29 ↔
åter till portalsidan
· portalsidan är www.UniversumsHistoria.se