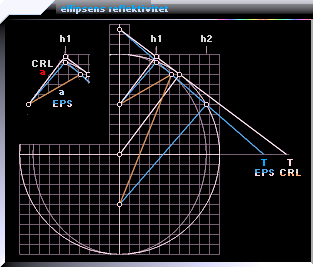
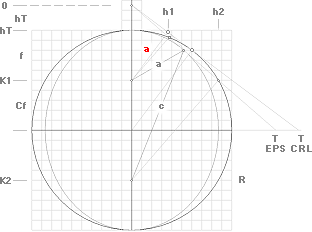
CEPH-EKVATIONEN
— UNIVERSUMS HISTORIA | a![]() production 2008XI26 | Efter sammanställningar från 1982 | Senast uppdaterade version: 2022-12-09 · Universums Historia
production 2008XI26 | Efter sammanställningar från 1982 | Senast uppdaterade version: 2022-12-09 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla
webbsidor
CEPH-ekvationen | i sammanst. frn P2001_1.wps 2001IX25 baserat på tidigare
sammanställningar från 1982-84 | 2008XI26 sammanställning för Universums Historia
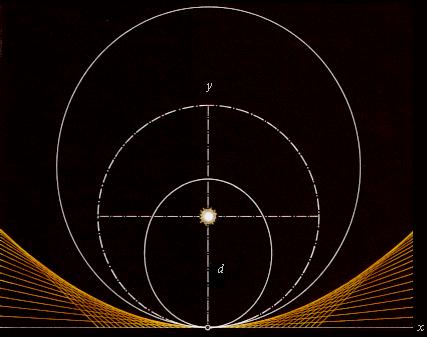
ekvation och tangent: cirkeln
| ellipsen | parabeln | hyperbeln · karaktär: ellipsen | parabeln | hyperbeln | perceptionsanalysen
| Dandelinsfärerna | De Koniska Sektionerna |
reflektiva egenskaper | parabeln
| ellipsen | hyperbeln
| cirkulärt interfererande
egenskaper | ellipsen
| hyperbeln
| parabeln
CEPH-ekvationen sammanfattar
matematikens fyra grundkurvor cirkel, ellips, parabel och hyperbel i en och
samma form tillsammans med ett karaktäristiskt excentricitetstal som skiljer
individerna åt. Sambandet är speciellt användbart i sammanhang som berör de
olika s.k. celesta rörelsebanorna, alltså typ planetbanor. Men CEPH-ekvationen
kan också med fördel användas i den elementära utvärderingen av t.ex. olika
resultat inom integralkalkylen (CEPH-ekvationen kan relativt enkelt användas
direkt för att få fram uttrycken för motsvarande ellipsoidiska, paraboloidiska
och hyperboloidiska formegenskaper — men den allmänna litteraturen tycks vara
sparsam i deras omnämnande). Speciellt i Universums Historia har
CEPH-ekvationen använts i utvecklingen av sambanden för beräkning av atomvikterna,
se från ATOMVIKTERNAS
ELLIPSEKVATIONER.
CEPH-ekvationen finns (här veterligt
December 2008) inte omnämnd i den etablerade litteraturen. Här följer en
generalgenomgång.
|
|
|
Alla
fyra kurvformerna CRL·EPS·PRB·HRB kan
sammanfattas i samma matematisk uttryck x = (2d[1+e]y – y2[1–e2])1/2
.............................. CEPH-EKVATIONEN Sambandet
ansluter speciellt till himlakropparna och de möjliga omloppsbanorna kring en
centralmassa via avståndet (d). Termen
e anger ett karaktäristiskt excentricitetstal för de olika
kurvtyperna: e=–1 ......................... fritt fall, rät linje utmed d –1>e<0
..................... ellipser,
apofokus e= 0
......................... cirkeln 0<e<1 ..................... ellipser, perifokus e= 1
......................... parabeln e > 1
......................... hyperblerna |
Ellips Cirkel Ellips Parabel Hyperbel
CEPH-EKVATIONEN
SATELLITERNAS
ELEMENTÄRA OMLOPPSBANOR
CEPH-ekvationen
sammanfattar alla de fyra s.k. klassiska kägelsnitten även kallade de
koniska sektionerna cirkel, ellips, parabel och hyperbel i ett enda
sammanhängande matematiskt beräkningsbart uttryck, sambandet ovan/nedan med
variabeln i y och funktionsresultatet i x.
x = (2d[1+e]y – y2[1–e2])1/2................. CEPH-EKVATIONEN
e = –1
...................... fritt
fall
0 > e >–1 ................ ellipser
e = ±0 ..................... cirkel
1 > e > 0 .................. ellipser
e = + 1 .................... parabel
e > 1
........................ hyperbler
CEPH-ekvationens sammanfattande form (typ ovan) har eftersöks på
webben @INTERNET men ännu (-November 2008) inte hittats. Flera webbkällor finns som beskriver Kägelsnitten eller De Koniska Sektionerna — med
tillhörande vidlyftiga matematiska utläggningar. Dock finns (här veterligt
ännu) ingen som sammanfattar alla fyra i någon (uppenbart) enkel direkt
praktiskt beräkningsbar form typ CEPH-ekvationen.
CEPH-ekvationen är — som det har visat sig
— trots allt elementär i både matematiken och fysiken och borde därmed finnas
väl representerad (men gör tydligen inte det); Då den framkommit i min egen
historia i samband med studiet av gravitationsfysiken, ges i följande
presentation den sammanhängande härledande berättelsen (ur mitt eget arkiv) som
beskriver i varje fall ett sätt på vilket CEPH-ekvationen tar form. Som
särskilt praktiskt exempel på hur CEPH-ekvationen framstår i Universums Historia,
se Härledningen
till Atomära massdefekterna genom Elliptiska Ekvationer enligt TNED.
CEPH-ekvationen har före denna
framställning (2008XII5) omnämnts i följande htm-filer med ställen i Universums
Historia enligt
ATOMTRIANGELN.htm .................... Intervallets oförstörbarhet II
ElektriskaLaddningen.htm .................. Ljusvägarna i gravitationsfältet
ExpBekr.htm .................................... SOLRANDSOBSERVATIONERNA FRÅN 1919
Fysiens7Principer.htm ....................... Upptäckten av mönstergeometrin för
kärnsyntesen, ellipsfunktionen, CEPH-ekvationen
index.htm ........................................ mekanikens indelning (pågående skisser)
REGISTER.htm ................................ länk till ovanstående i Fysikens7
UniversumsHistoriaInledning.htm ........ återstående
avsnitt, samma som ovan i Fysiken7, nu överflyttat dit 2008XII5
CEPHEKVATIONENS HÄRLEDNING OCH PRESENTATION
Ytmomentets
beteckning K, se Keplers ytmoment, har getts
historisk referens med association till Johannes Kepler (1571-1630). Han
introducerade begreppet genom sina berömda observationer av Solsystemets
planeter. Hans upptäckter har namngetts som de så kallade Keplers tre lagar för planeternas rörelse
(Keplers tre rörelselagar, eller bara Keplers tre lagar). Den andra av
dessa är den som (här) kallas ytmomentet (K=rv=vnd).
Eftersom de två fysikens centrala aspekter,
gravitationen
och elektriciteten,
uppför sig som fenomen under inverkan av en centralkraft, intar betydelsefullheten
hos K och dess tillämpbarhet en enorm omfattning.
Tillämpning i PREFIXxSIN
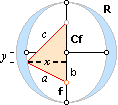
ELLIPSENS ANSLUTNING TILL
KEPLERMOMENTET
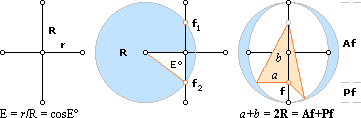
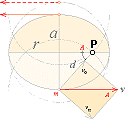
Ellipsen kan ritas och relateras som visas i ovanstående
illustration.
r
................................ lillaxeln
R
............................... storaxeln
Af .............................. Apofokus, den längst bort, förenklad
beteckning A
Pf ............................... Perifokus, den närmast, förenklad beteckning P
E
................................ stora
excentricitetstalet, r/R
E° .............................. ellipsvinkeln
Cf
............................. centrum
till fokus
e ................................ lilla excentricitetstalet, Cf/R
Planeternas omloppsperiod
Av särskilt intresse för Keplers
ytmoment är den celesta mekaniken
(himlakropparnas rörelser).
Figuren nedan visar en elliptisk
omloppsbana. m är omloppskroppen kopplad till den centrala fixpunkten P
där m ändra riktning beroende på inverkan från P utmed den
lokala s.k. ortsvektorn d, dvs., den linje utefter
vilken kraften på m verkar.
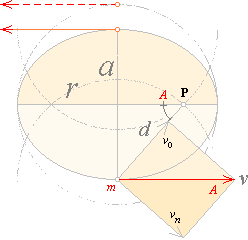
Ytmomentet i Ellipsen — PREFIXxSIN
— för ytmomentet enbart, se utförligt i Ytmomentet
K=vnd ; vn/v=cosA ;
K=vd·cosA ;
A=Ellipsvinkeln, d=r ; K=vr·cosA=vr·(a/r)=va
K=2(EPSAR)/T, EPSAR= 2pr2E/T, [E=cosA=a/r]
; K= 2par/T, = va ;
2pr/T= v
När m intar positionen som i
figuren, är vinkeln A lika med ellipsvinkeln där d=r. Som
cosA=E=a/r=vn/v=a/d finner vi direkt från de bägge sista
delarna att
vnd = va = K = 2A/T
Den totala ellipsytan är EPSAR= pr2E = pr2a/r = pra —
vilket vi ser enklare genom att betrakta ellipsen som en vridning av cirkeln;
på samma sätt som vi vrider en kvadrat aa en vinkel A (via en
axel utmed ena a-sidan) och därmed ena sidan förkortas enligt b=a·cosA
och därmed den totalt projicerade ytan ab, så gäller också för hela
cirkelskivans vridning: EPSAR=CRLAR(cosE°=E). Således
vnd = va = K = 2(pra)/T
Från den andra och sista delen får vi v=2pr/T där den totala perioden T blir
T
= 2pr/v ; T/2p = r/v
v
= r · 2p/T
Som vi ser, är detta samband identiskt
med sambandet för en helt cirkulär bana med v som en konstant hastighet helt igenom;
Känner vi v och T, kan r bestämmas.
För att ellipsen med sambandet ovan ska
gälla, måste v avgränsas till ändpunkten hos ellipsens lillaxel a.
[Andra, mera allmänna samband blir mera krävande]. Emellertid, eftersom det
finns en sådan v-konstellation för varje ellipsbana som arbetar under
inverkan av en centralkraft, kan vi använda den för att erhålla ett allmänt
samband som gäller för det celesta och varje annat elliptiskt omloppsobjekt.
Men för att förverkliga denna detalj måste vi först känna till ett samband med
den cirkulära accelerationen, se särskilt i centralaccelerationen om ej redan
bekant. Vi förutsätter här full bekantskap.
Tillämpning Centralaccelerationen
(samma som Centripetalaccelerationen)
ELLIPSENS KOPPLING TILL GRAVITATIONEN
Som visades i ytmomentet delar cirkel och ellips samma
betingelser för hastigheten när omloppskroppen i ellipsen intar positionen vid
lillaxelns ändpunkt.
v = r · 2p/T0 = rw
Genom denna unika koppling kan
ellipsbanan anslutas direkt till gravitationen genom likheterna för v.
För centralaccelerationen fann vi
tidigare att
å = rw2 ............................. centralaccelerationen
Från gravitationslagen får vi därmed
direkt det cirkulära sambandet
F = ma = må = mrw2 = r–2Gm2m som ger oss
r3w2 =
Gm2
där den centrala och cirkulära
accelerationen å=v2/r=rw2 neutraliseras av
den gravitella accelerationen a.
w anger vinkelaccelerationen från v=2pr/T0=(2p/T0)r=wr som ger w = v/r.
m2 är centralmassan eller centralkroppen i P, en av
ellipsens bägge fokuspunkter. Som vi ser är omloppskroppens massa egal: liten
eller stor omloppsmassa fungerar på samma sätt.
TILLÄMPNING
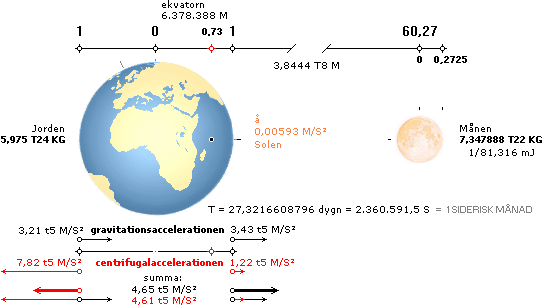
Med tillämpningen av den allmänna
gravitationslagen på celesta objekt i allmänhet, förutsätts det att endast två
kroppar åt gången framträder i ett i övrigt tomt kosmos. Då detta aldrig är det
praktiska fallet, speciellt i observationen av Månens omloppsbana, måste vi
acceptera allmänna (mindre) avvikelser i de enkla beräkningarna. Bara med en
mera djupgående inspektion och observationer under längre tidrymder (hundratals
år) kan mera precisa och realistiska förhållanden fastställas.
Månen är till att börja med (starkt) påverkad av Solen, men också av de
omgivande planeterna. Den ideala Månellipsen kring Jorden kommer då att uppvisa
flera extra rörelser. De två främsta är
1. Månellipsen själv roterar
2. hela Månelliptiska planet roterar
Tillsammans med den aktuella Månbanans
ellips, kan dessa rotationer förorsaka åtskilliga svårigheter i bestämningen av
den aktuella omloppsperiod (T0) som Månen
behöver för att fullborda ett helt varv i sin egen ellips. Vi måste vara klara
över att endast med en högt driven undersökning kan naturen i dessa detaljer
klarläggas — bara så att ingen läsare (här) ska få för sig att ämnet på något
som helst sätt är enkelt avklarat.
I det följande exemplet ska vi förutsätta att perioden T0 är (approximativt) lika med den så kallade nodmånaden eller drakmånaden. Utöver fasperioden (som är längre med två dygn), är denna period den enklaste att observera då den helt enkelt betyder varannan gång som Månen passerar ekliptikan; Ekliptikan är planet som Jordbanan kring Solen finns till i; Månplanets ellips lutar ca 5° relativt ekliptikan, så Månen ”går upp” genom ekliptikaplanet och ”går ner” genom den två gånger per varv; perioden (T0) kan då (enklast) bestämmas där t.ex. Månen just är på väg upp.
Vi använder suffixet d för dygn (eng. days)
motsvarande tidrymd 24 timmar enligt
1 d = 86 400 S
Exempel
Genom observation ses Månen rotera 360
grader eller ett helt varv i sin ellips under
T0 = 27d 5t 5m 34,08s
= (27,2122)d = 2,351134 T6 S
..................... nodmånaden
[BAs167sp2ö]
Använd Encartavärdet (ENCARTA 99 Earth)
för Jordmassan 5,97 T24 KG för att beräkna medelavståndet (R) till Månen genom
det nyligen härledda sambandet
r3w2 = Gm2 med
G
= 6,67 t11 M3(S2KG)–1
Svar: r = (w–2Gm2)1/3 = [(2p[2,351134 T6]–1)–2(6,67 t11)(5,970 T24)]1/3 = 3,8203 T8 M
Medelavståndet (R) till Månen
specificeras generellt i den allmänna facklitteraturen enligt R=3,844 T8 M [BAs166,
384 390 KM] .
Medelavståndets värde för alla planeter
Genom att använda samma relation som i
föregående exempel
r3w2 = Gm2
kan de ungefärliga omloppsdimensionerna
för planeterna i vårt Solsystem beräknas — om man först kan bestämma
avståndet Jorden-Solen (RSUN). Med RSUN ges då centralmassan m2, sambandet ovan, och
därifrån kan alla andra planeters R beräknas om man känner deras period T0.
Avståndet Jorden-Solen (RSUN) framkom först i samband med mera noggranna metoder för bestämningen av ljushastigheten (c, från slutet av 1800-talet). Det standardiserade värdet är (från 1978)
RSUN = 1AU = 1,49598 T11 M [BAs9ö].
Om vi bryter ut perioden ur det
föregående uttrycket
[r3w2 = r3(2p/T)2 = r3(2p)2/T2 = Gm2] får vi
r3T0–2 = k = (2p)–2 · Gm2 ............................... @ 3,36 T18 M3S–2 med m2 som
Solmassan 1,989 T30 KG
Det var denna k-proportionalitet
benämnd Keplers tredje lag som Kepler (1571-1630) fann genom sina
extensiva undersökningar under 1600-talet — och som senare inspirerade Isaac
Newton i dennes formulering av allmänna gravitationslagen.
Keplers tre
lagar [ref. BKLVIsp744n, FMs68sp2n,
BAs159sp2ö, m.fl.]:
I Varje
planet rör sig i en ellips med Solen i ena fokus
II Linjen
Solen-Planeten översveper lika stora ytor på lika långa tider
III Relationen
R3/T02 är konstant för alla planeter, R banellipsens storaxel,
T0 omloppstiden
Efter andra världskriget (från runt
1945) när radarn utvecklades, kunde mera noggranna mätningar
göras av avståndet Jorden-Solen. Nuvarande värdet
(från 1978 i källan nedan) för RSUN kallas en astronomisk enhet och betecknas
1AU med värdet
1
AU ................................. 1,495 9787 T11 M [BAs161]
RSUN
Exempel — bestämning av Solmassan
Perioden för Jordens rotation kring
Solen relativt fixstjärnorna, det så kallade sideriska året, är känd
enligt
T0 = 365,25636 d = 365d 6t 9m 9,54s .................... sideriska året, ”stjärnåret” [ENCARTA 99 Year]
Använd detta värde tillsammans med
standardvärdet RSUN=1AU ovan för att
bestämma Solmassan.
Lösning:
Vi använder uttrycket r3w2=Gm2 med w=2p/T0 som ger
r3w2G–1 = m2
Svar: m2 = (1,495 9787 T11)3 · (2p/[365,25636 · 86400])2 · (6.67 t11)–1 = 1,98969
T30 KG
Kommentar
Värdet från gängse fackverk [BAs9]
är
1,989
T30 KG .................. Solmassan, standardvärde [BAs9]
Konstanten k i Keplers tredje lag gäller som
nyligen omnämndes strängt taget bara med två kroppar åt gången. I den verkliga stjärnvärlden påverkar planeterna
varandra och k varierar något [i storleksordningen 3,3616 T18
till 3,3648 T18 M3S–2] beroende på planet. I översiktlig mening blir (alltså,
och emellertid) värdet 3,36 så exakt det kan bli.
Vidareutvecklingen av ellipsen i gravitationsfysiken
Elliptiska omloppsbanor
Genom att utveckla den unika
kopplingen mellan ellipsen och cirkeln som visades i ELLIPSENS ANSLUTNING TILL KEPLERMOMENTET,
kan vi finna en mera exklusiv samling samband för att bestämma elliptiska banor
under inverkan av en centralkraftsverkan. Resultatet ger
oss grunderna i beräkningen av satellitbanor. Glöm emellertid inte bort att
dessa samband är elementära och på intet sätt exakta i motsvarande
praktiska fall — även om man KAN använda de enkla sambanden för att initiera
verkliga banor.

v = r · 2p/T0 = rw
För de perfekt cirkulära omloppsbanorna
gäller som nyligen härletts att
F
= mv2/r = r–2Gm2m
v2/r = a = r–2Gm2
v2 = r–1Gm2
Centrifugalaccelerationen i ellipsen
vid r från P är samma som i en omskriven cirkel med radien r.
I denna del av ellipsbanan tar således g-kraft ma och å-kraft mv2/r precis ut varandra.
I den följande utvecklingarna ska vi i PREFIXxSIN
använda termen R för r och en förenklad beteckning för produkten
Gm2h–1 som D2 med
h =1M/S2
vilket ger accelerationen a i
numeriska enheter
D2 = Gm2 · h–1
=
aR2 · h–1 ; UNIT M3S–2KG–1 S2M–1=M2
Gm2
= D2h
v2
= R–1D2h
Vi får först
Med anslutning till ytmomentet
substituerar vi med RcosA
(2) RcosA vD–1
= (R–1h)1/2 RcosA
där vinkeln A räknas från
toppvertikalen som 0°. I figuren nedan indexerar också denna position den
centrala cirkulära vinkelreferensen C=0°.
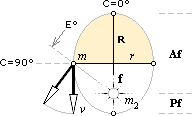
Vid C=90° är
vinkeln A lika med ellipsens
E° så att E=cosE°=cosA. I den första delen i (2)
ger produkten v cosA likhet med normalhastigheten vn i ytmomentet (inte utritat i illustrationen),
v
cosA = vn
Det reducerar (2)
till
där vnR=K från ytmomentet. Som detta gäller för alla
lokala distanser (d) i ytmomentet, inkluderat R, har vi
Från denna relation tillsammans med de
aktuella ellipssambanden får man ekvationerna för ellipsbanorna när tre av de
fyra parametrarna
D,
e,
v (vAf eller vPf) och
d (Af eller
Pf)
är kända.
Resultaten ges i ekvationstablån nedan
där beteckningarna har förenklats något (för att öka lärbarhet och översikt).
ELLIPSBANOR UNDER CENTRALKRAFTSVERKAN
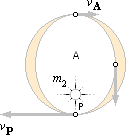
D = [Gm2 · h–1]1/2, D i meter;
h =1M/S2;
e = Cf/R, E=r/R, Af+Pf=2R, G= 6,67 t11 M3(S2KG)–1=JM/(KG)2;
w = 2p/T0;
Satellitsambanden
— ideala elliptiska omloppsbanor
Förenklade
beteckningar: A och P ersätter Af och
Pf; d ersätter R
h = 1M/S2,
D = [Gm2 · h–1]1/2, D i meter
|
® known wanted ¯ |
e|d |
e|vn |
d|vn |
|
|
|
vn |
D |
D |
D |
||
|
e= |
|
|
|
1 – A(vA//D)2/h |
0 |
|
P(vP/D)2/h
– 1 |
1 |
||||
|
d= |
|
|
(1–e)(D/vA)2h |
|
A |
|
(1+e)(D/vP)2h |
P |
||||
|
vn= |
|
DÖ[(1–e)/A]h |
|
|
vA |
|
DÖ[(1+e)/P]h |
vP |
||||
|
D= |
vAÖ[A/(1–e)]/h |
|
|
|
|
|
vPÖ[P/(1+e)]/h |
|||||
Sambandet
för D kan framställas tillsammans med ekvivalenta alternativa
vidareutvecklingar enligt
vA(A[1–e]–1h–1)1/2
vA(R[1–2(e–1+1)]–1h–1)1/2
D = w(R3h+)–1/2 ........................... Allmänt ................... vAvP = (Rw)2 = v2C=90°
vP(R[1–2(e–1+1)]h–1)1/2
vP(P[1+e]–1h–1)1/2
Exempel
Jordelliptiska banan kring Solen är
känd genom följande parametervärden
e 0,0167
R 1,495
9787 T11 M
A 1,52096 T11 M =R(1+e)
P 1,47099 T11 M =R(1–e)
Använd dessa värden med den
standardiserade centralmassan lika med Solmassan m2=1,989 T30 KG tillsammans med de tabellerade ekvationerna
ovan i standardiserade fysikaliska enheter för att bestämma
a. hastigheten hos Jorden runt Solen vid
apohelium (A)
b. Jordens hastighet vid perihelium (P)
Lösning:
D = [Gm2 · h–1]1/2
= [(6,67 t11)(1,989 T30)]1/2 = 1,1518 T10 M
Svar: a. vA= D(A–1[1–e]h)1/2
= 29 286,294 M/S
b. vP= D(P–1[1+e]h)1/2
= 30 281,114 M/S
ELLIPSBANORNA FRÅN DERAS GEMENSAMMA
MASSCENTRUM
Inledande utveckling av det centrala
sambandet
a+c = 2R ..................... allmänt elliptiskt samband
Från utvecklingen a2–b2=x2=c2–(2Cf–b)2 finner vi den
resulterande kopplingen
c2–a2=4Cf(Cf–b)=4Cf · y. Med c=2R–a
visar oss en vidare utveckling att
y = (R–a)R/Cf
där R/Cf=1/e med e som ellipsens lilla excentricitetstal. Då är
a = R–ey
vilket vi finner också gäller lika väl för c-distansen genom c = R–ey.
Vinkeln mellan b och a
betecknas här F° så att b/a=sinF i PREFIXxSIN.
Som b=Cf–y insätter vi
föregående samband för y och får då
(eCf – R+a)/a = e
sin F. I vänstra delen ersätter vi e med Cf/R så att vi får
(Cf2/R – R+a)/a = e sin F = Cf2/aR
– R/a + 1 = (Cf2/R – R)/a
+ 1.
Efter transformation mellan de bägge
delarna får vi
1 – e sin F = (R – Cf2/R)a–1 = R(1 –
Cf2/R2)a–1 = R(1 –
e2)a–1
= RE2a–1.
Därmed a = RE2(1
– e sin F)–1. Med r
som gemensam för endera a eller c har vi
r = RE2(1 – e sin F)–1.
Betrakta i PREFIXxSIN
ellipsens
r
= RE2/(1 – e sinF)
mellan m1 och
den centrala m2 separerad
av centralavståndet r. R betecknar som tidigare halva ellipsens
storaxel,
E=a/R ellipsens stora och e=Ö1–E2 dess lilla excentricitetstal med a som halva
ellipsens lillaxel, samt F° vinkelrotationen hos r. Det kan också
skrivas
r
= (r1+ r2)E2/(1 – e sinF)
= r1E2/(1 – e sinF) + r2E2/(1 – e sinF)
=
d1 + d2
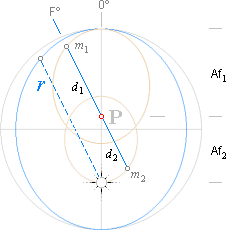
Detta avbildar en principiell delning
av den ursprungliga så kallade relativa ellipsen i två separata ellipser
med samma excentricitet. Om, och endast om d1 och d2 lyder
komponenterna i hävstångslagen
(notera att htm-dokumentet till den länken är ett experimentdokument som
upptar 1,6MB enbart i textdelen — om man försöker ladda upp den med en
mobiltelefon får man bereda sig på en lång väntetid, flera tiotal minuter i
sämsta fall; hävstångslagen utgår från ekvivalenta kraftvägar eller energier
Fd=mad inom ett s.k. Galileiskt rum, som betyder att accelerationskonstanten a
är idealt densamma överallt i det avgränsade rummet, därmed kan ekvivalenterna
behandlas enbart på faktorerna md)
m1d1 = m2d2
finns en centralpunkt P för
jämvikt och som kan kallas massans gemensamma centrum eller tyngdpunkten
för tvåkropparssystemet m1m2. Var och en
av de skilda distanserna d12 relaterar således banmässigt
likvärdiga som den ursprungliga ellipsen till en (dess) elliptiska fokalpunkt
(fokus) — men nu genom två mindre ellipser med halva deras storaxel som r12.
Då summerar r = d1+ d2 genom P
som de gemensamma fokalpunkterna för bägge de splittade ellipserna.
Figuren nedan komprimerar detaljerna
illustrativt.
Som
d1/d2 = r1/r2 = 2r1/2r2
= M1/M2
där M (eng. major) betecknar
storaxeln i respektive ellips, har vi också från hävstångslagen
d1/d2 = m2/m1 = r1/r2 = M1/M2
I respekt till största avståndet r mellan massorna,
är P lokaliserad som skild från endera massan via apofokus Af (största elliptiska avståndet mellan m och P).
I ellipsen har Af sambandet
Af
= R(1+e)
Som de parametriska relationerna i
originalet och de splittade ellipserna är desamma, har vi motsvarande
Af1
= r1(1+e) och
Af2
= r2(1+e)
Som R = r1 + r2 vilket ger
kvoten r1/r2
= (R–r2)/r2
= R/r2 – 1 har vi
m2/m1 = r1/r2 = R/r2
– 1
Första och sista delarna ger
m2/m1 = R/r2
– 1 ;
m2/m1 + 1 = R/r2
r2
= R[m2/m1
+ 1]–1
Insättning med Af2(1+e)–1
= r2 från
ovanstående, har vi därmed lokalen för P från m2 som
Af2(1+e)–1 = R[m2/m1 + 1]–1 ;
Af2
= R(1+e)[m2/m1 + 1]–1
Genom en simpel utveckling för Af1
får vi lokalen för P från m1 på
motsvarande sätt som
Af1
= R(1+e)[m1/m2 + 1]–1
Applikation
Med m2 som vår
Sol, kommer det gemensamma g-centrumet för P
mellan vilkensom planet och Solen att ligga innanför Solsfärens yta. Den planet som ligger närmast Solen är Merkurius.
Bestäm avståndet mellan Solcentrum och P
som Af2 genom följande specifikationer för
planeten Merkurius:
1AU 1,495 97 870 T11 M
R 0,387099 AU
e 0,2056
m1 0,3303 T24 KG
m2 1,989 T30 KG
;
Svar: Af2 = 11,593 T3 M, @ 12 KM
Utvidgning av banorna till paraboliska och hyperboliska
CEPH-EKVATIONEN i PREFIXxSIN
Från tidigare arbeten 1982-84
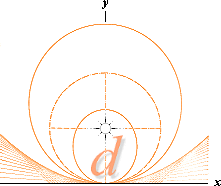
Utgående från en specifik distans d
från en centralmassa (m2) med en
given initiell vektornormal hastighet vn förefaller det tydligt att omloppskroppen måste bryta varje
sluten bana med ett tillräckligt stort vn. Med förmodan om ett bestämt värde för D kan vi beräkna ett motsvarande e-värde genom
typsambandet
genom att ta olika värden på vP. Men detta
tillval introducerar två optioner för e, vilket vi finner obekvämt. När vn utgår från noll, passerar kvantiteten för e från
apofokus (A) till perifokus (P). Mittpositionen är där D2/A=vA2 vilket visar en cirkulär bana med det valda d=R. Med ännu en
ökning i vA erhåller vi negativa värden för e — det relevanta är istället att använda
sambandet för P. Det visar
sig emellertid att vi genomgående kan använda sambandet för P i
samtliga fall enligt
e
= d(vnD)2h–1 – 1
För alla negativa e, från –1 upp till 0, kommer då d att relatera ett apofokus (A) — vilket är det enda att komma ihåg för att få allt rättvänt. Alla de positiva e, från 0 till 1, ger då d som den aktuella perifokus (P). För att beräkna ellipsens storaxel R använder vi det allmänna sambandet från ellipsens geometri via P enligt (d=f=R–Cf; e=Cf/R; d/R=(R–Cf)/R=1–Cf/R=1–e)
R
= d(1–e)–1
Med ett negativt e ger oss detta
direkt R genom sambandet för A [som är R = d(1+e)–1]. Den motsvarande vn-ekvationen blir då
den som gäller för P,
e=–1: vn = 0 ................................. fritt fall
vn
= D(d–1[1+e]h)1/2 e= 0: vn = D(d–1h)1/2 ................... cirkel
e= 1: vn = D(d–12h)1/2 ................. parabel, se nedan
Resultatet av denna
undersökning, min historia från runt 1981, ledde fram till upptäckten att hela
komplexet gömmer en mera allmän sambandsform som innefattar alla fyra möjliga
omloppsbanorna cirkel, ellips, parabel och hyperbel.
CEPH-EKVATIONEN
FRAMTRÄDER
SPONTANT uppstår frågan:
— När e passerar från 0 till 1
möter vi en allt smalare ellips. Med 0 framträder cirkeln, med 1 återstår bara
en rak linje …
— HUR?
— Det är inte en rät
linje, utan en parabel. Faktiskt.
— Visa.
Att linjen är rak för e=–1 är lätt att förstå eftersom det då gäller ett rakt och
fritt fall utan någon hastighet v. Men ett positivt 1, vad är det?
För att rätt belysa den frågan måste vi undersöka var banan försvinner
då e närmar sig 1.
Resonemanget (1982) genomfördes (i min historia) så här:
— Kan man inte utgå ifrån ett bestämt
värde (y) mellan utgångspunkten d och centralmassan, relatera
detta till ellipsens geometri
— x=E(R2–y2)1/2
— och sedan beräkna x-värdet
i anställningen att vn-värdena närmar sig e=1-vn-värdet?
— Värdet för y i
ellipsekvationen närmast ovan är nollrelaterat till ellipsens lillaxel. Vi kan
då välja y-värdet i x-ekvationen som skillnaden mellan varje R vi
får för banorna och en distans från utgångspunkten mot centralmassan;
— Vi låter en rät linje passera genom
utgångspunkten, i normal (rät vinkel) till distansen mot centralmassan,
betecknar linjen som koordinatsystemets x-axel, normalen till denna
genom centralmassan som y-axeln, och väljer sedan godtyckliga värden för
y (se vinjettillustrationen).
— Förhållandet mellan detta y och det ovan (nu betecknat y0) kan då skrivas
y0+y=R som ger y0=R–y.
— Med utveckling av sambanden från den
givna x-ekvationen ges då
Ellipsen
x = E(R2–y02)1/2 .......... ellipsens ekvation [från y = ÖR2–(x/E)2 ges x=EÖ(R2–y2)]
=
E(R2–[R–y]2)1/2
= E(2Ry–y2)1/2
— Räkning på detta resultat från ett
antaget y i antagna värden hos den utgående hastigheten som närmar sig e=1-vn-värdet, leder oss till att vi närmar oss en ändlig gräns
för varje x via varje antaget y.
— Vi behöver emellertid inte explicit
räkna vidare på denna utflykt:
— Hela problemet kan lösas mera elegant
i utvecklingen av sambandet för x.
— Vi tar in E i parentesen, använder
den föregående R-kopplingen, och erhåller
x = (E22d[1–e]y–[Ey]2)1/2
E2
= 1–e2 = 1 –e+e –e2
= 1 – e + e(1–e)
=
(2d[1+e]y–[Ey]2)1/2 ;
x = (2d[1+e]y – y2[1–e2])1/2................. CEPH-EKVATIONEN
Cirkel Ellips Parabel Hyperbel — se
efterföljande specifika extrakt
En spontan kristallisation. Emellertid,
är vi inte förtrogna med den fulla innebörden av ”e” kommer sambandet
att verka ”mystiskt”.
Vi studerar upplösningen.
Cirkeln
Med e=0 får vi direkt d=r
som ger
x = (2d[1]y – y2[1])1/2 = (2dy – y2)1/2 = (2ry – y2)1/2 ;
Uttryckt i den vanliga y-formen ges då
2ry–y2 = x2 = 2ry–y2 +r2 –r2 = r2+2ry–y2 – r2 = (r–y)2 – r2;
x2+r2 = (r–y)2 ;
Ö(x2+r2) = r–y ;
y = r–Ö(x2+r2);
Lägger vi till +r för att relatera xy-origo till cirkelns centrum gäller tydligen
y
= r–Ö(x2+r2) +r
=
Ö(x2+r2) ...................................... cirkeln, CEPHe=0
Vi känner igen den formen som den
vanliga för cirkelns ekvation.
Parabeln
Med e=1 får vi direkt
x = (4dy)1/2
y = x2(4d)–1 ......................................... parabeln, CEPHe=1
vn =
D(d–12h)1/2
Det är samma uttryck som vi känner som parabelns ekvation från parabelns geometri.
Hyperbeln
Från hyperbelns
geometri känner vi motsvarande samband
y
= tan–1M[(r2+x2)1/2–r], t
= tanM = r/m
y
= t–1[(r2+x2)1/2–r]
(yt+r)2 = r2+x2
y2t2+2ytr+r2 = r2+x2
x2 = 2ytr + y2t2 ;
t
= r/m, tr = r2/m = m · r2/m2 = t2m
x2 = 2yt2m + y2t2 ;
m
= f[(sinM)–1–1]–1
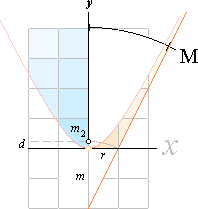
d motsvarar f
tan2M = t2
= (sinM)–2 – 1
t2m = [(sinM)–2
– 1]f[(sinM)–1–1]–1 = f[1+(sinM)–1]
x2
= 2yf[1+ (sinM)–1] + y2[(sinM)–2 – 1] ; f=d
=
2yd[1+ (sinM)–1] – y2[1 – (sinM)–2]
.................... hyperbeln,
M > 0°
Ersättning av (sinM)–1 i dessa likheter med e ger oss alldeles tydligt
CEPH-ekvationen
x = (2yd[1+e] – y2[1–e2])1/2 ........................................ hyperbel, CEPHe>1
vn = D(d–1[1+e]h)1/2
M
= asin(e–1)
För e=1 blir asymptotvinkeln M=0 vilket
raderar det hyperboliska alternativet. De giltiga e-värdena för en
hyperbolisk väg utgår således från större än 1.
På avståndet 1 T7 M från Jordens
g-centrum ges en kropp i relativ vila en hastighetskomponent vn rätvinkligt lodlinjen genom Jordytan. Bestäm om möjligt
det absoluta och ideala minimum för denna hastighet om kroppen ska gå i en
hyperbolisk kurva relativt Jordmassans centrum. Använd standardiserade
fysikaliska enheter (MKSA-systemet) och specificera de använda värdena.
Lösning:
vn =
D(d–1[1+e]h)1/2
d
= 1 T7 M
m2
= 5,97 T24 KG
G
= 6,67 t11 JM/(JG)2
D
= [Gm2 · h–1]1/2 = [(6,67
t11)(5,97 T24)]1/2 = 1,9954924 T7 M
eMIN
= 1
vn = 8,92411 T10 M/S
Svar: Minsta hastigheten måste vara
större än 8,92411 T10 M/S, vilket gäller för en parabolisk banform.
CEPH-kurvorna och deras tangenter
| KÄLLVERK |
CEPH-kurvorna — grundsamband
cirkelns speciella planprojektioner
så
härleds och framgår de fyra grundkurvorna och deras tangenter
CIRKEL
ELLIPS PARABEL HYPERBEL
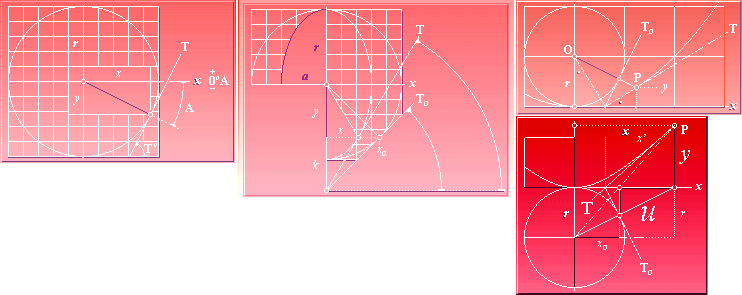
I de följande härledningarna används termen/beteckningen T° (»T-grader») för att beteckna tangentvinkeln såsom distinkt och skild från tangentlinjen (T). Samtliga följande härledningar utgår ifrån Pythagoras Sats a2+b2=c2. Med abc ersatta av xyr framstår Pythagoras sats speciellt som cirkelns ekvation enligt
r = Ö x2+y2 ............................ CIRKELNS EKVATION — direkt från Pythagoras
sats
Vinkeln T° beskriver en ordinär
systemvinkel med 0° i referens till det matematiska xy-systemets
positiva x-axel 0°. Se även utförligt från MATEMATIKENS GRUNDER om ej redan
bekant.
Cirkelns tangent · Härledning
CIRKELN (CRL)
y = Ör2–x2
............................................ cirkelns
ekvation
TANGENT: y/x = tanA ; x/y = tan(–T) = –tanT;
tanT = –x/y
Kommentar:
Bågvinkeln till inversen för tanA
som riktningen för tangentlinjen T, atan(x/y), refererar
T°=0 till negativa x-axeln. För att för korrekt polaritet för T°
måste den roteras 180 grader, vilket betyder samma som en multiplikation med –1.
Alternativt från grundtrigonometrin har vi det allmänna tan(–A)=–tanA och
1/tanA=cotA=tan(90–A). Då får vi med
tanA=y/x och T=A+90 sambanden
tanA=y/x=tan(T–90)=–tan(90–T)=–cotT=–1/tanT; tanT=–x/y
Se även från PERCPETIONSANALYSEN.
Ellipsens tangent · Härledning
Cirkeltangentens avbildning
ELLIPSEN (EPS)
x/x0 = a/r = E ; x/E = x0 ; y = Ör2–x02 = Ör2–(x/E)2
= (1/E)Ö(rE)2–x2 = (1/E)Öa2–x2 ;
y = Ör2–(x/E)2 ........................................ ellipsens ekvation
TANGENT: tanT0/tanT
= (k/x0)/(k/x)
= x/x0 = E ;
tanT = tanT0/E =
–x0/yE
= –(x/E)/yE ) =
–x/yE2
Kommentar:
Det finns åtminstone tre olika sätt att
finna grundkaraktären för ellipsens geometri (ellipsens ekvationer fyller
lätt en större mängd boksidor) [cirkelns vridning, reguljär konisk sektion,
koncentriska plancirklar]. Den enklaste av dessa är cirkelns vridning, vilket
är det alternativ som används här, figuren ovan. I cirkelns vridning kring y-axeln
genom ellipsvinkeln E° (den är 90 grader då ellipsen övergår i cirkel)
reduceras alla x-faktorer av samma faktor cosE° i PREFIXxSIN.
Det är samma som relationen mellan den reducerade cirkelns radie a
(ellipsens lillaxel) på x-axeln dividerat med
cirkelradien r (ellipsens storaxel); Förhållandet kallas här stora
excentricitetstalet,
cosE°=a/r=E. Genom E får
ellipsens ekvation samma form som cirkelns ekvation med enda skillnaden att xCRL reduceras av E till xEPS enligt xEPS=xCRL·E
med max a för EPS och max r för CRL. För att skilja de olika x-kvantiteterna åt i
härledningen, har cCRL indexerats x0.
Se även Ellipsens karaktär genom perceptionsanalysen — koniska sektionerna. Se även från PERCPETIONSANALYSEN.
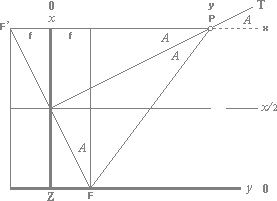
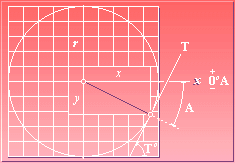
Parabelns tangent · Härledning
Cirkeltangentens avbildning
PARABELN · RadieUtvidgning genom
Cheops Rektangel, eller Räta vinkelns vridning genom x/2
(x/2)/r = y/(x/2)
;
y = x2/4r .............................................. parabelns ekvation
TANGENT: tanT = y/(x/2) =
2y/x = 2x2/4rx = x/2r
tanT = 2y/x
Kommentar:
Om vi tar x-skärningen (kallas
också x-interceptet) för cirkelns tangentlinje T, längden a, i
punkten aP (skärningen xT, f.ö. ej särskilt markerad i
figuren ovan) och relaterar det interceptet genom aP till en rät vinkel (O.aP.T), får vi de
symmetriska relationerna
a/r=y/a
som ger a2=yr. Som vi ser är detta identiskt med uttrycket från Cheops
Rektangel. Med figurens hjälp ser vi att diagonalen hos
denna rektangel är del av cirkelradien genom tangentpunkten där interceptet a
blir höjden hos den motsvarande Cheopstriangeln. Genom att relatera a
som en variabel x/2 erhåller vi då ändpunkten P hos varje
Cheopstriangel från utvidgningen av cirkelradien som en kontinuerlig kurva
kallad parabel. Se även parabeln från grundmatematiken
i samband med beräkningen av kvadratrötterna.
Se även Parabelns karaktär genom perceptionsanalysen — koniska sektionerna. Se även från PERCPETIONSANALYSEN.
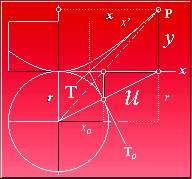
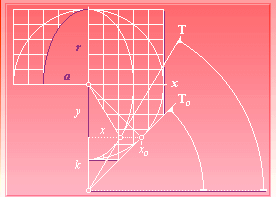
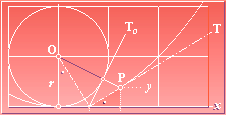
Hyperbelns tangent · Härledning
Cirkeltangentens avbildning
HYPERBELN (HRB) · EnhetsHyperbeln
med u=y
(y+r)/x = r/x0 ; y+r = xr/x0 = x/(x0/r) = x/(x/Ör2+x2) = Ör2+x2 = r+u ; y = u ;
y = –r + Ör2+x2 .................................. hyperbelns ekvation
TANGENT: tanT = y/x’, (y=u), = u/x’ = x/(r+u)
= x/(r+y) = x/Ör2+x2
tanT = x/(r+y)
EnhetsHRB Asymptot med x0= r, = 45º.
Kommentar:
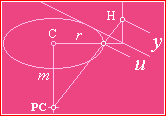
Se hyperbeln genom att sätta underdelen på en lampskärm
med
öppen cirkulär form mot väggen som antyds av
ovanstående illustration;
Ljuset från lampan i PC avbildar en hyperbel på väggen.
Betrakta normalen m till planet
C hos en cirkel med radien r och genom dess centralpunkt C. Från en
punkt PC på m under cirkeln föreställer vi oss linjer L som passerar
genom cirkelbågen totalt via en central- eller konisk projektion. Om vi
placerar ett plan (H) rätvinkligt C (som precis vidrör cirkeln C), skär
linjerna L planet H i motsvarande H-punkter i en kurva som kallas hyperbel.
Med figurens hjälp ser vi att relationen m/r=y/u kommer
att gälla för denna typ. Den mest elementära konstellationen finner man där m=r
som direkt ger oss y=u så att alla L bildar en
45-graders vinkel med m. I den här produktionen kallas en sådan
elementär hyperbel för enhetshyperbel. Som kurvtangenten i vilket fall
kommer att visa en avbildning (»mappning») mellan planen CH från cirkelns
reguljära tangent, kommer bägge planen CH att dela samma tangentföreningspunkt
(J, ej särskilt utmärkt i huvudfiguren ovan) där planen CH möts, alltså
någonstans utmed x-linjen. Med cirkeltangenten given, blir
hyperbeltangenten helt enkelt linjen T mellan JH.
Asymptotbegreppet
Den maximala vinkelrepresentationen av
»den yttersta konlinje L» som kan träffa H-väggen bildar en gränsvinkel (M°)
mellan m och L. I Enhetshyperbeln är M=45°. I detta maxläge är
motsvarande C-vinkel till L-skärningen med C-bågen (punkten mellan PC.H),
räknat från H-väggen som nollreferens, lika med 90°. Med då är också r
parallell med H, och L kommer strängt taget aldrig att träffa H. Hyperbelkurvan
kommer följaktligen att utsträckas obegränsat i det den närmar sig denna
konstanta gränsvinkel. Den begränsande linjen (L) genom M-vinkeln kallas då för
hyperbelns asymptot. M-vinkeln kallas analogt för hyperbelns
asymptotvinkel.
Se även Parabelns karaktär genom perceptionsanalysen — koniska sektionerna. Se även från PERCPETIONSANALYSEN.
KÄLLVERK TILL GRUNDKURVORNAS HÄRLEDNING
Det
finns (ännu veterligt November 2008) inga etablerade verk som beskriver grundkurvorna på det här presenterade sättet. Generellt är webben @INTERNET
som referenskälla mera inriktad på att ”förklara” grundkurvorna (cirkeln
frånsett) ellips-parabel-hyperbel genom högskolematematikens allmänna
formelapparat (jämför t.ex. Wikipedia Conic section 2008-11-28) — som därmed garanterat utestänger de allra flesta
människor från ämnet. Det tråkiga är — och som uppmärksammades redan tidigt i
min historia genom flödet i den allmänna bibliotekslitteraturen — att det
verkar inte finnas någon annan metod i modern akademi. Vilket vill säga:
ämnet ”förklaras av professurer inför doktorer”. Den vanliga befolkningen
lämnas (som vanligt) helt utanför ämnet. I den andan, och genom min egen
historia och dess utveckling, har ovannämnda (betydligt) enklare beskrivningar
framkommit (enligt min uppfattning, är det bäst att tillägga). Eller med andra
ord: källformerna till den här presentationen av grundkurvornas matematik och
geometri är varken mer eller mindre än de olika uppslagen från etablerade
källor genom den tillgängliga allmänna bibliotekslitteraturen — som dock tyvärr
helt tycks sakna perspektiv på ämnet. Vi hittar dem inte någon annan stans än
här, om iakttagelsen är korrekt uppfattad.
Editor2008XI26
DE KONISKA SEKTIONERNA PÅ
WEBBEN @INTERNET beskrivs på en uppsjö av ställen — på engelska. Det allmänna
intrycket (ännu November 2008, min personligt färgade mening) präglas
emellertid av en viss anda av diffushet, krånglighet och oklarhet. De koniska
sektionerna i etablerade framställningar tycks lida av en gemensam central
brist: avsaknad av en klar, tydlig och enhetlig referensgrund i det rent
beskrivande begreppet — som INTE använder högskolematematik. Det som fattas —
och också det som finns med, verkligen, men som inte lyfts fram tillräckligt
mycket och därmed förmörkar snarare än upplyser hela ämnet — är (alldeles
tydligt) perceptionsanalysen eller de från 1800-talet så
kallade Dandelinsfärerna (från
fransmannen-belgaren Germinal Pierre Dandelin 1794-1847, men som alls inte
beskrivs i termer av någon »perceptionsanalys») — ”Synkloten” beskriver själva
kärnpunkten i ämnets enkla och tydliga förklaring, men har tydligen tappats
bort (mer eller mindre); Även fast Dandelinsfärerna omnämns i flera eminenta webbkällor
tycks författarna ha svårt att lyfta fram huvudsaken i ljusets fokus: att det
är fråga om en fullödig 3D-perceptiv analys (se nedan). Utan den förklarande
perceptionsgrunden är och förblir (nämligen) alla beskrivningar av »de koniska
sektionerna» mer eller mindre rena hieroglyfer. Läsaren må emellertid döma
själv: Här följer den förklarande delen som (enligt min mening) sammankopplar
de kringspridda fragmenten till en begriplig och framförallt lättfattlig enhet
— utan konstiga (inblandade) högskolegrepp. Se även webbalternativen i
referensförteckning till jämförelse i KONISKA
SEKTIONER PÅ WEBBEN.
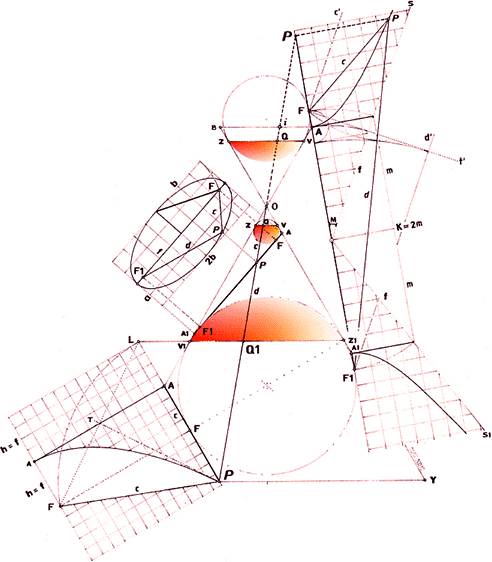
PERCEPTIONSANALYSEN
De Koniska
Sektionerna
Kägelsnitten
Dandelinsfärerna
Allting
som upptar någon utbredning skild från noll sett från en percpetionspunkt —
»användarens position» — ses och beskrivs i formen av en kon, även
kallad centralprojektion. Speciellt om synobjektet kan återföras på en cirkulär
planyta, som även gäller i fallet då objektet är ett geometriskt klot, kallas
synkonen cirkulär (rak eller sned). Vi utgår ifrån dessa detaljer som
givna och ”självbevisande” speciellt genom formernas ideala symmetri och
likformighet, och utan att vi lägger några som helst aspekter på det fysiska
rummets egenskaper varigenom sinnevärldens motsvarande detaljer framträder, kan
studeras, analyseras och klassificeras.
Från en perceptionspunkt (A) utanför ett geometriskt klot, är
alla avstånd till klotets horisont ekvivalenta. Är det någon »geometrisk sats»
som vi alla människor kan förstå intuitivt med excellent klarhet, så är det
just den: alla linjer som tangerar klotets yta och som går genom den gemensamma
strålpunkten (A), är lika långa, figuren ovan. I den sammanställda figuren
nedan får vi således att A.F = A.V, A1.Z = A1.F, osv. Den sammanställda figuren
beskrivs vidare utförligt med reducerade termbeteckningar längre ner för
respektive sektion parabel, ellips och hyperbel.
Karaktären för De
Tre Koniska Sektionerna
— genom Perceptionsanalysen:
|
PARABELN P.F = P.L
= c ELLIPSEN 2b = d+c HYPERBELN 2m = d–c |
|
Illustrationen ovan efter författarens sammanställningar
1987XII12 från tidigare.
De tre perceptiva sektionerna genomgås i tur och ordning nedan.
Vinklar betecknas typ D(O.B.A.O).
Parallella linjer betecknas || typ P.L är || med Y.O.
Beskrivningen görs utifrån de synbart allra enklaste, mest
uppenbara och direkt logiska 3D-egenskaperna i observationen av
perceptionslinjer via perceptionssfärerna även i dessa sammanhang
historiskt benämnda Dandelinsfärer vilket garanterar att ingen utesluts på grund av brist
på högskolemeriter.
Om det inte ger med
sig med en gång (även »vi proffs» måste också ta om det emellanåt, ibland): ta
en paus, ta om det igen — och igen, om det krävs. Det ger med sig. Det är
tillåtet att vila, men aldrig att ge upp. Hittar du ett bättre, enklare, sätt
att beskriva saken på, visa det, göm det inte.
perceptionsanalysen
P.F = P.L = c
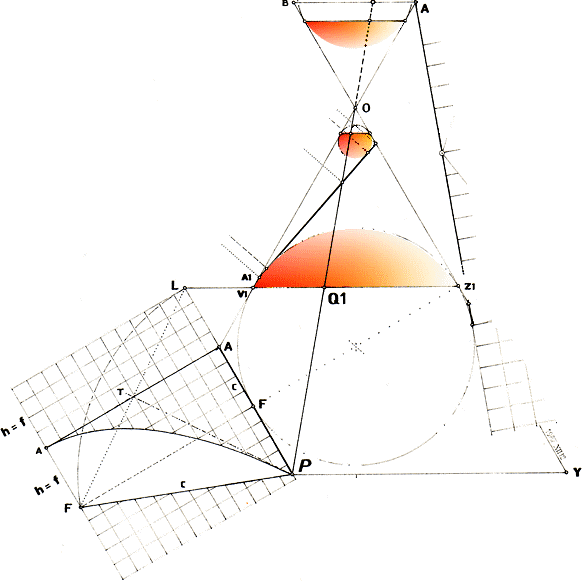
Strålpunkt A: A.F = A.V1. D(A.L.V1.A)
= D(O.B.A.O); A.V1 = A.L = A.F = f.
Snittplanet P.L är || och lika med konsidan Y.Z1, = P.Q1.
Parabelns karaktär får vi då genom strålpunkten P;
P.F = P.Q1 = Y.Z1 = P.L. Vilket vill säga P.F = P.L = c.
Se även Parabelns
ekvation och tangent genom cirkeln.
perceptionsanalysen
2b = d+c
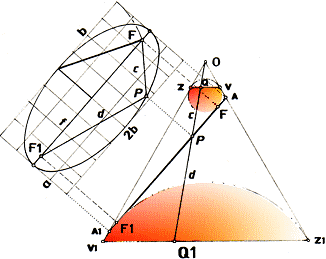
Vi klarlägger först att (A.F = A.V = h)ÖVRE = (A1.F1 = A1.V1 =
h1)UNDRE enligt följande:
V|F och V1|F1 är bägge sfärpunkter medan A|A1 är strålpunkter
över sfärytan;
Strålpunkt O: (O.V = O.Z); V.Z1(= h + A.Z1[= A.F1 = h + F.F1]) =
Z.V1(= Z.A1 + h1) = Q.Q1 = 2h + F.F1;
Z.A1 – F.F1 = 2h – h1;
Strålpunkt A1: A1.Z = A1.F(= h1 + F1.F); Z.A1 – F1.F = h1. Detta tillsammans med slutledet i strålpunkt
O ovan ger:
Z.A1 – F.F1 = 2h – h1 = Z.A1 – F1.F = h1; h1 = 2h –h1; 2h1 = 2h; h1 = h,
vilket skulle visas.
Vi har därmed också förtydligat att
A.A1 = 2h + F.F1, och A1.F(= A1.Z) = A.F1(= A.Z1).
Ellipsens karaktär 2b=c+d framgår då genom strålpunkt P, (h=h1):
(P.F = P.Q = c) + (P.F1 = P.Q1 = d) = Q.Q1 = konstant = V1.Z =
Z1.V = h1(=h) + A1.Z(= A1.F = A.F1) = A.A1 = 2b. Vilket vill säga
c + d = 2b.
Se även Ellipsens
ekvation och tangent genom cirkeln.
perceptionsanalysen
2m = d–c
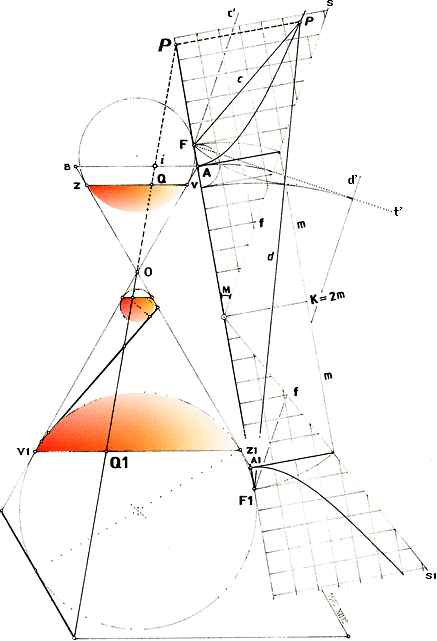
Vi sätter A.A1 = K, samt observerar via strålpunkt O att Q.Q1 = V.V1
= Z.Z1 = N.
Vi klarlägger på samma sätt som i ellipsens fall först att (A.F
= A.V = h)ÖVRE = (A1.F1 = A1.Z1 = h1)UNDRE enligt följande:
V|F och Z1|F1 är bägge sfärpunkter medan A|A1 är strålpunkter
över sfärytan;
Strålpunkt A1: A1.Z(= h1 + Z1.Z)
= A1.F(= K + h);
h1 = K – Z1.Z + h ........ = K – N + h.
Strålpunkt A: A.F1(= K + h1) = A.V1(= h
+ V.V1);
h1 = V.V1 – K + h
......... = N – K + h. Genom likheterna för h1 får vi då
K – N + h = N
– K + h; K – N = N – K; 2K = 2N; K = N; Således A.A1 = V.V1 = K = Z.Z1; Med K för
dessa i leden ovan för h1 får vi;
h1 = h, vilket skulle visas.
Hyperbelns karaktär 2m=d–c framgår så genom strålpunkt P
i kraft av resultaten ovan enligt;
(P.F1 = P.Q1 = d) – (P.F = P.Q = c) = Q.Q1 = N = K =
2m. Vilket vill säga d – c = 2m.
Se även Hyperbelns
ekvation och tangent genom cirkeln.
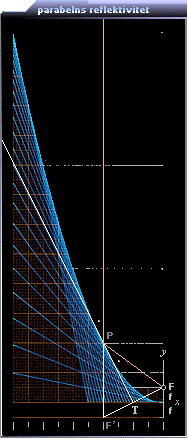
Parabelns optiska
egenskaper
|
|
|
Eftersom parabelns tangent T definieras som den symmetriska delningen av den likbenta triangeln P.F.F’ från PERCEPTIONSANALYSEN (de koniska sektionerna),
P.F = P.F’; P.F’ | | y (se PERCEPTIONSANALYSEN Parabeln),
framgår parabelns reflektiva egenskap direkt — inkommande A är lika med utgående A, se f.ö. Spegellagen:
Ena vinkelbenet (P.F’) i vinkelrummet för tangentvinkeln (A), ligger alltid parallellt med parabelns y-axel, analogt i normal till x-axeln; ljusstrålar som utgår från F återkastas av parabelkroppen rakt ut som parallella strålar i normal till parabelns x-axel.
Parabelkroppens användning som strålkastare blir därmed självskriven — liksom förmågan att samla upp parallellt inkommande strålar till ett koncentrerat fokus över ett större rymdområde, som i fallet med upptagande (mycket svaga) ljud- och ljusvågor över stora avstånd; vågbildens samlade effekt i fokuspunkten fungerar som en förstärkare. Jämför de jättelika rymdradioteleksopen med sina enorma parabolytor.
Ellipsens optiska
egenskaper
|
|
|
UTVECKLINGSEXEMPEL — vanligt rutat papper, måtten i cM: x=3; y=4; R=5; f=Cf=2,5; K1=3,75; K2=8,75; e=0,5; E=Ö 0,75; hT=1,25; a=3; c=7
Ljus som utgår (t.ex. c) från ellipsens ena fokus reflekteras av
ellipskroppen (a) så att ljuset samlas i motstående fokus.
För ellipsreflektivitetens matematiska bevisbarhet finns följande
observerade hållpunkter:
· Ellipstangenten T:s normaler dragna från skärningen med cirkeln genomskär ellipsens bägge fokuspunkter
· Cirkeltangenten T:s normal genomskär origo via R och via a (ellipsens kortaste fokusdistans) ellipsens ena fokuspunkt
· I fallet a=c är hT orepresenterad; då gäller reflexionssymmetrin kring x-axeln
· I fallet a=f är hT=0; då gäller reflexionssymmetrin kring y-xeln
· Reflexionssymmetrin saknar algebraisk bevisbarhet, se nedan (via a-faktorn markerad röd i illustrationen ovan: det finns två a med samma värde men olika lokal)
· Bevisningen kan bara ges kvantitativt numeriskt, se nedan, eftersom både cirkelns tangent och ellipsens tangent bägge ingår i lösningskroppen; det finns ingen specifik elliptisk lösning till de ekvivalenter som beskriver ellipstangentens ekvivalent med Spegellagen
Bevis för att
ellipsens tangent bildar reflexionsyta med lika vinklar mellan ellipslängderna
ac har eftersökts på webben (2008-11-30) men inte hittats. Många webbkällor
beskriver — nämligen — detaljen, dessutom i en del fall med avancerade
interaktiva animeringar — men ingen förklaring ges. Inte ens ett försök. Här
följer ett numeriskt exemplifierat utvecklingsblock som ger ett kvantitativt
bevis men indikerar att ett kvalitativt — algebraiskt — bevis INTE kan
existera.
Jämför följande utveckling, den ger överensstämmande
numeriska ekvivalenter:
Allmänna samband inom trigonometrin i PREFIXxSIN används:
y = RsinT .............. i utvecklingsexemplet är y=4, x=3, R=50mM
Cf=25mM=f, hT=12,5mM, E°=60, e=0,5 E=Ö
3/4, sinT=0,8
hT = R(secT – 1) ;
h = d/(1/tanA1 – 1/tanA2) ;
d = f+hT = K1 ger
h1 = K1/(tanT – 1/tanT) ;
d = R+Cf +hT = 2Cf+f+hT = K2 ger
h2 = K2/(tanT – 1/tanT) ;
OM reflektiviteten gäller, gäller att rektanglarna med diagonalerna ac blir likformiga så att ömsesidigt ekvivalenta förhållanden mellan alla motsvarande kopplande triangelsidor gäller. Därmed kan den reflektiva ekvivalensen för ellipsens del prövas/definieras genom följande utvecklingsled:
;
h2/h1 = K2/K1 = (2Cf+f+hT)/(f+hT) = 2Cf/(f+hT) + 1 | = c/a vilket föreligger som uppgift för bevisning = (2R –a)/a = 2R/a – 1 |;
OM likheten gäller, gäller tydligen att
2Cf/(f+hT) + 1 = 2R/a – 1 ;
2Cf/(f+hT) + 2 = 2R/a ;
Cf/(f+hT) + 1 = R/a ;
= (Cf + f + hT)/(f+hT) = (R+hT)/(f+hT) ;
a = (hT+f)/(1+hT/R)
= (hT+f)/secT
= (hT+f)sinT ........... OK
— Men denna ekvivalent kopplar till en NY a-lokal — i normal till CRL-tangenten. Se a-linjen markerad med röd text i figuren ovan.
— Därmed uppkommer frågan: Är det alls meningsfullt att söka en algebraisk ekvivalent?
— OM slutresultatet pekar på en geometrisk pinne med samma numeriska värde som den algebraiska ekvivalentens, men på annat ställe, är det uppenbarligen meningslöst att ens fråga efter en KVALITATIV ekvivalent då en sådan uppenbarligen INTE existerar;
=
(R[1/sinT – 1]+f)sinT
=
(R/sinT – R+f)sinT
= (R/sinT – Cf)sinT
= R – Cf sinT ............ 3 = 5 – 2,5×0,8 = 5 – 5/2 · 4/5 = 5 – 2
;
sinT = (R–a)/Cf = y(e/Cf) ;
y = (Cf/e) sinT
a = R – Cf sinT
Med dessa samband är det tydligt att rationella lösningar kan erhållas (i obegränsad mängd) som visar exakt ekvivalens genom motsvarande elliptiska xy-samband:
y = (R–a)/e .............. y ska stämma numeriskt exakt med ovanstående y från T
METOD:
Utgå lämpligen från rationella värden på a+c=2R, t.ex. a-värden; Beräkna sedan sinT genom
sinT = (R–a)/Cf .............. Cf=Re med e=Ö 1–E2=sinE° i PREFIXxSIN och E=b/R med b=ellipsens lillaxel, R=storaxeln.
Därmed får man
y = (Cf/e) sinT
som ska stämma exakt numeriskt med
y = (R–a)/e
Vilket vill säga, ekvivalensen
R – a = Cf sinT = ye
ska gälla — om den antagna ellipsens reflektivitet är korrekt uppfattad.
EXEMPEL:
Med 2R=10, Cf=2,5, e=0,5 och a=4 ges, via a+c=2R, c=6; Då är
sinT=(R–a)/Cf=1/2,5=0,4;
y = (Cf/e) sinT = 2,5/0,5 · 0,4 = 2
som ska stämma med
y = (R–a)/e = (5–4)/0,5 = 2
och vilket vi ser stämmer utomordentligt väl.
Hyperbelns optiska
egenskaper
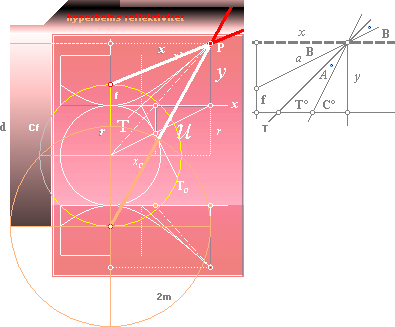
![]()
Hyperbelns tangentlinje (T) tudelar hyperbeldistanserna (ac) i två
lika vinkelrum (A°) vilket tilldelar hyperbelns reflektivitet extraordinära
fokuserande egenskaper, se vidare i resultatbeskrivningen längre ner.
Hyperbelns karaktär tecknas här med termerna 2m=c-a med
a som övre hyperbeldistansen i följande beskrivning.
Om spegellagen gäller med hyperbelns tagent (T) som bas och hyperbeldistansen c
via vinkeln C° som ljusstråle mot motstående hyperbelkropp, då gäller enligt
figurbeteckningarna ovan (höger) att reflexionsvinkeln A° ska vara lika med
A = 90–T – (90–C) = C–T;
Eftersom det också gäller generellt att T = B+A, analogt
A = T–B ges
A = C–T = T–B som ger
2T = C+B;
T = (C+B)/2
Hyperbelns tangent beräknas separat
T = atan x/(r+y)
Genom kontrollräkning finner vi att T-värdena överensstämmer
kvantitativt.
EXEMPEL:
Vi använder »enhetshyperbeln» som betyder att asymptotvinkeln
M=45° med r=m=1;
Vi använder sedan allmänna samband i hyperbelgeometrin enligt
f = Cf-r
y = (a–f)/(Ö 1+tan²M)
................ särskild
härledning;
Geometriskt — SCEN 1:
m+Cf=Xf; för illustration, se exv figurdelen till hyperbelns allmänna ekvation, Cf anger CentrumTillFokus, Xf anger
MotståendeXaxeltillNärliggandeFokuspunkt, hyperbelns karaktär 2m=c–a, cd här utbytta mot ac;
c–Xf=c–(m+Cf)=c–m–Cf;
Cf+c–Xf=c–m;
c–Xf=N;
Cf+N=c–m;
Geometriskt — SCEN 2:
Xf–f=2m;
Xf+N –f–N = 2m;
(Xf+N) – (f+N) = 2m;
c –
a = 2m = Xf–f;
c–Xf =
a–f
=
N;
I »3D-triangeln» med hypolängden (Cf+N) och kateterna r.(m+y) är
tydligen N tillskottet över konstanten Cf som
uppritar hyperbelkurvan på väggplanet
(H). Då
gäller tydligen i PREFIXxSIN att
y/N = sinM;
y = N sinM; sin = 1/Ö 1+
tan²;
y = (a–f)/(Ö 1+tan²M)
vilket skulle visas. Fortsättningen ger då
r/m = tanM
m/Cf =sinM
y = –r + Ö r²+x²
x = Ö y² + 2yr
som ger Cf=1/(1/Ö2)=Ö2 och f=(Ö2)–1=0,4142135;
Vi antar
a = 2 som ger
x = Ö3,5 = 1,8708286
y = (a+1=3)/Ö2 – 1 = 1,1213203
tanC = d/x = (y+r+Cf=Ö12,5)/x =Ö 12,5/3,5 = 1,8898223; C = 62,114433°
sinB = x/a = (Ö3,5)/2 = 0,9354143; B = 20,704811°
(B+C)/2 = 41,409622°
tanT = x/(r+y) = (Ö3,5)/(3/Ö2) = (Ö7)/3
= 0,8819171;
T = 41,409622°
Och som vi ser stämmer de antagna likheterna utomordentligt.
RESULTAT:
Hyperbelns tangentlinje T delar tydligen hyperbeldistanserna ac
i två lika vinkelrum (A°). Det betyder att ljus som riktas utifrån och in mot
ena hyperbelns fokuspunkt reflekteras av hyperbeln mot den andra
hyperbelgrenens fokuspunkt. Det är här inte bekant vilken praktisk
tillämpbarhet denna originella reflexionstyp besitter.
Kommentar:
Det är här inte känt om det finns något (enkelt) motsvarande
rent algebraiskt samband som bevisar hyperbelns reflektiva egenskap.
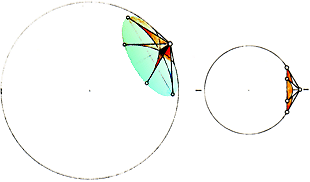
ELLIPSEN OCH HYPERBELN GENOM CIRKULÄR
INTERFERENS
Speciellt för hyperbeln
i nedanstående interferensmönster beskrivs utförligt i Ljusets
Interferens hur ljusets våglängd kan
grovberäknas med mycket enkla (helt primitiva) medel.

Studera
den högra illustrationsbilden från mitten: Formen av en ellips framträder
tydligt med växande omfång. Rätvinkligt ellipsens formkurva ser vi också
tydliga hyperboliska formationer. Matematiken för dessa ansluter till samma
karaktär som visas i perceptionsanalysen. Se även mera utförligt i Vattenvågornas Interferensmönster. Antalet hyperboliska stråk varierar med våglängden
(intervallet mellan cirklarna) och avståndet mellan fokuspunkterna och kan
användas för enkla beräkningar i elementära studier av ljusets vågnatur.
Genom ellipsens och hyperbelns karaktärer som summerande eller subtraherande en konstant bildas
motsvarande förutsättning för ellipsbildning och hyperbelbildning genom två
knippen koncentriska cirklar, figuren ovan. Speciellt hyperbelns framträdande
ur interferenserna är användbart i fysiken i studiet av ljusets vågnatur. Denna
del finns nu (från 2008XII5) i särskild framställning i Vattenvågornas Interferensmönster.
Även
parabeln har interferenskriterium — men det är (tydligen) inte lika känt som i
fallet ellips-hyperbel.
Den
Ungerska webbsidan (2008-12-03)
[http://www.komal.hu/cikkek/dandelin/dandelin.e.shtml]
datumreferens saknas,
KöMal
— Mathematical and Physical Journal for Secondary Schools, Conics and Dandelin
Spheres, Rita Kós
visar
principen och uppslaget till illustrationen nedan,
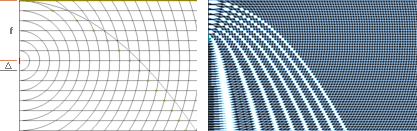
Parabelns
interferensekvivalent består av koncentriska cirklar och parallella linjer,
vänster. Interferenskriteriet framgår redan ur parabelns
karaktär genom att
fokusdistansens ekvivalent (P.F=P.L) tillväxer parallellt med parabelns y-axel. Därmed
kan tillväxten ställas ekvivalent på ett givet tillskott (D)
— som därmed omfattar både linjeintervallet och cirkelintervallet. Skärningarna
framkallar alltså parabeln. Illustrationen höger visar hur de successiva
parabelkurvorna framträder med växande fokuslängd (f).
Interferensen
som framkallar parabeln ges elementärt av ett koncentriskt cirkelknippe
tillsammans med ett knippe parallella ekvidistanta linjer med samma intervall
som de koncentriska cirklarna. Denna detalj är redan uppenbar genom parabelns karaktär (P.F = P.L = c); eftersom P.L alltid tillväxer i normal
till parabelns x-axel kan den tillväxten också ställas på ekvidistanta
tillväxtintervall (D), analogt de parallella linjerna och därmed även de koncentriska
cirklarna med samma intervall.
KONISKA SEKTIONER PÅ WEBBEN
Kommentar till en del webbkällor:
En del webbkällor som beskriver motsvarande ellipsens karaktär via Dandelinsfärer brukar använda enbart punkterna Q1.F1.P.F.Q —
naturligtvis i tanken att »förenkla beskrivningen»;
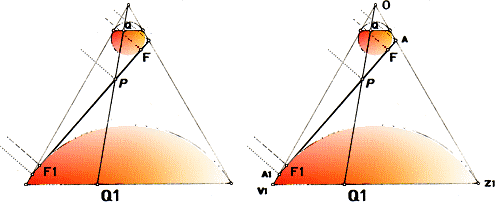
man inför då snittplanet (ovan vänster, se även illustrationen i
ellipsens karaktär) A.A1 i KONEN O.Z1.V1 mellan
Dandelinkloten övre-undre och postulerar att snittplanet rör vid de bägge
Dandelinkloten i punkterna F.F1. Med den förutsättningen blir det sedan enkelt
att påpeka — med perceptionsanalysen underförstådd men inte direkt
förtydligad — att P.F=PQ=c och P.Q1=P.F1=d och att summan av dessa är konstant
Q.Q1=2b. HUR fokuspunkterna F.F1 sammanhänger med den konstruktionen klargörs
dock inte närmare.
Se exv. enda svenska
webbkällan som enligt Google innehåller ordet Dandelinsfär,
[http://www.hh.se/download/1872626a1811b3f5b0bee8000142700/kegelsnitt.pdf]
s19-20,
KÄGELSNITT (ANDRAGRADSKURVOR), Högskolan i Halmstad (författare och datum saknas)
Det svenska utbudet är generellt (utöver ovan) ytterst magert.
Den enda reguljära svenska matematikkällan i ämnet koniska sektioner verkar
vara
[http://matmin.kevius.com/kagelsnitt.php] datum saknas,
Matematik minimum — Terminologi, Bruno Kevius
Mitt uppslag till den här
illustrerade sammanställningen (från 1987) kommer från boken LÄROBOK I GEOMETRI, DEL I, F. Carlsson
1943/1946. Boken använder Dandelinsfärer och ger sambanden, men utan
källuppgifter och utan något omnämnande i koppling till begreppet
”perceptionsanalys”. Termen ”perceptionsanalys” blev min egen spontana
omskrivning i ämnets reflexion genom Carlssons bok, samt insikten om att själva
typbeskrivningen (med klotens hjälp) är det rätta sättet om det gäller en
elementär beskrivning utan komplicerad algebra.
Utan kännedom om Dandelin (1822) som upphovsmannen bakom resonemangen
kan man tro att urkunderna sträcker sig åtskilligt långt tillbaka i tiden med
tanke på principens enkla form. Först nu (November 2008), i samband med den här
presentationen har emellertid upphovsmannen Germinal Pierre Dandelin (1794-1847) kommit i dagen (i min referens via
Wikipedia, se Germinal Pierre Dandelin).
Den engelska delen däremot är desto mera rikt representerad (se
»conic section» på t.ex. Google).
Nedan följer en mera omfattande (men ändå kortfattad
översiktlig) resultatöversikt från en genomgång av utbudet på webben i ämnet
matematikens fyra grundkurvor (December 2008).
WEBBESKRIVNINGAR VIA
INTERFERENSMÖNSTER
— ellipser
och hyperbler via koncentriska cirkelknippen
Webbkällor
som (December 2008) beskriver framträdandet av ellipser och hyperbler via
koncentriska cirkelknippen:
INTERAKTIV
SVENSK (översatt) animerad illustration av hyperbelbildningen (men inte ellipsformen)
via cirkulär interferens;
[http://www.walter-fendt.de/ph14se/interference_se.htm]
Last modification: January 18, 2003, 2008-12-03
Interferens
mellan två cirkulära eller sfäriska vågor,
URL:
http://www.walter-fendt.de/ph14se/interference_se.htm
© Walter
Fendt, May 22, 1999 — © Translation: Ronald Hedblad
I
övrigt är det (ytterst) tunnsått med svenska beskrivningar i ämnet — tyvärr ett
alltför ofta förekommande konstaterande i kunskapssammanhang i Sverige.
—
För att göra jämförelsen rättvis har jag dock inte kollat upp hur det är i
t.ex. Tyskland. Vilket vill säga; det är möjligen (minst) lika illa ställt där.
Osv. (utom England).
ENGELSK BESKRIVNING, utomordentligt tydligt beskrivande även för parabelns del via interferensmönster;
[http://www.komal.hu/cikkek/dandelin/dandelin.e.shtml]
datumreferens saknas,
KöMal
— Mathematical and Physical Journal for Secondary Schools, Conics and Dandelin
spheres,
Hungarian
Ministry of Education and Culture, Rita Kós
Webbkällan
nedan beskriver väl våginterferensen — men utan att i artikeln alls omnämna
orden ellips eller hyperbel. Dessa ord finns inte ens med;
[http://www.glenbrook.k12.il.us/GBSSCI/PHYS/CLASS/light/u12l1b.html]
2008-12-03
WIKIPEDIA,
artikeln nedan, uppvisar flera olika typbeskrivningar — men ordet ellip…
finns inte med; Ordet hyperbolic omnämns — en gång i samband med
mönsterbeskrivningen; En stor och tydlig interferensbild ellipser-hyperbler
finns också,
[http://en.wikipedia.org/wiki/Double-slit_experiment]
2008-12-03;
@INTERNET
Wikipedia Double-slit experiment
Också
på webbsidan
[http://www.physicsclassroom.com/Class/light/u12l3a.cfm]
beskrivs
interferensen (noga) illustrerat — men inte heller här förekommer ordet ellip…,
men väl ordet hyperbola — en gång.
Den här webbsidan beskriver ämnet illustrerat — i
tillbörliga termer — Bägge orden ellipse och hyperbola används,
men parabelns interferensform finns inte med;
[http://xahlee.org/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html],
Conic
Sections, 1995-2008, Xah Lee
I
övrigt finns inte heller så mycket mer att hitta i det ämnet på webben,
engelska sektionen (Jag har begränsat genomletningen på webben via Google till
koll på alla förekomsters artikelinnehåll inom max tre träffsidor för göra
framställningen kortfattad).
WEBBESKRIVNINGAR AV
REFLEXIONSEGENSKAPER
Webbkällor
som (December 2008) beskriver framträdandet av reflexionsegenskaperna hos
ellipsen, parabeln och hyperbeln
De
olika reflektiva-optiska egenskaperna för ellips, parabel och hyperbel beskrivs
(eller rättare sagt omnämns) f.ö. översiktligt illustrerat men utan vidare
bevis eller ingående beskrivning i
[http://www.math.uu.se/~lal/kompendier/Vektorgeometri.pdf]
s47,
VEKTORGEOMETRI
och ANDRAGRADSYTOR, LarsÅke Lindahl,
Matematiska institutionen, Uppsala universitet, 2000.
Parabelns
reflektiva egenskap,
[http://www.math.iupui.edu/m261vis/LMirror/parabola.html],
The
Reflective Property of the Parabola,
från
[http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Erbas/emat6690/Insunit/parabola/parabola.html],
University
of Georgia,
använder
vektoralgebra för ”ett elegant bevis”.
— Man
kan ta sig för pannan för mindre. Känner inte författarna till parabelns enkla geometriska tangentkonstruktion? Tydligen inte.
I
övrigt verkar det vara tunnsått med beskrivande bidrag, engelska delen. Den
svenska delen verkar, som redan omnämnts, i stort sett orepresenterad.
Ellipsens
reflektiva egenskap är desto mera representerad
på webben — på engelska.
ETT
svenskt exempel hittades — men det är rent bedrövligt;
Ellipsens reflektivitet omnämns s23 i
[http://www.hh.se/download/18.72626a1811b3f5b0bee8000142700/kegelsnitt.pdf]
(författare och datum saknas);
HÖGSKOLAN
I HALMSTAD (hittat separat via [www.hh.se]);
Författaren
framställer ”bevis”, men det är inte klart vad författaren avser med det — om
det gällde författarens diskussion i anslutning till DESCARTES BEVIS, eller om
det var något ANNAT. Författaren verkar inte avhandla något annat än ett
”bevis” för att ellipsbågen håller endast en tangentpunkt åt gången.
—
Författaren påstår
Ӂ
andra sidan ger vinkelräkning att F’ ligger på linjen P.F2” — vilket just är
bevisets centrala flaskhals: beviset går ut på att VISA ATT SÅ ÄR FALLET medan
författaren bara helt sonika PÅSTÅR DET UTAN BEVIS ELLER KLARLÄGGANDE.
—
Vilken ”vinkelräkning” avses?
Visa.
— Att
ellipsens båge bara innehåller EN tangentpunkt åt gången är f.ö. ingen särskild
angelägenhet att bevisa för ellipsens del; Den detaljen återfaller på cirkeln,
och sedan vidare därifrån ellipsen (samt parabeln och hyperbeln) genom cirkelns projektiva utvidgning.
— Men
som visas i BEVISET FÖR
ELLIPSENS REFLEKTIVITET handlar
saken inte bara om ellipsens tangent, utan även den omskrivna cirkelns tangent,
bägge krävs för att klarlägga beviset, men denna detalj omnämns inte i
Halmstadkällan ovan.
—
Exemplet säger en del om kunskapsnivån, om inga allvarliga felgrepp har gjorts
i den här framställningen.
För
att hitta vidare beskrivningar på ellipsens reflektivitet är man (tydligen)
hänvisad till andra språk:
Wolfram
MATHWORLD på Ellipse,
[http://mathworld.wolfram.com/Ellipse.html],
omnämner
visserligen ”Reflections” fokus-fokus, men ger ingen härledande beskrivning,
endast en referens (”Hilbert and Cohn-Vossen 1999. p. 3”).
I
ÖVRIGT VERKAR DET HELLER INTE FINNAS NÅGRA YTTERLIGARE ENGELSKA BIDRAG
—
konstaterat efter genomletning på 4 av de 62 funna träffsidorna i »geometry of
the ellipse» (2008XI29).
WEBBESKRIVNINGAR VIA KÄGELSNITT
Webbkällor
som (December 2008) beskriver formkaraktärerna som sådana hos ellipsen,
parabeln och hyperbeln
Denna del är (naturligtvis) den mest välrepresenterade i beskrivningen
av främst kurvorna för ellips, parabel och hyperbel. EMELLERTID — vilket
omnämndes från PERCEPTIONSANALYSEN, blir kägelsnitten eller DE KONISKA
SEKTIONERNA verkligt begripliga FÖRST med förklaringen av den ”mekanism” som
kägelsnitten visar sig innefatta — nämligen DANDELINS SFÄRER. Men inte alla ”kägelsnittsförfattare” inkluderar en samtidig
beskrivning av — eller ens omnämner — Dandelins sfärer. SAMT i den mån så är
fallet, återigen inte SÅ grundligt som den här framställningen blivit
tillägnad, se från PERCEPTIONSANALYSEN.
[http://xahlee.org/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html],
A
Visual Dictionary of Special Plane Curves,
1995-2008, Xah Lee
— ger
en allmänpresentation av de olika sätten som t.ex. ellips och hyperbel
framträder på, inkluderat Dandelinsfärer, men beskrivningen ger ingen direkt
klar och tydlig koppling till just en PERCEPTIONSANALYS — vilket vill säga:
själva den klargörande begreppsliga bevisningen tappas bort.
Dandelins
Sfärer beskrivs även på @ INTERNET
Wikipedia Dandelin spheres
[http://en.wikipedia.org/wiki/Dandelin_spheres]
2008XI28,
Wikipedia
Dandelin spheres,
med
ellipsen som exempel; där finns också länkar till en del av de webbsidor som
omnämnts här.
— Men
inte heller i Wikiwebbkällan ovan finns någon uttalad koppling till att ämnet
just beskriver en perceptiv analys (enligt sfäriska klotets geometri).
DANDELINSFÄRER
omnämns också i den redan omnämnda svenska webbreferensen
[http://www.hh.se/download/18.72626a1811b3f5b0bee8000142700/kegelsnitt.pdf],
—Emellertid
är (även här) presentationen helt fristående från PERCEPTIONSANALYSEN och dess
förklarande detaljer.
En av illustrationerna i källan ovan (s20, men
ingen källangivelse ges av författaren …) återfinns också på
[http://www.mathacademy.com/pr/prime/articles/dandelin/index.asp],
Platonic
realms — PRIME ARTICLES, Math Acadedmy
Online.
DANDELINS
BEVIS genomgås per i webbkällan
[http://www.liceomendrisio.ch/~marsan/matematica/materiale_vario/coniche/Dandelin/JDandelinEn.htm],
Java
applet JDandelin, © Slavomir Tuleja,
Jozef Hanc, 2002;
—
samma delar finns f.ö. återgivna i Halmstadkällan som ovan.
Emellertid
har källan bakat in s.k. ”applets” (specialprogram) men som inte verkar ha
någon representation i innehållet (vad författarna menar här blir en delvis
kaotisk röra).
— Ett
exempel på hur en presentation kan bli betydligt mera komplicerad än den är.
Dandelin
Spheres beskrivs även på
[http://mathworld.wolfram.com/DandelinSpheres.html],
Wolfram
MATHWORLD (-2008),
—
illustrerat med ellipsen som exempel, men ingen koppling till någon
”perceptionsanalys” ges där heller.
Omfattande
algebraiska samband som beskriver de koniska sektionerna finns (2008-11-28) bl.a. på
Wikipedia
Conic section
[http://mathworld.wolfram.com/ConicSection.html].
Wolfram MATHWORLD
[http://math2.org/math/algebra/conics.htm].
Math2.org
Math Tables: Conic Sections
[http://mathdemos.gcsu.edu/mathdemos/family_of_functions/conic_gallery.html],
Conic
Section Gallery
Den
svenska MATEMATIKLEXIKONKÄLLAN
[http://matmin.kevius.com/index.php]
Matematik
minimum - Terminologi, Bruno Kevius
(datum saknas)
omnämner
inte Dandelin överhuvudtaget, men ger i övrigt en relativt uttömmande allmän
översikt av de koniska sektionernas allmänna matematik.
RESUMÉ WEBBEN December 2008 CEPH
— Det finns
(veterligt, ännu) ingen heltäckande webbkälla som ensam tar upp alla aspekter
på matematikens fyra grundkurvor cirkeln, ellipsen, parabeln och hyperbeln. För
att få en sådan översikt måste vi (än så länge och med referens till
ovanstående allmänna men [mycket] kortfattade och översiktliga genomgång)
bläddra mellan olika (många) webbkällor — och dessutom sett över flera (många)
olika språk. Förhoppningsvis (men utan angiven organisation) uppvisar de
ovannämnda webbsidorna allt vi behöver veta i ämnet — då frånsett genomgången
med de olika RITINSTRUMENT som kan användas för att få fram kurvformerna rent
praktiskt på papperet. Också den delen är omfattande, men har inte alls tagits
med i den här presentationen.
CEPH-ekvationen
innehåll: SÖK på denna
sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla
webbsidor
CEPH-ekvationen
ämnesrubriker
innehåll
CEPH-kurvorna och deras
tangenter — cirkelns planprojektiva utvidgning
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen
i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn =
1,0086652u ...................... neutronmassan
i atomära massenheter (u) [HOP Table 2.1 s9–65]
me =
0,000548598u .................. elektronmassan
i atomära massenheter (u) [HOP Table 10.3
s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27,
1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG
............... atomära massenheten
[FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära
massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W
(2005)]
u = 1,6605402 t27 KG .......... atomära
massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27
KG ...... atomära massenheten [från www.sizes.com],
CODATA
rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe
on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten
i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på
1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.
[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)
t för 10–, T för 10+,
förenklade exponentbeteckningar
TNED (Toroid Nuclear Electromechanical
Dynamics), eller Toroidnukleära
Elektromekaniska Dynamiken är den dynamiskt ekvivalenta
resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn,
analogt Atomkärnans
Härledning. Beskrivningen enligt TNED är relaterad,
vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt
logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås
(således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.
Senast uppdaterade version: 2022-12-09
*END.
Stavningskontrollerat 2008-11-26.
rester
*
åter till portalsidan · portalsidan är www.UniversumsHistoria.se
PNG-justerad 2011-10-10
åter till portalsidan · portalsidan är www.UniversumsHistoria.se