Fysikaliska Grundbegrepp — Universums Historia

FYSIKALISKA GRUNDBEGREPP — UNIVERSUMS HISTORIA 2007XI5 | a production | Senast uppdaterade version: 2011-10-10 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

ljusets interferens

Se även hur ljusvåglängden kan grovberäknas ur helt enkla experiment med hjälp av Vattenvågornas interferensmönster.

ENKLA EXPERIMENT AVSLÖJAR LJUSETS NATUR

ÄNDRINGENS SNABBHET (frekvensen) sammanhänger med ljusets egenfärg. Vanligt ”vitt” ljus består i själva verket av många olika färger (frekvenser) som tillsammans bildar ”vanligt ljus” (vi ser det direkt genom regnbågen samt genom ett annat fenomen som inte är lika omskrivet). Genom ett ytterst enkelt experiment kan ljuset splittas upp och studeras på färgkomponenterna i detalj. Vi behöver ett stearinljus och två runda grässtrån, vi kan hämta dem från närmaste vildvuxna naturplätt. Bilden nedan visar hur det fungerar.

En enkel interferometer

DISPERSION — färguppdelning

Vi behöver ett stearinljus och två runda grässtrån, vi kan hämta dem från närmaste naturområde.

Tänd ljuset. För ihop två grässtrån och sätt dem rakt framför ögat. Genom att vrida på stråna mellan fingrarna kan man precisionsjustera den smala öppna spalten och därmed precisionen i färgseparationen. Ju mindre springa, desto högre upplösning.

Bilden som framträder genom springan ser ut ungefär så här (men mera diffus)

Genom att vrida på stråna och söka olika bilder kan man få väldigt stora och tydliga färgband.

Färgränderna på bägge sidor om ljuset har (i hög upplösning) utseendet

candle

vståndet från ljuslågans mittpunkt till första färgranden kan varieras genom att ändra spaltöppningen. Ett riktvärde för grov uppskattning är ca 15 mM. Den motsvarande upptagande synvinkeln på avståndet 1 meter från lågan blir då nära en grad (a=0,86°). Om vi tar denna vinkel som riktmärke tillsammans med en spaltöppning på fem hundradels mM (d=0,05mM) kan vi räkna ut ett grovt värde på våglängdens storlek (l) i PREFIXxSIN enligt l=d cosa [GFåk3Liber1980s150] som ger våglängden ca 750nM. Det motsvarar grovt sett det röda ljuset. Se utförlig beskrivning i Vattenvågornas interferensmönster.

ed en mikrometer som spalt kan vi kontrollera precisionen mera noggrant (spaltavstånd mindre än 0,02mM släcker ut bilden)

arje färg har sin frekvens (ändringshastighet).

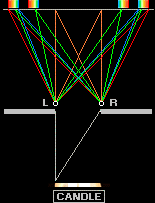
Från en given punkt på ljuslågan går synlinjer till den smala öppningen. Ljusstrålarna når materialpunkterna L och R som bildar nya ljuskällor i alla möjliga riktningar.

Frekvensens ändring över avstånd för alla färger i synlinjerna som utgår från LR bildar resonanser (går in i varandra) eller symmetrier i vissa punkter medan de i andra punkter bildar dissonanser (de tar ut varandra). Färgen framträder i resonansområdena och utsläcks helt i dissonansområdena. Vi kan se exakt samma principiella effekt med vattenvågor som korsar varandra i olika mönster: en del ställen förblir helt lugna, medan andra delar formas av summan av bidragen från enskilda vågfronter eller vågkällor. Den röda färgen har lägst ändringshastighet och har därför den bredaste eller största representationen (nära hälften av hela bandet).

Vattenvågornas interferensmönster | — med särskilt kopplande beskrivning till Ljusets Interferens | från MPcExempel 2004I6 | Spegellagen 2004I12 |

Vattenvågornas interferensmönster

EPS och HRB ur VATTENMÖNSTRET

Ellipser (EPS, konstant summa) och hyperbler (HRB, konstant skillnad) framgår direkt ur mönstret från två koncentriska knippen cirklar. Se mera utförligt i ELLIPSENS KARAKTÄR och HYPERBELNS KARAKTÄR.

Från två skilda centralpunkter ritas växande cirklar med ett fast intervall. Cirklarnas skärningspunkter tecknar två mönsterfigurer.

Den slutna figuren är ellipsen, den öppna är hyperbeln.

Ellipsen har summan av cirkelradierna konstant, samma som ellipsens storaxel. Hyperbeln har skillnaden konstant, lika med resten mellan centralpunkterna.

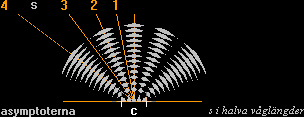
Mönstret är samma som ges av två (lika stora) vattendroppar som träffar vattenytan samtidigt (upprepat med exakt period). Markeras varannan cirkel med olika färg är det enklare att se hur vågmönstret bildas. Vattenvågorna förstärker varandra (grå områden) i mellanrum som gränsar till likadana cirklar i vågornas utbredningsriktning, och utsläcker varandra (ljusa områden) i mellanrum som gränsar till olika cirklar. Utsläckningen (olika cirklar) motsvarar en vägskillnad från centralpunkterna lika med cirkelintervallet (samma som en halv våglängd hos vattenvågorna).

Om de koncentriska cirkelknippena förskjuts med cirkelintervallet, uppstår 1, 3, 5, 7, 9, … tydliga vita hyperbelstråk. I figuren ovan är stråken nio.

Analogin mellan vattenvågor och ljus — samband i symbolisk algebra

Om cirkelintervallet anges i vattenvågornas referens, ett intervall d= ½ våglängd, och centrumavståndet c är ett helt antal d, c=n_cd, blir resten s i c för varje hyperbel lika med 1d, 2d, 3d, … n_sd. Allmänt för hyperbeln i PREFIXxSIN gäller dess asymptotvinkel sinA=s/c. A räknas då från c-linjen. Detta ger s/c=n_sd/n_cd=n_s/n_c.

I illustrationen är n_c=5. De möjliga hyperblerna via cirkelskärningarna blir då s/c={1/5, 2/5, 3/5, 4/5}. Den sista (5/5=1) blir den räta vertikalen.

allmänna samband

Räknas A från c-normalen som a° ges i PREFIXxSIN cosa c=s. Våglängderna s={2d, 4d, …} som ger vattenvågorna blir då i succession

cosa₂ c=s₂, cosa₄ c=s₄, cosa₆ c=s₆, … där s₂ i cosa₂ c=s₂ anger en hel våglängd.

Beräkning av våglängden. Om avståndet från c är stort relativt c kan man med god noggrannhet beräkna våglängden i PREFIXxSIN via första vågstråket enligt s₂=cosa₂ c genom att mäta eller uppskatta c med kännedom om normalvinkeln a.

Mera exakt enligt hyperblerna (Se Hyperbelns Ekvation) gäller

y=(s/2)Ö 1+x²/r² ............................................ absoluta hyperbelbågen (den som gäller räknat från mitten av c)

r=(s/2) tanA = (s/2) Ö (c/s)²–1 ...................... hyperbelns cirkulära öppningsradie (begrepp från raka konsnittet)

r²=(s/2)²[(c/s)²–1]=(1/4)(c²–s²)

; y=(s/2)Ö 1+4x²/(c²–s²) :

(c²–s²) c s stråk

24 5 1 lugn

21 5 2 vågor

16 5 3 lugn

9 5 4 vågor

^{(1/2)[1+4(x'2)/24]'0.5
MinGrafiskaEkvation}

Vattenmönstret (interferensmönstret) framträder endast med s som 0, 2, 4, 6, 8 … jämna antal halva våglängder. Dvs., endast i stråk där hela våglängder sammanträffar.

Artikeln nedan ger ett praktiskt exempel på hur ljusets våglängd kan bestämmas med hjälp av ovanstående beskrivna samband.

BERÄKNINGEN AV LJUSETS VÅGLÄNGD

Bilden av ljuslågan i det smala utrymmet mellan grässtråna — se den inledande beskrivningen från Ljusets Interferens — uppvisar periodiska färgband med regnbågens färger — blått innerst och rött ytterst. Genom att vrida på stråna justeras bilden. Väldigt stora och tydliga färgband kan på detta sätt ses direkt. Färgränderna på bägge sidor om ljuset har (i hög upplösning) utseendet

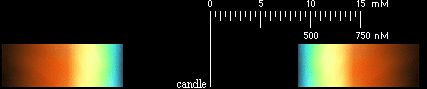
FÖRKLARINGEN TILL ljusfrekvensen f (Ljusets optiska natur) bildar exakt analogi med f i vattenvågor, deras periodiska rörelser och deras interferens. Genom att undersöka geometrin för hur sådana mönster bildas, får vi en direkt metod för att kunna göra en grov beräkning av de motsvarande ljusets våglängder vi ser i den enkla grässtråinterferometern. Grovberäkningen — som ska studeras i det följande — visar en våglängd för rött om ca 750 nM (n för nano- eller t9 M).

Separat beskrivning av interferensgeometrins grunder ges i VATTENVÅGORNAS INTERFERENSMÖNSTER.

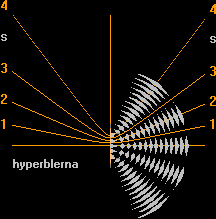
Banduppdelningen, figuren nedan (höger), uppvisar exakt samma fason som cirkulära vattenvågor som korsar varandra. Med spaltöppningen som c (som vi får uppskatta) och den upptagande synvinkeln (a°) mellan ljuslågan och första färgbandet, kan vi göra en grov, men rättvist orienterande uppskattning av storleken på

ljusvåglängden (2s). Avståndet från ljuslågans mittpunkt till första färgranden kan varieras genom att ändra spaltöppningen. Ett riktvärde för grov uppskattning är ca 2s=15 mM. Den motsvarande upptagande synvinkeln på avståndet 1 meter från lågan blir då nära en grad (0,86°). Om vi tar denna vinkel som riktmärke

tillsammans med en spaltöppning c på fem hundradels mM får vi grovvärdet i PREFIXxSIN 750nM@(5 t5 M)cos(0,86°)=7,50463 t7 M.

Med en mikrometer som spalt kan vi kontrollera precisionen mera noggrant: för ögats del släcks bilden ut av spaltavstånd mindre än 0,02mM — vilket visar att grovvärdet på 0,05 mM är rimligt.

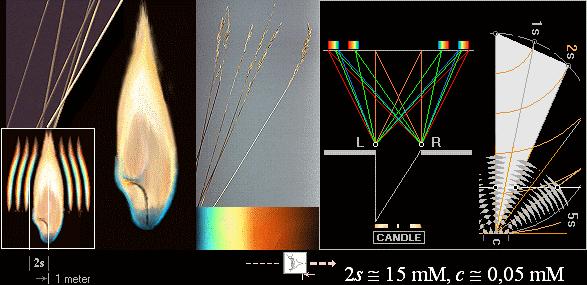
Illustrationen ovan sammanfattar beräkningen som beskrivs mera utförligt nedan;

— Avståndet till första färgbandet från ljuslågans centrum mäter ca 15 mM med ett betraktelseavstånd om ca 1 meter genom en spaltöppning av ca 0,05 mM: (0,00005)(0,015)/1=7,5 t7 M=750 nM.

Interferensgeometrins grunder beskrivs utförligt i VATTENVÅGORNAS INTERFERENSMÖNSTER — i sammanfattning enligt figurens högerdel.

Vi ser spaltöppningens referenspunkter LR (ovanifrån) som illustrationens markerade punkter L (vänstra, eng. Left) och R (högra, eng. Right). Punkterna LR bildar nya vågkällor som sprids genom spaltöppningen (c) på samma sätt som cirklar som utgår från respektive LR. Med en grov kännedom om avstånden samt interferensmönstrets geometri, kan vi göra en rättvis grovberäkning av storleksordningen av det aktuella ljusets våglängder, här företrädesvis det röda ljuset som upptar största delen av färgbanden.

Är cirkelintervallet (s) en halv våglängd och centrumavståndet (c) ett helt antal s, blir resten i c för varje hyperbel lika med 1s, 2s, 3s, … ns. Udda s (1,

3, 5, 7, 9 …) ger lugna stråk, jämna s (0, 2, 4, 6, 8 …) ger stråk med vattenvågor.

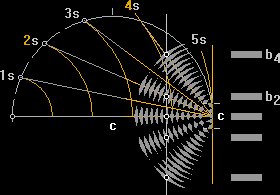
Ritas vinkelstråken upp på en plan rityta med centrumcirkeln (c) till jämförelse med cirkelintervallen, ser man tydligt hur våglängden (2s) definieras/beskrivs av ett godtyckligt fast avstånd (det förstorade c) via vinkelstråket. Den sanna våglängden (2s) är alltså den man får om det förstorade c förminskas till det aktuella c (matematiken är så här ”löjlig” i ena delen: i andra höjer man strax på ögonbrynen).

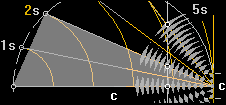
I PREFIXxSIN kan vi alltså beräkna våglängden 2s=l om vi känner den lilla öppningen c samt vinkeln (a°) till första vågstråket enligt

l/c=cosa;

l = c cosa ............. våglängden från c och a

För små a (från 1° och mindre) är cosa @ tana.

Med avståndet till första färgbandet från ljuslågans centrum som ca 15 mM, med ett betraktelseavstånd om ca 1 meter, genom en spaltöppning av ca 0,05 mM får vi

l = (0,00005) · (0,015)/1

= 7,5 t7 M

= 750 nM.

Detta värde är också vad man vanligtvis ser i facklitteraturen som ett generellt våglängdsvärde för det röda ljuset.

Interferensgeometrins grunder beskrivs f.ö. utförligt i VATTENVÅGORNAS INTERFERENSMÖNSTER.

LJUSVÅGLÄNGDENS GROVBESTÄMNING

GENOM ALTERNATIV METOD

Med fortsättning från Den Elementära Vågmekaniken

I en mera avancerad omgivning kan vi också grovmäta området för det visuella ljustes våglängder. Figuren nedan visar detaljerna.

Vi behöver 1. en tunn remsa aluminiumfolie, 2. en mikrometer för att mäta foliens tjocklek, 3. två plana glasskivor ca 20 cM långa, 4. en millimetergraderad linjal, 5. en konventionell arbetslampa, 6. en stel stång av trä eller plast (med rundad ände, typ handtaget på ett förstoringsglas).

Förklaring

Som är uppenbart från föregående experiment och den grundläggande vågteorin genom reflexionslagen i Elementära Vågmekaniken, genomgår färger som reflekteras av vatten från luft en fasändring — jämför det inledande repexperimentet i Elementär Vågmekanik där den reflekterade vågpulsen ligger i motfas relativt den inkommande. Färger som reflekteras av vattnet inifrån vattnet självt påverkar inte de omnämnda djupvektorerna i vågutbredningen. Vågfasen i dessa reflexioner bevaras, således.

Låt oss därmed betrakta två motsvarande (idealiserade) isblock, eller mera avancerat två plexiglasskivor. Färger som reflekteras (från lampan ovanför) inifrån topplattan motsvarar reflexion inifrån vattnet — Vilket betyder att fasen bevaras. Färger som passerar genom den ytan och sedan fortplantas den korta distansen i luftskiktet mellan plattorna och sedan reflekteras från bottenplattans toppyta, motsvarar en ordinär reflexion av färger från vattenytan — Vilket betyder att en fasändring uppstår.

Om de bägge glasplattorna har nolldistans i ena änden (figuren ovan vänster), och bara en ytterst liten separation i andra änden (höger ovan), tvingas färgerna interferera i sekvenser om 1/2 våglängd som vi avancerar från vänster till höger med växande vinkelrum. Vilket vill säga: Plattorna tvingas uppvisa ringar eller linjer som repeteras varje 1/2 våglängd om vi undersöker glasskivorna någonstans i området där de möts.

Placeras arbetsbelysningen approximativt rakt ovanför glasplattorna och vi tittar på plattorn från nära deras horisontella projektion, alltså med blicken strykande utmed endera glasytan, samt att vi använder trästången för att bilda en mjuk tryckpunkt som förstärker glasplattornas föreningspunkt, kommer vi (idealt) att se något som liknar färgringarna i ovanstående illustration. Cirklarna som framträder runt den tryckande stångspetsen kommer att synas påfallande »violett-gröna». Genom att placera linjalen överst på den övre glasskivan, kan vi bekvämt inspektera och läsa av distansen mellan två närliggande lika färger. Beroende på omständigheterna, finner vi någonting i storleksordningen 1,5 till 2,0 millimeter som intervallet mellan två lika färger med övriga data enligt figuren ovan.

En enkel beräkning ger då

0,02/180 = tan = 1,1 t4 tangentvinkeln mellan glasplattorna

2mM · tan = l/2 halva våglängden

4 t3 × tan = l = 444 t9 M hela våglängden

Resultatet ger en approximativ våglängd på runt 450 nM, eller avrundat 0,5 µM. I mera avancerade mätningar (genom riktlinjer som utvecklades runt 1900), uppvisar det synliga ljusets spektrum våglängder från 375 nM (violett) till 800 nM (rött) med grönt ungefär i mitten med ca 500 nM — vilket också är vad ovanstående grovmätning visar.

I sammanställning från föregående arbeten 2001IX17

FÄRGUTBREDNINGENS HASTIGHET

Ljushastigheten

Mot mitten av 1800-talet gjordes mera precisa bestämningar av ljushastigheten genom en rad sinnrika experiment av fransmännen Fizeau (1849, snabbroterande kugghjul, speglar, @INTERNET Wikipedia Speed of light 2008-12-13) och Foucault (1862 BKL IV sp433m, roterande speglar, GYMNASIETS FYSIK åk3 Liber 1980 s146). Foucaults roterande spegelprincip, figuren nedan, visar hur ljushastigheten kan bestämmas i princip — experimentet som beskrivs längre ner har veterligt explicit aldrig genomförts i denna stora skala, men väl i mindre format.

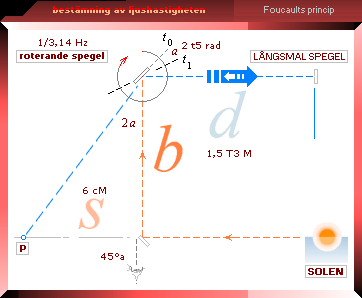
b=d=1,5 KM i figurens exempel. Om speglarna kan göras smala, typ 5mM, kan toleranserna i resultatet helt säkert garanteras för att rent kvalitativt fastställa ljusets ändliga hastighet även med en relativt liten tillgänglig kvadratyta för mätning (b=d=250 M) och en relativt låg rotationsfrekvens för den roterande spegeln (2-10 Hz).

Anordningen blir speciellt enkel att justera och ställa in om speglarna är smala: Man följer bara den fast monterade källspegeln med blicken och går sedan utåt sträckan b (inte helt kritiskt): Strålvinkeln från den smala källspegeln garanterar då precisionen i motsvarande rät vinkel: Är spegelns bredd säg 5mM och b=250 meter blir bågvinkelprecisionen lika med atan(0,005/2)/250 = 5,73 t4° eller 2,06 bågsekunder.

Experimentet kräver tre långsmala plana speglar. Som den mätande distansen här måste vara relativt stor, grovt ental eller delar av kilometer, blir enda praktiska ljuskällan Solen. Två av speglarna monteras fasta medan den tredje monteras roterande. Figuren ovan visar hur Solljus riktas mot den roterande spegeln via en mellanliggande fast bottenspegel. Bara i punkten t₀ kan ljuset nå den rakt utåt liggande toppspegeln överst till höger. Under den tid ljuset kräver för att nå dit, samt därifrån och tillbaka mot den roterande spegeln, hinner denna rota en liten vinkel a. Den resulterande reflexionen kommer då att hamna något till vänster om den första fasta spegeln via dubbla a-vinkeln;

Spegeln flyttas a på t vilket bildar infallsvinkeln 45°–a vid d-linjen; samtidigt flyttas spegeln relativt b-linjen 45°+a åt vänster utmed baslinjen s;

eftersom infallsvinkeln ska vara lika med reflexionsvinkeln, alltså 45°–a sett från spegelytans plan i bägge riktningarna, måste den reflekterade strålen ligga vinkeln 45°–a till höger om spegelytans förlängda linje ner mot s så att strålen från den roterande spegeln mäter vinkeln från b-linjen enligt 45+a – (45–a) = 2a.

Se vidare resultatvärdena i uppställningen sist.

Figuren anger en medurs vinkelrotation på 0,318 Hz (1/p Hz eller 1 varv på ca 3,14 sekunder) för den roterande spegeln [Varje enkel men stadig vattendriven hjulanordning kan fungera]. Genom rotationen blir det fullt möjligt att observera avvikelsen från den markerade ögonpunkten och vänsterut med a-vinkelns uppritade belopp under den korta tid som den roterande reflexen utbildas. Om b=d är 1,5 kilometer kommer den reflekterade toppspegelns puls att ritas ut för observation runt 60 millimeter till vänster om bottenspegeln — fullt mätbart med lämpliga förberedelser och justeringar för referenspunkter. Förutsatt Solreflexerna är tillräckligt starka (vilket de garanterat är även med små handhållna speglar över några få kilometer) borde det vara möjligt att avläsa vänsterdragningen från rotationsreflexionen — inte bara konstatera det faktum att en sådan utdragning visas. Experimentet (utan vidare anordningar) måste göras i Soluppgången eller Solnedgången, dessutom på något område som är relativt slätt över mätytan.

Resultatvärdena visar att bara en kvadratyta med sidan 250 meter och en rotationsfrekvens på 10 Hz kan ge fullt avläsbara värden.

beskrivning

TIDEN det tar för ljuset (eg. färgerna) att tillryggalägga vägen d från den roterande spegeln till den sista spegeln — överst i illustrationen, fram och åter — ger från grundformen v=d/t med v=c och d:=2d enlig

t = 2d/c

Under den tiden t har den roterande spegeln vridit sig en vinkel som kan bestämmas ur grundrelationerna

A°/360 = l/2pr = t/T

s anger delen av hela omkretsen 2pr som bildas på omloppstiden T; Det ger oss motsvarande radianvinkeln (a) ur de bägge första leden enligt

A°2p/360 = l/r = a = A° ·p/180

och radianvinkeln via tiden t ur de bägge sista leden enligt

l/2pr = t/T = a/2p = t/T som ger

a = 2p t/T = 2p t f = wt

med f rotationsfrekvensen och 2pf som vinkelfrekvensen,

w = 2pf = 2p/T ................................. S^–1

Tangens för dubbla a-vinkeln har vi enligt figuren ovan som

tan 2a = s/b

För små a-värden, vilket är fallet i den här tillämpningen, kan tangensvärdet sättas praktiskt taget lika med radianvärdet självt, 2a.

Därmed sammantaget

tan 2a = s/b @ 2arad

w = 2p/T = 2pf = a/t

f = w/2p

t = a/w

c = 2d/t = 2d/(a/w) = 2dw/(a » s/2b), @ 4bdw/s ;

c = 4bdw/s ;

2a = s/b = 4dwc–1 = 4d(2pf)c–1 = f · 8pdc–1

c betecknar färgernas utbredningshastighet i luft, alltså motsvarande ljushastigheten. I avrundade termer används här det enklare värdet

3 T8 M/S (mera exakt 2,99792458 T8 M/S), vilket ger följande data till jämförelse:

c = 3 T8 M/S:

2a = f · 8pdc–1

w f, Hz d=b, M 2a = 4dwc–1 = s/b s, M instrumentering

20p 10 250 2,09439 t4 0,052 enkel

2p² p 250 6,57973 t5 0,016 enkel

4p 2 250 2,09439 t5 0,005 enkel

2 1/p 1,5 T3 4 t5 0,06 enkel

500 250/p 2 1,33 t5 2,67 t5 avancerad

500 250/p 5 3,33 t5 1,67 t4 avancerad

500 250/p 10 6,67 t5 6,67 t4 avancerad

De sista tre exempelvärdena ansluter grovt till de aktuella dimensioner som användes av Foucault. Bara för jämförelsens skull, visas i resultatet nedan att Foucaults metod är relativt begränsad fastän högt driven i utformningen som sådan [Foucaults instrumentmikroskop i avläsningsapparaten tillåter en precision i området hundradels millimeter (t5 M), med möjliga bråkdelar beroende på utrustningen].

c = 2,99792458 M/S:

500 250/p 2 1,33425 t5 2,66851 t5

Mera noggranna mätningar av ljushastigheten kräver mera noggranna tidmätare. Idag [2001] kan varje person som kan hantera grundläggande elektronik i princip genomföra sådana mätningar på egen hand — med elektronikens många avancerade men billiga komponenter.

LJUSBRYTNINGEN

GENOM EN VATTENDROPPE

I APPLIKATION 4 Experiment 1 i Elementära Vågmekaniken användes en droppflaska för att få fram en serie koncentriska vattencirklar. Som vi kan ha observerat i dessa undersökningar, bildar rekylen en påfallande sfärisk större droppe inte sällan åtföljd av en serie mindre droppar. Den sfäriska formen framträder tydligt om vi studerar rekylen från nära vattenytan med arbetsbelysningen placerad vid sidan.

Den sfäriska droppens tvärsnitt via droppens största diameter kan relateras till en cylindrisk sektion motsvarande en rak bägare av glas eller plast. Ljusgenomgången i tvärsnittet ger då en karaktäristisk geometri för en ideal ljusstråle som kommer in vid droppens kant, markerat med IN till vänster i nedanstående illustration.

Vattendroppens grundanalys uppvisar en del enastående karaktärer. Vi studerar först grundrelationerna — De verkar komplicerade, men är enkla.

Vi utgår ifrån den reserverade vattenvinkeln som beskrevs i Elementära Vågmekaniken, se VATTENVINKELNS GRÄNSVÄRDE, och betraktar detta intervall i vattendroppen.

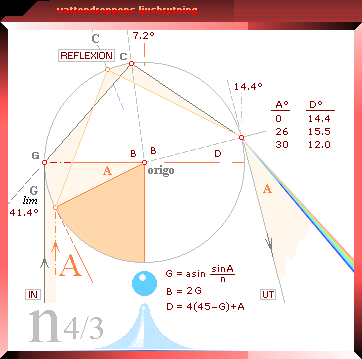
Vi sätter radien R; Kordapunkterna GC avdelar en likbent triangel GC.R.R vars halva origovinkel (B) är lika med vinkeln G eftersom GC delas på mitten rätvinkligt; Då är B=2G, och det gäller att vinkeln C vid REFLEXIONSPUNKTEN (C) fås C=B–A; Detta gäller tydligen i vilket fall, både för den betecknade gränsvinkeln limG där A=0 och alla övriga G som är större än limG, från minsta 41,4° till största 90°.

Den inkommande strålen IN i figuren med idealt exakt noll tjocklek touchar droppens yta, vilket ger en motsvarande gränsbrytningsvinkel A=0°: inget ljus kommer då in i vattendroppen (stråltjockleken är noll och ingen strålenergi kommer in i själva vattenvolymen). Varje med IN-linjen högerdragen parallell begränsningslinje för en motsvarande förtjockad ljusstråle betyder då ATT ljus inträder droppen. Ingångsstrålen bestäms av tangenten till ytan, alltså radienormalen, och den är lika med A relativt den begränsande IN-strålens bredd. På A-vinkelns linje (markerad orange i figuren) bryts då ljuset in i droppen i PREFIXxSIN enligt

sinG = n–1sinA .................................. se Ljusbrytningen i Vatten

Den brutna strålen möter sfären från insidan i REFLEXIONSPUNKTEN markerad överst i illustrationen, och blir därifrån basen för en liksidig triangel med de bägge lika vinklarna (G’, ej utritade). Toppvinkeln fås enligt

180–2G’=180–2(90–G)=2G. A-vinkeln subtraherad från denna toppvinkel ger VINKELN FÖR REFLEXIONSPUNKTEN C i respekt till horisonten (vänster). Vilket vill säga,

C = B–A som med B=2G — se figuren — ovan ger

= 2G–A

= 2(asin n^–1sinA) – A;

sin (A+C)/2 = n^–1sinA

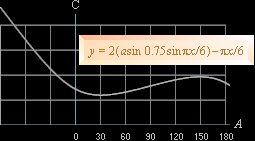
Grafen ovan visar C-funktionen i PREFIXxSIN med ett lägsta bottenvärde via A » 30° genom brytningsindex n=4/3.

Vertikalskalans enhet är 1 radian = 180/p = 57,295779°.

Som REFLEXIONSPUNKTEN bildar en symmetrisk kopia från den brutna IN-strålen, har vi bara att dubbla B-vinkeln för att få vinkeln där strålen lämnar vattendroppen. För att erhålla den vinkeln (D) i respekt till noll grader på högra sidan om horisonten subtraheras först A och sedan hela summan från 180. Alltså,

D = 180–(2B–A) = 180–(2[2G]–A) = 180–(4G–A) = 180–4G+A = 4(45)–4G+A

= 4(45–G)+A

Som strålen i denna punkt bara är en symmetrisk kopia av IN till REFLEXIONEN får vi direkt den slutliga returnerade luftstrålen relativt sfärytan som A. Verkligen. I respekt till IN-riktningen således helt enkelt

UT = D+A = 4(45–G)+A + A = 4(45–G)+2A = 2[2(45–G)+A]

Vi summerar;

Om vi följer den enkla relationen för B från noll och uppåt [i PREFIXxSIN], B=2G, finner vi (strax) att REFLEXIONSPUNKTEN vänstersveps till ett minimum (A»30°) — och sedan vänder och går tillbaka. Detta reflexionsområde blir koncentrerat till nära en och samma utgående ljuspunkt med D grovt som 14°.

Minsta C — genom aritmetisk prövning — n=4/3:

a = 0,17p ..................... A i radianer

A = 0,17p · 180/p

= 3060/100

= 30,6° ..................... mindre/större A ger större C (decimalrepresentationen här ej exakt känd)

C = 68,985171°

D = 11,429656°

D+A = 42,029656

Genom vinkelspridningen över A uppdelas ljuset på olika långa vägar som via de olika ljusfrekvenserna vid samlingspunkten D bildar en relativt IN-strålen asymmetrisk UT-stråle och som därmed uppvisar en färgspridning med blått innerst och rött ytterst.

Observera att en mera exakt räkning på vinkelgränserna rött-violett kräver motsvarande mera noggranna brytningsindex, vilken del här ej beaktats.

REGNBÅGEN — violett-blått innerst, rött ytterst

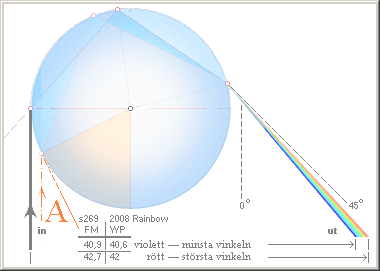
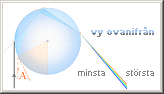
Överst: Tabellen FM/WP avser olika källuppgifter för gränsvinklarna för violett (minsta) och rött (största) i olika fackverk/epoker. FM avser FOCUS MATERIEN 1975 s269, WP avser @INTERNET Wikipedia Rainbow 2008-12-16.

Vattendroppen avbildad ovan med det ideala vita ljusets brytning via n=4/3 visar principen för den allmänt förhärskande tolkningen av regnbågens uppkomst; Förutsatt Solen (eller annan stark ljuskälla) ligger på, bakom betraktaren, och det finns en fuktighetsregion (vattendroppar i luften) som inbegriper vinkeln grovt runt 40-43° mellan infallande ljus och betraktarens position, finns förutsättning för en regnbåge att visa sig sett från betraktaren; Alla vattendroppar i regionen bryter regnbågens färger, men bara ljuset från den brytande del som stämmer i vinkel med betraktarens position når dit; Vilket vill säga; minsta vinkelrummet i vattendropparnas brytning sett från betraktaren är det avsnitt hos bågen som ligger längst inåt — som betyder färgen blått-violett; längre ut ökar vinkelbidraget och färgvisningen drivs mot rött.

@INTERNET Wikipedia Rainbow 2008-12-16 innehåller f.ö. en omfattande beskrivning med referenser av en stor mängd delfenomen i samband med regnbågen som fenomen.

Se även Svenska Wikipedia Regnbåge 2008-12-16 (Artikeln är ännu väldigt dåligt relaterad, en tyvärr alltför vanlig åkomma i webbsammanhang); en illustration antyder (möjligen oavsiktligt) att regnbågen är ett fenomen som ”hänger i luften” som en reguljär »optisk synvilla» som kommer ifrån typ »närliggande moln».

ATT färgernas källa tvunget måste vara konkreta brytobjekt — vattendroppar — på stället kan (möjligen) klargöras på följande sätt (här utan vidare härledning);

Varje droppe bidrar (nämligen) i princip med ett litet i sig obetydligt vinkelområde för just sin specifika färgvinkel mot betraktaren; kontinuiteten i färgobservationen bygger på att många närliggande sådana vattendroppars små samverkande bidrag bildar ett synligt färgband över ett visst vinkelintervall — och som per tillräcklig ljusenergi kan ge en viss intensitet i den aktuella färgen. Vilket vill säga: Regnbågen framträder i försorg av vattendropparna på stället där regnbågen faktiskt syns — och vilken position ändras med betraktarens och ljuskällans ändrade positioner, förutsatt mellanliggande luftrum har tillräcklig fuktighet.

EXPERIMENTELLT BEVIS:

Med Solen i ryggen en klarblå dag kan man själv frammana MinEgenRegnbåge med en vattensprayflaska (typ för blommor) — eller en trädgårdsslang för bevattning, där man kan reglera strålen till en fin spray. Regnbågen framträder i vattensprayens små vattendroppar. Inte på något annat ställe.

FÄRGAURAN — INUTI ÖGAT

Ett omnämnande av fenomenet har eftersökts på webben men ännu inte hittats

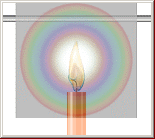
MÅNGA AV OSS HAR SÄKERLIGEN sett »en svag diffus aura» kring månen — med en mycket grovt skiss ungefär som i nedanstående bildillustration.

FÄRGAURAN är emellertid ytterst ljussvag och så svår att upptäcka (för normalt jäktade storstadsfolk som knappt har tid över att ens gå ut och titta på den klara stjärnhimlen — om en sådan alls kan ses på grund av omgivande [stads-] belysning) att man måste öva sig en stund om man är ovan aurabetraktare. När man väl vet hur det fungerar, kan man sedan till och med obehindrat se färgauran kring ett tänt stearinljus, även mitt på ljusa dagen, i fullt dagsljus. Längre fram nedan visas hur man enkelt kan mäta färgaurans vinkelupptagande spektrum, se Färgaurans uppmätning.

En beskrivning har eftersökts genom åren i tillgänglig bibliotekslitteratur, samt på senare tid även på webben som rapporterar fenomenets kännedom. Men ingenting har ännu hittats. Det närmaste man kommer är ögonmedicinska beskrivningar av olika (obehagliga, tydligt besvärliga, irriterande) auroafenomen i ögat — kallas typ inre ögonhalo — som kan upplevas av vissa personer som genomgått ögonoperation, men det är uppenbarligen inte den här artikeln. Därutöver finns en beskrivning av något som på engelska kallas ”Airy disk”, sv. Airys skiva eller Airyskiva;

”Airy disk | The central spot in the diffraction pattern of the image of a star at the focus of a telescope, named after George Airy.”,

[http://www.daviddarling.info/] -2008,

THE WORLDS OF DAVID DARLING — The Internet ENCYCLOPEDIA OF SCIENCE

Min översättning:

Airyskiva | Centralpunkten i böjningsmönstret hos bilden av en stjärna vid teleskopets fokus, uppkallat efter George Airy.

Svenska motsvarigheten kallas Airy-mönster och Airy-skiva — men själva fenomenformen verkar var dåligt representerad i beskrivningen.

Fenomenet kopplar (tydligen) till flera olika linsoptiskt/stråltekniska fenomen, bl.a. parabolantenner och deras begränsningar i fokuspunkten. Fotografier av fenomenet visar ett koncentriskt ringmönster med flera breda mellanliggande (mörka) band — av samma typ som böjningsmönstret kring en (laser-) ljusstråle som får passera ett litet hål. Detta är dock heller inte den här artikeln — färgauran uppvisar bara två färgcirklar — och det talas dessutom heller inte något om termen FÄRG överhuvudtaget i sammanhanget med Airys skivfenomen.

Ytterligare ett fenomen omnämns på @INTERNET Wikipedia Halo, optical phenomenon 2008-12-16, isbåge, eng ”Icebow” — där däremot färger omnämns tillsammans med ett fotografi på Månen ”22 degrees halo around the Moon”. Det är emellertid ett närmast otroligt skarpt singulärt ringfenomen (med en svag färgeffekt), dessutom fotograferbart. Totalt omnämns (December 2008) 23 olika halofenomen i Wikipediaartikeln, varav många kopplar till (fantastiska) fotografier.

FÄRGAURAN i den här artikeln är emellertid garanterat inte fotograferbar; fenomenet kan inte fotograferas.

BEVIS 1:

Genom att använda en blompinne som förs utmed synlinjen, finner man att färgaurans intensitet avtar med allt mindre avstånd mellan ögat och blompinnen. Vid en viss distans släcks praktiskt taget hela färgauran ner

Med hjälp av en blomsticka eller en bit styv kartong som sätts mellan ljuskällan och ögat finner man strax att färgauran ligger parkerad konstant framför — närmare ögat — än varje föremål; färgauran är inte ett rumsobjekt; fenomenet finns uppenbarligen inuti ögat.

BEVIS 2:

Återknyt till de bägge inledande illustrationerna i den här artikelns början; Använd med fördel en lång blompinne och sikta in den mot det tända stearinljusets ljusaste punkt — för pinnen allt närmare ögat; Med spetsen precis i den ljusaste centralstrålen, släcks plötsligt färgauran ner, helt och hållet när en viss minsta kritisk distans uppnås: färgauran kommer i läge AV.

BEVIS 3:

Genom att kika på stearinljuset genom olika inre reflekterande/speglande metallrör kan den cirkulära färgauran studeras alternativt — även i en helt kvadratisk rörprofil. Verkligen. Vid ett försök användes en ihålig blank rörprofil av aluminium (ca en halv meter lång) och som trots sitt kalejdoskopiska spegelmönster av rutnät bevarade färgaurans cirkulära form: cirkeln/cirklarna växer eller avtar i radie med synriktningens ändring i vridning mot eller från ljuskällans centrum. Som knappast ett fyrkantig rör kan bilda cirklar av sig själv, måste fenomenets förklaring uppenbarligen sökas på annat håll.

SLUTSATSER:

1. Färgauran är inte ett objekt kring ljuskällan.

2. Fenomenet arbetar (erhåller energi) på centrallinjen mellan ljuskällans centraldel och det uppfattande ögat, inte av omgivande områden.

3. Aurans intensitet, med en given fix distans ljuskälla till öga, är en funktion av ett avstånd från ögat, inte från ljuskällan.

Färgauran kan inte fotograferas — men den kan mätas:

Anordningen nedan visar hur man enkelt kan mäta färgaurans upptagande synvinkel — ringdiametern växer med växande avstånd till ljuskällan så att ett synbart konstant upptagande färgvinkelspektrum gäller; Genom att mäta den yttre ringens diameter via en given distans från stearinljuset (en linjallängd i mätningen nedan) finner man att den upptagande vinkeln visar ca 4°, figuren nedan.

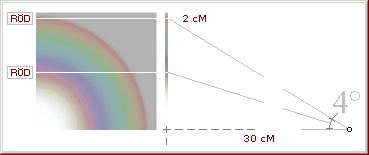
(atan 2/30)/2 ger spektrumvinkeln blått till rött omkring 1.91 grader — ungefär samma som gäller i fallet färgspridningen genom vatten.

Färgerna sprids approximativt 2° från violett-blått till rött.

Brytningsfenomenet tillhör uppenbarligen områden inuti ögongloben, men inget ytterligare omnämnande i ämnet är här känt.

accelerationsbegreppet

a = v/T

ACCELERATIONSBEGREPPET

se även ACCELERATIONEN, en alternativ beskrivning

Ett exempel på ett kontinuerligt integralt skeende är den s.k. naturliga accelerationen (a=dv/dt) som dessutom är ett alldeles utmärkt exempel: i varje tidpunkt dtÛ0 — och som inte finns i form och fenomenvärlden, erinra differentialens definition i nollformsalgebran — råder en viss hastighet v; kontinuiteten ligger i PUNKTBEGREPPET och variationen i v kan bara beskrivas så snart det finns ett bestämt intervall. Ett exempel på ett skeende som INTE är kontinuerligt I INTEGRAL MENING är f.ö. en gränsvärdesprocess. Jämför Atomtriangeln (se Gränsvärdesresonemang).

Nollformsalgebran — Så härleds accelerationen i detalj

s/v = T ............................ gäller för konstant hastighet i varje tidpunkt (v=s/T ) ..................................... mängdoberoende

v/a = T ............................ gäller för variabel hastighet över varje T-intervall (a=v/T)

dv/da = T ........................ gäller för variabel hastighet i varje tidpunkt (da=dv/T) ................................. mängdoberoende

; s/v = dv/da .............. variationsekvationen (varianten)

; s da = v dv ................. differentialekvationen

; ò s da = ò v dv ............... differentialekvationens integralekvivalent — integration genom den mängdoberoende enheten enligt tillståndets princip

; sa = v²/2 ................. variantens integrala lösning (från Formlagarna i nollformsalgebran, eller direkt från INTEGRALENS ARITMETIK)

; a = v²/2s ............... = v/T .................................... den linjära, likformiga accelerationen

; v = 2s/T

Klassisk Logik — Så härleds accelerationen i detalj

För konstant hastighet följs distans och tid åt. Ändras hastigheten kontinuerligt, kommer också distansen att växa (acceleration) eller avta (retardation) kontinuerligt i förhållande till tiden. Den enklaste ändringen är att distansändringen relativt tiden är konstant: Släpp ett föremål och studera rörelsen; Föremålet börjar från noll, och ökar sedan hastigheten (v) successivt som tiden (T) går. Enklaste formen för hastighetens ökning blir alltså att hastigheten (v) tillväxer som tiden (T) gör det. Vi kan härleda uttrycket för den så kallade linjära accelerationen (a=v/T) utifrån grundformen för accelerationen (a) — den principiellt uppnådda hastigheten (v) efter tiden (T) enligt a=v/T — samt formen för konstant hastighet v=s/T på följande sätt. Vi använder två linjaler L1 och L2.

L2 glider på L1 och L1 glider relativt Tiden (stranden, L) med samma distansändring som L2 mot L1. Därmed får vi ett fullständigt linjärt likformigt ändringsförhållande mellan distans och tid i syntesen:

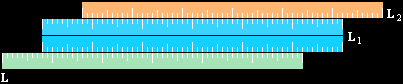
På L1 åker L2 med konstant hastighet v₂=s/T. Men L1 ändras relativt tiden T (stranden L). Om L1 ändras relativt T som L2 ändras relativt L1 så att L1:s hastighet relativt T är samma v₁=v₂=s/T, då ändras L1+L2 relativt T sammantaget

v=v₁+v₂=2s/T ; v/T = (2s/T)/T = 2s/T²= a ; v/2s=1/T ; v²/2s=v/T=a

Resultatet är alltså detsamma som fås från integralen genom nollformsalgebran.

alternativ beskrivning

ACCELERATIONEN

HASTIGHET (v) = DISTANS (d) / TID (T) = meter per sekund = d/T = v

ACCELERATIONSBEGREPPET ÄR DEN MATEMATISKA FYSIKENS GRUNDVAL

All rörelseändring — start från noll — kräver acceleration (a): noll till v på T

ACCELERATION (a) = HASTIGHET (v) / TID (T) = v/T = a

VY: håll ett (lätt) föremål ovanför marken. Släpp det. Föremålet börjar accelerera.

Från noll till v på T bildas en hastighetsökning från noll. Hastighetsökningen kallas acceleration. Accelerationen tecknas i matematiken a = v/T, se figur 1 nedan. OM a är LINJÄR, som betyder att v/T är konstant överallt, säger man att a är KONSTANT (och linjär, vilket är samma sak).

Fig:1

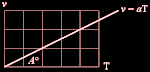
Accelerationens matematiska fysik bygger helt på geometrins elementära ytbegrepp. Se MATEMATIKEN FRÅN BÖRJAN för grunderna.

YTAN

under v-funktionen [se figur 1 ovan, den kan också förstås uppdelad i smala vertikalremsor vT=(d/T)T=d, de summerar hela resan under T] — höjd v gånger bredd T dividerat med 2, triangelytan —

ger en associerad resulterande fysikalisk storhet DISTANS (T förkortas bort, återstår d) enligt

(v)T = (d/T)T = d = distans

eftersom hastigheten (v) uttryckt i fysikaliska storheter är distans (d) per tid (T), v=d/T.

Uttryckt i v = aT blir produkten eller hela REKTANGELYTAN vT lika med (v=aT)T= aT². Den aktuella ytan under funktionsgrafen v=aT, halva rektangeln, blir då

A = xy/2 = Tv/2 = TaT/2 = aT²/2 = d

Därmed har vi, via v-funktionen v=aT, funnit den viktiga faktorn distans som är associerad med en LINJÄR acceleration. Vi får den

d = aT²/2 som för accelerationen betyder

a = 2d/T²

första- och andraderivatan av d

v | a

Nu kan alla möjliga samband lösas för den linjära accelerationen genom de bägge hörnstenarna a=v/T och a=2d/T².

I integralkalkylen har vi den motsvarande varianten v=aT=d(d)/dT som ger differentialekvationen d(d)=aT·dT med integrala lösningen d = a·T²/2. Genom dessa ordningar blir förstaderivatan för distansen lika med hastigheten, eftersom d’=(aT²/2)’=aT=v, och andraderivatan för distansen blir accelerationen, eftersom v’=(aT)’=a=d’’.

centralaccelerationen

v₀/T = a = w²/r

Centralacceleration

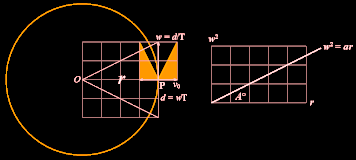
Relationerna genom de rätvinkliga och likformiga trianglarna ger

v₀/w = d/r = wT/r; v₀/T = a = w²/r = a_w = å

Figurer och samband ovan

I en cirkulär rörelse är accelerationen också närvarande och LINJÄR om periferihastigheten w i respekt till ringradien r matchar w²/r=a=å=konstant. Beteckningen å (a med cirkel) här endast förtydligar ringens aspekt. Cirkelaccelerationen eller centralaccelerationen betecknas med typen centripetal- med v₀ riktad inåt och centrifugal- med v₀ riktad utåt.

massbegreppet

MASSBEGREPPET

Med begreppet massa (m) för en kropp förstås i den praktiska vardagen det motsvarande begreppet tyngd (ma) eller vikt

Gravitationen — konvergensen eller i vardagligt tal tyngdkraften

· visar sig genom den ACCELERATION (a_G) en kropp uppvisar då den attraheras (faller) mot en annan kropp

· definieras genom den CENTRIFUGALACCELERATION (a_w) som bildar JÄMVIKT med a_G

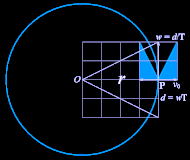
Centrifugalaccelerationen (a_w) definieras (i P):

centrifugalaccelerationen

v₀/w = d/r = wT/r; v₀/T = a = w²/r = a_w = å

Centrifugalkraften (F_w) definieras (i P):

med given rotation (w) och radie (r) ändras KRAFTEN (F) proportionellt mot MASSAN (m):

a = a = a(m/m) = (ma)/m = F/m = w²/r = massoberoende

kraftlagen

F = ma

HÄRUR framgår KRAFTLAGEN

F = ma

Kraften över vägen motsvarande produkten av kraft (F) och distans (d) som ger

Fd=mad=(KG)(M/S²)(M)=KG(M/S)²=J, Joule

kallas också ibland för kraftvägen (eller Vridande Momentet), eller bara arbetet, detsamma som rörelseenergin.

RÖRELSEENERGIN eller KINETISKA ENERGIN E=Fd=mad kan också skrivas

E(kin) = mv²/2 = mad = m(v/T)d = mv(d/T) = mv · v/2

eftersom a = v/T = 2d/T² som ger v = 2d/T med d/T = v/2.

Se även räknelagarna i MATEMATIKEN FRÅN BÖRJAN

DÄRMED kan massan specificeras:

konvergenskraft F

massa = gravitation = konvergens = ——————————————— = —— = m

konvergenskraftens fältstyrka a

gravitationslagen

F = ma = Gm₂m/r²

GRAVITATIONSLAGEN

Ur kraftlagen F=ma härleds och framgår den allmänna universella gravitationslagen med hjälp av centralrörelsen:

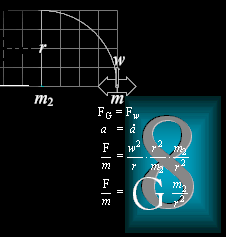se beskrivning nedan

GRAVITATIONEN

TYNGDKRAFTEN

Gravitationslagen

KONVERGENSKRAFTEN

DEFINIERAS GENOM CENTRALKRAFTSVERKAN

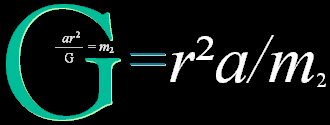
gravitationskonstanten 6,67 t11 JM/(KG)² uppmättes första gången 1798 av Henry Cavendish

tyngdpunktens definition

CENTRIFUGALKRAFTEN

· bildar ideal jämvikt med konvergenskraften utmed ortsvektorn (r)

· definierar ortspunkten lika med centralmassans tyngdpunkt (m₂)

· definierar massringen genom tillståndets princip
absolutverkan av r överallt (i planet) kring (m₂)
massringen i sin tur överallt i rymden kring (m₂) definierar sfäriska g-systemet

Hålls r fix och m₂ ändras i massringen måsta a ändras lika eftersom a beror av r:

konvergenskraftens fältstyrka (a) är för givet r direkt proportionell mot centralmassan (m₂)

w²r/G=m₂

Med a=å=w²/r ändras alltså centralmassan m₂ med w² för givet r: w²/m₂ för givet r är konstant.

Tillväxer r med m₂ konstant avtar w² så att vi kan skriva

w²/m₂ · r = G = r · w²/m₂ = r² · w²/r · 1/m₂ = r²a/m₂

Då är

w² = Gm₂/r

och alltså gäller

w²/r = Gm₂/r² = a = å = F/m

Därmed

GRAVITATIONSLAGEN — KONVERGENSKRAFTENS ALLMÄNNA FORM

F = ma = Gm₂m/r²

Eller enklare, direkt i syntes från kraftlagen:

F=ma=mw²/r=(w²/rm₂)m₂m=(w²/m₂)m₂m/r=(w²r/m₂)m₂m/r²=Gm₂m/r²

KEPLERS TREDJE LAG

w² = Gm₂/r = (2pr/T)² = 4p²r²/T² ; Gm₂/4p² = r³/T² ; m₂ = (4p²/G)(r³/T²)

FLYKTHASTIGHETEN

E = mv²/2 = Gm₂m/r = Fr ; v² = 2Gm₂/r = 2w² ; v = Ö 2Gm₂/r

FIZEAUS EXPERIENT

FIZEAUS EXPERIMENT

ref. P2001_2.wps REVELATION OF LIGHT

INLEDNING

Ljusutbredning i mobila objekt i stationära gravitationsfält

Vi beaktar/erinrar först tröghetsbegreppets elementära egenskap i överföringen av ljus mellan olika material enligt induktionen genom elektriska laddningens fält med referens till en lokal gravitell dominans (typ Jorden, Jordytan); erinra att elektriska fältets definition bygger på divergensens g-beroende, dessa detaljer beskrivs utförligt från elektriska laddningens fält.

Varje Q-rörelse ändrar alltid tillståndet i de stationära rymdpunkterna, fördröjd av divergensen c mellan Q och varje stationär punkt. Ändringen utförs genom det mobila fasta elektrostatiska fältets referens som är bundet till varje Q genom c i gravitationens försorg, se även från Superpositionsprincipen. Denna ändring motsvarar energin eller mobila trögheten (ljuströgheten) i Q-rörelsen som därmed överförs via divergensen c över avstånd till andra elektriska system, det vi kallar för (elektromotorisk) induktion. I avkännandet av dessa överförda ändringar, med fördröjningen via c, kan laddningar i avlägsna materiella system uppvisa respons och därmed överföringen av ljus.

Som redan påpekats i LJUSFRIHETSSATSEN är ljushastigheten (divergensen c) inte additiv med mekaniska hastigheter (v). I de fall där ändå dessa bägge förekommer, krävs speciell aktsamhet för att lyckas. I den här artikeln, för att förbereda ovanstående experimentbeskrivning, studeras ett av de enklaste fallen: ett stationärt och dominant g-fält (den fasta Jordytan) med rörliga markobjekt som påförs ljus från en stationär källa (S).

ETT MOBILT OBJEKT i ett dominant g-fält erhåller den elektromobila ljuströgheten från en stationär ljuskälla S genom uttrycket

c_in=c₀±v. c₀ tillhör det stationära och dominanta g-systemet medan v tillhör rörelseobjektet. Dvs.:

v_MOBIL ändras relativt c_STATION. Detta beteende är analogt med effekten av ljud mellan en stationär källa och ett mobilt mottagande objekt i stillastående luft; Variationerna i ton motsvarar variationerna i färg. Tillsammans med brytningsindex gäller för det mobila materialet M att

c_in_M = (c₀±v)/n

Emellertid som nyligen noterades, när ljuströgheten från ljuskällan S når v-objektet genom den lokala divergensen c₀ absorberas ljuströgheten partiellt av dess interagerande massystem (materien i v-objektet) och som bär sin ljusutbredningskaraktäristik med sig. Således exponeras också den anlända trögheten till v-faktorn. Då blir den principiella ljusutbredningen i v-objektet den idealt medelmässiga

w = c_in_M+v = (c₀±v)/n + v

Dvs., refraktionsindex (samma som brytningsindex) n färdas tillsammans med v-objektet. Isolering av termen c ger oss

w = c₀/n ± v/n + v

w = c₀/n + v(1±1/n) .......................................... M/S

ljusutbredning (medelvärde) i tätare material som rör sig med v relativt ljuskällan med divergensen c₀ i ett stationärt g-fält (Jordytan)

Bort från S, (c₀–v):

w = c₀/n + v(1–1/n)

Mot S, (c₀+v):

w = c₀/n + v(1+1/n)

LJUSUTBREDNINGEN I MOBILT ELASTISKT MEDIUM

Ljus genom elastiskt material i ett stationärt g-fält

För en elastiskt substans M (typ vatten som inträder ett rör) där ljus från S äntrar M_v=₀ och accelererar upp till ett maximum M_v är det uppenbart att v-faktorn i föregående c_in=c₀±v måste reduceras innan ljuset har etablerat en konstant topphastighet för utbredningen i M_v. Som denna v-reduktion vidare och tydligen också beror på materialsammansättningen i M [högre brytningsindex n betyder lägre topphastighet], verkar det klart att reduktionen hos v står i beroende av brytningsindex n. Detta skulle ge oss, idealt,

c_in=c₀±v/n för en maximalt inkommande ansats hos ljusets utbredning i den elastiska substansen som färdas med topphastigheten v. Den modifierade sambandsformen inkluderat v till den totala utbredningen för ljuset i M blir då tydligen

c_in_M = (c₀±v/n)/n = c₀/n ± v/n²

w = c_in_M+v = c₀/n ± v/n² + v

w = c₀/n + v(1±1/n²) ......................................... M/S

ljusutbredning (medelvärde) i tätare elastiskt material M som färdas med topphastigheten v med start från 0 relativt ljuskällan med divergensen c₀ i ett stationärt g-fält, + för närmande och – for avlägsnande rörelse mellan station och objekt

Maximala differensen i ljus från S och ljus i det mobila materialet eller mediet M blir därmed, tydligen, en relation mellan den stationära divergensen c₀ och ljuset i M i dess rörelse bort från S (största differensen),

w = c₀/n + v(1–1/n²) .......................................... avlägsnande rörelse, M/S

I ett praktiskt fall, bör w vara (något) lägre då fördröjningen i rummet mellan massobjekten i M här bortsetts ifrån i förmodad ideal överföringskaraktäristik med respekt till ljusutbredningen i M.

^{_______________________________________________________________________________}

Notera att ”en klassisk tolkning” av ”ljushastigheten” jämförd med mekaniska objekt är irrelevant eftersom ljuset inte uppför sig som en åkande partikel (se ljusfrihetssatsen). Utgår man ändå ifrån sådana förutsättningar, blir slutsatserna felaktiga.

^{_______________________________________________________________________________}

Fizeaus experiment

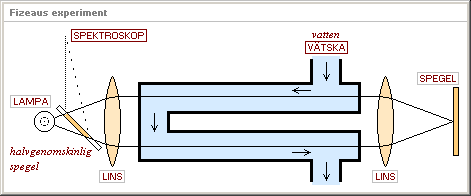
Fizeau’s experiment

EXPERIMENTELL BEKRÄFTELSE på Ljusutbredningen i mobila elastiska media

FIZEAUS EXPERIMENT. Denna figur är ett extrakt från flera typer av illustrationer från olika litterära källor (bibliotekslitteratur). Den visar principen bakom arrangemanget i mätningen av ljusutbredningen (1854) genom vatten som flyter i parallella rör (Varje rör hade längden 1,5 meter).

PÅ FÖRSLAG från Augustine Fresnel (1788-1827) år 1818, utfördes ett experiment år 1854 av Armand Fizeau (1819-1896). I referens till etablerade källor [McGRAW-HILL ENCYCLOPEDIA OF SCIENCE AND TECHNOLOGY 7th Edition 1992, Light s55], var anordningen av den form som visas i figuren ovan. Som det hävdas, matchade också resultaten det nyligen härledda/diskuterade sambandet

w = c₀/n + v(1–1/n²) ............................................ avlägsnande rörelse, M/S

Detta typuttryck föreslogs ursprungligen av Fresnel [ref. HANDBOOK OF PHYSICS · McGraw-Hill 1967 · 6-164.sp2mö]. Fresnel föreslog emellertid den motsatta rörelsen genom

(c₀/n) – v(1–1/n²) snarare än vårt föregående härledda

(c₀/n) + v(1+1/n²), således åberopande ett generellt

(c₀/n) ± v(1–1/n²) snarare än

(c₀/n) + v(1±1/n²). Fresnel stödde sig på 1800-talets eteridéer där ljusets gravitella beroende var helt okänt, därmed exkluderande innebörden av varje jämförande teoretisk undersökning på denna punkt. De olika uttrycken hos den närmande rörelsen interfererar emellertid inte med experimentet eftersom bara den största differensen eftersöks i det spektroskopiska resultatet. Dvs., bara relationen mellan c₀ och recessionen (frånrörelsen) w = (c₀/n) + v(1–1/n²) räknas.

FIZEAUS EXPERIMENT refereras till (stundtals) frekvent som en bekräftelse på den speciella relativitetsteorin i viss litteratur. Vi studerar anledningen till det i följande korsreferens.

Från en av relativitetsteorins specifika uttryck i kinematiken, formeln

w = (v + c/n)/(1+v/cn) ................................. formel från relativitetsteorin (boken nedan)

får man Fresnels ekvation genom en viss process: man utesluter vissa delar för ett få en förenklad slutform.

Metoden genomförs genom följande steg

[ref. FÖRSTÅ RELATIVITETSTEORIN, G. Lindahl, Biblioteksförlaget 1971, s36-39]

w = (v + c/n)/(1+v/cn) ; 1/(1+v/cn) » 1–v/cn

w = (v + c/n) · (1–v/cn) = v + c/n – v²/cn – vc/cn²

= v + c/n – 0 – v/n²

= c/n + v – v/n²

= c/n + v(1–1/n²)

Och, som vi ser, matchar resultatet perfekt Fresnels ekvation. Vilket vill säga, det nyligen härledda sambandet

w = c₀/n + v(1–1/n²) ............................................ avlägsnande rörelse, M/S

Den egenartade punkten i detta, som läsaren redan kan ha observerat, är att förmodan med den relativistiska delen i ämnet behandlar detaljer — inte analoga med diskussioner om mobila elastiska media, utan — beträffande en fast objektsform (typ BIL eller TÅG) som färdas med konstant hastighet v. Vilket vill säga, r-teorin förutsätter att ljuset inträder v-mediet direkt [vårt tidigare erhållna

w = c₀/n + v(1–1/n)].

Men detta är något helt annat än experimentets detaljer: ljusets faktiska acceleration in till vattnet.

Följaktligen tycks r-teorin, som det får förstås, inte ha något egentligt sammanhang att uppvisa i vattnets accelererande fenomenform från 0 till v i det aktuella experimentets ljus; stället där ljuset inträder och utträder anordningen. Den relativistiska delen i saken visar således snarare, eller möjligen »mera», ett laborativt (algebraiskt uteslutande) sammanträffande på föregivna uttryck: relativitetsteorin har, egentligen, inte mycket att göra med experimentet av Fizeau.

NOTERING

I den ovan angivna källan (Lindahl) omnämns ingenting om någon »avgörande accelerationseffekt» för resultatet. Källan beskriver experimentet enligt den visade illustrationen, antar vattnet som en motsvarande bil i rörelse, ger uttrycken, och sedan inget mera.

Referensen [FÖRSTÅ RELATIVITETSTEORIN, G. Lindahl, Biblioteksförlaget 1971, s39] hävdar bekräftelsen i övning 26c enligt

”c) Vid en upprepning av Fizeaus experiment fann Michelson att ljusets fart i vatten, som strömmade med en fart av några meter per sekund, på grund av vattnets rörelse ökade med ett värde, som var 0,434 av vattnets fart. Stämmer detta resultat med formeln ovan i b? [w = c/n + v(1–1/n²)]. Vattnets brytningsindex är 1,33.”

Svar till övningarna (s52)

”26c) n = 1,33 ger värdet 0,435 vilket stämmer utomordentligt väl med Michelsons resultat.”

se även i SAKREGISTER