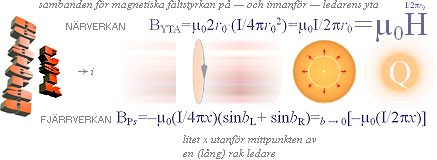INDUKTION OCH MAGNETISM APPENDIX | 2007IV15 | a production | Senast uppdaterade version: 2024-10-26 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

tre jämförande exempel · syntes av induktionen och magnetismen · e-fältets frihetssats

InduktionenOchMagnetismen

magnetiska fältvektorns matematiska uppkomst

MAGNETISKA FÄLTVEKTORNS MATEMATISKA UPPKOMST

DEN MATEMATISKA UPPKOMSTEN AV DEN MAGNETISKA FÄLTVEKTORN

*1996XII by 199XII Compilation of INDUCTION AND MAGNETISM 2007VI15

—————————————————————————————————————————————————————

extraherat från KRAFTLAGEN 1999XIII

Förklaring till den magnetiska fältvektorn B

TRIGONOMETRIN KOPPLAR REDUKTIONERNA ORDNAT MED B-VEKTORN

I de följande matematiska sambanden visas specifikt hur representationen för vektorer mellan vänstra delblocken (;® expansionsvektorer elektriciteten) och högra delblocken (;¯ tangentiella vektorer magnetismen) blir matematiskt ekvivalenta genom en negativ koordinatrotation (–i) på 90 grader. Det förklarar specifikt hur vektorrepresentationen för magnetismen har reduktionerna (expansionsvektorerna M) som ekvivalenta begrepp kontra den mera allmänna tangentiella representationen (B, enligt högerhandsregeln).

Vilket betyder: det konventionella B-vektorbegreppet är en matematisk konstruktion — inte en fysikalisk egenskap. Magnetismen i relaterad fysik förklaras enbart med hjälp av reduktionens vektorer (M). Reduktionsbegreppet förklaras utförligt från Kausalsambandet. Men det ingår inte i den moderna akademins lärosystem. Jämför inledande citat i inledningen till induktionen och magnetismen enligt relaterad fysik.

Det betyder att den konventionella föreställningen om ”vektorprodukt”

— som är en modern akademisk konvention (som underförstår vissa, av den moderna akademin under 1800-talet uppfunna idéer, om hur fysiken förmodas fungera — som om naturen skulle underordna sig mänskliga rådslag) och som används frekvent av högskoleingenjörer i »försöken att förklara magnetismen och induktionen»

— INTE är tillämplig på den elementära fysiken. Som “fysikalisk teori” är den konventionella föreställningen om ”vektorprodukt”, och förblir så, en matematisk sofism — med redan väl erkända kvantitativa kvaliteter. Märk också detta väl.

Se även i

Uppdagandet — The Revelation — vektorkalkylens grunder i modern akademi

EKVIVALENSEN MELLAN EXPANSIONER OCH TANGENTER

expansions och tangentekvivalenterna

EKVIVALENSEN MELLAN

EXPANSIONER OCH TANGENTER

i PREFIXxSIN

I utdrag och vidarebearbetning Från DYNAMIKENS GRUNDER 1995 Del III s23 Compaq Edition

vektorformerna till tvåkropparskomplexet för gravitationen, elektriciteten och magnetismen

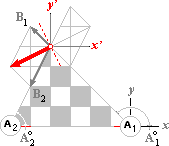
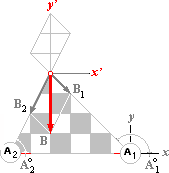
geometrisk vektorrepresentation

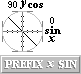
¯A2 A1
motsatta strömmar
B^2	B^2
= (å x’)^2 + (å y’)^2	= (å x’)^2 + (å y’)^2
= (B1sinA1 + B2sin[A2+180])^2	= ( B1sin[A1—90] + B2sin[A2+90])^2
+ (B1cosA1 + B2cos[A2+180])^2	+ ( B1cos[A1—90] + B2cos[A2+90])^2
= (B1sinA1 – B2sinA2 )^2	= ( B1cosA1 – B2cosA2 )^2
+ (B1cosA1 – B2cosA2 )^2	+ ( –B1sinA1 + B2sinA2 )^2
= B1^2 + B2^2 — 2B1B2sin(A1 — A2)	= B1^2 + B2^2 — 2B1B2sin(A1 — A2)
	Notering. ; (–a+b)^2 = (a–b)^2
EXPANSIONSVEKTORER	TANGENTIALVEKTORER
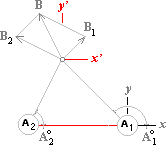
EXPANSIONSVEKTORER	TANGENTIALVEKTORER
Notering. ; (–a–b)^2 = (a+b)^2
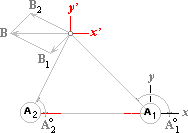
B^2	B^2
= (å x’)^2 + (å y’)^2	= (å x’)^2 + (å y’)^2
= ( B1sin[A1+180] + B2sin[A2+180])^2	= ( B1sin[A1+90] + B2sin[A2+90])^2
+ ( B1cos[A1+180] + B2cos[A2+180])^2	+ ( B1cos[A1+90] + B2cos[A2+90])^2
= (–B1sinA1 –B2sinA2 )^2	= (–B1cosA1 –B2cosA2 )^2
+ (–B1cosA1 –B2cosA2 )^2	+ ( B1sinA1 +B2sinA2 )^2
= B1^2 + B2^2 + 2B1B2sin(A1 — A2)	= B1^2 + B2^2 + 2B1B2sin(A1 — A2)
samriktade strömmar
¯A2 A1¯

Specifikt för magnetismen ser vi att de trigonometriska funktionerna automatiskt säkerställer de kvantitativa ekvivalenterna mellan resultanterna till expansionsvektorerna;® och tangentiella vektorerna ; genom summeringen av reduktionerna såsom omvänd i motriktade strömmar relativt summeringen i komplexet med samriktade strömmar: högerhandsregeln med det magnetiska fältets riktning är, tydligen, innefattad i logiken/matematiken av naturen — helt säkert betryggande skild från varje människoskapad institutionalism.

Illustrationerna och utvecklingarna i de ovan givna uttrycken visar hur vektorsummering utförs för fältvektorer som har källform i två skilda centra A₁ och A₂.

En grafisk representation av de resulterande fältformerna finns här längre ner i magnetiska fält.

Som är uppenbart från den vänstra blockdelen, expansionsvektorerna ;®, har dessa vektorformer exakt analogi med riktningsformerna för den elektriska fältstyrkan med källa i två olika punktladdningar. Speciellt för laddningar med lika tecken, blir vektoralgebran också ekvivalent med en vektorsummering för fälten mellan två idealt sfäriska graviterande kroppar A1 och A2, analogt överensstämmande expansionsvektorer vid samriktade strömmar. För det magnetiska fältets fysik ger analysen ett motsvarande PLANT SNITT genom de idealt bägge oändligt långa raka parallella ledarna A1 och A2 med de åtföljande fältringarna i det givna planet analogt med papperets eller bildskärmens plan med referensaxlarna (xy)’ enligt ovanstående uppställningar.

DEN ALLMÄNNA BETECKNINGEN B

För att strikt matematiskt understryka samhörigheten i detta sistnämnda fall mellan reduktioner som expansionsvektorer ;® (illustrationens vänstra delar) och reduktionernas resulterande interferens genom respektive fältrings tangent (analogt, rätvinkligt expansionens riktning och illustrationens högra delar ;¯), har BETECKNINGEN B valts kollektivt för dessa bägge olika vektorkomplex.

Som vi ser via de trigonometriska funktionerna (vi förutsätter deras bekantskap här) tar de automatiskt hand om de kvantitativa ekvivalenterna mellan resultanterna för de expansiva och tangentiella vektorerna genom reduktionssummering såsom reverserad i motriktade strömmar relativt summeringen på samriktade strömmar i det magnetiska fallet. Det beundransvärda i denna naturgivna ordning kan inte nog understrykas. Se även från Matematikens Grunder.

InduktionenOchMagnetismen

e-fältets frihetssats

fältstyrkefrihetssatsen

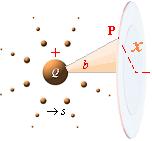
ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS

— Electric Field Strength Liberty Clause: X demands at least two Q

Betrakta först från elektriska kraftlagen leden nedan

(1) F = k(Q/r)² = ma = mc/dT = Rc(m/R)(A/dT)/A

(2) U = k(Q/r) = Fr/Q = E/Q

(3) U/r = kQ/r² = F/Q = X = kQ/r² .................. elektriska fältstyrkan

sats:

X kräver minst 2 Q

bevis:

INOM EN ENSKILD ELEKTRISK LADDNING

Q = Ö (m/R)(A/dT)

är ingen elektrisk fältstyrka — spänning U eller potential över en ändlig distans r — (3) möjlig;

En enskild laddning har bara att referera till sitt eget mobila momentana laddningsskal Q som återkopplar via c, och det skalets distansparameter är differentiell (ds=dr); intervallbegrepp — kraftverkan över distans — är för den enskilda laddningen ett abstrakt begrepp;

POTENTIALEN på r från Q-origo DÄREMOT i DET Q-skalet har den elementära formen i (2) i differentialer enligt U=Rc(dQ/dr), det som (således) i relaterad fysik kan kallas för potentialimpulsen på r från Q-origo via den lokala g-styrda divergensen c;

För att SÅLEDES realisera en elektrisk fältstyrka (X), måste den givna laddningen delas eller relateras till två separata laddningar (två skilda ds separerade av någon distans, ett INTERVALL), eller en annan laddning måste insättas eller relateras tillsammans med den givna, formande en allmän koppling åtskild av distans r, ett elektriskt fält (se denna elementära fältgeometri illustrerad längre ner),

F/q₁ = kq₂/r² = X

resultat

VILKET VILL SÄGA: Den interna kraften hos en fysiskt elementär laddning Q bevaras eller SKYDDAS således av kvadraten

(Q/r)² = Q²/A = m/RdT

vilket garanterar bevarandet av Q oberoende av tid och rymd.

Begreppet om ett elektriskt fält UPPKOMMER ALLTSÅ FÖRST ur begreppet om en rörelse (separation, delning, separering):

X = dU/dr = dF/dQ.

BETYDELSE:

Vilket betyder: X kräver minst två Q.

DETTA VIKTIGA KLARLÄGGANDE HAR EFTERSÖKTS I DEN MODERNA AKADEMINS LÄROSYSTEM, MEN INTE HITTATS.

Elementära elektriska fältet i relaterad fysik ges alltså som funktion av potentialimpulsen via 1/r;

I modern akademi tillämpas däremot en makromodell på den enskilda laddningen — genom införandet av s.k. provkroppar — som därmed likställs med ett makroskopiskt elektriskt fält och som således ges i funktion av 1/r². Se vidare nedan i ELEKTRISKA FÄLTETS GEOMETRI.

InduktionenOchMagnetismen

elektriska fältets

elementära geometri

5KB JPG

ELEKTRISKA FÄLTETS ELEMENTÄRA GEOMETRI

Q-systemets divergensfält

elektriska fältet

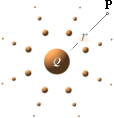
Elektriska fältet · grundläggande elektricitetslära

Avtagande sfärer markerar avtagande potential. Den övergripande bilden är idealt sfärisk till geometrin; fältbilden expanderar idealt mot oändligt med Q som en momentant mobil sfärisk yta som utvidgas fortlöpande från centrum med hastigheten c, uppdaterande systemets potential kontinuerligt.

det grundläggande elektriska divergensfältet

Den principiella c-bindningen till massan från ljusets eller divergensens g-beroende

Se utförligt grunden från superpositionsprincipen

definierar tydligen ett motsvarande grundläggande fält av fortlöpande ändlös c-utvidgning baserad på en gravitell kärna.

Vi kan därför kalla det fältet för ett divergensfält.

Notera att begreppet ”divergensfält” KAN ha en helt annan innebörd i den moderna akademins vektorkalkyl. Denna ingår dock inte i den här presentationen varför risken för sammanblandningar är helt utesluten.

Som den typen också ansluter till elektriska kraftlagen eller divergenskraften, representerar den också det fundamentala statiska elektriska fältet (e-fältet). Divergensen relaterad i endera riktningen definierar den elektriska polariteten ±. Den enkla illustrationen ovan avbildar e-fältet.

Längre ner visas den mera matematiskt avancerade elementära tvådimensionella fältformen.

MED KLARLÄGGANDE FRÅN ELEKTRISKA FÄLTETS FRIHETSSATS

Statiska elektriska fältet

Den laddade massan Q avbildar ett potentialDivergensfält U=kQ/r. Fältpotentialen U varierar proportionellt mot växande avstånd r från masscentrum (idealt förutsatt direkt proportionalitet mellan massa och laddning). Vi kallar I RELATERAD FYSIK det typiska ELEMENTÄRA ELEKTRISKA KRAFTVÄGSFÄLTET, under inverkan av divergensen, för det elementära statiska elektriska fältet eller enklare statiska e-fältet. Vi kan också kalla det elementära divergensfältet eftersom divergensen tydligen (genom c-flödet över intervall) definierar ±-egenskapen hos elektriciteten (inflöde eller utflöde, det finns bara två olika att välja på). De avtagande »sfäriska punkterna» i figuren ovan representerar avtagande fältpotential.

Matematiken för

ELEKTRISKA FÄLTET

Elektriska fältet (a) nedan illustreras genom en s.k. solfjäder. Alltså, en paragon (gen. geometriskt mönster) bestående av ekvidistanta radiellt dragna successiva vinkelrum från ett centralt origo.

Med två varandra skärande (interfererande) solfjädrar (b) framträder det elementära elektriska superponerade fältet från två lika (punktformiga) elektriska laddningar (c). Figurerna abc nedan illustrerar detaljerna för vidare diskussion.

INTERFERENSMÖNSTRET SOM BILDAS i (b) har två olika möjliga lösningar. Dessa visas illustrerat (förtydligat) i (c):

Antingen genom lika laddning (++ eller – –) ELLER genom olika laddningar (+– eller –+).

Plansnittet genom det idealt sfäriska elektriska fältet illustreras av figuren i (a); fältexpansionen motsvarar ökningen i divergensen c från ljusets g-beroende. I respekt till gravitationsfysiken (mekaniken) kallas samma typfält för ett gravitationsfält, eller enklare ett g-fält (ett gravitationellt fält).

Se även i EKVIVALENSEN MELLAN EXPANSIVA OCH TANGENTIELLA VEKTORER

De två olika mönstertyperna från (b) i (c) visas illustrerat förtydligat nedan.

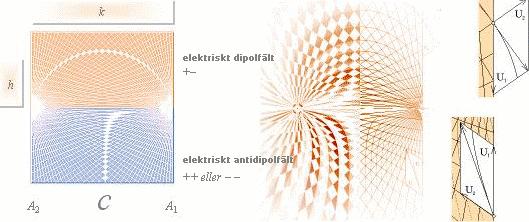
De bägge kurvsystemen betecknade respektive dipol- och antidipol-fält framträder markerade i figur (c), vidare förtydligade till höger ovan med motsvarande applicerade fältvektorer betecknade U. Grunden för hur dessa kan beräknas (funktioner av 1/r) beskrivs vidare nedan.

viktigt att observera:

Grundläggande begrepp i fysiken kan inte förklaras av den moderna akademins lärosystem

I MODERN VETENSKAP OCH AKADEMI anses penetrationen U=F/Q=k(Q/r) i det elementära Q-fältet vara en skalär. Från ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS i relaterad fysik är denna elementära U-form emellertid en väl differentiellt relaterbar vektorform, ingen skalär. Dess matematiska funktion är av distansen 1/r att särskilja från den elektriska fältstyrkans makroskopiska vektorform som är en funktion av 1/r². Superponering av två elementära Q-fält motsvarar således de bägge ovan avbildade kurvaturerna. Se vidare från beviset i ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS. Se också från POTENTIALBEGREPPET.

matematik, relaterat

Man finner de två olika kurvaturerna genom att fylla i varannan angränsande mosaiska kvadrat; en automatisk kurvatur framträder då, som sammanbinder typkurvan med respektive laddningscentrum.

Cirkulärfältets form [övre delen i (c), orange] kallas ett fält av typen

dipol (ett s.k. dipolfält). Det motsvarar fältet mellan två elektriska laddningar med

olika polaritet, ±.

Logaritmiska kurvaturen kallas (här) ett fält av typen

antidipol (ett s.k. antidipolfält). Det motsvarar fältet mellan två elektriska laddningar med

lika polaritet, (– –) eller (+ +).

dipol, relaterat:

Toppkurvaturen i (c) bildar cirkelbågar:

Varje fältpunkt bidrar till bågteckningen genom att ansluta

en Ökande r-distans till ett origo, och

en Minskande r-distans till det andra origot;

Laddningarna attraheras.

Cirkelradien (R) hos bågen med höjden h över kordan k som förbinder laddningarnas origo beräknas (här utan bevis)

R = [h²+(k/2)²]/2h .......................... dipolkurvans ekvation

R-origo är beläget på vertikallinjen mellan laddningarna i föreningspunkten mellan varannan mönsterkvadrat.

antidipol, relaterat:

Bottenkurvan i (c) formar en logaritmisk typkurva som emellertid måste ritas matematiskt med skilda ekvationer för x och y (en så kallad parametrisk ekvation): Varje fältpunkt bidrar till bågteckningen genom att ansluta

bägge Ökande r-distanser till bägge origo;

Laddningarna repelleras.

Den aktuella antidipolkurvan sätts matematiskt genom att välja en initierande fast vinkelskillnad V=A1–A2 vars skärande vinkellinjer utpekar en initierande fältpunkt relativt de bägge laddningarna. I figuren (c) ovan har origo för vinkeln A₁ valts som xy-systemets origo. Då blir, genom trigonometriska samband, kurvan formellt ritad parametriskt från xy-origo enligt

x = y/tanA₁ ................................... antidipolkurvans ekvation, x-delen

y = k(tanA₁^–1+anA₂^–1)^–1 ............. antidipolkurvans ekvation, y-delen med A₁=V+A₂

*How electricity descends from Gravitation by Principle · Compilation with mathematical derivations 2007VI19

InduktionenOchMagnetismen | Begreppen Fältstyrka och Potential

ALLMÄNNA (vanliga) VANFÖRESTÄLLNINGAR I MODERN AKADEMI OCH VETENSKAP OM ELEKTRISKA TERMER

förklarat enligt relaterad fysik

BEGREPPEN FÖR

FÄLTSTYRKA OCH POTENTIAL

INOM ELEKTROFYSIKEN

kraftvägen i elektriska fältet 1996XI27

POTENTIALBEGREPPET

POTENTIALBEGREPPET

U = k(dQ/dr) ................................................ Volt

Från det gravitella fältets (gravitationsfältets, eller enklare g-fältets) potential (ekvipotentialytan genom centrifugalaccelerationen w²/r) med formen

Fr/m = w² = Gm₂/r .......................... g-fältets potential, w är den perifera g-balanserande rotationshastigheten

svarar analogt men inte identiskt det motsvarande elektriska fältets potential i den individuella centralkroppens idealt sfäriska system enligt

Fr/Q = U = kQ/r

I det statiska elektriska elementära fältet är potentialen U en penetration, d[Fr]/[dQ], och som sådan en riktad differentiell impulsform:

U = k(dQ/dr) penetrerar en vektordifferential.

Inte en skalär.

Riktningen ges av divergensen (c i Rc=k=elektriska konstanten) i Q-flödet — positivt (utåt) eller negativt (inåt) beroende på polaritet.

vektor och skalär

Definitionen på en vektoriell storhet betraktas allmänt analogt med varje riktningsbestämd faktor, vad den än vara må: riktning betyder vektor.

Definitionen på en skalär storhet betyder vektordefinitionens negation: utan bestämbar riktning i 3D-rymden (t.ex. dagens högsta temperatur).

Referenser till allmänna definitioner på vektor (utsträckning) och skalär (reellt tal) finns exv i MATEMATIKLEXIKON W&W 1991.

Begreppet skalär för den elektriska potentialen håller först när laddningen sätts i rörelse och fältet har etablerats i ett makroskopiskt sammanhang.

Se även föregående beskrivna ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS.

begreppet fältstyrka

DEN ELEMENTÄRA ELEKTRISKA LADDNINGENS FÄLTDYNAMIK

DEN ELEKTRISKA FÄLTSTYRKAN

ELEKTRISKA FÄLTSTYRKAN

dU/ds = X V/M (X, Grekiska bokstaven X, xsi [eller symboliskt »e-f» som i Elektriskt Fält])

ett begrepp reserverat för uppkomsten av magnetiska fält — laddningar i rörelse — logistiken för potentialfälten i makroskopisk skala

· Formen dU/ds är reserverad för laddningar i rörelse — för uppkomsten av magnetiska fält

· Ett statiskt elektriskt laddningsfält har ingen dU/ds på någon enda punkt

· Ett statiskt elektriskt laddningsfält innehåller ingen elektrisk fältstyrka:
de differentialformer vi kan tala om för den ideala elektriska laddningens del, inkluderat elektrisk fältstyrka, har i vilket fall kvantitativ nollform enligt differentialens definition i relaterad fysik; ett statiskt elektriskt laddningsfält innehåller därmed hur man än räknar ingen elektrisk fältstyrka. Se även ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS, där ges den helt tydliga förklaringen.

Betrakta (X, xsi, eller e-f) för en singulär laddning Q elektrofysikens

F/Q = X = kQ/r² = U/r

i analogi till gravitationsfysikens

F/m = a = Gm/r² = w²/r

I g-fysiken gäller — enligt relaterad, klassisk fysik, se GcQ-teoremet — absolut verkan mellan alla kroppars tyngdpunkter, och därmed en direkt vektorrepresentation för den lokala gravitella fältstyrkan a ; a är en fysikaliskt riktad storhet, en vektor.

En absolut verkan över avstånd — F/Q — existerar emellertid INTE inom elektrofysiken.

Kraftvägen — kopplingen — mellan en fältpunkt och laddningens centrum är bruten av fältkopplingens begränsade ljushastighet c, vilket innebär att (F/Q)-formen är ett odefinierat begrepp — märk väl — det elementära elektrostatiska fältet. Det leder oss till de följande klargörande punkterna:

*forts. 1996XII by 199XII Compilation of INDUCTION AND MAGNETISM 2007VI15

—————————————————————————————————————————————————————

· det finns ingen elektrisk fältstyrka inuti ett elementärt statiskt elektriskt laddningssystem

· formen U/r = F/Q har varken någon vektoriell eller skalär substans inom ett statiskt laddningsfält, den existerar inte

POTENTIALENS VIKTIGHET

förklarande penetrationens aspekt i elektriciteten

FÖR ATT KUNNA relatera dynamiken i varje fältåterkoppling mellan fältpunkt och laddningens centralpunkt (Q), MÅSTE ändpunkterna i flödesvägen finnas innefattade. Det är grundvillkoret. Detta villkor uppfylls uppenbarligen av formen Fr/Q = U = k(dQ/dr) — ARBETET (Fr) genom fältmättnaden (Q, laddningsytan). Det ger potentialimpulsen i punkten P på r från Q-origo. Impulsidén ansluter till divergensformen för c vilket genom ljusets absolutacceleration a=c/dT genom Newtons tredje lag uppenbarligen betyder en otvetydigt motsvarande differentiell penetration i elektriska flödets riktning [dE/dQ = k(dQ/dr)]. Se även explicit i innebörden av begreppet differential enligt relaterad fysik till skillnad från konventionens differens.

Impulsen mc/dT som genom resistansen (R) över ytan (A) — enligt relaterad fysik [se GcQ-teoremet] — bildar ekvipotentialytorna i e-fysikens singulära laddningsfält (statiska elementära fältet från en punktladdning av idealt sfärisk modell), analogt laddningen Q fördelad och konserverad över varje ekvipotentialyta 4pr², ger i varje penetrerande punkt av den sfäriska ytan, och analogt, impulsvektorn k·dQ/dr. Den — utmed radien differentiellt riktade— aktiva impulsvektorn vars penetrerande punkt svarar mot differentialkvoten

dQ/dr

analogt den differentiella kvoten för arbetet Fr över fältmättnaden (laddningen) Q

d(Fr)/(dQ)

enligt (totalt för hela bollytan)

Fr/Q = U = kQ/r,

definierar således fältets riktning.

Vi kan (således) knappast få en tydligare illustration av vad, exakt, begreppet vektor har för konkret praktisk innebörd.

Det finns ingen annan faktor att hänföra fältets kraftåterkopplande utvidgning till, än densamma faktor som producerar penetrationen. Det är, den lokala(och genom ljushastigheten i fältet integralt återkopplande) divergensen — nämligen i dess impulsiva karaktär genom ljusets absolutacceleration a=c/dT i ändpunkten för r via laddningens elektriska flöde genom c enligt ljusets gravitella beroende och den därmed sammanhängande superpositionsprincipen som i allt definierar det statiska elementära elektriska laddningsfältet ENLIGT RELATERAD FYSIK; U=k[dQ/dr].

Penetrationen — fältriktningen, kraftvägen i fältet — och dess normal (rätvinkliga) yta produceras alltså identiskt. Vi erinrar att dessa begrepp i den här diskussion är differentiella. Se även differentialbegreppet i nollformsalgebran enligt relaterad fysik och matematik.

Potential ¯U via impuls genom [dQ/dr] — — definierar BÅDE en fältriktning OCH en differential till impulsytan Q. Genom denna dubbelform för U, och inget annat, superponeras fälten mellan skilda elektriska laddningar — och därmed kraftverkan.

Dessa grundfakta leder till följande allmänna punkter:

· begreppet skalär för U saknar representation i det elementära elektriska laddningsfältet

· penetrationen U — spänning d[Fr]/[dQ] — är en riktad impulsform i det elementära elektriska laddningsfältet, ingen skalär

· den samhörande normalytan till penetrationsresultanter i superponerande laddningsfält (samma som fältinterferenserna eller kurvorna rätvinkligt fältriktningen) är inga ekvipotentialytor; ekvipotentialytor följer helt andra vägar relativt sådana underförstått innefattade formaliteter (modern akademi har nämligen sina egna idéer på området och som ansluter till elektriska fältets kvantitativt makroskopiskt mätbara delar; relaterad fysik och modern akademi skiljer sig här fundamentalt åt i representationerna med elementära fältbildningar som funktion av 1/r respektive 1/r², se Magnetiska fältbilderna)

· de superponerade individuella VEKTOR-impulserna (U = kQ/r) bestämmer det resulterande fältets riktningsgeometri (kraftvägarna i fältet)

;

Det finns inget spänningsbegrepp av någon intervallmässig natur inom det elementära statiska laddningsfältet DÄRFÖR ATT DET INTE FLYTER NÅGON STRÖM DÄR — ingen energi krävs för att ”fylla” en laddning för att få den att fortsätta agera »oändligt laddningsfält i evighet» (därför att summan av alla krafter och moment i massa-laddningen är noll [se även utförligt från Atomkärnans härledning]) — bara ett pågående divergensflöde (se superpositionsprincipen), som återkopplar kraftvägarna inom flödets fältmässiga utvidgning. Den elementära statiska laddningens fält är inget spänningsfält, utan ett uttalat ljusimpulsfält upphängt på den centrala laddningskroppens g-fält. Se även grunderna enligt GcQ-teoremet.

;

Potentialen (spänningen) U, formen dQ/dr i det elementära elektriska fältet, arbetar INTE som det makrofysikaliska begreppet potential (spänning) och vilket senare begrepp är en skalär. Potentialen (spänningen) i det elementära elektriska fältet arbetar istället som en direkt impulsvektor inom en begränsad gravitellt relaterad punkts domän och vilken riktningsform definierar den lokala kraftåterkopplingen i fältet. (Det »stavas» i allt enligt U = kQ/r).

*forts. 1996XII by 199XII Compilation of INDUCTION AND MAGNETISM 2007VI15

—————————————————————————————————————————————————————

Se även mera utförligt i

ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS.

POTENTIALBEGREPPET

InduktionenOchMagnetismen

elektriska fältets begrepp

ELEKTRISKT FÄLT — elektrisk och magnetisk kraftväg

ELEKTRISKA FÄLTETS BEGREPP

central beskrivning av missuppfattningarna i modern vetenskap och akademi

Genom att införa i en godtycklig punkt (P) en »testkropp» (q) i det elementära statiska elektriska fältet kopplat till en centralladdning (Q), uppkommer en begränsad vektoriellt utvidgad elektrisk fältstyrka (X=F/q)med ett tillhörande makrofysiskt potentialbegrepp (U=Fr/q) genom vektorkraftens verkan (F=kQq/r²) mellan testkroppen och Q.

”Elektriskt fält

Ett elektriskt fält avgör vilken elektrisk kraft en testladdning skulle utsättas för i varje punkt.”

BONNIERS ASTRONOMI · The Cambridge Encyclopaedia of Astronomy · Bonniers 1978 · s477sp2n

Den vektoriellt likformiga fältbilden som ernås på den vägen — i allt funktionen av 1/r² — beskriver det elektrostatiska fältets MEKANISKA kraftväg (makrofältet, eller probfältet) med tillhörande »fältlinjer». Det elektrostatiska fältets ELEKTRISKA kraftväg, analogt det elektriska fältets struktur — i allt funktioner av 1/r — uppvisar å andra sidan en ordning där ingen testkropp är närvarande; Den elektriska kraftvägen bestäms enbart av hur det elektriska fältets flöde återkopplar mellan central laddning och omgivande rymdpunkter på en referensram som ENLIGT RELATERAD FYSIK bestäms av den lokala gravitationen enligt elektriska fältets definition (se superpositionsprincipen): energifördelningen över laddningen i varje fältpunkt enligt Fr/Q = kQ/r = U, = E/Q. Denna typ, typen 1/r märk väl, finns INTE närvarande inom den beskrivande moderna världsvetenskapens akademiska elementära elektriska litteratur. Den kan inte mätas, utan tillhör ett avsnitt av den elementära elektrofysikens grundteori som helt saknar representation i modern akademi, jämför elektriska laddningens härledning. Den omnämns aldrig.

Utgående från en sådan »testkroppsmekanik», nämligen i ett ensidigt fasthållande och erinrande av »experimentella resultat» — således i sig själva på intet sätt felaktiga förhållningssätt — och därigenom ovillkorligen framhållande och byggande hela teorin för elektriciteten på det fältbegrepp som extraherats härifrån, blir alla grundläggande missuppfattningar av de elementära formerna inom elektrofysiken så exakt likadant garanterat framgångsrikt cementerade. Undra sedan inte över kalabaliken. Den har en perfekt förklaring.

Med grund i detta närmande, når man heller inte den förklarande teorin till uppkomsten av magnetismen och induktionen, där impulsbegreppet E/Q (den elektriska laddningens radiellt riktade form och verkan i varje fältpunkt genom den lokala ljushastigheten c, se superpositionsprincipen enligt relaterad fysik) är central och helt avgörande — varigenom dessa nämnda två fenomen, 1/r kontra 1/r², istället förväxlas. Friskt. I RELATERAD FYSIK däremot får genom impulsbegreppet (dE/dQ) uppkomsten av magnetismen och induktionen en fullständig fenomenologisk förklaring — utan inre växelverkan (växelverkansfrihetssatsen). Se vidare från Induktionen och Magnetismen. Se även i PARALLELLEXPERIMENTEN i detta dokument.

EXEMPEL:

*forts. 1996XII by 199XII Compilation of INDUCTION AND MAGNETISM 2007VI15

KONVENTIONELLT SKOLEXEMPEL FRÅN EN TRADITIONELL SVENSK LÄROBOK SOM VISAR DEN KOMPLEXA NIVÅN PÅ DEN MODERNA AKADEMINS OCH VETENSKAPENS MISSUPPFATTNINGAR INOM ELEKTROFYSIKENS GRUNDLÄGGANDE ELEMENTÄRA BEGREPP

”

Exempel

Två punktladdningar med storlekarna –Q och +2Q är belägna enligt fig. 14.05 på avståndet a från varandra. Sök potential och fältstyrka i punkten P.

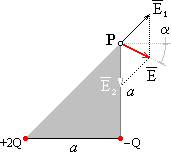
I Utdrag från modern undervisningslitteratur | originalets illustration här omritad av mig för bästa tydlighet

TEKNISK ELEKTRICITETSLÄRA E. Danielson Gleerups Lund 1965

Danielsons bok är f.ö. den i sitt slag allra förnämsta — helt utmärkta — svenska referens som alls finns i elektrofysikens grunder

Fig. 14.05

Potentialen är

V = 2Q/(4pe0 · a · Ö2) – Q/(4pe0 · a) V = Q(Ö2 – 1)/(4pe0 · a) volt

Elektriska fältstyrkan sammansättes av E₁ och E₂, varvid

E₁ = 2Q/(4pe₀ · 2a²) E₂ = Q/(4pe₀ · a²)

Resultanten E har en horisontalkomponent

E_x = E₁ · cos 45° = Q/(4pe₀ · a² · Ö2)

och en vertikalkomponent

E_y = E₁ · cos 45º – E₂ = Q/(4pe₀ · a² · Ö2) – Q/(4pe₀ · a2) E_y = [Q/(4pe₀ · a² · Ö2)][ 1 – Ö2 ]

\ E = ÖE²_x + E²_y = [Q/(4pe₀ · a²)] · Ö(2 – Ö2)

Vidare är i fig. tg a = –E_y/E_x = Ö2 – 1 \ a = 22,5°

Ekvipotentialytor.

Punktladdningar förekommer visserligen relativt sällan inom tekniska tillämpningar. Då det elektriska fältet från sådana laddningar är relativt enkelt, fortsätter vi dock undersökningen av dessa fält. Resultaten kan sedan tillämpas på mera komplicerade system.

”

TEKNISK ELEKTRICITETSLÄRA E. Danielson GLEERUPS Lund 1965 s122-123

—————————————————————

Kommentar:

I en ELEMENTÄR ELEKTRISK LADDNING finns ingen elektrisk fältstyrka F/Q. Se från POTENTIALENS VIKTIGHET samt förtydligat i ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS. Så, exemplet ovan skulle kunna vara ett högeligen praktiskt korrekt exempel på hur att beräkna och verifiera varje fysikaliskt möjlig mätning av en makroskopisk elektrisk fältstyrka. Men, återigen, det är i så fall inte en beskrivning av elektrofysiken på nivån elementär. Boken berättar (nämligen) ingenting om detta, eller ger i övrigt någon ledtråd till någon form av klargörande. Och så är böckerna generellt i vår kultur färgade av samma inneboende akademiska gestalt; Alla missar poängen. Den relaterade fysikens grundbegrepp kan inte beskrivas av den moderna akademins lärosystem; Grunderna finns inte ens omskrivna, utan sammanblandas (friskt) med makroskopiska fältbegrepp — typ ovan givna skolexempel.

Se utförlig beskrivning enligt relaterad fysik från Begreppen Fältstyrka och Potential.

InduktionenOchMagnetismen

magnetiska fält

MAGNETISKA FÄLT

Fältformerna i de tre ovanstående sammanställda samlingen kurvor visar magnetiska fältets form och struktur utgående ifrån två idealt oändligt långa raka parallella ledare. Som synes, uppnås ekvivalenta fältstrukturer för kraftfält med samriktade strömmar (övre vänster) och samhörande B-värden för motströmmar (nedre höger) Fältbilderna gäller också för ekvipotentialerna för elektriska antidipolfältet och gravitationsfältet mellan två lika massor, nedre vänstra bilddelen. Övre vänstra och nedre högra bilddelarna gäller även för elektriska antidipolnormalerna och dipolekvipotentialerna. Fältbilderna för elektriska dipol och antidipolfälten visas illustrerat i elektriska fältets matematik enligt relaterad fysik.

relaterad fysik

och modern akademi

1/r² KONTRA 1/r

Den mekaniserade fältbilden [F/Q, f (1/r²)] blir något annorlunda jämfört med den elektriska fältbilden [E/Q, f (1/r)] eftersom graferna för elektriska fältstyrkan X=F/Q är funktioner av 1/r² till skillnad från 1/r som gäller för det rena elektriska fältet (se föregående från POTENTIALENS VIKTIGHET) där X inte existerar. Grundformen med dipol och antidipolfälten får i runda linjer sagt nära samma utseende; cirklar i mekaniska dipolfältet är ”nästan cirklar” [Se exv FOCUS MATERIEN 1975 ill.s77]).

För fältbilderna till ekvipotentialkurvorna, blir emellertid relationerna helt annorlunda. Eftersom begreppet differentiella potentialer [se från POTENTIALENS VIKTIGHET] i det makroskopiska fältet alltid löper i samma riktning som elektriska fältet X, den elektriska fältstyrkan, blir alla ekvipotentialkurvor transversella (rätvinkliga) till vektorkurvorna för X.

Detaljerna som hör till de konventionella 1/r²-formerna (i den mening de alls visas) finns väl beskrivna i konventionell litteratur och avhandlas därför inte i den här presentationen, utöver vad som sagts ovan. Jämför föregående EXEMPEL.

InduktionenOchMagnetismen

Parallellexperimentet: Relaterad fysik och modern akademi

Se utvidgad delvis förenklad version i PEX2024Intro ¦ PEX1994OriginalDetails — induktionsfenomenet mera i detalj

PARALLELLEXPERIMENTEN FRÅN 1994

Note20Oct2024 — GoogleCHROME ignores link headlines — jumps down in text, ignores link context;

UH organized links in general: LINKlinkmarker (not visible): often followed by nearest previous link — GoogleCHROME has begun to jump over/skip this: the user now must scroll up to see the Chrome hidden original. As tested: Applies only for links outside the present htm-document, leading to it.

Other web readers still respond correctly (Microsoft Edge, Safari, Fiefox, Netscape ..). exposing the CONTEXTUAL linkage (if equipped with an end colon mark) without breaking the continuity.

AddedNoted 25Oct2024. We will watch to see if this GOOGLE Archive Intrusion becomes corrected.

Parallellexperimenten från 1994

För att bevisa induktionens friställning från magnetismen anställdes (1994) följande »enkla» experiment:

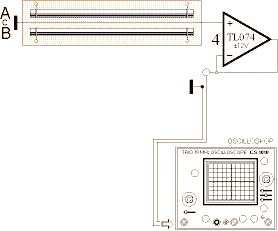
Två raka parallella strömledare AB är kopplade till en strömkälla som under kort tid kan generera (mycket) höga strömstyrkor på väl definierade stigande och fallande strömramper. Mellan AB-ledarna är magnetiska fältstyrkan noll om de lika stora AB-strömmarna är samriktade, och maximalt större än noll om AB-strömmarna är motriktade (Kretsen för uppmätning av magnetiska fältstyrkan visas separat längre ner i Hallelementet). På denna avgörande mittlinje finns alltså uppspänd en (mycket) fin koppartråd (C). Genom att mäta spänningen i C då strömmarna i AB ändras växande och avtagande, kan man avgöra vad det är som gäller i praktiken. I figuren ovan är C kopplad till en mycket känslig operationsförstärkare som i sin tur är direkt kopplad till ett oscilloskop där allt som händer i C-linjen kan studeras i detalj. Experimentkopplingen och resultaten beskrivs mera detaljerat nedan.

Experimenten har nu (2008) för länge sedan redovisats till ledande svenska universitet.

Man skickar tillbaka materialet med avhandlingen

»Vi har ingen möjlighet att ta del av dina skriverier». Heja Sverige.

experiment, utförande

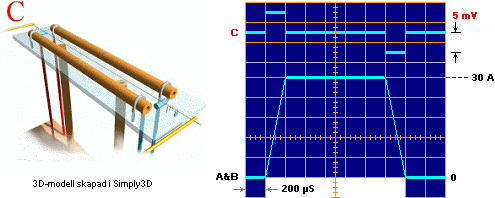
Parallellexperimenten 1994. I den tunna precisionsplacerade tråden C induceras en spänning då strömmen genom de samgående lika stora parallellströmmarna ändras — trots att den magnetiska fältstyrkan i C är konstant noll. Experimenten bevisar således att induktionen existerar oberoende av magnetismen — exakt så som förutsägs enligt relaterad fysik.

mekanik, anordning

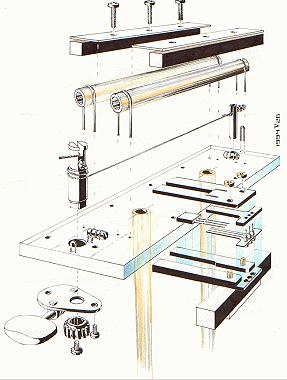
Den mekaniska anordningen (sprängskissen från 1994, förminskat A4-format).

Spännskruven anställdes som del i projektet för att samtidigt kunna genomföra experimentet med den elektromekaniska induktionen: den svängande strängen i det fasta magnetfältet. Den beräknade och förväntade effekten infann sig.

koppling, kretsschema

kretsbeskrivning

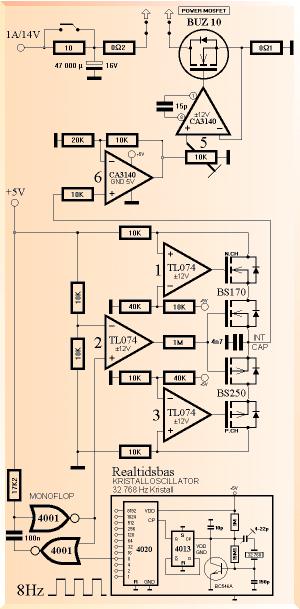
GENOM EN PRECISIONSSTYRD PowerMosfet-koppling skickas en exakt 8Hz repeterande hög toppström på 15Ampere precisionspuls med 1mS varaktighet och strömderivatan di/dt=75000 A/S genom de två parallella raka 5mM×0,1M mässingsrörledarna A&B. Den låga repetitionsfrekvensen med den korta strömpulsen gör att hela elektroniken kan byggas direkt på ett kopplingsdäck utan kylare. Centrumavståndet mellan A&B i experimenten var 15mM.

Genom en separat mätning på mittlinjen C mellan A&B (HALLELEMENT 3103 C) konstaterades noll magnetisk fältstyrka.

På C spändes sedan upp en fin 0,1mM koppartråd kopplad till en högresistiv (1 TW) operationsförstärkare som mätte spänningen i C mellan ändpunkterna. På respektive stigande/fallande strömflank registrerades då på ett oscilloskop en induktiv puls om ca ±5mV: Det induceras spänning där inga variabla magnetiska fält kan påvisas.

I C induceras alltså, verkligen, en spänning, helt utan koppling till någon påvisbar magnetisk fältstyrka.

Den inducerade spänningen i C visade sig vara helt oberoende av C-materialet, men beroende av A&B-materialet samt deras tvärsnittsdimensioner.

Sedan detta resultat kontrollerats genom flera försök, kopplades ena stången bort då det i vilket fall stod klart att magnetismen inte hade någon inverkan. Med en sålunda halverad ström halverades också amplituden på induktionspulsen i C till ca ±2,5mV.

uppmätning av

magnetiska fältstyrkan

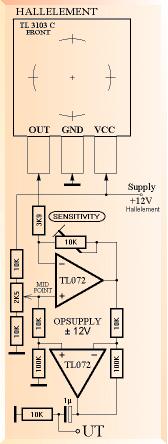
KRETSSCHEMAT ovan visar den separata kopplingen för hallelementet 3103 C för uppmätning av magnetisk fältstyrka.

Nedan visas hur oscilloskopet kopplades till operationsförstärkaren TL074 som mätte spänningen i den uppspända C-linjen.

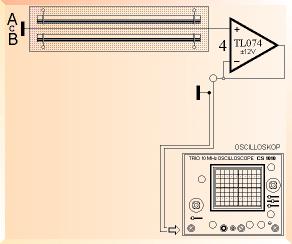
Med en fördubblad strömstyrka på 30Ampere i ena rakledaren, di/dt=150000 A/S, kunde så konstateras att induktionen i C återgick till föregående nivå ca ±5mV.

Med motvända 15A-strömmar i A&B, di/dt=75000 A/S, uppmättes maximal magnetisk fältstyrka (ca 0,8 mT).

I C blev då mätlinjen helt rak: noll. Ingenting kunde observeras trots i sammanhanget full magnetisk närvaro.

InduktionenOchMagnetismen

IndMagSyntes

Syntes av induktionen och magnetismen

Den sekundära induktionen och fjärrverkan i magnetismen (eng. far application)

De följande nio sambanden i min referens tillhör de ursprungliga utvecklingarna [från 1996XII]. De använder ett klassiskt matematiskt språk av enklaste och mest elementära slag i trigonometrins PREFIXxSIN. Sambanden har, såvitt här känt, absolut ingen konventionell representation eller motsvarighet. Uttrycken förklaras efter den följande sammanställningen. X (Grekiskans X, xsi) betecknar elektrisk fältstyrka (X=U/r).

(1) X_s/X_r = sinb

= (dU/ds)/(dU_c/dr) = (dU/dU_c)(dr/ds)

= sinb = (dU/dU_c)(1/sinb)

(2) (sinb)² = dU/dU_c

dU = dU_c(sinb)²

(3) Rc = R’ç = 1/e = ^®R_maxç₀ = konstant = k(4p), VM/AS

¯¯ ¯¯¯¯¯¯¯¯

(4) ç₀ = c – v .......................... kausalsambandet divergensens partiella reduktion

(5) P = dQ/(4p dr)

(6) U = U_c(sinb)²

= Rc · P(sinb)²

= ^®R_max · ç₀P(sinb)²

(7) = ^®R_max · (c – v)P(sinb)²

= ^®R_maxcP(sinb)² – ^®R_maxvP(sinb)²

= U_c + U_v

= U_c + (U + ¯Û)

= U_c + u + û

U_v = u + û = –^®R_maxvPsin²b

^®R_max := [^®R_max– ¯R] ; ¯R = û = 0 för konstant v

= – (^®R_max– ¯R)vPsin²b

= –^®R_maxvPsin²b + ¯RvPsin²b

(8) u = –^®R_maxvPsin2b ........... ReduktionsPotential, magnetisk fältPotential

(9) û = ¯RvPsin²b .................. ¯InduktionsPotential, induktiv fältPotential

*cont. 1996XII by 1999XII Compilation of INDUCTION AND MAGNETISM 2007VI15

—————————————————————————————————————————————————————

BESKRIVNING

I det följande kommer ovanstående samband att relateras.

Statiskt i laddningsfältet för Q gäller

U_c = Rc(Q/4pr)

Med förenklingen (5)

P = (Q/4pr)

ges

U_c = RcP

En ideal elementär elektrisk laddning Q⁺ som lägesändrar med ds/dt = v i riktningen iy med hänsyn till punkter (P) idealt fixerade av ett fasta tillståndets fysik i en lokal gravitell dominans, liknande referensen för ett laboratorium på den idealt fasta Jordytan,

producerar — tillsammans med den statiska fältimpulsen U_c i varje rymdpunkt P, i fältets framriktning y — en sammansatt impulsverkan i P av formen

U_c + U_v = U

Här sammansätter U_v formen för impulsen i P associerad med lägesändringen (v). Genom fältåterkopplingen i U_c på ändringen v, blir verkan av lägesändringen för Q⁺ ekvivalent med den positionsändrande impulsen U_v. Denna ändring producerar delvis en elektrisk fältspänning U [motsvarande en elektrisk spänning U som driver laddningen i dess rörelse] med en tillhörande elektrisk fältstyrka X [Grekiskans xsi, eller E-F], och delvis en induktiv resistans ¯R som strävar att motverka lägesändringen. Denna induktiva resistans motsvarar ett X motriktat elektrisk kraftfält med en tillhörande elektrisk dipolfältstyrka ¯Ð (D-E [Alt+0208]). ¯Ð är alltid riktad så att ändringen motverkas (se Tredje ändringslagen). Om ändringen ds/dt är konstant v, uppträder emellertid den induktiva resistansen endast differentiellt (dRÛ0, se differentialens definition), eftersom v då projiceras linjärt utmed den konstanta divergensen c som gäller i det lokalt dominanta g-systemets referens. I lägesändringen med ett konstant v = s/t uppträder således ingen motverkande kraft. Denna detalj innebär tydligen att

· R i riktningen v bevaras konstant, oberoende av magnituden i v

· en laddning i rörelse möter inget motstånd så länge rörelsen saknar variation

Som divergensen saknar koppling till kinetiken, adderas inte c med v. Den uppkomna effekten från v i en motsvarande rymdpotential hos laddningen — enda återstående alternativet — är istället given som en v tvärställd (rätvinklig) högre resistans ^®R’, och vilken kompression relativ den omgivande g-dominanta rymden (P) producerar den magnetiska fältringen i respekt till P. Som R’ strävar att uttömma sig i det omgivande tunnare rummet R, expanderar ringen sålunda i riktningen x® rätvinkligt strömlinjen y som R’ närmar sig R. Den magnetiska fältringen blir således en uttalad planvåg i riktningen x och vilken expandera fullständigt rätvinkligt v. (Jämförelsen med ringarna på vattenytan från den fallande vattendroppen ger en excellent liknelse).

· Genom oförmågan hos divergensen c att förena sig med laddningens hastighet v i den givna g-referensen uppkommer ett magnetiskt fält som expanderar inom den lokala gravitellt relaterade rymdens toppdivergens (c) i riktningen x® rätvinkligt v

Flödesfaktorerna Rc är, som nyligen omnämndes, således bevarade intakt i riktningen för strömvägen i analogt med laddningens hastighet v. För att denna i varje rymdpunkt bevarade Rc-konstant ska kunna matcha den uppkomna, partiellt (differentiellt) högre magnetiska fältvågsresistansen ^®R’ rätvinkligt strömriktningen i, gäller det tydligen att

Rc = ^®R’ç = ^®R_max · ç₀ = KONSTANT ............................. WM/S = VM/AS

Den magnetiska fältvågen utbildas alltså på ett motsvarande (normalt mycket marginell) lägre c-värde (ç₀) motsvarande den aktuella reduktionen och som därmed förklarar vågens expansion mot den omgivande normalrymdens c då fältvågens högre R uttömmer sig i normalrummets lägre R.

Termen ç förenklar här ett »c-komma». Rc-konstanten är (konventionellt) benämnd elektrisk permeabilitet, eller (i fri rymd) den elektriska konstanten (Eller ännu mera specialiserat, kapacitiviteten för vakuum, Rc = 1/e).

Analogt med den högre resistansen i fältvågen uppkommer således en motsvarande lägre divergens.

· Som R_max närmar sig R när ringen expanderar, närmar sig analogt ç toppdivergensen c från minimum ç₀.

Som framträdandet av ç₀ motsvarar magnituden för v, får man v = c – ç₀. Vilket vill säga,

ç₀ = c – v

Effekten av den totala fältimpulsen U_c + U_v , framkommande genom inverkan av v i strömriktningen i för Q⁺, kan därmed uttryckas

U_c + U_v = ^®R_maxç₀P

Resistansformen ^®R_max rätvinkligt strömriktningen i innefattar den induktiva resistansens verkan. Det beror på att summan av verkan och motverkan i strömriktningen alltid avbildar den aktuella strömstyrkan via kvantiteten ^®R_max och i varje rymdpunkt P. Är motverkan noll, samma som konstant v, räknas bara ett rent ^®R_max. Ändras v, uppkommer den induktiva resistansen ¯R som reducerar kraften i strömriktningen. Den totalt aktiva resistansens form kan då skrivas

R = [^®R_max– ¯R] ................................................... W = V/A

Denna form är den aktuella och fullständiga formen för den resistiva delen i komplexet. På liknande sätt kan vi betrakta impulsen U_v som sammansatt av fältspänningen U och den motriktade induktiva spänningen ¯Û (u-flex [Alt+0219]). Detta ger oss sambanden

U_v = U + ¯Û

U_c + U_v = U_c + U + ¯Û

Vi har därmed

U_c + U + ¯Û = [^®R_max– ¯R]ç₀P

Den induktiva impulsen ¯Û blir additiv då den, i sin verkan som impulsform, motverkar fältimpulsen U. Av samma anledning ges den induktiva resistansen ¯R som subtraherande — då ¯R uppenbarligen agerar skalär reducerande på verkan från ^®R_max. Därmed kan ledet skrivas mera komprimerat och summerande enligt

U_c + U + ¯Û = ^®R_maxç₀P

Impulsformen genom divergensen c på r från Q, [dQ/dr], bestämmer dynamiken i hela komplexet.

Impulsformen ger speciellt vinkelkomponenter för fältresistanserna — ^®R_max utmed x-axeln och ¯R utmed y-axeln — liksom för verkan av Q i lägesändringen utmed y-axeln [][uppPil; dess SymbolTeckensnitt visas inte i htm-dokumentet med Internet Explorer; anledning okänd].

Rätvinkligt strömriktningen i, ®, ges ändringen ds i y-riktningen analogt med en tangentiell del [ô ][dubbelriktad VertikalPil i Windings] av laddningens ekvipotentialyta. Verkan i denna del blir alltså noll. Vi ska nu närmare studera de här nämnda komponentdetaljerna i de skilda riktningarna xy.

På vägen ds i riktning v finns avbildat utöver dU_v också dU_c så att fältstyrkan i riktning v totalt blir

X_s = (dU_c+dU_v)/ds = d(U_c+U_v)/ds

Vi relaterar detta.

Är U_c inte associerad med U_v utgår förutsättningen för fältstyrkan i riktningen v för att övergå till den vilande dU_c/(ds=dr), vilket alltså gäller då v är noll. Är nämligen

v=0=U_v är det givet att

dU_c/ds = dU_c/dr

eftersom ansatsen i ett framträdande med ett figurerande v i vilket fall måste bygga på ett intervall (variationens, analogt integralens grundval) och därmed förutsätta en väg-tid-kvantitet större än noll, och vilken ordning vi — således — finner relevant.

Formen för X [elektriska fältstyrkan, här Grekiskans Xsi, X]_s är således väldefinierad.

Med denna överföring (eng. mapping) av U_c=k(dQ/dr) på s, analogt i riktningen för v, upphör emellertid inte U_c att agera som en potentialimpuls utmed r.

[Vi minns att det är den lokala divergensen c som bestämmer Q-potentialen från varje individuell massladdning (mQ), se superpositionsprincien, och termen »potentialimpuls» på r från Q-origo är alltså välrelaterad, och endast så].

Den rent dynamiska verkan i överföringen av U_c på s är, nämligen, en funktion av U_c i P. Vilket betyder; i ändpunkten av varje r. Därmed bör överföringen också totalt på s vara relaterad till den momentana verkan U_c på r (Från tidigare diskussioner vet vi att denna verkan inte är projektiv eftersom ingen rörelse existerar utmed r i det statiska fältet). Med denna i P momentana agerande punktfältstyrka

X_r= dU_c/dr

får vi relationen

[(dU_c+dU_v)/ds]/[dU_c/dr] = X_s/X_r

Med v=0 finner vi då ds=dr och därmed dU_c/dU_c = 1 eftersom då enbart dU_c=dU_c är relevant. Sambanden är alltså väl relaterbara.

Relationen [(dU_c+dU_v)/ds]/[dU_c/dr]=X_s/X_r motsvarar exakt den trigonometriska projektionen mellan s och r via vinkeln b som sinb i PREFIXxSIN. Vi får

[(dU_c+dU_v)/ds]/[dU_c/dr] = X_s/X_r = sinb;

[(dU_c+dU_v)]/[dU_c][dr/ds] = sinb;

[(dU_c+dU_v)]/[dU_c] = sinb[ds/dr] = (sinb)²;

Och vi har

U_c+U_v = U_c(sinb)² = ^®R_maxç₀P(sinb)² = U_c + (U + ¯Û)

författarens personliga notering

NOTE. In Kraftlagen 1999 is erroneously stated (typical ”tired-error”):

Relationen (dU_c+dU_v)/dU_c motsvarar exakt den trigonometriska projektionen mellan s och r via vinkeln b som sinb med PREFIXxSIN. Vi får

[(dU_c+dU_v)/dU_c][dr/ds] = sinb[dr/ds] = (sinb)²

Och vi har

U_c+U_v = U_c(sinb)² = ^®R_maxç₀P(sinb)² = U_c + (U + ¯Û).

The correction should be as stated above:

Relationen [(dU_c+dU_v)/ds]/[dU_c/dr]=X_s/X_r motsvarar exakt …

This compilation has been corrected 2002VIII31 on the above notified error.

Resultatet blir samma som en ”trigonometrisation” av de olika delarna;

Vinkelkomponenten till Q för alla b¹0 blir i PREFIXxSIN Psinb utmed y-axeln, och motsvarande ^®R_maxsinb för fältresistanserna i x-riktningen. Det ger de vidare leden

U_c + U + ¯Û = ^®R_maxsinb·ç₀·Psinb

U_c + U + ¯Û = ^®R_maxç₀Psin²b

Med förenklingen u = U och û = ¯Û, och insättningen ç₀ = c – v, (se Kausalsambandet) ges

U_c + u + û = ^®R_max(c – v)Psin²b

U_c + u + û = ^®R_maxcPsin²b – ^®R_maxvPsin²b

u + û = –^®R_maxvPsin²b

Den induktiva resistansen ¯R är, som nyligen omnämndes, differentiell [analogt kvantitativt=0, se begreppet differential om ej redan bekant] i resistanskomplexet med ett konstant v. Den är aktuell endast när v ändras, analogt när Q uppvisar en acceleration. Med det tidigare härledda sammansatta sambandet för resistanskomplexet totalt, får vi

u + û = – (^®R_max– ¯R)vPsin²b

u + û = –^®R_maxvPsin²b + ¯RvPsin²b

varav

u = –^®R_maxvPsin²b............ REDUKTIONSPOTENTIALEN magnetiska fältpotentialen

û = ¯RvPsin²b....................... ¯INDUKTIONSPOTENTIALEN induktiva fältpotentialen

Som tidigare, är P = (Q/4pr).

Som ^®R_(max) och ¯R arbetar i olika riktningar, har de ingen ömsesidig växelverkande koppling.

Se även särskilt i växelverkansfrihetssatsen.

Den komprimerade matematiska formalian i induktionens och magnetismens arbetande komplex kan förenklas utgående direkt från den elektriska fältstyrkans relation i (1) enligt

X_s/X_r = sinb

Resultaten i uttrycken (8) och (9)

(8) u = –^®R_maxvPsinb² ........... ReduktionsPotential, magnetisk fältPotential

(9) û = ¯RvPsinb² .................. ¯InduktionsPotential, induktiv fältPotential

kan utvecklas, vidare, till mera praktiskt användbara uttryck som följer:

Induktiv potential (9):

û = ¯RvPsin²b

û = ¯Rv(Q/4pr)sin²b

dû = ¯Rv(dQ/4pr)sin²b

¯RvdQ = ¯R(ds/dt)diT

dû = ¯RT(di/dt)(1/4pr)sin²b ds

dû/ds = X_induktiv:= Ð = ¯RT(di/dt)(1/4pr)sin²b

s/r = sinb

RT = L

Ð = L(di/dt)(1/4pr²)sinb · s

dÐ = L(di/dt)(1/4pr²)sinb · ds ............................ V/M, induktiva dipolFältstyrkan i P i PREFIXxSIN

Magnetisk potential (8):

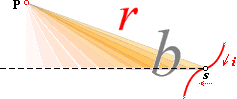
u = –^®R_maxvPsinb

u = –^®R_maxv(Q/4pr)sin²b

u/s = X = du/ds = –^®R_maxv(Q/4pr)sin²b/s

s/r = sinb

X = –^®R_maxv(Q/4pr²)sinb

v = ds/dT

X = –^®R_max(ds/dT)(Q/4pr²)sinb

X = –^®R_max(Q/dT4pr²)sinb · ds

dX = –^®R_max(dQ/dT4pr²)sinb · ds

dX = –^®R_max(I/4pr²)sinb · ds

dX/ç₀ = dB_P

dB_P = –(^®R_max/ç₀)(I/4pr²)sinb · ds

R₀c₀ = ^®R’ç = 1/e₀ = ^®R_maxç₀ = konstant, VM/AS

¯¯¯¯ ¯¯¯¯¯¯¯¯

^®R_max = R₀c₀/ç₀

^®R_max/ç₀ = R₀c₀/ç₀² = Rc/ç₀² = 1/e₀ç₀² |; fullständigt (ç₀/c₀)/e₀ç₀² = 1/e₀ç₀c₀ |

Med en förenkling av den medelmässiga reduktionen för små v relativt c enligt ç₀=c₀ får vi det enklare — men, att observera, det dynamiskt omöjliga —

^®R_max/c₀ = R₀c₀/c₀² = R₀/c₀ = µ₀

Vilket betyder: Med ett sant [ç₀=c₀–v]=c₀ får vi v=0 som betyder noll magnetisk verkan.

Var gärna noga med att erinra denna förenkling eftersom annars teorin för induktionen och magnetismen blir djupt bekymmersam.

I strikt mening finns inte ett µ₀ i magnetismen. Men det klargörandet finns inte upptaget eller ens omnämnt i modern akademi. Se vidare i µ₀.

Därmed — i erinran av dessa punkter och utan hänsyn till minustecknet — har vi i PREFIXxSIN

differentialekvationen för den magnetiska expansionsintegralen

OREPRESENTERAD I MODERN

AKADEMI OCH VETENSKAP

dB_Px = µ₀(I/4pr²)sinb · ds = d(dB_Ps/db_s) .......................... VS/M², magnetiska fältstyrkan i P i PREFIXxSIN

Sambandsformen är varken befintlig eller omnämnd i modern akademi eller vetenskaplig teori eller litteratur — därför att modern akademi använder begreppet vektorprodukt, se nedan, för att formulera sin del, och denna kan garanterat INTE kopplas bakåt via vektorproduktens definition.

Lösningen däremot

är känd som Biot-Savarts lag; den markerar grunden för modern elektrisk teori.

I konventionellt PREFIXxCOS skrivs lösningen till ovanstående givna integral (typiskt)

dB = µ₀(I/4px)sinb db_s eller mera generaliserat med användning av så kallad vektorprodukt

= (µ₀/4p) · I · ds × r/r³

InduktionenOchMagnetismen

treatise

EXAMPLES in

2001XI3

Advanced examples in induction and magnetism | a TREATISE ON

The fallacious modern academy interpretations in

INDUCTION AND MAGNETISM

TRE PRECISA EXEMPEL FÖR EXAKT JÄMFÖRELSE

EXEMPLIFIERING AV DEN MODERNA AKADEMINS FATALITETER INOM INDUKTION OCH MAGNETISM

Exempel i Induktion och Magnetism

Exempel 1

I artikeln om sekundära induktionen [Ringen och den cirkulära spolenTHE RING AND CIRCULAR COIL] härleddes det generaliserade uttrycket för den allmänna induktansen hos en (tunn) cirkulär spole med n varv och diameter d enligt

û_COIL(di/dt)^–1 =

L = d·n²·L_d /1M ..................... allmänna ringSpoleInduktansen ENLIGT RELATERAD FYSIK, VS/A

I den väletablerade eminenta svenska elektroniska fackreferensen ELFA [Faktasidorna, Induktansen, katalog 1998 (s624) och vidare — detaljerna har sedan medtagits i alla efterföljande årsupplagor av ELFA-katalogen] är den följande spolformen given med L i µH, d spoldiametern och l spolens bredd (eller höjd, se illustrationen ovan) i cM:

L = (0,08d²n²) / (3d + 9l) ................ µVS/A (= µVS/AcM · cM)

Med l << d kan faktorn 9l frånses. ELFA-sambandet blir då det enklare

L = (0,08d²n²)/(3d) µVS/AcM · cM

= 0,08d·n²/3 µVS/AcM · cM

= k · d·n² · 1M–1 µVS/A · M · 1M^–1

k·10⁶ = L_k ;

= d·n²·L_k · 1M^–1 VS/A

vilket vi ser är exakt samma principiella form och samband som det ovan från relaterad fysik.

NOTERING:

Från Ringen och den cirkulära spolenTHE RING AND CIRCULAR COIL har termen Ld ovan sambandet

L_d /1M =pKµ_L

M För detta exempel och de två följande noteras specifikt för vart och ett:

Men modern akademi har utvunnit sina uttryck från uppfattningen att magnetismen (F) kopplar till induktionen, medan den relaterade fysikens uttryck utgår från den rena induktiva effekten där ingen som helst magnetism existerar — se bevisen från parallellexperimenten om ej redan bekant, samt härledningarna till de aktuella sambanden: dessa är helt orepresenterade i den moderna akademins lärosystem.

Helt rent.

Hur förklaras då likheten?

OBSERVERA ATT TOTALA PRIMÄRA INDUKTANSEN PER METER µ_L — som det ser ut okänd av modern akademi — HOS LEDAREN MÅSTE VARA KÄND enligt relaterad fysik genom

µ_L = K(µ₀+µ_c) ..................... totala ledningsPrimära induktansen per meter , VS/AM

[För µ_L se PRIMÄRINDUKTANSEN I SAMMANFATTNING].

*cont. EXAMPLIFYING THE MODERN FATALS ON INDUCTANCE AND MAGNETISM

Exempel 2

I samma artikel som Exempel 1 erhölls också

L = µ_Ln² · A/h ...................................... allmänna ringspoleinduktansen

A är ytan av ringspolens tvärsnitt, h är spolens höjd och n är antalet spolvarv.

Låt oss nu göra ett fel:

Syftet är att jämföra slutresultatet med standardmeningarna i den modern akademins lärosystem genom de fackböcker vi kan läsa och studera på biblioteken. Vi ska (nämligen) »härleda» ovanstående L-typ genom att FELAKTIGT förmoda att faktorn F=B·A, vi kommer strax tillbaka hit, vilket vill säga i sammanhanget B, har koppling till induktionen — som det är omtalat, erkänt och praktiserat av modern akademi — vilket den (B) garanterat INTE har enligt relaterad fysik: magnetismen och induktionen växelverkar inte enligt relaterad fysik. Se den utförliga förklaringen och grunden till den detaljen i Uppkomsten av Induktionen och Magnetismen enligt Relaterad Fysik, om ej redan bekant, samt de experimentella bevisen i Parallellexperimenten.

I SEKTIONEN FÖR MAGNETISMEN

[Tillämpning B-styrkan i en lång rak spoleB-STRENGTH IN A LONG STRAIGHT COIL]

fann vi

B = –µ₀nI/s ............ fältstyrkan inuti lång rak spole i Tesla, VS/M²

n .............................. antal varv

I .............................. strömstyrkan

s .............................. spolens längd

µ₀ ............................ 1,25662 t6 VS/AM

Detta uttryck är också välkänt i det moderna lärosystemet.

Bara för erinran; en spänning induceras explicit i varje lindningsvarv eller ring från de totala n–1 ringarna genom strömderivatan (di/dt).

DET AVGÖRANDE FELET

Låt oss nu utföra det avgörande felet genom att hävda att lagen för elektroMEKANISK induktion

U₁ = dF/dT

beskriver den inducerade spänningen i en sådan spolring som den i exemplet [fix ledare som badar i variabelt B]. Vilket vill säga, vi identifierar FELAKTIGT FÖRST induktionen med magnetismen och tillämpar SEDAN ÄVEN FELAKTIGT ett samband från magnetismen på den så felaktigt påsyftade induktiva effekten. Då får N ringar den inducerade spänningen

U_N = N(dF/dT)

Som den allmänna induktionen gäller för alla möjliga fall oberoende av HUR spänningen induceras enligt U=L(di/dt), har vi därmed fått fram det centrala departementet i hela FelRestaurangen enligt

U_N = N(dF/dT) = L(di/dt) ................. centralEXEMPLIFIERADE FelRestaurangsDepartementet

Termerna Tt och Ii är inte avgörande i differenserna (lilla i [i] används ibland för att beteckna en variabel ström). Då gäller

NdF = Ldi = LdI som ger NF = LI. Som F = BA får vi NBA = LI och därmed

L = NBA/I. Insättning av föregående resultat för B låter oss anlända till

L = N(–µ₀nI/s)A/I = –Nµ₀nA/s. Vilket vill säga, med längden s som höjden h och n=N

L = –µ₀N²A/h ..................................... resultatet av felutvecklingarna

EXAKT.

Frånsett minustecknet och den alternativa indexeringen för µ₀ och µ_L ,

är det exakt samma uttryck som den ovan omnämnda relaterade fysikens allmänna ringspoleinduktansen,

L = µ_Ln² · A/h ...................................... allmänna ringspoleinduktansen

Exakt samma form. Exakt samma kvantitet.

Och vart ville vi komma med det?

L-uttrycket som vi nyligen härledde sensationellt genom de (dubbla) felgreppen,

refereras — verkligen — till

av modern akademi som

(exempel från en modern skolbok)

”Man kan visa att induktansen hos en spole växer med kvadraten på varvtalet.”.

Boken skriver i marginalen:

“L = µ₀N²·A/l

(Gäller för en lång spole utan järnkärna.)”.

GYMNASIETS FYSIK Åk2 Liber 1978/1980, s212

M Som vi ser, är uttrycken identiska (l = h). Man kan visa.

*cont. EXAMPLIFYING THE MODERN FATALS ON INDUCTANCE AND MAGNETISM

Exempel 3

I artikeln

induktionen på den primära ledarytanINDUCTION ON THE PRIMARY CONDUCTOR SURFACE

Simplified application for comparison

fann vi

L = –(µ_L/2p)s[ln(4s/d) – 2s/d] ......................... den relaterade fysikens samband

Allmänna självinduktionen på ytan av en rak primärledare,

sekundära induktionen

L = (µ₀/2p)s[ln(4s/d) – 3/4] .......................... modern akademi

rak ledare, modern akademi,

sista termen anges som en korrektionsfaktor, den varierar beroende på källa

För att utvärdera hävden, har modern akademi bland många andra de följande referenserna:

Källan Elektronikens Grunder Del 1, John Schröder 1971, s124 specificerar (här t för 10–)

L= 2t7·l[ln(4l/d) – 3/4]

där 2t7 @ µ₀/2p = (1,25662 t6 VS/AM)/2p = 1,99997 t7 VS/AM.

Samma specifikation finns i Electronics Equations Handbook, Stephen J. Erst 1989 s7.

ELFA-katalogen (1998-99, s624) specificerar

L= 0,002·l[ln(4l/d) – x]

med x som frekvensberoende [x=3/4 för låg frekvens] och L i µH med l och d i cM.

Frånsett x, samma som föregående ovan.

M Och återigen, som vi ser, är sambanden formellt identiska.

SlutPåExempelENDofExamples.

Orsakerna — från Tre jämförande exempel

Varför har det blivit så här?

Följande punkter sammanfattar observationerna sett från kausallogiken (för magnetismen och induktionen, se särskilt i Kausalsambandet), samma som relaterad fysik — varför, och hur, begreppen induktion och magnetism inte kan beskrivas med hjälp av den moderna akademins lärosystem:

Trots den uppenbara — men tydligtvis inte uppmärksammade »triviala» — väsensskillnaden mellan induktion och magnetism som visas i den äldre skolans begrepp Maxwells regel, verkar det inte finnas någon etablerad litteratur, inte alls överhuvudtaget, som uppmärksammar just den detaljen: Maxwells regel visar hur magnetismen i praktisk mening onekligen måste vara fenomenskild från induktionen: En noggrann genomgång har, tydligen och hur i sanning märkligt det än kan synas, inte genomförts — inom den moderna akademins kvarter. Jämför Parallellexperimenten från 1994. En motsvarande experimentform i konventionella referenser har eftersökts men inte påträffats.

Uppkomsten av induktionen och magnetismen i relaterad fysik

— grundbegreppen som förklarar och beskriver ljusets plats i fysiken (divergensen, DEEP) och gravitationen (konvergensen, GRIP) och som förklarar och beskriver grundbegreppen med rymdkompakthet (µ=R/c, konv. magnetiska konstanten, konv. se Vacuum permeability @INTERNET Wikipedia [2011-09-06]) och rymdlängdskompakthet (L=RT=µs, induktansens grundbegrepp i relaterad fysik), och som i relaterad fysik med en gång klargör väsensskillnaden mellan induktion och magnetism

— har ingen motsvarande beskrivningsgrund i den moderna akademins lärosystem:

Växelverkansfrihetssatsen klargör enligt relaterad fysik varför magnetism och induktion inte växelverkar — men har ingen motsvarighet i den moderna akademins lärosystem.

Anledningen varför man i modern akademi felaktigt identifierar µ0 med magnetismen

— och som i relaterad fysik utgör den egentliga grundorsaken till kalabaliken: ljusets grundläggande fysik

— framgår genom den nära analogin att förenkla divergensen (ljushastigheten) som ingår i rymdkompaktheten (µ) i magnetismen (Rmax/ç0) med fria rymdens motsvarande (i normala fall) obetydligt skilda kvantitet (R0/c0); Se särskilt i ovanstående Tre Jämförande Exempel, dessa ger direkta konkreta kvantitativa praktiska exempel med konventionella referenser till jämförelse på hur (och varför) »det fungerar» trots fel. (Modern akademi gestaltar en »dockskåpsteater»).

Expansionsintegralen för magnetismen klargör (i summa av ovanstående) ytterligare en anledning varför detaljerna har undgått den moderna akademins skarpsinnen: den moderna akademins vektoranalys — med generaliserande begrepp (Maxwells ekvationer): Modern akademi utgår ifrån den s.k. Biot-Savarts lag — integrala lösningen till magnetiska expansionsintegralen och vars differentialekvation INTE kan innefattas i den moderna akademins vektoranalys (begreppen skalär- vektorprodukt) med mer än den analysen havererar. Maxwells ekvationer är (med andra ord) en förenkling (genom att på ett sätt återföra induktionens fenomenfysik på magnetismen, och på ett annat sätt reducera magnetism till induktion: matematiska [be]grepp). Se särskilt Differentialelementet i MAC.

Se även i Epilog.

Editor2011IX6

InduktionenOchMagnetismen

Induktionen och Magnetismen i modern akademi

Den svenska delen i Wikipedia @INTERNET skriver på ämnet ”elektromagnetisk induktion”

”Induktion är ett begrepp inom fysiken som innebär att en spänning alstras (induceras) i en ledare om ett magnetfält i dess närhet varierar.”

”Om e är den elektromotoriska spänningen och F är det magnetiska flödet så gäller

e = – dF/dt

För en rak ledare som rör sig i ett magnetfält

e = B · v · l

Riktningen på en eventuell ström ges av Lenz’s lag som säger att den inducerade strömmen ska motverka sin orsak.”

@INTERNET Wikipedia Elektromagnetisk induktion 2007-06-22

Liknande bidrag bör vara välkända då dessa helt klär upp ytan på planeten Jorden med början från 1800-talet.

Vilket vill säga: Ingen grundläggande förklaring till induktionen och magnetismen som fenomen finns i den moderna akademins lärosystem. Verkligen.

Ingen vet hur det fungerar — och på många ställen råder heta debatter med djupa motsättningar som bara tycks fördjupas ju mera man anstränger sig (se exv Wikipedia Talkpages på Magnetic field — även generellt i många andra ämnen som berör grundfysiken) — utom RELATERAD FYSIK.

Modern akademi tycks — verkligen — ha ett steg vidare att ta innan den kan matcha benämningen fysikalisk vetenskap.

Se även ELEKTRISKA LADDNINGEN.

InduktionenOchMagnetismen

Epilog

Modern akademi bekymrade sig aldrig att undersöka induktionens och magnetismen fenomennatur från naturens utgångspunkt

Se även i

Uppdagandet — The Revelation — vektorkalkylens grunder i modern akademi

Det grundläggande felet som modern akademi gjorde, var att påtvinga föreställningen om induktion och magnetism en redan existerade mänskligt skapad matematisk byggnad, nämligen den som uppfanns under 1800-talet av just modern akademi — utan att förstå värdet av den grundläggande, naturliga matematiken. Se vidare belysande exempel i jämförelse mellan relaterad fysik och modern akademi i begreppet differential, med vidare.

Genom naturens kvalitet, existerar ingen ”elektromagnetisk induktion” (se från PARALLELLEXPERIMENTEN) fastän fenomenets kvantitativa natur klart visar att om ett sådant fenomen antas existera, blir det resulterande felet i varje kommersiell tillämpning så litet att det helt försvinner från scenen. Se exemplifierat i TRE EXAKTA EXEMPEL.

I modern teori och vetenskap härleds magnetismen på samma VEKTORIELLA basis som induktionen — VILKET sett från den relaterade fysikens synvinkel BETYDER utan expansionsintegralen. Modern akademi kallar det elektromagnetisk induktion. Denna är det centrala beviset. Se utförligt från EXPANSIONSINTEGRALEN.

MODERN AKADEMI UTESLUTER expansionsintegralen som förklarar skillnaden mellan induktionen och magnetismen

vektorprodukten gör det bekvämt att anställa magnetismen för induktionen: felkvantiteten är negligerbar i vilket fall

MODERN AKADEMI EXKLUDERAR expansionsintegralen som förklarar skillnaden mellan induktion och magnetism:

förklaringen utesluts ur lärosystemet.

Varför utesluts expansionsintegralen av modern akademi? Vi har studerat detaljerna i den här presentationen. (Svaret är, deprimerande: Därför att dess nivå på intelligens uppenbarligen inte räcker för andras ändamål). Men sanningen att säga: Fråga DEN.

*

Se även i KONSEKVENSER — ALLMÄNNA STYCKEN SOM BESKRIVER KONFLIKTEN mellan Modern Akademi och Relaterad Fysik speciellt angående magnetismen: Ampere, Maxwell och B i MAC.

Ampere, Maxwell och B i MAC — Tillägg 5Okt2011 · Länkar vänster

0 | 1 | | 2 | | 3 | | 4 | | 5 |

BILDKÄLLA: Författarens arkiv · Viken13Apr2010Bild201 · NikonD90 · Detalj

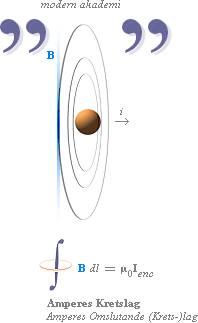
Amperes omslutningslag och magnetismen i modern akademi

2011IX20

Amperes omslutningslag och magnetismen i Modern akademi (MAC)

Angående Maxwells justering av Amperes Kretslag — konv. eng., Ampère’s Circuital Law, Amperes Kretslag, Amperes Omloppslag, Amperes Omslutningslag [helst inte »Amperes lag», det finns nämligen också en Ampère’s Force Law, kraftverkan mellan elektriska ledare]

Vilken relaterad innebörd har begreppet om »en magnetisk fältstyrka» via en av strömmen omsluten (godtycklig) tvärsnittsyta?

— Felet växer med avståndet.

:

— I relaterad fysik bygger hela magnetismens härledning på det som INTE finns i modern akademi: kausallogikens Kausalsamband (se Kausalsambandet). Nedanstående sammanfattar ämnet via ikoniserade samlingspercept från Grundläggande Magnetmatematik.

Alla samband i PREFIXxSIN. FotoBILDKÄLLA: Författarens arkiv · 21Aug2011Blom1_18Excur16 · NikonD90 · Detalj

VINJETTSAMBANDEN: Fysikaliska storheterna direkt från elektriska kraftlagen F=RcQ²/A ger B=F/Qc=RQ/A=(R/c=µ)(c=s/t)Q/A=µsI/A; Med s=2r och A=sfärytan — se Närverkan — ges µI/2πr. Se motsv. Rakledaren i Fjärrverkan.

— I modern akademi finns inte den kausallogiskt medhörande distinktion som skiljer på verkan INOM Q (närverkan) och verkan UTANFÖR Q (fjärrverkan).

— I (tydlig) följd av den omständigheten, ser vi stundtals i modern akademisk litteratur skriv- och beskrivningssättet (Omslutande Integralen [eng. contour integral] här som ○∫, något Unicodetecken med ringen inflyttad i integraltecknet tycks inte finnas)

○∫ B dl = µ₀I_enc .................. Amperes Omslutningslag

I engelsk litteratur kallas sambandsformen ovan Ampère’s circuital law, här försvenskat som »Amperes omslutningslag» [ref. @INTERNET Wikipedia Ampère’s circuital law], eller Amperes Kretslag.

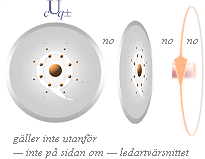
— I termer av relaterad fysik gäller ‘lagen’ INTE för annat än den direkt ledningsomslutande linjeintegralens yta. Alltså inte utanför själva ledarytan, och inte heller på något avstånd från tvärsnittscirkeln som skär ledaren.

Områden utanför r (ledaren) avbildar approximationer där felet växer med avståndet

— Sambandsformen (här differentierad) B=(µ/2π)(dI/dr) är som visats i Närverkan giltig sett med HELA strömflödet som EN idealt ihoppressad Q-skiva analog med strömledarens fysiska tvärsnitt och med idealt homogen i-fördelning över hela tvärsnittet. Sambandsformen har därför ingen direkt fenomenmässig koppling till områden utanför den fysiska ledaren. Det finns ingen sådan magnetfysik.

— Genom att B-vektorn i en TOROID omsluts av en motsvarande Q-form (ekvivalent normalt cirkulärt ledartvärsnitt), gäller (se B-styrkan i en lång rak spole) sambandet även (med god noggrannhet) toroiden med B-centralradien r enligt B=(µ/2π)(NI/r), N antalet lindningsvarv.

— Vi ser emellertid av den analoga gränsformen, i princip samma samband via Biot-Savarts lag med försvinnande b-vinkel B=(µ/2π)(I/x), att ÄVEN med viss utsträckning utanför ledarytan, »gäller sambandet approximativt».

— Följaktligen ser vi i modern facklitteratur en (stor) mängd applikationsexempel som söker »rättfärdiga Amperes kretslag» som fenomengrundad under olika betingelser, trots att den rent principiella — fenomenmässiga — fysiken som Amperes kretslag beskriver inte existerar i sammanhanget.

Jämför citatdelen nedan,

“Ampère's circuital law is now known to be a correct law of physics in a magnetostatic situation”,

@INTERNET Wikipedia Ampère's circuital law, Original Ampère's circuital law [2011-09-22]

http://en.wikipedia.org/wiki/Amp%C3%A8re's_circuital_law

— Magnetiska fältstyrkan utanför ett givet ledaravsnitt i förlängningen av strömleden, är ett direkt exempel som visar begränsningen i Amperes kretslag; Utanför en ledare, i dess strömleds förlängning, finns ingen som helst koppling till någon närvarande förorsakande elektrisk laddning, och därmed heller ingen omslutande kretsslinga att integrera på.

— Man skulle NORMALT SETT ÖVERGE uppfattningen om »lag» för »Amperes kretslag» ENBART med det exemplet som grund.

— DEN Föreställningen finns emellertid INTE i modern akademi (men det finns andra, på sätt och vis liknande, vidare nedan), varför man istället söker KOMPENSERA FELET med tillägg — och som leder till ytterligare fenomengrundade trassligheter i den moderna akademins lärosystem i ämnet magnetism och induktion.

— Wikipediaartikeln för sin del belyser »Amperes kretslag» med konsekvenser som kräver korrektioner och säger,

“James Clerk Maxwell conceived of displacement current as a polarization current in the dielectric vortex sea, which he used to model the magnetic field hydrodynamically and mechanically.[9] He added this displacement current to Ampère's circuital law at equation (112) in his 1861 paper On Physical Lines of Force .[10]”,

@INTERNET Wikipedia Ampère's circuital law, Shortcomings of the original formulation of Ampère's circuital law [2011-09-22]

http://en.wikipedia.org/wiki/Amp%C3%A8re's_circuital_law

— Men läser man Maxwells On Physical Lines of Force (1861) omnämner han ordet Ampere bara en gång, sidan 505 — och då endast i förbigående:

“The theory that electric currents are linear, and magnetic forces rotatory

phenomena, agrees so far with that of Ampere and Weber ...”,

James Clerk Maxwell, ON PHYSICAL LINES OF FORCE (1861), s505

THE SCIENTIFIC PAPERS OF JAMES CLERK MAXWELL, DOVER PUBLICATIONS, INC., NEW YORK [1890]

Finns som gratis PDF-dokument på Internet Archive,

http://www.archive.org/details/scientificpapers01maxw

— Maxwell omnämner Ampere bara i förbigående;

— Det finns — i den aktuella sektionen — inga speciellt namngivna samband som Maxwell refererar till som typ »Amperes ekvationer». Ingenting av den typen specificeras i Maxwells skrift.

Däremot omnämner Maxwell Amperes ekvationer i tappningen “laws of the attractions and repulsions of

electric currents” i ON FARADAY'S LINES OF FORCE s193.

[Deras formulering har här veterligt inget omnämnande eller hänvisning i Maxwells beskrivning i sektionen ON PHYSICAL LINES OF FORCE].

Maxwells extensiva utvecklingar beträffande “electric displacement” är desto mera omfattande. Det samband för STRÖMSTYRKA som Maxwell utgår ifrån (ekv.9 s462, “the strength of an electric current parallel to z through unit of area”), och som han refererar till (s496 Prop. XIV), har uppenbarligen ingen direkt koppling till just »Amperes kretslag», i varje fall inte sådan den ter sig i ovan citerade tappning.

— Maxwells utgångspunkt är istället, tydligen, enbart att rättfärdiga just begreppet deplacement, eller (elektrisk) förskjutning för ändamålet att inkludera i strömstyrkans definition (i Maxwells allmänna resonemang) detaljen med (motsvarigheten till) elektrisk polarisation, fenomenet att en viss energi i en ström åtgår för att polarisera explicit icke strömförande men spänningsavkännande delar. Som Maxwell själv uttrycker saken:

frn. s491n:

“These relations are Independent of any theory about the internal mechanism

of dielectrics ; but when we find electromotive force producing electric displacement

in a dielectric, and when we find the dielectric recovering from its state

of electric displacement with an equal electromotive force, we cannot help

regarding the phenomena as those of an elastic body, yielding to a pressure,

and recovering its form when the pressure is removed.”,

James Clerk Maxwell, On Physical Lines of Force (1861), s491n

— Ändamålet i Maxwells framställning kopplar tydligen till en ren strömteknisk, allmän, definition som innefattar alla möjliga fall (och — eller Men — som i efterhand utnyttjas frekvent i moderna kvarter för insättning i alla möjliga sammanhang, tydligen även sådana som Maxwell själv aldrig explicit formulerat).

— Grunden till »dielektriska förskjutningen» omnämns i början av boken, citatet nedan, genom dåtidens allmänt uppdagade experimentella resultat, att man inte kunde bortse ifrån just inverkan av dielektrikum i de allmänna sambanden;

“The investigations of Hertz have shewn that

electro-dynamic radiations are transmitted in waves with a velocity, which, if not equal to, is

comparable with that of light, and have thus given conclusive proof that a satisfactory

theory of Electricity must take into account in some form or other the action of the

dielectric.”,

THE SCIENTIFIC PAPERS OF JAMES CLERK MAXWELL, DOVER PUBLICATIONS, INC., NEW YORK [1890], inl. sidan xxii.n

— Därmed framgår tydligare Maxwells motiv med »displacement current»:

— Att Maxwells bidrag här skulle ha haft, alls, någon åsyftande koppling till att »justera Amperes kretslag», citatet från Wikipedia, det är i åsyftningens form, uppenbarligen, resultatet av en senare modern omskrivning som har föga med den historiska sanningen att göra, men som kanske är bekväm för de moderna snillen som också omarbetat Maxwells ursprungliga sambandsformer till den mera avancerade moderna akademins skrivsätt — och som (följaktligen) bara förvillar ytterligare.

Klargörande aspekt på

den modernt påstådda »Maxwells justering av Amperes Kretslag»

END.

Magnetiska kraften mellan parallella ledare — konv. Amperes Kraftlag

Magnetiska kraften mellan parallella ledare — konv. Amperes Kraftlag

Med magnetismens (magnetiska fältstyrkans B) definition i NÄRVERKAN från elektriska laddningens kroppsyta som B=µI/2πr=µH, med H som magnetiserande kraften (från eng. magnetizing force), tillsammans med magnetiska kraftlagen, F=BQu=BIℓ, ges direkt en förenklad form för kraftverkan mellan två (oändligt utsträckta, i praktiken mycket långa relativt deras inbördes avstånd) raka parallella ledare enligt

B = (µ/2π)I₁/r ;

F = B·I₂ℓ = (µ/2π)I₁/r · I₂ℓ

= (µ/2π)I₁I₂ℓ/r ....................... konv. Amperes kraftlag

Det är samma formalia som (Sep2011) beskrivs på artikeln

@INTERNET Wikipedia Ampère's force law

Sambandsformen påstås ligga till grund för definitionen av enheten 1 Ampere:

Med I=1Ampere, ℓ=1Meter och

µ/2π = r

= (1,99997 t7 VS/AM · 1A/VS)

~ 2 t7 M (vilket skulle kräva extremt tunna trådledare; < Ø0,1µM) ;

utverkas en kraft mellan ledarna på 1Newton (0,1019667 KP; tyngden på Jordytan av ca 1dL vatten).

Maxwells begrepp Magnetizing Force

— Begreppet magnetiserande kraft H=I/2πr i relaterad fysik är här tydligen av samma upphov som Maxwells från 1855:

“If we examine the lines of magnetic force produced by a closed current,

we shall find that they form closed curves passing round the current and

embracing it, and that the total intensity of the magnetizing force all along

the closed line of force depends on the quantity of the electric current only.”

;

James Clerk Maxwell, s184n ON FARADAY'S LINES OF FORCE (1855);

THE SCIENTIFIC PAPERS OF JAMES CLERK MAXWELL, DOVER PUBLICATIONS, INC., NEW YORK [1890]

— Det fins EMELLERTID (också) här en viss obskyr historia:

— “all along the closed line of force” är ett — trots definierat som B-riktningens sammanhängande utsträckning [Maxwell s158, “...and might be called on that account a line of force”] — milt sagt diffust begrepp i Maxwells beskrivning.

— I relaterad fysik (se från Närverkan) har omslutningen 2πr en begränsad betydelse TILL strömledaren: formen gäller endast med referens till gränsen för (förekomsten av laddningsmassa i rörelse) den aktuella strömledarens yta — inte utanför. Någon godtycklig B-kurva UTANFÖR denna gräns finns, i relaterad mening, ingen magnetiskt fenomenfysikalisk grund för — därför att heller ingen elektrisk laddning finns där.

— Det förefaller — NÄMLIGEN — som att Maxwell i sin beskrivning är ute och snurrar UTANFÖR LEDARYTAN när han (s185ö) talar om “number of unit lines of magnetic force” och “number of unit cells in each complete line of force is measured simply by the number of unit currents which embrace it.”. Inte PÅ (eller i) ledarytan.

— Men det sägs inte uttryckligt — men nära (direkt efter ovan, Maxwell s185ö):

“The unit cells in this case are portions of space in which unit of magnetic quantity is produced by unity of magnetizing force.”;

“The length of a cell is therefore inversely as the intensity of the magnetizing

force, and its section inversely as the quantity of magnetic induction at that

point.”,

James Clerk Maxwell, s185 ON FARADAY'S LINES OF FORCE (1855)

— Maxwells RYMDCELL har ingen motsvarighet i relaterad fysik, och inte heller något ANTAL magnetiska fältlinjer;

— Magnetiska fältlinjernas BILDLIGA praktik sammanhänger med de material [järnfilspån oftast] som formar dem [som i all annan naturligt våggenomströmmande verksamhet i formen av resonanser, stående vågmönster], och avspeglar ingen egenskap i »fältlinjerna» som sådana. Det finns ingenting sådant i relaterad fysik.

— B-linjerna, relaterad fysik, sprids från bildningen i sina lokalt dominant gravitellt relaterade rymdpunkter med den reducerat bildade något lägre ljushastigheten [reduktionen ç] mot den tunnare fria rymdens c, och bildar på den vägen mönster [fasta, sammanhängande magnetiska kraftfältslinjer] genom passagen i olika [magnetiska] material.

— Magnetiska fältlinjerna i relaterad fysik innehåller inga “celler” eller består av något “antal fältlinjer”. Det är emellertid den APPLICERADE MEKANIK som Maxwell använde för att beskriva ämnet matematiskt med dåtidens [runt 1860] fysikkunskaper — och som vi kan känna igen i (olika) ANALOGIER.

— Maxwells CELLANALOGIER grundas på hans beskrivning från s160, Theory of the Motion of an incompressible Fluid. Hela Maxwells elektrofysikaliska matematik bygger på analogier hämtade ur den upprinnelsen.

Jämför s162ö,

“(7) We have now obtained a geometrical construction which completely

defines the motion of the fluid by dividing the space it occupies into a system

of unit tubes.”;

s160ö;

“(1) The substance here treated of must not be assumed to possess any of

the properties of ordinary fluids except those of freedom of motion and resistance

to compression. It is not even a hypothetical fluid which is introduced to

explain actual phenomena. It is merely a collection of imaginary properties

which may be employed for establishing certain theorems in pure mathematics in

a way more intelligible to many minds and more applicable to physical problems

than that in which algebraic symbols alone are used. The use of the word

"Fluid" will not lead us into error, if we remember that it denotes a purely

imaginary substance with the following property :

The portion of fluid which at any instant occupied a given volume, will at

any succeeding instant occupy an equal volume.”, med vidare.

Citaten ovan från Maxwells ON FARADAY'S LINES OF FORCE (1855) ur

THE SCIENTIFIC PAPERS OF JAMES CLERK MAXWELL, DOVER PUBLICATIONS, INC., NEW YORK [1890]

GENOM den relaterade fysikens LJUSETS FRISTÄLLNING FRÅN KINETIKEN — frikopplandet av Maxwells matematiskt analoga cellmekanik från den praktiska fysiken — försvinner också motsvarande intervalldomäner [Maxwells virvelceller och liknande modellbyggen] ur Maxwells beskrivning.

Det är delvis svårt [och delvis lätt] att följa Maxwell i hans matematiska utsvävningar: termernas innebörd förefaller ofta förloras i ett kaos av abc, xyz, αβγ, XYZ, och liknande, och det blir sedan ingen enkel sak att hitta igen deras ursprung i en samling på 668 sidor utan direkta hänvisningar som hjälp — om ens det räcker. För att få en klar bild av vad Maxwell menar i sina detaljer måste man [nog] ställa upp en termatiskt välordnad och länkad nomenklatur till jämförelse. Det blir i vilket fall ett omfattande verk som ännu väntar på sin sammanställare.

— Maxwells beskrivning liknar här mera (som det ser ut) Amperes Kretslag [Bds=µI].

— Men vi kommer nog heller inte så mycket längre i dessa efterforskningar:

— OM vi (jag) inte hittar något mera klargörande citat från Maxwell, är det i vilket fall redan uppenbart ATT Maxwell ALDRIG kan klargöra sig på den berörda punkten: huruvida B-fältet ska förstås UTANFÖR ledarytan eller inte (moderna korridorers fackboksförfattare verkar se saken just så; utanför).

— Det står alldeles klart att det är så därför att såväl Maxwell som hans samtida inte SER att det finns en underliggande expansionsintegral (nedan, samt explicit i Vektorkalkylens sammanbrott inom magnetismen i modern akademi), en hela magnetismens grundval, som magnetismens grundläggande fenomenform utgår ifrån:

— Den relaterade fysikens elementära formulering av expansionsintegralens differentialekvation

— som inte omfattas av modern akademi utan som i stället används FÖRST från sin LÖSNING som den konventionellt benämnda Biot-Savarts lag, och vars differentialekvations utelämnande — tydligen — förklaras på grund av att sammanhanget ELJEST kommer i frontalkollision med DEN MODERNT AKADEMISKA VEKTORKALKYLENS FORMULERING i ämnet, se utförligt från Regelbrott i Vektorkalkylen

— utesluter varje begriplig, klar, entydig och koncis formulering i modern akademi.

— Varken Maxwell, Ampere, eller någon deras samtida eller nutida, tycks ha insett DET de BORDE ha insett med koppling redan mer än 100 år före Maxwell: James Bradley 1725 (publ. 1729), upptäckten av aberrationen: fenomenet som visar ljusets friställning från kinetiken, LJUSETS GRAVITELLA BEROENDE (som tydligen helt undgick den moderna akademins framväxt under 1800-talet); Magnetiska fält uppkommer från elektriska laddningar i rörelse (genom de elektriska laddningarnas statiska fälts ändrade potentialbilder i) fasta, fixa, omgivande lokalt dominanta gravitationsfälts rymdreferenspunkter och inget annat; Det är FÖRST därifrån som magnetismen som fenomen blir begripligt, beskrivbart och fullständigt förklarligt.

— Expansionsintegralen ingår inte i den moderna akademins föreställningsförmåga, ehuru tydligtvis grundläggande för den allmänna praktiken på lösningsformen Biot-Savarts lag.

Amperes Kretslag, konv. eng. Ampère’s circuital law

Magnetismen i modern akademi · BILDKÄLLA: Författarens arkiv · 21Sep2011UtsiktMoln_20Excur17 ·NikonD90 · Detalj

Amperes Kretslag — [ref. @INTERNET Wikipedia Ampère’s circuital law] — Magnetismen i modern akademi

http://en.wikipedia.org/wiki/Amp%C3%A8re's_circuital_law

Modern akademi, nedan mitten, verkar inte ha någon bestämd uppfattning om HUR den magnetiska fenomendetaljen bildas eller utvecklas (se även Citatblocket):

Det oerhörda i sammanhanget är att det, tydligtvis, också finns en FULLSTÄNDIGT UTTÖMMANDE FÖRKLARING till VARFÖR och HUR modern akademi heller inte kan ha eller få fram någon bestämd uppfattning i saken. Nämligen genom den relaterade fysikens grundbeskrivning från Expansionsintegralen med tillhörande Vektorkalkylens sammanbrott i MAC. I kort sammandrag: Modern akademi utesluter TVÅ av de TRE fullständigt beskrivande vektorformerna — i en och samma 3D-vektorkropp dessutom, de facto — som grundlägger magnetismens bildning och uppkomst — och börjar först med den resulterande tredje, sista, 3D-vektorn: Biot-Savarts lag. Se utförligt från Expansionsintegralen. Då man sedan ska förklara fenomengrunden, är det klart att högsätet för det uteslutna också lyser med sin frånvaro i de beskrivande festligheterna: Ingen kan begripliggöra något djupsammanhang; Ingen kan förklara detaljerna i magnetismens fenomenfysik eftersom de har uteslutits.

Trigonometriska samband här i PREFIXxSIN. Reg synkoperar den lokalt dominanta gravitationens rymdpunkter som referenser. Se utförligt från Kausalsambandet.

Konsekvenser till påseende INOM MAGNETISMEN — naturkonflikten mellan Modern Akademi och Relaterad Fysik	Modern akademi	Relaterad fysik
Parallellexperimenten induktion och magnetism växelverkar inte Förtydligandet till Faradays EMI Expansionsintegralen µ0 Vektorfelet i MAC Vektorkalkylens sammanbrott i MAC Ampere, Maxwell och B i MAC Tre Jämförande Exempel induktion och magnetism växelverkar inte
MAC, förkortn., Modern akademi	differentialelement: Biot-Savarts lag *	differentialelement: Magnetiska laddningsfältspotentialen som ovan

*Se utförlig beskrivning i Vektorkalkylens sammanbrott INOM MAGNETISMEN i modern akademi.

— Det ser ut som (men som, citatformen nedan frånsett, verkar omöjligt att få fatt på i direkt mening) att man i modern akademi tror att magnetiska fältringar bildas utgående ifrån, och alltså i bildningshänseende är begränsade till, den elektriska laddningens materiella kroppsyta. Det är i varje fall så den s.k. Amperes Krets(omslutande) Lag skrivs (och tolkas), integralformen ovan mitten med den angivna ringintegralen. Se @INTERNET Wikipedia Ampère's circuital law 2011-09-21. Den antydda »Avgränsningen» får också konsekvenser: man menar att det finns ett magnetisk fält typ mellan plattorna på en kondensator som laddas upp-ur, med — TROTS — hänvisning till att det inte finns någon ström av elektriska laddningar där. Jämför utdraget nedan:

”Although current is flowing through the capacitor, no actual charge is transported through the vacuum between its plates. Nonetheless, a magnetic field exists between the plates as though a current were present there as well.”,

@INTERNET Wikipedia Displacement current [2011-09-20]

http://en.wikipedia.org/wiki/Displacement_current

— Men det är också i princip OMÖJLIGT att hitta direkta utsagor som SÄGER det DIREKT: magnetfält bildas [UTESLUTANDE] som koncentriska ringar utgående ifrån en elektrisk laddning i rörelse.

Fullt allvar.

— I relaterad fysik (Kausalsambandet) bildas magnetismen som ringar på vattenytan (V) : V avbildas upphängd i den omgivande rymdens lokalt dominanta gravitationsfälts fasta och fixa rymdpunkter, figuren ovan höger. Fältringarna uppkommer då den elektriska laddningens statiska elektriska fältpotentialer ändras i de aktuella g-punkterna som följd av laddningens lägesändring. Magnetiska fältringar återfinns därmed i princip — förr eller senare, med ljushastighetens fördröjning — överallt i hela universum för varje minsta lägesändring hos en elektrisk laddning: i förlängda framriktningen, bakåt, och även åt sidorna (utom exakt rätvinkligt lägesändringen om laddningen avbildar ytan hos en idealt homogent sfäriskt formad kropp).

— Se den sammanställda vektorillustrationen i Magnetiska Laddningsfältspotentialen (förminskad nedan) med tillhörande 3D-vektorsatsbildningsblock för att orientera sammanhanget.

Magnetiska laddningsfältspotentialen

Det är ur den relaterbara magnetfysikens synvinkel alltså tydligt att Amperes Kretslag beskriver en direkt stympning av den aktuella fenomenformen: magnetfälten som finns UTANFÖR en ledare (avslutad eller böjd) utesluts tydligen i Amperes Kretslag: Den i Amperelagen omslutande B-formuleringen utesluter partier ur strömmens magnetiska fältbildning (man kan — enligt relaterad fysik — inte avgränsa magnetismen så som antyds av Amperes Ketslag med mer än man stympar fenomenfysiken i samma utsträckning), och som därför på olika sätt måste kompenseras för, för att sambandet ska framstå fullständigt.

— För att få med den av den begränsade B-slingan utelämnade strömdelen i Amperes Lag måste man, i termer av hur saken beskrivs i modern akademi, införa det som kallas (eng.) Displacement Current.

— Det finns emellertid (här) ingen direkt säker framställning i ämnet, eftersom den moderna akademins utläggningar i saken bygger på det som REDAN visats innehålla inkonsistens:

1. ingen uttalad uppfattning finns i modern akademi att magnetismen gäller med utgångspunkt från den lokalt dominanta gravitationens referenspunkter (se relaterad fysik utförligt från Kausalsambandet),

2. expansionsintegralen ingår inte i den moderna akademins föreställningssätt, men väl dess lösning som Biot-Savarts lag (man hoppar alltså över Kausalsambandet — den relaterbara förklaringen till magnetismens uppkomst — och Planvektorsumman — den allmänna trigonometriska fältekvivalensen mellan expansioner och tangenter; Se exempelframställningen i Vektorkalkylens sammanbrott inom magnetismen i MAC);

— I modern akademi börjar man således från Biot-Savarts lag — och som i ljuset av Amperes KretsOmslutandeLag (eng. Ampère’s circuital law) också får den moderna akademins stämpel att vara en begränsad formulering i magnetismens elementära fysik. Man säger att dessa samband, Biot-Savart och Ampere, gäller magnetostatiskt. Jämför citatet nedan;

“The law is valid in the magnetostatic approximation, and results in a B field consistent with both Ampère's circuital law and Gauss's law for magnetism.”,

@INTERNET Wikipedia Biot–Savart law [2011-09-21]

http://en.wikipedia.org/wiki/Biot-Savart_law

— Det komplicerar genomgången betydligt.

— Det finns här ingen allmänt känd form för hur tolkningarna i de olika korridorerna ska göras i den moderna akademins utsagor, utöver vad som här har påpekats.

— Jämför även citatet nedan;

“Few topics in modern physics have caused as much confusion and misunderstanding as that of displacement current.”,

@INTERNET Wikipedia Displacement current, History and interpretation [2011-09-20]

http://en.wikipedia.org/wiki/Displacement_current

Saken görs inte mindre komplicerad av att man (generellt) i modern litteratur illustrerar ämnet ur flera, till synes inbördes motsatta (kaotiska), synvinklar och utan att närmare förklara den (för en lekman) uppenbart obesvarade fenomengrunden; Bilderna nedan från Hyperphysics, Ampère’s Law som ovan och Biot-Savart Law;

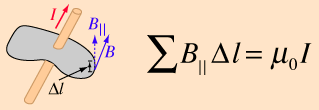
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/amplaw.html

— Å ena sidan, ovan, ser det ut som att man förstår B-fältet som AVGRÄNSAT till någon omskriven yta rätvinkligt själva den magnetbildande strömleden.

— Å andra sidan, nedan, ser det ut som att man medger GODTYCKLIGA lokationer för magnetiska fältstyrkan B relativt den strömledsdel som ansvarar för bildningen. I ingetdera fallen ges någon förklaring till hur man tänker sig fältstyrkans utbildning.

— Jag vill inte skriva under på att en sådan lärobild kan kallas UNDERVISNING. Jämför uteslutningarna i Vektorkalkylens sammanbrott inom magnetismen i MAC.

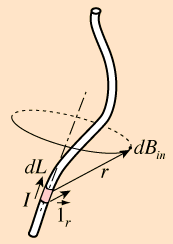
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/biosav.html

Saken kompliceras ytterligare av att Displacement Current i modern akademi anses uppkomma ur varierande elektriska fält — som någon slags superfenomengrund vid sidan av det övriga. Jämför citatet nedan, samma källa som närmast ovan;

“Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do.”;

“However it is not an electric current of moving charges, but a time-varying electric field.”.

Här framträder — tydligt — den inneboende konflikten i Magnetismen och Induktionen [konv. Faradays lag] i modern akademi — i ljuset av den relaterade fysikens härledning till Induktionen och Magnetismen, i vidare stöd av Parallellexperimenten med resultatredovisningens notation: Notera den exakta innebörden av den elektroMEKANISKA induktionen.

;

KOMMENTAR:

»A Time Varying Electric Field» återfaller i vilket fall på en energiräkning E=UQ:

— Med given laddning Q är ändringen i energi E och potential U direkt proportionella. Men potentialändring är samma som lägesändring [även ytdeformation] av Q;

— Fysiken för uppkomst, eller variation, av en elektrisk spänning U är omöjlig utan en förflyttning — acceleration — av elektrisk laddning [Q=E/U=Fd/U=mad/U]: det är uppkomsten av induktion i relaterad fysik, samt uppkomst av magnetism [B]; Från elektriska laddningen [Q] via elektriska kraftlagen F=RcQ²/A som B=F/Qc=RQ/A till den aktuellt påvisbara magnetiska fältstyrkan B=(R/c)(s/t)Q/A=µsI/A. Dvs., magnetisk fältstyrka definieras i relaterads fysik entydigt på en Q-rörelse relativt den lokala g-divergensen [c]. Inget annat.

— Citatmeningen ovan kan [alltså] göra anspråk på vad den vill, men den är i vilket fall tydligen INTE välrelaterad för energins räkning, “not an electric current of moving charges”. Här visas [således] ytterligare ett exempel på komplikationer i modern akademi.

— Ytterligare en annan detalj är just termen »varying»:

— Fenomenet skulle inte finnas för konstant ström?

— Här framträder således ännu en oklar detalj i modern akademi [se föregående citat]:

@INTERNET Wikipedia Displacement current [2011-09-20]

”Although current is flowing through the capacitor, no actual charge is transported through the vacuum between its plates. Nonetheless, a magnetic field exists between the plates as though a current were present there as well.”.

— En kondensator som uppladdas med KONSTANT STRÖM — konstantströmsgenerator, ofta förekommande elektronisk konstruktion i många praktiska applikationer — uppvisar en magnetisk fältstyrka ÄVEN mellan ett par kondensatorplattor. Det har ingen betydelse om strömmen som laddar kondensatorn är konstant eller variabel. Magnetfältet finns där i vilket fall, trots att någon direkt laddningstransport inte sker mellan kondensatorplattorna över deras separerande avstånd. Citatet längre upp talar emellertid om »time varying electric field» — SOM OM magnetfält mellan kondensatorplattor inte skulle finnas med konstant uppladdningsström.

— Någon utvikande förklaring eller beskrivning till [den SÅ för en lekman] uppenbarade, obesvarade, fenomenbeskrivningen ges inte.

— I modern akademi anser man som bekant att det är variabla magnetisk fält som bildar induktionen: dvs.: elektriska fält som ändras med tiden bildar också magnetiska fält, enligt modern akademi.

— DEN INDUKTIVA ASPEKTEN bara understryker den allmänna svårigheten att, med referens till den redan etablerade nomenklaturen, formulera KONSISTENTA MENINGAR i ämnet.

— Maxwell [1861] införde en Displacement Current — [s496 ekv.105 ON PHYSICAL LINES OF FORCE] för att KOMPLETTERA strömbildens helhet med sidoeffekten som innefattar elektrisk polarisation — [från Electric Displacement] — vilket Maxwellska införande enligt moderna källor emellertid skulle ha skett som ett JUSTERANDE TILLÄGG till Amperes Kretslag. Men den framställningen tycks från Maxwells sida emellertid, tydligen, inte vara av karaktären »feljustering av Amperes lag». Se relaterad, citerad, beskrivning i Ampere, Maxwell och B i MAC. Här framträder (således, om korrekt uppfattat) ytterligare en oklarhet som fördunklar och, högeligen, försvårar en begriplig översikt i sammanhangen — sådana de presenteras i moderna kvarter.

Associationerna leder (således, vidare) till den moderna akademins allmänna föreställning om »elektromagnetisk induktion»: vektorproduktens förenklade fenomenbeskrivning (se Vektorkalkylens regelbrott) som utesluter expansionsintegralen och sammanför magnetism och induktion under ett och samma matematiska tak. Konsekvenserna beskrivs i Tre Jämförande Exempel.

— Magnetismens fenomenfysik i modern akademi trängs, tydligen, undan till förmån för den moderna akademins mera viktiga matematiska övningar.

Också just begreppet Displacement current som en justerande faktor i Amperes Kretslag ges — påstås — i den moderna beskrivningens termer äga upphov i Maxwells framställningar.

— I dagens läge finns alla Maxwells vetenskapliga verk (’Maxwells papers’) samlade för gratis läsning, så vi kan själva kontrollera varje sådant påstående.

— I detta fall verkar sammanhanget snarare vara en modern omskrivning, än en historisk rapport. Se utförligt från Ampere, Maxwell och B i MAC.

Amperes Kretslag i Praktiken

Amperes Kretslag i Praktiken

Samma som NÄRVERKANS APPLIKATION i relaterad fysik

— I relaterad fysik är B-värdet endast ett punktvärde som kan mätas lokalt med (t.ex.) ett Hallelement;

— Men i den moderna akademins (alltmer komplicerade) vidlyftiga högskolebeskrivningar, förefaller det (allt mera) svårt att få KLARHET i exakt vad som menas GÄLLER från det moderna akademiska hållet. Jämför Citatblocket. Det finns inga verk i modern akademi som klarlägger detaljerna på ett språk som kan förstås av den som kan läsa.

— I (sålunda) takt med tidens växande brist på begripliga förklaringar, förefaller istället historien skriva den moderna vetenskapens sidor som en process av (allt mer) reducerat vett som bygger in sig i allt mer abstrakta hänvisningar, en sammankomst som är ägnad att konservera klubbens inre slutna cirkel, genom att (också framledes fortsätta) utestänga fysikens elementära förklaring.

— Det liknar en ljusnande horisont som avtecknar ett sjunkande fartyg.

I relaterad fysik är närverkan B=(µ/2π)(I/r) begränsad till strömledarens radie (r). Sambandet fråntas därmed sin direkt fenomenrelaterade grund utanför den fysiska ledarens r.

— B gäller avgränsat till (en idealiserad, omskriven cirkulär omkrets för) den fysiska laddningens kropp — närverkan — i idealiserad form som en hel, cirkulärprojicerad, idealt sfärisk, laddningskropp Q för hela strömstyrkan. Ingenting utanför.

— B är ett (idealt) punktvärde som gäller överallt i hela den Q-omslutande 2πr-ringen: Det är lika med motsvarande sambandsvärde i Biot-Savarts lag mitt på ytan av en rakledare OM dess längd är stor relativt ledardiametern.

— Ju längre ut från (den cirkulära) ledarytan på en begränsad ledare man mäter, desto större blir felet.

— Det är alltså i och för sig OK att differentiera enligt B=µ(dI/ds). Men att i den situationen också framställa en differentialekvation på formen (konv. Amperes Kretslag, eng. Ampère’s Circuital Law)

Bds = µdI ;

∫Bds = µI

i meningen av att distansen (s) skulle gestalta någon fysiskt godtycklig rymdomslutande linje för B, det BRYTER tydligen grundformen och inför en approximerad fysikform vars fel uppenbarligen växer med s-formens differens mot den aktuella strömledarens radie. Det är följaktligen i relaterad mening ingen riktig magnetfysik. Jämför moderna kvarter:

“Although this result

was calculated for the special case of a circular path surrounding a wire, it holds

for a closed path of any shape surrounding a current that exists in an unbroken circuit.”,

“The general case, known as Ampère’s law, can be stated as follows:

The line integral of B·ds around any closed path equals µ₀I, where I is the total

continuous current passing through any surface bounded by the closed path.”,

“Ampère’s law describes the creation of magnetic fields by all continuous current

configurations”,

frn.s945n [okänd källa, okänd datering, men ambitiöst snyggt utformad — verkar vara en rest från [nu 2011] utgången webbsida, möjligen från runt 2001,

CHAPTER 30 Sources of the Magnetic Field

http://200.105.152.242/olimpiada/file.php/1/LIBROS_OLIMPIADAS/FISICA SERWAY/30-SourcesoftheMagneticField.pdf

Källan ovan tycks inte exemplifiera någon (direkt) utpräglad tillämpning av det den påstår »Amperes kretslag» vara kapabel till;

— Källan exemplifierar samma typ av resultat (vi finner enklare) i den relaterade fysikens beskrivning grundad på just närverkans princip (se från Närverkan):

— B-fälten inuti kompakta och rörformade ledare, samt (motsvarande) toroider och (långa) spolar.

— Inget annat.

Vi finner samma exempeltyp i

(toroider, spolar)

Ampere’s Circuital Law and Applications 01.06.09

http://www.ssapunjab.org/sub%20pages/edusat/phy3.pdf

Samt i (till synes) alla övriga som finns på webben (Sep2011):

spolkonstruktioner: toroider, spolar av olika form och typ.

Med andra ord: Den moderna formuleringstypen av arten »around any closed path» tycks lysa med sin frånvaro i praktiska exempel. Man använder genomgående just den relaterade fysikbeskrivningens närverkande princip för Q-rörelsen (se från Närverkan).

Ampere, Maxwell och B i MAC — Tillägg 5Okt2011

InduktionenOchMagnetismen | AppENDix

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Induktionen och magnetismen APPENDIX

ämnesrubriker

innehåll

INDUKTIONEN OCH MAGNETISMEN APPENDIX

Magnetiska fältvektorns matematiska uppkomst

Den matematiska uppkomsten av den magnetiska fältvektorn

Ekvivalensen mellan expansionsvektorer och tangentvektorer

Den allmänna beteckningen B

Elektriska fältstyrkans frihetssats

Fältstyrkefrihetssatsen

Elektriska fältets geometri

Elektriska fältets elementära geometri

Det grundläggande elektriska divergensfältet

Matematiken för elektriska fältet

Den moderna akademins begränsade referenser

Elektriska fältets relaterade matematik

Dipol

Antidipol

Fältstyrka och Potential

Begreppen Fältstyrka och Potential

Vanliga vanföreställningar i modern akademi och vetenskap om elektriska termer

Potentialbegreppet

Vektor och skalär

Begreppet fältstyrka

Potentialens viktighet

Elektriska fältets begrepp

EXEMPEL — i jämförelse med modern akademi

Magnetiska fält

Relaterad fysik och modern akademi — 1/r² KONTRA 1/r

Parallellexperimenten

Parallellexperimenten från 1994

Utförande

Mekanik

Kopplingsschema

Kretsbeskrivning

Uppmätning av magnetisk fältstyrka

Syntes av Induktionen och Magnetismen

Beskrivning

Induktiv potential

Magnetisk potential

Tre precisa exempel för exakt jämförelse

Treatise

Jämförelse mellan relaterad fysik och modern akademi i induktion och magnetism

Exempel 1 · ringspoleinduktansen

Exempel 2 · induktionens felaktiga identifiering med magnetismen som leder till den moderna akademins matematiska formalia

Exempel 3 · allmänna självinduktionen på ytan av rakledare

Orsakerna

Induktionen och Magnetismen i modern akademi

Epilog

Ampere, Maxwell och B i MAC

Amperes omslutningslag och magnetismen i modern akademi

Amperes kraftlag

Maxwells begrepp Magnetizing Force

Amperes Kretslag, konv. eng. Ampère’s circuital law

Konsekvenser

Magnetiska laddningsfältspotentialen

Amperes Kretslag i Praktiken

Senast uppdaterade version: 2024-10-26

*END.

Stavningskontrollerat 2008-06-09 | 2011-10-05 | 2014-02-09.

rester

[uppPil; dess SymbolTeckensnitt visas inte i htm-dokumentet med Internet Explorer; anledning okänd]

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-09-06

åter till portalsidan · portalsidan är www.UniversumsHistoria.se