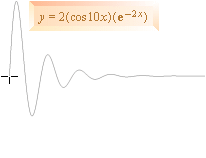ELEMENTÄR VÅGMEKANIK — UNIVERSUMS HISTORIA | a production 2008XI26 | Efter sammanställningar från 1982 | Senast uppdaterade version: 2017-08-13 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Elementär Vågmekanik | i sammanst. frn P2001_1a.wps 2001IX17 | 2008XII6-13 i sammanställning för Universums Historia

begreppet vågmekanik i modern akademi | våg-partikelfenomenet enligt TNED |

Den elementära vågmekanikens begrepp har (här veterligt) ingen vare sig svensk eller engelsk motsvarighet i en ELEMENTÄR beskrivning — av HUR vågbegreppet framväxer i fysiken ur de allra enklaste av förutsättningar: spegellagen, impulslagen, reflexionslagen. Det finns (veterligt) ingen webbkälla som beskriver ämnet från den synvinkeln. Ingen. Välkommen.

ELEMENTÄR VÅGMEKANIK

med tonvikt på vatten och ljus

Bilderna ovan illustrerar (vänster) Spegellagen som grundval för den vidare beskrivningen av den mekanism som sammansätter, formar och bildar vågbegreppet i fysiken i vidare mening (höger). Detaljerna bakom vågornas olika formationer kommer att beröras grundligt i denna presentation. Bilder och illustrationer ovan ur författarens privata arkiv.

Den elementära vågmekaniken beskriver ENLIGT RELATERAD FYSIK OCH MATEMATIK den fysikaliska uppkomsten av begreppet våg, vågens rent mekaniska fysik och dess växelverkan (interferens) med andra vågor utifrån de allra enklaste och mest primitiva redskapen för studium, analys och observation. Ämnet som sådant beskrivs i gängse lärobokslitteratur under rubriken VÅGRÖRELSER (vågrörelselära, skulle man kunna säga), se exv. GYMNASIETS FYSIK åk3 Liber 1980 som ger »en bra allmän översikt» — för att nämna ett konkret exempel.

Termen ”vågmekanik” i modern akademi har ingen liknande elementär koppling; Termen ”vågmekanik” associeras vanligen med den etablerade högskolefysiken på området kvantfysik och kvantmekanik. De senare är helt orepresenterade i den här framställningen. Jämför citaten nedan.

”Vågmekanik, detsamma som undulationsmekanik.”,

BKLXIIsp1037n (1928)

”Undulatio’n (av lat. u’ndula, liten våg), vågrörelse”,

BKLXIIsp85ö (1928)

”Undulationsmekaniken utgör en betydelsefull sida av den under namnet kvantmekanik kända generaliseringen av den klassiska mekaniken, som utvecklats under de senare åren i närmaste sammanhang med Bohrs atomteori. Med utgångspunkt i idéer, som framförts av fransmannen L. de Broglie (1924), har U. väsentl. grundlagts av österrikaren Schrödinger (1926).”,

BKLXIIsp85ö (1928)

För att särskilja begreppen benämns i denna presentation ovanstående citerade typ som kvantfysik, inte (elementär) vågmekanik. Den elementära vågmekaniken grundas i den här presentationen helt på Spegellagen — samma som impulslagen eller reflexionslagen (eller verkanslagen). Hur vågens mekanism därifrån framträder är vad följande beskrivning — enligt den elementära vågmekaniken — ska handla om.

Se även särskild korsreferens beträffande BEGREPPET VÅGMEKANIK i sektionen om Atomkärnan som elektromagnetisk transformator.

Elementär Vågmekanik | P2001_1a.wps 2001IX17 | Reflexionslagen

Experimentella Uppdaganden i Fysiken

Tillämpningar av Impulssambandet

REFLEXIONSLAGEN

Varje PUNKT i ytan på en kropp som deltar i någon energiomvandling (arbete, aktivitet)

— i beaktande av att punkten själv inte absorberar någon del av verkan

— kommer att returnera varje inkommande vektor tillbaka ut men omvänd enbart OM bevarandet av punktens eget vilotillstånd garanteras, och endast då.

Denna del med garanterat bevarad ytform motsvarar (således) rent mekaniskt ytpunkten som ”en idealt obegränsat hård ytpunkt”; den ändrar inte sin position under den inkommande vektorns inverkan.

Detta principiella beteende kan beskrivas i syntes som reflexionslagen — vilket i klartext betyder en mekaniserad ekvivalent version av Spegellagen:

inkommande = utgående;

reflexionslagen

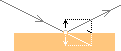
Reflexionslagen: Den resulterande verkan är summan av inverkans komponenter om ytan lämnas intakt; inkommande = utgående

Spegellagen utpekar grundbegreppen med linje, plan och punkt tillsammans med ovanstående geometriska satsbild. Därmed bildar också spegellagen den absolut beskrivande basen för vektorbegreppet (begreppen om en bestämd utsträckning [med bestämd längd]). Associeras vektorerna med massor (m) i rörelse (v) fås motsvarande impulslagen (p=mv) som utsäger samma som ovanstående men via kroppar som genomgår s.k. fullständigt elastisk stöt.

Spegellagen och Impulslagen eller Reflexionslagen bildar ALLTSÅ tillsammans med tillståndets princip — varje tillstånd eller ”kropp” bevaras så länge det inte genomgår en ändring — olika ekvivalenta uttryck för en och samma grundläggande princip och som absolut sammankopplar fysiken med matematiken-geometrin, illustrationen närmast ovan: inkommande är lika med utgående genom bevarandet av tillståndets princip; ingen verkan överförs till »materialet» som utför reflexionen. Impulslagen förklarar därmed hela den centrala mekanismen i fysiken i allmänhet (just vektorformerna) och vågmekaniken i synnerhet; hur en våg bildas och därmed hur den fungerar genom mekanikens begrepp.

Vi studerar hur.

I den ideala ytan — som alltså är helt noll i tjocklek — tar ingen punkt själv del i inverkan parallellt med ytan eftersom en ytpunkt är masslös: noll utsträckning och därmed heller ingen massa. Därmed KAN inkommande vektorer tillåtas GLIDA parallellt med ytan men inte att penetrera den men några bestämda intervall.

Denna symmetri av absolut reflexion för den penetrerande vektorn betyder att ytpunkten kommer att kasta tillbaka resultantvektorn i samma vinkelriktning den inkom; Om också den horisontella komponenten anses påverka ytan, kommer den inkommande vektorn att kastas tillbaka diametralt. Detta senare fall är aktuellt i det praktiska fallet när vi betraktar vissa ytnära referenspunkter (i fasta material), t.ex. på ytan av föremål med utpräglat oregelbunden ytjämnhet. Vi kommer dock här i fortsättningen endast att beröra de ideala ”plana” fallen.

TILLÄMPNINGAR 1

Kompakta kulor som träffar en solid idealt plan elastisk kropp

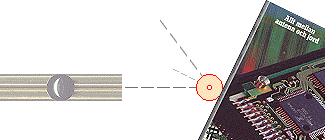
Utmärkt bekräftelse på reflexionslagen fås med några få relativt enkla hjälpmedel. Två metallrör tejpade tätt tillsammans, monterade i någon lutande vinkel mot t.ex. ett bord, ger hastighetens vektor för en metallkula. Denna infallsvektor riktas mot ett material som kan returnera den kolliderande inverkan från kulan. Det kan vara ryggen på en tjock katalog, eller bättre, sidan på ett tjockt skärbräde av trä. Förutsatt tillräcklig hastighet hos kulan och frånsett ett större eller mindre kulspinn som uppkommer vid träffen, kan vi observera att den utgående vinkeln är approximativt lika med den inkommande. Med hjälp av en penna och ett underliggande papper kan vi kontrollera att denna ordning gäller med god noggrannhet. Genom att testa olika material finner vi också att reflexionen blir mer eller mindre dämpad, analogt mer eller mindre vinkelavvikelse mellan utgående och inkommande. Vissa material absorberar nästan helt den penetrerande vertikala ytvektorn, och lämnar bara den ytparallella komponenten ensam kvar (efter träffen fortsätter kulan att rulla helt tätt intill träffmaterialet)

Vi kallar reflexionslagen i dessa sammanhang hellre för impulslagen då vi också kan visa att styrkan i träffen beror på produkten av kroppens massa (m) och hastighet (v) enligt

p = mv .............................. impulslagen

Impulsen (p) bildar en vektor (mv) som visar sig helt följa reflexionslagen förutsatt att hänsyn tas till hårdheten i träffytans material — idealt som ovan: ”obegränsat hårt”, vilket garanterar inkommande = utgående.

TILLÄMPNINGAR 2

Generering med Observation av en Reflekterande Puls

I detta enkla experiment kan vilket som helst rep användas knutet till ett dörrhandtag (den långa sladden till dammsugaren duger utmärkt). Vi ska först bara försöka observera hur dörrhandtaget returnerar en kort genererad puls genom repet. Om vi använder sladden till dammsugaren, kommer det mesta av pulsen att dämpas ut, men en tillräckligt stor del finns kvar för vår observation. Figurens vänstra del visar vyn ovanifrån med hur pulsen genereras, vilket vill säga i sidled. En vertikal riktning kommer inte att fungera så bra med ett vanligt rep (fastän ibland det illustreras så i en del litteratur, jämför till exempel ENCARTA 99 på artikeln Waves). Det vertikala hänget, figuren ovan höger, är vad vi behöver för att ge utrymme åt sidpulsen.

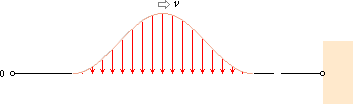
Figuren närmast ovan illustrerar en ideal toppvy för hur den sidsnärtade pulsen utbreder sig genom repet mot dörrhandtaget.

När vi genererar pulsen, överför vi kraft till repmaterialet genom att introducera mekaniska spänningskrafter (eng. tension forces); genom Newtons tredje lag vet vi generellt redan att sådana krafter strävar att motverka orsaken till sin uppkomst och därmed att dra ner utbuktningen till noll. De påförda krafterna är alltså noll vid utbuktningens ändar med ett maximum vid pulskrönet. Strävan att reducera pulskrönet mot noll etablerar alltså krafter som genomlöper materialet beroende på dess elasticitet och styrkan i den genererade pulssnärten, vilket bildar en motsvarande utbredningshastighet för pulsen eller som vi säger vågen genom repet.

Vi kallar generellt den observerade löpande pulsen för en våg

— hela förloppet en vågrörelse.

Den följande sekvensen av idealt erhållna inverkande vektorer på dörrhandtaget visar hur pulsen reflekteras i detalj — i full enhetlighet med reflexionslagen;

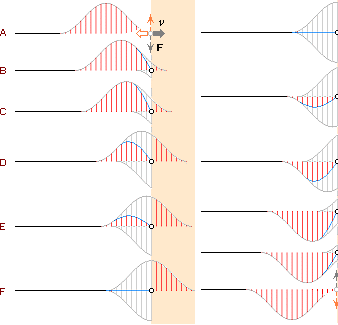
Sekvensen fortsätter samma från F och vidare genom de upp-och-nervända kopiorna av ovanstående delar (högra sidsekvensen); Pulsen reflekteras som en negativ kopia.

När pulsen når dörrhandtaget, börjar handtaget mata av kraftvektorerna och deras hastigheter ”en efter en” enligt reflexionslagen. Dörrhandtaget motsvarar en (via ett litet fast höjdavstånd från en ideal reflexionsyta, dörrblocket) upphängd infästnings- eller kraftreferenspunkt i dörrens idealt fasta yta som påverkas av pulskrafterna. De vertikala komponenterna (v) kommer således inte att kunna glida parallellt med dörrytan utan kommer istället att kastas tillbaka in i repet via infästningspunkten — för att bevara vilotillståndet hos den emottagande dörrytan inkluderat dess (närmonterade) handtag. Del (A) i sekvensen visar hur dessa vektorer reflekteras idealt tillbaka i repet, utan dämpning från handtaget. Därmed skickas en upp-och-nervänd kopia av de verkande krafterna tillbaka till repet: alla krafter och deras hastigheter bevaras eftersom ingen annan tillgänglig väg finns. Följaktligen måste dessa reflekterade krafter interferera med de allaredan befintliga när den ena delen går in och den andra ut. Det enastående resultatet är att amplituderna summeras. Det medför alltså att alla krafter har tagit ut varandra vid sekvens F. Denna situation är emellertid bara resultatet av en momentan (idealt differentiell) interferens; Krafterna fortsätter att utbreda sig i respektive riktningar tills alla har återvänt till repet via dörrhandtaget. Därmed avtar interferensen och vågpulsen har uppstått på nytt men nu i negativ tappning.

Generellt beträffande amplitudsummeringarna med interfererande (växelverkande) vågrörelser känner vi redan den bakomliggande förklarande principen som superpositionsprincipen: varje våg bibehåller sin identitet och (frånsett värmeförluster där sådana förekommer) utbreder sig oberoende av samverkan och interferens med andra vågor.

I experimentet med dammsugarsladden kan vi också verkligen observera denna återvändande negativa puls fastän den är starkt dämpad. Med ett mera elastiskt rep blir dämpningen (betydligt) mindre. Denna elasticitetsaspekt kan beskrivas mera fördjupat som följer.

Betrakta sekvensen vid F: Vågpulsens båglängd måste komprimeras till den (betydligt) kortare och idealt halt raka replinjen. Detta kan uppenbarligen bara komma ifråga om repet är just SÅ elastiskt — vilket garanterat dammsugarsladden inte är.

I nästa experimentella observation ska vi studera det praktiska beteendet hos denna speciella egenskap närmare, först via repet och senare via enkla experiment med vatten.

TILLÄMPNINGAR 3

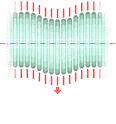
Observation av Reflexion hos repetiva pulser genom Stående vågor

Om vi börjar mata vårt experimentrep från TILLÄMPNING 2 med rytmiskt likadana repeterande sidvippande vågpulser, bör vi observera det följande sedan dörrhandtaget har matat av en våglängd, vilket vill säga två pulser (en vänster och en höger).

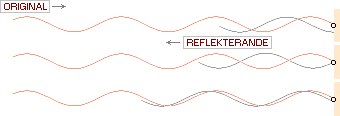
Efterhand, som dörrhandtaget matar av spänningskrafterna i repet och returnerar dem, superponeras amplituderna mellan inkommande och utgående som i föregående illustrerade sekvenser. Principen är alltså densamma som för en enskild puls i TILLÄMPNING 2 med enda tillägget att interferensen fortsätter kontinuerligt (tills energin som matar arbetet upphör) Figuren ovan illustrerar den ideala (förlustfria) returnerade våg som växelverkar med den aktuella. Figuren nedan visar det idealt renodlade resultatet.

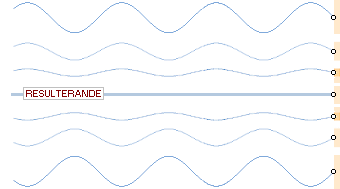
Del av repet i experimentet sett i olika ögonblick.

Om resultatbilden (se nedan) sammanförs framgår tydligt de så kallade NODPUNKTERNA som samtidigt markerar så kallade STÅENDE VÅGOR.

Idealt och momentant är kraftverkan noll — ingen ändring — i nodpunkten hos dörrhandtaget och alla övriga etablerade nodpunkter. Om amplituden (pulshöjden) är liten, kan vi studera de stående noderna med mycket tillfredsställande resultat även i det enkla experimentet.

Som vi kan se från de resulterande ideala interferenserna, blir den resulterande vågformen en rytmisk maximal dubbel/original och en minimum rät linje. Denna resulterande våg kommer emellertid inte att uppvisa några åkande pulser utmed replängden, utan istället stående vågor med växande och avtagande våghöjd med en idealt mellanliggande rät linje. De närliggande punktändar varemellan stående pulser uppstår och försvinner kallas den stående vågens noder, analogt vågens konstanta nollställen. Dörrhandtaget utbildar ett första sådant nodställe. Närmaste associationen till hela komplexet blir skuggbilden från en belyst fast vågkurva som får snurra kring en längsgående mittaxel.

I vårt experiment med dammsugarens elsladd knuten till dörrhandtaget, kan vi studera dessa fixa noder mycket precist om pulserna har liten amplitud — effekten visar sig med både snabba och långsamma sidvippningar. Nodpunkterna är fixa och därmed aldrig föremål för verkande krafter — vilket i sig är fascinerade att studera; nodpunkterna överför kontinuerligt kraftvektorer i bägge riktningar, men påverkas ingenting själva.

Stående vågor genom fixa noder i sladden till en dammsugare knuten till ett dörrhandtag, matad av sidvippningar som genererar kontinuerliga pulser. Sett ovanifrån.

Med tillräcklig amplitud i pulsen till dammsugarsladden börjar den rotera;

[Ge sladden ett tillräckligt häng, mata den sedan med mycket långsamma men långa sidvippningar (tre pulser totalt för hela sladdlängden)].

Förklaringen är (naturligtvis) att dammsugarsladden inte kan trycka in i sin egen begränsade elasticitet de aktuella båglängderna i formen av räta linjesegment; För att kompensera för denna oförmåga, då ingen annan lösning finns, måste de interfererande repkrafterna ge ut den överskottsenergi som man försöker lägga in — men som sladdens elasticitet inte klarar — i en transversell riktning, alltså rätvinkligt ”inpumpen”, vilket introducerar inre vridande moment, och därmed en ”överstegring av motoreffekten”; repet ”stallar” och börjar rotera.

Som vi ska se i ett senare experiment (Den roterande vattenvågen), bekräftas (ännu tydligare) samma princip i genereringen av vattenvågor.

TILLÄMPNINGAR 4

Observation av Reflexion av Vågor i vatten

UTOMORDENTLIG BEKRÄFTELSE på reflexionslagen uppnås genom att studera vattenvågor. I detta enkla experiment används en rektangulär vanligt diskbalja av plast, typiskt 35 cM lång, 25 cM bred, 15 cM hög, samt en droppflaska (samt ev. någon enkel arbetsbelysning) — och våra bumpande händer.

Experiment 1

CIRKULÄRA VÅGOR

Om vi låter vattendroppar falla i vår enkla diskbalja och justerar lampan för optimal inspektion, eller ljuset med kontrastverkan på annat sätt (bilden ovan tagen med vanlig enkel mobilkamera 1,3Mpixels JPG) kan vi se hur cirkulära vågor som sprids från droppträffen också reflekteras tillbaka som just cirkulära vågor. Med hjälp av viss extra belysning kan vågreflexionen studeras mera detaljerat mot baljkanten via vågkonturerna t.ex. mot baljans botten (experimentera gärna själv, det finns många olika möjligheter att studera).

Bilden nedan baseras på en mera avancerad (läs dyr) utrustning vilket krävs för mera noggranna studier. Vi ser visserligen i princip samma mönster med våra enkla medel — men att få det i bild är inte lika enkelt (!). Genom fotografiet nedan kan vi kontrollera (mycket) noga att reflexionslagen verkligen håller streck här. Vi kan emellertid också studera denna excellenta reflexionsprincip mera tydligt i nästa experiment.

Cirkulära vågor reflekterade mot en plan väggyta reflekterar cirkulära vågor

[GYMNASIETS FYSIK åk 3 Liber 1980 s58]

Experiment 2

RAKA VÅGOR

Genom att använda (t.ex.) ett plant plexiglas (20×15 cM) som reflekterande vågskärm som sätts ner i baljan med olika vinklar och samtidigt studera vågmönstret genom att generera vågor med kontinuerliga handbumpningar på baljkanten, kan vi studera hur fronter med raka vågor från endera baljväggen reflekteras mot det brytande-reflekterande plexiglaset — i full överensstämmelse med reflexionslagen.

Baljväggen kastar den penetrerande vektorkomponenten hos den inkommande vattenkraftens vektor tillbaka till vattnet. En spegelvåg från originalvågen reflekteras tillbaka ut.

Med olika försök att alstra korta eller långa vågor, kan vi studera den karaktäristiska symmetriska våginterferens som (t.ex.) bildar mönster på baljans botten med lämplig arbetsbelysning (placera belysningen lågt, inte högt, med ljuset strykande över vattenytan).

Vattenvågsfysiken

Från dessa simpla experiment kan vi förstå de grundläggande aspekterna på vattenvågens fysik.

Vattenvågen fungerar principiellt på samma sätt som i de föregående enkla repexperimenten. Enda skillnaden är att de motsvarande mekaniska spänningskrafterna i repmaterialet här i vattenmaterialet blir djupvektorer (»tryckvektorer»).

Försöker vi pressa ner något i vatten (figuren nedan), svarar vattnet som om det vore inkompressibelt; Vattnet tillåter inte någon vertikal kompression. Istället pressas ett deplacement utåt horisontellt i proportion till den störande inverkan (volymen) på vattnets normalyta. Eftersom vattnet inte svarar på denna puttning omedelbart överallt, påverkas omedelbart endast de mest närliggande delarna; pressas något ner i närområdet, svarar vattnet med att resa upp närmast liggande del, tillsammans med ett utbildat motsvarande horisontellt tryck (en slags förtätning) som längre fram säkerställer att störningen strävar att uttömma sig expansivt. Således åstadkommer inpressningen att närliggande delar välls över horisontellt på närmast närliggande delar (under viss tid med viss kraft) vilket bildar det partiella horisontella expansionstryck som ansvarar för den expanderande ringbildningen och därmed våghastigheten, samt delvis ett djuptryck som håller reda på våghöjdens komponent i kraftverkan.

Vattenvågen genereras på i princip samma sätt som i det inledande fallet med repet.

Den huvudsakliga inpressningen blir alltså mer eller mindre direkt analog med snärten i bildningen av vågpulsen i repexperimentet. I bägge fallen kan vi (lätt) förstå hur och på vilket sätt krafterna etableras på principiellt samma sätt. När väl en gång strukturen för spänningskrafterna har etablerats, fortsätter krafterna verka genom den karaktäristiska vågutbredningens material ända tills all vågenergi har uttömts.

HUR VATTENVÅGEN REFLEKTERAS

När en vattenvåg möter ytan på ett fast (hårt) ämne, baljväggen, kan baljväggen inte svara utbredningen från vattnet; Därmed kastar väggen tillbaka de ytinträngande vektorerna tillbaka till vattnet. Vilket vill säga, vattnet erhåller sina egna djuptryckande vektorer åter. Som vågen utbreder sig tillbaka till vattnet, interfererar den då med de redan etablerade vattenkrafterna. Genom denna verkan kommer en solid bergklippa att reflektera en vattenvåg på exakt samma princip och ideala vis som visades i fallet med repet i TILLÄMPNING 2. Enda skillnaden är att vi måste förstå hur de motsvarande vattenkrafterna agerar: amplituder ovanför vattnets normalnivå (vilonivån) besitter krafter som strävar att reducera neråt (alltså typ nedåttryckande); amplituder under normallinjen har krafter som strävar att reduceras uppåt.

Då kan vi också förstå hur djupfaktorn högeligen påverkar uppförandet hos en vattenvåg. En inkommande våg som är bildad på stort vattendjup kommer över grundare områden obönhörligen att pressa djupvektorerna upp allt högre till högre vågor; för att bevara vågenergin då djupdelen avtar tvingas våglängden kortare och våghöjden högre med bevarad vågrytm (antalet vågtoppar per sekund eller frekvensen) — vilket betyder lägre våghastighet. (v=d/t; t=d/v=konstant; avtar d måste också v avta).

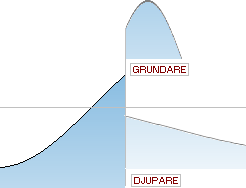
Vattenvågen anpassar sin våghöjd efter vågdjupet — därför att då vågen bildades fanns en viss energi som etablerades just i ett visst vågdjup och vilken energi (idealt) bevaras; Kommer vågen in över ett djupare område, fördelas energin på mera djupgående vattentryckande vektorer och våghöjden avtar i motsvarande grad. Om vågen istället kommer in på grundare område, överförs djuptrycket på våghöjden som därmed tilltar.

våghastighetsrelationen

Denna enkla vektorTryckande princip samlar vågteorin i de två enda möjliga ömsesidigt reversibla konfigurationerna som visas i illustrationen ovan. Med f som given vågrytm gemensam för bägge områdena, lika med inverterade värdet av tidsperioden för våglängdens utbildning, l (lambda) som våglängden och c våghastigheten, fås de enkla sambanden

cA cB

fA = —— = —— = fB

lA lB

som ger

cA lA

—— = —— = n

cB lB

Vilket vill säga: hastigheterna förhåller sig som våglängderna med bibehållen konstant frekvens.

Vi observerar explicit — i andra termer av det redan sagda — att en positiv förskjutning (från djupare till grundare) förstärker den inkommande pulsformen medan en negativ förskjutning (från grundare till djupare) reducerar (eller fullständigt reverserar) den. Termen n kallas generellt refraktionsindex, samma som brytningsindex.

Experiment 3

STÅENDE RAKA VÅGOR

Fotografierna överst visar den använda diskbaljan i experimenten samt ett exempel på stående vågor som framträdde ur ett visst rytmiskt bumpande med ena handen på baljkanten. Figurerna nedan är delvis stiliserade från ovanstående.

Den ljusa delen överst representerar spegelbilden från arbetslampan. Om den används ska den placeras ungefär som i illustrationen för att vi ska kunna studera vågbildningen så tydligt som möjligt i det praktiska fallet (som kräver ytterligare utrustning om det fallet också ska fotograferas, vilket här inte är fallet).

I detta experiment används bara baljan själv och våra händer (tillsammans med viss belysning) för att skapa stående vågor i raka fronter. Beroende på baljans plastmaterial, får vi helt gratis hela vågserier om ena baljkanten beslås med en hand. Genom att upprepa handslaget, samt reglera des styrka och snabbhet i rytmen, kan vi observera hur och när ett visst vågtåg kopplar genom ”ett rinnande vågmönster” som flyter rytmiskt genom det reflekterade ljuset. Figuren närmast ovan visar helt ideala raka vågfronter medan vi i det praktiska fallet inte får så väldigt jämna sekvenser — men nära. Med upprepade försök, kan vi studera de bildade till synes helt ”fasta vågmönstren” under allt längre och längre tidrymder ju skickligare vi blir som handbumpande vågvaktmästare.

Den första detaljen att studera (som också är den mest fascinerande) är de motsvarande repnoderna på baljväggen. I detta fall motsvarar dörrhandtaget hela baljväggen längd och vi ska studera hur nodlinjen kvarstår fullständigt lugnt medan vattenytan utanför den vippar upp och ner, in till närmast våldsamt (så att det börjar stänka om det) — medan baljväggens nodlinje ligger helt stilla, inte minsta rörelse.

Denna situation ansluter till TILLÄMPNING 3 med repet i de stående noderna enligt föregående illustrationer, här återkallad som nedan.

Stående vågor via fasta noder i vattnet hos en enkel diskbalja, matad med vår ena hand som bumpar på en av baljväggens kanter.

Den roterande vattenvågen

Om vi börjar med lätta vågalstrande handkantsbumpar, och sedan avancerar till mera tuffa attacker genom att öka vågamplituden, konstant i observation på motstående baljvägg, kan vi se det följande.

Normalt stående raka vattenvågor med liten våghöjd. Den ljusa delen i mitten motsvarar belysningen från arbetslampan.

Typ1 Typ2

Ökas amplituden uppkommer strax små fördjupningar utmed de första två eller tre vågfronterna. Fotografiet nedan ger en motsvarande uppfattning om det praktiska fallet i denna situation.

De framträdande små fördjupningarna har observerats vara av två grundläggande sorter enligt närmast föregående skisserade illustration, Typ1 (kvadratisk) och Typ2 (hexagonal). Vilken av dem som framträder beror på energimatningen, alltså häftigheten i vågkrafterna. Skillnaderna är emellertid delvis sublima, och det är inte lätt att behålla en viss formation under observation någon längre tid — fastän vi kan upprepa samma typform om och om igen, med vissa ansträngningar — på grund av att minsta lilla miss i den tillfälligt konstanta energimatningen nära omedelbart uppvisar ett annat mönster. Det förefaller dessutom som att fördjupningarna, när de väl visar sig, uppkommer helt plötsligt och abrupt, ingalunda ”mjukt och smygande”.

Medan dessa formationer uppträder kan vi studera baljväggens nodlinje och se att den verkligen kvarstår orörd — den ändras inte, inte ens med minsta lilla observerbara del. Det är (min uppfattning) fascinerade.

Det initierande framträdandet av fördjupningarna indikerar den föregående omnämnda elasticiteten hos mediet, i detta fall vattnet.

I figuren med de stående vågorna med de fixa noderna, måste vattnet pressa alla vågor till normalnivån och samtidigt behålla totala energin föregående en ny fas med framträdandet av nya nodpulser.

— Men vattnet kan inte vara helt plant överallt och samtidigt ha initiell energi för att resa upp vågor.

Detta är en helt omöjlig situation

— därför att när ytan är plan, har all energi uttömts.

Vi kan förstå anledningen för hur vattnet uppför sig i det praktiska fallet med de nämnda aktuella fördjupningarna (Typ1 och Typ2) som just en konsekvens av denna observerade omöjlighet;

— När vågenergin överskrider ett visst kritiskt värde, roterar vågen plötsligt och abrupt ner på motstående sidor om den ideala horisontella nodaxeln, vilket får fördjupningarna att framträda, och därmed motsvarande upphöjningar. Därmed befinner sig svängningen i (stabil) resonans — för just den matande vågenergin.

Det finns (till synes) många former och strukturer som bildas av denna komplicerade våginterferens. Vinjettfiguren till Experiment 3 visar ett observerat praktiskt fall (typ hexagonalt) av flera olika möjliga mönster. Mönstren generellt är med denna enkla anordning relativt svårfångande eftersom de kräver en (relativt) noga avvägd energimatning — vilket bevisas därmed att mönstret ändras omgående med minsta variation.

Verifikation av djupfaktorn

VÅGHASTIGHETENS ÄNDRING MED VÅGDJUPET

Genom att placera olika objekt i baljan kan vi bekräfta den föregående omnämnda slutsatsen att djupfaktorn påverkar våghastigheten. Figuren närmast ovan illustrerar den ideala förebild med vars hjälp vi kan studera en del av de grundläggande strukturer som visar sig i experimenterandet med vatten i den enkla diskbaljan. Frekvensen, analogt vågrytmen, konserveras medan våghastigheten och dess amplitud ändras med varierande vattendjup. Trots att baljan i exemplet är relativt liten, kan effekten med den varierande våghastigheten observeras tydligt — varierande våglängder som bryts i relation till objektens (upptagande) form och placering.

TILLÄMPNINGAR 5

Observation av Objektens Reflexion i vatten

Vi har redan härlett reflexionslagen som en speciell form av den mera naturligt elementära spegellagen. Bilden ovan är ett utmärkt exempel på den enda typiska naturvy vi behöver för att fullt ut kunna se, beskriva, förklara och härleda spegellagen — men som mycket enklare även kan göras över en helt enkel kopp te: det är samma princip, det enda som behövs är en speglande vattenyta. I följande experiment ska vi också se hur vi med relativt enkla medel kan kontrollera att spegellagen — eller reflexionslagen — verkligen håller streck.

I figur 1 nedan med vidare används diskbaljan från föregående experiment tillsammans med två ytterligare verktyg; Vi behöver en graderad linjal och en enkel men rak blomsticka.

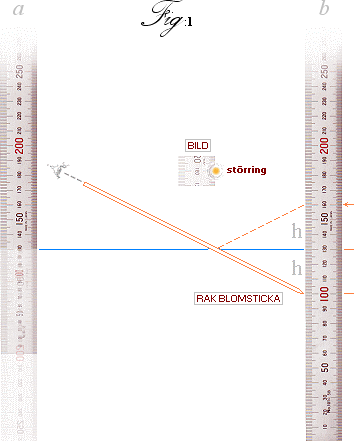
Figur 1. Anordning med verktyg.

Den högra figurdelen (b) visar den aktuella linjalen (en stålskala) som används i experimentet. Den är placerad som visas nedan i figur 2. Vänstra delen (a) illustrerar den motsvarande perceptionsvy vi ser med blicken riktad mot linjalen och utkikspunkt över vattytan från motstående baljkant. För korrekt funktion måste linjalen monteras stabilt och rätvinkligt vattenytan — vilket garanterar de geo-matematiska förutsättningarna i spegellagen eller reflexionslagen. Figuren nedan visar hur anordningen kan göras med enkla men stadiga medel.

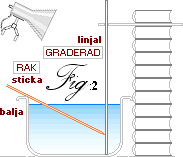
Figur 2. Monteringsarrangemang med böcker, linjal och blomsticka.

Med ovannämnda monteringsvillkor uppfyllda, kan baljkanten användas som en primitiv stödpunkt om spetsen på blomstickan försiktigt trycks mot den vertikala linjalen. Blomstickan kommer genom sin materialegenskap att försöka komma upp till ytan, men med några upprepade försök kan den fås att vila i en fix position med spetsen pekande mot en bestämd graderingspunkt. Därmed tillåts vi mera ingående att förbereda en mera noggrann inspektionspunkt i betraktelsen av vattenytans spegelbild av linjalens gradering.

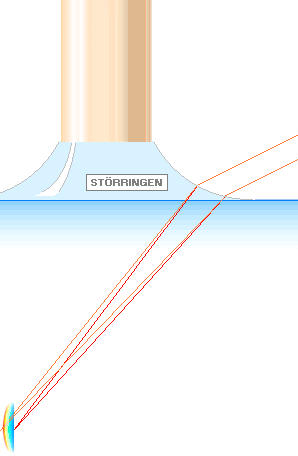
När vi blickar i blomstickans riktning ser vi en liten störring där stickan går ner i vattnet. Denna del kommer på visst sätt att störa observationen. Men om vi flyttar blickpunkten något sidledes, kan störringens mittdel ganska precis indikera ett skalvärde i vattenspeglingen. Figuren nedan (även i figur 1) visar principbilden för att få ut ett läsbart resultat.

Figur 3. Hur linjalens vattenspeglande gradering kan avläsas med hjälp av störringen.

RESULTAT

Genom upprepade experiment för olika avstånd mellan vattenytan och blomstickans pekande spets på linjalen under vattenytan, kan vi bara konstatera att distanserna markerade h i figur 1 är samstämmiga: delen under vattenytan motsvarar höjden ovanför vattenytan och vilka distanser kan ses sammanträffa genom störringen vid x.

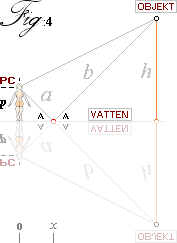
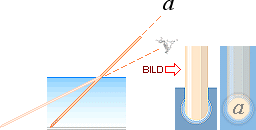
Figur 4. Spegellagen, samma som reflexionslagen. Resultaten bekräftar spegellagen: perceptionsvinkeln är samma som objektvinkeln. Ett objekt som reflekteras i vatten ses som en vänster-höger skiftad kopia som är frontroterad 180° — som om vyn ses med blickpunkten underifrån vattenytan på samma avstånd som blickpunkten över.

Som detta resultat uppenbarligen avbildar symmetrin i spegellagen, figur 4 ovan, är det en direkt bekräftelse på reflexionslagen: Perceptionsvinkeln (A) mot vattenytan är samma som objektsvinkeln A mot samma yta. Denna detalj innebär — tydligen också — att distanserna a+b bildar den kortast möjliga vägen mellan observatör (PC) och Objektet — om vägen ska vidröra ytan. Varje annan ytpunkt än den som motsvarar x-avståndet, figuren ovan, kommer att tillhöra en längre distans. Som kortaste vägen också betyder minsta arbetet, är det tydligt att reflexionslagen också konserverar en optimal energilag.

Men varför är vattenspeglingen så svag? Det är en genomgående observation i föregående experiment: vattenspeglingen är nära knappt synbar.

Figur 5. Vattenspeglingen tillhör avgjort inte det allra starkatse intrycket. Varför är vattenspeglingen så svag?

Som vi ser från vyerna under experimentens gång, är den speglande vattenbilden av linjalskalan påfallande svag. Det verkar som att det mesta av luftbildens tydliga bild bara »försvinner ner i vattnet» och kvarlämnar bara en liten del synlig som den aktuella vattenspeglingen.

Vi kan komma svaret på gåtan en bit på spåren om vi sänker blickpunkten och låter den stryka precis utmed vattenytan; Vi ser direkt att intensiteten hos vattenspeglingen nu ökar nära drastiskt och ger en mycket fin och tydligt spegelbild med blickpunkten helt nära vattenytan; Ökas synvinkeln, försvinner också speglingen och är nästan helt borta rakt över.

Om vi tillåter oss att tänka i analogier (alla modeller är tillåtna i fantasin) är det alldeles uppenbart att ljuset uppför sig som om det bestod av många cylindriska strålar, likt blomstickan men mycket smalare, och som i sig består av många godtyckligt orienterade VÅGPLAN, typ det nedan illustrerade:

Figur 6. Ljusets vågplansmodell. Det verkar som att ljuset beter sig som om det bestod av individuella cylindriska strållinjer med inre godtyckligt orienterade vågplan. Den reflekterade delen från vattnet (blått) är bara de plan som skär vattenytan parallellt med denna, medan resten fortsätter ner i vattnet. Om detta är en korrekt teori, förklarar den perfekt varför bara en liten del av ljuset reflekteras: bara en liten del av alla möjliga ljusplans orienteringar är parallella med just vattenytan. Den reflekterande delen stämmer då också excellent med den föregående beskrivna planvågens form enligt reflexionslagen: de penetrerande djupvektorerna från den inkommande strålen kastas tillbaka ut av ytan, precis som i fallet med den vinklade vattenvågen som möter baljväggen. Vågnaturen för ljus verkar således avgjort klar — men det är en högeligen avancerad vågnatur. Se vidare utförligt från Ljusets Polarisation.

Samlar vi alla möjliga sådana vågplan i två mot varandra rätvinkliga xy-riktningar med vattenytan som x-preferens — vilket betyder att vi med lämpligt xy-val kan ta fram vilkensom delplansriktning — kan den observerade intensiteten i vattenspeglingen förklaras galant genom att det med vattenytan parallella reflexionsplanet samlar mera energi på mindre synvinklar med början från vattenytan självt; Större vinklar betyder att energin i vattenspeglingen måste fördelas analogt reflekteras på större vinkelrum, vilket betyder svagare bild i en viss given riktning analogt mindre ljusenergi »per given ögonpixel». Observera dock att analogin inte får drivas för långt: naturligtvis finns det inga motsvarande rent fysiska vågplan; modellen är matematisk-geometrisk.

Vi ska inte föra denna diskussion längre i detta avsnitt. En vidare och mera detaljerad beskrivning av ljusets fysik ges dels i blocket om ELEKTRISKA LADDNINGEN i Elektriska Laddningens härledning genom Ljusbrytningen och dels mera utförligt i blocket om Ljusets polarisation — där ges också de vidare grunderna i ljusets reflektiva och refraktiva (brytande) uppförande enligt relaterad fysik — samt inledande generellt i Fysikens 7 Principer genom Divergensens princip.

Vad som däremot kan klargöras — men här ingalunda bevisas — med exceptionell experimentell tydlighet i dessa enkla experimentella sammanhang, är en annan aspekt på ljusets natur — och som också berör på andra ställen i Universums Historia men från andra utgångspunkter (Se Divergensens Princip): ljuset utbreds masslöst. Vi studerar hur.

LJUSSTRÅLAR ÄR MASSLÖSA

Att ljusets »strålvågor» inte består av någon ENSKILD partikel är klart från principen att ljusstrålens motsvarande cylinder eller den aktuella ljusstrålen faktiskt DELAS när den möter t.ex. vattenytan. Vilket vill säga, en del av strålen reflekteras, en del bryts.

Att strålvågorna inte består av några partiklar ALLS kan i sig klargöras på två sätt, ett logiskt och ett (delvis) experimentellt. Det första och enklaste är den grundläggande (”löjliga”) observationen att medan vattenytan reflekterar Solens färger och alla andra objekt och deras färger, reflekterar den INTE deras vikt — själva tyngden. Vikt, eller rörelse, hos ordinära objekt reflekteras i vilket fall inte. Det andra sättet: Om vi vet hur partiklar uppför sig när de kommer in i vatten från givna riktningar — i jämförelse med observationer hur ljusstrålar uppför sig — finns ett helt enkelt experiment som bekräftar det redan sagda: energin som krävs för att uppvisa färgerna använder INTE partiklar eller massor till färgernas fortplantning över distans mellan de olika massiva materieelementen (atomerna). Exemplet nedan visar oss att inget spår av någon sådan likhet med massbaserade transportmedel finns.

EXPERIMENT MED FYRA STÅLKULOR FÖR ATT BEVISA

att utbredningen av färgstrålar — ljus — över avstånd inte har någonting gemensamt med partiklar i rörelse

Min erfarenhet: Jag trodde jag hade en någotsånär grovt översiktlig uppfattning om hur fasta partiklar uppför sig när de färdas genom vatten från en inkommande luftväg — tills jag genomförde dessa enkla experiment. Jag blev högeligen förvånad. Vi ska använda diskbaljan från föregående experiment tillsammans med ett lutande plan (en vanlig glasskiva) samt fyra olika stora stålkulor med diametrarna i millimeter 19, 10, 5 och 2. Figuren nedan visar det enkla arrangemanget.

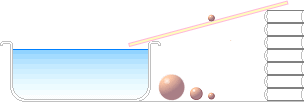
Figur 7. Arrangemanget.

För att tillåta förutsättningarna att alla kulor får en optimal och lika (idealt) hastighet oberoende av deras diameter består lutningsplanet i det här experimentet av ett vanligt ramglas 30×40 cM som ligger med en fast lutning ner mot diskbaljan, ca 10-15°, typ figuren ovan. Från en given position släpps varje kula så att den fritt får falla utmed fallplanet och sedan vidare ner i baljan. Med tom balja kan vi först observera att alla fyra kulorna träffar baljans botten approximativt i samma träffpunkt.

Men baljan vattenfylld och den största kulan kan vi bekräfta att den träffar baljans botten nära på samma ställe frånsett en liten differens. När så den minsta kulan, den med diametern 2 mM, ansattes och släpptes utför planet visade sig emellertid ett helt annat beteende. Illustrationen nedan visar den typiska rörelsekurvan för den minsta av kulorna som observerades under försöken.

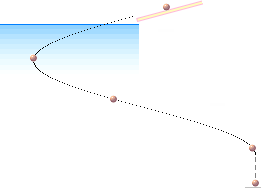
Figur 8. Den minsta kulan uppvisar ett chockerande rebelliskt beteende. Ljus som inträder vatten beter sig bara inte så här!

Kulan slutade sin bana till och med LÅNGT BAKOM fallranden. Samma principiella beteende kunde också iakttas för 5mM-kulan, men inte så tydligt. Rörelsevägen för 10mM-kulan skiljde sig knappast från den stora 19mM-kulan. Därmed stod resultatet klart.

Den minsta kulan avgör frågan om den utbredande naturen för energin hos färgerna (eller som vi säger, ljuset): ljus från luft till vatten uppför sig ingalunda som inkommande små partiklar — likt den minsta kulan i experimenten ovan. Ljus, även den tunnaste stråle, fortplantas rakt och solitt genom vattnet, utan de vrängningar vi skulle ha rätt att förvänta oss om ljusets fortplantning vore av ovanstående anmodade typform. Denna klarhet har också blivit speciellt tydligt framhävd genom alla föregående experiment där den ljusförmedlande bilden av alla föremål och deras delar under vattnet och genom det uppvisar samma renhetsgrader och utsträckningsfasoner som med föremålen i luft.

Slutsats:

Vilken naturförklaringen än är till färgernas förekomst och utbredning, har deras energi tydligen ingenting att göra med en transport av massor över avstånd. Vilket vill säga: Ljusenergin utbreder sig masslöst mellan föremålen.

Slutsatsen innebär att ljuset tvunget utbreder sig mellan föremålen utan användning av massa för överföringen (Se även utförligt från LJUSETS FRISTÄLLNING FRÅN KINETIKEN) — men också tvunget att föremålen måste innefatta (mycket små) massor (atomernas elektroner) som underhåller motsvarande vågsvängningar; därmed kan dessa bilda nya källor till den fortsatta masslösa överföringen. Se även i INDUKTIONEN, som beskriver själva fenomenformen bakom ljusenergins masslösa överflyttning över tomrummet mellan de olika materiesystemen.

Ljusets utbredningshastighet är ändlig

Vi har redan genomgått en del relativt enkel relationsmatematik i Våghastighetsrelationen; med också ljusvågornas tillämpning på den enkla relationsformen understryks endast att själva ljusets blotta brytförmåga i t.ex. vatten bevisar att det rör sig om två skilda utbredningshastigheter, en för luften och en för vattnet. Därmed är indikeringen också klar att ljushastigheten är ändlig.

Ljusets utbredningshastighet beror på den närvarande massan

Genom de allmänna observationerna att olika material uppvisar olika beteende inför värme och reflexion, berättar den masslösa energiutbredningen hos ljuset i andra ord att den energin distribueras och fortplantas olika i olika substanser: Det är substansen som dikterar genomsläppet, inte ljuset självt. Utan den förklaringen, har uppenbarligen de olika egenskaperna hos olika material beträffande värme och reflexion ingen substantiell mening.

Vi kan därför sluta oss till att ljusets uppförande beror på massorna — mera noga sagt: på gravitationen, analogt styrkan i massornas samlade inverkan. Som värme utbreder sig olika i olika material, skulle vi förvänta oss att också ljuset utbreder sig med olika hastigheter i olika material, i full enlighet med den föregående diskuterade (härledda) formen för Våghastighetsrelationen. Det blir då naturligt att förutsätta att tätare material generellt sett bör uppvisa en lägre ljusutbredningshastighet eftersom luften, eller mellanrummet mellan luftatomerna, är den lättaste av alla substanser och därmed borde uppvisa den snabbaste genomgången.

Dessa aspekter är också de allmänt och vanligt mest förekommande kända i ljusets fysik och som kan läsas i snart sagt varje fackbok i ämnet.

Det mest uppenbara beviset för att ljuset uppför sig olika i olika material, frånsett observationen med värme och reflexion (jämför t.ex. olika material som sätts mellan handen och en eldhärd: vissa ämnen täcker för värmen — men det finns också sådana som inte gör det) visas av den enkla bilden vi ser av föremål delvis täckta av vatten, som till exempel blomstickan i föregående experiment som framstår ”bruten” genom vattenlinjen. Genom att mäta denna avvikelse kan vi också finna de motsvarande hastigheternas förhållande i luft och vatten. Följande experiment ger ett exempel på hur en sådan mätning kan gå till.

LJUSBRYTNINGEN GENOM VATTEN

LJUSETS BRYTNING GENOM VATTEN — hur ljusbrytningen kan mätas med enkla hjälpmedel

Som vi redan observerat, om inte förr så mycket väl genom föregående experiment, uppvisar vattnet en bruten bild av ett föremål mellan luftsida och vattensida. Illustrationen nedan visar två typiska vyer vi ser med blicken i respektive riktning för blomstickans brutna partier.

Figur 9. Typiska vyer av bruten bild hos en rak pinne mellan luft och vatten.

Illustrationen nedan visar det enkla arrangemanget för att mäta de olika vinklarna i de skilda vyerna. Det finns emellertid en del (sublima) detaljer som framskymtar i anordningen och som vi måste vara klara över för att lyckas med mätningarna. Den främsta av dessa detaljer är den tidigare vidrörda störringen som ligger på blomstickan i övergången vid vattenlinjen; I figurbilden nedan är hela syftet med experimentmätningen att utnyttja störringen för att precis sikta in stället där skärmkanten träffar vattenytan vilket ger de aktuella mätdistanserna som vi måste plocka upp. För att genomföra det finns en del ytterligare detaljer att studera.

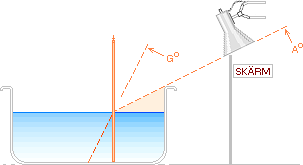
Figur 10. Bestämning av vattnets refraktionsindex, samma som brytningsindex (n).

Notera att också bildskärmens ljusinställningar (högeligen) påverkar läsbarheten i nedanstående fotografi. Jag har här försökt göra en kompromiss via en enkel mellantonsjustering i fotografiet för att styra ut ett mellanresultat i jämförelse med min arbetsskärm (något mörkare) och den som jag använder till Internet (något ljusare). Resultatet beror också på varifrån man tittar: ner på bildskärmen ger ett ljusare intryck, uppåt mot skärmen betydligt mörkare.

Övre: Störringens bild på baljans botten från blomstickan i Figur 10 ovan fotograferad med 1,3 Mpixels webbkamera i JPG-format, samt uppljusad 50% i mellantonen; bildljusets original är så svagt att det knappt syns i annat fall. Notera också att ljusstrimlans form ändras (drastiskt) med olika avstånd till skuggkanten samt med den primära förorsakande störringens olika lutning mot vattnet via föremålet som den bildas invid. Bilden nedan visar anordningen ovanifrån med den avskärmade arbetslampan till höger och det minimala ljusflödet vänsterut och ut över baljan med den knappt urskiljbara (ovan förstorade) störringens bottenprojektion alldeles ovanför skärmkantens skuggbild på baljans botten. I det fotograferande ögonblicket lades linjalen över baljan som stöd för blomstickan så att störringen kunde fotograferas. Störringen uppvisar regnbågens färger (rött längst ut till vänster) och är speciellt betydelsefull för noggrannheten i experimenten. Se vidare huvudtexten nedan i STÖRRINGENS BETYDELSE.

PLANSKÄRMEN ovan till höger precis under lampskärmen (se även illustrationen i figur 10) har följande betydelse: Normalt sett strålar en vanlig glödlampa ut ljus åt alla möjliga håll. Tittar vi på den skuggbild som ges från kanten på en rakt avskuren kartongbit från en sådan lampa ser vi en högeligen oskarp och diffus kantbild som knappast duger som mätreferens. Genom att begränsa lampstrålningens olika riktningar via planskärmen, så som visas i fotot ovan, får vi en optimalt rak ljusstrålare och därmed en långt skarpare kantbild av rakskärmen och som nu däremot helt klart kan användas i mätningarna. Men det sker till priset av att ljusstyrkan också reduceras märkbart.

Planskärmen kan göras behändigt med hjälp av en tom hushållspappersrulle som precisionshandtag; skär upp en passande skåra som en bit plexiglas kan skjutas in i; montera först en svart täckande klippkartong med dubbelhäftande tejp på glasets ena sida, precis kant i kant med glaset så att en skarp formkant fås. Denna anordning kan sedan monteras i en andra (mera fast monterad) pappersrulle (uppskuren) och därmed justeras/vridas t.ex. i höjd-längsled (mellan t.ex. en uppsättning tjocka böcker som stadigt monteringsstöd eller liknande).

STÖRRINGENS BETYDELSE

Genom vattnets ytspänning bildas en kurverad övergång från vattenytan till det nedstuckna föremålets yta. Ljusbrytningen i den delen ger en speciellt användbar referens som vi kan använda som en grov mätreferenspunkt.

Figur 11. Störringen och dess projicerade linskropp på baljans botten.

Den speciellt upplysta delen i störringen där blomstickan möter vattenlinjen kan (förnämligt) användas för att markera dels mätgränsen där ljuset möter vattenytan och dels där den brutna ljusstrålen i vattnet träffar baljans botten. Bilden ovan illustrerar vad som måste justeras in för hand för att få exakt precision: störringens ljusstrimla på baljbottnen ska precis röra vid kantskuggan. Detta kräver emellertid ett SÄKERT sätt att DELS garantera en mätmässig normal till vattenlinjen för blomstickans del och DELS en motsvarande siktnormal till kantskuggans linje på baljbottnen. Vi ska strax se hur dessa delproblem kan lösas galant med ytterst enkla medel. Låt oss emellertid först studera en ”bonusapplikation” från »störringens allmänna egenskaper» — den visar sig nämligen vara oberoende av föremålet som möter vattenlinjen och som vi därför kan utnyttja (galant). Vi studerar först den aktuella anordningen och diskuterar sedan de allmänna egenskaperna.

Figur 12. Mätsänke.

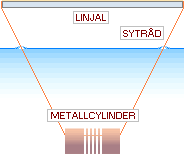
Istället för den delvis ohanterliga enkla blomstickan kan vi använda två betydligt finare sytrådar som automatiskt garanterar lodprecisionen; Ett metallrör genomträs med en sytråd som knyts ihop och träs över den graderade linjalen. Därmed har vi fått en så bekväm och precis mätanordning vi alls kan få, illustrationen nedan;

Figur 13. Precisionsmätning med ytterst enkla medel.

Störringens oberoende linskropp

Med sänkhänget monterat på linjalen (på ett godtyckligt utvalt ställe) behöver vi bara justera linjalens placering tvärs över baljan tills störlinjen på baljbottnen precis rör vid skuggkanten (figur 11). Denna positionsjustering kan göras ytterst precist (om vi inte är alltför darrhänta). I bilden ovan är detaljerna delvis idealiserade — till exempel skymmer linjalen delvis den ena eller andra sytrådsvattenpunkten i det praktiska fallet, men den detaljen är mindre kritisk då vi alltid kan ”kika lite vid sidan” och därmed i vilket fall ha full koll på situationen — eller göra en brett sänke som automatiskt placerar sytrådspunkterna utanför linjalens bredd.

Fotografierna nedan (som togs nyligen 2008XII9 för att förbättra presentationens tydlighet) bevisar hur störringens linskropp är oberoende av föremål — störlinsen är (nämligen) avgörande viktigt för den senare experimentella delen.

Vi studerar den detaljen.

Fotografierna övre-undre visar att störringen uppvisar samma linstjocklek oberoende av material; det är endast vattnets ytspänningsvall mot materialet som bestämmer störringens projicerade linstjocklek mot baljbottnen (i blomstickans fall ca 5mM tjock och 10-15mM bred, figur 11).

Övre fotografiet visar tre markant olika föremål som alla uppvisar samma störringsdimensioner: en sytråd monterad i ett kort metallrör som hänge över den graderade linjalen, blomstickan (Ø3mM) och ett markant grövre Ø10mM mässingsrör. De bägge övre — räknat från kantskuggan — små ljusstrimlorna tillhör mässingsröret från dess motstående sidor, och man kan t.o.m. precisionsjustera den inbördes höjden på dessa genom att vrida på röret. Den bortre ljusstrimlan vid kantskuggan tillhör sänklodets främre sytråd och den hitre ljusstrimlan kommer från blomstickan.

(Den ljusa bulan i mitten nederst tillhör plastbaljans design). För att förtydliga dessa detaljer, föregående fotografi, gjordes en mindre omorganisation enligt bilden närmast ovan; De bägge högra (svaga) ljusstrimlorna tillhör fortfarande mässingsröret; den synbarligt större hitre ljusstrimlan (”halvlinsen”) närmast under rörstrimlorna kommer från blomstickan, och de bägge nedre/bortre ljusstrimlorna kommer från de bägge sytrådarna på ömse sidor linjalen (den bortersta strimlan här knappt skönjbar). Att störlinsen synes större från blomstickan beror här på tillfälliga omständigheter; linskroppens storlek ändras med avståndet från skuggkanten samt beroende på hur föremålet lutas relativt ljuskällan. Med en mera noggrann justering sammanfaller alla tre objektens störlinser om de jämkas ihop precis på skuggans kantlinje. Denna detalj, som visar att linskroppen är oberoende av nedsänkt materialdimension (i vårt fall olika tråddiametrar), är viktig därför att störlinsen kommer att utnyttjas som preferens vid mätningarna i precisionsinställningen — med vidare.

Figur 14. Uppmätningen av skuggkantens avstånd.

Ytterligare en mätteknisk detalj återstår av de tidigare två antydda som vi måste ha garantier för: uppmätningen av skuggkantens horisontellt projicerade avstånd på vattenytan. För att få fatt på den detaljen måste vi konstruera NÅGON motsvarande fysiskt mätande KOPPLING mellan skuggkanten och vattenytan. Ett enkelt sätt att genomföra den saken på visas i figuren ovan: Genom att använda blomstickan med spetsen mot baljbottnen vid skuggkanten och andra änden uppe vid vattenytan kan en hyfsad precision måttas in visuellt mot linjalens skala.

Det finns emellertid en bättre metod — och samtidigt något mera krävande, fast fortfarande med enkla medel:

Den tunna linjen i mitten av baljan på fotografiet ovan är en sytråd som monterats med metallhängen i ändarna så att den hänger spänt och fint över baljan och störringarnas mätlinjal och dess skala. Ljuset överst i bilden kommer från ett tänt stearinljus; Genom att använda en separat (handhållen) glasplatta (eller en fickspegel) kan en separat ljusbild kastas tillfälligt över vattenytan från stearinljuset vilket är tillräckligt för att få sytrådens vattenspegling synlig; Därmed kan sytråden och dess spegelbild precisionsinpassas mot skuggkanten på baljbottnen så att en med dessa enkla medel mycket noggrann positionsbestämning fås; Sytråden, dess spegling och skuggkanten på baljbottnen ska precis täcka för varandra på gemensam lodlinje. Därmed är vinkelprecisionen garanterad för den slutliga uppmätningen, figuren nedan samt anordningen i bilden ovan (utom lampan till vänster med skärmen).

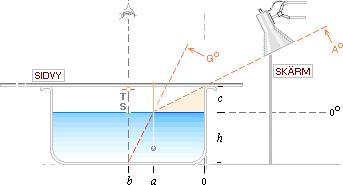
Figur 15. Beteckningarna T och S markerar sytråden och dess spegelpunkt för bestämningen av skuggkantens horisontdistans.

MÄTEXEMPEL i mM (upprepat experiment med ny uppmontering December 2008 till jämförelse med originalet September 2001):

c ................... 54

h ................... 96

a ................... 70

b–a ............... 71 (70,5)

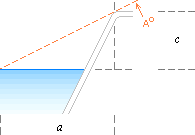
Notera ovan i figur 15 att baljväggens lutning INTE är kritisk; Förutsatt att vi endast observerar stället där skuggbildningen börjar vid baljkanten (referensnollan för a-värdet, figuren ovan) ger sig resten själv — oberoende av hur baljans väggform är designad; totala mäthöjden (till c) och vattenhöjden (h), som är relativt enkla att mäta, sköter resten automatiskt.

Vi bestämmer först kvantiteterna hc. Dessa är fasta och kommer att mätas på bara en gång. De enda ytterligare mätningar som måste göras är distanserna ab. Relationerna ger

h/(b–a) = tan G

c/a = tan A

Refraktiva indexet eller med samma mening brytningsindex n in PREFIXxSIN blir då:

sin A sin[atan c/a] 1 + [h/(b–a)]2

——— = n = ———————— = Ö ———————

sin G sin[atan h/(b–a)] 1 + [c/a]2

Med ovanstående mätvärden ges

h/(b–a) = tan G = (96)/(71) = 1,3521126; sinG = 0,5946265

c/a = tan A = (54)/(70) = 0,7714285; sinA = 0,7917822

sinA/sinG = 1,3315622 » 1,33

Med det mera noggrant avlästa b–a=70,5 ges

sinA/sinG = 1,3376744 » 1,34

Relationen n = sinA(sinG)^–1 kallas brytningslagen och n brytningsindex. Genom upprepade mätningar, delvis med samma lampvinkel och delvis med olika lampvinklar, finner vi ett n-värde på i runda tal 1,34.

VATTNETS GRÄNSVINKEL

Standardvärdet på n för vatten i facklitteraturen anges (vanligen) generellt som 4/3=1,33.

Med A som gränsen för 0° och n=4/3 blir den maximala brytningen i vatten avrundat i PREFIXxSIN räknat från vattenytan som nollvinkelreferens lika med

limes G = asin 3/4 = 41,4°

STÖRRINGEN OCH DET VANLIGA LJUSETS FÄRGUPPDELNING

SOM REDAN OMNÄMNDES i grundstudiet av vågnaturen genom vatten, bevaras vågfrekvensen även om våghastigheten ändras, se Våghastighetsrelationen. När vattenvågen inträder olika bottendjup — idealt en tvär övergång — projiceras frekvensen lika mellan de olika höjdnivåerna på övergångslinjen medan våglängden och hastigheten varierar över de skilda djupen. Med tillämpning av samma princip på ljusets utbredning leds man till följande slutsats; Om våglängden ändras tillsammans med våghastigheten för en given frekvens, då är uttrycket för brytningsindex giltigt endast för en specifik frekvens, eller som ett medelvärde för ett visst frekvensområde. Vi kan misstänka att denna detalj kopplar till ljusets olika färger, men hur finner vi en bekräftelse på det?

Om förmodan att färger motsvarar frekvenser är relevant, borde vi kunna se dessa olika färger när ljus går in i vatten från luft (eller uttränger omvända vägen). Finns något sådant framträdande i de experiment som genomgåtts i föregående framställning? Nej. Inte direkt — beroende på grad av observation. Det finns visserligen flera olika detaljer i vattenvågornas fysik som kopplar till färguppdelning även om dessa fenomen vanligen är (ytterst) diskreta och svaga vid normal observation, alltså utan direkt hjälp av det mycket starka Solljuset som primär ljuskälla. Om vi frånser dessa specialfall, finns det emellertid en detalj vi redan studerat (Se från Störringens betydelse) och som visar ”den hemliga ingången”, nämligen den tidigare omnämnda störringen, här återigen nedan i idealiserad och förtydliga illustration. En mera ingående granskning visar att störlinsen på baljbottnen uppvisar regnbågens färgskala.

Färgspridningen ligger med blått närmast skuggkanten — precis som regnbågens innersta del, bilden nedan. Men linskroppen är i det experimentella fallet så ytterligt ljussvag att den inte på långa vägar framstår med ovanstående bilds färgklarhet. En viss uppfattning om det praktiska fallet till jämförelse syns på föregående fotografi i samband med figur 10 (med viss reservation för den billigare webbkamerans teknik — som , från och till, ger relativt dåliga färgkanaler om det gäller precisionsdetaljer, i varje fall min modell, så jämförelsen är möjligen inte riktigt helt rättvis).

Foto av en enorm regnbåge sommaren 2008, författarens arkiv. Den såg ut att bara ”gå rätt upp i himlen”. Den var oerhörd.

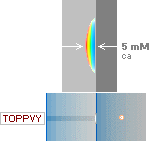
Mycket stiliserat uppvisar linsfiguren ovan den typiska bild man kan se av störringen kring blomstickan i vattenlinjen då den avbildas av ljusbrytningen på diskbaljans botten. Se även experimentanordningen från figur 10. Den motsvarande storleken är ungefärligt i skala 1:1; ca 5mM tjock och ca 15-20 mM vid — grovt sett som formen hos ett cirkulärt segment. Se även jämförande ljuskroppar från stänger med olika grovlek i Störringens oberoende linskropp.

varje frekvens har sitt särskilda brytningsindex

störringen

Störringen fungerar tydligen som ett ljussamlande instrument, vilket antyds av ovanstående illustration; För varje frekvens finns ett specifikt brytningsindex. Därmed samlar störringen de olika färgerna över (en del av) den primärt brytande linskroppen uppe vid vattenbrynet och åstadkommer så via de något skilda vinkelvägarna en uppdelning som presenteras närmare på baljans botten i formen av den aktuella »störlinsen». Som det visas, ligger blått närmast och rött längst ut. Brytningsindex för blått-violett blir det största-starkaste och för rött blir det minsta-svagaste med alla övriga färgers brytningsindex däremellan.

Som omnämndes tidigare i mätningarna, var det väsentligt att sikta in avståndspreferensen på störlinsens bottenpunkt mot kantskuggan så att själva linsbulan kunde ses ovanför. Denna del skulle därmed motsvara det blåa-violetta ljusets brytningsform med maxvärdet n=1,34.

Genom viss uppskattning av störlinsens tjocklek, ca 5 mM, med en strålväg i brytlinjen (September 2001) på runt 155 mM ges en vinkelavvikelse blått till rött på approximativt 2°, eller

atan (5/155) = 1,85°

Detta skulle ge den röda färgens brytningsindex i en grov approximation som n=1,3 [sec (limes G_{BLÅTT = 42°} – 1,9°) = 1,31 i PREFIXxSIN].

I den nuvarande upprepade experimentomgången (vattenhöjd h=96 mM) se linstjockleken markant mindre (närmare 4 mM) vilket med viss tolerans ger ungefärligen samma resultat

[atan 4/Ö(96²+70,5²) = 1,92°; sec (limes (asec 1,34) – 1,9°) = 1,3018265 » 1,31 i PREFIXxSIN].

RESULTAT:

blått ................................... 1,34

rött .................................... 1,31

medel ................................ 1,33 [= 4/3]

NOTERING. Dessa värden är grova referensvärden och med delvis idealiserade preferenser från icke optimerade mätningar.

Därmed är genomgången av den elementära vågmekaniken avslutad.

Framställningen fortsätter i Fysikaliska Grundbegrepp. Där beskrivs en ytterst enkel »interferometer» med vars hjälp ljusets våglängd kan grovberäknas tillsammans med detaljer ur Vattenvågornas Interferensmönster som också gäller för ljuset — samt ytterligare ett annat experiment som behandlar ljusets våglängdsbestämning via färgfenomen i tunna skikt. Där ges också en vidare beskrivning av Ljusbrytningen i Vattendroppar (som förklarar regnbågens bildning), samt en del ytterligare praktiska delar som berör ljusets fysik och som kan vara värda att känna till — om ej redan bekant.

Vågmekaniken i modern akademi

Den återstående delen i detta dokument tillägnas en allmän översiktlig genomgång av begreppet vågmekanik — i ljuset av den moderna akademins nomenklatur.

Elementär Vågmekanik | Atomkärnan som elektromagnetisk transformator | MPCompil.wps 2003I27 | Mac0.wps 2003II18 | TNED5.wps 2004I13 | RadioNUDE.wps 2004VII4 |

Denna framställning beskriver den moderna akademin och vetenskapen som innefattad i TNED — som en primitiv företeelse i de mänskliga kulturernas historia. Den enda praktiskt konkreta solida garanti som finns för säkerheten och kredibiliteten i det påståendet återfaller helt och hållet på den teoretiska jämförelsen mellan TNED och moderna akademi (MAC) i ämnet grundämnenas atomvikter i jämförelse med de experimentellt uppmätta värdena, och endast därigenom. Följande presentation innehåller länkar med avsikten att koppla ämnets allmänna förklaring vidare till de för ämnet särskilt avdelade avsnitten, såvitt oklarheter föreligger.

atomkärnans vågnatur

BEGREPPET VÅGMEKANIK

Om bakgrunden till uppkomsten av föreställningen att partiklar skulle besitta vågegenskaper

Se även RÄKNEEXEMPEL

Atomkärnans vågnatur

— enligt TNED

Det finns — ENLIGT TNED — inga partiklar i fysiken som uppträder SOM vågor — partiklarna (massa, laddning, spinn) EMITTERAR em-vågor vid mekaniska kontakter (stötar, kollisioner: våginterferens). Se från Atomkärnans härledning. Här följer en kort genomgång i resultatdelen.

Atomkärnan ENLIGT TNED gör sig av med den mekaniskt upptagna kollisionsenergin (återgår till sitt ursprungliga jämviktstillstånd) i samma mening som svängningens amplitud avtar. På motsvarande sätt kan kärnan exciteras genom inkommande strålning. Eftersom den moderna akademin, följdriktigt som konsekvens av att våldföra sig på energilagens första huvudsats (massa kan inte skapas kvalitativt därför att den kan förintas kvantitativt), anser att ”massa är högfrekvent ljus” tolkas ovanstående som experimentella bevis för att ”partiklarna har vågegenskaper” samt »massa kan skapas kvalitativt ur — inte utbytas kvantitativt mot — ljus». Illustrationens vågform beskrivs utförligt i huvudtexten, den härleds i Allmänna Svängningsekvationen. Atomkärnan enligt TNED härleds utförligt från PLANCKRINGEN.

Den större kompakta formen ovan till vänster motsvarar enligt TNED utseendet på alla atomkärnor från masstal 2 och uppåt. Enda skillnaden är omfånget. Kärnradierna följer i stort r₀A^1/3, r₀ protonradien och A masstalet. Eftersom även den minsta kärnans dimensioner vida överstiger dimensionerna hos elektronelementen (se Spektrum), kan elektronerna lätt förmedla alla de kärnsvängningar som uppkommer då olika partiklar på kärnnivå ”kolliderar”. Atomkärnan är enligt TNED genom sin strängt elektromekaniska konstruktion elastisk och fungerar därför som en helt perfekt transformator mellan elektrisk och mekanisk energi. Sambandet för dessa svängningar benämns genom den relaterade fysiken i TNED som det mass-interaktiva sambandet l=J/mv (MIC, mass-interactive connection). På atomär nivå har det formen l=h/mv (de Broglies vågekvation), h lika med Plancks konstant. Svängningarna är av tradition främst kända genom elektrondiffraktion (1927) och neutrondiffraktion (1932) — ”bilder av atomerna i en kristall” erhållna genom neutroners kollision med kristallatomernas kärnor.

Bakgrunden till sambandet l = h/mv

ATOMKÄRNAN se härledning från Planckringen SOM VÅGGENERATOR

Den effektiva massförstörelsen (Solen, m®g) i rörelsens bevarande (energilagen) anvisas av massa-energi-ekvivalenten enligt

Fdr=madr=m(c/dT)dr=mc²=mar=m(v/T)r=Jf ; c²/r=a ; mc²=Jf (massa-impulsmoment-ekvivalenten).

Om lokalen för m har någon koppling till divergensens impulstillstånd cr i en ringyta se Keplers ytmoment så att dess impulsmoment har ekvivalenten J=mcr vilket ger den möjliga massförstörelsen med rörelsens bevarande enligt mc²T=J=mcr, cT=r=c/f, då bildar r en våglängd (l) om T=1/f är periodisk (som den är i en cirkulär genomgång); c/l=f. Då gäller också för impulsen med massans bevarande mvl/T=Jf ; mvl=J.

Inverkan på varje m strukturerad av en ring J=mcr kommer alltså otvetydigt att generera en våglängd l=J/mv: alla kroppar (även t.ex. Jordklotet) uppvisar i princip ett specifikt l vid en specifik stötreaktion (mv). I TNED benämns denna viktiga koppling massinteraktiva sambandet (MIC, mass interactive connection). Sedan neutronen hade upptäckts år 1932 av James Chadwick, upptäckte man också strax neutrondiffraktionen; kristaller som får ”bada” i neutronstrålar uppvisar ett karaktäristiskt spridningsmönster som effektivt och noga kan bestämmas genom MIC. Men redan 1927 hade elektrondiffraktion observerats experimentellt i bekräftelse av MIC-sambandet (Davisson och Thomson, nobelpris 1937). I traditionell mening kallas MIC för de Broglies vågekvation. Men dess teori bygger på helt andra (läs: mera primitiva) föreställningar om fysiken och som ledde fram till uppfattningen om en våg-partikel-DUALITET snarare än en våg-partikel-HARMONI och som gör att alla i den studieklassen helt har missat det kvalitativa målet. Vi studerar hur.

atomkärnan uppträder som en perfekt förlustfri elektromekanisk transformator

mv-inverkan på en atomkärna åstadkommer svängningar i den elastiska kärnbyggnaden som återspeglas på de omgivande elektronmassorna vars svängningstillstånd definieras ur J=h=Plancks konstant 6,626 t34 JS. Man får alltså den rent praktiska fysiken (på elektronkvantumets nivå) enligt l=h/mv, utomordentligt väl experimentellt bekräftat sedan 1932 (eg. först 1927). Vilket vill säga; atomkärnan uppträder genom sin elastiska mekaniska konstruktion som en perfekt förlustfri elektromekanisk transformator — inom kärnelasticitetens gränser. Mekanisk stötenergi som tas upp av kärnan uttöms i elektromagnetisk strålning som dämpas av kärnans elastiska modul. Eller omvänt, inkommande em-strålning kan försätta hela kärnan eller delar av den i svängning beroende på våglängd. Eftersom kärnan inte innehåller någon mekanisk friktion (atomkärnan är förlustfri, den behöver ingen energipåfyllning för att fortsätta fungera), endast magnetiska-induktiva-kapacitiva dämpare mot självsvängningar, blir överföringarna fullständigt idealt förlustfria. Atomkärnan uppträder därmed som en helt ideal elektromekanisk transformator.

ELEMENTÄRT beskrivs atomkärnans elektromekaniska svängnissystem enligt TNED av den likaledes elementära s.k. svängningsekvationen enligt

d’’+Ad’+Bd = 0 (mekaniska delen) = u’’+Au’+Bu (elektriska delen). A=2a anger dubbla dämpfaktorn, B=w02 med w0 som vinkelfrekvensen. Lösningen till den dämpade svängningen är i PREFIXxSIN

y = C e^–at cos wt

med t som tiden för svängningsförloppet. Vågformen visas exemplifierat [y=2e^–2xcos10x] i illustrationen ovan.

Föreställningen om en våg-partikel-DUALITET i fysiken, alltså ett förment motsatsförhållande, blir följdriktigt därmed endast en i den moderna akademins egna spökslott förhärskande trångsynt missuppfattning, en ytterst primitiv och begränsad föreställning — på grund av en alltför ivrig strävan att uppfinna snarare än att härleda naturfysiken.

Visa.

Föreställningen om ”våg-partikeldualiteten i fysiken” fås alltså, som ovan, genom att eliminera massans kvalitet ur atomkärnan och bara se till kvantiteterna — elektromagnetiska svängningsformer utan några som helt kvalitativa egenskaper.

Därmed — och endast så, och inget annat, eller så inte alls — är det tydligt att modern akademi kan beskrivas såsom innefattad i TNED: som en primitiv företeelse i de mänskliga civilisationernas historia.

BEGREPPET VÅGMEKANIK

EN VIDARE RELATERAD GENOMGÅNG angående begreppet vågmekanik i modern akademi

— se särskild citatsamling för inledande bekantskap, om ej redan bekant

Begreppet VÅGMEKANIK i modern akademi

Materiefysiken är begränsad till elektronen som den förmedlande länken för all fysikalisk mätning; utan elektroner kan inga fysikaliska mätningar genomföras; All instrumentfysik bygger på elektronerna som förmedlare av ljus genom värme (rörelseenergi) och elektricitet (laddning genom ändlig hastighet).

Men elektronens bindning till sin atomkärna grundas på resonanser genom ett ytmoment (K=vr=h/m) och som grundlägger den enkla men i modern akademi tydligen helt orepresenterade härledningen till GRUNDÄMNENAS PERIODISKA SYSTEM med alla elektronkonfigurationer inkluderade; Resonanskriteriet bygger på endast hela antal våglängder, och så har det kommit sig att all makroskopiskt detekterbar fysikalisk elektromagnetisk strålning — elektronsvängningar — uppträder som om ljusenergi emitteras och absorberas i enskilda diskreta hf-kvanta; Inte därför att ”ljuset uppträder som partiklar” utan för att materiefysiken genom symbiosen elektron-atomkärna bygger på hf-resonanser: beviset är den fotoelektriska effekten: egenskaper hos materien, inte hos ljuset (Max Planck hade rätt; Se utförligt i Fotoelektriska Effekten). Rent kvantitativt — matematiskt — kan man alltså utmärkt använda begreppet ”foton” i ljusets beskrivning och dess materiella växelverkan. Men tar man den delen bokstavligt — kvalitativt — urartar beskrivningen eftersom ljusets utbredning över avstånd inte bygger på någon transporterande princip överhuvudtaget utan på en tillståndets princip genom gravitation; ljusets utbredning över avstånd sker masslöst och med ändlig hastighet i gravitationens inverkan via INDUKTIONEN vilket garanterar energins bevarande. Se även i COEI (Energins bevarande genom Induktionen).

Men massans fysik — främst kopplingen mellan atomkärnan och gravitationen, se Atomkärnans gravitella härledning, med massan som central aspekt — kan HELLER inte beskrivas med materiefysikens begrepp eftersom massfysiken också — verkligen — beskriver de element som bildar elektronen som massform, inte som kvantitet (odelbart »kvantum»), men vilken beskrivningsform anses »omöjlig» i modern akademi — och som förvisso redan till vissa delar behandlades av både Erwin Schrödinger och Werner Heisenberg mot mitten av 1920-talet (Heisenberg och Schrödingers berömda matris och vågekvationer som gav så glänsande resultat) men vars partikulärt glänsande inledningar strax förkastades redan år 1927 av Heisenberg med hänvisning till Einsteins relativitetsteori: bannlysningen av elektronmassans beståndsdelar [ref. TRETTIO ÅR SOM SKAKADE FYSIKEN, George Gamow Prisma 1966/68, s104]. Vissa bedrifter i modern akademihistoria är särskilt lysande.

Massfysiken beskrivs fullständigt härledningsbart relaterat enligt TNED via Planckringen h=mvr som en elektrogravitell struktur med atomkärnan i formen av ett elektromekaniskt svängningssystem; Se utförligt från Atomkärnans härledning; se även den kortare inledningen ovan i Atomkärnans vågnatur. Försöker man (nämligen) beskriva atom- och kärnfysiken ensidigt utifrån enbart materiefysikens horisont, utan att fästa något avseende vid massfysiken, kommer man fram till den modell av massa och materia som nu är den allmänt förhärskande och som sammanfattas i den moderna akademins begrepp VÅGMEKANIK — detsamma som »kvantfysikens allmänna beskrivning av fysiken på nivån atom och kärnfysik»: materiens väl experimentellt påvisade »våg-partikel-DUALITET».

Eller sagt på annat sätt sett från TNED: OM den rent KVALITATIVA egenskapen hos atomkärnan plockas bort och man enbart ser till den rent KVANTITATIVA (samt upphöjer DEN omformningen med begreppet kvalitet) — utraderas TNED fullständigt och ersätts av modern akademi: materiefysik: vågmekanik, typ modern akademisk: Materien uppvisar vågfenomen, ljuset uppvisar partikelegenskaper, och ingen förstår hur; en paradox framträder; en dualitet uppkommer; ”naturen” framstår som irrationell, ologisk, och möjligen därigenom också ”elak”.

Massfysiken (TNED) står emellertid helt orepresenterad i modern akademi, den är helt okänd — garanterat av uppfattningen om ”elektronens odelbarhet”; I materiefysiken är e helt säkert det: odelbar.

EXEMPEL: Ljusets polarisation, det enkla köksexperimentet som tydligen helt missats av modern akademi, gör det materiefysiken inte klarar av: massfysiken förklarar ljusets polarisation som förorsakad av inre strömmar och strukturer i elektronens massform. Se utförligt i Ljusets Polarisation. Bara av den anledning är det tydligt att det enkla köksexperimentet INTE anses välkommet i modern akademi (det avslöjar modern akademi som en ytlig anordning: fenomenformen kan inte integreras med lärostolen med mer än denna fragmenterar och sönderfaller: elektronmassans komponenter). En tekopp, vatten, en handhållen glasplatta, god belysning. Välkommen.

För en grundlig bekantskap med TNED som den fysikbeskrivning som — per exempel — tveklöst tycks innefatta, inte utesluta, modern akademi som en primitiv företeelse i mänsklighetens historia, se jämförelsen TNED/MAC (Modern akademi) i ATOMVIKTERNA. Det är — tydligen — ren utklassning. Men det finns mera.

Materiefysikens avgjort största begränsning — Planckstrålningens uppbyggnad från nollvåglängd

PLANCKSTRÅLNINGENS UPPBYGGNAD I MATERIEN är begränsad genom materiefysiken till elektronkomponenternas ändliga dimensioner; Den teoretiskt högsta frekvensen, frånsett tillskott från extra rörelseenergier, är via E=hf=mcc i elektronens fall (m=9,11 t31 KG) teoretiskt lika med

f=mcc/h=1,23739 T20 Hz vilket motsvarar vilofrekvensen i annihilationsstrålningen ±e; Materiefysiken kan varken förklara, beskriva eller härleda Planckstrålningens uppbyggnad från nollvåglängd, analogt och idealt motsvarande obegränsat hög frekvens, se Plancks strålningslag; Det som ställer upp det avgörande hindret är den kvalitativa tolkningen av sambandet för Plackenergin, E=hf: Med Plancks konstant h given kommer energin att växa över alla gränser om villkoret är att anställa obegränsat växande frekvenser. Materiefysiken klarar garanterat inte av den delen — men massfysiken gör det, galant;

Genom att atomkärnan via Planckringen h=mvr och massekvivalenten

m=[n®¥]^–1m·[n®¥] kan härledas EKVIVALENT som en obegränsad fraktal struktur av h-ringar i h-ringar utan ände — villkoret är att atomkärnan summerar nollmoment, nolladdning och nollkraft, den behöver ingen påfyllande energi för att fortsätta fungera på massa, laddning och spinn, samt att massan måste kunna upplösas fullständigt enligt E=mcc=hf — kommer också Plancks konstant h på motsvarande sätt att bli en STRUKTURKONSTANT:

hf = (h/n)nf; Med växande fraktaldjup i atomkärnan [n®¥] fragmenterar h alltmer samtidigt som f kan växa — och därmed anta obegränsat stora värden med i princip en obegränsat liten energimängd. No Problemo. Det finns en osäkerhetsprincip för varje fraktalnivå. Därmed är materiefysikens universalherravälde brutet och den moderna akademins kvalitativa vågmekanik — dualitetsbegreppet våg-partikel i modern akademi, själva motsättningen — utraderad. Därmed kan också Planckstrålningens uppbyggnad beskrivas i detalj — »ända nerifrån botten»; från de allra högsta frekvenserna [genom Comptoneffekten från den primära massförintelsen (m®g), typ Solenergin, som producerar allt längre våglängder och därmed lägre frekvenser] till de alla lägsta, se mera utförligt från Värmebildningen.

Massfysiken så introducerad leder (främst) till det som materiefysiken inte klarar av: Solfysiken; Solens fem värmegrader med härledningen till kärninduktiva strålningstrycket genom massfysiken — till skillnad från det redan väl kända elektrokinetiska strålningstrycket genom materiefysiken och som i dessa sammanhang är helt försumbart — men det enda modern akademi känner till. Av dessa fem är bara en känd av modern akademi: Planckvärmet. Resultaten leder till en (närmast galant) förklaring av Koronafysiken, tillsammans med en till synes exempellös perfekt allmänbeskrivning av Solens redan välkända observerade egenskaper i övrigt: Solperioden på 11 år, magnetiska cykeln på 22 år med Solmagnetiska fältets periodiska växling, se från Solens allmänna magnetfält, Solfläckarnas allmänna fysik, Solens allmänna vågfunktion (okänd i modern akademi), samt explicit Solens gravitella radie (6,97 T8 M okänd i modern akademi), den är ca 1000 KM större än Solens fotometriska radie (6,96 T8 M) och den är helt avgörande för Solperiodens härledning. Dessa resultat är, som det får förstås, tydligen helt omöjliga utan massfysikens bidrag — TNED — och de förlägger alla den nuvarande moderna akademins och vetenskapens uppfattningar om stjärnfysiken till nivån »dockskåpsteater med partikelacceleratorer»: fusionsmaskineriet i stjärnorna är inte höga hastigheter som får atomerna att kollidera, utan ett övergripande g-tryck — långt inne i Solcentrum över mantelytan på en liten kompakt städkärna: atomkärnan kan inte komprimeras, den står redan på noll enligt den enkla elektriska kraftlagen F = k(Q/[n®¥]r[n®¥]^–1)². Lugnt. Energiräkningen redovisar minutiöst;

Grundämnesbildningen i universum är något helt annat i praktiken än den moderna akademins uppfattning. Se vidare från GRUNDÄMNESBILDNINGEN, K-cellens värmefysik och Allmänna kosmiska tillståndsekvationen som förklarar helheten i detalj. Alla dessa resultat beskriver en fullständig kosmologisk matematisk-fysikalisk harmonisk enhet, relaterbar in i minsta detalj, som det har visat sig — helt utan inblandning av högskolematematik. Inget krångel. Raka rör. Järnet från start till mål.

CITATBLOCK

VÅGMEKANIKEN I SÄRSKILDA WEBBCITAT 2008-12-10/12

[http://www-istp.gsfc.nasa.gov/stargaze/Q7.htm] 2005-2006,

(Q-7) Wave Mechanics — From Stargazers to Starships, David P. Stern, 2005;

”That was the basic idea of what was called "wave mechanics"--meaning, not the mechanics of waves, but a re-formulation, in terms of waves, of the branch of physics known as mechanics, which deals with motions of matter.”;

Min översättning:

Det var grundtanken i det som kallades ”vågmekanik” — vilket vill säga, inte vågornas mekanik, utan en omformulering i vågtermiska begrepp av fysiken känd som mekanik vilken behandlar materia i rörelse.

”Newtonian mechanics treats matter strictly as localized particles, or of bodies and fluids consisting of such particles. Wave mechanics asserts that when one gets down to the atomic level, particles sometimes need to be treated as waves, spread out in space, their location and momentum not known until they interact. Even then, as Heisenberg showed in his uncertainty principle, one can never extract full information.”;

Min översättning:

Den newtonska mekaniken behandlar materien strikt som lokala partiklar, eller som kroppar och vätskor som består av sådana partiklar. Vågmekaniken försäkrar att när man kommer ner på atomär nivå måste partiklar ibland behandlas som vågor, utspridda i rymden, deras lokal och moment okända tills de växelverkar. Även då, som Heisenberg visade i sin osäkerhetsprincip, kan man aldrig få full information.

[http://www.faqs.org/faqs/] -2008,

INTERNET FAQ ARCHIVES Online Education

[http://www.faqs.org/docs/qp/chap07.html],

Chapter 7: Wave Mechanics and Wave Particle Duality

Källan ger tyvärr inga speciella referenser till materialet typ boktitlar, författare etc.

— Vi vet (ännu) strängt taget inte varifrån det här materialet kommer.

”Schrödinger's theory of the quantum world is called wave mechanics.”;

Min översättning:

Schrödingers teori om kvantvärlden kallas vågmekanik.

”In spite of this success, the very meaning of the waves remained unclear. Schrödinger believed that the intensity of the wave at a point in space represented the 'amount' of the electron that was present at that point. In other words, the electron was spread out, rather than concentrated at a point. However, it was soon found that this interpretation was untenable, because observations revealed that particles never spread out. For example, it follows from the wave equation that when a wave, representing an electron, strikes a target, it spreads out in all directions. Experimentally, on the other hand, the electron scatters in some specific direction but never breaks up.”;

Min översättning:

I ljuset av denna framgång, framstod den blotta innebörden av vågorna oklar. Schrödinger trodde att intensiteten hos vågen i en rymdpunkt representerade ’mängden’ för elektronen som fanns närvarande just där. I andra ord var elektronen utspridd snarare än koncentrerad som en punkt. Emellertid, upptäckte man snart att denna tolkning var ohållbar, därför att observationer avtäckte att partiklar aldrig sprids ut. Till exempel, så följer det av vågekvationen att när en våg, representerande en elektron, slår ett målobjekt, sprids den ut i alla riktningar. Experimentellt, å andra sidan, sprids elektronen i någon specifik riktning men delas aldrig upp.

[http://nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-lecture.pdf],

The fundamental idea of wave mechanics, ERWIN SCHRÖDINGER, Nobel Lecture, December 12, 1933

Vågmekanikens fundamentala idé

Schrödinger avslutar sitt föredrag så:

s316:

”I would define the present state of our knowledge as follows. The ray or the particle path corresponds to a longitudinal relationship of the propagation process (i.e. in the direction of propagation), the wave surface on the other hand to a transversal relationship (i.e. norma1 to it). Both relationships are without doubt real; one is proved by photographed particle paths, the other by interference experiments. To combine both in a uniform system has proved impossible so far. Only in extreme cases does either the transversal, shell-shaped or the radial, longitudinal relationship predominate to such an extent that we think we can make do with the wave theory alone or with the particle theory alone.”

Min översättning:

Jag skulle beskriva vår kunskaps nuvarande tillstånd sålunda. Strålen eller partikelvägen motsvarar en longitudell relation hos fortplantningsprocessen (alltså, i utbredningsriktningen), vågytan å andra sidan en transversell relation (alltså, i dess normal). Bägge relationerna är utan tvekan verkliga; den ena bevisas genom fotograferade partikelvägar, den andra genom interferensexperiment. Att kombinera bägge i ett enhetligt system har hittills bevisats omöjligt. Bara i extrema fall överväger antingen den transversella, skalformade eller radiella longitudella relationen till den grad att vi tror vi kan stå ut med vågteorin ensam eller med partikelteorin ensam.

Min Kommentar:

Det ser ut som en ”ångestdeklaration”: plågsamheten i att ”nödgas överge” Newtons mekanik för en ny, mera sublim och samtidigt rent förskräcklig vågteori — som på det hela taget gör att man begriper ännu mindre än tidigare — men som är det enda experimentellt överensstämmande alternativet som finns.

Det hade (således) varit bättre för vetenskapen omkring 1930 att kapitulera inför Naturen och inse att Hon är den smartare. Därmed hade man enklare kommit problemets lösning på spåren; härled fysiken, uppfinn den inte.

@INTERNET Wikipedia Wave-particle duality 2008-12-12

”In physics and chemistry, wave–particle duality is the concept that all matter and energy exhibits both wave-like and particle-like properties. A central concept of quantum mechanics, duality addresses the inadequacy of classical concepts like "particle" and "wave" in fully describing the behaviour of small-scale objects. Various interpretations of quantum mechanics attempt to explain this ostensible paradox.”;

Min översättning:

I fysik och kemi är våg-partikeldualiteten begreppet att all materia och energi uppvisar både vågliknande och partikelliknande egenskaper. (Som) Ett centralt begrepp i kvantmekaniken, adresserar dualiteten oförmågan hos klassiska begrepp som ”partikel” och ”våg” i ett fullständigt beskrivande av beteendet hos småskaliga objekt. Olika tolkningar av kvantmekaniken försöker förklara denna skenbara paradox.

BLANDADE CITAT — vågmekaniken

massa är ljus

”Skillnaden mellan materia och strålning är inte definitiv. Båda kan betraktas som en form av energi. Vid sin kortvågiga gräns närmar sig strålningen till och övergår i gripbar materia.”,

FOCUS MATERIEN 1975 s262sp1mö

begreppet vågmekanik

de Broglies vågekvation

”Planck och Einstein hade påpekat, att ljuset, om vars vågnatur tidigare ingen tvekan rått, ibland kunde uppföra sig som en ström av partiklar. År 1924 framkastade Louis de Broglie tanken att denna dualism våg-partikel kanske kunde tänkas gälla även sådana företeelser som man dittills betraktat som partiklar, t.ex. elektronerna. Hypotesen om sådana s.k. materievågor gav uppslaget till en ny och mycket fruktbärande utvecklingslinje inom fysiken som fått namnet vågmekanik.”,

FOCUS MATERIEN 1975, s97sp1ö

”Våglängden hos en materievåg skulle enligt de Broglies hypotes bero av den motsvarande partikelns impuls enligt relationen

h

l = —— (8)

mv

där h är Plancks konstant, m partikelns massa och v dess hastighet.”,

FOCUS MATERIEN 1975, s97sp2mn

elektronen inte i kärnan

”… sedan kvantmekaniken gjort sitt segertåg blev den viktigaste invändningen den att elektronen helt enkelt inte kunde rymmas i kärnan. Detta kan förefalla egendomligt med tanke på att elektronen ju är den lättaste av partiklarna. Det visade sig emellertid att våglängden hos den materievåg som är associerad med elektronen skulle bli större än kärnans egna dimensioner vid den energi hos partiklarna som det här rörde sig om.”.

FOCUS MATERIEN 1975, s116sp1mn

elektronen strukturlös

”Unlike α particles, electrons are structureless point-like objects”

DETERMINATION OF THE HELIUM-6 NUCLEAR CHARGE RADIUS USING HIGH-RESOLUSION LASER SPECTROSCOPY, s14

LI-BANG WANG, B.S., National Taiwan University, 1996;

Min översättning:

Till skillnad från alfapartiklar, är elektroner strukturlösa punktlika objekt.

elektronen oändligt liten

”Experiments in which electrons are scattered by other particles, however, effectively measure the size of the electron, and they indicate that the radius must be exceedingly small. Indeed, all experimental data gathered so far are consistent with the idea that the electron is a point particle, entirely without extension.”

”In the 1940’s these problems were resolved by abandoning the mechanical model of the electron and devising a new and more abstract theory, quantum electrodynamics. In quantum electrodynamics the electron is allowed to be a dimensionless point particle and its mass is allowed to be infinite, at least in principle.”

SCIENTIFIC AMERICAN August 1980 The Isolated Electron s92sp2;

Min översättning:

Experiment med elektroner som sprids av andra partiklar, emellertid, mäter effektivt elektronens storlek, och de indikerar att radien måste vara mycket liten. Alla samlade data är hittills, verkligen, samstämmiga med uppfattningen att elektronerna är punktpartiklar, helt utan utsträckning.

Under 1940-talet löstes dessa problem genom att bannlysa elektronens mekaniska modell och anvisa en ny och mera abstrakt teori, kvantelektrodynamiken. I kvantelektrodynamiken är elektronen tillåten att vara en dimensionslös punktpartikel och dess massa tillåts vara obegränsad, åtminstone i princip.

massa kan skapas

”Electron-positron pairs can be formed if gamma rays with energies of more than 1 million electron volts strike particles of matter.”.

ENCARTA 97/99 Positron

Min översättning:

Elektron-positron-par kan formas om gammastrålar med energier mer än 1 miljon elektronvolt träffar materiella partiklar.

”When a high-energy photon penetrates the electron shell close to the nucleus, it may create a pair of electrons, one of negative charge and the other positive; a positively charged electron is also known as a positron. Pair production is an example of the conversion of energy into mass.”.

ENCARTA 99 · X-ray, Pair Production

Min översättning:

När en högenergetisk foton penetrerar elektronskalet nära en atomkärna, kan den skapa ett par elektroner, en med negativ laddning och den andra positiv; en positivt laddad elektron är också känd som en positron. Parproduktion är ett exempel på omvandling av energi till massa.

”In classical physics, matter and energy were considered two separate concepts that lay at the root of all physical phenomena. Modern physicists, however, have shown that it is possible to transform matter into energy and energy into matter and have thus broken down the classical distinction between the two concepts (See Mass; Relativity).”

ENCARTA 97/99 Matter

Min översättning:

I klassisk fysik ansågs materia och energi två skilda begrepp som grundlade all fysisk fenomenalitet. Moderna fysiker, emellertid, har visat att det är möjligt att omvandla materia till energi och energi till materia och har således brutit ner den klassiska åtskillnaden mellan de bägge begreppen.

CITATBIHANG

RÄKNEEXEMPEL de BROGLIES VÅGEKVATION

TNED: våg-partikel-DUALITET i fysiken finns inte

Massa är ställen utan ljus ENLIGT TNED (se GRIP och DEEP) — Så: massa kan inte ”emittera ljus”, vilket ändå skulle vara ”våg-partikel-dualitetens definition”: partiklar ”uppträder som em-vågor”. Konfusionen har lett till uppfattningen att ”atomkärnans beståndsdelar” i formen av ”partiklar” skulle kunna anställas på föreställningar om ”partiklars vågegenskaper” och därmed en diskussion om »mekanismerna i den svåråtkomliga kärnfysiken» huruvida den och den partikelns våglängd inryms i den och den partikelns volym. I TNED finns inga partiklar alls i atomkärnan. Se från Atomkärnans härledning.

Modern akademi accepterar protonen och neutronen i atomkärnan — men inte elektronen i neutronen

Om vi endast för jämförelsens skull undersöker samma typargument på alla kärnor tyngre än protonen som modern akademi använder för elektronen (man sätter v=c i de Broglies vågekvation) mot neutronen som värd finner man i runda tal

kärna materievåglängd

protonen-neutronen ............ 1,32 t15 M = r₀

helium ................................ 0,33 t15 M

guld .................................... 0,007 t15

materievåglängden l=h/mc @ (proton-neutronradien)/masstalet = (1,32 t15 M)/A

Och så vidare. Materievåglängden skulle alltså minska med kärnans ökande massa. Därmed skulle heller INTE kärnorna kunna förklaras som sammanslagningar av fria neutroner och protoner. Trots att analogin alltså saknar konsistens som sådan, är det — som vi nu alla väl vet från de elementära skolböckerna — ändå just den uppfattningen av atomkärnan den moderna akademin uttrycker: den moderna akademin accepterar protonen och neutronen i atomkärnan — men inte elektronen i neutronen.

modern akademi accepterar protonen och neutronen i atomkärnan — men inte elektronen i neutronen

END.

Elementär Vågmekanik

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Elementär Vågmekanik

ämnesrubriker

innehåll

ELEMENTÄR VÅGMEKANIK

Inledning

Reflexionslagen

Tillämpningar 1 mekanisk stöt

Tillämpningar 2 pulsbildning

Tillämpningar 3 stående vågor

Tillämpningar 4 vattenvågors reflexion

Experiment 1 cirkulära vågor

Experiment 2 raka vågor

Vattenvågsfysiken

Hur vattenvågen reflekteras

våghastighetsrelationen

Experiment 3 stående raka vågor

Verifikation av djupfaktorn

Tillämpningar 5 vattenspegling

Ljusstrålar är masslösa

Experiment med Fyra Stålkulor

Ljusbrytningen genom vatten

Hur ljusbrytningen kan mätas med enkla hjälpmedel

Störringens betydelse

Störringens oberoende linskropp

Mätexempel

Vattnets gränsvinkel

STÖRRINGEN OCH DET VANLIGA LJUSETS FÄRGUPPDELNING

Störringen

Resultat

Atomkärnans vågnatur

Bakgrunden till sambandet l = h/mv

Begreppet vågmekanik

Citatblock

Citatbihang

RÄKNEEXEMPEL de BROGLIES VÅGEKVATION

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[BA]. BONNIERS ASTRONOMI 1978

— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.

[FM]. FOCUS MATERIEN 1975

[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2017-08-13

*END.

Stavningskontrollerat 2008-12-16.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se