innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Induktionen och Magnetismen kan [nära exakt] liknas
vid mekanikens hydrodynamik: En vattendroppe som efter träffen mot vattenytan
bildar expanderande ringar, magnetism, och fria droppserier via kraftrekylen, induktion.
Av ej närmare känd anledning [naturföraktet frånsett] varken omskrivs eller används
den analogin i den moderna akademins lärosystem.
Base • Fysikens
7 Principer | DIVERGENSEN | Ljusbrytningen
| Ljusfrihetssatsen
| Ljusets Gravitella
Beroende | Elektriska Kraftlagen
| Elektriska
Laddningen | Elektriska Fältet | Fältfrihetssatsen
|
Main • Induktionsdipolens
uppkomst | INDUKTIONEN | Närverkan och Fjärrverkan | Induktionslagen | Induktansbegreppet
från elektriska konstanten |
Induktionens specifika ekvationer · Ringen · Rakledaren ·
Transformatorlagen | Parallellexperimenten | Induktionsbegreppet
genom Parallellexperimenten | Allmänna
Materieinduktansen |
BILDKÄLLA: Författarens arkiv · Ovan: 21Mar2009VattenDrop10ABild46 · NikonD90 · TonMontage
med DELPHI4Test2011, originalbilden förminskad tillsammans med centraldetaljen
i fokus · Nedan: 17Maj2009StrandBild130
· Detalj
*Förklarande INDUKTIONEN OCH MAGNETISMEN 2007VI14
INDUKTIONEN
MED VIDARE FORTSÄTTNING FRÅN EN INTRODUKTION TILL
INDUKTIONEN OCH MAGNETISMEN
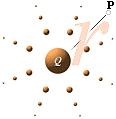
®i
I en given rymdpunkt P är vid varje tidpunkt givet en specifik fältmässig potential U=k(Q/r) från det ideala elektriska laddningssystemet Q. Ansatsen, från Q®v i analogi till en strömriktning ®i, att ändra U i riktningen i med en motsvarande resistans ®R, uppväcker enligt Newtons tredje lag ett reaktivt motstånd ¬R. Som detta reagerande ¬R är differentiellt så länge v är konstant, erbjuder det inget realt värdemässigt motstånd. Inverkan av ¬R påverkar således inte rörelsen hos Q med konstant v. Bara när Q lägesändrar genom att öka eller minska hastigheten (accelerera), kommer den differentiella reaktiva faktorn ¬R att ackumulera över den allmänna elektriska fältexpansionens hastighet c för att bygga upp en motsvarande induktiv dipolfältstyrka (Ð=û/r) i den omgivande dominanta gravitella referensen. Se utförlig separat beskrivning i INDUKTIONSDIPOLENS UPPKOMST.
Effekten på de omgivande laddningarna (q) från detta induktiva rymddipolfält (Ð) är att q attraheras av Ð i den naturliga totala verkan som alltid söker att motverka orsaken till uppkomsten av en ändring (accelerationerna, se Newtons tredje lag eller mera rudimentärt tredje ändringslagen), det vi kallar för (elektromotorisk) induktion.
Induktionens verkan kan beskrivas allmänt genom induktionslagen:
verkan
av en växande elektrisk ström strävar att motverka orsaken till strömökningen
genom en strömökningen motriktad induktionsspänning;
verkan
av en avtagande elektrisk ström strävar att bevara strömstyrkan genom en
strömminskningen medriktad induktionsspänning.
Induktionslagens kvalitativa fenomengrund har också en motsvarande allmän (generaliserande) kvantitativ matematisk form (û = L · di/dt).
Se Universella Induktionslagen.
*Förklarande INDUKTIONEN OCH MAGNETISMEN 2007VI14
basic
mathematics of induction
INDUKTIONENS GRUNDMATEMATIK
|
Från den elektriska kraftlagen F = kQ2/4pr2 med k=Rc, skrivs den induktiva fältstyrkan (Ð, Alt+0208, d-e, endast i denna presentation) från den allmänna fältstyrkan (X=U/r=FQ/r=kQ/r, med Grekiskans stora xi [X i Symbol] för X) differentiellt genom induktionspotentialen (û) som dû/r = kû · dQ/4pr, = d(dû/dr) = dÐ, V/M Eftersom û bildas differentiellt, skilt från c genom en laddningshastighet v, måste den ordinära elektriska konstanten genom divergensen k=Rc relateras kû=R’v för induktionens verkan via den i en pågående acceleration momentana laddningshastigheten v, a=dv/dt, där R’ är den ackumulerade induktiva resistansen närvarande bara när v är del i en acceleration: dû = R’v · dQ/4pr = R’v · diT/4pr = R’(ds/dt) · diT/4pr =
R’T · (di/dt)(1/4pr)ds De separata termerna it betyder den
aktuella strömmen för i och t tiden under vilken i-kvantiteten
ändras. Med differentialkvoten di/dt kallas termerna tillsammans för strömderivatan.
Mera noggrant för den induktiva fältstyrkans
del gäller då via dÐ
= d[dû/dr] att dÐ = R’v · dQ/4pr2 = R’v · diT/4pr2 = R’(ds/dt) · diT/4pr2 = R’T · (di/dt)(1/4pr2)ds Dvs., di/dt-kvoten framkommer ur den motsvarande induktivt verksamma delen R’v i elektriska konstanten (Rc) genom likheten v=ds/dt. Produkten R’T kallas induktans (L=RT) och varar under T bara så länge Q-rörelsen ändras. Vilket vill säga, bara så länge strömderivatan (di/dt) har någon lutning skild från exakt noll. Generaliserad av de nämnda termerna, kan den grundläggande differentiella induktiva ekvationen skrivas i termer av den induktiva dipolfältstyrkan enligt dÐ = L(di/dt)(1/4pr2)ds. Med vinkeln b (se vidstående illustration) mellan
linjerna 1. Q-origo till en godtycklig rymdpunkt P utanför Q-centrum och 2.
riktningen i s-förlängningen för lägesändringen (i) når vi
slutligen den fundamentala differentiellt induktiva komponenten i PREFIXxSIN dÐ = L(di/dt)(1/4pr2)sinb · ds ........................... V/M
induktiva dipolfältstyrkan i P |
|
Med en vidare termförenkling enligt
L = L(di/dt) med L som Grekiskans stola L [Lambda]
skrivs formen enklare
dÐ = (L/4pr2) sinb ds
...................................... V/M
L ...... aktuella ledarinduktansen, standardenheter,
H Henry (WS= VS/A)
Ð ..... speciell beteckning för
induktiv dipolfältstyrka X i V/M,
giltig i P
utanför ledaren från ds
L ..... Grekiskans
Lambda, förkortar komponenterna L(di/dt), V
*Förklarande INDUKTIONEN OCH MAGNETISMEN 2007VI14
Betydelsen och verkan av DEN INDUKTIVA DIPOLEN
I ovanstående härledda
led för den inducerade spänningen û
dû =
R’T · (di/dt)(1/4pr)ds = L · (di/dt)(1/4pr)ds
kan vi generalisera
induktionsbegreppet genom att bortse ifrån strömvägens förlängning eftersom den
fysiska enheten från faktorerna (1/4pr)s i vilket fall bildar en numerisk
koefficient. Därigenom, enbart i beaktande av en principiell bildning för den
inducerade spänningen û,
har vi det centrala sambandet
û = L = L · (di/dt)
Som vi ser från
denna likhet, bildar ackumulationen av resistans i P genom strömderivatan (di/dt)
en konstant spänningskälla. Från denna principiella bildning blir det
naturligt att kalla spänningsramen û genererad i P för en fältdipol
med den enkla innebörden av ett levande spänningsfall û till 0 i
P (från + till –).
Som spänningen û bildas motsatt
Q-fältets potentiella variation, utbildar också û en mekanisk tröghetskraft
med vilken den induktiva resistansen (R’) agerar och försöker motverka verkan
från Q-accelerationen.
Spänningen som
bildas av induktionen blir rymdspänningsrelaterad till g-ramens referens
relativt Q-rörelsen. Denna rymdspänning blir därmed fullständigt oberoende av
typen av ledare den ingriper i. En fin silvertråd kommer att uppvisa exakt
samma spänningsfall per längdenhet som ett hårstrå eller en grov kopparcylinder.
Experiment med raka ledare bekräftar också (trivialt) att så är fallet (se parallellexperimenten).
För att finna praktiska värden för den inducerade spänningen (û) ur den ovan härledda induktionens grundform, måste vi känna den aktuella kurvaturen för strömlinjen (s) — vilket betyder att vi måste utföra (åtminstone) en ytterligare integration. Se vidare i specifika Ð-ekvationer.
*1996XII by 1999XII Compilation of INDUCTION AND MAGNETISM 2007VI15
Extraherat från P2001_2,wps
NÄRVERKAN OCH FJÄRRVERKAN
Både induktionen och magnetismen uppvisar en närverkan [Q till insidan] och fjärrverkan [Q till utsidan]. För att särskilja dessa komplex i beskrivningen är induktionen i den här presentationen indelad i en primär och en sekundär del, medan magnetismen har bibehållit terminologin med närverkan och fjärrverkan. För den senare delen, se explicit i Magnetismen.
PRIMÄR OCH SEKUNDÄR
INDUKTION
ENLIGT RELATERAD FYSIK
Medan den primära induktionen »tar» direkt i den absoluta närytan av varje laddningsmassa när den lägesändrar (se utförligt i potentialbarriären),
vilar den sekundära induktionen på utvidgningen
av det elektrostatiska fältet hos varje laddning beroende på divergensen
c. Den sekundära induktionen refereras till en primärinduktionen
motsvarande men väsentligen fördröjd ändring genom varje laddnings
lägesändring i den omgivande rymdens individuellt g-relaterade fältpunkter.
I MODERN AKADEMI finns (här veterligt) ingen sådan åtskillnad presenterad, omskriven eller omtalad.
Induktionsbegreppet i modern akademi ställs helt på magnetismens framträdande: Man hoppar över expansionsintegralen som definierar den fenomenologiska skillnaden mellan induktion och magnetism — och kan därigenom [bekvämt] tillämpa den kvantitativa vektorkalkylens begrepp [som uppfanns av modern akademi under 1800-talet, se utförligt från Differentialelementet i modern akademi] enligt de berömda s.k Maxwells ekvationer. Se även TRE EXAKTA EXEMPEL där resultaten jämförs i noggrann korsreferens mellan relaterad fysik och modern akademi.
Grundläggande fysiska villkor för elektrisk ström — se även i Introduktion till Induktionen och Magnetismen
Grundbegreppen inom induktionen och magnetismen finns redan beskrivna i inledningsavsnittet till induktionen och magnetismen i
UPPKOMSTEN AV INDUKTIONEN OCH MAGNETISMEN från Ljusets natur i avsnittet om Elektriska laddningen. Vi förutsätter här bekantskapen med dessa grundbegrepp. De anges i vilket fall löpande genom länkar till de aktuellt förklarande och beskrivande avsnitten så att man obehindrat kan följa resonemanget i detalj. För harmonin i det löpande sammanhanget måste genomgången av dessa grundbegrepp här till vissa delar upprepas.
När divergensen c agerar lokalt genom »utvidgningen» ds
i rymdpunkten (P), relaterar också c en acceleration a=c/dT.
Enligt Newtons
tredje lag måste denna acceleration resultera i (eller, vara
resultatet av) en tröghet, ett divergensmotstånd R som motverkar
gravitationens absolutverkan — och därigenom ger den ändliga divergensen [Se utförligt i GcQ-teoremet].
Som c agerar genom R i ds som en konstant hastighet
c = ds(dT)–1, kan verkan av R och c tillsammans
uttryckas med substitutionen R/R=1 i c enligt
Rc = Rds(dT)–1. Överflyttningen ger
RdT = Rc–1ds. Med kvoten
Rc–1=µ som en konstant referens för den fria rymden rymdkompakthet
får vi
RdT = µds ......................... VS/A=VS/AM · M
Med konstant
divergens över s får vi RT=µs. Med beteckningen RT=L
ges då explicit för induktionen
L = µs ................................. den primära induktansen, VS/A (Henry)
µ = Ls–1
.............................. primärinduktansen
per meter, VS/AM
(Henry/Meter)
Detta är den
minsta möjliga elektriska tröghet eller primära induktans varje
elektrisk strömlinje kan och måste ha i elektrofysiken. Alla strömlinjer s som arbetar under divergensen c måste
utgå från denna grundläggande µ rymdprimära induktans per meter.
Som L uttrycker
produkten av resistans R och tid t, där R=ûPOTENTIAL/iSTRÖM, får L ekvivalenten ûti–1=L. Då är ût=Li, eller û=L(i/t). Om
strömmen i är konstant med hänsyn till tiden t, [i/(t®¥)], så att lutningen di/dt
närmar sig noll obegränsat, gör û det också. Således uppträder û,
och därmed också L aktivt endast genom en strömderivata (di/dt) > 0. Enligt Newtons tredje lag tvingas
spänningen û (u-flex) att växelverka med varje
annan närvarande spänning U så att den inducerade û motverkar U. Vilket
vill säga,
û = –L(di/dt) ...................... inducerad spänning
där L=µs.
Varje strömlinje får sin egen specifika
primärinduktans per meter, µ, med hänsyn till olika parametrar som material,
temperatur, kristallin struktur, och täthet. Det gör termen induktans i
praktisk mening till en högst utmanande och krävande term att hantera om vi
önskar en precis behandling. Se PRIMÄRINDUKTANSEN I SAMMANFATTNING.
Emellertid kommer bestämningen av L i det praktiska
fallet att bli så enkel som att mäta den genom den negativa spänning den skapar
tillsammans med strömderivatan: L = û/(di/dt). Den formen
gäller för varje typ av strömväg under alla typer av förhållanden.
För att etablera en
elektrisk ström
— en Q-rörelse över en ändlig distans s
bestämd genom divergensen c —
måste strömvägen
minst ha den absoluta rymdinduktansen L per meter s enligt L/s.
ELEKTRISK INDUKTANS MOTSVARAR MEKANISK TRÖGHET — Se Integrala Analogierna
Induktansfaktorn L
själv har en direkt matematisk motsvarighet till mekanikens massa
(m) som ansvarig för uppkomsten av det rent elektriska motståndet då (di/dt) > 0, se Integrala Analogierna. För
att etablera en given ström I, beror
induktionsspänningen û på tiden som krävs för att uppnå
(accelerera) I. Effekten och energin
blir då de sambandsformer som framgår i Integrala Analogierna: Energin
konserveras genom den etablerade rörelsen — och frigörs när den upphör.
Exempel
Betrakta en lång
elektrisk ledare (tråd, tiotal eller hundratals meter). Påförandet av en
spänning mellan trådändarna med en mellanliggande ändlig (låg) resistans
betyder att starta upp en ström genom tråden. Den induktiva energin som
användes vid strömmens uppbyggnad finns nu tillsammans med den konstanta
toppströmmen — som en boll i rörelse bevarar kraften som åtgick för att sätta
den i rörelse. När strömvägen sedan plötsligt bryts, introduceras en mycket
snabbt avtagande strömderivata (di/dt) i strömvägen där t-faktorn
tydligen närmar sig noll obegränsat; Den resulterande inducerade spänningen
enligt û=Ldi/dt tvingas då lika uppenbart att växa över alla
gränser. Om inte den upplagrade energin (genom någon lämpligt utformad
skyddsanordning) tillåts ta en lämplig utväg ur denna påtvingade situation,
kommer en urladdningsgnista att bildas någonstans där motståndet
är som lägst i trådvägens omedelbara närhet. Det sker, om inte annat, då û når isolationsspänningen för luft, ca 25 000 Volt per centimeter.
Därmed frigörs energin som användes vid den tidigare strömmen uppbyggnad.
Placera därför alltid en lämplig
skyddsresistans mellan ändarna på en spole eller generellt långa ledare med
speciellt höga induktanser så att AV-stötarna kan ebba ut mjukt och därmed
motverka en annars uppenbart äventyrlig förstörelse.
Som c/dT = a med c · ds/dT
= a · ds = c2 har
vi specifikt
µ0ds = R0 · dT = R0 · c/a
µ0 · a · ds = R0c0
µ0c02 = R0c0 = 1/e0
c0 = 1/Ö e0µ0
där
e0 = 1/R0c0 = 8,8543 0803 t12 C/VM
µ0= R0/c0= L0s–1= 1,25662 t6 VS/AM [1,2566370614 ENCARTA, Fundamental Constants];
c0 = 2,99792458 T8 M/S
DEN
PRIMÄRA INDUKTANSEN gäller
oberoende
av kurvaturen för
s.
Det är bara den
effektiva längden av s, strömmen väg, som räknas i primärinduktansen.
Denna grundläggande
egenskap är relevant bara i det att vi betraktar en ändring i en ström så att
ändringen ingriper eller »tar tag i» alla laddningar i en enda sekvens —
som vore laddningarna sinsemellan
knutarna på ett slutet rep som kan dras ändlöst runt två motsatta hjul likt
strömmen i en sluten elektrisk krets.
Denna situation är direkt tillämplig på den
mekaniska rörelsen hos laddningarna i en ledare. I det elektriska fallet där
alla laddningar i en ledare »dras» av en pålagd spänning, är den exakta
analogin till en motsvarande direkt respons här inte känd, men en sådan
ideal direktverkan antas här ändå.
i
sammanfattning
För att särskilja den primära induktionens huvudmässiga induktans (Lc) från varje annat allmänt induktansbegrepp (L), betecknas i denna presentation för klarhetens skull termerna kopplade till den primära induktansen enligt uppställningen i PRIMÄRINDUKTANSEN I SAMMANFATTNING.
Notera den mera
allmänna innebörden av µ som den tidigare relaterade rymdkompaktheten. Dess induktiva mening
manifesteras bara utmed en strömväg (s). I magnetismen är detta inte fallet
eftersom s och µ arbetar rätvinkligt varandra. Se speciellt Växelverkansfrihetssatsen. Exempel som
visar tillämpningen praktiskt ges utförligt i Tre Exakta Exempel.
Medan den primära
induktionen »tar» direkt i det absoluta närområdet av massytan till varje
elektrisk laddning (se Potentialbarriären)
när den lägesändrar, vilar den sekundära induktionen på en utvidgning av
det elektrostatiska fältet för varje elektrisk laddning beroende på divergensen (c). Den sekundära
induktionen relateras för varje berörd laddning till en fördröjd ändring av
tillståndet i den relativt primärledaren omgivande rymdens g-relaterade
fältpunkter.
För att en
centralladdning ska kunna kommunicera eller ”uppdatera” ändringen i dess egen
position till sina egna individuella fältpunkter, måste varje laddning använda
den begränsade divergensen (c) för att »rapportera» positionsändringen till potentialerna i dess eget
individuella Q-fält. Se även i Superpositionsprincipen.
För att relatera en verkan i denna, sekundära,
induktion måste vi studera situationen i respekt till ett givet tillstånd i en
godtycklig rymdpunkt skild från laddningens massyta. Som Q-fältet för varje
individuell laddning utvidgas oändligt från dess origo, påverkar den sekundära
induktionseffekten från varje individuell elektrisk laddning fälten och centrum
för alla övriga individuella elektriska laddningar.
Samtidigt introducerar oss detta studium
för den allmänna föreställningen om induktionens verkan — också giltig för den primära induktionen,
eftersom också den primära induktionen måste använda fältpunkter, ehuru i en
mera omedelbart närliggande mening, se Potentialbarriären.
Som vi ska se, har den
elementära inverkan av den sekundära induktionen praktiskt taget ingen
betydelse inom en ledare, men en högst vital betydelse utanför den: Den sekundära induktionen
påverkar vad som helst som har någon utsträckning utanför
primärledaren, därigenom »rapporterande» alla ändringar till alla andra som
befinner sig utanför den (en perfekt demokrati).
specifika Ð-ekvationer
INDUKTIONENS SPECIFIKA EKVATIONER
Från den introducerande genomgången av INDUKTIONENS MATEMATIK härleddes grundsambandet nedan:
dÐ = L(di/dt)(1/4pr2)sinb · ds ...... V/M, praktiska induktiva dipolfältstyrkans grundform i P
L = L(di/dt);
dÐds
®
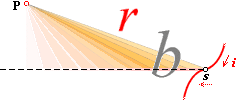
dÐ = (L/4pr2) sinb ds
......................................... V/M
L ...... aktuella
ledarinduktansen, standardenheter, H Henry (WS= VS/A)
Ð ..... särskild beteckning
för induktiv dipolfälstyrka X i V/M,
giltig i P
utanför ledaren från ds
L ..... Grekiskans Lambda, förkortar komponenterna L(di/dt), V
NOTERA
ATT L BLIR EN SAMMANSATT INDUKTANS OM s ÄR NÅGOT ANNAT ÄN EN EXAKT RAK
STRÖMVÄG. MED EN GIVEN KURVATUR FÖR s inte en rät linje KOMMER DEN
SEKUNDÄRA INDUKTIONEN ATT ADDERAS ELLER
SUBTRAHERAS BEROENDE PÅ DE OLIKA DELARNAS KURVATUR.
LTOTAL = Lc + LSKURVATUR
Se uppställningen i
PRIMÄRINDUKTANSEN I SAMMANFATTNING
För en rak ledare
är LSKURVATUR noll där Lc är dess primära induktans. För en ledare i
formen av en rät vinkel, ger ingendera av de motstående sidorna något bidrag
till sekundärinduktionen i strömmens riktning: induktionen verkar endast i
strömriktningen.
Den
generaliserade ringintegralen
RINGEN OCH DEN
CIRKULÄRA SPOLEN
Inverkan av den
sekundära induktionen i tillämpningen på elementära elektriska
ledare är speciellt uttalad i den cirkulära ringen. Med den föregående omnämnda generaliseringen
û = L(di/dt) blir den inducerade spänningen i ringen
ûRING = LK =
L · (di/dt) · K
................................. ringinduktionen
K ............................................................................ numerisk koefficient
K beror av ringens
dimensioner och induktionsvinkeln (normalt hela varvet 360°). K blir en
högeligen sammansatt koefficient som för sin rent matematiska beskrivning
kräver snart sagt en hel volym i sig [ref. CD Kraftlagen
1999 XII, Induktansen.wps 1999XI20]: ämnet är ypperligt komplicerat;
ingen direkt (enkel) sambandsform för K är här känd.
I en strikt term av mätande teknik, finns
för ringen del ingen möjlig väg att skilja den sekundära induktionen från den
primära. Med den mera precisa primärinduktansen Lc=µLs
för L där s=2pr, r ringens medelradie, blir ringens
allmänna induktion
ûRING = pµL2r · (di/dt)K ........................................ allmänna ringinduktionen, V
Med förenklingen 2r=d
som diametern med Ld · 1M–1=pKµL får vi det enklare
ûRING = d·Ld (di/dt)/1M
.......................................... allmänna
ringinduktionen, V
NOTERING. I
ALLMÄNHET ÄR DEN INDUCERADE SPÄNNINGEN û MOTRIKTAD HUVUDSTRÖMMEN OCH SKA
GES MED NEGATIVT TECKEN. MINUSTECKNET FRÅNSES DOCK I GRUNDFORMERNAS ENKLA
BESKRIVNING.
Allmänna
ringspoleinduktionen
Uttrycket för den
allmänna ringinduktionen är också grundvalen för ringinduktionen i formen
av en elektrisk spole — med följande enkla tillägg.
Betrakta en luftlindad (utan järnkärna)
spole med en fin isolerad koppartråd i n varv som en enda lång ledare.
Vi frånser de olika geometriska positionerna mellan ringarna — vi ser varje
lidningsvarv som en helt ideal exakt sluten individuell ring — vilket innebär
att ringens tjocklek måste vara liten relativt ringens diameter för att
sambanden ska gälla, analogt en tunn tråd lindad på en (betydligt) större
cylinder. Som samma ström flyter genom alla individuella cirkelvarven, påverkar
varje varv alla de övriga varven med en sekundär induktion som vi betraktar
ömsesidigt densamma för alla individuella ringar. Från
ûRING = d·Ld (di/dt)/1M
.................................... allmänna
ringinduktionen, V
finner vi då:
Induktionen i n
ringar, som inte påverkar varandra, blir
ûnRING = d·n·Ld (di/dt)/1M
Induktionen i n
ringar som påverkar varandra idealt blir då motsvarande en produkt med n
enligt
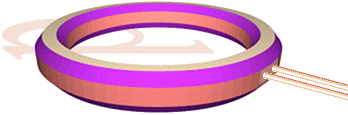
|¬ d
® |
ûCOIL = d·n2·Ld (di/dt)/1M
........................................ allmänna
ringspoleinduktionen, V
eftersom varje ring
erhåller en sekundär induktion beroende på strömderivatan (di/dt) i alla
n. Vilket vill säga: Induktionen i n varv växer med antalet n
ringar (primärinduktansens längd) och antalet n innefattade sekundära
induktioner. Precisionen i detta uttryck avtar med växande tvärsnitt hos
ringkroppens trådform. Allmänna induktansen L=U(di/dt)–1 blir då
ûCOIL(di/dt)–1 = L = d·n2·Ld /1M ..................... allmänna ringspoleinduktansen, VS/A
Med substitutionen
höjden h för spolen får vi
L = d·n2·Ld · h/(h · 1M)
= d·n2·pKµL · 1M · h/(h · 1M)
= d·n2·pKµL · h/h
Som d2r · pKh av princip tillåter pr2 (K-faktorn för ringen är högeligen flexibel i
respekt till alla möjliga fall av en rings dimensioner) får spolens allmänna
induktans också ekvivalenten
= µLn2 · pr2/h
L = µLn2 · A/h
...................................... allmänna
ringspoleinduktansen
med A som den
cirkulära ytan hos spolringen (r som origo till halva ringkroppen) och h
spolens höjd (eller bredd).
Lösningar till
induktiva dipolfältstyrkan i P
TRANSFORMATIONEN AV
INTEGRATIONSKONSTANTEN
För att kunna utföra integrationen med avseende på vinkeln b,
måste integrationskonstanten
ds transformeras till en dito db. Vi använder för detta ändamål
sambandet i PREFIXxSIN
som följer.
Integrationskonstanten ds kan
uttryckas analogt genom
x/s = tanb
s = x/tanb
Vi differentierar
med avseende på b och får genom formlagarna (se Bastablån, Dn synkoperat Derivatan)
ds/db = Dn s = Dn x/tanb = –x/(cosb)2
ds = (–x/cos2b)·db
Insättning i
sambandet för induktionen ger oss
dÐP = L(1/4pr2)sinb·ds, L=L(di/dt), se L:=Lc=µLs
= L(1/4pr2)sinb·(–x/cos2b)·db
= – L(1/4pr2)sinb·x(1/cos2b)·db
; x/r = cosb
x2/r2 = (cosb)2
r2/x2 = 1/(cosb)2
; = – L(1/4pr2)sinb·x(r2/x2)·db
= – L(1/4p)sinb·(1/x)·db
= – L(1/4px)sinb·db
dÐP = –(L/4px)sinb·db
............................. V/M
induktiva dipolfältstyrkan i P, se
figuren nedan
PUNKTINTEGRALENS
DIFFERENTIALEKVATION
riktningen för dÐP parallellt med Q-rörelsen
dÐPds ®
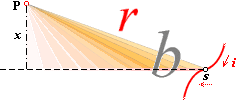
Sambandet för dÐP uttrycker den elementära
differentialekvationen för den induktiva dipolfälstyrkan. I detta uttryck
gäller Ð (d-e, Alt+0208) för bara en punkt P i normaldistansen x från
strömvägen ds och för bara ett singulärt värde på vinkeln b.
RAKLEDARENS
INDUKTION
Den integrala
lösningen för den raka ledaren s blir
òdÐP = –(L/4px) b®90ò sinb·db
ÐP = –(L/4px) b®90[cosb]
ÐP = –(L/4px) [cosb – cos90]
ÐP = –(L/4px) [cosb – 1] ;
ÐP =
(L/4px)(1–cosb)
............................. V/M
induktiva dipolfältstyrkans
punktintegral, rak ledare
ÐP är
medriktad huvudströmmen om denna avtar (se även Maxwells Regel)
ÐPds ¬
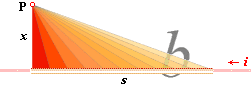
Punktintegralen uttrycker
den inducerade spänningen endast i P från s via b genom s-normalen
x och utanför ledaren [Se även vidare förklarande beskrivning i Inre Sekundära Induktionen].
Som vi enkelt kan förstå från denna enkla tillämpning, är
beräkningen av induktanser komplicerat även för det enklaste av alla fall: Vi
är fortfarande låsta vid endast en punkt P. För att finna en praktiskt lösning
där Ð kan mätas fysiskt, måste vi återigen utföra ännu en integration, nu över
en ändlig P-kurvatur.
*cont.
LINJEINTEGRALEN
GENOM P
Den enklaste
tillämpningen på en kurvatur genom P är (naturligtvis) den raka sekundära
strömlinjen (LP, se illustrationen nedan) parallell med den givna
primärledaren s.
LP
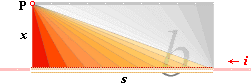
Om vi »sveper den
induktiva verkan i P» genom LP (inte illustrerat ovan), förstår vi strax att
det totala vinkelrummet för b som täcks av denna procedur kommer att
kräva dubbla b (illustrerat ovan genom de motvända diagonaldelade
symmetriska halvrektanglarna). Svepet motsvarar den linjeintegral som måste
användas; både »framsidan» från den ena svepriktningen, och »baksidan» sett
från den andra riktningens sfäriska halvdelar måste beaktas i en gemensam
totaldel som innefattar hela den primärledande ideala laddningssfärens yta.
Som ÐP = dU/ds med LP lika med s, har vi först i PREFIXxSIN varianten
dU/ds = ÐP = (L/4px)(1–cosb)
dU = ÐP ds = (L/4px)(1–cosb) ds
Med dubbla b,
enligt det nyligen beskrivna P-svepet över LP, får vi totalt
0®90dU = 2(L/4px)(1–cosb) ds
Från de föregående utvecklingarna erhölls ds=(–x/cos2b)db. Vi anländer då till
dU =
(L/2px)(1–cosb)·(–x/cos2b)·db
= (L/2p)(1–cosb)(–1/cos2b)·db
= –(L/2p)(1–cosb)(1/cos2b)·db
= –(L/2p)[(1–cosb)/cos2b]·db
= –(L/2p)(1/cos2b – 1/cosb)·db
Och vi har den preparerade differentialekvationen för linjeintegralen
enligt
dU = (L/2p)(cosecb – cosec2b)·db ...................
V, cosec = 1/cos i PREFIXxSIN
b räknas från b (mellan 0 och 90°) till 90 grader
LINJEINTEGRALENS DIFFERENTIALEKVATION
Lösningen genom
integralkalkylen blir (se även Bastablån)
ò dU =
(L/2p) 0®90ò (cosecb
– cosec2b)·db
ò dU =
(L/2p) [ 0®90ò cosecb
db – 0®90ò cosec2b db]
U = (L/2p) 0®90[ln tan(b/2) – – 1/tanb]
=
(L/2p) [ln tan(b/2) – ln tan45° + 1/tanb – 1/tan90°]
Från trigonometrin
minns vi att 1/tan90° är orepresenterat eftersom 1/(n®¥) aldrig uppnår 0. För exakta 90° blir alltså
den värdemässiga representationen exakt noll. Detta ger oss
=
(L/2p) [ln tan(b/2) – ln 1 + 1/tanb – 0]
Och vi har
sekundärledarens
induktion
SEKUNDÄRA
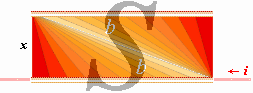
PRIMÄRA
U = (L/2p) [ln tan(b/2) + 1/tanb] ............................. V
inducerade spänningen i en rak
sekundärledare parallell med primären s med x/s=tanb
L
........................................................................................... Lc(di/dt)
OBSERVERA ATT
PRIMÄRINDUKTANSEN Lc FÖR s MÅSTE VARA KÄND.
[Se PRIMÄRINDUKTANSEN
I SAMMANFATTNING].
Sekundärledarens
material är fullständigt irrelevant.
NOTERING. I dessa samband räknas endast fullständigt linjära former;
Tidsförskjutningar mellan fältåterkopplingar i varje laddnings eget ideala
sfäriska system har bortsetts ifrån. Vidare underförstås rymdens resistivitet helt idealt homogen och
ekvivalent med ett idealt Galileiskt kraftfält (konstant gravitation
överallt) där också Q-hastigheten (v) är försumbar vid sidan av
ljushastigheten (c0).
RELATIVA MAGNITUDEN Sekundära induktionen
y = ln tan(b/2) +
1/tanb
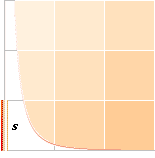 x
x
Den Relativa Magnituden för den sekundära induktionen utanför en rak
ledare, enheter i s med tanb=x/s.
I denna ideala y-ekvation är tjockleken för s idealt noll vilket betyder
att y-toppvärdet växer över alla gränser.
Om vi ritar upp grafen med vinkelberoendet (b) i induktionen för
en given ändlig ledare s, kan vi få en god uppskattande föreställning om
hur sekundärinduktionen varierar utanför rakledaren, illustrationen ovan.
Grafen ovan visar resultatet.
Som vi ser, avtar induktionen
(y) snabbt utanför ledaren. Beroende på ledarens tvärsnitt (se följande
artikel), kommer grafens toppdel att rundas av och sedan återvända till noll på
vänstra sidan. I artikeln nedan ges ett uttryck för sekundärinduktionens
toppgräns motsvarande ytan hos en praktisk ledare.
Från grafen inser vi utan svårighet att den sekundära
verkan passar perfekt för att överföra energin mellan olika strömmar mellan
tätt liggande strömledare.
primärledarens yta
Jämförande moderna resultat inom Induktionen
INDUKTIONEN PÅ PRIMÄRLEDARENS YTA
Förenklad tillämpning för jämförelse
Med små värden för vinkeln b (<1°) blir felet litet om tan(b/2) sätts
lika med tanb/2.
Felet med x på ytan av en Ø0,5mM×30mM tråd ligger närmast i
sjunde decimalen. Jämför
(0,25/30)/2 = 0,00416666…
tan(atan(0,25/30)/2)
= 0,00416659…
Med användning av denna förenkling på U-formen för sekundärinduktionen
får man
x/s = tanb
tan(b/2) Û tanb/2
U = (L/2p)[ln(tanb/2)
+ (1/tanb)]
= (L/2p)[ln(x/2s)
+ s/x]
ln a = –ln(1/a)
ln(x/2s) = –ln(2s/x)
Med tråddiametern d = 2x erhålles
ln(x/2s) = –ln(4s/d)
Därmed totalt
U = (L/2p)[–ln(4s/d)
+ 2s/d]
Och vi har
U = –(L/2p)[ln(4s/d) – 2s/d]
.............. V
Självinduktionen
på ytan av en rak primärledare, sekundärinduktionen
s ........................................................ rakledarens längd, M
d ........................................................ rakledartrådens diameter, M
L ....................................................... Lc(di/dt)
OBSERVERA ATT PRIMÄRINDUKTANSEN
Lc FÖR s
MÅSTE VARA KÄND.
[Se PRIMÄRINDUKTANSEN
I SAMMANFATTNING].
Som mängden parallella sekundära ledare nära ledarytan inte ändrar den
inducerade spänningen, avbildar uttrycken självinduktionen på ytan av en
rak ledare med längden s och cirkulära diametern d.
Med primära induktansen Lc=µLs
finner vi ett uttryck för den allmänna induktansen (L)
U = –[Lc(di/dt)/2p][ln(4s/d) – 2s/d] ;
U/(di/dt) = –[Lc/2p][ln(4s/d) – 2s/d] ;
L =
–(µL/2p)s[ln(4s/d) – 2s/d]
Se referenskällor i (Exempel
3) i Tre Exakta
Exempel
L = (µ0/2p)s[ln(4s/d) –
3/4]
rak ledare, modern akademi
sista termen anges som en korrektionsfaktor,
den varierar beroende på källitteratur
DEN NÄRA (principiellt
exakta) ÖVERENSSTÄMMELSEN MELLAN SAMBANDEN ÄR ANMÄRKNINGSVÄRD
— eftersom
induktionen och magnetismen är strängt åtskilda enligt relaterad fysik men
intimt förenade enligt modern akademi.
Bägge
föreställningssätten kan uppenbarligen inte vara riktiga.
Sammanhangen diskuteras vidare i Tre Exakta Exempel där resultaten jämförs mera ingående.
Se även artikeln om µ0: orsaken varför µ0 felaktigt identifieras med magnetismen i modern akademi.
sekundärinduktionen
Inre
Sekundära induktionen
PÅ STORT AVSTÅND från den inre rymden hos en elektrisk ledare (figurdelen
i a nedan) framstår dess samlade rum av bärande laddningar som »en
kontinuerlig laddningslinje». Totalmängden Q fördelad över hela strömlinjen ger
en laddningsdifferential som klart kan integreras i olika sammanhang och
tillämpningar.
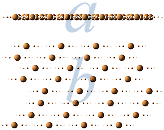
Inuti ledaren (figurdelen i b ovan) — med avståndsskalan mellan
de enskilda atomerna eller »ännu mindre»: mellan elektronmassornas enskilda
komponenter som laddningsbärare — upplöser sig denna form och är inte längre
tillämplig. Den följande översikten förtydligar sammanhangen.
Utgående ifrån
dÐ = (L/4pr2) dr
........................................... V/M
induktiva
dipolfältstyrkan i P
— som specificerar den induktiva fältdipolen (Ð) i en fix rymdpunkt (P) på
avståndet r rakt fram i Q-rörelsen under (di/dt)
— ser vi direkt att föreställningen om »integration» blir irrelevant om
strömlinjen saknar »laddningskontinuitet»;
Varje laddning ger ett bidrag dÐ, och en ändlig kvantitet för Ð
kan bara ges integralt: genom att laddningen ses homogent fördelad över
varje intervall.
Verkan från en laddning på alla andra inuti en ledare, är i den raka
ledarens fall styrd av avstånd mellan laddningarna — i den mån vi alls ska tala
om enskilda elementära elektriska laddningar som elektricitetsteorins
grundval. En sådan rymd framstår ”tät” utanför ledaren OM alla dess laddningar
betraktas komprimerade i en enskild ideal geometrisk linje som representerar
den ideala ledaren. Detta är emellertid inte (riktigt) fallet inuti (den
praktiska) ledaren. Om vi bara för exempelbeskrivningens del integrerar
differentialekvationen ovan, får vi dipolfältstyrkan i (P) som
ÐP = (L/4p)ò(1/r2)dr
; ÐP = –(L/4pr) = du/ds
ÐP motsvarar
inverkan från alla laddningar mellan noll till r i den fixa rymdpunkten
P (r-änden) och tagna över strömlinjen betraktad som
»laddningskontinuerlig». Denna dipolfälstyrka är emellertid differentiell; Den
får en ändlig form först med integration över ett ändligt s-intervall.
Emellertid finns, som nyligen omnämndes, ingen grund för integration i detta
fall eftersom den förmodade laddningskontinuiteten hos strömlinjen bestäms av
laddningar som med teorins föreställning om enskilda laddningar också
tvunget är separerade av inbördes avstånd. Bidraget från alla laddningar
på en given kommer därför — inom ledarens eget materiella ledningsrum —
att vara integral brutet genom laddningarnas inbördes avstånd och därmed under
alla omständigheter [frånsett oändlig masstäthet] bli en differential till Ð.
Den induktiva fjärrverkan (inverkan från alla andra laddningar på den enskilda,
den motsvarande sekundära induktionens verkan) kommer följaktligen att sakna
representation inuti det aktuella ledarmaterialets egenrum.
Slutsats:
Den sekundära induktionen har ingen signifikans inom
en ledare.
Med avseende på de relativa skillnaderna i rymdtäthet i anledning av
ovanstående resultat, och endast så, kan integralformerna för den sekundära
induktionen användas med god precision med början från den omgivande tomma
rymden (oändligt) och in till, men inte inkluderande, ytan hos den materiella
ledaren.
Notera dock att ovanstående utläggningar berör (den relativa) skillnaden
i relativ täthet mellan fasta tillståndets Jordfysikaliska solida ledare
och den allmänna ”tomma rymden” utanför sådana ledare. Om vi, till exempel,
betraktar elektrisk ledning på nivån joniserade atommassor (eller
elektronmassor) i stjärnornas yttersta materievärld där en helt annan
storleksskala gäller, måste vi iaktta en viss försiktighet i formuleringarna
(men inte nödvändigtvis med resultat i en sämre allmän precision).
estimated
secondary induction inside ring
UPPSKATTNINGEN AV RINGENS INRE SEKUNDÄRA
INDUKTION

Av speciellt
intresse är den sekundära induktionen utanför-inuti en ring då den frekvent
används i många praktiska konstruktioner.
Utgående ifrån den principiella grafen för
sekundärinduktionen utanför rakledaren (se föregående graf i RELATIVA MAGNITUDEN), kan vi göra en
grov uppskattning av hur sekundärinduktionen avtar inuti ringen men utanför
dess ringkropp. Illustrationen ovan antyder resultatet som här är sammanställt
med hjälp av två kopior av föregående nämnda illustration, tillsammans med
föregående resultat av induktionen genom ledarens begränsade tvärsnitt
(induktionsspänningens toppvärde).
Som varje Q-rörelse i ringledaren bidrar
till sekundärinduktionen utanför ledaren — men för vår analys här i ringens
inre centrala del — genom en del positiv induktion (närmast Q och starkast) och
en del negativ (längst bort från Q och svagast), och som lämnar ett positivt
netto, borde minskningen i sekundärinduktionen med ökande avstånd från
ledarcentrum avta än mera snabbt än i fallet med rakledaren. I ringens mitt och
i det närmast i området nära denna, borde därför den sekundära induktionen
teoretiskt vara helt säkert praktiskt noll, eftersom bidragen i centralpunkt
själva tar ut varandra symmetriskt runt om.
Resultatet utpekar en viktig funktionell
egenskap som bildar förutsättningen för och därmed berör en av elektroteknikens
verkligt avancerade detaljer — och som serveras oss helt gratis ur naturdjupen.
Nämligen möjligheten att transformera, överföra, elektrisk energi på olika spänningsnivåer utan några större
energiförluster. Sammanhanget beskrivs vidare nedan i Transformatorlagen samt särskilt i JÄRNKÄRNETRANSFORMATORN.
ENERGIÖVERFÖRING
MELLAN SPOLAR
![]()
Energiöverföringen
Som den induktiva
verkan härrör från energin som används för att bygga upp en primär ström, kan
vi söka ideal överföring mellan två spolar, en primär spole (P) och en
sekundär spole (S). Funktionen är att den senare (S) får den förras (P)
strömtröghet L som en maximal energimässig inmatning. För att relatera denna
koppling, betraktar vi återigen hela den primära ledarlängden (s) för
varje spole genom vilken energi manifesteras.
I en föregående
artikel Den
generaliserade ringintegralen erhöll vi för ringspolen
ûCOIL = d·n·nLd (di/dt)/1M
............................. allmänna
ringspoleinduktionen, V
Som
nLdd/1M = Lc = µLs = pKµLnd
har vi
ûCOIL = n·Lc (di/dt)
Effekten i Watt
blir
ûCOILI = n·Lc · I · (di/dt)
Energin,
differentialekvationen, är
ûCOILI dt = n·Lc · I · di
med lösningen
ûCOILIT = n·Lc · I2/2
ûCOILT =
n·Lc ·
I/2
ûCOIL =
n·Lc ·
I/T2
= n·Lc · di/2dt
[Utvecklingen är
trivial då den återvänder till originalet. Se även den motsvarande
grundläggande induktiva energiintegralen i Integrala Analogierna].
Med energin som
förflyttas mellan spolarna (ideal energiöverföring utan förluster) får
vi
ûP = nP·LcP · di/2dt =
ûS = nS·LcS · di/2dt
Om LcP=S (vilket inte är fallet såvida inte bägge
spolarna är identiska) har vi men en grov förenkling genom varje gemensam
strömderivata
ûP nP
—— = —— ......................... transformatorlagen,
förenklad ideal energiöverföring
ûS nS
Sambandet innebär rent teoretiskt-matematiskt att vi kan överföra varje möjlig spänning från en källa till en annan, förutsatt en ideal energiöverföring mellan spolarna, enbart genom att observera förhållandet mellan antalet spolvarv (n); nP/nS.
material
Ferromagnetiska material
Villkor
för ideal induktiv energiöverföring
VI
NOTERAR (2008) ATT INGEN ALLMÄNT ERKÄND TEORI FÖR UPPHOVET TILL
FERROMAGNETISMEN ÄNNU HAR SETT DAGEN I GÄNGSE KVARTER.
I vissa material, som Järn, Kobolt och Nickel, delar atomernas
elektronmassor på samriktade slutna strömleder i formen av inre cirkulerande
strömmar (Se dia-, para- och ferromagnetismen i relaterad fysik). Effekten framvisar en
lokal grupp atomer som formar så kallade magnetiska dipoler. Men dessa dipoler
är relativt små och är ömsesidigt isolerade i så kallade domäner som är slumpartat orienterade i
metallen. Genom att använda en yttre strömkälla, kan domänerna fås att
rätta in sig tillsammans. Inrättningarna samlar en växande mängd elektroner
från närliggande domäner vilket synkroniserar stora (motsvarande makroskopiska)
cirkulerande kollektiva inre järnströmmar. Dessa järnströmmar rör sig (idealt)
exakt som den yttre strömmen i en spole lindad kring metallen — vilket vi vet
ENBART på grund av likheten mellan de magnetiska fälten.
Se även i Allmänna teorin för ferromagnetiska material enligt
relaterad fysik.
Som påpekades ovan i RINGENS
INRE SEKUNDÄRA INDUKTION påverkas inte
centrum av den induktiva effekten från en överliggande spole: flera, separata,
sådana spolar kan »arbeta ostört» på och med hjälp av den närliggande JÄRNYTANS
stora kollektiva inre kärnmagnetiska elektronströmmar med att VIA DESSA
överföra energin mellan spolarna — som kan placeras godtyckligt på järnkärnan;
Järnet gynnar starkt transformatorlagen.
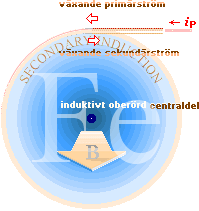
DEN AVSTÄMMANDE
MEKANISMEN för att samla järnströmmarna utförs alltså av strömmen iP hos en primär spole P. P är
lindad på en kärna av Järn (Fe 26), se även ovanstående illustration.
Den sekundära induktionen från P visar sig bara i närheten av P —
enligt RINGENS
INRE SEKUNDÄRA INDUKTION analogt bara närmast ytterdelen av
järnytan (IiS). Denna region, vilken vi betraktar som liten jämfört med
det allmänna tvärsnittet av järncylindern, utgör det huvudsakliga arbetsområdet
i överföringens mekanism.
Som en växande P-ström genererar en växande underliggande sekundär (S) ström motriktad P enligt induktionslagen, överförs tydligen idealt hela energin i P-ändringarna på S; genom att S-mediet bärs av Järnets inre elektronströmmar — som alltså är MYCKET större än motsvarande elektronströmmar vid normal elektrisk ledning i t.ex. kopparledare — kan S-strömmen nu i sin tur förmedla en omvänd sekundär induktion samriktad med S på en spollindning på ett helt annat ställe på järnkärnan, eftersom i vilket fall HELA järnkärnans ytmässiga S-strömmar följer P-strömmens ändringar; Energin i P överförs med andra ord med hög effektivitet på en separat S-spole i försorg av Järnets inneboende cirkulerande elektronströmmar som dessutom lämnar den centrala delen av järnkärnan praktiskt taget helt åt P-strömmens styrning eftersom den inre delen av en ring inte påverkas nämnvärt av sekundär induktion enligt RINGENS INRE SEKUNDÄRA INDUKTION.
Därmed kan alltså
en sekundär spole S erhålla (idealt) hela den induktiva effekt som
används av primärspolen P i dess egen strömbyggnad iP.
Men det finns ytterligare
en avancerad faktor som gynnar hela funktionen: en självreglerande ”elektrisk
ventil”:
Hela fördelen med
järnkärnans ytdel (IiS) som tar emot sekundärinduktionen från
primärspolen P är den följande. När strömmen iS flyter genom sekundärspolen S,
åstadkommer (naturligtvis) dess självinduktion en motverkan som löper i
samma orsaksriktning som P-strömmen, således matande iP. Detta resulterar (naturligtvis) i en
avtagande induktiv resistans i P. Resultat: Ju mera iS som tas ut ur S, desto mera iP flyter det in till P; Sekundäruttaget
STYR OCH REGLERAR primärflödet. Man kan (väl) knappast få ett tydligare
naturexempel på hur en öppen famn ser ut rent praktiskt.
Ingen
speciell reglerande anordning krävs, regleringen är helt självautomatisk.
Järnkärnetransformatorns
funktion beskrivs även separat i MAGNETISMEN på artikeln Järnkärnetransformatorn.
END induktionen.
BIHANG| GRUNDLÄGGANDE
ELEKTRISKA STORHETER
GRUNDLÄGGANDE ELEKTRISKA STORHETER
*Basic Electric Quantities · In extract 2007VI19 from Chapter 2 of Related Physics
P2001_2
the
electrical quantities
DE ELEKTRISKA STORHETERNA
Grundläggande elektriska
storheter
ström ·
resistivitet · termiskt beroende · strömtäthet · historia · spänning ·
kapacitans
Referens
KOMMUNICERANDE
SAMBAND Mekanikens Elektricitet
De följande
centrala korrespondenserna förklarar de grundläggande sambanden i behandlingen
av elektriciteten.
(X, Grekiskans xsi, min [lätt ihågkombara]
»grafiska akronym» för Elektrisk Fältstyrka [E-F])
Bastabell för jämförande samband i gravitationen och elektriciteten
kraft F = ma = Gm2/r2 = mw2/r ............... gravitationskraft konvergenskraft
F = ma
= kQ2/r2 = mc/dT ............... elektrisk kraft divergenskraft
energi E = Fr
= Gm2/r
= mw2 .................... gravitationsenergi konvergensenergi
E = Fr
= kQ2/r
= mc2 ...................... elektrisk energi divergensenergi
potential Fr/m
= Gm/r = w2
........................... gravitationspotential konvergenspotential
Fr/Q
= kQ/r = U
............................. elektrisk
potential divergenspotential
styrka F/m =
a = Gm/r2 = w2/r .................. gravitell fältstyrka
F/Q = X = kQ/r2 = U/r .................... elektrisk fältstyrka
I den här sektionen
presenteras de mest grundläggande formella storheterna i elektriciteten. Vi bör
känna till dem som grundvalen för de vidare beskrivningarna i Induktionen och Magnetismen,
med vidare.
Se även elektromekanikens grundbegrepp, där visas hur
ovanstående också framgår direkt ur g-fysikens grundbegrepp.
Elektrisk Strömstyrka
Elektrisk strömstyrka
Ström
I
........................................................ standardenhet A, Ampere
Med en elektrisk
ström (I) menas helt enkelt ett flöde av laddningar (Q) (motsv.
vattenmolekylerna i en vattenström) som passerar en referenspunkt eller en referensyta
(strömtäthet) per lika tider (T) enligt
Q
I = —— ............................................. elektrisk strömstyrka, Ampere
T
Som med ett
vattenflöde bestående av vattenmolekyler, består ett elektrisk flöde av
individuella elektriska laddningar [massor med elektriska fält].
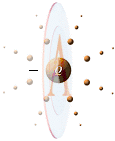
Den totala summan
av Q som passerar en ytsektion (A) i flödet per sekund definierar
strömmens kvantitet, det vi kallar för strömstyrkan.
*cont.
Elektriska kraftlagen i elektriska strömmen
understanding the electric current
ATT FÖRSTÅ DEN
ELEKTRISKA STRÖMMEN
Se även en rekapitulation av elektriska kraftlagen
Som potentialen
U i den elektriska laddningen Q är arbetet (kraften över vägen) eller energin Fr tagen över det
sfäriska Q-systemet, har vi U=E/Q=RcQ/r.
Med c=r/T får vi i absoluta storheter U=R(Q/T) eller U=RI
där I=Q/T definierar begreppet elektrisk ström.
Denna grundläggande och statiska form (I=Q/T)
visar uppenbarligen en motsvarande expansion av ett sfäriskt Q-skal från
en ideal centralpunkt med hastigheten c=r/T.
Det är också det ideala begreppet med ett
medelvärde för c för hur det statiska Q-fältet uppdaterar sitt
potentialfält genom en motsvarande sfärisk expansion där den elektriska
laddningen Q återspeglar sin existens genom varje fältpunkt. Mera grundligt
förklaras Q-fältets allmänna återkopplande, expanderande dynamik enligt superpositionsprincipen som ges från grunden i elektriska laddningens härledning.
Ser vi enbart till
den differentiella
(d) aspekten för Q som dQ, vilket ger oss
respektive dU=RdI där dI=dQ/T, avbildar emblemet
för denna differential åt oss en motsvarande partikel dQ som
färdas utmed r med hastigheten c i en rymdresistans R. Notera
dock att denna liknelse med ”differentiella partiklar” inte får drivas för
långt: differentialens värdemängd är noll och inget annat. Se
vidare grundbegreppen enligt relaterad fysik och matematik med differentialbegreppet
i Nollformsalgebran. Om vi betraktar alla möjliga värden för c,
från exakt noll och uppåt, avbildar de enkla uttrycken dU=RdI
och dI=dQ/T mera tydligt sambanden för rörelsen hos varje
kvantitet Q med hänsyn till tiden.
Med andra ord:
sambanden U=RI och I=Q/T gäller för samtliga fall med
Q-hastigheter mellan noll och den lokala divergensen c —
oberoende av material. U mäter det s.k. potentialfallet över
R-distansen passerad av Q. Med Q givet och dess motsvarande »statiska
fältimiterade godtyckliga divergens» — vilket som helst värde 0-c — avtar U med växande sfärradie i det motsvarande Q-skalets expansion. Sagt i
ett vidare sammanhang kan man därmed säga att det statiska Q-systemet
således DEFINIERAR »generella egenskaper» i elektrodynamiken: den
motsvarande skalutvidgningen med dess egenskaper. Vi kommer att återknyta till dessa delar på flera ställen, och under
olika synvinklar, under presentationens gång (speciellt i magnetismen och dess
stundtals till synes veritabla snårskog av svårfattlig dynamik).
Sambanden utpekar
tydligen en kvantitativ lag: ingenting sägs om kurvaturens
dimensioner, vägen som Q-kvantiteten tar. Sambanden är uppenbarligen giltiga
för alla möjliga fall under alla möjliga förhållanden inom intervallet 0-c.
Det enda som spelar någon roll (R och hastigheterna v mot c som
givna) är Q-kvantitetens passerande av en begränsad tvärsnittsyta under tiden
T. Det betyder att sambanden är giltiga för ett hårstrå lika väl som för en
grov kopparstång eller en enda ensam singulär elektrisk laddning som färdas
ensam i fri rymd med max
hastighet v=c. Detta sistnämnda är klart från den enkla
observationen i analogi med Q-modellen:
hur stort än U är mellan ledarändarna, kommer den påverkade laddade partikeln
aldrig att överskrida hastigheten v=c eftersom c grundlägger hela
det elektriska fältets »uppdateringshastighet» eller utbredningshastighet, den
elektriska strömmens inre motorik. Se även i divergensen.
Vilket vill säga:
elektrisk ström härledd ur elektriska
kraftlagen, lyder slutna elektriska system. Förflyttning av laddade partiklar utanför
sådana slutna system, förpassar också de motsvarande matematiska sambanden
utanför den elektriska kraftlagen och därmed till den allmänna mekaniken.
SUMMERING Elektrisk STRÖM | 2001X22
Strömbegreppet i
dess logiska form är strängt mekaniskt: partiklar per. Den
elektriska kraftlagen med dess centrala och ideala sfäriska Q-modell definierar
elektrisk strömstyrka med absolut precision inuti slutna elektriska
system. Vilket betyder; med förflyttning
av laddare partiklar i hastigheter fån 0 till den maximalt lokala divergensen c
— alltid med referens till det lokalt dominanta g-fältets fasta och idealt fixa
solida bas.
Se även vidare från
DEEP i Fysikens
allmänna förklaring.
Elektrisk Resistans
Se även om resistansen i Historia
Elektrisk resistans
Elektrisk resistans (R) eller elektriskt
motstånd uttrycks matematiskt inom elektrofysiken enligt
R =
(Fr/Q)/I
=
(E/Q)/I
=
E/(QI)
=
U/I
med elektriska kraften F från elektriska
kraftlagens F = k(Q/r)2 och I från elektriska strömstyrkan. Se även i Elektrisk effekt och energi.
Med
given laddning (Q) och strömstyrka (I) bildar varje materiellt
strömflöde ett motstånd (R) likt materialet som hindrar vattenflödet i en viss
vattenströmning. Med en viss materialform och ett visst strömningstryck (U) för
en given ström (I) finns ett motsvarande motstånd (R).
Genom ekvivalenten R=E/(QI) förstås att resistansen (R) omsätter energi:
Högre motstånd betyder högre energi med given laddning (Q) och ström (I).
Se
även om resistansen i Historia.
Elektrisk Resistivitet
resistivity
of electric conductors
RESISTIVITETEN I
ELEKTRISKA LEDARE
En ideal laddning i
fri rymd möter inget motstånd (R) eller resistans när den färdas
med konstant hastighet [Newtons
första lag]. Laddningar som färdas i elektriska ledare
har emellertid under normala förhållanden en specifik resistans beroende på typ av material.
Med en homogen (likformig) fördelning av
laddningar i en ledare (m) med given tvärsnittsyta (A), har ledaren en karaktäristisk
resistans i ytans tvärsnitt enligt
RmA–1 = W/1M2
Grekiska bokstaven omega
W anger enheten (”Ohm”) för R, också explicit
som Volt/Ampere. Med längden s för ledaren (cylindern
från A-spåret), blir den aktuella konduktiva resistansen eller ledningsresistansen
R över s
s · RmA–1 = W/1M
= R/1M ;
s · RmA–1 · 1M = R
.......................... konduktiva
resistansen
R = Rms/A · 1M
Termen Rm kallas resistiviteten för ledaren.
Resistiviteten mäts i Ohm-Meter eller (V/A)M. Den refereras stundtals till
genom den grekiska bokstaven rho (r, samma som r i teckensnittet Symbol den
symbolen används också stundtals för att beteckna täthet)
Rm · 1M = r = (R/s)A ...................... resistiviteten
i Ohm-Meter
Resistiviteten är temperaturberoende
[Se Strömmens
temperaturberoende nedan].
För Koppar (Cu),
vid rumstemperatur 20°C [20°K över vattnets fryspunkt 273°K], är
resistiviteten
rCu20°C = 1,78 t8 WM
................... resistiviteten för Koppar vid normal
rumstemperatur
I
facklitteraturen
[numera 2007 också via @INTERNET],
finns
utförliga tabeller över resistiviteten för olika material. Se t.ex. svenska Wikipedia Resistivitet, engelska Wikipedia Resistivity.
Generellt uppvisar alla
ledare mer eller mindre variationer i r även
med relativt små temperaturvariationer.
För Koppar ökar r omkring 0,4% per ökande värmegrad (max 1,745
vid 15°C).
[Min
ursprungliga referens här är KARLEBO HANDBOK upplaga 12 s1099].
Exempel
Bestäm resistansen
för en 0,1M lång kopparledare med cirkulärt tvärsnitt med radien 0,25 mM vid
normal rumstemperatur.
Använd ovan angivna
specifikationer.
Svar: R = RmsA–1 · 1M = (1,78 t8)(0,1)(p ·
[0,25 t3]2)–1 · 1M = 9,06546 mW.
STRÖMMENS
TEMPERATURBEROENDE
För temperaturbegreppets grunder, se Allmänna Gaslagen.
Alla material
uppvisar variationer med temperaturen.
Med en given
resistans R0 är den linjära ändringen i temperatur (°Kelvin) över varje ändlig ändring DR
DR
————
R0
—————— = d = n/°K
DT
Då är
DR/DT = R0n/°K ;
DR = R0nDT/°K ..................... resistansökningen med temperaturökningen
SAMBAND
RESISTANS-TEMPERATUR
DELTAFAKTORN (d, Grekiskans delta [d i Symbol]) kallas temperaturkoefficienten.
Tabellen nedan ger
några få standarvärden med temperaturkoefficienten i n t3 =
millienheter per grad Kelvin.
[ref.
ELFAKATALOGEN No49 2001, ELFA AB 2000, s579]
Al Fe Cu Ag Au
n t3 4.2 6.5 4.3 3.9 3.6
aluminium järn
koppar silver guld
Exempel
Föregående exempels
Ø0,5 mM × 0,1 meter långa koppartråd har resistansen R0= 9 mW vid rumstemperatur 20°C. Bestäm dess resistans
om temperaturen ökas med 450°C.
Lösning
Vi bestämmer först
den tillkommande resistansen från temperaturökningen.
DR = R0nDT/°K ger DR = (9 t3)(4,3 t3)450/°K = 17,415 t3 W.
Svar: Resistansen blir 9 t3 + 17,415 t3 =
26,415 mW.
Kommentar
Enligt specifikationer
i (vanliga) fackböcker gäller också sambandet ovan väl i de praktiska fallen
för alla metaller (sambandet förutsätter helt linjär giltighet).
Begränsningarna [förmodligen nära smältpunkterna] finns emellertid här inte
angivna.
STRÖMTÄTHET
Med giltigheten av
det centrala elektriska sambandet i slutna elektriska ledarsystem
U=RI och
I=Q/T,
giltiga för varje
strömväg under varje förhållande i varje material som vi kunde sluta oss till i
ATT
FÖRSTÅ DEN ELEKTRISKA STRÖMMEN, kan vi definiera
strömfördelningen inuti en given elektrisk ledare med en definierad
tvärsnittsyta (A). I de flesta praktiska fall är denna cirkulär.
Vi får
I
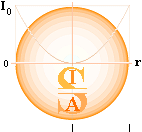
0 r0
r0
....................... ledarens
radie
A0
..................... ledarens
yta
r ........................ aktuell
radie inuti ledaren
A ....................... aktuell
yta inuti ledaren
I0
....................... elektrisk
ström genom A0
I ......................... elektrisk
ström genom A
A/A0 = pr2/pr02 = (r/r0)2
I0/A0 = S = I0/pr02
............................ strömtätheten
för den cirkulära ledaren,
A/M2
Förutsatt att denna
fördelning är idealt homogen gäller
I0/A0 = S = I/A
Då är
I = SA = AI0/A0 = I0(r/r0)2 ;
I = I0(r/r0)2
....................................... aktuell
ström inuti ledaren, Ampere
Eftersom materiella
ledare uppvisar resistans, kan de utveckla betydande värme (upp till
smältpunkten) om matning sker med höga strömstyrkor.
Standardtabeller
för olika ledare och diametrar rekommenderar maximala strömmar som specificeras
av S-parametern i AM–2.
Värmeeffekten som bildas av en resistans
följer av energiformen
E = U · Q = RI · IT
som formellt ger
E/T = PWATT = RI2
Om resistansen R är
känd och strömmen I som passerar genom den, kan vi beräkna temperaturen i
resistansen om vi också känner R-ledarens materiella temperaturkoefficient.
Exempel 1
I föregående exempel
beräknades totalresistansen R för en Ø0,5 mM × 0,1 M lång koppartråd med
temperaturen
(450+20=470)°C
som 26,415 mW. Bestäm effekten i Watt och minsta spänningen
i Volt över R som krävs för att driva strömstyrkan 10A genom R-ledaren.
Lösning
Vi bestämmer först
effekten:
PWATT
= RI2 ger PWATT = (26,415 t3)102 = 2,6415 Watt.
Vi använder sedan
det centrala allmänna sambandet i elektrofysiken (se ATT FÖRSTÅ DEN ELEKTRISKA STRÖMMEN)
U=RI för att bestämma den nödvändiga
spänningsfallet.
U=RI ger U=(26,415 t3)10 = 0,26415
Volt.
Svar: Effekten över R är 2,6415 Watt och minimum
spänning är 0,26415 Volt.
Exempel 2
För att träna på
tekniken i att hantera värdena, ska vi här upprepa föregående exempel men från
en annan startpunkt. Vi ska (nämligen) försöka bestämma temperaturen över R
enbart med vetskapen om dess basdata och med början från rumstemperatur och
nollström.
Frågeställning:
En konstant ström på 10A måste dras genom
en Ø0,5 mM × 0,1 M lång koppartråd R med temperaturkoefficienten 4,3 t3/°K.
Försök bestämma maximala ökningen i R-temperaturen orsakad av den angivna
strömmen om spänningsfallet över tråden inte får överstiga 0,1 Volt.
Lösning
Vi använder
sambandet resistans-temperatur
DR/R0n · 1°K = DT
för att bestämma
temperaturen. R0 är känd och n är given. Den resistiva ökningen DR får vi genom
R=U0,1V / I10A = 0,01 W.
Detta är den totala
resistansen R. Vi subtraherar sedan R för den aktuella ledaren vid
rumstemperatur som vi från exemplet tidigare i
RESISTIVITETEN
I ELEKTRISKA LEDARE vet
är 0,009 W. Då är
DR = 0,01 – 0.009 = 0,001 W.
Insättning av detta
resultat tillsammans med de övriga givna kvantiteterna ger då
DR/R0n · 1°K = DT = (0,001)/(9 t3 · 4,3 t3) = 25,839793 °C.
Totala uttrycket
ger oss
R= (UmaxImax–1) ;
[R–R0]/R0n · 1°K = (RR0–1 – 1)n–1 · 1°K = DT ;
DT = (UmaxImax–1R0–1 – 1)n–1 · 1°K ............ ledarens temperaturtillskott
n ................................................................... temperaturkoefficient, 4,3 t3/°K för
Koppar
Svar: Temperaturens maximala ökning i R=0,01W via strömmen 10A är 25,84 °C.
Elektricitetens centrala dramatik
Elektriska resistansen. År 1826 upptäckte den tyske fysikern Georg Simon Ohm (1787-1854) de resistiva förhållandena inom elektrofysiken genom att mäta spänningsfallet mellan två referenspunkter, i allt på olika elektrisk ledare (cirkulära metalltrådar). Han upptäckte att resistansen eller elektriska motståndet ändrades delvis beroende på strömmen och delvis beroende på kvoten
sLÄNGDEN/AYTAN. Efter Georg Ohm kallas sambandet
R = U/I
......................... Ohms lag,
efter Simon Ohm
också för Ohms
lag.


Ørstedts
revolutionerande upptäckt.
Upp till 1819 hade många experiment genomförts inom elektricitetens
fenomenfysik, men fortfarande litet var känt om dess natur. Året 1819 (publ.
1820) inträffade ett revolutionerande genombrott: Dansken Hans Christian Ørsted
upptäckte att en magnetisk nål reagerade på en elektrisk ström. Sedan
Andre-Marie Ampere (André-Marie Ampère) i September 1820 fick höra talas om
Ørsteds upptäckt [ref. @INTERNET Wikipedia, Andre-Marie Ampere 2010-08-28], hade han efter bara en vecka presenterat en
omfattande beskrivning av fenomenet inför franska vetenskapsakademin. Den teori
som ännu i våra dagar praktiseras generellt inom elektrofysiken grundas
fortfarande i allt väsentligt på de samband som ställdes upp av Ampere.
Den verkliga början på denna dramatiska
historia — den fascinerande utvecklingen med upptäckten av elektricitetens
detaljerade natur — startade emellertid med Michael Faraday år 1831. Efter hans
upptäckt att en elektrisk ström i en isolerad krets kunde uppväcka en ström i
en annan krets, utvidgades den experimentella grenen inom elektrofysiken
dramatiskt. Eftersom den elektriska strömmens natur inbegriper fundamentala
konserverande lagar för energi som frigörs när en ström stängs av, var
man strax i full färd med att inspektera och debattera uppkomsten av gnisturladdningar. Så, kan man säga, föddes elektrofysiken i
naturvetenskaplig mening.
Urladdningseffekten
studeras vidare. Från 1838 intensifierades
intresset för gnisteffekten. Det rent tekniskt instrumentella närmandet
utvecklades naturligtvis med ännu mer fördjupat intresse i takt med att
studierna generellt ledde fram till olika tekniska förbättringar. De olika
anordningarna utvecklades snart i total strävan att studera gnistfenomenet i evakuerade
glasrör, vilket blev förebilden till de senare s.k. katodstrålerören (de
numera [2008] föråldrade CRT-bildskärmarna [Cathod Ray Tube, sv.
katodstrålerör]). Upp till slutet av 1800-talet gjordes många förfinade
undersökningar och experiment i syfte att söka en djupare förståelse för
naturen bakom dessa nyupptäcka »strålar». Runt 1880 upptäckte man att strålarna
innehöll impetus (alltså rörelsemängd [mv], vilket indikerade att
strålarna bestod av små massiva partiklar). År 1897 visade Joseph John Thomson
att katodstrålen kunde förklaras som en ström av negativt laddade partiklar som
strax kom att kallas elektroner. Den avgörande metoden för att mäta
elektronens laddning gjordes från 1906 av Robert Andrews Millikan. Under
perioden från 1819 upp till denna punkt år 1906, hade elektrofysiken som
vetenskaplig gren utvecklats till en högt driven avancerad instrumentell
teknologi med många upptäckter vid sidan av det speciella studiet av den
elementära elektriska laddningen. Genom Millikan blev den elementära
elektronladdningen slutligen bestämd (år 1916, med en extrapolering 1938
beroende på ett systematiskt fel) till 1,602 t19 Coulomb [ref. FOCUS MATERIEN
1978 s666].
Atomkärnans
experimentella påvisande. År
1911 hade Ernest Rutherford genom experiment avtäckt att solida material bestod
av ypperligt små och täta partiklar — det vi kallar atomkärnor —
inbördes separerade av stora avstånd.
Tillsammans med upptäckten av elektronen (som tillskrivs Thomson) manifesterade
Rutherfords experimentella avtäckande flera mera precisa modeller av de fasta
ämnenas natur. En allmän idé framkom strax att alla material bestod av atomer
med en mycket hård och kompakt atomkärna omgiven av »mjuka moln av
elektroner» fördelade över stora volymer. Denna modell förklarade (i det
närmaste) perfekt alla kemiska reaktioner och det principiella beteendet hos
gaser, vätskor och fasta ämnen.
[Det ska dock här omnämnas att redan flera
hundra år före Kristus fanns liknande teorier i omlopp. Vår dokumentkälla på
denna punkt är Demokritos (460-360 f.Kr.)].
Källstoffet till
ovanstående historiska sammandrag finns mera utförligt i boken Upptäckten av
elektronen, David L. Anderson, Harvard University Case History, Aldus 1966.
Kompletterande
uppgift om Ørstedt;
”… beskrev i Experime’nta
ci’rca effe’ctum confli’ctus ele’ctrici in a’cum magne’ticam (1820) en
elektrisk ströms inverkan på en magnetnål”,
BONNIERS
KONVERSATIONSLEXIKON Band XII 1928 sp1631
Materialens
ledningsförmåga (konduktiviteten)
är numera känd att bero på sättet som atomerna i ett fast ämne tillåter de
yttre mer eller mindre löst bundna elektronerna (benämnda valenselektroner) att
förflytta sig fritt inom materialet. Hårt bundna elektroner bildar det vi
kallar för isolatorer medan mera löst bundna valenselektroner
bildar det vi kalla för goda elektriska ledare. De bästa ledarna är i tur och ordning Silver (Ag), Koppar
(Cu), Guld (Au) och Aluminium (Al).
Som vi kan bekräfta genom ganska enkla och
primitiva experiment, kan elektroner på ett högst enkelt sätt transporteras
från ett material till ett annat. Genom att gnugga en plan plexiglasskiva med
vanligt hushållspapper och sedan släppa (till exempel) vanliga risgryn på
glasytan, kan vi omedelbart få se många intressanta effekter (bara genom att
till exempel peka med ett finger nära inpå ett gryn).
Det allmänna studiet av elektriciteten genom olika mätningar beror
(generellt) av ett högt drivet instrumentellt utvecklat hantverk — även i de enklaste av alla mätningar. Basmaterialet
är (koppar)tråd med likformigt (cirkulärt) tvärsnitt som i sig bygger på en
avancerad industriell rening av metallmaterialet (i huvudsak koppar).
En av de första personer som konstruerade
instrument för mätning av elektriska strömmar [föregångaren till galvanometern]
var (som ovan) den berömde franske vetenskapsmannen André-Marie Ampère
(1775-1836), vilket skedde i nära anslutning till Ørsteds upptäckt 1819
[ref.
André-Marie Ampère, The Founder of Electromagnetism, 2009; http://www.juliantrubin.com/bigten/ampereexperiments.html],
[ref.
Radio-electronics.com, Resources and analysis for electronics engineers,
Andre-Marie Ampere, datumuppgift saknas;
http://www.radio-electronics.com/info/radio_history/gtnames/andre-marie-ampere.php],
[ref.
@INTERNET Wikipedia Galvanometer 2010-08-28].
För att förverkliga en sådan
instrumentering, i varje fall i någon mera avancerad mening, måste först en
rent metallurgisk (metallutvinnings-) teknik ha utvecklats och förfinats.
Metoden som används för produktion av elektrisk (koppar-) tråd utnyttjar en
speciellt konstruerad plan tjock stålplatta (ett s.k dragstål) med fint slipade
koniska hål. Genom att upprepat glödga-avkyla (för att bevara flexibiliteten)
och dra tråden genom sådana successivt allt mindre hål, får man den önskade
tråddiametern med hög noggrannhet.
Elektrisk Spänning
voltage
Spänning
U ............................................ standardenhet, V Volt (från
Fr/Q=E/Q=kQ/r, J/C)
Närhelst ett arbete
(E=Fr) utförs för att separera minst två (redan) skilda laddningar av ett
avstånd (r), produceras en laddningsspänning (U=E/Q=Fr/Q)
eller (makroskopiskt) en elektrisk potential eller som vi också säger en
elektrisk spänning mellan dem. Spänningsbegreppet vilar på den ensamma elektriska laddningen (Q) och dess
elementära elektriska fält genom fältets divergens (c)
såsom motsvarande en divergensspänning (Fr/Q=kQ/r=U)
eller divergenspotential med en formellt motsvarande strömstyrka I=U/R=([k=Rc]Q/r)/R=cQ/r=[r/T]Q/r=Q/T
relaterad till divergensen,
c=dr/dT.
Som denna ström, relaterad till
divergensen, INTE beskriver ett flöde av individuella laddningar per tidsenhet,
utan det interna divergensflödet
(dr/dT=c) utmed distansen (r) enligt superpositionsprincipen och därmed en intern divergensström
som närmar sig noll obegränsat med växande T=r/c enligt I=Q/(T®¥), kan spänningen U=kQ/r med
hänsyn till den singulära laddningen Q också relateras som en uttalad
divergensspänning inuti det interna Q-fältets fysik — att särskilja från varje
laddningsspänning där r separerar åtminstone två skilda laddningar.
Med en elektrisk
spänning (U) menas således
BÅDE en separation U=E/Q mellan olika belägna laddningar över
varje utvidgning (r), OCH
en (motsvarande) ström U=RI som dras (den aktiva delen
i I) över varje väg (r).
U = RI = E/Q ....................... elektrisk spänning, Volt
Specifikt kallas
också spänningen U för spänningsfall (eng. potential drop)över
distans.
Sambandet U=RI
är det mest omfattande, och enkla, i den tekniska-praktiska elektrofysiken
(elektroniken [från elektro-tekniken]). Det används inom
elektrofysiken i liknelse ungefär som lungorna använder luften vi andas och
ögonen vyerna vi ser.
Kondensatorlagen · kapacitans
Elektrisk kapacitans
Kapacitans
......................................................... standardenhet F, Farad (Coulomb/Volt)
Termen kapacitans
i elektrofysiken används i samma mening i den vanliga mekaniken som kapaciteten
(förmågan, abiliteten) att lagra (t.ex.) vatten i en cistern med motsvarande
geometriska dimensioner; Medan vattnet
använder volymen, använder elektriciteten ytan. Den elektriska anordningen
kallas kondensator (eng. capacitor); Kondensatorn som elektrisk
behållare för elektriska laddningen framgår direkt från sambandet för den
elektriska fältstyrkan enligt
F/Q = X = kQ/d2 = Q/eA = U/d ....... elektriska fältstyrkan
Den centrala delen
är ytan (A), som är flödessnittet mellan de motsatta elektrodernas
(anslutningsytornas) laddningssidor.
Från de två sista
delarna får man kondensatorlagen
kondensatorlagen
Q/U = e · A/d ......................................... kondensatorlagen, C/V, se även alternativt
sist nedan
e0 = 1/R0c0 ......................................... 8,85430803 t12 C/VM
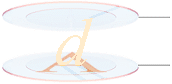
Med en given distans mellan de bägge (metalliska) plana
ytorna, separerade av deras gemensamma snittyta A, växer kapacitansen
Q/U proportionellt mot växande A. Planytorna har samma funktion som en
motsvarande vattencistern där istället volymen är det centrala.
Genom att använda
tunna material med litet d i en kompakt rullad cylinder kan mycket höga
C-värden erhållas. Samtidigt krävs en allt högre kvalitet för allt högre
spänningar hos det elektriskt isolerande skikten som garanterar att de ledande
delarna bevarar en elektrisk isolation. I många tillämpningar inom elektroniken
där små kapacitansvärden behövs, blir kondensatorn som fysisk komponent
emellertid just så »enkel» som illustrationen ovan antyder.
Sambandet för kapacitansen från
ledet ovan skrivs
Q
C = —— = e · A/d ........................................ elektriska kapacitansen, Farad
U
Med I=Q/T
som ger Q=IT kan kondensatorlagen (kapacitansen) också tecknas alternativt
U=Q/C= TI/C.
Induktionen
innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
Induktionen
ämnesrubriker
innehåll
Senast
uppdaterade version: 2024-09-09
*END.
Stavningskontrollerat
2007-11-21 | 2008-03-06 | 2008-06-11
rester
ref. CD Kraftlagen 1999 XII, Induktansen.wps 1999XI20
*
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se
PNG-justerad 2011-08-25
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se
