ELEKTRONMASSANS KOMPONENTER 2007XI25 a production | Senast uppdaterade version: 2023-11-30 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Efter sammanställningar från Fysikens 7 Principer 2002

Spektrum · Kvanttalen · Kärnmagnetiskt moment · KÄRNMAGNETISKA MOMENTET

J_0K + 3J_1K = 0

Atom- och Kärnfysikens två Kungsekvationer

F_BT + F_eZ = 0

Med fortsättning från Planckringen

ELEKTRONMASSANS KOMPONENTER

från toroidaggregatet N3m20

REDAN OMKRING ÅR 1925 framlades avgörande teoretiska bidrag som förutsatte ”vibratorer” i elektronmassan. Dessa teoretiska bidrag är kända som Heisenberg och Schrödingers ekvationer och som ledde fram till en närmast glänsande förklaring till atomens spektrum. Föreställningen om »beståndsdelar i elektronen» kunde emellertid inte förenas med den moderna akademins allmänna uppfattning, och ”vibratorerna” avskrevs därför av Heisenberg (år 1927) [ref. TRETTIO ÅR SOM SKAKADE FYSIKEN George Gamow, Prisma 1968, s104] med hänvisning till relativitetsteorin.

Allmänt från Planckringen

Neutronringens antal 1,0086652/0,000548598=1838,624 elektronmassor indelas enligt TNED i centralmassivet 1818e med förbrukningsmassan 18e och tillägget 2,624e. Sista delen är utfyllnadsmassa på grund av ringasymmetrin. 18e är förbrukningsmassa som omsätts i massdefekter (max 17,76 vid Järn).

TNED lämnar ingen upplysning om fraktalnivå No3, här används ett sämsta fallets värden för att få fram data på elektronmassans komponenter. r₀ anger neutron-protonradien.

t-ringen

STORLEKEN HOS Elektronmassans ringkomponent, t-ringen

max r₀ · 0,000 000 8

max r₀/50

framgår ur det från Planckringen härledda toroidaggregatet N3m20 genom delvis uppskattning då N3m20 bara beskriver de två översta nivåerna. Beräkningarna efter sämsta fallets förhållanden redovisas nedan illustrerat.

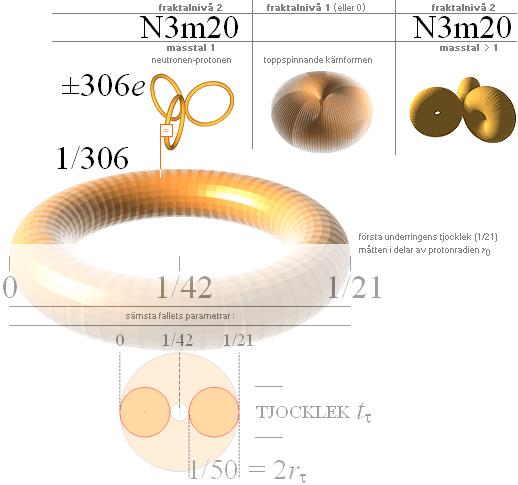
beskrivning

1/21-ringens underringar har gränsvärdet 1/42 för ringdiametrarna = noll mängd underringar. I praktiken måste de alltså vara (betydligt) mindre. Ett sämsta fallets största värde ENLIGT TNED utgår ifrån diametern 1/50 som absolut diametrala maxvärdet för elektronmassans komponentringar (t-ringarna). Med 1/50 givet kan antalet (n) t-ringar i e-massan beräknas genom resultaten från härledningarna i Spektrum.

Man finner värdet (avrundat) n=177062.

t-ringens tjocklek. Största omkretsen för 1/21-ringen är (0,1495996)@0,15. Fördelat på sämsta fallets 177062 ger det t-ringens tjocklek

t_t=0,15r₀/(177062)=r₀8,4716 t7. Inte ens i stark förstoring av neutronen-protonen blir den delen synlig i bild. Diametern 1/50 kan dock illustreras i skala enligt illustrationen nedan (en pixel).

e-massans ringelement

Figurbeskrivning

e^–-sfären: volymen av t-ringarnas 177062 spinnsfärer till jämförelse i samma skala som protonskalan nedan,

e-sfärens radie ca 56% av protonradien, elektronmassan uppträder dock (normalt) aldrig på den formen

® · ¬ e/177062

elektronelementet, diametern visar en pixel i samma skala som protonskalan nedan.

Packas t-ringarna cylindriskt upptar de (efter sämsta fallets beräkningar, se ovan) längden (max) ca 1/7 av protonradien — MAX.

elektronen i TNED

atomkärnan elektronen — här illustrerad med alla t-ringar toppspinnande i formen av närliggande sfärer som bildar e-sfären, se grundberäkningen ovan i t-ringen

proton

| r₀ | = 1,37 t15 M

e-sfären förekommer aldrig isolerad i fysiken i TNED, alla dess komponenter, t-ringarna, ligger utspridda kring atomkärnan, se även från Atomfysikens två Kungsekvationere.

Se även elektronladdningen i Härledningen till elektriska laddningen.

Eftersom laddningen hos e (elektronen) är massproportionell enligt atomkärnan som massans fundamentalform [PASTOM] har det (i allmänhet) ingen betydelse om vi anger hela e för beräkningar som i själva verket avser enskilda elektronelement (t-ringen), eller direkt e/n. Resultaten blir i vilket fall samma i slutänden. (Det finns dock fenomenområden som är undantagna från de allmänna fallen, men dessa är speciella och redovisas inte i den här presentationen).

Se även matematiskt i Kraftverkan på t-ringen.

Q-geometrin 4p

F = ma = m(c/dT) = m(c/dT)(RA)/(RA) = Rc(m/R)(A/dT)/A = Rc(Q/r)² elektriska kraftlagen

Generellt om elektriska laddningens geometri i elektriska kraftlagen

I materiefysiken är elektronen given som en odelbar elektriskt laddad enhet (e=1,602 t19 C) som grund för de olika atomerna enligt GRUNDÄMNENAS PERIODISKA SYSTEM genom resonansverkan. Speciellt i TNED genom POTENTIALBARRIÄREN och principalpartikeln, kan den elektriska laddningen (Q) generaliseras i formen av ett idealt punktobjekt motsvarande principalpartikelns mQ-karaktär med godtycklig orientering (spinn) i rymden. Det betyder att Q generellt kan betraktas genom en SFÄRISK YTA A=4pr² (speciellt på stort avstånd från laddningen). I den allmänna tillämpningen av materiefysiken används (således) elektriska kraftlagen

F = ma = m(c/dT) = m(c/dT)(RA)/(RA) = Rc(m/R)(A/dT)/A = Rc(Q/r)² elektriska kraftlagen

(mestadels) på formen

F = ma = m(c/dT) = m(c/dT)(RA)/(RA) = Rc(m/R)(A/dT)/4pr² = (Rc/4p)(Q/r)² = (1/4pe)(Q/r)² elektriska kraftlagen

med elektriska kapacitivitetstalet (även elektriska konstanten) e₀ = 8,8543 t12 C/VM för vakuum. Med motsvarande tomrummets

R₀c₀=1/4pe₀ = 8,98743 t9 VM/C skrivs vanligen elektriska kraftlagen (med således underförstådd SFÄRISK koppling)

F = (1/4pe₀)(Q/r)² elektriska kraftlagen

Generellt i Universums Historia används den mera allmänna formen F=k(Q/r)² med k=Rc från härledningen till Q, med i förekommande fall särskilda specifikationer.

Vektorhärledningarna till Spektrum och Kvanttalen enligt relaterad fysik

SPEKTRUM OCH KVANTTALEN

Atomfysiken Kärnfysiken 1818+18+k

ATOMENS ELEKTRONKONFIGURATION har redan härletts i separat artikel via Keplermomentet och bör redan därför vara bekant. Se GRUNDÄMNENAS PERIODISKA SYSTEM.

Spektrum

VÄTEATOMENS SPEKTRUM

Med början från impulsmomentet J=mvr med Plancks ekvivalenta konstant h=m_nc₀r_n, bestäms atomens dynamik enligt TNED av de bägge centrala impuls och kraftekvationerna (se Atomfysikens två kungsekvationer)

J_0K + 3J_1K = 0

F_BT + F_eZ = 0

Medan J-delen tar hand om kärnbalansen explicit, arbetar F-delen mera på den frigjorda elektronmassan (F_eZ). Den matematiska fysik som beskriver denna dynamiska kommunikation ges från den enklast och mest elementära av alla atomer, Väte-1-atomen med dess enda elektronmassa. Som detta centrala kärna-elektronsystem kommunicerar genom en elektrisk kraft (F_eZ), introducerar detaljerna från potentialbarriären också vissa energiekvivalenta kriterium. Som redan omnämndes i Keplermomentet med härledning till grundämnenas periodiska system från en rent resonant synvinkel, uppvisar systemet proton-elektron också utpräglade resonanta egenskaper baserade på den allmänna resonanta vågmekanikens heltalsstruktur. Vilket vill säga; elektronmassan (m) svänger i elektriska resonanser grundade på enbart hela tal (n) under inverkan av den lokala divergensen eller ljushastigheten (c) genom en grundläggande Planckimpuls mc och en allmän våglängd l. Kraftverkan från protonen når eller ”tar” elektronens masselement (t-ringen) i den definierade potentialbarriärens energizon

c₀/2 = c_z ........................................................... M/S

Det är till denna zon all dynamisk växelverkan måste relateras i elektrofysiken för att dynamiken ska kunna möta energiekvivalenterna såsom definierade genom potentialbarriärens energizon w=c.

energicirkeln

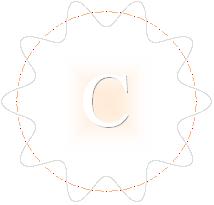
Atomens dynamik bestäms av hur kärnan kopplar till t-ringarna genom en energibaserad geometriskt ideal basring (C) med omkretsen l0; C bildar då den grundläggande ideala ekvivalenta vågenergicirkeln runt atomkärnan.

t-ringens karaktär beskriver elektronmassans egenskap

Se även inledningen längre upp i t-ringen — där förklaras den, här, fortsatta användningen av begreppet elektron — i generell ersättning av t-ringens karaktär med spinn (impulsmoment). Elektronen som sådan i TNED har ingen sådan egenskap: elektronen uppträder aldrig som partikel; elektronen är en hop, en mängd likadana delkomponenter som utgörs av impulsmomentringar (t) med massa (m), laddning (Q) och spinn (J=mcr), samma som impulsmoment. m ingår i Q, se Elektriska laddningen.

Det är med hänsyn till denna fasta våglängd l0 de mindre t-ringarna måste svänga för att kunna bevara Planckkonstanten h i elektronens impulsmoment, h=mc_z·l₀. C-cirkeln bildar alltså formen för en dynamisk ekvivalent eller jämviktsformen för ett impulsmoment (h=mc_z·l₀) via en ideal centralkraftsverkan. Denna centralkraftsverkan, utgående från atomkärnans laddning och spinn, bildar lokalen för elektronmassans eller C-ringens resonanser. Eller kort sagt, stående vågor (C_x), och som redan omnämnts i periodiska systemet på Keplermomentets enkla form.

Varken energizonen i potentialbarriären, eller atomkärnan över huvud taget med referens till Planckringen omnämns i modern akademi. Därmed finns inte heller den här följande presenterade elementära härledningen till atomens spektrum med, och som vi ska få se, innefattar samtliga redan kända aspekter i sig.

HÄRLEDNING — atomens spektrum genom ekvivalenta C-energicirkeln

elektronmassans komponenter · spektrum

Atomens dynamik bestäms av kopplingen kärna-elektron. Enligt relaterad fysik kan denna dynamik förstås som en speciell utvidgning av atomkärnan via elektronelementen [Se från Neutronens sönderfall]. Kärnan kan både ge ut och ta upp sådana element allteftersom dess energibalans så kräver. Den matematiska fysik som beskriver dynamiken baseras på det enklaste fallet med vätekärnan (p) och den enda elektronen (e).

Genom resultaten från härledningarna i PLANCKRINGEN består elektronen av en viss mängd ringar här benämnda (tau) t-ringar med totalmassan m=m_e. Genom de resultat som vi kommer att nå genom denna modell, kan vi senare genomföra mera noggranna beräkningar av t-ringarnas dimension och antal för vidare prövning. Atomens dynamik bestäms av hur kärnan är dynamiskt kopplad till dessa ringar genom en större grundring (C) med omkretsen l₀. C bildar formen för en dynamisk ekvivalent eller en jämvikt för ett rörelsemängsmoment, samma som impulsmoment, (h=mc_zl₀) via en ideal centralkraftsverkan som i inverkan av kärnans laddning och spinn bildar orten för elektronens (C-ringens) resonanser, dvs., stående vågmönster (C_x). Den matematiska fysiken för t-ringarnas massa-laddning tillhör resultaten från divergensens g-beroende (DGD) enligt principalpartikeln med radien r från PASTOM

r_c=0 = 2Gm/c₀² = 1,48427 t27 · m ................ M

för varje m finns ett motsvarande r

varur potentialbarriären härleds. Denna visar, beskriver och förklarar den elektriska laddningens exakta karaktär vilken här förutsättes bekant. Potentialbarriärens maximum är densamma ideala zon där inverkan från yttre e-fält griper tag i en laddad principalpartikel. Den definieras genom ekvivalensen mellan g-energin och divergensenergin och benämns här nollzon enligt

c₀/2 = c_z ......................................................... M/S, nollzonen (nollzonens energimaximum)

Det är till denna zon all dynamisk verkan måste hänföras inom elektrofysiken för att fungera i enlighet med energilagen. Jämviktscirkeln C för e definieras således på nollzonens form i impulsmomentet för C från kärnan p:s centralverkan enligt

h = mc_zl₀

Med hc_z fix kan ml₀ anta vilka som helst ömsesidigt inversa proportionaliteter varigenom jämviktscirkeln C kan definiera vilka som helst motsvarande slutna figurformer (C_x), dvs., olika svängningsformer.

I dessa grundhärledningar relateras även m=m_e fix. Med ett minsta r-värde för C_x, (rhå) r, och ett största divergensvärde (xsi) x i nollzonen ges de möjliga ekvivalenterna för konstant h enligt

h = mc_zl₀ = mc_z(2pR) = mx(2pr)

resonansvillkoret

Huvudkvanttalet n — mönsterfysikens grundval

Väsentligt för resonansverkan [Se ill. i Resonanserna] är att C_x måste bestå av ett helt antal (n) toppar eller dalar för att jämvikten eller resonansen i energin för banformens omkrets ska gälla:

h = mx(2pr)

h = mn^–1xn^–1 (2prn²), se Förklaringen till n^–2

xn^–1=v, rn²=d ;

d = rn² .......................................................... radien för motsvarande C_x-cirkeln

h = mn^–1v(2pd) ;

huvudkvanttalet

Grundvillkoret med n för resonansverkan betecknar huvudkvanttalet (n) inom atomfysiken.

Begreppet kvantfysik eller kvantmekanik introduceras alltså naturligt i atomfysiken via n med föreställningen om resonanserna.

Förklaringen till n^–2

Potentialbarriärens massa-laddning förklarar varför både massan och divergensen måste reduceras på samma kvantitet n:

Om divergensen — inom den energizon där ett yttre e-fält griper tag i principalpartikeln — reduceras, reduceras analogt också den motsvarande mängden affekterad massa: nolldivergens affekterar nollmassa — och därmed nollkraft. En analogi är att betrakta elektriska kraftlagen F=ma=k(Q/r)²=Rc(Q/r)², F/n=(c/n)K=(m/n)a: med divergensen c reducerad följer analogt (kraft)massans reduktion.

Förenklingen h=h/2p används ofta i atomfysiken

(h, eng., h-bar)

Vi har alltså

hn

n · h = n · mc_z·l₀ = mv(2pd) = mvl ;

nh(2pd)^–1 = mv, h=h(2p)^–1

mv = nh/d = J/d, J = mvd = nh

I den följande framställningen kommer kvoten J/h=n att bilda matematisk typform för atomens dynamik.

VÅGKOPPLINGEN i C_x , noll till 360° och som definierar hela energidynamiken mellan p och e via C och h, ges enligt (v=d/T)

c_z = l₀T₀^–1 ............................................ våghastigheten genom e bestäms av verkan i nollzonen

Därmed ges

h = mc_z·l₀ = mc_z²T₀ = mc₀²T = mc₀²T₀/4 = Ef ^–1 ;

hf = E

Den resulterande energin E_v mellan gravitationsenergin E_s och divergensenergin E i t-fältet ger som tidigare via ekvivalensen mellan de senare, w=c=c₀/2=c_z analogt E=E_s från potentialbarriären

E_v = E_s + E = mw²+mc² = 2E

elektronmassans komponenter · spektrum

KRAFTEN i det arbete E_v som definierar energibalansen i nollzonen [också bekvämt begrepp för intervallet mellan energizonens maximum, c=c(z), och noll], utgörs av den elektriska attraktionen F_z=k(e/d)² mellan p och t-ringarna i e, där ändpunkten för d relateras till c_z på varje t-ring i C, eller, generellt för samtliga fall till x/n via C_x.

kraften på t-ringen

Kraftverkan på t-ringen

KRAFTEN VIA ELEKTRONMASSANS ELEMENT ÄR DENSAMMA

Notera i fallet Väteatomen att formen

F_z = k(e/d)² avseende HELA elektronmassan blir identisk med formen

F_z/n = k·e_{KÄRNLADDNINGEN}·(e/n)_tRINGEN/d² som avser t-ringen, n antalet t-ringar i e.

[Formen gäller även i princip för hela atomen i samtliga Z-fall för Ze enligt ZF_z/n = k·Ze·(e/n)/d² som likväl ger F_z= k(e/d)²].

Vi kan alltså obehindrat använda hela elektronmassan (e) som illustrativ (ikonisk) representant för t-ringens räkning.

Se även ATOM- OCH KÄRNFYSIKENS TVÅ KUNGSEKVATIONER där redovisas grunden för F_z.

VÄGEN över vilken F_z verkar är avståndet d varigenom kraftvägen eller arbetet definieras på samma form som ett mekaniskt vridande moment

E_v = F_zd = ke²/d = 2E

Observera att arbetet E=Fd=mad via divergensen av princip beror av den lokala divergensen i varje rymdpunkt (d=ds) så att

energin inom elektrofysiken alltid, på ett eller annat sätt, tvunget måste hänföras till E=m(c/dT)ds=mc(ds/dT)=p(ds/dT).

Eftersom nollzonernas utsträckning är helt försumbara i den allmänna verkan mellan vätekärnan och elementen i e, kan vi behandla kraftvägarna analogt och bekvämt via konstant divergens c=ds/dT=s/T över finita intervall som ger det allmänna E=mc² [i TNED, Divergensenergin eller Primära massförstöraren].

Om alltså energin i grundcirkeln C ändras med något tillskott DE så att totala energin blir E₁=E+DE, kräver de av C uppsatta villkoren, konstant h, att DE avges enligt E₁–DE=E. Denna triviala balans medger alltså vilka som helst fluktuationer

E = hf

= E₁–E₂ = h(f₁–f₂)

atomens generella energidistribution

Energiformen

Den effektiva energin blir alltså 2E=E_v=F_zd=ke²/d varav divergensenergin E är

E = ke²2^–1/d = hf = h(f₁–f₂) = E₁–E₂ = ke²2^–1(1/d₁ – 1/d₂)

= ke²2^–1r^–1(1/n₁² – 1/n₂²)

grundformen till väteatomes emissionsspektrum

elektronmassans komponenter · spektrum

DEN chockerande KORTA KLASSISKA HÄRLEDNINGEN I EKVIVALENTER

Bohrmodellens enkla motsvarande kinematiska ekvivalent:

Resultatet ovan är detsamma som att relatera kraftjämvikten i väteatomen som given via den aktuella

divergensen x/n=v betraktad som en helt ideal kinetisk hastighet v för

elektronen e betraktad som en helt ideal liten laddad kula som färdas runt p;

mv²/d = F_z = ke²/d² ; mv² = F_zd = ke²/d ; mv²/2 = E = ke²/2d

elektronmassans komponenter · spektrum

Med d=rn² från resonansvillkoret, n ett helt tal från 1 och uppåt benämnt huvudkvanttalet, har vi alltså (c=lf)

hf = hc₀l^–1

= ke²2^–1r^–1 (1/n₁² – 1/n₂²)

Vätets Spektrum

och därmed det konventionellt redan välbekanta vätets enkla spektrala våglängder

l = 2k^–1e^–2hc₀r · (1/n₁² – 1/n₂²)^–1

R-värdet för den ideala jämviktscirkeln C får vi ur h=(mc_z l₀)=m(c₀/2)2pR=mc₀pR, R=h(mc₀p)^–1.

Med

c₀ = 2,99792458 T8 M/S

m_e = 9,11 t31 KG

h = 6,625 t34 JS

ges avrundat

R = 7,7214156 t13 M ........................................................... ideala C-cirkeln

antalet t-ringar i e

Om vi känner dimensionerna [Se t-ringen] i den kärnregion varifrån t-ringarna härrör, kan vi via R beräkna antalet sådana i e via pt-svepet i Elektronringens spinn — för vidare prövningar. N3m20-aggregatet ger resultatet att varje e består av 177062 t-ringar vardera med diametern ca 1/50 av protonradien r₀=1,37 t15 M:

n = m(e)/m(t)

= R(2p)/t(2r)

= (7,7214156 t13 M)(2p)/([1,37 t15 M]/50)

= (4,8515 t12)/(2,47 t17M)

= 177062,35

~ 177062

Tjockleken blir (sämsta fallet) i storleksordningen r₀t7: så tunn att den i kärnvyn framstår som helt osynlig.

Beräkningen av Väteelektronens Grundradie r och dess inre receptiva divergens v

—————————————————————————————————

Från hn=(2p)mvd ges d=hn(2pmv)^–1. Ur [centralrörelsen, mv²/d=F=k(e/d)²] mv²=ke²/d fås mvd=ke²/v=hn/2p varav hn=2pke²/v. Därmed ges

hn=(2p)mvd; (hn)²=hn(2p)mvd=(2pke²/v)(2p)mvd=(2pe)²mkd

varav

d = (hn)²[(2pe)²mk]^–1

Med

h ....................... 6,625 t34 JS (närmevärde)

e ....................... 1,602 t19 C

m ..................... 0,000549u = 9,11521 t31 KG (mera noggrant 0,000548598u=9,10853 t31 KG med u=1,66033 t27 KG)

k ....................... 8,98743 T9 VM/C = 1/4pe₀ ; e₀ = 8,8543 t12 C/VM; 4p från A=4pr² i F=([k’=Rc=1/e₀]/A)(m/R)(A/dT)=(1/4pe₀)(Q/r)²

får man r via n=1 ur d=rn²=r från d ovan enligt

r = h²[(2pe)²mk]^–1 @ 5,29 t11 M ............................. minsta r i C_x

I den traditionella akademins kulmodell kallas r för väteatomens grundradie.

Från hn=2pke²/v kan vi lösa ut divergensen v=xn^–1 enligt

v = 2pke²h^–1n^–1 = xn^–1 = (2,1875325 T6 M/S)n^–1

Som vi ser, ligger divergensen i komplexet på nersidan mot principalpartikeln innanför potentialbarriärens maximum. I den traditionella kulmodellen betecknas v som elektronkulans hastighet runt kärnan. Se BOHRANALOGIN.

kalkylkort · vätets spektrum · kalkylkortet fungerar inte aktivt tillsammans med htm-dokument ·

nedan visas endast kortets ytbild, det kan tyvärr (ännu 2007) inte aktiveras av någon webbläsare · Ordnat nedan (Apr2010):

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik 2 Kalkylkort — Vätets spektrum — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

termiska energiekvivalenter

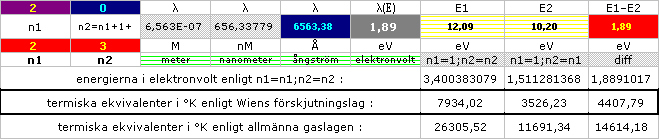
l = 2k^–1e^–2hc₀r · (1/n₁² – 1/n₂²)^–1 ; h f = h c₀l^–1 ; E = ke²(2r)^–1(1/n₁² – 1/n₂²)

E=(3/2)bT ; b=1,3805502 t23 J/°K; T=2E/3b [ref. Allmänna gaslagen via E=mv²/2, men temperaturvärdena blir galna]

T=k_{2,893 t3 M°K}l^–1=k_{2,893 t3 M°K}(hc₀/E)^–1

BALMERSERIEN ger vätets synliga spektrum med n₁=2 och n₂={3,4,5,6,7} med 3 vid rött och 7 vid violett.

Väteatomens jonisationsenergi är 13,6 eV

Med E = hf = ke²2^–1r^–1(1/n₁² – 1/n₂²), r = h²[(2pe)²mk]^–1 = 5,2927355 t11 M, kan Väteatomens energi beräknas då n₂ växer obegränsat (n₂®¥) med n₁=1:

E_VäteJON = (8,98743 T9 VM/C)(1,602 t19 C)²/2(5,29 t11 M) = 2,17893 t18 J = 13,601335 eV

Denna energi är (således) densamma energi som krävs för att HELT frikoppla elektronenmassans bindning till sin moderkärna (med moderkärnans motsvarande excitation i utbyte).

Denna energi kallas också allmänt för väteatomens jonisationsenergi.

Avslutning Spektrum med inledning till Kvanttalen

Med grundformen given via vätets enkla spektrum och kärnans masstruktur känd [Se Atomkärnans härledning], blir det nu möjligt — i full enlighet med energilagen — att härleda de olika kvanttal som är förknippade med den allmänna beskrivningen av atomens dynamik — och som kopplar till grundämnenas periodiska system.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

Kvanttalen

De återstående fyra kvanttalen q s_t µ_t F_t

Inkluderat N=3 UPPDAGANDET i N3m20

Begreppet kvanttal i relaterad fysik ansluter till den heltaliga analogt bestämt kvantiserad fenomengrund — resonanserna i atomerna — som beskriver ett specifikt kännemärke (karaktär) eller egenskap som elektronelementet uppvisar — i termer av elektriska och magnetiska fenomendetaljer:

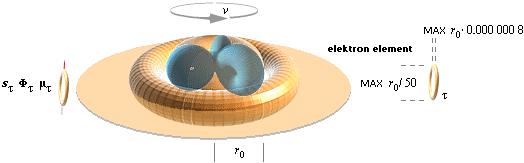
s_tF_tµ_t är elektronelementets olika kvanttal, de relaterar till hur t-ringarna kopplar till kärnan.

»Fetringen» i figuren kring atomkärnan motsvarar en stiliserad bild av kärnladdningens maximala potentialområde. Denna ring har ingen praktisk elektrisk-magnetisk betydelse, men klargör den traditionella svårigheten i att förstå begreppet fysikalisk precision på nivån »nära atomkärnan».

s_tµ_t kopplar till t-ringens ringström, F_t kopplar till t-ringens toppspinn. Dessa begrepp har ingen motsvarande formtolkning i moderna kvarter: ingen kan förklara dem, ehuru många använder dem.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

NOTERING — i tolkning enligt TNED. Runt år 1925 använde två berömda fysiker oberoende av varandra motsvarande t-ringar för elektronmassans komponenter för att förklara atomens allmänna spektrum, kända som Heisenberg och Schrödingers matris och vågfunktioner. Emellertid bannlystes dessa ”underliga vibratorer” från atomfysiken år 1927 av Heisenberg ”med hänvisning till relativitetsteorin” [ref. TRETTIO ÅR SOM SKAKADE FYSIKEN, George Gamow, Prisma 1968 s104]. Därmed eliminerades varje spår till kvanttalens mekaniska koppling — som också därmed blev helt abstrakt.

En del bedrifter i den moderna akademins historia framstår som särskilt lysande.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

ATOMENS DYNAMIK — kvanttalen q s_t µ_t F_t

Kvanttalen — Vågformernas finstruktur

Med allt vidare delar av masstrukturerna medtagna följer mera noggranna bestämningar av atomens dynamik. Specifikt följer härav Plancks konstant som en strukturkonstant [Se särskilt PLANCKS STRUKTURKONSTANT]. Denna detalj har emellertid ingen betydelse för beskrivningen av atomen på nivån för elektronernas koppling till atomkärnan utan berör explicit endast kärnfysiken (elektronens element i Atomkärnans härledning).

När e svänger mellan de olika E-nivåerna 1 till n [Se från ENERGICIRKELN] blir de olika energiöverföringarna lika många som antalet kombinationer mellan de n olika nivåerna.

Exempel: Med n=6 får man vågskuren

₆n₅, ₆n₄, ₆n₃, ₆n₂, ₆n₁; ₅n₄, ₅n₃, ₅n₂, ₅n₁; ₄n₃, ₄n₂, ₄n₁; ₃n₂, ₃n₁; ₂n₁; 5+4+3+2+1=15

Vågskuren ger antalet övergångar lika med summan av alla heltal från 1 till n–1 enligt 2^–1[(n–1)²+n–1]=2^–1(n²–n). Med n–1=q således 2^–1(q²+q).

Till denna vågskur kan följande tilläggas, och som visar att vågskuren som funktion av huvudkvattalet n kan uttryckas på dess dubbla form

f (n) = (q²+q)

pt-svepet

Eftersom vågkopplingen, som i elektronen (e) sker på divergensen (v) via c_z, bestäms av elektriska-magnetiska kopplingen pt

— protonkärnan-t-ringen, eller »pt-svepet» analogt med kärnspinnet och därmed »Coulombstråken» som sveper över elektronmassans t-ringar från atomkärnan

— kan vi med kännedomen om kärnans struktur (N3m20) sluta oss till att följsamheten för t inte är helt jämn. Som kärnringarna roterar och därmed drar t-ringarna med sig, »ser vi enkelt» med de tre kärnringarnas 120° spridning att t-ringarnas rörelser snarare bör uppvisa en accelererad-retarderad inåt-utåtgående periodisk form. Om vi tar med kärnans struktur kan vi alltså på detta sätt härleda en primär hastighetsvariation ±u för våghastigheten v i e och som därmed kommer att dela energiöverföringen vid varje n i (minst) två olika möjliga delar. Totala antalet övergångar blir alltså (q²+q). Vi sätter v±u=w. Faktorn w via n ansvarar alltså härifrån för hela vågdynamiken i atomen. Med ett absolutvärde för u får vi med hänsyn till alla möjliga ±u två kvoter, en för +u och en för –u enligt (u/w)+(u/w)=2(u/w). Eftersom (u/[w=v+u]) emellertid omöjligen kan bli större än 1 blir enda möjligheten för (u/w) att kunna trigga heltal att multipliceras med en heltalskoefficient C₀ så att villkoret 2C₀(u/w) > 1 uppfylls. Vi sätter 2C₀=C. De möjliga kombinationerna i förhållandet u/w kan därmed återfalla på de möjliga vågskurarna (q²+q) om

(q²+q) – C(u/w) = 0

och endast då. Under dessa förutsättningar gäller alltså

f (n) = (q²+q) = uC/w

För att kunna insätta denna vågskursfunktion i atomens dynamik, måste vi finna dess motsvarande impulsmoment. Eftersom t uppvisar både centrifugalkraft och inverkan från divergensen, kan vi för denna lösning tillämpa ELEKTRISKA FÖRSKJUTNINGEN, se nedan (se utförligt i Planeternas Perihelierotation) för det sfäriska systemet

f (w/c) = u_SPH/w = 3(w/c)² ............... sfäriska, se utförligt i Planeternas Perihelierotation, kortform nedan i ELEKTRISKA FÖRSKJUTNINGEN

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

Sambandet är elementärt för mekaniken (men vi måste kunna hantera infinitesimalkalkylen [Se NOLLFORMSALGEBRAN] för att förstå dess härledning och innebörd). Här följer en kort genomgång.

Den elektriska förskjutningens rotationsförhållande u/w ges som funktion av den vektoriella vinkelförskjutningen w/c=tanA så att u/w=f(w/c). Produkten mellan Keplers ytmoment K=wr och centrifugalaccelerationen å=w²/r, åK=w³, tillåter också vilken som helst principiella ekvivalent åK=w³=uc². Med centralformen w³ betraktad som integral [w³ innefattar komplexets totala impuls (p=mv), och bör därmed relateras som integral], erhåller man dess derivata d(åK)/dw som (åK)’=3w²=uc²w^–1. [Vi noterar att u/w gäller lika genom hela medelbancirkeln så att u/w=du/dw=u’ vilket ger

d(uc²)/dw = (uc²)’ = uc²d(1)/dw = uc²/w]. Från de två sista delarna får man u/w=f(w/c)=3w²c^–2.

Med w som en summa mellan u och vilken som helst annan konstanta hastighet v via w=u+v noterar vi att en ändring i w med avseende på v kan uttryckas [Û, motsvarar]

w’=d(u+v)/dv=(u+v)’=du+1 Û v’=1 så att dvÛdw.

Om vi uttnyttjar den treringade bastoroiden eller neutron-protonaggregatet N3m20 [Utförligt i PLANCKRINGENS DIMENSIONER], se utförligt från Planckringen, kan vi med hänsyn till en av ringarna definiera elektriska förskjutningen i detta speciella fall enligt u_SPH=3u_TOR. Föregående led får då ekvivalenten enligt

f (w/c) = u_TOR/w = (w/c)² ................. toroidnukleära sambandsformen för elektriska förskjutningen

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

Med given divergens (c) är förskjutningskvoten w/c begränsad till 1 då w®c. Vågkopplingen i e sker emellertid på en variabel divergens (se divergensen v från Spektrum) som kan anta alla värden mellan noll och c_z. Detta betyder att kvoten w/c i princip måste kunna bilda kvantiteter större än 1. Om vi skriver c_z=(c_z/A)A, betyder (c_z/A) alternativt den variabla divergensen noll till c_z, A en obestämd kvantitet större än 1. Elektriska förskjutningen på c-divergensen motsvarande (c_z/A) kan alltså skrivas

f (w/c_z) = u_TOR/w = (w/[(c_z/A)A])² = (Aw/c_zA)²

Med C=A² får man då

u_TORC/w = (Aw/c_z)²

= (Awc_z^–1)²

= (Amwl₀[mc_z·l₀]^–1)²

= (Amw2pRh^–1)²

= (J_u h^–1)²

där mc_z·l₀/2p=h/2p=h från Spektrum och AmwR=J_u. Därmed har vi funnit det eftersökta impulsmomentet enligt

_________

J_u = hÖ u_TORC/w

Med föregående u i uC/w=f (n)=(q²+q)=q(q+1) som u_TOR ges därmed det allmänna impulsmomentet

________

J_u = hÖ q(q+1) ................. energinivåernas allmänna impulsmoment

På denna bas, och endast där, kan man postulera att elektronen vibrerar. I modern akademi finns, vad vi vet, ingen motsvarande mekanisk modell. Sambanden har där i stället framkommit ur rent matematiska analyser i koppling till experimentella observationer (”för att få ekvationerna att stämma”). I modern akademi betecknas q som (ban)kvanttalet l och man skriver då konventionellt

______

J_l = hÖ l(l+1) ................. konventionella beteckningar

Andra konventionella benämningar för kvanttalet l är banimpulsmoment, bikvanttal och azimutala kvanttalet.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

elektronringens spinn (s_t)

s_t — »ELEKTRONENS SPINN»

FÖR ATT TRIGGA t-ringarnas dynamiska koppling till atomkärnan via energicirkeln C från Spektrum, tänker vi oss dessa lagda som små tvärställda cirklar runt den större C-cirkeln, så att varje t-ring motsvaras av en C-korda. Summan av t-ringarna runt C definierar elektronen. Vartefter pt-vektorn sveper över ringarna på C-periferin [se pt-svepet] och därmed vågformens element definieras eller vidrörs dynamiskt, bildas ett bestämt förhållande till kärnan via det givna impulsmomentet h=mc_z·l₀ för C. För ett varv 0-360° har alltså pt-vektorn via kärnans spinn triggat eller vidrört exakt halva e-massan i C, och därmed halva elektronens totala impulsmoment.

[Vi får tänka oss triggningen som att pt-vektorn vrider en fast visare 180 grader på varje fast t-ring, C-cirkeln runt, så att då denna fullbordats halva t-ringarnas totala moment vidrörts av pt-vektorns triggsvep].

Relativt h har vi då härlett (t-) spinnet — t-ringens roterande konstanta ringström i ringkroppen —

s_t=1/2

för varje t-ring motsvarande 180° rotation i dess egen ringström. Spinntalet för e totalt blir alltså detsamma s_t=h/2. Med h som enhet underförstått, refereras spinnet vanligen endast som det angivna s_t=1/2. Eftersom elektronen inte existerar utom som ett namn för en viss kvantitet t-ringar, kan vi utan risk för missförstånd hänföra e-spinnet till det egentliga t-spinnet. Då detta t-spinn s_t=1/2, relativt kärnans centrala B-fältsriktning, kan vara orienterat på två olika sätt [»±1/2»](fram eller back beroende på lokalt omgivande B-fält, se vidare nedan i Elektronringens magnetiska moment) får t-spinnets orientering — eg. s-spinnvektorns projektion relativt kärnspinnets riktning — den magnetiska magnituden »ms_t=±1/2=m_s». Om vi generellt betecknar elektronens spinnimpulsmoment med J_s=hs kan vi med hjälp av de olika energiövergångarna via q i det allmänna J/h=Öq(q+1) direkt insätta t-ringspinnets fasta impulsmomentsvektor via dess orubbligt fasta absolutvektor s_t=1/2 enligt

s-vektorn

_________

s = Ö s_t(s_t+1) = Ö (1/2)(1/2+1) = Ö (1/2)(3/2) = Ö 3/4 = (1/2)Ö 3

och därmed erhålla motsvarande »allmänna impulsmoment för elektronen»

_________

J_s = hÖ s_t(s_t+1) .............. energinivåernas allmänna elektronimpulsmoment — t-ringspinnets impulsmomentsvektors fasta längd

Med s_t=1/2 får man alltså rent J_s=hÖ(3/4).

Beteckningen [m_s] »ms_t=±1/2=m_s» — som ofta används i etablerad litteratur (även typen S_z i referenserna nedan, suffixet z refererar en preferensaxel [z] som i det experimentellt undersökande fallet motsvarar orienteringen av ett yttre pålagt magnetiskt fält [FOCUS MATERIEN 1975 s108.ill.ö, ”i förhållande till en riktning som t.ex. bestäms av ett yttre magnetfält”] — men inte alla webbkällor talar om vad som gäller …)

[Se exv.

HYPERPHYSICS — Electron Intrinsic Angular Momentum http://hyperphysics.phy-astr.gsu.edu/hbase/spin.html

HYPERPHYSICS — Electron spin http://hyperphysics.phy-astr.gsu.edu/hbase/spin.html#c1]

— betyder uppenbarligen i TNED att den fasta t-ringens s-vektor (i h-enheter ±1/2) varierar från minimum s_t=±1/2 [+Upp –Ner, parallellt med kärn-B-fältet] och sedan växande [beroende på resonansvillkor] till max J_s=hÖ(3/4) samtidigt som t-ringen därmed bringas i precession (»krängrotation» [konv. spinnbankoppling, eng. Spin-Orbit Interaction], se exv. HYPERPHYSICS http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydfin.html#c2 Spin-Orbit Interaction 2010-10-05) kring projektionsvärdets minimum ±1/2. Något annat tolkningssätt för t-ringens del föreligger (här veterligt) inte. Se även motsvarande vidare i Elektronringens toppspinn.

Justerat/Förtydligat 2010X6.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

elektronringens magnetiska moment (µ_t)

µ_t — »ELEKTRONENS MAGNETISKA MOMENT»

Elektronens magnetiska moment (µ_t) får vi direkt ur t-spinnet: ett helt varv för ringströmmen i t motsvarar (idealt) två varv i C och därmed en faktor 2h för t-ringens magnetiska moment. Vi tecknar det här

µ_t = 2h · b · s

där b anger tilläggsparametrar och s elektronspinnet.

Det magnetiska momentet (µ), utförligt i Begreppet magnetiskt moment, anges konventionellt i storheten Bohrmagnetoner där hb ovan motsvarar en Bohrmagneton. Källorna varierar i Bohrmagnetonens angivande. Om vi utnyttjar källan

eh(4e₀m)^–1 ........................ FOCUS MATERIEN 1975 s106sp1mö

ges elektronspinnets magnetiska moment mera exakt på formen

µ_t = 2h · e(4e₀m)^–1 · s

_________

= 2 · eh(4e₀m)^–1 · Ö s _t (s _t +1) ............ t-ringens magnetiska moment

I konventionell litteratur anges (i ofta resulterande obskyr association till spinnorienteringen s_t=±1/2) ett elektronens magnetiska spinnkvanttal med beteckningen m_s — Se exv.,

FYSIK, ELEKTRONHÖLJEN OCH ATOMKÄRNOR, Eve Staffansson, Akademiförlaget-Gumperts 1963 s31, ”Dessa två orienteringar brukar man klargöra genom att införa det magnetiska spinnkvanttalet m_s , vilket kan anta värdena +1/2 eller –1/2.”,

LINKÖPINGS TEKNISKA HÖGSKOLA — Kemi – Grundläggande begrepp. Kap. 1. (2010), ”magnetiskt spinnkvanttal m_s = + ½ eller – ½”,

ECYCLOPAEDIA BRITANNICA 2010 — magnetic spin quantum number, ”The spin quantum number is s = ½, so in the presence of a magnetic field an electron can have one of two orientations corresponding to magnetic spin quantum number m_s = ±½.”, m.fl. För innebörden av m_s — Se Beteckningen m_s.

Justerat/Förtydligat 2010X6 — med närmast nedanstående tillägg.

Elektronens magnetiska moment anges (vanligen) konventionellt med beteckningen (µ, mikro-), vanligen också med suffixet s (typiskt) enligt µ_s , nedan med Bohrmagnetonens beteckningssätt från FOCUS MATERIEN 1975 [s106sp1mö],

_______

µ_s = 2 · eh(4e₀m)^–1 · Ö s(s+1) ............ konventionella beteckningar

Se alternativt exv. HYPERPHYSICS — Electron spin http://hyperphysics.phy-astr.gsu.edu/hbase/spin.html#c1 med benämningen ”Magnetic moment” och typformuleringen

_______

µ_s = – (e/2m)g · Ö s(s+1)

I modern akademi känner man inte till t-ringen varför man heller inte kan ge någon resonabel förklaring till, eller ens disputera elektronspinnet [Elektronen betraktas generellt i modern akademi som en punktlik, strukturlös partikel]. Därmed kan man heller inte förklara eller beskriva toppspinnet (F_t) för t-ringen.

Vi studerar detta.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

elektronringens toppspinn (F_t)

F-SPINNET

Medan t-ringarnas ringströmmar är fixa egenskaper (ändras de, förstörs ringen), kan hela t-ringen även rotera på samma sätt som man snurrar ett mynt på högkant. Om vi använder pt-vektorn (se grovillustration från Kvanttalen) i koppling till en t-ring och följer kärnspinnet ett varv runt, ser vi enkelt att pt-kopplingen idealt kan få t-ringen att toppsnurra likaledes ett varv relativt en fix punkt i ett omgivande dominant g-fält. Med beteckningen (fi) F för detta ringspinn får vi alltså en grundform att relatera toppspinnet till enligt

F_t = h ................................................ t-ringens spinnimpulsmoment

Med de bägge spinnen s_t (fix) och F_t (variabel) givna, kan deras summa rent formellt skrivas på komplex form S(_sF)=s_t+iF_t: Sammansättningen betyder — tydligen enligt TNED — (långt) utanför atomkärnan (i dess spinnplan) att s_t strävar att ställa in sig parallellt med moderkärnans B-fält, medan iF_t söker lyfta upp t-ringen analogt med riktningen hos de övre tre kärntoroiderna (från s_t-spinnets definition; iF_t-vektorn roterad +90° relativt centrala kärn-B-fältet); Resultatet blir tvunget att t-ringen kränger (precesserar) som ett roterande mynt som just är på väg att lägga sig. Krängningen projicerar, tydligen, minst s_t=±1/2 på B-riktningen (konv. z) i moderfältet, med en största impulsmomentsvektor för t-spinnet lika med det föregående omnämnda J_s=hÖ(3/4). Detta är dock överkurs för modern akademi eftersom man inte känner ämnets dynamik [elektronen som punktlik, strukturlös, se bl.a. Citatet i Spinnbegreppet i Modern akademi] men det är, tydligen, ändå på den ovan uppdagande matematiska formen man beskriver kvanttalen i atomen i facklitteraturen. Eftersom begreppet om det magnetiska momentet (i modern akademi) bygger på föreställningen om en ensam partikels rotation (elektronen) kring ett centrum, får t-ringens toppspinn sitt motsvarande magnetiska moment definierat på Bohrmagnetonen tillsammans med relationen för energinivåernas allmänna impulsmoment J_u /h=Öq(q+1) i vågskurarna vilket medför att hela hemligheten med den krängande elektronmassans komponent, t-ringen, förloras i den moderna akademins lärosystem. Med konventionell beteckning l för q ges först

_____

µ_F = eh(4e₀m)^–1Öl(l+1) .................... t-ringspinnets magnetiska moment

I konventionella termer har F_t av förklarliga skäl ingen representation. Det figurerar emellertid ändå gömt via h genom föreställningen om en elektronbana och då som grund för ovanstående magnetiska moment via Bohrmagnetonen. I konventionella termer benämns detta µ_F som det magnetiska banimpulsmomentet för elektronen med beteckningen m_l [sambandsformen nedan från FOCUS MATERIEN 1975 s106sp1mö med beskrivningen ”Till det mekaniska impulsmomentet hör även ett magnetiskt moment eftersom elektronen är bärare av en elektrisk laddning. Detta magnetiska moment är”, sambandet nedan, högerledet] — trots att alla, även inom modern akademi, är på det klara med att några banor för elektronerna i atomerna varken existerar eller är möjliga att härleda någon dynamik för:

_____

m_l = eh(4e₀m)^–1Öl(l+1) ..................... konventionella beteckningar

Beteckningen m åsyftar på ’magnetisk’ och suffixet l är det man vanligen ser i facklitteraturen med totalsymbolen m_l , jämför

HYPERPHYSICS — The Magnetic Quantum Number http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydazi.html#c2 2010-10-05

där beteckningen m_l används i beskrivningen. Se även t.ex.

SVEN ERIKSONSGYMNASIET 2002 — Naturvetenskap - De fyra kvanttalen och atomorbitaler, ”Magnetiska kvanttalet, m_l”, http://www.utb.boras.se/uk/se/inst/naturvetenskap/Kemi/teori/atombind/kvantmodel/Fourqatumnr.htm

Justerat/Förtydligat 2010X6

F_t-spinnet är en medelform

Ingenting hindrar att hela elektronmassan med avseende på dess utspridda delar via t-ringarna kan uppvisa regionalt skilda toppspinn som följd av växelverkan mellan olika närliggande atomer. Ingenting hindrar heller att F_t-spinnen kan variera lokalt av andra skäl som inbegriper lokala em-effekter.

I det allmänna fallet frånser vi dessa inre mera avancerade möjligheter och betraktar F_t-spinnet som ett och samma för alla t-ringar relativt deras moderatomkärna.

Energinivåernas allmänna impulsmoment — »vågskursresonatorn»

Om vi med ”vågskurskvanttalet” q, konventionellt tecknat l, associerar t-ringarnas spinn ±1/2, vilket återför hela vågdynamiken just på t-ringarna, får vi en kombinationsfaktor eller en vågskursresonator j_l=l±1/2. Vi noterar att nollvärdet för u i elektriska förskjutningen — vilket motsvarar l=0=q — betyder grundtillståndet för huvudkvanttalet n som definierar den ideala C-cirkeln från Spektrum och på vars form hela komplexet vilar. Genom j-kombinationen får man alltså ytterligare ett kvanttal i familjen impulsmoment enligt

______

J_j = hÖ j(j+1) .................................... energinivåernas allmänt sammansatta impulsmoment

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

Periodiska Systemet

ATOMER MED FLERA ELEKTRONER

Föregående beskrivning i Spektrum och Kvanttalen av proton-elektronbindningen har lett fram till en generellt tillämpbar typform som (med bibehållen kärnstruktur) gäller för alla atomer.

Varför är detta klart?

Det är klart därför att det inte finns någon annan definition på en elektrons energibindning till en atomkärna (med den givna strukturen): alla föregående beskrivna tillstånd

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

kan ockuperas av exakt lika många elektroner. Ett annat sätt att säga samma sak på är elektronbindningskriteriet:

två olika elektroner inom samma atom kan aldrig helt besitta exakt samma uppsättning kvanttal — därför att varje sådan uppsättning representerar definitionen på endast en elektron

Historiskt — utan ovanstående förklaring — formulerades denna centrala (men triviala) sats av Wolfgang Pauli år 1925, benämnd Pauliprincipen eller uteslutningsprincipen.

Atomkärnans toppspinn, nukleära spinnkriteriet

Elektron(bindnings)kriteriet leder direkt på en annan fundamental och central egenskap som gäller lika för alla atomer — enligt TNED. Genom att alla möjliga elektronbesättningar definieras genom ett bestämt toppspinn från atomkärnan, den tidigare nämnda pt-vektorns triggsvep som definierar F_t =h, erhåller alla atomer samma toppspinnsdefinition för energistabila elektronkonfigurationer. Vilket vill säga: alla atomkärnor spinner på exakt samma vinkelrotation. För referens kallas den satsen här nukleära spinnkriteriet. Vi finner också detta resultat som en naturlig förutsättning för att olika atomers atomkärnor ska kunna förenas och delas genom kärnreaktionslagen.

Kärnreaktionslagens elementarform K1+K2–(m®g)=K förutsätter nämligen att inga yttre störande moment existerar då i annat fall ingen grund finns att garantera varje enskild nuklids eget rena impulsmoment 0= J_0K+3J_1K, till exempel en neutron efter fission. Se även separat artikel i SPINNBEGREPPET I MODERN AKADEMI.

Kärnbeskrivningarna för kvanttalen kan sammanfattas som nedan för de tre huvudaktörerna nqs;

n Som huvudkvanttalet n styr sina toppskurar till q=n–1 och därifrån successivt nedåt, kan vi relatera n till en koppling med q-nivåerna enligt

n–1, n–2, n–3, n–4, n–5, … 1

För varje sådan q-nivå kan dess genererande u/w-förskjutning via u anta såväl positiva som negativa värden motsvarande de tidigare beskrivna acceleration-retardationsfaserna för t-kroppen.

q Energitillståndet i varje sådant ±u eller med samma egentliga mening varje ±q, är definierad av t-ringens toppspinn F_t riktat av dess tillhörande spinnmagnetiska moment µ_F, konventionellt tecknat m_l. Varje rotvektor Ö q(q+1) för q får alltså de optimalt inkorporerade konventionellt projicerade nivåerna [i konventionen med l insatt för q]

q, q–1, q–2, q–3, q–4, q–5, … 0, –1, –2, –3, –4, –5, … –q

s Slutligen kan varje µ_F-värde (eller konventionellt m_l) ha t-ringens strömspinn s_t (konventionellt [kopplad till] m_s) riktad relativt kärnspinnets symmetri som fix preferens med endera ±1/2.

Resultat:

K L M N … konv.

n _F 1 2 2 2 2 3 3 3 3 3 3 3 3 3 4 … n

q _F 0 0 1 1 1 0 1 1 1 2 2 2 2 2 0 … l

µ _F 0 0 1 0 1 0 1 0 1 2 1 0 1 2 0 … m_l

s_t ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± … m_s

Understrykningarna motsvarar negativa värden

Denna »enkla» typorganisation kopplar till (grundkartan för) grundämnenas periodiska system. I mer avancerad form innefattar systemet olika grunddata för varje grundämne såsom atomnummer, masstal, täthet, smältpunkt osv. Tabellformen avbildar — dock utan att explicit definiera eller specificera — den exakta elektronkonfigurationen för alla möjliga grundämnen.

Vi når samma resultat genom det tidigare nämnda kombinationskvanttalet j_l=l±1/2 ,med l=±u=±q, genom att summera kvanttalen för (u=)l=q och s enligt nedanstående exempel.

Exempel:

n 4

l –3 –2 –1 0 1 2 3

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

j –5/2 –3/2 –1/2 +1/2 +3/2 +5/2 +7/2 l + 1/2

–7/2 –5/2 –3/2 –1/2 +1/2 +3/2 +5/2 l – 1/2

S = summa antal tillstånd = 2[2(n–1)+1] = 2[2n–1]= max antal elektroner

Tabellering av S specifikt för varje huvudkvanttal eller huvudskal visar oss att

n 1 2 3 4 5 6 7 8

2[2n–1] 2 6 10 14 18 22 26 30

beteckning s p d f g h i j

Om vi genomför en mera sammansatt kompression av ovanstående, bara för att få en skymt av hur systemet ter sig i stort, finner vi

n 1 12 123 1234 12345 123456 1234567

huvudskal K L M N O P Q

underskal s sp spd spdf spdfg spdfgh spdfghi

summa e 2 8 18 32 50 72 98

2 2+6 2+6+10 … … … …

/ 2 1 4 9 16 25 36 49

Ö 1 2 3 4 5 6 7

Editor2003I15 Sammanställt från Basic Principles of Related Physics efter arbeten från 1981IX.

Övriga observationer som bekräftar modellens ställning har tidigare framställts i DYNAMIKEMS GRUNDER 1995X (obs enbart författarens referens) där beskrivningarna av experimenten med spinnpolariserade protoner och kärnradierna är centrala. Genom efterföljande arbeten har den senare formen kunnat preciseras ytterligare, tillsammans med en allmän genomgång av materiens allmänna fysik, i enlighet med FYSIKENS 7 PRINCIPER.

EXAKT ELEKTRONKONFIGURATION för varje grundämnesatom kan inte ges av ovanstående härledda samband i Spektrum och Kvanttalen, endast den allmänna konfigurationens principform (själva grundkartan eller skelettet). Sambanden kan därmed heller inte i någon preciserad bemärkelse utpeka det periodiska systemets egentliga kontur, endast utpeka dess allmänna formgrund. Men det finns en annan, långt enklare matematisk form som klarar bägge dessa uppgifter med glans (men utan att lägga några som helst aspekter på t-ringarnas fysik). Se vidare i Periodiska Systemet genom Keplermomentet.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

KOLLEKTIVA IMPULS- OCH MAGNETISKA MOMENT I ATOMER

När vi introducerar flera elektroner samtidigt till samma kärnpott kommer de ideala singeltillstånden att blandas mer eller mindre häftigt. För den allmänna översikten kan dessa tillstånd samlas i grupper med samma kvanttal — på bekostnad av den beskrivande exaktheten. Följande sammanställning ansluter till konventionellt redan praktiserade ordning med tillhörande beteckningar.

l summerar L .................................................. l=q är alla heltal 0 1 2 3 4 5 …

s summerar S .................................................. S = Ns, N antal elektroner

L och S summerar J ........................................ totala atomära impulsmomentet

Summeringarna ger [ref. HOP 4-132col.2b, FOCUS MATERIEN 1975 s107sp1]

L = {0, 1, 2, 3, 4, 5, …}

S = {N₂, N₂–1, N₂–2, N₂–3, … 0 eller 1/2}

där N₂ betyder N/2, N antalet e

J = {a, a+1, a+2, a+3, … L+S} där a=L–S

Totala impulsmomentet J skrivs alltså på samma sätt som den föregående betitlade vågskursresonatorn i summeringen av l med s genom j_l=l±1/2 som ett allmänt kvanttal J med impulsmomentet

Jh = (L + S)h

Tecknet h (h-bar) är allmän förkortning för h=h/2p. Det åtföljande totala magnetiska momentet (i frånvaro av varje yttre B-fält) blir motsvarande i Bohrmagnetoner

[ref. HOP p4-132col.2m, källan skriver (2mc) för (4e₀m)]

µ = µ_L + µ_S = – eh(4e₀m)^–1 (L+2S)

där minustecknet vid –e indikerar riktningsreferens.

elektronmassans komponenter · kvanttalen n q s_t µ_t F_t

Spinnbegreppet i modern akademi

Klargörande 2004XII20 — de här använda termbegreppen förklaras i Spektrum och Kvanttalen

ATOMKÄRNANS SPINN OCH t-ringens toppspinn F_t blir identiska grundformer genom definitionen av Plancks konstant h. Spinnfaktorn är alltså 1. Denna grundfysik identifieras emellertid av modern akademi som ett 1/2-spinn. Vi behöver inte känna någon som helst oro inför denna detalj eftersom

1. modern akademi saknar uppfattning om en ”toppspinnande atomkärna”; man accepterar inte någon som helst åskådlig mekanisk modell för atomkärnan; Introduceras en sådan innebär det en total kollaps för modern fysikalisk teori som helt bygger på idén att massa är högfrekvent ljus — samtidigt som man, likväl, tillämpar olika tröghetsassocierade vektorbegrepp på atomkärnan (modern akademi kännetecknas av stark kluvenhet, citat i punkt 3 nedan)

2. spinnets grundläggande preferens i sig självt är endast ett relativt prefix som kan förstås ha vilken magnitud som helst blott vi konsekvent observerar originalets bevarande

3. kärnspinnet — h här men 1/2 i modern akademi — är inte kvantitativt avgörande för beskrivningen av atomens struktur (elektronskalen), men desto mera avgörande i den kvalitativa beskrivningen av atomen: atomkärnans fysik och därmed fysiken överhuvudtaget. Vi studerar denna punkt, explicit.

Toroidmodellen innefattar den moderna akademins preferenser som primitiva.

Modern akademi har varken kunskap om eller någon teori för ett s_t-spinn: — det infördes i modern akademi på 1920-talet på grund av spektroskopiska observationer ”för att få ekvationerna att stämma” [ref. ENCARTA 99 Spin]. Utan 1/2-värdet kollapsar energiräkningen. Jämför denna del med följande representativa citat som visar att modern akademi mera tycks intresserad av magi och mystik än naturvetenskap. Fetstilen är min markering.

Citat

”Experiments in which electrons are scattered by other particles, however, effectively measure the size of the electron, and they indicate that the radius must be exceedingly small. Indeed, all experimental data gathered so far are consistent with the idea that the electron is a point particle, entirely without extension.”

”In the 1940’s these problems were resolved by abandoning the mechanical model of the electron and devising a new and more abstract theory, quantum electrodynamics. In quantum electrodynamics the electron is allowed to be a dimensionless point particle and its mass is allowed to be infinite, at least in principle.”

SCIENTIFIC AMERICAN August 1980 The Isolated Electron s92sp2

En dimensionslös — och alltså masslös — partikel som å andra sidan kan ha oändlig massa, har ingen känd koppling till begreppet SPINN. Enbart med stöd i spinnbegreppet kan man alltså helt avfärda ovanstående typmeningar som tillhörande ett väl avsomnat intresse för begreppet naturvetenskap.

Se mera utförligt i ELEKTRONENS BUBBELKAMMARSPÅR där en mera handfast bevisning ges.

I vårt h-prefix och toroidmodellen, såväl som i den moderna akademins kvantitativa teori, har s_t-spinnet alltså värdet 1/2.

Så länge beskrivningen berör atomens yttre struktur, har kärntoppspinnets magnitud ingen som helst explicit avgörande betydelse. Inte heller TNED lämnar någon direkt upplysning om toppspinnets magnitud (h×J_T). Den moderna akademins »föreställning» om 1/2-spinnet för F_t — i toroidmodellen ett 1/1-spinn och som modern akademi alltså inte känner grunden för — är alltså inte alls avgörande för den fysikaliska beskrivningen av atomens yttre struktur, helt i enlighet med punkt 2. Vilket spinnprefix man än väljer återfaller atomens yttre fysik likväl endast på det centrala s_t-spinnet — av konventionen benämnt ”elektronens spinn” och som vi nu vet är ett vettlöst begrepp eftersom elektronen är en hop, en mängd, ett kvantum, och därför inte har några fysikaliska egenskaper alls, allra minst någon ”radie”.

Betydligt värre blir det när modern akademi ska beskriva kärnfysiken: den kvalitativa fysikens aspekt. Där totalhavererar modern akademi, och där urartar också den moderna akademins begrepp om spinn fullständigt. I sammanställning [Se även samma tabell i Jämförande tabell i Neutronfragmenten]:

Jämförande tabell — Spinnbegreppet i Modern akademi kontra Relaterad fysik

———————————————————————————————————

Relaterad Fysik (TNED)

SP+Se		SP	+	Se	+	0	.............	← summa inre ringspinn
0n^1	→	1H^1	+	e^–	+	(m→γ)	.............	massekvivalenten
0n^1	→	1H^1	+	e^–	+	(m→γ)	.............	energiekvivalenten
nτ	=	pτ	+	eτ		...........	.............	τ-ringströmmens spinnekvivalent
0		1/2	–	1/2		...........	.............	summan av alla spinn och moment är noll
Modern Akademi (MAC)
1/2		1/2	+	1/2	+	1/2	.............	← ”summa spinn”
0n^1	→	1H^1	+	e^–	+	v	.............	”energiekvivalenten”

———————————————————————————————————

Se även i Spinnbegreppet i Modern Akademi.

MAC-uppgifterna ovan på de olika detaljernas spinnvärden finns bl.a. i separat tabell i FOCUS MATERIEN 1975 s140. Spinnvärdena finns även infogade i tabellen för PARTIKELNOMENKLATUREN.

Den konventionella uppfattningen om fysiken har ingen jämförande referens med TNED (två skilda världar).

Den konventionella uppfattningen om ”spinn” blir särskilt obskyr eftersom man rent allmänt inte erkänner någon åskådlig BILD av atomkärnan, men likväl tvingas associera till en sådan på grund av vektorbegreppen. Vilket vill säga; atomkärnan kan varken beskrivas, härledas eller förklaras genom den moderna akademins lärosystem.

Se även från ENERGILAGEN.

Se även Jämförande tabell i NEUTRONENS FRAGMENT.

BT-fältet

B_T-FÄLTETS BETYDELSE FÖR ELEKTRONMASSORNA

För härledningen till atomkärnan, se från Planckringen

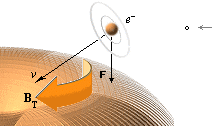
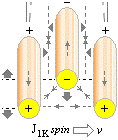
INKOMMANDE elektronelement (e^–) drivs mot kärnpolen eller skjuts bort ifrån den beroende på vilken pol incheckningen går på. Det som bestämmer till eller från är riktningen hos kärnans magnetiska topptoroidfält B_T — som bildas av den positiva laddningsdelen i deplacementet via J_1K. (J_1K härleds i ATOM- OCH KÄRNFYSIKENS TVÅ KUNGSEKVATIONER).

DEN LILLA PILEN TILL HÖGER OVAN pekar enligt TNED på ett elektronelement [max diameter ca 1/50 av protonradien, ringens tjocklek max ca 1/3 000 000 av protonradien enligt sämsta fallets beräkningar — ringen kan alltså i praktiken vara betydligt mindre]. Eftersom massa och laddning är proportionella genom kärnmassan som massans fundamentalform har det i de allmänna fallen (som inbegriper Q/m-funktioner) ingen betydelse om vi använder elektronbeteckningen (e^–) för samtliga fall istället för det mera egentliga ”e/n” med n som antalet t-ringar i e. Elektronelementets massa är enligt TNED max 1/177 062 av elektronkvantumets massa 9,11 t31 KG enligt dimensionerna i N3m20-aggregatet.

För B_T-fältet, se även i Atomkärnans allmänna magnetiska yttoroidfält.

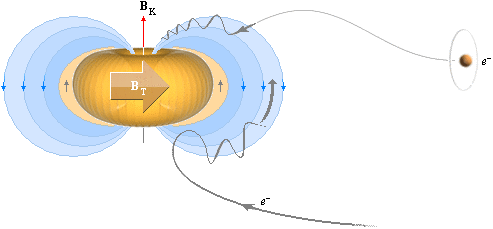
En atomkärna (här med positivt centralmagnetiskt kärnfält, ovan) tvingar ett inkommande elektronelement att gå i spiral in mot den korrekta kärnpol som anvisas av B_T-fältet enligt bilden ovan. Spiralbanor förekommer f.ö. alltid i samband med elektriska laddningar som kommer in i magnetiska fält i någon vinkel som skiljer sig från den exakt räta. Om vi känner högerhandsregeln (och kraftvektorlagarna inom magnetismen) kan vi räkna ut hur laddningen kommer att vrida sig om vi också känner laddningens polaritet och det yttre B-fältets riktning. Om B_K-fältet växlar pol blir den enda effekten på elektronelementet att det spiralsnurrar in mot kärnan åt andra hållet (moturs i stället för medurs eller omvänt).

Ett elektronelement som av någon anledning kommer in till kärnan vid ”fel pol” [‡1], tvingas 1. vända i försorg av det starka B_T-fältet vid kärnytan, 2. drivs ut från kärnytan och upp mot rätt kärnpol (kärnanoden, samma som J_0K-vektorn) där 3., B_T-fältet centrerar elektronelementet kring ”kärnstaven” i mitten, in mot kärnbrunnen. Alla dessa delar följer direkt av högerhandsregeln. Nollenergierna, analogt nollkrafterna i F_BT+F_eZ=0 säkerställer sedan beträffande elektronelementets vidare öde att det finns en ekvivalent till en sluten banform för ett elektronmassaflöde mellan kärna och hölje och som via krafvägen F_eZd följer härledningarna i Spektrum och Kvanttalen.

‡[1]: ”in the direction of its spin”

”The assumption of parity conservation — an expression for the reflection symmetry of the interaction — was dramatically shattered by the experiment of Wu, Ambler, Hayward, Hoppes and Hudson, following the theoretical suggestions of Lee and Yang. They showed that the electrons are emitted, by the decaying Co⁶⁰ nucleus, preferentially in the direction of its spin.”

[HOP 9-55col.1mt]. Vidare beskrivningar av samma experimentella art visar att positroner från kärnan emitteras i den motsatta riktningen

[ref. FOCUS MATERIEN 1975 s143sp1ö].

Min översättning:

Förmodan med paritetens bevarande — ett uttryck för reflexionssymmetrin i växelverkan — blev dramatiskt uppriven genom experimentet av Wu, Ambler, Hayward, Hoppes och Hudson, efterföljande ett teoretiskt förslag av Lee och Yang. De visade att elektronerna emitteras, av den sönderfallande kärnan Co⁶⁰, företrädesvis i riktningen för dess spinn.

NOTERING 2007-11-27: Sökning på @INTERNET Google »kärnmagnetiskt moment» ger noll svenska resultat. De facto. År tvåtusensju. Noll. Ingenting.

Kärnmagnetiskt Moment

Med direkt fortsättning från B_T-fältet

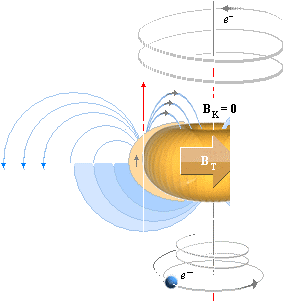
Grundläggande begrepp inom kärnfysiken ENLIGT TNED

KÄRNMAGNETISKT MOMENT

KÄRNMAGNETISKA MOMENTET

Referenser nedan visar några olika sätt som kärnmagentiska momentet skrivs i olika källverk

ipr²

Vad betyder kärnmagnetiskt moment?

KÄRNMAGNETISKA MOMENTET — utförlig beskrivning

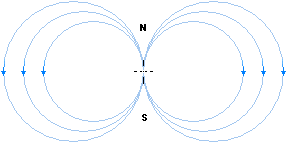
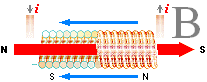
Eftersom atomkärnan utåt sett — enligt relaterad fysik med grund i B_T-fältet — uppför sig som en liten magnetisk stav — som en strömgenomfluten elektrisk spole — med utpräglade magnetpoler (en magnetisk dipol) kan man mäta den kärnmagnetisk dipolfältstyrkan eller kärnmagnetiska momentet genom olika metoder.

Man mäter på hur atomerna i ett visst ämne reagerar på styrningar från olika yttre (mycket starka) magnetfält. Metoderna är mångskiftande, men flera (många) använder allmänna samband som uttrycker resonansfrekvenser vid givna energier. Ett sådant (typform, HOP 9-90 sp1) är

v₀ = g₁H₀/2p = g_I µ_NH₀/h

(v anger transiteringsfrekvens). Likheten gäller när resonans inträder mellan atomkärnornas B-fält och B-fältet från det ytte H₀-fältet. Genom att avläsa data och mäta v₀ och H₀ kan de övriga parametrarna beräknas (g₁, magnetgyriciteten, g_I nukleära proportionalitetskonstanten mellan momenten för magnetism och impuls, µ_N kärnmagnetonen eh/2Mc, M anger [eller är kopplad till] nuklidmassan). Kort sagt; man mäter på atomkärnan som om den vore en liten kort rak enkellagrad elektrisk spole vars ström bestäms av kärnladdningen eZ.

Produkten av strömmen i genom spolen och tvärsnittsytan pr² ger (råformen för) det gängse begreppet magnetiskt (dipol-) moment, µ=ipr².

Eftersom cylinderns yta och sfärens ytan har samma ekvation 4pr² kan den korta spolens cirkulerande laddningar återföras på en spinnande sfär vars yta består av många små laddningar. Det är denna sfäriska modell som används i den traditionella föreställningen om atomkärnan.

Den sfäriska modellen är emellertid problematisk. Om man tillämpar differentialbegreppet på sfärens totala ytladdning Q får man automatiskt en fullständigt strukturlös homogen laddningsyta utan ojämnheter. En sådan sfärisk laddning som spinner kring en centralaxel ger varken någon magnetisk eller induktiv effekt och är därför helt värdelös som modell.

Jämför den magnetiska fenomenformens grundläggande differentialekvation ENLIGT TNED, dB_P=µ₀(I/4pr²)ds; ändringen utmed en väg s måste avse ett intervall för att B_P ska bli något annat än noll. En spinnande idealt slät Q-sfär innehåller ingen förutsättning för det.

För att en spinnande eller roterande sfär med laddningen Q ska ge någon effekt, magnetisk eller induktiv eller bägge, måste den vara en makrosfär, dvs., innehålla fördjupningar och upphöjningar, gropar och ojämnheter så att potentialbilden för givet r har möjlighet att ändras. Vilket vill säga; sfären (formen) måste vara strukturerad.

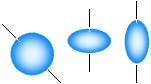
Q=eZ

Till vissa delar frånser man den här svårigheten i den konventionella kärnteorin och behandlar modellen som om den vore giltig i alla fall.

Genom att modifiera den sfäriska grundformen efter olika asfäriska teoretiska samband ges motsvarande ändringar i den raka spolformens geometri och strömtäthet. Laddningsasfäriteten kallas kärnelektriskt kvadrupolmoment. En positiv asfäricitet uttrycker laddningens utdragning utmed kärnspinnaxeln (polutdragen sfäroid), negativ asfäricitet en ihoptryckning vid polerna (avplattad sfäroid). Längre kommer man inte i modellhänseende i modern akademi.

Dessa modellbegrepp har ingen som helst koppling till TNED. Enligt TNED är och förblir varje sfärisk differentialanalogi till atomkärnan dödfödd redan från första punkt.

Matematiska samband

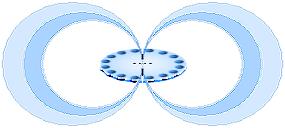
För en ring av ett stort antal mycket små idealt sfäriskt punktformade elektriska laddningar med summan Q=IT som drivs runt i ringen gäller förenklat den magnetiska fältstyrkan (B) i rotationscirkelns centrum

B=µI/2r=µQ/T₀2r=µQ/[T₀=2pr/v=2p/w]2r=µQv/4pr²=µQw/4pr ......................... VS/M²

B = w(µ/4p)Q/r ................. fältstyrkan avtar med växande r för given laddning Q och rotation w

Vi använder (Grekiskans lilla Ohmega) w=2p/T₀ som vinkelhastigheten med T₀ som tiden för ett varv; wr=v.

konventionella skrivsätt

Tre olika konventionella referenser

Begreppet magnetiskt moment (i gängse terminologi) grundas på följande [ref. HOP 8-112 sp2m].

Den strömstyrka (i) som den i en ring ensamma roterande laddningen bildar har formen

i=Q/T₀=Qv/2pr=Qw/2p .................... strömstyrkan är inte beroende av radien

Omloppet för Q bildar en magnetisk dipol.

Omloppets tvärsnittsyta, pr², bildar en ekvivalent som relaterar en viss strömtäthet för hela i. Genom att sätta ipr² får man

ipr²=Qvr/2 = Qmvr/2m = QJ/2m=(wQ/2)r²

Med Q=e och impulsmomentet J=h=Plancks konstant=6,625 t34 JS får man

ipr² = eh/2m ...................................... magnetiska momentets grundform

MAGNETISMEN via strömmen i beror I RELATERAD FYSIK av elektriska konstanten Rc med rymdresistansen (R) och ljushastigheten (c). Substitution med R₀c₀=1/e₀ ger

R₀c₀ ipr² = R₀c₀ eh/2m = eh/2e₀m

Med referens till halva topphastigheten för ljusets utbredning (energiekvivalenten som definierar potentialbarriären, se Potentialbarriären) ges

R₀ (c₀/2) ipr² = R₀c₀ eh/4m = eh/4e₀m = µ ............ WM³/C

vilket (med minustecken framför) är vad FOCUS MATERIEN 1975 s106sp1 anger som den s.k. Bohrmagnetonen, samma som enheten för magnetiskt moment.

KÄLLAN [HOP] Handbook of Physics, E.U. Condon, McGraw-Hill 1967 s.8-112, substituerar med 1/c i ipr² som ger

ipr²/c = eh/2mc = µ ................................................. CM

Också detta kallas av HOP-källan för magnetiskt moment.

I gängse bruk används elektronmassan m i elektronsammanhang och nuklidmassan M i kärnsammanhang [ref. HOP 8-112 sp2n].

EN TREDJE VARIANT (utan ekvation) ges av Encarta 99 (se Bohr Magneton) i enheten AM², vilket motsvarar råformen ovan ipr²=eh/2m.

Begreppet magnetiskt moment i gängse termer är alltså en ekvivalent till den enkla typformen avbildad ovan (!). Enkellagrad spole.

Men där stannar också analogin.

B=w(µ/4p)Q/r .................................... centralmagnetisk dipolfältstyrka, ringekvivalent

ipr²=(wQ/2)r² .................................... sfäriskt kärnmagnetiskt moment, kan ej tillämpas direkt på atomkärnan enligt TNED

ATOMKÄRNAN enligt MAC (modern akademisk teori) (Mycket förenklat, man vill inte vidkännas någon ÅSKÅDLIG modell för atomkärnan, men tvingas använda en ändå på grund av vektormatematiken):

MAGNETISKT MOMENT

MODERN AKADEMI

ENKELLAGRAD RAK SPOLE från ideala sfäranalogin 4pr² med magnetiska momentet ipr²:

ATOMKÄRNAN enligt TNED:

flerlagrade spolar med olika laddningar

MAGNETISKT MOMENT

RELATERAD FYSIK

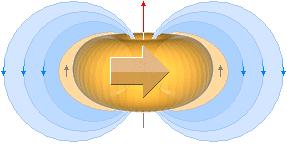
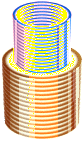
Det finns ingen jämförande matematisk fysik att tillgå.

Sagt på annat sätt: Fysiken kan inte beskrivas, eller förklaras, med den moderna akademins begrepp.

(Den moderna akademins begreppshorisont är för trång).

Begreppet magnetiskt moment som det är konventionellt definierat, kan enligt TNED mycket väl tillämpas på elektronens element — den toppsnurrande t-ringen — men definitivt inte på atomkärnan.

SAMMANFATTNING

Atomkärnans fysik och matematik enligt TNED kan inte anställas i någon egentlig jämförelse med konventionella föreställningar eller teorier. Det är som att försöka jämföra en vuxen människas tankevärld med ett barns (alltså i meningen: som att försöka diskutera äktenskapliga problem med människor som ännu inte har kommit in i puberteten).

Det är också så att den moderna akademins teori om kärnmagnetismen, och föreställningen om kärnspinnet generellt, använder begreppen från atomens hölje med elektronmassornas kvanttal [Se Spektrum och Kvanttalen]. Men atomkärnan är inte elektronerna, och därför kan man inte komma fram till sakens kärna på den vägen. Med andra ord beskriver det konventionella kärnmagnetmomentets begrepp, med stöd i experimentella uppmätningar, detaljer som sammanhänger med elektronmassornas koppling till kärnan — hela atomen — inte någon explicit kärnfysik. KärnSpinnKvanttalen som anges i de konventionella tabellerna över kärnmagnetiska moment är alltså, relativt TNED, irrelevanta kärntekniska begrepp. De beskriver atomen. Inte kärnan.

Vidare beskrivning nedan.

KÄRNIKONERNA

Stiliserade modeller (laddningsikoner) i TNED som visar totala laddningsstrukturen, kärncentrum i mitten, spinnande ringar:

NEUTRONEN:

negativt centralmagnetiskt dipolfält

MAC-sfäranalogi: negativt kärnmagnetiskt moment

PROTONEN samt alla övriga atomkärnor:

positivt centralmagnetiskt dipolfält

MAC-sfäranalogi: positivt kärnmagnetiskt moment

GÄLLER ALLA ATOMKÄRNOR UTOM NEUTRONEN

positivt, negativt eller inget centralmagnetiskt dipolfält; kärnan justerar allt eftersom via de inre delarna

MAC-sfäranalogi: positivt, negativt eller inget kärnmagnetiskt moment, motsvarande ovan

MOTSVARANDE SPOLMODELL:

flerlagrade »magnetiska momentspolar» med omväxlande positiva och negativa strömmar

µ=ipr² saknar enhetlighet

FÖRKLARING

ipr² — kan inte användas på ett sammansatt spolsystem

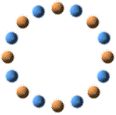
a b c

a. FÖR ETT SYSTEM av ett stort antal ekvidistanta, radiellt placerade lika stora men omväxlande positiva och negativa laddningar som roterar med w kring ett gemensamt centrum gäller att B=0, i centrum och på alla andra ställen, eftersom de ekvivalenta potentialerna ±Q/r tar ut varandra.

b. Är (–)-laddningarna i (a) förskjutna inåt är B i centrum negativt. UTANFÖR ringen är B positivt; B=w(µ/4p)Q/r:

magnetiska momentet ipr²=(wQ_RING/2)r² är positivt, =(wQ_RING/2)(r_POS² – r_NEG²).

c. Är (+)-laddningarna i (a) förskjutna inåt är B i centrum positivt. UTANFÖR ringen är B negativt; B=w(µ/4p)Q/r:

magnetiska momentet ipr²=(wQ_RING/2)r² är negativt, =(wQ_RING/2)(r_NEG² – r_POS²).

Slutsats:

ETT SLUTET ELEKTRISKT SYSTEM med summa noll i laddning kan alltså ha ett positivt, negativt eller noll B-värde i centrum.

Men titta här:

I b är magnetiska momentet ipr²=(wQ_RING/2)r² för den positiva, yttre, laddningen större än för den negativa eftersom r i ipr² är större;

systemet har i MAC-termer ett positivt magnetiskt moment — men i centrum gäller en negativ B-vektor,

B=w(µ/4p)Q/r

eftersom B växer med avtagande r.

I gängse verk heter det: neutronen har ett negativt magnetiskt moment: den uppför sig som en negativt strömstyrd magnetisk dipol. Systemet har emellertid som nyligen påpekades i MAC-termer ett positivt magnetiskt moment. Det går alltså inte att använda MAC-terminologin för att beskriva kärnfysiken, enligt TNED. Logiken spårar ur och ger galna resultat.

Slutstats, förtydligande

Det går inte obetingat att använda MAC-terminologin — begreppet magnetiskt moment ipr² — på ett sammansatt spolsystem

därför att MAC-terminologin klargör att det för modern akademi i atomkärnan inte finns några laddningar utöver eZ.

MAC-terminologin räknar bara med en spole och en laddningstyp. Med en sådan preferens blir naturfysiken enligt TNED definitivt vandaliserad. (Man vill ropa: sluta, bryt, avbryt misshandeln, sätt MAC på rymdfärjan till Månen och låt dem stanna där. Men ingen hör).

Modern akademi ser inte det inre NEUTRALA området,

det är mörkt för modern tanke; den ser bara det yttre med kärnladdningen eZ.

EFTERSOM ATOMKÄRNAN ENLIGT TNED TVUNGET REGLERAR SIN KÄRNMAGNETISM via just dessa inre, för modern akademi dolda delar, genom att fördela negativa eller positiva delar längre in eller längre ut, allt eftersom kärnbalansen och atomdynamiken så kräver det ur energihänseende, är det givet att

begreppet kärnmagnetisk moment INTE kan ha den praktiska aspekt som den moderna akademins rent matematiska fysik ändå är ägnad att mera ingående beskriva.

Uppmätningen av atomkärnans magnetiska moment genom föreställningen om ett ipr² är alltså på sätt och vis IRRELEVANT — för analysen av kärnfysiken.

Det säger, strängt sagt, ingenting om atomkärnan.

Det vill säga; det som bestämmer atomkärnans ”levande spolmagnetism”, analogt med de experiment som kärnan utsätts för via yttre B-fält och hur kärnans svarar på dessa, är naturligtvis summan av alla kärnmagnetiska bidrag, och inte enbart det som ges av den fjuttiga, försvinnande lilla kärnladdningen eZ.

För att kunna beräka ett netto kärnmagnetiskt moment som ansluter till den enkla raka spole som tänks reagera på yttre B-fält, måste man i den sammansatta TNED-strukturen först beräkna den motsvarande strömstyrka netto som sammanhänger med netto gällande centralmagnetisk fältstyrka.

I föregående exempel b

analogt

ser vi direkt bara genom att titta på strukturen och erinra B-formen för ringen att det här rör sig om en centrumnettostyrka som är negativ: de stora delarna är inbördes neutrala, de bortfaller direkt, återstående delar motsvarar en tvålagrad spole som med lika laddningar (+) drar lika stora strömmar i olika riktningar varav den spole som har minsta diametern ger största bidraget, analogt största fältstyrkan till centrum. Det effektiva magnetmomentet i ljuset av den enkla raka spolanalogin bestäms alltså i ringformerna närmast ovan av den inre negativa strukturen. I detta fall bestämmer B_NEG–B_POS enligt TNED strömstyrkans effektiva värde i det ideala, enkla magnetmomentet ipr² — som ligger till grund för beräkningsalgoritmerna i de experimentellt uppmätta värdena.

Korrektionen mot TNED skulle i detta fall och i grova drag se ut så här:

B = µI/2r; strömmarna är lika stora; netto B blir i ringens centrum

B = (µI/2)(1/r_NEG – 1/r_POS) ;

I = (2B/µ)(1/r_NEG – 1/r_POS)^–1

= (2B/µ)r_NEGr_POS(r_POS – r_NEG)^–1

EXPERIMENTELLA DATA som anger kärnmagnetiska dipolmoment med magnitud X betyder att atomkärnan reagerar på yttre magnetfält som om den vore en vanlig magnetstav med momentstyrka X.

———————————————————————————————————————————

Gängse begrepp kärnmagnetiskt moment efter experimentella uppmätningar, avser enligt TNED — som utpekar den verkliga fysiken — en centralt verkande B-styrka B=w(µ/4p)Q/r. Inget magnetiskt moment ipr²=(wQ/2)r².

———————————————————————————————————————————

Modern akademi säger: neutronens kärnmagnetiska moment är negativt medan protonens är positivt.

TNED säger: neutronens centrala magnetiska kärnfält är negativt medan protonens är positivt; momenten är omvända, men dessa finns inte för modern akademi eftersom man använder en (märklig) sfärisk modell.

Begreppet magnetiskt moment som det är konventionellt definierat, kan enligt TNED mycket väl tillämpas på elektronens element — den toppsnurrande t-ringen — men definitivt inte på atomkärnan.

MED REFERENS TILL TNED som atomkärnans förklaring, räknar man konventionellt på något annat än det man utför sina experiment på (Man avhandlar Afrika genom att tala om Sverige). Man tror att man mäter på det här (med eller utan centralt magnetfält):

Q=eZ

diamagnetism

paramagnetism

ferromagnetism

Kärnmagnetiska Momentets Grundbegrepp

DIA- PARA- OCH FERROMAGNETISMEN

diamagnetism · paramagnetism · ferromagnetism

MATERIEFYSIKENS GRUNDLÄGGANDE FENOMENFORMER ENLIGT TNED

Ikonerna ovan beskrivs i KÄRNIKONERNA.

VAD TROR DU, om du inte redan vet det?

Om vi räknar bort neutraldelen i vänsterikonen och endast ser till återstoden minus innanför och plus utanför enligt högerikonen, alla lika stora laddningar, vem av typerna kommer då att bidra mest med B-styrka utmed en axel placerad i storringens kant som laddningarna roteras kring?

Svar:

— Negativa vinner. Helt klart.

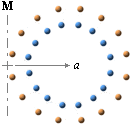
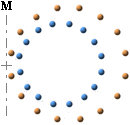
I den allmänna, övergripande, rent matematiska behandlingen av atomkärnans magnetism — med hänsyn till den allmänna laddningsfördelningen i atomkärnan — kan vi i en mycket enkel och bekväm form likna hela kärnan vid en enkel (kulformig) strömring motsvarande snittet av en rak (kort), flerlagrad, elektrisk makrospole.

Den magnetiska verkan från kärntoppspinnet J_0K på deplacementsringarna strävar att öka deras lamellavstånd. Större lamellavstånd innebär ökad diameter för hela den inre översta 3-ringkroppen;

Den sammandragande B-kraften mellan lamellringarna motverkas vilket medför att deplacementskraften gynnas. Den magnetiska, lokala, motverkan från atomkärnans allmänna impulsmoment J_0K (se utförligt i Atomkärnans härledning) beror emellertid av periferihastigheten och avtar alltså in mot kärncentrum — konstant vinkelrotation för toppspinnet förutsatt.

Samband —

ALLMÄN SAMBANDSKOPPLING

För B-styrkan nära ytan på en rak ledare med cirkulärt tvärsnitt med radien r₀ gäller förenklat B=µI/2pr₀=µH₀. Med laddningen q i en cirkulär rörelse med radien a och vinkelhastigheten w=v/a gäller för ett kort avsnitt d av båglängden under tiden Dt att I=q/(Dt=d/v=d/wa)=qwa/d. Då är B=µqwa/2pr₀d=µ(q/d)wa/2pr₀. Med givet (q/d)w/2pr₀ växer alltså B vid laddningsytan proportionellt med växande a. Det finns inget ytterligare att belysa med den saken, sambandet endast förtydligar att B-styrkan på laddningarna avtar in mot centrum i försorg av den konstanta vinkelrotationen från J_0K.

Med avseende på kärncentrums mittaxel M och ett deplacement i de tre inre tvärställda toppringarna mellan lika stora laddningar i skilda ideala koncentriska cirklar (vänster ovan) bildas en typförskjutning med den negativa laddningscirkeln in mot centrum som följd av B-verkan från J_0K (se även mera utförligt i Neutronens sönderfall i ATOMKÄRNANS np-STRUKTUR). Vi ska nu försöka undersöka denna typförskjutning för att få en säker kvalitativ uppfattning.

Matematiska samband —

CENTRALMAGNETISKA KÄRNFÄLTET

Eftersom B-styrkan i centrum [generellt via radien a enligt B=wa^–1(kQ)] växer med minskat centrumavstånd a för en given rotationsladdning Q och given vinkelrotation w kan vi med ringikonens förenklade bild samtidigt få en enkel kvantitativ översiktlig referensbild av hur vi (här) kan sluta oss till att B-styrkan i rotationscentrum för neutronen bör vara negativ. För att erhålla denna referensbild anställer vi en kvantitativ undersökning med den positiva yttre deplacementsdelen som referenscirkel.

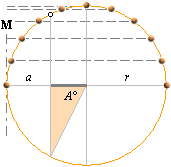
Eftersom B-styrkan för given laddning och vinkelhastighet växer med inversen på miskande avstånd (a) från centrum M kan vi jämföra en totalsumma för alla positiva 1/a-bidrag med totalsumman för alla negativa 1/a-bidrag med givet antal enhetsladdningar, alla lika stora. Med PREFIXxSIN a=r(1 – sin nA°), A°=180/n, ges summan S

S-formen

n

S = å [r(1 – sin nA°)]^–1

n=1

Om vi undersöker ikonformens magnetiska tillförlitlighet (största B-bidraget ges av största 1/a-summan analogt minsta a-värdet) genom att gentemot en kantaxel M summera alla inverterade avstånd a^–1=[r(1 – sin nA°)]^–1 för halvcirkeln (hela cirkeln ger dubbla summan) får vi ett konkret besked om huruvida ikonringen är elektriskt principkorrekt då den tillämpas på TNED-kärnans inre tre toppringar. Vi undersöker då summaformen betecknad S i ovanstående summaled.

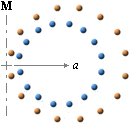
OM deplacementen i de inre toppringarna i TNED-kärnan vore exakt koncentriska motsvarande de två laddningsringarna, funnes ingen möjlighet att relatera ett negativt kärnmagnetiskt moment för neutronen

Vi finner först att S är strängt växande för strängt avtagande grundcirklar. Dvs., en liten laddningscirkel ger mot M-axeln ett större 1/a-bildrag, analogt större B-styrka totalt sett än en stor laddningscirkel. För två koncentriska cirklar gynnas emellertid den positiva delen av radieskillnaden; 1/a-formen för den inre, negativa laddningscirkeln får gentemot M-axeln formen

[Dd+r(1 – sin nA°)]^–1 där Dd är radieskillnaden. OM deplacementen i de inre toppringarna i TNED-kärnan vore exakt koncentriska motsvarande de två laddningsringarna, funnes alltså ingen möjlighet att relatera ett negativt B-värde i kärncentrum för neutronen.

Undersöker vi därmed summaformen genom att, i enlighet med B-effekten från J_0K-spinnet, något förskjuta den negativa deplacementscirkeln inåt M-axeln (vi gör Dd mindre än radieskillnaden), finner vi också att den negativa 1/a-summan blir den större.

Därmed är, i princip, ringteorin bekräftad.

För 150 likadana q-laddningar 0-180° ger den positiva grundringen summan S=230 282,641935053. OM deplacementet d_Q (skillnaden i radie mellan ±-ringarna) sätts till 1/10 000 ligger fördelen för det negativa övertaget i avståndet från M-axeln till minusringen från ca d_Q/2790 (S=230 282,940315631). Om minusringens framdel ligger exakt på M-axeln blir S=230 305,672502303 med

r_MINUS=r_PLUS(1–1/10 000). Övertaget för minusringen växer sedan (naturligtvis) med växande deplacement d_Q. Undersökningen visar att de olikheter som verifierar det negativa magnetiska momentets övertag bör avse mycket små metriska differenser mätt med atomkärnans dimension.

LADDNINGSIKONERNA I TNED

Se även från KÄRNIKONERNA där grunden till nedanstående stiliserade kärnikoner beskrivs.

IKONRINGARNA beskriver ingen kvantitativt exakt motsvarighet till bildningen av B-styrkorna tillämpade på atomkärnans inre toppringar.

Med ledning av föregående grova undersökning av förskjutningarna kan man emellertid ändå använda ringikonerna även för dessa fall — blott vi erinrar B-effekten från J0K-spinnet.

DEN NEUTRALA RINGDELEN, där alla Q ligger på samma centralring, ger för två motställda likadana ringar alltid ett central-B-fält lika med NOLL utmed rotationsaxeln (se föregående S-samband). I grundformen bortfaller alltså dessa ur betraktelsen. För protonens del bestäms B-styrkan i kärncentrum därmed (ikoniskt) enbart av kärnladdningen i det positiva, kvarvarande deplacementet. I detta fall (protonen) bör B i kärncentrum alltså bli positivt.

Dia-, para, och ferromagnetismens grunder

FÖR ALLA ÖVRIGA ATOMKÄRNOR behöver vi nu endast tillåta oss den (ytterst bekväma och) principiella ordningen att kärnan genom sin struktur kan ordna med en liten variation internt i den neutron-protonideala neutrala ikoniska mittringen:

DIA (nollpol)

en liten förskjutning av minuskulorna inåt kan nolla den positiva kärnpolen (diamagnetism),

PARA (svag negativ) och FERRO (stark negativt)

ytterligare inskjutning ger ett allt starkare negativt kärnmagnetiskt centralfält (para- och ferromagnetism),

IDEALT POSITIV

och en liten indragning av ytladdningsringarna ger ökat bidrag till kärnans ideala positiva magnetpol (idealt B-positiv atomkärna).

UTFÖRLIG BESKRIVNING

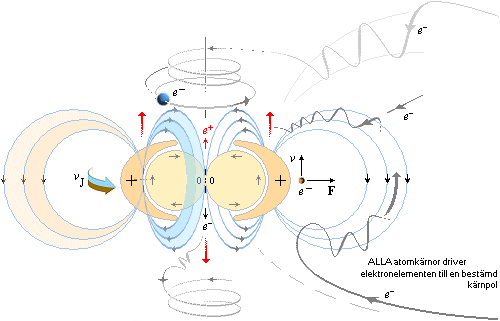
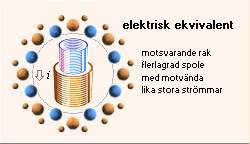
Sammanställd förenklad bild av atomkärna med negativt kärnmagnetiskt dipolmoment

Bilden ovan visar i förenklad kvalitativ syntes hur TNED beskriver närområdet kring en atomkärna med negativt kärnmagnetiskt moment.

Alla atomkärnor har ett gemensamt likriktat yttre magnetiskt toroidfält (B_T) med grundstyrka från neutronkärnan. B_T garanterar att varje inkommande MYCKET LITEN negativ laddning [Se t-ringen] drivs till korrekt kärnpol (kärnanoden) och i övrigt håller kärnans närområde intrinsiskt rent från sådana.

BT-fältet [se utförligt i B_T-FÄLTET] garanterar på detta sätt att eventuella positroner skickas ut från kärnan i diametralt motsatt riktning mot elektronmassorna. (Se även efterföljande artikel ATOMENS CENTRALREGELERANDE DYNAMIK, Centralkontakterna).

beskrivning

Genom att justera den inre (för alla akademiska proffs gömda) Q-kroppens laddningar, kan kärnan (från masstal 2) generera olika magnituder i det centralmagnetiska kärnfältet (B_K, se nedan). Inputtning av minusladdningarna mot centrum motverkar det positiva centralfältet B_K från det positiva grunddeplacementet på samma sätt som vi påför en växande motström i den inre av spolarna i en tvålagrad elspole. Därmed minskar B_K i mitten och går mot noll. Ytterligare inputtning av minuskulorna (blå) ger härifrån en övervikt åt det negativa hållet, och vi får en negativ riktning på det centralmagnetiska B_K-kärnfältet.

OM VI I EN MYCKET FÖRENKLAD BILD UTNYTTJAR den enkla strukturgeometrin för magnetfält från två parallella rakledare, kan vi göra en grov skiss på hur atomkärnan, enligt TNED, förverkligar de ovannämnda laddningsikoniskt illustrerade kärntyperna — rent magnetiskt.

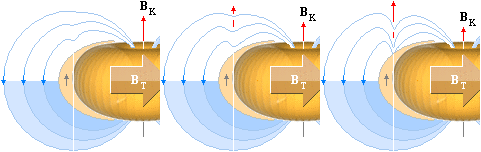
Längst till vänster utgår vi ifrån (i den rena oförvanskade nederdelen, blått) en kärna motsvarande protonformen med en positiv kärnmagnetisk centralfältstyrka B_K. Vi ökar sedan på strömmen i den inre minusspolen, analogt med att den negativa laddningsmassan i kärnan skjuts inåt mitten (se även resultaten från föregående S-form).

När det positiva B_K är helt motverkat och B-fältstyrkan i kärncentrum alltså är lika med noll har vi nått fram till följande skisserade situationsbild:

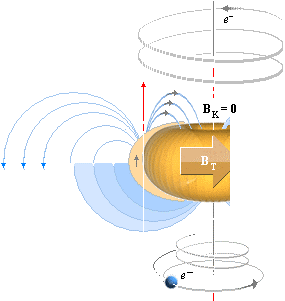
Atomkärnan har får ett kantmagnetiskt dipolfält med en utpräglad magnetpol (röda pilen) i formen av en cylindermantel.

En LITEN negativ laddning som har NÅGON hastighet rätvinkligt rödpilen, dvs., alla elektronmassor som tillhör kärnan i den allmänna matematiska fysken tidigare omnämnd, tvingas av B-cylinderns polstyrka in i en cirkulär moturs rörelse över kärnanoden. De så låsta elektronmassorna bildar i sig en spolström som ger kärncentrum en »artificiell» magnetisk polriktning.

Diamagnetism. OM ETT YTTRE B-FÄLT läggs på över materialet flippar hela atomkärnan på cylinder-B-polen och ställer in sig i det yttre B-fältets riktning eftersom den lokala kärn-B-cylindern är den starkare gentemot det elektronartificiella B-polfältet. Men då har också hela elektronspolen i kärnan flippat och uppvisar nu ett magnetisk motfält mot det yttre B-fältet. Hela atomen motverkar eller försvagar med andra ord det yttre B-fältet. Denna motverkan kallas diamagnetism.

PARA- OCH FERROMAGNETISM. Om kärnan i stället har ett ännu större negativt deplacement så att BK-styrkan i kärncentrum blir negativ blir situationen en annan. Härifrån kommer kärnan att överta det tidigare artificiella negativa B-fältet som ett standardfält i kärncentrum, allt mera ju mera negativ BK-styrkan är.

Paramagnetism. Om det negativa B_K-fältet är starkare än det motvända cylinderfältet kan kärnan harmoniera med ett yttre B-fält och därmed förstärka det med mängden atomkärnor som rättar in sig (mycket höga B-styrkor kan på detta sätt erhållas med lämpliga grundämnesatomer). Atomkärnor med tillräcklig negativ B_K-fältstyrka kan koppla ihop sig över (extremt) långa avstånd, medan svagare negativa B_K-fält inte räcker till för kopplingarna mellan flera atomer. Härifrån är det nu lätt att identifiera de svagare typerna som tillhörande gruppen paramagnetiska.

Ferromagnetism. De starkare kommer alltså att tillhöra gruppen ferromagnetiska.

modern teori

MODERN TEORI

Som redan påpekats (se ovan från Kärnmagnetiska Momentet) är den moderna kärnteorins matematiska fysik inte tillägnad någon fenomenförklaring som berör kärnmagnetismen ENLIGT TNED. Sökning på @INTERNET Google på »-magnetism» visar heller ingenting utöver allmänna materialbeskrivningar. (Det finns i etablerade kretsar ännu 2007/8 ingen direkt uttalad teori som hänför magnetismens orsaker direkt till atomkärnan).

Ett PDF-dokument @INTERNET från år 2000 som belyser (den fortfarande olösta) frågan om ferromagnetismens upphov finns på

[http://dpwww.epfl.ch/cours/ansermet/magweb/itinerant_ferromag.pdf].

centralkontakterna

CENTRALKONTAKTERNA

ATOMENS CENTRALT REGLERANDE DYNAMIK

Allmän beskrivning av resonans och dissonans i atomkärnan

Kort snabbgenomgång

ATOMKÄRNAN FRÅN PLANCKRINGEN se utförligt från Planckringen

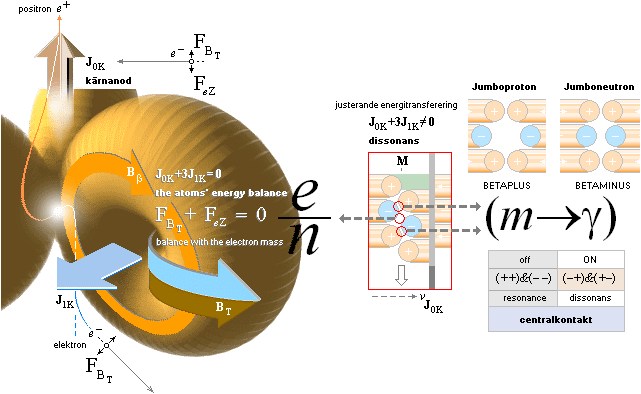
Atomkärnans geofysik framgår ur Planckringen med grund i jämförelser med massans volymära fundamentalform (vattendroppsmodellen som ger den elementära kubgrafens kärnradier r=r₀A^1/3) med motsvarande Planckringens fraktala strukturform (PASTOM) som bildar toroidaggregatet. Formen för N=3 i typformen N3m20 för toroidens formfaktor framgår direkt ur grundvillkoren (lägsta möjliga offset för kärnradierna se även i Atomkärnans dimensioner), vilket också direkt ger atomkärnornas geometri för alla masstal från A=2 och uppåt, proportionerna är desamma. Som den geofysiken grundas helt på laddningsdeplacementet (ringarna i understrukturen uppvisar inbördes förskjutning) framgår atomkärnans allmänna centraldynamik enligt följande framvisade detaljer.

Centralkontakterna

BESKRIVNING

off	ON
(++)&(– –)	(–+)&(+ –)
resonans	dissonans
centralkontakt

Atomkärnans centraldynamik kan återföras på en konventionell ELEKTRONISK SWITCH som styr hela verkningssättet.

Atomkärnans två centralkontakter — läge normal (resonans) och läge ombyggnad (dissonans)

I DEN STRÄNGT GEOMETRISKA MODELL SOM TNED FRAMSTÄLLER FÖR ATOMKÄRNAN framgår följande, speciella, grundkaraktäristik.

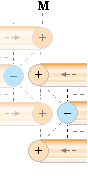
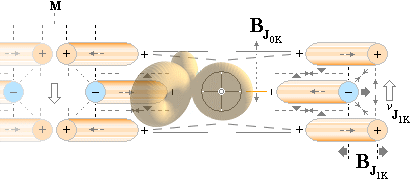
M betecknar mittaxeln i kärncentrum, analog med riktningen för J_0K.

Vi ser att det finns två principiellt olika sätt för de tre inre toppringarna att mötas på i kärncentrum. Men bara den ena av dessa satisfierar nollsumman J_0K+3J_1K=0. Nämligen den med centralkontakten enligt den motvända ordningen (++)&(– –), analogt ekvivalenta tyngdpunktsavstånd för de tre ringarna mot kärncentrum. Denna ordning motsvarar alltså ett stabilt tillstånd hos kärnan (resonans). Den andra delen, vänstra bilddelen, kan av symmetriskäl bara innehas av två ringar åt gången, aldrig alla tre. I vyn ovan, vänster, kan vi se den tredje ringen i bakgrunden med sina under-b-ringar placerade i läge mellan de givna: den kommer aldrig riktigt i samma läge (det skiljer på ett halvt ringavstånd i höjdled). Den tredje toppringen kan alltså i detta läge inte ha samma centrumavstånd som de andra två. Härav följer att centralkontakten (–+)&(+–) tillhör ett instabilt tillstånd: kärnan befinner sig i självsvängning (dissonans).

OM kärnans centralkontakt befinner sig i jobbläget (–+)&(+–)-läget OCH vi enbart vore hänvisade till krafter som verkar i ±-ringarnas plan (horisontellt i figuren), då vore vi rejält illa ute beträffande möjligheten att garantera någon semester för arbetslaget. Hur kommer ringarna tillbaka till viloläget? Det är tydligt att det 1. mellan nära angränsande toppringar måste finnas en motsvarande lyftkraft (vertikalleden) och 2. det inbördes avståndet mellan ±-ringarna i bilden ovan måste vara betydligt mindre. Svaret på frågan ligger i verkan av det yttre markerade BJ0K på de angränsande toppringarna. Vi studerar detta.

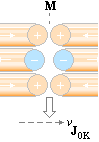
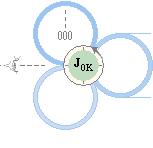
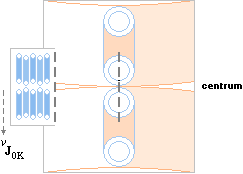
DEN ALLRA STARKASTE MAGNETISKA FÄLTVERKAN för en laddning (Q) som lägesändrar ligger alltid utan undantag rakt fram i lägesändringsriktning (här v_J0K). Det är samma fenomenala magnetiska fältkraft som i en strömlinje av lika laddningar söker inrätta alla på gemensam, rak strömlinje. Ju närmare två angränsande laddningar befinner sig i strömlinjen, desto större blir inrättningskraften rätvinkligt strömloppet. Därmed har vi, direkt, den rent kvalitativa dynamiska förklaringen till varför också centralkontakten

(++)&(– –) är den mest stabila — förutsatt att attraktionen mellan närliggande men i skilda toppringar befintliga ±-ringar inte överväger.

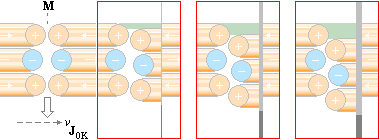
SOM VI RENT TEKNISKT SER AV (–+)&(+–)-läget, gynnar det också — kvalitativt dynamiskt korrekt — kärnans ombyggnad, justering och reglering. Nämligen just beträffande den möjliga kontaktpunkten mellan (±) som ensamt kan realisera arbetsenergin (m®g).

Om vi studerar denna konstellation mera ingående, ser vi att centralkontakten i dissonansläget (–+)&(+–) nödvändigtvis inte behöver ha en exakt ring-mot-ring position som i den föregående mera grova illustrationen. Förutsatt att avståndet mellan ±-ringarna i samma toppring är litet och därmed den möjliga förskjutningen mellan angränsande toppringar marginell räcker det med att endera toppringen är vertikalflyttad en halv b-ringtjocklek. Därmed uppfylls villkoret för arbetsläget som kräver (m®g) via ±-kontakt. När så minusandelen minskar, minskar också den Coulombattraktion som orsakade arbetsläget (minusdeplacementets allmänna centruminskjutning från den yttre B_J0K-verkan). Därmed återtar den lyftande, linjeinrättande vertikalverkande magnetiska fältkraften sitt övertag: centralkontakten (++)&(– –) uppnås och stabilt tillstånd inträder. Det väsentliga i saken är alltså själva närheten mellan de angränsande toppringarna; Den lyftande B-kraften är helt beroende av en sådan närhet eftersom inverkan av magnetismen, själva lyftkraften som bildar centralkontakten (++)&(– –), mellan de angränsande toppringarna via J_0K-spinnet avtar snabbt med avståndet.

DÄRMED KAN VI SE EXAKT var, och i princip HUR atomkärnan ombesörjer ett aktivt betasönderfall — själva stället där elektronmassan till atomens ytterhölje kommer ifrån (eller dras in till):

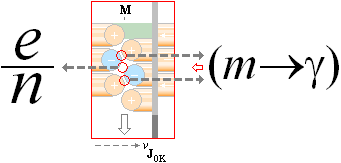
EXAKT HUR proceduren går till kräver en mera omfattande djupdykning i den fraktala ringstrukturens sublima elektromekanik, men den analysen kommer inte att ges här. Principen står emellertid klar.

SOM VI NU HAR SETT av den rent matematiska fysiken i TNED-kärnan bygger hela atomens dynamik, jämvikt och balans på en kontinuerlig (yttre, eller inre) elektromassagenomströmning genom kärnbrunnarna, från motsvarande kärnanoden (riktningen för J0K) till kärnkatoden enligt nollsumman F_BT+F_eZ=0 varav den senare faktorn F_eZ sammanhänger med härledningarna i Spektrum och Kvanttalen. För faktorn F_BT gäller explicit en balans mellan kärnans B_T-fält och elektronelementets B_t.

Positiv och negativ jonisation

F_BT-balansen återspeglas, naturligtvis explicit, på området i centralkontakten:

En för liten B_t-faktor innebär ett underskott, en försvagad totalverkan;

kärnan strävar att få tyngdpunkten längre ut, analogt ett exciterat tillstånd som söker förlägga befintlig elektronmassa längre bort från kärnan, motsvarande positiv jonisering, eller att internt avdela positiva elektronmassor som medför ett betasönderfall.

En för stor B_t-faktor innebär en större totalverkan än kärnresonansen tillåter;

kärnan söker dra in tyngdpunkten genom att koppla bort eller göra sig av med elektronmassa, internt eller yttre.

Kärnan kan på detta sätt avkänna, justera och reglera den totala balansen genom olika svängningstillstånd som innefattar olika energinivåer.

END.

Editor2008V

innehåll: SÖK på denna sida Ctrl+F ·sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Elektronmassans komponenter

ämnesrubriker

innehåll

ELEKTRONMASSANS KOMPONENTER

t-ringen

e-massans ringelement

Elektronen i TNED

Q-geometrin

Spektrum och kvanttalen

Spektrum

Energicirkeln

Resonansvillkoret

Huvudkvanttalet

Kraften på t-ringen

Energiformen

Bohranalogin

Divergensen v

Vätets Spektrum — sambandsformen

Antalet ringar i e

Väteatomens grundradie

Kalkylkort

Termiska energiekvivalenter

Väteatomens jonisationsenergi

Kvanttalen

pt-svepet

Elektriska förskjutningen

Elektronringens spinn

Elektronringens magnetiska moment

Elektronringens toppspinn

Periodiska Systemet

Elektronbindningskriteriet

Nukleära spinnkriteriet

Kollektiva impuls- och magnetiska moment

Spinnbegreppet i modern akademi

BT-fältet

Kärnmagnetiskt moment

Konventionella skrivsätt

Begreppet magnetiskt moment i konventionen · tre olika referenser

Kärnikonerna

Dia-, para- och ferromagnetismen

S-formen

Centralkontakterna

Atomens central reglerande dynamik

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

e₀ = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Plancks allmänna strålningslag 1

Stefan-Boltsmanns strålningslag

Wiens förskjutningslag

Planck-

Genomgående i den här framställningen möter man ”Planck-” med tillägg av olika fysikaliskt associerade fenomendelar.

Grunden för denna egenhet är enkel och beskrivs direkt av impulsmomentet J=mvr med historisk koppling till ganska precis år 1900: Max Planck lyckas genom olika empiriska grepp härleda sin numera berömda Plancks Allmänna Strålningslag. Den kräver en universell konstant (betecknad h och med äldre terminologi kallad det universella verkanskvantumet), senare benämnd Plancks konstant. Det visade sig strax att Plancks konstant bildar grundvalen för hela atom- och kärnfysiken. Närmare bestämt enligt grundformen som definierar neutronen, eller som den kallas här Planckringen enligt h=m_nc₀r_n, men som dock inte omnämns i den etablerade facklitteraturen av här ej känd anledning. När vi därför (här) härleder grunderna som sammanhänger med Plancks konstant (h) är det bekvämt att beteckna de olika sambandsdetaljerna med motsvarande kopplingar till och i Plancks konstant. Därav beteckningen ”Planck-” med tillägg av olika fysikaliskt associerade fenomendelar i denna presentation.

speciella fonter: MT Extra (h-bar)

Senast uppdaterade version: 2023-11-30

*END.

Stavningskontrollerat 2007-11-25 | 2010-05-18 | 2010-09-23 | 2010-10-06.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se