StjärnFysiken2005Pictures | 2008X20 — Universums Historia | Redigering och
sammanställning: BellDHARMA 1984-2008 | Senast
uppdaterade version: 2018-10-10 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Komplement till Stjärnfysiken DELII med dess förminskade bilder här i
original på PNG-JPEG-format — htm-tilläggsdokument till Universums Historia
frn. Sept 2008
GRUNDBEGREPP ENLIGT TNED
Stjärnfysiken DEL
I
.......................... Solfysiken,
basen för stjärnornas allmänna matematiska fysik, se från Solfysiken
Stjärnfysiken
DEL II
......................... rubrik
som nedan, se huvuddokumentets beskrivning i Solfysiken II
BILDBASER OCH DITO REFERENSER TILL HUVUDBESKRIVNINGEN I
STJÄRNORNAS
ALLMÄNNA FÖRDELNING, UTVECKLING, SPRIDNING OCH FÖREKOMST
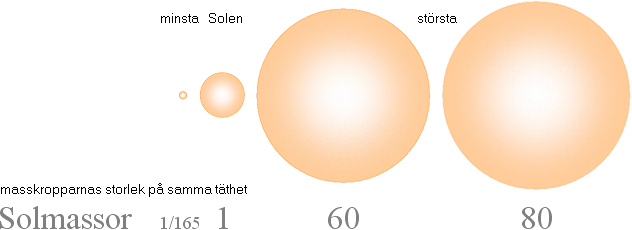
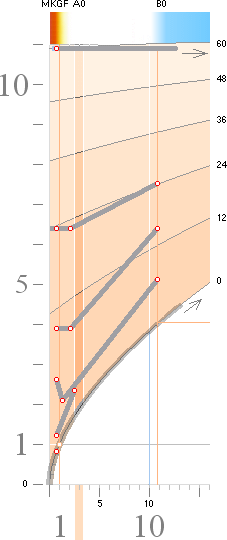
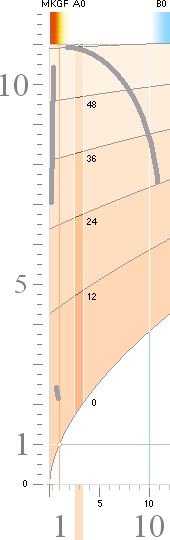
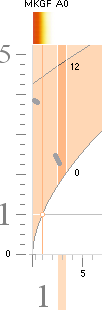
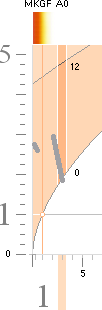
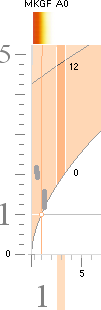
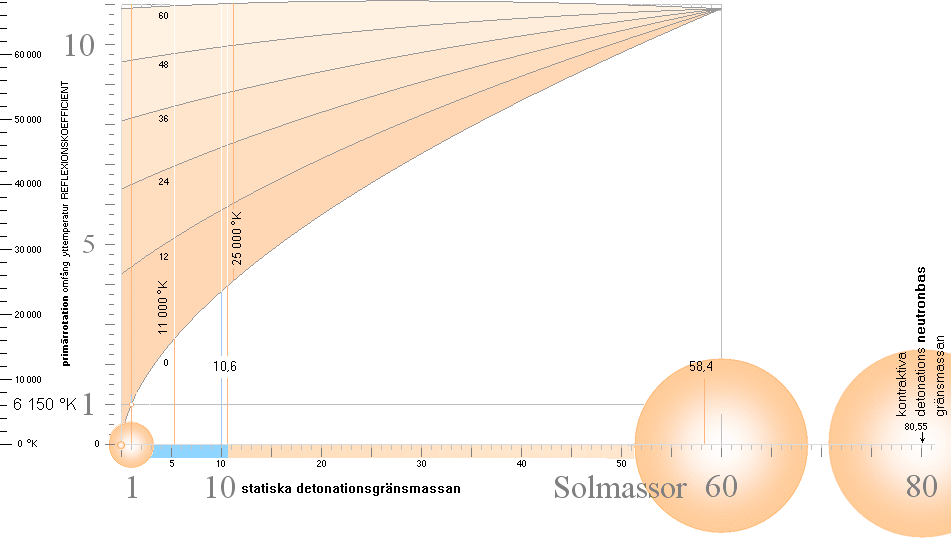
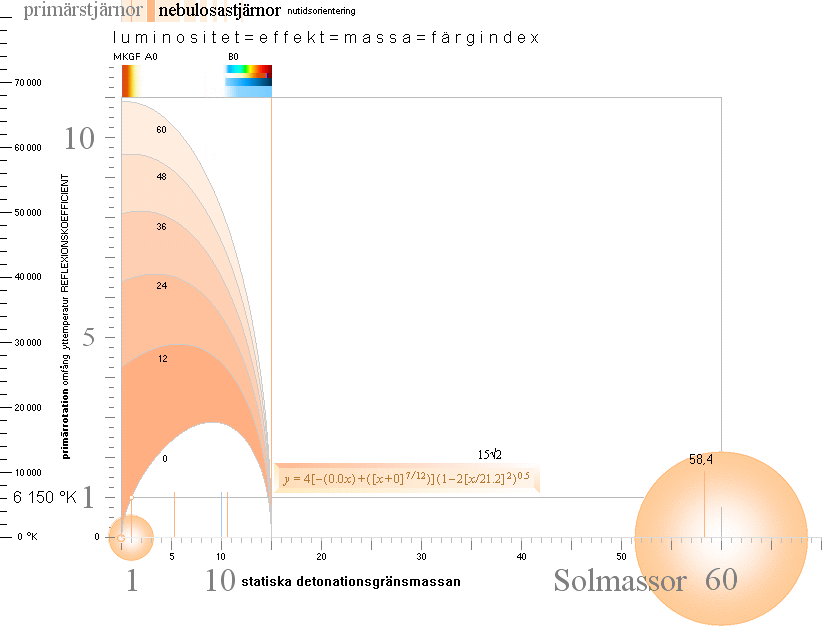
Stjärnfysiken enligt relaterad fysik och matematk (TNED) grundas på en besättning av primärt avdelade J-massor från K-cellens expansion med lägst 1/165 Solmassor (m0SLIM, absolut lägsta stjärngränsmassan) och högst 80 Solmassor (J80-massan). Se utförligt från stjärnornas gränsmassor. Genom massavyttring som sker under J-kroppens expansionsfas efter divergenständning reduceras J80-massan till nätt 60 Solmassor. Alla stjärnor utvecklas och fortbildas sedan på och inom den masstocken. GRÄNSMASSORNA specificeras i TNED enligt nedanstående översikt.
GRÄNSMASSORNA I STJÄRNFYSIKEN ENLIGT TNED insatta i masskala. Se särskild beskrivning för Statiska detonationsgränsmassan.
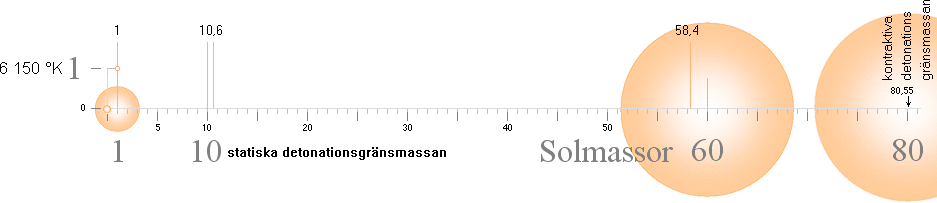
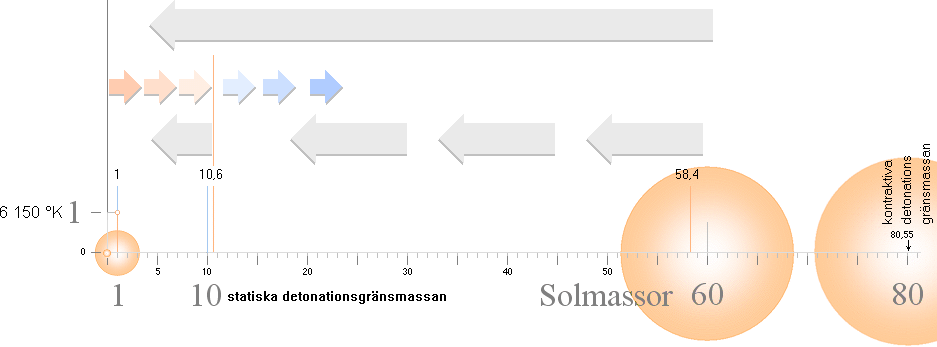
Stjärnmassor <10 Solmassor kan genomgå
flera energicykler med successivt växande massa mot brytpunkten och även
passera denna.
Se vidare från Brytpunkten vid 10 Solmassor.
Se även i stjärnspridningen från normalkurvan.
*funktionen för stjärnornas normalkurva
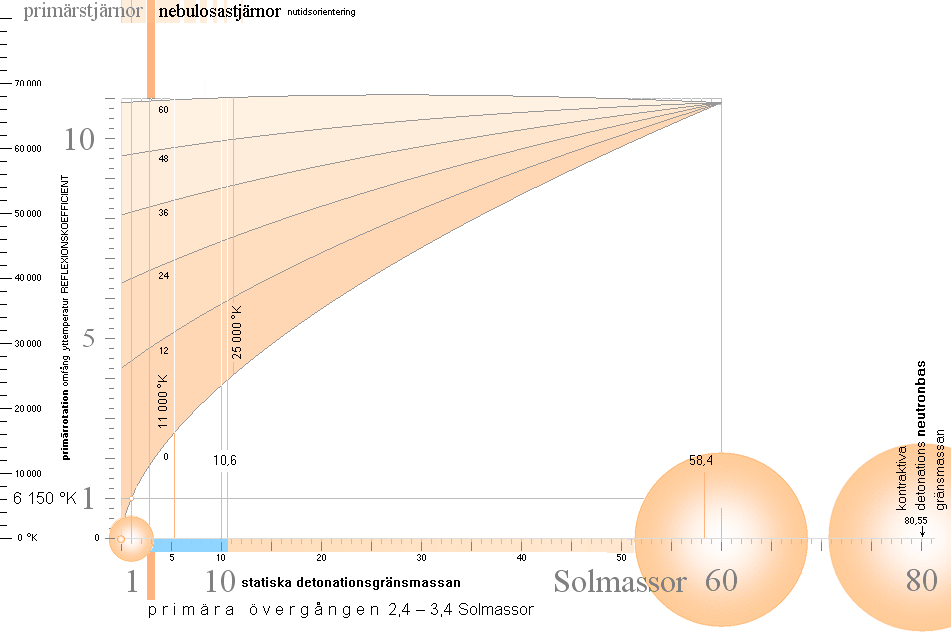
*primära övergången med
färgindex
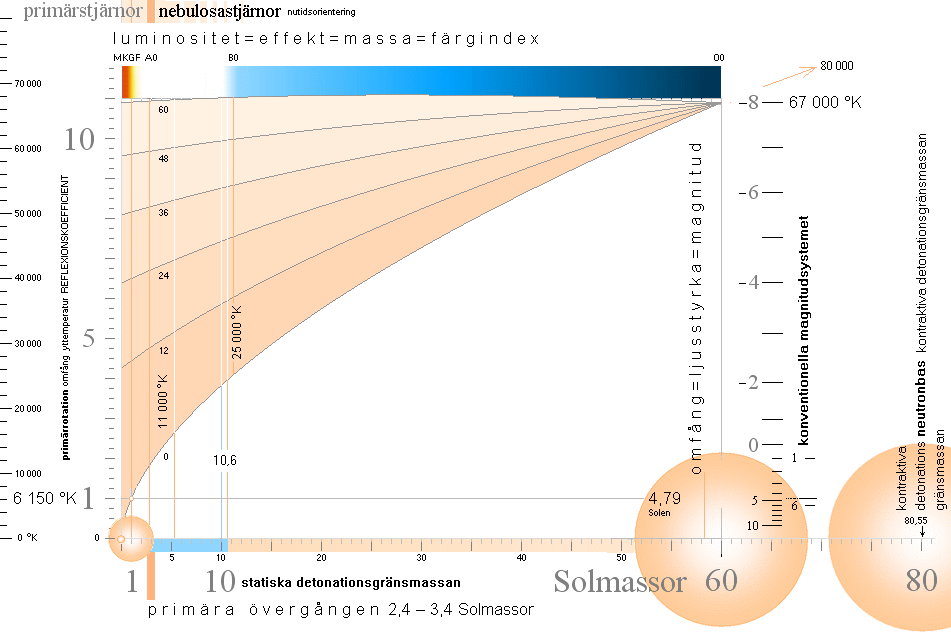
*Stjärnspridningen från normalkurvan
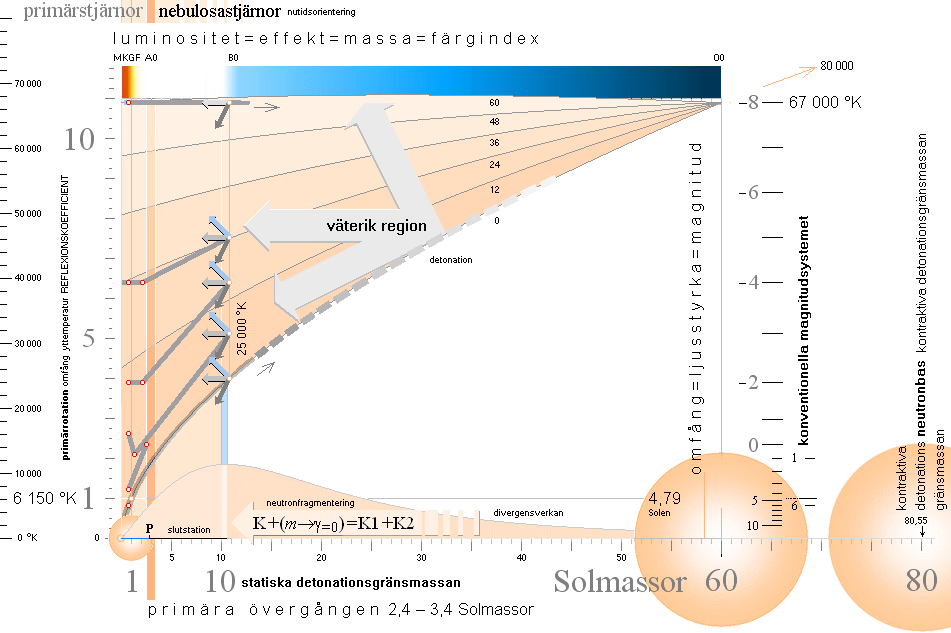
*Stjärnornas
fortbildning — samma bildobjekt
som föregående sida med inlagd illustration till en stjärnas periodiska
energicykler i väterika regioner.
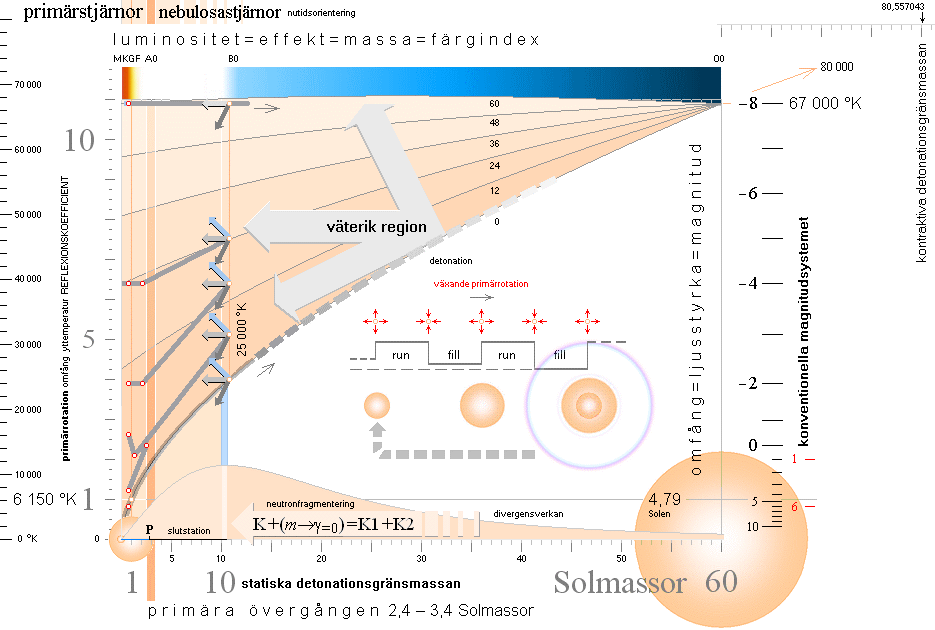
*stjärnornas fördelning i olika stjärnfält
|
[BAs62] [FMs618] |
||||||
|
|
|
|
|
|
|
|
|
spiralgalax |
klotformig stjärnhop |
öppen stjärnhop |
öppen stjärnhop |
öppen stjärnhop |
öppen stjärnhop |
öppen stjärnhop |
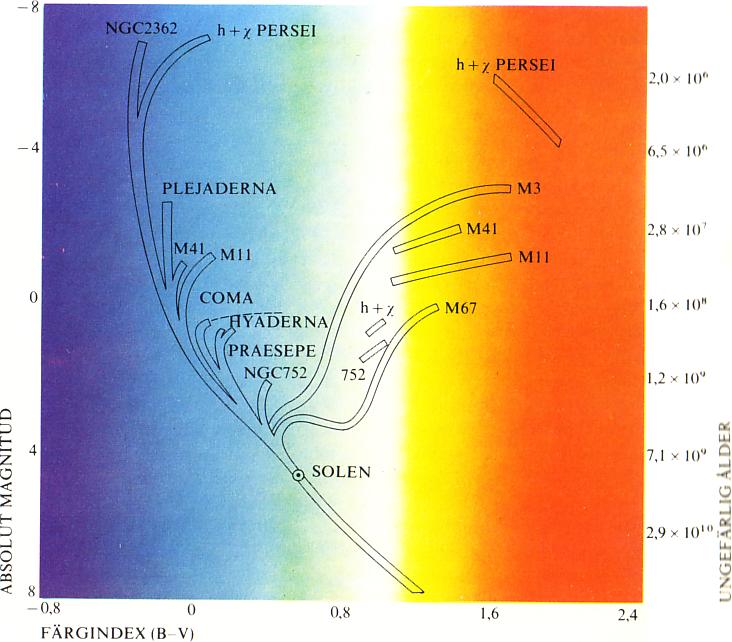
*BONNIERS ASTRONOMI 1978 s54, källreferenser. Observera att basskalorna TNED/HR-diagrammen är vänster-högerställda.
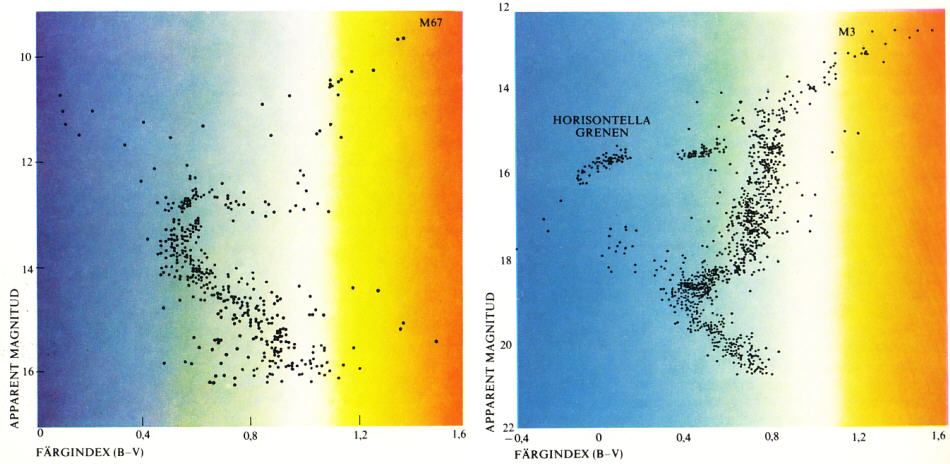
*BONNIERS ASTRONOMI 1978 s62, källreferenser — Observera att basskalorna TNED/HR-diagrammen är vänster-högerställda.
|
|
|
|
|
|
*BONNIERS ASTRONOMI 1978 s62, källreferenser — Observera att basskalorna TNED/HR-diagrammen är vänster-högerställda.
GRUNDDATA FÖR SOLEN
— i orienterande jämförelse med modern akademi
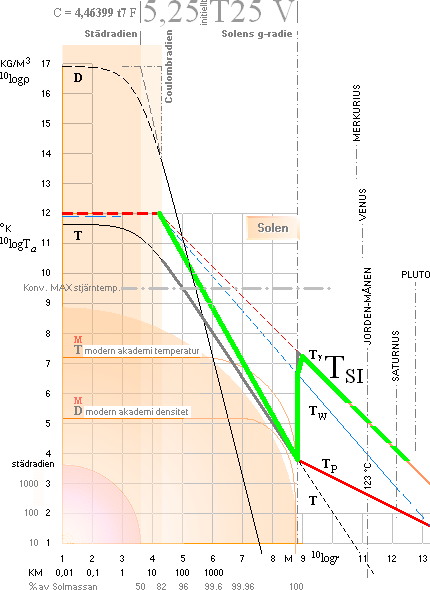
SOLENS INRE: D beskriver Täthetens Radiella Variation, T beskriver Temperaturens Radiella Variation. Motsvarande kurvor i modern akademi (MAC) är betecknade med MD och MT [ref. BONNIERS ASTRONOMI 1978 s128 Fig.8.1-8.2, här omräknade ungefärligt för anpassning till den logaritmiska skalan].
SOLENS YTTRE: Se utförligt från Solens Temperaturfysik (Solens Fyra
plus En Värmegrader).
Se även Solstädet · Värmegraderna ·
Med närmast anknytning: Från kortbeskrivning i Exotermiska Kärnreaktionslagen
——————————————————————————————————————————————————
Den matematiska grundvalen
till UNIVERSUMS HISTORIA —
EXEMPELBESKRIVNINGAR MED KALKYLKORT
TILL
Exotermiska Kärnreaktionslagen
Även EXOTERMISKA fusionslagen | fusionsekvationen
IF mDK2 + (mDK1–mDK)AK1/AK2 < mDK THEN OK .......... exotermiska fusionslagen
MED GRUND I Planckringen h=mcr eller NEUTRONEN från c0-kroppen enligt RELATERAD FYSIK bildas alla andra atomkärnor genom fusion [Se även utförligt från NUKLIDBARRIÄREN] enligt GRUNDÄMNESBILDNINGEN från maximal täthet genom atomkärnans inkompressibilitet efter K-CELLENS DETONATION genom K-cellens värmefysik och efter den matematiska fysik som anvisas av NEUTRONKVADRATEN enligt KÄRNREAKTIONSLAGEN som följer direkt från Allmänna Tillståndslagen. Neutronkvadraten visar hur — till noggrann jämförelse med den redan etablerade uppfattningen — ATOMVIKTERNA framkommer genom atomära massdefekterna. Exotermiska kärnreaktionslagen, ovan (Se särskild härledning nedan), är det rent matematiska instrumentet som grundlägger hela undersökningen: Exotermiska fusionslagen upplyser om exakt vilka föreningar som är EXOTERMISKT möjliga (sådana som ger energi), och förutsatt att inga yttre störande moment finns med i bilden (finns sådana tillkommer ytterligare parametrar). Analys och resultat av dessa detaljer är vad som bär hela ansvaret för fundamenten i UNIVERSUMS HISTORIA.
Varje atoms specifika atomkärna — nuklid — beskrivs detaljerat i TNED enligt
———————————————————————————————
|
ATOMNUMMER |
NAMN |
MASSTAL |
AtomärMASSDEFEKT |
———————————————————————————————
med ATOMNUMMER (Z) som atomens heltaliga elektriska laddning (antalet e, konv. samma som antalet kärnprotoner), NAMN som atomens internationellt kemiska beteckning, MASSTALET (A) som antalet primära neutroner (konv. protoner plus neutroner) som den bildade atomens atomkärna (nukliden) återfaller på i antalet elementära nuklidkvanta, AtomärMASSDEFEKT är skillnaden i massenergi mellan aktuell atom och dess primära neutronindivider som bildat just den atomen. Masstalet A i relaterad fysik är alltså samma som antalet bildningsneutroner (I modern akademi betraktas atomkärnan som en reell behållare för en summa av verkliga neutroner [n] och deras sönderfallsmakar protoner [p] medan atomkärnan enligt TNED i PASTOM helt saknar beståndsdelar; np-formalian används emellertid också av TNED i beskrivningen av KÄRNSTRUKTUREN men då mera exakt med referens till skillnaden mellan neutron och proton i kärnytan, se utförligt från LADDNINGSDEPLACEMENTET). Se utförligt från NEUTRONEN och NEUTRONKVADRATEN. Neutronen föreligger given från c0-kroppen enligt energiräkningen och energilagen från ALLMÄNNA TILLSTÅNDSLAGEN i TNED.
kalkylkortet nedan
DIREKT FRÅN DEN HÄR WEBBLÄSAREN Exoterm.ods — se
öppningsmanual
om ej redan bekant — eller kopiera
URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att
SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på
datorn)
http://www.universumshistoria.se/AaKort/Exoterm.ods
Kalkylkortet ovan i delbild från gratisprogrammet OpenOffice
SVENSKA VERSIONEN.
Tillämpningsexempel
visas efter
härledningen nedan.
Kopplar till (huvud-)
beskrivningar i
Nuklidbildningarna.htm | Exotermiska Kärnreaktionslagen —
Se även efterföljande UTFÖRLIGA EXEMPEL i manualen
Härledningen till exotermiska fusionslagen
2010IV18
Härledningen till EXOTERMISKA KÄRNREAKTIONSLAGEN — med kalkylkort i OpenOffice
OM föreningen (fusionen) mellan två atomkärnor (nuklider) GER ENERGI kallas fusionen (med lån från kemins reaktionsbeteckningar) EXOTERMISK. Kräver föreningen istället (mer) energi (än den ger ut) kallas processen ENDOTERMISK. Från sambanden för atomvikt och atomär massdefekt kan vi alltså skriva den typiska exotermiska fusionen mellan två komponenter (K1 och K2 som ger K) enligt
(1) exo = (UK1 + UK2 – UK)uc2
....................................................... i Joule
;
(2) exo/uc2 =
(UK1 + UK2 – UK) = EXO
;
Med atomära massdefekten (mD) i atomvikten (U) för nukliden med masstalet A
bortfaller först
neutronmassan (mn) eftersom den ingår i alla tre termerna:
EXO/mn = UK1 + UK2 – UK
(4) = AK1(1–mDK1me) + AK2(1–mDK2me) – AK(1–mDKme)
Räknat i
elektronenheter (1=me) ges ytterligare en förenkling enligt
EXO(e)/mn = AK1(1–mDK1) + AK2(1–mDK2) – AK(1–mDK) = X;
X = AK1–AK1mDK1 + AK2–AK2mDK2 – AK+AKmDK
(5) =
AK1 + AK2 – AK –
AK1mDK1 – AK2mDK2 + AKmDK
Eftersom
summan av masstalen (A) i vilket fall är (i denna del, ska vara)
noll gäller i samtliga fall att
(X) = 0 – AK1mDK1 – AK2mDK2 + AKmDK
(6) = AKmDK – (AK1mDK1 + AK2mDK2)
Vilket också kan skrivas med omvända termer om också summan är noll enligt
0 = (AK1mDK1 + AK2mDK2) – AKmDK
0 = (mDK1AK1 + mDK2AK2) – mDKAK
Dvs., som ovan; OM exo
i
exo
= mDK1AK1 + mDK2AK2 – mDK(AK)
................................ i
e-massor
(7) = mDK1AK1 + mDK2AK2 – mDK(AK1 + AK2)
= mDK1AK1 + mDK2AK2 – mDKAK1 + mDKAK2
= mDK1AK1 – mDKAK1 + mDK2AK2 + mDKAK2
(8) = AK1(mDK1 – mDK) + AK2(mDK2 + mDK)
är större än (eller
som ett extremt gränsfall, exakt lika med) noll gäller fusionen
FRÅN KÄRNREAKTIONSLAGEN
(K1+K2) – (m®g) = K
som en entydigt
given EXOTERMISK KÄRNREAKTION Se från Allmänna Tillståndets Ekvation —
alltså en förening av atomnuklider som entydigt ger energi. Termen ENDOTERMISK betyder i
motsvarande mening en process som KRÄVER energi ([inom kemin] för att
alls bli av).
För att avgöra genom prövning via
nuklidernas atomära massdefekter och
masstal behöver vi således endast kontrollera ekvivalensvillkoret
–
AK2(mDK2 + mDK) = AK1(mDK1 – mDK)
– mDK2 – mDK =
AK1(mDK1 – mDK)/AK2
–
mDK =
mDK2 + AK1(mDK1 – mDK)/AK2
(9) =
mDK2 + (mDK1 – mDK)AK1/AK2 ;
;
ÄR produktens
atomära massdefekt (mDK)
mindre än (eller lika med) högerledets summa av massdefekter och masstal
gäller tydligen villkorliga exotermiska fusionslagen enligt
(10) IF mDK2 + (mDK1–mDK)AK1/AK2 < mDK THEN
OK ............. exotermiska fusionslagen
Vi kan med denna
sambandsform nu pröva HURUVIDA alla möjliga fusioner också verkligen KAN
realiseras exotermisk på KÄRNREAKTIONSLAGENS MOMENTFRIA
VILLKOR med hjälp av
tabellvärden för nuklidernas masstal (A) och (OBS) atomära massdefekter (mD) —
företrädesvis med hjälp av ett KALKYLKORT (OpenOffice för gratis allmän
tillgänglighet).
MANUAL
MANUAL TILL EXOTERMISKA
KÄRNREAKTIONSLAGENS KALKYLKORT
KALKYLKORTET TILL EXOTERMISKA KÄRNREAKTIONSLAGEN ANVÄNDS exemplifierat SÅ HÄR:
Exempel:
Nukliderna K1 och K2 respektive med
———————————————————————————————
|
ATOMNUMMER |
NAMN |
MASSTAL |
AtomärMASSDEFEKT |
———————————————————————————————
ska prövas för exotermisk fusion med produkten K — enligt (lämpligast) uppställningen/redovisningen i typexempel
K1 + K2 =
K resultat
2He69,969 + 6C1614 = 8O2215 OK 23,8 MeV
Beskrivning:
EXOTERMISKA KÄRNREAKTIONSLAGEN utan — som här — direkt koppling till en ATOMVIKTSTABELL kräver en separat uppställning typ ovan för varje fusionsled som ska prövas;
GENOM EN SEPARAT ATOMVIKTSTABELL VID SIDAN AV ställs nukliderna först upp genom atomnummerNAMNmasstal enligt
K1 + K2 =
K resultat
2He6 + 6C16 = 8O22
Atomära massdefekten fylls sedan i separat för varje nuklid enligt typexemplet i fortsättning från ovan (hyfsad precision ges med förenklade värden i tre decimaler),
K1 + K2 =
K resultat
2He69,969 + 6C1614 = 8O2215
Med detta led som grund fylls kalkylbladets inmatningsrutor i manuellt med data för masstal (A, antalet ekvivalenta primärneutroner; konv. atomkärnans summa antal protoner och neutroner) och atomär massdefekt (mD) enligt de nedan markerade delarna,
K1 + K2 =
K resultat
2He69,969 + 6C1614 = 8O2215 OK 23,8 MeV
Masstalet för K räknas ut
automatiskt genom inmatningarna för K1 och K2

Är fusionen EXOTERMISKt möjlig visas OK i resultatrutan (annars ’notOK’). Den exotermiska resultatenergin visas i antal elektronmassor och dels i MeV (MegaelektronVolt).
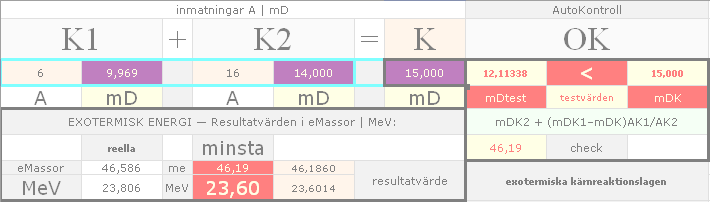
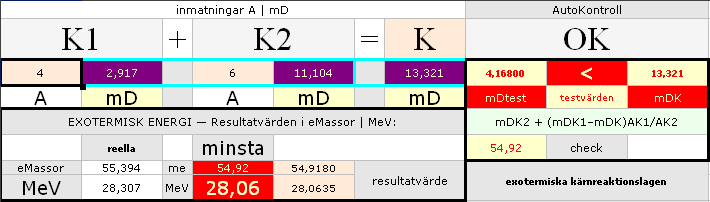
Ovanstående helt manuella inmatningsprocedur har använts genomgående i UNIVERSUMS HISTORIA vid prövning, analys och utveckling av alla angivna fusioner i alla htm-dokument.
Man kan ta med flera (i
princip hur många som helst) K1 genom att ange masstalet i dess
heltalsmultipel:
SAMMANSATTA EXEMPEL (Från Nuklidbildningarna.htm — udda nuklidgruppen, från första ledet):
K1 + K2 = K resultat me realt avgiven fusionsenergi per i MeV
21H22,917 + 1H22,917 =
3Li611,104 OK 49,548 25,319
Skärmdump av resultatet i kalkylkortet:

Masstalet för K1 med 2K1 blir dubbla
det normala — massdefekten är samma
;
K1 + K2 = K resultat me realt avgiven fusionsenergi per i MeV
21H22,917 + 3Li611,104 =
5B1013,321 OK 55,394 28,307
Skärmdump av resultatet i kalkylkortet:

Masstalet för K1 med 2K1 blir dubbla
det normala — massdefekten är samma
; …
Förklaring till resultatcellerna:
————————————————————————————————————————
eMassor reella = (U1 + U2 – U)/me
MeV reella = (U1 + U2 – U)(uc02/e)/(T6)
eMassor minsta från (6) [originalet från MsWorks 4.0]:
(6) (X) = mDKAK – mDK1AK1 – mDK2AK2
= mDK[AK2 + AK1] – mDK2AK2 – mDK1AK1
= AK2(mDK[AK2 + AK1] – mDK2AK2 – mDK1AK1)/AK2
= AK2(mDK[1 + AK1/AK2] – mDK2 – mDK1AK1/AK2)
eMassor minsta = AK2(mDK[1 + AK1/AK2] – mDK2 – mDK1AK1/AK2)
Se även tillämpningsexempel på UTANFÖRNUKLIDERNA — nuklider som (ännu) inte finns med i tabellerna, hur man ändå (med viss försiktighet) kan räkna med dem med kalkylkortets hjälp.
Se även de vidare, mera omfattande, resultatredovisningarna för grundämnesbildningarna generellt i FUSIONSBILDNINGEN GENOM EXEMPEL.
Nedanstående artikeldel SKULLE ha funnits med från början (2007) som inledande introduktion till Solfysiken — hur Solen fungerar som energimaskin. Men i takt med de allt mer fördjupade htm-författningarna — med främsta föresats att beskriva huvudgrenarna i ämnets övergripande matematiska fysik — »kom den bort». Här kommer den nu.
Editor2010VI18
HUVUDILLUSTRATIONEN TILL SOLENS ENERGIPRODUKTION
Artikelinnehållet kopplar till motsvarande (delvis mera utförliga) beskrivningar i
Konstantströmmen och SOLENS KAPACITANS
—————————————————————————————————
|
|
Stjärnfysiken
Del 1 — energiproduktionen i Solen KONSTANTSTRÖMMEN · VäteIN och HeliumUT — konstantströmmen Illustrationen nedan visar Solens energiproduktion i förenklad översiktlig sammanfattning. Läs illustrationen nedan från
höger till vänster: MAC: I DEN TRADITIONELLA KOSMOLOGIN utgår man ifrån att Solens energiproduktion genom H-H-fusionerna bildar en växande inre Heliumkärna med en termonukleärt aktiv väterand som drivs mot Solytan [‡1] (På grund av dess begränsade intervall kan inte hela vätebanken utnyttjas utan Solens livstid blir förhållandevis kort). Läs illustrationen nedan från höger till vänster. Beroende på initiell massa (och olika faser), kommer solkroppen in i en andra, hetare termonukleär fas där Heliumkärnan i sin tur kan bilda tyngre grundämnen (Kol, med vidare uppåt). Vid ett visst kritiskt skede säger man att den förtätade inre Heliumkärnan »kollapsar under sin egen tyngd» [‡2]. Man säger att solkroppen slutar med att den inre kärnan imploderar och höljet exploderar ([super]novautbrott).
Läs
illustrationen ovan från vänster till höger: TNED: I RELATERAD FYSIK är preferenserna helt omvända. Läs illustrationen ovan från vänster till höger. H-H-fusionerna sker i den inre hetaste delen (osynlig i denna skala). Vartefter Heliumprodukterna bildas från 41H1 till 12He4 ökar samtidigt den effektiva Coulombprodukten (cp=Z², Z anger atomens elektriska laddning, samma som atomnumret) mellan två närliggande kärnor från 1 till 4. Två He förenas inte, inte heller He och H (och inte heller He-neutron). Därmed söker sig de potentiellt överpositiva He-kärnorna till områden med lägre potential, vilket betyder att de (sakta) dras ut mot Solytan. Därmed kan motsvarande mängd friskt Väte strömma in till den heta värmecentralen. Funktionen garanterar att Solen »brinner stadigt in till sista vätedroppen». Se utförligt i Konstantströmmen och SOLENS KAPACITANS. Blandningen H-He i Solytan, tillsammans med luminositetsvärdet (i stort sett konstant under Solens hela livstid), indikerar Solåldern. Stjärnor som befinner sig i väterika regioner kan »nytanka» och bilda en andra (och n:te) generationens stjärnor. Utförligt från Stjärnornas Histogram i STJÄRNFYSIKEN Del II. Solens allmänna energiproduktion i TNED — från 100% Väte till 100% Helium Ordningen med den nyligen omnämnda konstantströmmen innebär med hela Solklotet som förenklad illustration att en optimal bränslezon med Väte drar sig krympande in mot reaktionscentrum (ej utritat) och ersätts av bildat Helium. Utanför bränslezonen bildas i motsvarande (ekvivalent mening) en blandzon av fusionsprodukter. I konventionell kosmologi läser man ovanstående från höger till vänster: reaktionscentrum flyttas hela tiden utåt på en inre växande Heliumsfär — med maxtätheten 1,5 T5 KG/M³ [‡3]. Det är 5,42 T11 gånger mindre än i TNED: Det finns inga jämförande paralleller. Blandzonen uppvisar successivt tyngre bildade grundämnen utåt, vilket är en ren konsekvens av inverkan från kärninduktiva strålningstrycket. Blandzonens uttunnade sammansättning i stjärnklotets yttre delar (se nedan) avspeglar (exakt) hur långt processen hunnit. |
|
|
|
|
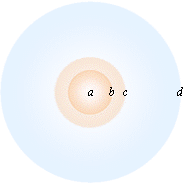
Stjärnans olika delar enligt TNED |
Andelen Helium-4 trycks ut utanför den effektiva Väte-1-bränslesfären (b) från städet (som i denna skala bara är en osynlig prick i a) i kraft av strålningstrycket, samt i motsvarande mening nedåt innanför städytan (vi frånser här delvis denna del i beskrivningen). Utanför Helium-sfären (c) vidtar huvudklotet (c–d) där gasen i huvudsak är ytterst tunn och som avspeglar blandningen mellan de (bägge) inre kärnornas sammansättning (Väte-Helium), allt eftersom tiden går. Den yttre ”storsfären” (c–d) med sin låga täthet måste finnas för att få fram den teoretiska basen som ”spegel” för den inre blandningens sammansättning. Annars går det inte. Den framgår också explicit ur sambandet för täthetens radiella variation [ρ=r–4(ρ0R4)]; Huvuddelen av Solens massa ligger väldigt långt in, sammanpressad mot centrum i en relativt liten kompakt (flerlagrad) sfär, se Stjärnstädet. Storsfärens yttersta del (d) består till stor del av fria elektroner och negativa joner i balans mot den inre starkt positivt joniserade delen. Mellandelen c–d kan innehålla en blandning av neutrala atomer och joniserade dito, allt beroende på lokala strömningar. Den stora elektrontätheten vid g-sfärens gräns (d) garanterar stjärnklotets avgränsande kontur (Se Opaciteten). |
|
|
|
Vid stjärnans första dag är innehållet i c–d 100% Väte-1. När stjärnan brunnit ut måste samma område tvunget ha 100% Helium-4. Allt annat är uteslutet om vi betraktar fritt rörliga partiklar inom hela d-sfären. Den enkla linjära funktionen beskriver då stjärnans brinntid i spegel av sammansättningen i området c–d. Består c–d i avrundade värden av — som i Solens fall härrör från spektrala observationer av Solytan — 25% Helium och 75% Väte är det tydligt att komponenten brunnit i 1/4 av sin totala livstid. Det finns ingenting att välja på. På samma stråltryckande grund måste sedan, konsekvent, varje tyngre bildad nuklid parkera sig i lager ovanpå Heliesfären (c), med vidare uppåt samt med tillbörlig del i storsfären. Den negativa klotytan med sitt överskott av elektroner — så länge strålningstrycket garanterar en positivt joniserad centralkärna — rekombinerar lättast och snabbast med den lättaste atomkärnan, alltså Väte-1. Tyngre nuklider placeras i prioritet djupare ner i sträng analogi med täthetens växande in mot centrum — i samtidig konkurrens med strålningstrycket som i rakt motsatt riktning verkar kraftigare på nukliderna ju större deras kärnladdning är, samt i förhållande till hur mycket strålningstrycket förmår jonisera en tyngre atom då den drivs ut från centrum. Vi bör därför under alla omständigheter finna en maximal medelvärdesbildning av grundämnesförekomsterna i klotets huvudvolym (c–d). Knappast i något annat område finns förutsättningen för en neutral blandning mellan ytterligheterna. Ovanför-utanför klotet gäller delvis andra förutsättningar. Konstantströmmen (I=Q/T) betyder att stjärnan brinner med konstant energiproduktion och konstant effektförbrukning (samma som luminositet) under hela sin livstid — i princip in till sista väteatomen. Se även i Konstantströmmen och Solens Kapacitans. Se även mera utförligt från Solens energiproduktion. |
|
|
———————————————————————————————
SÄRSKILDA citatREFERENSER TILL den ovanstående HUVUDTEXTEN
[‡]1: Den
växande Heliumkärnan
”Med tiden börjar kärnbränslet i stjärnans centrum därför ta slut och alltmer ersättas av helium.”,
”När bränslemängden minskar kan uteffekten av kärnenergi bara hållas uppe genom att kärnan drar sig samman, vilket leder till att temperaturen ökar. Av ännu ej helt klarlagda orsaker, som hänger samman med fördelningen av den totala gravitationella lägesenergin hos stjärnan, åtföljs denna kärnkontraktion av att det yttre höljet sväller.”,
”Huvudseriefasen i stjärnans utveckling karaktäriseras sålunda av tömning av kärnans väteförråd och en långsam expansion hos ytskikten, allt i den nukleära tidsskalan.”,
”Härvid sker en smärre ökning av energiproduktionen, och de yttre lagren svalnar något …”,
BONNIERS ASTRONOMI 1978 s61sp1mö
;
”Orsaken till att en stjärna expanderar till en röd jätte är att kärnprocesserna, där väte förvandlas till helium, flyttar ut från centrum av stjärnan till ett något längre ut beläget skikt.”,
”Samtidigt ökar då hettan i centrum och blir så stor att även helium kan förbrännas till tyngre ämnen, huvudsakligen syre, kol och neon.”,
”Resultatet blir att stjärnan producerar avsevärt mer energi än tidigare, och för att jämvikten mellan utstrålning och energiproduktion skall kunna upprätthållas måste stjärnans yttre delar expandera kraftigt.”,
FOCUS MATERIEN 1975 s622sp2m
[‡]2: Kollapsen
”Efter många olika fusionsstadier blir kärnan till slut instabil och
imploderar, varefter stjärnans yttre lager exploderar.”,
BONNIERS ASTRONOMI 1978 s65sp1mö
;
”Massiva stjärnor kan under sin utveckling nå centrumtemperaturer på
över 1 000 miljoner grader. I detta extrema tillstånd drivs kärnreaktionerna
mycket snabbt och en rad ovanliga fysikaliska processer kommer tillstånd.”,
”Stjärnan går in i en katastrofartad instabilitet där en stor del av
den kastas ut i form av ett supernovautbrott. De centrala delarna kollapsar.”,
FOCUS MATERIEN 1975 s622sp2m
[‡]3: Solkärnans täthet i modern akademi
”Beräkningar har visat att densiteten i solen varierar från 1,5×105 kg/m3 i centrum till 10–4 kg/m3 vid ytan.”,
BONNIERS ASTRONOMI 1978 s128sp1.Figur 8.2
END.
innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
innehållsförteckningen (fram till nedan) ansluter till bilderna i detta
dokument (komplement till Stjärnfysiken Del 2) — länkkällan till bilderna ges
löpande i den beskrivande huvudtexten, se från Stjärnfysiken
DEL II.
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]
me = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]
u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],
CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens elektriska laddning [ref. FOCUS MATERIEN 1975 s666]
TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska
Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som
följer av härledningarna i Planckringen h=mnc0rn,
analogt Atomkärnans
Härledning. Beskrivningen enligt TNED är relaterad,
vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt
logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås
(således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans
Härledning.
Senast uppdaterade version: 2018-10-10
*END.
Stavningskontrollerat 2008-10-23 | 2010-04-19 | 2010-06-18.
rester
*
åter till portalsidan · portalsidan
är www.UniversumsHistoria.se
PNG-justerad 2011-10-10
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se