TERMOFYSIKENS MATEMATIK 2007XI24 a BellDHARMA production | Senast uppdaterade version: 2021-07-19 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Plancks strålningslag · Stefan-Boltzmanns strålningslag · Wiens förskjutningslag · Konstanten i Stefan-Boltzmanns strålningslag

Efter sammanställningar från Fysikens 7 Principer 2002

Med fortsättning från Allmänna Gaslagen · Planckringen

Från grundbegrepp i Allmänna Gaslagen

STEFAN-BOLTZMANNS STRÅLNINGSLAG

Stefan-Boltzmanns strålningslag är given som om effekt P (=E/t, aktivitet eller energi per tid) alstras i en yta (A):

P®T; dP/dT=d(E/t)/dT=k₁T; dT_x=dT_y=dT_z ; effekt bildar temperatur ; temperatur=rörelseenergi gäller linjärt i alla xyz ;

ò dP_xyz= òòò k₁T · 1dT_x · 2dT_y · 3dT_z = P = k₂T⁴ = AkT⁴ ; a=1 ; Med absorptionskoefficienten a=(0®1) ges

P = aAkT⁴ ............................... Stefan-Boltzmanns strålningslag, A anger strålytan, W

Koefficienterna 1·2·3 är av samma typ som också förekommer i momentekvationen (Fd=E) i allmänna gaslagen

Absorptionskoefficienten a räknas från 0 till 1. Värmegraden T räknas från den s.k. absoluta nollpunkten i grader Kelvin (°K). Konstanten k anges

5,7 t8 WM^–2°K^–4 från experimentella mätningar.

Sambandet P = aAkT⁴ förutsätter att rummet/rymden utanför strålytan (A) är absolut rörelselöst tomrum motsvarande

T_YTTRE=0°K. Är så inte fallet, eller om temperaturen (T_YTTRE) ligger nära T måste Stefan-Boltzmanns strålningslag kompletteras enligt den mera fullständiga formen

P = aAk(T⁴ – T_YTTRE⁴)

EXEMPEL 1 [GYMNASIETS FYSIK åk3 Liber 1980 s113]

En wolframglödtråd till en vanlig glödlampa är ca 12 cM lång. Trådens diameter är ca 0,4 mM. Vid ett försök i ett rum med normal rumstemperatur (20°C) sändes elektrisk ström (P=UI) genom wolframtråden varvid den upphettades till runt 2500 °C eller i grader Kelvin

T=2500+273,15 » 2773°K. Wolfram är en s.k. gråstrålare med a=0,45. Uppgift: Beräkna effekten P i experimentet med hjälp av Stefan-Boltzmanns strålningslag från angivna data utan hänsyn till T_YTTRE. Lösning: Vi använder MKSA-enheter:

P=aAkT⁴=(0,45)(0,0004p · 0,12)(5,7 t8)(2773)⁴=228,7062 » 229 W.

Svar: Effekten i Watt blir avrundat 229 W.

HÄRLEDNINGEN ovan (P®T …) utgår (helt enkelt) ifrån förutsättningen att temperatur (T) bildas ur effekt (P): omvändningen gäller inte; T är massgrundad, inte materiegrundad, se vidare i Strålningstryckets Termonukleära Ekvivalent. Med

E=Pt som ger P=E/t=kT kan vi därmed bilda varianten med differentialer enligt

dP/dT=d(E/t)/dT=k₁T. Denna funktion är helt linjär, endimensionell. För att få den i 3D-rummets xyz använder vi samma temperaturdifferential dT för alla tre dimensionerna. Efter integration ges så Stefan-Boltzmanns strålningslag som ovan på den enkla formen

P=AkT⁴ med k som en proportionalitetskonstant.

k kan lösas ur Plancks strålningslag som dock först måste utvecklas ur Stefan-Boltzmanns strålningslag. Se vidare i

KONSTANTEN i Stefan-Boltzmanns strålningslag

— den saknar ännu en fullständig beskrivning i MAC

Stefan-Boltzmanns strålningslag (P®T) RELATERAD FYSIK

P = aAkT⁴

k = 5,7 t8 WM^–2°K^–4 ............. experimentellt [GFåk3LIB1980s112m]

= 2p b⁴p⁴/15h³c₀² ................ teoretiskt, från Plancks strålningslag (b, Boltzmanns konstant 1,3805502 t23 J/°K)

= 5,66893154148517 t8 WM^–2°K^–4

I Stefan-Boltzmanns strålningslag P=aAkT⁴ är utgångspunkten att effekt (P) ger temperatur (T) eller rörelseenergin. Man kan därmed postulera (P®T, ”P ger T”, eller P är generatris till T”):

mot varje temperatur T svarar en viss effekt P

Formgrunden för Stefan-Boltzmanns strålningslag är emellertid materiebaserad: P®T. Vilket betyder att den ges av materiella element eller atomer. Den som kan förklara värmegrunderna (…® P…) måste emellertid vara massbaserad, vilket betyder att den måste innefatta massans struktur eller atomkärnan (se från Planckringen) med neutrinospektrum med alla våglängder medräknade: m®^gp®P®T. Se Strålningstryckets Funktion. Denna detalj har aldrig klarlagts i den moderna akademins lärosystem — där man istället följdriktigt (friskt) sammanblandar flödesformerna typ T®P, vilket ger kaos. Det är bara en utpräglad masstruktur med Planckstrålningens samtliga våglängder medräknade (se Plancks strålningslag) som kan förklara generatrisen till begreppet effekt, och den grunden kan bara härledas, som det har visat sig, genom Planckringen, analogt atomkärnan med Plancks konstant som en strukturkonstant. Och som vi vet, finns inte den med i modern akademi.

Plancks strålningslag

inledning

En separat, komplementär härledning till Plancks strålningslag finns också i Plancks strålningslag från Plancks Entropisamband. Ett avsnitt som länkar de bägge härledningarna finns i Plancks Strålningslag. Nedan följer härledningen via Stefan-Boltzmanns strålningslag och grafläran.

Om det inte vore för GRAFLÄRAN — kunskapen om variationerna genom observationer av xy-funktionernas kurvfigurer — skulle vi (förmodligen) få det ytterst besvärligt med att härleda Plancks strålningslag. Denna för atomfysiken avgörande sambandsform har i gängse kvarter strängt sagt ingen direkt begriplig härledning alls (se vidare citat i slutet av den här artikeln). Nedanstående härledning beskriver detaljerna.

Från Stefan-Boltzmanns strålningslag

PLANCKS STRÅLNINGSLAG

N_l = l^–5hc²[e^hc/blT–1]^–1

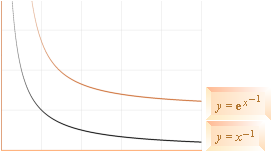
I GRAFLÄRAN FINNS BARA TVÅ kurvtyper att välja på: DELS den där funktionsvärdet (y) dels går mot oändligt då variabelvärdet (x) går mot noll, och DELS den där y går mot noll då x går mot oändligt. Den ena beskrivs av typen exponentialfunktion (xⁿ, variabeln i basen) och ges av funktionen y=x^–n. Den andra beskrivs av typen inverterad exponentfunktion (e^n/x, variabeln [inverterad] i exponenten) och ges av funktionen y=e^n/x. De bägge typerna visas ovan i respektive grafiska illustrationer med n=1. Typgraferna ovan är avgörande i den annars nära omöjligt begripliga härledningen av Plancks strålningslag. (Fackböckerna håller sig i allmänhet borta ifrån varje närmande).

I Stefan-Boltzmanns strålningslag P=aAkT⁴ är utgångspunkten att effekt (P) ger temperatur (T) eller rörelseenergin. Vi kan då postulera (P®T, ”P ger T”, eller P är generatris till T”):

mot varje temperatur (rörelsetillstånd) T svarar en viss effekt (aktivitet) P

Om vi utnyttjar frekvensenergin E=hf (samma som Planckenergin) kan vi också postulera — vidare — (lf=c):

mot varje temperatur T svarar en viss effekt P med en viss våglängd l;

P=E/t = hf/t = hf ² = hc²l^–2 = aAkT⁴

Vi ser att P och T växer obegränsat med avtagande våglängd (l), förutsatt konstant hcaAk; P = hc²l^–2 = aAkT⁴.

OM VI SÖKER temperaturfunktionens linjära aspekt — vi minns att temperaturen bara är ett annat »namn» för rörelseenergi och att dess rudimentära aspekt är linjär i OBS differentialformen, liksom allt övrigt i variationernas tillståndsfysik (se även grundbegrepp i atomtriangeln om ej redan bekant) — måste vi gå baklänges från Stefan-Boltzmanns strålningslag, tillbaka till den linjära grundformen vi utgick ifrån, men nu med andra termer. Det betyder en återderivering i tre nivåer. Med beteckningarna ovan får vi

(hc²)l^–2 = (aAk)T⁴ ;

a₁l^–2 = a₂T⁴ ;

Tredjederivatan, enligt ovanstående resonemang, kan då skrivas

d³(l^–2)/(dl)³ = (a₂/a₁) · d³(T⁴)/(dl)³ ; med lösningen (VL)

–24(l^–5) = 24(a₂/a₁) · f (y) · f (l,T) ;

(l^–5) = –(a₂/a₁) · f (y) · f (l,T) ;

Funktionen för y, f (y), är given som funktionsvärdet. Det ger oss

a1(l^–5)[–f (l,T)]^–1 = f (y) ;

VÅGLÄNGDSFUNKTIONEN f (l,T) måste, som vi nyligen antydde, ge ett obegränsat växande funktionsvärde med obegränsat avtagande variabelvärde (l), ända in till 0. Det finns bara två variationstyper inom matematiken som kan satisfiera det villkoret, se ovanstående beskrivna grafiska funktioner: antingen y₁=l^–n eller y₂=e^n/l. Men första alternativet finns redan i vänsterledet (VL) för hela f(y) och matchar dessutom inte funktionsparametrarna f(l,T). Återstår –f(l,T)=–y₂=–e^n/l. Eftersom villkoret är att partiella funktionsvärdet y₂=f (l,T) måste närma sig noll då variabelvärdet växer obegränsat (l®¥), måste vi dessutom justera den funna exponentfunktionen enligt y₂:=1–e^n/l.

Med –f (l,T) ges då y₂=–1+e^n/l. Vi har då, sammantaget i fortsättning från ovan,

a₁(l^–5)[–f (l,T)]^–1 = f (y) ;

a₁ = hc² ;

–f (l,T) = –1+e^n/l = y₂ ;

Därmed framträder Plancks strålningslag:

a₁(l^–5)[–f (l,T)]^–1 = f (y)

(hc²)(l^–5)[–1+e^n/l]^–1 = f (y)

analogt

hc² 1

—— · —————— = f (y) = y

l⁵ e^n/l – 1

Med våglängden (l=x) som variabel ges grafiskt kurvskaran

y = ax^–5(–1+e^n/x)^–1 ............... grafiskt

Illustrationen nedan visar en kurvskara med a=1 och n exemplifierat från 1,5 (toppkurvan) till 2 (bottenkurvan).

y

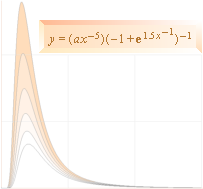x

y-formen anger typformen för Plancks strålningslag. n-värdet 1.5 ger illustrationens toppgraf med a=1.

Genom grafläran framträder alltså

linjära temperaturens elementära vågfunktion i effektbildningen

enligt y som ovan, liktydigt med PLANCKS STRÅLNINGSLAG.

koefficienten n

Koefficienten n i Plancks strålningslag

För att variationen i y₂=[–1+e^n/l] ska stämma med temperaturens växande då våglängden avtar, måste koefficienten n innehålla värmegraden T enligt n=k/T, k tills vidare obestämd. Detta ger oss

f (l,T) = [–1+e^k/lT]

Enheterna för lT är M°K. För att ta ut dessa så att exponenten till e blir oberoende (lika med 1) gäller substitutionerna

k₁/lT = k₁/(M°K) = k₂/[(M°K) J/°K] = [JM]/[(M°K) J/°K];

Enheterna J/°K och JS har motsvarande väl definierade fundamentala fysikaliska grundsamband enligt

J/°K .............. b, för Boltzmanns konstant (från allmänna gaslagen)

JS ................. h för Plancks konstant (Planckenergin E=hf)

JM ............... hc för Plancks konstant × ljushastigheten, JS×M/S=JM

Därmed

k₁/lT = [JM]/[(M°K) J/°K] Û hc/blT

Vi har då funnit totalt

hc² 1

—— · —————— = f (y)

l⁵ e^hc/blT – 1

Totala funktionsvärdet f (y) är det som i etablerad facklitteratur kallas strålningsradians (eg. spektrala radiansen) med enheten Watt per Kubikmeter (och Steradianer), W/M³(SRsteradianer)=N_l, eller kort sagt

sambandet

Plancks strålningslag:

strålningseffekten N_l i W(M³SRsteradianer)^–1

N_l

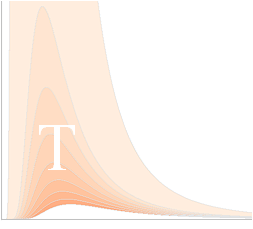l

Temperaturen T är vågfunktionen för, motsvarande genomströmningen av, alla möjliga våglängder (l) i en rymdpunkt.

Plancks strålningslag (W/M³)

y = ax^–5(–1+e^k/xT)^–1 ................................... grafiskt,

x är variabeln, a=k=1, T antar olika värden från minst 0

Planckvärmegraden (T) är den temperatur vid vilken en (ideal) kropp uppvisar ovanstående genomströmmande strålningseffekt som funktion av alla möjliga våglängder noll till oändligt.

Editor2007III17

historia

HISTORIA

Detaljerna i ovanstående härledning ingår INTE i den moderna akademins lärosystem (Det finns ingen liknande källa att plocka från, mig veterligt). Plancks strålningslag framkom (dessutom) INTE historiskt genom härledning. Det finns (här veterligt) ännu i denna dag i gängse litteratur ingen ENKEL beskrivning av hur Plancks strålningslag härleds. Det som visas i ämnet (se exv @INTERNET Wikipedia Planck law) är ytterligt svårtillgängligt för den som inte är expert på högskolematematik (det framstår närmast proppat med obesvarade frågetecken).

Max Planck kunde i början på 1900-talet genom experimentella detaljer, i samband med utarbetandet av ovanstående samband (som det får förstås ur källorna, se citat nedan) sluta sig till Planckenergin E=hf och vilket samband sedan i sig banade vägen för atomfysiken med kvantteorierna.

RENT HISTORISKT är emellertid den nyligen genomgångna härledningen till Plancks strålningslag OMÖJLIG. Härledningen BYGGER (nämligen) på att frekvensenergin hf MÅSTE vara noga kvalitativt känd i grundfysiken, annars går det inte. Men hf-formen (som källbeskrivningarna får förstås) framkom först tillsammans med framväxten av Plancks strålningslag [‡1]. I TNED (relaterad fysik) däremot är härledningen till frekvensenergin hf elementär grundfysik. Se PLANCKENERGIN. Därmed kan också Plancks strålningslag härledas begripligt, verkligen, ur mycket enklare premisser, som ovan.

‡[1] ”Max Planck originally produced this law in 1900 (published in 1901) in an attempt to improve upon an expression proposed by Wilhelm Wien which fit the experimental data at short wavelengths but deviated from it at long wavelengths. He found that the above function, Planck’s function, fit the data for alla wavelengths remarkably well. In constructing a derivation of this law, he considered the possible ways of distributing electromagnetic energy over the different modes of charges oscillators in matter. Planck’s law emerged when he assumed that the energy of these oscillators was limited to a set of discrete, integer multiples of a fundamental unit of energy, E, proportional to the oscillation frequency v:

E = hv

Planck made this quantization assumption five years before Albert Einstein hypothesized the existence of photons as a means of explaining the photoelectric effect.”

@INTERNET Wikipedia Wien-Planck law 2007-03-17

Min översättning:

Max Planck producerade ursprungligen denna lag år 1900 (publicerad 1910) i ett försök att förbättra ett uttryck föreslaget av Wilhelm Wien vilket stämde med experimentella data för korta våglängder men avvek vid långa våglängder. Han fann att ovanstående funktion, Planckfunktionen, stämde med data för alla våglängder anmärkningsvärt bra. I konstruerandet av en härledning för denna lag, beaktande han de möjliga sätten för distribution av elektromagnetisk energi över de olika laddningsoscillerande tillstånden i materien. Plancks lag uppkom när han antog att energin hos dessa oscillatorer begränsades till en mängd diskreta, heltalsmultipler av en fundamental energienhet, E, proportionell mot oscillationsfekvensen v:

E = hv.

Planck gjorde detta kvantiseringsantagande fem år före Albert Einsteins hypotetiserade existens av fotoner som ett medel för att förklara den fotoelektriska effekten.

”Then, in 1924, Satyendra Nath Bose developed the theory of the statistical mechanics of photons, which allow a theoretical derivation of Planck’s law.”

@INTERNET Wikipedia 2007-03-17 Wien-Planck law|Planck’s law of black body radiation

‡[2]:

8phc 1

u(l,T) = ———— · —————————

l⁵ e^hc/lkT – 1

@INTERNET Wikipedia Wien-Planck law 2007-03-17

Min översättning:

Då, år 1924, utvecklade Satyendra Nath Bose teorin för fotonens statistiska mekanik, vilken tillåter en teoretisk härledning av Plancks lag.

Wiens förskjutningslag

PLANCKS STRÅLNINGSLAG INNEFATTAR

TOPPVÄRDET FÖR l i given T-kurva i Plancks strålningslag ger Wiens Förskjutningslag:

WIENS FÖRSKJUTNINGSLAG

Formen för T-kurvornas toppvärden fås genom att derivera Plancks strålningslag med avseende på våglängden.

Vi studerar hur.

GIVET:

N_l = l^–5hc²[e^hc/blT–1]^–1 .......... Plancks strålningslag

Vi söker toppvärdet för l, analogt 0=N_l’;

0 = (l^–5[e^hc/blT – 1]^–1)’ ;

Vi använder produktderivatan ([AB]’=A’B+AB’) tillsammans med exponential- och exponentderivatorna med huvudräkning för att lösa den sammansatta derivatan:

0 = –5l^–6[e^hc/blT – 1]^–1 + l^–5(–1)(hc/bl²T)e^hc/blT(–1)[e^hc/blT – 1]^–2 ;

:

0 = –5l^–6[e^hc/blT – 1]^–1 + l^–5(hc/bl²T)e^hc/blT[e^hc/blT – 1]^–2 ;

0 = –5l^–6[e^hc/blT – 1]^–1 + l^–7(hc/bT)e^hc/blT[e^hc/blT – 1]^–2 ;

0 = –5l^–6 + l^–7(hc/bT)e^hc/blT[e^hc/blT – 1]^–1 ;

0 = –5 + l^–1(hc/bT)e^hc/blT[e^hc/blT – 1]^–1 ;

0 = –5 + (hc/blT)e^hc/blT[e^hc/blT – 1]^–1 ;

x = hc/blT ;

0 = –5 + xe^x[e^x – 1]^–1 ;

0 = –5 + x[1 – 1/e^x]^–1 ;

0 = –5 + x[1 – e^–x]^–1 ;

5[1–e^–x] = x ;

x kan lösas iterativt med början från x=1 ;

x = 4,9651142…

= hc/blT ;

lT = hc/bx = (6,626 t34 JS)(2,99792458 T8 M/S)/(1,3805502 t23 J/°K)(4,9651142…)

= 2,89794 t3 M°K = k ; [GFåk3LIB1980s114 anger 2,893 t3]

l = k_{2,898 t3 M°K}T^–1 .............................. Wiens förskjutningslag

Editor2007III17

Se även i @INTERNET Wikipedia Wien’s displacement law 2007-03-17

konstanten i Stefan-Boltzmanns strålningslag

Den till synes ”enkla konstanten k” i Stefan-Boltzmanns strålningslag

P = aAkT⁴

har en ytterst dramatisk historia i sin härledning. Vi studerar den detaljen.

KONSTANTEN i Stefan-Boltzmanns strålningslag

— den saknar ännu en fullständig beskrivning i MAC

Vi utgår ifrån härledningen till Plancks strålningslag från Stefan-Boltzmanns strålningslag enligt föregående genomgång.

(1) P = aAkT⁴ ................................ Stefan-Boltzmanns strålningslag GER

(2) N_l = l^–5hc²[e^hc/blT–1]^–1 .......... Plancks strålningslag som GER k i (1):

Värdet på k i (1) kan med viss finess bestämmas ur (2) — med återintegration av (2) till (1). Följande beskrivning visar hur.

fas 1

Om vi återknyter till Stefan-Boltzmanns strålningslag

P = aAkT⁴ med ekvivalenta P=E/t = hf/t = hf ² = hc²l^–2 = aAkT⁴ som ger hc²l^–2 = aAkT⁴ med l^–2 = aAkT⁴(1/hc²), kan k SIMULERAS fram på följande sätt:

I härledningen av fysikaliska grundsamband, använder vi naturkonstanter som direkta ersättare för fysikaliska enheter där så är möjligt

Genom att värmegraden (T) återfaller på ett rudimentärt begrepp om rörelse i materien-massan, och då ringen (2pr) är grundläggande för beskrivningen av materien-massan genom gravitationen (a=mw²/2) och impulsmomentet (J=mvr), är det naturligt att tänka sig effekten (eller aktiviteten) P i härledningen från k₁T i (1) som funktion av en ringdiameter (2r) enligt k₁T=1/2r=p/2pr=p/l så att T avtar med växande r. Dvs.;

I härledningen från k₁T i (1) kan vi först sätta k₁ = (p/lT = pb/hc = 1/M°K). Då är

k₁T = T(p/lT) = p/l. Om vi räknar i enheter, är 1/lT samma som 1/M°K=b/hc där c är divergensen (M/S), h Plancks konstant (JS) och b Boltzmanns konstant (J/°K). Då är

k₁T = T(pb/hc) med differentialformen

d(k₁T) = d(p/l) = dT(p/lT) = dT(pb/hc). Detta ger oss

k₁T d(k₁T) = T(pb/hc) dT(pb/hc) så att vi får sammansättningen

k₁T · 1dT_x · 2dT_y · 3dT_z = T(pb/hc)·1dT(pb/hc)·2dT(pb/hc)·3dT(pb/hc)

= T·1dT·2dT·3dT· (pb/hc)⁴ med integrala lösningen

; T⁴ · (1·2·3)/(4·3·2) · (pb/hc)⁴

I VÄNSTERLEDETS DEL till Plancks strålningslag (2) motsvarande grundformen till Stefan-Boltzmanns strålningslag (1), hade vi en motsvarande utgångsvariant av formen

l^–5d(l) · (K = hc²[e^hc/blT–1]^–1 d[l,T]) med integrala lösningen [integration enligt differentialerna 1d(l)_x2d(l)_y3d(l)_z]

l^–2(1·2·3)/([–4][–3][–2]) · K ; Vi återkommer strax till K-integralen (den kan inte lösas direkt algebraiskt utan ger oändlig serie). Frånsett tecken har vi då

HL = T⁴ · (1·2·3)/(4·3·2) · (pb/hc)⁴

VL = l^–2 (1·2·3)/(4·3·2) · K ;

l^–2K = T⁴ · (pb/hc)⁴

fas 2

Eftersom vi hade att P=E/t = hf/t = hf ² = hc²l^–2 = aAkT⁴ kan vi nu flytta över hc² från (pb/hc)⁴ så att vi får tillbaka P (faktorerna aA är inte signifikanta i de följande uträkningarna och vi kan därför frånse dessa med särskild markering), nu mera preciserat enligt

P = hc²l^–2 · K = aAT⁴ · p⁴b⁴/h³c² ;

P = hc²l^–2 = aAT⁴ · (1/K) · p⁴b⁴/h³c² ;

P = hc²l^–2 = aAT⁴ · (p⁴/K) · b⁴/h³c² ;

fas 3

Vi kan alltså i slutsumman skriva integralen, från (2) till (1) enligt

ò l^–5 d(l) hc²[e^hc/blT–1]–1 d(l,T) = aAT⁴ · (p⁴/K) · b⁴/h³c²

Vi kan skala bort konstanterna hcb genom att sätta dem lika med 1 för att på så sätt kunna studera den rena råa grafiska formen för att få fram dess matematiska koefficientvärde (K),

(3) ò l^–5 d(l) [e^1/lT–1]^–1 d(l,T) = aAT⁴ · p⁴/K

Vi ser nu, först, vilket är det centrala, att något ”l” inte förekommer i HL. Vilket vill säga: varje T i HL gäller [enligt (2)] för alla l från noll till oändligt. För att kunna utföra en numerisk beräkning av integralformen i (3), för varje givet T, måste vi alltså utföra integrationen på integranden l^–5[e^1/lT–1]^–1 med variabeln l i intervallet 0 till ¥.

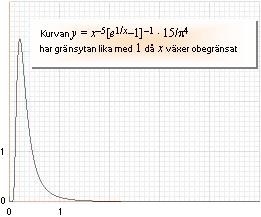
Kurvan y = x^–5[e^1/x–1]^–1 · 15/p⁴ har gränsytan lika med 1 då x växer obegränsat

Knappast före de snabba datorernas tid kunde en sådan uppgift lösas (inom rimlig tid). Men i dagens läge (i stort från 2000) är det möjligt. Metoderna ges av Simpsons formel eller alternativt Hyposerien. Om vi insätter integranden x^–5[e^1/xT–1]^–1 i någon av dessa metoder (ett särskilt datorprogram krävs) finner vi för T=1 — inom intervallet 0 till 10000 (vilket i stort sett kan betraktas som »hela grafen») och med 1 miljon delintervall — svaret

(3) _{x=0®10 000}ò x^–5[e^1/x–1]^–1 d(x) = 6,4939394022…

Värdet 6,49393940… är samma som p⁴/15, och alltså kan K sättas lika med 15;

(3) p⁴/15 = 1⁴ · p⁴/K ; 15 = K

Konstanten i (1) så långt således

k = b⁴p⁴/15h³c²

fas 3

Vi kan då säga att k på visst sätt härleds ur Plancks strålningslag (2). Det finns emellertid ännu en (gömd) koefficient som tillhör k i (1) innan vi är klara:

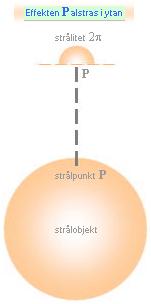
Lägger vi till högerledet (HL) en rymdvinkel 2p (halva rymdklotytan är 2p-enheter med samma intensitetsradie r=1) och som betyder att strålningen, då den utgår från en delyta (eg. en punkt) på strålobjektet — vilken som helst och runt om i ett halvklot med samma intensitet — så att säga garanterar att objektsytan inte också strålar på baksidan (eller insidan, eller olika långt åt olika håll), alltså själva ”stråliteten”, har vi den slutligt fullständiga koefficientform som brukar associeras med Stefan-Boltzmanns strålningslag i gängse facklitteratur,

k = 2p · b⁴p⁴/15h³c² ;

= 5,66893154148517 t8 WM^–2°K^–4

kT⁴ = WM^–2

AkT⁴ = W = P;

P = aAkT⁴; a = 0®1 absorptionskoefficient, numerisk

[NOTERING. »Strålitetsbeskrivningen» ovan finns (här veterligt) inte omnämnd i den etablerade facklitteraturen …].

I Wikipedia-beskrivningen på Plancks strålningslag (för att ge refererande exempel till jämförelse) används inte föregående typ med våglängden för att härleda k i Stefan-Boltzmanns strålningslag. Man använder istället en frekvensform där det ingår en integral

òx³(e^x–1)^–1dx vars ytvärde också ger p⁴/15=6,493939… då x®¥. Det är (tydligen) den typen det hänger på, men den ges ingen DIREKT förklaring. Saken görs inte bättre av att Wikipediaförfattarna dels anser att integrationerna är ENKLA och LÄTTA — vilket alla vet INTE är sant utom författarna — och dels inte lämnar fullständiga spårbara uppgifter om VARIFRÅN de integrala kopplingarna som sådana härrör.

Jämför återigen:

”Then, in 1924, Satyendra Nath Bose developed the theory of the statistical mechanics of photons, which allow a theoretical derivation of Planck’s law.”

@INTERNET Wikipedia 2007-03-17 Planck’s law of black body radiation

Teoretisk härledning av Plancks strålningslag skulle alltså vara ett erkänt svårbegripligt ämnesområde.

kärninduktiva värmemotståndet

Strålningstryckets Termonukleära Ekvivalent p = (akT⁴)2/c₀

STRÅLNINGSTRYCKET

Strålningstryckets Funktion (m®^gp®P®T)

RELATERAD FYSIK

p = ak_PT⁴ := ^gp ........... strålningstrycket, kärninduktiva värmemotst., N/M²

k_P = 2k/c₀

= 3,781904041 t16 NM^–2°K^–4

Strålningstrycket

Se även i

Vad betyder den moderna akademins term strålningstryck?

härledning

HÄRLEDNING

Från

P = aAkT⁴ .................... Stefan-Boltzmanns strålningslag, A anger strålytan, W

via sambandet för effekten

P=E/t=pV/t ges

p = Pt/V. Då är genom Stefan-Boltzmanns strålningslag som ovan trycket p lika med

p = Pt/V = (aAkT⁴)t/Ad = (akT⁴)t/d

Vi studerar tryckets (p=F/A, N/M²) principiella fysikaliska verkan genom massans fundamentala struktur från Fysikens Sjunde Princip enligt härledningarna i Planckringen eller Atomkärnan med avseende på den primära massförstöraren E=mc²:

Elektriska verkan på Q i atomkärnans alla delar sker enligt TNED alltid i energizonen med divergensen d/t=c₀/2=c_z där laddningspotentialen i Q är maximal [Se Potentialbarriären]. Med t/d=2/c₀ och verkan på Q enligt TNED i atomkärnans ytstruktur genom ett således härlett nukleärt strålningstryck p=F/A från massdestruktion (m®g) ges då p som ett kärninduktivt ytvärmemotstånd (gp) med generatrisens riktning från tryck till tryckets temperaturekvivalent ^gp®T, och endast så, enligt (p:=^gp);

p = (akT⁴)t/d = (akT⁴)2/c₀ = 2(ak)T⁴/c₀;

p = 2(ak)T⁴/c₀ .............. kärninduktiva värmemotståndet, N/M²

Därmed är generatrisen för temperatur (grunden för atomkärnornas och alla subatomära partiklars inbördes lägesändringar och därmed Planckvärmet eller materievärmen) ytterst återförd på massfysiken genom massdestruktion (m®g), analogt primär induktiv transmission (massan och laddningen försvinner medan energin överförs induktivt på omgivande mQ-system i form av värme och ljus, dvs., termiska svängningar).

forts.

NeutrinostrålningenBasic

Neutrinostrålningens grunder enligt TNED

Genom massdestruktion från de allra djupast liggande fraktala nivåerna med de allra högsta frekvenserna och de allra lägsta energierna

— enligt Plancks konstant som en strukturkonstant i härledningen av Planckringen och därmed fullständig förklaring av Planckstrålningens samtliga våglängder

— byggs värmestrålningen i en kropp upp med början från masstrukturen [PASTOM] [Atomkärnan]. llustrationen nedan antyder processen [COMPTONEFFEKTEN], från högre frekvenser till successivt lägre. Yttersta energikällan är alltså fusionerna typ Solen, samt i mindre omfattning de s.k. radioaktiva nuklidernas sönderfall. Generatrisen för effekt (P) och temperatur (T) blir alltså massdestruktionen som sådan: från högsta frekvenserna mot de lägsta. Erinra Plancks konstant som en strukturkonstant från härledningarna i Planckringen. Strålningen som bildas ur massdestruktionerna beskrivs generellt enligt TNED med termen neutrinostrålning (g).

Se även relaterat i

COMPTONEFFEKTEN,

NEUTRINOSPEKTRUM,

ALLA FYSIKENS KROPPAR VÄRMELÄCKER och

ORSAKEN TILL T INRYMS INTE I ALLMÄNNA GASLAGEN.

Plancks Strukturkonstant

E = hf = (h/n_F)n_F f = h_F f_F

Se även atomkärnans härledning · ATOMKÄRNANS GEOMETRI · atomkärnans elektrogravitation

v v

l = å l _v ; f = å f_v ; c₀ = l f

v=1 v=1

EFTERSOM PLANCKS KONSTANT h definieras på toroidaggregatets fraktala toppnivå — där elektronmassans bindning till atomkärnan lyder vektorledet F_BT+F_eZ=0, delen F_eZ kopplar explicit till Spektrum och Kvanttalen — är Plancks konstant också en strukturkonstant: h_N=m_Nc₀r_n=6,62559 t34 JS [HOP s7–155];

(h_N®0)=(m_N®0) vilket definierar tyngdcirkeln idealt på r_n.

Den strukturella aspekten på h visar sig emellertid explicit inte på elektronnivån, eftersom atomkärnans fraktalstrukturella system av spinnande mQ-ringar besitter en långt tätare och mera sammansatt vågmekanik än den som figurerar i atomens elektronhölje och därför (i allmänhet) arbetar på våglängder kortare än elektronelementets.

Denna strålningstyp benämns i TNED neutrinostrålning. Dess kvalitativa spektrum kan INTE efterhärmas artificiellt eftersom vårt enda arbetsverktyg på den punkten är elektronmassorna. Men dess rent kvantitativa energiekvivalent kan alltid bildas artificiellt genom elektronsvängningar och därmed påverka-försätta atomkärnan i motsvarande exciterade tillstånd enligt K+(m®g)=K1+K2, se KÄRNREAKTIONSLAGEN. Ovanstående enkla ekvivalentled visar hur toroidsystemets fraktalstruktur gömmer-inkluderar neutrinonivåerna i kvantitativa elektronekvivalenter. Neutrinostrålningens vågkaraktär kan på samma sätt syntetiseras på den enkla kvantitativa ekvivalenten c₀=f l enligt de vidstående angivna summaleden. Begreppet spektrum får därmed en något annorlunda karaktär än den konventionella.

VARJE UNIK FUSIONSNUKLID (ändringar i 1818e-massivet, se 1818-kroppen) erhåller därmed sin egen unika uppsättning

fusionsfrekvenser f=_v=1®vå f_v och

fusionsvåglängder l=_v=1®vå l _v vars ekvivalenter alltid kan återföras-gömmas kvantitativt på

energi-frekvensekvivalenten E=hf. Se även från PLANCKEKVIVALENTERNA.

forts.

Med isolerade koefficienter enligt

p = (2k/c₀)aT⁴ = k_PaT⁴ ;

k_P=2k/c₀=2(5,6689315 t8)/(2,99792458 T8)=3,7819 t16 [°K⁴WS/M³=JM^–3°K^–4=NM^–2°K^–4] ges

strålningstrycket

p = ak_PT⁴ := ^gp ................................. strålningstrycket, kärninduktiva värmemotståndet, N/M²

k_P = 2k/c₀

= 3,781904041 t16 NM^–2°K^–4

^gp anger strålningstrycket i N/M². Alla elektriska laddningar strävar dit där strålningstrycket är som lägst. Strålningstrycket som kärninduktivt värmemotstånd kan också kallas strålningstryckets termonukleära ekvivalent.

· strålningstrycket (gp) beräknas INTE från värmegraden (T). Strålningstrycket beräknas från massdestruktionen (m®g) som i stjärnornas fall bestäms av gravitella övertrycket i stjärnornas allmänna tryckekvation (p–p_e–^gp=0). Det gäller att strålningstrycket ^gp BILDAR värmegraden T:=Tg enligt ^gp®Tg. Omvändningen gäller INTE.

kraftjonisation

Strålningstryckets kraftekvivalent. Eftersom temperaturens generatris är INDUKTIV kan strålningstryckets funktion och dynamik återföras på en KÄRNREAKTANS. Ju högre temperatur, desto mera induktivt motstånd gör den laddade atomkärnan mot att BEFINNA SIG i området (värmemotstånd). Kärnan strävar att avlägsna sig från lokalen med strålningstryckets kraft, vilket innebär att atomkärnan på sätt och vis erhåller en högre RIKTNINGSBETINGAD Coulombpotential med växande temperatur. En elektriskt laddad partikel rör sig alltid mot det område som innehåller det lägsta strålningstrycket — häftigare ju större partikelns laddning är. Strålningstryckets PÅVERKAN är alltså proportionellt mot EKVIVALENTA (riktningsberoende) laddningen:

p = T⁴ · ak_P(c/c₀) = F/A = k(Q/r)²/A = k(Ze/r)²/A ;

Z² = T⁴ak_P(c/c₀)(A/k)(r/e)²

Z = T² · (r/e)(ak_PAc/c₀k)^1/2 ................ värmeladdningens ekvivalenta elektronmultipel (ZT)

Värmeladdningens ekvivalenta elektronmultipel (ZT) är direkt proportionell mot temperaturens kvadrat.

Genom den ordinära Coulombkraften kan man alltså skriva strålningsrepulsionskraftens ekvivalent som en produkt mellan värmeladdningens ekvivalenta elektronmultipel (ZT) och kärnladdningen (laddningsobjektet) (Z) enligt

F_T = Z_TZ · k(e/r)²

= T² · (r/e)(ak_PAc/c₀k)^1/2 · Z · k(e/r)² ;

F_T = T²(e/r)(ak_PAkc/c₀)^1/2Z = T²e(a _2/3k_P4pkc/c₀)^1/2Z = T²Z(8,54859 t22)(N^M–2°K^–4 VMC)^1/2(c/c₀)^1/2

ZerA är parametrar som tillhör atomkärnan (varav rA förkortas bort).

Se tillämpning i Koronafysiken.

Med noll strålningstryck är ZT=0 och därmed också FT=0.

Från Strålningstrycket

ABSORPTIONSKOEFFICIENTEN a

— Strålningstryckets fullständiga form

^gp = 2ak₀T⁴/c₀ = ak_PT⁴

Innebörden av absorptionskoefficienten a måste återföras på hela rummets xyz. Trycket p=ak_PT⁴ gäller bara i EN riktning p_x. I detta fall finns ingen förutsättning för brytning eller spridning varför också a=1. Ordningen ansluter därmed till samma typform som gäller för allmänna gaslagen där volymen V är inkluderad enligt pV=kT=2mw²=mv²=E_k=Mv₀²/2. I strålningstryckets fall kan V sättas på enhetsformen 1 M³ för att bilda en direkt ekvivalent med motsvarande ak_PT⁴V.

Enklaste sättet att relatera en utveckling, blir på den ekvivalenta enhetsformen 1=a som gäller för p_x. Eftersom p=p_x=p_y=p_z=p_xyz gäller i samtliga riktningar, får vi för p_xy enhetsformen 1=2a och för p_xyz enhetsformen 1=3a.

Eftersom dubbla g-energin motsvarar divergensenergin genom ljusets friställning från kinetiken (se även i Solrandsavböjningarna) (Vi observerar att denna detalj INTE ingår i modern akademi, se utförligt från Potentialbarriären med energizonen) (2mw²=mv²=E_k=Mv₀²/2, se TemperaturEnergiEkvivalenten i Allmänna Gaslagen) blir reala rörelseenergins 3D-ekvivalent halva enhetsformens ekvivalent enligt 1=3a/2 som ger

a = 2/3 .................................................. absorptionskoefficienten

Samma resultat men mera utförligt ges genom det endimensionella p_x=1ak_PT_x⁴, det tvådimensionella p_xy=2akPT_x⁴ och det tredimensionella p_xyz=3ak_PT_x⁴. Eftersom p=p_x=p_y=p_z=p_xyz gäller i samtliga riktningar gäller också p_xyz=k_PT_x⁴ så att vi får den enklare föregående enhetsformen 1=3a. Dubbla g-energin som ovan ger reala rörelseenergins 3D-ekvivalent genom en halvering enligt 1=3a/2 som ger

a = 2/3 ................................................. absorptionskoefficienten

eller utförligare p_xyzE=mv²/2V med p_xyzE=3ak_PT⁴/2=3p_x/2.

I stjärnornas fall — generellt i alla lokaler som behärskas av fusionsenergin genom massdestruktion (m®g) — behöver vi knappast bekymra oss om de olika s.k. frihetsgrader [ref. FOCUS MATERIEN 1975 s192sp1ö] som medföljer gaserna vid de lägre temperaturerna på grund av molekylbindningar och som här skulle göra a ytterst komplicerad. Inuti en stjärna (frånsett den allra svalaste typen) finns knappast annat än enskilda atomer, knappast molekyler. Därmed framstår a=2/3 som ideal för samtliga stjärnor.

Alla stjärnor får exakt samma absorptionskoefficient a=2/3.

a = 2/3 ........................ stjärnornas allmänna (enatomiga) absorptionskoefficient

Alla SYNLIGA stjärnor visar samma spegel.

1–a betyder motsvarande reflexionskoefficient. Alla enatomiga stjärnor reflekterar 1/3 av ljuset.

Vad betyder den moderna akademins term strålningstryck?

Vad avses då med den moderna akademins terminologi ”strålningstryck”?

Med uppfattningen att temperatur ger tryck T®p i p=ak_PT⁴ avses (MATERIEFYSIK) ett värmegradens kinetiska tryck, eller ett rörelseenergitryck, eller ett elektrokinetiskt tryck. Värmegraden T beskriver alltid en rörelseenergiekvivalent. Eftersom alla partiklar på atomär nivå (utom neutronen) är elektriskt laddade påverkar de också varandra sinsemellan genom sina inbördes rörelser. På detta sätt blir föreställningen om ett med T sammanhängande elektrokinetiskt tryck helt naturlig. Flera personer bidrog också (runt 1900) med experimentella iakttagelser av detta sublima fenomen. Inom stjärnfysiken är emellertid Planckvärmegradens kinetiska tryck fullkomligt oväsentligt; det har (mig veterligt) ingen som helst betydelse, och det används överhuvudtaget inte i beskrivningen av stjärnornas allmänna fysik ENLIGT TNED.

RÄKNEEXEMPEL

strålningstrycket i modern vetenskap

I modern vetenskap och akademi BONNIERS ASTRONOMI 1978 s52sp2 anges strålningstrycket på formen temperatur till tryck (p¬T) enligt

p_rad = (1/3)k₁T⁴ (rad för radiellt) med k₁=7,56 t16 J/M³/°K⁴.

Exempel:

Solytans temperatur ligger runt 6000 °K. Bestäm konventionella strålningstrycket vid den temperaturen.

Lösning:

p_rad = (1/3)(7,56 t16)(6000)⁴ = 0,3265919 (1Pa = 1N/M²).

Svar: p_rad = 0,3265919 Pascal.

RÄKNEEXEMPEL

strålningstrycket i relaterad fysik

I relaterad fysik (TNED) beräknas strålningstrycket i stjärnfysiken enligt stjärnornas allmänna tryckekvation

^gp = p – p_e ................................. strålningstrycket, kärninduktiva värmemotståndet, N/M²

med kärnyttrycket p_e= k(Ze/d)²/(pr₀)² och stjärnyttrycket p = G(m₂/2r²)²/p.

Exempel:

Bestäm strålningstrycket vid avståndet r=6,96 T8 M från Solens centrum med atombasen m_A=1,0078252u som Solens ämnesbas Väte-1,

Solmassan 1,989 T30 KG, k=1/4p(e₀=8,8543 t12 C/VM)=8,98743 T9 VM/C, G=6,67 t11 JM/(KG)², Z=1, e=1,602 t19 C och r₀=1,37 t15 M.

Lösning:

På grund av mängden parametrar, kräver lösningen för sin praktiska hantering ett kalkylkort: Konstanterna insätts i celler, och resultatet beräknas enligt (kalkylkortet kan tyvärr inte skickas med i det här htm-dokumentet, nedan visas endast ytbilden)

Kalkylkort — Strålningstryckets radiella variation för Solen

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik1 Kalkylkort 1 — Strålningstryckets radiella variation för Solen — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

kalkylkort MsWORKS · strålningstryckets radiella variation för Solen

dubbelklicka på kortet för att öppna det och utföra beräkningar, mata in r (gäller inte Windows Vista och senare | Gäller inte alls för webbläsare).

Kalkylkortet i denna display (dock här endast i bild) gömmer cellytor där konstanterna redan är inlagda.

^gp = (r/3)^4/3(4p)^1/3Gm₂^2/3 – r²k(Ze/[m_A/4r₀³ – 1]pr₀²)² = 8,94847 T13 N/M²

Svar: ^gp = 8,94847 T13 Pascal.

Kommentar:

Jämför föregående exempel p_rad = 0,3265919 Pascal från modern vetenskap. Det finns inga som helst paralleller.

Det är ren utklassning.

degenerationstrycket

Med utvidgad fortsättning från Strålningstrycket

DEGENERATIONSTRYCK

MODERN VETENSKAP IFRÅGASÄTTS — forts. strålningstryck — elektrondegenerationstryck

Modern akademi har tvingats uppfinna en hel del speciella artiklar för att kompensera dödläget i det naturliga gensvaret i strävan att beskriva universums fysik från den ståndpunkten att kunskapen INTE besitter en egen självständig väsensgrund, och som alltså samtidigt portförbjuder visdomen att hälsa på. En av dessa artiklar kallas konventionellt degenerationstryck. Vi studerar härledningen ENLIGT TNED, samt motsvarande resultat enligt etablerade källor.

TNED: Enligt atomens allmänna kraftled F_BT+F_eZ=0 BYGGER hela atomfysiken på samtliga möjliga kombinationer

(F_BT+F_eZ)₁+(F_BT+F_eZ)₂+(F_BT+F_eZ)₃+…+(F_BT+F_eZ)_n = 0

ELEKTRONMASSORNA DELAS GEMENSAMT av hela kroppens kärnmassa enligt kemiekvationen ovan.

Elektronen kan på detta sätt befinna sig hur långt från kärnmassan som helst, helt i enlighet med Bohrs enkla atommodell från 1913:

d = r_{5,29 t11 M}n², väteatomens enkla spektrum, d går mot oändligt då huvudkvanttalet n växer obegränsat.

Man kan undra varför modern akademi inte observerar den detaljen i DETTA sammanhang men väl i ANDRA:

ju mera atomen exciteras, desto längre bort förlägger den sin elektron; elektronen kan INTE innestängas.

Flera atomer kan obehindrat dela på sina elektronmassor i en gemensam typmolekyl (i princip en hel kropp) genom att ha flödesströmmarna gemensamt.

Därmed är elektronens absolut individatomära bindning eliminerad.

I atomens allmänna impulsmoment J_0K+3J_1K=0 är enligt TNED elektronelementet bundet till kärnan genom kraftverkan F_BT+F_eZ=0.

Eftersom hela elektronmassan (m) beskrivs generellt genom Plancks konstant (h) på impulsmomentet h=mvr=n(m/n)vr

får elektronelementet (m/n) samma allmänna status som hela elektronmassan, analog elementarkvantat e, vilket gör att vi kan räkna direkt på hela e.

INFÖR VI NU SÅLEDES FELAKTIGT en DEN Elektronmassans ABSOLUTA bundenhet till en atomkärna

— vi eliminerar således kraftekvationen F_BT+F_eZ=0 ur hela kärn och atomfysiken —

kan DEN FELAKTIGA bundenheten generaliseras som r analogt med en grovt förenklad form för »atomens radie».

DEGENERATIONSTRYCK FINNS INTE I FYSIKEN

— men vi kan härleda dess allmänna ekvation på samma felaktiga grunder som i modern akademi, för att beskriva sakinnehållet exakt

Vi uppfinner alltså begreppet kropp via en samling ballonger (atomerna) som hålls ihop av ett åtsnöpt överkast: Ju mera vi försöker tränga ihop atomerna genom att dra åt tyget allt hårdare, desto mera motstånd gör ballongerna, eftersom vi felaktigt förutsätter att elektronerna (ballonggasen) INTE kan rymma ur sin ballong (atomen). Leden nedan visar slutresultatet.

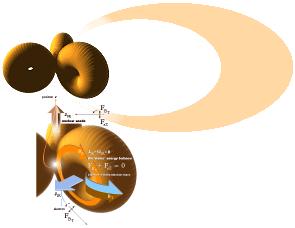
Elektronmassans frikoppling från kärnan med växande excitationsgrad garanterar att

begreppet ELEKTRON-DEGENERATIONS-TRYCK

inte har någon praktisk naturgrund. I Solens centrum är kraftverkan mellan kärna och hölje

F_BT+F_eZ=0

mycket försvagad på grund av den höga excitationen. Elektronmassan parkeras istället i Solhöljet.

degenerationstryckets härledning

till jämförelse med etablerade källor

En totalvolym V bestående av N atomer med kubisk medelradie r=(V/N)^1/3 ger då från v=h/mr: v = (h/m)(N/V)^1/3 = (h/m)n₀^1/3.

BALLONGatomTRYCKET _ep som utövas av n₀ atomer per volymsenhet kan skrivas grovt

_ep = n₀mv² (från p = F/A = m · v²/d · 1/A = mv² · 1/V). Då gäller

_ep = n₀mv² = n₀m(h²/m²)n₀^2/3 = (h²/m)n₀^5/3 = (h²/m)(N/V)^5/3 ;

_ep = (h²/m)(N/V)^5/3 ........................... absoluta BALLONGatomtrycket, N/M²

LJUSETS GRAVITELLA BEROENDE reducerar all makroskopisk elektromagnetisk verkan med avtagande lokal ljushastighet. I kosmologiska sammanhang måste vi därför ta med den allmänna ljusGravitella koefficienten (c/c₀). Därmed ges ABSOLUTA BALLONGATOMTRYCKET GENERELLT

_ep = (N/V)^5/3(h²/m)(c/c₀) ................. m elektronmassan, p i N/M²

_ep är alltså helt temperaturOberoende.

Med h=mc₀r=mc₀(N/V)^–1/3, som anger r=h/mc₀, ges (h²/m)(c/c₀)=h(mc₀r/m)(c/c₀)=h(r)(c)=hc(N/V)^–1/3. Därmed

_ep = hc(N/V)^4/3 ................................. absoluta BALLONGatomtrycket, N/M²

Exakt samma form (p) anges i BONNIERS ASTRONOMI 1978 s106 med benämningen ”Formeln för trycket hos en relativistisk, degenererad elektrongas”. Någon antydan om vad som menas med ”c” ges f.ö. inte (man förutsätter att ”samma c gäller överallt i hela universum”).

MODERN VETENSKAP IFRÅGASÄTTS — forts. elektrondegenerationstryck

förklaringen enligt TNED

Därför finns inget elektrondegenerationstryck i fysiken

Solen visar att elektronmassan läggs ut, utanför den inre täta centralkroppen (som i princip är elektronfri). e-massan tvingas inte till någon bestämd avgränsad bindning till sin atomkärna.

FÖRKLARINGEN ENLIGT TNED

modern akademi utestänger kraftekvationen

F_BT + F_eZ = 0

och uppfinner degenerationstrycket.

Ju mera upptagen (rörelseaktiv, em-aktiverad) kärnan blir, desto svagare blir krafterna som kopplar till kärnans avkänning och reglering av elektronmassans konstantström genom kärnbrunnen. Därmed blir elektronmassan allt lösare bunden till sin kärna.

I modern teori menar man att ett sådant frisläppande inte existerar — trots den redan kända Bohratomens enkla matematik med huvudkvanttalet n som obegränsat.

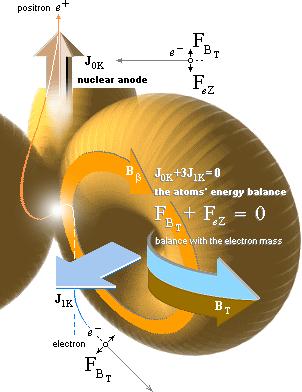
Höger: Bubbelkammarfotografi av s.k. parbildning, e^– e⁺

elektronen till vänster, positronen till höger,

SCIENTIFIC AMERICAN — August 1991 · s45

Kraftekvationen

F_BT + F_eZ = 0

utsäger att atomkärnans excitationsgrad är direkt proportionell mot elektronens frihetsgrad.

I modern vetenskap känner man varken till kraftekvationen eller atomen/atomkärnan den beskriver.

Frånsett mekaniska stötar kan atomkärnan bara exciteras av neutrinostrålning, detsamma som em-strålning från massdestruktion.

Ju mera atomkärnan exciteras

— den ingår i allt mera komplicerade rörelsescheman och svängningsfaser där fältstyrkorna i elektronmassans koppling försvagas på grund av olika (fördröjnings- och) skärmingseffekter

— desto mindre bunden blir elektronmassan till atomkärnan. Det betyder detsamma som att kraftverkan i bägge F_BT och F_eZ försvagas med atomkärnans excitation.

Därför finns heller ingen specifik volymär bindning mellan kärna-elektron och som degenerationstryckets teori tydligen felaktigt bygger på. Atomens volym kan i princip vara obegränsad enligt Bohrs enkla kvantvillkor.

BAKGRUND se ovanstående illustration, grunderna ges från Planckringen

Kraftekvationen

OM kärnfältet B_T utverkar någon influens på elektronmassan utöver vad som ingår i balansräkningen för atomkärnan — summan av alla moment och krafter är noll enligt

J_0K+3J_1K = 0

— måste B_T-kraften F_BT uppvägas av en lika stor och motriktad kraft, enligt Newtons tredje lag. Eftersom influensen bara kan komma ifråga om elektronmassan kommer utanför kärnan, kan motkraften bara vara kärnattraktionen F_eZ: kraftvägen blir i bägge fallen densamma, via c. Då gäller kraftekvationen

F_BT + F_eZ = 0

Därmed bibehåller kärnan balansräkningen i sin utvidgade form som atomen per exakt matematisk fysik.

Ekvivalenten mellan krafterna innebär, tydligen, en sluten NOLLRESISTIV bana som den kärnbundna elektronmassan följer. Elektronkomponenten bibehåller den hastighetskomponent (v_t) den hade då den lämnade kärnan, och återkommer med samma belopp. Den slutna banformen bestäms då av kurvaturen för komponentfältet

F_BT + F_eZ = 0

som verkar på vt.

ENERGIN i kraftvägen för F_eZ mellan kärna och elektronelement grundlägger vektorhärledningen till spektrum och kvanttalen (se Spektrum och Kvanttalen).

EXCITATIONSGRADEN

Men influensen av kärnfältet B_T på elektronmassan beror på graden av atomens excitation. På liknande sätt som då en elektrisk ledare påförs allt högre frekvens och därmed ledningselektronerna dras alltmer utåt mot ledarens yta, tappar också en atomkärna alltmer kontakten med sin elektronmassa då kärnan exciteras (strålningstryckets inverkan från stjärncentrum). Graden av excitation kan kopplas till styrkan hos krafterna i kraftekvationen

F_BT + F_eZ = 0

Maximala styrkan i respektive kraftformer F_BT och F_eZ ger en optimalt icke exciterad atom. Att styrkan i respektive kraftformer F_BT och F_eZ går mot noll betyder att atomen/atomkärnan exciteras alltmer, dvs., den ingår i allt mera komplicerade rörelsescheman och svängningsfaser där fältstyrkorna i elektronmassans koppling blir försvagade på grund av olika (fördröjnings- och) skärmingseffekter.

Därmed finns inte längre någon fysikalisk grund eller förutsättning för det i modern teori förmodade s.k. degenerationstrycket.

Eller sagt på annat sätt: excitationsgraden kan förstås vara detsamma som styrkan i den elektromagnetiska kopplingen mellan kärna och hölje. Excitationsgraderna motsvarar bindningsnivåerna i Spektrum. Man tycker att besättningarna i den moderna akademins korridorer borde veta det här, eftersom det är elementärt.

Värmebildningen

Från strålningstryck till värme — p®T

Se även i Strålningstryckets termonukleära ekvivalent

Massdestruktionen (m®g) från fusionerna K1 + K2 – (m®g) = K genererar en atomkärnbaserad (NUKLEÄR) em-strålning (h/n)nf. Den nuklidgenererade em-strålningen bildar ett STRÅLNINGSTRYCK, eller ett RIKTNINGSBASERAT KÄRNINDUKTIVT VÄRMEMOTSTÅND. Strålningstrycket fungerar som en värmebildande generatris:

Den nuklidgenererade em-strålningens energi

(h/n)nf₀ påför atomkärnorna svängningskomponenter = arbete genom kärnornas ±b-byggnad. Komponenterna är karaktäristiska för varje specifik fusion och som berör specifika avsnitt i atomkärnans byggnad.

ARBETET betyder att energin i svängningskomponenten reduceras från givna (h/n)nf₀ till den lägre (h/n)nf₁.

Strålningstryck ^gp (gamma-p) produceras ur massdestruktion (m®g) i fusioner enligt kärnreaktionslagen K1 + K2 – (m®g) = K genom stjärnornas allmänna tryckekvation p_G – p_e – ^gp = 0. ^gp fungerar som ett kärninduktivt värmemotstånd genom den högfrekventa kärn-em-strålningen. ^gp är genom kärnstrukturens ±b-väv (således enligt TNED) laddningsaktiv och alla laddade massor strävar dit ^gp är som lägst.

Det masslösa ^gp påtvingar materien värme T (rörelseenergi).

Energin som bildar kärnsvängningen och får atomkärnan att ändra sitt tillstånd och därmed i kärnelektrisk växelverkan med andra kärnor ändra sin position och därmed uppvisa VÄRME (svängningsrörelser i materien) kan alltså skrivas

E = hf₀ – hf₁ = h(f₀–f₁) = hf = (m®g)c² .................... värmets energi, Planckenergin

Värmestrålningen genom massa och material byggs på så sätt upp gradvis av den nukleärt bildade em-strålningen (m®g) från massdestruktionerna. Alla möjliga nuklidfrekvenser berörs.

Em-strålning från massdestruktion (även parannihilationer ±e) kallas här sammanfattande för neutrinostrålning med beteckningen (m®g) i kärnreaktionslagen

K1 + K2 – (m®g) = K. Se även Comptoneffekten.

Comptoneffekten

COMPTONEFFEKTEN I KORT SAMMANFATTNING

Massdestruktionen (m®g) från fusionerna genererar nukleär em-strålning. Den nuklidgenererade em-strålningen är samma som strålningstryckets värmebildande generatris. Em-strålningens energi påför atomkärnorna svängningskomponenter som leder till att kärnorna ändrar inbördes positioner. Därmed byggs värmestrålning upp gradvis av den nukleärt bildade em-strålningen från massdestruktionerna.

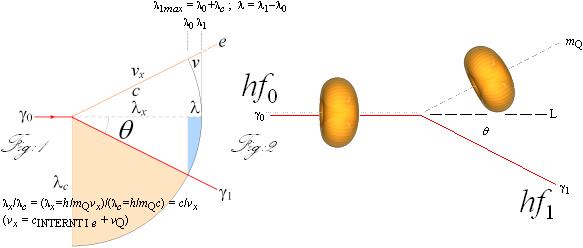
Energin som får Q-massan att ändra riktning är

E = hf₀ – hf₁ = h(f₀–f₁) = hf = (m®g)c²

Eftersom Plancks konstant h i TNED är en strukturkonstant gäller fraktalformerna med (i princip) godtyckliga heltalsvärden n enligt

hf = (h/n)nf₀.

Se även från NEUTRINOSPEKTRUM.

Se även från MASSFYSIKEN.

Materiefysik och massfysik — MATERIEFYSIK — MASSFYSIK:

BEGREPPSFÖRKLARINGAR ENLIGT RELATERAD FYSIK -- Förtydligande tillägg 6Jan2017

MATERIEFYSIK ......................... T→p

Materiefysiken beskrivs från temperatur (T) till tryck (p), T→p, typ allmänna gaslagen (pV=kT). Materiefysiken är utomordentligt väl representerad i modern akademi.

MASSFYSIK ............................................. p→T

Massfysiken däremot beskrivs från tryck till temperatur, p→T. Men den typen ingår inte i modern akademi (utom formellt kvantitativt men inte kvalitativt via massförstörarna E=mc²=hf) — därför att man inte kan härleda atomkärnan där. Massfysiken står helt orepresenterad/outforskad i modern akademi. Se särskilt från SOLFYSIKEN.

Massfysik och Materiefysik

EXEMPEL — massa är inte värme: massa är en värme-Generator

Notera att webbläsaren Firefox läser INTE teckensnittet Symbol — 64 av 118 htm-dokument 2016 i Universums Historia. I detta htm-fall har delvis ersättningar gjorts i efterhand med Times New Roman Unicode.

Materiefysikens värmeenergiinnehåll kan beskrivas med hjälp av Allmänna gaslagen; E=pV=kT:

temperatur (T) bildar tryck — omvändningen gäller inte, se ORSAKEN TILL T INRYMS INTE I ALLMÄNNA GASLAGEN:

— Energin (E) är direkt proportionell mot temperaturen (°K), k en proportionalitetskonstant (J/°K). Är temperaturen 0, är den med temperaturen förknippade energin 0. Men det betyder inte att också massan är noll:

Massfysikens energiinnehåll bestäms av massenergin (Primära och sekundära massförstörarna) E=mc²=hf.

ENERGI (temperatur) innefattar arbete (kraft över väg: E=Fd=ma·d)

ORSAKEN till någon påvisbar förekomst av temperatur kan alltså ytterst återföras på ett arbete.

ARBETETS ORSAK kan bara återföras ytterst på fysikalisk konkret vägbar massa (m): — Allt arbete E=mad utförs ytterst på kredit av massförstörelse (m→γ) som bildar värme och ljus.

ORSAKEN till en förekomst med någon påvisbar temperatur kan alltså ytterst sett INTE återföras på makrofysikens materiefysik, inte alls överhuvudtaget: Är temperaturen 0°K, är också värmeinnehållet i makrofysiken lika med 0:

tryck (p) som temperaturbildare kopplar endast till massfysiken via kärnreaktionsprocesser = strålningsbildning:

— Se massfysikens utförliga beskrivning särskilt (använd inte Firefox, se ovan) i relaterad fysik från SOLFYSIKEN.

Massa som sådan kan generera värme — också i princip direkt FRÅN 0°K. EXEMPEL: Finns ett par närliggande elektron-positronmassor ±e, annihileras dessa (Se Parannihilation). Annihilationsprocessen genererar Planckstrålning E=hf=mc² med m som de aktuella elektron-positronmassor som försvinner och i vilken process värmestrålning med frekvensen f bildas. Den strålningen är elektromagnetisk. Själva den aktuella makroskopiska värmebildningen — materiens påvisbara värmesvängningar: temperatur — uppkommer endast i omgivningen: där Planckstrålningen påträffar närliggande atomer och deras elektronskal. Därmed utbildas motsvarande impulser (mv) mellan atomerna, och de börjar svänga. Därmed bryts 0°K-tillståndet och en temperatur över 0°K bildas.

Följande beskrivning ger grundläggande referenser i begreppen massfysik (detaljerna som berör atomkärnans struktur) och materiefysik (den vi kan se direkt, mer eller mindre)

neutrinospektrum

Energibegreppet ur materiefysikens synpunkt har en gräns vid 1,23568 T20 Hz — atomhöljets maxfrekvens

NEUTRINOSPEKTRUM

Se även i Neutrinostrålningens grunder enligt TNED

Energibildning som går från kärnfysiken till atomfysiken, alltså den här vägen,

är inte samma som energibildning som går från atomfysiken till kärnfysiken, alltså den här vägen:

massfrihetssatsen

VILKET VILL SÄGA:

värme och ljus kan inte skapa massans struktur, bara massans kvantitativa energiekvivalent enligt (m®g) = (m¬g)

energibegreppet ur experimentell synpunkt: uteslutande baserat på materiefysiken (presentationer uteslutande genom elektronen)

Samma sak uttrycks mera avancerat i ENERGILAGEN.

Eftersom massans vägande struktur således inte kan skapas, och elektronen HAR vägande massa som utvecklar centrifugalkraft (se trådstråleröret), är det tydligt att elektronmassan måste härröra — avdelas — från (och åter kunna upptas av) atomkärnan.

Eftersom massa inte kan skapas, är således elektronens vägande massa en fundamental beståndsdel av atomkärnan.

ENERGILAGEN gör alltså detta klart redan från grunden.

I modern akademi finns inte begrppet struktur för Plancks konstant (se Plancks strukturkonstant) varför heller ingen uppfattning KAN finnas om elektronmassan som bestående av mindre element och som i sin tur härrör just från atomkärnan — trots att modern akademi mycket väl känner till att elektronen ligger utspridd kring atomkärnan. Allt återfaller på Q — den elektriska laddningens härledning och som modern akademi garanterat inte kan härleda. Se utförligt från elektriska laddningen.

beskrivning

objekt:

E = hf = (m®g)c²

I TNED ÄR PLANCKS KONSTANT EN STRUKTURKONSTANT

Se även efterföljande Atomkärnans fraktala frekvens- och våglängdsspektrum

Se även i Neutrinostrålningens grunder enligt TNED

Eftersom elektronspektrum är lika för alla atomer (betasönderfallen) men inte neutrinostrålningen (som »bygger upp» atomkärnornas struktur genom fusioner från lättare till tyngre), KAN massekvivalenta elektronenergier sönderdela alla atomkärnor enligt det kvalitativa sambandet E = hf = (m®g)c² = (m¬g)c². Samma kvantitativa sönderdelningsenergier, nämligen, som bildas från fusionerna garanterar att energierna som frigörs med bildandet av de tyngre atomkärnorna INTE sönderbryter de lättare atomkärnornas byggnad. Neutrinoenergierna som sammanhänger med atomkärnornas bildning, bildar TVUNGET olika fraktala nivåer i atomkärnan (se från Planckringen), och dessa är inbördes säkrade genom att de högsta neutrinofrekvenserna tillhör de lättaste atomkärnorna så att dessa inte sönderdelas på de tyngres bildning. Om energin vore elektronhomogen också för kärnfysiken, vore (alltså) de olika atomkärnorna en omöjlighet.

I naturliga lokaler säkras varje bildad nuklid från sönderfall — oberoende av temperaturens inverkan.

kärnspektrum

Atomkärnans fraktala frekvens och våglängdsspektrum i TNED

Betrakta

E=hf=(h/n₁)(n₁f)=(h/n₂)(n₂f)=(h/n₃)(n₃f)=(h/n₄)(n₄f)=…

E/hf=n₁/n₁=n₂/n₂=n₃/n₃=n₄/n₄=…

Om n₁ motsvarar den djupast liggande fraktalnivån, motsvarande den lättaste atomkärnan, n₂ den närmast högre liggande fraktalnivån motsvarande den närmast högre liggande nuklidbildningen, osv, ges en frekvenskarta exakt motsvarande nuklidbildningarna där frekvensen avtar från lättare till tyngre, analogt fusionsvåglängden är växande med tyngre nuklider. n-suffix med högre heltal motsvarar då atomkärnor med högre atomvikt: Fusionsfrekvenserna spärrar kvalitativt mot varandra så att frekvenserna från tyngre nuklider (längre våglängder) inte åstadkommer en sönderdelning av frekvenser från lättare nuklider (kortare våglängder).

Med ovanstående ekvivalent vinner man den excellenta fördelen, att en energiekvivalent (E=hf) alltid kan bildas kvantitativt genom (artificiellt genererade) elektronsvängningar, vilka ju gäller lika för alla atomer och för ändamålet att exakt kunna ”fejka” en nukleär uppdelning av vilka som helst nuklider i deras komponenter genom att låta en nuklid ”bada” i sin egen kvantitativa fusionsenergi (m®g)=(m¬g).

Nukliderna själva har under nuklidbildningarna ingen sådan finess, eftersom frekvenserna i den naturbaserade grundämnesbildningen alstras av kärnan (se Grundämnesbildningen, Nuklidbarriären).

Inte höljet.

Den lägsta frekvensen (tyngsta nukliden) har tvunget kortare våglängd än elektronelementet, vilket spärrar för elektronkopplingar — som i annat fall skulle överföra fusionsenergierna i ett blandat kvantitativt tillstånd, tillämpliga på alla atomkärnor, och därmed effektivt krossa hela byggnaden.

Därmed bevaras fusionsfrekvenserna säkert separerade i de lokaler där de termonukleära fusionerna utlämnas åt sig själva genom naturliga processer. Högre nuklidbildningar äventyrar inte de lättare komponenternas hållfasthet, vilket skulle vara fallet om fusionsfrekvenserna vore helt kvantitetsgrundade.

Därmed säkras grundämnesbildningen i samma termiska lokal med samtidig existens av lättare och tyngre nuklider — oberoende av temperaturens magnitud. Fusionerna kan alltså friska på bäst de vill med avgivandet av termiska bidrag via massdefekterna. I och med, nämligen, att dessa med allt tyngre nuklider förknippas med allt längre fusionsvåglängder, gynnas rörelseenergin för de lättare omgivande (på kortare våglängder baserade) nukliderna. Därmed kan också rejält höga temperaturer bildas (lokalt) som följd av fusioner från lägre till högre masstal.

Om man alltså artificiellt försöker att härma den naturliga, självutlämnade proceduren, kommer man grundligt att misslyckas med det, eftersom den enda artificiella svängningsgenerering som finns att tillgå är den som gäller lika för alla atomer. Nämligen den som ombesörjs av elektronsvängningar, analogt Plancks STRUKTURKONSTANT h på dess högsta fraktalnivå (No1).

Vad man med ovanstående energiekvivalent följaktligen kommer att finna i sådana experiment, blir just det att en strålenergi som kan sönderdela en viss atomkärna enligt E=hf, samtidigt också kan sönderdela samtliga lättare typer enligt ekvivalenterna

E/hf=…=n₄/n₄=n₃/n₃=n₂/n₂=n₁/n₁

Betasönderfall däremot hämmas generellt lika för alla atomer eftersom alla atomer i det avseendet grundas på exakt samma komponent: elektronen.

OBSERVERA att våglängdsbildningarna för atomkärnorna via neutrinospektrum INTE är analoga med den motsvarande konventionellt benämnda s.k. de Broglies vågekvation (l=h/mv) där våglängden avtar med växande masstal. I TNED är sambandet l=h/mv en interatomär elektromekanisk energiöverföringsform (MIC, mass interactive connection) mellan mekaniska och elektriska fenomen (jämför neutrondiffraktion), ingen beskrivning av materiens eller massans byggnad.

Neutrinofrekvensernas n-suffix beror på fraktalsystemets matematiska delning, och den algoritmen är enligt TNED bara känd i detalj för första underfraktalen enligt N3m20-aggregatet. Neutrinospektrums fraktala delning kan alltså fastställas av princip, ehuru (ännu 2007-01-22) inte i någon annan detalj än den som sammanhänger med atomvikternas inbördes relationer. Se vidare i NEUTRONKVADRATEN.

Comptongränsen

NEUTRINOSPEKTRUM

COMPTONGRÄNSEN

atomfysikens grundläggande begrepp i TNED

ARTIFICIELLT (utan hjälp av massdestruktion) kan ingen högre materiell temperatur än drygt 1 miljard grader Kelvin bildas i materien —

T_e = k_{2,893 t3 M°K}(l^–1=f/c=E/hc=mcc/hc=mc/h) = k_{2,893 t3 M°K}m_ec/h

= 1,19243 T9 °K

— enligt Wiens förskjutningslag

l =k_{2,893 t3 M°K}T^–1 och atomens maxfrekvens genom elektronmassan m_e

f_c =m_ec²/h

= c/l_c

= 1,23568 T20 Hz med motsvarande våglängd via c=lf

l_c = 2,42612 t12 M

För att högre temperaturer ska bildas måste strålning från massförintelse (m®g) eller s.k. annihilationsstrålning utnyttjas, men den kan inte bildas av materiesystemens svängande elektroner. I TNED benämns den gränsen Comptongränsen (2,426 t12 M). Strålningen på den högfrekventa delen om den gränsen klassificeras i TNED som neutrinostrålning, analogt strålning associerad med massförintelse.

Elektronmassans komponenter enligt TNED har emellertid begränsad utsträckning (1,37 t17 M) vilket gör att den verkliga gränsen för typen elektronstrålning blir flytande mellan T20 till T25 Hz. Men den flytningen inbegriper också Plancks konstant (h) som strukturkonstant.

Se vidare beskrivning i Atomkärnans fraktala frekvens- och våglängdsspektrum.

OBSERVERA dock att ovanstående gäller för elektronmassan idealt vilande. Med elektronens-positronens rörelseenergi tillväxer ekvivalenta frekvensen (E=hf). Därmed finns, i princip, ingen övre gräns varken för E eller f genererad med elektronernas (och positronernas) hjälp. Elektronmassans ökning genom partikelaccelerationen (MoveQ, se PLANCKEKVIVALENTERNA) kan f.ö. återföras på mr-faktorerna i impulsmomentet J=mvr: masschokningen (se PLANCKEKVIVALENTERNA) medför att r avtar i elektronelementet (t-ringen) vilket i sin tur möjliggör allt kortare våglängd i den elektrongenererade Planckenergin hf och därmed högre frekvens.

UPPGIFT OM nuvarande tekniskt HÖGSTA FREKVENS (T24 Hz) finns i

Citat:

”At the other extreme, photons of arbitrarily high frequency may be produced by colliding electrons with positrons at appropriate energy. 10²⁴ Hz photons can be produced today with man-made accelerators.”

@INTERNET Wikipedia Electromagnetic spectrum 2006-07-27

Min översättning:

I andra änden kan fotoner med godtyckligt hög frekvens produceras av kolliderande elektroner och positroner vid lämplig energi. 10²⁴ Hz fotoner kan produceras idag med människoskapade acceleratorer.

Se även i COMPTONEFFEKTEN.

Comptoneffekten

COMPTONEFFEKTEN

För grunderna till elektronmassan, se Elektronmassans komponenter

Comptoneffekten

Comptoneffekten:

em-strålningens energireduktion vid växelverkan med materia

Beviset för massans struktur — som inte kan förklaras av materiens struktur

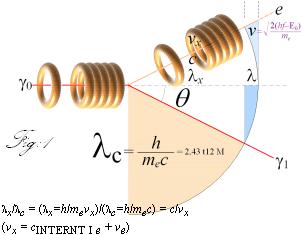
En inkommande em-stråle (g₀) böjer av (g₁) genom det arbete den utför om den råkar på en fri elektron med hastigheten v. Tillståndsändringen i elektronbanan gör att den också böjer av. Idealt (men inte helt korrekt) bryts g-strålen och e-cylindern på samma vinkel (q) men åt motsatta håll.

Comptonekvationen i PREFIXxSIN:

l = h/m_ec (1 – sin q) = l₁ – l₀

= l_c(1 – sin q)

l_c = h/m_ec = 2,42612 t12 M ............................. Comptonvåglängden

f_c = m_ec²/h = 1,23568 T20 Hz .......................... Comptonfrekvensen

= c/l_c

Härledande beskrivning

Em-verkan (em förk. elektromagnetisk-) i e-massan griper tag i e-massan genom l_c (från divergensimpulsen m_ec [se även Planckimpulsen] och Plancks konstant h). e-massan är i detta skede RESONANSLÅST (e-massan saknar bestämd form) vid atomen och släpper först vid E₀ (från FOTOELEKTRISKA EFFEKTEN) som ger e hastigheten

v_e = Ö 2(hf–E₀)/m_e med cylinderformen genom magnetisk verkan i strömflödesvägen v. Totala e-impulsen ökar då från vilolägets referens c via det fasta l_c med tillskottet +v_e till l_x. Som totala impulsen ökar med v_e och därmed energin, är tvunget l_x<l_c.

Em-verkan på e betyder ett arbete som kräver energi. Energin ges av

E = hf₀ – hf₁ = h(f₀–f₁) = hf som får e-massan att ändra riktning. Relationerna ger

l_x/l_c = (l_x=h/m_ev_x)/(l_c=h/m_ec) = c/v_x. Med l_x=l_c gäller v=0; Det aktiva våglängdsintervallet är l = l_c – l_x = l₁ – l₀. l är i praktiska våglängder skillnaden mellan längsta våglängden (l₁, efter växelverkan med e) och kortaste våglängden (l₀, före växelverkan med e). Med konstanten l_c gäller trigonometriskt i PREFIXxSIN

l_x/l_c = sinq = (l_c–l)/l_c = 1–l/l_c ; l/l_c = 1 – sin q. Totalt således Comptonekvationen som ovan.

Se även Comptoneffekten konv. i @INTERNET Wikipedia Compton scattering 2006-06-12

Hist., Comptoneffekten, upptäcktes 1922 av Arthur Compton, Encarta 99

Fotoelektriska effekten

[c0_1.doc s73 | MPcPeriodic1.wps s26 | Kärnstrukturen.doc]

PEFECT Photoelectric Effect

FOTOELEKTRISKA EFFEKTEN

MATERIENS STRUKTUR

Ur ljusets brytning framgår LJUSETS FYSIK — ljusets tre gestalter

—————————————————————————————————————————————————————

DIVERGENSEN: c = a·dT ;

c i ds, ljushastighetens punktvärde, ljusets fysikaliska motorik

LJUSHASTIGHETEN: c = s/T ;

c genom Ds, ljushastigheten bestäms av intervall

Färgerna (ljuset): c = l·f ;

c genom frekvensen f=1/T₀ — elektriska laddningarnas periodiska rörelser

fotoelektriska effekten · elektronernas hf-egenskaper · periodiska systemet

—————————————————————————————————————————————————————

modern akademin känner inte till dessa detaljer, varken år 1887 eller senare

—————————————————————————————————————————————————————

ÅR 1887 iakttas följande (ref. TRETTIO ÅR SOM SKAKADE FYSIKEN George Gamow Prisma 1968 s35ö):

Man hade observerat att vissa metaller avger elektroner om metallen bestrålas med lämpligt ljus.

Fenomenet fick namnet fotoelektrisk effekt.

Mätningarna på de frigjorda elektronerna visade

I. Vid given frekvens men variabel intensitet hos ljuset är elektronenergin konstant medan elektronmängden varierar proportionellt mot intensiteten.

II. Med variabel frekvens emitteras elektronerna — från en viss miniminivå som varierar för olika metaller — med en rörelseenergi som är helt linjärt proportionell mot frekvensen.

Planckenergin hf definierar elektronens materiella frekvensbindning

Är elektronens materialbindning E₀=hf₀ blir den utkastade elektronens energi

E = h(f – f₀) = hf – E₀ ............................................ fotoelektriska effekten, elektronenergin, J

förutsatt f >f₀. E₀ är f.ö. särskilt låg i gruppen alkalimetallerna (Z = {3, 11, 19, 37, 55, 87})

alkalimetallerna

Periodiska systemet härleds i GRUNDÄMNENAS PERIODISKA SYSTEM genom resonanser.

Sambandet för E är alldeles detsamma som för atomens generella energidistribution som grundlägger härledningarna i Spektrum och Kvanttalen.

FOTOELEKTRISKA EFFEKTEN påvisar ALLTSÅ egenskaper i materien —

INTE egenskaper hos ljuset: elektronens mönsterbindning genom bestämda vågkvanta — resonanser.

VERKNINGSSÄTTET tillämpat på verkanslagen, som följer direkt ur spegellagen eller reflexionslagen och som anger riktningarna i verkan — resulterande verkan från den inkommande verkan är i verkanspunkten summan av verkanskomponenterna —

tillger fotoelektriska effekten en motsvarande KVANTITATIV IMPULSANALOGI: inkommande hf-kvanta träffar elektronen som kickas ut tillsammans med en (eventuell, beroende på riktning) resulterande frekvensändring i ursprungliga hf-impulsen. Denna senare del påvisades 1923 (1922) av Arthur Compton (se Comptoneffekten). Verkanslagen (intervallets analogt energins oförstörbarhet) garanterar en sådan, kvantitativ, funktion.

Albert Einstein framlade impulsanalogin år 1905 i formen av fotonen som en fritt existerande (ljustransporterande) partikel — inget sagt om någon verkanslag eller kännedom om ljusets allmänna TRE gestalter. I kraft av den fotoelektriska effektens faktiska verkningssätt, ansågs det därmed bevisat att fotoner verkligen existerar. Den fotoelektriska effektens veritabla »turistbroschyr» till materiens struktur hade därmed hastigt förvandlats till en kvalitativ icke existerande egenskap hos ljuset. Och så presenteras saken ännu i denna dag i den allmänna lärobokslitteraturen: man anför fotoelektriska effekten som bevis för existensen av fotoner. Dvs., enligt relaterad fysik (TNED):

Fysiken innehåller inga fotoner. Fotonen är en matematisk modell. Ingen fysisk kvalitet. hf-energi är källenergi, på stället. Inte målenergi som färdas för att träffa. Men den kan beskrivas så, kvantitativt. Märk väl.

Max Planck menade att energipaketen hf INTE beror på någon egenskap hos ljusvågorna själva utan på att atomen kan emittera och absorbera strålning endast i bestämda hf-kvanta (Gamows bok sidan 33). Den moderna akademin antog INTE den uppfattningen.

”Einstein påvisade att ljuskvanta måste existera fritt rörliga i rummet för att man

skall kunna förklara de empiriska lagarna för fotoelektriska effekten, dvs. emissionen av elektroner från metallytor som bestrålas med violett eller ultraviolett ljus.”

TRETTIO ÅR SOM SKAKADE FYSIKEN George Gamow Prisma 1968 s34ö

Jämför ovanstående citat i en mera balanserad tappning:

”Einstein påvisade att ljuskvanta måste existera fritt rörliga i rummet för att man

I EN MATEMATISK-KVANTITATIV BESKRIVNING AV FYSIKEN

skall kunna förklara de empiriska lagarna för fotoelektriska effekten, dvs. emissionen av elektroner från metallytor som bestrålas med violett eller ultraviolett ljus.”

Albert Einsteins helt glänsande kvantitativa ”förklaring” har alltså ingen som helst kvalitativ fysikalisk motsvarighet; Den är endast en mycket bekväm MATEMATISK modell. Om den tas för en kvalitativ beskrivning av fysiken, är det klart att den leder vilse, att den leder till helt felaktiga grundföreställningar om fysikens natur.

Max Planck hade helt rätt. (Det är sedan en annan historia att Max Planck senare, och med honom många andra, ”omvände sig” och accepterade Einsteins uppfattningar). Den moderna akademin hade dock andra intentioner. Hela historien utmynnade i att man började ANSE att elektriska, magnetiska och gravitella fällt HAR energi — medan fysiken klart visar att så ingalunda är fallet: energin finns där massan finns, E=mc², och därutöver inte alls: dE Û 0 = (m=0)c².

Se även i Massfrihetssatsen.

;

det finns inga fotoner i fysiken, bara i matematiken

Fortsättning i Solfysiken.

END.

Editor2008V

Termofysikens Matematik

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Solfläckarnas uppkomst

ämnesrubriker

innehåll:

TERMOFYSIKENS MATEMATIK

Stefan-Boltzmanns strålningslag

Stefan-Boltzmanns strålningslag

Plancks strålningslag

härledning

sambandet

historia

Wiens förskjutningslag

Konstanten i Stefan-Boltzmanns strålningslag

Strålningstryckets Termonukleära Ekvivalent

Kärninduktiva värmemotståndets härledning

strålningstrycket

strålningstryckets funktion

neutrinostrålningens grunder

Plancks strukturkonstant

strålningstrycket

strålningstryckets termonukleära ekvivalent

kraftjonisation

strålningstryckets kraftekvivalent

sambandet

absorptionskoefficienten

Strålningstrycket i modern akademi

räkneexempel · jämförelse mellan modern akademi och relaterad fysik

Degenerationstrycket

obegränsat bindningsavstånd genom Bohrmodellen från 1913

förklaringen enligt TNED

Värmebildningen

från strålningstryck till värme

Comptoneffekten i kort sammandrag

materiefysik och massfysik

neutrinospektrum

massfrihetssatsen

kärnspektrum

Comptongränsen

neutrinostrålningens definition

Comptoneffekten

PhotoElectric efFECT · Fotoelektriska effekten

innehåll (föregående):

Stefan-Boltzmanns strålningslag · konstanten i Stefan-Boltzmanns strålningslag

Plancks strålningslag

Wiens förskjutningslag

STRÅLNINGSTRYCKET · Strålningstryckets Termonukleära Ekvivalent · Strålningstryckets kraftekvivalent · Strålningstrycket i modern akademi · degenerationstryck

Neutrinospektrum

REGISTER

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2021-07-19

*END.

Stavningskontrollerat 2007-11-21 | 2008-03-06 | 2017-01-06.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se