SOLFYSIKEN 2007XI30 a BellDHARMA production ·
Stjärnfysikens fundamentala grunder enligt TNED | Senast uppdaterade version: 2022-04-19 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Solens Temperaturfysik · Solens 3 Ekvationer · kvaliTATIVA Fotometriska Effekten · kvantiTATIVA Fotometriska Effekten · Solradien
Solens Fyra Värmegrader enligt TNED · T skalvärmegraden · TP Planckvärmegraden · Tw Wienvärmegraden · Tg strålvärmegraden · Koronafysiken · Joniseringen i Solkoronan räkneexempel
se även från Solsystemets uppkomst enligt TNED · ovan, bildkälla:
GoogleSearch Solsystemet, bildträffar
se även från Universums Födelse enligt TNED · grundämnesbildningen
· fusionsgränsmassan · nuklidbarriären · atomkärnans härledning · Fysikens 7 Principer
universums allmänna värmegrund
allmän
inledning till stjärnfysiken
STJÄRNORNAS ALLMÄNNA TRYCKEKVATION (p–pe–gp=0) innebär enligt TNED att en stjärna bildas primärt om
g-trycket [p = G(m2/2R2)2/p] är större än
e-trycket [pe= k(Ze/d)2/(pr0)2], och endast då. Differensen eller g-övertrycket (p–pe=gp) definierar det strålningstryck (gp) som stjärnan spänns upp på. Strålningstrycket i TNED är ett kärninduktivt värmemotstånd (enhet N/M2) som härleds ur Stefan-Boltzmanns strålningslag. Stefan-Boltzmanns strålningslag härleds separat enligt TNED tillsammans med Plancks strålningslag och Wiens förskjutningslag med (vidare) grunder i Planckringen, samma som atomkärnans härledning — som INTE ingår i moderna akademi. Dessa strålningslagar bildar teorins hela grundval. Se även Degenerationstrycket: det har ingen funktion i TNED men är centralt i den moderna akademins kosmologiska uppfattning.
Stjärnfysikens Grunder enligt
TNED — i fortsättning från Termofysikens Matematik
STJÄRNORNAS ALLMÄNNA TRYCKEKVATION
ELEMENTÄRA GRUNDSAMBAND
Genom det initierande neutronsönderfallet som sker från divergenständningen (tON) garanteras att alla stjärnor i universum ENLIGT TNED börjar från grunden med Väte-1-baserad stjärnmateria som omvandlas successivt till Helium-4. Vi studerar hur.
Stjärnornas allmänna tryckekvation framgår från de tidigare omnämnda fusionsgränsmassorna
med klarläggandet av GRUNDÄMNESBILDNINGEN genom DIAKVADRATEN som funktion av K-cellens expansion genom divergenständningarna, tillsammans med härledningen av massdestruktionens energifrigörande (m®g) via strålningstryckets termonukleära ekvivalent samt i klarläggandet av att det konventionellt betecknade degenerationstrycket saknar fysikalisk grund ENLIGT TNED, enligt
STJÄRNORNAS
ALLMÄNNA TRYCKEKVATION ENLIGT TNED:
gp = p – pe
Degenerationstryck saknar ENLIGT TNED fysikalisk grund, se DEGENERATIONSTRYCK
beskrivning
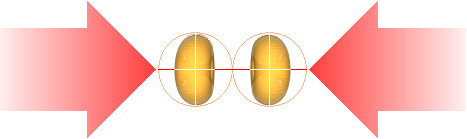
OM DEN IHOPTRYCKANDE GRAVITATIONSKRAFTEN (g-trycket, p) efter divergenständning i den avdelade J-kroppens massa är större än den kärnrepellerande Coulombkraften (Coulombtrycket, pe) mellan de maximalt närliggande atomkärnorna, pressar g-trycket atomkärnorna LUGNT (mycket långsamt) över varandras nuklidbarriärer i det centrala maximalt täta J-klotet.
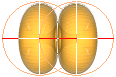
I fallet med atomkärnorna som spinnsynkroniserade Väte-1-kärnor (se Spinnsynkronisering), medför passagen över nuklidbarriären att atomkärnorna förenas (fusion) enligt KÄRNREAKTIONSLAGEN
K1 + K2 – (m®g) = K
.................................................................................. kärnreaktionslagen
Föreningen verkställer massförintelse (m®g) som bildar värme och ljus,
(m®g)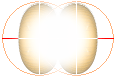 
värme&ljus
motsvarande ett termonukleärt strålningstryck (gp). Därmed har J-massan bildat en termonukleär energiproducerande enhet som vi kallar för en stjärna eller i vårt fall Solen. Strålningstrycket (gp) spänner upp stjärnan och bygger upp stjärnans allmänna Planckstrålning i försorg av massdestruktionen (m®g) — ända nerifrån närmast noll liggande våglängder enligt härledningarna i Planckringen. Vi noterar att modern akademi inte kan härleda denna del enligt Planckenergin E=hf eftersom energin växer över alla gränser då våglängden närmar sig noll obegränsat. Se även Alla våglängder i Planckringen.
GOOGLE-sökning
@INTERNET 2007-03-14 på »highest
possible frequency» leder bl.a. till ett frågeforum
[www.physicsforums.com/archive/index.php/t-109616.html] där frågan om kortast möjliga våglängd ventileras och
man kommer fram till i stort sett samma slutsats som här:
det går inte med de samband man känner till.
SourceRef.
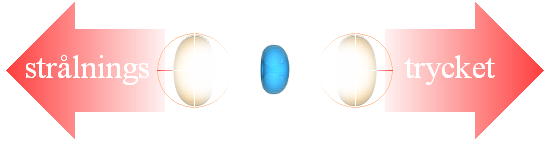
Strålningstrycket klingar av, nya fusionsagenter strömmar till …
… och g-trycket tar (återigen) över för att bilda en ny fusionsvåg …
STJÄRNGRÄNSMASSAN eller Solgränsmassan — J-massan där precis p=pe gäller — beräknas direkt ur de kärnfysikaliska parametrarna ENLIGT TNED med hänsyn till
den maximala centrala Coulombtätheten (r0=rC, kärnornas omskrivna sfärer vidrör varandra precis) enligt
pe = p
k(Ze/prd)2
=
Gm22/4pR4 ; r kärnradien, d avståndet
kärnyta-kärnyta, R stjärnradien, m2 stjärnmassan
r0 = 3m2/4pR3,
R = (3m2/4pr0)1/3 ;
Gm22/4pR4 = Gm22(4pr0/3m2)4/3/4p
= Gm22/3(4p)1/3(r0/3)4/3 ;
k(Ze/prd)2 = Gm22/3(4p)1/3(r0/3)4/3 ;
m22/3 = k(Ze/prd)2(4p)–1/3(r0/3)–4/3G–1 ....................................................... Solgränsmassan mSLIM
mSLIM bevaras på
den maximalt centrala Coulombtätheten (rätblock, atomkärnorna vidrör varandras omskrivna kuber);
r0 = mA/8r3 .......................... kärnkuben (2r)3
= 8r3
= rC= mA 1,0078252u/8(r1,37
t15 M)3, lika med 8,13444 T16 KG/M3
för Väte-1-bas
m2 = [k(Ze/prd)2(4p)–1/3(r0/3)–4/3G–1]3/2
= [k(Ze/prd)2(4p)–1/3(mA/8r33)–4/3G–1]3/2
= [k(Ze/d)2(1/r)2(1/p)2(4)–1/3(1/24)–4/3(p)–1/3(1/r3)–4/3(mA)–4/3G–1]3/2
= [k(Ze/d)2(r)–2(p)–2(4)–1/3(1/24)–4/3(p)–1/3(r)4(mA)–4/3G–1]3/2
= [k(Ze/d)2(r)2(4)–1/3(24)4/3(p)–7/3(mA)–4/3G–1]3/2
= [k3/2(Ze/d)3(r)3(4)–1/2(24)2(p)–7/2(mA)–2G–3/2]
= [(Ze/d)3(r)3(288)p–7/2mA–2(k/G)3/2] ; r=d ;
m2 = [(Ze)3(288)p–7/2mA–2(k/G)3/2] ;
m2 = mA–2Z3 · e3p–7/2(288)(k/G)3/2
=
mSLIM = mA–2Z3 · e1,602
t19 C3p–7/2(288)(k8,98743 T9 VM/C/G6,67
t11 JM/(KG)2)3/2
ATOMMASSAN mA
som utgör stjärnans ämnesbas (primärt Väte-1) ska egentligen associeras med atomkärnan — genom att max täthet inbegriper en aktiv fullständigt joniserad centralt opererande materialkärna. Denna detalj kan förbises i de översiktliga beräkningarna men är viktigt att känna till om mera exakta värden är kritiska.
Med ämnesbasen Väte-1 som har mA=1,0078252×1,66033 t27 KG ges stjärngränsmassan
m0SLIM = 1,204 T28 KG, eller ca 6 Jupitermassor (Jupitermassan är 1,89885 T27 kilo).
Lägsta möjliga gränsmassan ges enligt TNED på Deuteriumbas (1H2) som hamnar på ca 1,6 Jupitermassor.
OBSERVERA STRÄNGT SKILDA KOSMOLOGISKA GRUNDIDÉER:
enligt
modern akademi:
Stjärnbildningen enligt
MODERN AKADEMI:
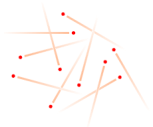
Stjärnorna antas bildas i ett expanderande universum ur omfattande stoft- och gasmoln som tänks sammandras under lång tid av gravitationen. Problemen med att beskriva stjärnbildningen enligt den modellen är ytterst komplicerad, innehåller en stor mängd obesvarade frågor, och kan bara i vissa avgörande delar simuleras lösningsvägen genom omfattande datorprogram. Fusionerna i stjärnan tänks verkställas genom slumpvisa kollisioner av samma typ som i högenergiforskningens partikelacceleratorer.
egenskap: gravitationen
vill komprimera mera — men HINDRAS AV DET INRE TRYCKET
från kallt till varmt — initiell temperaturekvivalent: 0 °K min
enligt
relaterad fysik:
Stjärnbildningen enligt
RELATERAD FYSIK (TNED):
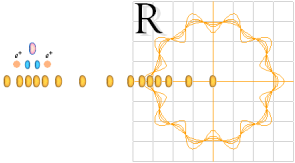
Stjärnbildningen utgår ifrån ett maximalt tätt materietillstånd där begreppet stjärna bestäms av balansen mellan inåttryckande g-kraft och mottryckande elektrisk Coulombkraft. Stjärna bildas om g-kraften är större, och fusionerna verkställs på en inre maximalt tät mycket liten stjärnkärna här benämnd stjärnstädet. Fusionerna verkställs periodiskt genom lugna mjuka g-tryck. Stjärnbildningens mekanismer återfaller på K-cellens allmänna värmefysik med enkla matematiska funktioner som kan beskrivas och förklaras i detalj.
egenskap: centrum
vill expandera mera — men HINDRAS AV GRAVITATIONEN
från varmt till kallt — initiell temperaturekvivalent: 9 T11 °K max
De två olika sätten har inga kvalitativa
beröringspunkter. De existerar i från varandra helt skilda
föreställningsvärldar.
Genom den följande presentationen kommer löpande
jämförelser att göras i resultatformerna med nu kända konventionella
föreställningssätt och teorier.
Värmegrunderna · se även från stjärnstädet
VÄRMEBILDNINGENS GRUNDER GENOM STJÄRNFYSIKEN
PLANCKSTRÅLNINGENS UPPBYGGNAD
FRÅN NOLL
Se även i jämförelse REFERENSERNA I DEN MODERNA AKADEMINS VÄRMETEORI
1. Städklotets fusionsmantel (se illustrationen ovan), äv. fusionsskiktet är stället där fusionerna sker — i städklotets tunna yta genom stjärnans hela energicykel; Städklotets fusionsmantel omsätter i Solens fall (Väte-1-bas) 6 T11 KG nuklidmaterial per sekund med effekten grovt P = 4 T26 W.
2. Massdestruktionen (m®g) genom
kärnornas förening ger em-strålning som bygger upp kroppens allmänna
värmestrålning — samma som den allmänna Planckstrålningen: från maximalt korta
våglängder, garanterat ända nerifrån noll enligt härledningarna i Planckringen, till allt längre med
successiv frekvensminskning.
Se utförligt från Neutrinospektrum och Plancks Strålningslag.
OBSERVERA SOLSTÄDETS FUSIONSMANTEL: Med medelvärdet 6 T11 KG per sekund för Solens del blir
fusionsskiktet extremt, ytterst tunt.
Vi bör inte räkna med (hur vi än räknar) att det skiktet någonsin
överstiger ens en ynka millimeter just på grund av den höga centraltätheten.
Det leder till flera konsekvenser för beskrivningen av Solfysiken och som inte
uppmärksammats i moderna kvarter just på grund av de strängt skilda
föreställningssätten; En skillnad på 40 nanometer i städet speglas av Solytan
som en kilometerstor skillnad.
I BESKRIVANDE ORDNING studeras först den allmänna matematiska fysik som fås för stjärnfysiken enligt TNED. Se nedan från STJÄRNFYSIKENS FUNDAMENTALTEOREM.
Se även (efter vidare nedan)
STJÄRNFYSIKEN ENLIGT TNED
STJÄRNFYSIKENS FUNDAMENTALTEOREM
Stjärnfysikens fundamentalteorem framgår KVALITATIVT Ur stjärnornas allmänna tryckekvation
ÖVERTÄTHETEN
(rmR) via stjärnans städradie (R) och centralmassa (m2)
rmR = m2/R3 · (3/4p) FRÅN G-TRYCKET — från max Coulombtäthet
r0=rC=mA/8r03=mR/VR=3mR/4pR3=8,13444 T16 KG/M3 för Väte-1-bas som sätter gränsen —
DEFINIERAR
DEN Primärt OROTERADE STJÄRNANS ABSOLUTA ARBETSTÄTHET
genom ett motsvarande förhållande mellan städradien R — den maximalt inre täta Solkärnan som fusionerna trycks fram på av g-trycket — och ytradien r enligt
R/r=krmR.
STÄDRADIEN är den maximalt täta centralkärna som stjärnan trycker fram fusionsenergin på.
Övertätheten (rmR) används här som preferens för relationen (R/r) med koefficienten k som justerande faktor och som vi kommer att lösa ut nedan.
Övertätheten
blir den del som garanterar stjärnans funktion.
Är r=R kan m2 INTE bilda SOL därför att det inte finns någon övertäthet, analogt ingen stötmassa och därmed ingen rekylkraft som kan igångsätta energiproduktion genom fusion. Genom att för detta gränsfall 1=k · rmR definiera
yttätheten (rr=mR/V),
mR =
rrV ;
1 = rrV/mR
samt
centraltätheten (r0=rC=mR/VR) och normal- eller
medeltätheten (rnom=rn=m2/V) enligt substitutionerna
= rrV/mR · VR/m2 · m2/VR = rrVR/mR · V/m2 · m2/VR = rr/rnr0 · rmR = k · rmR
ges totalt enligt TNED
stjärnfysikens fundamentalteorem
R/r=rmRk= m2/R3(3/4p)rr/rnr0
I ord utsäger stjärnfysikens fundamentalteorem
följande:
ALLA Primärt OROTERADE STJÄRNOR kan beskrivas genom en konstant centraltäthet (r0=rC),
en konstant medeltäthet (rn) och en konstant yttäthet (rr), lika för alla.
Ett annat sätt att uttrycka samma sak på är:
VOLYMENERGIN PER (KG)3 ÄR KONSTANT för stjärnor med samma ämnesbas. Se även MASSA-LUMINOSITETSRELATIONEN.
r0 = rC = mA/8r03 ........................................... mA anger atombasens massa, r0 anger kärnradien
= 8,13444 T16 KG/M3 ............................... maximala Coulombtätheten, Väte-1-bas
rn = 3mS/4prS3 ................................................. medeltätheten för alla (oroterade) stjärnor, från Solen
Då gäller i fortsatt utveckling ALLMÄNNA STJÄRNKONSTANTEN, M3/KG
R4/m2r = (3/4p) · rr/rnrC
....................................... allmänna
stjärnkonstanten
= (3/4p) · rr4pr3/3m2rC ; R4/r = rrr3/rC ;
TÄTHETENS RADIELLA VARIATION (r:=rr)
ges då enligt
(R/r)4 = rr/rC med
rr = rC(R/r)4 ................................................................ yttäthetskonstanten med r för hela stjärnradien, KG/M3
Yttäthetskonstanten skrivs mera allmänt i den här presentationen enligt
r = r0(R/r)4
YTTÄTHETSKONSTANTEN OCH SOLRADIEN
KAN BERÄKNAS — ENLIGT TNED
Se
utförliga beskrivningar nedan i yttäthetskonstanten
och Solradien
rr = Ö 18e0(E)/Gc0 ................................ YTTÄTHETSKONSTANTEN för primärstjärnor, (E) = 1VM–1C–1S–3KG
= 8,9277145 t5 KG/M3 konv. anger 0,0001 [BAs128fig.8.2];
värdet ger P=4,1
T26 W
e0 = 8,8543 t12 C/VM .......................... 1/R0c0, elektriska konstanten
= rr2Gc0/18 · 1MCS3V–1(KG)–1
rG = [rr(8/mA)–1/3/r0]–1/4(3/4p)1/3·[(1/m0SLIM)1/3
– (1/mS)1/3]–1
= 6,97063467 T8 M .......................... SOLENS MASKINRADIE
— större än synliga Solradien med ca 1000
KM
rF = 6,96 T8 M ...................................... SOLENS UPPMÄTTA FOTOMETRISKA RADIE (synranden, [BAs127.Tab8.1])
[Se även 6,955 T8 M ref. @INTERNET Wikipedia Solar radius 2010-04-12]
P = A2e0(E) ............... SOLENS RÅEFFEKT oberoende av temperatur och absorptionskoefficient
= (4pr2)2e0(E) = (4p[6,97 T8 M]2)2(8,8543 t12
C/VM)(E)
= 3,29993 T26 W, [jämför
ENCARTA(1999-2004-) P=3,83 T26 W; Wikipedia Sun 2009-03-23 3,846 T26 W] se även Fotometriska Effekten
e0 = 8,8543 t12 C/VM .......................... 1/R0c0, elektriska konstanten
= rr2Gc0/18 · 1MCS3V–1(KG)–1
rn = 3mS/4prS3, rS=rG, mS=1,989 T30 KG
= 1 402,3223 KG/M3 ........................ SOLENS MEDELTÄTHET rnom=rn
SOLRADIEN Solens Elektrogravitella Radie KAN INTE HÄRLEDAS AV MODERN AKADEMI
Stjärnfysikens fundamentalteorem grundas på stjärnstädet med stjärnans allmänna tryckekvation. Dessa detaljer säkerställer, garanterar och certifierar bortom allt tvivel att sambandet för Solradien ligger helt utom den moderna akademins räckhåll: sambanden kan inte härledas ur den moderna akademins lärosystem. Det finns inga som helst beröringspunkter.
MASSA-LUMINOSITETSRELATIONEN
(MLR)
stjärnornas energiproduktion
Den matematiska fysikens grundval för stjärnornas energi enligt TNED ges av massa-luminositetsrelationen (MLR). Den bygger på stjärnstädet (R) med maximala Coulombtätheten, enligt föregående beskrivningar.
Eftersom alla stjärnor med samma ämnesbas arbetar på samma typstäd, finns ingen ytterligare central maximal täthet att hämta hur stor stjärnmassan än blir. Endast kraften ökar och därmed också hastigheten i förbränningen. Alla OROTERADE stjärnor utgår följaktligen ifrån en och samma maximala inre täthet (rC) som sedan droppar av utåt tills jämvikt uppnås mellan strålningstryck och g-tryck. Medeltätheten för alla stjärnor med samma ämnesbas bör därför också verkligen vara en KONSTANT — oberoende av massan — densamma medeltäthet rn=1 402,1847 KG/M3 som gäller för Solen. Varje OROTERAD stjärna (med Solens ämnesbas) kan därmed beräknas sin ytterradie enligt
rSTAR = (3mSTAR/4prn)1/3 .......................... stjärnradien, primärt oroterad stjärna
rSTAR = mSTAR1/3(0,0554245 KG–1/3M) @ mSTAR1/3/18
Ökar kraften, vilket betyder att stjärnan har större massa, ökar också volymen i motsvarande grad så att nettomedeltätheten bevaras.
Ett annat sätt att säga samma sak på är
VOLYMENERGIN PER KG3 ÄR KONSTANT för stjärnor med samma ämnesbas.
härledning
ARBETET (E) som utvecklas i masslinjen (m) genom hastigheten (v) i den linjära konstanta accelerationen
a=v/T=(2d/T)/T=2d/T2 skrivs i mekaniken
E
= Fd = mad = m · v/T · d = mv · d/T = mv · v/2
= mv2/2
VARIATIONEN för E med avseende på masslinjen skrivs som varianten eller derivatan dEx/dmx=v2/2.
DIFFERENTIALEKVATIONEN skrivs då med given linjär hastighet dEx=dmx · v2/2.
VARIANTEN för E med avseende på massvolymen med förutsättningen att dmx=dmy=dmz kan då skivas totalt
dExyz/dmxdmydmz = v2/2 ; med differentialekvationen
dExyz = (v2/2) dmxdmydmz ; med lösningen
Exyz = m3v2/12 = (v2/2) òòò dmx dmy dmz ;
Om stjärnan utvecklar sitt arbete (värmet) likformigt divergent (sfäriskt) i varje lokal rymdpunkt genom en konstant linjär acceleration (a) genom ett konstant linjärt intervall (d=x=y=z), då förhåller sig volymenergierna E och Es för de olika massvolymerna m och ms enligt
EEs–1 =
(m3 · v2/12)(ms3 · v2/12)–1
= (m/ms)3 .............................................................................. volymenergirelationen
Tilläggskoefficienternas fysikaliska enheter för ytenergin (KG) och volymenergin (KG)2 bortfaller i
EEs–1 så att den vanliga linjära arbetsenergins ekvivalent återstår. Eftersom E=Pt får vi alltså
EEs–1 = PPs–1 = (m/ms)3, suffixet s refererar till Solvärdena.
Analogt med begreppet effekt (P) används i stjärnfysiken begreppet luminositet (L) så att vi får
MASSA-LUMINOSITETSRELATIONEN
PPs–1 = (m/ms)3 ....................................................... massa-luminositetsrelationen (MLR)
Med P=Ps(m/ms)3 ges från E=Pt tidsekvationen t=E/P=E/Ps(m/ms)3=(E/Ps)(ms/m)3.
VOLYMENERGINS FUNKTION bygger på en central exotermiskt termonukleär energikropp (exotermisk, som ger energi i motsats till endotermisk, som kräver energi) där det bildade Heliet genom sin större Coulombpotential drivs ut mot stjärnytan och därmed ersätts av motsvarande inströmmande Väte. Därmed hålls effekten (luminositeten) konstant. Utan den förutsättningen gäller inte sambanden. Denna detalj ansluter också helt till definitionen av strålningstrycket enligt TNED.
Tidsekvationen
tidsekvationen
STJÄRNORNAS LIVSLÄNGD
Med Solens effekt eller luminositet Ps som en ideal konstant över Solens hela livstid och dess massa ms som preferens för en fast, given och fullständigt definierad värmebildning av endast EN bestämd typ (Väte-Heliumförbränning), och inget annat i enlighet den generella sfäriskt likformiga divergens som ges av MLR, kan vi alltså bestämma luminositet och livslängd för varje annan solstjärna med utgångspunkt från dess massa.
Massdestruktionen (m®g) i förhållande till hela Solmassan är (i princip) helt försumbar (0,7%) varför vi kan sätta Solmassans preferens som konstant oberoende.
Med E=(m®g)c2=Pt — som i Solens fall med massdefekten i Väte-Heliumförbränningen per väteatom ger
E=1,065 t12 J — ges t=EP–1 [Se även räkneexempel i BAs56sp1m]. Energibidraget totalt per KG i Väte-Heliumfusionerna i Solens fall blir Es= 6,36347 T14 J. [Utförligt i Energibidraget i Solens fall]. För en godtycklig stjärnmassa m [max 60 Solmassor (se J80-MASSAN)] gäller då E=mEsKG–1. Med P = Ps(m3/ms3) ges därmed i fortsättning från ovanstående via t = EP–1 ekvivalenterna
t = mEsKG–1[Psm3/ms3]–1 = mEsKG–1ms3/m3Ps = EsKG–1ms3/m2Ps = m–2 · EsKG–1ms3/Ps = m–2K
= m–2K = (nms)–2K = n–2Kms–2 = n–2 · EsKG–1ms/Ps = n–2Ts .................. tidsekvationen, S
n anger antalet Solmassor ms=1,989 T30 KG. Luminositeten Ps kan beräknas exakt och diskuteras i efterföljande artiklar (Solens tre ekvationer).
Med Es=EsKG–1ms=(6,36347
T14)KG–1(1,989 T30)=1,26569 T45 J taget över 1 miljard år
(T9) ges
EST9 = (EsKG–1ms)/(T9 år)=4,01074 T28 J/(T9 år)
Dividerat med Ps i Watt ges då livslängden Ts för Solen direkt i T9 år så att man får
Ts = EST9/Ps = (4,01074 T28 J)(T9 år)–1 · Ps–1 ..................................... Solens livslängd i miljarder år
t = n–2Ts ............................................................................................... tidsekvationen, S
=
n–2(4,01074 T28
J)(T9 år)–1Ps–1
.................................................... n anger antalet Solmassor
t ges i antal miljarder år, n anger antalet Solmassor, Ps anger Soleffekten.
I gängse fackverk anges Ps=3,9 T26 W [ENCARTA 1999/2004 Sun anger 3,83 T26 W] som ger Ts=102,84 T9 år idealt med fullständig väteförbränning. [Se även motsvarande räkneexempel i BAs56sp1]. Med Solära Råeffekten Ps=3,3 T26 W ges (avrundat neråt) Ts=121 T9 år.
Strålningstryckets radiella variation
gp = p – pe
; allmänna
tryckekvationen,
gp anger strålningstrycket
p = (gr/3)4/3[(4p)1/3Gm22/3], p anger gravitationstrycket (g-trycket)
pe =
gr2[k(Ze/d)2/(pr0)2 = k(Ze/(mA/4r03
– 1)pr02)2], pe
anger Coulombtrycket (e-trycket)
Stjärnan spänns upp på strålningstrycket gp och är full utbildad vid jämvikten gp = p – pe.
Begreppet degenerationstryck förekommer inte i stjärnfysiken enligt TNED.
Se utförligt i degenerationstrycket.
beskrivning
Strålningstryckets utbildning ansvaras för av atomkärnorna, och det är deras geometri och ekvivalenta fysik som bestämmer täthetens medelvärdesform genom stjärnans tryckekvation
p – pe – gp = 0 ........................... stjärnans allmänna tryckekvation
pe ............................................... kärnYTtrycket eller Coulombtrycket, F/A
= k(Ze/d)2/(pr0)2, k=Rc0=(R0/4p)c0 @ 9 T9 VM/C
p ................................................. stjärnYTtrycket eller g-trycket, F/A
= G(m2/r)2/4pr2
gp ................................................ strålningstrycket, F/A
= (aP)2,53387
t16T4 (absorptionskoefficient
0,67), för aP se nedan
NOTERING: gp = (aP) 2,53387 t16T4 med
aP = akP =
2,53387... t16 (N/M2)°K–4
= (a=2/3)(kP=2k/c0=3,781904041 t16 NM–2°K–4)
är strålningstryckets funktion enligt grundformen
gp = akPT4 med absorptionskoefficienten a=2/3 och akP samma som aP. Se även Strålningstryckets funktion.
ANLEDNINGEN varför I DENNA ANALOGI det INTE går att räkna ”konventionellt” på d i elektriska kraftlagens F=k(Ze/d)2 är enkel: KÄRNytTRYCKET gäller inte UTANFÖR atomkärnan. Naturligtvis inte. Kärnyttrycket gäller endast i linje med toppspinnets axel, analogt kärnbrunnen där MAXIMAL Coulombisk ömsesidig elektrisk kraftverkan gäller — ENLIGT TNED.
BERÄKNINGEN AV STRÅLNINGSTRYCKETS VARIATION med avseende på stjärnradien blir alltså SPECIELL. Därmed dikteras den variabla täthetsparametern (r) av atomkärnans cylindriska, eller i total volymuppfyllande analogi rätblockiga, utsträckning V=(2r0)2(r0+d)=4r03(1+d/r0) [Se PLANCKRINGENS DIMENSIONER]. Det går alltså INTE att beräkna d från antagen täthet r=3m2/4pr3 genom d=(mA/r)1/3–r0; Resultaten blir galna (pe avtar långsammare än p och passerar p vid ca r=170 KM. Jämför pe = p – gp som för detta fall skulle kräva gp=0=stendöd stjärna).
Relationerna ger
medeltätheten med konstant massa (d refererar
ekvivalenta kärncylinderlängden), r0 anger
kärnradien (primärt protonradien 1,37 t15 M)
r = (1+d/r0)–1 · mA/4r03 ; ............................. tätheten, från Coulombdistansen, = rn
(1+d/r0) = r–1 · mA/4r03 ;
d = r0([ r–1mA/4r03 ]
– 1) ; ............................. Coulombdistansen, från tätheten, = gd
;
pe = k(Ze/dpr0)2 ........................ = F/A = k(Ze/d)2/(pr0)2 e-tryckets härledning
= r2 · k(Ze/([ mA/4r03 ] –
1)pr02)2
p = G(m2/r)2/4pr2
= G(rV/r)2/4pr2 = G(r4pr3/3r)2/4pr2
=
4pG(rr/3)2
=
4pG(r[3m2/4pr]1/3/3)2
=
(r/3)4/3(4p)1/3Gm22/3
;
p – pe = (r/3)4/3(4p)1/3Gm22/3
– r2k(Ze/[mA/4r03
– 1]pr02)2
= strålningstryckets radiella variation = gp ;
—————————————————
gp = (r/3)4/3aG – r2ae ............. från stjärnornas allmänna tryckekvation, N/M2 med
aG = (4p)1/3Gm22/3
ae = k(Ze/[mA/4r03
– 1]pr02)2
—————————————————
r = m2/V=3m2/4pr3 = rn ....... medeltätheten i stråltrycksbildningen dikteras direkt från
variabeln r
via den fasta stjärnmassan m2:
MED
GIVEN FIX MASSA (m2) bestäms stråltrycksrelaterade
medeltätheten rn via r
enligt r=m2/V=3m2/4pr3.
Samma som den fasta massa med dynamiskt varierande täthet som
stjärnan spänns upp på av strålningstrycket från dag ett.
NOTERING.
En termkonflikt har här uppstått: rn betecknar också normaltätheten från stjärnfysikens
fundamentalteorem. Beteckningen ovan för rn används dock knappast vidare.
Om vidare risk för missförstånd skulle uppkomma, anges detta särskilt i texten.
STRÅLTRYCKSTEMPERATURENS RADIELLA VARIATION
Genom separat härledning av Stefan-Boltzmanns strålningslag och
STRÅLNINGSTRYCKETS
TERMONUKLEÄRA EKVIVALENT
gp = 2ak0T4/c0 = akPT4 med
kP= 2k/c0 = 3,781904041 t16 NM–2°K–4
k = 5,7 t8 WM–2°K–4 ............. experimentellt
= 2p b4p4/15h3c02 ................ teoretiskt, från Plancks strålningslag
= 5,66893154148517 t8 WM–2°K–4
b = Boltzmanns konstant 1,3805502 t23 J/°K
ges därmed även
Stråltryckstemperaturens radiella variation
Tg = (gp/akP)1/4 ......................... gp
beräknas gp=p–pe
med gp som den egentliga variationen i strålningstryckets radiella utbredning enligt föregående härledning.
Absorptionskoefficienten a (se särskild artikel) härleds i samband med strålningstryckets termonukleära ekvivalent och är för alla normalstjärnor (enatomiga stjärnämnen) optimalt lika med 2/3.
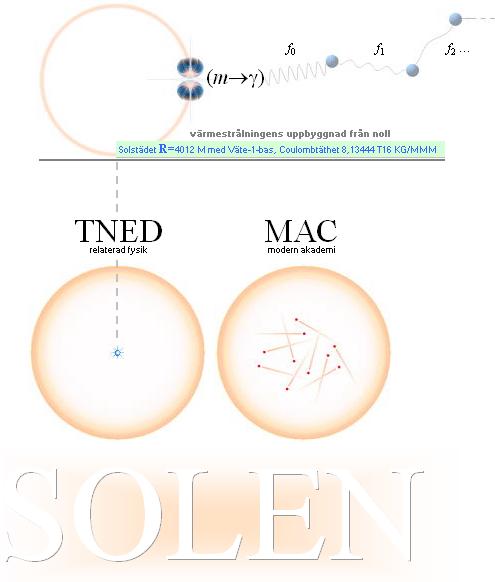
STJÄRNSTÄDET är ENLIGT TNED (cirkelcentrum ovan vänster) den lilla kompakta massiva kärna som avgränsar stjärnans arbetsyta (städytan), och som stjärnan bildas på och som energin produceras ifrån genom (ytterst långsamma) periodiska g-tryckvågor. I konventionell kosmologi (ovan höger) finns ingen teoretisk grund för den typen, utan man tänker sig istället Solen som en sluten behållare som innehåller gas av hög temperatur och tryck där fusionerna bildas kontinuerligt genom slumpvisa kollisioner.
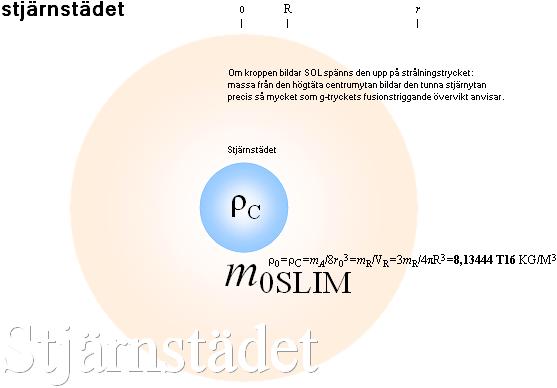
STÄDRADIENS EKVATION se även ovanstående illustration är given från stjärnfysikens fundamentalteorem enligt
R = r(rr/r0)1/4 ................................... stjärnstädets radie, r anger stjärnradien, r0=rC anger centraltätheten, rr anger yttätheten; R ingår inte i MAC
Solen omsätter drygt 2,5 ton Väte-1 till Helium-4 per sekund på varje kvadratmeter vid städytan med radien R=4012 meter som forslas in och ut med effektförbrukningen runt 3,3 T26 Watt. Tjockleken på ett sådant skal med (tätheten r0 och) 2,5 ton kärnmaterial per kvadratmeter kring R mäter 11 stycken omskrivna atomkärnsfärer på rad. En sådan hinna är långt ifrån synlig ens i det starkaste mikroskop. (En mera effektiv värmemaskin än Solen är [således] av allt att döma omöjligt att hitta i universum). Sambandsformerna leder till en energicykelkurva som i princip håller konstant brinneffekt hela Solens livstid — som ett (idealt) alkaliskt batteri med konstant spänning hela tiden.
Stjärnstädets ekvation innefattas i stjärnfysikens fundamentalteorem.
Se även Stjärngränsmassan m0SLIM.
Se utförlig härledning till STÄDRADIEN R.
STÄDRADIEN R
Gravitationens övervikt pressar atomkärnorna in över
varandras nuklidbarriärer. Fusion sker, SOL bildas.
Solsfären spänns ut som en tunn hinna precis på
strålningstrycket gp i stjärnans allmänna tryckekvation.
STÄDRADIEN blir den maximalt täta centralkärna som stjärnan trycker fram fusionsenergin på.
Med vidare beskrivning från stjärnfysikens fundamentalteorem
STÄDRADIENS EKVATION är given från stjärnfysikens fundamentalteorem enligt R
stjärnstädets radie, r anger stjärnradien, ingår inte i Modern akademi
R = r(rr/r0)1/4 ......................... M
Det finns emellertid en liten fördjupning i R som (eventuellt) kan åsamka bryderier om man inte känner till den. Nämligen den absolut minsta städradien.
Givna — r anger kärnradien, Z anger atomnumret ;
rC = r0 = mA/8r3 ...................... maximala Coulombtätheten från given atombas
= 8,13444 T16 KG/M3 ........ maximala
Coulombtätheten, Väte-1-bas
m0SLIM = mA–2Z3 · e1,602
t193p–7/2(288)(k8,98743 T9/G6,67 t11)3/2
= 1,204 T28 KG .................. minsta stjärnmassan med Väte-1-bas (6 Jupitermassor)
= (3m0SLIM/4prn)1/3 .............. rn=3mS/4prS3= 1402,3223 KG/M3 med rS=6,97 T8 M (se Solradien)
= rS(m0SLIM/mS)1/3 = rS(0,1822484)
= 3281,4823 M .................... initiellt minsta städradien
GRÄNSFALLET med 1 = k · rmR från R/r=krmR i stjärnfysikens fundamentalteorem medför följande.
Rmin avser en stjärna med endast 1/165 av Solens massa. SOLSTÄDETS RADIE bör därför vara något större än Rmin, motsvarande ett R+Rmin. (Fetstilen för R, absolut minsta städradien, används här av bekvämlighetsskäl för att slippa floran av suffix).
STRÅLNINGSTRYCKET (gp) UTGÅR FRÅN STÄDET (R=rmSLIM=3281 M för vätebas). Gasen tvingas därmed expandera — med MOTTRYCKET i konstant inåtriktad form på städkroppen (mSLIM=6 Jupitermassor för vätebas). Städets STÖTYTA utvecklar exakt den energi som differensen mellan initierande g-tryck (p) och Coulombtryck (pe) ger.
STÄDRADIENS EKVATION är given från stjärnfysikens fundamentalteorem enligt
stjärnstädets radie, r anger stjärnradien, ingår inte i Modern akademi
R = r(rr/r0)1/4 ........................... M
För att kunna bygga en stjärna som slutar på alla oroterade stjärnors konstanta medeltäthet rn=1402,3223 KG/M3 med rS=6,97 T8 M, från ett uns över gränsmassan 1,2 T28 KG med primärradien 3281 meter på ett arbetsstäd med maximala Coulombtätheten r0=8,13444 T16 och yttätheten rr=8,9277145 t5 KG/M3, och följaktligen radien
rmin=r0SLIM=1,27027 T8 M, MÅSTE dynamiken tvunget TA av den befintliga gränsmassan (m0SLIM) och kvarlämna ett centralt arbetsstäd i r0 med radien
R=r0SLIM(rr/r0)1/4=731,1384 M. (Fetstilen för R, absolut minsta städradien, används här av bekvämlighetsskäl för att slippa floran av suffix). Det är alltså uppenbart att R<Rmin i fallet med den allra minsta stjärnan.
Vi sätter RSOL= R+Rmin= R för Solens städradie som ger
R = R – Rmin
= rS(rr/r0)1/4 – Rmin = rS(rr/r0)1/4 – (3m0SLIM/4prC)1/3
= rS(rr/r0)1/4 – (3m0SLIM/4pmA/8r3)1/3
= rS(rr/r0)1/4 – (3m0SLIM8r3/4pmA)1/3
= rS(rr/r0)1/4 – (3mA–2Z3
· e1,602 t193p–7/2(288)(k8,98743 T9/G6,67 t11)3/28r3/4pmA)1/3
= rS(rr/r0)1/4
– (mA–2Z3 · e1,602 t193p–9/2(1728)(k8,98743
T9/G6,67 t11)3/2r3/mA)1/3
Med yttäthetskonstanten rr beräknad från kapacitivitetstalet, rr= 8,9277145 t5 KG/M3, beräknas Solradien från Solmassan 1,989 T30 KG som beräknas via kärnparametrar och Keplers tredje lag [Från avståndet Jorden-Solen 1,496 T11 M och Jordens anomaliska omloppstid (365,2596425 d) kring Solen][Se särskilt i Solmassan] enligt
re0S = [rr(8/mA)–1/3/r0]–1/4(3/4p)1/3[(1/m0SLIM)1/3
– (1/mS)1/3]–1
= 6,97063467 T8 M ............................ SOLENS MASKINRADIE
Därmed
R = 731,1384 M ...................... absolut minsta städradien, Väte-1-bas
Eller direkt från R-sambandet med r för re0S = 6,97063467 T8 M (värdena varierar något beroende på preferens),
R = r(rr/r0)1/4 ......................... stjärnstädets radie, r anger stjärnradien, R ingår inte i konventionen
= r(5,75576545 t6) =
4012,1338 M .................... Solens städradie
R =
R – Rmin =
731,0696 M ...................... absolut minsta städradien, Väte-1-bas
Yttäthetskonstantens
koppling till Solradien
YTTÄTHETSKONSTANTEN (rr) med Solen som referensstjärna kan skrivas rr=r0([R+Rmin]/rS)4 med RSOL= R+Rmin= R som ovan i rr=r0(R/r)4 från stjärnfysikens fundamentalteorem, och R som städradien. Med R=r0SLIM(rr/r0)1/4 ges rr=r0(R/r0SLIM)4. Därmed fås ekvivalenterna
rr = r0(R/r0SLIM)4 = r0([R+Rmin]/rS)4
Ur de bägge sista delarna framgår minsta stjärnmassans städradie R, samt därmed Solens städradie och därmed yttäthetskonstanten rr enligt
R/r0SLIM = [R+Rmin]/rS ;
rS/r0SLIM = 1+Rmin/R ;
Rmin/R = rS/r0SLIM – 1 ;
R = Rmin(rS/r0SLIM – 1)–1 ; .................. minsta städradien, Väte-1-bas
rr = r0([R+Rmin]/rS)4
Vidareutveckling ger
r0
CENTRALTÄTHETEN se nedan
R+Rmin = Rmin(rS/[rS – r0SLIM])
[R+Rmin]/rS = Rmin/[rS – r0SLIM]
rr = r0(Rmin/[rS – r0SLIM])4
Rmin = (3m0SLIM/4pr0)1/3
r0 = mA/8r03
.................................................... centraltätheten, kubiska block, se ill.
ovan
;
rr = r0((3m0SLIM/4pr0)1/3/[rS – r0SLIM])4
= r0–1/3((3m0SLIM/4p)1/3/[rS – r0SLIM])4
= (mA/8r03)–1/3((3m0SLIM/4p)1/3/[rS – r0SLIM])4
= (8r03/mA)1/3((3m0SLIM/4p)1/3/[rS – r0SLIM])4
= r0(mA/8)–1/3((3m0SLIM/4p)1/3/[rS – r0SLIM])4
m0SLIM = mA–2Z3
· e3p–7/2(288)(k8,98743 T9/G6,67 t11)3/2
r0SLIM = (3m0SLIM/4prnom)1/3
…
rr = r0(1/[rS/Rmin – r0SLIM/Rmin])4
= r0(1/[rS/Rmin – (r0/rnom)1/3])4
= r0(1/[(mSr0/m0SLIMrnom)1/3 – (r0/rnom)1/3])4
= r0(1/(r0/rnom)1/3[(mS/m0SLIM)1/3 – 1])4
= r0((rnom/r0)1/3/[(mS/m0SLIM)1/3 – 1])4
= r0–1/3(rnom1/3/[(mS/m0SLIM)1/3 – 1])4 .........................................
rnom = 3mS/4prS3
rnom1/3 = (3mS/4p)1/3rS–1
rr = r0–1/3((3mS/4p)1/3rS–1/[(mS/m0SLIM)1/3 – 1])4
= r0–1/3((3/4p)1/3rS–1/[(1/m0SLIM)1/3 – (1/mS)1/3])4
r0–1/3 = r0(8/mA)1/3
;
rr =
r0(8/mA)1/3((3/4p)1/3rS–1/[(1/m0SLIM)1/3
– (1/mS)1/3])4 ...............
Sambandet ovan används för beräkning av Solradien (rG) genom Solens Tre Ekvationer.
Yttäthetskonstanten · Solens Tre Ekvationer · Solens 3 Ekvationer · Solens Unikitet · Solens Gravitella Radie
2007XII16
Solens
3 Ekvationer
SOLRADIEN FRÅN YTTÄTHETSKONSTANTEN
— Hur yttäthetskonstanten beräknas
SOLENS TRE EKVATIONER
STJÄRNORNAS LUMINOSITET OCH VÄRMEGRADENS RADIELLA VARIATION
p ® T:
den enda temperaturgenererande faktor som en stjärna alls kan besitta ges från
strålningstrycket, som kommer från fusionsenergin;
jämvikten med g-trycket definierar funktionen
referenssamband
1=R0c0mS/M2t3; t @ 6 T13 S @ 2 miljoner år … se utförligt längre ner från Solen Identifieras
P
VM KG
rr2Gc0
——— = e0 ——— · ——— = —————
A2 C M2S3
18
beskrivning
STRÅLNINGSTRYCKETS FUNKTION p®T enligt p=akPT4 bildar fasta tillståndets värmezoner på varje sfärisk skalyta r med given lokal täthet r=dm/dV. Differentialformen gäller tydligen explicit VID r. Genom att utnyttja g-tryckets allmänna form vid randen av r för en given homogen innesluten massa m — FÖR EN VISS BESTÄMD STJÄRNMASSA (m) — enligt
p =
F/A=G(m/r)2/4pr2=G(m)2/4pr4 = akPT4
................. se STRÅLNINGSTRYCKETS
FUNKTION
kan täthetens homogena normalform r=m/V användas direkt eftersom den i vilket fall endast avser det g-tryck — och därmed det partiella strålningstryck — som gäller i klotytan.
Strålningstryckets värmebildning
kommer på detta sätt i vilket fall att arbeta på DEN LOKALA tätheten r=dm/dV. Vilket vill säga, exakt VID r.
TERMISKA JÄMVIKTEN bestäms då av det lokala g-trycket via lokala tätheten kontra lokala värmegraden.
Vi skiljer alltså — skarpt — mellan värmegrad (T) och stråltrycksgrad (Tg, strålningstryckets temperaturekvivalent):
OBSERVERA att strålningstryckets egen temperaturekvivalent (stråltrycksgraden Tg) har medelvärdestäthetens momentanvärde via stjärnans fasta massa som variabel. Värmegraden däremot (T) har den lokala vanliga tätheten r=r0(R/r)4 som variabel. Insättning av r=r0(R/r)4 i m från p ovan ger då via
m=rV=r · 4pr3/3 som ger
G(m)2/4pr4 = G(r4pr3/3)2/4pr4 = 4pG(rr/3)2 = p = akPT4 ;
(rr/3)2 =
p/4pG
= akPT4/4pG
r0=rC
e0=1/R0c0 elektriska
konstanten C/VM = A/VMS = 8,8543 t12 C/VM
Solparametrarna från kapacitivitetstalet för vakuum (e0=1/R0c0) — vidareutvecklingar från strålningstryckets samband
Täthetens
radiella variation r=r0(R/r)4 ger alltså (r · r/3)2=([r0(R/r)4]r/3)2=([r0R4/r3]/3)2=r–6(r0R4/3)2.
Därmed
p=akPT4=4pG(rr/3)2=4pGr–6(r0R4/3)2 som ger T4 = (akP)–1 r–6 4pG(r0R4/3)2 ;
(1) Ta = (4pG/akP)1/4 r–3/2
(r0R4/3)1/2 ...................... värmegradens radiella. variation, °K
VID YTAN gäller r0R4=rrr4 som ger
(2) Tar = (4pG/akP)1/4 r1/2
(rr/3)1/2 ........................... stjärnytans värmegrad, °K
Med Tar4 = (4pG/akP) r2 (rr/3)2 = a–1(4pG/kP) r2 (rr/3)2 ges slutligen från Stefan-Boltzmanns strålningslag
P = aAkTar4 ................................................. stjärnans allmänna effekt
= aAk · a–1(4pG/kP) r2 (rr/3)2 = Ak · (4pG/kP) r2 (rr/3)2 ; 4pr2=A ;
= A2 · k5,67 t8 · (G6,67 t11/kP 3,78 t16)
(rr8,98 t5/3)2 ; kP = 2k/c0;
SOLEN IDENTIFIERAS via e0=(rr)2(Gc0/18)CMS3V–1(KG)–1
(3) utpekar en
bestämd typstjärna:
P = A2e0(1VM–1C–1S–3KG)
= 3,3011376 T26 W .................................. se även Solens Fotometriska effekt (konv. 3,846 T26 W [Wikipedia Sun 2009-03-23])
beskrivning
rrGc0 i (3) är konstanter som ger P/A2=konstant=rr2Gc0/18.
Men P/A2 är ingalunda en konstant
i det allmänna fallet.
bevis
I det allmänna fallet gäller från Stefan-Boltzmanns strålningslag P=aAkT4 att P/A2=akT4/A=variabel. P/A=akT4 är variabel. Men enda sättet att eliminera en variabel v genom införande av faktorer är att införa variabelns invers enligt v·v–1=1. I fallet med substitutionen A/A och ledvis överflyttning ökas istället variabelns potens. Därmed är det klart att P/A2=akT4/A=variabel om P/A är det.
följdsats:
Det är alltså tydligt att P/A2=konstant=(KG/M2)/S3=(m/M2)/t3 utpekar en bestämd typstjärna med bestämd massa, MASSYTSKONSTANT (m/M2) och radie — och därmed också en bestämd primär egenrotation.
Utan den sistnämnda parametern är stjärnans exakta fysik obestämd: en högre primär egenrotation dämpar stötenergin i stjärnstädet på grund av centrifugalkraftens motverkande funktion och därmed en reducerad effekt.
MED
SUBSTITUTIONEN 1=(e0/e0) i P/A2=konstant=KG/M2S3
ges
P/A2
= (e0/e0)mS/M2t3
= (R0c0e0)mS/M2t3
= e0 · R0c0mS/M2t3.
Separat undersökning visar med konventionella Soldata som grund att Solens primära egenrotation inte får överstiga max 0,00023 Hz om Solradievärdet 6,96 T8 M ska vara korrekt i tredje decimalen. Högre primärrotation [Se ROTATIONENS INVERKAN PÅ STJÄRNANS FYSIK] betyder att stjärnytan drastiskt utvidgas och därmed en växande osäkerhet i mätningarna för Solens del. Det visar sig att t-faktorn i ovanstående samband uppfyller villkoret om man sätter
1 = R0c0mS/M2t3
som ger
t = (R0c0mS/M2)1/3
= 6,07892 T13 S
Primärrotationen f0 kan beräknas idealt ur slutvärdet (f=1/t) vid fullt utbildad stjärna [Se utförligt från STJÄRNORNAS OMFÅNG] enligt
f0 = (r/R0)2f ............ R0=(3m2/4prmax=1,82 T17)1/3
Solmassan beräknas klassiskt ur Keplers
tredje lag mSTARG/4p2=R3/t2 från den
kända anomaliska omloppstiden (365,2596425 dygn) och avståndet Jorden-Solen (1AU@1,496 T11 M). I Solens fall ges
mSTAR = 1,98941 T30 KG.
I rotationsfallet (f –1=6,07892 T 13 S) ges f0=4,20476 t5 Hz. Marginalen mot 2,3 t4 Hz är alltså god.
Därmed garanteras en nära helt ideal primär effektparameter med en maximalt avgränsad och fokuserad kroppsrand.
Antas ovanstående, ges
e0 = rr2(Gc0/18)·CMS3/V(KG) enligt
P
VM KG
rr2Gc0
——— = e0 ——— ·
——— = —————
A2 C
M2S3 18
rr2 = 18e0/Gc0 · VM–1C–1S–3KG ;
rr = 8,9277145 t5 KG/M3yttäthetskonstanten
rr
= 8,9277145 t5 KG/M3 .................... yttäthetskonstanten, primärt oroterade
stjärnor
DÄRMED KAN via Solradiella yttäthetsekvivalenten (separat beskrivning med härledning från Stjärnstädet)
rr = r0(8/mA)1/3((3/4p)1/3rS–1/[(1/m0SLIM)1/3
– (1/mS)1/3])4
den unika Stjärn(Sol)radien BERÄKNAS DIREKT (för prövning mot Solära fotometriska observationsvärdet rF=6,96 T8 M (±0,002 T8 M) för fastställande av unikiteten i ovanstående självutpekade sambandsformer) ur elektriska kapacitivitetstalet för vakuum (e0) via Keplers tredje lag från avståndet Solen-Jorden och omloppstiden för Jorden kring Solen. Man får då
Solens elektrogravitella radie rS=rG enligt
rG = [rr(8/mA)–1/3/r0]–1/4(3/4p)1/3
· [(1/m0SLIM)1/3 – (1/mS)1/3]–1
rG = [rr(8/mA)–1/3/r0]–1/4(3/4p)1/3·[(1/m0SLIM)1/3
– (1/mS)1/3]–1
= 6,97063467 T8 M .......................... SOLENS MASKINRADIE
— större än synliga Solradien med ca 1000
KM
rG-värdet blir ca 1000 KM större än synliga Solradien, vilket också stämmer kvalitativt med TNED (se vidare från Solens Vågenergi och Fusionsperioden). Därmed är Solen identifierad som den unika stjärnan som stämmer överens med ovanstående utpekade samband.
Den låga egenrotationen i Solens fall (f0=4,20476 t5 Hz) garanterar att rr kan likställas med en praktiskt taget primärt idealt oroterad stjärna som därmed får utgöra preferens.
Solens råa effekt (PS), oberoende av temperatur (T) och absorptionskoefficient (a) kan därmed beräknas enligt (3)
P = A2 · rr2Gc0/18 ...................................... effekten oberoende av T och a
= A2e0·1VM–1C–1S–3KG
= 3,3011376 T26 W
Se även Solens Fotometriska effekt (konv. 3,846 T26 W [Wikipedia Sun 2009-03-23]).
KVALITATIVA DELEN — från Solens fyra värmegrader
FOTOMETRISKA EFFEKTEN
Ytljusstyrkan vid Solytan påverkas mycket litet av strålningstrycket vid Solytan i förhållande till hur strålningstrycket påverkar de mycket tätare liggande atomerna i ett fast material, t.ex. en fotometer (på behörigt Solavstånd).
FOTOMETRISK MÄTNING på Solen ska realt avse strålningstryckets värmebildande effekt på Solytan (vars ljusstyrka ska mätas), analogt Solkroppstemperaturens koppling till ytljusstyrkan, eller med samma innebörd Solens effekt.
Inte på fotometerns betydligt tätare materierum.
Fotometern ska mäta på Solytans material. Inte på fotometerns
material. Men strålningstryckets värmegradsbildande funktion garanterar att
inverkan på fotometerns tätare materierum är större än inverkan på Solytans
betydligt tunnare materierum: Fotometern kan inte obetingat mäta på Solytans
materierum.
Fotometern ska idealt mäta på den VERKAN som strålningstrycket
åstadkommer på Solytan: verkan ska avse värmegraden med effekt och ljusstyrka
som kopplar till sambandsformerna (Stefan-Boltzmanns strålningslag) och som
studeras i den täta materiens Jordiska laboratoriemiljö — och vilken
värmegradsverkan antas utbredas från Solytan via em-strålning för att träffa
till exempel känselytan på en fotometer.
Men fotometern och alla andra föremål utsätts i verkligheten för strålningstryckets inverkan som en separat fenomenfaktor vid sidan av den (avlägset) sekundära värmebildning som strålningstrycket åstadkommer — som i fallet med Solytan.
Solytans
värmegrad (T) ges av strålningstrycket
(se Solens Fyra Värmegrader, Värmebildningen). Solytans värmegrad och dess emissioner blir
därför av en sekundär termisk ordning. Det är Solytan vi vill mäta på, men
fotometern kan inte gömma sig för strålningstryckets inverkan generellt utan
lägger denna till Solytsemissionerna. Fotometerns elektronemission — flödet av elektroner som
funktion av energin i det TOTALA inflödet av em-strålning — blir därför beroende inte
bara av emissionerna från Solytan som gavs av strålningstrycket där,
utan även av den lokala strålningstrycksverkan på själva fotometermaterialet.
Strålningstryckets värmegrad (Tg) och fotometriska objektets värmegrad (T Solytan) är INTE analoga. T bildas ur Tg, varav fenomenformen (Jordmaterialens experimentella motsvarigheter) T (som övergår i TP från Solytan) ska mätas via fotometer men vars materierum INTE kan frikopplas från Tg lokalt. Därmed åstadkommer lokala Tg på fotometermaterialet (som fotometern för sin del idealt INTE vill se) ett extra energigenomflöde och därmed ett elektronbaserat energiflödesfel i mätningen.
Tätheten vid Solytan är f.ö. runt en tiondels gram per kubikmeter. Det är 25 miljoner gånger mindre än Jordytans genomsnittstäthet 2,5 ton per kubikmeter.
Snarare än att mäta på ljuset från den glesa
Solytan, mäter fotometern på termonukleära strålningstryckets inverkan på den
fasta materiens täta atomavstånd: fotometern.
Fotometriska energiflödesfelet kopplar DÄRMED tvunget till de skilda atommedelavstånden (dC/dS) i de olika materierummen fotometern/Solytan.
Genom aritmetiska undersökningar framkommer följande
bild i beskrivande klarhet.
atomavstånden enhetsdistansens värmegrader
dS/dC (Tg/TP)LOC
——————— = ——————— = b
P/(Pmät – P) (Tg/TP)SUN
effektvärdena Solytans värmegrader
beskrivning
Förhållandet mellan Tg och Tw
(Solytan/AlltUtanför) är konstant (5,2561744519...) och oberoende av avståndet från Solytan. Förhållandet mellan
endera Tg-Tw och TP däremot
varierar med avståndet från Solytan.
Nu är det emellertid som nyligen omnämndes just T →TP samt TW som bildar preferens i mätdata
för Solens effekt och luminositet med motsvarande fotometriska (och
spektroskopiska) instrumentella mätobservationer — med Tg som värmegrunden för samtliga T.
Det faktum att (TgELLERTw)/TP
inte är analoga och inte oberoende av avståndet
till Solytan, samt att FOTOMETRISKA MÄTNINGEN enbart vill ha TP-formen och inget annat men att den ordningen INTE är fysiskt
möjlig, betyder att fotometriska mätningen påtvingas Tg. Men inverkan från Tg betyder ett högre
energigenomflöde än det som skulle mätas via TP. Därmed benämningen
fotometriska effekten: mätvärdet blir för högt.
Solytans
värmegrader kan beräknas först med kännedom om Solradien. Men Solradien kräver
förutom kärnfysikaliska parametrar kännedom om Solmassan, och den kan bara, vad
vi vet, ges från enhetsdistansen 1 AU — medelavståndet Jorden-Solen
1,496 T11 M — via Keplers III:e lag:
w2 = Gm2/r= (2pr/T)2 =
4p2r2/T2 ; Gm2/4p2 = r3/T2
; m2 = (4p2/G)(r3/T2).
Förhållandet mellan värmegradsgradienterna respektive vid Jordbanan/Solytan kan då sägas bilda en MODUL (grundpreferens) för anomalierna mellan ”den normala laboratoriets värmegrad” T(Planck) och den i moderna kvarter mindre bekanta strålningstryckets värmegradsekvivalent Tg.
Det visar sig nu att förhållandet mellan värmegradsgradienterna (Tg/TP) respektive vid Jordbanan/Solytan kan ställas i likhet med förhållandet mellan atommedelavstånden (dS/dC) Solytan/FastaMaterien och effektvärdena reala/uppmätta P/(Pmät – P) enligt
atomavstånden enhetsdistansens värmegrader
dS/dC (Tg/TP)LOC
——————— = ——————— = b
P/(Pmät – P) (Tg/TP)SUN 14,6497311
effektvärdena Solytans värmegrader
(Tg/TP)-värdena kan beräknas (kvoten ger b=14,6497311) liksom dS-värdet (kubiska, 2,65632 t8 M) samt P-värdet 3,3 T26 W. Pmät-värdet är känt [ENCARTA (1999-2004-) Sun 3,83 T26 W; Wikipedia Sun 2009-03-23 3,846 T26 W] ca 3,84 T26 W. Därmed kan atommedelavståndet dC i den fasta materien som motsvarar fotometriska anordningens materierum beräknas (eg. kontrolleras), och man finner värdet 2,96 Å. Det är en utomordentlig bekräftelse på sambandets giltighet.
Pmät = P[1+ b(dC/dS)] ......................................... fotometriska effekten
fotometriska effektvärdet med
dC
= 2,96 Å och
dS = (mAu/rr)1/3=2,65632 t8 M=266 Å och
b = 14,6497311 och
P = 3,3011376 T26 W
= 3,84087 T26 W ¦ Det uppmätta värdet enligt ENCARTA (1999-2004-)Sun anges 3,83
T26 W; Wikipedia [NASA] Sun (2009-03-23) 3,846 T26 W
KVANTITATIVA DELEN — Hur
Soleffekten beräknas från instrumentell spektroskopisk observation
FOTOMETRISKA EFFEKTEN
Se även KVALITATIVA DELEN ovan.
så räknar man
Uppmätt värde (typiskt) i intensitetsfördelningen för Solkroppens värmestrålning (Wientoppen eller Plancktoppen)
l = 4 983 Ångström = 4,983 t7 M;
Man använder Wiens förskjutningslag (toppvärdet för Planck-kurvskarans primärvärmekurva, se även Plancks strålningslag)
T = k2,898 t3 M°Kl–1
Det ger värmegradens ekvivalent
T = k2,898 t3 M°K(4
983 t10)–1 = 5806 °K
Antas T-värdet SOM OM Solen vore en absolut svart kropp — utan varje spår av reflekterande egenskaper — fås via Stefan-Boltzmanns strålningslag ytljusstyrkan
P/A = k5,7t8T4
= 6,44 T7 W/M2
Effekten blir med Solradien (fotosfären) r = 6,96 T8 M lika med
P = (4pr2)(6,44 T7) = 3,92 T26 W [BAs9 anger 3,9 T26 W].
Jämförande citat
”Solens effektiva temperatur,
5800 K, är direkt relaterad till dess ytljusstyrka, som är 6,44 × 107
watt/m2. Enligt Stefan‑Boltzmanns lag motsvarar nämligen detta
strålningsflöde det flöde man kan vänta sig från ytan av en s.k. svart kropp
vars temperatur är just 5800 K. Man bör emellertid hålla i minnet att
temperaturen varierar med djupet i solatmosfären. Det är i och för sig möjligt
att definiera en slags medeltemperatur för de synliga skikten i atmosfären —
den effektiva temperaturen är en sådan, och flera andra definitioner, som alla
ger något olika resultat, har kommit till användning — men alla dessa
definitioner har sina begränsningar.”
BONNIERS ASTRONOMI 1978 s130sp2n
BERÄKNINGEN kan (alltså) inte genomföras fullt ut därför att absorptionskoefficienten som normalt figurerar i Stefan-Boltzmanns strålningslag INTE är känd för Solytan — ehuru man vet att den i vart fall är mindre än 1. Jämför:
”S:s verkliga temperatur
undandrar sig beräkningar; den är emellertid större än S:s effekti’va
temperatur [den temperatur, som en absolut svart kropp (se Strålning)
med samma skenbara storlek som S. måste äga för att utstråla samma värmemängd
som S.], vilken beräknats till 5,600°—6,000°.”
BONNIERS KONVERSATIONSLEXIKON X 1927 sp1158
Se även utförligt i kvalitativa delen till
STJÄRNMASSANS RADIELLA VARIATION
— härledning
Med stjärnfysikens fundamentalteorem givet, med yttäthetskonstanten
r = r0(R/rR)4 = r0(1+r/R)–4
fås GRAFISKA
INTEGRALEN (för utförlig beskrivning av integral, derivata och
differentialbegreppen, se från Relaterad
Fysik och Matematik)
ò r0(1+r/R)–4 dr = –r0R(1+r/R)–3/3 + r0R/3
= (r0R/3)[1 – (1+r/R)–3]
................ ytan växer
med r mot gränsvärdet (r0R/3)
FYSISKA
INTEGRALEN är knepigare. Eftersom grafiska ytvärdet har ett bestämt gränsvärde
kommer också massan i varianten r=dm/dV att få ett högsta värde.
Eftersom ett sådant bara kan motsvara stjärnmassans absolut största värde (mMAX), måste en konstant (k) införas i varianten enligt
rk=kr0R4rR–4=dm/dV. Differentialekvationen blir då
dm = kr0R4 · rR–4dV
............................................................. rR=r+R
med V=4pr3/3. Differentialtransformationen från dV
till drR
blir dV/dr=V’=(4p/3)
Dn r3=(4p/3)
· 3r2=4pr2 som ger dV=4pr2dr med r=rR. Därmed den fullständiga differentialekvationen
dm = kr0R4 · rR–44pr2drR = k4pr0R4 · rR–2drR ;
ò dm = k4pr0R4 ò rR–2 drR ;
m = –k4pr0R4rR–1 ;
Arbetsmassan (m) är noll vid rR=R; vi bestämmer integralkonstanten vid motsvarande rR=R:
m(0) = –k4pr0R3 ;
Arbetsmassan
kan då skrivas på den bestämda integralen
m =
k4pr0R3 – k4pr0R4rR–1
=
k4pr0R3(1 – RrR–1)
=
k4pr0R3(1 – [1+r/R]–1)
Vid r=0
blir också m=0. För att få med mSLIM
gäller fullständigt stjärnmassans
radiella variation
m = k4pr0R3(1 – [1+r/R]–1) + mSLIM
m = kSTAR(1 – [1+r/R]–1) + mSLIM
................ stjärnmassans
radiella variation, OBS r räknas från
städradien R.
Med kända MAX m vid MAX r och städradien R och stjärngränsmassan mSLIM kan kSTAR därmed beräknas för varje OROTERAD stjärna direkt enligt
kSTAR = k4pr0R3 = (mSTAR – mSLIM)(1 – [1+(rSTAR–R)/R]–1)–1 KG = masskonstant för varje specifik stjärna
OBSERVERA ovan att r/R=(rSTAR–R)/R eftersom r måste räknas från R,
inte från 0;
kSTAR =
k4pr0R3 = (mSTAR – mSLIM)/(1 – R/rSTAR)
KG
Därmed stjärnmassans radiella variation mellan R och r som ovan enligt m.
kSTAR för Solen är 1,97697 T30 KG (Solmassan dividerad med 1,0060901) med R=4012 M, rG=6,97 T8 M och mSLIM=m0SLIM =1,204 T28 KG.
Med klarläggandet av SOLENS FOTOMETRISKA EFFEKT kan alla (primärt oroterade) stjärnor beskrivas generellt till sin allmänna effektförbrukning.
STJÄRNORNAS EFFEKTFÖRBRUKNING
Från Solens 3:e Ekvation gäller råeffekten
P = A2 · rr2Gc0/18 ............................. Solens totala temperaturoberoende råeffekt
= A2e0·1VM–1C–1S–3KG
= 3,3011376 T26 W
Med MASSA-LUMINOSITETSRELATIONEN (konstant volymenergi per kubikkilo) PPs–1= (m/ms)3 ges då för alla stjärnor (Väte-1-bas) motsvarande
P =
(mSTAR/mS)3 · AS2rr2Gc0/18
= (mSTAR/mS)3
· AS2e0·1VM–1C–1S–3KG
Solens
kapacitans · Råvärden · Från idealt statisk Solkropp
utan avskärmande effekter (HELA laddningsmängden
räknas) ·
C = Q/U = R4012
· (4pe0)1,11266 t10 = 4,46399 t7 F; Qbegin=2,46708 T19 C; Qend=Qbegin/2; Ubegin=Qbegin/C=5,52662 T25 V
SOLENS
KAPACITANS
Totalt ENLIGT TNED i Solen [Se Solens Energiräkning nedan] bildas i genomsnitt per sekund ca Ne+=15,4 T37 positronmassor e+ — av totala elektronladdningen 1,18865 T57 elektronmassor. IDEALT HÄLFTEN kvarstår vid Solenergins slut. Räkningen baseras på TNED-råvärdet från Soleffekten 3,3 T26 W [se fotometriska effekten 3,84 T26 W]. Per sekund och i genomsnitt under Solens hela livstid bränns alltså lika många Ne+=15,4 T37 positronmassor som elektronmassor.
Strålningstrycket garanterar att uppströmningen av det bildade, mera laddningstunga, 2+-joniserade 2He4 från det centrala Solstädets mantelyta uppvägs av ned- eller inströmmande joniserat Väte-1, dessa bägge strömriktningar (netto) tar (således) ut varandra. Återstår: den positronström (ie+ =Q/t) som bildas från städet, som transporteras till Solytan i kraft av strålningstrycket, och som annihileras i ytan tillsammans med motsvarande e–. Följaktligen, reala strömmar, finns i egentlig mening bara en konstantström ie+ enligt
forts.
Solens
energiräkning — allmän referens
4([14,5–1,5=13] me 9,11521 t31)c3T82=4,26591 t12 J .............................. energin från fyra väteatomer till en helium-4-atom
3,3 T26 W
........................................................................................... Energiutgivningen per sekund enligt
TNED, se Solens Råeffekt
Antal H-He-fusioner per S: (3,3 T26 W)/(4,3 t12 WS) @ 7,7 T37
He-4-massa:
4×1,66033 t27 KG × 7,7 T37 = 5,11381 T11 KG @ 5 T11 KG per S
Med konventionella
avrundade effektvärdet P = 4 T26 W ges
He-4-massa:
4×1,66033 t27 KG × 9,3 T37 = 6,17642 T11 KG @ 6 T11 KG per S
Antalet
7,7 T37 motsvarar också antalet bildade positronpar per sekund;
SEKUNDMEDELVÄRDET FÖR Antalet positroner som ska brännas av per sekund blir
alltså
Ne+
= 15,4 T37
Den
motsvarande elektronmängden ger laddningen
Qe– = 15,4 T37 × 1,602 t19 C = 2,46708 T19 C
Energibidraget totalt per KG i
Väte-Heliumfusionerna i Solens fall
FÖRKLARINGAR TILL SAMBANDSFORMERNA
Varje Väteatom bidrar med atomära massdefekten i elektronmassor (e) genom massdefekten för Helium (14,5) minus den för Väte (1,5) enligt
14,5–1,5=13
Massdefektens energibidrag explicit per Väteatom blir (värdena här blir mera noggranna än ovan)
E=mc2=me 9,11521 t31 C(13)c2,99792458 T8 M/S2 = 1,065 t12 J
Antalet likadana atomer i massan M KG med atomvikten U i atomära massenheter u är för samtliga fall
N=M/uU
Väteatomens atomvikt är (avrundat) 1,008 — eller approximativt 1 om vi bara söker grovvärden. För 1 KG Väte gäller antalet Väteatomer
N=(1KG)/u1,66033 t27 KGU1,008 =
5,97509 T26 @ 6 T26
Energibidraget totalt PER KG i massförbränningen från Väte till Helium blir alltså
E= N · mc2 = 5,97509 T26 · 1,065 t12 = 6,36347 T14 J
Detta värde kan användas genomgående i en grovberäkning för alla stjärntyper.
Maximala livslängden räknas sedan via L=E/t via tidsekvationen enligt
t =m2(E/KG)/L
med m2 som stjärnmassan.
forts
ie+ = Q/t = e(15,4 T37)/S =
2,46708 T19 A.
En sfär med halva Solradien genomträngs av denna ström (medelvärdet) med litet drygt 16 A per kvadratmeter.
KONDENSATORLAGEN C=Q/U med U=E/Q=Fr/Q=Q(r · 4pe0)–1 ger för spänningen varianten (se Derivata och Integral i Relaterad Fysik och Matematik)
dU/dr=X=F/Q=Q(4pr2e0)–1.
Då ges för en sfärisk kondensator [ref. Teknisk Elektricitetslära, E. Danielson Gleerups 1965, s138] differentialekvationen dU=Q(4pr2e0)–1 dr med lösningen
òdU=U=òQ(4pr2e0)–1 dr = –Q(r · 4pe0)–1
Spänningen går mot oändligt då r går mot noll. Distansen r=d måste alltså anställas på en minsta möjliga offsetradie, lika med städradien R=a, från vilken d utgår så att man får lösningen
U=–Q(4pe0)–1(a+d)–1. Integralens bestämda form blir då
U=–Q(4pe0)–1(a+d)–1
– –Q(4pe0)–1(a)–1 = Q(4pe0)–1[(a)–1
– (a+d)–1].
Kapacitansen C=Q/U blir
C = (4pe0)[(a)–1 – (a+d)–1]–1
= (4pe0)[a–1 – b–1]–1
= (4pe0)1,11266 t10 · ab(b – a)
med städradien a=R och stjärnradien b=R+d=r. Eftersom b–1 är försumbart relativt a–1 ges direkt praktiskt
C = a · (4pe0)1,11266 t10 ....................... stjärnklotets kapacitans, Farad, a anger stjärnans städradie
Solens städradie är a=4012 meter. Solklotets maximala kapacitans blir alltså
CSOL = 4,46399 t7 F eller 0,4464 µF.
Värdet motsvaras av en ordinär (liten, vanlig) avkopplingskondensator. Men kolla spänningen:
Eftersom Solen vid sitt slut idealt omvandlat allt Väte-1 till Helium-4, har utgångsladdningen i e–-stocken halverats genom avbränningen mot positrondelen som bildades från deuteriumfaserna i fusionerna. Med konstant kapacitans C=R(4pe0)1,11266 t10=Q/U ändras alltså Q från
Qbegin=2,46708 T19 C till Qend=Qbegin/2 med tillhörande spänning
Ubegin =
Qbegin/C = 5,52662 T25 V och slutvärde Uend = Ubegin/2 = 2,76331 T25 V
(Nuvärdet ger 5,0511479 T25 V via [SolensNuvarandeÅlder20,82]/[SolensIdealaLivslängd121], se Tidsekvationen).
från Strålningstryckets Kraftekvivalent
SOLKLOTETS
ELEKTRONFRIHET
SOLENS POLARISATION
STRÅLNINGSTRYCKETS KRAFTJONISERANDE INVERKAN garanterar INITIELLT ENLIGT TNED att alla existerande väteatomer i Solklotet från Solens primära bildning blir säkert fullständigt joniserade enligt sambandet
Se sambandet för STRÅLNINGSTRYCKETS KRAFTJONISERANDE INVERKAN.
kvantitativt
BERÄKNINGSEXEMPEL
H+-JONISATIONEN
Med Z=1 och Tg=24 T6 °K som gäller från Solytan ges
FT = 4,92398 t7 N ;
Väteatomens jonisationsenergi är 13,6 eV eller
EJ = 2,17872 t18 J;
Sämsta fallets kraftpotential (FT) som sammanhänger med atomens jonisationsenergi (EJ) kan helt säkert fastställas (med angivna d=ra=0,529Å för Väte och Helium) enligt sambandet
;
H+-jonisationen ger då värdet
FTH1 = EJ/(d = 0,529Å) = 4,11856 t8 N vilket vi ser ligger väl inom det teoretiska FT=4,92398 t7 N.
Vi kan därför påstå — helt säkert, med stöd av den ovan härledda matematiska fysiken — ATT det egentliga, huvudsakliga Solklotet är RENT på H-elektroner. De samlas vid g-ytan. (Se Solranden).
Hur är det då med Heliumelektronerna?
Heliums 2:a, inre elektron kräver enligt tabell i Wikipedia [@INTERNET Wikipedia Ionization energies of the elements 2007-03-09] minst
EJ=5250,5 KJ/mol = 8,71756 t18 J;
Vi får då
FTHe2 = (8,71756 t18 J)/(0,529 Å) = 1,64793 t6 N
Potentiella kraftjonisationen ges via Z=2 som ger teoretiska
FT = (24 T6)2 · 2 · (8,54 859 t22) = 9,84797 t7 N
Det är 1,6733692 ggr för litet och räcker inte.
;
Beräkningarna visar att FÖRST från ca halva Solradien
(Tg=44 T6 °K) och inåt är också Heliumatomen fullständigt (säkert) HELT joniserad.
resultat
Resultaten av beräkningarna visar att vi (helt säkert) kan räkna med att halva Solklotet, räknat inifrån och ut, är intrinsiskt RENT på elektroner överhuvudtaget — frånsett den obetydliga del som eventuellt sammanhänger med den lilla mängden tyngre grundämnen (ca 1% i 25%He och 75%H). Den enda elektronström som kommer från Solkärnan och går mot Solytan är f.ö. den positronmängd som frigörs ur deuteriumbildningen. För övrigt strömmar Helium-4-kärnor ut mot Solytan medan deras vakanser i Solkärnan fylls på av Väte-1-kärnor som är det primära stjärn- och kärnbränslet. Se vidare utförligt från SOLFLÄCKARNAS UPPKOMST, där beskrivs strömningsordningarna i detalj.
elektronerna ligger packade mot yttre Solranden
KRAFTEN som EN fri elektron strävar att förenas på med sin antingen Väte-1-kärna eller sin Helium-4-kärna, ovanstående räkneexempel, är på tok för LITEN för att elektronen ska överkomma den strålningstryckets kraftjonisation (4,92398 t7 N) som gäller inom Solklotet enligt ovanstående räkneexempel: den fria elektronen tvingas istället av strålningstryckets kraftverkan maximalt utåt — och skulle också försvinna HELT ur Solklotets grepp om det inte vore för g-kraftens inverkan i förening med den uppkomna potentialskillnaden: det positiva inre av Solklotet. Strålningstryckets inverkan bildar (tydligen) jämvikt vid g-radien, och sätter därmed en definitiv gräns för den fria elektronmassans utflykt. Utåt sett är Solen (vad man vet) helt elektriskt neutral.
Se även från Solvinden.
ELEKTRONSKIKTETS TJOCKLEK från Solens första dag kan beräknas ur sambandet för SOLENS ELEKTROGRAVITELLA RADIE — enbart genom att ändra värdet för atommassan i parametern mA för Väte-1 (hela atomen 1,0078252u) till kärnmassan netto (1,007276602u):
Frånräknas elektronmassan på 0,000548598u [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u] i beräkningen för centraltätheten rC ges
mA=1,007276602u med
rG = 6,974141205 T8 M; Diff=341 140 M.
Man kan i Solens fall tolka det som att elektronmassan i Solen upptar ett (extra) sfäriskt ytskal med tjockleken drygt 340 KM.
SOLENS SIKTDJUP anges till jämförelse i konventionell litteratur till ca 500 KM;
”Följden blir att större delen av den
strålning vi ser emitteras i ett bara 500 km tjockt lager. Innanför detta lager
är solen ogenomskinlig”
BONNIERS ASTRONOMI
1978 s130sp2ö
Se även i Elektrontätheten i Solytan, Solklotets Elektronfrihet, Solranden.
från Solklotets Elektronfrihet
SOLRANDEN
ÄMNESSAMMANSÄTTNINGEN VID SOLYTAN · OMVÄNDANDE SKIKTET
Från Solens primära bildning garanterar STRÅLNINGSTRYCKETS KRAFTJONISERANDE VERKAN enligt TNED att Solklotet blir helt rent på fria elektronmassor (se Solklotets Elektronfrihet): elektronmassorna tvingas till ett smalt område strax under Solklotets g-yta (rG) som ligger ca 1000 KM ovanför nominella värdet för Solens synliga yta (Solens fotometriska radie) rF=6,96 T8 M.
Illustrationen närmast nedan visar enligt TNED hur Solklotets yta, initiellt från Solens första dag, besätts med elektronmassa (blått) ända ut till g-randen (rG). Efter normalisering (se beskrivning nedan) uttunnas den yttre delen genom rekombination med atomkärnor från Solklotet (främst Väte-1), vilket driver den fria elektronförekomsten en bit inåt Solklotet (rF). Eftersom rekombinationen i princip ger helt neutrala atomer, framstår området som ”svalt”: ingen utpräglad emissionsfysik finns i detta område. Därmed kan dessa atomer ta emot strålningen längre in från Solklotet som då framstår i formen av ett absorptionsspektrum: ljusare (hetare) spektrallinjer mot en mörk (svalare) bakgrund. Detta område kallas också i en del (äldre) litteratur för det omvändande skiktet.
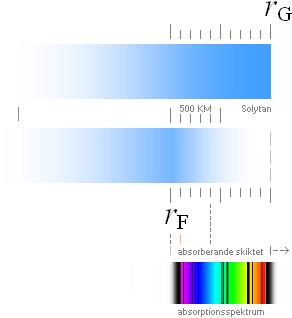
STRÅLNINGSTRYCKET garanterar generellt en hög allmän kraftjonisation (se även Jonisationen i Solkoronan) för alla grundämnesatomer i Solklotet. Dessa tyngre atomkärnor drivs mot Solytan av strålningstrycket — Notera att termen strålningstryck i modern akademi har en helt annan innebörd, se Elektrokinetiska strålningstrycket — och därmed en garanti för maximal rekombination mellan atomkärnor och deras elektronbesättningar, alldeles just uppe invid Solens g-yta. Därmed kan en utarmning ske av elektroner närmast under rG tillsammans med en fullständig atomär neutralisation vilket gör att området framstår »emissionslöst». Spektralt sett, tas energi upp i detta emissionslösa skikt från omgivande, mera utpräglat exciterade atomer, vilket leder till att området ser ut att vara ”markant svalare” än områdena under och över. Ett absorberande skikt har bildats; Spektrallinjerna tecknas mörka mot det underliggande, hetare kontinuerliga spektrumet. Dvs., atomerna i det absorberande skiktet absorberar energi från omgivande områdens atomer.
”Absorptionslinjespektret har hjälpt solforskarna att beräkna solatmosfärens sammansättning”
BONNIERS ASTRONOMI 1978 s132sp1m
Höger: Infälld inscannad bild från BONNIERS ASTRONOMI 1978
s136 som visar den experimentellt (delvis) uppmätta (spektroskopiska)
temperaturkurvan från Solytan till Solkoronan. Den branta temperaturövergången
kallas i engelsk litteratur för ”one of the classic problems of astrophysics”
[ref. ENCARTA 2004 Sun].
Se även värmegraderna för Tg och Tw enligt TNED till jämförelse.
Emissionslösa tillståndets princip
Det emissionslösa området betecknat absorberande i illustrationen ovan får alltså karaktären av en absorbator relativt de atomers energitillstånd som befinner sig utanför det absorberande skiktet. Vartefter elektrontätheten genom rekombination avtar in mot Solcentrum och jonisationskraften ökar, minskar också rekombinationerna och man finner (här helt i teorin) grundämnesatomer med allt mera utpräglat jonisationsspektrum, motsvarande en markant växande temperaturstegring in mot den djupare liggande Solkroppen. Därmed avtar det till synes emissionslösa området och ersätts av mera normalt spektrala förekomster med tydligt exciterade atomer.
I ändarna på det absorberande skiktet kan man (eller bör man enligt TNED) alltså i princip finna såväl negativa som positiva joner, beroende på den ”turbulens” som råder för tillfället i det starkt präglade rekombinationsskiktet.
Från området närmast rG och en bit inåt Solen varken utsänds eller mottas därmed knappast något ljus alls enligt TNED på grund av det ovan beskrivna emissionslösa tillståndets princip: ingen absorption, ingen reflexion. Området framstår som helt transparent.
ELEKTRONTÄTHETEN I SOLYTAN
Elektrontätheten i Solytan är
enorm jämfört med vanliga Jordiska material
RÄKNEEXEMPEL
Normala föremål:
Specifika vikten för Väte-1 till jämförelse är ca r=0,09 KG/M3. En Väteatom väger me=1,0078252u=1,67332 t27 KG. En M3 Väte-1 innehåller då 0,09/me eller
5,37852 T25 elektroner/M3
För t.ex. Järn (26Fe56) gäller motsvarande r=7870 KG/M3 med 26 me per atom som ger
1,80892 T29 elektroner/M3
Solytan till jämförelse:
Med idealt beräknade elektronskiktet i Solytan från ELEKTRONSKIKTETS TJOCKLEK, ca 340 KM, ges först volymen
V=4p([rG–340 000]3 – rG3)/3=4p(4,5355 T 23 M3)/3=1,89982
T24 M3 » 1,9 T24 M3.
Antalet elektroner i Solmassan 1,989 T30 KG med Väte-1-bas är (1,989 T30 KG)/me=1,18865 T45. Idealt med fullständig väteförbränning har den potten halverats vid slutet av Solens primära energicykel. Därmed elektrontätheten (initiellt) i det 340 KM tunna Solytskiktet (1,18865 T45 elektroner)/(1,9 T24 M3) som ger
6,25606 T32 elektroner/M3
Det är (6,25606 T32)/(1,80892 T29)=3458,4171 gånger högre elektrontäthet än den som gäller i vanligt Järn. Runt sagt 3500 gånger större. Vi skulle säga: enormt.
Den höga elektrontätheten i Solytan
garanterar maximal ljusspridning
— eller som man säger analogt med
Solens synrand:
opaciteten eller
»ljusogenomskinligheten».
SOLVINDEN
Hur materialet från stjärnan läcker ut i rymden
Genom den primära fusionsbildningen med efterföljande expansionsfas som ENLIGT TNED gäller för alla J-kroppar i K-cellens expansion (utförligt i J-kroppens expansion), expanderar alla himlakroppar mot ett (bestämt) gränsvärde — och i allt långsammare takt. Denna expansion är mycket snabb i början, den fortgår i princip under oändlig tid, men avstannar snabbt och utvidgas sedan med allt mindre belopp.
Planetkropparna avstannar snabbast och genererar de häftigaste egenrotationerna under den mycket korta fusions- och huvuddelen av expansionsfasen. De större gaskropparna expanderar mera långsamt med betydligt mindre egengenererad inledande rotation. En stjärna som från sin primära kroppsbildning har NÅGON egenrotation (i TNED utgår vi ifrån att så är fallet), producerar själv impulsmoment genom fusionsenergin; Skillnaden mellan den inre tätare delen och den yttre mera porösa garanterar att det hela tiden bildas vridande moment mellan inre och yttre delar. Därmed producerar stjärnan en successivt växande rotation i takt med att den förbrukar sitt bränsle. Eftersom den egenproducerade rotationen också medför en mera blygsam reduktion av effekten (g-trycket reduceras något genom den ökande centrifugalkraften), samt att stjärnan kontinuerligt genomgår inre täthetsändringar som följd av produktionen av tyngre nuklider från lättare, motverkas delvis den idealt oändliga primärexpansionen. Slutresultatet blir likväl (se Rotationens inverkan på stjärnans fysik) att stjärnan kan betraktas med bibehållen konstant radie. Men eftersom den initierade idealt oändliga expansionen inte kan upphävas (primärenergin till expansionen kan inte förstöras) utan likväl fortsätter, uppstår TVUNGET ett mindre massutflöde, ett läckage. Balansen mellan strålningstryck och g-tryck enligt den allmänna tryckekvationen tillåter nämligen i sig inget massutflöde alls, utan förutsätter att all materia stannar kvar inom stjärnkroppen. Det faktum att material lämnar stjärnan kontinuerligt kräver alltså en annan förklaring. En planet däremot, som helt saknar termonukleära energicentra och därför inte kan generera någon egenrotation utöver den som bildades under fusionsfasen, fortsätter att expandera i långsam takt med allt mindre belopp — så länge dess inre har någon smälta som håller kroppen elastiskt. Följdsatsen för en stjärna blir alltså den, att ju större egenrotation den producerar, desto större blir massutflödet; Strålningstrycket garanterar att massutflödet drivs eller ”blåser” iväg från Solytan:
Observationerna av det solära partikelutflödet — och dess egenskaper — grundlade benämningen solvind (Parker 1960, BAs151sp2mn).
UTANFÖR STJÄRNANS G-SFÄR kan strålningstrycket »blåsa på med full pedal». Den utläckande partikelmassan är explicit inte bunden av stjärnans g-sfär eller det potentialförhållande som råder innanför g-ytan och drivs därmed utåt av strålningstrycket och åstadkommer därmed den observerade partikelvinden eller solvinden.
Alldeles just VID g-ytan där strålningstryckets påverkan på ivägdrivningen av partikelutflödet hindras av stjärnans sammanhållande g-krafter (p – pe – gp = 0) är också strålningstryckets joniserande effekt (se Koronafysiken) i princip noll. Man har också i Solens fall observerat det nyligen ovan omnämnda s.k. omvändande skiktet [BAs132sp1]; en zon där temperaturen (jonisationsgraden) avtar något utåt mot den motsvarande gravitella eller kapacitiva Solytan rG — för att sedan, ännu längre ut, åter växa in i Solkoronans betydligt högre temperaturekvivalenter. Det omvändande skiktet bildar en spektral övergång mellan Solkroppens underliggande s.k. kontinuerliga spektrum och det längre ut liggande karaktäristiska (först absorptions-, sedan emissions-) linjespektrum som är typiskt för fria atomer. Se vidare i Solranden och Spektrala värmegraden.
MASSUTFLÖDET FRÅN SOLKROPPEN är genom observationer [BAs151sp2n] beräknat till ca 1 T9 KG/S. Även om vi räknar idealt på hela Solens livstid från 100% Väte till 100% Helium (120 miljarder år med Solens råeffekt) avverkas bara knappt 3,8 T27 KG i Solvindens form. Det är bara knappt 0,2% av hela Solmassan, eller runt 634 Jordmassor.
SOLVINDEN KAN DELVIS HINDRAS I SITT KONTINUERLIGA UTFLÖDE av ett laddningskonserverande solärt magnetfält (B); alla elektriskt laddade partiklar som befinner sig i ett magnetiskt fält och som uppvisar någon form av diversifierad rörelse i skilda riktningar (som fallet bör vara alldeles strax utanför Solytan), intvingas i spiralbanor av det yttre B-fältet; Så länge den lokala magnetiska solära ytkraften är större än det aktiva strålningstryckets kraftjoniserande komponent (se STRÅLNINGSTRYCKETS KRAFTJONISERANDE INVERKAN), kvarhålls en (växande) mängd material som normalt (utan B-fältet) skulle ingå i det kontinuerliga utflödet i Solvinden; OM B-fältet plötsligt upphör, frigörs den instängda laddningsmängden för STRÅLNINGSTRYCKET och genomgår då helt naturligt en explosionsartad acceleration. Utan att vi här genomgått någon som helst analys eller beskrivning av Solens allmänna magnetiska fysik, kan vi sluta oss till att OM det beskrivna förloppet är det som observerats i Solens fall (en s.k. koronal massutkastning, CME, eng. Coronal Mass Ejection), Solen också måste uppvisa en sådan motsvarande magnetisk brytdynamik enligt TNED (Den framställningen finns här ännu 2008-01-24 inte i färdigt skick — se dock vidare närmast nedan).
Solmagnetismen behandlas i separat dokument (se från Solens Energiproduktion; Det dokumentet innefattar Solmagnetismen enligt TNED men avsnitten har måst uppdelas på flera htm-domäner på grund av den begränsade Webbläsningsteknikens snabbhet. Se vidare orientering i registerdelen [innehåll] i Solens Energiproduktion).
Solens ämnessammansättning
Se även efterföljande artikel
(Väteytan) med tabell över uppmätta
grundämnen i Solvinden och fotosfären
EN NATURLIG FÖLJD av det omvändande skiktets övergångszon mellan g-kropp och icke-g-kropp, där alltså förekomsterna i stort sett endast påverkas av den lokala gravitationen, är att tyngre ämnen får större benägenhet än lättare att befinna sig i området. Om detta är en korrekt slutsats innebär den att direkt spektral mätning på förekomsterna i området kommer att uppvisa en övervikt av tyngre ämnen i förhållande till en allmän avspegling av Solklotets medelmässiga ämnessammansättning. Värdena kommer att visa en större andel av de tyngre grundämnena än den som är representativ för Solen som helhet. BONNIERS ASTRONOMI 1978 s126 anger (på här ej kända grunder) att Solen består av ca 75% Väte, ca 25% Helium, 0,8% Syre, 0,3% Kol, och 0,5% övriga. ENCARTA 99 Sun anger att Solen består av 71% Väte, 27% Helium och 2% övriga. Ovanstående representerar (här i förmodan) resultat av experimentella observationer av spektrum från Solytan (som bearbetats med statistiska metoder i korrelation mot en föregiven modell av atomfysiken med grundteorier för tryck och temperatur), men inga källdata på det finns här.
En bättre mätare på Solkroppens medelmässiga sammansättning vore att mäta solvindens partikelinnehåll, det material som stjärnan faktiskt läcker ut. Solvindens partikelnatur omnämns [BAs151sp2mn], men tyvärr finns inga uppgifter på den relativa förekomsten av främst andelen Väte (protoner) kontra andelen Helium (alfapartiklar). I ovanstående slutsats ljus och inom K-cellens allmänna teori, ska Heliumandelen i Solvinden vara (betydligt) lägre än 25-27% (17%) medan protoner-elektroner ska stå för (betydligt) mera än 71-75% (83%). [Solens nuvarande ålder dividerat med Solens livslängd ska IDEALT ENLIGT TNED ge andelen Helium]. Det finns dock en detalj som spräcker den möjligheten. Se artikeln nedan om Väteytan.
Med fortsättning från Solens ämnessammansättning
Väteytan
Genom den allmänna negativa höljesjonisation som strålningstrycket utverkar ligger det nära till hands att klassificera samtliga stjärnors yttre klotrand på följande enkla form.
Den negativa jonisationens största potential bildas av (nära) fria elektronmassor (e–). Dessa placerar sig ytterst, närmast under stjärnans g-skal. Närmast elektronerna i klotytan följer rekombinerat Väte-1 och-eller dito vätejoner. Dessa ger det minsta motståndet i elektronrekombinationerna på grund av minsta atommassan. Tyngre nuklider rekombinerar längre ner under skalet (tätheten växer med avtagande avstånd in mot centrum). Efter Väte-1-skiktet, vidare inåt mot Solcentrum, följer sedan övriga tyngre nuklider med en alltmer mindre utpräglad (negativ) jonisation i alltmer utpräglad mix inom klotets huvudsfär och som avspeglar stjärnans medelinnehåll av grundämnen. Därigenom kommer alla stjärnor att uppvisa en typisk väteyta, oberoende av det övriga innehållet. Genom denna kan sedan stjärnan läcka ut sitt material på grund av den allmänna expansionsfysiken (se Hur materialet från stjärnan läcker ut i rymden). Närmast g-ytan på ovansidan samlas (på vanligt sätt) de tyngre nukliderna i läckmassan längst ner, lättare över, och bildar på så sätt den ämnespool (turbulens) från vilken läckmaterialet sedan drivs ut av strålningstrycket (se Strålningstryckets kraftjonisation), ut i den omgivande rymden.
Även om alltså stjärnan praktiskt taget är fullproppad med Helium-4 i stjärnklotet KAN ytdelens tunna Väte-1-del bibehållas med elektronskiktet och ytpoolen (med varierande sammansättning) — så länge strålningstrycket garanterar den positiva jonisationen i centraldelen, och därmed den negativa i g-ytan.
Observerad Ämnessammansättning i Solen
ALLMÄNNA BEKRÄFTELSER
Den ovanstående beskrivningen bekräftas till vissa delar av observationer som gjorts på Solmaterialets förekomst och fördelning i olika regioner (ämneskoncentrationen He/H är större i Solytan än i Solvinden). Tabellen nedan är min sammanställning från den angivna engelska källan (Source). Originalet har här försvenskats och förtydligats. I originaltabellen finns noter till varje förekomst som ger en referens till vem-vilka som utfört mätningarna. Dessa referensnoter har här tagits bort då de i vilket fall inte bidrar till den kvantitativa överblicken.
Solytans och Solvindens ämnessammansättning
Table G1 — värden i förhållande till
förekomsten av Syre16
Sammanställning
av ämnesmängder i Solvind och fotosfär (von Steiger, 1994)
Source: [http://www.gps.caltech.edu/genesis/DocumentG.html
]@INTERNET2007XII31
X i X i X i X i
|
X |
eV |
Solvinden
i Ekliptikan |
tolerans |
Solvinden Från Koronala Hål |
tolerans |
SEP-baserad
Korona |
tolerans |
Fotosfären |
tolerans |
|
FJP |
± |
± |
± |
± |
|||||
|
H |
13.60 |
1900 |
400 |
824 |
80 |
|
|
1175 |
— |
|
He |
24.59 |
75 |
20 |
48.5 |
5 |
55 |
3 |
115 |
— |
|
C |
11.26 |
0.72 |
0.10 |
0.70 |
0.10 |
0.428 |
0.043 |
0.468 |
— |
|
N |
14.53 |
0.129 |
0.008 |
0.145 |
0.011 |
0.123 |
0.009 |
0.117 |
— |
|
O |
13.62 |
1 |
|
1 |
|
1 |
|
1 |
|
|
Ne |
21.56 |
0.17 |
0.002 |
0.136 |
0.011 |
0.142 |
0.014 |
0.138 |
— |
|
|
|
0.14 |
0.02 |
|
|
|
|
|
— |
|
Mg |
21.56 |
0.16 |
0.03 |
0.083 |
0.02 |
0.193 |
0.011 |
0.0447 |
— |
|
Si |
8.15 |
0.19 |
0.04 |
0.054 |
0.009 |
0.164 |
0.0099 |
0.0417 |
— |
|
|
|
0.18 |
0.02 |
|
|
|
|
|
— |
|
S |
10.36 |
0.038 |
0.009 |
0.019 |
0.003 |
0.0377 |
0.0016 |
0.0191 |
— |
|
|
|
0.05 |
0.02 |
0.022 |
0.008 |
|
|
|
— |
|
Ar |
15.76 |
0.004 |
0.001 |
0.0037 |
0.0006 |
|
|
0.00447 |
— |
|
Fe |
7.87 |
0.19 |
(0.10,0.07) |
0.057 |
0.007 |
0.172 |
0.023 |
0.0355 |
— |
|
|
|
0.12 |
0.03 |
|
|
|
|
|
— |
|
Kr |
14.00 |
3.4 t6 |
0.4 t6 |
|
|
|
|
1.89 t6 |
— |
|
Xe |
12.13 |
0.88 t6 |
0.12 t6 |
|
|
|
|
0.197 t6 |
— |
t6 = 10^–6 i värdena för Kr (Krypton)
och Xe (Xenon)
förklaring till tabellens termer
FJP första joniserande potentialerna (värden
i elektronvolt)
jonisationsenergin för ämnesatomens yttersta elektron
SEP-baserad Korona mängd X i
Solkoronan grundad på studier av solära energipartiklar
Solvinden i Ekliptikan mängd X i Jordbanplanet (ekliptikan), dvs. utmed synlinjen Jorden-Solen
beskrivning
Tabellvärdena ovan för de olika ämnenas förekomster
är angivna i förhållande till förekomsten av Syre16 (8O16) — men källan anger
ingen referens till de olika regionernas inbördes O-förekomst (ämneskoncentrationen
är i vart fall större i-vid Solytan än utanför). Anledningen (1994) KAN bero på
att det 1. är erkänt svårt att mäta förekomsterna absolut eftersom stundtals
(mycket) stora variationer förekommer och man ingalunda är på det klara med HUR
de varierar, och därmed 2. uppfattas svårt att ge en begriplig beskrivning i
klartext — den får vi stå för här!
Syre är den av de tyngre atomerna som är mest representerad i solvinden, källa: [www.cosmicrays.org/muon-rays.php]2007-10-30;
Den källan anger att av 100% solvindsmaterial upptas 95% av
protoner och elektroner, 4& av joniserat Helium, resten 1% av övriga
ämnesatomer.
Se även
ämnen i fotosfären:
Väte Helium Syre Kol
Järn Svavel Neon Kväve Kisel Magnesium
73,46% 24,85% 0,77% 0,29% 0,16% 0,12% 0,12% 0,09% 0,07% 0,05%
Källa: @INTERNETWikipedia Sun 2007-05-07
I jämförelse mellan Solvinden (He/H=75/1900 » 4%) och Solytan (He/H=115/1175 » 10%) framgår att skillnaderna är (remarkabelt) stora.
Som omnämndes ovan i Solens ämnessammansättning ska Heliumandelen i Solen enligt TNED vara ca 17%. Men eftersom Väteytan innebär en relativt sett (mycket) högre vätekoncentration där än Solmedelvärdet, är det uppenbart att de 17%:en Helium blir underrepresenterade. Siffrorna här antyder att Heliumandelen (då) skulle reduceras med grovt sett runt hälften, just i Solytan, samt sedan vidare utåt än mindre i själva det utläckande Solmaterialet (runt ytterligare en halvering).
Se även från Solklotets Elektronfrihet.
Från Tidsekvationen
ALLMÄNNA BEKRÄFTELSER
Den allmänt observerade stjärnfördelningen [BONNIERS ASTRONOMI 1978 |s31|Tabell 2.3| s50| se vidare nedan]
överensstämmer med TNED enligt följande grunddata:
Alla
primärstjärnor
med större massa än 2,4 Solmassor har slocknat och gått in i en andra
energicykelfas.
beskrivning
Från tidsekvationen (t) som utvecklades ur massa-luminositetsrelationen (MLR)
TS = EST9/Ps = (4,01074 T28 J)(T9 år)–1 · Ps–1 ..................................... Solens livslängd i miljarder år
t = n–2TS ............................................................................................... tidsekvationen, S
=
n–2(4,01074 T28
J)(T9 år)–1Ps–1
.................................................... n anger antalet Solmassor
ges från Solens 3:e Ekvation
P = A2 · rr2Gc0/18
(se yttäthetskonstanten),
som ger Solens råeffekt Ps=3,3011376 T26 W=A2e0·1VM–1C–1S–3KG,
tidsekvationen mera exakt preciserat enligt
= n–2(121,49569) ................................................................................ t i T9 år, n i mS
Med resultaten från K-cellens värmefysik är universums nuvarande ålder T=20,82 miljarder år. En beräkning av Solsystemets/Vintergatans ålder ingår och som med hänsyn till galaxernas nuvarande medelavstånd i beaktande under K-cellens expansion förlägger Vintergatans bildning till inte mera än max 10 miljoner år efter K-cellens detonation. Därmed är t i sambandet ovan liktidigt med T=20,82 miljarder år med två korrekta decimaler i antal miljarder år så att vi får
20,82 = n–2(121,49569)
;
n = Ö (121,49569)/(20,82)
= 2,4156837 Solmassor
Enligt BONNIERS ASTRONOMI 1978 |s31|Tabell 2.3| s50|, 26 uppmätta specificerade individer, ligger
huvuddelen av de optiskt observerbara stjärnornas mätbara massor mellan 0,34-2,4 Solmassor. Faktiskt.
Resultatet för övre gränsen i detta intervall överensstämmer med TNED enligt följande grunddata:
basdata
enligt TNED
SOL eller stjärna, friliggande kosmisk termonukleär exotermisk självunderhållande energikälla;
K-cellens ålder ................................. 20,82 T9 år K-cellens värmefysik.
Vintergatans galaxgrupp och Solsystemets ålder (ovan):
liktidiga minus max 10 miljoner år Medelavståndet mellan galaxerna (3 Mpc) i K-cellens expansion
Solens konstanteffekt ...................... PSUN=3,3011376 T26 W Solens tre ekvationer
Solens verkliga yttemperatur ............ T = 6150 °K Solens andra ekvation
Solens livstid ..................................... tSUN
= 121,49569 T9 år,
avrundat 120 miljarder år för sämsta fallens grovberäkningar (102,8 T9 år via konv. 3,9 T26 W)
NU EXISTERANDE PRIMÄRSTJÄRNOR
KAN HÖGST HA MASSAN (från Tidsekvationen
i MLR)
n = [(121,49569)/(20,82)]1/2 = antal Solmassor =
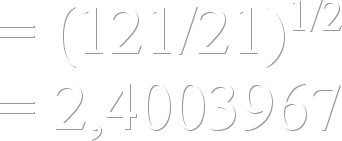
Därmed (så långt) bekräftas den allmänna tidsekvationen med stjärnfysikens fundamentalteorem och massa-luminositetsrelationen enligt TNED.
Generellt för hela det synliga stjärnfältet genom observation gäller tydligen
·
Huvuddelen av
de optiskt observerbara stjärnornas mätbara massor ligger mellan 0,34-2,4 Solmassor
[BAs31.Tabell
2.3, s50; 26 uppmätta specificerade individer].
· Stjärnor med låg luminositet och liten massa är oerhört mycket vanligare än högmassiva stjärnor [BAs30sp1mn].
· 80% av alla stjärnor är svala huvudseriestjärnor [BAs79sp2mö].
STJÄRNFYSIKEN MED HÄNSYN TILL STJÄRNFÄLTEN — stjärnornas spridning, utveckling och förekomst
Denna avslutande del i stjärnfysiken — med ovanstående inledning — behandlas mera utförligt i särskilda avsnitt:
För närvarande (våren 2008) under htm-utformning. [Färdigställt hösten 2008, se nedan].
Se från Stjärnfysiken Del II.
Fortsättning i SolfysikenTemperaturfysiken.
Editor2007XI21 | 2008V14
Solfysiken
innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
Solfysiken
ämnesrubriker
innehåll
Solgränsmassan
· stjärngränsmassan
skilda
grundteorier · jämförelse
med MODERN AKADEMI
Yttäthetskonstanten
och Solradien · allmän orientering
Tidsekvationen · stjärnornas livslängd
yttäthetsekvivalenten
· yttäthetskonstantens koppling till Solaradien · Solradiella
yttäthetsekvivalenten
Solens
fotometriska effekt · kvalitativa delen
Solens
fotometriska effekt · KVANTITATIVA delen
kapacitansvärdet för Solen · Solens kapacitansvärde
Solfysiken · Stjärnfysikens elementära grunder
enligt TNED
Stjärnfysikens grunder enligt TNED
Yttäthetskonstanten
och Solradien · generella samband för vidare
Solens Fotometriska Effekt kvantitativa delen
Fotometriska Effekten kvalitativa delen
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon,
McGraw-Hill 1967
Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]
me = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]
u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],
CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
t för 10–, T för 10+, förenklade exponentbeteckningar
PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER
Här används genomgående och konsekvent beteckningarna
förkortning för förenklad 10-potensbeteckning, t för
10–, T för 10+
m milli t3
µ mikro t6
n nano t9
p pico t12
f femto t15
Alla Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav — liksom nedanstående tusenprefix.
K kilo T3
M mega T6
G giga T9
T tera T12
Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM.
TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.
Senast uppdaterade version: 2022-04-19
*END.
Stavningskontrollerat 2007-11-21|2008-03-06
rester
*
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se
PNG-justerad 2011-10-10
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se