PLANCKLAGEN — UNIVERSUMS HISTORIA | enproduktion 2010III6 | Senast uppdaterade version: 2011-10-10 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

UnicodeStandard: TYPOGRAFIN I DETTA HTM-DOKUMENT HAR I DE FLESTA (MÖJLIGA) FALL UTNYTTJAT DEN TILLGÄNGLIGA (men krångliga) TECKENSNITTSSTANDARDEN FÖR UNICODE — SOM FINNS KOMPLEMENTÄRT TILL SYMBOL-TECKENSNITTET FÖR DET KLASSISKA GREKISKA ALFABETET SOM NORMALT ANVÄNDS I NATURVETENSKAPLIG LITTERATUR I OLIKA MATEMATISKT-FYSIKALISKT BESKRIVANDE SAMMANHANG med typexempel Ω Φ Σ Π Ξ Λ Θ Δ α β γ δ ε λ θ κ π ρ τ φ σ ν ω ∏ √ ∑ ∂ ∆ ∞ ∫ ≤ ≈ ≥ ← ↑ → ↓ . VISSA AV DESSA TECKEN UPPVISAR (med den här presentationens allmänna teckensnitt och storlek Times New Roman 9) EN NÅGOT SÄMRE REPRESENTATION ( t.ex. ett mindre tydligt pilhuvud, ett mera otydligt rottecken, m.fl.) OCH SOM GÖR ATT UNICODE-ALTERNATIVET (här ännu) INTE UTNYTTJATS FULLT UT. DET ÄR FÖR ÖVRIGT BARA WEBBLÄSARNA INTERNET EXPLORER OCH GOOGLE CHROME SOM LÄSER SYMBOLTECKENSNITTET (MOZILLA VISAR t.ex. Ö för rottecknet, etc.).

Alla kroppar värmeläcker Isolerade Systemet antas 1858 Stewarts bidrag · Kirchhoffs bidrag · Maxwells bidrag · Kosmiska bakgrundsstrålningen Frekvensformen · Temperatursambandet · Exemplet Solen Grundsatser Grundtermer · Webbreferenser ·

VÄRMESTRÅLNINGENS SPEKTRUM, OBEROENDE AV SPECIFIK KROPP

PLANCKS STRÅLNINGSLAG I PRAKTISK FYSIK

PLANCKS STRÅLNINGSLAG I PRAKTISK FYSIK

Plancks strålningslag (se särskilt Härledningen från Plancks entropisamband)

[Se även i FOCUS MATERIEN 1975]

1 hc²

N_λ = —— ——————

λ⁵ e ^hc/bλT – 1

beskriver den idealt i varje masskropp föreliggande odämpade rena interferenslösa temperaturstrålningen I DEN MASSLÖSA RYMDEN i varje masskropp, mellan alla masselement, oberoende av kropparnas specifika sammansättning, typ, art eller form:

Varje ljusvåglängd (λ=c/f ) utsänd från varje ljusaktivt masselement (h=mcr, m=[Q²/R][dt/A], se från Elektriska Laddningen) uppvisar en egen energi (N, spektrala radiansen) vid en bestämd temperatur (T). (E=mcc=hf=kT).

För direkt (exakt) praktiskt exempel, se DEN KOSMISKA BAKGRUNDSSTRÅLNINGEN.

För begreppet spektral radians, se RADIANS och SPEKTRAL RADIANS.

För härledningen till Plancks strålningslag, se PLANCKS STRÅLNINGSLAG FRÅN STEFAN-BOLTZMANNS STRÅLNINGSLAG och PLANCKS STRÅLNINGSLAG FRÅN PLANCKS ENTROPISAMBAND.

Masskomponenten h grundlägger materiefysiken

2010III26

Mera utförligt:

Masskomponenten h — Planckringen — grundlägger materiens ljusfysik:

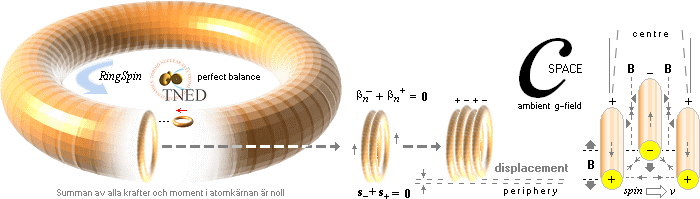
Med atomkärnans härledning från Plancks konstant (h) eller Planckringen [Se utförligt från ATOMKÄRNANS HÄRLEDNING]

h = mNEUTRONMASSAN1,0086652ucTOPPDIVERGENSEN2,99792458T8M/SrNEUTRONRADIEN1,3196611t15M

= 6,62559 t34 JS

som via MASSPRINCIPEN visar m=[n→∞]·m/[n→∞]

— som i sig krävs för att via massdestruktionen (m→γ) garantera massans fullständiga upplösning i värme och ljus via primära massförstöraren E=(m→γ)cc med garanterat icke stela beståndsdelar i massans sammansättning

— grundläggs också definitionen för h=(h/[n→∞])[n→∞] som en strukturkonstant i Planckenergin E=hf, samt därmed atomkärnan som massans fundamentalform, helt utan inre beståndsdelar. 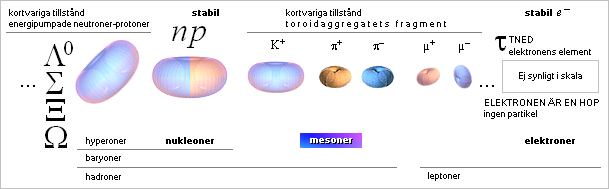Speciellt med ELEKTRISKA LADDNINGEN Q=√(m/R)(A/dT), dess koppling till massan och därmed i kraft av atomkärnan som massans fundamentalform med absolut proportionalitet mellan laddning och massa [Se särskilt i POTENTIALBARRIÄREN], ges alla, samtliga, särskilda komponenter i massfysiken

atomkärnan

från NEUTRONEN, dess vidare sammansättning till tyngre atomkärnor enligt NEUTRONKVADRATEN med ATOMVIKTERNA [Se även särskilt från NUKLIDBARRIÄREN],

neutronens fragment

elektronmassan via NEUTRONENS SÖNDERFALL

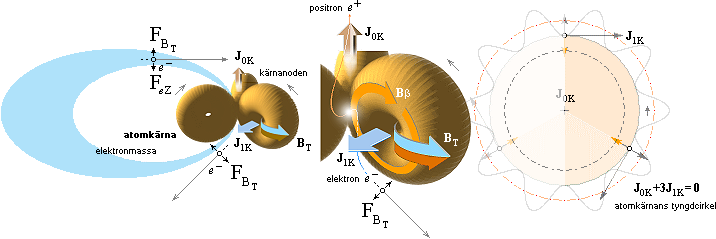
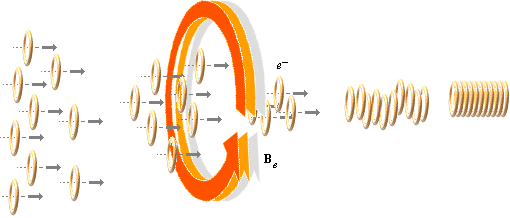
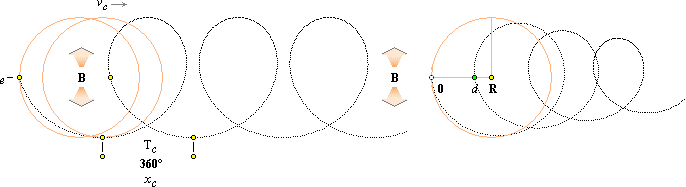
elektronmassans komponenter med exempel i

ELEKTRONENS BUBBELKAMMARSPÅR,

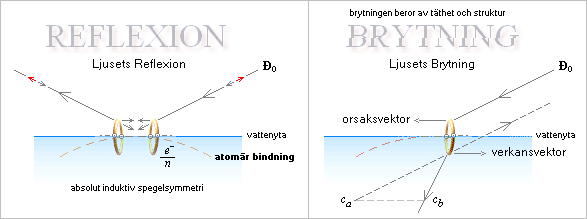
LJUSETS REFLEXION och LJUSETS BRYTNING,

LJUSETS POLARISATION,

MASSDESTRUKTIONEN, (parannihilation)

samt särskilt via Keplers Ytmoment enligt

GRUNDÄMNENAS PERIODISKA SYSTEM

sin grundliga förankring i Planckringens tre fysikaliska faktorer massa, laddning och spinn (impulsmoment): Massa, laddning och spinn bildar grundval för fysikens alla, samtliga utan undantag, möjliga sätt att förmedla gravitation tillsammans med elektromagnetisk strålning [Se även särskilt i NEUTRINOSPEKTRUM och LJUSETS GRAVITELLA BEROENDE och FOTOELEKTRISKA EFFEKTEN och LJUSETS OPTISKA NATUR och INDUKTIONEN OCH MAGNETISMEN om ej redan bekant]. Därmed framträder Plancks strålningslag — företrädesvis med härledning från Plancks entropisamband [Se Plancks strålningslag från Plancks entropisamband] — entydigt ur masskomponenten h.

Notera att den moderna akademins lärosystem helt, och alldeles uppenbarligen genom egen förskyllan som det får förstås, saknar möjligheter att förevisa, härleda eller ens påvisa dessa för fysikbeskrivningen helt avgörande detaljer. Se särskilt från HÄRLEDNINGEN TILL DEN ELEKTRISKA LADDNINGEN, PLANCKEKVIVALENTERNA och ATOMKÄRNANS HÄRLEDNING.

Genom att Planckenergin E=hf innefattar Planckringen (h=mcr) som grundlägger ATOMKÄRNANS HÄRLEDNING i relaterad fysik

— och därmed Planckringen med massa, laddning och spinn som grundvalen för fysikens allmänna elektromagnetiska fenomennatur med atomkärnan enligt massans struktur (Se PASTOM) som en förlustfri elektromekanisk komponent som inte behöver någon påfyllning för att fungera

— beskriver tydligen Plancks strålningslag

1 hc²

N_λ = —— ——————

λ⁵ e ^hc/bλT – 1

den föreliggande — från masselementen utgående — odämpade ljusenergin, utan specifik materiell hänsyn;

N(λ) beskriver tydligen energidistributionen (eg. spektrala radiansen) för varje bestämd energi vid varje bestämd temperatur vid varje bestämd våglängd

[i princip således genom varje möjlig Planckring]

för ett motsvarande bestämt antal likaberättigade energifördelningssätt

[som alltså också inbegriper tillståndsfysiken i varje möjligt massfysikens element; nämligen med dessa som agenter för radiansen].

[Se HÄRLEDNINGEN TILL PLANCKS STRÅLNINGSLAG från Plancks entropisamband för en mera detaljerad genomgång].

Enklare:

Plancks strålningslag beskriver och definierar tydligen

VÄRMESTRÅLNINGENS SPEKTRUM, OBEROENDE AV SPECIFIK KROPP

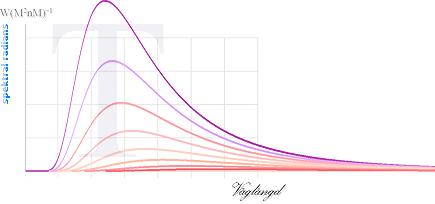
Ju högre grad av KONTINUITET i den spektrala distributionen som kroppen uppvisar, alltså ju färre avbrott och avvikelser mot Planckkurvans idealt fullständigt kontinuerliga spektrum, desto mera överensstämmer tydligen kroppens verkliga temperaturform med Planckkurvans ideala form.

Det finns, veterligt, ingen annan preferens (spektrala tätheten) att hänvisa urvalet till.

Planckstrålningslagens rent fysikaliska förankring kan därför INTE beskrivas (definieras) exakt utifrån föreställningen om SPECIFIKT olika (Jordlaboratoriska) kroppar (typ ideal hålrumsstrålare, absolut svart kropp) — även om dessa uppvisar exceptionellt överensstämmande AVSNITT i Planckkurvornas representation.

Det finns tyvärr — frånsett Kosmiska bakgrundsstrålningen och Solens Irradians — ännu (Apr2010) inga uppmätta grafer att förevisa till jämförande exempel, trots ett närmast enormt utbud av skrifter i ämnet på webben.

Så kan t.ex. ett upphettat ämne i en ljuslåga i ett vanligt Jordlaboratorium inte avge termonukleärt orienterade våglängder liknande ljuset från Solen — och är därmed också uteslutet som definitionsbas i Plancks strålningslag där tydligen närvaro krävs för alla våglängder.

Det som krävs är, tydligen, ett enhetligt masselement av princip, oberoende av material: Planckringen (h=mcr). Se utförligt från ATOMKÄRNANS HÄRLEDNING.

Inledande beskrivning, kompletterande

Plancks strålningslag [se även FOCUS MATERIEN 1975]

1 hc²

N_λ = —— ——————

λ⁵ e ^hc/bλT – 1

innefattar — beskriver — alla möjliga våglängder (λ).

Alla möjliga våglängder betyder, tydligen, detsamma som kontinuerliga spektrumets definition.

Planckenergin E=hf med Planckringen (h=mcr) garanterar I RELATERAD FYSIK (Se utförligt från ATOMKÄRNANS HÄRLEDNING om ej redan bekant) att Planckringen (atomkärnan, elektronmassans komponenter) av princip är den svängande agenten för strålningsradiansen på massprincipens form (Se PASTOM med PROPORTIONALITETEN MELLAN MASSA OCH LADDNING) enligt m=[n→∞](m/[n→∞]). Därmed förstås att ingen minsta massdel kan återfinnas i en given strömring (h=mcr). Den omständigheten framställer DELS Plancks konstant (Planckringen h=mcr) på formen av en strukturkonstant som kan förmedla Planckenergin E=hf=(h/n)nf på obegränsat korta våglängder med obegränsat liten energi, samt DELS garanterar att varje Planckring saknar stela beståndsdelar och därmed kan upplösas fullständigt genom massdestruktion enligt primära massförstöraren E=mcc, analogt (typiskt) Solens energiomsättning, och DÄRMED garanterar alla möjliga våglängder. Våglängder kortare än ringens utsträckning innefattas automatiskt i ringens egen fraktalstruktur som ovan (Se utförligt i ATOMKÄRNANS HÄRLEDNING), våglängder större än ringens utsträckning innefattar den normala induktionsverkan (Se INDUKTIONEN) med ringens längsförflyttning. Därmed blir varje möjlig Planckring (mcr) agent för alla möjliga våglängder.

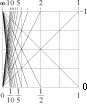
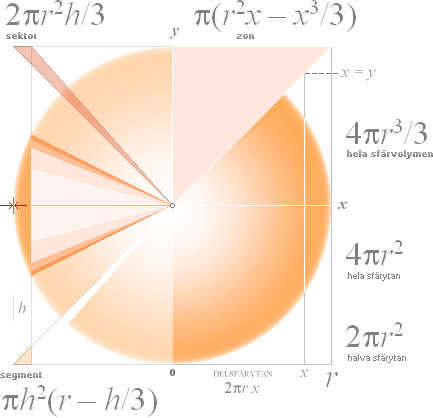
Bilden ovan (TANGENSKVADRATEN) illustrerar själva skalan — från noll, mot oändligt — för en bekväm, ändlig, översiktlig bild av själva omfattningen.

Med Planckringen h=mcr som ekvivalent med PRINCIPALRINGEN för massa, laddning och spinn, beskriver Plancks strålningslag med andra ord ENLIGT RELATERAD FYSIK en IDEALT obegränsat liten sfäriskt 4π RUNDSTRÅLANDE RADIATOR (»Planckradiatorn») med strålmassaenergin E=mcc=hf (spektral radians) — utan hänsyn till dämpning, interferens eller växelverkan med andra sådana radiatorer; Planckstrålningslagen tar endast hänsyn till strålningsagenternas kvantitativa summerande eller enskilda kvalitativt MASSLÖSA INDUKTIVA RYMDVERKAN (»själva ännu oanvända ljusenergin»). Se även i Satsen om alla kroppars värmeläckning.

Varje Planckradiator (h=mcr) kan alltså GENOM MASSPRINCIPEN (Se särskilt utförligt från ATOMKÄRNANS HÄRLEDNING om ej redan bekant) av princip förmedla alla möjliga våglängder. Men den förmågan upphör tydligen (slätas ut) med ATOMEN på grund av atomens RESONANSVILLKOR (elektronmassan), se utförligt från GRUNDÄMNENAS PERIODISKA SYSTEM.

Plancks strålningslag gäller därför endast beskrivande inom materiefysiken — och därmed strängt taget PÅ ATOMERNAS RESONANSVILLKOR. Plancks strålningslag kan alltså sägas gälla analogt med grund i ABSOLUTA TEMPERATURSKALAN: idealt noll rörelse mellan atomerna definierar temperaturens idealt absoluta nollpunkt, 0°K. Materiefysiken (atomernas inbördes rörelser, deras sammansättning och struktur) kan alltså av princip varken beskriva eller mäta massfysiken (Planckresonatorernas fysik, se ATOMKÄRNANS HÄRLEDNING).

Härav följer:

Ju högre grad av KONTINUERLIGT SPEKTRUM — Planckspektrumet alla våglängder — som en atomgrupp (en hel kropp, eller någon del) kan uppvisa, samt INOM EN MAXIMALT AVGRÄNSAD FRI RYMD MED MAXIMALT STORT AVSTÅND MELLAN MÄTKROPP OCH OBJEKTSKROPP för att minimera alla eventuella avvikelser, desto högre grad av överensstämmande noggrannhet ges med Planckkurvan.

Den kosmiska bakgrundsstrålningen

se utförligt från Inledande beskrivning

Den högsta formen av RENHET i Planckkurvan uppnås följaktligen för hela universum i K-cellen:

Den kosmiska bakgrundsstrålningen

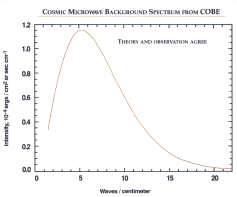
För förklaring,

se PLANCKS STRÅLNINGSLAG MED FREKVENSEN SOM VARIABEL

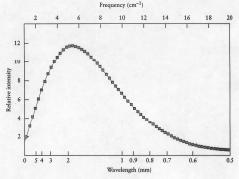
Bilden ovan; originalet förminskat 50%, inverterat, gråreducerat, från

@INTERNET Wikipedia Cosmic microwave background radiation 2010-03-23

http://en.wikipedia.org/wiki/File:Firas_spectrum.jpg

”The FIRAS data match the curve so exactly, with error uncertainties less than the width of the blackbody curve, that it is impossible to distinguish the data from the theoretical curve.”;

Min översättning:

FIRAS data matchar kurvan så exakt, med felosäkerheter mindre än bredden på svartkroppskurvan, att det är omöjligt att skilja data från den teoretiska kurvan.

Artikeln behandlar inte den öppna frågan varför mätkurvan slutar tvärt.

Jämför även

”Det var det mest perfekta svartkroppsspektrum man någonsin sett i naturen”.

UNIVERSUMS FÖDELSE, John D. Barrow, Natur och Kultur 1994,

s23(Figur 1.6, COBE-satellitens mätningar 1989)-24,

Den kosmiska bakgrundsstrålningen — Planckvärmestrålningen på (nu) ca 2,73 °K; Den varken mäts från eller strålar från någon särskild kropp, utan är, tydligen, den sammanlagda strålning som (per lång tid) samlats från alla universums kroppar med deras genomgång i universums totala värmeutvecklingshistoria (K-CELLEN I RELATERAD FYSIK). Se även utförligt från K-CELLENS VÄRMEFYSIK. Se även det jämförande diagrammet nedan från K-cellens värmefysik.

Effektgrafens matematiska form nedan (som påminner om Planckkurvans form) har formen

P = kT(a+T²)^–2 ...................... T betecknar tid, P betecknar effekt

Se mera utförligt från K-cellens värmefysik.

PLANCKVÄRMEGRADEN I K-CELLENS UTVECKLING

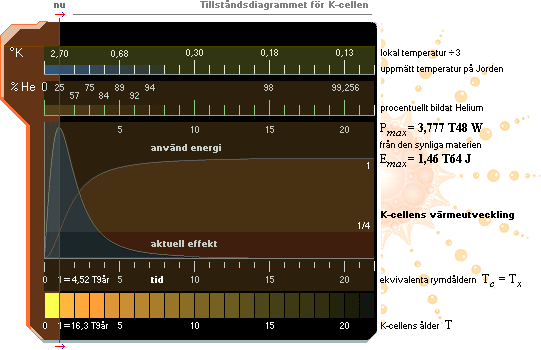
K-cellens tillståndsdiagram, se utförligt från K-cellens värmefysik

ABSOLUTA METRIKEN (ljushastighet och frekvens följs åt genom ljusets gravitella beroende) garanterar att Planckstrålningen inom K-cellen uppvisar en perfekt homogen ordning för varje lokal rymd som uppvisar en ljushastighet större än noll — oberoende av vilken den är. Observera att det INTE har något med RELATIVITETSTEORIN att göra. Se utförligt exempel i GPS-EXEMPLET, samt utförlig beskrivning i PLANCKEKVIVALENTERNA.

Solens irradians

SOLEN har också ENLIGT RELATERAD FYSIK (utomordentligt) bra förutsättningar för att uppvisa en perfekt Planckkurva (kortaste våglängderna från massdestruktionen i kärnomvandlingarna, längsta våglängderna via gashöljet) — men Solytans (strängt) reflektiva ytskikt fragmenterar (tydligen) resultatet:

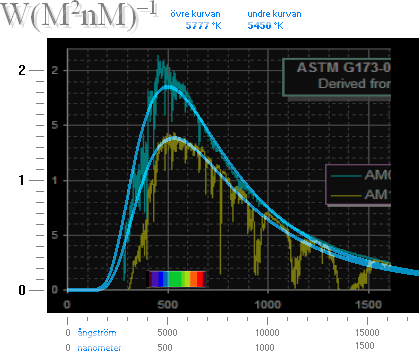
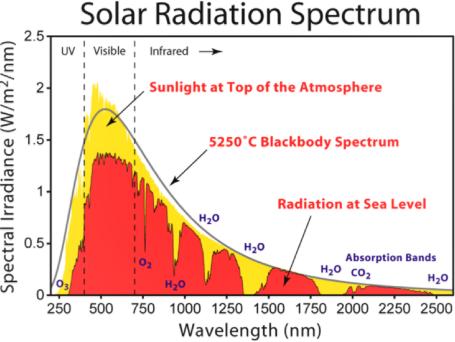
Originalet ovan från

Solar Spectral Irradiance & PV Cell Operational Regions (ASTM G173-03)

http://www.rfcafe.com/references/electrical/ASTM%20G173-03%20Reference%20Spectra.htm

tillsammans med ungefärliga genomskärande Planckkurvor respektive vid

T = 5777 °K ...................................... övre heldragna kurvan, från satellit (AM0)

T = 5450 °K ...................................... undre heldragna kurvan, från Jordytan (AM1.5)

N_λ = 8.4(x^–5)(–1+e^1/0.401x)^–1 .............. övre grafen, T=5777°K

Grafiskt övre (författarens privata grafritande program) unit200 T=5777°K

[0.55·8.4(x'–5)(–1+è'1/0.401x)'–1] ;

N_λ = 8.4(x^–5)(–1+e^1.06/0.401x)^–1 .............. undre grafen, T=5450°K

Grafiskt undre (författarens privata grafritande program) unit200 T=5450°K

[0.55·8.4(x'–5)(–1+è'1.06/0.401x)'–1]

Se även utförligt i Hur Plancks strålningslag beräknas för spektral irradians.

Den undre kurvans fragmentering (mätningar från Jordytan) beror på (främst) atmosfäriskt vatten i Jordatmosfären som absorberar i olika våglängdsintervall.

Den övre kurvans fragmentering (mätningar från satellit) beror på (den mycket komplicerade material-) brytningen från Solytan.

Tyvärr finns (ännu Mar2010) inga ytterligare praktiska mätexempel att visa upp med (enbart) tillgång till den öppna webben.

Genom att PLANCKS STRÅLNINGSLAG, WIENS FÖRSKJUTNINGSLAG och STEFAN-BOLTZMANNS STRÅLNINGSLAG hänger ihop som en enda matematisk kropp (nedan) blir det speciellt bekvämt för oss att (ofta oegentligt) idealisera alla möjliga kroppar och omständigheter i den allmänna fysikbeskrivningen på Plancks (bekväma) strålningslag — och därmed ofta bekvämt, men inte alltid så träffsäkert, göra påstående om olika kroppars temperatur i samband med olika spektrala våglängder (Wiens förskjutningslag, oftast). Det är viktigt att den bekväma (redan väl etablerade) ordningen står klart formulerad.

De tre nämnda strålningslagarna (se ovanstående länkar) sammanhänger så:

STEFAN-BOLTZMANNS STRÅLNINGSLAGs derivata leder till PLANCKS STRÅLNINGSLAG; PLANCKS STRÅLNINGSLAGs derivata leder till WIENS FÖRSKJUTNINGSLAG. Därutöver kan Plancks strålningslag också härledas alternativt från Plancks entropisamband med direkt koppling till allmänna gaslagens enkla samband (se särskild härledning i Plancks strålningslag från Plancks entropisamband). Dessa tre strålningslagar hör ihop som en enda matematisk enhet med samma fysikaliska grund och förutsättningar. Genom att någon av dem uppvisar experimentell verifierbarhet, gör de andra det också automatiskt. Se särskild experimentell referens.

Grundsatser

GRUNDSATSER

för den förklarliga översikten till Plancks strålningslag

2010III29

PROPORTIONALITETEN MELLAN MASSA OCH LADDNING

Eftersom atomkärnan I RELATERAD FYSIK är massans fundamentalform (Se PASTOM) — specifika beståndsdelar saknas helt: jämför 1=[n→∞](1/[n→∞]) — bygger hela framställningen i TNED på förutsättningen med exakt proportionalitet mellan massa och laddning. Proportionaliteten anställer helt och hållet Planckringen (h=mcr) för atomkärnans ekvivalenta strukturbyggnad. Se utförligt från ATOMKÄRNANS HÄRLEDNING. Frånsett beskrivningen med PRINCIPALPARTIKELN i Potentialbarriären

”Principalpartikeln leder oss till exakt principiell kunskap om hur den elektriska laddningen (Q) är konstruerad i förhållande till massan”,

finns (ännu Mar2010, frånsett här) inget särskilt avsnitt i UNIVERSUMS HISTORIA som rubricerar den detaljen, utan massa-laddningsproportionaliteten omnämns löpande i vart särskilt fall. En översiktlig listning med de centrala ställena där kopplingen omnämns särskilt ges nedan:

artikel

PLANCKRINGENS DIMENSIONER:

”Med exakt proportionalitet mellan massa och laddning är deplacementets storlek …”;

PLANCKRINGEN:

”en spinnande ring (J=mvr) med massa och laddning …”,

”Enda sättet för en sådan ekvation att gå ihop, är med en struktur av ±-laddningar (β) med ±-spinn som regleras av ett allmänt impulsmoment (eg., rörelsemängdsmoment) J=mvr …”,

”Solen FÖRBRUKAR MASSA KONTINUERLIGT. Massan förintas och dess inneboende energi överförs på andra massor genom värme och ljus (m→γ) enligt

e^– + e⁺ = 0 ............... laddning

s_e– + s_e+ = 0 .............. spinn (rörelse)

m_e– + m_e+ = 2m_e ......... massa

”,

”Laddningen är, som massan och spinnet, utan upphov”,

”… massan konserverar laddningen via Potentialbarriären …”,

”(proportionaliteten mellan massa och laddning vid fusion)”;

ELEKTRONMASSANS KOMPONENTER:

”Eftersom laddningen hos e är massproportionell …”,

”Potentialbarriärens massa-laddning förklarar varför både massan och divergensen måste reduceras på samma kvantitet n: …”,

”Eftersom massa och laddning är proportionella genom kärnmassan som massans fundamentalform …” …

Satsen om alla kroppars obönhörliga värmeläckning — Plancks strålningslag

alla kroppar värmeläcker

Beskrivning:

Varje elektriskt laddad kropp som befinner sig i en rymd där ljushastigheten är större än noll och som genomgår en positionsändring åstadkommer genom sitt lägesändrade elektriska fält och den däri kopplande (lokala) ljushastigheten en återverkan (se induktion) på alla omgivande elektriskt laddade kroppar med en motsvarande (se elektriska fältpotentialen) avståndsbetingad, induktiv, positionsändring. Se utförligt från Induktionen.

Genom att den elektriska fältpotentialen (U=E/Q=Fr/Q=k[dQ/dr]) avtar med avståndet från den laddade masskropp som medierar induktionen blir verkningsresultatet:

Ljusets induktivt verkställande styrka avtar med ljusets (divergenta) spridning. Det betyder i motsvarande mening:

Den effektiva ljusenergin ([n→1]hf) per fast rymdvolym avtar »i takt med tiden». I andra ord:

Ljusets styrka försvagas med divergensen (men inte frekvensen; för frekvensens avtagande se Comptoneffekten; Se även tillägget nedan, om ej redan bekant). Eller ännu enklare:

Alla fysiska kroppar värmeläcker.

Särskilt klargörande sammanfattande genomgång (om ej redan bekant) rörande masselementens ljusväxelverkande egenskaper — alla kroppar värmeläcker

Impulsmomentet, eller Planckringen h=mcr, motsvarar I RELATERAD FYSIK massfysikens absoluta principiella komponent (eller »det principiella masselementet») med de fysikaliska storheterna massa (m), laddning (Q) och spinn (J=mvr, v=c=lf). För spinnets del, se även i SPEKTRUM OCH KVANTTALEN. Se även SPINNBEGREPPET I MODERN AKADEMI.

Genom villkoret ENLIGT RELATERAD FYSIK i Fysikens Sjunde Princip, massans principiella struktur (PASTOM) och som krävs för att den primära massförstöraren E=mcc ska kunna upplösa materien in till sista prick (se utförligt i MASSDESTRUKTIONEN), bildar Planckringen ekvivalens med PRINCIPALRINGEN i POTENTIALBARRIÄREN; Principalringen definierar STÄLLET där ett yttre elektriskt fält griper TAG i massfysikens elektriskt laddade element, den här benämnda ENERGIZONEN [c(z)=c0/2]. Se utförligt från POTENTIALBARRIÄREN, om ej redan bekant.

Därmed grunden i TNED för ATOMKÄRNANS HÄRLEDNING från PLANCKRINGEN genom PASTOM i formen av ett oändligt fraktalt elektromekaniskt ringströmsaggregat. Aggregatets elementära toppform visar sig i formen av NEUTRONEN enligt PLANCKS KONSTANT

h = 6,62559 t34 JS = m(NEUTRONMASSAN)×c(LJUSHASTIGHETENS TOPPVÄRDE c0)×r(NEUTRONRADIENtyngdcirkeln), se utförligt från PLANCKRINGEN. Plancks konstant får därmed också egenskapen att vara en STRUKTURKONSTANT, se från NEUTRINOSPEKTRUM.

Planckringens frakta struktur med sin strängt bundna kraftväv för massa och laddning ger ringstrukturen funktionen av en ideal elektromekanisk transformator (se även SVÄNGNINGSEKVATIONEN): Ringen kan omvandla mekanisk energi (stötenergi) till elektromagnetisk (induktiv) strålning och omvänt uppvisa inre mekaniska svängningsrörelser som funktion av yttre induktiva (och magnetiska) fält.

Då ringen utsätts för induktiv påverkan från en yttre ljuskälla (se från INDUKTIONEN) och därmed omsätter växelverkan mellan inkommande induktion och intern elektromekanisk transformation, ändras ringens position enligt induktionsverkan. Samtidigt ändras, tvunget enligt energiräkningen, också den resulterande (efterföljande) induktionsriktningen (»ljusstrålens riktning») så, att summan av energierna före växelverkan är samma som energierna efter växelverkan. Dvs., ljusstrålens energi avtar|ökar på bekostnad av ringens induktivt erhållna|reducerade rörelseenergi. Fenomenet kallas konventionellt för COMPTONEFFEKTEN (Se även till jämförelse konventionellt exv. @INTERNET Wikipedia Compton scattering 2010-03-22). Verkan är naturligt som störst för masspartiklar jämförliga med atomkärnorna. Det ger Comptoneffekten karaktären att visa sig i det högfrekventa området (gammastrålning, röntgenstrålning). Principen gäller dock för samtliga elektriskt laddade masskroppar. Genom att ingen massform är helt och hållet fullständigt tät, att det finns mellanrum mellan alla massformer, kan heller ingen ljusenergi innestängas fullständigt i en rymd där ljushastigheten är större än noll; Mellanrummen (rymden) mellan masselementen (Planckringarna) garanterar i vilket fall att ljusenergin sprids divergent. Därmed totalt:

energin från en ljuskälla avtar obönhörligen med ljusenergins uppehållande i massa: alla kroppar värmeläcker.

För att bevara en kropps temperatur återstår därmed bara en, och endast en, möjlighet: att kroppen — en visst avgränsad region — tillförs lika stor energimängd som den värmeläcker. Jämför Solen.

Notera att ovanstående beskrivning av princip är omöjlig i modern akademi: elektriska laddningens härledning, induktionen, atomkärnans härledning.

Alla möjliga våglängder

Planckenergin E=hf tillsammans med STRUKTURKRITERIET (PASTOM) som grundlägger atomkärnans härledning i PLANCKRINGEN garanterar att varje strukturring (mcr) kan mediera ALLA MÖJLIGA VÅGLÄNGDER, alla möjliga frekvenser; Våglängder mindre än ringens utsträckning påverkar ringstrukturens underfraktaler (ringbyggnaden endast), medan våglängder större än ringens utsträckning ger motsvarande (makrorelaterad) ordinär induktionsverkan (hela ringen försätts i rörelse).

Med antalet P=E/hf Planckenergikvanta ges maximala antalet likaberättigade energifördelningssätt på potensformen (1+P)^(1+P) med aktuella antalet likaberättigade energifördelningssätt som W=(1+P)^(1+P)/P^P för varje singulär Planckring h=mcr för varje bestämd frekvens (f ). Se utförligt i HUR W BERÄKNAS. Det betyder i slutänden att varje bestämd frekvens för varje Planckring (h=mcr) besitter ett visst bestämt, och för varje materiell växelverkan ursprungligt odämpat, energifördelningsvärde av princip bland alla andra möjliga frekvenser (och Planckringar). Sätts W-formen in i PLANCKS ENTROPISAMBAND S=b(lnW), som bl.a. kan HÄRLEDAS på det enklaste från Allmänna Gaslagen (se även mera utförligt i HÄRLEDNINGEN TILL PLANCKS ENTROPISAMBAND) framträder direkt Plancks strålningslag som W-formens derivata. Se utförligt i Plancks strålningslag från Plancks entropisamband.

Planckstrålningens fysiska form

Men varje FYSISK KROPP är INTE en Planckring (h=mcr); Genom att alla materiella kroppar ENLIGT RELATERAD FYSIK består av en stor mängd PLANCKRINGAR (atomkärnor, elektromassaelement utspridda över hela atomvolymen) tvingas Planckringarna inbördes, ömsesidigt och sinsemellan uppvisa olika slag av växelverkan i de olika frekvenserna med, speciellt, de specifika atombesättningarna. Det betyder tydligen — i den praktiska fysiken, frånsett exemplet med den kosmiska bakgrundsstrålningen — att INGEN fysisk kropp är kapabel att uppvisa en exakt Planckstrålningskurva för alla möjliga våglängder — [men (oftast) med tydlig »allmän följsamhet» tillsammans med en (stor) mängd olika fragmenterade avsnitt (Se exemplet med Solens Irradians)]. Eftersom alla material består av en stor mängd atomer med elektriskt laddade elektronhöljen och därmed en stor flora av möjliga interferenser, finns följaktligen ingen DIREKT möjlighet INOM JORDFYSIKEN — någonsin — att få fram en exakt experimentell Planckkurva som stämmer heltäckande med den ideala odämpade teoretiska formen, inte för något material.

Trots att Plancks strålningssamband bistod de förfinade mättester [‡3] som genomfördes under 1911, fanns redan då en viss önskan om mera övertygande experimentella resultat. Eller som Max Planck själv uttryckte saken i sin nobelföreläsning från 1920 [‡2]: ”Även idag, ska det erkännas, kan vi inte tala om en slutlig exakt bekräftelse. I själva verket är ett friskt försök [som leder] till bevis trängande behövligt.”. Se även särskilt Planck från 1914 (The Theory of Heat Radiation); Planck understryker svårigheten att tolka innehållet, samma ämne [‡1] ”Att därför försöka dra slutsatser beträffande de speciella egenskaperna hos de partiklar som emitterar strålarna från de elementära vibrationerna i strålarna hos det normala spektrat skulle bli ett hopplöst företag.”.

Frånsett extremfallet med DEN KOSMISKA BAKGRUNDSSTRÅLNINGEN som gäller hela K-CELLEN vet vi emellertid från experimentell prövning av STEFAN-BOLTZMANNS STRÅLNINGSLAG att också Plancks strålningslag är certifierat genuin nämligen som STEFAN-BOLTZMANNS STRÅLNINGSLAGS DERIVATA, samt även WIENS FÖRSKJUTNINGSLAG som Planckstrålningslagens derivata. Alla dessa tre strålningslagar hör ihop tillsammans med deras (någon, vilkensom) bevisbarhet. Därmed är beviset stadfäst.

Men läckningen — emissionen — är ju strålningen. Och alltså är Plancks strålningslag läckningen: Satsen om alla kroppars värmeläckning är tydligen samma sak som Plancks strålningslag:

alla våglängder oberoende av kroppens sammansättning eller storlek

h

Plancks konstant, h = mcr — strömringen, masselementet: även atomkärnan

Satsen om alla kroppars värmeläckning övergår — då — tydligen i samma som definitionen för KONSTANT TEMPERATUR då energiinflödet som underhåller genomströmningen är (kan anses vara, med olika grader av idealisering beroende på typ av tillämpning) lika stort som det läckande utflödet. Se f.ö. (som utförligt exempel) i SOLFYSIKEN. Se även Plancks strålningslag från Plancks entropisamband.

Se även i Summerande Planckstrålningsexempel.

Den moderna akademin

DEN MODERNA AKADEMINS ANTAGANDE av begreppet »isolerat system» i termodynamisk mening

Varför uppmärksammades inte den ovan (ytterst enkla) ordningen i och med upptäckten av Plancks konstant (h), det universella verkanskvantumet (eng. universal quantum of action), med publikationen av Max Planck från år 1901?

Det tveklöst enkla (exakta) svaret är:

»isolerade systemet» stänger kunskapsvägen

ORDNINGEN UPPMÄRKSAMMADES TYDLIGEN INTE På grund av den då runt 1900 redan etablerade, sedan runt ett halvsekel bakåt, allmänna skadeglädjen i den UPPFINNING som alla dåvarande vetenskapare tydligen kastade sig över med hull och hår — då detaljen ställdes fram av Balfour Stewart år 1858, tydligen till allas JUBEL:

uppfinningen och antagandet av en ogenomtränglig strålande inneslutning (”impervious radiating inclosure”); ett isolerat system i termodynamisk mening.

Ett isolerat system i termodynamisk mening existerar inte i fysiken: alla kroppar värmeläcker. Plancks strålningslag.

Undantag existerar inte.

Det mest anmärkningsvärda är att den moderna akademin, strax, identifierade sitt ’system’ med universum: Jämför den moderna akademins sammanfattande termofysik med speciellt termodynamikens andra huvudsats; Den hade från början en helt glänsande klar formulering (se Clausius klassiska formulering från 1862: värme går alltid från varmt till kallt) men som senare omformulerades (exakt när finns här f.n. ingen exakt uppgift på). Det finns idag inget kvar av ursprunget. Inte ett spår. Se särskilt som ovan fackbokens enkla sammanfattning.

Se vidare utförligt från

ENTROPIBEGREPPET I RELATERAD FYSIK och

ISOLERADE SYSTEMETS URSPRUNG.

Det går inte att TEORETISERA — framställa matematisk fysik — PÅ BEGREPPET »isolerat system» i termodynamisk mening: det finns ingen fysikalisk referens, ingen preferens, ingen dynamisk utgångspunkt till vägledning. Ämnet beskriver FIKTION, pseudofysik, från början till slut.

Antagandet av »isolerat system» medförde att vägen stängdes automatiskt till ljusfysikens grundliga förklaring tillsammans med atomkärnans härledning; När det universella verkanskvantumet, Plancks konstant h, uppdagades omkring år 1900, förstod ingen innebörden. Och så är det ännu i dag (Apr2010). I 1800-talets ljus: Utvecklingen tog tydligen en väg den inte borde ha tagit.

Uppenbarligen — tydligen och relaterbarligen — ENBART genom att så TVÄRBRANT motsätta sig varje erinran om KUNSKAPEN SOM FRIDSAMHETSGRUNDAD, se särskilt från sanningsbegreppet — genom praktiska vardagliga exempel under lång tid i systematiska utdrivningar, förföljelser, förhör, rättegångar och upprepade frihetsberövanden, förebråelser och allmänna utskällningar, för att ställa fram hela skräckväldet i dess fulla vidd — kan man FÖRSTÅ grunden, orsaken och omfattningen till VARFÖR mänskligheten INOM MODERN AKADEMI — domstolsverksamheten inkluderat i synnerhet med FÖREDÖMET FÖR RÄTTSLOGIK — INTE förmått uppmärksamma KUNSKAPSGRUNDERNA, inte ens i minsta elementära mening:

DEN här tydligt uppmärksammade MODERNA AKADEMINS HELA NATURKONFLIKT grundas — tydligen närmast helt — på 1800-talets berömda idé att MÄNNISKAN HAR SKAPAT MATEMATIKEN: logik, intelligens, förnuft — herredeviser. Med den Europeiskt domstolsutnämnda VAPENMAKTENS DÖMANDE, BESTRAFFANDE OCH BELÖNANDE ÖVERHÖGHET ÖVER FÖRSTÅNDET och dess rättsutövande tillhyggen som främsta sevärda inslag blir det hur enkelt som helst att också FATTA DET ALLMÄNNA MODERNA AKADEMISKA INSLAGET av att UPPFINNA istället för att HÄRLEDA — skjut först, fråga sen — när det kommer till VETTET; I konsekvent EFFEKT är det alldeles tydligt att man också, automatiskt, utan att anstränga sig särskilt, utan någon direkt överläggning, genom dessa uppfinningar, deras blotta ANDA, har STÄNGT KUNSKAPSVÄGEN. Jämför atomkärnan som exempel, med redovisade jämförelser, med vidare [utförligt i ATOMKÄRNANS HÄRLEDNING]. Saken i den uppfinnande bemärkelsen gäller alltså INTE teknik, marknad och hantverk, utan en FÖRMENT FÖRNUFTSLOGIK, idéer om PÅTVINGAD ÖVERHÖGHET I SANNINGSBEGREPPET som bara grundas på typen ovannämnda citatexempel: genuint fridsamhetsförakt med äkta kunskapshat. Sanningshat. Fräsande, bespottande förakt med yttringar i dess allra mest folkligt förankrade, populära vidd. Om något barn försöker närma sig, haglar bannorna: ”HUR SKULLE DET VARA OM ALLA GJORDE SOM DU!”. Tala sedan om ORSAKERNA.

Se särskilt i

Demensförklaringen över Mänskligheten

Nationernas oavsiktliga Kunskapsförakt — om bakgrunden till Universums Historia och Den Relaterade Fysikens Innehåll

Införandet av den moderna akademins allmänna auktoritära överhöghet — INFÖRANDET AV LYDNADSTVÅNG 1870

DET BLIR SVÅRT ANNARS ATT FÖRKLARA HUR MAN SÅ INGÅENDE KAN MISSA KVINTESSENSEN AV VETTET. Se även i AGW.

1800-talets IsoleradeSystem-lära, betraktad som explicit grundval för termofysiken som vetenskap, attackerar alldeles tveklöst grundvalen för den exakta beskrivningen i Plancks strålningslag: alla kroppar värmeläcker.

— Veterligt ingen i modern akademi tänker på vad man gör, sysslar med, i samband med blotta användandet av begreppet »isolerat system» i termodynamisk mening. Den moderna akademin är alldeles uppenbarligen istället så helt, fullständigt, genomsyrad av den användningsformen, trots dess erkända obefintlighet, att hela ansvaret för att kunskapsvägen I DET ÄMNET ligger blockerad — här tveklöst — kan återföras på just den detaljen: »isolerat system».

Uppdagandet av Plancks konstant (från år 1900, se Plancks original) bildar förutsättningen för upplysningen. Men det uppdagandet medförde ingalunda att det tidigare uppfunna begreppet »isolerat system» (Stewart 1858) förkastades. Tvärtom hade det blivit så etablerat att det, tydligen redan då omkring år 1900 hade börjat framstå som den moderna akademiska lärobyggnadens grundval.

Jämför återigen fackbokens enkla sammanfattning.

Det faktum att alla masskroppar utverkar elektromagnetisk aktivitet — värmeläckning, strålning — genom blotta sammansättningen av fundamenten MASSA LADDNING SPINN (Planckringen h=mcr, m=[Q²/R][dt/A], se från Elektriska Laddningen) och med Planckringen (h=mcr) som grundvalen för hela strålningsfenomenet, helt oberoende av specifikt material, det faktum att alla kroppar värmeläcker, allt det körs över — utplånas — med användningen av »isolerat system»: förbudet att värmeläcka. De vetenskapliga publikationerna från det sena 1800-talet och framåt är också uppenbarligen fullproppade med just sådana beskrivningar typ ”impervious radiating inclosure” med tillhörande omfattande matematiska utläggningar: Stewart, Kirchhoff, Maxwell, Planck m.fl.

Se INTERNET ARCHIVE, i stort sett alla de klassiska 1800-talsverken (och senare) i värmeläran finns numera inskannade som digitalkopior på webben och kan läsas/nerladdas gratis (sök på typ Theory of Heat i INTERNET ARCHIVE, se även särskilda http-länkar som omnämns löpande i den här framställningen).

Den stympade fysikbild som återstår med antagandet av »isolerat system» blir — då — tydligen föga mer än en rent fiktiv pseudofysik, utan varje form av naturvetenskapligt grundad förankring: Bumpande — fiktiva — »ljusgummikulor» som kastas tillbaka från idealt supersensationella science fictionavskärmande kärlväggar i den moderna vetenskapens uppfunna inneslutningar med tillhörande »dockskåpsekvationer» (helt värdelöst material). I jämförelse med Planckringen ATOMKÄRNANS HÄRLEDNING finns inga paralleller.

I ljusets av den ovan (delvis) depraverade historieuppvisningen med andra ord:

Den moderna akademins uppsegling under 1800-talet missade inte bara förklaringen till ljusets fysikaliska fenomengrund, så som det framstår ännu i denna dag, utan än mer förklaringen till Plancks konstant: atomkärnans härledning. Alla kroppar värmeläcker. Det finns inga isolerade system i termodynamisk mening i fysiken. Man intygar det också själv, se särskilt citat (se även särskilt i citat från Maxwell). Likväl upphöjs det (därför att modern akademi inte har någon annan grund att återföra sin uppfattning om universum på, se särskilt i Entropibegreppet i Modern akademi).

Se vidare, mera utförligt, i

ENTROPIBEGREPPET I RELATERAD FYSIK och

ISOLERADE SYSTEMETS URSPRUNG och

ISOLERADE SYSTEMETS INNEBÖRD.

Plancks strålningslag

PLANCKS STRÅLNINGSLAG beskriver — TYDLIGEN GENOM VISS NÄRVERKAN — varje materiell kropps idealt odämpade rena interferenslösa temperaturstrålning som föreligger i rymden, i varje masskropp, mellan alla masselement, oberoende av kropparnas sammansättning, typ, art eller form.

För exakt praktiskt exempel, se den kosmiska bakgrundsstrålningen.

Mera sammansatt:

Planckstrålningen är tydligen grundläggande för hela fysiken: PLANCKS STRÅLNINGSLAG

1 hc²

N_λ = —— ——————

λ⁵ e ^hc/bλT – 1

beskriver energidistributionen (eg. spektrala radiansen) för varje bestämd energi vid varje bestämd temperatur vid varje bestämd våglängd [i princip således genom varje möjlig Planckring] för ett motsvarande bestämt antal likaberättigade energifördelningssätt [som alltså också inbegriper tillståndsfysiken i varje möjligt massfysikens element; nämligen med dessa som agenter för radiansen]: ljusenergins odämpade föreliggande — utan materiell hänsyn.

Således — definitionen av giltigheten för Plancks strålningslag:

Ju högre grad av SPEKTRAL alla våglängder REPRESENTATION en kropp kan uppvisa i sin energidistribution

med en bestämd energi

— uppmätt under längsta möjliga tid, således med minsta möjliga variation

— vid varje bestämd våglängd

desto högre grad av värmegradsbaserad noggrannhet kommer kroppens samlade radians (utstrålning) TYDLIGEN att uppvisa mot den ideala helt rena Planckstrålningskurvans värden (Se även Illustrerat Exempel).

BEVISET FÖR HÖGSTA MÖJLIGA RENHET i den rent PRAKTISKA tillämpningen av Plancks strålningslag blir, således tvunget, med hjälp av all tillgänglig elektromagnetiskt aktiv massa under längsta möjliga mätintervall med minsta möjliga variation — vilket tydligen vill säga: HELA UNIVERSUMS SAMLADE STRÅLNING i formen av den s.k. kosmiska bakgrundsstrålningen.

Se även beskrivningen av Plancks strålningslag från början och inledningen.

Se även i Summerande Planckstrålningsexempel.

Frekvensformen

PLANCKS STRÅLNINGSLAG MED FREKVENSEN SOM VARIABEL

Frekvensformen

MED EXEMPEL FRÅN DEN KOSMISKA BAKGRUNDSSTRÅLNINGEN

Plancks strålningslag

1 hc²

N_λ = —— ——————

λ⁵ e ^hc/bλT – 1

uttryckt på motsvarande frekvensform (f=v) blir via c=λv

h v⁵

N_λ = —— ——————

c³ e ^hv/bT – 1

h/b = (6,626 t43 JS)/(1,38 t23 J/°K)

= 4,80144 t11 S°K ;

h/c³ = (6,626 t43 JS)/(2,99792458 T8 M/S)³

= 2,45917 t59 JS/(M/S)³

BILDKÄLLA: THE TELESCOPE HISTORY

The 76.0 m Lovell radio telescope at Jodrell Bank Observatory

http://www.solarnavigator.net/telescope.htm

Med Plancks strålningslag på frekvensformen ges direkt grund för att mäta spektral radians direkt genom frekvensavkännande utrustning typ radioteleskop (bilden ovan vänster). Observera att frekvensformen börjar från nollfrekvens motsvarande oändlig våglängd medan våglängdsformen börjar från noll våglängd motsvarande obegränsad frekvens. Det tillgängliga webbutbudet av presentationsgrafer till den kosmiska bakgrundsstrålningen (eng. CMBR, Cosmic Background Microwave Radiation) visas typiskt som nedan;

Referenser för kurvornas tolkning saknas ännu, vidare nedan.

1	2

1 @INTERNET Wikipedia Cosmic microwave background radiation 2010-03-23

2 STOCKHOLMS UNIVERSITET — Institutionen för astronomi

http://ttt.astro.su.se/~ez/kurs/Cosmology08_handouts/Cosmology08_L7.pdf

Skalor och värden är (helt) olika jämfört med våglängden som Planckkurvans variabel. Anledningen till denna (till synes »bisarra») nyordning är i detta fall begriplig eftersom mätningarna gjorts »med konventionella radioantenner». Alltså, på radiofrekvensbas (typ radioteleskop, området T11 Hz [hundratal GHz]). Termen ”waves/centimeter” har f.ö. innebörden x = 0,01·1/λ. Emellertid (dessutom): I försöken att återskapa motsvarande ideala Planckstrålningskurva (för formell kontroll), stöter man direkt på patrull.

Det tråkiga är att ingen av källorna (ännu Mar2010) upplyser läsaren om vilken ekvationsform av de tillgängliga som använts i grafens presentation — eller ens hur den grafiska formen framställts i skalformen.

Olika webbkällor använder (nämligen, utan att säga det) olika frekvenssamband …

I den slutsatsens sken: Det är så dåligt som det alls kan bli. I andra sammanhang skulle dylika presentationer HELT refuseras (Utgivning av Aftonbladets huvudupplaga i Sverige på hebreiska: man ur huse). Det finns i själva verket (ännu, här veterligt) ingen beskrivning av CMBR-grafens form, inte i någon begriplig mening, inte i någon av alla de hittills (Mar2010) tillgängliga genomsökta webbkällorna (till hit upp till ett tjugotal genomgångna träffsidor med sökning på speciellt PDF-dokument med CMBR-grafer); Det förefaller, nära, som att »det professionella etablissemanget» INTE VILL HA den uppmärksamheten.

Vad som däremot visas (efter visst letande) är — den i våglängdsvariabeln ljus — till synes underliga uppgiften att Planckstrålningens värmegrad på 2,73 °K (2,728) har sin Wientopp vid — inte 1,06 mM utan — 1,9 mM.

Anledningen är följande.

Planckkurvan via frekvensvariabeln

y = x⁵(–1+e^x/T)

ger en (helt) annan funktionsform än

Planckkurvan via våglängdsvariabeln

y = x^–5–(–1+e^1/xT)

Därmed också en annan form för

Wientoppens våglängdsekvivalent

λ = (2,898 t3)/T ;

λ = (2,898 t3)/2,73

= 1,06153 t3 M

enligt

(ref. @INTERNET Wikipedia Wien's displacement law 2010-03-27)

Wientoppens frekvensekvivalent

f = T · [5,879 T10 Hz/°K] ;

λ = c/f = (2,99792458 T8 M/S)/(2,73 · [5,879 T10 Hz/°K])

= 1,8679 t3 M

OVANSTÅENDE KURVEXEMPEL är dock (helt säkert) INTE tecknade/beräknade på frekvensformen med v^5 (snarare v^2, men inte heller den formen ser ut att stämma särskilt bra).

Tills dess att författarna bakom hieroglyferna lägger sig ut i ämnet gäller tydligen:

precisa referenser saknas ännu.

Den kosmiska bakgrundsstrålningstemperaturen beskrivs detaljerat i relaterad fysik genom hela K-cellens utvecklingshistoria via Stefan-Boltzmanns strålningslag enligt

T = [P/(ak4πR²)]^0,25K^–1 ..................... kosmiska bakgrundsstrålningens temperatur, relaterad fysik

med K(=λ/λ0)=3 som rödförskjutningens medelvärdeskoefficient (se härledningen för EKVIVALENTA STRÅLYTAN i Samband i sammandrag i K-CELLENS VÄRMEFYSIK), R som K-cellens strålradie via konstanta ljushastighetens toppvärde c0=R/t. (Se även mera utförligt i Härledningen till K-cellens värmefysik; Ett helt öppet OpenOffice-kalkylkort finns även tillgängligt, alla parametrar, som kan studeras i detalj, samt ändras för prövning, analys och jämförelse). T-värdet 2,7 °K är det som gäller vid Pmax, analogt K-cellens utveckling vid 16,37 miljarder år (universums ålder minst). Med ljustiden för de mest avlägset synliga delarna till K-cellens centrum (vår lokala galaxgrupp) ges tilläggsvärden (som beror på aktuell lokal; max totalt 20,91 miljarder år för hela nuvarande universums ålder).

Noteringar

NOTERING 1:

HyperPhysics ger korrekt beskrivning

Webbkällan HYPERPHYSICS beskriver en korrekt (relevant, linjär) skalform för CMBR-kurvan med våglängdsvariabel (men utan motsvarande inprickade mätdata),

http://hyperphysics.phy-astr.gsu.edu/hbase/bkg3k.html

HyperPhysics ger även allmänna tillämpningsexempel på Plancks strålningslag

http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/planckapp.html#c1

NOTERING 2:

Inlägg som berör Wienlagens frekvensform

Webbkällan

@INTERNET Wikipedia Cosmic microwave background radiation 2010-03-23

har på sin TalkPage på rubriken Wien's Law doesn't apply?

http://en.wikipedia.org/wiki/Talk:Cosmic_microwave_background_radiation

ett inlägg/klargörande som också beskriver (den olustiga förekomsten med) Wienlagens frekvensform.

NOTERING 3:

Uppfattningen att CMBR beror på Jordoceanerna

I källan ovan (diskussionssidan till wikiartikeln) omnämns den originella uppfattningen om ursprunget till CMBR som (företrädesvis) drivs av Pierre-Marie Robitaille (PhD, Ohio State University); Robitaille driver uppfattningen att CMBR i själva verket skulle ha Jordoceanerna som upphov (!).

Robitaille hade (Mar2007) kontaktat wikidiskussionsgruppen och aviserat sin mening;

Mars2007 inbjöds Robitaille att delta i TalkPage-diskussionerna på Wikipedia;

Juni2008 (efter en lång paus) gav Robitaille ett utförligt, väl refererat, svar (som förmodligen fick/får alla att tappa andan):

”Along these lines, it should be noted that the production of any thermal spectrum requires a physical oscillator”.

Robitaille har (nämligen) också mycket riktigt påpekat (genom sina vetenskapliga publikationer) det som alla redan vet — att Plancks strålningslag i modern akademi saknar förklaringsgrund beträffande VAD som alstrar Planckstrålningen. Nämligen en någon oscillator (citatet ovan avspeglar delvis den detaljen): Planckstrålningens totala oberoende av kropp, ämne, substans och material. Det problemet är ett, i sig genomgående, »klassiskt problem» som även (på visst sätt) har tagits upp av Planck själv [‡1], Einstein och andra (Robitaille ger utförliga referenser med citat i sina skrifter). Men Robitaille driver saken hårt: Han menar att själva grundfysiken från Kirchhoff (omkr. 1860) är FELAKTIG (omnämns även på wikiTalkSidan, ”I have now prepared an extensive discussion of Kirchhoff's Law of thermal emission”), och som kräver att de tre strålningslagarna måste omvärderas: Stefan-Boltzmanns strålningslag, Plancks strålningslag, Wiens förskjutningslag. Hur som helst: Robitaille tar tillfället i akt och menar nu att den förlorade fysikaliska oscillatorn, här, har anställt vattenmolekylens vätebindning, ”For the microwave background that oscillator will turn out the [to] be the very weak hydrogen bond between water molecules.”. Och ’på den vägen är det’, resonerar Robitaille, kort sagt.

Med den omfattning som Robitailles framställning angriper etablerade begrepp är det förståeligt (men inte försvarligt) att diskussionsgruppen (mot sin vilja) tvingades ignorera hans inlägg: Robitailles inlägg (heller inget senare) står fortfarande (Mar2010) obemött. Huvudartikeln ger heller inget omnämnande.

Här görs bara den vidare noteringen att RELATERAD FYSIK lämnar Robitailles teser — helt — utan förankring;

K-CELLENS VÄRMEFYSIK ger separat, oberoende, bevis för den kosmiska bakgrundsstrålningen.

SOLFYSIKEN ger oberoende bevis för att huvuddelen av Solklotet har mycket lägre täthet än varje motsvarande Jordfysikaliskt ämne;

Solens yttäthet [BAs128.fig.8.2] — för att exemplifiera kort — anges konventionellt grovt 0,0001 KG/M³, i relaterad fysik mera noga 0,000089277145; det är tydligen ett vakuum med våra mått mätt, långt ifrån någon vätska;

Robitailles framställningar innefattar (nämligen) också, separat utom ovan, den originella ståndpunkten att Solytan skulle vara en vätska, 1000 gånger hetare än det etablerade värdet på runt 6000 °K; Se (citat nedan) The Liquid Model of the Sun i

THE COLLAPSE OF THE BIG BANG AND THE GASEOUS SUN (2002)

Pierre-Marie Robitaille, Ph.D., Professor of Biophysics, Chemical Physics and Radiology, Ohio State University

http://www.thermalphysics.org/pdf/times.pdf

Jämför:

”Thus, the real temperature of the photosphere is ~1,000 times higher than the currently accepted temperature [34, 35]. Similarly, the temperature for the source of the microwave background is ~100 times higher than the measured value [33, 39, 40].”, s51sp2ö

Hänvisningarna är till Robitailles egna (peer-review-publicerade) artiklar:

BLACKBODY RADIATION AND THE CARBON PARTICLE

Pierre-Marie Robitaille, Department of Radiology, Ohio State University, July 2008

http://www.ptep-online.com/index_files/2008/PP-14-07.PDF

— Har du sett SpiderMan 3 — Scenen där han sitter högt ovanför marken på ett hustak och tar igen sig efter matchen med SandMannen. SpiderMan tar av sig ena stöveln, det rinner sand ur, och säger (med luttrad själ) ”Where do all these guys come from …”.

Där man inte frågar efter sanningen, visar sig också alla möjliga typer. Det är teaterns eviga lycka (och förbannelse) att det är så. (Ju värre bovarna är, desto större dramatik).

Jämförande resultatvärden Solytan

PREFERENSER I DEN SPEKTRALA UTVÄRDERINGEN i fallet Solen

Jämförande resultatvärden för Solytans temperatur

RELATERAD FYSIK — Solens reflektiva yta fragmenterar Planckspektrum

Massdestruktion (m®g) garanterar alla våglängder från noll, samt sedan vidare genom Solens allmänna vågekvation alla övriga våglängder mot oändligt. Se utförligt från Solens allmänna vågekvation i Solens vågmekaniska reflexionsrand;

Våglängden växer och amplituden avtar från centrum och utåt i Solens Allmänna Vågfunktion. Solens g-radie bestämmer gränsen för de mekaniska SolYtvågornas divergens.

SOLEN SOM LJUSEMITTERARE (enligt relaterad fysik, beskrivningen ovan med länkar som beskriver referensgrunderna) kan betraktas som en kropp som emitterar alla möjliga våglängder. I den meningen skulle Solen vara en perfekt (ideal) s.k. »svart kropp». Emellertid uppvisar Solytan ett påtagligt ljusspridningsskikt, dessutom med (tydligt) komplicerade förvecklingar [Utförligt i Spektroskopiska Jonvärmegraden]. Det gör att ljuset som går ut från Solytan, helt säkert, INTE KAN uppvisa den ideala absolutemitterande kroppens perfekta Planckstrålningsspektrum, utan snarare ett dito fragmenterat på Solytans karaktär av olika absorberande och emitterande ämneslokaler; Solytan verkställer en viss reflektivitet — som delvis påverkar utgående strålning.

Utan vidare referenser än så skulle man därmed kunna förmoda att Solytans effektiva Planckstrålningstemperatur (Wientoppen, se Wiens förskjutningslag) borde vara en blandning mellan den maximala absorptionskoefficienten a=2/3 (gäller för alla stjärnor i relaterad fysik, härledningen grundas på en simpel »rymdspridning» via xyz, se utförligt i ABSORPTIONSKOEFFICIENTEN) och den ideala a=1 med ett medelvärde på grovt 0,833.

Tabellen nedan (kalkylkort i OpenOffice) visar jämförande resultat med de (möjliga) olika värden som finns att välja på. De bägge övre (blå) inmatningsraderna avser data från etablerade fackverk, se efterföljande redovisning.

Jämförande resultatvärden för Solytans temperatur

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik2 — Solytan T — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

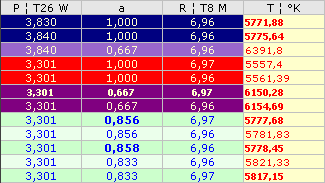
T = (P/aAk_{5,7 t8})^1/4 ............................. °K, Se Stefan-Boltzmanns strålningslag

k = 5,66893154148517 t8 ................. WM^–2°K^–4, Se Konstanten i ovanstående

P_SOL = 3,3011376 T26 ............................. W, Se Solens Råeffekt

P(SOL) från Solens råeffekt enligt TNED

SOM VI SER har knappast skillnaden i Solradievärdena (1000 KM) någon större betydelse. Skillnaden beror på värdena i Pa. Om T-värdet runt 5777°K avspeglar den uppmätta spektralmätningen (5016 Å, vidare nedan), finns bara en möjlighet för att resultatet i TNED ska stämma överens med den resultatformen: om a=0,856. Det ligger också nära det nyligen angivna medelvärdet på a=0,833 (5817,15°K; det skiljer på +40°C) och kan så långt förstås vara en rimlig bekräftelse. Emellertid finns (ännu, veterligt) inga direkt säkra referenser som kan ge närmare besked: Det skulle i så fall kräva ett fastställande av något (typiskt) medelvärde för Solytans reflektivitet (direkt observation upphör vid ca 500 KM in i Solkroppen). (Alla experter vet redan att den uppgiften i princip är omöjlig: det beror på skiktdjup. Men det är bara min tolkning). "sun surface reflectivity" ger ännu (Mar2010) noll sökresultat på webben.

Med Solen som exempel

Plancks strålningslag i praktisk fysik — med exempel från Solen

Genomgången I RELATERAD FYSIK (tillsammans med uppsamlade grunddata från Solobservationerna) i KORONAFYSIKEN för Solen visar att området just vid Solranden är (ytterst) komplicerat. Frånsett referensen med Solens gravitella radie finns i relaterad fysik ingen annan bestämd (idealt teoretiskt) värmegrad för Solytan att referera till. Se även Jämförande tabell.

Solytsvärden i etablerad litteratur

Solytsvärden i etablerad litteratur utgår från instrumentell mätning på Jordytan (även via ballong) och från satellit:

Spektroskopiskt (spektrograf, spektrofotometer, spektroradiometer, se allmänt [t.ex.] i @INTERNET Wikipedia Radiometry 2010-03-21; Någon exakt källreferens som beskriver metoden singulärt i detalj finns f.n. inte här);

Stellär klassifikation (spektral analys [som delvis innefattar ovanstående], se detaljerad beskrivning i @INTERNET Wikipedia Stellar classification 2010-03-21 och Sun, den senare artikeln beskriver hur värdet 5778°K kopplar);

5016 Å (5,016 t7 M), via Wiens förskjutningslag motsvarande

T = 5777 °K (se Tilley 2003 nedan);

Bestrålningseffekt (pyranometer, pyrheliometer, se @INTERNET Wikipedia Pyrheliometer 2010-03-21)

(1368 W/M²); Vid Jordbanan (OBS här medelbaserat efter årsmedelvärde, 4πR², R=1AU=1,496 T11 M) ges totaleffekten

P=3,84732 T26 W som via Stefan-Boltzmanns strålningslag (a=1) P=aAk_{5,7 t8}T⁴ ger

T = 5779 °K

Webbreferens: Se (bl.a.)

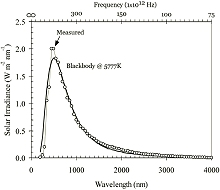
Spectral Transformities for Solar Radiation Reaching the Earth, David R. Tilley (2003)

Biological Resources Engineering and Natural Resources Management, University of Maryland

Fig.2 s10 förminskad med 50%

http://www.enst.umd.edu/tilley/emergy/SpectralTransformitiesTilley2003.pdf

Källan visar den uppmätta spektrala radiansen från Solen (”Howard et al. 1960”) i jämförelse med den ideala Planckkurvan vid T=5777°K.

Utbudet av jämförande liknande grafer från andra tillgängliga webbkällor är (ännu Mar2010) magert. Wikipedia har (naturligtvis) också en — vi ska återkomma till den senare (den innehåller av allt att döma vissa fel), se Webbfel i SolIrradiansen.

Soleffekten via Stefan-Boltzmanns strålningslag med a=1 och Solradien (fotometriska) R=6,96 T8 M blir med T=5777°K

P = aAk_{5,7 t8}T⁴

= (1)(4πR²)(5,7 t8)(5777)⁴

= 3,86467 T36 W

ENCARTA 99 Sun, Characteristics of the Sun anger 3,83 T26 W (via 5770 °K);

Wikipedia Sun 2009-03-23|2010-03-21 anger 3,846 T26 W (via 5778 °K).

Planckstrålningstoppen idealt för Solen presenteras i facklitteraturen generellt (genom [medelbaserad] spektralanalys) med a=1 vid ca 5016 Å (5,016 t7 M), via Wiens förskjutningslag motsvarande

T = 5777 °K. (En del webbkällor anger 5778). Se även i Jämförande tabell.

Fragmenteringen

Se även inledande illustrativt (sammanställt) exempel i Solens Irradians.

OVANSTÅENDE OMNÄMNANDE med Solytans reflektiva sammansättning, se Solens reflektiva yta fragmenterar Planckspektrum, (se även ELEKTRONTÄTHETEN I SOLYTAN, Opaciteten) betyder att man knappast kan utesluta en märkbar påverkan för utträdet av ljuset från det inre av Solen. Elektronmassan med dess elektriska enhetsladdning fungerar generellt som förmedlare av alla möjliga våglängder större än elektronelementets egen utsträckning, se från ELEKTRONMASSANS KOMPONENTER. Just för Solens ytskikt finns, här veterligt, ingen möjlighet att undvika effekten att den omständigheten tvunget måste skapa speciella spektrala övergångar. Observera elektrontätheten för Solytan enligt resultaten i relaterad fysik: Det finns ingen motsvarande Jordfysik att jämföra med.

OM man kan påstå att totalresultatet blir en påtaglig fragmentering av givna våglängder (energin bevaras, endast kurvformens yta ändras), blir den motsvarande totala effekten från en given totalenergi att amplituden för vissa våglängder i vissa intervall kan dämpas ut medan andra förstärks. Ett enkelt grafiskt exempel illustrerar principen, nedan.

Med en ursprunglig vågform (A) som tvingas passera ett våglängdsbrytande ’komponentgitter’ (B) (ELEKTRONMASSANS KOMPONENTER i Solytan) dämpas tvunget vissa partier ut medan andra förstärks för att bevara nettoenergin totalt. Om B hela tiden varierar (vilket fallet är i Solens fall) kan vi substituera med en variabel (periodisk) funktion (här godtyckligt) av formen i C,

y = x ^{b cos cx}

Vågformen i D blir då A genom B, analogt C överlagrad på A i formen av D;

CosinusFragmenteringen

Ju större b-värde, desto mera fragmenteras A.

Vi kan utnyttja datorns (bildskärmens) begränsade pixelenhet för att få fram »normalt omöjliga resonansmönster» i våginterferenserna med y(C)-sambandet genom att göra c-koefficienten (mycket) större än enheten som sambandet beräknas på. Ett exempel

y(D) = x ^0.5cos500x ..................................................... D-faktorn, PREFIXxSIN

visas nedan med A ersatt av sambandet för Plancks strålningslag enligt Planckkurvan

y(A) = 8.4(x^–5)(–1+e^1/0.401x)^–1 .................................... A-kurvan nedan

och som gäller idealt för solära irradiansen vid Jordbanan (1AU);

(Se utförligt i särskild beskrivning hur Planckstrålningslagen hanteras för ändamålet)

y(A) = 8.4(x^–5)(–1+e^1/0.401x)^–1[x ^0.5cos500x]................. D-kurvan nedan, PREFIXxSIN

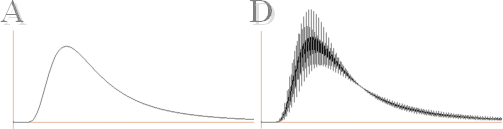
Grafiskt (författarens privata grafritande program) unit200; T=5777°K (Solirradiansen vid Jordbanan)

A = [0.55·8.4(x'–5)(–1+è'1/0.401x)'–1] ;unit200

D = [0.55·8.4(x'–5)(–1+è'1/0.401x)'–1][x'0.5cos500x] ;unit200

Se utförligt i Hur Plancks strålningslag beräknas för spektral irradians, om ej redan bekant.

Fragmenteringen (här i PREFIXxSIN) är i exempelfallet noll vid x=0 och x=1, samt alla

cos cx = 0 = cos nπ. Dvs., alla cx=nπ som ger x/n=π/500=0,00628318, n heltalen 1 2 3 … n:

x = n(0,00628318) ............................ ger noll fragmentering

Fragmenteringen förstärks periodiskt med växande x-värde, men överstiger aldrig x-värdet explicit genom att exponenten aldrig blir större än 1;

Fragmenteringen varierar alltså växande från x^0=1 (ingen inverkan) till x (max fragmentering).

Genom att kurvformen i D-grafen följer (överlappande) resonansmönster som inte direkt kan styras av funktionsvariabeln x (genom att det trigonometriska intervallet är mindre än det bildritande enhetsintervallet [en pixel]) finns här heller ingen direkt (enkel) garanti för att fragmenteringsfunktionen bevarar totala energiinnehållet i den ideala A-grafen. Det kräver i så fall generellt att högre amplituder tas ut av mindre så att nettoskillnaden blir noll;

För att avgränsa den växande x-MAXdelen krävs särskilda tillägg (i annat fall växer energifunktion med växande våglängd, vilket dock inte är fallet i Plancks strålningslag);

För växande våglängd x är det tydligt att amplituden växer med xMAX, även om huvudfunktionen dämpar ner den så att den inte (direkt) syns. En (enklare) funktionstyp (moderator) finns som kan begränsa tillväxten, men samtidigt innesluter helhetsvärdet mellan referensgränserna 1/2, 2/3 och 1. Funktionen (F) är

F = 1/(1+1/[x+1]); med x=0 ges F=1/2; x=1 ger F=2/3; x obegränsat ger F=1.

Om F används sätts den multiplicerande med huvudfunktionen (testadOK, se nedan).

Ungefär samma amplitudform ges i D-grafen med tillägget F = (1,7)/(1+ 1/[x+ 1]):

D = [0.55·8.4(x'–5)(–1+è'1/0.401x)'–1][x'0.5cos500x](1.7[1+1/(x+1)]'–1)

Resonansmönstret kan styras (D-grafen ovan), justeras och modifieras med tilläggen Offset1 och Offset2 enligt

[(x±Offset1)^0.5cos500(x±Offset2)]

Jämförande praktiska resultat

I webbkällan

Solar Spectral Irradiance & PV Cell Operational Regions (ASTM G173-03)

http://www.rfcafe.com/references/electrical/ASTM%20G173-03%20Reference%20Spectra.htm

”ASTM G173-03 Reference Spectra”,

finns en grafisk resultatbild från (omfattande) mätdata på solära irradiansen. Den röda toppdelen motsvarar mätningar utanför Jordatmosfären ”the radiation level outside of the Earth's atmosphere”, den blå undre grafdelen motsvarar mätningar på Jordytan, ”the radiation level after passing through the atmosphere 1.5 times, which is about the level at solar zenith angle 48.19°s, an average level at the Earth's surface (terrestrial).”. Källans referens är samma som nedanstående i NREL (National Renewable Energy Laboratory) från ASTM (American Society for Testing and Materials) med angivna internationella standardreferenser.

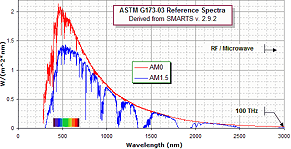
Originalet ovan från

Solar Spectral Irradiance & PV Cell Operational Regions (ASTM G173-03)

http://www.rfcafe.com/references/electrical/ASTM%20G173-03%20Reference%20Spectra.htm

förminskat 2ggr.

Webbkällan ovan har samma preferenser som i webbkällan nedan (den blå grafen ovan motsvarar den undre röda nedan),

National Renewable Energy Laboratory (Feb2010)

http://rredc.nrel.gov/solar/spectra/am1.5/

Beteckningssättet (enligt källan ovan) för AM0 AM1 AM1.5 etc., är standardiserade instrålningsreferenser: AM0 betyder ’genom noll atmosfär’ och gäller bara för satellit: AM1 gäller genom hela Jordatmosfären rakt ovanifrån; För övriga lutningar med Solen allt längre mot horisonten gäller högre värden (typ AM1.5), dvs., allt mer av Jordatmosfärens massa måste penetreras av Solljuset.

Luftens medeltäthet är f.ö. ca 1,2 KG/M³.

Se även @INTERNET Wikipedia Air mass coefficient 2010-03-21.

Med källgrafen justerad, ovan från rfcafe.com, med jämna pixelmått för 200pixels horisontellt för våglängdsskalan med enheten 1000nM och 110 pixels vertikalt för spektrala radiansenheten i W/M²nM (se utförligt i radians och spektral radians) ges grovjusteringen i xy-led 113%x;94%y som ger den något bredare jämförelsegrafen

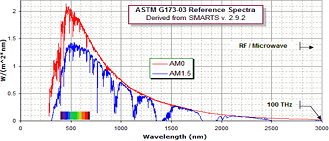
Med föregående fragmenterade Planckexempelgraf (inverterad nedan, sedan gråtonad över) lagd ovanpå/igenom framgår så hela PRINCIPEN DIREKT PRAKTISKT ILLUSTRATIVT med våglängdsfragmenteringen (separata delar överst, sammanfört nederst):

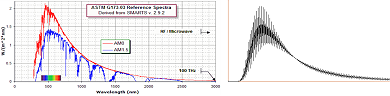
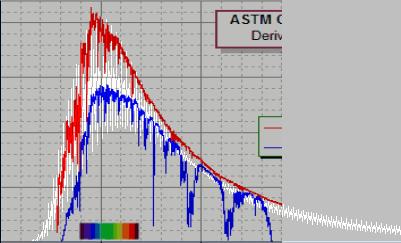
Föregående D-kurvan (vit) genomdragen till jämförelse med mätkurvorna för Solljuset (röd utanför Jorden, blå vid Jordytan)

y(A) = 8.4(x^–5)(–1+e^1/0.401x)^–1[x ^0,5cos500x]................. D-kurvan, PREFIXxSIN

SOM VI SER framträder onekligen en del (vissa) principiella likheter.

Komponenten som ger bredare (hela) dämpande våglängdsavsnitt kan också formuleras principiellt som en extra ytterligare faktor (det kräver dock en särskild beskrivning).

— De dämpade avsnitten underst kommer från främst atmosfäriskt vatten som absorberar solenergi i olika frihetsgrader och våglängdsintervall.

Reflexion medför dämpning

Den föregående tabellbeskrivningen med olika undersökande resultatvärden för Solytans VERKLIGA temperatur har tillsammans med reflexionen — Solytan representerar ett (starkt, extraordinärt) ljusspridningsskikt — samtidigt anställt en möjlig tilläggsfaktor till Plancks strålningslag.

Såvitt korrekt uppfattat, kan tilläggsfaktorn i fallet Solytan (möjligen) kompensera för den praktiska fysikens högre reflexionskoefficient (konv. albedo) än exakt 0. Resultatvärdena antyder med andra ord att absorbtionskoefficienten (a) ENLIGT TNED skulle vara ca 0,856 mot ideala a=1.

Då Solljuset växelverkar VIDARE med andra massor, till exempel vid inträdet i Jordatmosfären, bör vi ha en viss rätt att förvänta oss att samma dämpning (energiförlust via reflexion) uppkommer även där.

Den fullständiga giltigheten av Plancks strålningslag för motsvarande praktiska uppmätningar SKULLE följaktligen, i så fall för samtliga fall, inbegripa förekomsten av en absorptionskoefficient (a), idealt lika med 1, och som kan anta olika värden efter beroende på olika fall;

1 hc²

N_λ = —— —————— · a

λ⁵ e ^hc/bλT – 1

MEN:

Samtidigt med effektdämpningen sker en motsvarande energidämpning:

Jämför en total reduktion (a=nära noll): Om E=hf dämpas med konstant h måste f avta med minskande E, analogt längre våglängd på maximalt E;

Wientoppen förskjuts mot lägre frekvens, analogt längre våglängd;

Om den matematiken håller streck generellt blir resultatet i netto med andra ord i princip detsamma som en Planckkurva med lägre temperaturvärde — Vilket i princip gör att a-faktorn kan ersättas med alternativt lägre T-värde.

Planckformen får då (likväl) i slutänden sin vanliga innebörd — men med avtagande T-värden motsvarande inträngande materialdjup från ett toppvärde

1 hc²

N_λ = —— ——————

λ⁵ e ^hc/bλT – 1

De rena Planckkurvorna som stämmer ungefärligt med den ovanstående källgrafen från rfcafe.com visas inlagda i bilden nedan till jämförelse.

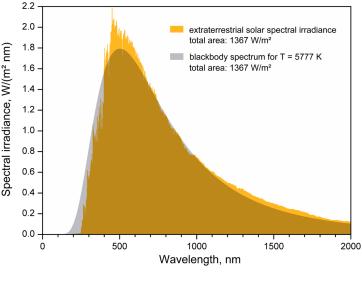
Originalet ovan från

Solar Spectral Irradiance & PV Cell Operational Regions (ASTM G173-03)

http://www.rfcafe.com/references/electrical/ASTM%20G173-03%20Reference%20Spectra.htm

tillsammans med ungefärliga genomskärande Planckkurvor respektive vid

T = 5777 °K ...................................... övre heldragna kurvan, AM0

T = 5450 °K ...................................... undre heldragna kurvan, AM1.5

N_λ = 8.4(x^–5)(–1+e^1/0.401x)^–1 .............. övre grafen, T=5777°K

Grafiskt övre (författarens privata grafritande program) unit200 T=5777°K

[0.55·8.4(x'–5)(–1+è'1/0.401x)'–1] ;

N_λ = 8.4(x^–5)(–1+e^1.06/0.401x)^–1 .............. undre grafen, T=5450°K

Grafiskt undre (författarens privata grafritande program) unit200 T=5450°K

[0.55·8.4(x'–5)(–1+è'1.06/0.401x)'–1]

Se utförligt i Hur Plancks strålningslag beräknas för spektral irradians.

OCH SOM VI SER:

Dämpningen med tillhörande förskjutning mot längre våglängder, framträder tydligt i den undre kurvan.

Notera att principiellt liknande förskjutningar också kan ses (i stor mängd) i den enklare cosinusfaktorn, se CosinusFragmenteringen.

;

Om temperaturdifferensen mellan Solytans ideala 5777°K och Jordytans medelvärdestemperatur (via termogravitella jämviktstrycket, 17°C=) 290°K utnyttjas fås

5777 – 290 = 5487 ............................ °K

Den grafen (illustrationen längre ner) skiljer sig knappt från den undre i bilden ovan — och kan därmed tas som indikation på (beviset för) en (inre) matematisk koppling:

En kropp (likt Jorden) som bestrålas av en annan hetare kropp (likt Solen) uppvisar i successivt olika inträngande djupskikt motsvarande lägre T-Planckkurva med allt större skärmning (reflexion) mot strålkällan

(Vilket alltså förutsätter att strålkällan INTE ges TID att värma upp objektet …).

Den lägre T-kurvan motsvarar lägre intensitet, vilket kan tolkas som att den lägre T-kurvan kopplar till högre reflektivitet (analogt mindre absorberad energi) vid en motsvarande genomgående konstant temperatur (sedan den yttre strålkällan, efter viss tid, värmt upp objektet … Formuleringarna kan, som vi ser, göras tämligen »krångliga»).

Ta nämligen följande belysande praktiska (teoretiska) exempel:

Summerande Planckstrålningsexempel

I en ihålig inneslutning (idealt sfärisk, men inte nödvändigtvis) med i det närmaste 99,999% reflekterande väggar släpper man in, under viss tid, en viss ljusmängd E=hf som garanterar en viss uppvärmning. Därefter tillsluts anordningen med förbehållet att det införda E kvarstannar i garanti av att endast 0,0001% tillåts absorberas av inneslutningens material. Följaktligen uppvärms därmed inneslutningens väggar inte omedelbart (med ljushastighetens distanspassage d=ct) via E, utan blott så småningom eftersom huvuddelen av E till 99,999% hela tiden reflekteras runt, runt, och bara 0,0001% absorberas av materialväggarna. Vi kan därmed (idealt) påstå: Bara mycket (mycket) sakta kommer alltså kärlväggarna att uppvärmas med minskningen i E — tills slutligen E-resten motsvarar inneslutningsanordningens totala värmeutstrålning (emissionen) (reflexionen undantagen, den bidrar aldrig till en kropps uppvärmning). Därefter eftersträvar den så uppvärmda anordningen att återgå till tillståndet före införandet av E genom att värmestråla mellanskillnaden till det omgivande rummet (vilket avslutar experimentet).

Om den införda E-mängden betraktas som ideal Planckstrålning (alla våglängder finns med) är det tydligt att kärlväggarna med tiden påtvingas en allt högre T-kurva (in till ett visst maximum) med start från det omgivande rummets initiella T-form.

Sett från det infallande ljusets ytskikt, kan förloppet då tydligen också liknas vid att E-mängdens högre T-form, och som hela tiden matar kärlkroppen under ytskiktet med de 0,0001%-en absorption, uppvisar (likt Jordatmosfärens olika djupskikt inför Solljusets E) allt lägre T-värden ju längre bort ifrån ytskiktet man anställer en motsvarande mätpunkt.

Så länge processen pågår med matning från E=Pt, kan man då tydligen också säga att varje särskilt djupskikt uppvisar en viss genomströmningsekvivalent, motsvarande ett visst bestämt energitillstånd, analogt en viss temperatur (och som långsamt ändras med minskningen i E).

Och, alltså, kommer vi bara tillbaka till utgångspunkten:

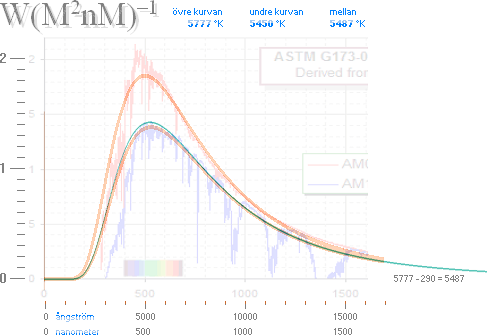
Originalet ovan från

Solar Spectral Irradiance & PV Cell Operational Regions (ASTM G173-03)

http://www.rfcafe.com/references/electrical/ASTM%20G173-03%20Reference%20Spectra.htm

tillsammans med ungefärliga genomskärande Planckkurvor respektive vid

T = 5777 °K ...................................... övre heldragna orangea kurvan, AM0

T = 5487 °K ...................................... mellankurvan, grön; 5777–290=5487

T = 5450 °K ...................................... undre heldragna orangea kurvan, AM1.5

Grafiskt (författarens privata grafritande program) unit200 T=5777°K

[0.55·8.4(x'–5)(–1+è'[5777/T]/0.401x)'–1] ;

Varje djupskikt (bestämt intervall) uppvisar — idealt momentant, som ett utdraget (oändligt) fast tillstånd — sin motsvarande Planckkurva med sin specifika temperatur (och sin specifika diversitet av våglängder), så, att kroppen internt uppvisar alla T-kurvor med alla E-nivåer från ytans maximala T vid ljusinfallet, neråt mot kroppens lägsta T-värde (med alla fragmenteringar inkluderat).

Skillnaden inbördes mellan de olika djupskiktens absorberande förmåga (i förhållande till ytskiktet) KAN då tydligen också återföras på en motsvarande (matematiskt kvantitativ ekvivalent) reflexionsfaktor; reflexionens ekvivalent är störst längst uppe vid ytan, och avtar sedan (snabbt) med djupet, analogt motsvarande högre absorption, så att summan av djupskiktens reflexer (självklart) ger ytans reflex (homogent material förutsatt).

Till viss del är det omöjligt att INTE associera (viss) transmission med reflexion i ljuset av ovanstående beskrivning. Transmissionen bortses dock helt ifrån i beskrivningen.

Exemplet har, tydligen, samma innebörd som följande:

1.

En (sfäriskt) ihålig kropp (K) med 99,999% reflekterande väggar hettas upp till T över Jordlaboratoriets normala rumstemperatur (J=20°C=293°K). Därefter avkyls K (snabbt) till J — med förbehållet att reflexionsstrålningen i den inre ihåligheten INTE hinner uttömma sig under avsvalningen utan finns kvar;

Därmed kan reflexionsstrålningen med sitt Planckspektrum vid ideala T uttömma sin ljusenergi via de 0,0001%-en absorption (1/0,000001=1 miljon gånger) till den underliggande kroppsinneslutningen, och därmed höja dennas temperatur, motsvarande föregående exempelbeskrivning. Principen är alldeles densamma.

Notera att omvändningen inte går an: Om K börjar från N=0°K och värms upp till J=293°K=20°C, kan inte samtidigt den sfäriska ihåligheten bevara N »i kraft av de reflekterande materialväggarna»; Den reflekterande materialytan kan inte hindra — utestänga — materialatomernas värmestrålning via väggarnas 99,999% reflektivitet. Den reflekterande innerväggen bildar en bottenyta sett från den uppvärmande energins synvinkel, och värmestrålningen kommer att tränga in i den sfäriska ihåligheten genom den bottenytan (vakuum) — utan hänsyn till bottenytans beskaffenhet. Därmed får ihåligheten samma Planckspektrum som J. Dvs., det går tydligen bara att anställa inneslutningen med de reflekterande materialväggarna från den värmande, energigivande, sidans reflektivitet. Vill man bevara det inte maximalt kallt med kroppens uppvärmning, får man alltså istället göra utsidan av kroppen maximalt reflekterande.

(»Reflexionsvingarna» i den svängande atomelektronmassan kan inte frikopplas från atomernas reguljära termofysik: energi strömmar alltid från varmt till kallt, aldrig omvänt).

2.

EN KORT LJUSPULS skickas in i

En (sfäriskt) ihålig kropp (K) med 99,999% reflekterande väggar (varefter insläppets ihålighet täpps till);

Ljuspulsen antas ha ett Planckspektrum motsvarande temperaturen T över Jordlaboratoriets normala rumstemperatur (J=20°C=293°K).

Därmed kan reflexionsstrålningen med sitt Planckspektrum vid ideala T uttömma sin ljusenergi via de 0,0001%-en absorption (1/0,000001=1 miljon gånger) till den underliggande kroppsinneslutningen, och därmed höja dennas temperatur, motsvarande föregående exempelbeskrivning. Principen är alldeles densamma.

3.

LJUS EMITTERAS I PULSINTERVALL till en plan

kroppsyta (K) med 99,999% reflekterande planyta;

Varje LjuspulsIntervall antas ha ett Planckspektrum motsvarande temperaturen T över Jordlaboratoriets normala rumstemperatur (J=20°C=293°K).

Därmed kan reflexionsstrålningen med sitt Planckspektrum vid ideala T uttömma sin ljusenergi kontinuerligt via flödet av ljuspulser via de 0,0001%-en absorption till den underliggande kroppen, och därmed höja dennas temperatur, motsvarande föregående exempelbeskrivning. Principen är alldeles densamma.

Dämpning i intervall

Möjligheten finns också att sammanföra Planckkurvan med en moderator (typ exponentfaktor, se nedan) som (likt ovanstående fragmenteringsexempel på Jordatmosfärens absorberande vattenångor) utesluter vissa avsnitt. För den (mera) fullständiga överblickens skull beskrivs den typen nedan.

grafiskt, se föregående D-kurva, unit200:

D = [0.55·8.4(x'–5)(–1+è'1/0.401x)'–1][x'0.5cos500x]

med intervalldämpande moderator (med offset vid 0,8 ovan)

([0.55·8.4(x'–5)(–1+è'1/0.401x)'–1][x'0.5cos500x])'[1+20(1+[80(x–0.8)]'10)'–1]

Moderatorn tillsammans med Planckkurvans ordinära form (D-kurvans cosinusmoderator utelämnad) blir

1 hc²

N_λ = [—— ——————] ^ [1+ amplitudenMotNoll(1+ 1/[bredden(x–offset)^flanklutningen])]

λ⁵ e ^hc/bλT – 1

= P^[1 + M]

För att få flera avgränsningar måste flera moderatorer summeras enligt

Totalt = P^[1 + M1 + M2 + M3 + …+ Mn]

Atomär närverkan

Webben uppvisar en del nyare rön som ansluter till ytterligare en aspekt på ovanstående fragmentering, avdelningar och uppdelningar i Planckkurvorna:

— Experimentellt påvisande att Plancks strålningslag visar för små värden då sändare-mottagare befinner sig mikroskopiskt nära varandra.

Se exv.,

IOP — A WEBSITE FROM THE INSTITUTE OF PHYSICS

— Exposing the flaw in Planck’s law, Aug6 2009

http://physicsworld.com/cws/article/news/40044

Artikeln berättar att den utstrålade värmen ligger i storleksordningen upp till ca tre gånger högre då ”två objekt är åtskilda av bara 30 nM”; Det motsvarar ca 120 medelatomavstånd (ca2,5Å) i fast materia (i normal luft är medelavståndet mellan luftmolekylerna ca 3 nM = 30Å, eller grovt 10ggr fasta atomavstånden).

Artikeln berättar att redan Planck själv hade framställt misstanke om att Planckstrålningslagen skulle vara begränsad till området för ”den termiska strålningen” (från ca 0,48µM och längre med referens till Solens yttemperatur på ca 6000 °K). Tidiga experiment gjordes (1950-talet), men undandrog sig resultat tills helt nyligen (2009 som ovan).

Resultatet utpekar att atomerna i ytpunkterna på ett (plant) material i praktiken framstår (betydligt) hetare (energirikare) än den medelform som anges av Plancks strålningslag.

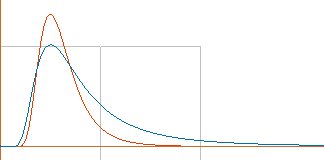
N_λ = 8.4(x^–5)(–1+e^1/0.401x)^–1 .............. övre grafen, T=5777°K

Grafiskt blå (undre) (författarens privata grafritande program) unit100 T=5777°K

1[0.55·8.4(x'–5)(–1+è'1/0.401x)'–1] ;

N_λ = a(8.4)(x^–10)(–1+e^b/0.401x)^–1 ........ undre grafen, T= komplicerad funktion

Grafiskt rödbrun (övre) ; godtyckligt modifierad

6[0.55·8.4(x'–10)(–1+è'2/0.401x)'–1]

Graftekniskt kan fenomenet återföras på samma energiinnehåll men via en motsvarande Planckkurva som uppvisar högre intensitet, alltså högre amplitud motsvarande högre temperatur, med motsvarande snävare ’kjol’ vid basen.

Möjlig förklaring

Specifikt för avtagande näravstånd mellan atomerna i ett material, speciellt vid ingången till materialytan, framstår ljusets uppförande tvunget mera märkbart beroende på materialets specifika atomgenomgångar (Jämför dubbel och tripelbrytande optiska material, för att exemplifiera). Ljushastigheten är den faktor som främst kan uppvisa markanta olikheter mellan atomerna i materialet och mellan materialet och en yttre mätpunkt, olika material uppvisar olika egenskaper (Se även Ljusbrytningen i vatten). Ljushastigheten, med tillhörande olika spektrala spridningar (vi minns att brytningsindex för ett material återfaller på varje specifik frekvens med en specifik utbredningshastighet), upphör visserligen med ljusets (värmestrålningens) utträde ur materialkroppen. Men just i det gränsområdet, då olika partier ännu väsentligen skymmer varandra, finns tydligen utrymme för (stora) anomalier (syn. avvikelser).

Med den anomaliska inverkan som allra störst i, inuti, materialet, är det rimligt att förvänta sig att det finns ett övergångsområde alldeles utanför kroppsranden där spektrala utjämningar sker, en homogenisering för hela den materialkroppen relativt en längre ut belägen mätpunkt. Den ideala (homogena) mätformen ska avse den ideala radiella utgången för materialets (spektrala, runt normalytan halvklotsformade) radians. Men om avvikelsen från den ideala normallinjen är stor bör också mätresultatet visa det.

Då mätpunkten (illustrerad ovan) befinner sig omedelbart utanför den strålande materialkroppen blir också inverkan från närliggande, vinklade, partier allt mera märkbar. Därmed undertrycks den strängt radiella, ideala, mätformen och mätpunkten tar emot till exempel olika specifika frekvensinterferenser som bara är just specifika för materialkroppens näryta.

Enda möjliga energiräkningen för att få ihop det med mätformen längre ut, där närverkans ytdifferenser inte är påtagliga, är uppenbarligen att varje atom eller atomgrupp i den strålande närytan uppvisar en högre ljusintensitet på bekostnad av ett fattigare Planckspektrum (den snävare kjolen), analogt en högre amplitud motsvarande en högre normaltemperatur med en snävare kurvbas. De bortfiltrerade bidragen med de våglängder som fattas, anställs då, tvunget, på den övriga atommassan — men som framkommer FÖRST när HELA materialkroppens strålningspott kan exponeras för mätpunkten.

Man kan också — enklare — se det så:

— Ett material som upphettas relativt en stationär Jordlaboratorisk mätutrustning, uppvisar motsvarande specifikt exciterade tillstånd i den atomärt interna strukturen: Varje atom (isolerad) uppvisar ett utpräglat linjespektrum. Atomernas inbördes värmeväxelverkan skapar emellertid en blandning som utjämnar vakanserna och skapar ett mer eller mindre påtagligt kontinuerligt spektrum — och som därmed bara kan SES med den samlade verkan från hela kroppens atommassa. Alltså »på tillbörligt avstånd». Nära ytan, fragmenterar den spektrala homogeniteten, och specifikt atomnära bidrag visar sig med analogt högre intensitet (»högre temperatur») på bekostnad av en fattigare spektral respresentation. Dvs., ytatomerna är »hetare».

En motsvarande teoretisk beskrivning (till jämförelse) har eftersökts på webben men ännu (Apr2010) inte påträffats.

EXEMPEL PÅ fel i Solgrafen på webben

Uppmärksammat felexempel i Solgrafen på webben

Ingen av de nedanstående webbgraferna är, tydligen, tillförlitliga. För säker referens, använd istället referenser (med överensstämmande) från

NREL (National Renewable Energy Laboratory) från ASTM (American Society for Testing and Materials), där specificeras internationell standard.

1	2

1 @INTERNET Wikipedia Sunlight, Composition, Solar irradiance spectrum 2010-03-29

http://en.wikipedia.org/wiki/File:Solar_Spectrum.png

reducerad till 59% från originalet för att få samma vertikalskala somk nedan

2 @INTERNET Wikipedia Effektiv temperatur, Composition, Solar irradiance spectrum 2010-03-29

http://sv.wikipedia.org/wiki/Fil:EffectiveTemperature_300dpi_e.png

reducerad till 50% från originalet

Felet:

samma toppvärden

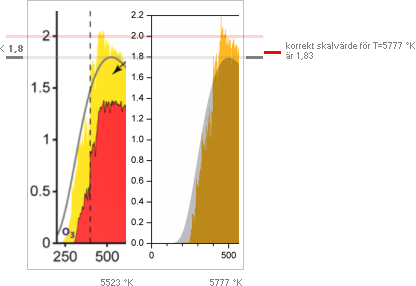
strängt olika T-värden

Graferna i 1 och 2 uppvisar samma typgraf, men temperaturvärdena anges olika;

För grafen i 1 lika med

T = 5250 °C + 273 °K

= 5523 °K;

För grafen i 2 lika med

T = 5777 °K ........................... det korrekta värdet, se nedan

Wikikällan till grafen i 1 skriver:

”The sun produces light with a distribution similar to what would be expected from a 5525 K (5250 °C) blackbody, which is approximately the sun's surface temperature.”,

@INTERNET Wikipedia Sunlight, Composition, Solar irradiance spectrum 2010-03-29

http://en.wikipedia.org/wiki/File:Solar_Spectrum.png

Det är tydligen fel uppgift:

Solytans temperatur, internationell standard

Korrekt värde enligt internationell standard (se nedan) är

T = 5777 °K

enligt

NREL (National Renewable Energy Laboratory) från ASTM (American Society for Testing and Materials) med angivna internationella standardreferenser.

Se särskilt

National Renewable Energy Laboratory (Feb2010)

http://rredc.nrel.gov/solar/spectra/am1.5/

Se även webbkällorna i Jämförande praktiska resultat.

Se även huvudartikeln på Wikipedia Sunlight

”The spectrum of the Sun's solar radiation is close to that of a black body with a temperature of about 5,800 K.”,

@INTERNET Wikipedia Sunlight, Composition 2010-03-29

Samt även mera exakt på Sun (de flesta webbkällor använder något av värdena 5777 eller 5778)

”In this spectral class label, G2 indicates its surface temperature of approximately 5,778 K (5,505 °C)”,

@INTERNET Wikipedia Sun 2010-03-29

Korrekta skalvärdet på Solära Irradiansen för toppvärdet via T=5777°K på avståndet 1AU=1,496 T11 M från Solen och belysningsytan 1 M² blir

N(λ) = 1,83275 t9 W/M³ = 1,83275 W/(M²nM)

Dvs., avrundat ca 1,83 enheter. Se även graferna med webbkällorna (Internationell standard) från Jämförande resultat och Tilley 2003, m.fl. Se även i Beräkningsexempel och Illustrerade exempel.

Solär Irradians — internationell standard

Solära Irradiansen — internationella standardreferenser

I webbkällan

National Renewable Energy Laboratory (Feb2010)

http://rredc.nrel.gov/solar/spectra/am1.5/

ges INTERNATIONELLA standardreferenser:

”The photovoltaic (PV) industry, in conjunction with the American Society for Testing and Materials (ASTM) (http://www.astm.org/) and government research and development laboratories developed and defines two, and only two, standard terrestrial solar spectral irradiance distributions. The two spectra define a standard direct normal spectral irradiance and a standard total (global, hemispherical, within 2-pi steradian field of view of the tilted plane) spectral irradiance. The direct normal spectrum is the direct component contributing to the total global (hemispheircal) spectrum. The current Standard Reference Spectra are both incorporated into a single document, ASTM G-173-03.

HISTORICAL NOTE : The reference spectra were first generated as separate standards, designated as E-891-82 and E-892-82 (for direct normal and global tilt, respectively.) As of June, 1999, ASTM Subcommittee G3.09 combined these two documents into a single standard "Standard Tables for Reference Solar Spectral Irradiance at Air Mass 1.5: Direct Normal and Hemispherical for a 37 Degree Tilted Surface" The relevant international standard is ISO 9845-1, 1992, based solely upon both E891 and E892. In January of 2003, the G159 standard was REVISED extensively, and REPLACED with G173-03. The older standards E-891, E-892, and G159 are WITHDRAWN and NO LONGER AVAILABLE except as historical standards. Downloads are provided here for reference and comparison with the new G173 spectra.”,

”The ASTM G173 spectra represent terrestrial solar spectral irradiance on a surface of specified orientation under one and only one set of specifed atmospheric conditions. These distributions of power (watts per square meter per nanometer of bandwidth) as a function of wavelength provide a single common reference for evaluating spectrally selective PV materials with respect to performance measured under varying natural and artifical sources of light with various spectral distributions. The conditions selected were considered to be a reasonable average for the 48 continguous states of the United States of America (U.S.A.) over a period of one year. The tilt angle selected is approximately the average latitude for the contiguous U.S.A.”,

About the Reference AM 1.5 Spectra

NATIONAL RENEWABLE ENERGY LABORATORY (Feb2010)

http://rredc.nrel.gov/solar/spectra/am1.5/

Absorption, emission, reflexion och transmission

GRUNDBEGREPP

Absorption, emission, reflexion och transmission

GRUNDBEGREPPEN I MATERIENS VÄXELVERKAN MED LJUSET

absorption, emission, reflexion och transmission

absorption kroppens effektiva uppvärmning, energins inströmning

emission kroppens effektiva avsvalning, energins utströmning

reflexion återkastning, påverkar inte kroppens uppvärmning (speglar, alla frekvenser)

transmission genomgång, påverkar inte kroppens uppvärmning (typ tunna material, frekvensberoende)

Den värmemängd som en kropp upptar blir den värmemängd kroppen måste emittera för att kroppen ska kunna upprätthålla det vi kallar för en konstant uppnådd temperatur via en konstant pålagd (upptagen, absorberad) energi. Den värmemängden plus den reflekterade är den totala värmemängd (infallande ljus) som kroppen presenteras för men vars energiräkning för kroppens del bara berör absorptionen, analogt uppvärmningen. Det ljus som reflekteras inräknas inte i det ljus som absorberas; Reflekterat ljus bildar en direktverkande förlustfri »specialemission» via motsvarande »specialabsorption» som bara berör de materieelement som garanterar reflexionens verkan (»reflexionsvingarna» i elektronmassan, se Ljusets Reflexion i Relaterad Fysik). Ev. transmissionsenergi ingår inte i kroppspåverkan.

Frånsett transmissionen:

Totalt infallande ljusmängd = absorberad ljusmängd + reflekterad ljusmängd

Totalt infallande ljusmängd	=	absorberad ljusmängd	+	reflekterad ljusmängd
		uppvärmer kroppen		uppvärmer inte kroppen polarisation ingår

Reflexionsfenomenet innefattar ytabsorption med omedelbar emission:

materialet uppvärms (självklart) aldrig av den ljusmängd som reflekteras

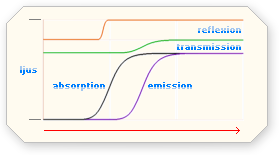
Graferna ovan sammanfattar ikoniskt de fyra olika faktorer som — utom brytning och polarisation — brukar förknippas med ljusets inverkan på och växelverkan med en masskropp: absorption, emission, reflexion och transmission. Transmissionen — belysningen minus absorptionen och reflexionen — omfattar främst optiska (och tunna) material och har ingen energirelaterad betydelse för beskrivningen av en kropps värmeenergiomsättning.

Det är endast absorptionen som berör värmepåverkan;

Ljusenergin som kroppen avkänner (absorption plus reflexion) minus den reflekterade delen är lika med den absorberade delen; Den delen måste också uttömmas ekvivalent med en lika stor mängd emission, lika med energin som åtgår för att hålla kroppen uppvärmd — till den momentant angivna temperaturen med den momentant pålagda energin. Se Summerande Planckstrålningsexempel.

Generellt i den här presentationen (och övriga i Universums Historia om inget annat anges) frånses transmissionen helt och hållet i analysen av kropparnas värmefysik. Det är enbart absorption (=emission) och reflexion som räknas.

Är kroppen helt ogenomskinlig (konv. opak, eng. opaque) gäller alltså formellt transmission = 0 med

absorption + reflexion = 1

Annars

absorption + reflexion + transmission = 1

med absorption = emission.

Experimentell bekräftelse på Stefan-Boltzmanns strålningslag

Experimentellt beprövad verifikation för Stefan-Boltzmanns strålningslag

EXPERIMENTELL PRÖVNING av Stefan-Boltzmanns strålningslag finns redovisad (bl.a.) i webbkällan

”The quality of the fits for both methods, the agreement of the exponent in the second method, and the correspondence of the two values of the constant σεA_s creates a strong argument for the support of Stefan-Boltzmann’s law.”,

Wooster College, Department of Physics — Stefan-Boltzmann Law, Austin R. Carter, May2004

http://www3.wooster.edu/physics/JrIS/Files/Carter.pdf

Flera (många, liknande) resultatredovisningar spärras dock (tyvärr) av vissa webbdomäner med krav på speciell behörighet alt. särskild betalning.

Plancks strålningslag med olika skrivsätt

De olika diversifierade PlanckstrålningsKällpreferenserna, som ovan, medför (naturligtvis) en motsvarande FLORA av specifikt uttryckta FORMLER för Plancks strålningslag.

Olika skrivsätt för Plancks strålningslag

Skrivsätten för Plancks strålningslag

De olika förekommande skrivsätten för Plancks strålningslag som florerar på enbart olika webbsidor (Mar2010) ges i översikt och sammanställning nedan i mittleden — tillsammans med orienterande beskrivning av aktuell typ, och ev. tillämpningsområde.

Sambandsformerna nedan anges här genomgående med våglängden som variabel [en del källverk använder frekvensen (f=)v=c/λ]. För beteckningen sr (steradianer), se efterföljande beskrivning i steradianer.

sfäriskt rundstrålande: används (typiskt) i samband med mätningar på Solstrålningen.

P hc²

—— = —————— · [(e ^ [hc/bλT]) – 1]^–1 = W(M³sr)^–1

4πM³ λ⁵

Se efterföljande beskrivning i Hur Plancks strålningslag beräknas för spektral irradians.

Ovanstående form för Plancks strålningslag är den som kopplar direkt i samband med olika praktiska mätdata (mätinstrument) av typen radiometriska, spektroradiometriska och (spektro-)fotometriska, (oftast) med upplösningen av radiansens enhetsdel M³sr till irradiansens enhetsdel M²nM. Se särskilda exempel i Illustrerade Exempel och Beräknande Exempel samt Hur Plancks strålningslag beräknas för spektral irradians.

I instrumentsammanhang används (typiskt, enligt webbuppgifter) spektroradiometriska instrument (i prisklassen typ 20-50 000 kr) för att mäta Planckstrålningens olika energi/effektvärden för olika våglängder. Dessa instrumentvärden presenterar den ursprungliga rundstrålande föregående typformen för spektral radians W/(M³sr) i spektral irradians W/(M³), vanligen som W/(M²nM), se Beräknande Exempel och Illustrerade Exempel.

halvsfäriskt rundstrålande: används för emission från plana ytor med trigonometriska tilläggssamband

P 2hc²

—— = —————— · [(e ^ [hc/bλT]) – 1]^–1 = W(M³sr)^–1

2πM³ λ⁵

Uppgift saknas ännu på specifika tillämpningar för ovanstående typuttryck. Se även i @INTERNET Wikipedia Planck’s law 2010-03-11 (m.fl.) där ovanstående sambandstyp anges.

Det är ännu (med webbkällornas hjälp enbart) okänt vilken (typisk exemplifierad) applikation som ovanstående form använder.

krafttäthet (normal): c=d/t ; P/c = Pt/d = E/d = mad/d = ma = F

P 2 hc

—— · — = —————— · [(e ^ [hc/bλT]) – 1]^–1 = E(M³srM)^–1 = N(M³sr)^–1

8πM³ c λ⁵

krafttäthet (åttaPi): c=d/t ; P/c = Pt/d = E/d = mad/d = ma = F

P 2 8πhc

—— · — = —————— · [(e ^ [hc/bλT]) – 1]^–1 = E(M³M)^–1 = N(M³)^–1

M³ c λ⁵

Planck (se Plancks original) skrev ovanstående år 1901, tredje kvoten, samb.13s7ö, men ger i sin skrift ingen särskild benämning (en sådan ges i Plancks motsvarande tredje kvot nedan, Plancks beteckning för vänstra delen ovan är E).

energifördelning: λ/c = 1/[f = v] = t

P 2λ² 8πh

—— · — = —————— · [(e ^ [hc/bλT]) – 1]^–1 = WS²(M³)^–1 = ES(M³)^–1

M³ c² λ³

Planck (se Plancks original från 1901) benämner ovanstående, tredje kvoten, för ’energifördelning’, ”energy distribution”, samb.12s6n, här med våglängden (λ) ersatt av Plancks frekvens (v) via c=vλ, 1/λ³=[v/c]³. (Plancks beteckning för vänstra delen är u).

Utöver ovanstående finns ytterligare varianter som kan ses i (flera) webbkällor (typ motsvarande 2h/λ³ för mellankvoten via frekvensformen [f=v] 2hv³/c³). Tyvärr verkar inte författarna bakom denna diversifiering (lika) intresserade av att berätta om anledningen till företrädet, själva tillämpningen.

[Det är verkligen rejält dåligt med berättarkonsten på det området på webben, generellt i ämnet Plancks strålningslag (ännu Mar2010)].

Uppmärksammandet är en av anledningarna till den här framställningen — de få GRATIS TILLGÄNGLIGA referenser som finns.

———————————————————————————————————————————

Referens:

Plancks original från 1901

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s3

http://bourabai.kz/articles/planck/planck1901.pdf

Radians och Irradians

Radians och Irradians

Orientering i sfärbegreppen med allmänna radiometriska (elektromagnetiskt mätorienterade) enhetsbeteckningar. Sfärens olika samband som ovan beskrivs utförligt i Elementarytorna. 1 steradian motsvarar ungefär rymdvinkeln hos den avskurna sfärytan längst till höger (1/4π).

radians ..................... från ljuskällan

irradians .................. det belysta objektet

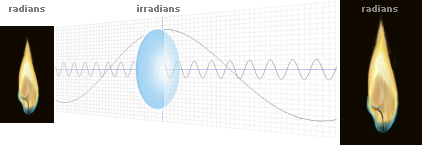
Radiansen innefattar rymdvinkeln — för sr se steradian

——————————————————————

radians W/(M²sr) ........................ utstrålningen

spektral radians W/(M²Msr) = W/(M³sr)

Utstrålningen med hänsyn till färg

radiant intensitet W/(sr)

Irradiansen innefattar inte (explicit) rymdvinkeln

——————————————————————

irradians W/(M²) ............................ belysningen

spektral irradians W/(M²M) = W/(M³); även ofta W/(M²nM)

Belysningen med hänsyn till färg

Se Illustrerade Exempel och Beräknande Exempel

intensitet används ibland synonymt med irradians

effekt W

luminositet används ibland synonymt med (ljus/värme)effekt

Ordstammen spektral kopplar till våglängd eller frekvens (samma som färg).

Se även grundfysiken i LJUSETS INTERFERENS [hur man konstruerar en primitiv spektrometer (färguppdelare) och hur man kan beräkna ljusets våglängder från (den enkla) grundmatematiken].

Referenser

—————————————————————————————————————————

Webben innehåller en stor mängd källverk som avhandlar ovanstående grundbegrepp. För allmän webbreferens till etablerade skrivsätt, se här särskilt (mest bekvämt)

@INTERNET Wikipedia

Radiance (äv. Spectral Radiance), Irradiance (äv. Spectral Irradiance), Steradian

Steradian

Steradian

För illustration, se Radians och Irradians

Beteckningen steradian

(av Grek. stereo, solid, och Lat. radius, stråle. ref. @INTERNET Wikipedia Steradian 2010-03-05)

är 3D-motsvarigheten till 2D-matematikens radian.

Den tvådimensionella geometrin har vinkelbegreppen

Gradvinkel (A°) och Radianvinkel (a)

;
A°/360 = s/2πr ; A°πr/180 = s ; s anger en del av cirkelbågens längd

Med enhetsradien r=1 ges radinavinkeln från gradvinkeln (A°)

A°(π/180) = a

och motsvarande gradvinkeln från radianvinkeln

a(180/π) = A°

Hela vinkelrummet för cirkeln (A=360°) är 2π radianer,

a = 2π

Den tredimensionella geometrin har motsvarande (enhetliga) rymdvinkelbegreppet

steRadianvinkel (sr).

Speciellt med referens till sfärens yta (A=4πr²) används termen steradian (sr) motsvarande rymdvinkeln i 3D [För illustration, se Radians och Irradians]:

(sr) = A/4πr² = (A/r²)/(/4π);

Totala rymdvinkeln är 4π steradianer.

A anger sfärens delyta (4πrx).

För illustration, se Radians och Irradians.

Spektralenheterna

HUR PLANCKS STRÅLNINGSLAG BERÄKNAS FÖR motsvarande uppmätande SPEKTRAL IRRADIANS

Hur Plancks strålningslag beräknas för spektral irradians

Särskild beskrivning — spektral radians och spektral irradians

Plancks strålningslag — sfäriskt rundstrålande:

P hc²

—— = —————— · [(e ^ [hc/bλT]) – 1]^–1 = W(M³sr)^–1 spektrala radiansen

4πM³ λ⁵

I instrumentellt mätande anordningar görs följande modifikationer för att kunna använda Plancks strålningslag tillsammans med effektiva mätvärden.

Vi genomför här först en allmän (formell) omskrivning enligt följande:

Mellanledet (ML) ger maximala värdet för HELA den sfäriskt (4π) rundstrålande effekten

[([4π]/[4π])(ML)]; För mindre sfäriska delytor gäller tydligen

[([sr]/[4π])(ML)] = [(A/[4πR²])(ML)] = [([A/R²]/[4π])(ML)] med R avståndet från strålkällan och A den bestrålade delsfäriska ytan.

Resultatet spektrala radiansen (»utstrålningen») kan då uttryckas med enheten i steradianer preciserat som [A/R²];

W/(MMM[A/R²])

Nu kan vi studera hur justeringen med steradianer måste slutföras för att matcha instrumentfysiken (cirkulärt mätande skivytor); Med

[([A/R²]/[4π])(ML)]

flyttas först [4π] över till vänsterledet så att man får

P hc²

—— = —————— · [(e ^ [hc/bλT]) – 1]^–1 · [A/R²] = W(M³)^–1

M³ λ⁵

Enheten totalt benämns nu spektrala irradiansen (»bestrålningseffekten»). Bestrålningsytan A anges sedan med hänsyn till den mätande anordningens (fotocell) cirkulära tvärsnitt enligt

A = πr²

som ger

[A/R²] = [πr²/R²] = [r/R]²π

Anges enheten r=1M ges tydligen

A = [1/R]²π

och därmed

P hc²

—— = —————— · [(e ^ [hc/bλT]) – 1]^–1 · [1/R]²π = W(M³)^–1

M³ λ⁵

Med Solen som exempelljuskälla (T ca 5800°K) och våglängder runt Wientoppen (ca 5000Å eller 500nM eller 0,5µM) ges maxvärden i storleksordningen t9 W/M³. Det utnyttjas för att specificera enheten (mera bekvämt, också tillsammans med den mätande kvadratskivan i M²) med uppdelning av M³ i M²M och sedan multiplikation med T9, analogt division med t9 för enheten Meter i nämnaren i W/(M²Meter) så att man får motsvarande nämnardelens Meterenhet i nanoMeter (t9 M) enligt

W/(M²nM)

Se även efterföljande jämförande illustrerade webbexempel i Illustrerade Exempel.

Spektrala radiansen

2010III5

Spektrala radiansen

Se även i Radians och Irradians

Spektral radians N(λ) beskriver genom Plancks strålningslag den idealt odämpade utstrålande kroppens ljusenergi i Watt per kubikmeter omsluten strålningsvolym med hänsyn till den sfäriska rundstrålningsgeometrins maximala 4π steradianer; W/M³sr. För förkortningen sr, se steradian.

Teknisk mätning av spektral radians anställer en motsvarande belysningseffekt (W) per kvadratmeter bestrålad yta (M²) och våglängdsmeter (M), spektrala irradiansen (W/M³). Hur omräkningen går till visas exemplifierat med jämförande webbexempel i Hur Plancks strålningslag beräknas för spektral irradians.

Teknisk mätning för spektral irradians

Den tekniska mätningen innefattar tre grundblock: färguppdelning (spektroskop), våglängdsmätning (spektrometer), intensitetsbestämning (spektrograf, fotometer). Se även i GRUNDTERMER.

I vårt eget vardagliga (primitiva) kök kan en ytterst enkel spektrometer konstrueras med mycket enkla redskap. Den lämpar sig dock inte för någon mera preciserad bestämning.

Illustrationsblock 1 motsvarar brytningsgeometrin för en vattendroppe. Vi kan se hur uppbrytningen sker i spektralfärgerna i ena kanten på ett vanligt (slätt) dricksglas med hjälp av en vanlig ljuslåga från ett stearinljus;

FOTO: Författarens arkiv · Jan2010 · Nikon D90

Illustrationsblock 2 motsvarar beskrivningen i LJUSETS INTERFERENS. Spektrum från den enkla ljuslågan blir synligt mellan spalten på två grässtrån med typen runda skaft som hålls tätt ihop framför ögat.

Illustrationsblock 3 motsvarar den spektrala bild av ljuslågan man får om man placerar en CD-skiva bakom ljuslågan.

Observera att den spektrala återgivningen via fotografiet INTE är varken rättvist eller exakt (fotografiets skarpa färgövergångar är i verkligheten mjuka, samt att färgerna delvis förvrängs av kameran: synligt violett blir utpräglat blått i fotografiet. m.m.). Den högra bilden visar (en del av) ljuslågans spektrum med lågan placerad (ca 0,5M) till höger om CD-skivan.

Våglängdsmätning kan genomföras (grovt) med grund i Illustrationsblock 2. Se särskild beskrivning i LJUSETS INTERFERENS.

För att slutligen också kunna mäta ljusets intensitet — varje spektralfärgs egen enskilda intensitet och därmed få en heltäckande bild av ljuskällans spektrala radians — krävs dock mera avancerade anordningar (se WebbExempel nedan).

Från början (från senare delen av 1800-talet) fanns bara optiska/fotografiska tekniker med olika jämförande spektrodiagram. Idag (utvecklingen under senare delen av 1900-talet) används (nästan) uteslutande halvledarbaserade komponenter tillsammans med mer eller mindre avancerad datorisering.

Instrumentmekanikens kraftiga utveckling under hela 1900-talet har medfört, speciellt med den kommersialiserade datoriseringen från grovt 1980 och framåt, att alla de olika delar som krävs för en fullständig mätning av spektral irradians numera (i allmänhet) finns i ett och samma apparathölje — Vilket också (i allmänhet) betyder (extremt) dyr utrustning. Se WebbExempel nedan.

Flera webbkällor finns som också beskriver hur man kan göra enkla. billiga hemmagjorda spektroskop av typen CD-skiva. Se vidare i Webbreferenser.

Webbexempel mätinstrument

WebbExempel:

Spektroradiometer Luzchems’s Spectroradiometers

BILDKÄLLA: http://www.luzchem.com/products/spectroradiometer.php

”Luzchem's spectroradiometers can be used for solar irradiance measurements, photobiology research, drug photostability testing, environmental dosimetry and curing applications.”.

Inga direkta prisexempel visas, man får begära sådana särskilt. Jämför nedan.

Spektroradiometer EDMUND OPTICS — Compact Spectroradiometers

BILDKÄLLA: http://www.edmundoptics.com/onlinecatalog/displayproduct.cfm?productid=2704

”Spectroradiometers are calibrated spectrometers with the correct geometry to characterize light sources. Our spectroradiometer has a quartz cosine receptor and is calibrated to measure absolute spectral irradiance of light sources. It can be used as a quick, handheld device to verify center, dominant, and centroid wavelengths, intensity, and color of LED and other light sources. In addition to LED calibration and color analysis, this spectroradiometer is useful for solar studies, photo-stability testing, and photobiology and photochemistry applications.”.

Prisexempel NT58650 (billigaste versionen) 4.270,25 Euro;

1 euro = 9,72456556 svenska kronor (Mar2010);

41.526,325 Skr

Övriga typer av (spektro)radiometriska mätinstrument

Crookes radiometer Crookes radiometer (eng. Crooke’s radiometer) [äv. ljuskvarn, eng. light-mill]

BILDKÄLLA: @INTERNET Wikipedia Crookes radiometer 2010-04-01

Funktion: I ett evakuerat glaskärl finns (fyra) fast förbundna skovlar med en fint axiellt vertikal montering så att skovlarna kan rotera horisontellt. Varje skovelskiva har ena sidan vit (maximal reflexion) och andra svart (maximal absorption). Närmas en ljuskälla till glaset, börjar skovlarna rotera (snabbare ju högre intensitet ljuset har).

(Finns att köpa från under 10 dollar).

Bolometer Bolometer (eng. Bolometer)

APEX — Technical description of LABOCA

BILDKÄLLA: http://www.apex-telescope.org/bolometer/laboca/technical/

Funktion: Noggrann ljusmätning typ termometer. En metallplatta (ovan en avancerad materialstruktur nedkyld till nära absoluta nollpunkten) bestrålas med ljus från objektet. Plattans temperatur ändras proportionellt mot den upptagna strålningens intensitet. Ändringen visar sig i en motsvarande elektrisk utspänning. Bolometern avkänner energi.

Se även allmän funktionsbeskrivning på

@INTERNET Wikipedia Bolometer 2010-04-01

(Bolometern i bild ovan ligger förmodligen i den dyrare prisklassen [specialkomponenter för satellitapplikationer], det finns dock relativt billiga halvledarbolometrar på webben, typ 5-20 dollar, och vidare uppåt).

Termoelement Termoelement (eng. Thermocouple)

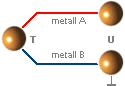
Funktion: Termoelektriska effekten (Seebeck-effekten). Om atomgittret i en rak isolerad (elektrisk ledare) metalltråd [—] avkänner olika värmegrader i respektive materialände, uppstår motsvarande elektronvandring; En elektrisk spänning uppkommer mellan ändarna. Genom att använda två olika metaller med en gemensam temperaturavkänningspunkt bildas en mätbar elektrisk potential i andra änddelen mellan de olika metalldelarna. Fenomenet kallas ibland Seebeckeffekt och upptäcktes 1826 av Thomas Johann Seebeck [ref. THE INTERNET ENCYCLOPEDIA OF SCIENCE

http://www.daviddarling.info/encyclopedia/S/Seebeck_effect.html

]. Se även funktionsbeskrivning på

@INTERNET Wikipedia Thermoelectric effect 2010-04-01

(ELFA säljer ett termoelementkit för 334kr+moms).

Termostapel Termostapel (eng. Thermopile)

Genom att seriekoppla många (flera hundra) termoelement kan hög noggrannhet uppnås (känsligheten är multipeln av halva antalet föreningspunkter).

En utförlig (uttömmande), illustrerad, beskrivning av termoelement och termostapel finns (bl.a.) på

CAPGO — Thermocouples

http://www.capgo.com/Resources/Temperature/Thermocouple/Thermocouple.html

Pyranometer Pyranometer (eng. Pyranometer)

BILDKÄLLA: @INTERNET Wikipedia Pyranometer 2010-04-01

Funktion: Mätning av Solär irradians i W/M² (genom halvsfärisk total instrålningsvy [2π sr]).

Pyranometer Pyranometer (se äv. ovan)

Global Water Instrumentation INC — WE300 SOLAR RADIATION SENSOR

BILDKÄLLA: http://www.globalw.com/products/we300.html

(Prisuppgift 807 dollar, vikt 114g)(Apr2010)

Pyrometer Pyrometer (eng. Pyrometer) [värmeTemperaturMätningskamera]

PENTRONIC — Teori » IR-pyrometrar

BILDKÄLLA:

http://www.pentronic.se/Theory/IRpyrometers/tabid/189/language/sv-SE/Default.aspx

Webbkällan ger också en uttömmande beskrivning av pyrometerns funktionssätt.

(Prisuppgift saknas).

Funktion: Mätning av temperatur/värme (ofta i industriella tillämpningar typ metallsmältor i stålverk). Pyrometern samlar ljuset på optisk väg (som en vanlig kamera) samt analyserar resultatet med olika typer av (avstämda) sensorer. Resultatet visar objektets yttemperatur.

Se även funktionsbeskrivning på

@INTERNET Wikipedia Pyrometer 2010-04-01

Beräknande Exempel

EXEMPEL 1:

Genom spektroskopisk observation hade man i ett fall kommit fram till att Wientoppen i Solens Planckspektrum ligger vid våglängden λ=4983Å (spektrala färggränsen mellan himmelsblått och havsgrönt). Det ger via Wiens förskjutningslag motsvarande Solens yttemperatur på ca

T = (2,898 t3 M°K)/(λ=4983 t10 M)

= 5815,7736 °K

≈ 5800 °K

Bestäm totala spektrala radiansen i W/(M³sr) för den givna Wienvåglängden

λ=4983Å vid den givna temperaturen

T=5800 °K.

Lösning:

Plancks strålningslag ger direkt med h=6,626 t34 JS, c=2,99792458 T8 M/S och b=1,38 t23 J/°K

N_λ = λ^–5hc²[e^hc/bλT–1]^–1 ........... Plancks strålningslag (W/M³sr)

= 1,34098 T13 för hela Solklotets indigogröna färg

Svar: se ovan!

KOMMENTAR:

Med våglängden 100Å, samma T, är spektrala radiansen reducerad till praktiskt taget noll (3,15 t93). Vilket vill säga: även med obegränsat kort våglängd ges praktiskt taget noll strålningsenergi.

Åt andra hållet, då våglängden växer obegränsat, ges via T=5800°K ett gränsvärde (1,91 T15 vid ca λ=0,001 M).

Totala stråleffekten till jämförelse (alla Planckvåglängders spektralradianser tillsammans) för hela Solen är grovt 4 T26 W. Se från Solens effekt.

EXEMPEL 2:

Bestäm med ledning av föregående exempel spektrala IRradiansen ute vid Jordbanan på avståndet

R = 1AU = 1,496 T11 Meter från Solcentrum. Använd en cirkulär referensyta med radien 1 Meter som objektet för den avkännande bestrålningsuppmätningen.

Lösning:

Vi använder direkt den i avsnittet Hur Plancks strålningslag beräknas för spektral irradians tidigare beskrivna sambandsformen för spektrala irradiansen i Planckstrålningslagen med

T = 5800°K och λ = 4983 t10 M = 4,983 t7 M enligt

P hc²

—— = —————— · [(e ^ [hc/bλT]) – 1]^–1 · [1/R]²π = W(M³)^–1

M³ λ⁵

= 1,86946 t9 [W(M³)^–1 = W(M²M)^–1]

= 1,86946 t9 [W(M³)^–1 = W(M²nM)^–1]

Svar: se ovan!

Se även den jämförande grafen med T=5777°K, nedan i Illustrerade Exempel.

Värdet blir

P/M³ = 1,83275 t9 W/M³

Illustrerade Exempel

Se även ovanstående Beräknande Exempel

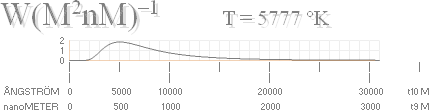
Solstrålningens idealt odämpade spektrala irradians (ideala Planckstrålningen) på avståndet vid Jordbanan (1AU=1,496 T11 M) per en kvadratmeter cirkulär belysningsyta.

Parametervärden:

R 1AU = 1,496 T11 M,

h 6,626 t34 JS

c 2,99792458 T8 M/S

b 1,38 t23 J/°K

T 5777 °K

P hc²

—— = —————— · [(e ^ [hc/bλT]) – 1]^–1 · [1/R]²π = W(M³)^–1

M³ λ⁵

Grafiskt med PixelUnit10 (författarens privata grafiska ritprogram)

y = 0.0000000000001·8.4(0.00000000000000001)([x10'–7]'–5)(–1+è'0.0144/5777x10'–7)'–1

= (8.4 t39)/([x/10⁷]⁵)/(–1+e^[0.0144/5777x/10⁷]) ;

Med 10ggr förstoring i vertikalled, för tydligare upplösning, ges grafen nedan:

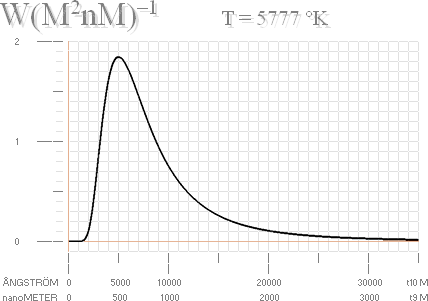
Solstrålningens idealt odämpade spektrala irradians (ideala Planckstrålningen) på avståndet vid Jordbanan (1AU=1,496 T11 M) per en kvadratmeter cirkulär belysningsyta.

Observera att graftypen INTE är någon specifik egenskap hos speciellt Solen utan gäller generellt för alla typer av ljuskällor som uppvisar den aktuella temperaturen: Plancks strålningslag gäller bara avseende våglängd (eller frekvens) och temperatur (inom rymdområden med ljushastighet större än noll), helt oberoende av ljuskällans sammansättning eller speciella egenskaper. Se även i Hur Plancks strålningslag beräknas för spektral irradians. Se även i Radians och Irradians.

;

Grafiskt med PixelUnit10 (författarens privata grafiska ritprogram)

y = 10·0.0000000000001·8.4(0.00000000000000001)([x10'–7]'–5)(–1+è'0.0144/5777x10'–7)'–1

; = 10·(8.4 t39)/([x/10⁷]⁵)/(–1+e^[0.0144/5777x/10⁷]) · (0.1)_SKALENHETEN ;

Grafen ovan fås också direkt (enklare) genom våglängdsenheter i mikrometer t6=1/10⁶ enligt PixelUnit100

y = 8.4(x'–5)(–1+è'1/0.401x)'–1 ; vertikalskalan direkt i nM för T=5777°K

[0.0144/5777x/10⁶] = 1/0,401 ;

(8.4 t39)/([x/10⁶]⁵) = (8.4 t9)(x'–5) ;

För att få ut andra temperaturer T görs omräkningen för 1-täljaren i e-exponenten enligt

5777/T

Jämförande webbkälla

Jämför

Många olika webbkällor finns som avhandlar Solstrålningen — en stor mängd Planckkurvor som visar Solspektrum finns på GoogleSök, se generellt via »solar spectrum» Bilder

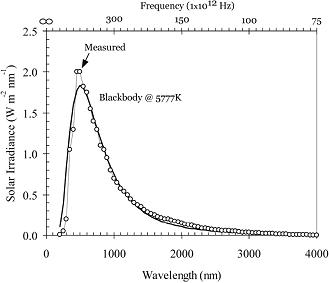
Spectral Transformities for Solar Radiation Reaching the Earth, David R. Tilley

Biological Resources Engineering and Natural Resources Management, University of Maryland

Fig.2 s10

http://www.enst.umd.edu/tilley/emergy/SpectralTransformitiesTilley2003.pdf

Med hänsyn till Solutstrålningens ytfragmentering (Se från Med Solen som Exempel), att därför Solen heller inte bör uppvisa någon exakt Planckstrålningskurva, framgår det ändå alldeles tydligt av ovanstående webbkällas mätresultat att överensstämmelsen med den ideala Planckkurvan är tämligen god.

Se även Webbfel som visar hur en del liknande grafer uppvisar korrumperade fel.

Citatsamling

CITATSAMLING

‡[1]

”On the contrary, it may just as correctly be said that in all nature there is no process more complicated than the vibrations of black radiation. In particular, these vibrations do not depend in any characteristic manner on the special processes that take place in the centers of emission of the rays, say on the period or the damping of the emitting particles; for the normal spectrum is distinguished from all other spectra by the very fact that all individual differences caused by the special nature of the emitting substances are perfectly equalized and effaced. Therefore to

attempt to draw conclusions concerning the special properties of the particles emitting the rays from the elementary vibrations in the rays of the normal spectrum would be a hopeless undertaking.”,

s107n

INTERNET ARCHIVE — The Theory of Heat Radiation, Max Planck (1914)

http://www.archive.org/stream/theheatradiation00planrich#page/n7/mode/2up

Min översättning:

Å andra sidan kan det lika gärna korrekt sägas att i hela naturen finns det ingen process mera komplicerad än vibrationerna för svart[kropps-]strålning. Speciellt, beror inte dessa vibrationer i något karaktäristiskt manér på de speciella processer som äger rum i centrum av strålemissioner, säg på perioden eller dämpningen hos emitterande partiklar; för det normala spektrat är utmärkt framför alla andra spektra av det blotta faktum att alla individuella skillnader förorsakade av den speciella naturen hos den emitterande substansen är fullständigt utslätade och utsuddade. Att därför försöka dra slutsatser beträffande de speciella egenskaperna hos de partiklar som emitterar strålarna från de elementära vibrationerna i strålarna hos det normala spektrat skulle bli [är] ett hopplöst företag.

Planck om giltigheten av Planckstrålningslagen

‡[2]

Max Planck om resultatet av Planckstrålningslagen, Plancks nobelföreläsning från 1920

”Thus the new radiation formula was found, which, in the face of its experimental proof, has stood firm to a reasonable extent until now. Even today, admittedly, we cannot talk of final exact confirmation. In fact, a fresh attempt at proof is urgently required.”,

MAX PLANCK, NOBEL LECTURE JUNE 2 1920

The Genesis and Present State of Development of the Quantum Theory

http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html

Min översättning:

Sålunda blev den nya strålningslagen funnen, vilken, i ljuset av dess experimentella bevis har visat sig hålla streck i rimlig utsträckning tills nu. Även idag, ska det erkännas, kan vi inte tala om en slutlig exakt bekräftelse. I själva verket är ett friskt försök [som leder] till bevis trängande behövligt.

‡[3]

”My radiation formula especially has so far stood all tests satisfactorily, including even the refined systematic measurements which have been carried out in the Physikalisch-technische Reichsanstalt at Charlottenburg during the last year.”,

förordet November 1912, sida vii

INTERNET ARCHIVE — The Theory of Heat Radiation, Max Planck (1914)

http://www.archive.org/stream/theheatradiation00planrich#page/n7/mode/2up

Min översättning:

Min strålningsformel har speciellt så långt bistått alla prövningar tillfredsställande, inkluderat även de förfinade systematiska mätningarna som har genomförts på fysisk-tekniska riksanstalten i Charlottenburg under förra året.

Citat från FOCUS MATERIEN 1975

”Strålningslagar

Definitionsmässigt skall en idealt svart kropp kunna absorbera all infallande strålning oavsett våglängden. Omvänt kan då strålning av alla våglängder emitteras. Den effekt som utstrålas inom ett visst våglängdsområde är en funktion av temperaturen och kan beräknas med hjälp av Plancks strålningsformel:

1 hc²

N_λ = —— ——————

λ⁵ e ^{hc/k λT} – 1

där konstanterna är respektive h = Plancks konstant, c = ljushastigheten i vakuum och k = Boltzmanns konstant.”,

”Från varje ytenhet på ytan av en kropp med absoluta temperaturen T utstrålas per tidsenhet en bestämd energimängd i form av strålning med våglängden λ. Denna strålning sprids i en halvklotformad volym kring ytenheten, dvs. över rymdvinkeln 2π steradianer. Vi kan då ange strålningseffekten (effekt = energi/tid) per ytenhet och per rymdvinkelenhet, beräknad per våglängdsenhet.”,

”Det är denna storhet, den s.k. spektrala radiansen, som betecknas N_λ i Plancks formel. Enheten för N_λ blir således om λ uttrycks i Å, watt m^–2 sr^–1 Å^–1, och om λ uttrycks i M, watt m^–3 sr^–1.”,

FOCUS MATERIEN 1975 s286sp2ö

Se även utförligt i Plancks strålningslag med olika skrivsätt.

Svart kropp

Fullständig strålningsabsorption kallas konventionellt för strålning från en ’absolut svart kropp’ (från 1862 efter Kirchhoff).

En absolut svart kropp [ref. FOCUS MATERIEN 1975 s90sp1] beskrivs i facklitteraturen som en kropp som kan absorbera all strålning utan att reflektera något, och som därmed också kan emittera all strålning utan någon energimässig dämpning. Vid ideala 0°K (se absoluta temperaturskalan) är den absolut svarta kroppen (således) helt svart (ingen signal), men antar färg allteftersom den upphettas: Från rödglödning till vitglödning (samt vidare, ytterst mot blåvitt med växande temperatur).

Experimentellt brukar den absolut svarta kroppen förknippas med en helt sotad (svart) kroppsyta, vanligen i formen av ett (väl isolerat) inre hålrum, hålrumsstrålare, med enbart en liten öppning för ljuset att tränga ut genom och som motsvarar den idealt (klotformiga) absolut svarta kroppens radiella ljusemission.

Isolerade Systemets Baneman

BALFOUR STEWART UPPFINNER ISOLERAT SYSTEM INOM TERMOFYSIKEN

Balfour Stewart uppfinner Isolerat System 1858

Uppfinningen gillas och antas av det moderna akademiska vetenskapliga etablissemanget

Upphovsmannen:

”But the most important advance was made by Balfour Stewart in establishing, not only a quantitative relation, but also a qualitative or selective one. By the introduction of his ingenious idea of an impervious radiating inclosure he demonstrated the equality between the emissive and the absorptive power of any wave length.”,

förordet sida v;

Från

ON THE RELATION BETWEEN THE EMISSIVE AND THE ABSORPTIVE POWER OF BODIES FOR HEAT AND LIGHT.

BY G. R. KIRCHHOFF.

Reprinted from "Investigations on the Solar Spectrum and the Spectra of the Chemical Elements," 2d. Edition, Berlin,

Ferd. Dummler's Publishing House, 1866, Gesammelte Abhandlungen, pp. 571-598, Leipzig, 1882.

i

XV THE LAWS OF RADIATION AND ABSORPTION — SCIENTIFIC MEMOIRS EDITED BY J. S. AMES;

MEMOIRS BY PROVOST, STEWART, KIRCHHOFF, AND KIRCHHOFF AND BUNSEN. COPYRIGHT, 1901, BY AMERICAN BOOK COMPANY. TRANSLATED AND EDITED BY D. B. BRACE.

Boken finns gratis på Internet Archive,

http://www.archive.org/details/lawsofradiationa00bracrich

Se vidare (ordet enclosure) i Stewarts beskrivning, samma källa som ovan

(1858¦s43 RADIATION AND ABSORPTION). Stewart använder inte ordet emission i sin beskrivning, endast ordet radiation.

I stort sett samtliga involverade i vetenskapen under 1800-talet fyller sedan i på samma vers. Nedan Kirchhoff:

Kirchhoffs bidrag till begreppet ISOLERAT SYSTEM i termodynamisk mening

”Let a body which satisfies these conditions be surrounded by an enclosure, having the same temperature, through which no heat rays can penetrate, whose temperature is kept constant and which satisfies the same conditions.”, s76

Från

ON THE RELATION BETWEEN THE EMISSIVE AND THE ABSORPTIVE POWER OP BODIES FOR HEAT AND LIGHT.

BY G. R. KIRCHHOFF.

Reprinted from "Investigations on the Solar Spectrum and the Spectra of the Chemical Elements," 2d. Edition, Berlin,

Ferd. Dummler's Publishing House, 1866, Gesammelte Abhandlungen, pp. 571-598, Leipzig, 1882.

i

XV THE LAWS OF RADIATION AND ABSORPTION — SCIENTIFIC MEMOIRS EDITED BY J. S. AMES;

MEMOIRS BY PROVOST, STEWART, KIRCHHOFF, AND KIRCHHOFF AND BUNSEN. COPYRIGHT, 1901, BY AMERICAN BOOK COMPANY. TRANSLATED AND EDITED BY D. B. BRACE.

Boken finns gratis på Internet Archive,

http://www.archive.org/details/lawsofradiationa00bracrich

I och med att det finns MELLANRUM mellan alla Planckringar (mcr) som medierar värmestrålning (gen. ljus, se Ljusets Optiska Natur), och att alla Planckringar värmeläcker, kommer man alltid, obönhörligt, till en punkt vid en kropps (värme-) bestrålning då den (efter en viss tid), tvunget, blir mättad; För varje ytterligare bestrålning tvingas då tydligen kroppen ge ut exakt lika mycket som den tar emot: emission är lika med absorption MED SAMTIDIGT GENOMFLÖDE AV VÄRMELÄCKNING. Denna situation definierar således tydligen begreppet temperatur med en given energi. Olika material uppvisar olika genomflödesstyrka (värmetröghet). Det gäller även för K-cellen. Alla kroppar värmeläcker.

Det finns inga idealt totalreflekterande fysikaliska ljusspeglar eller dito material.

Maxwells bidrag till begreppet ISOLERAT SYSTEM i termodynamisk mening

James Clerk Maxwell använder f.ö. samma typformalia (1871, The Theory of Heat)

”… and that both the cylinder and the piston are absolutely impermeable to heat, so that not only is heat prevented from getting out or in by passing completely through the cylinder or piston, but no heat can pass between the enclosed substance and the latter …”, s128ö;

”in the present case no heat is allowed to enter or leave the substance,”, s128n;

INTERNET ARCHIVE — JAMES CLERK MAXWELL 1871 The Theory of Heat

http://www.archive.org/details/theoryofheat00maxwrich

Maxwell klargör dock samtidigt att

”No substance in nature is absolutely impermeable to heat, so that the image we have formed can never be fully realised”, s128mö.

Samt (vilket visar att användningen av »isolerat system» redan är etablerad),

”One of the best established facts in thermodynamics is that it is impossible in a system enclosed in an envelope which permits neither change of volume nor passage of heat, and in which both the temperature and the pressure are everywhere the same, to produce any inequality of temperature or of pressure without the expenditure of work. This is the

second law of thermodynamics”, s338mö.

;

Alldeles för mycket teoretiserande i ett ämne som ännu ingen visste mycket om i grunden. Lägg till det dåtidens föreställning om ljusfenomenet i det »ämne» som kallades ’etern’.

Notera att de termodynamiska satserna om energi och temperatur och deras variation ÄR OMÖJLIGA ATT FORMULERA UTAN PLANCKS KONSTANT, UTAN PLANCKS ENTROPISAMBAND, UTAN sambandet för antalet likaberättigade energifördelningssätt, och därmed utom PLANCKS STRÅLNINGSLAG — och därmed omöjliga att formulera med användandet av ”an envelope which permits … no(r) passage of heat”, från Maxwell närmast ovan.

Termodynamiken I RELATERAD FYSIK kan inte formuleras i någon exakt, kunskapsteoretisk grund, varken på Maxwells horisont eller någon hans samtida. Se utförligt från ALLA KROPPAR VÄRMELÄCKER.

Att värme alltid strömmar från varm till kallt, att den fenomengrunden inte kan omvändas utan tillförande av energi, måste ovillkorligen använda Plancks konstant och därmed Plancks strålningslag med satsen om alla kroppars värmeläckning som grundval.

Maxwell hade — således, enklare — kunnat framställa saken med samma mening men mera korrekt:

Eftersom ljusets natur är att vara divergent, se utförligt i DIVERGENSEN och INDUKTIONEN, och med förutsättningen att materien består av massdelar med mellanrum, finns ingen fysisk möjlighet att omvända flödet av värme från varmare till kallare utan tillförande av energi. Utförligt från ALLA KROPPAR VÄRMELÄCKER.

Se även särskilt i HUR KROPPARNA VÄRMELÄCKER, om ej redan bekant.

Särskilda klargöranden

Plancks strålningslag täcker KVANTITATIVT bara materiefysiken

I utdrag från SOLENS FYRA VÄRMEGRADER ENLIGT TNED

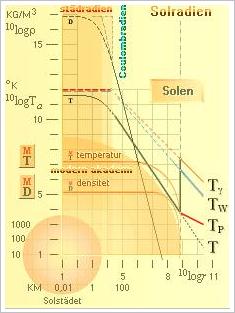
Ovanstående figurdelar i sammanställning visar: En regelrätt jämförelse mellan TNED och MAC (modern akademi) kan inte göras: TNED och MAC är två vitt skilda föreställningsvärldar: FRÅNSETT YTAN saknar de varje matematisk beröringspunkt. Av de fyra avbildade värmegraderna är det bara TP (PLANCKVÄRMEGRADEN, eg. Stefan-Boltzmanns strålningslag) som är känd i modern akademi. Se utförligt i VÄRMEGRADERNA.

Beteckningarna markerar den moderna akademins motsvarande funktionskurvor för respektive temperatur och täthet [BAs128].

RELATERAD FYSIK: Plancks strålningslag med grund i Planckenergin (E=hf) byggs visserligen med tvungen nödvändighet på massfysikens Planckring (h=mcr): alla våglängder finns representerade. Men som vi har sett genom HÄRLEDNINGEN TILL PLANCKS STRÅLNINGSLAG FRÅN PLANCKS ENTROPISAMBAND och som kopplar till ALLMÄNNA GASLAGEN, finns ingen koppling mellan allmänna gaslagens obefintliga T-generatris (T→p) och massfysikens dito uppenbara tryckfunktion som grundvalen för värmebildningen (p→T) (Se från Värmebildningen). Den senare gäller för Solens (stjärnornas) energiomsättning (generellt för massdestruktioner) genom STJÄRNORNAS ALLMÄNNA TRYCKEKVATION. Plancks strålningslag, analogt Stefan-Boltzmanns strålningslag (P=aAkT^4), kan därmed bara tillämpas kvantitativt först från stjärnkroppens (gravitellt) avgränsade kroppsyta (den röda TP-grafen ovan). Inte innanför. Det som finns innanför (den gravitellt definierade) stjärnytan blir med andra ord för Plancks strålningslag abstrakt — på samma sätt som punkten (differentialen, kristallens hörnpunkt) är ett abstrakt begrepp för intervallet; föremålet för Planckstrålningen, h i hf, massfysiken, inryms inte i tillämpningsområdet, materiefysiken. Massfysiken är abstrakt för materiefysiken.

Solen är genom sin massdestruktion och allmänna vågfunktion i relaterad fysik tvivelslöst källa för alla möjliga våglängder. Emellertid uppvisar Solytan (alldeles tydligt) en komplicerad anordning med reflexion i olika komplicerade (trånga) övergångar som, tydligen, fragmenterar representationen och därmed, bara av den anledningen, inte kan presentera någon exakt Planckstrålningskurva — men mycket väl en uppenbart medelvärdesorienterad dito. Se Solens Irradians i exempel.

Man kan (följaktligen, i ovanstående framställnings ljus) säga att Plancks strålningslag fragmenterar (urartar) på materiens explicit särskilda beståndsdelar, atomerna [Se även i Atomär närverkan]. Nämligen, och tydligen, så: På grund av att de enskilda atomerna via sina utspridda elektronbesättningar i sig uppvisar specifika frekvensegenskaper i olika s.k. exciterade avsnitt, olika för olika atomslag, försvinner samtidigt också varje möjlig idealt homogen Planckstrålningsrepresentation på DEN nivån — trots att Planckringens element i laddningsmassan (elektronen, se ELEKTRONMASSANS ELEMENT) genom sin blotta egenskap med MASSA LADDNING SPINN garanterar en övergripande utstrålningsfysik; Men den principdelen »övermönstras» med andra ord (körs över) alltså av atomens specifika frekvensnatur, elektronmassans laddningskvantitativa (resonansfrekventa) natur. Se även i GRUNDÄMNENAS PERIODISK SYSTEM. Dvs., atomen kan inte visa specifika strukturer (strömmar) i, inuti, elektronmassan då denna bara svarar på heltaliga resonansvillkor, trots att sådana inre strömmar av princip måste kunna existera i kraft av elektronmassans element, deras struktur på Planckringens princip via massprincipen E=hf=(h/n)nf. Se vidare utförligt i LJUSETS POLARISATION, REFLEXION OCH BRYTNING. Se även i Satsen om alla kroppars värmeläckning.

Därmed framstår Planckstrålningens ideala temperaturkurvor ALLTID, mer eller mindre — för samtliga specifika fysikaliska kroppar — som avskurna, fragmenterade och begränsade i det praktiska fallet — UTOM i det speciella unika fallet med HELA universum (K-cellen): den kosmiska bakgrundsstrålningen som inbegriper all existerande elektromagnetiskt aktiv massa i hela universum: universums temperatur genom dess utvecklingshistoria, nu (uppmätt) ca 2,73 °K. Den delen rapporteras också vara den mest perfekt uppmätta Planckstrålning som någonsin gjorts. Se Den kosmiska bakgrundsstrålningen.

Särskilda klargöranden

Planckstrålningens kontinuerliga spektrum föreligger alltid — ingen tidpunkt existerar då Planckspektrum inte finns

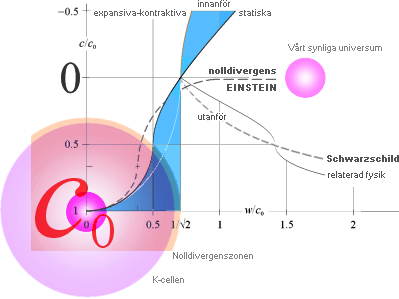
c0-kroppen med Grunddata från K-cellens värmefysik,

från UnivHistPrim.htm

K-cellens centrala kärna

Relaterad Fysik: K-CELLEN ÄR ALLTID TÄND I CENTRUM. Vid maximala tätheten (1,82 T17 KG/M³) strax före K-cellens detonation består den elektromagnetiskt aktiva centralkroppen i K-cellen av en sfär med massan 1,60227 T32 KG ≈ 80 Solmassor (Solmassan är 1,989 T30 KG) med radien 59455,481 M eller nära 6 mil. Den släcks aldrig ner, garanterat av det centrala toppvärdet för ljushastigheten, K-cellens tyngdpunkt. Inom den sfären finns garanterat av de inre pågående kärnreaktionerna alla, samtliga, våglängder och frekvenser representerade: från noll våglängd i centrum med de pågående massdestruktionerna, till oändlig våglängd i periferin där ljushastigheten går mot noll. PLANCKS STRUKTURKONSTANT garanterar att frekvenserna med våglängder mindre än ELEKTRONMASSANS ELEMENT också antar energier som går mot noll enligt Planckenergin E = hf = (h/n)nf. Det em-aktiva centralklotets innervägg som gränsar mot noll ljushastighet överför, slutligt och tvunget, all elektromagnetiskt aktiv vågrörelse till en (obegränsat) långvågig mekanisk dito. Se även ATOMKÄRNAN som ett elektromekaniskt svängningsaggregat via SVÄNGNINGSEKVATIONEN. Därmed garanteras att Planckstrålningens samtliga våglängder — Planckstrålningslagens kontinuerliga spektrum — alltid föreligger, samt dessutom genomtränger (med olika förtecken) alla kroppar som finns till i den elektromagnetiskt aktiva K-cellens kropp under dess expansion, vårt universum.

Illustrationen ovan sammanfattar i RELATERAD FYSIK beskrivningen av K-cellen genom LJUSETS GRAVITELLA BEROENDE med jämförande analys och exempel från modern akademi. Se särskilt utförligt från DET EKOLOGISKA UNIVERSUMET.

Man har nämligen annars — i viss grundfilosofisk mening — (väldigt) svårt för att ta till sig DET RENT FYSISKA BANKVALVET till Planckstrålningens — just — KONTINUERLIGA spektrum (även om man kan acceptera dess rent teoretiska allmängiltighet). Varifrån (nämligen) kommer det? Eller rättare sagt: HUR förankras det i naturboken?

Planckstrålningens kontinuerliga spektrum gäller, ju, för samtliga kroppar I HELA UNIVERSUM (om det ska vara någon vits med Plancks konstant, det s.k. universella verkanskvantumet).

En upphettad gas TILL EXEMPEL och som inte är alltför hårt komprimerad, visar oss alls inget kontinuerligt band av spektrala representationer utan istället diskret avgränsade linjer eller band med (stora) mellanrum.

Men om gasen komprimeras tillräckligt så att tillräckligt många atomer får vara med och summera ett mera komprimerat förhållande, uppvisar också gasen ett motsvarande kontinuerligt spektrum.

För kroppar som INOM en viss temperaturlokal, t.ex. ett teknisk laboratorium, uppvisar stora inbördes temperaturskillnader, t.ex. vid studiet av ett upphettat ämne i en liten gaslåga med temperaturen runt 1500°C i ett stort rum med temperaturen 20°C, tillkommer TYDLIGEN ämnesatomernas SPECIFIKA ELEKTRONRESONANTA BIDRAG i kontrast till att det övriga rummets föremål INTE genomgår samma uppvärmning. Endast om det upphettade ämnet uppvisar en maximalt hög inre atomär täthet — nämligen för att garantera det motsvarande avgränsat kontinuerliga spektrum som redan finns representerat för alla kroppar i hela universum och taget på en deras gemensamma historiska utvecklingspunkt, K-cellens värmefysik — kan jämförelserna bli rättvisa.

Den mest ideala anordningen är (således) den s.k. hålrumsstrålaren [Se även Svart kropp] med sin maximalt inre belagda sotade yta. Då dess inre kavitet (hålrum) uppvärms, utsänder strålaren alla möjliga våglängder (utom de termonukleära) genom ett litet upptaget hål som man kan mäta på.

SOLEN å andra sidan — RELATERAD FYSIK — är en helt perfekt naturkälla för alla möjliga våglängder. Men på grund av att Solytan är utpräglat reflekterande tillkommer (tydligen) vissa spektrala komplikationer som, enligt mätresultaten, visar sig i en utpräglad fragmentering: Planckkurvan framgår, helt klart, som medelvärdesformen, men ingalunda med någon exakt motsvarighet. Se Solens Irradians.

GRUNDTERMER — teknisk ljusmätning

GRUNDTERMER — teknisk ljusmätning

HISTORISK ORIENTERING

spektroskop ......................... visuell observation av färguppdelning

spektrometer ...................... samtidig våglängdsbestämning

spektrograf ......................... samtidig fotografisk/fotoelektrisk registrering

ref. FOCUS TEKNIKEN 1975 s494sp1ö

I dagens värld (Apr2010) finns en stor mängd instrumentella (oftast extremt dyra) lösningar för olika typer av ljusmätningar (gen. spektroRadiometri). En del visas i kort översikt i Webbexempel Mätinstrument. Detaljerade funktionsbeskrivningar för instrumenten finns på webben (ofta helt gratis) i form av datablad; Fabrikanten specificerar instrumentets eller komponentens tekniska data (och också numera oftast med förslag på kretslösningar i olika tillämpningsexempel där elektronik ingår).

I följande ges enbart en kort historisk överblick med de mest centrala instrumentbegreppen genom de (för vår tid) historiskt mest framträdande verken.

FOCUS TEKNIKEN 1975 beskriver generellt den traditionella ljusmätningstekniken enligt följande utdrag — till jämförelse:

”Spektralapparaterna består i princip av tre huvuddelar: en del som insamlar eller alstrar strålningen, en som delar upp den, och en som möjliggör observation eller registrering. Om denna tredje del medger endast observation (med ögat) är instrumentet ett spektroskop. Kan det också användas för att fastställa våglängden hos strålningen talar man om spektrometer. Registrerar instrumentet den uppsamlade strålningen antingen fotografiskt eller med fotoelektrisk metod (jfr Fotoelektricitet) kallar man instrumentet spektrograf.”

HUR ETT SPEKTRUM FRAMTRÄDER beskrivs kortfattat i avsnittet om Spektrala Radiansen. I UNIVERSUMS HISTORIA ges en enkel separat grundbeskrivning i LJUSETS INTERFERENS. Här ges en liten utvidgning.

Spektrala gittertyper

Transmissionsgitter och reflexionsgitter

De två enkla grässtrånas ljusuppdelning av stearinljuslågan i ett enkelt primitivt spektrum (Se LJUSETS INTERFERENS) får en mera avancerad teknisk motsvarighet i ett s.k. optiskt plangitter.

En slät glasskiva vars yta avdelas i parallella ritsor med jämna mellanrum bildar samma princip som i det enkla paret grässtrån mellan två närliggande ritslinjer. Den klara glasöppningen släpper igenom (transmitterar) ljuset, medan ritsornas oskarpa urgröpning sprider ljuset godtyckligt. Ju flera ritsade linjer som tas med, desto högre blir interferensbildens intensitet. Ett sådant optiskt plangitter kallas transmissionsgitter (eng. transmission grating). Görs ritsorna på en metallyta kallas plangittret för reflexionsgitter (eng. reflection grating).

En CD-skiva med sina täta spår (ca 600 per mM) kan (med viss finess) utnyttjas både som ett reflexionsgitter (skivan precis som den är via uppspelningssidan) och som ett transmissionsgitter (använd tejp för att dra bort färgmasken på den målade sidan, man ser rakt igenom) [En DVD-skiva har till jämförelse ca 1351 linjer per mM].

I Webbreferenser ges exempel på några webbkällor som visar hur man kan konstruera ett mera avancerat, men fortfarande helt enkelt och i princip helt gratis spektroskop med en allt finare, mera precisionsartad upplösning. Matematiken för att beräkna de olika våglängderna är alldeles precis densamma som i den enkla primitiva spalten från de bägge runda grässtråna i LJUSETS INTERFERENS.

Se även @INTERNET Wikipedia Diffraction grating 2010-04-03, konventionell beskrivning av de olika detaljerna i gittertekniken.

Den svenska representationen av basdokument i ämnet är (ännu Apr2010) (ytterst) mager [typ »optiska gitter»].

SCIENTIFIC AMERICAN February 1982 berättar i sin artikel från s118 om HENRY A. ROWLAND. Rowland gjorde sig känd i de olika forskningslaboratorierna världen runt för sina högpresterande spektroskop från senare delen av 1800-talet. Rowlands egna mätningar (extremt exakta Solspektrumdata) finns f.ö. dokumenterade i en del böcker som finns gratis på INTERNET ARCHIVE. Se bland annat

SPECTRUM ANALYSIS John Landauer 1898 — INTERNET ARCHIVE

http://www.archive.org/details/spectrumanalysis00landuoft

s33;

” Rowland's Concave-grating Spectroscope. — The development of spectrum analysis received a considerable impetus from Rowland's discovery of the concave grating in 1881. By its use measurements have attained a degree of accuracy otherwise unapproachable, and whilst this is specially true of the values obtained by the coincidence method, it also applies; to wave-lengths directly determined; it is the only instrument which is available for use with all rays, including the ultra-violet and the infra-red, and, as no lens is necessary between the slit and eyepiece, defects from loss of light or spherical aberration are avoided; the gratings being astig-[s34]matic, a luminous point, such as a spark, appears in the field of view as a line, thus greatly facilitating the comparison of solar lines with those of metals, and the enlargement of spectra. Photographs, both of the visible and invisible portions of the spectrum, are easily obtained, and their accuracy is necessarily far in excess of the drawings prepared from ocular observation …”

Boken ger en utförligt (grundläggande) beskrivning av grundbegreppen (våglängd, reflexion, refraktion, prismor, dispersion [färguppdelning], rent spektrum, ritsningar [med reguljära avstånd parallellt utförda raka fördjupningar, vanligen i glas eller metall, även benämnt [spektral-]gitter], diffraktion [spridning]) och vidare. Utförliga, illustrerade, beskrivningar genomgås av de olika spektroskopiska och spektrometriska instrumenten — de allra första precisionsinstrumenten i sitt slag.

Figuren nedan (från s33) visar ett spektroskop med en uppställning tillsammans med ett optiskt reflexionsgitter (reflex grating);

Bildtexten frn.s32:

”A simple form of spectroscope with a reflex grating is shown in Fig. 19. The telescope and collimator are situated close together on separate mountings; the grating is enclosed in a case with a plane parallel glass front to protect it from [s34] corrosive fumes, and is fixed on a revolving stand so that spectra of any desired order can be brought before the crosswires of the telescope.”,

SPECTRUM ANALYSIS John Landauer 1898 — INTERNET ARCHIVE, s33n

http://www.archive.org/details/spectrumanalysis00landuoft

En enklare anordning som också tydligare beskriver spektrometerns grundprincip visas av boken på sidan 32, nedan.

Boken ger många liknande väl illustrerade exempel. Med sin utförliga beskrivning blir den en helt genuin referens till den banbrytande spektrografiska instrumentmekanik som föregick vår egen tid och tog sin början under 1800-talet.

I mitten (M) sitter spektralgittret (här tydligen ett transmissionsgitter) som får sitt ljus från ljuskällan genom den övre anordningen (L) (kollimator [optisk anordning för parallellisering av ljusstrålar] med öppning [d] som ljuskällan riktas in mot). På en vridbar graderad cirkelskiva sitter ett teleskop (kikare, F) med hårkors (eng. cross-wire) som fokuserar på ritsbilden. Genom att vrida F framträder från M (i okularet [den med ögat betraktade slutbilden], o) olika spektrallinjer vilkas motsvarande skalvärden kan avläsas på den graderade cirkelskivan (och sedan omräknas enligt lämpliga samband).

En motsvarande nyare tids konstruktion av samma typ av spektrometer som ovan visas nedan.

nc technology Niagara Collage Canada — USING A SPECTROSCOPE (2010)

http://technology.niagarac.on.ca/sop/Spectroscope.html

Källan ovan beskriver anordningen mera ingående.

Webbreferenser

Webbreferenser

Fotometriska Grundbegrepp

FOTOMETRI — KTH Biomedicinsk fysik & Röntgenfysik, Kjell Carlsson 2003

http://www.biox.kth.se/kjellinternet/Fotometri.Komp.PDF

;

Källinnehåll: Källan behandlar linsoptiska detaljer med fotometriska och radiometriska termer tillsammans med deras matematik (integralkalkyl), samt ger en särskild exempelsamling med lösningar.

Hur man bygger ett enkelt (primitivt) spektroskop med en CD-skiva, kartong, rakblad, pappersrulle och tejp

1.

Science Toys You Can Make With Your Kids — BUILDING A SIMPLE SPECTROSCOPE

http://sci-toys.com/scitoys/scitoys/light/cd_spectroscope/spectroscope.html

;

Källinnehåll: Hur man bygger och använder ett spektroskop med enkla medel (i princip helt gratis med prylar som redan finns hemma).

2.

A Toy Spectroscope and its Operational Diagram, I.N. Galidakis (1998-2010)

http://ioannis.virtualcomposer2000.com/spectroscope/toyspectroscope.html

;

Källinnehåll: Som i 1 — men ännu enklare (i princip helt gratis med prylar som redan finns hemma) samt delvis (mycket) mera utförligt (direkt kvalitativa resultat uppnås).

;

Denna webbkälla visar också spektrala resultat från en vanlig stearinljuslåga — tillsammans med många andra — i

http://ioannis.virtualcomposer2000.com/spectroscope/amici.html#colorphotos

;

Källan ger även omfattande illustrerade grafiska spektroskopiska data på grundämnen,

THE SCIENCE OF COLOR, THE EMISSION SPECTRA OF THE ELEMENTS AND SOME LAMP ENGINEERING APPLICATIONS,

I.N. Galidakis (1998-2010)

http://ioannis.virtualcomposer2000.com/spectroscope/elements.html

Ljuslågans kemi

Ljuslågans kemi beskrivs i

SCAD The University for Creative Careers datum/författare saknas

s h a d e r w r i t i n g: c a n d l e f l a m e

http://sfdm.ca.scad.edu/faculty/mkesson/vsfx319/wip/best_spring2003/ca301.2/scott_dean/fire/flame.html

PLANCKS STRÅLNINGSLAG I PRAKTISK FYSIK END.

PlanckLagen

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Plancks strålningslag i praktiken

ämnesrubriker

innehåll

PlanckLagen

UnicodeStandard

PLANCKS STRÅLNINGSLAG I PRAKTISK FYSIK

Masskomponenten h grundlägger materiefysiken

Inledande beskrivning, kompletterande

Den kosmiska bakgrundsstrålningen

PLANCKVÄRMEGRADEN I K-CELLENS UTVECKLING

Solens irradians

Grundsatser

PROPORTIONALITETEN MELLAN MASSA OCH LADDNING

Satsen om alla kroppars obönhörliga värmeläckning

Alla möjliga våglängder

Den moderna akademin

Plancks strålningslag

Frekvensformen — Plancks strålningslag

CMBR

Noteringar

Jämförande resultatvärden Solytan

TABELL — Jämförande resultatvärden för Solytans temperatur

Med Solen som exempel — Plancks strålningslag

Solytsvärden i etablerad litteratur

Webbreferens Tilley

Fragmenteringen

CosinusFragmenteringen

Jämförande praktiska resultat

Betecknigssättet AM0 AM1 AM1.5

Reflexion medför dämpning

Summerande Planckstrålningsexempel

Dämpning i intervall

Atomär närverkan

EXEMPEL PÅ fel i Solgrafen på webben

Solytans temperatur, internationell standard

Solär Irradians — internationell standard

GRUNDBEGREPP

Absorption, emission, reflexion och transmission

Experimentell bekräftelse på Stefan-Boltzmanns strålningslag

Skrivsätten för Plancks strålningslag

Plancks strålningslag med olika skrivsätt

Sfäriskt rundstrålande

Halvsfäriskt rundstrålande

Krafttäthet normal

Krafttäthet åttaPi

Energifördelning

Radians och Irradians

Orientering i sfärbegreppen med allmänna radiometriska enhetsbeteckningar

Steradian

Spektralenheterna

Hur Plancks strålningslag beräknas för spektral irradians

Spektrala radiansen

Teknisk mätning för spektral irradians

Webbexempel mätinstrument

Spektroradiometer

Crookes radiometer

Bolometer

Termoelement

Termostapel

Pyranometer

Pyrometer

Beräknande Exempel

EXEMPEL 1 — spektral radians

EXEMPEL 2 — spektral irradians

Illustrerade Exempel

Solstrålningens idealt odämpade spektrala irradians

Jämförande webbkälla

Citatsamling — allmänna termer

Planck om giltigheten av Planckstrålningslagen

Citat från FOCUS MATERIEN 1975

Svart kropp

Isolerade Systemets Baneman

Kirchhoffs bidrag

Maxwells bidrag

Maxwell klargör

Särskilda klargöranden

Plancks strålningslag täcker KVANTITATIVT bara materiefysiken

Planckstrålningens kontinuerliga spektrum föreligger alltid — ingen tidpunkt existerar då Planckspektrum inte finns

GRUNDTERMER — teknisk ljusmätning

HISTORISK ORIENTERING

Spektrala gittertyper

Transmissionsgitter och reflexionsgitter

Spektroskop

Spektrometerns grundprincip

Webbreferenser

Fotometriska Grundbegrepp

Hur man bygger ett enkelt spektroskop

Ljuslågans kemi

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[BA]. BONNIERS ASTRONOMI 1978

TNED

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2011-10-10

*END.

Stavningskontrollerat 2010-04-06.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se