MATEMATIKEN Formlagarna 2008IV29 | Senast uppdaterade version: 2014-03-25 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Potensderivatan

Formlagarna

Med fortsättning från Nollformsalgebran

FORMLAGARNA

Formlagarna i utförlig genomgång finns i särskild beskrivning (ännu bara på ) engelska i HÄRLEDNINGARNA TILL FORMLAGARNA.

— Där ingår också nedanstående tabellBILD utformad i text MED interna länkar till avsnittet för varje härledd formlag.

bastablån i formlagarna i PREFIXxSIN

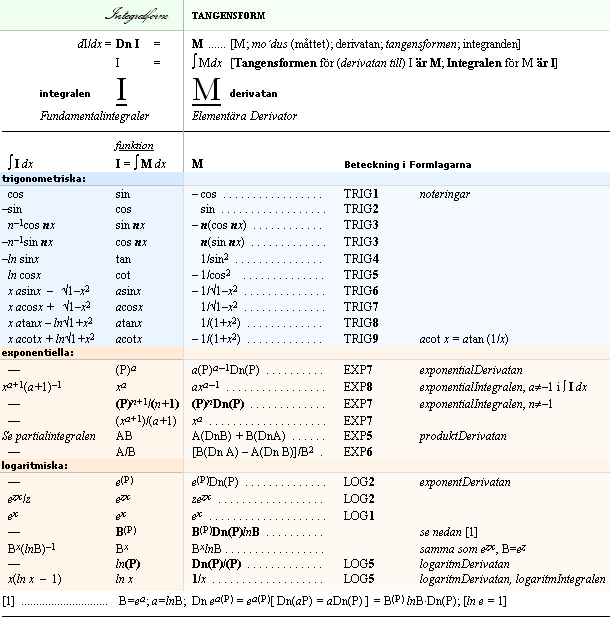
FORMLAGARNA

(konv. deriveringsregler) framgår ur positionsformen eller differentialkvoten

y’ = (y₀–y)/(x₀–x) ..................... positionsformen

positionsformens metod

Ekvivalent med tangensformen eller derivatan i relaterad matematik är också termen

positionsform eller differentialkvoten y’=(y₀–y)/(x₀–x).

Metod: UTVECKLA y-formen i Positionsformen dy/dx=(y₀–y)/(x₀–x) för att isolera differentialerna; därmed extraheras eller renas y-formen från associerade differentialer genom dxÛ0 och dyÛ0, där Û (övergår-i) betecknar övergångsformen från positionspunkter (dx) till värdemängder (0, noll, ingenting), vilket ger slutresultatet.

NOTERA: primtecknet (’) används med fördel för att förenkla skrivsättet TYP Dn y = y’:

»DerivataN till y är lika med y’»

genom att på den tillämpa matematikens alla grundfunktioner. Ovanstående bastablå visar resultaten i sammanställning.

Vi studerar här några allmänna grundexempel som visar hur formlagarna i tablån har utvecklats.

UTVECKLINGSEXEMPEL

produktderivatan

UTVECKLA y-formen i positionsformen dy/dx=(y₀–y)/(x₀–x) för att isolera differentialerna:

därmed extraheras eller renas y-formen från associerade differentialer genom dxÛ0 och dyÛ0

Funktion:

y = AB = y_Ay_B

Lösning:

y₀ = (A+dA)(B+dB) = AB + AdB + BdA + dAdB

dAdB Û 0

y₀ = AB + AdB + BdA

y₀ – y = AB + AdB + BdA – AB = AdB + BdA

(y₀ – y)/dx = A(dB/dx) + B(dA/dx) = AB’+BA’ = y’

Resultat:

(AB)’ = AB’ + BA’ ........................ produktderivatan, A och B godtyckliga funktioner

UTVECKLINGSEXEMPEL

exponentialderivatan

UTVECKLA y-formen i positionsformen dy/dx=(y₀–y)/(x₀–x) för att isolera differentialerna:

därmed extraheras eller renas y-formen från associerade differentialer genom dxÛ0 och dyÛ0

Funktion:

y = X^a , y₀ = X₀^a , (P) = X

Lösning:

dy/dx = [X₀^a – X^a]/dx = [[X + dX]^a – X^a]/dx
y₀=X₀^a=(X+dX)^a insatt för (a+b)ⁿ i binomialteoremet

(a+b)ⁿ = aⁿ[1 + n(b/a) + n(n–1)(b/a)²/2! + n(n–1)(n–2)(b/a)³/3! + … + (b/a)ⁿ]

ger
(X+dX)^a = X^a

+ X^aa(dX/X)

+ X^aa(a–1)(dX/X)²/2!

+ X^aa(a–1)(a–2)(dX/X)³/3!

+ X^aa(a–1)(a–2)(a–3)(dX/X)⁴/4!

+ … + (dX)^a
Efter minus X^a och division med dx, finns bara en ren term som inte innehåller dx i täljaren, X^aa(dX/X). Därmed
dy/dx Û X^aa(dX/dxX) = aX^a–1 dX/dx = aX^a–1 Dn X dx/dx = aX^a–1 Dn X ;

Resultat:

Dn (P)^a = a(P)^a–1 Dn (P) ................. exponentialderivatan,(P) en godtyckligt sammansatt funktion

UTVECKLINGSEXEMPEL

logaritmderivatan — med Beviset för e

UTVECKLA y-formen i positionsformen dy/dx=(y₀–y)/(x₀–x) för att isolera differentialerna:

därmed extraheras eller renas y-formen från associerade differentialer genom dxÛ0 och dyÛ0

Funktion:

y = B^x

Lösning:

y’ = dy/dx = (y₀–y)/dx = (B^xB^dx–B^x)/dx = B^x(B^dx–1)/dx

Med en graf för y, i exemplet y=2^x, ses relationerna enklare;

beviset för e

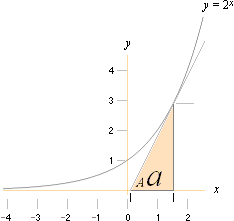
Man ser genom

tanA=y/a=dy/dx=(y₀–y)/dx ; y/a=(y₀–y)/dx ; a=y·dx/(y₀–y)=dx/([y₀/y] – 1)=dx/([B^xB^dx/B^x] – 1)

att

a = dx/(B^dx–1);

Vilket vill säga:

Eftersom dx är konstant beror a endast av B. Följaktligen finns ett och endast ett B för vilket gäller att a=1;

Vi söker B₁=e;

1=dx/(e^dx–1) ger då e=(1+dx)^1/dx. Vilket betyder,

e = (1+x/¥)^¥/x ..................... beviset för e

MED DIFFERENTIALENS DEFINITION ENLIGT NOLLFORMSALGEBRAN

NOTERING: Eftersom modern akademi sätter DIFFERENTIAL(dx)=INTERVALL(Dx) är härledningen ovan omöjlig att förstå i termer av modern akademi:

Det går inte att jämföra de olika sätten eftersom modern akademi INTE erkänner en skarp skillnad mellan punkt (dx) och intervall (Dx).

Alldeles samma resultat nås direkt med insättning av den mängdoberoende i den direkt beräkningsbara summaformen i Binomialteoremet (BT):

(a+b)ⁿ = aⁿ[1+ _m=0\n å [(b/a)(n–m)]_m![(m+1)!]^–1]

= aⁿ[1 + n(b/a) + n(n–1)(b/a)²/2! + n(n–1)(n–2)(b/a)³/3! + … + (b/a)ⁿ]

;

Med 1 för a, 1/¥ för b och ¥ för n som ger

(a+b)ⁿ = (1+1/¥)^¥

framgår att sigmatäljarens (b/a)(n–m) är de enda termer som påverkas;

Man får (b)(n–m) = (1/¥)(¥–m) = (1–m/¥). Eftersom m/¥=d(m)Û0 gäller alltså

(1–m/¥)Û1 och därmed (b)(n–m) = 1;

Genom separat analys i BT framgår speciellt att 1^¥=1 med potensen (1+b)^¥ om b=0;

(1+0)^¥ = 1^¥[1+ _m=0\¥ å [0]_m![(m+1)!]^–1] = 1 + 0 = 1

Dvs., a^¥=1 med a=1 som ovan.

Därmed resultatet

(1+1/¥)^¥ = 1[1+ _m=0\¥ å [1]_m![(m+1)!]^–1]

= 1+ _m=1\¥ å [m!]^–1

= 1+1+1/2!+1/3!+1/4!+1/5!+ …+1/m! = 2,718 28 18 28 45 90 45 …

Men alldeles samma resultat fås om b=x/¥ och n=¥/x enligt

(b)(n–m) = (x/¥)(¥/x–m) = (1–x/¥)Û1;

Eftersom mx/¥=d(mx)Û0 gäller alltså (1–mx/¥)Û1 och därmed likväl (b)(n–m) = 1.

Alltså gäller även att

(1+x/¥)^¥/x = 1[1+ _m=0\¥ å [1]_m![(m+1)!]^–1]

= 1+ _m=1\¥ å [m!]^–1

Och alltså gäller allmänt

Eulers ekvivalenter

exponentialekvivalenterna eller (här) EULERS EKVIVALENTER

(1+x/¥)^¥ = (1+1/¥)^x¥ .............................................. bonus, Eulers ekvivalenter

Benämningen ”Eulers ekvivalenter” finns (här f.ö. veterligt) INTE i modern akademi. Anledningen varför den beteckningen här valts framgår av de spår av Leonhard Eulers egna utvecklingar man finner i moderna referenser där Euler omnämns — men som sedermera (till vissa delar) förkastades av modern akademi i kraft av dess allmänna omdaning av logiken under 1800-talet.

Se vidare separat artikel i Eulers Ekvivalenter.

MACfelet e

NOTERA FELET I MODERN AKADEMI:

— Ovanstående insättningar kan INTE tillämpas på den moderna akademins lärosystem och dess matematiska satser.

Vi studerar detta.

Modern akademi skriver BT (typiskt, jämför exempelvis MATEMATIKLEXIKON W&W 1991 s46-47)

(a+b)ⁿ = aⁿ[_m=0\nå (b/a)^mn![(n–m)m!]^–1]

Vilken är skillnaden? Man har strukit strukturkomponenten. Genom att dividera den naturliga serieformen med

faktorn (n–m) får man den moderna akademins ovanstående uttryck [som följaktligen lämpar sig utmärkt för

statistik]. Därmed har också uttrycket upphört att gälla som beräkningsbart. Låt oss se resultatet.

Vi sätter a=1, b=1/¥ och n=¥. Man får

(1 + 1/¥)^¥ = _m=0\¥ å (1/¥)^m¥![(¥–m)m!]^–1 = _m=0\¥ å (1/¥)^m¥[¥]^–1 = 1/¥ Û 0

Sambandet kan inte användas.

Vad gör modern akademi för fel?
Felet — fullständigt relaterabart — återfaller på den moderna akademins uppfinningar under 1800-talet (här i generell referens utan exakta citat) som resulterade i att man började sätta likhet mellan punkt (differential) och intervall (differens) och därmed GARANTERA logisk vägran att erkänna den mängdoberoende (¥) och dess användning för definitionerna av differentialen (dx = x/¥) och differensen (Dx = x/[n®¥]):
Man skriver (nämligen, se citat) i modern akademi
dx = Dx
och tillämpar sedan ett gränsvärdesresonemang som alltså helt saknar logisk soliditet enligt
_n®¥limes n = ¥;
gränsvärdet för n då n växer obegränsat är den oändliga mängden ¥;
I relaterad matematik och fysik existerar inga oändliga mängder:
— (x/¥)(1+1+…)=dx¹x, punkter kan inte adderas, det finns inga oändliga mängder —
Därmed tillämpar man felaktigt i modern akademi också skrivsättet
_n®¥limes 1/n = 1/¥
med värdemängden noll, helt korrekt enligt
_n®¥limes 1/n = 0
vilket leder till att man också i modern akademi felaktigt skiver (och tänker)
_n®¥limes (1+1/n)ⁿ = (1+1/¥)^¥ = (1+0)^¥ = 1
och därmed
(1+1/¥)^¥ ¹ e
Saken förvärras genom att värdemängden för formen (1+1/n)ⁿ bildar partiella serieekvivalenter med e-serien enligt
exemplifierat för n som 1, 10, 100, 1 000, 10 000 … n®¥
värdena 2, 2.5937425, 2.7048138, 2.7169239, 2.7181459, … 2.7182818… ”=e”,
Härigenom luras man till uppfattningen att
”_n®¥limes (1+1/n)ⁿ = e”
Det korrekta sättet är, enligt relaterad logik — med grund i Atomtriangeln och dess grund i intervallets oförstörbarhet och därmed den mängdoberoendes framträdande i atomtriangelns entydiga definition av integralen som enhet utan delar — och därmed differentialens definition genom den mängdoberoende,
_n®¥ (1+1/n)ⁿ = ARITMETISKAVÄRDET(e) Û 1 + 1/1! + 1/2! + 1/3! + … = e = (1+1/¥)^¥

e tar inte gränsvärde — därför att e är en positionsform, ingen bestämd geometrisk mängd.

Tillämpar man, som modern akademi gör, gränsvärdesbegrepp på e hamnar man i direkt logiskt absurda resultat som ingen varken förstår, kan beskriva, eller förklara.
Jämför tillämpningen av den mängdoberoende direkt från serieledet för BT via (a+b)ⁿ= (1+1/¥)^¥,

= aⁿ[1 + n(b/a) + n(n–1)(b/a)²/2! + n(n–1)(n–2)(b/a)³/3! + … + (b/a)ⁿ]
= 1 + ¥(1/¥) + ¥(¥–1)(1/¥)²/2! + ¥(¥–1)(¥–2)(1/¥)³/3! + … + (1/¥)^¥
= 1 + ¥(1/¥) + ¥(¥)(1/¥)²/2! + ¥(¥)(¥)(1/¥)³/3! + … + [(1/¥)^¥=(1/¥)Û0]
= 1 + 1 + 1/2! + 1/3! + 1/4! + …

Varje härledning till e måste tvunget utnyttja Den ovanstående inneboende Logiskt underförstådda Innebörden av Den Mängdoberoende i ¥–N=¥. MEN eftersom den moderna akademin inte känner till 1/¥ som definitionen på enhetens differential kan den följaktligen heller inte härleda e utan logiska fel: den känner inte till skillnaden mellan positioner (dx) och värdemängder (0) och kan därför endast tolka 1/¥ som ”noll”; den ställer upp formalian genom ekvivalenter (liknande dem i leden närmast ovan), postulerar relaterbart felaktigt, se härvarande beskrivning, att (1+1/¥)^¥=(1+0)=1, och kan alltså inte relatera, = fattar ingenting av INNEHÅLLET.

Så länge uppräkneligheten m är försumbar mot givet n så att serien för dessa fall kan sättas analogt med termformerna
1 + ¥(1/¥) + ¥(¥)(1/¥)²/2! + ¥(¥)(¥)(1/¥)³/3! + …, får alltså serien partiell likhet med den exakta serien via (1+1/¥)^¥. Den oändliga processen (1+1/[n®¥])^n®¥ utelämnar alltså alltid en viss mängd termer från (1+1/¥)^¥ som helt säkert inte liknar (1+1/¥)^¥-seriens termer. Därmed spricker också föreställningen om likheten med ett förmodat gränsvärde.

Modern akademi innehåller ENBART exempel på läromedel som kan användas för att detaljstudera det ovan sagda till jämförelse. Ett utförligt exempel finns i
ITK-6 MATEMATIKBIBLIOTEK, Lennart Brandqvist, s42-43, INSTITUTET FÖR TEKNISKA KURSER, STOCKHOLM 1961.

Vilket vill säga: e kan inte härledas ur gränsvärdesresoneamang, ty “gränsvärdesresoneamanget” använder tvunget och utan insikt den mängdoberoendes ställning enligt
¥–N=¥, vilket den gränsvärdesresonerande — men modernt akademiskt sinnade personen — inte är medveten om eftersom han inte känner till grunderna: den mängdoberoende. Se vidare från Atomtriangeln.

Summering
Positionsformen (1+1/¥)^¥=e är alltså INTE lika med _n®¥ lim (1+1/n)ⁿ av exakt samma aritmetiska skäl som att
positionsformen 1/¥ INTE är lika med 1/(n®¥); (n®¥)¹¥; intervall ¹ punkt. Intervall är INTE punkt. Men modern akademi hävdar just det. Därav kalabaliken.

Värdemängden i _n®¥(1+1/n)ⁿ närmar sig alltså ARITMETISKAVÄRDEMÄNGDEN(e), alltid partiell, av exakt samma skäl som att
värdemängden i _n®¥ 1/n närmar sig 0 Û 1/¥. Se vidare från nollformsalgebran, där ges utförliga beskrivningar med exakta härledningar.

speciella

exponentderivatan

Därmed resultatet för hela uppgiften

e = (1+x/¥)^¥/x = (1+1/¥)^¥ = 1+ _m=0\¥ å [(m+1)!]–1 = 1+ _m=1\¥ å [m!]^–1

= 1+1+1/2!+1/3!+1/4!+1/5!+ …+1/m! = 2,718 28 18 28 45 90 45 …

y’ = tanA = y/a = B^x/a = e^x = d(e^x)/dx ............. delresultat, exponentderivatan

Eftersom (grundmatematiken) B=e^m, som ger m=lnB, ges B^x=e^mx. Då är d(B^x)=d(e^mx). Eftersom m är en zoomfaktor för x måste den också återfinnas i slutresultatet y som motsvarande zoomfaktor för detta, annars bevaras inte xy-systemets enhet. Man får alltså d(e^mx)/dx=me^mx och därmed

y’ = d(B^x)/dx = B^xlnB = tanA = y/a ................. exponentderivatans fullständiga form

varav således a=(lnB)^–1.

naturliga logaritmbasen

e benämns i gängse termer den naturliga logaritmen (eg. naturliga logaritmens bas).

Den är av avgörande betydelse för fysikens beskrivning genom matematiken

(variationer genom TID: dF/dt = F’).

Ännu ett steg återstår.

Med

e^x = 1 + x + x²/2! + x³/3! + x⁴/4! + x⁵/5! + … + x^m/m!

och insättning av en godtycklig funktion (P) för x, fås den mera allmänna funktionen y=e^(P)

e^(P) = 1 + (P) + (P)²/2! + (P)³/3! + (P)⁴/4! + (P)⁵/5! + …+ (P)^m/m!

Deriveringen term för term via exponentialderivatan ger

Dn e^(P) = 0 + Dn(P) + 2(P)Dn(P)/2! + 3(P)²Dn(P)/3! + …+ m(P)^m–1Dn(P)/m!
Dn e^(P) = Dn(P)[1 + (P) + (P)²/2! + (P)³/3! + (P)⁴/4! + …+ (P)^m/m!]

allmänna

exponentderivatan

Delen inom rakparentesen har samma form som e^(P). Därmed den mera allmänna exponentderivatans form

Dn e^(P) = Dn(P)·e^(P) ......................... exponentderivatan, (P) en godtyckligt sammansatt funktion

Därmed kan härledningen till logaritmderivatan slutföras:

Med (P):=ln(P)

[:= används inom datatekniken stundtals som ett s.k. tilldelningstecken; det kan användas bekvämt för att slippa flera index för en och samma bokstavsvariabel då den genomlöper ändrade innebörder; Jämför (P2)=ln(P1)]

ges direkt

Dn e^ln(P) = Dn ln(P) · e^ln(P) ; (P)=e^ln(P) eftersom ln(P)=ln(P) från e^a=(P) som ger a=ln(P)=(P);

Dn (P) = Dn ln(P) (P)

Resultat:

logaritmderivatan

Dn ln(P) = (P)’/(P) .............................. logaritmderivatan, (P) en godtyckligt sammansatt funktion

Dn e^(P) = (P)’e^(P) .............................. exponentderivatan, (P) en godtyckligt sammansatt funktion

UTVECKLINGSEXEMPLEN I SAMMANFATTNING

potensderivatan

Termen potensderivata har eftersökts i den moderna akademins lärosystem men inte hittats.

—————————————————————————————————————————————————————

POTENSDERIVATAN

—————————————————————————————————————————————————————

UTVECKLINGSEXEMPLEN I SAMMANFATTNING

I logaritmderivatan [ln(P)]’=(P)’/(P) sätter vi (P):=(P)^Q som ger [ln(P)^Q]’, [Q · ln(P)]’= (AB)’. Därmed ges

[ln(P)^Q]’ = [(P)^Q]’/(P)^Q = [Q · ln(P)]’ = Q[ln(P)]’+ Q’ln(P) = Q(P)’/(P) + Q’ln(P).

ALLMÄNNA POTENSDERIVATAN — P och Q godtyckliga funktioner eller konstanter — framgår därmed enligt

(1a) [(P)^Q]’ = (P)^Q[Q · ln(P)]’

(1b) [(P)^Q]’ = (P)^Q[Q[ln(P)]’ + Q’ln(P)]

(1c) [(P)^Q]’ = (P)^Q[(P)’Q/(P) + Q’ln(P)]

P och Q kan vara vilka som helst godtyckliga funktioner eller konstanter.

Allmänna potensderivatan kan sägas innefatta eller sammanfatta alla övriga derivator;

Produktderivatan Dn (AB) framgår explicit ur (1) genom Q=A och ln(P)=B;

Logaritmderivatan Dn ln(P) framgår explicit ur (1) genom Q=1;

Exponentialderivatan Dn (P)ⁿ framgår ur (1) genom Q=konstant=n;

Exponentderivatan Dn e^Q framgår ur (1) genom P=konstant=e.

Allmänna potensderivatan omnämns inte i gängse allmänna matematiska fackverk

(Jämför MATEMATIKLEXIKON W&W 1991)

Terminologin ”exponentialderivata”, ”exponentderivata” ,”potensderivata” och ”logaritmderivata” förekommer inte i gängse matematiska litteratur (se exv. MATEMATIKLEXIKON W&W 1991). Allmänna potensfunktioner (typ y=x^1/x) omnämns inte — det finns heller (mig veterligt) inga exempel i den allmänna lärobokslitteraturen. Sådana exempel har eftersökts men inte hittats.

tillämpningsexempel potensderivatan

POTENSDERIVATAN I EXEMPEL

ALLMÄNNA POTENSDERIVATAN

[(P)^Q]’ = (P)^Q[Q(P)’/(P) + Q’ln(P)] ..................................... Allmänna PotensDerivatan

Om i allmänna potensderivatan insättes Q=konstant=n ges

[(P)ⁿ]’ = (P)ⁿ[n(P)’/(P)] = n(P)^n–1Dn(P) ........................... ExponentialDerivatan (variabeln i Basen)

Om i allmänna potensderivatan insättes P=konstant=e ges

[eⁿ]’ = eⁿQ’ln(e)] = eⁿDn(Q) ............................................... ExponentDerivatan (variabeln i Exponenten)

P och Q kan vara vilka som helst uttryck, konstanter eller funktioner.

EXEMPEL:

Derivatan (till, för, av) förkortas här som tidigare Dn analogt med Dn y = y’.

[(P)ⁿ]’ = (P)ⁿ[Q(P)’/(P) + Q’ln(P)] ..................................... Allmänna potensderivatan

Exempel. Bestäm Dn x^x. Lösning: Med P=Q=x ges direkt [(x^x)]’ = x^x[1 + lnx], vilket är lösningen.

Exempel. Bestäm Dn 2^1/x. Lösning: P=2, Q=1/x ger direkt [2^1/x]’ = 2^1/x[(1/x)0/2 + (–1/x²)ln2]=–2^1/xx^–2ln2, som är lösningen.

Eulers ekvivalenter

Den enda person i vetenskapshistorien som synes ha uppfattat den övergripande enhetens existens (dock utan en vidare formulering) är Leonhard Euler (1707-1783).

Detaljer i hans funktionslära kördes EMELLERID SOM DET SER UT över av den moderna akademin under dess uppsegling under 1800-talet.

LEONHARD EULER (1707-1783) är f.ö. vår tids kända grundare av matematikens avancerade funktionsbegrepp med skrivsätten sådana vi använder dem numera [TYP y = f (x)] — samt (här veterligt) den historiska banemannen för den naturliga logaritmen (e).

Eulers Ekvivalenter

Exponentialekvivalenterna — Den mängdoberoende överenhetens ställning

¥-MATEMATIKENS ÖVERLÄGSENHET ÖVER MODERN AKADEMI

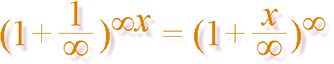
Det synes ha funnits en person i vetenskapshistorien som uppfattat något av matematikens verkligt enastående grunder, Leonhard Euler (1707-1783). Men mycket av hans arbeten kördes över i och med uppkomsten av den moderna akademin och dess herreidéer under 1800-talet; den moderna akademins grundläggande remarkabla förnekelse av skillnaden mellan punkt och intervall.

Eftersom vi tydligen ser, tänker och förstår punkten genom en mängdoberoende enhet (¥) och som, galant och utan risk för missförstånd NÄR VI väl KÄNNER GRUNDERNA, kan betecknas med symbolen ¥ — punkten finns inte som mängd, den är noll — medan intervall är mängd,

är tydligen förhållandet mellan mängd (intervall A) och punkt (P) oberoende av A;

A/P=¥=¥A=¥=¥(A®¥)=¥=¥+A=¥=¥^¥=¥, ¥–¥=0, ¥/¥=1, ¥=¥.

Passa överflyttningsfel. Exempel: ¥A=¥ ”ger” A=¥/¥=1. Här hade studenten felaktigt tänkt sig att ¥A¹¥. Saken gällde ¥/(¥A=¥)=1.

¥ är en ren läromästare i konsekvenslogik således.

Härav följer punktens definition som en position (vad vi ser, aspekten, begreppsliga formelementet) vars värdemängd är (övergår i, Û) noll:

A/¥=P=(1/¥)A Û 0

Vi skiljer alltså skarpt mellan positioner (uttryck med ¥) och värden eller kvantiteter (rena mängduttryck), av samma skäl som vi skiljer skarpt mellan förstånd och fenomen, mellan punkt och intervall. För att understryka denna distinktion används (här) dubbelpilen, Û (eller annat passande, ), då i annat fall beskrivningen kollapsar. Med (1/¥)=d för differentialen, som ger 1=¥/¥, ges dA som differentialen till eller för mängden A.

A/¥=dA

Genom den mängdoberoende överenheten ¥ definieras mängden A som enhetsintegralen ¥dA=òdA=A.

Se vidare mera utförligt från nollformsalgebran.

2001IX24

Den Gömda Upptäckten från Leonhard Euler

HISTORIA

MISSTANKEN att Euler skulle vara den ledande personen bakom e-sambanden, leder till en mera detaljerad undersökning. De imaginära trigonometriska sambanden upptäcktes och presenterades uppenbarligen av Leonhard Euler (Introductio 1748). Emellertid, som det ser ut, gav aldrig Euler någon underliggande begreppsanalys till den centrala och avgörande upptäckten av e. När den delen, under 1800-talet, ställdes under dåvarande matematiska idéer, demolerade dessa TYDLIGEN — genom att introducera gränsvärdesbegrepp — effektivt de fundament på vilka Euler hade upptäckt hela diamantgruvan. Därmed också svårigheten att alls spåra rötterna i den här (Hemliga, Gömda) historien: begreppen har ingen etablerad urkund. Det finns ingen litterär källreferens att ösa ur.

Nedanstående referens [‡1] [Euler, från sidan 110] ger en någorlunda detaljerad beskrivning av Eulers sätt att resonera i sin bok Introductio från 1748. Referensen ger inget direkt citat, snarare refererar väsentliga samband från Introductio via gängse ”moderna symboler”.

Den centrala aspekten [s111sp1ö] är Eulers uttryck enligt

e^x = (1+x/i)ⁱ;

”i”:et används inte här av Euler som beteckning för den komplexa enheten — enligt referensen [‡1], introducerades denna av Euler först 1777 — utan som en ”oändligt stor”. Referensen exemplifierar vidare Eulers sätt att hantera denna faktor enligt [”1–1/i = 1”]; Det antyder att Euler betraktade den som Enhetsfaktorn ¥, i full enlighet med nollformsalgebran och atomtriangeln. Vilket vill säga,

e^x = (1+x/¥)^¥.

Alltså enligt exponentialekvivalenterna, (1+x/¥)^¥ = (1+1/¥)^x¥.

Från denna enkla observation — i gängse litteratur väl GÖMD från direkt uppenbarlighet, integrerad med en explicit bibliografi i [‡1] av Euler — verkar det tydligt att Euler behandlade de formella sambanden korrekt, men var oförmögen att analytiskt formulera ”det oändligt stora” i dess sanna symboliska mening.

[Han använde Enheten korrekt, men avfärdade dess egentliga form som motsägelsefull då den tycktes strida mot den matematiska logiken …].

Efter honom, under 1800-talet, blev denna oförmåga att förstå eller beskriva sakgrunden cementerad enligt ”evigt död” med introduktionen av det sätt på vilket gränsvärdesbegreppen kom att tolkas.

Sagt på annat sätt: den principiella styrkan hos Enheten ¥ introducerades helt säkert i försorg av Leonhard Euler (1748). Men då den aldrig fick någon analytisk bakgrund, ingen förklaring, snarare överkörd av det senare 1800-talets ”frigörande idéer om logiken”, strandade hela konceptet. Istället för ett uppdagat grandiost och högst kraftfullt seglande skepp på matematikens vida oceaner, stängdes dörren till dess kungarike av händerna och idéerna i den mera fräckt uppseglande moderna akademin under 1800-talet.

‡1 [MATEMATIKLEXIKON W&W 1991, från originalet The Crescent Dictionary of Mathematics (1962) by W. Karush (Wahlström & Widstrand 1991)]

Potenslagarna och Logaritmlagarna | HÄRLEDNINGAR

Härledningarna till

POTENSLAGARNA och LOGARITMLAGARNA

2008IV9 | © BellDharma Copyright hem.passagen.se/belldharma

potenselementen

potensbegreppets element

	logaritm
bas	exponent
a	n	=	P
potens			produkt

POTENSLAGARNA 1987XII6 | 1994IV4 | 1996I5 Med införandet av kvadraterna inom geometrin, i vidare mening då vi betraktar en upprepad följd av ekvivalenta faktorer inom matematiken a1·a2·a3·a4·a5·…·an uppstår behovet av en smidig symbolik. Detta behov blir tillgodosett då vi istället för kvadraten a·a skriver a^2, och på samma sätt för kuben a·a·a skriver a^3. Vi kallar en sådan komprimerad faktorform för en potens. Termen a benämner vi som potensens bas och det övre index kallar vi för potensens exponent. Ett annat använt ord för exponenten är också logaritm (av grekiskans lo´gos, förhållande, och aritmo´s, tal) och till vilket begrepp vi ska återkomma i sektionen om logaritmlagarna. Potensens ekvivalent, P i uttrycket a^n = P, kallar vi på samma sätt som i den vanliga multiplikationen för en produkt. Vi ska här närmare studera hur de räknelagar man finner vid laborerandet med exponenterna är analoga med och följer mönstren för de ordinära matematiska relationerna. Om vi vidareutvecklar resonemanget kring faktorledet ovan kan vi teckna produktföljden av alla faktorer a1®n (index, ”1-till-n”) som a^n där exponenten n anger summan av n stycken a-faktorer. Vi kan alltså teckna ledet (1) a1·a2·a3·a4·a5·…·an = a^n För varje ytterligare faktor a som införs i denna produkt, växer naturligtvis n med 1. Vi kan skriva den fasen mera komprimerat som a^n·a = a^n·a^1 = a^n^+1. Inför vi m stycken sådana a-faktorer, kan vi med en ännu högre växel i maskineriet teckna det hela enligt (2) a^n · a^m = a^n+m Som ett enkelt numeriskt exempel kan vi förtydliga med ledet a^5 = a^3+2 = a^3·a^2. Låt oss därmed vidareutveckla sammanhangen. För varje division vi utför med a-faktorn, kommer n i (1) ovan givetvis att reduceras med 1. Vi skriver detta som a^n 1 (2.1) a^n^–1 = —— = a^n (——) = a^n · a^–1 a a Då vi på motsvarande sätt inför en division med m stycken a-faktorer får vi analogt leden a^n 1 (3) a^n^–^m = —— = a^n (——) = a^n · a^–^m a^m a^m Som a^n-potenserna tar ut varandra i de två sista leden, har vi därmed förtydligat att 1 1 (4) a^–^m = —— ; —— = 1/a = a^–1 a^m a Genom omflyttning mellan leden i den första delen i (4) ovan genom överflyttningslagen för division får vi även givetvis 1 (5) a^m = 1/a^–^m = —— a^–^m Genom att ställa potenserna i samma led finner vi speciellt genom (4) och (5) att (6) a^m–m = a^0 = 1 = a^m(1/a^m) = a^m/a^m Låt oss därmed avancera genom att lägga in en ännu högre växel i utvecklingarna. Om vi sätter a^n·a^n kan vi följaktligen betrakta varje a^n som en enskild produkt P, analogt P·P = P^2 = (a^n)^2. Men, a^n·a^n har vi också enligt (2) som a^n^+^n. Vi kan alltså utveckla det hela enligt (7) a^n·a^n = (a^n)^2 = a^n^+^n = a^n^· 2 Som vi ser, visar sammanhanget att om parentesen tas bort måste vi samtidigt utföra en multiplikation mellan inre och yttre exponent. Förtydligat, (7.1) (a^b)^c = a^bc Eller mera utförligt: Med fortsättningen på ledet ovan i (7) ges mera förtydligat (8) a^n·a^n = a^n^· 2 = a^2^n = (a^2)^n = (a · a)^n och som visar oss hur potenslagarna vill ha det med parenteserna. Om vi fortsätter på samma form är det givet att om vi tar med allt flera potenser a^n i (7), kan vi också skriva dessa sammantaget som (a^n)^m. Med tillämpningen av parenteslagen i (7) på den modellen, får vi således (9) (a^n)^m = a^nm Utnyttjar vi nu (4), alltså att 1/a är detsamma som a^–1, och om vi sätter a^–1 i stället för a^n i (9) ovan, får vi 1 (10) (——)^m = (a^–1)^m = a^–^m a Vi ser att nr (10) är inversformen för nr (5). Ställer vi samman detta med ekvivalenten 1/a^m i nr(4), finner vi förtydligat den eminenta potenslagen 1 1 (11) a^–^m = —— = (——)^m = 1/a^m = (1/a)^m a^m a Vi närmar oss därmed slutfasen i härledningen till potenslagarna. Vi börjar med att göra en sammansatt tillämpning av nr(9) ovan enligt (12) (a·a^n)^m = (a^n^+1)^m = a^(^n^+1)^m^=^nm^+^m = a^nm·a^m = (a^n)^m·a^m Sätter vi nu a^n=b får vi genom det första och sista ledet ovan (13) (a·b)^m = a^m·b^m Därmed är vi framme vid slutfasen. Vi ska genom parenteslagen i (9) och inverslagen i (11) härleda uttrycket för a om a^n=b. Genom att flytta över b till det vänstra ledet genom omflyttningslagen för division får vi först (14) a^n/b = 1 = (1/b)a^n = (1/b)^n^/n·a^n = [(1/b)^1/^n]^n·a^n = [(1/b)^1/^n·a)^n = 1^n = 1 = (1/b)^1/^n·a Tillämpar vi nu nr (11) på b-inversen ovan sist i nr (14), får vi (15) 1 = (1/b)^1/^n·a = [1/(b^1/^n)]a Genom att sedan flytta över uttrycket för b till vänstra ledet får vi (16) b^1/^n = a Den ovan härledda dramatiken kan vi nu uttrycka på det följande sammanfattande sättet: (17) OM a^n=b, DÅ ÄR a=b^1/n Nr (17) är den fullständiga potensformens matematiska grundform. Tilldelar vi nu en sammansatt exponent till a, kvoten n/m, kan vi upprepa berättelsen från nr(14) ovan enligt (17.1) a^n/m/b = 1 = (1/b)a^n/m = (1/b)^mn/nm·a^n/m = [(1/b)^m/n]^n/m·a^n/m = [(1/b)^m/n·a)^n/m = 1^n/m = 1 = (1/b)^m/n·a = (1/b^m/n)a = 1 Vi har således med andra ord och sammantaget funnit den motsvarande potenslagen (18) OM a^n/m = b, DÅ ÄR a = b^m/n Som vi ser av dessa sammanhang, lyder den brutna exponenten m/n samma lag vid skiftning mellan leden som då m/n fungerar som en separat ordinär kvotfaktor. Dvs, analogt med omflyttningslagen för division. Vi kan därmed omforma (18) ovan i satsen (19) OM a^n/m= b DÅ ÄR a^n= b^m OCH a^1/m= b^1/n Därmed är potenslagarna härledda. För att fullständiga greppet om den formella symbolikens detaljer relateras sambanden ovan mera ingående genom rottecknets användning. Rottecknet För att få den fullständiga bilden av potenslagarna ska vi här också ställa dem i relation till rottecknet — vilket ofta används som bärande symbol inom såväl algebran som aritmetiken. Konventionellt skrivs: Om a^2=x, då är a=Öx. Man läser högerledet som ”kvadratroten-ur-x”. Det korrekta sättet — i ljuset av exponentens många olika möjliga värden — är här att sätta ett index (^2) framför rottecknet (^2Ö), men just för kvadratroten-ur utelämnar man vanligen detta index (»kvadratroten-ur» är i de allra flesta och mest frekventa av matematikens sammanhang det centrala begreppet). För kubikroten-ur skriver man dock det korrekta ^3Ö, ”tredje-roten-ur”. Rottecknets användning i den allmänna matematiska algebran kan då, och i koppling till potensuttrycken, formuleras genom rotsatsen: OM a^n= x, DÅ ÄR a = ^nÖx ”n:te-roten-ur-x” Låt oss därmed ställa den sammansatta formen i nr(18) i koppling till rottecknet. Om vi allra först tillämpar rotsatsen ovan på (17) får vi (20) OM a^n= x, DÅ ÄR a = x^1/^n = ^nÖx Med den mera sammansatta formen i (18) får vi (21) OM a^n/m= x, DÅ ÄR a = x^m/n = ^n/mÖx Sista ledets sammansättning läser vi som ”(n-dividerat-med-m-)roten-ur-x”. Skriver vi om uttrycket för x något, via nr(9), får vi (22) x^m/n = (x^m)^1/^n Om vi nu betraktar (x^m) i nr(22) som x i nr(20) kan vi också se (22):an inuti (20):an på formen (23) (x^m)^1/^n = ^nÖx^m = x^m/n vilken form därmed ger oss den mera sammansatta bilden av nr(21). Förtydligat och via (23) ovan, har vi alltså (24) ^nÖx^m = x^m/n Därmed är potenslagarna härledda.

LOGARITMLAGARNA 1987XII6 | 1994IV4 | 1996I20 Idetta avsnitt fullständigas de matematiska sammanhang som är förknippade med potensalgebran från den föregående sektionen med potenslagarna genom de motsvarande uttrycken för potensens exponent, den så kallade logaritmen (från grekiskans lo´gos, förhållande, och aritmo´s, tal; ”förhållandetalet”). Som grundformerna redan förklarats i den föregående sektionen förutsätter vi här grundbegreppen med produkt, bas, exponent och potens bekanta. LOGARITMLAGARNA aktualiseras så snart vi önskar ge ett uttryck för exponenten n i sambandet (1) a^n = P Det konventionella sättet att uttrycka exponenten på genom den matematiska algebrans symboler är (2) n = ^alogP vilket i en del litteratur även skrivs n = loga P. Med uttydningen ”n är lika med a-logaritmen för (till) P”, används genomgående i denna volym skrivsättet i (2) med en ytterligare förenkling typ n=alogP. P betecknar här som tidigare potensens ekvivalenta produkt. Begreppet ”logaritmen” syftar alltså på exponenten (n), där a i nr(1) och i dessa sammanhang också benämns som potensens bas eller analogt potensens antilogaritm. Uttydningssättet för uttrycket alogP kan därmed formuleras specifikt förtydligat som; a-logaritmen för P är exponenten till basen a i potensen P. Det här skrivsättet är på sitt sätt knöligt och omständligt för den som är ovan (och även för övriga). Knöligheterna ger emellertid med sig i takt med att man bearbetar dem. Analogt med formuleringen ovan i (2), eller om vi direkt insätter uttrycket för n, nr(2), i (1) ges det mera sammansatta och klargörande uttrycket (3) a^a^logP = P Genom (1) kan vi även klargöra den viktiga logaritmlag som kommer fram då vi sätter P=a. Vi får då a^n = a = a^1. Vi tar fasta på de bägge sista leden, tillämpar nr(2) med n=1, och får då förtydligat att (4) 1 = aloga = ^alog a Vi utvecklar nu sammanhangen vidare genom att tillämpa potenslagarna, här främst P(10) och P(11) från motstående härledningar, dvs inverslagarna. Vi skriver då först P(10) på formen (5) (1/a)^n = P = a^–^n Tillämpar vi nu nr(2) ovan på detta, får vi de bägge logaritmerna, respektive (6) n = ^1/^alogP OCH –n = ^alogP Men, (5) kan också skrivas i formen som — enligt P(11) — 1/a^n = P. Inversen blir då (7) a^n = 1/P Med bruk av (2) på denna form, får vi även logaritmen (8) n = ^alog(1/P) Om vi nu omformar uttrycket för –n i nr(6) till n = –^alogP, kan vi sammanställa de så erhållna bägge n-ekvivalenterna i (6) med den i nr(8) vilket ger oss förtydligat (9) ^alog(1/P) = ^1/^alogP = – ^alogP Flyttar vi här över högra ledets minustecken till de bägge vänstra leden, kan vi även teckna nr(9) som (9.1) – ^alog(1/P) = ^alogP = – ^1/^alogP Vi går nu in på nästa fas i utvecklingarna. Vi betraktar potensen (10) a^n/m = P Vi tillämpar sedan i sedvanlig ordning först nr(2) som ger oss (11) n/m = alogP; n = m(alogP) Sedan tillämpar vi P(19) på nr(10) så att vi får (12) a^n = P^m Genom (2) får vi nu de bägge logaritmerna för dessa potenser respektive som (13) n = ^alogP^m OCH m = ^Ploga^n Ekvivalenten för n ovan är densamma som för n i nr(11). Vi får således förtydligat att (14) ^alogP^m = m(^alogP) Genom sambandet i (14) kan vi därmed också teckna m i (13) som m = n(^Ploga). Uttryckt i n blir detta; n = m/^Ploga. Med n-ekvivalenten i nr(11) får vi därmed (15) n = m(^alogP) = m/^Ploga Faktorerna m tar ut varandra i de bägge sista leden, och vi har (16) alogP = 1/Ploga Vi går nu in på ett mera avancerat område i utvecklingarna. Vi skriver först nr(1) i formen a^x = P, där vi sätter x som kvoten n/m. Vi ska därmed visa hur man finner ett samband mellan logaritmerna till olika baser, vilket vi genomför främst genom nr(4). Vi skriver (17) a^x = P; x = alogP = n/m = (n/m)(^eloge/^eloge) I sista ledet har vi som synes substituerat (1=något/något) in den främmande logaritmbasen e via ekvivalensen mot 1. Vi tillämpar nu (14) på detta sista led. Dvs, vi för in faktorerna n och m i logaritmen vilket ger oss (18) x = n/m = (^eloge^n)/(^eloge^m) = alogP Låt oss förtydliga dessa sammansattheter. I leden till nr(18) ovan har vi n = ^eloge^n och m = ^eloge^m via e^n = e^n respektive e^m = e^m enligt (1) och (2). Betraktar vi nu, till exempel, m-formen har vi också via (16) m = ^eloge^m = 1/^kloge med k = e^m, analogt 1/m = ^kloge, = (^alogP)/n i (18). För potensformen således via basen (e^m), logaritmen p = (^alogP) och produkten e; (e^m)^p/n = e, eller med omflyttning av n till högra ledet; (e^m)^p = e^n. Vi finner samma uttryck enklare genom n-formen emedan n = m(^alogP) = ^eloge^n som via sista ledets potensform ger e^mp = e^n, lika med (e^m)^p. Som vi ser, är detta endast en annan form för (3), dvs med a = e^m och P = e^n, vilket vi inte kan hysa tvivel om då termerna är distinkta. Med dessa ekvivalenter insatta i (18) får vi således transformationslagen mellan olika logaritmer enligt (19) a^x = P; x = alogP = (elogP)/(eloga) För att exemplifiera en del av logaritmbegreppets praktiska förankring kan vi här göra den enkla uppställningen nedan med successiva produkter av talet 2 som logaritmbas. Vi sätter produktledet som A och får tabellen nedan. A = 2 4 8 16 32 64 128 256 512 1024 ^2logA = 1 2 3 4 5 6 7 8 9 10 Ur ledet för A väljer vi sedan godtyckliga baser a och P enligt a^x = P. Vi exemplifierar med a=8 och P=256, dvs vi söker nu x i ledet 8^x = 256. Genom (19) får vi x=(^2log256)/(^2log8) som genom tabellen ovan ger oss ekvivalenta kvoten x=8/3. Med 8 = 9–1 får vi 8/3 = 3–1/3, avrundat 2,67. Dvs; 8^8/3 = 8^2,67. = 256. Om vi vill kontrollera detta, kan vi resonera så: Genom potenslagarna får vi ekvivalenterna 8^3–1/3 = 8^3/8^1/3. Som 2^3 = 8, som ger 8^1/3 = 2, har vi 8^8/3 = 8^3/2 = 256. 8^3 kan vi också dela upp genom potenslagarna enligt ekvivalenterna 8^3 = (2·4)^3 = 2^3·4^3 = 8·64 = 512. Som också 8^3 = 2·256 = 512, enligt resultatet ovan, är därmed överensstämmelsen uppenbarligen bekräftad. I runda tal således; 8^2,67 = 256. Därmed är vi framme vid slutfasen för utvecklingen av logartimlagarna. Ur det ovan framförda framkommer två av matematikens mycket förnäma arbetshästar. Nämligen de samband som svarar mot potenslagarna P(2) och P(3). Om vi skriver om P(2) i formen som (20) a^n · a^m = a^n+m = AB A B ; n+m = alog(AB) n=alogA m=alogB har vi summan av logaritmerna n och m enligt (21) n+m = alogA + alogB = alog(AB) Gör vi på samma sätt med P(3), samma relationer som i nr(20) ovan, dvs a^n = A och a^m = B, får vi motsvarigheten till P(3) enligt (22) a^n/a^m = A/B = a^n·a^–m = a^n–m n–m = alog(A/B) Här måste vi iaktta en viss försiktighet och förtydliga sammanhangen för den negativa exponenten m. Då vi har a^m = B, gäller enligt P(11); a^–m = 1/a^m = 1/B. Tillämpar vi nr(2) på detta får vi –m = ^alog(1/B). Vi flyttar över minustecknet till högra ledet och får genom nr(9) m = – [^alog(1/B)] = ^alogB. Därmed kan vi nu summera intrycken via (n–m) i nr(22). Vi får (23) (n–m) = alogA – alogB = alog(A/B) Därmed är härledningarna till logaritmlagarna slutförd. Sammanställning se även i Potenslagarna och Logaritmlagarna i särskild syntes i Matematiken från början. Potenslagarna a^0 = 1 1/a = a^–1 a^–n = 1/a^n = (1/a)^n a^n+m = a^na^m a^n–m = a^n/a^m (a^n)^m = a^nm (ab)^n = a^nb^n a^n=b ; a = b^1/n a^m^/n=b ; a = b ^n^/m a^m^/n = ^nÖ a^m Logaritmlagarna ^alog a = 1 a^a^log^P = P a^n = P; n = ^alog P n = ^elog P / ^elog a ^alog P = (^Plog a)^–1 ^alog (1/P) = –(^alog P) = ^1/alog P ^mlog A^n = n(^mlog A) ^mlog AB = ^mlog A + ^mlog B ^mlog A/B = ^mlog A – ^mlog B *

ITK-citatet

Citat (anteckningarna i gråmarginalerna ingår inte i citatkällan), se från e-analysen

KOLLA ”lim”: ® KOLLA 1/¥=0: ® ”man kan visa” KOLLA ”lim”: ®

” DERIVATAN AV y=lnx OCH y=^alogx Innan vi övergår till härledningen av logaritmfunktionens derivata skall vi först behandla ett uttryck som ständigt återkommer vid bestämning av gränsvärden. Betrakta uttrycket n®¥ lim (1+ 1/n)^n Vid bestämning av ovanstående funktions gränsvärde, får man akta sig för att göra felet n®¥ lim (1+ 1/n)^n = (1+ 1/¥)^¥ = (1+0) = 1 Fel! Om man i stället utvecklar funktionen (1+ 1/n)^n enligt binomialteoremet och därefter låter variabeln n gå mot oändligt, kan man visa att gränsvärdet kan bestämmas ur följande konvergenta serie n®¥ lim (1+ 1/n)^n = 1 + 1/1! + 1/2! + 1/3! … Summan av ovanstående konvergenta serie betecknas med e. Med tre decimalers noggrannhet blir talet e e = 2,718 Det är ovanstående tal e som används som bas i det naturliga logaritmsystemet. ”. ITK-6 MATEMATIKBIBLIOTEK, Lennart Brandqvist, s42-43 INSTITUTET FÖR TEKNISKA KURSER, STOCKHOLM 1961

n®¥ lim 1/n ¹ 1/¥ n®¥ lim 1/n = 0 lim (1+ 1/n)n = 1 ^n^®¥ (1+ 1/n)n = AV(e) ^n^®¥

ITK-6 MATEMATIKBIBLIOTEK, Lennart Brandqvist, s42-43, INSTITUTET FÖR TEKNISKA KURSER, STOCKHOLM 1961

AV(e) betyder här partiella aritmetiska värdemängden för e.

MATEMATIKEN FORTSÄTTER I DEN HÖGRE ANALYSEN.

Avsnittens htm(l)-formering är under utarbetande — men ämnet är omfattande och det kommer att ta TID att bygga länkarna och korsreferenserna till den nu rådande matematiska nomenklaturen för exakt jämförelse.

— Verkställt 2009-01-10. Se från Analysen.

Matematiken från början

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Formlagarna

ämnesrubriker

Bastablån

Utvecklingsexempel

Potenslagarna och Logaritmlagarna

innehåll

FORMLAGARNA

Bastablån

Positionsformens metod

Utvecklingsexempel

produktderivatan

exponentialderivatan

logaritmderivatan

beviset för e

Eulers ekvivalenter

Speciella exponentderivatan

naturliga logaritmbasen

Allmänna exponentderivatan

logaritmderivatan

potensderivatan

tillämpningsexempel

Eulers Ekvivalenter · historia

Potenslagarna och Logaritmlagarna

referenser

—

Senast uppdaterade version: 2014-03-25

*END.

Stavningskontrollerat 2008-03-06.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se