MATEMATIKEN1 2008IV29 A BellDHARMA production | Senast uppdaterade version: 2019-01-02 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Matematiken från Början

Grunderna i matematiken

MATEMATIKEN FRÅN BÖRJAN

Matematikens lagar framgår spontant ur det enhetsindelade xy-systemet — rutat papper.

Vi studerar hur.

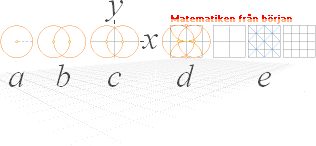
ENHETSSYSTEMET (samma som rutat papper) byggs upp teoretiskt med passare (vänster nedan) och linjal (höger nedan), sekvenserna ovan a–e.

Enhetssystemet, indelat efter ordningen xy (x horisontellt och y vertikalt) kan också kallas

det matematiska xy-systemet.

Lika antal rutor i bägge leden (xy) bildar en kvadrat (aa), olika x och y bildar en rektangel (ab),

Rektangelns diagonala delning ger två likadana figurer som var och en kallas rätvinklig triangel; snedsidan kallas hypotenusa (här enklare hypolinje), varje raksida kallas katet, pl. kateter.

geometrin

Begreppet geometri (av grek. ge, jord, och metrei’n, mäta) betyder traditionellt ”vetenskapen om rummet” och grundas därmed på ovanstående enkla planbegrepp med tillhörande enheter och deras inbördes ordning. Se även mera elementärt från Spegellagen.

I den här framställningen kallas varje rät linje i xy-planet som inte tillhör rutsystemet för en hypolinje (efter hypotenusan, samma som diagonalen i rektangeln ab).

grundlagarna

MATEMATIKENS FEM GRUNDLAGAR

Nedanstående algebraiska skrivsätt sammanfattar de fem grundlagarna på matematikens mest utvecklade skrivsätt, den s.k. symboliska algebran.

Efterföljande beskrivning visar hur de fem grundlagarna framgår utan hjälp av matematiska tecken, enbart genom att läsa mönsterformerna.

Längre fram visas hur de algebraiska teckningarna har uppkommit.

Se även vidare i DEN SYMBOLISKA ALGEBRANS GRUNDER I KORT SAMMANDRAG om ej redan bekant.

Pythagoras sats

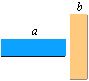
Enbart med hjälp av två likadana rektanglar

(som delas diagonalt i fyra lika rätvinkliga trianglar) framträder matematikens fem grundlagar

1 2 3 4 5

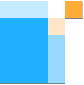
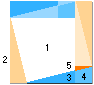
namn: 1. Cheops Rektangel 2. Första Binomlagen 3. Andra Binomlagen 4. Konjugatlagen 5. Pythagoras Sats

symbolisk algebra: h² = (r–x)_b(r+x)_d (a+b)² = a²+b²+2ab (a–b)² = a²+b²–2ab (a+b)(a–b) = a²–b² a²+b² = c²

= r²–x²

Hur den symboliska skrivformen framträder beskrivs i särskild del — se detaljerad sammanfattning.

Resonemang (typform):

2. FÖRSTA BINOMLAGEN: Med hjälp av förtydligandet av kvadratytorna aa (stora orangea, delvis skymd) och bb ser vi (direkt) att hela den större kvadraten (a+b)(a+b) har samma innebörd som summan av kvadraterna aa och bb tillsammans med de bägge vita rektanglarna ab + ab. Och alltså gäller

(a+b)(a+b)=aa+bb+2ab.

3. ANDRA BINOMLAGEN: Den orangea kvadraten i mitten har sidan (a–b); Vi får den kvadraten (a–b)(a–b) genom att ta bort de fyra rektanglarna ab från hela den yttre storkvadraten (a+b)(a+b). Om vi utnyttjar föregående resultat, behöver vi alltså enbart ta bort ytterligare 2ab för att få svaret:

(a–b)(a–b)=aa+bb-2ab.

4. KONJUGATLAGEN: Kvadraten aa minus kvadraten bb ger, som vi ser, en fragmenterad delyta som kan ställas på den illustrerade rektangelns högkant med basen (a–b) och höjden (a+b): Vi bara flyttar över den vertikalställda högerremsan (a–b)b till vänsterdelens a(a–b) så att vi får rektangeln (a+b)(a–b). Och alltså gäller:

(a+b)(a–b)=aa-bb.

5. PYTHAGORAS SATS: Tar vi bort de bägge rektanglarna 2ab från den yttre storkvadraten (a+b)(a+b),

återstår uppenbarligen bara den inre “tomma” kvadraten (cc); Eftersom första binomlagen redan visat oss att (a+b)(a+b)=aa+bb+2ab, så återstår alltså aa+bb sedan vi tagit bort 2ab. Alltså gäller det att (a+b)(a+b)–2ab=aa+bb, =cc vilket är Pythagoras Sats:

aa+bb=cc.

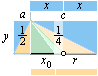
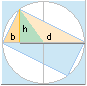
1. CHEOPS REKTANGEL: Cheops rektangel »framgår hur lätt som helst» — om vi känner till den symboliska algebran. Men för den som är nybörjare i matematiken krävs först en hel del studium innan man kommer så långt att man förstår “överflyttningslagen för division”. OM vi förstår den framgår Cheops Rektangel på följande sätt: Rektangeln i cirkeln visar två likformiga rätvinkliga trianglar, den större med höjden (h) och basen (d), den mindre med motsvarande (liggande) höjden (b) och basen (h). Med den symboliska algebrans hjälp förhåller sig alltså triangelsidorna i de två trianglarna som b/h=h/d; genom överflyttningslagen för division fås direkt bd=hh som är Cheops Rektangel. »Enkelt» för den som redan vet grunderna, en stor och smärtsam sorg för den som inte känner dem. Divisionsbegreppet beskrivs här utförligt i DIVISIONSBEGREPPET.

Från de fem grundlagarna utgår all övrig matematik.

Cheops Rektangel och Gyllene Snittet

En mera upplysande och fördjupad mönsteranalys explicit för Cheops Rektangel i koppling till CHEOPSPYRAMIDEN via Gyllene Snittets figurform finns nu Jan2018+ sammanställd i CHEOPS REKTANGEL 2017. Framställningen nedan från 2008.

BENÄMNINGEN CHEOPS REKTANGEL för formen bd=h² förekommer inte i gängse litteratur (det närmaste är ”geometriska mediet”). Formen bd=h² är (emellertid) avgörande för hela matematikens-fysikens utveckling för människans del; Spåras den baklänges via den retoriska algebran (bd=h² användes bl.a. av Galileo Galilei i dennes beskrivningar), hamnar man längst ut i historiens dimmiga horisonter vid Cheopspyramiden (daterad ca 2500 f.Kr.);

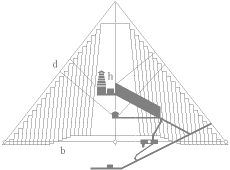
Cheopspyramiden vid Gize i Egypten visar att byggnaden beskriver sambandsformen bd=h² med stor precision. Cirkeln som omskriver Cheops Rektangel har sitt origo i den s.k. grottan, den med liten vit punkt markerade rektangeln i markplanet till höger om mittlinjen. Det finns bara en, och endast en sådan unik triangulär relation i matematiken.

Basvinkeln blir idealt 51,827292…° , se samband nedan. Cheopspyramidens motsvarande uppmätta vinkel skiljer sig enligt källmaterialet [‡1] från denna med en förvånansvärt snäv tolerans på endast (max) ±0,05°; Även om Pyramidens halva bas sätts som sidan på ett A4-papper (21 cM) ligger Cheopspyramidens vinkelavvikelse inom 0,2 mM längst ut (litet mindre än en pixel på skärmen), vilket även med en fint vässad blyertspenna ligger inom den ritade linjens tjocklek.

Bilderna ovan är min sammanställning efter studier av ett större antal litterära källor i ämnet Cheopspyramiden.

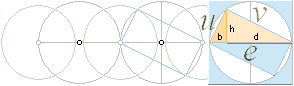
Den triangel som bildas då basdelen d är lika med rektangelns kortsida (pyramidens sida) bildar en unik triangelrelation i matematiken som kopplar till begreppet Det Gyllene Snittet:

gyllene snittet

Man får i fallet Cheopspyramiden

b/h = Ö [(Ö5) – 1]/2 varav

[(Ö5) – 1]/2 = 0,6180339

= a

= –1+1/a

Sambandet är känt som Gyllene Snittet eller Gyllene Förhållandet (a+1=1/a).

Det är (alltså, här veterligt) den äldst kända urkunden för den centrala sambandsformen bd=h².

pärlbåtssnäckan

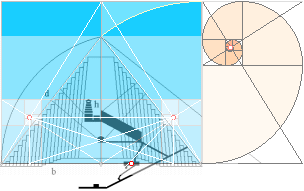
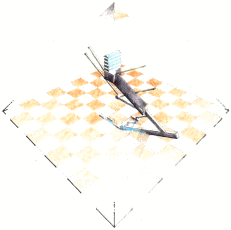
PÄRLBÅTSSNÄCKAN

Gyllene Snittet har (flera, mäktiga) naturkopplingar. Till höger ovan finns avbildat den spiralform som bildas av Gyllene Snittet genom serien av alla successiva kvadrater i all oändlighet. Enligt MATEMATIKLEXIKON W&W 1991 s158sp1 är den spiralen naturligt representerad av formen hos den s.k Pärlbåtssnäckan (Nautilus Pompilius, jag har letat efter en bild av den på Internet, flera fina Nautilusfotografier finns, men veterligt ingen på typen Nautilus Pompilius). Referenspunkterna som utpekas av den oändliga spiralformens geometri tycks f.ö. passa väl in på Cheopspyramidens inre planering, bilden ovan: en syntes av matematiken?

referenser

‡[1] A HISTORY OF ARCHITECTURE Sir Banister Fletcher, University of London 1961

480 ft high (146,304 M), 756 ft square (230,4288 M)

ger arctan 480/(756/2) = 51,779568° vilket är 0,047724° från idealet

Harmoniska trianglarna · Komplexa algebran · Ljusets g-beroende · Kvadratrötterna

Syntes av CheopsRektangel

SYNTES AV

betydelsen av

CHEOPS REKTANGEL

i matematiken och fysiken

MED INLEDANDE orienterande KORT BESKRIVANDE ARTIKLAR

Nedanstående textdelar är importerade från original i MsWORKS 4.0 som PNG-bilder eftersom det inte existerar (ännu 2008) en enda webbläsare på Jorden som TILLSAMMANS MED EN VETTIG ARBETSMILJÖ FÖR FÖRFATTAREN SÅ ATT HAN SER VAD HAN HÅLLER PÅ MED kan få fram DET originalet: matematikteckningen på enklaste sättet. Mera utförliga presentationer kräver mera utrymme och finns f.n. 2008IV inte i htm-form.

H-trianglarna

Komplexa algebran

Generella samband för i genom successiva 90°-rotationer i xy-systemet; positiv exponent roterar moturs i steg om 90°, negativ exponent roterar medurs i steg om 90°:

i⁰=1; i¹=i; i²=–1; i³=–i; i⁴=1; i⁵=i; …; i^–1=–i; i^–2=–1; i^–3=i; i^–4=1; i^–5=–i; …

ljusets g-beroende

kvadratrötterna

Den symboliska algebran

DEN SYMBOLISKA ALGEBRANS GRUNDER I KORT SAMMANDRAG

DEN SYMBOLISKA ALGEBRANS GRUNDER I KORT SAMMANDRAG

matematikens fem elementära operatorer · djupbeskrivning

+ – × ÷ Ö

plus minus gånger dividerat med kvadratroten ur

operatorerna

Den symboliska algebrans grunder i kort sammanfattning

Den formella matematik som vi kallar för algebra (a+b=c) och aritmetik (1+2=3) bygger på en avancerad symbolik. Den grundas på de fem operatorerna (plus, minus, gånger, dividerat med, [kvadrat]roten ur)

+ – × ÷ Ö

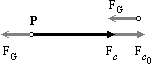
De fem operatorerna innefattar det mäktiga instrument med vars hjälp alla typer av mönsterformer kan beskrivas. De fem operatorerna följer ur det enhetsinrutade xy-planet. Deras lagar uppdagas med hjälp av de grundläggande flödesbegreppen via en fast nollpunkt P i xy-systemet med användning av de enkla flödesriktningarna stega åt höger (®) och stega åt vänster (¬). Man behöver alltså i grunden bara räkna rutor.

Genom enkla stegningsexempel kan man summera (+) och subtrahera (–) resultat från olika stegningsmängder genom att eliminera motsatta par-pilar:

®®® ¬¬¬¬ ger slutpositionen ¬. Med resultatets sammanställning eller likheten ersatt av likhetstecknet (=) skrivs samma led

®®® ¬¬¬¬ = ¬. Om särskilda tecken utvecklas för varje mängd, |=1, | |=2, | | |=3, | | | |=4, skrivs enklare samma sak

®3 ¬4 = ¬1. Med ersättning av (+=®) och (–=¬) skrivs enklast

+3–4=–1. I allmänhet utelämnas + framför en mängd om denna står först i sin del. Därmed får man det mera smidiga

3–4=–1.

Den tomma mängden (ursprungligen sunya från Indien) eller ingenting, detsamma som den fasta nollpunkten P, skrivs lika med noll (0). Genom att helt godtyckligt betrakta någon viss mängd (M) som en stegning

(®3 ¬4 = ¬1 = ¬[¬3®4]) kan man mycket enkelt och exakt ur mönsterlagarna härleda och kontrollera parenteslagarna (som den symboliska algebran garanterat inte klarar att beskriva), teckenlagarna

[–(a–b)=–a+b], samt

den allmänna överflyttningslagen för addition (se även nedan):

om a=a gäller a–a=0.

Likhetstecknet:

Matematiken grundas på visshet. Den identifieras i matematiken genom en jämförelse mellan minst två delar V (vänster) och H (höger). Om bägge är identiska gäller ekvivalensen V=H där ”=” garanterar vissheten (förutsatt elementen är korrekt givna från början). För ”icke lika med ” eller ”skild från” används symbolen ¹.

Teckenlagarna: preferens ®=+, ¬=–

Minustecknet (¬) är en polaritetsvändare, teckenvändare eller dito omkastare

– + = + – = –, – – = +, – – – = –, – – – – = + …

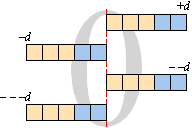
Udda minus ger minus, jämna ger plus

Överflyttningslagen för addition:

om d=d gäller d–d=0

En term ändrar tecken om den byter sida om likhetstecknet.

Parenteslagen:

–b + –c

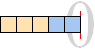
–[ b + c ] = –b–c ;

–(a₁ + a₂ + a₃ + … an) = –a₁ –a₂ –a₃ … –a_n

Varje mängd kan beskrivas som en summa av delar vars enhet kan isoleras från andra mängder genom en avgränsande parentes.

Enskilda termer i en negativ parentes ändrar tecken om parentesen tas bort.

Speciellt innebär parenteslagen att ett enskilt minus (–) kan skrivas ekvivalent –=–1 och behandlas som en separat faktor a=(–1). Se vidare i Distributiva lagen.

Ur ovan beskrivna +–-grunder framgår multiplikation (×): multiplikation betyder samma sak som serieaddition [3a=a+a+a]. Den framgår genom att återigen räkna rutor [a(a+b)=aa+ab] i givna större rektanglar.

Multiplikation

Multiplikation framgår ur xy-planet som en serieaddition med lika termer a₁ + a₂ + a₃ + … an enligt typexemplet

exempel 1 enligt figuren:

3 + 3 = 6 = ^y2 · ^x3, (= 1 · 6), = 2 + 2 + 2 = 2 · (1 + 1 + 1) = 3 · (1 + 1) = 3 · 2

exempel 2:

2₁+2₂+2₃+2₄+2₅ = 5·2 = 10

allmänt:

n_{MULTIPLIKATOR} · a_MULTIPLIKAND = na = produkt

Om a är multiplikanden är multiplikatorn n antalet a

Distributiva lagen: 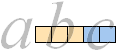a(b+c)_d=ab+ac ; ab=a(d–c)=ad–ac

a(a₁ + a₂ + a₃ + … an) = aa₁ + aa₂ + aa₃ + … aa_n

Produkten av en faktor med en parentes av fristående termer är faktorns produkt med de enskilda parentestermerna (multiplikation föregår addition)

Distributiva lagen betyder i klartext den maskinordning som igångsätter den formella matematikens egentliga algebra. Utan dess klarläggande kan matematikens inneboende mönsterordningar inte utvecklas. Den enkla rektangelkroppen, som f.ö. definierar hela parenteskomplexet, visar i sin egen självbärande syntes hur lagmatematiken arbetar på såväl positiva som negativa termer och hur de sammansätts av multiplicerande (a) och summerande [(b+c) och (d–c)] individuellt isolerade faktorkroppar.

DIVISIONSBEGREPPET

På motsvarande sätt är division (÷) en seriesubtraktion [3a/a(=)3a₀–a₁–a₂–a₃(=)3]:

MULTIPLIKATION DIVISION

2 · 3 = 6 = 2+2+2 = 3+3 6 / 3 = 2 = (3+3)/3 = 3/3+3/3 = 1+1

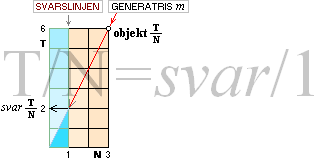
allmänt:

T_TÄLJARE / N_NÄMNARE = T/N = K = Kvot (“T-ÄN-K”)

Seriesubtraktion går ut på att se efter hur många gånger N ryms i T, (T – N Är resten noll? Nehej. T – N – N Är resten noll? Nehej …),

genom att kontrollera (testa) om skillnaden är noll efter varje subtraktion.

En mera utförlig beskrivning av divisionsbegreppet ges i

DIVISIONSALGORITMEN som innefattar fallen då svaret inte går jämnt ut.

Teckenlagarna för addition och subtraktion gäller lika för multiplikation och division.

Ur divisionsbegreppet framgår speciellt

Överflyttningslagen för division:

om a=a gäller a/a=1.

AddSubMulDiv

En enklare syntes av addition, subtraktion, multiplikation och division, enbart genom att räkna rutor, ges av följande två paragoner:

Enhetssystemet, indelat efter ordningen xy (x horisontellt och y vertikalt) visar oss RÄKNELAGARNA:

addition subtraktion multiplikation division

(det är i princip bara att »räkna rutor»; se även i följande TALSYSTEMEN och DIVISIONSALGORITMEN)

Se även mera utförligt från Den Symboliska Algebran

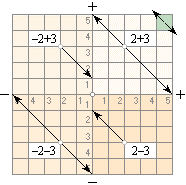
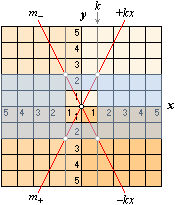
1. addition och subtraktion 2. multiplikation och division

serieaddition och seriesubtraktion

Speciellt för ADDITION används traditionellt termerna

addend + addend = summa

Speciellt för SUBTRAKTION används traditionellt termerna

minuend — subtrahend = summa

Speciellt för MULTIPLIKATION används traditionellt termerna

faktor · faktor = produkt

Speciellt för DIVISION används traditionellt termerna

täljare / nämnare = kvot ELLER

dividend / divisor = kvot ELLER bråk

TANGENS RELATION — matematikens mest elementära matematiska funktion

Med det utbildade xy-systemet grundläggs de relaterade begreppen för multiplikation och division genom relationer eller förhållandet mellan den rätvinkliga triangelns bägge rätvinkelsidor eller kateter, x och y. Ovan geometriskt illustrerade multiplikation (xy) och division (y/x) ges komprimerat på motsvarande algebraiska sätt i faktorlagen, se nedan. Relationen y/x kallas också allmänt i matematiken för tangens (ta’ngens).

Inversbegreppet

a/1 = 1/(1/a) 1/b = (1/b)/1

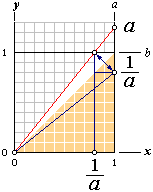
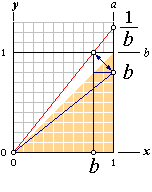
Illustrationen visar a=1,25 med 1/a=0,8

Kvantiteten n uttryckt som 1/n kallas explicit inversen, reciproka värdet eller inverterade värdet för n.

En kvantitet a kan alltid uttryckas på kvotformen y/x=a=a/1_=x. Om enheten 1 i stället relateras till x-parallellen y_=b=1 får man inversen till a där hypolinjen 0.a skär b, a=1/(1/a). ”(1/a)” är nu relaterad som en kvantitet på x-linjen (eller b-linjen). Som vi ser, är detta endast en simpel förminskning av den givna kvantitetstriangeln a/1. Principtriangeln ”a/1” själv har inte ändrats, vi ser den bara i nytt ljus genom en zoomning.

På samma sätt då man utgår från en kvantitet b, mindre än ett; på x-linjen blir den direktinverterad enligt 1/b=(1/b)/1 där ”(1/b)” blir relaterad som en kvantitet på y-linjen (eller a-linjen) genom triangeln y/x=(1/b)/1. Som vi ser är förhållandet intakt. (Att rita dessa detaljer geometriskt, se figurerna ovan, är betydligt mindre krångligt än att beskriva dem genom symbolisk algebra).

[Om b betraktas på x-linjen och är större än 1, blir resultatet principiellt detsamma som i a/1-figuren om denna vrids moturs 90°].

Faktorlagen:

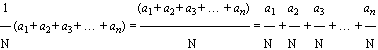
Den allmänna kvoten a=b/c tillämpad på distributiva lagen a(r+x)=ar+ax ger faktorlagen enligt

(b/c)(r+x) = (b/c)r+(b/c)x.

Den är matematikens mest fullständiga algebraiska beskrivningsform och fullständigar därmed den elementära genomgången av matematiken. Faktorlagen beskriver i sak utbrytning och insättning av gemensam nämnare.

SKRIVSÄTTET ovan för kvotformen 1/N är det tydligaste. I den raka skrivformen 1/N görs ibland (oegentligt) typteckningar av formen 1/ab som betyder 1/(ab), inte (1/a)b. På samma sätt tolkas 1/ab+c i enlighet med distributiva lagen där multiplikation (och division) går före addition (och subtraktion), förtydligat (1/[ab])+c.

Räknelagarna för potenser och deras omvändning som logaritmer framgår på samma typ av ”högre växel” som multiplikation och division från addition och subtraktion:

Potenslagarna följer av seriemultiplikationer från grundformen a₁a₂a₃ … a_n=aⁿ=P. Man har då terminologin BAS^exponent=Produkt där aⁿ(=P) explicit kallas potens. Om potensen (aⁿ=P) uttrycks i termer av exponenten (n) kallas uttrycket en logaritm, n=^alogP, eller enklare alogP om inga missförstånd uppkommer. Potenslagarna härleds (typiskt) på formen: om q=n+m, då gäller

a^q=(a·a·a·a·… aⁿ)·(a·a·a·a·… a^m)=aⁿ·a^m=a^n+m. Potenslagarna grundas alltså (väsentligen) på att återföra grundmatematiken på exponenten.

Potenslagarna — se utförliga härledningar i POTENSLAGARNA — i sammanställning är

a⁰ = 1

1/a = a^–1

a^–n = 1/aⁿ = (1/a)ⁿ

a^n+m = aⁿa^m

a^n–m = aⁿ/a^m

(aⁿ)^m = a^nm

(ab)ⁿ = aⁿbⁿ

aⁿ=b ; a = b^1/n

a^m/n=b ; a = b ^n/m

a^m/n = ⁿÖ a^m

Logaritmlagarna följer av potenslagarnas omvändning (genom exponenten). Med potensen aⁿ=P given skrivs exponenten n enligt n=^alogP eller av somliga n=log_aP, eller enklare (och snyggare) om inga missförstånd uppkommer n=alogP. Allmänt brukas för basen e förkortningen ln och för 10-basen log eller lg.

Om logaritmen efterfrågas eller påtalas, är det n man frågar efter eller hänsyftar på i en potens aⁿ=P. Termen antilogaritm hänsyftar på potensens bas, a. Denna kallas understundom i logaritmiska sammanhang även för logaritmens bas.

Logaritmlagarna — se utförliga härledningar i LOGARITMLAGARNA — i sammanställning är

^alog a = 1

a^{alog P} = P

aⁿ = P; n = ^alog P

n = ^elog P / ^elog a

^alog P = 1/(^Plog a)

^alog (1/P) = –(^alog P) = ^1/alog P

^mlog Aⁿ = n(^mlog A)

^mlog AB = ^mlog A + ^mlog B

^mlog A/B = ^mlog A – ^mlog B

Fakultet betyder i grundformen 1·2·3·4·5…·n = n!

Semifakultet n!! betyder för udda n detsamma som 1·3·5·7…·n = n!! och för jämna n motsvarande 2·4·6·8…·n = n!!

Produktsumma är en alternativ skrivform för potensen

a₁a₂a₃ … a_n=aⁿ=P= _n=1®nPa_n.

Indexeringen framför produktsummatecknet (stora pi), n=1®n, anger ”(med) n från 1 till n”. (Alternativt kan pilen [Alt+0174 i Symbol] ersättas med ett backslashtecken, \, eller annat passande bara det anges tydligt).

Seriesumma är av samma typ som P men med addender (termer) i stället för faktorer. Den skrivs då, samma typindexering,

a₁+a₂+a₃+ … +a_n=na=S= _n=1®nåa_n

BinomialTeoremet (BT) har en särskild ställning i matematiken. Det är lösningen på alla uttryck av typen (a+b)ⁿ [se första binomlagen]. Vi finner lösningen till dessa genom att metodiskt räkna ut ekvivalenterna för (a+b)²=a²+2ab+b², (a+b)²(a+b)=(a+b)³, (a+b)³(a+b)=(a+b)⁴, och så vidare och som ger

(a+b)¹ = a + b

(a+b)² = a² + 2ab + b²

(a+b)³ = a³ + 3a²b + 3ab² + b³

(a+b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a+b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

(a+b)⁶ = a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶

(a+b)⁷ = a⁷ + 7a⁶b + 21a⁵b² + 35a⁴b³ + 35a³b⁴ + 21a²b⁵ + 7ab⁶ + b⁷

… .......................................... negativa b (se andra binomlagen) ger varannan term negativ

I råformen är lösningen (vi hoppar över mellanräkningarna och går direkt på resultatet)

(a+b)ⁿ = aⁿ + na^n–1b + n(n–1)a^n–2b²/2! + n(n–1)(n–2)a^n–3b³/3! + … + bⁿ

= aⁿ[1 + n(b/a) + n(n–1)(b/a)²/2! + n(n–1)(n–2)(b/a)³/3! + … + (b/a)ⁿ]

där fakulteten N! i nämnarna betyder 1·2·3·4·5·…·N. Undersöks termerna enligt uppställningen ovan framgår att

1 n n(n–1) n(n–1)(n–2)

— + — + ——— + ————— + …

0! 1! 2! 3!

¯

Vi kan använda denna ordning med 0!=1 för att indexera n-parenteserna enligt

0! = 1 ;

n! = 1·1·2·3·4·5·…·n ............................................................ n från 0

(n–m)_m! = (n–0)₀(n–1)₁(n–2)₂(n–3)₃(n–4)₄(n–5)₅ … .......... m från 0

Totalt kan binomialteoremet därmed uttryckas på den betydligt enklare men mera sammansatta och fortfarande fullständigt beräkningsbara formen

(a+b)ⁿ = aⁿ[1+ _m=0®nå [(b/a)(n–m)]_m![(m+1)!]^–1]

= aⁿ[1+ _m=0®nå (b/a)^m+1[(n–m)]_m![(m+1)!]^–1]

= aⁿ[1 + n(b/a) + n(n–1)(b/a)²/2! + n(n–1)(n–2)(b/a)³/3! + … + (b/a)ⁿ]

TALSYSTEMEN och POSITIONSSYSTEMET

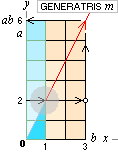
Generatrisbegreppet (snedlinjerna [/] i xy-systemet eller hypolinjerna som beskriver multiplikation och division, se föregående illustrationer för multiplikation och division) leder direkt till de olika talsystemen och talbaserna, hur de konstrueras, sammansätts och systematiseras genom sina naturliga periodiska avdelningar.

Talsystemet

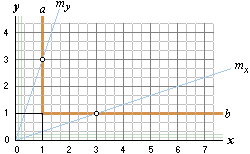
TALSYSTEMEN bildas genom talgeneratorerna eller talgeneratriserna (m) i det enhetsindelade xy-planet. Talgeneratrisen m är gömda linjen eller projektionen genom xy-origo och den heltaliga talbasen (T) på enhetsparallellerna ya och xb, således med exakt spegelsymmetri kring enhetsdiagonalen (linjen som ges av x=y, alltså rakt uppåt höger mellan xy-axlarna). Skärningen mellan m och xy-systemets enhetsparalleller delar enheten i T delar. Delningspunkternas gömda linjer återför projektionerna på motsvarande symmetrihalva, därmed utvidgas projektionerna. Genom projektionssymmetrin kring enhetsdiagonalen, som innebär att varje delenhet blir objekt till motstående symmetrihalvas projektioner, upprepas alltså delningen obegränsat så att enheten delas fraktalt enligt ordningen (1), 1/T, (1/T)/T, (1/T/T)/T, osv. Med T=3 får man alltså (1), 1/3¹, 1/3², 1/3³, 1/3⁴, 1/3⁵, osv. Detta är stommen i positionssystemet. Närmare bestämt den decimala delen. Heltalsdelen definieras på samma sätt men omvänt enligt exemplet 1, 3¹, 3², 3³, 3⁴, 3⁵, osv. Ett sådant system med givet heltal T kallas ett talsystem med talbasen T.

Positionssystemet är en naturligt inneboende fraktal delningsordning i xy-planet som följer naturligt ur talsystemens bildning. Delningsordningen grundas på ett heltal som kallas talbas (T). Enheten 1 består av T delar där varje delenhet består av T delar och vilken ordning sedan upprepas med obegränsad delning via T (se Talsystemen). Varje delningsnivå kallas en position. Den beskrivs matematiskt som en kvot K=N/T^p med heltalet p som positionens ordningstal, N anger heltal i täljaren och T talbasen i nämnaren. p=0 ger enhetspositionen K=N. N anger alltså positionens numeriska koefficient. N kan anta alla heltalsvärden från 0 till T–1. Värdet noll (tom mängd eller ingenting), 0, innebär att talets position i systemet ligger utanför (under) den aktuella positionens intervall, alternativt att det inte finns något tal alls.

Jämför exemplet (3-systemet, talbasen är 3)

0 1

0.20123

Ettan i en viss position 1/T^p har samma innebörd som N=T i närmast lägre position; T/T^p+1=1/T^p.

Positionssystemets allmänna form är

Varje delterm anger en enskild delningsnivå eller en position (p) i N/T^p. T anger talbasen och N positionens numeriska koefficient. Så skrivs till exempel 0,2012₃

Ytterligare Exempel: Talbasen 5 har decimalpositionerna 1/5, 1/5², 1/5³, 1/5⁴, … med motsvarande heltalspositioner 1, 5, 5², 5³, 5⁴, … och så vidare, med uppräkneligheten

1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, … och så vidare för att exemplifiera. Från Indien (via Araberna) har vi fått det decimala talsystemet med talbasen 10 med siffrorna 0123456789 och som mestadels används för att beskriva aritmetiken i allmänhet. För ett talsystem med basen 16, för att exemplifiera, fyller man på med andra tecken från 10 enligt

1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, … och så vidare.

Omvandlig mellan olika talsystem av givna tal T₁₀, alltså givna i det vanliga 10-systemet, görs genom (AdivB betyder heltalsdelen av kvoten A/B, div-operatorn beskrivs i Divisionsalgoritmen)

a = T₁₀ · [B^{(ln T) div (ln B)}]^–1

i successiva positioner på följande sätt. a bestämmer första positionen i svaret med B som talbas. Man följer sedan ordningen

a, – HELTALET i a, × B =_NYTTa

Man fortsätter på detta sätt att mata av den främsta siffran tills resten blir 0 där positionen analogt avtar med 1 för varje steg. Ordningen kan studeras på en enkel kalkylator (som inte har logaritmer), men man måste då känna nämnaren i nedanstående uttryck.

Exempel (ansluter till ovanstående illustrerade exempel med talbasen 3).

T=0,728395…₁₀

—————————— = 0.7283950… , – 0, × 3 =

3^{(ln T) div (ln 3)}

2.1851851… , – 2, × 3 =

0.5555555… , – 0, × 3 =

1.6666666… , – 1, × 3 =

1.9999999… , – 2, × 3 =

0 END.

(ln T) div (ln 3) ger högsta systempositionen, här 0.

Svar: 0,728395…₁₀ = 0,2012₃

Det är inte möjligt att utgå i T direkt från en godtycklig talbas, t.ex. direkt från 0,2012₃. T måste ges på 1-systemets form (och därifrån på 10-systemet) eftersom inte alla system är inbördes kommensurabla; jämför (1/3)₁ = (0,333…)₁₀ i all oändlighet.

Se vidare i Divisionsalgoritmen.

Kvadratrötterna Ö

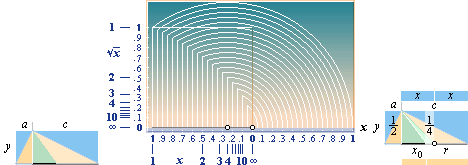
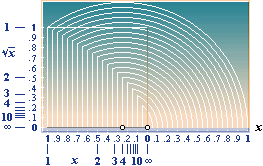
Cheops Rektangel — KVADRATRÖTTERNA

Från ac=y² ges direkt godtyckliga kvadratrötter med a=1 som y=Öc. Det metriska beroendet av c begränsar emellertid denna direkta metod som inte ger någon samlad överblick över alla möjliga kvadratrötter. Lösningen är att uttrycka diagonalen 2r alternativt via en konstant k enligt a+c=2r=2x+k. Detta ger ac=y²=2xk. Med a=k=1/2 får man då y²=x och därmed y=Öx. Genom att begränsa x till geometriska mängder på en skala mellan noll och ett tillsammans med skalans invers får man hela klassen (dvs., »alla» möjliga) kvadratrötter från 0 och uppåt obegränsat. Rotvärdet y blir alltså skärningen mellan cirkeln med radien r=x+1/4 dragen från vänstra (x=1/4)-punkten och y-linjen dragen från vänstra x. Funktionskurvan kallas parabel. I syntes

y²=r²–x₀²=(x+1/4)²–x₀²=(x+1/4)²–(x–1/4)², konjugatlagen, =(2x)(1/2)=x

Denna syntes av kvadratrötterna har knappast något aritmetiskt värde annat än som grovt orienterande. Som en syntes för den femte operatorn (Ö) i matematiken är resultatet emellertid suveränt.

Divisionsalgoritmen sammanfattar matematikens fullständiga divisionsbegrepp som giltigt för samtliga möjliga talsystem. Därmed innefattas även algebraisk division.

BESKRIVNING MED UTFÖRLIGA EXEMPEL

Varje bestämd kvantitet eller geometrisk mängd GM (=T) kan alltid likställas med en produkt mellan två bestämda kvantiteter, respektive N och K, enligt

T = NK ............................. divisionsalgoritmens grundform (”tänk”)

Kvoten T(täljare)/N(nämnare)=K har emellertid endast en bestämd aritmetisk värdemängd (GM=AV) i talsystem som är kommensurabla med talbasen N. Exemplet 100/30 ger exakt 100 lika delar i 30-systemet [=3,A₃₀=3+10/30=(90+10)/30], men 3,333… i 10-systemet, och 3+1/3 i enhetssystemet (talbas 1). Med T och N som godtyckliga bestämda GM, bestäms formen för K följaktligen av valet av talsystem: närmare bestämt med valet av dess talbas (N). Varje bestämd geometrisk mängd (GM) T kan alltså och följaktligen skrivas liktydigt med en summa a+b mellan två bestämda GM, respektive a (=NK) och b (en rest R) enligt

T = a + b

T = NK + Rest .................. divisionsalgoritmens fullständiga form (”tänker”)

En godtycklig GM=T kan alltså ge (b större än noll) eller inte ge (b=0) en rest (R) enligt exemplet

100 = K ................................ ingen rest

100 = 30·3 + 10 .................... med rest ; N=30, K=3, R=10

Formen eller värdet på K beror alltså på valet av talsystem.

Divisionsalgoritmens ekvation är T/N=K+R/N, mera utförligt

T NK + Rest Rest

T = NK + Rest ; —— = ————— = K + ———

N N N

¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯¯

Divisionsalgoritmens funktion framgår i två steg.

1. Då N i T=NK+R betraktas genom en godtycklig summa N=n₁+n₂; Om divisionen utförs på en godtycklig term i N enligt K=T/n₁

T = [n₁+n₂]K + R = [n₁+n₂]T/n₁ + R = T[1+n₂/n₁] + R

T – T[1+n₂/n₁] = R = T(1 – [1+n₂/n₁]) = T(1–1–n₂/n₁) = –T(n₂/n₁)

T = NT/n₁ – T(n₂/n₁) = (T/n₁)(N – n₂) = (T/n₁)(n₁) = T

blir resultatet alltid korrekt, förutsatt att resten R också behandlas korrekt enligt R=–T(n₂/n₁) där n₂ är alla resterande termer i N med n₁ eliminerad. Det betyder i klartext: med N givet på typformen N=a+b+c+d+e kan divisionen av T utföras på vilkensom av termerna a-e, alltså bara en enda, förutsatt R behandlas korrekt. Jämför exemplet med T=100 och N=15:

T 100 50 200

—— = ——— = 10 – ——— = 20 – ———

N 10 + 5 10 + 5 10 + 5

I första fallet sker divisionen på 10; T/10=10, resten R blir

–T(n₂/n₁) =–100(5/10) =–50.

I andra fallet sker divisionen på 5; T/5=20, resten R blir

–T(n₂/n₁) =–100(10/5) =–200.

2. Om också T utvidgas till summan T=T₁+T₂ och divisionen utförs på endast en av termerna T₁, ser vi att summan T fås tillbaka via R om man följer schemat enligt K=T₁/n₁

R = T–NK = T–N(T₁/n₁) = T₁+T₂–NT₁/n₁ = T₂+T₁(1–N/n₁)

= T₂+T₁(n₁–N)/n₁ = T₂+T₁(–n₂)/n₁ = T₂–T₁n₂/n₁

T–NT₁/n₁ = T₂–T₁n₂/n₁

T–T₂ = NT₁/n₁–T₁n₂/n₁ = (T₁/n₁)(N–n₂) = (T₁/n₁)(n₁) = T₁

Härav följer divisionsalgoritmen:

divisionsalgoritmen

en division T/N=(T₁+T₂+T₃+…+T_n)/(n₁+n₂+n₃+…+N_n) kan alltid utföras initiellt på endast två termer T₁/n₁=K
förutsatt att R=T–NK beaktas.

Det vill säga (trivialt), K gäller för vilka som helst två termer T_n och N_n. Jämför samma som föregående exempel, T=100 och N=15:

T 70 + 30 5 110

—— = ——— = 7 – ——— = 14 – ———

N 10 + 5 10 + 5 10 + 5

I första fallet sker divisionen på 10; 70/10=7, resten R blir

T–N(T₁/n₁) =100–15(70/10) =–5.

I andra fallet sker divisionen på 5; 70/5=14, resten R blir

T–N(T₁/n₁) =100–15(70/5) =–110.

Jämför motsvarande algebraiska division:

T x 1 x²

—— = ——— = 1 + ——— = –x + ———

N x – 1 x – 1 x – 1

I första fallet sker divisionen på x; x/x=1, resten R blir –T(n₂/n₁)=–x(–1/x)=1.

I andra fallet sker divisionen på –1; x/–1=–x, resten R blir –T(n₂/n₁)=–x(x/–1)=x².

Ett första fall på en mera sammansatt kvot visar den enorma styrkan i divisionsalgoritmen (ref. ITK Matematikbiblioteket Lennart Brandqvist 1961 Algebra II s10-11):

T 6x⁴ + x³ + 6x² + 7x + 1 x³ + x + 1

—— = ——————————— = 6x + ————— = 6x + 1

N x³ + x + 1 x³ + x + 1

I första fallet sker divisionen på x³; 6x⁴/x³=6x, resten R blir T–N(T₁/n₁)

= 6x⁴ + x³ + 6x² + 7x + 1 – (x³ + x + 1)(6x⁴/x³)

= 6x⁴ + x³ + 6x² + 7x + 1

–( 6x⁴ + 0 + 6x² + 6x + 0) = x³ + x + 1

Mera utförligt i Kalkyl_03

METODOPERATORERNA DIV OCH MOD

div erhålls från divisionsalgoritmens ekvation T/N=K+R/N som K-faktorn (skippa R):

T/N=K, skippa resten, betyder samma som INT(T/N) = T div N , INT för heltalet av.

mod erhålls från divisionsalgoritmens ekvation T/N=K+R/N som R-faktorn (skippa K):

T/N=R, skippa K, betyder samma som REM(T/N) = T mod N , REM för återstoden (mantissan) av.

Speciella samband: T/U mod N = T mod UN

Metodoperatorerna div och mod finner (särskilt kraftfulla) tillämpningar i (speciell) datorprogrammering och allmänna (komplicerade) algebraiska uttryck.

Ovanstående praktiska genomgång motsvarar den elementära matematiken:

hur matematikens fem operatorer

+ – × ÷ Ö

fungerar — med inblick i de grundläggande räknelagar som krävs för att förstå matematikens (vidare) utveckling.

Vägen därifrån leder sedan närmast vidare (efter nollformsalgebran, se nedan) till trigonometrin [sin|cos|tan] med den vidare funktionsanalysen — för en introduktion, se Historia — Leonhard Euler

[f (x)=y] och kalkylen (även benämnd ”analysen”, ò y’dx = y) där föreningen mellan matematik och fysik behandlas mera ingående.

NOLLFORMSALGEBRAN (motsv. konv. infinitesimalkalkylen eller bara analysen) är den relaterade fysikens och matematikens samlingsnamn för begreppen som beskrivs, förklaras och härleds tillsammans med differential-, derivata- och integralkalkylens grunder. Se vidare från Nollformsalgebran. Utan dessa begrepp kan vi inte beskriva vissa avgörande delar i den trigonometriska matematikens praktiska detaljer (som till exempel serierna för sinus och cosinus som vi måste känna till för att få ut, eller bara förstå hur vi får fram, konkreta värden).

Kunskapsmålet med matematiken ENLIGT RELATERAD LOGIK är ingenting annat än det här: att människan ska kunna formulera (läs: verkligen förstå) naturprocesserna i fysiken;

matematiken är enda sättet.

Människan kan (mig veterligt) inte komma längre än så i den praktiska matematikens tillämpning:

Bygga, lära, leka.

Skrivsätten för addition och subtraktion

Människor generellt i varje fall i den rika världens industriländer under större delen av 1900-talet har ända sedan småskolan fått de grundläggande elementära matematiska färdigheterna i ryggmärgen med nedanstående typiska (eller motsvarande) huvudräkningsscheman för addition och subtraktion. I dagens läge (2010) med datorer och tekniska kalkylatorer används de knappast alls längre — men kommer väl tillpass när »batterierna är slut» eller när »strömmen har gått».

Exempel

Skrivalgoritmen för subtraktion:

5 4 3 2 1 |position

1010 |minnesrader

1 2 3 10 |minnesrader

+ 1 2 3 4 5

- 9 9 9

———————————

= 1 1 3 4 6

Beskrivning: Man lånar från närmast högre position med 10 i varje.

1. 9FRÅN5 går inte: Måste låna från 4:an; Stryk 4:an, flytta upp 4–1=3:an, skriv ut lånet 10 i positionen 1 till höger överst; Utför (10+5) – 9 = 6.

2. 9FRÅN3 går inte: Måste låna från 3:an; Stryk 3:an, flytta upp 3–1=2:an, skriv ut lånet 10 i positionen 2 till höger överst; Utför (10+3) – 9 = 4.

3. 9FRÅN2 går inte: Måste låna från 2:an; Stryk 2:an, flytta upp 2–1=1:an, skriv ut lånet 10 i positionen 3 till höger överst; Utför (10+2) – 9 = 3.

4. 0FRÅN1 går inte: Måste låna från 2:an; Stryk 2:an, flytta upp 2–1=1:an, skriv ut lånet 10 i positionen 3 till höger överst; Utför (10+2) – 0 = 1.

5. 0FRÅN1 går inte: Måste låna från 2:an; Stryk 2:an, flytta upp 2–1=1:an, skriv ut lånet 10 i positionen 3 till höger överst; Utför (10+2) – 0 = 1.

6. KLART. Inga fler positioner finns.

Positionssystemets Förklaring (T=10^):

+ 1T4 + 2T3 + 3T2 + 4T1 + 5T0

-(0T4 + 0T3 + 9T2 + 9T1 + 9T0)

Genom att låna 10 från positionen närmast till vänster (4T1) återstår 3T1 — och sedan på samma sätt med övriga.

Exempel

Skrivalgoritmen för addition:

5 4 3 2 1 |position

1 1 1 |minnesrader

+ 1 2 3 4 5

+ 9 9 9

———————————

= 1 3 3 4 4

Beskrivning: Man lägger till 1 (minnessiffra) om över 9 till positionen närmast till vänster.

1. 5+9 = 14; För upp 1:an över positionen närmast till vänster;

2. 1+4+9 = 14; För upp 1:an över positionen närmast till vänster;

3. 1+3+9 = 13; För upp 1:an över positionen närmast till vänster;

4. 1+2+0 = 3; Ingen minnessifra finns att lägga till;

5. 0+1+0 = 1; Ingen minnessifra finns att lägga till;

6. KLART. Inga fler positioner finns.

Positionssystemets Förklaring (T=10^):

+ 1T4 + 2T3 + 3T2 + 4T1 + 5T0

+ 0T4 + 0T3 + 9T2 + 9T1 + 9T0

Genom att addera 10 till positionen närmast till vänster (4T1) ökas dess positionsvärde med 1 — och sedan på samma sätt med övriga.

Trigonometrin

Trigonometriska funktioner

TRIGONOMETRIN

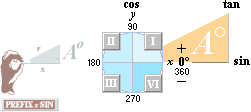
PREFIXxSIN

sinus, ursprungligen dji’va, korda (generellt linjen i cirkeln som tangerar bägge bågpunkterna), från Indien;

från ”boken om aritmetiken” som ursprungligen skrevs i Indien (800 e.Kr.) och som nådde Europa genom handelsvägarna och först översattes av araberna;

Med arabernas översättning blev det dja’ib vilket transkriberades som dji’ba, vik, som på latin översattes till si’nus

[ref. BONNIERS KONVERSATIONSLEXIKON BandX 1927 sp612, SIGMA Band4 1956 s1329].

sinusrelationen: minsta förhållandet mellan sidorna som greppas av tummen-pekfingret med origovinkeln (A) inåt; sinA=x/r

cosinusrelationen: minsta förhållandet mellan komplementsidorna; cosA=y/r

tangensrelationen: minsta förhållandet mellan rätvinkelsidorna; tanA=y/x=cos/sin

teorem

Trigonometrins formella grundteorem (lärosats) — med sinus på x-axeln:

För en viss given vinkel (A°) finns ett visst förhållande i enhetscirkeln r=1=Ö(x² – y²) mellan projektionerna x/r=sin, y/r=cos, och y/x=tan

Cirkeln, grundbegrepp

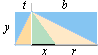
Plantriangelns vinkelsumma

Ta ut en godtycklig rektangel (vänster); dela den godtyckligt (mitten), markera respektive dels diagonal: varje rektangelhalva summerar två räta eftersom hela rektangeln summerar fyra räta; för ihop delarna (höger): de tre vinkelspetsarna tillsammans (A+B+C) summerar fortfarande två räta eftersom de inre två räta vid basen bortfaller, vilket är plantriangelns vinkelsumma.

Cirkelns omkrets — perimetern (P) — förhåller sig alltid till cirkelns diameter (Ø=2r) som talet PI (p; p i Symbol):

P/2r = p ;

P = 2pr ...................... cirkelns omkrets

Cirkelns yta (A för Arean) fås som triangelytan A = (P · r)/2 = Pr/2 = (2pr)r/2 = (pr)r = pr² ;

A = pr² ...................... cirkelns yta

Se även

A_YTAN = (2pr)/2 · r = pr²

cirkelytan, tyngdlinjens rotation,

även cylindermanteln och brutna konen

Radianbegreppet

CIRKELNS VINKELMÅTT

A_GRADER/360

= s/2pr

= (s/r)/2p

= a_RADIANER/2p ;

A°/a = 180/p

ALLMÄNNA 3D-SYSTEMET

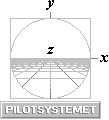
I MODERN AKADEMI används PREFIXxCOS, se vidare nedan.

Vinkeln (A) räknas genom hela cirkelns 360° (eller annan kvantitet) som förhållandet mellan det upptagande vinkelrummet och hela cirkelrummet, samma som bågdelen (s) relativt hela omkretsen (2pr) enligt A/360=s/2pr;

radianer

Med enhetscirkeln r=1 ges båglängden s i motsvarande vinkelenhet radianer (a) enligt

a = A°(p/180);

prefixXsin

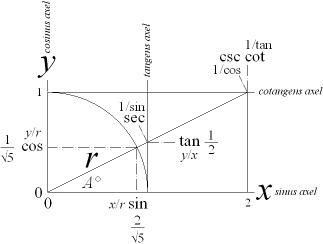
Figuren visar trigonometrins grundrelationer exemplifierat i PREFIXxSIN: x-axeln (horisontella) bildar sinus-axel.

I modern akademi används istället y-axeln (vertikala) som sinus axel. Se förklaring och jämförelse nedan.

I MODERN AKADEMI används (det krångliga sättet med) PREFIXxCOS (trigonometriska prefixet på x-axeln) enligt

PREFIXxCOS sin=y/r; cos=x/r; tan=y/x; [sec=1/cos; cosec=1/sin; cotan=1/tan] ................. icke harmoniska

Man har alltså secans som 1/cosinus, inte som 1/sinus, samt på samma omständliga sätt cosecans som 1/sinus.

Jämför

PREFIXxCOS sin=y/r; cos=x/r; tan=y/x; [sec=1/cos; cosec=1/sin; cotan=1/tan] ................. icke harmonisk

PREFIXxSIN sin=x/r; cos=y/r; tan=y/x; [sec=1/sin; cosec=1/cos; cotan=1/tan] ................. harmonisk

Secans skär tangens axel, cosecans skär cotangens axel. Gäller för bägge PREFIXxSIN|COS

Enklaste sättet att memorera blir naturligtvis efter PREFIXxSIN.

För att därifrån anpassa resultatet efter den moderna ordningen PREFIXxCOS behöver vi bara byta plats mellan termerna sin|cos. Inget annat. Resten sköter sig självt. Trigonometrin blir därmed “enkel”:

tre grundrelationer sin|cos|tan med harmoniska inverserna sec|csc|cot i PREFIXxSIN.

arcusbegreppet

ARCUSBEGREPPET

Med den goniometriska eller trigonometriska typformen a = |sin|cos|tan| A som betyder motsvarande relation mellan respektive triangelsidor (|x/r|y/r|y/x|) för givet vinkelrum (A) fås vinkeln som sådan enligt motsvarande så kallade arcusfunktion enligt A = arcus |sinus|cosinus|tangens|.

Exempel i PREFIXxSIN:

Med a = sinA = 0,5 ges A = arcsin 0,5 = 60°.

I den här presentationen används det (mycket) förenklade skrivsättet, samma typexempel

asin0,5=60°, om inga missförstånd uppkommer.

historia

Före 1970-talet användes TABELLER i skolorna (man köpte dem i bokhandeln) för att få fram korsreferenser på vinklar och deras motsvarande trigonometriska relationer — eller i enklare fall RÄKNESTICKOR som numera och sedan länge är helt utdöda på marknaden. Från senare delen av 1970-talet och framåt kom så de revolutionerande “tekniska räknarna” (som också kunde köpas i bokhandeln): Alla sin|cos|tan och deras arcus (vinkel-) funktioner fanns inbakade. Bara att trycka på knappen.

Cirkelns talsystem

Cirkelns talsystem — 1, 3, 5, 17, 257, …

enligt relaterad matematik

Trigonometrins formella grundteorem är emellertid beskaffad på samma sätt som talsystemen i det vanliga enhetsindelade xy-systemet: beroende på talbas är relationerna kommensurabla (mätbara med samma mått), eller så inte.

Exempel: Någon exakt vinkel typ “Ö 2 grader” finns inte i matematiken.

Exakt bestämda vinklar (A°) är bara de som satisfierar följande samband (här utan härledning):

M · (360/n)/2^m ..................... cirkelns bestämda vinkelrum, Mnm heltal, n anger polygontalbas

M.a.o.: BESTÄMDA VINKELVÄRDEN kan bara erhållas ur bestämda rationella tal (y/x, bägge bestämda GM) i xy-systemet genom operatorerna

+ – × ÷ — DÄRFÖR att inget annat sätt finns att dela 1 i någon bestämd delmängd så att summan av delarna kan återföras på 1. Sådana ”perfekta trianglar”, alla xyrA° bestämda, kan vi därför kalla för (absolut) fullständigt bestämda trigonometriska trianglar.

Sambandsformen ovan [M · (360/n)/2^m] är principiell: det går inte att ange den unika talbasföljden exakt: Vilka talbaserna är för cirkeln, i rakt följd efter 1|3|5|17|257|65535| …, kan (veterligt) inte uttryckas i någon direkt ekvation, utan de exakta talbaserna måste framräknas ur en (sådan exakt) successionsform som bygger på grundbaserna: alla högre talbaser extraheras ur dessa.

Anledningen är (på sitt sätt enkel): cirkeln runt mäter ingen bestämd geometrisk mängd.; Omkretsen beror på pi (p=3,1415926…) som är ett s.k. transcendent tal, vilket betyder att det aldrig slutar med decimalerna och att decimalerna aldrig upprepas i någon periodisk serie utan fortsätter i all oändlighet. Därmed beror också talbaserna på denna obestämdhet. Enda sättet att bestämma dem, är att använda grundbaserna och de som sedan följer av dem.

När vi, alltså, i allmänhet talar om sin|cos|tan för en viss vinkel (A°), vilket skrivs t.ex. sinA=2/Ö5, kan vi (i allmänhet) inte räkna med att få ut något EXAKT vinkelvärde A. Det finns dock olika trigonometriska och goniometriska serier som en viss vinkel kan beräknas ur, och som (sedan 1970-talet) lagts till i tekniska kalkylatorer. Bekvämt för oss, behöver vi bara trycka på tangenterna (typ INV sin|cos|tan) för att få redan på vinkelvärdet. Kom bara ihåg att all etablerad och kommersiell matematik använder PREFIXxCOS. Se beskrivning ovan i PREFIXxSIN.

vinkelsummateoremet

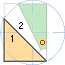
VINKELSUMMATEOREMET

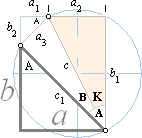
Praktiskt tillämpningsexempel på trigonometriska funktionerna

SAMBANDEN FÖR ADDERANDE VINKLAR i PREFIXxSIN

Genom att teckna upp rätvinkliga trianglar i cirkeln, kan de trigonometriska sambanden för vinkelsummeringar härledas ur de enkla grundfunktionerna.

Av de 14 centrala samband som bildas ur ovanstående illustrerade relationskropp behöver vi här endast beröra några av de första för att kunna koppla vinkelsummateoremet. De övriga är inte avgörande för det fortsatta sammanhanget.

HL betecknar HögerLed (VL VänsterLed). Vi använder de enkla trigonometriska grundrelationerna med rätvinkliga triangelns kateter ab och hyposidan c med vinkeln j (Grek. fi, j) och vinkelprefixet a/c=sinj, b/c=cosj, b/a=tanj=(b/c)/(a/c), samt Pythagoras sats a²+b²=c² som ger

a²/c² + b²/c²=1=(a/c)² + (b/c)²=sin²j+cos²j (som vi ofta skriver förenklat sin²+cos²=1).

Figuren visar relationerna

	a2	= a – a1 = cosA·c1 – sinA·a3	b1	= b + b2 = sinA·c1 + cosA·a3
	a2/c	= cos(A–B)	b1/c	= sin(A–B)
	a2/c	= cosA·c1c^–1 – sinA·a3c^–1	b1/c	= sinA·c1c^–1 + cosA·a3c^–1
	a2/c	= cosA·sinB – sinA·cosB	b1/c	= sinA·sinB + cosA·cosB
(4)	cos(A–B)	= cosAsinB – sinAcosB	sin(A–B)	= sinAsinB + cosAcosB	(5)
		sin–B=sinB, cos–B=–cosB ;	¬	projektionssymmetrierna
(1)	cos(A+B)	= cosAsinB + sinAcosB	sin(A+B)	= sinAsinB – cosAcosB	(2)

Beteckningarna (1)(2)(4)(5) refererar till ordningstalen i de totalt 14 samband som ovanstående är ett utdrag ur.

som tillämpade på ovanstående enhetscirkeln med r=1=r₁=r₂ med tillhörande x=sin och y=cos direkt ger komponenterna

y = y₁x₂ + x₁y₂ (1)(2) x = x₁x₂ – y₁y₂ ......... vinkelsumman

y = y₁x₂ – x₁y₂ (4)(5) x = x₁x₂ + y₁y₂ ......... vinkelskillnaden

Enhetscirkeln med r=1=r₁=r₂ medför att x/(HL)=y/(HL)=r/r₁r₂=1, (HL) respektive högerdelar.

Man har alltså ekvivalenterna totalt speciellt för sambanden i tabellen markerade (1) och (2) varur vinkelsummateoremet ges enligt

x=(x₁x₂–y₁y₂) ; y=(y₁x₂+x₁y₂) ; r=r₁r₂(=)D₁+D₂ ................ vinkelsummateoremet

summerande vinklar betyder multiplicerande hypomängder

resultat

Resultatredovisning för vinkelsummateoremet

Summering av två vinklar (eller två trianglar) A₁+A₂ motsvarar (Û) multiplikation med trianglarnas hyposidor r₁r₂

r₁r₂…r_n Û A₁+A₂+…+A_n

Är r₁=r₂=…r_n = rⁿ gäller tydligen

rⁿ Û nA ................... vinkelsummateoremets enklast sammanfattande form

Summeringen för sinusdelen betyder då för n lika trianglar (xyr)₁+(xyr)₂ med resultanten (xyr)_n att

x_n/r_n = sin(A₁+A₂+…+A_n) = x_n/rⁿ

Summeringen för cosinusdelen betyder på samma sätt för n lika trianglar (xyr)₁+(xyr)₂ med resultanten (xyr)_n att

y_n/r_n = cos(A₁+A₂+…+A_n) = y_n/rⁿ

Därmed kan de aritmetiska serierna för sinus och cosinus härledas direkt.

sinus och cosinus serier

SERIERNA FÖR SINUS OCH COSINUS

I VINKELSUMMATEOREMET (se föregående block) med x=sin och y=cos,

x=(x₁x₂–y₁y₂) ; y=(y₁x₂+x₁y₂) ; (r=r₁r₂) Û (D₁+D₂) ...................... vinkelsummateoremet

sätter vi vinklarna (a=D₁)=(b=D₂) i successiva vinkelsummeringar via teoremets

sin(a+b) = xx_n – yy_n = x_n+1

cos(a+b) = yx_n + xy_n = y_n+1

vilket till en första jämförande granskning ger oss

…

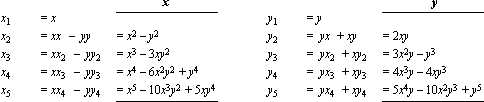
Vi ser att resultaten i kolumnerna markerade xy har exakt samma form som termerna (x+y)ⁿ i BT frånsett tecken.

(Vi studerar denna del separat genom jämförelser med leden i x och y mot BT-seriens varannan term):

Med BT-seriens faktorer _m=1®n(n–[m–1])_(m–1)! analogt n, n(n–1), n(n–1)(n–2), … som m₁, m₂, m₃, … enligt

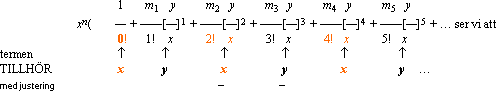
Vartannat par xy justeras alltså på negativt tecken. Det är (alltså) uppenbart att binomialteoremets serie innefattar vinkelsummeringarna i en del sinus (x) och en del cosinus (y). Vi söker en ORDNAD uppdelning.

Vi ser direkt från serieavsnittet ovan, frånsett första termen 1, att fakultets och exponenttalen k=1®2m_m=1®m (2,4,6,…) samlar alla x-termer enligt (y/x)^2m/(2m)! om m räknas från 1. De tillhörande fakultetsparenteserna för n,

n(n–1)₂, n(n–1)₂(n–2)₃(n–3)₄, n(n–1)₂(n–2)₃(n–3)₄(n–4)₅(n–5)₆, måste då skrivas med

p=1®(2m–1)_m=1®m — första x-termen med n(n–1) för m=1 i indexeringen 2m_m=1®m — enligt

n[(n–[1®p])_p!] = n[(n–p)_p!] vilket vi skriver förenklat och rakt n[n–(2m–1)]_(2m–1)!. Teckenändringen blir

(–1)^m.

EXTRAKTET för x-delen således

x_n = xⁿ(1+_m=1®nå(y/x)^2m(–1)^mn[n–(2m–1)]_(2m–1)!/(2m)!)

Alla y-termer samlas på motsvarande sätt genom en förskjutning med –1 i termpositionerna relativt x-delen.

EXTRAKTET för y-delen därmed

y_n = xⁿ(_m=1®nå(y/x)^2m–1(–1)^m–1n[n–(2m–2)]_(2m–2)!/(2m–1)!)

BÅGVINKELNS MINSTA ASPEKT fås med x=r=1 via cirkelbåglängdens (s) differential ds=dy=da vid motsvarande sina=1, analogt a=0Ûda, som ger y/x=da=a/¥ med a i radianer och aspekten genom den mängdoberoende via n=¥. Eftersom alla mängder N elimineras tillsammans med ¥ enligt ¥±N=¥=¥^c övergår fakultetsparenteserna i enbart ¥.

Vi får alltså för x-delen, med vidare,

(y/x)^2mn[n–(2m–1)]_(2m–1)! = (da)^2m¥ = (da)^2m¥^2m = (da¥)^2m = (a/¥ · ¥ = a)^2m = a^2m.

Med x_n=sina och y_n=cosa har vi alltså (xⁿ=1 via x=r=1)

sin a = x_n = 1+_m=1®m®¥ å a^2m–1(–1)^m–1/(2m)!

= 1 – a²/2! + a⁴/4! – a⁶/6! + a⁸/8! – a¹⁰/10! + a¹²/12! – a¹⁴/14!…

cos a = y_n = _m=1®m®¥ å a^2m–1(–1)^m–1/(2m–1)!

= a¹/1! – a³/3! + a⁵/5! – a⁷/7! + a⁹/ 9! – a¹¹/11! + a¹³/13! –…

enligt PREFIXxSIN med a i radianer;

s/2pr=a/2p=A°/360; a/p=A°/180=(s/r)/p.

Serierna konvergerar ytterst snabbt med praktiskt taget en korrekt decimal per beräknad delterm.

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Grundmatematiken

ämnesrubriker

Enhetssystemet

Matematikens 5 grundlagar

Syntes av Cheops rektangel

Symboliska algebrans grunder

Talsystemen och Positionssystemet

Trigonometrin

Matematikbeskrivningen fortsätter efter trigonometrin i analysen, se separat dokument från nollformsalgebran.

innehåll

MATEMATIKEN FRÅN BÖRJAN

Enhetssystemet

Matematikens grunder

Matematikens 5 grundlagar

Pythagoras sats · Cheops rektangel · Första binomlagen · Andra binomlagen · Konjugatlagen

Cheops rektangel och Gyllene snittet

Gyllene snittet

Pärlbåtssnäckan

Syntes av Cheops rektangel

Harmoniska trianglarna

Komplexa algebran

Ljusets gravitella beroende

Kvadratrötterna

Symboliska algebrans grunder

Matematikens 5 operatorer

Likhetstecknet

Teckenlagarna

Överflyttningslagen för addition

Parenteslagen

Multiplikation

Distributiva lagen

DIVISIONSBEGREPPET

Överflyttningslagen för division

Mönsterparagonerna för addition, subtraktion, multiplikation och division

Inversbegreppet

Faktorlagen

Potenslagarna

Logaritmlagarna

Fakultet, Semifakultet, Produktsumma, Seriesumma

Binomialteoremet

Talsystemen och Positionssystemet

Talsystemet

Positionssystemet

Positionssystemets allmänna form

Omvandling mellan olika talsystem

Kvadratrötterna

Divisionsalgoritmen

Divisionsalgoritmens ekvation

Algebraisk division

Metodoperatorerna div och mod

Skrivsätten för addition och subtraktion

Trigonometrin

Trigonometrins formella grundteorem

Cirkeln

Radianbegreppet

Radianer

PREFIXxSIN

Historia

Cirkelns talsystem

Vinkelsummateoremet

Serierna för sinus och cosinus

Dokumentöversikt till MATEMATIKEN i Universums Historia

referenser

Dokumentöversikt till MATEMATIKEN i Universums Historia

I UNIVERSUMS HISTORIA har högskolematematikens begrepp (vektoranalys, matrisalgebra) ingen representation.

Genom den allmänna granskningen har dock vissa (sådana) partier inte kunnat undgå omnämnande.

Se särskilt Vektoranalysen i ljuset av magnetismen och Vektorfelen i Modern Akademi.

Notera 2016 att webbläsaren Firefox läser INTE teckensnittet Symbol — 64 av 118 htm-dokument i Universums Historia 2016. Internet Explorer och Google Chrome läser Symbol.

FYSIKENS ELEMENTÄRA GRUNDER skall avhandlas kunskapsmässigt på ELEMENTÄR nivå. Inget annat accepteras.

— Därmed garanteras, nämligen, VARJE ELEMENTÄRT LÄSKUNNIG INDIVID fullständigt tillträde — och därmed yttrande — i ämnena.

Ingen enda individ i mänsklighetens familj får utestängas — på institutionellt framställda grunder.

— All matematisk fysik i UNIVERSUMS HISTORIA behandlas på nivån elementär

— med särskilda avsnitt som behandlar differential-, integral och derivatabegreppen utförligt från grunderna.

— För grundmatematiken, se från Matematiken från början.

— För derivata-, differential- och integralkalkyl, se från NOLLFORMSALGEBRAN.

— För n:te ordningens varianter och universaler [konv. (linjära) differentialekvationer], se från Den högre analysen.

— Alla htm-dokument

i UNIVERSUMS HISTORIA

som behandlar matematiken:

Matematiken1.htm Matematiken från början — detta htm-dokument

Matematiken1_1.htm Den komplexa algebran

Matematiken2.htm Formlagarna

Matematiken3D.htm Grundbegreppen i 3D-geometrin

ATOMTRIANGELN.htm NOLLFORMSALGEBRAN — differentialbegreppet och integralbegreppet från grunden

AllaTal.htm Oändlighetsbegreppet · Gränsvärdesbegreppet · Kontinuitetsbegreppet

CEPHekvationen.htm Cirkeln·Ellipsen·Parabeln·Hyperbeln

GalaktiskaKoordinater.htm Allmän orientering, jämförelse med olika webbkällor

MatElementarYtorna.htm Sfärens Yta Och Sfärens Volym i enkla klassiska härledningar

MatematikenAnalys.htm Den Högre Analysen — varianter och universaler

MatematikenAnalysEXEMPEL.htm Praktiska exempel

MatematikenAnalysEXPINT.htm Den Speciella exponentintegralens metod

MatematikenAnalysPALM.htm ELEMENTÄRA GRÄNSSNITTETS Metod för PARTIKULÄRA LÖSNINGAR, Del I

MatematikenAnalysPALM2.htm ELEMENTÄRA GRÄNSSNITTETS Metod för PARTIKULÄRA LÖSNINGAR, Del II

MatematikenEkvation.htm EKVATIONSLÄRANS GRUNDSATSER ENLIGT RELATERAD MATEMATIK — Ekvationslära

MatematikenEkvation2.htm EKVATIONSLÄRANS GRUNDSATSER ENLIGT RELATERAD MATEMATIK — Polynomdivision

MatematikenFunktion.htm FUNKTIONSKLASSERNA I RELATERAD MATEMATIK

MatematikenFormlag.htm UTFÖRLIGA HÄRLEDNINGAR TILL FORMLAGARNA med länkade tabellposter (Bastablån) — beskrivning delvis på engelska

MatematikenSinus.htm TRIGONOMETRINS GRUNDBEGREPP med utförliga beskrivningar från plangeometrins grunder

MatematikenSinusKinTrig.htm TRIGONOMETRINS GRUNDBEGREPP VIA KINEMATIKEN — trigonometrin via cirkelrörelsen i projektioner, kompletterande

Senast uppdaterade version: 2019-01-02

*END.

Stavningskontrollerat 2008-03-06 | 2016-12-17.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-09

åter till portalsidan · portalsidan är www.UniversumsHistoria.se