Matematiken|Analysen — Universums Historia

DEN HÖGRE ANALYSEN — UNIVERSUMS HISTORIA | a production 2008XII22 | Efter sammanställningar från 1997IX27 | Senast uppdaterade version: 2014-04-18 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Den högre analysen | närmast från MPcExempel.wps 2003XII6 | 2008XII22 | i sammanställning för Universums Historia

— Matematiken innehåller inga motsägelser.

Finner man sådana, är formuleringarna felaktiga.

Se från Sanningsbegreppet.

Grundläggande Rangkunskap — grundfunktionernas derivabilitet (deriverbarhet) och integrabilitet (integrerbarhet), begreppet elementärt gränssnitt

y’ = dy/dx ; d(dy/dx)/dx = d(dy)/dxdx = d²y/(dx)² = (1/¥)(1/¥ · y)/(dx)²;

s128|133 M2001_3.wps

Ledet ovan: Se HÖGREDERIVATANS ALLMÄNNA TECKNING — till jämförelse med modern akademi.

VARIANTER OCH UNIVERSALER

DEN HÖGRE ANALYSEN

VARIANTERNA OCH DERAS UNIVERSALER ENLIGT RELATERAD MATEMATIK

eller: — Speciellt tillägnat e-LOGARITMEN och DEN MATEMATISKA FYSIKEN

inledning

DEN HÖGRE ANALYSEN I RELATERAD MATEMATIK innefattar den allmänna beskrivningen, formuleringen och lösandet av motsvarande naturliga fysikaliska processer — variationer, med matematikens språk och verktyg — genom en Variant, variationsekvationen, och dess lösning som Universal, integralens mest allmängiltiga ekvation.

— Eller som det också heter i konventionella kvarter; »lösandet av linjära (eller icke-linjära) n:te ordningens differentialekvationer (med eller utan konstanta koefficienter)».

Inledande praktiska exempel visas i Praktiska utvecklingsexempel.

EN faktor finns som ensam bär ansvaret för den ÖVERGRIPANDE beskrivningen av den typ av presentation som utmärker den högre analysen: det är den naturliga logaritmbasen (e). Det är (nämligen) helt och hållet på dess formella natur och egenskap som hela den s.k. högre (matematiska) analysen vilar (konv. ”kalkylen” eller ”analysen”).

ALLA FYSIKALISKA PROCESSER kan (nämligen) uttryckas generellt som en funktion av tiden enligt F=f (t ) med derivatan DnF=dF/dt=F’. Differentialekvationen ger dF/F’=dt. Vi ser direkt att lösningen ansluter till logaritmintegralen, se Bastablån, och därmed till den naturliga logaritmbasen e.

Lösningen till i stort sett samtliga fysikaliska problem introduceras därmed — tvunget — på varianter som på ett eller annat sätt sammanhänger med e.

Men detta är inte allt:

MED DEN CENTRALA STÄLLNINGEN hos e visar sig också en inneboende — ytterst avancerad, förnämlig och mycket elegant — strukturalgebra som just det här avsnittet ska handla om; Strukturalgebran (via e) hjälper oss att verkställa lösningarnas formella uppställningar i konkreta, begripliga former med hjälp av kunskap om de matematiska grundfunktionernas deriverbarhet och därmed deras integrerbarhet — vilken förmåga vi också beskrivande kan kalla derivabilitet eller integrabilitet — dessa är nyckelord i den här presentationen.

Eftersom naturprocesserna allmänt bygger på elektriska och mekaniska grundbegrepp, måste just grundbegreppen och deras härledningar vara väl bekanta för den som vill studera de praktiska lösningarna; Det betyder i motsvarande grad att den högre analysen blir (ytterst) krävande — för den som inte redan är insatt; Alla vetenskaper har sina speciella tillämpningsområden i den högre analysen; Ju mera vi känner till grundbegreppen, desto mera tillämpningskraft kan realiseras på olika formuleringar som berör just naturprocesserna, samt de formuleringar som berör själva lösningarna. Den högre analysen berör alltså i stort sett »ingenjörsvetenskaperna»: alla grundkunskaper i matematik och fysik måste finnas med, upp till och med differential, derivata och integralkalkyl — och som omsätts på en (ännu) högre strukturväxel: ”analysen” eller ”kalkylen”.

Inledande orienterande beskrivning med allmän översiktlig genomgång av grundbegreppen

Differentialer (dy/dx) bildar varianter (y’=dy/dx) som kan skrivas som differentialekvationer (dy=y’dx) med lösningen eller integralen

(ò dy = y = ò y’dx = ò f ’ [x] dx = f [x]). Integralens fullständiga ekvation (y=f [x] + C) kan för kännedomen om dess allmänna universella giltighet kallas universal.

Genom att naturprocesserna — främst — avbildar krafter som verkar genom och under tidrymder (dF/dt=F’), intar den naturliga logaritmbasen (e) en naturlig ställning — eftersom den elementära integrala lösningen med variabeln i nämnaren tillhör logaritmintegralen (logaritmderivatans omvändning, se logaritmderivatan).

SÄTTET som e uppvisar den matematiska strukturen på visar sig nämligen GENERELLT kunna skrivas, för varje variant, på principiellt två allmänna typformer

se Inledande praktiskt utvecklingsexempel till jämförelse;

… ey’’’’ + dy’’’ + cy’’ + by’ + ay = 0 ..................... konv. homogen variant

… ey’’’’ + dy’’’ + cy’’ + by’ + ay = [·] ................... konv. inhomogen variant, [·] en godtycklig funktion inte lika med noll

— primtecknet ’’’… anger antalet derivatanivåer —

vilka kan återföras på e genom en transformator (konv. karaktäristisk ekvation) av motsvarande typ

… en⁴ + dn³ + cn² + bn¹ + an⁰ = 0 ......................... konv. homogen variant

… en⁴ + dn³ + cn² + bn¹ + an⁰ = [·] ........................ konv. inhomogen variant, [·] en godtycklig funktion inte lika med noll

och som härifrån kan beskrivas vidare genom olika lösningsklasser med olika metoder;

VARIANTEN — derivataekvationen som ovan — KLASSIFICERAS GENERELLT efter antalet primtecken, analogt variantens derivatagrad:

en variant med derivatagrad n betyder en n:te ordningens variant.

LÖSNINGARNA till de inhomogena varianterna klassificeras genom universalsatsen i en normal lösningsdel för den motsvarande homogena varianten (yH) och en speciell lösningsdel för den inhomogena varianten, eller den (konv.) s.k. partikulära lösningen (yP), summan av dessa ger hela lösningen (y = yH + yP).

Se vidare från Allmän klassifikation av varianter.

elementära gränssnittets funktionsranger

DEN HÖGRE ANALYSENS BESKRIVNING ENLIGT RELATERAD MATEMATIK står helt — och faller helt

— med beskrivningen av

elementära

Gränssnittets Funktionsranger

Tablå 0 — matematikens elementära grundfunktioner

RANGKARAKTÄRISTIK VariantAssocierade DERIVATOR

yP, formell rangterm. PREFIXxSIN för trigonometriska funktioner

exponentiella rang eller funktion DerivataImmunitet

yP = e^nx ; exponent JA|xⁿ *

y + y’+ y’’ = e^nx + ne^nx + n²e^nx variant å

yP = xⁿ ; bas nej

y + y’+ y’’ = xⁿ + nxⁿ^–1 + n(n–1)xⁿ^–2 variant

logaritmiska

yP = ln nx ; log JA|xⁿ

y + y’+ y’’ = ln nx + n(nx)^–1 – n²(nx)^–2 variant

trigonometriska

yP = sin nx ; sin nej|cos

y + y’+ y’’ = sin nx – n cos nx – n² sin nx variant å

yP = cos nx ; cos nej|sin

y + y’+ y’’ = cos nx + n sin nx – n² cos nx variant å

yP = tan nx ; tan nej|sin, cos

y + y’+ y’’ = tan nx + n(sin nx)^–2 + 2n²cos nx (sin nx)^–3 variant

yP = cotan nx ; cot nej|sin, cos

y + y’+ y’’ = cot nx – n(cos nx)^–2+ 2n²sin nx (cos nx)^–3variant

yP = asin x ; arc sin JA|xⁿ

y + y’+ y’’ = asin x – (1–x²)^–1/2 – x(1–x²)^–3/2 variant

yP = acos x ; arc cos JA|xⁿ

y + y’+ y’’ = acos x + (1–x²)^–1/2 + x(1–x²)^–3/2 variant

yP = atan x ; arc tan JA|xⁿ

y + y’+ y’’ = atan x + (1+x²)^–1 – 2x(1+x²)^–2 variant

yP = acot x ; arc cot JA|xⁿ

y + y’+ y’’ = acot x – (1+x²)^–1 + 2x(1+x²)^–2 variant

NOTifikationer till TABLÅ 0

* i produkt med f ’(x)e ^f^(x) om f ’(x)ÏC , f ’(x) aldrig skild från e ^f^(x)

å rangtermen är självsummerande

JA, nej | DerivataImmunitet JA betyder att ingen annan enskild rang kan forma den givna genom derivering

|xⁿ rangUttryck till höger om vertikalstrecket specificerar en formell derivata-(rangs)-transformerande rang

Allmänt bara rangerna e^nx (exponentRangen) och xⁿ (basRangen) är DerivataSolida: deras derivering inkräktar inte på andra ranger

Beskrivning till Tablå 0

GRUNDLÄGGANDE STRUKTURELL DERIVATAKUNSKAP eller Ranglära

Alla ranger utom xⁿ och ln nx bibehåller rangens FORM [derivataparametern] oberoende av derivering.

Rang e^nx xⁿ ln nx [sin|cos|tan|cot]nx arcus

derivataparameter nx n nx nx (1±x²)

Om vi i fallen ln nx även tillåter ln (nx+K) bibehålls (nx+K) genom deriveringarna. Kvar återstår därmed endast en enda funktionsrang som ändrar sin form vid derivering. Nämligen basfunktionen xⁿ. Vi kan alltså betrakta variabelpotenserna (xⁿ) som speciellt exklusiva. Det finns emellertid också andra sätt att klassificera exklusiviteterna;

Alla ranger utom de två första leder vid derivering som vi ser till explicita rot- [arcus sin|cos] och/eller potensuttryck [t ex ln nx].

Trigonometriska funktionerna delas i olika rangtyper som [beroende på sammansättning] endast alstrar yttre koefficienter

[jämför i PREFIXxSIN t ex (cosAx)’’ = A(sinAx)’ = –A²cosAx]. De trigonometriska funktionerna studeras därför speciellt i särskilda avsnitt;

De trigonometriska funktionerna genererar gränssnittsskift (för termen gränssnitt, se Elementära gränssnittets begrepp) genom att de uppträder som dubbelrangtermer, typ (sin|cos)’ = (cos|sin), denna detalj berör dock inte metoden med partikulärlösningarna eftersom denna helt grundas på det elementära gränssnittet med endast enkla osammansatta rangtermer.

Följande genomgång belyser detaljerna.

Rangtermen e^nx är den högsta

Den enda rangterm som under alla förhållanden aldrig raderar sin egen rang, vare sig deriverande (mot rang) eller deriverad (från rang) är e-logaritmens exponentfunktion e^nx. Denna rang blir därmed helt naturligt »den allra högsta» (renaste) av alla ranger (vi erinrar att termen rang här renderar betydelse endast för fundamentaltermens bestämning och därmed endast i deriverande sammanhang).

Kriterium: fundamentaltermen är av typen Ae^nx

Rangtermen xⁿ är den näst högsta (om |n|>0), därefter följer I AUTOMATIK logaritmfunktionen

Den enda rangterm som å den andra sidan aldrig inkräktar på annan rang genom sin egen deriverande karaktär är basfunktionen eller variabelpotensen xⁿ (x är variabeln). Vi ser av TABLÅ 0 att logaritmrangen resulterar i (negativa) variabelpotenser: Dn ln(P)=Dn(P) · (P)^–1. Men i jämförelse mellan dessa bägge (ln nx eller xⁿ) i en sammansättning av blandade ranger blir valet av företräde ändå lätt i och med att logaritmfunktionen har en egendefinierad grundpotens (–1) för sin del: Logaritmfunktionen kan aldrig derivera en positiv variabelpotens till en positiv variabelpotens. Förekommer sådana bör alltså basfunktionen finnas med i bakgrunden.

Utan att här ange några vidare ”regler” (ehuru de framgår självmant på det enklaste), kan vi därmed konstatera att någon risk för sammanblandning mellan basfunktioner och logaritmfunktioner knappast föreligger, under förutsättning att vi är observanta på aktuell potensstruktur i variantens inhomogen (högerledet).

[Vi frånser här sammansättningen av ev. f (x) och vilket fall vi ändå alltid måste beakta enligt dess egen signifikanta form].

Resultatet kommer alltid att ge basfunktionerna före logaritmfunktionerna om potensen n i fundamentaltermen är positiv . Är den negativ beror utfallet på fundamentaltermens insättning i varianten (det kan resultera i en logaritmrang, eller i en basrang). Med generell preferens till positiva variabelpotenser kan vi därmed säga att basfunktionerna intar den näst högsta termrangen. Därefter följer logaritmfunktionerna.

Kriterium: fundamentaltermen är av typen xⁿ med n i högsta grad

Rangtermerna i gruppen trigonometriska funktioner är olika för sin|cos och deras arcus

Arcusfunktionerna är i sin derivataparameter entydiga genom sammansättningen (1±x²). Genom att parentesen kan vara av två olika typer bör vi inte ha några egentliga svårigheter att skilja den ena ifrån den andra om bägge förekommer i samma inhomogen. Om vi fortsätter att hålla oss till högsta potensgrad som preferens för högsta rang om flera potensranger förekommer, blir alltså rangordningen för arcusfunktionerna identisk med den uppställda i TABLÅ 0.

För rangerna sin|cos, och frånsett första ordningens inhomogena varianter där partikulärlösningen ges exakt via integralkvoten, finns inget enhetligt rangbegrepp (!). Sinus och cosinus är nämligen (som vi redan observerat, successivt) växelderiverande och intar därför en extraordinär ställning inom hela derivatakalkylen.

I en förekommande blandning av de olika funktionsgrupperna framgår således av TABLÅ 0 hur [frånsett sin|cos] att förstå vilken term som via ett givet högerled hos varianten ska utväljas som högsta rang. Om flera termer av sinsemellan väsensskilda ranger förekommer blir alltså valet av fundamentalterm godtyckligt. Dvs., vilkensom rangterm kan (i princip) betraktas som den mest fundamentala [då den är bestämd, kan den frånses och den återstående bestämningen kan fortsättas på de återstående rangerna, se vidare från Partikulärlösningens allmänna metod (PALM)].

Med den mest fundamentala termen given ges en allmän och generell metod för att finna en partikulärlösning till den givna varianten enligt

ALLMÄNNA PARTIKULÄRA LÖSNINGSALGORITMEN.

;

Den finns inte upptagen i modern akademi — också av skäl som exponeras i framställningen tillsammans med granskning av tillgängliga läromedel i de olika exemplen till jämförelse.

Elementära gränssnittets begrepp

Se även Elementära gränssnittets funktionsranger

Elementära gränssnittets begrepp

ALLA OPERATIONER, deriverande eller integrerande, gjorda på de grundläggande formella rangtermerna

e^nx, xⁿ, ln nx, sin nx, cos nx, tan nx, cotan nx, asin x, acos x, atan x, acot x

kan beskrivas representera operationer på Det Elementära Gränssnittet (eng. interface).

Var och en av de ovannämnda matematikens 11 grundfunktioner kallas här för en rang, den karaktäristiska rangens teckning för rangterm.

ALLA OPERATIONER, deriverande eller integrerande, gjorda på de grundläggande rangtermerna representerade av de olika matematiska funktionerna kan refereras till som operationer på ett gränssnitt — en struktur av diskreta, noga definierade komponenter [grundläggande elementära integraler] i ömsesidigt beroende och innehållande de grundläggande rangtermerna (funktionens verkställande term). Detta gränssnitt kan betraktas som elementärt om alla komponenterna är icke-sammansatta. Vilket vill säga, inte komponerade av mixade ranger.

Jämför

xⁿ (a+x^m)^k en dubbelbasrang

x (sinx) en dubbelrang

e^x^sinx en (sammansatt) tripelrang

xⁿ e^x^sinx en (sammansatt) kvadrupelrang

TERMEN GRÄNSSNITT (interface) refererar då till en kopplande nivå av integrabilitet (integrerande styrka, integrerbarhet), dels i respekt till en allmän lösbarhet för varianter i finnandet av deras universaler, dels i främjande av en beskrivande klassifikation av integrander som sådana eftersom en given nivå eller gränssnitt av integrabilitet expanderar (med införandet av mixade ranger) eller kontraherar (med reducerandet av mixade ranger) proportionellt mot komplexiteten i mixade ranger i en given integrand. Denna typklassifikation, med användningen av gränssnittets terminologi, blir speciellt användbar i beskrivningen av (navigerandet genom) de eljest (enormt) komplexa strukturerna av kalkyl på nivån varianter och universaler.

VI KLARAR INTE BESKRIVNINGEN av integralkalkylen — centralkärnan i den högre analysen — UTAN GRÄNSSNITTETS TERMINOLOGI

— Det är i varje fall författarens allmänna intryck i ämnets uppdagande, och som läsaren själv kan kontrollera genom egna observationer.

högre gränssnitt

Elementära gränssnittet består av singulära elementära funktionsranger. Högre gränssnitt består av dubbel, trippel eller multipla rangtermer i samma rang eller mixade i skilda ranger. En inhomogen variants partikulära lösning växer i komplexitet med växande sammansättning i variantens funktionella gränssnitt.

EFTERSOM FUNKTIONSRANGERNA INTERNT INTE KAN kommunicera genom deriveringar på flera än max två ranger åt gången, kan Integrander som innehåller strikt sammansatta funktionsranger aldrig relatera till grundintegraler. Det är helt uteslutet.

För att lösa sådana sammansatta integraler finns det (främst) tre metoder:

1. Metod 1 i partiell integration (den enklaste), gäller för alla ranger i valfri mix

2. Metod 2 i partiell integration (den svåraste), gäller för alla ranger i valfri mix

3. Den speciella exponentintegralens metod, gäller bara för DerivataSoliderna* e^nx and xⁿ (i valfri mix)

* deras deriveringar inkräktar aldrig på andra ranger

INTEGRALEN

MED DEN RELATERADE MATEMATIKENS BEGREPP


		integralen
y	=	ò	y’	dx
lösningen			integranden	integrationskonstanten

ANLEDNINGEN TILL varför vissa integrander är svårare att lösa än andra är mycket en förklaring i termer av nivån på eller gränssnittets deriverbarhet för ett givet uttryck. När vi väl en gång sett skymten av strukturen bakom denna befriande insikt, lärande att särskilja mellan singulära och sammansatta rangtermer i ett givet uttryck, blir analysen av integraler eller integralevaluering i allmänhet och av alla typer och sorter (mycket) enklare.

PARTIELL INTEGRATION för att exemplifiera [från EXP(5) i Formlagarna][konstanter frånsett], arbetar av princip alltid på ett högre gränssnitt än det elementära. Vi kan se det direkt genom

f (x)[·] i Metod 1 och [·]òf (x) i Metod 2. Det vill säga, en partiell integrand i allmänhet kan inte direkt relatera till en grundfunktion. ALLTSÅ, högst elegant, används partiell integration för att expandera det elementära gränssnittet till högre nivåer av fundamentala integraler. Detta inte bara breddar den formella aspekten, utan också vårt vokabulär i förklarandet och förståendet av vad som egentligen pågår när vi integrerar.

Lösandet av integraler, från dem vi redan känner, betyder då helt enkelt att antingen expandera gränssnittet eller utveckla dess uttryckbarhet med resultat i möjligheten till en större mängd lösningar, samband och kombinationer. Från denna utgångspunkt kan vi också klassificera varje typ av integrand i två fundamentala kategorier : tillämplig — eller inte — inom ett givet gränssnitt.

Betrakta till exempel de två synbarligen olika integranderna

1 1

———————— ————

ax² + bx + c 1+x²

Är de kompatibla i gränssnitten? Det vill säga, kan den ena härledas ur den andra inom samma gränssnitt? Om ja, finns det en elementär lösning. Om nej, måste metoder utom det aktuella gränssnittet användas, se vidare exempel nedan i Integralkalkylen genom rangterminologin. I detta fall ser vi direkt att svaret måste bli ja helt enkelt genom att sätta a=1, b=0 och c=1 som ger 1+x². Dvs., alla gäller. Det betyder att integralen till den vänstra integranden kan utvecklas från integralen till den högra integranden. [Alla sådana lösningar görs genom mer eller mindre enkla differentialtransformationer].

Integralkalkylen genom rangterminologin

AVGÖRANDE SATSER INOM INTEGRALKALKYLEN

Alla integraler som sammansätts enligt någon metod måste tvunget bli rangbegränsade.

Denna viktiga och klargörande detalj sammanhänger med att funktionsrangerna sinsemellan inte kommunicerar genom derivering på flera än maximalt två ranger. En integralekvation kan med andra ord aldrig vara funktionsmässigt heltäckande för alla möjliga matematiska funktionstyper [enbart trigonometrin innehåller åtta grundtyper]. En integralekvation i generell mening kommer därför i ett eller annat avseende alltid att uppvisa ”luckor” eller ”stopp” i sin ”algebraiska kontinuitet” beroende på integrandens sammansättning.

Anledning:

Du vill förstå integralers ”allmänna sammansättning och mekanik” (men fattar inte riktigt sakens kärna).

Dessa luckor (som reducerar eller eliminerar den aktuella integralen för vissa parametervärden) omtalar att lösningen innefattar andra ranger. Vissa sådana integraler har en lucka (eller två — med förgreningar), och vissa har periodiska luckor.

Integralkalkylens MetodSats för täljar-nämnar-kommutativiteten

Denna sats erinrar lagen för integralutvecklingar på redan sammansatta systemintegraler

EXEMPEL PÅ EN SYSTEMINTEGRAL som utvecklats genom partiell integration

ò xⁿ/(Ö a–x) dx = –2(Ö a–x)[ xⁿ + _m=₁_®_n å x^n–m(a–x)^m2^m[ (n–t)_t_! ]/(2m+1)!! ] ; t = m–1

Om vi kollar upp denna integralform i ”världens mest kraftfulla interaktiva integrallösare på webben”

[http://www.integrals.wolfram.com/index/jsp] 2009-01-04,

Wolfram Online Mathematica Integrator — The world’s only full-power integration solver

får vi svaret

ò xⁿ/(Ö a–x) dx = –2(Ö a–x) xⁿ (x/a)^–n (hypergeometriska funktioner)

där termgruppen i ovanstående parentes ”hypergeometriska funktioner” motsvarar källans led av termer — som kopplar till en ICKE klargjord (serie-) beskrivning (som man måste studera särskilt för att få ut något begripligt av).

— Exemplet visar att även ”världens mest avancerade integrallösare (Januari 2009)” KAN vara problematisk att umgås med.

Eftersom integralsamband inte är operativt kommutativa för multiplikation

— inverserna behärskas av logaritmintegralerna och de ordinära basfunktionerna av exponentialintegralerna

— kan man heller inte godtyckligt sammanställa en integralekvation i tanken om att den ska kunna utföra ”alla möjliga produkter”.

Variabeln i täljare eller nämnare är en ytterst känslig detalj för integralerna medan de operativa funktionerna är helt okänsliga för sådana detaljer.

[Därför är kvotderivatans integralaspekt tämligen värdelös som integralt verktyg].

Satsen innebär att typformen, exemplifierat, x^c(P)ⁿ kommer att kräva ett särskilt integralkomplex för alla c större noll och ett särskilt integralkomplex för alla c mindre än noll.

EXEMPEL (här utan bevis)

Vi betraktar som ett exempel integrander av typen

xⁿÖ a–x²

Med n större än 0 är integralerna rangmässigt duala. Jämna n ger en blandning av arcusrangen och x-potenser, udda n ger rena x-potenser. En och samma integralmetod kan användas för att bestämma individerna.

Med n mindre än noll och heltaligt är rangerna triala. Logaritmrangen tillkommer till de bägge ovannämnda. Här måste man använda tre olika integralekvationer för att kunna bestämma individerna; med två I-ekv. erhålls endast individer med antingen jämna n eller udda n beroende på integrandens typform.

Metod:

1.Studera frekvent funktionsrangerna och deras deriverande karaktärer. En integral är aldrig annat än en derivatas omvändning.

Rangerna beskrivs utförligt i Gränssnittets Funktionsranger.

2. Studera (tal-) teorin med funktionsklasserna och funktionsbegreppen repeterande. Beskrivningen av matematiken på den här nivån är omöjlig utan en exakt kopplande nomenklatur.

Allmän klassifikation av varianter

Derivatans definition y’=dy/dx beskrivs i relaterad matematik såsom en ny funktion, variationsekvationen (eg. variationsfunktionen) eller varianten y’ med differentialekvationen dy=y’dx och därmed fundamentalintegralen eller ytintegralen òdy=òy’dx=y. Derivatan till en funktion (y) skrivs här explicit

Dn y = y’. Gränsvärdesbegrepp existerar inte. Se utförligt från Nollformsalgebran.

[HL anger högerdelen av ett led, VL vänsterdelen].

För en enhetlig klassifikation av alla typer av varianter, är det bekvämt att systematisera deras teckningar på den elementära formen

y’ + ay = 0 ................................ första ordningens variant

y’’ + ay’ + by = 0 ................................ andra ordningens variant

y’’’ + ay’’ + by’ + cy = 0 ................................ tredje ordningens variant

y⁽ⁿ⁾ + a₁ y^(n–1) + a₂ y^(n–2) + …+ a_n y = 0 ........... n:te ordningens variant

Homogena och inhomogena varianter

Antalet primtecken (n) motsvarar antalet deriveringsnivåer associerade med den aktuella varianten. Ovanstående elementära varianttyp med HL=0 kallas homogen. Om HL är något annat än noll, kallas varianten inhomogen.

y’’ + ay’ + by = 0 .............................................. homogen variant ;

y = yH ................................................................ Homogenen

y’’ + ay’ + by = [·] ............................................ inhomogen variant, [·] ¹ 0, [·] den obekanta ;

y = y_P ................................................................. Partikulären

Allmän form, linjära och icke linjära varianter

Punktparentesen [·], den okända, kan vara vilket som helst uttryck — skilt från noll.

Ett uttryck skrivet på ovanstående typform med noll i HL kallas också i allmänhet för ett uttryck skrivet på allmän form. Varianttypen ovan är klassificerad som linjär därför att alla y-termer är av en och samma grad ett. Om detta inte är fallet [vilken som helst av termerna kan skilja] är varianten klassificerad som en icke-linjär variant. Om alla vidhängande koefficienter i den aktuella varianten också är strikt numeriska kvantiteter, så som antyds i de ovanstående elementära leden, sägs varianten vara given med konstanta koefficienter (abc…) — i motsats till y-associerade faktorer av formen f(x). Om varianten har en eller flera sådana funktioner säger man att varianten är given med en eller flera variabla koefficienter.

Generellt — grundalgoritm

OM i en given variant … Ay’’’+By’’+Cy’+Dy=[·] y är känd, bildar varianten V=LP ett spår eller ett derivataprogram i HL=[·]. Känner man grundfunktionerna och deras deriverande egenskaper kan y på motsvarande sätt lösas genom att analysera [·], [·] den obekanta.

LÖSNINGARNA

LÖSNINGARNA — Homogena varianter

Fundamentala varianten dy/dx=y’=y ger den fundamentala differentialekvationen dy/y=dx med den integrala lösningen lny=x=F(x). Se även i Bastablån.

Generalisering av Denna fundamentalintegral ger universalen

lny = x+K. Uttryckt i funktionsvärdemängden (y) blir universalen

y = e^x+K

=C e^x, C ¹ 0.

Som (C e^x)’=C e^x, vilket ger ursprunget y=y åter, kan denna universals variant också skrivas på den allmänna formen y’–y=0.

Då kan typvarianten y’+ay=0 (1 i y’–1y=0 ersatt av det allmännare –a) direkt återföras på universalen

y = C e^–ax ............................ universalen till varianten y’+ay=0

Vilket vill säga, y’=–aC e^–ax=–ay.

TRANSFORMATORN

SPÅRAS UTVECKLINGEN BAKLÄNGES får man e^axy=C , =e^F(x)y, och därmed

[e^F(x)y] = [C ]

[e^F(x)y]’ = [C ]’ ..................... VL tillämpad på produktderivatan (AB)’=AB’+A’B ger:

e^F(x)y’ + f (x)e^F(x)y = 0 · e^F(x) ................ e^F(x) är optimal i HL för vilken som helst homogen variant ;

y’ + f (x)y = 0

EXPONENTFUNKTIONEN e^F(x) katalyserar uppenbarligen en principiell matematisk transformation [konv. karaktäristisk ekvation]. I RELATERAD — beskrivande — matematik kan därför e^F(x) kallas för en transformator (av lat. transforma’re, omvandla; omvandlare) [konv. integrerande faktor]. I relaterad matematik kan föremålet för omvandlarens produkt språkriktigt därför också benämnas verbalsubstantivt transform. Se även Varianternas Transformer nedan. Med förenklingen F(x)=nx som ger f(x)=n=–a katalyserar transformatorn e^nx transformationer (med tillhörande transformer) på följande form från givna enkla varianter:

VARIANTEN y’ + ay = 0:

I y insätts transformatorn e^nx=y med x som den beroende variabeln (funktionsvariabeln):

y’ + ay = 0

ne^nx + ae^nx = 0 ;

e^nx(n + a) = 0 ;

(n + a) = 0 ;

n = –a ;

VARIANTEN y’’ + ay’ + by = 0:

I y insätts transformatorn e^nx=y med x som den beroende variabeln (funktionsvariabeln):

y’’ + ay’ + by = 0 ;

n²e^nx + ane^nx + be^nx = 0 ;

e^nx(n² + an + b) = 0 ;

n² + an + b = 0 ;

Efter lösning [Se Andragradsekvationens Lösning]

n = –(a/2) ± [ Ö(a/2)²–b ]

Varianternas transformer

VARIANTER av högre ordning ger i syntes transformationerna (eller transfo´rmerna)

n + a	= 0	.......... första ordningens variant
n² + an + b	= 0	.......... andra
n³ + an² + bn + c	= 0	.......... tredje
n⁴ + an³ + bn² + cn + d	= 0	.......... fjärde
n^m+ an^m^–1+ bn^m^–2+ cn^m^–3+ dn^m^–4 +…	= 0	.......... m:te

Jämför den inledande mera förenklade beskrivningen.

Vilket vill säga: Föregående omnämnda »bekvämligheten att systematisera varianternas teckningar» på den elementära formen är tydligen REDAN en i matematiken (logiken) inneboende ordning — som utkristalliserar sig spontant med analysen av matematiken på denna nivå, enligt ovanstående genomgång.

Genom att lösa variantens transform finner varianten sin universal. Exponenten till n är VARIANTENS DERIVERINGSGRAD. I det första och enklaste fallet där n=–a blir lösningen alltså y=e^nx=e^–ax (den optimala konstanten C här utelämnad eller satt lika med 1).

Att finna universalen till en HOMOGEN variant har alltså reducerats till problemet att lösa variantens aktuella transform (y_H).

För att kunna hantera transformer av högre grad än 2 krävs omfattande insikter i EKVATIONSKUNSKAP;

De centrala begreppen är polynomstrukturer, faktoriseringar, partialbråksuppdelningar (lösandet av linjära ekvationssystem).

EMELLERTID finns (idag 2008, många) avancerade datorprogram som kan utföra (många av) dessa uppgifter rent maskinellt

— men som också (i allmänhet) är (extremt) dyra, och dessutom ingalunda enkla att använda för den som inte känner till ekvationslärans språk.

EMELLERTID (glädjande nog): UTVECKLINGEN PÅ WEBBEN går, tydligen, mot »mera allmängiltighet»

— allt flera interaktiva (kraftfulla) matematiska verktyg ser dagens ljus och som kan användas helt gratis.

Så finns t.ex. för direkt integrala lösningar webbkällan (dock ännu Januari 2009 enbart på engelska)

[http://www.integrals.wolfram.com/index/jsp] 2009-01-04,

Wolfram Online Mathematica Integrator — The world’s only full-power integration solver

För (enklare) partialbråksuppdelning finns webbkällan (också tyvärr ännu enbart på engelska)

[http://www.calc101.com/webMathematica/partial-fractions.jsp] 2009-01-07,

WebMATHEMATICA — Step-by-Step Partial Fractions, Sam Blake;

länk från @INTERNET Wikipedia Partial fraction, automatic step-by-step partial fractions 2009-01-07

Utnyttja med fördel dessa som KOMPLEMENT om uppgiften gäller att kontrollera egna lösningar — till studium och jämförelse.

Terminologi i beskrivningen av lösningen till en variant

TypExempel Konventionellt (konv.)

VARIANT y’’ + ay’ + by = [·] ”differentialekvation”

TRANSFORM n² + an + b = [·] ”karakteristisk ekvation”

Tablå för Lösningarna Till

HOMOGENA VARIANTER

lösningarna till 1:a ordningens varianter

lösningarna till 2:a ordningens varianter

lösningarna till n:te ordningens varianter

Universalerna till första och andra ordningens Homogena Linjära Varianter

LÖSNINGARNA TILL HOMOGENA VARIANTER genom transformatorn e^nx i PREFIXxSIN

variant V	transform	lösning (rötter)	universal lösningen till y i V
y’ + ay = 0	n + a = 0	n = –a	y = Ce^–ax
y’’ + ay’ + by = 0	n² + an + b = 0	n = –(a/2)±[Ö(a/2)²–b]	se [‡1] nedan
lösningen till andra ordningens Homogena Linjära Varianter:
‡[1] Ro	n+= u ; n–= v	reala, olika rötter	y = Ce^ux + De^vx
‡[1] Rd	n=u=v=r	real, singulär dubbelrot	y = e^rx(Cx + D)
‡[1] C	n₊= a+ib ; n_–= a–ib	komplexa, olika rötter	y = e^a^x(Csinbx + Dcosbx)

Universalerna till m:te ordningens Homogena Linjära Varianter

LÖSNINGARNA TILL HOMOGENA VARIANTER av godtycklig grad (m) härleds från lösningarna till andra ordningens homogena varianter, se ovan.

Detta sker genom den allmänna polynomform som transformen för m:te varianten uppvisar. Genom Ekvationskunskapen finns metoder som kan uttrycka varje polynom genom ordningen av polynomets rötter. Resultatet har direkt koppling till andra gradens polynom, med tillägg av begreppet multiplicitet. Lösningen till n:te ordningens homogena varianter (vars komplexa del garanterat inte kan härledas/begripliggöras i modern akademi) skrivs då

y^(m)	+	a₁ y^(m–1)	+	a₂ y^(m–2)	+	…	+	a_m y	= 0	... m:te ordningens variant
n^m	+	a₁ n^m–¹	+	a₂ n^m–²	+	…	+	a_mn	= 0	... m:te ordningens varianttransform, reguljärt polynom

;

transformens rottyp universalen till V via y ; LÖSNINGEN

—————————————————————— ——————————————————————

reala olika rötter y = C₁eⁿ1^x + C₂eⁿ2^x + C₃eⁿ3^x + C₄eⁿ4^x …

Index för C och n specificerar m:te ordningens variant

reala multipla rötter y = e^rx(C₁ + C₂x + C₃x² + C₄x³ + … + C_mx^m^–1)

Index för C specificerar (m:te ordningens variant om alla rötter är identiska, och) den singulära rotens multiplicitet

komplexa olika (s.k. parvis konjugerade) rötter y = e^a^x(C sinbx + D cosbx)

C = C₁ + C₂x + C₃x² + C₄x³ …

D = D₁ + D₂x + D₃x² + D₄x³ …

Index för C&D specificerar parmultipliciteten (max m:te ordningens variant div 2)

EXEMPEL i PREFIXxSIN

Kort orienterande illustrerande exempel

— se även i EXEMPEL|Komplexa olika (s k parvis konjugerade) rötter i Lösningarna till n:te ordningens homogena varianter:

Bestäm universalen till den homogena varianten

y’’’’’ + y’’’’ + 2y’’’ + 2y’’ + y’ + y = 0

y⁽⁵⁾ + y⁽⁴⁾ + 2y⁽³⁾ + 2y⁽²⁾ + y⁽¹⁾ + y⁽⁰⁾ = 0

Lösning

Transformen är n⁵+n⁴+2n³+2n²+n+1 = (n+1)(n²+1)². Rötterna är

(n+1) ......................... en singulär rot med värdet –1

(n²+1)² ...................... 2 par komplext konjugerade rötter, faktoriserade rotvärdet ±i1

Inre transformens rötter till n²+1 blir [Andragradsekvationens allmänna lösning]

n = 0 ± i1 ................. inre transformens komplexa rötter

Deluniversalen för den singulära roten blir C e^–x.

Deluniversalen för parrötterna, via a=0 (exponentkoefficienten a i e^a^x) och b=1 (vinkelkoefficienten n i [sin|cos]nx) med parmultipliciteten lika med 2, blir alltså

y = e^0x([C₂x + C₁]sin 1x + [D₂x + D₁]cos 1x)

y = [C₂x + C₁]sinx + [D₂x + D₁]cosx

Svar: Universalen till homogenvarianten y’’’’’ + y’’’’ + 2y’’’ + 2y’’ + y’ + y i PREFIXxSIN är

y = C e^–x + [C₁ + C₂x]sinx + [D₁ + D₂x]cosx

Universalerna till

n:te ordningens Homogena Linjära Varianter

Universalerna till n:te ordningens Homogena Linjära Varianter

— Från M2001_4.wps | UniVar.wps s78

n:te ordningens varianter

Generalisering av lösningarna från

2:a ordningens varianter

(1) reella olika rötter

y = C₁eⁿ1^x + C₂eⁿ2^x + C₃eⁿ3^x + C₄eⁿ4^x …

Index för C och n specificerar m:te ordningens variant;

Summan av alla de m partiella universalerna sammansätter den totala universalen om kvoten mellan delarna är variabel, se universalsatsen, kvoterna ansluter här till de olika n-exponenter som ger kvoten dess form Ae^(a–b)x, kvoten således x-beroende och därmed variabel.

Exempel [Jmfr. ITK 9 Brandqvist, 1962 s47]

y’’’ – 2y’’ – y’ + 2y = 0 ............. den homogena varianten

n³ – 2n² – n + 2 = 0 .................. den homogena variantens transform

Insättning för iteration genom omflyttningen n³ – 2n² + 2 = n ger oss direkt en rot lika med n₁=1 [Iterationer initieras allmänt via kvantiteten 1, eller noll]. Det ger oss en divisionsfaktor (n–1) som, via faktorsatsen, kan användas för att analysera (uppdela) tredjegradens ekvation i den givna divisionsfaktorn och ett annat faktorblock som motsvarar faktorerna i typekvationer av andra graden. Analysen utförs då genom polynomdivision. Vi kan emellertid, i detta fall, nå ett direkt rakt-på resultat; antingen genom iterationsalgoritmen [vilken mestadels men inte alltid är den enklaste och mest effektiva metoden] — i vårt exempel ger initieringsvärdet 0 direkt ett rotvärde n=2 — eller genom »direkt undersökning» (alltså mer eller mindre intuitionsgrundat genom enkla prövningar i huvudet) i den givna formen som visar att också n=–1 är en lösning. Om vi utnyttjar överflyttningen explicit som leder till andra ekvationsgradens iteration, (n³ – n + 2)/2 = n², ser vi enklare att den redan anmälda roten n=–1 är en giltig lösning. Därmed har vi funnit transformens alla tre lösningar:

n₁=1 .......................................... transformens första rot

n₂=–1 ........................................ transformens andra rot

n₃=2 .......................................... transformens tredje rot

Vi finner också dessa rötter direkt från

n³ – 2n² – n + 2 = n²(n–2) – (n–2) = (n–2)(n²–1) = (n–2)(n+1)(n–1); (n=2), (n=–1), (n=1).

Svar: Universalen till den homogena varianten y’’’ – 2y’’ – y’ + 2y är y = C₁e^x + C₂e^–x + C₃e^2x .

(2) reella multipla rötter (singulära dubbelrötter i fallet 2:a ordningens varianter)

y = e^rx(C₁ + C₂x + C₃x² + C₄x³ + … + C_mx^m^–1)

Index för C specificeras (m:te ordningens variant om alla rötter är identiska, och) den singulära rotens multiplicitet, exemplifierat;
m

1. y = e^rx(C )

2. y = e^rx(Cx + D)

3. y = e^rx(Cx² + Dx + E)

4. y = e^rx(Cx³ + Dx² + Ex + F)

m. y = e^rx(polynom av grad m–1 med konstanta koefficienter)

Polynomet motsvarar generaliseringar av fundamentalintegralen i lika många steg (m) som multipliciteten anger, dock högst variantens ordningstal.

Exempel [Jmfr. ITK 9 Brandqvist, 1962 s48n]

y’’’– 3y – 2y = 0 ................................. den homogena varianten

n³ – 3n – 2 = 0 ................................... den homogena variantens transform

Insättning för iteration via utbrytningen n(n² – 3 – 2/n) = 0 ger oss via iterationen n² = 3+2/n med n från 1 en entydigt positiv rot lika med n=2 enligt n² = 5; 3,89; 4,013; 3,99; … 4. Iterationsalgoritmen enligt omskrivningen n²–3 = 2/n ger oss med n från 1 direkt den andra roten n=–1. Någon ytterligare rot kan vi inte få ut av den givna transformen. Någon av rötterna n=2 eller n=–1 bör alltså vara en dubbelrot. Faktoriseringen görs, som vi vet, på rotens negativa värde. De bägge rötternas engradiga faktorformer blir alltså (n–2)(n+1). För att pröva vilken av faktorformerna som är dubbelroten undersöker vi vilket av alternativen (n–2)²(n+1) eller (n–2)(n+1)² som ger transformen

n³ – 3n – 2. Vi finner att det senare alternativet (n–2)(n+1)² ger transformen. Det är alltså n=–1 som är dubbelroten. Därmed har vi funnit samtliga tre transformens lösningar:

n₁₂=–1 ............................................... transformens enda dubbelrot

n₃=2 .................................................... transformens tredje rot

Dubbelrotens monala multiplicitet m är lika med 2 vilket för dubbelroten betyder deluniversalen

y = e^rx(Cx + D) med r=–1. Singulärrotens deluniversal är Ae^rx med r=2. Med enhetliga beteckningar C för de godtyckliga konstanterna blir alltså universalen totalt lika med y = C e^2x + e^–x(C₀ + C₁x).

Svar: Universalen för den homogena varianten y’’’– 3y – 2y är y = C e^2x + e^–x(C₀ + C₁x) .

(3) komplexa olika (s k parvis konjugerade) rötter

y = e^a^x(C sinbx + D cosbx)

C = C₁ + C₂x + C₃x² + C₄x³ …

D = D₁ + D₂x + D₃x² + D₄x³ …

Index för C&D anger parmultipliciteten (max m:te ordningens variant div 2)

HÄRLEDNING:

Om tolkningen är riktig i

SATSEN OM PARVISA KOMPLEXA RÖTTER

betyder ett givet heltaligt polynom med reella [ej i-tecknade] koefficienter att komplexa rötter till detta alltid uppträder parvis.

En multiplicitet i fallet komplexa rötter måste därmed alltid vara av parform. Alltså typ, 2, 4, 6, 8 … rötter, aldrig ett udda antal.

Om vi återknyter till ovanstående härledning till 2:a ordningens varianter med komplexa rötter, kan vi av centralledet nedan sluta oss till hur den vidare strukturen kommer att te sig då parformerna utvidgas. Se följande förklaring, ehuru den inte omedelbart framgår.

parmultiplicitet

y = ay₁ + by₂ 2:a ordningens varianter 1

y = (a₂x + a₁)y₁

+ (b₂x + b₁)y₂ 4:e ordningens varianter 2

y = (a₃x² + a₂x + a₁)y₁

+ (b₃x² + b₂x + b₁)y₂ 6:e ordningens varianter 3

På samma sätt som i fallet singulära dubbelroten för 2:a ordningens varianter måste vi här anta en stegvis generalisering av fundamentalintegralerna motsvarande dubbelstegen — i annat fall ”hänger vi bara på” lösningen till 2:a ordningens varianter. För att t ex härleda en parmultiplicitet 3 måste vi förutsätta minst en 6:e ordningens variant, men inte 6 generaliseringar!, utan endast 3, eftersom rötterna inte kan avse alla fundamentalsteg, endast vart annat!

[

I annat fall, SATSEN OM PARVISA KOMPLEXA RÖTTER, skapar vi förutsättning för flera komplexa rötter än vad varianten har utrymme för. Detta är också helt i sin ordning för universalernas del, eftersom de inget annat är än den mest generella ekvation [för y], se Universalen, vars derivataprogram [ay+by’+cy’’+…] den givna varianten utpekar

denna detalj är — således — omöjlig att beskriva för den moderna akademin i anledning av dess idé om ”integrationskonstanten C”

— denna detalj är en av anledningarna varför modern akademi garanterat inte förmår förklara ämnet för studenten

Om detta är riktigt ges då Motsvarande slutlösningen exemplifierat enligt

y = e^a^x(C sinbx

+ D cosbx) 2:a ordningens varianter 1

y = e^a^x([C₂x + C₁]sinbx

+ [D₂x + D₁]cosbx) 4:e ordningens varianter 2

y = e^a^x([C₃x² + C₂x + C₁]sinbx

+ [D₃x² + D₂x + D₁]cosbx) 6:e ordningens varianter 3

…

[Jmfr. ITK9 Brandqvist, 1962 s56, äv. s52ö, noterat skriv/tryckfel s50ö (y₁= y₂)]

Exempel

Vi observerar, med en given variant, att det på inget sätt måste vara så att hela variantens form nödvändigtvis måste ansluta till, till exempel, kategorin komplexa rötter. En variant kan innehålla en godtycklig mix av alla de ovannämnda typformerna. Vi ska här studera ett exempel med utgångspunkt från den faktoriserade transformens polynom (n+1)(n²+1)².

Bestäm universalen för den homogena varianten

y’’’’’ + y’’’’ + 2y’’’ + 2y’’ + y’ + y = 0

y⁽⁵⁾ + y⁽⁴⁾ + 2y⁽³⁾ + 2y⁽²⁾ + y⁽¹⁾ + y⁽⁰⁾ = 0

Lösning

Transformen är

n⁵ + n⁴+ 2n³ + 2n² + n + 1. Detta polynom har ekvivalenten

(n+1)(n²+1)².

[Erinra divisionsalgoritmen; Genom en enkel — när vi väl känner till hemligheten — huvudräkning finner vi »direkt» att divisionen av den givna transformen med n+1 ger n⁴+2n²+1. En kort begrundan över detta resultat (se första binomlagen) ger ekvivalenten (n²+1)²].

Vi har därmed i exemplets ljus

(n+1) ......................................... en singulär rot med värdet –1

(n²+1)² ...................................... 2 par komplext konjugerade rötter, rotvärde ±i1

Inre transformen för n²+1 blir motsvarande andra gradens ekvation

n² + 0n + b = 0 ......................... 2:a gradens ekvation, normalform, preparerad

n² + an + b = 0 ......................... 2:a gradens ekvation, normalform, allmän

n = – (a/2) ± Ö(a/2)²–b ............ 2:a gradens ekvation, lösningen preparerad

n = – (0/2) ± Ö(0/2)²–b ............ 2:a gradens ekvation, allmänna lösningen
a=0, b=1;

n = 0 ± Ö–1 ................................ inre transformens rot

n = 0 ± i1 ................................... inre transformens komplexa rötter

Deluniversalen för singulärroten blir

C e^–x.

Deluniversalen för parrötterna, via a=0 (exponentKoefficient a i e^ax) och b=1 (vinkelKoefficient n i [sin|cos]nx) med parMultipliciteten lika med 2, blir således i PREFIXxSIN

y = e^0x([C₂x + C₁]sin 1x + [D₂x + D₁]cos 1x)

y = [C₂x + C₁]sin x + [D₂x + D₁]cos x

Svar: Universalen till den homogena varianten y’’’’’ + y’’’’ + 2y’’’ + 2y’’ + y’ + y i PREFIXxSIN är

y = C e^–x + [C₁ + C₂x]sin x + [D₁ + D₂x]cos x.

END n:te ordningens varianter

inhomogena varianter

PARTIKULÄRA

Lösningarna Till

INhomogena VARIANTER

partikulära lösningarnas allmänna metod

END.

UNIVERSALENS DEFINITION

GENERALISERINGSBEGREPPET I RELATERAD MATEMATIK FÖR FUNDAMENTALINTEGRALEN

Definition ENLIGT RELATERAD MATEMATIK:

Universal, den mest allmänna primitiva ekvation från vilken en variant [variationsekvation, samma som derivata dy/dx=y’] kan erhållas.

En universal är av den enkla och allmänna formen

y = f (x) + C ...................... universalen

REFERERA till Integral-funktion-identitetens kriterium. Där ges fullständig förklaring.

Konstanten C — ekvationskonstanten — införs ENLIGT RELATERAD MATEMATIK manuellt efter våra egna önskemål och är ingen »egenskap i matematiken». Införandet av ekvationskonstanten C kallas i RELATERAD matematik att generalisera en integral, en variant eller annat funktionsuttryck för att därmed erhålla dess universal. Erinra IntegralFunktionsIdentitetsKriteriet.

Observera att

· termen ”generaliserad integral” har en helt annan innebörd i den moderna akademins lärosystem
[ref. MATEMATIKLEXIKON W&W 1991 s142sp1m];
[ref. ITK-8 s58];
Funktionskurvor med xy-axlarna som asymptoter (kurvan närmar sig axeln obegränsat utan att någonsin nå fram) blir exempel på generaliserade integraler i konventionell mening: skillnaden ligger enbart i en särskild gränsdefinition för integralintervallet som skiljer bestämda integraler från obestämda. I relaterad matematik [Se Fundamentalintegralen] behövs ingen sådan särskild formalia då varje särskild integral i vilket BESTÄMT fall alltid måste utvärderas via en sin eventuella integralkonstant. Se vidare i bestämda och obestämda integraler.

· termen universal (som ovan — och därför) inte är representerad i den moderna akademins lärosystem

Termen Universal

I relaterad matematik kan vi alltid lägga till en ekvationskonstant (C) till en viss funktion eller integral, vilket i motsvarande relaterad logik kallas att generalisera integralen. Det betyder att funktionen placeras i vertikalled och därmed antar den mest allmängiltiga form som funktionen kan behandlas på. Den kan då kallas universal, med den meningen. Det finns också en universalsats som gäller för alla funktioner. Denna sats har endast betydelse inom den högre analysen, vilken behandlas här. Se Universalsatsen.

Examineringsexempel:

Nedanstående termer används genomgående i beskrivningen; Exemplet är en normalmall. Tillförsäkra dig om att du förstår, kan relatera och beskriva i detalj var och en av de följande fem fundamentala uttrycksformerna. Exemplet använder hyperbelns ekvation y=(1+x²)^0,5 med dess tangensform eller derivata y’=x(1+x²)^–0,5, så du behöver inte utföra annat än enkla huvudräkningar till lösningarna.

Exempel och övning:

Här används grundbegreppen från Atomtriangeln och avsnitten i Matematiken1 och Matematiken2;

Följande exempel ger en viss orientering till bekantskap; Visa för den nedan givna varianten

y’ = x(1+x²)^–0,5

dess

a universal

b lokala universal med y(Ö3)=3

c obestämda integral (fundamentalintegralen)

d fundamentalintegrals integralkonstant (Q)

e bestämda integral

Svar:

a y = (1+x²)^0,5 + C

b y = (1+x²)^0,5 + 1 ; [ 3 = (1+(Ö3)²)^0,5 + C , C = 1 ]

c y = (1+x²)^0,5

d y(0) = 1

e y = (1+x²)^0,5 – 1

Metod, samtliga fall

Man söker först alltid fundamentalintegralen (variantens enda singulära unika primitiva funktion, c ovan) till den givna varianten. Sedan beror de vidare lösningarna på vilken information som efterfrågas.

UNIVERSALSATSEN

Universalsatsen är helt avgörande för den högre analysens LED

Universalsatsen. EN UNIVERSAL y=f (x)+C sammanfattar obegränsat många OLIKA lösningar eller positioner: en universal kan omöjligen ha två lika lösningar: en positionspunkt kan omöjligen uppdelas i ”flera lika”. En position (lösning) är och förblir EN UNIK position. En universal y=f (x)+C kan alltså uppdelas i minst två olika deluniversaler eller LÖSNINGAR y_a och y_b enligt y=y_a+y_b. Jämför universalen y=f (x)+C med dellösningarna y_a=x+1 och y_b=x–1. Bägge är dellösningar i universalen

y=f (x)+C, summan av bägge (y=2x) ingår också i universalen y=f (x)+C. Den ena kan erhållas ur den andra genom KVOTEN

y_a/y_b = (x+1)/(x–1) = 1 + 2/(x–1) = g(x) som alltså i sig själv är en funktion, en variabel. Är KVOTEN däremot en konstant enligt y_a/y_b=C (jämför y_a=y_b) får man en annan funktion (y_a=Cy_b) och därmed gäller INTE dellösningarna som deluniversaler: x+1 kan inte erhållas ur C(x–1);

En variabel kan inte erhållas från en konstant. Härav följer UNIVERSALSATSEN

universalen är summan av alla deluniversaler om kvoten mellan dessa är variabel, och endast då

Om det finns n stycken olika lösningar till en variant av TILL EXEMPEL en faktoriserad form typ

(P₁)(P₂)(P₃)(P₄)…(P_n), kan alltså den totala eller universella lösningen likväl skrivas på summan av dellösningarna enligt

(p₁)+(p₂)+(p₃)+(p₄)+…+(p_n) eftersom varje dellösning i vilket fall, oberoende av utseendet, gäller självständigt enligt universalsatsen.

EXEMPEL:

En universal y = Ae^nx har två (inre) rötter y_a=C e^ax och y_b=De^bx, ACD godtyckliga konstanter. Kvoten y_a/y_b är INTE konstant [Ee^(a–b)^x].

Resultat: Universalens sammansatta form med bägge lösningarna (deluniversalerna) innefattade kan då skrivas korrekt y = Ce^ax + De^bx.

Universalsatsen antyds i vissa matematiska läromedel — men den beskrivs inte. Jämför:

En variabel kan inte erhållas från en konstant. Resultat: satsen kan INTE härledas från MAC.

Integral-funktion-identitetens kriterium:

IntegralFunktionsIdentitetsKriteriet (IFIK)

Se från INTEGRALENS DEFINITION i Atomtriangeln

en integral är alltid ett singulärt unikt funktionsmässigt uttryck;

en integral kan aldrig addera, bygga eller skapa konstanter

— intervallbegreppet för en konstant kan inte skapas eller förintas

— således refererar en integral alltid till en funktion,

— aldrig till ett uttryck med isolerade separata konstanter:

en integral är bara en enda primitiv unik funktion

Jämför derivatan till funktionen y=kx genom positionsformen;

y=kx, y₀=kx₀; y’=dy/dx=(y₀–y)/(x₀–x) = (kx₀–kx)/(x₀–x) = k(x₀–x)/(x₀–x) = k

Om k=0 är även derivatan 0.

För en fristående konstant uttryckt av y=k=y₀ ges på samma sätt

y’=dy/dx=(k–k)/dx = 0/dx = 0

Eller som tidigare konstaterats via samma typled: y=k har ingen tangent.

y=k har ingen tangent

Se även vidare förtydligande nedan i Nollintegralen.

NOLLINTEGRALEN

DEN BESTÄMDA Integralen för noll är noll: dy/dx = y’ = 0 ;

ò dy = y = ò 0·dx = 0 ò dx = 0x = 0

Det som saknar intervall har heller ingen integral.

Derivatan till en konstant C är noll — inte därför att derivatan ÄR noll, utan

— därför att derivatan till en konstant inte existerar:

y₀=y=C; dy/dx = y’ = (y₀–y)/dx = (C–C)/dx = 0/dx = y’= 0

Derivatan till en konstant finns inte

— därför att det inte finns någon funktionsbyggnad, inget relationsmässigt intervall att beskriva någon variation för.

Jämför modern akademi — som omöjliggör ovanstående klargörande:

ò 0dx = 0

Särskilt Relaterad beskrivning

DEN MODERNA AKADEMINS ALLMÄNNA VÅLD PÅ INTEGRALKALKYLEN

Integralen för noll är noll

Betrakta följande exempel. Eftersom modern akademi inte kan hantera ¥-grunderna

— se Den Mängdoberoende och Mästarlogikens huvudsats i Nollformsalgebran

— kan den heller inte förstå funktionsbegreppets grunder och därmed heller inte förstå konsekvensen av satsen att

en konstant kan inte relatera en variation.

Resultat:

”Eftersom derivatan till en konstant C är lika med noll gäller det att ò 0 · dx = C”, se vidare jämförande citat nedan.

Gängse modern akademisk matematisk litteratur påstår (typiskt) det ovannämnda.

Beskrivning med utförligt bevis

YTAN (y) för det område som begränsas av x-axeln (L₀, figuren nedan) och en rät linje (L) parallell med denna som går genom en punkt k på y-axeln bestäms enligt

y = kx

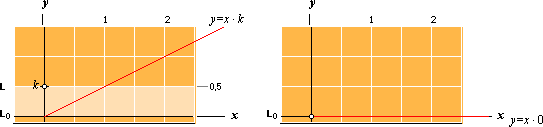
Vänster. Så länge tangenten k eller derivatan är skild från noll finns också en bestämd ändlig rektangelyta kx.

Höger: Med k=0 upphör emellertid rektangeln att existera och ingenting alls finns kvar: 0x=0.

Om k=0 finns inget område — det är noll. Och alltså är också ytan noll enligt

y = 0x = 0

ETT BARN KAN INSE DET — men tydligen inte modern akademi — att det inte längre finns någon varken yta eller område att räkna på:

Området är noll.

Ytan är noll.

Finns inte.

Integralen för noll är noll: dy/dx = y’ = 0 ; ò dy = y = ò 0·dx = 0 ò dx = 0x = 0

Det som saknar intervall har heller ingen integral.

SLUTSATS:

Modern akademi kan uppenbarligen och relaterbarligen varken relatera, hantera, förklara, beskriva eller härleda analysen.

Jämför den moderna akademins allmänna anspråk på att besitta kompetens:

”Människan har skapat matematiken, därom är alla lärde överens”,

Sveriges Radio Vetandets Värld 25 mars 1988.
”matematik Enligt en etablerad uppfattning är matematiken läran om tal, om rummet, och de många generaliseringar av dessa begrepp, som skapats av det mänskliga intellektet.”,

MATEMATIKLEXIKON W&W 1991 s278sp2ö.

EXEMPLET MED KONSTANTEN C visar att

· Den konstant C som modern akademi uppfinner kallas ”integrationskonstant” (constant of integration);

· I modern akademi finns ingen uppfattning om den inneboende integralkonstanten (Q). Dess faktiska existens sammanblandas med ovanstående.

· I den högre analysen garanterar detta
att den moderna akademin i sin undervisande fattningsnivå förlorar vitala beskrivande delar som därmed, i modern akademis regi, omöjliggör varje exakt, klar, tydlig och förklarande beskrivning av hela analysen;

· Den moderna akademin »förkväver mänskligheten» med sin primitiva uppfattning av begreppet logik: den härleds inte, den uppfinns, och vilken ytliga tankekonst därmed kan uppfattas så att den pådyvlas mänskligheten. Visa.

DEN MODERNA AKADEMINS INTEGRALBEGREPP

För att matcha ut de egna uppfinningarna i kraft av att förkasta blotta tanken på en redan befintlig naturkunskap, jämför ovanstående citat, så sammanblanda integralkonstant med ekvationskonstant (C), samt i övrigt förvisa tillståndets princip från logiken och därmed påtvinga analysen begrepp den inte känner till, tvingas den moderna akademin också analogt uppfinna en definition på såväl derivata som integral genom begreppet gränsvärde; I stället för en integral finner vi i modern akademi EN HEL BUTIK som definieras på olika summationstyper — Lebesgue, Stieltje, Riemann …

Jämför gängse framställningar:

”Vid användandet av obestämda integraler får man inte glömma att addera en konstant, en s.k. integrationskonstant C, till resultatet, ty eftersom derivatan av en konstant C är lika med noll, så blir följaktligen

ò 0dx = C

”

ITK-8 MATEMATIKBIBLIOTEK INTEGRALKALKYL Lennart Brandqvist

Institutet för Tekniska Kurser, Stockholm 1962, s147

” If F is any integral of f, the most general integral of f is F + c, where c is an arbitrary constant called the constant of integration; this is because a constant has derivative 0, so (F + c)’ = F ’ + c’ = f + 0 = f. ”

ENCARTA 99 Calculus

Min översättning:

Om F är någon integral till f, är den mest allmänna integralen till f lika med F + c, där c är en godtycklig konstant kallad integrationskonstanten; det är därför att en konstant har derivatan 0, så att (F + c)’ = F ’ + c’ = f + 0 = f.

Det måste sägas i sanningens namn — i anslutning till ovanstående genomgång i Nollintegralen:

Den moderna akademins TYDLIGT primitiva matematiska intelligens leder — tydligen, per exempel — till de vandaliseringar av matematiken som FÅR de väsentliga avsnitten i den vidare analysen ATT FRAMSTÅ SOM omöjliga att förstå — per modern akademi. SUMMAN visar FÖLJDRIKTIGT att den nu rådande allmänna matematikundervisningen knappast renderar högre omdöme än det här: rent bedrövligt.

Det finns gott om hjärna i modern akademi.

Men vettet förefaller, som det får förstås, praktiskt taget orepresenterat. EXEMPEL: se ovan samt (därmed, analogt) facit i den allmänna matematikundervisningen: få, om ens några, klarar den delen. Men det beror naturligtvis inte på att kunskapen som sådan fattas utan på att det saknas personer som kan beskriva den, förklara den och framför allt härleda den.

^{_______________________________}

En bestämd integral — yta — räknas alltid från noll.

^{_______________________________}

Se vidare konkreta exempel i Härledningen till n.te ordningens homogena varianter, ämnet Komplexa Rötter;

Se även Härledningen till Partikulära Lösningarnas Allmänna Metod — modern akademi står utanför pga ovanstående — eleverna uppmanas ”gissa lösning”;

Se explicit i ALLMÄNNA LÖSNINGAR till InHomogena varianter — Partikulärlösningarna.

ANDRAGRADSEKVATIONENS LÖSNING

Binomlagarna — ANDRAGRADSEKVATIONENS LÖSNING

Om binomlagen skrivs generellt enligt (a+A/2)²–(A/2)²=a²+Aa=K med A/2=b från 2ab i a²+b²+2ab, kan a lösas i alla uttryck av typen

K = a²+Aa alternativt a²+Aa – K = 0

om KA är känd. Ovanstående led ger lösningen ±(a+A/2)²=K+(A/2)², ±(a+A/2)=Ö K+(A/2)², a+A/2=±Ö K+(A/2)²;

a = –A/2 ± Ö K+(A/2)² ........................... andragradsekvationens lösning

DIFFERENTIALTRANSFORMATIONER

EXEMPEL

Se Fundamentaltermen i partikulärlösningarna till inhomogena varianter.

Se METOD 1 i Partiell integration.

Se även ett par praktiska referensexempel i Magnetismen på Differentialtransformation

1. För att integrera dB_P över vinkeln b måste vi först anpassa …

2. Som cirkelbågen i radianer b är b = s/x, får vi differentialtransformationen db=d(s/x)=ds/x

Den högre analysen

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Den högre analysen

ämnesrubriker

innehåll

DEN HÖGRE ANALYSEN

inledning

orienterande beskrivning

Elementära gränssnittets funktionsranger

Tablå 0 — funktionsrangerna

Elementära gränssnittets begrepp

Termen Gränssnitt

Högre gränssnitt

Integralkalkylen genom rangterminologin

Allmän klassifikation av varianter

Homogena och Inhomogena varianter

Allmän form, linjära och icke linjära varianter

Lösningarna

Homogena varianter

Transformatorn

Transformatorns transform

Varianternas Transformer

Tablå för lösningarna till homogena varianter

första ordningens homogena linjära varianter

andra ordningens homogena linjära varianter

n:te ordningens homogena linjära varianter

EXEMPEL

n:te ordningens homogena varianter — lösningarna

Universalerna till n:te ordningens homogena linjära varianter

reella olika rötter

Exempel

reella multipla rötter

Exempel

komplexa olika rötter

Exempel

Inhomogena varianter

Lösningarna till inhomogena varianter

Universalens definition

Termen universal

Universalsatsen

INTEGRAL-FUNKTION-IDENTITETENS KRITERIUM (IFIK)

NOLLINTEGRALEN

ANDRAGRADSEKVATIONENS LÖSNING

DIFFERENTIALTRANSFORMATIONER

referenser

[ITK]. ITK 1-10 MATEMATIKBIBLIOTEK 1962 Lennart Brandqvist,

INSTITUTET FÖR TEKNISKA KURSER Stockholm, Victor Pettersons Bokindustriaktiebolag, Stockholm 1962

[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2014-04-18

*END.

Stavningskontrollerat 2009-01-09.

rester

PNG-justerad 2011-07-18

åter till portalsidan · portalsidan är www.UniversumsHistoria.se