SOLGALAKTISKA OCH JORDEKVATORIELLA KOORDINATER 2008X18 | Senast uppdaterade version: 2011-10-10 · Universums Historia

 

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

Koordinatomvandlingarna (KOWIOR) i relaterad matematik | webbsambanden |

 

 

GALAKTISKA KOORDINATER

 

 

Webben @INTERNET (November 2008) är ännu ypperligt fattig på beskrivande och förklarande matematik i ämnet omvandling från Jordekvatoriella till Solgalaktiska koordinater (och omvänt) — även i den engelska delen. Trots flera (eminenta) källverk på webben finns (flera) som uppvisar tydliga brister i den matematiska hanteringen; Sambanden man refererar till visar sig gälla bara delvis — utan att författarna ger minsta notis i saken. En del av exemplen kommer att visas här. Det finns dock en del (säkra) standardverk som kommer att refereras till i den följande framställningen. Följande presentation i Galaktiska Koordinater ger en utförlig och uttömmande beskrivning och förklaring av sambandsformerna enligt relaterad matematik genom vinkelsummateoremet och rotationssatsen. Ett redovisande kalkylkort ingår (se GalKord) som kan användas för konvertering där det också finns testresultat och ett separat rotationskort för allmän användning för den som är intresserad.

 

 

inledning

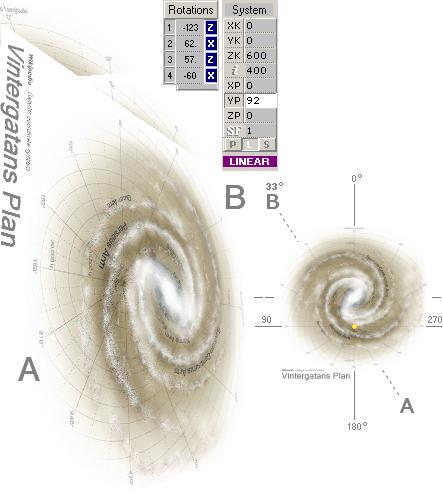
Översikt Vintergatan — plan och vinklar

Översikt Vintergatan — plan och vinklar · för källdata, se från grunddata i efterföljande illustrationsblock

 

 

Källreferenser för basdata, se från grunddata i efterföljande angivna källverk

 

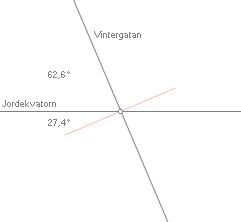
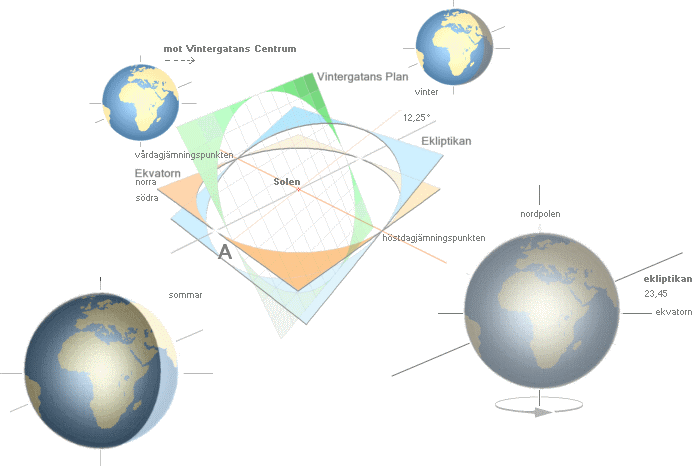
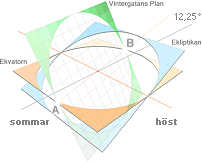
Om vi börjar från vårdagjämningspunkten — överst vänster ovan, skärningen ekvatorn(orange)-ekliptikan(blå) — och vrider den linjen (JL) via origo runt i ekvatorsplanet (orange) till den angivna vinkeln 12,25°, då markerar den linjen (GL) skärningen mellan Jordekvatoriella planet (orange) och Vintergatans plan (grön), vinkeln är fastställd (med årsreferensen [ekvinoktium] 1950) till rektascensionsvinkeln 282,25° eller 18h49m (18 timmar 49 minuter). Galaxplanets lutning är samma som att kring GL  vrida upp ekvatorsplanet 62,6°. Linjen Solen-Vintergatans centrum fås slutligen genom att i det så uppvridna Vintergatsplanet vrida GL en  vinkel –33°. Se vidare nedan.

   Vinklarna [se exv. @INTERNET Wikipedia Galactic coordinate system 2008-11-06] 282,25 62,6 och 33 är fastställda från 1950 års s.k. ekvinoktium (B1950). Det finns också ett ekvinoktium från 2000 (J2000) med marginellt andra vinklar (282,75 | 62,87 | 32,93). Driften beror på att vårdagjämningspunkten vandrar medurs i ekliptikan ett varv på 28 500 år [BAs441sp2ö], det är den s.k. precession som Jordaxeln utför med väsentligen bevarad konstant lutning mellan ekvatorn och ekliptikan.

 

REK och DEK

 

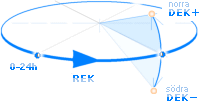
REKtascensionen räknas astronomiskt med Jordekvatorn som skivplan och vårdagjämningspunkten (20 Mars) som nollvinkel 0-24h. Siktvinkeln precis utmed ekvatorn motsvarar DEKlinationsvinkeln noll grader. Står vi på nordpolen och tittar ner på ekvatorn som illustrationen ovan antyder, räknas deklinationsvinkeln positiv från horisonten och uppåt norr mot vår plats, och negativ under horisonten ner mot södra polen; DEKlinationsvinkeln räknas 0-±90° med + för nordlig och – för sydlig latitud. Tänk den som ett halvlock som kan vikas uppåt eller neråt från ekvatorn kring REK-normalen (ej utritad ovan). Rotationsriktningarna är exakt desamma som i det allmänna matematiska xy-planet med positiv rotation moturs — vilket motsvarar utsikten från nordpolen; Jorden roterar moturs = matematiskt positivt kring sin egen axel sett från nordpolen, och Jorden roterar också moturs kring Solen sett därifrån. I (den allmänna) astronomin sätter man Solen »i mitten» av Jordekvatorns (oändligt utsträckta) plan och använder den referensen som »allmän astronomisk nollpunkt» t.ex. i Solgalaktiska koordinatsystemet. Se vidare nedan.

 

grunddata

SOLGALAKTISKA OCH JORDEKVATORIELLA

KOORDINATER

25 000 lå  ........................          Solens ungefärliga avstånd från Vintergatans centrum (ref. @INTERNET Wikipedia Milky Way — Sun’s location 2008-10-18)

 

 

 

”Den linje genom jorden som går vinkelrätt mot det galaktiska planet skär himmelssfären i norra och södra galaktiska polerna. Den förra är belägen vid rektascensionen 12h 49m och deklinationen +27,4 grader (ekvinoktium 1950 0)”,

VÄRLDSRYMDEN, B. Ernst, T. de Vries, Norstedts 1966

Beteckningarna för REKtanscension och DEKlination används här stundtals (inom avgränsade delblock) med den engelska förkortningen motsvarande RECtascension och DEClination.

grundtermer

 

EKLIPTIKAN — kurvan och planet som Jorden omsluter på sin årliga bana runt Solen.

JORDAXELN — lutar 23,45° mot ekliptikans normal; Jordekvatorn lutar 23,45° mot ekliptikans plan.

EKVATORIALPLANET — Jordekvatorns plan används traditionellt som det astronomiska huvudreferensplanet.

Ekliptikan/ekvatorn skär varandra i två punkter: vårdagjämningspunkten och höstdagjämningspunkten.

VÅRDAGJÄMNINGSPUNKTEN — astronomisk nollpreferens för rektascensionsvinkeln (REK) 0 till 24 timmar;

Rectascensionen (REK) eller timvinkeln räknas moturs sett från norra hemisfären

— samma som Jordens naturliga rotationsriktning kring Jordaxeln

— i hela timmar (nnh), minuter (nnm) och sekunder (nns) med typformen 12h46m00s. 00h00m00s är vårdagjämningspunkten.

Deklinationen (DEK) eller höjdvinkeln är »kikartubens höjdvinkel över horisonten», räknas ±90° med +(plus) för norra och –(minus) för södra hemisfärerna.

 

Jordlokalens grundbegrepp

 

Med ovanstående citerade uppgift blir timvinkeln 12h49m = 192,25° = 180° + 12,25°; Med den linjen som bas för höjdvinkelns vridningsaxel, ligger då Vintergatans polaxel parallellt med höjdvinkeln 27,4° (se uppgiften ovan i citatet);

Vintergatans planskiva, rätvinkligt polaxeln, lutar 90–27,4 = 62,6° mot Jordekvatorns obegränsat utsträckta referensplan.

   Med hjälp av dessa referensvinklar kan Jordekvatoriella koordinater REC|DEC (konv. ekvatoriella eller celesta koordinater) på formen typ 1913+16 (REC 19h13m, DEC +16°) omvandlas till Solgalaktiska koordinater (med origo i Solen, med Jordekvatorns referensplan till stöd) att skilja från centralgalaktiska koordinater (med origo i Vintergatans centrum). Solgalaktiska koordinaterna kallas emellertid mera allmänt (och något oegentligt) för galaktiska koordinater.

För att undvika missförstånd används här hellre den mera beskrivande benämningen Solgalaktisk.

 

Solgalaktiska

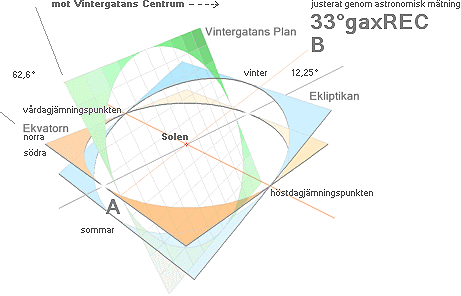
Solgalaktiska koordinatsystemet

 

 

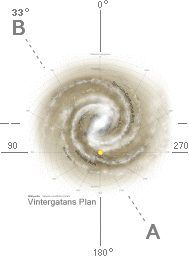
Delvis ombearbetad originalbild från @INTERNET Wikipedia Milky Way 2008-10-18 för att förtydliga strukturen mot vit bakgrund

 

Grundlinjen som avviker 12,25° från ekvatorsplanets motsvarande sommar(6h)-vinterlinje(18h) och som ligger i Vintergatans plan, träffar inte precis i Vintergatans centrum. Genom astronomisk observation (här utan källangivelse) har man uppskattat att en tilläggsvinkel på minus 33° ger riktningen ganska precis till Vintergatans centrum. Med ytterligare kännedom om Solens ungefärliga avstånd från Vintergatans centrum (ca 25 000 lå, i en del [äldre] litteratur ca 30 000 lå) framgår Solgalaktiska koordinatsystemet enligt figuren ovan.

 

gyromodellen

 

I studier av geometrin rekommenderas (här) läsaren starkt att införskaffa sig en gyromodell typ ovanstående författaroriginal (från Maj 1981): modellen är utskuren med passepartoutkniv i 1mM och 2mM vit passepartoutkartong i enskilda cirklar. Hela anordningen har sammanfogats med enkla egenkonstruerade kopparnitar, knappnålar, vattenbaserat lim och 2mM skruv med mässingsmutter (fanns en gång i tiden på Clas Ohlson). Samtliga cirklar är vridbara och roterbara. I mitten sitter en axiellt vridbar kub. Skalorna har ritats med tusch, vattenbaserade färgpennor och gnuggisar (numera en i princip helt utgången teknik som användes mycket av många under 1970-talet), samt förseglats med fixativ för att ge ytan ett plastiskt skydd mot fukt och damm. Du kommer garanterat att få mycket glädje av en sådan modell i olika trixiga analyser inom 3D-geometrin. Modellen har hängt med i 27 år — här återigen till hjälp, nu i analysen av Vintergatan och Solsystemet.

 

Med ovanstående citerade grunduppgift kan »en första enklare analys» genomföra som visar hur Solgalaktiska koordinater fås från Jordekvatoriella med nolldeklination.

 

För grunderna i 3D-geometrin se 3D-GEOMETRINS GRUNDER, om ej redan bekant. Där ges en utförligt illustrerad kortfattad beskrivning som förklarar grundbegreppen. Vi förutsätter här full förtrogenhet.

 

nolldeklinationssambanden

 

 

I PREFIXxSIN med (C)=62,6° och (R)=JordekvatoriellaRectascensionsvinkeln

— med nollpunkten från skärningen Jordekvatorn/Vintergatsplanet ges

— med sambandsformerna (gax i illustrationen förkortar galax-, nedan förenklat till g)

 

             tan gREC          = tan(R) · sin (C)

             cos gDEC         = – cos(R) · cos (C)  ...........................   negativt med negativt x enligt illustrationen

 

— direkt ur nedanstående hjälpillustration

 

 

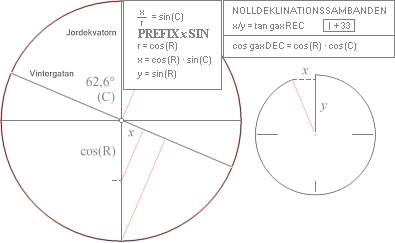
             gREC = atan[tan(R) · sin (C)]  ........................   i PREFIXxSIN det som är enklast att förstå i den elementära trigonometriska analysen

             gDEC = acos[–cos(R) · cos (C)]  ....................   i PREFIXxSIN det som är enklast att förstå i den elementära trigonometriska analysen

 

             gREC = atan[tan(R) · cos (C)]  .......................   i PREFIXxCOS det som gäller i kommersiella räknare

             gDEC = asin[–sin(R) · sin (C)]  ......................   i PREFIXxCOS det som gäller i kommersiella räknare

 

TRIGONOMETRISKA KVADRANTVILLKOR:

 

x/y = tan gaxREC måste framställas på villkor:

(R) måste formateras varvoberoende och positivt 0-360° för konsistenta entydiga resultat;

OM (R)>90 OCH (R)<=270

— (R) ligger mellan 90-270

— ADDERA 180+33; 

OM (R)>270 ADDERA 360+33; annars ADDERA 33;

 

 

Vinkeloffseten på 33° är den restvinkel som (fastställt i internationell astronomisk standard efter särskild astronomisk observation) måste subtraheras (vridning medurs i trigonometrin) från skärningsvinkeln Jordekvatorn/Vintergatan för att få en referenslinje i Vintergatsplanet som precis genomskär Vintergatans centrum, denna referenslinje markerar då Solgalaktiska koordinatsystemets nollinje.

 

 

Ovanstående utveckling ger en enkel men säker grundreferens för att kontrollera omvandlingen mellan Jordekvatoriella till Solgalaktiska koordinater, dock i ett begränsat område. För en mera fullständig genomgång är vi hänvisade till vinkelsummateoremet tillsammans med rotationssatsen från den elementära 3D-geometrin. Vi studerar hur.

 

 

 

koordinatomvandlingarna enligt relaterad matematik

 

 

Koordinatomvandlingar genom vinkelsummateoremet och rotationssatsen (KOWIOR)

 

Vintergatans plan

Vi använder Pilotsystemet xyz från den elementära 3D-geometrin som ovan.

 

 

 

Eftersom Jordekvatoriella systemet och Solgalaktiska systemet bägge har en och samma centralpunkt — Solen — motsvarande Pxyz=(0;0;0) finns bara en enda given entydig riktning från den origopunkten i bägge systemen. För att realisera omvandlingen mellan systemen matematiskt, kan vi alltså använda oss av en hjälpsfär med radien lika med 1 och med den specifika motsvarande initierande positionen P(xyz)=(1;0;0) med början från Jordekvatoriella referenspunkten (vårdagjämningspunkten). Hjälpsfärens radiekoordinater xyz hjälper oss sedan via rotationerna att få ut rätt slutvinklar i konverteringen.

 

Med vyn sett (snett) ovanifrån enligt astronomisk standard med utsikt över ekliptikans norra planhalva blir det (då) naturligt att sätta Jordekvatoriella planet som Y-planet; Vårdagjämningspunkten blir vår absoluta nollreferens (REKtascensionens nollgraderslinje) med enhetskoordinaterna P(xyz)=(1;0;0),

 

P

x

y

z

1

0

0

 

Härifrån ska den enhetslinjen enligt grunddatat först roteras 282,25°yW (12h49m + 90°) till positionen motsvarande 12,25°-linjen i illustrationen ovan;

Därifrån ska sedan ett parallellplan till ekvatorsplanet — galaxplanet — vikas upp 62,6°xW;

Slutligen ska därifrån 12,25°-linjen vridas ner –33°yW för att få skärning med Vintergatans centrum.

 

Rotationsordningen skulle alltså bli totalt

+yW282,25°

+xW62,6°

–yW33°

vinkelminus

Förtydligande:

 

Rotationstransformationen från ekvatoriella till galaktiska — vilket betyder att Jordekvatoriella vinkelvärdena i den givna rymdriktningen räknas om i Solgalaktiska systemets referens — ges baklänges från galaxsystemet till ekvatorialsystemet och måste alltså tas därifrån — med vinklarna baklänges och negativa:

+yW33°

–xW62,6°

–yW282,25°

Detta är emellertid en systemrotation; bildrotationen vet vi är omvänd så att vi i slutänden får

–yW282,25°

–xW62,6°

+yW33°

 

Eller mera omständligt sagt:

 

Rotationsvinklarna (yW, xW, yW) flyttar galaxsystemet relativt ekvatorialsystemet;

— För att relatera ekvatorialsystemet till galaxsystemet så att vi i slutänden får galaxkoordinaterna, måste vinklarna ändra tecken;

— jämför en linje L som roteras säg 30°zW relativt horisontnollan 0°; den senare måste i förhållande till den förra tillskrivas en negativ vinkelrotation, annars blir det fel.

Rotationsordningen blir då totalt

–yW282,25°

–xW62,6°

+yW33°

 

Nu ser vi emellertid att ordningen ovan INTE kommer att ge korrekt resultat

— därför att nämligen t.ex. –282,25° INTE relaterar till samma rotation som +282,25°; –282,25° blir fel ställe.

För att få korrekt värdeform är vi därför tvungna att tillämpa en omvänd ordning (vilken sett från galaxsystemet blir den enda logiskt korrekta) enligt

 

+yW33°

–xW62,6°

–yW282,25°

 

så att den negativa rotationens sista värde garanterat placerar nollreferenslinjen enligt den motsvarande positiva rotationens första värde, alltså räknat från vinkelnollan vid P(xyz)=(1;0;0).

 

Nu är — slutligen — emellertid dessa rotationer också systemrotationer, alltså typ RotII;

— Eftersom beräkningarna görs efter vinkelsummateoremets RotI-system, blir med kännedom om rotationssatsen därmed tvunget ordningen i RotI LIKVÄL den omvända enligt

 

–yW282,25°

–xW62,6°

+yW33°

 

TILL DESSA TRE ROTATIONER ska nu läggas den aktuella Jordekvatoriella vinkelrotationen respektive REKtanscensionen och DEKlinationen;

Vi har dem i Pilotsystemet som ovan med Jordekvatorn som Y-planet enligt

1. yW REK

2. zW DEK

 

Emellertid är också dessa systemrotationer — så att vi i RotI-beräkningarna måste relatera omvändningen

1. zW DEK

2. yW REK

 

Med uppställningen efter | REK | DEC | 282,25 | 62,6 | –33 | i den fasta ordningen enligt

 

1

2

3

4

5

yW

zW

yW

xW

yW

REK

DEC

282,25

62,6

–33

 

får vi därmed koordinatomvandlingen från Jordekvatoriella till Solgalaktiska enligt den exekverande (verkställande) ordningen

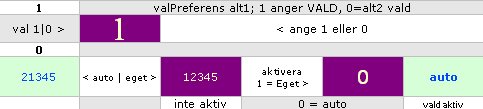
21345

För att omvandla från andra hållet — från Solgalaktiska åter till Jordekvatoriella — behöver vi bara ändra tecken i den fasta ordningens 345-värden med multiplikation av –1, samt sedan tillämpa den verkställande ordningen

21543

 

ALLMÄNT KALKYLKORT FÖR STUDIUM finns i GalKord

Separat kalkylkort finns där ovanstående system kan studeras och manipuleras i detalj

 

I kalkylkortet GalKord finns på fliken Tabell2 (det finns totalt tre tabellflikar att välja på) en uppställning som visar hur hela ordningen verkställs i matematik;

Enbart genom att styra köordningen (12345) i rotationsordningen kan exakt samma ekvationsblock användas både för ekvatoriella till galaktiska som galaktiska till ekvatoriella.

   Tabell2-kortet i GalKord är särskilt uppställt som ett exempel för att (på-) visa exakt hur den ordningen verkställs, samt att den verkligen också fungerar;

— För att göra inmatningen säker och pålitlig används fasta indata typ nedan

 

Tabell2 GalKord

 

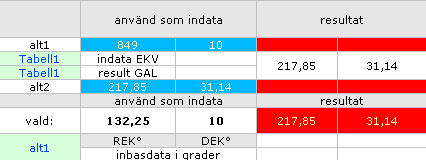
från resultaten i Tabell1-kortet så att man fritt kan välja utgångspunkten: antingen Jordekvatoriella (övre) eller Solgalaktiska (undre).

Dessa indatavärden (himmelsblått ovan) ändras alltså med val av indata i Tabell1.

— Valet görs genom att sätta 1 eller 0 i två markerade inmatningsceller typ nedan,

 

 

inmatningresultat

 

Resultatet ska bli samma värden som i den del som inte är vald;

Väljs Jordekvatoriella (1) ska resultatet bli Solgalaktiska;

Väljs Solgalaktiska (0) ska resultatet bli Jordekvatoriella; det är endast ordningen 21345 eller 21543 som tillsammans med minustecknen för vinklarna bestämmer resultatet — ekvationerna är exakt desamma.

En tillvalsruta finns också (högra violetta ovan) med vars hjälp man kan överrida den automatiska inmatningen av ordningarna 21345 | 21543 och själv knappa in önskad ordning för studium — eller använd kortet och skriv om cellkoden som du själv vill.

Se även en kortfattad beskrivning här längre ner för Tabell1-kortet i GalKord.

 

I Tabell3-kortet i GalKord finns ett renodlat fritt inmatningsblock med fem rotationer som man själv kan bestämma ordningar och värden i och använda för olika tester och studier.

 

Tabell3 GalKord

 

De enskilda rotationerna kan utöver Köordningen styras genom individuell nollställning (raden överst, aktiverad 1). Kortet beräknar slutkoordinaterna för ingångsvektorn xyz i max 5 rotationer i Rotationskomplex I.

 

kvadrantvillkoren

I BÄGGE FALLEN LÖSER VI UT transfereringsresultatet — här relaterat i PREFIXxSIN — via xyz-slutledet enligt

y/(R=1) = cos gDEK|DEK  .........................................    y-värdet, plus eller minus, ger deklinationsvinkeln direkt

z/x med kvadrantvillkoren via arctangens  ............    se vidare beskrivning nedan

 

 

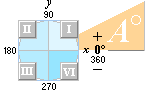
Koordinatsystemet xy med de fyra kvadranterna I II III IV. ArcTangens för tangensrelationen (y/x) kan inte specificera om vinkeln ligger i I eller III och inte heller om den ligger i II eller IV. För att få fram vilken kvadrant som koordinatpunkten Pxy ligger i, måste kvadrantvillkoren nedan beaktas.

 

kartan för kvadrantvillkoren · slutvinkel genom arctangens med följande tilläggsvillkor:

 

POS y

NEG y

 

y=0

x=0

POS x

NEG x

NEG x

POS x

 

POS x

NEG x

POS y

NEG y

I

II

III

IV

 

0

180

90

270

 

+180

+180

+360

 

 

 

 

 

 

 

för att få ut rektascensionsvinkeln.

— Vinkelvärdet från Y-planets atan z/x

— som motsvarar Z-planets y/x och som avses i tabellen ovan

— löses alltså ut enligt ovanstående kvadrantvillkor.

 

Dessa uppställningar visas

mera ingående i kalkylkortet GalKord.

 

I många nyare dator- och kalkylprogram finns redan en sådan tangensbaserad kvadrantVillkorsFunktion inlagd;

— den brukar kallas ARCTANGENS2; Man anger då respektive xy-parametrar enligt (typ)

ARCTAN2(x; y), vilket ger korrekt slutvinkel direkt, dock enligt ordningen 0±180°.

 

DEN FULLSTÄNDIGA UPPSTÄLLNINGEN i PREFIXxSIN GENOM VINKELSUMMATEOREMET

x = xx1 – yy1                   ;  y = yx1 + xy1

med x1 = sinus för rotationsvinkeln (W) och y1 = cosinus för rotationsvinkeln (W) enligt

x = x sinW – y cosW     ;  y = y sinW + x cosW

blir för samtliga xyz|W i ordning

 

 

x

y

z

xW

x

y sin xW + z cos xW

z sin xW – y cos xW

yW

x sin yW – z cos yW

y

z sin yW + x cos yW

zW

x sin zW – y cos zW

y sin zW + x cos zW

z

 

zW-delen (sett rakt framifrån) med xy-axlarna är grundprefixet;

yW-delen (sett ovanifrån) med zx-axlarna fås med zW-delen ersatt med z för y;

xW-delen (sett från sidan [höger]) med zy-axlarna fås med zW-delen ersatt med z för x;

 

Ovanstående tre ekvationsblock är precis vad varje 3D-beräknande avancerat datorprogram använder som kärnan i alla vektorberäkningar som innefattar godtyckliga rotationer av godtyckliga punktmängder. Genom indirekt adressering, kan matrispunkterna till alla objekt matas in i blocket för att få fram slutvärden för bildpresentation.

 

I fallet med den verkställande ordningen 21345 för Jordekvatoriella till Solgalaktiska blir uppställningen

— som tidigare i PREFIXxSIN

 

 

 

x

y

z

xyz

 

 

1

0

0

start

2

zW

x sin zW – y cos zW

y sin zW + x cos zW

z

DEC

1

yW

x sin yW – z cos yW

y

z sin yW + x cos yW

REK

3

yW

x sin yW – z cos yW

y

z sin yW + x cos yW

–282,25

4

xW

x

y sin xW + z cos xW

z sin xW – y cos xW

–62,6

5

yW

x sin yW – z cos yW

y

z sin yW + x cos yW

+33

 

där varje successivt nytt xyz tas från resultatdelens led närmast ovanför.

Sista ledets xyz-del innefattar resultatet gDEK|REK vilket utlöses enligt föregående kartbeskrivning i kvadrantvillkoren.

 

FÖRENKLING KAN GÖRAS — som vi ser — med ihoptagning av leden i 1 och 3 eftersom rotationsplanet Y är samma i bägge fallen. Men vi genomför inte den delen här.

 

Uppställningarna ovan finns

sammanfattande i kalkylkortet GalKord.

 

Innan vi kan få fram ett verkligt användbart kalkylkort med konsekvent visning och presentation i koordinatomvandlingar Jordekvatoriella-Solgalaktiska-Jordekvatoriella, finns en del ytterligare detaljer att »fylla i». Dessa finns samlade i kalkylkortet GalKord — samt en del andra användbara kortblock för rotationsberäkningar generellt.

 

I GalKord finns ett kalkylblock sammanställt med ordningarna

21345

21543

[samt ett tillval med fria inslag]

som kan ändras manuellt och man därigenom kan styra resultatet på alternativt sätt.

 

Det finns också ett separat kalkylkort med valfria xyz-värden där man själv kan ange (max) 5 rotationer som sedan kan köras i valfri ordning.

Till kalkyldelen i Tabell1-kortet i GalKord speciellt finns också en del motsvarande noteringar med jämförelser från de etablerade verk som kan hittas på webben (November 2008).

 

 

 

 

 

WEBBSAMBANDEN

— Jämförelse med konventionellt angivna sambandsformer

 

Vi kan testa det »enkla resultatet» i nolldeklinationssambanden samt ovanstående mera reguljära resultat enligt relaterad matematik mot olika webbkällor som erbjuder interaktiv koordinatomvandling ekvatoriella-galaktiska

— här främst

 

DIREKT KONVERTERING ekvatoriella till galaktiska koordinater PÅ WEBBSIDAN (se infälld förminskad bild nedan)

[http://fuse.pha.jhu.edu/support/tools/eqtogal.html].

Vi utgår ifrån att kontrolldelen i ovannämnda webbkälla ÄR korrekt (det är en astronomisk standardform).

 

Det finns flera interaktiva webbsidor som har konverteringskort där man kan skriva in ekvatorialvärdena och få ut Solgalaktiska motsvarigheten; De flesta av dem ger DOCK intryck av krånglig navigering (som man snabbt bläddrar förbi för att »hitta något enklare»)

— men en finns som är rakt på sak (den bästa, men det finns bara en precision att välja på vilket betyder att man måste knappa in max 12 siffror för varje gång).

 

 

NOTERA FÖR DENNA WEBBKÄLLA:

 

·          Rutan med B1950 avser standardpositionerna från epokpreferensen år 1950 (Jordaxeln vrider sig sakta, ett varv på 25 800 år vilket marginellt ändrar referenserna något över seklerna). Det finns också en nyare version från år 2000 (J2000) med marginellt andra vinkelpreferenser om man vill vara extra noga och ”up-to-date”. Här förutsätter vi att B1950 används genomgående (skillnaden är helt marginell och utan betydelse i översiktliga sammanhang).

·          Resultaten presenteras i gREK som LII och gDEK som BII

·          Med gDEK=±90° har gREK ingen betydelse, 0-360° gäller då, men källan ovan kan t.ex. visa
LII=103.9509 BII=89.9999 (webbkällan kan inte visa exakt gDEK=90°)
för 1247+27,4 (slås in som 124700 i ruta ett och 272400 i ruta två);
i GalKord visas konsekvent 0-360±90 och i förekommande fall omvänt gal-ekv 0-24±90

 

 

Den webbkällan verkar för tillfället vara den minst omständliga (och mest tillförlitliga).

 

 

 

EN MERA DIREKT ÖVERSIKTLIG GRAFISK KURVKARTA

Jordekvatoriella-Solgalaktiska-Jordekvatoriella FINNS PÅ WEBBEN till jämförelse i Webbkällan

— http://web.njit.edu/~gary/321/Lecture18.html — datumreferens saknas, Physics 321 Astrophysics II:  Lecture #18 Prof. Dale E. Gary, NJIT, The Milky Way Galaxy - I

— Den ger en bra översiktlig fast grafisk kurvkarta som visar konverteringen i intervall om 10° (fast det tar en liten stund innan man fattar hur kartan ska läsas).

 

 

 

Söker vi på webben @INTERNET mera fördjupat efter SAMBANDEN till ”galactic coordinates” ges främst följande sökträffar:

Sambanden nedan i konventionella PREFIXxCOS:

 

[http://scienceworld.wolfram.com/astronomy/GalacticCoordinates.html],

Wolfram Research — Eric Weisstein’s World of Astronomy

”

Given equatorial coordinates d (declination) and a (right ascension), the galactic coordinates (b, l), can  be computed from the formulas

             cosb cos(l – 33°)           = cosd cos(a – 282.25°)

             cosb sin(l – 33°)            = sind sin 62.6° + cosd sin(a – 282.25°) cos 62.6°

             sinb                               = sind cos 62.6° – cosd sin(a – 282.25°) sin 62.6°  .................   OK

”,

”

”;

 

 

Även källan nedan ger samma galaktiska koordinatomvandlingsuppgifter,

[http://web.njit.edu/~gary/321/Lecture18.html],

Astrophysics II, Lecture #18. Prof. Dale E. Gary, New Jersey’s Science & Technology University

”

”;

 

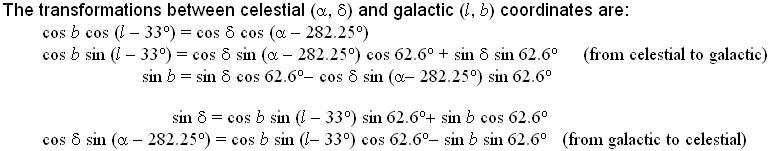
             cosb cos(l – 33°)           = cosd cos(a – 282.25°)

             cosb sin(l – 33°)            = sind sin 62.6° + cosd sin(a – 282.25°) cos 62.6°

             sinb                               = sind cos 62.6° – cosd sin(a – 282.25°) sin 62.6°  .................   OK

 

             sind                                = cosb sin(l – 33°) sin 62.6° + sinb cos 62.6°

             cosd sin(a – 282.25°)   = cosb sin(l – 33°) cos 62.6° – sinb sin 62.6°

;

Och även

[http://faculty1.coloradocollege.edu/~sburns/Courses/08-09/PC361/chpt1.pdf],

Chapter 1, Astronomical Coordinate Systems, Colorado Collage

”

”;

 

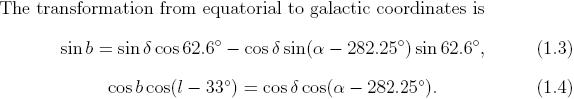
             sinb                               = sind cos 62.6° – cosd sin(a – 282.25°) sin 62.6°  .................   OK

             cosb cos(l – 33°)           = cosd cos(a – 282.25°)  ..........................................................   Colorado-sambandet

 

 

 

Med sambandet ovan i PREFIXxSIN, b = gDEC, l = gREC,

             cosb                               = cosd sin 62.6°            – sind                cos(a – 282.25°) cos 62.6°  ...............   OK

             cosgDEC                       = cosDEC sin 62.6°      – sinDEC          cos(REC – 282.25°) cos 62.6°                           

ser vi att föregående nolldeklinationssambanden övergår i samma led med DEC=0 och offsetvinkeln 282,25°=0 som ger

             cos gDEC                      = 0                                 – 1                    cos(REC – 0) cos(C)

                                                   = –cos(R) cos(C)

 

 

 

Sambandet för galaktiska DEKlinationen, sinb ovan, fungerar genomgående.

Däremot fungerar inte de övriga sambanden tillfredsställande

— utom i vissa partier, och då med tillfogande av villkorssatser (kvadrantvillkor)

— som bara tycks kräva en allt vidare komplicerad struktur för att ge relevanta resultat, dock ständigt med uppdagade felintervall. Eftersom författarna bakom de citerade sambanden heller inte tycks vara benägna att berätta för läsaren hur de hade tänkt sig att sambanden ska tolkas, blir det ingen lätt uppgift att få ihop det.

Slutomdöme:

— Något är fel med dessa samband;

 

 

EXEMPEL ekv-gal (avrundade resultatvärden i två decimaler) värdena är kontrollerade mot standardWebbkällan:

0720+10 ska ge

207,55+11,41

Coloradosambandet visar

218,45+11,41

Gränsformen för Coloradosambandets felform ligger 

mellan 0649 = 102,25° och 0809 = 122,25°;

alla inslagsvärden REK+10 i det intervallet ger fel resultat i gREK:

Utanför det felfönstret är Coloradovärdena OK (i en första preliminär granskning).

Coloradosambandet uppvisar alltså mycket väl relevanta värden, man bara i vissa avsnitt, inte alls genomgående.

För den som inte känner till någon prövningsteknik, introduceras en ytterst påfrestande hantering — och som garanterat få klarar av att genomlysa.

Andra DEK-värden ger naturligtvis andra felintervall;

Så ger till exempel

0809+20 som ska visa

203,00+26,28

Coloradovärdet

223,00+26,28

DET ÄR (således) TYDLIGT att »ColoradoUniversitetet» haft mindre möjligheter att studera alternativa lösningsmetoder;

Sambandet är inte tillförlitligt. (Eleverna undervisas bara i begränsad omfattning).

 

Även New-Jersey-Astrofysikens samband och Weisstein-sambanden innehåller ovanstående felsamband

— vi ser också i vidare jämförelse (se nedan närmast) att dessa sistnämnda INTE matchar de samband som visar genomgående relevanta resultat

— och de uppvisar också genomgående felintervall

— även om man använder bägge sambandsalternativen för att söka en arcustangensform via sluttransformation z/x med kvadrantvillkor.

EXEMPEL ekv-gal:

Med 0720+10 som ska ge gREK|DEK

207,55+11,41

visar New-Jersey-Astrofysikens samband och Weisstein-sambanden felaktigt

38,51+11,41

via arctangens med kvadrantvillkor.

Sambandsformerna i New-Jersey-Astrofysikens samband och Weisstein-sambanden är alltså INTE generellt giltiga.

 

 

Generellt uppvisar sambandet

             sin(l – 33°)       = (sind sin 62,6° + cosd sin(a – 282,25°) cos 62,6°)/cosb  ..............             OK

i ovanstående källverk I PRINCIP relevanta värden; Den trigonometriska projektionen på vertikalaxeln kan emellertid INTE skilja mellan typ 5° och 175°, värdet är i bägge fallen detsamma. Därmed kan sambandet som sådan inte heller ENTYDIGT användas för att få fram gDEK-vinkeln (l) — det som krävs är ett tangensvillkor: både sinus och cosinus måste stämma.

Däremot uppvisar ”kompanjonen” i källverken ovan, sambandet

             cos(l – 33°)       = cosd cos(a – 282,25°)/cosb  ..........................................................             error, ger fel

genomgående felvärden; Jämför källverket nedan (Duffett-Smith), som tillämpar en annan procedurtyp.

Det är här inte känt vad felformen närmast ovan har för någon källgrund. I vilket fall elimineras möjligheten att få fram korrekt gREK-värde.

 

 

Webbkällan nedan däremot ger (så långt ännu testat) korrekta värden genomgående;

 

Google-Böcker med begränsad förhandsgranskning (sökning på ”galactic coordinates”)

Easy PC Astronomy, Peter Duffett-Smith, Cambridge University Press 1997, s43

”

”,

 

             sinb                               = cosd cos 27.4° cos(a – 192.25°) + sind sin 27.4°

                                                   = – cosd sin 62.6° sin(a – 282.25°) + sind cos 62.6°

                                                   = – cosd sin(a – 282.25°) sin 62.6° + sind cos 62.6°

                                                   = sind cos 62.6° – cosd sin(a – 282.25°) sin 62.6°

 

Källan ovan ger samma form för galaktiska deklinationsvinkeln som föregående källverk, men i övrigt en annan — mera precis — sambandsform för gREK;

 

                                                                      sind – sinb cos 62,6

             tan(l–33)                       = ————————————————  .............             Duffett-Smith-sambandet, ekv-gal REK

                                                                cosd sin(a–192,25) sin 62,6

 

                                                                     sinb cos 62,6 – sind

             tan(l–33)                       = ————————————————

                                                                cosd cos(a–282,25) sin 62,6

 

— och som visar sig vara samstämmig genomgående med webbKontrollkällan och Koordinatomvandlingen via vinkelsummateoremet och rotationssatsen. Observera att ovanstående samband är angivna i PREFIXxCOS (som vi skriver dem i kalkylbladen och datorprogrammen och i de tekniska räknarna generellt).

 

Även från galaktiska till ekvatoriella Duffett-Smith-sambanden ser ut att stämma med ovanstående bägge samstämmiga referenter enligt

 

             sind                                = cosb cos 27,4 sin(l – 33) + sinb sin 27,4

                                                   = cosb sin 62,6 sin(l – 33) + sinb cos 62,6

 

                                                                         cosb cos(l–33)

             tan(a–192,25)               = ————————————————  .............             Duffett-Smith-sambandet, gal-ekv REK

                                                        sinb cos 27,4 – cosb sin 27,4 sin(l–33)

 

                                                                         cosb cos(l–33)

             tan(a–192,25)               = ————————————————

                                                        sinb sin 62,6 – cosb cos 62,6 sin(l–33)

 

eller likvärdiga [tan A–a = cot(90–[A–a] = 90–A+a = 90+a–A = –[A–(90+a)]) = – cot A–(90+a)]

 

                                                        – sinb sin 62,6 + cosb cos 62,6 sin(l–33)

             tan(a–282,25)               = ————————————————

                                                                           cosb cos(l–33)

 

Observera att ovanstående samband är angivna i PREFIXxCOS.

 

forts.

 

 

GalKord

Huvuddelen av tester och jämförelser (ovan) finns inlagt i nedanstående kalkylblock

(blocket öppnas i separat fönster via OpenOffice förutsatt installerat, se länk med manual nedan närmast över bilden)

— tillsammans med ett konverteringskort av typen

(endast i bild nedan)

 

kalkylkort GalKord · Tabell1 · se öppningsmanual om ej redan bekant ·

 

Kalkylkortet kräver OpenOffice nyaste (svenska) version (3.0.0) · det KAN bli trixigt från Webbläsaren Internet Explorer om man inte känner till manualen

 

 

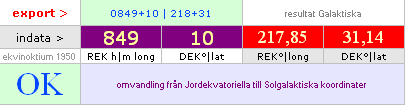
inmatningresultat

 

·          Indata REK anges konventionellt 0-24 i timmar|minuter (eng. hours|minutes) med positionerna TTMM,nn…;
typinslag av formen –REK ignoreras och justeras automatiskt internt till +REK

·          Indata DEK anges i 0-±90 grader med positionerna GG,nn… och justeras automatiskt över ±90°;
typinslag av formen 91 ignoreras och justeras internt till 89
— eftersom 91-värdet i annat fall skulle kräva att också REK-värdet måste justeras 180°, den vidlyftiga villkorssättningen tillämpas inte här

·          eftersom kortet är öppet för ändringar, kan den som själv så vill ändra delarna efter egna önskemål: det kort som visas är bara min egen grundskiss (utan alltför mycket påtande)

·          alla resultat kan kontrolleras manuellt mot den standardiserade astronomiska webbkällan
[http://fuse.pha.jhu.edu/support/tools/eqtogal.html]

 

OK-rutan visar OK endast om Duffett-Smith-värdena överensstämmer med Koordinatomvandlingen via vinkelsummateoremet och rotationssatsen (KOWIOR). Alla OK-värden ska då också stämma exakt med Webbens Astronomiska StandardKonvertering.

VärdeTestformen mellan Duffet-Smith och KOWIOR baseras på exakt maskinell jämförelse utan decimal avrundning (18 decimaler standard).

Om OK-rutan mot all förmodan skulle visa ”error” är antingen

1. något (allvarligt) fel — typ trasig dator (vilket garanterat aldrig händer inför ögonen på en normal användare), eller någonstans helt knäppa sambandsformer — eller

2. någon enkel villkorsform har missats; T.ex. har viss anpassning i cellkod gjorts för att matcha ut slutresultaten vid gränsvinkeln ±90°DEK som innebär att REK-värdet är egalt; Duffett-Smith-värdet (atan2-funktionen) har ingen parameter för det fallet utan kan i princip visa vad som helst 0-±180°. För att justera det (och andra liknande) måste alltså en villkorsform läggas till OM skylten ”OK” ska visas — inkluderat ev. missar från cellprogrammeraren, alltså mig.

   OM ”error” visas KAN det SÅLEDES bero på att någon gränsdetalj har missats. En del sådan cellkod KAN vara trixig, och bara i tidens längd får man till slut ihop ett väl fungerande cellprogram. Bli därför inte förvånad OM det plötsligt ev. kommer upp något FEL: kortet har ingen felfrihetsgaranti utan är bara en första fungerande skiss, inbilla dig inget annat. Hittar du något fel, är det bara att ändra (jag gör det med jämna mellanrum och löpande i alla mina egna kort när någon defekt visar sig).Samtliga kort har dock testats noga och genomgående eftersom resultaten i dem är avgörande viktiga för sammanhanget, och det bör inte finnas några större fel.

 

Se även en vidare beskrivning i ALLMÄNT OM KALKYLKORTET I GALKORD.

 

 

 

I fortsättning från huvudtexten

 

— Det finns alltså DELVIS OLIKA uppgifter på webben i ämnet.

Vad betyder det?

— TYP ”taskigt läge” för enskilda personer som VILL använda sambanden i olika datorsammanhang: det funkar inte — beroende på datakälla

Se för övrigt ett exempel i ett av de många olika frågeforumen på webben,

[http://www.shatters.net/forum/viewtopic.php?f=7&t=11650], obesvarad fråga från Maj 2005;

Här ställer en person den enkla raka frågan som kan besvaras av sambanden ovan i Duffett-Smith-källan, men som personen i frågan inte hittat — men väl de föregående citerade sambanden typ Weisstein och som att döma av EXEMPLEN inte fungerar genomgående; för att verkligen hjälpa den här frågaren måste i stort sett hela den här avhandlingen refereras till — så att läsaren SÄKERT får fasta referenspunkter och INTE utelämnas åt förtvivlans branter — på engelska.

Förhoppningsvis kommer vi dit, också.

Emellertid är också den här avhandlingen fortfarande under kritisk granskning. Inte med mer än en mera omfattande genomgång har gjorts av testvärdena kan en mera slutlig mening ges.

 

 

Hur härleds Duffett-Smith-sambanden?

 

 

EMELLERTID: Heller inte Duffett-Smith-källan har (veterligt) någon beskrivning av sambanden.

 

Ingen av författarna beskriver de använda sambanden mera ingående — i någon RELATERAD bemärkelse som INTE stödjer sig på typ »matristransponering».

Varför inte då?

— Därför (nämligen) att den läsare som INTE känner till »hemligheten» heller inte har en chans att reda ut snårigheterna. DET är taskigt.

— Därför att ingen i den moderna akademins korridorer tycks känna till de TVÅ OLIKA rotationskomplexen RotI och RotII.

— Jo (se vidare längre ner), man känner till dem — och ändå inte — genom algebraiska resonemang som garanterat ingen vanlig dödlig förstår något enda strå av. Modern akademisk tankevärld kan inte beskriva dem på något annat sätt.

 

Säg — till exempel — att ”felförfattarna” ovan typ Weisstein verkligen HAR genomfört praktiska räkningar på sambanden — just i de intervall där sambanden också ger korrekta resultat. Hur säger vi då? Har författarna fel när de säger att ”sambanden KAN användas för att beräkna …”? De säger ju inte typ ”sambanden ger GENOMGÅENDE KORREKTA RESULTAT”. Vi kan alltså strängt taget inte kritisera innehållet ”heller” eftersom det inte klart utsägs vad som menas. Å andra sidan är det uppenbart via EXEMPLEN att t.ex. Weissteins samband INTE OBETINGAT kan användas för att få en genomgående resultatform som stämmer överens med oberoende (etablerade) standardkällor typ AstronomiskaWebbReferensen. Det är alltså i vilket fall uppenbart att det saknas vissa grundläggande kunskaper i ämnet. Eller sagt på annat sätt: felformerna bevisar att ingen inom modern akademi i grunden kan ge någon KLAR OCH LÄTTBEGRIPLIG beskrivning och förklaring till ämnets omfattning eller struktur: rotationskomplexen I och II. I modern akademi känner man — tydligen i deras eget ljus, alltså utan hjälp av abstrakt algebra — inte till dessa. Man kan — tydligen — inte förklara ämnet för t.ex. en 12-åring. Jämför den elementära 3D-beskrivningen i relaterad matematik. Där går det.

 

Läs — till exempel — artikeln @INTERNET Wikipedia Rotation 2008-11-06.

— Inte ett ord om ’flera olika rotationskomplex’.

— Inte ens en antydan.

— Det är så bedrövligt som det alls kan bli; »Många» (läs, högskoleutbildade) KAN använda sambanden med matriser och determinanter för att få fram resultat i MÅNGA olika sammanhang — men det finns ingen som kan förklara innehållet så att det kan användas av till exempel en 12-åring.

— HÄR däremot går det i varje fall I PRINCIP. Rotationssatsen till exempel kräver inte någon direkt matematisk algebra för att förstås. Resten (se vinkelsummateoremet) är rena formaliteter.

 

Men de »skrifterna» typ Wikiexemplet närmast ovan (@INTERNET Wikipedia Rotation 2008-11-06) är också fulla av högskolematematikens matriser och determinanter och som man hänvisar till i moderna lärostolar när frågan om ROTATIONERNA kommer upp. Men den typen berörs över huvudtaget inte i Universums Historia.

 

 

 

 

 

KONVENTIONELL BESKRIVNING AV DE TVÅ ROTATIONSKOMPLEXEN GÖMMER SIG BAKOM MATRISTRANSPONERINGSBEGREPP

 

Upphittat:

 

[http://mathworld.wolfram.com/RotationMatrix.html],

”When discussing a rotation, there are two possible conventions: rotation of the axes, and rotation of the object relative to fixed axes.”;

Min översättning:

När man diskuterar rotation finns det två möjliga konventioner: rotation av axlarna, och rotation av objektet relativt fasta axlar.

 

— Jodå. Modern akademi känner visst till att det finns TVÅ olika rotationskomplex. Men kolla snacket — alltså vokabuläret:

Webbsidan avhandlar hela ämnet dels beträffande konversationen mellan de två sätten och dels rotationerna överhuvud genom matrisbegrepp, speciellt matristransponering mellan de två olika sätten — mera abstrakt och ljusår ifrån den enkla observationens logik går nog inte att komma. Och, som vi ser, finns ingen möjlighet för en icke-högskolefamiliär person att hänga med i det resonemanget. Vi kan alltså, i det upphittade resultatets ljus, fortfarande påstå: det finns ännu (November 2008) ingen allmän begriplig eller logisk varken beskrivning eller förklaring på webben @INTERNET i ämnet rotationer — inom den moderna akademins egna lärostolar.

— OM (nämligen) den moderna akademins matrisalgebra vore så förfärligt jätteduktig som vissa tycks vilja påskina, hur kommer det sig då att SÅ många människor står UTANFÖR den moderna akademin? Den borde vara lovprisad, men intet hörs på den fronten.

Visa.

— Det är inte matrisalgebran det är fel på, naturligtvis inte. Det är kunskapsnivån omkring.

 

 

 

 

 

ALLMÄN ÖVERSIKT

VINTERGATANS STJÄRNSYSTEM

SOLGALAKTISKA KOORDINATER (gREK 0-±360°, gDEK 0-±90°) används med fördel om det gäller att lokalisera de olika s.k. himmelsobjekten. Nedan visas några avancerade exempel på den astronomiska instrumentvetenskapens uppskattade resultat. Med blickpunkten riktad mot Vintergatans centrum — det mest klart lysande ljusbandet på stjärnhimlen — ser vi rakt mot nollpunkten i nedanstående panorama över SolGalaktiska vinkelskalan.

EXEMPEL 1: Örnnebulosan (+7000 lå, den med de helt fantastiska stoftbilderna) har JSg-koordinaterna (J, Jordekvatoriella, Sg Solgalaktiska) 1819–14|17±0; SgREK på 17° är lätt att hitta i bilderna nedan — vilket gör det enkelt att känna igen och komma ihåg lokalerna. Sedan på samma sätt med alla andra himmelsobjekt.

EXEMPEL 2: Krabbnebulosan (–6500 lå) har JSg-koordinaterna 0534+22|185–5; Den ligger alltså relativt lågt under Vintergatans skiva, samt rakt bakåt bort från centrum vid vinkeln

185°=–175°.

Krabbnebulosans markant avvikande position från Vintergatsskivan indikerar att originalstjärnan detonerade i ett relativt vätefattigt område, att stjärnan alltså låg (ligger) relativt isolerad från andra objekt. Men detta är bara lekmannens indikering.

 

                                                                                                     

 

                                                                         

 

                                                                          

 

                                                                                                                                 

 

Vinkelskalan ovan visar motsvarande Solgalaktiska REKtascension 0-±65°. Solgalaktiska DEKlinationen i ovanstående fotografiska remsa visas längst till vänster ovan i det smala intervallet 0-±1°.

 

BILDEN NÄRMAST OVAN (infraröda ljusets bild, eng. Infrared …) består i originalets kopia av 6 olika avlånga remsor som i sig består av en stor mängd mosaiskt sammanförda databilder baserade på omfattande observationer. Bilden ovan har här hämtats från webbkällan

@INTERNET Wikipedia Milky Way 2008-10-18

[http://upload.wikimedia.org/wkipedia/commons/3/3b/Ssc2008-11a.jpg]

den används också frekvent av (många) andra webbsidor.

 

Användning

 

Solgalaktiska koordinater är avgörande värdefulla referensmärken i den allmänna ÖVERSIKTLIGA analysen och utvärderingen av olika specifika stjärnobjekt; Olika regioner har olika lokala sammansättningar och den allmänna Solgalaktiska koordinatkartan ger en stor hjälp att lokalisera vad som hör till vem. Speciellt om det gäller jämförande analyser, som i fallet med pulsarerna, krävs enligt TNED en grundlig kännedom om den aktuella stjärnlokalen för att kunna avgöra grundaspekter som berör den avgörande ljuskurvans orsaksgrund. Med Solgalaktiska koordinater för objekten blir det mycket enklare att orientera sig. Se vidare i PULSARERNA.

 

 

 

 

 

 

Galaktiska Koordinater

 

innehåll: SÖK på denna sida Ctrl+F ·sök alla ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

Galaktiska Koordinater

ämnesrubriker

                      

 

innehåll

              GALAKTISKA KOORDINATER

 

                       Översikt Vintergatan — plan och vinklar

 

                                                         Ekvinoktium

 

                                                         REK och DEK

 

                       SOLGALAKTISKA OCH JORDEKVATORIELLA KOORDINATER

 

                                                         Grunddata

 

                                                         Grundtermer

 

                                                         Jordlokalens grundbegrepp

 

                                                         Solgalaktiska koordinatsystemet

 

                                                         Gyromodellen

 

                                                         Nolldeklinationssambanden

 

                       KOWIOR — koordinatomvanling genom vinkelsummateoremet och rotationssatsen

 

                                                         Vintergatans plan

 

                                                         Vinkelminus

 

                                                         Allmänt om kalkylkortet för studium av rotationerna

 

                                                         Kvadrantvillkoren

 

                       WEBBSAMBANDEN

 

                                                         Direktkonvertering

 

                                                         Weissteinkällan

 

                                                         New-Jersey-Astrofysiken

 

                                                         ColoradoUniversitetet

 

                                                         Felexempel

 

                                                         Duffett-Smith-källan

 

                                                         Kalkylkort GalKord

 

                                                         Rotationskomplexen i modern akademi

 

                       VINTERGATANS STJÄRNSYSTEM — allmän översikt

 

                                                         Användning

 

referenser

lå förkortning för ljusår, ljusets fria rymdväg under ett (sideriskt) år,

d           = vT = c0T = (299 792 458 M/S)(365,25 · 24 · 3600 S)

             = 9,46073 T15 M  ..............................  för T i T15, se T nedan

T för 10^+, t för 10^–, förenklade exponentbeteckningar

[BA]. BONNIERS ASTRONOMI 1978

 

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

 

 

Senast uppdaterade version: 2011-10-10

*END.

Stavningskontrollerat 2008-11-10.

 

rester

*

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG-justerad 2011-10-10

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se