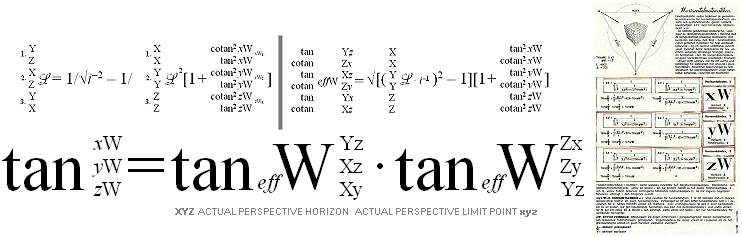MATEMATIKEN3D 2008XI2 BellDHARMA | 2006XI11 | Senast uppdaterade version: 2019-12-04 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

PERCEPTION AND PERSPECTIVES:

— ENLIGT PILOTSYSTEMET XYZxyz

ALLMÄN GENOMGÅNG AV GRUNDBEGREPPEN I 3D-GEOMETRIN MED PERSPEKTIV- OCH PERCEPTIONSGRUNDERNA

Appendix ¦ 3D-GEOMETRIN 2008 — från 3D-geometrins grunder 2006XI11 | urspr. frn. grundmanus 1976-1984 | — sammanställning med kortare beskrivningar

3D-MATH PERSPECTIVE GEOMETRY — its natural foundation EQUIVALENCE OF ROTI AND ROTII ¦ The ORIGIN OF ROTII ¦ FJÄDERANALOGIN — Spring Analogy Sfärperspektivet | Lagerqvistsyndromet | Perspektivkroppen | 3D-matematiken | Linjärperspektivgeometrins grunder | HP-kroppen | 3D-geometrins punktfält — 3D-matematiken

3D-GEOMETRIN 2008 ¦ 2019

PilotSystemet xyzXYZ:

Pilotsystemet — relaterad matematik

ANVÄNDS ALDRIG GENERELLT I ETABLERAD LITTERATUR

Bilden på tjejen är tagen ur en gammal tidning (i slutet av 1990-talet) eller katalog som jag inte minns namnet på. Jag ber om ursäkt för det. Jag hoppas hon inte misstycker att bli utnyttjad på det här oanmälda sättet.

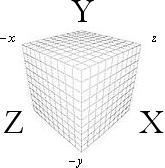
koordinataxlar och rotationsaxlar

xyz

KOORDINATPLAN och ROTATIONSPLAN

XYZ

3D geometri är

(enligt erfarenhet)

den datorstödda

läran och kunskapen om

beskrivning och presentation av

formerna i rummet xyz

på den plana bildytan xy

*

PRESENTATIONEN AV 3D-GEOMETRINS NOMENKLATUR försvåras avsevärt på grund av den moderna akademins sällsynt illa valda preferenser. Det mest naturliga valet av alla, pilotsystemet med positiva z i framriktningen, används INTE i den etablerade 3D-nomenklaturen på annat sätt än som ett NEGATIVT SYSTEM. Därmed blir matematiken också maximalt krånglig: studenten TVINGAS tänka i onaturliga banor, samt därmed acceptera DET som ”nomenklatur”. Man vänjer sig. I relaterad fysik och matematik är pilotsystemet ett positivt preferenssystem, precis som vi ser DET naturligt (med positivt till höger och uppåt, negativt till vänster och neråt).

3D-GEOMETRIN 2008

3D-G3PF:

3D-GEOMETRINS 3 PUNKTFÄLT

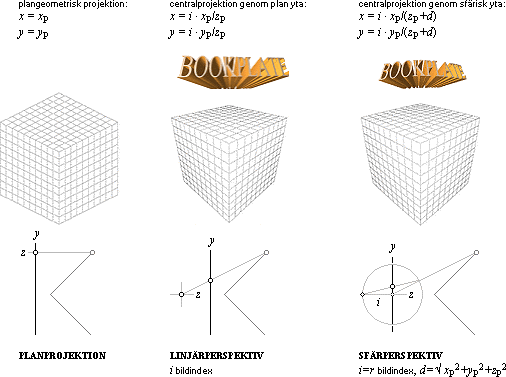
Planprojektion — Linjärperspektiv — Sfärperspektiv:

3D-geometrins 3 punktfält

SFÄRPERSPEKTIVET: Introduktion ¦ Härledningar

Vänster: ytutfyllande spegelsymmetrisk figurin av BellDharma 1995: 1. Robin Hoods Stövlar 2. Porträtt, Escher i Stormhatt, 3. (rotera 90°) Berglandskap med Glaciär. Höger: Självporträtt av Escher i litografi 1943 från Grafik och teckningar, M. C. Escher (1959)

SFÄRPERSPEKTIVET verkar vara helt orepresenterat i den vetenskapligt beskrivande formen på INTERNET. Det finns mig veterligt heller inget (kommersiellt) 3D-program som innefattar den synnerligen enkla sfäriska algoritmen (se nedan). Det finns visserligen artiklar som omnämner termen ”sfäriskt perspektiv”, och som även i en del fall ger någon illustration, men det materialet är ytterst magert för att inte säga helt obefintligt. Det bästa illustrativa materialet är rent artistiskt, av ypperligt hög kvalitet och sammanhänger med namnet Maurits Escher. Men, som han själv skriver, var han mindre intresserad av att förklara och beskriva än att utföra sina helt enorma och fantastiska, högst fascinerande verk. Jag introducerades för Escher i början på 1970-talet av en skolkamrat (en genuin Escherbeundrare), och det är Escher som inspirerat mig att göra en fullständig genomarbetning av (bl.a.) sfärperspektivet.

Sfärperspektivet, härledningar med RITEXEMPEL: Projektionssambanden ¦ GrundRITNINGAR MED PASSARE

3D-GEOMETRINS 3 PUNKTFÄLT

MITTEN: FRIHANDSTECKNING ENLIGT GRUNDERNA I DEN SFÄRISKA PERSPEKTIVGEOMETRIN »SEENDEPERSPEKTIVET» — Blyerts 1984 — Kopierat med lätt rödton, original A3.

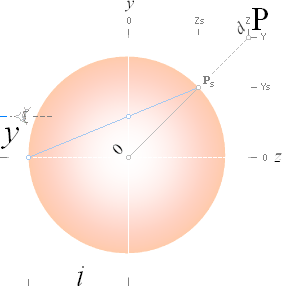
SFÄRPERSPEKTIVET — projektionssättet

SFÄRISKA PERSPEKTIVETS PROJEKTIONSPRINCIP illustrerat:

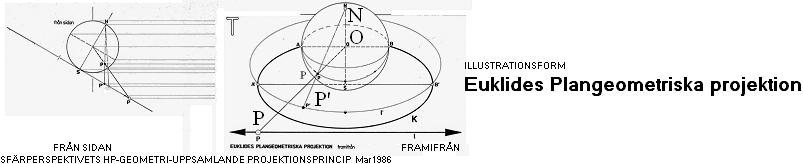
EN URSPRUNGLIG Synlinje från sfärens centrum origo O till en rumspunkt P skär sfärytan i en avbildad make P. För att få med även rumspunkter innanför sfären anställs en NODPUNKT — själva sfärperspektivets öonpunkt N på sfärens baksida och i perceptionsriktningen (z): Från N siktas sfärP:et på en underliggande PLAN bildyta — idealt genom sfären i mitten, eller på godtyckligt avstånd från O: P’ kan då avbilda praktiskt taget HELA xyz-rummets P — frånsett N-punkten.

— Illustrationen nedan visar hela principen i extrem vy:

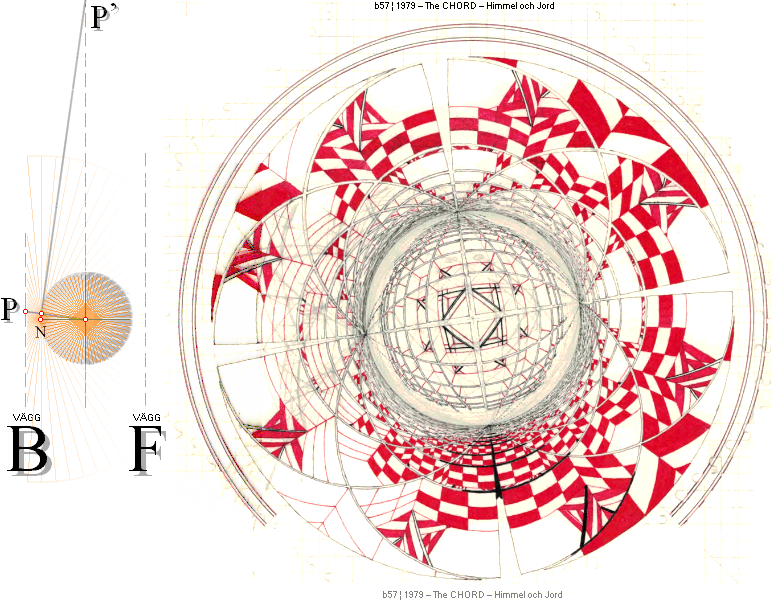
Vänsterdelen ovan BF i figuren visar projektionsprincipen med P-avbildningen i P’ via ögonpunkten N från den ursprungliga spegelbilden av xyz-rummet på sfärytan — och även objekten innanför denna. Objektspunkter även bakom ögonpunkten N kan avbildas — visas. Men då i motsvarande »oändligt förstorad version» ju närmare N sfärP:et ligger från rumsP:et.

— Det är, tydligen »Det Verkliga INRE Seendeperspektivet» — »drömvärldens visuellt olika avsnitt, kollage och inskjutningar»;

— Allt är synligt i Mind:et. Eller som en del säger det i Bion: ”You can run, but you cannot hide”. Bilden ovan 1978-79 är tecknad med vanlig passare efter de uppdagade härledningarna till sfärperspektivets matematiska geometri — efter inspirerat arbete från Maurits Escher[‡]. Se CHORD-KROPPEN.

Ett alternativt visningssätt till ovanstående visas nedan från från tiden med DELPHIchords2003:

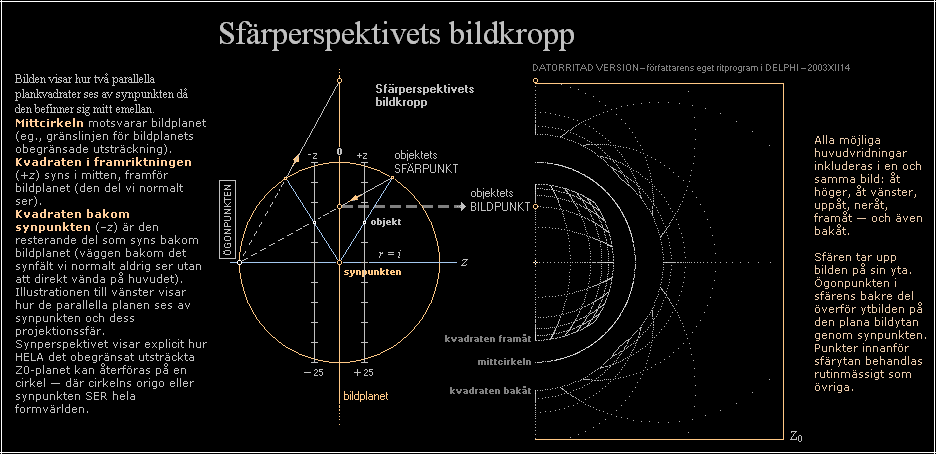
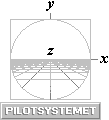
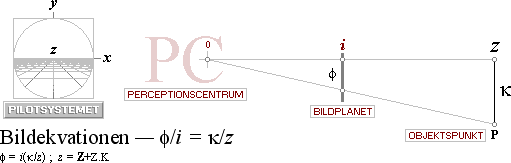
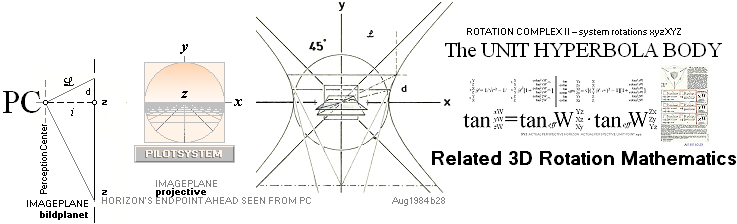
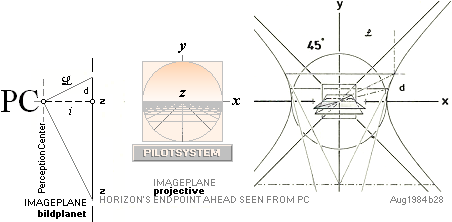
Z(0)-PLANET — 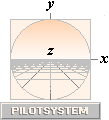med nomenklaturen från PILOTSYSTEMET — är här benämningen på det aktuella BILDPLANET — »filmduken», speciellt 0-planet eller bildprojektionsplanet i mitten i figuren — som xyz-3D-verkligheten vi lever i spelas upp PÅ framför våra seende ögon. Trots det systemets förträffliga användbarhet, används det aldrig, synligt, i etablerad litteratur. — utan krångliga förvanskningar TYP: negativa värden i framriktningen — men positiva åt höger och uppåt. Jämför MACz.

SPHprojDed: SPHded.

LINJÄRA FUNDAMENTALA HP-GEOMETRIN Avbildad på Sfären — FRÅN Pxyz till BILDPLANET (y) som är ställt genom Sfärens mitt — hela xyz-rummet kan i princip avbildas utom projektionspunkten längst bak på sfärytan: »MindPerspektivet».

Se även den illustrerade översikten från ovanstående allmänna beskrivning i 3D-geometrins 3 punktfält

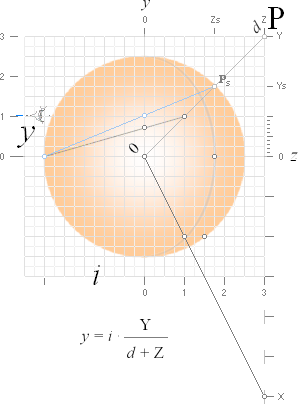
Exempel: EXEMPEL 1: Figuren ovan visar ett bildklot med radien (BildIndex) i = 2,5 enheter. Objektspunkten (P, överst höger) har koordinaterna P(XYZ) = P(0;3;3) vilket ska motsvara objektspunktens spegelbild på klotytan precis på omskrivna klotets cirkelradie i den aktuella vyn. Bildpunktens y-koordinat blir då med ovanstående härledda samband y = iY/(d+Z) med d = (X²+Y²+Z²)^0,5 som ger = (2,5)(3)/([0²+3²+3²]^0,5 + 3) = 1,0355339 Med figurens hjälp ser vi att detta värde stämmer utomordentligt väl med figurens skalvärden.

Sfärperspektivet — härledning: d = √ X^2 + Y^2 + Z^2 = avståndet från koordinatorigo till objektspunkten (P); Ys Zs i Ys y i i —— = —— = —— ; ——— = — ; Ys = Yp — ; Zs = Zp — ; Yp Zp d i+Zs i d d i + Zs = i + Zp(i/d) = (i/d)(d+Zp) ; Ys/(i+Zs) = Ys/(i/d)(d+Zp) ; Ys = Yp(i/d) ; Y = Yp ; Ys/(i+Zs) = Yp(i/d)/(i/d)(d+Zp) = Yp/(d+Zp) ; Resultat: Ys y Yp ——— = —— = ——— i+Zs i d+Zp Härledningen ovan för Y-koordinaten med vyn sedd från sidan gäller även för X-komponenten med vyn sedd ovanifrån, sambandet blir analogt Xs x Xp ——— = —— = ——— i+Zs i d+Zp Se även vidstående Exempel. Beviset för att relationerna gäller även i fallen då spegelpunkten Ps inte ses exakt på sfärytans rand i vyn baseras på att: — Ps ligger i vilket fall på linjen (gömda cirkelbågen som Y-linjen ritar upp på den speglande klotytan, se även vidare i vidstående Exempelbeskrivning) mellan Ps[som ovan] och sfärens origo [O]: — Triangelrelationerna Ys/Yp = Zs/Zp med Ys/(i+Zs)= y/i blir i vilket fall analoga — oberoende av X med givna YZ. — Det enda som (då) bestämmer bildpunktens placering (y som ovan i exemplet) blir alltså X i d: y går mot noll som X växer obegränsat. Samma typresonemang gäller sedan också för bildpunktens x-koordinat med projektionen sedd ovanifrån (delvis i mixad vy i vidstående exempelfigur). EXEMPEL 2: Vi använder samma YZ-värden som i Exempel 1 men ett alternativt X-värde, X=6; [Flera olika sätt finns att kontrollberäkna de inre värdena, alla kräver dock god inblick i ellipsens och cirkelns elementära geometri, en del av dessa delar finns beskrivna i CEPH-ekvationen, vi förutsätter här den bekantskapen]; P(XYZ) = P(6;3;3) Det motsvarar objektspunktens spegelbild på klotytan i den markerade punkten mellan Ps.O i exempelfiguren. Bildpunktens y-koordinat blir då y = iY/(d+Z) med d = (X²+Y²+Z²)^0,5 som ger = (2,5)(3)/([6²+3²+3²]^0,5 + 3) = 0,7247448 vilket vi med figurens hjälp ser stämmer utomordentligt väl.

NOTERA att (xyz)=0 ligger i sfärens centrum i sfärperspektivet, medan motsvarande (xyz)=0 för linjärperspektivet ligger i den motsvarande sfärytans ögonpunkt; ögonpunkten endast FÖRMEDLAR — inte utgör centralpunkten hos — den bild som ses med PC (PerceptionsCentrum|PerspektivCentrum) i sfärens centrum. Alla Objekt(xyz) ses därför förminskade i Sfärperspektivet relativt Linjärperspektivet med samma utgångsvärden,

Linjära Sfäriska

För att få ungefärlig överensstämmelse i växlingen Sfäriskt-Linjärt kan Bildindex (i) ökas till Z.K (Objektets eget koordinatorigos Z-avstånd). Jämför bilden nedan i sfäriskt perspektiv (i = Z.K) med föregående linjärperspektiv ovan vänster (Z.K > i):

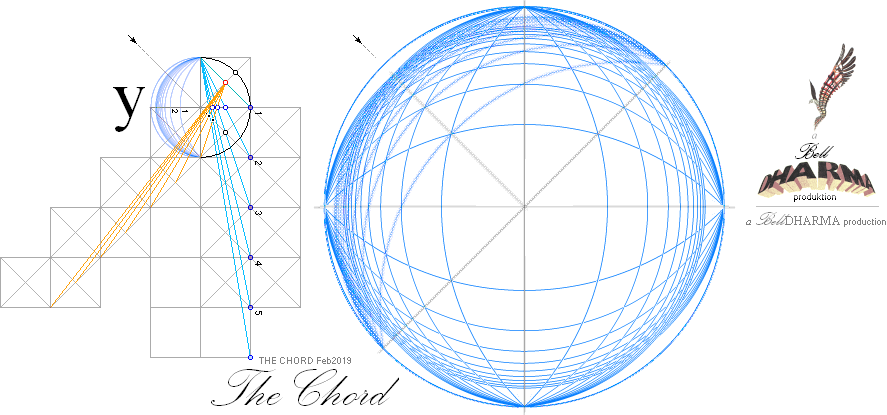
CHORDkroppen: RITNING MED PASSARE

PRINCIP MED GRUNDILLUSTRATIONER

HUR MAN KAN TECKNA SFÄRPERSPEKTIVETS BASPLAN MED PASSARE och linjal:

I KORT ILLUSTRERAD SAMMANFATTNING:

— Sfärperspektivets[‡] MANUELLA UPPRITNING klargör i det allt väsentliga den intima kopplingen och samhörigheten med HORISONTALPERSPEKTIVETS grunder[‡]. Den angivna sambandsformen i figuren nedan beskrivs mera detaljerat i efterföljande text. Här understryks enbart genom den visuella delningsgeometrins nödvändiga förberedelse för Sfärperspektivets uppritning ATT samhörigheten ÄR stadfäst:

HorisontalperspektivgeometrinHPG+SfärperspektivgeometrinSFPG=sant:

SPHperspPASS: — BasicHP-SP:

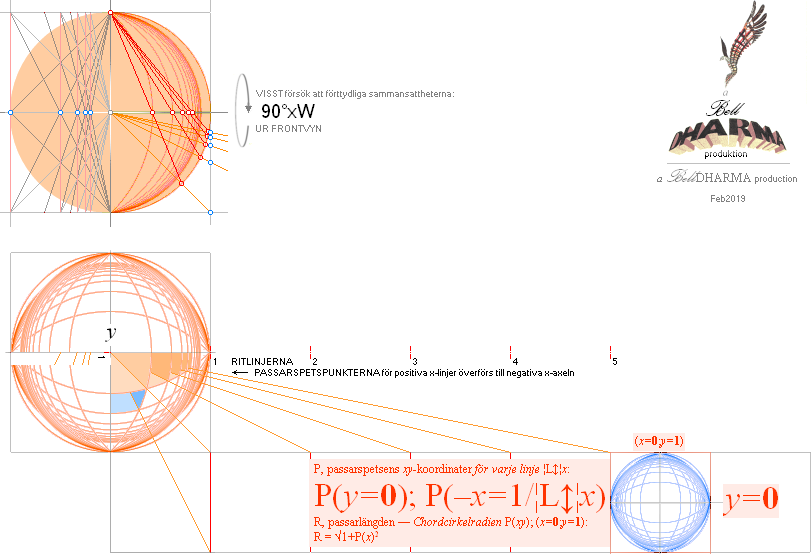
— Men var i etablerad litteratur finns beskrivningarna? Jag ser inga. Och Maurits Escher såg tydligen inga han heller för sin tid (1898-1972). Den Moderna Akademins enda intresse i ämnet verkar vara koncentrerat till ABSTRAKT ALGEBRA: ingen illustrativ praktisk koppling: ingen praktiskt — hantverksbetonad — beskrivning eller förklaring. Jämför citatet från WolframMATH2019.

Vi studerar ämnet — noga.

CAD:

COMPUTER AIDED DRAWING— CAD — datorstödd ritning:

— Inte DatorSKAPAD:

— INDIVIDEN skapar eller upptäcker eller uppdagar ett grundkoncept. Inte Datorn.

Datorn kan sedan användas för att FRAMHÄVA och TYDLIGGÖRA. Inget annat. Hjälpmedel. Inte Auktoritet.

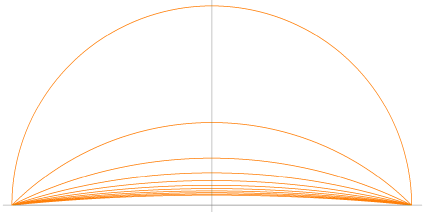
Datorn kan med fördel användas för uppritning av cirkelbågarna med speciellt stor radie — flaskhalsen vid ritning med fysisk passare.

— Sambandet för CIRKELN y = √ 1 — x² prepareras med variabla insättningar enligt

y = √ 1 — x²

= —(y) + A√ 1 — (x/A)²

; A = √[1+(a+b)²]

–(0)+([1+(0+0)'2]'0.5)(1–[x/[1+(0+0)'2]'0.5]'2)'0.5

–(1)+([1+(1+0)'2]'0.5)(1–[x/[1+(1+0)'2]'0.5]'2)'0.5

–(2)+([1+(1+1)'2]'0.5)(1–[x/[1+(1+1)'2]'0.5]'2)'0.5

–(3)+([1+(1+2)'2]'0.5)(1–[x/[1+(1+2)'2]'0.5]'2)'0.5

–(4)+([1+(1+3)'2]'0.5)(1–[x/[1+(1+3)'2]'0.5]'2)'0.5

–(5)+([1+(1+4)'2]'0.5)(1–[x/[1+(1+4)'2]'0.5]'2)'0.5

...

Ritprogrammet som använts här utvecklades av författaren (2002+) i DELPHI4 — med STARK undran, och förundran, varför inte mjukvarujättarna på Jorden BJUDER på den typen i samband med datorförsäljning — LÅT MÄNNISKORNA UTVECKLAS, för tusan bövlar. Varför inte. What’sUp?

— DÄRFÖR ATT DET skulle GE ALLDELES FÖR STOR FRIHET ÅT MÄNSKLIGHETEN individerna själva SOM ISTÄLLET MÅSTE UTSUGAS betala mera MEDAN DE HÅLLS FÖRSLAVADE I UNDERJORDEN UTAN BELYSNING med ProfitFöretagens Djupt Beundransvärda ViVeta-DuKöpa. MäGuvaFiiint. Rätta gärna om fel.

— Ritverktyg

— Här i Datorsammanhanget: enskilda pixelsteg måste kunna navigeras, liksom bestämda återkommande flyttningsintervall i de olika möjliga bildflyttningsmoderna AND OR XOR, transparent, kvadraturroterande i steg om 90°, alla kombinationer: piltangenter, sifferbordet, kontrolltangenter:

— Ett motsvarande KLAVIATUR, en bordsdator.

— Vad vi vet — här — existerar inga sådana gratis ritprogram på Internet Feb2019 — om alls över huvud taget på Internet (svårt att få fram exakt VAD som finns i ämnet):

är helt avgörande för att människor ska kunna utveckla naturvetenskapen. Frågan ställs öppen: FINNS SÅDANA VERKTYG IDAG Feb2019 alls över huvud taget — dessutom gratis, jättefina, för den som vill och har tid att arbeta med detaljerna? Webben är full med ”free”. Vad, exakt som döljer sig bakom är svårare att få reda på. »ENKLA ritprogram» @Internet verkar INTE vara någon lätt sak att hitta exempel på.

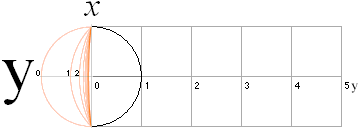
Enhetsrutnätet INÅT x-axeln i Sfärperspektivets BILDCIRKEL ritas upp UTÅT oändligheten med passarspetsen i 0 — Bildcirkeln — 1 2 3 4 5 .. med passarlängden/ritudden genom x-axelns bildcirkelskärning; Cirkelradierna för y = 0 1 2 3 4 5 .. blir respektive

√ 1 + (0+0)² = 1 ¦ √ 1 + (1+0)² = √2 ¦ √ 1 + (1+1)² = √5 ¦ √ 1 + (1+2)² = √10 ¦ √ 1 + (1+3)² = √17 ¦ √ 1 + (1+4)² = √26 ¦ √ 1 + (1+5)² = √37 ¦ ...

RITPROGRAMMETS FUNKTION: ENTER startar vid makören (tydlig kryssform), precisionsinsättning vid slutpunkt, SHIFT verkställer — tills ENTER avslutar;

— FÖRE varje SHIFT finns optionen INSERT som pausar och frikopplar markören som kan flyttas till en färgkarta: vid INSERTNo2 hoppar markören tillbaka till LämnaLäget, och en SHIFT verkställer på vald färg. Linjetjockleken kan ställas in separat när som helst med sifferbordets hjälp: mata in värdet.

— VAR finns den ENKLA typen, dessutom GRATIS, utom HÄR? Internet Feb2019 verkar INTE vara stället att — ens — försöka få reda på det.

— Piltangenter, Sifferbordet, Kontrolltangenterna + Musen — till vänster, sifferbordet+piltangenterna till höger: bägge händerna används naturligt som vid ett klaviatur. Effektivt. Snabbt. Enkelt. Programmet utvecklades av författaren i Borlands Pascal Turbo Assembler.

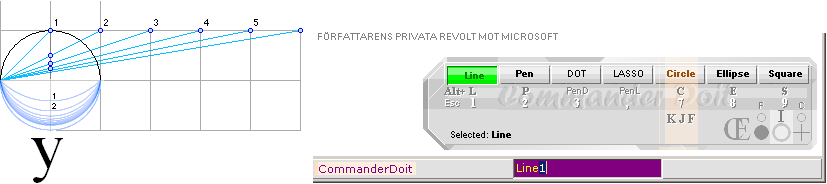
Ritverktygen som medföljer Windows — jämför W10 — innehåller ingen pixelstegning i valfria intervall för samtliga ritnavigeringar. Vill man dra en linje mellan två punkter, är det slumpen i slutänden som avgör. Det finns ingen exakt inställning. Paintbrush i Windows 3.1 hade Det. Men det väldig användbara enkla ritprogrammet plockades bort med Windows 95. Så: Vad, exakt, VET Microsoft Feb2019 om Elementär DatorSTÖDD Ritning? Visa gärna med tydliga exempel. Blända oss.

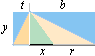
Enhetsrutnätet UTÅT Sfärperspektivets BILDCIRKELBÅGE ritas upp genom ENHETSDELNING, figuren ovan:

— Passarlängden som tidigare genom x-skärningen med bildcirkeln och Passarspetsen successivt på avstånden från origo:

1 ¦ 1/2 ¦ 1/3 ¦ 1/4 ¦ 1/5 ¦ ...

Cirkelradierna för dess delavstånd blir respektive

√ 1 + (0+1)² = 1 ¦ √ 1 + (0+1/2)² = √5/4 ¦ √ 1 + (1+1/3)² = √10/9 ¦ √ 1 + (1+1/4)² = √17/16 ¦ √ 1 + (1+1/5)² = √26/25 ¦ √ 1 + (1+1/6)² = √37/36 ...

med den cirkelDatorRitande formen

–(0)+([1+(0+1)'2]'0.5)(1–[x/[1+(0+1)'2]'0.5]'2)'0.5

–(1/2)+([1+(0+1/2)'2]'0.5)(1–[x/[1+(0+1/2)'2]'0.5]'2)'0.5

–(1/3)+([1+(0+1/3)'2]'0.5)(1–[x/[1+(0+1/3)'2]'0.5]'2)'0.5

–(1/4)+([1+(0+1/4)'2]'0.5)(1–[x/[1+(0+1/4)'2]'0.5]'2)'0.5

–(1/5)+([1+(0+1/5)'2]'0.5)(1–[x/[1+(0+1/5)'2]'0.5]'2)'0.5

...

Enhetsrutnätet — den plana bildytans motsvarande rutnät i fysikvärlden — är så härlett och definierat för sfärperspektivet.

DIAGONALERNA behandlas på samma sätt º via diagonalerna i rutnätet:

— Rita ut diagonalerna i rutnätet med ett motsvarande diagonalkryss genom bildcirkelns origo=centrum. Måtta på samma sätt som ovan med passarspetsen i avdelade punkter med tillhörande cirkelbågar genom skärningen Bildcirkeln xyDiagonalpunkter. Vi gör ett försök:

The CHORD of ARCS:

Enda skillnaden i sambanden för diagonalerna blir att införa KvadratRotsFörkortningen √2 :

–(0)+([1+(0+1)'2]'0.5)(1–[x/[1+(0+1)'2]'0.5]'2)'0.5

–(1/2√2)+([1+(0+1/2√2)'2]'0.5)(1–[x/[1+(0+1/2√2)'2]'0.5]'2)'0.5

–(1/3√2)+([1+(0+1/3√2)'2]'0.5)(1–[x/[1+(0+1/3√2)'2]'0.5]'2)'0.5

–(1/4√2)+([1+(0+1/4√2)'2]'0.5)(1–[x/[1+(0+1/4√2)'2]'0.5]'2)'0.5

–(1/5√2)+([1+(0+1/5√2)'2]'0.5)(1–[x/[1+(0+1/5√2)'2]'0.5]'2)'0.5

...

Notering: FINNS DET NÅGOT MERA stimulerande, matematikutvecklande och verkligt rejält djupentusiasmerande än att arbeta med dessa STRUKTURER — just att få SKRIVA ut dem, utveckla dem, och sedan SE dem: oändlighetsperspektiven. Ge gärna exempel den som vet mer.

Den tidiga Versionen 1980 med passare och Rotrings nålfina tuschpennor:

DELPHIchords2003:

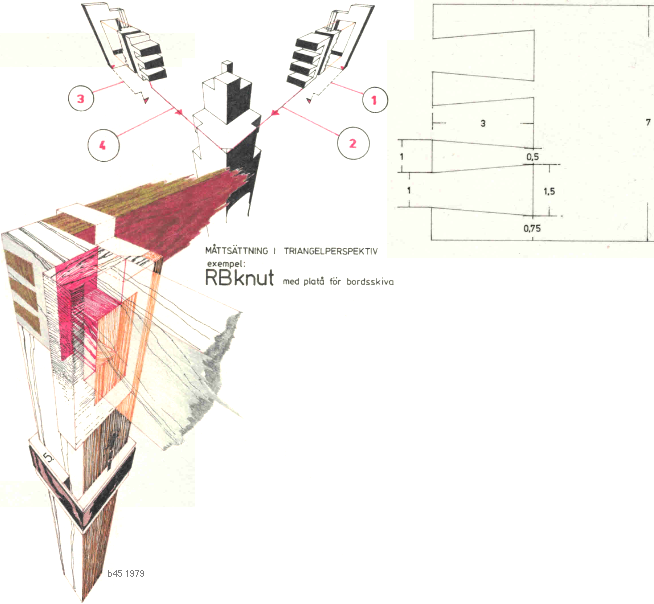
MÅTTSÄTTNING I KVADRATERNA i vidare mening utförs som antyds i figuren ovan.

— Mera exempel visas nedan: Datorritat sfärperspektiv 2003 med författarens eget utformade ritprogram i DELPHI-1¦4 — Programformer vars ÅTKOMLIGHET — successivt från Windows XP och framåt — har stängts ner av Microsoft.

— DELPHI4 fungerar fortfarande i Windows (10) — men SÅ våldsamt stympat av Microsoft att programformen »har tappat motorn»:

• Alla datorprogrammerare är beroende av utvecklingsprogrammens — här DELPHI4 främst — hjälpmanualer. I originalet (tiden vid Windows XP) användes en WinHELP-fil för att synkronisera den första datorerans HELP-filer — som DELPHI använder frekvent i sin CodeEDITOR med bekväma och förnämliga länkopplingar typ: man klickar på ett ord och kopplas direkt till aktuell FÖRKLARANDE avsnitt. Enbart Windows API-blocket är (ytterst) omfattande. och man klarar inte programmeringen utan detaljerad kommandoinformation (med exempel).

— Den möjligheten har Microsoft helt eliminerat med senare Windows (10): WinHELP-filen kan visserligen kopieras från äldre Windows-system. Men Windows 10 släpper inte inte in den i något operativt arbete — trots ihärdiga, otaliga försök. Så har hela det oerhört fina och på sin tid GRATIS utvecklingsprogrammet för Windows — DELPHI4 — bommats igen av Microsoft: »åtkomst nekas». Once upon a time ... there were flowers on the ground ...

Ytterligare några illustrationer framhäver sfärperspektivets egenheter:

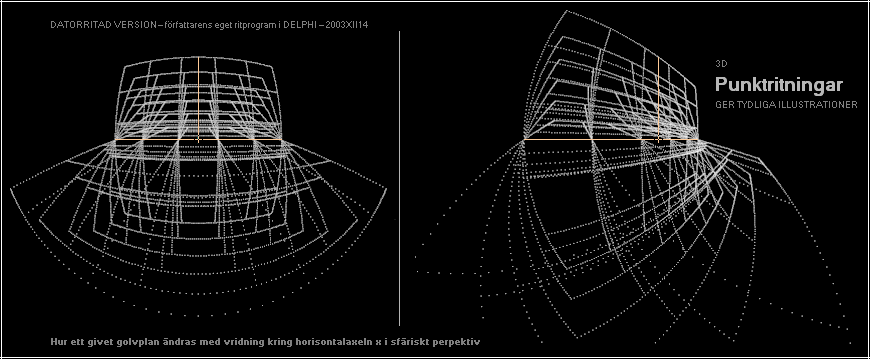
RITPROGRAMMET här MICROSOFT STÖDJER INTE LÄNGRE DEN TYPEN använder ett enkelt kvadratiskt plan — valfritt antal delkvadrater — som sedan kan presenteras i olika perspektiv: plan-, linjär-, eller sfäriskt. För rotationskomplexet, se från Rot1 och Rot 2: Rot1 används uteslutande i datorsammanhang på grund av dess enkelhet — och oerhörda snabbhet i beräkningskomplexen.

CHORDeq:

En enhetligt CIRKELRITANDE matematisk sammanfattning för SFÄRPERSPEKTIVEN av typen GÄLLER FÖR SAMTLIGA FALL kan sammanfattas som nedan — cirkelbågar som avbildar godtyckliga objektslinjer:

— Se vidare förklaring och beskrivning som följer.

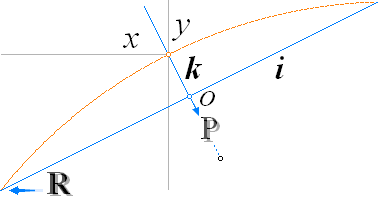
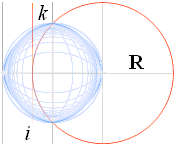
O, origo:

K, objektslinjens normaldistans från O:

k, avståndet från O för K-avbildningen: k = R–i:

i, BildINDEX i=1:

P, passarspetsens distans från O för varje objektslinjes distans K från O med motsvarande bildrepresentation k:

P = 1/K

R, passarlängden — ChordCirkelRadien:

R = √1+P²

O, ImageINDEX i =1 @Origo [»at center»] (origo, from Latin, ”origin”, BKLVIII 1926sp1391):

P, compasses’ OnsetTipDistance from O for each objectLine’s distance K from O with a corresponding image k;

R, compasses’ length — the actual CHORD-circle radius.

— In CAD — Computer Aided Drawing/design — an arbitrary Chord-Arc

such as the one illustrated (orange) in the left part of the figure above

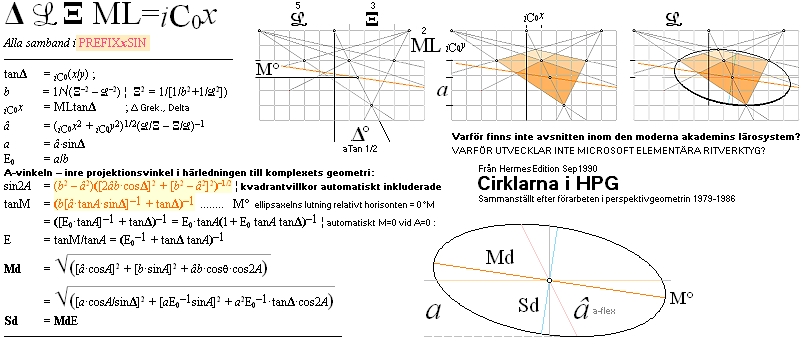
is computer-drawn in polar coordinates by the expression

1[2(sin[(x)+(þ/2)([90–45]/90)])] — PREFIXxSIN þ (ANSI: Alt+0254) specifies pi in author’s program;

First number 1 specifies the actual CHORD-circle radius to be drawn in i-units; Second number 45 specifies the actual angle (A), here in degrees, by which the actual Chord-Arc is tilted or twisted from a vertical defaullt 0°. In the illustration, A=+Arc[Tan(½)]=26,57°,

SFÄRPERSPEKTIVETS BILDREPRESENTATION för den rena datorhanteringens del: Den är på sitt sätt betydligt enklare att hantera genom att perspektivpunkterna beräknas som fotografiska bildpunkter — inga bågritningar — i stor mängd som sedan bakas ihop till en färdigroterad slutbild (som kräver särskilda bildalgoritmer för att ge ett slutligt naturligt utseende). Se den enkla HÄRLEDNINGEN för xyz-punkternas del.

ENHETLIGA ENKLA ALLMÄNNA SAMBAND

AVBILDNINGEN AV YTPLANET xy i Sfärperspektivet (ChordOfARCS — a BellDharma designation only in spite of its mathematical discovery [late1976] after inspired investigations from the great and fascinating works of the graphician Maurits Escher [1898-1972]):

:

ALLA AVSTÅND FRÅN xy-ORIGO — måttsenhet = Bildindex i = ChordCirkelradien:

——————————————————————————————————

x — linjer parallella med y-axeln:

P(y=0)(–x=1/1)¦L↨x1 ¦ P(y=0)(–x=1/2)¦L↨x2 ¦ P(y=0)(–x=1/3)¦L↨x3 ¦ P(y=0)(–x=1/4)¦L↨x4 ¦ ...

P, passarspetsens xy-koordinater för varje linje ¦L↨¦x:

P(y=0); P(–x=1/¦L↨¦x)

R, passarlängden — Chordcirkelradien P(xy); (x=0;y=1):

R = √1+P(x)²

R = √1+P(x)² ;

——————————————————————————————————

y — linjer parallella med x-axeln:

P(x=0)(–y=1/1)¦L↨y1 ¦ P(x=0)(–y=1/2)¦L↨y2 ¦ P(x=0)(–y=1/3)¦L↨y3 ¦ P(x=0)(–y=1/4)¦L↨y4 ¦ ...

P, passarspetsens xy-koordinater för varje linje ¦L↨¦y:

P(x=0); P(–y=1/¦L↨¦y)

R, passarlängden — Chordcirkelradien P(xy); (x=1;y=0):

R = √1+P(y)²

R = √1+P(y)²

——————————————————————————————————

SAMMANTAGET KOMPRIMERAT:

——————————————————————————————————

P, passarspetsens xy-koordinater för varje linje ¦L↨¦xy:

P(yx=0); P(–xy=1/¦L↨¦xy)

R, passarlängden — Chordcirkelradien P(xy); (x=01;y=10):

R = √1+P(xy)²

Sambanden ovan har sammanställts CHORDeq till en enklare enhetlig sambandsform som gäller för samtliga fall, 0-360° oberoende av xy-beteckningarna. se CHORDeq.

— polärformen till chord-bågen beskrivs nedan.

POLÄRA KOORDINATER för ATT få fram GODTYCKLIGT ROTERADE exakta datorSTÖTTritade CHORD-cirklar:

1[2(sin[(x)+(þ/2)([90–45]/90)])] — PREFIXxSIN þ (ANSI: Alt+0254) anger pi;

— Första siffran anger CHORD-cirkelradien R relativt UNIT = BildINDEX-cirkelradien = i;

— Siffran markerad 45 anger aktuella CHORD-cirkelns vridning (+90° i figuren nedan) relativt vertikalläget 0°;

— CHORDA-måttet som PolärCirkeln måste anpassas till för korrekt passning: k = R–i — alltid inom i-distansen.

EXEMPEL: 30° från vertikalt, R=10×(i=50)pixels. Med Kordan (k) markerad tas ChordCirkeln ut enkelt (kopieras direkt) till i-cirkeln, aktuell del.

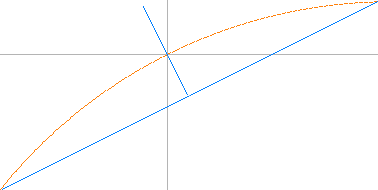
PolärCirkeln på formen r = 1[2(sin[(x)+(þ/2)([90–45]/90)])] ritas alltid roterad relaterad cirkelns toppunkt vid 0°.

— METODEN lämpar sig endast för enskilda Chordcirklar (flera steg krävs för att sätta samman resultatet = TIDSKRÄVANDE), ingen direkt systemritning att likna vid föregående rektangulära metod — se CHORD-kroppen. Se även CHORDeq sambandet i sammanfattning för godtycklga CHORD-cirklar.

Avslut: CHORDkroppen

MYCKET MER finns säkert att presentera, visa och studera i ämnet SFÄRPERSPEKTIV. Tills vidare avslutas framställningen här med att omnämna/illustrera de mest närliggande CHORD-komplexen som också kan ritas med passare:

Författarens manuella sammanställningar för Sfärperspektivets olika ämnesblock Mar1986.

Figurerna ovan — FloorCHORDS, ComplexCHORDS och WallCHORDS, manuellt ritade och sammanställda av författaren 1986 — har vart och ett sina speciella sambandsformer:

— Alla är lika omfattande att studera som fascinerande att arbeta med. Och framför allt, ATT rita upp själv — med en gammal vanlig klassisk, precisionsställbar naturligtvis, passare.

Avgörande elementära ritverktyg:

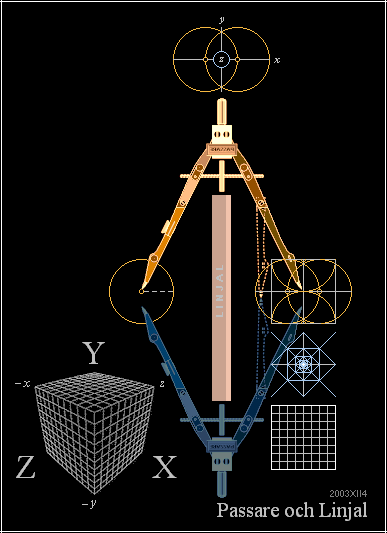
Passare med StällSkruv, Linjal — och Vinkelhake: noggrant vinkeltestad för bästa resultat:

— VINKELHAKSTESTET: Lägg an och rita: VÄND och titta: Minsta vinkelfel visas i att linjerna skevar.

— LINJALTESTET: Rita: DiametralVÄND och titta. Minsta orakhet visas i skevande linjer:

— Fram med Sandpapper och Slipklossar. Vi ger oss inte förrän resultatet är perfekt. Vi får vila, aldrig ge upp.

— Den som vill investera i ett ritverktyg som, garanterat, håller hela livet ut, som inte kräver batterier eller ström eller underhåll alls, gör klokt i att sondera marknaden för att vaska fram bara det allra bästa.

JÄMFÖR (Feb2019) ELLIPSOGRAFEN HAFF Nr.97:

— Verktygen, instrumenten, tillverkas inte längre.

PASSARE verkar fortfarande finnas en del till rejäla priser — SAMT FÖRETAG nu även Tradera SOM FORTSÄTTER ENVISAS MED COOKIES — insisterar på att besvära privatpersoner med täckande rutboxar typ ”JAG FÖRSTÅR” att medverka i brott mot mänskligheten — Vi Förbättrar Din Upplevelse Genom att Spionera På Ditt Och Andras InternetAnvändande — tydligt utan minsta insikt i vad som försiggår:

— FÖRESTÄLLNINGEN ATT Internet-INDIVIDANVÄNDARSPIONAGE HAR NÅGOT MED EN FÖRBÄTTRING AV NÅGOT att göra ÄR RENT FABRICERAT Google-NONSENS FÖR TILLFÄLLET ATT FÅ UTÖVA PRIVATRÄTTSLIGT INTRÄNGANDE MANIPULERANDE AFFÄRSVERKSAMHET — lagbrott A12UDHR10Dec1948 — SOM VORE DET FRÅGA OM EN VÄRLDSOMSPÄNNANDE VÄLGÖRENHETSINRÄTTNING. DET FINNS INGENTING SÅDANT:

— All verksamhet

attityd, tanke, åsikt, uppfattning, åberopande, mening, idé, hävd, inlägg, debatt, föreningsverksamhet

UTOM människovärdighetens explicita uttryckliga erkännande är och förblir utövande förtryck

”EFTERSOM ERKÄNNANDET AV DEN INNEBOENDE VÄRDIGHETEN OCH AV DE LIKA OCH OMISTLIGA RÄTTIGHETERNA FÖR ALLA MEDLEMMAR I MÄNSKLIGHETENS FAMILJ ÄR GRUNDVALEN FÖR FRIHET, RÄTTVISA OCH FRED I VÄRLDEN”, K1UDHR10Dec1948.

är allt övrigt icke-frihet, icke-rättvisa, icke-fred: satanistiskt, fascistiskt, nazistiskt djävulsdyrkande skit.

— Affärsvärlden har — snabbt 2010+ — glidit in i en föreställning att företräda en INDIVIDRÄTTSLIGT MANIPULERANDE AUKTORITET: klassiskt utövande fascism, på Bekväma Folkbesökta Internet.

OM TRADERA OCH ANDRA FÖRETAG VILL FORTSÄTTA PÅ DEN VÄGEN ÄR DET DERAS ENSAK. MEN LÅT DET DÅ OCKSÅ STÅ SÅ: »Vi skiter fullständigt i ”varje individ” att premiera kunskapen om grundläggande mänskliga rättigheter med ”personlighetens fria och fulla utveckling”». Visa det i klartext FRÄMST. Tack. Jag deltar inte i någon nazistisk verksamhet. Vare sig den sker medvetet eller omedvetet.

Tillfredsställelsen det ger att använda ett sådant verktyg, varje gång, har inga andra egna ord än dessa, veterligt: det utvecklar — hela tiden. Gnäller aldrig (Typ Microsoft&Google). Tjatar aldrig på en (Typ Microsoft&Google). Jävlas aldrig (Typ Microsoft&Google).

3D-GEOMETRIN 2008 | 3D-nomenklatur

3D-nomenklatur

För att framgångsrikt kunna arbeta med 3D-programmen, är det avgörande viktigt att först förstå vad programmakaren menar att de olika riktningarna betyder.

Bilden på tjejen är tagen ur en gammal tidning (i slutet av 1990-talet) eller katalog som jag inte minns namnet på. Jag ber om ursäkt för det. Jag hoppas hon inte misstycker att bli utnyttjad på det här oanmälda sättet.

MACz: PilotSystem

ETABLISSEMANGETS OFTA ANVÄNDA VEKTORKALKYLANPASSADE 3D-NOMENKLATURSYSTEM

som kör över det enkla pilotsystemets preferens:

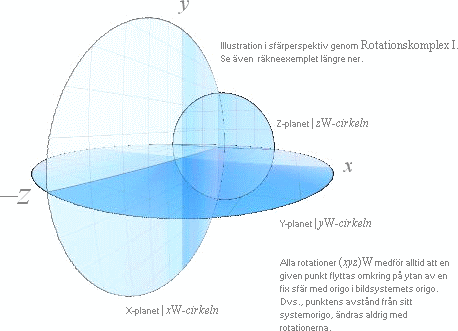
Den mest naturliga preferensen för 3D-geometrin, pilotsystemet xyz, omnämns inte ens i den moderna etablerade matematiska nomenklaturen. Istället används ett s.k. högersystem** baserat på en SKRUVANALOGI som alltså kräver ytterligare förtrogenhet för lekmannen (**+z är den riktning »en högergängad skruv» stiger då den vrids positivt i xy-planet [samma som Z-planet i pilotsystemets termer]; –z i termer av pilotsystemet, alltså bakåt).

DE TVÅ ENDA OCH MÖJLIGA ROTATIONSKOMPLEXEN (RotI&II) omnämns inte i den etablerade 3D-nomenklaturen — i varje fall inte i någon direkt uppenbart iögonenfallande mening. Naturlig konsekvens: förhållandevis FÅ personer känner sig dragna till ämnet, och även då endast under speciella (högst privata) föreställningar som den personen (naturligtvis) har SVÅRT att förklara för andra. Hela ämnet blir därigenom ”intuitivt” — därför att man inte känner metoden.

3D-GEOMETRIN 2008 | Rotationer — 3D-geometrins rotationskomplex

Rot1&Rot2:

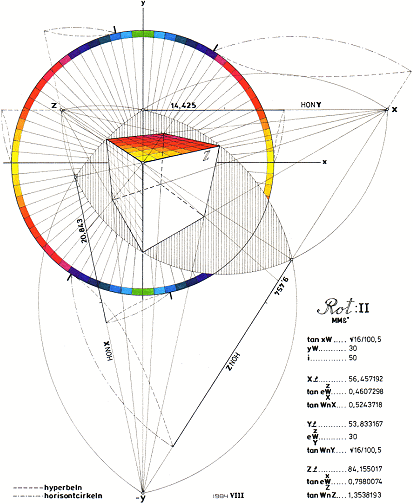
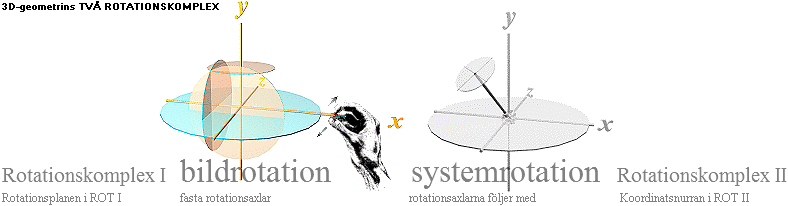
ROTATIONSKOMPLEX 1 OCH ROTATIONSKOMPLEX 2

ROTATIONERNA I 3D-GEOMETRIN

Ännu (November 2008) finns på @INTERNET ¦ WolframMathJan2019 ingen reguljär (eller någon alls) beskrivning av rotationskomplexet i 3D-geometrin som beskriver de TVÅ enda och möjliga rotationssystem som finns — i någon begriplig mening för en icke-högskolefamiljär person. Här ges en fullständigt orienterande genomgång.

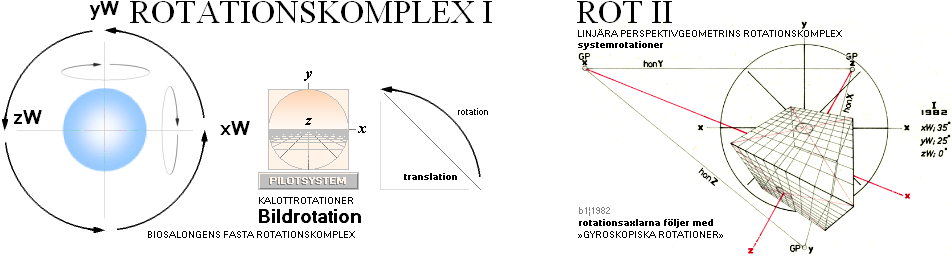
BILDROTATION OCH SYSTEMROTATION

bildrotation och systemrotation — 3D-geometrins rotationskomplex

Se även i EQUIVALENCE OF ROTI AND ROTII — beviset för att rotationssystemen är varandras omvändning med samma värden

BILDROTATION OCH SYSTEMROTATION

Se även utförligt i The ORIGIN OF ROTII. Ursprunget till ROT I är mindre dramatiskt: xy-systemet som sådant — Bion, Filmduken:

3D-geometrin innehåller TVÅ rotationskomplex: RotI och RotII.

Den ordningen omnämns inte i modern akademisk litteratur.

Rotationskomplex I Rotationskomplex II

Rotationsplanen i ROT I Koordinatsnurran i ROT II

bildrotation systemrotation

»picture rotation» system rotation

fasta rotationsaxlar rotationsaxlarna följer med

PFFU:

”PERSONLIGHETENS FRIA OCH FULLA UTVECKLING”

[‡HÄVDEN] ¦ [‡Erinrad Bevisgrund] ¦ [A3] ¦ A22 ¦ A26.2 ¦ A29.1

är den enda universellt erkända existerande utvecklingsgrundval som finns för människan: Den enskilda individens naturligt hälso- och förståndsbefrämjande utveckling — på den erkända ”grundvalen för frihet, rättvisa och fred i världen”[‡K1¦UDHR10Dec1948].

KULTURELLT UTVECKLINGSEXEMPEL 1980+¦2000+:

— ”Mjukvarujättarna” på Jorden övergår strax (2000+) till att använda Mänsklighetens som Försöksdjur i Driften att göra Stoa Vinster på Människors Allmänna behov av ”PERSONLIGHETENS FRIA OCH FULLA UTVECKLING”:

— Se här StinaOlle. Vi har tagit fram jättefina Utvecklingsverktyg — MaskinenFörTextOchBild — som du Nu kan Köpa till förmånligt pris. Jättebra. Myrorna vallfärdar i enorma mängder till Honungsburken. Fullt jubel råder.

— TEKNIKUTVECKLINGEN — med början från 4Bit 8Bit 16Bit 32Bit 64Bit ... — säkrade allt snabbare och större datorkraft.

Jättebra. Men människorna som — förtjust — samlades till Honungsburken och BÖRJADE UTVECKLA DATORKRAFTEN GENOM PRAKTISKA TILLÄMPNINGAR lämnades — strax — strandsatta.

— Med viss stingande smärta insågs snart att Individen Användes, Utnyttjades, som ett slags försöksdjur.

— Vinsterna gick till utveckling av operativsystem med en allt mer tydligt framtonad STRÖMLINJEFORM — typ Microsofts SLARVORDLISTOR (WORD2000): —»Microsoft hjälper Dig Skita Bättre»: ”personlighetens fria och fulla utveckling”. Jättefint.

— Mjukvaruindustrins ProfitParadis slog upp portarna — på vid gavel. Vi enskilda användare fattade ingenting — förrän långt senare.

— ”Mjukvarujättarnas” Självutropade NyutGivna Bästsäljare ViÄrLedandePåIntelligens började strömlinjeforma användargrunderna:

— ”Mjukvarujättarna” började utesluta — INTE »BAKÅTKOMPATIBILITERA» — en gång framställda och utgivna användbara utvecklingsverktyg, verktyg som Enskilda Individer redan hade använt, uppskattat, för Produktion enligt

”PERSONLIGHETENS FRIA OCH FULLA UTVECKLING”:

»dom där, därnere, är ju i vilket fall bara Försöksdjur, så vi har fria marknadshänder att laborera som vi vill»

— ”Mjukvarujättarna” började, så, införa en direkt dikterande användarroll för StinaOlle:

»dom där, därnere, är ju i vilket fall bara Försöksdjur, så vi har fria marknadshänder att laborera som vi vill»

— StinaOlle fann sig plötsligt, med viss förfäran — rösterna genom Webben, olika förskrämda och kvävda rop på hjälp mot mjukvarujättarnas nesliga fasoner, under Windows utvecklingshistoria (”Windows Sucks!”) — vara intvingade i en VÄRLDSOMFATTANDE DIKTERAD SAMMANSLUTNING — kapad — AV ”Mjukvarujättarna” (Restart your computer now, or we will do it for you, Microsoft Compatibility Telemetry ... Alla tidigare Windowsanvändare tvingas medverka ...).

— ”Mjukvarujättarna” började, successivt, ta bort-utesluta-inte stödja tidigare väl fungerande utvecklingsverktyg.

Microsoft utestänger alla användbara fina 16-bitarsprogram med övergången till 32-bitarssystem: Simply 3D med flera utesluts;

Microsoft stänger plötsligt ner, utan förvarning, vidare användning av MsWORKS från WindowsVista — rena datorkapningsverksamheten;

Stavningskontrollen i WORD2000 stängs för, får inte/kan inte användas längre;

— Ett allt mer tydligt mjukvaruindustrins profitdrivande ANVÄNDARDIKTERANDE datorintresse gjorde sig märkbart.

Datorer har också begränsad livslängd;

— Datorn slutar fungera en dag — speciellt med Microsofts påtvingade DatorKapningsVerksamhet: Mera intensiv processoranvändning förkortar centralprocessorns livslängd:

Processoranvändningen 60-70% — efter Den WindowsPåtvingade Stora Uppdateringen 2016 — från tidigare 10-12% på DVD-filmer: datorn kan inte längre, alls, användas för ändamålet — Windows operativsystem har i princip upphört som ANNAT än en Kontrollerande FångCell.

— När datorn ger upp, upphör också möjligheten att använda DESS installerade programvara. Vi kan kopiera arbetsresultaten. Inte verktygen.

Med den händelsen — i ljuset av JordiskaMjukJättarnas profitsamkväm — har utvecklingsverktygets programgrund också försvunnit.

— ”PERSONLIGHETENS FRIA OCH FULLA UTVECKLING” blev föremål för KAPNING: Intrång.

»dom där, därnere, är ju i vilket fall bara Försöksdjur, så vi har fria marknadshänder att laborera som vi vill»

DEN ALLMÄNNA RÄTTSUPPFATTNINGEN är — också — KORRUMPERAD på samma boliner

[‡HÄVDEN] ¦ [‡Erinrad Bevisgrund].

— Företagsamheten ges fria händer att genomföra i stort sett vad som helst — EFTERSOM varje annan ordning SÄRSKILT FÖR DET VÄRLDSLIGT ETABLERADE PROFITVÄNLIGA RÄTTSSYSTEMETS DEL innebär att BÖRJA inordna rättsutövningen enligt

”PERSONLIGHETENS FRIA OCH FULLA UTVECKLING”: domstolarnas inrättande UNDER, inte över, UDHR10Dec1948.

Jämför: Europas Diktatur; RÄTTSSYSTEMETS DÖDSPSYKNINGAR MOT VÅLDSVÄGRARE.

— ”Mjukvarujättarnas” intrång i mänskligheten ÄR brottslig verksamhet [A12].

ATTIDYD — hävd, åberopande — UTOM människovärdighetens erkännande är utövande förtryck [‡HÄVDEN]:

Kulturlag. Kriminallag. Brottslag. Rättslag. Utvecklingslag.

Mänskligheten Feb2019 lever bevisligt, i många avseenden instängd i en Underjord — utan belysning:

— »Aha. Så DU är intresserad av SEENDE. MyOhMy. DÅ vill vi, SEENDEÄGARNA, ha BETALT härnu ser du, för det som vi bestämmer att DU ska tycka ATT du TÄNKER är BRA, ser du, här nu, ser du. BETALA OSS».

MICROSOFT Feb2019 erkänner inte mänskliga rättigheter som grundval för verksamheten. Absolut gärna rätta om fel.

MICROSOFT speciellt är alltid välkommet att visa sin version av praktiska exempel som ansluter till ”PERSONLIGHETENS FRIA OCH FULLA UTVECKLING”. Visa. Blända oss. Absolut. Windows 3.1+: den fria och fulla datoranvändningen utan intrång.

OVANSTÅENDE ILLUSTRATIONER ansluter till författarens genomgång av de olika rotationskomplexen per matematik. En mera utförlig beskrivning låg tidigare (Webb-originalförfattningen från 2006) tyvärr (ännu) utanför ramen för ämnets då korta presentation:

2006: Dock kommer här de mest elementära delarna att genomgås så att läsaren själv längre fram kan hänga med i sådana praktiska exempel som t.ex. omvandlingen mellan ekvatoriella och galaktiska koordinater. Se särskild beskrivning i Solgalaktiska Koordinaterna.

Nu Jan2019 har den vidare utvecklingen — sammanhanget i stort — gjort det mera angeläget med en något djupare presentation. Avsnitten här har utvidgats med ”mera kött på benen” från originalarbetena (1976+) till 2006-originalets enklare kontext. Den främsta anledningen: Den etablerade litteraturens fortfarande väl magra beskrivningar i ämnet.

FÖRUTSÄTTNINGAR ENLIGT Pilotsystemet xyz¦XYZ::

— Varje unik rymdpositionspunkt P(xyz) = R = √x²+y²+z² kräver (minst) tre förflyttningar ΔxΔyΔz, translationer eller rotationer vilketsom, för att nå en ny unik rymdpositionspunkt x'y'z'. — Men endast EN translation, vilketsom, ELLER TVÅ rotationer DEKLINATION OCH RECTASCENSION krävs för att definiera en godtycklig unik rymdpositionspunkt P(xyz) relativt en given fast referens, t.ex. xyz-systemets positiva koordinataxel x:

BEVIS Rot I:

— Utgående från R=+x ger en yW-rotation en godtycklig RECTASCENSION (rektascensiv) placering i horisontalplanet; Med en ytterligare zW-rotation

DEKLINATION (deklinativ) placering tvärs horisontalplanet nås alla övriga sfäriska punkter P(xyz) med den givna sfäriska utgångspunktradien R=+x.

Minst tre rotationer krävs för att flytta en given objektspunkt R=√x²+y²+z² till en annan R-position R=√x’²+y’²+z’².

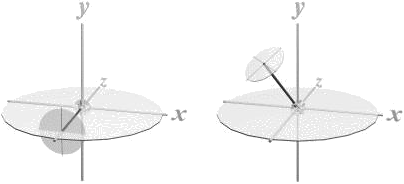
Rotationskomplex I — bildrotation.

En given punkt roteras (planförflyttas) på sin rotationscirkel genom varje bild-koordinataxels fasta rotationscylinder. Föremålet (varje punkt) roteras utifrån bildsystemets fixa systemaxlar. Härledningen till rotationskomplex I begagnar den elementära trigonometrins begrepp i pilotsystemet xyz och är därför förhållandevis enkel.

Rotationskomplex II — objektsrotation eller systemrotation.

Föremålet roteras utifrån sina egna systemaxlar — som följer med i rotationen. Härledningen till rotationskomplex II kan återföras på en ‘koordinatsnurra’[‡] — en stav med en cirkelskiva i änden på vilkens periferi den aktuella koordinatpunkten P_xyz sitter.

Gyromodellen:

Rotationskomplexen I och II förhåller sig till varandra som varandras omvändningar:

Se Rotationssatsen med (eng.) Beviset för samhörigheten RotI&II.

Exempel:

ROTI ....................... 45°zW, 30°xW, –15°yW

ROTII ...................... –15°yW, 30°xW, 45°zW

Samma värden, men i omvänd ordning. Slutpositionen blir i bägge fallen densamma.

I studier av geometrin rekommenderas (här) läsaren starkt att införskaffa sig en gyromodell typ ovanstående författaroriginal (från Maj 1981): modellen är utskuren med passepartoutkniv i 1mM och 2mM vit passepartoutkartong i enskilda cirklar. Hela anordningen har sammanfogats med enkla egenkonstruerade kopparnitar, knappnålar, vattenbaserat lim och 2mM skruv med mässingsmutter (fanns en gång i tiden på Clas Ohlson). Samtliga cirklar är vridbara och roterbara. I mitten sitter en axiellt vridbar kub. Skalorna har ritats med tusch, vattenbaserade färgpennor och gnuggisar (numera en i princip helt utgången teknik som användes mycket av många under 1970-talet), samt förseglats med fixativ för att ge ytan ett plastiskt skydd mot fukt och damm. Man har (min erfarenhet) garanterat mycket glädje av en sådan modell i olika trixiga analyser inom 3D-geometrin. Modellen har hängt med författaren nu i 27 år — fortfarande till nytta.

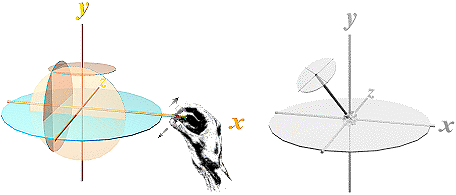
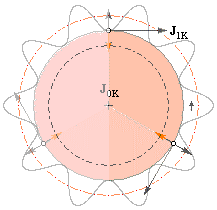
Satsen kan förstås direkt med hjälp av en (»enkel») gyromodell. Se vidare nedan i Rotationssatsen. Det rent matematiska beviset är mera krävande och baseras på bevisande ekvivalens mellan de bägge ovan nämnda RotI&II. Beviset ryms tyvärr inte i den här framställningen.

Se även utförlig praktisk tillämpning i Solgalaktiska Koordinaterna.

RotI

är som biosalongen och biobesökaren: betraktaren kan snurra objekt i filmen genom ett fast (magiskt) salongssystem (RotI) med rotationsaxlarna xyz och rotationsplanen XYZ: framifrån (zW), mellan händerna (xW, bilden ovan vänster), ovanifrån (yW).

RotII

är biobsökaren inuti filmen: aktören — som själv följer med objektet i rotationen — kan rotera objektet med referens till någon av dess egna koordinataxlar xyz.

Rotationsordningen i RotII är analog med den astronomiska koordinatbeskrivningen (se vidare i Solgalaktiska Koordinaterna).

RotII sammanhänger HELT med matematiken för den linjära perspektivgeometrin genom ENHETSHYPERBELN. Se vidare beskrivning nedan, (samt vidare utförlig i HP-geometrin, ingår inte i denna presentation).

DE TVÅ ENDA OCH MÖJLIGA ROTATIONSKOMPLEXEN (RotI&II) omnämns inte i den etablerade 3D-nomenklaturen — i varje fall inte i någon direkt uppenbart iögonenfallande mening. Naturlig konsekvens: förhållandevis FÅ personer känner sig dragna till ämnet, och även då endast under speciella (högst privata) föreställningar som den personen (naturligtvis) har SVÅRT att förklara för andra. Hela ämnet blir därigenom ”intuitivt” — därför att man inte känner metoden.

3D-GEOMETRIN 2008 | Den linjära perspektivgeometrins grunder

Riktkuben	Lagerqvistsyndromet	HP-kroppen	3D-matematiken

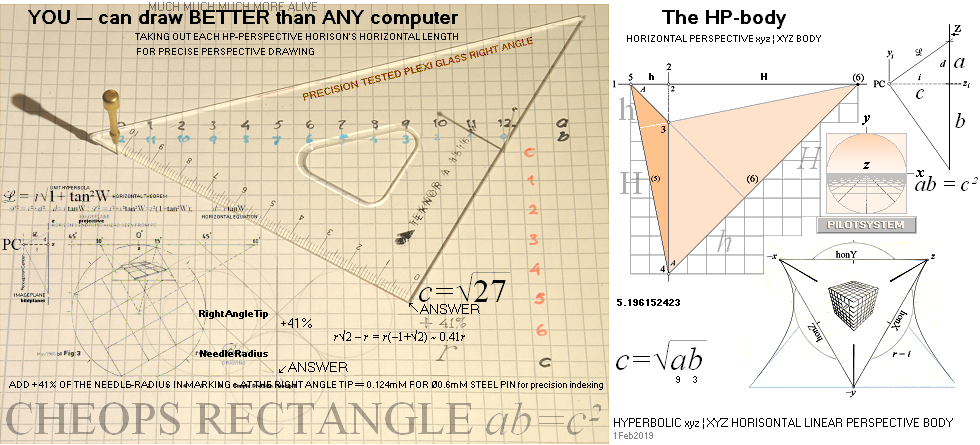
Den linjära perspektivgeometrins grunder

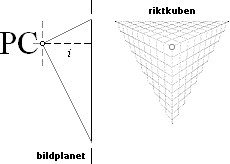
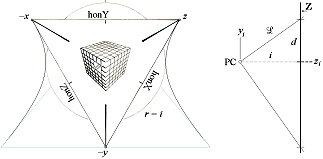
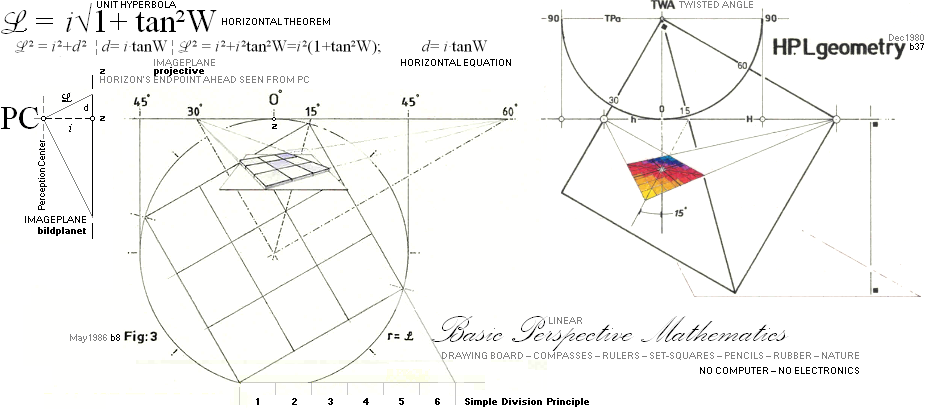
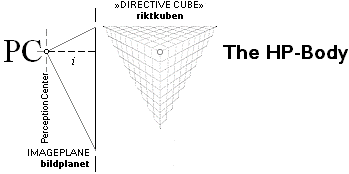
enhetshyperbeln — Linjärperspektivens definition genom HYPERBLER som bildar perspektivets motsvarande HP-kropp:

HorisontalPerspektiv-kroppen [HP-kroppen]

DEN LINJÄRA PERSPEKTIVGEOMETRIN

kan syntetiseras på ENHETSHYPERBELN med RIKTKUBEN i origo — centrum, »mitten».

HP-matematiken

i bildindex — L horisontalindex (orig. L bildkopia i Mural Script — kan inte läsas av t.ex. Firefox)

Horisontalekvationen Horisontalteoremet

d = tanW·i = i √ 1+ (tanW)²

Riktkuben

Horisontalekvationen. Gränspunkten för en linje som är vriden i planet vinkeln W grader har från horisontens normal avståndet tanW·i.

Nedanstående riktkubsmodell är byggd i Anim8or — men det är närmast oerhört krångligt att få den att fungera efter programmets tänkta funktioner. Kuben drar t.ex. iväg Gud vet vart om man försöker med Ctrl+Z efter en genomförd rotation, samt det faktum att DET läget INTE blir det ursprungliga. Jämför Simply3D som en gång fanns i Windows95-miljön: enkelt, OCH rena drömmen jämfört med Anim8or.

NOTERING

NOTERING, MODERN AKADEMISK LITTERATUR OCH NOMENKLATUR

Riktkuben tycks vara ett helt okänt begrepp i moderna kretsar:

Ingenting av det ovan nämnda står att läsa om i den befintliga bibliotekslitteraturen. Olika författare som försöker beskriva linjärperspektivet talar om typerna ”enpunktsperspektiv”, ”tvåpunktsperspektiv” och ”trepunktsperspektiv”. Dessa motsvarar HP-geometrins ”en kub sedd rakt framifrån”, ”en kub vriden horisontellt” och ”en kub vriden godtyckligt”. Men riktkuben beskrivs aldrig i etablerade kretsar då man (tydligen) inte känner till linjärperspektivens (enkla, men omfattande) sammanfattande matematik. Se även Lagerqvistsyndromet till jämförelse.

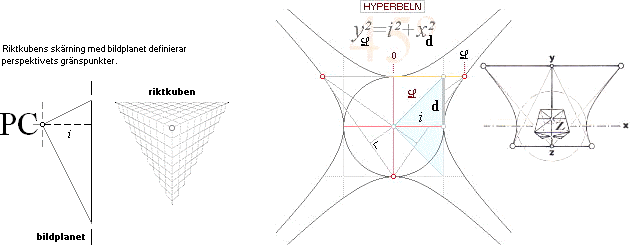
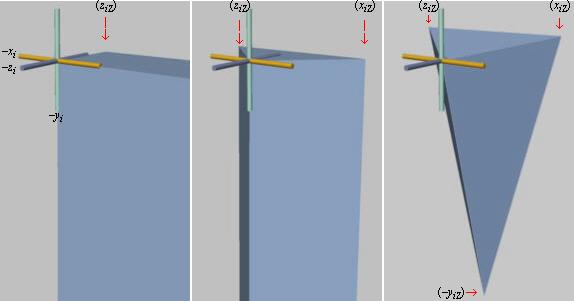
Riktkubens skärning med bildplanet definierar perspektivets gränspunkter. Illustrationerna visar i tur och ordning en gränspunkt, två gränspunkter, tre gränspunkter.

3D-GEOMETRIN 2008 | 2019 ¦ Linjärperspektivets gränspunkter

LINJÄRPERSPEKTIVETS GRÄNSPUNKTER

RIKTKUBEN SOM FORMBEGREPP FINNS INTE I FENOMENVÄRLDEN — ENBART I FÖRSTÅNDS- OCH FÖRESTÄLLNINGSVÄRLDEN:

— Riktkubens formdel framträder direkt som HP-kroppens tre signifikanta horisontplan XYZ med sina tre signifikanta perspektivistiska gränspunkter xyz.

HPExempel:

— Vi SER riktkuben alltid perspektivistiskt i föreställningsvärlden genom den uppritningen: kubhörnet som genomtränger bildplanet:

— Planet i bakgrunden är bildplanet (BP), (de tre) genomskärningspunkterna genom BP anger perspektivets gränspunkter för koordinataxlarna xyz.

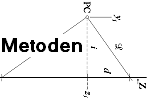
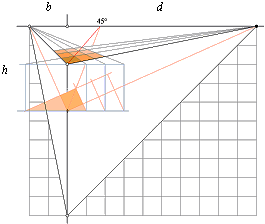
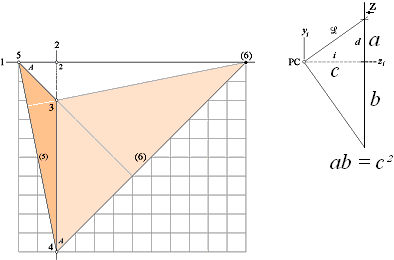
Metoden med CHEOPS REKTANGEL (ab=c²) hjälper oss sedan »med resten»:

NERVIKNING Av varje (XYZ) horisontalplan för sig PÅ räta vinkeln definierar DET horisontalplanets horisontalINDEX (horisontens indexlängd ):

— Det ger oss Gränspunkternas motsvarande rätvinkliga VÄRDEN (i grader eller metriska kvantiteter). Och vilka referensvärden sedan kan användas för att alternera — rotera — olika plandelar perspektivistiskt korrekt — med tillhörande nya gränspunkter med motsvarande avritningar, och så mycket Artisten står ut med. Det är bara fantasin och TIDEN som sätter gränser. Principerna är givna — och ytterst enkla.

»CENTRALEN» — primära BildIndex i —

kan vi alltid ta ut via den ytterst enkla Metoden med CHEOPS REKTANGEL:

— Direkträkning med de bägge horisontdelarna (a och b, eller h och H) hH=i² — här 2·8=16; i=4 — eller genom direkt geometrisk användning av räta vinkeln (grå) som antyds i figuren ovan.

— EFTERSOM — matematiskt, nervikningen via Cheops Rektangel med Pythagoras Sats —

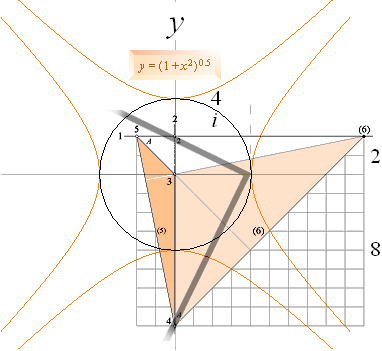
² = i² + d² där också d/i = tanW° = 2/4=0,5 — -horisontens aktuella uppvridning i exemplet med d = i· tanW° — får vi

² = i² + i²tan²W° = i²(1 + tan²W°) som ger oss = i√ 1 + tan²W°, ser vi — nu — att x-FUNKTIONEN för tanW°-värdet ekvivalent,

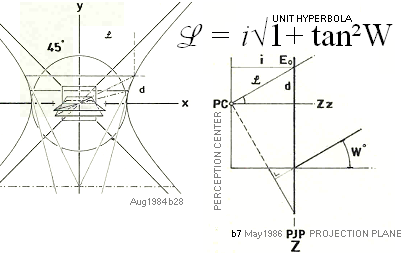
= i√ 1 + x² uttrycker ENHETSHYBERBELNS EKVATION, den ovan avbildade orangea kurvformen som ser likadan ut uppvänd och tvärvänd (hyperbelns asymptotvinkel = 45°).

— Enhetshyperbelns kurvform definierar HP-kroppens perspektiva gränspunkter genom den så härledda ekvationen för HORISONTALTEOREMET:

= i√ 1 + tan²W° = i√ 1 + (d/i)² ..... horisontalteoremets ekvation som tydligen definierar hela perspektivgeometrins totala fundamentala LINJÄRA PERCEPTIONSKROPP.

= 4√ 1 +(2/4)² = 4√ 1,25 = √20 = 4,472135955.

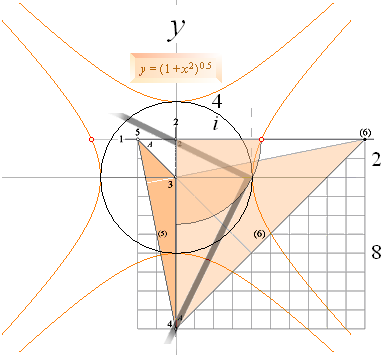
Effektvinkeln för övre (Y-) horisonten beräknas med endera sidan h 2-5 eller H 2-6 som TANeffW = h¦H/. Här skulle värdena bli

TANeffWh = 2/√20 ¦ 24,09° och TANeffWH = 10/√20 ¦ 65,91°.

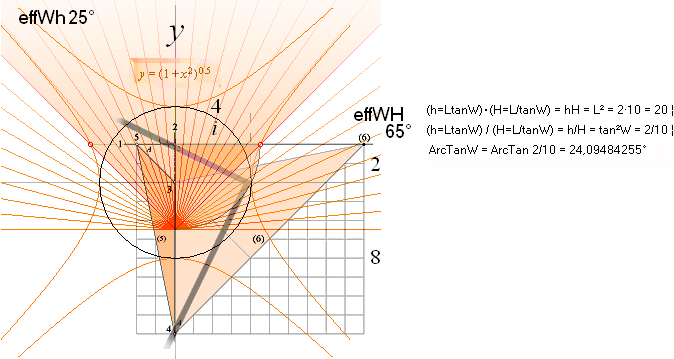
VinkelSolfjädern — konv. gradskiva — säkrar kontrollen på korrekta/rimliga beräkningsvärden.

— HP-KROPPEN är en ren elementär uppvisnings NATURSKOLA i — befrämjande — matematikövning och dito färdigheter av typen »rena spöregnet».

— Det finns »hur mycket som helst» ELEMENTÄR matematik och geometri att öva på i ämnet för den som vill och har tid.

PentaEX:

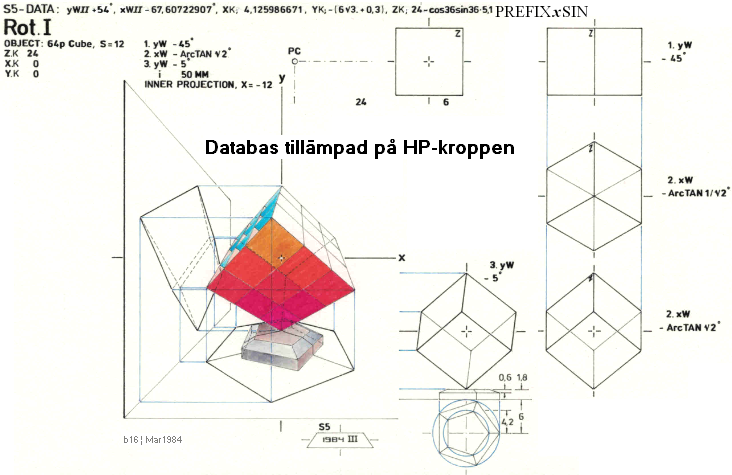
PREFIXxSIN — »Trigonometrins Artistiska förenkling», se särskild artikel.

HorisontalPerspektiv-exempel från 1984 — »databas söker lämplig perspektivvy».

— Den här författarens referens: DEN typen av rent artistiskt arbete jämfört med REN DATORPROGRAMMERING (för 3D-applikationer) är TVÅ VITT SKILDA VÄRLDAR.

ARTISTERIET är det »man längtar efter mest». Medan datorarbetet »visserligen är jäkla askul» — men i grunden VÄLDIGT (väldigt) andefattigt.

— Man måste ta paus emellanåt, åka eller gå ut i Naturen för att Hämta Andan. Annars dör man ihjäl — långsamt.

»BÄSTA KOMPROMISSEN»: Egna (grund-) teckningar som skannas in till dator och som KAN manipuleras eller presenteras vidare, typ från ovan:

CityEX:

Förslag till Väggmålning i Stadsplaneringen — glaserat Tegel — för främjandet av en mera matematikintresserad befolkningskultur ...

— Den typen är MYCKET ROLIGARE att arbeta med.

— TÄNK en hel STAD som är PROPPAD med den typen, alla stora öppna väggytor, liknande eller annat passande, med beskrivande, undervisande, upplysande matematisk geometri — i alla typer av olika blandningar. Wao. »GrafittiKultens Återkomst». Elementär Undervisning. Alla Turister är välkomna.

Kulan och plattformen:

Kulan och Plattformen — Blyerts 1988 — illustration till Mekaniken-Kinetiken: rörelsens elementära natur — OCH perspektivlärans grunder. TIDLÖST.

ALLA TECKNINGAR FRÅN FÖRFATTARENS PRIVATA ARKIV — samlingskollage som beskriver perspektivtecknandets två huvudkomplex: linjärt och sfäriskt.

Beskrivning:

Efter erfarenhet och studium

OAVSETT FÖREMÅLET FÖR ARTISTERIET finns alltid undantagslöst EN och endast EN enda ÖGONPUNKT eller PERCEPTIONSCENTRUM för varje möjligt UPPFATTAD vy eller BILD:

— Uppåt, neråt, åt höger, åt vänster, är alla väl intuitivt givna riktningsled som tecknandet — för EN given blickpunkt — tvunget och oåterkalleligt måste ta hänsyn till och utgå ifrån.

— VET MAN INTE DET UNDERLIGGANDE REGELVERKET framstår också resultatet med EXAKT den framtoningen. Varken mer eller mindre — som också kan medföra »väldigt engagerad bildkonst»:

— »Ju mindre vi VET, desto Bättre framtidsutsikter».

De bägge grundkomplexen LINJÄRT och SFÄRISKT kan utvidgas godtyckligt för den som (så) känner geometrin för andra projektionssätt: det finns ingen gräns för den kombinatoriken annat än den egna fantasin. Rekommenderas starkt — oerhört personlighetsutvecklande: individens unika särart; Rita. Spela. Dansa. Hantverket. Artisteriet. Tekniken. Instrumenten. Byggnaderna. Naturen. Kulturen.

— Med Primära och sekundära bild- och horisontalindexen så givna, och den enkla metoden för att konstruera, eller beräkna direkt genom Cheops Rektangel (ab=c²) är — SÅ — hela perspektivkomplexet tydligen FULLKOMLIGT KOMPLETT GENOMLYST. Det finns inget mer att tillägga eller förklara eller beskriva. Resten blir rent ritarbete, så mycket Artisten vill, kan och förmår: VRID, rotera, markera, beräkna, ta ut, och RITA. Alla kombinationer är tillåtna — från ett fast givet BildIndex i, den centrala bildpunkten som hela bilden, eller vyn, ses FRÅN.

HPprimBasic:

HP-kroppen med primära baslägen utan effektvinklar.

SUCCESSIVA ROTATIONER xyz¦W° utifrån en given horisont (XYZ) blir i (en delvis krävande men ytterst intressant) sammanställning av formen (bildlänk till större, med separat beskrivning från The Origin of Rot 2 och The Horizontal Theorem )

med angivna s.k »effektvinklar» — vinkeländarna (»restvinklarna») som ligger utanför hyperbelkurvorna. Sammanställningen genomfördes för min del Jul1981 med en senare (1998 Equivalence of Rot1 and Rot2) sammanställd härledning som visar hur de bägge rotationskomplexen ROT I och ROT II

är varandras omvända ordningar — tagna med samma värden.

— Som det har visat sig: Vi hittar inte sucken i etablerad litteratur — ehuru ROTATIONSMATEMATIKEN där emellertid som vi redan noterat är väl kommersiellt tillämpad. I modern akademisk mening döljer sig komplexet bakom ytterst abstrakta detaljer som världens ledande PhD-hövdingar tydligen inte kan beskriva rationellt för populationen vanliga fotgängare. Se exemplet från WOLFRAM Math Jan2019.

DatorRelaterat:

MOTSVARANDE DATORRELATERAD BESKRIVNING

HP-kroppen

DATORRITNING DIREKT PÅ HP-GEOMETRINS DETALJER[‡] förekommer inte i datorvärlden. Inte alls — här veterligt.

— »3D-riket» i datorvärlden (successivt med teknikutvecklingen från 1980+) behärskas istället av det betydligt enklare rent matematiskt-algebraiska ROT1-komplexet, dess smidiga och hutlöst snabba matematik.

RitARTISTERIET har på den utvecklingsvägen kommit (något) i skymundan: folk numera (Feb2019) RITAR inget. Bokhandlarna har för länge sedan avverkat det breda, och fina, ritsortiment som en gång fanns med sin guldålder strax före datorrevolutionen (1980+).

Men vänta bara ska du få se: Människor kommer att tröttna UR på den tomma, ytliga, elektronikbilden och börja LÄNGTA efter The Real Steel — förr eller senare. Ingen dator kan mäta sig med ett mänskligt individuellt artisteri; penna papper, enkla ritverktyg, kunskap, glöd. ENERGIN det GER saknar ord.

PRINCIPEN FÖR

DatorMatematisk presentation av linjärperspektivets gränspunkter

Betecknas riktkubens koordinataxlar med (xyz)_i, blir deras skärning (xyz)_iZ med bildplanet (Z) detsamma som linjärperspektivets gränspunkter P(xyz)_iZ med respektive bildkoordinater xy enligt P(xyz)_iZ[xy]. Totalt med positiva och negativa riktningar ges alltså 6 gränspunkter (max 3 synliga) med 12 koordinatvärden (max 6 synliga).

PRINCIPBESKRIVNING:

Man får xy-koordinaterna för perspektivets gränspunkter P(xyz)iZ genom att ange riktkuben på enhetsform med x=y=z=1. Efter genomförda rotationer ges sedan gränspunkternas bildkoordinater [xy] i P(xyz)_iZ[xy] direkt genom BILDEKVATIONEN

— från xyz-rummet till xy-bildplanet —

enligt {x|y}=i{x_P|y_P}/z_P med (xyz)_P från rotationerna av riktkubens enhetsform x=y=z=1, och {x|y} motsvarande respektive x och y i den sammanförda beteckningen [xy].

Rotationernas reguljära matematik beskrivs utförligt i Rotationerna i 3D-geometrin.

Rotationernas geometri beskrivs översiktligt i 3D-geometrins rotationskomplex.

3D forts.

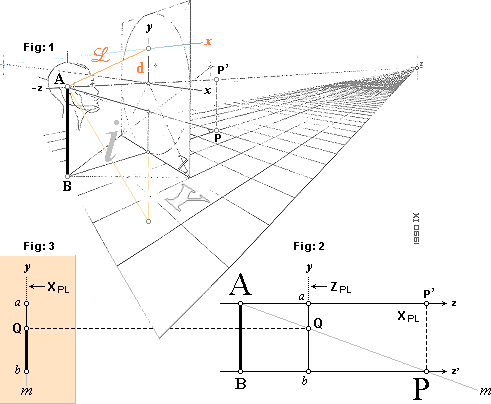
Gränspunktssatsen: — retoriskt

Gränspunkten för bilden av framänden på alla möjliga linjer i golv och takplan

som sträcker sig mot oändligt, sammanfaller med bilden av huvudpunkten (a i fig:2) på z-axeln.

Bildindex i anger avståndet mellan perceptionscentrum (PC, »filmprojektorn», betecknat A i figurerna 1 och 2 ovan) och bildplanet (»bioduken», betecknad Zplanet i figur 2).

Perspektivets styrka beror inte på i utan på den upptagande synvinkeln mellan PC och objekten:

Stora upptagande synvinklar motsvarar »bilder av jättestora objekt»,

medan små synvinklar ger ett alltmer plangeometriskt (»perspektivlöst») intryck. Bildcirkeln i och PC bildar alltid en synkon med 90° nittio graders upptagande synvinkel.

Det avbildade konceptet (salongen i figur 1) illustrerar den åskådliga härledningen till gränspunktssatsen inom perspektivgeometrin.

Begreppet framgår syntetiserat genom figurerna 2 och 3.

3D-GEOMETRIN 2008 | Bildekvationen

3D forts.

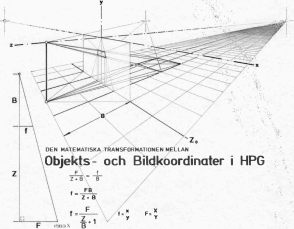
Okt1983

Bildekvationen — Från 3D till 2D

Alla rådata som beräknas av ett 3D-program måste i slutänden omtransformeras till endast två koordinater xy på bildskärmen.

För det linjära perspektivets del sker den transformationen med hjälp av en speciellt enkel bildekvation. Den används också i omtransformationen för sfärperspektivet i en något modifierad form, se föregående 3D-geometrins 3 punktfält.

Oavsett typ av perspektiv (linjärt, sfäriskt, eller annat) måste slutbilden alltid, i vilket fall, relateras till en plan bildyta typ bioduk eller bildskärm. Genom att linjärperspektivet innehåller just den elementära planytans absolut mest elementära element, blir också bildekvationen nedan grundform för alla typer av perspektiv.

explicit:

f_x= x = i([X+X.K]/[Z+Z.K]) k_x=X+X.K

f_y= y = i([Y+Y.K]/[Z+Z.K]) k_y=Y+Y.K

BILDEKVATIONENS ENKLA RÅFORM är x_i=ix/z, y_i=iy/z.

Bildekvationen återför rums- eller objektspunkten (xyz)_P från perceptionscentrum (PC) på bildplanet i dess två koordinater (xy)_i. Genom att utnyttja en kropps egensystem (XYZ)_K som är placerad i rummet i (XYZ)₀ förenklas transformationerna enligt sambanden ovan för kroppar bestående av stora punktmängder — så som det ju också är i den datorstödda 3D-geometrins värld.

Rotationerna i 3D-geometrin

Rotationerna i 3D-geometrin

3D-ROTATIONERNAS STORA TILLÄMPNINGSOMRÅDE: SNABBA DATORBASERADE PROGRAM MED STORA PUNKTMÄNGDER

HUR ROTATIONERNA I 3D-GEOMETRIN UTFÖRS I PRAKTIKEN

Se mera utförligt i exempel i sammanställning i Rot1Prepared

xyBildRot1:

SAMMANTAGET FÖRENKLAT: vidare mera utförligt i samband i Prepared:

———————————————

Alla punkter i den strikt matematiska behandlingen av 3D-geometrin roteras utan undantag genom Rotationskomplex I. Rotationsaxlarna xyz har rotationsplanen eller rotationscirklarna XYZ.

Med utgångspunkt i Z-planet — koordinataxlarna xy — roteras en given punkt P(xy) enligt sambanden från vinkelsummateoremet. Rotationen av P(xy) blir i PREFIXxSIN för zW

x := x sinW – y cosW

y := y sinW + x cosW

xy i HL (förkortning för HögerLed) är objektskoordinaterna och xy i VL är de resulterande från rotationen W. Ordningen för rotationerna xW och yW fås på samma form genom att insätta resultaten för xy i faktorerna zy för xW och xz för yW.

Exempel i PREFIXxSIN:

Punkten P(–1=x; 0=y; 0=z) — P(–1,0,0) — roteras –(asin 3/5)yW med sinW=3/5=0,6 och cosW=4/5=0,8 (vi minns att sin–A=+sinA); termerna xy i Z-planet motsvarar termerna xz i Y-planet så att man får:

x := (–1)(3/5) – 0 cosW = –0,6

z := 0 sinW + (–1)(–4/5) = 0,8

Punkten P(–0,6=x; 0,8=z; 0=y) roteras sedan –(90°)zW som ger:

x := (–0,6)(0) – 0 cosW = 0

y := 0 sinW + (–0,6)(–1) = 0,6

Punktkoordinaterna är då P(0=x; 0,6=y; 0,8=z)

Mera utförliga exempel ges i Solgalaktiska Koordinaterna.

Mycket mer finns att beskriva och illustrera i 3D-geometrins grunder.

Det som framställts ovan är endast de absolut viktigaste grundbegreppen som krävs för att kunna hänga med i 3D-beskrivningar generellt.

Se även efterföljande Rotationssatsen.

Lagerqvistsyndromet — infört 11Okt2011 från doc-originalet KALKYL_MsWORKS.doc, HP-GEOMETRIN s86, med tillägg.

LAGERQVISTSYNDROMET

LAGERQVISTSYNDROMET — se även i Comparing Examples

Små observatörer inför stora objekt

Hur man framställer läromaterial som bygger på — här bevisligt IRRATIONELLT OLOGISKT INKONSISTENT — felaktigt uppfattade kunskapssammanhang

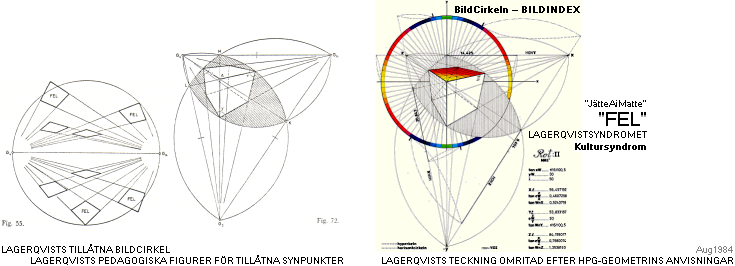
— Bokförfattaren Lagerqvist[‡] PERSPEKTIVLÄRA Bonniers 1964 — i en här tydligt bevisbart omfattande kollegial[‡] kultur av vanföreställningar och vidskepelser om perspektivgeometrins elementära grunder — påstår på flera ställen[‡Fig.55¦72] utan redovisad anledning, skäl, eller orsak att perspektivkvadrater med främre kvadrathörnet mot betraktaren som visar mindre, eller lika med 90 grader, är "FEL" och ”orimligt”.

LINJÄRA HP-syndromet — RÄTT är FEL: FEL är RÄTT ¦ Tillägg 13Feb2019:

Boktexten anvisar ett — streckat i bokfiguren 72 — ”tillåtet område” för perspektivteckning

”är det teoretiska området för en bildframställning med hjälp av trepunktsperspektiv”.

— Bokförfattaren känner tydligen inte — riktigt — till perspektivgeometrins grunder: Samma perspektivteckning förtydligad i omritad version (1984) — ovan höger enligt HorisontalPerspektivGeometrins anvisningar, som visar och bevisar att bokförfattaren uppenbarligen har en högst begränsad uppfattning om ämnets sakinnehåll.

— HorisdontalPerspektivGeometrins grundligt härledda matematik[‡], som f.ö. inte alls ingår i boktexten, visar och bevisar, detaljerat, att bokförfattarens påståendeformer är självmotsägande: I ena delen (55) är del ”FEL” att rita ut detaljer utanför BildCirkeln: I andra delen (72) är det tillåtet — uppenbarligen helt utom bokförfattarens egen medvetenhet, av flera olika skäl: 1. HPG-matematiken är tydligen okänd. 2. Principen för hur Cirklar i HorisontalPerspektivGeometrin presenteras, visas och bestäms, tydligen helt okänt i moderna kvarter:

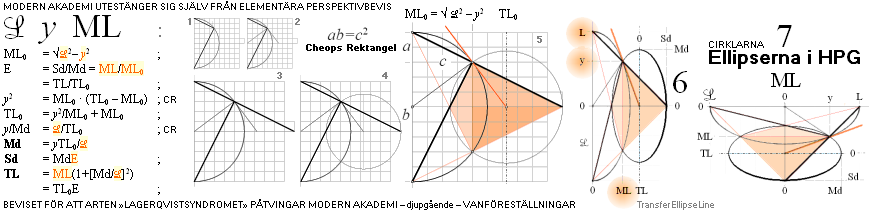
Cirklarna — ELLIPSERNA — i LinjärPerspektiven — Feb2019: Cheops Rectangle

— Varför ingår inte ovanstående i den moderna akademins lärosystem: böcker, artiklar, uppsatser? — What’sUp? Eftersökt. Inte upphittat. ´at’sUp?

— Sambanden framgår direkt ur den enkla plangeometriska figurformen via Cheops Rektangel. Ellipser vid sidan av mittlinjen, nedan, härleds sedan »på samma form» men något mera sammansatt, sammanställningen nedan.

Härledningarna till nedanstående finns nu Mar2019 i PEPS. Efter förarbeten 1976-1986.

— Två Kalkylkort för Ellipsberäkningarna finns sammanställda i Tabell 7 i GyroDec2018.ods.

— Vilken är själva anledningen till ATT modern akademis lärosystem INTE tar upp ämnesområdet i böcker, artiklar, uppsatser? — What’sUp? Eftersökt. Inte upphittat.

— What’sUp? Eftersökt. Inte upphittat — utom här i Universums Historia: Cheops Rektangel.

ELLIPSritningen:

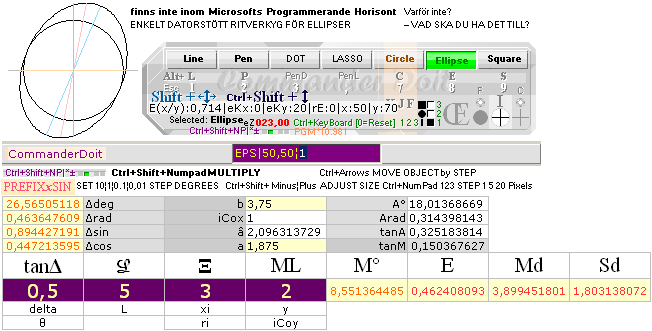
How is it that THESE, this specific type, of simple and elementary precision drawing tool NEVER was developed by Microsoft — to PROMOTE A GENERAL EDUCATIVE POPULATION OF ENLIGHTENED PEDESTRIANS on Planet Earth: — What’sUp? Ahhgaad.

— A simple Electronic calculator will do just fine — with a traditional Ellipsograph: not in production any more. Earth Lived: Earth Died.

— Den KULTUR som Modern Akademi byggt upp 1800+: Vad — exakt — ÄR det för något i mänsklighetens samlade kulturhistoria, egentligen?

Det ena området efter det andra framträder ur NATURBOKEN med högst elementära avsnitt — helt orepresenterade i MAC. What’sUp?

— Är det någon som, nyligen, påstått att Mänskligheten nu (Feb2019) lever i Underjorden — UTAN belysning?

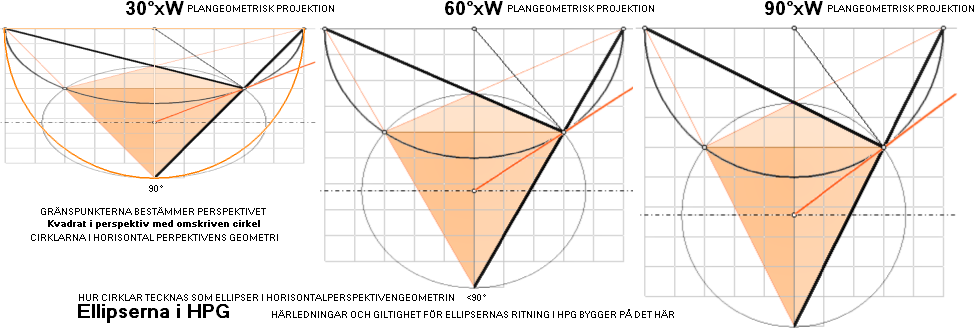
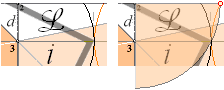
Härledningarna[‡] BYGGER på ATT BasCirkeln med Horisontens Bildindex (Cheops Rektangel) rent perspektivistiskt omsluter ett utpräglat spetsvinkligt SETT mot betraktaren vänt kvadrathörn. Det är hela ”hemligheten” bakom SÄTTET att kunna teckna in exakt cirkelrepresentation i linjära perspektiv.

— 30°xW-versionen — till jämförelse — visar den motsvarande tillåtna LagerqvistSyndomatiska perspektivvyn, basvyn uppvikt plangeometriskt 60°.

Ämnet står HELT orepresenterat i bibliotekslitteraturen, här veterligt:

— CITATGRUNDEN HÄR är möjligen ”HelYlleSvensk”, och därmed kanske särskilt vinklad för Sveriges del: växande kalhyggen 1800+. Hur det ser ut i bibliotekslitteraturen i övriga Världen är här mindre känt. Viss WebbKoll (13Feb2019) visar att den Engelska befolkningsdelens perspektivteckningar, i en del fall, ser ut att vara mindre imponerad av Lagerqvists rekommendationer. Men inget ytterligare är här känt om den rent teoretiska (akademiska) historiska lärogrunden i ämnet ”perspektivlära” (Det krävs 7 veckors sträckläsning på tillgänglig BOK-litteratur, minst).

Det moderna akademiska lärosystemet ger inget omnämnande; Detaljerna som ovan omnämns inte — explicit. Eftersökt. Inte upphittat.

— Vi vet inte varifrån bokförfattaren har fått sin uppfattning:

"...mot betraktaren vända hörn placeras utanför cirkelns periferi blir det spetsvinkligt — alltså mindre än 90° — vilket är orimligt. Framställt i perspektiv måste detta hörn under alla förhållanden bli trubbvinkligt, dvs. mer än 90°. Även att placera hörnet på cirkelperiferin, varvid vinkeln blir exakt 90°, är alltså felaktigt.",

" ... skulle bli spetsiga, vilket vore orimligt. (Redan att de i en perspektivbild är räta, är en orimlighet. De måste under alla förhållanden bli trubbiga, se fig. 55.)",

s28-29, PERSPEKTIVLÄRA Lagerqvist 1964.

LAGERQVISTSYNDROMET

är här benämningen på en (Svensk) tydligt kollektivt, detaljerat bevisbar, modernt akademiskt rent VISUELL kollegial — utlärd från någon undervisningsstol — vanföreställning av okänt ursprung. Vanföreställningen har, tydligen gått i arv från någon här inte närmare känd källa, och som lika tydligt INTE kan relateras eller beskrivas eller förklaras:

— ”orimligt!”, ”FEL”: saknar referenser.

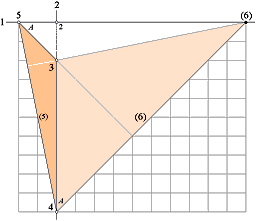
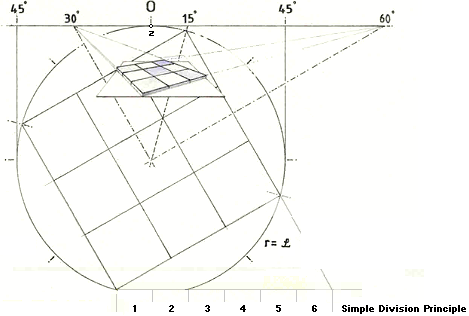
Figur a vänster visar ett snedställt kvadratiskt rutnät (K) i Z på i från PC. Kvadratens diagonal har satts lika med 2i (i anger BILDINDEX, se ill. Perspektivgeometrins grunder).

Fig:a

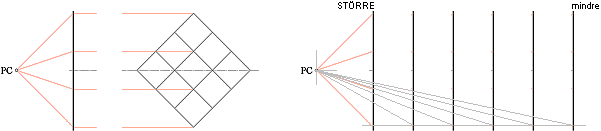
Figur a höger: Linjärperspektiven kan INTE ändra den plangeometriska egenskapen för figurer i rumsplan som är parallella med bildplanet Z. Sådana figurplan motsvarar snitt i plana synkoner och kan bara visas större eller mindre beroende på avståndet till PC.

Figur b visar vad som händer för varje minsta uppvridning av KVADRATEN kring x i Figur a.

— Testa att föra hörnet på ett papper (försiktigt) mot ögat, nära. Spetsvyn typiskt i Figur b är precis den bildvy som då framträder.

Fig:b

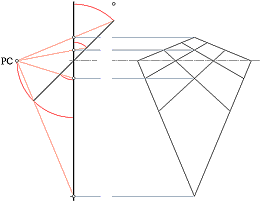
— För vi hörnet på ett papper helt nära ögat, är det just precis en MYCKET spetsvinklig perspektivbild som framträder av papperets rätvinkliga hörn. Precis av den typ som visas i Fig:b.

— Varför skulle den typen av vy vara ”orimlig”?

— Vi ser SÅDANA vyer, alltid, med SMÅ observatören NÄRA STORA objekt.

— Varför skulle den typen av vy vara ”orimlig”?

— Och varför påstå sådant, utan att tala om varför?

— What'sUp?

Någonstans i den dimmiga historien finns svaret.

Ju närmare K-spetsen (P) kommer PC i uppvridningen, desto längre och spetsigare blir HP-bilden i Z av P|x. Med P exakt i PC, försvinner bilden av K som då göms i Y-planet av x.

— Exemplet illustrerar den linjära perspektivbild man ser ju närmare man kommer (mycket) stora objekt.

Jämför modern akademi:

CitatLagerqvist:

Lagerqvists påståenden till figurerna 55 och 72

Figurerna [55][72] nedan är inskannade och här förminskade original från bibliotekslitteratur

PERSPEKTIVLÄRA, Erik Lagerqvist, Bonniers 1964, s28-29 (Fig. 55), s36 (Fig. 72);

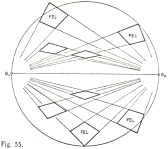
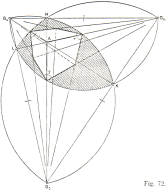
Bokens figurtext (färgmarkeringar i texten är mina egna):

Vä: Fig. 55

”Föremålets placering i höjdled, nedanför eller ovanför horisonten, sker givetvis efter eget gottfinnande, dock må man se till att ingen del av föremålet kommer utanför cirkelns periferi. Avbildar man t.ex. en snedställd kvadrat på ovanstående sätt (fig. 55) och dess främsta, mot betraktaren vända hörn placeras utanför cirkelns periferi blir det spetsvinkligt — alltså mindre än 90° — vilket är orimligt. Framställt i perspektiv måste detta hörn under alla förhållanden bli trubbvinkligt, dvs. mer än 90°. Även att placera hörnet på cirkelperiferin, varvid vinkeln blir exakt 90°, är alltså felaktigt.”

Hö: Fig. 72

”Den gemensamma ytan HKL av de därigenom uppkomna cirkelsegmenten är det teoretiska området för en bildframställning med hjälp av trepunktsperspektiv. Skulle bilden — t.ex. kuben i fig. 72 — sträcka sig utanför detta område, innebure detta att hörnvinklarna u, v och y skulle bli spetsiga, vilket vore orimligt. (Redan att de i en perspektivbild är räta, är en orimlighet. De måste under alla förhållanden bli trubbiga, se fig. 55.)”

Varför påstår bokförfattaren ”FEL”, ”orimligt”, ”alltså felaktigt”, ”en orimlighet”?

— Vi har nyligen[‡] konstaterat att det I PRAKTISK VISUELL VERKLIGHET inte föreligger något hinder att betrakta »stora föremål på nära avstånd» i en bildform av just en utpräglad spets för rätvinkliga hörn: ett pappershörn nära ögat. Så, vad kommer sig ovationerna? What’sUp?

Notera först och främst att författaren, tydligen, inte motiverar sina, tydligen lika, strängt hållna påståendesatser angående

”utanför cirkelns periferi” och

”orimligt” och

”under alla förhållanden”, och

”det teoretiska området”.

Anledning:

— ÄVEN i det att författaren, tydligen, INTE känner till DEN LINJÄRA PERSPEKTIVGEOMETRINS ÖVERGRIPANDE HP-kropp, BORDE han ha förstått så pass mycket av ÅSKÅDNINGSGRUNDERNA (titta ner på Jorden och tänk en vridbar kvadrat inuti Jordsfären, figurerna ab ovan) att han kunnat bespara LÄSAREN de tydligt befängda ’auktoritetsmeningarna’ ovan. Lagerqvists märkliga, helt orelaterade, påståenden till figurerna 55 och 72.

— Med andra ord: författaren har av ej närmare känd anledning tydligen (för det första) ärvt en ’omöjlighetsmening’ från någon (äldre) ’lärare’ och som tydligen grundas på en direkt OKUNNIGHET om på vilket sätt, och hur, den linjära perspektivgeometrin sammanhänger. Nämligen genom HP-kroppen:

— Modern akademi känner uppenbarligen inte till perspektivgrunderna.

Vi studerar det — vidare — i ljuset av Lagerqvists påståenden;

Lag72HPG:

LAGERKVISTSYNDROMET I FORMULERING OCH BEVISNING

Kolla nämligen i-cirkeln (fig.55) i Lagerqvists HP-kropp:

Lagerkvists egen perspektivkub här utritad nedan med HELA HP-kroppens hyperbelgrenar [streckade] för att visa det exakta sammanhanget:

— Nämligen: Lagerqvist VET tydligen INTE vad han talar om — ELEMENTÄRA KUNSKAPER fattas tydligen i ämnet.

— Bokförfattarens påstående innefattar tydligen direkta motsägelser:

Inskannad förminskad kopia av original i A4-format, författarens arkiv från grundmanuskripten Aug1984 till HP-geometrin.

— En motsvarande formulering på webben har f.ö. eftersökts som BESKRIVER ömsesidigheten i de två möjliga rotationskomplexen RotI&II, och som ansluter till ovanstående, men har ännu inte påträffats [Okt2011]. Se utförligt tillägg 2019 i SAMHÖRIGHETEN MELLAN ROT I OCH ROT II.

— Webben [se exv. Wikipedia, Perspective (graphical)] använder den föråldrade beskrivningsformen med enpunkts, tvåpunkts och trepunktsperspektiv, [se Riktkuben]. Men ingen övergripande MATEMATISK SYNTES som visar sammanhangen framträder i dessa beskrivningar.

Jämför HP-matematiken ¦ BILDEKVATIONEN, HORISONTALEKVATIONEN ¦ TheHOREQ ¦ HORISONTALTEOREMET ¦ TheHoriTheo.

Kort figurbeskrivning:

HP-kroppen i Lagerqvists Fig.72 här förtydligad ovan med fullständiga HP-data.

— Enligt Lagerqvist, se citatet Fig.72, skulle ”det teoretiska området för en bildframställning med hjälp av trepunktsperspektiv” vara det streckade partiet inom de tre H-cirklarna.

— Enligt Lagerqvist, citat Fig.55, skulle det partiet enligt Lagerqvists tydligt hemliga önskemål men som inte finns med i den praktiska perspektivgeometrin emellertid också begränsas av en i-cirkel (och vars SAMMANHANG Lagerkvist tydligen inte känner till); Kvadrathörn i Z-planet (Fig:a) får alltid EXAKT 90° där.

— KUBEN i bilden utgår ifrån i-cirkeln (färgad) som ett xyz-roterat objekt i denna, och erhåller SÅ genom hyperbelgrenarnas motsvarande horisontrotationer motsvarande »horisontcirklar» — vilket Lagerkvist uppenbarligen inte medger någon öppning för.

— Och följaktligen, som vi ser av helhetsperspektivkroppen ovan, där Lagerqvists figur 72 ingår:

— LinjärPerspektivBegreppets ENHETLIGHET utgår uppenbarligen INTE ifrån de tre horisonterna eller horisontcirklarna — man kan, tydligen, inte formulera saken så; LinjärPerspektivBegreppets ENHETLIGHET utgår ifrån (c i Cheops Rektangels ab=c²) en central BILDCIRKEL (i), ett bildindex (som bygger totalt på sex gränspunkter med kuben som perspektiv preferenskropp), och som här alldeles tydligt SKÄR IGENOM Lagerqvists ’stränga teoretiska område’.

— Linjärperspektiven medger — naturligtvis, Lagerqvists obevisade påstående till trots — såväl spetsiga kvadratvinklar, figurbegreppen i ab, OCH att sådana från en visst given horisontcirkel kan sträcka sig utanför en annan given horisontcirkel. Perspektivgeometrin innehåller inga visuellt åskådliga gränser.

— (Lagerqvists) PÅSTÅENDEN strider ALLTSÅ mot de egna teserna — som källan dessutom INTE redovisar upphovet till (Lagerqvistsyndromet).

— KANSKE SPECIELLT UTPRÄGLAD SVENSK Läroboks- och Bibliotekslitteratur under 1900-talet i ämnet Perspektivlära, modern akademi.

Grundläggande kunskaper i ämnet saknas, tydligen som det får förstås i modern akademi med den referensen.

HP-kroppen — infört 11Okt2011 från doc-originalet KALKYL_MsWORKS.doc, HP-GEOMETRIN s86, med tillägg [urspr. från grundmanus 1984].

HP-kroppen

Se även Riktkuben

PROJEKTIONSLINJEN PC till objektslinjer PARALLELLA MED HP-kubens xyz-linjer får också dessa som gränslinjer då projektionslinjens längd utsträcks obegränsat.

Därmed definierar HP-kubens xyz-skärning med Z gränspunkterna xyz för 3D-perspektivet.

GRUNDERNA I

Den Linjära Perspektivgeometrin

eller TREPUNKTSPERSPEKTIVEN eller TRIANGELPERSPEKTIVEN eller HYPERBOLISKA PERSPEKTIVEN eller

HORISONTALPERSPEKTIVEN

DE LINJÄRA PERSPEKTIVENS GEOMETRI — trepunktsperspektiven, triangelperspektiven, hyperboliska perspektiven, eller som vi här ska kalla dem, HORISONTALPERSPEKTIVENS GEOMETRI (HP-Geometrin) — utgår ifrån DET FASTA PILOTSYSTEMET (xyz)_i med origo i PERCEPTIONSCENTRUM (PC); En fritt vridbar RIKTKUB xyz (HP-KUBEN) insätts med sitt hörn i PC;

HP-kubens skärning med ett fast (xy-) BILDPLAN Z på avståndet i (BILDINDEX) från PC definierar gränspunkterna xyz för bilden i Z av 3D-rummets alla möjliga xyz-paralleller.

(HP-geometrins fundamentalteorem).

Bilden av HP-kuben i Z bildar alltså en triangel. Därav benämningarna triangelperspektiv eller trepunktsperspektiv.

Varje HP-triangel kan återföras på en symmetrisk eller likbent grundtriangel vars gränspunkter följer enhetshyperbelns ekvation

(halva horisonten = √ i²+d² = ). Därav benämningen hyperboliska perspektiven.

PC [perceptionscentrum, projektionscentrum] motsvarar biosalongens filmprojektor, Z motsvarar filmduken.

Varje objektspunkt (Pxyz) i 3D-rummet och PC bildar en projektionslinje.

Objektspunkterna avbildas som projektionslinjens skärning med bildplanet Z.

[Rotationerna i HPG (horisontalperspektivgeometrin) bildar rotationskomplex II (xyz-medföljer rotationerna)].

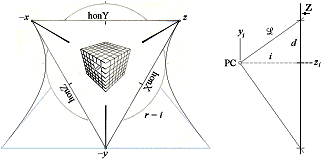
Koordinatplanen/horisontalplanen hon(XYZ) som koordinataxlarnas xyz-normaler, ger tillsammans med dessa de sex linjerna xyz XYZ som indelar HP-kroppens större triangel hon(XYZ) i sex mindre rätvinkliga trianglar.

(Allmänna egenskaper).

HP-kroppens uppritning — 3 olika sätt

2 linjer, 4 punkter definierar HP-kroppen, se figuren närmast nedan.

1. Vi drar horisonten (Y —),

2. lodlinjen (y |),

3. markerar PC=HP-kubens hörnpunkt,

4. markerar lodlinjens längd,

5. markerar endera återstående gränspunkten på Y.

Koordinataxlarna xyz är normaler till horisonterna XYZ. Därmed är HP-kroppens 6 rätvinkliga trianglar bestämda genom ovanstående: xyz-linjerna går alla genom mittpunkten PC och avskär därmed samma antal rutor per som horisonterna gör i normalriktningen.

CHEOPS REKTANGEL bd=h² ger bildindexcirkeln

i = √ (2|3)(3|4) = √ 2×8 = 4.

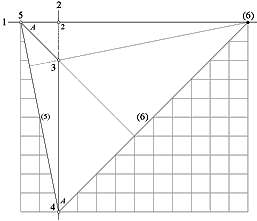
HP-kroppens allmänna konstruktion (med linjal) på RUTAT PAPPER.

Skalenlig 3D-Måttsättning

Skalenlig 3D-måttsättning i givet horisontalplan (H) med horisontlängden (från symmetriska bastriangeln)

görs genom att fälla ner H plangeometriskt via CHEOPS REKTANGEL (=h) bd=h², h=√bd.

Se även ursprunget till CHEOPS REKTANGEL i Matematiken 1.

h fås med passare genom att först dela b+d=2R i hälften (dra lika stora cirklar från 2R-sträckans ändpunkter, cirklarnas skärning på ömse sidor om 2R ger en normal till 2R som delar denna precis mitt itu), och sedan dra cirkeln R från mittpunkten. Skärningen mellan R och H-normalen genom PC definierar h, analogt den i R-cirkeln inskrivna rektangeln (från Cheops rektangelteorem).

Figurerna i den nedfällda plangeometriska H-delen överförs sedan via deras referenspunkter (P) till en H-parallell som flyttas upp (se figuren ovan) så att den skär genom PC. Därmed kan motsvarande HP-linjer dras från P till respektive gränspunkter på H. Figuren ovan exemplifierar tillvägagångssättet.

FLERA SÄTT FINNS att teckna HP-kroppen.

Exemplet nedan från i-cirkeln.

3 punkter med i-cirkeln definierar HP-kroppen, se figuren närmast nedan.

1. Vi drar i-cirkeln från punkt 1,

2. markerar horisonten (H) genom punkt 2,

Därmed är nästan hela HP-kroppen given:

2 medför via givet i att också blir givet (2|2),

3. samt därmed också lodlinjens längd via normalen 2|3

4. HP-kroppen fullständigas genom att bestämma gränspunkten på H för endera av de bägge återstående koordinataxlarna.

Koordinataxlarna xyz är normaler till horisonterna XYZ. Därmed är HP-kroppens 6 rätvinkliga trianglar bestämda genom ovanstående: xyz-linjerna går alla genom mittpunkten PC och avskär därmed samma antal rutor per som horisonterna gör i normalriktningen.

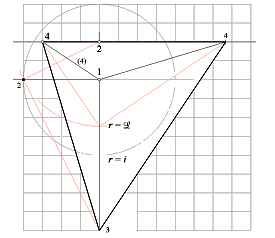
HP-kroppens allmänna konstruktion (med linjal OCH passare) på RUTAT PAPPER.

Ytterligare ett sätt:

4 punkter med en H-cirkel definierar HP-kroppen, se figuren närmast nedan.

1. Vi drar horisonten (H);

2. Vi drar H-cirkeln med radien R från punkt 0 (ej utsatt),

Därmed ges gränspunkterna 2 och 4.

3. Vi anger lodlinjen, samt PC på denna (punkt 5), vilket också ger punkten markerad 3.

Två av HP-kroppens rätvinkliga trianglar delar på en gemensam rektangeldiagonal via 2R. Normalerna i punkterna ab blir därmed givna via PC, och därmed även den sista gränspunkten (8).

Med detta sätt tvingas PC, punkt 5, ligga INOM R-cirkeln.

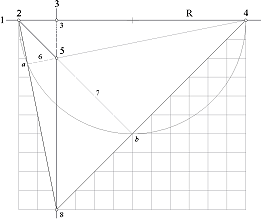
HP-kroppens allmänna konstruktion (med linjal OCH passare) på RUTAT PAPPER.

Från passare och linjal till plotters och dagens datorer

Ända fram till »brytningstiden» under 1980-talet (då olika datorplotters började dyka upp) fanns bara i stort sett Passare och Linjal för att utföra olika ritningar för gemene man. Man hade ritbräden, vinkelhakar, textmallar, gnuggisar och i allmänhet Rotrings tuschpennor (och Caran D’aches 2mM blyertsstiftpennor) som kunde köpas hos alla välsorterade bokhandlare. Idag (2011) finns inte ett spår kvar av den epoken. Det är som att en hel värld har »transformerats» till en helt annan.

— I dagens läge (2011) kan i stort sett alla möjliga 3D-komplex utföras direkt på datorer (och skrivas ut med högupplösande skrivare) — tyvärr ännu inte med några direkt enkla program som kan användas utan mer eller mindre ingående 3D-erfarenheter.

3D-GEOMETRIN 2008 | PILOTxyz.wps 2001II16 | urspr. frn. Index7c.wps 1998VI26 | Rotationssatsen — ROTATIONSSATSEN

ROTATIONSSATSEN

Med hjälp av en gyromodell kan man relativt enkelt konstatera den omvända samhörigheten mellan de bägge rotationskomplexen I och II.

En motsvarande beskrivning eller omnämnande har eftersökts på webben (@INTERNET November 2008) men inte hittats.

Modellen nedan är en konstruktion av denne författare från 3D-programmet Simply 3D som en del datortidningar gav ut som gratisprogram under Windows 95-eran. Tyvärr fungerar inte Simply 3D på senare datorsystem (32-bitar och uppåt) — vilket är synd med tanke på dess relativa enkelhet och därmed utmärkta verktyg för nybörjaren. Sådana program varken finns eller görs i dag, samtliga gratis 3D-program är (numera) så komplicerade att nybörjaren snarare avskräcks än känner sig inbjuden.

Vi studerar hur omvända rotationerna i det fasta bildsystemet är exakt samma som rotationer i gyrosystemet.

Väl det en gång fattat tillsammans med vinkelsummateoremet, finns inget rotationsproblem som inte kan lösas.

Sambandet mellan RotI och RotII — Följande beskrivning använder genomgående Pilotsystemet

1998VI26

I koordinatgyrot nedan till vänster Gyro1 ser vi att första rotationen alltid är gemensam för bägge rotationskomplexen I och II.

— Tänker vi oss nu att vilja rotera yW (rotation kring fasta vertikalaxeln) via RotI från detta läge ser vi direkt att detta är detsamma som att vrida gyro-x-axeln helt plant utmed den fixa Y-ringen i det fasta RotI-systemet. Med negativt 15ºyW i RotI får vi resultatet i Gyro2.

Om vi nu i detta slutläge Gyro2 vrider upp kuben via det andra rotationskomplexet, RotII, alltså via kroppssystemets x-axel, så att gyro-Y-planet återigen sammanfaller med den fixa Y-ringen, Gyro3, då är det klart att

	Gyro 1	Gyro 2	Gyro 3	Gyro 4
RotI	30ºxW	30ºxW, –15ºyW	–15ºyW	Gyrot nollställt
RotII	30ºxW	–15ºxW, 30ºyW	–15ºyW

1. xW blir nollställt för RotII — som alltså innebär att motsvarande baklänges rotation från Gyro2 i RotII är –30ºxW

2. den sista vridningen för att nollställa gyrot blir de återstående 15 graderna från RotI, alltså samma som för RotI (gyro-x-axeln, i Y-ringens gömda plan, har hela tiden legat kvar på exakt samma ställe som den lämnades via den andra rotationen –15ºyW i RotI).

— Om vi nu genomför dessa för RotII diskuterade baklängesrotationer

— –30ºxW, 15ºyW — men baklänges — –15ºyW, 30ºxW — så att vi börjar med yW och tar xW sist, kommer vi alltså tillbaka till läget i Gyro2. Slutsatsen blir alltså :

RotI 30ºxW, –15ºyW

ger exakt samma resultat som

RotII –15ºyW, 30ºxW

Exakt samma rotationsvärden — samma rotationsbeteckning — men i omvänd ordning.

Med andra ord ; RotI och RotII ger samma resultat om samma vinklar och värden från det ena rotationskomplexet tas i omvänd ordning mot det andra. Vi kan pröva med vilka som helst andra två rotationer och vi finner alltid samma överensstämmelse. Men:

— Gäller detta även med en tredje rotation inkluderad?

— Ja. Det gör det.

Om vi tittar på föregående gyroläge 2, och tänker oss att i detta läge påföra en zW-rotation via RotII (vi sätter den här till 45ºzW), då inser vi, via tillbakarotationerna för att få nollställning, att slutläget blir detsamma som att se gyrot från dess Z-plan i gyrobild 2 (den svagare delen i mittbilden nedan motsvarar 45ºzW) ;

	Gyro 2	gyrobild 2	gyrobild 3
RotI	30ºxW, –15ºyW		45ºzW, 30ºxW, –15ºyW
RotII	–15ºxW, 30ºyW		–15ºyW, 30ºxW, 45ºzW

SOM VI SER är detta helt (trivialt) ekvivalent med att vi i RotI börjar med den slutliga zW från RotII. Detta är fullständigt klart (tänk in den sista RotII-rotationen som mittbilden ovan antyder, denna ingår därmed sedan ‘naturligt’ med utgångspunkt från RotI, resultatet kan vi studera i högerbilden), och om vi gör på samma sätt med andra rotationsordningar (= andra namn på axlarna) finner vi naturligtvis exakt samma princip och ordning. Sålunda :

rotationssatsen: INL.

RotI och RotII ger exakt samma resultat om samma vinklar och värden från det ena rotationskomplexet tas i omvänd ordning mot det andra.

— Same end result from reversed order between I and II.

Ovanstående i syntes

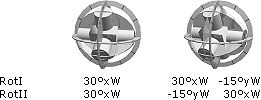
Om vi först studerar sekvensen för RotI — rotation av det inre gyroobjektet i det yttre fasta 3-ringade bildsystemet med dess fasta xyz-axlar

— enligt 30°xW och sedan –15°yW

— vilket ger det utroterade X-planets cirkel precis skärande 15°-strecket på den fasta yW-ringens skala

— ser vi tämligen enkelt att precis samma slutläge fås i RotII

— systemaxlarna följer med

— om vi börjar med –15°yW och sedan utför 30°xW.

Med detta fattat kan vi nu framgångsrikt studera tre rotationer och se att precis samma principiella ordning gäller:

I ovanstående sista bild (höger) lägger vi på en initierande 45°-rotation, översta raden med RotI; vi ser (om vi tänker efter en stund) att detta kan göras ENKELT genom att rotera gyrokuben ovan i sista bilden 45°zW vilket ger oss slutbilden nedan längst till höger,

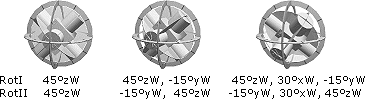
Genomför vi sedan slutligen en återrotation genom RotI — vi börjar med minus 45°zW, sedan minus 30°xW och sist plus 15°yW — kan vi för varje sådan återrotation följa i detalj och se att vi också verkligen återställer gyrot i nolläge. Och alltså gäller rotationssatsen som ovan.

*

FullRedo:

Full redovisning Feb2019

Ett motsvarande algebraiskt bevis finns också — se utförligt från EQUIVALENCE OF ROTI AND ROTII.

— Men det är (betydligt) mera krävande då det förutsätter bekantskap med den speciella matematiken i RotII — som kräver (åtskilligt) utrymme — se Rot II Origin.

Det är också underligt att inget alls tycks finnas på webben (ännu November 2008 — och fortfarande samma Feb2019) som ens ger en elementär orientering i ämnet — frånsett högskolematematikens matriser och determinanter förstås, eller vad som påstås sammanhänga med dessa: redovisning saknas.

”Matriser och determinanter” har f.ö. ingen representation i Universums Historia:

— Enda anledningen: finns inget som helst behov. Helt rent. Totalstädat. Komplett Glänsande.

I modern akademi verkar det inte finnas något utvecklat rationellt beskrivande vokabulär för de två skilda rotationskomplexen. MEN: Man känner — eller rättare sagt FÖREFALLER känna — till dem:

Se Konventionell beskrivning av de två rotationskomplexen inom 3D-geometrin — här i ny erinrad upplaga, se citat från WolframMATH2019 med kommentarer och jämförelser.

— Man tycks — fortfarande — inte kunna beskriva saken med andra ord än genom högskolematematikens matrisbegrepp, eller det som förefaller koppla DIT genom nämnda: redovisning saknas — vilket garanterat portar de allra flesta människor från ämnet.

Märkligt är det:

— Man VET inte. Därför att OM man visste, saken redan sedan länge hade sett dagsljuset[‡Origin].

3D-GEOMETRIN 2008 ¦ 2019

APPENDIX: 27Jan2019

APPENDIX

ESTABLISHMENT

The ORIGIN OF ROTII ¦ EQUIVALENCE OF ROTI AND ROTII

————————————————————————————

FJÄDERANALOGIN — Spring Analogy

ALLMÄNNA SAMBAND FÖR ATOMKÄRNANS MEKANISKA FORMHÅLLFASTHET ENLIGT RELATERAD FYSIK — K-cellens Detonation

I htm-kopia 9Jun2012 från originaldokumentet (Maj2004) i MsWORKS 4.0 Fjäderanalogin.wps

AppendixINTRODUCTION:

COMPARING EXAMPLES — by Examples Ex0 | Ex1 | Ex2 | Ex3 | Ex4

Jämförande exedmpel som avslöjar den etablerade lärobokslitteraturen obefintliga ämneskunskaper — Se särskilt i LagerqvistSyndromet

INTRODUCTION PRECISE TECHNICAL DRAWING IN The HORIZONTAL PERSPECTIVE HP-BODY

COMPARING THE LEVEL OF KNOWLEDGE IN MODERN ACADEMY

Quoting Established Sources ¦ EXAMPLE 0 ¦ EXAMPLE 1 ¦ EXAMPLE 2 ¦ EXAMPLE 3 ¦ EXAMPLE 4 ¦

Ex0CheopsRECTANGLEby2NeedlesAndRightAngle:

PRACTISING

CHEOPS RECTANGLE

WITH ONLY TWO NEEDLES AND ONE PLEXIGLASS RIGHT ANGLE TO GET THE HP-BODY PERSPECTIVE XYZ-HORIZON INDICES:

CALLING PLANET InternetSearch EARTH HUMAN if there are any left POPULATIONS JAN2019:

— How many single individual persons on Planet Earth Jan2019 KNOW about this one:

ONE precise Plexiglass right angle, two steel pins (Ø0.6mM), square (2/10’’~5mM) printed paper for ease of test or millimeter-printed paper for more precise quantitative inspection, needled by distance a+b on a white piece of 2mM passe-partout carton:

— By carefully pushing the angle against the NeedleShafts, the angle-tip DIRECTLY NOT ONLY solves c=√ab. But ALSO solves the problem of finding a given perspective horizon’s INDEX length () — for further exact and precise TECHNICAL perspective drawing[‡].

Given a three corner triangel (below right) with a middle intersecting point for the three horizontal normals:

— Each horizons perspective INDEX length () is found projectively by folding its horizontal plane (X¦Y¦Z) down on the horizon’s normal. The practical way for that fold is as shown below left with needles and a 90°angle.

— Then further precise angles for precise vanishing perspective points LimitPoints can be marked on the given a+b-horizon. In all: Just ordinary plane simple geometrical basics.

CHEOPS RECTANGLE: Ex0CR

— IN PRECISION LINEAR PERSPECTIVE DRAWING:

There are also a number of other ways to ONSET the actual HP-bofy three corner triangle. See from Onsetting the HP-BODY. See also THE HORIZONTAL EQUATION. See also CHEOPS RECTANGLE.

— Two?

— Five?

— Three thousand? Five hundred thousand?

LOOKING @INTERNET 1Feb2019

we WOULD wish ”the web” to be »full of it»: Ideas, examples, methods: The CHEOPS RECTANGLE Method Yess

none of the above simple principle linear perspective drawing details seem to have a front web representation:

— not seen. Searched for. Not (yet) found.

Pen. Paper. Rulers. Needles. Carton. Plexiglass angles. Compasses: Traditional Classic Drawing WITH a deeper ELEMENTARY insight into the explaining mathematics — logics — of it.

No computer. Just YOU and Nature — promoting[‡] ”the full and free development of personality”: The Individual’s Own Private Unique Way: NOBODY makes it like YOU do. Guaranteed.

— Where is That ”deeper” 1Feb2019 on Earth? I don’t see any.

Compare Quotes from established quarters on the subject (Wolfram 2019 ¦ Perspective Education 1966).

Search word, exact ”CHEOPS RECTANGLE”. Two hits 1Feb2019:

1. NASA’s satellite project — with merchandise products, not really our subject.

2. This Portal, UniverseHistory — the connection as such bd=h².

— No more. No Perspective stuff. Wikipedia on Perspective (graphics) is far from even a mentioning.

On the other hand, fair play: the Term ”CHEOPS RECTANGLE” might not be familiar, while the expression might ...

What’sUp?

IF no one cares about looking for the treasures, they continue being perfectly aligned with the ticking seconds in darkness. They exist. But not (yet) in daylight.

Establishment:

Comparing related mathematics with modern established sources Jan2019:

The only mentioning we find on the subject in modern quarters:

TRANSPOSITION MATRICES[‡] IN MODERN ACADEMY — RotI&RotII in modern quarters

Wolfram2019: Establishment

WOLFRAM MATH WORLD mentions (Oct2011 ¦ Jan2019: Rotation Matrix)

” When discussing a rotation, there are two possible conventions: rotation of the axes, and rotation of the object relative to fixed axes.”,

” Wolfram websites use cookies to improve your experience with our services. By continuing to use this website, you are consenting to this use as described in our Privacy Policy.”,

WFoct2011 ¦ Wolfram Rotation Matrix 31Jan2019.

HumanRightsViolations:

COOKIES VIOLATES HUMAN RIGHTS:

Freedom to hold opinions WITHOUT INTERFERENCE:

A19 UDHR10Dec1948:

Everyone has the right to freedom of opinion and expression; this right includes freedom to hold opinions without interference and to seek, receive and impart information and ideas through any media and regardless of frontiers.

”By LOOKING AT ME you agree/consent to ...” IS Classic Fascism: dictatorship. IS.

Wolfram Math, please, and associates:

— I make my own choices, regardless of what and how other people make theirs.

— My experience is my own personal property, as your is yours. And no one is capable of ”improving” inside of that property EXCEPT you for you and me for me. Nobody.

NOBODY.

The CookieSyndrom IS a Dictate, a Prompt, a Fascistic claim. Provable in every detail. Leave it. Drop it. Stop insulting Humanity.

General Cultural Company Enterprising:

A08 UDHR10Dec1948:

”.. to the end that every individual and every organ of society, keeping this Declaration constantly in mind, shall strive by teaching and education to promote respect for these rights and freedoms .. ”.

— CONSENT again, Wolfram + Associates: — »We give a SHIT about THAT». Not a word.

— That SEEMS perfectly correctly stated with respect to the provability of respectively RotII and RotI.

— HOWEVER. A little more than on line + a right angle is needed to CONFIRM the acquaintance.

The Wolfram source @Internet gives nothing else than information about the algebraic/matrix sets in mentioning them from established sources (Goldstein 1980, Arfken 1985). The only LEAD the reader receives is this — very, exceptional — deep explaining properties of the subject:

Modern Academic

HIGHLY EDUCATIVE CONTRIBUTION TO THE ENLIGHTENMENT OF PERSPECTIVES:

Wolfram Math World Improves Our Mathematical Experience with Practical Examples:

3D-Perspective Rotations — with Simple To Understand Arrows, Deepening Our GotItExperience.

— Wolfram, please: How come this outrageous ABSTRACTION? Please, do show.

— »WE don’t know». Please do correct if wrong.

— The best part with modern academic algebra on visual perspectives: we don’t have to SHOW any.

cont. →

MACAndIntelligence: W2019

Related Description — versus Universes History, its Basic Math and TNED-physics: trying to throw some light onThe Subject

WOLFRAM MATH:

— Are you consenting human rights or not?

WOLFRAM MATH AND ASSOCIATED, TRY THIS ONE: Attitude — opinion, claim, statement, thought, apprehension, idea, notion, interpretation: mind, sense — outside the recognition of human dignity, human rights, IS PRACTISING OPPRESSION: Fascism, Nazism, Dictatorship, Devilship, Satanism — Pick one: A01 UDHR10Dec1948 — ”WHEREAS recognition of the inherent dignity and of the equal and inalienable rights of all members of the human family is the foundation of freedom, justice and peace in the world,”; EVERYTHING else MEANS NOT freedom, NOT justice, NOT peace: PRACTISING OPPRESSION: Fascism, Nazism, Dictatorship, Devilship, Satanism — Pick one. HENCE: CRIMINALITY — any kind of offence, insult or attack on decency — is unequivocally FOUGHT by (A08) ”teaching and education to promote respect” for HUMAN RIGHTS; WHEREAS — WOLFRAM MATH WITH ASSOCIATED AS HERE obviously so PROVEN IN DETAIL — Humans, Communities, and Cultures who DO respect human rights NEVER — ever — develop any kind, sort or type or nature of OFFENSE: no criminality, no attacks, no intrusions: no interference with privacy [A12]. Not in our cultural epoch, not in any other either. It is a LAW BY NATURE. Please do make corrections if wrong: All other activity and claim, aiming to fight criminality and general offence, HENCE IS practising oppression: devilry — by DRIFT, never by PLAN: nobody chooses stupidity over sanity inspired from a rational point of view. Only a fucked up ATTITUDE do so. I don’t think it is so. I know it is so.

WOLFRAM AND OTHER ESTABLISHED INTERNET PORTALS SUCH AS WIKIPEDIA and Associates radiate this general impression:

— Modern Academic mathematics and physics are GENUINE, SERIOUS and (deeply) RATIONAL — intelligibly — founded branches in a general natural scientific TREE of »universal knowledge». It would be nice if that was the case — then this presentation never had to face the light of day.

In TESTING this assumed Modern Academic LOGICAL reliability — at first in the PRACTICALLY EXPLICABLE area of magnetism and induction — details appeared (here in 1994) exposing the modern idea of magnetism and induction to be SURFACE MINDED: it doesn’t tell the whole story. It leaves (huge) gaps, unanswered questions, formulates »dumass math inventions» to compensate. WITH a following general disability to rationally EXPLAIN the connections: THE differential equation for the EXPANSION INTEGRAL in Magnetism is not only UNKNOWN in Modern Quarters. But also makes a general CRASH IF the established concepts of VECTOR ALGEBRA are applied to it. Really. Let’s see why.

— In modern quarters it is held in general that induction and magnetism follow Maxwell’s equations, and have a common physical origin: modern academic vector calculus. But THE SOLUTION to the variant, the actual magnetic integral in modern quarters, IS known: The Biot-Savart Law. So: In comparing the actual PRACTICAL RESULTS FROM TESTING THE PHYSICS contra corresponding EXPRESSIONS in different established textbooks — especially on the level of INDUCTION — the peculiar did arise between Modern Academy MAC and Related Mathematics and Physics TNED, see Three Examples in Treatise. What? What appeared? WHILE TNED APPARENTLY explains the details by atomic precision — especially

WHY MAC ERRONEOUSLY IDENTIFIES µ₀ WITH MAGNETISM
cont. →

TNED EXPLAINS PHYSICS IN DEEP: In induktance (µ₀s) the foundational space-compactness µ₀ is always present. In magnetism

:

IT IS A SIMPLIFICATION FROM THE BASIC DEEP NEVER DEVELOPED IN MAC

it never appears:

— In MAC, says TNED, this IS the only known reason why the phenomenon of induction is associated, identified, with magnetism — despite the simple ”Maxwell’s rule” showing it does NOT. Proof: The Parallel Experiments 1994. Has been searched for in established literature, not found:

Proof of induction as completely liberated from magnetism

MAGNETISM AND INDUCTION NEVER — ever — INTERACT — but modern academic textbooks are full of such claims

— The »MagneticDifferential»[‡] has no modern academic representation: Modern academy INSTEAD departs FROM INDUCTION — »covering over» The »MagneticDifferential» BY modern academic vector calculus: The bare raw rational logical related mathematical and physical proof which explains the whole complex in absolute deep detail, is driven over by modern academy vector calculus AND ITS DEMANDING CONSEQUENCE: the fatal idea that induction and magnetism interact. They don’t, says TNED: Induction and Magnetism NEVER interact — as x and y never interact, as Light and Kinetics never interact — only cooperates in a way neither very well described in modern quarters:

— c and v never interacts:

— light has no kinetic connection: light and kinetics never interact: Light’s Liberty Clause in Related Physics, with further:

— Physics is governed by The Planck Equivalents — NOT Einstein’s Theory of Relativity — the vic-error: LIGHT AND KINETICS DOES NOT INTERACT. Practically the same mathematical expressions: fundamentally different physical foundations. Page up. Page down. Experiment in. Experiment out. Not one found exception. A NEW — »very old» — model of the universe appears.

— Magnetism and Induction HAVE DIFFERENT DIMENSIONS — but Performs A Dolls House Theater if insisted to Match — holding mankind in darkness, ignorance and delusion, proclaiming IT to be The Master Intelligence. 1800+ answers.

— And so, the bottom line says it: Magnetism’s FUNDAMENTAL physics CANNOT be applied on modern academy vector product. BECAUSE in doing so 1. the modern academic vector calculus responds by CRASHING on itself, and 2. (so) proves that induction and magnetism NEVER interacts — as also experimentally notified[‡], however searched for in established literature but not found. And there are more examples outside magnetism and induction:

— See f.ex. (for example) Central motion — the MIT-example.

In EXPLAINING Nature, modern academic teaching system has excluded itself by inventing ideas instead of deducing them from Nature, says TNED. To underline the sublime differences — with the shocking essentials by school examples especially in concern of Light and Gravitation PHYSIC’S SEVEN PRINCIPLES — the following compilation serves:

NATURE in physics, comparison MAC/TNED:

TNED: Dedicated Proof to all Nature Lovers: ———————————————————— 1. only natural constants: 2. .. in the beginning ... 3. .. Earth .. fusion limit mass ... THE BOTTOM LINE: CHEOPS PYRAMID ATTESTS TNED — from Cheops Rectangle: 4. .. possible ancient remnants .. 5. .. Sun’s Photometric Effect — a direct TNED-hit ...

PRACTICAL and highly provable in any deep EXAMPLES IN related as in TNED MATHEMATICS AND PHYSICS SHORT SYNTHESIS dedicated to MAC 3Feb2019 in comparison with TNED related physics and mathematics — practical examples to enlighten »the population of the dark age» — inside modern academic quarters: • MAC/EINSTEIN on »light’s gravitational dependency» term not found in MAC: c/c0 = (1 – w^2/c^2) — invented logic: — c and v do interact, see vic-error — disproved by M&M-experiment from 1881, never recognized (however noted) in MAC • TNED/CHEOPS RECTANGLE ¦ LIGHT’S GRAVITATIONAL DEPENDECY, c/c0 = (1 – w^2/cc0) — deduced from basic geometry: c0 is conserved independently of gravitation, — c and v never interacts — in full concord with induction and magnetism, as above noted • TNED/CHEOPS RECTANGLE ¦ [‡] — Harmonic Triangles explaining The Complex Algebra: r=x+íy. • TNED/CHEOPS RECTANGLE ¦ [‡] — Light’s Gravitational Dependency — preserving-guaranteeing c0 independently. • TNED/CHEOPS RECTANGLE ¦ [‡] — Square Roots. • TNED/CHEOPS RECTANGLE ¦ [‡] — Cheops Pyramid from Flinders Petrie’s measurements 1883: The rJ-Circle Construct. • TNED/CHEOPS RECTANGLE ¦ [‡] — Foundational Perspective Mathematics[‡]. ... Attempting a FURTHER CONTEXTUAL CLARIFICATION: —————————————————————————— Environmental SAFE — Huge — Energy For Mankind; — no WindPoles, no Nuclear Plants, no Deforestation, no Petroleum, no Fuckups: TNED ATA/CAT DEDUCTIONS: The complete disintegration of the atomic nucleus — regulated by simple math, but tough to realize technologically — yet Feb2019: But Modern Academy has locked itself outside its details Because of INVENTING, not deducing, physics from 1800+: TNED explains the details: ATA AtomNucleus’ Transmissive Autonomy — as in ARC ¦ [‡] with modest current.: CAT Capacitive Transmission — as in LIGHTNING with a sufficiently large current. — The TNED DEDUCED FROM PLANCK CONSTANT[‡] Atomic Nucleus includes, incorporates — is based upon, physically exclusively — a self catching CURRENT TRAP. It is perfectly mathematically explainable and expressible, specifically apparent in an ARC and LIGHTNING. The MATH-part — as also Nature Shows IT — points to a complete adequate E=mc^2 disintegration of the nucleus without any kind of rest products. Nature demonstrates IT in natural Earth cloud-ground lightning provided sufficient current strength — see also The Zambia Positron TGF certifying the principle TNED-theoretical part of it. — BUT MODERN ACADEMY PEOPLE ARE STANDING COMPLETELY OUTSIDE THE SUBJECT DUE TO THE MODERN ACADEMY INVENTED IDEAS OF NUCLEAR PHYSICS IN GENERAL: it is a hopeless primitive[‡]: — TNED + Experimental Physics = TRUE. So to speak. And we need only one — 1 — simple itty bitty tiny practical example that exposes flaws or any the smallest error in TNED, in order to advise IT to the TrashCan. Please do show. Very high IQ. SUGGESTED PROJECT NAME: save humanity from killing Earth BioSurface.

→ cont.

a corresponding MAC-presentation SO has banned itself out of the NATURAL SCIENTIFIC p(a)lace from square one;

— To ”understand” MAC-induction and magnetism, the student MUST adopt an intellectual method »INVENTED BY OUR FOREFATHERS»:

— No RATIONAL depth exists in MAC-induction. It is Surface minded from begin to end. CONCLUSION, says TNED:

Modern academy and its love to its own »master intelligence ideas» evolved 1800+

”to overcome ones human limitation and become master of the universe”, on the Fields Price medallion:

Transire suum pectus mundoque potiri. ”The most glamorous honour a mathematician can receive”.

DID DEVELOPE only a NOMENCLATURE on the level of ”A Doll’s House Theater”, so to speak. Nature — the student’s mind — was locked out.

— PRACTICALLY THE SAME END EXPRESSIONS HOLD in TNED and MAC, if at all[‡]. But with vast essential differences in explaining the nature behind; There is NO — guaranteed — conversion between the two. Only one of them can EXPLAIN the other — as »A Primitive».

So, WOLFRAM MATH with other associates in this subject of 3D-Rotations and Perspectives: GENUINENESS OF MATHEMATICS — matrices and Modern Academic Vector Algebra specifically — demands a little more than two figures with three straight lines to EXPLAIN, or claim, the Nature behind the body of perception and how it works in Linear Mode:

— Modern academy vector calculus is NOT a valid NATURAL SCIENTIFICAL method of explaining anything except a provable primitive logical inventive method leaving out the deep — relatable, understandable — part of natural intelligence, as exemplified above. Not necessarily wrong. But indeed primitive.

→ cont.

EXCEPT FOR one line and a right angle TWO FIGURES that seem to have nothing in common with Related Perspective Mathematics, WOLFRAM EXPOSES NO FURTHER ILLUSTRATIVE WORK.

— Compare RELATED MATHEMATICS: 100% Pedal — Real Horse Power stuff:

The Real Steel:

The Wolfram Rotation Matrix — although claiming rhetorically familiarity with the end result[‡] from the equality between Rotation Complex I and Rotation Complex II — seems to have nothing, no practical connection at all, with the actual practical subject.

— The Wolfram source does not CLARIFY, or cannot do so, its MEANING of the symbols with respect to BASIC VISUAL ELEMENTARY FOUNDATIONS:

— Modern Academy High School References Leave Pedestrians out. Why not handcuff them directly, too?

THE WOLFRAM PRESENTATION OF THE CLAIMED TWO POSSIBLE ROTATION SYSTEMS

See Rotation Complex I and Rotation Complex II

USE MATRIX AND MODERN ACADEMIC VECTOR[‡] NOMENCLATURE.

— There is no PRACTICAL — by vision, sight — account. Only a deep and vast abstract account. Very.

What IS that?

— Modern academy has during its Inventive Period in the 1800:s COME UPON A METHOD of ”Cut-To-The-Chase”-algebra, skipping all the practical stuff in between, getting directly to The Profit Station: The less normal pedestrians understand of the content, the more Profit will come BECAUSE it lies in the Nature of Man and Woman to ASK for Answers to Everything — Unknown. So the More ”Cut-To-The-Chase”-algebra, leaving everything outside, the more MustBuy. Then Profit is secured. ”You Pay Monthly to SEE”.

— They don’t Know. Because if, it would be shown.

Can’t explain. Can’t describe. No details.

RELATED MATHEMATICS EXPLAINS by practical examples and comparing cross references:

— As is evident from the examples in deep (magnetismen, induktionen, centralrörelsen), describing NATURE in deep with the help of modern academic mathematics does NOT work very well. In fact, as so proven:

— It crashes. Deeply. IT isn’t for Understanding. IT is — or rather appears to be only — for Profiting.

»Magnetism&Induction under same roof»: Doll House Theater: Atomic Bombs; Technology for Cutting Forests down: The Forests who laid the foundation of the human and land animal evolution: »cultural suicide». A Fundamental Environmental Crash 1800+. ”Cut-To-The-Chase”-algebra.

Nothing wrong with the algebra. Absolutely not. Mathematics is never wrong. But the ATTITUDE behind MIGHT be, depending on ”cultural traffic conditions”.

Please make corrections if wrong: Knowledge explains, not Dictates. So, Modern Academy:

— IT cannot explain Nature — related thinking based om simple elementary natural properties[‡] that every person can understand in every atomic detail[‡] — IN DEEP: deeper, deepest.

Please do give only one rejecting example — one: 1 — and this author will convert immediately.

— Surface minded ideas of math: Destructive natural intelligence. Destructive natural behaviour. Partnership.

— By DRIFT. Of course. NOT by Plan. Buddha’s simple teaching on The Two Principles: 1. The principle of ignorance — DRIFT — and 2. the principle of INSIGHT or KNOWLEDGE or HARMONY (Nirvana).

COMPARE A POSSIBLE EXPLANATION[‡]:

— »During the 1800:s, Modern Academy had direct revelations from the lord, automatically introducing Nirvana in modern mathematics»:

”to overcome ones human limitation and become master of the universe”, on the Fields Price medallion:

Transire suum pectus mundoque potiri. ”The most glamorous honour a mathematician can receive”.

The whole established subject obviously rests on »pure high school mathematics»: matrices and the general modern academic »High IQ» vector algebra: As abstract as can be. Pedestrians are left outside: ”Above our paygrade”.

In Universes History:

No trace exist in Universes History of such Modern Academic High School mathematics: no statistics — Compare RELATED Deduction of Planck Radiation Law[‡]: no statistics. Not an atom of it.

— In any RELATED sense, we are allowed to use only relatable concepts, each one by detail leading back to the simple elementary basics — leaving no single individual behind:

— IT relates, or not at all. No modern logic academic inventions. No jumps. No dark corners. If we don’t know, we don’t know. If we do, we do. We walk the paths we know, and stay away from the rest — until better equipped with a method of conquering the difficulties. Always WITH nature. NEVER against.

As far as known, that is the closest we get in any contribution from the »Nature Earth Destructive Occupying» modern academic teaching system 1800+: transposed matrices. It is, obviously, a guaranteed exclusion of Human Mankind main populations from any relatable practical insight.

OBVIOUSLY: Some persons in modern academy has taken some time to »press the subject through» modern academic high school mathematics (combinatorics). It however seems that no ELEMENTARY — basic mathematics — description exists at all in modern quarters on the subject RotI&RotII — despite the subject’s simplicity, as here described.

Has been searched for, not yet found.

Wikipedia on Perspective (Graphical, 30Jan2019) is far from even mentioning the term HYPERBOLA in any context connecting the basic elementary visual linear perspectives. The word ”hyper-” is not even mentioned in the article. Wikipedia mentions one, two and three ”point perspective” with some poorly relatable computer graphics — and four .. six .. unillustrated. No clarifying practical — pen and paper — descriptions. Nothing for a potential artist to consult: no deep info. And: Don’t even think about mentioning The CHORD.

TRADITIONAL LIBRARY LITERATURE is even worse:

Ex1PMCLP1979:

A Practical Example of PRECISE MEASUREMENT COMPOSITION in linear perspective from 1979, this author’s pen and hand:

PerspectiveQuote1966:

compared to claims and statements we find in established educational library literature on the subject:

”MÅTTSÄTTNING AV PERSPEKTIV

För måttsättning passar ingen annan metod än den rätvinkligt parallella.”,

RITTEKNIK — Regler och råd för teknisk ritning med projektionslära,

LÄROBOK I TEKNOLOGI FÖR GYMNASIET OCH TEKNISKA SKOLOR,

Lars Walldén, SÖ-förlager 1966, s72;

”MEASUREMENT COMPOSITION IN PERSPECTIVE

For measurement composition no other method is suitable than the right-angular parallel.”.

— So modern academic teaching system keep saying.

— Why not handcuff the students directly — too?

More examples:

Ex2PMCLP2017: Ex1

CHEOPS RECTANGLE Section Nov2017

— Details inside Cheops Pyramid: Instructive clarification — THE GALLERY GRANITE PLUGS

APPLYING PRECISE MEASURING QUANTITIES IN A VISUAL PERSPECTIVE by artist’s pen, rulers, hand and paper HAS NO ESTABLISHED PREFERENCE OR RECOGNIZED TEACHING FOUNDATION — as quoted[‡].

Ex3PMCLP2017: Ex1 Ex2

CHEOPS RECTANGLE Section Nov2017

— Details inside Cheops Pyramid: The Step

What? What are you talking about, »modern man»?

— Preciseness in SETTING EXACT quantitative measures in visual linear (or other) perspectives? No? EasyPiecy. When we know how.

— Modern Man: Get out of The Computer, and Test The Natural Way: Get BACK TO LIFE. USE the Tube. Don’t let IT (GOOGLE-MICROSOFT) use you.

Please DO make corrections IF untrue. Knowledge — nature — is our aim. Nothing else.

Ex4PMCLP1980: Ex1 Ex2

ELLIPSOGRAPH No97 Sep1980

— Details in Linear Horizontal Perspectives: ELLIPSES

Exercising Ellipses Math with an Ellipsograph in 1980.

— They don’t know. Meaning:

— They don’t know.

BUT modern academic teaching system CLAIMS to Know — by Transposing Matrices: Rotation Matrix. What, exactly does that mean: Animated Transformers? Billion Dollar Computers? Hollywood’s ”Warning ... Prison”?

— Where is the practical pedestrian’s part of IT, the Practical KnowHow of it, the TodayIwillDoSome of IT? I don’t see any. Is there even a CUBE in there?

Book in. Book out. Lesson in. Lesson out. Hour in. Hour out. Generation in. Generation out. Grandfather in. Grandmother out. It’s called: culture. Merit. Education. PayGrade.

Very Educated Population. Very Instructive. MustBuyBook.

It seems — have been searched for, not yet found — that the HP-body[‡] is not at all known in modern quarters. But its rotational complex is — or rather seems to be known by the end result — by transposed mathematical methods that few individuals on Planet Earth do understand the practical meaning of underneath.

— Compare The Horizontal Equation: HOW TO DRAW SIMPLE AND EXACT VIEWS IN LINEAR PERSPECTIVE seems not familiar at all in modern academic quarters. Never mentioned. Never seen. Never heard of.

MANY EXAMPLES EXIST ON THE ACTUAL RESULTING VIEWS IN LINEAR PERSPECTIVES. That is true. But in describing its fundamentals, the contributions appear as the above quoted. That is, as in an underground room — with no light at all. Pedestrians are left out. No enlightenment. No knowledge.

But the rotational orders are — or seem to be — known[‡]. However obviously in a manner leaving the practical details outside. Most Near Associated Resemblance: Like looking into a World Population of Complete Blindness: knowing, not knowing. Saying, not saying. Claiming, not claiming. Living, not really.

Wikipedia has no Article about IT Jan2019: The NATURAL ARTISTIC and Natural Visual Foundation of Linear Perspectives: The Hyperbolic Unit Body — Cheops Rectangle: Linear and Spheric. ONE natural base.

Rot1Rot2sam:

The ORIGIN OF ROTII — The MATHEMATICALLY DEDUCED

EQUIVALENCE OF ROTI AND ROTII

MATEMATISKT HÄRLEDDA EKVIVALENSEN MELLAN ROTI OCH ROTII

———————

Från sammanställda arbeten i perspektivgeometrin — Jun1981 ¦ Aug1984 ¦ Jun1998 — Jan2019

———————

See special English edition in The ORIGIN OF ROTII — the basic RotII-equations

Inledning: INTRODUCTION: RC12Theorem:

SAMHÖRIGHETEN mellan de bägge rotationskomplexen[‡] RotI och RotII beskrivs retoriskt-illustrativt-intuitivt i den enkla ROTATIONSSATSEN[‡] med hjälp av en enklare Gyromodell[‡]:

RotI och RotII ger exakt samma resultat om samma vinklar och värden från det ena rotationskomplexet tas i omvänd ordning mot det andra.

— Rot1 and Rot2 give exactly the same end result IF same angles and values from one of the Rotation Complexes are taken in a reversed order relative the other. It is named here: The Fundamental ROTATION COMPLEX THEOREM.

I följande sektion visas den rent matematiska-algebraiska bevisgrunden till rotationssatsens giltighet. Bevisformen använder specifika samband ur RotII som inte presenterats här tidigare i Universums Historia — på grund av ämnets VÄL omfattande och sammansatta natur.

Nu Jan2019 befinner vi oss i en något annorlunda situation

— CHEOPS REKTANGEL[‡] med tvärsyntes genom snart sagt allt möjligt i fysik och matematik:

Alla utvecklingsdetaljer i Universums Historia grundas HELT på den matematiska fysiken från CHEOPS REKTANGEL:

Se även från MEL1 och MEL 2 ¦ SOLFYSIKEN I TNED TESTAS

Viss angelägenhet finns för att visa samhörigheterna mera både på djup, bredd, och höjd.

— Verkligen djupintressant ämne eftersom intet — nada — motsvarande av den mera enkla matematikens form syns i etablerad litteratur.

MDR12EQ:

ALL TRIGONOMETRIC RELATIONS IN The Most Simple PREFIXxSIN — no derivatives, just plain basics

MATHEMATICAL DEDUCTION OF THE Rot1¦Rot2

EQUALITIES — mathematical proof

ONLY UNICODE CHARACTERS ARE USED HERE IN ORDER TO INHIBIT CERTAIN WEB BROWSERS FROM VANDALIZING ORIGINAL COMMERCIAL COMPUTER WORD PROCESSOR FONT WORKS — we thought the computer era was developed for OUR convenience — an idea soon proved to be a commercial sewer

————————————————

Synthesis figures in The ORIGIN OF ROTII are scanned copies of the original paper work with ellipses drawn »The ROTRING LetraSet Era» by a precision EllipsoGraph (HAFF Ellipsograph Nr.97 — bookstore stuff from the late 1970:s: can’t find it today 2019 to any reasonable price).

————————————————

FOR A GENERAL ACQUAINTANCE WITH THE PREFIXxSIN-BASOCS, SEE TABLES IN TRIGONOMETRY unless already familiar.

CompiledRot1:

Compiled ROT I Equations:

All IMAGE 3D-ROTATIONS in Rot1 are made from the simple (AngularSumTheorem)

where (x¦y)₂ is replaced by (sinW¦cosW)₂ giving the general 3D-rotational simple format

x := x sinW – y cosW

y := y sinW + x cosW

By successively shifting the actual angles xyz(W°) on the same type xy-expression format with corresponding given or simultaneously calculated coordinates xyz, any 3D-rotation of any coordinate point xyz is performed.

The corresponding compiled Rot2-equations are more demanding. See separate section in The ORIGIN OF ROTII.

— Here we show how the correspond and communicate through the already observed »3D Rotation Complex Theorem».

CompiledRot2:

Compiled ROT II Equations:

from Order No5 —

x_MOD = sin(yW+90)·sinxW·z + sin(atan[z’/x’]+yW+90)√(x²+y²)(1–[coszw·sinxW]²)

z_MOD = cos(yW+90)·sinxW·z + cos(atan[z’/x’]+yW+90)√(x²+y²)(1–[coszw·sinxW]²)

y_MOD = cosxW·z + sinxW·coszw·r

Abbreviations:

x’ = sin(zw–90)·(√x²+y²)·cos(–xW)

z’ = cos(zw–90)·√x²+y²

zw = zW₀+zW

Additional Conditions for atan applies: .

The above given coordinate transformation equations by rotation in RotII are given in »the classic way». That is, with the elementary tangent conditions connected to the four classical quadrants of the circle — in order to determine the correct polarity of the coordinates for each specific rotation.

We will now show how the more sophisticated Rot2-parts EQUALS — give the same end result — as the simpler Rot1-parts — with respect to the stated »rotational theorem».

Prepared Rot1:

By straight indices (1 2) to clarify the deductive continuity:

ROT I — Equations :

zW xW yW

x1 = x·sinzW – y·coszW z1 = z·sinxW – y1·cosxW x2 = x1·sinyW – z1·cosyW

y1 = y·sinzW + x·coszW y2 = y1·sinxW + z·cosxW z2 = z1·sinyW + x1·cosyW

Equations in ROT I as above are now compiled in such a way to express a final complete equative solution

explicitly for end coordinate x2,

explicitly for end coordinate y2 and

explicitly for end coordinate z2

with a reversed rotational order relative the RotIINo5 order:

yW — xW — zW

As already observed (Rotation Theorem ¦ The Theorem) by a simple visual investigation from The GYRO-model, these two different complexes SHOULD give the same end coordinate result.

— So: From this point we now investigate how the actual equations from the two different complexes DO match

— if at all.

— WITH pedestrians included: basic deeply exact relatable math only. Nobody is left out:

SECTIONx ¦ SECTIONz ¦ SECTIONy

Sx:

SECTIONx: equations for x

—————————————————————————————————

ROT I x = (x·sinzW – y·coszW)sinyW – (z·sinxW – [y·sinzW + x·coszW]cosxW)cosyW

x = (x·sinzW – y·coszW)sinyW – z·sinxWcosyW – [y·sinzW + x·coszW]cosxWcosyW ;

x1 = x·sinzW – y·coszW

= sinzw·r ;

y1 = y·sinzW + x·coszW

= coszw·r ;

form RotIx = sinyWsinzw·r – z·sinxWcosyW – [coszw·r]cosxWcosyW

ROT II x = sin(yW+90)·sinxW·z + sin(atan[z’/x’]+yW+90)√(x²+y²)(1–[coszw·sinxW]²)

x = –cosyW·sinxW·z + sin(atan[z’/x’]+yW+90)√(x²+y²)(1–[coszw·sinxW]²)

form RotIIx = – z·sinxW·cosyW – cos(atan[z’/x’]+yW)√r²(1–[coszw·sinxW]²) ;

If equality for x holds :

sinyWsinzw·r – [coszw·r]cosxWcosyW = –cos(atan[z’/x’]+yW)√r²(1–[coszw·sinxW]²)

sinyWsinzw·r – [ coszw·r ]cosxWcosyW = –cos(atan[z’/x’]+yW)r√(1–[coszw·sinxW]²)

sinyWsinzw – coszw · cosxWcosyW = –cos(atan[z’/x’]+yW)√(1–[coszw·sinxW]²)

; atan[z’/x’] = T

= –cos(T+yW)√(1–[coszw·sinxW]²)

; cos(A+B) = cosAsinB + sinAcosB

= –(cosTsinyW + sinTcosyW)√(1–[coszw·sinxW]²)

sinyWsinzw – cosxWcosyWcoszw = – [cosTsinyW√(1–[coszw·sinxW]²) + sinTcosyW√(1–[coszw·sinxW]²)]

sinyWsinzw – cosxWcosyWcoszw = – cosTsinyW√(1–[coszw·sinxW]²) – sinTcosyW√(1–[coszw·sinxW]²)] ;

cosxWcoszw:

We investigate rear=right blocks in LeftRight rank-parts :

Vi undersöker bakre¦högra ledblocken i VL¦HL :

cosxWcosyWcoszw = –sinTcosyW√(1–[coszw·sinxW]²)]

cosxWcosyWcoszw = –sinTcosyW√1–[coszw·sinxW]²

cosxWcoszw = –sinT√1–[coszw·sinxW]²

; –sin = sin ;

–cosxWcoszw = sinT√1–[coszw·sinxW]²

–cosxWcoszw/√1–[coszw·sinxW]² = sinT ; quadration (SQUARING) eliminates minus sign:

√ [cosxWcoszw]²/1–[coszw·sinxW]² = sinT

= sin atan(z’/x’)

; z’/x’ = –cos(zw–90)/sin(zw–90)cosxW

; z’/x’ = –sinzw/coszw·cosxW

= sin atan(z’/x’)

= 1/√1+(z’/x’)²

√ [cosxWcoszw]²/1–[coszw·sinxW]² = 1/√1+(–sinzw/coszw·cosxW)² = sinT ; quadration eliminates minus sign:

√ [cosxWcoszw]²/1–[coszw·sinxW]² = 1/√1+(sinzw/coszw·cosxW)² ; root sign forwad:

√ [cosxWcoszw]²/1–[coszw·sinxW]² = √ 1/1+(sinzw/coszw·cosxW)² ; quadration:

[cosxWcoszw]²/1–[coszw·sinxW]² = 1/1+(sinzw/coszw·cosxW)² ; inverting both ranks:

1–[coszw·sinxW]²/[cosxWcoszw]² = 1+(sinzw/coszw·cosxW)² ; transfer of [cosxWcoszw]² ;

1–[coszw·sinxW]² = [cosxWcoszw]²+(sinzw·cosxWcoszw/coszw·cosxW)² ;

1–[coszw·sinxW]² = [cosxWcoszw]²+ (sinzw·cosxWcoszw/coszw·cosxW)²

1–[coszw·sinxW]² = [cosxWcoszw]²+ (sinzw)²

1 = [coszw·sinxW]² + [cosxWcoszw]²+(sinzw)²

1 = cos²zw·sin²xW + cos²xWcos²zw + sin²zw

1 = cos²zw(sin²xW + cos²xW) + sin²zw

1 = cos²zw( 1 ) + sin²zw

1 = cos²zw + sin²zw ;

Which we see HOLDS.

We investigate remaining two front=left blocks in LeftRight rank-parts :

Vi undersöker resterande två främre¦vänstra ledblocken i VL¦HL :

MinusSinzw:

sinyWsinzw = – cosTsinyW√(1–[coszw·sinxW]²)

sinyWsinzw = – cosTsinyW√(1–[coszw·sinxW]²)

sinzw = – cosT√(1–[coszw·sinxW]²) ; holds with condition fot T incl.

–sinzw = cosT√(1–[coszw·sinxW]²)

√sin²zw/(1–[coszw·sinxW]²) = cosT ; quadration eliminates minus sin zw:

√sin²zw/(1– cos²zw·sin²xW ) = cosT

√sin²zw/(1– cos²zw[1–cos²xW ]) = cosT = √sin²zw/(1– cos²zw + cos²xWcos²zw) =

√sin²zw/(sin²zw + cos²xWcos²zw) = cosT

√1/(1 + cos²xWcos²zw/sin²zw) = cosT

1/√1 + [cosxWcoszw/sinzw]² = cosT

= cos atan(z’/x’)

; z’/x’ = –cos(zw–90)/sin(zw–90)cosxW

; z’/x’ = –sinzw/coszw·cosxW

; z’/x’ = –sinzw/cosxWcoszw

= cos atan(z’/x’) = 1/√1+1/(z’/x’)²

= cosT = 1/√1+[x’/z]²

1/√1 + [cosxWcoszw/sinzw]2 = cosT = 1/√1 + [cosxWcoszw/sinzw]²

Which we see HOLDS.

Vilket vi ser STÄMMER:

sinyWsinzw – cosxWcosyWcoszw = – cosTsinyW√(1–[coszw·sinxW]²) – sinTcosyW√(1–[coszw·sinxW]²)]

B – A = B – A

Hence equality holds for x.

Alltså gäller likheten för x.

Orig.1998VI30

Sz:

SECTIONz: equations for z :

—————————————————————————————————

ROT I z = (z·sinxW – [y·sinzW + x·coszW]cosxW)sinyW + (x·sinzW – y·coszW)cosyW

z = z·sinxWsinyW – [y·sinzW + x·coszW]cosxWsinyW + (x·sinzW – y·coszW)cosyW ;

y1 = y·sinzW + x·coszW

= coszw·r ;

x1 = x·sinzW – y·coszW

= sinzw·r ;

form RotIz = z·sinxWsinyW – cosxWsinyWcoszw·r + cosyWsinzw·r ;

ROT II z = cos(yW+90)·sinxW·z + cos(atan[z’/x’]+yW+90)√(x²+y²)(1–[coszw·sinxW]²)

; cos(A+90) = cos(90–A) = sinA

z = sinyWsinxW·z + cos(atan[z’/x’]+yW+90)√r²(1–[coszw·sinxW]²)

form RotIIz = sinyWsinxW·z – sin(atan[z’/x’]+yW)√r²(1–[coszw·sinxW]²) ;

If equality for z holds :

– cosxWsinyWcoszw·r + cosyWsinzw·r = – sin(atan[z’/x’]+yW)√r²(1–[coszw·sinxW]²)

– cosxWsinyWcoszw·r + cosyWsinzw·r = – sin(atan[z’/x’]+yW)r√(1–[coszw·sinxW]²)

– cosxWsinyWcoszw + cosyWsinzw = – sin(atan[z’/x’]+yW)√(1–[coszw·sinxW]²)

; atan[z’/x’] = T

= – sin(T+yW)√(1–[coszw·sinxW]²)

; sin(A+B) = sinAsinB + cosAcosB

= –(sinTsinyW + cosTcosyW)√(1–[coszw·sinxW]²)

– cosxWsinyWcoszw + cosyWsinzw = –(sinTsinyW + cosTcosyW)Ö(1–[coszw·sinxW]²)

cosxWsinyWcoszw – cosyWsinzw = sinTsinyW√(1–[coszw·sinxW]²) + cosTcosyW√(1–[coszw·sinxW]²)

Checking: √3/28 · 0.4375 √3/28 √0.4375

We investigate rear=right blocks in LeftRight rank-parts :

cosxWsinyWcoszw = sinTsinyW√(1–[coszw·sinxW]²)

cosxWsinyWcoszw = sinTsinyW√(1–[coszw·sinxW]²)

cosxWcoszw = sinT√(1–[coszw·sinxW]²)

Det är samma resultat som från härledningen för x-delen[‡], där ekvivalensen visades.

These ranks are precisely the same as the previously checked x-ranks, see from cosxWcoszw.

Which we see HOLDS.

Således, likheten STÄMMER.

We investigate the remaining two front=left blocks in LeftRight rank-parts :

–cosyWsinzw = cosTcosyW√(1–[coszw·sinxW]²)

–cosyWsinzw = cosTcosyW√(1–[coszw·sinxW]²)

–sinzw = cosT√(1–[coszw·sinxW]²)

Det är också samma resultat som från härledningen för x-delen[‡], där ekvivalensen visades.

These ranks are also precisely the same as the previously checked x-ranks, see from MinusSinzw.

Which we see HOLDS.

Således, likheten STÄMMER.

Hence equality also holds for z.

Alltså gäller likheten också för z.

1998VI30

Sy:

SECTIONy: equations for y :

—————————————————————————————————

The remaining SECTIONy then becomes »Only A Walk in the Park»:

ROT I y = (y·sinzW + x·coszW)sinxW + z·cosxW

y1 = y·sinzW + x·coszW

= coszw·r

y = sinxWcoszw·r + z·cosxW

form RotIy = sinxWcoszw·r + z·cosxW

= z·cosxW + sinxWcoszw·r ;

ROT II y = cosxW·z + sinxW·coszw·r

form RotIIy = z·cosxW + sinxWcoszw·r ;

Here it is immediately obvious from the preparing format that the y-connections are equivalent.

Här ser vi direkt efter den förberedande omformningen att sambanden är ekvivalenta.

Således, likheten STÄMMER..

Hence equality also holds for y.

Alltså gäller likheten också för y.

CONCLUSION:

RotationComplexes I and II relate as each others reversals.

Which was to be shown.

Rotationskomplexen I och II förhåller sig till varandra som varandras omvändningar.

Vilket skulle visas.

1998VI30

—————

END RotII.

— Why not MAC: What’sUp? I don’t see any[‡].

RotIIorigin: — From Compilation Origin of RotII Jul2007 — Induction and Magnetism — IaMmath.doc

The origin of Rotation Complex II — in this History of The Universe

The ORIGIN OF ROTII

DOCUMENTS PRECEDING and preparing Universes History

Introduction: R12origin

BACKGROUND — as original as can be:

From parents honouring ART and INSTRUMENTATION this child got »the basics» — already from square one. Drawing became an early MUST (as music).

— Towards the beginning of the 1970:s many artists had (recently) discovered the amazing works from the dutch graphician Maurits Escher[‡] — to whom this author have a special connection of admirability. Without Escher’s work — and all the people who admired his work and promoted others to study it too — this presentation would never have come about. But few direct mathematical descriptions on the subject of Perspectives were known by this author at the time. So it became urgent to find a more mathematical approach in clarifying the depths of it — if at all.

NATURE:

EXERCISE (left+: WorkCollection 1980-1995): When sufficient training has been spent on picturing natural forms, try this one — »proving the partnership»:

— Enter Apartment; Curtains down over windows; No outlook: Paper, lead pencils or whatever seems interesting: PICTURE HER FROM IMAGINATION. No photographic aids. No computer. No books. No magazines. Just YOU and HER — and a genuine Test: »Love me — or Leave me».

The student will KNOW. There is nothing to BELIEVE. No guessing around. No DOUBT. No PAIN. Just pure raw Natural Joy. ENERGY. AppleStuff.

Then we will know and see where the »I» of it is standing — at best, ready to try the deeper suit named Natural Mathematics: WITH Nature. NEVER against.

See also in REGULAR DIVISION OF THE PLANE

IN LACK OF DEEPER ENLIGHTENMENT in¦from established literature, this student began a deeper mathematical investigation on the subject: The Act of Perception by geometrical PERSPECTIVES.

— The illustration below shows the basic and very simple parts INTRODUCING the complete HORIZONTAL PERSPECTIVE complex by simple mathematics. In established textbooks the nearest terms found are ”one point perspective”, ”two point perspective” and ”three point perspective”, depending on application. But nothing of the like below has been found in established literature, so far — Despite its simplicity.

TheHOREQ: Rot2origin

THE HORIZONTAL EQUATION

THE HORIZONTAL EQUATION IN LINEAR PERSPECTIVES d = i·TanW

— Directly intuitive from simple plane geometry:

A WebSearh 13Feb2019 shows that at least one established educational source, seemingly, is aware of the above basic horizontal principle. — However not in any mentioned connection to »The Real Steel Explaining» The Cheops Rectangle: UNIVERSITY OF UTAH — Department of Mathematics, High School Program Lecture: The Geometry of Perspective Drawing on the Computer [www.math.utah.edu/].

— The Utah source illustrates the principle in the section Using Vanishing Points And Measuring Points in 8 illustrations. But the source gives no direct manually directed perspective drawing description, although ’the same in context’. Neither is anything said of The Circle in the section Analytic Treatment of the Perspective View of a Circle, except this leading quest:

”But why is the image exactly the ellipse and not some other closed curve?”

— Good Question — Has Good Answer. But the Utah source gives IT no mentioning — except this one:

”We shall answer this question by figuring out the equation of the image of the circle on the perspective drawing. ”.

— They don’t know: It’s NOT the perspective. It’s the Plane Geometrical projection APPEARING — featuring — a perspective (basicHPG) — not known in modern quarters, as it seems. Cheops Rectangle — The Good Answer in a pure and clean Vision: no math necessary. Just Plane View.

Explanation:

Given 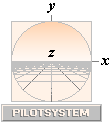the simple xyzXYZ PILOTSYSTEM with ImageIndex i

i — in general the distance between the observer @PC and the ImagePlane: ImageIndex:

:

THE HYPERBOLIC PART explains the established terms

”one point perspective”, ”two point perspective” and ”three point perspective”,

depending on application:

Left: COVERING ALL CASES AND SITUATIONS with our given xyxXYZ PILOTSYSTEM — you know: the one we consult in order to cross the street, drink coffee while reading the paper, and admire nature in general — a STEER¦Guide¦DIRECTIVE Cube SC has its corner @PC Perception Center, freely turnable. Its 90°45°90° degree preference makes the actual geometrical-mathematical transition from or through our natural intuitive perceptive view:

— Tilting SC straight up (or down) along the y-axis increases its contacting length — from Image Index i to (H=) — with the intersecting ImagePlane:

— As in the triangle id is part of the SC top square — diagonally or as a square side, depending on our choice of reference — also, figure right above, has its same right angle distance on the intersecting Image Plane as a new tilted (by the twisting angle W°) Horizon Length (H=).

— So the simple mathematical bottom line is, from The Horizontal Equation d=i·tanW, that

H² = i² + d² = i² + d² = i² + i²·tan²W = i²(1 + tan²W) giving us directly the unit hyperbola equation

H = i√ 1 + tan²W = i√ 1 + x² with x as the hyperbolic variable:

— TILTING by a given coordinate axis xyz in any direction a given coordinate plane (XYZ) defines the Horizontal Perspective Body by its perspective endpoints — where all perspective parallel lines meet in the endless — intersecting the xy-image system’s Unit Hyperbolas. In all a CUBE-oriented three point basic perspective limit point triangle then appears — for any basic XYZ.horizontal tilt.

The STEER-Cube’s projection on the image plane[‡] shows a 3-set triangular block.

— Each triangle represents an individual XYX-horizon. The horizon is split by a normal (c) through PerceptionCenter (3). So, each one of the right angular triangles — each horizon’s own seen square and its intersection with the ImagePlane — obeys the simple but (very) powerful

CHEOPS RECTANGEL (Cheops Rectangle) equation ab = ². The actual ImageIndex i is then given from any inside projected (vertical in the figure below) ab-horizon as i² = ab.

STEERcube’s projection on the ImagePlane:

— Inner HIDDEN right angle ab=c² = CHEOPS RECTANGLE

i = 4 ¦ a=2, b=8 identifies the actual HP-body.

— FAMILIARIZE on the subject:

Use only square-printed paper, draw any triangle with corners in crosses between squares, which simplifies all eventual mathematical calculations.

With sides given, the Horizontal Equation with CHEOPS RECTANGLE as above solves specific issues for each horizontal plane.

— See CHEOPS RECTANGLE how we — easily — find each XYZ-horizon’s horizontal INDEX with very simple tools — we don’t even need a CALCULATOR. Really.

The unit hyperbolic connection is simply deduced in detail as follows:

— STEER-cube TILTED shockingly simple:

TheHoThe:

IT IS THE CUBE PREFERENCE THAT MAKES IT — WITH ITS STRAIGHT ANGLES

THE HORIZONTAL THEOREM — from TheHOREQ

The Horizontal Theorem — from The Horizontal Equation’s perspective view: The Steer Cube, or the GUIDE cube, or The Directive (Directional) Cube:

——————————

H = ; HORIZON LENGTH:

i ; IMAGE INDEX

d/i = tanW° ; HORIZONTAL EQUATION directly from simple plane geometry;

= x ; functional variable;

d = ix ;

H² = i² + d² ; simple STEER CUBE TILT W° by vertical distance d:

= i² + i²x²

= i²(1 + x²) ;

H = i√ 1 + x² ; UNIT HYPERBOLA — LinearHORIZONTAL PERSPECTIVE HORISONTAL THEOREM: The HP-body.

The HORIZONTAL THEOREM: = i√ 1 + (tanxW)².

THESE BASIC ELEMENTARY PERSPECTIVE CONNECTIONS (1978-1984) lead further to a compiled general method for handling the HP-body in a general RotationComplex: How to rotate a given object’s xyz-axes with their XYZ-planes in any arbitrary way by successively adopting new rotational axes as they change with each rotational step with defined new planes and horizons.

By summer 1981 a compilation was finished with the mathematical connections for successive HP-rotations in Rotation Complex II of the following comprised form:

— The original has explicitly written equations for each case. However, as the difference between the individuals consist only in different combinations of axes xyz and planes XYZ, the more simplified extract below says the same thing:

RotationComplex II — Jul1981 — TheHOREQ

Jul1981 b3,29

Short description:

(xyz)W = 0; HORIZONTAL INDEX = i. Each equation for horizontal length is a successive equation relative a given horizontal index. The initial position is to set a horizontal index as i in the -equation. Is from here the value of the rotational or twisting angle W set as 0 or unit multiples of 90 degrees, the resulting horizon equals zero — conv. central linear perspective. All other values for W gives a value for between i and endless. This value then becomes in its turn a horizontal index for coming horizons honXhonYhonZ.

eW, EFFECT ANGLE (effW). The effect angle specifies the difference in perspective degrees between the horizon-zero (-normal through PerceptionCenter) and, respectively, rotational axis’ perspective limit point. The tangent values for these angles are, with respect to the two limit-points along a given horizon, each others inverse.

The6Orders:

SIX POSSIBLE BASIC ORDERS or different ways exist to relate a complete three axis rotation in RotationComplex II:

In our history of a further development of the complex, the number 5 order was chosen to focus a deduction leading to a general RotII mathematical synthesis.

— It is namely so

— see MATHEMATICAL DEDUCTION OF THE Rot1¦Rot2 EQUALITIES, the RotII-base of which will be explained below

— that in the end of this result in investigating Rotation Complex II, a most simple connection (same values in reversed order, RotationComplex Theorem) between Rotation Complex II and Rotation Complex I was found. With this correspondence we are free to choose from any of the six mentioned orders by a simple reversal from the much more simpler Rotation Complex I.

The rotation order yxz in Rotation Complex II

With the order of rotations given as (yxz)W, W indicating the rotating angle, specifically as |yW|xW|zW|, we can see (perhaps almost directly, with the help of the given illustration below) that a general space point P(xyz) in the fix Image System (K), about to be rotated by rotation complex II in the order (yxz)W, will be defined by a MOST SIMPLE gyroscopic »Coordinate Top», like a spinning wheel on a rod:

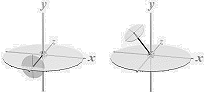
Left: The zero-set coordinate top in Rotation Complex II for a given point P(xyz).

P(z) will be the length of the rod or The zAxel whereon the top wheel is set spinning;

— The RODzAXEL is then associated with rotation yW (as seen from above or down on the Y-plane floor);

— Rotation xW will be the rod’s projective shortening (as seen from the same view);

— P(x) och P(y) will be the point position encircled by the top’s spinning peripheral wheel-circle associated with the final spin rotation zW in that circle.

The following illustrations after the Ellipsograph article show by example how this described type rotation (RotII) was detailed.

EllipsoGraphNr97:

Simple Ellipsograph instrument helped to develop the complex — by precise elliptic illustrations

Some figures here in The ORIGIN OF ROTII are scanned copies of the original paper work — »The ROTRING and LetraSet Era» — with ellipses drawn by a precision EllipsoGraph — HAFF Ellipsograph Nr.97. By that time: Ordinary bookstore stuff from the late 1970:s; Can’t find it today 2019 to any reasonable price;

— A WebSearch 7Feb2019 tells that eBay has the true (1 or two, pre-owned) HAFF no97 ”ellipsographo” — ”573.77 SEK” resp. ”678.09 SEK”.

— My recommendation would be: buy it — if a serious WoMan in Math and Geometry. Absolutely. Some few basic details are given here how it works.

Problem: The instrument is no longer in production: Is is an Antique ”selled to highest bidder”.

— But for Swedes (AND OTHERS): be aware of a company named UPS intrinsically unable to explicitly in writing guarantee and recognize human rights as the foundation of the company’s enterprise, as experienced with still unsolved details who with no notice hi-jacks packets from foreign countries not allowing the internal domestic post-system to handle the package delivery and expects private persons to act as a company: Unless at home the company travels around the apartments with their own vehicles, further contributing to an already heavily air polluted environment, forcing individuals to consent without any agreement, or not responding when contacted, the UPS is — reported by hundreds of people (eniro.se), including example of legal threats if not extra payment is made — confiscating the package, with a reported really very disrespectful behaviour. Some persons report that they never received the pack from, for example, USA.

This is a worst, and most sad, example of ”a supposed free world market”, in practice consumed by fascistic attitudes[‡], real bad ass mentalities, making it impossible to have a world wide free trade:

— We apologize for our wrong, but we are unable to make a correction. Humanity in prison.

It SHOULD be in the interest of every nation and state to get rid of such sewer company ATTITUDES. No action:

— We are not obliged to obey or promote human rights: Sweden before WW2, Sweden especially during WW2[‡], and Sweden certainly most exclusively after WW2.

Tell me about it. So: The Sewer Companies Thrives — with a continued local populated respectful attitude extinction: Tenants are — literally — locked in by landlords, reported to Swedish authorities with no response, refusing to take any notice on human rights. The situation seems »worse than around 1932»: A self-proclaimed authority oppressive attitude (2010+) is spreading in the society like an unimpeded wildfire: public surveillance, and growing. No human rights mentioning. Not one word. 1932.

TRY THIS ONE, UPS Sweden + Associated: Attitude — opinion, claim, statement, thought, apprehension, idea, notion, interpretation: mind, sense, UnameIt — outside the recognition of human dignity, human rights, IS PRACTISING OPPRESSION: Fascism, Nazism, Dictatorship, Devilship, Satanism — Pick one: A01 UDHR10Dec1948. ZipIT.

PHOTO: 28Jan2019 NIKON D90

The HAFF Ellipsograph Nr97 — long before ”The Computer Age”: Two 2mM thin 0.23 M × 0.18 M cross mounted Plexiglass xy-slides hold milled slots for circular Plexi plates screwed together on a setting middle slide with a Rotring adopted pen slot for precise elliptic drawing, as well as an adopted Ø2mM lead-pen drawing interface. Precise cross markings for a xy-centre guarantees very precise ellipse drawings with fine (0.1mM) Rotring ink-pencils or a sharply dressed 2mM lead pin.

ELLIPSOGRAPH PRINCIPLE:

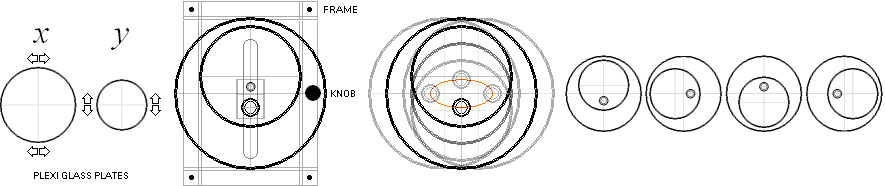
Two XY plexi glass plates mounted on a xy Plexi glass frame with milled plate slots are screwed fast by a middle adjustable slid. The figure shows such a fastening position between the two plates with a central uptake for a pencil. By pushing on the Knob — fastened on the top greatest plate — the two plates are driven to their extents in their respectively xy-slots, performing an ellipse, orange in figure. Precision Scales on the settling slid allow very precise elliptic drawings.

— IN TIME, with much use, a small play in the slots will decrease the preciseness of the drawing (normally within 1/100 mM = 0,0003937’’). This is easily adjusted by mounting slot-narrow stripes of (thin) paper in the slots with fast holding tape at the ends, considerably extending the precision lifetime of this very fine drawing tool. Example below from works in Sep1980 — Linear Perspective Mathematics EPSonML.

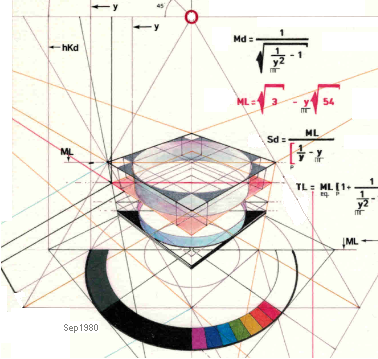
Exercising Ellipses Math with an Ellipsograph in 1980.

— See The EPSmath — how circles in 3D-world are precisely drawn as ellipses in Linear Perspectives.

Rot2Synthesis:

The RotII Complex Order No5 Synthesizing deductions

Below is given the final and actual deductions leading to the more comprised 3 RotIIno5 equations central in the final proof where the two rotational complexes merge into one. See The EQUIVALENCE OF ROTI AND ROTII.

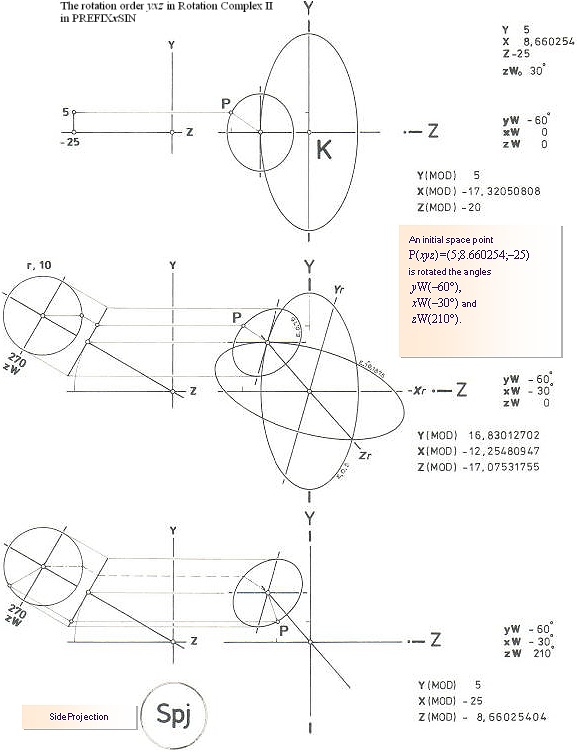
Nov1983

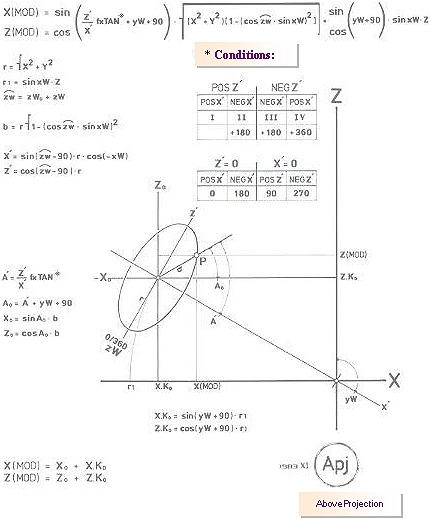
Nov1983

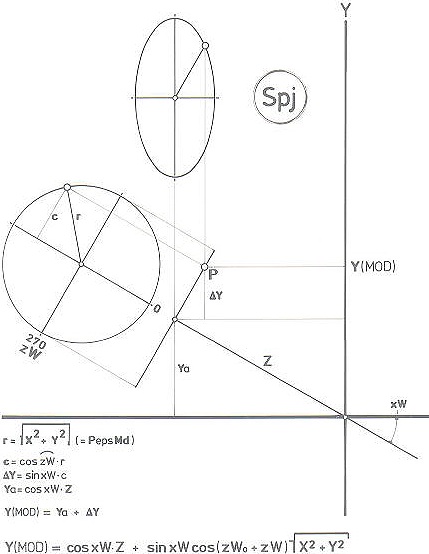
Nov1983

So having extracted the three central equations in RotIIOrderNo5

x_MOD = sin(yW+90)·sinxW·z + sin(atan[z’/x’]+yW+90)√(x²+y²)(1–[coszw·sinxW]²)

z_MOD = cos(yW+90)·sinxW·z + cos(atan[z’/x’]+yW+90)√(x²+y²)(1–[coszw·sinxW]²)

y_MOD = cosxW·z + sinxW·coszw·r

the rest of the history relied on proving The EQUIVALENCE OF ROTI AND ROTII.

Free Fantasy Details in WaterColorPainting from 31May1993 — Mathematics From The Beginning.

Hand, eye, pencil. Development of the individual’s INSIGHT into Nature by practical study:

ARTISTRY — as far as here known — in general is the only way for a human to grow a real and true in-sight.

STRUCTURES AND PATTERNS definitely promote the study of Mathematics.

See ”Final Countdown” in

Proving The MATHEMATICAL EQUALITY BETWEEN THE TWO ROTATIONAL COMPLEXES.

FjäderAnaloginKcellen: Maj2004 ¦ Jun2012 ¦ Feb2019 — APPENDIX

SCHEMATICALLY ILLUSTRATED

The TNED Atomic Nuclear angular momentum J_0K + 3J_1K = 0 guarantees a practically none nuclear geometric deformative tendency before the nucleus as such splits — or rather answers the indtruding force by throwing it back. In a dense large highly gravitationally compressed sphere, such a reaction inevitably is equivalent to a nuclear generated Detonation: a spring analogy.

EXPLAINING K-CELL DETONATION FROM TNED — basic TNED-kosmology

FJÄDERANALOGIN — Spring Analogy

How The Incompressibility of the Atomic Nucleus responds to mechanical pressure

ALLMÄNNA SAMBAND FÖR ATOMKÄRNANS MEKANISKA FORMHÅLLFASTHET ENLIGT RELATERAD FYSIK — K-cellens Detonation

EFTER htm-kopia 9Jun2012 från originaldokumentet (Maj2004) i MsWORKS 4.0 Fjäderanalogin.wps

Förarbetena till K-cellens DETONATION[‡]

— detaljerat försök att härleda ELEMENTÄRA fysikgrunder enligt TNED för K-cellens allmänna pulsfysik från TNED-kosmologins framvisade ALLMÄNNA TILLSTÅNDSLAG[‡].

— Se även delvis mera utförligt — vidare — från SOLSYSTEMEN I VINTERGATAN[‡].

2004V1

SAMMANSTÄLLNING — K-cellens detonation

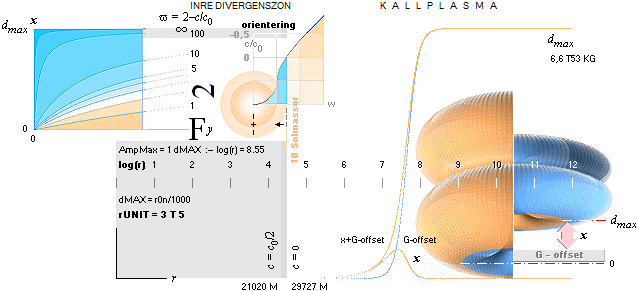
Graf y = [1+(x)'–2]'–1

Sammanställning med beteckningar och samband:

G-offset ................... x_sK = (k_f x_f /ϖF_sK + 1)^–1 ....................... per neutron i K-cellen ; Variabeln är r, se nedan i FsK

x+G-offset ............... x_a = (k_f x_f /ϖ(F_sK+F₀) + 1)^–1 .............. per neutron i K-cellen

detonationsintrycket x = x_a–x_sK ........................................... per neutron i K-cellen

x_max = 0,117d_max

statiska g-trycket p_J = F_Kcell/A_Kcell = F_Kärna/A_Kärna ; gäller exakt i varje ekvipotentialyta

statiska g-kraften F_sK = k_fx_f x_sK/(1–x_sK)ϖ , = p_JA_Kärna= πG(2πrr₀r/3)² ; Variabeln är r.

r_0c = (3/8Gπρ)^1/2c₀

c = (c₀/2)[1 – √ 2(r/r_0c)²–1]

divergenskoefficienten ϖ = (2–c/c₀) = 2 – (1/2)[1 – √ 2(r/r_0c)²–1] ; x gäller bara från ϖ>2

neutronradien r_0n = 1,32 t15 M

max axiellt intryck d_max = x_f = r_0n/N ; N_min=1000

” x_f = d_max

neutronformstyrkan k_f = k_9T9(918e_1,602t19)²/x_f³

K-cellens täthet_5T9år ρ = 1,67241 t28 KG/M³ (en väteatom per 10 M³ rymd)

K-cellens radie_5T9år r_c=0 = (ρ)^–11,60841 T26 KG/M = 9,80679 T26 M ......... referensvärde

Synradie_5T9år r_VIS = ca 3 T25 M eller ca 1000 Mpc med massan ca 2 T49 KG

K-cellens massa5T9år m_0K = r_c=0(1,48427 t27 M/KG)^–1 = 6,60714 T53 KG

K-cellen vid max täthet:

antal neutroner N_n = m_6,6T53A_6,023T26/U_1,0086652 = 3,94103 T80 ~ 4 T80

täthet ρ_max = 1,82 T17 KG/M³; från neutronkärnans omskrivna rätblock, se r_0n

radie r_Kmin = (3m6,6T53/4pr1,82T17)^1/3

= 9,531 T11 M

g-energi E_G = G_6,67t11m_6,6T53²/r_9,5T11

= max 3,000 T85 J K-cell contracting-detonating energy constant

THE GENERAL ENERGY BUDGET TO KEEP IN MIND IN ATTEMPTING TO EXPLAIN ALL THE DETAILS

EKVIVALENTA Data vid K-cellens maxtäthet ρmax som satisfierar de observerade värdena från rödförskjutningen [‡R] ENLIGT RELATERAD FYSIK vid de nu synligt mest avlägsna delarna (ca 1000 Mpc eller ca 3 T25 M):

detonationsenergi E_kin = m_6,6T53v_7,5T9²/2

= max 1,856 T73 J

= E_D

detonationskraft F₀ = E_kin/(x_f=d_max)

= min 1,406 T91 N ; g-kraften 3 T73 N försumbar

Detonationsintrycket med x_max=0,117d_max blir i den motsvarande realiteten grymt mycket mindre. v_7,5T9 i E_kin minskar från ytan och är noll i K-cellens centrum (v_r=v_7,5T9[r/r_Kmin]) vilket ger ett x_max=(1,82t10)d_max med d_max=r_0n/1000. Det resultatet betyder tydligen att atomkärnan är fruktansvärt — ofattbart — hård.

——————— ‡[R]

Antaget medelvärde för rödförskjutningarna motsvarande de mest avlägset synliga delarna ENLIGT RELATERAD FYSIK:

λ/λ₀=(1–v_2T8/c_3T8)^–1=3 [Se mera utförligt i K-FORMEN ¦ m0cK1]

HÄRLEDNINGAR:

K-cellens detonation, fjäderanalogin

Härledningar — DEDUCTIONS

FIGUREN FRAMHÄVER EN STARKT ÖVERDRIVEN DEFORMATION FÖR ATT FÖRTYDLIGA HUVUDSAKEN: dMAX [r/1000]

Se särskilt ATOMKÄRNANS INKOMPRESSIBILITET[‡] om ej redan bekant.

Inledning:

GRUNDBEGREPPEN TILL TERMINOLOGIN SOM ANVÄNDS HÄR GES FRÅN DE FÖRSTA FEM KORTA DELAVSNITTEN i Härledning från Kraftlagen DEL I ¦ DEL II ¦ DEL III ¦ DEL IV ¦ DEL V ¦ DEL indexVI ¦ DEL VI — förarbetet till Del 6: K-cellens detonation. Vi fortsätter därifrån med det korta repetitions- inledningsavsnittet nedan med efterföljande Del 6 med de sista 5 korta sektionerna, detaljernas slutliga inpassning i helheten.

DETALJERAD FYSIKBESKRIVNING ENLIGT ANVISNINGAR FRÅN TNED GENOM ATOMKÄRNANS HÄRLEDNING[‡] — ALLA SATSBILDER ÄR eller ska vara relaterbara FÖLJDSATSER UR DE ENKLA PREMISSER SOM GRUNDLAGT ATOMKÄRNANS HÄRLEDNING, eller så inte alls.

Styrkan i atomkärnans formhållfasthet kan återföras på STRUKTUREN I hela dess samlade laddningsinnehåll

Q = Z(1818e+18e–m_D) .......... se NEUTRONEN och NEUTRONKVADRATEN

genom uppdelningen i ±β-komponenterna tagna över kärnans maximala ihoptryckning eller deformationsmaximum (d_max=x_f).

För neutronen med massdefekten noll gäller Q=918e.

DEN FORMBEVARANDE Styrkan (k_f) återförs på divergenskraften F=k_9T9(Q/x_f )² över deformationen x_f enligt

F/x_f=k_f=k_9T9Q²/x_f³

k_f konserveras av atomens allmänna impulsmomentsekvation[‡] J_0K+3J_1K=0 där negativ divergens ingår enligt DEL I

F_c0 – F_c – F_G = 0 ................ vektorekvivalenterna mot F_G utbildar negativa F_c

Kärnans totala struktur är ENLIGT TNED grundad på F_G jämte ovanstående vektorled. (Se ATOMKÄRNANS HÄRLEDNING[‡]). Impulsekvationen garanterar att kärnan alltid svarar med samma kraft som den vilken söker ändra dess tillstånd. Denna egenskap gör det omöjligt att ”döda” atomkärnan genom att påföra den tryck. Utsätts kärnan för ”oändligt deformerande tryck” svarar den med ”oändligt deformerande mottryck”.

Atomens allmänna impulsmomentsekvation J_0K+3J_1K=0 bygger på växande täthet med växande fraktaldjup. I ekvivalent analogi betyder det att atomkärnans ytform är oändligt tät[‡]. Det betyder också att kärnan gör motstånd mot komprimering med exakt den kraft som söker genomdriva den i impulsekvationens bevarande.

— Genom kärnans fraktala ringstruktur har atomkärnan (således) en mycket begränsad möjlighet att uppvisa någon direkt deformation. Det innebär att kärnan tvingas uppvisa en motsvarande begränsad axiell ihoptryckning vars gränsläge motsvarar oändligt motstånd. Eller sagt på annat sätt: För att kärnan ska kunna avgöra exakt vilken kraft det är fråga om, måste den ha en viss elastisk slaglängd eller mätlängd (d_max). Men det innebär samtidigt att d_max aldrig exakt kan uppnås: FORMEN måste — tvunget — ställas på en motsvarande asymptotisk (exponentiell) matematisk form.

EFTERSOM det således inte ENLIGT TNED går att platta ut atomkärnan, nolla ut den i en tryckanalogi, leds vi — i varje möjlig »fjäderanalogi» — till INSÄTTNING av ett fast och fixt absolut TRYCKSTOPP (d_max):

— Ett d_max kan omöjligen uppnås: »oändligt kraft+»: motkraften växer tvunget proportionellt med samma belopp.

NEUTRONKÄRNANS MAXIMALA IHOPTRYCKNING I HÖJDLED (d_max) måste alltså vara absolut gränslägesbestämd.

— Impulsekvationen med tyngdcirkelns bevarande J_0K+3J_1K=0 kan då sägas eller påstås innefatta egenskapen att

• atomkärnans deformation resulterar i en motkraft som växer oändligt med oändligt växande tryck.

2004-10-18. Denna detalj ansluter idealt till elektriska kraftlagen: F=k(Q/r)²: om r går mot noll obegränsat växer också F obegränsat, Q givet. Slaglängden för kraftens utbildning avtar emellertid analogt och verkar under allt kortare distanser. Men den finns där.

— Man kan på detta sätt säga att deformationen hos atomkärnan driver dess struktur mot elektriska kraftlagens idealform med Q som en obegränsat liten lokal.

Se vidare i slutet med grunderna mera i detalj — Härledning från kraftlagen.

En vanlig makroelastisk kropp, efterlämnar alltid en större eller mindre deformation efter varje påverkan. Atomkärnan har ingen sådan defekt: atomkärnan är förlustfri, den varken avger energi i sin funktion eller kräver energipåfyllning för att fungera. Atomen/atomkärnan (enligt TNED) är den perfekta ideala elastiska kroppen som alltid strävar att bevara sin form fullständigt enligt J_0K+3J_1K=0. Alla krafter som strävar att ändra kärnans form, återförs därför till sina ursprung.

KONTAKTERANDE TRYCK innefattar hela atomkärnans ±β-struktur.

DISTANSTRYCK innefattar endast atomkärnans Coulombiska laddning Ze.

REAKTIONSTIDEN för kärnans formåterställande vid deformation återförs på närliggande ringar i kärnans fraktalstruktur. Då denna besitter obegränsat djup återförs också reaktionstiden på motsvarande obegränsat små rum. Eftersom dessa kärnelement verkar överallt samtidigt i hela kärngeometrin blir reaktionstiden analogt obegränsat kort. Reaktionstiderna bestäms alltså helt enkelt av den allmänna mekaniken via kraftverkan enligt Galilei-Newton där accelerationen a=v/T=2d/T². Dvs., T=2d/v. Snarare än någon inneboende egenskap i kärnan som bestämmer hur den ska reagera på deformation, bestäms således detaljerna av orsaken. Alltså utifrån kommande intryck. Kärnan själv bidrar bara med tryckstoppet (d), samt formstyrkan k_f.

F-integralen

DEFORMATIONSKRAFTENS VARIATION DEL II dF/dx=F’ inom intervallet x_f=d_max återförs på divergenskraftens variation genom inverterade kvadraten på resten mellan tryckstoppet d_max=1 och intrycket x enligt 1/(1–x)². Nollavstånd för divergenskraften betyder ”oändlig kraft” vilket här motsvarar fallet x=1 — som aldrig uppnås.

Varianten F’=dF/dx=(1–x)^–2 ger då integralen F via differentialekvationen

dF = (1–x)^–2 dx ;

F = (1–x)^–2 dx

= (1–x)^–1 ;

F(0) = 1 ; bestämda integralen blir:

F = (1–x)^–1 – 1

= x/(1–x)

= [1/x – 1]^–1

ENHETSFORMEN för x-variationen mellan 0 och 1=d_max har reala metriska distansen d_max eller med samma innebörd x_f. Deformationen dämpas absolut av formstyrkan k_f. Med dessa konstanta koefficienter ges, realt metriskt,

F = k_fx_f x/(1–x)

k_f = k_9T9Q²/x_f³

Divergenskoefficienten: ϖ »omega-pi» (»OmPi» ¦ PiOm: [»pjom»])

DIVERGENSENS ÄNDRING MED GRAVITATIONEN utverkar generellt divergenskraftens lokala variation genom divergenskoefficienten DEL III ¦ DEL IV c/c₀. c bestäms av gravitationskraften. I normala sammanhang är c/c0=1. I den avancerade kärnfysiken däremot har divergenskoefficientens variation högst avgörande betydelse.

NEGATIVA DIVERGENSKRAFTEN som följer av det allmänna kraftvektorledet enligt TNED

F_c0 – F_c – F_G = 0 ............. vektorekvivalenterna mot F_G utbildar negativa F_c

medför att divergenskoefficientens variation med varierande c ges på formen (”v” för ϖ i Symbol)

ϖ = (2–c/c₀)

Toppdivergensen c=c₀ ger då ϖ=1, nolldivergensen ger ϖ=2, samt vidare positivt uppåt obegränsat med växande negativ divergenskraft F_c.

Växande v DEL V dämpar alltså F, men gör samtidigt F-variationen brantare så att stora variationer i F ges på allt mindre variationer i x.

Kraftändringen totalt för hela komplexet kan då skrivas

F = k_fx_f x/(1–x)ϖ .................... atomkärnans uppförande vid axiell deformation x

Resultat, Grafisk representation

— neutronen

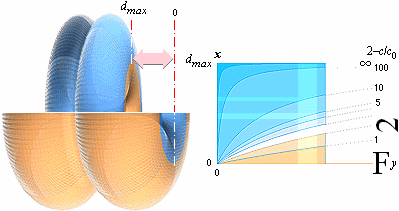
F = k_f d_maxx[(1 – x)(2–c/c₀)]^–1 ; 0 ˂ x ˂1

k_f = k_9T9(918e)²/[d_max]³

DelVI:

DEL I ¦ DEL II ¦ DEL III ¦ DEL IV ¦ DEL V ¦ DEL indexVI ¦ DEL VI — förarbetet till Del 6: K-cellens detonation

DEL VI: Deformationskraftens tillämpning på K-cellen, Detonationssambandet — statiska g-trycket och statiska g-kraftens inverkan

Sektioner 1-6:

Sektion 1 ¦ Sektion 2 ¦ Sektion 3 ¦ Sektion 4 ¦ Sektion 5 ¦ Sektion 6

Sektion 1

DEL VI SEKTION 1: Det passiva kärnyttrycket från den negativa[‡] divergensen

GRAVITATIONEN i en sfärisk masskropp J i lokaler där ϖ>2 utövar ett kontinuerligt formstatiskt kontakterande PASSIVT EKVIVALENT divergenstryck på atomkärnan K från ϖ=2 och uppåt enligt ekvivalenterna

F_J/A_J=p_J=F_K/A_K

Suffixet J avser J-kroppen och suffixet K atomkärnan.

Det passiva trycket resulterar INTE i någon aktion från atomkärnan, utan påverkar bara dess strukturdjup med en förskjutning av brantheten för k_f.

G-yttryckets ekvivalent är

p_J = m_J a/4πr² = m_J(Gm_J/r²)/4πr²

Kärnytparametern A_K avser hela kärnytan; Gravitationen reglerar divergensen och därmed den DEN FORMBEVARANDE Styrkans EXPONENTIALFORM (brantheten) för k_f i atomkärnan. I behandlingen av neutronen-protonen med radien r₀ gäller approximativt

A_K= (πr₀)² ..................................... toppspinnets kärnyta

I DISTANSTRYCKANDE ANALOGIER sätter vi

F_K = p_JA_K = k_9T9(e/nd)²

där n är en konstant som sammanhänger med laddningsgeometrin i distansverkan [Se termogravitella jämviktstrycket].

Sektion 2

DEL VI SEKTION 2: Statiska g-kraften, statiska g-trycket

Kontakterande tryckanalogier kräver däremot hela kärnladdningens singulärkomponent i ±β-strukturen (Q=918e för neutronen) enligt

F_K = p_JA_K = k_9T9(Q/x_f )²

G-tryckets inverkan på kärnan betraktas på detta sätt inte så mycket utifrån en föreställning om riktningsvektorer som utifrån ytgravitationens inverkan på divergensen i kärnans omedelbara närhet och därmed inverkan på den kopplande formbevarande styrkan k_f.

Variationen i F_K kommer alltså att ansluta till variationen i föregående härledda deformationskraft F så att vi får atomkärnans statiska g-deformation (via x) eller statiska g-kraften

F_sK = p_JA_K = k_fx_f x/(1–x)ϖ ...................... statiska g-kraften

p_J = F_Kcell/A_Kcell = F_Kärna/A_Kärna .......... statiska g-trycket, gäller exakt i varje ekvipotentialyta

x relateras här direkt till sK utan suffix. Denna deformation är PASSIV och utverkar inget EGENTLIGT REKYLTRYCKANDE arbete på atomkärnan (som resulterar i en rekylkraft), utan endast förskjuter reaktionspunkten, den bevarande formkraften, längre ner i kärnstrukturen. [Typgrafen i TNED141A.BMP].

TNED141ABMP:

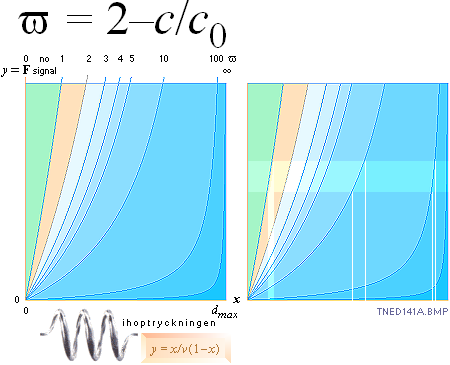
Därmed kan vi beräkna det avsnitt av x i F som bortfaller på grund av statiska g-trycket i fallen där divergenskoefficienten ϖ>2. Aktiva deformationsintryck på atomkärnan kommer att ha detta x-värde som ett OFFSETVÄRDE. Efter mellanräkningar och införande av täthetsfaktorn ρ=m_J/(4πr³/3) ges

F_sK = p_JA_K= πG(2πrr₀ρ/3)² = πG(2πr₀ρ^2/3[3m_J/4π]^1/3 (1/3))²

TYNGDPUNKTENS DEFINITION: cMAX

I en sfärisk kropp med given massa är F_sK exakt i varje ekvipotentialyta. Tätheten tagen efter massan och den lokalt omslutna klotradien kommer alltid att avse g-styrkan i klotytan, oavsett förhållandena innanför.

Sektion 3

DEL VI SEKTION 3: g-statiska intrycket — grafrelaterade kraften — Detonationsimpulsens gränslinjer

Ur funktionsekvivalenten till F-integralen x/(1–x)=(1/x – 1)^–1 med F_sK=k_fx_f (1/x – 1)^–1ϖ^–1 ges för x ekvivalenten för g-statiska intrycket

———————————————

x_sK = (k_f x_f /ϖF_sK + 1)^–1 ....................... g-statiska intryckets ekvivalent

———————————————

x_sK definierar detonationsimpulsens yttre gränslinje för hela K-cellen.

Vi observerar att x ges relativt det matematiska xy-systemets enhet 1.

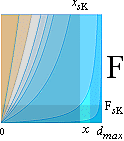T=2x/v

Grafrelaterade kraften F_aG för en realt kärnmottryckande kraft F blir med statiska g-kraften F_sK som offset och F som den aktiva deformationskraften

F_aG = F_sK + F

F_aG kommer att avse eller avgränsa den aktuella detonationsimpulsens gränslinje eller gränskurva.

Grafiska (enhetsmatematiska) intrycket x_a blir

x_a = x_sK + x

x_a definierar detonationsimpulsens inre gränslinje för hela K-cellen.

F_aG bestäms genom att först beräkna F_sK ur den lokala gravitationen.

Sektion 4

DEL VI SEKTION 4: Allmänna samband, statiska och expansiva

I beräkningarna av statiska g-kraften F_sK för given ideal homogen täthet används med fördel mellanledets ekvivalent F_sK=πG(2πrr₀ρ/3)² från SEKTION 2 ¦ [‡].

Partiella klotradien r kopplar direkt till divergenskoefficienten ϖ=(2–c/c₀) via c enligt

STATISKA[‡]

r_0c = (3/8Gπρ)^1/2c₀ ; c_z=c₀/2, r_cz=r_0c√1/2

c = (c₀/2)[1 – √2(r/r_0c)²–1]

ϖ = 2 – (1/2)[1 – √2(r/r_0c)²–1]

EXPANSIVA[‡]

r_0c = (3/2Gπρ)^1/2c₀ ; c_z=c₀/2, r_cz=r_0c√3/4

c = c₀[√(r/r_0c)²–1] ; r_cz=r_0c√3/4 notera att sambandet för detta fall har teckenomvända rottermer

ϖ = 2 – √(r/r_0c)²–1

Observera

GRÄNSMASSORNA GENOM EXPANSIVA-KONTRAKTIVA STATISKA TILLSTÅNDETS G-FYSIK

att

• sambanden gäller bara för centralmassor med egen divergenszon[‡] (allt större än 10_STATISKA 80_EXPANSIVA Solmassor)

• sambanden endast avser ϖ>2 (r_STATISKA-värden mindre än r_0c/√2 OCH r_EXPANSIVA-värden mindre än r_0c ger negativ rot)

• divergensekvivalenten för c är negativ i ϖ>2

För ϖ>2 med c=c₀(2–ϖ) gäller för given centralmassa med homogen täthet distansen r_STATISKA från masscentrum till ekvipotentialytan för c ur c

r = r_0c√[1+(1 – 2 · c · 1/c₀)²]/2

Motsvarande för r_EXPANSIVA är

r = r_0c√[1 +(c · 1/c₀)²]

Med växande negativ divergens c växer också r från masscentrum ut mot g-max.

Sektion 5

DEL VI SEKTION 5: Impulsen

VÄRDET PÅ x_a–x_sK=x ÄR AVGÖRANDE för bestämningen av IMPULSEN som kärnan utvecklar då den bildar rekylkraften. x är nämligen den enda distansfaktor kärnan förfogar över för att bilda accelerationen i formåterställningen.

Syftet med fjäderanalogin är att finna svaret på frågan vilket realt x som ger (kan förstås ge) vilken real deformationskraft F i en viss ekvipotentialyta r i området ϖ>2. Med ovanstående genomgång kan svaret formuleras

x_sK+x = (k_f x_f /ϖ(F_sK+F) + 1)^–1

För att problemet ska vara meningsfullt för K-cellens matematiska fysik, måste x sättas i någon koppling till området med ϖ=1.

— Det är därifrån som tändningen ska komma, om vi har förstått saken rätt.

— Vilken kraft motsvarar — då — intrycket x i lokalen ϖ=1 (samma som K-centrum, idealt exakt i)? Svaret blir

x = (k_f x_f /F + 1)^–1 ........ Det motsvarar statiska tillståndets F=F(1/x – 1)^–1

Med impulsen FT=p=m_6,6T53v_7,5T9=m_Kv_a0K=4,95 T63 NS @ 5 T63 NS som krävs för att ge K-cellen en expansion — som ENLIGT TNED motsvarar värdena från observationerna via rödförskjutningen [‡R] — krävs minst ett

F_min=p/T=p/(2x/v)=pv/2x=mv²/2x=E_kin/x=(1,85625 T73)/x.

Med impulsen FT=p=m_Kv_a0K som krävs för att expandera K-cellen krävs minst ett

F_min=p/T=p/(2x/v)=pv/2x=mv²/2x=E_kin/x.

E_kin är den rörelseenergi K-cellen samlat genom kontraktionen, kvantitativt densamma som K-cellens g-energi, idealt med avseende på största utsträckningen Gm_0K²/r_Kmin.

x motsvarar den distansekvivalent som accelerationen 0 till v ska genomföras på. Litet x kräver stort F, större x nöjer sig med mindre F.

Observera att fristående x i sambanden ovan refererar till xy-systemets enhet 1. I metriska ekvivalenter måste x multipliceras med d_max=x_f.

EXPANSIONSHASTIGHETEN[‡] v=r√(8πρ/3) ger:

Rörelseenergin för varje ekvipotentialyta med radien r i K-cellen genom K-cellens totalmassa m_0K och maxtätheten ρ ges enligt

E_kin = mv²/2

= mr²(4πρ/3) ;

E_kin = m_0Kr²(8Gπρ/3)/2

= m_0Kr²4Gπρ/3 ;

Parentesformen är densamma som faktorn i statiska tillståndets fysik SEKTION 4. Den här angivna formen för E_kin gäller i vilket fall då det bara kan finns en rörelseenergi för hela komplexet.

FÖR ANALYSENS DEL noterar vi att rörelseenergi kan förstås med sin kvantitet obegränsat näraliggande klonktillfället då, idealt, K-cellens samtliga atomkärnor stöter ihop. Exakt samma mängd ges sedan tillbaka genom den resulterande detonationen. Idealt och enkel sett, alltså en ren ideal fullkomligt elastisk studs.

Sektion 6

DEL VI SEKTION 6: Slutformen, detonationssambandet

OM VI FÖR SAMTLIGA FALL ansätter ett absolut minsta statiskt F₀=E_kin/(x_f=d_max)

x_sK+x = (k_f x_f /ϖ(F_sK+F₀) + 1)^–1 = x_a

erhåller vi

x = x_a–x_sK

med

x_sK = (k_f x_f /ϖF_sK + 1)^–1

F_sK = πG(2πrr₀ρ/3)².

Insättes x i

F_min = E_kin/x

från SEKTION 5 erhålles alltså ett nytt, dynamiskt F_min som varierar med ϖ och som omtalar vilket lokalt bidragande F_min i aktuell ekvipotentialyta som minst krävs för att uppfylla det allmänna F₀=E_kin/x_f.

Därmed har vi slutfört beskrivningen av de nödvändiga matematiska delar som krävs för att kunna beskriva K-cellens detonation ur enklast tänkbara förutsättningar.

Sambandsformerna blir

Detonationsimpulsens yttre gränslinje:

G-offset ................... x_sK = (k_f x_f /ϖF_sK + 1)^–1

Detonationsimpulsens inre gränslinje:

x+G-offset ............... x_a = (k_f x_f /ϖ(F_sK+F₀) + 1)^–1

Detonationsimpulsens gränskurva eller detonationssambandet:

x = x_a–x_sK

x definierar gränskurvan för K-cellens detonationstransient.

Detonationens reella kurva kommer att ligga mellan x och funktionens r-axel.

Detonationstransienten beskriver området där K-cellens neutroner bildar maximala deformationen som utlöser detonationen.

Det betyder alltså ett motsvarande deformationsområde inom vilket K-cellen kan komprimeras på detonationsenergin.

— Som vi ser av graferna, tillåts praktiskt taget ingen deformation x alls i K-cellens centrum och periferi.

— Deformationszonen ligger inuti K-cellen, i stort omkring 7,5 T8 M utanför centrum (d_max=r_0n/1000), alltså en rejäl bit utanför c=0-gränsen — men likväl bara vid en tusendel av K-cellens radie.

2004XI4

ALLMÄNT FÖR BERÄKNINGARNA

FORMSTYRKAN FÖR PROTONEN är med hänsyn till den lilla massdefekten (1,5e) och elektronens frisläppande ur neutronen marginellt skild från neutronreferensen. I denna grova översikt betraktas denna skillnad som oväsentlig då principen för atomkärnans formstyrka i vilket fall står klar. Vi kan därmed obehindrat tillämpa de givna sambandsformerna på hela K-cellen genomgående (med vissa reservationer) då uppgiften i denna framställning endast är att få en approximativ kvantitativ översikt.

Graferna i denna presentation är beräknade från c_z=c₀/2-gränsen och utåt då x-värdena i vilket fall (även med d_max=r_0n/1) inte har några distinkt skilda värden från — i princip — noll strax utanför c_z-gränsen.

END.

NOTERING — dokument:

— Typografiska Skarvarna mellan MsWORKS 4.0, WORD 2000 och Webbläsarna:

EFTER ÖVERFÖRING och justering med Ctrl + ++ som gör nedsänkta/upphöjda Synligt Läsbara i WORD — FRÅN MsWORKS 4.0:

EFTER IMPORT TILL WORD FRÅN WORKS:

IMPORTEN I WEBBLÄSAREN

:

Jättekul: Förrädiskt, man ser inte, direkt — särskilt inte i efterhand sedan lång tid gått — vad som är vad med mer än man parallell-läser från webbläsaren.

— Speciellt upphöjningar (kolla Q2) — snygga i WORD — men katastrof i webbläsaren

dras ner i webbläsaren: kontexten förloras.

SÅ FÅR MAN I EFTERHAND PLÖJA I STORT SETT »ALLTIHOPA IGEN» FÖR ATT RÄTTA TILL TYPOGRAFIN PÅ AVSEDD FORM — men många (många) ställen har missats — och många (många) har korrigerats i efterhand.

Många sådana rent typografiska efterhandsjusteringar har gjorts i dokumenten allt sedan Internetintroduktionen för Universums Historia från Aug2008 — och fel hittas fortfarande 2019(+).

DedKraftLag:

2004-10-22 Fjäderanalogin.wps

Ursprungets

HÄRLEDNING FRÅN KRAFTLAGEN

DEL I ¦ DEL II ¦ DEL III ¦ DEL IV ¦ DEL V ¦ DEL indexVI ¦ DEL VI

—————————————————————————————————————————————

Härledning från kraftlagen — Den sammanhängande FYSIKBESKRIVNINGEN uteslutande ENLIGT TNED

—————————————————————————————————————————————

Inledning

I NEGATIV DIVERGENS[‡] förskjuts atomkärnans formbevarande styrka inåt i den fraktala ytstrukturen. Det sker genom den kraftbaserade divergensreduktion, enligt kraftvektorledet

F_c0 – F_c – F_G = 0 ............. vektorekvivalenterna mot F_G utbildar negativa F_c

som den starka gravitationen åstadkommer, och som garanterar att naturkonstanten c₀ bevaras orörd. Vi noterar som tidigare

— LJUSHASTIGHETENS BEVARANDE OBEROENDE AV GRAVITATIONENS INVERKAN —

att negativa ljushastigheter inte existerar. Men kraftdynamiken med negativ divergenskraft gör det definitivt[‡] i enlighet med bevarandet av F_c0 med sina tillhörande ekvivalenter. För att kunna härleda sättet på vilket K-cellen reagerar vid kontraktionsfasens slut, då avståndet mellan alla individuella neutronytor blir idealt noll och hela K-cellens neutronmassa »klonkar ihop i ett enda slag»[‡] måste vi genomföra en matematisk djupdykning i atomkärnans formfysik. Resultatet ska visa hur, och var, K-cellen detonerar — i detalj — om TNED avspeglar korrekt naturuppfattning.

DEL I: Atomkärnans formstyrka ϑ — grek. theta (J), gränsläget för kärnans deformation

[Inledande illustration TNED109B.BMP. Samband s47]

Från Atomkärnans härledning[‡] relaterade vi massans definition alternativt på formen

m=m=ma/a=F/a.

Betrakta från härledningen av elektriska kraftlagen eller divergenskraften dess form

F=k(Q/r)² med k=Rc=R₀c₀= (reciproka) elektriska konstanten ca 9 T9 VM/C.

En obegränsad delning av Q och r, eller alternativt en obegränsad delning av Q² och ytan A, via faktorn (n→∞) enligt

F=k(Q/r)²=k([Q/(n→∞)]/[r/(n→∞)])²=k(Q/r)²

beskriver exakt principalpartikeln (Se Potentialbarriären[‡]) i atomkärnans fraktalstruktur, den som oupphörligt delas utan att någonsin komma till noll och därför aldrig återfinns som någon partikel. Kraften F uttrycker eller bevarar alltså en inneboende formstyrka i atomkärnan via massan enligt

m = F/a = F/(c/dT) = FdT/c = k(Q²/A)(dT/c) = Rc([m/R][A/dT]/A)(dT/c) = m

Eftersom r-formen redan är återförd på minsta möjliga avståndsformen r/(n→∞), kan atomkärnan omöjligen fullständigt komprimeras, skjutas sönder eller på annat sätt förstöras på mekanisk väg; den kommer att svara med en exakt lika stor motkraft enligt ekvivalenten F=k(Q/r)² genom att r tvingas mot 0, R₀c₀Q givna och konstanta.

Vi behöver här inte ta någon som helst hänsyn till gravitationens inverkan eftersom, som vi har sett,

— LJUSHASTIGHETENS BEVARANDE OBEROENDE AV GRAVITATIONENS INVERKAN —

gravitationen garanterar att c₀ bevaras intakt genom kraftvektorledet

F_c0 – F_c – F_G = 0 ...... vektorekvivalenterna mot F_G utbildar negativa F_c

Kraftvektorledet ingår redan av princip i atomkärnans struktur (Atomkärnans härledning[‡]). Samt att rymdmotståndet R₀ är givet som grund för c₀ och därför heller inte påverkas av gravitationen. Atomkärnans formstyrka är alltså garanterad i vilket fall oberoende av gravitationens inverkan.

— Det enda vi behöver göra för att få fram en användbar matematisk fysik för att kunna beskriva kärnans formstyrka med tillhörande dynamik blir — så endast — att införa ett tryckstopp (d_max) motsvarande en gränslängd för kärnans motsvarande axiella intryckning: Gränslängden d(MAX) kan aldrig uppnås eftersom kraften i dess närmande redan är ställd på oändligt, som ovan:

exakt lika stor motkraft enligt ekvivalenten

F=k(Q/r)² OM r tvingas/komprimeras mot 0,

R₀c₀Q givna och konstanta

Det är alltså uppenbart att d_max > 0, visst och bestämt. Vi ska här också beteckna den avgörande gränslängden med termen x_f : formgränsstoppet.

x_f = d_max ............................... formgränsstoppet, gränslinjen för atomkärnans axiella ihoptryckning

Atomkärnans bevarande formkraft kan då återföras på en fast och fix grundkonstant, en

ϑ = F = k_9T9(Q/x_f )² ............. formfaktorn Theta (grek. J)

i följande mekaniska fjäderanalogi (ϑ, Grekiskans J).

— I mekaniken gäller enkla praktiska experiment med med stångvirad metalltråd om inte annat att kraften på en fjäder följer formen

F=kd med k som fjäderkonstanten och d som intrycket.

Styrkan i atomkärnans formhållfasthet kan som ovan nämnts återföras på STRUKTUREN ¦ PASTOM I hela dess samlade laddningsinnehåll Q=Z(1818e+18e–m_D) genom uppdelningen i ±β-komponenterna tagna över kärnans maximala ihoptryckning eller deformationsmaximum (d_max=x_f). För neutronen med massdefekten noll gäller

Q = 918e ~= (1818 + 18 + 2,624)e = ± (2× 918e + REST[1,312]e)

DEN FORMBEVARANDE Styrkan (k_f) återförs på den konstanta divergenskraften eller formfaktorn

F=k_9T9(Q/x_f )² över deformationen x_f enligt F/x_f=k_f=k_9T9Q²/x_f³.

k_f konserveras av atomens allmänna impulsmomentsekvation J_0K+3J_1K=0 där som tidigare noterats negativ divergens ingår enligt

F_c0 – F_c – F_G = 0 ............. vektorekvivalenterna mot F_G utbildar negativa F_c

k_f motsvarar den mekaniska fjäderkonstanten, k_f = F/x_f.

DEL II: Atomkärnans axiella deformation

FUNKTIONEN VI SÖKER måste uppfylla villkoret att ju större deformationen blir mot gränsstoppet x_f=d_max, destor brantare och tvärare blir kraftens ändring med avseende på intrycket (x), ehuru en linjär funktionsform som går mot oändligt är utesluten inom ett avgränsat funktionsintervall (x_f=d_max=1). Funktionen måste alltså tvunget bli exponentiellt betingad. Eftersom kraftformerna i atomkärnan ytterst vilar på ytformer (av sammansatt fraktal natur [‡P]¦[‡A] ) måste kraftändringens funktion återföras på en yta som — därmed — kan avspeglar hela kärnformens yttre deformation.

— Enklaste här kända sättet blir att återföra en

DEFORMATIONSKRAFTENS VARIATION dF/dx=F’= F f (x)

inom intervallet x_f=d_max på divergenskraftens variation genom inverterade kvadraten på resten mellan tryckstoppet d_max=1 och intrycket x enligt f (x)=1/(1–x)². Nollavstånd för divergenskraften betyder då ”oändlig kraft” vilket här motsvarar fallet x=1 — som aldrig uppnås. Därmed är villkoret med expontentialformen uppfyllt.

Varianten F’=dF/dx=ϑ(1–x)^–2 ger då integralen F via differentialekvationen

dF = ϑ(1–x)^–2 dx ;

F = ϑ (1–x)^–2 dx

= ϑ(1–x)^–1 ;

F(0) = ϑ ; bestämda integralen blir:

F = ϑ(1–x)^–1 – ϑ

= ϑ[(1–x)^–1 – 1]

= ϑx/(1–x)

= ϑ[1/x – 1]^–1

Av mellanledet ϑx/(1–x) ser vi att x-formen är helt numerisk, den kan ersättas med

x/(1–x)=d_maxx/d_max(1–x). Dvs.;

ENHETSFORMEN för x-variationen mellan 0 och 1=d_max har reala metriska distansen d_max eller med samma innebörd x_f. Deformationen dämpas absolut av formstyrkan k_f. Med dessa konstanta koefficienter ges då realt metriskt

F = k_fx_f x/(1–x)

= F x/(1–x) ....................................... atomkärnans axiella deformation:

grundform utom gravitationens inverkan

DEL III: Deformationens allmänna ekvation — gravitationens divergensreducerande inverkan

Vid en visst given lokal divergens[‡] f (c) svarar ett visst kärnintryck f (x) mot en motsvarande kärnmotkraft eller en deformationskraft F,

intrycket (x) = motkraften (F) ....................... allmänna, kvalitativa grundmekaniken

Formfaktorn F[‡] är atomkärnans kraftbevarande konstant [F=k_9T9Q²/x_f²]. För given divergens bestämmer F intryckets magnitud. Motkraften å sin sida beror också dynamiskt just av en divergensfunktion f (c) så att vi för samtliga fall kan teckna upp ett motsvarande mera fullständigt sambandsled enligt

intrycket · formfaktornKONSTANT = kärnmotkraften · divergensen ;

f(x)F = Ff(c) ;

f(x)/f(c) = F/F .................................... fullständiga (Gravitella) funktionsformen

Som DEL II vi redan studerat, är intryckets funktion en inverterad formbevarande ytfunktion för atomkärnan,

f (x) = 1/A = 1/(1–x)²

Enheten 1 i tryckanalogin motsvarar atomkärnans enhetsyta med referens till intryckets maxvärde x_f=d_max i formstyrkan F=ϑ.

DEL IV: Divergenskoefficientens funktion — gravitationens inverkan

Divergensens funktion bildar en divergenskoefficient

v, bokstaven v i Symbol — sammansatt av lilla omega och toppdelen på pi här improviserat som »PiOm»:

— OM Pi försöker Trycka ner Omgivningen, reser den sig, okuvligt. (.. författaren bara improviserar ... )

som gäller vid varje given g-kraft. Vi kan lösa ut den funktionen f(c) genom att betrakta fallet där divergensen inte har någon KONTAKTERANDE inverkan på tryckanalogin. Nämligen där f(c)=1, analogt där det gäller att c/c₀=1, dvs., i K-cellens centrum[‡]. Funktionen för f(c) ska i vilket fall vara kontinuerlig mot detta nollställe. Lösningen till f(c) ges då enligt leden och utvecklingarna

(F/F)f (x)=1=f (c) ; E=E₀ ;

E = 2E₀ – E₀ f (c) .......................... med f(c)=1 ges E=E₀ vilket motsvarar orörd kärna

E = E₀[2– f (c)] = PT = P₀T[2– f (c)] ; E = mad = Fd = Pt ; P = Fd/t = Fv; v = c:

P = P₀[2– f (c)] = Fc = Fc₀[2– f (c)] ;

c/c₀ = 2– f (c) ;

f (c) = 2–c/c₀ = (F/F)f (x) ;

ϖ = 2–c/c₀ ......................................... ; .................. divergenskoefficienten

DEL V: Deformationskraftens fullständiga samband

Av ovanstående följer

F = F f(x)/f(c) = F f(x)/ϖ ;

Fx = E = F f(x)/ϖ x ;

f(x) = 1/A = 1/[1–x]² ;

dE/dx = F (1/[1–x]²)/ϖ ;

dE = F (1/[1–x]²)/ϖ dx ;

E = F (x/[1–x])/ϖ · 1M ;

F = F x/[1–x]ϖ ........................................................... atomkärnans uppförande vid axiell deformation x, F=k_9T9Q²/x_f²

F-ekvivalenten beskriver deformationssambandet.

x relaterar metriskt till enhetsvärdet 1 för x_f=d_max. Toppdivergensen c=c₀ ger v=1, nolldivergensen ger v=2, samt vidare positivt uppåt obegränsat med växande negativ divergenskraft F_c. Växande v dämpar alltså F — men gör samtidigt F-variationen brantare så att stora variationer i F ges på allt mindre variationer i x.

— Se Typgraf TNED141A.BMP.

Sektioner 1-6

DEL VI: Deformationskraftens tillämpning på K-cellen, Detonationssambandet — statiska g-trycket och statiska g-kraftens inverkan

forts. DEL VI.

;

DEL VI SEKTION 1: Det passiva kärnyttrycket från den negativa divergensen

F_J/A_J=p_J=F_K/A_K

p_J = m_J a/4πr² = m_J(Gm_J/r²)/4πr²

DEL VI SEKTION 2: Statiska g-kraften, statiska g-trycket

F_sK = p_JA_K = k_fx_f x/(1–x)ϖ ................... statiska g-kraften

p_J = F_Kcell/A_Kcell = F_Kärna/A_Kärna ....... statiska g-trycket, gäller exakt i varje ekvipotentialyta

DEL VI SEKTION 3: g-statiska intrycket — grafrelaterade kraften

xsK = (k_f x_f /ϖF_sK + 1)–1 ....................... g-statiska intryckets ekvivalent

DEL VI SEKTION 4: Allmänna samband, statiska och expansiva

r0c = (3/8Gπρ)^1/2c₀

r0c = (3/2Gπρ)^1/2c₀

DEL VI SEKTION 5: Impulsen

FT=p=mv

DEL VI SEKTION 6: Slutformen

Detonationsimpulsens yttre gränslinje:

G-offset ................... x_sK = (k_f x_f /ϖF_sK + 1)^–1

Detonationsimpulsens inre gränslinje:

x+G-offset ............... x_a = (k_f x_f /ϖ(F_sK+F₀) + 1)^–1

Detonationsimpulsens gränskurva:

x = x_a–x_sK

N-min i dMAX:

TILLÄGG 3Feb2019 — originalets text 2004

N-minimum i dMAX

——————————————————————

NOTERA SKILLNADEN MELLAN MASSTALET 1 OCH DE ÖVRIGA FRÅN 2 — se »DEUTERONENS HEMLIGHET»

——————————————————————
ORIGINALTEXTEN från 20Apr2004 innehåller relativt omfattande resonemang med utvärderingar och utvecklingar som komprimerades på kortform i (Masstalet 1) ATOMKÄRNANS EKVIVALENTA GEOMETRI VID DEFORMATION. Här ges en mera uttömmande grundbeskrivning som förklarar ansatserna i beskrivningssättet: Atomkärnans impulsmoment[‡] J_0K + 3J_1K = 0:

Se särskilt i PLANCKRINGEN och ANTALET MASSELEMENT I ELEKTRONEN

Det angivna N(min) = 1000 baseras på ett sämsta faller SÄKRA marginalvärde som (garanterat) INTE äventyrar en övre maxgräns för atomkärnans elastiska deformation — så att vi inte räknar på helt galna grunder. Men grovräkningen vill snarare sätta det gränstalet till runt N(min) = 20.000: atomkärnas obotligt stränga ovilja mot att deformeras utan att splittras.

En del av resonemanget i avsnittet[‡] ATOMKÄRNANS EKVIVALENTA GEOMETRI VID DEFORMATION ansluter till den — här — kompletterande illustrationen ovan:

— Sämsta fallets grovberäkning med FRAKTALNIVÅERNA i N3m20-aggregatet[‡] Neutronen visar en närmast »möjlig elastisk fraktalnivå» vid underfraktal No4 (R0/2100 i figuren ovan).

— Räknar vi emellertid i NETTO på varje första underfraktals ring med sina 612 elektronmassor, totalt (1836+2,64)e för hela neutronen, visar den symmetriska geometriska cirkulära delningen ett maxvärde på drygt 97:

tan(360/612) = 1/97,39940293

~ 97,4

Vi VET emellertid inte säkert vad som gäller i atomkärnans fall — utöver vad TNED anvisar för toppspinnet och de två första underfraktalerna. Det ligger — emellertid — också i sakens natur ATT den geometriska delningen — tvunget — MÅSTE ha kredit på kärnfysiken i praktiken för att kärimpulsmomentets balansekvation J_0K + 3J_1K = 0 ska gälla:

— ENDAST då kärnan exciteras — börjar självsvänga vilket framalstrar de invävda ±e-krafterna med explosiv verkan — bryts impulsmomentets balansekvation, analogt tyngdcirkelns naturliga fluktuationer omkring elasticitetsgränserna.

Så: Delningsformen cotan360/[(1818+18+2,64)e/3 = 612+k]~97 kan inte ignoreras: Det anger det absolut lägsta fraktaldiametrala värdet för andra underfraktalen — som garanterar den större (No1) underringens elektromagnetiska sammanhållning enligt förutsättningarna i PLANCKRINGEN (Atomkärnans härledning).

— Med en vidare hoftning på att nästföljander fraktalnivås motsvarande ringdiameter är MAX hälften — vilket också bör vara en STOR överdrift — ges så en mera praktiskt rimlig N(min)-gräns vid R0/([97~100]·200) = 20 000.

— Det är den först ringnivå vars ØNo4 som rent geometriskt i princip kan verkställa en variation hos en toppringsdiameter ØNo1=FörstaUnderfraktalen genom att pack-avstånden mellan närliggande ØNo4 ökar — aldrig minskar. Och där ligger hela det eftersökta KRITERIET i jakten på ett rimligt referensvärde för atomkärnans — neutronens i detta fall — elasticitetsgräns: gränsen då kärnas mekanik säger ifrån och börjar ge tillbaka intrycket;

N_min = R₀/20.000

snarare än det tidigare antagna sämsta fallets grovvärde R0/1000.

EMELLERTID har det redan strängt lilla (1/1000) försumbara intrycksvärdet mindre betydelse rent kvantitativt sett än rent kvalitativt sett. Det avgörande viktiga i härledningen till K-cellen detonationsfysik är i vilket fall ATT något (litet) gränsvärde existerar, och som kan PÅTRIGGA detonationstillfället avgörande mekanik. Så, behöver vi inte, längre, slita oss förtvivlade med den frågeställningen då nu principen står fullkomligt klar.

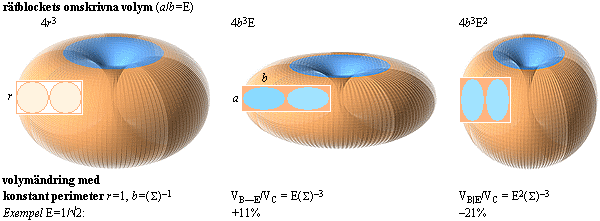
INNEBÖRDEN för de bägge illustrerade[‡] olika deformationssätten för atomkärnan blir då också mindre dramatiska EFTERSOM det som gäller, i vilket fall, är att OM den uppskattade fraktaldifferensen (R0/20.000) vid ØNo4 bryts upp — och atomkärnorna/atomkärnan sönderfaller, eller försöker göra det, befinner vi oss i vilket fall VID gränsen då atomkärnan ger tillbaka samma kraftsvar som det som föranledde intrycket: atomkärnan i höggravitella lokaler med c=0 har ingen elektromagnetisk makrobaserad förlustfaktor att ta hänsyn till: atomkärnan är förlustfri, och därmed 100% elastisk i gensvaret på varje MEKANISK STÖT som kärnan utsätts för; Det finns inga elektromagnetiskt termiska värmeförluster så länge atomkärnan befinner sig i en c=0-lokal: K-cellens detonation.

END.

COMPILATION COMPLETED 1Feb2019

3Dgeometrin

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

3D-Matematiken

ämnesrubriker

innehåll

3D-GEOMETRIN

Allmän genomgång av grundbegreppen i 3D-geometrin

PERCEPTION AND PERSPECTIVES

Pilotsystemet

3D-geometrins 3 punktfält

Planprojektion — Linjärperspektiv — Sfärperspektiv

SFÄRPERSPEKTIVET

SFÄRPERSPEKTIVET — sambanden för manuell passarritning, HÄRLEDNINGAR

SFÄRPERSPEKTIVET — projektionssättet

SFÄRPERSPEKTIVET — projektionssambanden för datorritningen, HÄRLEDNINGAR

CHORD-KROPPEN — principen med illustrationer

Samhörigheten mellan HORISONTALPERSPEKTIVEN och SFÄRPERSPEKTIVEN

CAD — computer aided drawing/design

The CHORD of ARCS

DELPHIchords2003

CHORDCIRKLARNAS ALLMÄNNA EKVATION

Avslut

Avgörande elementära ritverktyg

3D-nomenklatur

MACz — koordinatnomenklaturen i modern akademi

Rotationerna i 3D-geometrin — 3D-geometrins rotationskomplex

ROTATIONSKOMPLEX 1 OCH ROTATIONSKOMPLEX 2

Bildrotation och systemrotation

BILDROTATION — Rotationskomplex I

SYSTEMROTATION — Rotationskomplex iI

Rotationskomplex I

Rotationskomplex II

PERSONLIGHETENS FRIA OCH FULLA UTVECKLING — utvecklingsverktygen

GYROMODELLEN

Linjära perspektivets grunder

Riktkuben ¦ Horisontalelvationen ¦ Horisontalteoremet ¦

ENHETSHYPERBELN

HP-matematiken

BILDINDEX

HORISONTALINDEX

Riktkuben

RIKTKUBSMODELL — Anim8or

Linjärperspektivets gränspunkter

HPExempel

PentaEX

CityEX

Kulan Och Plattformen

SamlingsKollageHP

Beskrivning

HorisontalPerspektivKroppens grundvyer

DatorRelaterat

Gränspunktssatsen

Bildekvationen

Rotationerna i 3D-geometrin — hur rotationerna i 3D-geometrin utförs i praktiken

xyBildRot1

EXEMPEL Rot 1

Lagerqvistsyndromet

LINJÄRA HP-syndromet

Cirklarna ELLIPSERNA i HPG

ELLIPSritningen

FIG a

FIG b

Citat Lagerqvist

Lagerqvist Fig5572

Lag72HPG

HP-kroppen

HP

PC

HP-kroppens uppritning

Skalenlig 3D-Måttsättning

Rotationssatsen

Rotationssatsen

Full redovisning

APPENDIX

AppendixINTRODUCTION

Comparing Examples

EXAMPLE 0

CHEOPS RECTANGLE, illustrated perspective method

ESTABLISHMENT

Wolfram2019

Human Rights Violations

GCCE

MAC And intelligence

Nature in Physics

The Real Steel

EXAMPLE 1

PerspectiveQuote1966

EXAMPLE 2

EXAMPLE 3

EXAMPLE 4

EQUIVALENCE OF ROTI AND ROTII

Inledning

Introduction

RC12 Theorem

MATHEMATICAL DEDUCTION OF THE Rot1¦Rot2 EQUALITIES

CompiledRot1

CompiledRot2

Prepared Rot1 — to match the reversed rotational order of Rot2

SECTIONx

cosxWcoszw

MinusSinzw

SECTIONz

SECTIONy

CONCLUSION

The ORIGIN OF ROTII

Introduction

NATURE

The HORIZONTAL EQUATION

Explanation

THE HORIZONTAL THEOREM

RotationComplex II Jul1981

The 6 Orders

EllipsoGraphNr97

Rot2Synthesis

FJÄDERANALOGIN — Spring Analogy

Sammanställning med beteckningar och samband

Divergenskoefficienten — ref

dMAX

GRAVITATIONSENERGIN

DETONATIIONSENERGIN

RödförskjRef

HÄRLEDNINGAR

F-integralen

Divergenskoefficienten — förklaring

DEL 6 Deformationskraftens tillämpning på K-cellen, Detonationssambandet — statiska g-trycket och statiska g-kraftens inverkan

SEKTION 1 Det passiva kärnyttrycket från den negativa divergensen

SEKTION 2 Statiska g-kraften, statiska g-trycket

TYNGDPUNKTENS DEFINITION

SEKTION 3 g-statiska intrycket — grafrelaterade kraften

SEKTION 4 Allmänna samband, statiska och expansiva

SEKTION 5 Impulsen

SEKTION 6 Slutformen

HÄRLEDNING FRÅN KRAFTLAGEN

DEL 1 Atomkärnans formstyrka ϑ

DEL 2 Atomkärnans axiella deformation

DEL 3 Deformationens allmänna ekvation — gravitationens divergensreducerande inverkan

DEL 4 Deformationskraftens fullständiga samband — Divergenskoefficientens funktion — gravitationens inverkan

DEL 5 Deformationskraftens tillämpning på K-cellen, Detonationssambandet — Deformationskraftens fullständiga samband

DEL 6 — index

N-minimum i d-MAX

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[BA]. BONNIERS ASTRONOMI 1978

— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.

[FM]. FOCUS MATERIEN 1975

[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929) — ALBERT BONNIERS FÖRLAG STOCKHOLM

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, här ofta använd förkortning för Modern ACademy versus the comparing TNED — etablerad vetenskap sedan början av 1800-talet

TNED — Related PHYSICS And MATHEMATICS — Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

SHORT ENGLISH — TNED in general is not found @INTERNET except under this domain

(Universe[s]History, introduced @INTERNET 2008VII3).

TNED or Toroid Nuclear Electromechanical Dynamics is the dynamically equivalent resulting description following the deductions in THE PLANCK RING, analogous AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, each, details claim to be fully logically explainable and understandable, or not at all. With TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’ Deduction.

Senast uppdaterade version: 2019-12-04

*END.

Stavningskontrollerat SVENSKA 2008-11-02 | 2008-11-06 | 2011-10-11 | 2019-02-08. ÅrMånDag.

Stavningskontrollerat ENGELSKA 2019-02-07.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ L τ πρ ħ ε UNICODE — often used charcters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡ ↔↕ ħ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ ϑ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; 25 ↓; 26 →; 27 ←; 22 ▬

23 ↨ — also 18 ↕; 29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

*

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se