PULSARERNA 2008IX23 a BellDHARMA production · | Senast uppdaterade version:
2018-06-21 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Pulsarerna | I sammanställning för
presentation i webbDokument Från Stjärnfysiken2005 |
Inledning till pulsarmatematiken
|
hastighet |
|
distans |
|
v |
·1S= |
d |
|
|
|
|
|
v |
·1S= |
d |
|
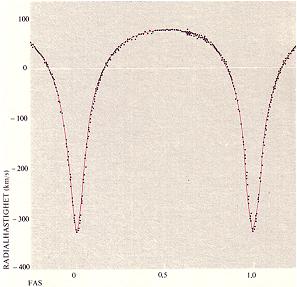
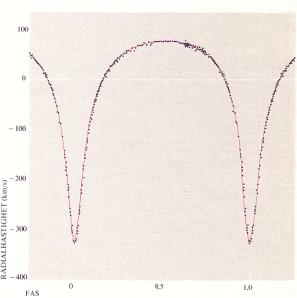
radialhastighetskurva PSR 1913+16 från BONNIERS ASTRONOMI
1978 s92 figur 5.11 |
|
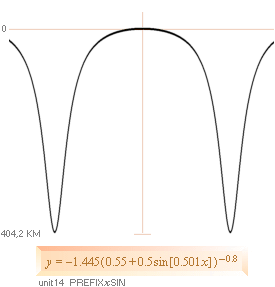
ideala radialdistanskurvan enligt TNED en av flera olika
kurvlösningar |
I modern akademi
och vetenskap finns ingen teori som beskriver ’hur en stjärna kastar ut och
drar tillbaka material periodiskt’ (se Så föddes
uppfattningen om den roterande neutronstjärnan). Rent matematiskt-fysiskt är emellertid det enda som skiljer
en sådan periodisk expansion och kontraktion ifrån dopplerkurvan för en
dubbelstjärna, som ovan vänster, en simpel multiplikation eller division med
enheten 1 Sekund; Med uppmätt grund i materialets ljusemission utmed synlinjen
Jorden-objektet, framgår direkt en väg-tid-kurva (d ovan höger) från en uppmätt
hastighet-tid-kurva (v ovan vänster, dopplerkurvan).
Kurvan blir exakt densamma. Exakt.
Ekvivalenter är ekvivalenter.
Enda sättet att avfärda den möjligheten är
att påvisa att varje objekt är TVÅ stjärnor, samt att
’pulsarekvivalenten’ (ovan enligt TNED, d) aldrig kan förekomma, se pulsarsambanden nedan enligt TNED.
Exemplet
ovan illustrerat visar objektet PSR 1913+16 som ligger ca 21 000
ljusår härifrån, nära utkanten på
Vintergatans centrala ansvällning — vi (nu levande) kommer med största
sannolikhet aldrig någonsin att få veta hur det objektet ser ut. Objektet
upptäcktes 1974 av Hulse och Taylor som tilldelades nobelpriset i fysik år 1993
för upptäckten (här utan vidare referenser, webben är full av dem, se exv.
nedan).
Det man ser av objektet PSR 1913+16 är
emellertid bara en ytterst svag radiosignal,
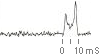
Källa:
[http://www.ias.ac.in/jarch/jaa/16/307-325.pdf] s312,
Binary Pulsars and Relativistic Gravity
Diamond
Jubilee Symposium on Pulsars 14-17 March
1994, Raman Research Institute, Bangalore
utspridd,
defokuserad och i stort sett »väldig illa tilltygad», i princip oläsbar som
sådan, ständigt varierande, aldrig lika, men ständigt återkommande efter ett
regelbundet signalmönster. Pulsformen ovan är en s.k. (statistisk) profil som
tas fram genom en avancerad apparatur med signaltekniska program och
beräkningar. Ur det datahavet fick de nobelprisbelönta pionjärerna Hulse-Taylor
fram den ovanstående radialhastighetskurvan, här i kopia från Bonniers
Astronomi 1978 sidan 92. Figuren visar en radialhastighetskurva, och man menar
att den förorsakas av den enda synliga komponenten av de två i ett (s.k.
trångt) dubbelstjärnesystem. Den synliga komponenten, en s.k. neutronstjärna,
utsänder pulser — primitiva exemplar av den ovan avbildade profilpulsen — som
anländer hit till Jorden periodiskt med (den statistiskt framräknade) frekvensen 17 Hz och som varierar i intensitet (frekvens) på det sätt som
radialhastighetskurvan antyder.
Eftersom
man redan från början i modern akademi och vetenskap (1967) uteslöt möjligheten
att en kompaktstjärna (konv. vit dvärg eller neutronstjärna) alls vore kapabel
att pulsera (vibrera), se Så
föddes uppfattningen om den roterande neutronstjärnan, har man heller aldrig räknat med den enkla möjligheten
som den renodlade figurformen ovan till höger visar: just en kompaktstjärna som
periodiskt kastar ut och drar ihop ett omgivande (väsentligen gasiskt)
material. Kurvformerna är identiska. OM den funktionen också hade fysisk grund
skulle man alltså direkt kunna påstå:
Objektet PSR 1913+16 visar inte två
stjärnor — bara en enda.
ENLIGT
TNED finns en sådan grund — helt med referens till resultaten från Solfysiken
med Fusionsperioden och Solens fyra periodiska funktioner.
Vi studerar det.
Modern akademi och vetenskap (MAC):
I
modern akademi (MAC) refererar man till sambandet 2p(Gr)–1/2 som — med maxtätheten grovt taget ca 1 T17 KG/M3
(Helium-4-stjärna) — ger ett största värde i sekunder
2p/Ö(6,67 t11 · T17) = 0,00243285
Med
referens till det uppmätta periodvärdet på 0,033 sekunder för Krabbnebulosan
är det värdet 0,002… tydligen alldeles för litet; ENBART på den matematiska
grunden avskrev man möjligheten med en pulserande ämnesbas, och man antog
istället en fast roterande dito. Se utförligt i Så
föddes uppfattningen om den roterande neutronstjärnan. Faktiskt.
Relaterad fysik (TNED):
Med
den framgångsrika beräkningsgrunden för Solens olika grunddata enligt TNED, här
främst Solperioden på 11,44 år
(från Solens dag 1, nuvarande värde är ca 11,1 år) men som dessvärre GARANTERAT
inte kan framräknas på den moderna teorins grunder, är det naturligt att pröva
sambanden vidare på andra områden som berör stjärnfysiken. Kan pulsarernas
fysik, generellt stjärnornas variabilitet, förklaras generellt av Solfysikens
grundläggande ekvationer sådana de är uppställda enligt TNED?
I TNED bestäms alla stjärnors periodiska
fysik av två grundläggande kommunicerande samband (se utförligt från Pulsarmatematiken
enligt TNED),
fD = (4Grmax/TPp2Ö3)1/3 ...................................
rotationsfrekvensen ur
pulsfrekvensen, rmax för Helium-4-stjärnan är 6,5 T17 KG/M3.
1/TP = fD3
· [4Grmax]–1p2Ö3 ..................
pulsfrekvensen ur
rotationsfrekvensen.
Eftersom
atomkärnan inte kan komprimeras enligt TNED (se atomkärnans inkompressibilitet) finns heller inga beröringspunkter för jämförelse
mellan den moderna akademins teori och sambanden ovan enligt TNED. I modern
akademi använder man
— som
bekant
— en
helt annan kärnfysikalisk grundmatematik
— Jämför
Planckringen i TNED med gängse tillgängliga beskrivningar på nivån
kärnfysik: webben @INTERNET är proppad med sådana.
Se
även jämförelse mellan MAC och TNED i atomvikterna. Där framgår orsakssammanhangen mera grundligt till direkt
jämförelse.
PSR
1913+16 är — i ovanstående ljus —
inte ett unikt exempel;
I
följande del visas ett antal ytterligare observerade ljuskurvor som (möjligen)
kan beskrivas med grund i ovanstående rotcykloidens grundform — och som därmed
(eventuellt) skulle kunna vara enskilda pulsarobjekt.
Vi
studerar hur.
Uppmätta mm-värden på
Hastigheterna för PSR 1913+16 i Bonnierskällan: (14,9LOW+61,9HIGH)/19UNIT=4,0421052 | × 100
KM/S » 404,2 KM/S max
Exemplen
som följer baseras helt på matematiskt definierade kurvformer — vi studerar först
deras enkla uppbyggnad
materialutkastningens
grundform i TNED
När
en gammal utbränd stjärna slocknar, tappar den också (enligt TNED) sitt
strålningstryck. Därmed sjunker den ihop för att sluta som en kompaktstjärna.
Kompaktstjärnan kan emellertid fortfarande vara aktiv — OM dess g-tryck är
tillräckligt stort för att åstadkomma kontakter mellan atomkärnorna då
kompaktstjärnan genom sin sammandragning når maximal täthet (ca 6,5 T17 KG/M3
enligt TNED med Helium-4-bas), se f.ö. stjärnornas allmänna tryckekvation. Är g-trycket större än det motriktade Coulombtrycket,
kan nuklidbarriärerna överkommas och atomkärnorna kan klonka ihop och därmed
också rekylera; Eftersom atomkärnan enligt TNED inte kan komprimeras, samt att
Heliumkärnor inte kan förenas i par, resulterar den sammanpressande g-kraften i
en lika stor återkastande rekylkraft. Därmed tvingas materialet (återigen)
expandera — för att strax vända tillbaka igen om expansionen inte är allt för
häftig. Därmed har kompaktstjärnan bildat det som enligt TNED kallas för en pulsar: en roterande OCH pulserande kompaktstjärna.
Kompaktstjärnans sätt att expandera sitt
material beskrivs i TNED av en ytterst enkel cykloidisk grundekvation (se rotcykloiden), sambandet överst nedan.
[(cos
ax)2]n
.......................................................................................... grundform, väg-tidgrafen (y) i PREFIXxSIN
[(cos ax)2]n + A[(cos a[x+b])2]m + B[(cos
a[x+c])2]u
......................... grundform
med tillägg
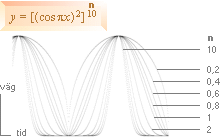
Rotcykloidens
råsamband tar emellertid ingen hänsyn till eventuellt omgivande material;
Omgivande material kommer otvetydigt att dämpa (eller alternera) expansionen
och därmed ljusemissionen på olika typer beroende på sammansättning och metrik.
Grundexemplet
—
såvitt tillämpligt, märk detta väl eftersom ännu ingenting är avgjort
— är
naturligtvis PSR 1913+16;
Gäller INTE den beskrivna väg-tid-analogin, kan också resten av den här framställningen
kasseras. Vi måste alltså anta den typbeskrivningen till en prövande förutsättning
för att komma vidare här
—
helt med referens till resultaten från Solfysiken med Fusionsperioden och Solens fyra periodiska funktioner och som i dessa resultats ljus just utpekar
rotcykloidens grundform som matematisk bas i alla normala primärstjärnor
— och
därmed även rimligtvis även i senare skeden. Sedan får vi se om de vidare
resultaten (också) är rimliga mot redan genomförda observationer
— typ
grundexemplet PSR
1913+16. Men därmed är också huvudfrågan i princip redan avgjord:
Rotcykloidens grundform kan alltså inte direkt
ge typfunktionen i exemplet med PSR 1913+16
—
även om den typkurvans partiella delar väl kan beskrivas av rotcykloiden
men då genom en tvungen alternering (dämpning) av n-faktorn [n=4Grmax/p4fD3] samt uppdelad på olika partier. Exemplet nedan visar det
med nära exakt träffsäkerhet.

Rotexempel i PREFIXxSIN. Jämför studieexemplets uppmätta graf enligt PSR 1913+16.
Överensstämmelsen är inte exakt, men mycket nära. Rotcykloidens råform i exemplet
PSR 1913+16 ger n=4900 till jämförelse via en helt odämpad kompaktstjärna.
Dämpningen i n-faktorn (samma som en täthetsreduktion och i den mån sambanden
är tillämpliga) blir på grund av det omgivande materialet tydligen som störst
omedelbart utanför stjärnytan vid dess minsta radie analogt högsta rotation
(längst upp i grafen ovan) och avtar sedan utåt; Om analogin gäller, är det
tydligt att de yttersta delarna påverkas minst, de inre delarna mest av ett
omgivande dämpande materialskikt, vilket vi också finner logiskt med
centralkraftverkans avtagande funktion med växande avstånd från centrum.
För
att kunna beskriva alla möjliga kurvformer som kan komma av alla möjliga
dämpningar med hänsyn till omgivande material, och i den mån den observationellt
uppmätta kurvformen alls avviker från den enkla rotcykloidens grundform, måste
vi alltså anta
—
utan möjlighet att bevisa något eftersom vi inte har koll på själva
stjärnobjektet
— det
omgivande materialet som ett allmänt svängningsmedium. Vilket (därmed)
vill säga: vi måste i princip kunna anta vilka som helst periodiska
kurvformer med referens till en centralt
matande energikälla, själva pulsaren. Eller med andra ord: vi kan för den
kvalitativa analysens del endast tillåta oss att anta alla möjliga
kurvformer som kan återföras på rotcykloidens grundform. Den enda egentliga hake som finns i den stjärnanalysen
är att de motsvarande alternativa kurvformerna måste kunna återföras på
motsvarande materialskikt och dess dynamiska fysik. Det är utmaningen — och
som vi aldrig direkt kan kontrollera exakt, bara göra mer eller mindre troligt
med (trolig) kännedom om den aktuella stjärnlokalen och dess materialbild. Har
vi ingen sådan, är analysen därmed också dödfödd. Enbart signaldata räcker
inte. Vi måste också veta (med trolig säkerhet) något om regionen.
I exemplet PSR 1913+16
visas direkt med koordinatbeteckningarna (rektascension 19timmar13minuter=1913,
deklination 16°Nordlig=+16) att objektet ligger i riktning mot Vintergatans
centrum — samt med ytterligare källuppgifter att avståndet är beräknat/uppskattat till ca 21 000 lå;
Med hjälp av en ungefärlig översikt över Vintergatan
— samt tillgång till ett konverteringsprogram som kan ge motsvarande Solgalaktiska koordinater —
finner vi att uppgiften med Jordekvatoriella koordinaterna 1913+16 placerar
objektet alldeles i utkanten på Vintergatans centrala ansvällning som ligger ca
25-30 000 lå härifrån. Vi VET naturligtvis inte hur det ser ut där. Då denna
del emellertid bör uppvisa en betydligt högre lokal gravitation än i
våra regioner — tillsammans med en betydligt högre stjärntäthet — och därmed
som vi kan förmoda men här alltså inte bevisa en mera påtaglig närvaro av
gasiskt material mellan stjärnkropparna i hela den regionen, finns det enbart
på den grunden sannolika skäl för att anta en utpräglad dämpfaktor. Därmed skulle
grund finnas för ovanstående kurvtolkning — själva n-dämpningen från
rotcykloidens råform — och längre än så kommer vi inte i den analysen.
Med ovanstående rotexempel
(PSR 1913+16) har vi alltså fullständig tillåtelse enligt analysvillkoret
att söka en motsvarande enhetlig (mera fullständig) kroppsrelaterad kurvform
till rotcykloidens mera primitiva skelett. Vi finner en sådan (naturligtvis)
genom analysen för de möjliga omloppsbanor som sammanhänger generellt med centralkraftsverkan, analogt Keplermomentet. Detta innefattar ellipsbanornas
matematiska fysik, och man finner (genom särskild analys) att funktionen
nedan (grå kurva) markerad ’ellipsfunktionen (2)’ — fortfarande inte helt exakt
men mycket nära — ansluter till den uppmätta Bonniersgrafen i exemplet PSR 1913+16
(integrerad svagt röd nedan med komplementgraferna i grått). Alla samband nedan
i PREFIXxSIN.
DIREKT KONVERTERING ekvatoriella till galaktiska koordinater PÅ WEBBSIDAN
[http://fuse.pha.jhu.edu/support/tools/eqtogal.html]
— men
tydlig beskrivning saknas (en TYVÄRR alltför vanlig attityd);
—
källan använder LII för galaktiska REC och BII för galaktiska DEC: man måste
mata in 6 siffror i två omgångar för varje konvertering:
—
hhmmss för REKtascensionen (»horisontalsnurren» 0-24 timmar) OCH DDMMSS för
DEKlinationen (»kikarhöjden» 0±90°).
y
= [(cos px)2]20
................................................................................. rotcykloidens väg-tid-kurva
y
= –0,028[([1 + (1,25tanx)2]1/2[0,92 + secx]–1)2]2,2
.................... ellipsfunktionen
1
y
= –0,87 · ([1 + (tanx /
0,88)2]1/2[0,9 + secx]–1)0,96
...................... ellipsfunktionen
2

cycGRAFEKVATION(unit175) –1.15(cosþx)'40 ....... n-faktorn
dämpad från 4900 till 20, endast yttre delen (tätheten reducerad ca 250 ggr)
eps1GRAFEKVATION(unit028)
–0.028([(1+[1.25tanx]'2)'0.5][0.92+secx]'–1)'2.2
eps2GRAFEKVATION(unit028)
–0.87([(0.9+[(tanx)/0.88]'2)'0.5][0.9+secx]'–1)'0.96
För att kompensera för samtliga möjliga
fall av kurvtyper är det enligt analysvillkoret
alltså tillåtet att
dels upprepa rotcykloidens råform i huvudformen genom
utfyllande komponenter av samma typ som råformens, analogt en eller flera förskjutningar
(sin|cos) med tillhörande adderande eller subtraherande kurvdelar, se
föregående grundform med tillägg, och
dels alternera hela kurvformen — exemplet närmast ovan med
direkt koppling till exemplet i PSR 1913+16
—
genom funktionsformer
som innefattar rotcykloidens formtyp
— och
därmed flera parametrar
— och
därmed mera avancerade funktionskurvor som kan ta hänsyn till en bredare materialbas
som medium för de energigenomströmningar som matas av centralens pulsar.
Rotcykloidens grundform blir skelettet, och
— de enligt analysvillkoret tillämpliga — matematikens övriga kurvfunktioner
blir kroppshöljet.
Dessa utfyllande komponenter sammantaget
tecknande i föregående grundform med tillägg, kan alltså anställas på samma form som rotcykloidens
grundform — med enda skillnaden att de tillagda komponenterna optimerar en
möjlig förskjutning inom hela perioden (koefficienterna bc), samt kan
både öka och minska olika bidrag med olika grader av amplitud (koefficienterna
AB) och dämpning (exponenterna mu).
På dessa nu redovisade grunder kan de
ovan beskrivna kurvkomponenterna användas för att söka en optimalform mot
observerade kurvdata från (vissa, inte alla) astro-tekniska-nomiska
observationer — för att få fram en grund för jämförande analys mot TNED. Som
tidigare noterats är PSR 1913+16 vårt absoluta grundexempel: Kan det
visas att dess formkurva i den beskrivna väg-tid-meningen inte gäller, gäller
heller ingen annan del av den här framställningen.
Notera
att den här enkla jämförande analysen aldrig kunde anställas i moderna
lärostolar
—
därför att man redan från början (1967)
uteslöt den pulserande aspekten
ENKLA EXEMPEL PÅ LJUSKURVOR
SOM ANSLUTER TILL
ROTCYKLOIDENS GRUNDFORM ENLIGT TNED
Förvånande
nog kan en synbarlig (markant) del av de konventionellt presenterade
ljuskurvorna från olika stjärnobjekt beskrivas tämligen träffsäkert enbart av
ovanstående typ enkla grundform med tillägg.
Som vi strax ska se: Det anmärkningsvärda
är INTE att man observerat ljuskurvor av arten PSR 1913+16,
utan istället sådana som helt klart mera ansluter till rotcykloidens enklare
skelett. Faktiskt. Vi studerar några exempel.
ASPIRANT
1:
Namn: TT Aurigae även HD 33088
Period: 1.332735 dygn
Avstånd : 3 360 lå (1 030 pc)
Lokal: »0502+39»
Magnitud:
KÄLLA,
bild:
[http://www.tass-survey.org/tass/refs/wilson/index.html] Spring 1994,
UNDERSTANDING BINARY STARS VIA LIGHT CURVES, IAPPP Communications R. E. Wilson, University of Florida
KÄLLA,
data:
[http://digital.library.pitt.edu/cgi-bin/parallax/viewitem.stable/07acr9511s/v0000/i000/01830177.tif?config=pitt&userID=NoUserID&dpi=4&booknotis=07acr9511s]
”
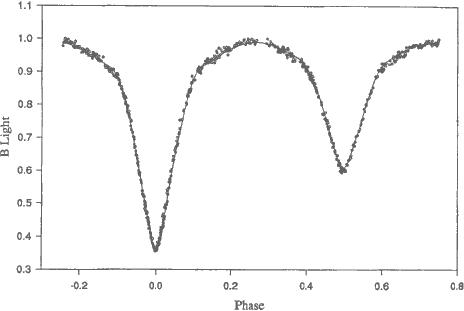
FIGURE 4. A good B light curve of TT Aurigae observed by Wachmann, Popper, and Clausen (1986) and fitted by Terrell (1991). Agreement between model and observations is not perfect, but make no apologies if you do as well as this.
”.
TNED;
lägg märke till den utpräglat kantiga typformen:
GRAFEKVATION
(unit800) –1.2(0.3–0.03[(sinþx)'8]–0.2[(sinþx)'2]+[0.5(cosþx)'20]+0.4(cosþ[x+1.5]/2)'80)
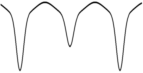
Flera
liknande typer som den ovan finns på
[http://www.rssd.esa.int/index.php?project=HIPPARCOS&page=c_example1]
(2007)
enligt
ASPIRANT
2:
Namn: HIP 48188 även HD 85207
Period: 0,888021 dygn
Avstånd : 815 lå (250 pc)
Lokal: 09 49 24,72;
–38 20 57,5
Magnitud: 8,68-9,23 (osynlig
för blotta ögat)
”HIP 48188 (HD 85207, XX Ant). This star is of spectral type A8/F0V. It varies between about 8.68 and 9.23 magnitudes, with a period of 0.888021 days. It is classified as an Beta Lyrae type eclipsing binary. The star is at a distance of about 250 parsecs.
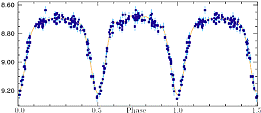
”,
ASPIRANT
3:
Namn: HIP 59683 även HD 106400
Period: 0,407528 dygn
Avstånd : 326 lå (100 pc)
Lokal: 12 14 20,97;
+11 49 10,3
Magnitud: 9,19-9,92 (osynlig
för blotta ögat)
”HIP 59683 (HD 106400, AH Vir). This star is of spectral type K2V. It varies between about 9.19 and 9.92 magnitudes, with a period of 0.407528 days. It is classified as a W Ursae Majoris-type eclipsing binary. The star is at a distance of about 100 parsecs.
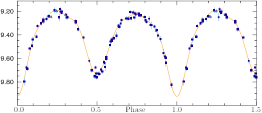
”.
I
webbkällan
Google-Böcker: Light curves of eclipsning and non-eclipsing binaries beskrivs illusterat i boken (s217)
An Introduction to Close Binary Stars, R. W. Hilditch, Cambridge
University Press 2001;
finner
vi ytterligare en
ASPIRANT
4:
Namn: PG1336-018
Period: uppgift
saknas ännu
Avstånd : uppgift saknas ännu
Lokal: uppgift saknas ännu
Magnitud: uppgift saknas ännu
”
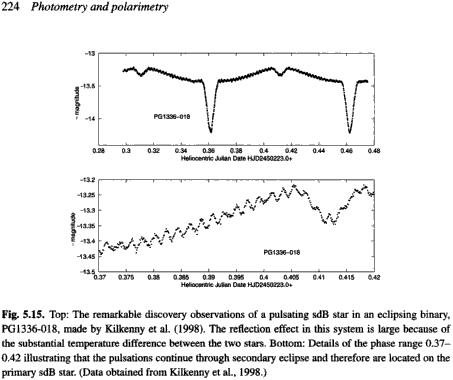
”.
TNED:
Fullständig
lösning utom den överlagrade delen — denna läggs till som separat addend
GRAFEKVATION (unit400) –1.2(0.2+0.05[(sinþx)'200]–0.08[(sinþx)'4]+[0.4(cosþx)'200]+0.0(cosþ[x+1.5]/2)'80):
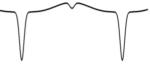
ASPIRANT
5:
Namn: Beta Persei även Algol
Period: 68,75 timmar (2,8646 dygn) [http://csep10.phys.utk.edu/astr162/lect/binaries/algol.html]
Avstånd : 93 lå @INTERNET Wikipedia Beta Persei
Lokal: 0308+41 @INTERNET Wikipedia Beta Persei
Magnitud: uppgift saknas ännu
[http://ocw.mit.edu/NR/rdonlyres/Physics/8-282JSpring-2006/FA6D75DC-760D-4B28-98FF-0423B27B3855/0/ps6.pdf] s4:
”“Eclipsing Binary” optional”,
”
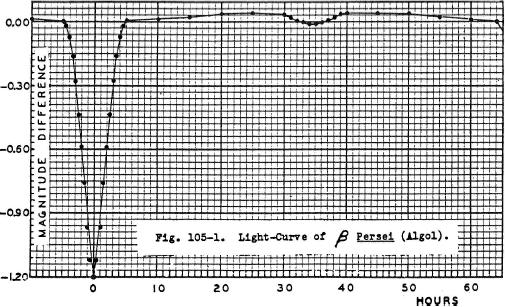
”.
TNED:
GRAFEKVATION
(unit800)
–(0.1+0.03([(sinþ[x])'2]'50)–0.02([(sinþ[x])'2]'0.8)+[0.5([cosþx]'2)'80]).

ASPIRANT
6:
Se Krabbnebulosan (särskilt avsnitt med mera utförliga TNED-data)
…
(Flera
exempel följer).
Men vi VET ingenting om det här (än).
Ett
avgörande skulle kunna ske OM vi till exempel fick fram ett enda astronomiskt
objekt med en väl observerad ljuskurva som matchar TNED-formens rotcykloid (typ
ovanstående grundexempel) där man klart kunde visa på att det består av två individer. Inte en. Därmed skulle saken vara avgjord: TNED gäller
inte.
I fallet Krabbnebulosan vet man redan att objektet är singulärt. Men det är inte
»lika enkelt» att avgöra för andra objekt — som också passar in på typen pulsar
enligt TNED.
Det
här relativt korta avsnittet tar upp hela 93 KB i htm-filen enbart (det är
tydligen tabellen som är kodkrävande):
Krabbnebulosans
pulsar enligt TNED. Krabbnebulosans
observerat utpräglade pulsform (—¯——) off-on-off från den centrala pulsaren kräver
enligt TNED för pulsbildningen en tillräckligt tung kompaktstjärna; Det ljus
som produceras genom atomkärnornas sammanstötande rekyl då stjärnan expanderar
måste grundas på en ljushastighet (cD) i stjärnytan som är lägre än
stjärnytans initiella expansionshastighet (vD). Bara ljusets gravitella beroende kan ge en sådan funktion, förutsatt stjärnmassan är tillräckligt
stor. Därmed kan stjärnan effektivt spärra av alla observatörer från en del av
ljusbildningen. Inget ljus kommer ut då. Istället för en konstant (avtagande)
ljusutveckling, uppvisas en bruten pulsform med mellanliggande mörka inaktiva
intervall — precis så som det är observerat.
Detta stämmer också enligt TNED med
förutsättningarna för Krabbnebulosans bildning (för ca 1000 år sedan): För att
en primärstjärna (stjärna som fortfarande befinner sig i den första
Väte-Helium-cykeln) precis i vår tid ska ha hunnit fram till sin novapunkt
(bränslekollaps) enligt stjärnornas allmänna histogram ska dess massa enligt tidsekvationen
vara grovt sett 3,4 Solmassor [tSOL/(tSTAR=tNU/2)=(mSTAR/mSOL)2].
Om vi räknar med att (i varje fall) 1/3 av
Krabbnebulosans centrala kompaktstjärna i formen av en Helium-4-stjärnmassa
»försvinner» vid den initiella novabildningen, alltså expanderar bort från
stjärnan och kvarlämnar en mindre massrest, återstår grovt sett 4,5 T30 KG
eller ca 2,3 Solmassor.
Gränsen enligt TNED för en Helium-4-kropp
med tätheten 6,5 T17 KG/M3 ligger vid 2,65 Solmassor för att det
utsläckande ljusvillkoret ska gälla vid expansionens initiering (idealt enligt
de enkla grundsambanden), samt ytterligare en gräns vid ca 1,85 Solmassor om
utsläckningen också ska innefatta statiska tillståndets g-fysik (dessa aspekter finns inte alls med i modern teori,
se utförligt från K-cellens detonation) — och som dessutom visar att överslagsberäkningen är
rimlig. Därmed släcks den första delen av pulsen ner effektivt. Dess senare del
kan framträda längre fram i perioden, men då som funktion av en lägre energi
eftersom primärpulsen redan gått. Tillsammans med olika resonansfenomen (här
utan vidare beskrivning) kan slutresultatet uppvisa i princip vilka
signaltyper som helst inom ett begränsat pulsintervall. Vad som är vad beror på
kompaktstjärnans sammansättning och det material den omger sig med, och vi kan
bara ange graden av den matematikens trolighet med grund i vissa antaganden om
lokalens sammansättning (och resultaten av datorsimulerade verkningssätt till
jämförelse).
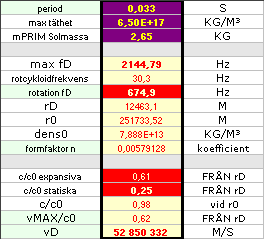
Tabellen nedan ger parametersamlingen
enligt TNED för Krabbnebulosans pulsar — enbart med grund i uppgiften på 33 mS
från den uppmätta periodtiden. Allt övrigt är TNED-resultat.
STÖTENERGIN (E) som krävs
för att belysa Krabbnebulosan är så obetydlig relativt huvudmassans totala
stötenergi att den i stort sett kan förläggas till ett (ekvivalent) tunt
ytskikt med massan m=2E/vmax2. I exemplets fall
med stjärnmassan (Heliumkärna) i enkla men grova termer 5 T30 KG, vmax=0,5c0
och E=T31 J/S [BAs111sp2mn] ges m=8,9 T14 KG med regionen förutsatt betingad
av toppdivergensen c0=2,99792458 T8 M/S. Det är bara
en del på 5×1015 för hela stjärnmassan.
|
orientering |
|
|
|
|
TNED — rotcykloidens råform |
|
observerad pulsform, se sep.
källa |
|
motsv. pulsform TNED |
|
|
Krabbnebulosan 0534+22
— 6 500 lå |
|
|
|
|
|
|
|
|
|
|
|
|
Krabbnebulosan |
|
källa |
|
|
|
||||
|
|
spektrum |
alla |
|
|
|
|||||
|
|
apprx pos Rec±Dekl |
0532+22 |
|
|
|
|||||
|
|
avstånd från Solen ±lå |
– 6500 |
|
|
|
|||||
|
|
period tP Sekunder |
0,033 |
|
|
|
|||||
|
|
rotcykloidfrekvens Hz |
30,30 |
TNED |
|
|
|
||||
|
|
rotation fD Hz |
674,90 |
TNED |
|
|
|
||||
|
|
rD M |
12463,10432 |
TNED |
|
|
|
||||
|
|
r0 M |
251733,5168 |
TNED |
|
|
|
||||
|
|
rmax KG/M3 |
6,5 T17 |
TNED |
|
|
|
||||
|
|
mPRIM Solmassa |
3,40 |
TNED |
|
|
|
||||
|
|
mNUV Solmassa prel. |
2,65 |
TNED |
|
|
|
||||
|
|
formfaktor n |
0,005791283 |
TNED |
|
|
|
||||
|
|
rotationsklass |
högroterande |
TNED |
|
|
|
||||
|
5 000 lå per streck |
|
c/c0 vid rD expansiva |
0,610144107 |
TNED |
väg-tid hastighet-tid |
|
pulsvidd ca 1,5 mS — period 33 mS |
|
|
|
|
1 lå = 1,46073 T15 M |
|
c/c0 vid rD statiska |
0,247290514 |
TNED |
|
|
|
|
|
|
|
1 pc = 3,26 lå |
|
|
|
|
|
|
|
|
|
|
tabellförklaringar
Krabbnebulosan Källa Pulsform: NASA
[http://imagine.gsfc.nasa.gov/docs/science/know_l2/pulsars.html], många
webbkällor visar den här källformen — i olika tappningar.
Weng, @INTERNET Wikipedia engelska
avdelningen Crab Nebula 2008-10-07.
TNED; Se sambanden generellt i PULSARMATEMATIKEN. Dessa finns här
sammanfattade i PSR-exemplet.
kalkylkort Pulsarerna i TNED — manual för
kalkylkortets aktivering
inmatningresultat
Matematikdelen som kortet bygger på beskrivs särskilt i PULSARMATEMATIKEN
ENLIGT TNED
Krabbnebulosans Pulsfysik i Modern Teori är till jämförelse erkänt svårlöslig (ref. @INTERNET
Wikipedia Crab Nebula 2008-10-08):
1.
principen med den roterande neutronstjärnans svepande fyrlika pulsstråle
stämmer dåligt: man räknar här med en typ ”vindpulsar” (eng. pulsar wind
nebula, pulsarvindsnebulosa) för att matcha observationerna med den
omgivande toroidringens periodiska energisättning (den framgår f.ö. direkt
naturligt enligt TNED-pulsarens teori: primär ringstruktur med sekundära
ringformationer) — som i sig heller inte kan förklaras på den roterande
neutronstjärnans bas;
2. den
teoretiska massan stämmer dåligt med observationerna: den teoretiska
ursprungsstjärnans massa (protostjärnan) anges till mellan 9 och 11 Solmassor;
resultatet ligger långt ifrån summan av det nu iakttagbara materialet som
beräknas till omkring 1,4-2 Solmassor för pulsaren plus 2-3 Solmassor för
materialet omkring, totalt och grovt sett max 4 Solmassor — men meningarna är
olika och ingen allmän konsensus finns.
Jämförande
EXPERIMENTEXEMPEL MED SOLEN
Formfaktorn för Solen blir med grundperioden tP = 11,44
år (Solperioden från dag 1 enligt TNED, den är nu 11,1 år) lika med n=63
356 289,98 med en rotationsfrekvens fD på 0,304020814 Hz. Den kurvformen är,
relativt Krabbnebulosans exempel ovan, helt omvänd med spetsarna uppåtvända och
en motsvarande ytterst lågprofilerad hastighet-tid-kurva, i princip en rät
linje med »induktionsspikar» endast vid periodens fusionspunkter. Emellertid
syns inte ett spår av någon sådan »spetsig» väg-tid-form i Solens ljusemission
eftersom Solens aktiva fusionskropp effektivt fyller ut alla sådana luckor.
GRAFISK EKVATION
(unit368)
0.1+0.6[(sinþx)'180]+0.11[(cosþ[1.1+x])'120]+0.05[(sinþ[1.57+x]/1)'20] — mitten
nedan
GRAFISK EKVATION
(unit410) 0.1+0.45[(sinþx)'180]+0.11[(cosþ[1.1+x])'120]+0.05[(sinþ[1.56+x])'30]+0.1[(sinþ[1.98+x])'50]
— höger nedan

Som jämförande exempel på formkänsligheten: Jämför närmast ovan vänster (Pulsen från Krabbnebulosans pulsar i det synliga frekvensområdet) med ovan mitten; Som vi ser återstår (ännu) en del att göra innan pulserna kan anses någorlunda likvärdiga. För att få bättre passning mot originalet är det tydligt att minst ännu en tilläggskomponent måste användas; Pulsen längst till höger visar ett närmande. Originalets pulsform (vänster ovan) visar dessutom en liten högerlutning (2°). En sådan kan också åstadkommas på hela formen genom att lägga till addenden +0,035x (= tan 2°) och sedan återrotera resultatet 2°. Originalpulsen är dessutom mera spetsformad … Och — så — vidare.
Avsikten är dock INTE här att få en helt exakt överensstämmelse med observationspulsen — denna är i vilket fall i sig föremål för olika vrängningar över de stora avstånd som signalen färdas och avspeglar därför heller inte »originalet». Syftet är här ENDAST att undersöka den rimliga formanalogin mot de grundsamband som utpekas av TNED i floran av universums olika ljuskällor.
allmänt om stjärnornas fördelning enligt TNED
Enligt
TNED kan alla ljusproducerande himlakroppar (generellt stjärnor) indelas i tre
typgrupper som kopplar till stjärnans SÄTT att emittera ljus:
1. normal stjärna, 2. variabel, och 3. pulsar.
Pulsaren
skiljer sig från de bägge övriga genom att dess ljus framträder som en distinkt
ljuspuls (intensitetspuls) typ noll-max-noll och sedan ingenting tills nästa puls.
De två andra typerna har inga sådana nollställen utan uppvisar en
tidskontinuerlig ljusaktivitet av större eller lägre magnitud, konstant (1)
eller varierande (2).
Pulsarens matematiska fysik enligt TNED
bygger emellertid på samma cykliska periodicitet som sammanhänger med det inre
i alla stjärnor genom STJÄRNORNAS ALLMÄNNA TRYCKEKVATION och teorin för det centrala STJÄRNSTÄDET
med dess fusionscykler och som (bl.a.) enligt TNED leder till den framgångsrika
teoretiska bestämningen av Solperioden (från max
11,44 år). I den meningen, alltså på den matematikens grund, kan alla stjärnor
utan undantag klassificeras som »pulsarer» — med olika karaktärer.
Speciellt i jämförelse med den moderna
akademins begrepp pulsar, som just betyder en stjärna som uppvisar en
motsvarande ”ensam isolerad ljusstråle” med mellanliggande nollvärde, förlorar
emellertid begreppet pulsar sin rent praktiskt historiska förankring om den
ovan antydda definitionen på pulsar antas (generellt) eftersom det var just på
ljustypens form — intermittent transient med mellanliggande nollvärde — som
begreppet pulsar grundades (1967, upptäckten av pulsaren CP 1919).
Om vi behåller den konventionella redan
väletablerade definitionsbasen kan en pulsar — se Stjärnornas Allmänna Histogram enligt TNED — klassificeras som en helt utbränd
stjärntyp som når sitt maximalt täta tillstånd genom sammandragningen under
slockningsperioden och som därmed uppvisar (periodisk) detonation på grund av atomkärnans inkompressibilitet då atomkärnorna klonkar ihop vid stjärnytans uppnådda
max täthet. Av naturliga skäl kan också en sådan stjärna kallas kompaktstjärna. Dvs., i TNED i princip samma som STJÄRNSTÄDET hos
normalstjärnan. Därmed kan alla stjärnor (enklare) klassificeras enligt TNED på
nedanstående illustrerade typform.
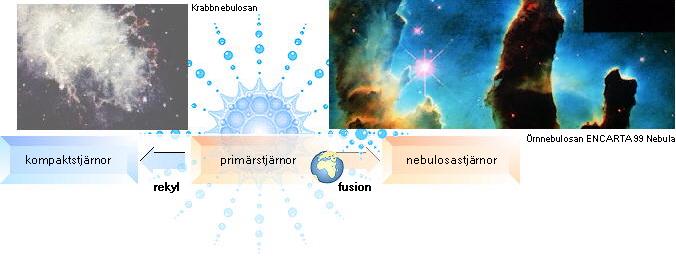
Se mera utförligt i STJÄRNORNAS
ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING.
Beroende på rotation, massa och typ av ämnessammansättning, kan en
kompaktstjärna via sin detonation åstadkomma en stor mängd olika möjliga
ljusemissioner. Basen för de ljusemissionernas beskrivning blir alltså (hur som
helst) pulsarmatematiken, och det är i kraft av denna som de olika objekten i
denna framställning kommer att belysas.
Se PULSARMATEMATIKEN utförligt i separat artikel: Pulsarmatematiken enligt
TNED beskriver den cykliska formgrunden för alla stjärnors ljusemitterande
egenskaper genom den absolut mest elementära, relaterbara, matematiska fysikens
grundbegrepp. Vi förutsätter här full bekantskap.
Kärnbegreppen är perioden (tP),
rotationsfrekvensen (fD) och formfaktorn (n). Dessa tre fungerar FORMELLT helt
oberoende av stjärnmassan — enbart beroende på stjärnans maximala täthet. HUR
stjärnan emitterar ljus, ankommer sedan på stjärnmassans storlek och massans
sammansättning — tillsammans med eventuellt omgivande vätebanker. Stjärnmassan
kan beräknas först med kännedom om den maximala detonationshastigheten (vD). Se
samband i PSR-exemplet.
pulsarens förklarande matematik
Den matematiska fysik som helt
förklarar
pulsarernas fysik ENLIGT TNED
grundform relaterad fysik ............ c/c0=[1–w2/cc0]
ingår inte i den moderna akademins
lärosystem. Helt uteslutet. Intrinsiskt rent.
Se
även Så
föddes uppfattningen om den roterande neutronstjärnan.
I relaterad fysik bevaras
naturkonstanten
c0 i energiledet E=Ec+EG
och kraftvektorledet Fc=Fc0–FG
genom ljusets gravitella beroende;
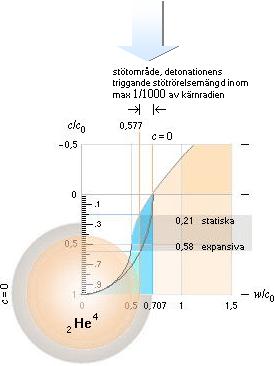
Se även i GRÄNSMASSORNA.
Einstein kunde inte
härleda den fysiken på grund av sin låsning vid v+ic-felet
och som sammanhänger med fysikens beskrivning via
Varför inte då?
Svar:
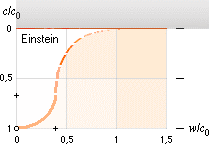
grundform
Einstein .................... c/c0=[1–w2/c2]
Se utförligt från v+ic-felet.
Einsteins relativitetsteori utesluter hela ämnet
— och
öppnar samtidigt en flod av motsvarande sensationella beskrivningar.
TNED: När en stjärna genomgått sin energicykelfas, vilket innebär att den gjort slut på sitt primära Väte som omvandlats till Helium-4, börjar stjärnan krympa som följd av att fusionsenergin upphör. Därmed försvinner stjärnans strålningstryck och den kan i princip sjunka ihop på sin maximala täthet — som i fallet Helium-4 enligt TNED är 7,22 T17 KG/M3. Så länge kontraktion (eller expansion) pågår gäller kontraktiva tillståndets g-fysik (den högra elliptiska kurvdelen i 2He4-grafen ovan till vänster, den relaterade fysikens grundform). När maximal täthet uppnås och därmed kontraktionen upphör, vilket i TNED betyder att atomkärna vidrör atomkärna, gäller inte längre kontraktiva/expansiva g-fysiken utan istället statiska tillståndets g-fysik (den vänstra mindre cirkulära kurvdelen i 2He4-grafen ovan; utförliga härledningar i expansionsmatematiken). Därmed förskjuts också referenspunkten för stjärnans g-tryck mot en punkt längre in i stjärnkroppen — som DÄRMED garanterar att stjärnan detonerar:
F=k(Q/r)2=k([Q/(n®¥)]/[r/(n®¥)])2=k(Q/r)2
Atomkärnan kan inte komprimeras, den står redan på noll. Varje tendens att försöka pressa ihop stjärnmaterialet från läge max täthet resulterar i en resolut motkraft: detonation. Kontraktionsfasen avslutas ALLTSÅ TVUNGET med en garanterad detonation som tvingar stjärnmaterialet att expandera [‡1].
Expansionen kan ske på många olika sätt, och en starkt bidragande faktor är om stjärnan också har en egen rotation — vilket genom centrifugalkraftens inverkan dämpar expansionens häftighet och därmed kan göra förloppet periodiskt. Därmed kan stjärnkroppen uppvisa tillhörande ljusemissioner av många olika slag och typer — genomgående över hela det elektromagnetiska spektret.
Kontraktionsfasen avslutas ENLIGT TNED med en
garanterad detonation som tvingar stjärnmaterialet att expandera
”De kärnfysikaliska processer som föregår ett supernovautbrott redovisas
på annat håll, så vi nöjer oss här med en kort sammanfattning. I det innersta
av en stjärna som hunnit långt i sin utveckling försiggår flera olika processer
som kan absorbera energi och därmed också initiera en gravitationskollaps.
Dessa processer klarlades på 1950‑talet. Problemet var hur denna kollaps
kunde vändas till den iakttagna expansionen hos supernovan och dess gasrester.
Uppenbart var att naturen på något sätt kunde åstadkomma en sådan omvändning,
och dennas konsekvenser för kärnsyntesen diskuterades mot slutet av 50‑talet
mycket grundligt av E. M. och G. R. Burbidge, W. A. Fowler och Fred Hoyle. På
den tiden trodde astronomerna att supernovautbrotten inte kvarlämnade några stjärnrester
alls. Detta antagande kullkastades mot slutet av 60‑talet genom
upptäckten av pulsarerna. Det stod snart klart att dessa pulsarer måste
vara snabbt roterande neutronstjärnor, sammanstörtade stjärnor med densiteter på över 1018 kg/m3. Det enda kända sättet att åstadkomma sådana
stjärnor var de
kollapsprocesser man räknat sig fram till i samband med supernovautbrotten.
Sedan knöts hela denna tankekedja prydligt samman genom upptäckten av en pulsar
i Krabbnebulosans centrum. Det sker mycket riktigt ett sammanbrott i stjärnans
centrum, men detta hejdas och kastas om i dess yttre skikt, genom processer som
uppträder vid gränsytan mellan dessa skikt och kärnan.”
BONNIERS ASTRONOMI 1978 s86sp2m
Kommentar:
Teorin för detonation genom gravitell kontraktion i modern akademi kunde inte utvecklas på 1950-talet och kan inte utvecklas nu heller (2007) på grund av felaktiga (djupt bristfälliga) föreställningar om massans grundfysik. Se vidare i Atomkärnans härledning enligt TNED. För att kompensera dessa brister, var man tvungen att uppfinna »motsvarande förklaringar», vilket lett fram till en — i termer av TNED väl etablerad — pseudofysik (Jämför Planckekvivalenterna).
Se vidare exempel på observerade ljuskurvor och jämförelserna i atomvikter mellan TNED och MAC (Modern Academy):
CITAT — fetstilen i citattexten är min markering
PSR B1913+16
”In 1974, Joseph Taylor and Russell Hulse discovered for the first time a pulsar in a binary system, PSR B1913+16. This pulsar orbits another neutron star with an orbital period of just eight hours. Einstein's theory of general relativity predicts that this system should emit strong gravitational radiation, causing the orbit to continually contract as it loses orbital energy. Observations of the pulsar soon confirmed this prediction, providing the first ever proof of the existence of gravitational waves. As of 2004, observations of this pulsar continue to agree with general relativity. In 1993 the Nobel prize in physics was awarded to Taylor and Hulse for the discovery of this pulsar.”
@INTERNET Wikipedia Pulsar 2007-02-28
Min översättning:
År 1974 upptäckte Joseph Taylor och Russel Hulse för första gången en pulsar i ett binärt system, PSR B1913+16. Denna pulsar går i bana kring en annan neutronstjärna med en banperiod på just åtta timmar. Einsteins allmänna relativitetsteori förutsäger att detta system skulle emittera stark gravitationsstrålning, förorsakande banan att sammandras kontinuerligt som den förlorar banenergi. Observationer av pulsaren bekräftade snart denna förutsägelse, tillhandahållande det första beviset någonsin för existensen av gravitationsvågor. Ännu 2004, fortsätter observationer av denna pulsar att överensstämma med den allmänna relativitetsteorin. År 1993 tilldelades Taylor och Hulse nobelpriset i fysik för upptäckten av denna pulsar.
”Werner Becker of the Max-Planck-Institut für extraterrestrische Physik recently said,
“The theory of how pulsars emit their radiation is still in its infancy, even after nearly forty years of work.””
@INTERNET Wikipedia Pulsar 2007-02-28
”PSR B1913+16
PSR B1913+16 (also known as J1915+1606) is a pulsar in a binary star system, in orbit with another star around a common center of mass. In 1974 it was discovered by Russell Alan Hulse and Joseph Hooton Taylor, Jr., of Princeton University, a discovery for which they were awarded the 1993 Nobel Prize in Physics.
Using the Arecibo 305m antenna, Hulse and Taylor detected pulsed radio emissions and thus identified the source as a pulsar, a rapidly rotating, highly magnetized neutron star. The neutron star rotates on its axis 17 times per second; thus the pulse period is 59 milliseconds.
After timing the radio pulses for some time, Hulse and Taylor noticed that there was a systematic variation in the arrival time of the pulses. Sometimes, the pulses were received a little sooner than expected; sometimes, later than expected. These variations changed in a smooth and repetitive manner, with a period of 7.75 hours. They realized that such behavior is predicted if the pulsar were in a binary orbit with another star.
The pulsar and its companion both follow elliptical orbits around their common center of mass. Each star moves in its orbit according to Kepler's Laws; at all times the two stars are found on opposite sides of a line passing through the center of mass. The period of the orbital motion is 7.75 hours, and the stars are believed to be nearly equal in mass, about 1.4 solar masses.
The minimum separation at periastron is about 1.1 solar radii; the maximum separation at apastron is 4.8 solar radii. In the case of PSR B1913+16, the orbit is inclined at about 45 degrees with respect to the plane of the sky, and it is oriented such that periastron occurs nearly perpendicular to our line of sight.
The orbit has evolved since the binary system was initially discovered, in precise agreement with the loss of energy due to gravitational waves predicted by Einstein's General Theory of Relativity.”
@INTERNET Wikipedia PSR B1913+16 2007-02-28
‡[2] @INTERNET 2007III1 [www.johnstonarchive.net/relativity/binpulsar.html] Data on the PSR B1913+16 system
DATA PSR1913+16
Data Givna Grunddata från ovan Beräknade Data enligt TNED
————————— ————————————— ——————————————
hastighet 402 KM/S [BAs93] 402 KM/S (vDmax)
cyklisk period 7,752 timmar 7,752 timmar (TP)
»pulsfrekvens» 17 Hz 7,14 Hz (fD)
massa 1,4 Solmassor 1,01 Solmassor Helium-4 | 6,5 T17 | 7,22 T17 | KG/M3 |
avstånd 21 000 lå [‡1]
NOTERINGAR:
Det beräknade värdet 7,14 Hz är fD-värdet (detonationsrotationsfrekvensen).
Hur stjärnan uppför sig generellt (i resonans totalt) finns här ingen framställning på.
Uppgiften i citat på 17 Hz är inte specificerad.
Citatet från Wikipedia uppvisar ingen graf.
Citatkällan anger inte i vilken region objektet finns, eller avståndet till det.
För att bemöta citatets uppgifter med TNED-analys, måste en mera noggrann redovisning ges av objektets mätdata.
—————————————————————————————————————————————————————
‡[1] @INTERNET 2007III1 [www.johnstonarchive.net/relativity/binpulsar.html]
Data on the PSR B1913+16 system
Ovanstående referens innehåller utförliga övriga data på PSR
1913+16 [Se »Binary pulsar PSR B1913+16» på Google].
SPÖKSTJÄRNORNA
GRUNDLÄGGANDE INVÄNDNINGAR MOT DEN MODERNA AKADEMINS DATATOLKNING?
Inledning
|
MED stjärnfysikens grund enligt TNED i · DETONATIONSGRÄNSMASSAN PÅ MAX 15 SOLMASSOR framträder MÖJLIGEN ENLIGT TNED — här ännu till prövning — stjärnfysikaliska fenomen vars matematiska fysik INTE kan härledas av konventionell kosmologi — eftersom man där anser att stjärnorna bildades ur kontraherande gasmassor i ett expanderande universum. Påstående: I konventionell kosmologi medför FELTOLKNINGEN av fenomenformerna bakom ovanstående punktstycke uppkomsten av motsvarande SPÖKSTJÄRNOR — uppfunna objekt — eftersom man inte kan härleda funktionen från STJÄRNSTÄDET. Exempel En normalstjärna på 10 Solmassor (m10) har ENLIGT TNED en ytvärmegrad på T=23 500 °K. Strålningstryckets starkt kalljoniserande värmegradsekvivalent vid stjärnytan är Tg=35,8 miljoner grader. Låt oss anta att stjärnan dämpas med en faktor 1000 på grund av reducerad ljushastighet genom stjärnytans starka gravitation. Detta ger stjärnyttemperaturen T=23,5 °K och strålningstryckets temperaturekvivalent Tg= 35 800 °K. Därmed motsvarande SPEKTRALA detaljer; Stjärnljuset kan omöjligen gömma undan den rent spektrala effekten från Tg i detta läge. Spektralkartan för den stjärnans ekvivalenta värmegrad som närmar sig gränsmassan m10 kan på detta sätt vid en direkt spektral genomgång av allt ljus som stjärnan utsänder förstås uppvisa (våldsamt) högre frekvenser relativt sitt sanna tillstånd; Stjärnans allmänna Planckkurva speglar en betydligt högre temperaturtopp. KÄNNER MAN INTE DESSA GRUNDER förvillas man dra slutsatsen att stjärnan har betydligt större massa än sin normalekvivalent. I exemplets enkla fall skulle värdet T=35 800 °K motsvara en normal stjärnmassa på [(35 800)/(6 150)]12/7=20,5 Solmassor. Inte 10. Felet blir alltså våldsamt. |
Den här artikeln kan MÖJLIGEN utvidgas med speciella — mera praktiskt jämförande — exempel som också ansluter till pulsarernas ljuskurvor enligt TNED, se det inledande exemplet med PSR 1913+16; Exemplet med just PSR 1913+16 är här ett skolexempel (För TNED:s del).
Vi vet emellertid ännu varken mycket om de bakomliggande objekten till långt avlägsna ljuspunkter som uppvisar periodiska variationer, eller om TNED-matematiken för dessa fall ens har någon fysikalisk motsvarighet alls.
Tills vidare får ovanstående stå som en (eventuell) introduktion till ev. vidare beskrivningar;
Endast OM ytterligare uppslag kommer fram, kommer en vidare beskrivning att genomföras.
PSR-exemplet
med allmänna samband
HUR
VÄG-TID-FUNKTIONEN I ROTCYKLOIDENS GRUNDMATEMATIK ENLIGT TNED KAN HARMONIERA
MED
EN
PRAKTISK HASTIGHET-TID-FUNKTION ENLIGT DET ILLUSTRERADE EXEMPLET MED PSR 1913+16
eller
GRUNDERNA
I LJUSKURVORNAS FUNKTIONELLA PRAKTIK ENLIGT TNED
Speciellt i översikt
beskrivs klassen pulsarer i TNED enligt nedanstående grundsamband
— se utförliga härledningar i Pulsarmatematiken
fD = (4Grmax/TPp2Ö3)1/3 ............... rotationsfrekvensen ur pulsfrekvensen
1/TP = fD3[4Grmax]–1p2Ö3 ................... pulsfrekvensen ur rotationsfrekvensen
vD = fD(6p2m2/rmax)1/3
......................... rotationshastigheten
via maxtätheten
given
centralmassa och max rotationsfrekvens
m2 = rmax(vD/fD)3/6p2
= rmaxvD3(TPp2(Ö3)/4Grmax)/6p2
= rmaxvD3TPp2(Ö3)/4Grmax6p2
= vD3TP(Ö3)/24G = vD3TP(1,08199 T9 KG2/JM)
=
vD3TP/GÖ192
y = [(cos ax)2]n ............ rotcykloidens allmänna ekvation, i PREFIXxSIN, vägen-tiden
n = 4Grmax/p4fD3 ..... n anger
rotcykloidens form
Studieexempel — den möjliga funktionsbeskrivningen för
objektet PSR 1913+16 enligt TNED genom pulsarmatematiken
|
BONNIERS ASTRONOMI 1978 s93 figur 5.11, PSR 1913+16: |
Figurförklaring — Den moderna akademins radialhastighetskurva genom en elliptisk analogi |
|
|
|
|
Illustrationens text: ”5.11: Radialhastighetskurva för pulsaren PSR 1913 + 16 som ingår i ett dubbelsystem. Radialhastigheten anges i km/s — positiva värden anger rörelse bort från jorden och vice versa. Omloppstiden är 0,323 dygn. Kurvan avviker kraftigt från en enkel sinuskurva på grund av banans höga excentricitet (e = 0,6).”. |
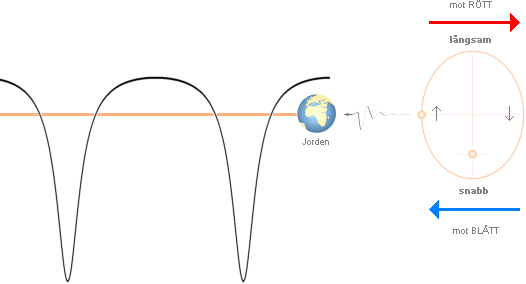
När objektet (PSR 1913+16) — som utsänder (radio-) strålning — rör
sig bort från Jorden förskjuts ”tonen” eller färgen mot längre våglängd
(rött). Denna del motsvarar den övre kurvdelen över nollinjen
(radialhastigheten 0 till ca +80 KM/S). När objektet sedan vänder och åter
börjar röra sig mot Jorden förskjuts tonen eller färgen mot kortare våglängd
(blått). Denna del motsvarar de undre kurvdelarna under nollinjen
(radialhastigheten 0 till ca –320 KM/S). |
Mätkurvan ovan vänster från Bonnierskällan motsvarar radialhastigheterna mot-från Jorden erhållna ur de olika våglängdsförskjutningarna i den mottagna strålningsändringen från objektet. Radialhastighetskurvan motsvarar den form som uppvisas av ett objekt som rör sig i en elliptisk bana med den angivna excentriciteten, illustrationen ovan till höger.
Genom att radialhastighetskurvan i varje sin kurvpunkt avspeglar funktionen v=d/T, gäller rent teoretiskt precis samma funktion i formen av en helt ren radialdistanskurva, alltså enbart genom att multiplicera med en tidskonstant T=1 Sekund som ger v·1S = d, vilket leder till att hastigheten (v) exakt kommer att motsvara en distans (d) — och därmed bilden av hur en kropp sväller och drar ihop sig periodiskt. Vilket vill säga: Den uppmätta Bonnierskurvan kan lika gärna ses som ett variationsdiagram över hur en kroppsrand kontraherar och expanderar periodiskt, här med perioden 7,752 timmar med totala hastighetsintervallet noll till 404,2 KM/S.
ENLIGT TNED kan rotcykloidens grundform INTE DIREKT ta hänsyn till eventuellt dämpande omgivande stjärnmaterial: Rotcykloidens grundform tar bara hänsyn till stjärnans g-rand i formen av en ideal ring.
I fallet PSR 1913+16 med perioden 7,752 timmar betyder det att rotcykloidens råform enligt TNED med n runt 4900 kommer att skilja sig föga från principgrafen
…|¯ |¯ |¯ |¯ |¯ |¯ |…
Med uppgiften från BONNIERS ASTRONOMI 1978 på sidan 93 på objektet PSR 1913 + 16 med perioden 0,323 dygn eller 7,752 timmar — ett FÖRMODAT s.k. trångt spektroskopiskt dubbelstjärnesystem — framgår radialhastigheten (största värdet) av källans illustration till max 405 KM/S (404,2 KM/S);
Vi tillämpar TNED-matematiken ovan med rmax= 6,5 T17 KG/M3 och får via
TP = 0,323 dygn = 27907,2 S för en ensam stjärna med max perifer rotationshastighet
vD = 405 KM/S
en Helium-4-baserad central restmassa på 2,00889 T30 KG eller runt 1,01 Solmassor,
med rmax= 6,5 T17 KG/M3; Cykloidfaktorn för den helt odämpade massutkastningsgrafen blir
n = 4897,53 och stjärnan uppvisar en max rotationsfrekvens
fD = 7,13687 Hz med detonationshastigheten
vD = 0,5731c0 och lägsta ytdivergensen (vid detonationsradien rD) lika med 0,8185c0.
Enligt uppgifter [‡1] ligger objektet strax utanför den runda centrala ansvällningen i Vintergatans centrum, sett härifrån ca 21 000 lå eller drygt 6,4 Kpc; Den helt odämpade råformen (n=4897,53) skulle därför kunna uppfattas som orealistiskt brant OM lokalen är väterik och därmed väsentligen dämpande — men vi har ingen som helst möjlighet att kontrollera den exakta lokalens beskaffenhet. Vi kan ingenting bevisa i det avseendet. Vi kan emellertid sluta oss till — eftersom lokalen tydligen befinner i Vintergatans mest turbulenta område, centrum eller i dess närhet — att objektet omges av vätgas som åstadkommer maximal dämpning — analogt en betydande reduktion i täthetsformen:
Se även från den beskrivande inledningen för objektet PSR 1913+16, samt vidare i EXEMPEL.
y = –0,028[([1 + (1,25tanx)2]1/2[0,92 + secx]–1)2]2,2 ........... PREFIXxSIN
Denna form kommer från ett grundsamband
v = (K/r)(1+ [tanx]/E)1/2(e + secx)–1 ............. ellipsfunktionen
med de elliptiska banparametrarna
v omloppskroppens banhastighet i ellipsens tangent
K Keplermomentets ytkonstant (M2/S)
r ellipsens storaxel
x centrumvinkeln mätt från ellipsens/cirkelns centrum
E ellipsens excentricitet, stora excentricitetstalet (lillaxeln/storaxeln)
e ellipsens excentricitet, lilla excentricitetstalet (fokuslängden/storaxeln)
e2+E2 = 1
y = –0,87([(0,9 + [(tanx)/0,88]2)0,5][0,9 + secx]–1)0,96 ........... PREFIXxSIN

epsGRAFEKVATION(unit028)
–0.87([(0.9+[(tanx)/0.88]'2)'0.5][0.9+secx]'–1)'0.96
Vi kan se FLERA AVVIKELSER i originalgrafens matchning (ovan) mot den ideala ellipsbanans v/t-form — och som i vilket fall DÄRMED aldrig kan garantera någon enkel exakthet med elementära funktioner. Dessutom är y-grafen ovan (y=–0,028…) INTE optimerad (vilket betyder att den KAN fås att passa ÄNNU bättre med ÄNNU flera parametrar).
Det finns (nämligen) också YTTERLIGARE funktionsformer som kan ses passa in tämligen noga (och som avslöjar en viss tydlig asymmetrisk skevhet i exempelgrafen från Bonnierskällan, övre rundningen, och som inte borde finnas där om objektet vore en ellipsbana);
Se alternativet
y = –1,445(0,55 + 0,5 sin 0,501x)–0,8 ........................ PREFIXxSIN

accGRAFEKVATION(unit028)
–1.445(0.55+0.5sin[0.501x])'–0.8
derivatan
–1.445(0.8·0.5·0.501·cos0.501x)[0.55+0.5sin0.501x]'–0.8–1
se även (möjligen enklare) 3.2–(1–0.9sinþx)'–0.5
Originalgrafen från BONNIERS ASTRONOMI 1978 s93 figur 5.11, PSR 1913+16, här återigen lagd ovanpå y-grafen ovan (underliggande svart).
Funktionsformen ovan (y=–1,445…) kommer ifrån en DELVIS grundform för accelerationskonstantens variation genom föregående ellipsfunktion (här utan bevis eller härledning). Grafen tjärnar endast att exemplifiera FLORAN AV MÖJLIGHETER — och vilken parameterbetsyckning vi i vilket fall ALDRIG KAN KONTROLLERA MOT DET FYSISKA OBJEKTET. Vi kan bara göra det mer eller mindre troligt att objektet HAR den och den funktionsmatematiken.
Eller sagt med andra ord:
TNED utpekar att ytdivergensen för objektet PSR 1913+16 vid
minsta radien (9 KM) är 0,82c0 med detonationshastigheten 0,57c0 vilket garanterar att objektet emitterar ljus kontinuerligt —
utan mörka mellanliggande intermittenta avbrott, om än med varierande frekvens
och intensitet:
Objektet är INTE ett
dubbelstjärnesystem. Objektet är EN stjärna.
Kompaktstjärnans pulserande period (tP) är de angivna
0,323 dygnen, analogt 7,752 timmar.
Inget annat. Det finns inga andra komponenter. Stjärnan
KAN FÖRSTÅS emittera sitt ljus PERIODISKT på (nära exakt) samma matematiska
form som en kropp som rör sig i en elliptisk bana kring en annan kropp — enligt
ovanstående matematiska exempel PSR 1913+16.
Se
även från Exemplet PSR1913.
Genom den konventionella teorin som
beskriver fenomenets grund i ett dubbelstjärnesystem, anges respektive stjärnmassor
till 1,441 resp 1,387 Solmassor.
[http://www.johnstonesarchive.net/relativity/binpulsar.html]2008-10-03 | 30 Aug 2004
Därmed skulle den SÅ beskrivna
ensamma stjärna OCKSÅ ansluta till samma principiella dubbelspektrum
som det vilket visas illustrerat i FOCUS MATERIEN 1975 (FMs617) — samt av samma typ i Bonnierskällan [BAs93fig5.10].
Den råa cykloidiska kurvformen för stjärnans
expansion-kontraktion i TNED kan alltså med de ovannämnda förutsättningarna
MÖJLIGEN förstås övergå i samma principiella karaktär som den i
Bonnierskällan illustrerade experimentellt uppmätta.
Uppgiften på 17 Hz i
Bonnierskällan — och övriga
Enligt uppgifter i alla (samtliga) fackböcker [BAs114sp2mö ”59,03 ms”] skulle ljusobjektet bakom PSR 1913+16 (en konventionellt benämnd s.k. neutronstjärna) uppvisa en superkonstant periodisk rotation på 17 Hz, eller mera noga 0,05903 S = 59,03 mS. Bonnierskällan ger ingen direkt redovisning på HUR den pulsen har uppmätts, eller visar någon BILD på hur den pulsen ser ut.
Om vi letar på webben (September 2008) hittar vi heller inget sådant basdata:
det finns ingen sådan — enskild — puls
Separat
sökning @INTERNET 24 September 2008 visar att uppgiften på 17 Hz gömmer ett
ytterst komplicerat observationskomplex: signalerna ligger ”utsmetade” inom
ett frekvensfönster på grovt hela 5 Hz
(170 mS): Högre frekvenser anländer före
lägre — fenomenet kallas (frekvens-) dispersion och sägs bero på varierande
elektrontäthet genom signalvägen hit till Jorden. ”FrekvensSmeten” måste
de-analyseras av speciella selektiva spektralinstrument med tillhörande
datorisering för att få ihop det på slutet.
Uppgifterna på ”den exakta ljuskurvan” är
alltså — och därmed, frånsett den allmänna dopplerkurvan som visar den stora
huvudperioden (tP) — dels ytterst knapphändiga — alltså i princip
instrumentellt helt obefintliga — och dessutom så diversifierade att vi inte
ens säkert kan tala om EN observerad ljusemission; Alltsammans är i vilket fall
i slutänden sammanställt (efter olika algoritmer) till ”en passande slutform”.
Vi vet inte hur signalen ser ut som lämnar objektets närmaste lokal, finns inte
en chans att avgöra det.
Med andra ord, uppgiften på 17 Hz är
statistiskt framräknad ur en stor mängd uppmätta frekvensdata med stor
spridning, inte
direkt uppmätt. Därmed är det också omöjligt att relatera den uppgiften.
THE DISCOVERY
OF THE BINARY PULSAR, Russel A. Hulse 1993
[http://nobelprize.org/nobel_prizes/physics/laureates/1993/hulse-lecture.pdf] s54:
”For
example, when observing at 430MHz at Arecibo, the differential time delay across
the available 8MHz bandwidth for a distant pulsar with DM N 200 cm-3pc would be 170 ms. Since this dispersion across the receiver bandwidth is much
larger than a typical pulsar pulse width or even the entire period of short-period pulsars, “de-dispersion” is usually part of
any pulsar observation.”,
Min
översättning:
Till exempel, när man observerar vid 430 MHz vid Arecibo [en stor radioteleskopstation i Sydamerika, Puerto Rico], skulle den differentiella tidsfördröjningen över den tillgängliga 8 MHz bandbredden för en avlägsen pulsar bli 170 millisekunder. Eftersom denna dispersion över mottagarens bandbredd är mycket större än en typisk pulsars pulsbredd eller även hela perioden hos kortperiodiska pulsarer, blir ”de-dispersering” vanligen en del av varje pulsars observation.
SÅ HÄR SER »PULSEN» UT:
[http://www.ias.ac.in/jarch/jaa/16/307-325.pdf],
Binary Pulsars and Relativistic Gravity
Diamond Jubilee Symposium on Pulsars 14-17 March 1994, Raman Research Institute, Bangalore
s312:
”
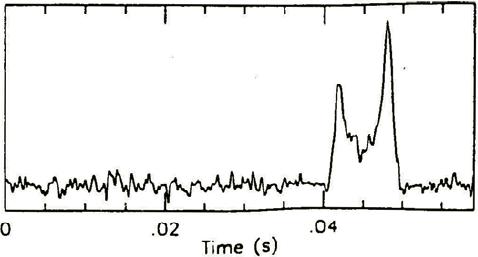
”;
”
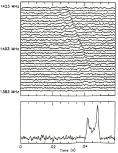
”, bilden ovan här förminskad
från originalet, jämför bilden överst
”Figure
4: Pulse profiles obtained on April 24, 1992 during a five-minute observation
of PSR 1913+16. The characteristic double-peaked shape, clearly seen in the
de-dispersed profile at the bottom, is also discernible in the 32 individual
spectral channels.”,
Min
översättning:
Figur
4: Pulsprofil erhållen 24 April 1992 under fem minuters observation av PSR
1913+16. Den karaktäristiska dubbeltoppade formen, tydligt synbar i den
disperserade profilen längst ner, är också skönjbar i de 32 individuella
spektrala kanalerna.
NOTERA PULSBREDDEN PÅ CA 10 mS i bilden ovan: I ljuset av TNED-teorin kan vi »lätt» se hur källan till den (dubbel-) pulsen ges vid tillfället då stjärnmaterialet kastas ut vid max rotation (fD, stjärnan hinner rotera drygt 25 grader under pulsbildningen). Pulsen avspeglar det korta statiska tillståndets avgörande rekyl, och kommer därför att integreras i hela materialkroppen tillsammans med expansionen och den påföljande kontraktionen — samt därmed innefatta all information som finns beträffande dopplerförskjutningarna och som beskriver den egentliga perioden (tP).
Ovanstående bildexempel visar inte SÅ tydligt olikheterna mellan de skilda pulserna, mera att de ligger förskjutna i frekvens (genom den omtalade s.k. dispersionen samma som spridning). En betydligt bättre illustrativ webbkälla som visar pulsernas principiella olikhet ges nedan (textmarkeringarna är mina).
[http://www.emis.de/journals/LRG/Articles/lrr-2003-5/download/lrr-2003-5Color.pdf],
Testing General Relativity with Pulsar Timing, Ingrid H. Stairs, University of British Columbia 2003
s6:
”
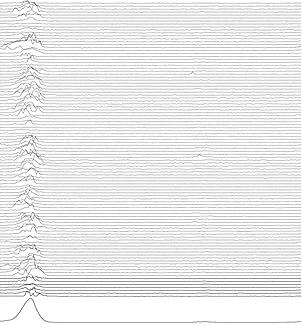
”;
”Figure
1:
Top: 100 single pulses from the 253-ms pulsar B0950+08,
demonstrating pulse-to-pulse variability in shape and intensity.
Bottom: Cumulative profile for this pulsar over 5 minutes (about 1200 pulses); this approaches the
reproducible standard profile. Observations taken with the Green Bank Telescope
[98]. (Stairs, unpublished.)”,
”The exact mechanism by which a pulsar
radiates the energy observed as radio pulses is still
a subject of vigorous debate.”,
”Radio
pulsars were firmly established to be neutron stars by the discovery of the pulsar
in the Crab nebula [120]; its 33-ms period was too fast for a
pulsating or rotating white dwarf, leaving
a rotating neutron star as the only surviving model [108, 53].”,
Min
översättning:
Figur
1: Överst: 100 enskilda pulser från 253 millisekundpulsaren B0950+08,
demonstrerande puls till pulsvariabilitet i form och intensitet. Nederst:
Ackumulerad (statistiskt framräknad) profil för denna pulsar över 5
minuter (omkring 1200 pulser); denna närmar sig den reproducerbara
standardprofilen. Observationerna tagna med Green Bank Teleskopet [98].
(Stairs, opublicerat).
Den
exakta mekanism med vilken en pulsar utstrålar energin observerad som
radiopulser är fortfarande ett ämne under vigorös debatt.
Radiopulsarer
blev stadigt etablerade som neutronstjärnor genom upptäckten av pulsaren i
Krabbnebulosan [120]; dess 33-millisekunders period var för snabb för en
pulserande eller roterande vit dvärg, lämnande en roterande neutronstjärna som
den enda överlevande modellen [108, 53].
NOTERA ATT MAN SOM LÄSARE I ALLMÄNHET FÅR JOBBA HÅRT FÖR ATT VASKA FRAM DET OVAN NÄMNDA: Bonnierskällan till exempel (Standardverket om Universum från Cambridge 1977) omnämner INTE den grundläggande — ovan i citat delvis exemplifierade — ytterst omständliga signalanalys som INTE I SAMTLIGA FALL krävs för att erhålla den konventionella facklitteraturens pulsardata. Som läsare får man istället intrycket att det som vetenskaparna mäter på är DIREKTA PULSER — alltid. Så är det alltså INTE. Det föregående exemplet PSR 1913+16 är ett exempel — uppgiften på 17 Hz-perioden. Det faktum ATT det verkligen finns pulsarer som också, verkligen, uppvisar en fast period, bildar (härifrån) i ljuset av TNED och ovanstående genomgång en selektiv spärr mot varje VIDARE (”allmänpulsariska”) litterära överseende: vi vill (härifrån, och NU allt framledes) veta exakt vilken den mätande observerade pulsformen är — typ ovan förevisade föredömliga exempel från Stairs.
»PULSEN» FRÅN PSR 1913+16 har alltså framkommit ur en enorm signalbank av OLIKA PULSER, utspridda över stora frekvensområden — med närmast enorma marginaler, en siffra på 170 mS omnämns; Pulsbankens individer, varje enskild puls, bearbetas i datamaskiner med olika speciellt anpassade signalbehandlingsprogram för att i slutänden få fram ett konstantvärde baserat på en s.k. statistisk pulsprofil. Den framräknas. Den existerar inte fysiskt observerbar.
I TNED finns bara en fast period i pulsarens fysik: detonationsperioden tP (TP), perioden som bestämmer intervallet för stjärnaktivitetens energiproduktion. Pulsarens rotationsfrekvens i TNED har sitt högsta värde (fD), men detta avtar naturligtvis då materialet kastas ut och når sitt minimivärde (f0) där materialet mäter sin största utsträckning. I PSR 1913+16-exemplet ovan är tP perioden mellan »bottenpelarna», lika med 7,752 timmar. Eller sagt på annat sätt — enligt TNED:
Det finns ingen annan fast period i pulsarens fysik att leta
efter;
Pulsen på 17 Hz är — i detta fall med objektet PSR 1913+16 —
uppenbarligen en spökpuls.
PULSARENS ALLMÄNNA FUNKTION
ENLIGT TNED
I modern teori uteslöt man redan från början (1967) en koppling mellan rotation OCH puls — därför att man inte kan relatera en sådan grund på kärnfysikens bas i modern mening. Därmed satte man sig också i sinnet att ur alla möjliga detekterade pulser med den kortaste perioden från universums rymdhav söka EN bestämd frekvens ur någon systematiskt stor spridning (den automatiserade anordningen letar systematiskt efter sådana) från en stor mängd detekterade skilda frekvenser genom att med grund i en VISS TEORI OM VAD PULSARFYSIKEN GÅR UT PÅ programmatiskt SYNTETISERA fram en sådan bestämd frekvens trots att ingen sådan direkt föreligger i den mätande anordningen enligt de citerade källverken, se Uppgiften på 17 Hz.
Insisterar man på att vaska fram en sådan bestämd frekvens ur frekvenshavet, är det tydligt — OM det nu är TNED:s pulsarfysik som gäller — att man har lyckats alldeles utomordentligt med att SKAPA sitt pulsarobjekt precis så som man vill ha det; Uppgiften på 17 Hz i PSR 1913+16-objektet är en uppfunnen fast (medel-) frekvens framräknad på statistisk bas; Den kan uppenbarligen ingen annan fysikalisk dynamisk källbas ha än rotfrekvensen — enligt TNED, fD — på max 7,14 Hz.
Så här fungerar det — enligt TNED:
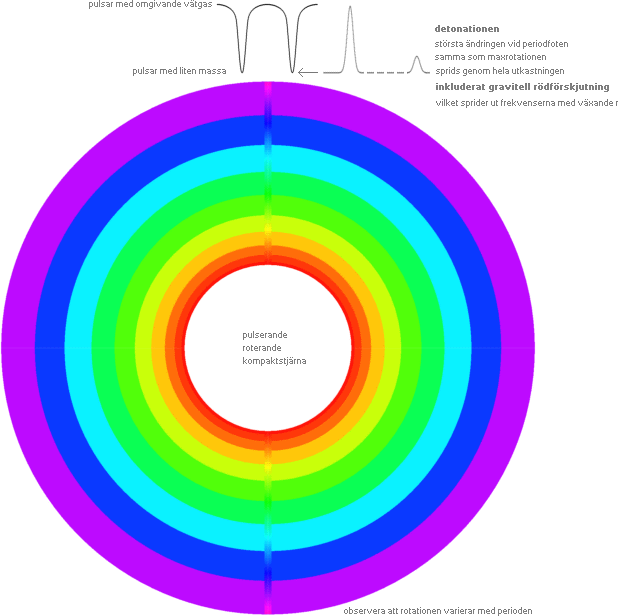
TNED: Den högtäta centrala
kompaktstjärnan spärrar alltid ljusvägen för det ljus som bildas bakom stjärnan
sett från en observatör framför stjärnan: ljuset bakom kommer inte igenom den
täta massan. Det observatören ser är (i princip) bara ljuset som stjärnan
producerar utmed kortaste ljusvägen observatör-objekt. För stjärnmassor som
tillsammans med rotationsfrekvensen uppvisar en högre detonationshastighet (vD) än stjärnytans ljusdivergens (cD) uppkommer helt mörka avsnitt i ljuset från
det material som expanderar — helt eller delvis — beroende på stjärnans
sammansättning och lokal. En sådan avgränsning vittnar om en kompaktstjärna med
relativt stor massa (och därmed i allmänhet en kort period). PSR 1913+16 är
inte ett sådant objekt — men pulsaren i
Krabbnebulosan är det, helt säkert.
När det omgivande materialet når sin minsta utsträckning från kompaktstjärnans centrum — analogt när detonation inträffar — bildar kärnrekylerna kraften till den ljusenergi som frigörs då materialet kastas ut på den samtidiga maximala rotationsfrekvensen — i PSR 1913+16-exemplet 7,14 Hz enligt TNED. Turbulensen i det utkastade materialskiktet garanterar i vilket fall att NÅGON (radio-) strålning ALLTID produceras med grund i centralkraftverkan via Keplermomentet, i detta fall garanterat av att utkastningshastigheten (0,57 c0) är lägre än ytdivergensen (c=0,82c0) vid stjärnytan omedelbart efterföljande detonationsögonblicket. Därmed garanteras ljussättning över hela tP-perioden (7,752 timmar). Den DETONATIONSPULS som bildas i detonationsögonblicket då stjärnans fysik växlar från kontraktiva till expansiva tillståndet — med det mellanliggande statiska tillståndets fysik där ytdivergensen MOMENTANT i detta exempel ligger på c=0,76c0 — återspeglar — »samplar», tar upp — naturligtvis OCKSÅ stjärnans karaktäristiska maxrotation (fD) vid tillfället. När sedan materialet expanderar, sprids naturligtvis också denna korta statiska tillståndets puls ut över samtliga differentierade frekvenser som materialet når allt längre ut — tillsammans med stjärnans gravitella rödförskjutning i materialutkastningen — och stjärnan via sitt impulsmoment roterar allt långsammare mot minimum f0. Det är KLART att det man SEDAN ser av denna kompott tvunget blir en historia av utspridda frekvenser, även på helt nära håll — och som alla sammanstrålar i en och samma övergripande period (TP), vilket är pulsarens enda fasta period (tillsammans med stjärnrotations maximum fD och minimum f0, men dessa återfinns aldrig kontinuerligt). Det är i varje fall vad som synes framgå helt klart och tydligt enligt TNED.
Periodfotens puls enligt TNED (idealt, efter rotcykloidens enklaste matematik) på 7,14 Hz eller 140,1175 mS är alldeles tveklöst grunden till uppgiften på 17 Hz eller 59,03 mS och som man — i resultatmässig konsekvens — påtvingat objektet genom en villkorsstyrd och dito programmerad, inte uppmätt, signalteknik — med grundföreställningen att objektet uppvisar en fast rotation. Enligt TNED, och ovanstående grafiska exempel, och i den mån det också verkligen håller streck, finns ingen sådan fast rotation: Inte hos Solen, inte hos någon enda stjärnkropp som uppvisar ett uns rotation över exakt noll. (Gäller alltså förutsatt att himlakroppen har en massa som överstiger eller tangerar stjärngränsmassan, den är för Väte-1-bas enligt TNED lika med 1/165:del av Solmassan). Alla roterande stjärnkroppar roterar variabelt — tillsammans med ett överliggande pulserande materialskikt, ända tills friktionen om inte annat helt reducerat varje spår av rotation.
Det skulle därmed inte finnas några fasta rotationsfrekvenser alls för stjärnkropparna i universum; Den föreställningen skulle — då — vara grundad helt på en DIKTERAD TEORI — som redan från början (1967) uteslöt annat än ”fast roterande neutronstjärnor”. En historisk överblick ges nedan i Så föddes uppfattningen om den roterande neutronstjärnan.
PULSAREN ENLIGT TNED
I
KORT SAMMANFATTNING

DEN VARIABELT
ROTERANDE OCH PULSERANDE KOMPAKTSTJÄRNAN ENLIGT TNED uppvisar ljusemissioner
radiellt med mellanliggande mörka intervall
—
distinkta pulser
— ENDAST OM stjärnytans divergens (cD) vid
detonationen är lägre (eller lika med) den initiella expansionshastigheten (vD).
Detta kräver generellt att kompaktstjärnan (generellt en gammal utbränd primärstjärna som slutat som en utpräglad Helium-4-kropp) måste vara
av typen tyngre
—
garanterat av den starka ytgravitationens inverkan som reducerar
ljushastigheten i stjärnytan.
PULSAREN
ENLIGT MODERN AKADEMI
I
KORT SAMMANFATTNING — en enskild roterande laserstråle?
I
modern akademi finns inte teorin om de cykliska funktionerna som baseras på expansionsmatematiken.
Se f.ö. Grundläggande
skillnader i de olika modellerna TNED/MAC i Stjärnfysiken.
I modern akademi anser man att stjärnornas
inre fysik bygger på analogier till en innesluten gas där fusionerna åstadkoms
på samma sätt som i partikelacceleratorer, alltså via höga hastigheter. Därmed
har man också helt andra utgångspunkter i teorin för pulsarerna;
Den tillfälliga pulsen hos pulsaren
»förklaras» i modern akademi med att en ljusstråle likt den från ett fyrtorn
tillfälligt sveper över Jorden. Ljuset i strålen som sådan anses kontinuerligt;
Man tänker sig i modern akademi alltså ljuset från pulsaren likt ljuset från en
ljusfyr — men man vet (ännu) inte hur den stråltypen bildas i detalj, eller hur
den fungerar dynamiskt; Ingen kan förklara den eller beskriva dess fysik;
Fetstilen min markering:
”På något sätt skapas någonstans i den rotande magnetosfären koherent (laserliknande) radiostrålning. Denna koncentreras till en smal stråle och ger liksom blänket från en fyr en radiopuls varje gång denna stråle sveper över jorden. Därutöver emitteras också mycket snabba (relativistiska) partiklar.”
BONNIERS ASTRONOMI 1978 s113sp2mn
”På något sätt matas rotationsenergin från pulsaren ut i den omgivande nebulosan, till en stor del i form av snabba partiklar som vid växelverkan med det omgivande magnetfältet alstrar synkrotronstrålning.”
BONNIERS ASTRONOMI 1978 s113sp2ö
NOT. Med synkrotronstrålning avses samma strålningseffekt som bildas av elektroner som går i cirkulära banor på grund av (starka) omgivande (starkt linjäriserade) magnetiska fält.
Man
medger dock öppet att man (ännu 2008) inte har förstått mekanismen (fullt ut)
bakom teorin om den ensamma kontinuerligt verksamma laserstrålen — som f.ö.
tänks wobbla (precessionsrörelse) runt någon axel genom kompaktstjärnan — och
som gynnsamt precis måste svepa över Jordklotet för att kunna observeras.
@INTERNET Wikipedia Pulsar 2008-10-09 Werner Becker 2006:
”The
theory of how pulsars emit their radiation is still in its infancy, even after nearly
forty years of work.”,
Min översättning:
Teorin
för hur pulsarer sänder ut sin strålning befinner sig fortfarande i sin linda,
även efter nästan fyrtio års arbeten.
Utförliga
beskrivningar till den moderna teorin om pulsarens fysik finns på (exv.)
@INTERNET Wikipedia Pulsar — med många vidare referenser.
En (bättre)
illustrerad beskrivning av hur man tänker sig ”laserstrålen” visas i
Pulsars — NASA’s Imagine the universe
[http://imagine.gsfc.nasa.gov/docs/science/know_l2/pulsars.html] Last Modified: December 2006
De
svenska webbreferenserna i ämnet är (ännu, September 2008, som vanligt) ytterst
dåligt representerade (i princip helt obefintliga).
En utförligt historisk beskrivning av hur man
resonerade i modern akademi för att utesluta det pulserande alternativet — så
föddes uppfattningen om den roterande neutronstjärnan
Varför räknar man i modern akademi inte med
en VARIABEL rotation hos pulsarobjektet? Därför att man inte räknar med atomkärnans inkompressibilitet: När max täthet uppnås, enligt TNED, detonerar kärnytan exakt på den kontraherande kraftens belopp:
materialet kastas ut, rotationen avtar, materialet återvänder, rotationen ökar
igen till sitt maximum, osv. DEN VARIABELT ROTERANDE STJÄRNAN PULSERAR. DEN
blotta möjligheten har man uteslutit redan från början i modern akademi, se
utdraget nedan. Som bekant, till exempel, anser man i modern akademi att om
stjärnmassan överstiger runt 5 Solmassor för en motsvarande kompaktstjärna [‡1], kommer den att förvandlas till ett s.k. svart hål — därför att
det inte finns något begrepp om STOPP genom atomkärnans inkompressibilitet i
modern akademi. DET SVARTA HÅLET blir då en naturlig teoretisk konsekvens i den
moderna akademins tankevärld: hur mycket massa som helst på hur liten volym som
helst. Därför kan man heller inte tänka sig den variabla rotationsfrekvensen:
det finns i modern tankevärld ingen dynamisk faktor — atomkärnans
inkompressibilitet — att ställa dynamiken på; man »dikterar» följaktligen att
objektet måste ha KONSTANT rotation. Så görs också »stjärnprogrammen» därefter
— som används för att leta efter pulser i universum som uppvisar JUST en
KONSTANT period.
Jämför:
[http://www.astro.umd.edu/~miller/teaching/astr688m/lecture16.pdf] sidangivelser saknas i det här pdf-dokumentet
ASTRONOMY COURSES TAUGHT AT MARYLAND 1999-
Rotation-Powered Pulsars — Shapiro and Teukolsky, Chapter 10
”The Nature of
Pulsars
We know now that they are rotation-powered pulsars, but it is very instructive to go through the chain of
logic leading to that conclusion. In 1968, there were three important facts
established about pulsars:
1. They
were fast, with periods between 0.033 s and 3 s. The pulses themselves could be
even shorter, <0.01 s in some cases.
2. They
were extremely stable, with P/P’ equal to thousands to millions of years.
3. They
always increased in period slightly, never decreased.
Let's
consider what this implies.
Ask
class: what does the first fact imply about the nature of the object? The fast
periods and short pulses imply something small. Barring beaming, the size of
the object would have to be < ct, if t is the time of the pulse. That
gives 3,000 km for 0.01 s. Barring relativistic beaming with g ~ 100
or more, this demands a compact object (white dwarf, neutron star, black hole)
instead of a normal star. The next question is
Ask
class: what are ways in which one can get a periodic signal from a star or
stars? Generically one might think of rotation,
vibration, or a binary orbit (indeed, all three are seen in various
circumstances). Let's focus first on white
dwarfs. Can they, by rotating, vibrating, or pulsating, give a 0.033 s period? No: for all three
processes, the minimum period is of the order 2p(Gr)–1/2, which is a minimum of ~seconds for r ~ 108
g cm–3 maximum densities of white dwarfs. Therefore, white dwarfs can't do it. Ask class: what
could one say about black holes? Can they produce periodic pulsations? No, but
the answer isn't as obvious as it used to be. Getting a periodic signal out
implies some fixed structure, and there just isn't any such place on a black hole.
Of course, quasiperiodic oscillations are seen, just nothing as coherent as
from a pulsar. That means we're down to
neutron stars. Is it rotation,
vibration, or a binary orbit?
Ask
class: what could one say against vibration? Here
the ultrahigh density means that the vibration period, of order 2p(Gr)–1/2, is a few milliseconds, much
too fast for the majority of pulsars.
Ask
class: what can be said against binary orbits? Two things. First, inspiral due
to gravitational waves would cause the period to decrease, not increase.
Second, a binary orbit with a period of seconds would cause the two to spiral
into each other in at most a few hours, whereas many pulsars have now been
observed for thirty years.
This line of argument, due originally to
Tommy Gold, indicates that pulsars must be rotating neutron stars. Therefore, remarkably, neutron stars are very
observable.”.
Min
översättning (textmarkeringarna är mina):
Pulsarernas Natur
Vi
vet nu att de är rotationsmatade pulsarer, men det är mycket instruktivt att
genomgå kedjan av logik som leder till den slutsatsen. År 1968 fanns tre
viktiga fakta etablerade om pulsarer:
1. De
var snabba, med perioder mellan 0,033 och 3
sekunder. Pulserna själva kunde vara ännu kortare, mindre än 0,01
sekunder i en del fall.
2. De
vara extremt stabila, med P/P’ lika med tusentals miljoner år.
3. De
ökade alltid något i period, minskade aldrig.
Låt
oss begrunda vad detta antyder.
Fråga klassen: vad antyder det första faktat beträffande naturen hos
objektet? De snabba perioderna och korta pulserna antyder någonting litet.
Bortsett från strålitet, skulle objektets storlek behöva vara mindre än ct,
om t är pulstiden. Det ger 3.000 KM för 0,01 sekunder. Frånsett
relativistisk strålitet med gamma ungefär 100 eller mer, kräver detta ett
kompakt objekt (vit dvärg, neutronstjärna, svart hål) istället för en normal
stjärna. Nästa fråga är
Fråga klassen: vilka är sätt på vilka man kan få en periodisk signal
från en stjärna eller stjärnor? Generiskt kan man tänka sig rotation, vibration
eller en binär omloppsbana (alla tre kan, verkligen, ses under olika
betingelser). Låt oss fokusera först på vita dvärgar. Kan de, genom rotation,
vibration eller pulsning ge en 0,033 sekunders period? Nej: för alla tre
processerna är minsta perioden av storleksordningen 2p(Gr)–1/2,
vilket ger ett ungefärligt minimum av sekunder för maximala tätheter r »
T14 KG/M3 hos vita dvärgar [2p/Ö(6,67 t11 · T14) = 0,0769337 min
notering]. Därför kan inte vita dvärgar
göra det.
Fråga klassen: vad skulle man kunna säga om svarta hål? Kan de
producera periodiska pulsningar? Nej, men svaret är inte så uppenbart som det
har varit. För att få ut en periodisk signal inbegriper någon fix struktur, och
det finns bara ingen sådan plats på ett svart hål. Självklart ses
kvasiperiodiska oscillationer, bara ingenting så sammanhängande som från en
pulsar. Det betyder att vi är nere på neutronstjärnor. Är det rotation,
vibration, eller en binär omloppsbana?
Fråga klassen: vad skulle man kunna säga mot vibration? Här betyder den
ultrahöga tätheten att vibrationsperioden, av storleksordningen 2p(Gr)–1/2,
är några få millisekunder [2p/Ö(6,67 t11 · T17) = 0,00243285 min notering], vilket är mycket för snabbt för majoriteten pulsarer.
Fråga klassen: vad kan sägas mot binära omloppsbanor? Två saker. Först,
inspiralering beroende på gravitationsvågor skulle förorsaka perioden att
minska, inte öka. Sedan, en binär omloppsbana med en period på sekunder skulle
förorsaka de bägge [objekten] att spiralera in till varandra inom som mest
några få timmar, då däremot många pulsarer nu har observerats under trettio år.
Detta led av argument, ursprungligen från
Tommy Gold, indikerar att pulsarer måste vara roterande neutronstjärnor.
Därför, remarkabelt, är neutronstjärnor mycket observerbara.
Ovanstående
utdrag besvarar frågan om orsaken till följande (annars gåtfulla) påstående i
(bl.a.) BONNIERS ASTRONOMI 1978 s111,
”Sedan 1967 har man upptäckt många fler pulsarer (ca 200), med perioder
varierande från fyra sekunder till 33 millisekunder — den sistnämnda är
perioden för pulsaren i Krabbnebulosan. Denna är särskilt intressant eftersom
den gav det slutgiltiga
beviset för att pulsarerna är neutronstjärnor med starka magnetfält; radiopulsernas
regelbundenhet åstadkoms genom dessa stjärnors snabba rotation”
BONNIERS ASTRONOMI 1978 s111sp1m
Man
stödjer sig alltså på sambandsformen 2p(Gr)–1/2
(se i citatet
ovan) som i fallet med tätheten för
en kompakt Helium-4-kropp (r = grovt T17 KG/M3) helt utesluter perioden i
Krabbnebulosan.
Jämför TNED — helt andra samband, helt
andra förutsättningar:
PULSARERNAS GRUNDMATEMATIK ENLIGT TNED
fD = (4Grmax/TPp2Ö3)1/3 .................... rotationsfrekvensen ur pulsfrekvensen
1/TP = fD3 · [4Grmax]–1p2Ö3 .................. pulsfrekvensen ur rotationsfrekvensen
atomkärnan kan inte komprimeras, se Atomkärnans inkompressibilitet
Stjärnornas allmänna tryckekvation finns inte i
modern akademi — därmed heller inte den tillhörande matematiska fysiken.
Själva ekvationsformen med fD OCH tP ingår inte i den moderna
akademins föreställningsvärld.
För mera förklarande
jämförelser på nivån elementär kärnfysik — roten till skillnaderna — se Bekräftelser på Atomkärnan enligt TNED.
‡[1] ref. @INTERNET Wikipedia Neutron star 2008-10-03,
”Gravitational
collapse will always occur on any star over 5 solar masses, inevitably
producing a black hole.”;
Min
översättning:
Gravitationell
kollaps uppkommer alltid på varje stjärna större än 5 Solmassor, ofrånkomligen
producerande ett svart hål.
Avsnittet nedan är överflödigt.
Detaljerna ges enklare direkt i Stjärngränsmassan
via c0.
GRÄNSMASSAN FÖR NOLLDIVERGENS I KROPPSYTAN VIA MAX HOMOGEN TÄTHET ENLIGT TNED
Vid c=0 gäller tydligen från ljusets gravitella beroende
0 = (1/2)[c0 – Ö |–c02+4w2 | ] ;
0 = c0 – Ö |–c02+4w2 | ;
–c02+4w2 = c02 ;
4w2
= 2c02 ;
2w2 = c02 = 2Gm2/rc0 = 2rc02(4pGr/3) = rc02(8pGr/3) ;
rc02 = c02(3/8pGr);
rc0 = c0(3/8pGr)1/2; .................................................................... OK
m = rV = r·4pr3/3 .................................................................... OK
= r·4p[c0(3/8pGr)1/2]3/3
= r·4p · c03(3/8pGr)3/2 · 1/3
= r–1/24c03(8G)–3/2 Ö 3/p ........................................................ OK
= r–1/24c03(8G)–3/2 Ö 3/p
= r–1/2c03(8G)–3/2 Ö 48/p
= r–1/2c03G–3/2 · 1/8Ö8 · Ö 48/p
= r–1/2c03G–3/2 · 1/Ö512 · Ö 48/p
= r–1/2c03G–3/2 · Ö 3/32p
= r–1/2(c0/ÖG)3Ö 3/32p ........................................................ OK
= r–1/2(8,54444 T39)(KG/M)3/2
Med maxtätheten r = 6,5 T17 KG/M3 som ENLIGT TNED gäller för en ideal Helium-4-kropp blir gränsmassan m drygt 5 Solmassor:
m = (6,5 T17 KG/M3)–1/2(8,54444 T39)(KG/M)3/2 = 1,0598 T31 KG; m/(1,981 T30 KG) = 5,3283426.
För en Väte-1-baserad stjärnkropp blir motsvarande gränsmassa ca 10 Solmassor.
Se mera utförligt (och enklare) från Stjärngränsmassan via c0.
PRIMÄRSTJÄRNORNAS FUSIONSPERIODER
— ENLIGT TNED
Med
inledande begrepp och härledningar från Solfysiken i Solperioden.
TILLFÄLLIG
DEPOSIT FÖR UTVECKLINGAR SOM KOMMER
— i
det närmaste är på väg ATT INTEGRERAS MED UNIVERSUMS HISTORIA:
2008X4
—
vidareutvecklingar med en utarbetad sammanställning för samtliga
primärstjärnor:
FUSIONSPERIODEN FÖR SAMTLIGA
PRIMÄRSTJÄRNOR
tP = ARm0TRANSIT–1hr[(r)C(r)r]1/2 · 1S
kolla
Webbformateringsexemplet ovan: tas parenteserna bort kring r-termen (Symbol, r) åker
nedsänkta tecknen upp — om teckenstorleken är mindre än 25. Noterat 2008-10-25.
AR = 4pR2 ; R = r(rr/rC)1/4 ;
= 4pr2(rr/rC)1/2 ;
tP = ARm0TRANSIT–1hr(rCrr)1/2 · 1S
= 4pr2(rr/rC)1/2m0TRANSIT–1hr(rCrr)1/2 · 1S
= 4pr2m0TRANSIT–1hr(rCrrrr/rC)1/2 · 1S
= 4pr2m0TRANSIT–1hrrr · 1S
;
m0TRANSIT ;
EFUSION = 4([14,5–1,5=13] me 9,11521 t31)c3T82=4,26591 t12 J
= 4([14,5–1,5=13]me)c2
= Pt ; t = 1S ;
1S = EFUSION/P
Antal H-He-fusioner per sekund
N = P/EFUSION
SekundTransitMassa,
He-4-massa:
m0TRANSIT = N· mHe4
= (P/EFUSION)mHe4
= mHe4P/EFUSION
= mHe4P/[4([14,5–1,5=13]me)c2] , 4 anger masstalet för He-4 ; ................... noggrant 14,4834105 – 1,5180399 = 12,96537 » 13
= UHe4uP/[4[mDHe4–mDH1]Ueuc2]
= UHe4P/[4[mDHe4–mDH1]Uec2]
= (UHe4/Ue)P/[4[13]c2]
UHe4 »
4 ;
........................................................................................................... noggrant 4,0026031
m0TRANSIT = P/13Uec2
= P/13(0,000548598)c2
= P · (1,56013 t15 KG/W) .............................................................................. noggrant enligt ovan 1,56531 t15
Förbränningsmassan per Watt:
mP = 1,56013 t15 KG/W = konstant med energicykeln Väte-1 till Helium-4, gäller för alla primärstjärnor (från dag 1) ;
m0TRANSIT = P/mP ;
tP = 4pr2m0TRANSIT–1hrrr · 1S
tP = 4pr2PmP–1hrrr · 1S ;
P =
Solära råeffekten
= (4pr2)2e0 · (1VM–1C–1S–3KG);
tP = 4pr2PmP–1hrrr · 1S
= 4pr2mP–1(4pr2)2e0hrrr · 1S · 1VM–1C–1S–3KG
tP =
hrmP–1(4pr2)3e0rr · 1VM–1C–1S–2KG
tP = hrr6 · mP–1(4p)3e0rr · 1VM–1C–1S–2KG
; hr = elektronskiktets tjocklek i Stjärnytan ;
hr = STJÄRNRADIEN (rG) utan elektronmassan — STJÄRNRADIEN (rG) med elektronmassan; hr i Solens fall blir ca 340 KM;
= rG–e – rG+e ;
rG = [rr(8/mA)–1/3/r0]–1/4(3/4p)1/3/[(1/m0SLIM)1/3–(1/mS)1/3]
r0 = protonradien enligt Planckringen via Neutronkvadraten ............... 1,37 t15 M
m0SLIM = stjärngränsmassan ........................................................................ 1,204 T28 KG
mS = Solmassan ...................................................................................... 1,989 T30 KG
rr = yttäthetskonstanten .......................................................................... 8,9277145 t5 KG/M3
e0 = elektriska konstanten (kapacitivitetstalet för vakuum) ................... 8,8543 t12 C/VM
UTAN VIDARE UNDERSÖKNING framgår av variablerna ovan (hrr6) att perioden (tP) växer med stjärnmassan; tunga stjärnor har lång period, lätta kort.
Dessutom avtar perioden med
stjärnans livslängd så att Solen kommer att sluta på drygt 9 år — beräknat från
dag-1-värdet ovan och nuvarande medelvärde ca 11,1 år via stjärnornas allmänna tidsekvation och K-cellens allmänna värmefysik.
Alla oroterade primärstjärnor har ENLIGT TNED samma medeltäthet (se stjärnfysikens fundamentalteorem; alla oroterade primärstjärnor utvecklar en konstant volymenergi per kilo)
rn = 1 402,3223 KG/M3 ........................ SOLENS MEDELTÄTHET rnom=rn
vilket ger stjärnradien som funktion av stjärnmassan via volymen enligt
rSTAR = (3mSTAR/4prn)1/3
rSTAR = mSTAR1/3(0,0554227)
Därmed kan Solens (normala) massa 1,989 T30 KG och Solens gravitella radie 6,97 t8 M användas som primär referens för att beräkna alla övriga primära oroterade stjärnors radie:
;
rSOL = mSOL1/3(0,0554227)
rSTAR = mSTAR1/3(0,0554227)
;
rSTAR/rSOL = (mSTAR/mSOL)1/3 ;
rSTAR = rSOL(mSTAR/mSOL)1/3
Sambandet för elektronskiktets tjocklek (hr) kan då lösas ut på Solens fysik enligt
hrSTAR = rG–e – rG+e
= rSOL–e(mSTAR/mSOL)1/3 – rSOL+e(mSTAR/mSOL)1/3
= rSOL–e(mSTAR/mSOL)1/3 – rSOL+e(mSTAR/mSOL)1/3
= (mSTAR/mSOL)1/3(rSOL–e – rSOL+e)
= (mSTAR/mSOL)1/3(hrSOL)
Därmed
tPSTAR = hrSTARrSTAR6 · mP–1(4p)3e0rr · 1VM–1C–1S–2KG
= (mSTAR/mSOL)1/3(hrSOL)[rSOL(mSTAR/mSOL)1/3]6 · mP–1(4p)3e0rr · 1VM–1C–1S–2KG
= (mSTAR/mSOL)1/3(hrSOL)rSOL6(mSTAR/mSOL)2 · mP–1(4p)3e0rr · 1VM–1C–1S–2KG
= (mSTAR/mSOL)7/3(hrSOL)rSOL6 · mP–1(4p)3e0rr · 1VM–1C–1S–2KG
= (mSTAR/mSOL)7/3(tPSOL)
SAMMANFATTNING
Perioden
växer alltså med antalet Solmassor upphöjt till 7/3 »
2,33.
För
Solen ges ENLIGT TNED
tP = 11,44112839 år (med de enklare värdena ovan), se mera
utförligt i Solperioden
Minsta
stjärnmassan (Solmassan dividerat med 165) ger tP = 2418 S, eller ca
40,3 minuter.
Största praktiska stjärnmassan (ca 15 Solmassor
enligt TNED) får tP = 6 348 år.
Se
även allmänt för stjärnornas gränsmassor enligt TNED i
Se
även generellt för stjärnornas yttemperatur som funktion av stjärnmassan
i
Pulsarerna
innehåll: SÖK på denna sida Ctrl+F ·sök alla ämnesord överallt i SAKREGISTER
Pulsarerna
ämnesrubriker
innehåll
Illustrerat exempel ·
PSR 1913+16
ENKLA EXEMPEL PÅ LJUSKURVOR
· TT Aurigae · HD 85207 · HD 106400 · PG1336-018 · Beta Persei (äv. Algol) ·
Krabbnebulosan
Pulsarens
förklarande matematik enligt TNED · jämförande grunder med modern
akademi
Hur
pulsaren föddes i modern akademi — citerad historisk sammanfattning
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]
me = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]
u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],
CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.
t för 10–, T för 10+, förenklade exponentbeteckningar
TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.
Senast uppdaterade version: 2018-06-21
*END.
Stavningskontrollerat 2008-10-25.
rester
*
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se
PNG-justerad 2011-10-10
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se