PLANCKRINGEN 2007XI11 · I fortsättning från Fysikens Sjunde Princip · a production · | Senast uppdaterade version: 2024-03-26 · Universums Historia • HUMAN RIGHTS HEADLINES

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

atomära massenheten u |

FYSIKENS SJUNDE PRINCIP (PASTOM Principal Structure of Mass) är en direkt följd av energilagen (tredje principen), gravitationen (femte principen) och elektriciteten (sjätte principen) och vilka delar definierar den primära massförstöraren E=mc² som krävs för bildningen av värme och ljus från massförbränningen (m®g) med Solen som det närmast strålande exemplet. Villkoret för en sådan total massupplösning är att massan av princip inte får innehålla några (stela) beståndsdelar. Detta villkor uppfylls av den sjunde principens massekvivalent m=m[n®¥]^–1[n®¥] som visar att massan av princip får förstås som bestående av ett obegränsat antal obegränsat små delar som oupphörligen delas så att någon minsta beståndsdel inte kan återfinnas.

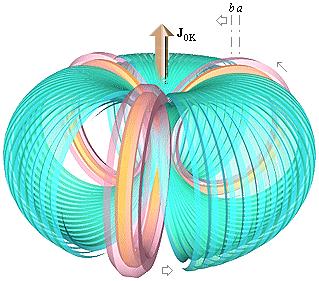
Genom det ytterligare villkoret att materien som sådan, tydligen, inte behöver någon energipåfyllning för att vara just materia, är det lika tydligt att materiens minsta beståndsdelar, atomerna, tvunget summerar nollmoment: en spinnande ring (J=mvr) med massa och laddning som fortsätter att snurra i evighet om den inte omvandlas till värme och ljus. Ringformens elementära matematik skrivs som J=mvr med J som det s.k. impulsmomentet eller rörelsemängdsmomentet (Eng., angular momentum), vilket är samma som Keplermomentet K=vr med massan m inbegripen. Dess mest eminenta form är känd som Plancks konstant h = m_nc₀r_n = 6,62559 t34 JS [ref. HOP s7–155] (t för 10^–, T för 10⁺): m_n betecknar neutronringens massa, r_n neutronringens radie (tyngdcirkeln) och c₀ ljushastighetens toppvärde c₀=2,99792458 T8 M/S, samma som divergensen c enligt resultaten från Ljusets Grundläggande Fysik. Därav den naturliga benämningen Planckringen för atomkärnans mest elementära individ: neutronen.

— Benämningen ”Planckring” finns (här veterligt 2007XI14) inte i gängse kvarter. Det gör inte heller den följande framställningen som beskriver atomkärnans härledning i detalj.

Atomkärnans geometriska härledning — PlanckEkvivalenterna — PotentialBarriären — Nuklidbarriären — Ljusets Gravitella Beroende

atomkärnans härledning -- PLANCKRINGEN 1 -- atomkärnans gravitella härledning, se PlanckRingen 2 ¦ THE ATOMIC NUCLEUS —— TAN: Aug2023 — Explaining the primitive idea of the atomic nucleus

Resolution 217 — Golden Section Matrix Systems Solutions ¦ Resolution 217(A) — UDHR10Dec1948¦ Resolution217Short — English editions Jan-Mar2024

TheAtomicNucleus [ I ] Jun2023 — DeducingTHErZ ¦ TAN II Sep2023 — comparing nuclear physics ¦ TAN III Nov2023 — relating Earth crust isotopic compositions ¦ TAN IV Dec2023 — FusionLimitMass FULIMA

Atomkärnans Geometriska Härledning · Atomkärnans Gravitella Härledning

ATOMEN OCH ATOMKÄRNAN DEFINIERAS ELEMENTÄRT FRÅN

NEUTRONEN — h = 6,62559 t34 JS	1,0086652u = 1,67481 t27 KG	2,99792458 T8 M/S	1,3196611 t15 M
PLANCKRINGEN h =	mn	c0	rn
NEUTRONEN — h = 6,62559 t34 JS	neutronmassan	toppdivergensen	neutronradien

1,67481 t27 KG × 2,99792458 T8 M/S × 1,3196611 t15 M värdena varierar marginellt beroende på standardiserad epok och institutionell metod

För Inledning, se ovan.

Se även TNED sammanställd utvecklingshistoria i TNED FRÅN BÖRJAN.

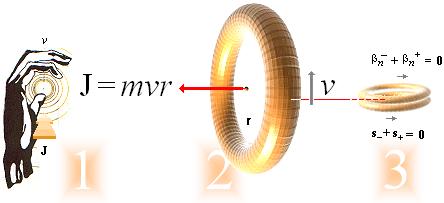
1. Högerhandsregeln. Tummen pekar i kraftvektorns riktning J, fingrarna i rotationsriktningen v. 2. Planckringen med impulsmomentet J=mvr. 3. Planckfraktalerna som krävs för att definiera summa nollmoment: ringar i ringar i evighet utan slut definierar massekvivalenten m = m[n→∞]–1[n→∞], n är antalet ringar som växer obegränsat:

Planckringen innehåller i grunden inga beståndsdelar. Bara ren, strukturerad, kraft.

J i praktiken. Ett cykelhjul som hålls mellan händerna i axeländarna och roterar ger ett utmärkt exempel på innebörden av kraftvektorn J. Varje försök att ändra hjulets position i rotationsplanet stöter omedelbart på starkt motstånd.

Planckfraktalerna

Förklaring:

Atomen (kärnan och dess elektronmassa) behöver inte vridas upp eller tankas för att fortsätta snurra: Summan av alla krafter och moment i atomen är noll (Atomfysikens två kungsekvationer). Enda sättet för en sådan ekvation att gå ihop, är med en struktur av ±-laddningar (b) med ±-spinn som regleras av ett allmänt impulsmoment (eg., rörelsemängdsmoment) J=mvr som ovan: mvr + –mvr = 0 = J₀+NJ₁. Eftersom ingen stel del får finnas — på villkor som bestäms från den primära massförstöraren E=mc², se vidare nedan — måste varje ring uppvisa en liknande understruktur (Planckfraktaler), totalt med ringar i ringar i all oändlighet enligt den ekvivalenta massformen m = m[n→∞]–1[n→∞] så att ingen beståndsdel kan återfinnas i m, analogt oupphörlig delning. Vi ska här löpande studera hur ringstrukturen fungerar med de angivna sambanden, och i slutänden se att allt stämmer galant. De närliggande motställda ringarnas förmåga att förinta eller annihilera varandra fullständigt är avgörande för giltigheten av den primära massförstöraren E=mc² som ger värmen och ljuset (m→γ), se Solen nedan, och som produceras genom induktionens inverkan ur massdestruktionen: motsatta spinn och laddningar tar ut varandra. Som redan formulerats i Energilagen bevaras accelerationen som komponent i massan genom induktionen (motsv. Newtons tredje lag) medan den gravitella eller kvalitativa massdelen försvinner med m-strukturen. Observera att denna beskrivning är högeligen allmän och elementär.

TNED

— De beskrivna Planckringarnas oändliga toroidala fraktala struktur, genom de elektriska (Q) och mekaniska (m) detaljerna, framställer hela ämnet naturligt på akronymen TNED (Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken. Därmed framstår impulsmomentet (J=mvr) med Plancks konstant i ringen h=mcr som en strukturkonstant. Se även särskilt i Plancks strukturkonstant.

Solen FÖRBRUKAR MASSA KONTINUERLIGT. Massan förintas och dess inneboende energi överförs på andra massor genom värme och ljus (m→γ) enligt

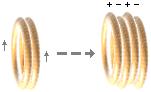
e^– + e⁺ = 0 ............... laddning

s_e– + s_e+ = 0 .............. spinn (rörelse)

m_e– + m_e+ = 2m_e ......... massa

Överföringen sker INDUKTIVT (se induktionens elementära definition) enligt COEI (Conservation of energy by induction)

U_ind = E=^UQ/Q_s = L(di/dt)k = Lk = kRTQ/T² = kRQ/T = kRI = kU. Massans kvalitativa struktur (E/c²) förintas, men energin bevaras. Jämför även från Energilagen:

Då m en gång förintats, kan det sedan inte återskapas. Dock kan massans energiekvivalent substituera massan enligt den redan experimentellt välkända kvantitativa ekvivalensen

E = (m→γ)c² = (m←γ)c²

Dvs., ett kvantitativt utbyte massa-energi kan alltid bildas. Formen (m→γ) som sådan är dock kvalitativt irreversibel: m kan förintas, men inte återskapas.

Primära massförstöraren, E=mc² där m omvandlas till ljus och värme (här generellt gamma, γ) genom induktionen (m→γ), utgör Planckringens grundval: den allmänna energiförsörjningen. Ytterst för vår del har den upphov i Solen och stjärnorna (och i mindre omfattning från de naturligt radioaktiva grundämnena i Jordkroppen).

De konstant spinnande ringarna i Plackstrukturen (illustrationen ovan, detalj 3) sammanhålls, tydligen, inbördes av magnetiska krafter liknande den sammandragande magnetiska kraften mellan lindningsvarven i en vanlig teknisk elektrisk spole. Enda principiella skillnaden är att Planckringarnas olika laddningsringar med motsatta spinn i netto ger motsvarande ekvivalenta lika ringar med samma spinn och laddning. Den magnetiska effekten i netto är densamma som i en normal enkellagrad elspole.

deplacementet

NEUTRONENS NEGATIVA KÄRNMAGNETISKA MOMENT

+ protonens kärnyta + neutronens kärnyta

| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |

– –

Bildkopia nedan av ovanstående textoriginal i WORD 2000 — efter upptäckt Apr2010 att SAMTLIGA TESTADE WEBBLÄSARE Internet Expolorer 7, Internet Expolorer 8, Google Chrome, Netscape, Mozilla Firefox, Opera vill ha det på annat sätt: Är webbläsaren korrekt utformad av programmakaren ska skillnaden mellan bildoriginalet nedan och textalternativet ovan vara noll. Se även en tydligare illustration i LADDNINGSDEPLACEMENTET. Kommer det internetverktyg snart som kan visa naturfysiken? Därför att nu är det — tydligen — så dåligt som det någonsin kan bli.

Genom ett ytterst litet (positivt) deplacement mellan ±-ringarna, alltså en liten toppförskjutning så att ringarna inte ligger helt jämnt med varandra i ytan och vilken detalj bekräftas av det faktum att neutronen uppvisar ett negativt kärnmagnetiskt moment, uppvisar Planckringen en ytterst sinnrik elektrodynamisk mekanik som hindrar ±-ringarna att attraheras fullt ut inbördes, vilket skulle leda till omedelbar förintelse; Deplacementet fungerar tydligen så, i försorg av ringens toppspinn och därigenom dess magnetism, att ±-laddningarna drivs ifrån varandra med negativa inåt och positiva utåt så att deplacementet tenderar att förstärkas. Nettoeffekten blir att den inbördes elektriska attraktionen mellan ±-ringarna motverkas. Se utförligt i CENTRALKONTAKTERNA. Se även i Neutronens Sönderfall.

Deplacementets ytterligare förskjutning innebär emellertid att jämvikten eller tyngdcirkeln i Planckringens J=mvr rubbas: Då m strävar att dra in sig mot centrum är det tydligt att r strävar att reduceras. Men det går inte enligt det konstanta J=mvr. För att motverka ändringen och därmed återställa balansen J, svarar alltså neutronen på enda tillgängliga sättet: Att föra ut precis så mycket ekvivalent kärnmassa att balansen i tyngdcirkeln återställs, medräknat energiförlusten i ombyggnadsarbetet (m→γ) som motsvarar en viss massdefekt.

Resultat: Neutronen är instabil och sönderfaller (inom 12-14 minuter) till en Väteatom i formen av atomkärnan eller protonen med sin omgivande elektronmassan eller elektronen. Kärnan ansvarar alltså för att den slutliga balansen netto i laddningsfördelningen kärna-elektron är exakt noll. Därmed framstår kärnladdningen (+e) som omvänd på elektronladdningens belopp (–e). Så börjar historien.

atomkärnans

inkompressibilitet

Planckmomentet J=mvr garanterar att ringen inte kan komprimeras: Enda sättet att minska r i det konstanta mc₀r är att öka m. Atomkärnan, konstant m, kan inte komprimeras. Men det står också klart redan genom elektriska kraftlagen F=k(Q/r)² via massekvivalenten m = m[n→∞]^–1[n→∞]; Med analogt obegränsat avtagande r är det tydligt: atomkärnan står redan på noll. Se även i ATOMKÄRNANS FORMBEVARANDRE KRAFT.

Med högerhandsregeln tillämpad genom hela den fraktala ringstrukturen, så att varje närliggande två fraktalnivåer summerar nollspinn enligt grundformen

mvr + –mvr = 0 = J₀+NJ₁, kommer varje ytterligare lägre fraktalnivå för v-faktorn att växa från toppvärdet v genom ledformen nedan där k betecknar en principiell fraktal delningsfaktor för varje fraktalnivå,

v, vk₁, vk₁k₂, vk₁k₂k₃, vk₁k₂k₃k₄, vk₁k₂k₃k₄k₅, …

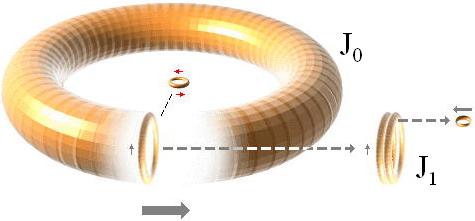
Byggnaden för de fraktala ringspinnen summerar en bild med en nettoeffekt som visar HUR en godtycklig punkt på toppringens yta inte uppvisar någon rörelse alls enligt de omväxlande riktningarna i v-faktorns spinn och som tar ut varandra då fraktaldjupet avancerar mot oändligt och vi växlar betraktelsen mellan de bägge rätvinkliga fraktala orienteringarna. Detta är också det villkor som måste uppfyllas för att vi ska kunna betrakta bara ett spinn åt gången — därför att varje annan ordning kommer att splittra hela byggnaden på de individuella spinnen (erinra varje försök att ändra riktning på det roterande cykelhjulet: det går inte utan tillförande av energi, och någon sådan bensinstation har inte atomen), som betyder ingen modell alls. Hela toppringen kan med detta resultat därmed förstås rotera (spinna) på en ekvivalent stel ringkropp. Vilket vill säga: spinnet relaterar till toppringens bägge närmast inre rätvinkliga spinn, alltså som redan noterats 0 = J₀+NJ₁. J₀ längst upp med J₁ närmast under och N antalet (stela) ringar i J₁:

n(m/n)(v·k)(r/k) = mvr ;

NJ₁ = J₀ ;

J₀ + NJ₁ = 0

Med andra ord: Enbart genom framträdandet av Plancks konstant (h=mvr), får atomkärnan inte förstås som en statisk solid homogen substans innehållandes en samling partiklar. Atomkärnan enligt Plancks konstant måste istället förstås som en dynamisk, ihålig fraktal ringbyggnad helt utan beståndsdelar, en massans fundamentalform, helt omöjlig att relatera till någon materiell modell. Den främsta egenskapen, således, hos Plancks konstant h:

alla våglängder

h är fraktalt: E=hf=(h/n)nf. Vilket betyder — samt upplöser en stor klassisk svårighet i modern teoretisk kärnfysik: Våglängder direkt från noll innefattas i Plancks strålningslag. De finns redan där, men i modern akademisk teori kan man inte förklara dem, eller ens beskriva dem, därför att deras blotta närvaro kräver oändlig energi enligt E=hf: Med konstant h och obegränsat växande frekvens f=c/l, analogt obegränsat avtagande våglängd l, måste tydligen Planckenergin (E=hf) växa över alla gränser. Ett fraktalt h däremot löser den knuten galant: kortaste våglängderna motsvarar de minsta och mest sublima energierna Atomkärnan med toppringen J₀ bildar gränsformen. Ekvivalenter är ekvivalenter.

ATOMKÄRNANS EXAKTA FORMBILD

hur atomkärnan ser ut, forts. frn. atomkärnans härledning

kärnfysikens

J_0K + NJ_1K = 0

HUR BILDEN AV ATOMKÄRNAN

FRAMTRÄDER

PLANCKRINGEN eller analogt det allmänna sambandet för impulsmoment J=mvr visar hur atomen måste definieras med utgångspunkt från

NEUTRONEN h=m_nc₀r_n,

den primära massförstöraren E=mc²,

samt den därav följande massans principiella struktur som inte tillåter några beståndsdelar enligt

m = m[n®¥]^–1[n®¥]. Vilket vill säga: Atomen måste skrivas på nollformen

0 = J₀+NJ₁

Därmed är i princip atomkärnans byggnad identifierad. Dess exakta form kan beräknas genom Planckstrukturens fraktala toroidsystem via TOROIDMATEMATIKEN på de bägge toppnivåerna J₀ och J₁, enligt bestämningen av N-faktorn i den senare, och med hjälp av kubgrafen r=r₀A^1/3 som den approximativa grunden för atomkärnans tillväxt från grundindividen A=1 och därmed radiella grundreferens. Kubgrafen har (också, nämligen) visat sig approximativt korrekt enligt experimentella observationer [HOP]. Kubgrafens härledning är ytterst enkel och ges i särskild artikel som här förutsätts bekant.

derivering

Råsambandet för summan av A stycken ihåliga toroider som bildas av toroiden A=1

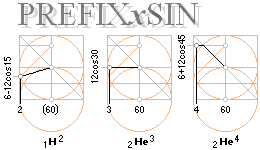
R_A=r_A[(cos 180°/N)^–1–1]+2(r_A+r²mA/r_A) i PREFIXxSIN

beskriver Plancktoroidens formfaktorer genom de bägge variablerna N, antalet underringar, och m, förhållandet i underringen mellan dess ringtjocklek och den närmast längre ner i strukturen liggande ringtjockleken. R_A (=r) anger toppradien, och r_A anger radien i underfraktalen. För att kunna lösa ut formfaktorerna, måste R_A-sambandet deriveras (se r-sambanden nedan) för att i slutprodukten få fram mesta möjliga kompakta produkt och därmed mesta möjliga energihushållning. Därefter måste parametrarna slutligt bestämmas med hjälp av någon mätpraktiskt förankrad referens, vilket sker med hjälp av den nyssnämnda approximativa kubgrafen. Resultatet redovisas nedan.

KÄRNRADIERNA 2007XI11 | Grundredovisning i sammanställning från DYNAMIKENS GRUNDER 1995X

Kärnradierna — Del I

ATOMKÄRNANS EXAKTA GEOFYSIK eller — Atomkärnans härledning I —

KÄRNRADIERNA GENOM PLANCKRINGEN

Så framträder bilden av NORMALTILLSTÅNDETS atomkärna. Se även från Inledningen.

Se även Kärnradierna i Resultatredovisning.

KÄRNRADIERNA GENOM PLANCKRINGENS NÖDVÄNDIGA MASSFRAKTALER m=m·[n®¥]^–1·[n®¥] för att satisfiera fullständig massupplösning utan stela beståndsdelar enligt E=(m®g)c² (Principal Structure of Mass) [från Fysikens 7:e princip]

r = f (A)₁ · f (A)₂ · f (A)₃ · … ju flera parametrar som tas med, desto noggrannare blir beskrivningen … Vi börjar med den första:

r = f (A)₁

= [2r₀/(2[m+1]+K)]Ö 2mA(2+K) = k · r₀A^1/2 .......... råsambandet för toroidradierna efter deriveringen, gäller från A=2

k = [Ö 2m(2+K)] · [1/(m+1+K/2)]; växande m ger avtagande k (mot 0), växande N ger växande k (mot 1)

K = [(cos 180°/N)^–1–1] i PREFIXxSIN

N = antalet underringar i första underfraktalen, teoretiskt minst 3 för att bilda ett spinnplan (J)

m = toroidens formfaktor i första fraktalen (ringdiametern/ringtjockleken), teoretiskt större än minst 2

A = masstalet

r₀ = neutron-protonradien (skillnaden mellan dessa är marginell och frånses här), gäller för A=1

0 = J_0K + NJ_1K, atomkärnan-atomens allmänna impulsmomentsekvation (»impulsekvationen»)

N3m20

0 Ø₁ Ø₂

| | |

: tillståndsbild INTERN STRUKTUREKVIVALENT utan toppspinn. I PRAKTIKEN:

N3m20

m-FAKTORN Ø₂/Ø₁

m bör idealt vara (relativt) stort (vilket betyder en spinkig inre kärntoroid):

Stort m garanterar (nämligen) att den massförskjutande inverkan från neutronens negativa kärnmagnetiska moment får så liten slaglängd som möjligt (vilket återfaller på Ø₁) och därmed under så kort tid som möjligt, vilket begränsar det momentets metriska dynamik på atomen som helhet och därmed effektiviserar (optimerar) sönderfallets inre dynamik (på tid och distans, och därmed ett minimum av ombyggnadsenergi, analogt minimal massdefekt).

N3m20

Faktorn k: Växande m ger avtagande k (mot 0), växande N ger växande k (mot 1); m måste vara teoretiskt större än minst 2, och N måste vara minst 3 för att kunna bilda ett spinnplan för impulsmomentets ekvivalenta atomära grundform J_0K + NJ_1K=0: summan av alla moment i atomen är noll; En atom kräver ingen påfyllning för att fungera, den är ett passivt perpetuum mobile: den spinner i evighet (om den inte omvandlas till värme och ljus).

— Men hur framkom N=3?

— Eftersom, teoretiskt, matematiskt, enklaste vägen att pröva fram Nm blir att hålla N på minimum (alltså 3)

— då N i annat fall leder till att toroidgrafen (r=kr₀A^1/2) drar iväg uppåt, långt över grundgrafen (kubgrafen, orange) till jämförelse och vilket skulle leda alldeles fel med just kubgrafen som approximativ jämförande grundreferens

— blir det givet att den faktor som per störst precision bestämmer mittpunkten i balansen mot kubgrafen (r=r₀A^1/3) blir m-faktorn:

N=3 är alltså i princip redan givet från grunden: minsta möjliga nominella avvikelse från kubgrafens grundreferens.

Med skärningarna mellan graferna ungefär i mitten av nuklidspektrat (A_max ca 270, men egentligen max 240 med Uran-238 som det naturligt tyngsta grundämnet), ges

m=20 med N=3 analogt k = 0,440460982.

Alla prövningar hittills (i min historia från 1993 till nu 2007) har enbart bekräftat den bilden. Se vidare i

RESULTATREDOVISNING KÄRNRADIERNA.

FRÄMSTA EXEMPEL: se neutronkvadraten: Atomvikterna.

Det finns också en annan (oberoende) del som verifierar N=3-modulen. Se vidare i Kvanttalen

— utan N=3 blir det svårt att få ihop det rent matematiskt.

h=m_nc₀r_n

Se härledning från Planckringen.

Atomkärnan 3Dmodell Simply 3D °

Därmed är atomkärnan känd — J_0K + 3J_1K = 0

SE även i ATOMKÄRNANS DIMENSIONER.

Se även i KÄRNRADIERNA Resultatredovisning nedan.

ATOM- OCH KÄRNFYSIKENS TVÅ KUNGSEKVATIONER

J_0K+3J_1K = 0 impulsekvationen

F_BT + F_eZ = 0 kraftekvationen

atomens impulsekvation

J_0K+3J_1K = 0

tyngdcirkeln

Atomens tyngdcirkel — med början från härledningarna i Planckringen

ATOMKÄRNANS GEOMETRI tillsammans med de primära toppspinnen

(J_0K och J_1K) definierar ett nollmoment som återfaller på en ekvivalent tyngdcirkel: tyngdcirkeln definierar medelradien (r) för ringmassan (m) genom toppdivergensen (c₀) enligt impulsmomentet J=mvr. Riktningen för de tre toppringarnas samlade impulsmoment 3J_1K tas ut av toppspinnets impulsmoment J0K så att summan blir noll på tyngdcirkeln enligt J_0K+3J_1K = 0.

BTfältet

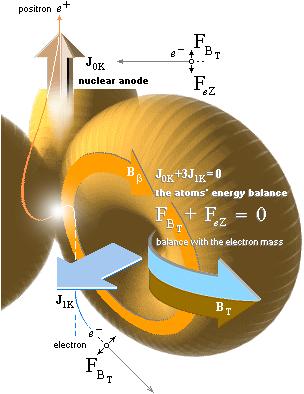
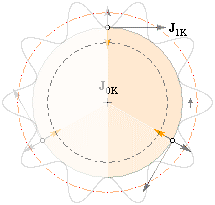
Vänster: atomens kraftekvation F_BT + F_eZ = 0. Höger: tyngdcirkeln enligt J_0K+3J_1K = 0.

Atomkärnans allmänna magnetiska yttoroidfält (B_T)

Ringspinnet enligt högerhandsregeln bildar genom impulsmomentet J₁ på kärnstrukturen ett magnetfält (B_T) med den riktning som utpekas i ovanstående illustration enligt topptoroidfältet B_T. Genom den svagt positivt laddade atomkärnans toppspinn (samma riktning som för B_T ovan) ges ett motsvarande magnetiskt topptoroidkärnfält (B_K) med samma riktning som för J genom kärnbrunnen.

atomens kraftekvation

F_BT + F_eZ = 0 ....................... se även ovanstående illustration

Kraftekvationen

OM B_T utverkar någon influens på elektronmassan utöver vad som ingår i balansräkningen för atomkärnan — summan av alla moment och krafter är noll enligt J_0K+3J_1K = 0 — måste B_T-kraften F_BT uppvägas av en lika stor och motriktad kraft, enligt Newtons tredje lag (se ändringslagarna). Eftersom influensen bara kan komma ifråga om elektronmassan kommer utanför kärnan, kan motkraften bara vara kärnattraktionen F_eZ: kraftvägen blir i bägge fallen densamma, via c. Då gäller kraftekvationen

F_BT + F_eZ = 0

Därmed bibehåller kärnan balansräkningen i sin utvidgade form som atomen per exakt matematisk fysik.

Ekvivalensen mellan krafterna innebär, tydligen, en sluten NOLLRESISTIV bana som den kärnbundna elektronmassan följer. Elektronkomponenten bibehåller den hastighetskomponent (v_t) den hade då den lämnade kärnan, och återkommer med samma belopp. Den slutna banformen bestäms då av kurvaturen för komponentfältet F_BT+F_eZ=0 som verkar på v_t. Se vidare i elektronmassans komponenter.

ENERGIN i kraftvägen för F_eZ mellan kärna och elektronelement grundlägger vektorhärledningen till spektrum och kvanttalen (se Spektrum och Kvanttalen).

Kemikopplingen. ALLA ATOMER som satisfierar balansräkningen F_BT+F_eZ=0 är atomer som beskriver slutna elektriska flödessystem motsvarande en ideal elektrisk isolator. FLERA ATOMER kan då forma atomsystem om, och endast då, deras summadynamik satisfierar ovanstående enkla balansräkning. Det betyder att de kan dela på elektronmassor antingen i 1. ett gemensamt centralflöde via F_BT eller i 2. en gemensam energidelning via F_eZ, eller 3. en kombination av dessa enligt

(F_BT+F_eZ)₁+(F_BT+F_eZ)₂+(F_BT+F_eZ)₃+…+(F_BT+F_eZ)_n = 0

KÄRNRADIERNA resultatredovisning

Se härledning från Kärnradierna genom Planckringen.

KÄRNRADIERNA 2007XI11 | Grundredovisning i sammanställning från DYNAMIKENS GRUNDER 1995X

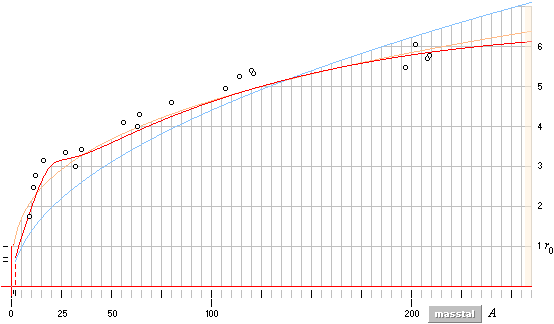
Svarta ringar, mätdata på 19 nuklider från NUCLEAR PHYSICS (år?) av Irvin Kaplan s387 Table 16–5 (från prof. Otterlund Lunds Univ. 1996)

Kubgrafen : r = r₀A^1/3 ................................................... räknas från A=1

YtToroiden : r = (0,4404609)r₀A^1/2 ............................... räknas från A=2

Linjära: r = r₀(1,15–A/900) ............................... räknas från A=2, se massa-spinnkompensationen

Transient: r = r₀[1+x(3+x⁵)^–0.7] .................................. x = (A – 2)/15, räknas från A=2, se massa.täthetskompensationen

Slutgrafen : r = (1,15–A/900) · [1+x(3+x⁵)^–0.7] · (0,4404609)r₀A^1/2, räknas från A=2, r₀=1,37 t15 M

KUBGRAFEN r=r₀A^1/3 (orange kurva) är den approximativa grunden och utgångspunkten i härledningen till atomkärnans formfysik. Den härleds helt enkelt med föreställningen — till att börja med som en grov referens — att atomkärnan är en homogen kropp likt en (sfärisk) vattendroppe. Alla atomkärnor bildas som en summa av en minsta kärnindivid A=1 (neutronen-protonen), vilket leder direkt på kubgrafen, sambandet r=r₀A^1/3, se särskild härledning.

PLANCKRINGENS YTTOROID kr₀A^1/2 (blå kurva) nödvändiggörs ur energilagen som leder till massans struktur och som krävs för att kunna förklara den primära massförstöraren E=mc²: Omvandlingen till värme och ljus från massa (m®g) som tas till energin för arbetet som omsätts då atomerna byggs upp, eller generellt massdestruktion enligt E=mc², kräver att massan inte får innehålla (stela) beståndsdelar. Massans rörelseform beskrivs elementärt på impulsmomentet eller ringen J=mvr generellt. Plancks konstant (J=h) innefattar redan grundindividen i den analysen enligt h=m_nc₀r_n, neutronmassan · toppdivergensen · neutronradien, och är därför självskriven här. Därav toroidmatematiken: atomkärnorna förenas primärt på yta, inte på volym.

ATOMENS GRUND DEFINIERAS h=m_nc₀r_n med

m_n = 1,0086652u ..................... neutronmassan, 1u=1,66033 t27 KG [ENCARTA 99 Molecular Weight]

c₀ = 2,99792458 T8 M/S ....... toppdivergensen

r_n = 1,3196611 t15 M ............ neutronradien

Definitionen gäller neutronens ekvivalenta tyngdcirkel med Plancks konstant h=6,62559 t34 JS [ref. HOPs7-155].

ATOMEN DEFINIERAS AV PLANCKRINGEN h=m_nc₀r_n

kärnrad. forts.

Parameterdelarna i sambandet kr₀A^1/2 (Planckradierna) specificeras ur en derivering av ringens (toroidens) formfaktor då flera ringar förenas till större — vilket hur man än räknar leder till att atomkärnan med masstalet A=2 får ett yttre omfång som är mindre än grundindividens A=1. Detta beror på att grundformen A=1 är (betydligt) mindre kompakt än produkterna från A=2. Se utförlig beskrivning i m-FAKTORN.

Se även nedan i särskild verifikation genom HOP-källan i Deuteronradien i HOP.

Deuteronradien i HOP. Referensen HOP [s9-210sp1ö] visade sig innehålla ett avgörande svar. Grundformen för toroidmatematiken förutsäger en radie på 62% av r₀ för ₁H². HOP avhandlar i aktuell artikel bestämning av deuteronradien genom spridningsförsök, uttryckt via olika matematiska samband. Något direkt värde anges inte, enbart ett allmänt uttryck vars lösning dock är en andragradsekvation. Lösningen ger tvenne svar på deuteronens radie. Det ena är 315% av r₀, det andra 77%. Medan det förra är osannolikt stort, är det senare en ren kvalitativ fullträff — betydligt mindre än 1. Toroidmodellen kan alltså inte (enkelt) avfärdas på den punkten: den innefattar resultatet.

Eftersom kubgrafen (orangea kurvan) också enligt observationer sägs uppvisa en approximativt hyfsad experimentell motsvarighet, kan Planckradiekurvan (blå) avstämmas ungefärligt mot kubgrafen (orange) för att därigenom bestämma Planckringens, alltså atomkärnans, motsvarande formfaktor. Med en ungefärlig delning av (det kända) kärnspektrat i två lika hälfter, med skärningen mellan Plackradierna och kubgrafen ungefär i mitten (här ca A=135), framgår så Planckringens formfaktorer Nm enligt toroidaggregatet N3m20 för A=1. Värdet på k blir då 0,440460982.

Faktorn k har (nämligen) parametrarna [Ö 2m(2+K)] · [1/(m+1+K/2)] med K = [(cos 180°/N)^–1–1] i PREFIXxSIN: växande m ger avtagande k (mot 0), växande N ger växande k (mot 1); m måste vara teoretiskt större än minst 2, och N måste vara minst 3 för att kunna bilda ett spinnplan för impulsmomentets ekvivalenta atomära grundform J_0K + NJ_1K=0: summan av alla moment i atomen är noll; En atom kräver ingen påfyllning för att fungera, den är ett passivt perpetuum mobile: spinner i evighet (om den inte omvandlas till värme och ljus).

Eftersom, teoretiskt, matematiskt, enklaste vägen att pröva fram Nm blir att hålla N på minimum (alltså 3) då N i annat fall leder till att den blå grafen drar iväg uppåt, långt över grundgrafen (orange) till jämförelse, blir det givet att den faktor som per störst precision bestämmer mittpunkten i balansen mot kubgrafen blir m-faktorn (»ungefär 20» ger ovanstående), analogt k = 0,440460982.

JUSTERADE PLANCKRADIERNA (röd kurva) bildas ur grundkurvan (blå) med beaktande av att ytformen inte inbegriper någon massfördelning i Planckringen med växande A: med hänsyn till den nödvändiga fraktala ringstrukturen i Planckringen går masstätheten mot oändligt i toroidytan då antalet fraktala nivåer går mot oändligt (se Atomkärnans Gravitella Härledning). Det finns (främst) två allmänna justeringar som måste genomföras för att kompensera yttoroidens brist på denna punkt och som i slutänden medför den ovan avbildade röda funktionskurvan, se Masstäthetsdistributionen och Yttäthetskompensationen. De svarta ringarna till jämförelse är kärnradievärden från experimentella mätdata (Kaplan-Otterlundbidragen) [från den stora experimentalepoken under 1950-talet].

Från resultatet av Planckringen i KÄRNRADIERNA GENOM PLANCKRINGEN

ATOMKÄRNANS ALLMÄNNA

ELEKTROGRAVITELLA EGENSKAPER

Från Energizonen i Potentialbarriären från Ljusets Gravitella Beroende

ATOMKÄRNANS ALLMÄNNA ELEKTROGRAVITELLA EGENSKAPER

I särskilt resultat från KÄRNRADIERNA GENOM PLANCKRINGEN

Eftersom naturkonstanten c₀ bevaras oberoende av gravitationens inverkan enligt kraftvektorledet F_c = F_c0 – F_G, samt även elektriska konstanten bevaras enligt

R₀c₀=(±1)R_max(±1)ç₀, kan tydligen — oberoende av gravitationens inverkan — Planckringen, eller »atomkärnans egen inre övergripande elektrogravitella-magnetiska oändligt fraktala massfysik», likväl beskrivas på energizonens ekvivalent c₀/2=c_z MED ett motsvarande internukleärt ekvivalent fristående w=c (enligt redan tidigare berörda grundsatser)

1a. varje masskropp (m) har sitt eget särskilda g-fält oberoende av samverkan och interferens med andra kroppars g-fält (superpositionsprincipen)

1b. divergensen bestäms lokalt av gravitationen genom kraftvektorledet F_c0 –F_c– F_G=0 som en med gravitationen förbunden egenskap, oberoende av interferens och samverkan med andra kroppars gravitella, elektriska eller magnetiska fält, vilket garanterar bevarandet och konserverandet av c₀

Dvs., atomkärnans fysik kan beskrivas I EKVIVALENS MED KONSEKVENSEN att atomkärnans fraktala ytstruktur — en direkt konsekvens av Plancks konstant, se från Planckringen — konserverar en egen absolut och fristående strukturell g-dominans i bevarandet av c₀ och som inte kan förstöras eller ändras, oberoende av interferens och samverkan med makrofysikens övergripande yttre dominanta g-fält. Energizonen kan alltså sägas bevaras EKVIVALENT oberoende av makrogravitationens styrka — därför, nämligen, att atomkärnan, som härletts ovan, grundas på en obegränsad toroid fraktal ihålig ringstruktur där tätheten går mot oändligt med växande fraktaldjup. Detta gör det (nu) möjligt att i detta skede härleda atomkärnan också på dess strikt gravitella form — och som garanterat ligger utanför den moderna akademin möjligheter (Se Einsteins Ekvation), se Atomkärnans Härledning II. Det betyder alltså att atomkärnan är okänslig för makrogravitationens inverkan.

Eftersom principalringen med c₀/2=c_z närmar sig noll obegränsat med växande fraktaldjup och därmed med obegränsat växande täthet innefattar alla möjliga grader av motsvarande yttre makrogravitationer, finns ingen möjlig makrogravitation, hur stark den än är, som kan ”döda” eller ”stänga av” atomkärnans elektromagnetiska funktion.

Det enda som händer om makrogravitationen växer obegränsat är att atomkärnan bara blir ”hårdare”, analogt mera em-avstängd i sin näryta. Energizonerna c₀/2=c_z bevaras i vilket fall inom atomkärnans fundamentala massform.

Ekvivalenter är ekvivalenter.

Hur kan Q koppla till massytans c=0?

Dynamiken

I och med att divergensen, analogt det elektrostatiska fältet, bygger på massans g-fält, nämligen genom divergensens g-beroende och därmed bevaras i samma mening som massan bevaras — e-fältet definieras av g-fältet — finns alltid en dynamiskt levande och med gravitationens verkande garanti (Se GcQ-teoremet) absolut koppling mellan potentialbarriären och massan. Om partikeln påverkas elektriskt, vilket innebär att fältpunkternas potentialer påverkas, dras centralmassan automatiskt med eftersom e-verkan ytterst sett grundas på partikelns g-fält. Och omvänt, om partikeln påverkas rent mekaniskt följer dess omgivande potentialbarriär med allt eftersom kroppens g-fält antar andra positioner med kroppens förflyttning.

Innan det stod klart att denna avancerade dynamik saknar upphov (Se Energilagen: om energin saknar upphov, gör massan det också) uppstod (i min historia) den till synes dräpande svåra frågan hur man skulle förklara den elektriska verkan i potentialbarriären då ju barriärens kontakt med partikelytan går via c=0. I och med energilagen som säger att massan saknar upphov därför att energin gör det, och därmed att dynamiken redan är uppkopplad via g-fältet och därmed e-fältet som grundat på divergensen c, samt det avgörande kraftvektorledet F_c0 –F_c– F_G=0 som förklarar c i detalj genom gravitationens samtliga möjliga fall, elimineras denna svårighet fullständigt. Laddningen är, som massan och spinnet, utan upphov. Med dessa klarlägganden förklaras alla elektrofysikens fenomen med utomordentlig skärpa och exakthet.

[c0.docs99].

Atomkärnans gravitella härledning — PlanckEkvivalenterna — PotentialBarriären — Nuklidbarriären — Ljusets Gravitella Beroende

atomkärnans g-härledning -- PLANCKRINGEN 2 -- atomkärnans geometriska härledning, se PlanckRingen 1

Se även Atomkärnans Härledning I i KÄRNRADIERNA GENOM PLANCKRINGEN

ATOMKÄRNANS GRAVITELLA HÄRLEDNING — Atomkärnans härledning II — MASSANS Eller

GRAVITATIONENS FUNDAMENTALFORM

ATOMKÄRNANS MASSA LIGGER INTE I DESS VOLYM UTAN I DESS YTA: Planckringens strukturfraktal h=mvr med massekvivalenten m = m[n®¥]^–1[n®¥] garanterar att masstätheten går mot oändligt som fraktaldjupet ökar: Atomkärnan är en utpräglad (oändligt ihålig) skalbyggnad vars yta i princip är oändligt hård men samtidigt oändligt tunn. Vi studerar hur.

Se även TNED sammanställd utvecklingshistoria i TNED FRÅN BÖRJAN.

ATOMKÄRNAN HÄRLEDS ENLIGT TNED från PLANCKRINGEN h=m_nc₀r_n ur gravitationen=massan

från den primära massförstöraren E=mc² som enligt energilagen grundlägger en massans fundamentalform genom Planckringen (J=mvr) med massekvivalenten m = m[n®¥]^–1[n®¥].

ATOMKÄRNANS GRAVITELLA HÄRLEDNING ENLIGT RELATERAD FYSIK görs från gravitationslagen

F=ma=Gm₂m/r² genom energilagen (POM) som en fundamental massform (PASTOM) genom potentialbarriärens ring J=mvr.

m = [n®¥]m/[n®¥] = [n®¥]m’; m’= n^–1(F/a) = F(an)^–1 = F/a’ .............. basic (PASTOM)

a’ = an = nGmr^–2=Gmn^–1(rn^–1)^–2=Gm’(r’)^–2 ; a I FORMYTAN växer OBEGRÄNSAT med n®¥

a’ = Gm’(rn^–1)^–2 ........................................................................... aktuella fallet, m&r®0

= nGmr^–2 .................................................................................. fast r, m®¥

· Den fundamentala massformen m = m[n®¥]^–1[n®¥] innehåller alltså inga partiklar;

· massa består av ett obegränsat antal masselement som oupphörligen delas så att någon minsta massdel inte kan återfinnas

· massa är ställen utan ljus c=0 — som bevarar det GENOM GRAVITATIONEN F

· Atomkärnan består inte av några partiklar, utan en ytterst sammansatt GRAVITERANDE kraftväv F/a’ med utanpåliggande elektriska och magnetiska fält — som följd av att hela kärnmassan fragmenterar på ringfraktalerna där a’®¥ så att någon minsta beståndsdel inte kan återfinnas, m’®0

· Plancks konstant är SÅLEDES en fraktal strukturkonstant E=hf=hn^–1nf=h_n f_n, n®¥;
högsta frekvenserna i djupaste delarna med lägsta energierna

· det finns ingen våg-partikeldualitet i fysiken kärnan är ett elektromekaniskt svängningssystem (mvl=h)

· massan konserverar laddningen via Potentialbarriären (c₀/2)

· masstätheten r I FORMYTAN växer obegränsat med växande n

r = n²m · [V_tor=(2p)²r_T²r]^–1 ............................................................. r>r_T, fast V, m®¥

= n2m · [V_tor=(2p)²r_T²n^–2r]^–1 ...................................................... fast m, V®0

= n2mn^–1[V_tor=(2p)²r_T²n^–2rn^–1]^–1 ............................................... aktuella fallet, m&V®0

FRAGMENTERINGSKRAFTEN kan bara upphävas genom en ±bn-struktur: SUMMA NOLLSPINN, SUMMA NOLLADDNING: attraherande massor som upphäver fragmenteringskraften F och därmed nollzonerna (m®g):

· a överförs på andra massor via induktionen (COEI), således går ingen energi förlorad

Giltigheten av den primära massförstöraren (E=mc²) från energilagens andra huvudsats (m®g) beskriver massan på en obegränsat fraktalt delbar total form utan partikulära beståndsdelar vars fundamentala matematiska fysik innefattar ett impulsmoment J=mvr eller ringen. Atomkärnans form är därmed given som ringar som består av ringar i all oändlighet. Den aktuella ihåliga toroidformen framkommer genom att jämföra den idealt kompakta toroidformens multiplicitet (proportionaliteten mellan massa och laddning vid fusion) via en heltalsbaserad (A) kubanalogi

r = r₀A^1/3 (r₀ atomkärnans grundradie) med yttoroidens matematik, kr₀A^1/2. Medelformen (en atomkärna drygt i mitten av det naturliga nuklidspektrat, runt A=135) motsvarar N3m20-aggregatet eller grundnukliden som beskriver neutronens-protonens fysiska geometri. Se från KÄRNRADIERNA GENOM PLANCKRINGEN (Atomkärnans härledning I). Övriga tyngre kärnor följer sedan av grundnuklider som förenas till större kärnor.

N3m20 verifierades (1994) speciellt i analysen av kollisioner mellan spinnpolariserade protoner (från artiklar i Scientific American 1979 och 1987, Alan D. Krisch: May 1979 The Spin of The Proton frn. s.58 och August 1987 Collisions between Spinning Protons frn. s.32). Neutronkvadraten ger toroidmodellen dess slutliga bekräftelse genom matematiken för atomvikterna, samt vidare i K-cellens allmänna värmefysik (se från Universums Historia) som helt bygger på dessa resultat.

[c0_I.doc s29]

neutronens sönderfall

NEUTRONEN

Med fortsättning från

NEUTRONENS NEGATIVA KÄRNMAGNETISKA MOMENT

efter resultatet i KÄRNRADIERNA GENOM PLANCKRINGEN

Neutronens sönderfall — se även i Neutronens nolladdning

Neutronen innefattar elektronen och protonen genom massdefekten 0. Neutronen är emellertid instabil; den sönderfaller till en kärna (protonen) och ett hölje (elektronen) i formen av en väteatom inom 12-14 minuter. Orsaken är deplacementet.

1. Den magnetiska effekten från J_0K på laddningsdeplacementet bildar en förskjutning in mot kärncentrum M mellan ±-ringarna i de inre toppringarna (nedan t.h.). Ett inåtdragande moment ¬ bildas då, bort inåt centrum från ideala tyngdcirkelns tyngdlinje som därmed också rubbas.

2. För att bibehålla jämvikten måste ett lika stort men motriktat moment bildas.

3. Kärnan genomför det — arbetet — genom att dels bränna av massa (m®g) som krävs för energin till arbetet, och dels genom att FÖRA UT — inte skapa — NEGATIV DEPLACEMENTELEKTRONMASSA från ringstrukturen ut, utanför kärnan, bort från den inre dislokationen. Därmed flyttas tyngdcirkelns tyngdlinje tillbaka utåt bort från kärncentrum till läge jämvikt.
Kärnan svarar alltså med att bygga en exakt balanserad atom. Dess kraftekvation är F_BT + F_eZ = 0, där FeZ definierar Spektrum och Kvanttalen i detalj. Kraftledet reglerar hela kommunikationen mellan den centrala atomkärnan och de yttre elektronmassorna och är ansvarig för alla kemiska bindningar och varje annan strömstyrd verksamhet som inbegriper atomen.

4. Alla atomkärnor, även neutronen, får genom ovanstående ordning en utpräglad kärnpol: negativa och positiva elektronmassor avges i diametralt motsatta riktningar enligt en strängt bestämd ordning [‡1]. Se även i Elektronens Bubbelkammarspår.

5. Atomkärnan justerar, reglerar och anpassar deplacementet dynamiskt per dia, para och ferromagnetiska kärnmagnetiska typmoment.

ATOMKÄRNANS n-p-STRUKTUR

Med neutronens sönderfall till en protonkärna och en elektronmassa (Väteatom), framkommer också en ny kärnstruktur. Det finns därmed totalt två olika ytstrukturer

neutronens kärnyta protonens kärnyta

enligt neutronsönderfallets mekanism,

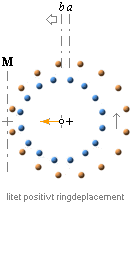
Höger (ba): Underringarna har här ikoniserats med små sfärer för att förtydliga principen. Blå sfärer för minus och orangea för plus. De inre blå sfärerna representerar de negativa ringarna som bär ansvaret för neutronens negativa kärnmagnetiska moment. På grund av magnetismen från toppspinnet, i kraft av det redan existerande positiva deplacementet, strävar dessa negativa delar att separera de positiva och negativa ringarna ytterligare — med följd i att de senare drivs inåt. Därmed skapas obalans och som neutronen återställer genom att droppa av minusmassa. Den resulterande kärnan, protonen, uppvisar i följd härav en mera utpräglad ringstruktur med positiva delar längre ut, precis uppvägande den utförda minusmassan, samt med nettoresultatet att också protonens kärnmagnetiska moment övergår i ett positivt dito. (Kärnmagnetiska momentets matematiska fysik beskrivs i särskild artikel).

där massan i neutronens negativa kärnmagnetiska moment (se texten under ovanstående illustration) som förorsakade neutronens instabilitet flyttas ut i formen av elektronmassan. Därmed uppvisar den resulterande centrala kärnytan en mera utpräglad elektriskt laddad ytstruktur (+) genom att skillnaden mellan de positiva och kvarvarande negativa ringarna blivit något större. På den grunden kan kärnstrukturen relateras i varje atoms särskilda s.k. nuklid;

OBSERVERA GRUNDVILLKORET FRÅN PASTOM: atomkärnan som enhetsform är helt fri från inre partikulära beståndsdelar. Men för att kunna beskriva den enheten som grundad på nollkraft och nollmoment (atomkärnan behöver ingen energipåfyllning för att fungera) måste vi — som exemplifierats ovan — använda en termuppdelning (med förgreningar) av typen J0+NJ1=0 (typ –5+5=0) och som därmed anställer en viss uppfattning om partikulära (inre) beståndsdelar. Notera (därmed) också den kvantitativa ekvivalensen mellan massa och energi generellt: Alla kärnmodeller som uttrycker kärnenergins ekvivalenter har tvunget fysikalisk giltighet, vare sig vi gillar det eller inte. Men det betyder INTE att ”energipartiklarna” existerar som beståndsdelar i atomkärnan, även om man kan påvisa att de existerar under mycket kort tid genom speciellt höga kollisionsenergier. Vilket vill säga: I TNED har ”kvarkteorin” ingen som helst ställning därför att atomkärnan inte innehåller några beståndsdelar av någon som helst kvalitativ art. Atomkärnan (från neutronen) är en harmonisk enhet, helt utan beståndsdelar. Se även explicit i Neutronens fragment.

Se även Allmänt om den moderna Kvarkteorin.

npStrukturen

Nukliden är atomens specifika kärndel, såsom komponerad av typen n-struktur (n) och p-struktur (p). En viss nuklid med dess speciella kärnstruktur kan därmed återföras på n-p-typerna som nukleoner, alltså atomkärnans grundläggande strukturelement: atomkärnans bildning kan återföras på dessa som komponenter, och atomkärnan kan också sönderfalla i sådana. Varje p-nukleon bidrar med en elektronmassa. Vi noterar att termen nukleon i konventionell kärnfysik används ungefärligen på samma sätt (men inte riktigt), samt att den där betecknar en beståndsdel i atomkärnan. I TNED finns ingenting sådant: atomkärnan innehåller inga beståndsdelar. Se vidare från Planckringen.

DEPLACEMENTSFÖRSKJUTNINGEN avbildad ovan gäller också, delvis vidare, för alla tyngre atomkärnor i deras olika och möjliga n-p-skepnader genom att kärnan, allt efter energiinnehåll och balans, kan justera deplacementet och därmed också reglera det kärnmagnetiska momentets form, fason och magnitud. Endast vissa n-p-strukturer bildar de stabila nukliderna i formen av atomernas centrala kärnbyggnader. Utöver dessa finns en stor flora av instabila nuklider som ligger spridda omkring det stabila huvudstråket.

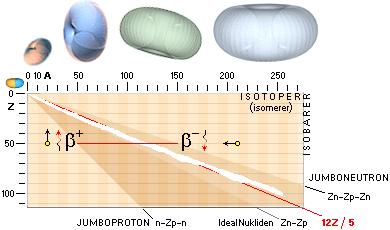
NUKLIDKARTAN (AZ) i TNED

Nuklidstatiska medelvärdeslinjen A=12Z/5 skär med god approximation nuklidfältet (vitt i AZ-kartan nedan). Där återfinner vi de naturliga grundämnenas stabila atomer. Genom att n-p-strukturen kräver vissa utfyllnader med växande atomnummer Z, kommer en del av grundämnesatomerna att uppvisa isotoper: samma Z men med olika masstal A. Atomer med samma masstal (A) men olika atomnummer (Z) kallas isobarer.

Individer vid sidan av de stabila är mjukt instabila (masstalet bevaras under sönderfallet):

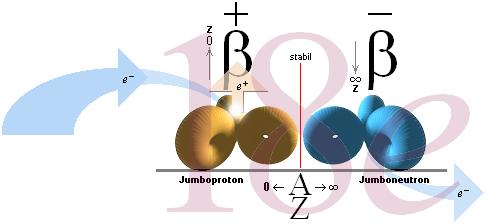Betasönderfallets mekanism

Termen beta avser elektronmassans bägge polariteter (både elektron och positron).

Jumboneutroner till höger och Jumboprotoner till vänster. Jumboneutronen är för tung för sitt atomnummer, den strävar att göra sig av med en (eller flera) elektron för att komma in på rätt läge längre ner i kartan via ett högre Z. Jumboprotonen är för lätt för sitt Z; genom att bränna av +b-ringar, eller alternativt dra in en (eller flera) elektron, kan den minska sitt Z och därmed förflytta sig uppåt i läge korrekt balans. AZ-kartan innefattar också gränser för atomer som är hårt instabila (masstalet ändras under sönderfallet, generellt från Z=83). Beskrivningen för den delen är mera utrymmeskrävande och behandlas inte i denna korta översikt.

forts.

RADIOAKTIVITETENS MATEMATISKA FYSIK ENLIGT TNED

Kort beskrivning (särskilt avsnitt [‡] under utarbetande) [Från ENERGY_Spark][utf. RadioNUDE]

Enligt TNED beskrivs alla instabila atomkärnors ändring mot ett stabilt tillstånd via de två typleden

(K) – E_hf18 = K = (K1+K2 – (m®g) + _b0_gm) – E_hf18 .............. betasönderfall, betainstabila atomer, betanuklider

[K] – E_hf1818 = K = [K1+K2 – (m®g) + _T 0_gm] – E_hf1818 .......... nuklidsönderfall, nuklidinstabila atomer, radionuklider

Tas den neutrinostyrda radiokomponenten E_hf1818 bort ur kärnreaktionslagen, får man endast uttrycket för en stabil nuklid, vilket INTE är radiofallet.

Av den anledningen vet vi helt säkert ATT neutrinoinfluenserna spelar en avgörande roll för radionuklidernas sönderfall. Men teorin — DEN ÄR OMFATTANDE — ingår inte i konventionella led.

Se utförligt med beskrivning av samband och teori, med härledningar, analyser och jämförelser mot etablerade termer och begrepp från

RADIOAKTIVA SÖNDERFALLETS ALLMÄNNA SAMBANDSFORMER

Se även avsnitten i syntes i det kortare registerblocket Radioaktiva Sönderfallets Fysik i RegisterR.

Varje radionuklid har sitt särskilda neutrinospektrum, och olika radiotyper interfererar därför INTE i sina respektive sönderfall. BETASÖNDERFALLEN däremot har ömsesidiga influenser eftersom neutrinoemissionerna ÄR av samma typ för alla betasönderfall och motsvarande energier därför också kan genereras av elektronsvängningar. I radiosönderfallen däremot är neutrinonivåerna isolerade från elektrongenererade effekter.

forts.

Nuklidkartan AZ i TNED

beskrivning

[Från c0_I]

KÄRNSTRUKTUREN, toroidens system av ±b-ringar, beskrivs i TNED genom protonens typstruktur med beteckningen p och neutronens typstruktur med beteckningen n. KOMBINATIONERNA p-n bestämmer aktuell atomnuklid. Beteckningen Z används allmänt för atomnummer, samma som antalet ekvivalenta protonindivider. Beteckningen A används allmänt för masstal, samma som antalet ekvivalenta p och n i samma atombyggnad: A=p+n.

KÄRNSTRUKTUREN ENLIGT TNED

neutronens kärnyta protonens kärnyta anti-protonens kärnyta

Om vi fyller på p-formen med omgivande (integrerade) n-former — en Zn-Zp-Zn-nuklid, en s.k. JumboNeutron — ser vi direkt varför den resulterande kärnbyggnaden förr eller senare måste mista sin karaktäristiska kärnladdning; Neutronmassorna tvingar resultanten att dra in det positiva b-deplacementet. För att kärnan ska kunna uppvisa en stabil laddning måste den därför och för detta fall spädas ut med mera p-ämne. Om p-kärnan å andra sidan växer jämnt med ett minimum av n-massa — idealt en n-Zp-n-nuklid, en s.k. JumboProton — ser vi lika enkelt att kärnladdningen tvunget måste växa i magnitud; Kärnan tappar också här sin grundharmoni från den enkla protonen, analogt väteatomens kärna. En ideal Zn-Zp=Z(n-p)-nuklid skulle ge exakt balans — förutsatt ringen hade n-form. Att så inte är fallet leder fram till en medelvärdeslinje — nuklidstatiska medelvärdeslinjen. Nuklidstatiska medelvärdeslinjen (röda diagonalen ovan) beskriver i stort VAR vi återfinner grundämnenas stabila atomer och kärnor i hela den möjliga n-p-kartan.

Sambandet för nuklidstatiska medelvärdeslinjen är medelvärdet av koefficienterna för ideala Z(n-p)-nukliderna via k=1/2 med Z=A/2, och Jumboneutronens Z(n-p-n)-nuklider via k=1/3 med Z=A/3. Medelvärdet blir [(1/2)+(1/3)]/2=5/12 med Z=5A/12, eller A=12Z/5.

neutronen

Neutronkvadratens Uppdagande

ALLMÄNNA RESULTAT från härledningarna i Planckringen FÖR JÄMFÖRANDE EXEMPEL

h=m_nc₀r_n

Från resultatet av Planckringen i KÄRNRADIERNA GENOM PLANCKRINGEN

NEUTRONEN — (1818+18+2,624)m_e

neutronmassan m_n=1,0086652u [HOP Table 2.1 s9–65]

elektronmassan m_e=0,000548598u [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

m_n/m_e=1838,264

Se illustrationens förklaring i Nuklidkartan AZ

OM NEUTRONMASSAN 1,0086652u uttrycks i elektronmassan 0,000548598u fås värdet

1838,264 elektronmassor som kan skrivas på uppdelningen

1818 + 18 + k

1818 .................. centralmassivet

18 ...................... förbrukningsvara, omsätts i atomära massdefekten

k ........................ löpande (»smörjmedel») 2,624 e-massor

Talet 18 markerar en viktig detalj i kärnfysiken —

ENLIGT TNED

Atomära massdefekten — i fortsättning från beskrivningen närmast ovan:

Skillnaden mellan 1. neutronmassan som krävs för att bilda hela den atomen, samma som masstalet (A) gånger neutronmassan och 2. atomens aktuella egenmassa (som bara kan erhållas genom praktiska experiment [genom en s.k. masspektrograf]), med skillnaden uttryckt i antalet elektronmassor per neutronnukleon, hela nuklidkartan igenom,

är max 18 ELEKTRONMASSOR. Atomära massdefektens formella grund beskrivs utförligt i Atomära Massdefekten.

Järntoppen

Järnindividen ₂₆Fe⁵⁶ ligger högst med värdet 17,759142e.

· Atomära massdefekter större än 18 förekommer inte

· Begreppet ATOMÄR MASSDEFEKT finns inte med i modern akademi

I modern akademi har man antagit en annorlunda massdefektsdefinition;

Den grundas på kärnmassan — inte på hela atomen.

Därmed fås delvis andra värden, med en helt annan ordningsföljd mellan maxima och minima i kärnfysiken.

massdefekterna

Jämför (se även mera utförligt längre ner)

RELATERAD FYSIK

m_D: 1.₂₆Fe⁵⁶_17.759142, 2.₂₈Ni⁶²_17.748159, 3.₂₈Ni⁶⁰_17.744140, 4.₂₆Fe⁵⁸_17.738285.

m_Dn: 3.₂₆Fe⁵⁶_17.168214, 1.₂₈Ni⁶²_17.176463, 4.₂₈Ni⁶⁰_17.149481, 2.₂₆Fe⁵⁸_17.171605.

MODERN AKADEMI (MAC)

— MAC-värdena ovan omräknade från en webbkälla som jag lyckats missa … Se dock exempelräkningen nedan, samt citatet från Wikipedia med vidare referenser som styrker ordningen (MAC-värdena ovan fås identiskt i tre decimaler om man använder elektronmassan 0,0005497126u tillsammans med de nedan övrigt angivna parametrarna …).

Räkneexemplen nedan använder »en vanlig gammal klassisk kalkylator» med sju fasta decimaler.

Exempel MAC, viktsenheter i u=1,66033 t27 KG, A=56, p=1,0078252u–0,00054598u=1,0072756u, n=1,0086652u:

antal 0,51103373 MeV

atomen kärnan, k 26p+30n, j massdefekt, j–k (j–k)/A=a a/m_eu ger a i e-massor

26Fe56 55,9349363 55,920672 56,449121 0,5284488 0,00943658 17,201277

Notera att man får något olika värden beroende på noggrannheten i valet av antalet decimaler: t.ex. elektronmassan avrundat 0,000549 mot det mera noggranna 0,000548598 ger märkbara skillnader i dessa jämförelser; det är här inte känt exakt vilka basreferenser som använts för de ovanstående fyra representanterna i MAC-värdena; I exemplet närmast ovan har använts TNED-preferenserna.Kör man exemplet ovan i ett kalkylblad (MsWORKS) blir slutvärdet 17,2021173 beroende på högre noggrannhet. Till jämförelse anges MeV-värdet 8,7946 för Ni-62 i @INTENET Wikipedia Nickel 2008-10-30, som ger likvärdiga 17,210305 elektronmassor. I vilket fall hamnar vi märkbart långt ifrån den relaterade fysikens detaljupplösning.

”At the peak of binding energy, nickel-62 is the most tightly bound nucleus, followed by iron-58 and iron-56.^[1]”,

@INTERNET Wikipedia Binding energy 2008-10-30

Min översättning:

Vid toppen för bindningsenergin, är nickel-62 den hårdast bundna atomkärnan, följd av järn-58 och järn-56.

Exempel TNED, viktsenheter i u=1,66033 t27 KG, A=56, n_u=1,0086652, m_eu=0,000548598:

atomen, a a/A/nu=b (1–b)/m_eu=c

26Fe56 55,9349363 0,9902573 17,759142

c = massdefekten per neutron uttryckt i elektronmassaenheter i u

Har dessa skillnader någon betydelse?

Ja. Verkligen. Stor betydelse. Vi studerar det.

Om man använder gängse tabeller över atomvikter U för givna masstal A [HOP Table 2.1 s9-65 – 9-86] och uttrycker U i den atomära massdefekten

— skillnaden mellan

1. neutronmassan som krävs för att bilda den atomen

[vi minns att neutronen innefattar hela väteatomen och därmed elektronmassan, vi behöver aldrig bry oss om den på något särskilt sätt, den ingår automatiskt med max en per neutron] och

2. den aktuella atomens massa,

allt uttryckt i elektronmassaenheter per neutron

atomära massdefekten

ekvation

m_D = (1–U/Am_n)/m_e ................... atomära massdefekten, U = Am_n(1–m_Dm_e) med

m_n = 1,0086652 ........................ neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598 .................... elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

begreppet atomär massdefekt beskrivs mera utförligt och vidare i Atomära Massdefekten.

eller mera egentligt med m_nm_em i enheten KG och med m_D=n_e som antalet elektronmassor, m aktuella atommassan och A masstalet

n_e = u(1–m/Am_n)/m_e ................... atomära massdefekten,

ALLMÄNNA RESULTAT FÖR JÄMFÖRANDE EXEMPEL

h=m_nc₀r_n

Från resultatet av Planckringen i KÄRNRADIERNA GENOM PLANCKRINGEN

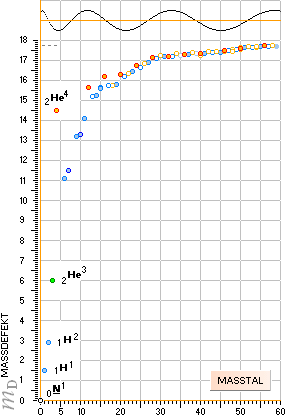
får man nedanstående kartbild. Nuklidkarta Ae visar atomära massdefekten för de stabila nukliderna (de instabila ligger spridda omkring huvudspåret). Maximum vid 18m_e bestäms teoretiskt av sambandet ovan genom

18/1,0086652=17,845366 .......................... teoretiska maxgränsen, praktiskt max 17,759142 för ₂₆Fe⁵⁶

Begreppet atomär massdefekt beskrivs mera utförligt och vidare i Atomära Massdefekten.

DÄRMED KAN Ae-KARTAN ANSTÄLLAS TILL JÄMFÖRELSE MED ETABLERAD TEORI.

Läsaren, om inte redan förtrogen, kommer alldeles strax att få exakta besked.

GRUNDKARTA

Nuklidkarta Ae. De stabila nukliderna inprickade efter deras atomära massdefekt. Skalan 0-18 anger antal elektronmassor som bränts av per primär neutronindivid (masstalet A, som också kan uppfattas som en summa av neutron-protonindivider eftersom neutronen av princip redan innefattar hela väteatomen) för att bilda den atomen.

I konventionella beskrivningar används inte atomära massdefekten utan istället en nukleär massdefekt som ger delvis annorlunda värden eftersom elektronerna inte ingår där. Detaljerna beskrivs vidare i huvudtexten.

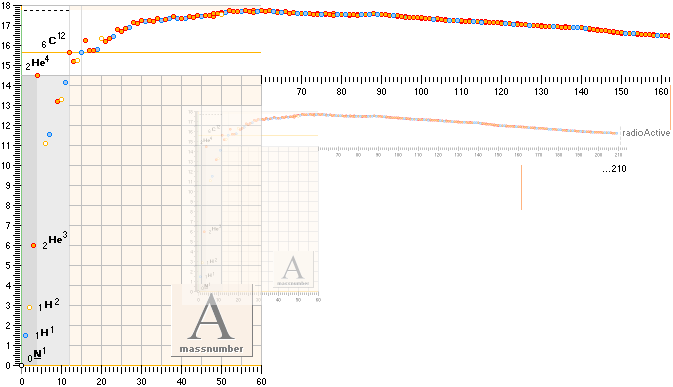
Viktigheten i den beskrivningen framkom (i min historia) inte förrän betydelsen av Ae-kartan uppdagats:

Går det att, på något sätt, beräkna motsvarande atomvikter teoretiskt enligt Planckringen för att på så sätt kontrollera precisionen mellan experiment och teori? Finns det någon sådan grund?

Javisst gör det det. Det är det som är det anmärkningsvärda, det enastående. Det finns en mönstergeometri, som här kommer att kallas neutronkvadraten. Med den grunden är, tydligen, helt okänd av modern vetenskap. Helt komplett fördold. Resultatet, i samma skala som den ovan visade, blir nämligen:

SAMMA KARTA.

Hur? Vi ska strax studera detaljerna närmare i neutronkvadraten.

Först:

Vad visar den moderna akademins teoretiska värden till jämförelse?

Notering: Följande jämförelse bygger HELT på nedanstående redovisade data från Weizäckerekvationen. Någon annan representant för den moderna akademins teori är här inte känd.

atomkärnans energibindningar

jämförelse · jämförelser mellan TNED och Modern Akademi

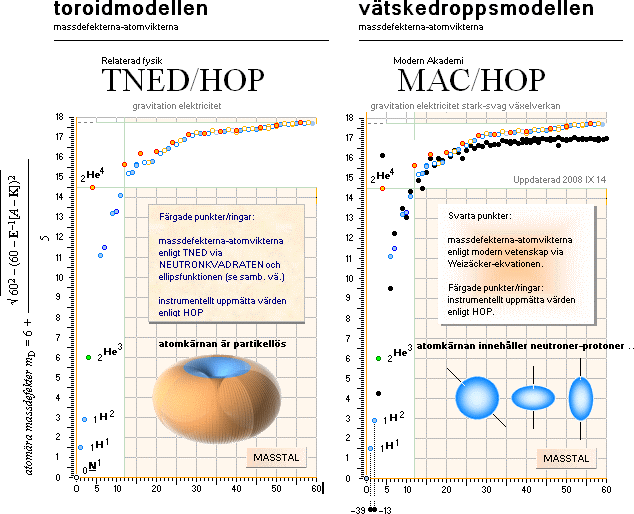
Se även Atomvikter i jämförande tabell som ansluter till ovanstående grafiska presentation.

Se även kompletterande delvis mera utförlig jämförande beskrivning HOP/TNED/MAC i Bekräftelser på Atomkärnan enligt TNED.

De svarta punkterna i högra delen visar de teoretiska värden man får enligt Weizäckerekvationen i modern akademiskt teori och som ansluter till vätskedroppsmodellen. (Genom en tidigare felräkning, min historia, hamnade Weizäckervärdena på tok alldeles för högt upp; Felet: en exponent A^–1/3 hade feltecknats i kalkylbladet [–^1/3 istf. korrekt ^–(1/3)]. Se även beskrivningen i Weizäckerekvationen).

Frånsett de tre första nuklidvärdena (som ger helt horribla värden, antydda med siffror nederst) ansluter Weizäckerekvationens resultat ”hyfsat” till de experimentellt uppmätta värdena (se även annan illustrerad jämförelse nedan). Ser man emellertid till en mera noggrann test av teorin är det tydligt att Weizäckerekvationens värden i vilket fall INTE har förutsättningen för just en noggrann stämning. Planckringens värden däremot håller sig (nära) som ett plåster till experimentalfysiken via HOP-tabellens värden. Felet med Weizäckerekvationen är att den grundas på en volymär analogi; Korrekt sätt är (enligt TNED) en ytanalogi — om inget annat revolutionärt uppkommer som kan uppvisa en ännu mera avancerad precision.

En mera ingående redovisning av hur TNED-värdena framräknats finns i PRECISIONEN I ATOMVIKTERNA ENLIGT TNED.

Ett annat sätt att visa samma resultat:

MAC (modern vetenskap och akademi): röd; EXPERIMENTELLA OBSERVATIONER (HOP): svart; TNED: svart

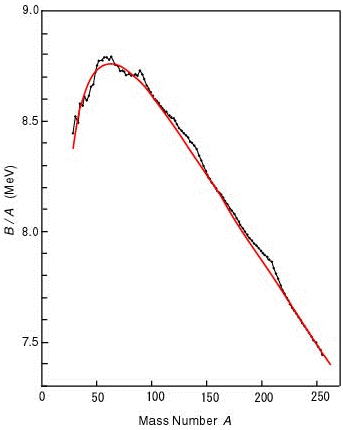
Röd kurva motsvarar Weizäckerekvationens värden, den svarta är de experimentellt uppmätta värdena.

Illustrationen samt nedanstående citat är hämtade från

Internet Seminar MICROSCOPIC WORLD –3– The World of the Atomic Nucleus

English translation of "The Internet Seminar (Microscopic World -3- The World of the Atomic Nucleus)"

from the original Japanese version,

Jan. 1, 2006 · Dr. Kenjiro Takada · Emeritus professor of Kyushu University

“2-4: The Liquid Drop Model [Comparison with Experimetal Data]

In order to confirm how well the Weizsaecker-Bethe mass formula can reproduce the experimental data of nuclear binding energies, the comparison with experiment is shown in the following figure, in which the red curve shows the values of the binding energy per nucleon obtained by the Weizsaecker-Bethe formula, and the black points indicate the experimental data, which are equivalent to those in the figure at the bottom of the preceding page.”

Internet Seminar MICROSCOPIC WORLD –3– The World of the Atomic Nucleus, Dr. Kenjiro Takada 2006

Min översättning:

2–4. Vätskedroppsmodellen [Jämförelse med Experimentella Data]

För att bekräfta hur väl Weizäcker-Bethe massformeln kan återge de experimentella data på nukleära bindningsenergier, visas jämförelsen med experiment i den följande figuren, i vilken den röda kurvan visar värdena för bindningsenergin per nukleon erhållen från Weizäcker-Bethe formeln, och de svarta punkterna indikerar experimentella data, som är ekvivalenta med dem i figuren längst ner på föregående sida.

Texten till Figuren:

“As seen in the above figure, the Weizsaecker-Bethe mass formula can reproduce well the experimental data for a wide range of nuclei. We can therefore conclude that the liquid drop model is enough valid in nuclei.”

Min översättning:

Som ses i figuren ovan, kan Weizäcker-Bethe massformeln återge väl de experimentella data för ett brett område av nuklider. Vi kan därför sluta oss till att vätskedroppsmodellen är tillräckligt giltig i atomkärnor.

Jämför återigen TNED via NEUTRONKVADRATEN: den svarta grafen. Det är det mest anmärkningsvärda i hela den här historien: TNED och experimentalfysiken tycks här gå helt hand i hand. Där kan man — tydligen — tala om precision. Se även ovanstående jämförande grafer.

massdefekterna i grafisk sammanställning

Grafen nedan som visar den atomära massdefekten för de stabila nukliderna sammanfattar jämförelserna mellan de olika teoretiska kärnmodellerna i modern akademi (Weizäckerekvationen — vit) och relaterad fysik (TNED — blå) med referens till de experimentellt uppmätta basvärdena (HOP — röd). Diagrammet har ritats av MsWORKS 4.0 Kalkylprogram med grund i resultatdata från respektive teorier enligt Weizäckerekvationen och allmänna massdefektsekvationen enligt TNED.

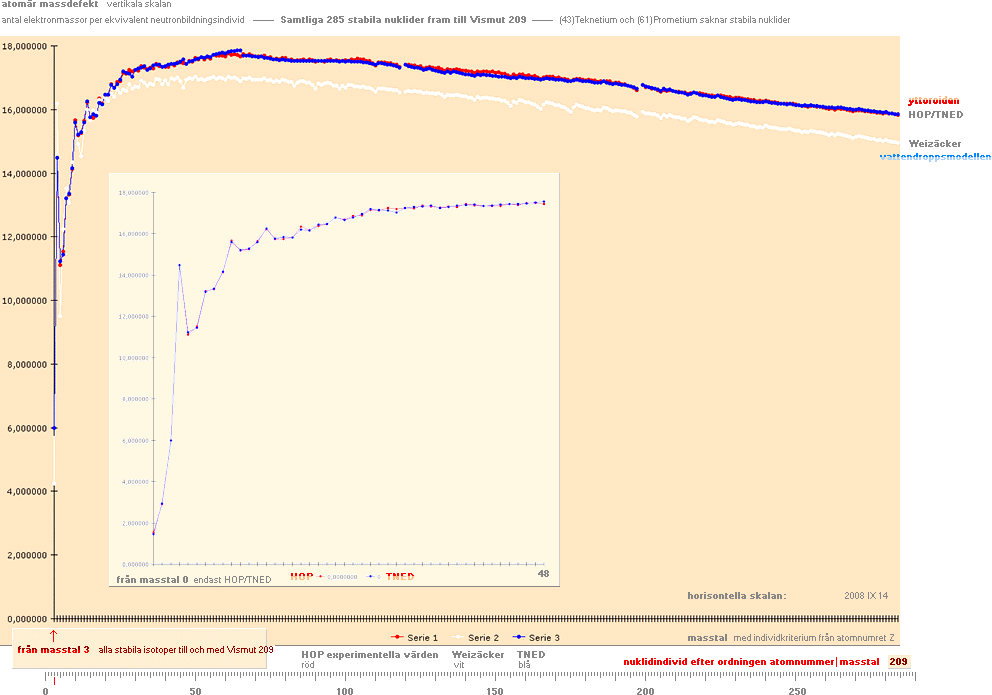
Det lilla glappet som syns mellan TNED/HOP vid Järntoppen (omkring masstal 60) beror på att TNED-värdena här framräknats delvis genom de allmänna medelellipser som bildar Neutronkvadratens mönsterkropp snarare än via de mera noggranna reguljära elliptiska massdefektsekvationer som finns för ändamålet (men som är krävande då ännu ingen uttömmande genomgång finns i författning); Om vi studerar vågfunktionen för medelellipserna ser vi (genom separat överlagrande bildanalys) att dessa kurvor ligger aningen för högt mot slutet; den sista vågkammen slutar också i samma avsats, vilket ger en liten ”läpp” på slutet. (Se även Allmänna massdefektsekvationen). Ytterligare sådana förenklingar finns i TNED-grafen — vilket innebär att en fördjupad analys bör göra precisonen ännu mera markant. En fördjupning av dessa detaljer är dock inte av nöden i detta skede. Lägg för övrigt märke till att Weizäckerekvationen garanterat INTE klarar de allra första grundnukliderna utan närmast våldsamma fel. TNED däremot prickar in värdena med excellent glans.

ENBART med grund i ovanstående träffsäkerhet från TNED är saken avgjord: frågan om äktenskapet gäller (tydligen) mellan experimentalfysiken och TNED. Helt klart är det så — tydligen från första till sista prick.

Se även en del av ovanstående motsvarande sifferdata i JÄMFÖRANDE TABELL MED ATOMVIKTER.

Se även kompletterande beskrivning (diagrammet ovan mera utförligt) i Bekräftelser på Atomkärnan enligt TNED.

Observera att jämförelsen i massdefekter mellan modern akademi (nukleära) och TNED (atomära) INTE besitter linjäritet: resultatskalorna är förskjutna och man får olika maxima och minima:

modern akademi

I den moderna akademins lärosystem beskrivs begreppet massdefekt i atomfysiken med referens till atomkärnan — inte hela atomen — enligt typformen

MASSDEFEKTEN I MODERN AKADEMI

m_Dn = Zm_P + [A–Z]m_N – m_K ............... konventionella massdefekten, berör endast atomkärnan

Z anger atomnumret (atomens elektrontal, samma som antalet p-nukleoner), m_P protonmassan 1,0078252u, m_N neutronmassan 1,0086652u, m_K totala kärnmassan, och A masstalet. Z motsvarar ”antalet protoner i kärnan” och A–Z ”antalet neutroner i kärnan”. De olika sätten, m_D i relaterad fysik och m_Dn i modern akademi, bildar inbördes förskjutningar som gör att respektive maxima och minima INTE är analoga.

Atomära massdefekten från nukleära massdefekten

m_D = (m_Dn + Z[m_n – m(₁H¹)])/Am_em_n

visar att sambandet beror på tre parametrar, m_Dn Z A, och därför inte enkelt kan översättas från det ena sättet till det andra:

det finns ingen enkel korsreferens mellan de olika sätten.

De beskriver alltså väsentligen olika egenskaper i fysiken och kan därför inte jämföras med varandra i någon direkt mening.

EXEMPEL:

Till jämförelse visas nedan de fyra atomindivider som har de högsta massdefekterna i de två olika definitionssätten. Värdena anges på formen

_ATOMNUMMERATOM^MASSTAL_MASSDEFEKT. Siffrorna först anger ordningstalet för massdefekten från högsta (1) till lägsta (4), samma individer till jämförelse.

RELATERAD FYSIK

MODERN AKADEMI

Som framgår av ovanstående jämförelse: Det är alldeles tydligt att den moderna akademins vetenskapliga lärosystem har »problem med definitionen av den atomära massenheten» — numera (2007) välkänd sedan 1960 års nyare standard.

(Tidigare användes Syreindividen ₈O¹⁶ — och dessförinnan Väteatomen ₁H¹ från början).

Se även historia i

[www.sizes.com/units/atomic_mass_unit.htm]).

Se även Konventionella Kärnmassdefekten (m_Dn som ovan men i mera matematik med direkta konventionella referenser).

neutronkvadraten

Jämförelserna ovan sammankopplas genom Neutronkvadraten — se även från Neutronkvadratens grundform:

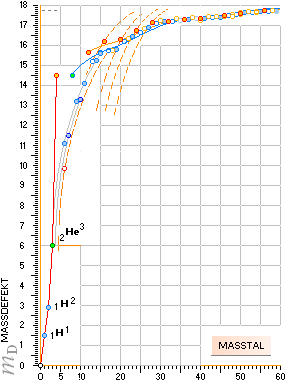
NEUTRONKVADRATEN

Neutronkvadraten ingår inte i den moderna akademins litteratur. Det finns heller ingenting i ämnet på @INTERNET.

NEUTRONKVADRATEN FRAMKOMMER (i min historia) genom att

1. teckna upp konventionellt tabellerade atomvikter U för givna masstal A uttryckta i atomära massdefekter enligt

n_e = u(1–m/Am_n)/m, se Nuklidkarta Ae

2. konstatera den råa mönstergeometrin som utpekas av Ae-skalorna enligt figurformen

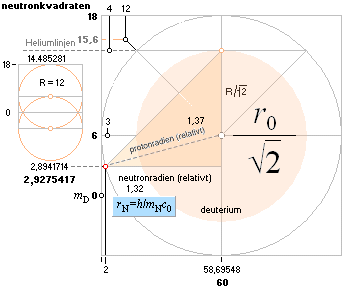
tillsammans med den anmärkningsvärda precisionen i de tillhörande kvantitativa värdena som visar

grundkärnradierna

genom neutronkvadraten

och deras koppling till

atomvikterna

med experimentellt jämförande grunddata [HOP Table 2.1 s9-65 – 9-86]

grundnukliderna

I PREFIXxSIN	atomär massdefekt neutronkvadraten		tabellvärde, HOP	differens
1H ^2	mD = 6 – 12cos15°	= 2,8941716	2,9169332	0,0227616
2He^3	mD = 0 + 12cos30°	= 6	6,0033368	0,0033368
2He^4	mD = 6 + 12cos45°	= 14,485281	14,4834105	–0,0018705

De fyra första grundnukliderna, masstalen 1 till 4 har speciella, fasta, kopplingar i neutronkvadraten. Tre av dem framgår som ovan. Kopplingen för Väte ₁H¹ kan göras till masstalet för Helium-4 — eftersom kärnradierna för protonen (med förstoringsfaktorn från neutronen Ö8/(1+Ö3)=1,0352761) och Helium-4-kärnan får förstås (nära) identiska. Se även i KÄRNRADIERNA.

Neutronkvadraten utpekar kärnradievärdet 1/Ö2 för deuteronen (₁H²), se från HELIUMLINEN, och 1 för Helium-4 (₂He⁴). För den enda stabila atomkärnan med masstalet 3 (₂He³) ligger kärnradien mellan 0,71r₀ och 1r₀. Sambandet för toroidaggregatets kärnradier ger den värdet 0,9r₀; En mera bekväm värdeform (men kanske inte helt korrekt, exakt referens saknas här veterligt) via neutronkvadratens mönsterform ger 0,95r₀ (1–3/60=0,95).

Väte-Heliumkopplingen ger då atomära massdefekten för ₁H¹

(m_D= 1,4610753)×(1,0352761)=1,5126164. HOP-tabellen anger 1,5180399. Differensen blir 0,0054235.

; jämför differensvärdet i tabellen ovan med maximala upplösningen 0,05e för skärmbilden i Ae-kartan, analogt samma bild: precisionen i neutronkvadratens enkla råvärden ovan tål alltså att förstoras ytterligare tillsammans med de experimentellt grundade värdena utan att någon skillnad kan ses, faktiskt (precisionen är rent ut sagt läskig …)

3. konstatera den fortsatta anmärkningsvärda kvantitativa överensstämmelsen genom att söka en djupare härledning för atomära massdefektsekvationen som leder till ELLIPTISKA EKVATIONER — såväl horisontella som vertikala — som beskriver den matematiska-geometriska kärnformen i neutronkvadraten tillsammans med resultaten från exotermiska kärnreaktionslagen (fusionslagen) som visar vilka nuklider som kan bildas ur dem redan givna och som tydligen uppvisar hela nuklidkartan, även vidare från masstal 60:

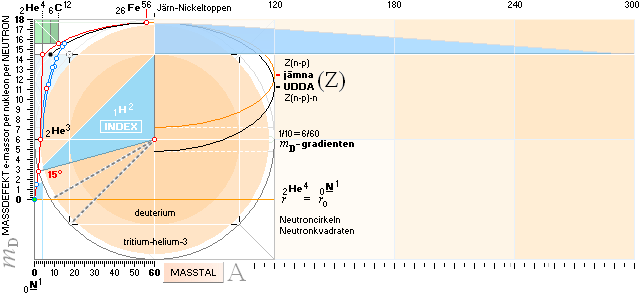
Max masstal enligt TNED är A=300. Det bestäms med speciell referens till Heliumlinjen ovan vid mD=6+12/Ö2 genom en hyperbel som framgår ur ovanstående mönstergeometri. Beskrivningen ges utförligt i särskilt avsnitt i Nuklidkartans gränsvärde.

beskrivning

NEUTRONKVADRATENS ELLIPTISKA FUNKTIONER — se även från punkt 3 ovan

Lätta nukliderna N60-GRUPPEN — mDmax toppsätter horisontalellipserna

En mera djupgående beskrivning av hur ellipserna kopplar till Neutronkvadraten finns i

ATOMVIKTERNAS PRECISION GENOM NEUTRONKVADRATEN

samt i

Ellipsekvationernas härledning genom NEUTRONKVADRATEN.

Här följer endast korta sammandrag som överlåter den djupare bekantskapen på nämnda avsnitt.

Toppellipserna avgränsar medelformen för de stabila nuklidernas exotermiska bildning ur EXOTERMISKA FUSIONSLAGEN genom två olika ellipser, en JÄMNA-ellips för nuklider med masstal som slutar på 0 2 4 6 8 och en UDDA-ellips för nuklider med masstal som slutar på

1 3 5 7 9 — tillsammans med en, integrerad, helt enkel i PREFIXxSIN COSINUSERAD vågfunktion

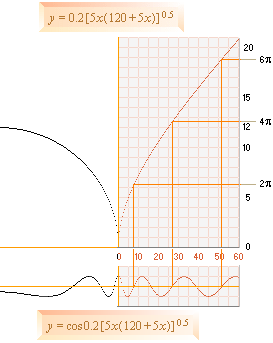
0,1 · cos 0,2[5x(120+5x)]^0,5

Den härrör från neutronkvadratens horisontalelliptiska grundekvation

0,1 · 0,2[5x(120+5x)]^0,5 ..................... A=5x, gäller för den grafiska skalanpassningen

med typutseendena

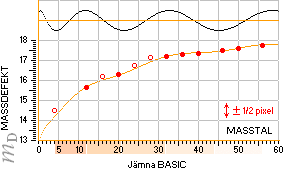
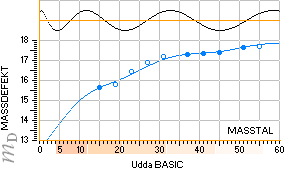
Ringarna markerar de experimentellt uppmätta värdena. Kurvorna från Neutronkvadratens mönstermatematik.

Följsamheten är alldeles tydligt utpräglad.

Tunga nukliderna N60+-GRUPPEN

HORISONTALELLIPSERNAS EKVATION I NEUTRONKVADRATEN är (E anger ellipsens stora excentricitetstal lillaxeln/storaxeln)

y = offset + E(1/5)Ö 600x–25x²

Direkt ur denna form får man en hyperbel genom att eliminera x i 600x samt sätta +E som –E med inre variabeln positiv,

y = offset – E(1/5)Ö 600+25x²

Resterande delar bestäms av 18-gränsvärdet för Järn-Nickeltoppen. Efter mellanräkningar ges en rå datahyperbel

y=–0,0146(600+25x2)^0,5

Utan överlagrad vågfunktion visas i nedanstående graf hur råhyperbeln följer de experimentellt uppmätta stabila nuklidernas atomära massdefekter i den tunga nuklidgruppen [nukliderna över masstal från runt 200 och uppåt blir alltmera utpräglat tungt radioaktiva (kärnorna sönderfaller) och har här utelämnats].

m_D = 18 – 0,0146Ö 600 + (A–60)² ......................... aktuella massdefektsekvationens råhyperbel

Råhyperbelns kurvform utgörs av den vita linje som genomskär färgringarna.

Det är utan vidare uppenbart av följsamheten att de stabila nuklidernas förekomst beskrivs väl av neutronkvadratens basgeometri.

VERTIKALELLIPSERNAS FUNKTION

TVÄRELLIPSERNA beskriver explicit de nuklider som ligger utanför vågfunktionens linje enligt neutronkvadratens allmänna massdefektsekvation:

Från DE STABILA GRUNDNUKLIDERNA beräknas ALLA ANDRA ATOMER genom elliptiska ekvationer (tvärställda ellipser) enligt

allmänna massdefektsekvationen

_____________________

Ö 60² – (60 – E^–1[A – K])²

mD = 6 + ————————————— ............. A, masstal

5

Massdefektsexcentriciteten

E = 1 – (A_REFERENS)/6 ............................................ definierar ellipsbågen

Masstalsoffseten .............................................................. placerar ellipsen, enhet i masstal

K = A_REFERENS[1+ (NUKLIDREFERENS_MASSDEFEKT)/6]

K beror på vilken/vilka nuklid som är »förälder» i fusionerna

En och samma nuklid kan bildas på flera (många) olika vägar

Allmänna massdefektsekvationen beskrivs mera utförligt i PRECISIONEN I ATOMVIKTERNA ENLIGT TNED.

exempel

Exempel

Helium-3-nukliden som AREFERENS omspänner totalt en primär fusionsbildning av fem grundämnen med masstalen {6,9,11,14,15}. Vi finner den delen genom särskild fusionsanalys (hänsyn till kärnstrukturen enligt TNED). Vi genomför inte den analysen här utan förutsätter bekantskap.

Vi får då massdefektsexcentriciteten E = 1 – (A_HELIUM-3)/6=1/2. Nuklidreferensen i K är för alla grundnuklider (som t.ex. ₂He³) lika med neutronbasens massdefekt 0 vilket ger oss

K = A_HELIUM-3[1+(0)/6] ..................................................... = 3

Vi får alltså massdefektsekvationen

m_D = 6 + (1/5)[60² – (60 – 2[A–3])²]^0,5 ............................ A={6,9,11,14,15}

med värdena — HOP-tabellens värden a till jämförelse

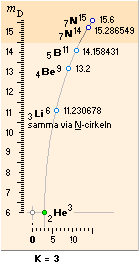
nuklid m_DHOP=a m_Dnk=b a–b 1/E K

₇N¹⁵ 15,6465044 15,6000000 0,0465044 2 3

₇N¹⁴ 15,2626269 15,2865494 –0,0239230 2 3

₅B¹¹ 14,1307300 14,1584312 –0,0277010 2 3

₄Be⁹ 13,2126736 13,2000000 –0,0126736 2 3

₃Li⁶ 11,1039987 11,2306787 –0,1266800 2 3

Det är endast Litiumindividen som kommer att synas något avvikande i samma illustrationsskala som ovan.

Generellt måste man först göra en utvärdering för en viss nuklid för att se om den gäller som en exotermisk dito (som ger energi vid bildningen). Därmed får man grunddata på referenserna

A_REFERENS och NUKLIDREFERENS_MASSDEFEKT

som krävs för att genomföra beräkningen för m_D. Alla sådana beräkningar utgår ifrån det tidigare nämnda grundnukliderna som själva framgår direkt ur neutronkvadratens mönstergeometri.

Nedan till jämförelse de värden som hör ihop med föregående jämförande illustration i Ae-kartan.

atomvikter — jämförande tabell

Jämförande Tabell med teoretiskt beräknade atomvikter för jämförelse mellan TNED och MAC

relativt experimentellt uppmätta i Tabelldata HOP. Nedanstående tabelldata ansluter till den jämförande illustrationen i Ae-kartan.

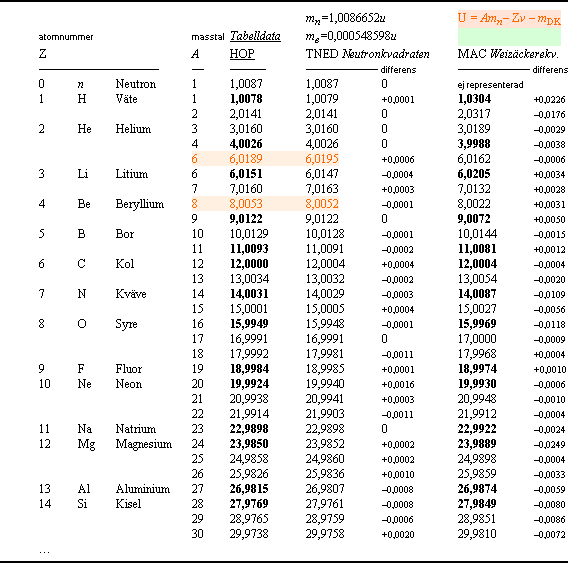
Tabelldata HOP (HANDBOOK OF PHYSICS, E.U. Condon, McGraw-Hill 1967) anger experimentellt uppmätta atomvikter enligt

Table 2.1 s9-65–9-86. ₂He⁶ och ₄Be⁸ är instabila och har här medtagits endast för jämförelse. Tabellvärdena avrundade till 4 decimaler.

Tabellen visar tydliga skillnader mellan MAC och TNED. Skillnaderna framgår dock tydligare i motsvarande graf, se den jämförande illustrationen (MAC med svarta punkter) i Ae-kartan.

WEIZÄCKEREKVATIONEN

beskrivs bland annat i HOP-källan [HOP s9–8] och även i FOCUS MATERIEN 1975 s125.

I sammandrag lyder den

+dA^–3/4......... even_n-even_p

B = a₁A – a₂A^2/3 – a₃Z(Z–1)A^–1/3 – a₄[(N–Z)/2]²A^–1 ±0 ............... HOP s9-8sp2m

–dA^–3/4.......... odd_n-odd_p

med

a₁ a₂ a₃ a₄ d (=a₅)

MeV 14.0 14.0 0.61 84.2 ~34 FOCUS MATERIEN 1975 s125sp2n anger d=33.5 MeV

som efter strukturell analys ger

Weizäckerekvationens praktiska form

B = a₁A – a₂A^2/3 – a₃Z(Z–1)A^–1/3 – a₄(A/2–Z)²A^–1 + a₅(1–Amod2)(–1)^Zmod2A^–3/4

nukleära massdefekten (bindningsenergin) MeV

där Xmodn betyder samma som den heltaliga resten av divisionen X/n (från divisionsalgoritmen, grundmatematiken).

HOP-källan skriver:

”A number of fairly good semiempirical binding-energy or mass functions have been constructed which give a good approximation to the true masses over the wide range of both stable and unstable nuclei in terms of relatively few empirical constants. Perhaps the simplest such formula is that of Weizäcker: (2.1) …”

HOP [HANDBOOK OF PHYSICS McGraw-Hill 1967, E.U. Condon, s9-8sp2]

Min översättning:

Ett antal hyfsat bra semiempiriska bindningsenergi- eller mass-funktioner har konstruerats som ger en god approximation till de sanna massorna över det breda området för både stabila och instabila nuklider i termer av relativt få empiriska konstanter. Kanske den enklaste sådan formel är den av Weizäcker.

HOP-källan beskriver de fem termerna sålunda (s9-8sp2). Första termen representerar en ”volymeffekt”, en bindningsenergi proportionell mot antalet nukleoner. Andra termen uttrycker volymenergibidragets avtagande som beror på yteffekter. Tredje termen uttrycker ”the fact that the binding energy is diminished by the electrostatic repulsion between the protons. There are ½Z(Z–1) interactions between the charges which are taken to be uniformly distributed over the volume of the nucleus. The A^–1/3 factor expresses the dependence of this energy contribution on the radius of the nucleus which is assumed to be proportional to A^1/3.”. Fjärde termen beaktar effekten av kärntillståndens symmetriegenskaper och hur dessa modifieras när nukleonantalet hålls konstant och neutronöverskottet varierar. Femte termen representerar också en symmetrieffekt som sammanhänger med jämna-udda fördelningar av kärnnukleonerna. Termer liknande de tre första uppträder också i samband som uttrycker energin för en laddad vätskedroppe.

Om koefficienterna i Weizäckerekvationen uttrycks i atomära massenheter genom (litet t för 10^–)

u_ENCARTA = 1,66033 t27KG · (2,99792458 T8 M/S)²/(1,602 t19 C) · 1t6

= 931,4794669 MeV

kan vi anställa en direkt jämförelse mellan MAC-ekvationens värden (Modern ACademy, m_DK) och Neutronkvadratens (analogt HOP-tabellens, m_D) via

m_D = (m_DK+ Zv)(Am_nm_e)^–1

Så kan Weizäckerekvationens nukleärvärden omräknas för jämförelse med atomvärdena

KärnMassdefekten m_DK (konventionella massdefekten, den som garanterat missar Neutronkvadraten):

m_DK = Zm_P + [A–Z]m_n – m_K

———————————————————————————————————

den skrivs (t.ex.) i FOCUS MATERIEN 1975 s124sp2ö

DM = ZM_p + NM_n – M_kärna

———————————————————————————————————

= Z[m_n–m_e– (m®g)_medelvärde] + [A–Z]m_n – m_K

= Z[m_n–m_e–v] + Am_n–Zm_n – (U– Zm_e) ; v = (m®g) = m_n–(m_P+m_e) ;

= Zm_n – Zm_e – Zv + Am_n– Zm_n – U + Zm_e

= Am_n– Zv – U ; U = Am_n– Zv – m_DK

Atomvikten genom atomära massdefekten m_D, enligt Neutronkvadraten,

U = Am_n(1 – m_Dm_e) ;

= Am_n– Zv – Am_n(1 – m_Dm_e) ;

m_DK = – Zv + Am_nm_Dm_e ;

Atommassdefekten (m_D) per neutronnukleon uttryckt i antal elektronmassor genom kärnmassdefekten (m_DK) för kontroll av MAC-ekvationen:

m_D = (m_DK+ Zv)(Am_nm_e)^–1

neutronkvadraten

Se även från NEUTRONKVADRATENS UPPKOMST

NEUTRONKVADRATENS GRUNDFORM

Den enkla figurgeometrin visar att individerna med masstalen 4

(Helium, via Ö2-linjen) och 12 (Kol, neutronkvadratens diagonal) intar speciella ställningar.

HELIUMLINJEN (6 + 12/Ö2 = 14,485281) bildar en speciell preferens som kommer att kallas Heliumpreferensen eller Heliumnivån i denna presentation. Motsvarande experimentellt uppmätta värde enligt HOP Table 2.1 s9-65 – 9-86 är 14,4834105.

Beskrivning

Via en helt enkel geometrisk figurkropp typ ”Pythagoras sats för kärnfysiken” enligt ovanstående grundform, framkommer en hel skur av atomära massdefektsvärden som visar sig stämma förvånansvärt väl med motsvarande omräknade värden enligt HOP-tabellens atomvikter via sambandet

U = Am_n(1–m_Dm_e)

Mönsterformen och dess grund kommer här att refereras till som »neutronkvadraten».

Med ytterst enkla matematiska samband beskriver neutronkvadraten, först och främst, de stabila nuklidernas positioner i den atomära massdefektskartan.

Neutronkvadratens matematiska geometri är omfattande (och vi ska därför endast blott så småningom avtäcka detaljerna).

Deuteronens radie (₁H²) r_D ges från neutroncirkelns r_N (samt även från kärnradierna enligt N3m20) enligt r_D=r_N/Ö2 (urspr. r₀/Ö2 med r₀ för protonradien).

Linjen från deuteroncirkeln genom 1/Ö2-linjen till neutroncirkeln bildar en diagonal halvkvadrat med sidan r_N(1+Ö3)/Ö8=r_N0,9659258@1/1,035.

Om vi vänder på preferenserna (neutronkvadraten kan inte visa större än sitt eget) och ser den mindre sidan (0,966) som r_N och den aktuella r_N som den reella, något större protonradien får vi ett förhållande 1/0,966=1,035. Rent empiriskt (utan härledning) fås neutronradien ur impulsmomentet h=m_Nc₀r_N enligt

r_N=h/m_Nc₀=(6,626 t34)(1,67472 t27)^–1(2,99792458 T8)^–1 @ 1,32 t15 M.

Med analoga uppgifter från spridningsförsöken inom partikelfysiken (perioden ca 1950-1980) och grunddata från HOP (1967) som ovan anges vätekärnans största radiella utsträckning konventionellt till r₀=1,37 t15 M [standardvärde i HOP, Table 1.4 s7–27].

Det är alldeles samma avrundade värde som fås genom 1,32·1,035=1,3662 @ 1,37.

Sambanden överensstämmer alltså.

60-skalan

MED R=12 och masstalet A=2 som INDEX-referensen för första fusionsbildningen, deut(e)ronen, utpekar neutroncirkeln i ovanstående kvadratur ett maxvärde för A på funktionscirkelns radie lika med

58,695486=2/(1–sin15°) i PREFIXxSIN.

Det motsvarar massdefekten 6–12cos15°=2,8941714 e-massor per ekvivalent neutronbildningsnukleon, per neutron, enligt figurgeometrin

m_D = R[1/2 – ([1+3^0,5]8^–0,5 – 2^–0,5)] = 2,8941714

= R(0.5 – cos15°) = 2,8941714

= 6 – (1/5)[60² – (60 sin15°)2]^0,5 = 2,8941716

DEN LINJÄRA GEOMETRISKA bildningen av deuteronradien r_D i neutronkvadraten utpekar alltså genom masstalet 2 ett största masstal A för r_N lika med

A_max/A₂ = r_N/(1–[1+Ö3]/Ö8) ;

A_max = r_N2/(1–[1+Ö3]/Ö8)=2×29,34774 = r_N58,69548

Om r_N återställs via faktorn 1,035 till ursprunget blir A_max=1,035×58,69548=60,7 avrundat.

I m_D-enheter är r_N redan fastställd från den givna 18-skalan till 12e av den enkla neutronkvadratens rent geometriska bildning (som inte är någon egentlig härledning utan en ren mönsterfunktion av samma art som den som grundlägger den formella matematiken).

A_max-skalan justerad på heltalig kommensurabel form med massdefektsskalan, ger A_max=60 för r_N.

Transfereringsfaktorn blir då bekvämt 1/5.

Justeringen med A_max från 58,7 till 60 medför att 2-punkten för r_D något skjuts in mot nollpunkten för A. Därmed ges ett motsvarande högre m_D-värde för deuteriumatomen enligt

6–(1/5)Ö(60²–58²)=2,9275417.

Medelvärdet av de bägge blir

(2,9275417+2,8941716)/2=2,9108565. Tabelldata från HOP visar 2,9169332. (En sådan precision är oöverträffad i teorin …).

Och det är just det anmärkningsvärda med neutronkvadraten — som vi redan sett en del imponerande exempel på i föregående jämförelse. Den följer den experimentellt förankrade tabellprecisionen som ett plåster. Homogent, likadant överallt. Inga hopp eller skutt eller avvikelser av någon större ordning. Det visar i sig att den underliggande ordningen är välformulerad och välförankrad.

INDEX-referensen i neutronkvadraten inkluderar en speciell serie som sammanfattar de allra första exotermiska fusionerna (som ger energi i motsats till endotermiska som tar energi) genom neutronkvadraten enligt följande motsvarande mönsterformer (massdefekten för Helium-3 och Tritium ₁H³ sammanfaller i neutronkvadraten)

I PREFIXxSIN	atomär massdefekt neutronkvadraten		tabellvärde, HOP	differens
1H ^2	mD = 6 – 12cos15°	= 2,8941716	2,9169332	0,0227616
2He^3	mD = 0 + 12cos30°	= 6	6,0033368	0,0033368
2He^4	mD = 6 + 12cos45°	= 14,485281	14,4834105	–0,0018705

De fyra första grundnukliderna, masstalen 1 till 4 har speciella, fasta, kopplingar i neutronkvadraten. Tre av dem framgår som ovan. Kopplingen för Väte ₁H¹ kan göras till masstalet för Helium-4 eftersom kärnradierna för protonen (med förstoringsfaktorn från neutronen Ö8/(1+Ö3)=1,0352761) och Helium-4-kärnan är identiska.

Väte-Heliumkopplingen ger (m_D= 1,4610753)×(1,0352761)=1,5126164. HOP-tabellen anger 1,5180399. Differensen är 0,0054235.

NEUTRONKVADRATEN INNEFATTAR ELLIPTISKA EKVATIONER med vars hjälp massdefekterna kan beräknas — tillsammans med en särskild fusionsanalys som krävs för att garantera den aktuella individens sammansättning (exotermiska kärnreaktionslagen). Vi studerar exempel och härledningar i separat artikel som ovan i NEUTRONKVADRATENS ELLIPTISKA FUNKTIONER.

PLANCKRINGEN | atomära massenheten u | atomära massdefekten mD | se även molbegreppet

atomära massdefekten

atomära massenheten

Den atomära massenheten (u=mKOL12/12) sammanhänger ENLIGT TNED intimt med definitionen av den atomära massdefekten (mD) — det sistnämnda begreppet förekommer överhuvudtaget inte i den moderna akademins lärosystem: där tillämpas istället den nukleära massdefektens matematik. Se den inledande specifikt utförliga exempeljämförelsen i atomära massdefekten. Här följer en fullständig genomgång.

MED NEUTRONKVADRATEN INFINNER SIG AUTOMATISKT EN NOGGRANN DEFINITION AV

begreppet ATOMÄR MASSDEFEKT (mD) tillsammans med

begreppet ATOMÄR MASSENHET (u=mKOL12/12).

Den här artikeln beskriver hur dessa begrepp kommunicerar.

Neutronkvadraten är inte känd i modern akademi, vilket innebär att man tvingas tillskriva atomära massenheten (u=mKOL12/12) en godtycklig grund, se citat.

»Från början» användes Väte-1-nukliden, senare (fram till 1960) Syre-16-nukliden som u-agent. Genom att fysiker och kemister använde något olika preferenser enades man till slut (1961) att använda Kol-12 som internationell standardnuklid för atomära massenheten (amu, eng. atomic mass unit). Se även i Litterära referenser.

DEN ATOMÄRA MASSDEFEKTENS matematiska formulering visar sig medföra en naturlig formulering av begreppet atomär massenhet (u). Innebörden av den atomära massenheten u — som en förmodad exakt universell referens — visar sig emellertid också ha mening endast om det också existerar en fast motsvarande bestämd mönstergeometri för massdefekternas kvantiteter — en slags »kärnfysikens Pythagoras sats»: neutronkvadraten.

Genom indelningen av atomens minsta bestämda enhet — neutronen — i ett fast centralmassiv (1818e+k) som aldrig påverkas av massdestruktionen (m®g) i grundämnenas uppbyggnad, se Grundämnesbildningen, och dels ett förbrukningskapital (18e) som enheten får disponera fritt i byggandet, se utförlig inledande beskrivning från neutronen, finns förutsättningen för en sådan antydd »kärnfysikens Pythagoras sats»: neutronkvadraten.

Koefficienten k är ENLIGT TNED en tilläggsmassa på (HOP-tabellen, se förhållandet mellan neutronmassan och elektronmassan 1836+) 2,624e. Den fungerar som utfyllnadsmassa eller »smörjmedel» (en del på 735 av massan för alla rörliga delar). Kärnstrukturen är (nämligen enligt TNED) inte helt exakt symmetrisk i spinnformerna och kräver därför en liten utjämningsmassa som kan löpa fritt mellan de olika delarna och därmed garantera en optimalt jämn och mjuk gång (»motorspinnet»). I den elementära behandlingen av atomen figurerar inte k i ombyggnaderna utan förutsätts som en fristående del under alla förhållanden.

Framträdandet av mönstergeometrin måste emellertid också, tvunget, bygga på en samtidig rent teknisk, experimentellt grundad, kvantitetsmätning av massdefekterna. I annat fall har mönstergeometrin, vilken den än är, uteslutande ett rent teoretiskt (konstnärligt) värde. Först tillsammans med de praktiskt uppmätta värdena (HOP-tabellen från 1967) kan mönstergeometrin hävda sin egen, oberoende, ställning. Aldrig förr. Föreningen, tillfället då praktiken möter teorin, är vad den följande artikeln berättar om:

definitionen av den atomära massenheten (u=mKOL12/12) genom neutronkvadraten — tillsammans med experimentellt uppmätta atomvikter.

ATOMÄRA MASSENHETEN u GRUNDLÄGGER

atomära massdefektens definition

För klarläggande av korsreferenser med modern akademi, se inledande jämförande exempel.

ATOMÄRA MASSDEFEKTEN definieras som det arbete (m_D) per neutron som åtgår för att bilda just den atomen — med neutronen i impulsmomentet h=m_nc₀r_n som referens för alla möjliga atomära individer.

Eftersom enhetsformerna är givna genom neutronen och dess elementära sönderfall till en Väteatom med den givna elektronmassan (m_e) blir det naturligt att uttrycka neutronmassan och det arbete som åtgår i enheten m_e i sammanhang som beskriver arbetet (m_D) för samtliga atomnuklidbildningar.

Från konventionellt given atomvikt (U) och masstal (A) kan atomära massdefekten då tecknas förenklat enligt

m_D = (1–U/Am_n)/m_e ................... atomära massdefekten, U = Am_n(1–m_Dm_e) med

m_n = 1,0086652 ........................ neutronmassan i atomära massenheter u [HOP Table 2.1 s9–65]

m_e = 0,000548598 .................... elektronmassan i atomära massenheter u [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66033 t27 KG .............. [1,66043 t27 i HOP Table 1.4 s7–27]

Eller, mera egentligt med m_nm_em i enheten KG och med m_D=n_e som antalet elektronmassor, m aktuella atommassan och A masstalet

n_e = u(1–m/Am_n)/m_e ................ atomära massdefekten

Nedan följer en mera utförlig beskrivning med en mera fullständig definition.

atomära massdefektens förklaring

DEN ATOMÄRA MASSENHETEN — Rörelsen i materien kräver någon minsta massenhet som partikulär referens; vilken ska man välja?

masstal, massdefekt, massenhet och atomvikt

DEN ATOMÄRA MASSENHETEN

— Rörelsen i materien

En viss minsta massenhet (u) måste förutsättas som rörelsen kan anställas på för att kunna beskriva kinetiken — annars havererar fysikbeskrivningen. Den enheten visar sig också (alldeles bestämt) ha (säker) koppling till neutronkvadraten: den atomära massenheten u genom en alldeles särskild central atomnuklid: Kol-12.

FÖR ATT FÖRSTÅ RÖRELSEN I MATERIEN — som innefattar massan, vilket beskriver kinetiken (rörelsen utan massan innefattas i kinematiken) — måste vi förutsätta

en viss minsta massenhet (u) som rörelsen kan anställas på. Den kan i princip vara hur liten som helst, men den måste vara bestämd. Så återstår då endast frågan vilken denna grundläggande massenhet är (eller bör vara). Svaret ges ENDAST ENLIGT TNED MED NEUTRONKVADRATENS HJÄLP med hög precision på ett oväntat sätt. Nämligen DELS genom själva formuleringen av den atomära massdefekten, se nedan, och DELS genom summan av alla de 282 stabila nuklidernas gemensamma bidrag; Massenheten u identifierad som 1/12 av massan hos Kol-12-nukliden infinner sig automatiskt. Vi studerar hur.

HÄRLEDNINGEN TILL u = mKOL12/12

2004IX30|2004X1|

atomära massdefekten, atomvikten

Alla atomer kan bildas av ett helt antal A stycken grundnuklider eller neutronmassor (m_N=m_n). Liktydigt med antalet neutronbildningsindivider används benämningen masstal för A.

Atomens massa m fördelad över masstalet A är aldrig större än neutronmassan m_N. Skillnaden motsvarar den atomära massdefekten:

massdefekten är den massavbränning (m®g), (»inbränningsmassan»), som varje neutron måste bränna av under ombyggnaden för att bilda m via A neutronmassor.

ATOMÄRA massdefekten per ekvivalent neutronnukleon för en atom med massan m fås alltså

(1) m_N – m/A

Massdefektsdelen av hela neutronmassan blir då

(2) (m_N – m/A)/m_N = (1 – m/Am_N)

För att kunna uttrycka denna massdefektsdel i den enda kända mindre återstående massenhet som finns — elektronmassan (m_e), i ett antal n_e elektronmassor m_e — måste vi tillfoga en korrektionsfaktor u eller en massenhet så att vi får ekvivalenta fysikaliska massenheter i KG. Vi har då formulerat atomära massdefektsekvationen:

(3) (1 – m/Am_N)u = n_em_e .............................................. u = n_em_e(1 – m/Am_N)^–1

Med given massenhet u kan alla massor m skrivas som ett antal U massenheter u enligt m/u=U, analogt uU=m. U betecknar då atomvikten i u-enheter. Med m_e/u=U_e , m=uU, och m_N=uU_N kan därmed ovanstående led tecknas (1 – Uu/AU_Nu)u = n_eU_eu = (1 – U/AU_N)u som ger n_eU_e = (1 – U/AU_N) och därmed

(4) (1 – U/AU_N)/U_e = n_e

Om vi tillåter oss att tolka m-beteckningen också som en U-form, samt tillåter oss att skriva massdefekten retoriskt (massDefekt) i antalet elektronmassor n_e som m_D ges den mera behändiga och överskådliga teckningen

(5) m_D = (1 – U/Am_N)/m_e ............................................. atomära massdefekten

Här gäller alltså m_N och m_e underförstått i u-enheter med U som den aktuella atomens atomvikt i samma u-enhet.

Atomvikten beräknas sedan med kännedom om faktorerna Am_Nm_Dm_e enligt

(6) U = Am_N(1–m_Dm_e) .................................................. atomvikten

Reala massan fås härifrån, som ovan föregående (4), enligt

(7) m = uU ...................................................................... ekvivalenta atommassan

Massenheten u

u i olika källverk

ATOMÄRA MASSENHETEN u=m(₆C¹²)/12

OLIKA KÄLLVERK anger den atomära massenheten (nu 2007) något olika beroende på instrumentell besättning;

källa Signifikanden i t27 KG:

HOP 1967 1,66043;

FOCUS MATERIEN 1975 1,66041;

ENCARTA 99 1,66033;

SHARP (2005) 1,66053886; … teknisk kommersiell räknare från 2005 Sharp EL-506W med inbyggda fysikaliska konstanter

CODATA (2008) 1,660538782

MASSENHETEN u — hur den framkommer ur neutronkvadratens mönstergeometri

Vi noterar att neutronkvadraten även ger atomära massdefekten 15,6e för den stabila nukliden Kväve-15 [HOP 15,6465044e] — den mönsternukliden skiljer sig från Kol-12 [HOP 15,6594799e] endast genom den horisontella masstalsskalan, 15 för Kvävet och 12 för Kolet. Neutronkvadratens inre kvadratdiagonal (ovan höger) har bara Kol-12-nukliden som enda ekvivalenta nuklidform. Genom att Kol-12-linjen också skär Helium-4-linjen i Neutroncirkeln (som därmed omskriver samtliga nuklidbildningar), får Kol-12-linjen via neutronkvadratens mönstergeometri en genomgående »access» till samtliga nuklider i fysiken. Hur Kol-12 utskiljs från Kväve-15 beskrivs i det följande.

Av sambandet i (3) ovan framgår för en given atom med atomära massdefekten (1 – m/Am_N) att dess enda variabla ekvivalent — n_e — beror på valet av u.

OM det finns en fast och bestämd inneboende mönstergeometri [neutronkvadraten] som beskriver alla massdefekter i ett bestämt antal elektronmassor, med givna skalor och relationer — för varje bestämd atom — är det också givet att det bara kan finnas en, och ingenting annat än bara en och endast en enda — exakt — massenhet u, absolut.

absoluta atomära massenheten

Absoluta Atomära Massenheten ingår Naturligt i Neutronkvadraten

neutronkvadratens 12-18-60-skala bygger på en absolut massenhet u

Sambandet i nr(3) för u, u = n_em_e(1 – m/Am_N)^–1, kan skrivas u = n_euU_e(1 – uU/AuU_N)^–1 som ger oss

(8) 1 = n_eU_e(1 – U/AU_N)^–1

F

ör att massenheten 1u ska gälla för samtliga fall, oberoende av vilken atom UA det gäller, kommer det explicita värde på n_e=n_u som bestämmer u=1 tvunget också att satisfiera massenheten för samtliga möjliga fall via U=A enligt

(9) u = 1 = n_uU_e(1 – 1/U_N)^–1

Därmed, nämligen, blir u oberoende av såväl atomvikt som masstal, den gäller lika för alla, och återfaller då endast på de fasta och fixa referenserna

(10) m_N/m_e = konstant = K_Ne = uU_N/uU_e = U_N/U_e = 1838,623546… = (1,674717092 t27 KG)/(9,108537173 t31 KG)

Referensvärdena i (10) anger ekvivalenta antalet elektroner i neutronen (1818+18+k_2,623546). 18e-delen är den del som tillhör arbetskapitalet för m_D, 1818e-stocken (+k) tillhör neutronens centralmassiv. Största m_D ges för Järnindividen ₂₆Fe⁵⁶ med m_D=17,7591423e via de ovan angivna värdena för m_N/m_e.

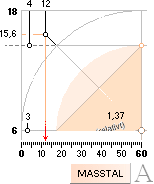
Neutronkvadratens mönstergeometri gör inte direkt någon hemlighet av särställningen för Kol-12 — den framgår exceptionellt tydligt. Men hur framgår den särställningen rent numeriskt?

U=A-villkoret

Emellertid kan det bara finnas ett och endast ett exakt fall för vilket gäller att U=A. Detta är klart av flera skäl. Först därför att atomerna vid sina bildningar till högre system i annat fall inte skulle kräva någon massdefekt alls och därmed vara regelrätta »kulsamlingar» av u. Vore alla atomer dessutom bildade av U=A är det tydligt att u=1 måste vara neutronen. Men detta motsägs av (9): med U_N=1 ges u=n_uU_e/0 som antyder att u i så fall skulle gå mot oändligt, vilket vi vet INTE gäller. Sambandet alltså inte bara antyder en unik förekomst U=A; Definitionen av u kräver tydligen en sådan unik förekomst enligt (9). Den framgår på följande (överraskande) sätt:

Med U=A i u(1 – m/Am_N) = n_em_e ges — via m=Uu=Au som ger u(1 – Au/Am_N) = n_em_e = u(1 – u/m_N) —

n_e = u(1 – u/m_N)/m_e

— Vi genomgår FÖRST samtliga 282 stabila nuklider och ger var och en chansen att ikläda sig agenten för en TYP atomär massenhet u(x) med ett motsvarande resulterande n(e) som ska föreställa mD-värdet för u-agenten; u(x) beräknas då för varje nuklid i ett givet u-system (CODATA-tabellen från 1993 eller HOP-tabellen från 1967, vilketsom) enligt

u(x) = m/A = Uu/A ............................ A anger masstalet för u-agenten

— Vi tillämpar sedan en statistisk medelvärdesform:

₆C¹² framgår klart som enda kandidaten för u:

Tabellutdrag · kalkylkortet till atomära massenheten · öppningsmanual

Utdrag (endast resultatdelen i botten) från kalkylkortets tabellresultat visar att även olika tabellepoker (1967 för HOP kontra 2001 för CODATA) är samstämmiga i neutronkvadratens referens. Bägge tabellreferenserna uppvisar en precision i bestämningen av atomära massenheten för aktuell nuklidagent, alltså Kol-12, med bättre än en del på en miljon. Därmed är atomära massenhetens nuklidagent entydigt bestämd: det är Kol-12 som gäller, ingen annan.

CODATA (The Committee on Data for Science and Technology) sammanhänger med den i kalkylkortet extraherade tabellen från NIST (National Institute of Standards and Technology). CODATA ger (eller rekommenderar) standardiserade värden på fysikaliska konstanter och som (sedan 1966) rekommenderas (internationellt) av olika referensverk.

För generell källverksreferens till CODATA/NIST-tabellen se Källreferensen till Codatatabellen i slutet av den här artikeln.

Så här genomförs beräkningen:

— 2008XI19. MEDELVÄRDESFORMEN för alla de 282 stabila nukliderna från Väte-1 till Vismut-209 genom ovanstående samband blir enligt CODATA-tabellen lika med 15,6505999; Med skaltoleransen för neutronkvadratens masstalsskala via 60-modifieringen 58,69548=2/(1–sin15) ges ekvivalent för Kväve-15 (se Exempel Elliptiska ekvationer)

m_D = 6 + (12/60)(60² – [60 – 2(15 – 3)]²)^1/2 ................... 58,69548 ersätter 60

och Kol-12 via elliptiska funktionen för Kol-12

m_D = 6 + (12/60)(60² – [60 – 3(12 – 4)]²)^1/2 ................... 58,69548 ersätter 60

motsvarande mD-värdet 15,6790922 vilket därmed bildar ett motsvarande absolut övre skalgränsvärde;

— Slutvärdet bör ligga mellan dessa — alltså över 15,65.

— Därmed elimineras Kväve-15-nukliden som aspirant: den har i CODAT|HOP-tabellerna mD-värdet 15,64… medan Kol-12 framträder klart över målsnöret på 15,659…

— Några andra aspiranter finns inte (övriga ligger klart under 15,64).

— Med marginella skillnader ges samma typresultat via HOP-tabellen.

— Kol-12 framgår alltså klart som den slutliga enda kandidaten genom att alla övriga bortfaller.

Att Kol-12 och Kväve-15 bägge ”tävlar” om positionen för atomära massenhetens nuklid (u-agenten) får vi tydlig koll på rent grafiskt på följande sätt:

grafanalysen He4

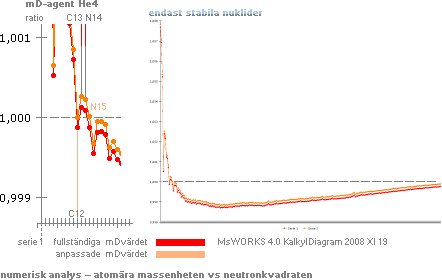
Med prövning på samtliga 282 stabila nuklider som agenter för u(x), från Väte-1 till och med Vismut (₈₃Bi²⁰⁹), finns rent numeriskt bara fyra nuklider vilkas n(e)-värden i det allra närmaste ansluter till det givna Helium-4-mD-värdet på 14,485281, röda grafdelen ovan. Den röda grafdelen (neutronkvadraten) är emellertid orealistisk som exakt fysiskt alternativ. Normalformen, orange, är mera realistisk (experimentalvärdena) vilket bara lämnar två kandidater kvar: Kol-12 och Kväve-15.

— 1-strecket motsvarar mD-referensen för Helium-4 i prövningen.

— Den orangea grafdelen är den normaliserade värdefunktion som ges med förutsättningen att det är mD-värdet hos Helium-4 från de experimentellt uppmätta atomvikterna som gäller.

— Den röda grafdelen utgår från att neutronkvadratens mD-värde är det som gäller.

— Skillnaden mellan de bägge indikerar precisionen i mD-nuklidens värdeform.

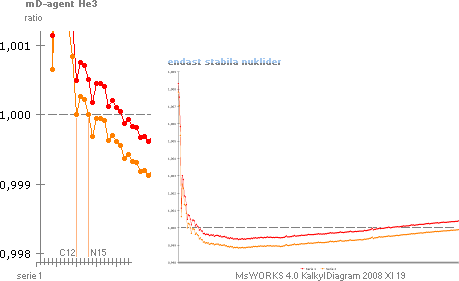
— Andra referenser än Helium-4 ger typiskt större vertikal differens mellan grafdelarna röd-orange

— den röda drar iväg uppåt som här, ovan, med Helium-3 som alternativt mD-referensexempel (mD=6).

Från (3) ges

n_e = u_x(1–U/AU_n)/m_e

Sambandet kan användas för att testa precisionen i varje given nuklids fasta mD-värde via en godtyckligt vald nuklid som agent för atomära massenheten — precis samma numeriska analysbas som i prövningen ovan för u-agenten som sådan:

— Uppslaget bygger på Helium-4-nuklidens mD-värde, det är i neutronkvadraten helt oberoende av neutronkvadratens masstalsskala enligt

mD = 6+12/Ö2 = 14,48… ........................ se från Heliumnivån

— Vi sätter in mD-nukliden He4 för (U/A) och får då via (1–U/AU_n)/m_e en fast referenskoefficient (K). Då gäller det tydligen att

n_e = u_xK

där n_e betyder motsvarande mD-värdet via agenten u_x:

— u(x) kan i varje givet u-system enkelt bestämmas för vare given nuklid enligt u(x) = m/A = Uu/A.

— OM det finns en bestämd u-agent u(x) sådan att också n_e ger PRECIS prövningsnuklidens mD-värde (här Helium-4), är det tydligt att agenten u(x) — genom U=A-villkoret — BÖR vara analog med den atomära massenhetens nuklidagent.

— Vi kan emellertid inte räkna med att får en exakt överensstämmelse mellan Helium-4-nuklidens fasta mD-värde i neutronkvadraten och prövningsvärdet n(e) — eftersom det förra bygger på ren fast geometrisk mönstergeometri och det senare på experimentellt uppmätta atomvikter: på ett eller annat sätt måste någon skillnad finnas (fysiken innehåller av princip inga fasta referenser, allt varierar).

— Men vi kan titta efter HUR liten den skillnaden blir, och därigenom sluta oss till huruvida någon agent för u alls är uppenbar.

— Vi dividerar alltså resultat med mD-värdet (idealt i neutronkvadraten, fullständiga mD-värdet) vilket ger den röda grafdelen ovan.

— Vi kan sedan jämföra det resultatet med att anta det mD-värde som det nominella som ges från den experimentellt uppmätta atomvikten, den orangea grafdelen ovan.

— Som vi ser, visas tydligt (orange) att bara Kol-12 och Kväve-15 kan komma ifråga som aspiranter.

— I HOP-tabellen ges respektive mD-värdena för Kol-Kväve-nukliderna som 15,6594799 för Kol-12 och 15,64650442 för Kväve-15 — De ligger alltså mycket nära varandra.

— Så framgår (alltså) Kol-12 som enda slutliga kandidaten för u:

Medelvärdesbildningen 15,65… för samtliga möjliga ingående stabila nuklider tillsammans med neutronkvadratens tolerans i masstalsskalan

— som medger bestämning av ett absolut största toppgränsvärde för u-agentens mD-värde lika med 15,679…

— avgör alltså den slutliga separationen mellan de två enda möjliga kandidater

— Kol-12 och Kväve-15

— som kan komma ifråga för bestämningen av u-agenten genom det unika villkoret U=A

— och som kräver en mD-individ mellan 15,65 och absoluta toppgränsvärdet 15,697;

— Avgörandet faller entydigt till fördel för Kol-12 genom att dess experimentellt uppmätta mD-värde 15,659… ligger över medelvärdesbildningens 15,65 och därmed mot toppvärdet 15,679… medan Kväve-15-kandidaten uppvisar 15,64 och därmed bortfaller med klar marginal.

— Därmed framstår Kol-12 klart som Solen som enda alternativet för atomära massenhetens nuklidagent.

Medelvärdet av CODATA-tabellmedelvärdet och skaltoppvärdet blir 15,66484607 vilket bör motsvara ett »medelvärdets övre toppgräns»; slutvärdet »bör» ligga under detta toppvärde, vilket ger ett sannolikt statistiskt slutmedelvärde på

(15,65059995+15,66484607)/2=15,65772301 som blir det »mest sannolika nominella slutvärdet» för neutronkvadratens mest sannolika motsvarighet till det experimentellt uppmätta värdet (15,6594946). Detta räcker för att — säkert — separerar Kväve-15-värdet (15,6463743) från Kol-12-värdet (15,6594946); Kväve-15-värdet blir klart för lågt. Emellertid är Kol-12-värdet redan säkrat genom skaltoppvärdet 15,6790922 — tillsammans med tabellmedelvärdet (15,6505999) vilket säkrar att slutvärdet kommer att ligga över Kväve-15-värdet (15,64…). Tabellmedelvärdet definierar undre gränsen via skaltoppvärdet som absolut övre gränsen.

neutronens atomviktsvärde

Med givna mD=n_u för u-agentens nominella slutvärde från ovanstående resultat (15,6577…e) och kvoten K_Ne mellan neutronmassan och elektronmassan (1838,6…e) beräknas U_N (atomviktsvärdet för neutronen) enligt följande:

Nr(9) ger efter mellanräkningar U_N= (1–n_uU_e)^–1. Med U_e=U_N/K_Ne ges

n_uU_e=n_uU_N/K_Ne=U_N/(K_Ne/n_u). Med förkortningen K₀=K_Ne/n_u leds vi så vidare till andragradsekvationen

U_N²K₀ – U_N= –1. Med negativa rotens lösning ges

(11) U_N = K_Ne/2n_u – Ö (K_Ne/2n_u)²–K_Ne/n_u

K_Ne motsvarar kvoten neutronmassan/elektronmassan, och n_u motsvarar typ 15,6e; U_N anger neutronmassan i u-enheter:

(11) U_N = (K_Ne/2n_u)[1 – Ö 1 – (K_Ne/4n_u)^–1]

U(N)-värdena visas i tabellutdraget.

I slutänden kan vi jämföra de så — mycket elementärt — statistiskt framräknade resultaten för u-värdet med det som ges av respektiver tabellepoker (här HOP från 1967 och CODATA/NIST från (senast) 2001). Med värdet för neutronmassan m(n)=Uu givet från experimentalfysiken ges

u = m(n)/U:

HOP:

u = 1,6604316 t27 KG .................... teoretiska statistiska övre gränsvärdet enligt neutronkvadratens u-agent

u = 1,66043 t27 KG .................... experimentellt baserade värdet

CODATA:

u = 1,6605404 t27 KG .................... teoretiska statistiska övre gränsvärdet enligt neutronkvadratens u-agent

u = 1,660538782 t27 KG .................... experimentellt baserade värdet

Se även u i olika källverk i sammanställning.

Grafisk representation av

differensen mellan HOP (1967) och CODATA (tidigast från 1995)

1967 u = 1,66043 t27 KG 1995-2001 U = 1,660538782 t27 KG

HOPtabellens data / CODATA

mD-värdena — endast stabila nuklider medtagna

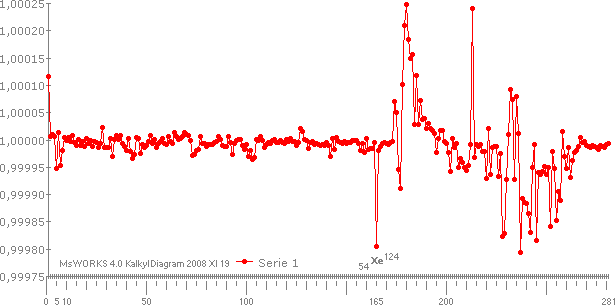
nummer 104 missad — 38Sr84 — totalt 282 stabila nuklider

Skillnaderna har ingen praktiskt betydelse i den rent grafiska jämförelsen motsvarande exempeljämförelsen, även CODATA-värdena ansluter till den bilden. Det är emellertid uppenbart att det finns en del frågor att finna svaret på i studiet av den rent tekniska lösningen för tillvägagångssätten i de olika tabellepokerna. Det är här inte närmare känt vilka dessa svar är.

atomära massenheten

Atomära massenheten u definieras för en enda unik stabil nuklid som har U/A=1; Kol-12-nukliden

ATOMÄRA MASSENHETEN ENLIGT TNED

ATOMENS GRUND DEFINIERAS h=m_nc₀r_n — se från Planckringen — med

m_n = 1,0086652u ..................... neutronmassan, 1u=1,66033 t27 KG [ENCARTA 99 Molecular Weight]

c₀ = 2,99792458 T8 M/S ....... toppdivergensen

r_n = 1,3196611 t15 M ............ neutronradien

Definitionen gäller neutronens ekvivalenta tyngdcirkel med Plancks konstant h=6,62559 t34 JS [ref. HOPs7-155].

ATOMEN DEFINIERAS AV PLANCKRINGEN h=m_nc₀r_n

Neutronen bildas inte av andra atomer och uppvisar därför heller ingen massdefekt (gen., föreningsarbete): neutronens massdefekt är noll. Neutronen har emellertid ett påtagligt negativt kärnmagnetiskt moment. Neutronens negativa kärnmagnetiska moment påtvingar neutronen en massförskjutning in mot kärncentrum som rubbar jämviktscirkeln: neutronen är instabil. För att motverka förskjutningen och återställa balansen, tvingas neutronen flytta ut en del av sin massa längre ut. Men för det åtgår ett visst arbete (m®g): neutronen sönderfaller till en Väteatom. Väteatomen är den ursprungliga neutronkärnan i formen av en s.k. proton eller vätekärna med positiv elektrisk laddning tillsammans med en omgivande elektronmassa med negativ elektrisk laddning, elektronen. Sönderfallet till den stabila Väteatomen sker (normalt) inom 12-14 minuter. Under den tiden övergår också det ursprungliga negativa kärnmagnetiska momentet till ett positivt. Neutronen upptäcktes år 1932 av James Chadwick. Neutronen uppvisar ingen synbarlig elektrisk laddning. Elektronmassan (m_e) är 9,10908 t31 KG eller i HOP-referensens värden 0,00054598u [HOP Table 10.3 s7–155 för m_e och Table 1.4 s7–27 för u]. Neutronmassan uttryckt i antalet elektronmassor är 1818+18+2,624 = 1838,624. I denna presentation används generellt värdet för u=1,66033 t27 KG från ENCARTA 99 Molecular Weight.

Se även vidare i Atomära massenheten genom litteraturen nedan.

Massenheten från Kolkopplingen i Neutronkvadraten

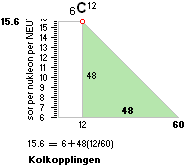
I neutronkvadraten finns bara en nuklid som kopplar enhetligt till alla andra nuklider. Nämligen genom enhetskvadratens diagonal:

Kolindividen med masstalet 12. Det finns heller ingen annan stabil nuklid med det masstalet. Massdefekten i neutronkvadratens grundskala är 15,6e som ovan (HOP-tabellens värden ger 15,6594799). Den fås också genom massdefektsekvationens allmänna ellipsfunktion enligt 15,6=6+(1/5)Ö(60²+[60–3(12–4)]²) med

A_REFERENS=4 för Helium-4-nukliden och NUKLIDREFERENS_MASSDEFEKT=0 för neutronen som gäller för alla grundnuklider,

vilket ger massdefektsexcentriciteten 1/3 och MasstalsOffseten 4,

Massdefektsexcentriciteten

E = 1 – (A_REFERENS)/6 ......................................... definierar ellipsbågen

Masstalsoffseten .............................................................. placerar ellipsen, enhet i masstal

K = A_REFERENS[1+ (NUKLIDREFERENS_MASSDEFEKT)/6]

med massdefektsekvationen

mD = 6 + (60² – [60 – E^–1(A – K)]²)^1/2/5 ............ A, masstalet

Neutronkvadraten erbjuder genom sin unika ställning ett utomordentligt tillfälle att pröva just ”riktigheten” i valet av atomär massenhet. Man menar nämligen i konventionella kvarter (eftersom neutronkvadraten är okänd där) att valet av atomär massenhet är godtyckligt.

”The Atomic Mass Unit, or a.m.u., is an arbitrarily defined unit of mass created by scientists for measuring the masses of atoms and molecules.”

@INTERNET BCPL.NET A Service of Baltimore County Public Library 2000

[www.bcpl.net/~kdrews/introterms/intro2.html]

Min översättning:

Den atomära massenheten, eller amu, är en godtyckligt definierad massenhet som är skapad av vetenskapare för mätning av atomära och molekylära massor.

Se föregående delar i jämförelse med ovanstående påstående: det är tydligt att ”godtyckligt definierad massenhet” tillhör en mindre upplyst verksamhet.

Se även i följande Atomära massenheten genom litteraturen.

ATOMÄRA MASSDEFEKTEN

MASSDEFEKTEN = OMBYGGNADSENERGIN

Alla atomer kan rått beskrivas som bildade ur A stycken neutroner (1818+18+2,624)m_e. Varje atom har en atomär massdefekt som räknat i elektronmassor per bildningsneutron är max 18 (eg., 18/1,0086652=17,845366), se utförligt från atomära massdefektens definition.

atomära massenheten genom litteraturen

Atomära massenheten genom litteraturen. Värdet för atomära massenheten (u) är något olika beroende på i vilken epok i vetenskapshistorien man befinner sig, samt vilket referensverk (med vetenskaplig metod) som används. För enhetligheten i de tabellverk jag själv använt som exempelgrunder genom hela min författning har jag (något oegentligt) valt Encartavärdet

u = 1,66033 t27 KG (från ENCARTA 99 Molecular Weight). HOP-källan, som tabellerna över atomvikterna i min referens hämtats från

[HOP Table 2.1 s9-65–9-86], anger själv

u = 1,66043 t27 KG.

FOCUS MATERIEN 1975 använder värdet

u = 1,66041 t27 KG [FMs124sp1mn].

I den tekniska kalkylatorn SHARP EL-506W (2005) används i listan med konstanter värdet

u = 1,66053886 t27 KG för u;

En sökning på @INTERNET (2007) uppvisar ett värde

u = 1,6605402 t27 KG (Sv. Wikipedia); en annan källa visar samma som Sharpvärdet ovan (markerat med fetstil i rubrikvärde under Google-boxen med sökning på »atomic mass unit»), samt ytterligare ett värde

u = 1,660538782 t27 KG [från www.sizes.com] som specificerar det värdet som en CODATA rekommendation från 2006 med toleransen

±0,000 000 083 t27 KG (Committe on Data for Science and Technology).

På samma webbsida, samma artikel

[www.sizes.com/units/atomic_mass_unit.htm],

berättas vetenskapshistorien om hur atomära massenheten kom till

— speciellt varför man till slut valde Kol-12:

— bästa kompromissen mellan kemister och fysiker.

Se även i u i olika källverk i sammanställning.

Hur vet folket i modern akademi att U/A=1 kopplar till Kol-12-individen?

— I modern akademi tillämpar man ju inte den atomära massdefekten, utan istället den nukleära typen (m_Dn, se från Jämförande exempel) och som inte kan anställas i någon direkt jämförelse. Hur vet man? Vilket är kriteriet?

Man vet det inte. Man har, slutligt från 1960, kommit överens om det genom olika kongresser, institutionella utredningar, samt praxis genom historiens gång — genom den centrala ställning som Kol-12 intar naturligt i kemin och atomfysiken. En beskrivning av historien finns f.ö. på

@INTERNET [www.sizes.com/units/atomic_mass_unit.htm] History of the atomic mass unit.

Man »vet» alltså inte att Kol-12-individen »har egenskapen U=A», utan tror — fullt och fast, vilket man tvingas göra utan fasta referenser — att den formen är en godtyckligt vald konvention.

Jämför (återigen):

”The Atomic Mass Unit, or a.m.u., is an arbitrarily defined unit of mass created by scientists for measuring the masses of atoms and molecules.”

@INTERNET BCPL.NET A Service of Baltimore County Public Library 2000

[www.bcpl.net/~kdrews/introterms/intro2.html]

Min översättning:

Den atomära massenheten, eller amu, är en godtyckligt definierad massenhet som är skapad av vetenskapare för mätning av atomära och molekylära massor.

Tydligen inte.

AtomviktsTabellen från NIST/CODATA

[http://physics.nist.gov/cgi-bin/Compositions/stand_alone.pl?ele=&ascii=html&isotype=some] 1995-2001;

(NIST) National Institute of Standards and Technology — Physics Laboratory (2005)

[http://physics.nist.gov/]

Atomic Weights and Isotopic Compositions for All Elements

NIST kopplar till

[http://physics.nist.gov/cuu/Constants/],

The NIST Reference on Constants, Units and Uncertainty

CODATA (Committee on Data for Science and Technology) Internationally recommended values of the Fundamental Physical Constants

[http://physics.nist.gov/cuu/Constants/] uppdateras löpande, senast oktober 2008 2008XI20;

med grunddata enligt

me = 9,109 382 15(45) t31 KG ........................ elektronmassan

mn = 1,674 927 211(84) t27 KG ...................... neutronmassan

u = 1,660 538 782(83) t27 KG ...................... atomära massenheten

Värdena inom parentes (standardnomenklatur som man tyvärr också får leta febrilt efter referenser för) anger toleransen med början från sista värdesiffran (lägg parentesvärdet med ± över värdets sista siffra).

och noteringarna

”

Notes: Notes for Representative Isotopic Composition and Standard Atomic Weight

a Air reference material used for the best measurement.

b Commercially available Li materials have atomic weights that range between 6.939 and 6.996; if a more accurate value is required, it must be determined for the specific material.

Note: The range given in Atomic Weights of the Elements 1995 was 6.94 to 6.99.

c The range of 2H in tank hydrogen is 0.0032 - 0.0184 atom %.

d Materials depleted in 6Li and 235U are commercial sources of laboratory shelf reagents. In the case of Li such samples are known to have 6Li abundances in the range 2.007 - 7.672 atom %, with natural materials at the higher end of this range.

e The Commission on Atomic Weights and Isotopic Abundances recommends that the value of 272 be employed for 14N/15N of N2 in air for the calculation of atom % 15N from measured 15N values.

f Evaluated isotopic composition is for most but not all commercial samples. Some isotopes are altered because of the contribution of a daughter product from the radioactive decay of another element. These isotopes are: 40Ca, 87Sr, 138Ce, 143Nd, 176Hf, 187Os, 206Pb, 207Pb, 208Pb, and 235U. Because the abundances must add up to 100 percent the abundances of all isotopes of an element are affected.

g Geological specimens are known in which the element has an isotopic composition outside the limits for normal material. The difference between the atomic weight of the element in such specimens and that given in the table may exceed the stated uncertainty.

h An electron multiplier was used for these measurements and the measured abundances were adjusted using a square root of the masses.

m Modified isotopic compositions may be found in commercially available material because it has been subjected to an undisclosed or inadvertent isotopic fractionation. Substantial deviations in the atomic weight and isotopic composition of the element from that given in the table can occur.

r Range in isotopic composition of normal terrestrial material limits the precision of isotopic composition and atomic weight. The tabulated values should be applicable to any normal material.

w Fresh water reference material used for the best measurement.

”;

Det är här inte känt varför NIST/CODATA-tabellen bara innehåller ett fåtal vissa instabila nuklider — dessa har (i kalkylkortet, under utformning) markerats särskilt med referens till den mera utförliga och omfattande HOP-tabellen från 1967 där varje nuklid specificeras.

Jämför till exempel grundämnet Teknetium (Z=43): alla nuklider är instabila, ingen stabil nuklid finns; Men medan NIST/CODATA bara tar upp en mindre del av även de instabila nukliderna sett totalt, tar HOP-källan upp desto flera. Varför är som sagt här okänt. Dessutom anges inte typ ämnets ev. instabila karaktär i NIST/CODATA-tabellen: ingen särskild notering finns. Det är bara tack vare HOP-källan som preferens som denna detalj här uppmärksammats.

En motsvarande senare mera fullständig tabell över (samtliga) isotopa nuklider, även de (kända) instabila, finns på webben interaktivt PER (inte i tabellform) på

[http://atom.kaeri.re.kr/ton/],

2000 Nuclear Data Evaluation Lab, Korea Atomic Energy Research Institute,

man får klicka sig fram per individ.

Från webbkällan

[http://ie.lbl.gov/toimass.html]

finns en pdf-fil från 1993 där en mera fullständig isotop tabell över nuklidmassorna ges i

”b. The 1993 atomic mass evaluation : (I) Atomic mass table”, som kopplar till pdf-filen

[http://ie.lbl.gov/mass/1993AWMass_1.pdf],

The 1993 atomic mass evaluation, G.Audi A.H. Wapstra,

tabellen börjar på sidan 22, men ingenting kan kopieras direkt därifrån (filen är ingen typ textfil).

Förord till atomfysiken

I den moderna akademins lärosystem är de flesta för att inte säga samtliga kärn- och atomfysikens »elementära delar» omöjliga att härleda. Verkligen. Deras fattningsgrund är i stort sett helt experimentell, och ingen enkel form finns för deras allmänna förklaring. I relaterad fysik (TNED) är det helt annorlunda; NEUTRONKVADRATEN bildar kärnfysikens syntes — med exempellös utklassning av den moderna akademins kärn- och atomteori, per redan genomförda experimentella observationsvärden till exakt jämförelse. Men »neutronkvadraten» är helt okänd i modern akademi — och den kan heller inte härledas på den moderna akademins lärostol med mer än den stolen fragmenterar total. Se t.ex. jämförelsen i massdefekterna.

FÖRST för atomfysikens del:

Att teoretisera sig fram till atomfysikens olika aspekter är visserligen, på sitt sätt, möjligt. Men utan en praktisk, instrumentellt grundad experimentell observation är varje teori i princip värdelös. Det är, dessutom, inte speciellt upphetsande att studera utvecklingen av en teori i dess egna anspråk på sensationella samband, vartefter detaljerna avtäcks. Det är först när teorin visar sig överensstämma väl med noggranna praktiska observationer som man börjar känna rysningarna utmed ryggraden, mera ju högre precisionen är. Idealläget är, således, en redan väl utbyggd instrumentmekanik med många noggranna observationer, helst uppställda i tabellform, men vars fenomengrunder man i allmänhet inte är lika överens om. Därmed kan varje teori prövas och vägas noga.

Därmed skulle man också vara benägen att säga så här: INTE FÖRRÄN det finns en redan väl utbyggd experimentalfysik med många avancerade mätinstrument, kan en mera avancerad bild av fysikens grunder komma i dagen.

Den här presentationen baseras helt på redan existerande noggranna mätdata. Om det finns någon del i teorin som inte stämmer överens med dessa, ska den inte vara här. Kort och gott.

kubgrafens härledning

KUBGRAFENS HÄRLEDNING

Notering: Följande del på engelska finns även på TalkPage (discussion) i Wikipedia Nuclear Size.

Den infördes där av mig (15 September 2007) för att understryka DET Wikipedias begränsade referenssystem som redan påpekats i Grunder och Policy (Jag hoppade av på egen begäran då jag till slut insåg att Wikipedia INTE är forum för den här typen av framställningar). Bidraget nedan i Wikipedia står som ett varnande exempel — i modern akademi finns garanterat ingen som kan härleda »atomkärnans radie». Se vidare från Planckringen.

Tillägg 2011-07-06: Wikipediaartikeln »Nuclear size» finns inte längre. Den har numera (Jul2011) tagits bort och ersatts av Charge radius: föregående arkivdelar på TalkPage återfinns inte, inkluderat nedanstående engelska version. Se även tillagd beskrivning i Nuklidradierna Del II i Wikipedia Nuclear Size.

Konstant kärnmassatäthet avseende yttre formens kubiska ekvivalent.

Illustrationen visar kvadraterna i masskuberna som bildas om man adderar dem successivt i steg om 50 genom en grundindivid 1K.

Med föreställningen att alla atomkärnor består av en homogen substans likt vatten och är uppbyggda av n stycken enkla (idealt) identiska grundindivider K, blir atomkärnornas kroppsradier lika med sidan på den resulterande kuben nK enligt

AK/K=(Ar₀³)/r₀³=A=(A^1/3r₀)³/r₀³=(r/r₀)³;

r=r₀(A)^1/3 ....................................... kubgrafen

Sambandet beskriver en motsvarande approximation för atomkärnornas (sfäriska) radie med föreställningen att atomkärnorna kan liknas vid adderade vattendroppar från en grundindivid av bestämd storlek. A anger masstalet eller antalet sådana A=1 individer för varje större bildad kärna enligt

r = r₀A^1/3

med

A .................. kärnans masstal, samma som antalet A=1 individer

r₀ .................. radien hos A=1-individen

r .................... kärnradien hos den bildade individsumman

Sambandet har använts under en stor del av 1900-talet som approximativ referens för kärnradierna, inkluderat olika teoretiska modeller som berör kärnfysiken. Nedan följer en kort genomgång (fram till slutet av 1900-talet då vissa nyordningar inträffar).

Kubgrafens Historia — med Referenser

r₀ uppträder tidigt, redan 1936. Enligt en avhandling daterad av APS (American Physicist Society) vid mottagandet 17 September 1936, hävdade H. A. Bethe (tysk-amerikansk fysiker 1906-2005) att “The nuclear radius is found to be 13 · 10^–13 cm ±10 percent, as compared to 9 · 10^–13 in the older theory.”, (APS Copyright 1936).

r₀ är också neutron-protonradien, beskriven “roughly 1 Fermi” (10^–15 M = t15 M) från spridningsförsök (SCIENTIFIC AMERICAN May 1979, The Spin of the Proton, s66 ill. största grafvärdet ca 1,1 Fermi), (SCIENTIFIC AMERICAN August 1987, Collisions between Spinning Protons, s34 sp3m).

I traditionella vetenskapliga källor under 1900-talet är r₀ mera noggrant specificerad som standardreferens 1,37 Fermi i Table 1.4, Adjusted Values Of Constants, Nuclear radius (s7–27, ref. HOP 1967), där r=r₀A^1/3 anges som “approximate relation”. Denna senare källa rapporterar också “A variety of methods can be used to explore nuclear radii and are found to provide consistent results” (1. The Size of the Nuclei, s9–11). Följande sådana fem (5) olika experimentella metoder redovisas av HOP, här summerade i korthet [HOP, s9–11-12]:

1. neutron scattering

2. a-decay, energy observations

3. mirror-nuclei, energy observations

4. mesic atoms, energy observations

5. high-energy electron scattering, diffraction

Källan informerar att metoderna (1) och (2) bara ger ”semiquantitative measures”. Metod (3) ger approximationen 1,37×A^1/3 t15 M, men metoden begränsas till de lättare kärnorna. Metod (4) ger approximationen 1,2×A^1/3 t15 M ”if the nucleus is assumed to have a uniform charge distribution” [s9–12 sp2ö], men den metoden är å andra sidan bara ”accurate” för tyngre atomkärnor. Metod (5) refereras ”The best high-energy electron scattering experiments have been made by Hofstadter and his collaborators.”, [s9–12 sp2n].

Resultaten totalt summeras av HOP-källan:

“Since R is proportional to the cube root of A, the densities of all nuclei are approximately the same.”, (HOP s9–12 sp1m),

samt

”The general agreement of the radii obtained by the different methods serves also to substantiate theories of barrier penetration and the theory of the equivalence of neutron-neutron and proton-proton interactions.”, (HOP s9–13 sp1ö).

Min översättning:

Eftersom R är proportionell mot kubroten ur A, är tätheterna för alla atomkärnor approximativt densamma.

Den allmänna överensstämmelsen hos radierna erhållna ur de olika metoderna tjänar också att ge substans åt teorier om barriärpenetration och teorin för ekvivalensen för neutron-neutron och proton-proton-växelverkan.

Under 1990-talet …

Någonting händer (uppskattningsvis) under 1990-talet.

Om man (nu, runt 2007) söker på webben på typ “nuclear radius” hittar man en uppsjö av till synes helt nya, andra referenser — och som INTE verkar vara medvetna om “den tidigare historiens standard”. Man har tydligen (genom datoriseringens snabba utveckling) fått fram en mera avancerad instrumentering som kan belysa kvantiteterna mera ur det vågmekaniska perspektivet snarare än ur “klassiska spridningsförsök”. Numera (nämligen) används laser i många avancerade sammanhang. Därmed får man en annorlunda preferens — och som gör att någon direkt jämförelse med “den gamla skolan” inte låter sig göra — och som därmed också sätter punkt för varje vidare upplösning av den historien: Atomkärnornas dimensioner genom kvantitativ mätning är ENLIGT TNED, och förblir, begränsad vara genom de begränsade dimensionerna hos elektronmassans komponenter. Därmed (nämligen) blir också de metriska uppgifterna med laserns hjälp på “atomkärnornas radie” motsvarande “vågmekaniskt svulstiga”. Emellertid, jag är ingen experimentell expert på det området och det finns (ännu, veterligt) heller ingen beskrivande referens på webben som gemene man kan läsa. Så, orsakssammanhangen här antydda står bara för min räkning. Kort sagt: vi vet litet om det här. De som vet bättre, håller (ännu) tyst i leden.

ENLIGT TNED bygger atomkärnans härledning via PLANCKRINGEN på en redan definierad radie för neutronen (1,32 Fermi). Genom NEUTRONKVADRATEN och därmed protonkärnan som neutronsönderfallets produkt, visas (galant ENLIGT TNED) hur ”det klassiska värdet” på 1,37 Fermi för protonradien stämmer med Planckringens neutronradie 1,32 Fermi och som ökar något till just 1,37 på grund av sönderfallet.

Därmed har TNED (ytterligare) distanserat sig från ”den nyare tidens moderna akademiska preferenser” där det tycks mera viktigt än någonsin att framhäva bilden av atomkärnan som något diffust och högeligen oklart — trots att den är materiens i särklass hårdaste och tätaste materiedel och enbart därför borde vara den mest självskrivna i kategorin extremt tydlig.

Det var bättre förr. Liksom.

APPENDIX

spinn-massa kompensationen

SPINNMASSA-

YTTÄTHETSKOMPENSATIONEN

+…=

beskrivning

(A=1)+(A=1) med noll ingångsmoment tvingar processen att konservera impulsmomentet (med fixt v) i J=mvr: När massan (m) dubblas måste r halveras, samma v. Men i successiva fusioner (föreningar A+A+…), där föreningsprodukten dessutom skiljer sig mycket från formen i A=1, drivs m följaktligen mera häftigt in mot centrum för de lägre A-produkterna än för de högre. Dvs., (A=1)-aggregatet disponerar mera radieförskjutande kraft på lättare än på tyngre atomkärnor. Därmed kompensationen för spinnmassan, (1,15–A/900 med delvis ledning av Deuteronradien i HOP). Atomkärnan med masstal A=2 kommer då att börja på 0,71r mot grundtoroidens 0,62r.

mera ingående

[IaM_TNED2 s19]. Med deriveringen av grundaggregatet A=1 (vänster ovan) till produkten mellan två eller flera sådana grundindivider och som ger en maximalt kompakt toroidform (höger), är det speciellt klart att bildningen av de senare via den förra bidrar mera till en massförskjutning in mot centrum för de lättare än de tyngre atomerna. Dvs., med växande A får inverkan av ytterligare +1A allt mindre inverkan på slutformens massdistribution. Om m i J=mvr dras längre in mot centrum så att tyngdcirkeln r blir snävare, bevaras inte längre J med fixt v. För att kompensera för denna skillnad mellan lättare och tyngre, måste vi införa en linjär justering (1,15–A/900) som något ökar radiebidraget i början och minskar det med allt växande A. Med en ungefärlig uppskattning, som delar de lättare och tyngre atomerna i ungefär två lika halvor i kärnradieskalan (främst masstalen från 1 till grovt 250 som motsvarar de på Jorden naturligt förekommande grundämnena) kan den negativt lutande kompensationsgrafen förläggas med sin mittpunkt ungefär där toroidgrafen skär kubgrafen. Denna detalj innebär att toroidgrafen (i stor utsträckning) på sätt och vis närmar sig kubgrafen.

masstäthetsdistributionen

JUSTERADE PLANCKRADIERNA

Med resultat från härledningarna i Kärnradierna genom Planckringen. Se särskilt från RESULTATREDOVISNING KÄRNRADIERNA

MASSTÄTHETSDISTRIBUTIONEN

eller massa-täthetskompensationen

Massdistributionen (KG/M³) i toroiden är inte proportionell mot ytgrafen kA^1/2, utan ökar i täthet med allt större antal inbegripna fraktalnivåer varav toroidformen bara beaktar de två längst upp. Om den resulterande produkten blir alltför kompakt relativt dess initiella spinn-massa balans, får den tillskott av rotation vilket våldför det konstanta impulsmomentets princip: summan av alla moment i atomen är noll. Vilket betyder: som alla atomer idealt byggs från neutronen J_0K + NJ_1K=0, kan inga adderande spinn uppkomma från aggregat som förenas. Det betyder att alla atomkärnor tvingas ha en och samma magnitud i toppspinnet. De facto. Detta stämmer också med resultaten i härledningarna från Spektrum och Kvanttalen, se särskilt i Nukleära spinnkriteriet.

Alternativt: Massans fördelning i toroidaggregatet, massdistributionen, är inte proportionell mot yttoroidens toppytsform k · r₀A^1/2. I det praktiska fallet är massdistributionen i Plancktoroidens fraktalsystem en funktion av den obegränsat växande masstätheten med allt finare ringnivåer i fraktalstrukturen; Ju flera nivåer man tar med i beräkningen, desto högre masstäthet uppnås i slutresultatet eftersom varje ring är ihålig och denna ihålighet bortfaller då man tar med den aktuella ringfraktalens nivå. Den råa toroidytformen kr₀A^1/2 tar ingen hänsyn till denna detalj eftersom den bara arbetar på de två översta nivåerna. Se även Atomkärnans Gravitella Härledning.

MED MASSA-SPINN(yttäthets)KOMPENSATIONEN (eller, spinn-massakompensationen, vilketsom) kommer atomkärnan med masstal A=2 att börja på ca 0,71r mot grundtoroidens 0,62r (eller 0,63r beroende på avrundning, vi väljer här det senare värdet). Minskningen från 1 för den senare betyder en optimal effekttransient med toppvärdet 1–0,63=37%. Den ändringen tvingas tydligen genomlöpa samtliga möjliga fusioner med bildningen av de successivt tyngre atomkärnorna med toroidaggregatet N3m20 som basagent (se från Nuklidbildningarna). Därmed är det tydligt att kärnradierna måste kompenseras på en motsvarande ytterligare något större tyngdcirkel (som ansluter till 0,71r) än grundtoroidens teoretiska (0,62r-nukliden). Av skäl som berör fusionsfysiken måste denna justering som vi också kan kalla massa-täthetskompensation dessutom vara av typen transient, alltså pulsformig. Vi studerar hur.

Eftersom fusionsbildningarna i sig betingas energimässigt av en toppreferens vid Järntoppen med max atomär massdefekt vid A=56, samt att den effektstyrda transientens energifunktion som sådan uppmäter effekttoppen vid 1/4 av energimaximum (A=14) — f.ö. exakt samma funktionsform och typ som i K-cellens värmefysik, y=x[a+bx²]^–2 — måste uppenbarligen också massa-täthetskompensationens funktion styras av samma parameterkomplex. Emellertid är effekttransientens funktion som sådan betingad av en obegränsat utsträckt variabelskala; I detta fall måste denna komprimeras så att transienten planas ut rimligt mot noll inom nuklidkartans begränsade intervall. En ungefärlig motsvarighet med ovannämnda gränser (som justerar A till mellan 15 och 20) ges av typfunktionen x(3+x⁵)^–0,7.

+…=

Mera om massa-täthetskompensationens pulsform. Av skäl som nu bör framgå av kärnans nödvändiga formfysik (se från Planckringen, KÄRNRADIERNA GENOM PLANCKRINGEN, Atomkärnans Gravitella härledning), måste kärnans relativa masstäthet variera som mest från masstal A=2 — upp till en viss gräns som funktion av den utfyllande neutron-protonformen (N3m20, vänster ovan). Dvs., ändringen i masstätheten bör vara som mest utpräglad i nuklidspektrats allra lägsta regioner där formfaktorn mellan de mera kompakta kärnorna från A=2 och det ”spinkiga” neutron-protonaggregatet (N3m20) spelar den största rollen. Denna variation bör alltså uppvisa en utpräglad pulsform (från noll till ett utpräglat maximum) i kärnspektrats låga del. Någon exakt teoretisk kvantitativ bestämning för denna pulslika variation finns emellertid (ännu) inte — frånsett 1. vissa symmetrier hos atomerna med masstalen 1-20 (period 1, se Härledningen till Grundämnenas Periodiska System); alla elektronskal är fyllda från botten — den symmetrin är unik för hela periodiska systemet — och 2. atomkärnorna från runt masstalen 15-20 (ungefär från Neon) bildas på en allt ökande andel bildningsneutroner som blir allt flera än motsvarande antalet bildningsprotoner. Där bör också transienttoppen ligga.

Pulsformens kompensationsgraf med större r för de lättaste nukliderna har här insatts på formen [1+x(3+x⁵)^–0,7]_b med x = (A–2)/15. Den pulsformen ansluter också ungefärligt till delvis experimentellt angivna referensvärden (bidragen från Kaplan-Otterlund). Möjligen finns också flera (mindre) andra liknande pulser i nuklidspektrat, men ingen analys finns ännu (för min del) på den punkten. Det finns (nämligen) ytterligare kompensationer som sammanhänger med (till exempel) massdefekterna; de har inte alls berörts här, men också dessa påverkar grafbilden och gör den mera komplicerad.

REGISTER

Planckringen

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Planckringen

ämnesrubriker

Atomkärnan härledning

Atom- och kärnfysikens två kungsekvationer

Kärnradierna, resultatredovisning

Atomkärnans allmänna elektrogravitella egenskaper

Atomkärnans gravitella härledning

Neutronens sönderfall

Neutronen

Neutronkvadraten

Neutronkvadratens grundform

Atomära massdefekten utförlig beskrivning

Atomära massenheten (u)

Kubgrafens härledning

Appendix

innehåll

förord

PLANCKRINGEN

Atomkärnans härledning

Planckringen

Högerhandsregelen

Planckfraktalerna · strukturkriteriet

Impulsekvationens grundform

Laddningdeplacementet

Neutronens negativa kärnmagnetiska moment

Atomkärnans inkompressibilitet · atomkärnan kan inte komprimeras

Alla våglängder

Atomkärnans utseende

Derivering

Toroidradierna · råform

Kärnradierna genom Planckringen

Plancktoroidens ytform

m-faktorn

N3m20

Atomkärnan · illustrerad

Atom- och kärnfysikens två kungsekvationer

Atomens impulsekvation

Tyngdcirkeln

Atomkärnans allmänna magnetiska yttoroidfält · BT-fältet

Atomens kraftekvation

Kemikopplingen

Kärnradierna, resultatredovisning

Kaplan-Ottlerund bidraget

Deuteronradien i HANDBOOK OF PHYSICS

Atomkärnans allmänna elektrogravitella egenskaper

Dynamiken

Atomkärnans gravitella härledning

Gravitationens Fundamentalform

Neutronens sönderfall

Atomkärnans n-p-struktur

n-p-Strukturen

Nuklidkartan [AZ] i TNED — inledning · isotoper · isobarer

Jumboneutroner och Jumboprotoner

Radioaktivitetens matematiska fysik

Nuklidkartan AZ i TNED

Neutronen — neutrokvadratens uppdagande

Atomära massdefekten · inledande beskrivning med jämförande exempel

Järntoppen

Massdefekterna · jämförelse mellan TNED och Modern Akademi

Atomära massdefekten · samband

Max mD

GRUNDKARTAN

Nuklidkartan Ae i TNED

Atomkärnans energibindningar · direkt jämförelse mellan TNED och modern vetenskap

Massdefekterna i grafisk sammanställning

Massdefekten i modern akademi · allmänt

Neutronkvadraten

Neutronkvadratens uppkomst i min historia

Grundkärnradierna

Grundnukliderna

Beskrivning

Neutronkvadratens elliptiska funktioner

Allmänna massdefektsekvationen

EXEMPEL

Atomvikter · jämförande tabell

Weizäckerekvationen

Kärnmassdefekten

Neutronkvadratens grundform

Beskrivning

Protonradien

60-skalan

Atomära massdefekten utförlig beskrivning

Atomära massdefekten — definition

Atomära massdefekten — förklaring

Atomära massenhetens grundekvation

Ekvationen

Atomvikten från atomära massdefekten

Inledande samband

Inledande definition · grundbeskrivning med korsreferens mot föreställningarna i modern akademi

Inledande beskrivning · Grundkartan — nuklidkartan med atomvikter via masstal

Atomära massenheten (u) — atomära massdefekten (mD)

Atomära massenheten — atomära massdefekten

Atomära massdefektens definition

Atomära massdefektens förklaring · de 7 främsta sambanden

Massenheten u · hur den framkommer ur neutronkvadraten

U=A-villkoret

Tabellutdrag HOP/CODATA

Kalkylkort atomära massenheten

Grafanalysen Helium-4 mD

Neutronens atomviktsvärde

HOP/CODATA-differensen i grafisk representation

Atomära massenheten — allmän samlingsbeskrivning

Atomära massenheten genom litteraturen

Källreferenser till CODATA/NIST-tabellen över atomvikterna för de 282 stabila nukliderna

Förord till atomfysiken

Kubgrafens härledning

Historia

Appendix

Masstäthetsdistributionen

Spinn-massa-yttäthetskompensationen

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

gen. förkortn. generellt

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Irvin Kaplan | Källuppgiften från prof. Ingvar Otterlund Lunds univ. 1996 är tydligen felstavad — av allt att döma. Otterlund ger varken eget datum i sin korrespondens, eller anger boktryckets kronologiska referens. Sökning på webben @INTERNET (2008) ger heller inga träffar på ”Irvin Kaplan Nuclear Physics” (utom två träffar i den spanska delen, med obskyr innebörd) — men väl på Irving Kaplan Nuclear Physics;

IRVING KAPLAN

(1912-1997), amerikansk kemist, en 2nd Edition Nuclear Physics finns från år 1962 (med flera, [originalet från 1955]),

samt en senare publicerad 1997;

Källa: @INTERNET Wikipedia | Nuclear physics | Irving Kaplan | 2008-08-04.

Senast uppdaterade version: 2024-03-26

*END.

Stavningskontrollerat 2008-03-06 | 2008-11-17 | 2008-11-21.

rester

*

PNG-justerad 2011-06-25

åter till portalsidan · portalsidan är www.UniversumsHistoria.se