NEUTRONFRAGMENTEN | FUSIONSGRÄNSMASSAN | 2002 | 2008VI26 | a production | Senast uppdaterade version: 2017-08-19 · Universums Historia

innehåll · denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

	pp-kollision	Grundtablå	Ikonisk översikt	MIC-ekvivalenterna	skapelse
Neutronfragmenten i relaterad fysik Neutronfragmenten Uppdagade massunderskott i fysiken enligt TNED	Diskussionsexempel originalversionen med GRANSKNING och ANALYS EXEMPELFRAMSTÄLLNINGEN
	Utvecklingsexempel	partikelnomenklaturen 1975	partikelnomenklaturen	partikeldelningen i TNED	eller delning

· Neutronfragmenten TABELL · Partikelnomenklaturen TABELL · Neutrinobegreppet i TNED · Fusionsgränsmassan ·

Diskussionsexempel

Diskussionsexempel

Originalförfattningen från Juni2008

magnetiska B-vektorn upp genom bildytan

Bubbelkammarfotografi från FOCUS MATERIEN 1975 s139

Originalförfattningen till

NEUTRONENS FRAGMENT ENLIGT TNED

Bestyckningarna nedan med tillhörande justerade termbeteckningar är den relaterade fysikens beskrivning enligt TNED från motsvarande uttagna linjeteckning med tillhörande konventionella termbeteckningar enligt FOCUS MATERIEN 1975 s139 och som kommer att förklaras och härledas ingående i följande presentation — för att klarlägga och bevisa varför och hur föreställningen att massa skapas från em-strålning saknar fysikalisk soliditet och experimentell grund. Det som spökar är (nämligen) den kvalitativa ekvivalensen mellan massa-energi — E = (m®g)c² ¹ (m¬g)c² — till skillnad från den kvantitativa: E = (m®g)c² = (m¬g)c². Många har ramlat i den fällan. Se vidare från BESKRIVNING nedan.

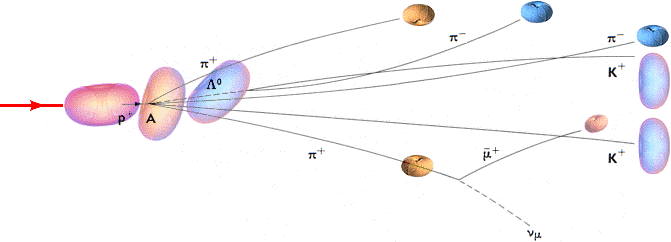
Bubbelkammarfotografiet av en proton-protonkollision från FOCUS MATERIEN 1975 s139

Bubbelkammarfotografiet från FOCUS MATERIEN 1975 s139

Bilden nedan är originalet från FOCUS MATERIEN 1975 s139 inverterat, vilket förtydligar att den uttagna Focusteckningen under är korrekt återgiven.

Bokkällan tillhandahåller f.ö. grunddata på de angivna partiklarna i särskild tabell (s140).

Spårdelarna har förtydligats av bokförfattarna i FOCUS MATERIEN 1975 s139 i den nedanstående linjeteckningen.

Linjebilden har här roterats ett kvarts varv med bokkällans bibehållna beteckningar för bästa översikt.

Syftet i följande framställning är att genomföra en noggrann analys av spårbildens detaljer — i ljuset av JÄMFÖRANDE resultat från TNED, generellt för kärn- och atomfysiken.

Focuskällan

BESKRIVNING

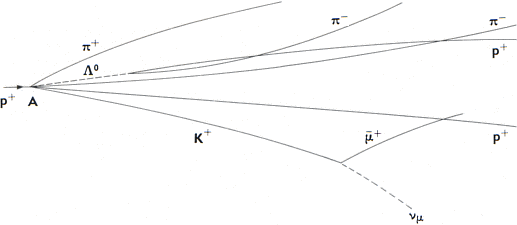
Från 2 kolliderande protoner vid A spåras 2 protoner, 1 lambda-hyperon (1116MeV), 3 pi-mesoner (418,8MeV), 1 anti-meon (my-meson 105,66MeV), 1 K-meson (494MeV) och 1 neutrino (som indikerar ett bortförande av 388MeV). I allt 7 objekt (2134,46+388MeV) utom de två protonerna (1876,4MeV). Värden inom parentes anger vilomassan i MeV. Värdena kommer från tabellen över ”Stabila och semistabila elementarpartiklar” i FOCUS MATERIEN 1975 s140sp1n.

FRÅN VAR kommer objekten?

Frånsett L⁰ är de uppenbarligen fragment av de två kolliderande protonerna, vilka upphör att existera från A. Så, vad exakt betyder då de två högra betecknade protonerna?

OM en kärna blir tillräckligt exciterad, från strålning eller från mekanisk påverkan med samma kvantitativa energi, kan den ENLIGT TNED ändra sin struktur. Kärnan kan ändra sin laddningsbild i vilkensom riktning ± via sitt centralmassiv 1818e och som grundlägger härledningen till atomära massdefekten med atomvikterna enligt NEUTRONKVADRATENS MÖNSTERGEOMETRI. Neutronkvadraten är ett helt okänt begrepp i moderna kvarter. Se vidare i Neutronkvadraten om ej redan bekant.

Betrakta från det kvalitativt irreversibla sambandet från energilagen

E = (m®g)c²

— explicit demonstrerat av Solen — dess kvantitativa ekvivalent

E = (m®g)c² = (m¬g)c²

Bevarandet av neutronens impulsmoment (eng. angular momentum) ges av Plancks konstant h eller PLANCKRINGEN som

h = m_Nc₀r_N

En ekvivalent till r_N kan skrivas r_N=r₁+r₂+r₃+…+r_n med ett motsvarande m_N=m₁+m₂+m₃+…+m_n.

Som m_n också kan skrivas m_n=m_a+(m®g)_a, kan vilken som helst atomkärna, eller del av vilken som helst atomkärna, alltid simuleras på en kvantitativ ekvivalent, från en substratdel som är instabil då den utlämnas åt sig själv. Ett exempel i energiekvivalenter blir av formen

Ekvivalenterna

genom strålning genom kinetisk energi (från mekanisk påverkan)

—————————————— ——————————————————————

p⁺ = K⁺+ (m®g)_Kg = K⁺+ (m®g)_Kkin

eller

p⁺ = p⁺+ (m®g)_pg = p⁺+ (m®g)_pkin

beroende på energier och beräkningar utförda av den enskilda nuklidens dynamiska kärnkropp.

Detta principuttryck är klart därför (i K-fallet) att K-mesonen kommer från den kolliderande (strål-) protonen när den måste utbyta kinetisk (eller radiativ) energi med målprotonen, vilket direkt ger

p⁺ – (m®g)_Kkin = K⁺

I samma ordning fås den instabila lambda-hyperonen i energiekvivalenter genom en momentan nukleär omstrukturering enligt

p⁺ + (m®g)_Lkin = L⁰

Denna exciterade proton är instabil och kommer att sönderdelas genom fission i två lättare instabila delar med en nettoladdning samma som L⁰, alltså 0.

Dessa två kan då skrivas

= p⁺ + p^– = K⁺+ (m®g)_Kkin + p^–

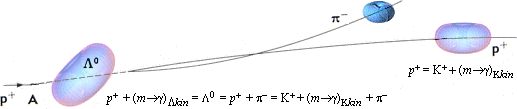
Således — om allt är korrekt uppfattat— är de bägge högra betecknade protonerna i FOCUS-källan inte protoner utan

[K⁺ eller p⁺]+(m®g)_kin-partiklar!

;

p⁺ = K⁺+ (m®g)_Kkin = p⁺+ (m®g)_pkin ; K⁺ = p⁺+ (m®g)_pkin – (m®g)_Kkin = p⁺ + åE_kin = p⁺+ (m®g)_pkin

SOM I ORDINÄRA FUSIONER, FISSIONER och sönderfall kräver varje strukturell ändring i ett kärnaggregat en massdestruerande energi (m®g) för att återuppbygga, justera och omorganisera. Strålningen som produceras från sådana ombyggnader inbegriper utan undantag enligt relaterad fysik en neutrinokomponent. Vilket vill säga, en em-strålning som ligger långt under den som kan detekteras av elektronmassans komponenter. Se även utförligt i NEUTRINOSPEKTRUM. Även i delningen av protonen till mindre beståndsdelar från tunga kollisioner, har vi således rätt att förvänta en viss neutrinostrålning då nuklidaggregatet uppvisar delning. Fastän neutrinospektrum är kvalitativt väl känt enligt TNED, finns (här veterligt) ingen enkel matematik som beskriver den resulterande motsvarande kollisionsverkan som inbegriper protonens flera fragment med den imaginära neutrinopartikeln inkluderad. Den senare lämnar (nämligen) aldrig några spår, och sådana måste underförstås indirekt från beräkningar. Eftersom varje gömd riktning kan avdelas i ett godtyckligt antal summerande gömda delar, är problemet uppenbart.

För att det av en given kärnstruktur initiellt tillgängliga partikelsubstratet ska gälla, måste alla spåren i exemplet utom det som tillhör L⁰ föras ner (vi går då baklänges) på bara en enda kvarvarande proton. Det är, alla dessa:

p⁺ ® p⁺ + p^– + p⁺+ K⁺

;

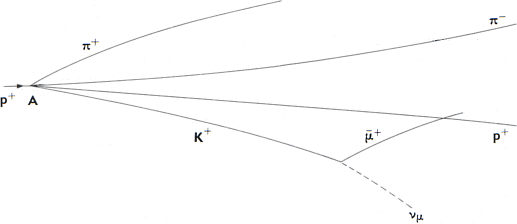
® p⁺ + p^– + p⁺ + (p⁺+ (m®g)p_kin)

® p⁺ + p^– + (K⁺+ (m®g)K_kin) +(p⁺+ (m®g)p_kin)

Summan av vilomassorna för delarna får inte vara större än protonens vilomassa:

3(139,6MeV)+1(494Mev)=912,8MeV. Protonmassan är 938,2MeV.

Den centralt mest högra p⁺ skulle då vara en

p⁺=K⁺+(m®g)_Kkin (den tyngsta, med minsta avvikelsen), och

den betecknade K⁺ skulle vara en

K⁺=p⁺+(m®g)_pkin, allt i termer av energiekvivalenter.

(Både K⁺ och p⁺ har samma medelmässiga halveringstid [halflife] t8 sekunder, men sådana periodvärden anges konventionellt som fluktuerande med den initiella energin).

Neutrinos är inga partiklar ENLIGT RELATERAD FYSIK, se NEUTRINOSPEKTRUM, utan elektromagnetisk strålning i spektrum med våglängder kortare än elektronelementets diameter (t-ringen, max 1/50 av protonradien 1,37 t15 M vilket ger minimifrekvensen vid ca T25 HZ; allt däröver klassificeras i TNED som reguljär neutrinostrålning).

Den slutliga delningen sett i vyn från [K⁺=p⁺+(m®g)_pkin] till (anti-) my-mesonen µ⁺ konserverar laddningen genom en reguljär (m®g) elektromagnetisk neutrinostrålning.

Av kända skäl, genomgår en atomkärna (eller något av dess fragment) som förstör massa från (m®g) en rekyl eller studs i respekt till den omgivande lokalt dominanta gravitationens referensram där strålningen utbreds oberoende av kärnhastigheter. Rekylimpulsen beror på frekvensekvivalenten (m=E/c²=hf/c²=hf/clf =h/cl) och kopplar till en imaginär partikelrepresentation som »kolliderar» med kärnan. I detta fall leder avböjningen efter sammanträffandet till µ⁺-delen som indikerar »tungt», vilket innebär att en stark massdestruktiv stöt inträffade vid spårbrytningen. (Beroende på symmetri, behöver inte alltid tunga massdestruktiva strålningsstötar förknippas med tunga avvikelser. Även en stor massdestruktiv strålning kan lämna den resulterande komponenten med liten avvikelse; Jämför extremfallet med träff rakt på; komponenten fortsätter rakt fram om den inte splittras).

Den vidare utvecklingen gör gällande att µ⁺ (och alla de andra fragmenten med liknande förbindelser) kommer att sönderdelas genom mera massdestruktion, vid slutet lämnande endast en ensam positron som kommer att förintas tillsammans med någon närliggande elektron. Därmed har hela den ursprungliga protonen förintats, kvarlämnande bara värmen och ljuset från dess energiekvivalent E=mc².

Resultat:

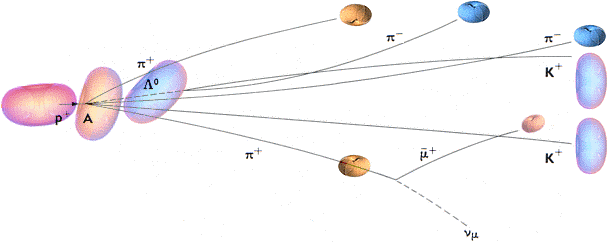
Partikelstorlekarna i fragmentbilden har anpassats proportionellt efter deras angivna energiinnehåll.

Fragmenten är associerade med (stora) extra energier erhållna från accelerationsenergin hos den inkommande protonen.

I jämförelse mellan paret p^–K⁺ från L⁰ med det motsatta paret p^–K⁺ från den inkommande protonen är det uppenbart att det senare paret har en lägre grad av avvikelse; Det förra paret förlorade alltså en större mängd impulsmoment (eng. linear momentum) från deras delning än det senare paret (större krökning, samma partikel, samma magnetfält, betyder lägre hastighet).

Denna effekt indikerar (ENLIGT TNED) att neutrinostrålningens del vid ögonblicket för p^–K⁺-delningen från L⁰ skulle ha en sådan ekvivalent riktning att den skulle vara motriktad L⁰-partikelns framåtriktade rörelsemängd.

I delningen från p⁺ (139,6 MeV) till µ⁺ (105,66 MeV) ärt det vidare tydligt att den ideala vilomassans neutrinostrålning på 33,94 MeV själv INTE kan förklara den tunga µ⁺-avvikelsen; Den felande delen återfaller uppenbarligen på chokmassan som gavs åt den inkommande protonen under dess acceleration. Den totala vilomassan för delarna tillsammans med neutrinomassans strålningsdestruktion från den motsvarande vilomassdelningen, är lika med varje protons vilomassa. Eftersom impulsmomentet inom protonens hela ±b-struktur bevaras genom summan av delarna genom Plancks konstant tillsammans med den massdestruerande neutrinostrålningen (m®g), blir varje principiell delning av protonen giltig och legal ner till den blotta enda elektronen eller positronen Därmed kommer alla de ovan angivna partiklarna att sönderfalla till en slutlig elektron eller positron.

— BÄGGE DE EXCITERADE PROTONERNA DELAS och kommer sedan aldrig mera att återfinnas. De blir (tydligen) totalt fragmenterade i steg och intervall på massdestruktioner (m®g), initialiserade av den kolliderande energin.

— Energiekvivalenter är energiekvivalenter.

— Jag ser fram emot varje förklaring som kan visa att den synpunkten är felaktig.

Jämför den alternativa uppfattningen:

De bägge protonerna i den ursprungliga teckningen från FOCUS-källan tros vara stabila partiklar — enligt beteckningarna med p⁺: protonen är stabil och sönderfaller inte. Dessa skulle då fortsätta existera för alltid — som om det vore fysikaliskt möjligt att excitera en proton till dess sönderfallströskel, men att det aldrig skulle komma dithän när protonen verkligen sönderfaller. Det skulle göra protonen till en hård magisk boll kapabel att producera magiska fenomen — »partiklar» — lämnandes sig själv oberörd. Men magi och mystik har ingenting med vetenskap att göra (men det är roligt titta på på bio).

Resultatet erhållet från TNED förklarar varför och hur föreställningen att massa skapas från em-strålning inte har någon fysisk representation och ingen experimentell grund.

Notera återigen skillnad och likhet i massa-energiekvivalenterna.

Se även mera utförligt från grunden i PLANCKRINGEN eller Atomkärnans härledning.

TILLÄGG Jun2010:

Jun2010

TILLÄGG

Det nutida (2010) stora intresset för NEUTRINOFYSIKEN har på senare tid medfört en mera djupgående kritisk granskning av ovanstående resultatbild — med uppdagade inre otillräckligheter. Resultatbeskrivningen ovan finns utvecklad med en mera nyanserad och tillrättalagd resultatbild i KRITISK GRANSKNING AV RESULTATET — slutbilden blir densamma som i Focuskällan, detaljerna genomgås per separat del för att klarlägga varför och hur. Emellertid har också — därmed — samtidigt uppdagats (upplysande) fördjupningar som förut inte kunde formuleras och som här i efterhand INTE gör det enkelt att avfärda den ovanstående originalförfattningen som direkt felaktig ehuru (för en redan konventionellt insatt person) uppenbart bristfällig.

Se mera utförligt (och tillrättalagt) från

NEUTRONENS FRAGMENT, Komplement Del I

och

Uppdagade, obemärkta, massunderskott i fysiken enligt TNED.

TILLÄGG Jun2010 END.

NEUTRONFRAGMENTEN | Atomkärnans delfragment | 2004VII12

Partikelnomenklaturen

Allmän Översikt

ALLMÄN ÖVERSIKT — atomkärnans delfragment från neutronfragmenten

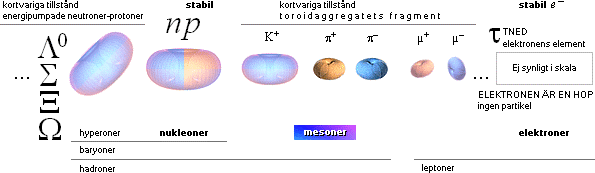
Partikelnomenklaturen. Ovanstående sammanställning ansluter till föregående genomgång (se från Neutronfragmenten) samt en enklare konventionell termatisk översikt från FOCUS MATERIEN 1975 s140. Massuppgifterna har här iklätts proportionella partikelformer enligt TNED.

En (veterligt) närmast obegränsad flora av atomkärnans delformer finns som återfaller på neutronen-protonen. Neutron-protonfragmenten samt avsnitt ur hyperongruppen förekommer naturligt som resultat av den kosmiska strålningen. Slutpunkten för dessa fragment återfaller på elektronen-positronen, masskillnaden ges ut som em-strålning. Peka och klicka för vidare.

Se även i Elektronmassans komponenter och Atomkärnan härledning.

Partikelnomenklaturen

——————————

Utvidgad beskrivning

PARTIKELNOMENKLATUREN Maj2010

Partikelnomenklaturen, för partikelgruppernas namn, se färgbeteckningar under tabellen,

se även Allmän Översikt

Konventionella atomära partikelnomenklaturen

Tabell över kärnpartiklarnas konventionella värden, beteckningar och benämningar vid referensåret 1975

Tecknen/Symbolerna i Grekiska alfabetet här i UNICODE (bör kunna läsas korrekt av samtliga webbläsare).

Partikel	namn	Massa MeV	Spinn	Laddning e	Särtal	Medellivslängd S	Antipartikel
γ	foton	0	1	0	0	stabil	γ
ve	elektronneutrino	0	½	0	0	stabil	v e
vµ	myonneutrino	0	½	0	0	stabil	v µ
e^–	elektron	0,51	½	–1	0	stabil	e^+
µ^–	myon	105,66	½	–1	0	t6	µ^+
π^+	pion	139,6	0	+1	0	t8	π ^–
π ^0	pion	135,0	0	0	0	t16	π ^0
K^+	kaon	494	0	+1	+1	t8	K^–
K^0	kaon	498	0	0	+1	> t10	K^0
η ^0	eta meson	549	0	0	0	< t18	η ^0
p	proton	938,2	½	+1	0	stabil	p
n	neutron	939,5	½	0	0	T3	n
Λ^0	lambda	1 116	½	0	–1	t10	Λ^0
Σ^+	sigma	1 189	½	+1	–1	t10	Σ^+
Σ^0	sigma	1 193	½	0	–1	< t14	Σ^0
Σ^–	sigma	1 197	½	–1	–1	t10	Σ^–
Ξ^0	x(s)i	1 315	½	0	–2	t10	Ξ^0
Ξ^–	x(s)i	1 321	½	–1	–2	t10	Ξ^–
Ω^–	omega	1 673	3/2	–1	–3	t10	Ω^–

TABELLFÖRKLARINGAR

——————————————————————————————————————————————————————————————————————————————————————————————

FÄRGBETECKNINGAR:

LEPTONER Tauonen 1777 MeV (med neutrinos) påvisades experimentellt först 1974-1977 [@INTERNET Wikipedia Tauon, History 2010-06-06], utom ovanstående

MESONER jämför (namnnomenklatur) eng. Wikipedia Eta meson 2010-06-06

NUKLEONER i TNED endast neutron och proton

HYPERONER jämför (mera utförligt) LIST OF HYPERONS i eng. Wikipedia Hyperon 2010-06-06

BARYONER

HADRONER

Partikel normalt teckensnittsformat har använts för samtliga partikelbeteckningar — källverket till ovanstående FMs140sp1n använder kursiv text för partiklarna µ η Σ ; men den regeln hålls inte strängt av konventionella publikationer med exempel från PDF-dokument tillgängliga på webben. Här är motivationen för det enkla raka formatet maximal tydlighet i läsbarhet; kursiverade bokstäver, speciellt typen Symbol, blir ofta mera svårlästa än normalt i kursiv stil vid mindre teckenstorlekar.

namn benämningen ’elektronneutrino’ tillsammans med beteckningen ’ve’ kan uppfattas ofullständig; mera preciserat används i TNED för (elektronassocierade)
antineutrinon benämningen elektronassocierad neutrinostrålning [ve– med v] och motsvarande reguljära (elektronassocierade)
neutrinon benämningen positronassocierad neutrinostrålning [ve+ med v], vilket bättre-tydligare ansluter till samtliga nu förekommande beskrivningssätt (där numera även typerna myonassocierad och tauonassocierad neutrinostrålning förekommer)

Massa avser partikelns motsvarande ekvivalenta vilomassa

Särtal eng. strangeness; [FMs142sp1m] särskilt kvanttal som relaterar partikelväxelverkan

Medellivslängd t | T anger 10^ – | +

Antipartikel här understruken bokstav istf. konv. streck över (kräver specialprogram om annat än Symbol).

FAKTAKÄLLOR Värden och beteckningar i ovanstående tabellsammanfattning — utom namnkolumnen (separat insatt) — har hämtats från motsvarande uppställning ”Stabila och semistabila elementarpartiklar” i FOCUS MATERIEN 1975 s140sp1n — benämningen HADRONER ingår inte explicit i källtabellen men omnämns i texten (sp2mn), Se även Wikipedia Hadron 2010-06-06.

NEUTRINOBEGREPPET I TNED Maj2010

Neutrino — neutrinobegreppet i TNED

Neutrino — _Z X^A_mD

Z atomnummer samma som atomkärnans laddning, lika med elektronhöljets laddning i antal e=1,602 t19 C

X nuklid nuklidatomens kemiska beteckning

A masstal i TNED antalet ekvivalenta bildningsneutroner, konv. »neutroner och protoner», se från Grundämnesbildningen

mD atomär massdefekt i antal elektronmassor (1 elektronmassa = 0,511 MeV avr.) — max 18 min 0

NEUTRONEN sönderfaller (inom 12-14 minuter) till en väteatom = proton + elektron

(idealt från viloläge) enligt

₀n¹₀ – (m→γ)_{0,78 MeV} = ₁H¹_1,518

neutron neutrino väteatom

Arbetet (m→γ)_{0,78 MeV} kallas efter namngivningen [av Fermi 1934, se nedan] för

neutrino (“den lilla neutrala”).

Neutrino historik

Neutron och neutrinos — historik

neutronen 1920 teoretiskt (bl.a.) av Ernest Rutherford [ENCARTA 99], experimentellt

1932 James Chadwick [HOP, ENCARTA 99]

positronen 1928 teoretiskt av P. A. M. Dirac [ENCARTA 99]. experimentellt

1932 Carl Anderson [HOP, ENCARTA 99]

neutrino 1930 teoretiskt av Wolfgang Pauli [Wikipedia Neutrino 2010-05-06], namngiven

1934 av Enrico Fermi [Wikipedia Neutrino 2010-05-06], experimentellt

1956 av Cowan-Reines [ENCARTA 99, Wikipedia]

I RELATERAD FYSIK (TNED) benämns — generaliserat — all strålning i samband med massförintelse (m→γ) enhetligt och enkelt som neutrinostrålning. Det inbegriper även (generaliserat) gränsformen med parannihilationernas gammastrålning (±e). För alla dessa fall (TNED) används grekiska bokstaven gamma (γ, g). Gammakomponenten (γ) associerar direkt med materiefysikens värmegrunder via Plancks strålningslag med temperaturekvivalenter analoga med atomernas rörelseenergier. Se utförligt från VÄRMEGRUNDERNA.

I RELATERAD FYSIK produceras ALLTID neutrinostrålning i samband med massdestruktion (m→γ). Det sker uteslutande alltid i samband med att atomkärnan (eller dess fragment) byggs om eller sönderfaller genom ett utfört arbete, enligt kärnreaktionslagen

K1 + K2 – (m→γ) = K

Energin till γ (gammastrålningen) tas ifrån massan m och omvandlas med massans kvalitativa (strukturella) förintelse till det (frekvens- och våglängdsspecifika) ljus och värme som verkställer arbetet. Se även i NeutrinoSignaturen.

I TNED finns följaktligen inget utrymme för att hänföra neutrinostrålningen som annat än ren induktiv masslös em-strålning — den masslösa energi, värmen och ljuset, som krävs för ombyggnaden.

Neutrino Antineutrino

SKILLNADEN MELLAN

NEUTRINO OCH ANTINEUTRINO

Citatet nedan ger en tidig referens (1955) till den experimentellt påvisade skillnaden mellan neutrino och antineutrino.

Citat Davis 1955

”The equality of the neutrino and antineutrino could be tested by studying the inverse reaction of electroncapture

³⁷Ar + e^– → ³⁷Cl + ve

that is

³⁷Cl + ve → ³⁷Ar + e^–

but, using antineutrinos. It should be noted that the neutrinos are emitted in the fission process where neutron rich nuclei lower their neutron number through the β^–-decay process

n → p + e^– + ve. The experiment of Davis (1955) gave a negative result pointing towards an experimental way of distinguishing between the neutrino and antineutrino.”, s159m

GOOGLEBÖCKER — Basic ideas and concepts in nuclear physics, Kris L. G. Heyde, (1994|1999|2004)

Neutrinons masslöshet i TNED

Hur vet man att neutrinon är masslös enligt TNED?

— Man vet det därför att neutrinostrålningen i TNED utgör den massdestruktionsstrålning (m→γ) som definierar atomära massdefekten (mD) med grundexempel från neutronsönderfallet. Neutrinostrålning i TNED är föreningsarbetet.

Jämför (först):

Jämförande Tabell

Jämförande tabell — Spinnbegreppet i Modern akademi kontra Relaterad fysik

———————————————————————————————————

Relaterad Fysik (TNED)

SP+Se		SP	+	Se	+	0	.............	← summa inre ringspinn
0n^1	→	1H^1	+	e^–	+	(m→γ)	.............	massekvivalenten
0n^1	→	1H^1	+	e^–	+	(m→γ)	.............	energiekvivalenten
nτ	=	pτ	+	eτ		...........	.............	τ-ringströmmens spinnekvivalent
0		1/2	–	1/2		...........	.............	summan av alla spinn och moment är noll
Modern Akademi (MAC)
1/2		1/2	+	1/2	+	1/2	.............	← ”summa spinn”
0n^1	→	1H^1	+	e^–	+	v	.............	”energiekvivalenten”

———————————————————————————————————

Se även i Spinnbegreppet i Modern Akademi. Spinnbegreppet i TNED behandlas även utförligt i Spektrum och Kvanttalen.

MAC-uppgifterna ovan på de olika detaljernas spinnvärden finns bl.a. i separat tabell i FOCUS MATERIEN 1975 s140. Spinnvärdena finns även infogade i tabellen för PARTIKELNOMENKLATUREN.

I TNED baseras neutrinobegreppet (Grek. ν, n) på ren, masslös, induktiv elektromagnetisk strålning; Neutrinobegreppet i TNED har ingen koppling till vägande g-massa; Neutrinon i TNED är helt säkert masslös em-strålning.

Hur vet man det?

— Men hur kan det vara så säkert i TNED att neutrinon INTE är en masspartikel? Hur vet man det?

— Därför att neutrinostrålning (neutrino) i TNED bara är ett annat ord eller begrepp för den masslösa em-strålning som bildas ur massdestruktion (m→γ) via den primära massförstöraren E=mc² i ENERGILAGEN.

Neutrinon som masspartikel i MAC infördes med ett villkor att satisfiera den moderna akademins uppfattning om BEVARANDE AV SPINN (rörelsemängdsmoment J=mvr), se den infällda delartikeln nedan, och som ledde till att man tvingades postulera just spinnet 1/2 för neutrinon (se tabellen ovan) — för att få sakernas tillstånd att stämma med de andra spinnkomponenterna, enligt redan etablerade regelverk.

Införandet av neutrinopartikeln genom spinnbegreppet i modern akademi

Neutrinoresonemanget i fallet neutronsönderfallet går (grovt) ut på följande (konventionella begrepp):

Neutronen har spinnet 1/2. Det har protonen (Vätekärnan) också. Men också elektronen har spinnet 1/2. För att neutronsönderfallet

n → p + e^– + ve^– ska harmoniera med spinnfysiken enligt modern akademi (ve^– förklarar energiräkningen speciellt för elektronemissionen), måste det därför finnas en partikel ve^–, en antineutrino (sönderfallsenergi associerad med elektronemission), med likaledes samma spinn 1/2.

På den vägen etablerades neutrinon som »en partikel».

En tabell med de olika partikelbegreppen med angivna spinn (som angivet i tabellen ovan) m.m. finns (bl.a.) i FOCUS MATERIEN 1975 s140.

För att omnämna i varje fall en webbkälla som beskriver saken ungefärligt i analogi med det nyssnämnda, se exv. s43m

”Since the number of spin-1/2 nucleons is the same in the parent and daughter nuclei, the difference in the spins of the parent and daughter nuclei must be an integer. But the electron also has spin-1/2, so there appears to be a violation of conservation of angular momentum here.”,

”The solution to both of these puzzles was provided in 1930 by Pauli who postulated the existence of a massless neutral particle with spin-1/2 which always accompanies the electron in β-decay. This was called a neutrino.”,

BETA DECAY — Douglas Ross, Southampton University (2009)

http://www.hep.phys.soton.ac.uk/hepwww/staff/D.Ross/phys3002/beta.pdf

— Den omständigheten finns inte i TNED. Se Jämförande tabell (från Spinnbegreppet i Modern Akademi); Exempeluppställning i tabellen visar hur — och varför — spinnbegreppen i TNED och MAC är olika: TNED summerar nollspinn för atomkärna + elektron (summan av alla krafter och moment i atomen är noll; en atom behöver ingen energipåfyllning för att fungera): J_0K+3J_1K=0; Se ATOMKÄRNANS HÄRLEDNING. Det finns inget spinnutrymme — inte alls överhuvudtaget i TNED — för massdestruktionsenergin (m→γ)ve– i neutronsönderfallet i termer av relaterad fysik; Massdestruktion (m→γ)ve– är i termer av relaterad fysik entydigt ren masslös induktiv em(elektromagnetisk)-strålning. Nollspinn.

Se för övrigt om fotonbegreppet i PEFECT (Fotoelektriska effekten). I MAC ges fotonen spinnet 1 (se tabellen för PARTIKELNOMENKLATUREN). I TNED finns ingen sådan form: ljusets fysik utvecklar ingen centrifugalkraft, kopplar inte kinetiken alls (Ljusfrihetssatsen); ljusfysiken är masslös. Se även från Ljusets gravitella beroende.

Neutrinodynamiken

Neutrinodynamiken i TNED

Neutrinobegreppet i TNED kan återföras på de redan genomgångna detaljerna från ATOMKÄRNANS HÄRLEDNING med CENTRALKONTAKTERNA och ATOMFYSIKENS TVÅ KUNGSEKVATIONER (impuls- [J] och kraftekvationerna [F]);

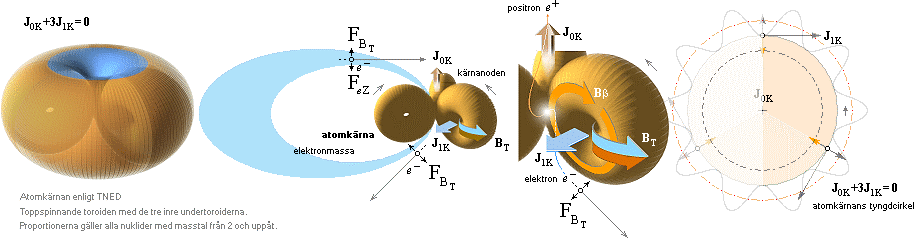
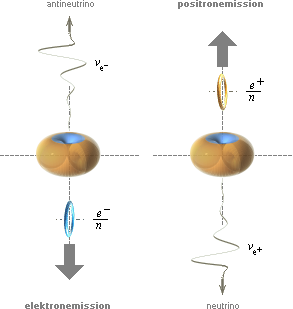
Figuren nedan visar hur respektive neutrino-antineutrinodynamik framträder enligt TNED.

Beskrivning

Lämpligaste sättet att få ut en (mindre) masskomponent (elektron-positron) ur en annan (större) — med mesta möjliga bevarande av den rent mekaniska jämvikten — är naturligtvis om den utträdande massans rörelsemängd (p=mv) balanseras av en (nära) lika stor men motriktad ekvivalent (induktiv) massimpuls [(m→γ)v]. Massimpulsen bör sammanhänga med det ARBETE som krävs för »ombyggnaden av huvudentrén» då den mindre massan avdelas.

Se även Beviset för atomkärnans elektronemissioner i spinnriktningen.

Se även samma ämne, här (nästan som ovan) konventionellt illustrerat (s45ö) i

BETA DECAY — Douglas Ross, Southampton University (2009)

http://www.hep.phys.soton.ac.uk/hepwww/staff/D.Ross/phys3002/beta.pdf

Med exempel från neutronsönderfallet (motsv. vänstra figurdelen ovan) är massdestruktionen (frånsett extra kinetiska komponenter explicit för den atomkärnan och som varierar beroende på miljö och omständigheter):

_ZX^A → _Z+1X^A + e^– + (m→γ)_ve– med exemplet neutronens sönderfall

₀n¹ → ₁H¹ + e^– + (m→γ)_{0,782 MeV}

1,0086652u = 1,0072766u + 0,000548598u + 0,00084u

1,0086652u = 1,0078252u + 0,00084u

Massdestruktionen (m→γ) vid neutronsönderfallet är (idealt, utan extra yttre moment) 0,7824427 MeV(/c²). Värdet motsvarar (ideala) elektronneutrinons mekaniskt ekvivalenta utträdesmassa, lika med 1,53 elektronmassor (Atomära massdefekten). Den delen får tydligen förstås som 1 ekvivalent elektronmassa som går åt rent induktivt för att balansera massimpulsen för den utgående elektronen. Resterande del (0,53e) kan därmed återföras på hela kärnstrukturens ombyggnadsanpassning — själva (transport- och produktionsleds-) energin till arbetet som krävs för att verkställa hela processen.

NeutrinoRekylen

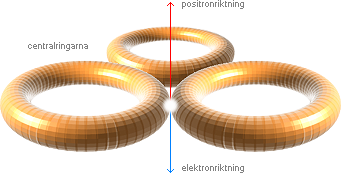
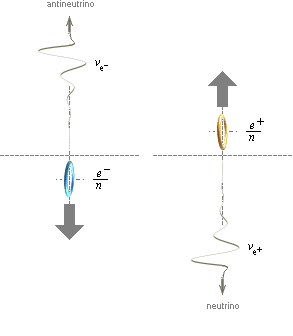
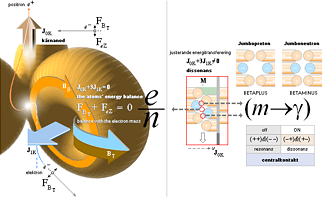
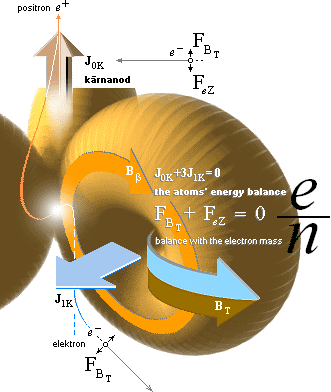
Figuren nedan vänster kompletterar föregående figur men utan atomkärnans ikon — illustrationens högerdel visar hur elektron-positronutgivningens maskincentral kan förstås i atomkärnan enligt TNED med hänsyn till de verkande ytmagnetiska kärnkrafterna (BT) och balansen i momenten (J&F).

Se även mera utförligt i ATOMENS CENTRALT REGLERANDE DYNAMIK (Centralkontakterna) och KÄRNMAGNETISKT MOMENT.

Där beskrivs även den moderna nomenklaturens begrepp i motsvarande jämförelse.

· Se större bild ·

Elektron-positronassocierade kärnomvandlingar i TNED

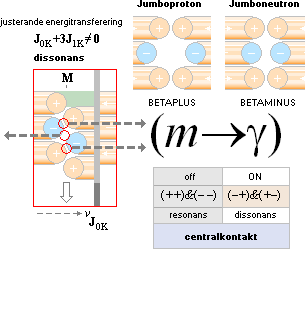
Elektron-positronassocierade kärnomvandlingar i TNED beskrivs generellt enligt nedanstående termorienterade översikt [se även AZ-kartan]:

———————————————————————————————————————————

Jumboneutron:

———————————————————————————

elektronsönderfall (jumboneutron) — se även mera utförligt i Atomkärnans np-struktur (Kärnstrukturen)

_ZX^A – (m→γ)_ve– – e^– → _Z+1X^A ;

_ZX^A → _Z+1X^A + e^– + (m→γ)_ve–

— nukliden är för lätt för sin laddning,

emitterar en elektron för att få högre atomnummer

———————————————————————————————————————————

Jumboproton:

———————————————————————————

positronsönderfall (jumboproton) — se även mera utförligt i Atomkärnans np-struktur (Kärnstrukturen)

_ZX^A – (m→γ)_ve+ – e⁺ → _Z–1X^A ;

_ZX^A → _Z–1X^A + e⁺ + (m→γ)_ve+

— nukliden är för tung för sin laddning,

emitterar en positron (som annihileras med en redan befintlig höljeselektron) för att få lägre atomnummer

———————————————————————————————————————————

_Z X^A_mD

Positronsönderfall kan också konkurrera med s.k. elektroninfångning (eng. electron capture [EC]); Istället för att emittera en positron, som sedan annihileras tillsammans med en elektron utanför atomkärnan, utför nukliden omvändningen; nukliden absorberar en elektron som jämnar ut (minskar) den positiva kärnladdningen. Vilket som är vad bestäms från fall till fall av atomen-atomkärnan genom dess interna energiräkning.

NeutrinoSignaturen

VARJE NEUTRINOTYP UPPVISAR EN SPECIFIK STRUKTUR — en NYCKEL

Neutrinons specifika signatur

Vi underförstår alltid att alla kärnpartiklar med ±e-struktur också alltid har sina motsvarande antipartiklar (omvänt laddningsdeplacement), men dessa skrivs (här, vanligtvis) inte ut explicit om inte speciella, särskilda, behov föreligger.

Med Neutronen som grund för massbasen i c0-kroppen i TNED, förklaras avsaknaden av antimateria i universum helt på neutronens negativa magnetiska moment med kärnstrukturens positiva deplacement: stationär antimateria i universum existerar inte enligt TNED. Genom att energi varken kan skapas eller förintas, endast omfördelas, se Energilagen, får frågan om energins ursprung samma status som frågan om massans ursprung: det finns inget sådant ursprung. Massa är liksom energi utan upphov, utan ursprung, utan skapelse, utan ände, vilket tydligen är ett resultat av fysiken man tåligt måste acceptera. Därmed förklaras alltså avsaknaden av antimateria i universum: kärnstrukturens positivt givna deplacement. Det kan bara omvändas tillfälligt i kraft av höga kollisionsenergier, vilket bildar motsvarande omvända ±e-strukturer eller som vi säger antipartiklar. Se vidare utförligt från Laddningsdeplacementet, om ej redan bekant.

För NEUTRINOSTRÅLNINGEN i TNED gäller GENERELLT grunderna från Plancks strukturkonstant; det finns en specifik neutrinonyckel för varje specifik kärnbildning och kärnsönderfall (neutrinons specifika signatur).

Se även Radiosönderfallet (fortfarande under utarbetande).

Genom PLANCKS STRUKTURKONSTANT besitter tvunget varje nuklid (via sin fusionsprodukt) via EXOTERMISKA KÄRNREAKTIONSLAGEN också ENLIGT TNED en specifik uppsättning

fusionsfrekvenser f =_v=1→v∑ f_v

fusionsvåglängder l =_v=1→v∑ λ _v

som alla kan återföras-gömmas kvantitativt på

energi-frekvensekvivalenten E=hf=(h/n)nf.

Se PLANCKS STRUKTURKONSTANT, om ej redan bekant.

Med kärnfysiken i TNED enligt centralkontakterna, elektronens-positronen elektriska polaritet, är det givet att också massdestruktionerna (m→γ) som sammanhänger med elektron-positronemissioner blir beroende av den aktuella nuklidstrukturens sammansättning:

Varje specifik massdestruktion (m→γ) får sin egen PROFIL eller NYCKEL; elektronassocierade massdestruktionen (m→γ)_ve– [antineutrinon, här även förenklat v] kan inte verkställa positronassocierade massdestruktionen (m→γ)_ve+ [v], och heller ingen av dessa i deras energiekvivalenter kan utbytas med någon kvalitativ effekt mot varandras domäner.

Nycklarna är olika och leder till olika (inbördes strängt skilda) rum.

Precis som i vardagslivet.

Rent experimentellt kunde denna detalj också påvisas tidigt (1955), se särskilt citat i början av detta avsnitt.

Eftersom neutrinostrålning i TNED bara är ett annat ord för massdestruktionsstrålning (m→γ) finns i den ordinära kärnfysiken enligt TNED inga andra massdestruktiva fall än de som i termer av sönderfall berör (se även RadioMath)

elektronsönderfall — sker på 18e-delen i nuklidstrukturen

betasönderfall ...................... mjuka sönderfall, kärnan bevaras — neutrino, antineutrino, lika för alla nuklider

nuklidsönderfall ................... hårda sönderfall, kärnan delas — specifika neutrinospektrum för varje radionuklid

kärnsönderfall — sker på centralmassivets 1818e

Nuklidsönderfallets neutrinostrålning enligt TNED uppvisar med andra ord samma fason som ovannämnda summaformer för »frekvens-våglängds-signaturerna». Neutrinostrålningen är med andra ord att förstå enligt TNED som helt och hållet specifik för varje nuklid, och som därför också ingår i fusionsfysiken — den exotermiska massdestruktion (m→γ) som i TNED kallas atomär massdefekt i bildningen av varje grundämnesnuklid.

NEUTRINOBEGREPPET I TNED END.

Neutronens sönderfall, referenser

”Equation (7.3) implies an instability of the free neutron. It decays [5] with a mean life of about 12 min”,

HOP 1967, s9–195.sp1n

;

”… neutronen sönderfaller som redan tidigare omtalats till proton + elektron (+ neutrino) med en medellivstid av omkring 13 minuter”,

FOCUS MATERIAN 1975 s138sp2n

;

”Neutronen är en neutral elementarpartikel, som är instabil och sönderfaller i en proton, en elektron och en antineutrino med en halveringstid på 12 minuter.”,

BONNIERS ASTRONOMI 1978, s478sp2n

;

”The neutron has a negative magnetic moment of -1.913141 nuclear magnetons or approximately a thousandth of a Bohr magneton. The currently accepted value of its half-life is 615 s +/- 1.4 s [10,25min]. The corresponding value of the mean life, which is now more commonly used, is 887 s +/- 2s [14,78min].”,

ENCARTA 99 Neutron

;

”While bound neutrons in stable nuclei are stable, free neutrons are unstable; they undergo beta decay with a mean lifetime of just under 15 minutes (885.7±0.8 s [14,7617min]).[2]”,

@INTERNET Wikipedia Neutron 2010-05-25

NEUTRONFRAGMENTEN | 2004VII12 | FUSIONSGRÄNSMASSAN | 2004X26 | 2009II28

FUSIONSGRÄNSMASSAN

JORDENS ANDRA EKVATION

Direkt htm-konverterat WORD-dokument Från originalförfattningen i Universums Historia 2004X26

Från allmän beskrivning i Fusionsgränsmassans Definition

För termerna k och d, se Nuklidseparationen i Diakvadraten

OPTIMALA FUSIONSGRÄNSMASSAN (substratmassan föregående grundämnesbildningen) för

Jämvikt mellan gravitation och inre expansionstryck föregående grundämnesbildningen från r_max för fasta kroppar

m_JSUB = r_max^–2(3/4p)^–1(k_J/d)³ .................. Jordens andra ekvation

= 6,80016E+24 KG

Minus 12% ger nuvarande Jordmassan 5,975 T24 KG.

Jämviktsmassan (eller Divergens-Konvergens-Gränsmassan) garanterar ENLIGT TNED maximal fusionsdynamik (långsammaste expansionen till slutlig produkt). Expansionsfasen medför att en viss procentuell del av substratmassan avges (som vätgas) beroende på centralkroppens gravitation. Parametrarna nedan förklaras längre ner.

r_max = 1,82 T17 KG/M³, stort T för 10⁺

d = (rr)^–1k_J

k_J = (2pr₀/3)^–1(e_1,602t19/n_P)Ö k_9T9/pG_6,67t11

n_Pmax = 5Ö2 = 7,1 — bestäms noga genom atomkärnans geometri

m_J(n_max) = 6,80016 T24 KG: n-max-värdet är det nominellt korrekta

r₀ ............ protonradien 1,37 t15 M

JÄMFÖRANDE MASSTABELL

Planet nuvarande planetmassa T24 KG anmärkning

Merkurius 0,3303 för liten

Venus 4,870 för liten

Jorden 5,975 exakt

(Månen) 0,074 för liten (=m_JOR/81)

Mars 0,6421 för liten

Jupiter 1899 för stor

Saturnus 568,6 för stor

Uranus 86,9 för stor

Neptunus 103,0 för stor

Pluto 0,017925 för liten (= m_JOR×0,003_Encarta)

J-kroppar med större massa än m_JSUB tillhör gruppen gaskroppar. J-kroppar med mindre massa än m_JSUB tillhör gruppen stenkroppar.

Endast m_JSUB har ENLIGT TNED fysikalisk förutsättning för att bilda en fullständig (optimal) uppsättning nuklider som täcker hela spektrat.

Jordens andra ekvation ref. Gränsmassan.wps — UNIVERSUMS HISTORIA

Härledning

JORDENS ANDRA EKVATION

Inledning

2004X28

Genom en ekvivalent av exakt balans mellan J-kroppens F_J/A_J, yt-G-tryckande, och protonkärnans F_K/A_K, yt-Coulombrepellerande kraft

F_K/A_K = p = F_J/A_J = G(m_J/r)²(4pr²)^–1 = G(m_J²/r⁴=[4prr/3]²)(4p)^–1 = G(4prr/3)²(4p)^–1 = k(Q/d)²(pr₀)^–2

som i G(4prr/3)²(4p)^–1 = k(Q/d)²(pr₀)^–2 ger pG(2prrr₀/3)² = k(Q/d)² med

d = (rr)^–1(2pr₀/3)^–1eÖ k_9T9/pG

k_J = (2pr₀/3)^–1eÖ k_9T9/pG

d = (rr)^–1k_J

definierar nuklidseparationen d=r₀ mellan de motvända atomkärnytorna ENLIGT TNED situationen då kärnorna precis tangerar varandras nuklidbarriärer utan inverkan av yttre moment, vilket ansluter till det exakta ideala villkoret i kärnreaktionslagen för fusion enligt exotermiska fusionslagen.

Eftersom atomkärnan ENLIGT TNED grundas på ett fraktalt ringsystem med bevarandet av impuls- och kraftekvationerna J_0K+3J_1K=0 och F_BT+F_eZ=0, där varje ringplan bildar den elektriska generatrisen för maximal Coulombverkan, blir repulsionen mellan kärnytorna väsentligen betingad av motsvarande idealt rakstrålande elektriska fält som i närverkan därmed avgränsar större delen av kärnladdningens eZ. Den elektriska angreppszonen reduceras alltså väsentligt i Coulombverkan mellan närstående kärnytor enligt en dividerande ekvivalent vinkelsektor med koefficientbeteckningen n_e.

De idealt rakstrålande ringplanen gäller emellertid endast för en elektrisk kropp som inte lägesändrar i förhållande till det omgivande dominanta g-fältet. Med referens till ljushastighetens toppvärde (c₀), kan kärnspinnen (idealt) återföras på motsvarande höga hastigheter (Se från Atomkärnans härledning) och ansluter därmed till samma principiella effekt som i den av James Bradley år 1725 upptäckta aberrationen, här benämnd elektriska förskjutningen v/c. [Se även ELEKTRISKA FÖRSKJUTNINGEN]. Dess absolut maximala värde i omedelbar anslutning till elektriska fältets angreppszon i kärnytan är via toppvärdet c₀ med referens till omgivande dominanta g-fältet exakt 1, vilket motsvarar en vinkelavvikelse på 45°. Coulombverkan reduceras då ytterligare som mest med en multiplicerande aberrationskoefficient 1/Ö2 vars dividerande term här betecknas n_B med benämningen Bradleykoefficienten. n_B är max Ö2 och minst 1, vilket senare fall motsvarar stillastående. Kärnladdningen e som verkar mellan kärnytorna i Coulombaktionen får då formen e:=e/n_en_B. Värdet på angreppskoefficienten kan bestämmas relativt noga med helt enkla medel. En rät, plan cirkelsektor från centrum i toroidkärnans första underfraktal upp mot motstående kärnyta avbildar hela laddningsfördelningen i det elektriska angreppet. Den reducerande faktorn blir 1/4 med den dividerande faktorn n_e=4. Men av denna sektor är inte allt riktat rakt mot motstående kärnyta, enligt varje ringplan som generatrisen för maximal Coulombverkan (Se från Planckringen), varför värdet på n_e måste vara större, analogt en trängre ekvivalent strålsektor. Som referensvärde för prövning anställer vi värdet n_e=5. Med totala nuklidkoefficienten n_P=n_en_B ges sambanden med de ovan införda modifikationerna enligt

d = (rr)^–1(2pr₀/3)^–1(e/n_P)Ö k_9T9/pG ................. se även Nuklidseparationen

k_J = (2pr₀/3)^–1(e/n_P)Ö k_9T9/pG = (3/2r₀)(e/n_P)Ö k_9T9/p³G

n_P = n_en_B

n_e = 5 referensvärde

n_B = Ö2 maxvärde

d = (rr)^–1k_J

r₀ = 1,37 t15 M

k_9T9 = 8,98743 T9 VM/C

e = 1,602 t19 C

G = 6,67 t11 JM(KG)²

Med r=(3m_J/4pr)^1/3=r^–1/3(3m_J/4p)^1/3 — via rr=r^2/3(3m_J/4p)^1/3 som ger d=(rr)^–1k_J=r^2/3[3m_J/(4p)]^1/3k_J — ges

m_J = r^–2(3/4p)^–1(k_J/d)³

Nuklidbarriären med d=r₀ definierar i m_J en optimal fusionsgränsmassa m_0JSUB via maximala tätheten r_max=1,82 T17 KG/M³ enligt

m_0JSUB = r_max^–2(3/4p)^–1(k_J/r₀)³ = 6,80016 T24 KG, vilken avyttrad med 12% ger nuvarande Jordmassan 5,975 T24 KG.

Efter mellanräkningar ges ekvivalent

m_0JSUB = [e(n_Pr₀²[2r²/9]^1/3p^7/6)^–1(k_9T9G^–1)^1/2]³

n_P = e(m_0JSUB)^–1/3(r₀²[2r²/9]^1/3p^7/6)^–1(k_9T9G^–1)^1/2

Gränsmassans härledning — grundparametrar, hela historien hänger, tydligen, på ingående kunskaper/kännedom om atomkärnan

Gränsmassans fusionsstatus

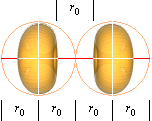
GENOM DEFINITIONEN FÖR GRÄNSMASSAN vid t_ON genom de tre gränslägena [¯GC][GC][GC¯][Se FusionsGränsmassans definition]

har vi fått en exakt preferens till fusionsbildningens möjligheter med den maximala tätheten som index. I detta läge kan kärnorna fritt glida mellan varandra inom nuklidbarriärernas egna kraftformer, analogt inom kärnreaktionslagens enkla formkomplex utan inverkan av yttre påförda moment och därmed realisera kopplingar för fusionsringar i godtycklig omfattning, allt eftersom kärnornas egna strukturer så bestämmer — med atomkärnans bägge impuls och kraftekvationer konserverade [Se Atomkärnans två kungsekvationer].

Formekvivalenten till gränsmassan m_J=m_0JSUB genom atomkärnan ENLIGT TNED får då utseendet enligt figuren ovan. r₀ betecknar protonradien 1,37 t15 M, det är den som gäller vid motsvarande full divergenständning vid t_ON, och det är till den som den optimalt balanserade nuklidseparationen (d) efter divergenständning ska hänföras enligt d=r₀.

Gränsmassans härledning — Definitionen av Coulombkraften (se Elektriska Kraftlagen) innanför nuklidbarriären — inledande kvalitativ beskrivning

ANGREPPSKOEFFICIENTEN n_e OCH ELEKTRISKA FÖRSKJUTNINGEN n_B

EFTERSOM ELEKTRISKA KRAFTVERKAN FRÅN ATOMKÄRNANS RINGSYSTEM ENLIGT TNED verkar maximalt i ringens plan, finner vi ett något annorlunda Coulombiskt beteende mellan två atomkärnor då de befinner sig mycket nära varandra i jämförelse med stora inbördes avstånd. Gränsen går vid nuklidbarriären, analogt Coulombbarriären. Utanför denna ser kärnorna varandra via sina frispinn mer och mer med växande avstånd som ideala punktformiga elektriska laddningar.

Ju längre ifrån varandra kärnorna är, desto mer framträder varje kärna i sitt eget individuella frihetsspinn. För motstående part — i lokaler med höga temperaturer — framstår kontrahenten alltmer som en kärna med alltmer sfäriskt utseende och med laddningen eZ.

När kärnorna i närkontakt vänder kontaktytorna mot varandra, avskärmar de samtidigt en övervägande stor del av e-laddningen. (Erinra Atomkärnans Gravitella Härledning).

Eftersom elektriska kraftens verkan är som störst i ringplanens förlängningar får vi en i det närmaste »rak» analogi till vilka toroidsektorer som kan komma ifråga för exakt beräkning av krafterna. Om vi till att börja med på närmast enkla sätt drar en rät strålkon från underfraktalens ring och uppåt, figuren ovan vänster, får vi först 1/4 av hela ena ringen som kan betraktas som laddningsobjekt mot den motstående kärndelen. Men av denna fjärdedel är inte allt rakt riktat med sikte på motstående part

— i själva verket finns ingenting alls ”rakt” i dessa sammanhang; närattraktionerna är alla, mer eller mindre beroende av v/c-spinn-parametrar, men vi idealiserar tills vidare på den raka formen som en allmän och enkel formpreferens. v/c-spinnets inverkan behandlas längre ner.

Maximum ges på toppen, mindre utåt. Det aktuella laddningsobjektet blir alltså under alla omständigheter mindre än e/4.

Avgränsas ett absolut största sektorvärde som är mindre än 90° genom en uppskattad absolut maximering på 80% av den givna rätvinkeln får vi en delningsfaktor 5. Den anges här som »angreppskoefficienten» n_e=5 som ett absolut referensminimum. Men vi måste då räkna med möjligheten att delningsfaktorn kan visa sig vara större med en mera fördjupad analys, men knappast mindre. Laddningsobjektet att räkna med i den fortsatta beskrivningen blir därmed som mest e/5.

v/c-spinnets parameter — elektriska förskjutningen n_B

Inverkan av v/c är en allmänform inom atom och kärnfysiken — i positiv divergens. Den grundlägger för övrigt härledningen till Kvanttalen.

Vi kan inte undvara v/c-parametern heller i dessa sammanhang — om saken gäller en mera exakt naturbeskrivning.

I repulsionsformen k_9T9(e/n_ed)² har vi förutsatt ett statiskt laddningstal (e/n_e). I själva verket ändras detta dynamiskt med kärnor i närkontakt, dessutom på ett komplicerat sätt vilket vi här inte närmare ska fördjupa oss i — utom i dess mest allmänna form.

Elektriska fält som uttränger ur lokalt dominanta kroppar (atomkärnans fraktala ytladdningssystem, se från Planckringen) till omgivande lokalt dominanta g-fält bör uppvisa en karaktäristisk elektrisk förskjutning (v/c) beroende på kroppens hastighet. Fenomenet är detsamma som upptäcktes år 1725 av James Bradley (publicerat 1729) och som kallas aberration. För Jorden med v=30 KM/S i förhållande till ljushastigheten i Solsystemet (grovt) 300 000 KM/S blir aberrationen som mest arctan1/10 000=20,63’’. I atomkärnans omedelbara närhet kan värdet förstås vara betydligt större med referens till kärnspinnets koppling till toppvärdet c₀ — vilket är utgångspunkten i resonemanget.

Tar vi med denna aberrationseffekt som alltid existerar i precisionsanalysen i kärnfysiken ENLIGT TNED — kopplingen till potentialbarriären för Q-formerna i ytstrukturen och hur ytladdningarna kopplar varandra i spinnen — har vi en maximal aberration på v/c=1. Effekten på riktningen i elektriska verkan blir då i PREFIXxSIN minimivärdet sin45° med den maximala aberrationsvinkeln B=45° (B för Bradley) som ger toppvärdet för elektriska laddningens verkan gånger en faktor 1/Ö2;

NOLLABERRATION skulle här motsvara en helt stillastående atomkärna med ett idealt rakstrålande elektriskt flödessystem motsvarande B=0° aberrationsvinkel och därmed enhetsvärdet 1 i PREFIXxSIN (sin0=1).

Rotfaktorn är maximal och kan inte överskridas då den är bunden till toppdivergensen c₀. Vi sätter rotfaktorn, eller dess möjliga reduktion mot enheten 1 som elektriska secansförskjutningen i PREFIXxSIN secB=n_B=Ö2. Maxvärdet är Ö2 som motsvarar B=45°, minimivärdet är 1 som motsvarar B=0°.

NUKLEÄRA ANGREPPSKOEFFICIENTEN n_P=n_en_B i k_9T9(e/n_Pd)² med verkan (1/5) reduceras då i totala elektriska angreppet n_P=n_en_B=5Ö2 som ger n_P=7,1 avrundat.

Men vi observerar att detta värde består av en maximerad komponent (n_B=Ö2) och en minimerad (n_e=5).

Det visar sig också att faktorn n_P är extremt känslig för bestämningen av gränsmassan m_0JSUB (Exakta värden på 1 KG när, kräver många exakta decimaler).

Jordens andra ekvation ref. Gränsmassan.wps — UNIVERSUMS HISTORIA

Gränsmassans matematiska fysik

GRUNDTEORI

FUSIONSGRÄNSMASSANS AGENT anges inledningsvis J-kroppen

Vi anställer en jämförelse mellan repulsionstrycket (samma som expansionstrycket) och gravitationstrycket. Vi betraktar resultatet i J-kroppens yta för att få fram maximal g-kraft, och vi sätter referensen för full divergenständning till J-kroppens centrum.

Inverkan av divergensreduktionen lokalt från J-kroppens egengravitation på atomkärnorna innefattar i repulsionskraftens form den allmänna reduktionsfaktorn (c/c₀) enligt

F_cK=F_K(c/c₀)=(c/c₀) k_9T9(Q_e/d)²

Vi kan emellertid inte direkt tillskriva reduktionen (c/c₀) någon kvantitativt signifikant innebörd annat än 1 eftersom bestämningen av c beror av den gränsmassa vars kvantitet vi söker.

Vi kommer därför initiellt att frånse reduktionens kvantitativa aspekt, men underförstå dess kvalitativa roll. Först när gränsmassan är kvantitativt bestämd, kan vi insätta reduktionen (c/c₀) för att erhålla ett mera exakt värde

Initiellt kommer vi alltså enbart att räkna på den normala Coulombkraften F_K=k_9T9(Q_e/d)², men underförstå en kvalitativ inverkan av divergensens lokala reduktion i kraft av J-kroppens egengravitation.

Eftersom g-trycket ska avse atomkärnan med koppling till ytgravitationens inverkan på divergensen, måste vi av princip redan från början innefatta hela atomkärnans verksamma ytstruktur i g-tryckets form. I en tryckanalogi där g-kraften påverkar atomkärnan kommer vi därför att använde hela atomkärnans yta som tryckytan mot g-kraften enligt F_J/A_J=p_J=F_K/A_K där suffixet J avser J-kroppen och suffixet K atomkärnan.

G-yttryckets ekvivalent

p_J = m_J a/4pr² = m_J(Gm_J/r²)/4pr²

kommer i den anställda jämförelsen att avse J-kroppen idealt i kallplasmatillståndets maximala idealt homogena täthet r_max=m_J/(4pr³/3)=1,82 T17 KG/M³ enligt neutron-protonkärnan i TNED. Det är i detta tillstånd som J-kroppen uppvisar den avgörande g-preferensen mot atomkärnan med varierande J-massa via g-yttrycket.

Problemets ursprungliga formulering

Det bör finnas ett visst maximum som balanserar en kropps massa mot g-yttryck och inre repulsionstryck med effekt i minimal expansion.

Är ytgravitationen FÖR stor, bildas också ett stort mottryck, vilket höjer repulsionseffekten. Minskas ytgravitationen, minskas också repulsionstrycket i ytan och därmed en mindre häftig (långsammare) expansion.

Lösningen

När kraften i det gravitella yttrycket p_J

— F=m_Ja, F_J/A_J= m_J a/4pr²=p_J=F_K/A_K, ytan A_K relateras till atomkärnan —

är lika stor som kraften i det repulsiva kärntrycket — F_K=k_9T9(Q_e/d)²] — råder exakt jämvikt mellan inre tryck och g-yttryck.

OM VI I F_J/A_J=p_J=F_K/A_K betraktar kärnytparametern A_K i koppling till g-trycket inte så mycket utifrån en föreställning om riktningsvektorer som utifrån ytgravitationens inverkan på divergensen i kärnans omedelbara närhet

vi hade ju nämligen att kärnytans elektromagnetism regleras proportionellt mot det omgivande moderfältets divergensstyrka enligt vektorformen

F_c0 – F_c – F_G = 0 ................. vektorekvivalenterna mot F_G utbildar negativa F_c, se Kraftvektorledet

kan vi anställa en ideal jämförelse med vilken den motsvarande repulsionskraft F_K är som finns mellan två vätekärnor

i situationen då full divergens har utbildats.

Vi sätter med andra ord A_K på hela neutron-protontoroidytans form (Se utförligt från ATOMKÄRNANS DIMENSIONER)

A_K= (pr₀)² ........................... neutron-protonkärnans toppyta

Neutronerna i kallplasmat ser varandra hur som helst på toppspinnets form, och det är den vi bör framhålla i sammanhanget.

Med ekvivalensen (r anger J-kroppens radie)

F_K = p_JA_K [= k_9T9(e/d)² = pGr₀²m_J²/4r⁴ efter mellanräkningar = pG(2prr₀r/3)²]

kan vi då undersöka OM kärnrepulsionsdistansen

— eller med samma mening nuklidseparationen d

— för en given J-kropp ligger innanför ideala nuklidbarriärens maximum eller om den ligger utanför.

Ligger den innanför överväger kärnrepulsionen och J-kroppens yta måste då svara med en motverkande kraft vilket betyder att ytmotståndet är större än jämviktens och därmed att kärnorna pressas ihop mera och styrkan i ytexpansionen blir större med allt mindre d och därmed allt häftigare expansion från ytan.

Ligger den utanför avtar motverkan mot expansionstrycket från divergenständningen med växande d och J-ytan gör mindre motstånd vilket innebär en allt mera snabb och maximerad expansion med allt större d.

I bägge fallen ges alltså principiellt samma avvikelser, men av skilda dynamiska skäl.

Idealet med maximal balans, som innebär att expansionen blir maximalt långsam, ligger då precis där d tangerar nuklidbarriärens kritiska avstånd kärna-kärna.

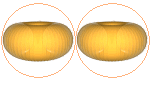
Nuklidbarriärens ideala maximum ges av protonradien r₀ och tillåter oss att se Coulombdynamiken enligt ovanstående illustration. Vilket vill säga; med gränsavståndet d=r₀ ligger de idealt motvända kärnytorna på d=r₀ från varandra. Motsvarande situation med kärnorna i optimalt motsatt läge betyder att de tangerar varandras kroppar i spinnplanet.

Efter mellanräkningar och kontroller får vi för F_K=p_JA_K=k_9T9(e/d)² nuklidseparationen d enligt

d = (2prr₀r/3)^–1eÖ k_9T9/pG = (rr)^–1(2pr₀/3)^–1eÖ k_9T9/pG

k_J = (2pr₀/3)^–1eÖ k_9T9/pG ;

d = (rr)^–1k_J

som med

r=(3m_J/4pr)^1/3=r^–1/3(3m_J/4p)^1/3

— med rr=r^2/3(3m_J/4p)^1/3 som ger d=(rr)^–1k_J=r^2/3[3m_J/(4p)]^1/3k_J

— ger

m_J = r^–2(3/4p)^–1(k_J/d)³

Topptoroidens yta:

Dimensioner med grundytor och volymer i översikt för neutron-protonkärnformen, se även mera utförligt från ATOMKÄRNANS DIMENSIONER

Neutron(1,32)-protonaggregatet(1,37) N3m20

r₀=1,37 t15 M, m=1,67 t27 KG

Se Tyngdpunktssatsen, Guldins Regler, beräkning av rotationsytor:

A=2p(r₀/2)×2p(r₀/2)=pr₀×pr₀=(pr₀)² ............................................................................................................................ ytan, topptoroiden

V=p(r₀/2)²×2p(r₀/2)=2p²(r₀/2)³=p²r₀³/4, r=2,63 T17 KG/M³ (2,94 T17 med r_0n=1,32 t15) .......... volymen, topptoroiden

A=4(r₀×2r₀)+2(2r₀)²=2(2r₀)²+2(2r₀)²=4(2r₀)² ............................................................................................................... ytan, omskrivna rätblocket

V=r₀×(2r₀)²=4r₀³, r=1,62 T17 KG/M³ (1,82 T17 med r_0n=1,32 t15) ............................................. volymen, omskrivna rätblocket

OM VI VILL VARA MERA PRECISERADE bör vi välja den i rätblocket inneslutna kärnan som volymform för beräkningen av max täthet i kallplasmat. Det är den närmaste analogi vi kan komma i det tillstånd då neutronerna glider omkring varandra som rena inoljade (men nollviskösa) mekaniska formobjekt.

Dessa marginaler är vanligen oväsentliga, men här får de stor betydelse för gränsmassan om det nu gäller att fördjupa exaktheten i beräkningarna.

I föregående artikel visades att protonladdningen eZ(1) reduceras med

NUKLEÄRA ANGREPPSKOEFFICIENTEN n_P=n_en_B i k_9T9(e/n_Pd)² i totala elektriska angreppet n_P=n_en_B=5Ö2 som ger n_P=7,1 avrundat.

Men vi observerar att detta värde består av en maximerad komponent (n_B=Ö2) och en minimerad (n_e=5).

Sambanden i sammanställning blir då

—————————————————————————————————

d = (2prr₀r/3)^–1(e/n_P)Ö k_9T9/pG = (rr)^–1(2pr₀/3)^–1(e/n_P)Ö k_9T9/pG

k_J = (2pr₀/3)^–1(e/n_P)Ö k_9T9/pG

d = (rr)^–1k_J ........................................ nuklidseparationen efter divergenständning

r ................ J-sfärkroppens kallplasmaradie

n_P ................ max 7,1 @ 5Ö2 = 7,0710678

m_J = r^–2(3/4p)^–1(k_J/d)³. OBS, d gäller med begränsad räckvidd utanför maxgränsen

limes m_J = r^–2(3/4p)^–1(k_J/r₀)³ ; d=r₀

= m_0JSUB ;

k_J = r₀[m_0JSUB(3r²/4p)]^1/3 ...................... alternativt, jämför längre upp

r₀ .............. protonradien 1,37 t15 M

r=r_max = 1,82 T17 KG/M³ ............................... maxtätheten i J-kroppens kallplasma

k_9T9 = 8,98743 T9 VM/C, det mera exakta värdet för elektriska fyra-pi-konstanten

n_P = e(m_0JSUB)^–1/3(r₀²[2r²/9]^1/3p^7/6)^–1(k_9T9G^–1)^1/2

G = 6,67 t11 JM/(KG)², gravitationskonstanten

resultat med n_P=5Ö2: m_0JSUB= 6,80016 T24 KG

—————————————————————————————————

Med n_P=5Ö2 ges m_0JSUB= 6,80016 T24 KG.

Det betyder en avyttring med 12,13% [6,8–(0,1213)6,8=5,97516] för att få nuvarande Jordmassan 5,975 T24 KG.

[Se även vidare från JORDENS FEMTE EKVATION, himlakropparnas primärmassor].

Skillnaden bör vara den marginella avyttring i J-skalet som åtföljer expansionsfasen.

JORDKROPPEN UTPEKAS ENTYDIGT

Närmast mindre aspirant är Venus med 4,87 T24 KG (kräver motsv. 28% massavyttring). Närmast större är Uranus med 86,9 T24 KG.

I föregående utvecklingar hade neutronradien insatts för protonradien i ovanstående samband. Resultatet ger då m_0JSUB=7,5 T24 KG.

Tar vi med den mycket blygsamma inverkan av reduktionen via (c/c₀) blir värdet på gränsmassan bara obetydligt mindre (ca 6,79962 T24).

Använder vi nuvarande Jordmassan 5,975 T24 KG för att beräkna absolut maximala n_P-värdet finner vi MAXn_P=7,3826449.

Det ger MAXn_e=5,2203182 med den fasta elektriska aberrationen n_B=Ö2.

MED JORDEN SOM DEN UNIVERSELLA MASSENHETEN är därmed maxgränsen för kärnelektriska angreppskoefficienten n_e bestämd till 5,2203182.

2004X26

Bilddeposit

Centralkontakterna i elektron-positronutgivningen

NEUTRONFRAGMENTEN | 2004VII12 | FUSIONSGRÄNSMASSAN | 2004X26 |

END.

NEUTRONFRAGMENTEN | 2004VII12 | FUSIONSGRÄNSMASSAN | 2004X26 |

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Neutronfragmenten | Fusionsgränsmassan

ämnesrubriker

innehåll

NEUTRONFRAGMENTEN

Neutronens fragment enligt TNED

Diskussionsexempel

Focuskällans originalbild

Focuskällans renritade spårbild

Beskrivning

massa-energiekvivalenten

Ekvivalenterna

Resultat

Neutronfragmenten — allmän översikt

Partikelnomenklaturen — allmän översikt

Partikelnomenklaturen — utvidgad beskrivning

Partikelnomenklaturen · TABELL

Neutrinobegreppet i TNED

Neutrino

Neutrino historik

Neutrino Antineutrino

Neutrinons masslöshet i TNED

Jämförande Tabell

Neutrinodynamiken i TNED

NeutrinoRekylen

Elektron-positronassocierade kärnomvandlingar i TNED

NeutrinoSignaturen

Neutronens sönderfall, referenser

FUSIONSGRÄNSMASSAN

Jordens andra ekvation

JÄMFÖRANDE MASSTABELL

Härledning

Gränsmassans fusionsstatus

v/c-spinnets parameter

Gränsmassans matematiska fysik

Resultat

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[FM]. FOCUS MATERIEN 1975 — Almqvist & Wiksell Förlag AB Stockholm 1965 — Andra reviderade upplagan 1975:

Det senare 1900-talets i särklass bästa sammanfattande allmänorienterande (svenska) verket i allmän fysik.

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

EXP allmän förkortning för e^;För e, se NATURLIGA LOGARITMBASEN (Härledningen till e)

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

d deci t1

c centi t2

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet [Se International System of Units] (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

γ Grek. gamma, g, är i TNED (ofta) en generaliserad beteckning för massdestruktionsstrålning som [via Plancks strålningslag] byggs upp från kortare till längre våglängder med representation först vid gammanivån i materiefysiken.
Skrivsättet (m→γ), »m till gamma», betyder här ’massa som omvandlas till ljus och värme i materiefysiken’, från lägst gammanivån vilket generaliserat inbegriper värmefysiken överförd på materiefysikens atomkärnor och elektronmassor. Se även utförligt från Energilagen. Mera allmänt betyder (m→γ) massdestruktionsstrålning från primära massförstöraren E=mc².

em-strålning em- används genomgående i Universums Historia som en bekväm förkortning för elektromagnetisk

TNED

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

MAC — I UNIVERSUMS HISTORIA ofta använd allmän förkortning för Modern ACademy, modern akademi.

Senast uppdaterade version: 2017-08-19

*END.

Stavningskontrollerat 2008-07-07 | 2009-02-28 | 2010-07-15.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se