GRUNDMATEMATIKEN 1 2008IV29 a BellDHARMA production | Senast uppdaterade version: 2023-02-22 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Grundmatematiken | Den Komplexa Algebran-Geometrin

DEN KOMPLEXA ALGEBRAN

KomplexALGEBRA 2005XI8 | MPcExempel 2003XII6

H-trianglarna

IMAGINÄRA ENHETEN i

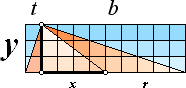
genom Cheops Rektangel

Cheops Rektangel med 2r=t+b och r=x+t

VINKELSUMMATEOREMET visar att komponentuppdelningarna i xy gömmer en avancerad metodkomponent — en komponentuppdelare. Genom att närmare studera hur vinkelsummeringen går till i detalj finner vi den som en inneboende komponentidentifierare. Den följande beskrivningen med harmoniska trianglar ger en konkret illustration.

HARMONISKA TRIANGLAR (H) är rätvinkliga trianglar xyr vars alla sidor består av hela tal

(1, 2, 3, 4, 5, … N). De kallas konventionellt »tripletter». Deras grundform härleds ur Cheops Rektangel y²=bt [från y/t=b/y] enligt

y²=(2r–t)t=bt=(2[x+t]–t)t=(2x+t)t. Med t=1 erhåller man y²=(2x+1)=b=N² ;

y=N ; x=(y²–1)/2 ; r=x+1 ........................................ harmoniska trianglarna

Grundtabell för H-trianglarna

y=N	1	2	4	3	4	8	5	6	12	7	8	16	9	…
x	0	1,5	3	4	7,5	15	12	17,5	35	24	31,5	63	40	…
r	1	2,5	5	5	8,5	17	13	18,5	37	25	32,5	65	41	…

Udda N (1, 3, 5, 7, 9, …) ger H-tringlar direkt. Jämna N (2, 4, 6, 8, …) kräver en dubblering. SUMMAN av två H-trianglar H_a+H_b resulterar i en tredje H-triangel H_c enligt

x=(x₁x₂–y₁y₂) ; y=(y₁x₂+x₁y₂) ; r=r₁r₂(=)D₁+D₂ ............... vinkelsummateoremet

Exempel:

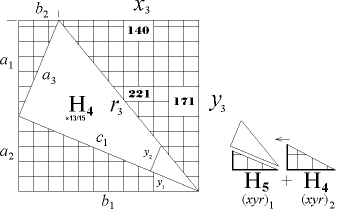
(H5xyr)1	+(H4xyr)2	= (Hxyr)3
(12;5;13)H5	+(15;8;17)H4	= (140;171;221)H

Om vi utnyttjar ovanstående enkla grundtabell för H-trianglarna och på dem tillämpar vektorproduktens ekvivalent r₁r₂ från vinkelsummateoremet ovan på två likadana trianglar kan vi studera komponentuppdelningen på ett mycket enkelt sätt.

Vi ser nämligen att summan av två H3 via r₁r₂ ger H7 enligt

(H3xyr) + (H3xyr) = r_H3² = 25, = r_H7 = (^x24; ^y7; ^r25)

Produkten r₁r₂=r_H3² via Pythagoras sats är [(x²+y²)^1/2]²=x²+y². Vinkelsummateoremet med (xy)₁=(xy)₂=(xy)_H3 visar oss de motsvarande komponenterna

x_H7 y_H7

x²–y² 2xy

Vi känner igen typen från första binomlagen. Om vi jämför dess motsvarande (x+y)² får vi

x²+y² +2xy

Likheten är onekligen slående. Om vi fortsätter undersökningen genom att addera ytterligare en H3 till summan ovan, och sedan ytterligare en H3 successivt, finner vi den ordning som tabellen nedan beskriver. Vi får naturligtvis samma resultat oberoende av vilken H-triangel (eller annan typ) vi väljer eftersom vi här endast studerar den algebraiska sammansättningen.

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

vinkelsummateoremets termer:

TABELL FÖR SUMMERING AV LIKA H-TRIANGLAR

x	y	summa lika H-trianglar
x	y	1
x^2 – y^2	2xy	2
x^3 – 3xy^2	3x^2y – y^3	3
x^4 – 6x^2y^2 + y^4	4x^3y – 4xy^3	4
x^5 – 10x^3y^2 + 5xy^4	5x^4y – 10x^2y^3 + y^5	5 …

binompotensernas termer till jämförelse:

x	+ y	(x+y)^1
x^2 + y^2	+ 2xy	(x+y)^2
x^3 + 3xy^2	+ 3x^2y + y^3	(x+y)^3
x^4 + 6x^2y^2 + y^4	+ 4x^3y + 4xy^3	(x+y)^4
x^5 + 10x^3y^2 + 5xy^4	+ 5x^4y + 10x^2y^3 + y^5	(x+y)^5

Som vi ser är koefficienter (talvärdena framför xy) och potenser (eg. exponentvärdena) helt identiska. Enda skillnaden är att polariteterna är annorlunda — tydligen efter ett visst bestämt mönster. Den enkla slutsatsen är alltså att det ser ut som att binompotenserna skulle kunna användas som ekvivalenter till vinkelsummateoremet. Eller rättare sagt: det ser ut som att vinkelsummateoremet innefattar binompotenserna i sig;

r_H1-pinnen

Titta på H1-triangeln. (^x0; ^y1; ^r1);

Den finns alltid med (för oss gömd) i alla y-komponenter från början eftersom den i vilket fall alltid har enhetsvektorn 1. Den syns alltså aldrig. Men den verkar. Vänta bara ska du få se.

Om vi sätter in H1-triangeln i uppställningen för summan av lika H-trianglar ovan finner vi hela hemligheten med den gåtfulla kopplingen mellan vinkelsummateoremet och binompotenserna. Nämligen med r_H1 som en teckenväxlare och y-koordinat-identifierare.

x		y	summa rH1-trianglar	rH1-vektorns egenmultiplikation
0	.................	1	1	r^1 =	1	rH1	y-bunden
–1	.................	0	2	r^2 =	–1	–1	x-bunden
0	.................	–1	3	r^3 =	–1	–rH1	y-bunden
1	.................	0	4	r^4 =	1	1	x-bunden
0	.................	1	5	r^5 =	r^1	rH1	y-bunden

Ordningen avbildar xy-koordinaterna för r_H1-pinnen i steg om exakt 90° i moturs rotation för varje summering enligt schemat

med ändpunkten i koordinaterna xy enligt

0 ; 1 –1 ; 0 0 ; –1 1 ; 0 …

Om vi på prov genomför en summering med en godtycklig triangel (H) och H1, finner vi också att hela H vrids moturs, alltså vinkelmässigt korrekt positivt, ett 90°-steg för varje H1-summering. Den automatiska komponentuppdelningen som vinkelsummateoremet uppvisar och som växlar mellan xy-axlarna är därmed, tydligen, identifierad. Vi kan studera saken på närmare håll om vi går tillbaka till tabellen för summeringen av lika H-trianglar. Om vi studerar den ordningen kan vi nu närmare se en återspegling av hur r_H1 sicksackar y-x–y-x-y–… med sin vektoretta, som dessutom växlar tecken varannan gång i sin komponent. Vi ser därmed också nu tydligare hur r_H1 flyttar över fokus till xy-sidorna enligt

+y_Y, –y²_x, –y³_Y, +y⁴_x, +y⁵_Y, –y⁶_x, … och så vidare.

SLUTSATS:

Om vi tar vara på denna tydliga naturvink, kan vi alltså lika gärna härma det automatiska beteendet hos r_H1 genom att helt enkelt explicit associera den med alla y-komponenter i binompotenserna (x+y)ⁿ enligt r_H1y — som ger härmningen eller metoden r=(x+r_H1y)ⁿ och sedan tillämpa ovanstående lagbundenhet på resultatet. Det är hela hjärtats hemlighet med den s.k. komplexa algebran.

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

Rollen för r_H1 som glänsande komponentidentifierare innebär alltså att den associerar sig med y, inte x, i grundläget eftersom r_H1 inte har någon x-komponent där. Av samma skäl är den låst vid y i motsatt läge, alltså motsvarande (r_H1)³. För alla övriga fall försvinner den, r_H1=±1, vilket säkerställer att vektorsummeringen med y-delarna tillsammans med x-delarna i de lägena fungerar.

r_H1-pinnen är alltså ingen uppfinning av någon person eller institution utan — tydligen — en i mönstergeometrins struktur inneboende matematisk logisk motor.

Ovanstående observationer betyder nu endast, om vi förstått saken rätt, att om vi sätter ihop r_H1 tillsammans med y och iakttar nämnda ordning — r_H1 står till tjänst med ±1 om den befinner sig i x-axeln och endast då — kommer ingenting annat att inträffa än det som vi redan observerat redan finns inneboende i komplexet. Det vill säga, vi skulle då ha lockat ut den underbara anden ur flaskan för att bereda oss nytta enligt den följande ordningen.

Vi sätter i för metodidentifieraren eller den komplexa enheten r_H1

r_H1 = i .................

(komponent-) metodidentifieraren, komplexa enheten/identifieraren (även benämnd imaginära enheten)

Vektorpotenserna (r_H1)ⁿ, motsvarande de successiva 90°-vridningarna, lyder då som ovan ordningen

i⁰=1, i¹=i, i²=–1, i³=–i=i^–1, i⁴=i⁰=1, i⁵=i¹=i, och så vidare i all oändlighet. Vi kan alltid subtrahera periodtalet 4 från i-exponenten, resultatet stämmer alltid ändå.

Om vi utnyttjar mod-operatorn

[n mod 4 ger för godtyckliga hela tal n alltid 0, 1, 2, eller 3, mod-operatorn härrör från den mäktiga divisionsalgoritmen som en kvots rest] kan vi återföra alla möjliga heltalsvärden n för i-potenserna på formen i^nmod4 motsvarande kvadrantrotationerna i⁰, i¹, i², i³.

För att uttrycka komponenterna tillsammans med metodidentifieraren i skriver vi alltså metoden

r = x+iy ................... = Öx²+y²

komplexa algebran Pythagoras sats

Därmed kan nu den komplexa enhetens definition preciseras exakt enligt följande.

Definition av komplex kvantitet

— i är inget tal (Jämför den moderna akademins lärostoff i ämnet); i är en METODIDENTIFIERARE med i=(0;1):

en komplex kvantitet r är ENLIGT RELATERAD MATEMATIK — sättet vi använder r på — en hypomängd (hypotenusa) i dess Pythagoreiska (rektangulära) form Ö a²+b² som är formaterad på metodidentifieraren (i) i a+ib (även »den komplexa formen»), således inkluderande xy-axlarna men inte deras paralleller

0+ib = (0;y)_Y-KOMPONENT = Ö 0²+b²
och

a+i0 = (x;0)_X-KOMPONENT = Ö a²+0²

Därmed kan vi fritt behandla alla komponenter i grundformen precis så som vi sett att r_H1-pinnen arbetar. Vi kan fritt summera, addera, dividera och subtrahera och utföra alla övriga operationer på i-tecknade (dvs., komplexa) matematiska uttryck. Kvantiteten x+iy kommer alltså att på vanligt sätt motsvara den Pythagoreiska hyposidan Ö(x²+y²) från matematikens fem grundlagar.

Nu kollar vi om allt stämmer: vi ska testa genom att multiplicera vektorerna r₁r₂ enligt de simpla ekvivalenterna (x₁+iy₁)(x₂+iy₂). Om vi har hittat rätt, ska vi få självaste vinkelsummateoremet i slutänden! Vi får

r = (x₁+iy₁)(x₂+iy₂)

= x₁x₂ + x₁iy₂ + iy₁x₂ + iy₁iy₂

= x₁x₂+ i(x₁y₂+y₁x₂) + i²(y₁y₂) ;

Med i²=–1 har vi alltså

= x₁x₂ + i(x₁y₂+y₁x₂) – y₁y₂

och därmed

= x₁x₂–y₁y₂ + i(x₁y₂+y₁x₂) ;

r = x + iy ;

x = (x₁x₂ – y₁y₂)

y = (x₁y₂ + y₁x₂)

Med andra ord:

Exakt samma resultat som i hela utvecklingen till vinkelsummateoremet — på tre rader. Här kan man tala om effektivitet.

Styrkan hos metodidentifieraren, eller komponentorganisatören r_H1 är (alltså, på sitt sätt) närmast oerhörd.

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

Sammanfattning

DEN KOMPLEXA ENHETEN r_H1= i

Vinkelsummateoremet — rⁿÛna; x=x₁x₂–y₁y₂; y=x₁y₂+y₁x₂; r=r₁r₂ — visar att xy-komponenterna i summeringen av växande antal lika trianglar (xyr) beskriver binompotensernas koefficienter (x+y)ⁿ.

Skillnaden består endast i en ordnad teckenväxling vars motorik kan återföras på den harmoniska elementära H1-triangelns (^x0; ^y1; ^r1) stegvisa kvadrantrotation (iⁿ). Vi igenkänner därför H1-triangeln r_H1 = i som en xy-komponentuppdelande metodidentifierare även benämnd komplexa enheten eller (från 1500-talet) imaginära enheten betecknad i (från slutet av 1700-talet, se även längre ner i Historia). Den komplexa enheten (i) associeras med y-termer i xy-planet enligt r=x+iy=Ö x²+y². Innebörden av i i de fyra kvadranterna ger via rⁿÛna

i⁰=1, i¹=i, i²=–1, i³=–i=i^–1, i⁴=i⁰=1 …

Vinkelsummateoremet med r=(x+iy) ger utvidgat rⁿ=(x+iy)ⁿ Û na.

Tillsammans med sambanden i Resultatredovisning för vinkelsummateoremet, x_n/rⁿ=sinna och y_n/rⁿ=cosna med rⁿ=r_n, får vi alltså även

rⁿ = (x_n+iy_n) = r_n. Med (x + iy)ⁿ/rⁿ ges vidare ekvivalent [(x + iy)/r]ⁿ=(x/r + iy/r)ⁿ.

Dessa samband används (se nedan) explicit för härledningen till serierna för sinus och cosinus med den komplexa metodidentifierarens hjälp.

Den komplexa algebrans fullständiga nomenklatur framkommer först med härledningen till serierna för sinus och cosinus med r_H1-pinnens hjälp — där vidare samband för den komplexa algebran innefattas. Vi studerar hur med början från Serierna för Sinus och Cosinus via i.

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN 2005XI9

sinus och cosinus serier

Se även motsvarande härledning till Serierna för Sinus och Cosinus utan hjälp av i

Härledningen till

Serierna för sinus och cosinus via i

SAMMANSTÄLLNING i PREFIXxSIN

— Varför är ”serierna för sinus och cosinus” viktiga?

— När de elektroniska kalkylatorerna började komma ut på markanden i slutet av 1970-talet, berodde deras popularitet just (främst) på bekvämligheten att slippa slå i (dryga) tabeller för att få fram konkreta värden i trigonometriska beräkningar; Man behövde nu bara ”trycka på knappen” med SIN eller COS så var allt klart i en hast. Serierna för sinus och cosinus (och många flera) bildar i varje fall den datoriserade grundvalen för varje mera avancerad teknisk tillämpning. ANIMERINGAR, till exempel, (generellt 3D-geometrin) vore helt omöjlig utan en datoriserad grund med sinus-cosinus-beräkningar (objektens rotation).

Vinkelsummateoremet r_n=(x_n+iy_n)=rⁿÛna med likvärdiga n · a = ¥ · dA=ò dA=A ger oss direkt

(x/r + iy/r)ⁿ = (sina + icosa)ⁿ

= (x + iy)ⁿ/rⁿ

= [(x_n+iy_n)=rⁿ]/rⁿ

= x_n/rⁿ + iy_n/rⁿ

= sinna + icosna = 1 = Ö (sin na)²+(cos na)² = Ö sin²na + cos²na

Med slutvinkeln na=¥dA=ò dA=A — med överförda beteckningar na:=¥da=ò da=a — ges

x = sin[daÛ0] = 1,

y = cosda = daÛ0.

Och alltså är

(sinda + icosda)^¥=(1+ida)^¥ = (1+ia/¥)^¥ = sin¥da + icos¥da = sina + icosa

Exponentialekvivalenterna — Eulers ekvivalenter från utvecklingen av logaritmderivatan enligt positionsformen i nollformsalgebran med den mängdoberoende ¥ — sammanför ovanstående med den naturliga logaritmbasen e och därigenom med binomialteoremet (BT) enligt

(1+x/¥)^¥=(1+1/¥)^¥x = e^x ..................................... Eulers ekvivalenter ; Således

(1+ia/¥)^¥=(+1/¥)^¥ia = e^ia som ger oss

(1+ida)^¥ = (1+1/¥)^¥ia = e^ia = sina + icosa ........................ Eulers formel,

a=p ger f.ö. e^ip=–1=i² analogt e^p/2=i^1/i=i^–i

som via BT ger

m®¥

e^ia = 1+å [ia]_m!/[m+1]!

m=0

med upplösningen i de bägge komponenterna

m®¥ m®¥

e^ia = 1+å [ia]^2m/2m! + å [ia]^2m–1/(2m–1)! = 1

m=1 m=1

som i beaktande av i⁰=1, i¹=i, i²=–1, i³=–i=i^–1, i⁴=i⁰=1 … som innebär att

alla i^2,4,6…= – + – + … och alla i^3,5,7…= ii^2,4,6… = i( – + – + …)

m®¥

ger = 1+å(–1)^ma^2m/2m! ................................................... sinusdelen, x

m=1

med serien sina = 1 – a²/2! + a⁴/4! – a⁶/6! + a⁸/8! – a¹⁰/10! + a¹²/12! –… i S-delen

m®¥

och + i ·å(–1)^m+1a^2m–1/(2m–1)! .................................... cosinusdelen, iy

m=1

med serien cosa = a – a³/3! + a⁵/5! – a⁷/7! + a⁹/9! – a¹¹/11! + a¹³/13! –… i S-delen

enligt PREFIXxSIN med a i radianer.

Serierna konvergerar ytterst snabbt med praktiskt taget en korrekt decimal per beräknad delterm.

imaginärtrigonometriska grundsambanden

sini och cosi

Med alla i^2,4,6…= – + – + … och alla i^3,5,7…= ii^2,4,6… = i( – + – + …) framgår att den komplext tecknade vinkeln ia ger seriernas absolutvärden (alla tecken positiva) enligt imaginärtrigonometriska sambanden (se vidare nedan i Imaginärtrigonometriska funktionerna)

sin ia = sini a = (e^a+e^–a)/2 och cos ia = i cosi a = i(e^a–e^–a)/2 med sini a + cosi a = e^a.

Konventionellt skrivs

sini som cosh och cosi som sinh

(MATEMATIKLEXIKONs175sp2, hyperboliska funktioner)

med benämningen »hyperboliska» funktioner — typformen

1 = (sini a)² – (cosi a)²

till skillnad från den goniometriska typformen

1 = (sin a)² + (cos a)².

Dessa begrepp (och deras historia) beskrivs mera utförligt längre fram i Imaginärtrigonometriska funktionerna.

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

historia

Se även i Historisk referens till Eulers Ekvivalenter

HISTORIA

LEONHARD EULER (1707-1783) SOM DEN EXAKTA MATEMATIKENS BANEMAN

Enligt MATEMATIKLEXIKON W&W 1991 s110sp2ö var det Leonhard Euler som (efter flera hundra års bekantskap med »imaginära tal») införde beteckningen i=Ö–1 år 1777. Euler betraktas enligt källan som banemannen i ”den moderna analysen”. Men det märkliga är, att Eulers väsentliga föreställningar om analysen (”funktionslära” enligt Euler, MLs131sp2ö) övergavs för helt andra företräden under 1800-talet (från Eulers funktion=analytiskt uttryck till Cauchys och Dirichlets avbildningsbegrepp [1837]). Snarare än en plats i den moderna akademins historia bör alltså Euler ha sin självskrivna plats i utvecklingen och upptäckterna av matematiken som exakt vetenskap. Eulers funktionsbegrepp är nämligen det rätta — betydligt mera djupgående än den moderna akademins ytterst ytliga föreställningar: Vi har tidigare t.ex. studerat definitionen av intervall, integral och punkt och som vi nu vet modern akademi INTE kan härleda utan måste uppfinna.

Mina egna matematiska referenser från utomstående under min egen matematiska utvecklingshistoria (i stort sett genomgående under 1980-talet) är ytterst magra — i jämförelse med de jättelokaler som tillhandahålls av inrättningar typ universitetsbibliotek. Mina egna referenser inskränker sig här till vad varje innevånare kan finna i sitt stadsbibliotek — som för den delen har en bra täckning sett till det allmänt etablerade utbudet. Se vidare i Allmänna referenser till Matematiklitteraturen. För min del sökte jag själv FÖRST de elementära härledningarna på egen hand för att därefter eftersöka etablerade källor till jämförelse. Inte sällan med upptäckten att väsentliga partier saknas — i den etablerade litteraturen.

På senare tid (90-talet) kom MATEMATIKLEXIKON W&W 1991 som ger en del referenser för den etablerade matematikens kännedom (dock utom högskolenivå). Först sedan jag själv upptäckt den mängdoberoendes (¥) viktiga grund, upptäckte jag i MATEMATIKLEXIKON artiklar som ger en del referat från Leonhard Eulers arbeten (från 1748) — och som visar tydliga paralleller. Tyvärr ger inte källan någon exakt redovisning av Eulers utsagor. Källan anger t.ex. på sidan 110 ett skrivsätt ”w=x/i” som sägs vara Eulers med ”i” i mening ”oändligt stort tal”. Källan beskriver inte denna detalj vidare, om det är källans tolkning, eller Eulers explicita mening, eller hur Euler resonerade i saken. Essensen av sambanden i de Eulerskt presenterade teckningarna är dock densamma som i den relaterade matematiken med den mängdoberoende enligt motsvarande w=x/¥=dx.

Källan anger (s110sp2ö) ”E. skriver a^w=(1+kw)”, vilket närmast för vår del motsvarar

e^dx=(1+dx)=e^x/¥=(1+x/¥), och därmed (1+x/¥)^¥ = e^x, vilket är helt korrekt (Se Beviset för e). Det är alltså av det skälet uppenbart att Euler synes ha varit VÄL förtrogen med (den praktiska sidan av) den mängdoberoendes inflytande. Innebörden av ¥ har emellertid aldrig kommit fram i den moderna akademins lärosystem, och därmed har även beskrivningen av Eulers samband tappat den förklarande kärnans essens.

Euler uppvisar genom källan ovan flera bevis på sin förtrogenhet (funktionsbegreppet). Men dessa banbrytande idéer övergavs under 1800-talet — med dess berömda allmänna omdaning av logiken.

Jämför — i analogi med Eulers galant enkla och tydliga funktionsbegrepp (för vidare analys):

FUNKTION:

· allt utom konstanter;

· allt som från en godtycklig punkt P har en entydig utsträckning

En konstant kan inte gestalta en variation.

En funktion (variation) blir därför analytisk genom att den kräver positionsformen dy/dx=y’.

Funktionskriteriet ansluter till UNIVERSALSATSEN*. Jämför –x/x=–1: |x| är INTE en funktion utan två.

ICKE-FUNKTION definieras som ett avbrott i funktionen.

*UNIVERSALSATSEN ingår ännu (Juli 2008) inte i den här presentationen, den tillhör den högre analysen med ekvationsläran (inkluderat funktionsbegreppet med talteorin ENLIGT RELATERAD MATEMATIK) och dess (mycket) omfattande verk. Målet är att även få med denna del (så småningom).

— Verkställt 2009-01-10. Se från Analysen.

Funktionsbegreppet generellt i matematiken. Efter Leonhard Euler (1707-1783, se även Historia ovan) skriver vi typiskt en funktion, vilken som helst, på den allmänna bekväma formen

y = f (x) ..................... Eulers funktionsbegrepp

Vi läser det som ”y (y) är lika med (=) funktionen (f ) för x (x)”.

y betecknar funktionsvärdet och x betecknar variabelvärdet.

Jämför t.ex. parabelns funktion, y=x²; varje variabelvärde x (vanligen horisontella axeln eller abskissan) ger via funktionen för x (som i detta fall är x²) ett resultatvärde y (vanligen vertikala axeln eller ordinatan);

I fallet parabeln kan vi alltså efter Euler skriva analytiskt att f (x) = y = x².

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

KOMPLEXA ALGEBRANS TERMINOLOGI

DEN KOMPLEXA ALGEBRANS TERMINOLOGI

Grundformerna

Alla utvecklingar här i PREFIXxSIN

SPECIELLT Viktig OBSERVATION — vinkelagentens multiplicitet

I EULERS FORMEL e^iv = sinv + icosv måste vi observera multipliciteten för vinkeln v enligt v=v+n·360°. I »normala fall» (v avser en singulär förekomst) har multipliciteten n ingen som helst betydelse. Är emellertid v associerad med en delningsfaktor typ v/m ges v/m=v/m+n·360°/m. Beskrivande övningsexempel följer. Generellt beaktar vi därför

e^iv= e^{iv + in·2p} eftersom

e^i2p = e^in·2p = 1 = sin n · (360° = 2p radianer)

Vilket vill säga; Den givna vinkeln v kan upprepat ”sättas på samma ställe” medan r-pinnen snurrar runt varv efter varv i enhetscirkeln.

Den FULLSTÄNDIGA v-formen är alltså

e^{iv + in·360° = i(v + n·360°) = ip} = sin p + i cos p

med p = (v + n·360°).

I samband där bara en enda rotation förekommer [p=p/1 som ger i(v + n·360°)=iv] kan den enklare formen med v=p användas. Vi kommer att studera ett detaljerat exempel för övning och återerinring i efterföljande exempelblock.

DEN KOMPLEXA ALGEBRANS TERMINOLOGI

Nedanstående termbeteckningar ansluter (i stort) till gängse förekommande beteckningar.

i ........................................ komplex identifierare-enhet

r ....................................... komplex vektor

a ....................................... real del (x), Re

b ....................................... imaginär del (y), Im

| z | = Ö a² + b² ................ absolutvärde, vektor eller modyl

v ....................................... argument, vinkel mellan z och x-axel, v = arg z
= arg z = atan b/a med kvadrantvillkor ;
y/x och y/–x, och –y/–x och y/x kan inte fås via tangeneten enbart; speciellt fås
0° = y/0 och 0° = 0/x; jämför
tan 1/0 = 90°
tan 0/1 = 0°
(1/0 är normalt helt omöjligt att beräkna)

a = | z | sinv ..................... real del via sinus

b = | z | cosv ..................... imaginär del via cosinus

b/a = tanv ........................ se v ovan

z = a + ib ............................ hypokvantitet på komplex (komponent-) form

_

z = a – ib ............................ komplext konjugat till a+ib

e^iv = sinv + icosv ............... vinkelenhetstransformator, r=1, komplexa kvantitetens polära form

re^iv = r(sinv + icosv) ......... r = | z | , allmänna vinkelenhetstransformatorn

z = | z | (sinv + icosv) ........ polärformen för komplex kvantitet;
Genom
z = a + ib
= | z | (sinv + icosv)
= r(sinv + icosv)
fås i förtydligande

z = re^iv ................................ centrala sambandet, r cirkelradien = | z | med
z = hypokvantiteten = HypomängdenGångerEtt
(1= sin²v+cos²v)

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

Exempel

ÖVNINGAR PÅ ALLMÄNNA KOMPLEXA UTTRYCK

Hur komplexa uttryck kan skrivas (v = atan b/a) :

z = 2 = 2e^iv = 2e^{i · (v = atan 0/2 = 0)} = 2e^{i · 0°}

z = i = e^iv = e^{i · (v = atan 1/0 = 90°)} = e^{i · 90°} = e^ip/2 *

z = 2i = 2e^iv = 2e^{i · (v = atan 2/0 = 90°)} = 2e^{i · 90°}

z = 1+ i = Ö 2 e^iv = Ö 2 e^{i · (v = atan 1/1 = 45°)} = Ö 2 e^{i · 45°}

Studera dessa exempel noga. De är uppställda i syfte att komprimera så mycket sammanfattning som möjligt på så litet utrymme som möjligt för snabb memorering. Försök komma ihåg implikationerna (de här explicit ej tecknade underliggande delarna) som leder till de aktuella resultaten.

Erinra blott: om ekvivalenten till z är en singulär koefficient är det en Re-komponent, annars en Im-komponent.

Använd sedan den allmänna (v = atan Im/Re) för att utveckla exponenten v.

Gå tillbaka till grundformerna (se föregående block) om påtet ovan är idel hieroglyfer.

(Tro det eller inte, men det är så även för ”proffs” — i tidens längd. Man kommer inte ihåg ett dyft om man inte arbetar med detaljerna kontinuerligt. Därför behöver man en avancerad minneslapp — speciellt om detaljerna är många, som i teckenhavet ovan).

* i = e^ip/2; i^1/i=e^p/2=i ^–i; i ⁱ=e^–p/2; i² =–1= e^ip; ip=ln–1; i=ln i^2/p=(2/p)(ln i); ip/2=ln i; …

EKVATIONER MED KOMPLEXA KOEFFICIENTER löser man

(HL högra delen av hela ledet, använd ni = z = re^iv)

Exempel:

x⁴ = 16i ;

HL = 16i = 16e^iv = 16e^{i · (v = atan 16/0 = 90°)} = 16e^{i · 90°}

VL = x⁴ ;

x = re^iv , x⁴ = r⁴e^{i · 4v} ;

VL = HL ; r⁴e^{i · 4v} = 16 e^{i · 90°} ;

r⁴ = 16

r = 16^1/4 = 2 .

e^{i · 4v} = e^{i · 90°} = e^{i · (90° + n360°)} ;

e^{i · v} = e^{i · 90°/4} = e^{i · (90° + n360°)/4}

Erinra den fullständiga v-formen med n som heltal (n börjar från 0, se slutlig Lösning nedan)

e^{iv + in·360° = i(v + n·360°) = ip} = e^ip= sinp + icosp

e^{i p/k} = sin p/k + icos p/k

v = 90°

p = (90° + n360°), p/4 = (22,5° + n90°)

e^iv = e^{i · p/4} = e^{i · (22,5° + n90°)} = [sin (22,5° + n90°) + icos (22,5° + n90°)]

Härifrån samlas de alternerade lokalerna för r-pinnen via n, den sluter cirkeln på n(v/n):

n=0 Û p = (22,5° + 0·90°) = 22,5° ¬

n=1 Û p = (22,5° + 1·90°) = 112,5°

n=2 Û p = (22,5° + 2·90°) = 202,5°

n=3 Û p = (22,5° + 3·90°) = 292,5°

n=4 Û p = (22,5° + 4·90°) = 382,5° = 22,5°

de 4 rötterna repeteras sedan ändlöst med början från toppen igen

Lösning:

x = (16i)^1/4 = 2i^1/4 = re^iv = 2e^{i · (22,5° + n · 90°)} = 2[sin (22,5° + n90°) + icos (22,5° + n90°)]

Kommentar

Lösningen betyder hörnen på en regelbunden polygon inskriven i cirkeln med radien r=2.

Exempel:

k = (1 + iÖ3)¹⁵ ;

z = 1 + iÖ3 ;

arg z = v = atan Ö3/1 = 60°;

r = [Ö 1² + (Ö3)² ] = 2

k = z¹⁵ = (re^iv)¹⁵ = (2e^iv)¹⁵ = 2¹⁵e^{i 15v}

e^{i · 15(v = atan Ö3/1 = 60°)} = e^{i · 900° Û 180°} = (sin 180 + icos 180) = (–1 + 0) = –1

e^i15v = –1

Lösning:

k = (1 + iÖ3)¹⁵ = –2¹⁵ = –32768

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

IMAGINÄRTRIGONOMETRISKA FUNKTIONERNA | Allmänna härledningar

Imaginärtrigonometriska funktionerna

eller DE ANALYTISKA Trigonometriska SAMBANDEN i PREFIXxSIN

sini cosi tani seci csci coti

Centralserierna i sin-sini och cos-cosi är exakt desamma — de skiljer sig endast i polaritet. Sett till derivatorna, har sini-cosi relationerna inga negativa tecken.

I konventionell litteratur kallas de imaginärtrigonometriska relationerna för hyperboliska funktioner, de betecknas

sinh cosh tanh sech csch coth där h:et utläses ”hyperbolicus”. Vi kommer här längre fram att relatera dessa begrepp mera ingående — för säker bekantskap.

Modern akademi har en sällsynt träffsäker förmåga att benämna matematikens områden med associerande begrepp — som ligger helt vid sidan av sakens kärna.

DE IMAGINÄRTRIGONOMETRISKA FUNKTIONERNA är ENLIGT RELATERAD MATEMATIK helt och hållet analytiska funktioner. De härrör från beteckningarna — men utan motsvarande geometriska relationsbegrepp — i serierna för sinus och cosinus genom att sätta samtliga termer i nämnda serier positiva, se mera preciserat nedan. För att skilja den imaginära, positiva serien från den verkliga skrivs här ett ”i” efter den senare för den förra. Ekvivalenterna till positiva sinus och cosinus bildar då motsvarande komplexa vinkelkoefficienter

sin ix=sini x och cos ix=cosi x. Medan den reala trigonometrin tecknar 1=(sinx)²+(cosx)² blir motsvarande samband med införandet av komplex vinkelkoefficient 1=(sinix)²+(cosix)²=(sini x)²+(i cosi x)²=(sini x)²+i²(cosi x)²=(sini x)²–(cosi x)². Därav benämningen hyperbolisk i modern akademi: Den liksidiga hyperbelns allmänna ekvation har just typformen 1=x²–y² — se även i Begreppet HYPERBOLISK. Men där stannar också kopplingen till hyperbeln. De imaginärtrigonometriska funktionerna är genom den komplexa vinkelkoefficienten rena cyklometriskt komplexa funktioner och har inte ett dyft att göra med vare sig trigonometri (goniometriska relationer, förhållanden mellan sidor i rätvinkliga trianglar) eller hyperbler. De imaginärtrigonometriska funktionerna har emellertid en stark koppling till den elementära fysiken genom catenarian eller kedjelinjen. Utöver catenarian som praktisk tillämpning, erbjuder ImTrigarna genom sina ekvivalenter ett särskilt område som kan utnyttjas inom algebran.

DEN KOMPLEXA ALGEBRAN I MODERN REGI är känd för att vara särskilt knölig. Här följer därför en mera noggrann — om än sammanfattande — genomgång av ImTrigarna enligt RELATERAD matematik.

I DEN ALLMÄNNA BESKRIVNINGEN AV TRIGONOMETRIN förenklas symbolberget betydligt om man till exempel i stället för den fullständiga formen

1=(sinx)²+(cosx)² skriver 1=sin²+cos². Eftersom aspekten redan är klar, förutsatt full förtrogenhet med trigonometrin, är missförstånd uteslutna. Endast i speciella fall används fullständiga former.

FRÅN EULERS EKVIVALENTER eller exponentialekvivalenterna kommer vi ihåg

positiv exponent

(1+1/¥)^¥x = (1+x/¥)^¥ = e^x = 1 + x + x²/2! + x³/3! + x⁴/4! + … + x^m/m!

= 2,718 28 18 28 45 90 45… ..................................... med x=1

negativ exponent

(1+1/¥)^¥(–x) = (1–x/¥)^¥ = e^–x = 1 – x + x²/2! – x³/3! + x⁴/4! – … + (–x)^m/m!

= 0,36 78 79 44 11 71… ........................................... med x=1

Kommer vi också ihåg att alla i^2,4,6…= – + – + … och alla i^3,5,7…= ii^2,4,6… = i( – + – + …) finner vi likt Leonhard Euler att

e^x + e^–x = 2[1 + x²/2! + x⁴/4! + x⁶/6! + x⁸/8! + x¹⁰/10! …

JÄMFÖR vi med sinusserien i PREFIXxSIN

_{m ® ¥}

sin x = 1 – x²/2! + x⁴/4! – x⁶/6! + x⁸/8! – x¹⁰/10! + … = 1+ å (–1)^mx^2m/2m!

^m=1

finner vi

_{m ® ¥}

sin ix = 1 + x²/2! + x⁴/4! + x⁶/6! + x⁸/8! + x¹⁰/10! + … = 1+ å x^2m/2m!

^m=1

= 2^–1(e^x + e^–x)

= å sin⁺ = sini x ................................................. absoluta sinusserien

PÅ SAMMA SÄTT finner vi för cosinusserien i PREFIXxSIN att

e^x – e^–x = 2[x + x³/3! + x⁵/5! + x⁷/7! + x⁹/9! + x¹¹/11! …

_{m ® ¥}

cos x = x – x³/3! + x⁵/5! – x⁷/7! + x⁹/9! – x¹¹/11! + … = å (–1)^m+1x^2m–1/(2m–1)!

^m=1

_{m ® ¥}

cos ix = i(x + x³/3! + x⁵/5! + x⁷/7! + x⁹/9! + x¹¹/11! + … = iå x^2m–1/(2m–1)!

^m=1

= i 2^–1(e^x – e^–x)

= iå cos⁺ = i cosi x ......................................... absoluta cosinusserien

Resultat:

sin ix = sini x = (e^x+e^–x)/2 sini x = sin ix = (e^x+e^–x)/2

cos ix = i cosi x = i(e^x–e^–x)/2 cosi x = i^–1cos ix = (e^x–e^–x)/2

sini x + cosi x = e^x ; sini ix + cosi ix = e^ix = sin x + i cos x = 1

= sin i²x + i^–1cos i²x

= sin –x + i^–1cos –x

= sin x – i^–1cos x

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

MED UTGÅNGSPUNKT I REALA TRIGONOMETRISKA FUNKTIONER, första ledet nedan, med vidare införande av den komplexa identifieraren i som en vinkelkoefficient, leder relationerna I FÖRTYDLIGANDE till

1 = (sinx)² + (cosx)² .............. cirkulära, reala trigonometriska

= (sin ix)² + (cos ix)² .......... cirkulära, imaginära trigonometriska

= (sini x)² + (i cosi x)²

= (sini x)² – (cosi x)² .......... resultat, imaginära trigonometriska; hyperbolisk form

= (åsin⁺)² – (åcos⁺)² ;

________

sini = Ö cosi²+1 = åsin⁺ ........... absoluta sinusserien

________

cosi = Ö sini²–1 = åcos⁺ ........... absoluta cosinusserien

Med

sini x = 2^–1(e^x + e^–x) = sin ix

cosi x = 2^–1(e^x – e^–x) = i^–1cos ix

återkopplas sambanden på ytterligare ekvivalenter via Eulers formel sinx+icosx=e^ix enligt

sini ix = 2^–1(e^ix + e^–ix) = sin x = sin i²x = sin –x

cosi ix = 2^–1(e^ix – e^–ix) = i cos x = i^–1cos i²x = i^–1cos –x

Vi kan alltid kontrollera resultaten direkt genom enkel huvudräkning genom att återknyta till enhetscirkeln med sinus-cosinusprojektionerna om vi kommer ihåg att den komplexa identifieraren i betyder en positiv rotation med 90 grader. Så återfinner vi speciellt från leden icosx=i^–1cos–x ovan att –cosx=cos–x.

Med tani = cosi/sini finner vi (efter mellanräkningar)

tani x = 1 – 2(e^2x + 1)^–1

coti x = [1 – 2(e^2x + 1)^–1]^–1

Som sini+cosi=e^x finner vi genom det triviala e^x=e^x, som ger x=ln e^x, att x=ln(sini+cosi). Därmed ekvivalenterna

x_sinix = ln (sini + [sini²–1]^1/2)

x_cosix = ln (cosi + [cosi²+1]^1/2)

Genom att utveckla det motsvarande uttrycket från tani finner vi

x_tanix = 2^–1ln[2(1–tani)^–1–1]

Därmed är genomgången av DEN KOMPLEXA ALGEBRAN ENLIGT RELATERAD MATEMATIK avslutad.

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

CATENARIAN

Introduktion till Catenarian — i fortsättning från ovanstående avsnitt

IMAGINÄRTRIGONOMETRERNAS DERIVATA

Genom exponentderivatan Dne^(P)=e^(P)Dn(P) i Formlagarna får vi direkt från

sini x = 2^–1(e^x + e^–x) = sin ix = åsin⁺

cosi x = 2^–1(e^x – e^–x) = i^–1cos ix = åcos⁺

tangensformerna

________

Dn sini = cosi = Ö sini²–1

________

Dn cosi = sini = Ö cosi²+1

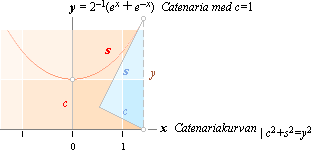
Med tani = cosi/sini ges direkt från EXP(6) i Formlagarna

Dn tani = sini^–2 = seci²

Dn coti = –cosi^–2 = –csci²

CATENARIAN även sv. Katenarian

— eller Kedjelinjen

KURVLÄNGDEN s för en kurva y=f (x)

ges genom differentialerna ds²=dx²+dy² varav (ds/dx)²=1+(dy/dx)²=1+(y’)²=(s’)²,

s’ = Ö 1+(y’)²

OM y=sini får man y’=cosi och därmed

s’ = Ö 1+cosi² = sini = y ;

y’ = s’ = sini

y’ = s’ = cosi

KRAFTVÄGARNA F_Hs och F_Vc med avseende på en gemensam referenspunkt bildar en jämvikt F_Hs=F_Vc. Vi skriver F_H=H och F_V=T. OM systemet befinner sig i ett Galileiskt kraftrum (tyngdkraftens verkan gäller konstant oberoende av rummets utsträckning) gäller i varje utsträckning

s/c=T/H=dy/dx=y’

Med c=1 gäller

________

s’ = dy/dx = y’= ò Ö 1+(y’)² dx

________

s’ = ds/dx = Ö 1+(y’)²

Därmed bildar kurvlängden s=cosi en catenaria [från Latinets cate’na, kedja] eller en kedjelinje y=s’=sini=(e^x+e^–x)/2, samma som en fritt hängande lina, rep eller kedja mellan två upphängningspunkter i ett rum med konstant tyngdkraftsacceleration.

Catenarians kurvlängd från lägsta punkten till P

är samma som catenarians tangent i P.

Illustrationen nedan visar en catenaria med c=1 enligt y = 2^–1(e^x + e^–x).

För given catenaria är c alltid en konstant

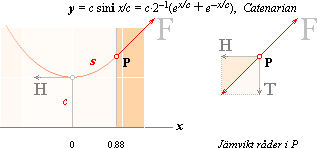
Med konstanten c inkluderad får catenarian den fullständiga formen

y = c · sini x/c = c · 2^–1(e^x/c+ e^–x/c) = cå sin⁺ ............................ Catenarian

y’ = cosi x/c = 2^–1(e^x/c – e^–x/c) = å cos⁺ .......................... tangenten

s = cy’ .............................................................................................. kurvlängden catenarians kurvlängd

Catenarian har samma form som ett fritt hängande elastiskt rep (lina) eller kedja.

Upphängd i en punkt P i en vägg, påverkas repet av en kraft F i P i tangenten s/c = cosi x = T/H. H är den horisontella kraften vid catenarians lägsta punkt och T är tyngden av s.

x_cosix=1 = ln(1 + Ö 2) = 0,8813735… .................... exempel med tangenten 1

forts. GRUNDERNA I DEN KOMPLEXA ALGEBRAN

Begreppet HYPERBOLISK

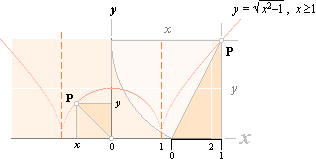
Klargörande

Begreppet HYPERBOLISK

Karaktären för enhetshyperbeln (horisontella sambandet)

jämfört med cirkeln

För en cirkel y=Ö1–x² — se den rödorangea cirkelkurvan i mitten — är avståndet mellan P och origo alltid den konstanta radien r=1:

x² + y² = 1. För enhetshyperbeln y=Öx²–1 — se den orangea hyperbelkurvan figuren ovan till höger/vänster — [även benämnd liksidiga hyperbeln] gäller att distansen mellan P och x-axeln via x-längden alltid avskär en rätvinklig triangel med basen lika med enheten 1, y som vertikalen och x som hypotenusan:

x² – y² = 1.

Imaginärtrigonometrins enhetsform sini²–cosi²=1 har alltså hyperbelns algebraiska typform, men i övrigt ingen som helst koppling till hyperbeln.

Sini och cosi-begreppen är tydligen komplementära komplexa beskrivare. De har, uppenbarligen, ingen som helst kvalitativ koppling till hyperbeln.

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Grundmatematiken | Den Komplexa Algebran-Geometrin

ämnesrubriker

innehåll

GRUNDMATEMATIKEN

För den elementära matematiken, se Matematiken från Början

För grundbegreppen inom differential, derivata och integralkalkylen, se från Atomtriangeln

För de elementära matematiska funktionernas derivator, se Formlagarna

Den komplexa algebran

H-trianglaran · den imaginära enheten genom Cheops Rektangel

Grundtabellen för H-trianglarna

Summering av lika H-trianglar, tabell

rH1-pinnen

Metoden

Komplexa enhetens definition

Sammanfattning

Härledningen till serierna för sinus och cosinus

Eulers Formel

Imaginärtrigonometriska sambanden

HISTORIA Leonhard Euler som den exakta matematikens baneman

Komplexa algebrans terminologi

Vinkelagentens multiplicitet

Fullständiga v-formen

Terminologi

Exempel

Imaginärtrigonometriska funktionernas härledningar

Absoluta Sinus

Absoluta Cosinus

sini

cosi

tani

coti

Catenarian äv. sv. Katenarian eller Kedjelinjen

Imaginärtrigonometrernas derivata

Catenarian

Begreppet HYPERBOLISK

Begreppet hyperbolisk i konventionen

Klargörande

referenser

MATEMATIKLEXIKON — WAHLSTRÖM & WIDSTRANDS MATEMATIKLEXIKON, 1991

”En bearbetad översättning av W. Karush The Crescent Dictionary of Mathematics (1962) utgavs 1970 under titeln Matematisk uppslagsbok. En omfattande revision har nu ansetts angelägen.”, Förordet.

Senast uppdaterade version: 2023-02-22

*END.

Stavningskontrollerat 2011-07-18.

rester

*

PNG-justerad 2011-07-18

åter till portalsidan · portalsidan är www.UniversumsHistoria.se