ATOMENS TOTALA ENERGITRANSFERERING · ATOMENS TOTALA ENERGIOMVANDLING · ATOMKÄRNANS TOTALA UPPLÖSNING | SAMMANSTÄLLNING 2008II13 | VII18

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

ATA CAT | Senast uppdaterade version: 2021-03-30 · Universums Historia

Atomens Transmissiva Autonomi · Kapacitiv Transmission

ATOMKÄRNANS TOTALA UPPLÖSNING

Atomkärnans fullständiga upplösning | 2008II13 | ENERGY_Spark | TNEDbasics | TNEDbasicsII |

Med inledande grunder från Atomkärnans härledning i Universums Historia genom K-cellens värmefysik med särskild tillämpning på Solfysiken enligt TNED och Blixturladdningens Fysik, se även i Kort Resumé av Blixturladdningens Fysik om ej redan bekant.

ATOMKÄRNANS FULLSTÄNDIGA UPPLÖSNING

Inledning

Grundmaterialet till följande framställning förutsättes här bekant enligt närmast ovan rubricerade detaljer.

Observera att framställningens grund helt saknar referenser i den moderna akademins lärosystem.

framställning

TEORETISK GRUND — 1818e-massivet

summa nollmoment — summa nollkraft — summa nollspinn — summa nolladdning — nollresistans — nollinduktans

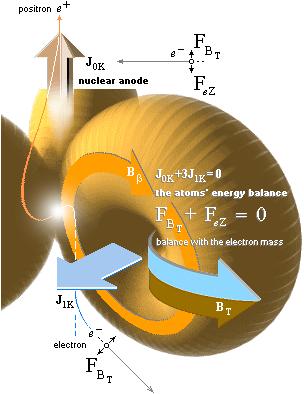
Atomkärnan består, från Neutronen genom Plancks konstant h=m_nc₀r_n enligt TNED, av positiv och negativ elektronmassa med summan ±e=0 — med fördelningen via elektronmassan 0,000548598u genom neutronmassan 1,0086652u enligt (1818+18+k)e med k=2,624e. Huvuddelen av laddningarna döljs och endast en liten del framträder genom kärnstrukturens laddningsdeplacement som exponerar atomkärnans positiva laddning (Ze), alltid exakt lika stor som den kärnan omgivande elektronmassans laddning. Atomkärnan enligt TNED beskrivs och härleds utförligt från Planckringen.

GENOM DEN MATEMATISKA FYSIKEN TILL TEORIN FÖR ATOMKÄRNANS HÄRLEDNING

finns bara ett, endast ett, och inget annat än bara ett enda unikt praktiskt sätt på vilket atomkärnan kan upplösas fullständigt och idealt i divergensenergin E=mc² — DET som alla energiingenjörer har som högsta önskedröm: energiutvinning ur materien utan restprodukter; Inga rester. Men det sättet är — och förblir — garanterat helt okänt av (och obegripligt för) modern akademi. Även fast härledningen kan presenteras i detalj på helt lättbegriplig (enkel) matematik, kommer den aldrig att tas upp av den moderna akademins lärosystem, därför att härledningens grunder söndersmular den moderna akademins grunder: föreställningen att intelligens bestäms av människor, inte av naturen. Kunskapen är, och förblir, fridsamhetsgrundad (se från sanningsbegreppet).

Atomkärnan är en strömstyrd komponent: Den innehåller en sin egen STRÖMFÄLLA.

Grundformen ges från TNED — garanterat fullkomligt helt okänd av modern akademi — enligt atom- och kärnfysikens två kungsekvationer

J_0K+3J_1K = 0 ............. impulsekvationen

F_BT+F_eZ = 0 .............. kraftekvationen (ström- och kemiekvationen)

förklaring

Eftersom atomkärnan är LÅST vid kraftekvationen enligt villkoret F_BT+F_eZ = 0, tvingas den reglera elektronflödet kärna-hölje via avkänningen av den magnetiska kraften i kärnbrunnen, F_BT; Eftersom atomen är förlustfri — den behöver ingen påfyllning för att fungera, summan av krafter, moment, spinn och laddningar i atomen är noll — innehåller den heller ingen elektrisk ledning av materiell natur (som alltid är resistivt och induktivt betingad); atomens (inre) är nollresistivt och nollinduktivt; förluster finns inte i atomen, som annars skulle kräva energipåfyllning för att hålla atomen vid liv; massan, laddningen och spinnet. Tillväxer F_BT (genom kärnbrunnen) som följd av en elektrongenomströmning (kemisk koppling, gnisturladdning) som är större än den som normalt kopplar till atomens egen yttre elektronmassa, tvingas kärnan, att av kraftekvationen F_BT+F_eZ=0, avdela motsvarande matchande elektronmassa så att balansen _iF_BT+_iF_e–_Z=0 bevaras. Ekvivalenter är ekvivalenter. Det finns ingen möjlighet för atomen-atomkärnan att smita från den fällan: Atomkärnan innefattar en strömfälla. Gränsen bestäms av atomens laddning, alltså atomens atomnummer (Z). Över denna gräns måste kärnan avdela elektronmassa från centralmassivet 1818e. Därmed är initieringen (men inte fullbordandet) av atomkärnans upplösning ett faktum.

Varje ENHET F_BT+F_eZ=0 uppträder som en sluten elektrisk isolator. Den betingas INTE av materiefysikens begrepp och besitter därför strömningsvägar som har inre nollresistans och inre nollinduktans.

gränsspänningen UG

EXPLICIT FÖR KEMISK KOPPLING, tillfället då två eller flera enheter förenas,

(F_BT+F_eZ )₁+(F_BT+F_eZ )₂+(F_BT+F_eZ )₃+…+(F_BT+F_eZ )_n = 0

finns en viss gränsspänning (U_G). Gränsspänningen bestäms av hur det enskilda elementet (t=e/n) ser respektive modercentraler enligt F_BT+F_eZ=0, INTE av hopen eller kvantat (e).

Märk denna detalj väl, eftersom den tydligen inte kan härledas av den moderna akademins lärosystem där begreppet om elektronmassans komponenter inte ens existerar. Se vidare detaljerat i Spektrum och Kvanttalen.

U_G = k_9T9(Q₁/r) = k(e_{1,602 t19}/rn₁₇₇₀₆₂) = Fr/Q₂=Fr/eZ

U_G = k(e/rn) .................. kemiska kopplingens absoluta gränsspänning

Den är i TNED bestämd (sämsta fallets parametrar) till 54µV för normala atomavstånd (runt 3Å) enligt fasta tillståndets fysik;

U_G = (9 T9 VM/C)(1,602 t19 C)/((177062)[3 Å]/2) .................. kemiska kopplingens absoluta gränsspänning

= 5,4286 t5 V

» 54 µV

DET KEMISKA FÖRENINGSTILLFÄLLET kopplar alltså en gemensam strömbana för e på inre nollresistans och nollinduktans vid U_G.

Vi återkommer senare till hur den teoretiska funktionen kan observeras genom praktiska experiment, men infogar redan här att området innefattar redan välkända fysikfenomen som emellertid är erkänt svårformulerade (citat följer) och läsaren bör INTE invaggas i föreställningen att ENS experimentet, hur enkelt det än kan verka, uppvisar någon enkel manual till en motsvarande rent teknisk fullskalig lösning: funktionen är ypperligt sammansatt, lika ypperligt svår att dissekera, och i princip omöjlig att upptäcka i naturen utom under vissa extremt sällsynta betingelser — eftersom funktionen i grunden kräver material som bara människan kan råvaruförädla ur naturens skafferi: goda elektriska ledare. Naturen har råvaran, men inte produkten (utom som sagt i vissa mycket sällsynta speciella fall). Ämnet är som klippt och skuret för människans kultur — i harmonisk samvaro med naturen.

ATOMKÄRNANS FULLSTÄNDIGA UPPLÖSNING | ATA

ATA

ATA

I verkningssättet ingår en atomens- eller atomkärnans transmissiva autonomi (ATA) enligt följande:

Atomens-Atomkärnans Transmissiva Autonomi

J0K+3(n)(J1K/n)	= 0 .............	toppringarna kan delas obegränsat
3^–1J0K+(n)(J1K/n)	= 0 .............	momentet kan delas med toppringarnas delning
(3n)^–1J0K+(J1K/n^2)	= 0 .............	ytterligare ekvivalent
J – mwr^2	= 0 .............	radien kan växa med avtagande massa, konstant toppspinn
FBT+FeZ	= 0 .............	bägge term. försv. med e-elem. upplösning, balansen bev.

Impuls- och kraftekvationerna innefattar ekvivalenter, se ovanstående uppställning, som tillsammans med den teoretiskt beskrivna strömgenomgången i kärnbrunnen kan åstadkomma en

REGLERING AV TOPPTOROIDENS RINGFORM. Se följande beskrivning nedan.

Genom positronringens starka Coulombiska attraktion på omgivande atomers elektronmassor, sker en stark ansamlig av elektroner mot kärnringen med tillhörande materieupplösning. Se vidare från ATA-karaktärisktiken.

beskrivning

Fysisk självreglering med hänsyn till kemisk koppling — ATA

Atomkärnans transmissiva autonomi

NORMALT SETT regleras den yttre elektronmassans elektriska kraftverkan (F_eZ) i balans med inverkan från atomkärnans magnetiska fält (F_BT) genom reglering, justering och avkänning via atomkärnans kärnbrunn i den slutna krets som elektronmassan (Ze) bildar med atomen eller molekylen. Det finns emellertid fall (elektrisk ljusbåge) då atomkärnorna HÄR ENLIGT TNED tvingas koppla motsvarande linjära stormolekyler (utförligt från Blixturladdningens fysik) med MAKROSKOPISKT CENTRALA ELEKTRONFLÖDEN katod-anod (samma som ljusbågsströmmen). I dessa fall påtvingas kärnbrunnarna e-flöden större än det normalt slutna Ze. För att kunna reglera balansen F_BT+F_eZ=0 för dessa fall måste atomen reducera sin elektronbesättning — Se kärnstrukturen med sammansättningen 1818e + 18e + k — i samtidig kärnexpansion enligt ekvivalenterna (ATA) i ovanstående uppställning.

Orsaken till toppringens växande radie ligger helt på den alltmer exponerade kärnytans positiva elektriska laddning som därmed ansvarar för ringens utvidgning proportionellt mot brunnströmmen. Kärnstrukturen enligt TNED beskrivs f.ö. utförligt i Planckringen.

Eftersom atomkärnans härledning inte ingår i den moderna akademins lärosystem och därmed heller inte uppfattningen om atomkärnans inneboende laddningsneutrala kropp (utförligt från Neutronen, se även i ATOMENS CENTRALT REGLERANDE DYNAMIK) förblir hela ämnesområdet fullständigt fördolt för den moderna vetenskapen.

Ingen känner till minsta prick i ämnet.

Jämför det ytterst enkla — men som tydligen aldrig föll den moderna akademins genier i smaken:

ATOMKÄRNAN FRÅN NEUTRONEN gömmer ett centralmassiv på 1818e med fördelningen ±909e plus en förbrukningsvara på 18e som sammanhänger med atomära massdefekten (samt en »smörjdel» på 2,624e, se Plancks Strukturkonstant ). Laddningssumman fördelas lika på ±e så att villkoret med atomens/atomkärnans nollmoment och nollkraft uppfylls: atomen kräver ingen påfyllning för att fungera. Atomkärnans fundamentalform (neutronen) uppvisar utåt laddningen noll.

NÄR NEUTRONEN SEDAN SÖNDERFALLER (se Neutronens sönderfall) uppvisar den exakt balans mellan den avdelade elektronmassan laddning (e^–) och den kvarvarande atomkärnans motsvarande positiva del (e⁺) i formen av protonladdningen — i fortsatt nollsumma. Sedan vidare på samma princip genom sammanslagning (fusion) av neutronindivider enligt KÄRNREAKTIONSLAGEN, analogt neutron-positronindivider eller analogt p-n-strukturer och som perfekt förklarar hela ämnets inneboende geofysik — enligt TNED.

Man känner inte ens till möjligheten att strömmen vid ljusbåge också är en utpräglad kärnström, en ström som går rakt genom atomkärnorna i strömvägen (se även nedan i Gnisturladdningens teori). Man lever (fortfarande) i den föreställningen att strömmen vid ljusbåge (och gnisturladdning) passerar mellan atomerna. Därmed garanteras att man också, enligt TNED, fortsättningsvis befinner sig långt ifrån en lösning till de uppmärksammande teoretiska svårigheterna. Citat följer längre fram.

Högre brunnström medför växande ringradie (r) med avtagande normal elektronbesättning (m), analogt högre KALLjonisationsgrad (J–mwr²=0). Kärnan differentieras alltmer i en isolerad positronstock (e⁺) med allt växande brunnström.

När brunnströmmen överstiger nukleära sönderfallets gränsströmstyrka

I_N = Q/T_N = A·918e/T_N

är positronstocken mättad. A anger kärnans masstal.

Därmed är gränsen nådd och restkärnan e⁺ expanderar enligt ovanstående övriga ATA-ekvivalenter.

Positronstocken annihileras tillsammans med omgivande atomers elektroner. Men experimentet är okänt i modern akademi.

Därmed är atomkärnan fullständigt upplöst.

T[N]: tillägg 30Mar2021

T_N = 317,11385 × 3 × 2πr₀/c₀ ¦ r₀ = 1,37 t15 M protonradien

= 2,732 t20 S

~ 3 t20 S .................... NUKLEÄRA ELEKTRON GENOMSTRÖMNINGENS TIDSEKVIVALENT

T(N) beskrivs utförligt med härledningar i NEGE (nukleära sönderfallets tidsfaktor ¦ Nukleära Elektron Genomströmnings Ekvivalenten).

Talet 317,11385 kommer från härledningen till NUKLIDKARTANS GRÄNSVÄRDE (förenklat talet 300 i NEGE).

För protonradien 1,37 t15 M (1,37 Fermi), se särskilt i KUBGRAFENS HISTORIA om ej redan bekant.

ATOMKÄRNANS FULLSTÄNDIGA UPPLÖSNING | ATA-karaktäristiken

ATA-KARAKTÄRISTIKEN

Atomkärnans speciella expansion med kärnringens växande, blottlagda positiva laddningsring och därmed attraktion av omgivande elektronmassor, se även från Inledningen

3D-modellen mitten ritad med hjälp av det äldre 3D-programmet Simply3D

Med initieringen av atomkärnans upplösning enligt TNED bildas positronringen via ATA (figuren ovan mitten). Hur sker parannihilationerna ±e? Uppenbarligen INTE så som parannihilationer sker mellan FRIA ±e. Detta är uppenbart därför att ATA-positronringen INTE kan expandera oändligt p.g.a. de magnetiskt sammanhållande ringkrafterna i ringkroppens (närmaste) underfraktal: ringspinnen garanterar en sammanhållande struktur OAVSETT moderringen bygger på omväxlande ±e eller e av endera slaget.

ATA-ringen representerar med sina A909e en enorm Coulombisk attraherare för alla omgivande e^–; Elektronmassorna drivs mot ATA-ringen på den fria elektronmassans enda vis (den normala cylindriska ordningen för fria elektronmassan, se även i Elektronens Bubbelkammarspår). Kärnringens magnetfält är emellertid också påtagligt mot de enskilda e-cylindrarna, vilket i näravståndet tvingar in dem i absolut synkronisering (se även illustrerat i Elektronförintelsen i CAT i Gammastrålningens uppkomst genom Blixturladdning).

Vid närkontakten avstannar naturligtvis attraktionsrörelsen abrupt och elektronmassan måste agera som den gör vid mötet med en ordinär fristående positronmassa (se annihilationsstrålningen):

Den häftiga inbromsningen vid kollisionsögonblicket [û=L(di/dt)] garanterar av princip en motsvarande »induktiv stoppstrålning» (konv. brehmsstralung eller s.k. bromsstrålning) med energin E=hf=hT^–1; Stoppstrålningen (och accelerationsstrålningen) underhålls nödvändigtvis stötvis genom att de attraherade elektronmassorna trycker på utifrån i takt med att massförintelsen fortlöper på insidan.

Generellt och grovt sett (olika källverk har något olika referenser) ges den lägre gränsen för termen gammastrålning vid ca f = T19 Hz (men observera att den gränsen ofta betraktas flytande mot den lägre röntgenstrålningens frekvenser). Det motsvarar E=6,626 t15 J eller drygt 41 KeV. För att nå den gränsen får T inte vara större än 1/f eller t19 S.

Med de ypperligt små dimensioner som sammanhänger med t-ringarna enligt TNED, synes den gränsen helt rimlig. Mera exakta beräkningar krävs dock för att säkerställa den referenten.

Em-strålningen från e^–-annihilationerna (i stötar mot kärnringen) blir därmed — och tydligen tvunget — planriktad utmed attraktionsriktningen för e^–, rakt in mot ATA-ringen.

Den em-strålningen går alltså, också tydligen i huvudsak, RAKT PÅ de cirkulärt omgivande atombesättningarnas elektronmassor som bör besitta exceptionellt hög elektrontäthet i kärnringens närhet, märk den detaljen väl — som därmed naturligtvis rycks med i resonansen från den häftiga plancirkulära gammaduschen, se även illustrationen nedan.

Totalt sett bör alltså CAT bilda kalljonisation (elektronrippning) med kraftig lokal gammaexcitation.

EMELLERTID: Inga som helst experimentella data är kända på den strålningstypen. Vi vet intet om typen av materialdämpning (strålabsorptionen), eller andra detaljer.

OM den plancirkulära gammastrålningen är effektivt absorberande i ringplanet som den verkar i — vilket eventuellt skulle kunna vara fallet med hålteorins energiräkning enligt TNED — finns i princip i varje fall inget enkelt sätt att mäta den gammastrålningen genom experimentet: ingenting kommer ut, inte ens utanför hålrandens cirkel. Det möjliga scenariot kan alltså skisseras enligt följande;

Det inre av hålbildningens förlopp förblir garanterat förseglat i kraft av den höga elektrontätheten i ringplanet och som effektivt täpper till gammaläckaget utåt;

3D-modellen ritad med hjälp av 3D-programmet Wings 3D

gammastrålningen dämpas ut internt effektivt via Comptoneffekten med resultat i motsvarande stark »elektronvärmebildning», analogt (mycket) lägre frekvenser utanför det bildade hålet.

Det finns ingen motsvarande materiefysik som kan beskriva ett sådant ämne.

En motsvarande utdämpningseffekt i luft via atmosfärisk blixturladdning med ATA/CAT är inte lika kritisk då atomavstånden i luft är ca 10 ggr större än i ett fast material, analogt tätheten (minst) 1000 gånger lägre — och därmed i princip dämpningen också (minst) 1000 gånger mindre.

— Finns det EVENTUELLT någon rapport i observationen av gammastrålning från blixturladdningar (TGF, Terrestrial Gamma ray Flashes, JordGammaFlashar) som gjorts och som tyder på att gammastrålningen skulle vara av typen dämpad (då den går genom särskilt täta molnlager typ vid ekvatorn innan den registreras av satelliten [RHESSI, nu 2008])?

— Ja. Det finns det. Men det är också bara antydningar (märk väl). Noteringen finns i källan @INTERNET nedan enligt

[http://scipp.ucsc.edu/seminars/experimental/davidsmith11_1_05.pdf] 1 November 2005,

{Gamma Rays from Lightning; [SCIPP, U. C. Santa Cruz]: David M. Smith, Brian Grefenstette, Jacob Stanley; [SFSU]: Liliana I. Lopez; [U. British Columbia]: Robert P. Lin, U. C. Berkeley, Christopher P. Barrington-Leigh}

”This suggests the TGFs we do see are highly diminished by atmospheric absorption”.

Min översättning:

Detta tyder på att de TGFs vi verkligen ser är högeligen försvagade av atmosfärisk absorption.

Det återstår emellertid en hel del klargöranden innan vi kan koppla ihop ovanstående antydan med den här framställningen.

Författarna ovan har SINA preferenser, och det finns här absolut ingenting som säger att dessa HAR någon som helst koppling till de HÄR antydda enligt TNED. Framtiden får utvisa mera ingående beskrivningar. Antydningen är emellertid och så här långt, intressant.

Se även mera om ATA-RINGENS ANNIHILATION i Resumé över Blixtbildningens Fysik enligt TNED.

ATOMKÄRNANS FULLSTÄNDIGA UPPLÖSNING |

CAT

Fenomengrunden bakom atomkärnans upplösning kommer här fortsättningsvis att benämnas CAT (Capacitive Transmission), Kapacitiv Transmission, termen förklaras i särskild artikel längre fram.

Anledningen

varför fenomenet undgått upptäckt:

tabell ljusbåge

gnisturladdning

ljusbåge och gnisturladdning

strömstyrkor

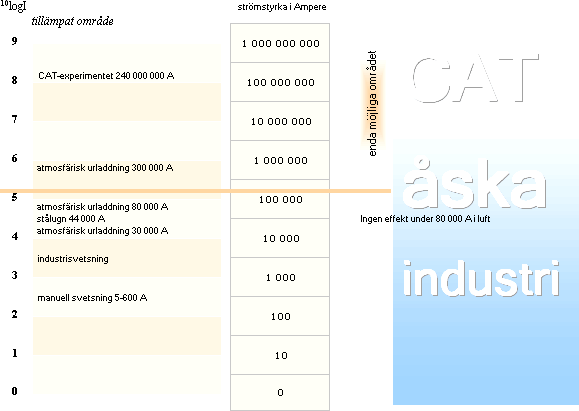
Tabellen visar hur CAT/ATA (frånsett vissa atmosfäriska urladdningar) göms effektivt bakom/ovan kommersiella och industriella tillämpningar.

Med undantag för vissa extremfall av atmosfäriska urladdningar (samt en mindre mängd potentiella atmosfäriska kandidater) finns inga egentliga naturliga förutsättningar för en fullständig utveckling enligt ATA — som innebär strömtryck över 80 000 Ampere med ämnesbasen Syre (O16) som exempel. Industriella tillämpningar (ljusbågsugnar i ståltillverkningen) ligger som mest runt 50 000 A.

De allra flesta laboratorieurladdningar omsätter alldeles för låga strömtryck: CAT träder inte i kraft — men väl ATA som innebär röntgenemissioner. Gränsen för luft ligger teoretiskt vid ca 78 000 A. Under den gränsen är det dött. Tillämpningar inom industrin (ljusbågsugn för stålsmältning) ligger som högst runt 50 000 A.

— Man har (alltså) helt enkelt inte (ännu) observerat ämnets dynamik.

gnisturladdningens teori

GNISTURLADDNINGENS ALLMÄNNA TEORI I JÄMFÖRELSE

Den främsta anledningen enligt TNED varför fenomenet ungått upptäckt är emellertid brist på teoretisk inblick:

GNISTURLADDNING I MODERN AKADEMI (MAC)

beskrivs-uppfattas som att elektronerna strömmar ner till marken PÅ SIDAN OM OCH MELLAN ATOMKÄRNORNA (ill.vä. ovan). Notera dock att just den meningsbeskrivningen här helt saknar citerande referenser: Vi VET ändå att det är så, därför att den andra delen för tillfället är ockuperad av TNED. Och den delen vet vi, helt säkert, är INTE representerad i modern vetenskap och akademi. Se särskilt klarläggande på den punkten i ATOMVIKTERNA: NEUTRONKVADRATEN med grundkärnradiernas koppling till atomvikterna och därmed TNED, inte MAC.

Förklaringen till mekanismen som åstadkommer överslaget är ännu okänd. Se även i citat.

GNISTURLADDNING ENLIGT TNED

se även särskilt utförligt om blixtbildningen i atmosfären i BLIXURLADDNINGENS FYSIK ENLIGT TNED

sker genom att elektroner som rivs från en kopplad centralstam av atomer strömmar ner till marken GENOM ATOMKÄRNORNA (ill.hö. ovan): blixtbanan kopplas av parallellspinnande atomkärnor på urladdningslinjen, som en ordinär kemisk koppling över längre avstånd, enligt kraftekvationen som formar den CENTRALA BLIXTSTAMMEN efter speciella villkor (mera utförligt nedan). Centralstammen döljs effektivt av plasmalokalen (minst 30 000 °K), bara inverkan från den yttre jonströmmen eller barkströmmen syns. Den initierande elektronrivningen, innan själva ljusurladdningen syns, åstadkommer obönhörligt gammastrålning om, och endast då, också atomkärnans geofysik påverkas (se ATA). En blixtbana på grovt sett 1 KM tar ca 1 mS för att utbildas med full elektrondrivning genom stammen innan ljusutvecklingen börjar. Den så starkt elektronrippade atomkärnstammen föranleder själva ljusfenomenet då omgivande elektroner söker rekombinera med atomkärnor nära stambanan.

Jämför:

ELEKTRONTÄTHETEN för Koppar är ca 8,4 T28 e/M³: elektrontätheten för atomkärnan är ENLIGT TNED minst

8,83775 T46 e/M³ (atomkärnans masstal gånger 909e dividerat med kärnvolymen).

förklaring

ELEKTRISKA LEDNINGENS TVÅ GRUNDFORMER

ELEKTRISKA LEDNINGENS TVÅ GRUNDFORMER

Se även från Teoretisk Grund

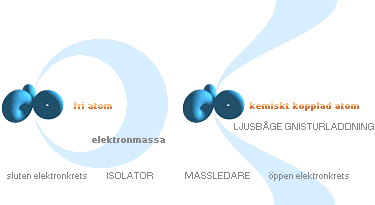
F_BT+F_eZ = 0 | (F_BT+F_eZ )₁+(F_BT+F_eZ )₂+(F_BT+F_eZ )₃+…+(F_BT+F_eZ )_n = 0

NOTERING. Kemiska kopplingar finns i flera (ytterst komplicerade) former. Den ovan illustrerade (höger) är den enklaste. Alla atomer i samma molekyl delar gemensamt på samma kollektiva elektronmassa.

ATOMENS KRAFTEKVATION F_BT+F_eZ=0 garanterar att i princip hur många atomer som helst kan förenas på en gemensam elektronmassa eftersom varje enskild atom i vilket fall summerar nollmoment. På samma grund som två eller flera atomer ingår kemisk förening, bildar (en eller) flera atomer en gemensam kedja (en plasmatisk centralstam) för att säkra elektrondraget vid ljusbåge och gnisturladdning. I modern akademi finns ingen uppfattning om atomkärnans geofysik (här främst den centrala kärnbrunnen) varför heller ingen uppfattning finns om fenomengrunden överhuvudtaget. Se även vidare i citat nedan.

I den ordinarie materieledningen är det materialatomernas gemensamma yttersta elektronmassor som bildar transportnätet för ledarens elektriska strömgenomgång. Därmed liknar materialledningen i princip samma typ som den enskilda (ovan vänster) atomens slutna elektronledningssystem. Se mera utförligt från grunden med atomkärnans härledning i Planckringen, om ej redan bekant.

citat

ÄMNETS OMVITTNADE SVÅRIGHETSGRAD

Se även sammanställda citat från allmänna uppfattningar i Blixturladdningen i Modern Akademi

”It is difficult to make accurate and meaningful measurements because of the high temperature and large current. Thus there is much that is not understood or substantiated.”

ENCYCLOPEDIA OF SCIENCE & TECHNOLOGY McGraw-Hill 1992, Band-2.s42sp2m Arc discharge

Min översättning:

Det är svårt att göra noggranna och meningsfulla mätningar på grund av den höga temperaturen och den stora strömmen. Det finns mycket som man inte har förstått eller substantierat.

”Although the arc type of discharge has very great commercial value, the mechanism of its operation is not very well understood.”

ENCYCLOPEDIA OF SCIENCE & TECHNOLOGY McGraw-Hill 1992, Band6 p84col.2m

Min översättning:

Fastän ljusbågens typ av urladdning har mycket stort kommersiellt värde, är inte mycket förstått av mekanismen bakom dess operation.

”Generally, the situation is so complicated that the theory can yield only qualitative predictions. Accordingly, most of the information concerning the various forms of gaseous conduction is empirical.”

ENCYCLOPEDIA OF SCIENCE & TECHNOLOGY McGraw-Hill 1992, Band6 p84col.1t

Min översättning:

Generellt är situationen så komplicerad att teorin bara kan åberopa kvalitativa förutsägelser. Följaktligen är det mesta rörande informationen av gasledningens olika former empirisk.

MÄTNINGAR KAN i generell mening INTE GENOMFÖRAS EXAKT — därför att materialet fragmenterar, fluktuerar, ändrar sammansättning och position från gång till annan på sätt som inte kan förutsägas.

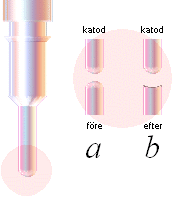
ANODEN FRAGMENTERAR. Vänster: Kontaktstift-elektrod av förtennad koppar över mässing, Stiftets längd ca 7 mM.

a: Kontaktstiftens utseende före urladdning.

b: Samma stiftändar efter ett antal urladdningar.

Anodelektroden urgröps märkbart. Efter ett antal urladdningar ser man tydligt hur anodelektroden gröpts ur efter katodelektrodens form.

ENDA TEORETISKA CHANSEN att få en fullständig bild av förloppet — under en specifik urladdning — är tydligen via en ytterst avancerad instrumentering som kan generera mycket snabba samplingssekvenser: fysiska data inom minst picosekunder, helst femtosekunder. Men inte heller den delen är »enkel» — eftersom ingen känner till hur mätobjektet ska anordnas på något meningsfullt sätt: allt brinner sönder; plasmadetaljerna (minst 30 000 °K) döljer och omöjliggör en fullständig inspektion.

Det är här (fortfarande 2008) inte ens känt OM sådan utrustning finns. OM den finns, är den i så fall emellertid INTE tillgänglig för personer utanför de allra dyraste och förnämligaste inrättningarna. Jag själv tillhör INTE det klientelet. Och så har det ju hetat genomgående i den naturvetenskapliga utvecklingen: nöden är uppfinningarnas moder.

experimentanordningen

Av den anledningen finns i den här presentationen i stort sett ingen annan instrumentellt fysikaliskt mätande observation att referera till än den digitala avläsningen av kondensatorspänningen efter varje urladdning, tillsammans med följande ytterst enkla experimentanordning med (inskannad kopia, se nedan, av) resultatet:

Experimentanordningen är ytterst enkel: ett kontaktstift (vänster, ca 7,5 mM långt) närmas ytan på en Aluminiumfolie (vanlig ugnsfolie går alldeles utmärkt). Metalldelarna är kopplade till en uppladdad kondensator (max 24 Volt matningsspänning, använd inte högre experimentmatningar, även denna enkla anordning ÄR äventyrlig, iaktta försiktighet, använd minst 50V kondensatormärkning). När kontakt sker, bildas omedelbart ett överslag; Ett alldeles runt hål i folien bildas, tillsammans med en liten intensivt lysande ljusbula av den avbildade typformen (även en mindre ljusbula kan ibland ses tillsammans med den större, men denna uppgift är ännu osäker). Från hålet syns också en viss mängd ljust orangea raka glödspår som bildas av heta sammankittade anodfragment (+). En enklare analys visar att glödspårens energibidrag är försumbart. Se vidare i huvudtexten.

Ljusbubblan i ovanstående illustration är delvis idealiserad och kan i praktiken i vissa fall uppvisa en märkbar oregelbundenhet (avvikelser i formen både utåt och inåt).

hålbildningen

Ovan: Ett av de mindre hålen (Ø ca 0,2 mM) nedan i den vänstra delen ungefärligt avbildat genom observation i 30 ggr förstoring. Notera att avbildningen ovan gjorts helt godtyckligt (med inspektion på ett utvalt hål i högen), och att inget som helst statistikt underlag finns för att påstå att den ovan avbildade formen är genomgående representativ (läsaren får här nöja sig med författarens obevisade påstående att »alla hålen ser i stort sett likadana ut» — i väntan på direkt fotografiskt avbildande mikroskop och som f.n. ligger helt utanför författarens ramar).

Nedan: En del av Aluminiumfolien som användes vid försöken.

Aluminiumfolien (tjocklek 0,017 mM) efter ett antal genomslagsurladdningar. De mindre hålen (uppmätta med 0,2 mM transformatortråd som lätt passerar igenom) ansluter till experimentkopplingen. De mindre hålen visar drygt 0,2mM i diameter, de ses i mikroskop som nära helt runda, som om de vore direkt urborrade (med kantsmältor) ur folien. Den inskannade bilden ger inte helt rättvisa åt hålens utseende också beroende på svårigheter att alls få fram någon läsbar inskannad bild.

Detaljerad beskrivning

Hålbeskrivningen enligt TNED, se även från Experimentkopplingen. Det inre TEORETISKA hålet Ø0,14mM i den 0,017mM tjocka Al-folien motsvarar grundformen för de atomer som joniseras lokalt i underskott av de 1,5 T16 kondensatorelektronerna med medeljonisationsgraden Al¹⁺. Den teoretiskt ENKLASTE energigrunden kräver (således i ekvivalenter) exakt motsvarande ekvivalent mängd positroner som frigörs ur urladdningsstammens (1,5 T16)/(27×918)=6 T11 atomkärnor och som tillsammans med motsvarande elektronmängd frigör energin 2453 J och därmed den idealt medeljoniserade mängden Al-atomer av graden Al¹⁺ som bildar det hålet. Hur elektronmängden rivs från nuklidagenterna beskrivs enligt TNED i ATA.

Effekten från den intensiva ±e-annihilationen emellertid inte bara river elektronerna i området utan bildar också en aktiv källa för atomär excitation; Den häftiga energiutvecklingen (2453 J) i den primära hålbildningen medför (tydligen för att förklara det praktiska större hålet, den ovan markerade extra ringytan) att också en lika stor mängd Al-atomer exciteras av strålningen från ±e-annihilationerna och därmed dras med i turbulensen som totalt ger de 3,2 T16 Al-atomer som bildar hela det uppmätta hålet på drygt Ø0,2mM. Flera typbeskrivningar i den här presentationen genomsöker andra förklarande alternativ, men (ännu) utan positivt resultat. Se särskilt från beskrivningen av försöken med Silverfolien. En mera noggrann genomgång av anordningens möjliga energidetaljer ges i ENERGIRÄKNINGEN.

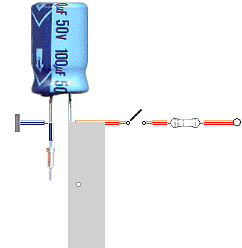
Se även EXPERIMENTKOPPLINGEN längre ner. Ovan visas experimentanordningens elektrolytkondensator (50V 100µF) med en remsa vanlig ugnsfolie, kopparledare och motstånd. Separat strömkälla med max 24V matningsspänning. Genom att kretsen kommer i elektriskt avbrott omedelbart då hålet bildas, kan kondensatorspänningen avläsas direkt efter varje urladdning. I medeltal urladdas kondensatorn till hälften, med vissa fluktuationer beroende på den manuella påtriggningen av förloppet. Den öppna switchen används efter varje urladdning för att fylla på kondensatorn. Experimentanordningens urladdning med gnistbildning har iakttagits ner till i varje fall 2 Volt matningsspänning (men rummet måste då vara fullständigt mörkt, gnistbildningen syns ypperligt svag). Teoretiskt kan enligt TNED urladdning ske ner till 54µV. I modern teori däremot, som baseras på aktiv jonisation, skulle för Aluminiumfallet absolut lägsta gränsen gå vid ca 6 Volts matningsspänning, se nedanstående redovisning.

OBSERVERADE GNISTURLADDNINGAR NER TILL 2V UTESLUTER JONISATIONSTEORIN

Enligt

@INTERNET Wikipedia Ionization energies of the elements 2007-03-09

krävs 577,5 KJ/mol = (577,5 J)(1,66033 t21) = 9,5884 t19 Joule för att frigöra Aluminiumatomens första elektron från moderatomen, eller i elektronvolt

(577,5 KJ/mol)(1,66033 t21 KG)/(1,602 t19 C) = 5,985272 eV;

OM hålet bildas på grund av att Aluminiummaterialets atomer exciteras på minst Al¹⁺ som grundval för atomernas Coulombiska repulsion, är det tydligt att absolut lägsta matningsspänningen för den med hålbildningen associerade gnistbildningen måste vara just 6 Volt; E=UQ. Inte mindre. Men gnistbildning på materialet Aluminium kan iakttas ända ner till (i varje fall) 2 Volts matningsspänning (i fullständigt mörklagt rum), enligt här genomförda observationer. Därmed är jonisationsteorin — som är den konventionellt mest populära, men också erkänt ofullständig — helt och hållet utesluten som grund för gnisturladdningen.

experimentkopplingen

EXPERIMENTKOPPLINGEN — se även hålbildningen

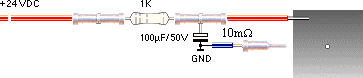Aluminiumfolie

Så länge kretsen inte bryts, strömmar normalt elektronmassor från katodstiftet (– vänster) till anodmaterialet (Aluminiumfolien höger).

För kopplingens funktionella resultat, se beskrivning i experimentanordningen.

Glödspårens energibidrag

GLÖDSPÅRENS ENERGIBIDRAG ÄR FÖRSUMBART

—————————————————————————————————————————————————————————————————

Se nyligen [DEC2012-Mar2013] tagna fotografier av speciellt aluminiumfolieurladdningarna i URLADDNINGSSERIERNA123.

Se även i IMPULSANALOGINkalkyl: beräkningarna med stöd av fotografierna visar att glödpartiklarna är partiklar i storleksordningen nanometer.

DIREKT OBSERVERADE GLÖDSPÅR (särskilt typiska) från experimentkopplingen visas nedan. Genom en separat uppsättning metallstänger som anodmaterial kan olika karaktäristiska glödspår detaljstuderas på enklaste sätt.

Längd ca 3 cM.

Knivskarpa spikraka typiska glödspår från experimentets gnisturladdningar. Efter direkt observation.

Glödspårens längd för Järn vid 24V matning 100µF 10mW ca 3-6 cM.

Anodmaterial överst till underst: Aluminium, Koppar, Järn.

Nyligen färdigställd anordning [Dec2012-Mar2013] för fotografisk dokumentation [AnordningenDec2012] [URLADDNINGSLÅDAN] ger motsvarande bilder i URLADDNINGSSERIERNA123 särskilt för Aluminium — se speciellt i KOLLIDERANDE NANOPARTIKLAR — samt för järnets del i SparkJärn och för kopparen i SparkKoppar.

Bakåtstudsen i luft efter en flera centimeter lång spikrak bana, Aluminium endast, förekommer inte alltid men kan observeras.

Al-spåret uppvisar aldrig delning (enligt hittills gjorda observationer).

Al-spåret slutar alltid tvärt (enligt hittills gjorda observationer), men kan dessförinnan uppvisa närmast otroliga banoriginal.

Delningen i 2 till 5-8 delspår (Järn, nästan alltid), i vissa fall med dubbelkronor (bilden), visar att glödpartiklarna delas upp på flera mindre.

Samma typ av glödspår men kortare ses från den roterande rivcylindern på en vanlig cigarettändare.

Motsvarande bilder i för järnets del i SparkJärn visar att ”dubbelkronan” förmodligen är en visuell sammanblandning mellan krondelningen från ibland flera närliggande enskilda spår. Test på olika järnlegeringar (tekniskt rent järn, silverstål/automatstål, verktygsstål) visar hittills ingen dubbeldelning på de hittills tagna fotografierna [Apr2013].

Kopparmaterialets glödspår är alltid raka (något kortare än i Järnfallet före dess ändring) med uttonad ände, uppvisar aldrig studs eller delning (enligt hittills gjorda observationer).

Ytterligare försök med andra material (mässing, silver, stål) visar att krondelningen är förbehållen järnet. För silver är f.ö. glödspåren praktiskt taget obefintliga. Tendens: glödspåren tillväxer med avtagande elektrisk ledningsförmåga (obevisat).

Glödspårens längd ligger grovt sett omkring 3 cM. Försök med olika material uppvisar olika typer av glödspår. Silver avviker från mängden genom att inte uppvisa några glödspår alls. Bilderna ovan är avbildningar baserade på en stor mängd naturligt perceptiva observationstillfällen för att därur syntetisera spårens karaktärer. Bilden av Järnspåren ansluter till vad som kan observeras från rivstiftet på en vanlig cigarettändare.

Hastighetskomponenten i glödspåren är för övrigt låg, vilket avslöjas med luftdraget från en vanlig hårtork; spåren böjer av märkbart.

Bevis — NeTOT

Antalet Aluminiumatomer i det bildade 0,2 mM-hålet med Aluminiumfoliets tjocklek 0,017mM är (N)

kalkylkort · urladdningshålets atomantal

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik6 Kalkylkort 1 — Urladdningshålets atomantal — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

N = m/Au = rV/Au = r[pr²h]/Au = 3,2 T16 stycken avrundat med A=27»U, r=2700 KG/M³ och u=1,66033 t27 KG.

A-värdet är här förenklat som det mera egentliga atomviktsvärdet (U) som skiljer sig marginellt (U för Al-27 är 26,9815389, differensen kommer att ligga i tredje decimalen).

För att hänga hela mängden hålatomer 3 T16 stycken på de grovt och som mest befintliga 100 glödspåren

(från ca 40 observerade baserat på delvis uppskattning med jämförande bildbaser)

med varje glödpartikels rörelsemängd ekvivalent med luftmolekylens rörelsemängd

(sämsta fallets beräkningar)

mv = 50u(500 M/S)_{LUFTMOLEKYLERNAS MEDELHASTIGHET} = 4,15 t23 NS

skulle glödpartikelns hastighet (v) i Aluminiumfallet (förgrovat 25u) bli

50u(500 M/S) = 25u×(3 T16/100)_{ATOMANTALET PER GLÖDSPÅR}×v ; vi löser ut v ;

v = 50u(500)/(25u×3 T14) = 25000/(7,5 T15) = 3,33 t12 M/S

För att den partikeln ska avverka den observerade sträckan på tre centimeter krävs tiden

T = d/v = 0,03/(3,33 t12) = 9 T9 sekunder = 285,19279 år

Även om antalet glödspår vore hundra gånger större, alltså 10 000, så tätt att begreppet glödspår vore utsuddat, skulle den observerade vägen tre centimeter för glödpartikeln kräva 2,85 år. I det praktiska fallet avverkas den på bråkdelar av sekunden, så snabbt att man inte ens hinner se någon rörelse, bara hela flashbilden av den totala rörelsebanan.

Därmed är det helt säkert, bortom varje tvivel, och förutsatt att inga dolda försmädliga sakfel ligger gömda som kan kullkasta hela den slutsatsen, att mängden glödspårsatomer — alltså de atomer som ingår i de större partiklar som bildar glödspåren — INTE har någon som helst signifikant betydelse för energiräkningen; Vi kan helt bortse ifrån deras bidrag.

Huvuddelen av atomerna lämnar tydligen materialet på annat sätt.

Den enklaste (första) förklaringen är, nämligen, att hålatomerna just lämnar området som ”stora (osynliga) glödande utsprättande fragment”. Hålets observerade utomordentliga jämnhet motsäger den förmodan — samt speciellt försöket med den mycket tunna silverfolien där inga glödspår alls förekom och som efterlämnade tydliga hängande svarta silver(di)oxidridåer i luften utanför det bildade hålet; bara det utesluter av princip glödspårsteorin.

Silverfolien

SÄRSKILDA FÖRSÖK MED SILVERFOLIE UNDERSTRYKER FUNKTIONEN

Ett fast material som utsätts för ultraviolett belysning (Solljus) och som då uppvisar elektronemission, uppvisar ingalunda någon samtidig tendens att upplösa sig (förångas) för att ingå kemisk förening med den omgivande luften. De exciterade materialatomerna stannar kvar i materialet. För att få ut dem i luften — en och en, motsvarande (som vi har förstått saken) experimentets hålbildning — krävs betydligt mera energi. Försöken med Silverfolien som anodmaterial, och som ger en direkt visuell bekräftelse på att hålatomerna förenas kemiskt per med luftens molekyler (de svarta hängande draperierna i luften alldeles utanför det stora bildade hålet efter urladdningen), ger det tveklöst säkraste experimentella belägget för att hålatomerna just avges på grunden PER atom, inte i grupper. Hålatomerna avges alltså analogt med grund i en medeljonisation för hela hålgruppens atomer på X¹⁺. Som emellertid konstateras i energiräkningen med en homogen energifördelning per atom förutsatt, räcker inte jonisationsenergin som sådan, inte ens på långa vägar, för att få ut hålatomerna ur materialet. Se även i kondensatorenergin.

Beskrivning

SILVERURLADDNINGEN ger en praktiskt taget glödspårsfri direkt omvandling från fasta gitterbundna silveratomer till kemiskt luftförenade dito.

Ett 1µM tunt metallskikt av Silver (17 ggr tunnare än Aluminiumfolien i experimenten) uppvisar inga observerade glödspår vid urladdningen. Efter urladdningen, syns tjocka hängande svagt böljande band eller ridåer, uppenbarligen av metallens oxid i luften strax utanför folien.

Den tunna Silverfolien (Bladsilver 1µM) är generellt olämpligt som experimentellt anodmaterial (i en öppen laboratoriemiljö av flera skäl, inte enbart den obehagliga [giftiga] silveroxiden); minsta luftrörelse får den extremt tunna folien att bölja och därmed åstadkomma dubbel och tripelpulser istället för en enda.

PRAKTISKT TAGET HELA HÅLMATERIALET INGÅR KEMISK FÖRENING MED OMGIVANDE LUFT

Iakttag därför särskild varsamhet vid experimenten med metallerna: tungmetaller i höga koncentrationer i människokroppen klassificeras som gift.

Glödspåren som fenomen är som redan omnämnts praktiskt taget obefintliga i fallet Silver: det syns inga glödspår. Efter urladdningen med Silverfoliet som anod uppträder emellertid tydliga svarta hängande långa draperier av silveroxid (eller möjligen silvernitrat) just intill folien och som mycket långsamt driver iväg (observationerna beror av aktuell luftcirkulation, samt urladdningsenergin). Förekomsten visar tydligen att silveratomerna, samtliga som avgick ur det stora uppkomna hålet, ingår kemisk förening med luftens atomer — de tydligt synliga långa, lodrätt hängande ridåerna och långsamt böljande slöjorna.

Men för att kunna ingå i kemiska reaktioner — enstaka atomer som förenas till flera — måste silveratomerna berövas elektronmassa (eller för den delen, påföras elektronmassa). Enda möjliga sättet att genomföra en sådan påverkan med början inifrån materialet är uppenbarligen följande:

att varje ENSKILD atom i princip påverkas av en motsvarande elektronberövande (joniserande) effekt.

Silveratomernas kemiska förening med luften ger alltså en ypperligt stark indikation som pekar på att den nödvändiga elektronberövande jonisationseffekten är en fälteffekt: elektronberövningen bildas eller översveper området — PER atom.

Därmed gynnas hela den detaljerade förklaringen enligt TNED, inkluderat den exakta energiräkningen (se närmast nedan):

exakt energiräkning

EXAKT ENERGIRÄKNING | Se även Energiräkningen i Syntes — räkningen i syntes med tillhörande kalkylkort

Hålbildningen enligt TNED

inledning

Se Experimentkopplingen för kretsdata.

ENKEL ENERGIRÄKNING VISAR ATT VARKEN KONDENSATORNS ENERGI ELLER ENS JONISATIONSENERGIN Al¹⁺ RÄCKER FÖR ATT FÖRKLARA HÅLBILDNINGEN

HÅLDIAMETER 0,2 mM

ANTAL Al-ATOMER 3,2 T16

Med uppfattningen om en jämn absolut homogen energifördelning i materialet per atom, frigörs det bildade drygt Ø0,2mM-hålet i den 0,017 mM tunna Aluminiumfolien genom att hålatomerna lämnar lokalen PER individ. Inte i grupp (frånsett smärre avvikelser). Resultat: Al-atomerna ingår kemisk förening med luftmolekylerna (se även Silverfolien) — och antar därmed deras medelavstånd.

Energin som krävs för denna process återfaller — tydligen — på Al-atomens ekvivalenta (kubiska) volymära rumsuppfyllande expansion; Från Al-metallens medelavstånd (2,55 Å) till luftens (30 Å). För att förklara hålets uppkomst måste processenergin i vart fall ombesörja Al-atomens medelmässiga xyz-förflyttning enligt den förutsättningen;

I jämförelsen är massorna för Al-atomen (27u) och luftmedelmolekylen ([2×16_SYRE+2×14_KVÄVE]/2=30u) grovt sett lika stora; Rörelsemängden (mv) som den medelmässiga Al-atomen minst måste utveckla för att expandera sin volym till luftmolekylens ska (minst) vara lika många gånger större än luftmolekylens rörelsemängd som förhållandet mellan volymerna Al-luft anger;

Al-atomen måste förflyttas, och energin för detta måste förklaras (basuppgifterna nedan från allmän skolboks- och facklitteratur):

beräkningar

ALUMINIUM (ill. vä.) har kubiska atommedelavståndet ca 2,55 Å.

LUFTMOLEKYLERNAS MEDELAVSTÅND (ill. hö.) är ca 30 Å;

LUFTMOLEKYLERNAS MEDELHASTIGHET är ca 500 M/S (vid 20 °C)

LUFTMOLEKYLERNAS MEDELFRIVÄG är ca 100 nM (vid 20 °C)

LUFTMOLEKYLEN KOLLIDERAR ca en gång per 200 pS

Tillgänglig kondensatorenergi 0,0216 J = mv²/2

Eftersom atommassorna Al-luft grovt sett är lika, blir motsvarande relationstal enbart beroende av hastighetskomponenten (v) enligt villkoret

(v_Al/v_LUFT)_min = _xyz(30/2,55)³

= 1628,3329

Den tillgängliga kondensatorenergin på E_CAP=0,0216 J ger max v per medelatom för Ø0,2mM-hålets totalt 3,2 T16 Al-atomer enligt

v_max = Ö 2E_CAP/(27u)(3,2 T16) = 5487,6675 M/S från E_CAP=mv²/2;

Men det är bara

(5488)/(500)

=10,976

eller nära 11 gånger luftmolekylernas medelhastighet:

Villkoret var att den siffran skulle vara minst 1628, enligt ovannämnda förutsättningar.

Energin från kondensatorn är alltså — för att kunna förklara den process som realiserar Al-atomerna snabba expansion till luften från foliet, som det får förstås med ovannämnda förutsättningar — våldsamt mycket för liten.

Därmed är slutsatsen klar — under den ovannämnda förutsättningen med homogen energifördelning, och endast då (Det finns här inte något explicit experimentellt klarläggande bevis för »homogen energifördelning» [frånsett Silverfolien], men vi utgår ifrån det i fysiken generellt i alla elektriska sammanhang eftersom elektronmassorna delas lika mellan alla atomer — och också uppvisar samma beteenden mellan alla atomer): experimentanordningen producerar energi, tydligen. Mängden omsatt energi är, enligt experimentkopplingen, uppenbarligen i förhållande till den energi som är förknippad med kondensatorns urladdning dessutom också exceptionellt stor:

v_min = Ö 2E_HÅL/(27u)(3,2 T16) = (1628)(500) = 814 000 M/S;

E_HÅL = v_min²(27u)(3,2 T16)/2 = 475,2553 J

E_HÅL/E_CAP = (475)/(0,0216) = 21990,74 » 22 000 ggr

Hålets uppkomst kan, uppenbarligen, inte förklaras med mindre energi: Al-atomen måste förflyttas, och för det krävs ett arbete vars kraft någonstans måste tas ifrån.

Varifrån tas energin? Utom TNED är fenomenet helt mystiskt, fullständigt obegripligt.

TNED visar på grunderna: Den moderna vetenskapen har, tydligen, missat grundläggande aspekter på den elementära fysikens grunder; För att förklara fenomenet krävs vad modern vetenskap inte känner till (och aldrig brydde sig om att studera): massfysik. Inte materiefysik.

Materiefysiken är redan välkänd i moderna kvarter.

Massfysiken (TNED) ger en helt ny syn på materiens minsta beståndsdelar: atomkärnan MED elektronmassan. Energiräkningen stämmer exakt. Trots det är jag ändå INTE (helt) säker. Det krävs mera bevis. Vetenskap är vetenskap.

Editor2008III7.

huvudartikeln

ENERGIRÄKNINGEN ENLIGT TNED

kondensatorn initieras

ANSATSEN i strömrusningen från T=0 [I(T=0)=U₀e^–T/RC/R=U₀/R] från kondensatorns laddningsmängd

Q_IGN=Q₀=U₀C₀=0,0024 C med elektronmängden

N=U₀C₀/e_{1,602 t19}=Q₀/e=(0,0024)/e=1,49812 T16 @ 1,5 T16 elektroner driver genom tändtiden tIGN

[v_AirIGN=d_GAP/T_IGN=1000/0,001=1 T6 M/S ; T_IGN=d_GAP/v_AirIGN=10 pS] upp maximal strömstyrka

I_IGN=Q_IGN/T_IGN=240 000 000 Ampere som ingen materiell krets klarar (se Materiella strömgränsvärdet): Kondensatorns elektronmängd 1,5 T16 elektroner tvingas av ansatsens induktans att dras till kondensatorns anod, och enda tillgängliga källan för den elektronmängden ligger enligt TNED i ATOMKÄRNANS TRANSMISSIVA AUTONOMI (ATA), anodsidan; Atomkärnans 1818e-stock övergår från ATA till CAT på grund av att strömmen överskrider gränsvärdet

I_N = Q/T_N = A·918e/T_N och frigör, tillsammans med anodsidans e-mängd som kondensatorn kräver, en lika stor positronmängd 1,5 T16.

Positronmängden annihileras tillsammans med omgivande atomers elektroner med frigörandet av energin

Elight

E_out = (m®g)c² = (N_{1,5 T16} · 2m_e)c² = (Q₀/e · 2m_e)c² = 2453 J = E_LIGHT;

Rörelsemängden kräver den avgjort största energidelen

De 1,5 T16 Al¹⁺-rippade atomerna drivs ut från området som bildar det absolut minsta grundhålet med diametern

2r = 2Ö N_{1,5 T16}(A₂₇u_{1,66033 t27 KG}/phr_{2700 KG/M}3) = Ø

= 0,14mM avrundat. h anger Al-foliets tjocklek 0,017 mM; det praktiska hålet är typiskt drygt 0,2 mM, se vidare nedan

Grundhålets 1,5 T16 Al-atomer

RÖRELSEMÄNGDEN p=mv=FT=maT=m(v/T)T som utvecklas (idealt) av de 1,5 T16 Al¹⁺-rippade hålatomerna under den aktiva energibildningstiden

T_IGN =10 pS, genom underskottet på 1e per atom, beror av den lokala Coulombiska kraftverkan

F =k_9T9VM/C(e/d₀)² genom det lokala atommedelavståndet

d₀ = [U_Alu/r]^1/3=[(26,981539)(1,66033 t27)/2700]^1/3=2,55054 t10 M

» 2,55 Å

enligt ekvivalenterna för rörelsemängdens kvadrat som ger rörelseenergin per medelatom (m) eller

rörelsemängdens energiekvivalent

(FT)² = (mv)²; (FT)²/m = mv²; (FT)²/2m = mv²/2 = E_kin = [kT(Q/d₀)²]²/2m ;

E_kin = [k_9T9T_1t11(Q_{1,602 t19}/d_{0 2,55 t10})²]²/2m_{27(1,66033 t27)} = 1,40729 t14 J;

Totalt för Ø0,14mM-hålets N_e=1,5 T16 hålatomer med E_kin(1,5 T16)=E_kinAl därmed rörelseenergin avrundat

E_kinAl » 210 J

Större T-värde ger högre E-värde.

Jämför minsta jonisationsenergin (Vridande momentets Absolut minsta separationsenergi). ARBETET (E=Fd) som utbildas med uppkomsten av kraftverkan (F=k_{9T9 VM/C}Q²/d²) mellan atomerna över gitteravståndet (d), analogt gitterenergin (eng. lattice energy) motsvarar en absolut statisk fältrelaterad (icke tidsberoende) rörelseenergi mv²/2 vid fullt utbildad kraft; Med minsta möjliga Coulombrepulsion via lägsta möjliga jongrad — Al¹⁺, som ger Q= 1e = 1,602 t19 C via d=2,55Å) — ges
E_JON = Fd = k_{9T9 VM/C}Q²/d = 9,05789 t19 J. Division med 1/(1000)(1000)(u=1,66033 t27 KG)=1/(1,66033 t21 KG) ger gängse enhetsstandard i KJ/mol med värdet
E_JON = 545,54757 KJ/mol eller 5,6541136 eV.
För Ø0,2 mM-hålets 3,2 T16 Al-atomer i den 0,017 mM tunna Al-folien ges E_JON(3,2 T16) = 0,0289852 J.
Krafttiden för E_JON fås ur ovanstående samband från rörelsemängdens ekvivalenter (se även sammanställning längre ner) enligt
T = (2m_27uE_JON)^1/2/k(Q/d₀)² = 8,02269 t14 S » 80 fS
I den inledande jämförelsen med luftmolekylernas rörelsemängd kontra den frigjorda Al-atomens, visades tydligt att storleksordningen i ovanstående E_JON-värde inte på långa vägar räcker till för att föra Al-atomerna ut till luftmolekylernas medelavstånd. Kraftbildningens tidsfaktor (se även efterföljande resultatredovisning i kalkylkortet) måste minst vara i storleksordningen tiotal pS med motsvarande rörelseenergin drygt 450 J för att få en förening med luften av de 3,2 T16 Al-atomerna.
Jonisationsenergin Al¹⁺ är alltså alldeles för liten i sig för att kunna förklara fenomenet.

Resterande Hålmassa på 1,7 T16 Al-atomer

RESTERANDE ENERGIMÄNGD (2453 – 210 = 2243)J åtgår (tydligen) för att bilda rörelsemängden till det resterande hålmaterialets (3,2–1,5=1,7)T16 atomer samt energin för ljusbulan, glödspåren, ljudknallen och den aktuella men i sammanhanget obetydliga jonisationsenergin (1816,7 KJ/mol eller 18,828473 eV per Al²⁺, se vidare nedan);

Med bibehållen energitid T_IGN=10 pS kan totala ekvivalenta medeljonisationsgraden bestämmas

idealt ur E_LIGHT=E_kinAl=2453 J från hela hålets atommängd N_eTOT=3,2 T16 enligt

Q² = (2m_27uE_LIGHT/N_eTOT)^1/2/kT(1/d₀)² ;

Medeljonisationsgraden (Q/e) blir

Q/e = 1,5284892 ....................... ekvivalenta effektiva jonisationsgraden för hela hålets medelatom

vilket grovt sett ger att de extra 1,7 T16 Aluminiumatomerna jonexciteras på i medeltal runt 2e: (e+2e)/2=1,5e.

Jonisationsenergin för Aluminium för att avlägsna den andra elektronen (Al²⁺) är enligt tabellreferesen lika med 1816,7 KJ/mol eller atomärt 3,01632 t18 J (18,828473 eV); För de återstående 1,7 T16 atomerna betyder det den i sammanhanget helt försumbara energin 0,0512774 J.

Därmed är det praktiskt uppmätta hålet på ca 0,2 mM fullständigt förklarat enligt TNED.

sambanden i syntes

Energisambanden i sammanställning med tillhörande kalkylkort

RÖRELSEMÄNGDEN (mv) GRUNDLÄGGER ENERGIRÄKNINGEN:

E_kinAl = m_27uv²/2 ;

v = k_{9T9 VM/C}T(Q/d₀)²/m ; från F=ma=mv/T=k_9T9(Q/d₀)² som ger v=kT(Q/d₀)²/m ;

E_kinAl = m_27u[kT(Q/d₀)²/m]²/2 = [kT(Q/d₀)²]²/2m_27u ;

T = (2m_27uE_kinAl)^1/2/k(Q/d₀)² ; Q² = (2m_27uE_kinAl)^1/2/kT(1/d₀)²

E_kinAl = [k_{9T9 VM/C}T_{10 pS}(e/d₀)²]²/2m_27u

FT=maT=m(v/T)T=mv; (FT)²=(mv)²; (FT)²/m=mv²; (FT)²/2m=mv²/2=E_kin;

E_kinAl(1,5 T16) = 210 J avrundat för Ø0,14mM-hålet

kalkylkort

Kapacitiva Transmissionens Energiräkning

ENERGIRÄKNINGEN ENLIGT CAT

kalkylkort · kinetiska energiräkningen Ekin · Aluminium · kretsresistans 10 mW

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik6 Kalkylkort 2 — Kinetiska energiräkningen — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

resultat

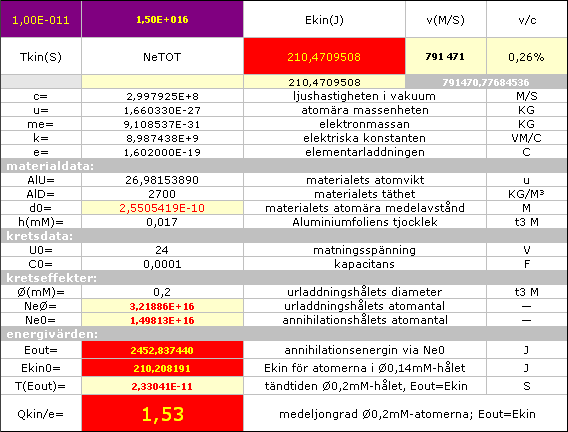
RESULTAT:

Experimentkopplingen producerar

E_LIGHT/E_CAP = 2453/0,0216 = 113 564,81

gånger den energi som krävs för att starta förloppet

— eller mera allmänt:

Om som i experimentfallet kretsresistansen är låg — i storleksordningen max tiotal mW; för låga kretsresistanser (R₀) gäller 1=e^–R0^/k — gäller tydligen från

E_CAP = E₀–E₁ = 3(U₀ – U₀/2)²C₀/2 = 3(U₀/2)²C₀/2 = (3/8)U₀²C₀ = 0,0216 J

förhållandet

E_LIGHT/E_CAP = 2m_ec²(U₀C₀/e)/(3/8)U₀²C₀ = (16/3)m_ec²/U₀e = U₀^–1(16/3)m_ec²/e = U₀^–1(16/3)(511007,77) ;

Energivinsten blir alltså i rånettoförhållandet mellan energi som åtgår för att underhålla/trigga processen och energi som utvinns

= U₀^–1(2 725 374,7 V)

Teoretiskt minsta U₀-värdet enligt TNED är 54µV. U₀ i experimentkopplingen är 24 V, men har testats manuellt med observerade urladdningsgnistor i mörklagt rum ner till 2V. Test på lägre spänningar visar knappast gnistspår och kräver därför (tydligen) en mera avancerad utrustning för reguljär detektering.

MINST RUNT HÄLFTEN AV HÅLATOMERNA ingår alltså enligt TNED kemisk förening med den omgivande luften, den resterande delen bildar teoretiskt ett potentiellt (mycket finfördelat) metalliskt damm i området (rekombination efter excitationstidens upphörande).

Försök med urladdningar i vatten (Al-foliets undersida mot vattenytan, elektrodkontakten från luftsidan) bekräftar uppdelningen; efter många försök bildas en mindre mängd bottenslam av typen (mycket) finfördelat; Samtidigt med urladdningarna ökar vattnets elektriska ledningsförmåga märkbart, vilket förklaras av den del av det elektriskt ledande anodmaterialet som förenas kemiskt med vattenmolekylerna. Emellertid finns (här ännu) inga mera noggranna uppgifter på de relativa mängderna varför ändå en viss försiktighet bör iakttas för att undvika ev. förhastade slutsatser.

Sammanfattning — hålbildningens energiräkning

För att rörelsemängden (mv) ska räcka till för att driva de 3,2 T16 Al-atomerna ut ur Ø0,2mM-hålet, måste medelatomens initiella hastighet (v = Ö 2E/Uu) vara minst tusentalet gånger större (500 KM/S) än luftmolekylernas medelhastighet (ca 500 M/S) så att en vägsträcka på minst 1000(100 nM)= 0,1 mM motsvarande minst runt halva håldiametern garanteras för att få hålatomerna bort från hålområdet.

Jämför:

ABSOLUT LÄGSTA GRUNDENERGIN med förutsättningen Al¹⁺ mellan Al-atomerna separerade av medatomavståndet 2,55 Å i metallen är

E_min = k_{9 T9 VM/C}(e_{1,602 t19 C})²/d_{2,55 Å} × 3,2 T16 = 0,0289852 J

Men denna ger (från E=mv² med v=Ö E/m) bara max utgångshastigheten

v_max = Ö 2E_min/(27u)(3,2 T16) = 6356,954 M/S;

Totala väglängden i luften skulle bara bli grovt sett (100 nM)(6357 M/S)/(500 M/S)=0,0012714 mM.

Rörelseenergin som ges enligt TNED ger en betydligt bättre beskrivning av det praktiska fallet via T_IGN=10 pS enligt sambandet

E_kinAl = [k_{9T9 VM/C}T_{10 pS}(e/d₀)²]²/2m_27u

Energivärdet blir drygt 475 J för samtliga 3,2 T16 Al-atomer med ett

v_max = 790 KM/S

som ger väglängden d(xyz)=0,158 mM.

Värdet d(xyz) motsvarar då antalet medelväglängder i luft (100 nM) på 1580, motsvarande (d_LUFT/2,55)³ som ger d_LUFT=29,7.

Se mera utförligt från energiräkningen.

energigrunder

LQ²/t²=E=konstant

Induktansen reduceras i CAT med utvecklingen av Q från atomkärnan: LQ²/t²=E=konstant

Matematiken är densamma som för K-cellens allmänna värmefysik

Försvinner Q via (m®g) måste makroinduktansen öka (massan överförs masslöst på andra massystem genom värme och ljus);

Utvecklas Q ur atomkärnans normalt dolda Q-bank (centralmassivet 1818e), måste makroinduktansen på något ställe istället minska. Produkten bevaras konstant enligt energilagen.

Induktansen förknippad med kondensatorns initierande strömrusning från T=0 och vilken ledningsväg praktiskt omedelbart bränns av, REDUCERAS av Q-bildningen i urladdningsstammen ENLIGT ENERGILAGEN. Således: inga som helst matematisk-fysikaliska konstigheter. Helt (hutlöst) enkla grejer.

utförlig beskrivning

Energiräkningen som bekräftar hålbildningen — se Experimentkopplingen separat

Vid T=0 uppkommer plötslig nollresistans i kretsens överslagspunkt, förorsakad av kemisk koppling mellan elektrodändarna, atomens fysik ENLIGT TNED.

Elektrodspänningen bildar en kortvarig kemisk förening mellan atomerna i elektrodändarna.

Strömöppningen vid T=0 initierar en MOMENTAN TOPPSTRÖM

I(T=0)=U₀e^–T/RC/R=U₀/R

som beror av kondensatorns elektronmängd i Q

N=U₀C₀/e_{1,602 t19}=Q₀/e=(0,0024)/e=1,49812 T16 @ 1,5 T16

och kretsens totala resistans (10 mW). Är resistansen liten, som i experimentfallet (grovt ca 10mW) gäller Q=UC.

Se även separat härledning i Kondensatorkretsens varierande resistans.

HELA Q=UC=0,0024 Coulomb sätts alltså — momentant — i rörelse vid T=0.

Men motståndet i överslagspunktens atomkopplande blixtbana (d=d_GAP= 0,01 mM uppskattat) är noll, atomens kemi och fysik ENLIGT TNED, vilket medför att hela Q-mängden måste dras över eller igenom d — därför att totala kretsinduktansen L kräver det; Energin i toppströmmen I(T=0), via nollresistansen i d, MÅSTE uttömma sig genom d, analogt kondensatorns egen garanterade urladdning på full Q-pott — i det kondensatorkretsinduktiva motståndets försorg;

Induktansen, den elektriska strömstyrkans tröghet, styr dynamiken. Är kretsresistansen högre, blir Q-potten motsvarande mindre. Jämför droppen som just BÖRJAT falla: initieringen (induktansen, trögheten) kan omöjligen elimineras. Se även separat härledning i Kondensatorkretsens varierande resistans.

grunddata, experimentkopplingens fall

T_IGNITION — tiden för gnistlinjens utbildning, se vidare i T_IGN

v_AirIGN=d_GAP/T_IGN=1000/0,001=1 T6 M/S ; T_IGN=d_GAP/v_AirIGN

Från atmosfäriska kända mätningar på en 1KM lång blixtbana som bildas på ca 1/1000 sekund.

d_GAP = 0,01 mM ;

T_IGN = (t5 M)/(T6 M/S) = t11 S

villkor

I_IGN = Q_{0,0024 C}/T_{IGN = t11 S} = 2,4 T8 Ampere ................ = U₀e^–T/RC/R=U₀/R, T=0

I_{N Aluminium} = A_{Al 27}·918e/T_{N=3 t20 S} = 1,32357 T5 Ampere ............... I_IGN>I_N: CAT gäller

MEN ENDA TILLGÄNGLIGA KÄLLAN för DEN nollresistiva taxibanan är ENLIGT TNED atomkärnan:

MED I_IGN>I_N måste de N=1,5 T16 elektronerna i Q, kondensatorns egenurladdning, som dras över nollresistansen d tas från områdets atomkärnor ±e=0 — HUR VI ÄN RESONERAR I ÖVRIGT. Om alltså N elektroner –e tas för att säkra kondensatorns egenurladdning, I_IGN>I_N, måste I ENERGIMÄSSIG KONSEKVENS motsvarande N positroner +e friläggas: ±e=0.

Den frigjorda positronstocken +e annihileras tillsammans med omgivande atomers N=1,5 T16 stycken elektroner, vilket ger energin

E_out = (m®g)c² = (N_{1,5 T16} · 2m_e)c² = (Q₀/e · 2m_e)c² = 2453 J = E_LIGHT

Mellan de e-rippade atomerna, medeljonisationsgrad av minst ordningen Al¹⁺, bildas häftig Coulombisk repulsion (F=ma) — samt extra joniserande energi på grund av strålningen från parannihilationerna;

Atomerna lämnar området, ingår kemisk förening med den omgivande luften, och kvarlämnar ett absolut minsta hål

2r = 2Ö N_{1,5 T16}(A₂₇u_{1,66033 t27 KG}/phr_{2700 KG/M}3) = Ø = 0,14 mM avrundat

[pr²h=V=m/r=NAu/r]

Det uppmätta hålet visar drygt 0,2 mM; den extra atommassan på ca 1,7 T16 atomer som skiljer grundhålet (Ø0,14mM) från det praktiskt uppmätta (Ø0,2mM) kan därmed bara förklaras av den extra strålenergi (2453–210=2243)J som KAN tillföras (1,7 T16)-delen från ±e-förintelsen.

Försök med lägre spänningar som ger mindre hål bekräftar det teoretiska sambandet.

Det praktiskt observerade hålets diameter, drygt 0,2 mM, bildas alltså genom E_LIGHT, inte genom E_CAP. h anger Al-foliets tjocklek 0,017 mM.

HÅLDIAMETERN drygt 0,2mM har f.ö. uppmätts genom en 0,2mM transformatortråd som lätt passerade hålen.

(Mättrådens diameter visar med mikrometer ca 0,22mM).

En mindre mängd av hålets atomer frigörs som glödpartiklar med låga hastigheter; Glödspåren böjs tydligt i luftströmmen från en vanlig hårtork.

Glödspårsbildningen varierar med material, störst för Aluminium och Järn, ringa för Koppar, obefintlig för Silver.

Separat analys visar att energin för glödspåren är försumbar och helt kan bortses ifrån i den allmänna energiräkningen.

Se även Ljusbulan och Silverfolien.

urladdningsförloppet

För atomkärnan ENLIGT TNED generellt om ej redan bekant, se Teoretisk Grund.

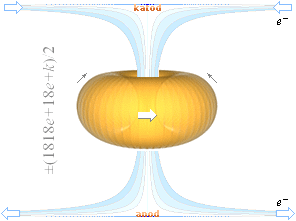
Situationen vid ljusbåge är enligt TNED av samma principiella typ som i kemisk koppling:

Kraftekvationen F_BT+F_eZ=0 garanterar att flera atomer i samma byggnad — även under fusion — kan dela på samma elektronmassa: summan av momenten och krafterna är noll för alla atomer. Atomen är förlustfri och kräver ingen påfyllning för att fungera. Atomens Transmissiva Autonomi garanterar att atomkärnan upprätthåller sin balansräkning per krafter och moment med bibehållen strömväg genom kärnbrunnen som också gäller för den enskilda atomen med sin enskilda uppsättning elektronmassor.

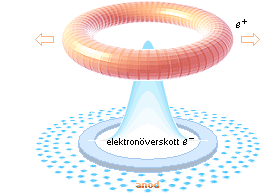
Situationen då Nukleära sönderfallets gränsströmstyrka (I_N) uppnås åstadkommer en brytning i det inre kärnflödet: det normala elektronflödet genom kärnbrunnen, som gäller vid normal funktion samt vid ljusbåge och även gnisturladdning, upphör då den enskilda atomkärnan i strömlänken inte längre kan förmedla mera elektroner till strömbanan. Därmed är atomkärnan eller PLANCKRINGEN fullständigt frikopplad i formen av en positronring (e⁺), lika med atomkärnans halva totala elektriska laddning och som normalt sett inte syns utåt utom via en bråkdel (Z). I_N-värdet (ca 80 000 A för luft) ligger emellertid så högt att fenomenformen knappast ens alls förekommer i naturen (tills människan kommer in på scenen med råvaruförädlingen och de elektriska komponenterna) — utom i ytterst sällsynta fall. Det är teorins grund enligt TNED.

Positronringen expanderar till en början starkt cirkulärt över anoden (Aluminiumfolien) i följd av sin positiva elektriska struktur, men hindras också i sin snabba expansion av den sammanhållande magnetismen i underringarna. Genom den starka Coulombiska attraktionen på omgivande elektronmassor, annihileras kärnringen sedan tillsammans med de lika starkt attraherande elektronmassorna, se vidare i ATA-karaktäristiken. Genom den så lokalt uppkomna häftiga kalljonisationen, som alltså blottlägger anodatomernas positivt laddade atomkärnor, drivs atomerna bort ifrån varandra, ut från en superhet centralpunkt, och bildar det observerade hålet i experimentkopplingen.

Kopplingsögonblicket — som betyder att massledning, analogt nollresistiv elektrisk ledning initierats — tvingar materialledningens kontaktställe katod-anod att brännas av; Materieledning är resistiv och bränns av på grund av (den höga) strömstyrkan (2,4 T8 A i experimentkopplingen, se även separat kalkylkort i Materiella Strömgränsvärdet). Resterande del av händelseförloppet läggs därmed i stort sett och praktiskt taget helt på anodsidan.

Vid T=0 uppkommer plötslig nollresistans i kretsens överslagspunkt, förorsakad av kemisk koppling mellan elektrodändarna, atomens fysik ENLIGT TNED.

Den enda komponent som kan förverkliga I_IGN=2,4 T8 A under 10pS med nollresistans och nollinduktans är den som summerar en struktur av ±e grundad på just nollresistans och nollinduktans, analogt

den komponent som är utan innehåll av inre beståndsdelar, som inte behöver någon påfyllande energi för att fungera, som har summa noll i krafter, spinn och moment och som därför är förlustfri: atomkärnan.

Bara atomkärnan besitter den höga elektrontätheten minst 8,84 T46 e/M³ som kan klara jobbet. EKVIVALENT dras därmed Q₀(e^–) direkt från elektrodatomernas atomkärnor, ner till anoden via en försumbar region av elektrodområdet (6 T11 Al-kärnor från [1,5 T16]/[27×918] eller grovt runt 1/24700 av hålmaterialets primära atomstock) och för att säkra kondensatorns urladdningsenergi E₀. Resterande frilagda, starkt expanderande positronstock Q₀(e⁺) tvingas annihilera med omgivande atomers elektronmassor. Därmed drivs de N elektrodatomerna ut från området av den lokalt påförda positiva Coulombrepulsionen (kalljonisationen), minst av graden X¹⁺.

Urladdningen U=U₀e^–T/RC av huvudkondensatorn (C₀) initieras vid T=0 vid kontakten mellan katodstiftet och anodytan;

MAX ström I=U₀e^–T/RC/R₀=U₀/R₀=2 400 Ampere gäller då.

Men »i samma ögonblick» tänds centralstammen med dess nollresistans;

En betydligt högre strömstyrka

i_IGN = Q₀/t_IGN= 240 000 000 A .................... Q_IGN frigörs

startar själva gnisturladdningen;

Men, som vi redan konstaterat, en sådan nollresistiv taxibana kan ingen materiell ledare ombesörja (240 miljoner Ampere under 10 pS); dess materiella koppling brinner av (garanterat avbruten från 14 nM ledardiameter, se Materiella Strömgränsvärdet) och påtvingar därmed kretsen ett reaktivt induktivt förlopp där den igångsatta men kretsbrutna laddningen någonstans måste tas ifrån: atomkärnans laddningssumma ±e=0 (utförligt från Neutronen). Det finns inget annat att välja på.

Den initierade induktansen flyttas över på nollresistiva massledande taxibanan.

Genom att atomkärnan kan frigöra laddning, kan lokala induktansen därmed reduceras och ekvationerna fås att stämma med urladdningsförloppets energisamband.

ELEKTRONTÄTHET Koppar ca 8,40 T28 e/M³.

ELEKTRONTÄTHET Atomkärnan minst 8,84 T46 e/M³.

Huvudkretsens initierade strömväg kommer i avbrott utan att någon elektronström har dragits explicit från katod till anod i C₀-kretsen.

URLADDNINGSVÄGEN för den frigjorda Q-stocken Q_IGN ligger nu beredd på anodsidan mot kretskondensatorn (C₀) — vilket för den strömvägens vidkommande innebär en halvering av totala kretsresistansen. Samtidigt (idealt) har bildningen av Q_IGN medfört en kapacitiv halvering.

Vi studerar hur kapacitanserna fungerar vid huvudkondensatorns urladdning.

tidsschema

TIDSSCHEMA FÖR GNISTURLADDNINGEN

— preliminära basdata

Kretsdata: 24V 100µF 10mW · anod, aluminiumfolie (vanlig ugnsfolie 0,017 mM), katod, kontaktstift (tennad Cu över mässing) ·

elektrodavstånd ca 0,01mM

tIGN 10pS

Tiden 10pS för själva gnisturladdningen är beräknad från uppgifter på konventionella (fotografiska) mätningar av den vanliga atmosfäriska blixturladdningen: en ca 1 KM lång blixtbana bildas på ca 1/1000 sekund [BKL II sp75m], vilket linjärt räknat ger 10pS på 0,01 mM.

0 10pS 1µS 100µS

| | | |

0 a b c

Överslaget initieras vid 0 med max strömstyrka enligt I=U₀e^–T/RC/R=U₀/R, T=0.

a. Efter 10pS — öppningen drar lokalt I=Q/T=240 000 000 Ampere — har Al-foliet bildat hål och kretsen är bruten. Intensiv ljusutveckling pågår.

b. Efter 1µS har 100µF-kondensatorn laddat ur.

c. Efter 0,1 mS har ljusutvecklingen från urladdningen med ljuskulan och glödspåren falnat bort (separat mätning med fotokomponent BPW22).

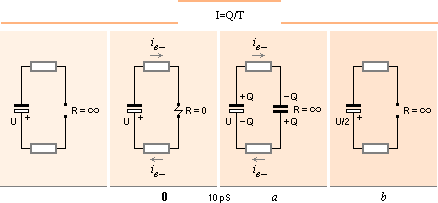
Förklaring

Vid 0 gäller elektrodisk kontakt med nollresistans R=0 — garanterat av atomkärnans matematiska fysik — vare sig strömvägen går i ett eller annat material. Vid a har från katodelektrodspetsen (idealt) dragits kondensatorns urladdningsmängd UC=Q. Det atomära område (anoden) som försörjer eller initierar Q-mängden 0,0024 Coulomb mäter (för Aluminium, U@27, r=2700) en kub med sidan (V=[m=Uu·6T11]/r)^1/3=2,15 tusendels millimeter, eller via folietjockleken 0,017mM ett hål med diametern 0,86 tusendels millimeter. Omärkligt. Avbrottet skapar en ny kapacitans, en elektrodisk kondensator (idealt med samma kapacitans som den givna), som tvingar den fasta elektroniska kondensatorn att urladda till hälften. Förloppet för den fasta kondensatorn kan då skrivas

U=Q/C ; C:=C/2 ; U=Q/(C/2)=2Q/C ; U/2=Q/C

med C:=C/2 vid a. Mätningarna visar också att kondensatorn i genomsnitt urladdas till hälften (med vissa fluktuationer beroende på experimentens manuella osäkerheter) .

Kondensatorns urladdning till a blir U₀–U_C=U₀–U₀e^–T/RC=24–23,99976=2,4 t4=0mV24: Kondensatorn hinner knappt ens reagera.

Den maximala strömstyrkan I=U/R från triggpunkten 0 med energin E=LI²/2 garanterar att kondensatorn måste urladda med referens till elektrodpunkterna där kretsen bröts, och därmed genom totala resistansen mellan dessa och kondensatorns materialkropp (här ca 10mW).

Bakomliggande resonemang, teori

· Kondensatorn i experimentkopplingen uppvisar en bruten strömväg (efter t_IGN=10pS, teoretiskt, instrument saknas här för direkt mätning)

· Kondensatorn visar att kondensatorspänningen stannar på 12V, vilket är halva matningsspänningen enligt Experimentkopplingen

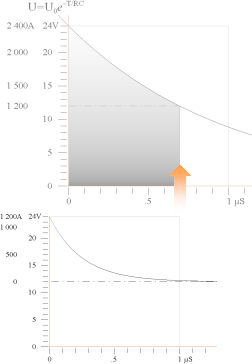
Övre kurvan antyder vad kretsen ställer upp i den praktiska kopplingen: urladdningen stannar plötsligt av mitt på. En sådan funktion finns — här veterligt — emellertid inte i fysiken, varför vi måste eftersöka en mera grundlig förklaring till urladdningsförloppet. Nämligen det som den undre kurvan visar: urladdningen avslutas mjukt.

DET ANTYDDA FÖRLOPPET I DEN NEDRE KURVAN innebär (uppenbarligen) att vi måste förutsätta följande, och som här inte direkt kan mätas:

urladdningen avslutas mjukt

därför att den är självutlämnad, inte reglerad av switch.

Vi (författarens referens) vet strängt taget inte det här genom någon samplad mätbild; vi utgår ifrån det därför att teorin kräver det;

kondensatorurladdningen från 24 till 12V genom 10mW tar (idealt) ca 0,7µS

— vilket vi förutsätter är en händelse EFTER hålbildningen. Hela tolkningen hänger på den förutsättningen.

Men för att kondensatorspänningen ska plana ut vid 12V — så som tydligen experimentkretsen uppför sig — måste induktansdelen som motsvarar den normala urladdningens avbrott, som i figuren ovan, helt elimineras. Det finns ingen annan elektrisk fysikalisk möjlighet för kondensatorspänningen att på annat sätt stanna mjukt och lugnt på halva matningen. Det är också precis vad energiräkningen ställer fram åt oss:

induktansargumentet

Enda sättet som stöds av ENERGILAGEN för att reducera en makroskopisk, materiell, induktans (L) är att öka den materiella laddningen.

Enligt ENERGILAGEN gäller nämligen (och som även påvisats i vid mening i K-cellens värmefysik)

LQ²/t² = E = konstant = LI²

Kondensatorns blotta, faktiska, urladdning MJUKT ner till nivån halva matningen — induktansens eliminering — är därmed i sig inte bara BEVISET utan även kriterium för ATT en laddningsmängd FAKTISKT frigörs och adderas till materiefysiken som tidigare INTE fanns uppackad där.

(Vi ser alltså, att hela energiförklaringen hänger ihop och är konsistent på alla punkter; Det finns egentligen inga frågetecken).

Vilket vill säga:

Urladdningsfenomenet kan INTE förklaras, beskrivas eller härledas ur materiefysiken.

Inte alls överhuvudtaget.

Massfysiken — TNED — klarar det. Men den ingår inte i modern vetenskap.

Det gör inte teorin till energiproblemets lösning heller. Tydligen.

händelsen

efter hålbildningen

Hålet bildas från mitten (vi förutsätter det) och utåt. Minsta början = HÅL betyder kretsavbrott.

HÄNDELSEN EFTER HÅLBILDNINGEN

— Hur kan hål bildas när kondensatorkretsen inte leder ström?

— Vi skulle, likväl, kunna vända på resonemanget och fråga så här: Hur SKULLE ett hål kunna bildas OM vi förutsätter ATT kondensatorkretsen leder ström? Försöket med Silverfolien har visat att kondensatorenergin i vilket fall inte räcker till för hålbildningen, räknat i jonisationsenergi per avdelad Aluminiumatom, själva sättet som hålet bildas på.

Eftersom vi ännu inte har tillgång till mätande instrument som kan visa förloppet, är vi hänvisade till resonemang.

— Det FINNS instrument, men herregud: hundra tusen kronor. Lägg av. Bara VISSA AVANCERADE fotodioder KAN kosta flera tusentals kronor. Det är, alltså och tydligen. bara RIKA PERSONER som FÅR.. Men även om vi håller oss till RELATIVT ENKLA EXPERIMENTANORDNINGAR (diskreta kopplingar med mindre dyra halvledare) är det fortfarande VISSA PROBLEM att få tag på kretsar: halvledarkomponenterna finns, ja — men inte här. Idel käppar i hjulet.

KAPACITANSEN (som kondensatorn ska laddas ur på från observerade 24V till 12V) bildas från e-massan Q_IGN från centralstammen. Det är teorin enligt TNED. Vi studerar sammanhanget i stort och sedan detaljerna.

— Varför kan man inte tänka sig att hålbildningen kommer efter urladdningen?

— Därför att efter urladdning — om vi med hålbildning tänker oss ett aktivt skede och inget efterklingande verksamhetseko — finns ingen energiomsättning; Energiomsättningen är noll efter urladdningen.

— Kom ihåg energin E=UQ=RIQ: är I noll finns ingen förutsättning för aktivitet. I, strömstyrka, måste under alla omständigheter vara större än noll för att kunna påvisa/påstå aktivitet. Därför är det helt säkert så att hålbildningen föregår eller existerar jämsides med urladdningen.

— Men i detta fall, experimentkopplingen, betyder hålbildningen också kretsbrott vilket komplicerar frågan ytterligare.

— Vi kan nämligen inte tänka oss att OM hålbildning och urladdning försiggår samtidigt den verksamheten fortsätter under HELA hålbildningen. Det är nämligen uppenbart att kretsen bryts i hålbildningens allra första skede — långt innan håldiametern 0,2mM drygt utbildats (se även illustrerat i Hålbildningen).

— Frågan om HÅLET är i detta fall en fråga om ELEKTRODAVSTÅND. Direktkontakt ger koppling, men varje (större) distans ger avbrott. Gränsformen i detta fall ligger i luftens överslagsspänning (idealt ca 25V/0,01mM). Varje avstånd mellan elektroderna större än 0,01mM betyder alltså avbrott i experimentkretsens fall. Eller sagt på sättet som innefattar hålbildningens geometri:

varje minsta öppning i anodmaterialet betyder omedelbart avbrott. Se även i Materiella Strömgränsvärdet.

Precis när katodstiftet (–) nuddar anodsidans Al-folie (+) sker urladdningen genom att materialen kommer i (kemiskt via spänningen, och) mekanisk kontakt med varandra. Hålet börjar bildas från den punkten — vilket samtidigt medför ett avbrott i den initierande kontaktpunkten och därmed totalt kretsavbrott i hela kondensatorkretsen:

kondensatorkretsen leder aldrig

— den bara initierar

Det är vad som tycks vara den stora hemligheten i teorin enligt TNED — och samtidigt den stora svårigheten i varje form av aktiv mätning.

I följd av kontakten katod-anod tiden tIGN, uppkommer avbrott då hålbildningen antar minsta möjliga skillnad från ingenting. Energin till hålbildningen tvingas följaktligen frammanas under den mycket korta tidrymden tIGN. Efter den är det, tydligen, kört: kretsen är bruten. Inget kommer fram. Men det här är (ännu enbart) teori, och inga direkta mätningar har (ännu) genomförts som kan säkra de här antydda resultaten — utom energiräkningen som sådan, och i den mån den är korrekt tolkad.

— Frågan ”HUR LÄNGE KAN DÅ hålet bildas SAMTIDIGT med urladdningen?” är därmed irrelevant för kondensatorkretsen del: Kondensatorkretsen leder aldrig. Den bara initierar.

— Det finns ingen möjlighet för någon materiell krets att dra I_IGN=Q_IGN/T_IGN=2,4 T8 A under T_IGN=10 picosekunder. Allt brinner av. Det betyder att kondensatorkretsen med SIN kretsresistans 10 mW visserligen KAN leda under max 10 pS med max 1200 A från 24 till 12V MEN att den möjligheten är obefintlig via de 240 miljonerna Ampere som ligger i drag på tIGN-sidan och därför BÖR befinna sig i avbrott i princip omedelbart från urladdningens första kopplingsögonblick.

Urladdningen sker DÄRMED inte på något som helst konventionellt sätt genom kondensatorkretsen som en vanlig sluten elektrisk kretskoppling. Den kretsen är, frånsett initieringen via de 10 pS, aldrig sluten. Spänningsfallet idealt under den tiden är f.ö. helt försumbart och har ingen betydelse för helheten:

U=U₀e^–T/RC = 23,99976 V.

— Hålet kan alltså inte bildas samtidigt med urladdningen utom under ANSATSEN i det initierande strömdraget, tiden 10 pS, då den centrala strömstammen öppnas. Därefter är helt enkelt varje materiell strömkrets avbränd. Se Materiella Strömgränsvärdet.

— Avbränningsfasen kräver att induktansen reduceras — vilket bara kan realiseras genom ökad laddning, E=LQ²/t²=konstant. Det är en strömmatematik som materiefysiken inte kan hantera — men som klaras galant av massfysiken. Och, som vi redan har sett enligt TNED, är massfysiken helt orepresenterad i modern vetenskap medan materiefysiken däremot är utomordentligt väl representerad.

Fyra argument

Fyra enkla argument visar att

varje konventionell föreställning om urladdningsfenomenet är dödfödd

Punkterna visar sammantaget att hålets uppkomst inte kan förklaras av konventionell materieledning. Det som krävs är massfysik (TNED). Men den ingår inte i modern vetenskap. Se från Planckringen.

Vi utgår ifrån att hålet bildas från centrum och utåt:

Högre kretsresistans ger mindre hål och en slutspänning längre upp mot matningsspänningen, enligt genomförda observationer.

Följande punkter ansluter till experimentkopplingen.

1. energin till hålbildningen inte CAP:en

· Hålbildningen visar att kondensatorkretsen bara leder initiellt vid T=0 enligt I=U₀e^–T/RC/R=U₀/R=2 400 A, T=t₀=0: Minsta hålbildning bryter kretsen vid katod-anodkopplingen. Energin till den vidare hålbildningen måste därför sökas utom kondensatorkretsens energiflöde. Med andra ord i hålmaterialet.

2. CAP-energin som sådan räcker inte för hålbildningen — inte ens på långa vägar

· Medelvärdet räknat per atom av materialmängden 3,2 T16 Al-atomer genom minsta möjliga jonisation Al¹⁺ ger genom kondensatorenergin 0,0216 J bara 11 av de drygt 1600 rörelsemängdsmultiplikander som krävs enligt den enkla energiräkningen för att omvandla Al-atomens kubiska metallbindningsvolym (2,55 Å)³ till luftens (30 Å)³; Kondensatorenergin som sådan på 0,0216 J räcker inte ens för att ge den elementära första Al¹⁺-jonisationen för Ø0,2 mM-hålets 3,2 T16 Al-atomer 0,029 J — energin till ljusbulan och det övriga fråntaget.
Men vi vet, dessutom, redan från FOTOELEKTRISKA EFFEKTEN att ENBART en jonisationsenergi typ Solljus som träffar en metallyta INTE förorsakar någon samtidigt förångning av metallens atomer så att metallytan börjar fragmentera — som den gör i vårt experimentfall. Vilket vill säga: ÄVEN MED jonisationsenergin som sådan (Al¹⁺) sker alls ingen hålbildning. Den energi som krävs för det är tydligen (betydligt) högre. Därmed är kondensatorenergin utagerad — helt!

3. CAP-systemet matchar inte hålet

· För att förklara det tydligt cirkulära hålets begynnande centrumbildning (här förutsatt) måste uppenbarligen en motsvarande betydligt högre central jonisationsspänning finnas än matningens 24 V: en centralt mycket hög (flera kilovolt, se illustrationen nedan) jonisation kan bryta upp hålbildningen och sedan bilda ett medelvärde minst Al¹⁺ taget för hela mängden. Men i experimentkopplingen finns ingen förutsättning för en sådan ordning.

Jonisationsenergin för samtliga Aluminiumatomens 14 elektronmassor är enligt tabellverk 257 923 KJ/mol eller

E=(257923 J)(1,66033 t21)/(1,602 t19 C) = 4,28237 t16 J = 2 673,1416 eV;

För hålbildningens symmetri är det mera relevant att utgå ifrån ett elektronunderskott motsvarande grafen ovan med största (14) i centrum och minsta (0) i periferin; genom successiv utjämning fördelas medelvärdet på Al¹⁺ i sluträkningen. Men några ”två kilovolts matningsspänning” finns inte i experimentanordningen.

4. jonisationsfenomenet inte primär orsak

· Jonisation med matningsspänningar under 3,98V (Cesium Z55, grundämnet med lägsta jonisationsenergin för yttersta atomelektronen) förekommer överhuvudtaget inte i fysiken. Alkalimetallerna uppvisar den lägsta jonisationspotentialen för frigörande av en elektron, runt 4-5 eV. Aluminium ligger runt 6 eV. Men urladdningar i experimentkopplingen har observerats i mörkt rum i varje fall ner till 2 volts matning (teoretiskt enligt TNED ner till 54 µV för fasta ämnen, sambandet E=UQ). Detta utesluter varje föreställning om jonisationsprocessen som primär förorsakande agent som sådan till urladdningsfenomenet.

Kondensatorenergin räcker inte

Kondensatorenergin räcker inte till hålet

HÅLDIAMETERN (se Hålbildningen) drygt 0,2mM har uppmätts på ett godtyckligt mindre antal hål genom en 0,2mM transformatortråd som lätt passerar hålen. (MÄTtrådens diameter visade i själva verket ca 0,22mM mätt med en mikrometer).

kondensatorns energi:

E=UQ=RIQ; dE/dI=RQ=RIT; dE=RITdI ............... E₀=RTI²/2=UQ/2=U²C/2=LI²/2

E=UQ; dE/dU=Q=UC; dE=UCdU .......................... E₀=U²C/2

E_CAP = E₀–E₁ = (C/2)(U₀² – U₁²)

Är U₁ halva U₀ vilket i experimentkopplingen förutsätter låg kretsresistans ges

lågresistiva kondensatorenergin

E_CAP = E₀–E₁ = 3(U₀ – U₁)²C/2 = (3/8)U₀²C

kondensatorns urladdning:

I=U₀e^–T/RC/R=U₀/R från T=0 .................................. full pedal från noll; E₀=LI²/2

Konventionell räkning på kondensatorspänningen från matningen 24 V till värdet efter hålbildningen 12 V ger kondensatorenergin 0,0216 J med experimentkopplingens komponenter.

Kondensatorns energi (räknat per atom) räcker inte som energikälla ens till hålatomernas jonisation Al¹⁺

jonisationsenergin

ENBART JONISATIONSENERGIN PER ATOM med jongrad lägst Al¹⁺ är enligt tabellreferens drygt

E_NAlJON = 6 eV = 9,612 t19 J per Al-atom

mera exakt E_NAlJON = 5,985272 eV = 9,5884 t19 J per Al-atom

Totalt för de 1,5 T16 Al-atomerna som bildar »grundhålet» 0,14mM krävs alltså en verklig ABSOLUT MINSTA jonisationsenergi som bildar förutsättningen för en Coulombisk repulsion enligt

E_AlJON = 9,588 t19 · 1,5 T16 = 0,01482 J

KONDENSATORENERGIN

E_CAP = 3(12 V)²(100µF)/2

= 0,0216 J

klarar DEN biten — men inte energin till ljusbulan + den resterande hålmängden;

3,2 T16 Al-atomer totalt för 0,2 mM-hålet; det fattas ca 53% atommängd; 1–(1,5 T16)/(3,2 T16)=0,53125;

Motsvarande E_AlJON för hela hålets 3,2 T16 Al-atomer skulle här bli

E_CAP = 9,5884 t19 · 3,2 T16

= 0,0306828 J

Det är dryga 1,42 ggr kondensatorenergin

— energin till ljusbulan frånsett (denna är av allt att döma inte helt obetydlig, men den är svårberäknad, se Ljusbulan).

ÄVEN MED JONISATIONSENERGIN SOM FAKTOR INBERÄKNAD (se vidare nedan) står det alltså klart att kondensatorenergin på 0,02 J INTE kan försörja HELA hålets enskilda Al¹⁺-medelvärde för jonisationsenergin på 0,03 J.

Detta resultat — grundat på den rena förmodan om energi PER atom — utesluter i sig att hålet uppkommer genom någon klassisk form av jonisationsprocess: Kondensatorenergin räcker inte ens till själva den Coulombiska förutsättningen. Förklaringen till hålet måste därför sökas på annat håll.

Utöver denna detalj framgår också i försöken med Silverfolien att ÄVEN sedan jonisationens Al¹⁺ realiserats för hela hålgruppens atomer (0,031 J), denna energi likväl INTE löser frågan: en metallyta förångas INTE bara för att den utsätts för joniserande strålningsenergi: atomerna stannar kvar medan elektronerna kickas ut. Det krävs, tydligen, betydligt mera energi för att få ut atomerna ur hålet än 0,031 Joule. Nämligen enligt den inledande energiräkningen drygt 450 J.

Se även vidare nedan från JONISATIONSARGUMENTET.

referenser

ENLIGT TABELLREFERENS ligger alla alkalimetallernas E_JON för yttre elektronen runt 4-5 eV

— sedan i växande med högre kemiskt gruppnummer. Helium ligger högst med runt 25 eV.

Jonisationsargumentet

JONISATIONSENERGIN

Argumentet för att hålbildningen sker enligt CAT

NORMALT SETT INNEBÄR EN ATOMS JONISATION att till exempel ljus med en viss minsta våglängd riktas mot en viss materialyta vars atomer ska joniseras (FOTOELEKTRISKA EFFEKTEN); Genom Planckenergin E=hf=hc/l (i eV E/e=hc/le=[JM/C][1,24 t6]/l) kan minsta våglängden (l) bestämmas för en känd minsta jonisationsenergi — eV-värdet; GRUNDÄMNESATOMERNAS JONISATIONSENERGIER finns numera i referenstabeller på @INTERNET. Värdena i den referenstabell som här används anges av referenskällan i enheter KJ/mol (1mol = 0,001KG/[u=1,66033 t27 KG] = 6,02289 T23 = Avogadros Tal). För att få värdet i eV räknas

EeV=E_KJ/mol·u(T6)/e=E_KJ/mol(1,66033 t21 KG)/(1,602 t19 C);

För Aluminiumatomens första elektron gäller (idealt) jonisationsenergin (i eV) ca 6 eV (577,5 KJ/mol) som kräver den ultravioletta våglängden

l = (1,24 t6)/(eV=6) = 2 067 Å = 2,067 t7 M;

MEN DEN JONISATIONEN GÄLLER BARA SÅ LÄNGE ATOMEN BADAR I DET PÅLAGDA LJUSET.

Då ljuskällan tas bort, försvinner också excitationsgraden.

I experimentfallet, se experimentkopplingen, finns emellertid VARKEN någon sådan liknade ljuskälla ELLER skulle närvaron av en sådan ljuskälla ENS ALLS föranleda någon avdunstning av Al-atomer från det belysta partiet; Enligt redan väl kända experimentella resultat berör jonisationen för fasta material nämligen bara deras yttersta elektronmassor som kickas ut från materialytan; Atombesättningen stannar kvar. Jonisationsenergin som sådan given betyder alltså inte någon ekvivalent lösning på experimentanordningens uppförande. För att få ut atomerna ur hålet krävs uppenbarligen (betydligt) mera energi än så.

I TEORIN FÖR EXPERIMENTFUNKTIONEN, det bildade hålet enligt TNED, tas (i medeltal) hela atomens yttersta elektron bort (förintas) genom annihilation. Det kvarlämnar — KONTINUERLIGT — en elektronrippad atom med en positiv elementarladdning i överskott i atomkärnan (tills moderatomen finner en yttre elektron som återställer balansen). Men energin för att ta bort den elektronen är i gengäld hela drygt 1 MeV (2m_ec₀²), vilket är något helt annat än 6 eV. I gengäld kan moderatomen — fortfarande KONTINUERLIGT, så länge som behövs och i den takt den själv bestämmer — utverka sin repulsionsfysik med omgivande atomgrannar och på den vägen utbilda den aktuella kinetiska energin (mv²/2) som bildar hålet.

Vilket vill säga: Hur man än räknar, går det inte ENBART att härleda experimentanordningens hålbildning på en typ ”joniserad medelatom”, Ty, jonisationsprocessen måste motsvara en kontinuerlig energimatning så länge hålbildningen varar. Med andra ord:

jonisationsenergin som sådan räcker inte för att förklara hålbildningen.

Men en elektronrivning gör det definitivt, därför att då kan atomen obehindrat, så länge den själv vill, eftersträva sin normala balans med full Coulombisk kraft ända tills den träffar på en utfyllande elektron — och den hittar inte moderatomen utom i rummet utanför de elektronrippade hålagenterna. Elektronrippningsprincipen fungerar alltså perfekt — även energitekniskt i totalräkningen.

Och alltså kommer vi (återigen) fram till samma resultat igen fast sagt på annat sätt:

Experimentkopplingens pulsresultat uppvisar långt mera energi än den som krävs för påtriggningen.

Hur mycket rörelseenergi krävs det då för att få ut de runda 3,2 T16 Aluminiumfoliets hålatomer ur hålet? Se vidare i ENERGIRÄKNINGEN ENLIGT CAT. Det är det remarkabla: Energiräkningen stämmer.

ATOMKÄRNANS FULLSTÄNDIGA UPPLÖSNING | Ljusbulan

ljusbulan

LJUSBULAN

Al-folie 0,017 mM; 24V; 10 mW; 100 µF; yttre ljusbulans diameter < 1-2 mM

Färgindex; Färgen motsvarar en viss temperatur som kan användas för grovberäkning av ljusbulans effekt.

kalkylkort · ljusbulans effekt enligt Stefan-Boltzmanns strålningslag

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik6 Kalkylkort 3 — Ljusbulans effekt — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

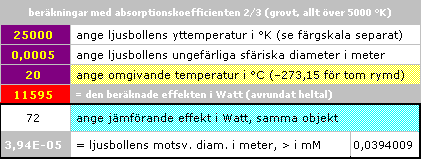
P=a_2/3k_{5,66893154148517 t8}A(T⁴–T₀⁴)

ENERGIN FRÅN EFFEKTEN beräknas på den TID (t_ON) under vilken effekten antas verka;

Sämsta fallet är här den maximalt uppmätta ljustiden t_ON=0,1 mS (1 t4 S).

Med den uppskattade temperaturen på 25000 °K för ljusbulan Ø=1 mM ges då

E = (11595 W)(1 t4 S) = 1,1595 J

vilket är 53 ggr det tillgängliga värdet på kondensatorenergin E_CAP=0,0216 J.

Detta resultat utpekar (återigen, se energiräkningen) att kondensatorenergin INTE kan förklara fenomenet.

Ljustiden för ljusbulan explicit (t_ON) är emellertid svår att bestämma närmare (om den nu skulle vara kortare än det uppmätta 0,1 mS) och innebär därför en ännu inte avgjord osäkerhet i experimentresultatet.

Det finns här (2008-02-15) heller inga ytterligare uppgifter av rent visuell experimentell art som skulle kunna vägleda oss i vad som är rimligt.

LJUSBULANS DUBBELFORM (eventuella förklaringen till den mindre delen)

Den mindre ljusbulans förklaring

Graf: 2+a([sinx]+[sin2x])'2.5

r=2+a([sinx]+[sin2x])2,5, a={0,1;0,5;1;2}

CENTRALT I HÅLET berövas atomkärnorna elektroner; kärnorna utbildar inbördes repellerande Coulombkrafter och eftersträvar att expandera utåt;

Jonisationsekvivalenterna påförs (eller överförs till) luftmolekylerna; de elektronberövade luftmolekylerna emitterar ljus då deras moderatomer får tillbaka elektroner (som tas ifrån eller delas med omgivande luftmolekyler);

Spektraltemperaturen för blåvitt på ca 30 000 °K motsvaras av energin ca 13 eV (via Wiens förskjutningslag lT=k och Planckenergin E=hf), vilket också är ekvivalenta jonisationsenergin för syreatomens första elektron.

DEN INRE MINDRE LJUSBULAN: OM katodstiftet inte fanns från tidpunkten omedelbart efter hålbildningen = ledningsbrytningen borde ljusbulan uppträda symmetriskt på bägge sidor kring Al-foliet; Stifttoppen betyder att den delen hindras; de atomer som är på väg utåt vid baksidan, kastas tillbaka mot framsidan och kan därmed förmedla en mindre ljusbula.

ATOMKÄRNANS FULLSTÄNDIGA UPPLÖSNING | Ljustiden

ljustiden

LJUSTIDEN 0,1 mS max

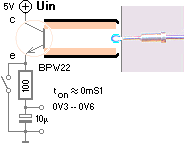
KOPPLINGEN OVAN visar hur tiden för ljusbildningen uppmättes i experimentet.

VILKEN den komponent är som bidrar med längsta ljustiden — glödspåren eller ljusbulan — är helt omöjligt att avgöra genom synintrycket; bägge delarna tycks uppträda i ett och samma flashtillfälle.

Med misstanken att ljusbulans varaktighet är betydligt kortare än glödspåren, krävs dock en mera avancerad (snabbare) fotokomponent (stigtider på max nanosekunder). Det finns (här) heller ingen direkt kunskap om en motsvarande ögats fysiologiskt kortaste reaktionstid för en absolut tidsminimal ljusflash som skulle kunna vägleda oss i någon uppgift på minsta rimliga möjliga tidsvärde; Är (nämligen) ljusflashen allt för kort hinner ögat likväl inte uppfatta detaljerna. Det krävs alltså en viss minsta varaktighet för ljusbulan (som förmodligen i den här fallet INTE är av typen nanosekunder), men vi vet här strängt taget inte vad som gäller för den delen.

INFORMATIONEN PÅ @INTERNET 2008-02-15 [för en introduktion, se exv http://webvision.med.utah.edu/temporal.html] är också sparsam på området: Väl finns en uppsjö av typen ”flash visibility”-artiklar med ”Bloch’s law” och ”Broca-Sulzer effect”. Men dessa artiklar beskriver mätningar och försök med repeterande pulser med varaktigheten i området 1-1000 mS. Ingenting omnämns om mätningar på visibiliteten av enskilda pulser (med långa mellanrum) som matas av vissa effekter med definierade stig och falltider.

beskrivning

Fototransistorn BPW22 har en 3mM toppkula som precis passar i ett 5mM mässingsrör (urspr. från Clas Ohlson). Paketet skjuts in i en (svart) krympslang som värms; Frånsett bottenöppningen har man då fått en helt ljustät och mekaniskt stabil förslutning [märk anslutningsbenen med rött(c)-blått(e) först så att kopplingsvägarna lätt hittas].

MÄTNINGEN. Genom att lägga aluminiumfoliet (anoden, se experimentkopplingen) tätt mot röröppningen (i normalt ljus) kan man kontrollera att fototransistorn är helt strypt. Spänningen över 10µ-capen ska då visa stabilt 0 (eller annat). När katoden (stifthylsan på bilden) förs mot foliet (separat kretskoppling) uppstår överslag (inom 10 pS): ett hål uppkommer i folien, anod-katod-kretsen bryts automatiskt och ljusbulan, tillsammans med glödspåren, drar in i röret.

ON-TIDEN. Minsta stig-falltid för BPW22 är enligt datablad (Philips) 2µS. Om transistorn hinner reagera, laddas kondensatorn upp över motståndet 100W så länge BPW22 drar. Genom att avläsa spänningen U över 10µ-capen via en separat voltmeter efter urladdningen kan ON-tiden beräknas enligt

t_on = R₁₀₀C_1t5 ln(1–U/U_5V)^–1

Genom upprepade försök (24V anod-katod, 100µF, 10mW, se experimentkopplingen) visade sig U variera runt 0,3 till 0,6V — dels beroende på osäkerheten i den manuella precisionen (experimenten måste delvis utföras i mörker) och dels beroende på att olika energimängder omsätts från fall till fall. Medelvärdet ger avrundat 0V5 som ger t_on=0,00010536 S, eller 100µS avrundat.

Nukleära sönderfallets gränsströmstyrka

NUKLEÄRA SÖNDERFALLETS GRÄNSSTRÖMSTYRKA

I_N = Q/T_N = A·(1836/2=918)e/T_N ; m_n/m_e » 1836; Vi frånser här tilläggsdelen på k=2,624e; Se vidare från Teoretisk Grund.

= A · 4902,12 ........................ fullständiga kärnsönderfallets minsta ström

beskrivning

Om antalet elektronmassor (Z) beaktas utöver nuklidinnehållets elektronstock (Z förkortas bort i Z·A·918e/[T_ZN=ZT_N]) gäller nedanstående.

I_N = Q/T_N = A·918e/T_N

= A · 4902,12 ............ fullständiga kärnsönderfallets minsta ström

I anger minsta strömstyrkan för fullständigt kärnsönderfall (se CAT) för kärna med masstal A.

Om I gäller, gäller också CAT (Kapacitiv Transmission), detsamma som atomkärnans fullständiga upplösning. Se utförligt från CAT.

918e är ENLIGT TNED (utom massdefekter) nuklidens största elektronmängd per ekvivalent neutronnukleon (Tilläggsmassan för nukliden på 2,6e frånräknad).

Se utförligt från PLANCKRINGEN.

Sambanden gäller samtliga nuklider och som garanterar att nukliden INTE delas genom uppdelning på skilda massdefekter. Strömstyrkor <I_N kärnregleras enligt ATA.

Nuklidinnehållets elektronstock refererar till atomkärnans sammansättning av ±e=0 enligt atomkärnans härledning från Planckringen, och som baseras på grunddatat från Neutronen; Neutronens elektronstock har sammansättningen 1818e+18e+2,624e. Se utförligt från Neutronen, om ej redan bekant.

CAT

CAT

KAPACITIV TRANSMISSION

Följande illustrerade beskrivning är med referens till experimentkopplingen (– katod, + anod)

När två spänningsförande elektroder närmas varandra och deras kemiska (spänningen förutsatt lämplig) och mekaniska kontakt realiseras, sker ett överslag. Om den lokala kapacitansen och resistansen i överslagsögonblicket är av sådan natur att en strömstyrka initieras som tangerar eller överstiger nukleära sönderfallets gränsströmstyrka (den är ca 78 000 Ampere för Syre, ungefär samma för luft), genomgår den kopplade strömstammens atomer i överslaget fullständig upplösning enligt följande funktionsbeskrivning (se även mera förklarande från inledningen).

1 centralstammen kopplar vid tiden T=0

2 e^–-massa dras »direkt» till anoden (ATA) som tvingar atomkärnan att exponera e⁺

3 e⁺-massan framtvingar g-emission

4 centralstammens jonisation ger ljusfenomen genom tillströmmande omgivningselektroner

Centralstammens anodatomkärnor i kopplad urladdningslinje i förenklad illustration enligt TNED.

I en motsvarande kontinuerlig ljusbågsström flyter elektronströmmen från katoden (vänster) till anoden (höger).

e^–-strömmen Q_IGN från katodens toppunkt (anodatomkärnan längst fram mot katoden) släpps aldrig fram — ledaren (Koppar) är garanterat avbränd från Ø28 nM

e^–-strömmen Q_IGN tas istället från urladdningsstammens atomagenter (anodmaterialet, Al-folien i experimenten): strömvägarna garanteras nollresistans med hög elektrontäthet:

Q_IGN till anoden bildar tillsammans med avbrottskatoden en extra kapacitans som sedan hela materialkretsen (längre fram) urladdas på tillsammans med huvudkapacitansen.

Q_IGN-rippningen (anodkärnornas elektronrivningar som transporteras till anodbasen för vidare transport till den påbörjade men tidigare avbrutna kondensatorurladdningen) frilägger motsvarande positronmassa med atomkärnans funktion enligt ATA som expanderar och annihileras tillsammans med omgivande atomers elektronhöljen. Sekundäreffekten bildar en stark lokal Coulombisk repulsion som bär ansvaret för att ett hål uppkommer (se från experimentkopplingen).

elektronrivningstiden

TIDEN FÖR ATT ELEKTRONRIVA HELA ATOMKÄRNAN (A·918e) bestäms av divergensen (c₀) idealt i Planckringen h=m_nc₀r_n med den specifika kärnradien (förenklat från A>4)

r=r₀A^1/3 med r₀=1,37 t15 M för protonradien (eller mera korrekt r_n=1,32 t15 M från hm_nc₀);

Med första underfraktalens toppspinn (se utförligt från Atomkärnans härledning) idealt via toppdivergensen c₀ måste spinnet avverka hela omkretsen (P), idealt P=2p(r/2)=pr på tiden

T(MINIMUMeNUC)=P/c₀=pr/c₀=pr₀A^1/3/c₀=(1,43565 t23 S)A^1/3;

För Aluminiumatomen med A=27 ges för varje neutronnukleon mängden 1836e/2=918e, med

T(MINIMUMeNUC)Al-27 = (1,43565 t23 S)(3) = 4,30696 t23 S;

I experimentkoppling används ca 6 T11 Al-atomer [(1,49812 T16)/(27×918)=6,04421 T11] för energitransfereringen på t_IGN=10 pS, vilket för en enskild centralstam ger medelvärdet per atom

(6 T11)/(1 t11)=6 t22 S och som därmed ligger väl inom gränsvärdet 4 t23 S.

materiella strömgränsvärdet

MATERIELLA STRÖMGRÄNSVÄRDET

OM strömhastigheten för givet ledartvärsnitt är given

här … … och här, är det uppenbart att strömhastigheten

här

måste vara högre OM tvärsnittet är mindre, samma laddningsmängd, given strömstyrka.

STRÖMHASTIGHETEN [v=I(nepr²)^–1] i varje elektrisk ledare med given elektrontäthet (n=e/M³) och givet ledartvärsnitt (pr²) tvingas växa i partier med trängre strömväg relativt den givna. Övre gränsen för v är c₀=2,99792458 T8 M/S. Därmed kan en absolut minsta MATERIELL ledarradie (rLIMc₀) bestämmas för en given strömstyrka (I) och som garanterat inte kan bli mindre. För en kopparledare (kondensatorns tilledningsben) med diametern ca 1 mM som drar strömmen 1 Ampere uppnås den gränsen om strömvägen tvingas in i ett tvärsnitt mindre än 3 Ångström (eg, 2,8 t 10 M).

I fallet med experimentkopplingen (I=2400 med Kopparledare) blir materiella ledarens gränsdiameter ca 28 nM (2,8 t8 M).

Kalkyl rLimc

kalkylkort · absolut minsta ledarlinjen (rLIMc) för given materiell ström

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik6 Kalkylkort 4 — Absolut minsta ledarlinjen — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

v = I(nepr²)^–1; n(e/M³) atomkärnan min 8,83775 T46 e/M³ ; n Koppar ca 8,4354 T28 e/M³; r = Ö I/vnep ;

Jämför:

Centrumcirkeln i atomkärnans kärnbrunn för alla atomkärnor med masstal 2 och uppåt är 1/28 av kärnradien (se Atomkärnans Dimensioner enligt TNED).

För en syrekärna O-16 gäller approximativt centrumcirkelns radie r=1,2 t16 M, för en Al-kärna ca 1,47 t16 M; ingen materiell ledarfysik kan konkurrera med den standarden. Max strömstyrka utan nukleär fragmentering är I=A(4902) A med elektrontätheten (alla nuklider, minst) 8,8 T46 e/M³.

Med experimentets kondensatorkoppling I=2400 A initiellt via Cu-ledare, sätts ledningsgränsen mellan kondensatordel och gnistled vid en ledarlinje med radien 1,4 t8 M (se resultat från kalkylkortet ovan). Nedanför denna gräns (r = 14 nM) är kretsen definitivt bruten. Därmed matas (tas) huvuddelen av det nukleära sönderfallet från elektrodens anoddel — genom dess kärnkopplade centrala urladdningsstam. Se även Elektronrivningstiden.

Kondensatorkretsens varierande resistans · resistiva sambandet

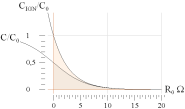
Kondensatorkretsens varierande resistans

GRUNDUTFÖRANDET I EXPERIMENTREDOVISNINGEN förutsätter en låg kretsresistans (R=10mW).

Test med R=10W ger gnistbildning, men den är då mycket försvagad (och måste studeras i mörker).

Energiomsättningen beror tydligen av R=R₀: R₀ STYR Q_IGN.

Vi söker funktionen för Q_IGN med R₀ som funktionens variabel.

Beteckningar

C₀ ............................. huvudkondensatorn

C_i ............................. urladdningskapacitansen

C_IGN ........................ alternativ till ovan

T_IGN ........................ bildningstiden för urladdningsgnistan

R₀ ............................ kretsresistansen, totalt

Kretsresistansen totalt (R₀) måste innefatta primärt induktivt resistiva delar. Fysikbeskrivning av material generellt på den nivån tillhör emellertid inte den enklaste uppgiften.

Vi gör därför här bara en grov funktionsskiss med viss ledning av direkt praktiska mätningar på C₀ för olika R₀ (vidare nedan), grundkrets som tidigare enligt experimentkopplingen.

Grundform:

Q_IGN = Q₀e^–R0^/kIGN

k_IGN = 3 ·1W .................... approximerat från praktisk mätning, vidare nedan

Härledning:

TI = T(U/R) = TU/R=Q =UC =TR^–1U=Q ; T/R=C ; T=RC ; R=T/C ;

i_IGN = Q_IGN/T_IGN = Q_IGN/(RC)_IGN = dQ/dT ;

dQ/Q_IGN = dT/(RC=k) ;

INTEGRALEN FÖR Q_IGN ges direkt från Q₀ över varje närmast mot T=0 liggande TIDSINTERVALL ;

_Q0\QIGN ò dQ/Q_IGN = lnQ₀ – lnQ_IGN

= T/RC = ln(Q₀/Q_IGN) ;

Q_IGN = Q₀e^–T/k ;

Toppströmmen initieras vid T=0 motsvarande vid i_IGN enligt I=U₀e^–T/RC/R₀=U₀/R₀.

För att kunna relatera situationen vid i_IGN måste T följaktligen omformas på statiska (icke tidsberoende, linjära) ekvivalenter.

T = R₀C_a , (RC=k)=R_bC_b

Vi känner inte gruppen C_aR_bC_b, men den kan bestämmas grovt genom experimentell mätning (nedan).

Med T/k ges (T)/(k)=(R₀C_a)/(R_bC_b)=R₀(R_bC_b/C_a)^–1=R₀(k)^–1. Därmed

Q_IGN = Q₀e^–R0^/k .......................... för små R₀ ges Q_IGN=Q₀

MÄTNING AV k_IGN. Med R₀=11W urladdades C₀ på knappt en volt (24,3–23,4=0,9);

En grov bestämning av k (försöken redovisas inte här) ger därmed k=3W (se separat beräkning);

Totala urladdningskapacitansen C=(C₀^–1+C_i^–1)^–1 avtar med avtagande Q_IGN. Det innebär att C₀ urladdas allt mindre med växande R₀, analogt minskande i_IGN.

Med C_IGN=Q_IGN/U₀ och C₀=Q₀/U₀ vid T=0 (innefattat T_IGN=10pS vilken obetydliga del vi frånser) ges C_IGN/C₀=Q_IGN/Q₀=n.

; Vid T_IGN=10pS är spänningen över C₀ fortfarande praktiskt taget U₀, och därmed även över C_IGN ;

C_IGN=Q_IGN/U₀ ; C₀=Q₀/U₀ ; U₀=Q_IGN/C_IGN=Q₀/C₀ ; C_IGN/C₀=Q_IGN/Q₀=n=e^–R0^/k ;

nC₀ = C_i ;

C = (C₀^–1 + n^–1C₀^–1)^–1 = C₀(1 + n^–1)^–1 ;

C₀/C = 1 + n^–1 ........................................ n<1 ;

Totala urladdningskapacitansen (C) förhåller sig till huvudkapacitansen (C₀) som spänningsfallet (U=U_DROP) från toppspänningen (U₀) förhåller sig till U₀: laddningsmängden (Q_IGN) i kondensatorkretsen dras över spänningsfallet (U_DROP) i samma krets ;

C₀/C = U₀/U = 1 + n^–1

U_DROP = U₀(1 + n^–1)^–1

= U₀(1 + e^R0^/k)^–1

= U₀–U_FINAL

;

U₀/U_DROP = 1 + e^R0^/k ;

U₀/U_DROP – 1 = e^R0^/k ;

R₀/k = ln(U₀/U_DROP – 1)

Med R₀=10mW ges U_DROP= 12V avrundat, vilket är väl i överensstämmelse med observationerna.

Överslagsstället (separata anodstänger) oxiderar stundtals från och till, vilket gör att U_DROP i vilket fall fluktuerar mellan olika urladdningar.

k-beräkningen från mätning

Q_IGN = Q₀e^–R0^/k

C_IGN/C₀ = Q_IGN/Q₀ = U/U₀; U=U_DROP

U = U₀e^–R0^/k

U₀/U = e^R0^/k

R₀/k = ln(U₀/U)

k = R₀/ln(U₀/U)

= (11 W)/ln(24,3/0,9) = 3,3375437 W » 3 W

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Atomkärnans Totala Upplösning

ämnesrubriker

innehåll

Atomkärnans Totala Upplösning

Atomkärnans fullständiga upplösning

Teoretisk Grund

Gränsspänningen UG

ATA

Beskrivning

T[N]

ATA-KARAKTÄRISTIKEN

CAT — definition

Anledningen varför fenomenet undgått upptäckt

Tabell — ljusbåge gnisturladdning

Gnisturladdningens teori

ELEKTRISKA LEDNINGENS TVÅ GRUNDFORMER

Citat

Experimentanordningen

Hålbildningen

Detaljerad beskrivning

Experimentkopplingen

Glödspårens energibidrag

Antal hålatomer

Kalkylkort — Hålet

Silverfolien

Beskrivning — Silverfolien

Exakt energiräkning

Energiräkningen Enligt TNED

Minsta jonisationsenergin

Sambanden i syntes

Kalkylkort — Energiräkningen enligt CAT

Resultat

Energigrunder

t-IGNITION

Urladdningsförloppet

Tidsschema

t-IGNITION 10pS

Bakomliggande resonemang, teori

Induktansargumentet

Händelsen efter hålbildningen

Fyra argument

Kondensatorenergin räcker inte

Lågresistiva kondensatorenergin

Jonisationsenergin

Konventionella Jonisationsenergin

Jonisationsargumentet

Ljusbulan

Kalkylkort — Ljusbulan

Den mindre ljusbulans förklaring

Ljustiden

Nukleära sönderfallets gränsströmstyrka

Nuklidinnehållets elektronstock

CAT — KAPACITIV TRANSMISSION

Centralstammen

Elektronrivningstiden

Materiella strömgränsvärdet

Kalkylkort — Absolut minsta ledarlinjen

AVNE-sambandet — I = Avne

Kondensatorkretsens varierande resistans

R0-sambandet

Märning av k-IGN

k-beräkningen från mätning

referenser

@INTERNET Wikipedia Ionization energies of the elements 2007-03-09. Se även [GYMNASIETS FYSIK Liber 1980 åk3s207].

[BKL]. BONNIERS KONVERSATIONSLEXIKON Band I-XII 1922-1928

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ....................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

ε₀ = 8,8543 t12 C/VM ............. (di-)elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

[BA]. BONNIERS ASTRONOMI 1978

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM.

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2021-03-30

*END.

Stavningskontrollerat 2008-03-06.

rester

Det finns här (2008-02-15) heller inga ytterligare uppgifter av rent visuell experimentell art som skulle kunna vägleda oss i vad som är rimligt.

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se