Blixturladdningens Fysik 2012-13 | 2012XII a BellDHARMA production | Senast uppdaterade version YearMonthDayTime 2021-05-04
innehåll · | webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
BILDKÄLLA: Författarens arkiv ·
13Sep2012 E29 Bild222
• Nikon D90 · Detalj

Teorin i TNED för de tre
fenomenområdena ATMOSFÄRISK URLADDNING, LJUSBÅGE
OCH ALUMINIUMFOLIEURLADDNING
uppvisar ENHETLIGHET genom utförda laddningsmätningar.
Slutliga, direkta, gammabevis återstår.
1. ![]() Kolliderande
nanopartiklar: Första fotot [Gtrack1_001.JPG]
(2Feb2013) med den nya
kamerasynkade urladdningsenheten XYcoAlFEDU
Kolliderande
nanopartiklar: Första fotot [Gtrack1_001.JPG]
(2Feb2013) med den nya
kamerasynkade urladdningsenheten XYcoAlFEDU
— tydliga spår [ImpulsKALKYLgrund]
från glödpartiklar [utgångshastighet
800.000 M/S] som kolliderar med luftmolekyler [500 M/S], kalkylkort
ger värden.
2. ![]() Bilder UrladdninghålenFOTO
— Jan2013 på urladdningshålen från urladdningsexperimenten
via USB-mikroskop.
Bilder UrladdninghålenFOTO
— Jan2013 på urladdningshålen från urladdningsexperimenten
via USB-mikroskop.
3. INSTRUMENTERINGEN
för påvisande av noll laddningsrester [Se JFET-sensorn].
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
LuftBASIC | IMPULSANALOGIN | Urladdningslådan | AnordningenDec2012 | Bevis i CAT-räkningarnas rimlighet | JÄMFÖRELSER KONV. REF. | Positronfrågan | GammaWeb |
Inledning [”ABSTRACT”]
BLIXTURLADDNINGENS FYSIK — positronförekomst [Se TGFintro] i samband med blixturladdning
RUBRIKERNA SOM BESKRIVER
NATURFENOMENET
— teorins enhetlighet enligt TNED:
·
gammastrålning
i samband med urladdningsfenomen
[Blixturladdningens fysik, resumé med gammastrålningens
uppkomst]
·
positronförekomst
i urladdningsfenomen
[TGFintro]
TEORINS ENHETLIGHET i relaterad mening för atmosfärisk urladdning [ABU], ljusbåge [LB] och aluminiumfolieurladdningarna [AlFU] [Se ABULBAlFU] kräver noll — ingen — restladdning: inte i något som helst mätbart avseende.
— Speciellt i samband med experimenten med aluminiumfolieurladdningarna [EXPERIMENTKOPPLINGEN] infann sig (mot slutet av 2012, med uppslag från olika webbkällor, se JFET-sensorn från Webbreferenser) ett enastående, utomordentligt tillfälle att kunna kontrollera just närvaron av eventuell restladdning i — just — experimentanordningens olika delar och detaljer — och därmed ett slutligt, otvetydigt, absolut avgörande i frågan om själva teorins praktiskt möjliga förankring. OM man kunde påvisa enhetlighet via ett laddningstest i experimentanordningen, skulle också en motsvarande praktisk — oåterkallelig — enhetlighet i alla de tre nämnda fenomenformerna vara bevisad. I så fall, och endast då, skulle också en vidare teknisk grund, verkligen, finnas (kunna föras i argument) för ytterligare i ljuset av den enhetliga teorin med atomkärnans fullständiga upplösning [ATA/CAT].
Se även kort sammanställning i BASFAKTA.
Hur
teorins enhetlighet har framkommit
— Med en känslighet på uppmätning av (se Exempelräkning i JFET-sensorn) hundra miljoner gånger mindre elektronladdning (T8 e) än den som omsätts (1,5 T16 e) i aluminiumfolieurladdningarna [AlFU] har nyligen genomförda testmätningar (se JFET-mätningarna) visat fullständig överensstämmelse med den ovannämnda teorins enhetlighet: ingen restladdning förekommer, eller kan påvisas, i samband med de experimentellt utformade aluminiumfolieurladdningarna.
— Det resultatet ger det enda (slutliga) utomordentliga stöd vi behöver för just FENOMENDETALJERNAS TEORETISKA ENHETLIGHET — motivet för att alls fortsätta. Det betyder i sin tur att det inte längre finns någon som helst uppenbar eller påvisbar grund, varken praktisk eller teoretisk, för misstanken om att teoretiska (praktiska) FEL skulle föreligga i den totala fenomenformens beskrivning [ABULBAlFU]: enhetligheten utpekar, tydligen, en korrekt praktik.
Men ännu är vi inte framme vid målet.
— Det enda som — nu (Apr2013) — fattas är ett direkt påvisande av gammastrålning också i aluminiumfolieurladdningarna [AlFU]. Enhetligheten kräver det. Det ska finnas påvisbar gammastrålning i aluminiumfolieurladdningarna av exakt samma skäl som det finns påvisad gammastrålning i de atmosfäriska blixturladdningarna [Blixturladdningens fysik, resumé med gammastrålningens uppkomst], i allt under gränsströmstyrkans förutsättningar [Strömstammens CAT-geometri].
Webben innehåller flera uppslag på — mer eller mindre känsliga — gammasensorer som vi (numera, möjligen) kan bygga själva (med viss elektronisk erfarenhet). Det ligger i sakens natur att i varje fall försöka utnyttja dessa uppslag för att få fram ev. resultat, självklart.
— I den mån konstruktioner kan förverkligas (och förutsatt inget oförutsett kommer emellan) kommer beskrivning av resultaten från byggen och tester med sådana gammasensorer att genomföras löpande härifrån, och när tid och tillfälle infinner sig.
»GammaTestet» hade — egentligen av mig själv — betraktats som uteslutet på grund av de mycket speciella komponenter (PIN-dioder) och konstruktioner som måste till för att få påvisbara resultat. Jag lutar fortfarande åt det hållet — verkliga, rejäla, gammatestare med höga känsligheter är INTE en uppgift för någon elektronikamatör. Utvecklingen av kretstekniken generellt i vår tid (och dess kännedom) har emellertid, och möjligen, ändrat på oddsen. Jag kommer i vilket fall att FÖRSÖKA genomföra kretskonstruktioner och mätningar.
När, och om några resultat visar sig kommer särskild presentation.
Instrumentbygge färdigställt
för fotografier av aluminiumfolieurladdningarna — med urladdningshålen i
USB-mikroskop
Ytterligare stöd för att ENERGIRÄKNINGEN i urladdningsfenomenet enligt TNED är rätt uppfattad ges av de fotografier [IMPULSANALOGIERNA] som nyligen (Feb2013) framkommit i försorg av särskilda instrumentbyggen. Huvuddelen av denna presentation är ägnad den delen — glödspåren, deras uppförande och frågan om deras energibidrag, samt ljusbulan och dess roll i urladdningsfenomenet. Resultatbilden totalt FÖREFALLER därmed enbart peka åt ett håll: TNED-teorin för ATA/CAT håller. Det ska finnas en verklig — framtida i princip helt garanterat avfallsfri (Nollrest) — energilösning av verkligt avancerad natur.
|
1. Glödspåren i foto |
2. Urladdningshålen i
foto |
3. Instrumenteringen
(Mar2013) |
4. ImpulsBASIC |
5. LuftBASIC |
|
1. |
2. Positronfrågan |
3. JFET-sensorn
|
4. |
5. |
1. ![]() Första fotot [Gtrack1_001.JPG]
(2Feb2013) med den nya
kamerasynkade urladdningsenheten XYcoAlFEDU —
tydliga spår från glödpartiklar som kolliderar med luftmolekyler, kalkylkort ger värden.
Första fotot [Gtrack1_001.JPG]
(2Feb2013) med den nya
kamerasynkade urladdningsenheten XYcoAlFEDU —
tydliga spår från glödpartiklar som kolliderar med luftmolekyler, kalkylkort ger värden.
2. ![]() Bilder UrladdninghålenFOTO
— Jan2013 på urladdningshålen från urladdningsexperimenten
via USB-mikroskop.
Bilder UrladdninghålenFOTO
— Jan2013 på urladdningshålen från urladdningsexperimenten
via USB-mikroskop.
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Avgörande
argument för giltigheten av TNED-ATA/CAT-teorin —
atomkärnans fullständiga upplösning · fysikgrunderna
till energiproblemets lösning ·
Genom en förhållandevis enkel instrumentering (InstrumenteringenMar2013 Dec2013-Mar2013)
har funktionsbilden för folieurladdningsfenomenet (från 2005/Web2008-) klarnat (betydligt — fullständigt) i
konturerna.
— Enhetligheten generellt i alla
tre fenomenformerna blixturladdning (ABU),
ljusbåge (LB) och folieurladdning (AlFU) har (äntligen, Mar2013) stadfästs
— enhetlig fysikgrund i fenomenformerna utan innehåll av frågetecken: en
fullständig förklaring — tillsammans med teorin (Kirchoffs
första kretslag — PotentialArgumentet)
med exceptionellt god förankring i mätresultaten (JFET-sensorn)
och de framkomna fotografierna (XUcoAlFEDU) (ImpulsanalogiernaKALKYL) som nu
(äntligen) möjliggjort mera direkt praktiskt kontrollerbara beräkningar.
Beräkningarna visar (ImpulsBASIC),
som redan tidigare noterats (Glödspårens Energibidrag), att
glödspårens energibidrag tydligen kan förstås ges av så små partikelmassor (nanokuber — direkt bakåtstuds [Kolliderande Nanopartiklar] syns tydligt och ofta i kollisionen med en luftmolekyl [ImpulsanaloginKALKYL]) att glödspårens
energiräkning i energiräkningen som helhet framstår
HELT försumbar. Teorin för giltigheten av enligt TNED
är att hålbildningen grundas på en jonisation
PER aluminiumatom, och den förutsättningen verkar (än så länge) stämma med
helhetsbilden. Se särskild sammanställd illustrerad fenomenbeskrivning i Folieurladdningen i
detalj.
— Enhetligheten i beskrivningssättet — tillsammans med det
faktum att inga direkta insteg (ännu Mar2013) har visat sig som kan
ifrågasätta djupteorins (helt glänsande) överensstämmelse med praktisk fysik
— lämnar därmed inte längre några som helst synbara tvivel på ATT ATA/CAT-teorin, verkligen, är naturkorrekt:
överensstämmelsen teori-praktik utpekar att en teknisk lösning är ofrånkomlig —
såvitt inga revolutionerande nya rön visar sig. Frågan blir därmed inte längre
Om, utan När.
Grundlig fenomenbeskrivning enligt TNED — Folieurladdningen i detalj
Folieurladdningen i detalj
Sammanställd detaljerad komprimerad snabbgenomgång av
ATA/CAT-grunderna i TNED — fenomenbeskrivningen i folieurladdningarna
— För den enkla experimentkopplingen, se EXPERIMENTKOPPLINGEN om ej redan
bekant.
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
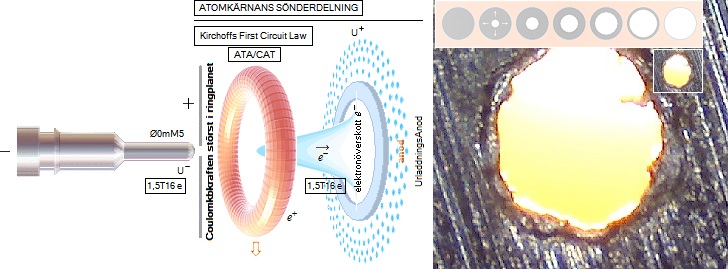
Från början är kondensatorn uppladdad — i originalexperimenten till 24V; i de här aktuella experimenten via de tre 9V-batterierna (till drygt 26V, med marginellt fallande som batterierna förbrukas). Bilden ovan vänster visar katodstiftet (MINUS [U–]) som urladdningarna kommer att ske igenom via dess (nära) beröring med den underliggande tunna (0,017 mM) aluminiumfolien (PLUS [U+]). Högra delen i bilden ovan visar detaljer från urladdninganordningen (Mar2013) med urladdningslådan och dess omspända aluminiumfolie till höger;
När katodstiftet berör aluminiumfoliens yttersta molekylskikt
— idealt via ett minsta [1/100 mM] avstånd via
urladdningen i luft med hänsyn till urladdningsspänningen runt 25V (24V i
originalexperimenten som är preferens i beräkningarna)
— inträffar själva urladdningsögonblicket [AlFU]: den ytterst komplicerade och sammansatta kärnan i hela händelsen; Se även utförligt i ENERGIRÄKNINGEN;
— Hålbildningen garanterar att Kondensatorns urladdningskrets omedelbart bryts: kondensatorn hinner inte urladda något alls. Men induktansen bakom ansatsen till den »påbörjningen» framtvingar det komplicerade händelseförloppet i den avbrutna, hålbildade anoddelen: elektronresten (1,5 T16 e–) på katodsidan kan inte nå kondensatorns anodsida på grund av hålbildningens kretsavbrott, utan kondensatorn måste istället återta den elektronmängden från urladdningsstammen i anoddelen via en sönderdelning av atomkärnan (ATA/CAT): induktansdraget i urladdningsansatsen som avbröts är den faktor som framtvingar de 1,5 T16 elektronerna att rivas ner ur urladdningsstammen och återlämnas till kondensatorns anodsida, på kredit av en lika stor frilagd positronstock på 1,5 T16 e+ (helt omöjlig att härleda i MAC, se utförligt från Atomkärnans härledning om ej redan bekant);
— Laddningsbalansen återställs (bilden nedan) genom att positronstocken först annihileras tillsammans med en lika stor elektronmängd som nu tas från den närliggande lokalens atomer — främst de närmaste aluminiumatomerna, och sedan successivt den närliggande luftens atombesättning; De så positivt joniserade (luft-) atomerna kommer att harmoniera perfekt i balans med den tidigare kvarlämnade, nu återstående, kretsavbrutna, katoddelens restelektronmängd 1,5 T16 e–; Den katodelektronresten kan rekombinera med luftjonerna från parannihilationerna (±e) på samma sätt som i fallet med ljusbågens jonströmmande luftatomer som återfår sina elektroner i kontakten med katodområdet [Se ett Räkneexempel via konventionella samband]. Därmed är balansen fullständigt återställd, och ingen elektronrest existerar. Den enhetligheten avgör hela den teoretiska förklaringsgrunden (Kirchoffs första kretslag; Potentialargumentet).
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
I flera av fotografierna (även bilden ovan [Kolliderande nanopartiklar]) framgår tydligt att (i varje fall en del av) glödspåren börjar på en ort som förefaller vara ljusbulan — skild i avstånd (och centrum) från urladdningsstiftet och själva urladdningshålet; Ljusbulan framträder på framsidan, strax utanför urladdningsfolien. Det är också den teoretiskt mest naturliga orten för det (i teorin framskjutande, avgörande) starkt joniserade närområdets aluminiumatomer att söka återställa sina elektronbesättningar. Nämligen i matning av elektronmassorna hos den närmast omgivande luftens atomer.
— Genom att Coulombkraften i positronringarnas expansion i sönderfallshändelsen [teorin enligt ATA/CAT] är som störst i ringplanet, är det naturligt att de atomer som påverkas starkast (först och mest) av den positronannihilerande baskraften är just den pågående hålbildningens diameterutsträckta förekomst av aluminiumatomer: ythålet, inte via materialets tjocklek: hålbildningen kan förstås genom att foliematerialets atomer i materialets ytutsträckning förlorar sina elektronbesättningar, med sekundär följd i stark inbördes Coulombisk repulsion (utåt, bort från katodstiftet, vidare nedan).
Elektronrivningen
från urladdningsstammens atomkärnorna bildar ett lokalt elektronöverskott i
anodmassan, men vilket överskott i själva verket är precis det som kondensatorn
kräver för sin urladdning som initierades via induktansen i hålbildningsögonblicket
då urladdningsledningen bröts. Det är en krävande, ytterst sammansatt
fysikförklaring, och försåvitt den också verkligen stämmer överens med
naturgrunderna: Helhetsbilden i de tre fenomenformerna (ABULBAlFU)
tillsammans med grundfysikens potentialargument
(Kirchoffs första kretslag) utsäger att
så är fallet.
— Katodstiftets fasta längsposition för sin del spärrar för positronringarnas (e+, illustrationen närmast ovan) inbördes, i urladdningsstammens riktning, längsriktade Coulombiskt repellerande expansion (ATA/CAT) den vägen: Enda öppna längsmässiga expansionsvägen är utåt, bort från katodstiftet, genom urladdningshålet. Samtidigt är katodstiftet föremål för den kvarvarande elektronresten (1,5 T16 e–) från den avbrutna initierande kondensatorurladdningen, och vilken elektronrest (Potentialargumentet, Kirchoffs första kretslag) i vilket fall kommer att återförenas med motsvarande joniserade atomer.
Kraftbilden i hålbildningen kan därmed förstås så att de frilagda atomerna i hålet drivs utåt, bort ifrån katodstiftet, tillsammans med hela den initierande urladdningsstammen i urladdningsögonblicket. Katodstiftet motsvarar i den meningen en »absolut fast rekylvägg» som tvingar materialet att avlägsna sig bort ifrån katodstiftet och söka sig utåt, åt andra hållet.
— Därmed grundteorin till ljusbulans uppkomst:
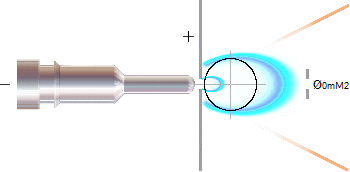
— Ljusbildningen kan förstås uppkomma då luftatomerna omedelbart utanför urladdningshålet, den markerade millimetersfären i Figur 3 vänster, dels berövas sina elektroner från de längre in mot katodstiftet utåtströmmande mera starkt joniserande atomerna, och dels då den jonisationen återställs via rekombinationer (även i lokal turbulens, samt) med restelektronladdningen från katodsidan (vars elektrondel måste förstås strömma till från katodstiftet då ingen annan väg finns).
— ENDAST I KRAFT AV rekombinationsområdets maximalt starka värmeutveckling (Ljusbulan), finns förutsättningarna för de tyngre glödpartiklarnas (kemiska sammansvetsningar och) bildning; antingen i grupperingar med en möjlig aluminiumoxid (Al2O3) eller aluminiumnitrid (AlN). Det finns dock här ingen som helst kemisk analys på kvarlevorna: dessa har ingen (direkt) synbarlig representation i folieurladdningarna i luft.
Se vidare detaljbeskrivningar i ABULBAlFU.
SÖNDERDELNINGEN I URLADDNINGSSTAMMEN GER noll RESTPRODUKTER
Vissa aspekter på en ev.
tekniskt genomförbar apparatkonstruktion
· Det finns inga restprodukter i energiräkningen.
· Det finns inget radioaktivt avfall.
· Det finns ingen restmassa som kan ställa till problem.
Problemet med »tillgången på brännbart
material»
Urladdningsstammen måste koppla elektrisk ledning (kemisk förening: atomfysikens två kungsekvationer). Eftersom alla ämnesatomer karaktäriseras just av den egenskapen — kemisk föreningsbarhet — kan i princip, och förutsatt man kan lösa problemen rent tekniskt — vilka förbränningsmaterial som helst komma i fråga som motsvarande »anodmaterial» — inte enbart goda elektriska ledare som experimentfallets Aluminium.
Är katodstiftet format med ett inre hålrum i formen av en hålkatod, samma som principen för en positronkanon, reduceras DELS det föregående beskrivna katodstiftets rekylfasta mekaniska bas, och DELS ges den nödvändiga förutsättningen för att samla upp positronmassorna INNAN de (okontrollerat) annihileras med omgivande atomers elektronbesättningar.
DEN TEKNISKA GRUNDLÖSNINGEN är just den, och förutsatt att praktiken också handlar om TNED-teorin: att hindra den okontrollerade positronspridningen i urladdningsögonblicket, Figur 2, att samla upp positronmassorna, och leda dem in i en kontrollerad jonkammare för kontrollerad energiutvinning. Det är hela målet med den rent tekniska lösningen.
Positronfrågan i urladdningsexperimenten
Vi
— varje kritisk observatör på Webben som studerat innehållet i Universums Historia till hit (23Mar2013)
— skulle säga:
— Javisst. Men var finns positronerna, och hur har man kunnat påvisa dessa i urladdningsexperimenten?
Svaret är, till hit: inte alls. Det är sant att OM inga positroner existerar i urladdningsfenomenet, är hela framställningen körd.
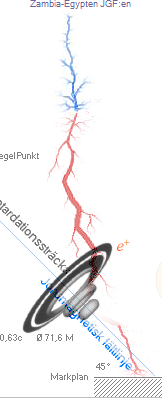
— Påvisandet av positroner i urladdningsexperimenten ansluter i TNED-teorin till samma svårighet i den atmosfäriska blixturladdningen (ABU): positronbildningen sker rätvinkligt urladdningsstammen [BlixtTGF2011], inte uppåt/neråt;
— I fasta material (0,3nM) är atomavstånden runt tio gånger mindre än i luft (gas, 3nM [LuftBASIC]) och dämpningen (Comptoneffekten [PARANNIHILATION] [ATA-KARAKTÄRISTIKEN]) i positronringplanen måste bli därefter: effektiv, i princip omöjlig att detektera utan avancerad instrumentering (som inte finns här [än]). Det finns ingen »konventionell rundstrålningseffekt» att relatera till.
— Positronförekomsten i urladdningsexperimenten är
därför en ren teoretisk konsekvens (TNED) som ännu inte kunnat påvisas av nämnda
skäl — i full praktisk enhetlighet med redan påvisade
positronförekomster i JordGammaFlasher (TGF:s). Se speciellt ZambiaTGF:en.
— Tills vi får mera klara besked om positronförekomster också i urladdningsexperimenten, är det enbart TNED-teorin (än) som står för positronkrediten i folieurladdningarna. Vi VET inte, men den enhetliga teorin för den enhetliga praktikens förklaring kräver det.
— Det är svaret på frågan. (Vi står i startgroparna, beredda till språng, men ingen vet åt vilket håll loppet ska gå — än).
Rekapitulation:
— ENERGILAGEN ENLIGT RELATERAD FYSIK
— massa KAN förintas DÄRFÖR ATT DEN
INTE KAN SKAPAS, speciellt förtydligat i PARTIKELBEVISET FÖR ATT ENERGI INTE KAN SKAPA MASSA
— klargör i relaterad mening bortom
varje tvivel, fråga och misstanke ATT den observerade positronförekomsten från
blixturladdning
— se särskilt ZambiaTGF:en
— INTE fungerar som man tror och påstår
i den moderna akademins led: »positroner-elektroner skapas ur energi».
Ovanstående sammanhang utpekar — helt absolut fullkomligt säkert — att det INTE
finns något sådant i naturen. Det är en vanföreställning som grundas på den
moderna akademins uppenbart trånga uppfattning om kärnfysiken: Se särskilt från
ATOMKÄRNANS HÄRLEDNING med speciell
tillämpning på ATOMVIKTERNA,
om ej redan bekant. Se även jämförande beskrivning TNED/MAC i Skapelse
eller Delning — neutronfragmenten.
— Därmed basfakta — enligt relaterad
fysik:
Positronförekomst i urladdningsfenomen — BASFAKTA
positronförekomst i urladdningsfenomen
TNED
utgick ifrån det (1993VII — N3m20)
via ATOMFYSIKENS
TVÅ KUNGSEKVATIONER där sambanden (ATA/CAT) uppdagar HUR atomkärnan
innehåller en sin egen strömfälla: grunden till framställningen om atomkärnans
sönderdelning, och därmed en helt ny möjlig kandidat — helt, fullkomligt, okänd
i MAC — till en lösning på det trängande
globala energiproblemet. Det var också för min del (långt) innan den faktiska
kännedomen framkom [2006 — efter tretton år] om dels gammastrålning från
blixturladdningar [1994] (som otvetydigt följer på positronförekomster), och
dels den senare upptäckten att också positroner visar sig [2009] (BlixtTGF2011) [Se viss inledning i
BLIXTURLADDNINGENS FYSIK i SNABBRUBRIKER].
— Enhetligheten i dessa detaljer (nu
Mar2013) lämnar (inte längre) något tvivel om DET FÖRKLARANDE SAMMANHANGET — om
inget revolutionerande är på väg att visa sig runt den omedelbara knuten:
— TNED
med teorin för blixturladdningen via ATA/CAT, innehåller här veterligt ingen
fråga eller motsägelse eller annan detalj som lämnar minsta tvivel om
funktionssättet, ehuru sådana detaljer ständigt eftersöks.
— Därmed (närmaste framtidens) facit:
Inte OM utan NÄR är frågan då sammanhangen avtäcks, slutligt.
— Om det inte vore för resultaten i ATOMVIKTERNA
från NEUTRONKVADRATEN
— urgamla hörnstenar i Kunskapen, tydligen — skulle varken jag (här) eller
någon annan ha något egentligt fysikbevis att komma med, alls. Hela Universums
Historia bygger på den delen: Planckringen.
Säkert.
Se även Termen
antipartikel i TNED : Universum innehåller ingen stationär antimateria.
Helt säkert. Laddningsdeplacementet: Neutronens negativa magnetiska
moment: energilagen. No way.
Att modern akademi (därmed,
ofrånkomligt) står inför ett fullständigt sammanbrott, råder här inget
tvivel om.
— Men menar du att positronbildning pågår i varenda bilmotor eftersom alla förbränningsmotorer använder GNISTAN I TÄNDSTIFTEN som trigg för motorkraften?
— Det vore nåt. AntiMercedes.
— Nej. Gränsen (i Jordatmosfären) för sådan verkan att positronbildning uppkommer ligger på strömstyrkor runt 80.000 Ampere (NUKLEÄRA SÖNDERFALLETS GRÄNSSTRÖMSTYRKA). Det är (nästan) så långt ifrån verkningssättet i en bilmotors topplock som att försöka åka till Arlanda och vänta på nästa flyg till Centrum i Vintergatan (30.000 ljusår härifrån). Det fungerar inte så.
BILDKÄLLA: Författarens arkiv · 21Sep2011 Excur17
UtsiktMoln Bild20

— Den förklarande och beskrivande enhetlighet som enligt TNED nu (Mar2013) framkommit i
fenomengrunderna för blixturladdning [ABU],
ljusbåge [LB] och folieurladdning [AlFU], med deras specifika
detaljförklaringar, gör att varje
vidare oklarhet i funktionsfysiken för SPECIELLT folieurladdningarna
[AlFU] nu HELT — fullständigt,
fullkomligt, absolut — har eliminerats. Detta sagt trots att det (här) ännu
inte framkommit något direkt experimentellt belägg som verkligen visar att
positroner — eller ens gammastrålning — verkligen, existerar i experimentformen;
inga sådana mätningar har (ännu) genomförts.
— Det enhetliga förklaringssättet
utpekar — fortfarande med den avgörande stora begränsning i experimentella
detaljer som ännu inte visat sig — att inget som helst tvivel, oklarhet eller
frågetecken finns i samband med funktionssättet: ATA/CAT-teorin håller streck. Absolut.
Se explicit POSITRONFRÅGAN
— den helt avgörande i slutänden.
— Se särskilt ZambiaTGF:en som belyser TNED-teorin i positronbildningens ljus
— och som ansluter till helhetsbilden (detaljen med motsvarande positronbildning) särskilt för
folieurladdningsteorins del. Teorin kan, veterligt, inte bli mer enhetlig än
så.
— Avsaknaden av direkta experimentella bevis för
positronförekomst (gammastrålning) i folieurladdningarna är ändå det som
framträder mest, och också det som med påfrestande intensitet verkar motsätta
sig experimentell inspektion:
— Det är här inte ens känt på vilket sätt
en t.ex. gammamätning skulle kunna genomföras i folieurladdningsfallet.
— OM teorin för parannihilationer i det
speciella CAT-fallet är riktig [Blixturladdningens fysik, resumé med gammastrålningens
uppkomst], måste varje strålmätning bli
komplicerad (omöjlig) eftersom strålningen (teoretiskt idealt HELT) dämpas
ut/absorberas inom planskiktet.
— I vidare begrundan av denna
experimentellt deprimerande låsning (Mar2013), infann sig plötsligt en alldeles
strålande lösning, i varje fall teoretiskt. Se särskild beskrivning med
fotografier i CATtestMar2013:
— OM man låter katodstiftet nudda vid
en foliekant, måste — tvunget — ljusbulan och hela urladdningsområdet blotta
ett urladdningshål i formen av (idealt) en halv cirkel — och därmed drömläge
för ett regelrätt gammatest: luften på kantens ovansida ligger fri för
inspektion. Det BORDE gå. Vi återkommer när och om resultat visar sig.
Ingenting kommer därför att stå slutgiltigt säkert förrän
sådana bevis framkommer, hur enhetlig, glänsande och överväldigande teorin än
är i övrigt.
— Som en ytterligare bekräftelse på
teorin för folieurladdningarna kom resultaten av de första fotografierna [Urladdningslådan] av glödspåren [utgångshastighet 800.000 M/S]:
aluminiumpartiklar från hålbildningen kolliderar alldeles tydligt med
luftmolekyler [500 M/S]. Se ImpulsKALKYLgrund för aktuella värden.

BILDKÄLLA: Författarens arkiv · 2Feb2013 Bild Serie1En10_7 · Nikon D90 ·
Exponeringstid 1/10 S · Bländartal F/20 · ISO 400,
— Här framgår tydligt hur glödpartiklar
(Aluminiumoxid, Aluminiumnitrat) stöter emot något — luftmolekyler — som ändrar
rörelsebanan i vissa (många) fall högst dramatiskt.
— Kretskopplingens RC-konstant är
T=(1KΩ)(100µF)=0,1S, samma som exponeringstiden i bilden ovan.
— Det garanterar det uteslutet att glödspåren
i bilden skulle vara en följd av flera, successiva urladdningstillfällen.
ETT FOTODOKUMENT [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
MED DET FÖRTYDLIGANDET kunde en
grundräkning anställas [ImpulsanalogiernaKALKYL]
på rörelsemängdens kredit (som
möjliggör en tämligen snäv bestämning av partikelmassorna med kännedom om
luftens parametrar [LuftBASIC]);
— Alldeles entydigt, med hänsyn till
den synliga mängden glödspår, är deras energibidrag försumbart. Därmed styrks
(ytterligare) energiräkningen med grundteorin enligt TNED att aluminiumatomerna avdelas ur
det kretsbrytande urladdningshålet
från urladdningstillfället PER atom, och därmed fullständig giltighet för
energiräkningen.
En viss reservation finns naturligtvis alltid hos varje seriös
experimentator, tills mera rådata framkommer: huruvida en viss praktik
verkligen HAR en viss teori som relevant förklaringsgrund. I detta fall finns
här veterligt inget känt insteg till något ifrågasättande (än) — men vi letar
alltid efter uppslag.

BILDKÄLLA: Författarens arkiv · 14Mar2013 BFConst2b
Bild3 · Nikon D90.
JFET-mätningarna med tillhörande mätinstrument och anordningar. Se särskilt
från JFET-sensorn.
— Se XUcoAlFEDU, Anordningen Dec2012.
Den på sitt sätt mest viktiga och
avgörande aspekten i ett SÄKERT EXPERIMENTELLT PÅVISANDE av fenomengrunderna i folieurladdningarna — och därmed hela
teorin bakom blixturladdningens och ljusbågens fysik genom ATA/CAT enligt TNED
— är HURUVIDA de synliga partikelfragmenten i glödspåren i själva verket skulle
utgöra så stora massdelar att teorin
Hålbildningen — AlFU
— hålbildningen anställs av
aluminiumfolieatomernas avdelande ur hålet PER atom via en jonisationsprocess
som baseras på ATA(ljusbågsfysiken)/CAT(atomkärnans upplösning med positronbildning som
grund), vilket grundlägger energiräkningen —
HELT kan avskrivas. Därmed skulle INTE
heller den framlagda energiräkningen gälla. Och därmed adjö till
energiproblemets lösning, i varje fall enligt TNED.
— IMPULSANALOGIN
i ljuset av mängden experimentellt observerade — fotografier — ger efter vad
som kan utläsas i mängden glödspår ett entydigt besked på den punkten:
Massdelen som upptas av glödpartiklarna i glödspåren är så mycket mindre i
förhållande till massdelen i hålbildningen att glödspårens massdel helt kan
bortses ifrån. Det var också vad som låg på bordet från början (2005). Men då
ingen mera exakt dokumentation fanns på området, fanns heller ingen grund för
någon mera definitiv slutsats.
Se utförligt från Impulsanalogierna.
ABU • LB • AlFU — SE
ÄVEN FRÅN INLEDNINGEN
|
Atmosfärisk BlixtUrladdning [ABU] |
LjusBåge [LB] |
AluminiumFolieUrladdningarna [AlFU] |
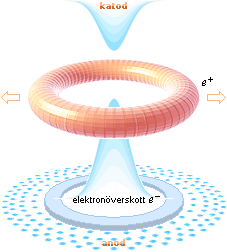
ELEKTRONÖVERSKOTTET I ANODDELEN bilden ovan höger
— omsättningen i folieurladdningarna: laddningsmängden [Se INDUKTANSARGUMENTET] för funktionssättets och energiräkningens sammanhängande enhet och förklaring som FAKTISKT frigörs och adderas till materiefysiken och som tidigare INTE fanns »uppackad» där, illustrationen ovan höger från Urladdningsförloppet
— är den del Q0(e–) som direkt från elektrodatomernas atomkärnor dras ner till anoden via en försumbar region av elektrodområdet (6 T11 Al-kärnor från [1,5 T16]/[27×918] eller grovt runt 1/24700 av hålmaterialets primära atomstock) för att säkra kondensatorns urladdningsenergi E0.
— Själva överskottet i netto i hela urladdningsproceduren läggs — emellertid — på katoddelen som inte tillåts föra tillbaka den föregående uppladdningsmängden till kondensatorn på grund av kretsbrottet via hålbildningen. Coulombattraktionen mellan katodöverskottet och det efterföljande urladdningsområdets starkt joniserade luftatomer utjämnas emellertid i slutänden, som det får förstås [POTENTIALARGUMENTET], och efterlämnar en helt neutral, restladdningsfri anordning.
— Formuleringen explicit av denna (avgörande) detalj i funktionssättet har tidigare inte framställts i Universums Historia. Här ges den mera fullständiga beskrivningen/upplösningen; Alla tre ovan nämnda fenomenformer lyder, tydligen, ATA-karaktäristiken enligt TNED — men den begreppsgrunden står (vad vi vet) orepresenterad i den moderna akademins lärosystem.
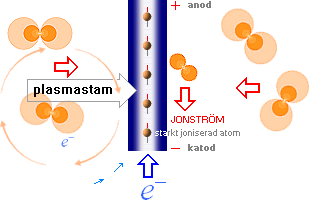
ABU: Atmosfärisk BlixtUrladdning
— Molnlokalen berikas på negativ laddning via Solljusets inverkan (vattnets avdunstning från Jordytan), i tidens längd; Potentialen Moln (minus) och Mark (plus) utjämnas då blixturladdning sker, och Marken återfår sin minusdel via Blixtstammens CAT (enligt TNED); det kvarvarande överskottet på elektroner i luftdelen, rekombinerar med blixtstammens yttre joniserade luftatomer som då neutraliseras (själva blixtljuset).
— Därmed är laddningsbalansen återställd till exakt ursprunglig jämvikt: noll spänning.
LB: LjusBåge
— Centralstammens absolut joniserade atomkärnor regleras [enligt TNED] enligt ATA av strömstyrkan i ljusbågen; Omgivande luftatomer berövas sina yttre elektroner sekundärt via centralstammen som drar elektroner till anoden. De så passivt joniserade moderatomerna bildar en jonström [barkström] — den enda fysiskt möjliga mätbara delen — mot katoden där de återfår sina elektroner: Barkströmmen fortsätter så länge ljusbågsspänningen är aktuell.
— Därmed är laddningsbalansen återställd till exakt ursprunglig jämvikt: noll spänning.
AlFU: AluminiumFolieUrladdningarna
— När Urladdningskondensatorn i EXPERIMENTKOPPLINGEN laddas upp (från 12V till 24V), leds (1,5 T16) elektroner från kondensatorns anod till dess katod: I anoddelen uppkommer ett underskott (1,5 T16 st.) på elektroner och ett lika stort överskott (1,5 T16 st.) på elektroner i katoddelen, separationen elektroner mellan anod-katod bildar den uppladdade kondensatorns spänning (24V); När urladdning inträffar bryts kondensatorkretsen vid katodstiftet: elektronöverskottet på katodsidan ges aldrig tillfälle att återlämnas till anodsidan på grund av det starka strömdraget som bränner av kretskontakten med följd i uppkomsten av ett hål; Anoddelen får istället tillbaka sin elektrondel (1,5 T16 st.) via CAT — atomkärnans upplösning [närmast anodmaterialets aluminiumatomer] med positronbildning och lokal parannihilation som [i förening med det millimeterlokalt närmaste luftområdet] garanterar [via elektronrekombinationer] ljusbulans centrala jonisationsområde och från vilken lokal glödspåren utgår [Glödspåren från ljusbulan]; det starkt luftjoniserade området utövar motsvarande Coulombisk attraktion med [kontakten via katodstiftet i] den avsnöpta katoddelens elektronöverskott (1,5 T16 st.); katoddelens tidigare avsnöpta elektronöverskottet kan därmed fritt rekombinera med det närliggande starkt joniserade luftområdets atomer [Se LJUSBULAN] strax utanför aluminiumfolien, i hålbildningens anslutning. Därmed — som det får förstås — återlämnas katoddelens (avbrutna) elektronöverskott till luftjonerna.
— Därmed är laddningsbalansen återställd till exakt ursprunglig jämvikt: noll spänning.
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Teorin i MAC, hålbildningen — AlFU
I modern
akademi [MAC] finns ingen ATA/CAT-fysik:
— Enda
tvivelslösa möjligheten att åstadkomma och påvisa återställd laddningsbalans
efter urladdning — elektronrestladdningar lika med noll — är att kondensatorkretsen
ges tid att ladda ur på vanligt konduktivt konventionellt sätt — FÖRE
hålbildningen — vilket garanterar bibehållen elektronbalans.
— Men: Även för
fotfolket i MAC torde följande stå utomordentligt klart: Kondensatorn kan inte
urladda på något vanligt sätt OM nu kretsen — som förklaringsgrunden har visat
sig i folieurladdningarna — verkligen är bruten via ett
uppkommet HÅL;
— OM
kondensatorn ska ladda ur på vanligt sätt måste
urladdningen ske FÖRE hålbildning.
— Antar vi den
möjligheten till prövning återstår frågan varifrån — då — energin till
hålbildningen ska komma, sedan kondensatorn laddat ur. Nämligen i ljuset av
Konsekvensen att — då — heller ingen energi finns tillgänglig.
— Det scenariot
är, naturligtvis, helt uteslutet i praktisk fysik.
— Enda,
logiska, rationella och relevanta fysiklösningen till det dilemmat är, här
veterligt, att
1. hålbildningen föregår
kondensatorns urladdning (kan inte förklaras eller beskrivas i MAC) och därmed
2. att
kondensatorns urladdning tvunget blir av typen icke konventionellt-konduktiv
natur (kan heller inte förklaras
eller beskrivas i MAC), eftersom ingen sammanhängande ledning finns
etablerad mellan kondensatorelektroderna ±.
— Den
möjligheten ligger, här veterligt helt, utanför den moderna akademins teoretiska
ramar — den kräver en helt annan bild av speciellt kärnfysiken (massfysik) än den nu förhärskande (materiefysik). Nämligen TNED. Den delen är alltså utesluten i MAC.
— Enda —
kufiska — möjligheten i MAC skulle då vara
— i ljuset av
att hålbildningen, tvunget, måste föregå urladdningen, samt oaktat händelsen
med ljusbula och glödspår
— att en
elektronrestladdning på kondensatorns katodsida (i MAC utan förklarlig anledning) kvarlämnas,
garanterat av hålbildningens kretsavbrott;
— OM den elektronrestladdningen
DESSUTOM INTE ska kunna påvisas efter en folieurladdning, måste den, tydligen,
på något sätt rekombinera med den resultatmassa som verkar i
urladdningstillfället.
— Men det leder
oss tveklöst samtidigt in på fysik- och hela fenomenförklaringen enligt TNED: ljusbulan med bildningen av
glödspår och de utspridda aluminiumatomerna från hålbildningen.
— Om vi går
potentialvägen baklänges, skulle situationen i netto före
elektronrestrekombinationen (katoddelens
elektronöverskott från kondensatorns uppladdning) vara att en
motsvarande positivt joniserad atombank finns i närheten: ett något, som
följaktligen bildats genom någon form av elektroneliminering ur den bankens atombesättningar.
— Frågan
varifrån en sådan elektroneliminering skulle härstamma är i termer av modern
akademi höljt i djupt mörker, och är tydligen förbehållen endast TNED: i MAC
har den frågan inget svar: Kondensatorns anod återfår sin elektronmängd — inte via katoddelens
elektronöverskott från uppladdningen, utan — via
elektroner som dras från urladdningsstammens atomer/atomkärnor (ATA/CAT) — enligt exakt samma
fysikgrunder som i fallet med atmosfärisk blixturladdning (marken återfår elektroner via
blixtstammen, molnelektronöverskottet överförs till stammens yttre jonområden,
luften, i form av själva blixtfenomenet) och ljusbåge (luftatomerna som joniseras vid anoden
och återfår sina elektroner vid katoden), och som i CAT-fallet
blottlägger atomkärnornas positrondelar, och vilka positrondelar sedan ansvarar
för elektronreduktionerna via parannihilationer (med utdämpning av
gammastrålning via Comptoneffekten [ATA-karaktäristiken] och den speciella
planvågsform som tydligen också kan tillämpas i förklaringen av det speciella
TGF-fallet [ZambiaTGF:en]),
och därmed den urladdningsstället omgivande luftens jonisation: luftjonerna(+)
elektronrekombinerar med elektronrestladdningen på katodsidan(–). Förklaringen
beskriver tydligen perfekt enhetlighet utan frågetecken. Exakt. Noll
frågetecken.
— Möjligheten i
MAC att någon elektronrestladdning på
kondensatorns katodsida skulle kvarstå efter en folieurladdning
— i anledning
av att ingen (uppfattning i MAC
finns angående) exakt balanserad omsättning i rekombinationer finns
mellan (det i MAC, här veterligt) oförklarliga jonisationsförloppet (ljusbulan
+ glödspåren) och elektronrestladdningar på katodsidan i följd av kretsbrottet
via hålbildningen
— skulle kunna vara ett speciellt föremål för direkt experimentell uppmätning [JFET-sensorn].
— TNED för sin del — exakt laddningsbalans —
utsäger att ingen som helst restelektronladdning i så fall ska finnas efter en
eller flera eller hur många som helst folieurladdningar.
Motsvarande utsaga i MAC har ingen, här
veterligt, uttalad litterär (eller annan) referens till den detaljen, och
därmed heller ingen säker teoretisk status.
— Mätningarna —
med hundra miljoner gånger större känslighet än den aktuella
elektronrestladdningen — visar ingen elektronrestladdning efter
folieurladdning. Laddningsharmonin och jämvikten bevaras, tydligt.
CAPföreHålet — från AlFU
Frågan om kondensatorns urladdning FÖRE hålbildningen, explicit:
Möjligheten att felgrunder
skulle finnas i ATA/CAT-teorin — Se även i Händelsekonstanten T
—
Kretsresistansen (10mΩ) [EXPERIMENTKOPPLINGEN] sätter en gräns
för kondensatorns urladdningstid via tidskonstanten [KONDENSATORN OCH SPOLEN]
RC=T=(10t3)(100t6)=1t6=1µS:
— En
elektronmängd (1,5 T16)
måste tydligen finnas tillgänglig för transport åter till kondensatorn för dess
urladdning via anodmassans ledningsmaterial. Är emellertid kretsen entydigt
bruten via ett uppkommet hål, finns ingen sådan återförande elektronmängd
DIREKT närvarande; I konventionell mening, alltså utom TNED,
finns då heller ingen fysisk möjlighet för kondensatorn att verkställa en
urladdning.
— Alternativet
— det som förefaller ligga närmast — skulle då vara att kondensatorn urladdas
FÖRE hålbildningen, enda här veterligt återstående fysiska alternativet, att
alltså hålbildningen uppkommer först efter ca 1 µS. Oaktat övriga aspekter på
den möjligheten, finns en speciell aspekt som stänger vägen;
— Om
kondensatorn via sin energi (E=UQ=[Q/C]Q=Q²/C=LI²)
har laddat ur finns uppenbarligen ingen närvarande energi på vars kredit en
hålbildning — kretsavbrott — skulle kunna uppkomma, inkluderat ljusbula och glödspår.
— Därmed
framstår kondensatorns urladdning såsom förmodad FÖRE hålbildningen HELT
utesluten.
— Jag (för min
egen del) vill ÄNDÅ inte utesluta »till synes omöjliga alternativ». Men så
länge alternativen inte har annat att erbjuda än fragment av ev. underliggande
helhetsförklaringar som helt lyser med sin frånvaro, har heller de enskilda
invändningarna inget DIREKT övergripande värde.
Tills någon ALTERNATIV (begriplig)
helhetsbeskrivning framkommer tillsammans med de olika (förmenta)
»förklaringsalternativen» (typ, ’kondensatorn urladdas före hålbildningen’), är
det tydligt att den nu, enligt TNED, aktuella
helhetsbilden perfekt beskriver alla tre fenomengrunder (ABULBAlFU) utan frågetecken. Det är DEN
INBÖRDES ENHETLIGHETEN i dessa fenomens naturförklaring, och beskrivning, som
(i varje fall för TNED:s vidkommande — sanningsbegreppet och dess
konsekvenser) är den avgörande detaljen: Finns det en enhetlig beskrivning,
utan frågetecken, finns självklart ingen anledning att förkasta den harmonin
till förmån för partikulärt ifrågasatta partier som (för tillfället) inte kan
uppvisa någon sammanhängande bild. Men också det gäller ju: Vi VET ännu inte
säkert. SÅ: I princip finns ALLTID möjligheten att någon mindre bemedlad
argumentflisa åstadkommer att hela ekipaget välter och försvinner ut i
intighetens tomheter. Det är alltid den RISK vi får leva med så länge ingen
absolut visshet finns på bordet. Dörren står alltid öppen i Universums
Historia.
Alla ovan beskrivna tre fenomenformer inbegriper och baseras på samma PotentialArgument — samma enhetliga, principiella funktionsfysik:
—
enhetligheten i ljusbågsfysiken, atmosfäriska blixturladdningen, CAT
ingen känd fysikalisk process finns som via en fri (ledande)
utbytesväg kan hindra ett neutraliseringsförlopp mellan potentialskillnader i
närliggande positiva och negativa områden: finns en sådan skillnad, sker ALLTID
en utjämning, snabbare eller långsammare.
Se RÄKNEEXEMPEL via konventionella samband
i koppling till urladdningsexperimenten.
Formuleringen ovan
är alldeles densamma som i Kirchoffs första kretslag:
— Alla strömflödesvägar, kontinuerliga eller avbrutna,
summerar noll elektrisk potential: FINNS FLÖDE GÄLLER OVILLKORLIGEN ATT
inströmmar = utströmmar;
laddningar som flödar utåt = laddningar som flödar inåt;
summan av alla
krafter och moment i atomkärnan är noll. Se Atomfysikens
två Kungsekvationer i TNED.
Det betyder SPECIELLT i de (med våra naturjordiska mått mätt) NATURSTYRDA urladdningssammanhangen, att ingen elektronrest kan förekomma efter urladdning: inte i området, inte i anordningar, inte i mätinstrument, med andra ord: inte alls över huvud taget;
Ingen elektrostatisk restladdning kan bildas som
följd av naturligt utlämnade urladdningsförlopp.
Satsbilden har avgörande betydelse för hela teorins övergripande enhetlighet [ABU-LB-AlFU] med speciellt tillämpad mätkontroll i samband med folieurladdningarna via JFET-sensorn. För den resultatredovisningen, se JFET-mätningarna.
För kontroll av energiräkningen generellt i urladdningsexperimenten, se speciellt från Impulsanalogierna.
Glödspåren tycks utgå från ljusbulan
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Nedan finns ett särskilt fotografi som tycks visa att glödspåren (i varje fall i en del fall) utgår från ett område utanför urladdningsfolien i glödspårens framriktning och som förefaller uppvisa en rätvinklig orientering mot urladdningsstiftets längsutsträckning:
— Genom att urladdningsstiftet befinner sig längre bakåt/inåt är det tydligt att orten för glödspårens ursprung i detta bildfall entydigt är den längre fram befintliga ljusblåvita ljusbulan — inte någon geometrisk vägsträcka som börjar på urladdningsstiftet.

BILDKÄLLA: Författarens arkiv · 2Feb2013
Serie2En5_002 · NIKON D90 · Bländartal:
F/20 — Exponeringstid: 1/5 S — Filmkänslighetstal ISO: 400
— Se även fotot i AlFUglödRef som mera tydligt visar ett exempel på ett glödspår som utgår från ljusbulan: glödspåret som sträcker sig bakåt, inåt i urladdningslådan, bakom urladdningsspetsen.
HÄNDELSETIDSKONSTANTEN (T) MED KAPACITANSENS HALVERING OCH INDUKTANSENS REDUKTION
Förtydligande från Tidsschemat
— folieurladdningsexperimenten, se Experimentanordningen
— Den avgörande brytpunkten ges vid a (se kopierad bild nedan Kapacitanserna i serie).
Sambandsformen generellt ges från kondensatorlagen
U = TI/C
= Q/C
= RI ;
R = T/C ;
RT = T2/C
= L
= µs ;
LC = T2 ;
T =
10pS = 10 t12 S; T² =
1 t22 S²
med koppling till energin (E) [sambanden i syntes i FYSIKENS ALLMÄNNA FÖRKLARING] enligt
E = UQ ; 2453 J
= RI·Q
= RI·IT
= RT·I2
= LI2
= L· I2T2/T2
= LQ2/T2 ; Q=1,5 T16 e ~= 2,4 t3 C; L = (2453 J)(1 t11 S)²/(2,4 t3 C)² = 4,26 t14 H
= PT
= UIT ;
— Vid kretsavbrottet (a), fullt uppladdad kondensator, har kondensatorns anod ett underskott (–Q) på N = 1,5 T16 elektroner och kondensatorns katod ett motsvarande elektronöverskott på lika mycket. Ingenting kan ändra den bilden i och med — och försåvitt korrekt fysikbeskrivning — kondensatorkretsen också verkligen är bruten genom det uppkomna hålet i urladdningsögonblicket.
— Laddningsbilden för den kommande urladdningens jämvikt i den situationen är alltså alldeles precis densamma som att en elektronladdningspotential på N elektroner tvunget måste ligga färdig i anslutning till anodmassan för att därmed tillföras kondensatoranoden, och en lika stor mängd N i kondensatorkatodens massdel.
— Men urladdningsvägen sådan den var vid uppladdningen är bruten och visar — alltså — följande laddningsfördelningsschema med hänsyn till den brutna kretspunkten, hålbildningstillfället:
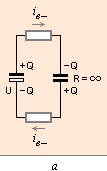
— Två lika laddningsmängder (UC=Q) i gemensamt strömflöde (urladdningsflödet, utan hänsyn till annat) kan skrivas
U = (U=Q/C)/2 + (U=Q/C)/2
Det betyder, uppenbarligen, att varje skänkel för sig, och därmed själva den faktiska urladdningskondensatorn, avkänner ett halverat spänningsvärde som sin slutprodukt, delsambandet ovan (U=Q/C)/2. Kretskondensatorn och den motstående, »fiktiva» eller tillfälligt bildade avbrottskapacitansen uppvisar samma fason.
Försök till djupförklaring
———————————
Delningen av Q via avbrottspunkten i två lika halvor
— en elektronöverskottsdel i katoddelen som inte längre kan nås av kondensatorn för urladdningsprocessen, och en elektronunderskottsdel i den också av avbrottspunkten isolerade anoddelen och vilken del måsta återtas via anodmassans bidrag
— innebär uppenbarligen också en reduktion till hälften av urladdningsspänningen: U/2 = (Q/2)/C.
— Men den matematiken [RCbasic] är alldeles densamma som i fallet för två seriekopplade, lika stora kapacitanser:
C = (1/C1 + 1/C2)–1 ; C1 = C2 = C12 ;
C = C12/2
Avbrottet skapar en kapacitansreduktion (C12/2) som yttrar sig i en reducerad urladdningspotential (U/2). Nämligen i försorg av att den verkliga fysiska kretskondensatorn aldrig får tillfälle att ladda ur som den laddades upp.
NOTERA vår EGENTLIGA svårighet här, i orsaksbeskrivningen:
— MATERIEFYSIKEN har
ingen här känd motsvarande fenomenform att jämföra med.
— Hela ämnet berör massfysik [ATA/CAT], och den finns inte (uttalat)
representerad i den moderna akademins lärosystem.
Halva spänningen återlämnas i två skilda sekvenser: den ena till kondensatorn via elektronstocken i anodmassans gnisturladdningsväg (CAT), och den andra återlämnas [POTENTIALARGUMENTET] via katodstiftets kontakt med den omgivande luftens positivt joniserade atomer.
Genom laddningsökningen (Q) i produkten av energi (E) och händelsetidskonstant (T), ET2=LQ2=konstant, tvingas induktansen (L) i händelseförloppet reduceras — samma som att den med induktanshändelsen associerade kapacitansen — inte den fasta elektroniska kapacitansen som sådan, märk väl — tvingas öka enligt sambandsformen LC=T2=konstant händelsetid: avtar L, ökar C (LC=T2=konstant), analogt Q (ET2=LQ2=energihändelsekonstant). Nämligen med en extra, avbrottstillagd kapacitans [Kapacitanserna i Serie], lika med den redan givna fasta (C=Q/U).
— Exakt räkning på händelsetillfällets LC-komponenter ges i Räkneexempel.
— En FÖRMODAD kapacitiv motsatsbild, »C ökar» och »C=C12/2» (’C avtar’) finns alltså inte; Förklaringen är bara den att hålbildningen genom sitt kretsavbrott bildar en tillfällig induktiv-kapacitiv koppling mellan den fasta elektroniska kondensatorn i experimentkopplingen och den tillfälliga avbrottskapacitansen som, nytillkommen, konserverar katoddelens elektronöverskott (tills detta utjämnas i kontakt med den urladdningslokalt omgivande luftens joner) och hindrar detta överskott från att nå den fasta kretskondensatorn.
— Hur komplicerad bilden än är, är denna typförklaring den här enda kända (djupform) som finns: Den tecknar en enhetlig förklaringsbild utan frågetecken.
Editor2013III18
Induktansen i urladdningstillfället (t[IGN]=10pS)
RÄKNEEXEMPEL:
— Genom sambanden i Händelsekonstanten T ges induktansen (L)
Q =1,5 T16 e
~ 2,4 t3 C ;
L = ET2/Q2
= (2453 J)(1 t11 S)²/(2,4 t3 C)²
= 4,26
t14 H ;
Via induktionslagen [u=L(di/dt)] fås motsvarande makroekvivalenta induktionsspänning (materiefysikens begrepp) i urladdningsstammen enligt
u = L(di/dt)
= (4,26 t14 H)([2,4 T8 A]/[10pS=1 t11 S])
= 1 022 400 V ;
Återräkning för energin via de 1,5 T16 elektronerna ger
E = UQ
= (1 022 400 V)(1,5 T16 · 1,602 t19 C)
= 2456,8272 J
Det är samma energivärde (2452,83744 J) som i energiräkningen [Elight] (skillnaden kommer från avrundningarna).
— Om vi jämför en konventionellt beräknad rakledarinduktans för urladdningsvägen
InduktansKalkylator för Rakledare enligt konventionell teori finns på webben i
The Inductance of Your
Electrode!
http://www.consultrsr.com/resources/eis/induct5.htm
Värdena man får fram kräver en del (di/dt)-elektronik för att kunna testas [enligt Kirchoffs kretslagar [INDUKTIONSLAGEN], u=L(di/dt)], från U=RI=RTI/T=L·I/T. Jämför f.ö. grundteorin:
1. ”The algebraic sum of
currents in a network of conductors meeting at a point is zero”;
”At any node (junction) in an
electrical circuit, the sum of currents flowing into that node is equal to the
sum of currents flowing out of that node”
2. ”The algebraic sum of the
products of the resistances of the conductors and the currents in them in a
closed loop is equal to the total emf available in that loop.”,
@INTERNET
Wikipedia, Kirchoff’s circuit laws [2013-03-20]
http://en.wikipedia.org/wiki/Kirchhoff's_circuit_laws
— Speciellt är Kirchoffs andra kretslag
(U=RI) I RELATERAD FYSIK samma som »POTENTIALVANDRINGSLAGEN»:
alla
spänningsfall från plusmatningen till minusmatningen summerar noll.
ges värdet (genom hela aluminiumfoliens tjocklek 0,017 mM, samt via tvärsnittet för en Al-atom grov 2,5 Å)
s = 0,017 mM
Ø = 2,5 t10 M
= 2,5 t7 mM
= 0,00000025 mM ;
Lkonv = ”0.0399961199738997 nH”
~ 0,04 t9 H
Det senare värdet är (0,04 t9 / 4,3 t14) = 930,23255 ggr högre än makroekvivalentens värde via induktionslagen.
— Enligt TNED måste också makroinduktansen tvunget reduceras kraftigt (»nollas») för att urladdningstillfället ska bli av, se Energigrunderna i CAT.
— Notera dock »den korrumperade induktionsmatematiken» i MAC: Det finns ingen jämförande grund mot den relaterade fysikens begrepp.
— Se särskild exempelsamling som beskriver sammanhangen i Tre Exempel.
— För induktionsbegreppet i vidare mening (djupanalysen), se INDUKTIONSBEGREPPET I RELATERAD FYSIK.
Meningsfullheten i ovanstående kommer fram först om vi har någon praktisk anordning att testa teorivärdena på. Webben har (här veterligt efter genomsökning 21Mar2013, »straight conductor inductance, experimental test») ingen direkt uttalad sådan i fallet rakledare. Jämför:
”The first dilemma which Rosa faced is that there is no unambiguous definition of how to define the inductance of a straight wire.”,
INDUCTANCE
OF A STRAIGHT WIRE — Tim Healy, Santa Clara University
http://www.ee.scu.edu/eefac/healy/indwire.html
Det är (med andra ord) ’grymt’ att [2013] försöka få någon klar uppfattning i ämnet experimentellt uppmätta induktansvärden för givna rakledare med utbudet av den moderna akademins begrepp, och försåvitt något alls finns gratis tillgängligt med Webbens hjälp.
ElectronRESET — Återställning av elektronbalansen — AlphaLAB
Återställning av elektronbalansen
— Restladdning i både metaller (snabbare) och isolatorer (långsammare, i vissa fall inte alls), neutraliseras i kontakt med luften, vilket redan är välkänt i etablerade kretsar:
ALPHA LAB INC — Electrostatic Effects
[14Mar2013-03-14]
http://www.trifield.com/content/electrostatic-effects/
”… the ion-enriched air will generally have a conductive time constant of a second or less, and is thus capable of discharging any charged object rapidly.”.
Fuktighetens inverkan — ElectronRESET
— Inverkan av lokal fuktighet påskyndar neutralisationsförloppet:
”Paper and cardboard [sv, papp] are slightly conductive, and are better conductors if the humidity is high.”,
AlphaLAB — Electrostatic Effects, Overview
Källan hänvisar i länk (”There are formulas for the number of ions, discharge time, and resistivity of air.”) till annat avsnitt som beskriver samband för neutralisationstiden:
ALPHA LAB INC — Electrostatic Effects —
[14Mar2013-03-21]
— Formulas for discharge by air ions (or by
immersion in a fluid), ion imbalance, charge plate detector
http://www.trifield.com/content/electrostatic-formulas/ -
8
”Discharge by air ions or fluids: Air is very slightly conductive if ions are present. (See About Air Ions). Generally, both + and - ions are present in air, and the two polarities can co-exist. Each polarity is measured separately, in terms of number of + ions per cc (cubic cm) and number of - ions per cc.”,
;
”Call "N" the lesser of the number of + ions per cc or - ions per cc.”,
;
”The resistivity of air is approximately Resistivity = 6×1018/N, in units of ohm cm.”,
;
”If a compact object, like a sphere or cube, is in air or a fluid, the discharge half-life time (in seconds) is approximately
T1/2 = 2×10–13 × resistivity of the air or fluid (in ohm cm).”,
;
”Therefore in air, T1/2 = 1.2×105/N, due to ions.”,
;
”Discharge by air (or by dipping into a grounded fluid) can remove all charge on a surface, including an overall charge imbalance (self-discharge by an object due to its own conductance can redistribute charges over its surface but cannot "bleed off" a charge imbalance of excess + or - unless the surface is connected to ground.) Dipping a charged insulator in water will immediately remove all surface charge.”
AlphaLAB, Räkneexempel — i området picosekunder — från AlphaLAB
RÄKNEEXEMPEL — de aktuella 1,5 T16 Al+1-jonekvivalenterna omsatt på den omgivande närmaste luftkuben med sidan ca 1mM som ger volymen 0,001 (cM)³ utanför urladdningsfolien:
— Vi tillämpar sambandet ovan från AlphaLAB med 1,5 T16 positivt laddade luftjoner per kubikcentimeter, N=(1,5T16/0,001cc)=1,5T19/cc, i närheten av katodstiftet som står i kontakt med uppladdningsöverskottet på lika många 1,5 T15 elektroner på den avbrutna minussidan:
T1/2 = (1,2 T5)/([1,5 T16]/[0,001 (cM)³])
= (1,2 T5)/(1,5 T19)
= 8 t15 S = 8 fS (åtta femtoSekunder)
1,5 T16 elektronladdningar har drygt 53 halveringar (53,735812 = ln[1,5 T16]/ln2) ner till praktiskt taget noll — 253=9,00719 T15 — vilket skulle betyda en totalt (ideal) neutraliseringsperiod på drygt 53 halveringsperioder eller
T = 53× 8 t15 S
= 4,24 t13 S eller 0,424 pS
Det finns här (med nuvarande utrustning) ingen möjlighet att studera något experimentellt (motsvarande) mätvärde (Vi har fullt sjå med att få fram experimentdata enbart i mikrosekundområdet).
— Exempelräkningen visar emellertid på huvudsaken: återställningen är snabb.
I det praktiska urladdningsexperimentet med katodstiftet, spelar (förmodligen) kontaktgeometrin viss roll, vilket (möjligen) ger en något längre period: »i området picosekunder».
BILDKÄLLA: Författarens arkiv · Kollage
NikonD90 · FÖRSOMMAR:RF24Maj2010VikBild133·VÅRVINTER:R16Apr2010VikBild201


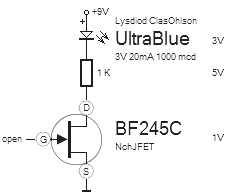
BILD43 1Nov2012 Nikon D90
— Anordningen i arbete via 9V-batterimatning med det enkla
kopplingsschemat till höger (se Webbreferenser)
— här (ovan) med den maximalt korta JFET-gateAntennen — en senare version
inkluderar JFET-transistorn monterad i en separat en skärmad prob [JFETgnd] som ansluts i den ovan
provisoriska antennens ställe.
— Anordningen har i efterhand byggts på med en OnOFF-enhet,
samt anslutning för 9V-batterieliminator (med särskild omkopplare för val av strömkälla).
Dessa detaljer beskrivs inte här explicit, och har heller ingen betydelse för
JFET-sensorns mätfunktion.
JFET-mätningarna klargör fenomenets allmänna
enhetlighet
INGEN RESTLADDNING KAN PÅVISAS EFTER FOLIEURLADDNINGARNA — VILKET i relaterad mening STADFÄSTER URLADDNINGSTEORINS ALLMÄNNA ENHETLIGHET, se speciellt från Blixturladdningens fysik, resumé med gammastrålningens uppkomst
Särskilda mätningar (20Mar2013) med JFET-sensorn gjordes speciellt för att kolla ev. effekter med sensorantennen precis i närheten av urladdningspunkten:
— Mätningar gjordes dels i framriktningen i glödspårens utsträckning, och dels rätvinkligt dessa, samt både på framsidan och baksidan (inuti urladdningslådan) av urladdningsfolien.
MÄTRESULTAT:
— Enda synbara effekten vid urladdningsögonblicket var OM
— vilket med JFET-sensorns exceptionella känslighet
är mera regel än undantag på grund av (typiskt) statisk elektricitet i kläderna
man har på sig och som JFET-sensorn (lätt, via visarutslaget i spänningen över 1K-motståndet) känner
av i centimeterrörelser —
det fanns något litet visarutslag (typisk minus 0-0V5 från toppvärdet 5V0, se JFET-sensorn) i spänningen över sensorkopplingens 1K-motstånd:
— Vid urladdningsögonblicket (alla testade urladdningsindivider) gick visarutslaget (inom några sekunder) upp på prick toppvärdet: samma som en motsvarande »elektronreststädning» i området: urladdningen neutraliserar (effektivt) all elektrostatisk obalans i närområdet. I övrigt ingen reaktion.
12Mar2013
Den avgörande experimentella
undersökningen
[JFET-sensorn] HURUVIDA ATA/CAT HAR VERKLIG PRAKTISK FYSIKALISK GRUND
Vad ska JFET-mätexperimentet gå ut på?
————————————————————————————————————————————————
— Att påvisa eventuella laddningsrester i området efter folieurladdning. Finns sådana, är teorin definitivt körd.
— Vad visade mätningarna?
— Helt rent. Inte ett liv.
Den avgörande experimentundersökningens syfte är helt enkelt att påvisa — eller inte påvisa — en elektronmängdsrest (1,5 T16 e–) i anordningens omedelbara närhet, efter varje urladdning.
Fram till hit (2012-13) fanns ingen bestämd uppfattning om HUR en dylik
mätning av ev. elektronrester skulle kunna genomföras:
— Gammastrålningseffekten [Se Gammastrålningens uppkomst genom Blixturladdning] är i teorin ytterst svåråtkomlig (se TGF-exemplet från Zambia, enligt TNED samt ATAKARAKTÄRISTIKEN: gammastrålningen
dämpas ut internt effektivt via Comptoneffekten), och därmed utesluten som kandidat för att på något praktiskt
genomförbart SÄKERT sätt kunna avgöra funktionssättet (med de enklare medel som i princip ligger öppna för var och
en). Däremot erbjuder närvaron av extra elektrisk laddning ett fullt
praktiskt möjligt mätobjekt — här, tydligen, med väl tilltagna marginaler via
den känsliga JFET-komponenten [BERÄKNINGSEXEMPEL].
Med vidare undersökningar har ett praktiskt mätinstrument konstruerats [ESLT] — och som därmed tar viss
huvudroll i denna presentation.
SENSORKRETSEN som används för att mäta närvaron av elektroner visas utförligt i ELEKTROSTATISK LADDNINGSSENSOR — med utförlig apparatkonstruktion och beskrivning i Konstruktionen.
Förberedelser för aktuell mätning:
0. MÄTOMRÅDET
KONTROLLERAS MAXIMALT NOGA före varje nytt försök för eliminering av varje
möjligt påvisande av elektrostatisk laddning som inte hör till
experimentanalysen:
— Flera olika sätt finns för att »rena området elektrostatiskt»; En fuktad
Wettexduk (köksdiskduk) som får beröra olika påvisade elektrostatiskt aktiva
materialpartier (trä, plast, textilier) har visat sig besitta en reducerande
eller helt elektrostatiskt utjämnande funktion.
— Det viktiga här är att eliminera alla tänkbara möjliga felkällor i omedelbar
anslutning till experimentanordningen och som sedan längre fram kan luras eller
falsktrigga på grund av (lömska) gömningar (som, möjligen, kan vara svåra att upptäcka med en gång);
1. KOPPLINGSPINNEN [JFETGND]
— som nollställer JFET-sensorn
och ställer denna i vänteläge — insätts först, före varje ny urladdning, och
tas sedan inte bort förrän en ny urladdning har verkställts:
— Detta moment är inte helt nödvändigt:
villkoren uppfylls i vilket fall om U[RJFET] visar fullt utslag (5V0) före varje urladdning;
2. Efter verkställd urladdning
inspekteras dels urladdningslådan
(UL) och urladdningskondensatorn (UK, konstruktionen
i översikt) [samt
allt övrigt närliggande] genom att föra JFET-sensorns Gate-antenn i
olika närrörelser invid objekten: JFET-sensorn ger [Okt2012] enligt Inledande
Test utslag för (i varje fall gott och väl) runt T8
elektroner [PENSELDRAGET],
vilket är mer än hundra miljon gånger mindre fri elektronmängd än den (1,5 T16
e–) som här enligt TNED-teorin (ATA/CAT) ligger på katodsidan
omedelbart före hålbildningen i urladdningsögonblicket [EXPERIMENTKOPPLINGEN]
— OM överskottsladdning finns (som ansluter till ATA/CAT), FÖREFALLER
den detaljen absolut omöjlig att missa.
— Därav, som här förmodas, det omöjliga i att missa mätresultatets avgörande i
status — för hela ATA/CAT-teorin; JFET-sensorn får därför
(här) uppfattas som en »SuperUltraEnormKänslig» sensorkropp — omöjligt att
missa;
Hur JFET-sensorn reagerar på ±e
Överskott på e(–):
— Dras ett objekt med e(–)-överskott bort ifrån JFET-sensorn är den induktiva verkan [NewtonIII] att samma mängd e-laddning med samma polaritet i JFET-sensorn lägesändrar åt motsatt håll: elektroner [e(–)] strömmar inåt i JFET-Gate:en — samma som att positiva laddningsbärare [e(+)] strömmar utåt i JFET-Gate:en, samma som positiv ström ut ur JFET-Gate:en: JFET-transistorn går mot ett alltmer strypt tillstånd (–5V):
OFF-läge.
Underskott på e(–):
— Dras ett objekt med e(–)-underskott bort ifrån JFET-sensorn är det samma som att en motsvarande e(+)-laddning i samma lokal lägesändrar åt motsatt håll:
— Dras ett konventionellt strömobjekt e(+) bort ifrån JFET-sensorn är det samma som att en motsvarande e(+)-laddning i JFET-lokalen lägesändrar inåt i JFET-lokalen:
— Den induktiva verkan [NewtonIII] blir i detta fall — bort från JFET-sensorn — att positiva laddningsbärare strömmar inåt i JFET-Gate:en — samma som att negativa laddningsbärare strömmar utåt i JFET-Gate:en: positiv ström flödar inåt i JFET-Gate:en: JFET-transistorn går mot ett alltmer öppet tillstånd (0V-högre):
ON-läge.
InledandeJFETtest — Mätningarna inleds — 14Mar2013
Vi testar allra först HUR eller OM JFET-sensorn reagerar på manuella upp- och urladdningar av urladdningskondensatorn;
— Tyristorkopplingen med den induktiva Touch-switchen [INDUKTIVATouchREF] verkställer uppladdningen, och en separat kabelkoppling med ett 1K-motstånd verkställer urladdningen [Den delen skulle här egentligen också ha varit en Touch-komponent — men den visade sig inte fungera [med den aktuella experimentlokalens förutsättningar]]. Vi får samtidigt se om eller hur JFET-sensorn reagerar på de (minimala) armrörelser som måste utföras för att verkställa Touch- och 1K-anslutningen:
INGEN RÖRELSE MELLAN JFET-SENSORN OCH URLADDNINGSKONDENSATORN:
— Det visar sig (första observationerna) att JFET-sensorn
— med analoga mätinstrumentet inkopplat för maximal koll (instrumentet visar +5V med JFET-sensorns lysdiod i full ljusstyrka)
— inte tycks reagera alls på urladdningskondensatorns uppladdning via tyristorkopplingen, eller urladdningen via 1K-motståndet; Bägge dessa besitter f.ö. samma tidskonstant RC=T=(1K)(100µ)=0,1S.
— Däremot visar JFET-sensorn utslag i minskning av sensormotståndets (1K) spänning från max 5V: spänningen avtar marginellt ner mot 4V via armrörelserna (mina kläder och deras marginella elektronladdningsöverskott spelar in, vilket JFET-sensorn känner av [lätt som en plätt]) i samband med Touchberöringarna.
— Dessa variationer är emellertid små, och ingen motsvarande ändring syns i JFET-sensorns UltraBlå lysdiod. För att skillnad ska ses i lysdiodens ljusstyrka, måste spänningen över sensormotståndet avta ner mot runt 1-2 Volt. Det är också vad vi skulle förvänta OM det skulle finnas runt T16 separat frigjorda elektronmassor i närheten — förutsatt någon rörelse genomförs mellan dessa, antingen av JFET-sensorn eller anordningen.
RÖRELSE MELLAN JFET-SENSORN OCH URLADDNINGSKONDENSATORN — via långsam vridning av assistenten som JFET-sensorn sitter på:
— U[RJFET] varierar 4V6 - 5V05 med minimal förflyttning (långsam vridning av Assistenten som håller JFET-proben) av JFET-sensorn alldeles nära den TÖMDA (0V5) urladdningskondensorn.
— Vid/efter TouchUppladdningen vandrar U[RJFET] ner till 4V4 och sedan långsamt upp mot 5V0 igen — men det kan (som sagt) bero på den marginella närvaron av min armrörelse med textilierna som jag bär.
— Samma typvridning på Assistenten nära den nu fullt uppladdade urladdningskondensatorn (24V7) ger här ett något mindre utslag: U[RJFET] varierar 4V8 - 5V0 — som också i princip kan hänföras till de rörelsemoment jag måste genomföra via min textilbeklädda arm för att vrida Assistenten (och dess koppling till kabelhärvorna i närheten av hela anordningen).
Alla dessa variationer är emellertid av underordnad betydelse: Som vi har sett av de inledande testerna — JFET-sensorns lysdiod slocknar helt med ändring av runt T8 elektroner i JFET-sensorns närhet — skulle T16 elektroner, hundra miljoner gånger mer, i närheten definitivt och avgjort få lysdioden att slockna om sensorn lägesändrar något.
Därmed behöver vi inte längre och mera göra flera försök på separat manuell upp-och urladdning av urladdningskondensatorn för att SÄKERT veta att dessa visserligen är förknippade med smärre variationer i JFET-sensorns utspänning, men att dessa är helt försumbara vid sidan av huvudmålet för mätningarna;
Resultat:
Huvudmätningarna — resultaten MED gnisturladdning
Huvudmätningen
Ingen reaktion. Inte livet.
Där flög resterna av den slutliga TNED-kraschens fiktiva reservkrafter ner i mörkrets avgrunder — och de lär nog heller aldrig mer, någonsin, visa sig igen: Insteg till verksamma ifrågasättanden mot ATA/CAT enligt TNED saknas: Jag känner inte till några — men det vore intressant (och berikande) om det alls existerar några att visa upp. Visa. Please.
— U[RJFET] varierar ungefär som ovan i den manuella förtestningen — samt något (0V5) just via urladdningstillfället (vilket vi redan vet gäller i alla typer av snabba laddningsförlopp, den delen saknar här betydelse).
— Urladdningsförloppet överrider f.ö. den tidigare införda tyristorkopplingen, och kondensatorn laddas i vilket fall omedelbart upp efter varje urladdning:; Vi kopplar bort tyristorkopplingen (kondensatorn får serieuppladda bäst den vill via sitt därmed något högre toppvärde [26V5] — ju flera, desto bättre underlag för mätdata):
— Efter upprepade folieurladdningar står resultatbilden omisskänneligt klar:
— JFET-sensorn beter sig som om ingen som helst extra elektronladdning kommer till i samband med folieurladdningarna.
Helt rent.
Inte en flämtning.
Inte minsta lilla.
— JFET-sensorn har förts omkring i närheten av alla tre huvudkomponenter: Urladdningskondensatorn, Urladdningslådan, De tre 9V-batterierna på tät rad. I samtliga dessa fall lyser JFET-sensorns UltraBlå lysdiod med full pedal.
Med andra ord:
ALLMÄNT OTVETYDIGT MÄTRESULTAT:
— Ingen nämnvärd extra elektronmassa synes tillkomma
i området efter verkställda folieurladdningar, varken efter enstaka eller
flera.
9V-batterierna innehåller ett smalt område i höljet på ena
långsidan som visar på en rätt stor restelektronladdning — även ett helt
(gammalt, flera år) urladdat dito
— En kraftig e–-laddning visade sig (strax
efter mätningarna ovan) i det smala utrymmet mellan 9V-batterierna (en extra koll, bara i förbigående):
Hastig dragning utåt med JFET-sensorn, bort från batterierna, nollade —
parkerade — mätvärdet (0V) samt släckte sensorlysdioden helt. Fullt mätvärde
U[RJFET]=5V0 visades sedan efter (runt) ett par, tre
minuter.
— De tre PHILIPS ALKALISKA 9V-batterierna uppvisar på sin minussida i höljesbottnen på ena långsidan en (märkbar) elektronmassa i överskott: När JFET-sensorn skjuts in där, eller bara berörs via det vita Gate-höljet, tänds sensorlysdioden, och släcks när JFET-sensorn dras ur.
— Test på ett fristående typ ENERGIZER 9V-batteri visar samma fenomen: ett elektronöverskott finns i batterifoten på negativa långsidan: Sensorlysdioden tänds vid JFET-sensorns rörelse in dit, och slocknar vid utåtrörelsen.
— Ytterligare test på ett gammalt (sedan länge, flera år urladdat) PHILIPS-9V-batteri visar samma fenomen.
Genom att återhämtningstiden verkar vara förhållandevis kort (några minuter) är det via grovräkningen INTE fråga om någon större mängd (i dekader ungefär samma som i exemplet med PENSELDRAGET [Penselelektronladdningen]):
Q = U·T/R
= (5V)(120S)/(2,5
T12 Ω)
= 2,4
t10 C;
= UC ; Se exempelräkningen i PenselElektronLaddningen
N = Q/(e=1,602 t19
C)
= 1,49812
T9 elektroner ; det observerade elektronöverskottet i fotsidans minusdel hos
9V-batterier — alla fabrikat
DÄRMED FÖREFALLER RESULTATET AV HELA MÄTUPPGIFTEN ENTYDIGT KLART:
Ingen som helst direkt påvisbar, signifikant, elektronmassa i överskott finns i testanordningen efter folieurladdningarna enligt den ytterst känsliga JFET-sensorns utslag (JFET-sensorn avkänner [LÄTT] hundra miljoner gånger mindre fri elektronmassa än den katodelektronrestladdning [1,5 T16 e–] som folieurladdningen i ATA/CAT-teorin förutsäger).
Resultatbilden därmed i full enlighet med ATA/CAT-fenomenformerna:
— TNED-teorin (även i detta sublima fenomenområde) verkar vara svår att hitta verkliga angreppspunkter på.
— ATA/CAT verkar vara en med naturfysiken helt överensstämmande beskrivning;
— Inget här [Mar2013] känt insteg finns som visar på något enda ifrågasättande — men vi letar alltid efter avgörande motbevis.
Impulsanalogierna — Kalkyl — ImpulsKALKYLgrund
— Första fotot [Gtrack1_001.JPG]
(2Feb2013) med
den nya kamerasynkade urladdningsenheten [koAFUE (XUcoAlFEDU), koordinerad AluminiumFolieUrladdningsEnhet]:
BILDKÄLLA: Författarens arkiv · CATfeb2013· 2Feb2013 Bild
Gtrack1_1 — NikonD90 · ISO: 400; Bländartid: 1/2 S; Bländartal: F/20
SKALMÅTTEN SKILJER SIG MED KAMERADJUPET:
Skalan underst ovan mätt med urladdningslådans front
som referens (katodspetsen 10 mM
innanför denna referens);
Skalan överst motsvarar ungefär samma intervall 20
mM inåt i bilden (katodspetsen
10 mM framför denna referens).
— Glödspåren ser »renare ut»: färre till antalet, starkare
per, större skillnad mellan långa (50mM) och korta (10mM).
— Vi vet inte närmare orsaken till dessa smärre variationer
relativt den föregående HELT manuella matningen. Vidare analys följer.
Se separat
beskrivning i XYcoAlFEDU (XY-coordinated Aluminium Foil Electric Discharge Unit)
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Bevisen för CAT-räkningarnas rimlighet (31Dec2012)
En vidare beskrivning (Jan2013) baserad på nya observationer
(Dec2012) från fotografier av folieurladdningarna.
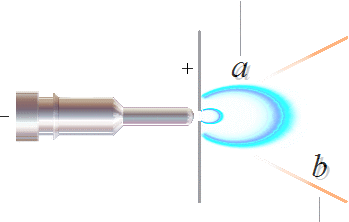
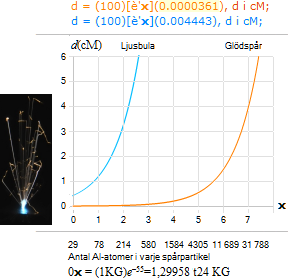
— Bägge fenomenområdena LJUSBULA(a) och GLÖDSPÅR(b) kan beskrivas med förutsatt teoretisk grund i PER FRIGJORD ALUMINIUMATOM med samma grundsamband (d=mv/R — Se HÄRLEDNINGEN);
— I fallet glödspåren visas mer
eller mindre direkt fullträff med spår som framträder på fotografi (spårlängd, kollisioner med
luftmolekyler — motsvarande fotobas — bilder
på webben— icke joniserade partiklar
finns veterligt inte i den nu kända litteraturen, ehuru många exempel finns på
typen Browns rörelser [rökpartiklar, pollen];
— Foton på enskilda kollisioner mellan en partikel [större, typ tusentals atomer, runt Ø5nM] och lufthavets molekyler finns här veterligt inte alls i den etablerade litteraturen; förekomster har eftersökts I DET GRATIS TILLGÄNGA WEBBUTBUDET Dec2012 — genomsökning på GoogleImages »particle collisions, air» m.fl. — men ännu inte påträffats).
— Grundsambandet ger samma resultat i netto som i den tidigare beskrivna »impulsvolymen» [(vAl/vLUFT)min = xyz(30/2,55)3] [Exakta Energiräkningen 2008II3].
Se utförligt med sammanställningen nedan i BESKRIVNING.
Impulsanalogierna — KALKYLGRUNDERNA [Kalkylkortet] — Inledning
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
a: d = mv/R: Omsättningen [osynlig] i området i och omkring ljusbulan — KubImpulsAnalogin
b:
d = mv/R: Glödspåren och deras partikelagenter: Linjära IMPULSANALOGIN — se Impulsanalogin
(a): Primärt plasmaområde — snabb
kemisk rekombination
på minimal distans — Kemiska MEDELkubImpulsAnalogin
(b): Sekundär bildning i glödspår — långsam
kemisk rekombination
på maximal distans — Impulsanalogin — glödpartiklarnas
totala antal ska i TNED-teorin vara försumbart mot huvudmängden som omsätts
enligt (a).
FOTOT
VÄNSTER BILDKÄLLA: Författarens arkiv · Spark2012main· 16Dec2012 Bild
Ljusbula003 — NikonD90 · ISO: 2000; Bländartid: 1/2 S; Bländartal: F/20. Anodmaterial: 0,017mM Aluminiumfolie, i övrigt samma
kopplingsbild som i CAT-experimenten. Ljusbulans utsträckning ca 3-5mM. Spårlängderna
grovt 1-3 cM.
NOTERA
i detta fall att den tillgängliga kondensatorenergin är 0,0216 J enligt den
härledda sambandsformen E(cap) = U²C·3/8. Se utförligt i Kondensatorenergin. Det är bara ca 70%
av ovanstående med hänsyn till det uppmätta urladdningshålets 3,22 T16
Al-atomer i förutsättningen om
deras utgivning i aktiv jonisationsenergi PER atom — att bevisas vidare.
(a) Ljusbulan — PLASMATISK HÖGENERGIBILDNING:
Kemiska
MEDELkubImpulsAnalogin ...................... (vAl/vLUFT)min
= xyz(30/2,55)3
(b) Glödspåren — Lokal elekektronrekombination som bildar en mindre mängd större atomgrupper, glödpartiklarna
Impulsanalogin
........................................................ d = mv/R
Beskrivning — Impulsanalogierna
BESKRIVNING
I Inledningen till Exakt energiräkning i ATA/CAT-dokumentet (2008II3) genomfördes en energiberäkning för folieurladdningarna grundad på »impulsvolym» enligt (från Al-atomens rymd till slutstationen med luftmolekylens rymd, energin för att förklara den utvidgningen)
(mv·V)ALUMINIUM = xyz(mv·V)LUFT ................. Volymformen
Via den sambandsgrunden kunde sedan primärenergin (475 J) grovberäknas enligt E=mv2/2.
Men:
— Hur VET vi (säkert) att den formen har någon RELEVANT koppling till ämnet?
Med grovt lika molekylära atommassor (mAl/mLUFT), samt medelatomavståndet 2,55Å för Aluminium och 30 Å för luftmolekyler, gavs sambandet
(vAl/vLUFT)min = xyz(30/2,55)3 ....................... Kemiska MEDELkubImpulsAnalogin
= 1628,3329
~ 1628
Med luftmolekylernas medelhastigheter i rumstemperatur på ca 500 M/S skulle motsvarande utgångshastighet för en Aluminiumatom från folien bli
vAlmin = vLUFT · 1628
= 500M/S · 1628
= 814.000 M/S
— Hur rimlig är den räkningen?
Vi känner (f.n.) ingen motsvarande teknisk applikation till jämförelse som skulle kunna ge vägledande upplysning:
— Atomer som utgår ur, eller avdelas från, ett material PER joniserad atom (vilket är den teoretiska, fortfarande obevisade, teorin bakom fenomenbeskrivningen enligt TNED och som hela framställningen är ägnad att testa, undersöka och pröva) har, här veterligt, ingen motsvarande känd teknisk beskrivning; Sambandsformen ovan (Kemiska MEDELkubImpulsAnalogin) är unik för materialändringen i folieurladdningen. Dvs., »det finns ingenting att jämföra med» — enligt här kända referenser.
— Vi kan kontrollera rimlighet och visshet genom att
volymformen (verkligen) kopplar (säkert) till en enklare linjär (»endimensionell»)
impulsanalogi.
— Med den nyligen uppmärksammade IMPULSANALOGIN (b) har en jämförande, förklarande, bild visat sig.
Nämligen så:
— Volymformen, värderesultatet, kan återföras på den linjära impulsformen — exakt samma kalkylform — bara med justeringen att beräkningen avser EN Aluminiumatom på en matchande energi (435 J) som ska ge stoppvärde över små distanser (millimeter eller deras bråkdelar: ljusbulans plasmaområde);
— Det faktum att den resultaträkningen visar RIMLIGA d-värden
d = mv/R ; RLUFT = mv/s = (28,24u)(500 M/S)/(0,1µM=1 t7 M) = 2,34 t16 NS/M
= (27u·804303 M/S)/(2,34 t16 NS/M)LUFT
= 0,154085 mM
är ett (indirekt, eller möjligen direkt) bevis för att impulsräkningen är analog och konsistent med volymformen.
Teorin:
— De högjoniserade Al-atomerna i området kring den plasmatiska ljusbulan rekombinerar snabbt med den omgivande luftens molekyler, inom ett sfäriskt område med radien runt 0,15 mM. Impulsanalogin kräver för det energin drygt 400 J (435 J), med resulterande initialhastighet drygt 800.000 M/S (804303 M/S) för Al-atomen.
— Matematiken (kalkylkortet) för glödspåren är EXAKT densamma. Enda skillnaden är att deras ANTAL per glödpartikel är högre (1000-50000) — dessa Al-atomer (kan förstås) strömmar/flödar till (med sammansmältning till större, tillsammans med luftmolekyler — totalt i större grupper med typ AluminiumOxid Al2O3 och AluminiumNitrid AlN) från urladdningshålets periferi i efterklangen av den häftiga centrala omsättningen — och därmed också deras hastigheter lägre (5-15000 M/S).
— ENERGIERNA PER PARTIKEL — den enskilda Al-atomen i fallet (a), gruppen Al-atomer tillsammans med luftmolekylerna som glödpartiklar i fallet (b) — är i bägge fallen (enligt kalkykortets resultat) i stort sett lika: runt 1,5-2,0 t14 J (94-125 KeV).
IMPULSANALOGIN SPECIFIKT FÖR GLÖDSPÅREN per fotografi [ImpulsanalogiernaKALKYL] visar särskilt beräkningsgrundens rimlighet:
— Det faktum att glödspåren slutar med tydliga, abrupta, avvikelser, visar att glödpartiklarna stöter emot — vad vi har förstått de enda tillgängliga kandidaterna — luftmolekyler, och därmed beräkningsgrunderna för impulsanalogin; Glödpartiklarna slutar på långsamma (millimeterlånga) medelrörelser (låga medelhastigheter, ental cM/S) i sammanstötningen med de omgivande luftmolekylerna (500M/S, samma rörelsemängder netto);
— Resultaten är samstämmiga med fotografiernas glödspår: längderna (b) i de mest synliga spåren varierar grovt 1-3 cM.
TEORIN — generellt för glödspår:
All bildning av glödspår utgår ifrån (kan återföras på) att ett material i det avskiljande snittet berövas en del av sin elektronbesättning (den sammanhållande materialkraften): materialets hållfasthet reduceras, grupper av atomer lämnar materialet i motsvarande joniserade (»starkt upphettade») partier. Exakta metriska data saknas här.
— SÄTTET med avverkning kan dock variera: från enskilda atomer till grupper (täljning med sammansmältning) från korn till större bitar.
— Beskrivningen (Dec2012), detaljerad, av processen verkar i princip vara helt orepresenterad i den gratis tillgängliga litteraturen på webben. Många beskriver fenomenet med glödspår från verktygsslipning (Skyddsföreskrifter, verktygsmanualer, spårkaraktärer för olika stålsorter [eng., spark testing]). Men ingen verkar ha någon detaljerad (direkt synbar på webben) teori om verkningssättet — utöver ”det är järnet som brinner i luften”.
Glödspåren (Järn) är lika (CAT-experimenten kontra webbdokument), men
energierna i avverkningen skiljer (10-100
ggr); materialavverkningsdimensionerna är inte analoga, men ljusbilderna
är det;
— TEST MED STARKA MAGNETER NÄRA ANODSTÅNGEN (18Dec2012; Järn mot Neodymmagneter [finns på Clas Ohlson], mycket starka) visar ingen som helst effekt (avböjningar som funktion av ev. jonisationer i strålpartiklarna). OM det verkligen håller streck, betyder det att VARJE TÄNKBAR teori om »strålpartiklarna som joniserade» kan avskrivas.
”Consequently, most commercial explosives are organic compounds containing -NO2, -ONO2 and -NHNO2 groups that, when detonated, release gases like the aforementioned (e.g., nitroglycerin, TNT, HMX, PETN, nitrocellulose).[1]”,
http://en.wikipedia.org/wiki/Explosive_material
@INTERNET Wikipedia — Explosive material [2012-12-18]
I närheten av materialytan på en neodymmagnet — Ø32mM, lyftkraft 31 KG (Clas Ohlson 2012) — är (största) magnetiska fältstyrkan (B) drygt 1 Tesla [Wikipedia 2012-12-18 http://en.wikipedia.org/wiki/Neodymium_magnet, ”The compound also has a high saturation magnetization (Js ~1.6 T or 16 kG) and typically 1.3 teslas.”];
— Med sambandet r = mv/BQ
[från MAGNETISKA KRAFTLAGEN F=BQv; Fr=BQvr; BQr=Fr/v=mår/v=m(v2/r)r/v=mv]
skulle en e-laddning (1,602 t19 C) med hastigheten 1 M/S (ett sämsta fallets lägsta värde) och massan hos en Aluminiumatom (27u~4,5 t26 KG) uppvisa en krökt bana med radien r ~ 2,8 t7 M = 0,00028 mM: spåret skulle vara så kraftigt avböjt att det inte ens skulle synas.
— Test med ett par handhållna neodymmagneter i absoluta närheten av gnisturladdningsanordningen (Järn, Aluminium) uppvisar ingen som helst tendens till avböjning hos glödspåren. Absolut ingen som helst synbar eller märkbar ändring framträder i jämförelse med urladdningarna då de studeras utan magneternas närvaro.
Därmed står det klart bortom allt vidare tvivel, att
glödspåren INTE sammanhänger med joniserade partiklar — annars, för övrigt, en
bekväm teori som utan magneternas hjälp är ytterst besvärlig (nära omöjlig, som det ser ut)
att befria sig ifrån.
ParticleSizeData
http://www.epa.gov/apti/Materials/APTI%20435%20student/Student%20Manual/Chapter_4_noTOC-cover_MRpf.pdf
— Se
från ImpulsanaloginBASIC
• ImpulsanalogiernaKALKYL
Impulsanalogin — härledning
UPPSLAGET FÖR SAMBANDET TILL DEN (här) BENÄMNDA
IMPULSANALOGIN är i min referens från ett Utvecklingsexempel i Lennart
Brandqvist 1962 ITK 9 — Differentialkalkyl s96 — Fisk som slutar simma och då glider en stoppsträcka d i vattnet. Härledningen nedan enligt
nomenklaturen från NOLLFORMSALGEBRAN
i UniversumsHistoria.
Härledningen — enligt nomenklaturen i Derivata, Differential- och Integralkalkylen i UniversumsHistoria: se utförligt från NOLLFORMSALGEBRAN om ej redan bekant — Se särskilt från Allmän klassifikation av varianter.
ACCELERATIONSKRAFTEN (FACC=ma) på vilken partikeln (P) får sin begynnelsehastighet (v) motsvaras av en lika stor men omvänt riktad retardationskraft från det material (R) som P genomfar, FRIKTIONEN (P)
P = FFRIC = FT/T = p/T = [p/x]x/T
= Rx/T
Det ger ekvationen (varianten)
FACC + FFRIC = 0
= m(d 2s/[dt]2) + R(dx/dt)
som beskriver tillståndet då P helt har stannat.
Med s=x och dx/dt=b är TRANSFORMEN (konv. karaktäristiska ekvationen) till ovanstående andra ordningens homogena linjära variant [konv. andra ordningens homogena linjära differentialekvation] (accelerationen a=d 2s/[dt]2=[ds/dt]’’) lika med
mb’’ + Rb’ = 0
mb2 + Rb = 0
b2 + (R/m)b
= 0 ; transformen
Transformens lösning (se andragradsekvationens lösning [andra ordningens homogena linjära variant]) är (reella, olika rötter)
b = –([(R/m)]/2) ± [ Ö([(R/m)]/2)2]
= –R/2m ± R/2m ;
b1
= u =
–R/2m + R/2m
= 0 ;
b2
= v =
–R/2m – R/2m
= –R/m ;
Hela variantens lösning [Jämför Tablån
för lösningarna till Homogena Varianter] med u=b1 och v=b2 och exemplets variabel t för den allmänna variabeln x
i beskrivningarna och motsvarande x för y,
x = Ceut + Devt
blir då
x = Ce0t + De–(R/m)t
= Cu + Cve–t(R/m)
Bestämning av koefficienterna CD:
— Då partikeln (P) uppnår begynnelsehastigheten (v) vid t=0 VID inträdet till mediet (R) är också x=0:
x(0) = C + De–0(R/m)
= C + D ;
D = –C ;
x = C – Ce–t(R/m)
= C(1 – e–t(R/m))
— Partikelns utgångshastighet v=x/t=dx/dt vid t=0 fås ekvivalent ur ovanstående genom derivatan [Se även utförligt i FORMLAGARNA]
v = dx/dt = [C(1 – e–t(R/m))]’
= C(0 – –[t(R/m)]’e–t(R/m))
= C[R/m]e–t(R/m) ; t=0 ger e–t(R/m) = 1 ;
v(t=0) = C[R/m]
Därmed koefficienten C enligt
C = mv/R
LÖSNINGEN TOTALT därmed
x = (mv/R)(1 – 1/etR/m)
R-faktorn bör bero på
partikelstorleken hos m i förhållande till partikelstorleken i R.
— Det finns f.n. här ingen allmänt känd formalia att referera till i den
matematiken.
— En hållpunkt är att
tillåta översiktliga beräkningar upp till gränsen för
R-partikelmedelavståndet (s) — då det är tydligt att
m-partiklar större än detta (s) möter allt mera
impulsmotstånd per längdmeter i R.
— Sista termen 1/etR/m kan bortses ifrån OM etR/m är mycket större än 1.
Vi studerar det.
TIDEN FÖR LJUSUTVECKLINGEN [LJUSTIDEN] I GLÖDSPÅREN har redan (preliminärt) uppmätts via fotokomponenten till (max)
t = 0,1 mS =1 t4 S. Med luftens impulsmedelmotstånd (R=mv/s) för normal luft vid 20°C gäller
RLUFT = mv/s = (28,24u)(500 M/S)/(0,1µM=1 t7 M)
= 2,34 t16 NS/M
.................. molekylära
medelimpulsmotståndet per spårmeter för normal luft vid 20°C
För olika (relevanta, möjliga) mängder Aluminiumatomer (U=27u) som agenter för glödpartiklar (P) gäller
m = ρV
= (2700 KG/M3)(k=PartikelKubsidan)3 ;
Tabellen nedan ger några värden för vägledande översikt:
k m N=m/Uu 1/etR/m, t=0,0001 S
— —— —— ——
1 2,7 60 0
10 27 000 60 000 0,000169
100 2700 0000 60 000 000 0,991
k PartikelKubsidan i nM,
Partikelmassan m i t24 KG, N antal atomer i P
Beräkningarna enligt d=mv/R för de möjliga glödspårslängder om max 3cM som gäller i folieexperimentet (b) visar via d=31,27 mM ett största antal Al-atomer N=25.000, motsvarande en Al-kub med sidan 7,46 nM. Det är (omkring d) den experimentellt observerade maxgränsen.
— Det är också på gränsen till precisionen som kan antas UTOM e-faktorns närvaro; För större partiklar måste den, uppenbarligen, tas med. Se även nedan vidare i JämförandeGRAFER.
I andra änden — ljusbulan — gäller å andra sidan bara räkningen för EN enda Al-atom (m=27u=4,48 t26 KG). TIDEN för den utvecklingen är här inte närmare känd, frånsett att den bör vara betydligt kortare än tiden (0,1µS) för glödspåren.
— ÄVEN om vi använder samma tidsfaktor för detta fall, t=1 t4 S, ges likväl inverterade e-faktorns värde praktiskt lika med 0.
— För att e-faktorn ska visa någon påverkan måste t-faktorn här minskas ner till runt t=1nS; e-faktorvärdet inverterat blir då 0,00534. Ännu kortare t-värden ökar (drastiskt) på e-faktorn; t=0,1nS ger inverterade e-faktorvärdet 0,593.
— Vi kan jämföra LINJÄRT med den beräknade utgångshastigheten v=814000 M/S vis t=1nS;
— vägen blir d=vt=0,000814 M = 0,814 mM. Det är drygt 5ggr längre än resultatsträckan via grundformens d=mv/R=0,15 mM (via E=435J och v=804303 M/S).
— Om utgångshastigheten är drygt 800.000 M/S och sluthastigheten i storlek som luftmolekylernas medelhastigheter (500 M/S vid 20 °C, normal luft) bör också hela vägtiden vara (betydligt) större än optimala linjära vägtiden.
— Den resultatbilden antyder, om relevant, att t bör ligga just vid 1nS eller längre.
— Vi skulle därmed, för samtliga fall ljusbulan och de synliga glödspåren kunna använda det förenklade slutsambandet (d=x)
d = mv/R
Distansen (d) som
partikeln (P) med massan (m) och begynnelsehastigheten (v) färdas med i mediet
med friktionen (R) innan P smälter samman med (stannar i) R
Används e-faktorn, kan t-värdet lösas (om x-värdet är känt, endast) enligt
x = (mv/R)(1 – 1/etR/m) ;
x(R/mv) = 1 – 1/etR/m ;
1/etR/m = 1 – x(R/mv) ;
etR/m = [1 – xR/mv]–1 ;
tR/m = ln[1 – xR/mv]–1
= ln[1 – x/d]–1 ;
t = (m/R)ln[1 – xR/mv]–1
NOTERING 1: Är xR/mv lika med eller
större än 1 ges irrelevant logaritmvärde: e-logartimen för 1/0,999… =1,000…1
går mot noll, och därmed t mot noll.
NOTERING 2: Är tR/m (beräkningen av x) större än flyttalslängden [Se exv.
OpenOfficeKALKYL] visas typ #NUM! för e^tR/m
motsvarande obegränsat; för dessa fall gäller det enklare d = mv/R direkt.
Graferna nedan visar de teoretiska spårlängderna enligt den enklare IMPULSANALOGIN (d=mv/R). Fotografiet till vänster i vertikalskalan [FotoGlödspår] är inlagt i ungefärlig motsvarande skala. Ytterligare foton krävs för att få en mera precis uppfattning om ljusbulans (genomsnittliga) dimensioner [instrumentell utformning pågår (Jan2013) för anpassning till fotografering för större bildmängder — se XYcoAlFEDUöversikt].
Glödspåret orange
graf (variabel partikelmassa via
t = 0,1µS och v=6500 M/S):
y = (100)x(6500)[1/(2.34[10^–16])](1–1/è^(0.0001)(2.34[10^–16])/x)
x(m)MIN = [1(10^–24)] ~= è^–55 ;
y i cM (y ggr 100):
y = (100)[è^–55+x](6500)[1/(2.34[10^–16])](1–1/è^(0.0001)(2.34[10^–16])/[è^–55+x])
y = (100)[è^–55][è^x](6500)[1/(2.34[10^–16])](1–1/è^(0.0001)(2.34[10^–16])/[è^–55][è^x])
y = (100)[è^x](0.0000360995)(1–1/è^(0.0001)(2.34[10^–16])/[è^–55][è^x])
x = (100)[è^x](0.0000360995)(1–1/è^(18005.797)/[è^x])
d = (100)[è'x](0.0000361), d i cM;
Ljusbulan
graf (variabel partikelmassa via
t = 1nS och v=800000 M/S):
y = (100)[è^–55][è^x](800000)[1/(2.34[10^–16])](1–1/è^(0.000
000 001)(2.34[10^–16])/[è^–55][è^x])
x = (100)[è^x](0.00444301)(1–1/è^(0.1800579)/[è^x])
d = (100)[è'x](0.004443), d i cM;
Översiktlig jämförelse
x e^– m, t24 KG N(Al) [m/27u] s(AlKUBsida) [V=s3=m/(ρAl=2700 KG/M3)], nM
0 55 1,3 29 0,8
1 54 3,5 78 1,1
2 53 9,6 214 1,5
3 52 26 580 2,1
4 51 71 1584 3,0 luftmolekylmedelavståndet [större friktion:]
5 50 193 4305 4,1 större än luftmolekylmedelavståndet
6 49 524 11 689 5,8 större än luftmolekylmedelavståndet
7 48 1425 31 788 8,1 större än luftmolekylmedelavståndet
8 47 3874 86 417 11,3 större än luftmolekylmedelavståndet
9 46 10531 234 915 15,7 större än luftmolekylmedelavståndet
10 45 28625 638 539 22,0 större än luftmolekylmedelavståndet
Motsvarande grafer via x-sambandet visas nedan till jämförelse.
Glödspåren
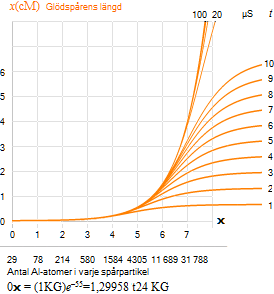
Ovan: De orangea graferna visar hur x-sambandets TEORETISKA funktion framträder mera tydligt via kortare ON-tider för glödspåret. Referensvärdet i det praktiskt uppmätta fallet är 0,1mS (orangea toppgrafen, 100 µS [LJUSTIDEN]) från de inledande mätningarna.
— Notera också (den uppenbara) möjligheten vid växande partikelstorlek: Ju större glödpartikeln blir — större träffyta — desto större blir den omgivande luftens impulsmotstånd per längdmeter. För växande glödpartikelstorlekar (större än luftmedelmolekylernas medelavstånd, ca 3 nM) bör därför kurvskaran ovan böja av alltmer mot x-axeln. Dvs., spårlängden bör avta från en viss kritisk gräns (ca x=5). Vi vet dock här inte närmare hur [Se i UtvidgningTVÄRSNITT — x-sambandets formgraf ovan].
— Vi kan därför räkna med att antalet Al-ekvivalenter i det aktuella glödspåret kan vara 10-200 ggr större än det som antyds av grafbilden ovan för (runt) x=6 [AAl/ALUFT=(rAl/rLUFT)2].
Frågan om antalet glödspår behandlas vidare i UtvidgningTVÄRSNITT.
Ljusbulan
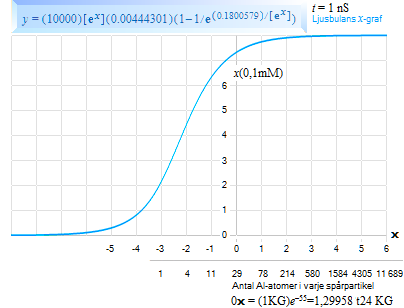
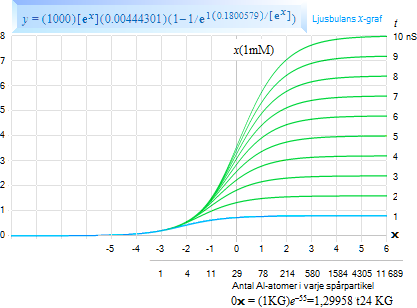
Mera exakta mätdata på ljusbulan (tidrymden) saknas ännu — enda svårigheten i den änden är (i princip) att få tag på fotokomponenter med korta stigtider [helst i området pS] (arbete med försök att utforma olika lösningar pågår).
— Ovanstående grafer visar (mera ingående) hur (väl) x-formens samband stämmer med den ursprungliga »impulsvolymanalogin»,
[(vAl/vLUFT)min = xyz(30/2,55)3] [Exakta Energiräkningen 2008II3].
— Det beräknade värdet i det senare fallet kräver (via energikvoten v2=2E/m) en begynnelsehastighet (v) på i storleksordningen 800.000 M/S. Då Ljusbulan i vilket fall inte sträcker sig ut i rymden mer än högst några millimeter, måste partikelstorleken (per »radiell ljusemission» [ett hypotetiskt ljusspår i den lilla ljusbulan], idealt) vara motsvarande liten jämfört med de längre glödljusspåren: Med tidsbilden för ljusbulans bildning i storleksordningen nS (1 t9 S) ges som i graferna ovan en utsträckning grovt omkring 1 mM. Det är också i grova drag vad experimenten visar (Se Ljusbulan):
— Med ON-tiden för ljusbulan omkring 1-4 nS stämmer metriken hyfsat (1-3 mM) med den (hittills mestadels manuellt) observerade ljusbulans utsträckning (Mera utförligt via fotografi i FotoGlödspår).
Vidare följer.
Den färdigställda kamerasynkade
urladdningsanordningen [XYcoAlFEDU]
kom endast att understryka det redan manuellt i huvudsak observerade och ovan
formulerade.
Se även generellt teori/matematik/begrepp om ”air friction” på HyperPhysics
HYPERPHYSICS
— Air Friction
http://hyperphysics.phy-astr.gsu.edu/hbase/airfri.html
Se särskilt ”penetration depth” (analogt med IMPULSANALOGIN)
HYPERPHYSICS
— Motion with Linear Drag
http://hyperphysics.phy-astr.gsu.edu/hbase/lindrg.html -
c1
UtvidgningTVÄRSNITT — Jämförande Grafer
UTVIDGNING 3Jan2013-01-03
[AAl/ALUFT=(rAl/rLUFT)2]:
— Tar vi med ovanstående sambandsform för tvärsnittets variation får vi en (säker) övre gräns för sämsta fallets räkningar:
Glödspåren via den enkla impulsanalogin
Vi använder grundformen från IMPULSANALOGIN
d = mv/R
Distansen (d) som
partikeln (P) med massan (m) och begynnelsehastigheten (v) färdas i mediet med
friktionen (R) innan P smälter samman (stannar) med R
med variabelt impulsmotstånd per längdmeter (R=mv/s) via en tilläggsfaktor [LuftBASIC] som vi ska kalla a-flex (â):
AAl/ALUFT
= (rAl/rLUFT)2
= â ; [Alt+0226, â; »a-flex»]
rLUFT = (3,4 t9 M)/2
=
1,7 nM .............................. tvärsnittsradien
idealt för medelluftmolekylen vid 20°C normal luft
Glödpartiklarna (mP, idealt Aluminiumekvivalenter) kan med stor sannolikhet ses/förstås som perfekt sfäriska via smälttillståndet;
V = mP/ρ
= 4πr3/3 ;
rAl = (3mP/4πρ)1/3 ; ρAl = 2700 KG/M3
= (mP · 8,84194 t5 M3/KG)1/3
mP = NAl ·27u
= NAl ·4,48 t26 KG ;
rAl = (NAl ·4,48 t26 KG · 8,84194 t5 M3/KG)1/3
= (NAl ·3,96 t30 M3)1/3
= (NAl)1/3 · 1,582 t10 M ;
â = (rAl/rLUFT)2
= ([(NAl)1/3 · 1,582 t10 M]/[1,7 t9 M])2
= (NAl)2/3 · 8,66 t3 ;
R := Râ ;
Tillväxten i impulsmotståndet per meter (R=mv/s) som den allt större glödpartikeln möter kan ses/förstås omvänt som en och samma glödpartikelstorlek som möter ett allt tätare luftmolekylbestånd (â, a-flex), analogt växande impulsmotstånd per spårmeter.
— I omvänd mening — Al-atomens tvärsnitt är mindre än medelluftmolekylens — passerar glödpartikeln genom luften allt lättare ju mindre den är: enstaka Al-atomer relativt den omgivande materiens partikelmedelsnitt.
— Sambandsformen totalt modifierad för partikeltvärsnittets variationer med glödpartikelns storlek därmed
d = mPvP/Râ
Distansen (d) som
partikeln (P) med massan (m) och begynnelsehastigheten (v) färdas i mediet med
friktionen (R) innan P smälter samman
(stannar) med R
= mPvP/R(rAl/rLUFT)2
= mPvP/R([(3mP/4πρ)1/3]/rLUFT)2 ; ρAl = 2700 KG/M3
= mPvP/R([mP1/3(3/4πρ)1/3]/rLUFT)2
= mPvP/RmP2/3([(3/4πρ)1/3]/rLUFT)2
= mP1/3vP/R([(3/4πρ)1/3]/rLUFT)2
= (NAl·27u)1/3vP/R([(3/4πρ)1/3]/rLUFT)2
= [NAl·4,48 t26 KG]1/3vP/R([(3/4πρ)1/3]/rLUFT)2
= NAl1/3[4,48 t26 KG]1/3vP/R([(3/4πρ)1/3]/rLUFT)2
= NAl1/3vP[4,48 t26 KG]1/3/R([(3/4πρ)1/3]/rLUFT)2
=
NAl1/3vP(2,21 t8 S)
............................................ CHECKED
OK
Glödpartikelns utgångshastighet (v[P]) då den inträder luftgränsen från metallexpansionen beror på den tillgängliga energin.
— Vi VET (ännu) inte mekanismen, säkert, för detta. För prövningens del har vi, främst, bara att räkna på principen en Al-metallexpansion PER Al-atom, vilket innefattar Al-atomens allra minsta excitationsenergi (Al+1), ca 6eV (~9,6 t19 J).
— Som tidigare: För att frigöra 3 T16 Al-atomer ur det observerade urladdningshålet (>Ø0,2mM) måste energin minst vara ca 0,03 J. Via rörelseenergin (E=mv2/2) ges då per Al-atom utgångshastigheten ca 6500 M/S (6541 M/S).
Därmed
d = NAl1/3(6541 M/S)(2,21 t8 S)
= NAl1/3(0,000144 M)
RESULTAT (Tabell3 KalkylMeanFree.ods):
— För spårlängden d=31,09 mM är glödpartikeln lika med
NAl = T7
(tio miljoner Al-ekvivalenter) med sfärradien 34,1 nM; Partikeln stannar vid uppnådda d på v(SLUT)=5,23 t5 M/S.
— Komplementärt via x-formen
x = (mv/Râ)(1 – 1/etRâ/m)
visas samma värde via t=0,0001S, t samma som det ursprungligt uppmätta medelvärdet (100µS) för glödspårsljusens varaktighet via fototransistorn [LJUSTIDEN].
— OM, sämsta fallet, hela Al-mängden 3 T16 atomer skulle delta i glödspårsbilden skulle antalet glödspår (med samma intensitet via längden ca 3 cM) bli drygt 2 T9 stycken.
— Den mängd glödspår vi kan observera — tydligt,
direkt med kamerans ögonbild utan vidare bestyckning — är tiotal (ned till
möjligen hundratal) glödspår mellan starkaste till svagaste [Se FotoGlödspår].
— Det FÖREFALLER således (fortfarande) högst osannolikt, enbart i beaktande av den klart synliga antalsmängden, att hela atomutgivningen från urladdningshålet skulle grundas på atomer som uppvisar tydliga glödspår; Vi är av den (vägda, tills motbevisat, men föga upplysande) uppfattningen att antalet glödspår och dess atommängd är försumbar vid sidan av huvuddelen som, vi tror, omsätts i den centrala ljusbulan. Mera direkta bevis är alltså angelägna.
— Utöver aspekten (ännu grundad på intryck, utan bevis) med antalet glödspår finns (som tidigare) ljusbulans energiräkning: Bara den, enbart, kräver mer energi än vad kretskopplingens kondensator och matningsspänning kan leverera. Emellertid finns heller inte för ljusbulans del, ännu, någon helt säker energiräkning (mera avancerade mätvärden saknas ännu, Apr2013).
— Den, möjligen, enda säkra indikation vi har är som tidigare att OM Al-atomerna avdelas ur urladdningshålet PER joniserad Al-atom (6eV), i vilket fall kondensatorenergin (U2C·3/8) på 0,0216 J INTE räcker till: Det krävs minst 0,031 J (0,030845152 J). Det fattas ca 30% — ljusbulans energiräkning oaktat (samt också oaktat energin i själva ljusbilden från glödspåren: glödpartikeln emitterar ljus, och den energin måste veterligt återföras på en extra del vid sidan av den initierande impuls som driver partikeln i spåret — ännu en olöst svårighet).
— Men det finns ett betydligt säkrare sätt att spåra avgörande argument:
Men TYP tio miljoner Al-atomekvivalenter [dFORMENtvärsnitt] (massan) i ett
glödspår stämmer ingalunda med spårbilden av glödspåren från ett (typiskt) foto
[IMPULSBILDEN].
— I ImpulsBASIC visas att ett glödspår som uppvisar bakåtstuds efter kollision med en luftmolekyl INTE — garanterat, helt säkert — kan ha större massa än 25.000 ekvivalenta medelluftmolekylmassor (28,24u).
— Felbilden ovan (T7
atomer) grundas (således) på energin (som användes för att
beräkna v[P]) bakom partikelaccelerationen; Den energin måste, tydligen,
återföras på en kraftigare bas än den rena, förmodade, Al(+1)-grunden — vilket
också teorin enligt TNED kräver.
TEORIN FÖR PARTIKELIMPULSERNA glödpartiklar/luftmolekyler som använts i denna framställning beskrivs utförligt i Impulsbilden.
IMPULSBILDEN 2013-01-03
IMPULSBILDEN — med fotografiskt jämförande exempel
ImpulsBASIC — ImpulsanalogiernaKALKYL
Basmatematik i
xy.planet för resulterande rörelsemängder — jämför IMPULSBILDEN
Grunderna i HUR vi kan se/förstå impulsfysiken i praktiska
exempel
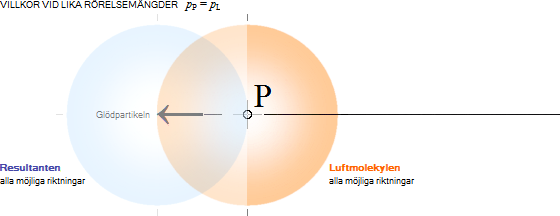
Är rörelsemängderna lika stora för
respektive luftmolekyl (L) [LuftBASIC] och
glödpartikel (P) kan den resulterande riktningen efter sammanstötningen i
impulspunkten (P) bara finnas i glödpartikelns framriktning. Aldrig, synbart,
rätvinkligt eller motsatt den riktningen.
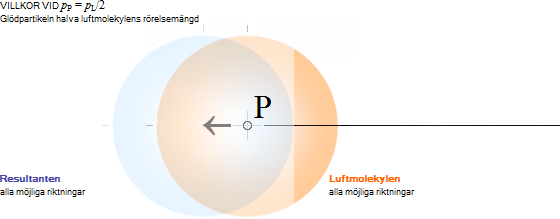
Impulsformen ovan visar det möjliga
resultantområdet (ljusblått) om glödpartikelns rörelsemängd är halva
luftmolekylens (p[L]=mv=[28,24u][500M/S]=2,3 t23 NS).
— Längden på bakåtresultanten ökar
sedan vidare med luftmolekylens övervägande rörelsemängd.
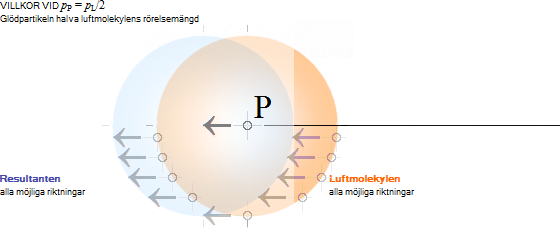
Bilden ovan visar mera ingående hur man
(på enklaste sättet) kan se/förstå den möjliga resultantverkan via
2D-representationens grunder (3D-komponenten framstår som projicerad på
2D-planet):
— Glödpartikelns impulspil (pilens
längd) förflyttas och placeras med impulspunkten (P) vid luftmolekylens
pilspets (luftmolekylens
pilspets ej utritad, samtliga fall på periferin till den orangea cirkeln/sfären),
Den flyttade impulspilens spets pekar då på impulsresultantens spets.
Utritat exempel för förtydligande av
principen:
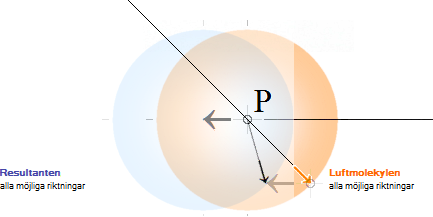
Figuren ovan visar (i 2D) hur
resultanten framträder utritad tillsammans med en vald riktning för
luftmolekylens infall om luftmolekylens rörelsemängd är dubbla glödpartikelns.
— Om vi studerar ett (typiskt, IMPULSBILDEN) glödspårsfotografi
(enligt ANORDNINGEN)
kan vi ofta (mera av regel än undantag)
se (flera) exempel på, just, bakåtresultanter.
— Den detaljen bevisar i sig, enligt
grundmatematiken ovan, att glödpartikelns rörelsemängd är MINDRE än den
kolliderande luftpartikelns.
— På den basen, fotografierna
tillsammans med LuftBASIC-värdena,
kan man fastställa — helt säkert — GRÄNSVÄRDEN för glödpartiklarnas storlek:
Glödpartiklarnas storlek visar sig, då, ligga i storleksordningen grovt runt
1-10 nM (1000-100.000 atomer).
Vi studerar det.
Glödpartikeln pP=mPvP
Luftmolekylen pL=mLvL
——————————————
GRUNDSAMBAND VID LIKA RÖRELSEMÄNGDER
pP = pL
= mLvL
= mPvP ;
mP/mL = vL/vP
= (500 M/S)/vP ;
mP = mL · (500 M/S)/vP ;
:
Foto:
——————————————
AVBÖJNINGEN I RÄT VINKEL: 2 mM per min 1/10 S = 0,02 M/S
; mP = mL(500/0,02) = 25 000 mL MAX
— se fotografiet nedan med
exponeringstiden (effektiva) 0,1 S:
BILDKÄLLA: Författarens arkiv:
Inverterat foto
med urladdning mot Aluminiumstång (26V 100µF) Spark2012_3
· 19Dec2012 Bild 5
— NikonD90 · ISO: 400; Bländartid:
1/5 S; Bländartal: F/9
sammanfört med
separat bild —
kameran i samma position — på anordningen med inlagd mätskala · Bild13, samt
bild på hela anordningen, Spark2012_2
· 18Dec2012 Konstr_001:

ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
FOTOGRAFERINGSTEKNIKEN, bilden ovan,
för tillfället:
— Separat handhållen kabelkopplad
utlösare i ena handen, katodstiftets anordning i den andra: Efter aktivering av
fotoutlösaren löper ca halva exponeringstiden (Exponeringstid för bilden ovan: 0,2 S) innan
kontaktstiftet träffar aluminiumstången och glödspåren framträder.
— Det betyder i netto runt (max) 0,1 S
för det praktiska tidsfönstret som ljusdetaljerna i bilden har att utveckla sig
på.
— Vi ser tydligt att glödpartikeln i
fallet med rätvinklig
avböjning uppvisar i varje fall spårlängder på runt 2 mM (eller
mera).
— Det betyder i netto [ImpulsBASIC] en ansvarig mobil
ljuspartikel med hastigheten MINST (0,002 M)/(0,1 S) = 0,02 M/S.
— Med impulsvillkoret för lika
rörelsemängder
pP = pL
= mLvL
= mPvP ;
mP/mL = vL/vP
= (500 M/S)/vP ;
mP = mL · (500 M/S)/vP ;
= mL · (500 M/S)/(0,02 M/S)
= mL · 25 000
betyder det att glödpartikelns massa i
fallet synlig
rätvinklig avböjning (som kräver att luftmolekylens rörelsemängd är den större, ImpulsBASIC) under alla
(genomsnittliga) förhållanden måste ligga under maxgränsen 25 000 gånger
luftmolekylens medelatomvikt (28,24u).
— Gränsmassan betyder då en
Aluminiumekvivalent (hel glödpartikel) med sfärradien
rAl = (3mP/4πρ)1/3 ; ρAl = 2700 KG/M3
= (3[25000·28,24u]/4π[2700 KG/M3])1/3
= 4,6973 t9 M
~ 4,7 nM .............................
glödspårets partikelstorleksgräns MAX i Al-ekvivalenter för
SYNLIG avböjning i rät vinkel mot ursprungsriktningen
Glödspår som avviker MER än räta vinkeln kräver i
motsvarande mening [ImpulsBASIC]
att glödpartikelns rörelsemängd är mindre än luftmolekylens: glödpartikelns
massa reduceras (med än högre utgångshastigheter) ju mer (och längre) spåret
avviker bakåt.
De spår som avviker mindre från
ursprungsriktningen kan i gengäld ha tyngre agenter (med lägre
utgångshastigheter).
— På den bildbasen (enbart) kan vi konstatera (med god
tillförlitlighet, enligt IMPULSMATEMATIKEN)
att glödpartiklarna i aluminiumurladdningsfallet bör ligga i storleksordningen
1-(max)10 nM [grovt 1000 till
(max) 100.000 Al-ekvivalenter].
Den resultatbilden har också
KONSEKVENSER (i energibilden) för beräkningarna i stort (IMPULSANALOGINS
SAMBAND med
partikeltvärsnittens variationer):
OM gränsen för N(Al) ligger runt 30000
aluminiumatomekvivalenter finns ingen möjlighet för ett glödspår att hinna
längre än 4,5 mM (se sambandet för dFORMEN tvärsnitt):
— De signifikanta glödspårens längder (se FotoGLÖDSPÅR speciellt i Aluminiumfoliefallet,
vårt experimentobjekt) ligger grovt (mest synliga) runt 1-3 cM.
— För att den d-matematiken ska
fungera, är det tydligt att INGÅNGSHASTIGHETEN för glödpartikeln måste vara
betydligt större än de angivna runt 6500 M/S — på kredit av en betydligt mindre
andel Al-atomekvivalenter än de d-sambandets
10 miljoner som annars krävs för att få värden för glödspårens längd runt 30
mM.
— Nämligen ca 50.000 M/S via
N(Al)=25000, som ger d=32,26 mM.
Uppgiften, föregående, på ingångsvärdet v(P)=6500 M/S för
glödpartikeln baserades på en minsta Al-jonisation per materialfrikopplad atom
(~6eV för Al+1) tagen energivägen via rörelseenergin (E=mv²/2).
— För att, via samma väg, få v(P)=50000 M/S (runt 10 ggr
mer) krävs, tydligen, en större energibas än Al+1.
— Den konsekvensen ligger också i linje med energiräkningen [Exakta Energiräkningen 2008II3].
— ENERGIN för att accelerera en
Al-partikel på 30.000 Al-atomer (eller motsvarande kemiskt bildad oxidpartikel)
upp till 50.000 M/S beskrivs elementärt av sambandet för elektronens massökning
[ELEKTRONENS
MASSÖKNING]. Termerna UQ=E anställer den ekvivalenta energin
för partikelaccelerationen i accelerationsanordningen.
(UQ=E lika med den tillgängliga accelerationsenergin:
Laddningen
Q kan anges godtyckligt för en godtyckligt elektriskt laddad partikel,
tillsammans med en godtycklig [tillgänglig, eller behövlig]
accelerationsspänning U, dessa bägge UQ anger ekvivalenta energin till den
accelererade partikelns massökning enligt PLANCKEKVIVALENTERNA).
Vilomassan m0 är den elektriskt laddade
partikel (glödpartikeln på jonbas) som ska accelereras av anordningens U. Sambandsformen
nedan gäller idealt för vakuum endast (idealt mellan atomerna). Se härledningen
i länken nedan, om ej redan bekant.
u = c√ 1 – 1/[(UQ/m0c2) + 1]2 ........................ laddningshastigheten
u
från accelerationsspänningen U
UQ/m0c2 = Δm/m0 = (E/c2)/m0 ; Δm anger den accelererade partikelns ekvivalenta massökningsenergi — UQ är inbördes godtyckliga med givet Δm
För att få u=50.000 M/S för en partikel med m0=25000 stycken
Al-atomer — övre glödpartikelmassagränsen för bakåtstuds vid spårlängden 30 mM [ImpulsBASIC] — måste energin
E=UQ=Δmc² vara i storleksordningen 10 MeV (1,6 t12 J). Dvs., runt 400 eV
per Al-ekvivalent.
— I Wikipediatabellen [2013-01-04]
över IonizationEnergies, 13 Aluminium (CRC),
http://en.wikipedia.org/wiki/Ionization_energies_of_the_elements_(data_page)
motsvarar det en jonisation på
elektronnivån +10 [skrivs konv. Al+10].
— I TNED
finns bara ett sätt för den typen; från ett maximalt hett, plasmatiskt, centrum
(ljusbulan, FotoGLÖDSPÅR)
med en STOR jonisation [ATA/CAT], och som sedan sprids utåt,
naturligt på TID, med avtagande grad.
— Glödpartiklarna kan i den bilden
förstås vara resterna i periferin av jonisationerna; de avdelade Al-atomerna
kan bilda sammansatta atomgrupper tillsammans med Syret (20%) som (kanske)
AluminiumOxid (Al2O3) och med Kvävet (78%) som
AluminiumNitrid (AlN). [Kemisk
analys på luftresterna efter urladdningarna saknas f.n.].
Ovan: IDEALISERAD TECKNING (2008) efter
upprepade observationer enligt EXPERIMENTANORDNINGEN. Jämför FotoGLÖDSPÅR nedan.
Nedan: Aktuellt (typiskt) exempel efter
direkt fotografering:
AlGlödspårenFOTOmain — Ljusbulan
Se
även tydligare i Fig.3
BILDKÄLLA: Författarens arkiv · Spark2012main· 16Dec2012 Bild
Ljusbula003 — NikonD90 · ISO: 2000; Bländartid: 1/2 S; Bländartal: F/20
Anodmaterial, 0,017mM Aluminiumfolie, i övrigt samma
kopplingsbild som i CAT-experimenten.
— Ljusbulans utsträckning ca (1-)3-5mM beroende på färggräns. Spårlängderna (de mest framträdande) grovt 1-3 cM.
— Se även i Kolliderande
nanopartiklar.
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
DEN SVARTA CIRKELN i Ljusbulan Ø1,3mM — inlagd till
jämförelse — motsvarar utrymmet för ca 3 T16 medelluftmolekyler [LuftBASIC] i rumstemperatur (20°C),
rL = (3mL/4πρ)1/3 ; ρl = 1,2 KG/M3
= (3[3 T16·28,24u]/4π[1,2 KG/M3])1/3
= 6,54088 t4 M
~ 0,65 mM ...........................
Upptagande
sfärradie i luften
[LJUSBULAN] utanför urladdningsfolien
för de motsvarande 3 T16 stycken
medelluftmolekyler vid 20°C som kan matcha de 3 T16 Al-atomerna som frigörs ur
det 0,2mM vida urladdningshålet [EXPERIMENTANORDNINGEN] via 24V 100µF [försumbar kretsresistans (max 10
mΩ)].
Vi kan (just) se scenariot — via
jonisation PER avdelad aluminiumatom från den 0,017 mM tunna aluminiumfolien
[Se även i AlFU]:
— URLADDNINGEN resulterar i en liten
kärna (ljusbulan) av starkt centraljoniserade Al-atomer; Elektronströmmen i
urladdningen från katoden (minus) till anoden (+, Al-folien), samt
katodstiftets fasta position bidrar till en rekylbildning i riktning ut från
katodstiftet; Luftmaterialet strax utanför folieytan/hålet blir en (ytterst)
stark attrahent till Al-jonerna; Al-atomerna dras till, och förenas med,
luftmolekylerna under stark ljusemission (ljusbulan);
— Huvudmängden Al-atomer förenas inom
ljusbulans millimeterdomän (inom nS) via höga hastigheter (800.000 M/S, ImpulsKALKYL) och små massor (enstaka [ljusspår 0,15mM] till tiotal
[ljusspår 1,54mM], knappast hundratal [ljusspår 15,38mM] Al-atomer; REF., Tabell2 (Via matchande omsättningsenergi)
KalkylMeanFree.ods):
— I Al-jonernas periferi (de Al-atomer som släpas med sist i
svansen in till ljusbulans luftatomer utanför folien) är jonisationen
som lägst [tidsspridningen från
centrum når periferin sist], och därmed en större tendens (mera tid) att
forma mera sammansatta luftföreningar (tyngre partiklar);
— De synliga glödpartiklarna bildas
(och falnar inom ca 100 µS [LJUSTIDEN])
i utkastningsriktningen (på den
resterande totaljonisationens accelerationskapital [ljusbulans främre del kan
agera accelerationselektrod för delarna längre bak]) som en mindre mängd
materialpärlor (hundratals
direkt synliga, tiotal speciellt ljusstarka [FotoGLÖDSPÅR])
med större (genomsnittlig) partikelmassa (1000-30.000 Al-atomekvivalenter) än i
ljusbulans fall (1-10);
— Glödpartiklarnas utgångshastigheter
måste förstås växa med avtagande partikelmassa för en bestämd spårlängd som
uppvisar tydlig avböjning i kollision med någon luftmolekyl: Se ImpulsBASIC. Dessa hastigheter kan (veterligt, som ovan) bara
förklaras i det efterklingande ljuset av den centrala ljusbulans starka
jonisationspotential.
Den energiräkningen utesluter i sig att ALLA MÖJLIGA
glödspår (ur hela materialpotten
på 3 T16 Al-atomer) skulle kunna återföras på samma
medelglödspårsenergikapital: antalet glödspår för hela 3 T16 Al-besättningen
skulle här via 25.000 Al-atomer per glödspår ge drygt T12 glödspår, och därmed
totalt T12 · 1,6 t12 J = 1,6 J. Den energin finns definitivt inte i den
aktuella experimentkopplingen (0,0216 J; 74 ggr mindre [KONDENSATORENERGIN]).
Bilder på urladdningshålen (>Ø0,2mM) från de
första urladdningsexperimenten — via USB-mikroskop
USB-mikroskopet (fabr. Plexgear) Finns på Kjell&Company
(2013) för 499:-; OMDÖME: Efter priset: perfekt för ändamålet — men lite svårnavigerat
(i 200 ggr förstoring) med den medföljande enklare stativfoten.
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Se även urladdningshålen
här utan förstoringar — främst på grund av att vissa webbläsare
[Firefox-gruppen kan inte läsa
”/”-katalogtecken på sätt som INTE ger ”NotFound”, medan GoogleChrome, IE,
m.fl. kan det utan problem] i princip omöjliggör navigering i ENKLA katalogstrukturer: katalognamnen måste skrivas på sådant
sätt — hela http://-www.-URL:en måste anges — att jag som författare inte kan
redigera — NÅ — dokumenten från min dator utan måste göra det via min
internetserver; Genom att förenkla presentationen på portalsidans mera
komprimerade htm-form (inga underkataloger får anges)
kan detaljerna visas även via typen Firefox webbläsare.
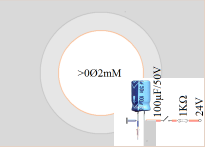


Ovan: Idealiserad teckning efter manuell observation
genom ett handhållet mikroskop (Clas Ohlson) i 30 ggr förstoring av de första
observationerna från urladdningarna 24V/100µF, foliedelen ovan (Aluminiumfolie
0,017 mM) höger med de mindre hålen till vänster:
Nedan: 0,017mM Aluminiumfolien från samma
typexperiment i senare upprepning (annat folieexemplar) med USB-mikroskop
20Jan2013, förstoring enligt mikroskopets skala 20
ggr
(hålets diameter i den 200 ggr förstorade bilden nedan drygt 40 mM — bredd ca
168pixel: 1pixel 0,2645833 mM via 96dpi; i sanna bildvärden med 0,265/0,2=1,326
ges förstoringsvärdet 168×1,325=222,6 ggr, vilket visar att skalan på
USB-mikroskopet håller god klass):

Al-folien upphängd i ASSISTENT; bakgrundsbelysning med
separat diodlampa justerad för den orangea bakgrunden, centralhålet (något
större än 0,2mM) i exempel.
Stora bilden ovan förstoring 20
ggr —
avståndet USB-mokroskopet(plasthöljet)-AlFolien ca 7 mM; Lilla infällda bilden
ovan vänster förstoring 4 ggr.
Nedan: Samma som ovan, centralhålet, men i förstoring
220 ggr:

Inslaget av
kantsmälta är alldeles tydligt: [Aluminium
smälter vid 660 °C]. Se även GlödspårenFOTO.
— Not bad. Idealteckningen
inte helt tokig (men
»UTSTANSNINGSFÖRESTÄLLNINGEN» är inte korrekt [fast det såg så ut i det enkla
mikroskopet]) — Vidare fotografier med en mera mekanisk (alla manuella
handrörelser uteslutna) krävs för att få bättre besked OM den ev. rundheten är
representativ för flertalet EXAKT STABILISERADE katodstiftpositioner.
Instrumentbyggen pågår (Jan2013).
Anordningen —
kopplingar och detaljer till fotografierna | Järn
| Aluminium | Koppar | Dec2012

Materialstängerna (mitten) borrade med Ø2mM hål,
preparerade med en kombination av 2mM mässingsrör (Järnia, alfer-profiler; finns bland sortimentet för rör,
stänger) och Elfas kontaktstift.
Matningsspänning från 3st 9V-batterier;
Batterihållarna för 9V-batterierna finns (sedan
länge) på ELFA (Bilden nedan Dec2012);

Katodstiftet från ELFA (kontaktresistans omkr. 1
mOhm, särskilda test).
[I stort sett all elektronik, alla komponenter, i denna framställning
är inhandlade från ELFA om inget annat anges].
Anordningen (efter
sammanställning)
BILDKÄLLA: Författarens arkiv · Spark2012_2· 18Dec2012
BildKonstr1 — NikonD90

Spänningskällan med komponenter och
experimentmaterial monterat på hyvlat och slipat träblock (3×7cM). I huvudsak
för manuella experiment. Se EXEMPEL i IMPULSBILDEN
— tydliga spår av luftmolekyler som kolliderar med glödpartiklar från
aluminium.
KATODSTIFTET (ytterst användbar detalj med många praktiska tillämpningar): Från ELFAKATALOGEN (nr50s426):
Kontakthylsa Fabr Scott Electronics SA; Hylskontakt: Berylliumkoppar, guld över nickel; Stift: Mässing, tenn över koppar;
Typ 01-445 Art.nr. 48-178-62 (ca 50:- per 100st [Man behöver dem (lätt, min referens) i 1000-tal vad tiden lider OM intresset för elektronik är STORT]).
Spårteckningarna, originalen efter observationer
Manuella teckningarna efter de första
observationerna från experimentell gnisturladdning via 24V/100µF
ALUMINIUM och KOPPAR uppvisar ingen krondelning (efter observationer från gnisturladdningen i CAT):

Från GLÖDSPÅRENS ENERGIBIDRAG i CAT [ATOMKÄRNANS TOTALA UPPLÖSNING]
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
NOTERA
DUBBELKRONDELNINGEN i den manuella avbildningen ovan i järnfallet :
— DUBBELKRONDELNINGEN är av allt att döma en (min egen
producerade) visuell sammanblandning — enbart på det tidigare obeväpnade
synintryckets basis — från mängden krondelningar som delvis täcker för
varandra;
— I de fotografier [SparkJÄRN]
som hittills tagits (från Dec2012) har inget enda exempel på dupletter i
krondelningen observerats: testade järnämnen: verktygsstål, silverstål, rent
(tekniskt) järn. Jämför fotografierna i SparkJÄRN.
XYcoAlFEDU
XY-coordinated Aluminium
Foil Electric Discharge Unit
— 2Feb2013
Urladdningslådan för Fotografisk Dokumentation
Inledande kort beskrivning — Konstruktionen
GRUNDRITNINGEN XY-DELEN TILL URLADDNINGSENHETEN FÖR SERIELL FOTOGRAFISK
DOKUMENTATION AV GLÖDSPÅR FRÅN ELEKTRISKA URLADDNINGAR GENOM ALUMINIUMFOLIE —
notera det skissartade i »On-The-Fly-Konstruktionssättet» [som nog är det mest vanliga vid alla
typer av prototyptillverkning]: vartefter detaljerna utformas, modifieras
konstruktionen (den ursprungliga
idén), och i slutänden krävs snart sagt mer jobb på ritningen [OM ENS EN SÅDAN ALLS FINNS] än
konstruktionen för att visa alla detaljer. Jämför bilderna av slutformen längre
ner.
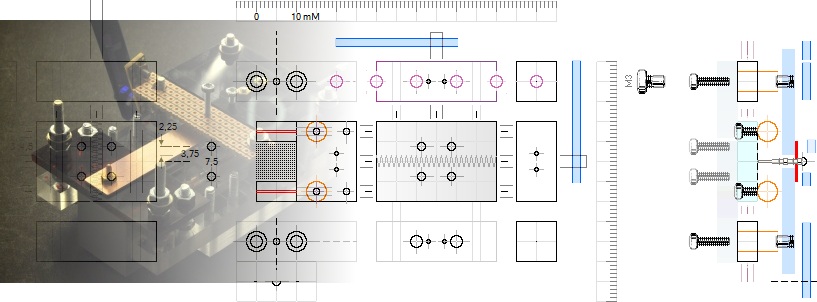
X-delen (överst) skruvas ihop med Y-delen (underst) via de
fyra centralskruvarna; Y-delen och det fasta fundamentet hör ihop; Y-delen bär
X-delen med sig — det konventionella sättet att bygga XY-bord. XY-blocken
flyttas genom en M3-gängad stång, 0,5mM per varv; Gängstångens ändar är fixerade
i respektive block via enkla koppartrådsmärlor (1mM) via filsvarvade
motsvarande urtagningar i gängstångens ändar. XY-blocken glider på 2mM
stålaxlar (silverstål) i 3mM kopparrör; rören är uppslipade med kryss i ändarna
som kan spännas ut något och därmed säkert fixeras i plexiglasblocken relativt
de löpande stålaxlarna. Konstruktionen kräver borrning av flera långa 20-30 mM
hål med Ø1,5-3mM borrar — hålpassningen är avgörande, vilket kräver en väl
inställd XYZ-utrustning (pelarstativ, koordinatbord).
DET URSPRUNGLIGA SYFTET
Urladdningslådan — XYcoALFEDU
DET URSPRUNGLIGA SYFTET var att få fram
en effektiv urladdningsyta på 10×10mM med intervall om 0,5mM (gängstigningen per varv för M3-gänga)
mellan varje par urladdningspunkter; totalt 20×20=400 tätt liggande
urladdningspunkter — med runt 0,3mM mellan varje par, kant till kant. Den
förebilden grundas på de manuella observationerna från de första
CATEXPERIMENTEN (med tillhörande
teorier): urladdningshålen visade runt Ø0,2mM med 0,017mM Al-folie och
spänningen U=24V med C=100µF.
BILDKÄLLA: Författarens arkiv · CATfeb2013· 2Feb2013 Bild
coAFUE_52 — NikonD90

URLADDNINGSLÅDAN — konstruktionens avgörande slutmål.
— I den färdiga konstruktionen,
20mM-aluminiumfyrkantprofilen,
i bild ovan med den påspända Al-folien
som hålls fast i flankerna av dubbelhäftande tejp;
— Al-profilen (ytelektriskt isolerad från fabrikanten, fabr. alfer på JÄRNIA) är avputsad i
kanterna för att ge säker ledande kontakt,
vilken separat testade funktion avgjorde den lösningens användbarhet; ena
flanken har ett M2-gängat hål för skruv där tilledaren ansluts. Hela Al-lådan
ansluts till XY-blocket via två delvis gängade Ø2mM kopparstänger som skymtar i
bilden ovan; stängerna sitter fastgängade på Al-lådans baksida och har separata
stoppskruvar för fixering i XY-blocket.
finns plats för 19×19=361
urladdningspunkter;
De stora urladdningshålen — XUcoAlFEDU
— Men TANKEN OM URSPRUNGSFUNKTIONEN —
ca Ø0,2mM urladdningshål — visade sig INTE hålla;
— På grund
DELS av den något (på tiondelar/hundradelar)
ojämna Al-foliens slutläge över urladdningsöppningen (uppsidan på folien i bilden ovan), trots
fastspänningen, och
DELS (mest) på grund av att de tätt
liggande urladdningspunkterna också visade sig deformera folieytan (de buktar så sakteliga inåt med
växande mängd hål)
blev funktionen hos kontaktstiftet
snarare av typen PLOG som delvis trycktes ner i folieytan;
— Runt dubbla urladdningshåldiametrar
visade sig, typ Ø0,4mM.
Det hade vi inte förutsett. Se bild på folien i URLADDNINGSHÅLEN.
UrsprungetHålbildningen, jämförelse
BILDKÄLLA: Författarens arkiv · 7Feb2013 Bild XYcoAl7Feb_001;002 · NikonD90

ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Separat test 7Feb2013 på
XYcoAlFEDU-anordningen — FÖRSÖK TILL kontroll av den ursprungliga manuella
originalfunktionen:
ORIGINALFUNKTIONEN:
— Katodstiftets beröring (strax
ovanför) aluminiumfolien åstadkommer en urladdning som bryter strömkretsen: Den
uppladdade kondensatorn urladdas inte helt, endast till hälften. [I XYcoAlFEDU-anordningen körs den
finstämning delvis över].
— Den delen har här, bilderna ovan,
realiserats BEHJÄLPLIGT på XUcoAlFEDU
genom att DELS justera stoppavståndet (krävande, trixigt, de fyra M3-skruvarna) och sedan DELS HASTIGT
MED ENA FINGRET PÅ MOTSATTA STIFTSPETSEN (bilden ovan) föra det fjädrande kopparplanet med
kontaktstiftet mot den uppspända folien — med stora mellanrum (5varv=2,5mM) mellan
urladdningsställena (för att
undvika den annars observerade lokala folieytdeformationen med många
närliggande hål). Anordningen är EMELLERTID definitivt INTE lämpad för
den typen av analys.
— Bilden ovan visar tre urladdningshål
som åstadkommits på det sättet; Kondensatorn uppladdas till ca 26,3V (det som f.n. finns kvar av 3×9V efter
viss användning); Efter uppladdningen tas R-anslutningen bort (så att kondenstorn inte kan
serieurladda/uppladda), och stiftets fjädrande kopparplan förs hastigt
mot folien; urladdning sker;
— Separat uppkopplat mätinstrument — för att kontrollera överensstämmelsen
— visar (med variationer) att kondensatorspänningen efter urladdning ligger på
ca halva matningen (omkring 13-15 V).
Det är samma typresultat som i de ursprungliga helt manuella
experimenten.
— Minsta lilla buktning i folieytan
gynnar fastbränning i kontaktstiftet (händer också i den manuella experimentdelen, men mera sällan).
Den defekten kan bara elimineras om folieytan (som i experimentfallet ovan i bild) är (maximalt) spänd (vilket
konstruktionen i XUcoAlFEDU
inte riktigt medger).
Ytterligare försök 8Feb2013 —
för att kontrollera föregående resultatbild — som bara understryker hela
anordningens (extrema) känslighet:
— Av ytterligare 19 testade (bilden nedan, raderna 2 3 [4
senare, ej i bild]) gav alla urladdning utan fastbränning — med FÖRSIKTIGT
NÄRMANDE av katodspetsen.
BILDKÄLLA:
Författarens arkiv · 8Feb2013
CATfeb2013 Bild
XYcoAl8Feb_001;002;005 · NikonD90 [i förekommande fall samtliga med tillagd
SHARPENING i separat DELHI-program (Författarens arkiv)]

Urladdningskondensatorns
Uppladdning — XYcoAlFEDUöversikt
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Den provisoriskt insatta Tyristorkopplingen (EC 103A, bilden ovan höger nedre, del av XYcoAlFEDU)
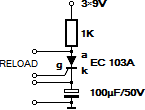
Genom att kortsluta de två
första tyristorbenen (Anod, Gate) med en smal metallpincett tänder tyristorn,
och kondensatorn laddas upp (inom 1/10 S) — varefter uppladdningskretsen
autobryts av tyristorns VGT-spärr.
insattes separat i förtestningen (InledandeJFETtest)
av JFET-sensorns ev. utslag i ev. kringliggande elektronladdningar under
manuella upp och urladdningar — för att eliminera, och observera, ev. mätfel.
Den provisoriska tyristorkopplingen (bilden nedan med kopplingsschemat) byttes sedan ut mot en mera stadigvarande
typ
INDUKTIVATouch i Inledande JFETtest
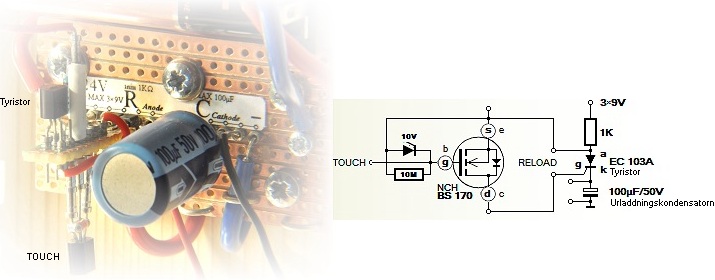
BILDKÄLLA: Författarens arkiv · 13Mar2013 CATfeb2013
Bild XYcoA13Mar_3 · NikonD90
— Provisoriska anordningen ersatt av en mera stabil dito. I
mitten urladdningskondensatorn 100µF/50V.
— Vänds
MOSFET-Touchtransistorn »rättvänd» — Drainelektroden vid TyristorAnoden,
Sourceelektroden vid TyristorGate:en — leder tyristorn hela tiden: Kondensatoruppladdningen
pågår då kontinuerligt och Touchfunktionen har ingen inverkan.
Den tillfälliga insättningen togs sedan bort då det visade sig att
induktionstransienten i de aktuella urladdningarna i vilket fall också triggade
tyristorn i läge ON så att kondensatorn, likväl, laddade upp direkt efter
urladdning i vilket fall.
— Syftet med den tillfälliga insättningen av tyristorn och den
induktiva Touch:en fick emellertid sin kredit av att vi, säkert, nu fick veta
hur JFET-sensorn reagerade i de olika manövrer som vi måste utföra i samband
med aktuella urladdningar: små variationer beroende på textilierna vi bär i de
små (minimala) armrörelser vi måste utföra för att manövrera anordningens
detaljer.
— DEN INDUKTIVA TOUCH-komponenten är separat utprovad (sedan många år
tillbaka av mig) och har använts, och används fortfarande ofta (och förnämligt)
i många olika tillfälliga (bekväma) switchlösningar i olika elektronikprojekt.
En redovisning kräver särskilda htm-dokument — som innefattar
elektronikgrunderna generellt. En del i dessa detaljer är (sedan länge) redan
utformat, men kräver (betydligt) mera tid för en enhetlig presentation. Tills
vidare refereras därför Touchkopplingen här endast till ovanstående
kopplingsschema.
— Därmed —
äntligen [Mar2013], efter alla mödosamma undersökningar, konstruktioner och
genomgångar (så man trodde att
man aldrig skulle komma fram) — VET vi nu SÄKERT vad det är vi ska mäta
på (restelektroner i
storleksordningen T16 st.) via den exceptionellt
känsliga JFET-sensorn, VAR vi ska leta (metallanslutningar), och HUR letningen ska gå till (föra JFET-proben i minimala rörelser
nära intill).
JFET-sensorns nollställning
och vänteläge
BILDKÄLLA: Författarens arkiv · 13Mar2013 BFprobe
Bild ProbeGND · NikonD90
— JFET-sensorn i apparatbygget beskrivs utförligt i separat htm-dokument,
se kopplingsbilden i JFET-sensorn och JFET-proben.
Hur man kan grovräkna närvarande
elektronladdning (Q) om JFET-sensorn ger något spänningsutslag (–U[GS], grovt
lika med [minus-] mätspänningen
över 1K-motståndet) som återhämtas under en tid (T):
— Exemplet nedan med minimalt
synlig känslighet
[typiska små utslag från arm- och kroppsrörelser på
halvmetersavstånd från JFET-sensorns ingångsantenn beroende på
textilbeklädning: vissa textilier är mer benägna än andra att lagra
elektrostatisk laddning] [går
kontinuerligt mot noll]
via U=0V2
[U(R=1K)=4V8] [1K-spänningen visar 4V8] se kopplingsbilden i JFET-sensorn
som återställs till 0V0
[U(R=1K)=5V0] [1K-spänningen visar 5V0] se kopplingsbilden i JFET-sensorn
inom T=1 sekund:
Q = U·T/R
= (0V2)(1S)/(2,5
T12 Ω)
= 8
t14 C;
= UC ; Se
exempelräkningen i PenselElektronLaddningen
N = Q/(e=1,602 t19
C)
= 499.375,78 elektroner ;
~
5 T5 elektroner ;
spänningsmätningen över 1K-motståndet
återställs från 4V8 till 5V0 på 1 sekund
Med högre instrumentupplösning kan ännu mindre
variationer observeras.
— Se även räkneexemplet i OriginelltMätresultat på den
observerade restladdningen hos 9V-batterier i höljesfoten.
JFET-sensorns
nollställning och vänteläge — under tiden som explicita
variationer pågår i upp- och urladdningar som alltid, i vilket fall, triggar
JFET-sensorn och därmed, här, blir oönskade utslag — verkställs på
enklaste sättet som visas i bilden ovan:
— En kort
kopplingstråd (isolerad röd, bilden ovan) placeras mellan JFET:ens
Gate(G)-Source(S) så att metalltråden kortsluter GS. Det garanterar att JFET:en
leder och lysdioden i indikeringen lyser med max ljusstyrka. Det isolerande
(vita, i bilden) höljet till GateAntennen ger tillräckligt moment för att
fasthålla den (röda i bilden) kopplingspinnen (man kan hantera proben
godtyckligt i xyz utan att pinnen ramlar ur). Strax före aktuell mätning
plockas pinnen bort (med metallpincett):
— Friktion
mellan metaller innehåller ingen elektronisolerande faktor; Elektroner kan
fritt strömma/fördelas jämnt (neutralt) mellan metallytorna, och ingen
elektrostatisk laddning kan uppkomma på den vägen. Att plocka bort
kortslutningspinnen för metallkontaktens del medför alltså inget äventyr (eller bör i varje fall inte göra det i
teorin) i ev. bildning av lokal elektrostatisk laddning.
— Däremot
får man vara försiktig med hand- och armrörelser, samt kläderna man har på sig
(kontrolleras alltid först) så att man SÄKERT vet att ingen nämnvärd
elektrostatisk effekt introduceras till den ytterst känsliga JFET-sensorn
enbart på grund av att man RÖR sig i närheten.
TENDENS — enligt observation:
— Restspänningen över kondensatorn
efter urladdningarna (liksom
storleken på utladdningshålen) varierar mellan 12-20V — om man utandas
vattenånga (som möjligen gynnar
urladdningsgränsavståndet i mikroområdet i urladdningsområdet) i urladdningslådan (före varje
urladdning) — Se särskild webbreferens i samband med Fuktighetens
Inverkan för Elektrostatisk Urladdning.
Det som spelar in FÖR
URLADDNINGSKONTAKTERINGENS DEL i konstruktionen (XYcoAlFEDU)
är att urladdningslådan är något (på
delar av tiondels millimeter) LITET ojämnt riktad topp/botten; de övre
urladdningspunkterna funkar OK, medan de undre inte alls går (i detta folieinspänningsexperiment får
man kompensera genom att trycka in folien utifrån för de nedre fallen).
— Urladdningarna skedde utan
fastbränning för alla de ytterligare 19 testade med kopparplanet försiktigt
fört emot folien.
— Restspänningen stannar ganska precis på halva den
uppladdade kondensatorspänningen (25V
med separat tyristorenhet till de 3×9V-batterierna [26V3]; restspänningen
typiskt 13V), vilket ansluter till originalexperimenten [EXPERIMENTKOPPLINGEN från 2008] — men
vissa variationer finns, liksom storleken på urladdningshålen.
FASTBRÄNNING förorsakas (veterligt i
teorin) av att folieytan lokalt uppvisar märkbara (inom tiondels mM)
variationer;
— när urladdningen sker, och hålsmälta
bildas i hålkanterna, finns möjligheten att smältan tränger upp (bakåt mot
stiftet) och på den vägen smetar fast. En (hårt) spänd folieyta bör eliminera
den typen helt. Det krävs dock en (ännu) mera finstämd anordning för att få en
tydligare djupbild av sammanhangen.
— För att studera detaljerna med
hålbildningen — via minimala kontaktavstånd i den manuella fysikens motsvarande
finmekanik — krävs en mera precist utformad anordning (under utformning Feb2013).
— För dokumentationens del, själva funktionssättet —
glödpartiklarnas tydliga kollisioner med luftmolekyler (och närliggande konstruktionsdetaljer) — har
de större hålen (urladdning sker
i allmänhet ända ner till 0V) ingen direkt betydelse:
AlFU — glödspårens ursprung, ref.
BILDKÄLLA: Författarens arkiv · CATfeb2013 CAT2 2Feb2013
Bild Serie2En5_12 —
NikonD90 · ISO: 400; Bländartid: 1/5 S; Bländartal: F/20

TYDLIGHETEN I GLÖDPARTIKLARNAS KOLLISIONER MED LUFTENS (och
anordningens) PARTIKLAR framträder bestämt. Därmed kan mera säkra
grovberäkningar göras för att bestämma glödpartiklarnas impuls.
— Se utförligt från LuftBASIC
och IMPULSANALOGIN.
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
— Blotta möjligheten att KUNNA
fotografera urladdningar i serier, själva
glödspårsbildningen med den centrala ljusbulan
på samma fasta fokus, var själva huvudsyftet med XYcoAlFEDU,
och den funktionen har i sammanhanget framträtt utomordentligt, typ bilden
ovan. Se även vidare i URLADDNINGSSERIERNA123.
— Däremot lämpar sig hela anordningen
(således) INTE för en mera exakt utvärdering av urladdningstillfällets minsta
möjliga avgörande elektrodavstånd; ojämnheterna i den uppspända Al-folien (och den i det sammanhanget klumpiga
inställningsmekanismen) krossar effektivt den möjligheten. En annan,
mera noggrann konstruktion krävs för det.
XYcoAlFEDU
XY-coordinated Aluminium
Foil Electric Discharge Unit
— 2Feb2013
BILDKÄLLA: Författarens arkiv · CATfeb2013· 2Feb2013 Bild
Gtrack1_1 — NikonD90 · ISO: 400; Bländartid: 1/2 S; Bländartal: F/20
Den allra första
bilden, första uppkopplingen efter konstruktionen, av den kameraanpassade
urladdningsenheten
(tidig morgon 2Feb2013).
— Al-partiklarna kolliderar, tydligen, med luftpartiklar;
tydligt märkbara avvikande rörelsebanor framträder. Se matematiken från IMPULSANALOGIERNAkalkyl.
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
ETT FOTODOKUMENT [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av aluminiumfolieurladdningarna (FENOMENFORMEN i CAT): glödspåren och ljusbulan i Aluminiumfolieurladdningarna.
— Bildsviterna visar GROVBILDERNA hur det ser ut i det praktiska experimentet.
— Nedan visas i sammanställning hur anordningen till fotografierna har gjorts.
BILDKÄLLA:
Författarens arkiv · CATfeb2013· 2Feb2013 Bild coAFUE_1;3;6;14;15;62;66;67
— NikonD90

KONSTRUKTION — grovbeskrivning:
Ett XY-block med M3-skruv (0,5mM stigning per varv)
transporterar ett mobilt urladdningsblock, anoddelen (AluminiumFyrkantRör 20mM i kub med påmonterad Al-folieremsa)
i XY-led:
— Ett katodstift (bilden ovan höger) monterat på
en remsa fjädrande kopparplåt (bilden
ovan vänsterNedre) förs ner mot Al-folien inom ett snävt intervall
(atan
5/17,5 ~ 16°; y-rörelse över hela
5mM-intervallet 0,5GÄNGSTIGNINGEN/22,5CIRKELDELEN =
0,022 mM)
för varje varv (0,5mM stigning i y-led) som Y-blocket
avancerar;
— När stiftet möter Al-folien, sker
urladdning.
— PRINCIPEN I SYFTET med hela
konstruktionen var att få en FAST KAMERAFOKUSERAD URLADDNINGSPUNKT för noggrann
dokumentering av själva fenomenformen — perfekt uppnådd funktion:
— Man håller utlösarkontakten (separat kamerakabel) till
kameran i ena handen, och den andra handens ena finger på XY-blockets
Y-visarhjul; Y-visaren är så konstruerad att man (lätt) kan känna ett litet
motstånd strax innan ansatsen verkställs och stiftkontakten löser ut;
— Man trycker på kamerautlösaren, och
sedan (inom en tiondels sekund,
läget är skarpt) direkt en liten ytterligare rotation på Y-pinnen (blå plexiremsan i bilden ovan nederst
vänster), vilket omedelbart resulterar i en urladdning FÖRUTSATT KORREKT
INSTÄLLNING (bilden nedan).
— Därmed kan fotografier tas (enkelt) i
serie av en ensam operatör: en bild per Y-varv.
— Konstruktionen ovan ger 19 varv per
kolumn i totalt 19 kolumner.
— När en kolumn (19 urladdningsställen) är
avverkad i Y-led (blå vevarmen i
bilden nedan), frikopplas fjädersprinten (man skjuter in den över den närliggande M3.skruven, kretskortsdelen
i mitten i bilden nedan), och man vevar tillbaka till toppläget — samt
vrider X-blockets del ett varv för nästa kolumn. Med återställning av
fjäderblocket är det sedan OK för nästa runda.
BILDKÄLLA:
Författarens arkiv · CATfeb2013· 2Feb2013 Bild coAFUE_8 — NikonD90 — XYcoAlFEDU

DEN KÄNSLIGA INSTÄLLNINGEN (röda 3mM-plexiplattan till höger)
— f.ö. hela konstruktionens absolut mest avgörande del: max stabilitet — visas
ovan i bilden till höger:
— Samma princip som för inställningen
av PLANPARALLELLITETEN HOS ett XY-koordinatbord på verkstadsgolvet i industrin
— eller hemma hos oss i vår privata finmekanikerverkstad (för engagerade amatörer):
— Man precisionsjusterar (in till hundradels millimeter)
största höjdläget för katodstiftets kontakt och dess kopparplan (0,5mM-CuPlåt) via ett ABSOLUT
STOPPLÄGE, de fyra ställskruvarna (röda
plexiplattan) med de motstående stoppskuvarna;
— När Y-vevens (blå plexiglaspinnen i bilden ovan vänster nedre)
beröringssprint kommer fram till fjäderplanet (kretskortsdelen i mitten), trycks kopparplanet med
katodstiftet (nära) RAKT ner i urladdningsblocket; kopparplanet och därmed
katodstiftet kommer inte längre än det inställda stoppläget; Det är viktigt att
katodstiftets yttersta kontaktspets INTE vidrör folien så mycket att denna
deformeras: stiftet ska bara nudda (stryka) över folieytan (fininställning på hundradels
millimeter).
BILDKÄLLA:
Författarens arkiv · CATfeb2013· 2Feb2013 Bild coAFUE_17 — NikonD90

Den avgörande fjädersprinten, den korta M2-skruven med
mutter vänster i bilden ovan (samhörande
med Y-veven som syns otydligt i bild längst till vänster), som berör
fjäderblocket (kretskortsdelen
ovan i mitten), anslutet till kopparplanet (se föreg. bild) där
katodstiftet sitter fast monterat.
OMLADDNINGEN:
— När en kolumn är avverkad (här 19st urladdningspunkter),
trycker man upp fjäderblocket (kretskortet
i mitten i bilden ovan) på toppen av M3-skruven, så att fjädersprinten
får plats under vid tillbakavevningen. Med en X-justerting på ett varv och
återställning av fjäderblocket, är så enheten klar för nästa urladdningskolumn
(här totalt max 19 st).
— Med ytterst liten vridning medger
inställningsskruvarna (M3
närmast på bägge sidor omkring röda plexiplattan, närmast föregående bild)
fininställning på 1/100 mM (1/50 varv eller drygt 7°).
DEN STABILA MONTERINGEN
— TILLSAMMANS MED KAMERA PÅ STATIV för
säkert slutresultat
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
BILDKÄLLA:
Författarens arkiv · CATfeb2013· 2Feb2013 Bild coAFUE_40 —
NikonD90

Prototypen underst tillsammans med den färdiga —
betydligt mindre — enheten överst. I mitten de tre 9V-batterierna med
RC-komponenterna. Bilden nedan visar kopplingsblocket med en inlagd
etikett — 32% utskrift med 96dpi ger 354 pixels per 30 mM, vilket kan användas
för att göra (snygga) etiketter [och
apparatfronter] till olika små bruksdetaljer TILLSAMMANS med
dubbelhäftande tejp [baksidan]
och bokplast [framsidan];
man använder bokplastens »oljepapper» som temporärt skydd till motstående sida
på den dubbelhäftande tejpen; tejpen på baksidan av printen, oljepapperet över
tejpen, man vänder på printen, lägger bokplast på fronten, och sist skär ut
etiketten med papperskniv och avlägsnar oljepapperet; den färdiga etiketten kan
sedan monteras som en ordinär självhäftande, inplastad, dekal.

BILDKÄLLA:
Författarens arkiv · CATfeb2013· 2Feb2013 Bild coAFUE_71 — NikonD90
STABILITETEN I SLUTMONTERINGEN ÄR
AVGÖRANDE:
— Här, BildcoAFUE_40,
har urladdningsenheten [BildcoAFUE_8]
monterats längst upp på den ursprungliga enkla »manuella anordningen» [AnordningenDec2013] — tillsammans med
extra stödplan (en centrumpelare
med ställskruvar, en vertikalstödplatta av en remsa rak, slipad spånplatta för
att eliminera vertikal elastisk töjning mellan det stora träblocket och den
plexiplatta det monterats på, i allt relativt bottenfoten): alla moment
som anställs i samband med beröringen måste GARANTERAT ABSORBERAS av den
underliggande blockmassan. Annars uppkommer/fortplantas darrningar i
materialkopplingarna (fjäderblockets extra moment) från handrörelserna: små
rörelser som stör exakt kamerafokus.
— Den större konstruktionen som syns underst,
under urladdningsenheten i BildcoAFUE_40,
är den föregående PROTOTYPEN: här var det avgörande viktigt att genomgå alla —
samtliga — detaljer AV PRINCIP i större skala (på delvis alternativa metoder) för att få SÄKER
kunskap om material och hållfasthet i konstruktionen som helhet — och om det
ALLS skulle gå att genomföra (med
amatörens begränsade verkstadstekniska utrustning …).
— Den stora smala plexiplattan i
förgrunden finns där som ett (ställbart
i z-led) kameraskydd — för att, säkert, eliminera varje äventyr i
eventuella skador från glödspåren på de olika kameralinser som används vid
fotograferingen.
2012-12-15
ALLMÄNNA GASLAGEN — p(1 atm) = 1,01325 T5 [Pa=N/M2] = 1,01325 (bar=760 mM Hg=torr) — k = 370,95002 J/°K
inledande LuftBasic för inomhusändamål i laborationer — Kalkylkort i KalkylMeanFree.ods
Beräkningarna för luft
ρ = m/V ;
pV = kT
= pm/ρ ;
ρ = pm/kT
= p/(k/m)T
= (p/T)/(k/m) ; [ref. Wikipedia Density of air 2012-12-23]
— Man använder STP-standardvärdet (Standard Temperature and Pressure) vid havsytan p=1 atm och T=0°C=273,15°K som referens (R) för att sedan beräkna alternativa täthetsvärden via alternativa temperaturer;
k/m = p/ρT = (1,01325 T5 Pa)/(1,2922 KG/M3)(273,15 °K)
= 287,06858 [J/°K]/KG = J/KG°K (Wikipedia anger 287,058)
= R ;
ρ = (p/T)/R ;
— Vid p=1atm och rumstemperaturen 20°C=273,15+20=293,15°K är luftens täthet
MedeltäthetenLUFT — LuftBASIC
ρLUFT = p/TR
= (1,01325 T5 Pa)/(293,15 °K)(287,06858)
= 1,2040403 KG/M3
............ luftens täthet vid 20°C
— Medelluftmolekylernas atomvikt (eg. molekylvikt) baserad på uppgifter om luftens sammansättning 78% Kväve (7N14), 20% Syre (8O16) är (approximativt) med två atomer per luftmolekyl i medeltal
UmedelLUFT — LuftBASIC
ULUFT = (0,78)(28)u + (0,2)(32)u
= 28,24u ................................ medelluftmolekylens atomvikt
— Antalet medelluftmolekyler per kubikmeter luft (1,2040403 KG vid 20°C) är då
NLUFT = m/Uu
= (1,2040403 KG)/(28,24 · 1,66033 t27 KG)
= 2,56792 T25 ........................ antalet luftmolekyler per kubikmeter
— Medelmolekylavståndet vid 20°C, den omkring varje medelluftmolekyl omslutna ideala kubvolymen, är då för täthetens 1 M3 lika med
VMOL = (1 M3)/(2,56792 T25)
= 3,89419 t26 M3
med kubsidan eller medelmolekylavståndet (mittpunktsavståndet för två kuber)
sMedelLUFT — LuftBASIC
s = VMOL1/3
= 3,38952 t9 M ...................... luftmolekylmedelavståndet
~ 34 Å
MEDELHASTIGHETEN [Momentekvationen] för medelluftmolekylen i rumstemperatur 20°C är
vMedelLUFT — LuftBASIC
v = √ 3RT/U ...................... via atomvikt och temperatur R=8314,9148 J/[KG°K]
= √ 3(8314,9148 J/KG°K)(293,15 °K)/28,24
= 507,42902 M/S ................. luftmolekylmedelhastigheten
Med medelavståndet 0,1 µM och hastigheten 500 M/S, ges medelfria vägtiden t=d/V som 2
t10 S= 0,2 nS.
Fria medelväglängden
TOTALA TRÄFFYTAN A (tvärsnittet σ=πr2 hos varje potentiell målform), gånger antalet n möjliga målobjekt per ytenhet, σn i M2n, kan via substitution med en approximativ fri medelväglängd l utvecklas via totalt inneslutna målobjektsrymden V=σl så att man får
V/l = σn · l/l som ger
V = σn · l ;
V/σn = l = (σn/V)–1 ; [ref. Wikipedia Mean free path 2012-12-23]
Det är samma (förenklade —VILANDE MÅL) formalia som anges (utan härledning) i Wikipedia (Mean free path).
— Med antagen medelmolekylutsträckning på samma typ (r ~ 3Å = 0,3 nM) som den mellan atomerna i fasta ämnen (grovt 1/10 av gasernas medelavstånd i markluften) och antalet målobjekt per kubikmeter som 2,56792 T25 ges
l = (σn/M3)–1
.............. genomsnittligt
kollisionsfria medelvägen, luftmolekylerna, vilande mål
= (σ[m/Uu]/M3)–1
= (σ[ρV/Uu]/M3)–1 =
(σ[ρ/Uu])–1 = Uu(σρ)–1
= (π[1,5 t10 M]2[2,56792 T25]/M3)–1
=
5,50916 t7 M ....... luftmedelmolekylens fria medelväglängd
~ 0,6 µM
DEN MERA SAMMANSATTA BERÄKNINGSFORMEN
Det är i storleksordning en tiopotens större än det värde (68 nM = 0,068 µM) som anges i Wikipedias tabell (Mean free path in kinetic theory) på den mera sammansatta beräkningsformen för rumstemperad luft vid normalt tryck;
Gasmedelbollens diameter samma
som medelatomavståndet i fasta ämnen, här ca 3Å/2 = 1,5 t10 M:
l = bT/20,5πs2p ; b=1,3805502 t23 J/°K Boltzmanns konstant
= (1,3805502 t23 J/°K)(293,15 °K)/(√2)π(1,7 t10 M)2(1,01325 T5 Pa)
= 3,11 t7 M ............ luftmedelmolekylens fria medelväglängd
~ 0,3 µM
Wikipediavärdet (68 nM) fås
mera bestämt nära om s sätts lika med medelmolekylavståndet (3,4 nM):
;
dFRIAMedelLUFT — LuftBASIC
Gasmedelbollens diameter samma
som medelmolekylavståndet i luft ca 30Å vid 20°C:
l = bT/20,5πs2p ;
= (1,3805502 t23 J/°K)(293,15 °K)/(√2)(3,4 t9 M)2(1,01325 T5 Pa)
= 7,78 t10 M ........... luftmedelmolekylens fria medelväglängd
= 77,8 nM
~ 0,08 µM
Vi använder (här) förenklat värdet 0,1µM i grovräkningen
;
RÖRLIGA
MÅL kan i sambandsformen för det aktuella tvärsnittet (σREST=πr2)
(Wikipedias artikel Mean free path) återföras (förstås) på metriska xy-utsträckningar
enligt följande algebraiska schema — förutsatt homogent fördelade
medelhastigheter inom medelmolekylbeståndet:
σMOVE2
= 2(σREST)2
= 2(σRestXσRestY)
= (σRestXσRestY)X
+ (σRestXσRestY)Y ; Kombinatoriskt
σMOVE
= (σREST)√2 ;
l = ([√2]σn/M3)–1
=
Uu([√2]σρ)–1
= (Uu/ρ)([√2]σ)–1
;
Uu/ρ =
bT/p ;
ρ = Uu/V0 ; (Se utvecklingarna
i Boltzmanns konstant)
Uu/ρ
= Uu/(Uu/V0)
= V0
= k0T/p
= (k/N[Loschmidts tal])T/p
= b[Boltzmanns
konstant]T/p ; (Se
sambandsformerna i Konstanternas värden)
l = bT([√2]σp)–1
=
bT/([√2]πr2p) ; Den
aktuella sambandsformen i Wikipedia (24Dec2012, ej härledd där)
Se även viss koppling till ovanstående detaljer [”the mean squared displacement”]
från den moderna akademins vetenskapshistoria (via Einstein) i
http://en.wikipedia.org/wiki/Brownian_motion
@INTERNET
Wikipedia Brownian motion, Einstein’s theory [2012-12-24]
— Det är för en praktiskt inriktad experimentalist YTTERST svårt att ta till sig dessa »statistiska matteteorier» om det gäller att använda dem I PRAKTISKA TILLÄMPNINGAR: inte en enda praktiskt redovisad, begriplig, experimentell framställning finns, här veterligt, som VISAR sambandens kredibilitet — enbart teoretiska beskrivningar med tillhörande »MonteCarloSimuleringar». LottoProgram. VAR FINNS DET PRAKTISKA FALLET? Vart tog naturvetenskapen vägen.
PRAKTISKA TESTER (luftpartiklar studeras) SOM STYRKER den teoretiska MATEMATIKEN:
En upphittad som redovisar experiment med olika sfäriska
plaskulor — 0,5µM-5µM — finns i PDF-dokumentet
http://physlab.lums.edu.pk/images/3/31/Ref3.pdf
THE TIME, SIZE, VISCOSITY, AND TEMPERATURE
DEPENDENCE OF THE BROWNIAN MOTION OF POLYSTYRENE MICROSPHERES, Jia et al., 2006
PARTIKELSTORLEKAR (vid experimentellt påvisande av Brownska rörelser):
TUTOR.VISTA.COM — Brownian Motion [2012-12-24]
http://chemistry.tutorvista.com/physical-chemistry/brownian-motion.html
”Brownian movement is seen in the colloidal solution.
Colloidal solutions are those which have particle size in between that of the
true solution and the suspension. The
diameter range of the particles is between 1nm to 1000nm.”
THE ENCYCLOPEDIA OF SCIENCE - Brownian motion
[2012-12-24]
http://www.daviddarling.info/encyclopedia/B/Brownian_motion.html
”Brownian motion of smoke particles
Brownian motion occurs in liquids and gases because of the
random motion of the molecules. In gases, Brownian motion is best observed by
illuminating from the side under a microscope a shallow box containing smoke. A
dark background is put behind the box. The illuminated smoke particles seen as
bright spots of light execute a zigzag walk against the dark background. The smoke particles have smaller
diameters than the wavelength of light but they can easily be seen as
they scatter light into a diffraction halo.”
Oavsett orsaken till de
(delvis) tydligt olika resultaten (>3ggr skillnad):
— KÄRNAN i teorin är »målets tvärsnitt». Dvs., den teoretisk TRÄFFYTAN. Men den matematiken är också SVÅR att veta;
— Atomernas elektronhöljen fungerar som delvis inbördes (idealt elastiska MJUKA) stötdämpare, och ingalunda som några skarpa, hårda bildjardbollsskal: atomernas elektronhöljen samverkar.
— Vi VET heller inte närmare HUR den dynamiken ter sig på aktuell molekylnivå: praktiska redovisningsexempel saknas.
— Det vi vill VETA här, är mera ingående EXPERIMENTELLA RESULTAT — så att v i få veta.
— Emellertid verkar webben urfattig på den typen av beskrivningar: knappast alls (inget enda) finns i redovisning på HUR luftens molekyler I PRAKTISK MÄTNING/observation uppför sig inbördes: moment, steglängder.
— Desto mera material finns på den s.k. Brownska rörelsen: luftmolekyler som puttar typ pollenkorn och rökpartiklar.
— Ingen BESKRIVANDE koppling verkar emellertid finnas som uppehåller sig invid den ev. samhörigheten mellan teori och praktik. (Generellt verkar teorin vara i övervikt).
— Det är nämligen svårt att få fram rent praktiska
observationer på typ lufthavets molekylära rörelser: positioner, impulser via
BILDER. Luftmolekylerna syns inte, per.
Teori på Webben — avsnittet om ”medelhastigheterna” inte möjligt att detaljbeskriva, annars bra uppslag
MOLECULAR
COLLISIONS — Michael Fowler 7/21/08
http://galileo.phys.virginia.edu/classes/152.mf1i.spring02/MolecularCollisions.htm
KALKYLKORTEN till IMPULSANALOGIERNA
Kalkylkortet
kalkylkortet nedan DIREKT FRÅN DEN
HÄR WEBBLÄSAREN KalkylMeanFree.ods
— se öppningsmanual
om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare
(vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN
OFFICE finns installerad på datorn)
http://www.universumshistoria.se/AaKort/KalkylMeanFree.ods
Tabell1 — allmänna konstanter
Tabell2 — Impulsanalogin d = mv/R — i luft 20°C
Tabell3 — komplement till Tabell2
Huvudtexten refererar vilken kalkylkortstabell (Tabell2, Tabell3) som används i
vilket sammanhang.
Dokumenten som
format presentationen i Blixturladdningens Fysik 2012 [10Apr2013]:
————————————————————————————————————
http://www.universumshistoria.se/BlixtTGF2012.htm
http://www.universumshistoria.se/BlixtTGF2012JPG.htm
http://www.universumshistoria.se/AaKort/KalkylMeanFree.ods
BlixtTGF2012BF245.htm
JÄMFÖRELSER MED KONVENTIONELLA REFERENSER
bilden
nedan med slipskivan
JÄMFÖRELSER MED KONVENTIONELLA REFERENSER
Materialavverkning genom ren mekanisk nötning (»täljning») — ingen direkt jonisation PER atom
— Materialstycket SLITS — täljs eller trycks
— av genom (en linje av) sammanhängande atomlager som I VILKET FALL måste bryta
hållfastheten i atomgitterbindningarna i materialet, och därmed, likväl, en
VISS begränsad lokal jonisation i ekvivalens med det utbrytande arbetet.

BILDKÄLLA: @INTERNET Wikipedia — http://en.wikipedia.org/wiki/Spark_(fire)
Järn — tekniskt rent, 7mM stång
Materialavverkning genom ren jonisation — ingen direkt mekanisk nötning
BILDKÄLLA: Författarens arkiv · Spark2012main · 16Dec2012 Bild
Järn014 — NikonD90 · ISO: 2000; Bländartid: 1/2 S; Bländartal: F/9
JÄMFÖR NYLIGEN FOTOGRAFERADE GLÖDSPÅR FRÅN ELEKTRISK URLADDNING (föregående CAT-experiment upprepade med fotografisk dokumentation) — glödspåren utgår från a:
JONISATION
— elektronreduktion (Jämför Teorin i MAC) som skapar repulsioner
mellan gitteratomerna
— är ENDA SÄTTET för fragmenten, vilka
de än är, att ta sig ut från materialet.
—
Att fragmenten i
jänfallen INTE tycks uppvisa någon direkt kollision med luftens
molekyler
[Jämför Aluminiumspåren där sådana kollisioner framträder övertydligt] (medelatomvikt grovt runt 30u, 500 M/S
medelhastighet, rörelsemängd medel p=mv=2,49049 t23 NS),
endast
inbördes delning i spårsluten, tyder på att järnfragmenten är av den tyngre
arten: analogt att rörelsemängden är mycket större än luftmolekylernas.
Magnettestet avgör: Partikelgruppen inte joniserad.
—
Istället kan fenomenet förklaras så:
—
I urladdningspunkten gäller helt säkert
PLASMA. Därifrån rekombinerar atomerna snabbt: Järnatomerna
förenas till större smältpärlor i plasmazonens utkant, tillsammans med den
omgivande luftens 78% Kväve (N) och 20% Syre (O), med ev. övriga;
—
Kväveföreningar med syre är kända för att ingå generellt i explosiva föreningar
[Wikipedia Explosive
material, Chemical, Dec2012]: föreningarna MED JÄRNET SOM
KARAKTÄRISTISKT CENTRALÄMNE kan tydligen förstås bilda tidsinställda
fyrverkeriutbrott (om ingen
annan förklaring gäller), vilka avlöper i de här benämnda
krondelningarna (i eng, ofta
gafflingar, fork eller flower-detaljer): metallpärlorna
delas tydligen upp i mindre på kredit av (kväve-)krevaderna.
—
INTRYCKET UTAN FOTO (Spårteckningarna)
är att krondelningar förekommer i flera nivåer på samma glödspår.
—
Fotografierna visar (hittills) att den typen av allt att döma är en
(tankemässigt visuell) överprojektion mellan två eller flera synligt
närliggande/vinkellika glödspår.
—
I inget fall har (hittills) någon tydligt skönjbar dubbelkrondelning iakttagits
på de fotografier som f.n. tagits på glödspåren från järn och stål som
anodmaterial.
Olika typer har testats (med växande
kolhalt/hårdhet):
Tekniskt rent järn (0% C), Silverstål
(1% C), Filstål (verktygsstål 1,2% C). Enda skillnaden mellan dessa
— om alls någon: olika urladdningar på
samma material uppvisar inbördes relativt stora skillnader
— är att antalet glödspår (och
intensiteten) MÖJLIGEN varierar med stålets hårdhet (högre kolhalt).
BILDKÄLLA: Författarens arkiv · Dec2012
· Nikon D90

KORNSTORLEKEN
hos glödpartiklarna i järn/stålfallen ligger förmodligen (ingen direkt beräkningsgrund finns här)
upp mot mikroområdet [Jämför ALUMINIUMFALLET].
Buzzard 1933 visar för sin del mera
industriellt anpassade mekaniskt anställda analyser från sliptester (eng. spark testing, olika stål testas
via högvarviga slipskivor) som lämnat sfäriska kulrester från glödspåren
runt Ø0,1-0,2mM — kornstorleken torde variera med energin i avverkningen:
smältkornens storlek växer med avverkningsenergin; Den rent jonbaserade
avverkningsenergin i detta fall, urladdningarna ovan via 100µF och 26V [Se ANORDNINGEN], är relativt ringa och
ligger i storleksordningen grovt (kapacitivt E=UQ) omkring tiondels Joule:
26V·1 T16 · 1,602 t19 C = 0,041652 J; 1 T16 atomer med första
jongrad, analogt lika många elektroner i jonisation, approximerat från
CAT-experimenten med Al-folie.
— Det motsvarar ungefär antalet atomer som
försvinner från den lilla märkgropen i materialet: 0,1mM i kub gånger tätheten,
7870 KG/M³ för Järn, ger 7,87 t9 KG material via
N=m/Uu=56·1,66033 t27 KG=8,5 T16 stycken Järnatomer;
—
Storleken hos avverkningsgropen, ca
0,1mM, och antalet glödspår (flera hundra) visar att metallpartiklarna här bör
vara betydligt mindre än Buzzards 0,14 mM-partiklar.
— Mera ingående, (molekylärt)
detaljerade beskrivningar av speciellt järn/stål-krondelningarna har eftersökts
på webben (Dec2012). Det verkar dock inte finns några sådana, i varje fall inte
i det gratis tillgängliga utbudet. Många beskrivningar finns dock på själva
slipspåren i olika tester från verkstadsindustrin (eng. spark
testing).
Men ingen underliggande teori verkar ens beröras eller omnämnas: anledningen
till krondelningarna, kornstorlekarna i de olika energifallen. Det är bara Buzzards framställning från 1933 som
syns, och den är också mager i teorin.
— Det finns i detta fotogalleri ingen säker tendens till
iakttagbar skillnad mellan de olika testade fallen Järn/Silverstål/Filstål;
— De individuella urladdningarna kan variera högst betydligt
inbördes i strålskurens mångfald (antal spår), styrka (längd) och intensitet
(ljus).
— Förgreningstypen som sådan (kronbildningen, som i de
typiska bilderna ovan) ser likadan ut i samtliga fall Järn/Silverstål/Filstål.
— Glödspårens beskaffenhet att sluta på
egna utbrottslinjer (liknande en rödaktig spjutspets) tyder på att
partikelstorleken (eller partikulära rörelsemängden) är betydligt större än den
omgivande luftens molekylmedelvärden. Någon jämförelse med Aluminiumfallet — som däremot
(övertydligt) visar interferens med luftmolekylerna — finns tydligen inte i
Järnfallet. Och av allt att döma heller inte i Kopparfallet.
BILDKÄLLA: Författarens arkiv · Spark2012main · 16Dec2012 Bild Järn006 — NikonD90 · ISO: 2000; Bländartid:
1/2 S; Bländartal: F/9

Typisk elektrisk urladdning från katodstift mot järnstång (tekniskt
rent järn) via 26V och 100µF. Se ANORDNINGEN.
Fotograferingsteknik manuell: Via en
separat handhållen utlösningsknapp aktiveras först kamerans utlösare. Man har
sedan bländartiden på sig för att nudda katodstiftet vid anodmaterialet. Med
viss övning ger sig en viss rytm. Enda svårigheten är (i början) att hitta
anodstången i mörkret. Också det går, med viss träning.
ANODMATERIAL: Järnstång (tekniskt rent järn), stångens diameter Ø~7mM.
Katodstift [‡]: ![]() Samma som i CAT-experimenten [Se EXPERIMENTKOPPLINGEN i CAT].
Samma som i CAT-experimenten [Se EXPERIMENTKOPPLINGEN i CAT].
Matning [Se ANORDNINGEN]:
3st 9V-batterier (ca 27V), 100µF 50V elektrolytkondensator (1K
uppladdningsresistans, RC=0,1S).
Glödspårens längd, ca 1-5 cM.
Total materialavverkning (här delvis uppskattat från folieurladdningarna i CAT-experimenten):
V = 0,017mM×π(0,1mM)2=(1,7 t5 M)π(1 t4 M)2
= 5,3407 t13 M3; ρ(Järn)=7870 KG/M3; m(Järn)=ρV~4,2
t9 KG = 4,2 µGram;
ca 4,5 T16 Fe-atomer (N=m/Uu).
Bilden nedan visar millimeterskalan på en stålskala som lagts vid
järnstången.
BILDKÄLLA: Författarens arkiv · Spark2012noCap · 15Dec2012 Bild Järn001 — NikonD90 med tilläggslinser · ISO: 400; Bländartid:
1/5 S; Bländartal: F/25

De små punkterna (små urgröpningar
i järnstången, överst, ca 0,1-0,2mM i diameter) bildas av
urladdningarna.
Skalan i millimeter från en stålskala som placerats vilande intill
järnstången.
Glödspåren är — tydligen, i detaljerna — av exakt samma typform (ökad mängd kol i järnet påstås konventionellt ge en rikare/starkare spårbild [”As the carbon content of the steel is increased, the number and intensity of the "carbon bursts" increase.”, Buzzard 1933 s529n]). Skillnaden är bara längden (spårbilden ovan [30mM] jämförd med Wikipedias slipbild [500mM] är runt 500/30=17ggr mindre, men spårtypen ser nära exakt likadana ut) och tjockleken — på grund av den betydligt lägre överföringsenergin;
E=UQ
— urladdning för hela matningsspänningen (här ca 26V), Q från CAT-beräkningarna (2×1,5 T16 × 1,602 t19 C = 4,803 t3 C) —
ger
E ~ 0,125 J ~ 7,8 T17 eV = 7,8 T11 MeV.
Slipbilden omsätter en (betydligt) högre magnitud (17 gånger mer; (minst) ca 2 J drygt [JÄMFÖRELSE: tyngden av ett dricksglas med vatten (0,1 KG) som stöts mot ett hårt föremål med hastigheten 10 M/S ger rörelseenergin 5 J).
— Det är — uppenbarligen — inte att tänka på några större partikeldimensioner som grund för glödspårsljuset i BildJärn006-bilden ovan.
— Vi kan grovräkna (BildJärn006) antalet grundlinjer i spårskuren till (över) 50 st. Men det finns (här) i järnfallet inget direkt sätt att avgöra den aktuella kornstorleken.
EFTER GENOMFÖRD ANALYS (Dec2012) —
Bilder på
Glödspår från Aluminiumatomer (möjligen
AlN/Al2O3) i kollision med luftmolekyler
Aluminiumatomens
elektronkonfiguration [Periodiska systemet] 2-8-3; Kväveatomens elektronkonfiguration 2-5; Föreningen kan bilda
elektronresonans via AluminiumNitrid
(AlN) — kristall (minst 8 atomer per);
—
DOKUMENTATIONEN PÅ ALUMINIUMNITRID PÅ SVENSKA är (ännu Dec2012) urusel.
Knappast ett enda ord om VAD eller HUR.
—
MOLEKYLÄRT fylld yttre elektronresonans kan också verkställas av AluminiumOxid
Al2O3: Syreatomens 2-8-6 har 2 vakanser (8–6=2); 3ggr dessa ger 6 platser;
Aluminiumatomens 2-5 har 3
vakanser (8–5=3);
2ggr dessa ger de tillgängliga 6. Övervikten för Kvävet (78%) mot Syret (20%) i
luften torde betyda att andelen AlN överväger (4 på 1). Atomvikten för U(AlN) =
(27+14)u=41u; För U(Al2O3) ges (2×27+3×16)u=102u.
BILDKÄLLA: Författarens arkiv · Spark2012main· 16Dec2012 Bild
Alum013 — NikonD90 · ISO: 2000; Bländartid: 1/2 S; Bländartal: F/9

Anodmaterial, 2mM Aluminiumstång.
— Gör din egen experimentutrustning [utan större dramatiska utflykter]
och ta urfina kort (om du har en systemkamera). Se ANORDNINGEN.
— Min rekommendation för maximal säkerhet:
planera anordningen omsorgsfullt; använd ingen högre spänning än runt max 24V,
ingen högre kapacitans än max 100µF;
— Är du det minsta tveksam: avstå.
Bilden ovan visar det typiska draget med ALUMINIUM SOM URLADDNINGSANOD (spårlängd ca 1-5 cM):
— Glödspåren från Aluminiummaterialet uppvisar ibland enorma tivolin av krumbukter åt alla möjliga håll — inkluderat direkt bakåtstuds. Ytterligare originella exempel nedan.
— Se även mera tydligt i Fig.3.
FotoGlödspår — se äv. Fig.3 — AlGlödspåren
BILDKÄLLA: Författarens arkiv · Spark2012main· 16Dec2012 Bild Ljusbula003 — NikonD90
· ISO: 2000; Bländartid: 1/2 S; Bländartal: F/20


Anodmaterial, 0,017mM Aluminiumfolie, i
övrigt samma kopplingsbild som i CAT-experimenten. Ljusbulans utsträckning [ännu osäkert i medeltal utan vidare
foton] ca (1-)3-5mM. Spårlängderna grovt 1-3 cM:
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
— Med rörelsemängdernas
ekvivalenter m[L]v[L] = mv, som ger m/m[L] = v[L]/v följer att förhållandet
mellan hastigheterna för luftens medelmolekyler (v[L]) och Partikelns
sluthastighet (v — Partikeln puttas
kontinuerligt omkring av luftmolekylernas värmerörelser) motsvarar
massförhållandet mellan Partikeln och medelluftmolekylen (ca 50u). Rimligheten efter
fotografiet ovan antyder [här utan vidare utläggningar] att Partikelns sluthastighet
bör ligga någonstans inom 0,1-0,5 M/S — men det är högst osäkra värden. Det ger ett
största förhållande
v[L]/v = 500/0,1 = 5000,
och ett minsta
v[L]/v = 500/0,5 = 1000,
som TILL JÄMFÖRELSE kan användas i den översiktliga grovräkningen. Se vidare beskrivning
i huvudtexten (nedan).
FÖR SPÅRBILDEN SOM SÅDAN
framgår följande av princip:
![]()
Ju
längre tid Glödpartikel vistas i spåret, desto mera dämpas dess hastighet på
grund av kollisioner med luftmolekyler; Kollisionerna framstår som — är — helt omärkliga
i början.
—
Först när Glödpartikelns hastighet avtagit märkbart, framträder impulserna från
luftmolekylerna mera tydligt: Glödpartikeln avviker märkbart från sin raka
bana.
PARTIKELSTORLEKAR
anges på webben bl.a. i webbkällan [2012-12-20]
http://www.engineeringtoolbox.com/particle-sizes-d_934.html
THE ENGINEERING TOOLBOX
Exempel
som anger partiklar mindre än 1µM=1000nM: — diameter i mikroMeter [t6 M = µM]:
Smoldering or Flaming Cooking Oil 0.03 - 0.9
Corn Starch 0.1
- 0.8
Sea Salt 0.035
- 0.5
Bacteria 0.3
- 60
Bromine 0.1
- 0.7
Lead 0.1
- 0.7
Radioactive Fallout 0.1 - 10
Rosin Smoke 0.01
- 1
Combustion 0.01
- 0.1
Smoke from Natural Materials 0.01 - 0.1
Burning Wood 0.2
- 3
Coal Flue Gas 0.08
- 0.2
Oil Smoke 0.03
- 1
Tobacco Smoke 0.01
- 4
Viruses 0.005
- 0.3
Typical Atmospheric Dust 0.001 to 30
Det
finns alltså många typer i nanostorlek.
Jämför även BROWNIAN MOTION-animeringarna på Wikipedia:
onekligen slående likheter.
— För metaller är atommedelavståndet grovt
2,5-3 Å eller approximativt 0,25 nM = 0,25 t9 M = 2,5 t10 M; en kub med sidan
10 nM (dammpartikel) kan då som mest (metalliskt stoft) innehålla antalet
atomer
N = [(10 t9 = 100 t10)^3]/(2,5 t10)^3 = (40)^3
= 64000. Är dammpartikelns kubsida 1 nM ges
motsvarande endast 64 atomer.
Är Partikelhastigheten
hög i början, har den omgivande luftens partikelimpulser praktiskt taget ingen
inverkan. Partikelspåret är helt rakt, spårillustrationen som ovan:
![]()
Men vartefter Partikeln
tappar rörelsemängd, alltså minskar i hastighet, blir den allt mer känslig för
de omgivande luftmolekylernas stötar. Vid en viss kritisk gräns, börjar en
märkbar avvikelse visa sig i Partikelbanan, och med allt vidare avtagande
hastighet blir den avvikelsen till slut märkbart dramatisk. Historien slutar
med att Partikeln puttas omkring slumpartat i lufthavet av luftmolekylerna på
deras rörelsemängd.
DEN KRITISKA
TIDSASPEKTEN:
— Fotografiet nedan är
taget (rytmiskt, flera) genom att taktmässigt först trycka in kamerautlösaren
(separat handhållen kabelanslutning) och först därefter, snabbt, anbringa
katodstiftet. Med bländartiden 1/2 sekund betyder det ett rimligt fönster på
max ca 0,25S fram till urladdningsljusets första delar. Därmed totalt
återstående ca 0,25S max för hela ljusbilden. Med max 3cM spårlängd ges idealt
0,03M/0,25S=0,12M/S. Det blir absolut lägsta partikelhastigheten i längsta
spåret. För att säkert få vetskap om en minsta tidsgräns, måste bilden tas på
och analyseras via kortare bländartider — en angelägenhet som INTE nuvarande
anordningar medger.
— Separat (preliminärt) fototest
Exponeringstid 1/5S — Spark2012_3
Bild7&14 19Dec2012 Bild7: ISO: 400; Bländartid: 1/5 S;
Bländartal: F/9 —



Aluminiumanod
visar osäkerheterna:
— En bild (ovan) kommer fram som visar ofullbordade glödspår
(inga avslutningar).
— Men hur vet vi tidsfönstret NÄR den bilden togs in av kameran?
Det KAN vara inom den första hundradelen (reaktionstiden max för vanliga dödliga
ligger just inom hundradelar [mina egna test via stoppur] om det gäller
intervall för reaktion på mekaniska tryck). Men vi
VET inte det. Det skulle i så fall vara gränsformen; Säg 5mM oavslutade spår
visas under 0,01S, vilket ger 0,5 M/S; Var FotoFönsterTiden istället 0,05S är
spårutvecklingshastigheten på 5mM lika med v=0,005/0,05=0,1M/S.
— Ju högre spårhastighet, desto mindre förhållandetal mellan
Partikelmassan och Luftmolekylen; För 20mM spår på 0,005S ges v= 4M/S; 500/4=125 Al-atomer per
SpårPartikel.
— Uppskattning av spårbildningshastigheten är också i sig äventyrlig: FÖSTA DELEN är snabbast, MITTDELEN
medel, SLUTDELEN långsammast.
Det visar (MÖJLIGEN i vilket
fall) att prövningsvärdena ovan (0,1-0,5 M/S) är någotsånär rimliga (och
ändå kanske inte — INTRYCK är bra för översikten, men inga bra precisionsmätare).
— En mera precis uppskattning via matematisk kalkyl ges i IMPULSANALOGIERNA — med stöd i ytterligare fotografier från
aluminiumfolieurladdningarna. Resultatet endast bekräftar ovanstående antydda
grova överblick.
Nedan visas hur
impulsanalogin kan beskrivas utifrån enklast möjliga förutsättningar. Se även mera
utförligt i HÄRLEDNINGEN.
FÖRENKLAD GROVBERÄKNING —
krummelspåret i FOTOglödspår öv.vä.

— (mv)P/d =
(mv)L/x; (mv)P/(mv)L = d/x; x·(mv)P = d·(mv)L:
— Partikeln (P) med rörelsemängden p=mv bromsas av (metriska impulsmotståndet, R) det
genomfarande mediets (L, luftens) partikulära metriska rörelsemängd (p0/s)d=Rd;
Rörelsemängdernas ekvivalenter efter tillryggalagd väg (d) motsvaras idealt av
att Partikeln helt har bromsats upp (eg, antagit samma status i impulser som
mediets partiklar).
— Då gäller [mv = p0 · d/s]: mv = (p0/s)d = (R=metriska ImpulsMotståndet)d, som ger
d = mv/R ....................
d, sträckan som Glödpartikeln färdas innan den når luftmolekylernas
medelrörelsemängd [då glödpartikeln har »stannat»]
m, Glödpartikelns massa vid bildningstillfället
v, Glödpartikelns utgångshastighet vid bildningstillfället
R, »metriska impulsmotståndet», p0/s; Luftmolekylernas
medelimpuls (p0) över luftMolekylMedelavståndet
(s) — styrkan i HUR Glödpartikeln kommer att tappa fart i den löpande kontakten
med luftmolekylerna
Ref., Utvecklingsexempel
från Lennart Brandqvist 1962 ITK 9 — Differentialkalkyl s96 — Fisk som
slutar simma och då glider en stoppsträcka
d i vattnet.
Se vidare i den mera utförliga Härledningen.
Vi behöver I GROVRÄKNINGEN inte ta med någon (direkt)
friktionsyta OM Partikeln är mindre (eller lika med) genomgångsmediets
genomsnittliga partikelavstånd [max fria
medelväglängden] (s = x = 0,1µM
i inomhusluft [20°C]).
— Om vi antar den förutsättningen för vidare prövning betyder
det i Partikeln=Aluminiumfallet att den inneslutna kuben med sidan 0,1µM
innefattar gränsfallet i antalet Aluminiumatomer lika med
N(Al[0,1µMKUB])=(m=ρV)/Uu=(2700 KG/M³ · [1 t6 M]3)/(27
· 1,66033 t27 KG) = 6,02289 T10 st
— Förbehållet här, med
ledning av ovanstående typfotografi, är att Partikeln inte får vara så stor
relativt den enskilda medelluftmolekylen [LuftBASIC], att luftmolekylen inte kan putta Partikeln (inom synbarheten
för fotografiets bilddata) — vilket (här), vad vi kan förstå, vore fallet om
Partikeln bestod av runt T10 atomer (Jämför:
att kasta 1 KG på en oceanångare [miljontals KG = förhållandet 1 till T6] gör
inte mycket åt båtens position).
— Ett mera ingående sätt
att uppskatta den gränsen är genom följande aritmetiska impulsanalogier:
— Luftmolekylens
medelatomvikt är grovt räknat U=30u med medelhastigheten 500 M/S [20°C]:
— Partikeln slutar i
vilket fall på samma rörelsemängd som luftens medelmolekyler, och dessa kan
därför anställas i analogin:
10-10.000?
30u · 500 M/S = 3000u · 5 M/S; Partikeln är 100ggr större/tyngre än
medelluftmolekylen;
30u · 500 M/S = 3000000u · 5 mM/S; Partikeln är 100.000ggr större/tyngre än
medelluftmolekylen;
— Fotografiet (FOTOglödspår
öv.vä.) på bländartiden 0,5S

visar i varje fall NÅGON
rörelse i den aktuellt krumlade spårbilden.
— Med den förutsättningen
skulle Partikelgränsen som ansvarar för spårbilden ligga grovt och ungefär vid
omkring (absolut) max 100.000 Al-atomer (med
största sannolikhet betydligt mindre antal; kanske 1 till 1000 max, vidare
nedan).
— Med rörelsemängden via
medelluftmolekylen enligt
p = mv = (30u · 500 M/S) = 2,5 t23 NS
och därmed R=metriska
ImpulsMotståndet (s = fria medelväglängden
grovt i luft vid rumstemperatur)
R =
mv/(s=0,1µM=1 t7 M) = 2,5 t16 NS/M
ges för sträckan d=1cM via massan 100.000
Al-atomer utgångshastigheten
v = Rd/m = (2,5 t16 NS/M)(0,01 M)/(T5 · 27 · u) = 558 M/S;
— RÖRELSEENERGIN för v via
m = T5 · 27 · u = 4,5 t21 KG motsvarar
E = mv2/2 = (m
= T5 · 27 · u = 4,5 t21 KG)v2/2 = 7 t16 J (~=4373eV;
0,043eV/atom);
För
d=5cM ges motsvarande ca 1eV per Al-atom, också det för lite.
— OM Al-utflykten baseras på jonisation
måste energin per Al-atom
minst [Al+1] vara ca 6eV (Se Tabell Wikipedia Ionization
energy of the elements); För 100.000 Al-atomer således minst 600.000 eV.
— Den räkningen (alldeles
för lågt v-värde [558 M/S]) styrker slutsatsen att antalet Al-atomer i
Partikelexemplets glödspårsindivid bör vara (betydligt) lägre än 100.000 — OM
Al-utflykten baseras på jonisation: utgivning med frikoppling PER individ.
Den observationen styrks
också via sambandsformerna i den mera omfattande Härledningen
till Impulsanalogin och det tillhörande Kalkylkortets resultat. Antalsgränsen (absolut, Nmax) går vid ca 25.000.
;
— Med N(Al)=1000 ges
motsvarande
v = Rd/m = (2,5 t16 NS/M)(0,01 M)/(T3 · 27 · u) = 55.800
M/S;
E = mv2/2 = (m
= T3 · 27 · u = 4,5 t24 KG)v2/2 = 7 t15 J (~=43.731eV;
43,7eV/atom [räcker till Al+3])
— Den resultatbilden
FÖREFALLER mera rimlig.
— PARTIKELKUBEN får då
kubsidan d=([m=4,5 t24 KG]/[ρ=2700 KG/M³])1/3=1,1856 t9 M,
eller ~1 nM,
— Dvs., en Nanopartikel (på gränsen [0,001µM] till [EPA-standard] klassificerad gaspartikel).
;
30u · 500 M/S = 30.000u ·
0,5 M/S; Partikeln är 1000ggr större/tyngre än medelluftmolekylen;
— Partikeln »stannar», i
vilket fall, på samma medelrörelsemängd som luftens medelmolekyler.
— Är glödspårens antal
runt 100 (vilket FÖREFALLER vara i överkant
[svaga spår syns inte, värdeformen kan vara äventyrlig]) blir
totala antalet Al-atomer i spårskuren lika med 100.000 — fortfarande en helt
försumbar mängd jämfört med hela områdets runt T16 Al-atomer som frigörs ur
Al-folien. Dvs., som tidigare: glödspårens energibidrag i hela räkningen
FÖREFALLER försumbart.
Se även mera utförligt om antalet glödspår
i UtvidgningTVÄRSNITT.
BILDKÄLLA: Författarens arkiv · Spark2012main· 16Dec2012 Bild Koppar022 — NikonD90
· ISO: 3200; Bländartid: 1/2 S; Bländartal: F/9

Bildhöjden motsvarar grovt ca 1 cM.
Kopparspåren (bilden ovan) framstår starkare i verkligheten än i den fotograferade bilden (mitt personliga intryck);
— Bilden ovan visar det typiska draget för glödspåren med KOPPAR SOM URLADDNINGSANOD (spårlängd 2-15mM):
— Glödspåren är alltid raka med spår som tonar ut mjukt i slutet.
— Se även SPÅRTECKNINGARNA till jämförelse med detaljerna ovan (mina datorteckningar efter de första observationerna).
Många bildexempel på webben på olika
materials glödspår finns f.ö. under rubriken
spark testing, spark characteristics
(spark streams)
GLÖDSPÅREN kallas (eng) streaks, spark pattern, spark streams
— men ingen verkar intresserad att
FÖRKLARA/relatera
SPÅRSTRUKTUREN PÅ/till
ATOMÄR/molekylär NIVÅ.
Inte ett endaste dokument ännu upphittat (15Dec2012).
— Många beskrivningar av fenomenet
finns. Ingen teori bakom.
— Det man hittar på webben berör:
Föreskrifter för stålarbetare. Skyddsföreskrifter. Apparatbeskrivningar.
Verktygsmaterial.
— Inte ett enda ord om den
bakomliggande teorin.
— EN upphittad — från 1933 (Ett kort
stycke s529 ”4. THEORY OF SPARK STREAM”):
[OBS: Speciella villkor gäller för experimentet: högvarvig
slipskiva (15000rpm)].
s529:
”The characteristic appearance of the spark stream is apparently
to be attributed chiefly to the oxidation of the carbon in the steel.
Alloying elements may contribute minor
characteristics to the stream.
It
appears probable that as the grinding wheel tears off small particles
of
steel the work done causes the
temperature to rise. This
rise in
temperature
may also be increased by a "pyrophoric" oxidation
effect
resulting from the rapid surface oxidation of small particles
which
are torn away from the steel specimen with perfectly clean
oxide-free
surface. The particles of steel are heated to such a degree
that they
become fused, at least superficially, and tend to become
spherical. Oxygen and carbon react in the heated
portions of the
particles
to produce C02 and perhaps CO.
The oxide scale formed on a plain carbon steel is not very tenacious
and easily flakes off. The gas which forms within the heated spherical
particles escapes through
this easily fractured skin and gives rise to
the "series spark
bursts." A comparatively
smooth pellet which
shows a slight
pattern on the surface remains
after the particle
cools.
Alloying elements in the steel may change the characteristics
of the
oxide film in such a manner as to give the various spark
characteristics.
The entire spark stream consists of the
trajectories of a multitude
of glowing particles
with the accompanying "bursts." As the carbon
content of the steel is increased, the
number and intensity of
the "carbon bursts"
increase.”, s529,
”Silico-manganese steel produced
badly blown pellets which, although
spherical in shape, had
holes
blown entirely through them (table 11).”, s538n,
THE UTILITY OF THE SPARK
TEST AS APPLIED TO COMMERCIAL STEELS, R. W. Buzzard 1933
http://nvlpubs.nist.gov/nistpubs/jres/11/jresv11n4p527_A2b.pdf
NOTERAT:
CAT-experimenten med TEKNISKT RENT JÄRN —
krondelningarna — har ingen kolfaktor att återfalla på (”in the steel”).
Medelavståndet mellan atomerna i fasta material är grovt ca 3Å = 0,3 nM:
— ”The
particles of steel are heated to such a degree that they become fused”
behöver inte betyda annat än att FRÅN BÖRJAN PYTTESMÅ MATERIALFRAGMENT (i storlek nano [tiotal atomer] eller bråkdelar av
mikro [hundratal atomer]) »sammansvetsas» på föregående beskrivna grund
(på sätt som här inte närmare är känt i detalj);
Dessa bildar de slutligt iakttagna materialpärlorna i formen av det iakttagna
slipdammet (ca Ø0,14mM). Huruvida dessa sfäriska pärlobjekt är objekten bakom
glödspåren finns ingen närmare beskrivning på.
s538:
”It has been found on
examining the metallic "dust"
from the spark stream of a steel that
the individual burned particles are globules or pellets
and that the
pellets from one steel often differ
quite characteristically from those
of another kind of steel.”
;
”The "dust" from the spark streams in the foregoing
examinations
was collected and the spherical pellets
separated from the more irregular
particles by rolling on a sheet of
paper. The spherical pellets were
then sieved. All of the pellets which did not pass a 100-mesh
screen
were collected and examined under the
microscope (x 35, fig. 28).”
;
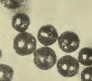
Ovanstående ger realmåtten för metallpärlorna (ca 5mM i
bilden med 35ggr förstoring) ca Ø=0,14 mM
Webbreferenser som
ansluter till blixturladdningens fysik (2012-)
1Vsensitive StaticChargeMeter — JFET MPF102 Nch
http://amasci.com/emotor/chargdet.html
Se även projektbyggare med
BF245
http://users.otenet.gr/~meteo/project_static-electricity-detector.html
Intense Positron Beam
http://www.ne.ncsu.edu/nrp/ips.html
MHD generator
http://en.wikipedia.org/wiki/MHD_generator
Relativt STORA MÄNGDER NEUTRONER BILDAS OCKSÅ I SAMBAND MED BLIXTURLADDNINGAR
En av läsarkommentarerna
föreslår InverseBeta, samt,
”Nuclear transmutations and fast neutrons have been observed to emerge from large electrical
current pulses passing through wire filaments which are induced to explode.”,
http://arxiv.org/pdf/0709.1222v1.pdf
ENERGETIC
ELECTRONS AND NUCLEAR TRANSMUTATIONS IN EXPLODING WIRES, Widom et al.,
2007
:
Gränsen (källan ovan s1sp1n)
går vid ca 17 000 Ampere — vilket är helt rimligt (i TNED).
Lightning strikes produce free neutrons, and we're not sure how, 26Mar2012
”The new detectors also allowed the researchers to calculate the neutron flux from the storm activity. In the previous experiments, it had been assumed that each detection event corresponded to a single neutron. In a surprising turn up, the new data show that up to 5000 neutrons per cubic meter are produced every second by lightning strikes.
This is very high, and not very compatible with the
alternate explanation, neutron production by high energy photons (gamma rays).
To generate the number of neutrons the researchers observe would take about 10
million gamma ray photons m-3s-1. Unfortunately, lightning strikes only generate
a tiny fraction of that.
At the moment, this research is not of Earth-shattering importance. But it does point to things going on thunderstorms that we just don't know about yet. And that is quite exciting. It is also important to realize that this isn't going to revolutionize our understanding of nuclear physics, so these observations aren't going to lead to new reactor designs or free energy. Still, we will learn more about thunderstorms, which is pretty cool.”,
http://arstechnica.com/science/2012/03/nuclear-lightening/
med uppslag/länk från
”Scientists confirm that lightning strikes generate low energy neutrons, but eliminate both of the explanations we had for how this might work.”,
Ars
Technica > Forums — Lightning strikes produce free neutrons, and we're not
sure how
http://arstechnica.com/civis/viewtopic.php?f=2&t=1170476
RC-matematikenBASIC — Resistanser
• Kapacitanser
Följande grundsamband är centralt för grunderna [STRÖMSTYRKA] inom elektroniken.
RESISTANSER:
![]()
Lika resistanser i serie
summeras:
U = RI = U[R1] + U[R2] = R1·I + R2·I = I(R1 + R2) ;
R = R1 + R2
;
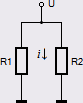
Lika resistanser i parallell
subtraheras:
U = RI = R·I1 + R·I2 = R(I1 + I2) ;
R = U/(I1+I2) = 1/[I1/U + I2/U] ;
R = 1/[1/R1 + 1/R2]
;
KAPACITANSER — RCbasic
KAPACITANSER:
R = T/C ;
![]()
Lika kapacitanser i serie subtraheras:
U = TI/C = U1 + U2 ; se Kondensatorlagen
C = TI/(U1 + U2) = 1/[U1/TI + U2/TI] ;
C =
1/[1/C1 + 1/C2] ;
C1 =
C2 ger C = C12/2
;
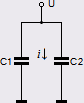
Lika kapacitanser i parallell summeras:
U = (T/C)I = T(I1 + I2)/C ;
C = T(I1 + I2)/U = TI1/U + TI2/U ;
C = C1 +
C2
Urladdningsfenomenets autobenägenhet
23Mar2013-03-23
Aluminumurladdningarna har i vissa fall uppvisat »självmotorik» — ett uppslag som visar att lokal omsättning via luftmolekylerna i urladdningsområdet själva ombesörjer en viss omsättning, och som därför (såvitt relevant i någon teknisk lösning) ger vissa tekniska uppslag. Bilden nedan från oscilloskopets mätning av spänningen Anod-Katod via spontana serier av ur- och uppladdningar.
OSCILLOSKOPETS INSTÄLLNINGAR: VERT. 5V/DIV;
HORIZ. 2mS/DIV: INTtrig.
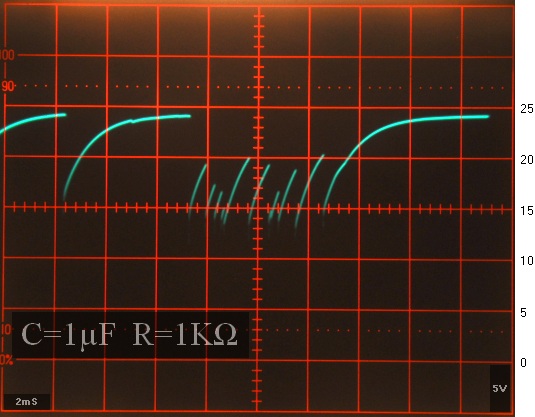
BILDKÄLLA: Författarens arkiv · 23Mar2013 AlRodDisch
Bild5 · Nikon D90 · Exponeringstid 1S · Bländartal F/22 · ISO 400
Genom att lägga
katodstiftet helt lätt mot en separat aluminiumstång gjordes i experimentens
början (2005) observationen att urladdningsförloppet ibland kan självtrigga
med, periodvis, spontana serieurladdningar.
—
Fenomendetaljen har nyligen försökt återupprepas för fotografisk dokumentation
(23Mar2013) — men det är svårt att hitta ett tillräckligt känsligt
beröringsområde.
— Fotografiet
ovan (från en serie på runt 50 bilder) är taget genom att, efter maximalt liten
beröringsanliggning, snäppa med fingrarna i närområdet för att alstra små mekaniska
vibrationer. Dessa är tillräckliga för att trigga motsvarande
serieurladdningar.
— Försöken här
gjordes med en urladdningskapacitans på 1µF med samma 1K-motstånd som i
originalkretsen, tillsammans med tre 9V-batterier i serie för
strömförsörjningen.
För ev. vidare.
Glödspåren sprids i riktning som hålexpansionen
26Mar2013
— Test med folieurladdningar på överkanten av ett (hårt) uppspänt aluminiumfoliestycke (maskinskruvstycke, dubbelhäftande tejp) visar att glödspåren (de visuellt mest synliga) INTE förekommer uppåt, endast neråt.
— Enklaste förklaringen är (då) att atomagenterna till glödspåren generellt genereras riktningsanalogt med hålbildningens expansion;
— Eftersom ingen sådan expansion finns över överkanten, är också (logiskt följdriktigt) glödspåren orepresenterade där (frånsett yttersta svaga korta spårlinjer som framgår på fotografierna i stark förstoring).
Därmed glödspår endast i förlängningen av den aktuella foliedelen: över kanten syns inga (direkta) glödspår.
Urladdningshålen i foliekanten visar sig också vara (regelrätt) halvcirklar.
BILDKÄLLA: Författarens arkiv · 26Mar2013
CATmar2013 Bild26 •
Exponering 1S · Bländare F/9 · ISO 400 · Nikon D90 · Detalj

NOTERA ljusbulans lätt uppåtriktade form: (nära) samma identiska form upprepas på foto efter foto — som om ljusbulans 3D-fysik vore (extremt) metriskt fastnaglad. I princip noll variation.
BILDKÄLLA: Författarens arkiv ·
26Mar2013 CATmar2013 Bild5;16
• Exponering 1S · Bländare F/9 ·
ISO 400 · Nikon D90
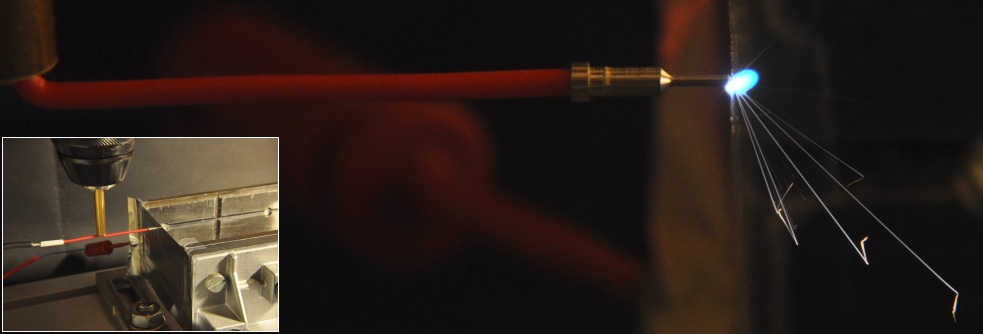
ETT FOTODOKUMENT Kolliderande Nanopartiklar [URLADDNINGSSERIERNA123] med 3×20 bilder tagna i tidsserie i separata block med exponeringarna 1/10, 1/5 och 1/2 sekund finns bifogat för grundstudium av glödspåren och ljusbulan i Aluminiumfolieurladdningarna [AlFU].
Den som redan har ett koordinatbord med
maskinskruvstycke och pelarstativ med inspänd borrmaskin (bilden ovan nedre vänster) (samt en systemkamera med stativ och
separat kamerautlösare) (samt
enklare attiraljer med kontaktstift, kopplingstråd och 3st serieanslutna
9V-batterier kopplade till en 100µF/50V kondensator som uppladdas via ett
1KΩ motstånd) kan omgående montera upp en köksaluminumfolie (typ för frys/och/eller ugn) med
dubbelhäftande tejp på maskinskruvstycket, precisionsspänna folien via
skruvstycket, och få samma typbilder som ovan inom kaffekvarten.
Toppspänningen hos kondensatorn på runt 26-27V via de tre 9V-batterierna,
hamnar efter varje kanturladdning (enligt
grovtest som ovanstående fotografier) strax ovanför mittpunkten (13V),
vid ca 14-18V, om urladdningen är av typen singulär.
När vi nu har kommit på hur att testa folieurladdningarna via en öppen kant, ska GAMMASTRÅLNINGSARGUMENTET inte längre innebära något hinder:
— Med en fotosensor (BPW34 eller bättre) samt förstärkningskrets, ska ev. närvarande gammastrålning MÖJLIGEN kunna avslöjas via folieurladdningarna i den öppna delen uppåt:
— Inget annat än omgivande ÖPPEN FRI LUFT finns där. FINNS gammastrålning i ljusbulans bildning och association, finns här veterligt heller inget som kommer att hindra ett påvisande.
Kanonläge för gammatest
Mar-Apr2013
Med arrangemanget i foto enligt CATtestMar2013 har det nu äntligen, slutligen, öppnat sig ett avgörande mättillfälle:
— DETEKTORER FÖR GAMMASTRÅLNING kan numera (med hyfsad känslighet och till synes imponerande resultat, enligt GammaWebben) byggas med relativt enkla, och billiga, medel. Se webbexempel i Gammamätning.
I kort sammandrag med speciell referens till ZambiaTGF:en
— principen enligt TNED i ATA/CAT är densamma:
— IDEALLÄGET för gammamätning — av EXAKT samma form
som enligt TNED skulle gälla i atmosfärisk urladdning — är en VINKELRÄTT
monterad gammasensor (foto-PiN-dioden
BPW34 eller bättre) precis över urladdningsstället med mellanliggande
fri luft: gammautbredningen garanteras på samma sätt som i det atmosfäriskt
påvisade fallet — enligt relaterad fysik.
— Det kanonläget finns nu — uppenbarligen — med testarrangemanget i CATtestMar2013.
Därmed finns — absolut — inte en suck, någonstans, att kunna missa mätresultatet förutsatt tillräcklig känslighet i gammasensorn:
— Webbexemplens gammasensorlösningar (Gammamätning) visar delvis imponerande resultat — typ utslag från vanlig GRANITSTEN. Det var intressant.
— Skulle mot all förmodan ändå INTE en enda ynka lilla mätpuls visa sig i millimeterområdet omedelbart utanför KANTEN på folieurladdningen enligt CATtestMar2013, har vi bara att konstatera faktum:
Medan positronförekomst är påvisad i
blixturladdningar [TGFintro],
finns ingen motsvarande förekomst i gnisturladdningar — inte ens med
strömstyrkor (240.000.000 A under 10 pS) många gånger de som atmosfäriska
urladdningar uppvisar (max 100.000 A under 1 mS).
I så fall generellt för TNED — ingen gammadetektering — förutsatt INTE så låga gammanivåer existerar att sensorn lik f-t inte reagerar:
1.
— ATOMVIKTERNA — Neutronkvadraten — kan vi inte rå på. Neutronkvadraten, väl en gång uppdagad, är tydligen omöjlig att frigöra sig ifrån i kraft av dess överlägsna samhörighet med experimentellt uppmätta data för atomvikterna.
— Någonstans, då, finns det utvecklingsfel (från min sida) i TNED-teorin för atomkärnans allmänna funktionssätt (ATA/CAT). Uppgiften blir (därmed för min del) att försöka penetrera den detaljen och presentera en förklaring, om det alls går.
2.
— Energiproblemets lösning kommer INTE att innehålla något bidrag från TNED.
Den avancerade energigrunden finns inte.
POSITRONBOLLEN i TNED-beskrivningen — fenomenet i samband med blixturladdning som en del sett — gäller INTE.
— Energifrågans lösning för mänskligheten har med det (enligt TNED) bara de redan välbekanta alternativen att välja på: kärnkraft, vindkraft, solceller, eller generellt Fred Flintstone-apparater (handvevad batteriuppladdning).
— Bästa underhållningen vi såg på den punkten blev IronMan på bio.
HARMONIBEGREPPET med sanningsbegreppet berörs, vad vi vet, inte.
KÄNSLIGHETSGRÄNSEN för gammanivåerna (Gammamätning) ska enligt det speciella webbexemplets påstående [MAXIM — APPLICATION NOTE 2236 Gamma-Photon Radiation Detector] vara runt
60 KeV = 9,612 t15 J
från Americium 241 i [de numera äldre] rökdetektorerna
SOM TESTOBJEKT
Se även grunddata på de atmosfäriskt uppmätta gammanivåerna från TGF:s i Blixturladdningens fysik, resumé med gammastrålningens uppkomst (0,03-10 MeV).
Webbreferenser
Mar/Apr2013
Kompl.htm:
C:\Dok11\CopVista\iNET\UnivHist\HTM\AatPEM\aFuseBoxA.htm
Min kommentar (9Apr2013) —
GoogleSökningar på elektronikkomponenter blir allt svårare
INKLUDERA RADEN NEDAN VID SÖKNING PÅ ELEKTRONIK — enormt irriterande databastablåer med kopiösa reklam- och fragmenterade datalänkar som leder till andra liknande som leder till andra liknande …, om och om igen. Dessa har poppat upp på sistone (Feb-Mar2013) — för att göra livet EXTRA surt för oss:
-www.datasheetarchive
-www.datasheets -www.alldatasheet -www.datasheetdir …
Olika ASSOCIATIONSAMATÖRER blockerar webben med
annonsbaserat SKRÄP — fragmenterat, uppdelat på miljoner olika delavsnitt …
UTAN DESSA HITTAR MAN SNABBT exakt angiven komponent.
Detecting gamma radiation with op amps
Webbreferenser
— INTE MYCKET KÄNSLIGHETSDATA presenteras i de följande gammasensorbyggena. Vi är i stort utlämnade åt ev. presentationer som visar utspänningsområden i detektorpulserna (0V2 i MAXIM-applikationen; 60KeV-gamma från Americium 241, citat nedan) tillsammans med uppgift (om alls) på anordningens förstärkning. Det är allt.
I BPW34-applikationen (längre ner här, den enkla transistorförstärkaren) finns ingen uppgift alls på förstärkning: pulsamplituderna i slutänden anger i artikeln approximativt 50-100 mV. Transistorförstärkningen för BC549/550 är nominellt (separat datablad) runt 600 till 800.
»Gamma-Photon Radiation Detector - AN2236 - ELEKTOR.nl»
Man får klicka på en separat
stripe för att öppna PDF-filen
MAXIM
— APPLICATION NOTE 2236 Gamma-Photon Radiation Detector
Samma som ovan i annan form
DESIGN
IDEAS — Circuit forms gamma-photon detector, Bruce Denmark, Maxim Integrated
Products, Sunnyvale, CA
http://www.edn.com/contents/images/42403di.pdf

”You can test the circuit with a cheap smoke detector. The ionizing types of smoke detectors use americium 241,
which emits a 60keV gamma photon. (The more expensive photoelectric smoke detectors do not contain
americium.) A 60keV gamma is close to the circuit's noise floor, but should be detectable.”,
;
”Small signal levels make this design an interesting challenge. It requires very low-noise circuitry, both because the amount of charge generated by individual gamma photons is extremely small, and because lowering the overall noise level allows the circuit to detect lower-energy gamma photons. Special attention must paid to the first stage, which is the most noise-critical.”.
OP MAX4477 — 2 OP i samma kapsel — verkar vara svårt att få tag på (se LittleDiode nedan). ELFA har MAXI-typen men med bara en OP per kapsel — MAX4475 — och då endast för ytmontering (SO-8);
ELFA:s pris på MAX4475 SO8 är 18,40 +moms., Art. 73-864-12 — sök på »max44».
PIN-dioden QSE773 (fabr. Fairchild) finns också att få tag på,
LittleDiode
— Components for All
http://www.littlediode.com/components/QSE773.html
— £2,99/st, men räkna med tot. ca 100:- för två st inkl. shipping och övrigt.
— LittleDiode har också MAX4477, typen SO8 — men till priset (Apr2013) av £10.99 per (~107kr/st).
Se även alternativ:
Utförlig beskrivning
MEASURE
GAMMA RAYS WITH A PHOTODIODE RADIATION DETECTOR USING A BPW34, Burkhard Kainka
(Germany)
http://xa.yimg.com/kq/groups/10603698/1658129756/name/Elektor-rivelatore+gamma+pin+diode.pdf
”The semiconductor
sensor we describe below also has
a relatively low sensitivity, only being able
to detect fairly intense sources of radiation,
but it is nevertheless an interesting
device for carrying out experiments and
measurements.”,
— GRANIT innehåller små mängder
radioaktiva ämnen — som projektet ovan redovisar gammautslag på.
Kopplingen är enkel (BC559C är
f.ö. likartad med BC550 [Finns på ELFA]):
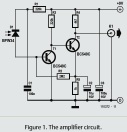
BPW34 (också av typen PiN-diod) finns (4 olika [för hålmontering och ytmontering] i IR-området 850nM-950nM) på
ELFA
DISTRELEC — Elektronik &Automation,
https://www.elfa.se/elfa3~se_sv/elfa/init.do?sq=fotodiod&cat=0
(19,50+moms, Art. 75-000-44).
Se även ett byggexempel (med begränsad åtkomst)
Construction
of an Alpha- Beta and Gamma-Sensitive
Radiation Detector on the Basis of a Low-Cost
PIN-Diode — Bernd Laquai, 12.6.2012
http://www.opengeiger.de/ABGDetektor_en.pdf
— Men framställningen innehåller ingen kretsbeskrivning på den presenterade anordningen.
Se även utförligt om fotodiodens tekniska/matematiska fysik (hur den svarar på inkommande strålningskvanta — dock utan praktiska värdeexempel) i
AN
INTRODUCTION TO SEMICONDUCTOR RADIATION DETECTORS — C. W. Thiel, Physics
Department, Montana State University (1999)
http://www.physics.montana.edu/students/thiel/docs/Detector.pdf
— Författaren använder
symboler och beteckningar i angivna led — utan direkt beskrivning av VAD
symbolerna betyder: man får LETA (om alls) i hela framställningen efter
LEDTRÅDAR till vad författaren håller på att beskriva (om alls). Tyvärr —
beskrivningen saknar praktiska exempel.
ETT KOMPLEMENT till ovanstående (»något bättre» — exempel finns), samma tema — OBS texten kan inte kopieras:
4.7
Photodiodes
http://ecee.colorado.edu/~bart/book/book/chapter4/pdf/ch4_7.pdf
EN BETYDLIGT MERA UPPLYSANDE BESKRIVNING — fotokonduktorer (PIN-dioden backspänd) med karaktärer, praktiska värdeexempel integrerat med beskrivningen — finns på
LADYADAnet
— Photoconductive Cells
http://www.ladyada.net/media/sensors/APP_PhotocellIntroduction.pdf
Se även
SKYWORKS
— PIN Diode Basics
— men (liksom i andra liknande webbexempel), författaren visar — utom i Figure 9 s4; man får leta i kopplingsschemat, se nederst höger — INTE PIN-diodens schemasymbol, inte alls över huvud taget, trots att dess ekvivalenta kopplingsschema diskuteras (ingående).
Även instruktiva (MED korrekt, upplysande schemasymboler)
— ytterst förnämlig, instruktiv, presentation:
— här får man [möjligen] DIREKT inblick i vad DEN ERFARNE
ELEKTRONIKBYGGAREN har sett i ämnet;
PIN-diodens två grundkopplingar — med trixiga förstärkaraspekter:
NATIONAL
SEMICONDUCTOR — Photodiode Amplifiers, Changing Light to Electricity
http://ecee.colorado.edu/~ecen4827/hw/hw1/PhotodiodeAmplifers.pdf
Se även (förnämliga — men också delvis »expertabstrakta»)
SKYWORKS
— Design With PIN Diodes
http://www.skyworksinc.com/uploads/documents/Design_With_PIN_Diodes_200312D.pdf
”When the PIN diode is forward biased, holes and electrons are injected into the I region. These charges do not immediately annihilate each other; instead they stay alive for an average time, called the carrier lifetime, t. This results in an average stored charge, Q, which lowers the effective resistance of the I region to a value RS.”.
— även här saknas (delvis
TYDLIGA) schemasymboler: artikelförfattaren envisas med att representera
PIN-dioden ![]() med den vanliga
diodsymbolen
med den vanliga
diodsymbolen ![]() — inga speciella
förklaringar finns — samt använder (också utan förklaring, här är det ”gissa lösningen själv” som gäller)
en pilsymbol ► (ibland fylld, ibland inte, ingen förklaring ges)
för GND (eng. GROUND, eller sv. jord),
det som oftast brukar representeras symbolvägen med en normal
— inga speciella
förklaringar finns — samt använder (också utan förklaring, här är det ”gissa lösningen själv” som gäller)
en pilsymbol ► (ibland fylld, ibland inte, ingen förklaring ges)
för GND (eng. GROUND, eller sv. jord),
det som oftast brukar representeras symbolvägen med en normal ![]() eller (»nergrävd
jordplatta»)
eller (»nergrävd
jordplatta») ![]() .
.
Se även
Microsemi-Watertown
— THE PIN DIODE CIRCUIT DESIGNERS’ HANDBOOK, 1998
http://www.qsl.net/n9zia/pdf/pin_diode_handbook.pdf
Se särskilt avsnittet
THE SILICON PIN DIODE RADIATION DETECTORS: UM9441 & UM9442;
— Det är (möjligen) den TEORI för PIN-dioden som påstås fungera i gammatest — men avsnittet är kort, inte mycket sägs utom det centrala:
”The PIN diode is reverse biased so that the entire I-layer is swept out ( depleted of free carriers). This reverse bias
creates an electric force field across the I-layer so that the electrons are swept to the P+ layer and the holes, to the
N+ layer. This flow of carriers in response to a pulse of radiation, constitutes a photocurrent that can be measured.
To maximize this photocurrent, the I-region must be as large as possible.”, citatkällan som ovan.
Även Wikipedias PIN-diodartikel saknar (11Apr2013) schemasymbol för den komponent som faktiskt beskrivs, se
@INTERNET
Wikipedia PIN diode [2013-04-11]
http://en.wikipedia.org/wiki/PIN_diode
BILDKÄLLA: Författarens arkiv ·
MONTAGE [Miljö2012]
21Mar2012 Bild2Viken • 15Sep2012
E32 Bild153 •
Nikon D90 · Detalj

END — Blixturladdningens Fysik 2012
FRÅN Blixturladdningens Fysik 2011 | JGF
| Ljusbågens fysik — Universums Historia
innehåll:
| SÖK
äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
Blixturladdningens
Fysik 2012
ämnesrubriker
innehåll
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]
me = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]
u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],
CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
e = 1,602 t19 C ...................... [ref. FOCUS MATERIEN 1975 s666]
ε0 = 8,8543 t12 C/VM ............. [ref. FOCUS MATERIEN 1975 s666]
[BKL]. BONNIERS KONVERSATIONS LEXIKON Band I-XII med SUPPLEMENT, Alb. Bonniers Boktryckeri, Stockholm 1922-1929
t för 10–, T för 10+, förenklade exponentbeteckningar
PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER
Här används genomgående och konsekvent beteckningarna
förkortning för förenklad potensbeteckning — t för 10^–,
T för 10^+
d deci t1
c centi t2
m milli t3
µ mikro t6
n nano t9
p pico t12
f femto t15
Alla Enheter anges här i MKSA-systemet [Se International System of Units] (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:
förkortning för förenklad potensbeteckning — t för 10^–, T för 10^+
K kilo T3
M mega T6
G giga T9
T tera T12
Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).
MAC, modern akademi (Modern ACademy): i Universums Historia ofta använd bekväm förkortning för den moderna akademin, med associerade
(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också
RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.
SHORT ENGLISH — TNED
in general is not found @INTERNET except under this domain
(Universe[s]History, introduced @INTERNET 2008VII3).
TNED or Toroid
Nuclear Electromechanical Dynamics is the dynamically (related)
equivalent — resulting description — following the deductions in THE PLANCK RING, analogous AtomNucleus’
Deduction.
— The description according to TNED is related,
meaning: all, each, details claim to be fully logically explainable and
understandable, or not at all. With TNED is (hence) also understood
RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’
Deduction.
Senast uppdaterade version: 2021-05-04
*END.
Stavningskontrollerat 2013-04-12.
*
√
τ ρ π ħ ε UNICODE — often used charcters in
mathematical-technical-scientifical descriptions
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω → ∞ ≡
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫
≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑
→ ∞ ↓
ϑ
ζ ξ
Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25
↓; Alt+26 →; Alt+27 ←; Alt+22 ▬
Alt+23
↨ — also Alt+18 ↕; Alt+29 ↔
Alt+1-49:
☺☻♥♦♣♠•◘○
◙♂♀♪♫☼►◄↕‼
¶§▬↨↑↓→←∟↔
▲▼ !”#$%&’
()*+,-./01 …
*
PNG-justerad
åter till portalsidan · portalsidan
är www.UniversumsHistoria.se