BlixtTGF2011 | LightningTGrFs2011 | 2011VII | Senast uppdaterade version YearMonthDayTime 2021-03-30

innehåll · | webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Blixturladdningens Fysik 2011 | JGF | Ljusbågens fysik — Universums Historia

Jul-Aug2011

Utvidgad beskrivning från resumé av

Blixturladdningens Fysik 2008

av BellDharma för UniversumsHistoria

POSITRONBILDNING I SAMBAND MED särskilt kraftiga BLIXTURLADDNINGAR SLUTLIGT BEKRÄFTAD — se TGF intro.

Se även huvudbeskrivningen i TNED av BLIXTURLADDNINGENS FYSIK [2008].

JGFs 2011	JGFs 2011	T(N)=3 t20 S	Ljusbågens fysik	JGFs 2011
Zambia-Egypten JGF:en	Höjdvinkeln: Fältlinjen Zambia-Egypten: Alternativ 1: Alternativ 2: Positronens Expansionshastighet:	NEGE Nukleära ELEKTRON genomströmnings Ekvivalenten	Efter nyligen [Jul2011] upphittade äldre [1800-1900] utomordentliga referenskällor men SOM INTE ENS OMNÄMNS AV ETABLERADE FACKVERK under 1900-talet — möjligen på grund av att portalfiguren är TJEJ: Mrs Hertha Ayrton [The Electric Arc 1902]. Hon erkändes inte av Royal Society, just därför. ÅmajGaad. Det blir bara bättre och bättre.	Zambia-Egypten JGF:en
Positroner från Blixturladdningar	Olika Sätt	Förtydligande	Sammanställning	Positroner från Blixturladdningar

TGF från engelskans Terrestrial Gamma ray Flashes, här försvenskat »JordGamma[stråle]Flashar», JGF

Nu återstår bara att klarlägga verkningssättet.

Konturerna klarnar

1. Mera detaljerad TNED-beskrivning av blixturladdningens fysik i anledning av ytterligare upphittade källor (Jul2011) som verifierar positronförekomst från blixturladdningar (konv. eng. TGFs).

2. Upphittade (Jul2011) ingående detaljbeskrivningar av ljusbågens fysik från sekelskiftet Ewald Rasch (1913, ELECTRIC ARC PHENOMENA) och Mrs. Hertha Ayrton (1902, THE ELECTRIC ARC).

3. Förtydligad, mera relaterad beskrivning av nukleära elektrongenomströmningskonstanten T(N) i TNED som krävs för att förklara ljusbåge och gnistbildning enligt relaterad fysik.

TGFintro

2011-07-24 | YearMonthDayTime | ÅrMånadDagTid

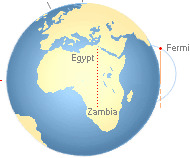
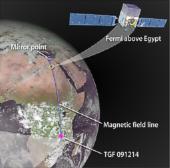
Fermi-satellitens Zambia-Egypten JGF-positron-detektering 14Dec2009

Kort INTRODUKTION med grund i uppmärksammad artikel den 3Jul2011 av BellDharma, om ej redan bekant.

JGF här försvenskningen av engelskans TGF Terrestrial Gamma ray Flash [»officially discovered» 1994 by CGRO] motsv. JordGamma(stråle)Flash

Positronförekomst från blixturladdning klarlagd

NASA-artikeln från 10Jan2011 — med observationsdata från 14Dec2009 — först observerad av mig 3Jul2011

— Till och med SÅ mycket klarlagd att det följande NUMERA framhålls:

”In fact, scientists now think that all TGFs emit electron/positron beams.”,

http://www.nasa.gov/mission_pages/GLAST/news/fermi-thunderstorms.html

Min översättning:

I själva verket tror vetenskapsmännen nu att alla JGFs emitterar elektron-/positronstrålar.

Genom det genombrottet har föregående beskrivning i

Blixturladdningens fysik, resumé med uppkomsten av gammastrålning från blixturladdning

hamnat i ett nytt — mera detaljerat beskrivande — ljus.

Föregående framställning fokuserade (nämligen) helt på den observerade gammastrålningen (utan avseende på någon påvisbar positronförekomst) som rapporterats från en del blixturladdningar (med början från 1994) och som givit upphov till benämningen (sv.) JGF.

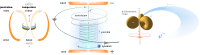
— I den framställningen fanns/finns inga andra aspekter på Jordens ytmagnetiska fält än de helt ideala (och därmed delvis förenklade) som redovisas i Möjliga Praktiska Fall, figuren vänster nedan.

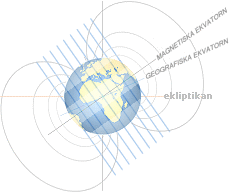
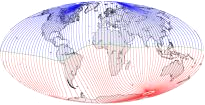
Den magnetiskt ideala — den redovisade	Den mera praktiska [mitten]	Jordmagnetiska Ytfältet enligt CIRES

Ekvatorialbältets Jordmagnetiska ytfältlinjer, mitten och höger, följer i stort samma riktning som Jordkroppens indelade longituder.

— Diskussionen av Positronringens Utvidgning gjordes därmed heller inte till föremål för någon större/vidare metrisk expansion.

(Genom ATA, också generellt beskrivet i Elektronens Bubbelkammarspår, se från Elektroncylindern, kommer positronringen, om den inte strax annihileras [vilket författaren (möjligen något förhastat) utgick ifrån i föregående förenklade fall], att fragmentera dels på positronelementens egna inre Coulombiska repulsioner [elektroncylindern av princip] och dels i växelverkan med Jordens ytmagnetism, vidare nedan).

— Vissa tillägg har nu i efterhand (Jul2011) gjorts till den ursprungliga framställningen (särskilt markerade stycken i särskilda indrag i nämnda dokument) för att förtydliga dessa detaljer, samt förbereda för den här artikelns mera detaljerade beskrivning.

— Vi kommer i den följande huvudtexten att studera Jordmagnetiska ytfältet mera i praktisk detalj i anslutning till det noterade observerade fallet, samt speciellt matematiken (dock även den till att börja med delvis idealiserad till riktningsparametrarna) för Jordmagnetiska fältets växelverkan med elektriskt laddade partiklar (elektroner, positroner).

— V bör redan känna till (de främsta) grunderna i den magnetiska nomenklaturen i ämnet ENLIGT RELATERAD FYSIK från ELEKTRONENS BUBBELKAMMARSPÅR. Se även från MAGNETISMEN om ej redan bekant.

Förtydligande angående gammmastrålningens möjliga riktning

Först: Förtydligande angående gammmastrålningens möjliga riktning

Positronförekomst observerad från atmosfärisk blixturladdning 14Dec2009, artikel först 10Jan2011

TGFs2011 — enligt relaterad fysik

Med vidare Från grundförfattningen i Blixturladdningens Fysik

ATA/CATref

	Relaterad Fysik förklarar JGF-urladdning	JGF sannolikast från blixtens topp eller fot	JGF-associerade gammariktningen
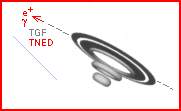
Se utförligt grunderna från ATA/CAT — om ej redan bekant. Endast under vissa betingelser — exceptionellt höga urladdningsströmmar — bildas enligt TNED förutsättningen för en JGF, analogt ett förlopp som beskrivs som ett atomkärnans sönderfall. De berörda atomkärnorna tvingas lämna ifrån sig sin elektronstock och efterlämnar en blottad positronstock som expanderar cirkulärt — inte sfäriskt — med stor kraft från urladdningspunkten, den här benämnda positronringen, bilden ovan vänster. JGF-Urladdningen enligt TNED innefattar en serie sådana efterföljande, koncentriska ringbildningar. Därmed bildas analogt gammastrålning från påföljande parannihilationer [elektroner dras dit från närliggande atomer], se särskilt illustrerad beskrivning från CAT-annihilationerna.	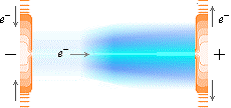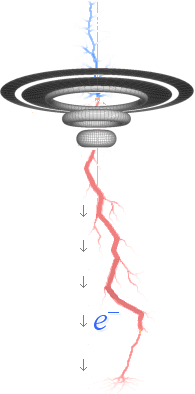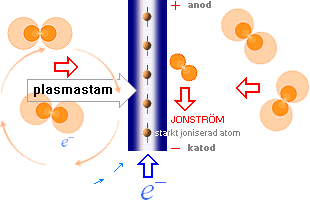katod ATA/CAT TNED Blixturladdning anod
	Vidare från Blixturladdningens Fysik	JGFs uppkommer från strömmar ca 80 000 A	Gammastrålningen från JGF är intrikat

MED POSITRONRINGENS VIDARE EXPANSION, högra bilden ovan, glesas de positiva ringkomponenterna nödvändigtvis ut samtidigt som de tvingas växelverka med det närvarande Jordmagnetiska ytfältet.

— Denna detalj har delvis tidigare förbisetts, se framställningen särskilt i ATA-karaktäristiken: de magnetiskt sammanhållande ringkrafterna, i TNED enligt ATOMKÄRNANS HÄRLEDNING, tvingar den övergripande ringformen att bevaras, ja. Denna idealt STARKT sammanhållande del är emellertid naturligt avgränsad, begränsad, till relativt små områden [främst atomkärnan som sådan, max utsträckning grovt nära 7 neutrondiametrar för största masstalet] med hänsyn till ljushastighetens [eg. DIVERGENSENS] begränsade arbetskapacitet för motsvarande fraktala strukturer [se PASTOM] över större avstånd.

[Jämför Atomkärnans Gravitella Härledning: kärnstrukturen innehåller också NOLLZONER som sätter definitiva gränser för omfattningen av hur en ljushastighetsbaserad konstruktion förmår synkronisera alla detaljer].

— OM DEN EXPANDERANDE POSITRONRINGEN INTE ANNIHILERAS via tillströmmande elektroner, kommer kvarvarande positronmassor förr eller senare att kunna lämna ringen som just enskilda positronmassor [se särskilt första sambandet i ATA (toppringarna kan delas obegränsat) som medger i princip oändlig uppdelning i bevarande av toppspinnets impulsmoment]. Särskilt under inverkan från de mest närliggande dominanta MAGNETISKA fältkrafterna, i vårt fall Jordens ytmagnetism, kommer positronmassorna i vilket fall att påverkas av avböjande krafter.

Därmed finns heller inte längre någon förutsättning för den helt ideala gammastrålningsplanhet som tydligtvis ändå enligt TNED måste gälla från själva urladdningsområdet, och in till något visst minsta avstånd. Med andra ord, finns förutsättningar att parannihilationerna, som alstrar gammastrålningen, kommer att — mer och mer — anta godtyckliga riktningar ju längre bort ifrån urladdningsstället positronerna hamnar.

— Denna detalj kunde inte diskuteras i föregående framställning i

Blixturladdningens fysik, resumé med uppkomsten av gammastrålning från blixturladdning

— Här har emellertid gammastrålningens godtyckliga riktningsmöjligheter funnit en vidare, mera relaterad, beskrivningsgrund.

Ju längre ut positronringen expanderar, ju mera öppnas möjligheten för enskilda positronmassor att bryta sig ur ringen i kraft av, främst, närliggande magnetiska kraftfält. I vårt fall, Jordens ytmagnetism. Därmed bryts också i termer av TNED-teorin den ursprungliga gammastrålningens planhet, se detaljerat från ATA-karaktäristiken. På ett visst avstånd från urladdningsstället finns (viss) möjlighet för gammastrålningen från parannihilationerna att uppvisa alla möjliga riktningar, och med uppvisande av de karaktäristiska ordinära diametrala jetstrålar som utmärker parannihilation ±e, dock inte precis i urladdningsområdets närhet. Exakt vilka metriska gränser som gäller, finns för närvarande ingen framställning på.

Zambia-Egypten JGFen

Se även från INTRODUKTIONEN [hur TNED ansluter till JGF] om ej redan bekant

Fermi-satellitens

Zambia-Egypten JGF-positron-detektering 14Dec2009

ETT TILLFÄLLE ATT TESTA TNED-teorin har visat sig genom ovanstående tillkännagivna nyhet.

Artikeln observerad av mig: 3Jul2011

Artikelns datum: ”01.10.11”, NASA

http://www.nasa.gov/mission_pages/GLAST/news/fermi-thunderstorms.html

bör betyda 10Jan2011, knappast 1Okt2011, men källan upplyser inte om sin dateringsteknik

Observationens datum: 14Dec2009 — observerat av Fermi-satelliten

resultatpresentation efter ca 1½ år

Se även den något [delvis] mera beskrivande artikeln i SCIENCE DAILY 11Jan2011.

NASA-vinjetten

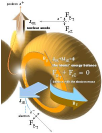
fältlinjer	orientering	TNED-alternativ 1	TNED-alternativ 2
Jordytans magnetiska fältlinjer 6magnetic mirror point 34.38° PitchAngle	Fermi satellit 550KM altitud
45°ca MagnetiskInklination 43µT2 Egypten	Zambia-Egypten, nära vertikala B-fält	45°ca MagnetiskInklination 32µT1 Zambia TGF	mest dynamiskt optimala alternativet

Uppgifterna om Orternas Magnetiska Inklinationer från Webbkällan nedan:

——————————————————————

Egypten Lat30°N Lng30°E Inc 44°04’DN 43,2µT

Zambia Lat10°S Lng30°E Inc 44°47’UP 32,1µT

——————————————————————

NOAA — National Geophysical Data Center [sampl. 2011-08-07], Compute Magnetic Field Values

http://www.ngdc.noaa.gov/geomagmodels/struts/calcIGRFWMM

Angående uppgiften ”100 trillion positrons”, = T14 positroner;

— Enligt TNED-CAT frigör varje deltagande Syreatomkärna minst 16·909=14544 positroner vid JGF;

— T14/14544 = 6,87568 T9 Syreatomer;

— Per cirkulärt lufttvärsnitt pi·r² med höjden 3nM (medelavståndet mellan luftmolekylerna) motsvarar det en cirkelskiva med diametern

2r = 0,248759 mM — ungefär som en pixel på bildskärmen [25,4mM/96dpi=0,2645833mM/d].

— Det är vad som krävs enligt TNED: en datorpixel luftatomer vars ±e-stock friläggs på sin positronbank ca T14 positroner [elektrondelen dras genom blixtkanalen som ansvarar för urladdningen].

— Från etablerat håll verkan man alltså (ytterst) förvånad över den ymniga förekomsten, vilken upplysning källan ovan bidragit med.

Se gärna (först) den animerade beskrivningen i NASA-artikeln för att få grundbegreppen.

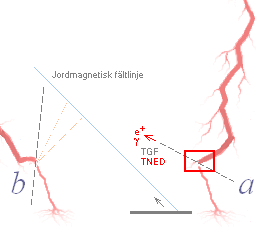
— Med den ±90° möjliga lokala variationen i utsträckning hos en blixtbana relativt en marknormal (gäller bägge urladdningstyperna MolnMark, MolnMoln), blir bägge alternativen ab i figuren ovan höger (här MolnMark) möjliga som riktningsmässiga kandidater för Fermisatellitens positrondetektering; Satelliten (för tillfället över Egypten) befinner sig under blixturladdningens horisont sett från Zambia; Förbindningen, skärande satellitens position, kan bara ske genom det lokala Jordmagnetiska fältet, antydd av bilden ovan i mitten, se även en mera detaljerad illustration i JGF under synhorisonten.

Magnetiska Spegelpunkten

— När positronerna inträder Jordmagnetiska fältet (lokalt i styrka ca 30-40 µT) fungerar de på samma sätt som i beskrivningen av spiralbanorna i ELEKTRONENS BUBBELKAMMARSPÅR.

— Skiljer sig ingångsvinkeln litet från 90° mot fältlinjens utsträckning utåt rymden från Zambia, kommer också positronerna att följa de (svagt) divergenta fältlinjerna i spiral relativt långsamt (vB). Med fältlinjernas konvergens där de går in i Jordytan igen (någonstans i eller i närheten av Egypten) tvingas positronernas vB mot ett nolläge genom att fältkraften ökar på de konvergerande fältlinjerna; Positronerna bromsas in, stannar, och vänder tillbaka, se vidare generella samband nedan.

— Vändpunkten kallas MAGNETISK SPEGELPUKT (eng. magnetic mirror point), MSP. Känner man latituden (ideal magnetism med Jordgeometrin, som det också turligt är i det aktuella fallet) för en viss MS-punkt, kan motsvarande ingångsvinkel, den s.k. (eng.) Pitch Angle (sv. höjdvinkeln) bestämmas.

— Illustrationens blixttyp, MolnMark är inte avgörande, det aktuella fallet kunde lika gärna vara ett MolnMoln-fall. De möjliga riktningarna täcks i vilket fall genom blixtbanans möjliga variation.

För magnetiska spegelpunktens matematik används här (tills vidare) referenskällan i Höjdvinkeln.

ZambiaJGF:en

2011-08-06

ZambiaJGF:en

Magnetiska kraftlagen

F = BQv = mv²/r

ger BQ = mv/r som ger

r = mv/BQ

Med Q=e=1,602 t19 C, m=9,11 t31 KG, och B=30µT som ett ungefärligt medelvärde för Jordmagnetiska fältstyrkan på Jordytan, ges

r = v(m/BQ = 1,93716 t7 S)

Med c=v=2,99792458 T8 M/S ges idealt

r = 58,07465 M

Lägre v ger mindre r. Ökar B, avtar r, mv/Q konstant.

ALTITUDGRÄNSEN FÖR MAGNETISK SPEGLING

Grovt sett räknar man med att altitudgränsen ca 100 KM (höjden över Jordytan) markerar gränsområdet för partiklar som kan studsa fram och tillbaka mellan de magnetiska polerna eller magnetiska spegelpunkterna (se från MSP ovan, vidare nedan). Under den gränsen börjar Jordatmosfären göra sig alltmer påmind, och partiklarna förlorar sin rörelseenergi genom kollisioner med den allt tätare atmosfären.

För altitudreferensen, se

@INTERNET Wikipedia, Van Allen radiation belt, Inner belt [samplat 2011-08-06]

http://en.wikipedia.org/wiki/Van_Allen_radiation_belt

MSP — magnetiska spegelpunkten

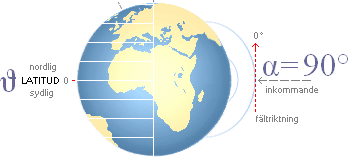
EKVATORIELLA HÖJDVINKELN α (eng. equatorial pitch angle) definierar partikelns inkommande riktning relativt den magnetiska fältlinjens längsriktning. Referenspunkten är (magnetiska) ekvatorialplanet (»mitt på»). Med α=90° kommer partikeln in via magnetiska ekvatorn — på samma sätt som en partikel rusar in i en BUBBELKAMMARE genom att skära kammarens pålagda magnetfält. Resultatet i Jordfallet blir att partikeln böjs av i en cirkel ovanför Jordytan (r = mv/BQ), en helt idealt cirkulär bana, utan att uppvisa någon drift mot magnetpolerna.

Skiljer sig däremot höjdvinkeln (α, alfa) från 90°, uppvisar partikeln en motsvarande hastighetskomponent parallellt med Jordmagnetiska fältlinjen. Därmed kommer partikelns cirkulära bana att börja vandra utmed Jordfältlinjen, snabbare ju mindre α är.

Genom att emellertid Jordfältlinjerna konvergerar, packas, mot polerna, ökar också fältstyrkan (B) som partikeln avancerar mot endera magnetpolen. Resultatet blir, som ovan (r = mv/BQ, mv/Q konstant), att r tvingas avta med växande B.

Men enligt centralkraften F=ma=mv²/r tvingas F (analogt a) öka om r avtar; accelerationens ändring kräver i vilket fall enligt ÄNDRINGSLAGARNA en motsatt reaktionkraft. Den yttrar sig i partikelfallet i att partikelhastighetens hastighetsvektor parallellt med Jordfältlinjen viks in rätvinkligt mot fältlinjen så att partikelns polvandring avstannar; Partikeln vänder åt andra hållet. Den kritiska vändpunkten kallas MAGNETISK SPEGELPUNKT (MSP, eng. magnetic mirror point [MMP]).

Höjdvinkeln

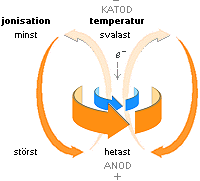
Magnetiska SpegelPunktens motsvarande magnetiska Jordlatitud (ϑ, theta) sammanhänger med ekvatoriella höjdvinkeln (α) enligt sambandet nedan (konv.). Magnetiska och Jordära vinkelindelningarna förutsätts här idealt analoga — som också, nära, är fallet, i varje fall omkring ekvatorialbandet, se Jordmagnetiska ytfältlinjerna i källan CIRES.

Magnetiska spegelpunktens matematik

(sin α)² = (cos ϑ)⁶/√(1+3[sin ϑ]²)

Magnetiska höjdvinkeln från magnetiska spegelpunktens latitud

För sambandets referens, se

@INTERNET Van Allen Radiation Belts, Richard Fitzpatrick 2011-03-31, [samplat 2011-08-06]

http://farside.ph.utexas.edu/teaching/plasma/lectures1/node22.html

Med uppgiften ϑ=30°N (MSP över Kairo, se NASA-vinjetten) ges

α = 34,38°

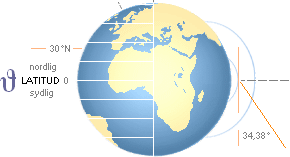
JGF under satellitens synhorisont

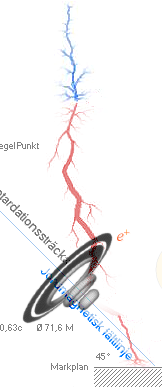
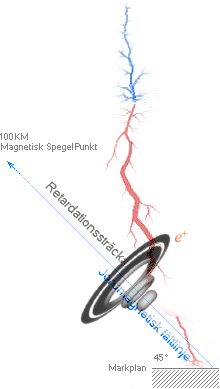
Vi kan reda ut begreppen vidare genom att beakta nedre atmosfärsgränsen på ca 100 KM — grovgränsen för aktiva magnetiska spegelpunkter: Under den altituden ökar Jordatmosfärens täthet (drastiskt) och partiklarna förlorar sin rörelseenergi genom kollisioner. Figuren nedan relativt noga efter aktuella lokaler i observationstillfället.

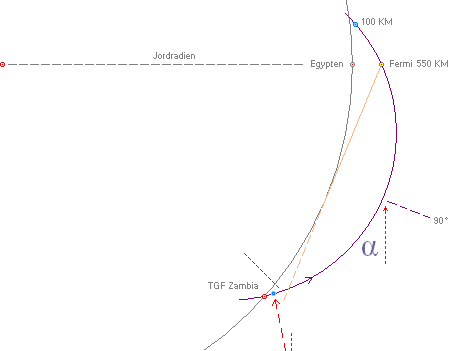
Ungefärligt metriska värden i Zambia-Egypten-JGF-exemplet. Källa, se originaldata från NASA-artikeln.

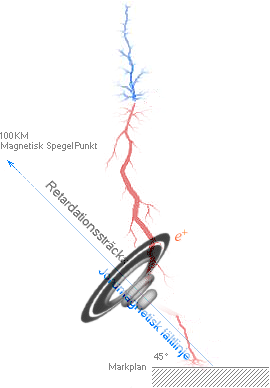
— De blåmarkerade punkterna på Jordfältlinjen (mörkviolett) markerar de lägsta möjliga magnetiska spegelpunkterna (här idealt symmetriska) på altituden ca 100 KM.

— Högra streckade rödpilarna markerar den möjliga positronriktningen som måste finnas med avseende på spegelpunkten över Egypten OM partikelvägen skulle ha bildats inkommande UTIFRÅN och in mot Jorden. Genom att höjdvinkelpunkten (α) idealt måste vrida sig mot symmetriska (Zambia-) spegelpunkten och där uppvisa exakt rät vinkel mot Jordfältet för ideal magnetisk partikelstuds mellan spegelpunkterna, blir varje infall UTIFRÅN, nedanför ZambiaBlåpunkten, utesluten: OM positronbildningen ska komma ovanifrån och ner mot Jordytan måste den under alla omständigheter ligga till höger om ZambiaBlåpunkten och dessutom vara något vinklad för att komma ur och vidare mot EgyptenBlåpunkten.

— Men man har redan övergivit föreställningen att TGFs skulle bildas på höga altituder (därför att energitätheten där i sig inte räcker — se citatblocket Gammastrålning från åskväder — ScienceDaily, May 2, 2005 i Blixturladdningens fysik i modern vetenskap och akademi, citatsammanställning).

— Enda alternativet är alltså att positronriktningen måste bildas underifrån, nerifrån markytan och uppåt mot Jordfältlinjen.

Retardationssträckan

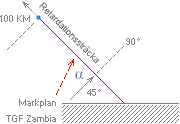
Här ser vi enklare de möjliga alternativen.

— OM positronriktningen händelsevis bildas EXAKT genom ZambiaBlåpunkten (övre streckade grå linjen), rätvinkligt Jordfältlinjen ut från Zambialokalen (här ca 45° enligt NOAA, se referenserna under NASA-vinjetten), då är därmed också motsvarande Egyptiska (symmetriska) spegelpunkt definierad.

Men för att komma dit måste positronriktningen ha NÅGON avvikelse från ideala rätvinkliga riktningen, analogt någon hastighetskomponent utmed Jordfältlinjen.

— Men vilken den komponenten än är, motsvarande vilken den riktningsvinkel än är som måste skilja sig från exakt 90°, kommer motsvarande spegelpunkt — där riktningen ÄR exakta 90° relativt fältriktningen — att förskjutas neråt marken i motsvarande grad.

— Enda möjligheten skulle då vara att positronriktningen börjar STARKT, med hög hastighet och stor kraft, från marknivån (ju längre ner desto bättre förutsättningar, större dynamik) med en relativt stor variabel infallsvinkel mot Jordfältlinjen, och att den hastigheten sedan DÄMPAS UT (via lokala parannihilationer, retardationssträckan) som positronerna spiralerar upp mot ZambiaBlåpunkten.

— Positronerna kan då, idealt, nå ZambiaBlåpunkten med reducerad utgångshastighet, idealt SOM OM infallet skulle ha skett där under exakta 90°.

— Därmed är motsvarande EgyptenBlåpunkt i andra fältänden säkrad.

— Galant förklaring.

De bägge olika blixurladdningstyperna MolnMoln och MolnMark kan därmed, i vilket fall, ALLTID komma ifråga som aspiranter för en möjlig JGF. Figuren nedan visar hur TNED — möjligen — beskriver förekomsterna.

Alternativ 1; Nersidan

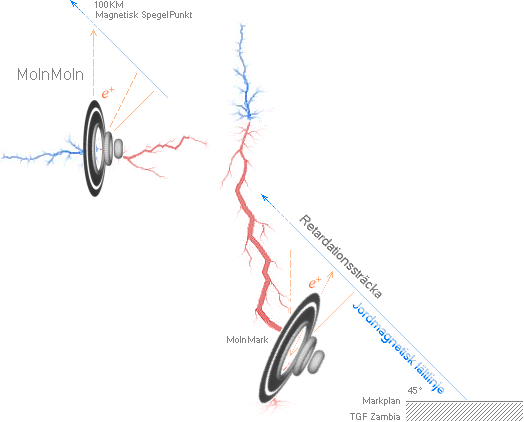
I MODERN AKADEMI brottas man med (den enorma — omöjliga) svårigheten att hitta utlösande faktorer som INTE ansluter till ovanstående (TNED).

— Hur man än kommer att bemöta dessa svårigheter är det (nu) uppenbart att man, för att kunna förklara förekomsten, måste finna en motsvarande RIKTNINGSANALOGI. Den måste, tydligen i vilket fall ansluta till ovanstående (galanta förklaring) — och försåvitt inga fel här har begåtts i framställningen: (annihilations-) bildning genom (successiv) dämpning.

— I annat fall kommer man inte upp till den nödvändiga magnetiska spegelpunkten, OVANFÖR ATMOSFÄRSGRÄNSEN (100 KM) — den som garanterar åtkomst till motsatta fältpunktens magnetiska spegelpunkt (Egypten i exempelfallet)..

Alternativ 1, bägge sidorna; Nersidan och Ovansidan

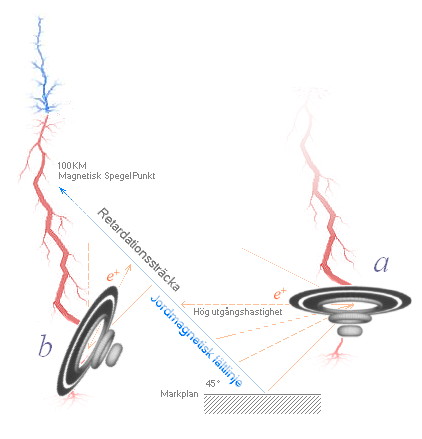
— Med ovanstående klargörande framstår strax i stort sett alla möjliga riktningsfall — i och med att den kritiska punkten ligger på begreppet DÄMPNING. I stort sett alla riktningar kan komma ifråga initiellt.

Sedan beror det på.

— Figuren ovan visar hur i princip vilka primära riktningar som helst (ab) kan komma ifråga då det nu i vilket fall står klart att

· positronstrålen, tydligen främst av energitekniska skäl, måste initieras nerifrån marknivån, under första spegelpunkten

· en DÄMPNING utmed retardationssträckan i vilket fall (därmed) är nödvändig för att få upp positronförekomsten till magnetpunkten per NOLL (helt utdämpad) hastighet i den riktningen, alltså utmed Jordmagnetiska fältlinjen.

Se även vidare nedan i Olika sätt att nå spegelpunkten.

— Men är det rimligt att den teoretiskt TNED-frilagda positronmängden hinner upp till spegelpunkten 100 KM längre upp, utan att annihileras på vägen; Hur kan vi veta det säkert, TNED-teoretiskt?

— Fria medelvägen i luft [R. Westöö ELEKTRON- OCH ATOMFYSIK, ESSELTE STUDIUM 1975 s8sp1m] ligger på ca 100 nM (1 t7 M eller 0,1µM). Men det gäller då för luftpartiklar med medelatomvikten (för luft) ca U=29u.

— För en positron- (eller elektron-) massa (med betydligt mindre tvärsnitt), samt beroende på hastighet (energi), gäller delvis andra värden.

— En fri elektron attraheras (kan infångas) av en atomkärna om elektronen kommer in på lämpligt sätt.

— En positron däremot repelleras av atomkärnan — och attraheras av atomens elektronmoln PÅ STORT AVSTÅND: på näravstånd finns ingen bestämd motsvarande attrahent.

”When emitted in the medium, positrons start a process of slowing down and thermalization. They loose energy and change direction by elastic scattering with atomic electrons and nuclei. This process lasts until the positron reaches thermal equilibrium with the surrounding matter: at this point it interacts with an electron. Consequently, positron mean free path in matter depends on two factors: the initial energy of the emitted particle and the properties of the surrounding matter in which positron is thermalized.”,

s1n;

Characterization of Silicon Photomultiplier as a photodetector for Positron Emission Tomography, 2005

(Fluor18) http://www.df.unipi.it/~fiig/theses/dascenzo.pdf

Källan ovan anger tabellvärden (s2ö Table 1.1) för positronernas fria medelväglängd i VATTEN, emitterade av olika nuklider (i samband med Positron Emission Tomography, PET, den medicinska tekniken som används för att studera det inre av organismen):

— Från lägst (Fluor[F]18) 0,6 till högst (Rubidium[Rb]82) 5,9 mM via motsvarande olika energier (resp. 0,633 och 3,40 MeV).

— I vatten. I luft blir värdena nödvändigtvis (grovt minst 10ggr) större (med än större ingångsenergier).

— Dessa detaljer är delvis svåra att grovberäkna:

— Jämför bubbelkammarfotografier av utdragna elektroner som uppvisar många cirklar; kammarvätskan är flytande väte, alltså betydligt tätare än luft, men likväl snurrar elektronmassan på, varv efter varv, ofta, utan att möta något hinder.

— En positronmassa har delvis andra förutsättningar.

— Om vi använder den föreslagna formen för FRIA MEDELVÄGLÄNGDEN i Wikipedia Mean free path [sampl. 2011-08-07]

http://en.wikipedia.org/wiki/Mean_free_path

L = 1/(σn) med σ=πr² med r=kollisionsobjektets skugg(cirkel)radie och

n=1/(atommedelavståndet)³=antalet kollisionsobjekt per kubikmeter, ges med

MedelLuftMolekylen (r=1,37 t15 M ·[A=29]^1/3=4,20907 t15 M) som kollisionsobjekt den fria medelväglängden

L = 485,1106 M;

— Något annat, direkt, målobjekts träffskugga finns inte att räkna på.

— Värdet är förmodligen helt orealistiskt alldeles för stort. Men låt oss ändå utnyttja tillfället:

— På en rät linje 0-100 KM går det avrundat

N=206 st 485,1106M-distanser;

— Teoretiskt, på en rät sådan linje, skulle det bara behövas just 206 front-positroner som vill offra livet för att den 207:e ska nå upp till första magnetiska spegelpunkten.

— Med tanke på att varje Syreatomkärna som genomgår CAT frilägger minst 16·909=14544 positroner, är andelen 260 nära försumbar. Är andelen Syreatomer som genomgår CAT av storleksordningen förekomsten på en luftmeter (3 T8 stycken med medelmolekylavståndet i luft 3 nM), bättras marginalerna på än mera.

— Det krävs dock mera avancerade beräkningar innan mera precisa besked kan ges. Grovräkningen visar dock det väsentliga:

— Genom att den primära positronförekomsten enligt TNED från en JGF bör vara tämligen ymnig, finns i vilket fall de allra bästa förutsättningarna för att återfinna positronmängder även långt från bildningslokalen.

— Det finns, av princip enligt TNED, knappast någon mera riklig positronförekomst i fysiken att upptäcka. Så, skulle det visa sig att TNED-teorin INTE håller, är man nog generellt rejält illa ute — om det gäller att finna en vettig förklaring.

— Varje ca 3,5 µM luft (3,43784 t6 M) med (Syre-) atomer som genomgår CAT (atomkärnans fullständiga upplösning enligt TNED i massa-laddningekvivalenter ±e=0) med minst 16·909=14544 frilagda positroner för varje Syreatom, är det som krävs per ideal hinderfri längdlinje för att FRILÄGGA distansen 100 KM upp till första spegelpunkten via det grovt uppskattade antalet N=16 666 666 st 6mM-intervall — medelfrivägen för positronen i luft, ca 6 mM (10 ggr källvärdet ovan för vatten via Fluoremission). Alla dessa N »underatmosfäriska» positroner försvinner (annihileras tillsammans med omgivande elektronmassor från närliggande atmosfäriska atomer), då, som aspiranter på uppvägen och kvarlämnar en friväg för (eventuella kvarvarande) övriga uppströmmande som kandidater för att vandra mellan de magnetiska spegelpunkterna i den övre Jordatmosfärens inre Van Allenbälten, enligt Fermisatellitens observerade exempelfall Zambia-Egypten 14Dec2009.

— Det är vad som krävs, och det är vad som måste förklaras och redovisas — OM bildningen relateras till normalområdet för blixturladdning moln-mark (som också innefattar urladdningar moln-moln, vilketsom).

Se även uppgifter i artikeln Runaway breakdown i Wikipedia [sampl. 2011-08-08] — uppgiften saknar dock referenser:

http://en.wikipedia.org/wiki/Runaway_breakdown

”Electrons in air have a mean free path of ~1cm. Fast electrons which move at a large fraction of the speed of light have a mean free path up to 100 times longer.”.

— It better.

Annars är vi illa ute.

Olika sätt att nå spegelpunkten

Olika sätt

OLIKA SÄTT ATT NÅ SPEGELPUNKTEN — teorins utvidgning

För att nå magnetiska spegelpunkten ca 100 KM ovanför Jordytan, och därmed garantera motsatta spegelpunktens återstuds, enligt Fermisatellitens rapporterade mätdata i fallet Zambia-Egypten-JGF:en från Dec2009, är det mest fördelaktigt om (de från en positronring idealt avdelade) positronerna har relativt hög utgångshastighet — OM det gäller en markbaserad JGF:

— Vartefter positronerna avancerar uppåt spegelpunkten (i spiral) parallellt med Jordmagnetiska fältlinjerna (så snabbt som möjligt för att, just, minimera förlusterna på vägen), kan parallellhastigheten dämpas ut successivt;

— Positronernas elektriska växelverkan med atmosfärens atomer på uppvägen (delvis elektrisk attraktion motsatt färdriktningen kan dämpa hastigheten), kan ge ett lämpligt lägre värde (idealt noll med hastigheten istället riktad rätvinkligt fältlinjen) då första spegelpunkten passeras. Därifrån bildas sedan samma principiella förlopp som i motsatta spegelpunkten: positronen stannar, vänder, och söker sig tillbaka till andra sidan igen, osv, p.g.a. att Jordfältet konvergerar mot spegelpunkterna.

Kärnringens expansion

↑ →

Om vi, figuren ovan, återvänder till illustrationerna med den expanderande kärnringen från JGF:ens CAT via ATA, allt enligt TNED, ser vi att ringen besitter precis de ideala förutsättningar som fenomenformen tycks kräva:

— DELS finns en expansionsriktning (som kan ge positronerna hastighet tvärs Jordmagnetfältet), med även DELS också en möjlighet (nu alltmera uppenbar) med en hastighetskomponent rätvinkligt expansionsriktningen.

— När kärnringen blottläggs alltmer på sin positronstock, vilket enligt teorin ska ske nerifrån anoddelen och uppåt [Moln-Mark-urladdning, marken anoden, se utförligt från BLIXTURLADDNINGENS FYSIK enligt TNED], blottläggs samtidigt teoretiskt en successivt växande Coulombrepulsion i ATA/CAT-strömstammens längsriktning.

— Därmed finns, i varje fall principiellt, möjligheten att hela den blottlagda positronringen KAN repelleras uppåt av den underliggande kärnstocken (som fungerar som ett rekylstöd, ev. med ytterligare stöd från marken om JGF:en är av den typen).

Alternativ 2

Ideala separationstiden via divergensen [c] och två Syrekärnringar [uppriktningen]

F = (k=9 T9 VM/C)([Q=A₁₆909e/3]/[d=3 t9 M])²

= 6,03184 t4 N ; 1,50796 t4 N med halva besättningen

= ma ;

a = F/[m=16(1,66033 t27 KG)]

= 2,27057 T22 M/S² ; 1,13528 T22 med halva besättningen

v = aT = c (idealt) ; likformig acceleration över korta avstånd

T = v/a

= 1,32033 t14 S

Ringrepulsionen bör [således] i vilket fall frambringa maximala upphastigheter.

Endast 1/3 av hela kärnpositronladdningen här beaktad [kärnkropparna skymmer delvis varandras Coulombfält].

— Liknande grovberäkning för EN expansionspositron relativt den övriga poistronringen ger grovt sett samma resultat: maximala hastigheter uppnås nära omedelbart vid CAT-urladdning.

— Vi ska dock här genomföra en mera avancerad grovberäkning för att se efter OM ALLS förutsättningarna existerar. Se Positronens Expansionshastighet.

— Situationen skulle därmed bli närmast ideal (figuren ovan):

— Jordmagnetiska fältlinjerna i ekvatorialbandet bildar i stort sett och förgrovat vinkeln 45° med markytan (NASA-Exemplet Zambia-Egypten). Ligger blixtbanans CAT-urladdningsdel ungefärligt i linje med denna riktning, och vi antar nyssnämnda repulsion-expansion, finns alla ideala förutsättningar för ringen att nå ut till första spegelpunkten ca 100 KM ovanför marken, samt då, med garanterade positronhastigheter (vidare i Positronens Expansionshastighet) rätvinkligt Jordfältlinjerna på ringexpansionens räkning.

Positronernas Observerade Hastighet

”“Even though Fermi couldn’t see the storm, the spacecraft nevertheless was magnetically connected to it,” said Joseph Dwyer at the Florida Institute of Technology in Melbourne, Fla. “The TGF produced high-speed electrons and positrons, which then rode up Earth’s magnetic field to strike the spacecraft.”

The beam continued past Fermi, reached a location, known as a mirror point, where its motion was reversed, and then hit the spacecraft a second time just 23 milliseconds later. Each time, positrons in the beam collided with electrons in the spacecraft. The particles annihilated each other, emitting gamma rays detected by Fermi’s GBM.

”,

GBM, Gamma-ray Burst Monitor,

NASA's Fermi Catches Thunderstorms Hurling Antimatter into Space 01.10.11

http://www.nasa.gov/mission_pages/GLAST/news/fermi-thunderstorms.html

;

v = d/T = (910 T3 M)/(23 t3 S) = 3,95652 T7 M/S = 0,1319753c

GBM, Gamma-ray Burst Monitor.

910 KM, ungefärligt från figurproportionerna i JGF under satellitens synhorisont.

— Genom uppvägen till spegelpunkten, kan den initiella upphastigheten dämpas ut successivt tillsammans med pågående annihilation mellan ringens positroner och ditattraherade elektroner från omgivningen.

— Det skulle förklara ideala läget med nollhastighet i fältlinjens riktning då positronerna når första spegelpunkten. Därmed garanteras motsatta fältsidans (symmetriska) spegelpunkt.

Ytterligare uppgifter från Fermiexemplet 14Dec2009 gör att vi (nu, för första gången, äntligen) kan precisera detaljerna än mer rent matematiskt — för TNEDs del. Vidare nedan från Positronens Expansionshastighet.

Positronens Expansionshastighet

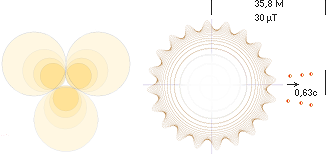
Från magnetiska kraftlagen F=BQv=mv²/R ges med v=0,63c och B=30µT radien R=35,80106 M för den ideala positronen i Jordmagnetiska ytfältet [Zambiavärdet 32,1µT] — positronen drar iväg på Jordfältlinjen via en cylinder med diametern 71,6 meter. Figurerna ovan antyder hur positronerna kan expandera/avdelas, förutsatt kärnringarna vid bildningen är flera [minst två i samma plansnitt] och trängs ihop i ett centrum [naturligt p.g.a. Coulombrepulsionen]. Vidare i huvudtexten.

Positronens Expansionshastighet — 0,63c

I beräkningarna nedan används förenklat t|T för 10^—+

Hastigheten rätvinkligt Jordmagnetiska fältlinjen har bara en, och endast en, chans att utbildas enligt CAT i TNED via en JGF: ögonblicket då kärnringen ligger helt frilagd på sin positronstock (minst A909e, störst A918e).

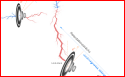
Figuren nedan visar först hur vi får fram grunddata från Fermiexemplet 14Dec2009:

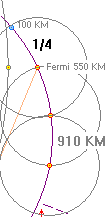
Grovfiguren Zambia-Egypten som visar ungefärliga avstånd på den ungefärligt sammanbindande Jordmagnetiska fältlinjen [violetta]. Se originalfiguren i JGF under synhorisonten.

Avståndet mellan spegelpunkten MSP(Egypten) och höjdvinkelns magnetiska ekvator (M) är ca 4 enheter Fermi-MSP, enheten grovt ca 910 KM enligt grovfiguren ovan. Enligt artikelkällan skulle positronens medelhastighet MSP-Fermi vara ca 0,13c; Höjdvinkeln når sitt maximum (α=34,38°) vid M, analogt ca 4 gånger avståndet MSP-Fermi. Vi kan därmed grovräkna sluthastigheten vid M som

v = 4×0,13c = 0,52c.

Positronens hastighetsriktning i Jordmagnetiska fältlinjens utsträckning är NOLL i spegelpunkten [blå i figuren ovan]. Vid ideala fältlinjens magnetiska ekvator är positronens hastighetsriktning nära parallell med fältlinjen, så när som på höjdvinkeln 34,38°. Vi antar här förenklat att vridningen på de 90–34,38=55,62 graderna är helt proportionell mot fältlinjens längsutsträckning, och därmed analogt hastighetsrelationerna 1:4.

— Om den hastigheten antas vara maxhastighetens vektorprojektion på fältlinjens utsträckning vid M, ges (i PREFIXxSIN) som en första approximation till prövning värdet

vMAX = v·secα

= 0,52c·1,2116649

= 0,6300657c

0,63c är den expansionshastighet vi måste lämna säker redovisning för — oavsett teori.

Vi kan undersöka grovfallets förutsättningar enligt TNED genom att utnyttja de enklast redan befintliga sambanden:

· elektronens hastighet (u) i vakuum som funktion av en accelerationsspänning (U) enligt Planckenergins ekvivalenter

________________________

u = c√ 1 – 1/[(UQ/m₀c²) + 1]² ........................ laddningshastigheten u från accelerationsspänningen U

m0 = 9,11 t31 KG, elektron-positronVilomassan

c = 2,99792458 T8 M/S

· accelerationsspänningen (uppskattad) via elektriska kraftlagen

U = Fr/Q = k(Q/r)

k = 9 T9 VM/C

Q = minimum A909e/3

r = minimum minst från kärnradien för A-nukliden, men [sannolikt minst, grovt) 10ggr större;

10[r0=1,37 t15 M][A=16]^1/3 = 3,45218 t14 M

Reduktionen med 3 för hela det frilagda Q-kapitalet är här en ren hoftning med grund i att, i vilket fall, hela kärnringens totalladdning aldrig kan ses från någon enskild punkt på ringen (realt en funktion av avståndet); Kärnkroppen självskymmer en del av sin egenladdning, här således endast i en grov uppskattning.

Om vi anställer ett KALKYLKORT med kalkylceller (OpenOffice) för att utföra beräkningarna,

Se Kalkylkortet Tabell1 Tillgängliga spänningen och Laddningshastigheten u

finner vi

A r Meter U Volt v/c0

16 1,0 t10 6,99 T4 0,48

16 5,0 t11 1,40 T5 0,62

16 4,7 t11 1,49 T5 0,63

0,63c satisfieras om den frilagda positronringen motsvarar en ekvivalent repulsionsradie på r=0,47 Ångströmenheter, motsvarande en accelerationsspänning på nära 150 000 Volt.

— I det praktiska fallet kan vi räkna med att accelerationsförloppet kräver en något trängre ringradie. Den bör också finnas tillgänglig från minimala grovt rMIN=3,5 t14 M (10ggr masstalsradien med Syreatomen som kärnagent, masstal 16).

vMAX avslöjar detaljer om blixtbildningen …

Resultatvärdet ovan förutsätter att vMAX ges med referens till en FAST preferens. I det aktuellt (fria) expanderande ringfallet skulle hastigheten strängt taget bara bli halva värdet (0,315c), ringcentrum idealt vilande. Hur vi än räknar på den vägen, skulle vMAX i vilket fall aldrig kunna bli mer än exakt 0,5c.

— Den upplysande omständigheten betyder bara för TNED-CAT-teorins del, att kärnringen, tydligtvis, måste trängas med andra, närliggande (i stor mängd dessutom) för att få en lämplig stabil (inre ringkropp) som yttre högpositrontäta kärnringar kan repelleras ifrån. Endast med den förutsättningen är det tydligt att värdet 0,63c kan uppnås. Annars bara max halva c.

Resultat

(från grovberäkningarna)

— Grovräkningarna för positronens expansionshastighet visar, tydligen, inga direkt uppenbara hinder eller svårigheter för TNED-CAT-teorins kvantitativa förutsättningar i matchningen av Fermisatellitens observationer i exempelfallet.

MAC — modern akademisk blixtbildningsteori

MAC förkortar Modern ACademy i UniverumsHistoria

Med dessa till synes helt glänsande grovresultat är det tydligt att den moderna akademins positronbildningsteorier upplever djupgående problem.

— Själva blixturladdningsElektronDraget beskrivs (eller associeras ofta) i MAC via eller i analogi med den s.k. Townsend avalanche-effekten.

— Karikerat: Man tänker sig en tillräckligt energirik primär elektron som kan dra ut en elektron från en närliggande atom, och vars energi också räcker för att i sin tur dra ut ytterligare en elektron, osv, så att man till slut »får» en enorm skur av elektroner som vräker sig fram katod-anod.

— Du menar att den utlösande primärelektronen skulle ha den originella egenskapen att summera totalenergin för alla sekundärt utdragna elektroner ...

— Man hänför varje ny elektrons energi till en redan etablerad elektriskt fältstyrka som ansvarar för varje frigjord elektrons acceleration. Resonemanget söker med andra ord förlägga den utlösande faktorn till materiefysiken: elektronström m e l l a n atomerna. För att få fram den utlösande elektronen, tvingas man anta (den föga smickrande naturvetenskapliga premissen med) inkommande kosmiska partiklar: dessa skulle då bära ansvaret för blixturladdningarnas påtriggning ...

Se exv, Wikipediaartikeln om Lightning, Lightning initiation

http://en.wikipedia.org/wiki/Lightning

”the mechanism by which the lightning discharge begins is not well known”.

Townsend discharge

Se även Townsend discharge i Wikipedia,

http://en.wikipedia.org/wiki/Townsend_discharge

Se även CITATSAMLINGEN angående modern akademi generellt i blixtljuset, samt speciellt den särskilda citatsamlingen i Blixturladdningens fysik i modern vetenskap och akademi.

Se även en etablerad beskrivning i National Geographic DAILY NEWS 20Apr2010, hur man tänker sig funktionssättet,

http://news.nationalgeographic.com/news/2010/04/100419-lightning-natural-particle-accelerators-lhc/

Townsend avalanche-effekten enligt TNED

sv. TownsendLavin-effekten

För en innesluten gas mellan två elektroder (kondensatorplattor) med en etablerad atomtråd (ATA) mellan plattorna åtskilda av distansen d, finns (med hänsyn till gasens täthet och temperatur) ett visst antal mellanliggande gasatomer som kopplar den centrala strömstammen (elektrondraget katod-anod). Dessa atomer blir i motsvarande grad joniserade. Ökas d (plattspänningen hålls konstant), tvingas naturligtvis strömstammen dra till sig ytterligare gasatomer för att (från anoden) fylla ut strömstammen, motsvarande en totalt ökad jonisation: strömstyrkan ökar med växande avstånd mellan kondensatorplattorna, konstant plattspänning. Den högre strömstyrkan i sig, medför att jonisationspotentialen också ökar (per längdmeter) så att proportionsvis en allt växande (lavinartad) mängd gasatomer kommer att delta i jonströmmen anod-katod.

FORMEN är i princip densamma som följer LJUSBÅGSMATEMATIKEN.

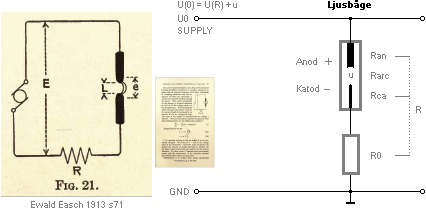
EXEMPEL (Ayrtons Kolelektrodsamband i Ljusbågsfysiken i sammandrag):

U₀ = 100 V

Rserie = 5 Ω

u = 98,06 V ............... bågspänningen

I = 0,398 A ............... bågströmmen

s = 1 mM .................. båglängden

;

U₀ = 110 V

Rserie = 5 Ω

u = 98,97 V ............... bågspänningen

I = 2,207 A ............... bågströmmen

s = 8 mM .................. båglängden

;

Med (nära) oförändrad spänning (u) mellan ljusbågselektroderna, ökar strömstyrkan (I) med ökande elektrodavstånd (s).

Fenomenformen är alltså välbekant — men ingen i MAC förstår/kan förklara innehållet.

— Medan man UNDERFÖRSTÅR att elektronströmmen katod-anod är ett fenomen MELLAN atomerna, har man ingen som helst teoretiskt grundval för att kunna förstå att den strömvägen i själva verket är en KÄRNBRUNNSTRÖM som kräver sammankoppling (via en viss gränsspänning, U[G] i TNED) av flera atomers atomkärnor.

— Fenomenet kan inte förstås utifrån materiefysiken. Inte alls överhuvudtaget.

— Massfysiken (TNED) förklarar saken. Men den är orepresenterad i MAC — och kommer så att förbli. För att förstå fysiken totalt, måste MAC överges: förstås som en primitiv konstruktion.

Strömstammens CAT-geometri

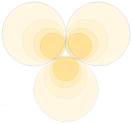
9Aug2011

Strömstammens CAT-geometri

Strömstammens möjliga geometri vid positronbildningen

Strömstammens möjliga tvärsnittsgeometri i blixturladdningen generellt enligt TNED har delvis tidigare berörts översiktligt med kvantitativa grunddata i UniversumsHistoria i sektionerna (främst) Blixtbildningen och Urladdningen och Blixtbanans bildning i syntes (BlixturladdningensFysik.htm).

Dock finns ingen föregående beskrivning som explicit behandlar strömkanalens formgeometri vid CAT — atomkärnans sönderdelning med exponeringen av positronringarna. Grunduppgifterna från Fermisatellitens Zambia-Egypten-fall har visat sig ge en möjlig vägledning i tolkningssätten.

Gränsströmstyrkan vid CAT för luftens två främsta nuklider

nuklid masstal gränsströmstyrka för CAT, Ampere

Kväve 14 14·909·IN = 67 956,84

Syre 16 16·909·IN = 77 664,96

IN = 5,34 A, se Nukleära Elektrongenomströmningens Makroekvivalent i Nukleära ElektronGenomströmningsEkvivalenten

Blixturladdningens minsta kanaltråd enligt TNED kan bara vara EN sammanhängande atomtråd: sammankopplade atomer/atomkärnor, samma princip som i kemisk koppling via KRAFTEKVATIONEN: atomerna/kärnbrunnarna delar på samma elektronbesättning.

För blixtbildningens stamkanaler (»blixtträdet») i sig (se Stegade ledaren) finns dock i princip (här veterligt enligt TNED) ingen begränsning för antalet parallella atomtrådar i en gemensam blixturladdningsväg. Begränsningarna i antalet parallella trådar uppkommer först vid själva urladdningstillfället. Tabellen ovan anger, enligt TNED, riktvärden för de strömstyrkor som gäller för EN urladdningskanal vid CAT, analogt vid JGF (eng. TGF).

Enligt (referensuppgift från Wikipedia Lightning)

MITIGATING LIGHTNING HAZARDS — Science & Technology Review May 1996 — s7n

”The average electrical discharge of lightning is about 15 coulombs; the highest charge transfer is estimated to be about 350 coulombs.”,

ligger (den observerade) totala laddningsmängden i en blixturladdning i stort mellan Q=15-350 Coulomb. Med en ungefärlig blixtbildningstid på totalt T=1 mS (Se fotografi av stegad ledare, blixtbanans utbildning, Zhang 2006) för en 1 KM lång blixtbana ges motsvarande strömurladdningar

I = Q/T 15.000-350.000 Ampere.

OM CAT gäller (samma som atomkärnans upplösning enligt TNED: positronbildning från blixturladdning) blir alltså maximalt antal parallella atomtrådar respektive (idealt samma nuklider)

5 för Kväve (350.000/67.956,84) och

4 för Syre (350.000/77.664,96), förutsatt hela urladdningsmängden till CAT. Inte mera.

Genom att alla nuklider i samma tråd delar på samma strömdrag, finns ingen direkt matematik på exakta antalet nuklider som kan delta i CAT per atomtråd — frånsett blixtbanans längd i sig (max 1KM) som sätter gränsen med antalet innefattade luftmolekyler/atomer (via medelavståndet 3nM, normal luft vid Jordytan: drygt 3 T8 nuklidagenter per luftmeter, endast grovt sett ca 1/5 av dessa, 60 miljoner nuklidkandidater per idealt längsgående luftmeter, kommer ifråga för blixtbanan, se Antalet Atomagenter).

Det enda riktmärket för kontrollerande beräkning som finns för tillfället, är uppgiften om (den möjliga) positronmängden från SCIENCE DAILY 11Jan2011 i fallet Zambia-Egypten-JGF:en

”the lightning flash detected by Fermi appeared to have produced about 100 trillion positrons”;

Hundred trillion = hundred thousand billion = hundred thousand thousand million = 100 000 000 T6 = T14 positroner med enbart Kvävenuklider betyder max

N = (T14)/(14·909) = 7,85792 T9 Kvävenuklider; Per ideal luftmeter (3 t9 M mellan varje) ges luftlängden för EN atomtråd

N·3nM = 23,573785 M — eller med max 5 atomtrådar, längden (komprimerat) nära 5 luftmeter;

För Syre motsvarande

N = (T14)/(16·909) = 6,87568 T9 Kvävenuklider med

N·3nM = 20,627062 M — eller med max 4 atomtrådar, längden (komprimerat) nära 5 luftmeter;

Således i vilket fall grovt MAX:

Fem luftmeter 4-5-kanals CAT (Delningen med 5 frånsett) — OM max urladdningsmängd (350 C) gäller.

GRUNDFÖRUTSÄTTNINGEN för att nå upp till hastigheten (av allt att döma) 0,63c för positronerna i det rapporterade Zambia-Egyptenfallet, se Positronernas Expansionshastighet, är otvivelaktigt — OM det är TNED som gäller — att FLERA, minst två, atomtrådar måste finnas. Annars kan bara max 0,5c komma ifråga (ideal urladdningsriktning parallellt med Jordfältlinjerna ut från markbasen).

— Det är tydligt i ovanstående beskrivnings ljus att TNED inte direkt kan avfärdas som kandidat till förklaringen av Zambia-Egyptenfallet.

SUMMERING

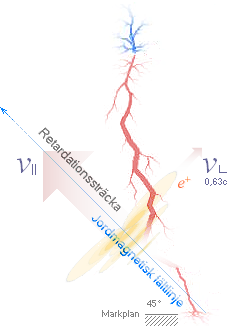
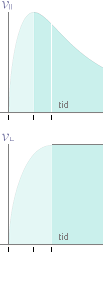
POSITRONMÄNGDEN frigörs enligt TNED via CAT , vilket motsvarar upplösningen av atomkärnans ekvivalenta ±e-bank, se utförligt från CAT. Positronexponeringen bildar dels en inbördes repellerande expansion mellan restnuklidringarna, idealt/optimalt uppåt från markytan parallellt med Jordfältslinjen [här idealt antagen lika med blixtbanans riktning], vPARALLELL, och dels en denna direkt rätvinklig ringexpansion vNORMAL. Vi förutsätter att vPARALLELL [i det ideala illustrerade fallet] dämpas ut då ringarna repelleras med hög hastighet upp mot första magnetiska spegelpunkten ca 100 KM över Jordytan. Den återstående positrondelen antas därmed bevarad på sin expansionshastighet [i exemplet 0,63c], se Positronens Expansionshastighet. Därmed är också motsvarande spegelpunkt i andra fältänden säkrad, och positronen kan nu vandra mellan dessa punkter, enligt Fermisatellitens registerade rapport 14Dec2009, se Zambia-Egypten-JGF:en. De bägge graferna ovan höger visar principen för hur de bägge hastigheterna bör utbildas.

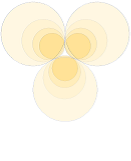
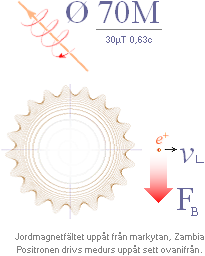
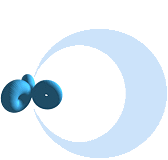
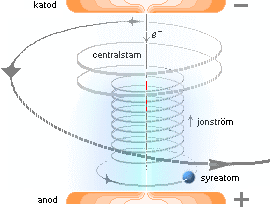
Figurdelen ovan höger illustrerar positronens expansion i den frilagda nuklidringen sett ovanifrån marken [Zambia]. Magnetfältets riktning uppåt [32,1µT]. Riktningen betyder att positronen [idealt] böjer [F(B)] av medurs. Sambandsformen F=mv/BQ ger omloppsdiametern 71,6 meter med periferihastigheten 0,63c, se beräkningarna i Positronens Expansionshastighet.

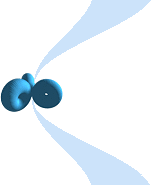
Figurdelen till vänster visar ett idealt snitt genom tre möjliga inbördes expanderande frilagda positronringar från motsvarande tre atomtrådar som enligt TNED utbildat CAT. Se översiktliga grundberäkningar i Strömstammens Geometri. Inte mer än max 5 atomtrådar [max 350 Coulomb totalt] kan bildas i Jordatmosfären med samtidig positronbildning [som då sker över endast grovt och idealt räknat 5 luftmeter av hela blixtbanan] — enligt TNED.

Vad återstår?

Vad återstår?

— Mera datauppgifter för vidare kontroll. Ovanstående genomgång ger onekligen visst perspektiv åt TNED. Men än är vi inte framme vid målet.

Strategiska argument

DEN FRÄMSTA ANLEDNINGEN varför just markbaserade blixturladdningar har använts i den här framställningen som objekt tillsammans med teorin för positronbildningen i CAT är (naturligtvis) den observerade förekomsten av s.k. »ljusbollar» eller »eldsklot» (eng., ball lightning). Just nere vid marken, och i samband med särskilt häftiga urladdningar skulle det, enligt ATA/CAT i TNED finnas en passande förklaring för uppkomsten av en sådan fenomenform [Se en tidigare exempelräkning i POSITRONBOLLEN]. Knappast annars. Även om en sådan fenomenform också (naturligtvis) skulle kunna bildas längre upp, vid molnroten, finns här veterligt inga observerade tillfällen för den delen. Markbaserade urladdningar blir alltså det naturliga valet i den övergripande förklaringen till samtliga fenomenformer i samband med blixturladdningar.

— En alternativ förklaring till »positronbollen» visar sig mera (reguljärt) med ovanstående genomgång av den möjliga positronexpansionen från en marklokal (se från Positronens Expansionshastighet):

— Istället för en reguljär positronbaserad luftboll, kan man lika gärna, och med principiellt samma resultat tänka sig att de snabbt expanderande positronerna från en lokal CAT-urladdning kvarlämnar en central, mindre (basketbollstor) luftboll av joniserade luftatomer. Då ytan på den luftJonbollen strävar att återneutralisera sina atomer genom att ta elektroner från mindre joniserade atomer utanför sfärytan, finns förutsättningar för uppkomsten av ljusfenomen under en viss kortare tid — likt det intensiva skenet från en ljusbåge. Om inte en direkt fenomenförklaring, kan LuftJonBollen därmed, möjligen, vara ett alternativ till den rena föreslagna fenomenformen i POSITRONBOLLEN.

Slutord

Vi VET naturligtvis inte (riktigt, än) exakt HUR de (tillsammans med omgivande atomer), enligt TNED, förmodade frilagda nuklidpositronringarna (figuren ovan, idealt) uppför sig från repulsionstillfället — utöver faktum ATT (grymt stark) repulsion otvivelaktigt bör ske. Fermiexemplet kan vara unikt.

— VÄRDET AV JUST DEN aspekten, positroner som expanderar ut från en liten medelpunkt, ansluter direkt i TNED till framställningen om POSITRONBOLLEN: den möjliga förklaringen till de s.k. »eldsklot» en del personer har observerat i samband med (särskilt häftiga) blixturladdningar i markområden (men som aldrig har funnit en tillfredsställande förklaring).

Kort översikt av ATA/CAT i TNED

BellDharma 2011VII26

Kort översikt av ATA/CAT i TNED:

· 1991-2006: Med början från 1991, i avtäckningen av de mera betydelsefulla matematiska djupen i den senare benämnda CAT-teorin, krävde TNED gammastrålning från vissa (särskilt kraftfulla) atmosfäriska blixturladdningar — gammastrålning från blixturladdning upptäcktes (officiellt) från 1994 (CGRO). Jag gjordes inte uppmärksam på det förrän 2006 (ScienceDaily 2May2005) — min sjösättning till INTERNET. Det kom som en länge saknad bekräftelse;

· 2010: Som emellertid CAT-TNED också kräver direkt positronförekomst från de aktuella kandidaterna (numera benämnda JGFs), uppmärksammades jag (lägligt) på sådana formella observationer 31Aug2010 från en artikel daterad 26Nov2009,
Mystery Terrestrial Gamma Rays May Destroy Matter DISCLOSE.TV,
”Fermi’s observations of terrestrial gamma rays have deepened the mystery. At least one of the flashes contain an unmistakable pattern of positrons — the antimatter counterpart of electrons. “It was a surprise, and now we have to explain it,” said Fishman”;

· 2011: NASA-artikeln från 10Jan2011, observerad av mig 3Jul2011, ger full bekräftelse på en direkt Fermisatellit-registrerad positronförekomst daterad 14Dec2009 (se Zambia-Egypten-JGF:en). Källuppgifterna medger nu, för första gången, en mera ingående matematisk-teoretiskt prövningskoll: Ingenting övergripande (inom synhåll) ser ut att motsätta sig TNED-teorin. Se från ZambiaJGF:en.

ScienceDaily-artikeln

Se även en något mera beskrivande (delvis mera kött på benen-) artikel i SCIENCE DAILY 11Jan2011 [här obs. 8Aug2011],

Thunderstorms Shoot Antimatter Beams Into Space

http://news.nationalgeographic.com/news/2011/01/110111-thunderstorms-antimatter-beams-fermi-radiation-science-space/

”Scientists wouldn't have been surprised to see a few positrons accompanying any intense gamma ray burst, added Dwyer, of the Florida Institute of Technology in Melbourne.

But the lightning flash detected by Fermi appeared to have produced about 100 trillion positrons: "That's a lot," he said.

”; [100 T12 = T14 positroner]

”Considering the amount of positrons in the beam Fermi detected, the thunderstorm was briefly creating more radiation—in the form of positrons and gamma rays—than what hits Earth's atmosphere from all other cosmic sources combined, Dwyer noted.

”

Källan ovan anger f.ö. NAMIBIA [sydvästra Afrika] — NASA-artikeln anger ZAMBIA [bilden nedan] med kartredovisad ortsframställning — men utan vidare referenser.

END TGFs2011.

Antalet MolnMark och MolnMoln

Justerad uppgift relativt föregående — andelen blixturladdningar av typen MolnMark är minst

The 2009 American Geophysical Union

http://europa.agu.org/?view=article&uri=/journals/jd/98JD01461.xml

:

”Depending on the assumption made concerning the latitudinal variation of the ratio of cloud flashes to total flashes, the mean rates of occurrence are between about 51 s⁻¹ and 55 s⁻¹ for cloud flashes and between about 10 s⁻¹ and 14 s⁻¹ for ground flashes. The uncertainty in these estimates is a factor of 2 in either direction.”.

Cloud(Cloud) ........................ ca 53 Hz

(Cloud)Ground ..................... ca 12 Hz

Det gör ett förhållande 12/53=0,226415 eller ca 23% CloudGround, med en majoritet 77% CloudCloud.

END TGFs2011.

NEGE — nukleära elektrongenomströmningsekvivalenten enligt TNED

se även NEGE i förtydligande

Tidsfaktorn T(N)=3 t20 S

kräver en närmare kvantitativ förklaring

I(N)ref

I ATA-delen i ATA/CAT omnämndes

I_N = Q/T_N = A·(1836/2=918)e/T_N, A anger masstalet, e = 1,602 t19 C

Nukleära sönderfallets gränsströmstyrka

Samt, mera specificerat, men utan djupare förklaring tidsfaktorn T(N) i Gränsspänningen i Blixturladdningens fysik.

Tidsfaktorn T(N), eller

Nukleära ElektronGenomströmningsEkvivalenten

Komprimerat (t=10^–):

T_N = [3·(2πr₀)/c₀]×300 ≈ 3 t20 S

kräver en närmare beskrivning — och förklaring.

— Det verkar finnas flera olika »medelvärdessätt» att relatera ovanstående resultatbild för T(N) i TNED:

1. Via atomkärnan som sådan i särskilt beaktande av kärnans första underfraktala ringar enligt impulsekvationen (inte tidigare redovisat i UNIVERSUMS HISTORIA), se efterföljande beskrivning;

2. Via en medelnuklid med utgångspunkt från dess kärnradie enligt kubgrafen (R/r0=A^1/3), tidigare redovisat i UNIVERSUMS HISTORIA i fusionslängden: max masstal (antalet max fusioner med Väte, se Nuklidkartans gränsvärde) avr. A=300 på divergensomloppet (ljushastigheten som absolut verkans preferens i analogi med Plancks konstant h=mcr) för vätekärnans radie (r0), detta resultat på en uppskattad medelnuklid (R) via kubgrafens samband R/r0=A^1/3; talet 3 ligger ganska precis i mitten av nuklidkartan om den räknas upp till sista stabila nukliden (Vismut, A=209; 209^1/3=5,9344721), analogt en praktisk övre referens för ett medelnuklidbegrepp 6/2=3, som ger resultatet som ovan. Eller omvänt sagt: den medelnuklidens kärnradieomlopp via c [(R/r0=209^1/3≈3)·([2πr0]/c0)] gånger max antal fusioner 300.

I avsnittet ATA/CAT ges en uttömmande grundbeskrivning enligt TNED av funktionssätten för ljusbåge och gnisturladdning, inkl. grundsamband. Vi förutsätter här den presentationen bekant. Här följer en delvis kompletterande beskrivning — speciellt för T(N), Nukleära ElektronGenomströmningsEkvivalenten. Den — såvitt alls tillämplig — har tidigare framstått mindre tydlig i Universums Historia.

— Eftersom (således, i fortsättning från grundbeskrivningen i ATA/CAT) en given nuklid (atomkärna) enligt TNED med givet masstal (A) inte kan innehålla mer än (via noll massdefekt idealt) max A918e eller minst (via max massdefekt 18e) A909e, kommer analogt maxvärdet för kontinuerlig strömgenomgång utan kärnupplösning, alltså explicit för maxLJUSBÅGE eller initiellt vid gnisturladdning, att ligga vid just den motsvarande makroskopiska strömstyrkan I(NCAT), Nukleära sönderfallets gränsströmstyrka.

— I(NCAT) blir då den makroströmstyrka som, ur idealt en (1) specifikt nuklid, förmår DRA UT A909e till den centrala strömstammen — från en enda A-nuklid, märk väl, och som formar gemensam atomkoppling med övriga atomkärnor, enligt Kraftekvationen, (se även ill. grundform)

F_BT+F_eZ = 0 ............ kraftekvationen

och som ingår i den strömstammen;

I_NCAT = Q/T_N = A·(1836/2=918)e/T_N, A anger masstalet, e = 1,602 t19 C

Nukleära sönderfallets gränsströmstyrka

För att kunna beräkna makrovärdet INCAT måste vi först veta värdet på TN = [Q=e]/IN:

;

T(N) beskriver tydligen FÖRHÅLLANDET mellan kärnströmmen (den enda elektronen explicit, Q=e) i en godtycklig medelnuklid och makroströmmen (I generellt). T(N) benämns i TNED nukleära elektrongenomströmningsekvivalenten,

T(N) = Q/I(N) .................... nukleära elektrongenomströmningsekvivalenten

HÄRLEDNINGEN

OM vi föreställer oss att SÄTTET på vilket en elektronmassa kan plockas ut ur den spinnande atomkärnan (för att kunna delta i stamströmmen i ljusbåge och gnistbildning enligt TNED), är det först också främst tydligt att uttaget sammanhänger med kärnstrukturens allmänna sammansatthet. Denna sammansatthet, enligt PASTOM, kan INTE sägas vara väsentligen olika för olika nuklider, inte ens i jämförelsen mellan den lätta neutronen-protonen och den tyngsta av alla atomkärnor (A=max317 enligt TNED). Strukturen enligt TNED (se PASTOM), nämligen, bygger på en oändligt fraktal struktur. Och så måste alla atomkärnor, alla nuklider, bli av samma strukturella typ, och därmed avspegla samma strukturberoende i detta sammanhang.

— Därmed är, i varje fall den principiella, lösningen till bestämningen av T(N)-faktorn klar;

Max antal fusioner enligt TNED är bekvämt avrundat 300. Genom en fusionsring bestående av 300 elementära väteatomer kan därmed totala, maximala, struktursammansättningen bestämmas idealt som referens, och för vidare prövning, på fusionstiden för 300 enskilda, ideala, spinnomlopp för vätekärnan enligt TNED och taget via DIVERGENSEN (analogt med den allmänna användningen av divergensformen c i Plancks konstant h=mcr) enligt (r0=1,37 T15 M) (t för 10^–)

T = (2πr₀)/c₀

= 2,8713 t23 S ........ idealt absolut teoretiskt kortaste fusionstiden = spinnomloppet för en vätekärna

Alla kärnpartiklar med kortare varaktighet än detta tidsvärde har, med vätekärnans preferens, ingen bestämd partikelstruktur — den är uppenbarligen under utveckling — och måste [därför] uppfattas som en KORTVARIG KRAFTFORM, ingen [kärn-]partikel.

Men varje (väte-)kärnas övergripande toppspinn har sin ekvivalent i atomkärnans första underfraktala spinnform enligt impulsekvationen

J_0K+3J_1K = 0 .......................... impulsekvationen

Det betyder att T-faktorn ovan får associeras med endast EN av de tre underringarna EFTERSOM deras sammansättning bygger på en ömsesidig dynamisk växelverkan. Dvs., hela kärnan kan, tydligen om inget hinder finns, förstås sammansatt med avseende på sina närmast inre ekvivalenter enligt minst T+T+T så att vi får minsta fusionstiden

T(1) = 3(2πr₀)/c₀

= 8,61392 t23 S

Därmed totalt för hela strukturen maximalt (t för 10^–)

• talet 300 här förenklat från nuklidkartans gränsvärde (317,11385)

T(300) = 300·3(2πr₀)/c₀

= 2,58417 t20 S ; avrundat med marginaler,

~ 3 t20 S ;

T(N) = 3 t20 S

NEM

Därmed också motsvarande makroströmstyrka för nukleära elektrongenomströmningen,

I(N) = Q(e)/T(N)

= 5,34 A

Allmänna Nukleära ElektronEkvivalenta UtväxlingsStrömstyrkan [NEEUS] för ljusbåge och gnistbildning, eller

Nukleära Elektrongenomströmningens Makroekvivalent [NEM]

Se även Effektkoefficienten P[0] i Ljusbågsmatematiken — en möjlig koppling.

Denna värdeform är också medelformen för (den knapphändiga, etablerade informationen om) (MINSTA medel-) ljusbågsströmmen från källorna ENCARTA (10A) och EST (2A), grovt 5A, se citaten i NEGE förtydligande, i förhållandet mellan elektronladdningen och nukleära elektrongenomströmningen, och som grundlade föregående (mindre specificerade) omnämnanden (Citaten nedan från grundmanuset, inte medtagna tidigare i UniversumsHistoria).

NEGE, förtydligande

Förtydligande till föregående angående — bakgrund 2011VII28

Nukleära ElektronGenomströmningsEkvivalenten

Kan inte härledas från eller återföras på materiefysiken — T(N) är, tydligen, exklusivt relaterbart endast för massfysiken

T_N-värdet 3t20 S

I_N=Q_e/T_N=5,34 Ampere

Allmänna Nukleära ElektronEkvivalenta UtväxlingsStrömstyrkan [NEEUS] för ljusbåge och gnistbildning

Citaten ENCARTA och EST

GENOM DELVISA UPPSKATTNINGAR, och delvisa jämförelser (genom delvisa citat som inte finns med i grundversionen till webbdokumentet, nedan [Encarta, EST; ENCARTA anger ca 10A, EST anger från ca 2A; grovt ca 5A som referensvärde]),

“To start an arc, the ends of two pencil-like electrodes, usually made of carbon, are brought into contact and a large current (about 10 amp) is passed through them. This current causes intense heating at the point of contact, and if the electrodes are then separated, a flame-like arc is formed between them.”

ENCARTA 2004 Arc (electricity)

“Unless the external resistance is sufficiently great to make the overall resistance positive, the discharge will change suddenly to the arc mode. Typical values in this region are a potential drop of a few tens of volts and a current ranging from a few amperes to thousands of amperes.”

ENCYCLOPEDIA OF SCIENCE & TECHNOLOGY McGraw-Hill 1992, Band-2.s42sp1m Arc discharge

användes i grundförfattningen (från 2008) beskrivningssättet för T(N) enligt

Från

BlixturladdningensFysik.htm#Gränsspänningen

T_N (för luft) kan beräknas approximativt med kännedom om parametrar vid ljusbåge:

man får approximativt T_N=3 t20 S enligt = Q_{1,602 t19 C}/I_5A — detta värde är också enligt TNED samma som det övre gränsvärdet för atomkärnans ändring vid fusion;

Strömstyrkan I=5A är grovt minsta strömmen för kontinuerlig ljusbåge (enligt gängse referensverk — men vissa källor antyder snarare runt 1 Ampere);

Q=1,602 t19 C är minsta atomladdningen för minsta strömmen.

Utöver den rent fusionskopplande referensen till T(N)=3 t20 S, vidare här i NEGE, finns (här veterligt) ingen annan. Omnämnandet med ljusbågens fysik gjordes endast med observationen att värdeformen är analog (via separata överslagsberäkningar och grovkoll på grundvärden [grovvärdet 5A från Encarta/EST som ovan] som faktiskt omnämns i den kända litteraturen, för jämförelsens del, samt till prövning för vidare).

T(N)-faktorn är en ren massfysikalisk term — och massfysiken — TNED — är som vi nu redan vet helt orepresenterad i MAC. T(N)-formen kan, här veterligt, inte härledas från eller återföras på materiefysiken, liksom heller inte elektronmassans komponenter kan det.

— Utöver det som (möjligen) framkommit explicit i den här framställnings ljus (Se Effektkoefficienten) fanns i föregående framställningar ingen direkt ljusbågsrelaterad, förmodad, empirik som kopplar T(N)-faktorn: ingenting var tidigare känt i saken. Heller finns inte i ljusbågsfysiken som sådan någon specifikt minsta ljusbågsström, vidare nedan. På grund av ämnets (mycket) knapphändiga referenser i facklitteraturen i den föregående framställningen, hade just detaljen med ljusbågsströmmen inga andra direkta referenskällor än de ovannämnda i citat.

LJUSBÅGSFYSIKEN EXPLICIT har (här, särskilt, i efterhand nu Jul2011) framkommit i nytt ljus genom den (länge efterlängtande och äntligen) upphittade »LJUSBÅGSBIBELN» från år 1913, se ELECTRIC ARC PHENOMENA, samt vidare från »ljusbågsfysikens moder» Hertha Ayrton (1895). Hennes bok The Electric Arc från 1902 är ren befriande läsning — men omnämns inte i typ det svenska uppslagsverket BKL från 1920-talet (Bonniers Konversations Lexikon). Faktiskt. Inte heller FOCUS MATERIEN 1975 ger något omnämnande: ordet ljusbåge finns inte ens med. I FOCUS TEKNIKEN 1975 finns dock orden Ljusbågemotor→Raketer Ljusbågskol→Kol Ljusbågsugn→Järn och stål upptagna. Ingen direkt beskrivning av fenomenet som sådant finns där.

Ayrton däremot öppnar alla portar — till hela ljusbågshimmelriket. Se vidare från Ljusbågsfysiken i sammandrag.

Jämförelser MAC|TNED — gnistbildning, ljusbåge

Jämförelser MAC|TNED

GNISTBILDNING, LJUSBÅGE

Nedanstående illustrativa kompression bör vara bekant från grundbeskrivningarna i ATA/CAT

instans	MAC	(MAC) | TNED	TNED
fenomentyp:	gnisturladdning, ljusbåge	fri atom	gnisturladdning, ljusbåge
illustration:
förklaring:	förklaring saknas ännu 2011	isolator — sluten elektronkrets	massledare — öppen elektronkrets
minsta gränsspänning gnisturladdning idealt vilande atomer, fasta ämnen	—		k([e/n]/r) = 54 | 14 µV
minsta gränsspänning gnisturladdning idealt vilande atomer, luft	—		k([e/n]/r) = 5,4 | 1,4 µV
minsta gränsspänning ljusbåge idealt vilande atomer, fasta ämnen	—		k([e/r]) = 9,612 V

MAC allmän förkortning i UniversumsHistoria för Modern ACademy

Mitten: Frånsett kärnmodellen och själva kopplingen [TNED, se kraftekvationen] kärna-elektron är uppfattningen om den fria atomen som en ISOLATOR principiellt densamma som i TNED.

Framställningar saknas i MAC

I MAC finns, här veterligt, inga TNED motsvarande (eller andra, liknande) angivna kvantitativa värdeformer som beskriver principen för gnistbildning och elektrisk ljusbåge. Se särskilt sammanställt citatblock i Blixturladdningens fysik i modern vetenskap och akademi.

Gränsspänningarnas förklaring i TNED

I TNED förklaras explicit gnisturladdningens fysik på kraftekvationens motsvarande koppling, inbördes via det enskilda elektronelementet, mellan flera atomer enligt gränsspänningen för kemisk koppling, och via spänningsformen för Coulombs allmänna ekvation (F=k[Q/r]², se Elektriska kraftlagen) enligt

U_G = k([e/n]/r)

= (1/4πε₀)([e/rn])

Gnisturladdning enligt TNED

Grundräkningen för elektronmassans antal komponenter i TNED ges från SPEKTRUM tillsammans med atomkärnans härledning som minst n=177062, se Elektronmassans komponenter. En möjlig justering i avsnittet om Casimireffekten ger n=673026, se Inverkan av n på föregående beskrivningar.

— För fasta material med medelavståndet grovt 3Å (0nM3) ges avrundat (räknat från medelpunkten för halva medelavståndet [r=0nM3]/2)

U_G = 54 µV ................... n=177062

= (9 T9 VM/C)(1,602 t19 C)/[(177062)[r]/2]

= 54,286 µV

U_G = 14 µV ................... n=673026

= (9 T9 VM/C)(1,602 t19 C)/[(673026)[r]/2]

= 14,2817 µV

En grovkoll med tidigare beräkningar på blixturladdningens olika parametrar gör det troligt att det senare värdet är det mera sannolika. Men inga direkta bevis finns ännu att peka på. Värdena gäller (fortfarande) till prövande verifierbarhet.

— Värdet (typ) 54 µV är enligt TNED den teoretiskt (förgrovat) lägsta spänning som krävs för att kunna observera ginsturladdning mellan fasta material (idealt vilande atomer förutsatt, ingen hänsyn till atomens specifika egenskaper).

— I de enkla gnistexperimenten som genomfördes i samband med EXPERIMENTKOPPLINGEN med Aluminium som anodelektrod och katoden som den förtennade mässingskontaktstifthylsan har gnisturladdningar iakttagits i varje fall ner till 2 Volt (men då under stora svårigheter på grund av den svaga ljusblixten som kräver absolut mörker för att kunna ses).

— För luft (medelavståndet mellan luftmolekylerna grovt och idealt vilande, r=3nM=30Å) blir värdena 10 ggr större.

Ljusbåge enligt TNED

Det enda som skiljer den tillfälliga gnisturladdningen från den kontinuerliga ljusbågen, enligt TNED, är att minst en hel elektronmassa måste delta i den motsvarande kemiska kraftkopplingen för att ljusbågen ska tända — analogt, kunna upprätthållas på elektronladdningens minsta belopp.

— Motsvarande gränsspänning för ljusbåge enligt TNED skulle i så fall, om sambandsformen har någon fysikalisk förankring, vara (r=3 Å, ca atommedelavståndet i fasta ämnen)

U_G = k(e/r)

= (1/4πε₀)([e/r])

= (9 T9 VM/C)(1,602 t19 C)/[(r)/2]

= 9,612 V

Notera att ingen hänsyn tagits till atomens rörelsetillstånd, eller dess specifika elektriska-termiska egenskaper. För det praktiska fallet bör alltså observerade värden ligga (något) högre.

— Under den spänningen kan ingen ljusbåge utbildas. Inte för något grundämne — enligt TNED.

— Jämför tabellen nedan (omskriven), experimentellt uppmätta värden för olika elektrodmaterial i samband med studiet av ljusbågens fysik, här från Raschs bok 1913 (s79 Table 15, högra kolumnen lägsta ljusbågsspänningen i Volt);

Carbon	38.88
Silver	14.19
Iron	15.73
Nickel	17.14
Cobalt	20.78
Gold	20.82
Copper	21.38
Palladium	21.64
Platinum	24.29

H. Ayrton

C.E Guye and L. Zebrikoff (1907)

Atomkärnans upplösning enligt TNED

Eftersom, enligt TNED, ljusbågen och gnisturladdningen bägge bygger på en central elektronström som delas gemensamt av de via gränsspänningen U(G) strömkopplade atomerna, samt att den elektronbesättningen därmed också tvunget kopplar atomkärnans allmänna strömkoppling med sin yttre elektronbesättning (kraftekvationen), finns analogt en viss övre gräns för elektronströmningen med hänsyn till atomkärnans elektronströmkapacitet. Nämligen i kraft av den enligt TNED via atomkärnans härledning befintliga ±e-struktur som atomkärnan bygger på, se särskilt i centralmassivet. Varje neutronindivid bygger på ett centralmassiv av ±909e som tillsammans med en förbrukningsstock på 18e, samt en överskjutande »smörjmassa», definierar neutronens antal elektronmassor som 1836+2,624=1818+18+2,624=1838,624. Förbrukningsstocken på 18e kopplar till atomära massdefekten, se utförligt från NEUTRONEN och NEUTRONKVADRATEN om ej redan bekant.

— Med den kvantitativa definitionen av gränsströmstyrkan I(N) för atomkärnans upplösning (CAT) via nukleära elektrongenomströmningskonstanten T(N) är fysikbeskrivningen i TNED fullständigad. Det finns, här veterligt, inget mer att beskriva i fysikens mera övergripande mening.

Ljusbågsfysiken i sammandrag

Ljusbågsfysiken i sammandrag

Se även GRUNDTEORIN ENLIGT TNED

Se även Justerade samband enligt Ewald Rasch 1913 frn. s76ö

u = u₁ + αs + δs/I

Sammanställning 2011-07-31

KolelektrodLjusbågens allmänna samband

I Kalkylkortet Tabell1 finns nedanstående Ayrton-baserade samband sammanställda.

Silent Solid Carbon (typ Apostle ref. Ayrton 1902 s119n) Ø11mManod Ø9mMkatod enligt Ayrton 1902 — Stabila tillstånd:

Kolstavarnas längdmotstånd ca 65 Ohm per meter

Grundsambandet (förmodl. frn. 1895) från Mrs. Hertha Ayrton (1854-1923, ref. Wikipedia), VoltMillimeterAmpere

u = u₀ + αs + (γ + δs)/I

= 38.88 + 2.074s + (11.66+10.54s)/I

Koefficienterna enligt Ayrton [1902] s183

u₀ 38,88 V

α 2,074

γ 11,66 V

δ 10,54

;

Kretskopplingen

Kretskoppling:

Fasta kretsresistansen R [‡]

R = (sδ + γ)^–1[([u₀ + U₀ + αs]/2)² – U₀(αs + u₀)] ;

Från matningsspänningen U0 i Volt och båglängden s i mM — R i Ohm

Båglängden s [‡]

s = –[α(u₀ – U₀) – 2δR)]/α² – √ ([α(u₀ – U₀) – 2δR)]/α²)² + [4γR – (U₀ – u₀)²]/α²

Från matningsspänningen U0 i Volt och fasta kretsresistansen R i Ohm — båglängden s i mM

Maximala bågspänningen u [‡]

u = (U₀ + u₀ + αs)/2 +√ ([U₀ + u₀ + αs]/2)² – (s[αU₀ + δR] + γR + u₀U₀) ;

Från matningsspänningen U0 i Volt, fasta kretsresistansen R i Ohm och båglängden s i mM

StartStröm Imax

Imax = U₀/R

Ljusbågen startas upp med kolelektroderna sammanförda, sedan separerade till MAX 6mM [Ayrton 1902 s244m; s244mn; s245n],

”in other words, 6mm. is the maximum length of arc that can be maintained under the given conditions of generator and external resistance.”

Nominella Bågströmmen I

I = (U₀ – u)/R

Samma som lägsta kretsströmmen vid uppnådd båglängd s

Riktmärke: Kolelektrodernas (Ayrtons typ) spänningsgränskoefficient u0 är 38,88V. En absolut lägsta matningsspänning U0 bör därför vara ca 50V — vilket ger R=0,92Ohm med max båglängd s=1mM: ljusbågsströmmen 4,16 Ampere med ljusbågsspänningen 45,4 Volt, startström 50 Ampere.

(Inte direkt inbjudande att experimentera med hemma på köksbordet — avancerad strömförsörjningselektronik, samt väl genomtänkt laboratorieplats: glasinbyggnad på eldfast underlag, mekaniska anordningar för bågkretsens reglering, optiska filter — krävs för att minimera risken för äventyr).

GraferARC

Optimalt stabil ljusbåge — konstant matningsspänning, variabel serieresistans

Exemplifierad dynamik vid konstant matningsspänning U0=100V — Efter samband från Herta Ayrton 1902 och Ewald Rasch 1913.

Genomgående solida kolelektroder Ø9-11mM enligt Ayrton — max 6mM ljusbåge [därefter instabil]

Bågspänningen:

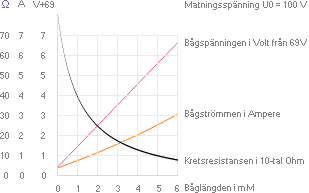
y = –69+[1.037x+(38.88+100)/2]

u = (u₀ + αs + U₀)/2

Bågströmmen:

y = [100–(38.88+2.074x+100)/2](10.54x+11.66)([([(38.88+2.074x+100)/2]'2)–100(2.074x+38.88)])'–1

I = [U₀ – [u₀ + αs + U₀]/2]((sδ + γ)^–1[([u₀ + αs + U₀]/2)² – U₀(αs + u₀)])^–1

Kretsresistansen [dämpad 10ggr] — måste varieras dynamiskt enligt sambandet nedan för stabil ljusbåge och fast matningsspänning U0:

y = 0.1[(10.54x+11.66)'–1]([(1/4)(38.88+100+2.074x)'2]–100[2.074x+38.88])

R = (sδ + γ)^–1[([u₀ + U₀ + αs]/2)² – U₀(αs + u₀)]

Koefficienterna enligt Ayrton 1902:

u₀ 38,88 V

α 2,074 V/mM

γ 11,66 V

δ 10,54 W/mM

———————————————————

s båglängd i millimeter

Sambanden från H. Ayrton

Bågspänningen

Bågspänningen u från båglängden s, kretsmatningen U₀ med fasta kretsresistansen R

;

U₀ matningsspänningen (supply voltage)

u bågspänningen

U₀–u kvarvaran8de resistansspänning (kolektroderna Ran Rca + serieresistansen R₀)

I strömmen genom alla kretskopplingens komponenter

;

(U₀ – u)/R = I

R fasta seriemotståndet + kolelektroderna — alla minus Rarc

Grundsambandet (förmodl. frn. 1895 föreg.) från s176 i THE ELECTRIC ARC (1902) av Hertha Ayrton, VoltMillimeterAmpere

V = a + bl + (c + dl)/J

med motsvarande beteckningar från s72 ekv5 i ELECTRIC ARC PHENOMENA (1913) av Ewald Rasch

e = g + αL’ + (γ + δL’)/J

med här använda beteckningar

u = u₀ + αs + (γ + δs)/I

Se motsv. grafer i Ayrtons bok s120 (Fig. 38, figurbeteckning saknas).

Notera att graferna idealt bryts praktiskt av den s.k. hissing-point, Ayrton s123mn.

Ayrton beskriver upptakten till härledningen av ovanstående hyperboliska sambandsform från sidan 176.

Sambandets slutform (i Watt) sidan 183, här med nutida beteckningar

P = I(38.88) + 11.66 + x[I(2.074) + 10.54]

Ayrton mätte, systematiskt, tålmodigt, upp hela komplexet, och redde ut värdena med en beskrivande sambandsform [publ. 1902] — allt gällande »Silent Solid Carbons»;

”is the general equation connecting the power expended in a

silent arc in watts, the current flowing in amperes, and the

apparent length of the arc in millimetres for the solid carbons

184 THE ELECTRIC ARC.

used.”,

Ayrton 1902 s183n

;

”(it cannot be too carefully borne in mind that this law does

not apply to cored carbons) ; ”,

”but before it can be accepted as

a universal law, it must be shown to apply to the results

obtained by other experimenters with solid carbons.”,

Ayrton 1902 s188ö

Arton ger ingen definition på »cored carbons», separat webbsökning upplyser att typen användes till ljusbågslampor för att få bågen mera centrerad; cored står för en central inre kärna av (pressat) kolpulver med lägre täthet rel. höljet. Ordinarie kolelektroder av s.k. solid typ genomgående homogen täthet.

”The values

of the constants in the equation does, however, depend on the

hardness of the carbons, and perhaps on their size.”,

Ayrton 1902 s188mö

;

Koefficienterna enligt Ayrton [1902] s183

:

u₀ 38,88 V

α 2,074

γ 11,66 V

δ 10,54

;

Härledningen här [mera detaljerad] ansluter till utvecklingarna från Ewald Rasch s72:

Från grundformen

u = u₀ + αs + (γ + δs)/I

med [m = u₀ + αs] och [C = γ + δs] ges

u = m + C/I ;

(u–m)I = C ;

C = (u–m)I

= (u–m)(U₀ – u)/R ;

CR = (u–m)(U₀ – u)

= uU₀ – u² – mU₀ + mu

= uU₀ + mu – u² – mU₀

= u(U₀ + m) – u² – mU₀;

CR + mU₀ = u(U₀ + m) – u²

= –[– u(U₀ + m) + u²]

= –[u² – u(U₀ + m)] ;

u² + u(U₀ + m) = – CR – mU₀ ;

u² – u(U₀ + m) + mU₀ + CR = 0 ;

u² – u(U₀ + m) = – (mU₀ + CR) ;

Andragradsekvationens lösning

K = a²+Aa alternativt a²+Aa – K = 0

om KA är känd. Ovanstående led ger lösningen ±(a+A/2)²=K+(A/2)², ±(a+A/2)=Ö K+(A/2)², a+A/2=±Ö K+(A/2)²;

a = –A/2 ± Ö K+(A/2)² ........................... andragradsekvationens lösning

u² – uA = – B ;

= (u – A/2)² – (A/2)² ;

– B = (u – A/2)² – (A/2)² ;

(u – A/2)² = (A/2)² – B ;

u = A/2 ± √ (A/2)² – B

= (U₀ + m)/2 ± √ [(U₀ + m)/2]² – (mU₀ + CR) ;

ROTLÖSNINGEN ÄR POSITIV enligt Ayrton:

u = (U₀ + m)/2 + √ [(U₀ + m)/2]² – (mU₀ + CR)

Lösningen samma som Ewald Rasch s107 ekv8, (men han har glömt mU₀-faktorn i slutparentesen);

= (U₀ + m)/2 + √ [(U₀ + m)/2]² – (mU₀ + (γ + δs)R)

u = (U₀ + u₀ + αs)/2 + √ [(U₀ + u₀ + αs)/2]² – ([u₀ + αs]U₀ + (γ + δs)R)

u = (U₀ + u₀ + αs)/2 +√ ([U₀ + u₀ + αs]/2)² – (s[αU₀ + δR] + γR + u₀U₀) ;

Ljusbågens negativa resistans

BÅGSTRÖMMEN MED KONSTANT BÅGSPÄNNING

Bågströmmen I via båglängden s — ljusbågens negativa resistans

— med konstant bågspänning u:

CR = (u–m)(U₀ – u) ;

CR/(u–m) = (U₀ – u) ;

CR/(u–m) + u = U₀ ;

U₀ = u + CR/(u–m)

= u + (γ + δs)R/(u–[u₀ + αs]) ;

u = konstant ;

U₀ = u + (γ + δs)R/(u – u₀ – αs)

= RI + u ;

RI = (γ + δs)R/(u – u₀ – αs) ;

I = (γ + δs)/(u – u₀ – αs)

= (γ + δs)/(K – αs) ;

y=I Ampere, U=75V konstant, x=båglängden i mM

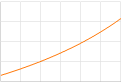
y = (11.66+10.54x)/(75–38.88–2.074x)

y-axeln bågströmmen i Ampere, x-axeln båglängden i mM, konstant u = 75 Volt [stabil ljusbåge]

;

Konstant kretsresistans R, variabel matningsspänning U0

U₀ = RI + u

Konstant matningsspänning U0, variabel kretsresistans R

(U₀ – u)/I = R

KONSTANT MATNINGSSPÄNNING

negativa resistansens aspekt

För att hålla bågspänningen konstant med växande båglängd, måste kretsresistansen minskas, vilket medför att bågströmmen också växer med växande båglängd.

— Denna detalj visar, explicit, att ljusbågen som strömkomponent uppvisar negativ resistans.

— Hur då?

Sambandet för spänningen,

RI = (U₀ – u)

gäller uppenbarligen också för ljusbågens strömfysik — men på ett sätt som ändå skiljer ljusbågsfysiken (markant) från den vanliga materiefysikens strömflöde.

;

— OM man tänker sig konstant bågspänning (u), och att bågströmmen (I) regelrätt skulle MINSKA när båglängden (s) ökar, är det underförstått att ljusbågen betraktas som en konstant resistans (typ en bit koppartråd) vars längd dras ut — och därmed ett mindre strömtvärsnitt erhålls: motståndet ökar i I=Q/T-tvärsnittet: Strömmen avtar.

— Resistiviteten [R(m)]

R = R_ms/A · 1M

i den vanliga materiefysiken gäller per längdmeter (s) via tvärsnittsytan A=πr².

— Ljusbågen beter sig inte så. När ljusbågen dras ut, och för att bibehålla bågspänningen (stabil ljusbåge enligt Ayrton), måste istället bågströmmen också ökas på (genom att anordningen, på något sätt, måste minska fasta kretsresistansen, given fast matningsspänning U0).

— Analogin visar att strömflödet i ljusbågen INTE (enkelt) kan liknas vid det vanliga materiella strömflödets fysik och mekanik.

— ÄVEN OM »tvärsnittsytan minskas» (vilket vi inte vet, men underförstår för ljusbågen) proportionellt mot växande båglängd s så att s/A tar ut varandra, måste likväl båglängdens resistivitetsfaktor [R(m)] också avta med växande s för att förklara den högre strömstyrkan (analogt underförstått, lägre bågresistans).

— Ett annat sätt att säga det på blir: ljusbågens strömfysik uppvisar negativ resistans.

Herta Ayrton beskriver saken sålunda:

”The Apparent Negative Resistance of the Arc is caused by the

true Positive Resistance Diminishing More Rapidly than the

Current Increases.”,

s400mn The Electric Arc, H.Ayrton 1902

Ayrton redovisar en noggrann experimentell analys på »koldimmornas» (eng, mist resp. vapour) olika resistiva uppförande tillsammans med kolelektroderna, och det blir ingen enkel uppgift att fastställa någon direkt enklare principfunktion än just Ayrtons — sett enbart till materiefysikens jonströmmar. Jonströmmens starkt upphettade delar spelar in på flera olika sätt med anpassningar i förångad materialmängd beroende på hur, och när, strömmarna varieras. Emellertid används (numera) även i modern nomenklatur beskrivningssättet med negativ resistans för ljusbågen t.ex. i Wikipedia,

”An electric arc has a non-linear relationship between current and voltage. Once the arc is established (either by progression from a glow discharge [5] or by momentarily touching the electrodes then separating them), increased current results in a lower voltage between the arc terminals. This negative resistance effect requires that ...”,

@INTERNET Wikipedia Electric arc, Overview [2011-08-12]

http://en.wikipedia.org/wiki/Electric_arc

ANALOGIN TILL TOWNSENDs URLADDNING (eng. Townsend discharge) är emellertid uppenbar: samma typ av samband, men i andra proportioner:

— John Townsend studerade högspända urladdningsströmmar i gasfyllda rör och fann (1897) att jonströmmen (I) mellan två kondensatorplattor (elektroder) åtskilda av varierande avstånd (s), men med konstant elektrodspänning (u, flera hundra volt), ökade med växande s. Townsends originalsamband är (Wikipedia Townsend discharge, Quantitative description of the phenomenon [2011-08-12], d för s)

I/I₀ = e^α_nd

Kurvformen (små värden på I0, höga αn-tal) är nära lika föregående (figuren nedan)

y = (11.66+10.54x)/(75–38.88–2.074x)

om man lägger till en offset (Y), en dämpkoefficient (k) samt sätter u=konstant lågt

y = k[Y+(11.66+10.54x)/(45–38.88–2.074x)]

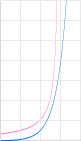
y-axeln strömstyrka, x-axeln elektrodavstånd, konstant elektrodspänning

y = 0.01è'2x

I = I₀e^αn^s

y = 0.05[5+(11.66+10.54x)/(45–38.88–2.074x)]

I = (γ + δs)/(u – u₀ – αs)

Denna — rent KVALITATIVA, principförklarande/beskrivande — detalj (min tolkning, de principiellt samhörande kurvformerna i ljuset av Townsends betydligt materietunnare anordning) lägger (möjligen) mindre vikt vid Ayrtons materiella kolångeteori och mera tyngd åt den kopplande strömvägens inre (egentliga) fysik (som definitivt lägger viss vikt vid begreppet negativ resistans):

— Fenomenformen kan inte förklaras enbart med materiefysikens begrepp. Det som krävs är, enligt TNED, en INRE STAMBANA (se Kemikopplingen) som bestämmer den underliggande dynamiken.

— Medan Townsends teori använder ELEKTRONEN MELLAN ATOMERNA som joniserande agent tillsammans med elektrodspänningen för att förklara fenomenet med växande ström över växande elektrodavstånd, använder TNED själva den inre kemiskt atomkopplade strömstammen, dess egen inre strömhållfasthet, GENOM atomerna/kärnbrunnarna som automatisk generatris för att öka eller minska jonisationsgraden beroende på elektrodavståndet.

Materiefysiken klarar inte en sådan beskrivning. Det är bara massfysiken — TNED — som kan det.

— Vi kan av ovanstående översiktliga jämförelser i vilket fall se att alla typer av elektrodstyrda urladdningsfenomen — gnist, glöd eller bågstyrda — i stort bör följa samma grundmatematik.

Den inre strömstammens karaktär — atomernas inbördes kemikopplingar enligt TNED — är att vara nollresistiv: det finns ingen materiell strömledningsfysik där. Med en sådan strömbana som grund, blir det naturligt DESS fysik som bestämmer formerna: ökas längden, ökas också inslaget av nollresistivitet: den yttre materieströmmens resistans tvingas avta med växande längd på stambanan.

— Omvänt med fast avstånd och växande strömstyrka: Även i detta fall ökar inverkan av stambanans strömgenomflöde via den högre strömstyrkan, analogt ett större beroende av nollresistiviteten i den centralt uppehållande men utåt sett dolda stambanan och med följd i att makroresistansen också tvingas minska.

— Eller som Ewald Rasch uttrycker saken i kretskopplingen till ljusbågen:

”If by reducing the

series resistance the current of an arc

of constant length be increased by an

amount dJ, the arc voltage will drop;

vice versa, if the current be decreased the arc voltage e

will rise.”,

s71m, ELECTRIC ARC PHENOMENA, Ewald Rasch 1913

Men den negativa resistansen karaktär framgår redan av själva grundsambandet till ljusbågsfysiken, enligt Ewald Rasch (1913), nedan (grundformen u = m+C/I). Herta Ayrton (1902), se från s175, omnämner inte den delen explicit. Hon arbetade sig systematiskt fram till lösningen genom att via experimentella mätningar utgå ifrån grundformen med spänningen som funktion av ström och distans U=f (I,s), och sedan vidare genom effektsamband (P=UI) tillsammans med geometriskt analytiska samband till motsvarande slutform (u = m+C/I) u = a + b + (c + d)/I.

HÄRLEDNINGEN

— grundsambandet ljusbågens fysik

— enligt Rasch (1913) s71m från Sylvanus Thompson [Ayrton namnger honom konsekvent Silvanus]

— med koefficienter och beteckningar [mestadels] enligt Rasch (1913) s72 [se även tabellen nederst], här i utvecklade fysikaliska storheter

För kretskopplingen, se Kretskopplingen. Beakta först grundsambanden inom elektrofysiken

P = (U=RI)I = RI² ; U/I = R = P/I² ;

En variant kan tecknas

du P

—— = – ——

dI I²

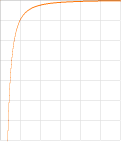
Bågspänningens (u, y-axeln) ändring med avseende på bågströmmen (I, x-axeln) motsvarar NEGATIVA inverterade strömstyrkans kvadratfunktion (–1/I²) — dvs, negativa — enligt TNED inre stamelektronstyrda — bågspänningen avtar mot noll med växande bågström.

Vi vet inte anledningen till insättningen av minustecknet i högerledet, enligt teckningen från Rasch [Thompsons ursprungsvariant]. Elimineras minustecknet, kommer det i vilket fall åter via integrallösningen — man får i vilket fall ett omvänt bågspänningsvärde i utgångspunkten. I TNED — ATA — är den delen naturlig: elektronströmmen, den nollresistiva inre strömbanan, är omvänd relativt yttre jonströmsbaserade materieströmbanan. Den detaljen [ATA] kan inte relateras i modern akademi.

;

du = – PI^–2dI

;

∫ du = – P ∫ I^–2dI ;

u = – PI^–1/(–1)

= PI^–1 ;

Relaterade fysikaliska storheter

Bestämda integralen kräver en (sammansatt) offset för x=0 via y=0;

;

u = u₀ + Ξ₀s + PI^–1 ;

;

P = UI = RI² ;

PI^–1 = U = RI ;

U = (U)d^–1d

= (U₁+U₂)d^–1d

= U₁d^–1d + U₂d^–1d

= U₁ + U₂d^–1d ;

P = P₁ + P₂d^–1d ;

P = γ + δs ;

Beteckningar vänster från Rasch s72 och Ayrton s184

Ayrton	Rasch	Här
b	α	α	Ξ0	2,074	V/M, här i V/mM [2,074 KV/M]
c	γ	γ	P1	11,66	W
d	δ	δ	P0/M	10,54	W/M, här i W/mM [10,54 KW/M]
a	g	u0		38,88	V
L	l	s		båglängd	mM
V	e	u		bågspänning	V

u = u₀ + Ξ₀s + (P₁ + δs)I^–1 ; Ξ, grek. xsi för ElektriskaFältstyrkan Ξ=U/d

Koefficienterna — möjliga kopplingar enligt TNED

LÄGSTA TÄNDSPÄNNINGEN (u0) beror (se tabell nedan) på elektrodmaterialet (38,88 V enligt Ayrton 1902). TNED har, möjligen, koppling till u0 via Elektriska Kraftlagen direkt enligt (se Ljusbåge enligt TNED)

U_G = k(e/r)

med lägsta, atomvilande, värdet 9,612 V (med fasta ämnens medelatomavstånd ca 3Å). Det värdet skulle, i så fall, vara alla elektrodmaterials absoluta grundvärde (direkt ljusbåge på lägre tändspänning går inte), och som sedan bildar ett praktiskt högre värde med beaktande av temperatur och elektro-termiska materialegenskaper.

ELEKTRISKA FÄLTSTYRKAN Ξ=U/s i Ξ0s kan möjligen ansluta till ideala, atomvilande, gränsspänningen U(G) i luft [atommedelavstånd ca 3nM i normal luft] enligt TNED 1800 V/M från grundräkningen n=177062:

— Här har vi, möjligen, ett exempel som (möjligen) kan illustrera sammansattheterna:

— Med det senare n-värdet 673026 skulle motsvarande idealt atomvilande gränsspänningsvärde bli avrundat ca 475 V/M;

— Eftersom, enligt utläggningarna, bägge värdena 1800 V/M via n=177062 och 475 V/M via n=673026 i vilket fall skulle vara för låga genom att temperatur (och elektro-termiska egenskaper) kommer till som kräver ett (betydligt) högre värde, finns en viss möjlig koppling;

— Med ett praktiskt U(G)-värde på 2074 V/M [2,074 V/mM], enligt Ayrtons (s184) uppmätta koefficient, skulle med det mera troliga n=673026 »kolångeluftens anpassningskoefficient» i den aktuella ljusbågens experimentmiljö bli ca

2074/475 ~ 4,37

— Det verkar rimligt. Men vi VET det inte här (men kan misstänka en koppling).

DELVIS TILL VÅR HJÄLP ger Rasch s79 en redovisad tabell (TABLE 15) över då (1913) nyligen genomförda experiment på olika elektrodmaterial.

Rasch-tabellen 1913

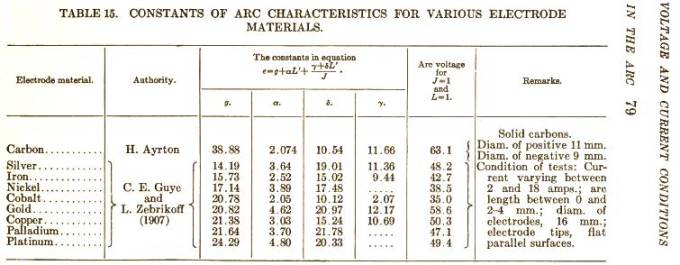
s79 Ewald Rasch 1913

Tabellen visar — tydligt — (förutsatt tillförlitliga värden) att typ Ξ0-koefficienten (Ayrtons 2,074) varierar med elektrodmaterial (»ElektrodÅngLuftKoefficienten»).

Men:

— Nu är begreppet gränsspänning i TNED, som ovan, reserverat (i teorin) för GNISTURLADDNING, alltså motsvarande kemisk koppling på elektronmassans enskilda komponent.

— Här kan emellertid vissa (betydelsefulla) uppslag till en fördjupad insikt i fysiken finnas, och som är (snart sagt) omöjliga att utrannsaka i teorin — utan experimentella stöd. Skulle, möjligen också, gnisturladdningskoefficienter vara signifikanta för ljusbågens tekniska fysik? Ser så ut det.

— Vi VET det inte här. Det är bara, än så länge, ett uppslag till en möjlig koppling.

”For instance, when experimenting with oxide arcs at

relatively low voltages (220 > e > 120 volts; E = 220

volts) the author observed sudden changes of the arc discharge

into spark discharge. Under certain conditions

a stream of crackling bluish sparks passed between the

white-hot oxide electrode tips (magnesia, thoria, zirconyttria,

calcium oxide, etc.), sparks which under other

circumstances between cold or metallic electrodes -

would have required many thousand volts to produce.”,

s110n Ewald Rasch 1913

Rasch omnämner också (s80n) samband liknande ljusbågens som ”med goda resultat” beskriver gnisturladdningar,

”It should be mentioned that, lately, J. Stark has ap

VOLTAGE AND CURRENT CONDITIONS IN THE ARC 81

plied to glow discharges, and Koch to spark discharges,

the equation of the arc characteristic, with good results.

Thus, seemingly, a greater measure of validity should be

given to this equation than would be due to it as a mere

empirical interpolation formula.

For spark discharges of not too great length, according

to Koch's observations,

C

e = m + —— (volts)

J

m = 300 + 86.4 L (volts),

C = 0.600 L (watts)

The numerical constants, naturally, are dependent on

the electrode material and signify, respectively, the

anodic voltage drop and the conductivity of the gases

in the discharge path.”,

s80n Ewald Rasch 1913

EFFEKTKOEFFICIENTEN P(1), Ayrtons värde 11,66, är tydligen — med ledning av Rasch-tabellen — en (lägsta) effekt-materialparameter. Vi känner den dock inte närmare här.

EFFEKTKOEFFICIENTEN P(0) i P0/M däremot kan, möjligen, också koppla till ATA-matematiken i TNED:

— Nukleära Elektrongenomströmningens Makroekvivalent I(N)=5,34 Ampere i Nukleära ElektronGenomströmningsEkvivalenten T(N)=3 t20 Sekunder, ligger väldigt nära

10540/2074 ~ 5,082

Vilket skulle betyda:

(Ξ₀)×(5,082 A = I_N) = P₀/M = (Ξ₀)Q(e)/T(N) = (U/d)e/T_N = ([k(e/d)]/d)e/T_N = ([k(e/d)²])/T_N = F/T_N

— OM en koppling skulle finnas, skulle T(N)=e/I(N) kunna specificeras närmare enligt

T(N) = (1,602 t19 C)/(5,082 A)

= 3,1523 t20 S

Vilket skulle betyda:

— En direkt experimentell bekräftelse på TNED-teorin i ljusbågsfysiken

OM VI PRÖVAR uppslaget på RASCH-tabellen (från 1913) som funktion av alfavärdena gånger I(N)=5,082A får vi motsvarande för deltavärdena δ=I(N)α

material	u0	α	Beräknat δ	Rasch δ	Ber/Rasch
Carbon	38,88	2,074	10,54	10,54	100%
Silver	14,19	3,64	18,50	19,01	97%
Iron	15,73	2,52	12,81	15,02	85%
Nickel	17,14	3,89	19,77	17,48	113%
Cobalt	20,78	2,05	10,42	10,12	103%
Gold	20,82	4,62	23,48	20,97	112%
Copper	21,38	3,03	15,40	15,24	101%
Palladium	21,64	3,70	18,80	21,78	86%
Platinum	24,29	4,80	24,39	20,33	122%

H. Ayrton

C.E Guye and L. Zebrikoff (1907)

— Avvikelserna ligger, tydligen, anmärkningsvärt väl samlade omkring 100% [+22%–15%].

— Här kan (och bör) det alltså finnas ytterligare en koppling.

För vidare.

Rotgränspunkten

Kretsresistansen

max 6mM enligt Ayrton (11mMAnod 9mMKatod)

ROTGRÄNSPUNKTEN

Fasta Kretsresistansen

Vi söker i rottermernas ekvivalenter

([u₀ + αs + U₀]/2)² = s[αU₀ + δR] + γR + u₀U₀

ett gränsvärde med given båglängd (s) och matningsspänning (U₀) för totala kretsens serieresistans (R).

R är kretsens fasta serieresistans frånsett bågresistansen (R+Rarc=Rtot);

;

([u₀ + αs + U₀]/2)² = s[αU₀ + δR] + γR + u₀U₀ ;

([u₀ + αs + U₀]/2)² = sαU₀ + sδR + γR + u₀U₀ ;

([u₀ + αs + U₀]/2)² = sαU₀ + u₀U₀ + sδR + γR ;

([u₀ + αs + U₀]/2)² = sαU₀ + u₀U₀ + R(sδ + γ) ;

R(sδ + γ) = ([u₀ + αs + U₀]/2)² – (sαU₀ + u₀U₀) ;

R_sLIM = (sδ + γ)^–1[([u₀ + U₀ + αs]/2)² – U₀(αs + u₀)] ;

LjusbågsKretsens fasta motstånd

Kretsresistansen (R/10 nedan y-axeln: 10 Ω per enhet) måste justeras enligt R-sambandet (rotgränspunkten) för stabil ljusbåge, här U=100V:

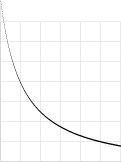
y = 0.1[(10.54x+11.66)'–1]([(1/4)(38.88+100+2.074x)'2]–100[2.074x+38.88])

Se även sammanställningen i GraferARC. x-axeln = Båglängden i mM, y-axeln kretsens fasta ledningsresistans i 10Ω/enhet för stabil ljusbåge enligt Ayrtons grundsamband, se Sammanställning.

Båglängden

Nytt försök 2011-07-31:

Båglängden s från U₀ och R

([u₀ + αs + U₀]/2)² = (u₀ + U₀ + αs)²/4

= (U + αs)²/4

= (U² +2Uαs + α²s²)/4

= (U² +2Uαs + α²s²)/4

;

([u₀ + αs + U₀]/2)² = s[αU₀ + δR] + γR + u₀U₀

= (U² +2Uαs + α²s²)/4 ;

U² +2Uαs + α²s² = 4(s[αU₀ + δR] + γR + u₀U₀) ;

U² +2Uαs + α²s² = s[4(αU₀ + δR)] + 4γR + 4u₀U₀ ;

U² +2Uαs + α²s² = s[A ] + B ;

2Uαs + α²s² = s[A ] + B – U² ;

2Uαs – sA + s²α² = B – U² ;

s(2Uα – A) + s²α² = B – U² ;

s(D ) + s²E = C ;

s(D/E ) + s² = C/E ;

s(F ) + s² = G ;

s² + sF = G ;

= s² + sF + (F/2)² – (F/2)²

= (s+F/2)² – (F/2)² ;

(s+F/2)² – (F/2)² = G ;

(s+F/2)² = (F/2)² + G ;

s+F/2 = ±√ (F/2)² + G ;

s = –F/2 ± √ (F/2)² + G ; ......... negativa roten gäller

;

s = –F/2 – √ (F/2)² + G

F = D/E

= (2Uα – A)/E

= [2Uα – 4(αU₀ + δR)]/E

= [2Uα – 4(αU₀ + δR)]/α²

= [2(U₀+u₀)α – 4(αU₀ + δR)]/α²

= [2αU₀+2αu₀ – 4αU₀ – 4δR)]/α²

= [2αu₀ – 2αU₀ – 4δR)]/α²

= 2[α(u₀ – U₀) – 2δR)]/α² ;

F/2 = [α(u₀ – U₀) – 2δR)]/α² ;

;

G = C/E

= (B – U²)/α²

= [4γR + 4u₀U₀ – (U₀+u₀)²]/α²

= [4γR + 4u₀U₀ – U₀² – 2u₀U₀ – u₀²]/α²

= [4γR + 2u₀U₀ – U₀² – u₀²]/α²

= [4γR – U₀² + 2u₀U₀ – u₀²]/α²

= [4γR – (U₀² – 2u₀U₀ + u₀²)]/α²

= [4γR – (U₀ – u₀)²]/α² ;

s = –[α(u₀ – U₀) – 2δR)]/α² – √ ([α(u₀ – U₀) – 2δR)]/α²)² + [4γR – (U₀ – u₀)²]/α²

Kvoten u/s

Kvoten (u–k)/s=konstant via R = f (s)

Från bågspänningen:

u = (u₀ + αs + U₀)/2 +√ ([u₀ + αs + U₀]/2)² – (γ + δs)R – (u₀ + αs)U₀ ;

Från fasta kretsresistansen (ROTGRÄNSPUNKTEN):

R(sδ + γ) = ([u₀ + αs + U₀]/2)² – (sαU₀ + u₀U₀)

= ([u₀ + αs + U₀]/2)² – U₀(sα + u₀) ;

;

u = (u₀ + αs + U₀)/2 +√ ([u₀ + αs + U₀]/2)² – ([u₀ + αs + U₀]/2)² + U₀(sα + u₀) – (u₀ + αs)U₀

= (u₀ + αs + U₀)/2 +√ 0

u = (u₀ + αs + U₀)/2 ; ....... line

= (αs + u₀+U₀)/2

= αs/2 + (u₀+U₀)/2

= s(α/2) + (u₀+U₀)/2 ;

= s(1,037) + (38,88+U₀)/2 ;

u–(u₀+U₀)/2 = s(α/2)

u–k = s(α/2) ;

[u–k]/s = α/2

= 1,037 ;

u i Volt, s i millimeter

MKSA-enheter, s i Meter:

[u–k]/1000s = α/2 ;

[u–k]/s = 1000α/2 ;

α = 2074 ; MKSA-enheter

;

(u–k)/s-Grafen (offset –69V x-axeln), U0=100V:

y = –69+[1.037x+(38.88+100)/2]

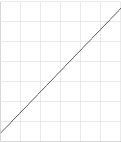
y-axeln bågspänningen i Volt med y=0 vid –69V, x-axeln båglängden i mM, U0=100V, R.

Kurvan ser likadan ut för samtliga fall, endast offsetvärdet varierar.

;

Bågströmmen

I:

u = (u₀ + αs + U₀)/2

; nominella bågströmmen:

I = (U₀ – u)/R ;

= [U₀ – (u₀ + αs + U₀)/2]/R

= [U₀ – P ]/R

; fasta kretsresistansen:

R = (sδ + γ)^–1[([u₀ + U₀ + αs]/2)² – U₀(αs + u₀)]

= (sδ + γ)^–1[(P)² – U₀(αs + u₀)] ;

I = [U₀ – P]((sδ + γ)^–1[(P)² – U₀(αs + u₀)])^–1

= [U₀ – P](sδ + γ)([(P)² – U₀(αs + u₀)])^–1 ;

;

P = (38,88 + 2,074s + U₀)/2

I = [U₀ – P](10,54s + 11,66)([(P)² – U₀(2,074s + 38,88)])^–1

I-Grafen:

y = [100–(38.88+2.074x+100)/2](10.54x+11.66)([([(38.88+2.074x+100)/2]'2)–100(2.074x+38.88)])'–1

y = [200–(38.88+2.074x+200)/2](10.54x+11.66)([([(38.88+2.074x+200)/2]'2)–200(2.074x+38.88)])'–1

y = [300–(38.88+2.074x+300)/2](10.54x+11.66)([([(38.88+2.074x+300)/2]'2)–300(2.074x+38.88)])'–1

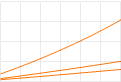
y-axeln bågströmmen i Ampere, x-axeln båglängden i mM, konstant matningsspänning (övre-undre) 100V, 200V, 300V med justerad fast kretsresistans (R) enligt R-sambandet (rotgränspunkten).

[Alla samband samma som de redan kända från Ayrton 1902].

Av sambanden, och graferna närmast ovan relativt [u–k]/s-grafen, framgår generellt att bågströmmen [nästan raka linjer, men inte riktigt] ökar i något [marginellt] växande med båglängden, analogt växande bågspänning som ovan.

Se även BÅGSTRÖMMEN MED KONSTANT BÅGSPÄNNING.

Justerade samband

Se från Ljusbågsfysiken i Sammandrag

— Justerade samband enligt Ewald Rasch 1913 frn. s76ö

Med grundsambandet från Ayrton (1902) s184:

u = u₀ + αs + (γ + δs)/I

= 38.88 + 2.074s + (11.66+10.54s)/I

Beteckningar vänster från Rasch (1913) s72 och Ayrton (1902) s184, se Relaterade Fysikaliska Storheter

Ayrton Rasch Här

b α α Ξ₀ 2,074 V/M, här i V/mM [2,074 KV/M]

c γ γ P₁ 11,66 W

d δ δ 10,54 W/M, här i W/mM [10,54 KW/M]

a g u₀ 38,88 V

L l s båglängden millimeter

V e u bågspänningen V

;

u – u₀ = αs + (γ + δs)/I ;

I(u – u₀) = Iαs + (γ + δs) ;

I(u – u₀) – Iαs = (γ + δs) ;

γ + δs = I(u – u₀ – αs) ;

— Med I=0 ges

γ + δs = 0 ;

s = – γ/δ ;

= – 11,66/10,54

= – 1,1062618 mM

Figuren nedan från sidan 74, Ewald Rasch (1913) ELECTRIC ARC PHENOMENA

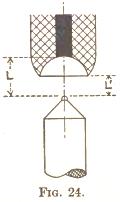
Rasch (Fig. 24s76 ovan) hänför den negativa koefficienten – 1,10 mM till kolelektrodanodens konkava urholkning. Därmed ges en något lägra bottenspänning [u(0)], samt ett något enklare grundsamband.

”Hertha Ayrton's equations (3 to 5, page 72) are open

to the objection that they unnecessarily complicate and

do not, as will be made evident below, quite correctly

describe the physical relations concerned.”,

s76ö, Ewald Rasch (1913) ELECTRIC ARC PHENOMENA

;

”The introduction of the true arc length L results in the

following correction and simplification of Hertha Ayrton's

equation.

(g = 38.88; α = 2.074- γ = 11.66; δ = 10.54.)

...

10.54 L

e = 36.59 + 2.074 L + ————

J

”,

s77m, Ewald Rasch (1913) ELECTRIC ARC PHENOMENA

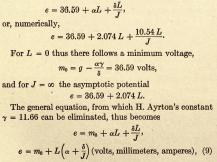
Dvs., bågspänningssambandets något justerade grundform

u = u₁ + αs + δs/I

= 36.59 + 2.074s + 10.54s/I

I beräkningarna som gjorts i detta dokument har Herta Ayrtons ursprungliga koefficienter och samband från hennes bok 1902 använts genomgående.

Grundformerna för gnisturladdning och ljusbåge enligt TNED

Kraftekvationen och Impulsekvationen i TNED

Energy_Spark.wps

Ljusbåge/gnisturladdning

GRUNDSAMBAND ENLIGT TNED — kort illustrerad översikt och snabborientering

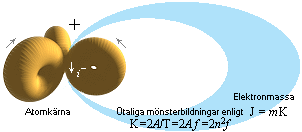
Isolerade [neutrala] atomer

Grundläggande fenomensamband i TNED

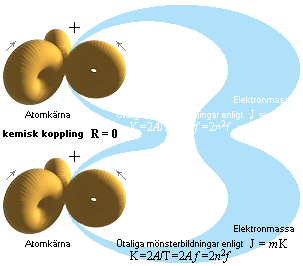
Kemisk koppling. När flera atomer förenas delar de på samma elektrongenomströmning. Kraftekvationen för varje atom bevaras enligt kraft- och kemiekvationen

(F_BT+F_eZ)₁+(F_BT+F_eZ)₂+(F_BT+F_eZ)₃+…+(F_BT+F_eZ)_n = 0

Ledet ingår automatiskt då atomer byggs upp från lättare till tyngre genom fusioner där atomkärnornas impulsmoment bevaras via impulsekvationen enligt fusionsringen

(J_0K+3J_1K)₁+(J_0K+3J_1K)₂+(J_0K+3J_1K)₃+…+(J_0K+3J_1K)_n = 0

Massdefekterna omsätts i värme och ljus (spektrum) med energins bevarande genom induktionen [COEI Conservation of energy by induction, U_ind=E=^UQ/Q_s=L(di/dt)k=Lk=mc²/Q_s]

enligt

β– + β+ = 0 ................................................... laddning

s_β– + s_β+ = 0 ................................................... spinn (rörelse)

m_β– + m_β+ = 2m_β ............................................... massa

Grundteorin enligt TNED

Sammanställd illustrerad kort översikt 11Aug2011

LJUSBÅGE OCH GNISTURLADDNING ^ENLIGTTNED

För ljusbågens grundsamband, se Ljusbågsfysiken i sammandrag

flöde	koppling	gnisturladdning	ljusbåge
		UG = k([e/n]/r)	UG = k([e/1]/r)

SOM I KEMISK KOPPLING grundläggs gnisturladdning/ljusbåge enligt TNED genom att gräns- eller isolationsspänningen [U(G)] mellan minst två närliggande atomer bryts. Fenomenformen, samma som i kemisk koppling, bygger HELT på att minst två atomer delar på samma elektronmassa. Därmed har en kärnbrunnström genom atomernas atomkärnor etablerats enligt TNED — se utförligt från Atomkärnans härledning enligt TNED om ej redan bekant.

Notera att principen för funktionssättet, tvunget, UNDGÅR modern akademi eftersom man där helt saknar den nödvändiga uppfattningen om ATOMKÄRNAN som en strömstyrd komponent (Se Kraftekvationen särskilt). I modern akademi tvingas man därför, då inget annat är känt, förklara fenomenet via en (icke nollresistiv, uteslutande jonbaserad) materieström (elektronström MELLAN atomerna) kontra TNED:s förklaring med e-strömmen som en (nollresistiv) masström GENOM atomerna, analogt med »atom- och kärnfysikens två kungsekvationer» i TNED.

Figurerna ovan visar grundbegreppen med samband. Det enda som — enligt TNED — skiljer gnisturladdning (momentan strömdrivning) från ljusbåge (kontinuerlig strömdrivning) är att gnisturladdningens gränsspänning är känslig på elektronmassans komponent (tau-ringen, ingår inte i modern akademisk teori, förkastades från 1927 sedan den använts för att beskriva atomens spektrum via Heisenberg-Schrödingers ekvationer, se särskild NOTERING i Kvanttalen), se ELEKTRONMASSANS KOMPONENTER ENLIGT TNED samt SPEKTRUM och KVANTTALEN om ej redan bekant, medan ljusbågen däremot (kontinuerlig strömdrivning) kräver hela elektronladdningen för att fungera.

U(G)-värdena som fås från de enklast tänkbara sambandsformerna ovan (från elektriska kraftlagen) gäller idealt för helt vilande atomer (0°K) samt utan hänsyn till specifika termiska-elektriska materialegenskaper.

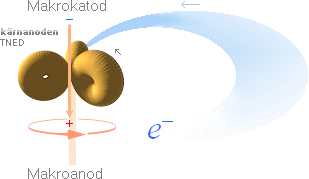
För ljusbågsmatematiken explicit (se från Ayrton 1902) är det bara direkt experimentella studier av den yttre jonströmmen som kommer ifråga. Se särskild sammanställning i Ljusbågsfysiken i Sammandrag.

Den — enligt TNED — inre strömstammen med elektronflödet genom de kopplade atomernas kärnbrunnar är omöjlig att penetrera materiellt med (någon större mängd) strömbärande atomer mellan elektroderna (plasmatillståndet upplöser allt som kommer in där). I evakuerade rör emellertid, där avståndet mellan de strömbärande atomerna i princip kan utsträckas till avståndet mellan elektroderna [vilket kräver motsvarande högre tändspänning], framgår elektronströmmen specifikt som en elektronstråle (konv. katodstrålerör). Det är i varje fall så som funktionerna får förstås enligt TNED.

FUNKTIONSSÄTT — ljusbåge enligt TNED

Flödesbilderna i figurerna nedan [utom TNED] ansluter i stort till redan kända, presenterade och studerade detaljer i ljusbågsfysiken, här i översiktligt sammandrag.

Centralstammens elektronlinje döljs effektivt av barkströmmen [jonströmmen] och kan därför inte inspekteras eller undersökas med några direkta [kända] metoder: allt som förs in där förångas.

Ljusbågen i sammandrag

fördelning: ström	fördelning: jonisation och temperatur	turbulens
Fig:1	Fig:2	Fig:3
Centralstammens absolut joniserade atomkärnor regleras vidare enligt ATA av strömstyrkan i ljusbågen. Därmed berövas omgivande luftatomer sina yttre elektroner sekundärt via centralstammen som drar elektroner till anoden. De så passivt joniserade moderatomerna bildar en jonström [barkström] — den enda fysiskt möjliga mätbara delen — mot katoden där de återfår sina elektroner.	Temperaturen är som störst där den joniserande inverkan på luftatomerna från centralstammen är som störst, alltså vid anodbasen (De berörda moderatomerna söker rekombinera sinsemellan och utsänder därmed ljus). Därifrån utgår också huvuddelen av ljuset (85% enligt ENCARTA [99]).	Situationen vid fast ljusbåge Den centrala plasmastammen bildar huvudströmleden (e–) genom kemisk koppling enligt atomens kraftekvation. Atomernas-kärnornas spinn i centralstammen driver i vilket fall en motsvarande rotation hos ljusbågen, dess ingående element. Figuren ovan ger en karikerad uppfattning om hur materieflödet möjligen fungerar.

För de experimentellt observerade, mycket detaljerade beskrivningarna av ljusbågens olika detaljer, se främst gratisboken The Electric Arc från år 1902 på Internet Archives av Mrs. Herta Ayrton (»ljusbågsfysikens moder», min benämning). Se även (den, främst) kompletterande boken från 1913 av Ewald Rasch, Electric Arc Phenomena.

Ingen av dessa (utomordentliga) referenser tycks ha uppmärksammats i det senare1900-talets facklitteratur.

FOCUS MATERIEN 1975 för att nämna exempel, tar inte ens upp ämnet till beskrivning;

Herta Ayrton omnämns inte ens i Bonniers uppslagsverk från 1920-talet; ljusbågen som fenomen omnämns KNAPPT.

kn

k = (1/4πε₀) ~ 9 T9 VM/C

n = 177062 (absolut orealistiskt) MINIMUM, se beräkningarna från Spektrum (Nov2007)

n = 673026 (praktiskt) nominella, se Antalet tau i beräkningarna från avsnitten om Casimireffekten och Lambväxlingen

Värdet på n [673026] som framkommit genom Casimireffekten och Lambväxlingen (Jul2010) är fortfarande (Aug2011) under prövning. De exempelräkningar som gjorts i BLIXTURALDDNINGENS FYSIK (Jun2008) har genomgående använt det ursprungliga [absolut minsta] n-värdet [177062]. Se till exempel i GRUNDRÄKNINGEN, som visar U(G)=5,4µV med medelavståndet 3nM mellan idealt vilande luftatomer — analogt 1800 V/M.

— Används det högre n-värdet ges istället ett lägre U(G)-värde på ca 1,4µV med motsvarande ca 475 V/M.

— Genom att grundräkningen — i vilket fall — INTE beaktar annat än idealt vilande atomer, utan hänsyn till specifika elektriska och termiska materialegenskaper, bör slutvärdena hur som helst bli multipler av grundvärdena.

— Som exempelvärdena visat sig, »stämmer kvantiteterna hyfsat» med antagandet av det lägre n-värdet som grund.

— Det betyder bara att det ännu lägre resultatvärdet via det högre n-värdet gynnas som ett grundvärde mot det resultatredovisade närmare praktiska ca 3,8 ggr större värdet [673026/177062=3,8010753]. (Vilket också visar att proportionerna i resultatframställningen överlag är harmonisk).

— Vidare prövningar får försöka avgöra vad som gäller. Se även Inverkan av n på föregående beskrivningar i Förklaringarna till begreppen i den moderna akademins kvantelektrodynamik.

Editor2011VIII12

Kalkylkortet

kalkylkortet DIREKT FRÅN DEN HÄR WEBBLÄSAREN ARC.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

AaKort/ARC.ods

Referenser

Electric Arc Phenomena

Electric Arc Phenomena

ELECTRIC ARC PHENOMENA

EWALD RASCH — NEW YORK · D. VAN NOSTRAND COMPANY 1913

TRANSLATED FROM THE GERMAN BY K. TORNBERG GENERAL ELECTRIC COMPANY

och som innefattar upplysningen att ljusbågskunskaperna i stort baseras på arbeten från Hertha Ayrton, en brittisk vetenskapare verksam kring sekelskiftet 1800-1900 som tycks ha utelämnats generellt från uppslagslitteraturen (enbart på grund av att nämnda var kvinna — fan ta dem, dessa 1800-talets vetenskapsfolk),

Ayrton hedras

”According to Hertha Ayrton, whom principally we have to thank for most of our accurate knowledge of the carbon arc, the minimum voltage m' is greater the longer the arc L'.”,

s72ö.

Fysiken 1900

”A REMARKABLE revolution is taking place in the fundamental

conceptions of Physics.”,

s[Romersk sidnotering i INTRODUCTION] v.ö.

Motsägelser

”It is not within the scope of the present monograph

to give an exhaustive review of the extensive literature

which has accumulated on the subject of the electric arc

and in which one is likely, quite often, to meet with contradictory

statements.”,

s.v.mn.

Dålig samordning

”Unfortunately, the arc-lamp industry is subdivided, one

viii INTRODUCTION

manufacturer building the lamps and another making carbons,

while to quote the words of a witty lawyer — "the

light is made by the janitor " (who trims the lamps and

switches them on). There is a great deal of truth in this

last statement.”,

s.vii.n.

Den allmänna utbildningsbristen

”At any rate, schools of technology offer to the student

neither a special course in light engineering nor even opportunity

for suitable laboratory work which might take

the place of such a course”,

s.viii.m.

Stora studiesvårigheter

”As matters now stand, it is hard for a student to be sure

of just what he must know, and still more difficult, for

reasons already stated, to acquire thorough knowledge of

the various branches of physical chemistry, of the theory

of radiation, the electronic theory, physiology of the sensory

organs, spectrum analysis, and to apply, independently,

these studies to the particular problems which he

has to solve. Very often he experiences more hindrance

than help from the self-contained and academically perfect

style in which the subject matter has been presented

to him by the lecturer.”,

s.ix.ö.

Maxwells ekvationer huvudbry

”Maxwell's electromagnetic theory of light, the ingenuity

and elegance of his differential equations, the

applications of these to Hertzian radiotelegraphy and

the reverence for the logical perfection of the system

presented, lead the student with appropriate horror

for forces acting across space and for the atomic conception

of electrical units to devote himself to speculations,

or even to actual experimenting on the direct

generation of light (Tesla's "Light of the Future").”,

”Woe be to him if his faith has been great, for his failures

will discourage him into a sceptical frame of mind

toward all theoretical knowledge. In many cases the

effect will be to retard industrial progress. Judging from

our present knowledge it is safe to say that even the most

obstinate efforts in that direction are, from the very start,

doomed to failure.”,

s.ix.m.

Maxwells teori föråldrad

”It can be fearlessly 'asserted in these days without

x INTRODUCTION

detracting from the reverence due the great genius of a

Maxwell, a Helmholtz, a Hertz that "Maxwell's electromagnetic

theory of light" is not a theory of light

at all*”,

”* Note added by the author during revision of manuscript:

At the eighty-first meeting (Salzburg, Sept. 21-25, 1909) of German

Scientists and Physicians, it was unanimously agreed by the highest

authorities on theoretical physics (Einstein, Planck, Born-Minowski, A.

Sommerfeld and others) that " Maxwell's theory of the universe and his

ether hypothesis must plainly be considered as obsolete."”

”Maxwell's curl equations may be true, indeed, in regard

to the phenomena of propagation of electromagnetic

waves of great length; but they are inapplicable and

apparently fundamentally so in case of shorter wave

lengths and higher frequencies, i.e., in case of phenomena

pertaining to light proper. They give not the least hint

as to the ultimate physical cause of light, which is of such

importance for the technical problems of light production.”,

s.ix.n.

Ljusbågen 1900

”It seems remarkable that the electric arc was known

only in the very form which it retained up to the beginning

of the present century”,

s2mö.

Ljusbåge-Gnisturladdning

”Electric spark discharges between metallic electrodes,

such as were obtained by Volta by means of the galvanic

pile named after him, differ in principle from the electric

arc as we know it, by the enormous resistance of the gaseous

path the spark gap necessitating high potentials

at the electrodes.”,

s2m.

Strömvägen

”In the case of spark discharges

between metallic terminals, the path for the

current consists mainly of the poorly conductive atmospheric

gases. Carbon electrodes, on the other hand,

give off incandescent vapors and solid particles which

GENERAL OUTLINE 3

offer a path of good conductivity, in which relatively

large amounts of energy can be transformed.”,

s2n.

Davy — »ljusbågens fader»

”It is, however, proven by the manuscript notes of Davy

that a stable flame discharge of considerable current density

between carbon electrodes was first produced and

4 ELECTRIC-ARC PHENOMENA

studied by him sometime in the years 1808 and 1809.

But not until the year 1812 does he give a complete and

clear description of the arc.”,

s3n.

Davy, ingen fullständig referens ges av Rasch.

Herta Ayrton [The Electric Arc 1902, s20mö] ger dock mera information:

Sir Humphry Davy:

”Sir

Humphry Davy, towards the end of October, 1800, was the

first to try tha effect of using as conductors two pieces of

well-burned charcoal”,

s20mö

”Whether W. Petroff as claimed by E. Smirnoff -

in the year 1802 had already discovered and known the

electric arc, may be left undecided.

In any case, it is the indisputable merit of Davy, by

virtue of his intuitive penetration, to have found out that

discontinuous spark discharges can be changed to stable

flame discharges of great current density by the employment

of carbon electrodes, a series resistance and the

selection of a suitable voltage.”,

s4ö.

The Electric Arc

Hertha Ayrton

[1854-1923, ref. Wikipedia]

Ytterligare upphittad LjusbågsBibel i samband med den upphittade delen från Ewald Rasch 1913, PDF-kopia

Finns på Internet Archive

THE ELECTRIC ARC

MRS. HERTHA AYRTON (1902) — NEW YORK · D. VAN NOSTRAND COMPANY

Bokens titelblad tycks sakna tidsuppgift

Tidsuppgiften 1902 finns angiven i Internet Archive:s rubrikpresentation av boken

Ayrton, ljusbågsfysikens moder

”According to Hertha Ayrton, whom principally we have to thank for most of our accurate knowledge of the carbon arc, the minimum voltage m' is greater the longer the arc L'.”,

s72ö, Electric Arc Phenomena, Ewald Rasch 1913

Historik, Wikipedia

”On 6 May 1885, she married one of her teachers at the Technical College at Finsbury, William Edward Ayrton. She assisted him with experiments in physics and electricity, and began her own investigation into the characteristics of the electric arc.”,

Ayrtons beskrivningar från 1895

”In 1895, Hertha Ayrton wrote a series of articles for The Electrician, explaining that these phenomena were the result of oxygen coming into contact with the carbon rods used to create the arc. In 1899, she was the first woman ever to read her own paper before the Institution of Electrical Engineers (IEE). Shortly thereafter, she was elected the first female member of the IEE.”,

Tjejer inte likaberättigade

”She was not as well received by the Royal Society. She was proposed as a Fellow of the Royal Society in 1902, but was turned down when the Council of the Royal Society decreed that married women were not eligible to be Fellows.”,

@INTERNET Wikipedia Herta Marks Ayrton [2011-08-11]

Citat från Ayrtons bok

AnodKolElektrod Ø11mM, KatodKolElektrod Ø9mM, samtliga fall.

s119mn:

”Accordingly, my experiments were

conducted with solid carbons for both positive and negative,

the positive carbon being 11mm. and the negative 9mm. in

diameter in all cases.”.

s105 :

Hur CoredCarbon påverkar bågspänningen vid ändring

;

s115:

”With the arc (with the above exception), a sudden rise of

current is in every case accompanied by a sudden fall of

potential, and a sudden fall of current by a sudden rise of

potential, even when, as in the case of an arc of 1mm. with

a cored positive carbon (lower curves, Fig. 36), the final steady

value of the P.D. is higher with the larger current than with

the smaller.”.

Ayrton, vidare i texten, hänför fenomenet till motsvarande ändringar i elektrodgeometrin (strömtvärsnittet); för höga bågströmmar (30A och vidare) märks knappast fenomenet.

s131 — konstant bågspänning; bågresistansen avtar med båglängden:

”Hence, for a constant P.D., the apparent

resistance of the silent arc, when in the normal condition,

diminishes rapidly as the arc is lengthened.”.

ENDBlixturladdningens Fysik 2011

Blixturladdningens Fysik 2011 | JGF | Ljusbågens fysik — Universums Historia

innehåll: | SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Blixturladdningens Fysik 2011 | JGF | Ljusbågens fysik

ämnesrubriker

innehåll

Blixturladdningens Fysik 2011 | JGF | Ljusbågens fysik

Översikt

TGFintro

JGF

Positronförekomst från blixturladdning klarlagd

Förtydligande angående gammmastrålningens möjliga riktning

ATA/CATref

Zambia-Egypten JGFen

NASA-vinjetten

Orternas Magnetiska Inklinationer

Magnetiska Spegelpunkten

ZambiaJGF:en

Höjdvinkeln

Magnetiska spegelpunktens matematik

JGF under satellitens synhorisont

Retardationssträckan

Alternativ 1; Nersidan

Alternativ 1, bägge sidorna; Nersidan och Ovansidan

OLIKA SÄTT ATT NÅ SPEGELPUNKTEN

Kärnringens expansion

Alternativ 2

Positronernas Observerade Hastighet

Positronens Expansionshastighet

Townsend discharge

Strömstammens CAT-geometri

Vad återstår?

Kort översikt av ATA/CAT i TNED

ScienceDaily-artikeln

Antalet MolnMark och MolnMoln

NUKLEÄRA ELEKTRONGENOMSTRÖMNINGSEKVIVALENTEN [NEGE] T(N) enligt TNED

I(N) — Nukleära sönderfallets gränsströmstyrka A·(1836/2=918)e/T_N

HÄRLEDNINGEN till T(N) = 3 t20 Sekunder

NEM — Nukleära Elektrongenomströmningens Makroekvivalent = 5,34 Ampere

NEGE, förtydligande

Citaten ENCARTA och EST

Jämförelser MAC|TNED — gnistbildning, ljusbåge

Framställningar saknas i MAC

Gnisturladdning enligt TNED

Ljusbåge enligt TNED

Atomkärnans upplösning enligt TNED

LJUSBÅGSFYSIKEN I SAMMANDRAG Jul-Aug2011

KolelektrodLjusbågens allmänna samband

Kretskopplingen

GraferARC

Sambanden från H. Ayrton

Bågspänningen

Ljusbågens negativa resistans

Bågströmmen via Båglängden

KONSTANT MATNINGSSPÄNNING — negativa resistansens aspekt

Härledningen — grundsambandet ljusbågens fysik

Relaterade fysikaliska storheter

Koefficienterna — möjliga kopplingar enligt TNED

Rasch-tabellen 1913

Rotgränspunkten — Kretsresistansen

Båglängden

Kvoten u/s

Bågströmmen

Justerade samband enligt Rasch 1913

Grundformerna för gnisturladdning och ljusbåge enligt TNED

GRUNDSAMBAND ENLIGT TNED — kort illustrerad översikt och snabborientering

Grundteorin enligt TNED

LJUSBÅGE OCH GNISTURLADDNING ENLIGTTNED

Ljusbågen i sammandrag

Elektriska konstanten och elektronmassans komponenter

Kalkylkortet

REFERENSER — böckerna finns gratis på Internet Archive

ELECTRIC ARC PHENOMENA — Ewald Rasch 1913

THE ELECTRIC ARC — Hertha Ayrton 1902

Senast uppdaterade version: 2021-03-30

*END.

Stavningskontrollerat 2011-08-19.

rester

*

√ τ π ħ ε UNICODE — often used charcters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓

ϑ ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — also Alt+18 ↕; Alt+29 ↔

*

PNG-justerad

åter till portalsidan · portalsidan är www.UniversumsHistoria.se