PERIODISKA SYSTEMET · GRUNDÄMNENAS PERIODISKA SYSTEM eller Periodiska Systemet genom Keplermomentet · 2007IV17 · Periodiska Systemets Härledning | Senast uppdaterade version: 2022-12-28 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
a BellDHARMA production 2007IV17
Periodiska
Systemet genom Keplermomentet (Keplers Ytmoment) och Keplerresonanserna, ger den fullständiga härledningen till atomernas
exakta elektronkonfiguration genom elementär grundskolematematik, och går
därmed förbi den traditionella kvantfysikens dunkla detaljer. Termerna
”Keplermoment” och-eller ”Keplerresonans” finns inte på webben. Man använder
istället traditionellt ”Keplers II.a lag” för Keplermomentet
(vr eller A/T), som dock INTE
är känt i någon traditionell mening i samband med periodiska systemet. Här
följer den beskrivningen.
Grundämnenas
Periodiska System genom Keplers Ytmoment
Tänk om jag hade sett det här när jag var
tolv.
![]()
Se
även från INLEDNINGEN
i den mera utförliga ORIGINALFÖRFATTNINGEN FRÅN
2003
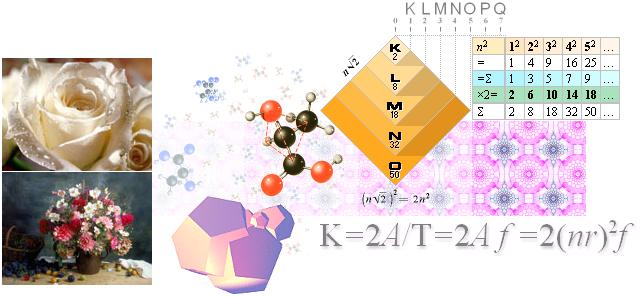
Bildkällor: De snygga
Fotografierna ovan t.v. är från @INTERNET [http://bilder.alltinggratis.se/].
Molekylmodellen i mitten
(mjölksyra) kommer från FOCUS MATERIEN 1975 s357. Övriga delar från
författaren.
Med föreställningen om den elektriska laddningen kan all materia
förklaras som sammansatt av atomer;
Atomen karaktäriseras av massa,
laddning och
spinn (rörelse). För
att rörelseformen (spinnet) ska fungera måste spinnet vara av typen resonant
(som ger en ton
eller en färg):
krafterna måste harmoniera, samverka och samarbeta, vilket betyder resonans:
Atomen behöver ingen påfyllning för att fungera: summan av alla krafter och
moment i atomen är noll: Varje atom består av en liten positivt laddad kärna, atomkärnan,
som omges av en lika stor negativ elektrisk laddning, elektronmassan eller elektronen.
Elektronmassan upptar bara en liten bråkdel av atomkärnans massa (elektronen
ligger runt atomen som ett tunt moln som kan anta olika mönster beroende på
spinnkopplingen eller resonansen till moderkärnan, och övriga). Genom att dela
gemensamt på elektronmassorna, sammanlänkas atomerna i ett material till en
enhetlig kropp.
De sammanhållande elektriska krafter som verkar mellan
atomerna kan återföras på centralkraftsverkan,
vilket innebär att det är den tunga centrala atomkärnan som avkänner, styr och
reglerar ordningen. Centralverkan grundas på en enkel princip som klargjordes
först genom Johannes Kepler
(1571-1630). Den är känd som Keplermomentet
eller Keplers ytmoment
(Keplers andra lag), K=vr=2A/T. Genom
att tillämpa Keplermomentets resonansform på de ytor som sammanlänkar atomerna
(endast hela tal motsvarande hela våglängder), framkommer en mönstersyntes som
i matematikens termer beskriver hela grunden bakom alla ämnens sammanhängande
egenskaper, de s.k. kemiska egenskaperna eller grundämnenas periodiska system.
Mot varje kärnmassa svarar en specifik
elektronmassa som definierar perfekt
balans och harmoni för hela den atomen. Eftersom elektronmassan kan återföras
på en YTA, likt vattenvågorna, samt att den lyder under centralkraftsverkan,
kan hela svängningskomplexet också återföras på Keplermomentet K=2A/T
Resonanserna — Keplermomentets
atomära grunder

QTEK WindowsMobile 1,3 MegaPixel. Författarens Fotografier 2007IV17
Grundämnenas periodiska system är inte ens enkelt att
»härleda» för folk som ”begriper kvantfysikens matematik”. Här ges emellertid
en långt enklare beskrivning (som
kan förstås med grundskolans matematik och fysik). Slutresultatet är precis detsamma.
Med bara en enkel diskbalja fylld med vatten, se
foto ovan, och en periodiskt bumpande hand som energigivare, samt de enklaste
av fysikens grunder iklädda matematikens former, framgår hela hemligheten med
grundämnena genom resonanser, samma som stående, fasta, vågmönster. Vi
kan se dem överallt i naturens underbara berättarbok — bara vi vet hur
boken ska läsas.
K=2A/T=2A f =2(nr)2f
Från enkla experiment hemma i köket med vattenvågor i resonans (se ovanstående illustration), framgår en direkt matematisk koppling till Keplers ytmoment K=vr=2A/T=2A f. Med elektronmassan (m) innefattad, vilket betyder samma som impulsmomentet (Plancks konstant, h=mvr), etableras koppling till elektronmassans kärnbindning genom centralkraftverkan enligt
centralkraftsverkan — systemkarta för Keplerresonanserna
J = m(K=2A/T=2A f =2n2fr2 )KEPLER AREA resonance MOMENTUM; J/(mfr2)=2n2

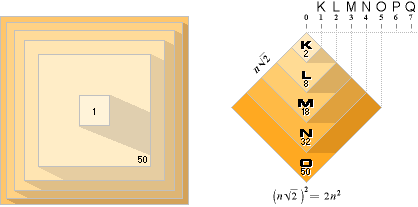
Denna struktur framvisar grundämnenas periodiska system via en heltalsbaserad algoritm, samma som resonanser enligt heltalen n = 1 2 3 … N. Illustrationen ovan visar grundprincipen. Vi studerar hur.
KEPLERKVADRATURENS
NUMERISKA UPPDELNING VISAR:
Talen 2,6,10,14,18 … i Keplersystemet markerar resonansgrupper (»atomtoner»). Talen 2,8,18,32,50 … markerar motsvarande primär resonansyta. Varje kvadrat eller resonansyta 2,8,18,32,50 … definieras av en gruppsammansättning
2, 2+6, 2+6+10, 2+6+10+14, …+4n–2.
Antalet elektronmassor (Z) i 2A som bestäms av resonansverkan via tiden T i resonanstalet n blir maximalt Z0=2n2={2,8,18,32,50,72,98…};
Atomkärnan avdelar eller BESTYCKAR elektronmassa till atomen med växande atomvikt på ETT, bara ett, och ingenting annat än bara ett enda sätt,
P 2 6 10 14 18 22
O 2 6 10 14 18
N 2 6 10 14
M 2 6 10
L 2 6
K 2
aldrig utan undantag: från KÄRNAN
(högre) till höljet (lägre). Mesta möjliga energihushållning. Vi
studerar den sammansättningen mera i detalj nedan.
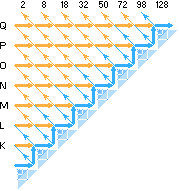
Tillväxten i ovannämnda enkla serieform framvisar en kärnmatrisisk algoritm som helt grundas på den tidigare nämnda centralverkan. Den beskriver, tydligen, hur resonansmassorna organiseras från atomkärnans centrala kraftcentrum. Figuren nedan illustrerar kärnmatrisiska algoritmen i dess tillväxtform (k för KÄRNAN), samma som föregående 2-6-10-14…-serie:
k-2; k-2;
k-6-2, k-6-2, och sedan vidare på samma sätt i par:
k-10-6-2, k-10-6-2;
k-14-10-6-2, k-14-10-6-2;
k-18-14-10-6-2 …
Ordningen är förtydligad nedan genom de tvärställda siffrorna som kopplar till algoritmens vertikalkolumner:
1 2 3 4 5 6 7 8 . . kärnnivå (steg) s
1 1 2 2
3 3
4 4 transmission t
Med beteckningarna K L M N O … för motsvarande resonansytor och kärnnivåerna indexerade som nedsänkta siffersuffix kan hela ordningen skrivas förtydligat
Z – (2K1 + 2L2 + 6L3+2M3 + 6M4+2N4 + 10M5+6N5+2O5 + 10N6+6O6+2P6 + 14N7+10O7+6P7+2Q7 +… = S
steg
1 2 3 4 5
6 7 8 9 10 11
12 13 14
15 16 = s
1 1 2 2 2
2 3 3
3 3 3 3 4 4
4 4 = t
Z anger atomens atomnummer eller atomens totala antal elektronmassor eZ. Slutsumman S är en strukturform som anger atomens exakta elektronkonfiguration. Den kan skrivas nK-nL-nM-nN-nO-… .
Atomens Exakta
Elektronkonfiguration
Metod: Med givet Z dras resonanstalen 2,6,10… successivt bort från Z enligt ledet ovan tills resten är noll.
Exempel: Z=26 (Järn, Fe) ger 2K1 + 2L2 + 6L3+2M3 + 6M4+2N4 = 20 med + 6M5 som ger 2K-8L-14M-2N.
lösningen:
Z–resonansgrupp kärnnivå
26–2=24 K +2 1
24–2=22 L +2 2
22–6=16 L +6 3
16–2=14 M +2
14–6=8 M +6 4
8–2=6 N +2
6–10=–4 M +10–4=6 5
summa 2K8L14M2N
Svar: 2-8-14-2
Se
även Jämförande Exempel från FOCUS MATERIEN och ENCARTA
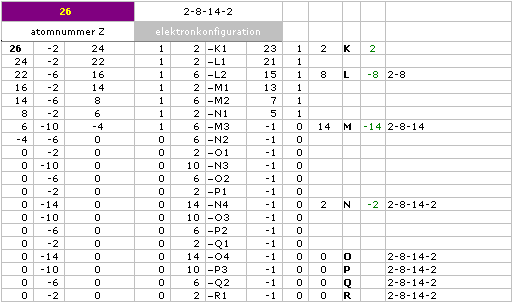
Med hjälp av ett kalkykort
— ovanstående cellbild urspr. från MsWORKS 4.0
— en motsvarande version som kan öppnas i OpenOffice ingår nu [från November 2008] i kalkylkortet till periodiska systemet, se längre ner
— kan kärnmatrisiska algoritmen eller enklare »atomalgoritmen» insättas i maskinordning för att beräkna godtyckligt ett visst grundämnes elektronkonfiguration. Uppställningen ovan anknyter till exemplet med Z=26.
Genom kärnmatrisiska algoritmen, framgår hela kartan till grundämnenas periodiska system genom aritmetiken via Keplers ytmoment, som ovan. Vi studerar närmare hur.
Med villkoret att den sekventiella elektronfyllningen av kvadraterna från minsta (n=1) till största genomförs från lägre till högre resonansgrupp 2+6+10+14+18+22+… kommer fyllningen på varje grupp (vilken som helst, hur som helst, allmänform för hela atomkomplexet) att slutföras (principform, numeriska uppdelningens 2-6-struktur) enligt ordningen
…2
…2+6
…2+6 + 2
…2+6 + 2+6
…2+6 + 2+6 + 2
…2+6 + 2+6 + 2+6 …
som betyder (mönsteraritmetiken för 2-6-strukturen ses enklare med hela kvadratkomplexet utskrivet enligt)
2 2 2 2
6 6 8 2+6
10 2+6 + 2 18 2+6 + 2+6 + 2
14 2+6 + 6 32 2+6 + 2+6 + 2+6 + 2+6
18 2+6 + 2+6 + 2 50 2+6 + 2+6 + 2+6 + 2+6 + 2+6 + 2+6 + 2
22 2+6 + 2+6 + 6 72 …
Det vill säga: 2-6-strukturen kan, i princip, komponeras från vilka som helst godtyckliga resonanskvadrater i hela komplexet.
Tillväxtordningen är som vi ser utpräglat binär(2)-hexal(6)-oktal(6+2=8). Binärdelen kan skrivas 10 med fetnollan som markör för fylld 2-grupp. Med 6-gruppen inkluderad i tillväxten blir ordningen oktal. Fetnollan markerar då fylld 8-grupp enligt 12345670.
Atomens Resonanta Arkitektur, de 7 Perioderna
Med indexerade inbrytningar inkluderade kan fyllningen i sekvens av resonanskvadraterna skrivas med hjälp av binär-hexal-oktalgruppen 1(234567)0 i komprimerad sammanfattning
period
1 10 2 K fullbordad
2 12345670 2-8 L fullbordad
3 12345670 2-8-8 M påbörjad
4 1239410511612713814815816117218345670 2-8-18-8 M fullbordad, N påbörjad
5 1239410511612713814815816117218345670 2-8-18-18-8 M fullbordad, N O påbörjad
6 1231932032132232332432532632732832933033133239410511612713814815816117218345670 2-8-18-32-18-8
7 1231932032132232332432532632732832933033133239410511612713814815816117218345670 2-8-18-32-32-18-8
Förklaring:
Betrakta tillväxten i period 4 (hur atomen bygger sin struktur enligt kärnmatrisiska algoritmen):
1239410511612713814815816117218345670:
Orsaken bakom de tre utfyllande åttorna (eller annat, passande tecken) är en ren logisk konsekvens av den inledande inbrytningen:
12.................................. 1 2 345670;
TY resonansgruppen (den som svarar mot M-kvadraten) måste tvunget avslutas enligt ordningen
… 9 10 11 12 13 14 15 16 17 18
vilket resulterar i den nödvändiga 888-utfyllnaden.
Samma princip gäller sedan för alla liknande inbrytningar (nummer 3 i period 7).
888-gruppen markerar f.ö. grundämnena Järn(Z=26, Fe), Kobolt(Z=27, Co), och Nickel(Z=28, Ni), alla av typen s.k. ferromagnetiska grundämnen (grundämnen med stor magnetisk potential).
MERA INGÅENDE BESKRIVNING AV STRUKTURENS
SAMMANSÄTTNING
För den som önskar en mera
ingående djupbeskrivning, har (Dec2012) den mera utförliga
originalförfattningen (från 2003) lagts till i slutet av detta dokument;
— Se utförligt i
Avslutning
Sjunde perioden är i naturen ofullbordad. Med de 92 naturliga grundämnena slutar den teoretiskt
12319320321322 2-8-18-32-22-8-2 KLMN fullbordade, OPQ påbörjade
Den verkliga konfigurationen för 92:an är (enligt gängse tabeller) 2-8-18-32-21-9-2, alltså samma slutsumma.
Vi ska dock redan här understryka att olika traditionella tabeller har något olika beskrivningssätt. Den exakta orsaken till det är (ännu) här inte känd. Se vidare i Jämförande källor nedan.
SAMMANSTÄLLNING
GRUNDÄMNENAS PERIODISKA SYSTEM
Ovanstående fyllnadsserier i sammanställning motsvarar grundämnena i de 7 perioderna enligt
————————————————————————————————————————
a b a
123456788812345678 ....................... den klassiska (horisontellt logiska) gruppindelningen i a och b
————————————————————————————————————————
resultat:
resultatsammanställning
1 ¯ elektronisk period, systemets 7 perioder
123456789012345678 ¬ kemisk grupp

Uppställningen nedan motsvarar ovanstående resultat med grupperna 1-18 i perioderna 1-7. Heltalen i rutorna anger atomnumret Z = atomens elektronantal (eg., ”KeplerResonansTalet”).
Historiskt gavs
periodiska systemets grundform på kemisk historisk bas av Dimitrij Mendelejev
från 1869.
Ett snyggt
fotografi på Mendelejev (2007-10-30) fanns tidigare [före Aug2011] på @INTERNET
på adressen
http://www.chemheritage.org/pubs/ch-v25n1-articles/feature_mendeleev.html
Den adressen
kopplar inte längre. Den aktuella bilden [om jag minns rätt],

finns
[21Aug2011] på
http://www.chemistry.co.nz/mendeleev.htm
![]() traditionella beteckningsformen i grupperna a och b
traditionella beteckningsformen i grupperna a och b
summa 13 14 16 17
18 19 tabellavvikelser
1 2 2 2 2
2 2
2 2
2 2
2 3 4 5 6
7 8 karaktäristiska e-nivåerna, övre
8 8 9 10 11 12 13 14 15 16 17 18 18 18 18 18 18 18 närmast undre
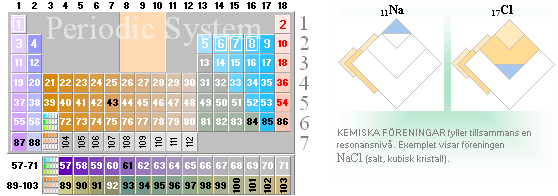
Svartmarkerade
siffror anger radioaktiva grundämnen.
De
tre mittfälten (26,27,28) motsvarar ”de tre åttorna” (Järn, Kobolt, Nickel) som
diskuterades i tillväxten i period 4, hela gruppen 26-28, 44-46, 76-78 kallas
Järn- och Platinametallerna.
Exempel som ovan:
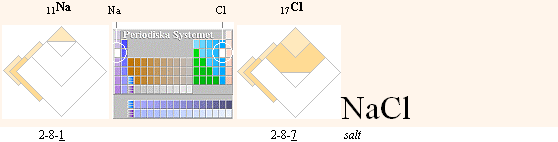
Har man en gång hajat grunderna till ovanstående blir det (nästan) generande
enkelt att förstå grundkonceptet i olika ämnens olika kemiska egenskaper — de
berör (i stort sett) bara de två yttersta resonanserna eller ”skalen”.
Ett slående exempel är föreningen NaCl (salt,
kubisk kristall). Även HCl (saltsyra) fungerar utmärkt, liksom H2O (vatten) och H3N (ammoniak, skrivs vanligen NH3) och CH4 (metan,
naturgas).
Alla
dessa (med många fler exempel) fyller tillsammans helt en resonansnivå.
De
mest reaktiva ämnena (direkt explosiva, farliga) är de som ligger i grupperna 1
(alkaligruppen) och 17 (halogenerna). Deras häftiga reaktion garanterar att
inte ens vissa av dem förekommer isolerat i naturen.
kalkylkort PerSyst · se öppningsmanual
om ej redan bekant

Kalkylkortet
(PerSyst) i bild ovan kan öppnas från [alla] webbläsare i ett separat fönster
via OpenOffice.
— Kortet kopplar
till en sammanställd tabell med grunddata som insamlades från flera olika
källverk i bokform
— i huvudsak
före webbdatoreran (t.o.m. 1981) enligt specifikationerna
Van Nostrand’s Scientific
Encyclopaedia, 4th edition 1968, 5th edition 1976
The Atomic Universe, Mihajlo Velimirovich
(PERIODIC TABLE OF THE ELEMENTS), Routhledge & Kegan Paul, London 1974
Richard Westöö FYSIK; Elektron- och
atomfysik för elteknisk gren, 3dje upplagan 1975, Esselte Studium
FOCUS MATERIEN 1975 s114 tabell
Bonniers Lilla Uppslagsbok 1973,
Periodiska systemet
Karlebo Handbok, 12te upplagan 1977
(Grundämnenas periodiska system,
s92-93)
ENCARTA (97-99-) Periodic System — se
speciella källverk längre ner

I kortet ingår
även ett delkort som ovan i bild
— endast för
ångor och gaser
— där läsaren
själv kan beräkna ett sammansatt ämnes atomvikt
— enbart genom
att ange grundämnets kemiska bokstavsbeteckning och atomantal i den sammansatta
kemiska molekylen, typ bildexemplet ovan.
— Se även andra
(interaktiva) webbexempel i SYSTEMET PÅ
NÄTET.
Skrivs perioderna ut enligt 32-bitarssystemet, som innefattar lantan(o)iderna och aktin(o)iderna utan utbrytningar, fås nedanstående karta: den är mera överskådlig, har ingen traditionell förankring, men har ändå på senare tid fått allt större användning just på grund av överskådligheten.
Enligt @INTERNET susning.nu/Periodiska_systemet (2007-10-30) har 32-bitarssystemet (på senare tid) antagits av IUPAC (International Union of Pure and Applied Chemistry). IUPAC bildades 1919 (ref. Wikipedia Sw. IUPAC), men uppgift saknas här om när IUPAC antog den nya nomenklaturen. Att döma av exv FOCUS MATERIEN 1975, som är ett (det bästa 1900-talets) standardverk i fysik-kemi där periodiska systemet anges på den ovannämnda traditionella formen, är IUPAC-normen nedan ett senare verk. Exakta uppgifter saknas dock här på den punkten.

FOCUS MATERIEN 1975 s114 tabell (elektronkonfigurationerna hos de
92 grundämnen som förekommer i naturen)
parentessiffror =
osäkra ENCARTA
(97-99-) till jämförelse — anger samma som i kärnmatrisiska algoritmen:
anger 2-8-18-(19)-(9)-(2) för 58Ce 2-8-18-20-8-2
anger 2-8-18-(20)-(9)-(2) för 59Pr 2-8-18-21-8-2
anger 2-8-18-(21)-(9)-(2) för 60Nd 2-8-18-22-8-2
anger 2-8-18-(22)-(9)-(2) för 61Pm 2-8-18-23-8-2
anger 2-8-18-(26)-(9)-(2) för 65Tb 2-8-18-27-8-2
anger 2-8-18-(27)-(9)-(2) för 66Dy 2-8-18-28-8-2
anger 2-8-18-(28)-(9)-(2) för 67Ho 2-8-18-29-8-2
anger 2-8-18-(29)-(9)-(2) för 68Er 2-8-18-30-8-2
anger 2-8-18-32-18-(9)-(2)
för 89Ac samma
men utan parenteser 2-8-18-32-18-9-2
anger 2-8-18-32-18-(10)-(2) för
90Th samma men utan parenteser
2-8-18-32-18-10-2
anger 2-8-18-32-18-(11)-(2) för
91Pa 2-8-18-32-20-9-2
anger 2-8-18-32-18-(12)*-(2) för 92U 2-8-18-32-21-9-2
*feltryck 2-6-(9) ska vara (4) för rätt Z
Exempel på originella feltryck (om jag inte har missat något …)
FOCUS MATERIEN 1975 s114 (elektronkonfigurationerna hos de 92 grundämnen som
förekommer i naturen)
anger 43Tc med
beteckningen Ma (!)
anger 61Pm med
beteckningen II (!)
Någon ”härledning” till periodiska systemet finns inte i traditionell
mening. Internetsökning ger noll.
PERIODISKA SYSTEMET PÅ WORLD WIDE WEB (@INTERNET) har stor representation med många (fina) uppställningar i tabellform — se träffarna på »periodic system» och »periodiska systemet» på Google. Källan med den bästa bredden och referensen bör (naturligtvis) vara Wikipedia (största editoriella potentialen för den fria viljans initiativ, dock med villkor). Emellertid känner man (inte heller där) till Keplerresonanserna — och de får heller inte beskrivas i någon artikel i Wikipedia eftersom det inte finns någon redan publicerad källa på den punkten.
Utöver den mera komplicerade akademiska kvantfysiken, som helt ligger utom ramen för den här nivån, finns ingen egentlig »härledning till periodiska systemet» i traditionell mening, i varje fall ingen som kan förstås på något enkelt sätt av lekmannen (med grundskolekompetens).
SVENSKA Wikipedia (2007-10-30) har f.ö. historiska (bild-) referenser som beskriver hur periodiska systemet vuxit fram historiskt-traditionellt.
internet
En extremt fin interaktiv svensk presentation av periodiska systemet med grunddata finns (2007-10-30) på
[http://strangnet.se/periodiskt/]
*
GRUNDLÄGGANDE
FYSIKBEGREPP
KEPLERS YTMOMENT — Keplermomentet
K=vr=2A/T
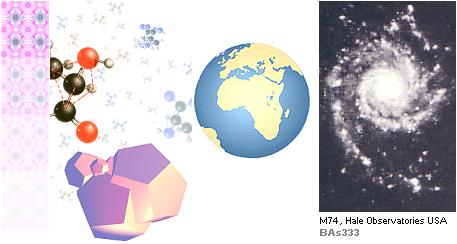
Utan Keplermomentet går det inte
Keplermomentet utsäger att
förbindningslinjen (d) — mellan två kroppar som lägesändrar
genom en kraft som verkar utmed d — översveper lika stora ytor på lika långa tider
Förbindningslinjen d kallas ortsvektor, och hela principen kallas centralverkan eller mera exakt centralkraftsverkan. Principen gäller alltså (idealt) speciellt såväl för himlakropparna med gravitationen som den verkande kraften, som för atomerna-atomkärnorna med elektriciteten som den verkande kraften.
härledning
Härledning — Keplermomentet — ytmomentet, centralverkan
Fysikens i särklass mest genomträngande sambandsform är K=vr=2A/T. Denna sambandsform, stundom benämnd ytlagen, framkom historiskt genom Johannes Kepler (1571-1630). Tillsammans med massan m ger den impulsmomentet eller rörelsemängdsmomentet J=mvr.
grunden:
Förbindningslinjen (d) mellan en fix punkt P (ortspunkten) och en kropp (B) som färdas rakt fram med konstant hastighet (v) visar att
d översveper lika stora ytor på lika långa tider;
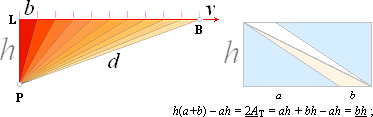
Denna remarkabla men enkla slutsats är en ren konsekvens av den elementära geometriska matematiken (förskjutningssatsen, bh/2=A, se figuren ovan t.h.);
Om den tillryggalagda vägen (s) delas i lika delar (b) har alla trianglar b.P nämligen exakt lika stora ytor (A=bh/2).
Från 2A=bh ges K=2A/T=bh/T=vh som anger ytmomentet eller Keplermomentet (efter Keplers andra lag).
En vidare undersökning visar att så länge ändringen i rörelseriktningen kan återföras på en impuls utmed d kan rörelsebanan relativt fixpunkten, ortspunkten eller centralpunkten P ha vilken form som helst (lagen för ytkvantitetens bevarande, se nedan):
Lagen för ytkvantitetens bevarande
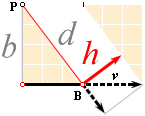
H
Hastigheten v i en godtycklig banpunkt (B) kan uppdelas i vinkelkomponenterna h(=vn) och H (=v0) utmed ortsvektorn d. För varje B gäller då enligt förskjutningssatsen och relationerna genom räta vinklar att
b/d = h/v ; bv = hd
Komponenten H utmed d kallas explicit för centripetalacceleration (inåt) eller centrifugalacceleration (utåt).
Om H ändras till H’, vilket avbildar v som v’, bibehålls likväl resultanten med v’ inom det givna intervallet h så att ytan H’h genom förskjutningssatsen är konstant:
h bildar i varje tidpunkt (T) ett fast, orubbligt, tak som definierar/innesluter varje resulterande v från varje möjligt förorsakande H.
Följaktligen kommer vilken som helst rörelseändring från B, oberoende av tidsaspekten och förutsatt att ändringen sker utmed d, att bevara det linjära ideala ytmomentet. Eftersom h gäller som plannormal till d i hela 3D-rummet, gäller tydligen lagen för ytkvantitetens bevarande alla möjliga 3D-banor.
TILLÄMPNINGAR Keplermomentet
Centrifugalacceleration
och Centripetalacceleration
Ortsaccelerationen utmed d (ändringen i H), eller centralaccelerationen (centripetal inåt, centrifugal utåt), som betyder att omloppskroppens läge ändras relativt den fixa ortspunkten eller centralpunkten (O), får sin exakta syntes från Keplermomentet genom likheten mot den linjära accelerationen a=v/T och med stöd av figuren nedan.
begrepp:
Begreppet acceleration (a) betyder att väg (d) och tid (T) separerar under rörelsen — till skillnad från konstant hastighet (v) som betyder att väg och tid hela tiden följs åt (v=d/T=konstant). Accelerationens grundform är (alltså) att hastigheten (v) ändras konstant och likformigt med tiden enligt a=v/T, en s.k. konstant likformig acceleration.
praktik:
Exempel: Håll ett föremål. Släpp det; Föremålet börjar från noll, ingenting, och antar sedan allt högre hastighet som det faller mot Jordens (eg., omgivningens lokala) tyngdpunkt. En sådan rörelse är (alltså) accelererad.
beskrivning:
En kropp (P) som beskriver en cirkulär rörelsebana, r=konstant, (d för cirkelns del närmar sig noll obegränsat) kan tecknas (idealt) på den nedanstående figurens enkla form. Sambanden ger:
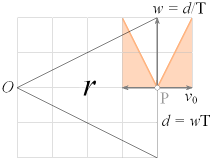
Den
cirkulära rotationen på en fast radie beskriver egentligen en
centripetalacceleration, men vi kallar (oftast) kraften för en centrifugalkraft
och därmed (oegentligt) cirkuläraccelerationen för en centrifugalacceleration.
Synonymer:
centralacceleration, ortsacceleration.
samband:
Med figurens beteckningar (w för den cirkulära tangentialhastigheten) gäller relationerna genom räta vinklar enligt
v0 d wT v0 w2
—— = — = —— ; —— = a = —— = aw = å
w r r T r
v0/w = d/r = wT/r ; v0/T = a = w2/r = aw = å
centralalaccelerationens
härledning
Beteckningen å (läs, ”a med cirkel”) enbart förtydligar att det är fråga om en cirkulär rörelseform.
förklaring:
Formen v/T uttrycker en linjär acceleration. Keplermomentet gömmer/avtäcker genom de geometriska relationerna på detta sätt den linjära accelerationen analog med ytmomentets centralacceleration.
För den helt cirkulära rörelsebanan närmas d=wT till 0 obegränsat. Centralaccelerationen skrivs alltså direkt för den cirkulära rörelsebanan enligt
å = v0/T
= w2/r ......................... centrifugalaccelerationen (allmän
referens)
TILLÄMPNINGAR Keplermomentet
Varje kropp (m) vars rörelsebana bestäms av kraftverkan eller ortsaccelerationen utmed förbindningslinjen till en centralkropp (m2) sägs lyda under centralkraftsverkan eller centralverkan. Ortsaccelerationen kallas även centralacceleration. Se även (alternativ) beskrivning i CENTRALACCELERATIONEN.
Keplermomentet i Ringströmmar och Ytresonanser
Keplermomentet i Ringströmmar och Ytresonanser
(Atomfysikens elementära grunder)

Om B består av delkroppar i en ring med radien r gäller Keplermomentet också för denna. Om varje delkropp ändrar sin position utmed r i en utåt-inåtgående rörelse som fullbordas (n gånger) på ett ringvarv T0, ges Keplermomentet för hela ringens ytmoment analogt periodiskt under T0/n. Vi har då ekvivalenten till en polärresonans
(ra=rin+[rout–rin][sin(n/2)a]2 i PREFIXxSIN, a i radianer) med grund i ringen förutsatt att T0 omfattar det exakta antalet hela inre våglängder (n) i ringen. Med ringmassan m ges då rörelsemängdsmomentet eller impulsmomentet med avseende på varje våglängd enligt J=mK/n=mvl0/n (totalt, hela ringen, Jn) där l0=2pr och v=l0/T0, J=mv2T0/n. (Se vidare i Spektrum och Kvanttalen).
Om ringmassan har godtycklig spridning och centralkraftsverkan gäller, kan den också fördelas på en godtycklig plan eller rymdyta vilketsom. Därmed har Keplermomentet i viss mån kommit tillbaka till sin ursprungliga (egentliga) elementarform: periodiska genomgångar för bestämda ytor (ytresonanser): K=2A/T0.
(Se vidare i Spektrum och Kvanttalen).

Johannes Kepler. Samtida kopparstick. Från BKL VII sp743.
Ytmomentets Princip upptäcktes av Johannes Kepler (1571-1630). I samband med utarbetandet av den nya världsbild som beskriver Solsystemets geometri, efter Tyge Brahes observationer (Astronomi’a no’va 1609, Harmo’nices mu’ndi 1619, [ref. BKL VII sp745]), fann Kepler de efter honom uppkallade tre lagarna (Keplers tre lagar): 1. Planeterna beskriver ellipsbanor kring Solen med denna i ena brännpunkten, 2. Linjen Solen-Planeten översveper lika stora ytor på lika långa tider (K=A0/T0), 3. Förhållandet mellan planetens omloppstid (T0) i kvadrat och kuben på medelavståndet (r) från Solen, är konstant (T02/r3=konstant).
GRUNDÄMNENAS PERIODISKA SYSTEM originalet från 2003 i MsWORKS — Den mera utförliga beskrivningen
Inledning
2003V15 — från MsWORKS 4.0
[MPcPeriodic1.wps] — (Microsoft tillåter inte längre att det programmet får användas —
fr.o.m. Windows Vista; se Microsofts ProgramVandaliseringar)
den skamligt enkla Härledningen till
GRUNDÄMNENAS PERIODISKA SYSTEM
eller Keplerresonanserna — (UR) den mera
utförliga originalförfattningen från 2003
central force
dynamics
J = m(K=2A/T=2A f =2n2f )KEPLER AREA resonance MOMENTUM, J/(fm)=2n2
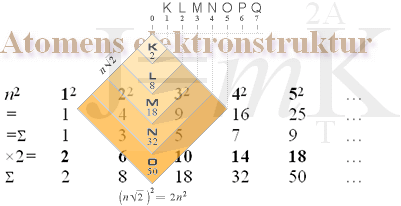
Atomic Building Algorithm:
insert available electrons (units) in sequence from lowest resonance
group (2) in any available square (n) and then outwards with priority from
lowest unfilled square. Can you do it?
… 2-8-8-1, 2-8-8-2, got
it: 2-8-9-2, 2-8-10-2, … 2-8-18-2, I’m
on: 2-8-18-3, 2-8-18-4, …
1239410511612713814815816117218345670
.... 2-8-18-8 ...... period4
Ovanstående Keplermomentets fullständiga resonansvillkor (ABAM, Atomic
Building Algorithm, gäller idealt för en isolerad atom) är tillräckligt för att
själv, i exakt sekvens, kunna teckna upp hela periodiska systemet med exakt
elektronkonfiguration för samtliga grundämnen. Algoritmens helt enkla dynamiska
grund visas längre fram. Ett enkelt praktiskt exempel visar hur vi kan förstå
det avgörande resonanskomplexet utan komplicerad matematik. Beskrivning följer.
Elektronen
uppträder kring atomkärnan som en elektrisk gas. Dess element är de berömda vibratorer som år 1927 förkastades av
modern akademi — därför att de inte passade in i en redan långt gången kvantiserad
verklighetsuppfattning — men som det till trots låg till grund för de
berömda Heisenberg och Schrödingerekvationerna. Med nära nog perfekt
träffsäkerhet förklarade de atomernas spektrala beteenden. Detaljer som legat
till grund för resultat som uppvisade nära nog exakt överensstämmelse med
praktiska experimentella observationer, satte man alltså igång med att
systematiskt avliva.
I traditionell
mening är man — i stort sett — hänvisad att arbeta sig igenom
hela spektralanalysen med kvantfysiken för att komma fram till någon ”begriplig
enkel” »förklaring» till grundämnenas periodiska system. Men då är till
slut hela arbetet så inbäddat i matematik att många av studenterna drunknade i
Algebraiska Havet.
Finns det inget enklare sätt?
Visst. Det finns en väg, men …
Den inkluderar — innefattar — modern akademi som primitiv
i sitt allmänna föreställningssätt. Det är också precis vad man kan förutsäga
för en attityd som med petitessig nogsamhet anser sin egen tanke stå så högt
över naturförnuftet [HerrefolksCitatet]
att den tycker sig ha rätt att anse fysikens grundläggande element såsom icke
existerande [VIBRATORERNA omnämnda ovan, se mera utförligt i ELEKTRONMASSANS KOMPONENTER]. För eller
senare kommer räkningen.
Utan några
speciella antaganden kommer grundämnenas periodiska system fram
spontant ur den allra enklaste ”barnsliga” föreställningen:
1. atomkärnan är en Kub
2. elektronmassan är en
Kvadrat
;
·
atomkärnan är en Kub [KUBANALOGIN],
en byggklots, som består av ett antal (A) mindre byggklotsar (K) så att totala
volymen för A(K=1) ger motsvarande kubsida A1/3.
·
men föreningen AK ger en ny, unik kub, som två vattendroppar förenas
till en större, som därför tvingar kärnan att byggas om, och för det åtgår ett
arbete (m→γ), massan m
måste tas från K och därmed en massdefekt; alltså är individen K inte
helt stabil (K är neutronen),
det blir den först när den, massdefekten frånsett, lämnar ut en liten del av
sig själv kallad elektronen, som ett hölje kring den egna kroppen, som
en elektrisk gas, då först uppnås ett stabilt motsvarande tillstånd av harmoni,
av balans och jämvikt; därmed lyder elektronens element under centralkraftsverkan och därmed
under impulsmoment
och därmed en resonansverkan;
olika stabila (s.k. stående) vågmönster och vågformer som genomströmmar
elektrongasen i dess kärnbindning
·
[Använd kökets bästa
diskbalja i plast (BILD), fyll
den med vatten nästan ända upp, ha god [justerbar] belysning så att effekterna
kan studeras i detalj; bumpa med ena handen periodiskt [jämnt, stadigt] på baljkanten
för att generera vågor, pröva dig fram, var inte rädd för att klappa på rejält;
man får se en mängd olika stående vågmönster beroende på mängden
tillförd vågenergi; missar man ett bumpslag så att det är märkbart svagare
eller starkare än föregående, försvinner mönstret omedelbart och ersätts av
något annat, helt fantastiskt, ungefär på samma sätt fungerar ”elektronernas
molekyler” kring atomkärnan; de stående vågmönstren kallas resonanser,
minsta störning i energin bryter mönstret]
·
elektronen är kan
förstås liknande en gas eller motsvarigheten till ett vatten som kan
bilda olika mönster eller resonanser över en viss begränsad yta (A),
den lyder under centralkraftsverkan via Keplers
ytmoment K=2A/T (vi skiljer Kepler från
Kuben).
·
kvadraten A har sidan som ett helt tal, motsvarande ett
övergripande resonanstal (n, som innehåller underavdelningar, vi
kommer tillbaka till det senare) som garanterar resonanskopplingen i ett helt
antal toppar och dalar, inte 1/2 eller 1/3 eller något annat fult
·
när AK bildas och elektronmassa avges tvingas den genom kärnans
begränsade energi att parkera sig i 2A efter villkor:
·
elektronmassan fördelas på de resonansnivåer som bestäms av 2A
via perioden T i försorg av n så att
·
fördelningen alltid genomförs, utan undantag, på den minst energikrävande summan resonansnivåer:
·
från lägsta
resonansgruppen (2, se nedan) och vidare utåt för att fylla 2A och med början från minsta ytan (n=1)
____________________________________________________________________________________
Resonansgrupperna är en delad resurs för hela atomkomplexet medan
elektronbesittningarna är privata.
____________________________________________________________________________________
Med således A=n2 och totalytan 2A=2n2 finner man (kan man se en förklaring till)
hur resonansnivåerna är uppdelade enligt
n2 12 22 32 42 52 … halva
ytan
= 1 4 9 16 25 … ”
=Σ 1 3 5 7 9 … talsummans
udda element (1+3+5=9 osv.)
×2= 2 6 10 14 18 … skalgrupperna (resonanskvanta, eller
resonansgrupp)
Σ 2 8 18 32 50 … totala
kvadratytan, antalet elektroner
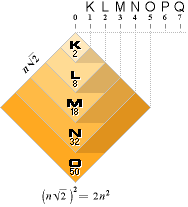
Resonanskvadraterna fylls nerifrån (n=1) och utåt — från lägsta resonansgrupp (2), strunt samma n-värdet, och från minsta resonanskvadraten (n=1) —
i steg om en enhet (1 elektron) lika med 1 ytenhet med växande AK, allteftersom
ordningen i skalgrupperna 2+6+10+14+18+22+…
inryms i de aktuella kvadraternas successiva totalsumma 2-8-18-32-50-….
Fyllningen på varje skalgrupp eller resonansgrupp (vilken som helst, hur som helst, allmänform
för hela atomkomplexet) med växande AK kommer följaktligen att slutföras
enligt ordningen
…2
…2+6
…2+6 + 2
…2+6 + 2+6
…2+6 + 2+6 + 2
…2+6 + 2+6 + 2+6 …
den framgår ur hela kvadratkomplexet utskrivet enligt
2 2 2 2
6 6 8 2+6
10 2+6 + 2 18 2+6 + 2+6 +
2
14 2+6 + 6 32 2+6 + 2+6 +
2+6 + 2+6
18 2+6 + 2+6
+ 2 50 2+6 + 2+6 +
2+6 + 2+6 + 2+6 + 2+6 + 2
22 2+6 + 2+6
+ 6 72 2+6 + 2+6 +
2+6 + 2+6 + 2+6 + 2+6 + 2+6
+ 2+6 + 2+6
26 2+6 + 2+6
+ 2+6 + 2 98 …
30 2+6 + 2+6
+ 2+6 + 6 128 …
Det vill säga: 2-6-strukturen kan, i princip, komponeras från vilka som
helst godtyckliga resonanskvadrater i hela komplexet.
Eftersom 2-gruppen inte innefattas i skalgrupperna ovanför denna, 6+10+14+18…,
kommer stegfyllningen enligt resonansvillkoret att innebära att större
kvadrater (från n=3) påbörjas
utan att de mindre ännu är helt fyllda. Med exemplet 2-8-8 givet innebär
det att nästa steg initieras på 2-8-8-1 i stället för på 2-8-9. På samma sätt har
alternativet 2-8-8-3 inte ens en statistisk chans att etablera sig utan
parkerar elektronen helt regelmässigt exakt enligt 2-8-9-2. Först från
2-8-18-2 är det okej med 2-8-18-3.
EXEMPEL:
Efter denna ordning kan också
kärnan, när den behöver det för sin egen interna balans (betecknas EC, electron
capture, elektroninfångning), fiska åt sig en enhet från minsta kvadratytan
med följd i att ovanförvarande enheter rättar in sig exakt efter
resonansvillkoret, i princip t.ex. från 2-8-18-2 med nettoresultatet
2-8-18-1 via (den snabba) transiteringen 2-7-18-2, 2-8-17-2,
2-8-18-1, stabilt tillstånd.
Med tillgång till en nuklidtabell kan vi kontrollera de olika möjliga EC-omvandlingarna som Keplerresonanserna förutsäger. (Resultatet är exakt). Beteckningarna nedan betyder
atomnummer ÄMNE
neutroner masstal;
EC Electron Capture (sv. elektroninfångning),
(m→γ) arbetet för kärnombygganden;
Exemplet ovan motsvarar omvandling från en radioaktiv isotop i zink
(Zn, 2-8-18-2) till en stabil nuklid i koppar (Cu, 2-8-18-1 = 2-8-17-2, den
senare är den teoretiska från Keplerresonanserna)
(30Zn3565)EC –
(m→γ)neutrino → 29Cu3665
Ett annat exempel (FMs126) är från järn
(Fe, 2-8-14-2) till Mangan (Mn, 2-8-13-2)
(26Fe2955)EC – (m→γ)neutrino → 25Mn3055
Fortsättningen
flyter på direkt med ändpunkt i grundämnenas periodiska system
med en exakt motsvarande karta över de naturliga grundämnenas
elektronkonfiguration. Vi kommer att förstå (eller i varje fall få en detaljerat förklarbar enkel
aritmetisk grundbeskrivning till) grunderna till varför och hur
olika grundämnen har olika egenskaper — utan att blanda in några som
helst begrepp från den gängse kvantfysiken (som man behöver flytväst och
nödradio för att navigera i). Exakt.
Jag ska inte föregå den
kommande härledningen vidare, ovanstående var tänkt enbart som en introduktion.
Resultatet i slutet kommer (säkerligen) att lyfta upp insikterna betydligt
beträffande redan befintligt material i olika faktaböcker (det finns mig veterligt inget liknande
i den konventionellt kända vetenskapliga litteraturen).
Det anmärkningsvärda är att
man inte behöver göra några särskilda antaganden för att komma fram till målet.
Det är i stort sett som att läsa en redan befintlig »helt enkel matematisk-logisk
karta» innantill och bara följa stigen till templet med de underbara skatterna.
Rena äventyrsfilmen, fruktansvärt spännande upplösning. Men nu tar vi det från
början.
För att kunna inhysa en viss elektronmassa i atomen, måste kärnan (genom
fusionsanalogin från lättare till tyngre) ha gjort sig av med en för dynamiken
motsvarande avpassad massdefekt (Atomära Massdefekten). Därmed begränsas kärnans
möjlighet att ge utrymme för de olika möjliga skalfyllningarna.
Inledning till grundämnenas periodiska system
Atomen
ATOMEN beskrivs galant utan större vidlyftigheter genom kubanalogin för kärnan och ytkvadraturen
(KEPLERS YTMOMENT) för den omgivande
elektronmassan (Elektronmassan frigörs i samband med Neutronens sönderfall). Den förra
förklarar hur (och varför) den senare uppkommer, denna i sin tur leder direkt
på grundämnenas periodiska system. Vi ska studera denna senare detalj
mera ingående i denna skrift.
GRUNDTEORI kubgrafen
(atomkärnornas radie)
konstant kärnmassatäthet för yttre kärnformens kubiska ekvivalent
(vänster) med (höger) elektronmassans resonansytor
Om vi tänker oss en helt ideal kubisk grundvolym (K) för massans
fundamentalform (atomkärnan, K motsvarar neutronen-protonen vilkensom)
som genom föreningar med kopior av sig själv bildar tyngre massor, finns det i
teorin och logiken en alldeles speciell, helt enkel matematisk ordning som
visar det enkla sättet. Vi betraktar då en helt ideal genomsnittlig konstant
kärnmassatäthet med avseende på den yttre formen för samtliga möjliga
kompositioner. Figuren ovan (vänster) visar kvadraterna i de masskuber som
bildas om man adderar dem successivt som 1K, 2K, 3K, …AK. A anger masstalet
eller antalet grundboxar. Figuren ovan t.v. visar kubkvadraterna för A från 1
till 250 i steg om 50. Sambandsformen blir då
AK/K=(Ar03)/r03=A=(A1/3r0)3/r03=(r/r0)3;
r=r0(A)1/3 ....................................... kubgrafen
Sambandet för r är samma som den avgörande approximerade
experimentalkurvan för atomkärnornas radier som har använts som grund för
härledningen till N3m20-aggregatet
(Se Kärnradierna).
r0 är grundradien, samma som neutronradien [Se
PLANCKS
KONSTANT] eller protonradien.
Härledningen
till atomkärnan (separat skrift) bygger på den enkla
elementära ringformen med impulsmomentet J=mvr [PLANCKRINGEN]. Den
aktuella metriska bestämningen av den motsvarande ideala grundringen, eller
toroiden för N3m20, blir
då beroende av experimentella observationer. Massan blir den motsvarande
neutronmassan (obetydligt skild från protonmassan) mn. Elementarformen för v genom GRIP och DEEP blir toppdivergensen c0. Ringradien blir toroidaggregatets grundradie r0. Impulsmomentet J, som
måste vara en universell konstant, blir Plancks
konstant (h). Med hmnc0 kända
beräknas r0=h(mnc0)–1 och man finner r0@1,32 t15 M. Den
experimentellt uppmätta protonradien anges [HOP] som
1,37 t15 M.
Arbetet
I den verkliga fysiken reduceras kubanalogin till en ideal (men viktig)
grundform. Den aktuella sammanslagningen 1K, 2K, 3K, …AK innebär nämligen en ombyggnad
som kräver ett arbete.
Energin för detta måste tas från kärnkomponenterna enligt energilagen via (m→γ)
vilket innebär att resultanten tappar massa, massdefekten (mDEF = mNUKΣNUK – mRES). Därmed är den
ideala kubanalogin bruten.
Detta leder direkt på den motsvarande ideala K-individen; För att denna
ska stämma överens med resultanternas möjliga balanserade dynamik och som
alltså innefattar en viss massdefekt, måste den tydligen själv vara instabil.
Vi identifierar denna K-individ med neutronen. Stabilt tillstånd uppstår först då
den, frånsett massdefekten, avgivit en del av sin massa som elektronen [ELEKTRONMASSANS KOMPONENTER] och därigenom
bildat en atom [ATOMFYSIKEN
TVÅ KUNGSEKVATIONER]. Först då gäller ett stabilt tillstånd.
Stabilitetsvillkoret måste alltså grundas på hela atomen, inte enbart på
kärnan. Därmed förklaras elektronmassan som en symbiotisk del av kärnan och som
med denna bildar den nödvändiga balansen och jämvikten.
Jämför massdefektsbegreppet
i modern akademi: det grundas på
atomkärnan, inte hela atomen, och därmed missas hela poängen: neutronkvadraten som framträder ur atomära
massdefekten;
NEUTRONKVADRATENS FASTA MÖNSTERGEOMETRI leder till de avgörande teoretiska ATOMVIKTERNA;
atomvikterna från neutronkvadraten utklassar, tydligen, grundvalen i den
moderna akademins teoretiska värden (Weizäckerekvationen). Det är på den vägen UniversumsHistoria funnit sin grundläggande förankring: noggrann kärnfysik från
ruta ett. OM det skulle visa sig att något härledande FEL finns i den delen,
faller också hela innehållet.
För att kunna bevara
individerna (K) på jämvikten i massformen med laddning, massa och spinn måste
alltså resultanten till nK ge ut en del av sin egen massa som elektroner.
Därmed kan atomens elektronstruktur med hänsyn till sin moderkärna (atomnumret
eller ”resonansnumret”) härledas ur centralverkan genom impulsmomentet [KEPLERRESONANSERNA]. Det
anmärkningsvärda är att denna härledning, som leder till grundämnenas
periodiska system, dessutom är enkel.
Genom den följande
härledningen till grundämnenas periodiska system finner vi exakt samma
resultat som ges genom den betydligt mera omfattande spektralanalysen med kvanttalen.
Dessa senare innehåller emellertid detaljer som sträcker sig långt utöver
enbart en grundkarta (själva tabellformuläret) till periodiska systemet och kan
därför inte jämföras i någon djupare mening med följande framställning.
2003V25
Kärn-Atombyggnadsalgoritmen
De utvändiga elektronytornas komplexitet och sammansättning växer (kan förstås växa) med
växande kärnmassa.
Om vi tänker oss att det mot varje kärnmassanivå svarar »en specifik
elektronnivå»
så att e-nivåerna växer uppåt-utåt med tyngre kärna
kan vi bilda en dynamiskt beskrivande (mycket enkel) matris som
beskriver hur elektronytorna styrs och kontrolleras av kärnan.
atomens hölje
atomens kärna atomkärnan
utan toppspinn från masstal 2,
nuklidaggregatet
från N3m20
enligt kubgrafen
från J-ringen
mvr
Eftersom hela kärnbyggnaden enligt PASTOM (Principle structure of mass)
är fraktal kommer hölje-kärna-kopplingarna i vilket fall att utspänna en
obegränsad matris vars botten saknar slut. För att förenkla matrisbilden har
den obegränsade kärnfraktaldelen (blått) i ovanstående illustration avslutats
med en antydd kvadratisk oändlighetsindelning. Dess exakta form är här inte
känd ehuru principen framgår.
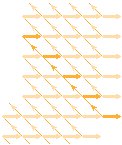
Vartefter kärnmassan ökar, ”elektronscannar” kärnan korrekta
elektronnivåer med exakta massbesättningar:
från lägsta ofyllda resonansyta och uppåt via närmast lägre
resonansgrupp i närmast högre elektronyta, dvs. i enlighet med pilriktningarna
i matrisen; en diagonal i taget, från vänster till höger. När toppen nås längst
upp i diagonalen, börjar scanningen om nerifrån kärnan igen men en
kärnresonansgrupp högre upp. På detta sätt »scannas» hela elektronsystemet av
genom en analog, sekventiell fyllning i varje resonansgrupp när balansen så
kräver.
När kärnan behöver elektronmassa (EC electron capture), bygger
den (kan, tydligen, den
kärnfysikaliska ordningen förstås så att kärnan bygger) om
elektronfyllningen genom att packa besättningarna helt regelmässigt enligt
matrisformen: plocka utifrån och in så att de yttersta delarna samlar sig så
nära kärnan som möjligt.
På samma schema kan en tyngre
kärna fylla elektronytorna inifrån och ut genom att på ovan beskrivet sätt
följa matrisordningen: från lägsta ofyllda elektronytor och uppåt genom närmast
högre ytor via närmast lägre resonansgrupp.
![]()
Atomen-kärnan kan alltså ”i lugn och ro” kontrahera-expandera
regelmässigt bäst den vill genom diagonalriktningen i den dynamiska matrisen,
allt eftersom energibalanserna så kräver. Det finns ett otal exempel på dylika
kontraktioner genom sönderfall från tyngre till lättare kärnor-atomer som visar
hur elektronkonfigurationerna hänger med enligt diagonalalgoritmen. Några
exempel visades i inledningen [REGELINITIERINGEN].
Det enda vi ”ser” av hela scanningssystemet är atomhöljet, alltså
elektronytorna (K, L, M, …).
Höljesfyllningarna i dessa sker alltså (kan förstås ske) sekventiellt med växande kärnmassa
(mellandelarna ej utskrivna) enligt
K2
L2L8
M2M8N2
M2M8M18N2
M2M8M18N2N8
M2M8M18N2N8O2
M2M8M18N2N8N18O2O8
M2M8M18N2N8N18O2O8P2
M2M8M18N2N8N18N32O2O8O18P2P8
osv.
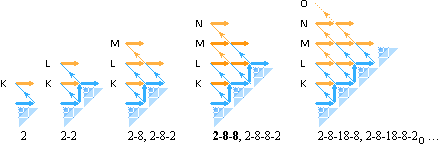
Eller i matrisformen som ovan, direkt med exempel från 2K-8L-8M; 2-8-8-1,
2-8-8-2, 2-8-9-2, 2-8-10-2, … 2-8-18-2, 2-8-18-3,
2-8-18-4, … 2-8-18-8, osv.
Algoritmens generella förklaringsgrund
Genom kärnans elektromekaniska system av verkande krafter i
kärnstrukturen (alltsammans följer i rakt nedstigande led från energilagen
som vattnet man häller ur kärlet matar av luftrummet ner till marken), bildas
analogt ett resonanssystem av Keplermoment
(se inledningen, samt vidare) i nivåytor
som (kan förstås)
ihopkopplas efter en enkel algoritm: håll kärnan-atomen så kompakt
(energisnål) som möjligt — med utgångspunkt från grundkärnans form.
Nivåytorna är, tydligen,
uppdelade i en yttre form (yttre elektronytorna, atomens hölje) och en inre
form, själva atomkärnan.
Nivåytorna i den senare är
optimalt kompakta genom motsvarande ringfraktaler som innesluter kärnans totala
±βn-struktur (β, grek. beta, används
ofta konventionellt som förkortning för elektron-).
Nivåytorna i den förra kan
alltså förstås som de senare utspridda (”uppsplittade”) över mycket stora
områden (i princip från kärnan och utåt obegränsat).
REDAN FRÅN ÅR 1877 upptäckte man grunderna i det här (enkla men
omfattande) massystemet. Eller rättare sagt, man tittade på detaljerna,
men begrep (med den här
framställningens preferenser) icke ett smackum av innehållet. Man
ansåg (1905) i stället att hela frågan handlade om ”egenskaper hos ljusvågorna”
— trots att det fanns åtminstone en viss person [Max Planck] som fattat
vad hela saken handlade om (nämligen han som likt titulaturen för Galilei som
”mekanikens fader” borde kallas ”atomfysikens fader”). Se vidare beskrivning i
senare del PEFECT
(Photoelectric effekt).
Grundämnenas
periodiska system
2003V14
Grundämnenas
periodiska system
Villkoren för resonansverkan [RESONANSVILLKORET] (kan förstås bilda) bildar
grundvalen för dynamiken bakom grundämnenas periodiska system.
Vartefter atomkärnan växer i
massa, bildas en motsvarande dynamisk balans genom kopplingen
kärna-elektronmassa enlig energibindningarna som definierar resonanserna [STÅENDE fasta VÅGMÖNSTER].
Elektronmassan
som svängningsmassa
För att massformen (atomkärnan) som typindivid ska uppvisa stabilitet
krävs att kärnan avger en noga bestämd del av sin massa (elektronen) som en omgivande ”elektrisk
gas”. Dennas stabila dynamik med kärnan, och endast då, bildar genom centralkraftsverkan en jämvikt
eller en energikoppling genom ett konstant universellt impulsmoment (J). Tillsammans med Keplers ytmoment (K=2A/T=v0d) kan det tecknas
J = mK = m(2A/T)
= m2A f
Med uppfattningen att elektronmassan m upptar ytan (2A) ges via
perioden T en resonansverkan i 2A (fasta stabila vågmönster genom en
stor mängd små vibratorer som följer Keplers allmänna ytmoment enligt
centralkraftsverkan). Med variationen av A genom ett heltal n som
kopplar resonansverkan periodiskt genom T för ytan A, och endast då, får man
A=n2
Icke heltaliga n betyder instabilitet i resonanserna och därmed
bruten jämvikt [RESONANSVILLKORET].
Med uppfattningen att
elektronmassans koppling med kärnan kan återföras på en fast, bestämd ytenhet i
A bildar ytan 2A också det numeriska antalet elektronenheter eller elektronkvanta
analogt med totalmassan m fördelad över elektronmassan. Antalet
elektroner (Z) i 2A som bestäms av resonansverkan via T av n blir alltså
Z0=2n2
Ytan hos varje successiv kvadrat (ZKLMNO…) anger numeriskt
det maximala antalet möjliga e-kvanta i atomen enligt uppställningen

Numerisk uppdelning av kvadraturen visar
n2 12 22 32 42 52 … halva
ytan
= 1 4 9 16 25 … ”
= Σ 1 3 5 7 9 … talsummans
udda element
×2= 2 6 10 14 18 … skalgrupperna (resonanskvanta, eller
resonansgrupp)
Σ 2 8 18 32 50 … totala
kvadratytan, antalet elektroner
Med växande kärnmassa växer dess avgivna elektronmassa.
Resonanskvadraterna fylls enhetligt för hela komplexet från lägsta resonansgrupp (2) och minsta ytan utåt och uppåt:
analogt nerifrån och upp, från lägre till högre resonansgrupper, i steg
om en elektron lika med 1 ytenhet, allteftersom ordningen i skalgrupperna 2+6+10+14+18+22+…
inryms i de aktuella kvadraternas successiva totalsumma 2-8-18-32-50-….
Atomens
elektronstruktur
Fyllningen motsvarar uppbyggnaden av de naturliga grundämnena från
lättaste till tyngsta i steg om 1 med en exakt motsvarande elektronkonfiguration
som vi här närmare ska studera. Successionen av enheter (Z) motsvarar
grundämnets atomnummer. Ren mönstergeometri således.
Med villkoret att den sekventiella elektronfyllningen av kvadraterna
från minsta (n=1) till största genomförs från lägre till högre
resonansgrupp 2+6+10+14+18+22+…
kommer fyllningen på varje grupp (vilken som helst, hur som helst, allmänform för hela atomkomplexet) att slutföras
(principform, numeriska uppdelningens 2-6-struktur) enligt ordningen
…2
…2+6
…2+6 + 2
…2+6 + 2+6
…2+6 + 2+6 + 2
…2+6 + 2+6 + 2+6 …
Mönsteraritmetiken för 2-6-strukturen ses enklare
med hela kvadratkomplexet utskrivet enligt
2 2 2 2
6 6 8 2+6
10 2+6
+ 2 18 2+6 + 2+6 +
2
14 2+6
+ 6 32 2+6 + 2+6 +
2+6 + 2+6
18 2+6
+ 2+6 + 2 50 2+6 + 2+6 +
2+6 + 2+6 + 2+6 + 2+6 + 2
22 2+6
+ 2+6 + 6 72 …
Det vill säga: 2-6-strukturen kan, i princip, komponeras
från vilka som helst godtyckliga resonanskvadrater i hela komplexet.
Eftersom 2-gruppen inte innefattas i skalgrupperna ovanför denna, 6+10+14+18…,
kommer stegfyllningen med resonansvillkoret iakttaget att innebära att större kvadrater påbörjas utan att de
mindre ännu är helt fyllda. Med exemplet 2-8-8 givet innebär det att
nästa steg initieras på 2-8-8-1 i stället för på 2-8-9. På samma
sätt har alternativet 2-8-8-3 inte ens en statistisk chans att etablera
sig utan parkerar elektronen helt regelmässigt exakt enligt 2-8-9-2. Först från 2-8-18-2 är det okej
med 2-8-18-3.
Ordningen är som vi ser
utpräglat binär(2)-hexal(6)-oktal(8). Den binära delen kan skrivas 10 med fetnollan som en markör för fylld
2-grupp. Inkluderas 6-gruppen, som därmed fullständigar beskrivningen av
ovanstående fyllnadsserier, blir ordningen oktal. Fetnollan motsvarar då fylld
8-grupp enligt 12345670.
Atomens
resonansmässiga arkitektur, de 7 perioderna
Fyllningen i sekvens av de två första kvadraterna kan då skrivas med
hjälp av binär-hexal-oktalgruppen 1(234567)0, vi kallar den fortsättningsvis oktalgruppen
oktalgruppen skalkonfiguration,
totalt för hela komplexet
10 2 K fullbordad
12345670 2-8 L fullbordad
Fyllningen av den tredje kvadraten kan bara göras på ett sätt i de två
första skalgrupperna, samma som ovan enligt 2-8-1, 2-8-2 och
vidare 2-8-3, … 2-8-8. Oktalgruppen upprepas alltså en gång
12345670 2-8-8 M påbörjad
Med ovannämnda fyllningsvillkor blir nästa steg för att fylla den
ofullbordade M-kvadraten (understruket) 2-8-8 att gå via 2-8-8-2.
Efter 2-8-8-2 fortsätter sedan fyllningen på det ofullbordade 8-skalet i full
enlighet med resonansvillkoret.
Med start från 2-8-8-1,
2-8-8-2, med vidare fortsättning kommer oktalgruppen alltså att bli föremål för
en inbrytning. Efter den fyllda 2-gruppen i L-kvadraten får vi alltså
typformen
12inbrytning345670
Den inbrutna fyllningen kan uttryckas sekventiellt med en separat oktal
ordning som fortsätter från 2:an med (inom parentes) 12(345…812)345670 så att hela sekvensen kan läsas oktalt i
ett sammanhängande sekventiellt led av typen 1234567812345678123…8. Vi måste dock
acceptera att sista 8:an får upprepas flera gånger för att fylla ut luckor, vi
ska strax se hur det ser ut.
Vi får då den fjärde oktala
sekvensen som arbetar på M-fyllningen från läget 2-8-8 enligt sekvenserna
2-8-8-1, 2-8-8-2, och sedan vidare 2-8-9-2, 2-8-10-2,
… 2-8-18-2 med fortsättningen 2-8-18-3, 2-8-18-4, … med
slutresultatet
1239410511612713814815816117218345670 2-8-18-8 M fullbordad, N
påbörjad
De tre åttorna motsvarar de tre grundämnena järn, kobolt och nickel
(ferromagneterna) — exakt elektronkonfiguration — enligt
respektive 2-8-14-2Fe, 2-8-15-2Co, 2-8-16-2Ni. Verkligen.
I den femte perioden gör vi på precis samma sätt: vi börjar från
O-kvadraten 2-8-18-8-1, fyller 2-gruppen längst ut, fortsätter sedan med den
ofullbordade 8-delen, och slutför med en O-oktett. Vi får då exakt samma
sekvens som ovan enligt
1239410511612713814815816117218345670 2-8-18-18-8 M fullbordad, NO påbörjad
Nu blir det spännande. Sjätte perioden kräver nämligen en ny
inbrytning. Den kommer att initieras efter 2:an i gruppen för
inbrytningsoktettens första element, 3:an i 123 och avse
(understruket) 2-8-18-18-8-2. Eftersom denna sekvens måste fylla upp
från 18 till 32 måste vi på samma sätt som tidigare med de tre åttorna fylla ut
luckor enligt typformen
12(345…888123456788812)345670
[Den aktuella sekvensen skulle här bli 12(345678888888123456788812)345670].
För att emellertid inte införa flera komplikationer än nödvändigt ska
vi här förenkla inbrytningen och beteckna dess element genomgående med
inbrytningsindividens siffra, trean, så att vi får typformen
12(333…333333456788812)345670
Vi kan sedan bekvämt associera 3-gruppen till ett separat block efter
12-sekvensen i period 6. Vi ska senare se hur hela paketet ser ut i den galant
enkla sammanställningen.
Vi får då för sjätte perioden totalt
1231932032132232332432532632732832933033133239410511612713814815816117218345670 2-8-18-32-18-8
För sjunde perioden får vi exakt samma sekvens en gång till vilket ger
oss
1231932032132232332432532632732832933033133239410511612713814815816117218345670 2-8-18-32-32-18-8
Avslutning
Här slutar vi. Sjunde perioden är i naturen nämligen ofullbordad. Med
de 92 naturliga grundämnena slutar den teoretiskt
12319320321322 2-8-18-32-22-8-2 KLMN fullbordade, OPQ
påbörjade
Den verkliga konfigurationen för 92:an är (enligt gängse tabeller)
2-8-18-32-21-9-2, alltså samma slutsumma.

21-9 nivån uppför sig som om kärnan snappat åt sig en elektron men inte
förmått avsluta återställningen av ompackningen korrekt i toppen från 21-9 till
den ideala balansens 22-8. 21-9-nivån är alltså ”taskig kommunikation”: atomen
är radioaktiv (Instabil).
Dock har inte alla radioaktiva ämnen en sådan disharmoni (instabiliteten
återspeglas då explicit i kärnnivåerna …).
— De instabila nuklidernas
fysik är (komplicerat) intrikat; de kräver en (ansenlig) volym för sig. Se
vidare från RadioMath.
Med transuranerna inkluderade (93-103, artificiellt producerade
genom högenergifysiken) blir slutdelen
1231932032132232332432532632732832933033133239 2-8-18-32-32-9-2
Av de återstående 15 ämnena i period 7 har nio framställts genom högenergiforskningen
(men de är mycket kortlivade). Den teoretiska slutdelen blir då
1231932032132232332432532632732832933033133239410511612713814815816117218 2-8-18-32-32-18-2
Visst är det jätteenkelt? Nästan som att räkna på fingrarna.
![]()
SAMMANSTÄLLNING
Slutvärdena i ovanstående resultat motsvarar grundämnena i de 7 perioderna

Med perioderna 4-5 som tabellradindex och de övriga perioderna kolumniserade
därefter, 3-grupperna speciellt indragna bakom (i tredje dimensionen) eller
under huvudtabellen, får man den (från slutet av 1800-talet, främst via ryssen
Dimitrij Mendelejev 1869) gängse välkända uppställningen för grundämnenas
kemiska gruppering, det s.k. grundämnenas periodiska system enligt
a b a
123456788812345678 ....................... den klassiska (horisontellt logiska)
gruppindelningen i a och b
GRUNDÄMNENAS
PERIODISKA SYSTEM
resultatsammanställning

NOTERING I konventionell litteratur används (mig
veterligt, frånsett Encarta på artikeln Periodic Table) inte nollan (0) som gruppreferens, den anges i stället med
grupptermen 8a (klassiska) eller 18 (matrisiska) [Se 32BitSYSTEM].
Ädelgaserna var inte alls kända då
Mendelejev 1869 (och Meyer, 1870) påvisade de första reguljära delarna i
periodiska systemet, tre av dem upptäcktes först 1894-1898 (Encarta Periodic
Law) — i sanning en fascinerande historia.
Den ursprungliga tablån för
periodiska systemet grundades på jämförande atomvikter, vilket är naturligt med
tanke på att upptäckterna kom genom kemin. Denna tablåtyp modifierades sedan från
1913 med framgångarna för Bohrs atomteori. Därifrån har tabellen sedan i gängse
referenser (i olika omgångar, successivt) omarbetats med referens till
atomnummer snarare än atomvikt.


INDELNINGEN (traditionellt i konventionell facklitteratur under 1900-talet):
1
alkalimetallerna ............................. grupp1
starkt basiskt reaktiva ämnen — begreppet alkalisk (alkali, av
arabiskans kaljun,, aska) kommer från ämnets förmåga att neutralisera syra.
Ämnena förekommer alltså knappast isolerade i naturen som rena grundämnen, de
reagerar f.ö. (häftigt) med vatten, har stor betydelse för organismerna, både
som gift och medicin.
2
alkaliska
jordartsmetaller ............. grupp2
besläktade med alkalimetallerna (men inte lika reaktiva, dock
tillräckligt för att inte uppträda isolerat i naturen). Exempel är magnesium,
metallen brinner direkt i luft med ett starkt intensivt lysande sken om man
sätter en ljuslåga till metallen, askan blir helt vit.
13
17
icke-metaller ................................... grupp13-17
gemensam benämning för gruppen av gaser (utom ädelgaserna) och fasta
ämnen. De mest framträdande är kol, syre och kväve som är de centrala för
organismerna. De som gränsar till metallavdelningen via trappstegsdiagonalen
kallas (ibland) halvmetaller, vi finner dessa typiskt som halvledarmaterial.
3
sällsynta
jordartsmetaller ............. grupp3
........ lantaniderna och
aktiniderna
generellt starkt paramagnetiska metaller i ringa
förekomster i naturen. De består av grupperna lantanoider (även lantanider) och
aktinoider (även aktinider), den förra har en radioaktiv komponent, den senare
har alla komponenter radioaktiva (periodiska systemets sista och tyngsta ämnen)
Se vidare i Tabellsammanställningarna.
Grundämnenas Periodiska System
innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
INNEHÅLL — Grundämnenas Periodiska System · Keplerrelaterade Periodiska Systemet
Periodiska systemet
ämnesrubriker
GRUNDÄMNENAS PERIODISKA SYSTEM,
sammanställning · SYSTEMET PÅ NÄTET — flera snygga uppställningar finns, men ingen
känner till någon härledning
innehåll
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
BKL, BONNIERS KONVERSATIONSLEXIKON 1922-1929
t för 10–, T för 10+, förenklade exponentbeteckningar
Senast uppdaterade version: 2022-12-28
*END.
Stavningskontrollerat 2008-03-06 | 2012-12-09.
rester
*
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se
∫
√ τ πε ħ UNICODE — often used charcters in
mathematical-technical-scientifical descriptions
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω →∞ →γ ≡ ↔↕ ħ ℓ
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈
≥ ← ↑ → ∞
↓
ζ
ξ
Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25
↓; Alt+26 →; Alt+27 ←; Alt+22 ▬
Alt+23
↨ — also Alt+18 ↕; Alt+29 ↔
Alt+NumPad 0-25, 26-...
☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓
→←∟↔▲▼
!”#$%&’()*+,-./♦812...
PNG-justerad 2011-08-21
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se
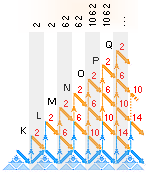 kärnmatrisiska
algoritmen
kärnmatrisiska
algoritmen