UNIVERSUMS HISTORIA — K-CELLENS VÄRMEFYSIK 2008XI16 · a production · Efter sammanställningar från 2004 | Senast uppdaterade version: 2021-07-22 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

K-cellens värmefysik | Utförlig beskrivning med härledningar | 2004V7 MPcNeutronkvadraten.wps | 2004X10 UniversumsHistoria.doc | 2008XI15 i sammanställning för Universums Historia

K-CELLENS VÄRMEFYSIK

UTFÖRLIG BESKRIVNING MED FULLSTÄNDIGA HÄRLEDNINGAR

K-cellens värmefysik — härledningar

HELIUMBILDNINGEN · TEMPERATURSTRÅLNINGEN · RÖDFÖRSKJUTNINGEN

K-cellens värmeeffektutveckling och universums allmänna historia

Inledning

Separat resultatredovisning visas i K-cellens värmefysik tillsammans med en illustrerad kortare beskrivning av vad K-cellens värmefysik går ut på.

Detaljerad resultatredovisning ges enligt nedanstående kalkylkort.

kalkylkortet K-cellen

Kalkylkortet nedan (kan öppnas från webbläsaren om OpenOffice finns installerat, se öppningsmanual om ej redan bekant) innehåller hela K-cellens beräkningsblock. Här kan samtliga parametervärden testas och kontrolleras. Sambanden beskrivs löpande utförligt i den följande texten.

kalkylkort K-cellens värmefysik · öppningsmanual ·

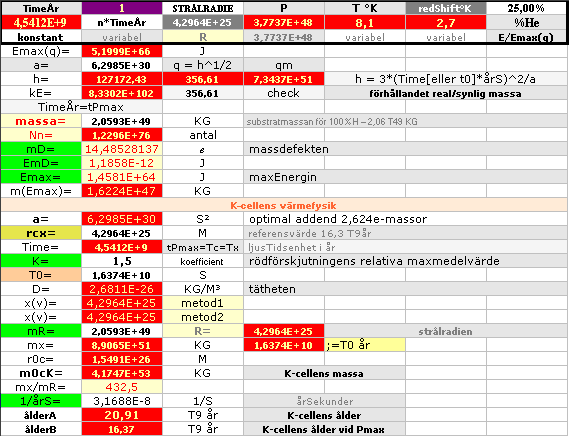
inmatningresultat

K-cellens effektfunktion

HÄRLEDNINGAR

Inledning

K-cellens totala effektutveckling (P=E/T) under expansionsfasen bygger på energiutveckling genom successiv divergenständning. Energiutvecklingen bildar värme och ljus. När hela K-cellen är divergenstriggad, sker ingen ytterligare effektökning. Från denna punkt avtar effekten och planar ut mot noll genom K-cellens begränsade massa och solarnas och stjärnornas begränsade livslängd som värmegivare. K-cellens effektutveckling kan därför liknas vid en lampa som tänds, eller en fyrverkeripjäs som bränns av och som sedan falnar mot ett utslocknande. Med viss kännedom om grafläran, beskrivs en sådan funktion enklast enligt y=x(a+x ²)^–2 med x som tidsvariabeln.

effektkurvan

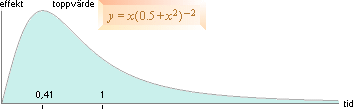
Toppvärdet ges från y-derivatan enligt

y’(0)=tP_max=Ö a/3.

— Om vi spårar typfunktionen för y för att finna eventuella kopplingar med en energihärledning finner vi också en väg.

— Energin är generellt effektens integral (effekten P = E/t; Pt=E som ger varianten dE/dt=P; dE = P dt). [E‡1].

Här skulle den ge

y_E = ò y_P dx = (1/2)[a^–1 – (a+x²)^–1] = (1/2a)[1 – (1+x²/a)^–1].

Vi ser att denna integral är bestämd direkt (se bestämda och obestämda integraler) och gränsvärdet är

E_max=[2a]^–1 då x®¥. Förhållandet mellan energin vid P_max och energin vid E_max är exakt 1/4.

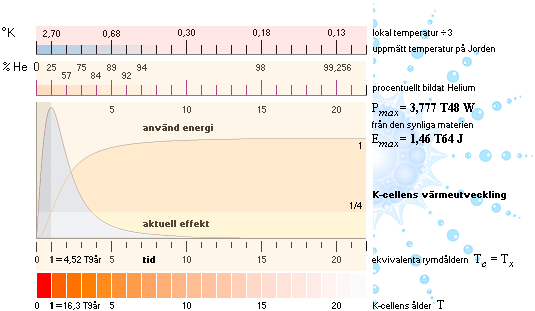
Eftersom värmeutvecklingen i den synliga materien idealt går från grundkapitalet 100% väte till slutstocken 100% helium, avspeglar förhållandet

E_aktuell/E_max i energifunktionen också den genomsnittliga heliumhalten i hela lokalen (energierna förhåller sig som massorna). 25% helium [BAs124sp2n] är också precis (grovt, approximativt; helium anses f.ö. svårt att upptäcka i universum) vad som har uppmätts och observerats som den genomsnittliga heliumhalten i vårt nuvarande synliga universum: funktion och observation överensstämmer. Hur otrolig den detaljen än kan synas, och förutsatt att sambandet kan härledas exakt och återföras på reala fysiska parametrar, är K-cellens totala värmefysik därmed given, och vi har här endast att spåra en härledning på detaljerna med utgångspunkt från givna observationella data.

Vi ser att energifunktionen med x=T beror av en faktor k/T².

Vi ser också att koefficienten a har formen av en kvadrattidskonstant.

Vi betecknar den a=t².

Faktorn k/T² är också precis vad K-cellens effekthistoria handlar om. Energin kan förutom sin effektfunktion E=PT nämligen och just också skrivas på formen

E=k/T² med k=LQ², vilket är huvudet på spiken i hela saken. Vi studerar detta.

Innebörden av LQ² i K-cellens värmefysik — se även förtydligat i Energilagen i relaterad fysik samt från Energilagen i Fysikens 7 Principer

Hur massan och laddningen förintas ömsesidigt — enligt relaterad fysik

MASSDESTRUKTIONENS FULLSTÄNDIGA MATEMATISKA FYSIK — enligt TNED

ENERGI uttrycks i storheterna

E=mad=U·Q=U·IT=PT=RIQ=RT·I²=RT(Q/t)²=LQ²/t² med centralenheterna

KG(M/S²)M=(KG·M²)S^–2=J=WS. Sambandet mellan energi (E) och effekt (P) i elektriska system beräknas generellt genom

E=PT.

I ett system där massa och laddning kontinuerligt förintas, överförs massans inneboende energi [(m®g)] på andra massystem enligt relaterad fysik genom (COEI Conservation of energy by induction, energins bevarande genom induktionen, se COEI)

U_ind=E^=UQ/Q_s=L(di/dt)k=Lk. Massans kvalitativa struktur förintas, men energin bevaras genom en proportionellt växande induktans L med avtagande Q-yta (A), analogt växande L med avtagande m, genom E=LQ²/t² så att LQ²=konstant=L(m/R)(A/dT) bevaras.

Konstanten ger formellt

k = LQ² = L(m/R)(A/dT) = Lm (A/d[RT]) = Lm · (k_RT); (nL)(m/n)=k_Lm.

Laddningen förintas tydligen via sin kvadrat proportionellt mot den med laddningen associerade massan. Därmed tillväxer induktansen så att produkten LQ² hålls konstant. Det betyder att massförstörelsen på Q ändar på rymdinduktansen µs=L=[R₀/c₀]s=[R₀dt/ds](s=ds)=[R₀dt], analogt

([m=0 Û 1/¥]/R)([A=0 Û 1/¥]/dT) = (1/¥)(1/dRT) = 1/RT.

Därmed är den induktiva primärformen i Q återförd på exakt samma allmänna bas som den som används av de omgivande Q-systemen i deras reaktion på den masslöst överförda energin. Hur den tillgängliga energin utnyttjas beror inte på energikällan utan på den mottagande parten (Q_s): dess fysik. (Detaljerna beskrivs f.ö. utomordentligt i PEFECT Photoelectric Effect, fotoelektriska effekten).

Synliga och totala massan

Se utförligt från härledningarna i RESULTAT från mK/mVIZ med värdebeskrivning i mK/mVIZh.

Eftersom K-cellens effektutveckling med omvandlingen Väte-Helium bara utvecklas i den strängt synliga delen av materien, men att effekten av värmeutvecklingen via Plancks konstant omfattar HELA K-cellens massa, bildas en spontan inre »koefficientstyrd matematisk analogi» som i slutänden serverar oss en exakt kvot (den är runt 355) mellan K-cellens totalmassa och dess synliga del. Det är produkten-konstanten LQ² som bär ansvaret för den ordningen. Se vidare utförligt i efterföljande härledningar.

Se även i Den mörka materien — där beskrivs ENLIGT TNED den teoretiska grundaspekt som visar varför bara en liten del av totalmassan är synlig.

KONSTANTEN LQ² innefattar ALLTSÅ hela energikapitalet för massavbränningen (m®g). Men vätemassan 100% vi utgår ifrån i den termonukleära värmeeffektbildningen utgör endast den synliga delen av materien, inte hela den massa som Planckstrålningen är uppbyggd på. Vi kan därför sätta LQ²-konstanten på en form (qq)LQ² med q som numerisk Q-koefficient. (qq)=h kan därmed sättas fritt som en allmän numerisk koefficient vilket ger oss friheten att utveckla LQ² efter dess fysikaliska enheter (KG · M²).

[Se vidare längre fram i Numeriska koefficienten h].

Energihärledningen

Energihärledningen kan därmed göras självständig på följande sätt.

Med k/E=a=t² ser vi att k/a=LQ²/t²=E=konstant.

Energin förbrukas aldrig, den bara omfördelas genom induktionen (L) via massförbränningen (m®g) som ger värmen och ljuset.

Konstanten a ger den OFFSET (associerad med kapitalstocken eller E_max) som energiutvecklingen utgår ifrån.

Med T som den egentliga tidsvariabeln ges tidsfunktionen k/E=a+T² som med T=0 ger a.

Då är E/k=1/(a+T²) och vi har E=k(a+T²)^–1, T för tiden. Vi kan sätta energin direkt negativt eftersom den är massreducerande enligt E=–k(a+T²)^–1. Massförlusten återhämtas sedan av K-cellen i nästa fas genom den tidigare beskrivna allmänna kosmiska tillståndsekvationen. E uttrycker en energiintegral. Den har från T=0 integralkonstanten

E(0)=–k(a+0)^–1=–k/a som måste subtraheras från huvudintegralen så att T=0 ger P&E=0. Därmed integralens bestämda form

E = – k(a+T²)^–1 – –k/a = k[1/a – (a+T²)^–1] = (k/a)[1 – (1+T²/a)^–1].

Och som vi ser är det alldeles samma typfunktion som ges av grafläran.

MAXIMALA ENERGIN (T®¥) är totalt

E_max = (k/a)[1 – 0] = (k/a) = E_G = mw2 = (E_kin) = (mv²/2) = [k_E/2]/a = k_E[2a]^–1 som alltså ger

E_max=(k/a). Med dessa införda beteckningar kan vi skriva

k_E=E_max[2a]=mv²=2E_G. Och vi har

E = E_max[1 – (1+T²/a)^–1].

n(3+n²)^–2 — n-enheten

Med tidsenheten t_Pmax=(a/3)^1/2 från effektgrafen kan T uttryckas i enheter n·t_Pmax via

T=n(a/3)^1/2 enligt E = (3E_max)[1/3 – (3+n²)^–1] med E_max=k/a=k_E[2a]^–1.

EFFEKTFUNKTIONEN fås direkt genom E-derivatan (se Derivata om ej redan bekant)

E’=dE/dT=dE/dnt_Pmax=P.

Deriveringen med avseende på n-enheten enbart ger

dE/dn=Pt_Pmax=P[Ö a/3]=(3E_max)[1/3 – (3+n²)^–1]’=(3E_max)2n(3+n²)^–2=2E_max3n(3+n²)^–2. P-funktionen således

P = 2E_max3[Ö 3/a]n(3+n²)^–2

=2E_max(27/a)^1/2n(3+n²)^–2.

Effektfunktionen kan ställas på ekvivalens med de bägge strålningslagarna Stefan-Boltzmanns strålningslag och Wiens förskjutningslag som sammanhänger intimt med Plancks allmänna strålningslag och som leder till parametrarna i värmebildningen. Stefan-Boltzmanns strålningslag ger ekvivalens med effektfunktionen enligt

P=P₀= a_0,67k_5,7t8A_STRÅLYTANt₀⁴, t för temperaturen här, där strålradien r_x i A kan beräknas med kännedom om den lokala temperaturstrålningen t₀. Tillsammans med Wiens förskjutningslag och den observerade rödförskjutningen (K=1,5) kan därmed den observerade temperaturstrålningen på 2,7 °K kontrolleras.

Se sambanden i sammandrag i slutet.

Numeriska koefficienten h. Om tidsskalan för a optimeras genom en koefficient h ges koefficientformen i P som

(27/a)^1/2=(27 h/ah)^1/2=(Öh) (27/ah)^1/2. h har alltså ingen som helst specifik innebörd för effektsambandet utöver h=1.

BETYDELSEN AV h FÖR ENERGISAMBANDET

Inkluderas den numeriska koefficienten h i uttrycket för t_Pmax ges explicit

t_Pmax=(ah/3)^1/2=T med h=3T²/a. h-värden andra än 1 har alltså bara betydelse för energisambandet, inte för effektsambandet.

h=1 i koefficienten a ger substratmassan eller den synliga massan i effektutvecklingen. T-faktorn som bestämmer h och därmed K-cellens realmassa (^qm) inom strålsfären måste bestämmas separat ur strålradien r_x vid effektmaximum enligt T= r_x(2/c₀)Ö[K² + 1].

r_x i sin tur bestäms explicit ur Stefan-Boltzmanns strålningslag.

Sambanden i sammandrag beskriver sambanden mera komprimerat i slutet av den här genomgången.

Numeriska koefficienten h framgår tydligare i Resultat.

Nedan följer en mera utförligt beskrivande detaljredovisning av ovanstående

— med särskilt indelade sambandsblock.

K-cellens värmefysik | Utförlig beskrivning med härledningar | 2004V7 MPcNeutronkvadraten | 2004V17 INTEGRALER_K-cell.wps | 2008XI15 sammanställning för Universums Historia

Inledning

K-CELLENS VÄRMEUTVECKLING

Med Solen som exempel

SOLEN FÖRBRUKAR MASSA. Massan förintas och dess inneboende energi överförs på andra massor genom värme och ljus enligt

e^– + e⁺ = 0 ................................................... laddning

s_e– + s_e+ = 0 ................................................... spinn (rörelse)

m_e– + m_e+ = 2m_e ............................................... massa

Vilka primära faktorer styr massförintelsen (m®g) som bildar värmen och ljuset?

Det är impulsmoment, induktans och laddning.

Impulsmomentet (J=mvr) grundas på ytmomentet eller Keplermomentet vr (M²/S). Det grundlägger ENLIGT TNED all centralkraftsverkan, i synnerhet den verksam i atomkärnan genom dess allmänna impulsmomentsekvation J_0K+3J_1K=0 (i denna presentation stundtals förenlat »atomens impulsekvation»). Den bygger helt på att atomkärnans tyngdcirkel bevaras.

Induktansen (L=RT) är ENLIGT TNED avgörande för värmets och ljusets (energins) masslösa överföring på andra massor genom

U_ind=E^=UQ/Q_s=L(di/dt)k=Lk (se COEI, energins bevarande genom induktionen) då massans kvalitativa struktur förintas.

Laddningen [Q=Ö (m/R)(A/dT)] är energibasen i den masslösa överföringen av värme och ljus på omgivande fasta Q-system. Detta gäller såväl under massans förintelse i synnerhet som under induktivt överförda moment i allmänhet. Laddningen förintas via sin kvadrat proportionellt mot den med laddningen associerade massan. Därmed tillväxer induktansen så att produkten LQ² hålls konstant. Det betyder att massförstörelsen på Q ändar på rymdinduktansen µs=L=[R₀/c₀]s=[R₀dt/ds](s=ds)=[R₀dt] analogt

([m=0 Û 1/¥]/R)([A=0 Û 1/¥]/dT) = (1/¥)(1/dRT) = 1/RT. Se även Den Mängdoberoende (¥) om ej redan bekant.

Notera att fysiken INTE kan utvecklas EXAKT om man inte känner den mängdoberoende enhetens ställning inom matematiken, ledet närmast ovan m.fl.

Därmed är den induktiva primärformen i Q återförd på exakt samma allmänna bas som den som används av de omgivande Q-systemen i deras reaktion på den masslöst överförda energin. Hur den tillgängliga energin utnyttjas beror inte på energikällan utan på den mottagande parten (Q_s): dess fysik.

Energiutvinningen i allmänhet

NEUTRONMASSAN BILDAR GRUNDEN

Eftersom all energiutvinning grundas på massförintelse (m®g) är det också den fundamentala massform som har massdefekten noll — neutronen — som utgör grundvalen i bildningen av värme och ljus (Planckstrålningen). I härledningen av K-cellens värmeutveckling blir det därför en primär neutronmassa som ska anställas som grund i den matematiska fysiken. Neutronen uppträder emellertid inte (normalt) som en stabil atomkärna, utan det är i stället vätekärnan eller protonen som bildar den synliga materiens fasta preferens.

Enligt gängse beskrivna observationer består den synliga materien av 75% väte, 25% helium med en obetydlig bråkdel (1%) övriga grundämnen. I härledningen av K-cellens värmeutveckling utgår vi därför ifrån en grundmassa 100% Väte vid tidpunkten noll enligt (i strukturkomponenter)

₀N¹ – (m®g) = ₁H¹ som successivt omvandlas till 100% Helium, restväte lika med noll och massdifferensen utgiven som värme och ljus. Energiutgivningen kommer alltså att grundas på massdefekten Neutron-Helium fast vi stundtals mera bekvämt (men något oegentligt) beskriver den på formen Väte-Helium.

allmän utförligt beskrivande noggrant uttömmande härledning

K-cellens värmeutveckling

Den kosmiska massförbränningens totala värmeenergiutveckling

ELEMENT:

ytmomentet K (Kepler), induktansen L och laddningen Q

GRUNDFORM:

E = k/t² ........................ KG · M² · S^–2 = J

a = t²

k = LQ² ....................... KG · M² ;

E = k/a

LADDNINGEN:

Q=Ö (m/R)(A/dT) arbetar momentant och gravitellt punktlokalt under divergensaccelerationen c/dT=a via E=mad=m(c/dT)d=mc² enligt

F=ma · (RA/RA)=m(c/dT)(RA/RA)=Rc(mA/RdT)/A=RcQ²/A=(1/4pe₀)(Q/r)² med A=4pr².

Se mera utförligt från ELEKTRISKA LADDNINGEN.

Konstanten k:

k = LQ² = L(m/R)(A/dT) = Lm (A/d[RT]) = Lm · (k_RT); (nL)(m/n)=k_Lm

;

Om induktansen (L) växer proportionellt med avtagande Q-yta A (k_RT konstant), motsvarande att induktansen växer proportionellt med avtagande Q-massa (k_Lm konstant), bevaras också produkten LQ² konstant=k. Dvs, k ändras inte under massförintelsen (m®g) som utvecklar energin och som överför den masslöst på andra massor genom värme och ljus. Det betyder att massförstörelsen på Q måste sluta på rymdinduktansen µs=L enligt

L = [R₀/c₀]s: med c₀=ds/dt ges

L = [R₀dt/ds]s. Och då s bara kan sluta på ds ges

L = R₀dt; Dynamiken tillhör uppenbarligen tomrummet för divergensens räkning

— vilket betyder: inget annat än gravitation-elektricitet

— i full enlighet med förutsättningarna i Fysikens 7 Principer.

Se särskilt GRIP och DEEP.

KONSTANTEN k=LQ² innefattar hela energikapitalet för massavbränningen (m®g) [se från Allmänna Kosmiska Tillståndsekvationen].

Men vätemassan 100% vi utgår ifrån är INTE HELA den massa som bidrar till Planckstrålningen:

Varför är det klart?

Kallplasmats avgjort största massavyttring ges inte som Väte-Helium — se specialartikeln i Den Mörka Materien om ej redan bekant.

Å andra sidan utgörs (alltså) inte den delen av någon lysande materia. Men den bidrar till temperaturstrålningens uppbyggnad UNDER DEN INITIERANDE HÄFTIGA FUSIONSFASEN (se K-cellens detonation och Himlakropparnas bildningstid) som följer av divergenständningen.

Vi kan därför sätta LQ²-konstanten på en form (qq)LQ² — vilket gör att vi fritt kan framställa (qq)=h som en numerisk koefficient med optionen att LQ² kan utvecklas rent efter sina fysikaliska enheter, respektive KG gånger M². Denna detalj leder i slutänden till bestämningen av kvoten mellan totala och synliga massan (den blir runt 355).

Konstanten a:

IMPULSMOMENTET (J=mvr)

Et = h = m_nc₀r_0n = neutronmassan · toppdivergensen · neutronradien = 6,626 t34 JS, se utförligt från Planckringen

innefattar energin

E = m_nc₀(r_0n/t) = m_n(r_0n/t)² = m_n(r_0n/t)²(r_0n²/r_0n²) = (m_n/r_0n²)(r_0n/t)²(r_0n²)

= (m_n/r_0n²)(r_0n⁴/t²)_konstant = (m_n/r_0n²)(K_{KEPLERMOMENTET})² = (m_n/r_0n²)(M²/S)²

så att vi får

= (m_n/r_0n²)(K)² = h(LQ²)_konstant/t² = k/a = KG · M² · S^–2

h=qq med q=(Öh) fördelas lika på induktans L och ytmoment K

med nyligen införda

a = t²

k = LQ²(Öh) = mA(d1)^–1 (Öh) = E_max t² (Öh) = E_max [a](Öh)

k/a = (m_n/r_0n²)(K)²(Öh)^–1 ..................... fortsättning från sista ledet i stycket ovan

a = r_0n²k · (Öh)(K²m_n)^–1 = r_0n² · (Öh)LQ²(Öh)(K²m_n)^–1 = r_0n² · (Q_n · Q_n^–1) · hLQ²(K²m_n)^–1

= r_0n² · Q_n · Q_n^–1 · hLQ²(K²m_n)^–1 · N_n/N_n

= r_0n² · Q_n · N_n · Q_n^–1 · hLQ²(K²m_nN_n)^–1

= r_0n² · Q_n · N_n · Q_n^–1 · hmA(K²m d1)^–1

= r_0n² · Q_n · N_n · hA(K² dQ_n)^–1

= r_0n² · Q_n · N_n · hA(A²T^–2 dQ_n)^–1

= r_0n² · Q_n · N_n · hT²(A dQ_n)^–1

= r_0n² · Q_n · N_n · hS²(M² dQ_n)^–1

I massförbränningens ljus råder exakt proportionalitet mellan massa och laddning;

Q_n = 1836e_1,602t19 + (k_e=0) ................. k_e varierar beroende på referensverk, högst 2,6 och lägst 0,5 ca

N_n = m/u_{1,66033 t27 KG}/U_1,0086652KG

;

————————

a = r_0n² · (1836e)N_n · hS²(M²dQ_n)^–1

————————

; dQ_n = (1836) dC ;

dC = dÖ (KG/R])(M²/dS)

= dÖ (KG)(M²/d[RS=WS=L=KG M²/C²])

= dÖ (1/d[1/C²])

= dÖ (C²/d1)

= Ö (d1)²(C²/d1)

= Ö dC² = (Öd1) C = (Ö 1/¥) C = (1/¥) C

= dC

Notera att fysiken INTE kan utvecklas EXAKT om man inte känner den mängdoberoende enhetens ställning inom matematiken.

hS²(M² dQ_n)^–1:

Betrakta hLQ²(K²m_nN_n)^–1.

Q² har alltid en ekvivalent som inbegriper en differential enligt Q²=(m/R)(A/dT). Formen

hLQ²(K²m_nN_n)^–1=hS²(M² dQ_n)^–1

är alltså egal genom LQ²=L(m/R)(A/dT)=RT(m/R)(A/dT)=mA/d1.

Energisambandet:

Vi ser att k/a=E=konstant med k/E=a=t²; Energin förbrukas aldrig, den bara omfördelas genom induktionen (L) via massförbränningen (m®g) som ger värmen och ljuset. Konstanten a (se närmast föregående ovan) ger den OFFSET (kapitalstocken eller E_max) som energiutvecklingen utgår ifrån. Med T som den egentliga tidsvariabeln ges tidsfunktionen

k/E = a+T² ; ................................ T=0 ger a ;

E/k = 1/(a+T²) ;

E = k(a+T²)^–1

Vi kan sätta energin direkt negativt eftersom den är massreducerande enligt

E = –k(a+T²)^–1

Massförlusten återhämtas sedan av K-cellen i nästa fas genom allmänna tillståndets ekvation där konstant täthet bevaras för hela klassen (den successiva följden) K-celler. (Se Allmänna Tillståndsekvationen).

Denna energiintegral har från T=0 integralkonstanten

E(0) = –k(a+0)^–1 = –k/a

Den måste subtraheras från huvudintegralen så att T=0 ger P&E=0. Därmed integralens bestämda form

E = – k(a+T²)^–1 – –k/a = k/a – k(a+T²)^–1

= k[1/a – (a+T²)^–1]

————————

E = (k/a)[1 – (1+T²/a)^–1]

————————

MAXIMALA ENERGIN (T®¥):

E_max = (k/a)[1 – 0] = (k/a) = E_G = mw² = (E_kin) = (mv²/2) = [k_E/2]/a = k_E[2a]^–1

;

E_max = (k/a) ................................................................................................................

;

k_E = E_max[2a] = mv² = 2E_G

;

Divergensenergin i E överförs ekvivalent på g-energin mw² som dubbla denna enligt kinetikens friställning från divergensen (dubbleringen av g-massan eliminerar kinetikens inverkan på divergensen). Jämför fallet med divergensnollzonen c=0 i den expanderande K-cellen som ombesörjs av expansionsekvivalenterna

v²+(c=0)²=c₀²=v²; k_E=mc₀². Därmed återförs energin E totalt på idealt g-fritt rum med toppdivergensen c₀ bevarad.

————————

E = E_max[1 – (1+T²/a)^–1]

————————

Effektsambandet:

SAMBAND:

E = Pt

P = E/t

VARIANT:

Effekten är energins variation med avseende på tiden:

P = dE/dT = E’ = d(E)/dT = Dn E ;

E = k/a – k(a+T²)^–1 ............................ energisambandet ;

Dn E = Dn [k/a – k(a+T²)^–1] = [0 – –k(a+T²)^–2(2T)] = 2kT(a+T²)^–2 ;

= P ;

P = 2kT(a+T²)^–2

k = aE_max = k_E/2 ...................... från maximala energin i energisambandet

E_max = k/a = k_E[2a]^–1

k_E = 2E_max[a]

————————

P = k_ET(a+T²)^–2

————————

Effektens toppvärde:

VARIANT:

Toppvärdet (ett eller flera) är nollvärdet (ett eller flera) för funktionens tangensform P’;

SAMBAND:

P = k_E T(a+T²)^–2

TANGENSFORMEN (samma som varianten eller derivatan, konstanter kan alltid inkluderas):

P’/k_E = Dn [T(a+T²)^–2]

= T · Dn(a+T²)^–2 + (a+T²)^–2

= T · (2T)(–2)(a+T²)^–3 + (a+T²)^–2

= –4T²(a+T²)^–3 + (a+T²)^–2 ;

P’(0) = –4T²(a+T²)^–3 + (a+T²)^–2 ;

4T²(a+T²)^–3 = (a+T²)^–2 ;

4T² = (a+T²)³(a+T²)^–2

= a+T² ;

4T²–T² = a ;

3T² = a ;

————————

t_Pmax = (a/3)^1/2

————————

Om en koefficient h associeras med a gäller tydligen

————————

t_Pmax = (ah/3)^1/2

————————

K-cellens värmeutveckling

K-CELLENS MATEMATISKA FYSIK

Energianvändningen vid t_Pmax:

Vi sätter energin vid E(t_Pmax) som toppvärdet Ê (Alt+0202);

T = t_Pmax = (a/3)^1/2 ........................... från P-toppvärdet ; [3T² = a]

E = (k/a)(1 – (1+T²/a)^–1) .................. från energisambandet ;

E_max = (k/a) .............................................. från energisambandet ;

Ê = (k/a)(1 – (1+a/3a)^–1)

= (k/a)(1 – (1+1/3)^–1)

= (k/a)(1 – (3/4)) ;

————————

Ê = (k/a)(1/4) ;

————————

Ê/E_max = (k/a)[1/4]/(k/a) ;

4 = E_max/Ê

Vid tiden t_Pmax för effektmaximum är 1/4 av totala energin omsatt enligt Ê.

K-cellens värmeutveckling

K-CELLENS MATEMATISKA FYSIK

Tidsenheten t_Pmax i energisambandet och effektsambandet:

Med

t_Pmax = (a/3)^1/2

som tidsenhet kan T uttryckas i enheter n·t_Pmax via T=n(a/3)^1/2 enligt

Tidsenheten t_Pmax=(a/3)^1/2 i

ENERGISAMBANDET:

E = (k/a)(1 – (1+T²/a)^–1) .................. från energisambandet ;

= (k/a)[1 – (1+n²/3)^–1]

= (k/a)[1 – 3(3+n²)^–1] ;

————————

E = (3k/a)[1/3 – (3+n²)^–1] ;

————————

E_max = k/a = k_E[2a]^–1 .......................... från energisambandet ;

————————

E = (3E_max)[1/3 – (3+n²)^–1]

————————

Tidsenheten t_Pmax=(a/3)^1/2 i

EFFEKTSAMBANDET:

P = k_ET(a+T²)^–2 ................................ från effektsambandet ;

T(a+ T² )^–2

= T(a+[n(a/3)^1/2]²)^–2

= T(a+n²a/3)^–2

= n(a/3)^1/2(a+n²a/3)^–2

= (a/3)^1/2(a/3)^–2n(3+n²)^–2

= (a/3)^1/2(3/a)²n(3+n²)^–2

= ([3/a]⁴a/3)^1/2n(3+n²)^–2

= (3³a^–3)^1/2n(3+n²)^–2

= (27/a³)^1/2n(3+n²)^–2 ;

————————

P = k_E (27/a³)^1/2 n(3+n²)^–2

————————

k_E = 2E_max[a] ...................... från maximala energin i energisambandet

P = 2E_max[a] (27/a³)^1/2 · n(3+n²)^–2

P(n) = P/n(3+n²)^–2 ;

P(n) = 2E_max (27a²/a³)^1/2

= 2E_max (27/a)^1/2

Om tidsskalan för a (Se Konstanten a) optimeras genom en koefficient h ges

= 2E_max (27 h/ah)^1/2

= 2E_max(Öh) (27/ah)^1/2

= 2E_max(Öh) (27/ah)^1/2;

P = 2E_max(Öh) (27/ah)^1/2n(3+n²)^–2

h har ingen specifik innebörd för effektsambandet utöver h=1.

Resultat:

K-cellens värmeutveckling

K-CELLENS MATEMATISKA FYSIK

Tidsenheten t_Pmax=(a/3)^1/2 i ENERGISAMBANDET och EFFEKTSAMBANDET

h ändrar (eller preciserar) E_max med (Öh) i bevarande av en effektenhetsfunktion.

h har ALLTSÅ ingen explicit betydelse för effektfunktionen.

h får i stället sin betydelse genom energisambandet (se Konstanten k) enligt

k = k_E/2

= E_max[a](Öh) ;

————————

^qE_max = E_max(Öh)

= E_max q ;

q = ^qE_max/E_max ;

mK/mVIZ

q = ^qm/m ............ K-cellens totalmassa dividerat med effektmassan = den synliga massan

————————

t_Pmax = (ah/3)^1/2 = T ;

————————

h = 3T²/a ;

————————

E_maxc^–2 = m ;

E_max(Öh)c^–2 = m(Öh)

m(Öh) = mq

= ^qm

= ^qE_max/c² ;

^qE_max = ^qmc²

T-faktorn som bestämmer h och därmed ^qm måste bestämmas separat.

Innebörden av h

E är den aktuella energi som utvecklas som värme och ljus genom massförintelsen (m®g).

t_Pmax=(ah/3)^1/2 (se tillämpningen på effektsambandet) har ingen specifik innebörd i effektsambandet utöver h=1.

Därav benämningen enhetsfunktion för effektsambandet (P).

Därmed ges den originella egenheten via P-sambandet att t_Pmax(h=1) explicit för P-formen definieras av a-konstanten enligt

t_Pmax= (a/3)^1/2

helt oberoende av h. I energisambandet däremot har h avgörande betydelse liksom t_Pmax=(ah/3)^1/2 har det.

Därmed definieras h som ovan ur effektsambandets enkla tidsenhet t_Pmax=(a/3)^1/2 i kraft av energisambandets specifika tidsenhet

t_Pmax= (ah/3)^1/2

vilket ger att tidsskalorna för bägge sambandsformerna kan ställas på ekvivalenta och analoga former.

Det är (tydligen) denna (lilla) detalj som markerar hela vikten, innebörden och betydelsen av K-cellens matematiska värmefysik

— själva höjdpunkten i kopplingarna.

Observera emellertid (och alltså) att t_Pmax= (a/3)^1/2 är ett meningslöst begrepp för den reella tidsskalan.

Den reella tidsskalans t_Pmax motsvarar hela K-cellens ålder (T) vid effektmaximum. Därmed kan inte

T=t_Pmax beräknas direkt ur a via

t_Pmax= (a/3)^1/2.

T måste i stället beräknas helt separat ur den observerade temperaturstrålningens rödförskjutning via strålradien r

r² = (8[(3t_2,7)⁴(a_0,67k_5,7t84p)])^–1(27/a)^1/2E_max

vid effektmaximum enligt

T = r (2/c₀)Ö[K² + 1] = 16,29216 T9 år

Först därefter kan REELLA h beräknas enligt

h = 3T²/a

(Se efterföljande separat beskrivning, T-faktorn).

Man kan säga att a FÖRST definierar EN OBUNDEN tidpunkt för effektmaximum t_Pmax enligt (a/3)^1/2, h=1, och SEDAN — med mellanräkningar som berör andra delar och som ger ett SPECIFICERAT t_Pmax=T — magnituden h för den massa som Planckstrålningen byggs upp på enligt 3T²/a.

Konstanten a kan alltså PÅ VISST SÄTT sägas styra hela verksamheten enligt föregående härledda

a = r_0n² · (1836e)N_n · hS²(M²dQ_n)^–1

För P har h bara innebörden 1, vilket visar att matematiken på den här nivån — såvitt korrekt fattad — är avancerad. Urgamla hörnstenar.

T-faktorn:

T-faktorn är samma som K-cellens ålder vid effektmaximum analogt med tidsenheten T=(ah/3)^1/2.

T-faktorn kan (veterligt) bara bestämmas ur värdet på den observerade temperaturstrålningen (t=2,7 °K) som innefattar rödförskjutningen (K-sambandet) vid effektmaximum.

Vi kan här fråga oss: Vad i K-cellens historia säger att effektmaximum sammanfaller med den observerade temperaturstrålningen på 2,7 °K?

Frågan kan preciseras på följande sätt:

— Hur kan vi vara säkra på att den temperaturstrålning vi nu iakttar från de mesta avlägset synliga [eg. K-radien] delarna sammanföll med effektmaximum?

— Vi kan vara helt säkra på det av två lika starka och sammanhängande skäl: den nu observerade [BAs124sp2n] heliumhalten på (grovt) 25% tillsammans med effektfunktionens formgraf (P). P-funktionens integral (energifunktionen) ger nämligen en motsvarande exakt heliumförekomst 25% från

^E(t_Pmax)/E_max=1/4 vid P_max, samt att ljuset som transporterande informatör förmedlat den observerade temperaturstrålningen på (avrundat)

2,7 °K via rödförskjutningen K=1,5 hit till Jorden på tiden

t_Pmax=4,52 T9 år över avståndet (max) till de mest avlägset synliga delarna [eg. K-radien]

r_x=4,28 T25 M (strålsfärens ideala radie i effektberäkningen). Effektmaximum gäller vid 25%He, och det är precis (grovt sett) det observerade medelvärdet taget över hela det synliga universum.

Det är alltså »ett sammanträffande» mellan observationella data och en elementär matematisk funktion som beskriver effekt och energi som gör att vi helt säkert kan säga att den temperaturstrålning vi nu iakttar från de mesta avlägset synliga delarna [eg. K-radien] också verkligen sammanföll med effektmaximum.

Denna ”tillfällighet”, hur otrolig den än kan synas, leder också till följande klargörande.

Effektmaximum eller energiomsättningens största häftighet bör vara som störst just då hela K-cellen har passerats av nolldivergenszonen. Det betyder att hela K-cellen i princip då är divergenstriggad (elektromagnetiskt aktiverad) om än inte helt divergenständ eftersom de yttersta delarna fortfarande ligger på c=0. Det innebär att ingen ytterligare massa finns för K-cellens del som kan delta i effektutvecklingen, och den avtar därför i magnitud från denna punkt. Fastställandet av nolldivergenszonens passage ut från K-cellen innebär därför också att hela K-cellens massa fastställs genom de härledda sambanden och funktionerna.

Editor2004VIII2

Förutsättningen med effektmaximum som den informationsbild från de mest avlägset synliga delarna [eg. K-radien] vi nu ser serverar oss en uppsättning data på hela K-cellen inklusive totalmassa. De främsta faktorerna i denna parameterlista är

· ekvivalenta radien (r) av den strålsfär som värmebildningen beräknas på

· K-cellens ålder (T=t_Pmax=Ö ah/3) vid effekttoppen

· reella massan (^qm) och energin (^qE_max) som styr effekten

Med grund i de föregående härledda delarna, med medelvärdet ENLIGT RELATERAD FYSIK av galaxernas rödförskjutning inkluderat

[(1–v_{R 2T8}/c_{0 3T8})^–1=3], samt helt i försorg av uppgiften (ca)

2,7 °K för den isotropiska observerade kosmiska temperaturstrålningen tillsammans med den nu synligt observerade massan

2,05802 T49 KG (efter vätekärnans massa enbart) baserat på uppgiften för medeltätheten

1 väteatom per 10 M³ rymd [BAs381sp2mn] inom radien (grovt)

1000 Mpc eller ca 3 T25 M beräknas ovanstående parametrar enligt nedanstående resultatlista.

K-radien r = 1000 Mpc

Avståndet till de mesta ljussvaga galaxerna är ca 6 miljarder ljusår = 5,67643 T25 M eller ca 1900 Mpc enl. ENCARTA Cosmology, Evolution of the Universe.

Med uppgifterna i 1 och 2 nedan

1. medeltätheten för den synliga materien på 1 väteatom per 10 M³ rymd, r = 1,67 t28 KG/M³ [BAs381sp2mn], och

2. ett uppskattat grovt medelavstånd till de galaxer som motsvarar rödförskjutningens medelvärde [BAs375fig18.14] motsvarande c₀/v=1,5 (K-sambandet)

— med ledning av diagrammet på sidan 378 i BONNIERS ASTRONOMI 1978 som visar avståndet i Mpc till de (då) uppmätta galaxerna som sträcker sig ut till max runt

r = 1000 Mpc = 1000 · 3,0856 T22 M = 3,0856 T25 M = K-radien

— ges

3. den ungefärliga massan inom den synsfären via r=m/V enligt

m = 4prr³/3 = 2,05505 T49 KG — eller mera noga med

r = 1,0078252u_{1,66033 t27 KG} /10M³ = 1,67332 t28 KG/M³ referensmassan (max)

m = 2,05914 t49 KG.

Det antagna värdet på r = 1000 Mpc eller K-radien anger INTE det synliga universum gränsradie, utan den uppskattade radie vid vilken de flest observerade högsta (K=1,5) rödförskjutningarna ligger. Alltså inte helt och hållet allra längst ut (ca 1840 Mpc eller 6 miljarder ljusår enligt ENCARTA 99/2004 Cosmology · Evolution of the Universe med de allra senaste och mest avancerade tekniska mätanordningarna); Universums synliga del sträcker sig ända ut till c=0, vilket betyder att den gränsen aldrig kan observeras exakt. K-radien 1000 Mpc avser endast referensvärdet för motsvarande (uppskattade) K-värdet på 1,5. Vi måste hur som helst utgå ifrån vissa (mer eller mindre grovt) hoftade basdata. Beräkningarna kommer sedan att visa mera extrapolerade data för motsvarande r-värde (nära 1400 Mpc för K=1,5, se nedan).

Se även i Illustrationer till K-sambandet.

Kosmiska bakgrundsstrålningen — K-cellens Planckstrålning

OBSERVATIONSVÄRDET 2,7 °K anges i flera källor. Se exv. ENCARTA 99 Infrared Astronomy, FOCUS MATERIEN 1975 s642sp1mö, UNIVERSUMS FÖDELSE John D. Barrow 1994 Natur och Kultur s23.

———————— basdata

m_s = 2,05802 T49 KG ......................... 100% Väte (eg. neutronmassa), substratmassan m_s i K-cellen

N_n = 1,23 T76 ....................................... antalet neutroner i m_s, = mA/(U·1KG), A=6,02289 T26 = 1/u, U_n=1,0086652u

mD = 14,5e ............................................. ATOMÄRA massdefekten för Helium (motsv. ca 29,6 MeV per bildad He-kärna):

E_mD = 1,18953 t12 J ............................... med mD i Joule

E_max = 1,46 T64 J .................................... = N_n(E_mD), samtliga [₀N¹ – (m®g) ® ₁H¹] till ₂He⁴, restväte=0

a_h=1 = 6,298 T30 S² ................................ = r_0n² · (1836e) · N_n · hS²(M²dQ_n)^–1

————————

l₀ = k_{2,898 t3 M°K}t₀^–1 ......................................... Wiens förskjutningslag ........ M

l/l₀ = (1–v_{R 2T8}/c_{0 3T8})^–1 ........... = 3 = 1/(1–1/K)

K = c/v_x = (c₀/Ö2) Ö w^–2–2c₀^–2 = 1,5

l₀ = k/t₀

l = k/t

l/l₀ = (k/t)/(k/t₀) = t₀/t .......... = 3 ;

t = t₀/3 .............................................................................................................. °K

t = 2,7 °K ;

3t = t₀

P = a_0,67k_5,7t8A_STRÅLYTANt₀⁴ ............ Stefan-Boltzmanns strålningslag ........... W

= 2E_max (27/a)^1/2 n(3+n²)^–2

; n=1 ; P_n=1=P₁ ;

P₁ = (1/8)E_max (27/a)^1/2 ;

3t = t₀ = [P₁(a₀k₅4pr²)^–1]^1/4 = [(P₁/r²)(a₀k₅4p)^–1]^1/4 ;

(3t)⁴ = (P₁/r²)(a₀k₅4p)^–1 ;

P₁/r² = (3t)⁴(a₀k₅4p) = (2,06585 t3) ;

a₁ = 2,06585 t3 = (3t)⁴(a₀k₅4p) ;

P₁/r² = a₁ ;

a₁ = r^–2(1/8)E_max (27/a)^1/2 ;

r^–2 = 8a₁(a/27)^1/2E_max^–1 ;

r² = (8a₁)^–1(27/a)^1/2E_max ; E_max= 1,46 T64 J ; a=6,298 T30 S² ;

————————

r = 4,28 T25 M = 1387 Mpc ;

m_K = 4,174662 T53 KG

————————

T = r (2/c₀)Ö[K² + 1] = 16,29216 T9 år

h = 3T²/a = 126042, q = 355 = Öh

^qE = E_max q ......................................... reella energin

Medelmässiga Rödförskjutningsradien eller K-radien (1000 Mpc) med ledning från K-sambandet och rödförskjutningens medelvärde (K=1,5), samt Väteatomens medelrymd (10 M³) och den uppmätta Planckstrålningen (2,7 °K) är högeligen känsliga för slutvärdet — inga praktiskt mera noggranna värden är kända. Så ändras t.ex. resultatet för K-cellens beräknade totalmassa till

m_K = 4,14391 T53 KG med 2,71 °K. Alternativt en något större Vätekub på 10,5 M³ ger

m_K = 4,124051 T53 KG. Även ett något mindre K-värde (1,48) ändrar resultatet till avrundat 4,14. Och så vidare.

Med värdet 2,73 °K

[John D. Barrow Universums födelse 1994 Natur och Kultur s23]

blir resultatet avrundat

m_K = 4,08 T53 KG.

Medelvärdet baserat på högsta och lägsta (med en maxvärdesextrapolering på 4,18) blir (4,18+4,08)/2 = 4,13.

K-cellens teoretiska massa baserat på separata samband (via Solmassan och Neutronmassan) är till jämförelse

m_K = 4,13816 T53 KG

Se utförlig beskrivning i K-cellens massa från Solmassan och Neutronmassan.

Faktorerna m_s, K och t styr resultaten; den synliga massan, galaxernas expansion, den nu observerade kosmiska temperaturstrålningen.

Upplägget och termernas innebörd förklaras kort i följande Sammandrag.

samband i sammandrag

Ekvivalenta strålytan (samma som den expanderande sfärytan i K-cellen via den synliga massan) växer med massförbränningen enligt LQ²=mA=konstant. Vi skriver här t (tau, Grekiskans t) för temperaturen med t₀ som lokal då vi använder T (och t) son tidsbeteckning.

VÄRMEEFFEKTENS EKVIVALENT är Stefan-Boltzmanns strålningslag enligt

P₀ = a_0,67k_5,7t8A_STRÅLYTANt₀⁴ = k_ET(a+T²)^–2 .......................... W

Temperaturen ges då IDEALT LOKALT (med konstant divergens) ur P från

t₀ = [P₀(a_0,67k_5,7t8A_STRÅLYTAN)]^1/4 ....................................... °K

VÅGLÄNGDEN I TEMPERATURSTRÅLNINGENS MAXIMUM (Planckstrålningens maximum) beräknas enligt Wiens förskjutningslag enligt

l₀ = k_{2,898 t3 M°K}t₀^–1 .................................................................. M

RÖDFÖRSKJUTNINGEN följer som tidigare EKVIVALENTA medelvärdet

l/l₀ = (1–v_{R 2T8}/c_{0 3T8})^–1 = 3

för de mesta avlägset synliga delarna [eg. K-radien] ENLIGT TNED via K-sambandet

K = c/v_x = (c₀/Ö2) Ö w^–2–2c₀^–2

som sammanhänger med bestämningen av ljusvägens integral (Se separat härledning, T_c=T_x).

Med

l₀ = k/t₀

l = k/t

ges alltså

l/l₀ = (1–v_{R 2T8}/c_{0 3T8})^–1 = 3 = (k/t)/(k/t₀) = t₀/t ;

t = t₀/3 ...................................................................................... °K

Strålradien beräknas helt linjärt efter r_x=c₀T_x med T_x=T_c via K-cellens konstanta expansionshastighet för divergensnollzonen enligt

r_x = c₀T_x = (r_0c/T₀)T_x = r_0cT_x/T₀ .............................................. M

som ansluter till A i Stefan-Boltzmanns strålningslag enligt

r_x² = [8(3t_2,7)⁴(a_0,67k_5,7t84p)]^–1(27/a)^1/2E_max.

Konstant c/c₀ bevarar konstant rödförskjutning. Det innebär att K-(medel)värdet på 1,5 är genomgående representativt för ljuset från de mest avlägset synliga delarna [eg. K-radien] helt oberoende av rymdens omfattning — genomgående i hela K-cellens historia.

K-SAMBANDET — se även K-värdet 1,5

v=v_x

w=w_x

;

v_x = w_xÖ2 ................................................................................... ekvivalensen mellan kinetiska och gravitella energin

;

c = c₀ Ö 1 – 2(w/c₀)² ................................................................. Divergensens Expansiva G-beroende

;

c/v = (c₀/wÖ2) Ö 1 – 2(w/c₀)²

;

c/v_x = (c₀/wÖ2) Ö 1 – 2(w/c₀)² = (c₀/Ö2) Ö w^–2–2c₀^–2 = K ;

beskrivning

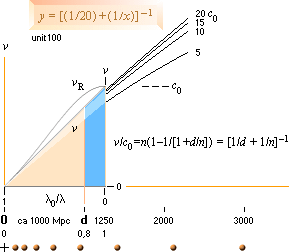
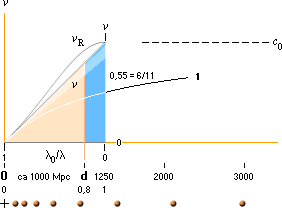
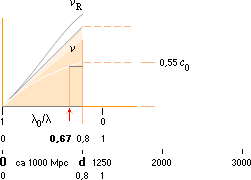
Expansionen v ENLIGT RELATERAD FYSIK blir lägre relativt v_R, se Galaxernas Rödförskjutning. v_R betecknar den moderna akademins värden. Ovanstående illustration, den uppljusade smala delen mellan v_R och v, visar det ungefärliga området där den reducerade galaxexpansionen arbetar. Det avtagande v utpekar ett gränsvärde (som motsvarar K-cellens expansionshastighet i sin ytdel om vi följer galaxobjekten vidare utåt).

Med en övre gräns på 5 [BAs375fig18.14] och ett hoftat medelvärde på 3 för observationerna av våglängdsförhållandet i galaxernas rödförskjutning l₀/l

— motsvarande v/c₀=0,8=1–l₀/l respektive v/c₀=2/3=0,67 som »den medelbaserade dopplergränsen» [K-radien] för vårt synliga universum, grovt 1000 Mpc eller 3 T25 M, notera att den reellt synbara delen sträcker sig (en bra bit) utåt ytterligare — se mera utförligt i K-radien —

— ges ett observationsvärde 1/(l₀/l)=1,5=c₀/v. Vi utnyttjar det observationsvärdet som ett allmänt medelvärde enligt

K = 1,5 ......................... = c₀/v = c/v_x = 1/(1 – l₀/l) = 1/(1–L) = K (se Dopplereffekten i Relaterad Fysik)

med ovanstående kopplingar enligt K-SAMBANDET.

RÖDFÖRSKJUTNINGEN K motsvarar (via c=c₀) inversen till objektets hastighet relativt c₀ i en idealt vilande statisk g-kropp med försumbar divergensreduktion. K-ekvivalentens invers motsvarar alltså analogt den ideala kvoten v/c₀. I RELATERAD FYSIK — ljusutbredningen i givet g-fält är exakt matematisk analog med ljuDutbredningen i stillastående luft, det enda som skiljer är topphastigheten (se Dopplereffekten i Relaterad Fysik) — får man för frånrörelse

lSTÖRSTA/l₀minSTA

l/l₀ = (1–v/c₀)^–1 ............... v = c₀(1 – l₀/l)

som ger värden större än 1,

l den längre våglängden.

I modern akademi [BAs375] — där man anser att ljuset bestämmer över kinetiken — tillämpas i stället

v_R = c(2[1–L²]^–1–1)^–1, L = l₀/l < 1; c=c₀

l/l₀ = Ö (c+v_R)/(c–v_R)

= Ö 1+2/(c/v_R–1)

= 1+z ........................ = 1/(1 – 1/K)

med (c=c₀)

v/v_R = (2 – [1–L²])/(1+L)

= 2/(L+1) + L – 1 ; L=l₀/l, c=c₀

där z benämns rödförskjutningen.

Enligt gängse verk [BAs375 1978] känner man (högst) z=4, motsvarande l/l₀=5 som ger v/c₀=0,8. Antalet av dessa objekt är dock relativt få.

@INTERNET Wikipedia Redshift, Highest redshifts [2012-03-06] ger till nyare jämförelse [34 år senare] den senaste uppgiften (2012) på högst uppmätta galaktiska rödförsljutningen, z=8,6.

Den största andelen ligger runt z=2 som motsvarar v/c₀=0,67. Se även nedanstående kopplande illustrationer (Illustrationer till K-sambandet).

illustrationer till K-sambandet

r = K-radien

|

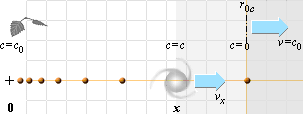neutronkallplasmaområde

r = ([8(3t_2,7)⁴a_0,67k_5,7t84p]^–1[27/a]^1/2E_max)^1/2 = T · c₀/2Ö[K² + 1] = c₀/Ö (8pGr/3)[K² + 1]

a = r_0n² · (1836e)N_n · hS²(M²dQ_n)^–1

Samtidigt som ljuset avancerar från x till 0 med variabel divergens expanderar hela K-cellen. Därmed sker en kontinuerlig divergensökning under x-resan som snabbar upp ljustiden. Matematiken i slutänden visar dock, trots ett komplicerat sammanhang, att man praktiskt taget kan sätta ljustiden för ljusvägen x på den helt enkla formen t=x/c₀. Trots ett förmodat komplicerat ämne blir matematiken helt enkel. Se utförligt i Ljusvägens Integral.

K-värdet 1,5

RÖDFÖRSKJUTNINGEN på K=1,5=c₀/v [eg. c/v_x=c₀/v, se K-SAMBANDET] har sin grund i att v är BETYDLIGT LÄGRE än vad v ser ut att vara i föreställningen att v-objektet existerar i en c₀-lokal.

Den reducerade lokala divergensen c bildar genom c/c₀ den extra kvot som sänker våglängden och ”speedfejkar” v. I slutänden hamnar vi inte på det förmodade v=0,67c₀, utan snarare på v=0,55c₀. GRÄNSVÄRDET med c₀ som utpekas av det reducerade v stämmer f.ö. (tydligen) perfekt med den övriga matematiken. Det utpekar att den yttersta delen i K-cellen expanderar (sammanfaller) med zonsvephastigheten v=c₀. Det betyder sammantaget att universums expansion verkligen befinner sig i ett inbromsande skede (men det sker långsamt), rejält långt ifrån Hubbles förmodade linjära hastighetsökningar. Se även Beräkningen av K-cellens period. ”Hubbles linjäritetslag” innefattas (alltså) »galant» i den matematiska fysiken till hela förklaringen

— Nämligen som en alltför primitiv uppfattning om Nivån på Naturintelligensen: K=1,5=c₀/v.

— De mest avlägsna objekten befinner sig inte i ett c₀-rum utan i ett markant divergensreducerat c-rum. Det är tydligt att vi måste skilja på transportföretag och stjärnkonstruktörer.

Se även mera utförligt från Galaxernas rödförskjutning.

K-cellen | HÄRLEDNINGARNA TILL K-CELLENS VÄRMEFYSIK | T_x = T_c

Ljusvägens integral

LJUSINTEGRALENS FORMULERING

Ljusintegralen är komplicerad. Men komplikationen är enkel att beskriva.

Uppgiften:

Härled ett samband för ljustiden (T_c) från x (lokalen c) till 0 (lokalen c₀).

Använd de härledda sambanden i K-cellen för att utveckla lösningen.

Lösning med diskussion

Uppgiften är komplicerad därför att ALL integration kräver ett bestämt intervall (x) under tillståndets begrepp;

— Men något fast tillstånd över ett x finns inte i K-cellen.

Men så är det ju också med fysiken i alla andra integrala problem; tillståndsändringar sker kontinuerligt över varje metriskt rymdavsnitt, och man måste därför från fall till fall tillgripa olika idealiseringar för att få fram (vettiga) lösningar. Integralformerna inom induktionen och magnetismen är alldeles utmärkta ”basexempel” som visar hur det fungerar i detalj.

Intervallet x är bestämt och ändras inte och ges omedelbart och absolut med givet T. Men varje integrationsintervall x innebär att förutsättningarna ändras: K-cellen expanderar för varje T+t och sönderbryter därmed själva förutsättningen för integrationen. Men vi är tvingade att integrera över ett fast x. ”Räddningen” är att divergenskroppen (ljusutbredningens variationskomplex totalt — för divergensbegreppet, se Divergensen om ej redan bekant) i K-cellen ändras med konstant hastighet. Därmed kan vi LIKVÄL genomföra en »primär integration» över ett fast x där inga tillståndsändringar sker, med en slutlig justering som tar hänsyn till K-cellens samtidiga expansion. Denna medför, som vi vet, att ljustiden över x i den stela ideala formen blir kortare därför att tätheten avtar och därmed gravitationens divergensreducerande inverkan.

lösningen

Ljusintegralen över x i den fixa (frysta) K-cellen

Momentanvärdet vid T₀ för c på x=r från K-centrum ges av c = dx/dt enligt

VARIANTEN: c = dx/dt

= c₀ Ö 1 – 2(w/c₀)² ........................... Divergensens Expansiva G-beroende

= c₀ Ö 1 – x²(2/r_0c)²

= c₀ Ö 1 – x²(2/c₀T₀)² ;

b = (2/c₀T₀)² ;

= c₀ Ö 1 – x²b

Differentialekvationen för divergensändringen c över x i fix K-cell med konstant T=T₀ blir

DIFFERENTIALEKVATIONEN:

dt = dx/c

= (c₀ Ö 1 – x²b)^–1 dx

= c₀^–1(Ö 1 – x²b)^–1 dx

INTEGRALSAMBANDET:

ò dt = c₀^–1 ò (Ö 1 – x²b)^–1 dx

LÖSNINGEN I PREFIXxSIN:

t = ò dt = c₀^–1(1/Öb)acos(xÖb) ..................... PREFIXxSIN

t anger tidsintegralen för ljusvägen x till centrum från en fast punkt i en fast och stel ekvivalent till K-cellen vid en given tidpunkt T₀.

Integralen är direktbestämd genom t(0)=0.

x_max = 1/Öb = r_0c/2

Under ljusvägen x via t har divergensdynamiken i K-cellen reducerats.

Under tiden som ljusvägen utbildas genom x via t i den idealt fixa K-cellen vid T₀ åldras x-rymdsfären med tiden T_x. Den benämns här rymdåldern för x-sfären, och det gäller att

T_x = T₀(x/r_0c) = x/c₀

Ljustiden t i den idealiserade integrallösningen ligger då som en fristående överskjutande del mot T_x, realt innefattas den.

Summan av t och T_x får alltså inte överskrida K-cellens ålder T₀ som ljusintegralens preferens.

Totala ljustiden T_c0 i den fixa K-cellen vid T₀ över ljusvägen x kan då skrivas genom en medelvärdesform. Den garanterar att summan aldrig överskrider T₀ enligt

T_c0 = (t+T_x)/2

= (1/2)(c₀^–1(1/Öb)acos(xÖb) + x/c0)

= (1/2c₀)((1/Öb)acos(xÖb) + x)

Slutsumman

T_c0+T₀ bildar en ny maximaltid (T₀) som utpekar övre maxtidgränsen för K-cellens ålder vid x-resans tidsreella slut.

T_c-vägen x är given av den initierande tidpunkten T₀₁, den ändras inte, men T_c-tiden kommer realt sett att förkortas på grund av den successivt lägre tätheten, analogt svagare gravitationen som följd av T_c0+T₀₁. Denna tidssumma kommer alltså att skjuta över målet liksom föregående missade åt andra hållet. Lösningen ska alltså — om inga missgrepp har gjorts — ligga mellan de skilda tiderna genom ett nytt, slutligt T₀-värde enligt

T₀ := (T₀+T_c)/2 ................................... aritmetiska medelvärdet

T₀ := Ö T₀[T_c+T₀] ............................... geometriska medelvärdet

Geometriska medelvärdet är alltid något (marginellt) lägre än aritmetiska.

Eftersom funktionen (tydligen) kan återföras på typen iterativa ekvivalenter (med reservation för feltolkning), kan vi välja geometriska medelvärdet för beräkningen av den slutliga b-faktorn. Detta kommer att optimera ljustiden mot ett maximum (aritmetiska medelvärdet kommer att ge en något kortare ljustid).

T₀₁ = Ö T₀[T_c+T₀] .............................. geometriska medelvärdet

b-faktorn och ljustiden över x blir alltså med dessa förutsättningar slutligt

b = (2/c₀T₀₁)²

= (2/c₀[T₀(T_c+T₀)])² ;

T_c1 = (1/2c₀)[(1/Öb)acos(xÖb) + x]

K-CELLENS ÅLDER vid ljusresans slut över x framgår därmed explicit som

T = T₀+T_c1

Resultat: T_c1/T_x = 1

LJUSINTEGRALEN för T_c1 (med referens till K-sambandet och K-värdet 1,5 som grundexempel) visar sig praktiskt taget identisk med den tidigare nämnda och helt enkla rymdåldern T_x=x/c₀. Skillnaden ligger i 16:e decimalen, och den figuren har ingen som helst praktisk signifikans.

Men när vi nu vet vilka hemligheter som denna enkla praktiska ekvivalent gömmer, blir det enklare att betrakta innehållet med viss tillbörlig respekt.

För vidare presentationer kan vi alltså sätta det helt enkla

T_c = T_x = x/c₀

ENERGILAGEN I RELATERAD FYSIK — se även Energilagens grundform från Fysikens 7 Principer

Energilagen — i relaterad fysik

ENERGILAGEN

RÖRELSENS PRINCIP [POM (Principle of motion): det är omöjligt att få fram en kraft utan att utgå ifrån något som redan befinner sig i rörelse; impulsen föregår kraften]

grundlägger energilagen [intervallets oförstörbarhet]. Ett intervall måste finnas för att kunna påvisa en rörelse; kraften förutsätter rörelsen; intervallet är vilket som helst Dd med optimal variation a=dv/dt. Eftersom intervallet är oförstörbart (APARC Absolute physical reference), så är också rörelsen (a_0tilld ), och därmed energin: energi kan varken skapas eller förintas utan måste förutsättas. Energilagens 2 huvudsatser:

POM1: m i a=am/m=F/m kan inte skapas eller bildas därför att a i m=ma/a=F/a måste förutsättas ............. m kan inte skapas

POM2: m i a=am/m=F/m kan förintas genom att a i m=ma/a=F/a är oförstörbar ........................................ m kan förintas

I det senare fallet flyttas a endast över på andra massor (värme, ljus) utan hjälp av någon transporterande massa (induktionsverkan [COEI Conservation of energy by induction]). varigenom energin bevaras (Jämför Solen). Massan förintas (m®g) och med den dess gravitation, laddning och elektriska fält. Se även mera fördjupat i MASSDESTRUKTIONEN (m®g) — annihilationsstrålningens grunder. Den kan alltså sedan inte återskapas därför att a i den måste förutsättas. Möjligheten att skapa eller bilda m genom a är alltså utesluten genom att det inte finns någon bindning mellan a och m; a kan frigöras ur m, a kan överföras på m men m kan varken frigöras ur a eller överföras på a och därmed heller inte skapas eller bildas av a.

Massdestruktionen (m®g) [Se även Divergensenergi E=mc²] kan bara återföras på lokaler där energin kan påvisas, analogt där det finns en vägbar, mätbar g-massa > 0.

Eftersom varje g-massa > 0 är självmotsägande i en förmodad självdestruktion, som innebär att ett värde större än noll inte kan realiseras, krävs uppenbarligen minst två distinkt skilda g-massor K1>0 och K2>0 för att en massdestruktion ska kunna realiseras. För att bilda produkten K, tillfälligt eller stadigvarande, analogt utföra en ändring i tillståndet, krävs ett arbete (m®g) vars enda energikälla bara kan vara de bägge g-massorna. Skillnaden mellan summan av komponenternas g-massor (K1+K2) och produktens (K) definierar kärnreaktionslagen och utgör alltså arbetet eller massdestruktionen (m®g) som åtgår för föreningen enligt

K1+K2 – (m®g) = K ....................................................................... kärnreaktionslagen

där K >0.

Omedelbar konsekvens:

Eftersom massa inte kan skapas, är elektronen (avdelas ur atomkärnan [NEUTRONENS SÖNDERFALL]) en fundamental beståndsdel i atomkärnan (på samma sätt som vattendroppar kan avdelas ur en större vattenmassa, och sedan åter förena sig med denna utan att ändå ses som fristående partiklar inuti):

BILDKÄLLOR: Författarens arkiv — 5Jul2012 E15 Bild144/138 · Nikon D90 · Detalj — STRANDVÅGOR bryts periodiskt mot en sten och bildar rekyler som bryts upp i mindre fristående vattendroppar, som strax återförenas med modermassan.

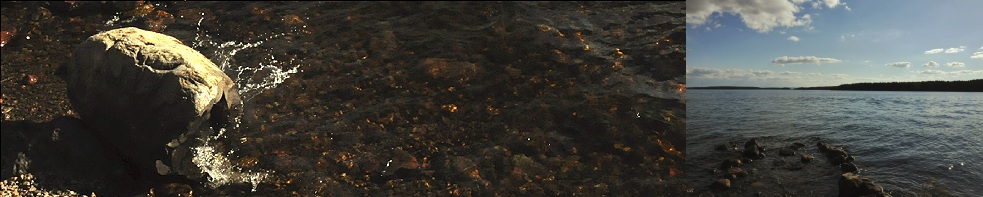
NATUREN illustrerar sig själv i PRINCIPER.

Jämför — neutronsönderfallet i komponenter

RELATERAD FYSIK:

S_P+S_e S_P + S_e + 0 ¬ summa inre ringspinn

₀n¹ ® ₁H¹+ e^– + (m®g) ............................ massekvivalenten

₀n¹ ® ₁H¹+ e^– + (m®g) ............................ energiekvivalenten

n_t = p_t + e_t ....................................................... t-ringströmmens spinnekvivalent

0 1/2 –1/2 ...................................................... summan av alla spinn och moment är noll

MODERN AKADEMI:

1/2 1/2 +1/2 + 1/2 ¬ ”summa spinn”

₀n¹ ® ₁H¹+ e^– + (m®n) ............................ ”energiekvivalenten”

Den konventionella uppfattningen om fysiken har ingen jämförande referens med TNED (två skilda världar);

Den konventionella uppfattningen om ”spinn” blir särskilt obskyr eftersom man rent allmänt inte erkänner någon åskådlig BILD av atomkärnan, men likväl tvingas associera till en sådan på grund av vektorbegreppen (Jämför Spinnbegreppet i modern akademi). Vilket vill säga; atomkärnan [PLANCKRINGEN] kan varken beskrivas, härledas eller förklaras genom den moderna akademins lärosystem.

Se mera utförligt från Planckringen — atomkärnans härledning.

Se även i Spinnbegreppet i modern akademi.

K-cellen | HÄRLEDNINGARNA TILL K-CELLENS VÄRMEFYSIK

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

K-cellen

ämnesrubriker

innehåll

K-CELLES VÄRMEFYSIK | HÄRLEDNINGAR

Inledning

Kalkylkortet K-cellen

K-cellens effektfunktion

Inledning

Effektkurvan

Innebörden av LQ² i K-cellens värmefysik

Synliga och totala massan

Energihärledningen

nEnheten

Numeriska koefficienten h

K-cellens värmeutveckling

Inledning

Energiutvinningen i allmänhet

K-cellens värmeutveckling

Konstanten a i energiledet

konstanten k

konstanten a

Energisambandet

Effektsambandet

Effektens toppvärde

Energianvändningen vid tPmax

Tidsenheten tPmax

Resultat

Tidsenheten tPmax=(a/3)^1/2 i ENERGISAMBANDET och EFFEKTSAMBANDET

mK/mVIZ = 355/1

Innebörden av h

T-faktorn

K-radien

Kosmiska bakgrundsstrålningen

Synliga massans andel i K-cellen, 1/355

Sambanden i sammandrag

K-SAMBANDET

Beskrivning

Illustrationer till K-sambandet

K-radien — illustration till K-sambandet

K-värdet 1,5

Ljusvägens integral

Härledning

ENERGILAGEN I RELATERAD FYSIK

Massdestruktionen

Kärnreaktionslagen

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[BA]. BONNIERS ASTRONOMI 1978

— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.

[FM]. FOCUS MATERIEN 1975

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2021-07-22

*END.

Stavningskontrollerat 2008-11-16.

rester

*

PNG-justerad 2011-06-25

åter till portalsidan · portalsidan är www.UniversumsHistoria.se