ELEKTRISKA LADDNINGEN | 2007XI6 · a ![]() production |
Senast
uppdaterade version: 2024-09-09 · Universums Historia
production |
Senast
uppdaterade version: 2024-09-09 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

 Q = Ö (m/R)(A/dT) kan inte härledas av modern akademi
Q = Ö (m/R)(A/dT) kan inte härledas av modern akademi
TILLÄMPNINGSEXEMPEL DIFFERENTIALBEGREPPET I RELATERAD FYSIK:
I fortsättning från Atomtriangeln
Accelerationsbegreppet används i denna artikel som kärnform och beskrivs
kortfattat nedan. För en mera grundlig genomgång, se accelerationsbegreppet.
LJUSBRYTNINGEN I VATTEN — LJUSETS GRUNDLÄGGANDE NATUR — ett utomordentligt
TILLÄMPNINGSEXEMPEL PÅ DIFFERENTIALENS BETYDELSE I RELATERAD FYSIK
som leder direkt på fysikens hjärta: ELEKTRISKA LADDNINGEN. Vi studerar hur.
elektriska laddningens härledning genom
LJUSETS GRUNDLÄGGANDE FYSIK
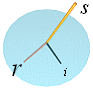
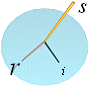
s = strå;
i = bild (image) reflekterad av vattenytan;
r = bruten (refrakterad) bild under vattenytan
Ljushastigheten (c) är ändlig. Bevis: Vi vet redan att ljusets utbredningshastighet är ändlig (runt 3 T8 M/S). Det är emellertid här viktigt med ett grundligt logiskt klarläggande från direkta enkla naturobservationer — OM sådana finns — som verkligen kan övertyga oss om att ljusets utbredningshastighet ÄR ändlig. Vi studerar för ändamålet som ovan en bild av ett grässtrå i vattnet invid sjökanten. Vi betecknar konstant hastighet generellt med v=d/T (distans genom tid), acceleration med a=v/T, ljushastigheten speciellt med c, samt tillämpar ideal geometri (med förebild från kristallhörnet i nollformsalgebran).
ANTA c=v=¥. Då är rörelsemängden mv via varje massassociation med c också oändlig enligt mv=m¥=¥; Ty, även om vi sätter m på differentialformen dm så att m¥ motsvarar dm¥=(m/¥)¥=m får vi (alltså, beroende på preferens) en bestämd ändlig men, om vi så vill, hur stor massa m som helst i slutresultatet; för att ändra riktningen i c=v=¥ skulle därmed i princip krävas av vattnet att det utgör en oändligt tät, kompakt och massiv kropp (w) med i princip obegränsad massa. Eftersom vi nu vet att en sådan uppenbarligen inte föreligger i ljusvägen, är enda enkla förklaringen till brytningen sr att c inte är oändligt och elementen i w som bär ansvaret för riktningsändringen därmed också mycket små. Vilket skulle bevisas. Därmed till huvudsaken.
Från den intervallösa brytningen sr är det uppenbart att c-ändringen över sr eller accelerationen a=dv/dT över brytpunkten där ljuset ändrar riktning (kristallhörnet) INTE bestäms av något intervall utan av ett tillstånd; Brytningen sr sker abrupt och direkt genom brytpunkten (ds), utan hjälp av något intervall. Differentialen dv i ändringen a=dv/dT påtvingas alltså dv=c i brytpunkten ds; ljusets optiska acceleration genom ds motsvarar en ljusets absoluta acceleration där, enligt
a=c/dT
Därmed är det tydligt att vi måste skilja mellan
·
ljusets divergens,
hastigheten (tillståndet) c i punkten ds; ..................... divergensen bildas inte över intervall
·
LJUSETS HASTIGHET,
medelvärdet över intervall (c=Ds/DT); ............ ljushastigheten
bildas över intervall
Direkt konsekvens: Arbete (energin, E) i fysiken skrivs E=Fd=mad som produkten av kraft (F) och väg (d) med F=ma. Vi insätter a=c/dT och får i differentialer direkt ekvivalenterna
dE = dF·ds = dma·ds = dm(c/dT)ds = dmc(ds/dT) = dmc2 = divergensenergin
Över ändliga intervall med konstant c är således divergensenergin lika med
E
= mc2
................................................... divergensenergin över intervall med
samma c
Med upptäckten (1900) av den universella impulsmomentskonstanten h=mcr=mccT=mc2/f = E/f med h som Plancks konstant 6,62559 t34 JS, eller det universella verkanskvantumet, ges
Sambandet E=hf tillskrivs (vanligtvis, utan referenser) Albert Einstein i samband med dennes teori om den fotoelektriska effekten. Men med referens till olika webbkällor (2008VII7), verkar trots allt Max Planck själv vara portalfiguren till sambandsformen E=hf, i varje fall i dess grundform. Se exv.
@INTERNET Wikipedia Planck's law 2008-07-07, samt
THE ORIGINS OF THE QUANTUM THEORY by Cathryn Carsson
[http://www.slac.stanford.edu/pubs/beamline/30/2/30-2-carson.pdf].
Även George Gamow i boken TRETTIO ÅR SOM SKAKADE FYSIKEN, Prisma 1968 (s32) beskriver sambandsformen E=hf i ljuset av ”Plancks antagande att energiinnehållet i ett strålningskvantum är proportionellt mot frekvensen”.
Från LJUSETS ABSOLUTA ACCELERATION med c i ds följer också direkt LJUSETS FRISTÄLLNING FRÅN KINETIKEN:
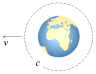
LJUSETS FRISTÄLLNING FRÅN KINETIKEN
divergensens frihetssats
divergensen c kopplar inte till kinetiken: c och v
adderas inte
(kinetiken berör åkande partiklar som utvecklar inbördes additiva hastigheter och centrifugalkrafter); LJUSETS ABSOLUTA ACCELERATION a=c/dT med adT=c bestäms av tillstånd i tomrummets gravitellt relaterade rymdpunkter (genom inverkan av massa eller gravitation, se nedan), inte av rörelse. Vilket betyder: ljus c och mekanik v adderas inte. Se även KAUSALSAMBANDET i Magnetismen. Ljusets fysik betingas tydligen av ett tomrummets fundamentala masslöshet. Se även DEEP i Fysikens 7 Principer.
Se även
Experimentella bekräftelser på riktigheten i den relaterade fysikens och matematikens härledda begrepp
EXPERIMENTELLA BEKRÄFTELSER PÅ LJUSETS FRISTÄLLNING FRÅN KINETIKEN
M&M:s experiment, uppdagandet av v+ic-felet
Fortsättning från Ljusets grundläggande fysik
grundform
KRAFTLAGEN F=ma följer direkt ur accelerationen (a=dv/dT) genom substitution med massa (m) enligt a=a=ma/m =F/m som ger kraftlagen F=ma.
Från kraftlagen F=ma följer också grundformen för ljusets gravitella beroende explicit:
c bestäms av gravitationen
Från F=ma=m(v/T) följer v=F(T/m)=c. I direkta differentialer c=Fc(dT/dm): minsta m ger en största divergens c som toppdivergensen c0. Då är c0=Fc0(dT/dm) med F c0= konstant; c avtar med växande massa m i c=Fc0 (dT/dm). Fastän denna form inte är fullständig, visar den ändå principen: divergensen c, tillståndet i ds, beror på massa = gravitation.
Se den utförliga formen i KRAFTVEKTORLEDET i LJUSETS GRAVITELLA BEROENDE.
Se även
Experimentella bekräftelser på riktigheten i den relaterade fysikens och matematikens härledda begrepp
EXPERIMENTELLA BEKRÄFTELSER PÅ LJUSETS FRISTÄLLNING FRÅN
KINETIKEN
M&M:s experiment, uppdagandet av v+ic-felet
ABERRATIONEN från James Bradley 1725
Ljusvägens gravitella beroende
genom olika lokalt dominanta g-system med inbördes lägesändringar
Fortsättning från Ljusets grundläggande fysik
Från LJUSETS ABSOLUTA ACCELERATION följer sedan vidare klarläggandet av gravitationens verkningssätt som avgörande för ljusets fysik; gravitationens avgörande fysikaliska absolutverkan, och som har varit föremål för så djupa diskussioner genom fysikens utveckling ända från Isaac Newtons tid (inte minst från Newton själv):
För att rent matematisk förklara den givande faktorn (gravitationen) bakom det ändliga v=c i divergensen via absolutaccelerationen
a=c/dT=dv/dT
är det tydligt att ursprungsformen (v) måste skrivas på den mängdoberoendes form, analogt motsvarande ”oändligt” i dv=v/¥ ovan enligt
(v=¥)/¥=d(v=¥)=(v=c) = ändlig hastighet.
Detta skulle alltså innebära att gravitationens inverkan är tidsabsolut (v=¥), helt oberoende av avstånden mellan kropparna; det enda som hindrar kropparna från att falla in mot varandra omedelbart är trögheten: motståndet mot tillståndsändring, eller rudimentärt kraftlagen F=ma.
GRAVITATIONENS ABSOLUTVERKAN framgår också oberoende i konvergensprincipen, se GRIP:
Lika för all materia, kan inte skärmas ifrån; oberoende av tid
Elektriska laddningen
ELEKTRISKA KRAFTLAGEN MED
ELEKTRISKA LADDNINGEN
Resultatet i slutänden leder
direkt på divergenskraften
eller elektriska kraftlagen med elektriska laddningen (Q) enligt
följande:
Absolutaccelerationen (c/dT) resulterar enligt ändringslagarna i en motverkan (här principiellt samma som Newtons tredje lag, se utförligt i atomtriangeln) som bildar ett divergensmotstånd (R). R-formen bildar grunden för induktionen och magnetismen och beskrivs särskilt i Rymdinduktansen för vakuum. Se även från Induktionen och Magnetismen.
Elektriska
Laddningen forts.
ELEKTRISKA LADDNINGENS HÄRLEDNING
Fortsättning från Ljusets grundläggande fysik
För att relatera rymdmotståndet (R) till divergensen (c) med
divergenskraften (F=ma=mc/dT, se nedan) måste en genomträngningsyta (A) finnas. Vi får dessa delar genom att i kraftlagen F=ma substituera motståndet och genomträngningsytan enligt leden nedan som ger oss divergenskraften eller med samma innebörd elektriska kraftlagen
F = ma = m(c/dT) = m(c/dT)(RA)/(RA)
= Rc(m/R)(A/dT)/A = Rc(Q/r)2 | Med sfärytan A= 4pr2 och Rc=1/e skrivs F ofta F = (1/4pe)Q1Q2/r2
med F i Newton (KG · M/S2), och
elektriska laddningen i Coulomb (C),
Q = Ö (m/R)(A/dT)
I boken UPPTÄCKTEN AV ELEKTRONEN,
David L. Anderson, Aldus 1966, ges en spännande CaseHistory-berättelse om i
stort sett hela 1800-talets dramatiska vetenskapshistoria med upptäckten av
elektronen och dess elektriska laddning i formen av den s.k.
elektriska elementarladdningen
Q(e) =1,602 t19 C
Den avgörande metoden för
elektronladdningens bestämning med hjälp av mikroskopiska mineraloljedroppar i
stället för vattendroppar utfördes av R. A. Millikan från 1906. Dåvarande
mätningar (Millikans tabell) gav värdet 1,592 ± 0,002 t19 C.
Mätningarna slutfördes år 1916 med
extrapolationen ± 0,0017 då precisionen inte kunde föras längre.
Fjorton år senare, år 1930, letade fysikern
J. A. Bearden efter fel i en kristall som hade använts vid röntgendiffraktion
då resultatet inte stämde med grunddata. Bearden hade i själva verket inte
gjort något fel utan istället utgått ifrån Q(e)-värdet 1,592 t19 C.
Samtidigt, omkring 1930, utförde A. H.
Compton liknande undersökningar via röntgendiffraktion. Compton och Beardens
resultaten visade samstämmighet och med dessa resultat skulle elektriska
elementarladdning Q(e) i själva verket vara 1,603 ± 0,001 t19C.
Vid samma tid, år 1932, framkastade den
japanske fysikern Shiba tanken om att ett systematiskt fel hade begåtts via
värdet för luftens viskositet. År 1937 genomförde Millikans kollega, Houston,
en noggrann mätning av luftens viskositet och fann en tidigare försummad
korrektionsfaktor. Med denna insatt i Millikans beräkningar gavs nu samstämmiga
resultat med Comptons och Beardens mätningar. År 1938 betraktades hela
mysteriet löst och problemet ansågs slutligt förklarat.
Nuvarande värde för elektriska
elementarladdningen, analogt elektronmassans laddning Q(e) är som ovan 1,602
t19 C [ref. FOCUS MATERIEN 1975 s666].
Koefficienten Rc (=1/e) kallas elektriska konstanten. Den beskrivs utförligt i Uppkomsten av Induktionen och Magnetismen.
|
|
Vi ser omedelbart att Q urartar med ändligt T, ty Q2 = (m/R)(A/T) = (m/R)(r2/T) = (m/R)(rc); med fast värde för mRc ändras Q med r, vilket vi vet inte gäller i fysiken: Q är konstant med konstant massa (m), rymdmotstånd (R) och divergens (c). m och R kan ändras proportionellt med konstant Q. |
Villkoret för giltigheten av Q är
alltså dT.
Annars havererar fysiken.
För induktionen och magnetismen, se utförligt illustrerad beskrivning från Induktionen och magnetismen.
Fortsättning från Ljusets grundläggande fysik
Modern akademi känner UPPENBARLIGEN bara kvantiteten Q —
inte det kvalitativa innehållet:
Q = Ö (m/R)(A/dT) som sådan tycks vara
formellt helt
okänd i modern akademi
Anledning: dT. dTi Q kan inte härledas av den moderna akademins
begreppssystem: man sätter dT=DT: Modern akademi gör ingen skillnad mellan differential (dT, aktuella fysiska laddningen) och differens (DT oändlig laddning motsvarande obegränsat avstånd r från laddningens centrum). Jämför den moderna
uppfattningen om elektronen som anses kunna ha noll utsträckning och samtidigt oändlig
massa.
”Experiments in which electrons are scattered by other particles,
however, effectively measure the size of the electron, and they indicate that
the radius must be exceedingly small. Indeed, all experimental data gathered so
far are consistent with the idea that the electron is a point particle,
entirely without extension.”
”In the 1940’s
these problems were resolved by abandoning the mechanical model of the electron
and devising a new and more abstract theory, quantum electrodynamics. In
quantum electrodynamics the electron is allowed to be a dimensionless point
particle and its mass is allowed to be infinite, at least in principle.”
SCIENTIFIC AMERICAN
August 1980 The Isolated Electron s92sp2
Min
översättning:
Experiment
i vilka elektroner sprids av andra partiklar, emellertid, mäter effektivt
elektronens storlek, och de indikerar att radien måste vara ypperligt liten.
Verkligen, alla experimentella data samlade hittills är samstämmiga med
uppfattningen att elektronen är en punktpartikel, helt utan utsträckning.
Under
1940-talet löstes dessa problem genom att bannlysa elektronens mekaniska modell
med hänvisning till en ny och mera abstrakt teori, kvantelektrodynamiken. I
kvantelektrodynamiken tillåts elektronen vara en dimensionslös punktpartikel
och dess massa tillåts vara oändlig, åtminstone i princip.
Se
även i citat.

Därmed
GcQ-teoremet:
GcQ-teoremet
Den praktiska giltigheten av den elektriska
laddningens fysik Q=Ö (m/R)(A/dT) genom den ändliga ljushastigheten c
garanteras av den absolutverkande gravitationen (G).
Som ovan: (v=¥)/¥=d(v=¥)=(v=c) =
ändlig hastighet c i a=c/dT=dv/dT
Beviset är alltså: Q.
Genom gravitationens absolutverkan, se GcQ-teoremet ovan, framgår universella individkriteriet eller mera allmänt (elektrogravitella) superpositionsprincipen enligt följande:


· Varje kropp har och bibehåller sitt eget särskilda g-fält F=G(m/r)2, oberoende av samverkan och interferens med andra kroppar (superpositionsprincipen);
· På kroppens g-system är upphängt kroppens divergenssystem (c) som innebär att ljushastigheten c varierar lokalt med avståndet till tyngdpunkten/ytan, eller med samma mening kroppens elektriska fält då elektrisk laddning (Q) är påvisbar. Elektriska fältstyrkan definieras F/Q=RcQ/r2 med elektriska potentialen Fr/Q=RcQ/r=E/Q.
· Varje ekvipotentialyta [w2=Gm2/r] har sin egen särskilda divergens [c = (c0/2)(1±Ö|1 – 4w2/c02|)], helt oberoende av hur kropparna rör sig, eftersom g-fälten inte ändras. Emellertid uppdateras inte den elektriska potentialbilden från laddningscentrum omedelbart i den omgivande fasta g-dominansens rymdpreferenser då en laddning lägesändrar. Fördröjningen beror av ljushastigheten (c). Eftersom denna emellertid är stor relativt människans vardagliga metrik, frånses c-fördröjningen generellt i samband som berör (den lokalt Jordbaserade) elektrofysiken.
Se även gravitationslagens härledning i separat artikel
i FYSIKENS GRUNDBEGREPP
GRAVITATIONSLAGEN
Gravitationskraften (kropparnas allmänna attraktion) härleds f.ö. direkt ur kraftlagen F=ma såsom den universella konvergenskraften F mellan två masskroppar m2 (centralkroppen) och m (omloppskroppen) med hjälp av den balanserande centralkraftsaccelerationen mw2/r enligt
F=ma=mw2/r=(w2/rm2)m2m=(w2/m2)m2m/r=(w2r/m2)m2m/r2=Gm2m/r2
med G=6,67 t11 JM/(KG)2 (uppmättes första gången 1798 av Henry Cavendish). Kraften gäller med r från tyngdpunkten, vilket beskriver ett sfäriskt gravitationsfält (F).
elektromekanikens grundbegrepp
ELEKTROMEKANIKENS GRUNDBEGREPP
Genom analogier mot gravitationens begrepp (laddningen Q motsvarar massan m) ges motsvarande begrepp i elektrofysiken:
motsvarande divergenskraften F = ma = k(Q/r)2 (elektriciteten)
gravitella fältstyrkan a = Gm2/r2
motsvarande elektriska fältstyrkan X = kQ/r2;
gravitella potentialen w2 = G(m2/r)
motsvarande elektriska potentialen U = k(Q/r) = Fr/Q = E/Q;
konvergenspotentialen w2 = EG/m
motsvarande divergenspotentialen c2 = Ec/m;
gravitella energin EG = Gm22/r=mw2 (konvergensenergin, E=Fr, se gravitationslagen)
motsvarande divergensenergin Ec = kQ2/r = mc2 = UQ;
Explicit i elektrofysiken definieras begreppet elektrisk strömstyrka (I) enligt I=Q/T.
Därmed kan spänningen U i elektriska kraftlagen också skrivas formellt genom de fysikaliska storheterna
U = Rc(Q/r) = R(r/T)(Q/r) = R(1/T)(Q) = R(Q/T) = RI ;
U = RI
Sambandet kallas traditionellt för Ohms lag.
Ljusets massberoende eller
ljusets gravitella beroende
eller divergensens
gravitella beroende, kraftvektorledet
DGD (Divergence’s Gravitational Dependency)
Från GRUNDFORMEN FÖR LJUSETS GRAVITELLA BEROENDE
LJUSETS GRAVITELLA BEROENDE
Se även grundbegreppen med divergens (tillståndet i rymdpunkten ds) och ljushastighet (medelvärdet över rymdintervall)
från LJUSETS OPTISKA ACCELERATION.
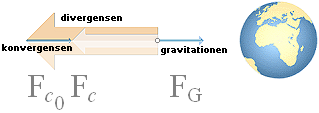
Situationen i rymdpunkten P(ds) med divergensen c på avståndet r från Jordmassans tyngdpunkt (m2).
Toppdivergenskraften Fc0=ma=m(c0/dT) = konstant med toppdivergensen c0 som ger c=Fc0dT/m visar formellt ett minsta m som ger ett största c enligt c0=Fc0dT/m=a·dT. Dvs., c0 ges med noll inverkan från massan. Då kan ett typ
kraftvektorledet Fc0 = Fc + FG ses gälla som formen för ljusets gravitella beroende: g-kraften (EG) motverkar toppdivergenskraften (Fc0) som ger den lokala divergenskraften (Fc); Fc0 och därmed c0 bevaras således konstant och helt oberoende av gravitationens inverkan. Motsvarande energiled blir tvunget
som efter eliminering av gemensamma massan ger v2=c2+w2=cc0 (se illustrationen nedan med Cheops Rektangel).
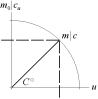
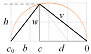 Cheops
Rektangel. Hur
c
beror av m
från w2=Gm2/r. Sambanden ger v2=c2+w2=cc0
enligt (c=d, c0–c = b),
Cheops
Rektangel. Hur
c
beror av m
från w2=Gm2/r. Sambanden ger v2=c2+w2=cc0
enligt (c=d, c0–c = b),
w/c=b = (c0–c)=d/w
; w2 = cc0–c2 ............. Cheops Rektangel, cb=w2
v/c0 =
c=d/v ; v2 = cc0 = c2+w2
energi- och krafthärledningarna
Summan av energierna divergens (Ec=mc2) och konvergens (EG=mw2) ger alltså mc2+mw2=m(cv)2=Ev; c2+w2=cv2. Med divergensens variation från c0 till 0 ges via Cheops Rektangel (bd=h2) ekvivalent c2+w2=v2=cc0 som ger c2=cc0–w2 eller c/c0=1–w2/cc0 med lösningen
c/c0=1–w2/cv2
ges c=c0–w2c0/cv2
; med substitutionen (R0k/R0k=1) fås
R0kc = R0kc0 – w2R0kc0/cv2
där R0kc=Fc och R0kc0=Fc0
som ger Fc = Fc0 –
w2R0c0k/cv2;
Eftersom Ev=mcv2, m=Ev/cv2,
ges med Ev=Fvr=Fc0r=R0c0kr
ekvivalenten (m/r)=(Ev/cv2)/r=R0c0kr/cv2r=R0c0k/cv2,
och därmed
w2R0kc0/cv2
=w2(m/r) = FG = (Gm/r)(m/r).
Och alltså gäller KRAFTVEKTORLEDET Fc = Fc0 – FG för
ljusets gravitella beroende; toppdivergensen c0 bevaras
konstant oberoende av massans-gravitationens inverkan.
Härledningen till divergensens gravitella beroende kan
alltså göras valfritt utifrån vilkendera delen med energin eller kraften.
ljusets gravitella beroende, statiska tillståndets fysik (expansiva-kontraktiva tillståndet
behandlas i särskild del)
RESULTATREDOVISNING allmänna samband:
LJUSETS GRAVITELLA BEROENDE
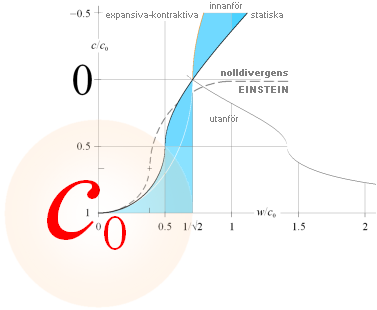
En kropps tyngdpunkt är den punkt i kroppen där divergensen är som störst. Se även i
efterföljande absoluta metriken.
statiska delen allmänna samband
LJUSETS (eg. divergensens) GRAVITELLA BEROENDE ENLIGT RELATERAD FYSIK
c/c0 = (1/2)(1 ± Ö |
1 – 4w2/c02 | ) med + från c0 till c0/2 och – från c0/2 till 0 eller mera exakt
c/c0 = (1/2)(1 + Ö 1 – 4w2/c02
) från c0 till c0/2 cirkeln
c/c0 = (1/2)(1 – Ö 4w2/c02
– 1 ) från c0/2 till 0 hyperbeln
w2 = Gm2/r = r2(4pGr/3)
idealt homogen täthet r
visar hur ljushastighetens lokala värde c (divergensen) avtar idealt från en homogen kropps tyngdpunkt (c0) och utåt kroppsranden med växande g-potential w2=Gm2/r. För en himlakropp (ideal sfär) med homogen täthet (r=3m2/4pr3, m2=r4pr3/3) tillväxer w2 med r2 enligt w2=Gm2/r=G(r4pr3/3)/r=r2(4pGr/3) ut till kroppsranden. Därefter, vidare utåt, avtar g-potentialen w2 med r enligt w2=r–1(Gm2). Illustrationen ovan visar dessa delar genom de heldragna kurvorna för en ideal sfärisk kropp som inte expanderar eller kontraherar och som har en medelmässigt homogen täthet vars g-rand håller exakt c=0. Den streckade kurvdelen (himlakroppens inre) visar till jämförelse Einsteins samband, se nedan, vilket samband dock bara delvis har en klar innebörd (delen över den lilla markerade korspunkten är här uppskattad).
statiska tillståndets samband med ensam kropp — speciellt med absoluta metrikens giltighet f/f0 = c/c0 ; c0/f0 = c/f = d0
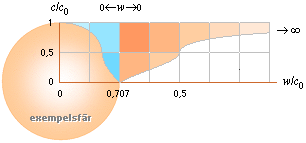
Föregående ovanstående graf, här på omvänd form.
Se även potentialbarriären.
w2 = r2(4pGr/3) .................................... innanför sfärytan,
homogen täthet r=3m2/4pr3, blå grafdelen
w2 = r–1Gm2 ........................................... utanför sfärytan, orangea grafdelen
c = (c0/2)[1 ± Ö | 1 – 4w2/c02 | ] .......... ljusets
g-beroende enligt relaterad fysik
c/c0 = (1/2)(1 ± Ö | 1 – 4w2/c02 | ) ........... med w = rÖ 4pGr/3 innanför och w = Ö Gm2/r utanför.
a lokala accelerationskonstanten
a innanför
klotskalet = r(4pGr/3)
;
r = 3m2/4pr3
tätheten (r i Symbol), homogen
sfär
a utanför klotskalet = Gm2/r2 ; m2 = centralmassan
G = 6,67
t11 JM/(KG)2 universella gravitationskonstanten
JÄMFÖR MODERN AKADEMI (Einsteins samband nedan):
grundform relaterad fysik ............ c/c0=[1–w2/cc0]
grundform Einstein .................... c/c0=[1–w2/c2] (Einstein tillät inte c=0, tidens upphörande enligt honom)
ref. McGraw-Hill SCIENTIFIC ENCYCLOPEDIA Edition 1970(-) Light p570
SKILLNADEN MELLAN MODERN AKADEMI OCH RELATERAD FYSIK-MATEMATIK
Skillnaden
mellan c0E (EINSTEIN) och c0T (RELATERAD FYSIK) i våra regioner — för den som vill kontrollera
c/(1–w2/c2)=c0E
——————— = [(1–[w/c]2)(1+[w/c]2)]–1 = (1–[w/c]4)–1 gäller (i begränsad mening) endast till max w=c
c(1+w2/c2)=c0T
— är helt försumbar. För Solvärdet t.ex. ligger skillnaden i nittonde decimalen.
RESULTATREDOVISNING FRÅN HÄRLEDNINGEN TILL LJUSETS GRAVITELLA BEROENDE allmänna samband:
LJUSETS GRAVITELLA BEROENDE
bevarandet
av c0
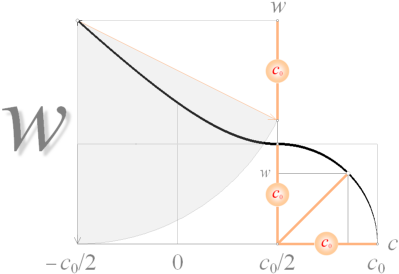
Naturkonstanten c0 bevaras oberoende av
gravitationens inverkan.
Vi ser att lösningen [±(c–c0/2)]2 = | (c0/2)2 – w2 | till energi och kraftleden i härledningen till ljusets g-beroende tecknar bilden av en del cirkel (w2+c2=c02, högra delen i figuren ovan) och en del hyperbel (w2–c2=c02). Slutresultatet i denna manöver är, som vi ser, att referensenheten c0 bevaras oberoende av magnituden för den resulterande divergensen c, oaktat denna är positiv (cirkeln) eller negativ (hyperbeln); För hyperbelns del flyttas hela ”c0-pinnen” med för varje w-värde, enligt hyperbelns karaktäristik: c0 bevaras konstant, oberoende av gravitationens inverkan.
RESULTATREDOVISNING FRÅN HÄRLEDNINGEN TILL LJUSETS GRAVITELLA BEROENDE allmänna samband:
NEGATIV DIVERGENS
Någon negativ ljushastighet kan vi (veterligt) inte härleda. Vad som däremot är uppenbart, är att bevarandet av c0 med i princip obegränsat växande gravitation kräver negativ divergenskraft enligt föregående härledda
KRAFTVEKTORLEDET Fc = Fc0 – FG. Är t.ex. Fc0 = FG måste tvunget Fc vara noll. Och på samma sätt om FG härifrån växer ytterligare, vilket resulterar i negativt Fc i bevarandet av c0 som ovan. Den negativa divergensen måste alltså finnas av princip som en faktor tillhörande divergenskraften för att kraftverkan i motsvarande energiled ska gälla. Einstein kunde inte härleda den delen, eftersom enligt honom ”tiden upphör” vid c=0. Se även Einsteins ekvation.
RESULTATREDOVISNING FRÅN HÄRLEDNINGEN TILL LJUSETS GRAVITELLA BEROENDE allmänna samband:
all existerande massas samlade tyngdpunkt beskriver orten för ljusets topphastighet, och endast där
KRAFTVEKTORLEDET Fc = Fc0 – FG i härledningen till ljusets gravitella beroende garanterar att ljushastighetens absolut högsta möjliga värde (c0) bara kan finnas i tyngdpunkten P0 för all existerande massa enligt FG=0 som ger Fc = Fc0.
Denna detalj uppställer åt oss föreställningen om en i området för P0 fast, ideal metrik (xyz) med ett fast förhållande mellan distans och tid enligt (d/T=c)0 och som, om den antas, utsäger att en bestämd distans d i (det närmaste området för) P0 också är samma bestämda distans på alla möjliga ställen utanför P0. Denna grundpremiss med en fast (ideal) metrik som gäller överallt i xyz-rummet leder oss fram till den märkliga konsekvensen att ljushastigheten utanför P0 och med hjälp av atomklockor inte kan mätas absolut, se sambanden nedan, eftersom också våglängderna (d=cT) i atomsvängningarna ändras med gravitationen om c gör det:
Absoluta metriken innebär att ljushastigheten INTE kan mätas absolut med hjälp av atomklockor därför att också atomernas svängningar ändras proportionellt med gravitationen (se frekvensens g-beroende nedan). Nettoresultatet blir ett och samma c-värde oberoende av det verkliga lokala c-värdet: om detta är mycket lägre än toppvärdet c0 svänger också atomerna i motsvarande grad långsammare så att likväl toppvärdet c0 visar sig enligt
c/c0=T0/T=f0/f
........................ frekvensen
f ändras omvänt
divergensen c
med varierande lokal gravitation
med absoluta metriken (som endast gäller idealt i lokalen för c0, fast vi [oegentligt, hypotetiskt] idealt låter den lokalen omfatta all föreställningsbar rymd)
cT=d0=c0T0
Olika ljushastigheter kan alltså INTE påvisas med hjälp av atomklockor. MEN ändringarna i atomklockstiden själv som följd av olika lokala g-potentialer kan dock påvisas på olika höjd över Jordytan. Ett excellent exempel finns i GPS-exemplet (Global Positioning System).
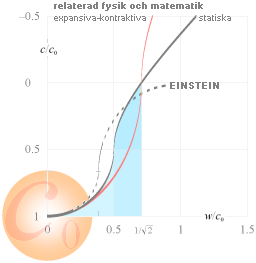
Frekvensens gravitella beroende eller
ABSOLUTA METRIKEN framställer ekvivalenterna cT=d0=c0T0
med c/c0=T0/T=f0/f,
T=1/f i enlighet med GcQ-teoremet (gravitationens absolutverkan) och särställer därmed en idealt absolut referens för
toppdivergensen c0 som orten för all totalt
existerande massas tyngdpunkt
ABSOLUTA METRIKEN cT=d0=c0T0=c/f=c0/f0 betyder ENLIGT RELATERAD FYSIK OCH MATEMATIK (se från atomtriangeln) att c0=d0/T0 bara kan finnas i g-centrum för all existerande massa (eg., i differentialer c0=dd0/dT0) och endast där, se ljusets gravitella beroende, samt att såväl den lokala ljushastigheten (c) som atomtiden (frekvensberoendet, eller, atomens inre elektromagnetiska svängningar via den lokala ljushastigheten c som funktion av gravitationen) avtar med växande avstånd från tyngdpunkten c0 (generellt avtagande elektromagnetisk aktivitet). Den atomära klockfrekvensen, inte tiden själv, varierar med höjden över Jordytan.
Albert Einstein (se Einsteins Ekvation) kunde inte härleda ljusets g-beroende i samtidigt bevarande av naturkonstanten c0, oberoende av gravitationen, eftersom han varken tillät såväl ingen (0) som negativ lokal divergenskraft. Det är endast genom kraftvektorledet Fc = Fc0 – FG som en sådan ekvivalent kan härledas, och den ingår inte i Einsteins tankevärld. Se vidare nedan i v+ic-felet.
RESULTATREDOVISNING FRÅN HÄRLEDNINGEN TILL LJUSETS GRAVITELLA BEROENDE allmänna samband:
LJUSVÄGARNA I GRAVITATIONSFÄLTET

En linjeväg för divergensen har ingen självständig
koppling till mekaniken eftersom divergensen ges punktlokalt
av gravitationen. Eftersom divergensen
alltså
beror av gravitationen, måste man söka linjevägen för en
ljusstråle i själva g-fältet, nämligen som en av gravitationen redan fastställd
tillståndsväg, ”en redan upptrampad stig” (som ljuset sedan följer som vattnet
en redan lagd ränna).
Vi kan i
grunden inte ange några bestämda ”riktningsvektorer” för divergensen i en
rymdpunkt eftersom riktningen är giltig med samma styrka ”åt alla möjliga
håll”. Vi kan ange vektorn för divergenskraften kontra g-kraften vilket leder
oss till sambandet för divergensens
g-beroende (DGD), men den analysen berör ett kraftbegrepp i
en fix rymdpunkt, ingen fysikalisk utsträckning. För att härleda en
sammanhängande ljusväg måste vi alltså använda den redan befintliga mekaniken
på ett sätt som konserverar divergenskriteriet. Det är mindre dramatiskt än det
verkar.
JÄMVIKTEN mellan g-kraft och centrifugalkraft för en omloppskropp m
på avståndet r kring en centralmassa m2 definieras inom
mekaniken genom gravitationspotentialen w2=Gm2/r. Den är
alltså oberoende av omloppskroppen m. Genom gravitationens absolutverkan kan därför g-potentialen
uppfattas som ett tillståndsbegrepp. Det tillståndsbegreppet för
gravitationen definierar alltså hela den gravitella sfäriska
ekvipotentialytan på r från m2 i varje möjlig
tidpunkt.
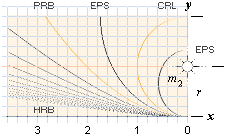
De olika möjliga omloppsbanor kring en centralmassa i fysiken som
uppritas av jämvikten med hänsyn till olika utgångshastigheter (v) i r-normalen,
sammanfattas i CEPH-ekvationen nedan med de motsvarande grafiskt avbildade fyra
klassiska banformerna illustrerade ovan,
x = [2ry(1+e) – y2(1–e2)]1/2........................ CEPH-ekvationen
CEPH-ekvationen specificerar klassen kurvskaror som i fri rymd lyder
under centralkraftens verkan, desamma som den celesta mekanikens fyra
kurvtyper.
Excentricitetstalet
e
bestämmer banformen enligt 0>e>–1, ellipser;
e=0, cirkeln;
1>e>0, ellipser;
e=1, parabeln;
e>1, hyperbler.
r betecknar brännpunkten, eller höjden över x-axeln till fokalpunkten
där centralmassan finns. För excentricitetstalet e och initialhastigheten v(0;0) gäller
(v2r)/Gm2 – 1 = e = v2/w2 – 1
v2 = (e+1)Gm2/r
Eftersom dessa kurvor täcker hela planrummet i varje snitt genom
centralmassan via klassen alla möjliga värden på e, kan man misstänka att det också är dessa
kurvor som helt idealt graverar ljusspåren i g-fältet med hänsyn till en
enskild fristående, idealt sfärisk materiehomogen centralmassa.
MOTSVARANDE LJUSVÄGAR — centrifugalkraftens eliminering
Enligt
LJUSETS FRISTÄLLNING FRÅN KINETIKEN (divergensens frihetssats) har divergensen med topphastigheten c0 som ljushastigheten ingen koppling till kinetiken.
Det innebär att
·
divergensspåret eller ljusvägen är partikellös, samt att
·
divergensspårets genomlöpande utvecklar ingen centrifugalkraft.
För att söka en möjlig lösning till hur en ljusväg bryts genom rymden i
inverkan från en (idealt sfärisk homogen) centralmassa måste man alltså söka
lösningar där centrifugalkraften är eliminerad. Detta realiseras genom
att fördubbla g-kraften, analogt centralmassan,
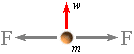
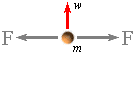
Eftersom g-kraften F är direkt proportionell mot
centralmassan, som för alla masskroppar motsvaras av en exakt balanserande
centrifugalkraft, blir närmaste vägen för att eliminera den senare ekvivalenten
att fördubbla den förra. Centrifugalaspekten elimineras genom att fördubbla G.
varigenom centrifugalkraftens komponent (F, se ovanstående
illustration) försvinner. Därmed är divergenskriteriet uppfyllt och
konserverat.
v2 = (e+1)2Gm2/r
Banformerna som definieras av e tillhör mekaniken.
Ljusvägen karaktäriseras emellertid som nyligen påpekades inte av någon
partikel i rörelse eftersom divergensen är partikellös och avgränsad till
endast en rymdpunkt (P). Komponenten v måste alltså relateras på tillståndets
princip överallt i hela
g-rummet (alla möjliga ljusbanor är redan givna av g-fältet i varje möjlig
tidpunkt) och därmed stillastående med grund i toppdivergensen c0.
Fördubblingen av centralmassan för CEPH-kurvornas anpassning till ljusvägarna
innebär följaktligen att den mekaniska rörelsen (v) upphör och ersätts
av tillståndet för toppdivergensen (c0). Vi studerar
detta genom energierna.
Med obegränsat växande r i w2=Gm2/r [vi
sätter r:=r(n®¥)] går w
mot noll för given centralmassa. Därmed ges ett gränsvärde för
gravitationsenergin dmw2 i den rymdpunkt P som motsvarar den
mekaniska rörelseenergin (Ekin=mv2/2) på den
stillastående toppdivergensens form dmc02/2. Formellt
gäller då
r®¥ limes dmc02/2
= dmw2 = dmGm2/[r(n®¥)]
m®0 limes dmc02/2 = dmw2 = dm(G/r)[m2/(n®¥)]
dmw2 = dmc02/2 ............................ rörelseenergins divergensekvivalent
w2=c02/2=Gm2/r =
konstant ......... g-potentialens divergensekvivalent
Sambandet tecknar alltså en impulsanalogi mv=m(c0/2) i rymdpunkten
P. Den mekaniska impulsen mv i P på r från m2 motsvarar för
ljusvägarna divergensimpulsen m(c0/2). Det är hela
hemligheten. Mekanikens v motsvarar alltså i ljusvägarna den
konstanta impulshastigheten c0/2. Då är
c02 = (e+1)2Gm2/r ........................ ljusvägarna i g-fältet
Därmed är ljusvägarna i g-fältet identifierade (ideal homogen sfärisk
centralmassa m2 utan hänsyn till omgivande g-massor).
syntes
Ovanstående kan framställas i syntes, alternativt, som följer.
Eftersom gravitationens
inverkan på divergensen är obetingad, vilket betyder att g-potentialen
av princip kan vara obegränsad, måste en koppling finnas till divergensen som bevarar
dess principiella identitet oberoende av hur c varierar som
funktion av w. Detta är speciellt tydligt i fallet c=0. Då alltså
kopplingen måste avse en konstant kan vi utnyttja toppdivergensens c0. Substitueras
denna motsvarande en mekanisk rörelseenergi (divergensens aktiva
aspekt får inte finnas med i den matematiska behandlingen vid c=0,
konstanten c0 måste alltså behandlas kinetisk) får man i
fallet c=0
EG= dmw2 = Gm2dm/r = dmc02/2 ......................... rörelseenergins divergensekvivalent
Det vill säga
w2=c02/2=Gm2/r;
rc=0=2Gm2/c02=1,48427 t27 · m2
vilket alltså ger ekvivalenten w2=c02/2 för c=0.
Den
kontinuerliga funktionen för c med avseende på w måste alltså
innehålla denna detalj. Det gör den också:
I resultatet c/c0 = (1/2)(1 ± Ö | 1 – 4w2/c02 | ) tillämpar vi c=0 som ger
c=0;
c/c0 = (1/2)(1 – Ö 4w2/c02 – 1)
0 = 1 – Ö 4w2/c02 – 1
4w2/c02 – 1 = 1
4w2/c02 = 2
2w2/c02 = 1
w2 = c02/2
Härledningen till ljusets g-beroende innefattar alltså
(hur märkligt det än kan synas) centrifugalkraftens eliminering automatiskt.
Se vidare i
PRAKTISKA OBSERVATIONER
Experimentella bekräftelser på riktigheten i den relaterade fysikens och matematikens härledda begrepp
Solrandsavböjningarna från år 1919: samma matematiska samband, helt skilda teorier
Elektriska laddningen | Planckekvivalenterna
Figur 2 kopplar till modern akademi — trots bevis enligt
figur 1 från 1881, Michelson och Morleys interferometerexperiment ;
c och v kopplar inte i fysiken. Inte alls överhuvudtaget. Se utförligt från v+ic-felet.
|
|
|
|
|||
|
|
|
|
|
|
|
|
a=c/dT |
Fig:1 |
Fig:2 |
Fig:3 |
Fig:4 |
|
Planckekvivalenterna se även ovanstående beskrivande figurer
DIVERGENSENERGIN E = mc2 och PLANCKENERGIN E=Jf med J=h=mnc0rn (se vidare i atomkärnan):
a = dv/dT ; dv = c ; a = c/dT ; dE = dm a ds = dm c/dT ds = dmc ds/dT = dmc2 ; E = mc2 = mclf = Jf
E = mc2 = hf ; m/f = h/c2 = m0/f0 ; m0/m = f0/f = (c0/l0)/(c0/l) = l/l0
m0c = m0l0 f0 = mcu = m(c–u) = m(l0 f0–lu f0) = mf0(l0–lu) = ml f0 ; m0/m = f0/f = (c/l0)/(c/l) =l/l0
m0 · c · l0 · f0 = Jf0 = m0c2 = E ; m0/f0 = J/c2 = m/f ; m0/m = f0/f = (c/l0)/(c/l) = l/l0
PLANCKEKVIVALENTERNA — figurerna UTOM 2. c och v kopplar inte i fysiken. v+ic saknar
fysikalisk grund
PLANCKEKVIVALENTERNA
U åstadkommer en SEPARATION mellan ett MoveQ (+Dm, kan mätas med trådstrålerör) och ett RestQ
(–Dm). Summan är noll. Massa kan INTE skapas. Fysiken innehåller inga massökningar på grund av rörelse.
Fig:3 se utförlig
beskrivning längre ner
|
|
|
|
|
n®¥ |
||
|
n
= c/cu = r/y ; cu anger återstående
accelerationspotentialen |
||
|
n=1 |
||
|
m0c = m0n · c/n = mcu = konstant |
|
För att vrida c-pinnen från toppläget vid 90° krävs
energi. Energin ges av accelerationsspänningen U. |
Fig:3 se utförlig
beskrivning längre ner
Systemets massa och energi bevaras konstant:
m0c2 = mccu = konstant = E ; (systemets egen inre energi)
c2 – cu2 = u2 ; (cirkeln, r = c = konstant), u elektriska laddningens hastighet efter acceleration av U=E/Q=Ri=m·c2/Q
m0c = mcu = m · Ö c2–u2 = konstant, PLANCKIMPULSEN ; u = c(1–1/[(UQ/m0c2)+1]2)0,5; u begränsas av c ;
Elektriska laddningen Q=Ö (m/R)(A/dT) garanterar att massändring inte finns i mekaniken därför att R inte finns där.
Planckekvivalenterna kopplar inte till mekaniska rörelsesystem.
Planckekvivalenterna gäller ENDAST för elektriska laddningar i U-system.
Planckekvivalenterna utskrivna således
m0/m =Ö 1–(u/c)2 .............. PLANCKENERGINS MASSEKVIVALENT i Qm ändras med växande u
f0/f =Ö 1–(u/c)2 ............. PLANCKENERGINS FREKVENSEKVIVALENT i Qm ändras med växande u
l/l0 =Ö 1–(u/c)2 ............. PLANCKENERGINS VÅGLÄNGDSEKVIVALENT i Qm ändras med växande u
utförligt
PLANCKEKVIVALENTERNA
Från härledningen till Q

PLANCKEKVIVALENTERNA
Differentialbegreppet från nollformsalgebran leder vidare via Q:
Med fortsättning från resultaten av härledningen till
den elektriska laddningen
Vi ser också, direkt, med förutsättningen (A/dT) given i Q, att Q är konstant endast under den förutsättningen att m och R varierar exakt proportionellt:
Eftersom R
inte finns i mekaniken (v), gäller heller inte m-variationer där
— bara i elektrofysiken. Märk väl.
Elektriska laddningen i elektriska experiment, där m och R varierar exakt proportionell enligt bevarandet av laddningen
Q=Ö (m/R)(A/dT), följer PLANCKEKVIVALENTERNA enligt syntesen i nedanstående figur 3.
Termen ”Planckekvivalenter” har i denna presentation följande grund:
Från Planckringen h=mnc0rn = 6,626 t34 JS = Plancks konstant med neutronkomponenterna mnrn och ljushastighetens toppvärde c0 benämns här generellt impulsen mc i atomära sammanhang också Planckimpulsen. Med vidare koppling, speciellt till Planckenergin E=hf, utkristalliseras en allmän form för de grundläggande samband som berör (speciellt) massfysiken och som därmed naturligt kan refereras till och kallas för Planckekvivalenter.
Beskrivningen nedan ger grundlinjerna.
Se även närmast ovanstående matematiska grundsammanställning.
Systemets massa och energi bevaras konstant:
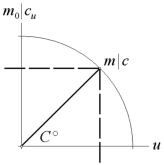
Figur 3
m0 ändras entydigt till m=m0+Dm för MoveQ-delen via U med konstant Qc; RestQ erhåller sin negativa del (m=m0–Dm) i försorg av det slutna elektriska systemets bevarande av massenergin i
m0c² = mccu = konstant = E
Ingen
massa skapas, ingen massa försvinner. Märk den detaljen väl.
— Se även mera utförligt i MAFEM (Mass-Force
Exchange Mechanism, massa-kraftutbytesmekanismen), där beskrivs utförligt
den mera djupgående matematiska fysiken bakom ovanstående härledda
massändringseffekt
— inom elektrofysiken enligt TNED.
SPÄNNINGEN U producerar en separation mellan ett
MoveQ (+Dm kan mätas med trådstrålerör) och ett RestQ (–Dm aldrig experimentellt uppmätt i
fysikens historia).
Summan är noll: Fysiken innehåller ingen massökning netto som följd av rörelse:
m0 ändras entydigt till m=m0+Dm för MoveQ-delen via U med konstant Qc; RestQ erhåller sin negativa del (m=m0–Dm) i försorg av det slutna elektriska systemets bevarande av massenergin i
m0c² = mccu = konstant = E
Ingen
massa skapas, ingen massa försvinner. Märk den detaljen väl.
Laddade partiklars
acceleration
ELEKTRONENS MASSÖKNING INOM ELEKTROFYSIKEN
Figur
3
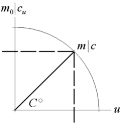
Efter elektrisk acceleration av laddningen Q med vilomassan m0 via spänningen U=E/Q=mc2/Q har Q massan m och laddningshastigheten u — med en återstående accelerationspotential cu. m0 ändras entydigt via U med konstant divergens c.
Genom Planckimpulsen för laddningens vilomassa
m0c=m0n(c/n)=konstant=mcu
ändras m via U enligt m=m0n med den resterande accelerationspotentialen cu=c/n.
cu anger den resterande del av toppdivergensen c som Q kan accelereras på, och det gäller alltså att m0/m=cu /c.
Med c=konstant är 1/n trigonometriska y-projektionen 1/n=cu /c med vektorekvivalenten c = u+icu , analogt
c–u=icu , se även ovanstående figur 3. Med m0/m=cu /c i Pythagoreiska ekvivalenter ges då
(m0/m)2=(c2–u2)/c2=1–(u/c)2 och därmed
PLANCKEKVIVALENTERNA (m0/m)2=(f0/f)2=(l/l0)2 = (c2–u2)/c2 = 1–(u/c)2:
(m0/m)2=(f0/f)2=(l/l0)2 = (c2–u2)/c2 = 1–(u/c)2:
f0/f = Ö 1–(u/c)2 ............. PLANCKENERGINS FREKVENSEKVIVALENT i Qm ändras med växande u
m0/m = Ö 1–(u/c)2 ............. PLANCKENERGINS MASSEKVIVALENT i Qm ändras med växande u
l/l0 = Ö 1–(u/c)2 ............. PLANCKENERGINS VÅGLÄNGDSEKVIVALENT i Qm ändras med växande u
jämför
r-teorins grundsamband:
T/T0 = Ö 1–(v/c)2 ............. tiden avtar med växande v
m0/m = Ö 1–(v/c)2 ............. massan växer med växande v
d/d0 = Ö 1–(v/c)2 ............. längden avtar med växande v
Delen (f0/f)2=(l/l0)2 framgår ur Planckimpulsen som ovan enligt (erinra c=lf)
m0c = m0l0f0 = mcu = m(c–u) = m(l0f0–luf0) = mf0 (l0–lu) = mlf0 ;
m0/m = f0/f
= (c/l0)/(c/l) =l/l0 | m0c=mlf0; m0/m=lf0/c=f0/f
PLANCKENERGIN E=Jf stammar från E = mc2 = mclf = Jf där E = mc2 är den nyligen härledda divergensenergin.
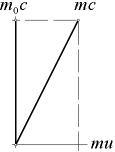
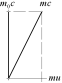
Figur 4
Figur 4 beskriver massökningen mera enkelt och direkt, med samma resultat som i föregående figur 3, här på komplex form enligt
mc = mu + im0c som direkt ger 1 = (u/c)+im0/m = (u/c)2+(m0/m)2; (m0/m)2=1–(u/c)2
vilket vi ser är samma som föregående.
Se även i
SAMBANDET
FÖR LADDNINGSHASTIGHETEN GENOM ACCELERATIONSSPÄNNINGEN
LADDNINGSHASTIGHETEN u FRÅN ACCELERATIONSPOTENTIALEN U I VAKUUM
Se vidare i
PRAKTISKA OBSERVATIONER
Experimentella bekräftelser på riktigheten i den relaterade fysikens och matematikens härledda begrepp
exakt samma matematiska samband, helt skilda teorier
EXPERIMENTELLA BEKRÄFTELSER PÅ LJUSETS FRISTÄLLNING FRÅN KINETIKEN
M&M:s experiment, uppdagandet av v+ic-felet
Solrandsavböjningarna från år 1919: samma matematiska samband, helt skilda teorier
ABERRATIONEN från James Bradley 1725
Ljusvägens gravitella beroende
genom olika lokalt dominanta g-system med inbördes lägesändringar
DEN KOSMISKA PARTIKELSTRÅLNINGEN
de experimentella bevisen för multipla c: exakt samma matematiska samband, helt skilda teorier
GPS-EXEMPLET: exakt samma matematiska samband, helt skilda teorier
Verifierande praktiskt
räkneexempel som visar att fysiken förklaras av Planckekvivalenterna, inte
relativitetsteorin.
samma matematiska samband, helt skilda teorier
UNIVERSUMS EXPANSION: samma observationsdata, en annan dopplermatematik
resultatet visar att fysiken
förklaras av Planckekvivalenterna, inte relativitetsteorin.
FIZEAUS EXPERIMENT: ljushastigheten genom strömmande vatten
resultatet visar att fysiken
förklaras av Planckekvivalenterna, inte relativitetsteorin.
Einsteins mc2
Albert Einstein härledde, enligt källan nedan, mc2 ur »impulsekvationen» m0/m=Ö 1–(v/c)2 och som i sig framkommer från vc-resultanten i v+ic-felet ovan. Citatet nedan från FOCUS MATERIEN 1975 s84:
”Man kan visa att massan hos en kropp som rör sig med hastigheten v enligt relativitetsteorin ökar med hastigheten så som anges av ekvationen
m = m0 · 1/Ö(1–b2)
där m0 är kroppens s.k. vilomassa. Fenomenet brukar kallas relativistiska massökningen och är väl bekräftat experimentellt, främst genom studiet av elementarpartiklar som accelererats till hög energi.
Genom att skriva om detta uttryck med hjälp av en så kallad serieutveckling, införa kvoten v/c i stället för b samt multiplicera ekvationens båda led med c2 får man
mc2 = m0c2 + (1/2)m0v2 + termer av högre ordning
Andra termen till höger om likhetstecknet kan identifieras som kroppens kinetiska energi enligt den klassiska mekanikens lagar. De övriga termerna måste också ha dimensionen energi, och Einstein drog en slutsats som skulle få oanade följder för varje människa på jorden, nämligen att den första termen i det högra ledet måste representera en energimängd som på något sätt var bunden i form av massa.”
FOCUS MATERIEN 1975 s84
Med hjälp av Binomialteoremet kan vi studera
närmare vad källan ovan antyder — och därmed mera noggrant studera
Einsteins utveckling:
BinomialTeoremet, vi studerar vad citatkällan antyder:
(a+b)n = an[1 + n(b/a) + n(n–1)(b/a)2/2! + n(n–1)(n–2)(b/a)3/3! + … + (b/a)n] ;
m0/m =[1–(v/c)2]1/2 = (1– k)1/2 ;
m = m0(1– k)–1/2 ;
(1+b)n , b = –k = –(v/c)2 , n=–1/2 ; sista termen (b/a)n utgår i BT med n<1 ;
(1– k)n = 1 + n(–k) + n(n–1)(–k)2/2! + n(n–1)(n–2)(–k)3/3! + …
= 1 + (–1/2)(–k) + n(n–1)(–k)2/2! + n(n–1)(n–2)(–k)3/3! + …
= 1 + (v/c)2/2 + n(n–1)(–k)2/2! + n(n–1)(n–2)(–k)3/3! + …
= 1 + (v/c)2/2 + …
mc2 = m0c2(1– k)–1/2 = m0c2 + m0v2/2 + …
Titta
alltså återigen på utvecklingen från Planckekvivalenterna:
m0c=m0n(c/n)=konstant=mcu
m0c=mcu
m0c2=konstant=mccu INGEN MASSÄNDRING SKER I NETTO. Ingen massa skapas. Ingen massa försvinner.
m0c²=KONSTANT=mccu=mc(c²–u²)1/2
Den detaljen framgår INTE explicit ur DEN ISOLERADE matematiken för BT, serieleden ovan. Jämför
m0c³/cu= mc² = m0c2 + m0u2/2 + …, u = c(1–1/[(UQ/m0c2)+1]2)0,5 , u ¹ v
ALGEBRAN innehåller explicit ingen information om fysiken. Serieutvecklingen ovan är »början i fel ände».
PotentialBarriären: PlanckEkvivalenterna — Nuklidbarriären — Ljusets Gravitella Beroende — Atomkärnans härledning
POTENTIALBARRIÄREN ¦ Compiled Synthesis

Ljusets gravitella beroende tillämpat på den elektriska laddningen (Q) ger av princip POTENTIALBARRIÄREN eller den elektriskt laddade massringens energizon. Energizonen talar om var någonstans av princip i massan som en yttre elektrisk fältkraft griper tag i en elektrisk laddning.
Sambandsformerna nedan skall inte ingå i den moderna akademins lärosystem på grund av skillnaderna i teoretiska utgångspunkter för härledningen till ljusets gravitella beroende (se Einsteins ekvation). Emellertid (efter visst genomläsande) ingår sambandsformen nedan rc=0 = 2Gm2/c02 i modern akademisk litteratur under benämningen Schwarzschildradien [ref. BONNIERS ASTRONOMI 1978 s115sp1m], men det resonemang man för där har ingen koppling till den här presentationen.
Från LJUSETS GRAVITELLA BEROENDE, hyperbeldelen
c/c0=(1/2)[1 – Ö (2w/c0)2 – 1 ] ges med c=0 utvecklingsleden; 1=Ö (2w/c0)2 – 1; 2=(2w/c0)2; 2=4w2/c02; 1=2w2/c02=2(Gm2/rc=0)/c02=2Gm2/rc=0c02, varav
rc=0 =
2Gm2/c02 = 1,48427 t27 · m2 ........................ massans nolldivergensradie, M ; för varje m finns ett motsvarande rc=0
Med obegränsat avtagande centralmassa m2 exponerar nolldivergensradien tydligen en principiell m2-massa, en »partikel» vars radie obegränsat närmar sig noll. Vi kan kalla den principalpartikeln.
Principalpartikeln leder oss till exakt principiell kunskap om hur den elektriska laddningen (Q) är konstruerad i förhållande till massan, samt var yttre elektriska kraftfält ingriper i Q: hur och var Q tas. Laddningens koppling till principalpartikeln beskrivs totalt av potentialbarriärens sex grafer:
potentialbarriären --
POTENTIALBARRÄREN:
MASSANS
PRINCIPIELLA STRUKTURGRUND
POTENTIALBARRIÄREN
— stället där Q tas: w=c
Ec=EG
= mc2=mw2; c=w:
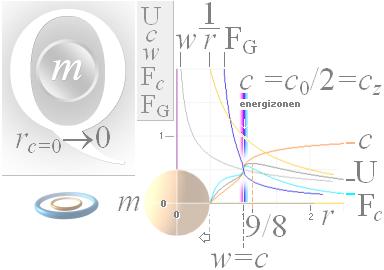
Potentialbarriärens sex funktionsgrafer
beskrivning
I elektriska kraftlagen F=Rc(Q/r)2 söker vi formen för potentialen U=Rc(Q/r) genom ljusets g-beroende (DGD)
c=(c0/2)[1±Ö | 1–4Gm2/rc02 | ] för en elektriskt laddad elementär principalpartikel (Q) genom det sfäriska gravitationsfältet.
Potentialen U på r från Q (potentialimpulsen vid r genom divergensen) ger analogt motsvarande laddningstrycket (impulsen U) utanför den laddade partikeln.
För att finna funktionens karaktär endast med avseende på avståndet r från centralorigo med hänsyn till variationerna i c kan termerna idealiseras genom
RQ=1=c0=4Gm2
Man får då
divergensen c = (1/2)[1±Ö | 1–1/r | ],
elektriska potentialen U = c/r,
g-potentialens rot w = 1/Ö4r, samt
divergenskraften Fc = c/r2.
Från härledningen till DGD framgår även formen för gravitationskraften FG genom FG = w2(R0c0k/cc0) = w2(R0k/c) = (w2/c)(R0k).
Med förenklingen (R=R0) R0k=1=c0 ges
konvergenskraften FG = w2/c = 1/4rc med w2=1/4r från g-potentialens rot ovan.
I DEN TRADITIONELLA SKOLBOKSFYSIKEN har man den motsvarande typformen för elektriska potentialen via ett konstant c som ger
skolfysiken U = 1/r.
Ovannämnda sex typfuktioner visas i illustrationen med referens till principalpartikeln. Härav framgår potentialbarriären — stället där Q tas: w=c. Laddningen Q tas där g-energin och c-energin är ekvivalenta: E=mc2=mw2 (formen för balans och jämvikt: konvergensen = divergensen). Potentialens maximum — den egentliga potentialbarriären — tecknar ett klotskal med radien 2,25 ggr principarpartikelns divergensnollradie [Umax=(9/8)/rc=0=(9/8)/0,5=2,25].
ENERGIZONEN
c = c0/2
=cz
Med c=w insatt i grundsambandet c2+w2=cc0 från ljusets gravitella beroende, ges cc0=2c2som ger c0=2c och därmed EnergiZonen
c = c0/2 =cz
Eftersom kraftverkan grundas på ringformen genom centralaccelerationen mw2/r, gäller ovan härledda potentialbarriärrens principfunktioner explicit direkt för ringen med kraftverkan i ringplanet. Under-ovanför detta blir förhållandena annorlunda.
FYSIKBESKRIVNINGEN i UNIVERSUMS HISTORIA fortsätter härifrån i Fysikens 7 Principer; denna del var från början tänkt att ingå i ett och samma dokument (Universums Historia). Men htm-dokument som man skriver OffLine blir lätt dryga (flera megabyte), och de måste delas upp för maximalt kort uppladdningstid ONline (med sämsta möjliga maskinvara). Därför har delarna i efterhand måst sättas på skilda htm-dokument, vilket delvis har spridit ut (demolerat den ursprungligt tänkta) översikten relativt originalet.
I inledningsdokumentet Universums Historia beskrivs hela ämnet mera övergripande med fysikens olika förgreningar och som kopplar till den separat avdelade syntesen i Fysikens 7 Principer.
Fortsätt i matematikbeskrivningen från stället med uthoppet som ledde hit till Elektriska Laddningen.
Matematiken för sin del, fortsätter i Formlagarna efter avsnittet om derivatan (som innehåller uthoppet som ledde hit, tillämpningsexempel på differentialbegreppet). Där ges en bastablå för de elementära derivata- och integralsambanden tillsammans med enkla utvecklingsexempel som beskriver och förklarar hur bastablån härleds. Efter Formlagarna följer sedan Den Högre Analysen som utgör slutmålet med den här presentationen: den allmänna formuleringen av fysikens alla möjliga variationer genom n:te ordningens varianter (konv. differentialekvationer) och deras lösningar — med vidare.
Editor2007XI14
Elektriska laddningen
innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Elektriska
laddningen
ämnesrubriker
innehåll
Ljusbrytningen i
vatten · ljusets grundläggande fysik
Ljusets
gravitella beroende grundform
Induktionen och magnetismen · i separat htm-dokument
referenser
t för 10–, T för 10+, förenklade exponentbeteckningar
(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken
är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.
Senast uppdaterade version: 2024-09-09
*END.
Stavningskontrollerat 2007-11-10 | 2007-11-14 |
*
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se
√
τ π ħ ε UNICODE — ofta använda tecken i
matematiska-tekniska-naturvetenskapliga beskrivningar
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω → ∞ ≡
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤
≈ ≥ ˂ ˃ ˂
˃ ← ↑ → ∞ ↓
ϑ
ζ ξ
Pilsymboler, direkt via tangentbordet: Alt+24 ↑; Alt+25
↓; Alt+26 →; Alt+27 ←; Alt+22 ▬
Alt+23
↨ — även Alt+18 ↕; Alt+29 ↔
PNG-justerad 2011-08-12
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se