ENTROPIBEGREPPET — UNIVERSUMS HISTORIA

ENTROPIBEGREPPET — UNIVERSUMS HISTORIA | enproduktion 2010II21 | Efter sammanställningar från 2009 | Senast uppdaterade version: 2015-01-09 · Universums Historia

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Entropibegreppet I RELATERAD MATEMATIK OCH FYSIK

med den fullständiga härledningen till Plancks strålningslag från Plancks entropisamband

EntropibegreppetsMultiUniversellaHarmoni

VERKANSKVANTUMSGRUNDADE PLANCKENTROPIN | PLANCKS STRÅLNINGSLAG FRÅN PLANCKS ENTROPISAMBAND

FOTO&MONTAGE: Författarens arkiv — Molekylmodell från FOCUS MATERIEN 1975 s357 · Vänster PLANETS REGULJÄRA INDELNING · Övriga: Kub och Pentagondodekaeder i Simply3D · Maskros Våren 2009 Nikon D90

Plancks entropisamband

inte Boltzmanns

Entropibegreppets innebörd

Feb2010 — utförlig genomgång

Entropibegreppet

Dec2009 — kortare, utan detaljer

kärnblock

utvalda huvudrubriker (börja här)

W finns inte i statistiken

TERMEN entropi (av grek. entre’pein, vända om [transformation]) infördes (1865) av Clausius (Rudolf Julius Emanuel Clausius, 1822-1888, BKL.II.sp1314ö).

Begreppet ENTROPI — som tillsammans med modern akademi uppkom under 1800-talet — har för många kommit att förknippas med en särskilt »elak» kosmologisk översiktskarta: oordning (se citat nedan): alltings absolut yttersta meningslöshet. Följande framställning visar de rent matematiska grunderna tillsammans med en utförlig genomgång av begreppen — i ljuset av den relaterade matematikens och fysikens resultat. För de sistnämnda, se särskilt från Atomkärnas Härledning i Universums Historia. För sammanfattning, se sammanfattning.

Först — inför åsynen av all prakt — kan vi till inledande jämförelse studera »Elakhetens Sal»:

Inledande citat

All textmarkering (färg, fetstil etc.) i citat är separat tillagda (för nyckelmeningar) i den mån de inte redan framhävs i originalen.

Min översättning:

Entropins idé hade en avgörande filosofisk och politisk betydelse. Entropi är vad ändrar klockans tickande till en förstörare för alla ting. Det är vad underligger den oundvikliga övergången från ungdom till ålder. Entropi är sönderfall. Och med sönderfall varar inget för evigt. Boltzmann hade i summa fångat dödligheten i en ekvation. Fysiken tillkännagav nu att ingen ordning, inte ens given av Gud, varar för evigt. Att det inte fanns någon naturlig ordning som Gud skulle ha stensatt, hade redan påpekats av den vetenskapare Boltzmann mest beundrade, Charles Darwin.

Från filmen om Cantor, Gödel, Boltzmann och Turing

http://www.supranaturalis.se/index.php?option=com_seyret&task=videodirectlink&Itemid=40&id=1689

PHILOSOPHY, PHYSICS, MATHEMATICS - DANGEROUS KNOWLEDGE (BBC FOUR)

All textmarkering (färg, fetstil etc.) i citat är separat tillagda (för nyckelmeningar) i den mån de inte redan framhävs i originalen.

Med denna inledande bredsida av verbalt kanonbestyckad angreppseld på dygdernas alla mekanismer — med tillhörande reklam för alla de goda tingens slutliga utplånande, i ljuset av en så tydligt upphöjd dödsdans kring mänsklighetens hopp — ser det rejält kört ut.

Men håll ut. Reklamen är inte så storvulen som den ser ut. I den här presentationen ges en fullständig genomgång.

KOMPLEMENT TILL UNIVERSUMS HISTORIA

ENLIGT RELATERAD MATEMATIK OCH FYSIK

Harmonibegreppet

FOTO: Författarens arkiv — Maskros · Våren 2009 · Nikon D90

Angående Frågan om

ENTROPIBEGREPPETS MULTIUNIVERSELLA HARMONI

eller

ÅTERERÖVRINGEN AV MÄNSKLIGHETENS EVIGA HOPP

— jämför ovan, det uppmuntrande inledningscitatet.

Santa Maria — Frihandsteckning · Författarens arkiv

Se även

ENTROPIBEGREPPET I KORTARE GENOMGÅNG FRÅN DECEMBER 2009

Alternativ rubrik till ENTROPIBEGREPPET (för att samla största möjliga verbala potential under bredast möjliga uppslutning)

DÖDSKALLARNAS RIKSDAG

eller

Boltzmanns entropibegrepp

UPPFATTNINGEN ATT KOSMOS EXISTENS BYGGER PÅ VÄXANDE OORDNING

Om den moderna akademins uppsegling i mänskligheten under 1800-talet

kärnblock

S = b(lnW) är Plancks entropisamband — inte Boltzmanns

HÄRLEDNINGEN TILL PLANCKS ENTROPISAMBAND

Hur W beräknas — antalet likaberättigade energifördelningssätt

HÄRLEDNINGEN TILL PLANCKS STRÅLNINGSLAG FRÅN PLANCKS ENTROPISAMBAND

W finns inte i statistiken

Åldrandets princip

BOLTZMANNS H-TEOREM

Entropibegreppets innebörd — detaljerad historisk genomgång

PRAKTISKA EXEMPEL

— ämnet gäller (också) tillfället att få understryka Ludwig Boltzmann och Max Planck som atomfysikens grundare: Boltzmann för uppslagen, Planck för formuleringarna; Ett (som det har visat sig) erkänt svårt formuleringsområde med många meningsriktningar.

Inledning till entropibegreppets innebörd

2010II9

S = b(lnW) är Plancks entropisamband — inte Boltzmanns

S = b(lnW) blev Max Plancks (verkanskvantums-)entropi — på Ludwig Boltzmanns matematiskt uppdagade atomism

S = b lnW ...................................................... J/°K, Plancks entropisamband

— modifierat och utvecklat av Max Planck omkring 1900 med inspirerad grund i Boltzmanns (garanterat erkänt besvärliga) atomistiska H-funktion (från Boltzmanns H-teorem 1872)

H[f_t] = ò f (r; v; t) ln f (r; v; t)d³rd³v .............. Boltzmanns H-funktion

Genom otaliga webbkällor framställs »Boltzmanns entropisamband» (eng. Boltzmann entropy formula, Boltzmann formula, Boltzmann equation) på typformen som ovan ofta enligt

S = k log W; S = k log_e W; S = k ln W

Se exempel på typcitat i W finns inte i statistiken, ”Boltzmann’s formula S = k logW”.

Men den sambandsformen är (långt ifrån) någon matematisk form som kommer från Ludwig Boltzmann: S-formen, ovan, växte tydligen fram genom Max Planck år 1900 (Se Plancks original) — också han från början en ihärdig motståndare till Boltzmanns atomistiska banbrytande idéer, liksom de flesta andra hans samtida vetenskapare (och med historiens stora sannolikhet för vilkas hätska attacker och kritik från vetenskapsfolket Boltzmann begick självmord år 1906, se särskild citatsamling); Men också Max Planck själv fick erkänna sig besegrad (se citat) på den punkten i samband med den berömda upptäckten av det universella verkanskvantumet år 1900 (Plancks konstant, h=mcr=6,62559 t34 JS) och som framkom i uppdagandet av det som numera kallas Plancks (allmänna) strålningslag

N_l = l^–5hc²[e^hc^/b^l^T–1]^–1 ............................... W(M³SRsteradianer)^–1, Plancks strålningslag

svartkroppsstrålningslagen · se även den relaterade fysikens fullständiga härledning i Plancks Strålningslag från Plancks entropisamband

Se även FOCUS MATERIEN 1975 s286sp2ö, samma form som ovan

Se även separat webbkälla med Plancks egen beskrivning

— Max Planck visar hur strålningsekvationen ovan framkommer, samt grunden till

sambandet (s6) för Planckenergin E=hf — från år 1901 på engelska i

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s3

http://bourabai.kz/articles/planck/planck1901.pdf

I samband med ovanstående har detaljer framkommit som har ställt ämnet i ett betydligt klarare ljus: en fullständig förklaring har visat sig, se separat artikel Härledningen till Plancks strålningslag från Plancks entropisamband. En kompletterande beskrivning finns i Flaskhalsarna i Plancks härledning där luckorna i Plancks härledande framställning beskrivs och förklaras i detalj. Vidare nedan.

För att få fram det sambandet tvingades Planck avhandla ämnet inspirerad av ”Boltzmann's trend of ideas” som Planck själv uttrycker saken i sin nobelföreläsning från 1920.

Planck använde i själva verket den efter honom uppkallade Plancks konstant h, som han själv också bestämde tillsammans med Boltzmanns konstant b, för att få fram entropisambandet. Eller, som Planck själv uttrycker saken i sin nobelföreläsning från 1920 angående h,

”Whilst it was completely indispensable for obtaining the correct expression for entropy - since only with its help could the magnitude of the "elementary regions" or "free rooms for action" of the probability, decisive for the assigned probability consideration, be determined”.

I klartext: Boltzmanns matematiska uppställning i Boltzmanns H-teorem blir i ljuset av Plancks härledning till allmänna strålningslagen »före sin tid»: det går inte utan Plancks konstant (h), inte utan Plancks (verkanskvantums-)entropi, inte utan Plancks strålningslag.

Citatet närmast nedan, med vidare, beskriver historiens kärndel:

”Guided by Boltzmann's kinetic theory of gases, Planck formulated what he called a "principle of elementary disorder" that did not rely either on mechanics or on electrodynamics. He used it to define the entropy of an ideal oscillator (dipole) but was careful not to identify such oscillators with specific atoms or molecules.

”,

”In November 1900 Planck realized that his new entropy expression was scarcely more than an inspired guess. To secure a more fundamental derivation he now turned to Boltzmann's probabilistic notion of entropy that he had ignored for so long. But although Planck now adopted Boltzmann's view, he did not fully convert to the Austrian physicist's thinking. He remained convinced that the entropy law was absolute - and not inherently probabilistic - and therefore reinterpreted Boltzmann's theory in his own non-probabilistic way. It was during this period that he stated for the first time what has since become known as the "Boltzmann equation" S = k log W, which relates the entropy, S, to the molecular disorder, W.

”,

MAX PLANCK: THE RELUCTANT REVOLUTIONARY Dec 1, 2000

http://physicsworld.com/cws/article/print/373

Man måste logga in på PhysicsWorld för att få tillgång till artiklarna från GoogleSökningen — men det är helt gratis

Brytpunkten

Citatet närmast ovan använder på flera ställen ordet ”probability”, sv. sannolikhet. Det är en del av den märkliga historien — därför att det visar sig vid en noggrann genomgång att hela den fullständiga härledningen till Plancks strålningslag enbart är en studie i tillståndsekvationer: inget spår av sannolikhet. Den delen beskrivs särskilt i Andra flaskhalsen. För att — ytterligare — klargöra den delen finns en särskild genomgång i W finns inte i statistiken — där också (en del av) anledningen framkommer varför begrepp från statistiken (tydligen felaktigt) har kommit in i bilden.

Som Max Planck själv visar i sin framställning från 1901 (webbkällan, med vissa utdrag, visas i Plancks original) kan Plancks strålningslag härledas utomordentligt väl relaterbart och elementärt utan den sedvanliga vidlyftiga universitets- och högskolematematikens utflykter från W-kvoten

W = (n+P)ⁿ⁺^P/(nⁿP^P) (med n för Plancks beteckning N).

Men som också Planck beskriver utomordentligt tydligt (och utöver den källan finns mig veterligt ännu ingen annan som klargör den saken) är utgångspunkten inte en potensfunktion (N^N) i W-kvoten utan en fakultetsfunktion (N!). Planck skriver den (s3n) som

R = (N+P–1)!/(N–1)!P!

— varefter Planck gör den (ytterst) märkliga (och bevisligen felaktiga, se räkneexemplet nedan) kopplingen

”Now according to Stirling's theorem, we have in the first approximation: N!=N^N”;

Jämför exemplet med n=50, avrundade värden, T för 10^+;

50! = 3 T64

50⁵⁰ = 9 T84

Det ”Stirling's theorem” som Planck omnämner har i själva verket formen

n! = (2p)^1/2 nⁿ⁺^1/2 e^–n [ref. MATEMATIKLEXIKON W&W 1991 s395sp2ö].

Den formen däremot stämmer mycket bra medan Plancks hoftning är uppenbart felaktig.

Men inte bara Max Planck använder (de därmed tydligt uppdagade felaktiga) fakultetsfunktionerna som grund för W-formen: i stort sett (här veterligt) alla etablerade webbkällor gör det. Se till exempel

@INTERNET Wikipedia Ludwig Boltzmann 2010-01-31

Även på webbsidan

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

Där beskrivs W-faktorn i citatets ”S = k log_e W” enligt

”W can be counted using the formula for permutations

bildkopia

”.

Det finns ingen varken logisk eller relaterbar koppling från permutationsmatematiken (N!) — alla möjliga positioner för abc — till potensmatematiken (N^N) — alla möjliga kombinationer i abc — den senare innehåller betydligt flera möjliga sätt än den förra, jämför räkneexemplet längre upp. Se även mera utförligt exempel längre ner. Citatkällan närmast ovan använder också ordet ’”sannolikhet” med, tydligen, grund i tyskans ”W is the Wahrscheinlichkeit”, med tyskans Wahrscheinlichkeit liktydigt med engelskans probability och svenskans sannolikhet. Källan fortsätter med W-beskrivningen som

”the frequency of occurrence of a macrostate[9] or, more precisely, the number of possible microstates corresponding to the macroscopic state of a system — number of (unobservable) "ways" in the (observable) thermodynamic state of a system can be realized by assigning different positions and momenta to the various molecules. Boltzmann’s paradigm was an ideal gas of N identical particles, of which Ni are in the i-th microscopic condition (range) of position and momentum.”,

med efterföljande ovanstående bildkopierade citatutdrag.

Men den W-formen, fakultetsfunktionen ovan i citat, har ingen matematisk koppling till W-formen med den relaterbara sammansättningen av potensfunktioner; potensfunktioner har uppenbarligen ingenting med ”Boltzmann’s paradigm” att göra: fakultetsfunktionerna. Den här uppmärksammade motsättningen, om allt är korrekt uppfattat, leder till den oundvikliga slutsatsen att begreppet sannolikhet — statistisk, i W-formen och därmed statistik i Plancks strålningslag — tydligen helt utesluts ur fysiken — och med den för den här författaren obehagliga och föga avundsvärda ställningen att ovanstående citatkälla, och alla liknande tydligen, (ännu) inte har uppfattat den ordningen.

Plancks helt utmärkta beskrivning visar också exakt var Planck själv begår felet:

”Now it is evident that any distribution of the P energy elements among the N resonators can result only in a finite, integral, definite number. Every such form of distribution we call, after an expression used by L. Boltzmann for a similar idea, a "complex." If one denotes the resonators by the numbers

1, 2, 3, ...N , and writes these side by side, and if one sets under each resonator the number of energy elements assigned to it by some arbitrary distribution, then one obtains for every complex a pattern of the following form:

bildkopia

”,

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s3

http://bourabai.kz/articles/planck/planck1901.pdf

Det enkla exemplet med abc i potensfunktionen (n+P)^(n+P) med (n+P)=3 visar det här: man kan i matematisk mening inte ställa upp ett sådant led som Planck ovan exemplifierar i fallet n partiklar och P Planckenergikvanta:

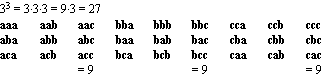
Vi kan i exemplet abc med (n+P)=3 inte precisera n för sig och P för sig — typ »en atom och två Planckkvanta» — endast TILLSAMMANS: alla fysikaliskt möjliga kombinationer gäller, ingen får utelämnas. Med andra ord: permutationsformen (N!)

— som just bygger på att utelämna (till och med) huvuddelen (tydligen)

— är uppenbarligen att förstå problemet på fel sätt. Korrekt sätt är, helt solklart, potensformen (N^N) med den betydligt rikare representationen jämfört med den betydligt trängre permutationsformen, (n+P=3)!=6={abc acb bac bca cab cba}; Potensformen, inte permutationsformen, leder direkt på Plancks strålningslag genom helt elementära utvecklingar, se utförligt i Härledningen till Plancks strålningslag från Plancks entropisamband.

Den kritiska frågan lyder:

— Kan man se kombinationskartan ovan i exemplet 3^3=27 som en BILD av alla möjliga kombinationssätten för TRE Planckenergikvanta i EN atom?

[(1+3)^(1+3)=4^4=256 stämmer ju inte med 3^3=27 …].

— Absolut, ja — enligt följande förklaring:

Betrakta det praktiska resonansexemplet med stående vattenvågor i en vanlig diskbalja från HÄRLEDNINGEN TILL GRUNDÄMNENAS PERIODISKA SYSTEM via Keplers ytmoment eller Keplerresonanserna:

Resonansexemplet

Varje abc i de 27 möjliga mönstersätten kan ses som en resonans, ett fast s.k. stående vågmönster, ett specifikt mönster som är unikt INOM atomen: Eftersom EN atom — via sitt UTSPRIDDA VÅGRESONANTA elektronhölje — kan anta vilka som helst — alla — typer av stående vågmönster (Se även i Härledningen till Spektrum och Kvanttalen) kan vi också därmed i antalet möjliga kombinationssätt i exemplet (n+P)=3 verkligen se de 3^3=27 kombinationerna i EN atom: atomen som kvantiteten atom räknas naturligtvis inte som kvaliteten resonans, eftersom en atom — elektronhöljet — kan anta alla resonanser, och vilket därmed (galant) förklarar att även kvantiteten n=0 är tillåten i det kvalitativa utfallet i (n+P), energins resonansmönster, men att den formellt kvantitativa ordningen kräver, självklart, ett minsta n=1: minst en atom måste finnas för att gestalta typ P=3 Planckenergikvanta (abc …).

Med Plancks W-form

W = (n+P)ⁿ⁺^P/(nⁿP^P) (med n för Plancks beteckning N)

gäller — således — i fallet n=1 kvalitativt för nämnarens (n+P) det optimala (0+P) med minsta (via c>0) P=1 och kvantitativt i nämnaren, tvunget, n=1 för den enda atomens elektronhölje, totalt Wmin=1.

Men vadå? Det står ju där, genom resultatet i Plancks strålningslag — med utomordentligt experimentellt bekräftad giltighet från W-formens potensfunktion, som ovan — att det tydligen är W-formens potensfunktion som gäller. Varför har man då inte sökt förklaringen från den utgångspunkten?

UtellMe.

Märkligt som det är: vid en allmän genomletning på webben (Feb2010, engelska delen) efter LIKNANDE PROPÅER från andra författare — och som därmed skulle leda till en (ytterst) enkel härledning av Plancks strålningslag, se Webbkällor som härleder Plancks strålningslag — finns knappast annat än »den sedvanliga och utspridda floran» av mer eller mindre högskolestämda, (djupt) komplicerade, avhandlingar som på olika sätt försöker begripliggöra Plancks strålningslag (alla misslyckas med det — inför åhörare som befinner sig under universitetsstrecket): långt ifrån den enkla beskrivning

(som — dock först från den korrekta W-kvoten — också beskrivs utomordentligt klart i Plancks härledning från 1901, se Plancks original)

man kunde förvänta sig OM någon hade uppmärksammat »sannolikhetssyndromet» i den etablerade beskrivningen av Plancks strålningslag. Som redan omnämnts, även Max Planck själv använder ordet ”probability” för W i sitt motsvarande S=b(lnW) i originalet från 1901 (se Plancks original)

(trots att han av flera källor [se exv. den nyligen ovan citerade i THE RELUCTANT REVOLUTIONARY] sägs ha varit emot det statistiska betraktelsesättet).

Det faktum att en fullständig härledning till Plancks strålningslag från Plancks entropisamband nu, och tydligen som det får förstås, har framkommit genom dessa uppdaganden och som, garanterat, visat sig inte ha något med sannolikhet att göra, samt att ingen verkar ha uppmärksammat den möjligheten — inte ens Planck själv, se Plancks original — gör att användningen av ’sannolikhet’ i koppling till härledningen av Plancks strålningslag, uppenbarligen och förutsatt att inga felslut finns, ser ut som en »allmän vetenskaplig låsning»: det finns tydligen ingen sannolikhetsgrund i Plancks strålningslag. Ingen permutationsmatematik. Bara rena tillståndsekvationer som uttrycker och beskriver rena entydiga energiekvivalenter på entydiga potensfunktioner. Hur man sedan, därifrån, ska ’förklara’ den strida strömmen av författare och studenter som använder matematisk statistik med sannolikhetsparametrar i beskrivningen av detaljer som sammanhänger med Plancks strålningslag, det förtäljer inte den här historien.

Vidare om Plancks, inte Boltzmanns, entropisamband:

S = k ln W;

”The formula is a modified or reduced form of Austrian physicist Ludwig Boltzmann's H-function and was first put in this shorthand form by German physicist Max Planck in his 1901 paper “On the Law of Distribution of Energy in the Normal Spectrum.” [1] Specifically, Planck explains that the entropy SN of the system [resonator] is proportional to the logarithm of its probability W, within an arbitrary additive constant:

S = k log W + const

”,

ENCYCLOPEDIA OF HUMAN THERMODYNAMICS kronologisk uppgift saknas

http://www.eoht.info/page/S+%3D+k+ln+W

Boltzmann;

”His formula, ∫(dq/T) = 2Ω/3, is, however, better known in the form S = k log W, which Max Planck gave it in 1901.

”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

”Boltzmann further introduced the H-functional (denoted E in the 1872 paper,

but later widely called H, including by Boltzmann):

H[f_t] = ò f (r; v; t) ln f (r; v; t)d³rd³v (2)

”,

Boltzmann’s H-theorem, its limitations, and the birth of (fully) statistical mechanics,

Harvey R. Brown and Wayne Myrvold, September 8 2008, s4

http://philsci-archive.pitt.edu/archive/00004187/01/Reversibility08.pdf

Således:

Boltzmanns H-funktion, som ovan från Boltzmanns H-teorem,

ÄR UPPENBARLIGEN NÅGOT HELT ANNAT ÄN Plancks Entropisamband

S = b lnW ...................................................... J/°K, Plancks entropisamband

— tydligen modifierat och utvecklat av Max Planck omkring 1900-1901 med inspirerad grund i Boltzmanns (garanterat erkänt besvärliga) atomistiska H-funktion (från Boltzmanns H-teorem 1872)

H[f_t] = ò f (r; v; t) ln f (r; v; t)d³rd³v .............. Boltzmanns H-funktion

Ännu i denna dag finns I MODERN AKADEMI ingen varken begriplig eller ens tillgänglig LOGISK beskrivningsgrund för att tala om vad, exakt Plancks konstant (h) går ut på, vad Plancks konstant är — utöver »det universella verkanskvantumet».

I RELATERAD FYSIK däremot VET vi (genom UNIVERSUMS HISTORIA) genom enkel analogi på nu redan välkända fysikaliska kvantiteter, nedan, att Plancks konstant ÄR — definierar — neutronen (dess tyngdradie och massa) på divergensen (ljusets topphastighet c0) enligt (1u=1,66033 t27 KG, se atomära massenheten)

PLANCKRINGEN — neutronen — Plancks konstant h

h = mcr = (1,0086652u)(2,99792458 T8 M/S)(1,31966 t15 M) = 6,62559 t34 JS

Genom den, så OCKSÅ, uppdagade NEUTRONKVADRATEN (helt okänd i modern akademi) kan atomvikterna via elliptiska funktioner bestämmas — med exemplifierad, tydlig, direkt tabelljämförande utklassning mot den moderna akademins teori;

h grundlägger med andra ord atomkärnans härledning ENLIGT RELATERAD FYSIK (dessutom galant, min mening). Se utförligt från Planckringen.

Se även (vidare, utförligt) från Boltzmanns H-teorem.

Entropibegreppets Innebörd

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Entropibegreppets Innebörd

2010II8

Se även INLEDNING TILL ENTROPIBEGREPPETS INNEBÖRD.

ENTROPIBEGREPPETS INNEBÖRD

Clausius inför termen entropi år 1865 — dess innebörd i modern akademi och relaterad fysik

Alla textmarkeringar i citaten är separat tillagda om inte samma i originalet (för markering av nyckelmeningar);

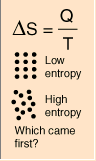
Entropibegreppet i modern akademi har tydligen, citat nedan, sitt definitiva ursprung i Clausius framställning från år 1854, med sambandsformen (beteckningen S kom senare [1865])

S = Q/T ................................... J/°K, Clausius ursprungliga sambandsform

Enheten J/°K är samma som den som i facklitteraturen används för värmekapacitet: en kropps förmåga att ta upp värme. Se även i allmänna sambandsformer.

BILDKÄLLA: @INTERNET Wikipedia Steam engine 2010-02-08

Steam engine, Stott Park Bobbin Mill

Clausius framställning 1854

HISTORIEN I LJUSET AV VÄRMEKAPACITETENS FENOMENFORM J/°K kopplar till den, i modern akademi centrala och numera berömda, s.k. termodynamikens andra huvudsats eller termodynamikens andra lag (citatutdrag följer nedan — i historisk succession)

— naturligtvis med direkt koppling till utvecklingen av ångmaskinen från slutet på 1600-talet (första kommersiellt fungerande från 1712, ref Wikipedia Steam engine).

Formuleringarna avlöser varandra under 1800-talet.

Citatet nedan är från Clausius framställning av år 1854 och ger oss den (i den här framställningen, centralt) vetenskapshistoriska grunden:

”He stated:^[3]

the second fundamental theorem in the mechanical theory of heat may thus be enunciated: If two transformations which, without necessitating any other permanent change, can mutually replace one another, be called equivalent, then the generations of the quantity of heat Q from work at the temperature T , has the equivalence-value:

$\frac {Q}{T}$

”,

”3. ^ Published in Poggendoff’s Annalen, Dec. 1854, vol. xciii. p. 481; translated in the Journal de Mathematiques, vol. xx. Paris, 1855, and in the Philosophical Magazine, August 1856, s. 4. vol. xii, p. 81”,

@INTERNET Wikipedia History of entropy, 1854 definition 2010-02-08

Min översättning:

Han påstod:

det andra fundamentala teoremet i den mekaniska teorin för värme kan sålunda formuleras: Om två transformationer vilka — utan att kräva annan bestående ändring, [än att de] kan ömsesidigt ersätta varandra — kan kallas ekvivalenta, då har bildningen av kvantiteten värme Q från arbete vid temperaturen T ekvivalensvärdet: Q/T.

Syftet med citatdelarna från Clausius är här främst att belysa DEN KLASSISKA grunden till den nuvarande moderna akademins »termodynamikens andra huvudsats» lärosystem, nämligen den helt enkla och ENLIGT RELATERBAR FYSIK KLASSISKT korrekta (»triviala») observationen att

värme går alltid från varmt till kallt

Den delen i huvudsatsens nuvarande formulering har, nämligen, helt gått förlorad. Det finns ingenting kvar av den delen;

Medan Clausius klassiska formulering helt klart ansluter till digniteten NATURLAG — divergensen, Plancks strålningslag, induktionen och magnetismen — är det tydligt att den moderna »isolerat system»-andra-termodynamikens-huvdsats INTE gör det.

Ett formuleringsbrott inträffande med andra ord — tydligen någon gång under 1800-talets sista dagar, eller möjligen i början på 1900-talet — och i tydlig ovetskap för alla inblandade. Tydligen: utom RELATERAD FYSIK omöjligt att fokusera.

Jämför — till att börja med — sådana påståenden som ”The second law can never be proven …”, sv., ’andra lagen kan aldrig bevisas’ från Ludwig Boltzmann någon gång under 1800-talets senare hälft

[”Boltzmann 1895, cited from Emch and Liu (2002), 103” från Kinetic Theory of Gases and Statstical Mechanics, Christian Wüthrich 2008,

http://philosophy.ucsd.edu/faculty/wuthrich/teaching/2008_285/LectureKinThyStatMech.pdf

];

— Vad menas med ”second law” — i Boltzmanns 1895-association?

Verkligen, och alldeles tydligen inte det som står att läsa om ”second law” i dagens »termodynamikens andra huvudsats». Vi ville — alltså — gärna veta vad, exakt, som avsågs.

Ytterligare längre fram.

Tydligen: Många — inte få — fackverk gör det felet vid den historiska resumén av termofysikens grunder att ikläda dåtidens beskrivning en senare tids nomenklatur och begrepp — utan att explicit tala om det. Resultatet blir att det historiska spåret sopas igen, och man får spendera åtskilliga timmar med förbryllande grimaser inför böckernas alla upptänkliga nymodigheter, utan varje spår av ursprunget.

Se Exempel på felskrivningar i etablerade källverk.

Jämför även (här mindre kritiskt), till exempel, fackverket nedan — framstående för sin tid:

”I intimt samband med andra huvudsatsen står tillståndsvariabeln entropi’ S, av Clausius definierad därigenom att ökningen i entropi dS hos en substans är lika med den vid en reversibel tillståndsändring tillförda värmemängden dQ, dividerat med den absoluta temperatur T, vid vilken den tillföres d.v.s.,

dS = dQ / T ”,

BONNIERNS KONVERSATIONS LEXIKON BandXI 1927 sp961ö

Vi VET (här) inte om skrivsättet ovan är Clausius eget eller den senare tidens omskrivning:

— Om det inte finns ett klargörande i källan att beteckningen ”d” framför storheten är NUTIDENS beskrivningssätt (och som numera identifieras med begreppet differential OCH SOM I MODERN AKADEMI också OFTA IDENTIFIERAS MED intervall, se särskilt citat), kan man få den uppfattningen att termbeskrivningen i sin CaseHistory möjligen återfaller på Clausius — inte på en nyare tids omskrivna begrepp — och varje användande av citatkällan i en analys i strävan att klargöra vad ursprungsförfattaren har avsett blir en helt värdelös handling; ENBART MED REFERENS TILL UTDRAGET LÄNGRE UPP är det tydligt att citatet närmast ovan just är en sådan, nyare tids omskrivning, inte Clausius ursprungliga beteckningssätt.

Det finns dock ingen vidare bevisning i den saken i den här presentationen (och vi behöver den, här, inte heller) — men exemplet pekar på vilka närmast enorma svårigheter som kan infinna sig i användningen av även etablerade källverk.

Se längre ner i Exempel på felskrivningar i etablerade källverk, som däremot verkligen anknyter till ämnet.

Drivkraften bakom intresset för termofysiken under, speciellt, 1800-talet var naturligtvis intresset för ångmaskinerna: deras uppenbart stora utvecklingspotential för industriella processer. Så framväxte också formuleringarna inom termofysiken mot en mera stringent och koncist vetenskaplig form vartefter forskningen fortskred:

Clausius framställning 1862

”In 1862, Clausius stated what he calls the “theorem respecting the equivalence-values of the transformations” or what is now known as the second law of thermodynamics, as such:

The algebraic sum of all the transformations occurring in a cyclical process can only be positive, or, as an extreme case, equal to nothing.

”,

@INTERNET Wikipedia History of entropy, 1862 definition 2010-02-07

Min översättning:

År 1862 framställde Clausius vad han kallar ”teoremet rörande ekvivalensvärdena till transformationerna” eller vad som är känt som termodynamikens andra lag, som sådan:

Den algebraiska summan av alla transformationer som förekommer i en cyklisk process kan bara vara positiv, eller, som ett extremt fall, lika med ingenting.

Den enkla omskrivningen av innebörden i ovanstående, och som kan ses i en del (webb-)källor är av den citerade typen nedan:

”A second formulation, due to Rudolf Clausius, is the simplest formulation of the second law, the heat formulation or Clausius statement:

Heat generally cannot flow spontaneously from a material at lower temperature to a material at higher temperature.

”,

@INTERNET Wikipedia Second law of thermodynamics, Versions of the Law 2010-02-10

Min översättning:

En andra formulering, enligt Rudolf Clausius, är den enklaste formuleringen av andra lagen, värmeformuleringen eller Clausius formulering:

Värme kan generellt inte flyta från ett material vid lägre temperatur till ett material med högre temperatur

Eller enklare:

värme flyter alltid, spontant irreversibelt, från varm till kallt

Den typformen kommer här, för bekväm referens, att kallas den klassiska andra värmelagen. Man kom (nämligen) att identifiera den med en TIDENS PIL (termen myntades först in på 1900-talet) och som tilldrog sig stort centralt naturfilosofiskt intresse under 1800-talet: naturlagarnas allmänna formulering, med hur och varför.

Clausius framställning 1865

entropibegreppet införs 1865 av Clausius

”In 1865, Clausius gave irreversible heat loss, or what he had previously been calling "equivalence-value", a name:[5][6]

“ I propose to name the quantity S the entropy of the system, after the Greek word [τροπη trope], the transformation. I have deliberately chosen the word entropy to be as similar as possible to the word energy: the two quantities to be named by these words are so closely related in physical significance that a certain similarity in their names appears to be appropriate. ”

”,

@INTERNET Wikipedia History of entropy, 1862 definition 2010-02-07

Min översättning:

År 1865 gav Clausius irreversibel värmeförlust, eller vad han tidigare hade kallat ”ekvivalensvärde”, ett namn:

”Jag föreslår att kalla kvantiteten S systemets entropi, efter Grekiskans ord [entre’pein, vända om, ref. BKL], transformationen. Jag har avsiktligt valt ordet entropi att vara så lika som möjligt ordet energi: de två kvantiteter att kallas med dessa ord är så nära besläktade i fysisk innebörd att en viss likhet i deras namn framstår ändamålsenlig.”

Clausius entropibegrepp

Vi ser nu — för det första och alldeles tydligt — ATT Clausius beskrivning »entropi = energi» — med synonymen värmeförlust — i renskrivning, tydligen, ska vara

entropi = energiFÖRLUST .................................... J/°K, Clausius entropibegrepp

Här visar sig — alltså — den första FÄLLAN i DEN OBETINGADE användningen av begreppet entropi

Jämför ett typsnitt ur tillgängliga webbreferenser (otaliga liknande finns) som bekräftar förtydligandet:

”Time's arrow points in the direction the second law operates – toward the inevitable rise of entropy and the loss of useful thermodynamic energy.”,

THE INTERNET ENCYCLOPEDIA OF SCIENCE David Darling ”up to date”

http://www.daviddarling.info/encyclopedia/Q/quantum_theory_origins.html

Min översättning:

Tidens pil pekar i den riktning som andra lagen opererar — mot den oundvikliga ökningen i entropi och förlusten av användbar termodynamisk energi.

Clausius sambandsform S=Q/T med enheten Joule per grader Kelvin, J/°K, är av samma form som den fundamentala gaskonstanten (k) vi finner i allmänna gaslagen

E = pV = kT = (F/A)Ad ................................ J, allmänna gaslagen

k = E/T = bN .............................................. J/°K, fundamentala gaskonstanten

b, Boltzmanns konstant (den idealt fundamentala materiegasbollens fundamentala värmeenergiinnehåll 1,38 t23 J/°K), eller fundamentala enheten för värmekapacitet

N, Loschmidts tal (N=2,6869722 T25 som kopplar till det mera namnkända Avogadros tal, se utförligt i Konstanterna i Allmänna gaslagen)

Beteckningen E för energi och Q för värme är alltså analoga:

S = Q/T ................................... J/°K, Clausius ursprungliga sambandsform

S = E/T ................................... J/°K, Allmänna gaslagens motsvarande sambandsform

Entropibegreppet i modern akademi blir (därmed och således med ovannämnda klargörande) utomordentligt enkelt att förstå — OM man samtidigt bara kommer ihåg den moderna akademins utgångspunkt i föreställning om UNIVERSUMS UPPHOV (nedan kort, utan vidare referenser):

BILDKÄLLA: @INTERNET Wikipedia Open Cluster 2010-02-08

NGC 346 · Öppen stjärnhop

I MODERN AKADEMI hoppas tillfället med BIG BANG över; Man väntar tills allt har spritts ut, maximalt, och börjar först sedan därifrån, alltså från maximalt KALLT: S=0/T=0, med noll värmemängd, E=0, analogt nollentropi;

Från utspridda gas- och stoftmoln bildas himlakropparna genom gravitell sammandragning; Sammandragningen (kollisioner) frigör värme (E>0), samma som att Clausiusentropin S=E/T tillväxer med den motsvarande förbrukade värmestrålningen och som sedan omöjligen kan återvinnas: Clausius energiFÖRLUST; Entropin växer med universums utveckling.

Det enda som fattas för att den beskrivningen — i full modern akademisk anda — ska bli fullständig är föreställningen om hela universum som ett »isolerat system»: om inte den utvecklade värmen kan komma ut, måste den stanna kvar. Därmed framgår själva bakgrunden och förklaringen till den numera allmänt förhärskande meningen med typformen ’entropin i universum ökar’. Jämför:

”Som minnesregler för termodynamikens två huvudsatser brukar ofta följande formuleringar användas:

Första huvudsatsen: Universums energi är alltid konstant.

Andra huvudsatsen: Universums entropi strävar alltid att öka.”,

FOCUS MATERIEN 1975 s325sp2mn

Jämför korrekt formulering;

’ Första huvudsatsen: Idealt slutna|isolerade materiesystems energi är alltid konstant.

Andra huvudsatsen: Idealt slutna|isolerade materiesystems entropi strävar alltid att öka.’

I praktisk fysik finns inga idealt isolerade system i termodynamisk mening.

Se även den nu rådande uppfattningen om »termodynamikens andra huvudsats».

Se även mera utförligt i ENTROPIBEGREPPETS SPRÅKFÖRBISTRING.

Se vidare utförligt från TILLSTÅNDSBEGREPPET I MODERN AKADEMI och ISOLERAT SYSTEM I TERMODYNAMISK MENING.

Exempel på felskrivningar i etablerade källverk

EFTER CLAUSIUS FRAMSTÄLLNING 1862 är händelsebilden diffus:

Föregående källor har, med tydlighet, klargjort att sambandsformen S=b(lnW) framkom först år 1901 genom Max Planck, samt att han också beräknade Boltzmanns konstant (b) som Boltzmann själv aldrig varken använde (eller ens skrev ut). Citatet nedan från Plancks nobelföreläsning från år 1920;

”This constant is often referred to as Boltzmann's constant, although, to my knowledge, Boltzmann himself never introduced it - a peculiar state of affairs, which can be explained by the fact that Boltzmann, as appears from his occasional utterances, never gave thought to the possibility of carrying out an exact measurement of the constant.”,

MAX PLANCK, NOBEL LECTURE JUNE 2 1920

The Genesis and Present State of Development of the Quantum Theory

http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html

Min översättning:

Denna konstant refereras ofta till som Boltzmanns konstant, fastän, vad jag vet, Boltzmann själv aldrig introducerade den — ett märkligt sammanträffande, vilket kan förklaras av det faktum att Boltzmann, vilket framgår från hans förekommande yttranden, aldrig gav tanke till möjligheten att genomföra en exakt mätning av konstanten.

WIKIPEDIAARTIKELN PÅ HISTORY of ENTROPY emellertid påstår följande — utan referenser (som fortfarande, tyvärr, är vanligt på Wikipedia):

”In 1877, Ludwig Boltzmann formulated the alternative definition of entropy S defined as:

$S = k_B \ln \Omega \!$ bildkopia

where

k_B is Boltzmann's constant and

Ω is the number of microstates consistent with the given macrostate.

Boltzmann saw entropy as a measure of statistical "mixedupness" or disorder. This concept was soon refined by J. Willard Gibbs, and is now regarded as one of the cornerstones of the theory of statistical mechanics.”,

@INTERNET Wikipedia History of entropy, Statistical thermodynamic views 2010-02-10

Det inlägget är (alltså) definitivt inte historiskt korrekt: artikelförfattaren är, tydligen och med referens till referenserna i föregående källor (Se från Inledning till entropibegreppets innebörd), inläst på Boltzmanns SENARE OMSKRIVNA SAMBAND och som — liknande en del föregående, här vidrörda, liknande exempel — har spritts ut över 1900-talet (i stor mängd, tydligen), med vidare.

Wikiartikeln slutar f.ö. sin historiska exposé där: vi får aldrig veta den slutliga kopplingen till den nu gällande formuleringen av »termodynamikens andra huvudsats» som beskrivs på annat ställe i Wikipedia:

entropin i ett isolerat system som inte befinner sig i jämvikt tenderar att öka med tiden, närmande sig ett maximalt värde vid jämvikt

från den svenska översättningen i Wikipedia Second law of thermodynamics 2009-12-11

Det är på pricken en formulering som helt klart ansluter till resultatet av utvecklingarna i Boltzmanns H-teorem — men ingenting omnämns (i Wikiartikeln) i den riktningen (heller); Boltzmanns H-teorem, i sin tur, är — nämligen — så (erkänt) komplicerat att reda ut, att ingen i den moderna akademins kvarter, ännu i denna dag, har förmått ge ämnet någon enhetlig eller entydig framställning — men flera (många) bidrag finns. Tydligt är (därmed, min mening) att man (förmodligen) i början på 1900-talet — och genom turer som få, om ens någon, kan reda ut i den moderna akademins anda — omformulerade »termodynamikens andra huvudsats» (på grund av vissa bekväma skäl) med grund i Boltzmanns PARTIKULÄRA resultat från just det berömda H-teoremet (den matematiska atomismens först formulerade grunder), och till den form som beskrivs i »termodynamikens andra huvudsats». Därmed försvann också de sista spåren av Clausius ursprungliga — klassiska, klara — framställning, se Clausius klassiska formulering från 1862.

Därmed lämnar vi den moderna akademins »andra huvudsats» åt sitt eget öde.

Se vidare utförligt från Boltzmanns H-teorem.

Se även i SAMMANFATTNING — vad betyder entropi.

I RELATERAD FYSIK däremot — se från Detonationen i K-cellens värmefysik — börjar universums historia VID motsvarande »BIG BANG»:

Se utförligt från K-cellen

Vad betyder det för entropibegreppets del?

Jämför Entropibegreppet i Modern akademi

Med alldeles precis samma oförändrade matematik som från Clausius grundform (S=E/T) från 1854 — ingenting ändras i matematikdelen — bildar nu värmekapaciteten (S) här, istället, en värmegrundad arbetspotential HELT identisk med energin — inte enrgiFÖRLUSTEN — i den ovan citerade Clausius entropianalogi »entropi = energi».

Med andra ord förvandlas INNEBÖRDEN — »kausalriktningen» — I Clausius ENTROPIBEGREPP, tvunget, till sin motsats — därför att utvecklingen av alla strukturer börjar från MAX VÄRME = max entropi — det finns inget annat alternativ att välja på — och går sedan tillbaka mot noll i takt med strukturens utveckling — analogt, hela universums expansion:

den relaterade fysikens entropibegrepp

entropi = värmegrundad arbetspotential, J/°K

FOTO: Författarens arkiv · Vattendroppe efter rekyl mot vattenyta · 1/4000 S

Drop10A · Mar2009 · Nikon D90

Matematiken är fortfarande alldeles densamma som redan används — men innebörden blir den diametralt omvända:

MED BÖRJAN FRÅN MAXIMALT VARMT utvecklas (naturligtvis) hela universums struktur med himlakroppar och deras utveckling, och allt som sker, i termer av arbete på avtagande entropi, avtagande värme, samma som högre ordning, mera ändamålsenlighet. Alltid.

FOTO: Författarens arkiv

Sommaren 2009 · Nikon D90

Undantag existerar inte. Se utförliga konkreta vardagliga exempel i Arbetsexempel med vidare i PRAKTISKA EXEMPEL — som också relaterar till den nu gängse etablerade moderna akademins föreställningssätt med dito referenser för exakt jämförelse (En del av exemplen — från den moderna akademins verkstäder — måste ses, verkligen, innan man tror det …).

Allmänna transientfunktionen

Alla processer är periodiskt återkommande.

Det finns inga undantag.

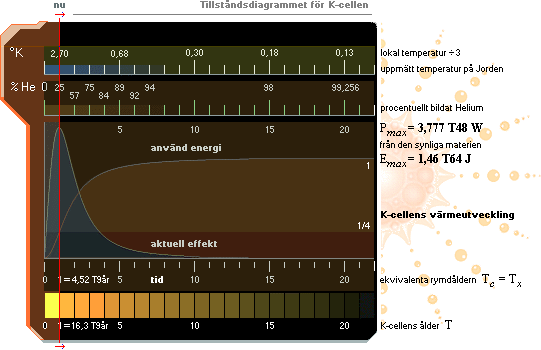
K-cellens tillståndsdiagram, se utförligt från K-cellens värmefysik

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

Alla processer och deras delprocesser, i sin tur deras delprocesser och så vidare ENLIGT RELATERAD FYSIK, utvecklas med andra ord på samma typ av effekttransient (aktuella effektgrafen ovan vänster) med tillhörande energianvändningsfunktion: massfysiken (p®T) — ytterst Solen och kärnomvandlingarna — matar energigrunden till materiefysiken (T®p) med den primära massförstöraren via massförintelsen E=(m®g)cc: Från K-cellens expansion som kallplasma med den efterföljande divergenständningen, se Himlakroppsbildningen, påförs alla himlakroppar en initiellt hög entropi från (m®g) och som sedan bildar det avtagande arbetskapitalet i takt med att arbetet utförs, analogt högre ändamålsenlighet, lägre entropi, högre ordning; Allt som finns på Jordens yta utvecklas på Jordkroppens avtagande temperatur: Clausiusentropin — kvantitetsvärdet S=E/T — utvecklas avtagande i takt med det organiska livets utveckling. Se EXEMPLET JORDEN. Sedan på samma sätt med allt övrigt: från ordinära naturfenomen till artificiella fyrverkeripjäser, se PRAKTISKA EXEMPEL: alla resultat utvecklas, visas och framträder på avtagande, inte ökande, entropi, på högre, inte lägre ordning

— med exakt bibehållen samma matematik som från Clausius grundsamband, se särskilt Arbetsexempel.

Varifrån man börjar i entropiänden är alltså egalt? Nej. Inte riktigt — tydligen.

I och med att allt återvänder till nollentropi med universums eller K-cellens periodiska pulsning — och maxentropin är förutsättningen, själva den arbetsmässiga utgångspunkten, för den diversifierade individordningens utveckling — men att inget motsvarande enhetligt »återvändande till maxentropi» finns i fysiken, bara en mängd olika individuella delprocesser — från K-cellens detonation och sedan vidare med samma princip för varje enskild himlakropp, med vidare — ligger det I DEN RELATERADE FYSIKENS MENING närmare till hands att betrakta nollentropin som »alltings ursprung och slutmål» snarare än ett slutmål med maxentropi. Dessutom, med hänsyn till den allmänna struktur av kallplasma (neutroner, se utförligt från NEUTRONEN) och dess grund för K-cellens vidare existens som sammanhänger med c0-kroppen blir valet av nollentropi (fullständig vila) det naturliga alternativet — om det gäller en översiktlig beskrivning.

Med vidare fortsättning i TILLSTÅNDSBEGREPPET I MODERN AKADEMI.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Sammanfattning

Från Keplers ytmoment till Plancks strålningslag — enligt relaterad fysik

KEPLERS YTMOMENT K=vr grundlägger den avancerade matematiska fysiken med sin koppling till CENTRALACCELERATION och CENTRALVERKAN. Tillsammans med massan (m) formar Keplermomentet ett rörelsemängdsmoment eller impulsmoment (Km=mvr=J). Impulsmomentets centrala matematiska formfysik känner vi som Plancks konstant h=mcr=6,626 t34 JS, som I RELATERAD FYSIK betyder NEUTRONEN

h = mNEUTRONMASSANcTOPPDIVERGENSENrNEUTRONRADIEN

= (1,0086652[u=1,66033 t27 KG])(2,99792458 T8 M/S)(1,31966 t15 M) = 6,62559 t34 JS

med massan m och tyngdcirkelradien r genom toppvärdet c för divergensen, och som grundlägger ATOMKÄRNANS HÄRLEDNING. Primära massförstöraren E=mcc, som följer ur POM i DEEP från GRIP, får sin formella ekvivalent med c=rf som ger Planckenergin E=mcc=mcr·f = hf, och därmed atomkärnan som ett på Plancks konstant h fraktalt strukturbaserat elektromekaniskt (eg. elektrogravitellt) svängningsaggregat med alla möjliga våglängder l=c/f från minsta närmast noll till största lika med kärnans utsträckning, därifrån vidare genom atomens omgivande elektronmassa som tydligen grundlägger materiefysikens värmedynamik.

Med grund i Planckenergin E=hf och den naturliga logaritmbasen e och dess naturliga koppling till den matematiska fysikens variationsuppställningar, härleds så Plancks entropisamband S=b(lnW) med utgångspunkt i föreställningen om likaberättigade energifördelningssätt: en materiell kropps bestämda egenenergi (hf) kan fördelas inbördes mellan materialets atomer på ett bestämt antal likaberättigade sätt. Därifrån härleds sedan Plancks strålningslag genom inverterade temperaturen som Planckentropins derivata (dS/dE=1/T) och som beskriver alla kroppars absorption och emission av värme med alla möjliga våglängder. Se även Max Plancks egen härledning i Plancks original från 1901.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

SAMMANFATTNING

BILDKÄLLA: Vänster; Friteckning, författarens privata arkiv. Höger; Kollage från Encarta99 — Galaxy, A Chorus Line

PÅ SAMMA SÄTT som människan måste ha en fysiologiskt fungerande nervmassa (hjärna) för att kunna bli varse sin egen förnimmande intelligens — TROTS att det finns avstånd, vakuum, mellan atomerna i hjärnan och därmed i princip avbrott, så kan vi snacka om sammanhanget sedan — så kan också, tydligen, alla individers summa av tänkande och förnimmande liknelsemässigt beskrivas, och relateras, som innefattad genom den övergripande kropp av materia (se c0-kroppen) som fenomenvärlden av princip består av. Alltså den kosmiska masskroppen totalt. Med den liknelsen som grund, enbart i kraft av vårt eget förnimmande exempel, kan man, tydligen, förstå ett motsvarande »kosmiskt övermedvetande».

Eftersom det individuella mänskliga medvetandet, således, kan förstås ingå som del i det förra, kan ett sådant kosmiskt övermedvetande emellertid inte (direkt) liknas vid vårt eget (personliga) individuella medvetande — utom i liknelsen med våra (personliga, [underbara]) fantasi- och drömfigurer: De som bara finns i våra egna (personliga) fantasier och drömmar, och som sedan »försvinner» för varje gång vi vaknar upp till vardagen — men som (lika troget) återkommer, igen, ständigt, alltid, när vi återgår till drömlägets [underbara] evighetsriken efter dagens aktiviteter. (En del repriser är helt enkelt otroliga).

BILDKÄLLA: Windows Media Center — MovieTime

Människans individuella medvetande kan, således, beskrivas liknelsemässigt från människans födelse som ett ([underbart] uppvaknande, och) och vid människans s.k. död som ett motsvarande (underbart) insomnande eller (mera drastiskt) »upphörande», helt säkert och visst som slutet på en film, och med den personens (rollfigurens) kroppsliga död. Termen »död» mister därmed (en stor del) av sitt normala innehåll typ »dödstråkigt»; Kroppsdöden bli (»bara») en övergång. Men formen för medvetandet som sådant upphör i liknelsens kraft och ljus alls inte, på samma sätt som också filmduken står kvar även sedan publiken gått hem. Formen för medvetandet övergår tydligen bara i den övergripande intelligensens egen universalkropp. (Således går inte ens någon ”tankeenergi” förlorad, den endast omfördelas). Nämligen i den dimension där individen inte längre har någon egen möjlighet att påverka innehållet, utan vilket innehåll i stället och tydligen bestäms av summan individrelaterade delar med enhetens totala del — på samma sätt som en artist som deltar i en föreställning med många samspelta kolleger [delad glädje är dubbel glädje]. Endast om de olika delarna harmonierar med varandra, att delarna beskriver en enhet utan inbördes motsättningar, motsvarande att ingen fråga längre finns därför att alla fått sina svar, vilar också individen i densamma absoluta fridens princip. Är så inte fallet, krävs en slutlig upplysning, och en sådan kan bara förverkligas, vad vi vet, genom att födas som en självmedveten varelse, en människa, och därmed genom att aktivt begrunda sanningens — harmonins — grundvalar.

BILDKÄLLA: Författarens privata arkiv — livets bok

Eftersom alla varelser strävar efter enhet, ljus och lycka, blir alla varelsers slutliga mål också, således tvunget, den mänskliga gestalten, eller i vilket fall den form som förmår förmedla individens insikt om sanningen, den eviga, absoluta fridens princip (speciellt av Buddha benämnd nirvana — den veterligt enda referent som närmat sig ämnet med beskrivande utläggningar [Diamantsutran]). Förvissningens grund, se från sanningsbegreppet, garanterar att det inte finns någon möjlighet att undkomma den ordningen, att den uppvisar lagbundenhet: ordningen är evig, oförstörbar. Lagen blir med dessa detaljer alltså identisk med begreppen (och handlingarna) sanning (visshet) och kärlek (fridsamhetssträvan, omsorg, medlidande, inlevelse, m.fl.).

ENTROPIBEGREPPETS SPRÅKFÖRBISTRING

Orsaker till UPPKOMSTEN AV

ENTROPIBEGREPPETS SPRÅKFÖRBISTRING

HIMLAKROPPARNAS ENTYDIGA UTVECKLING PÅ VÄXANDE KRISTALLORDNING: Jordkroppens avsvalning

TROTS att man uttryckligen inom den moderna akademins lärostolar intygar, se explicit citat, att det inte finns några »isolerade system» i den kända, synliga, observerbara fysikens värld, har man (inte minst Boltzmann själv [‡7], se från Boltzmanns H-teorem) ändå inte bara antagit en sådan idealism utan, tydligen, citatet nedan, även upphöjt den till ett slags kosmologiskt centraltempel för allmänglobalt vallfärdande i betygande av den övergudens allmänna respekt.

”Som minnesregler för termodynamikens två huvudsatser brukar ofta följande formuleringar användas:

Första huvudsatsen: Universums energi är alltid konstant.

Andra huvudsatsen: Universums entropi strävar alltid att öka.”,

FOCUS MATERIEN 1975 s325sp2mn

Jämför korrekt formulering;

’ Första huvudsatsen: Idealt slutna|isolerade materiesystems energi är alltid konstant.

Andra huvudsatsen: Idealt slutna|isolerade materiesystems entropi strävar alltid att öka.’

Men i praktisk fysik finns inga idealt isolerade system i termodynamisk mening.

Med ovanstående citatbrygd i ljuset av K-cellens värmefysik — Plancks strålningslag som garanterar att alla kroppar värmeläcker — betyder det tydligen att den moderna akademins nuvarande »termodynamikens andra huvudsats» är precis så »korrumperad» som den inte kan förstås, vilket vill säga, i avsaknad av varje form av naturvetenskapligt grundad observation: alla kroppar värmeläcker: alla möjliga olika sammanhang.

Se även i Naturtermiskt läckage.

— Se även (återigen), till jämförelse, den explicita formuleringen av nuvarande »termodynamikens andra huvudsats».

Planckentropin S=b(lnW) i kraft av Planckstrålningen utsäger tydligen — i varje fysikaliskt materiellt observerbart system — att alla fysikaliska kroppar emitterar (och absorberar) värmestrålning kontinuerligt, VÄRMEN LÄCKER ut — »isolerade system» finns inte i fysiken. Följaktligen verkställs oundvikligen en motsvarande absolut värmedöd för varje massändlig form — just på grund av att värmegivningen förr eller senare tvingas upphöra; Speciellt för universums fall, då alla stjärnor slocknat och alla radioaktiva ämnen sönderfallit, blir den slutformen samma som en total elektromagnetisk ljus- och värmedöd.: absolut nollstrålning.

Den nu förhärskande entropitolkningen, citatet ovan, utsäger, tydligen, något helt annat — just i kraft av begreppet »isolerat system». Tydligen också så till den milda grad att denna senare uppfattning

— med påstått stöd i »Boltzmanns entropi» [S=b(lnW)]

”Entropin S definieras nu

S = k ^elog W

där W betyder den termiska sannolikheten och k är den tidigare införda Boltzmanns konstant. Att entropin definierad på detta sätt verkligen överensstämmer med den termodynamiskt definierade entropin (se s. 324)[S=Q/T] kan sägas vara kronan på verket i arbetet att tolka termodynamikens fenomenologiska beskrivningar av olika experimentella resultat med den statistiska mekanikens hjälp.”,

FOCUS MATERIEN 1975 s193sp1mn:

”2. Boltzmann entropy: axiomatic characterization. In statistical mechanics, we are interested in the disorder in the distribution of the system over the permissible microstates [1]. The measure of disorder first provided by Boltzmann principle (known as Boltzmann entropy) is given by

S = KlnW, (2.1)

where K is the thermodynamic unit of measurement of entropy and is known as (p244)

Boltzmann constant. K = 1.33×10⁻¹⁶ erg/°C. W, called thermodynamic probability or statistical weight, is the total number of microscopic complexions compatible with the macroscopic state of the system. We avoid the name thermodynamic probability for the term W as it leads to many confusions [10]. Following Carnop [2], we, however, call the quantity “W” the “degree of disorder”.”,

Boltzmann-Gibbs Entropy: AXIOMATIC CHARACTERIZATION AND APPLICATION,

C. G. CHAKRABARTI and KAJAL DE, 1997 s243n, 2009-12-10

http://www.emis.de/journals/HOA/IJMMS/23/4243.pdf

som i själva verket, när allt kommer omkring, visar sig vara Plancks entropisamband

— antagits för ett slags »vetenskapligt religiöst» talesätt: oordningen ökar alltid i universum. Tar man bort, nämligen och som vi redan studerat på flera ställen i den här framställningen, den av här ej exakt närmare naturvetenskapligt känd anledning införda komponenten »isolerat system» ur den moderna akademins lärosatser — i enlighet med redan erkända meningar, se citat — förvandlas i en hast samma preferensmening, tydligen, till sin motsats:

oordningen avtar alltid i universum — underförstått med början från högre mot lägre temperatur.

Se vidare utförliga praktiska exempel i ENTROPIN i Konkreta Praktiska Exempel.

För upphovet till ISOLERAT SYSTEM i modern akademi, se även en nytillkommen (Apr2010) källreferens i Införandet av Isolerat System 1858.

ENTROPIN i Konkreta Praktiska Exempel

Med grund i beskrivningen för ENTROPIGEBREPPET I RELATERAD FYSIK från S = b(lnW) som är Plancks entropisamband — inte Boltzmanns och HÄRLEDNINGEN TILL PLANCKS STRÅLNINGSLAG FRÅN PLANCKS ENTROPISAMBAND ges i följande sektion ett urval i

klassen konkreta praktiska exempel:

Jorden

Arbetsexempel

Gravitationen

Den kastade bollen

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Jorden · Himlakroppsbildningarna

Jorden

Planckentropin (W) ökar snabbt från noll (1) upp till ett maximum	Planckentropin S=b(lnW) går mot noll
Processen initieras:	Den aktuella fysiska processen

J-kropparnas värmefysik	Jordens ålder	DNA	Gestalten	Galaxbildningen

Se utförligt från J-kropparnas värmefysik.

Alla fysikaliska processer utvecklas|initieras på en effekttransient med tillhörande energianvändningskurva: från ideal nolltemperatur|nollenergi snabbt upp till max värme, därifrån sedan långsamt åter mot noll.

Se även från K-cellens värmefysik.

För att åstadkomma en ändring i ett givet tillstånd krävs en kraft (F=ma) som också måste föras en viss distans (d) eller tid (T), därmed en viss energi E=Fd=mad eller rörelsemängd p=FT=maT=mv. Ändringen som följer är direkt proportionell mot kraften, och varaktigheten i ändringen, själva processen, bestäms av lokalens materialegenskaper. Det finns inga undantag. Alla fysikaliska processer — tillståndsändringar — lyder samma lag. Genom materiens bestånd av atomer, kommer alla naturliga processer att innehålla en stor mängd underprocesser som är specifika för varje materiell domän och dess specifika egenskaper. Dessa detaljer har, i olika nivåer, varit välkända allt sedan Keplers, Galileis och Newtons dagar under nu mer än tre hundra år.

Jorden utvecklas tydligen AVSVALNANDE — oberoende av vilken himlakroppsteori som finns — enbart i stöd av observationen med heta magmor från Jordens inre: Observationerna visar att det inre av Jordkroppen är varmare än ytan: Plancksambandets entropi för Jordkroppen avtar och går mot noll med Jordens åldrande; Och på samma sätt, med samma analogi, med varje annan himlakropp, frånsett stjärnornas aktiva perioder (konstant ordning) med nära konstant producerad lampeffekt (temperaturen hålls praktiskt taget konstant). Eller med andra ord: Jorden utvecklas på växande ordning, analogt avtagande S-värde, samma som avtagande molekylär oordning relativt den ideala perfekt ordnade kristallens 0°K. Trots att Planckentropin S=b(lnW) avtar med tiden i alla observerbara fall — det finns, här veterligt, inget observerat undantag just på grund av att alla kroppar värmeläcker enligt Plancks strålningslag: S ökar inte, S minskar — tillämpas ändå — likväl — uppfattningen i ovanstående citat.

Märk väl.

Enbart med Jorden som exempel ENLIGT RELATERAD FYSIK, se från J-kropparnas expansion:

S=b(lnW) utgår tydligen från ett motsvarande initiellt högt värde (»Jordens tillblivelse», se illustrationen ovan vänster, från motsvarande nolltemperatur med efterföljande snabba temperaturhöjning upp till toppvärdet) motsvarande en hög ingångstemperatur; Vartefter Jordkroppen svalnar, avtar S=b(lnW) med tillhörande alltmer ordnade former med ytbildningar, bergskedjeutvecklingar, och senare (tydligen) levande organismer med allt mera avancerad sammansättning. Jorden, och varje annan himlakropp, slutar därmed och alltså (idealt) som en helt stel kropp på nollenetropi — utan någon som helst värmegenomströmning:

S = b(ln[W=1]) = b(0) = 0

Med, sålunda, ovannämnda praktiska exempelgrund

— tillståndsändringarnas effekttransienter och deras energianvändningskurvor

— kan de naturliga processerna tydligen mera generellt formuleras på följande, men mot moderna hävder, rebelliska sätt:

Ordning — växande grad av [naturharmonisk] ändamålsenlighet — uppkommer alltid, uteslutande alltid, utan undantag, där materien går från varmt (mera oordnat: basenergi) till kallt (mera ordnat: nyttoeffekt):

Kristallernas värld är naturligtvis sinnebilden för den perfekta ordningen, och den finns i den kallare delen, motsvarande fasta tillståndets fysik. Arbetet i materiefysiken utförs utan undantag (den klassiska »termodynamikens andra huvudsats») på fallande temperatur från massfysikens energikapital som matar alla termiska toppvärden:

allt arbete i materien utgår från en Planckgrundad nollentropi S=0 — via massfysikens (m®g) upp till ett toppvärde i materiefysiken, och på vilket kapital arbetet utförs på divergensens natur som garanterar en irreversibel, spontan, strömning från varmt (toppvärdet) till kallt:

massfysikens garanterat entropilösa energigrund är S=0.

Praktiska exempel · se även Jorden · Se även Utförliga exempel genom Wikipedia

PRAKTISKA EXEMPEL

Varje tillståndsändring i fysiken måste, tvunget, föregås av en ökning i PlanckEntropi

S=b(lnW), analogt en temperaturhöjning som garanterar växande W, analogt en värmegrundad arbetspotential. Eller med samma (triviala) mening: för arbete krävs energi. Den så etablerade entropitoppen (Smax) garanterar sedan den efterföljande tillståndsändringens effekt (ändringens verkan) enligt allmänna transientfunktionen (P=E/t) och som i sig bildar en process med avtagande S (idealt och som mest tillbaka till tillståndet före ändringen). Summan av alla entropiminskningar — analogt, summan av alla delenergier som verkställer alla individuella arbetsprocesser — är alltid lika med den maximala toppentropins värde, samma som toppenergin som alla processer anställs på; Det är (trivialt) samma formulering som Clausius framställning från 1862, och i princip bara ett annat sätt att uttrycka energilagen: energi kan varken skapas eller förintas utan måste förutsättas.

PRAKTISKA EXEMPEL:

Med analog koppling till Plancks entropisamband S=b(lnW) från Clausius grundform S=Q/T:

Bilmotorn

4-taktsotto · V8-motor · principer 1981 · Författarens arkiv

Fallet med bilmotorn

För att kolven i en bilmotor ska kunna tillföra motorn kraft, måste en initierande hög temperatur tillföras som garanterar kolvens nedrörelse, analogt bränsleblandningens explosionstillfälle i cylindern. På den toppvärmen utvecklas kraften genom en motsvarande temperatursänkning, analogt avtagande entropi (S), och som sedan återtas med en ny kompression med åtföljande tändning och explosion med topptemperatur, och vilket förlopp upprepas periodiskt.

Salt&Peppar

FOTO: Författarens arkiv — Feb2010 · Nikon D90

Fallet med Salt&Peppar

En hög med salt för sig och en hög med peppar för sig hälls över i samma kar som sedan skakas om. Skakningen innebär att ett arbete utförs på blandningen, analogt att blandningen påförs en temperaturökning under blandningsprocessens gång. Varje positionsändring för varje partikel i respektive partikelhögar måste utföras på en motsvarande tillförd arbetskraft, samma som en initiellt tillförd värmegrundad arbetspotential och vilken initiellt tillförda arbetspotential tvunget avtar med positionsändringens verkställighet, analogt avtagande entropi (S) så att en motsvarande värmemängd följaktligen måste tillföras kontinuerligt (upprepat) för att blandningsresultatet, analogt avtagande entropi, ska kunna fortskrida.

Skakningsprocessen betyder dessutom ett extra värmetillskott till skakningskaret och blandningen tillsammans; för att få ut något resultat måste skakningen upphöra — och därmed en motsvarande temperatursänkning genom materialens naturliga värmeläckning — analogt en entropireduktion för att överhuvudtaget få ut något resultat.

Graden av ordning ([naturharmonisk] ändamålsenlighet) är större efter blandningen än före, och kan följaktligen bara uppnås genom lägre entropi från ett initierande högre S-(process-)toppvärde.

Meningen (Jämför Wikipedia Entropy) som påstår att ordningen i blandningen är lägre efter skakningen än före, erkänner inte ändamålsenligheten i blandningen som primär över komponenternas enskilda bidrag — på samma sätt som en mening som påstår att ordningen i en metallurgisk smälta av olika legerande grundämnen är lägre efter smältans avsvalnande än ordningen med separata ämnen i det svala tillståndet före blandningen, vilket uppenbarligen är ett problem för ändamålsenlighetens erkännande, inget problem för begreppet entropi.

Metabolism

FOTO: Författarens arkiv — Björklöv · Våren 2009 · Nikon D90

Fallet med metabolismen (ämnesomsättningen)

För att metabolismen i en organisk cell ska kunna utföra arbete måste cellen, tillfälligt, tillföras energi ([kemisk] värmegrad, entropi) och på vars kapital cellen sedan utför sin tjänst. Entropin (värmen) ges alltså som energigrund, som ett arbetskapital, medan tillväxten (cellens arbete, den egentliga strukturbyggnadens organisation, det enskilda arbetssteget) utförs på kapitalets avtagande, analogt entropins minskning. Även denna process upprepas tvunget periodiskt för cellens arbetssätt.

Fotboll

Från Googlesökning på ”football” Bilder

http://www.wiiwii.tv/wp-content/uploads/2008/07/football.jpg

Fallet med fotbollen

För att göra mål, måste fotbollslagets målgörare tillföra bollen en kraft. Det sker genom en spark som betyder att bollens material tillförs entropi, analogt värmemängd, och som sedan fördelas i bollens elastiska material med resultat i motsvarande utjämning; Det sker en entropiminskning då bollen far iväg genom luften och slutligen omsätter utgångsentropins huvuddel genom (mekanisk friktions-) värme då bollens impuls (rörelsemängden mv) dämpas av annat kontakterande, stationärt material.

Mekaniken generellt

momentekvationer generellt

Fallen generellt i mekaniken

För att ändra rörelsebanan hos en projektil, måste projektilen tillföras kraft under tid, analogt påföras en viss värmemängd, analogt entropi, och vilken tillförda värmemängd sedan avges med projektilens ändrade färdväg eller färdsätt, analogt en återgång för entropin mot det lägre värdet före tillståndsändringen.

Brevvågen

FOTO: Författarens arkiv — Feb2010 · Nikon D90

Fallet med brevvågen

För att väga ett brev måste vågen utföra ett arbete: det anställs av brevets massa och rörelsemängd som påför vågens rörliga delar ett motsvarande värmetillskott, ökad entropi, och på vilket avtagande kapital vågen sedan ställer in sitt avläsningsvärde genom massjämvikt: för att väga brevet måste entropin avta från ett initiellt påfört högre entropivärde.

Iskuberna

FOTO: Författarens arkiv — Feb2010 · Nikon D90

Fallet med iskuberna

ÅTERBILDNING AV IS (lägre entropi) från vatten (högre entropi) [generellt all kristallbildning] sker spontant enligt Plancks entropisamband S=b(lnW): den värmebaserade arbetspotentialen, entropivärdet S, tappas automatiskt via divergensen från en högre nivå till en lägre nivå; Iskuberna bildas genom att entropin avtar från den kropp eller lokal som isbildningen sker i, analogt en högre grad av kristallin ordning mot absoluta nollpunkten 0°K.

SMÄLTNING AV IS kräver på motsvarande sätt först att en värmegrundad arbetspotential tillförs lokalen och på vars avtagande entropi den fasta isen bildar smält vatten, analogt avtagande entropi med avtagande smältvärme.

I VILKET FALL avtar alltså entropinivån och går mot noll vid den aktuellt arbetande resultatprocessen.

Enklare — se även från massfysikens nollentropi — enligt relaterad fysik:

allt verkställande arbete utförs på avtagande entropi;

utgångskapitalet är (typ Solen) massdestruktionen (m®g) — från massfysiken som inte omfattas av materiefysiken — analogt samma som nollentropi: allt utgår från nollentropi (massfysik, »noll materiefysik»), allt återvänder dit

Alla dessa exempel (och varje annat naturligt, praktiskt fysiskt) kan alltså återföras på PlanckEntropin

S=b(lnW); Entropiökning (S ökar) betyder initiellt samma som matningen, energin, till den förestående tillståndsändringen, analogt ett högre W-tal (högre temperatur); På det beloppet utförs sedan ändringen samtidigt som entropin (S-värdet, motsvarande W-värdet) minskar eller återgår till värdet före ändringen.

Alla tillståndsändringar måste, tvunget och tydligen, följa den ordningen, utan undantag: nyttoarbete = entropiminskning

Arbetsexempel

ARBETSEXEMPEL

För att lyfta en kropp (m) med massan 1 KG höjden (d) 1 Meter över markytan via Jordytans tyngdkraftsacceleration a=9,81 M/S² (internationella medelbaserade standardvärdet för Jordytan) i en lagerlokal med temperaturen 17°C=290°K krävs en absolut MINSTA tillförd värmegrundad arbetspotential — entropi — på

S = (E=mad)/T = (1KG·9,81M/S²·1M)/290

= [(9,81)/290]J/°K

= 0,0338275 J/°K ...................... minsta mängden tillförd värmegrundad arbetspotential

SLÄPPER MAN TILLBAKA kroppen från den nivån, omsätts HELA den värmegrundade arbetspotentialen — entropin — i värme: dels till den omgivande luften i form av en mindre andel friktionsenergi då kroppen faller, och dels till underlaget i formen av kontakterande (mekaniska) värmesvängningar som överförs med motsvarande deformationer av det underliggande materialets atommassor — olika mekaniskt resonanta tryckfenomen — och som därmed, ytterst sett i materiegrunden, också inbegriper elektriska svängningsförlopp på ett eller annat sätt, analogt Planckvärmestrålningseffekter.

Men ANORDNINGEN som ska utföra arbetet med att lyfta m-kroppen en meter upp i luften (frånsett energin som går åt för att framställa anordningen) innefattar OCKSÅ material — någon form av konstruktion, och därmed (i allmänhet) rörliga delar (ytterligare arbetsmoment, de rörliga delarnas masströghet som måste övervinnas) som ofrånkomligt betyder att ytterligare entropi (S) måste tillföras för att överhuvudtaget få något gjort. Den andelen kommer följaktligen att sammanhänga med anordningens energieffektivitet.

Totala entropiökningen som kan garantera att arbetet blir utfört blir då

S(totalt) = S(arbetet) + S(värmeförluster i den utförande anordningen)

OM uppgiften just är att SLÄPPA TILLBAKA m-KROPPEN — typ industrihammare för någon detaljbearbetning — avtar alltså entropin från S(totalt) tillbaka till noll via d=0 som ger S=0 samtidigt som arbetet utförs (själva det bearbetande momentet). För att upprepa arbetsmomentet måste alltså samma mängd entropi S(totalt) åter (och åter) tillföras kroppen (och dess lyftande anordning, friktionsförlusterna) för att sedan återigen, upprepat, avta med arbetets utförande:

Entropin — den värmegrundade arbetspotentialen I DEN VERKSTÄLLANDE PROCESSEN — avtar ALLTSÅ med växande bearbetning.

Alltid. Undantag existerar inte.

Clausius entropibegrepp med energiFÖRLUST [för S(totalt)] fungerar alltså precis lika bra här som värmegrundad arbetspotential. Verkställigheten är densamma Det är (alltså och för den delen) bara en fråga om val av preferenser — självklart i fallet K-cellen.

Atomismens grunder — praktiskt entropiexempel

FOTO: Författarens arkiv Feb2010 Nikon D90

Enkelt experiment för påvisande av materiens atomära beståndsdelar

En kort (5-10cM) metallstång (koppar ovan) placeras med ena änden (H) (höger ovan) frilagd för åtkomst av en underliggande värmekälla, en vanlig ljuslåga räcker. Andra stångänden (V) ligger fast på underlaget med hjälp av enkla vikter (mynt) som placerats ovanpå. Nära H-änden, före utfallet, placeras en smal rund nål som får genomtränga en visare (kan vara en bit papper eller bättre ett vanligt grässtrå av den långa vanliga typen runt tvärsnitt, i ovanstående experiment virad tennad 0,5mM koppartråd).

När ljuslågan anbringas under den utskjutande stångens ände och denna uppvärms, utvidgas kopparstångens material: stången rullar på den tunna nålen som därmed vrids och ger ett tydligt observerbart utslag. Se även fotografier längre ner som visar utslagen.

Utan (många små) materiella komponenter med (bestämda, temperaturstyrda) avstånd emellan, blir det svårt att förklara fenomenet.

Boltzmann, citatsamling

Utförde man inte experiment inom de akademiska skikten under 1800-talet av ovan avbildade typ?

— Experimentellt påvisande av materien i meningen sammansatt av atomer.

— Tydligen inte.

När blotta idén framkastades av Ludwig Boltzmann (omkring 1870), att materien skulle bestå av verkliga atomer och molekyler, se från Boltzmanns H-teorem, bemöttes han (starkt) avvisande.

”Boltzmann's kinetic theory of gases seemed to presuppose the reality of atoms and molecules, but almost all German philosophers and many scientists like Ernst Mach and the physical chemist Wilhelm Ostwald opposed their existence.”,

@INTERNET Wikipedia Ludwig Boltzmann 2010-02-08

Min översättning:

Boltzmanns kinetiska gasteori verkade förutsätta realitet för atomer och molekyler, men nästan alla tyska filosofer och många vetenskapsmän som Ernst Mach och fysikkemisten Wilhelm Ostwald motsatte sig deras existens.

”Others objected even more strenuously to Boltzmann’s atomism. Much of Boltzmann’s later career was dominated by a debate with Ernst Mach, the Austrian physicist and philosopher. Mach distrusted excessive theorizing and felt that science should be based only on what could be experienced through plain observation. Therefore, he found Boltzmann’s belief that atoms actually existed to be a wild speculation.”,

THE CHEMIST’S BOOKSHELF; ATOMISM ARGUED; Gary J. Weisel

Boltzmann’s Atom: The Great Debate That Launched a Revolution in Physics, David Lindley

http://pubs.acs.org/subscribe/journals/tcaw/11/i08/pdf/802books.pdf

Min översättning:

Andra opponerade sig mera energiskt mot Boltzmanns atomism. Mycket av Boltzmanns senare karriär dominerades av en debatt med Ernst Mach, den österrikiske fysikern och filosofen. Mach misstrodde överdrivet teoretiserande och menade att vetenskap skulle baseras bara på det som kunde erfaras genom direkt observation. Därför fann han Boltzmanns uppfattning att atomer verkligen existerade vara vild spekulation.

”Boltzmann's theory, which presupposed the existence of atoms and molecules, was challenged by Wilhelm Ostwald and other "energeticists", who wanted to free physics from the notion of atoms and base it on energy and related quantities.”,

MAX PLANCK: THE RELUCTANT REVOLUTIONARY Helge Kragh Dec 1, 2000

http://physicsworld.com/cws/article/print/373

Man måste logga in på PhysicsWorld för att få tillgång till artiklarna från GoogleSökningen — men det är helt gratis

Min översättning:

Boltzmanns teori, som förutsätter existensen av atomer och molekyler, utmanades av Wilhelm Ostwald och andra ”energetiker” som ville befria fysiken från inslaget av atomer och basera den på energi och relaterade kvantiteter.

»atomexperimentet»

”Attacks on his work continued and he began to feel that his life's work was about to collapse despite his defence of his theories. Depressed and in bad health, Boltzmann committed suicide just before experiment verified his work.”,

LUDWIG BOLTZMANN — J J O'Connor and E F Robertson, Sept 1998

School of Mathematics and Statistics, University of St Andrews, Scotland

http://www-history.mcs.st-and.ac.uk/Biographies/Boltzmann.html

Min översättning:

Attackerna på hans arbete fortsatte och han började känna att hans livsverk var på väg att kollapsa trots hans försvar för sina teorier. Deprimerad och vid dålig hälsa, begick Boltzmann självmord strax innan experiment bekräftade hans arbete.

Experimentets resultatförklaring. De normala atomavstånden i fasta material (generellt runt och grovt ca d=2,5Å = 2,5 t10 M; [V/N=(m/ρ)/(m/Uu)=Uu/ρ]^1/3; EX: Järn Fe56 ρ=7870KG/M³, u=1,66033 t27 KG ger d³=56u/7870; d=2,27755 t10 M = 2,3 Å) utför kontinuerligt svängningar omkring sina kristallbindande inbördes medelavstånd. Påförs materialet värmegrundad arbetspotential — entropi — som i fallet med den anställda ljuslågan, påförs också de berörda atomerna denna värmemängd; den extra tillförda energin påtvingar de atomära medelavstånden ett litet tillskott; Med summan av ändringen i medelavstånden tagna över den berörda stångens längd tvingar värmetillskottet tydligen materialet att uppvisa en volymökning: Är materialet, som i experimentfallet, en lång rak stång, visas största effekten också i den största metriska utsträckningen, analogt i stångens längsriktning. Visarnålens utslag syns märkbart (ovan höger).

Då värmekällan tas bort, återgår visaren till ursprungsläget (inte riktigt i den aktuella anordningens fall, en del av återkrypningen läggs på motsatta nålvisarsidan tillsammans med värmeöverföringen till metallmynten och syns därför inte) — vilket bevisar principen att normalavstånden mellan komponenterna, atomerna, av princip återtas;

Materialet kan tydligen förstås som bestående av (en stor mängd små) komponenter med inbördes, bestämda, mellanliggande (små) avstånd.

Entropin. Ljuslågans kontinuerliga brinnande motsvarar den kontinuerligt tillförda värmegrundade arbetspotentialen — entropin — som utför det atomavståndsutvidgande arbetet och som hela tiden måste fyllas på för att avstånden inte ska återgå. Tas ljuslågan bort, kan den så upplagrade värmegrundade potentialen — entropin — i stången användas till arbete typ (här trivialt) att återföra visaren till utgångsläget: entropin tvingas, återigen, avta för att arbetets nyttoeffekt ska kunna uppvisas.

Ljuslågans motsvarande entropiräkning grundas på (motsvarande samma sätt genom) kemisk energi som frigörs genom stearinet (kolväten) som sugs upp av tygveken och som omsätts i den redan förkolnade (förbrända) vektoppen tillsammans med luftens syreinnehåll då förbränningen, samma som kemiska föreningen, bildar koloxid CO (som strax blir koldioxid, COO); Ljuslågans olika färger motsvarar olika våglängder som de ingående atomerna emitterar i de olika regionerna och efter sina lokala domäner; Ljuslågan utgör ett lokalt termokemiskt reaktionscentrum som, via ett katalyserande reaktionstemperaturområde, ljuslågans form, frigör värme ur föreningar mellan de kemiskt skilda atomerna med kolet (C) i stearinet och syret (O) i luften.

Entropiökningen för att åstadkomma föreningsarbetet motsvarar tillförseln av de separerade ämnena kol och syre; Sedan förening skett — föreningen kol-syre motsvarar entropitoppen då den kemiska bindningsenergin frigörs — avtar den delentropin med den lokalt avgivna värmeutvecklingen vilken dels sprids genom luften via omgivande luftmolekylers erhållna högre rörelseenergi [via molekylernas lokalt inbördes stötar (mv)] och dels masslöst genom induktionsverkan via divergensen (hf) tillsammans med den elektromagnetiska strålningens allmänna avtagande i energi enligt Comptoneffekten; Förloppet upprepas så med den påfyllande strömmen av kol från veken och syre från luften.

I alla sammanhang kan, alltså, samma metod och princip identifieras: entropin, den värmegrundade arbetspotentialen, avtar alltid med ett arbetes utförande: allt byggande och utförande, all konstruktion, går alltid från lägre till högre ordning, analogt från högre entropi (större molekylär oordning relativt ideala perfekta kristallordningen vid 0°K) till lägre. Det finns, tydligen, inga undantag. Bara exempel.

Se även i Arbetsexempel och PRAKTISKA EXEMPEL.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Isolerade systemets ursprung

Se även från Isolerat system i termodynamisk mening samt Naturtermiskt Läckage

Inledning — allmän beskrivning

FOTO: Författarens arkiv · HP-scanner

Isolerade system förekommer bara idealt (i analysen) i momentana (noll) tidpunkter: idealt, obegränsat, utsträckta fysiska-geometriska rum med kroppar som uppvisar bestämda kvantiteter över begränsade eller obegränsade volymer.

ftersom fysiken grundas på variationer som dock måste beskrivas med det som inte finns i fysiken, tillstånd, måste vi i motsvarande mening alltid använda oss av vissa s.k. idealiseringar, alltså frånse olika grader av olika detaljer i fysiken, för att kunna beskriva motsvarande naturliga förlopp — typ fallrörelsen på Jordytan utan hänsyn till Jordens rotation (då denna i vilket fall är försumbar i de allra flesta översiktiga experiment).

Vi måste alltså använda oss av olika grader av idealiserade system (kroppar, anordningar) i fysikbeskrivningen.

Hur dessa system är idealiserade måste vi också försöka klargöra i det enskilda fallet för att ge soliditet åt beskrivningen. Denna detalj stöter heller vanligtvis inte på något egentlig problem. Problem uppkommer, emellertid, då man söker beskriva eller förklara fysiken utifrån ett omvänt fall — med föreställningen om ett i fysiken befintligt typ »isolerat system» då inget sådant existerar i fysiken, eller en analog strävan att söka beskriva ett fysiskt föremål för det ideala begreppet tillstånd då inget tillstånd existerar i fysiken. Följande framställning försöker beskriva problemställningen — för termofysikens del.

Isolerade systemets innebörd

PLANCKSTRÅLNINGENS ALLMÄNNA FÖRANKRING I ENTROPIBEGREPPET

Isolerade systemets innebörd

ISOLERADE SYSTEMETS URSPRUNG

ALLMÄNNA GASLAGEN tar ingen hänsyn till orsaker till temperaturändringar; I materiefysiken är temperaturen generatris för tryck (p) [och volym V] (T®p), temperaturen tar ingen matematisk funktion av trycket (eller volymen) i allmänna gaslagen; Allmänna gaslagens momentana samband förutsätter ett »idealt isolerat system»: ingen T-läckning vid ett givet tillstånd (vilket i det praktiska fallet alltså idealt och enbart motsvarar »det helt läckfria» tillståndet i en viss tidpunkt).

EXEMPEL — allmänna gaslagen

pV = kT ............................................... allmänna gaslagen

p = 1 atm .......................................... trycket

= 1,01325 T5 Pa

= 1,01325 T5 N/M²

= 1,01325 bar (i äldre standard ca 760mM Hg eller »1 torr»)

V = 1M³ ........................................... volymen

T = 0°C ............................................ temperaturen

= 273,15°K

k = pV/T

= 370,95002 J/°K ........................ fundamentala gaskonstanten

MED FUNDAMENTALA GASKONSTANTEN k GIVEN SAMT GIVEN TEMPERATUR T, analogt given rörelseenergi E=pV=kT=(F/A)Ad hos gasbollarna i den inneslutna volymen V med trycket p är alla möjliga kombinationer pV likvärdiga som ger E=kT.

Det betyder, tydligen, att p och V kan ändras, hur som helst, i vilken som helst mening, alltid med samma likvärdiga resultat för given energi kT — men att ARBETET som förknippas med ändringen inbördes mellan pV inte ingår, täcks, av gaslagen. Det arbetet förutsätts bortsett ifrån, som om ett konstant termodynamiskt tillstånd råder (fast volym, fix temperatur). Så är med andra ord allmänna gaslagen en tillståndsekvation. Den säger ingenting om anordningen, bara den (momentana) inneslutningen V vid p med temperaturen T.

Statiskt och hydrostatiskt tryck — allmän beskrivning utan vidare referenser

Vad som behandlats ovan i allmänna gaslagen gäller det statiska trycket. Det statiska trycket p avser enbart den ideala gasens eget inre tillstånd där p gäller åt alla möjliga håll och riktningar i en godtycklig punkt i gasen, samt att gastätheten r=m/V är konstant i hela gasvolymen.

Tar man med i beräkningen också tyngdkraftsfältet med tyngdkraftsaccelerationen a (standard 9,81 M/S² vid Jordytan) blir sambanden mera komplicerade. Eftersom en gas är högeligen kompressibel, uppvisar en mycket hög gaspelare (flera tiotal meter) en markant högre täthet vid botten än vid toppen beroende på inverkan av gasens totala tyngd via a. I sådana fall gäller inte allmänna gaslagen. Vi får alltså iaktta en viss försiktighet i allmänna gaslagens tillämpning och begränsa den till relativt ”normala” volymer, kärl och inneslutningar som i stort ansluter till våra vardagsrum som maximala gasrum.

När vi kommer in på motsvarande samband för vätskor blir förhållandena delvis (mycket) enklare i och med att en vätska betraktas idealt som inkompressibel (en vätska har en viss kompressibilitet, men denna är mycket liten). Därmed blir tätheten (idealt) genomgående en och densamma även över stora höjder (flera kilometer) vilket förenklar den rent matematiska behandlingen.

Man brukar termen hydrostatiskt tryck där en gas eller vätska också påverkas av den lokalt dominanta gravitationen, alltså tyngdkraftsaccelerationen (a). Även fast också denna uppvisar variationer med avståndet från Jordens (ideala) medelpunkt betraktas den i alla elementära tillämpningar via ett Galileiskt kraftfält, dvs., med konstant tyngdkraftsacceleration. [I det ideala g-fältet avtar a med kvadraten på avståndet enligt a=Gm₂/r²].

Förståelsen av hur gaser och vätskor (luft och vatten) fungerar har flera inbördes paralleller. Vi studerar dem vidare i alla allmänna beskrivningar som handlar om vätskors tryck (allm., hydrostatik [”vattenkunskap” i grovt förenklad mening]).

Termerna statiskt tryck (in-trycket) och hydrostatiskt tryck (tyngdtrycket) är centrala i den elementära beskrivningen av de olika materietillstånden.

Förtydligande till allmänna gaslagen

Med temperaturen (T) som givare för tryck (p) och volym (V) gäller alltså allmänna gaslagen endast under den förutsättningen att eventuella värmeeffekter på gasen som orsakas av eventuella arbeten som verkställer inbördes ändringar i pV helt bortses ifrån (s.k. adiabatiska [utan värmeflöde] tillståndsändringar). Sådana ändringar, nämligen, beror tvunget på inneslutningens material och processens arbetssätt (tid) och har därför ingen generellt entydig eller enkel matematisk form. Därmed framstår också allmänna gaslagens tillståndsekvation enbart som en idealt momentan kvantitetsbild med fast given energi E=pV=kT och som i princip bara gäller i praktisk fysik (med [mycket] god noggrannhet) då gasen inte genomgår några (större) ändringar — eller som ett idealt momentanvärde i någon viss anordnings tidpunkt (beroende på olika grader av idealisering).

Det finns dock en del relativt enkla analogier som visar ansatsen till hur ändringar i gasens volym — som medför ändringar i gasens temperatur på grund av det utförda volymändrande arbetet — påverkar slutvolymen (och därmed sluttrycket enligt allmänna gaslagen).

Betrakta en innesluten mängd luft i en cylindrisk pelare med höjden h0, illustrationen ovan vänster. Om gasen plötsligt komprimeras, analogt h0 minskas genom att bottenytan (kolv/vattenyta) skjuts upp, kommer bottenytan att utföra ett accelererande arbete på gaspartiklarna under uppskjutningen: varje gasboll som möter uppväggen får ett extra energitillskott i proportion till uppskjutande (idealt stela) väggens hastighet. Detta arbete betyder alltså en högre rörelseenergi hos den berörda gasbollen, och som därmed överförs — främst — till den lättrörliga gasens snabba partiklar: det sker en liten temperaturökning motsvarande ihoptryckningen. Då kompressionsfasen sedan avstannar, kommer den lilla extra uppvärmningen (snabbt) att återgå till den (inledande) omgivningstemperaturen, vilket betyder att avsvalningen, enligt gaslagen, medför en ytterligare marginell slutkompression.

Vi kan studera den slutfasen i stor skala om vi har en gammal frysbox med inte helt färska tätningslister: Öppna dörren några sekunder för att släppa in varm luft (låg täthet). Då sedan dörren stängs och den varma luften kyls av (högre täthet), vilket betyder minskande medelavstånd mellan gasbollarna i den insläppta luftkroppen, minskar också lufttrycket inuti frysboxen; det bildas ett lokalt mindre vakuum som strävar att utjämnas genom att suga in luft utifrån — man kan höra hur det viner och visslar i tätningslisten när luften strömmar in. Är tätningen exakt, minskar istället volymen (plåtväggarna dras inåt), analogt kolven dras uppåt ett litet stycke till.

Utsätts istället gasen för en dekompression, alltså en utvidgning genom att öka h0, utför den frånskjutande bottenytan ett motsvarande decele(re)rande (retarderande) arbete på de gasbollar som träffar bottenytan då den skjuts neråt, vilket betyder att gasbollarna i motsvarande mening tappar rörelseenergi: det sker en motsvarande temperaturminskning. Sedan volymökningen avstannat och temperaturen åter stabiliseras (höjs till normalläget före ändringen) innebär tydligen den lilla extra återgången också en liten extra utvidgning så att bottenkolvens slutläge hamnar en liten bit ännu längre ner, eller analogt motsvarande högre tryck.

Enkla experiment i kökets normala rumstemperatur med PVC-slang och primitiva inneslutningar ger hyfsade experimentella bekräftelser på de samband man kommer fram till. Ingen matematisk beskrivning av dessa detaljer ges dock här då genomgången också kräver en utförlig genomgång av hydrostatiska tryckets matematiska fysik, vilket leder långt från huvudämnet i denna framställning. Syftet är här endast att påpeka möjligheterna och uppmärksamma observationerna.

Jag kollade just på webben (13Feb2010): SOM VANLIGT ÄR (ÄNNU Feb2010) DET SVENSKA UTBUDET MAGERT, här ämnet ELEMENTÄR GRUNDLÄGGANDE HYDROSTATIK.

Plancks entropisamband från Allmänna gaslagen

Allmänna gaslagen och Plancks strålningslag delar tydligen samma kvantitativa grundvillkor:

För en given temperatur (T) gäller en bestämd energimängd (E).

Se samband nedan. Villkoret gäller tydligen oberoende av om T kan anses gälla under något visst tidsintervall, eller om man eftersträvar att hålla T konstant under något visst tidsintervall, eller att T generellt gäller momentant i en viss tidpunkt. Eftersom (emellertid) alla kroppar värmeläcker kan bara T gälla strängt exakt i det sistnämnda fallet.

Allmänna gaslagen

pV = kT = E

har direkt (matematisk) koppling till Plancks entropisamband

S = b(lnW)

från Clausius grundform

S = E/T

genom allmänna gaslagens fundamentala gaskonstant

k = bN = E/T ............................................ J/°K

med

b, Boltzmanns konstant (den idealt fundamentala materiegasbollens fundamentala värmeenergiinnehåll 1,38 t23 J/°K), eller fundamentala enheten för värmekapacitet

N, Loschmidts tal (N=2,6869722 T25 som kopplar till det mera namnkända Avogadros tal, se utförligt i Konstanterna i Allmänna gaslagen)

Kopplingen ges via naturliga logaritmbasen (e) som allmänt känd »kopplare» till naturliga variationsordningar generellt

(eftersom variabeln visar sig ligga i en kvots nämnare, och därmed självservering på logaritmvariantens integral- och derivatamatematik, se logaritmderivatan);

Med Loschmidts tal N som Plancks ln(W) och fundamentala gaskonstanten k som Planckentropin S ges direkt

S = b(lnW) = E/T .................................... J/°K, Plancks entropisamband

Varianten dS/dE=1/T leder till Plancks strålningslag (se från Entropiderivatan); Och som baseras, just, på den enskilda atomens bidrag i W med grund i antalet Planckenergikvanta (hf) och begreppet (W) likaberättigade energifördelningssätt.

Allmänna gaslagen OCH Plancks strålningslag harmonierar utomordentligt väl i den allmänna beskrivningen av materiefysiken (Vilket redan är välkänt i experimentalisternas kretsar); Men helkass i massfysiken — därför att allmänna gaslagen, materiefysiken, inte innefattar orsaker till T vilka orsaker istället, ytterst, kommer från massfysiken via massdestruktion; se utförligt från värmebildningen. Se även i Massfysikens nollentropi.

Med andra ord:

Därmed har »isolerat system», i vilket fall, ingen som helst RELATERBAR funktion — tidsmässig utsträckning — att fylla i den praktiska fysiken.

Se även utförligt i MASSFYSIKENS NOLLENTROPI.

I MODERN AKADEMI HAR emellertid GENOM EN SERIE OLYCKLIGA OMSTÄNDIGHETER just »isolerat system» kommit att inta en HUVUDROLL i grundfysiken, nämligen i den s.k. »termodynamikens andra huvudsats».

Se vidare utförligt från Isolerat system i termodynamiken i Termodynamisk jämvikt.

För upphovet till ISOLERAT SYSTEM i modern akademi, se även en nytillkommen (Apr2010) källreferens i Införandet av Isolerat System 1858.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Åldrandets princip

ÅLDRANDETS PRINCIP

Inledande jämförande exempel

”

· Time reversal: Many laws of physics describe real phenomena when the direction of time is reversed. Mathematically, this is represented by the transformation, $t \, \rightarrow - t$ . For example, Newton's second law of motion still holds if, in the equation $F \, = m \ddot {r}$ , t is replaced by − t. This may be illustrated by describing the motion of a particle thrown up vertically (neglecting air resistance). For such a particle, position is symmetric with respect to the instant that the object is at its maximum height. Velocity at reversed time is reversed.

”,

@INTERNET Wikipedia Symmetry (physics), Discrete symmetries 2010-02-27

Min översättning:

Tidsomvändning [Tidsreversi(bili)tet]: Många lagar i fysiken beskriver verkliga fenomen när riktningen för tiden omvänds. Matematiskt är detta representerat av transformationen t→ –t. Till exempel gäller fortfarande Newtons andra rörelselag om i ekvationen F=md’’ t ersätts av –t. Detta kan illustreras av rörelsen hos en partikel som kastas upp vertikalt (frånsett luftmotståndet). För en sådan partikel är positionen symmetrisk i respekt till det ögonblick då objektet befinner sig vid sin maximala höjd. Hastigheten vid omvänd tid är omvänd.

Artikelns r med två prickar över betyder distansens andraderivata med Newtons beteckningar;

i relaterad fysik d = aT²/2; d’ = aT; d’’ = a, samma som acceleration, se accelerationsbegreppet

I RELATERAD FYSIK OCH MATEMATIK är accelerationen a=dv/dt beroende av ett INTERVALL som krävs för att beskriva den accelererade kroppens positionsändring från v=0 till v: Kroppen accelererar genom ett tids- och distansintervall från en bestämd utgångspunkt. Men en sådan kvalitativ rörelseform föreligger inte om vi vänder på tidsbilden (t→ –t; a=d[–v]/d[–t]) och kör filmen baklänges: den verkliga fysiska kroppen börjar inte, av någon mystisk anledning, retardera INNAN den nått fram till utgångspunkten från vilken den utgick i framhistorien, utan behåller hastigheten v ÄNDA IN TILL UTGÅNGSPUNKTEN. Och sedan, på liknande sätt, för fysikens övriga fenomengrunder:

Fysikens lagar uppvisar bara ett, och endast ett, och inget annat än bara ett entydigt verkningssätt.

I relaterad fysik och matematik kallas det (också) LOGIK.

Se utförligt från Kausalordningen, med särskild beskrivning i Utförligt Arbetsexempel 1;

Påståendet ovan i citatet från Wikipediaartikeln saknar tydligen — helt och hållet — en naturvetenskapligt grundad förankring:

Fysikens lagar kan I RELATERAD MENING omöjligen tidsomvändas.

Frågan NÄR den tydligt befängda uppfattningen uppstod som förmenar FYSIKENS LAGAR »tidssymmetri» — vilket i stort sett upprepas i varenda etablerad webbkälla [‡5] (ännu Feb2010 — men vilken ordform t.ex. inte ens finns upptagen i FOCUS MATERIEN 1975, och inte heller i det äldre omfattande uppslagsverket BONNIERS KONVERSATIONSLEXIKON 1922-1929, för att nämna exempel …) — verkar dessutom ypperligt svår att reda ut: förmodligen med ansats någonstans under senare delen av 1800-talet. Newtons PRINCIPIA (1687) innehåller i varje fall inget spår (ordstammarna ’symmetr’|ic|y och ’revers’|ible|al finns inte i Andrew Mottes översättning från 1729).

Orsaksriktningen i en tillståndsändring kan inte ändras

Orsaksriktningen — kausalordningen med ändringslagarna och den centrala accelerationen som tillståndsändringens grundval — från ett givet tillstånd till ett annat tillstånd kan omöjligen ändras. Det är åldrandets princip. Jämför personen som just gjort uthoppet från trampolinen: det finns ingen möjlighet att ångra orsaksriktningen. I den följande presentationen ges utförliga exempel med jämförande analyser och argument för att ge en genuin praktisk exempelgrund till den ovan rubricerade enkla (men tydligen sällan uppfattade, urgamla) åldrandets princip.

BILDKÄLLA: Bilder.AlltingGratis.se

2010I30

DEN MODERNA AKADEMINS FÖRYTLIGADE FYSIKKUNSKAPER

”Like other scientists of his day, Planck was intrigued by why the universe seemed to run in only one direction, why time had an arrow, why nature was apparently irreversible and always running down.”,

THE INTERNET ENCYCLOPEDIA OF SCIENCE David Darling ”up to date”

http://www.daviddarling.info/encyclopedia/Q/quantum_theory_origins.html

Se översättning

I LJUSET AV OVANSTÅENDE: Den moderna akademins etablissemang lever, tydligen som det får förstås, i en värld av föreställningar med EN DEL detaljer som FÖRMODLIGEN inte många människor i den vanliga vardagliga världen (Feb2010) känner till: föreställningen att fysikens lagar — alltså även före Einstein — tidsmässigt SKULLE »fungera lika bra framåt som bakåt»; Uppfattningen [‡5] att fysikens lagar skulle vara »tidssymmetriska» eller tidsreversibla. Den här framställningen gör anspråk på att ge en översiktlig genomgång med citat, exempel, jämförelser och argument.

ÅLDRANDETS PRINCIP ENLIGT RELATERAD FYSIK

STRÄNGT REVERSIBLA PROCESSER FINNS INTE I DEN RELATERBARA FYSIKEN

ÅLDRANDETS PRINCIP ENLIGT RELATERAD FYSIK

Smältande is i dricksglas — Nikon D90

FOTO: Författarens arkiv · Februari 2010

ENBART MED KÄNNEDOM OM universums expansion (Se utförligt från Dopplereffekten) finns rent naturlogiskt ENLIGT RELATERAD FYSIK uppenbarligen ingen grund för föreställningen om att någon enda fysikalisk process, alltså naturligt skeende, skulle vara »tidsmässigt omvändbar» (tidsreversibel, konv. tidssymmetrisk) — alltså som en film som spelas upp baklänges — men modern akademi hävdar det [‡5]. Expansionens momentana tillstånd, relaterad fysik, i varje tidpunkt garanterar att förhållandet mellan alla kroppar, elektriskt och gravitellt, också av princip ges en och endast en unik identitet som skiljer sig från varje tidpunkt både före och efter den givna. I fallet universums kontraktion, se K-cellens kontraktion enligt relaterad fysik, finns heller ingen förutsättning för expansionsfasens direkta tidsomvändning i och med att kontraktionsfasen (idealt) bygger på att alla stjärnor har slocknat och därmed en helt elektromagnetiskt kall kontraktiv processhistoria till skillnad från den utpräglat varma expansionshistorien. Därmed får begreppet åldrande ENLIGT RELATERAD FYSIK en naturlig, helt säker, rent matematisk preferens som inte kan omvändas (se även från EXPANSIONSMATEMATIKEN).

VID ETT FÖRSTA YTLIGT PÅSEENDE verkar det dock finnas vissa idealiserade ’gränsvärdesfall’ — typ is till vatten (värme tas från det omgivande varmare rummet till den kallare isen) och åter till is (… en mystisk temperatursänkning sker i en avgränsad del av rummet där plötsligt is visar sig med följd i att rummets temperatur höjs något) och som, just, tämligen omgående visar sig också vara, just, ett första ytligt påseende; Fysiken fungerar inte så (men det är alltid roligt att titta på filmen baklänges); Det finns i grunden inget enda exempel på naturprocesser som är fysikaliskt tidsmässigt omvändbara — men många finns som lever i den villfarelsen.

Låt oss därmed studera exempel.

— Vad säger webben?

Se även direkt i exemplen med Gravitationen och Den kastade bollen.

EXEMPEL:

”Den som känner biljardbordets utseende samt läge och rörelse hos biljardbollarna kan förutse hur dessa kommer att röra sig. Det är fråga om förutbestämda, mekaniska rörelser. Dessa lagar är också omvändbara i tiden. Solsystemet skulle gå lika bra baklänges. Men vi människor är inte omvändbara i tiden, och världen omkring oss är det inte heller. En förklaring är termodynamikens andra lag: oordningen i världen, ”entropin”, tilltar med varje energiprocess och detta är inte reversibelt; därför finns det en ”tidspil”.

”,

Att uppfinna det heliga på nytt eller Guden som vi inte behöver tro på Av Erland Lagerroth

Datumuppgift saknas

http://www.lagerroth.com/Kauffman

JÄMFÖR RELATERAD FYSIK:

Kausalordningen

FYSIKENS LAGAR ÄR ORSAKSBASERADE

Med samma mening: fysikens lagar är Deterministiska — kausalordningen är icke omvändningsbar, till jämförande studium i följande presentation

— Men vad allt detta tal om »tidssymmetri», vad menas med det?

— Ytterligare en svårighet i 1800-talets geniala samkväm.

Man hade nämligen uppfattat saken så

— eftersom TYP beskrivningen av en partikels rätlinjiga bana inte förändras om man kör filmen baklänges

— att »fysikens lagar är tidssymmetriska», alltså generellt »omvändbara».

— Men »fysikens lagar» är, här ENLIGT RELATERAD FYSIK, inget annat än ändringslagarna, analogt Newtons tre rörelselagar, och ur vilka hela fysikens flora av fenomen härleds, induktionen och magnetismen inkluderat.

— Men ändringslagarna, just,

1 tillståndet kvarstår tills ändrat

2 ändringen är proportionell mot den tillståndsändrande kraften

3 varje ändring strävar att bevaras

tecknar alldeles tydligt en bestämd, icke omvändningsbar ordning, särskilt excellent demonstrerat av magnetismen (kausalsambandet) och induktionen. Från vila (v=0) till rörelse (v>0) kräver en acceleration (a=v/T): Vi måste — tvunget — utgå från tillståndet (vilan), inte accelerationen, för att kunna definiera variationen (som ombesörjs via accelerationen).

Efter träff av vattendroppe mot vattenyta

FOTO: Författarens arkiv · APR2009 · Nikon D90

Magnetismen har ingen fysikalisk reversibilitet, på samma sätt som ringarna som bildas på vattenytan heller inte har det — och på samma sätt för induktionen: Heller hoppar inte vattendroppar upp från en plan rörelselös vattenyta, utan de intränger (faller) från materierummet utanför så att ringarna (utträngningarna, divergensen), magnetismen, kan bildas.

Jämför alltså återigen modern akademi [‡5]:

”In fact, all the fundamental laws of physics are purely time-symmetric, including the laws of electromagnetism and the wave equation of quantum mechanics.”,

MATH PAGES

http://www.mathpages.com/home/kmath552/kmath552.htm

Min översättning:

I själva verket är fysikens alla fundamentala lagar renodlat tidssymmetriska, inkluderat lagarna för elektromagnetism och kvantmekanikens vågfunktion.

Vi avhandlar tydligen just en relaterad, exemplifierad, beskrivning som uppenbarligen bevisar att ovanstående påstående helt saknar naturvetenskaplig förankring.

Fysikens lagar i RELATERAD MENING blir därmed och alltså entydigt kausalt (orsaksmässigt) bestämda, icke omvändbara — men som inte finns med i modern akademi.

Jämför, återigen, RELATERAD fysik:

Centralkraften — centralkraftsverkan — är inte omvändningsbar.

Orsaksgrunden ligger i centralpartikeln (gravitationen), inte i periferin.

Accelerationsbegreppet — generellt — är inte omvändningsbart.

Impulsen p=mv — rörelsen och dess massa — föregår kraften: intervallets oförstörbarhet.

Se från FYSIKENS TREDJE PRINCIP och INTERVALLETS OFÖRSTÖRBARHET.

Se utförligt beskrivande exempel i Utförligt Arbetsexempel 1.

Se även utförliga exempel till jämförelse med modern akademi i GRAVITATIONEN och DEN KASTADE BOLLEN.

Men det är, tydligen, ingen »tid» som bestämmer den ordningen, utan enbart orsakssammanhang —och som, tydligen, gått det moderna akademiska skarpsinnet helt förbi (Kausalordningen). Man kan alltså säga: fysikens lagar (Se från Ändringslagarna) är tidsoberoende — alltså, inte tidssymmetriska utan tydligen, strängt kausalstyrda: impulsen (samma som rörelsemängden mv) bestämmer riktningen; Jämför kärnreaktionslagen K1+K2–(m®g)=K: processen är kvantitativt, inte kvalitativt, omvändbar (Se även från NEUTRINOSPEKTRUM). (Och ännu i denna dag kvarstår, ju, dessa oklarheter högeligen inom den moderna akademins lärosystem. Se t.ex. den observerade omöjligheten från vektoranalysen inom magnetismen). Att skeendet i fysiken generellt ENLIGT RELATERAD FYSIK verkligen är irreversibelt — till skillnad från den moderna akademins fysikuppfattning — garanteras (således, kausalt) DELS av de ytterst enkla ändringslagarna som sådana (Newtons tre rörelselagar: accelerationen är icke omvändningsbar, se ovan) och DELS, mera övergripande, av universums expansion: varje momentant tillstånd — varje NU — garanteras en och endast en unik förekomst och med en utvecklingsriktning som garanterat skiljer på förflutet (mera komprimerat) och framtid (mindre komprimerat) i varje givet expanderande universum, samt DELS av divergensen som sådan, ljusets UTstrålande natur.

— Men den uppfattningen fanns, tydligen, ingalunda under den berörda epok under det berömda 1800-talet då frågan om ’naturlagarnas riktning’ tydligen fick stort utrymme (tydligen omkring tiden för Boltzmanns arbeten, mot 1800-talets senare hälft). Man var — tydligen allmänt [‡5] — av den uppfattningen att alla fysikaliskt beskrivande premisser HADE »tidssymmetri» — som det är ännu i denna dag i modern akademi.

Utförligt Arbetsexempel 1 — impuls föregår kraft

FOTO: Författarens arkiv

Stålkulor · Feb2010 · Nikon D90

Intervallet som kulan accelereras upp på från en yttre impuls får inte samma fysikaliska karaktär om ’man spelar filmen baklänges’ — men många lever i den villfarelsen

En kropp (m) utsätts vid incidenspunkten och tidpunkten t₀, och endast där i elementär ideal skolboksvälkänd fysikalisk mening, för en impuls (p=mv=Ft=mat=m[v/t]t); Kroppen m befinner sig i rörelse FÖRST vid tidpunkten t₁ så att tidrymden t₁–t₀ motsvarar INTERVALLET t; Då kroppen m genomgår intervallet t genomgår kroppen m samtidigt en acceleration a=dv/dt; Från hastigheten noll till hastigheten v betyder uppenbarligen en hastighetsökning, en acceleration, och uppnås med andra ord FÖRST genom (efter) intervallet t, vid tidpunkten t₁, och som kan betraktas som obegränsat näraliggande noll — men likväl ett intervall och som INTE kan fås att »övergå mjukt i noll» (se intervallets oförstörbarhet).

Ovanstående accelerationsanalys finns inte i modern akademi.

— Se särskilt från ATOMTRIANGELN (delen närmast noll kan aldrig delas) och INTERVALLETS OFÖRSTÖRBARHET, där ges utförliga exempel, samt explicit MÄSTARLOGIKENS HUVUDSATS, punkter (noll) kan inte adderas, det finns inga oändliga mängder. Se även Dedekinds Låda, Cantors fel (Cantors decimala algoritm i Cantors resonemang), och Härledningen till e för ytterligare exempel, om inte redan bekant.

I elementär fysik överförs HELA impulsen till kroppen i incidenspunkten »omedelbart». Men vi kan lika gärna studera ett mera praktiskt exempel med verkliga elastiska fysiska kroppar, resultatet blir ändå detsamma. Se utförligt i efterföljande exempel med Newtons vagga.

roppen m kan alltså, idealt, sägas ha uppnått sin acceleration under intervallet t=t₁–t₀ med den uppnådda hastigheten v vid t₁; Genom intervallet t har kroppen m alltså färdats en distans (d) som skiljer kroppen m från den incidenspunkt (orsakspunkten) där kroppen m (idealt) påfördes sin impulsvektor (mv);

en »spelas filmen baklänges» finns alls inga sådana, högst märkliga, fysikaliska lagar: ’Filmen baklänges’ med m som närmar sig incidenspunkten med hastigheten v och massan m, impulsen mv, har ingen ideal fysikalisk motsvarighet till att kroppen m, av någon mystisk oförklarlig anledning, SKULLE börja sakta av inom ett distansintervall (d) under ett tidsintervall (t), INNAN den når incidenspunkten vid t₀;

I den ideala elementära fysiken finns ingen sådan procedur: Kroppen m fortsätter idealt enligt förutsättningarna ända in till incidenspunkten t₀ och överför FÖRST där — absolut — sin impuls mv på incidenspunktens ideala kinetik. Och alltså kan man inte med något naturvetenskapligt förankrat stöd påstå att fysikens lagar uppvisar »tidssymmetri».

Accelerationsbegreppets kausallogik sönderbryter, tydligen, varje sådan uppfattning — utförligt relaterat och exemplifierat som ovan. Se även mera praktiskt nedan i Newtons vagga.

Utförligt Arbetsexempel 1.1 — Newtons vagga

Bildkälla: @INTERNET Wikipedia

Newtons vagga 2010-02-12

Newtons vagga

MOTSVARANDE FENOMEN I PRAKTIKEN ansluter till kropparnas materiella elasticitet. Med exempel från den (berömda) Newtons vagga (ovan vänster) — som är en (trivial) make till PENDELN (med mellanliggande kulor som impulsen överförs till, istället för en enda svängande kula):

den verkliga fysiken accelereras motstående kula av den överförda impulsen (mv); Det sker genom att materialet, tvunget, deformeras internt i orsaksriktningen för mv; Därmed åstadkoms att den utputtade kroppens tyngdpunkt, genom de inre sammanhållande atomära krafterna som bildar kroppen, påförs motsvarande utskjutning; Och med tillhörande, mera komplicerad, initierande acceleration:

en utkastade kulan uppvisar tvunget för den relaterade fysikens förklaring en elastiskt bula (en chockvåg som först fortplantas genom hela kulledet som ett sammanhängande material genom ledets centrala tyngdlinje) i den initierande riktningen mv och som orsakar accelerationen hos ändkulan. Körs filmen baklänges ser vi, plötsligt, hur samma men nu kausalt omvända bula uppkommer motsatt rörelseriktningen, samtidigt som kulan retarderar, utan att kulan ens har nått fram till vaggans kulstapel, och vilken detalj definitivt saknar en motsvarande fysikalisk grund:

Fysiken fungerar inte så — typ mystiska krafter som åstadkommer inre materiell, riktningsmässigt omvänd, deformation, dessutom innan kroppen ens har nått stötmålet.

ysiken har ingen sådan fenomengrund. Och alltså återigen: man kan, tydligen inte heller i detta fall, inte med något som helst naturvetenskapligt förankrat stöd, påstå att fysikens lagar skulle uppvisa »tidssymmetri» då förloppet spelas upp baklänges. Det finns, uppenbarligen, ingen sådan fysik.

Utförligt Arbetsexempel 2 — Gravitationen

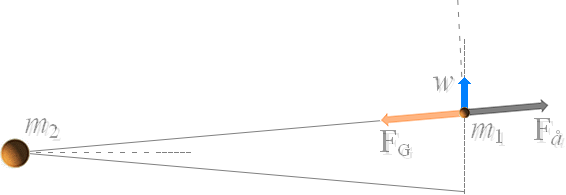
I den här framställningen (relaterad fysik) används beteckningen å (=mww/r, normalt a) som särskild beteckning för centralacceleration (centripetal- inåt, centrifugal- utåt) med den speciella beteckningen w (normalt v) för omloppshastigheten, för att särskilja termerna från fallet linjär rörelse.

utgångspunkt

Konvergensen — Gravitationen

GRAVITATIONSPRINCIPEN ENLIGT RELATERAD FYSIK — oberoende av material; kan inte skärmas ifrån; tidsoberoende, se utförligt från GRIP — definieras kvantitativt på formen Newtons allmänna gravitationslag med hjälp av impulsbegreppet i centralkraftsverkan (Keplers ytmoment; rörelser under inverkan av en centralkraft som verkar utmed förbindningslinjen, ortsvektorn, mellan centralkropp och omloppskropp, se utförligt från Ytmomentet) via centrifugalkraften (F=må=mw²/r) enligt

F=ma=mw²/r=(w²/rm₂)m₂m=(w²/m₂)m₂m/r=(w²r/m₂)m₂m/r²=Gm₂m/r² ....... gravitationslagen

;

Omloppskroppen (m1) — från en given konstant linjär hastighet w — ändrar sin rörelseriktning med elementär ideal fysikalisk laggrund i en sammandragande impulsverkan (p=mw), gravitationsvektorn, riktad från den ena kroppen (omloppskroppen m1) mot den andra (centralkroppen m2) — med omedelbart resulterande verkan från impulspunkten

(gravitationsprincipens tidsoberoende, se ovan, se även explicit från GcQ-teoremet enligt relaterad fysik)

i en lika stor men omvänt riktad centrifugalvektor; balansen mellan inåtriktad (konvergent) impuls och utåtriktad centrifugalkraft(sImpuls) definierar tydligen gravitationens vektoriella kvantitativa orsaksfysik.

effekt

KÖR VI FILMEN BAKLÄNGES måste gravitationsimpuls och centrifugalkraftsimpuls, tydligen, relateras med motsvarande omvänd riktning: centrifugalkraften strävar att driva m1-kroppen inåt, och gravitationskraften strävar att återställa balansen med en motriktad, utåtriktad, kraftimpulsvektor. Men någon sådan, högst märkvärdig, fysik vet vi finns inte; Gravitationen verkar entydigt konvergent, sammandragande och kan inte på något som helst sätt efterliknas eller härmas EXAKT med hjälp av andra fysikaliska fenomen.

(Centrifugalkraften kan simulera g-kraft lokalt, men inte över motsvarande lodavstånd eftersom centrifugalkraftens idealt vektoriella lodlinjer är divergenta, bort från centralpunkten, till skillnad från gravitationens lodlinjer som är konvergenta, in mot centralpunkten).

Med andra ord: centrifugalkraft och gravitationskraft kan inte ersätta varandra.

Därmed bortfaller också i detta fall möjligheten med tidssymmetri för fysikens lagar.

Jämför föregående citat (det är INTE signifikant för just den personen, utan snarare hela den moderna akademin, se citatreferenserna i [‡5]);

”Solsystemet skulle gå lika bra baklänges.”

Uppenbarligen INTE. Det finns ingen sådan fysik.

Utförligt Arbetsexempel 3

Divergensen — Ljusfysiken

DIVERGENSPRINCIPEN — beroende av material; kan skärmas ifrån; tidsberoende — definieras som konvergensprincipens fullständiga omvändning, se från DEEP.

Eftersom ljusets fenomenmässiga utbredning ENLIGT RELATERAD FYSIK (divergensprincipen, se DEEP) grundas på en idealt sfärisk »strålitet» med grund i induktionsfysiken och atomhöljenas elektronsvängningar

— DELS genom att Planckenergin per vinkeldistribution relativt materiens fasta atomvolymer avtar med växande spridningsvinkel [se särskilt i Hur värmen avtar med tiden] och DELS i ljusets växelverkan med atomerna genom Comptoneffekten [Planckenergin E=hf för det aktuella ljuset AVTAR ständigt med divergensens, ljusfortplantningens, tidsmässiga fortgående] som lämnar allt längre våglängder på allt växande stråltid för given utgångsljusenergi

— finns ingen som helst praktisk fysikalisk möjlighet att SPELA DEN FILMEN BAKLÄNGES utan tillförande av motsvarande energi. Ljusets divergensbaserade spridningsfysik — utstrålningen —kan inte återkomprimeras utan att energi tillförs. Då, således, den verkliga praktiska fysiken uppvisar en energiomsättning från högre till lägre, den naturliga ljusutstrålningen, visar filmen baklänges motsvarande energipumpning från lägre till högre; Vi vet att det finns ingen sådan fysik. Ljuset natur är att vara divergent, inte konvergent;

em-strålning kan inte komprimeras utan tillförande av energi

Vi kan inte heller kasta om preferenserna inbördes för GRIP (gravitationen) och DEEP (elektriciteten) eftersom gravitationen är tidsoberoende medan ljusfysiken begränsas av topphastigheten c₀=2,99792458 T8 M/S.

Så kan till exempel som redan omnämnts magnetismen inte fungera baklänges av samma skäl som att inte heller vattenringarna kan fungera baklänges i den verkliga fysiken — och sluta med att en vattendroppe hoppar upp från vattenytan; induktionen triggar magnetismen genom laddade kroppars lägesändring. Inte omvänt. Se utförligt från Induktionen och Magnetismen. Se även RESULTATEN FRÅN PARALLELLEXPERIMENTEN. Se även i Tre precisa exempel för exakt jämförelse, där ges exakt jämförande korsreferens mot moderna akademi per exakt praktisk matematik.

Och alltså även i detta fall bortfaller möjligheten med tidssymmetri för fysikens lagar.

Finns inte.

DÄRMED ÄR SAMTLIGA FALL UTTÖMDA enligt relaterad fysik: det finns bara gravitation (mekaniken, accelerationen, ändringslagarna, Newtons tre rörelselagar) och elektricitet (Planckenergin, Plancks strålningslag, Plancks konstant) att välja på. Som belysts ovan, förhoppningsvis uttömmande fullständigt, kan tydligen ingen av dem fås att uppvisa en bevarad fenomenkaraktär med en baklänges uppspelning typ »filmen baklänges». Med andra ord: föreställningen om »tidssymmetri för fysikens elementära lagar» [‡5] är alldeles uppenbart en utbredd vanföreställning (en myt) i modern akademi med, tydligen, följande allmänna raketbränsle som energigrund: fråga aldrig efter sanningen.

Slutsats

Det finns, i ljuset av ovan framställda elementära grundexempel och alldeles tydligt, ingen som helst relaterbar fysikalisk grund för något sådant som tidssymmetri för fysikens lagar. Till direkt jämförelse, se föregående citat.

Tydligen bara om man gör väldigt översiktligt summariska framställningar som bortser ifrån det mesta av fysikens avgörande djupdetaljer, kan man få fram meningar som gör gällande att fysikens lagar skulle uppvisa tidssymmetri.

FYSIKENS ELEMENTÄRA GRUNDER ENLIGT RELATERAD FYSIK har ingen förankring i modern akademi. Som redan påpekats, har modern akademi inte utmärkt sig för annat än att, redan från ruta ett med början under det berömda 1800-talet, framställa MÄNNISKAN SOM MATEMATIKENS och logikens SKAPARE — och följdriktigt, inte att härleda fysiken utan att uppfinna den.

Att vi — med andra ord — »spelar filmen baklänges» betyder inte att också DEN VERKLIGA kausalordningen UNDER FILMENS UPPSPELNING spelas upp baklänges så att vi, i så fall, skulle tycka att det är lika roligt framåt som bakåt. I det verkliga fallet kan vi SKRATTA enbart åt baklängeskonsterna DÄRFÖR att de, just, är overkliga — och därför att den verkliga kausalordningen, just, fortsätter även då vi spelar upp filmen baklänges. Det roliga inslaget med baklängesfilmningen FORTSÄTTER att förlöpa enligt universums expansion med ett unikt tillstånd i varje unik tidpunkt. Således är ENLIGT RELATERAD FYSIK, ovanstående genomgång, omvänd kausalordning eller »tidssymmetri» av alla, tydligen samtliga, relaterbara skäl en fundamental omöjlighet.

ALLTSÅ GENERELLT I SAMMANFATTNING, SAMTLIGA FALL ENLIGT RELATERAD FYSIK

— Intervallets oförstörbarhet, tillståndets princip; gravitation (F=ma) kan inte utbytas mot eller ersättas av centrifugalkraft ehuru centrifugalkraften definierar gravitationskraften kvantitativt på en cirkulär rörelse: kausalomvändningen gäller inte; rörelsemängden föregår kraften; rörelsemängdens intervall (tillståndet, den bestämda kvantiteten) måste först finnas för att accelerationen ska kunna definieras (a=dv/dt): kausalomvändningen gäller inte, och därmed tydligen heller inte omvändningen per tid;

Fysikens lagar är, tveklöst och helt säkert, irreversibla.

Eftersom induktionen, och därmed magnetismen, härleds med utgångspunkt i samma principiella grundmekanik, impulsen föregår kraften, är samtliga fall berörda med ovanstående sammanfattning. Se särskilt från Induktionen och Magnetismen.

EXEMPLEN befäster naturvetenskapen.

Se även sist i Partikelexperiment verifierar den naturliga ordningen.

Upphovet till uppfattningen om tidssymmetri

UPPHOVET TILL uppfattningen om tidssymmetrin för fysikens lagar?

Det som kan vara intressant att få veta är NÄR idéerna FÖRST framkom, eller framkastades, själva argumenten som ledde till eller antydde nuvarande, ovanstående [‡5] konstaterat felaktiga, omdöme att fysikens lagar skulle vara tidssymmetriska, att fysikens lagar lika väl skulle gälla om man spelade verklighetsfilmen baklänges.

Förmodligen inte med början från Aristoteles (384-322 f.Kr.) och dennes påföljande nära tvåtusenåriga världsuppfattning — heller inte, veterligt, med Galileo Galileis arbeten, och heller inte, veterligt, med Isaac Newtons arbeten.

Sökning bland nu (Feb2010) tillgängliga källor enbart på webben ger inga direkta referenser, bara antydningar som pekar på samma område: Boltzmanns H-teorem som den tändande gnistan. — Före den punkten fanns, veterligt (heller), ingen direkt »begreppspotential» för argumentutbyte. Argumenteringen är i vilket fall känd i samband med Loschmidts paradox, alltså efter 1872.

Citatkällorna i mängd på webben visar (eller rättare sagt, antyder) att tidssymmetrins begrepp för fysikens lagar åtminstone var i (nära) etablerat omlopp från grovt 1800-talets mitt i samband med formuleringen av andra värmelagen. Se särskilt Loschmidts paradox (från Boltzmanns H-teorem 1872) som helt grundas på ordformer typ »naturlagarnas reversibilitet».

Var finns referenserna?

Var finns referenserna?

OBS. Vissa av webb-källorna som visas i GoogleTräffarna kan inte kommas åt på grund av krav på särskild behörighet — eller att man betalar särskilt.

Det verkar som att man FÖRE ANDRA VÄRMELAGEN hade kommit fram till (eller hoppade in i) uppfattningen att den klassiska fysikens lagar var DETERMINISTISKA — kausalstyrda — och DÄRFÖR »tidsoberoende» — med (i så fall) felaktiga underförståddheter: tidssymmetriska. (Här kan man alltså skönja, men ännu inte bevisa, hur flera begreppsgrunder sammanblandas, tydligen, utan särskiljning).

TIDENS PIL SOM NATURVETENSKAPLIGT BEGREPP — alltså begreppen om naturskeendets irreversibilitet kontra dess reversibilitet (syn. tidssymmetri) — uppkom alldeles klart, entydigt och helt säkert med formuleringen av värmesatserna till termodynamiken, studiet av ångmaskinen och strävan att utveckla den nymodigheten för industriella ändamål — och därmed samtidigt med Clausius införande ev termen entropi.

Inte före det. Alltså, rätt och slätt, inte före Clausius mera direkta formulering av andra värmelagen från år 1862 enligt

värme flyter alltid, spontant irreversibelt, från varm till kallt

»Varför inte omvändningen?» uppväckte, tydligen (men det är tills vidare bara min tolkning, obs, i brist på mera exakta uppgifter) frågan om »naturlagarnas irreversibilitet» och därmed grunden till nuvarande uppfattningar.

”Newton's laws were quickly accepted because they led to correct predictions about the world. They did contain several puzzles, however, one of which was that they simply described the way that the world is, and do nothing to say why it is so. Their most puzzling aspect as far as time is concerned is that they work equally well if time runs forward or if time runs backwards. There is a complete time symmetry in the laws, yet human experience leads to the belief that time always flows forward. It was only in the middle of the 19th century that the second law of thermodynamics was proposed by Clausius and this was the first law to lack symmetry in the direction of time, see [7].”,

Referensen till not 7 (vi vet inte vad som står där, tyvärr):

”G Bierhalter, Zyklische Zeitvorstellung, Zeitrichtung und die frühen Versuche einer Deduktion des Zweiten Hauptsatzes der Thermodynamik, Centaurus 33 (4) (1990), 345-367.”,

A HISTORY OF TIME: CLASSICAL TIME — J J O'Connor and E F Robertson, Aug2002

http://www-history.mcs.st-and.ac.uk/HistTopics/Time_1.html

Min översättning:

Newtons lagar accepterades snabbt därför att de ledde till korrekta förutsägelser om världen. De innehöll dock flera problemnötter, av vilka en var att de helt enkelt beskrev sättet på vilket världen är, och inte gör något för att tala om varför det är så. Deras mest förbryllande aspekt så vitt tiden anbelangar är att de fungerar lika bra om tiden flyter framåt eller om tiden flyter bakåt. Det finns en fullständig tidssymmetri i lagarna, trots att mänsklig erfarenhet leder till uppfattningen att tid alltid flyter framåt. Det var bara i mitten på 1800-talet som termodynamikens andra huvudsats föreslogs av Clausius och detta var den första lag att sakna symmetri i tidens riktning.

Det ser alltså ut som att hela saken uppdagades genom en överraskande upptäckt — tidigare helt utan formulering.

Var finns referenserna?

NOTERA att citatets essentiella kärnmening — påståendet ATT ”they WORK” — helt saknar referenser. Varifrån har författaren fått denna uppfattning? Finns det en, verklig, historisk källa? Var?

”The origin of time asymmetry in the physical universe has exercised the attention of many of the world's greatest physicists since the time of Maxwell and Boltzmann.”,

”The problem is easily stated. Almost all physical processes display a unidirectionality in time, yet the underlying laws of physics (with a minor exception in particle physics) are symmetric in time. How does asymmetry arise from symmetry? Most investigators conclude that the explanation can be traced to the initial conditions of the system concerned. Seeking the ultimate origin of time asymmetry in nature inevitably takes one back to the origin of the universe itself, and the question of the cosmic initial conditions. It seems reasonable to assume that the universe was born in a low-entropy state, like a wound clock, from which it is sliding irreversibly toward a high-entropy state, or heat death, like a clock running down.”,

THE GLOBAL SPIRAL (1997-2008) — Science & Ultimate Reality, Paul Davies

http://metanexus.net/Magazine/ArticleDetail/tabid/68/id/8571/Default.aspx

Min översättning:

Ursprunget till tidsassymmetri i det fysiska universumet har anställt uppmärksamheten hos många av världens största fysiker sedan tiden för Maxwell och Boltzmann.

…

Var finns referenserna?

NOTERA ÅTERIGEN att citatets essentiella kärnmening — påståendet ATT de ”ARE symmetric” — helt saknar referenser. Jämför även det inledande exemplet. Varifrån kommer den tydligt tvärsäkra meningen i uppfattningen?

Är det Boltzmanns H-teorem från 1872?

Och den därmed uppmärksammande Loschmidts paradox.

Det ser så ut — men ännu utan någon säker referens.

”Boltzmann taught us that for familiar physical systems the thermodynamic arrow of time is deeply linked with very special "initial conditions":

Systems that start out far from equilibrium have an arrow of time as they are drawn toward the equilibrium. Systems that already are in equilibrium do not.”,

THE GLOBAL SPIRAL (1997-2008) — The arrow of time, entropy and the origins of the universe, Andreas Albrecht

http://metanexus.net/Magazine/ArticleDetail/tabid/68/id/8571/Default.aspx

Var finns referenserna?

NOTERA ÅTERIGEN att citatets essentiella kärnmening — påståendet ATT ”Boltzmann taught us”, sv., Boltzmann lärde oss — saknar tydliga, klara, referenser. Var finns satsbilden? Visa.

Observera att 1. citatkällan närmast ovan ger påståenden utan referenser, att 2. citatkällan närmast ovan i ljuset av ’Boltzmann’, underförstått, utan att berätta om det för läsaren, avhandlar fysikbeskrivningen på begreppet »isolerat system», Boltzmanns H-teorem [‡7] och som hela ämnet med Boltzmann initierades på från år 1872, och vilket »isolerat system» vi redan vet inte existerar i fysiken garanterat av Plancks strålningslag: alla kroppar värmeläcker, Boltzmanns H-teorem kan inte diskuteras i termer av praktisk fysik; entropibegreppet S=b(lnW) leder ENLIGT RELATERAD FYSIK till Plancks strålningslag och därmed ett entydigt S-värde för varje kropp med ett bestämt energiinnehåll vid en bestämd temperatur; Boltzmanns H-teorem (1872), som uppställdes flera decennium före kännedomen om Plancks strålningslag (1901), har följaktligen ingen reell koppling till fysiken. Citatkällan närmast ovan, dess egna meningar, omsluter tydligen inte den bilden, ”Systems that already are in equilibrium do not”, men ger ett bra exempel på komplikationerna ikring den. (Jämviktsbegreppet i relaterad fysik är ett momentanbegrepp, ett tillståndsbegrepp: inget fysikaliskt skeende finns i relaterad mening inom tillståndets begrepp, se utförligt från FUNTOP).

För frågan om ursprunget och upphovet till »tidssymmetrin» får vi, tydligen, typ ”gissa lösning” — förmodligen därför, och som vi redan anat i ljusets av Boltzmanns H-teorem (det var, förmodligen, den tändande gnistan) att en kakofoni av diskussioner PLÖTSLIGT uppstod (runt 1872) på en stor mängd fronter och med många olika argument. Och så, lika plötsligt, FANNS det bara någon strömlinjeformad mening där, gud vet varifrån.

Alla förutsätter det — ingen kan säga varifrån.

”The arrow of time expresses the fact that in the world about us the past is distinctly different from the future. Milk spills but doesn't unspill; eggs splatter but do not unsplatter; waves break but do not unbreak; we always grow older, never younger. These processes all move in one direction in time - they are called "time-irreversible" and define the arrow of time. It is therefore very surprising that the relevant fundamental laws of nature make no such distinction between the past and the future. This in turn leads to a great puzzle - if the laws of nature permit all processes to be run backwards in time, why don't we observe them doing so?”,

”Put another way: how can time-reversible motions of atoms and molecules, the microscopic components of material systems, give rise to the observed time-irreversible behavior of our everyday world? The resolution of this apparent paradox is due to Maxwell, Thomson and (particularly) Boltzmann.”,

”Thermodynamics makes no reference to atoms and molecules, and its validity remains independent of their existence and nature—classical or quantum. The high point in the development of thermodynamics came in 1865 when Rudolf Clausius pronounced his famous two fundamental theorems: 1. The energy of the universe is constant. 2. The entropy of the universe tends to a maximum.”,

SCHOLARPEDIA Time's arrow and Boltzmann's entropy 2010-02-12

http://www.scholarpedia.org/article/Time's_arrow_and_Boltzmann's_entropy

Var finns referenserna?

ÅTERIGEN SAMMA. ”THAT”. Var finns referenserna? Varifrån kommer uppfattningen?

Här ställs alltså kadrer av pseudofysikaliska paradoxfrågeställningar upp i närmast oerhörd exekverande ordning.

Jämför även det inledande exemplet.

Citatkällan närmast ovan verkar dessutom väl euforisk:

1. ”Thermodynamics makes no reference to atoms and molecules”. Var finns referenserna?

2. ”when Rudolf Clausius pronounced his famous two fundamental theorems”, med ”universe”. Var finns referenserna?

Vi har citatuppgift från FOCUS MATERIEN 1975 som stämmer med ovanstående punkt 2, se citat, men det är uppenbarligen en senare skrivning;

Vi har uppgifter om att Clausius formulerade saken för en motsvarande ångmaskins materiesystem, men inte för aspekten om universum. Källan ovan lämnar heller inga referenser. Källan kan i det faktaljuset alltså milt sagt uppfattas som spekulerande.

Det fortsätter på samma sätt — genom otaliga webbkällor: Man påstår ATT något SENSATIONELLT gäller, men har ingen REFERENS att anföra:

”The problem of the direction of time arises directly from two contradictory facts. First, the fundamental physical laws are time-reversal invariant. In other words, anything that can happen moving forward through time is just as possible moving backwards in time. Or, put in another way, through the eyes of physics, there will be no distinction, in terms of possibility, between what happens in a movie if the film is run forward, or if the film is run backwards.

”,

@INTERNET Wikipedia Philosophy of space and time, The direction of time 2010-02-12

http://en.wikipedia.org/wiki/Philosophy_of_space_and_time#The_direction_of_time

Återigen ”are time-reversal invariant”, sv. är tidsreversibelt oförändrade, ”are”: Ingen referens — ingen relaterbar, begripbar, förklaringsbar, fattningsbar, bevisbar grund — ges till de tydligt avgörande påståendena.

Jämför även det inledande exemplet.

Det finns uppenbarligen inget ”two contradictory facts”

Se från Kausalordningen med utförliga praktiska exempel.

Fysikens lagar är entydigt icke omvändbara

gravitation · elektricitet · magnetism · induktion · acceleration · centralkraftsverkan · Keplers ytmoment · impuls (rörelsemängden mv)

En annan wikipediaartikel, samma tema, uttrycker sig något mera försiktigt — men fortfarande utan referenser:

”In the natural sciences, arrow of time, or time’s arrow, is a term coined in 1927 by British astronomer Arthur Eddington used to distinguish a direction of time on a four-dimensional relativistic map of the world, which, according to Eddington, can be determined by a study of organizations of atoms, molecules, and bodies.

Physical processes at the microscopic level are believed to be either entirely or mostly time symmetric, meaning that the theoretical statements that describe them remain true if the direction of time is reversed; yet when we describe things at the macroscopic level it often appears that this is not the case: there is an obvious direction (or flow) of time. An arrow of time is anything that exhibits such time-asymmetry.

”,

@INTERNET Wikipedia Arrow of time 2010-02-12

http://en.wikipedia.org/wiki/Arrow_of_time

Citatkällans ”the theoretical statements that describe them remain true if the direction of time is reversed” är f.ö., tydligen, i ljuset av den relaterbara fysikens mening, osann:

Det finns inga relaterbara referenser till ’time-symmetry’ för fysikens lagar

Se från Kausalordningen med utförliga praktiska exempel.

Fysikens lagar är entydigt icke omvändbara

gravitation · elektricitet · magnetism · induktion · acceleration · centralkraftsverkan · Keplers ytmoment · impuls (rörelsemängden mv)

Artikelkällan närmast ovan omnämner/tar upp följande exempel:

GRAVITATION:

”Overview

The symmetry of time (T-symmetry) can be understood by a simple analogy: if time were perfectly symmetric then it would be possible to watch a movie taken of real events and everything that happens in the movie would seem realistic whether it was played forwards or backwards.[1]

An obvious objection to this assertion is gravity: after all, things fall down, not up. Consider first, some bodies interacting in space. Perhaps one asteroid approaches another, loops part-way around it, and slingshots off in another direction. In this case the forward-recording and the backward-recording look equally realistic.

”,

@INTERNET Wikipedia Arrow of time, Overview 2010-02-12

http://en.wikipedia.org/wiki/Arrow_of_time

— Att baklängesfilmningen SER likadana ut, ”look equally realistic”, kan nog var och en intyga, helt säkert. Men som också artikeln påstår, citatet längre upp,

”the theoretical statements that describe them remain true if the direction of time is reversed”

Min översättning:

de teoretiska påståenden som beskriver dem gäller fortfarande om tidsriktningen omvänds

nämligen att lagarna för skeendet skulle vara desamma även med en omvänd tidspil, stämmer alls inte med CENTRALKRAFTENS FYSIKALISKA VERKAN, se KausalExempel 2 (Gravitationen), i koppling till GRAVITATIONENS PRINCIP; Förutsättningen för att wikipåståendet skulle kunna gälla är att gravitation och centrifugalkraft kan utbytas mot varandra, i enlighet med impulsverkan i det fysikaliska skeendet som, just (centralkraftsverkan), definierar himlakroppens rörelse enligt Keplers ytmoment (K=vr). Men som vi vet, finns ingen sådan fysikgrund: lodlinjerna i gravitationen är konvergenta, i centrifugalkraftens motsvarande referens divergenta; centrifugalkraft kan inte härma gravitation, och gravitation kan inte härma centrifugalkraft. Fysiken ligger fast.

Med andra ord: Artikelförfattaren skriver, alldeles uppenbart, på en (väl inövad, extremt omfattande) MYT — med alldeles uppenbart tillhörande förytligade fysikkunskaper som har gått i arv med betygssättningens skolade meriter och karriärer. Det finns ingen tidssymmetri i fysiken.

Jämför även det inledande exemplet.

Helt rent. Se ytterligare exempel nedan (och alla andra …).

Nästa:

DEN KASTADE BOLLEN

”One could film a tossed ball as it moves up, slows gradually to a stop, and then falls back down into the catcher's hand. This is another case where the forward- and backward- recordings clearly look equally realistic. One might expect it to take the same amount of time for the ball to go up in reverse as it did for it to go up going forward, but as it turns out the film would show it taking slightly longer going forward than going backward. This is not because gravity is asymmetric but because when the ball is going forward in time it loses energy to air molecules it bumps into, but when the ball is going backwards in time the air molecules are bumping into it, giving it energy.”,

”Note that this inequality doesn't contradict the definition of time reversal because forward-up is a different leg of the trip from backward-up. So the system is strictly T-symmetrical

”,

@INTERNET Wikipedia Arrow of time, Overview 2010-02-12

http://en.wikipedia.org/wiki/Arrow_of_time

— You say so?

I alla TILLSTÅNDSFÖRÄNDRANDE FÖRLOPP måste varje utgångsläge, hur man än resonerar och vilken matematik man än använder, utgå ifrån ett visst bestämt tillstånd vars ändring går via en acceleration. Det spelar ingen roll om det är fråga om ”luftfriktion” eller ”kastade bollar”, eller vad annat som helst. Varje sådant exempel ansluter, tydligen perfekt principiellt med förorsakande impuls (mv) och resulterande acceleration (a=dv/dt), till det motsvarande exemplet med Newtons vagga (Kausalexempel 1.1): det idealt utgående intervallet som tillståndsändringen förlöper på, initieras av en riktningsbestämd impuls (mv) som överförs till den accelererande, läges- eller generellt tillståndsändrande kroppens rörelseform: kroppen accelererar under ett tidsintervall (t) via ett distansintervall (d) och uppnår först EFTER (vid) t sluthastigheten (v): spelas filmen baklänges krävs en helt annan fysik: innan kroppen nått impulspunktens ideala incidensposition uppvisas, tydligen, en oförklarlig retardation hos kroppen — som någon slags mystisk magisk »magnetisk» kraft som förmår kroppen att bromsa upp innan den träffar det vilande utgångsstället — då i, det verkliga fallet, för detta baklängesfall, kroppen skulle ha tillryggalagt även distansen d baklänges med bibehållen hastighet v, utan några magiska och mystiska inbromsningar FÖRE incidenspunkten/utgångspunkten i den verkliga framriktningen. Se även utförligt från Kausalexempel 1.

Med andra ord: Även i detta fall förbiser artikelförfattaren kausaldetaljerna i fysikens incidenspunkter — luftfriktionen i exemplet, och dess förmodade omvändning.

Det finns ingen sådan fysik.

Jämför även det inledande exemplet.

Artikelförfattaren anför ytterligare ett ”the final case of this example” enligt följande:

”What if you record somebody simply dropping a ball? It falls for a meter and stops. Certainly someone watching this recording in reverse would notice an unrealistic discrepancy: a ball falling upward! But imagine the forward-recording carefully. When the ball lands, its kinetic energy is dispersed into sound, shaking the ground, and some heat. That is what allows the ball to be moving one moment and still the next. Now think of the recording in reverse. Those sound waves, those ground vibrations, and that heat, are all rushing back into the ball, imparting just enough energy to propel it upward into the person's hand. With this understanding, the backward recording appears perfectly realistic. The only way that someone can tell the video is in reverse is by making the statistical prediction that it's unlikely that these forces could incidentally interact to propel the ball upward into your waiting hand.”,

@INTERNET Wikipedia Arrow of time, Overview 2010-02-12

http://en.wikipedia.org/wiki/Arrow_of_time

— Ovanstående markerade meningar understryker att författaren har det svårt — på flera olika plan.

Vi studerar hur.

”With this understanding” var inte artikelns huvudsakliga mening: I artikelns början klargörs, nämligen, uttryckligen

”the theoretical statements that describe them remain true if the direction of time is reversed”

Min översättning:

de teoretiska påståenden som beskriver dem gäller fortfarande om tidsriktningen omvänds

Artikelförfattaren har alltså tydligen — för det första — i påståendet ”With this understanding” nu plötsligt frångått ovanstående villkor för de fysikaliska lagarnas tidssymmetriska giltighet och menar att OM MAN FRÅNSER DETTA ”the backward recording appears perfectly realistic”. Men det var inte vad frågan handlade om:

På samma sätt — för det andra — som i föregående klargörande, förbiser artikelförfattaren kausaldetaljerna i fysikens incidenspunkter; jämför även det inledande exemplet (författaren förutsätter, underförstått och tydligen, i exemplet att hela bollens rörelseenergi omsätts i marken, dvs., bollen uppvisar ingen studs): ett föremål som läges- eller positionsändrar från en bestämd vilopunkt — ett föremål som lämnar markplanet och far uppåt — måste tvunget genomgå en acceleration (a=dv/dt) under en viss tid (t) genom en viss distans (d). Den fallande bollen i exemplet emellertid, når idealt enligt vad som påstås markplanet utan någon motsvarande retarderande rörelseform för d under t (den idealt helt stela bollen/marken), ”That is what allows the ball to be moving one moment and still the next”. Märk väl. Det är alldeles korrekt, att inte ens den mest sofistikerade videoutrustning skulle kunna filma en sådan sekvens, och därmed skulle heller ingen kunna »märka skillnaden» — utom den skrattande publikfriaren i bakgrunden som kunde plocka poäng på att publiken helt missade exemplets rent IDEALT MEKANISK teoretiska natur: omöjligheten med en retardation innan kroppen når markpunkten. Det finns ingen sådan fysik. Lägger vi dessutom till värmestrålningens fysik med divergensen, se Kausalexempel 3, blir hela exemplet direkt omöjligt: När bollen tappas ges motsvarande rörelseenergi ut som värmesvängningar (genom atomernas elektronhöljen, markens deformation) och vilken Planckstrålning divergerar med ständigt avtagande energi hf genom växelverkan med materiens element (atomerna), se VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK. För att åstadkomma en omvändning, filmen baklänges, måste däremot energi i motsvarande mening tydligen TAS någonstans ifrån — på tydligen alldeles samma sätt som en person som försöker frammana en splitter ny Mercedes genom att knäppa med fingrarna i luften. Vi vet att en sådan fysik inte existerar. Ljus SPRIDS UTÅT PÅ VÄXANDE VOLYM med avtagande energitäthet per given volym (med minimal spridning i typen laser), inte omvänt, och vilken fenomennatur ligger i divergensen, se från DEEP.

Med åter andra ord: Även i detta fall förbiser alltså artikelförfattaren kausaldetaljerna — ändringslagarna, omöjligheten att ändra, mixtra med, ändringens riktning — i fysikens incidenspunkter — både mekaniska och elektrodynamiska.

Ingen fysik fungerar så.

Se Kausalexempel 1 som det främsta mest elementära skolexemplet.

Det finns ingen tidssymmetri i fysiken. Det är en ren och skär myt, en (väl inövad) vanföreställning.

Jämför även det inledande exemplet.

Det verkar, i stort, vara snittet i de exempel som (med webben som referens) brukar ställas fram i ämnet ”referenser” till uppfattningen att fysiken skulle vara ”tidssymmetrisk” eller ”tidsreversibel”. Vilket med andra ord vill säga: intet. Noll. Ingenting. Finito. End. Se utförligt från Åldrandets princip. Det finns alldeles tydligt och uppenbart med jämförande referens till de praktiska jämförande exemplen (se särskilt från Kausalordningen) inget utrymme för någon förmodad tidssymmetri i giltigheten för fysikens lagar, inte på något som helst sätt. Det är, alldeles tydligt och uppenbarligen, väl relaterbart in i minsta detalj, en ren vanföreställning

(tydligen grundad på SLARVET att inte ta reda på — tillförsäkra sig personligen om, RELATERA — detaljerna: förytligade fysikkunskaper).

UTÖVER FYSIKENS FUNDAMENTALTEOREM (FUNTOP) och RÖRELSENS PRINCIP (POM), determinismens hela grundval, se även den rent matematiska (kinematiska) delen i FYSIKENS ELEMENTÄRA GRUNDER ENLIGT RELATERAD FYSIK, ovanstående exempel.

Summering

SUMMERING — åldrandets princip

I ljuset av ovanstående genomgång (Se särskilt från Kausalordningen)

— det finns ingen relaterbar naturvetenskaplig grund för den påstådda uppfattningen att fysikens lagar skulle vara tidsmässigt omvändbara, alltså precis lika giltiga som i en film som spelas upp baklänges

— är det alldeles lika tydligt att hela den moderna akademins nuvarande engagemang i frågor om ”tidens symmetri” är helt irrationellt, helt irrelevant.

Uppfattningen att fysikens lagar skulle vara tidssymmetriska [‡5] innehåller, tydligen och väl relaterbarligen (Se särskilt från Kausalordningen), ingen naturvetenskapligt grundad substans. Det finns ingen tidssymmetri i fysiken. Fysikens lagar är alldeles uppenbart entydigt och skarpt omöjliga att kasta om tidsmässigt typ filmen baklänges. Se särskilt de genomgångna exemplen ovan i Gravitationen och Den kastade bollen, samt från Kausalexempel 1.

Ändringslagarna garanterar att ändringens riktning i varje beskrivning av en variation, spelar ingen roll vilken, är och förblir entydig.

Vad beror avsaknaden av INSIKT i denna naturgrund, sett från den moderna akademins sida?

Som redan påpekats i den rent matematiska (kinematiska) delen i FYSIKENS ELEMENTÄRA GRUNDER ENLIGT RELATERAD FYSIK, ovanstående exempel: Modern akademi grundades under 1800-talet för tillfället att få upphöja MÄNNISKAN, inte NATUREN, som ”skapare av matematiken och logiken”, se särskilt citat. På område efter område trädde olika »nyskapare» in på scenen, den ena med till synes mera sensationella påståenden än den andra. Festligheterna gick tydligen ut på att uppfinna, inte härleda, fysiken och matematiken. Genom STATSSTYRD UNDERVISNING (se även Införandet av den moderna akademins allmänna auktoritära överhöghet, angående Nationernas Kunskapsförakt) — akademiskt grundad organisation, preferens och ordning — kom, så tydligen, hela samhällen att MATAS ENSIDIGT med ”den intelligenta överhetens ideal” med HerreDeviser, se citat, och annat liknande. Jämför arbetarklassens ställning under (första delen av) 1900-talet: fattiga människor, mer eller mindre livegna. Helt, fullkomligt chanslösa att komma med invändningar. Det som gällde var att kunna göra KARRIÄR — SOM REDAN BEKANT. Och så har det rullat på nu i runt 200 år.

Det finns också (inre) exempel på hur etablissemanget i modern vetenskapsakademi bemöter NYA radikala SYNPUNKTER: Ludwig Boltzmann. Det finns inga direkta bevis för det, se Citatsamling. Men flera författare tycks (allmänt) vara av den uppfattningen att Boltzmann år 1906 begick självmord, stort tack vare det nedvärderande bemötande han fick — genomgående, hela Boltzmanns livsverk, av dåtidens ledande vetenskapstrust, vetenskapsetablissemanget — för uppfattningen att materien består, verkligen, av atomer och molekyler: naturvetenskapens verkliga genombrott. Att finna sig stå mer eller mindre helt ensam mot ett så omfattande etablissemang kan under inga som helst omständigheter förstås avundsvärt: ingen uppmuntran, bara kritik. Time att stänga butiken med andra ord. Tre år senare bekräftande experiment hans teorier: Rutherfords direkt experimentella påvisande av atomkärnan (1909-1911) som ledde fram till den första atommodellen.

Resten av historien känner vi (väl).

SVENSKA WEBBKÄLLOR SOM OMNÄMNER TIDSSYMMETRIN

Feb2010

SVENSKA WEBBKÄLLOR SOM OMNÄMNER TIDSSYMMETRIN

I fallet (traditionella) fackböcker med referens till 1900-talets svenska bidrag i FOCUS MATERIEN 1975 finns inte ens ordet ”tidssymmetri” upptaget. Det omnämns inte.

Det svenska utbudet av webbkällor som beskriver ordet tidssymmetri ur (entropisk) matematisk-fysikalisk synvinkel — och som innehåller någon minsta grad av referenser, inte enbart (en skur av) påståenden — är (ännu Feb2010, ypperligt) magert. I stort sett ingenting alls.

Det som omnämns (av värde) ingår redan i fysikbeskrivningen ENLIGT RELATERAD FYSIK:

Partikelexperiment verifierar den naturliga ordningen

1. upptäckten att den förmodade »allmänna symmetrin» för partiklar-antipartiklar INTE gäller i praktiken

FYRA FORSKARE OM FORSKNING — Brutna symmetrier - årets Nobelpris i fysik, Okt 2008

http://lagerbladet.blogspot.com/2008/10/brutna-symmetrier-rets-nobelpris-i.html

;

Påvisande att antipartiklar och vanliga partiklar INTE är fullständigt symmetriska;

Nobelpriset i fysik 2008: Yoichiro Nambu, Makoto Kobayashi, Toshihide Maskawa

Det finns dock i modern akademi ingen teori som kan förklara den ensidiga förekomsten av vanlig materia till skillnad från antimateria. I relaterad fysik ges den förklaringen automatiskt genom neutronens kärnstruktur och Allmänna Kosmiska Tillståndsekvationen.

Lee och Yang (med flera 1956), påvisade brott mot den förmodade symmetrin att betaaktiva atomkärnor skulle avdela elektroner med symmetrisk fördelning: Elektronerna emitteras istället, rebelliskt helt enligt relaterad fysik, företrädesvis i spinnriktningen (motsvarande experiment visade att positroner emitteras i motsatta änden).

Bägge ovanstående är i full enlighet med RELATERAD FYSIK. Se från atomkärnans härledning.

Se speciellt från atomkärnans positiva laddningsdeplacement — förklaringen till varför universum bara består av vanlig materia med noll stationär förekomst av antimateria (deplacementets laddningsmässiga omkastning som för att visa sig kräver extremt höga kollisionsenergier och därför bara kan finnas under exceptionella, kortvariga, förhållanden). Se även i NEUTRONENS FRAGMENT.

Allmänt om tidssymmetri

2. tidsymmetrin i allmänhet (källan innehåller många påståenden)

ENTROPI I TERMODYNAMIKEN uppgift om författare och datum saknas

http://www.saunalahti.fi/~borgbros/artiklar/entropi.pdf

Angående den, tydligen, allmänna uppfattningen (källan ovan saknar sidnumrering) att

”Också elektromagnetismens ekvationer är tidssymmetriska.”:

Om det påståendet grundar sig på MAXWELLS EKVATIONER (se Vektorkalkylens regelbrott i modern akademi) och Faradays lag är det mycket möjligt att citatkällan uttrycker saken korrekt. I RELATERAD FYSIK DÄREMOT, se från magnetismen, gäller inte »Maxwells ekvationer» på grund av expansionsintegralen som

1. EXPLICIT inte ingår i den moderna akademins lärosystem i ämnet induktion och magnetism

2. visar att begreppet vektorprodukt i den moderna akademins vektoranalys gör våld på det beskrivande och förklarande sammanhanget, se utförligt exemplifierat från vektoranalysen i magnetismen.

Källan ovan skriver (något om Maxwells roll i förhistorien till begreppet statistik, men inga referenser ges, samt) mycket om entropi och Boltzmann, även sambandet S=b(lnW) och även i meningen av ”statist”|isk, men ingenting om Plancks strålningslag. Källan krediterar dock S-formen i namn av Max Planck, men kallar den ”Den logaritmiska relationen mellan entropi och termodynamisk sannolikhet”. Se utförligt från W ingår inte i statistiken.

Källan ovan (den enda som finns i sitt slag, faktiskt) antyder ursprungsaspekter från Maxwell, dock utan referenser;

GoogleSökning på »maxwell +irreversibility» ger:

http://philpapers.org/rec/COLTFO-4

som innehåller nedanstående:

Two Faces of Maxwell's Demon Reveal the Nature of Irreversibility,

John Collier, Department of Philosophy, University of Calgary 1990

http://www.nu.ac.za/undphil/collier/papers/twofaces.pdf

Utmärkt beskrivning med utförliga referenser — utom på den här punkten:

”that the fundamental (and hence presumably objective) laws of dynamics are time reversible”:

Lämnat utan referens.

Källan beskriver den kända ’Maxwells Demon’ som en del av historiens upprinnelse (1867): delvis nya aspekter kommer fram — men fortfarande oklart i stort.

EN aspekt, som framskymtar, är den här:

”Loschmidt also discovered the reversibility paradox which bears his name. Because the laws of mechanics are time reversible in the sense that replacing time with negative time in the equations describing a mechanical system also gives a mechanically possible system, for any system in which statistical entropy increases there is a corresponding mechanical system in which it decreases. This shows that the time reversal of a thermodynamic system is dynamical, but anti-thermodynamical.”,

http://www.nu.ac.za/undphil/collier/papers/twofaces.pdf

Two Faces of Maxwell's Demon Reveal the Nature of Irreversibility,

John Collier, Department of Philosophy, University of Calgary 1990

Om man enbart ser till »fysikens lagar» i ren algebraisk mening typ v=d/t finns naturligtvis ingenting som hindrar uppfattningen om en »omvändning»: ±v är egalt. Därifrån BLIR det sedan ’enkelt’ att koppla någon SLAGS motsvarande »kvalitetsmening». Men då ingen direkt uttalad ANALYS finns att beskåda i den förmodade historiens ljus, finns heller inget bestämt att fastslå i saken.

Vilket vill säga:

Det verkar GRYMT svårt att (enbart med webbens hjälp) få fram ETT KONKRET UPPHOV till föreställningen om begreppet tidssymmetri i fysiken. Newtons skrifter för att anställa någon rimlig jämförelse runt 1700 (Newtons Principia 1687), innehåller inget uppslag.

Vad som däremot står klart, är mängden författare som i dagen ljus (Feb2010) intygar och fastslår »tidssymmetrin» för fysikens lagar — som ovan (se från Åldrandets princip) fortfarande utan redovisad grund.

— Som vi redan VET: fysiken handlar inte om tillstånd utan om variation: en kropps likformiga, rätlinjiga rörelsebana kan inte beskriva någon händelse i ett kärl med en innesluten gas: partiklarna som kolliderar med varandra och kärlets väggar. Den mera praktiska sidan av fysiken, ändringarna, befinner sig med andra ord långt ifrån några rätlinjiga eviga rörelsebanor som aldrig ändras: gasen innesluten i en behållare med oändlig volym där partiklarnas banor är evigt desamma ±v=d/(±t).

— Endast om man bortser ifrån ÄNDRINGSTILLFÄLLENA (se särskilt från Kausalordningen) skulle »fysiklagarnas tidssymmetri» hålla. Men då talar vi, tydligen, inte längre om en verklig fysik. Märkligt är det att så många författare ändå ids ägna sig åt den typen av uppenbarligen helt meningslösa, uppenbart naturfysiskt grundlösa framställningssätt. Se särskilt i jämförelse med etablerade synsätt från det inledande exemplet i Åldrandets princip.

Generellt:

— Mycket, för att inte säga alltsammans i de inledande »vetenskapliga diskussionerna» tydligen omkring 1800-talets mitt handlar (tydligen) om HETSEN i att ENS diskutera SLUTGILTIGHETSASPEKTER på fysikaliska fenomengrunder — VÄRMESTRÅLNINGEN: ljusfysikens natur, Plancks strålningslag, avgörande för hela framställningssättet — vars innebörd ÄNNU inte ens hade upptäckts. DET är det märkliga; Det faktum att »isolerat system» i termodynamisk mening inte existerar i fysiken och att därför föreställningen om att det SKULLE, alls överhuvudtaget, finnas någon som helst fysikalisk substans i exempel som FÖRUTSÄTTER »isolerat system» i termodynamisk mening — Boltzmanns H-teorem — är och förblir fysikaliska meningslösheter. Ännu i denna dag tycks, emellertid, betydande intresse finnas för att FORTSÄTTA på den linjen. Sådana garanterat utomfysiska övningar faller helt utom ramen för den här framställningen vars enda intresse berör praktisk naturbeskrivning: relaterbar fysik. Se även särskilt i Alla kroppar värmeläcker.

Antar man den här källans betraktelsesätt (också tyvärr utan referenser),

Irreversibility (1867 - 1875) — Professor Dave Lebermore, University of Maryland (Aug 2001)

http://www-users.math.umd.edu/~lvrmr/History/Irreversibility.html

”Boltzmann's Viennese colleague Josef Loschmidt pointed out in 1876 that according to Newton's laws one should be able to return to any initial state by merely reversing the molecular velocities. There seems to be a fundamental contradiction between the reversibility of Newton's laws and the irreversibility we see in nature. This contradiction became known as the "Reversibility Paradox"; it had already been discussed two years earlier by William Thomson, in a paper that attracted little notice.”

skulle det ha varit Johann Loschmidt som (år 1876, ref. @INTERNET Wikipedia Loschmidt’s paradox 2010-02-28) i direkta ordalag formulerade »tidssymmetrin i fysikens lagar enligt Newton», själva föremålet för den här undersökningen. Men citatkällan ovan anger ingen referens.

Källan nedan,

http://www.tim-thompson.com/entropy2.html

”And again, later on in The Theory of Heat (page 328), Maxwell has this to say:

One of the best established facts in thermodynamics is that it is impossible in a system enclosed in an envelope which permits neither change of volume nor passage of heat, and in which both the temperature and pressure are everywhere the same, to produce any inequality of temperature or of pressure without the expenditure of work.”;

Sidangivelsen ska vara 338, boken finns att läsa på

INTERNET ARCHIVE

http://www.archive.org/details/theoryofheat00maxwrich

En mycket fin, avancerad, bokpresentation — med (nästan) riktig blädderupplevelse

antyder f.ö. att termen, begreppet eller beskrivningssättet »isolerat system» skulle haft James Clerk Maxwell (The Theory of Heat, 1871 ref. @INTERNET Wikipedia Theory of heat 2010-02-28) som upphovsman.

;

Genomletning av Maxwells bok från 1871 visar att ordstammen ’irreversib’|le|ility| med ordet ”irreversible” omnämns endast en gång (s151)

”The other mode of transfer, which takes place of itself whenever a hot and a cold body are brought near each other, appears to be irreversible, for heat never passes from a cold body to a hot one of itself, but only when the operation is effected by the artificial engine at the expense of mechanical work.”,

INTERNET ARCHIVE — JAMES CLERK MAXWELL 1871 The Theory of Heat s151mn

http://www.archive.org/details/theoryofheat00maxwrich

I övrigt verkar det svårt att binda upp Maxwell till någon portalfigur för begreppet »tidssymmetri» för »fysikens lagar», inga av de ordstammarna ger (veterligt) några träffar i Maxwells bok.

Däremot använder Maxwell ordet ”reverse” frekvent genom hela boken, alltid i samband med ”heat”, sv. värme, aldrig i samband med ”time” — naturligt då ämnet gäller beskrivning av värmemaskinens arbetssätt.

Det vidare sökandet fortsätter efter ev. konkreta (webb-)källor som (ev.) kan klarlägga upphovet till uppfattningen om tidssymmetri för fysikens lagar. Av det som hittills framkommit och som synes stå klart bortom varje tvivel är att begreppet »fysikens lagar är tidssymmetriska» i varje fall INTE fanns under Newtons tid, se Newtons referens i Principia.

Editor2010III3

Sammanfattning — vad betyder entropi

SAMMANFATTNING — vad betyder entropi

entropi — Clausius original (från år 1865): värmeFÖRLUST, S=Q/T, J/°K

entropi — Plancks entropisamband (från år 1901): värmekapacitet, S=b(lnW), J/°K

entropi — 1. generellt kvantitativt i nyare tid: Med viss erkänd anknytning till S-formen ovan måttet på atomär/molekylär omvänd ordning (oordning) relativt en perfekt inre rörelselös kristall (materiell kropp vid exakta 0°K), ofta (med få undantag) i association med orden sannolikhet och statistik; en stor flora av olikartade beskrivningar av ordet »entropi» finns

entropi — 2. generellt kvalitativt i nyare tid: godtyckligt olika beskrivningar på »oordning» typ »ostädat rum» m.fl.

entropi — 3. i relaterad fysik samma som Plancks entropisamband: Värmegrundad Arbetspotential garanterat utan statistisk anknytning med RELATERADE praktiska ARBETSEXEMPEL

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Massfysikens nollentropi

MASSFYSIKEN STÅR HELT OREPRESENTERAD I MODERN AKADEMI se från ATOMKÄRNANS HÄRLEDNING

Massfysikens nollentropi — utgångspunkten

Massfysikens tillståndsmatematik representerar nollentropi

Värmefysiken kan inte beskrivas eller förklaras enhetligt med entropibegreppets hjälp

— massfysiken ingår inte i materiefysiken = entropibegreppet: massfysiken är, tydligen, ett abstrakt begrepp för materiefysiken på samma sätt som differentialens begrepp, punkten i relaterad fysik och matematik, noll (0), är abstrakt för intervallet, ett (1)

Med analog koppling till Plancks entropisamband S=b(lnW):

För att utföra ARBETE — se även Arbetsexempel — måste en kropp påföras energi — HÖGRE entropi (S=E/T) — från ett begynnelsetillstånd med LÄGRE entropi och vilken högre entropiform sedan AVTAR MOT BEGYNNELSELÄGET då ARBETET UTFÖRS. Se PRAKTISKA EXEMPEL.

Det finns inga undantag: Sedan värmen byggts upp från en massdestruktion (m®g) — ytterst från Solen eller direkt från kärnkraft — flyter alltid VÄRME spontant från en varmare till en kallare kropp (se Clausius klassiska grundform); omvändningen, från kallt till varmt, kräver (följaktligen alltid utan undantag) tillförande av energi; Den klassiska formuleringen omformades f.ö. sedermera till nuvarande »termodynamikens andra huvudsats» där varje spår av Clausius grundform— som synes — är helt utraderad.

Utgångskapitalet i energin, massan (m) i E=(m®g)cc, besitter INGEN KOPPLING TILL ENTROIPIBEGREPPET I RELATERAD FYSIK, Plancks entropisamband S=b(lnW), därför att DET enbart berör materiefysiken (T®p), atomerna och molekylerna, inte massfysiken (p®T), atomkärnan, de absoluta energigrunderna och därmed också Planckstrålningens absoluta härledningsgrund: från noll (Se även från NEUTRINOSPEKTRUM).

Massfysiken står helt orepresenterad i modern akademi, de facto.

Se utförligt från ATOMKÄRNANS HÄRLEDNING och NEUTRINOSPEKTRUM. Massan i massförintelsen (m®g) som bygger upp värmen som energins, arbetets, utgångskapital har alltså noll — ingen — entropirepresentation: S=0 för m. Vid (m®g) — processen då värmebasen från massgrunden påförs materiens atomer — TILLVÄXER således S med värmebildningen (g, generellt gamma i relaterad fysik, neutrinostrålningen inkluderad) och bildar sedan en maximal värmetopp, analogt entropimaximum med Plancks entropisamband S=b(lnW) som entropipreferens — och från vilken toppunkt sedan värmen, analogt entropin eller energin, utför arbetet, se PRAKTISKA EXEMPEL; Följden blir genom divergensen och Comptoneffekten avtagande värmestrålning (förlustvärmet, Clausius entropi), analogt minskande entropi [Se Hur värmen avtar med tiden], och vilken mängd sedan måste påföras igen för att processen — arbetet — ska kunna utföras igen. Se även utförligt i Arbetsexempel. Det finns inga undantag. Alla fysikaliska, naturliga, processer följer samma schema. (Jämför även typillustrationen med JordenBegin som exempel). Följaktligen, följdriktigt, logiskt, KAN alla, samtliga processer sägas börja från läget S=0: energigrunden (m®g) via massan. Nollentropi. Perfekt ordning.

BILDKÄLLA: Modellering i Simply3D

Eftersom fysiken inte innehåller något enda »isolerat system»

— Plancks strålningslag, som förutsätter kontinuerlig emission och absorption i alla, samliga fall: alla kroppar, system, värmeläcker, se även Isolerade systemets ursprung

— finns heller ingen grund för föreställningen om »totalt växande entropi». Den detaljen är uppenbarligen en ren vanföreställning (Se även från Boltzmanns H-teorem [‡7]).

Dessa resultat harmonierar också perfekt med K-cellens värmefysik (universums periodiska pulsning).

Inledning till Boltzmanns H-teorem

Användningen av »isolerat system» i Boltzmanns H-teorem saknar fysikalisk förankring

Se även särskilt utförligt beskrivning från Termodynamisk Jämvikt.

Oavsett vilka slutsatser man än kommer fram till i övrigt — enbart i beaktande av att Plancks strålningslag utesluter »isolerade system» ur fysiken, det faktum att alla kroppar både värmeemitterar och absorberar, dessutom med (för materiens del) alla möjliga våglängder, se utförligt från resonanserna — står det helt klart att användningen av »isolerat system» i Boltzmanns H-teorem saknar fysikalisk förankring:

Att, matematiskt, söka »efterlikna» en detaljerad (statistisk) bild av något som inte existerar i praktisk fysik, ett »isolerat system», kan uppenbarligen INTE innehålla begripliga, inte relaterbara, inte förklarbara argument till områden SOM avhandlar praktisk fysik: Plancks strålningslag, det faktum att alla kroppar både värmeemitterar och absorberar, utesluter »isolerade system» — Boltzmanns H-teorem — ur fysiken.

Med andra ord kan Boltzmanns H-teorem bara av DET skälet inte diskuteras, oavsett vad resultatet av H-teoremet än utpekar: all argumentering med/mot H-teoremet är, således i det icke existerande isolerade systemets termodynamiska ljus, meningslös. Det finns ingen praktisk fysikalisk preferensgrund att peka på. Alla system värmeläcker: entropin [Plancks entropisamband S=b(lnW)] i alla kroppar avtar spontant om kropparna inte tillförs energi. Det är, tydligen, den praktiska vardagliga fysik vi genomlever, utan undantag. Se även i PRAKTISKA EXEMPEL.

Då, alltså, »isolerade system» inte existerar i fysiken, kan naturligtvis heller ingen formulera begripliga meningar om hur atomerna i ett materiellt system som inte existerar i fysiken »fungerar».

Expeditionen är dödfödd redan från början.

Men döm inte ut Boltzmanns H-teorem för det — utan det som inspirerande grund, atomismens första reguljära matematiska uppställning, hade med största sannolikhet inte Plancks strålningslag heller kommit fram. Vidare i huvudtexten.

Med åter andra ord (Se hela citatet):

Andemeningen i

”the entropy of an isolated system which is not in equilibrium”

@INTERNET Wikipedia Second law of thermodynamics 2009-12-11

Min översättning:

entropin i ett isolerat system som inte befinner sig i jämvikt

KAN uppenbarligen ingen — säkert, entydigt — uttala sig om: inte formulera säkra, entydiga premisser för, JUST på grund av att »isolated system» inte existerar i fysikens värld, garanterat av just Plancks strålningslag. Därför kan heller ingen säkert, entydigt, varken Boltzmann eller någon annan, ställa upp någon likaledes säker eller entydig matematisk formalia för att beskriva föremålet för det oklara. Dvs., H-teoremet, mera utförligt nedan i huvudtexten, är — hur det än ser ut matematiskt, just på grund av ingrediensen »isolerat system» — en »återvändsgränd». Det finns ingen utgång, bara ingång.

Därmed bortfaller också den ingrediensen ur »termodynamikens andra huvudsats» — vilket blottlägger den moderna akademins lärosystem som helt i avsaknad av en fast grund: avsaknad av kunskap om massfysiken: atomkärnans härledning, Planckekvivalenterna. Se även i UNIVERSUMS HISTORIA från Allmänna Tillståndslagen.

PRESENTATIONEN NEDAN genomgår detaljerna.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Boltzmanns H-teorem

Se även (med början) från ovanstående INLEDNING

Boltzmanns H-teorem från 1872

Boltzmanns H-funktion [‡1]:

H[f_t] = ò f (r; v; t) ln f (r; v; t)d³rd³v .............. Boltzmanns H-funktion

Boltzmanns H-teorem [‡2]:

—— < 0 ..................................................... Boltzmanns H-teorem

H-termen beskrivs i källreferenserna [‡3] med benämningen »negentropi», samma som entropins omvända innebörd. Därmed Boltzmanns H-teorem i motsvarande ord 7.1[‡]:

entropin i ett isolerat system

(med tillägget: som inte befinner sig i termodynamisk jämvikt)

växer irreversibelt

(med tillägget: mot ett toppvärde som uppnås vid jämvikt efter oändlig tid)

Förutsättningar:

Med tillkännagivande från år 1872 [‡1] [‡7] sökte Ludwig Boltzmann bevisa att dåtidens »värmefysikens andra lag», se Clausius framställning 1862 (nuvarande »termodynamikens andra huvudsats» där Clausius framställning helt försvunnit) eller andra värmelagen med (efter vad som hittills framkommit) dåvarande innebörd

värme flyter alltid spontant och irreversibelt från varmt till kallt

kunde bevisas ur mekanikens lagar [‡7.3] — vilket skulle betyda ett atomistiskt bevis för tidens pil [‡4]. En »TIDENS PIL» var (nämligen) den med särskilt stort intresse under 1800-talet observerade naturens lag som uppvisade skeende efter en bestämd tidsriktning som inte kan omvändas.

Vad var det, och hur?

En av H-teoremets grundförutsättningar var den att dåtidens vetenskapsfolk — nämligen, och så är det ännu i denna dag — ansåg att mekanikens lagar kunde förstås vara — just — tidsreversibla [‡5].

Se även särskild artikel i Åldrandets princip.

ANORDNINGEN I BOLTZMANNS H-TEOREM

Boltzmanns uppställda H-teorem bygger på typen »isolerat system» [‡7]:

Som grund för sin atomistiska H-funktion tänkte sig Boltzmann [‡8] en idealt innesluten gas i en idealt isolerad behållare som inte påförs några, vidare, tillståndsförändrande krafter utifrån. Gasbollarna antas idealt sfäriska och gasen förutsätts precis så uttunnad att bara binära (par-) kollisioner kan förekomma inbördes mellan gasbollarna. H-teoremets funktionsform, H-funktionen ovan, anställer den matematiska formen för gasbollarnas motsvarande positioner xyz och rörelsemängder mv (Sambandsleden uttrycks på flera olika sätt beroende på källverk).

Resultatet:

Resultatet av Boltzmanns H-teorem [‡9] gör gällande att den isolerade gasmassan uppvisar en

icke tidsmässigt omvändbar — tidsenkelriktad — ökning i antalet (energimässigt likafördelningsberättigade) sätt som gasbollarnas (xyz)(mv) kan kombineras på [‡7.1]. Alltså: att entropivärdet (med referens till Plancks entropisamband S=b[lnW]) ökar med tiden och närmar sig (oändligt) ett toppvärde motsvarande termodynamisk jämvikt.

Men enda fysikaliskt möjliga sättet att DEFINIERA antalet likaberättigade energifördelningssätt mellan de givna gasbollarna, atomerna, med given energi vid given temperatur framkom FÖRST i och med Plancks strålningslag (publ. år 1901). Där framgår det klart och tydligt att entropin (S) är en och endast en bestämd kvantitet för en kropp med en bestämd temperatur med ett bestämt energiinnehåll, se Härledningen till Plancks strålningslag från Plancks entropisamband: Ett bestämt entropivärde (S).

Men som resultatet ovan utpekar, ETT entropivärde i Boltzmanns (resultatmässigt hävdade [‡9]) H-teorem FINNS INTE. Den observationen ansluter (således) bara till det som redan påpekades i inledningen till Boltzmanns H-teorem: H-teoremet är en återvändsgränd. Helt fysikaliskt meningslöst, just via »isolerat system»:

Boltzmanns H-teorem förutsätter [‡7] egenskapen hos den inneslutna gasen PER TID att INTE värmeläcka; Men enligt Plancks strålningslag är alla fysikaliska kroppars natur PER TID (E=hf) just ATT värmeläcka, ljusfysikens divergenta natur [Se även explicit i DIVERGENSEN] — och som, tydligen, inte heller uppmärksammats av modern akademi; Boltzmanns förutsättning med HÄNDELSER, processer, inuti ett isolerat system i termodynamisk mening med konstant energi och temperatur saknar, med andra ord — helt — naturvetenskaplig grund.

Men de ovannämnda avgörande detaljerna

— ljusets divergens och Plancks strålningslag tillsammans med Comptoneffekten, mera utförligt i VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK; alla dessa krävs för att förstå termofysikens elementa

— kände inte Boltzmann eller hans då samtida till

— och det verkar inte vara mycket bättre ställt nuförtiden heller. Se från W finns inte i statistiken.

Bemötande:

Loschmidt påpekade [‡6], med sedermera benämning Loschmidts paradox, att det är omöjligt att ur mekanikens reversibla lagar kunna komma fram till en naturens irreversibilitet: reversibilitet kan inte bilda irreversibilitet.

Det fanns också andra invändningar [‡10] (som även Boltzmann själv erkände längre fram), men dessa beskrivs inte här, DELS på grund av att huvudsumman i vilket fall står klar, vidare nedan, och DELS på grund av att argumenten som finns, och dokumenten i deras ljus, representerar en ENORM litterär volym [‡7.2]. Dock ges en liten orientering längre fram, se Kritiken mot H-teoremet.

Alla tycks dock numera vara på det klara med [‡7.3] att Boltzmanns huvudsyfte misslyckades: att bevisa andra värmelagen från mekaniken.

Boltzmanns presentation från 1872 väckte stor debatt, och de ledande vetenskapsmännen tillbakavisade, generellt, Boltzmanns uppfattning att atomer och molekyler skulle vara, verkliga, materiella komponenter. Se Citatsamling. Vartefter experimentalfysiken utvecklades under 1800-talets senare del, svängde emellertid opinionen till Boltzmanns fördel, vilket ledde till att också Boltzmanns H-teorem blev en inspirationskälla med resultat i verkligt avancerade framsteg; Det främsta bidraget är nog (med Plancks egen erkända inspiration från Boltzmann) upptäckten av det universella verkanskvantumet (Plancks konstant), se utförligt med citatkällor från Plancks entropisamband.

Den allmänna utvecklingen efter Boltzmanns H-teorem

SOM VI SER är formuleringen av resultatet i Boltzmanns H-teorem

”In thermodynamics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the increase in the entropy of an ideal gas in an irreversible process”,

@INTERNET Wikipedia H-theorem 2010-01-30

Min översättning:

I termodynamiken beskriver H-teoremet som introducerades av Ludwig Boltzmann år 1872 ökningen i entropi för en ideal gas i en irreversibel process.

i princip identiskt med formuleringen i »termodynamikens andra huvudsats»

”The second law of thermodynamics is an expression of the universal principle of entropy, stating that the entropy of an isolated system which is not in equilibrium will tend to increase over time, approaching a maximum value at equilibrium”,

@INTERNET Wikipedia Second law of thermodynamics 2009-12-11

Min översättning:

Termodynamikens andra huvudsats är ett uttryck för entropins universella princip, vilken fastslår att entropin i ett isolerat system som inte befinner sig i jämvikt tenderar att öka med tiden, närmande sig ett maximalt värde vid jämvikt.

Men inte ett knyst hörs på den upplysande punkten i mängden beskrivande (webb-)källor (och andra, ännu Feb2010) beträffande upphovet till ovanstående formulering — från det klassiska originalet av Clausius från 1862. Och för en lekman är det dessutom verkligen inte, direkt, lätt att se likheten heller i det litterärt entropiska myllret:

entropin i ett isolerat system ökar

Jämför, direkt:

”Som minnesregler för termodynamikens två huvudsatser brukar ofta följande formuleringar användas:

Första huvudsatsen: Universums energi är alltid konstant.

Andra huvudsatsen: Universums entropi strävar alltid att öka.”,

FOCUS MATERIEN 1975 s325sp2mn

Se även »andra huvudsatsen» mera reguljärt i citat.

Ursprunget till omformuleringen

Överensstämmelsen framtvingar alltså, uppenbarligen och tveklöst UTAN annan referens än ovanstående generalgenomgång, ett konstaterande att det var Boltzmanns H-teorem som föranledde nuvarande, ovanstående, omformulering av den tidigare klassiska andra värmelagen — och vars tydliga och klara, entydiga, formulering därmed också gick förlorad: värme flyter, spontant och irreversibelt, från varmt till kallt. (Klaga sedan inte över att eleverna inte matchar kursinnehållet).

Plancks strålningslag

eliminerar Boltzmanns H-teorem

Plancks strålningslag eliminerar »isolerat system» ur termodynamiken — och utraderar därmed Boltzmanns H-teorem

Men, som vi redan kunde konstatera från den härledande beskrivningen och förklaringen till Plancks verkanskvantumsgrundade entropi S=b(lnW), garanterar Plancks strålningslag att ett »isolerat system» i termodynamisk mening inte kan existerar inom något som helst fysikaliskt reellt tidsintervall, se utförligt från Isolerat system i termodynamisk mening i Termodynamisk jämvikt:

S = b lnW = E/T = hfT^–1 .................................. Plancks verkanskvantumsgrundade entropisamband

S/b = lnW = (h/b)(fT^–1) » (4,8 t11 °K·S)(fT^–1) ;

Sambanden klargör alltså med grund i Plancks strålningslag:

Mot varje frekvens (f ) som sammanhänger med en viss Planckenergi E=hf — en kropps värmestrålning (Planckstrålningens derivata, Wiens förskjutningslag l=k/T, k=2,898 t3 M°K, f=c/l) — svarar, idealt, en bestämd genomströmningstemperatur (T);

Varje bestämd temperatur T garanterar för varje givet energitillstånd (W=e^S/b) att också Planckentropin (S) — antalet likaberättigade, idealt frysta momentana tillståndsbilder (likaberättigade mikrotillstånd) som visar/definierar/exponerar materieelementens positioner och rörelsemängder — förblir konstant.

Boltzmanns H-teorem — som tydligen [‡7] helt föregick (bortsåg ifrån) vad varje termodynamiskt materiellt system emellertid måste iaktta, nämligen Plancks strålningslag och därmed den ovannämnda verkanskvantumsbaserade Planckentropin S=b(lnW)=hf /T med Plancks konstant (h=mcr) — hade redan från ruta ett, därmed, eliminerat den praktiska fysiken ur teoremets förmodade praktiska förutsättningar: gasens kontinuerliga flöde av emission och absorption, eliminerat av den förmodade detaljen »isolerat system»: det finns inget sådant i termodynamisk mening i fysiken. Se särskilt från Isolerat system i termodynamisk mening. Se även till jämförelse i konventionellt citat, som nedan.

Därmed utraderas fysikens praktiska koppling till Boltzmanns H-teorem

Truly isolated physical systems do not exist in reality (except perhaps for the universe as a whole)”,

@INTERNET Wikipedia Isolated system 2009-12-11

Min översättning:

Verkligt isolerade system existerar inte i verkligheten (utom möjligen för universum som helhet).

I den moderna akademins lärosystem, emellertid, kan man inte, enkelt, bara ta bort detaljen »isolerat system» (alla vet redan, och intygar per citat som ovan, att »isolerat system» inte finns i fysiken: trots det, upphöjs likväl den delen …) — utan att rasera andra, väsenliga delar i hela lärosystemet. Ett (»enkelt») exempel: Uppfattningen att ’entropin i universum ökar’ harmonierar perfekt med den i modern akademi grundmurade uppfattningen att himlakropparna bildas från läge kallt: entropin ökar med universums åldrande (den kristallint perfekta ordningen från 0°K avtar); Skulle det vara en felaktig premiss, skulle det också med stor sannolikhet uppfattas som en högst absurd insinuation, en ren och djup förolämpning i modern akademi och som skulle rasera hela syndikatets lärostol. Ingen närmar sig den frågeställningen (explicit) i moderna kvarter; Här, i relaterad fysik, är den attityden mindre kritisk då utgångspunkten är en helt annan. Se utförligt från Atomkärnans härledning, analogt PLANCKRINGEN h=mcr. Se även utförligt i den här framställningen från Entropibegreppets innebörd.

Inre kritik mot Boltzmanns H-teorem

KRITISKA RÖSTER I MODERN AKADEMI MOT BOLTZMANNS H-TEOREM

Det finns (emellertid, även) exempel inom modern akademi [‡10] [‡11] — med PRINCIPIELL anslutning till samma resultat som ovan — som anför (mera matematiskt orienterade) invändningar mot själva uppställningen i Boltzmanns H-teorem — och det också ända från Boltzmanns dagar (Loschmidts paradox och Zermelos paradox). Nämligen just beträffande den underliggande, praktiska, fysiken: Boltzmanns H-teorem har föga att göra med den delen [‡11.1].

Det är klart att om man (ovetande) ställer upp en matematik för ett sådant förmodat fysikaliskt system som dock inte existerar i fysiken i termodynamisk mening, »isolerat system» [‡7], man heller inte kan räkna med att sambanden ska innehålla begripliga matematisk-fysikaliska fokus: frågan om vad som händer i det som inte finns i fysiken, isolerat system i termodynamisk mening, är av naturliga skäl omöjlig att avgöra — eftersom det inte existerar några naturvetenskapligt grundade förutsättningar för någon tidsintervallbaserad typ »isolerat system» i termodynamisk mening. Man intygar det också, verkligen, i modern akademi, men använder det, likväl, i övergripande mening.

»FELET» Boltzmanns gjorde med sitt H-teorem var, tydligen i ovanstående genomgångs ljus, att han var före sin tid. Boltzmann föregrep, alldeles tydligt, den utveckling på matematikens (och experimentalfysikens) område som, inspirerad av Boltzmann, ledde fram till det rätta sättet (ännu i denna dag, UTOM den relaterade fysikens beskrivning i modern akademi) — och som därmed förlägger Boltzmanns H-teorem till samlingen särskilt användbara instrument — verktyg — för naturvetenskapens utveckling. Därmed bildar också Boltzmanns H-teorem den praktiska (termo-) fysikens skiljelinje mellan termodynamik utan och med den Plancks konstant som framkom i svallet efter H-teoremet. H-teoremet som sådant är alltså »deadPhysics», död fysik. Tillstånd gäller bara under nolltid (tidsdifferential, se differentialen i NOLLFORMSALGEBRAN enligt relaterad matematik). Och i noll tid existerar ingen variation. Se även från Den verkanskvantumsgrundade Planckentropin.

Loschmidts paradox försvinner

Med upplösningen i Åldrandets princip att fysikens lagar är irreversibla — något som 1800-talets snillen tycks ha missat helt (se även Ändringslagarna) — försvinner också Loschmidts paradox. Den detaljen ger dock, likväl, ingen (vidare) kredit åt Boltzmanns H-teorem.

För grunderna — med utförligt jämförande exempel — till den moderna akademins uppfattning om fysikens lagar som »tidsreversibla» [‡5] och »tidssymmetriska», se utförligt från Åldrandets princip.

Referenser till beskrivningen i Boltzmanns H-teorem

Citatreferenser till Boltzmanns H-teorem

All textmarkering (färg, fetstil etc.) i citat är separat tillagda (för nyckelmeningar) i den mån de inte redan framhävs i originalen.

1[‡]

s4:

”Boltzmann further introduced the H-functional (denoted E in the 1872 paper,

but later widely called H, including by Boltzmann):

H[f_t] = ò f (r; v; t) ln f (r; v; t)d³rd³v (2)

which is large for narrow distributions and small for wide ones. Since the number of molecules in a gas is so large, Boltzmann treated the density function as continuous and differentiable. Now given the transport equation, and assuming

SZA holds at time t₀, it can be shown that

2[‡]

—— < 0. (3)

Boltzmann assumed that SZA holds at all times, thus ensuring the monotonic

behaviour of H over time. Equality in (3) holds when the gas reaches equilibrium

(the Maxwell-Boltzmann distribution, which is the unique stationary distribution consistent with the assumptions). This is Boltzmann’s H-theorem, one of whose assumptions we take to be the validity of SZA at all times.⁷

”, s4:

3[‡]

”The theorem gives a mechanical underpinning to both the spontaneous, monotonic

approach to equilibrium⁸ and its associated entropy increase, H playing the

role of the negative of the entropy (’negentropy’).

”, s3:

”… later known as the Stosszahlansatz

[eng. »ImpulseNumber Inception | Presumption»] (’assumption about the number of collisions’, now sometimes abbreviated to SZA …

”,

Boltzmann’s H-theorem, its limitations, and the birth of (fully) statistical mechanics,

Harvey R. Brown and Wayne Myrvold, September 8 2008, s4

http://philsci-archive.pitt.edu/archive/00004187/01/Reversibility08.pdf

Alla textmarkeringar i citaten är separat tillagda om ej redan befintliga i originalet (för markering av nyckelmeningar).

4[‡]

THE INTERNET ENCYCLOPEDIA OF SCIENCE David Darling ”up to date”

http://www.daviddarling.info/encyclopedia/Q/quantum_theory_origins.html

Min översättning:

Liksom andra vetenskapsmän av sin tid, var Planck nyfiken på varför universum tycktes gå i bara en riktning, varför tiden hade en pil, varför naturen uppenbarligen var irreversibel [icke-omvändningsbar] och alltid nöts ner.

Folket vid den tiden verkade inte överdrivet imponerade av att OM man skär sig, såret LÄKS: running UP...

Alla textmarkeringar i citaten är separat tillagda om ej redan befintliga i originalet (för markering av nyckelmeningar).

5[‡] tidsreversibilitet

”… Therefore, from the point of view of mechanics, which obeys time-reversal symmetry, there is not preferred direction for the flow of time.

Yet our everyday experience tells us that there are plenty of situations in which a system seems to evolve in a certain direction and not in the reverse direction, suggesting that there actually is a preferred direction in time. Some common examples are a glass falling to the ground and smashing into tiny pieces or the sudden expansion of a gas into a large box. These processes would always seem to occur in the same way and never in the reverse (the glass shards never reassemble themselves and jump back onto the table forming an unbroken glass, and the gas particles never suddenly all gather in one corner of the large box). This seeming inconsistency with the reversible laws of mechanics is known as Loschmidt's paradox. Indeed, the second law of thermodynamics, itself, would seem to be at odds with the reversibility of the laws of mechanics. That is, the observation that a system naturally evolves in such a way as to increase its entropy cannot obviously be rationalized starting from the microscopic reversible laws of motion.

Reversible laws of motion and the arrow of time, Mark Tuckerman (2009)

http://www.nyu.edu/classes/tuckerman/stat.mech/lectures/lecture_3/node2.html

;

”In fact, all the fundamental laws of physics are purely time-symmetric, including the laws of electromagnetism and the wave equation of quantum mechanics.”,

MATH PAGES

http://www.mathpages.com/home/kmath552/kmath552.htm

;

”T Symmetry is the symmetry of physical laws under a time reversal transformation”,

”Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.”,

@INTERNET Wikipedia T-symmetry 2010-01-30

;

”Tait were aware that the result was hard to reconcile with the time reversal invariance of the dynamics of a gas.”,

Boltzmann's H-theorem, its limitations, and the birth of (fully) statistical mechanics,

Harvey R. Brown and Wayne Myrvold, September 8, 2008, s7

http://philsci-archive.pitt.edu/archive/00004187/01/Reversibility08.pdf

;

”This puts the time reversal symmetry of (almost) all known low-level fundamental physical processes at odds with any attempt to infer from them the second law of thermodynamics which describes the behaviour of macroscopic systems. Both of these are well-accepted principles in physics, with sound observational and theoretical support, yet they seem to be in conflict; hence the paradox.”,

@INTERNET Wikipedia Loschmidt's paradox 2010-01-30

6[‡] Loschmidts paradox

”Loschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics.”,

@INTERNET Wikipedia Loschmidt's paradox 2010-01-30

Min översättning:

Loschmidts paradox, också känd som reversibilitetspardoxen, är invändningen att det inte är [ska vara] möjligt att sluta sig till en irreversibel process från [en] tidssymmetrisk dynamik.

Se även i citatreferens [‡10].

Alla textmarkeringar i citaten är separat tillagda om ej redan befintliga i originalet (för markering av nyckelmeningar).

7[‡] H-teoremet

”In the attempt to justify the postulate of entropy increase in the second law of thermodynamics, Boltzmann’s H-theorem used equations which assumed a system (e.g., a gas) was isolated: i.e., that all the mechanical degrees of freedom could be specified, treating the walls simply as mirror boundary conditions. This inevitably lead to Loschmidt's paradox. However, if the stochastic behavior of the molecules in actual walls is considered, along with the randomizing effect of the ambient, background thermal radiation, Boltzmann’s assumption of molecular chaos can be justified.”,

@INTERNET Wikipedia Isolated system 2010-01-30

7.1[‡]

”In thermodynamics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the increase in the entropy of an ideal gas in an irreversible process, by considering the Boltzmann equation.

It appears to predict an irreversible increase in entropy, despite microscopically reversible dynamics. This has led to much discussion.”,

@INTERNET Wikipedia H-theorem 2010-01-30

7.1.1[‡]

@INTERNET Wikipedia Second law of thermodynamics 2009-12-11

Min översättning:

Termodynamikens andra huvudsats är ett uttryck för entropins universella princip, vilken fastslår att entropin i ett isolerat system som inte befinner sig i jämvikt tenderar att öka med tiden, närmande sig ett maximalt värde vid jämvikt.

;

Notera likheten i formuleringarna:

1. ”the increase in the entropy of an ideal gas in an irreversible process”,

2. ”the entropy of an isolated system which is not in equilibrium will tend to increase over time”

7.2[‡]

”Although Boltzmann’s H-Theorem is 135 years old, presentday mathematics is unable to prove it rigorously and in satisfactory generality.”,

”For the moment we have to live with this shortcoming.”,

H-Theorem and beyond: Boltzmann’s entropy in today’s mathematics, C´edric Villani (2007)

http://www.umpa.ens-lyon.fr/~cvillani/Cedrif/P11.Boltzmann.pdf

Min översättning:

Fastän Boltzmanns H-teorem är 135 år gammalt, är dagens matematik oförmögen att bevisa det rigoröst och med tillfredsställande allmängiltighet.

För tillfället måste vi leva med detta tillkortakommande.

7.3[‡]

”In the latter part of the nineteenth century, Ludwig Boltzmann almost single-handedly established the field now known as statistical mechanics. One of his major contributions, and undoubtedly the most controversial, was his H-theorem. This work was published in 1872 with the intent of showing that the second law of thermodynamics derives from the laws of mechanics. While it is now generally agreed that the attempted proof was unsuccessful, the controversy attending this work was ultimately beneficial to the burgeoning field of statistical mechanics because it forced the workers to think through and refine the statistical and probabilistic concepts that were introduced by Boltzmann.”

CHAPTER 6 BOLTZMANN'S H-THEOREM — ALL ABOUT ENTROPY,

Benjamin G. Kyle, Chemical Engineering Kansas State University

Chemical and Process Thermodynamics (3rd Edition) 1999

http://www.che.ksu.edu/~bgkyle/Book_Chapters/6.PDF

8[‡] Anordningen

” 2.1 The theorem

The H-theorem was based on a model of a gas consisting of N hard, spherical

molecules of a single species, in a container with perfectly elastic walls.² The

gas is sufficiently dilute that only binary collisions need be taken into account

in the dynamics. Let the distribution (or density) function f(r; v; t) be defined

such that f(r; v; t)d³rd³v is the number of molecules within a volume element

d³r about r and with velocity lying within the velocity-space element d³v about v.³ Boltzmann's transport equation determines how f(r; v; t) evolves in time.

In deriving the transport equation, Boltzmann assumed that for the initial

state of the gas, the momentum distribution is isotropic: f₀(r; v; t) = f₀(r; v; t).

He also assumed that no external forces act on the gas and that at all times

the distribution is independent of position (homogeneous): f(r; v; t) = f(v; t).

”,

Boltzmann’s H-theorem, its limitations, and the birth of (fully) statistical mechanics,

Harvey R. Brown and Wayne Myrvold, September 8, 2008, frn.s2n

http://philsci-archive.pitt.edu/archive/00004187/01/Reversibility08.pdf

9[‡] Resultatet

s1n:

”Boltzmann’s H-Theorem

The so-called Boltzmann equation models the dynamics of rarefied gases via a time-dependent

density f (x, v) of particles in phase space (x stands for position, v for velocity):

bildkopia

Here v·Ñ_x is the transport operator, while Q is the bilinear collision operator:

bildkopia

and B = B(v−v*, s ) ≥ 0 is the collision kernel. The notation v′, v′* denotes pre-collisional velocities, while v, v* stand for post-collisional velocities (or the reverse, it does not matter in this case). I refer to my review text in the Handbook of Mathematical Fluid Dynamics [19] for a precise discussion, and a survey of the mathematical theory of this equation.

According to this model, under ad hoc [sv. »för ändamålet»] boundary conditions, the entropy S is nondecreasing in time. That is, if one defines

bildkopia

then the time-derivative of S is always nonnegative.

”,

H-Theorem and beyond: Boltzmann’s entropy in today’s mathematics, C´edric Villani (2007)

http://www.umpa.ens-lyon.fr/~cvillani/Cedrif/P11.Boltzmann.pdf

Kommentar:

Slutresultatet beskrivs så att sambandets S-värde (entropin) påstås icke-avtagande med tiden, ”S is nondecreasing”, analogt växande S-värde.

Tecknet Ñ (Symbol, Alt+0209 Ñ) kallas »nabla» och används i den moderna akademins vektorkalkyl som (vanligen) representerar en »vektordifferentiell operator» (’del’, se exv. eng Wikipedia på Del). Genom att vektorkalkylen i modern akademi innefattar detaljer som ENLIGT RELATERAD FYSIK omöjliggör en detaljerad beskrivning av grundfysiken i Induktionen och Magnetismen, se dessa, faller en strikt matematiskt behandling av ämnet ovan här helt utanför ramen för denna framställning (vektorkalkylen ingår över huvudtaget inte i Universums Historia). Den delen är heller inte av nöden då sammanhangen framgår på annat sätt. Se vidare från huvudtexten i Boltzmanns H-teorem.

;

Med alternativa beteckningar finns flera (många) webbkällor som visar samma resultat som ovan. Se till exempel

@INTERNET Wikipedia H-theorem 2010-02-10

http://en.wikipedia.org/wiki/Boltzmann%27s_H-theorem

Mera utförligt:

CHAPTER 6 BOLTZMANN'S H-THEOREM — ALL ABOUT ENTROPY,

Benjamin G. Kyle, Chemical Engineering Kansas State University

Chemical and Process Thermodynamics (3rd Edition) 1999

http://www.che.ksu.edu/~bgkyle/Book_Chapters/6.PDF

;

Se även [‡2] och [‡3] (som beskriver samma sak men på termatiskt kortare form).

10[‡] Kritiska röster

”6.2 THE PARADOXES

The scientific community was initially skeptical of Boltzmann's result and a lengthy controversy ensued.6 For the most part, the attacks on the H-theorem centered on two features which are now known as paradoxes associated with the names of Zermelo and Loschmidt.

Zermelo's paradox, also known as the recurrence paradox, calls Boltzmann's result into question because, according to a theorem proved by Poincaré: any mechanical system of fixed energy and volume obeying the laws of classical mechanics (the type of system considered by Boltzmann) must eventually return arbitrarily close to its initial state. Thus, Boltzmann's H should eventually increase as the system returns to its initial state and therefore H can not be said to never increase. It turns out that the key word here is eventually; Poincaré's theorem specifies a finite recurrence time, but estimates show this time to be astronomically large. Thus, while accepting the validity of Zermelo's claim, Boltzmann was able to argue that because of very long recurrence times, no one would ever observe a system with increasing H and therefore his H-theorem would not conflict with experience. Boltzmann also used the argument that the Second Law is statistical in nature and stated that while systems with increasing H were possible, their occurrence could be assigned an extremely low probability.”,

CHAPTER 6 BOLTZMANN'S H-THEOREM — ALL ABOUT ENTROPY,

Benjamin G. Kyle, Chemical Engineering Kansas State University

Chemical and Process Thermodynamics (3rd Edition) 1999

http://www.che.ksu.edu/~bgkyle/Book_Chapters/6.PDF

11[‡] Kritiska röster

s6–6:

”We conclude that a change of state, occurring in an isolated system in

which the gas remains macroscopically homogeneous, is difficult to imagine.”,

”In this regard, ter Haar⁹ in his treatment of the H-theorem states that "if a distribution differs appreciably from the equilibrium distribution, the return to

equilibrium is quite rapid." His estimate of the relaxation time for this process in

a gas at 300 K and atmospheric pressure is 10^–9 seconds which clearly indicates

that the changes we have considered for H do not correspond to observable

changes in entropy.”,

11.1[‡]

”Thus, the H-theorem has little to do with entropy and mainly demonstrates the stability of the equilibrium distribution.”,

s6–7:

”The failure of molecular theory to provide a proof or explanation of the second law may be due to incompatible descriptions of reality.¹¹ In the molecular view, ideality is found in the motion of particles which, as we have seen, is reversible and operates in a timeless fashion independent of human presence. On the other hand, ideality in thermodynamics is represented by the reversible process which never occurs naturally and can be approached only through the intervention of a human agent in reducing friction and potential gradients. Thus, Boltzmann's H-theorem may have failed because congruence is not possible in the mapping of one view of reality onto the other.

”,

CHAPTER 6 BOLTZMANN'S H-THEOREM — ALL ABOUT ENTROPY,

Benjamin G. Kyle, Chemical Engineering Kansas State University

Chemical and Process Thermodynamics (3rd Edition) 1999

http://www.che.ksu.edu/~bgkyle/Book_Chapters/6.PDF

Utförligt exempel genom Wikipedia

Slutexempel i Wikipedia — utförlig konkret beskrivning:

Exempel genom Wikipedia och andra webbkällor

DET BAKOMLIGGANDE RENT PEDAGOGISKA SYFTET med samliga retoriska entropiexempel som ställs fram i den etablerade facklitteraturen kan utläsas direkt ur följande korta citatkälla:

”Som minnesregler för termodynamikens två huvudsatser brukar ofta följande formuleringar användas:

Första huvudsatsen: Universums energi är alltid konstant.

Andra huvudsatsen: Universums entropi strävar alltid att öka.”,

FOCUS MATERIEN 1975 s325sp2mn

Jämför korrekt formulering — Med ovanstående citatbrygd i ljuset av K-cellens värmefysik: Plancks strålningslag som garanterar att alla kroppar värmeläcker;

’ Första huvudsatsen: Idealt slutna|isolerade materiesystems energi är alltid konstant.

Andra huvudsatsen: Idealt slutna|isolerade materiesystems entropi strävar alltid att öka.’

Men i praktisk fysik finns inga idealt isolerade system i termodynamisk mening.

”Universums entropi strävar alltid att öka.”.

Observera att rent KVANTITATIVT — beräknad värmemängd — finns absolut ingenting att invända mot de typexemplen eftersom de alla, som vi redan har studerat från Clausius klassiska framställning från 1854, utgår ifrån värmekapaciteten S=E/T J/°K med Q för värmeenergin E.

Däremot uppkommer problem med dessa typexempel — samtliga — i och med att de ansluter till Clausius begrepp för värmemängden Q som en energiFÖRLUST och som dessutom ackumuleras i den moderna akademins mystiska arkivlåda som inte tillåter någon värmeläckning — trots samstämmigt etablerat intygande att några sådana fenomenlådor inte existerar i fysiken, se citat.

Entropiexemplen som ställs fram i ovanstående ljus fungerar alltså så här — alla, inget undantag (jämför själv):

ENERGIN SOM KRÄVS FÖR ARBETET (whatever)

— speciellt den s.k. förlustenergi som sammanhänger med alla kroppars naturliga värmegenomströmning och som i samtliga fall kräver sin extra energi typ förluster för friktioner och värmegenomströmning i en maskins material

— »slits ner» genom ljusets naturliga divergens till en »energikvalitet» som blir allt lägre ju mera tiden lider, analogt större sektoriell spridning för ljusflödet och som sedan inte kan återanvändas på annat sätt än att det krävs extra energi för att återkomprimera till en högre användbarhetsnivå. Den värmeformen, menar man, trots intygat att ingen observerbar naturvetenskaplig grund finns för en sådan förmodad fenomenalitet, LAGRAS ADDITIVT »i universum» så att resultatet av all energianvändning resulterar i att, citatet ovan,

”Universums entropi strävar alltid att öka.”.

Alla, samtliga, etablerade entropiexempel — iskuber, salt och peppar, gasinneslutningar, ostädade vardagsrum, m.m. — går ut på att DRIVA exempelframställningen dit, enbart för tillfället att få understryka den meningen, den slutsatsen — trots, och som redan påpekats, att alla redan VET att en sådan ackumulerande naturvetenskapligt grundad fenomenform, ett förmodat »T-arkiv», inte har observerats. Plancks strålningslag, nämligen, garanterar att alla fysikaliska kroppar värmeläcker — även universum som helhet enligt relaterad fysik — just på grund av ljusets naturliga divergens. (Se även sammanfattande ljusets tre karaktärer i DEN FOTOELEKTRISKA EFFEKTEN). Det finns inga undantag: inga observerade, inte ens logiskt relaterbara, möjligheter existerar just med referens till Plancks strålningslag som garanterar alla kroppars kontinuerliga emission (och absorption) av värmestrålning; Alla kroppar värmeläcker; alla kroppars slutliga öde är noll värmegenomströmning, S=b(lnW)=0, noll entropi.

Universums em-strålning till c0-kroppen

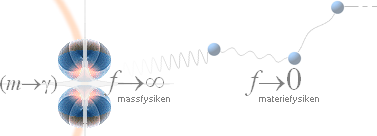
Se utförligt från Atomkärnans härledning

Från Solfysiken med värmebildningens grunder källbildas ENLIGT RELATERAD FYSIK värme och ljus som en högentropisk värmekvantitet (Emax) från massdestruktion (m®g) genom kärnenergi. Då sedan den strålningen avtar med divergensen [Se särskilt i VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK], samt växelverkar induktivt med omgivande massor (atomer), förloras samtidigt en viss del av strålningsenergin (f®0) — entropin avtar — med motsvarande vinning (massvärme) i mekanisk (kinetisk) rörelseenergi hos den aktuella laddade kroppen (atomen via dess elastiskt medföljande elektronhölje) och vilken växelverkan beskrivs av Comptoneffekten. Därmed avtar entropin genomgående, obönhörligt, i takt med att det återstående ljuset får allt längre våglängd med allt lägre frekvens: Materiefysikens Planckstrålning förstås alltså ytterst sett som en naturprocess genom ljusets naturgrundade divergens som går mot noll frekvens med våglängder som går mot oändligt: entropin S=b(lnW) går obönhörligt mot noll för alla fysiska kroppar då de utlämnas åt sig själva utan påfyllande värmegrundad arbetspotential.

c0-kroppen, se utförligt i Det ekologiska universumet

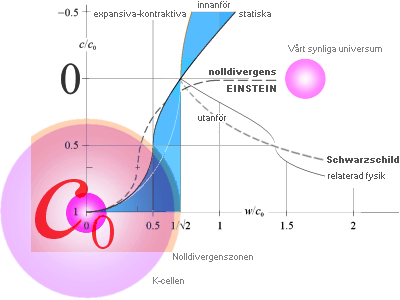
Se även från

Allmänna kosmiska tillståndsekvationen

Eftersom hela universum ENLIGT RELATERAD FYSIK, se från c0-kroppen, begränsas av LJUSETS GRAVITELLA BEROENDE via den växande massan räknat från den centrala gemensamma tyngdpunkten med toppvärdet c=c0, se även i GcQ-teoremet, och som innebär att ljushastigheten c avtar från toppvärdet c0 ut mot universums yttersta gräns, illustrationen ovan med tillhörande jämförande grundbegrepp i modern akademi, se utförligt i Ljusets gravitella beroende och Det ekologiska universumet, tvingas tydligen också all elektromagnetisk strålning som bildas i universum slutligt överföra den sista spillran långvågig Planckvärmestrålning till motsvarande långvågiga mekaniska svängningar, Comptoneffekten som ovan; alla kroppar värmeläcker. Således ÄVEN universum — summan av alla elektromagnetiskt aktiva kroppar och deras domäner och områden. Vilket vill säga ENLIGT RELATERAD FYSIK: Föreställningen om »isolerade system» i fysiken i termodynamisk mening är alldeles tydligt, klart och uppenbart en ren MYT — som av allt att döma introducerades (1872 [‡7]) i samband med Boltzmanns H-teorem (tydligen utifrån rena premisser, utan faktaunderlag). Alla kroppar värmeläcker, Plancks strålningslag, och det finns inga undantag.

»Isolerade system» i fysiken i termodynamisk mening, och i ljuset av dessa tydligen ytterst väl relaterbara detaljer, existerar inte. Se även i citat.

Följande exempelgenomgångar bara understryker det sagda.

All textmarkering (färg, fetstil etc.) i citat är separat tillagda (för nyckelmeningar) i den mån de inte redan framhävs i originalen.

’entropin ökar i ett isolerat system’

’entropin ökar i universum’

Wikipedias huvudexempel

Wikipedias huvudexempel med smältande is:

” Ice melting example

Main article: disgregation

The illustration for this article is a classic example in which entropy increases in a small "universe", a thermodynamic system consisting of the "surroundings" (the warm room) and "system" (glass, ice, cold water). In this universe, some thermal energy δQ from the warmer room surroundings (at 298 K or 25 °C) will spread out to the cooler system of ice and water at its constant temperature T of 273 K (0 °C), the melting temperature of ice. The entropy of the system will change by the amount dS = δQ/T, in this example δQ/273 K. (The thermal energy δQ for this process is the energy required to change water from the solid state to the liquid state, and is called the enthalpy of fusion, i.e. the ΔH for ice fusion.) The entropy of the surroundings will change by an amount dS = −δQ/298 K. So in this example, the entropy of the system increases, whereas the entropy of the surroundings decreases.

It is important to realize that the decrease in the entropy of the surrounding room is less than the increase in the entropy of the ice and water: the room temperature of 298 K is larger than 273 K and therefore the ratio, (entropy change), of δQ/298 K for the surroundings is smaller than the ratio (entropy change), of δQ/273 K for the ice+water system. To find the entropy change of our "universe", we add up the entropy changes for its constituents: the surrounding room and the ice+water. The total entropy change is positive; this is always true in spontaneous events in a thermodynamic system and it shows the predictive importance of entropy: the final net entropy after such an event is always greater than was the initial entropy.

As the temperature of the cool water rises to that of the room and the room further cools imperceptibly, the sum of the δQ/T over the continuous range, at many increments, in the initially cool to finally warm water can be found by calculus. The entire miniature "universe", i.e. this thermodynamic system, has increased in entropy. Energy has spontaneously become more dispersed and spread out in that "universe" than when the glass of ice water was introduced and became a "system" within it.

Notice that the system will reach a point where the room, the glass and the contents of the glass will be at the same temperature. In this situation, nothing else can happen: although thermal energy does exist in the room (in fact, the amount of thermal energy is the same as in the beginning, since it is a closed system), it is now unable to do useful *work*, as there is no more heat. Unless an external event intervenes (thus breaking the definition of a closed system), the room is destined to remain in the same condition for all eternity. Therefore, following the same reasoning but considering the whole universe as our "room", we reach a similar conclusion: that, at a certain point in the distant future, the whole universe will be a uniform, isothermic and inert body of matter, in which there will be no available energy to do work. This condition is known as the "heat death of the Universe".”,

@INTERNET Wikipedia Entropy 2010-01-31

http://en.wikipedia.org/wiki/Entropy#Ice_melting_example

FOTO: Författarens arkiv · Smältande is i glas Feb2010 · Nikon D90

Om rumstemperaturen SJUNKER något på grund av att rummet ger ut värme till den smältande isen i glaset, blir slutläget vid jämvikt nödvändigtvis det att motsvarande antalet likaberättigade energifördelningssätt eller mikrotillstånd (W) i rummet, sedan isen smält, S=b(lnW), har blivit MINDRE, mera drivet mot 0°K, inte större, än vid utgångsläget; W kopplar till Plancks strålningslag genom temperaturen enligt dS/dE=1/T, se Entropiderivatan i Härledningen till Plancks strålningslag från Plancks entropisamband. Finns inte en chans att komma ifrån den matematiken.

OAVSETT vad — således — artikelförfattaren kan uppvisa i den påstådda men ej redovisade referensen till ”can be found by calculus” är det tydligt att artikeln innehåller felaktiga påståenden — OM vi med entropi entydigt kan förstå Plancks entropisamband S=b(lnW) i ljuset av Plancks strålningslag och som inte tillåter »isolerat system» i termodynamisk mening.

Jämför (nämligen) fallet med rummets temperatur initiellt lika med energipotentialen i smältvärmet (n), analogt en något högre temperatur och därmed högre entropi i exempelfallet

S₁ = b(ln[W=1+n])

relativt absoluta nollpunktens

S₀ = b(ln[W=1+0]);

Sedan smältvärmet (n) avgivits från rummet till ’isbiten n’ har rummet (idealt) antagit den LÄGRE entropin

S₀ = b(ln[W=1]) = 0

från den högre entropins utgångsläge

S₁ = b(ln[W=1+n]) > 0

Eftersom S0 är lägre än S1, kan omöjligen S0 vara HÖGRE (citatexemplets ”the final net entropy after such an event is always greater”, ’högre entropi efter issmältningen) än S1.

Entropin TOTALT efter issmältningen enligt Plancks entropisamband S=b(lnW) måste, analogt, bli LÄGRE, inte högre som citatet påstår: värme går ALLTID från varmt till kallt, alltid med åtföljande entropiminskning — i full analogi med giltigheten av Plancks entropisamband S=b(lnW). Se även exemplet med Iskuberna i PRAKTISKA EXEMPEL.

Varför framstår inte det klart i citatexemplet?

”… some thermal energy δQ from the warmer room surroundings (at 298 K or 25 °C) will spread out …”;

— Artikelförfattaren i Wikicitatet kan uppenbarligen inte tänka sig det här, eller har möjligen aldrig tänkt i de banorna:

»0°K-is» som införs i rummet och som får smälta, vartefter ytterligare »0°K-is» införs som får smälta osv., och med den uppenbara slutklämmen att rummets Planckentropi S=b(lnW), analogt sluttemperatur, till slut, tvunget måste bli (gränsvärdet ) S=0 med W=1. Nollentropi. Entropin avtar alltid, tvunget, utan undantag, i varje naturlig arbetsprocess från ett initiellt toppvärde som matar processenergin. Se även i PRAKTISKA EXEMPEL.

— INGENTING HINDRAR NATURLIGTVIS EN MATEMATISK BESKRIVNING som går ut på det här: summan av alla ÄNDRINGAR, lämpligt formulerade, kan för alla termodynamikens skeenden och processer visas vara av den arten att ett motsvarande begrepp om åldring (»användning») ges entydigt, irreversibelt, och därmed i strängt växande kvantitet. Men en sådan, matematisk, formalia är i så fall av en helt annan art är den som gäller i fallet Plancks entropisamband S=b(lnW) där begreppet entropi är liktydigt med en bestämd uppsättning likaberättigade mikrotillstånd, energifördelningssätt (W) för alla ingående materieelement i en given kropps makrotillstånd (kroppens bestämda energi) vid varje given möjlig tidpunkt.

Planckentropin (S) kan, således, både öka och minska, och vilken formalia bevisas genom att begreppet »isolerat system» INTE ingår i S-formen, garanterat av just Plancks strålningslag som kräver kontinuerlig värmeemission (och absorption) för alla kroppar via divergensen (VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK) och Comptoneffekten. Se även sammanställt i Värmebildningen. Se även länk till en mera uttömmande beskrivning i INLEDANDE NOTIS.

Det entropibegrepp som ovanstående Wikicitat tydligen anspelar på, är således och i vart fall INTE Plancks entropisamband S=b(lnW).

Det bara understryker den redan uppmärksammade språkförbistringen i ämnet »entropi».

Se även i ENTROPIBEGREPPETS SPRÅKFÖRBISTRING.

Se även i Naturtermiskt Läckage.

— Citatexemplet använder, tydligen och således, ett entropibegrepp som uppenbarligen i varje fall inte sammanhänger med Plancks entropisamband S=b(lnW).

Notera också: Citatexemplet ger heller inga referenser;

På Wikiartikelns diskussionssida står bl.a. att läsa:

”The ice melting example has to count as original research unless it is sourced. As it's apparently used in many textbooks, this won't be hard to fix.”,

@INTERNET Wikipedia Talk:Entropy 2010-01-31

http://en.wikipedia.org/wiki/Talk:Entropy

Min översättning:

Issmältningsexemplet måste räknas som ursprungsforskning om inte källad. Då det uppenbarligen används i många textböcker bör den saken inte vara svår att ordna.

Värme från stek till tallrik

Värme från stek till tallrik

Nedan ges ytterligare ett citatexempel som visar på, också tydligt, hur man resonerar i modern akademi — och som (återigen) ger en ovärderlig inblick i »den moderna akademiska logiken» för den som intresserar sig för den typen, här av samma typ som i Wikicitatet ovan men något modifierat:

”When heat flows between a steak and a plate there is no violation of energy conservation; the energy lost by the steak is gained by the plate. However, conservation of energy does not explain why the heat always flows from the hot steak to the cold plate; this is where the second law of thermodynamics comes in. Suppose the steak is at temperature T, the plate is at a slightly lower temperature 0.95T, and that a small amount of heat Q is transferred from the steak to the plate.

you will never see heat flowing spontaneously from a cold body to a hotter one

Then the entropy of the steak decreases by Q/T while the entropy of the plate increases by Q/0.95T. It is easy to see that the entropy lost by the steak is smaller than the entropy gained by the plate, so the total entropy of the Universe has increased; this process is therefore consistent with the second law of thermodynamics. If, on the other hand, heat Q had flowed from the cold plate to the hot steak, the entropy lost by the plate (Q/0.95T) would have been greater than the entropy gained by the steak (Q/T), and the total entropy of the Universe would have decreased. This violates the second law of thermodynamics, so we can be sure that the process is impossible. Heat flow is said to be an irreversible process - you will never see heat flowing spontaneously from a cold body to a hotter one.

”,

3 The irreversible Universe

3.1 Thermodynamics and entropy

http://www.physicalworld.org/restless_universe/html/ru_3print.html

Författaren säger bara att om man lägger en het stek på en kall tallrik, tallriken värms upp — och att det skulle vara en rättvis beskrivning av att »entropin i universum ökar». Vilket vill säga, författaren lämnar inget utrymme för tallrikens naturliga avsvalning, bara för avsvalningen från stek till tallrik:

Bara inkomster. Inga utgifter: ”Rösta på mej. Jag vinner alltid”. Ungefär så.

Exempelbeskrivningen är alltså ofullständig — bara en del av värmekonverteringen i fallet stek-tallrik beskrivs, inte hela, ända från start och ner tillbaka till värmejämvikt. Exemplet ovan kan verkligen uppfattas som rejält fult — en lekman har inte en chans att värja sig.

Återigen: begreppet om att entropin skulle avta eller öka är, uppenbarligen, inte samma som ett begrepp om en ÄNDRING i värmekapacitet eller värmegrundad arbetspotential Q/T. Jämför 0/T=0 som visar Q=0; Men betyder det att själva entropin också är noll? [Med referens till Plancks entropisamband S=b(lnW), den enda säkra referens som tydligen finns till entropibegreppet från Clausius klassiska samband S=Q/T].

Om ingen värmemängd finns tillförd till föremålen, vad ska man då relatera begreppet entropi (S=Q/T) till?

(Jo. Plancks entropisamband. Och alltså framgår citatförfattarens inkonsistenta beskrivningssätt):

Entropin är då uppenbarligen noll=0/T=0. Alla arbetsprocesser skulle då i slutänden, sedan värmeflödet utjämnats och termisk jämvikt inträffat och med citatförfattarens entropiuppfattning, alltså definiera nollentropi för alla kroppar — vilket dock är absurt enligt citatets ”so the total entropy of the Universe has increased”. Och därmed; I VARJE FALL I LJUSET AV Plancks ENTROPISAMBAND S=b(lnW) — det enda relaterbart begripliga som finns i ämnet:

— Varken steken eller tallriken besitter naturligtvis någon »nollentropi» då bägge har samma (rums-)temperatur med samma relaterade (relativa) värmemängd (Q) relativt 0°K — vilket dock och alltså tydligen skulle vara fallet om man tillämpar citatförfattarens nomenklatur.

Matematiken i citatexemplet med Q/T är naturligtvis i sig OK. Men den relateras, tydligen, inte fullt ut;

Felet yttrar sig — som redan påpekats i inledningen — via syftet att låta allt gå ut på

”Universums entropi strävar alltid att öka” och vilken meningsuppfattning HELT tydligen grundas på det »isolerade system» som vi också sett genom Plancks strålningslag från Plancks entropisamband S=b(lnW) helt saknar naturvetenskaplig grund — alla kroppar emitterar och absorberar värmestrålning kontinuerligt; Felet man gör i sina »pedagogiska entropiexempel» yttrar sig med andra ord och tydligen i ett bevisligen irrationellt sätt — Plancks strålningslag som garantin för att isolerade system i »termodynamikens andra huvudsats» inte existerar ignoreras — och följaktligen med samma principiella (»korrumperade») resultat som oförmågan att se skillnad mellan derivata (ändring) och integral (funktionsvärde, »summan av alla ändringar»), exemplet ovan med noll=0/T=0.

Citatförfattaren uppvisar, emellertid, ingen unik företeelse: i underförstådd, logisk, mening florerar, tydligen och relaterbarligen, i själva verket FLERA entropibegrepp (med outtalade underförstådda innebörder) och som inte sällan hamnar på kollisionskurs med varandra, som i ovanstående fall.

Personerna använder på visst sätt korrekt matematik (S=Q/T), men kan, tydligen, inte beskriva föremålet utom på »det galna sätt» som våldför sig på det faktum att ISOLERAT SYSTEM inte existerar i fysiken i termodynamisk mening, bevisat genom Plancks strålningslag från Plancks entropisamband S=b(lnW); Alla kroppar värmeläcker, undantag existerar inte. Därför saknar alla utläggningar som går ut på att ”entropin i universum ökar” helt — med bestämt entydig säkerhet — naturvetenskapligt observerbar grund; Just garanterat av Plancks strålningslag och som, just, visar att alla kroppar värmeläcker: undantag existerar inte. Angelägenheten för de författarnas räkning introducerar (tydligen och således) ett nytt entropibegrepp (som oftast blir det som avses, underförstått, utan samtidig beskrivning): »processentropi», motsvarande en kristalls åldring vid upprepad uppvärmning och avsvalning.

Varför kan etablissemangets författare inte uttrycka sig bättre?

UNIVERSUMS HISTORIA innehåller MÅNGA PROPÅER till modern akademi som visar på inkonsistenser på flera olika plan, se särskilt från ATOMKÄRNANS HÄRLEDNING. Om man inte har den insikten — här helt grundad på den övertygande jämförelsen med atomvikterna från NEUTRONKVADRATEN— är det klart att också allt det övriga blir därefter.

Det rent kvalitativt knäppa etablerade sättet att beskriva entropi, exemplen ovan, beror (alltså) inte på något förståndshandikapp, någon »skillnad i intelligens». Bristen på klarhet beror snarare på — i den här framställningens skärande laserljus — att den modern akademins lärosystem aldrig har förmått utveckla de förståndsverktyg som matchar individens verkliga inneboende resurser, de som uppenbarligen krävs för naturbeskrivningen; Jämför »herrecitatet» med flera — och därmed heller inte förmått utbilda eleverna generellt efter deras VERKLIGT inneboende glänsande förmågor (vilket betyder att DE genierna är i [nära] antågande): Istället har den moderna akademins övergripande synsätt tydligen mer eller mindre medfört att hela mänskligheten stängts in i en nermörkad bur som få vågar sig utanför. Det är i varje fall så det ter sig — i den här framställningens ljus.

Förklaringen till varför värme går från varmt till kallt har — således — ingenting med »entropi» att göra (som helt och hållet är ett begrepp som hör till materiefysiken: från 0°K via W=1 och S=0 och uppåt i Planckentropin S=b(lnW)) utan är en ren massfysikalisk fenomengrund med grund i ljusets natur (se även Ljusets g-beroende): Allt arbete utgår från en topptemperatur som tilldelas olika materiesystem från en massdestruktion (m®g), från Solen eller kärnkraft direkt, och på vars avtagande värde arbete utförs, se särskilt i PRAKTISKA EXEMPEL. Se även Hur värmen avtar med tiden.

Som redan tidigare beskrivits i den här framställningen:

När em-strålningen växelverkar med materiens element förloras samtidigt (Comptoneffekten) en viss energi i den växelverkan, vilket lämnar den återstående em-strålningen på LÄGRE energi: Planckentropin S=b(lnW) avtar med arbetets utförande — tillsammans med den naturliga strålningsdivergensen som ger allt lägre energi per given belysningsyta, se VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK. Alltid. Där ligger hela förklaringen: Värme — Planckentropi S=b(lnW) — tappas spontant i själva verksamheten med blotta påvisandet av värme. Den irreversibiliteten — att varmt alltid »töms» mot kallt — återfaller, således på divergensen: ljusets fenomennatur som inte kan återkomprimeras (utan tillförande av energi).

Divergensen finns (emellertid) inte formulerad i modern akademi liksom också massfysiken står helt orepresenterad där, se från ATOMKÄRNANS HÄRLEDNING. Med referens till materiefysiken — i entydig analogi med Planckentropin S=b(lnW) — betyder det samma som att entropin ständigt minskar för varje kropp på vilken arbete utförs. Dvs., värmen läcker ut: Plancks strålningslag från Plancks entropisamband. Se utförligt i Härledning till Plancks strålningslag från Plancks entropisamband.

Det är, tydligen, precis raka motsatsen till det som påstås gälla i »termodynamikens andra huvudsats»: entropin påstås öka med VERKSAMHETEN (tiden) I UNIVERSUM, samma som den i relaterad fysik praktiska övergången från varmt till kallt — men modern akademi SER inte universum på det sättet (kort uttryckt: därför att massfysiken står orepresenterad i modern akademi, se särskilt från Massfysikens nollentropi).

GENOM Planckentropin S=b(lnW) som också gäller i den relaterade fysikens ljus, och som UTESLUTER TYPEN ISOLERAT SYSTEM I TERMODYNAMISK MENING — således oberoende av ’modell’ för universum — finns uppenbarligen bara ett och endast ett och ingenting annat än bara ett enda entydigt sätt: Entropin — motsvarande Plancks entropisamband S=b(lnW) — minskar. Alla kroppar värmeläcker. Det gäller ÄVEN för universum som helhet ENLIGT RELATERAD FYSIK. Se särskilt sammanställningen med c0-kroppen. För att utföra arbete måste en kropp först påföras ett entropikapital, en värmegrundad arbetspotential [massdestruktion (m®g)] — i entydig analogi med det enkla Plancksambandet S=b(lnW) — och som sedan förbrukas med arbetets utförande. Se även PRAKTISKA EXEMPEL. Se även i Allmänna transientfunktionen.

Det är alltså, och tydligtvis, INTE ett motsvarande entropibegrepp enligt Plancksambandet S=b(lnW) som avses med »entropi» i typexemplen ovan, märk väl (och som visar att modern akademi i dessa sammanhang befinner sig långt ifrån verkligheten …). Plancks strålningslag — alla kroppar värmeläcker — sätter punkt för alla andra formuleringar av »termodynamikens andra huvudsats» än den rena klassiska Clausius form med

värme flyter alltid från varmt till kallt

Den formuleringen, tydligen och för övrigt, gick helt förlorad med den moderna akademins uppfinning av »isolerat system» — någon gång under 1800-talets mitt eller mot 1800-talets slut och som det ännu (Feb2010) inte framkommit några konkreta urkunder för, ehuru väl etablerat i dagens litteratur.

Det verkar f.ö. grymt svårt att försöka reda ut, var, exakt brytpunkten ligger i det sena 1800-talets turbulenta diskussioner i ämnet. Av det som hittills framkommit (i den här presentationens ljus) verkar det som att källpunkten sammanhänger med det berömda Boltzmanns H-teorem — den första reguljära matematiska uppställningen som i varje fall försöker beskriva materiens atomism detaljerat — och som helt bygger på förutsättningen »isolerat system» [‡7]. Se även i Den allmänna utvecklingen efter Boltzmanns H-teorem.

Man tänker sig, således tydligen generellt i etablerade kretsar, att »entropi» är något som SKULLE mäta »graden av åldrande» eller irreversibilitet — av princip. Alltså samma som »divergensitet» (men ingen sådan framställd formulering av entropibegreppet finns, här veterligt, i den etablerade litteraturen).

Men det är (i så fall) ändå inte Plancks S=b(lnW) där alla mikrotillstånd (W) inom ett givet makrotillstånd är likaberättigade. Se även från HUR W BERÄKNAS; Plancks S=b(lnW) både ökar (för att göra en maskins [även Solens] arbete möjligt) och minskar (för att verkställa arbetets process). Se PRAKTISKA EXEMPEL. Planckentropin som sådan har alltså ingen allmän, kategorisk, »enkelriktning»; »TIDENS PIL» ligger inte där. Men divergensen har en sådan enkelriktning, ljusets fysikaliska fenomennatur, samt därmed sammanhängande universums expansion, K-cellens värmefysik, och som i sig per relaterad fysik och matematik garanterar en »tidens pil». Men det gör även Ändringslagarna: kausalordningen. Se utförligt från Åldrandets princip.

Inneslutna gasmassor

Ett exempel som diskuterar isolerat system och processer i inneslutna gasmassor

Ytterligare en upphittad:

”Even when a system is entirely isolated from external influences, its microstate is constantly changing. For instance, the particles in a gas are constantly moving, and thus occupy a different position at each moment of time; their momenta are also constantly changing as they collide with each other or with the container walls. Suppose we prepare the system in an artificially highly-ordered equilibrium state. For instance, imagine dividing a container with a partition and placing a gas on one side of the partition, with a vacuum on the other side. If we remove the partition and watch the subsequent behavior of the gas, we will find that its microstate evolves according to some chaotic and unpredictable pattern, and that on average these microstates will correspond to a more disordered macrostate than before. It is possible, but extremely unlikely, for the gas molecules to bounce off one another in such a way that they remain in one half of the container. It is overwhelmingly probable for the gas to spread out to fill the container evenly, which is the new equilibrium macrostate of the system.

This is an example illustrating the Second Law of Thermodynamics:

the total entropy of any isolated thermodynamic system tends to increase over time, approaching a maximum value.

”,

@INTERNET Wikipedia Entropy (statistical thermodynamics) 2010-02-01

Först: Citatkällan ovan beskriver tydligen det som redan tidigare påtalats inte finns i fysiken: isolerat system i termodynamisk mening: en pseudofysik: variationer i tiden inom något som inte existerar i fysiken. Se även etablerade citat med samma innebörd. I en sådan exempelbeskrivning, finns alltså heller inga säkra fysikaliska preferenser, och därmed heller inga säkra belägga för någon enda slutsats eller påstående.

Exemplet beskriver (uppenbarligen, till att börja med) inget tillstånd utan en INITIERANDE PROCESS: när startskottet går, sker en rusning, en tillståndsändring.

Sedan, för det andra — och därmed till exemplets orimliga fysikaliska förmodanden:

— Vad vet man om värmedistributionen i »partitionerna» gas/tomrumsdel? Är temperaturen samma? Om så, hur så, varför, och enligt vilka premisser?

— Det är naturligt för ansamlingen av kroppar till skillnad från tomrum att temperaturen via Plancks strålningslag (kropparnas allmänna värmespektrum) kvarstannar längre i, inuti, kroppen än i tomrummet. Dvs. OM gaspartition och tomrumspartition delar ’samma utgångspunkt’ med »samma temperatur» måste man i så fall förutsätta ett uppmätt termiskt randflöde i gaspartitionens kroppsperiferi — ett något lägre värde än i gaspartitionskroppens mitt — och därmed, i vilket fall, en (obotlig) temperaturskillnad av princip. Eller sagt på annat sätt:

UTJÄMNINGEN i gaspartitionens utspridande över tomrumspartitionen betyder ett ARBETE: värmemängd.

Obönhörligt.

Värmemängden — analogt Planckentropin S=b(lnW) — FÖRE, vid början, innan gasdelen strömmar in i tomrumsdelen och börjar homogeniseras, är alltså relaterbarligen STÖRRE än efter utjämningen.

Följaktligen:

PlanckEntropin S=b(lnW) avtar. Inte ökar;

Allt arbete kräver en avtagande PlanckEntropi — från ett initiellt högre värde.

Undantag existerar inte. Se PRAKTISKA EXEMPEL.

Återigen, således citatet ovan, ett exempel på en författare som »applåderar sig själv»: Exemplifiering av detaljer som, tydligen väl relaterbarligen, inte existerar.

Se även ytterligare allmänna praktiska exempel till jämförelse i ENTROPIN I KONKRETA PRAKTISKA EXEMPEL.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Tillståndsbegreppet i MAC

2010II1

ENTROPIBEGREPPETS FUNDAMENTALA GRUND

TILLSTÅNDETS FÖRBISTRING

och entropibegreppets heliga innebörd

I MODERN AKADEMI

TERMOFYSIKENS GRUNDBEGREPP ENLIGT RELATERAD FYSIK

Tillståndsbegreppets Förbistrade Användning i Modern Akademi

Naturfysikens absoluta irreversibilitet definieras av divergensen LJUSETS FYSIK

— BEKANT men helt utan formulering i modern akademi:

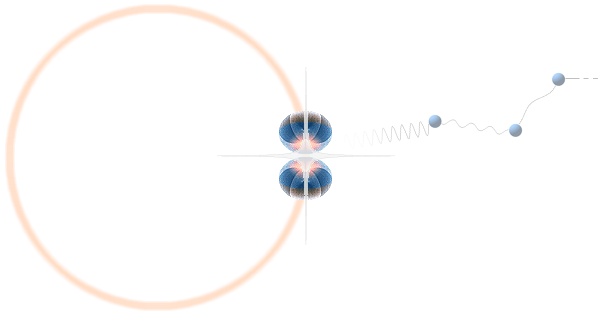
Värmebildningens grunder ENLIGT RELATERAD FYSIK —

Energin i Planckstrålningen avtar med tiden (Comptoneffekten).

Se även utförligt från Solfysiken.

Värmebildningens grund i fysiken är ENLIGT RELATERAD FYSIK den primära massförstöraren i massdestruktionen E=(m®g)cc med Solen som närmaste exempel, eller analogt (ekvivalent) energi från kärnomvandlingar generellt enligt

KÄRNREAKTIONSLAGEN K1+K2–(m®g)=K. Dessa elementära begrepp i den relaterbara fysikens värmegrunder berör massfysiken (p®T) med ATOMKÄRNANS HÄRLEDNING från Planckringen h=mcr såsom energigrund för samtliga processer och fenomengrunder i materiefysiken (T®p) och med beskrivande, matematisk, grund enligt Plancks strålningslag, generellt kropparnas allmänna värmestrålning.

Se även

TERMODYNAMISK JÄMVIKT · ISOLERAT SYSTEM I TERMODYNAMISK MENING

ALLMÄNNA SAMBANDSFORMER I TERMOFYSIKEN

som beskrivande referensgrund, om inte redan bekant.

Vi studerar nu hur entropibegreppet i ljusets av K-cellens fysik harmonierar perfekt med Plancks strålningslag och Plancks entropisamband som härleds nedan

Med förmågan (potentialen) att utföra arbete (E=Fd=mad) menas i termodynamiken (värmeläran) tydligen en ekvivalent värmegrundad arbetspotential

S = E/T .................................. värmegrundad arbetspotential

Beteckningen för energi (E) används f.ö. i värmeläran ofta med beteckningen Q (värme). För att ett arbete ska kunna utföras måste en viss värmemängd (E), vid en viss temperatur (T), först tillföras. Divergensen i ljusets natur (VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK) garanterar tillsammans med Plancks strålningslag och Comptoneffekten att alla kroppar emitterar (och absorberar) värme och på vars, således tvunget, avtagande belopp arbetets process kan utföras. För att kunna upprätthålla en viss arbetsprestation måste med andra ord en viss minsta värmemängd (E) kontinuerligt tillföras kroppen. Se även utförligt i Arbetsexempel.

entropi = värmegrundad arbetspotential

Uppenbart likvärdigt — ekvivalent — med begreppet värmegrundad arbetspotential (värme[arbets]kapacitet, J/°K) infördes termen entropi år 1865 av Clausius enligt föregående citerade genomgång, se från Clausius framställning 1854;

S = Q/T ................................... J/°K, Clausius ursprungliga sambandsform

Med intervallets eller tillskottets term (Delta, D) kan Clausius grundform också skrivas ekvivalent

DS = DQ/T ........................................... intervallformen

Tillförs ingen värmemängd (DQ) är också DS=0: inget arbete utförs.

Den värmegrundade arbetspotentialens kvantitet (S) framgår också i

Allmänna Gaslagen,

E = pV = kT = Fd = (F/A)Ad .............. allmänna gaslagaen

genom fundamentala gaskonstanten enligt

k = E/T = bN ...................................... fundamentala gaskonstanten

med (se Konstanterna i Allmänna gaslagen)

b ......................................................... Boltzmanns konstant

N ........................................................ Loschmidts tal

b, Boltzmanns konstant (den idealt fundamentala materiegasbollens fundamentala värmeenergiinnehåll 1,38 t23 J/°K), eller fundamentala enheten för värmekapacitet

N, Loschmidts tal (N=2,6869722 T25 som kopplar till det mera namnkända Avogadros tal, se utförligt i Konstanterna i Allmänna gaslagen)

PLANCKS ENTROPISAMBAND S=b(lnW) framgår på flera sätt.

I efterföljande beskrivning visas hur Plancks entropisamband S=b(lnW) framväxer naturligt ur uppfattningen om materien som bestående av atomer tillsammans med den naturliga logaritmbasen (e) och dess matematik — välkänd som grund för den matematiska fysikens allmänna variationsformer:

dy/dx = y’; dy/y’ = dx; òdy/y’ = lny’ = x ;

y = ln(P) ;

[ln(P)]’ = d[ln(P)]/dx = dy/dx

= (P)’/(P) = Dn ln(P) ;

d[ln(P)]/dx = d[(P)]/(P)dx ;

d[ln(P)] = d[(P)]/(P) ;

ò d[ln(P)] = ò d(P)/(P) ;

ln(P) = ò d(P)/(P) ;

Se även utförligt i logaritmderivatan och logaritmderivatans härledning.

Plancks entropisamband S=b(lnW) framgår också från allmänna gaslagen med hjälp av ovanstående e-logaritmen och dess kända koppling till naturliga variationer;

Genom matematisk analogi härleds

S = b(lnW) .......................................... Plancks entropisamband

från logaritmderivatan [Dn ln(P) = (P)’/(P)] från grundformen k=bN

k = bN = E/T ............................................ J/°K

i allmänna gaslagen.

Se mera utförligt från Plancks entropisamband från Allmänna gaslagen.

W — utan sannolikhet, i exakt energiekvivalent — anger antalet möjliga och likaberättigade energifördelningssätt eller mikrotillstånd för varje kropps unikt energibestämda makrotillstånd (»den frysta tillståndsbilden» med given energi vid given temperatur). Vid idealt absoluta nolltemperaturen 0°K, materiefysikens grundnivå, gäller tydligen

S=b(ln[W=1])=b(0)=0 .

Därmed framgår, i summa, Clausius klassiska entropisamband S=Q/T (i relaterad fysik värmegrundad arbetspotential) och Plancks entropisamband S=b(lnW) (arbetspotentialens absolut materiella makrotillstånd) som samhörande inom samma termodynamiska begreppsgrunder och dito definitioner. Sambanden är — tydligen — entydiga, harmonierande, helt fria från inre motsägelser eller ouppklarade innebörder.

Härledningen till Planckentropin

HÄRLEDNING TILL PLANCKS ENTROPISAMBAND

S = b(lnW) .......................................... Plancks entropisamband — inte Boltzmanns

ENLIGT RELATERAD FYSIK

Innan den aktuella härledningen: Jämför (först) angående Boltzmanns motsvarande entropimatematik:

”It now remained to give this conclusion a rigorous derivation and quantitative applicability, which Boltzmann did in his memoir submitted to the academy on Oct. 11, 1877, "On the Relation between the Second Law of the Mechanical Theory of Heat and the Probability Calculus with respect to the Propositions about Heat-Equivalence." He concluded that the entropy of a state is proportional to the probability of the configuration of its component particles. His formula, ∫(dq/T) = 2Ω/3, is, however, better known in the form S = k log W, which Max Planck gave it in 1901.

”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

Samt, det upplysande vid tillfället omkring 1900, Max Planck:

”…therefore reinterpreted Boltzmann's theory in his own non-probabilistic way. It was during this period that he stated for the first time what has since become known as the "Boltzmann equation" S = k log W, which relates the entropy, S, to the molecular disorder, W.

”,

MAX PLANCK: THE RELUCTANT REVOLUTIONARY Dec 1, 2000

http://physicsworld.com/cws/article/print/373

Logga in på PhysicsWorld för att få tillgång till artiklarna från GoogleSökningen — det är helt gratis

Jämför typutdrag från en webbkälla (ur högen), mera av regel än undantag: i stort sett på samtliga webbkällor:

”The logarithmic connection between entropy and probability was first stated by Boltzmann in his kinetic theory of gases. This famous formula for entropy S is

S = k log W”,

http://www.myphasespace.com/Teaching/UHCL/StatisticalMechanics/2009/Spring/Lectures/history-lecture1.pdf

Man får

— felaktigt av typcitatet närmast ovan, och det är många det på webben

— uppfattningen att sambandets FORM

S = b(lnW)

skulle ha Ludwig Boltzmann som upphovsman (eng. Boltzmann’s formula).

Men: Enligt ANSWER-källan ovan ställde emellertid Boltzmann fram sambandsformen (integralen, ofullständigt beskriven)

∫(dq/T) = 2Ω/3

S-formen, tillsammans med Plancks beräkning av Boltzmanns konstant (b), kom fram först i samband med Max Plancks beräkningar (runt år 1900, se citat) för att få fram den numera benämnda Plancks allmänna strålningslag. Se även mera utförligt i den sammanställda artikeln Plancks entropisamband.

Att det skulle ha förekommit en formulering från Boltzmann typ LOGARITMISKA sambandet mellan entropi och sannolikhet påstås även av ANSWER-källan i artikeln på

http://www.answers.com/topic/kinetic-theory

men inget explicit samband visas — utöver det ovan visade ∫(dq/T) = 2Ω/3.

Jämför UPPSLAGET (efter ändlöst letande bland hundratals, tusentals …):

”

4.1 The second theorem — a law?

In his kinetic theory of gases, Boltzmann considered a transport equation for the

distribution function f(q, p, t) in phase space and was able to describe entropy as

S = −H(f (q, p, t)) = − ∫ d³qd³p f (q, p, t) log f (q, p, t). (2)

His aim was to arrive at a proper microscopic underpinning of macroscopic thermodynamics — and in particular to obtain a microscopic version of the second

law.”, s11;

”From a mathematical point of view, the close analogy between Boltzmann's formula

S = −k_B Σ_i p_i ln p_i (in different notation than (2) …

”, s14;

PHILOSOPHY DEPARTMENT, UNIVERSITY OF BONN 2008

Holger Lyre: Time in Philosophy of Physics: The Central Issues

http://eldorado.tu-dortmund.de:8080/bitstream/2003/25146/1/012.pdf

;

MÅNGA FÖRFATTARE I ÄMNET KÖR alltså och tydligtvis HELA TIDEN MED BEKVÄMA OMSKRIVNINGAR med underförstådda kopplingar — som sällan kommer fram utom i ovanstående raritet av citat — som tydligen ger ett uppslag till vad som EGENTLIGEN menas med »Boltzmanns entropisamband», om allt är korrekt uppfattat, den markerade remsan med ekvation (2) ovan; Boltzmanns transportekvation som kopplar till Boltzmanns H-teorem från 1872 — och som, här veterligt, är den enda funna orsaken till varför den klassiska formuleringen från Clausius för ’andra termolagen’ sedermera omformulerades med referens till ISOLERAT SYSTEM och ENTROPI:

»termodynamikens andra huvudsats»

”The second law of thermodynamics is an expression of the universal principle of entropy, stating that the entropy of an isolated system which is not in equilibrium will tend to increase over time, approaching a maximum value at equilibrium”,

@INTERNET Wikipedia Second law of thermodynamics 2009-12-11

Min översättning:

Termodynamikens andra huvudsats är ett uttryck för entropins universella princip, vilken fastslår att entropin i ett isolerat system som inte befinner sig i jämvikt tenderar att öka med tiden, närmande sig ett maximalt värde vid jämvikt.

Det är på pricken resultatet av utvecklingarna i Boltzmanns H-teorem.

Se vidare i Boltzmanns H-teorem och Utvecklingen efter H-teoremet.

Härledningen — Plancks entropisamband

Se även från inledning till Härledningen till Planckentropin

Se även Härledningen från Allmänna Gaslagen

DEN MATEMATISKA FYSIKENS KOPPLING TILL e-logaritmen är välkänd med otaliga tillämpningsområden. Se till exempel GLOBALA VATTENFLÖDETS ALLMÄNNA EKVATION som ett (avancerat) exempel och som f.ö. innefattar direkta kopplingar till induktionen och magnetismen. Då vi alltså redan känner typformen med y=e^x — som för x skrivs x = ln y och med tangensformen eller derivatan dy/dx = y’ = d(e^x)/dx = e^x = Dn e^x, se från logaritmderivatan — kan vi, tydligen, TILLÄMPA alla matematiskt relaterbara samband som kopplar till någon naturprocess (whatever) genom att byta ut xy mot lämpliga naturvariabler — förutsatt vi KAN formulera naturprocessen.

Likaberättigade energifördelningssätt

Med insikten att alla kroppar består av atomer med ett myller av olika rörelseformer inom en kropps givna materialgränser, se särskild citatsamling, förstås tydligen i ögonblicksbilden ett motsvarande ekvivalent antal likaberättigade energifördelningssätt — inbördes mellan atomerna och som är egalt, vilketsom, för energitillståndet som helhet — ungefär som vardagsbilden av folk i olika situationer som säljer och köper inom en fast marknadsbudget. Ögonblicksbilden motsvarar, tydligen, ett bestämt energiinnehåll för hela kroppen vid en viss bestämd temperatur, analogt en viss bestämd medelmässig rörelseenergi hos varje atom.

Med antalet likaberättigade energifördelningssätt som y=W

— genom variabel värmegrundad arbetspotential, samma som värmekapacitet (S=E/T, J/°K, se Clausius framställning) vilket motsvarar kroppens energiinnehåll vid en viss given temperatur,

x = S = värmegrundadeArbetspotentialen = värmekapaciteten,

— får vi ekvivalent W=e^S med

S=lnW. Med Boltzmanns konstant b=1,38 t23 J/°K som den värmegrundade arbetspotentialens fundamentala minsta enhet (»värmekapacitetens energikvantum») ges

S = b·lnW ................................ J/°K, Plancks entropisamband

— vilket är Plancks entropisamband. Med Plancks egna beteckningar

S_N = k log W + const, se Plancks Original.

S-formen beskriver, tydligen exakt, en värmegrundad arbetspotentiell tillståndsekvivalent.

Se även vidare i Härledningen till Plancks strålningslag från Plancks entropisamband.

Alternativt — delvis mera utförligt

Med grund i allmänna gaslagen E=pV=kT: Mot varje bestämd temperatur (T) svarar, för varje given kropp, tydligen en entydigt bestämd energi (E=kT):

Vid (obegränsat nära) 0°K finns då, tydligen, bara ett och endast ett entydigt motsvarande mikrotillstånd

(W, antalet möjliga likaberättigade energifördelningssätt

[positioner xyz med antalet möjliga rörelsemängder mv] för kroppens aktuella energiinnehåll vid just den aktuella temperaturen)

motsvarande (obegränsat nära) noll värmegrundad arbetspotential med funktionen (f ) för W vid W=1 enligt

S = f (W=1) = 0 ...................... inget materiellt arbete kan utföras vid noll entropi

Från grafläran

(grundas på personlig erfarenhet från matematiken, varierar alltså med person)

är det känt att en sådan funktions begynnelseform stämmer utomordentlig väl överens med exponentfunktionen

y = e^x ..................................... exponentfunktionen

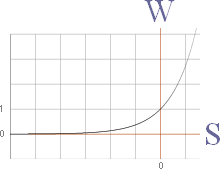
Exponentfunktionen

Därmed är härledningen redan i princip fullbordad:

Med motsvarande beteckningar S för x och W för y ges

e^S = W = e^S;

S = ln(W=1) = 0 ................................. värmegrundade arbetspotentialen

Eftersom den absolut minsta arbetsenheten i allmänna gaslagens matematiska fysik är Boltzmanns konstant eller enheten för värmekapacitet

b ......................................................... J/°K, Boltzmanns konstant

Boltzmanns konstant (den idealt fundamentala materiegasbollens fundamentala värmeenergiinnehåll 1,38 t23 J/°K), eller fundamentala enheten för värmekapacitet

måste naturligtvis den värmegrundade arbetspotentialen generellt ha Boltzmanns konstant (b) som enhetsbas. Därmed anpassningen som ger

S = b(lnW) ......................................... J/°K, Plancks entropisamband

Det enda som skiljer mot grundgrafen ovan (S) blir att S-formen här uppvisar en betydligt brantare stigning (S/b).

Med formell härledning i differentialer således varianten

dW/d(S/b) = W;

Härledningen med differentialer

Ändringen i det totala antalet möjliga likaberättigade energifördelningssätt (W) som [positionerna och rörelsemängderna (xyz)(mv) för] materialets komponenter (atomer, molekyler) kan uppvisa för ett givet energiinnehåll

— således med avseende på just energins aspekt (S/b)

— har uppenbarligen ingenting annat att återfalla på i fysikens värld än just ett specifikt antal likaberättigade energifördelningssätt (W) med grund i ett bestämt antal variabler (Planckenergikvanta) för det bestämda energiinnehållet (S).

Den masslösa utbredningen av ljus och värme genom materien

— atomerna och deras elektronhöljen, se från PERIODISKA SYSTEMET och FOTOELEKTRISKA EFFEKTEN, som grundad på induktionen (energins bevarande genom induktionen, se COEI), och därmed enbart genom divergensen som ljusets natur i kraft av att alla kroppar genomträngs, mer eller mindre, av värmeströmningar och därmed är oförmögna att HELT utestänga sådana

— garanterar att fysiken är intrinsiskt ren från typen isolerade system i termodynamisk (värmegenomströmmande) mening. Det gäller även för universum som helhet i relaterad fysik.

Denna aspekt INGÅR således i villkoret för ändringen i likaberättigade energifördelningssätt i (W): »isolerat system» i termodynamisk mening i fysiken existerar inte i något tidsmässigt utsträckt fysikaliskt skeende. Det är samma resultat som beskrivs (enklare) genom Plancks strålningslag, men som i strikt härledande ordning följer först ur Plancks entropisamband.

Entropivariantens differentialekvation blir alltså (helt odramatiskt)

dW/W = d(S/b) som vi vet från logaritmderivatan är identisk med logaritmintegralen

ò dW/W = ò d(S/b)

med lösningarna för första och andra integralen (förutsatt att W [materiefysikens nollgrund] räknas från lägst 1 med S=0, just vårt fall)

lnW = S/b ;

S = b(lnW) ......................................... J/°K, Plancks entropisamband

Det är, tydligen och uppenbarligen, i all sin chockerande enkelhet den relaterbara fysikens härledning — den relaterbara förklaringen — till Plancks entropisamband; För varje bestämt energiinnehåll i en kropp finns ett bestämt W-tal lika med summan av alla möjliga likaberättigade energifördelningssätt [positioner xyz vid alla möjliga rörelsemängder mv] som kroppens beståndsdelar (atomer, molekyler) kan anta — därför att materiefysiken inte uppvisar någon annan komponentgrund att välja på.

Eller med andra ord:

Planckentropin i S-formen uttrycker multipliciteten lnW av Boltzmanns konstant (b) [tagen över (de Planckenergiekvivalenta) variablerna (xyz)(mv) för de ingående komponenterna] — och därmed en ren energiekvivalent — eftersom inget annat finns att välja på: Varje kropp har sitt bestämda antal komponenter (atomer) och en bestämd energi vid varje tidpunkt, analogt vid varje given temperatur, och därmed ett bestämt W-tal.

Tillståndsbilden vid en viss tidpunkt kallas konventionellt för ett mikrotillstånd, samma som ett specifikt likaberättigat energifördelningssätt inbördes mellan alla ingående komponenter; W-talet innefattar alla möjliga likvärdiga sådana ’frysta tillståndsbilder’, unika mikrotillstånd, med kroppens komponenter [via de möjliga (xyz)(mv)]. Liktydigt med W-talet och summan likvärdiga mikrotillstånd används konventionellt termen makrotillstånd: ett bestämt energivärde för en bestämd temperatur med ett bestämt W-tal.

OBSERVERA DOCK att de konventionella begreppen i dessa sammanhang inbegriper (obskyra) detaljer som beskriver W-talet i S=b(lnW) i termer av STATISTIK och SANNOLIKHET — men som inte alls ingår i den relaterade fysikens framställning i ämnet Plancks entropisamband med koppling till Plancks strålningslag. Se utförligt från W finns inte i statistiken samt Flaskhalsarna i Plancks framställning.

Se även vidare (närmast nedan) i tilläggsartikeln Hur W beräknas.

Hur W beräknas

Med grund från Härledningen till Planckentropin

Hur W beräknas — allmänna referenser

antalet likaberättigade energifördelningssätt

Se även mera elementärt från HUR W BERÄKNAS FRÅN ENSKILDA ATOMERS POSITIONER (xyz)

I Plancks entropisamband

S = b(lnW) ......................................... J/°K, Plancks entropisamband

b, Boltzmanns konstant (den idealt fundamentala materiegasbollens fundamentala värmeenergiinnehåll 1,38 t23 J/°K), eller fundamentala enheten för värmekapacitet

har termen W följande innebörd:

W anger totala antalet likvärdiga energifördelningssätt eller mikrotillstånd (xyz)(mv) för kroppens eller systemets materiekomponenter i det givna makrotillståndet.

Se även explicit från Härledningen till Plancks entropisamband.

Det finns bara en ordning att välja på:

2010II21

Grundformen för

MATERIEFYSIKENS ALLMÄNNA STRÅLNINGSLAG — Plancks strålningslag

Hur W beräknas

För materievolymer som är små relativt ljushastigheten gäller tydligen följande:

Antalet likaberättigade energifördelningssätt inom en kropps givna energiinnehåll och temperatur, uttrycker som det har visat sig, i samtliga fall en tillståndsekvation med exakt kvantitativ definition av de inbördes olika (energi-)mängderna.

Det finns ingen sannolikhetsaspekt — men många påstår det, se lista med exempel i W finns inte i statistiken.

Det är — av allt att döma — en feluppfattning.

Se även särskild genomgång i W finns inte i statistiken.

Bevis:

W =

maximala

antalet olika

partikelenergier

aktuella antalet

likaberättigade

—————————————————————————————————————————————

energifördelningssätt

———————————————

aktuella

antalet olika

partikelenergier

— Varför då?

Det primära svaret är (delvis trivialt): Därför att det, uppenbarligen, inte finns några andra sätt att välja på med förutsättningen att S=b(lnW)=0 via W=1 vid T=0°K och S=b(lnW)=max via W=MAX vid T=max°K.

Olika partikelenergier är förutsättningen för flera inbördes olika energifördelningssätt via olika partikelenergier, vilket förefaller självklart. Eftersom ett antal energifördelningssätt förutsätter alla fysiskt möjliga kombinationer mellan tillgängliga olika partikelenergier, vilket enligt exempel återfaller på en matematisk potensfunktion N·N·N·…, synes enda rimliga förutsättningen för urvalspotten till de möjliga kombinationerna vara OM maximala antalet olika partikelenergier reduceras DIVIDERANDE via aktuellt antal olika partikelenergier n·n·n·…, alltid lika med eller mindre än maxantalet olika, SÅ att den kombinerbara återstoden, olikhetskvoten, bildar råstocken med egala N som därmed kan sägas bilda antalet energifördelningssätt med variation från max till 1 enligt förutsättningarna med varierande temperatur som påverkar variationerna i det aktuella antalet olika partikelenergier, materiens värmefysik.

Se även en mera utförligt genomgång i W finns inte i statistiken.

Det sekundära svaret (som bevisar riktigheten i det primära svaret) är att ovanstående W-form (nämligen) leder direkt på Plancks strålningslag — från Plancks entropisamband S=b(lnW) och Planckenergin E=hf: värmestrålningens fysik för alla kroppar. Med redan (excellent) experimentell bekräftelse på det sambandets allmänna giltighet i den termogravitella fysiken, blir det svårt att uppresa några direkt uppenbara invändningar. Då, följaktligen (ännu), inga sådana invändningar (här veterligt) syns, kan saken relateras i bevisets förklarande ljus på följande sätt.

Beskrivning:

MAXimum antal olika partikelenergier gäller alltid av princip vid (obegränsat nära) 0°K: partiklarna kommunicerar inte genom inbördes impuls (eller gör det per typ oändlig tid): noll rörelse.

MINimum antal olika partikelenergier gäller alltid vid max temperatur: partiklarnas skilda energier kommuniceras ’omedelbart’ över kroppsvolymen så inga direkt olika partikelenergier kan urskiljas.

Se även mera utförligt i den elementära genomgången i LIFE-satsen.

0°K:

aktuella antalet olika partikelenergier är lika med maximala antalet olika partikelenergier:

antalet likaberättigade energifördelningssätt är 1:

S=b(ln[W=1])=b(0)=0=minS;

max°K:

aktuella antalet olika partikelenergier är lika med 1:

antalet likaberättigade energifördelningssätt sammanfaller med maximala antalet olika partikelenergier: alla partiklar uppvisar (idealt) varandras energier (endast en gång):

S=b(ln[W=max])=maxS;

ANTALET OLIKA PARTIKELENERGIER (E=hf) — se utförligt från FOTOELEKTRISKA EFFEKTEN — bestäms, tydligen, av antalet (n) partiklar (atomer) tillsammans med antalet (P) Planckenergikvanta (hf): Det finns ingenting annat att välja på; E/hf=P betyder varje atoms totala svängningsenergi (E) fördelad över aktuella Planckfrekvensenergin hf, lika med antalet Planckenergikvanta (P). Så, antalet olika partikelenergier, speciellt i fallet med en atom (n=1), kan också betyda antalet (lika) Planckenergikvanta (P).

Om vi erinrar den elementära vågmekaniken (matematiken för vågorna och deras utbredning) med den centrala superpositionsprincipen, blir det enklare att förstå hur också en atoms elektronmassa kan fungera som ett motsvarande »vatten» som kan genomkorsas av alla möjliga (stående) vågmönster med alla möjliga energiinnehåll: alla möjliga P och deras fysikaliskt möjliga kombinationer. Dvs., i praktiken är varje enskild atom alltid föremål för genomströmning av alla möjliga våglängder som kan påverka elektronmassans komponenter, det vi kallar för »materiefysikens termodynamik».

Med exemplet (n+P)=3 kan summan av partiklar (ospecificerat) och Planckenergikvanta (ospecificerat) tydligen uppvisa totalt 27 olika möjliga inbördes partikelenergier (eg. partikelenergikombinationssätt) — alla fysikaliskt möjliga tänkbara kombinationer för (n+P)=3, inget mindre — enligt den exemplifierade uppställningen med abc (ett kombinationsexempel av 27)

Potensformen

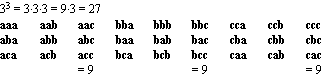
Antalet totalt möjliga kombinationer för n och P tillsammans kan alltså skrivas på potensfunktionen (se även Plancks W-form)

(n+P)ⁿ⁺^P = (n+P)ⁿ(n+P)^P ................ totala antalet möjliga kombinationer för n+P

Antalet likaberättigade energifördelningssätt (W) kan då i fallet W=1 vid 0°K skrivas formellt

(n+P)ⁿ⁺^P

W = ————— = 1

(n+P)ⁿ⁺^P

För att W, härifrån, ska kunna avta i nämnardelen och därmed tillväxa i kvoten finns med tillgängliga (n+P)ⁿ⁺^P=(n+P)ⁿ(n+P)^P tydligen bara ett sätt att välja på:

(n+0)ⁿ(0+P)^P: n är konstant för given kropp, det är bara P som kan varieras.

Det finns inget annat att välja på.

Nollningen av n i andra parentesen:

Lägsta antalsvärdet för P är 1 därför att exakt noll värmestrålning inte förekommer i materiefysiken: alla kroppar värmeläcker. Därmed ges lägsta W-talet (korrekt praktiskt) obegränsat närmast större än 1 (med antalet atomer n mycket större än 1) enligt

Generaliserade W-kvoten

(n+1)ⁿ⁺¹

W = ————— Û nⁿ/nⁿ = 1 ............. gäller vid 0°K

nⁿ1¹

GENERELLT skulle man kunna påstå: Eftersom antalet atomer (n) även i den minsta materiella kropp är (mycket) stort, garanteras att W praktiskt taget blir lika med 1 vid ideala 0°K.

Det finns emellertid en, visst avancerad, belysande aspekt som i fallet med endast en atom och P=1 Planckenergikvanta medger kvoten (0+P)/1=1. Nämligen i beaktandet att de möjliga kombinationerna i P ligger kvalitativt i atomens elektronhölje som en mönsterform, en s.k. resonans. Exemplet ovan med 3^3=27 möjliga mönsterbilder är, uppenbarligen, helt fysiskt möjliga i en atoms elektronhölje — (0+P)^(0+P) med W=(0+P)^(0+P)/[(n=1)(P^P)]=1, samtliga fall med endast en atom.

Atomen själv (eg. atomens elektronmassa) räknas inte (0) som någon specifik resonans (optimalt n=0 i W-täljaren) eftersom atomen med sin elektronbesättning kan uppvisa alla möjliga resonanser, men måste ändå finnas med som en W-kvotens kvantitativt minsta grundenhet (minst n=1 atomelektronbesättning i W-nämnaren) för att sambandet alls ska kunna uppvisa någon mönsterform i fysikalisk mening. Det är i varje fall den förklaring som framträder mest uppenbart.

En (delvis) mera utförlig (illustrerad) beskrivning finns i Den kritiska frågan från Plancks W-form.

I det praktiska fallet kan alltså W-formen, slutligt och generellt för n atomer och P Planckenergikvanta (hf), förstås och därmed skrivas allmänt

(n+P)ⁿ⁺^P

W = ————— ................................. antalet möjliga energifördelningssätt i n via hf

nⁿP^P

W-formen beskriver då, tydligen exakt — en tillståndsekvivalent:

W-formens samband uppvisar, synbarligen, ingen som helst koppling eller anknytning till begreppet sannolikhet.

Vilket skulle visas.

Sambandet för W ovan motsvarar föregående retoriska uppställning med de stora rutorna.

MED PLANCKS ENTROPISAMBAND S=b(lnW) blir det sedan mer eller mindre »ren motorväg» (fri hastighet) till målet (elementära deriveringar, logaritmlagar). Inga som helst problem:

Med dS/dE=1/T från grundformen S=E/T (allmänna gaslagen eller Clausius grundform) med E=hf och P=E/(hf) ges först från Plancks entropisamband S = b(lnW); e-logaritmen för W-kvoten kan utvecklas genom logaritmlagarna vilket för varje atom n=1 ger ledet

S = b[(1+P)ln[(1+P)] – P·ln(P)]

Insättning av P=E/(hf) och derivering med avseende på E ger efter utveckling och sammanräkning

dS/dE = (b/hf)·ln[1 + hf/E] = 1/T

Därmed (frekvensen f=c/l med våglängden l)

hf/bT = ln[1 + hf/E] = hc/bTl

som ger

e^hc^/bTl = 1 + hc/El

och som i fullständiga enheter ger

strålningseffekten per kubikmeter våglängd [som motsvarar den s.k. spektrala radiansen, W(M³SRsteradianer)^–1] som ger Plancks fullständiga allmänna strålningslag

hc²

N_l = ——————— ......................... W/(M³SRsteradianer)

l ⁵ · (e^hc/b^Tl – 1)

Se även den mera utförliga härledningen i Plancks strålningslag från Plancks entropisamband.

Med den enkla utgångspunkten från enbart n antal komponenter visas nedan — till viss jämförelse — en utförlig (elementär) beskrivning av grunderna i HUR W BERÄKNAS FRÅN ENSKILDA ATOMERS POSITIONER (xyz). Men, observera, att den, trängre, beskrivningen via enbart n atomer eller materiekomponenter inte leder till Plancks strålningslag. (Beskrivningen ger dock grundläggande inblick i den allmänna översikten).

Hur W beräknas från de enskilda atomerna

2010II16

HUR W BERÄKNAS FRÅN ENSKILDA ATOMERS materiekomponenters POSITIONER (xyz)

Antalet olika delenergier för energikroppens masskomponenter

Om vi väljer ett (idealiserat) tidsintervall (t) för att »ta en situationsbild» över en kropps tillfälliga innehåll av komponenter (atomer, molekyler) kan vi (lätt) förstå hur bilden blir tydligare om partikelhastigheten är låg:

ju mera partiklarnas medelhastighet (idealt) växer (mot oändligt) desto mera måste varje partikel, alltmer, uppvisa en homogent fördelad medelbaserad partikelenergi — alltmer lika för alla partiklar.

För en given, bestämd volym:

Ju högre medelhastighet kroppens materiekomponenter (atomerna) har och därmed högre medelbaserad sammanstötningsfrekvens med växande temperatur, desto snabbare genomströmmas kroppen tvunget av alla olika möjliga förekomster av alla möjliga olika partikelenergier. Så, den verkställande potentialen för att skillnaden inbördes mellan partiklarnas skilda energier tenderar att utjämnas på allt kortare tid växer då också med växande temperatur; Därmed ett allt större antal likartade partikelenergier med hela kroppens analogt växande totala energiinnehåll.

Ju högre partikelhastigheten är, desto svårare får vi (varje mätande anordning) att urskilja partikulärt inbördes olika delenergier. Analogin är densamma som inom fotografin: ju högre hastighet ett objekt har som passerar linsen desto svårare blir det att få en skarp bild. Största skärpan fås med helt rörelselösa objekt; En genomgående låg partikelhastighet betyder att partiklarna i motsvarande grad får god tid på sig att utveckla maximalt olika inbördes partikelenergier i den inbördes fördelningen av hela kroppens totala energiinnehåll.

Matematisk analogi

FRÅN DE FORMELLA EKVIVALENTERNA E=UQ=RIQ=RI·It=L[I=Q/t]²,

[LQ²]_k/[t₀²]_a=E=(konstant för varje massa)=mc²=hf=k/a med k=LQ² och a=t₀² gäller k/E=a+t² DÄR t=0 ytterst sett i värmefysiken definierar (massdestruktiva) villkor tillsammans med det nödvändiga tidbaserade Emax-OFFSETintervall a>0 som varje fysisk energi-massa transferering måste börja ifrån. Då är E/k=1/(a+t²), och vi har E=k(a+t²)^–1. Se även mera utförligt i K-cellens värmefysik.

Energiderivatan bildar TRANSIENTEFFEKTEN

dE/dt = P = (–)kt(a+t²)^–2. Konstanten a motsvarar det (korta) intervall (tändningen) som finns innan den aktuella massa-energi transfereringen verkställs.

Med P/kt=(a+t²)^–2 kan vi tydligen, inom ett avgränsat effektfönster t, detaljstudera den relativa energifördelningen i kroppsmassan genom att studera växande funktioner GENERELLT för alla typer av effektfunktioner via högerledets t-form enligt P/kt=(a+[f (t)]²)^–2. Med f (t) = tⁿ ges därmed motsvarande tillräckliga villkor för att studera den matematiska motsvarigheten till fallet då kroppens inre energiinnehåll växer med växande n och därmed energiskillnaderna internt i kroppen inom det givna t-intervallet.

Grafen nedan visar kurvskaran med (a=1) funktionen y=(1+xⁿ)^–2 motsvarande

(P/kt)S^–n=(a+[tⁿ]²)^–2=(E/[t²]ⁿ)/k för olika n, analogt mera homogen inre fördelning med växande n. Illustrationens n-värden visar n={1,2,3,4,5} där klockformen (n=1) alltmer går mot den omgivande rektangeln då n växer uppåt obegränsat.

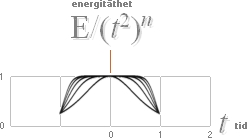
Ju kortare tid, analogt högre temperatur och högre totalt energiinnehåll, desto större mått av likafördelning i energi mellan partiklarna inbördes inom det givna tidsfönstret (0-1 ovan), analogt allt mindre inbördes skillnad i partikelenergi.

LIFE

Genom att, på så beskrivet sätt, den genomsnittliga partikelhastigheten för komponenterna i en kropp kan förstås öka med växande temperatur, analogt växande energiinnehåll [T = E/k = (mv²/2)/k] och därmed högre effekt P=E/t, kan vi alltså och därmed också postulera en ’självklar’ »LikaFördelningsdelEnergiantalssats» [LIFE]

generellt för en kropp med givet energiinnehåll beträffande energins fördelning över kroppens masskomponenter att

antalet lika partikelenergier växer med ökande temperatur

LIKAFÖRDELNINGSDELENERGIANTALSSATSEN

Ju »bredare tidsfönster» som anställs för mätning av partiklarnas energi vid given temperatur, desto flera lika partikel(medel-)energier visas; Med ett »oändligt tidsfönster» ges medelpartikelenergin lika för alla. Men vi använder i praktiken snarare ett så kort mätfönster som möjligt (och som i praktiken i materiefysiken begränsas med hänsyn till atomens begränsade utsträckning). Med givet (kortast möjliga) mätande tidsfönster, och förutsatt små medelavstånd (normala Jordlaboratorium) mellan atomerna i förhållande till ljushastigheten, utplånas således skillnaden mellan olika partikelenergier med deras växande medelhastighet. Vilket vill säga: mätningen kommer att visa allt flera lika (inom angivna marginaler) partikelenergier med allt växande temperatur.

För max temperatur blir antalet inbördes lika partikelenerginer idealt lika med antalet ingående partiklar (atomer, molekyler) och därmed ett och samma (ideala) delenergivärde för varje partikel,

nLIFE = n ..................................... antalet lika partikelenergier max temperatur

nLIFE – n = 0 .............................. antalet olika partikelenergier max temperatur

För (obegränsat nära) ideala 0°K — analogt i princip noll partikelhastighet — blir antalet inbördes lika partikelenerginer också (idealt) lika med noll — alla olika — så att varje partikel får ett eget unikt delenergivärde (oaktat vilket detta än är) med totalsumman lika med kroppens totala energiinnehåll för alla partiklarna tillsammans,

nLIFE = 0 ..................................... antalet lika partikelenergier min temperatur

nLIFE – 0 = n ............................... antalet olika partikelenergier min temperatur

Antalet totalt energibevarande likvärdiga SÄTT som de maximalt n olika partikelenergierna kan finnas till på inom den givna kroppen med den givna totalenergin blir, uppenbarligen, lika med det enkla exemplet med de tre delenergierna abc som bara kan sättas om inbördes genom att anta varandras värden/platser — positioner (xyz) — enligt fakultetsfunktionen (3!, »3-fakultet[-en]»)

3!=1·2·3=6={abc acb bac bca cab cba}; det finns inga andra möjliga (xyz)-SÄTT.

Och för n partiklar med givna (xyz) därmed n! sätt.

Varje (sådan) uppräkning/uppställning av ett antal element i en viss ordning kallas konventionellt för en permutation. [ref. MLs334sp2n].

Exemplet med de n=tre delenergierna abc uppvisar alltså totalt n!=sex inbördes (xyz)-permutationer.

Antalet likaberättigade mikrotillstånd

I det härledda sambandet för ändringen i antalet likvärdiga energifördelningssätt W (i en kropp med n materiella komponenter) med avseende på entropin S — via positioner (xyz) och rörelsemängder (mv) — hade vi för 0°K att

S_MIN = b(ln[W=1]) = b(0) = 0 .................... bara ett enda energifördelningssätt, T_MIN

I andra änden kan maxvärdet för W tydligen bara bli antalet likvärdiga energifördelningssätt n! med S-maxvärdet

S_MAX = b(ln[W=n!]) ................................... maximalt n! energifördelningssätt, T_MAX

Antalet likaberättigade energifördelningssätt eller som vi säger likaberättigade mikrotillstånd kan då tydligen skrivas för samtliga fall och med ovanstående nyligen genomgångna förutsättningar (LIFE) enligt [för skrivsättet f (v), se även Funktionsbegreppet]

W = ——————— = ₁_®_n_![f (v)]

n! · [f (v)]^–1

Genom att partikelhastigheten (v) ökar med temperaturen, analogt kroppens totala energiinnehåll, kommer divisionen med v-funktionen f (v) i nämnaren att betyda samma sak som att antalet olika partikelenergier, räknat med max från 0°K, minskar i den variabla n!-stocken med ökande v — vilket i förhållande till ideala tillståndets absoluta nollnivå med n! uppenbarligen betyder att allt flera partiklar uppvisar likartade energier och som därmed sänker antalsdelen i den jämförande n!-stocken (nämnardelen) i förhållande till ideala tillståndets absoluta nollnivå med n! i täljaren.

Observera att uppställningen med W= (n!)/(n!)[f (v)]^–1 följer tvunget, som ovan, på grund av att W=1 (med lägsta möjliga v=1) måste gälla vid 0°K och motsvarande W=n! vid max (här ospecificerad) temperatur. Med n som enda variabel finns tydligen inget annat att välja på.

T-funktionen

W-formen för växande temperatur (T) från 0°K kan då i princip även lika väl och helt formellt skrivas

W = _T=0→Tmax (1→n)!

Antalet likaberättigade energifördelningssätt (W) med given kroppsenergi (E) växer från W=1 vid temperaturen T=0°K och går sedan mot W=n! vid max (ospecificerad) temperatur för kroppen med antalet n masskomponenter (atomer, molekyler). Eller, alternativt,

n! n!

W = ——— = ——————— …

n! – T n₁!n₂!n₃!…n_m!

n_m-ekvivalenternas produktfakulteter motsvarar (här) bara ett alternativt uttryckssätt med användning av ytterligare permuterande villkor, nämnardelen alltid mindre eller lika med täljardelen n! — den typskrivningen kan ses i flera konventionella webbkällor;

Webbreferenser

@INTERNET Wikipedia Ludwig Boltzmann 2010-01-31

Även på webbsidan

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

En liknande (mera utförlig) beskrivning finns också i boken

Information measures: information and its decription in science and engineering,

Christoph Arndt 2001, s95-96

Finns på GoogleBöcker — med begränsad granskning

En motsvarande mera utförlig (men samtidigt mera krävande) beskrivning finns på

http://hyperphysics.phy-astr.gsu.edu/HBASE/quantum/disbol.html#c2

FRÅNSETT DIREKTKOPPLING TILL MAX PLANCK — vi återkommer strax dit — och att döma av det allmänna utbud som (ännu Feb2010) finns på webben skulle nog de allra flesta i detta skede säga att, na, något vidare enhetligt generellt samband för W finns nog inte

— och därmed heller ingen direkt (enkel) koppling från

antalet likaberättigade energifördelningssätt W till ett specifikt entropivärde S.

VI KAN (nämligen) från det ovan sagda SKÖNJA ATT

T-funktionen med andra ord tvunget och för samtliga praktiska fall, tydligen, måste bli »någon form av en motsvarande temperaturfunktion», alltså med speciella parametrar som, tydligen lika tvunget, för den aktuella kroppens atomtyp (elektronkonfiguration [värmedistribuerande förmåga: emission, absorption]) och sammansättning (energiupptagande frihetsgrader) betyder specifika förutsättningar, och därmed »särskilda lösningar» för varje kropp, ämne och substans. Känner man ett S-värde (exempel nedan) får man W-värdet generellt enligt

W = e^S/b .................................. antalet likvärdiga energifördelingssätt för givet S/b

EXEMPEL:

Den experimentellt uppmätta värmekapacitiviteten (vid rumstemperatur ca 20°C) för vatten är grovt sett ca

S_VATTEN/m = 4000 (J/°K)/KG .......... värmekapacitiviteten för vatten

För ca 1 liter = KG vatten ges då värmekapaciteten eller motsvarande entropitalet

S = 4000 (J/°K) ...................... värmekapaciteten för 1 KG vatten

Antalet motsvarande likaberättigade energifördelningstillstånd (W) blir då

W = e ^ 4000/(1,38 t23) = e ^ 2,89855 T26

Exemplet visar att kvantiteten för W (generellt) bildar helt opraktiskt otympligt stora tal — som blir helt omöjliga att »kontrollera»:

W-talet som matematisk kvantitet har alltså, knappast, någon direkt praktisk användbarhet.

Men hur många (på planeten Jorden) känner (ännu Feb2010) till att W-formen leder till Plancks strålningslag? — Och det bara med en liten »modifikation». Nämligen tillsammans med Plancks konstant (h) i Planckenergin E=hf, samt insatt »på tillbörligt sätt».

ATT DÖMA AV DET ALLMÄNNA UTBUDET PÅ WEBBEN (ännu Feb2010) har jag än så länge bara hittat en (1) enda person som tycks ha förstått den möjligheten. Nämligen Max Planck själv i hans framställning från år 1901 (se Plancks original) — med uppslag från Ludwig Boltzmann; Boltzmann och Planck är tveklöst de avgjort två främsta förgrundsfigurer som kan förknippas med grunden till atomfysiken som en matematiskt naturvetenskapligt etablerad gren: Boltzmann för uppslaget, Planck för formuleringarna. Se speciellt från S = b(lnW) är Plancks entropisamband — inte Boltzmanns.

Detaljerna i Plancks egen framställning beskrivs särskilt i Flaskhalsarna i Max Plancks framställning.

Den fullständiga härledningen ENLIGT RELATERAD FYSIK till Plancks strålningslag från Plancks entropisamband beskrivs detaljerat i Härledningen till Plancks strålningslag från Plancks entropisamband.

Resultatet av en direkt insättning av Planckenergin hf i Plancks entropisamband beskrivs vidare nedan i Impulsmomentets Planckekvivalenter.

För den vidare beskrivningen av W-kvoten, hur den slutligen leder till Plancks strålningslag, infinner sig en (närmast) radikal scenändring då — utöver de ovan beskrivna n komponenterna (atomerna) — det avgörande argumentet inträder som säger att varje atom också tvingas uppvisa antalet P=E/(hf) Planckenergikvanta (hf). Nämligen, med följd i att permutationsmatematiken (N!, antalet möjliga positioner) ersätts av den betydligt rikare potensmatematiken (N^N, alla fysiskt möjliga kombinationer). Se utförligt från HUR W BERÄKNAS.

Impulsmomentets Planckekvivalenter

INSÄTTS Planckenergin E=hf och därmed den på Plancks konstant h baserade allmänna verkanskvantumsbaserade värmevariationen (f ) som funktionsbaserad entropivariabel i Plancks entropisamband S=b(lnW) tillsammans med en temperaturenhet (T₀) som variationerna i f refereras till enligt

S = b(lnW) = E/T₀ = hf /T₀

får man mera praktiskt orienterade entropivärden för S.

Via f=T₀S/h och Wiens förskjutningslag (Planckstrålningens derivata, kroppstemperaturen) T=k/l som ger l=k/T med c=lf ges först

f = c/l = cT/k = T₀S/h

Se även sammanställningen i Den verkanskvantumsgrundade Planckentropin.

Med entropin lika med värmekapaciteten (J/°K) per kilo material som värmekapacitiviteten (J/°K/KG),

S/m ....................................... (J/°K)/KG, värmekapacitivitet

kan värmestrålningens Planckfrekvens f skrivas likvärdigt med avseende på kroppens motsvarande idealt homogena atom eller molekylkomponent (m=Uu, u=1,66033 t27 KG, atomära massenheten)

f = c/l = cT/k = T₀S/h = T₀[S/m]m/h = T₀[S/m]Uu/h

Är T=T₀ gäller tydligen

cT/k = T₀[S/m]Uu/h ;

c/k = [S/m]Uu/h ; (× T₀/T)

och man får kroppens ideala (fiktiva, FIC) medelbaserade atomviktskomponent enligt

U_FIC = (ch/ku)/[S/m] ; U = hc₀k^–1u^–1(S/m)^–1

Eller, analogt, kroppens värmekapacitivitet eller specifika värmet från U enligt

S/m = (ch/ku)/U_FIC

= (41283,767)/U_FIC

Eftersom ingen hänsyn tagits till kroppens atomtyp (elektronkonfiguration) och sammansättning (energiupptagande frihetsgrader), kommer värdena man får heller inte att ge någon exakt överensstämmelse för det specifika värmet med motsvarande experimentellt uppmätta värden. Dock ges tydligt orienterande värden. Se exempel nedan.

Jämförande exempel

EXEMPEL (J/°K)/KG — Vatten; atomvikt U=18

——————————————————————————————————

teoretiskt ovan experimentellt från tabell Wikipedia Specific heat capacity

S/m = 2293,5426 2080 +100°C

4181,3 +25°C

2050 –10°C

EXEMPEL (J/°K)/KG — Luft; medelatomvikt U=29

——————————————————————————————————

teoretiskt ovan experimentellt från tabell Wikipedia Specific heat capacity

S/m = 1423,5781 1003,5 ±0°C

1012 +23°C

EXEMPEL (J/°K)/KG — Guld; medelatomvikt U=197

——————————————————————————————————

teoretiskt ovan experimentellt från tabell Wikipedia Specific heat capacity

S/m = 209,56226 129 +25°C

De teoretiska värdena har, som vi ser generellt, ingen vidare rent precisionskopplande analogi till de experimentellt uppmätta värdena. Ser man emellertid till det faktum att det teoretiska värdet använder en FIKTIV MEDELATOM (U_FIC), utan hänsyn till den mera praktiska atomens specifika sammansättning och därmed egenskaper, är de teoretiska resultatvärdena ovan verkligen inte SÅ tokiga ändå. I mycket grova drag ges en hyfsad bild av hur det fungerar. Generellt avtar tydligen S/m med växande U_FIC.

Specifika värmets temperaturberoende

Med föregående separata T (kroppstemperaturen via Wiens förskjutningslag) och T0 (temperaturenheten) insatta fås motsvarande

S/m = (T/T₀)(41283,767)/U_FIC ............................. (J/°K)/KG

Om värmekapaciteten (S/m) generellt är experimentellt uppmätt vid en viss enhetsvärmegrad vid T0, kan alltså sambandet ovan för specifika värmet tolkas med referensen T0 mot varje avvikande temperatur T och som tydligen beskriver att specifika värmet ökar med växande kroppstemperatur och avtar med avtagande kroppstemperatur relativt referenstemperaturen T0.

Dvs., värmekapacitiviteten (analogt entropin S) beskrivs tydligen generellt med ökande kroppstemperatur (T).

Verkanskvantumsgrundade Planckentropin

Med giltigheten av föregående introducerade Plancks entropisamband S=b(lnW) via temperaturenheten T0 (1°K),

S = b(lnW) = E/T₀

= f (h/T₀)

fås direkt proportionalitet mellan entropin (S) och den värmestrålande energins frekvensekvivalent (f ) och som ger kroppskomponenten (atomen) dess värmegrundade arbetspotential; f arbetar på den enskilda kroppens masskomponent (atomen); är frekvensen noll, är också den värmegrundade arbetspotentialen, entropin, noll. Summan av alla enskilda f summerar kroppens totala energiinnehåll E=hf_SUMMA.

Idealt, med hjälp av Wiens förskjutningslag (l=k/T=c/f; f=cT/k) fås då för varje givet f en motsvarande, ideal, ekvivalent »atomens kroppstemperatur» T och som därmed också motsvarar den, i relaterad fysik analoga, värmegrundade arbetspotentialen eller entropin S enligt

S = f (h/T₀) = b(lnW)

= (cT/k)(h/T₀)

= hcT/T₀k

= T(hc/T₀k)

Med given temperaturenhet (T0) finns en ekvivalent bestämd temperatur (T) för varje bestämd energigenomströmningsfrekvens (f ), motsvarande ett bestämt entropivärde (S) med ett bestämt antal energifördelningssätt (W) bland kroppens n materiella komponenter:

entropin förblir entydigt konstant för varje givet tillstånd

Se även sammanställningen i Den verkanskvantumsgrundade Planckentropin.

Verkanskvantumsgrundade entropin

Istället för att betrakta hela mängden komponenter (atomer, molekyler) via hela den kroppens energiinnehåll, kan man med samma energimässiga, kvantitativa, innebörd använda varje komponents (atomens eller molekylens) medelmässiga genomsnittsvärde i alla möjliga mikrotillstånd:

Eller rättare sagt:

För varje kropps bestämda energiinnehåll finns (naturligtvis) bara ett och endast ett motsvarande kvantitativt — inte explicit statistiskt — medelvärde (E/n) som gäller likvärdigt, ekvivalent, för det tillståndets alla likvärdiga mikrotillstånds komponentenergi.

Se även från HUR W BERÄKNAS

DEN IMPULSMOMENTSGRUNDADE PLANCKENTROPIN

Den verkanskvantumsgrundade Planckentropin

S=b(lnW)

Med fortsättning från (närmast ovan) föregående HÄRLEDNING till Plancks entropisamband kan resultatet preciseras mera exakt och uttömmande för fysiken generellt enligt följande.

entropin (S) förblir konstant för varje givet energitillstånd

— i annat fall mister, tydligen, begreppet tillstånd sin entydiga fysikaliska innebörd: noll rörelse: ingen energibaserad variation

h = m_nc₀r_n = 6,62559 t34 ............................. JS, Plancks konstant, se från Planckringen

E = hf .............................................................. J, Planckenergin

Mot varje ljus|Värmebärande utbredning (f=c/l) svarar en bestämd energi (E=hf), se FOTOELEKTRISKA EFFEKTEN

;

S = b lnW = E/T = hfT^–1 ................................. J/°K, Plancks verkanskvantumsgrundade entropisamband

S/b = lnW = (h/b)(fT^–1) » (4,8 t11 °K·S)(fT^–1) ;

Frekvensen f avser summan av alla enskilda komponenters bidrag via totalenergin

energitillstånd i relaterad fysik: fysikaliskt bestämd kvantitet — således med varaktighet under nolltid eftersom fysiken inte innehåller några tillstånd utan enbart variationer, se från tillståndets princip

Beskrivning

Som redan visats i föregående sektion Impulsmomentets Planckekvivalenter kan Plancks entropisamband S=b(lnW) beskrivas mera ingående med hjälp av Planckenergin som ovan.

Speciellt genom S=E/T med differentialformen dS/dE=1/T bildas grunden för en direkt härledning till Plancks strålningslag från Plancks entropisamband S=b(lnW).

Plancks strålningslag grundlägger materiefysikens värmebeskrivning genom att garantera att alla kroppar kontinuerligt utesluter »isolerat system» ur termodynamiken genom att alla kroppar kontinuerligt emitterar och absorberar värmestrålning utan undantag; Varje kropp uppvisar i varje momentan tidpunkt en (idealt) bestämd energi vid en (idealt) bestämd temperatur, och som (därmed) ingår som definitionsgrund i kroppens partikulära sammansättning av atomer och molekyler med avseende på de enda tillgängliga positioner (xyz) och rörelsemängder (mv) som finns att välja på för den kroppen med det energiinnehållet vid den temperaturen enligt Plancks entropisambad.

Med avgränsat exemplifierad, konkret praktisk, tillämpning enligt Plancks entropisamband S=b(lnW) gäller med andra ord:

varje fysikaliskt entydigt bestämt tillstånd inom en bestämd kropp

— i varje nu och därmed

(ENLIGT RELATERAD MATEMATIK, se från differentialbegreppet med punkten eller differentialen, NU, och intervallet som strängt skilda begrepp)

på bas av en bestämd mängd energi, temperatur, volym och tryck

— motsvaras av ett lika entydigt bestämt W-tal, analogt en entydigt bestämd uppsättning av makrotillståndets inre energifördelningssätt (mikrotillstånd), och därmed av ett entydigt bestämt S-tal eller entropi, se särskilt i Härledningen till Plancks strålningslag från Plancks entropisamband S=b(lnW).

Med andra ord:

entropin (S, den värmegrundade arbetspotentialen) förblir konstant för varje givet tillstånd.

;

S = b lnW = E/T = hfT^–1 .................................. Plancks verkanskvantumsgrundade entropisamband

S/b = lnW = (h/b)(fT^–1) » (4,8 t11 °K·S)(fT^–1) ;

Sambanden klargör alltså med grund i Plancks strålningslag:

Mot varje frekvens (f ) som sammanhänger med en viss Planckenergi E=hf — en kropps värmestrålning (Planckstrålningens derivata, Wiens förskjutningslag l=k/T, k=2,898 t3 M°K, f=c/l) — svarar, idealt, en bestämd genomströmningstemperatur (T); Varje bestämd temperatur T garanterar för varje givet energitillstånd (W=e^S/b) att också Planckentropin (S) — antalet likaberättigade, idealt frysta momentana energitillståndsbilder (likaberättigade mikrotillstånd) över materieelementens positioner och rörelsemängder — förblir konstant.

Det betyder att fysiken per termodynamik (all verksamhet som inbegriper värme) FÖRST genom just Plancks strålningslag blir fullständigt förklarad och beskrivbar och därmed GILTIG — inte förr.

Först år 1900 (December) lyckades Max Planck (Nobelpriset i fysik 1918) avtäcka den efter honom uppkallade s.k. svartkroppsstrålningslagen eller Plancks (allmänna) strålningslag (se Plancks original). Plancks strålningslag kom som en befriande dusch över hela den dåtida vetenskapsvärlden; Seger från ruta ett, skulle man kunna säga [‡3][ref. Max Planck från 1912, The Theory of Heat Radiation] — men också med vissa förbehåll, inte minst från Planck själv [‡1] [‡2].

MIKROTILLSTÅNDENS LIKABERÄTTIGANDE

Ytterligare klargörande beträffande

MIKROTILLSTÅNDENS LIKABERÄTTIGANDE

MIKROTILLSTÅNDETS INNEBÖRD

Varje stel eller fryst tillståndsbild som uppvisar en särskild översiktsbild med särskilda positioner och rörelsemängder (för atomer och molekyler) kallas konventionellt ett särskilt mikrotillstånd. Alla mikrotillstånd är — med en given kropps momentant givna energiinnehåll — likvärdiga ur energisynpunkt. Summan av alla likaberättigade mikrotillstånden definierar hela makrotillståndet (S): en total BILD över alla möjliga (likaberättigade) kombinationer (xyz)(mv), analogt (materie-) tillståndets värmegrundade arbetspotential.

— Genom Clausius antagna grundsamband (S=E/T, J/°K) och Plancks (i konventionell litteratur ofta refererad som Boltzmanns redan etablerade) enkla s.k. entropisamband S=b(lnW), ges alltså här direkt ekvivalens mellan begreppen tillståndets värmegrundade arbetspotential och entropi.

För begreppet MIKROTILLSTÅND i modern akademi används i stort sett samma beskrivningsform, frånsett inslaget av STATISTIK och som inte finns med i den relaterade fysikens framställningssätt. Se utförligt i W finns inte i statistiken. Till jämförelse ges nedanstående citatutdrag:

”In statistical mechanics, a microstate describes a specific detailed microscopic configuration of a thermodynamic system that the system visits in the course of its thermal fluctuations.”,

@INTERNET Wikipedia Microstate (statistical mechanics) 2009-12-12

Min översättning:

I statistisk mekanik beskriver ett mikrotillstånd en specifikt detaljerad makroskopisk konfiguration hos ett termodynamiskt system [t.ex. atomernas lägen i en innesluten gas] som systemet besöker i loppet av dess termiska fluktuationer.

Entropi (S) för en viss kropp blir ENLIGT RELATERAD FYSIK kroppens förmåga att utföra arbete

— men den definitionen finns inte i modern akademi

det finns (frånsett framställningen här Feb2010) ingen sådan beskrivning på webben

entropi = värmegrundad arbetspotential ............... förmågan att utföra arbete

S = E/T ........................................................... Clausius Grundform (S=Q/T)

= k = bN ....................................................... Allmänna gaslagens konstanter

S = b(lnW) ...................................................... Plancks entropisamband

b, Boltzmanns konstant (den idealt fundamentala materiegasbollens fundamentala värmeenergiinnehåll 1,38 t23 J/°K), eller fundamentala enheten för värmekapacitet

N, Loschmidts tal (N=2,6869722 T25 som kopplar till det mera namnkända Avogadros tal, se utförligt i Konstanterna i Allmänna gaslagen)

W, totala antalet mikrotillstånd för alla positioner (xyz) med alla rörelsemängder (mv)

Med förmågan (potentialen) att utföra arbete (E=Fd=mad) menas således ENLIGT RELATERAD FYSIK i termodynamiken (värmeläran)

en ekvivalent värmegrundad arbetspotential S=b(lnW) i det speciella fallet med Plancks entropisamband och i det allmänna fallet med Clausius klassiska entropisamband S=Q/T,

alltså entydigt likvärdigt med begreppet entropi.

Därmed råder entydig ekvivalens mellan begreppen entropi och värmegrundad arbetspotential. Med andra ord:

Varje arbetande process kräver tillgång till ett energikapital, en toppvärdesentropi, för att kunna utföra processen och under vilken entropin, analogt den tillförda värmemängden, den värmegrundade arbetspotentialen, entydigt avtar från högre till lägre.

Se PRAKTISKA EXEMPEL.

Planckentropin S=b(lnW) avtar med växande ordning mot S=0 vid 0°K

Samma formella mening tillämpas också i modern akademi — men med andra preferenser: ordningen avtar — oordningen ökar — med större avstånd från 0°K

Notera att entropin i grundfallet S=b(ln[W=1])=b(0)=0 betyder en perfekt ordnad kristall: noll rörelse. Entropins alla nivåer över detta idealläge kan i motsvarande mening betraktas som ’oordnad’ med växande S-värde, analogt högre värmegrad. Men, återigen, den innebörden av entropibegreppet blir ändamålsenligt positiv eftersom varje arbete som utförs tvunget måste utföras på avtagande S, analogt avtagande entropi med sjunkande värmegrad från ett initiellt toppvärde, se PRAKTISKA EXEMPEL. Alltså ’ökande ordning’: all verksamhet i materiefysiken är, tydligen, ändamålsenlig med avtagande oordning=entropi;

Allt (naturligt) arbete resulterar i växande ordning = högre ändamålsenlighet.

Se PRAKTISKA EXEMPEL.

Isolerat system i termodynamisk mening finns inte i fysiken

Men hela den moderna akademins lärosystem i ämnet går ut på att ha formulerat »termodynamikens andra huvudsats» efter den premissen, se citat.

Se även EXEMPLEN I WIKIPEDIA.

Plancks strålningslag betyder att alla kroppar värmeläcker: det finns inga isolerade system i fysiken i termodynamisk mening. Se även illustrerat i Universums strålning går mot noll.

Därmed står det också klart att den moderna akademins »termodynamikens andra huvudsats» i nutida tappning inte gäller i relaterad fysik: den formuleringen är, tydligen, en pseudofysik.

Det som däremot helt säkert gäller i den relaterade fysikens mening är, helt säkert, den klassiska, ursprungliga, klara innebörden från Clausius framställningar (1854-1862):

värme flyter alltid från varmt till kallt.

Men det uppmärksammades redan tidigt i UNIVERSUMS HISTORIA i samband med K-cellens värmefysik. Se särskilt allmänna tillståndslagen.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Plancks entropisamband

Se även utförligt från Den relaterade fysikens härledande förklaring till Plancks entropisamband

Plancks entropisamband S=b(lnW) — inte Boltzmanns

——————————————————————————————————————

2010II6

GENOMBROTTET

Boltzmanns teori omtolkades av Max Planck på dennes eget icke-sannolikhetsmässiga sätt, citat nedan, och som ledde honom till det som numera kallas för »Boltzmanns entropisamband» S = b(lnW).

— Men den S-formen är Plancks samband och entropibegrepp, citat nedan, även särskilt i Plancksambandets särskilda citatreferens, inte Boltzmanns.

(Se Boltzmanns H-teorem, vilket strider mot Plancks entropisamband — enligt Plancks strålningslag — se särskild beskrivning från Plancks strålningslag eliminerar Boltzmanns H-teorem).

Noggrann citatgenomgång

”To achieve his fundamental derivation, Planck had to make what was, for him, a major concession. He had to yield ground to some of the work that Boltzmann had done. At the same time, he wasn't prepared to give up his belief that the entropy law was absolute, so he reinterpreted Boltzmann's theory in his own nonprobabilistic way. This was a crucial step, and it led him to an equation that has since become known as the Boltzmann equation, which ties entropy to molecular disorder.”,

THE INTERNET ENCYCLOPEDIA OF SCIENCE David Darling ”up to date”

http://www.daviddarling.info/encyclopedia/Q/quantum_theory_origins.html

Darling ger tyvärr inga explicita källreferenser.

”Although Boltzmann is often credited with inventing the entropy equation (1) [S=klnW], and k is now called ”Boltzmann’s constant,” Planck was the first to recognize the fundamental importance of both the equation and the constant.”,

Great physicists: the life and times of leading physicists from Galileo to Hawking

Oxford University Press, William H. Cropper 2002, s233n (Google BokSökning)

Min översättning:

Fastän Boltzmann ofta krediteras med att ha uppfunnit entropiekvationen S=klnW, och att k nu kallas ”Boltzmanns konstant”, var Planck den förste att inse den fundamentala betydelsen av både ekvationen och konstanten.

Mera konkret:

”In November 1900 Planck realized that his new entropy expression was scarcely more than an inspired guess. To secure a more fundamental derivation he now turned to Boltzmann's probabilistic notion of entropy that he had ignored for so long. But although Planck now adopted Boltzmann's view, he did not fully convert to the Austrian physicist's thinking. He remained convinced that the entropy law was absolute - and not inherently probabilistic - and therefore reinterpreted Boltzmann's theory in his own non-probabilistic way. It was during this period that he stated for the first time what has since become known as the "Boltzmann equation" S = k log W, which relates the entropy, S, to the molecular disorder, W.

”,

MAX PLANCK: THE RELUCTANT REVOLUTIONARY Dec 1, 2000

http://physicsworld.com/cws/article/print/373

Man måste logga in på PhysicsWorld för att få tillgång till artiklarna från GoogleSökningen — men det är helt gratis

KOMMENTAR:

”the entropy law” avser naturligtvis »termodynamikens andra huvudsats» — vid tiden omkring 1800-talets slut då Planck genomförde sina mest banbrytande arbeten och med innebörden:

värme går alltid från varmt till kallt, se uppslaget nedan.

— Nutida skribenter förbiser [tydligen, alltid den] distinktionen mellan nuvarande tolkning/lydelse och den aktuella historiens synsätt, vilket garanterat gör ANALYSEN AV sammanhanget helt obegripligt för en icke redan insatt.

UPPSLAG:

”Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law during 1850, in this form: heat does not flow spontaneously from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).”,

@INTERNET Wikipedia Second law of thermodynamics, History 2010-02-07

Exakt:

”In 1862, Clausius stated what he calls the “theorem respecting the equivalence-values of the transformations” or what is now known as the second law of thermodynamics, as such:

The algebraic sum of all the transformations occurring in a cyclical process can only be positive, or, as an extreme case, equal to nothing.

”,

”In 1865, Clausius gave irreversible heat loss, or what he had previously been calling "equivalence-value", a name:[5][6]

”,

@INTERNET Wikipedia History of entropy, 1862 definition 2010-02-07

Se vidare från Clausius framställning.

Wikipediakällan ovan [@INTERNET Wikipedia History of entropy] påstår vidare att Boltzmann införde sambandet

”S = kB ln Ω” år 1877, men ingen referens ges — och de referenser som finns här påstår att det var Planck som gav den formen 1901.

Jämför (om Boltzmann):

”His formula, ∫(dq/T) = 2Ω/3, is, however, better known in the form S = k log W, which Max Planck gave it in 1901.

”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

e-logaritmen (ln eller log_e eller ^elog) är inte samma som 10-logaritmen (log) — i vissa sammanhang används en generaliserad form för bägge (”log”);

I ett rent historiskt beskrivande perspektiv där frågan gäller klarhet i källreferenserna, finns alltså enbart med ovanstående citatdelar ”kB ln” och ”k log” ingen möjlighet att avgöra vad som kommer från vem, om den äldre beteckningen var ”log” och ”ln” är en nyare omskrivning, eller om förklaringen har någon annan källgrund.

Se Plancksambandets särskilda citatreferens (längre ner): Citatkällan

ENCYCLOPEDIA OF HUMAN THERMODYNAMICS

rubricerar sin artikel med ”S = k ln W”, källan påstår, med referens, att ”the formula”, alltså den formen, infördes 1901 av Max Planck — med hänvisning till Planck ”Specifically, Planck explains that” enligt ”S = k log W + const”.

Men log (10log) och ln (elog) är inte samma sak — men vi vet inte om också källförfattaren skiljer på dessa delar eller ’generaliserar’ med ’log’ för bägge.

Plancks log

Se dock explicit ett nyligen upphittat originaldokument från Planck år 1901 i Plancks Original (s3ö): Planck skrev precis som ovan

— S = k log W — och vilket skrivsätt log Planck klargör (s6n samband11) enligt

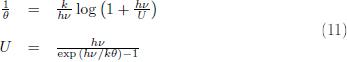
— vilket bevisar (exp skrivs förkortat för e^) det formella betraktelsesättet: Plancks entropisamband lyder alltså, enligt Max Planck som ovan

S = k ^elog W = k ln W

Dvs., i klartext: Planck härledde strålningsekvationen (Plancks strålningslag) från Planckentropin S=b(lnW), b Boltzmanns konstant 1,38 t23 J/°K.

Citatet ovan mera fullständigt:

”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

Detaljen ovan

”His formula, ∫(dq/T) = 2Ω/3”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

som tydligen bara ges en översiktlig summarisk referens som associerar till ”Oct 11 1877” och ”On the Relation …”, har dock en liknande, något annorlunda formulerad referens i webbkällan nedan:

”Boltzmann was, however, already back in Graz, as professor of experimental physics, when this momentous breakthrough came in the history of physics. In 1877 he submitted two memoirs to the Academy of Sciences in Vienna. In the first of these, presented on Jan. 11, 1877, "Remarks on Some Problems of the Mechanical Theory of Heat," Boltzmann made an incisive analysis of the formula ∫( dQ/T ) ≥ 0 and argued that its validity was not based on the inherent laws of nature but rather on the choice of the initial conditions.”,

REFERENCE PUBLICATIONS — Ludwig Boltzmann, UXL Newsmakers, (2005)

http://findarticles.com/p/articles/mi_gx5221/is_2005/ai_n19135100/

Sambandsteckningarna i de bägge webbkällorna är identiska ”∫(dq/T)” och artiklarna refererar till samma epok (1877) i Boltzmanns arbeten.

DÄREMOT

”In 1877, Ludwig Boltzmann formulated the alternative definition of entropy S defined as:

S = kB ln Ω”,

@INTERNET Wikipedia History of entropy, Statistical thermodynamic views 2010-02-18

http://en.wikipedia.org/wiki/History_of_entropy

rimmar Wikipediaartikeln illa, närmast ovan, med föregående två samstämmiga, inre referenter; Med tillägget att Wikikällan inte ger det påstådda sambandet från 1877 någon källreferens är det tydligt att Wikiartikelns påstående är felaktigt.

Det är, tyvärr, också — och tydligen fortfarande — ett av grundproblemen med Wikipedia: olika ”experter”, i tyvärr alltför invanda diskussionsrum, kastar ur sig mängder med påståenden som visserligen, någonstans i historien har en källform, men vars verkliga Case History är mera detaljerad än vad experten för tillfället har koll på i det varierande munvädret (vilket gör det verkliga fallet betydligt mera intressant).

Jämför Plancksambandets särskilda citatreferens längre ner:

sambandsformen S = k ln W framkom först 1901.

Planck om Boltzmanns konstant

Max Planck (Nobelpriset i fysik år 1918) skriver själv dels angående Boltzmanns konstant (k:et ovan efter likhetstecknet)

och dels angående Boltzmanns inflytande på utvecklingen av sambanden som ledde till Plancks strålningslag (utan att gå in på ovan antydda detaljer) i sin nobelföreläsning från år 1920:

”However, even if the radiation formula should prove itself to be absolutely accurate, it would still only have, within the significance of a happily chosen interpolation formula, a strictly limited value. For this reason, I busied myself, from then on, that is, from the day of its establishment, with the task of elucidating a true physical character for the formula, and this problem led me automatically to a consideration of the connection between entropy and probability, that is, Boltzmann's trend of ideas; until after some weeks of the most strenuous work of my life, light came into the darkness, and a new undreamed-of perspective opened up before me.”,

MAX PLANCK, NOBEL LECTURE JUNE 2 1920

The Genesis and Present State of Development of the Quantum Theory

http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html

Det betyder i klartext (som man redan kunde förmoda — om nu också uppgifterna verkligen är korrekta) att det i grund och botten är Max Planck, INTE Ludwig Boltzmann, som ska betraktas som upphovsmannen till sambandets väsentliga sakinnehåll (och som ovan, intygat på erkänt, inspirerat, uppslag från Boltzmann) enligt

(k här ersatt av b för Boltzmanns konstant b=1,38 t23 J/°K, samt som i ovanstående klarlagda citatutdrag från Plancks framställning att Planck i sitt samband från 1900-1901 använde e-logaritmen för ”log”, inte 10-logaritmen)

S = b(lnW) ........................... J/°K, Planckentropin, Plancks entropisamband

Sambandet ovan rimmar, nämligen (också), ILLA med Boltzmanns H-teorem som, ju, gör gällande att entropi är FÖRÄNDERLIG inom ett visst energiinnehåll, Boltzmanns väsentliga poäng och H-teoremets syfte [‡7.1], nämligen att påvisa ’entropins irreversibla ökning i isolerade system’ (som inte befinner sig i jämvikt) (och som — tydligen — föranledde ändringen av formuleringen i den äldre termodynamikens andra huvudsats, se från Ursprunget till omformuleringen).

Sambandsformen S=b(lnW) är alltså, verkligen, inte något original från Ludwig Boltzmann utan istället från Max Planck.

Plancks original från 1901

2010II18

Originaldokumentet från Max Planck år 1901

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s3

http://bourabai.kz/articles/planck/planck1901.pdf

Planckenergin E=hf — upphovet

På sidan 6 källan ovan införs E=hf med Plancks beteckning ε=hv enligt

” … we then find that the energy element ε must be proportional to the frequency v, thus: ε=hv”.

— Planck skrev uttryckligen exakt S_N = k log W + const:

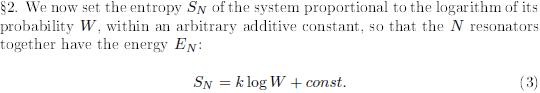
”§2. We now set the entropy S_N of the system proportional to the logarithm of its probability W, within an arbitrary additive constant, so that the N resonators together have the energy E_N:

S_N = k log W + const. (3)

”,

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s3

http://bourabai.kz/articles/planck/planck1901.pdf

Planck ger ingen härledande beskrivning, han bara inför sambandsformen i (3), och skriver sedan vidare, direkt efter, samma sida 3ö:

”In my opinion this actually serves as a definition of the probability W, since in the basic assumptions of electromagnetic theory there is no definite evidence for such a probability. The suitability of this expression is evident from the outset, in view of its simplicity and close connection with a theorem from kinetic gas theory.[8]”,

”8 L. Boltzmann, Proceedings of the Imperial Academy of Science,

Vienna, (II) 76 (1877 ), p. 428.”

Planck säger alltså (på stället) ingenting om huruvida (den här uppmärksammade försmädliga frågan om originaldetaljerna) ”proportional to the logarithm” ska avse e-logaritmen eller 10-logaritmen (eller någon annan bas). Dock ges svaret på frågan i (samband 11 sidan 6) Plancks framställning,

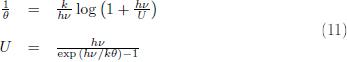
On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s6

http://bourabai.kz/articles/planck/planck1901.pdf

— vilket bevisar (exp skrivs förkortat för e^) det formella betraktelsesättet: Plancks entropisamband lyder alltså, enligt Max Planck som ovan

S = k elog W = k ln W

Dvs., i klartext: Planck härledde strålningsekvationen (Plancks strålningslag) från Planckentropin S=b(lnW), b Boltzmanns konstant 1,38 t23 J/°K.

Därmed är frågan fullständigt besvarad: Det är S=b(lnW) som gäller.

Utöver ovanstående:

Det enda, uttydbara, som tycks komma fram i försöken att få ut vad Planck refererar till ovan från Boltzmann 1877 ges från föregående

”His formula, ∫(dq/T) = 2Ω/3”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

Det finns flera (hutlöst MÅNGA »Boltzmann distribution equation 1877») webbkällor som också refererar Plancks referens till Boltzmanns Proceedings från 1877 — men som (de mera akademiskt orienterade av dessa) nekar direkt åtkomst. Ovanstående från Answers (och andra med samma referens) verkar ännu (Feb2010) vara enda bidraget.

Då uppstår frågan:

— Vad gör Plancks entropisamband på Boltzmanns gravsten?

— Det moderna akademiska etablissemanget fick dåligt samvete i samband med Boltzmanns tragiska självmord 1906 då man under i stort sett hela hans arbetsperiod mer eller mindre behånat honom för hans banbrytande men då ännu illa erkända uppfattning att materien bestod av atomer och molekyler. Verkligen. Så, man beslöt, tydligen, att bättra på oddsen för sitt dåliga samvete i efterhand med att dels sätta upp en präktig bronsbyst av Boltzmann vid hans grav — och dels rista in Plancks entropisamband, inte Boltzmanns, på gravstenen för att understryka respekten och, framförallt, hedern: Äran av att ha slitit ihjäl sig för att få de andra dödskallarna att åtminstone uppvisa vertikal orientering vid anblicken av atomismens matematiska grunder. Boltzmann, ratad och undanskuffad, banade vägen genom den taggiga häcken, Planck formulerade sammanhangen. Min tolkning. Garanterat utan andra referenser. Se även i Citatsamling.

Då kan i varje fall jag, med referens till ovan utforskade detektivgrunder (med särskilt stort tack riktat till genombrottet med uppslag från David Darling, webbkällan ovan) gå i väl relaterbart godo för att sambandet S=b(lnW) med dess entydiga entropimening i direkt harmoni med Plancks strålningslag

— som just eliminerar »isolerade system» ur fysiken i termodynamisk mening och därmed direkt punkterar Boltzmanns H-teorem

— är Max Plancks entropibegrepp, inte Ludwig Boltzmanns;

Se även i Verkanskvantumsgrundade entropin.

Det är tydligen Plackentropin S=b(lnW) saken gäller och som uttrycker principiellt samma sak (värmekapacitet), samma entropisambandsFORM, som Clausius kvantitativt grundade sambandsform (S=Q/T): I RELATERAD FYSIK värmegrundad arbetspotential; en bestämd entropinivå (S) för en bestämd energi (W); entropin avtar med varje utförd arbetsprocess — utan undantag i alla fysikens processer, se PRAKTISKA EXEMPEL, även taget för universum som helhet enligt c0-kroppen med den centrala periodiskt återkommande K-cellens värmefysik; Allt återvänder till ursprunget — för att sedan börja ett nytt kretslopp. Se utförligt från Hur K-cellen utvecklas. Se även från Massfysikens nollentropi — »begynnelsen».

HUR »Boltzmanns entropibegrepp» tydligen inte ansluter till Plancks entropisamband beskrivs utförligt från Boltzmanns H-teorem (den första atomistiskt-matematiska uppställningen, och som tydligen startade hela debatten om inga andra dolda källverk kommer i dagen).

— OCH vilket därmed introducerar oss för den redan antydda allmänna språkförbistringen i ämnet entropi. Det är, av allt att döma, just begreppet »isolerat system» som givit upphov till upploppet.

Se även mera utförligt i ENTROPIBEGREPPETS SPRÅKFÖRBISTRING.

Se även nytillkommen upphittad referens (Apr2010) i Uppfinningen av Isolerat system 1858.

Om man letar på webben (Feb2010) på ordet entropi (eng. entropy) sammanhänger träffarna (nästan) uteslutande med namngivning av personen Boltzmann.

Se även från S = b(lnW) är Plancks entropisamband — inte Boltzmanns.

Sambandet S=b(lnW) som sådant kommer alltså EGENTLIGEN från Max Planck (1901), inte från Ludwig Boltzmann — men många webbkällor kallar det typ »Boltzmann entropy», »Boltzmann’s formula». Det finns dock en del undantag:

”The iconic terse form of the equation S = k log W on Boltzmann's tombstone is in fact due to Planck, not Boltzmann.”,

@INTERNET Wikipedia Boltzmann constant 2010-02-05

Min översättning.

Den ikoniska kortformen för ekvationen S = k log W på Boltzmanns gravsten kommer i själva verket från Planck, inte Boltzmann.

” History

Although Boltzmann first linked entropy and probability in 1877, it seems the relation was never expressed with a specific constant until Max Planck first introduced k , and gave an accurate value for it (1.346 × 10⁻²³ J/K, about 2.5% lower than today's figure), in his derivation of the law of black body radiation in 1900–1901.[2] Before 1900, equations involving Boltzmann factors were not written using the energies per molecule and Boltzmann's constant, but rather using a form of the gas constant R, and macroscopic energies for macroscopic quantities of the substance. The iconic terse form of the equation S = k log W on Boltzmann's tombstone is in fact due to Planck, not Boltzmann.

As Planck wrote in his Nobel Prize lecture in 1920,[3]

This constant is often referred to as Boltzmann's constant, although, to my knowledge, Boltzmann himself never introduced it — a peculiar state of affairs, which can be explained by the fact that Boltzmann, as appears from his occasional utterances, never gave thought to the possibility of carrying out an exact measurement of the constant.

This "peculiar state of affairs" can be understood by reference to one of the great scientific debates of the time. There was considerable disagreement in the second half of the nineteenth century as to whether atoms and molecules were "real" or whether they were simply a heuristic, a useful tool for solving problems. Nor was there agreement as to whether "chemical molecules" (as measured by atomic weights) were the same as "physical molecules" (as measured by kinetic theory). To continue the quotation from Planck's 1920 lecture:[3]

Nothing can better illustrate the positive and hectic pace of progress which the art of experimenters has made over the past twenty years, than the fact that since that time, not only one, but a great number of methods have been discovered for measuring the mass of a molecule with practically the same accuracy as that attained for a planet.

”,

@INTERNET Wikipedia Boltzmann constant 2010-02-05

Plancksambandets särskilda citatReferens

S = k ln W;

”The formula is a modified or reduced form of Austrian physicist Ludwig Boltzmann's H-function and was first put in this shorthand form by German physicist Max Planck in his 1901 paper “On the Law of Distribution of Energy in the Normal Spectrum.” [1] Specifically, Planck explains that the entropy SN of the system [resonator] is proportional to the logarithm of its probability W, within an arbitrary additive constant:

S = k log W + const

”,

ENCYCLOPEDIA OF HUMAN THERMODYNAMICS kronologisk uppgift saknas

http://www.eoht.info/page/S+%3D+k+ln+W

Se även citatdelarna från början i Plancks entropisamband

Boltzmanns ursprungliga samband

BOLTZMANNS URSPRUNGLIGA ENKLA ENTROPISAMBAND

enligt nedanstående källa skulle ha varit

∫(dq/T) = 2Ω/3

Boltzmann:

”His formula, ∫(dq/T) = 2Ω/3, is, however, better known in the form S = k log W, which Max Planck gave it in 1901.

”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

2010II9

Upphittat/klarlagt tillsammans med föregående ovanstående citerade ”Boltzmann's H-function”:

”Boltzmann further introduced the H-functional (denoted E in the 1872 paper,

but later widely called H, including by Boltzmann):

H[f_t] = ò f (r; v; t) ln f (r; v; t)d³rd³v (2)

”,

Boltzmann’s H-theorem, its limitations, and the birth of (fully) statistical mechanics,

Harvey R. Brown and Wayne Myrvold, September 8 2008, s4

http://philsci-archive.pitt.edu/archive/00004187/01/Reversibility08.pdf

DET ÄR UPPENBARLIGEN NÅGOT HELT ANNAT DET ÄN PLANCKS ENTROPISAMBAND

S = b lnW ...................................................... J/°K, Plancks entropisamband

således modifierat och utvecklat med inspirerad grund i Boltzmanns (garanterat erkänt besvärliga) atomistiska H-funktion (från Boltzmanns H-teorem 1872)

H[f_t] = ò f (r; v; t) ln f (r; v; t)d³rd³v .............. Boltzmanns H-funktion

Jämför — beträffande (den fullständiga) innebörden i närmast ovanstående:

”Although Boltzmann’s H-Theorem is 135 years old, presentday mathematics is unable to prove it rigorously and in satisfactory generality.”,

”For the moment we have to live with this shortcoming.”,

H-Theorem and beyond: Boltzmann’s entropy in today’s mathematics, C´edric Villani (2007)

http://www.umpa.ens-lyon.fr/~cvillani/Cedrif/P11.Boltzmann.pdf

Min översättning:

Fastän Boltzmanns H-teorem är 135 år gammalt, är dagens matematik oförmögen att bevisa det rigoröst och med tillfredsställande allmängiltighet.

För tillfället måste vi leva med detta tillkortakommande.

Kommentar till Plancks original

s2ö:

”Thus another condition must now be introduced which will allow the calculation

of S, and to accomplish this it is necessary to look more deeply into the meaning of the concept of entropy.”,

s2n:

”If amplitude and phase both remained absolutely constant, which means completely homogeneous vibrations, no entropy could exist and the vibrational energy would have to be completely free to be converted into work.”

s3mö:

”Moreover, it is necessary to interpret UN not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts.”,

Se Plancks Original

Med uppfattningen att materien består av diskret avgränsade materieelement

(atomer, molekyler — vilket var Boltzmanns avgörande arbetsbidrag)

reduceras tydligen hela problemet med bestämningen av en kropps värmegrundade arbetspotential — entropin S — till en bestämning av den aktuella kroppskomponentens (atomens) värmegenomströmningsenergi (E=hf);

Grunderna i dessa tankegångar beskrivs i citat nedan av banemannen själv på området, Max Planck av år 1901 (här utan svensk översättning):

Planck, s1;

”… the principle persists that the law of energy distribution in the normal spectrum is completely determined when one succeeds in calculating the entropy S of an irradiated, monochromatic, vibrating resonator as a function of its vibrational energy U. Since one then obtains, from the relationship dS/dU = 1/q, the dependence of the energy U on the temperature q, and since the energy is also related to the density of radiation at the corresponding frequency by a simple relation,[5] one also obtains the dependence of this density of radiation on the temperature. The normal energy distribution is then the one in which the radiation densities of all different frequencies have the same temperature.”

;

”Consequently, the entire problem is reduced to determining S as a function

of U, and it is to this task that the most essential part of the following analysis

is devoted.”,

Se Plancks Original

Den enkla lösningen blev, med de nu för oss redan kända sambandsgrunderna, lika med Impulsmomentets Planckekvivalenter

S = b(lnW) = E/T₀ = hf /T₀

Entropin (S) — i relaterad fysik den värmegrundade arbetspotentialen — hos Plancks Boltzmanninspirerade ’vibrator’ eller ’resonator’ — [Se särskild beskrivning i Masskomponeten h grundlägger materiefysiken, om ej redan bekant] beror, räknat från en given temperaturnivå (T0) eller med referens till en given temperaturenhet (T0), enbart på värmestrålningens frekvens (f ). Summan av alla atomernas enskilda bidrag ger kroppens totala entropi (S_n = n · S).

[I Plancks Original ges analogin på sidan 2, sambanden (1) och (2)].

Med andra ord: entropin (S) förblir konstant för varje givet tillstånd (f ) — värmestrålningens frekvens vid en viss unik tidpunkt, en viss kropps bestämda energiinnehåll.

Se även (mera) sammanfattande från Verkanskvantumsgrundade entropin.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

TIDENS PIL

Se även från Åldrandets princip

För att ENLIGT RELATERAD FYSIK beskriva saken konkret

— från den enda minutiöst relaterbara referens som tycks finnas:

K-cellen

Se även i ALLMÄNNA TRANSIENTFUNKTIONEN

K-cellens tillståndsdiagram, se utförligt från K-cellens värmefysik

Varje tidpunkt (nu) i K-cellens historia, universums expansion, innehåller ett, endast ett och ingenting annat än endast ett enda unikt momentant — differentiellt— tillstånd.

Expansionen med variationerna i elektriska, magnetiska och gravitella fält garanterar i sträng mening att den unika tillståndsbilden inte någonsin återkommer. Aldrig.

Se även i Åldrandets princip.

entropin (S)

den värmegrundade arbetspotentialen

förblir konstant för varje givet tillstånd

— i annat fall mister, tydligen, begreppet tillstånd sin entydiga fysikaliska innebörd: noll rörelse: ingen energibaserad variation

Se även utförligt från Plancks verkanskvantumsgrundade entropisamband och tillståndsbegreppet.

Boltzmanns H-teorem, som tydligen helt föregick (bortsåg ifrån) vad varje termodynamiskt materiellt system emellertid måste iaktta, nämligen Plancks strålningslag och därmed Plancks (verkanskvantums-)entropi, Plancks konstant (h), hade redan från ruta ett, därmed, eliminerat den praktiska fysiken ur teoremets förmodade praktiska förutsättningar: gasens kontinuerliga flöde av emission och absorption, eliminerat av den förmodade detaljen »isolerat system», det finns inget sådant i termodynamisk mening i fysiken.

Den detaljen har (alltså) fortsatt att ligga OBEMÄRKT i modern akademi ända sedan Plancks dagar. Först med en mera ÖVERGRIPANDE analys av fysiken — typ UNIVERSUMS HISTORIA ENLIGT RELATERAD FYSIK och som ställer upp en helt annan grund för fysikbeskrivningen i kraft av ATOMKÄRNANS HÄRLEDNING — infinner sig en avtäckande ridå, tydligen.

Se även vidare beskrivning i Plancks strålningslag eliminerar Boltzmanns H-teorem.

Med andra ord: entropin (S) förblir konstant för varje givet tillstånd.

Med kännedom om bakgrundshistorien är den meningen som en direkt riktad, fruktansvärd, dementi rakt i ansiktet på modern akademi där det istället hävdas:

entropin i ett isolerat system ökar

Se även EXEMPLEN I WIKIPEDIA.

I härledningen till Plancks entropisamband S=b(lnW) (med grund i allmänna gaslagen) — materiefysiken med generatrisen T®p via samhörigheten med Clausius S=E/T — ingår villkoret för giltigheten av den härledda Planckentropin S=b(lnW) att en bestämd energi (E) gäller entydigt för en bestämd temperatur (T). Se särskilt i Plancks entropisamband från Allmänna gaslagen.

Eftersom alla kroppar värmeläcker, se Hur värmen avtar med tiden, finns heller ingen fysisk grund för begrepp om kroppar i någon tidsmässig utsträckning som INTE värmeläcker: alla kroppar värmeläcker.

Med andra ord (dementi nummer två):

Plancks entropisamband S=b(lnW) kopplar INTE till (något realt i tiden utsträckt befintligt) »isolerade system»;

Boltzmanns H-teorem (entropin i ett isolerat system [som inte befinner sig i jämvikt] växer) är följaktligen fysikaliskt irrelevant — OM det är Planckentropins S-form som gäller i entropibegreppets definition. I annat fall är det fråga om helt olika entropibegrepp, med inbördes olika preferenser.

Isolerade system förekommer bara idealt i analysen i momentana tidpunkter: situationsbilder under nolltid: idealt, obegränsat, utsträckta fysiska rum med kroppar som uppvisar bestämda kvantiteter över begränsade eller obegränsade rum.

Med andra ord (dementi nummer tre) och i själva verket:

Det finns — termodynamiskt, Plancks strålningslag som ovan — inga »isolerade system» i fysiken: Plancks entropisamband kopplar inte till »termodynamikens andra huvudsats».

Och, följaktligen (dementi nummer fyra):

Entropibegreppet (inte matematiken) är, tydligen, felaktigt formulerat i modern akademi:

Entropibegreppet har, tydligen, inte den I RELATERAD MENING — med matematiksambanden orörda — innebörd som påstås i den moderna akademins lärosystem — dessutom, tydligen, långt ifrån.

RELATERAD FYSIK:

Entropi betyder värmegrundad arbetspotential S = E/T = b(lnW) = hf/T och grundas på Plancks entropisamband — utan association till »statistik» eller »sannolikhet». Se särskilt i W finns inte i statistiken och från entropibegreppets innebörd. Entropi måste alltid tillföras en kropp för att arbete ska kunna utföras, se PRAKTISKA EXEMPEL: entropin avtar alltid med utfört arbete: ordningen mot den perfekta kristallens perfekta ordning vid 0°K ökar alltid för alla processer med universums expansion med början från ett initiellt toppvärde för S: Jorden utvecklas avsvalnande på en initiellt hög kroppssmälta, för att exemplifiera närmast. Se även utförligt i PRAKTISKA EXEMPEL. För hela universum, se K-cellen:

Entropin i universum avtar från ett initiellt toppvärde.

MODERN AKADEMI:

Se inledande citat:

Entropin i universum ökar: »Ordningen avtar». Jämförelser med modern akademi görs löpande på förekommande ställen i denna presentation.

Se speciellt PRAKTISKA EXEMPEL.

Se utförligt med jämförande grundbeskrivning i modern akademi i ENTROPIBEGREPPET I RELATERAD FYSIK.

Plancks strålningslag

Se även från HUR W BERÄKNAS

Plancks strålningslag från Plancks entropisamband

Se även sist i Flaskhalsarna i Plancks egen framställning från 1901

Hur Plancks strålningslag

N_l = l^–5hc²[e^hc^/b^l^T–1]^–1

framträder ur Plancks entropisamband

S = b(lnW)

A bokstäver kan byta plats med varandra (anta varandras platser) på A! sätt,

inga andra sätt finns:

EXEMPEL

3! = 1·2·3 = 6

abc bca cab

acb bac cba

= 6

A bokstäver kan väljas (i sina A positioner) på A^A sätt,

inga andra sätt finns:

EXEMPEL:

3³ = 3·3·3 = 9·3 = 27

aaa aab aac

aba abb abc

aca acb acc

= 9

bba bbb bbc

baa bab bac

bca bcb bcc

= 9

cca ccb ccc

cba cbb cbc

caa cab cac

= 9

;

Då gäller tydligen också med A = a+b att

(a+b) bokstäver kan väljas [i sina (a+b) positioner] på W = (a+b)^(a+b) = (a+b)^a·(a+b)^b sätt:

På samma sätt som i det enklaste fallet i HUR W BERÄKNAS FRÅN ENSKILDA ATOMERS POSITIONER (xyz) med det rena antalet n materialkomponenter (atomer) med maximala antalet n! permutationer (eller sätt) och grundkvoten som garanterar antalet likaberättigade energifördelningssätt

W = 1 (från lägst v=1) enligt

W = ——

n! · [f (v)]^–1

kan vi nu genomföra samma typresonemang men med en utvidgad kombinationsform för n; Ett fast antal masskomponenter (n) tillsammans med en variabel energikvantitet (E=hf) och vilken vi här ger antalsbeteckningen P = antalet Planckenergikvanta (hf), se Planckenergin.

a = n = antalet masskomponenter (atomer)

b = P = antalet Planckenergikvanta (hf)

W-formens potensfunktion

I genomgången HUR W BERÄKNAS visas hur

— för Plancks entropisamband S=b(lnW) med

S = b(ln[W=1]) = b(0) = 0 vid 0°K

— den växande funktionen för W-kvoten kan härledas genom växande antal lika partikelenergier genom växande temperatur enligt LIFE-satsen från maxantalet

(n+P)ⁿ(n+P)^P

så att man får Plancks härledda ekvivalent (se Plancks original) för W-kvoten enligt

(n+P)ⁿ⁺^P

W = ————— .................... antalet möjliga energifördelningssätt i n via hf

nⁿP^P

Eller i andra ord, uttryckt mera sammansatt:

För att ur antalet maximala grundsätt

(n+P)ⁿ(n+P)^P

— som, på ovan exemplifierat sätt, definierar alla kombinationer (n+P)

— säkerställa en nämnarfaktor i W-kvoten

— med den funktionen att endast de sätt frikopplas

(ur den tidigare, ovan nämnda, motsvarande fasta n!-stocken och som därmed reducerar denna och därmed — via nämnardelen — åstadkommer ett högre W-tal n!/[n! – T])

som via det så avtagande nämnarvärdet motsvarar ökningen i den extra tillagda variabeldelen P i (n+P), med P från minsta 1 (noll värmestrålning hf förekommer inte i materiefysiken) och uppåt obegränsat,

— kan, tydligen, bara alternativet

(n+0)ⁿ(0+P)^P

komma i fråga så att man får nämnardelen (n)ⁿ(P)^P — därför att P är den enda variabel som finns för kombinationssätten eftersom n är en fast konstant för varje given kropp. Den motsvarande enkla funktionsdelen från utvecklingarna i HUR W BERÄKNAS blir alltså

[f (v)]^–1 = (n)ⁿ(P)^P ;

Det ger oss W-formen

(n+P)ⁿ⁺^P

W = ————— .................... antalet möjliga energifördelningssätt i n via hf

nⁿP^P

Det är också det fullständiga, praktiskt fysikaliska, sambandet för antalet likaberättigade mikrotillstånd (W) eller likaberättigade energifördelningssätt för vilken som helst kropp med n stycken (idealt) likadana masskomponenter — eftersom, tydligen, inga andra fall finns att välja på med förutsättningen att antalet P motsvarar ett antal h·f. För varje bestämd frekvens f finns via Plancks konstant h=6,62559 t34 JS, tydligen, bara en viss minsta bestämd energimängd hf och som följaktligen bara kan växa uppåt i energi via ett bestämt antal (P) hf-kvanta. Varje masskomponent (atom) besitter energiinnehållet E_P=P·hf, hela kroppen totalenergin E=nE_P.

Entropiderivatan

Med den tidigare härledda (»enkla») formen för Planckentropin S=b(lnW) ges då via lnW och logaritmlagarna

lnW = ln[(n+P)ⁿ⁺^P] – ln[nⁿP^P]

= (n+P)ln[(n+P)] – (ln(nⁿ) + ln(P^P))

= (n+P)ln[(n+P)] – n·ln(n) – P·ln(P)

med — från Clausius grundform S = Q/T motsvarande allmänna gaslagens grundform k=E/T och som vi här skriver direkt enklare på den allmänna energibeteckningen (E) S=E/T —

dS/dE = 1/T

För varje Planckkomponent n=1 gäller då tydligen att

lnW = (1+P)ln[(1+P)] – 1·ln(1) – P·ln(P)

= (1+P)ln[(1+P)] – 0 – P·ln(P)

= (1+P)ln[(1+P)] – P·ln(P)

Och därmed Planckentropin

S = b lnW

= b[(1+P)ln[(1+P)] – P·ln(P)]

Med E_P/hf=P=U/hv (samma som Plancks beteckningar i Plancks original från 1901) ges vidare

S = b[(1+U/hv)ln[(1+U/hv)] – (U/hv)·ln(U/hv)]

Med föregående dS/dE = 1/T, med Plancks beteckningar (frånsett T) dS/dU = 1/T ges Planckentropiderivatan S med avseende på totalenergin U via produktderivatan enligt

dS/dU = b[(1+U/hv)ln[(1+U/hv)] – (U/hv)·ln(U/hv)]’

= b[(0+1/hv)ln[(1+U/hv)] + (1+U/hv)[(0+1/hv)/(1+U/hv)]

– [(1/hv)·ln(U/hv) + (U/hv)·(1/hv)/(U/hv)]]

= b[(1/hv)ln[(1+U/hv)] + (1+U/hv)[(1/hv)/(1+U/hv)]

– (1/hv)·ln(U/hv) – (U/hv)·(1/hv)/(U/hv)]

= b[(1/hv)ln[(1+U/hv)] + (1/hv) – (1/hv)·ln(U/hv) – (1/hv)]

= b[(1/hv)ln[(1+U/hv)] – (1/hv)·ln(U/hv)]

= (b/hv)[ln[(1+U/hv)] – ln(U/hv)]

= (b/hv)·ln[(1+U/hv)/(U/hv)]

= (b/hv)·ln[(1/(U/hv) + 1]

= (b/hv)·ln[1 + hv/U]

= 1/T

Därmed (frekvensen v=c/l med våglängden l)

hv/bT = ln[1 + hv/U] = hc/blT

som ger

e^hc/bl^T = 1 + hc/Ul

med totala (»strålkompakta») energin (U=E),

E = ——————— ......................... J, Plancks energirelaterade strålningslag

l · (e^hc/bl^T – 1)

Strålningseffekten (P=E/t=Ef=E·c/l) blir motsvarande

hc²

P = ——————— ......................... W, Plancks effektrelaterade strålningslag

l ² · (e^hc/bl^T – 1)

VOLYMÄRA strålningseffekten — strålningseffekten per kubikmeter våglängd den totalt volymärt massomslutna strålningseffekten — ger tillsammans med rymdvinkeln i (sr) steradianer Plancks fullständiga allmänna strålningslag som totalt motsvarar den s.k. spektrala radiansen, W(M³SRsteradianer)^–1 enligt

hc²

N_l = ——————— ......................... W/(M³SRsteradianer), Plancks fullständiga allmänna strålningslag

l ⁵ · (e^hc/bl^T – 1)

h 6,626 t34 JS, Plancks konstant

c 2,99792458 T8 M/S, ljushastigheten i vakuum

l M, våglängden

b 1,38 t23 J/°K, Boltzmanns konstant

T °K, temperaturen

Planckvärmekurvorna

Nl = l^–5hc²[e^hc^/b^l^T–1]^–1 ........... Plancks strålningslag (W/M³SR)

y = ax^–5(–1+e^k^/xT)^–1 ............... grafiskt

För utförlig beskrivning, se Plancks strålningslag i praktisk fysik.

Kort beskrivning. För varje bestämd temperatur (T) ges i Plancks strålningslag en bestämd Planckkurva som innefattar alla möjliga våglängder (l=l); Från kortast möjliga närmast noll till längsta möjliga mot oändligt. Planckkurvans derivata, samma som Wiens förskjutningslag, l = (k=2,898 t3 M°K)/T, definierar Planckkurvans högsta punkt, samma som totala värmestrålningens centrala våglängd för T.

Enbart med hjälp av materiefysiken kan värmestrålningens totala Planckspektrum INTE förklaras fullständigt därför att Planckenergin E=hf=hc/l i fallet med våglängdsområdet närmast noll tvunget uppvisar obegränsat växande energivärde, hc konstant: E växer över alla gränser då l går mot noll. Förklaringen ENLIGT RELATERAD FYSIK ligger i massfysiken tillsammans med värmens fysikaliska uppbyggnad, ytterst från massförstörelse (m®g): Plancks konstant (h) är en strukturkonstant; E = hf = (h/n)nf = (hc/n[l/n]), se utförligt från atomkärnans härledning. De djupast liggande, kortaste, våglängderna med de högsta frekvenserna tillhör atomkärnan (se utförligt i NEUTRINOSPEKTRUM) och faller därför utanför ramen för materiefysiken, analogt våglängdsområdet i atomernas elektronhöljen (se Comptongränsen) och som arbetar på den normala grundnivån (h). Därmed får också energimatematiken bakom grundämnenas uppbyggnad från lättare till tyngre, enligt relaterad fysik, en fullständig förklaring därmed att de lättare kärnornas strukturer garanteras intakta utan att de sönderbryts på de (betydligt högre) energier som frigörs vid de tyngre kärnornas bildning. Se utförligt från NUKLIDBARRIÄREN och GRUNDÄMNESBILDNINGEN.

Plancks strålningslag blir på detta sätt både kärn- och atomfysikens absolut främsta laggrund.

Max Planck visade år 1901 för sin del, utförligt i Plancks original, hur Planckstrålningslagen framväxer ur Plancks entropisamband S=b(lnW). Innebörden av termen eller begreppet ”statistisk” eller ”sannolikhet” i samband med gängse förekommande beskrivning av termen W — antalet likaberättigade energifördelningssätt se från HUR W BERÄKNAS — mister därmed, tydligen, sin (enligt modern akademi förmodade) självständiga betydelse; W saknar, tydligen, relaterbar koppling till något som, alls, skulle ha med sannolikhet att göra: W-formen, tydligen, avspeglar en helt ren tillståndsekvation, Se utförligt från W finns inte i statistiken. S-formen, dess ekvivalens med det bestämt övergripande energitillståndet med sitt bestämda energiinnehåll och bestämda temperatur — och vars speciella derivata som temperaturens invers dS/dE=1/T — bildar, tydligen, den temperatur- och våglängdsfunktion vi kallar för Plancks strålningslag. Det finns, tydligen — se ovanstående härledning i detalj — ingen statistisk parameter i den formen, bara rena tillståndsbeskrivningar. Se mera utförligt från W finns inte i statistiken.

Jag har alltid tyckt, så långt tillbaka jag kan minnas, att blotta ordet ”statistik” i samband med atomfysiken har verkat knäppt. S, se Härledningen till Plancks entropisamband, uttrycker tydligen ingen sannolikhet, inte av något som helst slag, och det gör tydligen inte W heller, se W finns inte i statistiken, enbart antalet likaberättigade energifördelningssätt bland n atomer och P Planckkvanta: de enda tillgängliga sätt som det aktuella fysiska tillståndets materiekomponenter har att välja på för att vara vad de är. Det finns, uppenbarligen, ingenting statistiskt i det: alla likaberättigade energifördelningssätt W är precis lika sannolika vid varje T °K och E Joule: inget sätt mer och inget sätt mindre. Plancks entropisamband S=b(lnW) är alldeles tydligt en tillståndsekvation med entropin S som en entydigt definierad värmegrundad arbetspotential, S=E/T=hf/T.

Och kan du tro: GoogleSök på energifördelningssätt. Ett (1) svenskt ord. Skammen går på torra land. Inte en enda träff. Inte en. ”energy distributional way”: 0. Lika illa där.

Editor2010II19

W finns inte i statistiken

2010II20

W saknar koppling till statistiken

I många webbkällor kan man se beskrivningar av entropisambandet S=b(lnW) som påstår att termen W sammanhänger med statistiska begrepp med tonvikt lagd på ordet sannolikhet (eng. probability):

Svenska webbkällor, sannolikhet — entropi (»entropi s = k log w +sannolikhet») 105 träffar:

http://www.saunalahti.fi/~borgbros/artiklar/entropi.pdf

http://130.235.7.155/publikationsdb/docs/5167.pdf

. . .

Engelska webbkällor, probability — entropy (»entropy s = k log w +probability») 71000 träffar:

http://en.wikipedia.org/wiki/Ludwig_Boltzmann

http://ask.metafilter.com/128814/Help-me-Understand-Boltzmanns-entropy-formula-S-k-log-W

http://pubs.acs.org/doi/abs/10.1021/j150304a012

http://www.tim-thompson.com/entropy1.html

http://dictionary.babylon.com/Entropy

http://chemed.chem.wisc.edu/chempaths/GenChem-Textbook/Thermodynamic-Probability-and-Entropy-626.html

http://mit.edu/6.976/www/handout/math_inforev.pdf

. . .

med typcitat från den sista källan ovan, s4:

”Boltzmann’s formula

S = k logW ,

which says that the entropy S of an observed macrostate is equal to the logarithmic probability

of its occurrence up to some constant k.”

Men: W i Plancks entropisamband S=b(lnW) har — uppenbarligen — ingen som helst koppling eller anknytning till, eller samband med, begreppet sannolikhet:

Härledningarna visar — nämligen — en genomgående beskrivning av tillståndsekvationer

— från e-logaritmen vid start till Plancks strålningslag vid mål.

Vi studerar innehållet i detalj i den följande framställningen.

Låt oss börja med den aktuella Härledningen till Plancks entropisamband fram till ”Alternativt — delvis mera utförligt”, alltså fram till sambandsformen

S = b·lnW ................................ J/°K

Den härledningen bygger helt på faktorn W i betydelsen av antalet likaberättigade energifördelningssätt tillsammans med e-logaritmens matematiska fysik. Och, som redan påtalats: Ögonblicksbilden motsvarar, tydligen, ett bestämt energiinnehåll för hela kroppen vid en viss bestämd temperatur, analogt en viss bestämd medelmässig rörelseenergi hos varje Planckkomponent.

Inte ett spår av någon ”sannolikhet” finns i den beskrivningen.

TITTAR VI INUTI W ser vi, i grundformen bland kroppens n atomer, bara den enkla möjligheten med faktorn n att varje enskild atom kan anta — byta plats med — varje annan atoms position (xyz). Det ger oss med grundexemplet n=3 med atomindividerna abc totalt antalet sådana platsbyten {abc acb bac bca cab cba}=6=1·2·3=3! (’tre-fakulteten’). På fakultetens funktionsform därmed generellt

n!=1·2·3·…·n, varje platsform kallas en permutation [ref. MLs334sp2n].

För kroppens n atomer och vid en bestämd kroppsenergi vid en bestämd temperatur skulle vi alltså kunna påstå att

antalet likaberättigade energifördelningssätt inbördes mellan de n atomerna är lika med n!.

Eftersom kroppsenergin redan är given, har det ingen betydelse hur de enskilda atomernas olika partikulära delenergier ligger fördelade, de kan med samma energiresultat i vilket fall kombineras (permuteras) på de angivna n! sätten. Beskrivningen via n! är alltså fortfarande bara en energiekvivalent.

För att kunna beskriva hur W ändras med växande temperatur, analogt högre S-tal, finns tydligen bara en, och endast en, och ingenting annat än bara en enda entydig utgångspunkt:

S = b(ln[W=1]) = b(0) = 0, vilket gäller vid exakta 0°K: ingen arbetspotential finns i någon materiell kropp om heller ingen rörelseenergi (temperatur) finns.

Med hjälp av n! ges därmed enda möjliga sättet, från absolut perfekt ideal kristallin ordning vid 0°K,

W = ——— = 1 ................................. antalet likaberättigade energifördelningssätt vid 0°K

Jag ser fortfarande inte röken av någon ”sannolikhet”.

Vartefter temperaturen ökar från den perfekta kristallordningens 0°K är det tydligt att allt flera atomer lämnar det ideala nolläget: Vi kan, tydligen, utnyttja den värmefysiken för att tilldela »värmeökningsatomerna» W-kvotens nämnare: Vartefter temperaturen ökar och allt flera atomer lämnar det ideala kristalltillståndets 0°K, avtar i motsvarande grad mängdvärdet i nämnarens »n!» så att W-kvoten ökar från lägst 1 och närmar sig maxvärdet max n! — med den fasta referensformen för den perfekta kristallordningens n! i kvotens täljare. Vi kan skriva det formellt

W = ——— = 1®n! ......................... antalet likaberättigade energifördelningssätt

n! – T

T betyder en (här) ännu ospecificerad temperaturfunktion som sänker nämnarvärdet från n! mot 1 så att hela W-kvoten med konstant täljare n! växer från lägst 1 mot max n!.

Vi ser nu, genom nödvändigheten för oss att precisera den fysikaliska dynamiken för HUR W ändras — allt flera viloatomer lösgör sig från nolläget och bildar alltmer en summa mot max n! i takt med att temperaturen, analogt S-värdet tillväxer — har medfört en liten ändring i bilden:

Istället för ett entydigt

antalet likaberättigade energifördelningssätt

som vi utgick ifrån för W gäller nu istället mera exakt en KVOT mellan

en fast högsta bestämd kvantitet (n!) lika med

max likaberättigade energifördelningssätt

och

en variabel kvantitet (n! – T) lika med

avtagande likaberättigade energifördelningssätt

med resultatet, den ursprungliga definitionen för W,

aktuellt antal likaberättigade energifördelningssätt.

OM den matematiken ska besitta någon mera begriplig fysikalisk motsvarighet är det tydligt att en mera korrekt beskrivning av den värmedynamiken måste bli:

en fast högsta bestämd kvantitet (»n!») lika med

max olika antal partikelenergier

och

en variabel kvantitet (»n! – T») lika med

aktuellt antal olika partikelenergier

med resultatet, den ursprungliga definitionen för W,

aktuellt antal likaberättigade energifördelningssätt.

maximala antalet olika partikelenergier

———————————————— = aktuellt antal likaberättigade energifördelningssätt

aktuella antalet olika partikelenergier

Se även BLOCKKVOTEN i HUR W BERÄKNAS

På annat ställe i denna framställning (LIFE-satsen, om inte redan bekant) visas generellt hur man för en given kropp med bestämd volym kan förstå att

antalet olika partikelenergier avtar med växande rörelseenergi:

Ju högre temperatur, desto snabbare utjämnas alla olikheter inom kroppens begränsade volym — och förutsatt att medelavstånden mellan atomerna är litet i förhållande till ljushastigheten, i annat fall gäller inte analogierna. Vi talar alltså om metriska utsträckningar jämförliga med föremål på Jordytan, knappast genomskärningar av stjärnor och planeter generellt.

Vid (obegränsat nära) 0°K är antalet olika partikelenergier nödvändigtvis maximalt lika med alla möjliga kombinationer (n!) mellan alla möjliga delar på grund av den maximalt obegränsad tid för varje atom att överföra sin partikelenergi till någon annan atom som råder på grund av den idealt obegränsat närliggande noll rörelseenergin. Atomerna kommunicerar inte.

MEN SOM VI SER betyder, tydligen, införandet av faktorn »partikelenergi» en ny aspekt till vår uppfattning om »kombinationer»:

MED ATOMKÄRNANS HÄRLEDNING ENLIGT RELATERAD FYSIK finns tydligen för bildningen av ljusets spektrum ingen särskild materiell eller massbaserad partikel som n skulle kunna återföras på: med alla möjliga våglängder i massfysikens ljus innefattade finns tydligen bara en principiell (fraktal) struktur att välja på: Planckkomponenten — Plancks strukturkonstant: Planckringen h=mcr. I relaterad fysik bildar (således) h inte bara grunden för LJUSETS FYSIK genom proportionaliteten mellan massa och laddning utan även grunden för ATOMKÄRNANS HÄRLEDNING, massans fundamentalform — och därmed hela grunden för Plancklagens kontinuerliga spektrum;

Det föregående använda begreppet »atom» för n — och därmed hela utläggningen med fakultetskomplexet — mister med andra ord [blir för trångt för] sin innebörd. Det går inte att anställa härledningen till Plancks strålningslag på den fakultetsrelaterade — statistiska — grunden: n! räcker inte.

Det enkla exemplets »partikelenergier och Planckkomponenter» abc MED partikelenergierna a, b och c kan nu (således, i rikare mening) också uppvisa den betydligt rikare typen aaa och cca osv., eftersom Planckkomponenten (h) saknar bestämd storlek eller antalsform [Se PASTOM] och därför, tydligen, bara kan räknas genom alla fysikaliskt möjliga sätt. Dvs., »atomerna» abc får genom energierna (abc) »färg» som just Planckkomponenter: Totala antalet kombinationer blir nu inte n! utan det betydligt rikare nⁿ.

Se även beskrivningen från Den kritiska frågan.

Med exemplets n=3 ges kombinationerna

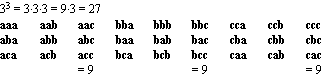
Med n Planckkomponenter och P Planckenergikvanta (hf) ges alltså totala antalet kombinationer

(n+P)ⁿ⁺^P

Sambandet för W kommer då, tydligen, att modifieras till

(n+P)ⁿ⁺^P

W = ————— .................... antalet möjliga energifördelningssätt i n via hf

nⁿP^P

FÖRKLARING: Av samma skäl som i föregående fall med W variabelt från 1 och uppåt, här med tillgängliga (n+P)ⁿ⁺^P=(n+P)ⁿ(n+P)^P, finns bara ett sätt att välja på med den faktorn i nämnaren. Nämligen genom att sätta (n+0)ⁿ(0+P)^P: n är konstant för given kropp, det är bara P som är variabel. Det finns inget annat att välja på. Lägsta antalsvärdet för P är 1 (därför att exakt noll värmestrålning inte förekommer i materiefysiken): alla kroppar värmeläcker. Det ger lägsta W-talet obegränsat närmast större än 1 enligt

(n+1)ⁿ⁺¹

W = ————— Û 1

nⁿ1¹

Se även mera allmänt i Generaliserade W-kvoten.

W-formen beskriver, tydligen exakt och fortfarande, en tillståndsekvivalent.

Jag ser fortfarande ingen ”sannolikhet”.

Med dS/dE=1/T från grundformen S=E/T (allmänna gaslagen eller Clausius grundform) med E=hf och P=E/(hf) ges först från Plancks entropisamband S = b(lnW); Härifrån kan sedan e-logaritmen för W-kvoten utvecklas genom logaritmlagarna vilket för varje Planckkomponent n=1 tydligen ger ledet

S = b[(1+P)ln[(1+P)] – P·ln(P)]

Insättning av P=E/(hf) och derivering med avseende på E ger efter utveckling och sammanräkning (utförligt i Härledningen till Plancks strålningslag från Plancks entropisamband)

dS/dE = (b/hf)·ln[1 + hf/E] = 1/T

Därmed (frekvensen v=c/l med våglängden l)

hf/bT = ln[1 + hf/E] = hc/blT

som ger

e^hc/bl^T = 1 + hc/El

och som i fullständiga enheter ger

strålningseffekten per kubikmeter våglängd (som motsvarar den s.k. spektrala radiansen, W(M³SRsteradianer)^–1) som ger Plancks fullständiga allmänna strålningslag

hc²

N_l = ——————— ......................... W/(M³SRsteradianer), Plancks fullständiga allmänna strålningslag

l ⁵ · (e^hc/bl^T – 1)

Se den mera utförliga härledningen i Plancks strålningslag från Plancks entropisamband.

Jag ser fortfarande ingen ”sannolikhet”.

Vi har nu, som ovan och uppenbarligen, genomgått alla detaljer i hela härledningen med W från grunden till Plancks allmänna strålningslag tillsammans med en särskild, fullständig, beskrivning av betydelsen, detaljinnehållet och innebörden av och i W-faktorn. Men ingenting har (tydligen, ännu) framkommit som visar någon koppling till eller ens en antydan till anknytning till begreppet ”sannolikhet” (Plancks [möjligen ironiska] ”probability”, se Plancks original).

Det är, alltså och förutsatt att inga övergripande fel begåtts i den här framställningens ljus, tydligt att uppfattningen att W-faktorn i Plancks entropisamband S=b(lnW) skulle ha någon anknytning till begreppet ”sannolikhet” helt saknar en naturvetenskapligt grundad soliditet.

Varifrån kommer feluppfattningen?

Varifrån kommer då bruket? Är det en missuppfattning?

Milt sagt tydligen nej. Snarare en (svårrelaterad) sammanblandning.

Betrakta sambanden för W och S nedan från den enkla genomgången i HUR W BERÄKNAS,

W = ——— = 1®n! ........................... antalet likaberättigade energifördelningssätt

n! – T

S = b(lnW)

Det finns (här utan vidare referenser) en allmän, principiell GREN av matematiken som behandlar nämnarformens typ

n! – T

på en mera generell fakultetsform

n₁!n₂!n₃!n₄!…n_m!

och som bygger på olika urvalskriterium inom kombinatoriken (generellt) och som därmed också ansluter till just statistiken och de olika begreppsrum som berör olika utfall — sannolikheter.

Ett (sådant) sätt att skriva ut W på är det som man också kan se (i flera olika webbkällor, här utan särskild referens) i samband med beskrivningen av ”Boltzmanns entropiformel” med bestämningen av W typ

P_n = n! ;

P_n₍₁₎_{, n(}₂₎_{, n(}₃₎_{, … n(}_m₎ = _i₌₁_®_m P P_n₍_i₎ ;

n ................................................................ antalet ingående element

n(i) ............................................................. antalet element i m-variabelns block

W = n!/_i₌₁_®_m P P_n₍_i₎ = n!/_i₌₁_®_m P n_i! = P ;

P_n

W = ——————————

P_n₍₁₎_{, n(}₂₎_{, n(}₃₎_{, … n(}_m₎

Se till exempel (GoogleBoksökning)

Information measures: information and its decription in science and engineering,

Christoph Arndt 2001, s95-96

Det är, vad jag vet, grundformen i Boltzmanns entropibegrepp (citat nedan) och som, enligt webbkällorna, figurerar i sambandsformer som ställdes upp först (från 1872 av Ludwig Boltzmann) — Men som det (också, frånsett nedanstående exakta utdrag, tydligen) är (hejdlöst) svårt att få fram historiskt exakta källredovisningar på: DELS på grund av att en del ARKIV inte tillåter GRATIS insyn och DELS eftersom mängden nutida författare, tydligen, blandar upp terminologin med senare tiders nymodigheter varav den främsta är att benämna Plancks entropisamband S=b(lnW) som Boltzmanns — det finns dock en del författare som understryker den missuppfattningen, men de verkar (ännu 2010) vara i minoritet.

Plancks approximation

Planck skriver uttryckligen i sin härledning från publikationen 1901sidan 3:

Boltzmanns entropikomplex

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s3

http://bourabai.kz/articles/planck/planck1901.pdf

Min översättning:

Nu är det uppenbart att varje fördelning hos de P energielementen bland de N resonatorerna kan resultera i ett ändligt, heltaligt, bestämt antal. Varje sådan form av fördelning kallar vi, efter ett uttryck använt av L. Boltzmann för en liknande idé, ett ”komplex”. Om man betecknar resonatorerna med talen 1, 2, 3, ...N …

Vad än Max Planck sysslar med i ovanstående fakultetsutläggning (n!), är det klart och tydligt att det INTE berör potensformen n^n — som Planck senare konverterar till på den sistnämnda (dessutom ofullständigt uttryckta) ”Stirling’s theorem” (se även längre ner i Plancks underliga approximation, tydligen observerat av flera):

Plancks

”any distribution of the P energy elements among the N resonators” [Se även i Den Kritiska Frågan],

— tydligen certifierat med uppslag från Boltzmann enligt

”Every such form of distribution we call …” och som därmed och i så fall, tydligen, skulle kunna betecknas Boltzmanns entropibegrepp

— är, tydligen, INTE en beskrivning av alla fysisk möjliga kombinationssätt mellan n »atomer» [Planckkomponenter] och P Planckenergikvanta. Ty, en sådan kan bara ges via den betydligt rikare potensformen (n+P)^(n+P) över den betydligt fattigare fakultetsformen (n+P)!. Se även utförligt från HUR W BERÄKNAS.

Jag vill (med det) inte utmåla Max Planck för någon oegentlighet. Ämnet är (och var då för över hundra år sedan ännu) alltför komplicerat (i all sin enkelhet) för det (ingen behärskar ämnet). Och det är LÄTT för mig att sitta här i efterhand med alla facit på hand (och stormodigt, på axlarna av mera eminenta existenser än min egen, dela ut favörer till höger och vänster, vilket jag därmed ödmjukt men bestämt avböjer).

Alla (förtrogna) vet att ännu i denna dag dras »kvantteorin» med vissa »besvärliga problem», och ett av dem är alldeles uppenbart den, enligt relaterad fysik lika uppenbart felaktiga förmodan om STATISTIK i naturdjupen (Men det uppfattas som HÄDELSE att säga det HÖGT i klassrummet). Enbart (tydligen) med en väldigt VID översiktskarta över fysikens naturvetenskapliga utveckling speciellt på atom och kärnfysikens område (som man fått privilegiet att fingra på under decennium), är det möjligt att (så här i efterhand) komma med de påpekanden som görs här — i ljuset av ATOMKÄRNANS HÄRLEDNING: PLANCKRINGEN mcr. Att Plancks beskrivning, som ovan med grund i »Boltzmanns entropikombinatorik», INTE beskriver ämnet korrekt matematiskt bevisas genom den korrekta potensformen som Planck senare använder och som leder rakt på slutmålet, se Plancks strålningslag från Plancks entropisamband, men som INTE sammanhänger med permutationsmatematiken (n!); det finns ingen koppling mellan n! och n^n. Det är den senare som gäller. Vidare nedan med exempel.

— Vad gör Planck för fel (vad är det han och de andra missar)?

— Ungefär som Boltzmann: »före sin tid». Tydligen.

— Planck, och med honom hela den moderna akademin, missar alldeles tydligt att ”resonatorn” är den allmänna strömringen h=mcr (PRINCIPALRINGEN massa laddning spinn) som I RELATERAD FYSIK, tydligen, konstituerar hela den tekniska byggnaden i atomkärnan och atomkärnans komponenter — med excellent demonstration i neutronens sönderfall till väteatom (spektrum och kvanttalen); Strömringen h=mcr är i relaterad fysik en strukturkomponent (se från PASTOM), se särskilt i Plancks strukturkonstant. Den krävs också för att kunna förklara/innefatta Planckstrålningen ända nerifrån noll våglängd — utan att sambandet E=hf havererar på oändlig energi — och ingår därmed automatiskt i atomkärnans härledning.

Atomkärnan behöver ingen påfyllning för att fortsätta uppvisa sitt SPINN, motsvarande aktiviteten i impulsmomentet eller PLANCKRINGEN mcr.

För den enskilda atomens del ENLIGT RELATERAD FYSIK: atomen besitter en stor mängd enskilda mcr-element — elektronmassans element, utspridda över hela atomen; Eftersom också hela atomkärnan i relaterad fysik motsvarar en strömring h=mcr, se från atomkärnans härledning, finns ingen GENERELL möjlighet i det allmänna elektromagnetiska utbudet att särskilja den ena strömringen ifrån den andra (utom genom våglängd) eftersom de alla samverkar och växelverkar. Strömringens allmänna form kan alltså kallas generellt (från neutronen) Plancks resonator i formen av (speciellt för materiefysiken) den övergripande atomen — och som gör att VARJE permuterande analogi (n!) missar (»förfjuttigar») det beskrivande målet: alla fysiskt möjliga kombinationer; Det som gäller är n^n. Inte n!. Se illustrerat, utförligt, från Den Kritiska Frågan.

Varken Planck eller hans samtida hade, tydligen, någon som helst inblick i den formen (och det har tydligen inte dagens moderna genier heller, se från ATOMKÄRNANS HÄRLEDNING); Kännedomen om den möjligheten SKULLE ha introducerats i samband med Heisenberg och Schrödingers våg och matrisekvationer (omkring 1925) som också begagnade ”resonatorerna” i beskrivningen av atomens spektrala resonansfysik. Men de elementen UTESLÖTS — förkastades — år 1927 efter en uppsats av Heisenberg som hänvisade till relativitetsteorin. Se även utförligt från ELEKTRONMASSANS KOMPONENTER. Som sagt var. En del bedrifter i modern akademi är särskilt lysande: Man hade hela lösningen rakt framför näsan, men förkastade de element vars matematik förklarade hela historien: atomspektrum. Se även från vic-felet. Se även i Spektrum och Kvanttalen.

Men den typformen har ingen koppling till fysikens entropibegrepp enligt Plancks entropisamband S=b(lnW): termodynamikens grund med Planckenergin E=hf och som definitivt inte kopplar till något som helst begrepp om ’sannolika utfall’ utan som bara, som vi har sett ovan, är en ren ekvivalent tillståndsbeskrivning. Plancks entropisamband S=b(lnW) har uppenbarligen ingenting med »sannolikhet» att göra; Den motsvarande W-kvoten i Plancks härledning

(s4ö i Plancks Original, Planck använder R för W och N för n)

(n+P)ⁿ⁺^P

W = ————— .................... antalet möjliga energifördelningssätt i n via hf

nⁿP^P

handlar, tydligen, INTE om permutationer (n!) utan om POTENSFUNKTIONER (P^P) för kombinationen antal-atomer-plus-antal-Planckenergikvanta (hf): (n+P)ⁿ⁺^P. Det finns uppenbarligen ingen koppling till statistiken — sannolikhet, olika utfall — i den uppställningen.

Med andra ord: Det statistiska inslaget i ämnet berör i vilket fall inte den värmegrundade arbetspotentialen, entropin S, Plancks entropisamband S=b(lnW).

Även Max Planck själv talar emellertid om ”probability” i sin beskrivning från 1901, se Plancks original — över en hel sida dessutom (s3) — och som avslutas med en märklig övergång till ovanstående korrekta W-form: Planck försöker inbilla oss (se även i Plancks underliga approximation) att kopplingen från »Boltzmanns statistiska W-form» (typ P-kvoten längre upp) med Plancks N!-termer skulle vara (s3n)

”Now according to Stirling's theorem, we have in the first approximation: N!=N^N”. Se även den mera utförliga beskrivningen i

Andra flaskhalsen — varför det är svårt att hänga med i Plancks egen beskrivning

Den kopplingen är utesluten: Jämför exemplet med n=50, avrundade värden;

50! = 3 T64

50⁵⁰ = 9 T84

Felet är så stort att det omöjligen går att ta Planck på orden. Medan formen N^N är korrekt, är kopplingen till n!-variablerna tydligen felaktig; Kroppens energitillstånd med avseende på de enskilda atomernas Planckenergikvanta (hf) beskrivs tydligen inte via permutationer n! (»Boltzmanns statistiska entropibegrepp») utan via potensfunktioner n^n (Plancks tillståndsekvivalenta entropibegrepp): atomerna har »färg»; n^n är betydligt rikare än n!.

Därför har heller inte W-faktorn någon koppling till statistiken:

Det är tydligen Planckentropins potensfunktioner N^N som gäller för fysiken — inte Boltzmanns statistiska permutationer N!.

Det finns dock, här veterligt, inget sådant känt klargörande i den nu etablerat tillgängliga litteraturen.

Om inte ens Max Planck själv kunde hålla ordning på de lösa trådändarna, ska man nog kanske heller inte vara alltför sträng mot de övriga korkflötena runt omkring. Men det är som möjligen redan framskymtat enkelt att säga för mig som redan står på axlarna på dem som gjort grundjobbet: historiens verkliga hjältar, med alla sina brister.

Se även utförligt från HUR W BERÄKNAS.

Plancks underliga approximation

Flera samtida med Planck använde samma underliga approximation

En nyligen (Mar2010) upphittat webbkälla omnämner (liksom här) uppmärksammandet av den ovannämnda högst besynnerliga koppling som Planck gör i påståendet med n!(=)n^n (s3n) i

”Now according to Stirling's theorem, we have in the first approximation: N!=N^N”,

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s1-8

http://bourabai.kz/articles/planck/planck1901.pdf

Källan, nedan, påstår att inte bara Planck använde den typen utan flera andra samtida skribenter, samt att 1. svaret på frågan VARFÖR står öppen och 2. detaljerna kopplar vidare till obesvarade frågor som sammanhänger med den moderna akademins kvantteori;

Citatet nedan t.v. utan svensk översättning:

”

The use of Stirling's formula in the theory of black body radiation

Interestingly, Planck, followed by some other early twentieth-century writers on the black-body radiation such as Debye and de Broglie, used the "first order" Stirling's approximation in a rather unusual way. Instead of using the expression n! ≈ (n/e)ⁿ the writers, who all were excellent physicists, preferred either to write it as n! = nⁿ or leave some components out immediately below. Two other eminent physicists, Einstein and Bose each took a different approach in their dealings with the problem and used other approximations. Although the left side of the equation n! = nⁿ is obviously not equal to its right side, which would lead to a gross error in simple calculation (for n=1, 1=1; for n=2, 2=4; for n=3, 6=27 etc., which does not seem reasonable), the substitution n! = nⁿ should be considered in terms of the mathematical operations that followed.

For Planck, they were: (1) n=n+1, (2) substitution to the fraction, (3) neglecting certain terms, (4) differentiation, and (5) integration. Planck's approximation resulted in a kind of "approximation of shape". The relationship between the idea of "energy elements" and the curve that was verified by measurement was demonstrated, but the elements were not separated. In fact the total of the approximations provided a far greater number of "complexions", as Planck called the system states, than the number calculated from the idea of completely separated system elements. This implied some extra microstates or interactions between the elements. The approximation was strongly nonlinear for a small number of elements. The same applies to the derivation of the photoelectric equation by Albert Einstein (the 'light quanta' were not separated).

Actually, none of the papers in question was devoted to the radiation of microsystems and that was perhaps why the writers chose not to give the reason for the approximation. One can only speculate that it could have been equivalent either to a kind of distant interaction being a joint effect of some variables or phenomena not yet known at the time of their writing and discovered later in quantum mechanics, such as spin or the uncertainty principle, or to some still unknown hidden variables . However, a relationship between the lack of separability implied by the early 20th-century thermodynamical analyses of the black body and the contemporary quantum entanglement theories is still missing.

”,

StateMaster ENCYCLOPEDIA — Planck's law of black body radiation; datum och författare saknas

http://www.statemaster.com/encyclopedia/Planck's-law-of-black-body-radiation

KOMMENTAR — till ovanstående citatutdrag:

Författaren påstår

”Instead of using the expression n! ≈ (n/e)ⁿ”;

EXEMPEL avrundade värden med n=50;

(1) 50! = 3,0 T64

(2) 50⁵⁰ = 8,9 T84

(3) (50/e)⁵⁰ = 1,7 T63 ; e = 2,718 28 18 28 45 90 45 …

Förhållandet (1)/(3) ger 17,754096. Vilket visar att även den angivna förenklingen är oacceptabel — ännu värre än »Plancks förslag» med ”N!=N^N” eftersom n! ligger närmare n^n än (n/e)^n. Ämnet gällde, tydligen, n^n, inte n!. (Exemplet bara understryker ämnets hutlöst svåra analytiska navigering, trots enkla pusselbitar. [Läs: det är, tydligen, bara den relaterade fysikens härledning till atomkärnan via Planckringen, med alla tillhörande detaljer, som klarar av helheten]).

Tillägg 2010IV6 — också Planck använder formen ovan i sin bok från 1914

I boken THE THEORY OF HEAT RADIATION av Max Planck (1914) — Hela boken finns i gratisupplaga på INTERNET ARCHIVE — har Planck gjort en senare utveckling av originalet för Plancks approximation från 1901.

I kapitlet ENTROPY AND PROBABILITY (från sidan 113) genomför Planck samma principiella uppställning som i Plancks approximation, men bara mera omständligt — och med precis samma slutresultat som tidigare: potensen från fakulteten. Planck använder på sidan 124 precis samma samband som ovan,

n! = (n/e)ⁿ (samband 171 s124)

— och ställer sig därmed i samma fotspår som ovannämnda källförfattare: ännu värre än Plancks ursprungliga »förslag» med ”N!=N^N”.

Alldeles uppenbart är det (således) att INGEN I MODERN AKADEMI förstår felet: det går inte att använda fakultetsformen, inte alls över huvud taget. Det är potensformen DIREKT som måste tillämpas. Se f.ö. W finns inte i statistiken.

Se utförligt i Planckresonatorn som förklarar VARFÖR ingen bestämd massform eller materialkomponent (typ atom eller elektron) bär ansvaret för Plancks strålningslag. Se även från Antalet likaberättigade energifördelningssätt och Brytpunkten och HUR W BERÄKNAS som förklarar varför potensformen gäller.

Se även särskilt i Plancks strålningslag i praktisk fysik, där genomgås ytterligare förtydliganden (separat bihang till detta htm-dokument), om ej redan bekant.

Flaskhalsarna i Max Plancks framställning

Originalframställningen från år 1901, Max Plancks original, finns på engelska på webben i PDF-dokumentet

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s1-8

http://bourabai.kz/articles/planck/planck1901.pdf

Med förutsatt tillgång till det åttasidiga PDF-dokumentet ges här motsvarande refererad genomgång med stöd av föregående separata artikel i Plancks strålningslag från Plancks entropisamband.

Första flaskhalsen — varför det är svårt att hänga med i Plancks egen beskrivning

Planck INTRODUCERAR (s3ö) entropisambandet (Plancks egen beteckning)

”S_N = k log W + const”

och med dåtidens beteckning ”log” för nutidens enklare ln, se särskilt klarläggande från noggrann citatbeskrivning i Plancks original.

Man får ingen klarhet i varifrån sambandets form kommer.

Deprimerande.

Men — som framgår i Härledningen till Plancks entropisamband — finns, verkligen, en både begriplig och klar, entydig, enkel och logisk grund som visar hur och varför just sambandsformen med e-logaritmen för W alls har någon betydelse för fysiken: e-logaritmens allmänna (berömda) koppling till fysiken, här genom hur variablerna står i det samband som beskriver variationen i antalet likaberättigade energifördelningssätt — och den gynnsamma ställning som termerna uppvisar i allmänna gaslagen (energin) med kopplingen energi-temperatur, maxvärden och minvärden. »Piece of cake».

Andra flaskhalsen — varför det är svårt att hänga med i Plancks egen beskrivning

Planck HOPPAR tydligen ÖVER DEN ENKLA ATOMANALOGIN (hela s3);

Planck ’är ute och snurrar i kombinatoriken’, hela sidan 3, och ’får ihop det på slutet’ med vad han kallar ’Stirlings teorem’ — helt obegripligt för en lekman. Och (MEN) vi behöver heller inte bekymra oss vidare i det, se utförligt nedan. Se även i W finns inte i statistiken. Det kan dock vara av visst intresse att relatera sammanhanget (vad Planck inte berättar om, fullt ut, då han helt säkert året 1901 skriver för sina kolleger som redan är införstådda …).

Stirlings formel finns omnämnd i MATEMATIKLEXIKON W&W 1991 s395sp2ö:

”Följande uppskattning av n! = 1·2·3·…·n för stora n:

n! = (2p)^1/2 nⁿ⁺^1/2 e^–ne^qn/12ⁿ

där 0 < q_n < 1 för alla n. Detta betyder att

_n_®¥ lim ——————— = 1

(2p)^1/2 nⁿ⁺^1/2 e^–n

”,

MATEMATIKLEXIKON W&W 1991 s395sp2ö

Prövar man med olika värden (typ n=3 och n=50 som extremfall på en enklare teknisk räknare) finner man mycket god överensstämmelse om den sistnämnda bråkformens nämnardel används direkt i jämförelse med n!.

Denna mycket goda överensstämmelse är dock, tydligen, INTE den som Planck beskriver (s3n) i

”Now according to Stirling's theorem, we have in the first approximation: N!=N^N”; Det (grovt) förenklade — och grovt felaktiga — ’närmevärdet’ n!=nⁿ stämmer inte alls, värre ju större n är: Med n=50 ges avrundat

50!=3 T64

mot

50⁵⁰=9 T84.

Här är det alltså tydligt att Planck gjort en grov miss, helt klart.

Men: Lösningen är enkel, även i detta fall. Formen med Plancks införda (men, som nyligen exemplifierats, alldeles tydligt felaktigt relaterade) N^N är nämligen helt korrekt: RELATERAR man (nämligen) antalet möjliga likaberättigade energifördelningssätt (W) å ena sidan via ett bestämt antal materiekomponenter (atomer) n får man, som visas i HUR W BERÄKNAS, maximalt n!. Men det är ju inte det enda sättet: RELATERAR man, nämligen å den andra sidan samma principiella komplex med flera ingående variabler — antalet principiella komponenter n TILLSAMMANS MED antalet Planckkvanta (P), kan antalet olika SÄTT nu istället tydligt beskrivas på en annan fason, nämligen som sätten på vilka TYP antalet bokstäver (ASCII n=26) kan skrivas i alla de 26 positionerna, men nu uppdelat på TVÅ skilda variabler (n+P), och med den extra egenskapen att varje n kan uppvisa »färg» och därför permutationsmatematiken (n!) inte kan tillämpas. Se utförligt i början från Plancks strålningslag från Plancks entropisamband. Sambandet är — just — (n+P)^(n+P).

Det förefaller (här) underligt att man (Planck med kolleger år 1901) inte kände till den möjligheten (som betyder detsamma som att VARJE Planckresonator (i Plancks N) kan förstås som en besättning, nämligen den enskilda KOMPONENTEN i varje atoms särskilda (elektron-)laddningsbesättning, och vilken formalia inte ingår i modern akademi, se från Elektronmassans komponenter). Därmed (nämligen) elimineras hela Plancks utläggning i ämnet ’kombinatorik’ — vi kan helt enkelt hoppa över den delen — och man kommer direkt på målet i Plancks motsvarande korrekta potensform (s4ö)

Se utförligt från början i Plancks strålningslag från Plancks entropisamband.

Också här (min mening): »Piece of cake. No Problemo». Se även illustrerat i Den Kritiska Frågan.

Se även vidare i Plancks underliga approximation.

Tredje flaskhalsen — varför det är svårt att hänga med i Plancks egen beskrivning

DERIVERINGEN AV DET SAMMANSATTA LEDET I PLANCKS ENTROPISAMBAND

Den minsta svårigheten (för den som känner till nollformsalgebran)

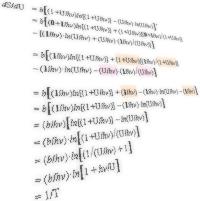
På sidorna 4-6 går Planck igenom Wiens förskjutningslag (med dåvarande preferenser från år 1901) och ur vilken framkommer den avgörande Planckenergin E=hf med Plancks konstant (h), med Plancks beteckningar (s6mn),

— som redan känner Planckenergin som en mera grundläggande hörnsten i RELATERAD FYSIK, nämligen via impulsmomentet (Keplers ytmoment K=vr tillsammans med massan mK) som bildar Plancks konstant mK=h=mcr eller PLANCKRINGEN och därmed grundlägger ATOMKÄRNANS HÄRLEDNING

— kan helt hoppa över det avsnittet och gå direkt på resultatledet (med Plancks beteckningar, s6n)

Notera att Planck använder beteckningssättet ”log” för »e-logaritmen till/för», se särskild utredning i Plancks Original.

Med grundformen (Plancks beteckningar utom temperaturen T för Plancks q) dS/dU=1/T deriveras så ledet ovan via produktderivatan, som efter sammanställning (logaritmlagarna) och vidare förenklingar ger slutresultatet

(Plancks samband.11 s6n, här frekvensen f för Plancks v och temperaturen T för Plancks q [grek., lilla theta, q] och b för Boltzmanns konstant, Plancks k)

U = ——————— ......................... J, Plancks energirelaterade strålningslag

e^(hf / bT) – 1

’Piece of Cake’ för den som är erfaren, bevandrad och förtrogen. En ’totalt omöjlig gåta’ för den som inte känner »den hemliga ingången». Se utförligt från Plancks strålningslag från Plancks entropisamband.

Avslutning

I GRUNDFYSIKEN däremot

— relaterad fysik och efter något annorlunda förutsättningar, med Planckenergin E=hf innefattad som utgångspunkt (omöjligt i vetenskapshistorien)

— härleds Plancks strålningslag alternativt med utgångspunkt från Stefan-Boltzmanns strålningslag som bildar termodynamikens grund, och sedan därefter Wiens förskjutningslag som är Planckstrålningslagens derivata. Se utförligt från PLANCKS STRÅLNINGSLAG i TERMOFYSIKENS MATEMATIK.

Termodynamisk jämvikt

Med huvudreferens till Tillståndsbegreppet i modern akademi

Termodynamisk jämvikt

I RELATERAD FYSIK

Se även praktiskt entropiexempel i ............................ Atomismens Grunder

Se även ...................................................................... Isolerade systemets ursprung

OBSERVERA FÖRST FÖR UNDVIKANDE AV MISSFÖRSTÅND: I RELATERAD FYSIK, SE FYSIKENS FÖRSTA PRINCIP (APARC), GÄLLER ATT FYSIKEN HELT OCH HÅLLET ÄR I AVSAKNAD AV TILLSTÅND, SÅDANA EXISTERAR INTE I FYSIKEN, MEN ATT FYSIKENS BESKRIVNING ÄR OMÖJLIG UTAN TILLSTÅNDETS BEGREPP. VI SKILJER DÄRFÖR PÅ FENOMENVÄRLD (VARIATION) OCH FÖRSTÅNDSVÄRLD (TILLSTÅND) I NATURBESKRIVNINGEN. SE ÄVEN FRÅN ATOMTRIANGELN OCH NOLLFORMSALGEBRAN I MATEMATIKEN. DEN DISTINKTIONEN FINNS INTE UTTALAD I MODERN AKADEMI, VILKET DIREKT UTESLUTER EN RÄTTVIS JÄMFÖRELSE I BEGREPPSGRUNDERNA.

TERMODYNAMISK JÄMVIKT i relaterad fysik kan, tydligen, bara definieras av det tillstånd — en bestämd temperatur — som råder då en kropp uppvisar en (efter olika tolkningsföreträden, beroende på grad av idealisering) stabil temperatur (punktmätning)

— minsta möjliga ändring under längsta möjliga period

— enligt Plancks strålningslag med kroppens emissioner och absorptioner av alla möjliga våglängder i det elektromagnetiska spektrumet. Med den tillgängliga graden av noggrannhet i mätningen som alls är fysikaliskt möjligt, kan vi säga att det tillståndet motsvarar ett bestämt energitillstånd, analogt en bestämd kroppstemperatur. Se Wiens förskjutningslag (Planckstrålningens derivata).

I MODERN AKADEMI antas i princip (nära) samma grundmening men med explicit tonvikt lagd på termisk jämvikt enligt (typcitat)

”Thermal equilibrium occurs when a system's macroscopic thermal observables have ceased to change with time.”,

@INTERNET Wikipedia Thermal equilibrium 2010-02-07

Min översättning:

Termisk jämvikt uppträder när ett systems makroskopiskt termiska observabler har upphört att ändras med tiden.

I relaterad fysik finns alltså inget sådant tillstånd — garanterat just av Plancks strålningslag (den moderna akademins idé är en [akademiskt] matematiserad konstruktion av fysiken: uppfinning, snarare än härledning); alla kroppars kontinuerliga emission och absorption garanterar att varje verkligt termodynamiskt system (kropp) alltid uppvisar olika grad av fluktuationer, mer eller mindre. Ett generellt statiskt (utan ändring) referenstillstånd i fysiken existerar f.ö. inte i relaterad fysik. Se utförligt från Tillståndsbegreppet i modern akademi och tillståndets princip i relaterad fysik.

Notera också följande:

TERMODYNAMISK JÄMVIKT i meningen idealt homogen gasblandning kan ALDRIG existera i någon EXAKT praktisk fysikalisk mening (men mycket nära för relativt små gasvolymer) — på grund av divergensens maxvärde i gasmassans tyngdpunkt enligt ljusets gravitella beroende: »temperaturvärdet» i, inuti, gasmassan är, tvunget, alltid störst i mitten, lägst längst ut, analogt störst elektromagnetisk mobilitet, minst tröghet, i centrum. Den aspekten, emellertid, intar knappast någon betydelse i normala praktiska tillämpningar i Jordfysiken. En helt annat situation uppkommer om gasinneslutningen omfattar STORA volymer, som typ stjärnor. Emellertid (och återigen) har dessa sistnämnda fall (p®T) ingen koppling till allmänna gaslagen (T®p) enligt relaterad fysik. Se utförligt från Solfysiken.

Isolerat system i termodynamisk mening

Se även från Isolerade systemets ursprung

Begreppet »isolerat system» I TERMODYNAMISK MENING — frånvaro av varje form av emission och absorption — har därmed (Se TERMODYNAMISK JÄMVIKT ovan) och tydligen följaktligen bara en, och endast en, och ingenting annat än bara en entydig innebörd i praktisk RELATERAD fysik:

exakta tillståndets fysik i varje bestämd tidpunkt:

noll varaktighet: existerar inte i fysiken.

Plancks strålningslag — kontinuerlig emission och absorption för alla kroppar — punkterar varje intervallbaserad tillståndsfysik för en kropp på ANNAT sätt än som just en kropp som värmeläcker. »Isolerat system» I TERMODYNAMISK MENING har därmed ingen fysikalisk representation: »isolerat system» I TERMODYNAMISK MENING finns inte i fysiken.

När vi alltså talar om en kropps tillstånd, analogt den momentana situationsbild som gäller i varje möjligt observerar tidpunkt — som en tänkt utsträckning i vår föreställande förståndsvärld — menar vi en absolut stel och fast, orörlig, fryst översiktsbild av alla kroppars inbördes positioner och rörelsemängder vid just den tidpunkten. Samt — OM ämnet också gäller en samtidig tillståndsbeskrivning av energin i den aktuella tidpunkten — varje annat sådant ENERGIMÄSSIGT (kinetiska energin, rörelseenergin E=mvv/2) LIKABERÄTTIGAT s.k. mikrotillstånd; Vilket avser positioner (xyz) och rörelsemängder (mv) och som avspeglar en och samma givna energimängd — och som vi kan associera till i sammanhang som speciellt berör tillståndsutvecklingen hos gaser och ångor, men även för kroppar och substanser i allmänhet. Plancks entropisamband beskriver, tydligen särskilt tillståndsbegreppet (W) för dessa fall med garanterat bevarande av Plancks strålningslag som därmed, helt säkert och grundligt, utesluter termen, föreställningen, uppfattningen och blotta idén om »isolerat system» I TERMODYNAMISK MENING.

I korthet: Den redan allmänt välkända allmänna gaslagen (se även i HISTORIA)

E = pV = kT = (F/A)Ad .......................................................... allmänna gaslagen

bildar atomismens (materiefysikens) naturvetenskapliga grundval med speciell giltighet för gaser och ångor räknat idealt från absoluta nollpunkten T=0°K=–273,15°C motsvarande ideal absolut materiell rörelselöshet: nollvärme. Men sambandet gäller bara med temperaturen (T) som generatris till tryck (p) [och volym V] enligt (T→p): T tar ingen funktion, varken av trycket eller volymen — därför att den fysikdelen berör olika sätt beroende på material. Den delen innefattas inte i allmänna gaslagen. Därför måste man också vara uppmärksam på HUR sambandet används, från fall till fall; det finns för olika material ingen enhetlig, enkel, matematik som beskriver hur T varierar om tryck och/eller volym ändras.

En (kort) beskrivning (utan matematiska samband) ges i Förtydligande till allmänna gaslagen där en viss orientering ges i hur man kan beräkna hur (snabba) ändringar i pV påverkar T med återverkan på pV (termisk rekyl) och approximativt enbart med hänsyn till gasmassan (omgivande material bortses ifrån). Observera att den framställningen inte är tillägnad att förstås som någon typ »bidrag till allmänna gaslagen».

Man skulle kunna säga att allmänna gaslagen, därmed, representerar »ett idealt slutet eller isolerat system». Men det visar sig vara mera beskrivande, upplysande och förklarande att säga som det är: allmänna gaslagen beskriver ett bestämt idealt momentant tillstånd för varje givet T — där man givit »tillbörlig tid» för pV att anpassa sig efter ändringen i T. Med andra ord: Allmänna gaslagen gäller med en idealt omedelbar verkställande koppling till faktorerna pV — i det praktiska fallet ALLTSÅ MOTSVARANDE förutsatt att tillbörlig TID ges för pV att anpassa sig.

För normala [små] Jordlaboratoriska gasvolymer [typ kubikmeter] innebär det relativt snabba anpassningstider [runt mikro- eller nanosekunder] då gasbollarnas medelhastigheter i typ rumstemperatur också är relativt höga.

Om (alltså) intervallet för pV-anpassningen beaktas, stämmer (alltså — väl bekant för alla experimentalister) allmänna gaslagen utomordentligt väl överens med praktiska fall. Begreppet »isolerat system» i allmänna gaslagen övergår då, mera korrekt, till innebörden av den momentana tillståndsbild som gäller vid den tidpunkt i det praktiska systemets fall då ändringen i pV från ändringen i T kan anses verkställd (»i allmänhet omedelbart»). Beroende på omständighet måste alltså alltid och i vilket fall varje särskild situation (noga) övervägas för att sambandet i allmänna gaslagen ska kunna användas.

Generellt, för hela universums fysik, har för övrigt I RELATERAD FYSIK allmänna gaslagen föga betydelse utanför Jordfysiken (mänsklighetens tekniska kultur). För dessa utomplanetariska fall, se utförligt från Stjärnfysiken.

Se även (vidare) från ISOLERADE SYSTEMETS URSPRUNG.

typen »isolerat system» — med någon som helst förmodad real matematisk-fysikalisk grund — utesluts ur termofysiken av Plancks strålningslag

Se även från Plancks entropisamband från Allmänna gaslagen.

Därmed är typen »isolerat system» I TERMODYNAMISK MENING helt säkert utesluten ur fysiken: det finns ingenting sådant som ett »isolerat system» I TERMODYNAMISK MENING i fysiken;

Pseudofysik

Varje mening som, ändå, på något sätt försöker göra gällande att »isolerat system» har, eller skulle ha, någon, alls överhuvudtaget tidsmässigt berättigad existens, praktiskt eller teoretiskt — någon som helst typ av praktisk, reell, fysikbeskrivning — kommer följdriktigt att avhandla pseudofysik: Synpunkter, uppfattningar, meningar och argument (enorma utläggningar) som ingen KAN ha någon naturgrundad uppfattning om; Varken säker eller observerbar eller alls överhuvudtaget någon enda naturlig fysikalisk grund som kan uppvisa någon som helst bekräftande fenomenalitet för typen »isolerat system»: En sådan fenomenalitet existerar inte; Därför, återigen, att Plancks strålningslag med kontinuerlig emission och absorption, kropparnas blotta termofysik, utesluter »isolerat system» I TERMODYNAMISK MENING i fysiken:

»isolerat system» I TERMODYNAMISK MENING existerar inte.

Det intygas också från etablerat håll, se särskilt i citat — men används likväl som FUNDAMENT i t.ex. »termodynamikens andra huvudsats».

Ursprunget till »isolerat system» i modern akademi

Historien berättar inte varifrån i modern akademi uppslagen till »isolerat system» i förening med UNIVERSUM har kommit; Det troligaste är, i brist på exakta källor, att ämnet kom ’smygande’ med intresset för värmemaskinerna under 1800-talet, med tillhörande resonemang om ideala förhållanden [typ »vi frånser ev. värmeförluster»] — ett resonerande som i termofysikens ljus TYDLIGEN blir ytterst äventyrligt om det inte finns en MYCKET VÄL RELATERBAR förtrogenhet med grundfysiken (att grundfysiken kan relateras minutiöst i detalj):

Att diskutera fysikaliskt skeende INOM »isolerat system» i termodynamisk mening är (således) med referens till Plancks strålningslag och ljusets blotta natur UTESLUTET: alla kroppar värmeläcker. Tänk inte ens tanken — därför att inga motsvarande fysikaliska observerade fenomengrunder existerar. Ren fiktion. Noll naturvetenskapligt intresse. End. Finito. Drop it. Se även [‡7] och [‡7.2].

Ett exempel på hur ’nära’ källan nedan rör vid ett ev. ursprung till »isolerat system» i termodynamisk mening — men utan att ändå direkt VARA ursprunget, vilket framgår av sammanhanget (här utan vidare utläggningar) — ges av James Clerk Maxwell i hans The Theory of Heat s338 (Maxwell beskriver dåvarande andra värmelagen):

”One of the best established facts in thermodynamics is that it is impossible in a system enclosed in an envelope which permits neither change of volume nor passage of heat, and in which both the temperature and pressure are everywhere the same, to produce any inequality of temperature or of pressure without the expenditure of work.”, s338

INTERNET ARCHIVE — JAMES CLERK MAXWELL 1871 The Theory of Heat

http://www.archive.org/details/theoryofheat00maxwrich

En mycket fin, avancerad, bokpresentation — med (nästan) riktig blädderupplevelse

Min översättning:

En av de bäst etablerade fakta i termodynamiken är att det är omöjligt i ett system som är inneslutet i en hölje som varken tillåter volymändring eller värmepassage …

Ämnet (Maxwells värmeteori) framtvingar naturligt typen »isolerat system» i beskrivningssättet, men utan att fördenskull inlägga några aspekter på UNIVERSUM.

(Upphovsmannen är alltså, knappast, Maxwell).

Se även mera allmänt (idealiserade begrepp) i Isolerade systemets ursprung.

Därmed är också motsättningen mellan RELATERAD FYSIK och MODERN AKADEMI fullständigt avtäckt; Sett ur den relaterade fysikens perspektiv går det inte att avhandla pseudofysik:

»isolerat system» I TERMODYNAMISK MENING existerar inte.

Förmodade detaljer som inte existerar har naturligtvis inget som helst naturvetenskapligt intresse. Det är ingen idé att ens tänka på ett närmande. Det är med andra ord viktigt att försöka klassificera intressegrunderna — inte alltid en helt enkel uppgift.

Allmänna sambandsformer i termofysiken

Med huvudreferens till Tillståndsbegreppet i modern akademi

Allmänna sambandsformer — termofysiken

Se ARBETSEXEMPEL och PRAKTISKA EXEMPEL

S₀ = E/T ................................................................ J/°K, värmekapacitet

S₁ = E/T/KG ......................................................... (J/°K)/KG, värmekapacitivitet (specifika värmet)

S₂ = E/T/mol ......................................................... (J/°K)/mol, molär värmekapacitivitet, S₁×atomvikten/1000

S₃ = b(lnW) ........................................................... J/°K, Planckentropin, Plancks entropisamband

Benämningen Plancks entropisamband (»Planckentropin») används här för sambandsformen

S = b(lnW) ............................................................. J/°K, Planckentropin, Plancks entropisamband

Historiska uppgifter, nedan, gör gällande att Max Planck, inte Ludwig Boltzmann, införde den numera berömda sambandsformen S=b(lnW). Det skulle ha skett år 1901, från Ludwig Boltzmanns ursprungliga sambandsform ∫(dq/T)=2Ω/3 — i sin tur från Rudolf Clausius S=Q/T 1865. Citatet nedan angående Boltzmann;

”His formula, ∫(dq/T) = 2Ω/3, is, however, better known in the form S = k log W, which Max Planck gave it in 1901.

”,

ANSWERS.COM — THE WORLD’S LEADING Q&A SITE (2010)

http://www.answers.com/topic/ludwig-boltzmann

;

S = k ln W;

”The formula is a modified or reduced form of Austrian physicist Ludwig Boltzmann's H-function and was first put in this shorthand form by German physicist Max Planck in his 1901 paper “On the Law of Distribution of Energy in the Normal Spectrum.” [1] Specifically, Planck explains that the entropy SN of the system [resonator] is proportional to the logarithm of its probability W, within an arbitrary additive constant:

S = k log W + const

”,

ENCYCLOPEDIA OF HUMAN THERMODYNAMICS kronologisk uppgift saknas

http://www.eoht.info/page/S+%3D+k+ln+W

Den rent historiska tillkomsten av Plancks entropisamband beskrivs i särskild genomgång med utförliga citat;

Efter relativt omfattande sökarbeten: Historiska basfakta i ämnet berättar hur Planck inspirerades av Boltzmanns resultat, hur sambandens form växte fram, och en del (men inte allt, ännu) hur det utvecklades ur föregående begrepp, samt vidare.

Se utförligt från Plancks entropisamband S=b(lnW).

Webbkällor som härleder Plancks strålningslag

EXEMPEL PÅ WEBBKÄLLOR SOM HÄRLEDER PLANCKS STRÅLNINGSLAG

Härledningen till Plancks strålningslag på webben

Utöver det redan omnämnda och i vissa partier redan citerade från Plancks original 1901 i webbkällan

On the Law of Distribution of Energy in the Normal Spectrum, Max Planck

Annalen der Physik vol.4, p.553 ff (1901), s3

http://bourabai.kz/articles/planck/planck1901.pdf

se från

S = b(lnW) är Plancks entropisamband — inte Boltzmanns

;

En till synes stor mängd exempel finns på webben som, efter olika sätt, försöker härleda Plancks strålningslag — men på sätt som knappast är begripligt av personer som inte är invigda i universitets- och högskolematematiken med alla dess vidlyftiga referenser och etablerade teorem. Till direkt jämförelse med dessa, se den helt på elementära begrepp grundade Härledningen till Plancks strålningslag från Plancks entropisamband. Den härledningen är helt och hållet identisk med huvudinnehållet i Plancks framställning från år 1901, som ovan, men först från W-formens potensfunktion — som emellertid även Planck och andra, tydligen felaktigt, använder permutationsmatematiken för att nå fram till; Brytpunkten beskrivs mera utförligt i S = b(lnW) är Plancks entropisamband — inte Boltzmanns. Se även i W finns inte i statistiken.

Med GoogleSökning Feb2010 på »Planck radiation law +derivation» ges följande, godtyckligt, uttagna webbreferenser (med syftet att undersöka om och hur källorna kopplar till Plancks entropisamband).

Webbreferenser — härledning till Plancks strålningslag

Webbkällan nedan ger inget omnämnande av Plancks entropisamband S=b(lnW) i samband med den härledande beskrivningen.

WIKIPEDIA

http://en.wikipedia.org/wiki/Planck's_law

@INTERNET Wikipedia Planck’s law, Derivation 2010-02-22

”

According to quantum theory, the energy levels of a mode are given by:

$E_{n_{1},n_{2},n_{3}}\left(r\right)=\left(r+\frac{1}{2}\right)\frac{hc}{2L}\sqrt{n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}. \qquad \mbox{(1)}$ bildkopia

…”.

DESSUTOM: Blotta ansatsen i ovanstående försök ”quantum theory” lämnar DIREKT huvuddelen av alla intresserade utanför partyt; Citatkällan fortsätter sedan på samma fason: ”Casimir effect”, ”statistical mechanics”, ”partition function”, ”Bose-Einstein statistics”, … .

Uppgiften gällde att härleda Plancks strålningslag — HELST med referens till Plancks entropisamband S=b(lnW) — enbart på elementära matematisk-fysikaliska grunder: derivering, integrering, differentiering, elementära räknelagar, allt det man (enkelt, i vardagslivet, beroende på tid och intresse) kan komma ihåg med relativt enkla huvudräkningsövningar väl en gång studerat i grunderna. Se även utförligt från ANALYSEN och MATEMATIKEN FRÅN BÖRJAN om inte redan bekant.

Nästa.

Citatkällan ovan refererar också Plancks strålningslag till en annan, särskild artikel i Wikipedia benämnd ”Gas in a box” — med en grundform som i sin tur hänvisar till en annan artikel benämnd ”Particle in a box”, som i sin tur (återigen) grundas på ”quantum mechanics” med tillhörande beskrivningar av matematiken för olika typer av vågfunktioner … . Innan den intresserade, men inte universitets/högskoleutbildade, läsaren har hunnit gå igenom alla dessa myllrande detaljer har det (säkert) hunnit bli julafton om flera gånger. Referensen är (med andra ord) definitivt varken enkel eller elementär.

Nästa.

Också webbkällan nedan utelämnar Plancks entropisamband S=b(lnW), samt använder sig av ”statistical mechanics”,

”To derive the energy density in this photon gas, we first need to know the relative probability with which a given energy state E(N) is occupied at a given temperature. Here, we turn to statistical mechanics, which reveals this probability as …”,

THERMAL HUB — Derivation of Planck's Law (Jul 2009)

http://thermalhub.org/topics/DerivationofPlancksLaw

vilket ansluter till föregående: framställningen är svårgripbar utom för universitets- och högskoleutbildade. (Universums Historia förenar nytta med nöje: från passare och linjal till grunderna i ingenjörsmatematiken).

Nästa.

Också webbkällan nedan (som avhandlar ämnet via vågfunktioner) utelämnar Plancks entropisamband S=b(lnW), samt använder sig av ”statistical mechanics” enligt ”The average energy per oscillator was calculated from the Maxwell-Boltzmann distribution” och som enligt Wikipedia Maxwell–Boltzmann distribution 2010-02-22 ”describes the probability of a particle's speed”,

SONOMA STATE UNIVERSITY, J. S. Tenn

Planck’s Derivation of the Energy Density of Blackbody Radiation, datumuppgift saknas

http://www.phys-astro.sonoma.edu/people/faculty/tenn/p314/BlackbodyRadiation.pdf

Utan att, således ens behöva, gå närmare in på detaljer är det tydligt att även denna webbkälla ansluter till de förra.

Nästa.

Inte heller följande webbkälla (som också avhandlar ämnet via vågfunktioner) omnämner eller använder Plancks entropisamband S=b(lnW). Dessutom figurerar även här begrepp från statistiken med ”sannolikhet” och som redan, som ovan, konstaterats ligger vid sidan av ämnet.

”The only flaw in the derivation of the Rayleigh-Jeans law is the classical assumption that each radiation mode can have any energy E. Then the continuous Boltzmann probability distribution …”

NATIONAL RADIO ASTRONOMY OBSERVATORY — Blackbody Radiation (2009)

http://www.cv.nrao.edu/course/astr534/BlackBodyRad.html

Webbkällan har figurer som inte kommer fram i Internet Explorer. Använd istället webbläsaren Mozilla Firefox eller Google Chrome (eller annan), där syns figurerna.

Heller inte den källan ger alltså något upplysande bidrag i ämnet.

Fortsätter man så mata av träffsidorna (de som har åtkomliga artiklar), tycks även alla följande övriga följa i stort sett samma mönster; Det är ”probability” och ”Boltzmann probability density”, termer och begrepp som alltså inte berör ämnet. Se beskrivningen utförligt från W finns inte i statistiken och

S = b(lnW) är Plancks entropisamband — inte Boltzmanns.

Det finns, tydligen (och således därmed, ännu i etablerade led), ingen som har noterat ”sannolikhetssyndromet” i Plancks strålningslag. Alla etablerade fackbeskrivningar (här veterligt) tycks använda sig av det. Alla tycks gå i samma, väl upplöjda fåror.

Frånsett UNIVERSUMS HISTORIA finns i varje fall ett svenskt exempel,

Plancks strålningslag — uppgift om författare och datum saknas

https://studentportalen.uu.se/uusp-filearea-tool/download.action?nodeId=124226&toolAttachmentId=49689.

som också ansluter till samlingen ovan enligt ”Bose-Einstein-fördelningen” — Och som enligt en annan svensk webbkälla (s4)

KTH-ELECTRUM KISTA — Viktiga samband i den statistiska fysiken, Ulf Ekenberg 2005

http://www.ict.kth.se/courses/IM2691/statfyssamm05.pdf

sammanhänger med att ”Kvantpartiklar med heltaligt spinn lyder Bose-Einstein-statistik.”. Inte heller denna källa lämnar, således, något bidrag.

Härledningen till Plancks strålningslag i UNIVERSUMS HISTORIA i Termofysikens matematik, utgår för sin del ifrån Härledningen till Stefan-Boltzmanns strålningslag — garanterat helt rent på statistiska förekomster — genom helt formellt matematiska-fysikaliska grundbegrepp utan någon inblandning av Plancks entropisamband S=b(lnW). Den härledningen är dessutom mera fullständig då den också innefattar/associerar härledningen till (den, annars, ytterst besvärliga) konstanten i Stefan-Boltzmanns strålningslag, samt vidare Wiens förskjutningslag. Motsvarande ordning finns, här (fortfarande) veterligt inte i någon etablerad fackbeskrivning. Där går man (här veterligt, samtliga fall) istället omvända vägen och härleder Stefan-Boltzmanns strålningslag ur Plancks strålningslag genom integration.

Den etablerade ordningen är alltså generellt den, som exemplifierats i ovannämnda webbkällor, att Plancks strålningslag, tydligen, härleds genomgående etablerat ur statistisk matematik — med, här, enda kända undantaget i Plancks framställning från år 1901: W-formen framställs tydligt på potensform, se Plancks W-form. Se även i W finns inte i statistiken.

ENTROPIBEGREPPET I GENERALGENOMGÅNG FRÅN FEBRUARI 2010

Hur värmen avtar med tiden

VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK

Hur ljuset — VÄRMEN — tvunget avtar med ljusets naturliga spridning

värmen tvingas avta med den sektoriella uttunningen av ljusenergin (hf) i kraft av elektriska potentialens naturliga avtagande med avståndet: hf-energin som sådan avtar också — och då med inbördes växelverkan mellan infallande ljus och elektriskt laddad kropp via Comptoneffekten

Beskrivning

Elektriska fältet garanterar att elektriska potentialen avtar med växande avstånd från den elektriska laddningen genom divergensen (LJUSHASTIGHETEN) och divergensens gravitella beroende. Induktionen ansvarar för FÄRGERNAS UTBREDNING genom de elektriska laddade kropparnas inbördes växelverkan då de svänger, oscillerar och positionsändrar — det vi kallar för ljuset: frekvenserna, våglängderna i värmefenomenet.

Varje elektriskt laddad kropp som genomgår en positionsändring åstadkommer genom sitt lägesändrade elektriska fält och den däri kopplande (lokala) ljushastigheten (DIVERGENSEN) en återverkan (se induktion) på alla omgivande elektriskt laddade kroppar med en motsvarande (elektriska fältpotentialen) avståndsbetingad, induktiv, positionsändring. Se utförligt från Induktionen.

Genom att den elektriska fältpotentialen (U=E/Q=Fr/Q=k[dQ/dr]) avtar med avståndet från den laddade masskropp som tar emot och vidarebefordrar (medierar) induktionen, avtar analogt ljusets induktivt verkställande styrka TVUNGET med ljusets (divergenta) spridning; Vilket i motsvarande mening betyder: allt mindre effektiv ljusenergi ([n→1]hf) per fast rymdvolym »i takt med tiden». Dvs., ljusets styrka försvagas med divergensen — men inte frekvensen; För frekvensens avtagande se Comptoneffekten.

Värmestrålningens (E/hf) sektoriella avtagande med avståndet från ljuskällan

Generellt kan man alltså säga att värmen tvingas avta med den ljussektoriellt expanderande uttunningen av ljusenergin (hf) i kraft av elektriska potentialens naturliga avtagande med avståndet — så länge det finns någon omgivande fri rymd för ljuset att tränga in i. Eller enklare:

— Värmen avtar med divergensen.

Det innebär tydligen detsamma som att varje försök att OMVÄNDA (komprimera) den naturliga spridningen obönhörligt kräver energi. Fenomenformen är alltså samma som att en ljuskälla syns allt svagare ju större avståndet till den är. I perceptionsanalysen betyder det detsamma som att föremålen förefaller minska med avståndet på grund av att också den upptagande synvinkeln minskar med ökat avstånd och därmed avtagande ENERGI (entropin, den värmegrundade arbetspotentialen) i det upptagande synfältets ändyta. Det finns här veterligt ingen allmän litterär framställning om någon person som uppfattat den fenomenformen som anmärkningsvärd i meningen att OMVÄNDNINGAR skulle vara möjliga — men den moderna akademin uppvisar (från senare delen av 1800-talet) en till synes stor flora av meningar, se särskilt citat, som förundras över att ’värme alltid går från varmt till kallt’, Clausius framställning från 1862. Se även från Åldrandets princip.

ENTROPIBEGREPPET I GENERALGENOMGÅNG FRÅN FEBRUARI 2010

Genomgången från Feb2010

END.

ENTROPIBEGREPPET I KORTARE GENOMGÅNG FRÅN DECEMBER 2009

Entropibegreppet

ENTROPIBEGREPPET I KORTARE GENOMGÅNG FRÅN DECEMBER 2009

2009XII11

ENTROPIBEGREPPET

——————————————————————————————

Notera f.ö. termerna ENLIGT RELATERAD FYSIK:

massfysiken (p®T) beskriver Planckstrålningens uppbyggnad från noll;

materiefysiken (T®p) beskriver (mass)Planckstrålningens (materie)distribution, den här benämnda »Planckstrålningen».

——————————————————————————————

Massfysiken står helt orepresenterad i modern akademi.

Se särskilt från Atomkärnans Härledning i Universums Historia.

FOTO: Författarens arkiv — Björklöv · Våren 2009 · Nikon D90

bakgrund | HISTORIA

Allmänna gaslagen

pV = kT = E .................................... J

grundlades med individuella bidrag från Boyle (1622), Charles (1787) och Gay-Lussac (1809), ref. @INTERNET Wikipedia Gas laws 2009-12-12. Clausius entropisamband S=Q/T introducerades 1865 ref. @INTERNET Wikipedia Rudolf Clausius, Entropy 2009-12-12, Plancks entropisamband S=b(lnW) infördes 1901, ref., se Plancks original. Många webbkällor kallar det för »Boltzmanns entropisamband», se t.ex. @INTERNET Wikipedia Boltzmann’s entropy formula 2009-12-12.

Naturtermiskt läckage

INLEDANDE NOTIS till mera omfattande klarläggande (Angående Plancks strålningslag som grundvalen för alla kroppars värmeläckning) — om ej redan bekant:

Angående Plancks strålningslag som grundvalen för alla kroppars värmeläckning

Med ytterligare genomsökning på webben i ämnet URSPRUNGET TILL ISOLERAT SYSTEM har flera 1800-talskällor uppmärksammats på INTERNET ARCHIVE — Flera (många) inskannade gratis digitalupplagor finns av bokpionjärerna bakom värmeläran (Stewart, Kirchhoff, Maxwell, Planck m.fl.).

För ändamålet har därför sammanställts ett separat htm-dokument i

PLACKS STRÅLNINGSLAG I PRAKTISK FYSIK där också bakgrunden till

Införandet av Isolerat System 1858 beskrivs ingående — tillsammans med övriga betydelsefulla detaljer i Plancks strålningslag. Se främst

Satsen om alla kroppars värmeläckning för en mera detaljerat relaterad beskrivning med förankring i Plancks strålningslag, dess grund, sammanhang, sammansättning, innebörd, betydelse och tillämpning, om ej redan bekant.

Se även Isolerat system i Termodynamisk mening

Det finns FLERA entropibegrepp i omlopp — beroende på det etablerade begreppet isolerat system:

Efter fri fantasi · Tuschteckning · Författarens arkiv

VARJE termodynamiskt system — materiell kropp — i den verkliga praktiska observerbara fysiken VÄRMELÄCKER, se även citat nedan. Undantag existerar inte — just på grund av ljusets divergenta, utstrålande natur, att materien består av ATOMER vars elektronhöljen alltid genomkorsas av olika strålningsmönster. Se även i VÄRMEDIVERGENSENS FÖRKLARING I RELATERAD FYSIK. Ytterst sett för varje sådant system, alltså kropp av atomer som utelämnas åt sig själv i rymden, avtar likaledes Planckstrålningen hos materiedelen också slutligt, obönhörligt: all materiebaserad elektromagnetisk strålning i varje givet expanderande universum går, tvunget, mot noll, analogt mot noll entropi S=b(lnW). Det gäller för samtliga fria kroppar motsvarande termofysikaliska system — därför att energin bakom strålningsgivningen i varje universum är ändlig: alla stjärnor måste en gång slockna då allt bränsle (stjärnornas vätebas) tagit slut: allt återvänder till ursprunget.

Vi ser det kretsloppets princip partikulärt i alla naturprocesser, i alla mekaniska och elektriska förlopp som innefattar ett naturligt motstånd mot förändring — svängningar, oscillationer, resonanser, mönstergrunderna genom atomerna — vi ser det (således) genom kvalitativa mönsterstrukturer hos alla fröbärande växter, från mullen och åter till mullen, vi ser det ständigt i naturens biologiska kretslopp, vi påminns om det i våra egna lekamliga kroppars förgänglighet och död med den ständiga födelsen av nya kroppar, vi kan se det i alla återkommande (periodiska) naturprocesser typ is och snö till vatten och åter till is och snö.

Motsvarande praktik med alla stjärnors utslocknande i ett massändligt universum, stundtals benämnt universums värmedöd, se exv. @INTERNET Wikipedia Heat death of the universe, motsvarande T=0°K, blir alltså i ljuset av Plancks entropisamband S=b(lnW) en återgång till S=0: all atomär inbördes rörelse utslocknar, allt återvänder till nollentropi. Nollentropi blir med andra ord idealt DET HELT KVANTITATIVA tillståndet då all atomär och molekylär rörelse helt har upphört. Det finns ingen kvalitetsaspekt i det.

— Men i den etablerade uppfattningen beror, tydligen, omskrivningen med »Boltzmanns entropisamband» från Plancks entropisamband S=b(lnW) istället på DET UPPFUNNA BEGREPPET isolerat system inom »termodynamikens andra huvudsats», citat nedan — vilket betyder en ANNAN tolkning:

”The second law of thermodynamics is an expression of the universal principle of entropy, stating that the entropy of an isolated system which is not in equilibrium will tend to increase over time, approaching a maximum value at equilibrium”,

@INTERNET Wikipedia Second law of thermodynamics 2009-12-11

Min översättning:

Termodynamikens andra huvudsats är ett uttryck för entropins universella princip, vilken fastslår att entropin i ett isolerat system som inte befinner sig i jämvikt tenderar att öka med tiden, närmande sig ett maximalt värde vid jämvikt.

Jämför isolerat system i etablerad litteratur:

”In the natural sciences an isolated system, as contrasted with a open system, is a physical system that does not interact with its surroundings. It obeys a number of conservation laws: its total energy and mass stay constant. They cannot enter or exit, but can only move around inside. An example is in the study of spacetime, where it is assumed that asymptotically flat spacetimes exist.

Truly isolated physical systems do not exist in reality (except perhaps for the universe as a whole)”,

@INTERNET Wikipedia Isolated system 2009-12-11

Min översättning:

I naturvetenskaperna är ett isolerat system, i motsats till ett öppet system, ett fysikaliskt system [material] som inte växelverkar med dess omgivningar. Det lyder ett antal konservationslagar: dess totala energi och massa förblir konstant. De kan inte inträda eller utträda, utan kan bara förflytta sig omkring inuti. Ett exempel är i studiet av rumtid, där det förmodas att asymptotiskt plana rumtider existerar.

Verkligt isolerade system existerar inte i verkligheten (utom möjligen för universum som helhet).

Felet i MAC

FELET man gör (i etablerade kvarter) i användningens av entropibegreppet I ETT SLUTET/isolerat UNIVERSUM är, således, inte att idealisera i sig, utan att felaktigt tillämpa den antagna idealiseringen — Jordfysikens idealiserade laboratorium — PÅ ETT OBJEKT SOM UPPENBARLIGEN STRIDER MOT ALLA ÖVRIGA AV ERFARENHETEN VERIFIERADE OBJEKTS VERKNINGSSÄTT: universum som helhet:

termodynamiska system, kroppar i värmesammanhang, som INTE värmeläcker

existerar inte i fysiken

Det finns ingen som helst varken kvalitativ eller kvantitativ observationell grund för att anta något dylikt (vilket också, faktiskt, understryks av konventionella källverk):

all materia absorberar och emitterar elektromagnetisk strålning, värme och ljus, genom att all materia består av atomer med elektronhöljen vars fysik baseras på elektromagnetiska svängningsresonanser av typen Planckenergi E=hf.

Därmed finns HELLER ingen som helst grundad anledning att utgå ifrån att universum som helhet skulle uppföra sig på något ANNAT sätt. Med andra ord:

— I ETT ÖPPET massändligt UNIVERSUM där energin alltså är begränsad, avklingar också för varje kropp tvunget ENLIGT OBSERVERAD ERFARENHET UTAN UNDANTAG värmestrålningen till (idealt) noll när all tillgänglig användbar energi omsatts och ingen längre finns kvar att underhålla någon värmestrålning — analogt noll entropi enligt Plancks entropisamband.

Det är också precis vad som uttrycks i enlighet med K-cellens värmefysik.

Uppfinningen av det isolerade universumet

UPPFINNINGEN AV DEN MODERNA AKADEMINS ALLMÄNT SLUTNA|isolerade förnekarUNIVERSUM

Med fortsättning från föregående.

I den moderna akademins unika universella uppfinnarverkstad — däremot — menar man att universums entropi växer: jämför eminensernas parad:

”Som minnesregler för termodynamikens två huvudsatser brukar ofta följande formuleringar användas:

Första huvudsatsen: Universums energi är alltid konstant.

Andra huvudsatsen: Universums entropi strävar alltid att öka.”,

FOCUS MATERIEN 1975 s325sp2mn

Man menar, tydligen, att entropin aldrig kan minska eller avta sett totalt — att ett massändligt universum inte kan betraktas PÅ SAMMA SÄTT som en fristående Sol som falnar, slocknar och till slut helt förlorar varje form av atomär rörelse

— trots att varenda naturbild bara utpekar den typen, tydligen och veterligt helt utan undantag

;

ISTÄLLET, tydligen, menar modern akademi att värmestrålningens uttömmande på något sätt skulle möta en MYSTISK VÄGG och sluta i ett slags konstant medelmässigt rörelsetillstånd av här okänd natur, se föregående citat från @INTERNET Wikipedia Second law of thermodynamics, samt även närmast ovan från FOCUS MATERIEN 1975.

Det är, tydligen runt år 2009, DEN bilden av begreppet entropi — den tydligen helt felaktiga uppfattningen om universum som ett isolerat system,

inte entropibegreppet som sådant med referens till GILTIGHETEN av Plancks strålningslag som visar HUR alla kroppar värmeläcker utan undantag

— som besitter den allra mest förnäma innebörden — applåderas mest — hos de allra mest förhärdade i den moderna akademins beundrarskara:

Man underförstår, tydligen, ett universalbegrepp, ett idealt slutet — isolerat — Jordfysikaliskt system (laboratorium) där ingen strålenergi kan läcka ut, men som i ljuset av föregående påpekanden, tydligen och uppenbarligen helt saknar varje spår av erfarenhetsmässig fenomengrund. Pseudofysik.

Därför, och endast med kännedomen om denna omständighet, denna tydligt falska förmodan med relaterad referens till den observerbara erfarenhetens praktiska fysik, kan man numera helt säkert avfärda den typen av OBS KVALITATIV entropitolkning som, helt säkert, fullständigt naturvetenskapligt ogrundad. Eller i andra ord:

all erfarenhetsmässig observation visar entydigt att alla naturliga kroppar och »system» återvänder till den grund varifrån de uppkommit: den i yttre elektromagnetisk mening absoluta vilans begrepp, den absoluta rörelselöshetens tillstånd:

noll entropi i full enlighet med Plancks entropisamband

— men inte enligt den etablerade uppfattningen om innebörden i begreppet entropi. Så upprepas tydligen, och utvecklas, alla naturprocesser. Ständigt, oupphörligt.

Men: Säg den som INTE redan observerat det.

Skillnaden i begreppsgrunderna hänger alltså, och tydligen, på »isolerat system».

Se även i Massfysikens nollentropi.

Citatextrakt i summa

Citatextrakt i summa:

”Som minnesregler för termodynamikens två huvudsatser brukar ofta följande formuleringar användas:

Första huvudsatsen: Universums energi är alltid konstant.

Andra huvudsatsen: Universums entropi strävar alltid att öka.”,

FOCUS MATERIEN 1975 s325sp2mn

Jämför korrekt formulering — Med ovanstående citatbrygd i ljuset av K-cellens värmefysik, således:

’ Första huvudsatsen: Idealt slutna|isolerade materiesystems energi är alltid konstant.

Andra huvudsatsen: Idealt slutna|isolerade materiesystems entropi strävar alltid att öka.’

Men i praktisk fysik finns inga idealt isolerade system i termodynamisk mening.

Den allmänna nedtrampningen av livet

Etablissemangets elaka entropibegrepp

entropibegreppet

EXEMPEL

EXEMPEL, JÄMFÖRELSER och ARGUMENT i ljuset av RELATERAD FYSIK som berör entropins etablerade begrepp

Med inledande utförlig beskrivning och genomgång från ENTROPIBEGREPPET I RELATERAD FYSIK.

Etablissemangets elaka entropibegrepp

modern akademi trampar ner den lilla plantan genom att slå den i huvudet med resten av universum

FOTO: Författarens arkiv · Våren 2009 · Nikon D90 · Förminskad och Bildbehandlad med lätt Sharpening

ORDNING AV PRINCIP är en UTOPI

— försök inte sticka upp: det faktum ATT den lilla plantan uppreser sig, rebelliskt MOT den moderna akademin, och påvisar faktum ATT entropin minskar — växande ordning, plantans utveckling — tillbakavisas med argumentet att JAMEN det gör ingenting åt saken eftersom TOTALA entropin i universum LIKVÄL ökar.

Den uppfattningen grundas alltså bara på ett simpelt, underförstått, men sällan insett preferensval: uppfattningen att universum är isolerat

— tydligen med förebild från ett idealiserat Jordlaboratorium.

Se även särskilt från Felet i modern akademi.

Med grund i den praktiska fysikens observerade samtliga fall att alla materierum uppvisar strålningsläckage och att därför uppfattningen om universum som ett slutet|ISOLERAT system helt saknar naturvetenskaplig grund, kan man — tydligen, som det får förstås — sammanfatta alla påståenden om universum som annat än en historia av växande ordning, ökande ändamålsenlighet, som naturvetenskapligt ogrundade.

Sådana uppfattningar har (följdriktigt, tydligen) ingen annan grund än i uppfinningen|FÖRNEKELSEN att naturen är intelligenslös.

Den moderna akademins allmänna våld på naturen

Som redan tidigare påpekats i ljuset av den relaterade fysikens beskrivning (se ENERGILAGEN, Fysikens tredje princip):

det finns inga isolerade system i termodynamisk mening.

Men hela den moderna termodynamiska lärogrunden bygger på den förutsättningen, citat.

Därmed radas också de felaktiga, falska — rent lögnaktiga — påståendena upp: i mängd.

Den moderna akademins uppfattningar generellt om tillvaron bara understryker den redan observerade traditionella moderna akademins alldeles tydliga AVERSION mot att (ens, tydligen) försöka SE att intelligens handlar om något som tillhör naturen, inte människan, något som människan är DELAKTIG i, inte herre över.

Jämför:

1. »alla tiders jag-är-bäst-deklaration»

”Transire suum pectus mundoque potiri”,

”Att övervinna sin mänskliga begränsning och bli herre över universum”,

”Fieldspriset är den förnämsta utmärkelse en matematiker kan få”,

MATEMATIK 2000 Lärobok 3 · NT | Naturvetenskapsprogrammet

Björk · Borg · Brolin · Ljungström · Natur och Kultur 1991, s219

Kommentar:

Texten står på medaljongen till Fieldspriset (»matematikens nobelpris»).

2. alla tiders DödSkalleRiksdag nummer ett

— demensförklaringen (demens, själlösa) över hela mänskligheten:

Ur filmen om Cantor, Gödel, Boltzmann och Turing (1tim29min från BBC FOUR) från

http://www.supranaturalis.se/index.php?option=com_seyret&task=videodirectlink&Itemid=40&id=1689

Philosophy, Physics, Mathematics - Dangerous Knowledge (BBC FOUR)

”The idea of entropy had a profound philosophical and political significance. Entropy is what changes the ticking of a clock into the destroyer of all things. It is what underlies the inexorable passage from youth to old age. Entropy is decay. And with decay, nothing lasts forever. Boltzmann had in essence captured mortality in an equation. Physics now declared, that no order, not even a God given one, will last forever. That there was no natural order, that God had set in stone, had already been pointed out by the scientist Boltzmann most admired, Charles Darwin.”, vid ca40min;

Min översättning:

Entropins idé hade en avgörande filosofisk och politisk betydelse. Entropi är vad ändrar klockans tickande till en förstörare för alla ting. Det är vad underligger den oundvikliga övergången från ungdom till ålder. Entropi är sönderfall. Och med sönderfall varar inget för evigt. Boltzmann hade i summa fångat dödligheten i en ekvation. Fysiken tillkännagav nu att ingen ordning, inte ens given av Gud, varar för evigt. Att det inte fanns någon naturlig ordning som Gud skulle ha stensatt, hade redan påpekats av den vetenskapare Boltzmann mest beundrade, Charles Darwin.

Se även i Två argument mot uppfattningen att ingenting varar för evigt.

Slutsats:

Modern akademi har tydligen formulerat naturgrunderna så maximal »övergripande» som det alls kan göras: Tydligen och uppenbarligen fel förutsättningar — på samtliga avgörande punkter.

Varför då? — eller Se även — Läs innantill (som ovan, med många flera):

”Människan har skapat matematiken, därom är alla lärde överens”.

Inte

”Människan UPPTÄCKER matematiken, därom är alla lärde överens”.

Det är stor skillnad det.

DELNINGSPRINCIPEN I MASSANS STRUKTUR GARANTERAR EN MOTSVARANDE RESONANSFYSIK INOM ATOMEN OCH I ALLA MOLEKYLÄRA FÖRENINGAR OCH DERAS BYGGNADER ANALOGT ALLA ORGANISKA CELLER OCH DERAS FUNKTION; DELNINGSPRINCIPEN KOPPLAR DIREKT TILL EXPANSIONSPRINCIPEN, INDIVIDKRITERIET ELLER STRUKTURKRITERIET SOM OCKSÅ GRUNDLÄGGER UNIVERSUMS HIMLAKROPPSBILDNING MED GALAXERNAS BILDNING OCH UTVECKLING; OCH SÅ UPPREPAS HISTORIEN GENOM HELA KRETSLOPPET PÅ EN GRUNDLÄGGANDE HARMONI SOM BYGGER PÅ RESONANSER, MÖNSTER, STÄNDIG VARIATION — MED GRUND I TILLGÅNG PÅ OÄNDLIG OSKAPAD MASSA

Varje unikt universum utvecklas ur varje föregående universum på DESS efterklang — och garanterar därmed att inte två identiskt efterföljande eller, någonsin alls, två identiska universum uppkommer. Varje universum är då, tydligen, som varje människa en unik individ. Se utförligt från K-cellens värmefysik.

Entropibegreppets Innebörd · Plancks entropisamband · Boltzmanns H-teorem · Plancks strålningslag från Plancks entropisamband ·

Massfysikens nollentropi · Åldrandets princip · Tillståndsbegreppet i MAC · Isolerade systemets ursprung · K-cellens tillståndsdiagram ·

Argument mot allmän sanningsförnekelse

Två argument mot uppfattningen att ingenting varar för evigt

I filmen Dangerous Knowledge

framförs den inledande allmänna existentiella åskådningsuppfattningen, likt en dom uttalad över hela mänskligheten — generellt beträffande individens förmåga att uttrycka hoppfullt tänkande (dessa vet möjligen, i sin tvärsäkerhet, också telefonnumret till adressaten — f.ö. enda anledningen varför den citatdelen medtagits [UNIVERSUMS HISTORIA omfattar inte religion och politik, men OM någon har direktnumret till Högsta ort, så gärna för mig:]):

’det finns ingen naturlig ordning som Gud skulle ha stensatt’

Anledningen till uppmärksammandet är, garanterat, inte att den här författaren har religiös anknytning. Det finns ingenting sådant. Däremot är intresset betydligt större i att relatera en vettig, livsbejakande grund av allmän harmoni och generellt fysiologiskt välbefinnande i enlighet med livets övriga underbara uppenbarelser och som ger vardagen dess många egenskaper med påtagligt utpräglad guldkant. Jag accepterar ingen förnekelse av det.

Se särskilt citatblocket från Dangerous Knowledge:

”Entropi är vad ändrar klockans tickande till en förstörare för alla ting. Det är vad underligger den oundvikliga övergången från ungdom till ålder. Entropi är sönderfall. Och med sönderfall varar inget för evigt.”.

Från citatblocket i Dangerous Knowledge

DET LINGVISTISK -LOGISKA ARGUMENTET

För det första:

DET LINGVISTISK -LOGISKA ARGUMENTET

”Ingenting varar för evigt” (eng. nothing lasts forever) är, tydligen, en självmotsägande mening. Ty, om INGENTING varar för evigt, när upphör då meningen ”Ingenting varar för evigt” att gälla? Meningen ”Ingenting varar för evigt” är alltså självmotsägande, en reguljär exixtensförnekarmening, vilket visar att det komplex man försöker beskriva INTE är väl genomtänkt.

Varje meningshävd, med meningens hävdande nödvändighet, vare sig sann eller falsk, bygger på visshet; Sanning. Alltid. Obrutet. Annars är meningen uppenbarligen ingen mening. ATT alltså ens FÖRSÖKA formulera någon enda mening som utesluter vissheten som meningens blotta grundval, typ ovanstående eminenta exempel, är och förblir en fundamental omöjlighet. Meningen motsäger (utplånar) sig själv. Se utförligt från Sanningsbegreppet.

DET MATEMATISK-FYSIKALISKA ARGUMENTET

För det andra:

DET MATEMATISK-FYSIKALISKA ARGUMENTET

Med James Bradleys upptäckt (1725, publ. 1729) av aberrationen, framgår med all önskvärd tydlighet det allra första påvisandet av ljusets gravitella beroende. Tillsammans med gravitationens absolutverkan i GRIP (konvergensprincipen) med efterföljande DEEP (divergensprincipen), se från Fysikens 7 Principer, och därmed elektriska laddningens härledning, se specifikt GcQ-teoremet, finns ingen möjlighet att undkomma faktum med universums allmänna c-kropp och innebörden av massans allmänna tyngdpunkt i ljuset av elektromagnetismens fysik:

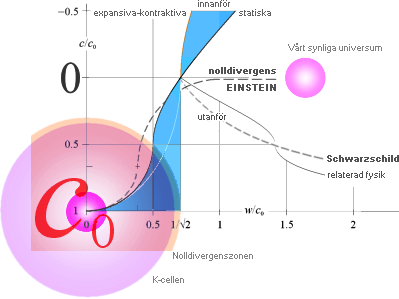
c0-kroppen med Grunddata från K-cellens värmefysik, från UnivHistPrim.htm

ljushastigheten (c) avtar från ett toppvärde i tyngdpunkten och utåt med växande massa; Universum är INTE elektromagnetiskt homogent, c gäller INTE överallt, vilket betyder att Jordfysikens formulerade »termodynamikens lagar» inte är tillämpliga på universum som helhet. Det hade man, som sagt, uppenbarligen förstått redan på Boltzmanns tid OM man hade beaktat James Bradleys upptäckt av aberrationen, i ljuset av FYSIKENS PRINCIPER (centralt från Johannes Kepler, Galileo Galilei och Isaac Newton, se även Ändringslagarna) — mer än hundra år före Boltzmann (1844-1906).

SÅLEDES:

Enbart av ovanstående (två enkla) skäl kan man avfärda alla ”vetenskapliga” påståenden som använder DET KVALITATIVA begreppet oordning i samband med entropins S-form som liktydigt med en, den primitiva uppfattningens, speciellt trång existenssyn: föreställningen om ett elektromagnetiskt homogent universum med ändlig massa. Det är uppenbarligen inte vårt fall.

Webbreferenser

Webbreferenser entropibegreppet

Särskilda Referenser

APPENDIX

Entropibegreppet i gängse verk

Det mest framträdande på webben (idag runt 2010) beträffande begreppet entropi är (naturligtvis den ännu oupplösta) motsättningen mellan »evolutionister» och »kreationister» — i ljuset av den moderna akademins »termodynamikens andra huvudsats». Som också redan har framskymtat i UNIVERSUMS HISTORIA, generellt, ges bägge dessa parter både fel och rätt — och det är relativt enkelt att se varför och hur i vart enskilt fall — med innehållet i denna presentation som facit. Utförligt från början i ENTROPIBEGREPPET. Här följer några typiska utdrag — utan vidare kommentarer — med citat från både svenska och engelska webbsidor (samt övrigt) som visar ett ungefärligt snitt genom ’världsmeningen’ i ämnet entropi.

All textmarkering (färg, fetstil etc.) i de följande citaten är min egen (för nyckelmeningar) i den mån dessa inte redan framhävs i originalen.

FOCUS MATERIEN 1975 s193sp1ö

”

Entropi

En av de viktigaste termodynamiska storheterna är entropin som i den statistiska mekaniken förknippas med den grad av ordning eller oordning ett materialtillstånd (inte nödvändigtvis gasformigt) uppvisar.

”.

http://www.holon.se/folke/kurs/Distans/Ekofys/fysbas/LOT/LOT_sv.shtml

2009-01-31, källreferens och datum saknas,

termodynamikens lagar;

”1. Energi kan inte skapas eller förstöras

2. Vid alla energiomvandlingar förbrukas energins kvalitet

Detta är naturlagar.”

”Termodynamikens andra lag säger oss att energins kvalitet (dvs. dess arbetsförmåga) minskar varje gång en energiomvandling sker.

Detta gäller alla energianvändningar, fysiska, metaboliska, interaktioner osv.

Detta betyder att energins kvalitet alltid minskar i universum som helhet, även om lokala ökningar kan ske på bekostnad av minskningar någon annanstans. I sin tur betyder detta att alla verkliga processer i universum är irreversibla.

En del tycker inte att detta är något vidare...

Energikvaliteten benämns exergi, och kan beräknas som summan av alla fria energier i ett system.

Till skillnad från energi kan exergi alltså konsumeras.”.

Källan ovan kopplar bl.a. till en webbsida där man beskriver hur vissa kristna församlingar starkt upprörs över formuleringar av typen ”oordningen ökar med tiden” eftersom det strider mot den gudomliga ordningens ideal (bibeln).

http://gluefox.com/skap/skev/termo.shtm

2009-01-31,

gluefox.com termodynamikens andra lag

Krister Renard 2007;

”Evolutionistens standardinvändning mot det sistnämnda argumentet är att -- oftast aggressivt och hånfullt -- påpeka att termodynamikens andra lag endast gäller för slutna (isolerade) system. Jorden utgör inget sådant slutet system, eftersom energi hela tiden tillförs från solen. Alltså bygger evolutionskritikerns hänvisning till andra lagen på bristande kunskap (eller illvilja alternativt dumhet).”.

http://www.evolutionsteori.se/kreationism_termodynamik.asp

2009-01-31,

evolutionsteori.se — Termodynamik, 2008

”Den ökade komplexiteten hos växter och djur följs därför av en entropiökning hos resten av universum, helt i överenstämmelse med termodynamikens andra huvudsats.[#3] [#4] Faktum är att ett flertal vetenskapsmän anser att termodynamikens andra huvudsats utgör en drivkraft för evolutionen, t.ex. utvecklas organismer för att fylla tomma ekologiska nischer på ett sätt som kan liknas vid den fria expansionen av en gas i en tom behållare.”.

http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/seclaw.html#c4

”Since entropy gives information about the evolution of an isolated system with time, it is said to give us the direction of "time's arrow" . If snapshots of a system at two different times shows one state which is more disordered, then it could be implied that this state came later in time. For an isolated system, the natural course of events takes the system to a more disordered (higher entropy) state.”.

http://www.icr.org/index.php?module=articles&action=view&ID=245

2009-01-25,

Institue for Creation Research — Does Entropy Contradict Evolution? by Henry Morris, Ph.D. March 1985;

”The popular syndicated columnist, Sydney Harris, recently commented on the evolution/entropy conflict as follows:

There is a factor called "entropy" in physics, indicating that the whole universe of matter is running down, and ultimately will reduce itself to uniform chaos. This follows from the Second Law of Thermodynamics, which seems about as basic and unquestionable to modern scientific minds as any truth can be. At the same time that this is happening on the physical level of existence, something quite different seems to be happening on the biological level: structure and species are becoming more complex, more sophisticated, more organized, with higher degrees of performance and consciousness.

”;

”This, indeed, is a good question, and one for which evolutionists so far have no answer. Some have tried to imagine exceptions to the Second Law at some time or times in the past, which allowed evolution to proceed in spite of entropy, but such ideas are nothing but wishful thinking.”.

@INTERNET Wikipedia Second law of thermodynamics 2009-01-25

”Pressure differences, density differences, and particularly temperature differences, all tend to equalize if given the opportunity. This means that an isolated system will eventually come to have a uniform temperature.”,

”Evidence indicates that biological systems and evolution of those systems conform to the second law, since although biological systems may become more ordered, the net change in entropy for the entire universe is still positive as a result of evolution.[10] Additionally, the process of natural selection responsible for such local increase in order may be mathematically derived from the expression of the second law equation for non-equilibrium connected open systems,[11] arguably making the Theory of Evolution itself an expression of the Second Law.”.

@INTERNET Wikipedia Entropy 2009-01-25

”The role of entropy in cosmology remains a controversial subject.”.

Solens massdefekt

Massan som Solen bränner av på en miljard år (T9 år) med nuvarande luminositet grovt 4 T26 W är så (löjligt) liten relativt Solmassan (grovt m_S=2 T30 KG) att man knappt tror det är sant:

SAMBAND m=E/c²=[PT]/c²;

[(4 T26 J/S)(1 T9år · 31557600 S)]/(3 T8 M/S)² = (4,44 T9 KG/S)(3,1557 T16 S)
@ (1,4 T26 KG)(1 T9 år)^–1;

Det är bara grovt sett (1,4 T26)/(2 T30)=0,00007 delar av hela Solmassan.

Inte ens på 100 miljarder år (för Solens del ENLIGT RELATERAD FYSIK eg. idealt ca 120 T9 år, se Tidsekvationen) skulle skillnaden vara mera än 0,007 — 0,7%.

Entropibegreppet

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Entropibegreppet

ämnesrubriker

ENTROPIBEGREPPET I GENERALGENOMGÅNG FRÅN FEBRUARI 2010

innehåll

ENTROPIBEGREPPET I RELATERAD FYSIK

Entropibegreppets MultiUniversella Harmoni

Inledande citat

kärnblock — huvudrubriker i sammanställning

Inledning till Entropibegreppets innebörd

S = b(lnW) är Plancks entropisamband — inte Boltzmanns

Brytpunkten

Resonansexemplet

Entropibegreppets innebörd

Clausius framställning 1854

Clausius framställning 1862

Clausius framställning 1865

Clausius entropibegrepp

Entropibegreppet i modern akademi

Entropibegreppet i relaterad fysik

Värmegrundad arbetspotential

Allmänna transientfunktionen

SAMMANFATTNING

Entropibegreppets Språkförbistring

HIMLAKROPPARNAS ENTYDIGA UTVECKLING PÅ VÄXANDE KRISTALLORDNING

ENTROPIN i Konkreta Praktiska Exempel

Jorden

PRAKTISKA EXEMPEL

Arbetsexempel

Atomismens grunder — praktiskt entropiexempel

Boltzmanns uteslutning ur det vetenskapliga samfundet, citatsamling

Isolerade systemets ursprung

Isolerade systemets innebörd

Statiskt och hydrostatiskt tryck

Förtydligande till allmänna gaslagen

Plancks entropisamband från allmänna gaslagen

Åldrandets princip

Inledande jämförande exempel

Orsaksriktningen i en tillståndsändring kan inte ändras

DEN MODERNA AKADEMINS FÖRYTLIGADE FYSIKKUNSKAPER

STRÄNGT REVERSIBLA PROCESSER FINNS INTE I DEN RELATERBARA FYSIKEN

Kausalordningen

Utförligt Arbetsexempel 1 — impuls föregår kraft · Kausalexempel 1

Utförligt Arbetsexempel 1.1 — Newtons vagga · Kausalexempel 1.1 · Newtons vagga

Utförligt Arbetsexempel 2 — Gravitationen · Kausalexempel 2

Utförligt Arbetsexempel 3 — Divergensen | Ljusfysiken · Kausalexempel 3

Slutsats

Upphovet till uppfattningen om tidssymmetri

Var finns referenserna?

GRAVITATIONEN

DEN KASTADE BOLLEN

SUMMERING — åldrandets princip

SVENSKA WEBBKÄLLOR SOM OMNÄMNER TIDSSYMMETRIN

Partikelexperiment verifierar den naturliga ordningen

Sammanfattning — vad betyder entropi

Massfysikens nollentropi

MASSFYSIKEN STÅR HELT OREPRESENTERAD I MODERN AKADEMI

Inledning till Boltzmanns H-teorem

Inledning

Användningen av »isolerat system» i Boltzmanns H-teorem saknar fysikalisk förankring

Boltzmanns H-teorem

Boltzmanns H-funktion

Den allmänna utvecklingen efter Boltzmanns H-teorem

Ursprunget till omformuleringen

Plancks strålningslag eliminerar Boltzmanns H-teorem

Inre kritik mot Boltzmanns H-teorem

Loschmidts paradox försvinner

Citatreferenser till Boltzmanns H-teorem

Exempel genom Wikipedia — och andra

Universums em-strålning till c0-kroppen

c0-kroppen

Wikipedias huvudexempel med smältande is

Värme från stek till tallrik

Inneslutna gasmassor

Tillståndsbegreppet i MAC (ModernACademy)

TILLSTÅNDETS FÖRBISTRING och entropibegreppets heliga innebörd I MODERN AKADEMI

Härledningen Till Plancks Entropisamband

Härledningen Till Plancks Entropisamband ENLIGT RELATERAD FYSIK

Härledningen

Likaberättigade energifördelningssätt

Hur W beräknas

Bevis

Generaliserade W-kvoten

Hur W beräknas från de enskilda atomerna

LIFE-satsen, beskrivning

LIFE-satsen

Antalet likaberättigade mikrotillstånd

T-funktionen

Impulsmomentets Planckekvivalenter

Jämförande exempel

Specifika värmets temperaturberoende

Verkanskvantumsgrundade Planckentropin

Den verkanskvantumsgrundade Planckentropin S=b(lnW)

DEN IMPULSMOMENTSGRUNDADE PLANCKENTROPIN

MIKROTILLSTÅNDENS LIKABERÄTTIGANDE

MIKROTILLSTÅNDETS INNEBÖRD

Plancks entropisamband

Noggrann citatgenomgång

Plancks log

Planck om Boltzmanns konstant

Plancks original från 1901

Plancksambandets särskilda citatReferens

Boltzmanns ursprungliga samband

Kommentar till Plancks original

Tidens Pil

K-cellen

Plancks strålningslag

Plancks strålningslag från Plancks entropisamband

W-formens potensfunktion

Entropiderivatan

Planckvärmekurvorna

W finns inte i statistiken

W saknar koppling till statistiken

Varifrån kommer feluppfattningen?

Plancks approximation

Boltzmanns entropikomplex

Plancks underliga approximation — från andra webbkällor

Flaskhalsarna i Max Plancks framställning

Första flaskhalsen — varför det är svårt att hänga med i Plancks egen beskrivning — sambandets form

Andra flaskhalsen — varför det är svårt att hänga med i Plancks egen beskrivning — fakultetssyndromet

Stirlings Formel

Tredje flaskhalsen — varför det är svårt att hänga med i Plancks egen beskrivning — deriveringen

Termodynamisk jämvikt

Termodynamisk jämvikt I RELATERAD FYSIK

Isolerat system i termodynamisk mening

Pseudofysik

Allmänna sambandsformer — termofysiken

Allmänna sambandsformer i termofysiken

Webbkällor som härleder Plancks strålningslag

EXEMPEL PÅ WEBBKÄLLOR SOM HÄRLEDER PLANCKS STRÅLNINGSLAG

Hur värmen avtar med tiden

Hur ljuset — VÄRMEN — tvunget avtar med ljusets naturliga spridning

ENTROPIBEGREPPET I KORTARE GENOMGÅNG FRÅN DECEMBER 2009

Entropibegreppet — i kortare genomgång från december 2009

Bakgrund

Naturtermiskt läckage — Flera Entropibegrepp i omlopp

Sönderfallets Kretslopp

Termodynamikens andra huvudsats i modern akademi

Isolerade System — citat

Exempel — citat

Felet i Modern Akademi

Värmeläckaget — huvudsats

Uppfinningen av det isolerade universumet

Termodynamikens två huvudsatser i kort sammanfattning enligt FOCUS MATERIEN 1975

Dangerous Knowledge

Citatextrakt i summa

Den allmänna nedtrampningen av livet

Etablissemangets elaka entropibegrepp

Argument mot allmän sanningsförnekelse

Två argument mot uppfattningen att ingenting varar för evigt

DET LINGVISTISK -LOGISKA ARGUMENTET

DET MATEMATISK-FYSIKALISKA ARGUMENTET

Webbreferenser

APPENDIX

Entropibegreppet i gängse verk

Solens massdefekt

referenser

[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)

[ML]. MATEMATIKLEXIKON Wahlström&Widstrand 1991

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2015-01-09

*END.

Stavningskontrollerat 2010-03-12.

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-06-25

åter till portalsidan · portalsidan är www.UniversumsHistoria.se