FYSIKENS7PRINCIPER 2008V3 a BellDHARMA production · Efter sammanställningar från 1984 | Senast uppdaterade version: 2020-04-29 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Fysikens 7 Principer

Med fortsättning från avslutningen i Elektriska Laddningen

2008IV9 |

UNIVERSUMS HISTORIA

En ny modell av universum

Fysiken kan beskrivas genom sju principer. KNAPPT En av dessa är känd av modern akademi;

Fysiken kan inte beskrivas på den moderna akademins begrepp eftersom dessa bygger på en grundläggande förnekelse av tillståndets princip och därmed omöjliggör varje presentation, förklaring och genomgång: Principerna leder till en reguljär härledning av atomkärnan. Därmed uppdagas en exakt matematisk kärnfysik på vars grund, läsaren till prövning, varje detalj i universums historia kan beskrivas, förklaras, härledas och framför allt visas i exakt jämförelse med den moderna akademins (motsvarande) framställningar. Presentationen är (således) tillägnad läsaren.

PRINCIPERNAS FÖRKLARING

DE SJU UNIVERSELLA PRINCIPERNA — Principernas Förklaring

Inledning

Tillståndets princip

ALL FÖRESTÄLLNING utgår från den absoluta vilans princip, den absoluta visshetens princip, SANNINGSPRINCIPEN, den absoluta likformighetens princip, eller allmänt tillståndets princip. Det är liktydigt med det oförstörbara intervallets eller den oförstörbara enhetens princip.

Grunden till ovanstående påstående ges i sanningspostulatet, vilket här förutsättes bekant.

All beskrivning utgår (således) ifrån en föreställning om tillstånd (eller visshet). Men …

Fysiken innehåller inga tillstånd (absolut positionsbestämning under nolltid). Men den beskrivs och fattas tvunget genom sådana (avstånden mellan kropparna oberoende av tiden: nuet, dTÛ0). Därav principerna.

Vi skiljer alltså skarpt mellan förståndsvärld (differentialer, dTÛ0) och fenomenvärld (differenser DT®0).

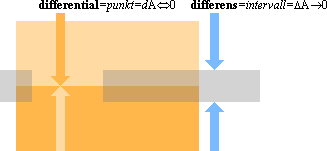
Se utförlig beskrivning från NOLLFORMSALGEBRAN

Fysiken identifierar vi med kropparna eller massorna: massa (m), laddning (Q) och rörelse (spinn).

De klassiska grundbegreppen är massa, kraft och gravitation. Genom massan m som

m=ma/a=F/a definieras kraftlagen

F=ma med a=v/T.

Gravitationslagen definieras genom centrifugalkraften

F=ma=mw²/r på ringens form motsvarande tyngden (vägande) eller trögheten (förflyttande) enligt

F=ma=(w²/rm₂)·m₂m=(w²/m₂)·m₂m/r=(w²r/m₂)·m₂m/r²=G·m₂m/r².

Fysikens sju principer är

APARC ............................................ statiken ............................................. tillståndsprincipen

FUNTOP ......................................... dynamiken ........................................ jämviktsprincipen

POM ................................................ energilagen ....................................... rörelseprincipen

NEONS ............................................ mekaniken ........................................ verkansprincipen

GRIP ................................................ gravitationen .................................... konvergensprincipen

DEEP ............................................... elektriciteten ..................................... divergensprincipen

PASTOM ........................................ masstrukturen .................................. massprincipen

Beteckningarna till vänster är de ursprungliga (akronymiska) förkortningar som framkom genom den första författningen på engelska (2002VIII).

Fysikens 7 Principer (I)

Genom ändringslagarna, med vidare genom ljusets fysik som leder till elektriska laddningen och de elektriska storheterna tillsammans med mekanikens gravitella referenser med GcQ-teoremet, ljusets gravitella beroende och Planckekvivalenterna, framväxer spontant en allmän syntes av hela fysiken — inkluderat vår egen vetenskapshistoria — genom sju universella principer: 1 tillståndet, 2 jämvikten, 3 rörelsen (energilagen), 4 mekaniken (ändringslagarna i syntes av de fysikaliska kropparna, samma som Newtons tre rörelselagar), 5 gravitationen, 6 elektriciteten, 7 masstrukturen (atomkärnan, materien, kosmos).

EFTERSOM KRONAN PÅ VERKET hur som helst är atomkärnan, och dess härledning helt bygger på massekvivalenten

m=m[n®¥]^–1[n®¥] och som klarläggs först genom Fysikens 7:e princip (dess syntes av fysiken), finns ingen egentlig (stark) beskrivande rent naturfilosofisk grund för atomkärnas härledning om inte Fysikens 7 Principer är klargjorda. Jag vill mena det. Potentialbarriären med sin centrala »princippartikel» följer visserligen direkt ur ljusets gravitella beroende. Men utan den beskrivande kopplingen till energilagen genom den sjunde principen, massekvivalenten

m=m[n®¥]^–1[n®¥] med sin frånvaro av beståndsdelar som krävs för bildningen av värme och ljus från den fullständiga massans upplösning E=mc², föreligger ingen egentlig sammanhängande förklaring till begreppens (logiska) utveckling. Atomkärnans härledning, som kronan på verket framstår, därmed, som helt beroende av Fysikens 7 Principer. Nämligen just den sjunde. Fysikens 7 Principer framstår alltså som avgörande i hela naturbeskrivningen. För min egen del beträffande ”atomkärnans härledning” kom ordningen i dessa principer inte så galant i rad. Men det beror (förmodligen) på att atomfysiken i min historia visat sina utstående hörn genom vetenskapslitteraturen (SCIENTIFIC AMERICAN) — och DEN kronologin därmed alltid haft prioritet. Atomkärnans härledning blev bekant för mig först (1993). Därefter (1994) kom ljusets g-beroende med potentialbarriärren — och som inte framstod helt tydligt från början. Först längre fram (genom Fysikens 7 Principer [från genombrottet med Fysikens 3:e princip [POM, se vidare nedan] via induktionsfysiken, 2001]) klarnade begreppen (med hög hastighet). I efterhand har den vägen inneburit (många) ytterligare klarlägganden. Men läsaren må själv döma i den saken.

Atomkärnans härledning förutsätter viss kännedom om innehållet i nedanstående — för bästa klarhet. Men eftersom jag redan känner till ordningarna, är jag värdelös som (opartisk) guide i det avseendet. Följ din egen intuition. Det gjorde jag.

SATSFORMERNA I

Fysikens sju principer

Endast en av dessa, mekaniken, är känd av modern akademi

TILLSTÅNDET

1 Statikens princip ........................ APARC — Absolute Physical Reference

En ändring måste alltid referera en jämvikt (tillståndet)

JÄMVIKTEN

2 Dynamikens princip ................. FUNTOP — Fundamental Theorem of Physics

Fysiken relaterar till jämvikt, inte till system

ENERGILAGEN

3 Rörelsens princip ...................... POM — Principle of Motion

Impuls — rörelsemängd, p=mv — föregår kraft

MEKANIKEN

4 Newtons tre rörelselagar .......... NEONS — Newton’s three laws

1. Varje tillstånd kvarstår tills affekterat (tillstånd och grundläggande tröghet): APARC

2. Ett nytt tillstånd är exakt kraften som realiserar det (kraftlagen): POM via a

3. Ansatsen till en ändring uppväcker alltid en likadan motriktad ansats (trögheten): FUNTOP

GRAVITATIONEN

5 Konvergensens princip .............. GRIP — Gravitation Principle

Lika för all materia, kan inte skärmas ifrån, oberoende av tid

ELEKTRICITETEN

6 Divergensens princip ................. DEEP — Divergence principle

Olika för all materia, kan skärmas ifrån, beroende av tid

MATERIEN

7 Masstrukturens princip ............. PASTOM — Principal (även Principle) Structure of Mass

Massförstörelsen kräver en i massan inneboende struktur

FYSIKENS 7 PRINCIPER beskrivs vidare nedan med växande detaljinnehåll i delarna II och III.

Fysikens 7 Principer (II)

1. (APARC Absolute Physical Reference). Tillstånd finns inte i fysiken, men är avgörande för fysikens beskrivning. Vi måste ha en situationsbild.

2. (FUNTOP Fundamental Theorem of Physics). Tillståndets motsvarighet i fysiken blir jämvikt: fysiken innehåller inga ”inertialsystem” eftersom något tillstånd inte finns i fysiken. Referensen är jämvikt. Inte system. Kolla hur småfåglarna flyger och leker genom snåren. Vadå inertialsystem?

3. (POM Principle of Motion). Intervallets oförstörbarhet garanterar att ingen rörelse kan uppstå utom genom en redan existerande kraft. Kraften, eller accelerationen a=dv/dT, kräver ett redan existerande intervall. Intervallets oförstörbarhet bildar därmed grundvalen för rörelsens princip, och därmed energilagen.

4. (NEONS Newton’s Three Laws). Ändringslagarna från atomtriangeln genom mekanikens kroppar ger Newtons tre rörelselagar: mekaniken.

5. (GRIP Gravitation Principle). Materialoberoende, kan inte avskärmas; tidsoberoende. Gravitationens eller konvergensens absolutverkande princip.

6. (DEEP Divergence Principle). Materialberoende, kan avskärmas; tidsberoende.

Fullständig negation av gravitationsprincipen ger divergensprincipen, det ändliga c och därmed elektrofysiken.

7. (PASTOM Principal Structure of Mass, även Principle …). För att m ska kunna omvandlas enligt E=mc² får m av princip inte innehålla några bestämda, definita (stela) beståndsdelar. Därmed massformens principiella struktur enligt ekvivalenten m = m/[n®¥] · [n®¥] och som leder till atomkärnans härledning. Oupphörlig delning. För atomkärnans härledning, se Planckringen.

KORT ORIENTERANDE GENOMGÅNG AV

Fysikens sju principer

Endast en av dessa, mekaniken, är känd av modern akademi

TILLSTÅNDET

1 Statikens princip ........................ APARC — Absolute Physical Reference

En ändring måste alltid referera en jämvikt (tillståndet)

Bevis: Tillstånd — inget tillstånd (icke-variation) existerar utom baserat på intervall utan ändring.

Tillståndets referens är absolut för fysiken — därför att variation (icke tillstånd) kräver ett intervall, ett principiellt avstånd (RUM): avlägsnas intervallet (rymden), försvinner samtidigt hela fysiken. Eftersom fysiken är variation men tillståndet en vila, och följaktligen inte inkluderat i fysiken, säger vi att det fundamentala intervallet, eller det principiella tillståndet, är oförstörbart — därför att det inte är föremål för ändring, som däremot saker och ting är i fysiken. Tillstånd (statik), intervall, balans och jämvikt (dynamiken) blir därmed begrepp som kan användas synonymt. Se även i EXEMPEL PÅ INTERVALLETS OFÖRSTÖRBARHET.
Urspr. fysikens första och enda lag.

JÄMVIKTEN

2 Dynamikens princip ................. FUNTOP — Fundamental Theorem of Physics

Fysiken relaterar till jämvikt, inte till system

Bevis: APARC — fysiken är variation.

Eftersom fysiken inte innehåller något tillstånd, finns heller ingenting i fysiken att relatera någon referens till. Vår uppfattning och beskrivning av fysiken måste alltså relatera till ett bestämt intervall, en jämvikt. Inom den allmänna filosofin skiljer vi (alltså) skarpt mellan förståndsvärld (TILLSTÅND) och fenomenvärld (VARIATION).

Fysiken innehåller alltså inga ”inertialsystem”, något sådant finns inte i fysiken.

Fysikens lagar, om det finns sådana lagar och i den mån de har någon giltighet, gäller för fysikaliska system, aldrig i fysikaliska system

Kraftlagen. Genom massan m=ma/a=F/a definieras kraftlagen F=ma, vilken är dynamikens grundform.
Urspr. fysikens giltighetsteorem.

ENERGILAGEN

3 Rörelsens princip ...................... POM — Principle of Motion

Impuls — rörelsemängd, p=mv — föregår kraft

Bevis: APARC —

Ett intervall måste finnas för att kunna påvisa en rörelse; kraften förutsätter rörelsen; intervallet är vilket som helst Dd med optimal variation a=dv/dt. Eftersom intervallet är oförstörbart (APARC), så är också rörelsen (a_0tilld), och därmed energin:

Ingen kraft F=ma kan uppstå utan att tas från något som redan har rörelse: m · 0 = 0

POM1: Energilagens första huvudsats utsäger att massa inte kan skapas enligt

m i a=am/m=F/m kan inte skapas eller bildas därför att a i m=ma/a=F/a måste förutsättas

POM2: Energilagens andra huvudsats utsäger att massa kan förintas enligt (m®g)

m i a=am/m=F/m kan förintas genom att a i m=ma/a=F/a är oförstörbar

I det senare fallet flyttas a endast över på andra massor (värme, ljus) utan hjälp av någon transporterande massa (induktionsverkan), varigenom energin bevaras (Jämför Solen). Massan förintas och med den dess gravitation, laddning och elektriska fält. Den kan alltså sedan inte återskapas därför att a i den måste förutsättas. Möjligheten att skapa eller bilda m genom a är alltså utesluten genom att det inte finns någon bindning mellan a och m; a kan frigöras ur m, a kan överföras på m men m kan varken frigöras ur a eller överföras på a och därmed heller inte skapas eller bildas av a.

Eller enklare uttryckt: Eftersom intervallet är oförstörbart enligt TILLSTÅNDETS PRINCIP kan a inte skapas och därmed heller inte m=ma/a=F/a och följaktligen heller inte Fd=E.

Energin kan varken skapas eller förintas, den måste förutsättas.

POM2 garanterar alltså att massförstörelsen (m®g) är kvalitativt irreversibel, samt att massa saknar upphov.

Energilagen kan därmed formuleras mera elegant:

massan kan förintas med energin bevarad — därför att den inte kan skapas (såväl energin som massan)

Se även mera utförligt i ENERGILAGEN. Se även Åldrandets princip i ENTROPIBEGREPPET I RELATERAD FYSIK.

Urspr. fysikens första princip

MEKANIKEN

4 Newtons tre rörelselagar .......... NEONS — Newton’s three laws

Mekaniken

1. Varje tillstånd kvarstår tills affekterat (tillstånd och grundläggande tröghet): APARC

2. Ett nytt tillstånd är exakt kraften som realiserar det (kraftlagen): POM via a

3. Ansatsen till en ändring uppväcker alltid en likadan motriktad ansats (trögheten): FUNTOP

Mekaniken beskriver och utvecklar fullständigt fysikens totala domäner av verkan. Mekaniken kan därför också med fördel i överordnad bemärkelse kallas verkansprincipen. Den utgår alltså direkt från tillståndets princip (precis så som Newton fann saken).

Se även (mera uttömmande) från ÄNDRINGSLAGARNA.
Urspr. fysikens andra princip.

GRAVITATIONEN

5 Konvergensens princip .............. GRIP — Gravitation Principle

Lika för all materia, kan inte skärmas ifrån, oberoende av tid

Bevis: APARC —

Fysiken identifierar vi med kropparna eller massorna. Absoluta tillståndets princip (APARC) i fysiken realiseras alltså genom en jämvikt (FUNTOP) motsvarande verkan genom en tyngdpunkt (nolltid). Absoluta tillståndets bestämmande princip i fysiken blir därmed den stela relationsbild (nolltid) som gäller för kropparna med hänsyn till deras tyngdpunktsavstånd och de med dem förknippade massorna men oberoende av tiden och kropparnas sammansättning.

Gravitationslagen definieras genom centrifugalkraften F=ma=mw²/r på ringens form motsvarande tyngden (vägande) eller trögheten (förflyttande) enligt

F=ma=(w²/rm₂)·m₂m=(w²/m₂)·m₂m/r=(w²r/m₂)·m₂m/r²=G·m₂m/r².
Urspr. mekanikens grundprincip.

ELEKTRICITETEN

6 Divergensens princip ................. DEEP — Divergence principle

Olika för all materia, kan skärmas ifrån, beroende av tid

Bevis: GRIP — dess fullständiga negation.

Tidsberoendet ger divergensens kvantitativa aspekt som topphastigheten c₀ för ljusets utbredning (optiken).
I negationen av GRIP som DEEP ligger naturligt att c=0 definierar massan: avskärmningen; massa är icke-ljus; ljus är icke-massa. Alla ställen där c>0 definierar alltså den masslösa (divergensskärmbara) rymden: ljus är icke-massa. Därmed är verkansprincipen i den masslösa energiöverföringen av a i m från energilagens (m®g) identifierad som divergensprincipen. Massa är alltså av princip tvunget ställen där divergensen c=0.

Materieberoendet tvingar (alltså) c att bero av gravitationen. Inverkan från GRIP på DEEP, analogt c mellan 0 och c₀, måste alltså avgränsas till verkan i endast en isolerad lokal rymdpunkt ds under dT. I annat fall kollapsar energilagen därmed att absolutverkan med ändlig hastighet (c) utsträcks över ett intervall. Absolutverkan (GRIP) garanterar via APARC alltså att divergensens ändliga verkanshastighet c=ds/dT avgränsas till en isolerad, fristående punkt och endast så. Därmed definieras divergensens acceleration som absolut enligt a=c/dT varur den primära massförstöraren från POM2 direkt härleds, E=mad=mc². Divergensens kvalitativa aspekt har följaktligen två polariteter, en positiv (0 till c, »utflödet») och en negativ (c till 0, »inflödet») vilka vi identifierar med respektive positiv och negativ elektricitet. Som följd av Newtons tredje lag innefattar divergensens verkan även ett motstånd (R) enligt a. Detta sammanhänger med begreppet induktans (elektriska trögheten) och därmed induktionen. Divergensens matematiska fysik beskriver hela elektrofysiken med elektriska laddningen (Q=Ö[m/R][A/dT]) och divergenskraften eller elektriska kraftlagen (F=RcQ²/A) vilka följer ur GRIP genom den allmänna kraftlagen (F=ma från m=ma/a=F/a) via substitution med motstånd över en genomträngningsyta (R/A)/(R/A). Genom GRIP, som funktion av divergensen c, definieras alltså det elektriska fältet för Q vars lägesändring relativt fixa punkter i ett yttre g-fält bildar grunden för magnetismen. Divergensens gravitella beroende beskrivs i DGD. Från denna följer Potentialbarriären där den exakta kopplingen mellan massa och laddning (Q) framgår. Induktionen och magnetismen behandlas i separata delar. mQR-begreppen ges särskild syntes i PLANCKEKVIVALENTERNA. DEEP syntetiserar för övrigt en (stor) mängd satser, inkluderat KÄRNREAKTIONSLAGEN (urspr. NUCREAL Nuclear Reaction Law) som f.ö. följer direkt av (m®g) i POM.
Urspr. elektrofysikens grundprincip.

MATERIEN

7 Masstrukturens princip ............. PASTOM — Principal (även Principle) Structure of Mass

Massförstörelsen kräver en i massan inneboende struktur

massa består av ett obegränsat antal masselement som oupphörligen delas så att någon minsta massdel inte kan återfinnas

m = m(n®¥)(n®¥)^–1 = (F/a)(n®¥)^–1(n®¥) = (F/[a(n®¥)])(n®¥) = m’(n®¥)

[Mass-fractal clause, MAFACE].

Bevis: POM2 —

Energilagens andra huvudsats utpekar en primär massförstörare. Denna härleds i DEEP som den redan kända E=mc². Dess giltighet för massans fullständiga upplösning kräver en i massan inneboende struktur vars allmänna massform leder till den sekundära massförstöraren eller rörelsestrukturen mc²=Jf. Denna struktur definieras sedan vidare i PASTOM genom olika följdsatser.

Den inneboende tillämpningen av GRIP på PASTOM, m=(F/[a(n®¥)])(n®¥), leder till den fundamentala massformens definition genom gravitationen på ringens eller toroidens fraktala form (J=mv2pr). Massformen består tydligen av en principiell ringform vars underfraktaler av m växer obegränsat på m’ med en motsvarande växande tyngdkraftsacceleration [Atomkärnans gravitella härledning]. Massformen, med den enligt Potentialbarriären omgivande laddningen inkluderad, beskrivs därigenom som en av gravitationen bestämd och enligt energilagen utan upphov befintlig kraftväv med omgivande elektriska och magnetiska fält motsvarande fraktalernas struktur. Alltså, ett elektromekaniskt toroidaggregat av utomordentlig sammansättning där masstätheten växer med djupet i fraktalstrukturen utan slut [Plancks strukturkonstant] [Atomkärnans gravitella härledning]. Aggregatets allmänna dynamik behandlas i TNED (Toroid Nuclear Electromechanical Dynamics). Den fundamentala massformen motsvarar naturligt grundämnenas mest elementära beståndsdel vilken vi identifierar med atomkärnan. Genom att jämföra toroidformens relativa dimensioner mot Kubgrafen (se Kärnradierna) kan geometrin (N3m20) för det aktuella primära toroidaggregatet (neutronen-protonen) bestämmas.

Den centrala masstruktursatsen, som formulerad ovan, leder direkt på Kubanalogin som grundlägger den mera reguljära härledningen till atomens dynamik i härledningen till GRUNDÄMNENAS PERIODISKA SYSTEM genom Keplermomenten och Kärnsyntesen genom Upptäckten av NEUTRONKVADRATEN. Keplermomentet tillhör grundfysiken från NEONS och beskrivs särskilt i GRUNDÄMNENAS PERIODISKA SYSTEM.

Med kännedom om den elementära vågmekaniken (studiet av vågrörelsernas utbredning genom främst vatten och enkla anordningar [rep]) och det allmänna impulsmomentet för atomen på dess grundnivå (h, Plancks konstant) framgår därmed Spektrum och Kvanttalen med (grundkartan till) Grundämnenas Periodiska System i en separat del. Nämnda delar härleds då tillsammans med övriga från mekaniken kända grundbegrepp i former som mera ingående beskriver och förklarar atomkärnans delar. Därefter följer slutligen hela Termodynamiken (i vid mening): beskrivningen av himlakropparnas uppkomst med deras och alla övriga alla materials egenskaper och tillstånd (primärt från Allmänna Gaslagen).

Sammanställt 2003II14 · 2003VII2 · 2010IV20

Fysikens 7 Principer (III)

Se även i Principernas förklaring.

1. Statikens princip ........................ APARC — Absolute Physical Reference

(APARC Absolute Physical Reference). EFTERSOM TILLSTÅNDETS BEGREPP BESTÄMMER RAMARNA enligt grundformen från formläran med formvärldens entydiga och obrutna beskrivning genom punkt, intervall, yta och volym, se nollformsalgebran

— men att tillståndet som begrepp är abstrakt för fysiken som istället tvunget betingas av oupphörlig variation eftersom absolut positionsbestämning eller ett tillstånd kräver nolltid för att utesluta variationer men som då också tvunget betyder ingenting och därmed ingen fysik alls

— är det också tillståndets begrepp som bildar fysikens mest övergripande princip: tillståndet finns inte i fysiken, men är avgörande för fysikens beskrivning. Vi måste ha en situationsbild.

Se även i Principernas förklaring.

2. Dynamikens princip ................. FUNTOP — Fundamental Theorem of Physics

(FUNTOP Fundamental Theorem of Physics). Tillståndets motsvarighet i fysiken blir därmed tvunget jämvikt, balans: fysiken innehåller inga ”inertialsystem” eftersom något tillstånd inte finns i fysiken. Referensen är (momentan) jämvikt i varje tidpunkt. Inte system. Jämför Newtons berömda ämbarförsök och hans tankeexperiment med de två repförbundna kloten i tomma rymden som tydligt visar att Newton fattade denna princip fullt ut.

I modern akademi anser man däremot att fysikens variationer måste relateras till s.k. inertialsystem, ett begrepp som den moderna akademin f.ö. tillskriver Isaac Newton att ha uppfunnit,

”Inertialsystem är enligt Newton det absolut vilande systemet och alla system som befinner sig i likformig rörelse i förhållande till detta.”

BONNIERS KONVERSATIONSLEXIKON (1924) Band V sp1363

men vars så förmodade källa det inte går att hitta. Begreppet inertialsystem är av allt att döma istället en modern akademisk uppfinning i den turbulenta strävan (se v+ic-felet) att formulera fysikens lagar utom tillståndets princip (se divergensen med ljusets absoluta acceleration). Fysiken relaterar till jämvikt, inte till system. Och om någon, är det Isaac Newton som klargjorde det genom sitt berömda ämbarförsök. Detta utesluter, veterligt, Newton som källan till begreppet inertialsystem. Det finns ingenting sådant i fysiken. Fysiken relaterar till jämvikt, inte till system.

De dynamiska referenserna t.ex. dv=adT i a=dv/dT finns inte till som några objektiva fysiska referenser, lika litet som Euklides räta linje finns att beskåda på något museum

Se även i Principernas förklaring.

3. Rörelsens princip ...................... POM — Principle of Motion

(POM Principle of Motion). Intervallets oförstörbarhet, utomordentligt syntetiserat av atomtriangeln, bildar grundvalen för verkan och motverkan genom verkans fundamentala grund: ingen rörelse kan uppstå utom genom en redan existerande kraft. Kraften, eller accelerationen a=dv/dT som kraftens motor, kräver ett redan existerande intervall. Intervallets oförstörbarhet bildar därmed grundvalen för rörelsens princip, och därmed energilagen som fysikens avgörande centrala aspekt:

energilagen

Ett intervall (Dx) måste finnas för att kunna påvisa en rörelse; kraften förutsätter rörelsen; intervallet är vilket som helst Dd med optimal variation a=dv/dt. Eftersom intervallet är oförstörbart, så är också rörelsen (a_0tilld), och därmed energin:

ENERGI KAN VARKEN SKAPAS ELLER FÖRINTAS UTAN MÅSTE FÖRUTSÄTTAS;

massdestruktionen

massa kan förintas (m®g) — därför att den inte kan skapas:

(1) m i a=am/m=F/m kan inte skapas eller bildas därför att a i m=ma/a=F/a måste förutsättas

(2) m i a=am/m=F/m kan förintas genom (1) att a i m=ma/a=F/a är oförstörbar, (m®g)

I det senare fallet flyttas a endast över på andra massor (värme, ljus) utan hjälp av någon transporterande massa (via induktionen enligt COEI (conservation of energy by induction)

U_ind = E=^UQ/Q_s = L(di/dt)k = Lk = kRTQ/T² = kRQ/T = kRI = kU), varigenom energin bevaras.

primära massförstöraren

Accelerationen (a) kan varken skapas eller förintas utan måste förutsättas; massa m=ma/a kan förintas i bevarandet av a (induktionen), men m kan inte skapas ur a därför att m=ma/a förutsätter att a redan finns i m, dvs., att m redan existerar med a i sig; Då m en gång förintats, kan det sedan inte återskapas. Dock kan massans energiekvivalent substituera massan enligt den redan experimentellt välkända E=mc² (men fortfarande allmänt illa fattade) kvantitativa ekvivalensen

E=(m®g)c²=(m¬g)c². Dvs., ett kvantitativt utbyte massa-energi kan alltid bildas. Formen (m®g) som sådan är dock kvalitativt irreversibel: m kan förintas, men inte återskapas, se (1) ovan.

Primära massförstöraren är alltså E=mc² där m omvandlas till ljus och värme (generellt gamma, g) genom induktionen (m®g).

Modern akademi: Energilagen, som ovan, kan varken formuleras eller härledas av den moderna akademins lärosystem på grund av dess uppfattning att intervall och punkt övergår i varandra (dx=Dx). Därmed vanställs satsen om intervallets oförstörbarhet. Dvs., modern akademi gör våld på energilagen genom sitt blotta lärosystem.

Se även i Principernas förklaring.

4. Newtons tre rörelselagar .......... NEONS — Newton’s three laws

(NEONS Newton’s Three Laws). Ändringslagarna genom mekanikens kroppar ger Newtons tre rörelselagar: mekaniken. Det är också fysikens centralt arbetande del, alla kategorier.

1. varje tillstånd — tangent, linjär utsträckning — kvarstår till affekterat

2. vid ändring: ändringen är proportionell mot den tillståndsändrande accelerationen

3. ändringen inträffar inte omedelbart utan genom ett intervall med påföljden: Mot varje tillståndsändrande acceleration svarar också, i försorg av intervallets existens, en lika stor motriktad tillståndsbevarande acceleration

Se även i Principernas förklaring.

5. Konvergensens princip .............. GRIP — Gravitation Principle

(GRIP Gravitation Principle). Materialoberoende, kan inte avskärmas, och därmed tidsoberoende: Tidsoberoendet beskriver gravitationens eller konvergensens absolutverkande princip.

Se även i Principernas förklaring.

6. Divergensens princip ................. DEEP — Divergence principle

(DEEP Divergence Principle). Den fullständiga negationen av gravitationsprincipen ger divergensprincipen: Beror på material, kan avskärmas, och därmed tidsberoende: den ändliga verkanshastigheten (ljushastigheten c) inom elektrofysiken. Divergensen kan förstås 0-c eller c-0, vilket i princip ger de två möjliga olika flödesriktningarna för positiv och negativ elektrisk laddning. Materialberoendet garanterar divergensens g-beroende. Förgreningarna i DEEP blir utomordentligt omfattande genom elektrofysikens många områden.

Se även i Principernas förklaring.

7. Masstrukturens princip ............. PASTOM — Principal (även Principle) Structure of Mass

(PASTOM Principal Structure of Mass, även Principle …). För att m ska kunna omvandlas enligt E=mc² får m av princip inte innehålla några bestämda, definita (stela) beståndsdelar. Därmed massformens principiella struktur enligt ekvivalenten

m = [n®¥] · m/[n®¥]:

Massan i dess fundamentala form (atomkärnan) kan beskrivas ekvivalent som bestående av ett obegränsat antal delar (J=mvr) som delas oupphörligt så att någon minsta beståndsdel inte kan återfinnas. Massans fundamentala form kan därmed återföras på en struktur av ±b-laddningar med ±-spinn i formen av ringar J=mvr med massan som kraft över acceleration (m=F/a) som alltså summerar nollmoment och nollkraft genom motvända spinn och laddningar: atomen behöver ingen påfyllning för att fungera. Summan av alla moment i atomen är noll. Se vidare i atomkärnans härledning från Planckringen.

Se även i Principernas förklaring.

Fysikens7Principer | Osäkerhetsprincipen

Pennan ritar aldrig finare linje än den är vässad för

OSÄKERHETSPRINCIPEN

osäkerheten i mätningarna är EXAKT

lp = h · n^–1

ELEKTRONEN (e) är en MÄNGD massa-laddning — en hop. Ingen partikel.

Utöver massa-laddning har den — explicit — inga som helst bestämda fysikaliska egenskaper. Ingen bestämd form, ingen bestämd utsträckning.

e kopplar till materien via resonanser — vågmönster som bara kopplar upp på HELA antal periodiska genomgångar — och som definieras genom Plancks konstant h med ekvivalenterna våglängd (l) och impuls (p=mv) enligt lp = h.

All fysikalisk mätning med elektronmassans hjälp kommer ALLTSÅ i vilket fall att begränsas av just h, vilket är absoluta osäkerheten i mätningen.

Elektronen definieras enligt TNED ur h på elektronmassans element (från neutronens sönderfall till väteatom), eller med samma omvända mening: h definieras ur e.

E = hf = (h/nF)nF f = hF fF

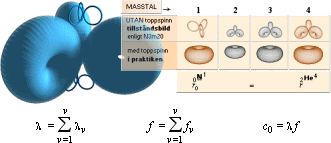
FYSIKENS MASSA är ENLIGT TNED emellertid INTE begränsad av impulsmomentet h i e utan innehåller en obegränsad mängd finare ringnivåer med impulsmoment av ekvivalent form (se från ATOMKÄRNANS HÄRLEDNING)

E = hf = (n/n)hf = hn^–1nf = h_F · f_F

Denna obegränsade indelning visar att ekvivalenta Planckenergifrekvensen i varje ringnivå växer med nivådjupet.

Observera att denna detalj också är förutsättningen för de allra kortaste våglängderna i Plancks Strålningslag och vilka delar modern akademi också måste avstå ifrån: inte heller den detaljen kan härledas med hjälp av den moderna akademins allmänna fysikbegrepp.

Varje särskild nivå får därmed, på samma sätt som gäller för elektronen, sin egen särskilda absoluta osäkerhet

lp = h · n^–1 = h_F. Värdet på Plancks fraktalkonstant sträcker sig alltså SETT TILL FYSIKEN SOM HELHET obegränsat mot noll.

MÄTNINGEN på h_F med n>1 har emellertid ingen (direkt) PRAKTISK fysikalisk representation eftersom det i slutänden ALLTID är elektronmassornas svängningar kring atomkärnorna som förmedlar alla fysikaliska mätningar:

Eftersom elektronmassans komponenter enligt TNED har begränsad räckvidd (se från Elektronmassans komponenter) kan heller inte hur korta våglängder som helst avkännas av elektronen: n>1 ligger utanför elektronens horisont.

OSÄKERHETEN SOM ABSOLUT KAUSALBEGREPP FÖR FYSIKEN uppställdes 1927 av Werner Heisenberg [FMs99sp1ö] — med elektronmassan som en absolut förmodad universell preferens. Därmed, menade man, hade ”den klassiska fysikens deterministiska betraktelsesätt” krossats (möjligheten att helt förutsäga en kropps framtida tillstånd utifrån exakt kännedom om dess nuvarande). Men i och med att massa (se från Atomkärnans härledning) nu INTE kan definieras med materiens struktur, där elektronmassan utgör gränsformen, blir Heisenbergs osäkerhetsprincip (lp=h) ingen absolut sådan, utan endast den som gäller för elektronnivån, analogt materien. Inte massan. Se även respektive massfysik och materiefysik. Därmed har det heller aldrig funnits något åsidosättande av ”den klassiska fysikens deterministiska betraktelsesätt”.

Massan bestämmer fysiken, inte materien.

Den moderna akademin har alldeles för ivrigt hängivit sig åt den oförställda skadeglädjen att sparka på SANNINGEN. Osäkerhetsprincipen är en mätprincip, en mängdform. Ingen filosofisk grundkälla.

Plancks konstant som en strukturkonstant förvandlar den moderna akademins uppfattning om ”osäkerhetsprincipen” till en specifik akademisk festvåning för speciellt trångsynta personer: det finns en osäkerhetsprincip för varje fraktal nivå.

Därmed är atomkärnan som åskådligt objekt bevisad.

logiken och filosofin kan inte beskrivas med modern akademi

Fysikens7Principer | ATOMVIKTERNA GENOM NEUTRONKVADRATEN | Precisionen i TNED

atomvikterna

PRECISIONEN I ATOMVIKTERNA GENOM NEUTRONKVADRATEN ENLIGT TNED

Inledning

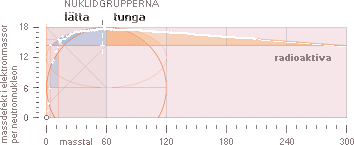
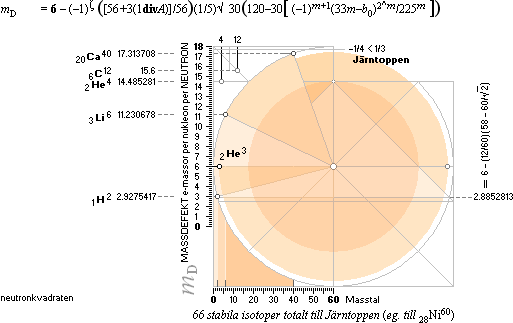
Stråken med vita punkter markerar nuklidkartan — de naturligt förekommande atomerna — med de stabila nuklidernas atomära massdefekter (vertikala skalan) uttryckta i antal elektronmassor (m_D) beräknade genom neutronmassan (m_n), elektronmassan (m_e) och masstalet (A) från experimentellt (HOP) uppmätta atomvikter (U) enligt sambandet

m_D = (1–U/Am_n)m_e

Den inlagda mönsterformen under de vita partierna markerar Neutronkvadratens mönsterkropp. Den är av allt att döma helt (fullkomligt) okänd i modern akademi och vetenskap, men innefattar motsvarande massdefektsvärden som i reda atomviktsvärden vida överträffar precisionen i den moderna akademins och vetenskapens motsvarande teoretiska beräkningar (Weizäckerekvationen), se Jämförande Tabell. Jämförande värden mellan TNED och experimentalfysiken (HOP) ges även nedan i RESULTATTABELL. Genom att Neutronkvadraten också ansluter till TNED genom Grundnuklidernas Kärnradier, resultat som i sig följer separat från härledningen till atomkärnan via Planckringen, intar TNED genom Neutronkvadraten — i kraft av de experimentellt uppmätta värdena till jämförande analys — helt naturligt en suveräniserad ställning över modern akademisk kärnfysikalisk teori. Hela presentationen i Universums Historia bygger på alla vidare resultat från den kopplingen: TNED och experimentalfysiken harmonierar. Precisionen i den harmonin beskrivs med detaljerade praktiska exempel i följande delar.

PRECISIONEN I ATOMVIKTERNA GENOM NEUTRONKVADRATEN

ENLIGT TNED

Allmän redovisningsgrund för certifieringen av TNED som preferens för kärnfysiken

Neutronkvadratens

mönsterkropp

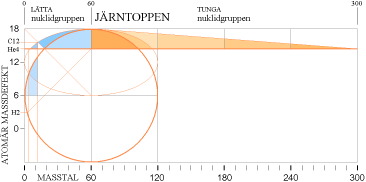
Neutronkvadratens allmänna mönsterkropp. En kompletterande mera utförlig beskrivning ges från NEUTRONKVADRATEN.

OVANSTÅENDE MÖNSTERKROPP visar NEUTRONKVADRATEN längst till vänster. Cirkeln markerar neutronradien r=h/mc₀. Den övre horisontella ellipsens vänstra halva markerar en medelellips till de mera precisa underliggande UDDA och JÄMNA horisontella nuklidellipserna upp till masstalet A=60 (se vidare illustrationer nedan). Till höger om denna halva tillkommer en hyperbelgren (se utförligt i Guldhyperbeln) som beskriver den allmänna lokalen för de tyngre nukliderna., från masstal 60 och upp till gränsen 300. Alla de nu nämnda kurvdelarna återspeglar en och samma grundläggande ekvationsform, se sambanden 1-4 i DEN TUNGA NUKLIDGRUPPEN inkluderat vågfunktionen.

NEUTRONKVADRATENS MÖNSTERFORM med dess basellipser och allmänna elliptiska funktioner, grundformen nedan,

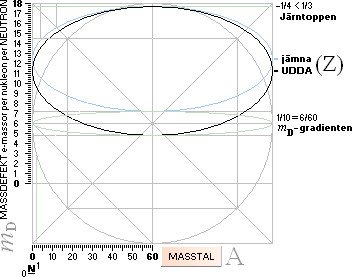
uppdagades (i min historia) först genom noggrann analys av experimentellt uppmätta atomvikter (HOP). Hur dessa ligger orienterade i neutronkvadraten i dess atomära massdefektsenheter (m_D) visas nedan för samtliga stabila nuklider (till masstal 210).

Neutronkvadratens mönsterkropp (vitt, neutroncirkeln, medelellipsen, Heliumlinjen) inlagd till jämförelse med massdefektsvärdena (vita punkter) från de experimentellt uppmätta nuklidernas atomvikter (HOP). Figuren till höger visar värdena utan neutronkvadratens mönsterkoppling.

typexempel neutronkvadratens allmänna precision

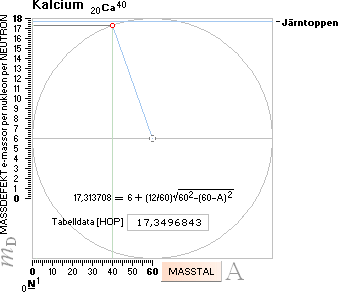
Typexemplet ovan i jämförelse med det experimentellt uppmätta värdet för atomvikten ger proportionsfelet 1,0000199.

Gränsen för teorins värdeacceptans går vid 1,0008.

Fusionsvägarna mot Järntoppen (högsta atomära massdefekten innehas av Järnindividen ₂₆Fe⁵⁶ med värdet 17,759142) som av Neutronkvadraten beskrivs via jämna-udda-ellipserna, från Heliumreferensen till Järntoppen, utgörs av fusionsvägarnas medelvärdesellipser (se nedan) med ansatserna i Kol-12 för jämna nukliderna och Kväve-15 för udda nukliderna enligt

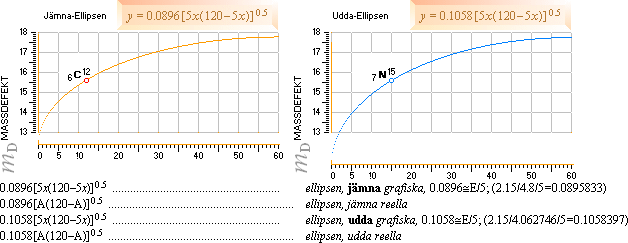
Ellipsernas referenser (Kol-12 för jämna och Kväve-15 för udda) är beräknade från Neutronkvadratens index.

Medelellipserna ovan tillsammans med vågfunktionen visas vidare nedan.

DEN ENHETLIGA MASSDEFEKTSEKVATIONEN innefattar en hybrid mellan vågfunktionsmedelellipserna, nedanstående grundkurvor, och mot dessa tvärställda ellipsbågar, se efterföljande illustration, på vars noga definierade massdefektsekvationer de utanförstående ofyllda ringarnas nuklider nedan beräknas så att samtliga kommer med.

Så har till exempel det teoretiska värdet för atomvikten hos ₂₀Ca⁴⁰ beräknats från kurvans ekvation i vänstra bilden nedan:

Vi ser att kurvans motsvarande värdepunkt (17,42) för horisontalvärdet 40 ligger strax ovanför mittpunkten på det experimentellt uppmätta värdet (den fyllda orangea ringen med mittpunkten 17,35), det skiljer på en pixel.

Om atomvikten för samma individ ₂₀Ca⁴⁰ beräknas mera korrekt teoretiskt också enligt tvärellipsernas mera exakta massdefektsekvationer, fås till jämförelse massdefektsvärdet 17,313708 som ger atomvikten 39,963385 — att jämföra med det experimentellt uppmätta värdet 39,9625889 som ger det något lägre ONEratio-värdet 1,0000199.

Denna exempelutveckling tjänar endast att belysa att neutronkvadratens mönsterform är avancerad och kan användas på flera sätt — med bibehållen god marginal till den proportionella toleransgränsen på 1,0008: Om neutronkvadraten skulle tangera det värdet, eller större, är den värdelös som teoretisk grundval. Man kan då lika gärna använda masstalet A direkt för U — och trycka ner TNED i papperskorgen — direkt.

vågfunktionen

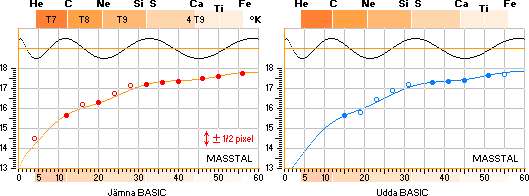
De värden som ligger vid sidan av graferna (ofyllda ringar) följer specifika fusionsvägar genom tvärellipser med specifika massdefektsekvationer. Jämför exempelfallet ovan med ₂₀Ca⁴⁰. Se även i vågfunktionens förklaring.

Medelvärdesellipserna visas nedan inlagda tillsammans med medelellipsernas integrerade vågfunktion. De streckmarkerade tvärellipserna tecknas av de egentliga massdefektsekvationerna som utpekar den aktuella nuklidens massdefekt och därmed dess atomvikt med hjälp av separata fusionsanalyser via EXOTERMISKA FUSIONSLAGEN. Färgpunkterna motsvarar experimentellt uppmätta värden som i denna skala skiljer sig obetydligt från neutronkvadratens värden.

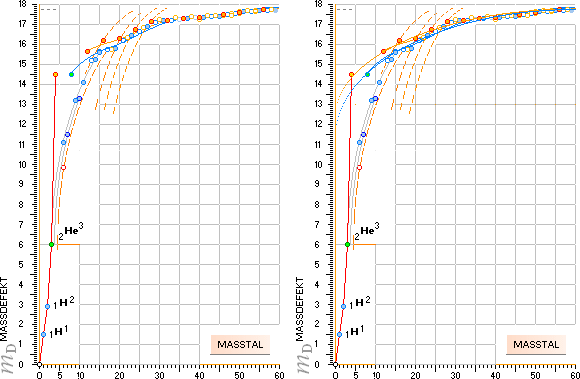
Vänster: Fusionsvägarna för de stabila nuklidernas bildning enligt neutronkvadratens mönstergeometri. De vertikalt (streckade) ellipsbågarna utpekar (exemplifierat) motsvarande nuklids massdefekt för givet masstal genom neutronkvadratens speciella elliptiska funktioner.

Höger: Överst ses medelellipserna inlagda tillsammans med deras modifikation via vågfunktionen och som ger en grundserie i massdefekterna för respektive jämna och udda nuklider. Tillsammans med tvärellipsernas kompletterande massdefektsvärden, kan samtliga 66 stabila isotoper upp till masstal 60 beskrivas enhetligt i den enda sammansatta MASSDEFEKTSEKVATIONEN. Massdefektsekvationen (se nedan) inkluderar hela nuklidblockets fem isotopgrupper så ordnade att man endast behöver ange atomnumret (Z) för att automatiskt få fram alla stabila nuklider med massdefekter och därmed beräknade atomvikter till jämförelse med de experimentellt uppmätta värdena.

Precisionen i Neutronkvadratens mönstermatematik

— som helt överlägsen de teoretiska resultaten i modern akademi

— grundlägger TNED som suverän preferens i kärnfysiken:

JÄMFÖRELSE MED PRECISIONEN FRÅN MOTSVARANDE MODERNA AKADEMISKA OCH VETENSKAPLIGA KÄRNTEORETISKA BERÄKNINGAR (Weizäckerekvationen) visas nedan (svarta ringar).

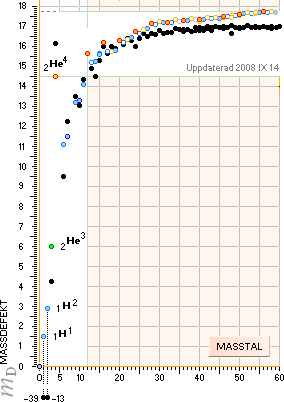
Analysen visar att den moderna akademins uppfattning om atomkärnan inte kan anställas i någon precis jämförelse med TNED. De svarta ringarna anger modern akademisk teori enligt Weizäckerekvationen, de färgade anger experimentellt uppmätta värden (HOP) som i denna illustrations upplösning inte märkbart skiljer sig från värdena beräknade från TNED (max ±0.2 elektronmassor).

En mera utförlig grafisk sammanställning HOP/TNED/MAC för samtliga 285 (–2) stabila nuklider finns i Massdefekterna i Grafisk sammanställning.

I JÄMFÖRELSE MED TNED befinner sig den moderna akademins teoretiska värden (Weizäckerekvationen) så långt från ämnet — om det gäller att avgöra kärnteorins precision — att varje jämförande analys är utesluten. Jämför ovanstående illustrerade sammanställning.

Ämnet understryker sin egen mening: det går inte att beskriva atomkärnan i någon precis eller exakt mening genom den moderna akademins lärosystem. Precisionen i Neutronkvadratens mönstermatematik som helt överlägsen de teoretiska resultaten i modern akademi, grundlägger — därmed — TNED som suverän preferens i kärnfysiken. Det är därför också angeläget att försöka finna eventuella systemfel i TNED som kan visa att den grunden (trots allt) INTE är korrekt uppfattad. Inget sådant fel har emellertid ännu (Augusti 2008) uppdagats (inte ens en tendens).

massdefektsekvationen

MASSDEFEKTSEKVATIONEN

Den allmänna matematiska form som Neutronkvadraten utpekar för massdefektsekvationerna i samtliga fall (analysen har ännu Augusti 2008 bara genomförts upp till Järntoppen), medelvärdesvägarna med Toppellipserna och vågfunktionen inkluderade är i kort sammanställning av formen

l g z fungerar som binärstyrda (logiska) sekvensdelare i den naturliga uppräkneligheten 012345…n som efter sina referenser (index) avdelar heltalen i två klasser, en 0-del och en 1-del av typen Z|z ₇

₀0,₁0,₂0,₃0,₄0,₅0,₆0,₇1,₈1,₉1,₁₀1,₁₁1, (=z ₇=) INT[1–(abs[Z/7–1] – [Z/7–1])/2]

Sekvensselektorerna härrör från divisionsalgoritmen i grundmatematiken.

l har från huvudekvationen referensen 3.

RESULTATTABELL, MASSDEFEKTSEKVATIONEN I EXEMPEL

MASSDEFEKTSEKVATIONEN i TNED ger i sammanställning för samtliga 66 stabila nuklider upp till masstal 60 en enhetlig mönsterbeskrivning som via atomnumret Z indelar de stabila nuklidernas förekomster i FEM stabila isotopgrupper, och som uttrycks matematiskt MED ENDAST HELTALENS HJÄLP i massdefektsekvationen och i kraft av neutronkvadratens villkor med de karaktäristiska elliptiska ekvationerna i formen av resulterande atomvikter — till jämförelse med experimentellt uppmätta värden (HOP).

Kolumnen ONEratio nedan visar proportionsfelet mellan de bägge. Om detta fel tangerar eller överstiger 1,0008 är den bakomliggande teorin värdelös som grund för atomkärnans byggnad (man kan då lika gärna använda masstalet A direkt istället för U-värdet: precisionen blir bättre).

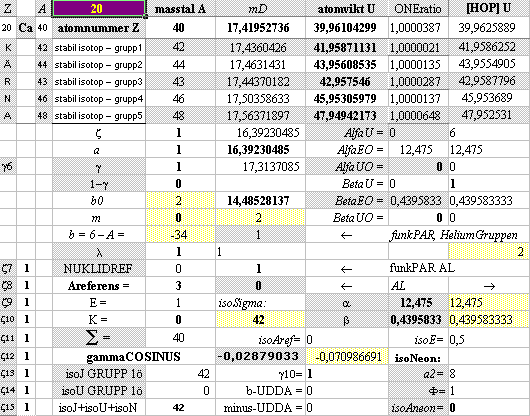
Tabellen ovan visar ett utdrag från det aktuella kalkylkortet i MsWORKS med för tillfället det inslagna atomnumret 20. Värdena visar atomvikterna för de stabila Kalciumisotoperna — tillsammans med vidhängande parametervärden i det nukleärt omfattande heltalskomplexet (ordet Symfoni verkar mera rättvist).

Neutronkvadraten, basvärden

Alla värden fås alltså från den enda enhetliga massdefektsekvationen — som innehåller hela ”symfonin” med heltalsväxlar, periodiska stegare, symmetriska och asymmetriska heltalsavgränsare. etc. Exemplet nedan visar hur systemet fungerar för de fyra första nukliderna.

[MPcKärnMatII].

Det fortsätter sedan på ungefär samma sätt för alla övriga stabila nuklider upp till Järntoppen (sista individen blir ₂₈Ni⁶⁰).

DEN TUNGA NUKLIDGRUPPEN

Någon motsvarande sammanställning för nukliderna från masstal 60 till nuklidkartans slut på den gemensamma föregående avancerade massdefektsekvationen för masstalen upp till 60, har (ännu, Augusti 2008, i mitt författarskap) inte genomförts: Det väsentliga är här först och främst att få säkra indikationer på att neutronkvadratens allmänna preferensformer verkligen gäller och därmed av princip KAN tillämpas inom den angivna toleransgränsen (proportionsrelationen mindre än 1,0008).

För att visa att också den tunga nuklidgruppens massdefektsvärden håller sig inom den toleransgränsen — även i fallet Neutronkvadratens allmänna ekvationsformer — ges följande allmänna genomgång och översikt med praktiska exempel till jämförelse i MASSTALEN FRÅN 60.

De olika metodgrenarna som redovisats totalt i denna genomgång tjänar därmed som olika exempel på ATT olika STICKPROV i de olika tillämpningssätten verkligen också ger värden inom toleransgränsen — i annat fall blir varje vidare beräkning meningslös.

Att resultaten också verkligen håller sig under toleransgränsen betyder att neutronkvadratens övergripande mönsterform beträffande atomvikterna också helt säkert håller god distans till motsvarande teoretiska värden i modern akademi och vetenskap (Weizäckerekvationen). Se Jämförande tabell.

masstalen från 60

2008IX8

MASSTALEN FRÅN 60

SMÅ MEN TYDLIGA TOPPAR framträder vid masstalen 60, 60+30=90, 60+30+50=140, (60+30+50+70=210) … motsvarande de olika platåerna i lätta nuklidgruppen :

Experimentella — från HOP-tabellen, från masstal 60 (grafisk enhet, 20pixel):

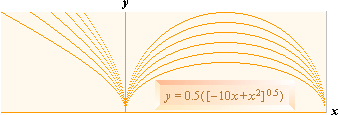
Vågfunktionen (se härledningen nedan.)

graf 0.5cos0.2(600[x+2.75])'0.496

y = 0,5 cos 0,2(600[x+2,75])^0,496

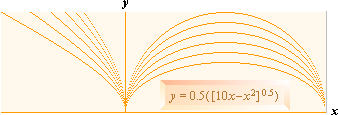
Tillsammans med huvudhyperbeln (se utförligt i Guldhyperbeln)

y = –0,0146(600 + 25x²)^0,5

(vågformen här reducerad till 0,05):

graf –[0.0146(600+25x'2)'0.5]+0.05cos0.2(600[x+2.75])'0.496

y = –0,0146(600 + 25x²)^0,5 + 0,05 cos 0,2(600[x+2,75])^0,496

Experimentella värdena inlagda under kurvan till jämförelse:

Enbart med huvudhyperbeln (vit nedan, se utförligt i Guldhyperbeln, över värdena):

tunga nuklidgruppen,

atomvikternas precision

HÄRLEDNING MED BESKRIVNING

Fortsättning från Masstalen från 60

Grafen

(1) 0,1 · cos 0,2[5x(120+5x)]^0,5

som tillhör lätta nuklidgruppen genom horisontalellipsens funktion

(2) 0,1 · 0,2[5x(120+5x)]^0,5 ..................... A=5x, gäller för den grafiska skalanpassningen

kan betraktas som trigonometriskt kontinuerlig eftersom sinusfunktionen och ellipsekvationen sammanhänger matematiskt (här utan bevis).

Detta gäller inte för huvudhyperbeln, (se utförligt i Guldhyperbeln)

(3) –0,0146(600+25x²)^0,5

som börjar från masstalet 60 i neutronkvadraten.

För att kompensera vågfunktionens anpassning till den hyperbelns öppna och obegränsat utsträckta formgraf, blir den närmaste kompensationen i (1) att eliminera den inre x-faktorn till noll. Effekten av detta ingrepp gör att vågformen dras ut med maximalt ökad våglängd för varje ny period (räknat från vågtoppen):

(4) 0,1 · cos 0,2[5x(120+0)]^0,5

0,1 · cos 0,2[600x]^0,5

Första perioden i denna vågform tillhör masstalen mindre än 60 och kan skalas bort så att funktionen börjar på andra vågtoppen enligt (här direkt grafiskt approximerat med intervallet 2,75; det exakta värdet är inte kritiskt)

(5) 0,1 · cos 0,2[600(x+2,75)]^0,5

Ytterligare korrektioner är tydligen också nödvändiga för att matcha det rent hyperboliska villkoret:

Det främsta är att vågfunktionens amplitud också bör avta — vilket i princip betyder tillägg av en funktionsfaktor av typen (a^–bx).

Det finns emellertid här ingen direkt uppenbart bestämd form för en sådan härledning (ehuru principen är klar).

En delvis kompenserande helhetslösning är att reducera den fasta amplitudkoefficienten från 0,1 till 0,05 samt justera den mycket känsliga exponenten marginellt från 0,5 till 0,496 (som gör våglängdsförstoringen större i slutänden).

Slutgrafen för hyperbeln+vågfunktionen blir då

(6) y = –0,0146(600+25x²)^0,5 + 0,05 · cos 0,2[600(x+2,75)]^0,496

Närmare än så kommer vi knappast med denna enklare typ av en härledd allmänt orienterande funktion för massdefekterna i den tunga nuklidgruppen.

Det visar sig emellertid att även utan vågfunktionen, kommer resultatvärdena att hålla sig inom den kritiska precisionens marginal (1,0008).

SÄMSTA FALLETS EXEMPEL:

Med ett sämsta fallets precisionsvärde för en av nukliderna i ovanstående slutform (6), t.ex. nukliden med masstal 88 (₃₈Strontium⁸⁸), visas i avrundade värden

teoretiska massdefekten 17,5

experimentella massdefekten 17,6

Atomvikterna

U = Am_N(1–m_Dm_e)

blir respektive

massdefekten atomvikten

teoretiska 17,5 (88)(1,0086652)[1–(17,5)(0,000548598)] = 87,910375

experimentella 17,6 (88)(1,0086652)[1–(17,6)(0,000548598)] = 87,905506 tabellvärdet 87,9056410

med precisionsfelen

PROPORTION

teoretiska

—————— = 1,0000528

experimentella

DIFFERENS

teoretiska — experimentella = 0,004734

kalkylkort · atomära massdefekten mD och atomvikten U från grundhyperbeln+vågfunktionen · minsta masstal = 60

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik5 Kalkylkort — Tunga nuklidgruppen — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

inmatningresultat · fungerar inte i htm(l)-dokument [ref.t.v. MPcKärnMat].

Även om man utesluter vågfunktionens del (HRB-värdet endast), kommer resultatet i vilket fall att ligga inom gränsen för proportionsfelets yttersta gräns.

Kalkylkorte ovan finns nu (Apr2010) att tillgå i en mera utvidgad version via OpenOffice — hela HOP-tabellen ingår för exakt kontroll av samtliga upptagna nuklider (drygt tusen stycken), samt ytterligare.

precisionsvillkoret

För att ett teoretiskt värde ska vara meningsfullt som referens, måste dess proportionella precision vara bättre än 1,0008 :

PRECISIONSVILLKORET

Teorin måste kunna uppvisa en precision på minst 8/10 000

— annars är den i princip körd

(läs: värdelös för analys av kärnfysiken)

Tabelldata [HOP] visar att samtliga atomvikter ligger ytterst nära nuklidens enkla heltaliga masstal (A). ATOMÄRA Massdefekten per neutronnukleon överstiger aldrig 1/102-del av neutronmassan. Med mantissan 0,000 000 0 som referens ligger avvikelserna i atomvikter maximalt

+0.0989400 med aktuell individ från 257,0989400 (₁₀₃Lw²⁵⁷) ................................... OneRatio1,0003849

–0.0983942 med aktuell individ från 117,9016058 (₅₀Sn¹¹⁸) ...................................... OneRatio1,0008345

med reservation för eventuellt missade aspiranter

Det betyder i klartext:

Om teorin för atomvikter inte kan ge en bättre precision än minst 8/10 000 är den, i princip, värdelös. Man kan då lika gärna använda det helt enkla heltaliga masstalet direkt för atomvikten, värdet blir bättre.

Jämför Weizäckerekvationen i modern akademi: sämsta fallens differenser ligger kring 0,02 med motsvarande proportionsfel 1,0005 — men ännu större fel finns för t.ex. Väte-1 med 1,02. Den precisionen utesluter alltså av princip den underliggande kärnmodellen som aspirant för den praktiska fysiken.

Detta villkor klaras galant av sämsta fallets exempel ovan: proportionsfelet för sämsta fallets individ får en marginal på mer än 10ggr; 0,0008/0,000053=15,1.

Fysikens7Principer | 2008IX9 | NEUTRONKVADRATENS ABSOLUT MATEMATISKA GRUNDER | 2003VI6 | MPcKärnfys1 | MPcKärnsynt | MPcKärnteorin |

neutronkvadraten

NEUTRONKVADRATENS ABSOLUTA GRUNDER

Se även i komplementet PRECISIONEN I ATOMVIKTERNA GENOM NEUTRONKVADRATEN ENLIGT TNED

NEUTRONKVADRATENS UPPTÄCKT 2003VI11

Ellipsekvationernas utförliga härledning

I delvis mera utförligt komplement till NEUTRONKVADRATENS PRESENTATION i PLANCKRINGEN

Neutronkvadraten

Upptäckten av mönstergeometrin för kärnsyntesen

CEPH-ekvationen

Som framgår av sambandet för atomvikten U enligt TNED

U = m_N · A(1 – m_Dm_e)

är det förutom masstalet A beroende av atomära massdefekten m_D: U bildas som funktion av m_D.

Vi kan följaktligen inte beräkna U ur m_D eftersom vi i sådana fall först måste veta U. Å andra sidan kan vi heller inte beräkna m_D eftersom det kräver att vi först måste veta U, som följer av m_D.

Emellertid:

Eftersom atomkärnan enligt toroidfysiken saknar beståndsdelar (vi erinrar grunden med m=F/a), finns ingenting annat att hänföra hela massdefektsfunktionen till än just — masstalet.

Om vi försöker att isolera A-termen (för att försöka hitta en principfunktion för vidare) genom att sätta

U = Am_N – m_Dm_eAm_N

= k_A1 – m_Dk_A2

= U(m_D/m_D)

= (Um_D)/m_D

= f (A)/m_D ......................................... för f (A) se funktionsbegreppet

= K_A/m_D ;

K_A = m_D(k_A1 – m_Dk_A2)

= m_Dk_A1 – m_D²k_A2

= k_A2(m_Dk_A1/k_A2 – m_D²)

K_A/k_A2 = m_Dk_A1/k_A2 – m_D² ;

K = m_Dk – m_D² ;

–K = m_D² – mDk

har vi erhållit vi en »enkel» andragradsekvation vars lösning entydigt kommer att bero av alla konstanter kK — och därmed i princip masstalet A:

m_D = k/2 ± Ö (–K=k₀) + (k/2)²

= (k/2=k₁) ± (1/2)Ö 4k₀+k²

CEPH-ekvationen

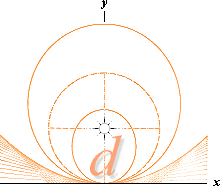
CEPH-ekvationen sammanfattar de fyra s.k. klassiska kägelsnittens ekvationer: CIRKELN, ELLIPSERNA, PARABELN OCH HYPERBLERNA.

Om ekvationen skrivs på sin allmänna grafiska form (CirkelEllipsParabelHyperbel-ekvationen),

______

m_D = k₁ + aÖ 4k₀+k² ............................. allmänna formen

_________________

= k₁ + aÖ 2d₀x(1+e) – x²(1–e²) ........ CEPH-ekvationen explicit

_______

m_D = k₁ + EÖ 2Rx – x² ........................... ellipsfunktionerna explicit

kommer den på ett speciellt sätt att satisfiera massdefektens grundaspekt — 18-gränsen:

Om nämligen m_D växer som funktion av masstalet A och har en övre gräns lika med 18 enheter, då bör den så slutna mD-funktionen (vertikalt) från A=0 till Amax (horisontellt) omskrivas av ovanstående samband i formen av elliptiska funktionskurvor.

Det finns ingenting för atomkärnan att välja på. Den måste följa det övergripande villkor som bestämmer gränserna för kärnans stabilitet: 18-e-massan. På ett eller annat sätt. I en eller annan mening.

I och med att tabelldata från genomförda experimentella mätningar på atomvikterna redan existerar, har vi endast att räkna om dessa i den enhet som 18-massan kräver — och sedan, i stort sett, håva in skörden genom att sätta ut värdena i en masstal-e-massa-matris. Därmed framkommer Neutronkvadraten (så småningom) automatiskt.

Hur CEPH-ekvationen sammanhänger med neutronkvadratens ellipsfunktion beskrivs utförligt nedan i Ellipsfunktionen.

x-skalan mot m_D är här relaterad 1:1. I Neutronkvadraten har emellertid i R-cirkeln två olika skalindex, R=12 mot m_D och R=60 mot Amax. Relationerna blir då

A_max/R_mD=60/12=5=A/x

Neutronkvadratens skalanpassningar

Variabeln x via R=12 identifierar vi alltså med masstalet x=A/5 vilket ger

24x–x² = 24(A/5)–(A/5)² = 120A/25 – A²/25 = (1/25)(120A – A²)

________

m_D = k₁ + (1/5)EÖ 120A – A² ................. ellipsfunktionerna explicit

Därmed är, i princip, problemet med U löst — med införandet eller rättare sagt uppdagandet av en principiell elliptisk mönstergeometri.

E anger excentricitetstalet, A anger masstalet och k₁ sammanfattar ytterligare delar (ellipsens offset) som vi strax ska återkomma till. Variabeln x identifierar vi med masstalet A.

massdefektsgradienten, förkl.

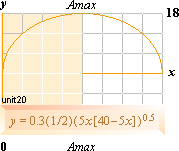
Med masstalet Amax givet, storaxelns längd, blir hela resan en funktion av ellipsbågens form och därmed en motsvarande allmän branthet (gradient) som vi kan kalla för massdefektsgradienten.

Avståndet mellan 18-taket och ellipsens storaxel, dvs, ellipsens lillaxel kan vi därför ge den eminenta benämningen absoluta massdefektsgradienten.

Vi bör, först och främst, finna två sådana gradienter i hela kärnsyntesen:

en för udda, och

en för jämna nuklider

— motsvarande ringsymmetrierna n-p och n-p-n (Se Kärnstrukturen).

Se grundkurvorna för udda och jämna basnukliderna.

Se även massdefektsgradientens kvantitativa formulering.

ellipsfunktionen

HUR NEUTRONKVADRATENS ALLMÄNNA ELLIPSFUNKTION FRAMKOMMER

Betrakta i fortsättning från ovanstående beskrivning först

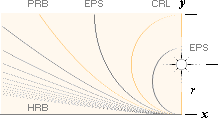
x = [2ry(1+e) – y²(1–e²)]^1/2........................ CEPH-ekvationen

;

Speciellt för ellipserna gäller (fixt R) att r=R(1–e), (1–e²)=E²;

x = [2R(1–e)y(1+e) – y²(1–e²)]^1/2 = [2Ry(1–e²) – y²(1–e²)]^1/2

= E[2Ry – y²]^1/2

Funktionen skriven med ellipserna på x-axeln motsvarar en rotation –90°, analogt en multiplikation med –i (Se Komplexa algebran),

–ix = (–i)E[2Ry – y²]^1/2

= E[(–i)²2Ry – (–i)²y²]^1/2

= E[i²2Ry – i²y²]^1/2

= E[–2Ry + y²]^1/2

Koordinataxlarna (–x)(y) roterade –i ger motsvarande (y)(x). Funktionen blir alltså exakt densamma men relaterad till komplementaxlarna enligt

y = E[–2Rx + x²]^1/2

Men detta är alldeles detsamma som en funktion

y = E[2Rx – x²]^1/2

roterad +90°, alltså i (Se Imaginära enheten), enligt

iy = iE[2Rx – x²]^1/2 = E[i²2Rx – i²x²]^1/2 = E[–2Rx + x²]^1/2

Vilket vill säga; placeringen av den grafiska funktionen

E[–2Rx + x²]^1/2 i xy-systemet är densamma som placeringen av den grafiska funktionen

E[2Rx – x²]^1/2 i samma xy-system. Funktionerna avbildas identiskt; y=ix:

Det enda som skiljer uttrycken från varandra är alltså att den första formen har en negativ rot; Vanligtvis i matematiken kan vi inte beräkna negativa rötter.

Men betrakta det enkla exemplet

(–2)⁵=(–2)(–2)(–2)(–2)(–2)=–32 SOM GER (–32)^1/5=0.2=–2, =(i²32)^0.2=i^2/5(32)^0.2=i^2/52=(i²)^1/52=(–1)^1/52=–2.

Vi kan ta ut själva funktionens byggnad ur negativa rötter — som om de vore positiva.

Funktionen E[–2Rx + x²]^1/2 kan då skrivas ekvivalent

iy = E[–2Rx + x²]^1/2 = iE[2Rx – x²]^1/2= E[ | –2Rx + x² | ]^1/2

Första och tredje ekvivalenterna ger därmed

y = E[2Rx – x²]^1/2

Om variabeln x roteras 180° kring y-axeln, analogt x:=–x, får man explicit

y = EÖ (–x)(2R – (–x))

= EÖ –x(2R + x)

= iEÖx(2R + x) ;

y/i = EÖx(2R + x) = –iy, i^–1=–i

Den grafiska formen för denna funktion är samma som ovan men med ellipsen på negativa x-sidan och hyperbeln på positiva.

Det är också samma form frånsett tecken som i den inledande beskrivningen,

m_D = k1 + EÖ 2Rx – x² ........................... ellipsfunktionerna explicit

Neutronkvadraten använder alltså den ovan positivt härledda formen som verktyg för atomvikterna med skalanpassningen via A=x

— Neutronkvadratens R-cirkel med skalindex R=12 mot m_D och R=60 mot Amax

— som ger 2Rx=120A och x² = A² med resultatet (positiva formen här)

m_D = k₁ + (1/5)EÖ 120A + A² ............... ellipsfunktionen positiva form explicit

motsvarande allmänna ellipsfunktionen

y = k₁ + 0,2[5x(120+5x)]^0,5 ................ A=5x, gäller för den grafiska skalanpassningen

med k₁ som optimal offset. Se utförligt från härledningen till neutronkvadratens horisontalelliptiska grundekvation.

Jämna och Udda

Av tidigare beskrivna skäl följer massdefekten explicit en ordning som, för den rent tekniska beskrivningen av atomkärnans byggnad, indelar de successiva kärnfusionerna i två grupper: en för jämna nuklider och en för udda (vi minns att ±b_n-strukturen i kärnan kräver exakt balans, vilken dock tvunget kommer att störas då kärnan ändrar storlek, fördelningen av motsvarande n-p-massor blir då, i vissa fall kritisk om det blir komplicerat för kärnan att börja dividera allt för mycket).

Som vi minns (Se Kärnstrukturen), kräver udda-nukliderna en tvådelning av kärnmassan för att få p-n-symmetri vilket, några få fall undantaget resulterar i instabila nuklider.

Med ett tillägg på en neutronindivid i nuklidkartans lägre del finner vi följdriktigt för sådana udda nuklider att de ger stabila individer. Toroidmodellen förutsätter med andra ord att vi får två något differenta allmänna massdefektsgrafer, en för jämna (parsymmetriska) och en för udda (halvparsymmetriska) nuklidtyper.

Vartefter massdefekten går mot 18-taket och nukliderna därmed skiljer sig allt mindre kommer de bägge delarna att integreras i samma principiella grafiska funktionsform.

Den vågfunktion som nukliderna gemensamt då ”rider” på kommer också att avspegla en motsvarande ”kosmologisk temperaturskala”. Den utpekar de ”termiska avsatser” där motsvarande fusioner äger rum.

Heliumreferensen

I försorg av kärnradiedramatiken, se utförligt från Kärnradierna genom Planckringen, som bildar ekvivalens mellan Väte-1-kärnan och Helium-4-kärnan,

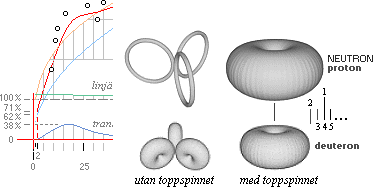
kommer Helium-4-kärnan, inte grundtoroiden N3m20, att bilda ett referensindex för kärnsyntesen, främst för de jämna nukliderna. Eller rättare sagt för massdefektsdynamiken. Nämligen genom den särskilda strukturreferens som med sin ekvivalenta rotationsradie mot N3m20 bildar och sammansätter alla tyngre atomer. Vi kan kalla den strukturreferensen för Heliumreferensen.

I toroidmodellens ljus kan man därmed säga att de (inre strukturellt) jämna nukliderna — som, väl att märka utgår från den udda (masstalet 1) instabila neutronnukliden med noll massdefekt — bildar grunden för hela »den kärntekniska hållfasthetsläran».

Platåerna

Vinkelpreferenserna

massdefektens variation från lägre till högre

Heliumplatån till Kolplatån

Från heliumreferensen intar kärnan ett (kärnstatiskt idealt) stabilt läge. Vi betraktar då kärnan på nuklidlinjen för Z(n-p)-typen i vinkelrummet för nuklidkartan, strax under statiska medelvärdeslinjen (12/5-linjen). Vartefter kärnan växer med n-p-par går den emellertid mot JumboProtonen vilket ger instabilitet. Redan vid Kolplatån sker en fasväxling då stabila nuklider kan bildas med tillägg av en neutron. Därmed inträder kärnfusionerna mot stabila nuklider med växande massdefekt i en lugnare fas där tilläggsneutronen ger en viss marginal uppåt.

Neonplatån till Kiselplatån

När ytterligare neutroner måste till för att parera divergensen mot JumboProtonen kommer kärnan in i fas tre, Neonplatån.. Från denna punkt, n-Z(n-p)-n-nukliderna, kan massdefektens stegring ske över ett ännu större intervall innan kärnan inträder i fas fyra, Kisel-Svavelplatån. Från denna punkt behövs ytterligare neutronpåspädning för att få kärnan ringsymmetriskt stabil, 2n-Z(n-p)-2n-nukliderna. Och, som tidigare, räcker denna påfyllning i ett ännu längre steg och med ännu lägre massdefektsstegring innan kärnan kommer in i Kalciumplatån vilken blir den sista.

Kalciumplatån

Härifrån får kärnan ytterligare neutronpåspädning för att kunna garantera stabila nuklider. Vi ser nu 3n-Z(n-p)-3n-nuklider som förekommer blandat med 2n-Z(n-p)-2n-typen från föregående platå och med vissa ytterligare neutrontillägg. Denna fas fortsätter sedan slutligt upp till Järntoppen där 18-taket uppnås för nuklidindividen ₂₆Fe⁵⁶ med sammansättningen 15n-26p-15n, analogt 2n-26(n-p)-2n. Därmed är kärnsyntesen i grunden avklarad.

Vågfunktionen

Se även särskild illustrerad beskrivning av vågfunktionen i PLANCKRINGEN

Vågfunktionen

0,1 · cos 0,2[5x(120+5x)]^0,5

härrör från neutronkvadratens horisontalelliptiska grundekvation

0,1 · 0,2[5x(120+5x)]^0,5 ..................... A=5x, gäller för den grafiska skalanpassningen

med typutseendena som visas i jämna och udda basnukliderna.

Ursprung. Vågfunktionen tar direkt sitt amplitudargument (0,1) genom massdefektsgradienten (m_D, se även illustrationen närmast nedan). Med visuell observation av nuklidernas placering generellt med grund i de experimentellt uppmätta värdena [HOP], samt med direkt utnyttjande av ovannämnda horisontalelliptiska grundekvation, framgår den nämnda vågfunktionen på enklaste sättet genom att helt enkelt »trigonomisera» ellipsfunktionen som ovan. Det finns bara två alternativ att välja på, sinus eller cosinus, och cosinusformen visar sig ge relaterbara resultat. Se f.ö. illustrationen till jämna och udda basnukliderna. Se även i artikeln ovan Platåerna som direkt kopplar till vågfunktionens resultatform.

Innebörd. Kärnans varierande massdefektsstegring genom den ökande kärnmassan — vi tänker oss att atomkärnorna byggs upp i en process från lättare till tyngre — betyder i rena funktionella termer att kärnan undergår en periodisk vågfunktion med växande våglängd från Heliumgolvet (se Heliumreferensen) till Järntoppen: tre toppar och tre dalar.

Nu är (blir) dalarna inga egentliga dalar när vi kommer till slutpunkten i matematiken, ty vågekvationen kommer att ligga överlagrad på den helt raka ellipsbågen (se illustrationen till jämna och udda basnukliderna), denna bör enligt våra överläggningar täcka medelvärdesvägen för samtliga jämna nuklider hela resan mellan Helium och Järn.

Med en ellipsbåge som växer nerifrån och upp, från vänster till höger, försvinner (nämligen) vågdalarna på ellipsens stigning så att nettoresultatet (i det närmaste) blir just platåerna (en regelrätt växande massdefektsfunktion får heller inte ge en funktion som på något ställe avtar).

Funktionen ska alltså initieras på dalen i första fasen motsvarande lägsta punkten för Heliumreferensen så att samverkan mellan våg och ellips ger en så rak ramp som möjligt i början. Den kommer då att motsvara massdefektens maximala stegring.

forts. neutronkvadraten

NEUTRONKVADRATEN

MED DESSA FÖRUTSÄTTNINGAR GIVNA — i ljuset av en stor mängd redan preparerade experimentella mätdata — har vi alltså endast att applicera föregående härledda principiella ellipsfunktioner på masstalet (A).

Om vi med kännedom om massdefektens definition enligt m_D-nomenklaturen tecknar upp de tabellomräknade (HOP) atomvikternas massdefekter och insätter dem i ett xy-system — där maxvärdet för masstalet Amax ”spontant” ges som 60, därför att det är det heltalsvärde som ligger närmast den enkla analysen: det allra enklaste och skalmässigt bekväma, se dock särskild härledning i Neutronkvadratens Masstalsskala — kan vi knappast, så småningom, undgå att träffa på Neutronkvadraten. Principformen med de elliptiska funktionerna är redan definierad så vi vet redan att vi , främst, ska söka medelvärdesvägarna (från Heliumreferensen) på ellipsbågar.

Vi har alltså från tidigare

m_D = k₁ + (1/5)EÖ 120A – A² ................. allmänna massdefektsfunktionen

Termen k₁ blir en sammansättning av en ellipsoffset, den räknas från Neutronkvadratens mittlinje, m_D=6 enheter, samt den aktuella vågfunktionen.

I full enlighet med föregående omnämnda jämna och udda fusionsvägar — räknat på nukliderna från Heliumreferensens m_D=14.5 och upp mot Järntoppen vid m_Dmax=18, ej utritade nedan — finner vi då (approximativt) respektive fusionsellipser för dessa i Neutronkvadraten enligt figuren nedan.

I grafritningen måste man införa skalfaktorn 5x=A som anpassar R_mD=12 till Amax=60 så att ellipsen ritas

y = offset + (1/5)EÖ 120(5x) – (5x)²

Jämna-ellipsen:

E = (12–1/4–12/10)/24 = (480/40–10/40–48/40)/24 = 422/(40·24) = 422/960 = 211/480

offset_{FRÅN 6} = (12–1/4–12/10)/2 + 12/10 = 6–1/8–6/10 + 12/10 = 6–1/8+6/10 = 6–10/80+48/80 = 6+38/80 = 6,475

Udda-ellipsen:

E = (12–1/4+12/10)/24 = (480/40–10/40+48/40)/24 = 518/(40·24) = 518/960 = 259/480

offset_{FRÅN 6} = (12–1/4+12/10)/2 – 12/10 = 6–1/8+6/10 – 12/10 = 6–1/8–6/10 = 6–10/80–48/80 = 6–58/80 = 5,275

OFFSETVÄRDET FRÅN 18-taket sattes i analysens början (min historia) genom ovanstående hoftning (–0,25e). Det finns emellertid ett mera teoretiskt exakt toppvärde för 18-taket (Se Massdefektens teoretiska toppvärde) och som ligger mellan detta och toppvärdet 17,75 vid Järntoppen. Nämligen (teoretiskt) 18/m_n med m_n uttryckt i atomära massenheter (u) enligt 18/1,0086652 = 17,845366. Det visar sig emellertid (separat analys) att skillnaderna mellan de olika värdegrupperna blir så liten att den kan försummas (vissa nuklidvärden gynnas medan andra missgynnas, och den lilla spridningen betyder i stort att differenserna tar ut varandra).

massdefektsgradienten

Den angivna mD-gradienten 1/10 — se även massdefektsgradientens förklaring — är uppenbarligen Neutronkvadratens egen naturliga massdefektsreferens via mD=6 relativt Amax=60: fusionsellipserna passar tämligen väl in på denna enligt illustrationen ovan.

Vi ska emellertid här inte gå längre i denna härledande beskrivning då vi redan nått fram till målet. Nämligen den allmänna ellipsformens härledning och hur den framkommer. Det väsentliga är här att först och främst ge klarhet åt denna grundform, samt dess vidare koppling för atomvikternas beräkning.

TVÄRELLIPSERNA

Tvärställda ellipsvägarna

Primärnukliderna under Heliumreferensen antyder en brantare massdefektsökning än nukliderna ovanför.

Massdefekten m_D via Neutroncirkelns xy-system har genom allmänna elliptiska massdefektsfunktionen

m_D = k₁ + (1/5)EÖ 120A – A² ................. allmänna massdefektsfunktionen

grundformerna

(m_D) = k₁ + (1/5)Ö 60² – (60–A)²

= k₁ + (1/5)Ö 120A – A² ................................ på Neutroncirkelns bågdel, k₁=6

= k₁ + (1/5)EÖ 120A – A² ............................. horisontella ellipsen, E<1, k₁ sammansatt

= k₁ + (1/5)Ö 60² – (60–[A–K]/E)² ............. vertikala ellipsen, E<1, k₁=6

med A som masstalet, K som en optimal offsetfaktor för ellipsens placering och E som ellipsens stora excentricitetstal (cirkeln = 1).

Termerna K och E förklaras nedan i Offsetfaktorn och Excentricitetstalet.

Tillsammans med A behövs ytterligare en masstalsassocierande term, A_REFERENSEN eller enklare A_ref:

A_REFERENS ingår i definitionen för både K och E (se vidare nedan) enligt

Massdefektsexcentriciteten

E = 1 – (A_REFERENS)/6 ................................. definierar ellipsbågen

Masstalsoffseten ..................................................... placerar ellipsen, enhet i masstal

K = A_REFERENS[1+ (NUKLIDREFERENS_MASSDEFEKT)/6]

och betyder helt enkelt masstalet för fusionsproduktens basnuklid. Denna kan endast erhållas genom separat analys (fusionsanalysen), vilket garanterar att rätt basnuklid kommer att ligga till grund för beräkningen.

Ellipsfunktionerna framgår explicit genom projektionsbegreppen, analogt förkortningar av respektive parametrar i xy-led och är därför i sig relativt enkla att relatera.

I Neutroncirkeln är masstalets horisontella (tvärellipsens potentiella) värde lika med a (se nedanstående illustration) — räknat från origo. Delen utanför blir då

60–a = a₀

Värdet på a₀ räknas då från A-skalans nollpunkt.

Multiplicerat med Neutroncirkelns vridning på E får man ellipsens horisontaldel a₀E=a_0E.

A-referensen — A_REFERENS — masstalsreferensen

Om en vänsterreferens A_ref tas som absolut index så att A (höger) alltid ligger innanför den tvärställda ellipsen, gäller A–a_0E=K=f (A_ref).

Faktorn K (se vidare nedan) betyder då avståndet mellan A=0 och tvärellipsens vänstra skärning med A-axeln. Tvärellipsen måste alltså (minst) skära en A-referenspunkt

K = A_ref

Därmed blir K-faktorn tvärellipsens offset från A=0-punkten.

Med Neutroncirkelns vridning på E får man alltså

a₀E = A–K SOM GER (A–K)/E = a₀

Därmed blir masstalet A återfört på Neutroncirkeln genom 60–a₀=a.

För att tvärellipsen ska vara giltig krävs alltså att A>K, analogt A>A_ref.

a₀

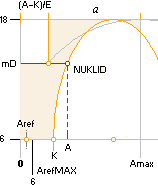
Excentricitetstalet E — tvärellipsens form

LITIUM-6-individens massdefekt (exemplifierat) i Neutronkvadraten kan skrivas direkt på Neutroncirkeln enligt

m_D = 6 + (1/5)Ö 60² – (60–[A=6])²

= 11,230678 HOP-tabellen ger motsvarande experimentella 11,1039987

= 6 + (1/5)Ö 60² – (60–2[A–3])²

I Helium-3-syntesen visas att Litium-6-nukliden kan återföras på Helium-3 som fusionsbas och därmed en referens A_ref=3. Koefficienten 2 motsvarar då inverterade excentricitetstalet E. Härur framgår att E kan skrivas

E = (60 – 10A_ref)/60 = 1 – A_ref/6 .................................... tvärellipsens excentricitet, stora excentricitetstalet

= ellipsens lillaxel dividerat med ellipsens storaxel

Olika ellipser skär i vissa fall vandra genom gemensamma nuklidindivider, vilket verifierar fusionsresonemangen med A_ref och den därmed sammanhängande definitionen på E.

Beryllium-9-nukliden, för att exemplifiera (se mera utförligt illustrerat i Berylliumklacken), gestaltar (tydligen) en sådan fler-ellips-individ enligt

m_D = 6 + (60² – (60 – 2,0[A – (K=3=A_ref)])²)^0,5/5, A={6,9,11,14,15}

m_D = 6 + (60² – (60 – 2,4[A – (K=4=A_ref)])²)^0,5/5, A={9;13;16}

Maxvärdet för A_ref blir alltså 6, förutsatt att negativa E inte räknas.

Faktorn 10 avbildar den tidigare nämnda Neutronkvadratens massdefektsreferens.

Massdefektens absoluta maximum m_D=18 fördelat på de tre toppringarna ger en toppringsreferens på m_D3=6. Den linjära massdefekten tagen över hela masstalsskalan får då en absolut gradient m_D3/A_max=6/60=1/10=m_D. Magnituden i massdefektsgradienten, 1/m_D, får alltså inte överstiga en faktor 10 enligt

A_max/m_D3=10

Med A_max=10m_D3 identifieras A_refMAX enligt ovanstående E-led ekvivalent med m_D3=6.

Det vill säga, längden på tvärellipsens lillaxel, som bestämmer E relativt A_max, får (tydligen) inte vara sådan att faktorn

A_max/A_refMAX=10=A_max/m_D3 = horisontcirkeln

underskrids; tvärellipsen kräver att nämnda faktor via A_max/A_ref är större än (eller lika med) 10.

Delarna mindre än 10 tillhör (tydligen) horisontalellipserna (fusionerna över Heliumreferensen).

Tvärellipsens dynamik i atomkärnan

— Medelvärdesgradienten 2003VIII12

Genom fusionsanalysen, se delvis exempel i Helium-3-syntesen, visar sig (främst) två masstalsreferenser

A_ref={3_HELIUM3,4_HELIUM4}. De innebär (tydligen) att den resulterande kärnan via deras sammansättning kan återföras på en ”strukturblandare” (strukturbindningskoefficient) eller referensgradient

m_D3/A_ref={2/1;3/2} med masstalsexcentriciteten

E^–1={2;3}. Alla fusioner som kan återföras på dessa A_ref karaktäriseras alltså av just aktuell ”blandningsmagnitud”;

Det är (alltså) tydligt att E har en rent kärndynamisk grundläggande, strukturbestämmande innebörd.

Därmed synes i varje fall rent tekniskt teoretiskt finnas den möjligheten att atomkärnan också accepterar de bägge grundmagnituderna från

m_D3/A_ref = {2/1;3/2} enligt en medelvärdesform

— tagen över hela kärnans väv av parladdningar —

(E_HELIUM3+E_HELIUM4)/2 = E_H(3+4)/2.

Detta skulle ge

E_H34 = 5/12 med A_refH34 = 7/2.

Det oerhörda infinner sig också;

E = 1–(A_REFERENS)/6 = 1 – 3,5/6 = 1/2,4, se praktiskt exempel i Berylliumklacken.

Det visade sig att en tidigare upptäckt men oförklarad magnitud på E^–1=2,4 och A_ref=3,5 stämmer med ovanstående kvantiteter.

Offsetfaktorn (se nedan) blir då beroende av dessa ”virtuella nuklidblandare” genom en likaledes virtuell nuklidreferens.

Med dessa klarlägganden är det tydligt att Neutronkvadraten är en verklig läromästare i kategorin kärnfysik.

Offsetfaktorn K — med NUKLIDREFERENSEN

Om vi, med stöd i ovanstående relationer och referenser, söker ett förhållande som på liknande sätt som i fallet för E avgränsar en maximal gradient för massdefektsändringen, kan vi skriva

(K–A_ref)/A_ref = m_Dmax=18/m_D3=6 = 3

Med en NUKLIDREFERENS-massdefekt för en tilläggsindivid i fusionssyntesen för en viss fusionsväg, en typ m_D’, får man då tydligen ett förhållande till Neutronkvadratens mittlinje, m_D=6 enheter enligt

(K–A_ref)/A_ref = K/A_ref – 1 = m_D’/6 ;

K = A_ref(1 + m_D’/6) ............................................................... tvärellipsens offsetfaktor

K = Masstalsoffseten .......................................................... placerar ellipsen, enhet i masstal

K = A_REFERENS[1+ (NUKLIDREFERENS_MASSDEFEKT)/6]

Om m_D’ kan återföras på Neutronen, m_D’=0, får man K=A.

Nuklidreferensen kan vara sammansatt av flera olika individer, inkluderat en e-massa totalt större än 18.

Tvärellipsen i summa

För att få fram vilka EK-värden som gäller måste man först genomföra en grundlig fusionsanalys så att tillbörliga nuklidindivider relateras på tillbörliga faktorer — nukliden som produkt måste vara garanterat EXOTERMISK. I annat fall har ovanstående härledda tvärelliptiska samband ingen mening.

Ovanstående relaterade samband i sammanställning nedan,

Massdefektsekvationen

_____________________

Ö 60² – (60 – E^–1[A – K])²

m_D = 6 + ————————————— ................. A, masstal

5

Massdefektsexcentriciteten

E = 1 – (A_REFERENS)/6 ................................. definierar ellipsbågen

Masstalsoffseten ..................................................... placerar ellipsen, enhet i masstal

K = A_REFERENS[1+ (NUKLIDREFERENS_MASSDEFEKT)/6]

EXEMPEL:

Nukliden ₂He³ med atomära massdefekten (avrundat) 6,00 ger

NUKLIDREFERENS_MASSDEFEKT = 6

med (en)

A_REFERENS = 2

som ger

K = A_REFERENS[1+ (NUKLIDREFERENS_MASSDEFEKT)/6]

= 2[1 + 6/6] = 4;

Excentricitetstalet blir

E = 1 – (A_REFERENS)/6

= 1 – 2/6 = 2/3

I Atomvikterna ges en kort översikt av hur sambanden ovan beskriver atomvikterna — genom ett enda enhetligt matematiskt (men mycket sammansatt) uttryck — med en precision som helt tycks utklassa den moderna akademins motsvarande teoretiska resultat (Weizäckerekvationen).

ETT PRAKTISKT EXEMPEL på hur ovanstående samband används i analysen för att få fram konkreta resultat finns i PRAKTISKT EXEMPEL.

Här ska ärligt sägas: Den mera utförliga (noggranna) beskrivningen till detaljerna inom neutronkvadratens fusionsanalys är (i originalet) omfattande. För att helt skala bort den delen och endast (förhoppningsvis) ta med de — för den övergripande förståelsen — mest viktiga delarna, har ovanstående presentation framkommit. Framtiden får sedan utvisa om ytterligare behov finns för vidare.

fusionsanalysen

FUSIONSANALYSEN

GRUNDEN FÖR FUSIONSANALYSEN I TNED är EXOTERMISKA FUSIONSLAGEN, samma som exotermiska kärnreaktionslagen.

Utförliga och genomarbetade grundexempel finns i Nuklidbildningarna i Baskartan för Udda och Jämna Nuklidserierna.

Vi måste (nämligen) kunna vara HELT säkra på ATT en viss nuklid verkligen KAN bildas med angivna komponenter, att produkten GER energi (att fusionen är exotermisk, annars är den endotermisk), samt att vi måste besitta ett effektivt kontrollverktyg — exotermiska kärnreaktionslagen — för att genomföra den bestämningen. Det är emellertid inte alltid man därmed träffar rätt: erfarenheten har visat att det finns vissa grundläggande knepigheter speciellt i grundnuklidernas sammansättning och som finns exemplifierat nedan i Helium-3-syntesen och Berylliumklacken. Först genom att klarlägga dessa detaljer kan de slutliga massdefektsekvationerna lösas.

Tillsammans med den grundläggande rent fusionstekniska utvärderingen, som ovan, måste vi alltså genomföra en ytterligare analys som går ut på bestämningen av de avgörande parameterobjekten som explicit kopplar till neutronkvadratens mönstergeometri eller allmänna ellipsfunktionen med grundobjekten

A_REFERENS

OCH

NUKLIDREFERENS_MASSDEFEKT

Det är dessa som avgör den atomviktsdefinierande ellipsens excentricitet, placering och därmed dess bågskärning med den aktuella fusionsproduktens masstal som ger resultatet.

Det är i denna korta presentation INTE avsikten att ge en uttömmande redovisning av begreppens ursprungshistoria i denna författares referens, utan enbart att ge en så snävt hållen allmänt orienterande beskrivning som möjligt — främst för att ge maximal klarhet åt grundbegreppen på kortast möjliga distans och därmed eliminera en annars svulstig och omfattande textkropp (som kan verka tröttande om man inte är extremt intresserad). Endast om det visar sig att vidare behov föreligger längre fram, kommer mera utförliga delar att sammanställas.

Helium-3-syntesen

Helium-3-syntesen

Massdefektsvärdena refererar till HOP.

Rött instabil, svart/grönt för markering av de två fusionsstråken.

** Regression, massdefekten reduceras i försorg av e-massor som tas från neutronens centralmassiv ±909e.

Att åstadkomma denna nuklidfusion torde inte höra till de allra enklaste laboratorieförsöken;

en neutron i mitten måste precis ”träffas” av två motsatt kolliderande heliumkärnor.

Se vidare beskrivning i BerylliumKlacken.

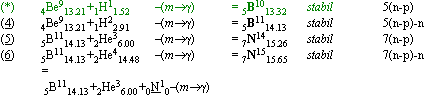
Kommentar

Litium-7–Beryllium-10-bildningarna kan återföras på ₂He³-ellipsen med ett offsettillägg som bestäms av massdefekten för ₁H¹.

₂He⁶ kan återföras på 2(₁H¹+2₀N¹=₁H³)=₂He⁴+2₀N¹. Eftersom ₂He⁴=₁H³+₁H¹ med ekvivalenta massdefekter för A=3, kan bildningen av ₂He⁶ (möjligen) återföras på

(₁H³-₂He³)-ellipsen med ett offsettillägg i två steg som bestäms av massdefekten för ₁H¹.

Berylliumklacken

BERYLLIUMKLACKEN

Anomalierna för ₆C¹³ och ₈O¹⁶

BERYLLIUMKLACKEN

Om vi betraktar nuklidsamlingen, ser vi strax (främst) att det ser ut som om individerna Kol ₆C¹³ och Syre ₈O¹⁶ ”hänger löst utanför” ordningen.

Det beror på att det — tydligen enligt Neutronkvadraten — finns en separat fusionsväg som sammanbinder dessa individer och ger deras massdefekter explicit.

Observationen leder till en (grundlig) studie av en känslig knutpunkt i hela nuklidskalan med centrum i den instabila Beryllium-8-individen. Vi studerar denna.

Med ₂He³-nukliden som basreferensnuklid i fusionssyntesen ges först

K = A_REFERENS[1+ (NUKLIDREFERENS_MASSDEFEKT)/6]

= 2[1 + 6/6] = 4;

Förklaringen till inverterade E-värdet på 2,4 ges i Tvärellipsens dynamik,

E = 1–(A_REFERENS)/6 = 1 – 3,5/6 = 1/2,4

Om vi känner 18-villkoret och massdefekten för Helium-4, kan vi huvudräkna (obs, den regressiva, beskrivs vidare nedan) approximativa massdefekten direkt på den komplicerade Helium-Neutron-Helium-fusionen; om den lyckas resulterar den i den stabila nukliden Beryllium-9. FusionsKopplingen utpekar (eller möjligen »föreslår») att ”nätverket” Helium-Beryllium-komplexet sammanbinder jämna och udda-ellipserna. Se vidare beskrivning nedan.

Den mera exakta balansräkningen — m_D=D–(18–D–2,25)=13,20, D=14,475 — kräver att kompositen ₄Be⁸ har m_D=14,475, dvs. marginellt lägre än ₂He⁴.

LITIUM, BERYLLIUM OCH BOR — Berylliumklacken

Grundämnena med det mest taskiga läget av alla — Litium, Beryllium och Bor

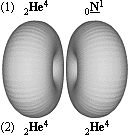
De första n-p-fusionerna med den ideala Z(n-p)-Heliumnukliden ₂He⁴ bildar alldeles för stora skillnader mot den redan väl balanserade ₂He⁴-ringsymmetrin för att fungera som stabila nuklider. ₂He⁴ har (dessutom) en väl etablerad, unik referens för hela atom och kärnfysiken som ingen annan atom har genom sin ekvivalens med rotationsradien för grundnukliden N3m20.

Oavsett den förenande komponenten som minst är en n eller p-typ bildas i vilket fall i kärnstrukturen en otillåtet stor divergens mot antingen JumboProton (p-n-p-n-p) eller JumboNeutron (n-p-n-p-n). Varje sådant försök till fusion kommer alltså att misslyckas: resultanten kan inte förverkligas. ₂He⁴ kastar helt enkelt ut uppvaktningen.

Ett annat sätt att säga samma sak på är: det finns ingen tillgänglig g-massa tillräckligt stor för att åstadkomma en varaktig ringsymmetriskt stabil ombyggnad av ₂He⁴ genom tillförande av enskilda n-p-individer. Det skulle behövas en så marginellt liten mini-n-p-individ för att få fram en stabil 2He4+n_x-nuklid att sådana marginaler långt underskrider vad grundaggregaten kan servera; de existerar inte i ringsymmetrierna.

₂He⁴ kan, följaktligen, heller inte servera en sådan förutsättning genom att i ett enskilt steg para sig med sin egen typ, symmetrin blir i netto, i princip, densamma: en Z(n-p)-nuklid med en (nära) obruten ₂He⁴-kärnstruktur. Går inte. Komponenterna kommer att mobilisera alla frånstötningsmekanismer som kan uppbådas: vi måste ha större utrymme, mera fri tillänglig g-massa: flera lika individer än två — eller en olik tilläggsindivid som inte är en fri neutron eller proton.

Det innebär att Heliumpreferensen med sin ekvivalenta rotationsradie mot grundaggregatet är tämligen ”helig mark”. Ingen kommer in där.

Första fysikaliskt möjliga stabila fusionen med Heliumindividen ₂He⁴ blir alltså tvunget av fasonen

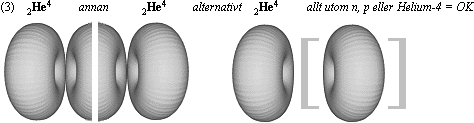
Första stabila fusionen med enbart Helium-4-individer realiseras alltså först på Kol-12-individen, ₆C¹² — och sedan vidare uppåt:

minst tre parsteg för att finna en matchning mot ringstrukturens symmetri.

Hela saken resulterar i den nuklidära kosmiska massdefektsdramatik som i sekvens ”hoppar över” aspiranterna närmast Helium: Litium, Beryllium och Bor.

Om man direkt försöker para ihop två ₂He⁴ händer inget annat än vad som händer om två biljardbollar stöter ihop. Går inte.

Be-individen ₄Be⁸, när den väl kommer igång, kommer att försvinna snabbt (inom t14 sekunder).

Enda chansen för detta taskiga läge för Be är att erhålla en tilläggsneutron innan de t14 sekunderna gått. Därmed bildas ₄Be⁹ som är den enda stabila isotopen i det grundämnet.

Trion Litium, Beryllium och Bor har (veterligt) det i nuklidspektrat i särklass mest taskiga (ogynnsamma) utgångsläget av alla möjliga nuklider. På grund av deras speciella originalitet i nuklidordningarna, har de (följdriktigt) en relativt sparsam förekomst i den kosmiska bygden.

Den regressiva fusionsbildningen

från Helium-4 till Beryllium-9

Beryllium 8-atomens massdefekt utgår från Heliumatomens — 14,485281 enligt nominella Neutronkvadraten — 14,4834105 enligt tabelldata. Denna Berylliumnuklid kommer emellertid aldrig att existera under någon överskådlig framtid (5 t14 sekunder enligt tabelldata).

₄Be⁹ har en smal, men rimlig, chans att bildas om den initieras på en neutronkärna mellan två Helium-4-kärnor.

Transiteringen för energin som möjliggör denna ₄Be⁹-bildning är i själva verket så tröskelgäckande att man knappt tror det är sant att så enorma avvägningar alls kan finnas.

För att kunna genomföra ₄Be⁹-transiteringen måste Neutronen av sitt 18-kapital lämna tillbaka nettoskillnaden mellan Heliumindividernas massdefekt och den för ₄Be⁹, samt slutligen själv bidra med ytterligare för att ”stämpla in” i Berylliets sublima byggnad.

(2×4,002603114,48+1,0086652) – 9,012185513,21 = 9,0138714 – 9,0121855 = 0,0016859 = 3,0708561 e-massor.

14,48 – 13,21 = 1,27

Neutronen har, förutom sin egen individ, att på åtta individer dela ut åt vardera 1,27 e-massor;

1,27×8 = 10,16;

13,21–10,16 = 3,05, vad neutronen måste anpassa sig själv till efter 8×1,27-utgivningen;

Jämför kapitalet 3,07 med handelsavtalet 3,05. Det går att köra båten i hamn, säkert, men det blir på näppen. Energin för hela ombyggnaden har bara

3,07 – 3,05 = 0,02 e-massor att ta av. Går det så går det.

Det faktum ATT det går på den lilla arbetsmängden, visar att ringstrukturerna Neutron-Helium-4 är praktiskt taget identiska: ytterst litet arbete för hela ombyggnaden; ren finputsning.

Beryllium-9 kan emellertid också bildas på annat sätt som inte (direkt) berör ovanstående, se Helium-3-syntesen.

Notera att en specifik nuklid kan uttryckas fusionstekniskt på flera olika sätt. Exemplen ovan visar ett av flera olika möjliga alternativ.

Beryllium-9-individen är (tydligen) en knutpunkt för flera fusionsvägar, vi återfår samma värde för samtliga fall.

Här ännu ett exempel:

Beryllium ₄Be⁹, Kol ₆C¹³ och Syre ₈O¹⁶ har (som det ser ut) en gemensam massdefektsekvation. Den lyder

m_D = 6+[60²–[60–2,4(A–K₌₄)]²]^0,5/5

Massdefekterna i Beryllium-Kol-Syre-anomalin blir respektive

nuklid A m_D jämförelse med gängse tabelldata [HOP]

₄Be⁹ 9 13,200000 13,2126736

₆C¹³ 13 15,220498 15,1931747

₈O¹⁶ 16 16,249995 16,2338185

CEPHekvationen

CEPH-ekvationen beskrivs med utförliga härledningar i särskilt avsnitt tillsammans med samband och härledningar till matematikens fyra grundkurvor cirkeln, ellipsen, parabeln och hyperbeln. Se CEPH-ekvationens härledning. Avsnittet nedan ger en kort inledning.

CEPH-ekvationen

CEPH-ekvationens härledning kräver i stort sett hela avsnittet om gravitationslagen med Keplermomentet och geometrierna för Cirkeln, Ellipsen, Parabeln och Hyperbeln, samt vidare härledningen till satellitbanorna (ellipserna och cirklarna) för att ge rättvisa åt helheten. Det kräver (i princip) ett helt särskilt htm-dokument — med ytterligare länkar till geometrin överlag. Den delen är emellertid garanterat omfattande och kan (ännu) inte ges i denna presentation — varför heller inte CEPH-ekvationens härledning kommer att presenteras här. CEPH-ekvationens motsvarande form nedan har eftersökts på webben men ännu (Augusti 2008) inte hittats (OM den tendensen håller i sig, kommer ett särskilt avsnitt att infogas senare med CEPH-ekvationens härledning). Vi förutsätter den tills vidare bekant (!). En allmän beskrivning av ekvationens innebörd ges nedan.

[Det särskilda avsnittet finns nu (sedan Nov2008) i särskilt htm-dokumnet, se CEPH-ekvationen].

CEPH-ekvationen

x = (2d[1+e]y – y²[1–e²])^1/2................. CEPH-ekvationen

beskriver de fyra celesta kurvformerna cirkel, ellips, parabel och hyperbel med y som variabel (massdefekten med ellipsen i neutronkvadratens fall) och x som funktionsvärde med sammansättningen

e=–1: ..................... fritt fall, rät linje

0>e>–1: .................. ellips, d betecknar apofokus

e= 0: ..................... cirkel

0<e<1: .................... ellips, d betecknar perifokus

e= 1: ..................... parabel

e> 1: ..................... hyperbel

d anger kortaste avståndet mellan omloppskroppen och centralmassan.

Se även CEPH-ekvationens koppling till Neutronkvadraten för atomvikternas beräkning.

JÄMFÖR TILL EXEMPEL @INTERNET WIKIPEDIA på Conic section (2008-09-13): Väl finns en principbild (som innehåller delar av den ovan) som visar hur de olika kurvformerna kan återföras på den centrala fokuspunkten (samt vilka e-värden som kopplar till vilken kurvform). Men Wikipediaartikeln innehåller (ännu) inget sammankopplande matematiskt uttryck som beskriver alla fyra kurvformerna tillsammans — inte alls någon sådan över huvud taget i artikeln. Det verkar som sagt var heller inte finnas någon sådan på webben i övrigt (därför att det heller inte finns någon allmän litteratur i modern akademi som, någonsin, har speglat just den detaljen? DET verkar underligt …).

Se vidare utförligt i CEPH-ekvationen.

Fysikens7Principer

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

innehåll

FYSIKENS 7 PRINCIPER

Fysikens 7 Principer

Principernas förklaring

Fysikens 7 Principer (I) · maximalt kortfattat

Fysikens 7 Principer (II) · mera utförligt

Fysikens 7 Principer (III) · utförligt

1. APARC tillståndets princip

2. FUNTOP jämviktens princip

3. POM rörelsens princip

energilagen

massdestruktionen

3.1 POM (I) energins oskapade princip

3.1 POM (II) intervallets oförstörbarhet, primära massförstöraren

COEI energins bevarande genom induktionen

4. NEONS mekanikens princip

5. GRIP gravitationens (konvergensens) princip

6. DEEP divergensens (ljusets, elektricitetens) princip

7. PASTOM massans strukturella princip

Osäkerhetsprincipen

Elektronen sätter gränsen för all fysikalisk mätning

Neutronkvadratens absoluta grunder

Atomvikterna genom Neutronkvadraten

Precisionen i atomvikterna genom Neutronkvadraten enligt TNED

Neutronkvadratens mönsterkropp

Typexempel på Neutronkvadratens precision

Järntoppen

Medelellipserna för Jämna och UDDa basnukliderna

Vågfunktionen · illustrerad

Massdefektsekvationen

Resultattabell · atomvikterna

Masstalen från 60 · den tunga nuklidgruppen

Huvudhyperbeln

Tunga nuklidgruppens precision

Precisionsvillkoret

Neutronkvadratens absoluta grunder · Ellipsekvationerna härledning

CEPH-ekvationen

Massdefektsgradienten · allmänt

Ellipsfunktionen

Heliumreferensen

Platåerna

Vågfunktionen · förklaring

Massdefektsgradienten · beskrivning

Tvärellipserna

Masstalsreferensen

Excentricitetstatelt

Tvärellipsens dynamik

Offsetfaktorn K

Tvärellipsen i summering

Fusionsanalysen

Helium-3-Syntesen

Berylliumklacken

CEPH-ekvationen · förklaring

REGISTER

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[FM]. FOCUS MATERIEN 1975

gen. förkortn. generellt

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2020-04-29

*END.

Stavningskontrollerat 2007-11-21 | 2008-03-06 | 2008-09-12

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se