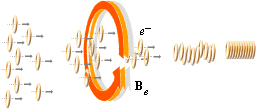
ELEKTRONEN LEC — UNIVERSUMS HISTORIA | 2010 |VII13|VIII18|XI2 | enproduktion | Senast uppdaterade version: 2014-02-02 · Universums Historia

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Kvalitativa Förklaringarna ·ELEKTRONEN · LEC · Casimireffekten · Lambväxlingen · Elektronens g-faktor · RESERVATION FÖR ÖVERFÖRINGSFEL

BILDKÄLLA: Författarens arkiv · BildR26Excur6 · 21JUL2010 · Nikon D90 · Detalj

Förklaringarna till begreppen i den moderna akademins kvantelektrodynamik (QED)från 1947

Begreppens förankring i fysiken, hur de uppkommit, och deras innebörd i relaterad fysik (TNED)

Antalet masskomponenter i elektronmassan

Lambväxlingen [eng. Lamb shift]	Elektronens g-faktor	Casimireffekten	Djupa motsägelser i MAC om elektronen	Elektronringens toppspinn
Atombrummet på elektronkomponenterna	Kärnan skymmer 1/1000 e	Materialen ytAttraherar — via e-komponenterna	e syns inte — för stor i kärnan	Jämförelser TNED-MAC

Allmänna artikelrubriker — Elektronen i materien

Elektronen och elektronringens toppspinn — Hur fysiken i MAC ersätts med vakuumfluktuationer

Elektronens g-faktor · Lamb-Retherfords Växling · Casimireffekten

Djupa motsägelser i MAC om elektronen — så liten att den inte syns alls, för stor för atomkärnan:

Värmetransporten kräver något mer än strukturlösa punktobjekt

Casimir-effekten — hur och varför tätt liggande materialytor suger

För Elektronelementet, se Elektronen, ELEKTRONMASSANS KOMPONENTER, Ljusets Polarisation, Spektrum och Kvanttalen.

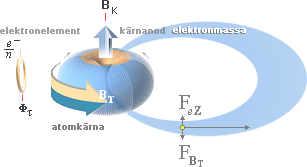
För BT, se Atomkärnans allmänna magnetiska yttoroidfält.

Elektronens frigörelse ur atomkärnan:

NEUTRONSÖNDERFALLET laddningsdeplacementet

NEUTRONSÖNDERFALLET kärnmagnetismen

ATOMKÄRNAN allmän formbeskrivning

ATOMKÄRNAN ELEKTRONMASSAN

ATOMKÄRNAN N3m20

kärnanod, BT-fältet.

KVALITATIVA FÖRKLARINGARNA

Kvalitativa förklaringarna

KVALITATIVA FÖRKLARINGARNA — enligt TNED

———————————————————————————————————————————————

ELEKTRONMASSANS KOMPONENTER	—	Elektronens g-faktor	·	Casimireffekten	·	Lambövergången
översikt ......................................................		Elektronens g-faktor		Casimireffekten		Lambövergången
detaljer ..........................................................		Elektronens g-faktor		Casimireffekten		Lambövergången
utförligt .......................................................		Elektronens g-faktor		Casimireffekten		Lambövergången

Elektronens g-faktor: [detalj]

…

I MAC blir det svårt — över huvud taget — att härleda »elektronens dubbla magnetism», se Elektronringens magnetiska moment [Jämför FOCUS MATERIEN 1975 s106sp2mn], utöver att den dessutom inte är exakt dubbel. (I MAC är det [således] experimentalfysiken [hantverket] som har fått bestämma takten i teorin [medan den för TNED bestämmer takten i framgångarna]).

I TNED är en del av elektronmassan skymd av atomkärnan via strömningsflödet i kraftekvationen [F(BT)+F(eZ)=0] och elektronmassan i atomär bindning kan därför inte uppvisa sin fulla magnetiska kraft med avseende på alla elektronmassans komponenter. Den isolerade elektronen däremot, som innehåller samtliga elektronringar, uppvisar följaktligen ett något högre värde (2,00231930…) på koefficienten (2), den s.k. elektronens g-faktor, till den idealt härledda elektronens magnetiska moment (»spinnflippkraften»). Nettoeffekten i praktiken blir att den atombundna elektronen uppvisar större eller mindre verkningsgrad beroende på hur stor andel som skyms av atomkärnan. Det betyder i allmänhet att verkningsgraden i elektronmassans svängningsenergi blir allt lägre ju närmare elektronen ligger kärnan. Den faktorn betyder en mindre reduktion av styrkan i Lambväxlingen och vilken faktor avtar med atomens växande excitation, analogt elektronmassan alltmera utspridd.

I MAC anser man att fenomenet istället beror på [Shpenkov 2004] ’vakuumets polarisation, elektronmassans renormalisation och anomalt magnetiskt moment’, där den sistnämnda [‡] intar samma funktion som den nyssnämnda reducerande nettoeffekten i TNED. Den teoretiska beräkningsgrunden beskrivs som ’exceptionellt komplicerad’, se eG-serien; MAC-värdet för elektronens g-faktor bildar en symbios mellan experiment och teori och anges [CODATA 2006] enligt

CODATA 2010-10-05 [Source 2006 http://physics.nist.gov/cgi-bin/cuu/Value?gem]

g_e = 2,0023193043622(15).................... nuvarande internationellt antagna värde [CODATA]

Det motsvarande TNED-värdet — iklätt de enkla heltalskoefficienterna från Neutronkvadraten — uppvisar motsvarande

b = 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22986]^–1)^–1

= 2,00231930436221 ....................... se beräkningar/jämförelser i Kalkylkortet

Se även en kortare resultatsammanställning i LEC.

Casimireffekten: [detalj]

Från illustration i LJUSETS POLARISATION.

F/A = ke²Z[d_z²d_xd_y]^–1[n]^–1 ...................... TNED

F/A = ħcπ²/240d_z⁴ ....................................................... MAC

Faktorerna Znd_x d_y ingår inte i MAC — dessutom finns ytterligare som här har utelämnats för den enkla framställningens skull (temperaturberoende, frekvensberoende, optiska parametrar …), se mera utförligt i artikeln om Casimireffekten.

DEN STORA SVÅRIGHETEN I TNED är att (oberoende) få fram exakta data på antalet komponenter — tau-ringar — i elektronmassan. Sämsta fallets beräkning genom N3m20-aggregatet ger lägst n=177062, Se Beräkningen av n, men det värdet är orealistiskt då en central öppning krävs i den aktuella deltoroidformens centrumhål, det sanna värdet måste under alla omständigheter vara högre. En möjlighet öppnar sig genom Casimireffekten — ett fenomen som yttrar sig genom atomattraktioner mellan närliggande materialytor, och som i MAC anses sammanhänga med VAKUUMFLUKTUATIONER. Enligt TNED kan effekten, tydligen, beskrivas (relativt enkelt) via Coulombkraften mellan elektronring-atomkärna då ringarna inbördes kan anta varandras motstående atombindningar (förstadiet till fullständig sammansmältning). Grundsambandet (för nära avstånd, typ 10 nM) blir som ovan — med sämsta fallets n=177 062. Motsvarande samband i MAC anges som ovan.

Med exempel på rumstempererat JÄRN ([kortaste, kubiska] atommedelavståndet är väsentligt för TNED-sambandet, men ingår inte [direkt] i MAC-sambandet) och normaltrycket vid havsytan på 1 atmosfär (F/A = 101 325 Pascal) ges till jämförelse

d(z) = 10,6 nM ................. MAC (10,642884)

d(z) = 8,82 nM ................. TNED (8,815724)

Här ska direkt sägas (efter genomläsning av flera rapporter som beskriver mätresultat Sep2010, se sammanställning i CasimirRef) att Casimireffekten är INGALUNDA överväldigande exakt representerad mellan teori och experiment. I flera fall omnämns relativa felprocent på 15-17% — medan i vissa andra fall siffror på runt 1% förekommer.

Relativa felet är 17%: (8,82)/(10,6) = 0,8320754, 83% träff, vilket just motsvarar ett relationsfel på nära 17%.

Antas resultatet, ges n = 4 × 177062 = 708 248 för antalet element i elektronmassan. Se mera utförligt i avsnittet om Casimireffekten.

Rent kvalitativt kan alltså fenomenet förklaras utomordentligt väl av TNED — medan MAC är hänvisad till sitt »fluktuerande vakuum» — via hf.

Se även en kortare resultatsammanställning i LEC.

Lamb-Retherford-effekten: [detalj]

Lambväxlingen (eng. Lamb shift), även Lambövergången, Lambskiftet — »ATOMENS MASKINLJUD» i TNED

Beteckningar i figuren återfinns i KVANTTALEN i Elektronmassans komponenter.

Elektronmassans INRE resonanser som funktion ENBART av varje ringkomponents koppling till atomkärnan [Se Elektronmassans komponenter], här på enklast sättet Väteatomen (1H1), kan PÅ ENKLASTE SÄTTET TILL PRÖVNING återföras på EN elektronring i direkt (kontinuerlig, vilket inte är riktigt korrekt, men vi frånser det här) påverkan från EN av toppspinnets tre undertoroider enligt N3m20-modellen i TNED. I TNED räknas NOLLENERGI för elektronmassan då den befinner sig på lägsta energinivån (n=1): atomen summera nollkraft [F(BT)+F(eZ)=0] och nollmoment [J(0K)+3J(1K)=0]. För att »befria» Väteatomen från elektronen krävs en excitationsenergi på 13,6 eV [Se Väteatomens Spektrum] — vilket i modern akademi anges som ett negativt talvärde för nivån n=1. Denna omvändning kan vara viktig att känna till (för nybörjaren i TNED). Väteatomens ENKLA emissionsenergier ges f.ö. [Se Väteatomens spektrum] enligt det redan välkända sambandet

E = ke²(2ρ)^–1(1/n₁² – 1/n₂²) .................... se utförligt i Väteatomens spektrum

med n1 som nivån närmast atomkärnan och n2 längst ut. I grundtillståndet med enbart E(n1=1) finns ingen excitationsenergi (E=0), och elektronmassan ligger därför låst vid kärnan via 13,6 eV. Lyfts elektronmassan upp till den första resonansen som tangerar närmast högre n-nivå vid n=2 ges excitationsenergin E=10,2 eV — lika med 0,75 × 13,6. Om den resonansenergin också innefattar en spegling av hur elektronringen ’vibrerar’ internt som följd av kopplingen till atomkärnan (»elektronmassans eller atomens maskinljud») kan vi räkna på enklaste sättet med nämnda förutsättningar — föregående antalsvärdet

708 248 från Casimirexemplet ovan —

(10,2 eV)/(708 248)/(3) = 4,80057 t6 eV .............. TNED; = 1160,65 MHz ............. obestämt grovvärde

Experimentellt Lamb-Retherford 1947 = 4,37200 t6 eV .............. MAC: = 1057,04 MHz ............. mätvärde

Fenomenet har fått namnet LambVäxlingen (eng. Lamb shift) efter experimentalisterna som uppdagade det (Lamb-Retherford 1947) [‡].

Relationsfelet är ca 9% — 91% träff. Andra nivåer ger andra värden — det finns MED OVANNÄMNDA ALLMÄNT KVALITATIVA FÖRKLARING ENLIGT TNED inre elektronresonanser för varje motsvarande enkel resonansgrupp i det konventionella atomspektrumet. TNED-värdet ovan, som exempelvärde, är ingalunda exakt, men ger den kvalitativt (PRINCIPFÖRKLARANDE) nödvändiga inblicken (även hyfsat kvantitativt, tydligen och förutsatt grundresultatet från Casimireffekten håller streck).

Genom vidare härledning i ABpEK — på redan känd matematisk formalia (QED) ehuru i nytt ljus via TNED — ökas träffprocenten ovan via TNED-frekvensen med 1160 ner till 1086 MHz med resultat i 97% träff och därmed ett absolutfel på mindre än 3% — tillsammans med en justeringsfaktor som inte är lika enkel att finna en exakt matematisk teori för. Se utförligt från ABpEK.

Se även en kortare resultatsammanställning i LEC.

Med andra ord: ELEKTRONMASSANS ELEMENT förklarar samtliga fenomen— se även i LJUSETS POLARISATION — det enkla köksexperimentet.

Se vidare utförlig beskrivning (för Lambväxlingen) i fortsättning från

Inledningen till ATOMKÄRNANS BRUM PÅ ELEKTRONMASSANS KOMPONENTER.

——————————————————————————————————————

[‡] ”Även elektronspinnet måste vara förknippat med ett magnetiskt moment, men på denna punkt överensstämmer inte formlerna exakt med de tidigare. Elektronen visade sig nämligen ha »dubbel magnetism»”,

FOCUS MATERIEN 1975 s106sp2mn

LEC — Lambväxlingen · Elektronens g-faktor · Casimireffekten

BILDKÄLLA: Författarens arkiv · Bild1Excur9 · 2OKT2010 · Nikon D90 · Detalj

LEC

Lambväxlingen, Elektronens g-faktor, och Casimireffekten

Se även en enklare genomgång i KVALITATIVA FÖRKLARINGARNA

I och med att den moderna akademin (från 1927) utestängde ELEKTRONMASSANS KOMPONENTER och istället valde att uppfinna fysiken allteftersom istället för att härleda den, har man följaktligen också — allteftersom — tvingats uppfinna olika »virtuella attribut» för att få ihop det med den rent KVALITATIVA sidan av experimentalfysiken: naturen tycks innehålla flera »maskindetaljer» än vad modern akademi hade tänkt sig från början. Matematikdelen däremot (i princip) är redan given — i den mån sambanden stämmer (någotsånär) med observationerna. Följande genomgång belyser de främsta ämnena i jämförelsen TNED-MAC.

Lamb

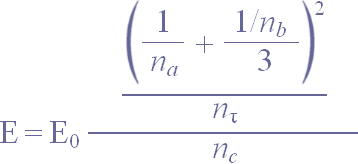
Lambväxlingen (eng. Lamb shift)

Även Lambskiftet, Lambövergången, Lambändringen, Lambvändningen, Lambomsvängningen, Lambkantringen, Lambbytet, etc.

Efter Willis Lamb och Robert Retherford 1947

MAC: ’vakuumfluktuationer’ (’vakuumets energi’ enligt QED) påtvingar elektronmassan en marginell extra svängningsenergi som inte ingår i matematiken för Vätets enkla spektrum; ”Thus, there exist small zero-point oscillations that cause the electron to execute rapid oscillatory motions”, ref. @INTERNET Wikipedia Lamb shift 2010-10-09. Experimentatorerna Lamb-Retherford [Schupp 1959, s1n] [Yung-Kyo Lim, 2000] uppdagade år 1947 att Väteatomens grundnivåer inte riktigt stämde energimässigt med Väteatomens enkla spektrum, mätningarna visade en marginellt högre frekvens med drygt 1000 MHz. Differensen har fått det engelska namnet Lamb shift. Fenomenet fick snart en teoretisk beskrivning (Bethe 1947, Schupp 1959 s2ö) genom (den senare) uppfinningen/benämningen av ett »vakuumets fluktuerande energi» och som markerar den egentliga ingången till kvantelektrodynamiken (eng. QED, Quantum electrodynamics). Wikipediaartikelns sambandsform (råformen, snarlik TNED-formen nedan) [@INTERNET Wikipedia Lamb shift, Derivation 2010-10-06] ger värdet 1024 MHz mot det uppmätta

[HYPERPHYSICS 2010-10-06 — Measurement of the Lamb Shift, http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/lamb.html]

1057 MHz för Väteatomens nivåskift 2s_1/2|2p_1/2 (överensstämmelsen är 96,88%).

Teori: växelverkan mellan elektronen och vakuum [ref. Wikpedia Lamb shift, ”interaction between the electron and the vacuum”]

Sambandsform: ΔE_Lamb = α⁵m_ec²([k(n,0)]/4n³) — Se LambWiki — men k(n,0) preciseras inte: artikeln ger istället en annan form (med delvis annat värde) enligt

Sambandsform: ‹ΔV› = (4/3)(e²/4πε₀)²(1/ħc)(ħ/mc)²(1/8πa₀³)ln(4ε₀ħc/e²)

kontroll visar att det fattas en faktor 2, med denna ges 1024 MHz, se Kalkylkortet Tabellflik 1

TNED: Kopplingen mellan atomkärnan och elektronmassan via Kraftekvationen F(BT)+F(eZ)=0 innefattar en marginellt extra strukturkomponent (via kärnstrukturen, se Atomkärnans härledning) mellan kärnan och det enskilda elektronelementet som inte ingår i matematiken för Vätets enkla spektrum. Kopplingen kärna-element alstrar en liten extra vibration av lägre frekvens

[i det markerade området 2 466 100 000 MHz] och som i TNED identifieras med »atomens maskinljud». Frekvensen kan bestämmas med kännedom om antalet enskilda elektronelement samt verkningsgraden i kraftverkan mellan kärnan-elementet (olika nuklider/maskiner uppvisar olika värden/»ljud» vid olika nivåer). TNED-värdet (råformen ₁H¹ n=2, l=1) ger 1086 MHz mot det uppmätta 1057 MHz för Väteatomens nivåskift 2s_1/2|2p_1/2 (överensstämmelsen är 97,33%), E=E₀[4/3]²/n³n, samma som nedan:

Teori: elektronmassans komponenter vibrerar marginellt som följd av varje komponents koppling till den spinnande kärnstrukturen enligt TNED

Sambandsform: E = α⁵m_ec₀²E₀/4n³e

Se mera utförligt i ABpEK.

Ele

Elektronens g-faktor

Även Elektronens gyromagnetiska förhållande (eng. Gyromagnetic ratio) — Väteatomens hyperfinstruktur

Från experimentella observationer omkring 1947-1948 [ref. Schupp 1959]

MAC: Någon direkt teori för denna detalj finns inte formulerad: Saken uppmärksammades genom experimentella mätningar i slutet på 1940-talet då man upptäckte differenser i elektronens magnetiska moment som inte kunde inpassas i den enklare spektralmatematiken, och fenomenet har sedan dess genomlöpt olika teoretiska beskrivningar enligt QED med benämningen Elektronens g-faktor, experimentellt uppmätt till 2,00231930… . Det finns dock en upphittad teoretisk sammanfattning enligt Shpenkov 2004 som hänför detaljerna enligt ’vakuumets polarisation, elektronmassans renormalisation och anomalt magnetiskt moment’.

Schupp [s2mö] (1959) beskriver fenomenet enligt ”the level splitting of the hyperfine structure of the ground state of hydrogen and deuterium for zero magnetic field”, sv., ’den hyperfina strukturnivådelningen i spektrum för grundtillståndet i Väteatomen (och Deuterium) vid yttre nollmagnetiskt fält’. Teoretiska sambandets matematiska form är inte enkelt uttryckbar (källa saknas ännu Okt2010). Delvis, enligt [Shupp 1956 från Sommerfields värde (1957)], ges (α=FSC motsvarar TNED-formen 1/n²)

g_e = 2(1 + α/2π – 0.328α²/π²) = 2(1.0011596) = 2,0023192 ..................... Sommerfields värde från 1957

CODATA-värdet [2006] är

CODATA 2010-10-05 [Source 2006 http://physics.nist.gov/cgi-bin/cuu/Value?gem]

g_e = 2,0023193043622(15)......................................................................... nuvarande internationellt antagna värde [CODATA]

Teori: experimentell observation från tiden 1947-1948 [ref. Schupp 1959]

Sambandsform: ingen generell (enkel) finns på webben (ännu Okt2010), ovanstående utgör första delarna

TNED: En del av elektronmassan (grovt 1/1000) befinner sig nära eller i (inuti) atomkärnan — på grund av den allmänna elektronströmningsfysiken i TNED [Kraftekvationen F(BT)+F(eZ)=0]. Sambandet garanterar enheten i kärna-elektron och vilken marginella del inte finns med i matematiken för Vätets enkla spektrum. (Idealt ligger hela e-massan utanför kärnan). [Alla (enelektron-) atomer uppvisar, därigenom, en marginellt lägre elektronmagnetisk kraft i jämförelse med mätningar på en enskilt infångad elektron]. Den enkla matematiken ger en ideal faktor 2 för elektronmassans totala magnetiska moment [Se Elektronringens magnetiska moment]. Tas den extra delen med som skyms av atomkärnan (beräknat efter Väteatomens parametrar) ges för den idealt isolerade elektronmassan ett marginellt större värde (2,00231930…) i överensstämmelse med uppmätta värden. Teoretiska sambandets grundform ger (med 9 korrekta decimaler mot det uppmätta värdet [CODATA 2006]), med n²=2h/e²R₀ och konstanterna enligt HOP-blocket

b = 2 + (πn² + ½ + 1/12)^–1 = 2(1,001159652) = 2,002319304

Med CODATA-konstanter genomgående och en vidare termutveckling ges den isolerade elektronens magnetfaktor

Värdet via Kalkylkortet ger motsvarande

b = 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22986]^–1)^–1

= 2,00231930436221

Teori: elektronmassans komponenter visar större magnetism utanför än i atomen — en mindre del passerar kontinuerligt genom kärnbrunnen som skyms/subtraheras

Sambandsform: b = 2 + 1/(πn² + ½ + 1/12) grundform — ingen slutgiltigt bestämd form är ännu (Okt2010) känd

Cas

Casimireffekten

Också uppmärksammad runt 1947-1948 — tätt närliggande materialytor »suger»

Efter Hendrik Casimir och Dirk Polder 1948

MAC: Det är återigen ’vakuumets energi’ som ansvarar för atomattraktion mellan två tätt närliggande (plana) materialytor. Sambandsformen för idealt plana parallella och elektriskt oladdade material anges konventionellt (från 1948)

[F/A] = ħcπ²/240d_z⁴ ........................ Casimir-sambandet i MAC, se exv. Wikipedia Casimir effect, Casimir’s calculation 2010-09-20

~ (1,3 t27)/d_z⁴ ........................ N/M²

Men teorin brottas med delvis stora svårigheter, och delvis, i vissa partier, relativt stora avvikelser mot uppmätta värden (upp mot drygt 15% fel). Något direkt jämförande konkret exempel mot TNED kan inte ges eftersom MAC-formen inte specificerar något material. ATT materialegenskaper har betydelse, är redan känt, men ingen övergripande beskrivning är ännu känd i ämnet i denna presentations referens (Okt2010). Wikipediaartikeln omnämner/exemplifierar ’ungefär 1 atmosfär’ (101 325 Pa) för avståndet ca 10 nM.

Teori: vakuumets nollenergi över små näravstånd skapar en attraherande kraft mellan närliggande materialytor [ref. Wikipedia Casimir effect]

Sambandsform: F/A = ħcπ²/240d_z⁴

TNED: Elektronmassans komponenter övergår delvis i och antar varandras atombindningar från ett visst minsta avstånd (förstadiet till materiell sammanfogning) vilket bildar en naturligt ömsesidig Coulombisk attraktion som kan härledas på vanligt sätt ur elektriska kraftlagen med kännedom om antalet element i elektronmassan, materialets täthet, samt övriga faktorer (termo-elektro-optiska) som berör det aktuella materialet. Sambandets grundform är (a-värdet [utanför detta spelar andra närliggande material allt större roll] nominellt 50-100 µM)

F/A = ke²Z[(d_xy+d)²(d_xy+[d+1]^d/a–1)²]^–1n^–1

För två idealt plana Järnplattor (26Fe56) vid rumstemperatur (20°C) med a=50µM ges F/A=1atm (101 325 Pa) för avståndet 8,94 nM, ekvivalenta värdet med MAC-formen ges vid 12,21 nM (~54 325 Pa), även vid avståndet 1000 nM (0,001 Pa), största avvikelsen visas i »kurvkölen» i intervallet 12,5-37,5 nM, störst vid ca 20 nM (38%), sedan allt mindre differens.

Teori: elektronmassans komponenter tränger in i varandras atomära materialdomäner (förstadiet till materiell sammansmältning) vid korta näravstånd

Sambandsform: F/A = ke²Z[(d_xy+d)²(d_xy+[d+1]^d/a–1)²]^–1n^–1

Se utförligt från CASIMIR| inledning.

Lambväxlingen — Lambskiftet

Lambväxlingen, Lambskiftet

Efter Willis Lamb och Robert Retherford 1947, se Schupp 1959 — Upptäckten av Väteatomens spektralt hyperfina struktur, ca en del på drygt 2 miljoner

Lambväxlingen

I MAC ’vakuumets vibrationer’ — i TNED ’atomkärnans spinnbrum på elektronmassans komponenter’ — i princip samma matematik [med smärre skillnader]

Lambväxlingen i Kort översikt.

Lambväxlingen i Mera komprimerad Jämförande översikt.

Lambväxlingen i TNED, Inledande härledning.

Lambväxlingen i TNED, Huvudrubrikens artikel.

AB PEK inledning

LAMBVÄXLINGEN

INLEDNING till ABPEK — Atomkärnans Brum På Elektronmassans Komponenter

KÄRNSTRUKTURSPINNET — »maskinbrummet» — PÅ ELEKTRONMASSANS KOMPONENTER [konv. eng. Lamb shift, sv., här Lambväxlingen]

I det normala — enkla, elementära — Väteatomens Spektrum gäller sambandsformen för energin i elektronhöljet till varje värde på huvudkvanttalet n = 1, 2, 3, … n enligt

E = E₀/n²

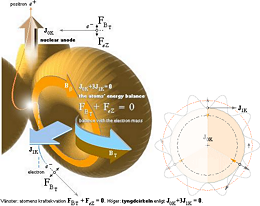
Grundnivån i Väteatomens energispektrum betyder noll (0) exitationsenergi [Erinra att atomen i TNED summerar nollmoment, nollkraft och nollspinn (s₁=s₂; 0=s₂–s₁) enligt de bägge centrala kraft- och impulsekvationerna resp.

F(BT)+F(eZ)=0 och J(0K)+3J(1K)=0]. I omvändning betyder den grundnivån lika med den potentiella energi som krävs för att Väteatomen ska släppa ifrån sig sin elektron [Se Väteatomens jonisationsenergi]. I fallet Väte är den energin ca 13,6 eV. De potentiella grundenergierna via sambandet ovan blir i succession för n-värdena

E(eV) 13,6 3,4 1,5 0,9 0,5 …

n 1 2 3 4 5 …

I den delen ingår inga aspekter på bidraget från elektronmassans komponenter — vilket är att förvänta enligt TNED på grund av deras extra rörlighet och som redan omnämnts i genomgången av KVANTTALEN, speciellt för kvanttalet Φ(τ): det ingår som sådant inte i MAC, enbart dess (trängre) aspekt i formen av det konventionellt benämnda s.k. elektronens magnetiska (banimpuls-) moment [vanligen m(l)]. Se utförligt enligt TNED i Elektronringens toppspinn.

[Konventionellt associeras m(l) med olika orienteringar — och därmed vektoriella projektioner — hos »elektronens impulsmomentsvektor». I TNED finns ingen motsvarighet till den modellföreställningen eftersom elektronen i TNED inte är EN partikel och l=q-talen därför handlar om övergångar mellan olika energinivåer som bildar olika »tonskurar» (resonanser, vågmönster) och som därför inte kan avsättas på någon enskild mekanisk kropp, endast ett system av (många) sådana kroppar. Vektoranalogin för m(l) i TNED kan därför bara vara analog med ett motsvarande mätinstruments totala mätutslag (magnituder och moduler i impulsmoment) för en viss massmängd som genomgår en viss process].

LambTNED

Snabbgenomgång. Kärnaggregatets minsta övergripande maskindetalj utgörs av en av de tre toroidunderfraktalerna — enligt TNED genom sambandet för Atomens impulsekvation [J(0K)+3(J1K)=0] som definierar balansräkningen i atomens övergripande impulsmoment. Den kärnstrukturen påverkar alla elektronelement [n] via kärnspinnet (h=mcr). Tar man med denna (första underfraktala) strukturpåverkan, kan den normalt enkla spektrummatematiken som verkar på enheten 1 enligt

E = E₀/n²

modifieras (eg. generaliseras) enligt

E = E₀[1 + 1//3]²/n³n

från

E = E₀/n²

= E₀(1/n²)

= E₀([1 + 0]/n²)

= E₀([1 + 0]/n²)/1

= E₀(1/n² + 0/n²)/1

= E₀(1/n_a + 0/n_b)²/n_cn

= E₀(1/n_a + 1/n_b)²/n_cn — om n_b→∞

= E₀(1/n_a + 1/3n_b)²/n_cn

;

= E₀[(1/n_a + 1/3n_b)]²/n_cn ;

= E₀[(1/n_a + K/3n_b)]²/n_cn ; faktorn K behandlas senare; [Se Avståndskompensationen]

;

Maskindetaljens struktur i TNED avsätts på/följer atomens huvudkvanttal [n(b)=n] genom att fördelas över detta [n(c)=n]. Dvs.,

n_a = n_b = n_c = n

som ger

TNED-Lamb

E = E₀[(1/n + 1/3n)]²/nn ....................... se från Sanbbgenomgången ovan

= E₀[1 + 1/3]²/n³n

= E₀[4/3]²/n³n

E₀ = k_e·e²/2ρ ................................ Väteatomens grundtillstånd, se Spektrum

= (1/4πε₀)e²/2ρ

= 2,179 t18 J ; ........ med konstanterna i HOP-blocket. se beräkningarna i Kalkylkortet Tabellflik 1

E₀/e = 13,601556278 eV ;

E₀/h = 3,2887174 T15 Hz ;

= 3,2887174 T9 MHz ;

r = h²[(2πe)²mk]^–1 .................... konv. Väteatomens grundradie, ~ 5,29 t11 M ;

n = 673 026 ............................. antalet komponenter i elektronmassan ;

——————————————————————————————

n E(MHz) uppmätt träffprocent [mera utförligt i Lambväxlingen]

—— ————— ———— ———————————————

1 8687,0473 8172 94

2 1085,8809 1057 97

3 321,74429 ? >97

4 135,73511 ? >(>97)

I annat fall [n(c)=1] föreligger endast Väteatomens rena enkla spektrum via n_a = n, n_b→∞, n_c = n = 1 som ger

E = E₀/n²

;

Väteatomens rena enkla spektrum: Kärnstrukturen i [(n_a^–1 + [3n_b]^–1)]²/n_cn bortses ifrån: n(b) följer atomkärnans fraktalsystem i PASTOM enligt n(b)→∞ vilket reducerar kärnstrukturbidraget till 0 via 1/∞; [3n_b]^–1 övergår i noll. Därmed utverkar också atomkärnan samma — identiska — fysik på samtliga elektronmassans komponenter [n=1], vilket medför att effekten avspeglas enhetligt på hela elektronmassan, utan hänsyn till inre komponenter; Kärnstrukturens inre elektronfördelning över n(c)=n parkeras på n=1 så att endast elektronmassans rena resonanser framträder utan strukturkomponenternas (kärnspinntoroidernas) bidrag.

Ett och samma grundsamband kan alltså användas för att beskriva bägge förekomsterna, med tillhörande inre kärndynamiska villkor, enligt

E = E₀[(n_a^–1 + [3n_b]^–1)]²/n_cn ........................... allmänna sambandsformen för Väteatomens huvudkvanttalsspektrum (q=0)

Med den teoretiska grundvalen, och med hänsyn till ytterligare faktorer som påverkan dynamiken (och som kommer att genomgås löpande), är det tydligt att ovanstående råform för antalet element i elektronmassan (n=673 026) beskriver det uppmätta ’atombrummet’ med god följsamhet. n-talets algebra ingår redan i MAC — men är inte känd på elektronmassans komponenter i TNED. Se utförligt i Härledningen till n.

Genom inverkan från Elektronens g-faktor ges totalt en mera avancerad beskrivning (»det sanna värdet» varierar beroende på avståndet [eg. graden av excitation, analogt elektronens grad av frikoppling från atomkärnan] mellan elektronelement och kärna).

Avståndskompensation eG

2010X10

LAMBVÄXLINGEN

Avståndskompensation — eG-faktorn

Faktorn som approximerar elektronens atombundna g-faktor och dess allmänna influens på (Väte-) atomens (enkla) energifysik

2010-10-11:

För Väteatomens huvudkvanttal endast

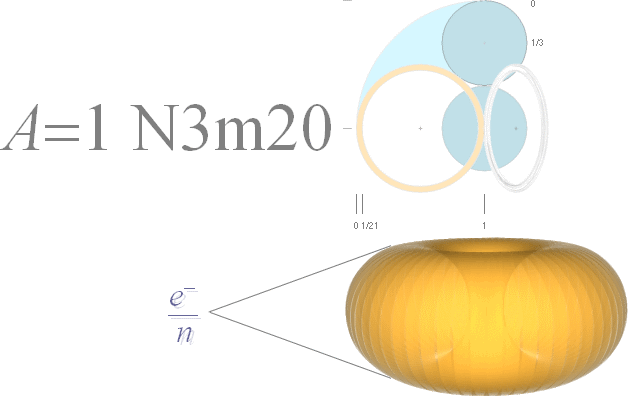
Genom elektronelementets (e/n) närmaste avstånd till atomkärnan (bilden ovan), avskärmas också största delen av kärnan i elektronelementets »synfält» från direkt Coulombisk åtkomst i den idealt linjära attraktionsvägen (största kraften över kortaste avståndet på minsta tiden). Först på stort avstånd från kärnan kan elementet »se» den maximalt största delen av kärnans elektriska attraktionsfält med referens till hur elementet kopplar resonanser med kortaste (snabbaste) ljusvägen via kärnladdningens idealt statiska elektriska fält på dess egengravitella lokala referens (se även Superpositionsprincpen).

Nettoverkan blir att Coulombiska verkningsgraden mellan elektronelement och moderkärnan ökar mot ideala 1 (från ett lägsta värde ca 0,88 i Väteatomens fall [vidare nedan]) med växande avstånd — inkluderat samtliga effektbidrag (temperatur, resonansskärmning, Elektronens g-faktor).

Genom att utnyttja experimentella observationsvärden, kan man söka olika teoretiska prövningar som (i detta fall visar sig) kan tangera de experimentellt uppmätta värdena.

Variationsfaktorn innebär tydligen en »modulerbar tolerans» i snart sagt alla möjliga PRESICIONSBESTÄMNINGAR — som mer eller mindre OMÖJLIGGÖR någon exakt värdebestämning i generell mening. Exakt HUR den detaljen ska tolkas [generellt], eller ens hanteras [generellt] finns här ingen som helst vidare framställning på utöver den här antydda aspekten.

[ALLA PRESICIONSTEORIER SOM BASERAS PÅ EXPERIMENT innehåller olika KORREKTIONSBLOCK — som mer av regel än undantag INTE erkänns generellt av samtliga forskare: det finns (alltid, smärre) olika tolkningar, olika korrektioner — större eller mindre].

Exempelutveckling

EXEMPELUTVECKLING

Betrakta (från ursprungliga sambanden via Lambväxlingen)

E = E₀[1 + (1–a)/3]²/n³n

med

a = b/n^c

och

b = 0,1201893

c = 0,1209440

;

Avståndsformen,

Lambväxlingen i TNED

E = E₀[1 + (1– b/n^c)/3]²/n³n

= E₀[1 + 1/3 – b/3n^c]²/n³n

= E₀[1 + 1/3 – (0,1201893)/3n^0,1209440]²/n³n

Reduktionsfaktorn [a] får löpa på huvudkvanttalets ändring tillsammans med en reciprok exponentiell korrektion [c] som verkställer att n-variationen växer långsamt från nära 1 och mot 1. Dvs., i stort samma som EN (starkt) REDUCERAD SPEGLING av n-variationerna, och som subtraheras avtagande mot 0 med växande n.

c-koefficienten summerar alla möjliga (medelmässiga) bidrag (inbördes skärmning, Coulombeffektivitet [resonansmönster], temperatur).

Lambväxlingseffekten — Väteatomen, l=0: se beräkningar i Kalkylkortet

n MHz med a utan a uppmätt

—— ————— ———— —————————————

1 8172,837 8687 8172,837 [Shpenkov 2007, s5m]

2 1057,844 1086 1057,844 [Shpenkov 2007, s5m], Lamb-Retherford 1947

3 316,642 322 (—)

4 134,213 136 (131,675) [Weitz et al., 1995]teoretiska

…

EXEMPLET visar — i varje fall med enstaka värden längst ner — att det GÅR att hofta GODTYCKLIGT med lämpligt valda funktionsvariabler för att tangera experimentella mätvärden.

I Exemplet ovan har funktionen y=(1– b/x^c) innebörden av en linje som från ett minsta värde (1–b, x=1) närmar sig 1 då x växer obegränsat.

Motsvarigheten i kärnfallet enligt TNED skulle vara att elektronelementets koppling till HELA kärndelen (1/3) växer (från lägst 0,88 vid max näravstånd) med växande avstånd (till störst 1), analogt med att elektronelementet SER alltmer av HELA kärnans Coulombfält.

JÄMFÖR (nämligen) med de matematiska utvecklingskoncepten i MAC — i princip alla liknande typer:

WIKIPEDIA

1. Det matematiska utvecklingskonceptet för Lambväxlingen från den etablerade forskarvärlden via Wikipedia,

med slutresultat i (exemplifierat för Väteatomens n=1, l=0) från originalledet i LambWiki

‹ΔV› = (1/3)h(32[π²ε₀m]²c³a₀³)^–1e⁴ln(4ε₀ħc/e²) .......... a₀ anger Bohrradien (5,29 t11 M)

som ger värdet 1024,23 MHz med internationella CODATA-konstanter, och som kräver ytterligare tillägg, se Telfer 1996 (källorna varierar något beroende på epok och metod) för att få det experimentellt uppmätta 1057 MHz från Lamb-Retherford 1947 (ref. Shpenkov 2007, s5n) — Eller enklare i samma wikiartikel med sambandet

ΔE_Lamb = α⁵m_ec²([k(n,0)]/4n³)

”for l = 0 with k(n,0) around 13 varying slightly with n”,

@INTERNET Wikipedia Lamb shift 2010-09-09

http://en.wikipedia.org/wiki/Lamb_shift

Sambandsformen är (med [k(n,0)]=E₀/e ~ 13,6 eV) samma som figurerar i beräkningen av n i TNED, =

(4/3)²[α^–5·e/m_ec₀²]/4.

Typformen med r + Δr är också principekvivalent med r ersatt av resonansvillkoret n² [Se Resonansvillkoret i Spektrum] eftersom (Vätets enkla spektrum) likheten ρn²=d gäller med ρ=Bohrradien (5,29 t11 M). Dvs., motsvarande ρn² + Δρn² = ρ(n² + Δn²).

SHPENKOV

2. Det matematiska utvecklingskonceptet för Lambväxlingen från Shpenkov 2007, s4.ekv.15, här förenklat för att visa det väsentliga (Shpenkovs lösning innefattar vissa lösningar av vissa vågfuktioner [konv. Bessel-funktioner], termerna ab)

λ^–1 = R^–1[n^–2 – (n + a – b)^–2]

med termerna ab sammansatta och n=(1, 2). Den andra, inre kvadratfaktorn i Shpenkovs samband ovan ansluter — här enbart i framställning för att belysa de snarliga sambandsformerna — i princip till Exemplets [1 + (1– b/n^c)/3]². Shpenkovs resultatvärden (Shpenkov 2007 s5 Table 3) är också (nära) desamma,

Väteatomen l=0 — Lambväxlingseffekten MHz

n Shpenkov uppmätt

1 8172,85200 8172,837

2 1057,84466 1057,8446

Shpenkov ger inga ytterligare.

Bägge utvecklingskoncepten ovan i 1(Wikipedia) och 2(Shpenkov) använder tydligen principen med utvecklingar baserade på

ρ(n² + Δn²) — och som därmed också ansluter till det här beskrivna Exemplet i TNED.

I ALLA TRE FALLEN — Wikipediaexemplet, Shpenkovanalogin och TNED — utför Väteatomens elektronmassa extra svängningsrörelser motsvarande den extra energin:

I Wikipediaexemplet, som markerar den etablerade forskarvärldens uppfattning (MAC), anses fenomenet bero av ’vakuumfluktuationer’ (som också anses vara orsaken till Elektronens g-faktor) tillsammans med ’vakuumets polarisation’ som påtvingar elektronmassan extra svängningsenergi. Se bidragstabellen i Telfer 1996.

I Shpenkovanalogin (Se Shpenkov 2007 s2ö men som inte betraktas riktigt »rumsren» i MAC) förklaras fenomenet av ’inter-atomära vibrationer’ med grund i en allmän, originell, universalpartikelmodell som är så abstrakt att man undrar hur författaren själv står ut, se Shpenkovs teorier — samt på en synbarligen väl underbyggd matematisk beräkningsgrund för vågfunktioner som (i varje fall i ett första påseende) förefaller vara ett mellanting mellan MAC och TNED.

I TNEDexemplet [‡] framträder fenomenet genom att elektronmassan ser kärnan via N3m20-aggregates struktur, en av de tre toroidarmarna [faktorn (1+1/3)]. Kärnspinnets koppling på den enskilda elektronkomponenten bildar en liten extra variation (som papperslappen mot ekrarna i cykelhjulet, atomens »maskinbrum»).

Jämför Wikipediaartikelns beskrivning:

”The fluctuation in the electric and magnetic fields associated with the vacuum perturbs the Coulomb potential due to the atomic nucleus. This perturbation causes a fluctuation in the position of the electron, which explains the energy shift.”,

@INTERNET Wikipedia Lamb shift 2010-09-09

http://en.wikipedia.org/wiki/Lamb_shift

Min översättning:

Fluktuationen i elektriska och magnetiska fält associerade med vakuum stör Coulombpotentialen från atomkärnan. Denna störning förorsakar en fluktuation i elektronens position, vilket förklarar energiändringen.

Det är — med följande minimala korrektion — EXAKT som klippt och skuret för TNED:

Fluktuationen i elektriska och magnetiska fält associerade med STRUKTUREN I ATOMKÄRNANS SPINN stör den normalt idealt sfäriska Coulombpotentialen från atomkärnan. Denna störning förorsakar en fluktuation i elektronens position, vilket förklarar den lilla extra växeln i energiändringen.

Notera för TNED:s del att kärnstrukturens alla möjliga formnyanser redan ingår i den enkla kraftekvationen.

Beskrivningen kan inte bli mera exakt förklarande [Vilket därmed också, tydligen, innefattar Shpenkovs ’inter-atomära vibrationer’].

MAC+Shpenkov+TNED

Med ytterligare en liten verkningsfaktor a i TNED-fallet enligt [1 + (1–a)/3]

— a-faktorn (=b/n^c) antar ett högsta värde (~0,12) och går sedan mot 0 då atomens excitation ökar (vilket innefattar inverkan av Elektronens g-faktor)

— ges tydligen en funktionsteknisk samstämmighet med stöd av experimentellt uppmätta värden för Väteatomens n=1, 2; l=0. Därmed, kan man säga (och så långt), innefattas samtliga fall i TNED: Se utförligt från Exempelutvecklingen.

SUMMERING

Avståndsformen (0,1201893)/n^0,1209440 i E = E₀[1 + 1/3 – (0,1201893)/3n^0,1209440]²/n³n som beskriver Lambväxlingen kvantitativt enligt Exempelutvecklingen är tydligen OK (För Väteatomens n=1&2 [med ev. vidare], l=0), vilket i varje fall till viss del belyser analogin i Lambväxlingens komplex. Som det ser ut av resultatet, är det (därmed) också tydligt att n-faktorn är välrelaterad: antalet komponenter i elektronmassan (nom. 673 026).

Nedan följer en vidare genomgång med bakgrund till ovanstående, samt jämförande korsreferenser med resultat i MAC.

Se även särskilt i härledningen till n-talet i mera precis algebra.

AB PEK, se även inledningen

Lambväxlingen

2010IX26

TEORI — E = E₀[(1/n_a + 1/3n_b)]²/n_cn_τ

———————————————————————————————————————————

ATOMKÄRNANS BRUM — »maskinsurret» — PÅ ELEKTRONMASSANS KOMPONENTER [konv. eng. Lamb shift, sv., här Lambväxlingen]

sambandsgrunden nedan från INLEDNINGEN

E = E₀[4/3]²/n³n .................................. för Väteatomens energier via huvudkvanttalet n

Se även E i Snabbgenomgång (kortform för nedanstående)

n = [(2h/e²R₀)⁵e/m_ec_z²](4/3)²

= [(1/α)⁵e/m_ec_z²](4/3)² ;

E = α⁵m_ec_z²E₀/en³ ; c_z = c₀/2 ;

= α⁵m_ec₀²E₀/4en³

E0/e ger energin direkt i eV; Med ytterligare division med h ges E=hf i f(Hz).

Väteatomens grundtillstånd (n=1) för väteatomens elektronmassa motsvarar en potentiell energi på 13,6 eV [atomen kräver den energin i utbyte mot att lämna ifrån sig elektronen; Se utförligt i Väteatomens spektrum] eller i våglängdsfrekvens (f )

f = (13,6 eV)(e=1,602 t19 C)/(h=60626 t34 JS) = [E=U(Q=e)]/h

= 3,28813 T15 Hz

= 3 288 130 000 000 000 Hz

Den färgmarkerade delen motsvarar det lägre frekvensintervall där man återfinner atomens motsvarande »maskinljud» (eg. maskinljus eftersom vågformen är elektromagnetisk), alltså i storleksordningen GHz eller tusental MHz. Området motsvarar alltså »själva maskinljudet» och som normalt sett inte ingår i den enkla räkningen för Väteatomens spektrum — kärnstrukturen, inkl. elektronmassans komponenter, framgår explicit inte i den enklare spektrummatematiken. Jämför Bohranalogin.

Genom jämförande utvecklingar i TNED/MAC har följande ordning visat sig (till prövning) [ENKLASTE utan inre kombinatorik] och som, tydligen, kan förklara det observerade fenomenet (från 1947 efter experimentalisterna Lamb-Retherford) — atomens maskinbrum. I MAC anser man att orsaken till fenomenet ligger i ’vakuumfluktuationer’. Som vi senare ska se är även i detta fall matematiken densamma; i MAC-fallet talar man om orsaken som ’vakuumfluktuationer’, i TNED-fallet är orsaken växelspelet mellan atomkärnan och elektronen med avseende på den inneboende strukturen — och ur vilken elektronmassans antal element kan härledas.

Genomgång

Vi studerar först grundsambandet som ovan,

E = E₀[(n_a^–1 + [3n_b]^–1)]²/n_cn_τ

som är en mera avancerad version av Vätets enkla (elementära) spektrum enligt [Se Energiformen i Spektrum]

E = E₀/n²

Beskrivningen nedan förklarar hur de olika parametrarna används och fungerar.

Väteatomen, q=0=l [betyder att sambanden endast gäller rena resonansnivåer i huvudkvanttalet n]:

; som ovan

Allmänna formen

Allmänna formen:

E = E₀[(n_a^–1 + [3n_b]^–1)]²/n_cn_τ ; E₀ = ke²/2ρ, /e ~ 13,6 eV, se Energiformen i Spektrum

»Väteatomens maskinljud» — konv. Lambskiftet eller Lambövergången (eng. Lamb shift):

n_a=n_b=n_c=n, n_τ=n antalet komponenter i elektronmassan (grovvärdet 4×177068 = 708 248 = n) ger »Väteatomens maskinljud»

E = E₀[4/3]²/n³n ;

Kärnstrukturen påverkar alla elektronelement [n(τ)=n] via kärnaggregatets minsta maskindetalj — en av de tre toroidunderfraktalerna i Atomens impulsekvation [J(0K)+3(J1K)=0] i TNED som definierar balansräkningen i atomens övergripande impulsmoment;

E(0) = 13,6 eV; E= (13,6 eV)(e/h)(t6)(16/9)/nn³ = (13,6 MeV)(4,29821 T8 C/JS)/nn³ = (5,84557 T9 MHz)/nn³ ;

(5,84557 T9 MHz)/(n = 708 248) = 8253,5575 MHz ; E1 = (8254 MHz)/n³ ; (e/h)(16/9)/n = 6,0688051 T8 C/JS=1/VS=Hz/V

(5,84557 T9 MHz)/(n = 691 292) = 8456,0006 MHz ; E2 = (8456 MHz)/n³ ; (e/h)(16/9)/n = 6,2176607 T8 C/JS=1/VS=Hz/V

(5,84557 T9 MHz)/(n = 673 026) = 8685,5039 MHz ; E3 = (8686 MHz)/n³ ; (e/h)(16/9)/n = 6,3864087 T8 C/JS=1/VS=Hz/V

n E1(MHz) E2(MHz) E3(MHz) Lambövergången för Vätespektrumets grundnivåer

———— ————————— ————————— ———————

1 8253 8456 8686

2 1032 1057 1086

3 306 313 322

4 129 132 136

… ................................................................

1057 efter Lamb-Retherford 1947

Maskindetaljens struktur avsätts på/följer atomens huvudkvanttal [n(b)=n] genom att fördelas över detta [n(c)=n], i annat fall [n(c)=1] föreligger endast Väteatomens rena enkla spektrum:

Väteatomens ordinära enkla spektrum:

n_a=n, n_b→∞, n_c=n_τ=1, Väteatomens rena ideala enkla spektrum, potentiella energin (störst närmast kärnan)

E = E₀/n² ; [3n_b→∞]^–1 övergår i 0 ;

Kärnstrukturen bortses ifrån: n(b) följer atomkärnans fraktalsystem i PASTOM enligt n(b)→∞ vilket reducerar kärnstrukturbidraget till 0 via 1/∞; Atomkärnan utverkar samma — identiska — fysik på samtliga elektronmassans komponenter [n(τ)=1] så att effekten avspeglas enhetligt på hela elektronmassan utan hänsyn till inre komponenter; Kärnstrukturens inre elektronfördelning över n(c)=n parkeras på n=1 så att endast elektronmassans rena resonanser framträder utan strukturkomponenternas (kärnspinntoroidernas) bidrag.

För atomer med flera elektronmassor tillkommer (här veterligt) vissa skärmningseffekter inbördes mellan elektronelementen, vilket gör bilden mera komplicerad. Ingen motsvarande sambandsform för dessa fall finns ännu formulerad sett från TNED.

EditRef., Sep2010.

ELEKTRONENS G-FAKTOR

BILDKÄLLA: Författarens arkiv · Bild7 RF2010/2· 5JUN2010 · Nikon D90 · Detalj

eG

2010X2

Elektronens gyromagnetiska faktor — b=2,00231930…

HÄRLEDNINGEN enligt TNED

Se även kortare sammansällning i Kvalitativa förklaringarna och LEC

— Kan elektronens gyromagnetiska faktorsamband härledas i TNED — med grund i fraktalsystemet från PASTOM och dess kraftväv av impulsringar enligt atomkärnans härledning — inkluderat acceptabel ekvivalens med experimentellt uppmätta värden?

— Vi gör ett försök:

n² = 2h/e²R₀

= 137,0580237 ; från cellresultaten i Kalkylkortet — avrundning från max 14 decimaler

a = 2πn² ;

= 861,1609609811 ;

b = 2(1+1/[a + 1 + 1/6])

= 2,0023193041 ; 2,00231930409728 .............. med 14 decimaler från Kalkylkortet

= 2 + 2/[a + 1 + 1/6] ; se nedan i Sammansättningen i m(e)/n

1

= 2(1 + ——————)

a + 1 + 1/6

1

= 2 + ———————;

πn² + ½ + 1/12

.................................... 2:an tillhör ordinarie enkelspektrum från hela m(e), inre kvoten tillhör elektronelementet, se Sammansättningen i m(e)/n.

Se även i Jämförande Resultatvärden.

c = 2/[a + 1 + 1/6] ;

b = 2 + c ;

d = 1/[a + 1 + 1/6] ;

c = 2d ;

1/d = [a + 1 + 1/6] ;

= e

= 862,3276276477 ;

;

_n→∞limes _n=1→n ∑ (e+1)^–n = (e)^–1 = d = (e+1)^–1 + (e+1)^–2 + (e+1)^–3 + …+ (e+1)^–n

; Se Reciproka Geometriska Serien — enklaste modellen för ett oändligt fraktalsystem: successiva halveringar.

e = a + 1 + 1/6

= 2πn² + 1 + 1/6

= 2(πn² + 1/2 + 1/12)

b = 2 + 1/e

= 2 + _n→∞limes _n=1→n ∑ (e+1)^–n

= 2 + _n→∞limes _n=1→n ∑ (2(πn² + 1/2 + 1/12) + 1)^–n

= 2,00231930409728 .............. med 14 decimaler från Kalkylkortet

;

Alla 1/d i fraktalbyggnaden för magnetiska momentets bidrag i TNED — 1 för hela elektronmassan och det extra 1/e för elektronmassans ringkomponent (med betydelsen av e-termen som ovan) —

1

= 2(1 + ——————)

a + 1 + 1/6

1

= 2(1 + ——————)

e

enligt (reciproka geometriska serien)

1 1 1 1

(——————)¹ + (——————)² + (——————)³ + …+ (——————)ⁿ

a + 1 + 1/6 a + 1 + 1/6 a + 1 + 1/6 a + 1 + 1/6

motsvarar — tydligen — ekvivalenten för (en aritmetiskt förenklad version av) ringfraktalsystemets obegränsade utsträckning, varje högre n-värde fördjupar och förfinar vågmönstret, utan att det finns något slut på finstrukturen [Jämför grundformen i PASTOM].

Summan blir som ovan, lika med d=1/862,3276276477 — och därmed totalt b=2,0023193041 i stället för det enkla rena 2 som gäller utan särskild hänsyn till elektronmassans ringelement (1/d).

Sammansättningen i m(e)/n

Sammansättningen i elektronelementet [m(e)/n]

Elektronens g-faktor — mera utförligt i eG utförligt

Sammansättningen [πn² + ½ + 1/12] i b

1

b = 2 + ———————;

πn² + ½ + 1/12

identifierar vi i TNED (på liknande sätt som gjordes i Lambövergången) enligt

2 ............................. ordinarie bidraget genom Spektrums elementära grundmatematik, se utförligt i Elektronringens spinn och Elektronringens magnetiska moment

övriga ...................... bidraget från varje enskild impulsmomentsring i elektronmassan enligt TNED:

;

πn² ......................... resonansvillkorets (n²) tvärsnittsyta för elektronringens magnetiska moment, se även Magnetiskt Moment

½ ........................... elektronringens strömspinn, se Elektronringens spinn ; τ-ringen definieras så i Kvanttalen

1/12 ....................... neutronkvadratens fasta formbas (1/12 av Kolatomen, se Atomära massenheten)
Även samma som »byggfaktorn» för kopplingen mellan masstalsradien (A=60) för hela neutronkvadraten och dess skala för atomära massdefekten (18), se även figuren i s-formens fysiska ekvivalent.

Alla termerna [πn² + ½ + 1/12] beskriver — uppenbarligen — komponenter till elektronmassans resonansmönster. Speciellt — enligt TNED — cirkulära snittytan πn² [samma som magnetiska momentet dividerat med strömstyrkan (i)] får via resonansvillkoret n²=2h/e²R₀ formen för neutrontyngdcirkelns omkrets 2πh/e²R₀ = mc·2πr/e²R₀ och därmed motsvarande vågimpulsmoment som ansluter till resonanserna i Keplermomentet — GRUNDÄMNENAS PERIODISKA SYSTEM.

— Vi minns från KVANTTALEN i TNED att elektronringens magnetiska moment härleddes på elektronringens spinn (s=1/2) genom »pτ-svepet» från atomkärnan — ett spinnvarv runt motsvarande Plancks konstant h. För hela strömspinnet i τ-ringen fann vi att ett motsvarande 2h följaktligen tvunget gäller för elektronringens magnetiska spinnmoment och med avseende på hela elektronmassans koppling till atomkärnan. Därav »2:an» ovan som gäller för hela elektronen, medan 1/d-kvoten gäller för τ-ringens del.

Jämförelser i resultat

Värdeformen — med jämförande precision

b = 2,0023193041

mera exakt via Kalkylkortet

= 2,00231930409728 = 2(1,00115965204864)

är känslig på grundvärdena i de fysikaliska konstanterna, värdet ovan (bl.a.) med elektriska konstanten

ε₀ = 8,8543 t12 C/VM från FOCUS MATERIEN 1975 s666

;

Jämför känsligheten:

Med Webbvärdet ε₀=8,85418782 t12 C/VM (direkt på Google via ”electric constant”) ges (utan vidare)

b = 2,0023193354

Generellt i Universums Historia används konsekvent fysikaliska konstanter från senare delen av 1900-talet, de finns redovisade under HOP-blocket [HANDBOOK OF PHYSICS, McGraw-Hill 1967].

Jämför precisionsvärdet på @INTERNET Wikipedia Gyromagnetic ratio, Gyromagnetic ratio for an isolated electron 2010-10-02

som anger det experimentellt uppmätta värdet (med långt flera decimaler än som normalt används i den här framställningen)

g_e = 2,0023193043617(15) = 2(1,00115965218085)

baserat på NIST/CODATA’s internationella standard, se webbkälla nedan — som bygger på åter andra konstanter.

— I varje fall för UNIVERSUMS HISTORIA: Om värdena, som ovan, överensstämmer in till nionde decimalen (som för sämsta fallet betyder ett max fel på 1 miljarddel) är saken alldeles definitivt avgjord. Det finns (då, veterligt) ingenting av princip att diskutera i saken. [Tveksamheterna ligger snarare i decimal nummer två (GROVREFERENS: 85% träff [0,15% fel] är hyfsat som en första approximation [men vi ser helst en skärpning på den punkten, runt 98% träff är bra resultat], 50% [50% fel] mera tveksamt om det gäller verifikation; 99,9999999% träff är excellent)].

— Med CODATA-konstanterna i tabell från 2004 som »MAC-värde» för b till jämförelse

(Tabellref. [http://pdg.lbl.gov/2004/reviews/consrpp.pdf])

via (FSC betecknas ofta i MAC med alfa-tecknet, α)

FSC = 7,297 352 568(24) 10⁻³

blir motsvarande b-värde via MAC

b = 2,0023196764 = 2(1,0011598382) .........................

att jämföra med TNED som ovan

b = 2,0023193043 = 2(1,00115965204864) = 2(1+1/[a + 1 + 1/6]), a=2πn²=2π·2h/e²R₀

Se även en annan källa (GoogleSökning 4Okt2010 visar totalt 163 träffar med samma siffror ”1.001159652”)

b = MAC = 2(1,001159652188 (4))

Chalmers BESTÄMNING AV FUNDAMENTALKONSTANTER Finstrukturkonstanten — Ingvar Lindgren (2002),

http://fy.chalmers.se/~f3ail/Letters/FysikAkt.pdf

s2mö:

”Det mest slående exemplet är den fria elektronens magnetiska moment (g-faktor), som påverkar energin i ett pålagt magnetiskt fält genom Zeemaneffekten. De noggrannaste mätningarna av denna effekt har utförts av Dehmelt och hans medarbetare vid Washington-univetsitetet i Seattle genom att studera en enstaka elektron fångad i en jonfälla. Dehmelt belönandes för dessa arbeten med (del

av) 1989 års Nobelpris. Elektronens g-faktor har bestämts till g_e = 2 × 1.001 159 652 188 (4), dvs med en relativ noggrannhet av 4×10^–12, vilket utgör den noggrannaste mätning som överhuvud taget har utförts.”.

Antydd serieform

VI KAN STUDERA den approximerade sambandsformen till jämförelse som visas på

@INTERNET Wikipedia Gyromagnetic ratio, Gyromagnetic ratio for an isolated electron 2010-10-02

g_e = 2(1 + FSC/2π + …)

eG-serien

;

Antydningen om flera termer i wikiartikeln ges ingen koppling där [‡], men letar man på webben kan man hitta i varje fall en historiskt beskrivande källa i referensen Arthur Schupp 1959, dock ingen regelrätt seriebeskrivning.

— Serieformen (S nedan) verkar svår att få tag på i MAC; Shupp ger vissa exempel på sidorna 2-3;

— Först med Shpenkov 2007 visas en reguljär (fullständigt principiell) form enligt (Shpenkov s3),

a_e(th) = 0,5(α/π) – 0,328478965579…(α/π)² + 1,181241456…(α/π)³ – 1,598(384)(α/π)⁴ + 4,382(19)·10^–12

= 1,1596521535(12)·10^–3 .................. från Shpenkov 2007, s3

Notera dock att formen ovan i sig är en förenkling; Shpenkov skriver i anslutning till ovanstående led ”The whole extended form of the equation on the “anomaly” ae(th), including functional expressions for factors of the α n terms, takes many pages. Therefore, we show here only the concise form of the equation derived now [6] up to the fourth order in the fine-structure constant [7] α”.

Serieformen i MAC för elektronens g-faktor skulle alltså och tydligen vara av typen

_n

S = ∑ k_n(α/π)ⁿ(–1)ⁿ⁺¹ = k₁(α/π)¹ – k₂(α/π)² + k₃(α/π)³ – … ± k_n(α/π)ⁿ(–1)ⁿ⁺¹

ⁿ⁼¹

eG-serien i MAC

med k(n) som olika koefficienter. Se Beräkningstekniskt Exempel för orientering.

CODATA [det på webben (Okt2010) mest färska värdet, ref. 2006] ger elektronens g-faktor enligt

CODATA 2010-10-05 [Source 2006 http://physics.nist.gov/cgi-bin/cuu/Value?gem]

g_e = 2,0023193043622(15)................................. nuvarande internationellt antagna värde [CODATA]

som i ovanstående termer ger (/2 – 1)

g_e/2 –1 = 1,15965218110 t3 ...................................... uppgiften ovan från Shpenkov är tydligen inte färsk

;

Jämförelsen mot Shpenkovs uppgift (serieformen längre upp) visar att korrektioner har införts (och införs löpande för att kunna matcha experimentella observationer), värdena stämmer bara in till sjunde decimalen.

I TNED — till jämförelse (se från Elektronens g-faktor) — finns (veterligt) ingen grund för någon direkt oändlig serieform som använder (FSC=) α-termen i (α/π)-potenser. Däremot — eftersom elektronmassan ingår i neutronaggregatet N3m20 från PLANCKRINGEN enligt TNED, och därmed kan (men kanske inte nödvändigtvis måste) återföras på PASTOM enligt Atomkärnans härledning, och enbart av det skälet en oändlig serie — är det (i varje fall tekniskt-matematiskt tydligen) möjligt att få samstämmighet med CODATA-värdet och via CODATA-konstanter i TNED tillsammans med [α=1/n²], en grundform (π/α + ½ + 1/12)^–1 och koefficienter från Neutronkvadraten enligt

b = 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22986]^–1)^–1

= 2,00231930436221 ....................... se beräkningar/jämförelser i Kalkylkortet

med

22986 = 18×1277 = 18·65 + 12·1818 = 18(60+5) + 12·1818 = 18(12·5 + 5) + 12·18·101

= 18·5 + 18·5·12 + 18·12·101

= 18·5 + 18·60 + 12·1818

— Alla koefficienter ingår i Neutronkvadraten, centrala i kärnfysiken enligt TNED. Det behövs inga superdatorer för att komma dit (eller så gjorde det det, enbart för att visa att det går utmärkt utan).

Se utförligt från Atomkärnans härledning, om ej redan bekant.

Sambanden beskrivs mera utförligt i Elektronens g-faktor utförligt.

;

Med den givna formen

g_e = 2(1 + FSC/2π + …)

ges motsvarande

b = 2,0023228195 = 2(1,0011614097)

vilket, som vi ser, inte matchar lika bra.

Se dock vidare i beskrivningen från Arthur Shupp 1959 där i varje fall ytterligare en serieterm omnämns (– 0.328α²/π²) och som ansluter bättre till TNED-värdet.

———————————————————————————— ‡

DEN ANTYDDA SERIEFORMEN i Wikipediaartikeln, se länk nedan

Wikipediaartikeln hänvisar till en separat artikel @INTERNET Wikipedia Precision tests of QED 2010-10-03 — men där ges heller ingen överväldigande beskrivning utöver följande:

”The current state-of-the-art theoretical calculation of the anomalous magnetic dipole moment of the electron includes QED diagrams with up to four loops. Combining this with the experimental measurement of g yields the most precise value of α:[4]

α^–1 = 137.035 999 070 (98),

a precision of better than a part in a billion. This uncertainty is ten times smaller than the nearest rival method involving atom-recoil measurements.”,

@INTERNET Wikipedia Precision tests of QED 2010-10-03

http://en.wikipedia.org/wiki/Precision_tests_of_QED

FermiLoop

Vad som menas med ’loop’ i Wikiartikeln (ovan) framgår i wikipediaartikeln om Anomalous magnetic dipole moment; Man använder Feynman Diagram [se dito i Wikipedia] med ett speciellt regelverk som förklarar att ”The reason loop diagrams are called loop diagrams is because the number of k-integrals which are left undetermined by momentum conservation is equal to the number of independent closed loops in the diagram”, sv.; Anledningen varför loopdiagram kallas loopdiagram är att antalet k-integraler som lämnas obestämda på impulsbevarandet [mv] är lika med antalet oberoende slutna loopar i diagrammet.

LOOPTEKNIKENS TEKNISKA BERÄKNING beskrivs bl.a. av Shpenkov 2007 [s3n]: En (exemplifierad) LOOP-koefficient i ’fjärde ordningen’ består av ’mer än hundra stora 10-dimensionella integraler’ som på grund av den exceptionella komplexiteten krävde ’utvecklingen av ett specialsystem med massiva parallellberäknande datorer’. Serieformen i bestämningen av elektronens g-faktor i MAC är med andra ord av typen ’extremely complicated’, väl distanserad i begripbarhet från och hanterbarhet för den medelmässiga trottoarfotgängaren: vi har inte en chans att hänga med i den algebran, det är uteslutet.

[Ett dylikt »beroende av experter (speciellt datoriserade sådana)» är INTE bra för naturvetenskapen: varje sakämne måste i sin ELEMENTÄRA GRUND kunna avhandlas på premisser, resultat och beskrivningar som KAN omfattas av den enskilda individens egen självständiga förmåga — annars blir begreppet NATURVETENSKAP värdelöst som en resurs för ALLA].

— Vilket inte alls visar samma översvallande överensstämmelse med TNED-värdet

(på grund av att konstanterna som används varierar något — vilket inte heller visar sig, nedan, vara det fullständiga svaret),

α^–1 = 137.05802373790500 ........................... TNED-värdet till jämförelse, se FSC=α

med konstanterna

α^–1 = 2h/e²R₀

= 2hε₀c/e²

= 2(6,62559 t34 JS)(8,8543 t12 C/VM)(2,99792458 T8 M/S)(1,602 t19 C)^–2 med t|T för 10–|+

Motsvarande i MAC via Wikipedia (Okt2010 — eller direkt från Google, ”Planck constant”, etc.) här avrundade till samma format:

= 2(6,62607 t34 JS)(8,8542 t12 C/VM)(2,99792458 T8 M/S)(1,602 t19 C)^–2 med t|T för 10–|+

som via Kalkylkortet visar

α^–1 = 137.06640505707400

att jämföra med ovan påstådda

α^–1 = 137.035999070 ................... Wikiartikeln

vilket inte stämmer mycket bättre i decimalpositionen än via TNED 137,05… .

Prövning med det mera noggranna e-värdet e = 1,60217646 t19 C ger direkt ett bättre resultat

α^–1 = 137.03621436771500

Tas också det MAC-värdet för Plancks konstant (direkt på Google) 6,626068 t34 JS fås

α^–1 = 137.03617300497200 ......... Via internationellt antagna standardvärden (CODATA) på webben

samt slutligen också inkluderat samt Standardwebbvärdet för elektriska konstanten 8,85418782 T12 C/VM fås

= 137.03602585818400 ......... Via internationellt antagna standardvärden (CODATA) på webben

att jämföra med ovan påstådda

α^–1 = 137.035999070 ................... Wikiartikeln

Det är allt — Men det är fortfarande träff på bara två decimaler relativt wikipediaartikeln påstående — Googlesökning på det värdet 137.035999070 ger f.ö. 195 träffar: helt säkert.

Utflykten bara understryker att det i MAC finns andra, underliggande (flera) faktorer som spelar in (och som inte framgår enkelt, direkt): inte ens med inbördes angivna referensvärden får man — tydligen — fram (någotsånär) verifierande resultat.

För ev. vidare.

Därutöver, samma wikiartikel, ges den generella upplysningen ”can only be obtained from another precision QED experiment” — som klargör att man INTE har någon färdig teori, och därmed heller ingen klar SERIEFORM att presentera:

”Precision tests of QED consist of measurements of the electromagnetic fine structure constant, α, in different physical systems. Checking the consistency of such measurements tests the theory.

Tests of a theory are normally carried out by comparing experimental results to theoretical predictions. In QED, there is some subtlety in this comparison, because theoretical predictions require as input an extremely precise value of α, which can only be obtained from another precision QED experiment. Because of this, the comparisons between theory and experiment are usually quoted as independent determinations of α. QED is then confirmed to the extent that these measurements of α from different physical sources agree with each other.”,

@INTERNET Wikipedia Precision tests of QED 2010-10-03

http://en.wikipedia.org/wiki/Precision_tests_of_QED

— Det finns dock en KLAR serieform [även om den verkar svår att hitta på webben] (Se eG-serien från Shpenkov 2007) — men den beskrivs ändå av typen ’extremely complicated’ då koefficienternas beräkning kräver (super-) datorer (i omfattande parallellsystem), se Shpenkov 2007 s3n.

;

VIDARE UPPLÖSNING — enligt TNED:

Eftersom atomen enligt TNED härleds från PASTOM [massans fundamentala struktur utan beståndsdelar] och bygger på en obegränsad struktur av allt finare impulsmoment, bör heller inte b-formen vara den absolut slutliga (vilket också antyds av värdejämförelsen underförstått att det experimentellt uppmätta värdet är något större [N,nnnnnnnnn140…]) än b-värdet.

Den aktuella b-formen skulle därmed (enligt TNED) syntetisera typutseendet

1

b = 2 + ————————— …

πn² + ½ + 1/12 + f

med f av samma typform som b (men med ytterligare karaktäristiska formfaktorer, här utan vidare fördjupning) och (således) med en serie som tecknar obegränsat avtagande bidrag — enligt fraktalformerna i TNED [elektronringens underfraktaler, sedan dessas i sin tur osv., se även Planckfraktalerna].

För b-termernas förklaring (utom f ), se Sammansättningen i elektronelementet [m(e)/n].

[Helheten visar att det blir allt svårare att bortse ifrån TNED …].

b-serien vidare

2010-10-04:

Serien för b — något vidare

Från Sammansättningen i elektronelementet [m(e)/n]

Med vidare prövningar i Kalkylkortet på ovanstående resultat (Tabellflik 2):

OM vi använder — genomgående — de fysikaliska konstanter som visas som »webbstandard» (typ Googles Kalkylator), stämmer TNED-värdena (med de angivna konstanterna som används i TNED) med följande tillägg till den antydda b-strukturen:

g_e = 2,0023193043617(15) = 2(1,00115965218085)

1

b = 2 + ———————————————————

1

πn² + ½ + 1/12 – ——————————

1 1

2 – —— + ————

18 22 800

= 2,00231930436171

= 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22800]^–1)^–1

CODATA 2010-10-05 [Source 2006 http://physics.nist.gov/cgi-bin/cuu/Value?gem] ger något annorlunda slutsiffror,

g_e = 2,0023193043622(15)

Värdet via Kalkylkortet ger motsvarande

= 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22986]^–1)^–1 ; 22986 = 18×1277

= 2,00231930436221

OBSERVERA att sifferexercisen ovan, alla termer efter kvoten 1/12, här har utvecklats helt godtyckligt och med sikte på att söka de mest framträdande — de enklaste — heltalskonstanterna som framträder i TNED.

— MINUSKOMPONENTERNA kan uppfattas som GYRODÄMPARE:

positiva värden .................... ger tillskott till Tauringens egenmagnetiska moment ................ — polfältstyrkan ökar;

negativa värden ................... ger reduktioner i Tauringens egenmagnetiska moment ............ — polfältstyrkan avtar.

n² = 2h/e²R₀

= 2hc₀ε₀/e²

Konstanterna ovan [från CODATA] finns (t.ex.) på Google direkt via ”Planck constant” etc., enligt [MAC-markeringen anger ett värde som avviker eller har flera decimaler ifrån det som normalt används i TNED, se HOP-blocket]

MAC-konstanterna

h_MAC = 6,62607000 t34 JS

c₀ = 2,99792458 T8 M/S

ε_0MAC = 8,85418782 t12 C/VM

e_MAC = 1,60217646 t19 C

R_0MAC = 376,730313 V/A = Ω .................... beräknat via 1/c₀ε₀

Kalkylkortet ger med dessa värden

b = 2,00231930436171

i jämförelse med MAC-värdet i Wikipedia

g_e = 2,0023193043617 (15)

Dvs., fullständig (exakt) överensstämmelse teori-experiment.

— Men vi får förstå (enligt TNED) att sista kvoten/nämnaren ALLTID kommer att kunna upplösas i flera underavdelningar.

— 18-talet finns också i NEUTRONKVADRATEN som atomära massdefektens maxvärde enligt Neutronkärnans indelning i TNED i e-block: centralmassivet 1818e + massdefektens kapitalstock 18e + ytterligare en rest (»smörjmedel») 2,624e.

EN ÖVERGRIPANDE TEORETISK BESKRIVNING MED ovanstående serieform som ansluter till fraktalbyggnaden enligt TNED [Se utförligt i ATOMKÄRNANS HÄRLEDNING] finns ännu (Okt2010) INTE i den här författningens ljus utom till föregående beskrivna kvoten 1/12, se Sammansättningen i elektronelementet [m(e)/n].

För ev. vidare.

Sammanställning eG

SAMMANSTÄLLNING (Okt2010):

Elektronens g-faktor

Kalkylkortet ger med MAC-konstanterna

b = 2,00231930436171

i jämförelse med MAC-värdet i Wikipedia (@INTERNET Wikipedia Gyromagnetic ratio, Gyromagnetic ratio for an isolated electron 2010-10-09 [LastMod 8Oct2010])

g_e = 2,0023193043617 (15) = 2(1,00115965218085)

med b enligt TNED på formen

1

b = 2 + —————————————————————

1

πn² + ½ + 1/12 – ———————————

1 1

2 – —— + ————

18 22 800

Det finns en mera noggrann värdeform via CODATA-värdet (Wikipedia har inte riktigt samma värde …),

CODATA [det på webben (Okt2010) mest färska värdet, ref. 2006]

ger elektronens g-faktor enligt

CODATA 2010-10-05 [Source 2006 http://physics.nist.gov/cgi-bin/cuu/Value?gem] Value — Concise form

g_e = 2,0023193043622(15)..................... nuvarande internationellt antagna värde [CODATA]

som i TNED

— med samtliga fysikaliska konstanter enligt CODATA, se Kalkylkortet Tabellflik 2

— ger (n²=1/α)

b = 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22986]^–1)^–1

= 2,00231930436221 ....................... se beräkningar/jämförelser i Kalkylkortet

med

22986 = 18×1277 = 18·65 + 12·1818 = 18(60+5) + 12·1818 = 18(12·5 + 5) + 12·18·101

= 18·5 + 18·5·12 + 18·12·101

= 18·5 + 18·60 + 12·1818

; överensstämmelsen gäller tydligen in till 13:e=sista decimalen:

1

b = 2 + —————————————————————

1

πn² + ½ + 1/12 – ———————————

1 1

2 – —— + ————

18 22 986 = 1836·12 + 18·53 ........... alternativt enklare till ovan

= 1836·12 + 18²·3 – 18

= (1818 + 18)·12 + 18²·3 – 18

;

Koefficienternas tolkning i TNED. Planckimpulsen h till 2 multipliceras in i högerledet som 2h + h(P) med ekvivalenta +(P)/(N/h); Vi kan därmed identifiera h-faktorn med undre termernas led enligt 2h — h/18 + h/(22986 = 1836·12 + 18·53). Därmed kan Planckimpulsen (h) identifieras [isolerad, var för sig] på dess PRINCIPIELLA fraktalformer enligt Atomkärnans härledning, i syntes i PLANCKS STRUKTURKONSTANT:

h/18 ........................... motsvarar neutronens mcr/18;

Med centralmassivet på (1818)e ges (1818)/18=101, alternativt centralmassivet + massdefektsdelen på (18)e som ger täljaren 1836 med kvoten (1836)/18=102; bägge associerar till kärndelens heltaliga gränsdelning via primtalet 101 och kan därför anses väl relaterbart i TNED;

h/1818 ...................... motsvarar neutronens mcr/1818; se Centralmassivet

h/1836 ...................... motsvarar neutronens mcr/1836; neutronmassans e-innehåll minus 2,624;

På samma sätt med centralmassivets (1818)e och totalstocken på (1818+18)e, vilket som passar; bägge motsvarar elektrondelen

(exakt 1/[1838,624 = 1818 + 18 + 2,624])e

i neutronaggregatet som definierar elektronmassan.

Koefficientvärdena är alltså väl igenkännbara, och kan relateras till elektronmassans olika kopplingar till N3m20-aggregatet (Neutronen elementärt).

För basgruppen πn² + ½ + 1/12, se Sammansättningen i m(e)/n.

— Vi vet inte hur koefficientsamlingen fortsätter i värdeformen — den kanske stannar vid ovanstående (eftersom alla centrala koefficienter redan är berörda), eller kanske fortsätter (men med ytterligare andra grupper av underfraktala koefficienter, här helt okända).

Resultatet ovan vilar enbart på de observationer som framkommit i den experimentella bestämningen och dess precision: den stämmer antingen med TNED, eller så inte. Tuff bransch.

Editor2010X9

;

Det anmärkningsvärda är INTE att TNED-komplexets koefficienter uppvisar en ekvivalent. Det anmärkningsvärda är att koefficienterna är dels enkla heltal — jämför eG-serien i MAC — och dels ansluter till TNED-komplexets kärnfysikaliska mönsterforms centralkoefficienter (elektronmassans del i neutronaggregatet N3m20) i komplexets mönsterbild för atomvikterna [1,2,3,5,6,12,18,60,1818]: neutronkvadraten. Se Beräkningstekniskt Exempel för jämförelse med motsvarande (ytterst komplicerade samling) i MAC;

— Man har i MAC-delen av komplexet [Se eG-serien i MAC] specialbyggt datorer för att kunna beräkna ’mer än hundra 10-dimensionella integraler i 4:e ordningens Fermi-diagram-loopar’ [‡] för att få fram de motsvarande, ytterst komplicerade koefficienterna i den relativt TNED omvända (och utsträckta) MAC-[α/π]-serien.

— Bara det faktum att en sådan (tekniskt) komplicerad algoritm, tydligen, har en betydligt enklare och dessutom heltalsbaserad koefficientform, som ovan enligt TNED, och som dessutom, tydligen, ansluter till en väl relaterbar genomgången härledning av atomkärnan [Se utförligt från PLANCKRINGEN om ej redan bekant], gör det lika svårt att frånse objektets faktum.

(Man kunde lika gärna säga att hela utredningen var tillägnad TNED — i en grymt stark teknisk bevisning, och på sätt som ingen hade kunnat förutsäga från början). Ekvivalenter är ekvivalenter.

eG utförligt

2010X6

elektronens g-faktor — TEORI

—————————————

elektronens magnetiska moment

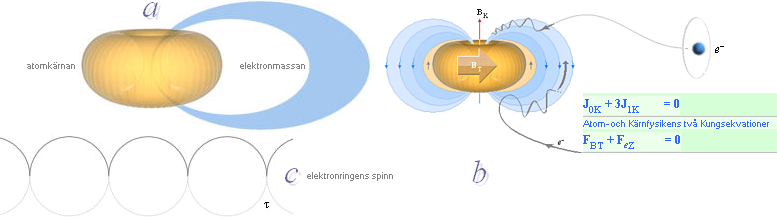
I TNED bildar atomkärna och elektronhöljets elektronmassa (a nedan) en sammanhängande enhet som summerar nollmoment och nollspinn. Elektronmassan frigörs elementärt ur atomkärnan genom neutronsönderfallet, och följer sedan strömningsvägen (b nedan) som utpekas av kraftekvationen [F(BT)+F(eZ)=0]. Atomkärnans volymära utvidgning genom elektronmassan till atomen betyder i TNED att atomkärnan emitterar en viss mängd impulsringar (J=mcr) som definierar elektronmassan. Elektronringens spinn härleds i KVANTTALEN som ringspinnet — motsvarande ringens konstanta strömstyrka — för varje sådan J-ring ([Tau] τ-ring i TNED) genom den ortsvektor som förbinder atomkärnan med en (vid en godtycklig punkt i det yttre fixa dominanta gravitationsfältet, detta ger också referensen för kärnans toppspinn enligt TNED, analogt laboratoriets referenspunkter) idealt fix τ-ring (långt) utanför atomkärnan (c nedan); Ett kärnspinnvarv definierar (»vidrör») halva τ-ringen, vilket definierar τ-ringens ringspinn på formen s(τ)=(1/2)h. Hela τ-ringens strömstyrka — analogt τ-ringens magnetisk moment — definieras därmed på två kärnspinnvarv; µ(τ)=2h.

Elektronens magnetiska moment — större än via spinnfaktorn 2h

Elektronens magnetiska moment — större än via spinnfaktorn 2h

Men som redan framgår i den nämnda a-delen, figuren ovan: Inte alla (n₀) τ-ringar finns med i atomperiferin motsvarande illustrationens c-del. En viss mindre andel (n₁, ca 1/1000 av hela elektronmassans antal τ-ringar, vidare nedan) befinner sig nära atomkärnan och i dess spinn-laddningsbrunn. Där kan inte elektronkomponenten åtkommas för någon direkt inspektion och inte heller deltar den uppenbarligen direkt i kollektivet för elektronmassans svängningsformer på samma sätt som sker längre ut. Den del som τ-ringens magnetiska moment definieras på kan därför inte riktigt motsvara den totala samlingen τ-ringar i elektronmassan men som ändå underförstås i den enkla (c ovan), ideala härledningen. En viss (mindre) mängd (n₁) kommer inte med i den praktiska delen.

Matematiskt [från idealt rena spinnfaktorn 2h] kan saken uttryckas

[2h/(n₀–n₁)]n₀ = 2h(n₀/[n₀–n₁] = 1 + 1/[P]) = 2h(1 + 1/[P]) = 2h(h + 1/([P]/h))

= 2(h + [P₁/h + P₂/h + P₃/h + … + P_m/h]^–1)

= 2(h + [N₁/k₁h + N₂/k₂h + N₃/k₃h + … + N_m/k_mh]^–1)

= 2(h + [(P₁ + P₂ + P₃ + … + P_m)/h]^–1) ; Eller direkt i h-enheter;

b = 2(1 + 1/[P₁ + P₂ + P₃ + … + P_m])

Förenklat:

b = 2 + 1/([P₁ + P₂ + P₃ + … + P_m]/2)

= 2 + 1/([N₁/k₁ + N₂/k₂ + N₃/k₃ + … + N_m/k_m]/2)

= 2 + 1/(N₁/2k₁ + N₂/2k₂ + N₃/2k₃ + … + N_m/2k_m)

= 2 + 1/(N₁/κ₁ + N₂/κ₂ + N₃/κ₃ + … + N_m/κ_m) , κ Grek. k, kappa.

n₀ anger antalet τ-ringar i elektronmassan, n₁ anger den vissa del som befinner sig nära atomkärnan eller i dess kärnbrunn — »i atomkärnan» — och som därför intar en speciell ställning som inte ingår i atomperiferins (enkla) matematik; n₀–n₁ blir då i själva verket antalet τ-ringar som underförstås i den enkla matematiken på impulsmomentets form

2h=[2h/(n₀–n₁)](n₀–n₁) och som gäller för ringspinnets ström (strömstyrkan [i] som definierar magnetiska momentet [iA=iπr²] för hela elektronmassan) via kärnspinnet eller motsvarande impulsmomentet h=mcr [=1] som gäller elementärt för Neutronen enligt TNED, och som via Neutronkvadraten bildar grunden för alla andra nuklider och deras atomer.

Ett grundvillkor för att lösa ut koefficienterna i k-formen (κ) är uppenbarligen att magnetiska momentets grundform (µ=iπr²) måste ingå som termen N₁ i grundkvoten (N₁/κ₁) i b-formen, hela komplexets bas.

Termen r i µ måste dessutom återföras (enhetligt, generaliserat numeriskt) på huvudkvanttalet (n); Formen n² motsvarar det allmänna resonansvillkoret och som därmed garanterar access till samtliga atomers nuklider och deras energibaser enligt härledningarna i Spektrum och Kvanttalen. »Spinnfaktorn» (κ₁) för detta fall kan bara vara κ₁=1, analogt med kärntoppspinnets 1h för ett spinnvarv;

(N₁/κ₁) = (πn²/1) = πn² = π2h/e²R₀ = m_nc₀·2πr_n /e²R₀

Som fristående kvot (alla andra N=0) skulle motsvarande impulsmoment fås 1/πn², vilket därmed kommer att motsvara storleksordningen totalt för det extra tillskottet utöver 2-faktorn.

Genom utvecklingen för ekvivalenten till resonansvillkorets faktorterm n²~137 [Se FSC i TNED] blir storleksordningen approximativt

2 + 1/πn² = 2 + 1/(3,1415)(137)

= 2,00232342

att jämföra med uppmätta (den s.k. elektronens g-faktor)

g_e = 2,0023193043622(15)

CODATA 2010-10-05 [Source 2006 http://physics.nist.gov/cgi-bin/cuu/Value?gem],

TNED-värdet motsvarar tydligen en 99,99903%=0,9999903 direktträff.

Masstalet 2 (2mcr=2h)

— motsvarande en impulsmomentskoefficient 2 räknat från grundnukliden som Neutronen i Neutronkvadraten och som grundlägger alla tyngre nuklidbildningar via atomära massdefekten [se även i Deuteronens Hemlighet]

— är centralt för bildningen av kärntoroidens ändrade formfaktorer [Se Planckringens dimensioner] för alla nuklider med masstal större än 1.

Adderas — således — också den nukleärt associerade koefficienten κ₂=2 med

(N₂/κ₂) = (1/2)

motsvarande den fristående kvottermens invers h/(1/2) = 2h = 2mcr

samt också κ₃=12 med

(N₃/κ₃) = (1/12)

motsvarande den fristående kvottermens invers h/(1/12) = 12h = 12mcr som kopplar till atomära massenhetens definition i TNED (1/12 av Kolatomens atomvikt i Neutronkvadraten), ges grundformen utvidgat enligt

b = 2 + (πn² + ½ + 1/12)^–1

Resultatet (med de delvis förenklade konstanter som redovisas i HOP-blocket) blir

b = 2,00231930409728 .............. med 14 decimaler från Kalkylkortet

att jämföra med föregående CODATA (internationella standarden, 2006):

g_e = 2,0023193043622

Det blir svårt att förneka en viss samstämmighet med den passningen.

Sammansättningen i m(e)/n, utförligt

(πn²/ [1/2]h) /2 = (2πn²/[1]h)/2 = πn²/ 1h ; 1 ...... är fundamentalt masstal; formfaktorer för A=1

(1/ [1]h) /2 = 1/2h = 1/ 2h ; 2 ...... är fundamentalt masstal; formfaktorer för A>1

(1/ [6]h) /2 = 1/12h = 1/ 12h ; 12 .... är fundamentalt masstal; atomära massenhetens masstalsfaktor

;

För fullständighetens skull, skulle man därmed också i Neutronkvadratens ljus kunna förvänta sig att också skaltermerna för atomära massdefekten (18e), centralmassivet 1818e, neutroncirkelns masstalsradie (60) och (som redan omnämnts ovan) massdefektsskalans transferkoefficient på 12 (och därmed 60/12=5) alla skulle finnas med i en mera fullständig P-serie för b-formen.

Då det (i varje fall för min del — till att börja med) är enklare att laborera med dessa koefficienttermer än att försöka utreda i vilken (EVENTUELL) impulsmomentsanalogi man ska relatera dem i TNED, visar sig följande vidare upplösning i b-formen:

Enligt TNED — om termblocket (πn² + ½ + 1/12) är representativt för τ-ringens släta ringyta — måste varje vald ringparameter förstås som ett STÖRRE värde än det praktiska därmed att masstätheten växer med växande fraktaldjup i ringstrukturen [Se Atomkärnans gravitella härledning] genom att varje ringnivå är ihålig. OM ytterligare förfining skulle krävas, kunde man därmed — enligt TNED — förmoda att ytterligare (serie) termer av första ordningen måste ges subtraherande — och sedan vidare i en möjlig fraktal serieform.

Det visar sig också fungera så — i varje fall vid en första ytlig anblick:

Används genomgående CODATA-konstanterna i värdebestämningen, ges för det första relativt ovan

b₁ = 2,00231930409728 .............. med 14 decimaler från Kalkylkortet

ett större värde

b₂ = 2,00231967590269 ............ samma ekvation men med CODATA-konstanter

och som — lägligt — visar sig »autojusteras EXAKT serietermiskt» med — just — en subtraherande påbyggnad efter 1/12 enligt

b₃ = 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22986]^–1)^–1 ;

22986 = 18×1277 = 18·65 + 12·1818 = 18(60+5) + 12·1818 = 18(12·5 + 5) + 12·18·101

= 18·5 + 18·5·12 + 18·12·101

= 18·5 + 18·60 + 12·1818

= 2,00231930436221

mot CODATA:s

CODATA 2010-10-05 [Source 2006 http://physics.nist.gov/cgi-bin/cuu/Value?gem],

g_e = 2,0023193043622

Utan att det (här Okt2010) finns någon uttömmande impulsmomentsanalogi till var och en av dessa koefficienttal (talet 18 anger f.ö. atomära massdefektsmaximum i Neutronkvadraten)

[resp. 2h, h/18, h/22986, … = h/18·1/36, h/18, h/18·1277, … = h/18·0,02777…, h/18·1, h/18·1277, …]

är det under alla omständigheter uppenbart att vilka ev. ekvivalenter det än kan finnas rent serietekniskt, de tvunget måste återfalla på ovanstående servicebutiks underbara hyllsortiment och som tydligen bara är unikt för just Neutronkvadraten — TNED. Det är det anmärkningsvärda i likheten.

g-faktorn i MAC

ÄMNET TILLDROG SIG INTRESSE redan från kvantfysikens början (främst under 1940-talet) [‡]. För att mäta HELA elektronens magnetiska moment måste man fånga in en elektron, ungefär som visas av spårbilden för elektroner i bubbelkammarfotografier, samt »justera frekvensen» så att man kan observera spinnflippet: Energin som åtgår för detta är svaret. Mot normalkoefficienten 2 som gäller i det enkla teoretiska fallet svarar då ett något högre praktiskt värde benämnt elektronens g-faktor (g_e).

Experimentbeskrivningen,

elektronens g-faktor

EXPERIMENTBESKRIVNINGEN finns i artikeln (SA) SCIENTIFIC AMERICAN August 1980, The Isolated Electron, Philip Ekstrom, David Wineland, från s90.

I korthet: Med bara storleken nära 4cM har man konstruerat en s.k. elektronfälla [monterad på toppen av en stark magnet som sedan kyls ner till 4 grader över absoluta nollpunkten]: elektroner leds in i ett centralt litet hålrum (ungefär Ø3cM) bestående av en hyperboliskt formad ringelektrod. Tillsammans med övriga liknande specialformer, bygger hela konstruktionen på att via elektriska och magnetiska fält hålla elektronerna/elektronen i en sluten bana (magnetronbanan) där man via olika energitillskott eller avdrag i fältbilden kan få elektronen att anta olika banradier, samt utföra spinnflippningar. Genom att justera energin mellan en bana med spinn-upp och en bana med spinn-ner kunde man läsa av det sökta svaret i apparaturens frekvensskillnad (hf-energin).

Den enkla bestämningen av g-faktorn enligt TNED i Elektronringens magnetiska moment ger exakt

g_e = 2

Artikeln från SA (Aug1980) ger till jämförelse (ca + 1/1000)

g_e = 2,0023193044

CODATA (internationella standarden, 2006):

g_e = 2,0023193043622

TEORETISKA VÄRDET i MAC sägs ansluta in till sista decimalen med det experimentellt uppmätta värdet. Men, som det också sägs,

s91sp1mn:

”Both the calculation and the measurement are difficult, but they have been refined to such an extent that the g factor of the electron is now known to greater accuracy than any other physical constant.”,

SCIENTIFIC AMERICAN August 1980, The Isolated Electron, Philip Ekstrom, David Wineland

Den enda upphittade webbkälla (Okt2010) som ger någon liten ledtråd till vilken typ av matematik det är fråga om i den teoretiska delen, kommer från Arthur Schupp 1959: Man använder typen

”The second order term in α, has been evaluated by Karplus and Kroll [10] and by Sommerfield [11]. The results are

g_e = 2(1 + α/2π – 2.973α²/π²) = 2(1.0011454) (Karplus - Kroll)

g_e = 2(1 + α/2π – 0.328α²/π²) = 2(1.0011596) (Sommerfield)

”,

Schupp 1959 s3ö, med α som den s.k. finstrukturkonstanten (eng. FSC Fine structure constant), beskriven av Schupp (s2mn) enligt ”α=e²/ħc=7.29719×10^–3”, ~ 1/137.

Den vidare serien finns inte beskriven (i några gratis tillgängliga verk på webben, Okt2010) på annat sätt än som nedan,

”The current state-of-the-art theoretical calculation of the anomalous magnetic dipole moment of the electron includes QED diagrams with up to four loops. Combining this with the experimental measurement of g yields the most precise value of α:[4]

α^–1 = 137.035 999 070 (98)

”,

@INTERNET Wikipedia Precision tests of QED 2010-10-03

http://en.wikipedia.org/wiki/Precision_tests_of_QED

Sammanfattning g-faktorn TNED

Sammanfattning g-faktorn TNED

Vilken matematik ger TNED till elektronens g-faktor? Det finns inte så mycket att välja på: Villkoret gäller tydligen HELA elektronen — vilket ställer upp bara enkla, elementära koefficienter att räkna på.

Andelen utelämnade τ-ringar — (g-faktorn i TNED)/2 – 1

Då vi söker HELA elektronmassans magnetiska moment, är det naturligt att räkna med samma grundparametrar som finns med i det som gäller lika för alla nuklider: huvudkvanttalet (n) med resonansvillkoret (n²), elektronkomponenterna inre ringspinn (1/2), samt koefficienten till atomära massenheten (1/12), samt vidare de enkla skalkoefficienterna som återfinns i Neutronkvadraten och som ingår för alla nuklider

1, 2, 6, 12, 18, 60 och därmed 60/12=5, samt centralmassivet 1818

Resonansvillkoret (n²) tillsammans med pi (π) bildar magnetiska momentets cirkulära omslutningsyta (πn², se magnetiska momentet).

Den elementära termsamlingen som gäller för alla nuklider kan då skrivas ut enligt

πn² + ½ + 1/12

Eftersom värdet 2 från Elektronringens magnetiska moment är för litet, söker vi en tilläggskvot på enklaste sättet enligt

b = 2 + (πn² + ½ + 1/12)^–1

Resultatet (med de delvis förenklade konstanter som redovisas i HOP-blocket) blir

b = 2,00231930409728 .............. med 14 decimaler från Kalkylkortet

att jämföra med föregående [Artikeln från SA (Aug1980)], samt efterföljande

g_e = 2,0023193044

CODATA (internationella standarden, 2006):

g_e = 2,0023193043622

Dvs., en direktträff (TNED/CODATA) på 0,99999999986769.

Används i TNED också mera noggrant de internationellt standardiserade konstanterna genomgående enligt CODATA

ges med deras g-faktorvärde ekvivalenten från Kalkylkortet (Tabellflik 2)

b = 2 + (πn² + ½ + 1/12 – [2 – 1/18 + 1/22986)^–1 ;

22986 = 18×1277 = 18·65 + 12·1818 = 18(60+5) + 12·1818 = 18(12·5 + 5) + 12·18·101

= 18·5 + 18·5·12 + 18·12·101

= 18·5 + 18·60 + 12·1818

= 2,00231930436221

mot CODATA:s

g_e = 2,0023193043622

— För min egen del vill jag nog inte kalla ovanstående resultat i ljuset av TNED någon regelrätt TEORI [kombination av olika givna Stadsskyltar — VALET är extremt välordnat, men innebörden är hieroglyfisk]. Det är snarare ett resultat av en viss vana att umgås med siffror. Att DÄRMED termvärdena ansluter till fysiska detaljer i TNED är en sak för sig. Att RELATERA dem till någon begriplig dynamisk ORDNING är — tydligen — en annan sak för sig.

CASIMIREFFEKTEN — inledning · utförlig beskrivning

Casimireffekten, kort översiktlig inledning,

vidare från huvudrubriken,

Se även kortform i CasEx

2010X13

Casimireffektens allmänna form — TNED-MAC

Efter holländaren Hendrik Casimir 1947 i samband med observationer vid industriell materialutveckling [Philips Laboratory], se Casimireffekten, Historia

TNED-sambandet totalt

F/A = ke²Z[(d_xy+d)²(d_xy+[d+1]^d/a–1)²]^–1[n]^–1

Se från Härledningen till Casimireffekten i TNED

Grafisk form

y = x^–2[(x)^m]^–2 — Casimireffekten typfunktionen ovan renodlad som nedan

m = 1 ........................ motsvarar MAC-formen med d ⁴ bruna grafen markerad ^ 4

m = x/a ..................... motsvarar TNED-formen med separerade typ d₁ ²d₂ ² ; n=n/4 ; ljusblå graferna markerade 1 | ∞

a=1 i figuren ger en snävare funktion än MAC-formens;

a→∞ i figuren ger max överskjutande avvikelse relativt MAC-formen;

max fel (38%) ligger vid ca 20 nM (1,64) med nedanstående exempelreferens, a=50µM

EXEMPEL med Järn (26Fe56) vid rumstemperatur (20°C), a=50µM [dessa ingår inte i MAC], distansenhet 12,21 nM, tryckenhet 5,43 T4 Pa

distansenhet distans ekvivalent attraktionstryck med värden i TNED = MAC

———————————— —————————— ——————————————————————————————————————————————

1 12,21 nM 54 325 Pa (ca ½ atm)

81,9 1 000 nM 0,001 Pa

;

SOM VI SER är maximala differensen (38TILL5)% TNED-MAC begränsad till ett område 1TILL4 distansenheter, i exemplet ca 12-48 nM, och som i princip kan MODULERAS med tillägg av olika materialparametrar:

Citatreferenserna till Casimiereffektens experimentella uppvisning

[Lisanti et al., 2005, PhysicsWorld 2002, ARXIV-källan Svetovoy-Lokhanin 2008 i Sfär-Platta-samband, (m.fl.)]

vittnar själva om önskemålet med en mera preciserad mätbild (på många olika material): Casimireffekten ger (ännu 2010) inte någon överväldigande exakt redovisad fenomenform i linje med sambandets (primära) MAC-form som ovan. Dvs., mätavvikelserna är i vissa fall relativt stora — vilket å andra sidan sammanhänger med att mätningarna är (ytterst) svåra att genomföra då vissa modifikationer (sfär-platta istället för ideala platta-platta) kräver att grundsambandet modifieras, och vilket ämne (ännu, i citatreferensernas anda) är delvis oklart i teorins uttolkning.

Artikeln i Wikipedia [‡] använder den ungefärliga distansen 10 nM för att exemplifiera attraktionstrycket på 1atm=101325 Pa, men utan angivande av något särskilt material eller (ens) specifika materialparametrar. Med Järnexemplet i TNED som ovan ges motsvarande distans för 101325 Pa som 8,936 nM — medan Nickel (28Ni59) för 101325 Pa ger 9,5545 nM ~10 nM. Kalkylkortet (Tabellflik 2, Casimireffekten) ger beräkningscellerna.

Med andra ord: Inte förrän man genomfört noggranna mätningar som klarar ut huruvida Casimireffekten är materialoberoende eller inte kan någon vidare slutsats dras.

Till viss del är en viss aspekt redan klarlagd i saken, se Lisanti et al., 2005, där man redan konstaterat att materialytans (underliggande) beskaffenhet har betydelse (den s.k. skineffekten). Det krävs dock vidare mätningar för att klara ut vad som gäller generellt.

Casimireffekten i TNED — härledningens form

Casimireffekten i TNED — härledningens form

Atomära attraktionskraften mellan mikroskopiskt närliggande materialytor vars elektronbesättningar börjar intränga varandras lokaler

F = k(Q/d)² ...................................................... ; k = R₀c₀ = 1/4πε₀ ..... hela elektronens rymdresistansform

F = kZe²/nd_z² ................................................... ; k = R₀c₀ = 1/ε₀ ......... enskilda elektronelementets rymdresistansform

F/A = kZe²/nd_z²d_x d_y

= ke²Z[d_z²d_x d_y]^–1[n]^–1 .................................. ; n antalet elektronelement i elektronmassan

d(xy) = (Uu/ρM³)^1/3 .............................................. ; kubiska atommedelavståndet [vid rumstemperatur], materialet måste specificeras

F/A = (ke²/u^2/3)Z[d_z²]^–1[n]^–1 (ρ/U)^2/3·1M ;

= ke²Z[(d_xy+d)²d_xy²]^–1[n/4]^–1 ; med preciserad distansparameter

= ke²Z[(d_xy+d)²(d_xy+[d+1]^d/a–1)²]^–1[n/4]^–1 ; avståndsverkan med maxgräns vid a ~ 50-100 µM (0,05-0,1 mM)

Härledningen till ovanstående samband genomgås utförligt från Härledningen till Casimireffekten i TNED och i de steg som i denna författnings referens framträdde vid den första genomgången (Sep2010).

Till jämförelse, se [‡]

F/A = ħcπ²/240d_z⁴ .................................................. Casimir-sambandet i MAC

se exv. Wikipedia Casimir effect, Casimir’s calculation 2010-09-20;

Inga primärt särskiljande materialparametrar ingår (atomvikt, täthet). ħ=h/2π.

Hur MAC-formen kopplar beskrivs i huvudtexten [Se Den springande punkten].

Formerna för hc och ke² är f.ö. fysikaliskt identiska [‡], bägge i JouleMeter (JM).

Härledningen till Casimireffekten i TNED

mera teoretiskt utförligt

Se även i Kort översiktlig inledning

HÄRLEDNINGEN

Se även i Praktisk teoretisk bakgrund — Se även mera utförligt i Casimireffekten — Se även allmän, kortare genomgång i LEC

Genom att utgå ifrån den enkla, raka rena råformen i elektriska kraftlagen F = k(Q/d)² ges — utan inblandning av den moderna akademins mystiska och magiska ’fluktuationer i tomrummet’ då vi redan har fattat grundpremissen med noll förekomst av massa i den masslösa rymden enligt nollenergin 0=0c² oberoende av akademiska överenskommelser som vill ha det på annat sätt — en RATIONELL sambandsform som kan användas för prövning mot experimentella mätvärden.

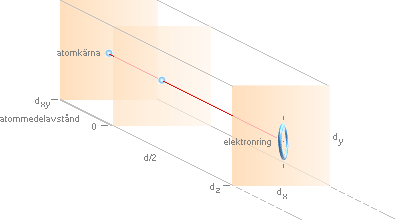
SPÄNNINGEN (U=E/Q) Fd/Q = k(dQ/dd) som motsvarar laddningen (Q) fördelad över den kraftverkande distansen (d) kan i fallet med den enskilda elektronmassans komponent (e/n) — Den förkastades från 1927 i MAC — byggas på en helt linjär idealt (kubisk) differentialgeometri (dQ/dd). Nämligen så att spänningsdifferentialen (dQ/dd) — utan inblandning av den ordinära sfäriska geometrins faktor 4π — kan FÖRDELAS DIREKT över den idealt kvadratiska tvärsnittsytan (A) d(x)d(y); A som kraftflödestvärsnittyta täcker idealt EN elektronring som enda agent längst ut i motsvarande atommodells sfäriska formblock (här idealt rymdtäckande kubiskt). Därmed ges bilden av den enda mobila kraftenhet som kan finnas i växelverkan med närliggande materieytors liknande elektronringar. Därigenom erhålls ett uttryck för ekvivalenta tryckkraften per kvadratmeter (F/A) som ringens attraktion på atomkärnan utövar på det lokala ytplanet, analogt »materialytornas ömsesidiga, inbördes atomattraktion».

Elektriska konstanten

Elektriska konstanten (k) associeras med andra ord i detta speciella fall enbart med den rena rymdresistansens form, dvs, utan den normalt extra nämnarfaktor 4π som ingår i materiefysikens elektronkvanta och som normalt associeras med det elektriska fältets idealt sfäriska geometri via laddningsytan 4πd²,

k = R₀c₀ = 1/ε₀ = 1/(8,8543 t12 C/VM)

Från elektriska kraftlagens grundform F = k(Q/d)² sätter vi då först QQ mera preciserat för samtliga atomer (e/n)Ze med avståndsfaktorn som d_z så att vi får kZe²/nd_z². Division med kvadratiska tryckytan (A) [d(x=y)]² ger F/A = kZe²/nd_z²d_xy²;

Distansparametern

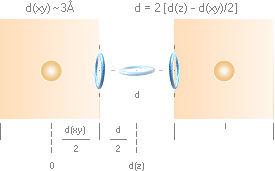
Med kraftavståndet (d_z) kärna-ring som halva materialdistansekvivalenten (d) mellan de bägge materialen ges först (d_z)=(1/2)[d_xy + d], analogt d=2(d_z)–d_xy ; Med materialytan idealt vid atomens kubgräns, analogt där elektronmassans medelavstånd från atomkärnan ligger, ges ett tillägg in till atomkärna på halva atommedelavståndet (d_xy/2) då d=0.

Medelatomavståndet via ämnets medeltäthet ρ=m/V ; Antalet atomer i m är N=m/Uu; Medelkubiska volymen för varje atom blir 1M³/N, kubiska medelavståndet blir d(xy)=(1M³/N)^1/3;

Därmed har sambandet modifierats till 4ke²Z[(d_xy+d)²d_xy²]^–1[n]^–1. Men elektronringen kan inte vara obetingat bunden till materialdistansen (d) via »kubKraftStrålytan» (d_xy²);

Vartefter d ökar, tappar ringen alltmer fokus på sin egen ideala kvadratyta (d_xy²). Kraftkopplingen kommer istället att spridas ut på alla möjliga underliggande kubsnittskvadraters atomstrålyta, typ (d_xy+Δd)² så att nettotrycket avtar. För att matcha det allmänna fallet, kan en enklare funktionsalgoritm utvecklas för ändamålet [Se Korrektion för växande avstånd]. Genom att ange en maxgräns (a ~ 50-100 µM [också grovt enligt vissa mätningar (220µM), se Citat från Hyperphysics]) för Casimireffektens verkan — med tanke på att också andra omkringliggande material får en allt större (mixad) inverkan med hänsyn till olika (minimala) medelavstånd mellan olika närliggande materialytor — får sambandet sin slutform enligt

F/A = ke²Z[(d_xy+d)²(d_xy+[d+1]^d/a–1)²]^–1[n/4]^–1

Se även grafiska jämförelsen i inledningen

För maximala näravstånd ([d+1]^d/a–1~0) ändras Δd bara marginellt; med växande d avtar kraftverkan alltmer med influens från Δd på d_xy och når max vid a-gränsen som ([d+1]^d/a–1~d) — vilket gör att hela sambandsformen närmar sig, MAC-sambandet nedan, funktionen för 1/d⁴ då d går mot a-gränsen. Se mera utförligt i Korrektion för växande avstånd.

Sambandet som anges i modern akademi är till jämförelse [‡]

F/A = ħcπ²/240d_z⁴ ........................ Casimir-sambandet i MAC,

se exv. Wikipedia Casimir effect, Casimir’s calculation 2010-09-20

~ (1,3 t27)/d_z⁴ ........................ N/M²

Materialparametrar anges inte i wikipediaartikeln (men antyds möjligen enligt ”the precise value depending on surface geometry and other factors”). Se även den grafiska jämförelsen mellan de olika typerna i inledningen.

Jämförande resultat

Jämförande resultat

Med referens till den tydligen allmänt generaliserade uppgiften från Wikipedia på d~10 nM med F/A = 101 325 Pa = 1atm kan vi pröva formen tillsammans med resultatet från sämsta fallets TNED-beräkningar för antalet elektronringar i elektronmassan som lägst 177062 genom att insätta det värdet som en första prövande grovform för n/4 (=177062), då vi inte har någon annan referens att utgå ifrån. Beräkningen finns i Kalkylkortet (Tabellflik 1, Casimireffekten). Beräkningarna visar (vid rumstemperatur) med värden i nanometer (nM=t9 M) för avståndet mellan idealt plana elektriskt oladdade materialytor respektive för ämnena Järn (26Fe58) och Nickel (28Ni59)

d, nM ämne Casimireffekten enligt TNED vid rumstemperatur och F/A = 101 325 Pa = 1 atm, n=708248

———— —— ———————————————————————————————

8,70832 Järn ₂₆Fe⁵⁶

9,26585 Nickel ₂₈Ni⁵⁹

för F/A = 101 325 Pa = 1 atm. Den jämförande uppgiften från Wikipedia är ospecificerad (material anges inte).

Med andra ord och sett enbart till den möjliga samhörigheten (9,26/10=92,6% träff), en mer eller mindre direkt fullträff.

Med det mera reguljärt härledda värdet på n [Utförligt i Antalet element i e] lika med 673 026 ges motsvarande värden

d, nM ämne Casimireffekten enligt TNED vid rumstemperatur och F/A = 101 325 Pa = 1 atm, n=673026

———— —— ———————————————————————————————

8,93588 Järn ₂₆Fe⁵⁶

9,50695 Nickel ₂₈Ni⁵⁹

för F/A = 101 325 Pa = 1 atm.

Med maxgränsen insatt vid ca 50 µM ges f.ö. ekvivalenta värden TNED-MAC då materialseparationen närmar sig den gränsen.

Resultatet endast understryker att man inte kan fälla något direkt avgörande om TNED-sambandet är det som verkligen gäller med mer än relativt omfattande materialtest har utförts i syfte att klarlägga den eventuella inverkan av olika material.

Men redan från en del av citatreferenserna [Lisanti et al., 2005, PhysicsWorld 2002, ARXIV-källan Svetovoy-Lokhanin 2008 i Sfär-Platta-samband, (m.fl.)] står det klart att de mätningar som redan gjorts på Casimireffekten uppvisar delvis stora differenser mellan teori och praktik.

Casimir-effekten | Casimir-kraften | Från Hendrik Casimir 1947

Casimir-effekten, utförligt enligt relaterad fysik

Se även från INLEDNINGEN med kort översikt

Från illustration i LJUSETS POLARISATION.

Casimir-effekten

Från 1948 (i samband med Lamb-Retherford-experimentet 1947 och förklaringen samma år från Bethe).

Alla materials uppvända utåtsida uppvisar ENLIGT TNED elektronmassornas τ-ringar — ELEKTRONMASSANS KOMPONENTER — som på olika sätt befinner sig i olika bindning till sina moderatomkärnor: Bilden infinner sig spontant: atomerna/materialen uppvisar gemensamt delade, kollektiva, elektronmassor.

Då avståndet mellan två (plana) materialytor kommer in i området för τ-ringarnas avståndskopplingar till atomerna, börjar också föreningsytan alltmer uppföra sig som en sammansvetsad enhetlig materialdel: en motsvarande attraherande kraft — atomattraktion enligt TNED — gör sig gällande mellan de åtskilda föremålen.

I MAC, där elektronmassans komponenter bannlystes från 1927 [‡5], kan man inte — följaktligen, då komponenterna inte längre beaktas — förklara fenomenet på något annat sätt än att tillskriva ett motsvarande fiktivt beteende hos tomrummet, ’vakuumfluktuation’ genom Plancks konstant (h) på Heisenbergs osäkerhetsprincip. Se särskilt jämförande citerad beskrivning i Teorin för elektronmassans komponenter, där beskrivs MAC-grunderna mera ingående till ’vakuumfluktuationerna’.

I TNED däremot kan fenomenet — denna framställning till vidare prövning för TNED — återföras på en regelrätt attraktion atomkärna-elektronelement tillsammans med signifikanta materialparametrar (atomvikt, täthet, medelatomavstånd, temperatur, värmeisolation och elektrisk ledningsförmåga), och som kommer att beskrivas mera detaljerat i denna presentation.

Enligt TNED: Från ett visst minsta avstånd (som beror på hur materialet uppvisar sin elektronringbindning) flyter τ-ringarna in i varandra, och det blir omöjligt att undvika att ringarna tar varandras materialatomkärnor för »sina». Därmed har en naturlig Coulombiskt grundad attraktionskraft etablerats mellan materialytorna.

Artikeln på Wikipedia anger ett exempelvärde typ 10nm (som betyder ca 30 medelatomavstånd i ett fast ämne).

Artikeln på Wikipedia (nedan) beskriver principen enligt MAC:

”In a simplified view, a "field" in physics may be envisioned as if space were filled with interconnected vibrating balls and springs, and the strength of the field can be visualized as the displacement of a ball from its rest position.”,

@INTERNET Wikipedia Casimir effect, Vacuum energy 2010-09-19

http://en.wikipedia.org/wiki/Casimir_effect

Casimireffekten, härledningen i TNED

Se även Mera Teoretiskt Utförlig Härledning

Praktisk teoretisk bakgrund

Casimir-effekten i relaterad fysik (TNED)

F/A = ke²Z[d_z²d_xd_y]^–1[n]^–1

————————————————————————————————

Faktorerna Znd_x d_y ingår inte i Casimirsambandets etablerade form — dessutom finns ytterligare (här veterligt ännu Sep2010 forskningstekniskt obeprövat i Casimireffektens ljus) som har utelämnats för den enkla framställningens skull (temperaturberoende, frekvensberoende, optiska parametrar …).

Vid genomgången av den (Aug2010) uppmärksammade s.k. Casimir-effekten (1947|48) med sambandet F/A=ħcπ²/240d⁴ [‡] — uppmärksammat i samband med den allmänna genomgången av artiklarna i MAC på ämnet PARBILDNING (’vakuumfluktuationer’) — TYCKS återigen TNED ha kommit till prövande undsättning i förklaringen av fenomenets fysik, nedan.

Praktisk teoretisk bakgrund:

Såväl beträffande de sammanhållande krafterna för förenade atomer till molekyler [Ström-, kraft- eller ’kemi-’ekvationen i TNED, F(BT)+F(eZ)=0)], som beträffande generellt sammanhängande atomgitterplan i ett ämne som bildar hela materialets sammanhängande hållfasthet, hänger hela den sammanhållande fysiken alldeles avgjort på elektronmassan, närmare bestämt elektronmassans komponent — massdelen — i formen av den här benämnda (τ, Grek. t, tau) τRingen. Från Spektrum tillsammans med Atomkärnans härledning är antalet beräknat till minst 177062; Dessa tillsammans formar — här till vidare prövning — det elektriska elementarkvantumet e=1,602 t19 C som vi kallar elektronen.

Om två normalt åtskilda material närmas varandra, är det givet — och ingenting kan hindra det — att domänerna med τRingar som vätter mot varandra och med visst näravstånd (inom hundratal-tusental atommedelavstånd, grovt tiondelar-hundradelar av mikrometer) kommer att börja anta varandras motsvarande moderatomkärnbindningar över materialgränsen (konv. Knudsen-skiktet) mellan de två föremålen. Ytterligheten, som vi får förstå saken, blir då föremålen pressas ihop så mycket att de har förenats i form av ett sammanhängande material [Se Kallfogningsgränser]. Och det är (om inte förr) uppenbart att den föreningsbilden påtvingar oss föreställningen om en ATTRAHERANDE sammanhållande KRAFT mellan materialdelarna åtskilda av ett geometriskt plansnitt genom materialet. Med hjälp av elektriska kraftlagen [F=k(Q/d)²] bör vi därför, och tydligen, också kunna formulera ett tämligen preciserat uttryck för hur den attraktionskraften ser ut rent matematiskt — Se HÄRLEDNINGEN.

WikiCasimirEx

”In fact, at separations of 10 nm—about 100 times the typical size of an atom—the Casimir effect produces the equivalent of 1 atmosphere of pressure (101.325 kPa), the precise value depending on surface geometry and other factors.[7]”,

@INTERNET Wikipedia Casimir effect 2010-09-20

Casimirsambandet

MAC

F/A = ħcπ²/240d_z⁴ ........................ Casimir-sambandet i MAC,

se exv.

@INTERNET Wikipedia Casimir effect, Casimir’s calculation 2010-09-20

~ (1,3 t27)/d_z⁴ ........................ N/M²

NOTERING 1. Inga primärt särskiljande materialparametrar ingår (atomvikt, täthet). ħ=h/2π.

NOTERING 2. För att inte d(z) ska urarta vid NOLLAVSTÅND måste d(z) vid noll betyda atommedelavståndet i materialets normala atomgitter så att nollavståndet får samma betydelse som ett ordinärt plansnitt genom materialet. Denna detalj omnämns inte i wikipdeiaartikeln (heller inte observerad på andra ställen).

NOTERING 3. Oberoende av Notering 2 ovan ges det orimliga resultatet att (t.ex. för Järn) materialets brottgränshållfasthet (4 T8 Pa för segjärn [‡]) uppnås innan materialets atommedelavstånd uppnås; sambandet ovan ger för 4 T8 Pa värdet drygt 1 nM [1,34 utan Noteringen i 2 och 1,115 med] att jämföra med råjärnets kubiska atommedelavstånd (vid rumstemperatur) 0,228 nM. [TNED-sambandet däremot ligger på den säkra sidan om brottgränserna; Det krävs extra inskjutningar för att uppnå brottgränsvärdets nivå [vilket också bekräftas av forskningen på området materialbildning under höga mekaniska tryck], se utförligt i Brottgränserna i Casimirsambandet].

Enbart av det skälet ser vi här tydligare vilka typiska teoretiska problem man har att brottas med i MAC för att få ihop det med Casimirsambandet, se även i Citatdelen. Av de studerade webbkällorna i ämnet, tycks dock ingen omnämna just detaljen med Casimirsambandets omöjliga koppling till materialens brottgränsvärden.

d_z anger avståndet mellan materialen (som förutsätts idealt plana, elektriskt oladdade).

hc-faktorn — leder till en approximation sett från TNED

AV PRINCIP kan vi se att varje material, materie- och massform i sin allmänna form (Planckstrålningen) innefattar en viss mängd egenenergi enligt Planckenergiformen E=hf. Med referens till neutronkärnan (mcd) och dess spinnradie (idealt d=c/f) ges till exempel totala genomströmningsenergin E=hf=mcd·c/d=mc². Varje motsvarande rymdavsnitt med motsvarande ’spinnradie d’ kan på samma sätt beskriva den aktuellt lokalt inneslutna egenenergin. På den vägen får man alltså en principiell sambandsform som uttrycker ekvivalens med elektriska kraftlagens form Fd²=ke² motsvarande Fd²=hc eftersom Fd²=Fd·d=Ed=hfd=mc²d enligt utläggningen nyligen ovan. Genom F=hc/d² ges alltså principiellt samma grundform som i fallet med elektronkomponentens (τRingens) elektriska attraktionsdel mot sin moderkärna. Dvs., sambandsformerna genom respektive elektriska kraftlagen (Fd²=ke²) och Planckenergin (Fd²=hc) blir analoga:

Analoga Fd²-former

Undersöker vi elektriska kraftlagen Fd²=ke² ser vi att analoga former ges via h·c=mcd·c=mc²d=Fd·d=Fd², så att

[Fd²]₁ = ke² = (1/[8,8543 t12] VM/AS)(1,602 t19 C=AS)² = 2,89848 t27 JM

[Fd²]₂ = hc = (6,626 t34 JS)(2,99792458 T8 M/S) = 1,98642 t25 JM (68,533326ggr [Fd²]₁);

[Fd²]₃ = ħc = hc/2π = 3,16148 t26 JM (10,907391ggr [Fd²]₁)

Den springande punkten

Den springande punkten i sammanhanget är emellertid att det, uppenbarligen enligt TNED (relaterad fysik), bara finns en och endast en enda komponent att upphänga hela dynamiken på — även med »enbart beaktande av alternativet Planckenergin Fd²=hc». Nämligen τRingen i e. Det finns, vad vi vet, ingen annan möjlig aktiv komponent i den relaterbara ordinära massfysikens elektronladdningsmassa som kan utverka en kraftvariation över avstånd. Frånses den möjligheten återstår bara det nu i MAC antagna alternativet med ’fluktuerande vakuum’.

Då τ-ringen i e inte finns observerad i modern akademi, måste man uppfinna en fiktiv kraftagent, en spektakulär ’vakuumfluktuation’, och som bara, tydligen, kan återföras på just Planckenergin Fd²=hc.

Därmed samhörigheten.

hc-faktorn — eller bara h-faktorn (tillsammans med 2|π; tecknet ħ brukas allmänt för h/2π) — brukar också användas generellt i MAC som substitutet för ’zero-point energy’ [Se även @INTERNET Wikipedia Zero-point energy, Varieties 2010-09-20], typ ħω: Genom Heisenbergs osäkerhetsprincip från 1927 [pλ=h=6,626 t34 JS (Gamow s108n)] lämnas — för samtliga MAC-fysikens fall — alltid en motsvarande kvantitativt obestämd del kvar mellan 0-h. I MAC har man tagit fasta på den öppningen som en ’tunnel’ till ’allt möjligt underbart’ som kan formuleras matematiskt och som kan studeras i något motsvarande verifierande experimentellt ljus.

Som framgår (för den som är bekant med TNED-grunderna) finns bara ett utfall av den historien: Förr eller senare kommer ett (kraftigt) genombrott.

Korrektion för växande avstånd

2010IX21

Korrektion för växande avstånd

CASIMIREFFEKTEN I TNED

Varje kvadratblock gömmer en ideal medelatomavståndskub, atomkärnan (inte synlig) i mitten.

Vartefter avståndet mellan materialdelarna ökar, och τ-ringarna kan fluktuera i mellanrummet, tappar den enskilda τ-ringen (ovan höger, idealt) alltmer fokus på sin individuella moderatomkärna: Istället för en alltmera noggrann ’kubstråle’ till moderkärnan, ges en medelfördelning på alla ingående kubytors atombidrag och som därmed försvagar den idealt närverkande en-till-en-kraftverkan med växande avstånd [Se även i Distansparametern]. I utvecklingsblocket nedan tas den distansbildningen som grund för att visa ett relativt enkelt sätt att funktionsbilda ett exponentiellt avtagande, och som kan användas som en första approximation i sambandsformen generellt.

Hur man öppnar (eller stryper) en variabel med variabelns linjära succession

Typformen

d_xy²

i föregående [‡] ke²Z[(d_xy+d)²d_xy²]^–1[n]^–1

skulle här behöva modifieras med den ordinära variabelparentesen

(d_xy+d)²

i formen med

d → 0 .................. maximalt näravstånd

d → d .................. maximalt fjärravstånd

med typfunktionen

(d+1)⁰ – 1 → 0 .................. maximalt näravstånd

(d+1)¹ – 1 → d .................. maximalt fjärravstånd

och som kan realiseras (en första approximation) enligt

(d+1)^m – 1 ;

m = d/a ;

d/a → 1 med d=a ;

d/a → 0 med d=0 ;

så att vi får faktorfunktionen

(d_xy+[d+1]^d/a–1)²

;

Sambandet totalt därmed, så långt,

F/A = ke²Z[(d_xy+d)²(d_xy+[d+1]^d/a–1)²]^–1[n]^–1

En första grovPrövning visar att a~50-100 µM ger hyfsad avstämning — men inom de typiska ’kaotiska’ referensvärden som Casimir-litteraturen (ännu Sep2010) uppvisar [Se jämförande grafer i Inledningen].

Se även de aktuella beräkningarna i Kalkylkortet.

Se även citatreferenserna till Casimireffekten, Lisanti et al., 2005, PhysicsWorld 2002, ARXIV-källan Svetovoy-Lokhanin 2008 i Sfär-Platta-samband, (m.fl.) — önskemålet framgår med en mera preciserad mätbild (på många olika material).

Maxgränsen i mätningar

CasimirDraget kan inte tillämpas i någon egentlig mening för avstånd över grovt 100 µM = 0,1 mM, se citat nedan. Andra närliggande material, samt även rumstemperaturen, spelar in alltmer då kropparna lämnar domänen för Knudsen-skiktet (den molekylära gränslokalen in till begreppet ’material’, speciellt mellan två olika dito).

[SYNBARHETSGRÄNSEN mellan två åtskilda plana hårdmetallytor ligger f.ö. runt 2µM med ett obeväpnat öga (testat med vanlig mikrometerskruv i ljusspringan mellan kontaktytorna)].

”Jens Gundlach and colleagues at Washington, for example, have used a torsion pendulum to determine the gravitational force between two test masses separated by distances from 10 mm down to 220 µm. Their measurements confirmed that Newtonian gravitation operates in this regime but that the Casimir force dominates at shorter distances.”,

(man måste logga in, men det är helt gratis)

PHYSICS WORLD — The Casimir effect: a force from nothing 2002

http://physicsworld.com/cws/article/print/9747

Kurvorna nedan visar de olika sätten MAC-TNED — och hur (liten) skillnaden är, se även från Inledningen:

y = x^–2[(x)^m]^–2 — Lambskiftet

x

ÖVRE m = 1 ........................ motsvarar MAC-formen med d ⁴

UNRE m = x/a ..................... motsvarar TNED-formen med separerade d₁ ²d₂ ² ; a=1 i figuren

Med a>1 kommer Undre kurvan att närma sig den Övre kurvan men skära denna (närmaste matchningen här är ca a=1,5).

Graf unit100

([x]'–2)([(x)'x/1]'–2)

Det verkar (ännu Sep2010 generellt ytterst) svårt att få fram några mera övergripande enhetliga CasimirMätData — ämnet verkar synnerligen kaotiskt på sitt sätt. Det är också erkänt svårnavigerat då känsligheten i mätningarna är stor och parametrarna delvis okända.

Jämför:

”But despite the intensive efforts of researchers in the field, many unsolved problems about the Casimir effect remain. In particular the seemingly innocent question of the Casimir force within a single hollow sphere is still a matter of lively debate. People are not even sure if the force is attractive or repulsive. Hendrik Casimir himself thought about this problem as early as 1953 while looking for a stable model for the electron. Half a century on, the mysteries of the Casimir force are likely to keep us entertained for many years to come.”,

(man måste logga in, men det är helt gratis)

PHYSICS WORLD — The Casimir effect: a force from nothing 2002

http://physicsworld.com/cws/article/print/9747

Avslutning Casimir

2010IX22

Avslutning

CASIMIREFFEKTEN

Citatreferenserna [Lisanti et al., 2005, PhysicsWorld 2002, ARXIV-källan Svetovoy-Lokhanin 2008 i Sfär-Platta-samband, (m.fl.)] i Casimireffekten vittnar själva om önskemålet med en mera preciserad mätbild (på många olika material). Det är en forskning som också en del (lyckligtvis) intresserar sig för, och som därför helt säkert inom den närmaste framtiden (enstaka år från nuv. 2010) kommer att få skörda en bättre naturvetenskaplig fenomenkontur.

Tills dess är ovanstående till synes i fördel för TNED (visserligen intressant, men strängt taget likväl) oavgjort.

CasimirEND.

ELEKTRONEN OCH ELEKTRONMASSANS KOMPONENTER · Antalet elektronelement i elektronen

BILDKÄLLA: Författarens arkiv · Bild46R2009· 17 MAJ2009 · Nikon D90 · Detalj

Antalet elektronelement i elektronen

Se även Inverkan av n på föregående beskrivningar.

Grundräkningen från ELEKTRONMASSANS KOMPONENTER ger ett sämsta fallets lägsta värde n=177062. Det mera avancerade resultatet här uppvisar n=673026. De enda föregående beräkningar som påverkas av det resultatet i TNED är den generella KEMISKA KOPPLINGENS GRÄNSSPÄNNING [U(G)]. Se särskild beskrivning i Inverkan av n på föregående beskrivningar.

Antalet masselement i elektronmassan

Se även sammanställning i ELEKTRONELEMENTETS ANTAL OCH DIMENSIONER i EelektronenIntro.

Det har påpekats vid flera tillfällen i Universums Historia att MASSFYSIKEN i MAC står orepresenterad. Likväl — vilket kommer att framgå i det följande — är massfysikens MATEMATIK (till viss del, men på ett kaotiskt sätt REDAN) representerad i MAC — men i former som (ännu Sep2010) saknar EXPLICIT formulering i gängse kretsar. Vi studerar innehållet.

2010IX27

TEORI — E = E₀[(1/n_a + 1/3n_b)]²/n_cn_τ

———————————————————————————————————————————

HÄRLEDNING TILL ANTALET ELEKTRONELEMENT I ELEKTRONMASSAN — preliminär framställning Sep|Okt2010

Från ATOMKÄRNANS BRUM PÅ ELEKTRONMASSANS KOMPONENTER

Genom Casimireffekten och Lambväxlingen har en möjlig metod visat sig för vidare prövning av och i TNED med en direkt bestämning av antalet masselement i elektronen (antalet τ-ringar). Följande sammanställning visar sambanden med utveckling och resultat.

FSC

OM med grund i den givna sambandsformen (1) nedan (FSC konv., Fine structure constant, sv. FinstrukturKonstanten, [ref. @INTERNET Wikipedia Fine-structure constant 2010-10-15] vi härleder den integrerat nedan i FSC i TNED)

(1) FSC = k_e·e²/ħc ; k_e = 1/4πε₀

= e²/4πε₀ħc ; ε₀ = 1/R₀c₀ ; ħ = h/2π

= e²R₀/2h ; R₀ = 376,72555 Ω=V/A

= 1/o ;

o = 137,0580237 ;

vi — tillsammans med TNED-villkoren för Lambväxlingen (4/3, se ATOMKÄRNANS BRUM PÅ ELEKTRONMASSANS KOMPONENTER) — utnyttjar den konventionella formen (@INTERNET Wikipedia, Lamb shift 2010-09-27)

(2) 1/n = [FSC⁵·m_ec²/4e] ;

så att vi får

(3) (4/3)²/n = [FSC⁵·m_ec²/4e] ;

med

1/n = [FSC⁵·m_ec²/4e](3/4)² ;

n = [FSC^–5·4e/m_ec²](4/3)² ;

n = [FSC^–5·e/m_ec²](8/3)²

= [FSC^–5·4e/m_ec²](4/3)²

= [FSC^–5·e/m_e(c/2)²](4/3)²

= [FSC^–5·e/m_ec_z²](4/3)²

= [(2h/e²R₀)⁵/(U_e=E_e/e)](4/3)² se utförligt i nr (15)

= [(2h/e²R₀)⁵/(m_ec_z²/e)](4/3)²

= [(2h/e²R₀)⁵e/m_ec_z²](4/3)² utförligt i nr (26)

= 673 026,65 ........................ från Kalkylkortet

kan vi också söka en möjlig härledning till det så erhållna n antalet elektronelement i elektronmassan i TNED genom att först utnyttja 3D-deriveringen för FSC-komponenten — med förutsättningarna i TNED, vidare nedan — enligt

(4) 60 = [1/x²]·(x⁵)’’’ = [1/x²](5·4·3)x² = 60

Om (1/FSC)² integreras genom d(xyz) bildas integrationskoefficienterna 3·4·5=60

och därmed sätta

(5) s = 60

i differentialekvationen (som strax ska förklaras)

(6) s·n² dn_x dn_y dn_z = ndU

n² tillhör Resonansvillkoret i Spektrum, hur det kopplar till FSC visas i FSC i TNED

(7) n² dn_x dn_y dn_z = ndU/s ; 1/s reduceras i HL om samma 1/s återfinns i VL

Vi förenklar

(8) dn_x dn_y dn_z = dn_xyz

så att vi får en enklare överblick genom

(9) n² dn_xyz = ndÛ

;

(10) n² = 2h/e²R₀ .................. Se FSC i TNED.

;

(n)²-formen ingår i atomens energispektrum genom RESONANSVILLKORET, formen n² — tillsammans med elektronmassans divergensenergi (E=Fr) i dess fördelning över elektriska laddningen (Q=e), analogt elektronens ekvivalenta elektriska (egen-)potential [E/Q=k(Q/r)]. Vi får då differentialformen i (11) och varianten i (12);

;

(11) (n²)(1V)/dU = n/dn_xyz ;

;

Elektronspänningen i neutronen — (n²)(1V)/dU — är lika med rymdutsträckningen hos elektronelementet i elektronmassan — n/dn_xyz;

Elektronspänningen i neutronen:

(n²) går ut på elektronantalet (m_n/m_e) i neutronen [Se FSC i TNED]; U avser masselektronspänningen E_e/e=Ue; Förenklat uttryckt kan man säga att kvoten (n²)(1V)/dU beskriver Elektronspänningen i neutronen.

Rymdutsträckningen hos elektronmassans elektronelement:

n är antalet elektronelement i elektronmassan och vars värde ska beräknas; n fördelat över den differentiella 3D-rymden [dn_xyz] för neutronelektronantalet (n²), dvs. varje elektronelement per 3D-rymd, kan då förenklat sägas beskriva Rymdutsträckningen hos elektronelementet (som finns i elektronmassan).

(12) n²/n = dU/dn_xyz(1V) ;

;

Atomkärnans impulsenhet (n²=2h/e²R₀) från N3m20-aggregatet i ATOMKÄRNANS HÄRLEDNING förhåller sig till det fasta antalet (n) delimpulsringar ([tau-]τ-ringen) i elektronmassan som elektronspänningen (U, se nr15 nedan) förhåller sig till varje elektronrings metriska 3D-fördelning i rummet via koordinaterna xyz;

Vi sätter n(xyz)-differentialen mera preciserat som 3D-differentialen

(13) dn_xyz = dn_x dn_y dn_z

så att vi får differentialekvationen

(14) n² dn_x dn_y dn_z (1V) = ndU

;

Spänningsformen m_ec_z² i (3) har sammansättningen

(15) U = E/Q

= mc²/e ;

m = m_e

c = c₀/2

= c_z ......................... se Potentialbarriären (w=c=c₀/2), ljusets g-beroende, stället där Q tas ;

U = m_e·c_z²/e

;

»Atomkärnans brum» på elektronmassan — men som inte ingår i den enkla matematiken för spektrum och som, tydligen, visar elektronmassans komponenter — betyder som ovan i ABPEK en tilläggsfaktor på (4/3)² till U-ledet så att dess fullständiga form blir

(16) U = (m_e·c_z²/e)(4/3)²

;

Den kommande 3D-integrationen över n²-enheten kommer att ge nämnarfaktorerna (3·4·5)=60 i vänsterledet. För att få ekvivalens med högerledet måste vi kunna härleda en motsvarande reducerande faktor (s=60) som omnämndes i början (5), motsvarande Û=U/s, och så att bägge leden blir ekvivalenta efter integrationen — och förutsatt att den här använda integralformen verkligen är relevant;

;

(17) s = 60 ;

(18) Û = U/s ;

= (m_e·c_z²/e)(4/3)²/s ;

(19) n²/n = dÛ/dn_xyz(1V) ;

(20) n²dn_xyz(1V) = ndÛ ;

;

s-formens fysiska ekvivalent

För att den redan observerade n-formen i (3), n=673 026=[FSC^–5·e/m_ec_z²](4/3)², ska bli härledningsbar måste vänsterledets integralnämnarkoefficienter i (20), n²dn_xyz, och som redan omnämndes i (4), 3·4·5=60, ha en väl relaterbar make i högerledets elektronspänningsekvivalent i (15), U=m_e·c_z²/e. I TNED — men inte i MAC —finns den möjligheten genom att NEUTRONKVADRATEN innefattar faktorerna (m_e/e) med grundläggande adress till samtliga atomer enligt (21) nedan.

2010IX28

Atomernas Materialsubstans — grundformen för m_e/e från NEUTRONKVADRATEN

— Om vi utnyttjar Neutronkvadraten i TNED

BILDKÄLLA: Författarens arkiv · MONTAGE: stora 17Jun2013 E19 Bild163 · Nikon D90 — lilla Neutronkvadratens grundform — Masstalsradien A=60 formar Neutronkvadratens byggnad i kärnfysiken enligt TNED.

Vattensplasharna [delelement från PARTIKELKOLLISIONER med höga energier] illustrerar också [ENERGILAGEN] atomkärnans odelbarhet [NEUTRONFRAGMENTEN] enligt TNED: Avdelade droppmassor som återförenas syns INTE som »snurrande objekt» inuti moderkroppen. Atomkärnan är partikelfri enligt TNED. Bergsäkert.

Genom att alla atomkärnor enligt TNED består av A(1838,624)e [minus delar som bränns av via massdefekterna] — från neutronens sönderfall med massan och laddningen för elektronen — får också alla atommassor samma effektiva massa-elektronladdningstäthet:

(21) 5,68572 t12 KG/C = m_e/e = m(A) · [A(1838,624)e]^–1

= m(A) · [A(m_n/m_e)e]^–1

= m(A) · [A(m_ne/m_e)]^–1

= m(A) · [Am_n(e/m_e)]^–1

= m(A) · (m_e/e)[Am_n]^–1

; det värdet beskriver alltså en ämneskonstant, »atomernas materialsubstans».

— kan neutronkvadratens specifika (m_e/e), via neutroncirkelns radie på masstalet r=60, uppfattas som

(m_e/[r]_Ae) = (m_e/60e)

med föregående

s = [r]_A=60

;

— Neutronkvadraten som sådan visar i sin neutroncirkel en obalans mellan å ena sidan den innefattade elektronladdningen (e) i neutronen och å andra sidan neutronradien med masstaletA=60 (eg. 58,69548); För enhetlighetens skull, skulle vi vilja att också A för neutronmasstalet vore satt på A=1, analogt ett enhetligt (m_e/e) via neutronen.

— Neutronkvadratens (m_e/e) alias (m_e/60e) kan alltså förstås ha antingen 60ggr högre massa än den verkliga neutronen [m_e/60], eller ha 60ggr för liten inneboende elektronladdning i förhållande till masstalsradien.

— För att få ut det enastående (m_e/e) i neutronen — och förutsatt framställningssättet är rationellt — måste alltså en motsvarande multiplikation med [r]_A=60 göras — och som därmed (perfekt) matchar villkoret med motsvarande integralkoefficienter 3·4·5=60 från vänsterledet. Överflyttningen skulle då ge

(m_e/e) = 60(m_e/[r]₆₀e)

(=) (m_e/e)

och därmed balans i härledningen.

Genom att neutronkvadratens massradie emellertid R=60 INTE är strängt exakt (58,69548), blir nettovinsten i utflykten att ALLA grundparametrar i kärnfysiken — alla atomer, alla ämnen, alla material — kommer med för optimal analys.

BILDKÄLLA: Författarens arkiv · MONTAGE: stora 20Aug2013 E25 Bild110 · Nikon D90 — lilla Neutronkvadraten — Grundnukliderna — alla atomer, alla ämnen, alla material — ALLA MÖJLIGA UNIVERSUM enligt TNED.

ANTALET n MASSELEMENT I ELEKTRONMASSAN

Med den kopplingen relevant, får högerledets U-form en väldefinierad betydelse endast om masstalet A=1 preciseras i neutronkvadratens (m_e/e); Antas sammansättningen fås alltså

(22) U[e] = (m_e·c_z²)/[r]_A=60e · (1V) ;

med nominella värdet för [r]_A=60=s lika med 60 .

Därmed är alla parametrar härledda [eg. relaterade på redan kända, beskrivbara grundformer].

Integrationen på differentialekvationen

(23) n²dn_xyz (1V) = ndÛ ;

skulle då ge

[Notera att antalet integrationer för högerledet kan göras godtyckligt genom att integrera successivt på integrationskonstanten (Se NOLLFORMSALGEBRAN) U/∞[x] /∞[y] /∞[z] /∞[å]… = d^nU; alla d[X]U behöver inte vara lika]

(24) ∫ n² dn_xyz(1V) = ∫ ndÛ ;

∫ ∫ ∫ n² dn_x dn_y dn_z = ∫ ndÛ/(1V) ;

(=) [n²⁺¹/(2+1)]; [n²⁺¹⁺¹/(2+1)(2+1+1)]; [n^2+1+1+1/(2+1)(2+1+1)(2+1+1+1)]

med lösningen = n⁵/(3)(4)(5)

(25) = n⁵/60 ;

n⁵/60 = nÛ/(1V)

= nU/s(1V) ; s = [r]_A=60 = 60

= nU/[r]_A=60(1V) ;

n⁵ = 60nU/[r]_A=60(1V) ; 60 = [r]_A=60 = 60

= nU/(1V) ;

n = n⁵U^–1(1V) ;

(26) = (2h/e²R₀)⁵(e/m_e·c_z²)(4/3)²(1V)

(27) = 673 026,65 = n₀ ;

(28) n = [n⁵·(1/60)[r]_A=60e/m_ec_z²](4/3)²(1V) ;

;

Tas optimala värdet för [r]_A=60=s lika med neutronkvadratens grundvärde 58,69548 ges ett motsvarande lägre n-värde

(29) n_A=58,7 = [(60)/(58,69548)=0,978258](673 026,65)

= 658 393,7 antalet masselement i elektronmassan

Exakta n-värdet

Det exakta n-värdet — 673 026

Optimalvärdet via masstalsradien 58,7 i samband (29) är inte realistiskt med referens till att värdet 60 är det som använts i framräkningen av atomvikterna (via atomära massdefekterna från neutronkvadraten). För enhetlighetens del, i varje fall, är det därför mera rimligt att utgå ifrån samma preferens i frågan om n-talet. »Exakta n-talet» bör alltså bli just 673026 (+0,65).

Epilog

Det som (ev.) kan avgöra värdet av ovanstående resultat är mera noggrant uppmätta värden för olika material i Casimireffekten — n-talet ingår i Casimireffekten enligt TNED som avgörande faktor, men har i dagens läge (Okt2010) ingen motsvarande bild i forskarvärlden.

Mätavvikelserna i Casimireffektens experimentella ljus är (enligt genomlästa rapporter, mer av regel än undantag heller) INTE marginella (som också kunde förväntas i ljuset av TNED: materialkonstanter preciseras inte konventionellt i Casimireffekten). Teorin är också delvis ofullkomlig i vissa avsnitt som berör aktuella mätanordningar (sfär-platta), och inga mera exakta besked finns därför ännu (mätfelen kan i vissa fall uppgå till mer än 15%). Se vidare i Casimireffekten.

Inverkan av n på föregående beskrivningar

Inverkan av n på föregående beskrivningar

KEMISKA KOPPLINGENS GRÄNSSPÄNNING

Det mera precisa (preliminära) värdet för antalet masselement i elektronen som n=673026 från föregående GRUNDBERÄKNINGARNA i Elektronmassans Komponenter [n=177062] har ingen direkt dramatisk inverkan på redan genomförda beräkningar utöver de som berör KEMISKA KOPPLINGENS GRÄNSSPÄNNING [U(G)].

De beräkningsresultat som direkt påverkas i UNIVERSUMS HISTORIA av det högre n-värdet (~3,8 ggr högre än grundformen via N3m20-aggregatets sämsta fallets beräkningar) är de som berör BLIXTURLADDNINGENS FYSIK — se GRUNDRÄKNING:

Med grundformen för n från enbart N3m20-aggregatets sämsta fallets beräkningar:

U_G = k(e/rn)

= (1/4πε₀)(e/rn)

U_G = (9 T9 VM/C)(1,602 t19 C)/((177062)[r]/2)

ges i sämsta fallets värden (n-faktorn här den absolut minsta möjliga) med r=3nM medelavståndet mellan luftmolekylerna

= 5,4286 t6 V ~ 5,4 µV

som ger 1800V/M med 3nM mellan luftmolekylerna

Med utvecklingarna för n genom Casimireffekten och Lambväxlingen:

U_G = k(e/rn)

= (1/4πε₀)(e/rn)

U_G = (9 T9 VM/C)(1,602 t19 C)/((673026)[r]/2)

ges med r=3nM medelavståndet mellan luftmolekylerna

= 1,42817 t6 V ~ 1,4 µV

som ger 467V/M med 3nM mellan luftmolekylerna

OM elektriska konstantens k-faktor istället räknas på det enskilda elektronelementets Coulombkoppling UTOM sfärgeometrin, dvs., frånsett faktorn 4π (vilket har utnyttjats i utvecklingarna för n, speciellt i Casimireffekten), ges istället

U_G = (1/ε₀)(e/rn) ;

U_G = (1/[8,8543 t12 C/VM])(1,602 t19 C)/((673026)[r]/2)

ges med r=3nM medelavståndet mellan luftmolekylerna

= 1,79219 t5 V ~ 18 µV

som ger 6000V/M med 3nM mellan luftmolekylerna

BLIXTURLADDNINGENS FYSIK SKULLE kunna vara den tänkbara observationsgrund som kunde AVGÖRA vad som är vad. Som redan påpekats i nämnda avsnitt, saknas emellertid (veterligt ännu Nov2010) avgörande observationsdata. Tills vidare får det ovan nämnda tjäna som referensgrund.

FSC i TNED

FCS i MAC betyder Fine Structure Constant, sv. FinStrukturKonstanten. FSC skrivs konventionellt i MAC (Se FSC)

α = e²/4πε₀ħc, i TNED mera reguljärt via ekvivalenten e²R₀/2h (Se utvecklingarna överst i FSC). Beskrivningen nedan visar hur termerna kopplar till resonansvillkoret med huvudkvanttalet i Spektrum för härledningen av antalet elektronelement i elektronmassan enligt TNED. Se även TNED-grundformen i Elektronmassans Komponenter.

2010-09-28

RESONANSKRITERIET FRÅN SPEKTRUM n² — vi utvecklar efter fysikens mest elementära sambandsformer:

Härledningen till Resonanskriteriets elementära ekvivalent

(n²) = 2h/e²R₀ = o = 1/FSC = 1/α

;

d = ρn² ; från Resonansvillkoret i Spektrum

n² = d/ρ

= mcr/mcρ ; h=mcr ;

= h/mcρ ;

Från Elektriska laddningen Q = √ (m/R)(A/dT) ges

m = Q²R(dT/A) ; Vi utnyttjar Q=e och R=R₀ i elektriska konstanten R₀c₀=1/ε₀ ;

m = e²R₀(dT/A) ; Från Divergensen i Ljusfysiken gäller a=c/dT med dT=c/a ;

m = e²R₀(c/aA) ; Fortsättningen blir då

n² = h/mcρ

= h/e²R₀(dT/A)cρ ; Vi utnyttjar A=ρ² ;

= h/e²R₀(c/aρ²)cρ

= h/e²R₀(c²/aρ) ; Vi utnyttjar att a=2ρ/T² och ρ/T=c vilket ger ;

= h/e²R₀(c²/[2ρ/T²]ρ)

= 2h/e²R₀(c²/[ρ²/T²=c²])

= 2h/e²R₀(c²/c²)

= 2h/e²R₀

= 1/FSC

= 1/7,296179915 t3 ........................ från Kalkylkortet till Casimireffekten

= 137,058023738

;

EKVIVALENTA SAMBANDSFORMEN UTVECKLAD — belyst — ALTERNATIVT

;

Elektronmassan (från elektronladdningens kvadrat i Elektriska laddningen, se nedan) i Neutronimpulsmomentet mcr (för neutronens ytterradie, eg. 1,9926606, se Toroidytan i Kärnradierna del 2) kan tydligen skrivas på formen

(10) o = 2h/R₀e² .................. numerisk enhet; nämnaren: (V/A)(C=AS)²=VAS²=WS²=JS; bägge faktorleden ger JS

= 2(6,626 t34 JS)/(376,72555 Ω=V/A)(1,602 t19 C)²

= 137,0665

= 2mcr/R₀[(m/R₀)(A/dT)]_{ELEKTRONLADDNINGENS KVADRAT}

= mc2r/(m_e)(A/dT)

= mcr/(m_e)(A/[dT=c/a])

= mcr/(m_e)(aA/c)

= mc²r/(m_e)(a[A=kπr²])

= mc²r/(m_e)(akπr²)

= m(r/T)²r/(m_e)([r/T²]kπr²)

= m/m_eπk

= (1,0086652)/(0,000548598)πk

= (1838,623545)/πk

= (585,25205)/k ;

k = 4,2698401 = 4(1,06746)

Vi måste — veterligt —alltid räkna med vissa minimala korrektioner inom atomkärnans komplicerade kraftväv eftersom ingen egentlig bestämt ändlig STATISK formstruktur existerar (PASTOM), samt med hänsyn till flödet i kopplingen mellan kärna elektronhölje. Konstanten k antyder den delen.

ELEKTRONEN · rubriker

Framträdande — vetenskapshistoriskt

Kraftekvationen

Framträdande — Tekniskt TNED

Allmänna länkar

Upptäckt

Elektronmassans komponenter, storleksordningar

Elektronen och positronen

Ingen våg-partikeldualitet i TNED

Elektriska laddningen, detaljinnehåll

Atomkärnan, storlek

Atomära massenheten

Tau-teorin

Elektronen och Φ

Massframträdandeproblemet

ELEKTRONEN — Rubriker

BILDKÄLLA: Författarens arkiv · BildS09RF2010/2· 5JUN2010 · Nikon D90 · Detalj

Framträdande vet.h. [Västerl.]

2010IX7

Elektronen i TNED

Q(e) = 1,602 t19 C

m(e) = 0,000548598u ~ 0,511 MeV

u = 1,66033 t27 KG = (₆C¹²)/12

ELEKTRONEN (efter Thomson 1896|97 [‡1]) framträder spontant ur NEUTRONEN (efter Chadwick 1932 [‡2]) genom NEUTRONENS SÖNDERFALL och bildar tillsammans med neutronkärnans sönderfallsprodukt (protonen) en hel ATOM, en Väteatom (efter Fermi 1934 [‡3]). Elektronen i TNED är inte en partikel, utan en hop partiklar.

Generellt kallas elektronutgivning från atomkärnor för BETASÖNDERFALL (Meitner, Hahn, Ellis, Chadwick, 1911-1932 [‡3]). I vetenskapshistorien observerades betasönderfallet [‡3] (radioaktiva isotoper) före neutronen [‡2].

I TNED grundlägger Plancks konstant neutronen enligt ATOMKÄRNANS HÄRLEDNING; Neutronen bildar den materiella substansen i c₀-kroppen vars centrala del — UNIVERSUM — beskrivs av K-cellens värmefysik på K-cellens Allmänna Tillståndsekvation som på neutronkroppens bas ger GRUNDÄMNESBILDNINGEN genom fusioner (atomkärnor som förenas, se Fusionsringen) enligt EXOTERMISKA KÄRNREAKTIONSLAGEN — UNIVERSUMS HISTORIA.

Enligt TNED är elektronen INTE en partikel utan (via CENTRALKONTAKTERNA) en ständigt fluktuerande elektriskt laddad Q(e) massenhet m(e) som framträder successivt ur atomkärnan i den yttersta delen från atomkärnans utvidgning till atom, ursprungligen från neutronens sönderfall till Väteatom.

Elektronens koppling till moderatomkärnan i TNED beskrivs på det enskilda elektronelementets massform [okänt begrepp i MAC, i TNED benämnd tau(τ)-ring, se utförligt i SPEKTRUM OCH KVANTTALEN och ELEKTRONMASSANS KOMPONENTER] enligt kraftekvationen

Kraftekvationen

F_BT + F_eZ = 0 ....................... atomens kraftekvation i TNED

Atomen summerar nollkraft och nollmoment — atomen kräver ingen påfyllande energi för att fungera

Elektronen och elektronmassans komponenter — framträdande

BILDKÄLLA: Författarens arkiv · Bild2Excur9 · 20OKT2010 · Nikon D90 · Detalj

Framträdande, Tekniskt TNED

Elektronen

ELEKTRONEN infinner sig naturligt i TNED genom neutronens sönderfall; NEUTRONEN eller Planckringen h=mcr bildar materiens grundelement genom ENERGILAGEN tillämpad på ALLMÄNNA TILLSTÅNDSEKVATIONEN för den kosmiska c0-kroppen: Neutronkärnan är till naturen instabil — med impulsmomentet Plancks konstant h = mcr = neutronmassan×ljusTopphastigheten×neutrontyngdcirkelnsRadie, se Planckringen. I TNED framträder neutronkärnan som en utåt sett neutral kraftväv av 1838,624 ekvivalenta elektronmassor

neutronen	neutronens sönderfall	grundämnesbildningen

[=1818centralmassiv+18massdektsstock+2,624smörjmedel]e. För att uppnå stabilitet i sin tyngdcirkelekvation [J(0K)+3J(1K)=0] måste neutronen föra ut en elektronmassa med balansräkning via kraftekvationen [F(BT)+F(eZ)=0]. Det sker genom en inre ombyggnad med massdestruktion (m→γ), i TNED benämnd NEUTRINOSTRÅLNING.

Neutronsönderfallet bildar en ATOM. Närmare bestämt en Väteatom: den centrala (väte)atomkärnan med det yttre elektronhöljet.

Genom att neutroner antingen direkt, eller vätekärnor direkt, eller en kombination av bägge kan förenas via fusion [Se EXOTERMISKA KÄRNREAKTIONSLAGEN], kan fysikens alla möjliga atomer bildas från neutronen som grundindivid.

		Brotthållfasthet Separat Dokument Kovalenta bindningens geometri MATERIENS BROTTHÅLLFASTHET Grundämnesmetallernas Brottgränser EXPERIMENTELLT — beräknat
elektronresonanserna	grundämnenas kemiska förening	materialens hållfasthet

De elektriskt laddade elektronmassorna fungerar som elektromekaniska svängningsmassor kring atomkärnorna (Se från Spektrum) och som tillsammans med resonansvillkor (Se även Keplermomentet) leder till härledningen av GRUNDÄMNENAS PERIODISKA SYSTEM.

Med utfyllande elektronmassor mellan atomerna bildas så förutsättningen för interna s.k. molekylära bindningar — kristallerna, atomgittren. Därmed grundläggs alla materials termiska, elektriska-kemiska och optiska egenskaper.

BILDKÄLLA: Författarens arkiv · Björklöv1| 03Excur1 · 3OMAJ2009 · Nikon D90

Elektronen och elektronmassans komponenter · allmänna länkar

	Elektronens frigörelse ur atomkärnan
Elektronen	Atomkärnan | Elektronmassan	Artiklar som anknyter till elektronmassan NEUTRONSÖNDERFALLET Kärnmagnetismen · Planckringen Laddningsdeplacementet Elektronen från Neutronen ATOMKÄRNAN · PLANCKRINGEN h=mcr Allmän formbeskrivning Elektronmassans element · Ljusets polarisation N3m20 · Planckringen, atomkärnans härledning BT-fältet · ATOMKÄRNANS KÄRNMAGNETISKA TOROIDFÄLT Atomkärnans allmänna magnetiska yttoroidfält BT-fältet · Elektronmassans komponenter KÄRNANODEN BT-fältet · Elektronmassans komponenter
	Elektronens element

Elektronen och elektronmassans komponenter · Elektronen — upptäckt

BILDKÄLLA: Författarens arkiv · Bild109R2009· 17MAJ2009 · Nikon D90 · Detalj

Upptäckt

Elektronens upptäckt

Genom sinnrika experiment som genomfördes under 1800-talet [Se ELEKTRISKA LADDNINGEN] lyckades man påvisa att den elektriska laddningen av princip alltid uppträder i en minsta bestämd kvantitet Q(e)=1,602 t19 C. Med identifieringen av e som Väteatomens enda negativt laddade elektronmassa (0,00054859u ~ 0,511 MeV), har bilden av atomen med enhetsladdningar på 1e växt fram som den etablerade bild vi idag har av atomfysiken.

Elektronmassan kring atomkärnan beskrivs etablerat i MAC i formen av s.k. orbitaler, alltså motsvarande olika geometriska domäner som elektronmassan uppfyller i den omgivande xyz-rymden. Dock erkänns i MAC ingen åskådlig FORM eller UTSTRÄCKNING för elektronmassans innehåll [‡4].

Ett grundstudium i TNED som visar en motsvarande (primitiv, tyngdpunktsbaserad) spridning av elektronmassans komponenter kring atomkärnan finns i avsnittet om Elektronmassans momentrelaterade tyngdpunktsavstånd från Vätekärnan.

I TNED — men inte i MAC — kan atomkärnan frigöra (eller infånga) såväl elektroner [e(–)] som positroner [e(+)]. Positronen är då bara elektronladdningsmassans omvändning: motsatt laddning, motsatt ringspinn. Se vidare i Atomfysikens två kungsekvationer. Se även i PARANNIHILATION.

Elektronen och elektronkomponentens storlek relativt atomkärnan

Elektronmassans komponenter

ELEKTRONRINGENS STORLEK OCH ANTAL — i skalenlig illustration nedan tillsammans med neutronen-protonen

Enligt resultat från beräkningarna i Antalet n i e

Grundformen från Atomkärnans härledning 2002VIII9 Principles of Physics τ-ringen TNED-Basic — skalenlig DIAMETER i vy med neutronen-protonen Ø=r0/50	Grundformen utvecklad 2010IX27 genom τ-ringen Casimir-Lamb — skalenlig DIAMETER i vy med neutronen-protonen Ø=r0/190,05376
°	°
↑Från Spektrum via PLANCKRINGENS DIMENSIONER via MAX r0/50 Antal elektronelement i elektronmassan: n = 177 062	↑Från separat härledning med n = 673 026 via Lambväxlingens matematik Ringens diameter justerad till Ø=r0/50(673026/177062) = r0/190,05376

atomkärnan N3m20 med radien [tyngdcirkeln] r₀=1,37 t15 M — neutronen-protonen skalenligt med elektronmassans komponent [tabellraden i mitten ovan] efter diameter.

Elektronringarna [ ° ° ] under den mörkblå rubrikremsan lagda tillsammans tätt intill varandra som cylinder [linjebilden nedan] upptar längden 0,15r₀:

För n, se utförligt i Antalet element i elektronmassan.

2r_τ = r₀/50, n = 177062: ; diameter r₀/50

d_pKUB = 2r₀ ; KUBsida protonkärnan med omskrivna kuben

d_τKUB = [(2r_τ)³(n)]^1/3 ; KUBsida summan av alla elektronmassans komponenter med omskrivna kuber

d_τKUB/d_pKUB = [(2r_τ)³(n)]^1/3/2r₀ ; n = 177062GER 56,15% | förhållandet mellan kubsidorna

d_pSPH = r₀ ; SFÄRradie protonkärnan med omskrivna sfären

d_τSPH = [(4/3)πr_τ³(n) · 3/4π]^1/3 = [r_τ³(n)]^1/3 ; SFÄRradie summan av alla elektronmassans komponenter med omskrivna sfärer [maximalt toppspinnande ringar]

d_τSPH/d_pSPH = [r_τ³(n)]^1/3/r₀ ; n = 177062GER 56,15% | förhållandet mellan sfärradierna

2r_τ = r₀/190, n = 673026: ; diameter r₀/190

d_τKUB/d_pKUB = [(2r_τ)³(n)]^1/3/2r₀ ; n = 673026GER 23,06% | förhållandet mellan kubsidorna

d_τSPH/d_pSPH = [r_τ³(n)]^1/3/r₀ ; n = 673026GER 23,06% | förhållandet mellan sfärradierna

Elektronen och positronen

Elektronen och positronen

Som redan framgår ur ENERGILAGEN med primära massförstöraren (E=mc²), förutsätter den övergripande toroidaggregaturen i N3m20 existensen av en (β, gen. elektrisk) ±βn-struktur som garanti för den möjliga massdestruktionen (m→γ) enligt COEI (energins bevarande genom induktionen), se exempelfallet med Solens energiproduktion; massa till värme och ljus.

;

Massan i (m®g) förintas kvalitativt (strukturen, gravitationen) men bevaras kvantitativt (energin) enligt

b– + b+ = 0 ............... laddning

s_b– + s_b+ = 0 .............. spinn (rörelse)

m_b– + m_b+ = 2m_b ......... massa

 via

COEI:

U_ind = E=^UQ/Q_s = L(di/dt)k = Lk = k·RT·Q/T² = kRQ/T = kRI = kU. Massans kvalitativa struktur (E/c²) förintas, men energin bevaras genom masslös, induktiv överföring på andra elektriskt laddade systems masströgheter (Conservation of energy by induction).

Se utförligt i PARANNIHILATION.

Från PASTOM (massans principiella struktur) följer då att elektronen (e=–βn) och positronen (e=+βn) bildar (föreställer) en integrerad struktur av impulsmoment — spinnande strömringar på impulsmomentets form (J=mcr), generellt i TNED benämnda τ-ringar (τ, tau; Grek. t) och som får förstås integrerade med atomkärnans fraktala struktur enligt PASTOM. Se utförligt i Elektronmassans komponenter. Den vidare prövningen för denna struktur i TNED är framställd i NEUTRONENS SÖNDERFALL, SPEKTRUM, KVANTTALEN och PERIODISKA SYSTEMET. Som framgår av dessa jämförande prövningar innefattas tydligen modern akademisk teori som en primitiv aspekt, och det ser ut som att det toroidfraktala systemet (TNED) beskriver atomens verkliga fysik i detalj.

Speciellt att notera för spektrum och kvanttalen enligt TNED är att graden av finstruktur är obegränsad enligt PASTOM: elektronmassans dynamik reflekterar hela kärnstrukturen genom Kraftekvationen (FBT+FeZ=0): det finns i princip hur många fingrader som helst.

Den främsta, och mest avancerade, bekräftelsen på TNED ges tveklöst genom jämförelse med MAC i ATOMVIKTERNA. Grunden ges från NEUTRONKVADRATEN — som resultat av ATOMKÄRNANS HÄRLEDNING ur PLANCKRINGEN genom toroidaggregatet N3m20; Deuteriumkopplingen som definierar impulsmomentets övergång mellan de två olika nukleära formfaktorernas dimensioner mellan masstalet A=1 till A>1, som innefattar Kärnradierna, är avgörande. Därmed ges hela grundvalen för Neutronkvadratens grundämneskarta via fusioner enligt Exotermiska kärnreaktionslagen genom de Elliptiska funktionerna baserade på Atomära massdefekten och som inte ingår i MAC.

Bekräftelsen är avancerad därför att den omedelbart — utan krav på specifikt institutionellt erkännande [och därmed på sitt sätt oberoende] — ger exakta besked i kraft av redan experimentellt uppmätta atomviktsvärden [HOP 1967]; Resultaten visar praktiskt taget »exakt» träff med TNED — men sett i de proportionerna med grova avvikelser via MAC-teorin, se Atomvikterna i jämförelse.

Med den sammansätta väv av samband som grundlägger värdena, deras härledning och sammanhang, som ovan, finns därför inte (längre) något tvivel i den praktiska fysikens val.

Därmed UNIVERSUMS HISTORIA.

[Det hör emellertid till god naturvetenskaplig sedvänja att alltid och främst leta efter de allra största felen i den egna meningen, att aldrig förutsätta något (vilket naturligtvis är orealistiskt), utan alltid eftersträva, så mycket man orkar (vilket också verkar väl optimistiskt), en väl relaterad förankring i varje enskild mening — och vilket vi alla vet ibland leder till frontalkrockar på grund av förhastade slutsatser. Förhoppningsvis överlever vi lidandets eldar, och kan lära av misstagen — då det tydligen inte går (direkt, kortaste vägen) genom förståndet].

——————————————

Förf.ref. Physics2001REST.wps s41|108

Ingen våg-partikeldualitet i TNED,

dynamiken kärna-elektron

Det finns ingen våg-partikeldualitet i TNED

Atomkärnan avkänner, styr och reglerar Q-flödet.

Positroner avges i kärnanodens riktning, elektroner avges i den motsatta kärnpolriktningen. Se utförligt i KÄRNMAGNETISMEN.

Via kraftekvationen avkänner, styr och reglerar atomkärnan kontinuerligt balansen mellan det centrala atomkärnans magnetiska toroidfält (BT) och spinnflödet hos komponenterna i elektronbesättningen (eZ). Se utförligt från ATOMFYSIKENS TVÅ KUNGSEKVATIONER och CENTRALKONTAKTERNA enligt TNED. I TNED benämns kraftekvationen därför också stundtals ström- och kemiekvationen.

Varken kraftekvationens sambandsform som sådan eller (här veterligt någon liknande) dess teori finns upptagen i den moderna akademins lärosystem.

I MAC [‡1] framställs elektronen sett som massbegrepp helt utan beståndsdelar; Man tillerkänner inte elektronmassan någon struktur, man beskriver den ”såvitt vi vet” av typen »punktlik» [‡4]. Det trots att man (från Heisenberg-Schrödinger, nedan) uppfattar (VET) elektronen som kapabel att ligga utspridd kring atomkärnan i formen av olika s.k. orbitaler [‡1][Quantum properties], samt i praktisk mening OCKSÅ kapabel att ANSVARA FÖR materialens olika termiska, elektriska, magnetiska och optiska egenskaper (vilket knappast kan vara utmärkande för objekt av typen ’såvitt vi vet’ »punktlik, utan struktur»).

Se även särskild artikel i ATOMKÄRNANS VÅGNATUR (Om bakgrunden till uppkomsten av föreställningen att partiklar skulle besitta vågegenskaper) — det finns ingen våg-partikeldualitet i TNED: elektronmassans element förklarar alla fenomen;

Våg-partikel-dualiteten finns inte i TNED

— Atomkärnan är ett elektromekaniskt svängningsaggregat. Se även SVÄNGNINGSEKVATIONEN.

Att elektronmassan enligt TNED verkligen kan förstås bestå av ett antal ringkomponenter på impulsmomentets form (J=mvr) visas explicit i LJUSETS POLARISATION och ELEKTRONENS BUBBELKAMMARSPÅR, samt i PARANNIHILATION.

Notera att begreppet »en elektron» (således enligt TNED) saknar en bestämd form eller utsträckning i fysiken eftersom elektronen genom sin komponentsumma (i princip) kan anta (alla möjliga) olika former och utsträckningar.

Se särskilt om elektronen i Resonanserna som enligt TNED grundlägger GRUNDÄMNENAS PERIODISKA SYSTEM.

Se även i Ljusets Polarisation, Neutronfragmenten och Skapelse eller delning.

[De nämnda artiklarna berör explicit korsrefererande jämförelser med MAC].

För elektronens vetenskapshistoriska upptäckt, se Elektronens upptäckt.

I TNED härleds ELEKTRONMASSANS KOMPONENTER som motsvarande fraktala ±e-strömringar (i TNED tau-ringar, τ-ringar) på impulsmomentets form (J=mcr) explicit i SPEKTRUM OCH KVANTTALEN. Tau-ringen som elektronmassans element är avgörande för härledningarna i BLIXTURLADDNINGENS FYSIK med ATA och CAT (ingår inte i MAC).

En liknande analogi med ’vibratorer’ i elektronmassan användes tidigt i MAC (omkring 1925 [‡5][Gamow]) konventionellt i samband med introduktionen av Heisenberg och Schrödingers resp. matris och vågfunktioner. Dessa ’vibratorer’ förklarade (nära perfekt) atomens spektrum — Men de förkastades strax (1927) tillsammans med en bannlysning av ’den mekaniska modellen’. Se särskilda referat i ELEKTRONMASSANS KOMPONENTER och ELEKTRONEN I MODERN AKADEMI, samt Atomkärnans åskådning i MAC [‡4]. Bannlysningen resulterade i QED.

Ljusets Polarisation — det fattas delar i MAC …

I TNED är f.ö. hela avsnittet i LJUSETS POLARISATION explicit tillägnat ELEKTRONMASSANS KOMPONENTER.

Jämför Det enkla Köksexperimentet: Det finns (fortfarande här veterligt Sep2010, efter viss genomsökning på webben) inte ens uppmärksammat i modern vetenskaplig litteratur — Alla (samtliga) »experimentatorer» tycks kräva ’rikedomens under’: lasrar, dyra uppmonteringskonsoler (»med elektrisk ström och grejer»), i en del exempel t.o.m. mikroskop, optiska linser (special), filter (optiska), och avancerade polaroidplasticerade material som garanterat lämnar huvuddelen av befolkningen i kö utanför Frågekiosken. Ingen av geniknölarna tycks omnämna (eller har kanske aldrig uppmärksammat) det enkla: en kopp te, en liten handhållen glasplatta, god belysning.

Vart tog Naturvetenskapen vägen?

Elektriska laddningen, detaljinnehåll

TNED:

Den elektriska laddningens existens bygger via Atomkärnans härledning på en integrerad, oändligt fraktal masstruktur (Kraftväv, F=ma, se Atomkärnans gravitella härledning) som enligt ENERGILAGEN omöjligen kan skapas, endast förintas enligt ekvivalenten [Se PARANNIHILATION]

e^– + e⁺ = 0 ....................... laddning

s_e– + s_e+ = 0 ....................... spinn

m_e– + m_e+ = 2m_e ................... massa

via primära massförstöraren E = (m→γ)c². Energin bevaras genom att [induktansen ökar på den reducerade laddningens räkning, se Kommutativa energiekvivalenten, med följd i att] massans energi överförs induktivt (elektriska fältets ändring relativt den lokalt dominanta gravitella referensen), masslöst via divergensen (c), på andra elektriskt laddade materiesystem [COEI].

En mera detaljerad beskrivning ges i PARANNIHILATION.

Se även särskilt i Partikelbeviset för att energi inte kan skapa massa.

Se även i DEEP från GRIP: ljus (c) är icke-massa, och kan inte skapa gravitation (massa, materia), ehuru gravitationen (massans närvaro) reglerar ljusets fysik.

Se även Ljusfrihetssatsen (Ljusets friställning från kinetiken): ljusvägarna utvecklar ingen centrifugalkraft (ljus är icke-massa): ljusvägarna är tillståndsbegrepp (»geodeser») i gravitationsfysiken.

Härledningar med praktiska resultat som är omöjliga utan TNED:

———————————————————

Solperioden — Solens energiproduktion

Solens magnetfält

Solfläckarnas fysik

PLANCKRINGEN — Atomkärnans härledning, massans fundamentalform, N3m20, elektronmassans komponenter, Spektrum och Kvanttalen, laddningsdeplacementet, kärnmagnetiska momentet, centralkontakterna [betasönderfallets fysik …]

[fusionerna, gemensamma toppkärnspinnet; deuteronkopplingen från N3m20, nukleära formfaktorns ändring, kärnradierna, fusionsringarna, grundämnesbildningen, himlakropparna]:

NEUTRONKVADRATEN — 1818e+18e-byggnaden, Atomvikterna

K-cellens värmefysik

Jordens 5 Ekvationer

ATA/CAT

Blixturladdningens fysik

Ljusets polarisation

Elektronens bubbelkammarspår

(Kosmiska strålningen …)

Om inga dolda felslut förekommer, verkar det främsta experimentellt verifierade beviset [frånsett ATOMVIKTERNA och Solperioden och Ljusets Polarisation och Elektronens Bubbelkammarspår] på att atomkärnans härledning enligt TNED är korrekt — en kraftväv av ±e-laddningar med tillhörande ±s-spinn — vara observationen av positroner (e+) i samband med Jordbaserad gammastrålning från vissa blixturladdningar (från Nov2009, Fermi Gamma-ray Space Telescope) och som krävs enligt TNED för att kunna förklara blixturladdningens fysik, men som inte ingår i den moderna akademins lärosystem.

Atomkärnan, storlek

ATOMKÄRNANS STORLEK avgörs genom PLANCKS KONSTANT

h = 6,62559 t34 JS

= mcr ....................... neutronens impulsmoment

som beskriver NEUTRONEN; Neutronmassan m (1,0086652u) [u=1,66033 t27 KG], neutronradien (tyngdcirkeln) r (1,3196611 t15 M) med toppvärdet för ljushastigheten c₀ (2,99792458 T8 M/S).

Med den förenklade kubanalogin som en approximation för atomkärnornas radier med hänsyn till masstalet (A, antalet neutroner [explicit utan neutronsönderfall] eller summan av antal neutroner och protoner [explicit med neutronsönderfallen inbegripna] som bildar den aktuella nukliden genom fusion) ges

r = r₀ A^1/3 .................... atomkärnornas approximativa kärnradier (tyngdcirklarna)

med r₀ som neutronradien (eller alternativt med protonradien r₀=1,37 t15 M).

Atomära massenheten

Atomära massenheten

Förutsättningen för en RÖRELSE (variation, v) i fysiken är ett INTERVALL (d=vT) som en KROPP (m) kan lägesändra (positionsvariera) på. Därmed kan en RÖRELSEENERGI (E=Fd=mad) utbildas enligt

E = mv²/2

GENOM ALLMÄNNA GASLAGEN [E=pV=kT, »Allmänna tillståndets rörelselag»] framgår att förutsättningen för en ENHETLIG fysikbeskrivning på E förutsätter att det finns en viss minsta massenhet (m=u) som alla materiella kroppar kan återföras på (samma som den atomära massenheten [u]). Genom NEUTRONKVADRATEN visas att den massenheten är den som erhålls från 1/12 av Kolatomens massa (U=12), och som ligger nära neutronmassan,

m(n) = 1,0086652u

u = 1,66033 t27 KG

För u, se utförligt i ATOMÄRA MASSENEHETEN.

TAU-TEORIN — elektronmassans komponenter i relaterad fysik

Tau-teorin

2010IX25

Teorin i Praktiken — elektronmassans komponenter

Alla de tre främsta fenomenformerna i den moderna akademins kvantelektrodynamik (QED)

— Lambväxlingen, Elektronens g-faktor och Casimireffekten, se LEC —

motsvaras i TNED av en förklaring som bygger på det som förkastades i MAC från 1927: elektronmassans inneboende masselement [‡]. I MAC anses däremot samtliga de tre nämnda fenomenformerna bero på ’vakuumets fluktuationer’ i fortsatt samtidigt förkastande av elektronmassans komponenter. Varje annan ordning i MAC innebär att dess lärosystem totalhavererar.

I materiefysiken garanterar ELEKTRONEN via RESONANSVILLKORET [n²] att bara hela elektronladdningar [elektronkvanta] kan studeras i fysiken. Genom sinnrika experiment kan man dock mäta energiernas Planckfrekvenser (f i E=hf) med en sådan precision att mindre skillnader (på miljondelar och mindre) framträder. Därmed kan också — enligt TNED — minimalt små störningar i elektronmassans detaljer påvisas [likt krusningarna på vattenytan] och som normalt inte ingår i den enklare fysikens spektralmatematik (Se Spektrum).

Tre experimentella områden ansluter dit:

Lambväxlingen [i TNED »atomens maskinljud» som papperslappen som pluttrar mot ekrarna i cykelhjulet, spinnstrukturkopplingen till atomkärnan],

Casimireffekten [i TNED materialytornas atomära attraktion genom delade elektronmassor i gränsskikten], och

Elektronens g-faktor [elektronmassans magnetiska moment i och utom atombindning].

hf

I TNED definieras gränslandet mellan materiefysik och massfysik av massans struktur [PASTOM].

I MAC kompenseras den uteslutning (från 1927 [‡5]) som genomfördes av begreppet STRUKTUR för elektronmassan [‡4] genom en motsvarande uppfinning av en vakuumfluktuation — för att matcha experimentella resultat — även benämnt Vakuumets Energi eller »Nollpunktsenergin», eng. Zero-Point Energy eller Vacuum-Point Energy.

Rent matematiskt resonerar man i MAC på följande sätt och med stöd av Plancks konstant (h, Heisenbergs osäkerhetsprincip):

”The energy levels of the photon ensemble are well known to be the energy levels of the harmonic oscillator problem:

En = (n + 1/2) ħω (20.10)

when there are no photons present (n = 0), there is a non-zero vacuum energy or zero-point energy:

En₀ = (1/2) ħω (20.11)

The photon ensemble is therefore regarded in the way that was originally inferred by Planck [26, 27], as a collection of harmonic oscillators.”, s357ö;

”Atkins [27] describes the vacuum energy as being due to fluctuating electric and magnetic fields when there are no photons present. Therefore in the absence of photons the electron records the influence of these vacuum fields in its zitterbewegung or jitterbug motion. The result is that the g factor is changed from 2 of the Dirac equation to the experimental value in Eq. (20.2). This means that the electron wobbles about its equatorial axis as it spins [27].”, s357mö,

ALPHA INSTITUTE FOR ADVANCED STUDY (AIAS) — 2010

Calculation of the Anomalous Magnetic Moment of the Electron from the Evans-Unified Field Theory (2005)

http://aias.us/documents/uft/a18thpaper.pdf

NOTERING: ħω = (h/2π)(2πf ) = hf = E = mc²

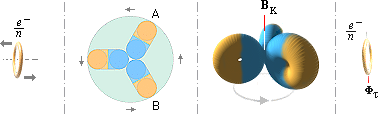
Från illustration till härledningen för de fem olika kvanttalen [n q s_τ µ_τ Φ_τ] i atomfysiken enligt TNED i

Spektrum och Kvanttalen i Elektronmassans komponenter.

Elektronmassans masskomponent måste liksom atomkärnan baseras på ett IMPULSMOMENT (J=mcr) med massa, laddning och SPINN, och får därför också karaktären — likt atomkärnan och dess tyngdcirkel [Se från PLANCKRINGEN] — som en RING: elektronringen.

Notera att skalförhållandet elektronring-atomkärna i illustrationen ovan ä starkt överdrivet: Vid atomkärnan i illustrationen ovan ses ringdiametern (sämsta fallets räkning i TNED) som max en pixel: · .

Som redan beskrivits i TNED i ELEKTRONRINGENS TOPPSPINN i Kvanttalen [Se även en kortare jämförande översikt i Elektronen och elektronens toppspinn], måste man i den enkla matematiska fysikens beskrivning frånse elektronelementets (τ[tau]-ringens) alla möjliga olika rörelsesätt för att få fram en översiktligt beskrivande och begriplig matematik. I dessa härledningar behandlas elektronmassan som EN enhet genom att varje elektronring uppvisar samma egenskaper och beteende som varje annan, vilket förenklar matematiken (betydligt). Eller, för att citera den egna framställningen,

I det allmänna fallet frånser vi dessa inre mera avancerade möjligheter och betraktar Φ(τ)-spinnet som ett och samma för alla τ-ringar relativt deras moderatomkärna.

UNIVERSUMS HISTORIA — Elektronmassans komponenter, BellDharma 2007|2010

http://www.universumshistoria.se/ElektronmassansKomponenter.htm#Kvanttalen_FiTau

I praktiken OCH GENOM ATOMKÄRNANS KRAFTEKVATION ENLIGT TNED [F(BT)+F(eZ)=0] — även med NOLL energigenomströmning enligt det ideala matematiska (förenklade) fallet — utför elektronmassan hela tiden inre oscillerande, vridande, krängande, vaggande och alla andra möjliga rörelser och deras kombinationer SOM FÖLJD av varje enskilt elektronelements kraftkoppling till atomkärnan och i den mån sådant utrymme finns för kraftekvationens balans — Se även figuren ovan som ger en översiktligt illustrativ orientering enligt TNED. Notera att elektronringens diameter i skalan är starkt överdriven (den är [enligt grundräkningen före detta dokuments tillkomst Sep2010], sämsta fallets räkning, max 1/50 av protonradien, i kärnvyn ovan skulle den synas som en pixelprick · ).

Genom τ-ringens elektromagnetiska (F[BT]+F[eZ]=0) koppling till atomkärnan, drivs ringen i de olika rörelser som speglar moderkärnans STRUKTUR — inte bara i toppspinnet, utan även i själva ytstrukturen som helhet (principen för ytfraktalerna beskrivs utförligt i atomkärnans härledning).

MED den dynamikens grund GIVEN — men som ovan orepresenterad i MAC på den tidiga historiens bannlysning av begreppet struktur ur elektronbegreppet — kan sedan den praktiska experimentalfysikens forskare postulera att den praktiska effekten ’måste bero på vakuumfluktuationer’ — eftersom det enda alternativet är bannlyst.

Det finns — med andra ord — ingenting annat att välja på — citatdelen ovan — OM man envisas med att bannlysa begreppet struktur ur elektronmassan.

Exemplen [LEC] — belysta i TNED — på effekter som anses härröra från ett ’vakuumets inneboende energi’) enligt MAC således:

· Elektronens observerade gyromagnetiska faktor (g-faktorn) — från härledningens ideala 2 till praktikens 2,0023193043768(86)
[ref.
Theoretical Basis and Proofs of the Existence of Atom Background Radiation, G. P. Shpenkov 2006
http://shpenkov.janmax.com/TheorBasis.pdf],

· Lambväxeln (Lambändringen eller Lambskiftet, eng. Lamb shift) och

· Casimireffekten (eng. Casimir effect),

Alla tre exempelfallen förorsakas av effekter från VAKUUMFLUKTUATIONER enligt MAC. Enligt TNED däremot handlar likaledes samtliga ovannämnda fenomenområden om den ELEKTRONENS INRE KÄRNKOPPLANDE STRUKTUR som uteslöts ur MAC från 1927 [‡5], och som bildar grunden för SPEKTRUM och KVANTTALEN i TNED . Se även från Tau-ringen och Antalet n i e.

MAC-matematiken i ämnet kallas/igenkänns f.ö. som typen ’Quantum field theory’, Quantum electrodynamics (QED).

För det vidare klargörandet av elektronmassans element i praktisk fysik enligt TNED, se ELEKTRONENS BUBBELKAMMARSPÅR, LJUSETS POLARISATION, CASIMIREFFEKTEN i relaterad fysik och Lambväxlingen.

En kortare översiktlig beskrivning av ovannämnda fenomengrunder ges i KVALITATIVA FÖRKLARINGARNA.

Elektronen och Φ

Elektronen och Φ

Vakuumfluktuationer i MAC ersätter elektronkomponenter i TNED

FLUKTUATIONER I VAKUUMET uppfanns av modern akademi (Bethe, 1947) för att kunna förklara den elektronens praktiska fysik som man från början (1925, Heisenberg-Schrödinger) hade antagit men som förkastades (1927) tillsammans med bannlysning av elektronens mekaniska modell

Elektronen — och

elektronringens toppspinn (Φ_τ)

Φ-SPINNET — TNED relaterad fysik förklarar

Se även utförligt i Elektronmassans komponenter, Elektronens bubbelkammarspår, Ljusets polarisation, Spektrum och Kvanttalen, Atomkärnans härledning

e-spinnet i MAC

Modern akademi (MAC):

Elektronen behandlas som en punktlik, strukturlös partikel [‡4] som roterar kring atomkärnan.

KVANTTALENS FÖRKLARING kan inte ges någon åskådlig modell, ytterst abstrakta beskrivningar, ingen förstår dem.

Tau-ringen

Relaterad fysik (TNED):

Se även i Antalet Tauringar i Elektronmassan och DIMENSIONER.

Se även ovanstående till jämförelse i MAC. Se även i Tau-teorin. Mera utförligt i ELEKTRONMASSANS KOMPONENTER.

Se även i VETENSKAPSHISTORIEN — hur man från år 1927 förkastade de ’vibratorer’ i e-massan som först användes:

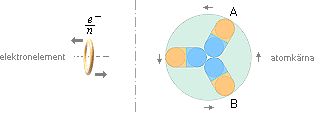
Elektronen är ett elementarkvantum, en hop, en mängd strömringar (mcr) som ligger utspridda runt atomkärnan (orbitaler).

Begrepp om »elektronen som en enskild partikel» finns inte. .......................... Elektronen är en hop — jämför Neutronens sönderfall.

Begrepp om »elektronens hastighet runt atomkärnan» finns inte. .................... Hastighetsaspekten tillhör DIVERGENSEN — stället där Q tas: Energizonen i Potentialbarriären.

Begreppet om »elektronens bana runt atomkärnan» finns inte. ....................... Elektronen formar YTRESONANSER kring atomkärnan — som kruset på vattenytan.

Utförligt i Spektrum och Kvanttalen.

Se även i Elektronmassans komponenter, Elektronens bubbelkammarspår och Ljusets polarisation.

Som framgår i KVANTTALEN, härledningen till elektronelementets toppspinn [Φ(τ), τ|Φ Grek. t, tau; F, Fi ] i relaterad fysik (TNED), kräver den enkla fysikbilden att τ-ringens alla möjliga rörelsesätt måste återföras på ett enklast möjliga impulsmoment, nämligen Plancks konstant h. Det DYNAMISKA resultatet av denna operation blir detsamma som att se τ-ringen som »en fast konduktörsskylt» som för spinnets definition får följa med i kärnspinnet som en fast roterande arm, vilket ger ett helt varvs topprotation för τ-ringen analogt med atomkärnans drivande spinnfysik. Analogin i det praktiska fallet blir att alla möjliga energiabsorberande bidrag som kan återföras på τ-ringen också återförs på dess lokala position: ringen topproterar (ytterst primitivt) ett helt varv som funktion av sin koppling till moderkärnan.

Φ_τ = h ............................. τ-ringens spinnimpulsmoment

Denna förenkling medför samtidigt — som vi strax inser — att ett visst möjligt energiabsorberade moment bortfaller, just på kredit från den förenklade formen Φ(τ)=h. Med andra ord: Noggranna mätningar bör uppvisa en viss (marginell) gradskillnad mellan den förenklade teoretiska modellens värden (mindre) och de praktiskt uppmätta (större).

Eftersom också det allmänna impulsmomentet i Spektrum (betecknat q i TNED, l i MAC, även benämnt banimpulsmoment, bikvanttal eller azimutala kvanttalet) tvunget kopplar till den egentliga finstrukturen, måste också detta kvanttal egentligen preciseras med inre uppdelningar. Syftet|Prövningen med Spektrum i TNED var just att försöka få fram en någotsånär ENKEL grundframställning, vilket gör att alla mindre fluktuationer tvunget måste uteslutas för att matematiken inte ska bli helt obegriplig. Kvanttalet q|l frånses därför (oegentligt) helt i den här framställningen.

Satsbild

r + Δr

Eftersom den förenklade vyn på alla elektronelementens ekvivalenta bidrag i princip bara medför/utsäger en ensam roterande kropp — »en primitiv laddning» kring atomkärnan, den moderna akademins ideala punktlika, strukturlösa elektron [‡4] — kan den praktiska verkan enligt modern akademi liknas vid följande [Welton 2, 1948]:

Den ensamma elektronpartikeln genomför dels sin vanliga rotation kring atomkärnan — och dels en ny, extra oscillerande rörelse som härrör från vakuumets polarisation eller vakuumets fluktuation — eftersom ingen annan förklaring synes föreligga med uppfattningen om elektronen som en punktlik, strukturlös partikel i MAC enligt [‡4].

Eftersom man SÅLEDES inte känner till den verkliga funktionen (TNED) i modern akademi, tvingas man FÖLJAKTLIGEN uppfinna en fysikalisk fiktion (en orsaksfaktor som inte existerar) — med samma principiella resultatfunktion som uppvisas av det experimentella resultatet (vilket tvunget framtvingar en PRIMITIV fysikuppfattning): ett vakuumets polarisation eller ett vakuumets fluktuation.

Modern akademi tvingas med andra ord UPPFINNA en fysikalisk FIKTION för att matcha experimentella resultat — därför och på grund av, som redan tidigare påpekats, att modern akademi sedan 1800-talet har uteslutit grundläggande, väsentliga detaljer och mekanismer i naturfysiken redan från ruta ett.

Jämför PLANCKEKVIVALENTERNA, för att nämna ett speciellt konkret praktiskt exempel.

Se även INERTIALSYSTEMET, för att nämna ytterligare.

Se också Magnetiska Fältintegralen för ännu ett praktiskt exempel [Magnetismen i modern akademi].

Se även ENTROPIBEGREPPET I RELATERAD FYSIK — här ges ytterligare exempel på fundamentala olikheter.

Jämför Wikipedia på artikeln om Lamb shift:

Sambandsformen är alldeles densamma som i citatet från Welton 1948 — samma typ som i den ovan markerade satsbilden. Genom den satsbilden blir det också alldeles tydligt att det är TNED (relaterad fysik) som förklarar fysiken i praktiken.

SPEKTRUMMATEMATIKEN — generellt med alla ingående parametrar — tillhör den mera avancerade fysiken. Sambandsformerna som leder vidare från den enkla satsbilden till de aktuella sambanden för Lamb-Retherford-övergången (eng. Lamb shift) innefattar avsnitt i den moderna akademins vektorkalkyl som explicit inte ingår i TNED [Orsaken till den åtskillnaden beskrivs utförligt exemplifierat från Magnetiska fältintegralen].

För att få fram motsvarande beskrivning i relaterad fysik (TNED) krävs en mera grundlig genomgång av motsvarande tekniska algebra, men ingenting av den delen finns (ännu Sep2010) framställt i min referens.

Det enda jämförande exempel som finns (på det rent spektrala området) är begränsat till Bohrekvivalenten i Spektrum. Jämförelsen ger en antydan om graden av komplexitet mellan de olika betraktelsesätten: Bohrekvivalenten avhandlas på runt sagt två rader, medan den relaterade fysikens spektrum kräver nära ett helt dokument.

Historia

Fenomenet som ovan »elektronens inre oscillation» upptäcktes (1947) experimentellt av Willis Lamb (1913-2008) och Robert Retherford (uppgift saknas) — Lamb-Retherford-växlingen (eng. Lamb shift), eller -övergången, -ändringen, -skiftet, etc.

‡ Uppmärksammad felstavning. Vissa källor kallar den aktuella (Robert) ’Retherford’ för ’Rutherford’, se citatreferensen. Det verkar inte finnas någon klar uppfattning vad som gäller, eller ens någon beskrivning alls på personen Robert Retherford (19Sep2010).

Här finns en upphittad källa som beskriver historien och använder stavningen Retherford,

INVESTIGATION INTO THE LAMB SHIFT — Crystal M. Moorman, 2010

http://www.physics.drexel.edu/~bob/TermPapers/Moorman_.QMProject.pdf

Genom mätningar på vätets spektrum visade sig en liten differens — där teorin däremot förespråkade samma värde. Resultatet har sedermera (med vidare) tolkats som ”strong evidence in support of quantum electrodynamics”, sv. starkt bevis i stöd för kvantelektrodynamiken (QED), citatet från Yung-Kuo Lim 2000.

Experimentet 1947 av Lamb-Retherford uppstod ur ett växande behov att klargöra påtagliga svårigheter i de dåtida teorierna (1940-talet) ikring kvantfysiken [Wikipedia, Quantum electrodynamics, History 2010-09-19]. Ett genombrott inträffade strax efteråt samma år (1947) då Hans Bethe lyckats härleda ett samband som gav överensstämmelse med Lamb-Retherford-resultaten.

Renormalisation

”The idea was simply to attach infinities to corrections at mass and charge that were actually fixed to a finite value by experiments. In this way, the infinities get absorbed in those constants and yield a finite result in good agreement with experiments. This procedure was named renormalization.”,

@INTERNET Wikipedia, Quantum electrodynamics, History 2010-09-19

http://en.wikipedia.org/wiki/Quantum_electrodynamics#History

;

Renormalisationen är den matematiska processen bakom ’vakuumets fluktuation’ som antas vara orsaken till Lambväxlingen. Ämnesområden: kvantfältteori (eng. quantum field theory), statistisk mekanik (eng. statistical mechanics), ref. @INTERNET Wikipedia Renormalizaion 2010-10-09:

”Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory.”.

Energin som utvecklas ur ’vakuumets fluktuation’ förknippas speciellt med termen självenergi (eng. self energy), ref. @INTERNET Wikipedia Self-energy 2010-10-09; Begreppet ’självenergi’ används också i beskrivningen av ’vakuumets fluktuationer’ i formen av ’vakuumets polarisation’ [ref. @INTERNET Wikipedia Vacuum polarization 2010-10-09] [fenomenet kräver speciellt starka elektriska fält i närheten av redan existerande materia] och som antas i MAC för att förklara typ positronbildning via laserbestrålning på olika målobjekt, se utförligt i Parbildning i MAC.

Ska man sätta något bokmärke i tiden för den definitiva uppkomsten av kvantelektrodynamiken (eng. QED Quantum electrodynamics) är det tydligt i samband med Bethes lösning (1947): man tvingades uppfinna fiktiva processer och dimensioner för att kunna förklara praktiska resultat — allt och tydligen enligt TNED med grund i uteslutningen (1927) av de väsentliga komponenterna: elektronmassans element.

Så har QED utvecklats vidare tillsammans med den fysik som sammanhänger med elektronmassans komponenter (Jämför t.ex. Feynmandiagrammen [enkla grafiska logocept i beskrivningen av partiklarnas kvantövergångar, ref. @INTERNET Wikipedia Feynman diagram 2010-10-09]).

Nobelpriset i fysik 1965 utdelades för dessa prestationer (Lamb-Retherford-experimentets efterföljande pionjärer: Tomonaga, Schwinger, Feynman).

MASSFRAMTRÄDANDEPROBLEMET

Massframträdandeproblemet

Elektronen och elektronens komponenter · Casimireffekten · ·

BILDKÄLLA: Författarens arkiv · Bild32Excur5 · 14JUL2010 · Nikon D90 · Detalj

MASSFRAMTRÄDANDEPROBELEMET — en av naturfilosofins grundfrågor, men orepresenterad i modern akademi:

— Med atomkärnans masstäthet på minst T16 KG/M³ [Protonmassan/omskrivna Kubvolymen], HUR kan vi alls SE några föremål då effektiva massvolymen inte ens upptar en synlig bråkdel av själva det synliga föremålet?

Massframträdandeproblemet — en av naturfilosofins grundfrågor, men orepresenterad i modern akademi

— Med klarläggandet av atomkärnan och dess masstäthet på grovt T16 KG/M³ uppstår frågan om HUR vi alls kan SE ett föremål, t.ex. en kubikmeter Koppar: Den effektiva volymen uppgår bara till en kub med sidan ca halva tjockleken av ett vanligt papper: Praktiskt taget helt osynligt.

Det är nämligen alldeles uppenbart att det måste finnas NÅGOT exceptionellt utfyllande material EMELLAN atomkärnorna och som får de olika materialens olika egenskaper i elektricitet, magnetism, värmeledning och optik att framträda.

Vad är det för något?

Svaret är naturligtvis: elektronmassorna. Se från ELEKTRONEN.

Jämför modern akademi [‡4]; Atomkärnan, åskådning i MAC:

— Där utesluts hela frågeställningen direkt från ruta ett.

— Ett PUNKTLIKT objekt kan naturligtvis INTE förklara massframträdandeproblemet.

Se även Djupa motsägelser om elektronen i MAC.

Medan modern akademi erkänner atomkärnan som en formkropp MED utsträckning, erkänner man inte mellanrummet mellan atomkärnorna som befolkat av massformer med utsträckning, citatet ovan [ett typexempel på en modern PhD]. Därmed kan man heller inte inlåta sig på frågan om HUR massorna kan ses eller förstås framträda eftersom rymden mellan atomkärnorna tydligen är avgörande för att kunna särskilja olika ämnens olika fysiska (termoelektrooptiska) egenskaper såsom t.ex. opacitet (optisk ogenomskinlighet) — som i exempelfallet Koppar.

Kalkylkortet

Kalkylkortet

RESERVATION FÖR ÖVERFÖRINGSFEL: Framställningen inkl. Kalkylkortet innehåller en stor mängd JÄMFÖRANDE-korsrefererande beräkningsresulat med DELS CODATA-konstanter och dels förenklade dito från facklitteraturen under 1900-talet (HOP-blocket) — och som MÖJLIGEN kan innehålla vissa överföringsfel eller felaktigt överförda eller insatta konstanter (rätt värde på fel ställe). Dessa fel är typiska för ämnet, och det är (enligt erfarenhet) omöjligt att utelämna dem från början om mängden är stor. Endast genom att pröva innehållet under en längre tid ges (successivt) möjligheter att upptäcka ev. försmädligt insmugna fel. Författarna ber om överseende ifall läsaren uppmärksammar något sådant fel — alla dokument i UNIVERSUMS HISTORIA är ständigt föremål för felsökning och kommer därför att rättas till om fel föreligger, förr eller senare.

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN Casimir.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/Casimir.ods

Kalkylkortet

Casimir.ods

KALKYLKORT ingår generellt i UNIVERSUMS HISTORIA för dokumentpresentationer där mera omfattande beräkningsarbeten ingår. Allt annat är uteslutet FÖR DEN RELATERADE FRAMSTÄLLNINGENS SKULL — man ska kunna följa framställningssättet i de avgörande partierna genom att själv utföra och kontrollera beräkningsprocedurerna — och ev. också kunna utverka egna utvecklingar om tid och intresse finns.

En fullständig manual till varje kalkylblock ligger emellertid utanför ramen för presentationen: endast partierna i huvudsak beskrivs, som nedan, illustrerat, med vissa förtydliganden. Kalkyldelarna är i vilket fall tänkta att kunna förstås (improviserat) av den som är insatt i framställningens detaljer.

Tabellflik 1

Casimireffekten — med

Platta-Sfärsamband enligt Prevenslik, Mohideen, Klimchitskaya

Kontrollräkning | Jämförande tabeller — Kovalenta bindningar | Väte

ÄMNESTABELL till Casimireffekten — Alla materialvärden vid rumstemperatur

Lambväxlingen [äv. Lambövergången el. Lambskiftet] | Okt2010 — med alternativa CODATA-konstanter

iteration Unit1 — Casimireffekten 23Okt2010

Tabellflik 2

Elektronens g-faktor — jämförande värden | Okt2010

Tabellflik 3

ELEKTRONENvdW — van der Waals krafter

Jämförande tabeller — Kovalenta bindningar

Jämförande metallbindningar

Casimireffekten Tabellflik 1:

Huvudkort

Inmatning | Resultat

REFERENSAVSNITT

REFERENSAVSNITT

Citatbihang till Elektronen

Vakuumets Polarisation

QED

Lambreferenser

Lambväxlingen i citat

Lambväxlingen, citatblock(2)

CasimirRef

Casimireffekten, historisk bakgrund

Citatbihang till Elektronen

Citatbihang till Elektronen

Citatbihang till Elektronen

[‡]1:

@INTERNET Wikipedia Electron, Discovery 2010-09-09

http://en.wikipedia.org/wiki/Electron#Discovery

ELEKTRISKA LADDNINGEN, kort historik om elektronens upptäckt,

ElektriskaLaddningen.htm#ELEKTRISKA_LADDNINGEN_härl

HISTORIA, Elektricitetens centrala dramatik — i resumé från Upptäckten av Elektronen, David. L. Anderson 1966,

IndMag_Induktionen.htm#HISTORIA_eFysiken

[‡]2:

@INTERNET Wikipedia Neutron, Discovery 2010-09-09

http://en.wikipedia.org/wiki/Neutron#Discovery

[‡]3:

@INTERNET Wikipedia Beta decay, History 2010-09-09

http://en.wikipedia.org/wiki/Beta_decay#History

BETA DECAY AND THE WEAK FORCE — The Development of an Entirely New Physical Force , 2008 Isaac M. McPhee

http://www.suite101.com/content/beta-decay-and-the-weak-force-a46284

Se även sammanställning i Neutrino-Neutron — Historia

Neutronfragmenten.htm#NeutrinoHistorik

[‡]4:

Kvarkar och leptoner såvitt vi vet punktlika,

Atomkärnans åskådning i MAC

———————————————————

Elektronen inte i kärnan [Se även RÄKNEEXEMPEL i citatbihanget],

Elektronen strukturlös,

Elektronen oändligt liten med oändlig massa,

BLANDADE CITAT, VÅGMEKANIKEN,

———————————————————

[‡]5:

’Vibratorerna’ i elektronmassan (1925) från Heisenberg-Schrödinger som avskrevs 1927;

”Så som vi beskrev i förra kapitlet föreställde sig Schrödinger att atomelektronernas rörelser styrdes av ett system av generaliserade tredimensionella de Broglie-vågor som omgav atomkärnan och vilkas former och vibrationsfrekvenser bestämdes av de elektriska och magnetiska kraftfälten.”, s97n,

”Heisenberg begagnade en mer abstrakt modell. Han behandlade atomen som om den vore sammansatt av ett oändligt antal lineära ”virtuella” vibratorer med frekvenser som sammanföll med alla tänkbara frekvenser som ifrågavarande atom kunde emittera.”, s97n,

”Den oväntade överensstämmelsen mellan resultat som erhållits med Schrödingers vågmekanik och Heisenbergs matrismekanik, vilka inte tycktes ha någonting gemensamt vare sig i de fysikaliska grundantagandena eller i den matematiska behandlingen, förklarades av Schrödinger i en senare uppsats. Han lyckades visa att hans vågmekanik, hur otroligt det i förstone kunde synas, var matematiskt identisk med Heisenbergs matrismekanik och att man i själva verket kunde härleda dem ur varandra.”, s103m,

”Men trots att kvantteorin både i vågform och i matrisform gav en utomordentligt god matematisk beskrivning av de atomära fenomenen, kunde den inte kasta det erforderliga ljuset i fysikens dunkel. Vilken fysikalisk innebörd skulle man tillskriva dessa egendomliga vågor och dessa underliga matriser?”, s104ö,

”Hur förhåller de sig till våra vardagsföreställningar om materien och världen? Svaret på dessa frågor lämnade Heisenberg i en uppsats som publicerades 1927.”, s104ö,

”Heisenberg inleder sitt resonemang med en hänvisning till Einsteins relativitetsteori, vilken då för tiden (och i viss mån än idag) av många framstående vetenskapsmän ansågs strida mot sunda förnuftet.”, s104mö,

Gamows fortsatta (längre) beskrivning via Heisenbergs uppsats 1927 utmynnar i Heisenbergs osäkerhetsrelation:

pλ=h=6,626 t34 JS (Gamow s108n);

Med föreställningen om elektronen som en partikel med impuls (p=mv) och position (λ) kan inte bägge bestämmas med godtycklig precision; Plancks konstant (h) sätter definitiva metriska gränser för varje exakt bestämning av position och impuls tillsammans; ’vibratorerna’ avskrevs som ’omöjliga’ med hänvisning till Plancks konstant enligt Heisenbergs osäkerhetsprincip (ref. @INTERNET Wikipedia, Uncertainty principle 2010-09-19).

I TNED elimineras den aspekten genom att Plancks konstant genom Planckringen i Atomkärnans härledning är en STRUKTURKONSTANT; Det finns en osäkerhetsnivå för varje fraktalnivå, där h-nivån är den som definierar materiefysiken. Genom att antalet nivåer är obegränsade (Atomkärnans gravitella härledning) försvinner osäkerhetsprincipen så som en förmodad övergripande princip helt ur fysiken.

TRETTIO ÅR SOM SKAKADE FYSIKEN, George Gamow, Prisma 1966/68

———————————————————

[‡]6:

Massa kan skapas,

BLANDADE CITAT, VÅGMEKANIKEN

Inledning till Vakuumets Polarisation

Inledning till Vakuumets Polarisation

Elektronen i TNED

Se även Djupa motsägelser om elektronen i MAC

– +

I MAC utgår man ifrån att elektronen är en punktlik partikel utan inre struktur [‡4].

I TNED är elektronen en hop, en mängd, bestående av (minst) 177062 enskilda J=mcr-ringar, se Elektronmassans komponenter (τ-ringen)

Eftersom τ-ringen ligger utanför h-kvantat på materiefysikens nivå, är det omöjligt att detektera τ-ringarna som enskilda objekt: de arbetar alltid i grupp genom RESONANSER.

Försöker man — således, fysiken enligt TNED — mäta elektronladdningen isolerat stöter man på patrull.

Elektronladdningen enligt TNED är en del av atomkärnan [m(n)/m(e)=(1,0086652)/(0,000548598)=1838,624], och kan inte separeras från denna som en isolerad, fristående fysisk faktor.

Genom att elektronmassan i vilket fall inte kan komprimeras till typen ’ideal punktladdning’ kommer den, om man försöker att isolera den i rummet (xyz) att uppvisa skilda egenskaper i jämförelsen isolerad-atombunden.

Av allt att döma är det också precis vad man har mätt på i det som konventionellt kallas för »vakuumets polarisation».

Se vidare i särskild artikel om Vakuumets polarisation.

Vakuumets polarisation, se även Inledning

Beskrivningen i MAC av ’vakuumets polarisation’ (och ’vakuumfluktuationer’) liknar mycket TNED-beskrivningen i Spektrum av den kvanttalsfaktor för elektronmassans element som tydligen inte MAC känner till:

elektronringens toppspinn (Φ_τ)

Φ-SPINNET

Så här låter det:

Se även SAMBANDSMATEMATIKEN TILL VAKUUMETS NOLLENERGI i separat citatblock.

VC1

”The fluctuation in the electric and magnetic fields associated with the vacuum perturbs the Coulomb potential due to the atomic nucleus. This perturbation causes a fluctuation in the position of the electron, which explains the energy shift. The difference of potential energy is given by

”, utan vidare beskrivning,

”Thus, there exist small zero-point oscillations that cause the electron to execute rapid oscillatory motions.”,

”The electron is "smeared out" and the radius is changed from r to r + δr”,

@INTERNET Wikipedia Lamb shift 2010-09-09

http://en.wikipedia.org/wiki/Lamb_shift

Min översättning:

Fluktuationen i elektriska och magnetiska fält associerade med vakuum stör Coulombpotentialen från atomkärnan. Denna störning förorsakar en fluktuation i elektronens position, vilket förklarar energiändringen. Skillnaden i potentiell energi är given av

sambandet.

Således existerar en liten nollpunktsoscillation som förorsakar elektronen att utföra snabba svängningsrörelser.

Elektronen ’smetas ut’ och radien ändras från r till r+δr.

”The vacuum has, implicitly, all of the properties that a particle may have: spin, or polarization in the case of light, energy, and so on.”,

@INTERNET Wikipedia Casimir effect, Vacuum energy 2010-09-09

http://en.wikipedia.org/wiki/Casimir_effect

Min översättning:

Vakuumet har, implicit, alla de egenskaper som en partikel har: spinn, eller polarisation i fallet med ljus, energi, och så vidare.

Anomalt magnetiskt moment

2010X9

Anomalous magnetic moment

ANOMALA MAGNETISKA MOMENTET

1947 i samband med uppdagandet av ’vätets hyperfina struktur’ eller den speciellt uppmärksammade [Welton 1948] »väteatomens energiväxling» som fick namnet Lambväxlingen (eng. Lamb shift, äv. Lambskiftet), även benämnd vätespektrums hyperfina struktur [Schupp 1959, s2mö], föreslogs [Breit 1947, samma källa] att fenomenet kunde förklaras med antagandet av ett elektronassocierat ”anomalous magnetic moment”, sv. anomalt [avvikande] magnetiskt moment.

Genom olika prövningar som inbegriper den s.k. finstrukturkonstanten [FSC] fann man ett värde som överensstämde med det från Lamb-Retherford-experimentet år 1947 experimentellt uppmätta 1057 MHz [Shpenkov 2007, s5m]. Teorin (QED) har sedan dess utvecklats med allt högre grad av förfining tillsammans med experimentellt uppmätta resultat. Se mera utförligt i Elektronens g-faktor.

En kortare genomgång av Lambväxlingen ges i LEC med jämförelser MAC-TNED.

Se mera utförligt i ABpEK för beskrivningen enligt TNED.

Vad går MAC-beskrivningen ”anomalous magnetic moment” ut på?

”In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle.”,

@INTERNET Wikipedia Anomalous magnetic dipole moment 2010-10-09

http://en.wikipedia.org/wiki/Anomalous_magnetic_dipole_moment

Min översättning:

I kvantelektrodynamiken är det anomala magnetiska momentet hos en partikel ett bidrag i verkningar från kvantmekaniken, uttryckt genom Feynman diagram med loopar, till den partikelns magnetiska moment.

Wikipediaartikeln ovan exemplifierar ”anomala magnetiska momentet” genom »första Feynman-loopen» i serien för elektronens g-faktor (α/2π ~ 0,0011614).

Det är också hela svaret på frågan — i ljuset av TNED: det är fenomengrunden bakom elektronens g-faktor.

”anomala magnetiska momentet” uppkommer i MAC enligt TNED på grund av att elektronmassans komponenter (grovt 1/1000) inte kan visa sig fullt ut i atombindningar på grund av att e-massan kontinuerligt genomströmmar atomkärnans kärnbrunn enligt kraftekvationen [F(BT)+F(eZ)=0] från Atomkärnans härledning — erinra att atomen inget annat är enligt TNED än en utvidgning av atomkärnan [Neutronens sönderfall] med en eller flera frigjord elektronmassa — och därför en del av e-massans atomära magnetiska moment absorberas (skyms) av atomkärnan; först genom mätning på den frigjorda elektronen [SCIENTIFIC AMERICAN 1980], där alla dess komponenter ingår, får man full pott: 2,00231930… mot den enkla matematikens rena 2 [Se Elektronringens magnetiska moment].

Med nettoeffekten i förklaringen enligt TNED i Elektronens g-faktor — ju närmare elektronmassan svänger kring atomkärnan, desto större närandel associeras elektromagnetiskt med atomkärnan och därmed motsvarande lägre verkningsgrad relativt den ideala elektronmassans svängningsenergi — kommer alla atomens excitationsnivåer, analogt elektronens energier, att innefatta en viss reduktion av den ideala elektronens totalenergi.

Exempel visas i Lambväxlingsfenomenet;

Som följd av att man (från 1947, Breit) sökte någon komponent som kunde förklara mellanskillnaden mellan det teoretiska MAC-Lambvärdet (1023 MHz) och det uppmätta (1057 MHz) — samt ytterligare (’vacuum polarization’ [Shpenkov 2004]) — uppfanns (tydligen) begreppet ’anomala magnetiska momentet’ för elektronen och som sedan figurerar i olika sammanhang som bidragande-reducerande faktor.

Se exempeltabell för Lambväxlingen från Telfer 1996, ”Anomalous magnetic moment +68 MHz”.

Se även motsvarande utdrag från Weitz et al., 1995, ”Vacuum polarization –215.168 MHz”.

Hur man resonerar matematiskt visas i utvecklingsexempel av Shpenkov 2007 (s5n) [men hans framställning är inte enkel att förstå utom universitetets-högskolans matematiska meriter].

Se vidare i Avståndskompensationen för eG.

Djupa motsägelser om elektronen i MAC

MAC uppvisar djupa motsägelser om elektronen

Först och främst: värmetransporten

Materialens termoelektrooptiska egenskaper motsäger uppfattningen i MAC om elektronen som »punktlik, strukturlös» [‡4]

Förutsättningen, rent kvalitativt, för att kunna påvisa de olika materialens termoelektrooptiska egenskaper [värmeisolation, elektrisk ledning, genomskinlighet (»keramik, spis, och fönster»)] är, tydligen, att utrymmet mellan de högtäta atomkärnorna består av något annat än den moderna akademins QED-objekt av typen »punktlika, strukturlösa» partiklar: elektronen [‡4].

Den bilduppfattning som presenteras av MAC för elektronen (nollrymd) är med andra ord uppenbarligen INTE förenlig med den faktiskt observerbara fenomenfysiken.

Dessutom innehåller MAC inre — tydligen djupa också — motsägelser om elektronen:

Å ena sidan [Elektronen inte i kärnan, FMs97sp2m] påstås att elektronen inte kan rymmas i kärnan med hänvisning till de Broglies vågekvation;

Å andra sidan påstås [Elektronen punktlik] att elektronen inte har någon utsträckning alls; Speciellt det sistnämnda framhävs generellt i elektronteorin i MAC enligt QED.

Bägge utsagorna kan uppenbarligen inte gälla samtidigt.

Se även i QED (Quantum electrodynamics, den moderna akademins samlade term för elektronteorin) där man redan från början (1927) fastslagit [QED1] att det är tillåtet att göra våld på fysikens lagar, speciellt lagen om energins bevarande [Jämför ENERGILAGEN i relaterad fysik], för att beskriva det fortsatta framhärdandet i ovanstående bevarade motsägelser.

I TNED finns ingen motsvarande motsägelse eftersom det redan från första början i Resonanserna (Grundämnenas periodiska system från Keplermomentet, ingår inte i MAC) och Atomkärnans härledning, ingår heller inte i MAC, står klart att elektronen som fysikaliskt begrepp inte är en partikel utan ett kvantum, en hop, en mängd bestående av ett antal mindre element [Se Elektronmassans komponenter] av formen impulsmoment med laddning, massa och spinn (J=mcr) och som får förstås bilda en kring atomkärnan kringliggande VÅGRÖRELSE — inte en roterande punktlik partikel — som betingas av ENDAST HELA ANTAL VÅGLÄNGDER (kvantfysiken i relaterad fysik) och som i TNED visas konsistent med väteatomens experimentellt observerade spektrum i Spektrum med vidare i Kvanttalen. Se specifikt för noggrann jämförelse analogin mellan TNED och Bohrekvivalenten i Bohrmodellens enkla motsvarande kinematiska ekvivalent.

Dessa detaljer ingår inte heller i MAC, ehuru resultaten gör det;

Elektronen uppträder — således enligt relaterad fysik (TNED) — aldrig som typ »punktlik partikel». Inte under några som helst omständigheter.

Att detta också gäller strängt i den praktiska fysiken visas enligt TNED i Elektronens bubbelkammarspår, samt i den övergripande beskrivningen och förklaringen till ljusets fysik genom aspekterna reflexion, brytning och polarisation, inkluderat förklaringen till fenomeneffekterna i Faradayeffekten och Kerreffekten, se LJUSETS POLARISATION: materialens termoelektrooptiska egenskaper generellt.

Med den — med experimentella observationer — tydligt enhetliga förklaringsgrunden, och förutsatt att inga felslut förekommer i framställningen som helhet, är det tydligt att elektronmassan i fysiken är JUST så övergripande uttömmande förklarad och beskriven som det alls är möjligt — dock utom MAC.

I andra ord sagt är det tydligt att modern akademi missar grundläggande aspekter på fysiken — som tydligen kompenseras med motsvarande uppfinningar med tillhörande fysikförklaringar som påstår det uppfunna vara verkligt — och med förklarande grund i de jämförande korsrefererade exempel som specifikt ingår i och varit huvudföremålet för Universums Historia. Se explicit i EXPERIMENTELLA BEKRÄFTELSER.

Ofta, men inte alltid, finner vi exakt samma matematiska formalia på två helt väsensskilda beskrivningssätt — vilket, tydligen som det får förstås, bara lämnar ett möjligt slutligt val: den av de bägge som mest utförligt innefattar den andra såsom en primitiv uppfattning.

Detta uppmärksammande har, speciellt i TNED, föranlett en ingående jämförande granskning av de klassiska (numera förlegade) bubbelkammarspåren från speciellt elektroner, se ELEKTRONENS BUBBELKAMMARSPÅR.

Analysen visar att spårtyperna som uppvisar tydliga drifter tvärs magnetfältets riktning

· definitivt inte kan åstadkommas av en ideal punktlik elektrisk laddning

· förklaras galant genom elektronmassans komponenter i TNED, elektriskt laddade strömringar (J=mcr); massa, laddning och spinn, här benämnda tau-ringar, i full enlighet med ATOMKÄRNANS HÄRLEDNING.

Men den främsta bevisbarheten i elektronmassans komponenter [τ-ringarna] visas ändå i TNED genom ljusets

· reflexion

· brytning

· polarisation

Se utförligt i LJUSETS POLARISATION. Varken konventionella partikelmodeller eller kvantfysikaliska vågbegrepp för sig har kunnat förklara ljusets alla olika fenomenformer. Man brukar i de olika fallen tillämpa dels vågmodellen och dels partikelmodellen beroende på problemställning.

En av pionjärerna på området, Erwin Schrödinger, skriver:

s316:

”I would define the present state of our knowledge as follows. The ray or the particle path corresponds to a longitudinal relationship of the propagation process (i.e. in the direction of propagation), the wave surface on the other hand to a transversal relationship (i.e. norma1 to it). Both relationships are without doubt real; one is proved by photographed particle paths, the other by interference experiments. To combine both in a uniform system has proved impossible so far. Only in extreme cases does either the transversal, shell-shaped or the radial, longitudinal relationship predominate to such an extent that we think we can make do with the wave theory alone or with the particle theory alone.”,

THE FUNDAMENTAL IDEA OF WAVE MECHANICS — Erwin Schrödinger, Nobel Lecture, December 12, 1933

http://nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-lecture.pdf

Min översättning:

Jag skulle beskriva vår kunskaps nuvarande tillstånd sålunda. Strålen eller partikelvägen motsvarar en longitudell relation hos fortplantningsprocessen (alltså, i utbredningsriktningen), vågytan å andra sidan en transversell relation (alltså, i dess normal). Bägge relationerna är utan tvekan verkliga; den ena bevisas genom fotograferade partikelvägar, den andra genom interferensexperiment. Att kombinera bägge i ett enhetligt system har hittills bevisats omöjligt. Bara i extrema fall överväger antingen den transversella, skalformade eller radiella longitudella relationen till den grad att vi tror vi kan stå ut med vågteorin ensam eller med partikelteorin ensam.

I varje fall med nedanstående källas tolkning skulle Schrödinger (som man kan vänta i anledning av hans vågekvationer för atomens spektrum) ha varit »en TNED-pionjär»:

”In spite of this success, the very meaning of the waves remained unclear. Schrödinger believed that the intensity of the wave at a point in space represented the 'amount' of the electron that was present at that point. In other words, the electron was spread out, rather than concentrated at a point. However, it was soon found that this interpretation was untenable, because observations revealed that particles never spread out. For example, it follows from the wave equation that when a wave, representing an electron, strikes a target, it spreads out in all directions. Experimentally, on the other hand, the electron scatters in some specific direction but never breaks up.”;

INTERNET FAQ ARCHIVES Online Education — Chapter 7: Wave Mechanics and Wave Particle Duality

http://www.faqs.org/docs/qp/chap07.html

Min översättning:

I ljuset av denna framgång, framstod den blotta innebörden av vågorna oklar. Schrödinger trodde att intensiteten hos vågen i en rymdpunkt representerade ’mängden’ för elektronen som fanns närvarande just där. I andra ord var elektronen utspridd snarare än koncentrerad som en punkt. Emellertid, upptäckte man snart att denna tolkning var ohållbar, därför att observationer avtäckte att partiklar aldrig sprids ut. Till exempel, så följer det av vågekvationen att när en våg, representerande en elektron, slår ett målobjekt, sprids den ut i alla riktningar. Experimentellt, å andra sidan, sprids elektronen i någon specifik riktning men delas aldrig upp.

SOM VI SER självbrottas MAC (som också lyckas med bedriften att kasta sig själv på mattan) med sin egen föregivna uppfattning om ’våg’ och ’partikel’ — med maximalt »olyckliga val».

[Grundfelet man gör i MAC är att INTE förstå begreppet RESONANS i den ELEMENTÄRA vågmekaniken: en ytform som, elementärt, definieras av Keplermomentet (K=vr) som tillsammans med massan (m) ger impulsmomentet (J=mK=mvr): GRUNDÄMNENAS PERIODISKA SYSTEM: elektronmassan ligger utspridd kring atomkärnan för att kunna satisfiera kvantfysikens/kvantmekanikens grundvillkor: endast HELA antal perioder ger resonans. Inget annat].

Schrödingers — tydligen enligt TNED helt korrekta — grundidé kunde aldrig utvecklas på grund av den moderna akademins favoriserade fasthållandet vid materiefysiken som den enda naturliga grundvalen: Plancks konstant (h=mcr) som ett enahanda universellt impulsmomentsVerkanskvantum utan något spår av STRUKTUR — trots Heisenberg-Schrödinger-ekvationernas framgång och som just förutsatte en sådan struktur: ’vibratorerna’ [‡5] i Schrödingers vågekvation.

Exemplet Schrödinger (och Heisenberg) visar bara att TNED-fysiken (hela tiden) försöker komma fram — men resolut motas tillbaka av krafter som mera är intresserade av att UPPFINNA än att HÄRLEDA. (Jag utnämner alltså härmed Erwin Schrödinger — i varje fall för min del — som Kvantmekanikens fader, 1925).

Tau-ringarna i TNED sammanför — tydligen — alla modeller och ger alla ljusfenomen en enhetlig förklaringsgrund, se Elektronens bubbelkammarspår, Ljusets polarisation — tydligen helt orepresenterad i MAC.

QuantumElectronDynamics — Kvantelektrodynamiken i MAC

QED

2010IX9

QED — Lambväxlingen · Casimireffekten · Elektronens g-faktor

Quantum ElectroDynamics — Kvantelektrodynamiken

Uppfattningen (från 1927 [‡5]) som antogs i modern akademi att ’elektriska laddningens fysik är i avsaknad av struktur’ samt uppvisar »punktlikhet» [‡4] skapar tydligen »sensationella föreställningar» — tillsammans med experimentella resultat — typ ’oscillerande vakuum’ och ’vakuumets polarisation’.

Ämnet är nog — således — inte direkt tillägnat trottoarfolket i den vanliga vardagens bestyr.

Genom att den blotta MÖJLIGA strukturdelen i elektronmassan utelämnades, återstod bara Heisenbergs osäkherhetsrelation (λp=h) att ta fasta på — när frågan (strax) bollades över på det här: Varje möjlig matematisk utgångspunkt för fenomenmässig beskrivning av möjliga fluktuationer i laddning Q(e) och massa m(e) — som rent experimentellt kan förekomma med hänsyn till just materiefysikens kvantiserade natur på nivån Plancks konstant (h). Det finns ingenting annat att välja på.

Sedan Heisenberg-Schrödingers matris- och vågekvationer framkommit (1925) som förklaring till atomens spektrum, utvecklades kvantiseringsbegreppen på elektronen vidare med resultat i det som kom att kallas QED (eng. Quantum electrodynamics, sv. kvantelektrodynamiken). En kort översikt av pionjärernas dagbild återges av Schupp 1959.

Speciellt utdelades nobelpriset i fysik år 1965 för de avgörande bidrag som kom att lyfta fram QED som en faktor att räkna med i den moderna fysikens utveckling, och då i allra största synnerhet med särskilt understrykande av dess experimentellt bekräftade ställning. Se exv. nobeltalet 1965 i

AWARD CEREMONY SPEECH —

The Nobel Prize in Physics 1965 — Sin-Itiro Tomonaga, Julian Schwinger, Richard P. Feynman

http://nobelprize.org/nobel_prizes/physics/laureates/1965/press.html

Genom arbetet med att få ekvationer och experiment att stämma, utvecklades samtidigt successivt allt mer avancerade matematiska modeller (1925-1965) som kunde inpassa elektronens beteende i de experimentella anordningarnas fysik. Utdrag som beskriver den exceptionella komplexiteten i den rent matematiska delen ges här av Shpenkov 2007 (s3n).

De experimentalområden som berör sakkärnan i QED (eng. Quantum electrodynamics, sv. kvantelektrodynamiken), och som vi nu känner som de främsta, är

Lambväxlingen

(eng. Lamb shift, sv. även Lambskiftet) [främst med den extra energin i Väteatomens n=2-skal på uppmätta 1057 MHz från Lamb-Retherford år 1947, förorsakat i MAC av ’vakuumets fluktuation’],

Casimireffekten

[med exempelvärdet p=1atm=101325 Pa vid ca 10 nM separation mellan två plana metallytor — atomär attraktion mellan närliggande elektriskt oladdade materialytor, också enligt MAC förorsakat av ’vakuumets fluktuation’] och

Elektronens g-faktor

[med värdet 2,00231930…, också enligt MAC förorsakat av ’vakuumets fluktuation’].

I TNED förklaras alla tre fenomenformerna dels genom atomkärnans struktur (N3m20-aggregatet från Atomkärnans härledning) och dels genom de ’vibratorer’ i elektronmassan som — korrekt från början i MAC — infördes omkring 1925 för att förklara atomens spektrum (Heisenberg-Schrödingers matris- och vågekvationer, se citat från Gamow), men som strax (1927) förkastades tillsammans med en allmän (slutlig, slutet av 1940-talet) bannlysning av någon mekanisk modell alls för elektronmassan [Se Citatet i Spinnbegreppet i modern akademi].

Med andra ord: Medan man i MAC har tvingats uppfinna agenter i tomrummet — vibrerande vakuum och polariserande vakuum — för de (enligt TNED korrekta) agenter som förkastades (1927), är dessa de enda rationella agenter som ALLS finns att förklara hela historien på och som också därför bildat utgångspunkten i TNED: atomkärnans härledning — från det universella verkanskvantumet eller Plancks konstant h=mcr (PLANCKRINGEN).

Konsekvensen av att utesluta ’vibratorerna’ från 1925 ur elektronmassan och i deras ställe ’införa virtuella partiklar’ medförde strängt obskyra former för beskrivning: Då dessa, virtuella, agenters egenfysik ENLIGT TNED inte finns representerad i verklighetens universum — samt under former som normalt är oacceptabla, främst direkta regelbrott mot energins bevarande, jämför citatet nedan — finns heller ingen rationell grund för att acceptera dem.

QED1

”Quantum mechanics allows, and indeed requires, temporary violations of conservation of energy”,

”… if any part of it were wrong the whole structure would collapse”,

SCIENTIFIC AMERICAN — 9Oct2006

Are virtual particles really constantly popping in and out of existence? Or are they merely a mathematical bookkeeping device for quantum mechanics?

http://www.scientificamerican.com/article.cfm?id=are-virtual-particles-rea&topicID=13

Min översättning:

Kvantmekaniken tillåter, och verkligen kräver, tillfälligt våld på energins bevarande …

… om någon del skulle vara fel skulle hela strukturen kollapsa

På den vägen har det alltså kommit sig dithän att modern akademi har etablerat en föreställning som går ut på att rymden, alltså tomrummet, och enligt osäkerhetsprincipen, kan innehålla alla slags nödvändiga fluktuationer (±e) — och vilkas sammantagna verkan, följaktligen, åberopas som orsaksgrunden för experimentellt påvisade resultat och som därmed i stöd av dessa påstås härröra ur osäkerhetsfluktuationer via Plancks konstant (h). För de rent matematiska grunderna i MAC, jämför citatet i Tau-teorin. Jämför citatet nedan.

QED2

”The vacuum has, implicitly, all of the properties that a particle may have: spin, or polarization in the case of light, energy, and so on.”,

@INTERNET Wikipedia Casimir effect, Vacuum energy 2010-09-09

http://en.wikipedia.org/wiki/Casimir_effect

Min översättning:

Vakuumet har, implicit, alla de egenskaper som en partikel har: spinn, eller polarisation i fallet med ljus, energi, osv.

I termer av TNED (relaterad fysik) upphör naturvetenskapen som rationell (förnuftsbaserad) verksamhet i samma stund och anda som man tillåter (organiserat, överenskommet) våld på olika förgreningar — enbart för att få ihop det i slutänden med experimentella observationer. En sådan formalism har spårat ur och må väl vara hur etablerad den vill, men har uppenbarligen ingenting att göra med verklig sann naturfilosofi. Analogin är regeringsmakten som inför en motvillig allmänhet börjar fängsla oppositionen för tillfället att få genomdriva diktatur.

Wikipedia skriver till exempel i sin artikel på Lamb shift

QED3

”The fluctuation in the electric and magnetic fields associated with the vacuum perturbs the Coulomb potential due to the atomic nucleus. This perturbation causes a fluctuation in the position of the electron, which explains the energy shift. The difference of potential energy is given by

”, utan vidare beskrivning,

@INTERNET Wikipedia Lamb shift 2010-09-09

http://en.wikipedia.org/wiki/Lamb_shift

Min översättning:

Fluktuationen i elektriska och magnetiska fält associerade med vakuum stör Coulombpotentialen från atomkärnan. Denna störning förorsakar en fluktuation i elektronens position, vilket förklarar energiändringen. Skillnaden i potentiell energi är given av

sambandet.

Jämför korrekt sentens enligt TNED:

Fluktuationen i elektriska och magnetiska fält associerade med STRUKTUREN I ATOMKÄRNANS SPINN stör den normalt idealt sfäriska Coulombpotentialen från atomkärnan. Denna störning förorsakar en fluktuation i elektronens position, vilket förklarar den lilla extra växeln i energiändringen.

Matematiken är — i vilket fall, i princip — densamma. Råformen i MAC-fallet

ΔE_Lamb = α⁵m_ec²([k(n,0)]/4n³)

”for l = 0 with k(n,0) around 13 varying slightly with n”,

@INTERNET Wikipedia Lamb shift 2010-09-09

http://en.wikipedia.org/wiki/Lamb_shift

är (nästan, i MAC tillkommer UTÖVER sambandsformen som sådan ytterligare detaljer men som inte explicit ingår i TNED) samma som råformen i TNED men med

1. c förtydligat ekvivalent av potentialbarriärens c_z=c₀/2 (från ljusets gravitella beroende (DGD) — ekvivalensen mellan gravitationsenergin [mw²] och divergensenergin [mc²]), stället där den elektriska laddningen TAS av princip i fysiken — som ger motsvarande α⁵m_ec_z²([k(n,0)]/n³), c_z finns inte upptaget i MAC, och DGD i TNED använder PLANCKEKVIVALENTERNA medan DGD i MAC använder RELATIVITETSTEORIN, se särskilt i Jämförelsen MAC/Relaterad fysik i Einsteins samband — vilket betyder att ömsesidigheten utesluts —

2. [k(n,0)] ersatt av Väteatomens grundenergi i eV, = E₀/e ~ 13,6 eV som ger motsvarande α⁵m_ec_z²([E₀/e]/n³),

3. faktorerna α⁵m_ec_z²/e=(4/3)²/n med n för antalet komponenter i elektronmassan (673 026,65), med

4. koefficienten (4/3)² från atomkärnans struktur [Utförligt från Atomkärnans härledning] med kärnspinnets strukturpåverkan på det enskilda elektronelementet via kärnaggregatet N3m20:s första primära underfraktal med delfaktorn (1+1/3), se härledningen i Lamb TNED, samt

5. den generellt approximerade allmänformen för N3m20-deltoroidens underfraktal i dess avståndspåverkan på det enskilda elektronelementet inkluderat effekten med Elektronens g-faktor (1 + 1/3 – b/3n^c);

Sambandet totalt i TNED blir motsvarande för Väteatomens huvudkvanttal (n, l=0) [Se beräkningarna i Kalkylkortet]

ΔE_Lamb = E₀[1 + 1/3 – b/3n^c]²/n³n. Koefficienterna bc — som generaliserar summan av alla effekter (temperatur, excitationsgradens inverkan på resonansmönstren, typ skärmning, elektronmassans totala magnetiska moment som funktion av excitationsgraden, se Elektronens g-faktor) utan vidare specifikation, för vidare prövning av sambandets allmänna praktiska giltighet — avstäms/kontrolleras genom prövning mot de experimentellt uppmätta värdena, se tabellredovisning i Avståndsformen. Och man finner att b=0,1201893 och c=0,1209440 satisfierar de bägge första Lambövergångarna i (n=1[8172,837 MHz], 2[1057,844 MHz]) — övriga här ej närmare kända — enligt det motsvarande totalsambandet

ΔE_Lamb = E₀[1 + 1/3 – (0,1201893)/3n^0,1209440]²/n³n

och som för det vanliga enkla Vätets huvudkvanttalsspektrum (idealt slät kärnstruktur, n=1) övergår i det enklare

E = E₀/n²

Se utförligt från utvecklingarna i Lamb TNED.

Sammansättningen — och naturen — i »moderatorerna i de fem punkterna» ovan är (här veterligt) helt uteslutna i härledning på något begripligt sätt utan kännedom om NEUTRONKVADRATEN: Vilket vill säga: (de förfärligt ytliga) MAC-analogierna (typ ’vakuumets fluktuationer’ [‡] som man verkligen undrar ifall någon, verkligen, tar på allvar, men det är ju så historien känner modern akademi) döljer den djupa sanningen. Se vidare i Avståndskompensationen för eG med jämförande resultatreferenser, samt Antalet element i elektronmassan.

NOTERING ——————————————:

‡ Energin finns där massan finns: E=mc²; i tomrummet är m=0, och sedan spelar det ingen roll vilka privata överenskommelser man gör, och hur dyrt man än bedyrar dessa: 0=0c². Enbart med den enkla matematiken är det tydligt att blotta idén om ’vakuumets nollenergi’, är, och förblir befängd, hur tilltalande de matematiska utvecklingarna än är, och hur än mycket dessa tangerar experimentella resultat: noll är och förblir noll. Men vadå? Man hade lösningen framför sig, ’vibratorerna’ i elektronmassan från 1925, men man förkastade dessa (1927) och bannlyste (1947) varje mekanisk modell för elektronen. Se Citat från Gamow och Citat i Spinnbegreppet i modern akademi.

Se även nedanstående citatexempel, som ansluter till samlingen.

QED4

”Physicists believe that empty space may be continually creating pairs of virtual particles, such as a positron and electron, which rapidly annihilate each other shortly thereafter.[78]”,

@INTERNET Wikipedia Electron, Virtual particles 2010-09-09

Min översättning:

Fysiker tror att tom rymd kontinuerligt kan skapa par av virtuella partiklar, såsom positron och elektron, vilka snabbt annihilerar varandra strax efteråt.

Anledningen till ovanstående (»kaxigt uttryckta») förankring i experimentalfysiken ligger numera (2010) väl synligt i laserteknikens kölvatten, se exemplet med positronbildning från guldatomer via laserbestrålning.

Summering QED

Summering

QED utvecklades i sin primära form från omkring 1925 och slutligt från ca 1947 genom att utesluta begreppet struktur ur elektronmassan.

Har man, generellt, matematiska samband som uppvisar analogi med experimentella resultat, men ingen adekvat, rationell teori som förklarar sammanhangen, är det tydligt att den teoretiska förklaringen ännu åstundar sin baneman, att den teori man har till dit är, och förblir, bristfällig.

LambReferenser

LambWiki

”The electron is "smeared out" and the radius is changed from r to r + δr”,

@INTERNET Wikipedia Lamb shift 2010-09-09

http://en.wikipedia.org/wiki/Lamb_shift

Teorin i modern akademi (via perturbationsteoi, »störningsteori») ger i Vätefallet (2p-2s) via Wikipediaartikeln sambandet

‹ΔV› = (4/3)(e²/4πε₀)²(1/ħc)(ħ/mc)²(1/8πa₀³)ln(4ε₀ħc/e²)

”This shift is about 1GHz, very similar with the observed energy shift.”. a anger Bohrradien.

Med en korrektion på ×2 ges frekvensen 1023,45 MHz (mätvärdet 1057 MHz).

= (4/3)(e²/4πε₀)²(h/2πm²c³)(1/8πa₀³)ln(4ε₀ħc/e²)

= (4/3)(e²/4ε₀)²(h/π⁴m²c³)(1/16a₀³)ln(4ε₀ħc/e²)

= (1/3)(e⁴/16ε₀²)(h/π⁴m²c³)(1/4a₀³)ln(4ε₀ħc/e²)

= (1/3)(he⁴/8²ε₀²π⁴m²c³a₀³)ln(4ε₀ħc/e²)

= (1/3)(he⁴/[8π²ε₀m]²c³a₀³)ln(4ε₀ħc/e²) .......... OK; men det ser ut att fattas en faktor 2 ;

= (2/3)(he⁴/[8π²ε₀m]²c³a₀³)ln(4ε₀ħc/e²)

= (2/3)h([8π²ε₀m]²c³a₀³)^–1e⁴ln(4ε₀ħc/e²)

= (1/3)h(32[π²ε₀m]²c³a₀³)^–1e⁴ln(4ε₀ħc/e²) ...... enda variabeln är a₀

= 1023,449866531 MHz (mätvärdet från Lamb-Retherford 1947 är 1057 MHz)

Wikiartikeln ger i ett samband längre ner den enklare formen

ΔE_Lamb = α⁵m_ec²([k(n,0)]/4n³) ”for l = 0 with k(n,0) around 13 varying slightly with n”, vilket i klartext associerar till Väteatomens grundnivå motsvarande jonisationsenergin 13,6 eV, alltså en division med e — men artikeln utsäger inte detta explicit, och vilket gör att den användningen här blir äventyrlig, trots ekvationens enkla form: sambandet är oklart. Se dock prövningen med

ΔE_Lamb = α⁵m_ec²(E₀/e)/4n³ enligt resultatredovisningen i Kalkylkortet (Tabellflik 1, Wikipedia Lamb shift)

Dessutom gäller, tydligen enligt MAC (samma artikel som ovan), bara Lambskiftet för s-orbitaler (enligt beskrivningens avgränsade förutsättningar, som dock inte omnämns explicit),

”For p orbitals, the nonrelativistic wave function vanishes at the origin, so there is no energy shift. But for s orbitals there is some finite value at the origin …”,

@INTERNET Wikipedia Lamb shift 2010-09-09

Se dock tabellcitatet från Weitz 1995, där anges också Lambändringsvärden för P-typen.

Lambväxlingen i citat

Lamb shift:

Även Lamb-Retherford shift — Källan nedan kan inte kopieras (1961)

Department of Physics, University of Delhi —

ON THE EFFEKT OF THE FINITE MASS OF THE PROTON IN LAMB SHIFT IN HYDROGEN ATOM — H.S. Mani, Jaidev Anand, 1961

http://www.new.dli.ernet.in/rawdataupload/upload/insa/INSA_1/20005ab7_244.pdf

”The Lamb Shift is interpreted as the difference between the self-energy of the electron and that of a free electron.”, s244mn.

Se även (2004)

Shpenkov 2004

Institute of Mathematics & Physics, UTA, Kaliskiego —

DERIVATION OF THE LAMB SHIFT WITH DUE ACCOUNT OF WAVE FEATURES FOR THE PROTON-ELECTRON INTERACTION —

G. P. Shpenkov 2004

http://www.unicentro.br/editora/revistas/recen/v6n2/Swp0000.pdf

”The main constituents of the energy “splitting”, called the Lamb shift, are the effects of vacuum polarization, electron mass renormalization and anomalous magnetic moment.”.

Eftersom elektronen i MAC anses och betraktas som en punktlik, strukturlös partikel [‡4], och därmed heller inte kan förklara den verkliga elektronens uppförande, måste man i MAC UPPFINNA MOTSVARANDE FIKTIVA FYSIK för att kunna förklara experimentella resultat.

Det ’vakuumets polarisation’ eller ’vakuumets fluktuation’ man talar om i MAC är i termer av relaterad fysik (TNED) uppenbarligen ingenting annat än resultatet av ELEKTRONMASSANS KOMPONENTER, dessa ingår inte i MAC.

Welton ref

PHYSICAL REVIEW — Some observable effects of the quantuum-mechanical fluctuations of the electromagnetic field, Theodore A. Welton, 1948

http://particle.korea.ac.kr/class/2005/phys602/p1157_1.pdf

Kan inte kopieras

;

Welton 1

s1157sp2n, II THE MEAN SQUARE FLUCTUATION IN POSITION OF A FREE ELECTRON:

”Our starting point is the observation that the quantuum-mechanical zero-point variation of the radiation field in empty space gives rise to fluctuating electric and magnetic fields whose mean square values at a pont in space are given by the well-known relation

In this equation the variable k refers to the wave number of a quantum, and the contribution to the mean square fluctuation arising from frequencies in the range cdk is therefore explicitly displayed.”.

Welton 2

s1158sp2, III THE LAMB SHIFT (V ersätter ’nabla-tecknet’):

” This can easily be seen in the following way. Consider the motion of an electron in a static field of force specified by a potential energy V(q). The coordinates of the electron consists of a part which varies smoothly in time with the orbital frequency plus a part which fluctuates randomly in time. We designate the smooth part by q and the random part by Δq. The instantaneous potential energy is then given by

V(q+Δq) = [1 + Δq·V + (1/2)(Δq·V)² + … ]V(q). (5)

The effective potential energy in which the particle moves will just be the average of (5) over all values of Δq.”.

———————

NOTERING. Nablatecknet (triangel med spetsen neråt) används i modern akademi för att beteckna en vektoralgebraisk operator (vektorkalkylen). Används ofta (men inte alltid) i meningen ’derivata’ eller ’gradient’. På grund av MAGNETISKA FÄLTINTEGRALEN i relaterad fysik kan den moderna akademins vektorkalkyl inte användas i TNED (generellt inte alls i samband med fysikens fenomengrunder, enligt relaterad fysik [TNED]).

Se @INTERNET Wikipedia Mathematical symbols, Nabla 2010-09-18

http://en.wikipedia.org/wiki/Mathematical_symbols

Lamb-Retherford experimentet

YungKuoLim —

Se även i

Uppmärksammad felstavning

World Scientific Publishing — 2000

PROBLEMS AND SOLUTIONS ON ATOMIC, NUCLEAR AND PARTICLE PHYSICS — Yung-Kuo Lim

http://kolxo3.tiera.ru/P_Physics/PG_General%20courses/Yung-Kuo%20Lim.%20(ed.)%20Problems%20and%20Solutions%20on%20Atomic,%20Nuclear%20and%20Particle%20Physics%20for%20U.S.%20PhD%20qualifiers%20(WS,2000)(ISBN%209810239173)(718s).pdf

Verkar inte finnas någon enklare URL …

”Lamb-Rutherford Experiment. In 1947, when Lamb and Rutherford measured the spectrum of H atom accurately using an RF method, they found it different from the predictions of Dirac’s theory, which required states with the same (n, j) but different l to be degenerate. Instead, they found a small splitting. The result, known as the Lamb shift, is satisfactorily explained by the interaction between the electron with its radiation field. The experiment has been interpreted as providing strong evidence in support of quantum electrodynamics.”, s39m.

Källan beskriver experimentet vidare i detalj.

Lambväxlingen, citatblock(2)

s2664sp1m,

Weitz 1995

PRESICISON MEASUREMENT OF

THE 1S GROUND-STATE LAMB SHIFT IN ATOMIC HYDROGEN AND DEUTERIUM BY FREQUENCY COMPARISON —

Weitz et al., 1995

http://www.nat.vu.nl/en/Images/Hlamb_tcm69-85353.pdf

Källan kan inte textkopieras.

NOTERA att tabellvärdet ovan typ 8172,802(40) MHZ är resultat av en SUMMERING med toppvärdet (”selfEnergy”) på 8396,456(1) MHz (Källan samma sida, samma spalt, längst ner, TABLE II);

NOTERA ”Vacuum polarization”-beloppet på minus 215 MHz:

VAKUUMPOLARISATION (experimentellt 1997 TRISTAN) är i MAC ett fenomen VID SIDAN AV VAKUUMETS FLUKTUATION (experimentellt 1947, Lamb-Retherford, »Lambövergången»). Vakuumfluktuationen i MAC associeras med ’vakuumets energi’ eller ’nollpunktsenergin’ och som (enligt vissa) grundlägger härledningen till (bl.a.) Lambövergången. Det är tydligt att källförfattarna ovan gör viss skillnad.

Se även

Telfer 1996

Johns Hopkins University —

EVERYTHING YOU ALWAYS WANTED TO KNOW ABOUT THE HYDROGEN ATOM (BUT WERE AFRAID TO ASK) —

Randal C. Telfer 1996

http://www.tcd.ie/Physics/People/Peter.Gallagher/lectures/js_atomic/hydrogen-essay.pdf

s20:

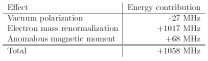
MAC-sambandet ger 1017 MHz, mätningen visade 1058 MHz; anomalous magnetic moment med +68 och vacuum polarization med –27 ger då 1058.

Man inför (ytterligare) olika justeringsparametrar typ vacuum polarization, anomalous magnetic moment — »fackartikelvärdena» är INTE rena värden, och ingen upplysning ges (oftast) heller.

Om de enorma beräkningsgrunderna för ’elektronens avvikande magnetiska moment’;

Shpenkov 2007

s3:

Institute of Mathematics & Physics, UTLS, Kaliskiego —

ANOMALOUS MAGNETIC MOMENT OF AN ELECTRON, LAMB SHIFT, AND MICROWAVE BACKGROUND RADIATION OF HYDROGEN ATOMS: WHAT DO THEY HAVE IN COMMON? — George P. Shpenkov 2007

http://shpenkov.janmax.com/CommonPhen.pdf

s2ö:

”caused by different constituents of specific wave motion of the electron in the intra-atomic wave field”

s3n:

”The derivation by QED (with participation of quantum chromodynamics) of Eq. (10) rests on the concept of virtual particles. The expanded form of the equation is extremely complicated.”,

”Actually, the coefficient 1.5098(384) of the α⁴ term (calculated with big uncertainty, ± 384 ) consists of more than one hundred huge 10-dimensional integrals.”,

”Therefore, because of the complicated mathematical structure of coefficients of the αⁿ terms, a special system of massively-parallel computers was developed to calculate (10) [6].”;

s5m:

”the most accurate experimental values obtained for the 1S and 2S Lamb shifts of the hydrogen

atom: L_1,s = 8172.837(22) MHz and L_2s−2p =1057.8446(29) MHz [12] (Table 3).”;

s5n:

”With allowance for the wave behavior of a proton and an electron, we have arrived at the simple, and precise, description of the anomalous magnetic moment of the electron, and also at the discoveries of the background spectrum of the hydrogen atom and the Lamb shifts nature.”.

Författaren beskriver i början hur AnomaliMomenten följer »högskolans vågvektormekanik»:

”In full agreement with the wave-particle duality, we can consider the hydrogen atom as a wave dynamic formation, namely as the simplest paired centrally symmetric proton-electron wave system”, s1mö.

Notera att Shpenkov (generellt) uttrycker delvis udda uppfattningar om olika fenomenformer i fysiken:

George Shpenkov [högutbildad fysiker-matematiker med många tekniska meriter och publikationer] hör till den typ av författare som med grund i den matematiska fysikens olika domäner ger en del originella aspekter på fysiken som INTE (direkt) ansluter till etablerade uppfattningar. Ett exempel beskrivs nedan:

”In particular, Shpenkov suggests that fundamental issues associated with the zero of energy can be used to significantly simplify how QED is applied in dealing with some of the more fundamental questions (for example, the anomalous magnetic moment of the electron) where it has been applied.”,

Issue 68 July/August 2006 — Infinite Energy Magazine — Concerning Truth and Justice in Science and What We Know About Science, Scott Chubb

http://www.infinite-energy.com/iemagazine/issue68/concerningtruthandjustice.html

QED är helig mark i MAC och släpps inte så enkelt ifrån sig. Shpenkovs »matematisk-fysikaliska originalitet» exemplifieras (till exempel) med hans »alternativa Planckkonstant» för elektronen, Shpenkov 2007 s2mn,

”where h_e = 2πm_eυ₀r_e is the proper action of the electron (analogous to the Planck action h)”

med förtydligandet s2ö,

”υ₀ is the oscillatory speed of boundary wave shell of the hydrogen atom equal to the Bohr speed”.

Matematiken är OK — men i modern akademi känner ingen till någon TEORI för dylika fysikaliska faktorer. Att också försöka INFÖRA någon slags ny konvention genom att, obetingat, anta »Shpenkov-begreppen» är definitivt INTE förenligt med naturvetenskapen.

Hur fel MAC än må ha i formuleringarna, måste varje framsteg i naturvetenskapen kunna innefatta föregående uppfattningar i en FÖRKLARING. Annars kommer ämnet inte fram.

Shpenkov för sin del — om jag inte helt har missuppfattat hans kärna i denna korta översikt — verkar mera intresserad av att införa en nyordning än att försöka HÄRLEDA vad den ev. skulle gå ut på, min mening. [Vilket TYVÄRR oftast är fallet med de originella bidragsgivarnas arbeten: för mycket MIG, för litet NATUR]. Nämligen, att MATEMATIKEN som Shpenkov (tydligen) framvisar »innehåller värdefull info» — om man känner grunderna i TNED. Men det vet/visste inte Shpenkov.

Motsvarande υ0 i TNED berör — tydligen — divergensen, energizonen i potentialbarriären, stället där e TAS och vilken detalj inte finns med i MAC då heller inte härledningen till elektriska laddningen (divergensens aspekt) finns med: Q=√(m/R)(A/dT). Dvs., Shpenkovs matematik — som det ser ut speciellt för Väteatomens spektrum och inkluderat inverkan från Lambväxlingen och Elektronens g-faktor — innehåller tydligen parameterfaktorer som explicit framgår tydligt i TNED (från Spektrum).

Nämligen: Shpenkovs RESULTAT överensstämmer med uppmätta värden.

Shpenkov omnämns inte i (några mera framträdande) forskningsrapporter i ämnet.

Shpenkovs teorier

Exempel på Shpenkovs eget framställningssätt i ämnet finns på webbsidan (2010-10-11)

http://shpenkov.janmax.com/LettEng.asp

Se även Shpenkovs teorier mera omfattande i

http://shpenkov.janmax.com/TheorBasis.pdf

Det är ”intra-atomic oscillations” och liknande — uttryckt på den avancerade matematikens vågfunktioner [jämförda med experimentella resultat] — en tydlig strävan från Shpenkov att övervinna den abstrakta QED-teorins logik.

Shpenkov gör dock ett uppenbart fel: Han »kommer fram till» [här f.n. utan annat motbevis än följande] att den kosmiska bakgrundsstrålningen [CMB] skulle ha sin grund i de ovannämnda ’interatomära oscillationerna’, och att BigBang-teorin därmed skulle vara grundlös. Vi VET att Shpenkov (och andra originella alternativ, se Pierre-Marie Robitaille) INTE har fog för sig: CMR sammanhänger helt tveklöst med ’universums temperatur’ [Se K-cellens värmefysik].

Däremot är Shpenkovs invändningar mot QED-teorins oscillerande vakuumenergi mera sympatiska — i varje fall sett ur TNED:s perspektiv — eftersom ämnet ansluter till ELEKTRONMASSANS KOMPONENTER och som avskrevs av MAC 1927 men som Shpenkov här veterligt inte känner till (eller så gör han det, men får inte bladet från munnen).

Shpenkovs allmänna teori om Universum-Antiuniversum och PartikelGrunderna är dock rent förfärlig läsning, min mening. Vart tog Naturen vägen Shpenkov?

I TNED finns ingen ’wave-particle duality’. Utförligt i Atomkärnans vågnatur.

Det är tydligen svaret på frågan om vilka underliggande komplex (enormt komplicerade datorstödda beräkningar som garanterat ingen enskild människa kan hänga med på) som finns i beräkningsgrunderna (som vi kunde förmoda men inte bevisa).

Webbkällan ovan ger också (alltså, s5n ovan) ett svar på kryptiken ’anomalous magnetic moment’; ytterligare en uppfinning i MAC för att matcha experimentet; MAC-sambandet ger 1017 MHz, mätningen visade 1058 MHz; anomalous magnetic moment med +68 och vacuum polarization med –27 ger då 1058.

CasimirRef

Citatreferenser till Casimireffekten

Lisanti 2005

OBSERVATION OF THE SKIN-DEPTH EFFECT ON THE CASIMIR FORCE BETWEEN METALLIC SURFACES — Lisanti et al., 2005

http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1189346/pdf/pnas-0505614102.pdf

Aspekter visar att överensstämmelsen mellan teori och experiment INTE är helt överväldigande

”The experimental results obtained with the thin metallic film are systematically smaller than those expected by the theoretical calculation also at larger separations.”, s11991sp1mö,

Lisanti et al., 2005

;

Sambandsformen

F = –π²hcR/720z³ [Se de oberoende källorna Preveslik, Mohideen, Lisanti i Sfär-Platta-samband]

ger med R=100µM [s11989sp2n, ”A 100-µm radius polystyrene sphere”] och z=0,1µM

F = 272,29 pN

— vilket visserligen ligger nära men ändå är tydligt för mycket relativt mätvärdena (tjockfilmen[svarta] ca 150 pN, tunnfilmen[grå] ca 100 pN).

Det finns tyvärr (ännu Sep2010) inget motsvarande TNED-samband utvecklat att jämföra med.

Dessutom är Sfär-Platta-sambanden inte Casimir-original (Platta-Platta) vilket ytterligare försvårar jämförelser.

OBS. Artikeln i Lisanti et al., 2005 utgår INTE ifrån Casimirs parallella-Plattor-samband, utan ifrån en version typ Sfär-Platta-samband som inte redovisas på något direkt enkelt sätt, man får söka i andra källor för att hitta förekomsten..

Artikeln utgår från andra samband: attraktionskraften sfär-platta (Lifshitz-ekvationen) — ingen direkt jämförelse kan ges.

Artikeln i Lisanti et al., 2005 går ut på att visa att Casimireffekten ändras med referens till den s.k. skineffekten (Fenomenet inom elektroniken då en ledare påförs hög frekvens och ledningselektronerna etablerar sig i ett tunt ’skin’ på ledarytan); Casimireffekten (för goda ledare) avtar om metallfilmsproverna understiger skin-djupet (ca 100Å för ”most common metals”). Resultatet endast understryker τ-ringarnas ställning enligt TNED.

Ytterligare uppgifter om Casimireffekten (vissa data) finns på

PhysicsWorld 2002

(man måste logga in, men det är helt gratis)

PHYSICS WORLD — The Casimir effect: a force from nothing 2002

http://physicsworld.com/cws/article/print/9747

Källan beskriver olika mätningar (man tycks använda koppar, aluminium, guld, krom …) — med diversifierade resultat och olika noggrannhetsgrader 1(sfärer)-15(plattor)% beroende på metod …

”It turns out that the measured Casimir force between real metallic mirrors that are 0.1 µm apart is only half the theoretical value predicted for perfect mirrors.”,

;

”We found that the simple solid-state models of the mirror match the real behaviour only above 0.5 µm.”,

;

”Another problem with calculating the expected Casimir force for a real system is the fact that experiments are never carried out at absolute zero - as originally envisaged in Casimir's calculations - but at room temperature.”,

;

”For example, the Casimir force between two plane mirrors 7 µm apart is twice as large at room temperature than at absolute zero.”,

”Fortunately, thermal fluctuations at room temperature are only important at distances above 1 µm, below which the wavelength of the fluctuations is too big to fit inside the cavity.”.

Casimireffekten,

historisk bakgrund

Bakgrunden (autobiografi) [Hendrik B. G. Casimir, holländsk fysiker, 1919-2000],

;

OF SOME THEORETICAL SIGNIFICANCE: IMPLICATIONS OF CASIMIR EFFECTS — Maclay et al., datumuppgift saknas (2001, sep. arxiv.org.)

http://www.quantumfields.com/casfin.pdf

Använd den här daterade källan istället:

http://arxiv.org/PS_cache/quant-ph/pdf/0105/0105002v1.pdf

från

http://arxiv.org/abs/quant-ph/0105002

;

”Let us first recall that Casimir discovered his effect as a byproduct of some applied industrial research in the stability of colloidal suspensions used to deposit films in the manufacture of lamps and cathode ray tubes. In the 1940s J.T.G. Overbeek at the Philips Laboratory studied the properties of suspensions of quartz powder, and experiments indicated that the theory of colloidal stability he had developed with E.J.W.”, s1n.

Kontexten tycks ha missat det deskriptiva objektets adjektivform här: ’and experiments indicated that the theory of colloidal stability he had developed with E.J.W. was valid’.

”Intrigued by the simplicity of the result, Casimir sought a deeper understanding. A conversation with Bohr led him to an interpretation in terms of zero-point energy. Then he went further with the idea of zero-point energy and showed that two perfectly

conducting parallel plates should be attracted to each other as a consequence of the change they create in zero-point field energy”, s2ö.

Med Casimirs egna ord, källan ovan:

”I mentioned my results to Niels Bohr, during a walk. That is nice, he said, that is something new. I told him that I was puzzled by the extremely simple form of the expresssions for the interaction at very large distance and he mumbled something about zero-point energy. That was all, but it put me on a new track.”, s2mö.

Tidsbilden ovan är omkring 1947-48 (”Summer or autumn 1947”), och Bohr hade (tydligen) nyligen hört/läst om Bethes publicerade lösning (1947) till Lamb-Retherford-experimentet, ref [Wikipedia, Quantum electrodynamics, History 2010-09-19].

Casimirs presenterade sitt resultat till Holländska vetenskapsakademin Maj 1948, och hans bidrag publicerades senare under året (källan ovan, s2m).

”The Casimir force between conducting plates is a more palpable consequence of zero-point field than, for instance, the Lamb shift. It is perhaps for this reason that it now appears to be the most widely cited example of how vacuum fields and their fluctuations can have observable manifestations.”, s2mn.

Med Casimirs egna ord, källan som ovan:

”The Casimir force, sit venia verbo, is the last but also the most elegant trace of cohesion energy [6].”, s3ö.

Ur de mera sensationella tolkningsföreträdena (typ ’omvänd gravitation’) strömmar sedan en vidare flora av mera avancerade »virtuella genier»:

”Zero-point field energy density is a simple and inexorable consequence of quantum theory, but it brings puzzling inconsistencies with another well verified theory, general relativity.”, s3mö,

;

”The discrepancy between theory and observation is about 120 orders of magnitude, arguably the greatest quantitative discrepancy between theory and observation in the history of science [12], [13]! There are numerous approaches to solve this “cosmological constant problem,” such as renormalization, supersymmetry, string theory, and quintessence, but as yet this remains an unsolved problem.”, s3mö.

Se även (kan markeras men inte kopieras)

PHYSICS TODAY — Casimir forces: Still surprising after 60 years — Steve K. Lamoreaux, 2007

http://palasantzas.fmns.rug.nl/Physics%20Today%20-%20S.%20Lamoreaux.pdf

En kopierbar version finns på

http://www.fen.bilkent.edu.tr/~bulutay/442-612/lamoreaoux-pt-07.pdf

”Casimir's conducting-plates paper is among the most important in the history' of physics, because it shows that the boundary conditions of a system can affect the zero-point energy of the system and, hence, the system's properties. The concept has wide application in physics, as attested by the thousands of citations to the paper.”, s41sp2m

”Casimirs result, equation 4, strongly suggests a reality of the electromagnetic zero-point energy. When Casimir told Wolfgang Pauli about the attraction of two conducting plates, Pauli rejected the notion as ”absolute nonsense.”⁵”, s42sp1n

”The question remains: Does the vacuum of free space contain zero-point energy manifested as a cosmological constant or other kind of dark energy?”, s43sp1mö.

Sfär-Platta-samband

Se även Casimirkälla (beskrivning) i

CASIMIR FORCE - NEUTRAL OR ELECTROSTATIC? — T. V. Prevenslik, datumuppgift saknas

http://www.esdjournal.com/techpapr/prevens/casimir/casmir.pdf

Där ges sambandet för sfär-platta (samband 2, dokumentet saknar siduppgift)

F = –π²hcR/720z³

— samt flera (mycket bättre, utförligare) experimentResultatBeskrivningar …:

inledningen:

”Since Casimir, the attractive force between neutral metal surfaces separated by an evacuated gap has been

attributed to the zero point energy (ZPE) of quantum mechanics. But the Casimir theory has difficulty in explaining how

contact of neutral surfaces in micro electro-mechanical systems (MEMS) devices can cause permanent adhesion without

the discharge of the build-up of static charge.”,

andra sidan:

”Since contact of neutral and otherwise chemically non-reactive surfaces under the attractive Casimir force is unlikely to cause permanent adhesion unless fusion bonding has occurred, the conclusion here is that electric charge is somehow produced in the Casimir effect, the permanent adhesion caused by static discharge. But in the standard formulation of the Casimir theory, the surfaces are assumed neutral and uncharged surfaces.”,

”Indeed, Casimir forces of any significance are only found at gaps less than about 0.2 µm corresponding to VUV wavelengths.

What this means is that the standard Casimir theory may need to be modified.”.

;

Källan ovan (ekv. 1, första sidan) ger även en något alternativ koefficientform till Casimirsambandet Platta-Platta enligt

F/A = hcπ/(240·z⁴) ....................... halva wikiversionen . . .

”The comparison of experiment with the theoretical Casimir force was within 15%.”,

att jämföra med Wikipedias version,

F/A = ħcπ²/(240·z⁴)

= hcπ/(480·z⁴)

OLIKHETERNA — aldrig förklarade – understryker bara ämnets (ännu Okt2010) obskyra natur. [Det är i princip i dagens läge omöjligt att få ut något ENHETLIGT från det etablerade hållet].

Se även

PHYSICAL REVIEW LETTERS — Precision Measurement of the Casimir Force from 0.1 to 0.9 µm — U. Mohideen, Anushree Roy, 1998

http://www.mit.edu/~kardar/research/seminars/Casimir/PRL-Mohideen98.pdf

Samma Sfär-Platta-typform (samband 1, s4549sp2m) som i källan ovan.

Se även

REVIEWS OF MODERN PHYSICS — The Casimir force between real materials: Experiment and theory — Klimchitskaya et al., 2009

http://rmp.aps.org/pdf/RMP/v81/i4/p1827_1

Samma Sfär-Platta-typform (samband 19, s1835sp1mn) som i källan ovan.

Se även (mera avancerade Casimir-aspekter [Lifshitz-teori — Casimirsambandets icke-plana tillämpning]) — men källan innehåller inte en enda graf, samt att mätområdet ligger i intervallet 0,1-6 µM, samt att mätningen avser Platta-Sfär:

ARXIV — Fulfillment of expectations of precise measurements of the Casimir force — V.B. Svetovoy, M.V. Lokhanin, 2008

http://arxiv.org/PS_cache/quant-ph/pdf/0005/0005085v1.pdf

”The main conclusion of the paper is that the upper limit is smaller than the observed force in the AFM experiments and the difference far exceeds experimental errors and theoretical uncertainties for small separations between bodies. The simplest modification of the experiment is proposed allowing to reveal origin of the discrepancy.”.

Se även (exempel på omvänd Casimireffekt — med lämpligt val av optiskt material: repulsiva nanomaterial: svävare),

NATURE — Measured long-range repulsive Casimir–Lifshitz forces — Munday et al., 2009

http://www.environment.harvard.edu/docs/faculty_pubs/capasso_measured.pdf

”We have presented detailed measurements, which unambiguously show that long-range quantum electrodynamic forces between solid bodies can become repulsive when the optical properties of the materials are properly chosen.”.

Lambväxlingen, Elektronens g-faktor — referenser

Lambväxlingen, Elektronens g-faktor — referenser

Schupp Ref.

Källan nedan (av typen klassiskt maskinskrivet manuskript) beskriver utvecklingen 1947-1959 i QED på området elektronens g-faktor

Källan nedan kan inte kopieras;

MEASUREMENT OF THE G-FACTOR ANOMALY OF FREE, HIGH ENERGY ELECTRONS — Arthur August Schupp 1959

http://deepblue.lib.umich.edu/bitstream/2027.42/7490/5/bad2186.0001.001.pdf

;

Många personer har arbetat med ämnet (sedan 1947), försökt sammanlänka teori och experiment, på den vägen har MAC-resultaten växt fram;

;

Kortare utdrag ur källtexten — Lambövergången (eng. Lamb shift)[Lambskiftet eller Lambändringen] — i TNED elektronmassans brum

Lambväxlingen,

Vätets hyperfinstruktur

s1n,

”In 1947, Lamb and Retherford [1] showed experimentally that the 2²S_1/2 state of atomic hydrogen did not coincide exactly withe the 2²P_1/2 state as predicted by Dirac theory [2].”,

s2ö,

”This was the first conclusive evidence of a difference between experiment and the existing theory and signaled the introduction of quantum electrodynamics to resolve the differences.”;

Notera (här) hur QED (eng. Quantum ElectroDynamics, sv. KvantElektroDynamiken) alltså växer fram ur observationerna — samt hur man tvingas anställa matematiken för att försöka hitta en teoretisk matchning — och hur hela den historien krediteras på »framgångarna inom QED»;

forts.,

”About a month after this discovery Bethe [3] reinterpreted the existing quantum electrodynamic theory and was able to explain the Lamb shift. By subtraction techniques he removed the divergences of the theory and found that the 2²S_1/2 state of hydrogen should be 1040 megacycles above the value due to Dirac theory. This value is in good agreement with the experimental value of 1000 megacycles and demonstrated the applicability of quantum electrodynamics.”,

Arthur Schupp 1959

Elektronens g-faktor

Elektronens g-faktor — ’den hyperfina strukturnivådelningen i spektrum för grundtillståndet i Väteatomen (och Deuterium) vid yttre nollmagnetiskt fält’

”the level splitting of the hyperfine structure of the ground state of hydrogen and deuterium for zero magnetic field”

;

s2mö,

”At about the same time Breit [4] suggested that the deviations of the level splitting of the hyperfine structure of the ground state of hydrogen and deuterium for zero magnetic field [5, 6] could be accounted for by postulating the existence of an anomalous magnetic moment for the electron. He found that the theoretical predictions would agree with experimental evidence if the magnetic moment of the electron was slightly larger than one Bohr magneton as predicted by Dirac theory.”,

Breit [4 (1947);

Hur serietermerna för elektronens g-faktor utvecklas vetenskapshistoriskt

;

s2mn,

”In 1948, Schwinger [7, 8] showed that the magnetic moment and g-factor of the free electron is modified by the quantization of the electromagnetic field. The g-factor is expressed as a series of radiative correction terms added to the Dirac value of 2. These terms are expressible in powers of the fine structure constant [9]

α = e²/ħc = 7.29719 × 10^–3

The first of these terms, the first order in α, was calculated by Schwinger and he found that the g-factor for the free electron should be

g_e = 2(1 + α/2π) = 2(1.0011638)

”,

Arthur Schupp 1959

s3ö,

”The second order term in α, has been evaluated by Karplus and Kroll [10] and by Sommerfield [11]. The results are

g_e = 2(1 + α/2π – 2.973α²/π²) = 2(1.0011454) (Karplus - Kroll)

g_e = 2(1 + α/2π – 0.328α²/π²) = 2(1.0011596) (Sommerfield)

Recently this difference has been resolved and the accepted value is 2(1.0011596). It is also in agreement with the bounds calculated by Peterman. [12]

Since then a number of experiments have been completed that determine the magnetic moment and g-factor of an electron when bound in an atom. Kusch and Foley [13] have shown that g_e = 2(1.00119 ± 0.00005) by atomic beam measurements of the Zeeman effect in the ground state of Ga, In and Na.”,

Arthur Schupp 1959

NOTERING:

Sommerfieldvärdet är också det som ansluter till TNED, 2(1,00115965204864)=.

Källtexten beskriver sedan hur olika experimentella-teoretiska bidrag avlöser varandra perioden 1949-1958:

Tsub och Kusch ................... 1949 [s3n],

Gardner och Purcell .............. 1949,

Franken och Liebes .............. 1956 [s4mn],

Hardy och Purcell ................ 1958 [s5mö].

Någon ytterligare seriebeskrivning, antydd av Shupp ovan, tycks inte finnas, i varje fall inte bland de gratis tillgängliga webbkällorna i ämnet elektronens g-faktor. [Se dock vidare i eG-serien].

SCIENTIFIC AMERICAN Aug1980s90

Däremot finns en 10-sidig illustrerad utförlig artikel i ämnet i SCIENTIFIC AMERICAN August 1980 s90, The Isolated Electron, Philip Ekstrom, David Wineland (2,0023193044) vs TNED 2,00231930409728.

s91sp1mn,

”Both the calculation and the measurement are difficult, but they have been refined to such an extent that the g factor of the electron is now known to greater accuracy than any other physical constant.”,

SCIENTIFIC AMERICAN August 1980, The Isolated Electron, Philip Ekstrom, David Wineland

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Elektronen — Casimireffekten · Lambväxlingen · eG-faktorn

ämnesrubriker

RubrikBilder

innehåll

ELEKTRONEN — Lambväxlingen · Elektronens g-faktor · Casimireffekten

Inledande länkar

KVALITATIVA FÖRKLARINGARNA

Översiktlig genomgång

Elektronens g-faktor

Casimireffekten

Lamb-Retherford-effekten

LEC — Lambväxlingen · Elektronens g-faktor · Casimireffekten

Mera utförlig beskrivning

Lambeffekten — Lambväxlingen

Elektronens g-faktor

Casimireffekten

Lambväxlingen

AB PEK — Atomkärnans Brum På Elektronmassans Komponenter — inledning

LambTNED · snabbgenomgång

TNED-Lamb · sambandsform

Väteatomens jonisationsenergi

Avståndskompensation — eG-faktorn

EXEMPELUTVECKLING

Avståndsformen

AB PEK — Lambväxlingen, TEORI

Genomgång

Allmänna formen

Elektronens g-faktor

Sammansättningen i m(e)/n

Jämförelser i resultat

Antydd serieform

eG-serien

FermiLoop

b-serien vidare

MAC-konstanterna

Sammanställning eG

Elektronens g-faktor — Teori

Sammansättningen i m(e)/n, utförligt

Experimentbeskrivningen, elektronens g-faktor

Sammanfattning g-faktorn TNED

Casimireffekten

Inledning

Casimireffekten i TNED — härledningens form

Härledningen till Casimireffekten i TNED — mera teoretiskt utförligt

Elektriska konstanten

Distansparametern

Jämförande resultat

Casimireffekten — utförligt

Casimireffekten, härledningen i TNED

WikiCasimirEx

Casimirsambandet MAC

Analoga Fd²-forme

Den springande punkten

Korrektion för växande avstånd

Maxgränsen i mätningar

Avslutning Casimir

Antalet masselement i elektronmassan

TEORI

FSC — Finstrukturkonstanten

s-formens fysiska ekvivalent

Exakta n-värdet

Inverkan av n på föregående beskrivningar

FSC i TNED

ELEKTRONEN

Rubriker

Framträdande — vetenskapshistoriskt

Kraftekvationen

Framträdande — Tekniskt TNED

Allmänna länkar

Upptäckt

Elektronmassans komponenter, storleksordningar

Elektronen och positronen

Ingen våg-partikeldualitet i TNED

Elektriska laddningen, detaljinnehåll

Atomkärnan, storlek

Atomära massenheten

Tau-teorin

Elektronen och Φ

e-spinnet i MAC

Tau-ringen

Satsbild

Renormalisation

Massframträdandeproblemet

Kalkylkortet

RESERVATION FÖR ÖVERFÖRINGSFEL

REFERENSAVSNITT

Citatbihang till Elektronen

Vakuumets Polarisation

Inledning

Anomalt magnetiskt moment

Djupa motsägelser om elektronen i MAC

QED

Summering

Lambreferenser

LambWiki

Lambväxlingen i citat

Shpenkov 2004

Welton ref

Lamb-Retherford experimentet — Yung-Kuo Lim

Lambväxlingen, citatblock(2)

Weitz 1995

Telfer 1996

Shpenkov 2007

Shpenkovs teorier

CasimirRef

Lisanti 2005

PhysicsWorld 2002

Casimireffekten, historisk bakgrund

Sfär-Platta-samband

Lambväxlingen, Elektronens g-faktor — referenser

Schupp Ref.

Lambväxlingen, Vätets hyperfinstruktur

Elektronens g-faktor

SCIENTIFIC AMERICAN Aug1980s90

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... [ref. FOCUS MATERIEN 1975 s666]

ε₀ = 8,8543 t12 C/VM ............. [ref. FOCUS MATERIEN 1975 s666]

t|T förenklad exponentbeteckning: t|T för 10^ – | +; EX.: t19 = 10^–19

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

d deci t1

c centi t2

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet [Se International System of Units] (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

MeV MegaElektronVolt; Ofta använd beteckning för (mass)energi från E=UQ; Man dividerar energin (E) med enhetsladdningen Q=e=1,602 t19 C, E/e motsvarande E/Q=U; Den kvarvarande enheten (U) i Volt kallas då elektronVolt. Efter ytterligare en division med T6 ges värdet i MeV.

MAC Ofta använd förkortning för modern akademi (Modern ACademy) i Universums Historia.

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning (Planckfraktalerna).
OM man ska försöka lyfta fram något CENTRALT — i syntes — i TNED kan det bara bli följande:
N3m20 — atomkärnans härledning — kopplar direkt till NEUTRONKVADRATEN via deuteronkopplingen [den centrala aggregattransformationen mellan de två olika nukleära formfaktorerna i TNED som definierar grunderna för fusionsfysiken] som kopplar ATOMVIKTERNA, vilka direkt visar jämförelsen TNED-MAC.

UTVIDGAD ORDLISTA — ElektronenLEC.htm 2010

Kvantelektrodynamiken i modern akademi [QED]

Vakuumets Polarisation, grundbegrepp i modern akademi

ELEKTRONEN [utvidgad, mera utförlig beskrivning]

Lambväxlingen [Kvalitativa förklaringarna]

Elektronens g-faktor [Kvalitativa förklaringarna]

Casimireffekten [Kvalitativa förklaringarna]

Antalet masselement i elektronmassan — utvidgad beskrivning Nov2010 [från Elektronmassans Komponenter, Nov2007]

FSC — Finstrukturkonstanten [eng. Fine Structure Constant]

Senast uppdaterade version: 2014-02-02.

*END.

Stavningskontrollerat 2010-11-12.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

τ π ħ √ ε UNICODE — ofta använda tecken i matematiska-tekniska-naturvetenskapliga beskrivningar

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ

Pilsymboler, direkt via tangentbordet: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — även Alt+18 ↕; Alt+29 ↔

PNG-justerad 2011-08-21

åter till portalsidan · portalsidan är www.UniversumsHistoria.se