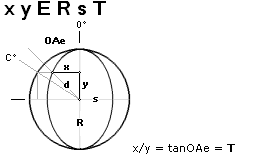
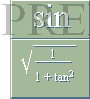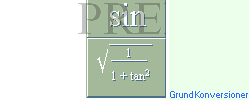MATEMATIKEN · ELEMENTARYTORNA 2009V26 en BellDHARMA produktion | Senast uppdaterade version: 2019-03-01 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

ElementarYtorna enligt relaterad matematik:

KLASSISKA ELEMENTÄRA HÄRLEDNINGSSÄTT MED INTEGRALA EXEMPEL 2009

KUBEN-KONEN-CIRKELN-CYLINDERN-SFÄREN

Inledning ¦ Sfärytan i 5 härledningar ¦ Sfärvolymen i 4 härledningar ¦ FÖRSKJUTNINGSSATSEN

———————————————————————————————————————————

———————————————————————————————————————————

HÄRLEDNINGARNA TILL ELLIPSERNAS PLACERINGSMATEMATIK I LINJÄRPERSPEKTIVEN 2019

PERSPEKTIVELLIPSERNA — Ellipsen

EPSonBesML ¦ Elliptic Polygonian ¦ Polygonian Arc ¦ Fractal Polygonian Arc ¦ Illustrated SUMMING CaseHISTORY 1978-2019 ¦

SYSVkh:

Sfärens Yta och Sfärens Volym

i enkla klassiska härledningar — förf. Apr2009

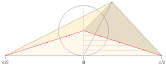
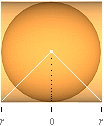
Figuren ovan beskriver sfärens volym och sfärens yta från konens volym med grund i (den urgamla) förskjutningssatsen — men många känner inte dessa grunder.

SFÄRYTAN och SFÄRVOLYMEN hör till matematikens och fysikens mest framträdande och viktiga formdetaljer. Men varken webben idag (April 2009) eller litteraturen generellt (grundskolan, gymnasiet) verkar vara begåvad i någon mera översvallande bemärkelse med klara och tydliga beskrivningar — av den gamla hederliga klassiska typen: ENKELHETEN, framför allt, i härledningssätten verkar som mest tillhöra ett passerat stadium — för runt 2 500 år sedan. Ämnet verkar i stort glömt och avsomnat; Man hänvisar till ’kalkylen’.

Med viss koll på den äldre bibliotekslitteraturen — i svensk referens i stort 1930-1960 — fanns, verkligen, en hel del genuina referensbeskrivningar, men som senare tiders läroboksförfattare verkar helt ha övergivit (se referensen i Fråga Lund som ett [avskräckande] exempel). Resultatet (naturligtvis) har blivit att inte ens elever på gymnasienivå längre verkar känna till ens den enklaste klassiska härledningen till sfärens yta och volym. Biblioteken har numera och för övrigt (sedan länge) magasinerat sina gamla läroböcker (typ LÄROBOK I GEOMETRI, DEL I, F. Carlsson 1943/1946), och inga spår finns (heller) längre kvar på dagens bokhyllor av dessa artefakter. I t.ex. svenska Wikipedia (och även den engelska motsvarigheten) på artikeln Sfärens yta, Klot eller Sfärens volym, hänvisar man (om alls) till integralkalkylen.

— I den här presentationen ges en illustrerad generalgenomgång av speciellt de klassiska sätten att härleda sfärens yta och volym, och vilka partier (April 2009) tydligen i övrigt är (nära) orepresenterade på den del av webben som syns främst.

Se även specifikt i Arkimedes lösning.

För elementarkurvorna cirkel, ellips, parabel och hyperbel, se även utförliga beskrivningar och härledningar till deras ekvationer och tangenter i CEPH-ekvationen.

Förteckning till härledningarna:

ElementarYtorna — Bildkälla nedan: Bilder.AlltingGratis.se

Alla härledningar till SFÄRENS YTA Sfärens Yta FRÅN cylindervolymen och konvolymen, PLANGEOMETRISKT elementärt från förskjutningssatsen, klassisk Sfärens Yta FRÅN tyngdlinjerna och elementarytorna, klassisk Sfärens Yta FRÅN cylinderytan, YTTEKNISKT, klassisk Sfärens Yta FRÅN konvolymen och cylindern, VOLYMTEKNISKT från förskjutningssatsen, klassisk Sfärens Yta FRÅN integralkalkylen, analytisk (via nollformsalgebran) Alla härledningar till SFÄRENS VOLYM Sfärens Volym FRÅN cylindervolymen och konvolymen, PLANGEOMETRISKT elementärt från förskjutningssatsen, klassisk Sfärens Volym FRÅN konvolymen och cylindern, VOLYMTEKNISKT från förskjutningssatsen, klassisk Sfärens Volym FRÅN atomtriangeln med integralernas aritmetik, klassisk Sfärens Volym FRÅN integralkalkylen, analytisk (via nollformsalgebran)

Förskjutningssatsen:

28Apr2009¦-04-28 efter föregående originalmanus från 2001 |M2001_1.wps|

FÖRSKJUTNINGSSATSEN

INOM DEN ELEMENTÄRA GEOMETRIN finns en framträdande lärosats (teorem) som mer än andra grundlägger speciellt kopplingen till fysiken. Den kallas här i relaterade termer för förskjutningssatsen, utförligt nedan, men den termen förekommer (veterligt) inte i modern akademi — i det sammanhanget;

Termen »förskjutningssats» i modern litteratur brukar återfinnas i ämnen som behandlar [matematiska] begrepp inom elektrofysiken. I engelskan används motsvarande namnform ”displacement theorem”, t.ex. om begreppet rotation som också kallas Euler’s Displacement Theorem, ref. [http://mathworld.wolfram.com/EulersDisplacementTheorem.html].

Men det finns också ”displacement theorem” som ansluter till andra ämnen. Dock finns (här veterligt) inget ”displacement theorem” i det engelska utbudet som ansluter till den elementära geometrin.

Den följande beskrivningen har, här veterligt (April 2009) ingen motsvarande varken litterär eller illustrerad make i det kända utbudet. Man kan tycka det är underligt — eftersom detaljerna är ytterst enkla, elementära och på intet sätt komplicerade, samt att de behandlar ett ämne som varje människa torde ha ett spontant intresse för: elementär (urgammal) matematik.

FÖRSKJUTNINGSSATSEN

inom den elementära geometrin utsäger:

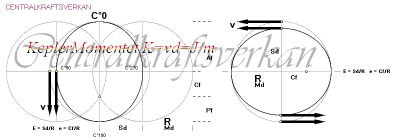
Se även FÖRSKJUTNINGSSATSEN alternativt beskriven i avsnittet om Periodiska Systemet (Keplermomentets grund till periodiska systemets härledning)

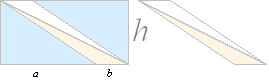
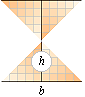
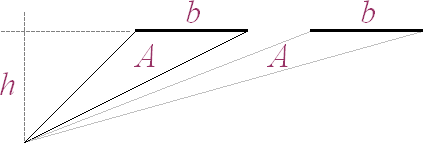
Med ytan för en plantriangel given som halva produkten av dess bas (b) och höjd (h), A=bh/2, bevaras relationerna mellan bas och höjd oberoende av förskjutning hos basen i dess förlängda plan:

b kan ha godtycklig position var som helst i rummet förutsatt h inte ändras

— ytan (ljusbeiga triangeln med basen b nedan) ändras inte

Förskjutningssatsen inom den elementära geometrin är formellt samma som triangelytan A=bh/2.

Tillämpning:

För tillämpning inom fysiken se FÖRSKJUTNINGSSATSEN som grundval för KEPLERMOMENTET i PERIODISKA SYSTEMET.

— Benämningen »förskjutningssatsen (inom elementär geometri)» förekommer (veterligt) inte i modern akademi — trots att den godtyckliga orienteringens princip i sammanhanget är grundläggande för att förstå de enkla »klassiska» härledningarna till typ konens volym och även sfärens volym.

— Vi studerar detta nedan.

Konvolymen:

Konens Volym

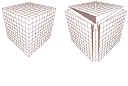
Om b gömmer en yta, kan denna med grund i förskjutningssatsen (följaktligen) ses på olika motsvarande godtyckliga ställen — och därmed i summa liktydigt med en godtyckligt MOTSVARANDE basyta, till exempel den som vi återfinner i KUBEN då den delas i sex lika delar:

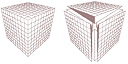
Vilket vill säga: Konvolymens ekvation kan återföras på ekvationen för en av de sex delpyramiderna i kuben:

V(CUB) = bbb = bb · 2h = 6 · V(PYR);

V(PYR) = V(CUB)/6 = bb · 2h/6 = bb · h/3 ) = V(CON);

V(CON) = Ah/3 = b²h/3 ........................ konvolymen är basytan gånger höjden dividerat med tre

Exempel:

EXEMPEL:

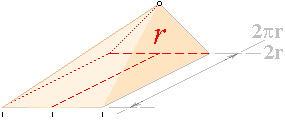
En Konvolym med cirkulär basyta kan idealt klippas upp (För Cirkeln, se även beskrivningen från Elementarytorna) via ett vertikalt (radiellt) snitt med utvikning av delarna i ett symmetriskt par som antyds i figuren ovan.

Koncirkelns variabla omkrets s = 2pr med olika höjd över basytan kan då likställas med motsvarande mera komprimerade pyramid (nedan) med rektangelytan

A = r · (s)/2

= r · 2(s/2)/2

= r · 2(2pr/2 ·r)/2

= pr² ................................... rektangelytan (s/2)·r motsvarande cirkelytan

analogt med nedanstående figur,

Konen med den cirkulära basytan pr² och höjden h kan alltså återföras på en pyramid med basytan A, höjden h och därmed volymen

V(CON) = Ah/3 ............................ ; konens volym

Cylindervolymen:

Cylinderns Volym

På samma sätt som i Konens Volym kan också cylindern klippas upp:

Cylinderns volym via de bägge symmetriska utvikta delarna blir på samma sätt lika med det ihopslagna markerade rätblockets volym (djupet = h)

V(CYL) = r(P/2) · h = r(2pr/2) · h = r · h(pr) = pr²h

Omsluter cylindern precis sfären, h=2r, skrivs cylindervolymen

V(CYL) = 2pr³ ............................ ; cylinderns volym

SfärvolymenMain:

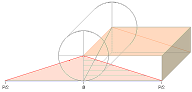
Sfärens Volym

Men cylinderns volym kan också klippas upp och bredas ut på ett annat, mera kompakt sätt:

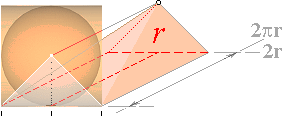
Här rullas hela cylindermantels omkretsar av direkt, successivt från största (r) till noll, motsvarande alla inre cylindriska skikt. Cylindervolymen bildar då, tydligen, precis 1/4 av rätblocket med basytan (2r)² och höjden 2pr vilket ger cylindervolymen

V(CYL) = (1/4)(2r)²2pr = 2pr³

Vi ser att detta stämmer utomordentligt väl med föregående erhållna resultat.

— Eftersom emellertid den av cylindern inneslutna sfärvolymen måste avta mot noll i den motsvarande uppklippta utbredningen, och därmed sluta på en motsvarande punkt, ges den i figuren ovan motsvarande (enda möjliga) sfäriska volymkroppen av den undre delen i takformens diagonala skärning — i förutsättning av att också sfärvolymens uppklippta utvikning bevarar ekvivalenta inre proportioner från r till noll.

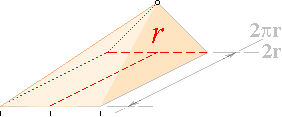
— Sfärvolymen kan då tydligen återföras på en konvolym med en basyta 2pr · 2r och höjd r enligt

V(KON) = V(SPH) = 2pr · 2r · r/3

= 4pr³/3 ..................... ; sfärens volym ur cylindervolymen och konvolymen från förskjutningssatsen

Sfärytan:

Sfärens yta

VI KAN INTUITIVT direkt förstå att om pyramidkroppen ovan representerar hela sfärvolymen och därmed varje plansnitt parallellt med bottenplanet också utgör en bild av en mindre sfär, då bör SFÄRENS YTA just vara bottenytan

A(SPH) = 2pr · 2r = 4pr² ............ ; sfärens yta, samma som omskrivna cylinderns yta

— Det finns en riktig »klassisk», mera utförlig beskrivning som också visar att så är fallet.

Se från Sfärytan och Cylinderytan. Se även Arkimedes lösning.

I följande delar beskrivs mera avancerade sätt att härleda de olika elementära ytorna och volymerna, dvs., ytor och volymer som berör figurerna/kropparna cirkel/cylinder, kon och sfär.

Elementarytorna:

ELEMENTARYTORNA

2009IV6

Från Integral0.wps 1997 IX · 2001 III | Till htm 2009 IV

Klassiska geometrins ytbegrepp:

Genomgång av den enkla, klassiska geometrins ytbegrepp

— i ljuset av den utvecklade integralkalkylens metoder;

En vidare syntes

— med en del studier i aritmetiska metoder till jämförelse

För den som (händelsevis) inte hänger med i de integrala exempel som visas i den här presentationen, se Integrala Exempel, finns ämnet grundligt beskrivet från Nollformsalgebran och Atomtriangeln — från de allra mest rudimentära logiska begreppen (Se INTEGRALBEGREPPET från grunden om ej redan bekant). Därifrån finns ytterligare vidare kopplingar till Den Högre Analysen där integralbegreppet ställs fram med mera allmänna (universella) utförliga exempel med relaterade lösningar (Se ANALYSEXEMPEL). Läsaren bör därmed (med dessa referenser) ha en god grund för studiet av integralkalkylens formella sammanhang (som även proffs ibland måste friska upp i minnet, från tid till annan) — se även de många konventionella webbkällor som (numera) finns att studera till jämförelse (sök t.ex. på integral-, differential- och derivata-, generellt kalkyl och analys).

— Rekommendation (vilket du säkert redan har fattat själv): Läs bara det som för tillfället behövs: friska upp det som har glömts genom att »slå upp det i läroboken»: Läroboken BÖR vara heltäckande, speciellt i de viktiga grundbegreppen; Är INTE Läroboken heltäckande i grundbegreppen har den misslyckats som Lärobok, och det är inte eleven det är fel på utan läraren.

Cirkeln:

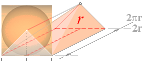
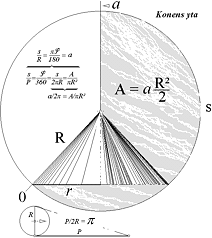
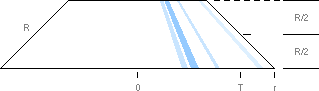
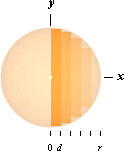
Cirkeln

Allmänt

Vi sätter cirkelradien som R. Cirkelns avrullning definierar pi (p) som förhållandet mellan omkretsen eller perimetern P

och cirkelns diameter 2R.

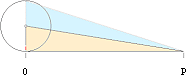
P/2R = p ;

P = 2pR ............................................... ; cirkelns omkrets, p » 355/113 = 3,14 15 92.

Alla P, noll till R, kan betraktas som ”smala remsor”. Halva rektangeln RP utfyller alltså cirkelytan enligt

A = R·P/2 = R·2pR/2 = pR² .................. ; cirkelns totala yta

På samma sätt blir bågdelen eller båglängden s av P cirkelns sektoryta.;

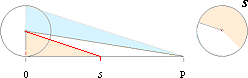
Cirkelytans mera allmänna ytekvation blir alltså från RP/2 det mera specifika

A = Rs/2 .............................................. ; cirkelns sektoryta

Vi ser att s=2pR ger cirkelns totala yta.

Konen:

Konen

Sektorn Rs/2 formar med s sluten en kon;

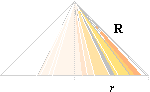
— Vi klipper ut resten ur cirkeln via två R-snitt och för ihop de bägge öppnade snitten;

— Det ger oss en trängre bascirkel med radien r i den kropp vi kallar för en rät cirkulär kon;

Från originalarbeten med grundmanus från 1989 XII;

första författningen 1992 V; andra författningen 1995 XI; tredje författningen i

BEGREPPSANALYSENS GRUNDFORMER 1996 II 22, dåvarande svartvita illustrationer anpassade för HP Deskjet 320

Konytan:

Med längden av konens bascirkel som s=2pr blir alltså konytan via sektorytan R·s/2

A = R·2pr/2 = Rpr .............................. ; konytan

Tyngdlinjen:

Tyngdlinjen

Om vi betraktar detta resultat på ett alternativt sätt ser vi att konytan också kan erhållas som

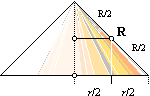
A = R · 2p · (r/2) = R · 2p · T ............ ; konytan

T ........................................................... ; tyngdlinjens tyngdpunktscirkelradie, här T=r/2

Om vi vrider upp R lodrätt med bibehållet T=r/2 och tillämpar sambandet R · 2pT får vi cylinderns yta

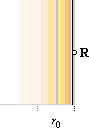
A = 2pT·R ............................................. ; cylinderns yta, r₀ = T

— eller vilken som helst alternativ del av en kon:

A = 2pT·R ............................................. ; stympade konens yta

Vi kan också förstå cylinderytan genom att klippa upp den och breda ut den. Den ges då som en rektangel med cirkelns

omkrets 2pr som längd och cylinders höjd h som bredd.

2prh ................................................... ; cylinderns yta

På samma sätt kan den stympade konytan förstås som en utbredd cirkulär yta ur vilken man tagit bort en inre cirkel och sedan snittat den yttre cirkelns R på vanligt sätt för att få konformen;

alternativ illustration,

Vi ersätter R i 2pTR mera allmänt med s (spatium) eller alternativt längden (l) så att vi får

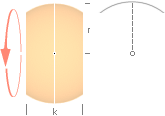
A = 2pTl ............................................ ; tyngdlinjens rotationsyta

Vi benämner s=l som tyngdlinjen och kallar ytan A för tyngdlinjens rotationsyta. Cirkeln 2pT kallar vi för tyngdpunktscirkeln.

Som visats i utvecklingarna ovan erhålls en rotationsyta A som produkten av tyngdlinjens längd s=l och

tyngdpunktscirkelns omkrets 2pT. För en rät linje med längden s=l ligger linjens tyngdpunkt i mitten.

Tyngdpunktssatsen:

Tyngdpunktssatsen utsäger då att

× tyngdlinjens längd l

× tyngdpunktscirkelns omkrets

= rotationsytan för l

A = 2pTl ............................................. ; tyngdlinjens rotationsyta

2pT .......................................................... ; tyngdpunktscirkeln

T .......................................................... ; tyngdpunktscirkelns radie

l = s ................................................... ; tyngdlinjens längd, ytans snittform

Motsvarande sats gäller också för en tyngdyta.

Tyngdlinjen motsvarar den geometriska centrumlinjen genom en tråd eller stång av homogen sammansättning. I den praktiska fysiken måste dessutom motsvarande konstruktion befinna sig i ett Galileiskt kraftfält (samma tyngdacceleration överallt i rummet). I annat fall gäller inte satsen.

— Inom den rena ideala geometrin är det just sådana, ideala begrepp om likformighet som gäller.

— Geometrins ”eget material” är just genomgående absolut homogent eftersom det är materielöst. Under förutsättning att vi kan konstruera mekaniska anordningar med hög grad av homogenitet kan också satsbilden ovan utnyttjas med motsvarande precision i praktisk fysik; En stor del av mekaniken ägnas (alltså) åt olika tyngdpunktsberäkningar.

Historia:

HISTORIA

Historiskt härstammar satserna om tyngdlinjer och tyngdytor (närmast) från schweizaren Paul Guldin (1577-1643), ofta benämnda Guldins Regler i facklitteraturen.

Satserna kan — som vi redan har sett — förstås intuitivt på enklaste sätt och också härledas utifrån de allra enklaste av geometrins och fysikens begrepp.

Cirkelbågens tyngdpunkt:

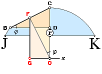
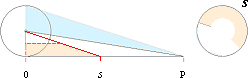
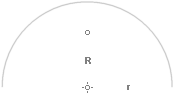
Cirkelbågens tyngdpunkt

Klassiska metoder för sfärens yta

Utan att direkt genomföra någon summering av olika delar visas i det följande hur SFÄRENS YTA kan bestämmas på ett förhållandevis enkelt klassiskt logiskt sätt.

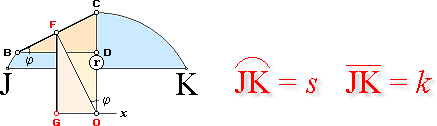
Figur till härledningen av cirkelbågens tyngdpunkt. Vinkeln j utläses ”fi” (j i Symbol). Cirkelradien OC=r.

Vi indelar cirkeln eller en bågdel s=l av cirkeln i n ekvivalenta delkordor BC. Varje korda motsvarar en rät tyngdlinje — tyngdpunkten på mitten — med tyngdpunkten i F.

— F projiceras på x-axeln i G.

— Roteras FG kring x-axeln uppstår en rotationsyta för BC

— sammanlagt för alla successivt sammanhängande BC som, då, alltmer liknar den yta som alstras av bågdelen s

— om BC tillåts gå mot noll obegränsat, analogt n®¥.

Vi benämner den totalytan som A. Varje delrotationsyta som bildas av en längd BC genom rotationspinnen FG benämns här A_n.

Betrakta svängarmen BC.FG:

— Eftersom FG alltid är rätvinklig BD är trianglarna BDC och FGO likformiga. Relationerna ger

BC/BD = FO/FG = secj

Minsta BC = Ds = s/(n®¥)

D = 1/(n®¥)

FG tyngdpunktscirkelns radie (R)

BC tyngdlinjen med sin tyngdpunkt i F

A_n = DA

= A/(n®¥)

= 2p(FG)Ds

= 2p(FG)(BC) ; rotationsytan för en tyngdlinje BC enligt tyngdpunktssatsen

Ekvivalenterna BC/BD = FO/FG ger (BC)(FG) = (BD)(FO). Därmed kan också A_n tecknas alternativt

A_n = 2p(BD)(FO)

Då BC går mot noll går FO alltmer mot cirkelradien r. Med denna gränsform insatt ges

A_n = 2pr(BD)

— Med obegränsat växande n antar tydligen BD samma gränsform som då kordan k delas obegränsat enligt

BD = Dk = k/(n®¥)

vilket blir minsta möjliga BD.

— Därmed har hela problemkomplexet tydligen automatiskt, självmant, fullständigt eliminerat alla aspekter som berör ’delsummeringar av BC för att få fram en hel motsvarande båglängd’; vi behöver tydligen inget sådant begrepp här:

A_n = DA = 2prDk ;

A = 2prk ; cirkelbågens rotationsyta; k=2r för halvcirkeln

= pr2k ; max cirkulär båglängd för rotationsyta är halva cirkeln, pr

SfärytanGuldin:

;

SFÄRENS YTA

SFÄRYTAN

;

För hela rotationscirkeln med max båglängd pr är k uppenbarligen lika med 2r. Därmed framträder hela sfärytan via sambandet för A = pr2k ovan enligt

k = 2r ;

A(SPH) = (pr)2(2r) ; sfärytan

A = 4pr² SFÄRYTAN

Detta är alldeles detsamma som den kring sfären omskrivna CYLINDERYTAN; längden 2r och diametern 2r med omkretsen 2pr som ger

A(CYL) = (2pr)2r ; cylinderytan

= 4pr²

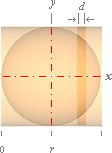
Sfärytan matchar exakt den omskrivna cylinderytan.

Se även vidare i SFÄRYTAN OCH CYLINDERYTAN.

ANALOGT ges direkt från origo med halva kordan k/2=x sfärytan

A(SPH) = (2pr)x ; sfärytan godtyckligt från origo

— Enligt tyngdpunktssatsen (A = 2pRl) ska det också finnas en tyngdpunktscirkel 2pR tillsammans med hela båglängden s=l med den angivna totalytan A = 2pRl.

Likheterna ger

A = 2prk = 2pRl ;

rk = Rl ;

R = l^–1kr ...................... ; cirkelbågens tyngdpunkt från origo via kordan k och båglängden l

R avståndet från origo

l båglängden (även s)

k kordans längd

r cirkelns radie

k beräknas från given båglängd s i PREFIXxSIN enligt

k = 2r cos s/2r

[Man har s/r = a, a i radianer; k/2 = b, b/r = cos a/2; b = r · cos a/2; k = 2r cos a/2 = 2r cos s/2r].

Med indelningen av cirkeln i ett helt antal sektorer n blir s = 2pr/n. Man får då den behändiga formen

k = 2r cos (2pr/n)/2r = 2r · cos p/n

;

s = 2r · acos(k/2r) = l ;

R = kr/[2r · acos(k/2r)] ;

R = k/2[acos(k/2r)] ; cirkelbågens tyngdpunkt från origo via kordan k och radien r, obs acos i radianer i PREFIXxSIN

;

R = s^–1(2r cos s/2r)r ;

R = s^–12r²cos(s/2r) ...... ; cirkelbågens tyngdpunkt från origo via båglängden s

;

Med radianvinkeln s/r = a = A°(p/180) som alternativ till båglängden s=l ges

R = (a/r)2r²cos(a/2) ;

R = a·cos(a/2)·2r .......... ; cirkelbågens tyngdpunkt från origo via radianvinkeln a = A°(p/180)

= (A°·180/p)·cos[A°(p/360)]·2r via gradvinkeln A° = a(180/p)

Halvcirkelns tyngdpunkt:

Med k=2r betraktar vi halvcirkeln med båglängden s=pr;

— Tyngdpunkten för halvcirkeln skulle då bli

R = l^–1kr = (1/pr)2r·r

= r(2/p) .................... ; halvcirkelbågens tyngdpunkt från origo

= r(0,6366197)

För sfärytan gäller halva cirkelbågen som rotationsytans båglinje l=pr;

— Med tyngdpunktens avstånd från origo för tyngdlinjen (l) som R=r(2/p) ges tydligen också sfärytan via sambandet för A ovan enligt

A = 2pRl = 2p(2r/p)(pr) = 4pr², vilket vi ser stämmer alldeles utomordentligt med föregående resultat.

Sfärytan och cylinderytan:

SFÄRYTAN OCH CYLINDERYTAN

Se även från Förskjutningssatsen

I detta klassiska exempel visas hur både sfärytan och cylinderytan framträder med hjälp av endast en elementär perceptiv analys och med kännedom om att sfären också kan förstås som »den allmänna rundeln» för cirkelns enkla grundsamband.

Perceptiv analys:

Om vi från sfärens mittcirkel (vertikalen) breder ut sfärytan via omkretsen av dess storcirklar bildas tydligen en cylinderyta:

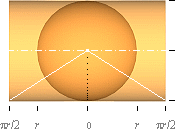
Varje kvartscirkel från vertikalnollan ( | ) får längden (2pr)/4 = pr/2. Men i denna cylinder finns bara en enda sfärcirkel som exakt avbildar sfärytan. Nämligen just den som förenar cylinder och sfär, alltså cirkeln för vertikalnollan. De övriga cirklarna överför sfärytan förstorat på cylindern med just beloppet p/2. Vi studerar detta mera ingående.

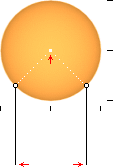
— Vi kan se anledningen till vrängningen enklare om vi tittar in i cylindern från sidan, figuren ovan. För avbildningen av två storcirklar från sfären mot cylindern bryts nodpunkten i mitten på sfären tvunget upp och breds ut mellan motsvarande parallella linjer på cylinderytan. Detta vränger alltså sfärytans avbildning sett med cylinderns begrepp. Minsta avståndet (”vrängvinkeln”) mellan två sådana storcirklar motsvarar tydligen en cirkel som gränsvärdet för en oändligt smal sfärisk sektoryta: sfärens ändpunkt som en motsvarande utbredd cylinderomkrets.

— Om vi prövar sammanhangen, kan vrängningen uppenbarligen främst återföras på den faktor p/2 som sfärcirklarna förstoras med vid utbredningen.

— Trycker vi konsekvensmässigt ihop (dividerar längden av) cylindern med beloppet p/2 bör alltså proportionerna återställas, såvitt korrekt uppfattat. Avbildningen från sfär till cylinder skulle därmed bli exakt;

Förstorade cylinderytans undre halva med 2 par kvadrater (pr/2)²

— Om vi alltså till prövning, figuren ovan, breder ut cylinderytan på den förstorade formen uppåt/neråt i det ursprungliga figurbegreppet får vi från origo och med vertikalnollan som symmetrilinje två halvor till höger och två till vänster i sfärens nedre del. På samma sätt ges i övre delen en spegelmake. Därmed inalles åtta delar (pr/2)² för hela den förstorade cylinderytan: fyra i undre halvan (figuren ovan) och fyra i övre halvan.

— Med resonemanget ovan skulle vi då få den verkliga sfärytan

SfärytanCylindern:

A = (pr/2)² · 8 · (p/2)^–1 = 4pr² ............. ; sfärytan, omskrivna cylinderytan

Och, som vi ser, stämmer detta alldeles utomordentligt med föregående resultat.

Ytprojektionen … från sidan	… motsvaras alltså av cirkulära vertikalprojektionen (cylinderprojektionen) framifrån, eller ovanifrån

Räknar vi direkt på den komprimerade formen via cylinderns yta, radien r och bredden 2r får vi analogt

A = 2pr · 2r = 4pr² ............................. ; sfärytan, omskrivna cylinderytan

Och som vi ser är detta alldeles samma resultat som i föregående utvecklingar.

Se även mera utförligt ytterligare »klassiska sätt» sätt för sfärytan från Elementarytorna, samt särskilt Sfärytan från Förskjutningssatsen.

Sfären och Cylindern genom Förskjutningssatsen:

SFÄRYTAN GENOM FÖRSKJUTNINGSSATSEN

KONENS BASYTA FÖRENAR SFÄREN MED CYLINDERN GENOM FÖRSKJUTNINGSSATSEN

OCH DEFINIERAR SAMTIDIGT SFÄRENS VOLYM FRÅN CYLINDERNS VOLYM

Ytterligare »enkla klassiska sätt» att härleda sfärytan visas i följande genomgång — där samtidigt sambandet för sfärens volym överraskande kommer fram som bonus från sfärytans samband.

Beskrivning:

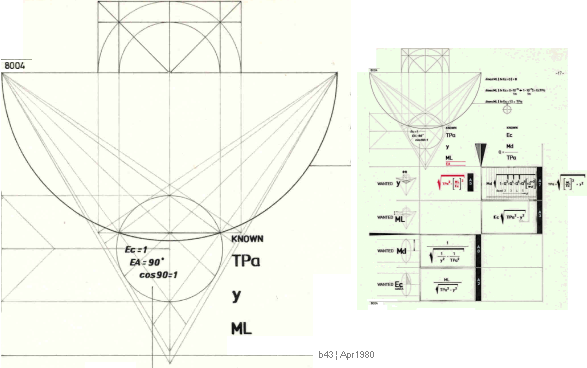
KUBEN har sex sidor i tre motsatta par; Volymen är bredden (x) gånger höjden (y) gånger djupet (z), alla samma (b) enligt

V = xyz = b³ ; kubens volym

Var och en av de sex sidorna bildar en pyramid med volymen

V = b³/6 ; kubpyramidens volym

Pyramidhöjden (h) kan skrivas som b/2 vilket med basytan b² ger

= b²·2h/6

= b²h/3

= Ah/3 ; pyramidens volym

Oavsett positionen för basytan b i triangeln med höjden h bevaras en och samma triangelyta A=bh/2. Se beviset i FÖRSKJUTNINGSSATSEN om ej redan bekant.

— Eftersom b tydligen DELS är förmögen att gömma basytor av godtycklig form, och att b DELS via förskjutningssatsen också kan vara fragmenterad eller utspridd på godtyckliga ställen med godtycklig uppdelning, och därmed i omvänd mening också sammansatt på basytor av godtycklig form, fortfarande med giltigheten i förskjutningssatsen, är det tydligt att det helt enkla sambandet för pyramidens volym kan återföras direkt på förskjutningssatsen via basytan som en allmän form för konens volym enligt

V = Ah/3 ; konens volym

— Konens basyta kan tydligen ha vilken som helt godtyckliga plana figurform.

Vi studerar hur detta resultat leder fram till sfärytan och sfärvolymen och deras samhörighet med cylindern.

Sfärytan, Cylinderytan, Sfärvolymen och Cylindervolymen:

SFÄRYTAN och CYLINDERYTAN,

SFÄRVOLYMEN och CYLINDERVOLYMEN

Med konvolymens klassiska innebörd klarlagd, framträder elementarytorna på än vidare (mera avancerade) enkla klassiskt logiska sätt. Konvolymens klarläggande leder dels vidare till ytterligare sätt för sfärytans härledning och dels till sfärens volym som därmed framträder som kanske den klassiska logikens allra enklaste härledning för just sfärvolymens del — retoriskt såväl som algebraiskt. Vi studerar hur.

Med sfärytans minsta möjliga LIKFORMIGA plana principalform genom uppdelning i ett obegränsat antal delytor

DA(SPH) = A(SPH)/(n®¥)

lika med cylinderytans minsta möjliga LIKFORMIGA plana principalform genom samma typuppdelning i ett obegränsat antal delytor

DA(CYL) = A(CYL)/(n®¥)

ges tydligen sfärens koniska principalvolym enligt

DV(SPH) = DA(SPH)h/3

och cylinderns koniska principalvolym enligt

DV(CYL) = DA(CYL)h/3

;

— Med principiellt likadana principalkonbasytor för DA(CYL) och DA(SPH) kan därmed, tydligen, sfärytan överföras identiskt på den omskrivna cylinderytan genom förskjutningssatsen enligt

SfärytanKonenCylindern:

DA(SPH)h/3 = DA(CYL)h/3 ;

A(SPH) = A(CYL) ; sfärytan är identisk med omskrivna cylinderytan genom förskjutningssatsen

4pr² = 2pr·2r; ; sfärytan och cylinderytan

Bonus — Sfärens Volym:

— Därmed framgår också att

sfärens volym är cylinderns volym minus de bägge kompakta ändkonerna

enligt

V(SPH) = 2r(pr²) – 2[V(CON)]

= 2r(pr²) – 2[(pr²)·r/3]

= 2rpr² – 2pr²r/3

= 2pr³ – 2pr³/3

= 6pr³/3 – 2pr³/3

= 4pr³/3 ; sfärens volym

Sfärvolymerna i sammanställning:

SFÄRVOLYMERNA I SAMMANSTÄLLNING

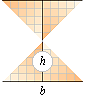
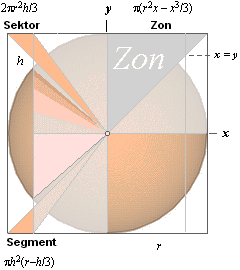
Fingranskning av projektionstriangeln för sfären mot omskrivna cylindern gör att man ur de ovan beskrivna detaljerna också kan härleda

volymen för sfäriska zonen [p(r²x – x³/3)],

volymen för sfäriska sektorn [2pr²h/3] och

volymen för sfäriska kalotten eller segmentet [ph²(r–h/3)] [h anger kalotthöjden].

Integrala exempel:

SFÄREN OCH KONEN GENOM INTEGRALKALKYLEN

Artiklarna nedan beskriver hur sfärvolymen, sfärytan, konvolymen och konytan kan hanteras i integralkalkylen.

För den om är obekant med integralkalkylens grunder, se utförligt från ATOMTRIANGELN och NOLLFORMSALGEBRAN.

Sfärvolymen via integralkalkylen:

SFÄRVOLYMEN VIA INTEGRALKALKYLEN

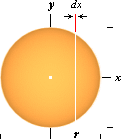
Sfärens volym via integralkalkylen

Sfärens differentialvolym dV kan skrivas som vertikalcirkelns yta, py², multiplicerat med positionen dx för x-värdet (skivans tjocklek).

y avtar från y_max= r till 0 vid x=r.

— Ekvationen för y är ekvationen för den storcirkel vi ser (rakt framifrån) av sfären enligt y=Ör²–x².

— Vi får alltså differentialekvationen

dV = py² dx

= p(r²–x²) dx ;

Integralen ger

V = p ò (r²–x²) dx = p (r² ò dx – ò x² dx)

ExponentialintegralenRef:

Vi ser att bägge integralerna i HL kan återföras på exponentialintegralen

ò (P)Dn(P) dx = (P)ⁿ⁺¹/(n+1) ....................... exponentialintegralen

(från omvändningen av exponentialderivatan).

— Således den integrala lösningen

a

V = p [r²x – x³/3]

b

Vi ser också att denna integral är av bestämd (definit) typ (Se Bestämda och Obestämda integraler). Den är alltså direkt beräkningsbar från noll utan vidare.

— Vi går enklaste vägen och väljer att tillämpa integralen i intervallet från origo fram till x=r. Detta ger volymen för halva klotet. Vi multiplicerar sedan resultatet med 2.

V = p [r²r – r³/3]

= pr³[1 – 1/3]

= 2pr³/3

Totala sfärvolymen blir alltså med denna lösning

V = 4pr³/3 ........................................... sfärens volym

Och som vi ser är detta alldeles samma resultat som i föregående utvecklingar.

Se även Sfärytan via Integralkalkylen.

Sfärytan via integralkalkylen:

SFÄRYTAN GENOM INTEGRALKALKYLEN

Nedan följer till jämförelse sfärytan från integralkalkylen.

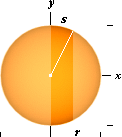
Sfärens yta via integralkalkylen

I integralkalkylen finner vi samma resultat. Vi sätter s som del av storcirkelns båglängd. Sfärens differentialyta dA kan då skrivas som omkretsen hos den variabla vertikalcirkeln, 2py, multiplicerat med båglängdens differential ds. Den variabla radien y har vi i PREFIXxSIN genom

y = r · sina

där r är sfärradien. a betecknar här vinkeln i radianer med vinkelnollan i y-axeln. a växer alltså från noll då x gör det. Radianvinkeln a är den inneslutna bågdelen s dividerat med r så att vi får a=s/r. Men för att kunna integrera på a måste vi först genomföra en differentialtransformation. Vi får denna enligt

da/ds = Dn a = Dn s/r = 1/r ; ds = r da.

Vi insätter detta i differentialekvationen dA = 2py ds tillsammans med y-formen ovan och får då

dA = 2p · r · sina · r da ; integrationen ger

A = 2pr² ò sin a da = 2pr²[cos a]

Nu är cosa = x/r i den utvalda del som integrationens intervall avser (bågen s). Detta ger oss

A = 2pr²[x/r] = 2pr[x]

Denna integralform är bestämd direkt eftersom den ger 0 om x är noll. Med x=r får vi halva sfärytan. Totala sfärytan blir alltså dubbla denna. Därmed

A = 4pr² ............................. sfärytan, omskrivna cylinderytan

Och som vi ser är detta alldeles samma resultat som i föregående utvecklingar.

Konen via integralkalkylen:

KONEN GENOM INTEGRALKALKYLEN

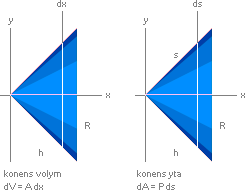
Konens volym genom integralkalkylen

R/h = k = y/x ;

y = kx ;

dV = A dx = py² dx = p(kx)² dx = pk²x² dx ;

V = pk² ò x² dx ; integration genom exponentialintegralen ger

= pk² x³/3 ; direkt bestämd integral,

x från 0 till h ger med insättningen av R/h för k resultatet

= pR²/h² h³/3

= pR² h/3 .......................................... ; konens volym

= Ah/3

vilket vi ser är samma resultat som i den enkla klassiska härledningen till konens volym.

Konens yta genom integralkalkylen

I DET FATALA CYLINDERFELET visas hur man genom en felaktig förmodan (genom [multipla] dubbelfel) ändå hamnar i rätt slutresultat. Tillämpas samma cylinderfel på konen ges emellertid direkt ett felaktigt resultat (vidare i slutet). Det är enkelt att förbise det kritiska differentialvalet — som lekman är det lätt att använda cylindrar som percept för allt möjligt, men det är inte alltid samma som det klokaste valet. Korrekt sätt är i konytans fall att relatera konmantelytans differential till hyposidan (s), inte till utsträckningen utmed x-axeln.

— Man får

R/(s) = k = y/s ;

y = ks ;

dA = P ds = 2py ds = 2pk s ds ;

A = 2pk ò s ds ; integration genom exponentialintegralen ger

= 2pk s²/2 ; direkt bestämd integral

= pk s² ;

Med s från 0 till hela mantelsidan (s) ges med insättningen av R/(s) för k resultatet

= pR/(s) (s)²

= pR(s) ................................................. ; konens mantelyta

A = pRÖ R²+h²

vilket vi ser är samma resultat som i den enkla klassiska härledningen till konens yta.

OM vi här, felaktigt hade satt mantelytans differential till dA=Pdx skulle slutresultatet med y=kx ha blivit det felaktiga V=pRh.

Cylinderfelet:

HUR EN FELAKTIG ANSATS FÖR SFÄRYTANS HÄRLEDNING LEDER TILL ETT KORREKT RESULTAT

DET FATALA CYLINDERFELET

DEN FÖRMODADE SFÄRYTAN GENOM CYLINDRAR

Från M2001_1.wps s53

Ansats (den är felaktig, se vidare nedan):

Vi sätter

a antalet cylindrar plus en

n räknare från 1 till a–1

d = r/a, varje cylinders bredd

A_n = 2p y_n d, the n:th cylinder-area

y_n = Ö r²–(nd)² = Ö r²–(nr/a)² = r Ö 1–(n/a)²

radien hos varje individuell cylinder

Ytan för den n:te cylindern blir då

An = 2prd Ö 1–(n/a)² = 2pr²(Ö a²–n²)/a²

Summan av alla a–1 cylindrar kan då skrivas via serien

2prd[ Ö 1–(1/a)² + Ö 1–(2/a)² + Ö 1–(3/a)² + … + Ö 1–([a–1]/a)² ]

EN OINITIERAD PERSON kommer (med största sannolikhet) att resonera så (frestad av uppenbarligheten i de första termerna när a är ett stort tal):

— Om a är stort, blir talen 1, 2, 3, 4, … n försumbara jämfört med a och varje rot erhåller då ett värde lika med 1.

Med generatorn (a®¥) som utsäger att a växer obegränsat, vilket betyder att d blir r/(a®¥), kommer vi fram till att

2prd [ 1 + 1 + 1 + … ] = 2pr · (r/[a®¥])[ [a®¥] ] = 2pr²

(Vi skulle få samma resultat genom att direkt referera seriesumman som a).

(Uppställningen ovan ger via differentialbegreppet i MÄSTARLOGIKENS HUVUDSATS endast ett resulterande 2p·dr med d=1/¥).

Därmed för hela sfären 2 × 2pr²

A_SPH = 4pr² ......................... ; sfärytan, samma som omskrivna cylinderytan

HÄRLEDNINGEN ÄR INTE KORREKT

— även fast svaret är det.

Se SFÄRYTAN GENOM INTEGRALKALKYLEN.

— Vad gör vi för fel?

— Rotserien Ö1–(n/a)² är frestande för att låta oss begå det fatala felet:

— Det är först och främst absolut uppenbart att ”de första” oräkneliga termerna blir praktiskt taget samma som 1 om a är mycket större än n.

— Vad man (som lekman) DÄREMOT INTE ser (enkelt) är att slutdelen i serien är långt från 1.

— Vår förmodan att seriesumman ovan dividerad med a skulle ha en gränsform lika med

1

visar i själva verket en gränsform lika med

0,7853981…

Se tabelluppställningen längre ner i HUR ROTSERIENS SUMMA BERÄKNAS.

— Det betyder att hela slutsatsresonemanget ovan är direkt felaktigt.

— Vilket vill säga, seriesummans gränsform är lika med p/4=0,7853981…, inte 1:

— Serien kan inte användas alls överhuvudtaget för det åsyftade ändamålet.

— Eller mera korrekt uttryckt:

ansatsen med cylinderindelningen är fatal i strävan att söka sfärytan

Vi kan se logiken i det också genom att cylinderbredden i själva verket aldrig har något samröre med sfärens yta

Cylindrarna vidrör aldrig sfärytan, som istället ges via kordor (stympade koner).

Rotseriens summa:

HUR ROTSERIENS SUMMA BERÄKNAS I BORLANDS PASCAL (Delphi)

Summering av rotserien Ö1–(n/a)² över a med växande n utförs i Borlands Pascal som följer (R real, A&M longint, Code integer, S string):

Val(Edit1.Text,A,Code); R:= 0;

for N:= 1 to A-1 do

begin

R:= R + Sqrt(1-Sqr(N/A));

end;

R:= R/A; S:= FloatToStr(R); ClipBoard.AsText:= S;

Värdet på a tas från en EditBox (kopplat till t.ex. FormClick). Efter avslutad summerande for-loop, divideras resultatet med a och transformeras sedan för presentation. Här skickas resultatet till Urklipp och kan sedan importeras (hit) till Ordbehandlingsprogrammet eller Anteckningar med det enkla Ctrl+V.

Den följande tabellen visar resultaten med olika a-värden till jämförelse:

a summan/a (direkt från Urklipp)

5 0,659262207220308

10¹ 0,726129581561509

10² 0,780104257944913

10³ 0,784888866729489

10⁴ 0,78534786939781

10⁵ 0,785393154196754

10⁶ 0,785397663385993

…

p/4 = 0,7853981…

Borlands Pascal DELPHI:

Borlands Pascal

DATORVÄRLDENS I SÄRKLASS MEST REVOLUTIONERANDE ProgramProgram — det är ett masterprogram som kan användas för att skapa Dator(Windows)Program — visade sig med lanseringen av Borlands DELPHI 1 (1995). Det kom som en (befriande) våg som sköljde över hela planeten.

Mot senare delen av 1990-talet gavs DELPHI 1 (versionen baserad på 16 bitars CPU) ut gratis av (flera) datortidningar (PC&Mac 4/97), totalt med hela den omfattande DelphiHjälpen — inkluderat utförliga referenser till Windows API (Windows Application Programming Interface) — samt några år senare (PC FÖR ALLA 5-2000) även DELPHI 4 (versionen baserad på 32 bitars CPU). Med den förlösande utgåvan kunde man plötsligt skriva egna, ytterst stabila, Windowsprogram med rasande finess och enkelhet (och många kom också att utveckla sina grundläggande datorprogrammeringskunskaper på den vägen).

Dessa (gratis) äldre (utgångna) versioner av Delphi är så mycket mer anmärkningsvärda eftersom de innefattar Borlands Assembler; Därmed ligger vägen öppen för den som vill att göra i stort sett allt som kan göras på en dator (med assemblerspråkets detaljer innefattat vilket i princip bara betyder att man använder den gamla DOS-skolans Assemblerlitteratur, se exv. USING ASSEMBLY LANGUAGE 3rd Edition, Allen L. Wyatt, QUE 1995). Kort sagt: i Delphi 1/4 finns allt man behöver för att utveckla precis vad som helst som alls KAN utvecklas på en dator, dessutom med maximal (via assemblerdelen, en garanterad) snabbhet.

Vilka VERKLIGT ANVÄNDBARA ELEMENTÄRA DATORORIENTERADE utvecklingsverktyg erbjuds GRATIS på Webben idag?

Efter en kort genomgång på webben (Maj 2009) visar sig emellertid en deprimerande resultatlista — för den som vill testa olika motsvarande masterprogram:

DELPHI med Borlands Pascal och Turbo Assembler: Delphi 1/4 finns (här veterligt) INTE längre att få tag på i någon gratisversion;

(Q)BASIC med Visual Basic (och liknande): Flera (många) (Visual) Basic-versioner finns GRATIS på webben idag (Maj 2009) — men det är inte lätt att få veta om ens avgörande funktioner finns med; EXEMPEL: Jämför t.ex. Microsoft Corporation med Office 2000; Där finns visserligen Visual Basic version 6 (VB6) med — men kommandohjälpen är så dålig, och dokumentationen så utspridd att det inte ens går att få fram det tidigare QBasic-kommandot för att rita ut bildpixels (PSET): PSET-kommandot finns inte i repertoaren, omnämns inte i hjälpen — men PSET-funktionen omnämns på webben i olika diskussionsforum där VB6 diskuteras. VAR finns alltså PSET i VB6?

— En nybörjare som (t.ex.) kommer över VB6 via Office 2000 — mitt exempel — har ALLTSÅ inte ens en rimlig chans att komma någonvart i en enkel elementär datorbaserad bildkunskap. Hur (då) andra personer kan påstå att (t.ex.) PSET skulle finnas på deras versioner, är här helt okänt; Det indikerar bara ett (mycket) depraverat allmäntillstånd.

Övriga programKompilerande program: Att (t.ex.) försöka få fatt på ett GRATIS C++-kompilerande masterprogram som garanterat INTE försöker pracka på ”nybörjaren” runt 50 olika demoVideos på 20 minuter vardera (med i vissa fall så grovt amerikaniserade dialekter hos inspicienten att det stundtals är svårt att höra vad som sägs) och som slutar med att nybörjaren lärt sig att skriva ut ”Hello World” på bildskärmen, eller LÄGGA BESLAG PÅ ALLT MÖJLIGT PÅ MITT SKRIVBORD OCH INFÖRA ÄNDRINGAR JAG INTE VILL HA, verkar vara en direkt omöjlighet (Maj 2009). Med den hastigheten gäller typ nästa istid innan vi kommer fram till motsvarande för PSET: elementär datorstödd bildbehandling. DELPHI skulle klara saken (lätt som en plätt, dessutom), men den programformen tillsammans med den omfattande Windows API-dokumentationen finns som sagt inte längre tillgänglig — i någon gratis upplaga. Fullversioner av Delphi är f.ö. definitivt inte billiga; från 400 till 4000 dollar (Maj 2009) — och då vet vi (här) inte vad de innehåller (om språket ens är begripligt för en nybörjare).

En sak att lägga märke till (som allmän referens): Ännu 2009 finns inte en enda webbläsare som klarar av att visa original från en traditionell ordbehandlare utan att förvanska den typografiska metriken, på ett eller annat sätt (Se exempel från Webbtest) — trots (extremt) dyra utvecklingsprogram, från Borland och andra.

ARKIMEDES LÖSNING:

SFÄRENS YTA OCH VOLYM — grundform

ARKIMEDES LÖSNING

Se även föregående i SAMHÖRIGHETEN MELLAN SFÄR OCH CYLINDER

Föregående beskrivningar av hur samhörigheten mellan sfären och dess omskrivna cylinder kan förstås, har en mera elegant allmän matematisk lösning känd som ARKIMEDES LÖSNING;

Lösningen som gavs av Arkimedes (Grekisk matematiker och filosof, 287-212 f.Kr., @INTERNET Wikipedia Arkimedes 2009-04-30) omtalas bl.a. i webbkällan

LundUnivRef:

http://www.maths.lth.se/query/answers/q200410.html#20041007095326

LUNDS UNIVERSITET — Fråga Lund om matematik, Frågor och svar oktober 2004 ¦2004, 2009-04-30¦

En gymnasielärare vill veta råd för sina elever i någon ’enkel härledning’ till sfärens volym …

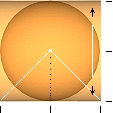
— Arkimedes lösning bygger helt enkelt på iakttagelsen att samhörigheten sfär-cylinder-kon i själva verket automatiskt innefattas i Pythagoras sats: ett snitt genom sfären-cylindern med den symmetriskt delade konkroppen innefattad (ljusa triangeln i figuren nedan) visar att cirkelytan, sfärens kalottcirkel [px²], och konens avgränsande ringyta [p(r² – y²)] i själva verket är identiska ytor via Pythagoras sats x² = r² – y² enligt

A(CRLSPH) = px² = p(r² – y²) = A(RINCON)

;

Dubbelkonen (endast halva utritad nederst) i mitten på kroppen sfär-cylinder, figuren nedan, överför y-snittvärdet symmetriskt på x-axeln så att konringens yta blir identisk med sfärkalottens snittcirkelyta via Pythagoras sats.

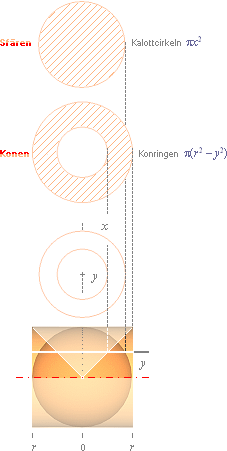
Arkimedes lösning till sfärens yta och volym.

— Genom att ytorna är identiska (de snedstrecksmarkerade delarna i ovanstående figur) och därmed den urholkade konkroppens snittyta tydligen kan överföras identiskt på sfärkalottens snittyta — och därmed dess variation från noll till max — är det tydligt att också volymerna blir identiska.

— Därmed bevisade Arkimedes samhörigheten mellan sfären och dess omskrivna cylinder med den inskrivna dubbelkonen. Se Sfärens Volym FRÅN konvolymen och cylindern.

— TYVÄRR finns inte denna (gamla klassiskt eleganta) elementära geometri beskriven i någon översvallande allmän litteratur: exemplet ovan från Lund visar i stort sett att ämnets kännedom är ett område förbehållet fåtalet.

Editor2009IV30 ¦ 2019II23

Ellipsen: Nov1979 ¦ 25Feb2019 ¦ — Se även Förteckning över Ellipsartiklar i Universums Historia -Feb2019

ELLIPSEN I UNIVERSUMS HISTORIA

Allmänna EllipsBeteckningar — med trigonometrins sinus axel som x-axeln enligt PREFIXxSIN:

— Konventionellt används x-axeln som cosinus, vilket TermFörkrångligar de annars helt enkla sammanhängande SinCosTanSecCscCotSiniCosiTani-relationerna.

— En gång fattat: byt ut konv. sin mot cos och vice versa för att få xSINprefixet. Inget annat. Se mera utförligt förklaring i prefixlänken, om ej redan bekant.

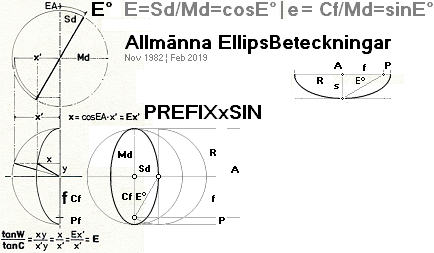
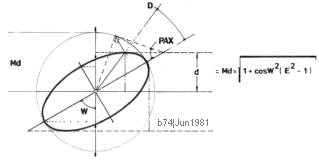
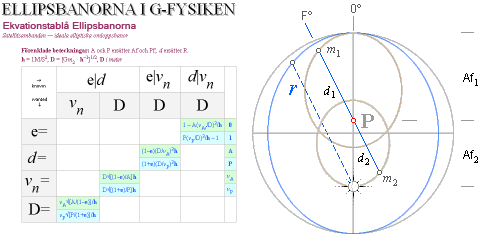
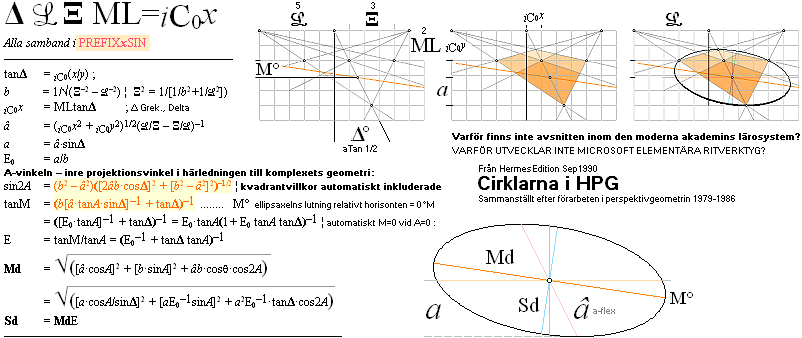
ELLIPSEN I UNIVERSUMS HISTORIA

acHärledningen: Tabell3

E = Sd/Md = cosE° = cosEA = s/R = S/M ;

e = Cf/Md = sinE° = f/R ;

f = Cf = Mde = Re ;

————————————————————

E = Xe/Xc ;

Xc² = R² – y² ;

Xe² = Xc²E² ;

a² = Xe² + (y – f)²

= Xe² + y² – 2fy + f²

= Xe² + y² – 2Rey + R²e² ;

Xe² = (R²–y²) – (R²–y²)e²

= R² – y² – R²e² + y²e²

a² = R² – y² – R²e² + y²e² + y² – 2Rey + R²e²

= R² + y²e² – 2Rey

= R² – 2Rye + y²e²

= (R – ye)² ; y = (R — a)/e.

Beskrivning, ac-sambandet:

Summan av fokaldistanserna a och c från en punkt P på ellipsbågen är konstant och lika med ellipsens storaxel 2R.

— Ellipsvinkelns E°-diagonal AC=Ø=2R genom ellipsens omskrivna bildningscirkel tecknar alltid en normalpunkt B

för punkten B på ellipsbågen mot vertikalaxelns y-värde vid D så, att normalskärningen AC¦DB delar cirkeldiagonalen 2R i fokaldistanserna a och c.

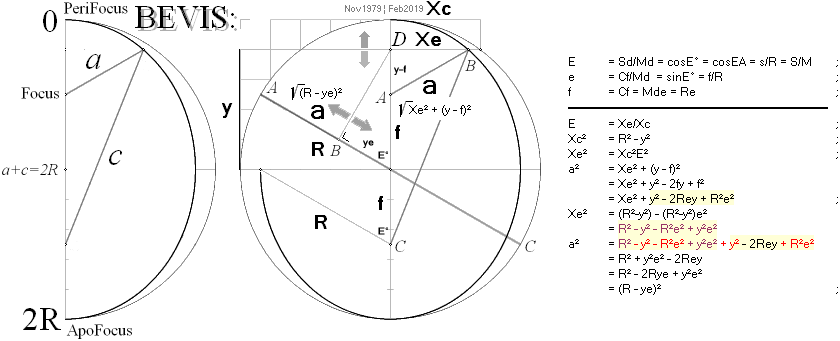
Diagonalnormalen DB glider på diagonalen AC med ändringen i y-värde från ellipspunkten B och delar, så, AC i fokaldistanserna a=BA och c(inteUtmärkt)=BC som, så, summerar AC=2R. Härledningen i figuren gäller explicit för a — men kan ses direkt också för c genom teckenändring i de givna sambanden: sätt y+f respektive R+ye för den återstående c-delen: Summan av a och c ger konstant 2R.

Samma resultatbild ges för Ellipsen i PERCEPTIONSANALYSEN

DandelinSfärerna, från G. P. Dandelin 1794-1847,

efter uppslag från en äldre LÄROBOK I GEOMETRI, Del 1, F. Carlsson 1943/1946

men på helt andra härledningsgrunder. Se även (2008) Webbreferenser särskilt ang. de koniska sektionerna.

ELLIPSGEOMETRINS MATEMATIK är utomordentligt omfattande med flera (många) olika tillämpningsområden. Vart och ett av dessa har (oftast) särskilda beteckningssätt. Och slutsumman i den turistbroschyren betyder (oftast) att helhetsbilden över ”ellipsens geometri” har en tendens att göra ellipskomplexet diffust: svårnavigerat, svåröverskådligt.

FÖR UNIVERSUMS HISTORIAs del är den här framställningen tänkt att försöka reducera den kryptiken genom en någotsånär översiktlig kartbild.

I den här framställningen ljus kan ovanstående ALLMÄNNA ELLIPSBETECKNINGAR användas som — eller är tänkt att kunna användas som — en »Ellipsgeometrins Portal»:

— Grundbeteckningarna ges här — med projektionssättet

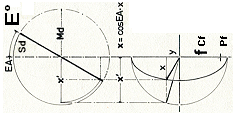
som visar hur ellipsen framträder från cirkelvridning kring cirkeldiagonalen via ellipsvinkeln (EA=E°).

Beteckningssätten 1979-2019

Beteckningssätten här är delvisa hybrider mellan beteckningar som använts från början (1978+) med en löpande tendens att försöka förenkla termfloderna för bättre översikt i ellipskomplexets många olika sambandsformer. Figurerna här syftar att samla de olika beteckningssätten.

— Ellipsens halva storaxel (Md, »MajorDistance», eller från planeternas omlopp MeanDistance) med halva lillaxelns »SmallerDistance» (Semi[Halv-]Dist.), Sd, var de första som användes i den här historien ljus. Andra mera termenkla beteckningar ersätter dessa stundtals, här som resp. R och s. Beteckningarna för Perifokus (Pf) och Apofokus (Af) tecknas här också enklare med resp P och A med centrum-till-fokus (Cf) som f.

Åsyftningen med beteckningssätten har hela tiden varit en ASSOCIATIV koppling mellan term och form — vars lämplighet oftast inte framträder förrän efter lång tids prövande användning.

Förteckning, EllipsArtiklarna i UH:

Förteckning över elliptiska tillämpningar och beskrivningar i Universums Historia -Feb2019

• TRIGONOMETRINS GRUNDBEGREPP — hur Ellipsen framträder »direkt från Köket»;

• Ellipsens omkrets — polygonserie med kalkylkort;

• CEPH-ekvationen — CirkelEllipsParabelHyperbel beskrivs ¦ basic;

• PERCEPTIONSANALYSEN — alternativ CEPH-genomgång ¦ basic;

• Ellipsens reflektivitet — ellipsens optiska egenskaper;

• KEPLERELLIPSERNA — beskrivning i samband med Solsystemets omloppskroppar;

• PERSPEKTIVELLIPSERNA — ellipserna i den linjära perspektivgeometrin;

• Som ovan med härledningar EPSbesOnML i det här dokumentet;

• EllipsProjektionerna — inledande EPSbasic grundsamband till ovan;

• EKVATIONSTABLÅER till ellipsgeometrins matematik — särskilt tillägg Feb2019:

Tab4: 90 ellipsekvationer

Tab5: 36 ellipsekvationer

d-sambandet.

TILLÄGGSAVSNITT Feb2019

PerspektivEllipserna:

PEPSIHPG — Se även ELLIPSEN med grundbeteckningar om ej redan bekant

UNICODE-BLOCK 16Feb2019

Härledningarna till PERSPEKTIVELLIPSERNA I HPG

— Matermatiken3D

EPSbasic ¦ EpsPJM ¦ ElliPole ¦ PARC ¦ FractPARC ¦ EPSonBesML ¦

—————————————————————————————

Illustrerad SUMMERANDE UTVECKLINGSHISTORIA: 1978-2019

ALL djuprelaterad MATEMATISK GEOMETRI — exakt härledningsbar — är utomordentligt omfattande, utrymmeskrävande och exceptionellt RIK på STRUKTURER. Här ges en del tidiga exempel ur författarens arkiv (ca 1980-1990) med de nödvändiga utvecklingar som ledde fram till perspektivgeometrins matematik. Ämnesområdet här gäller främst CIRKLARNA i linjärperspektiven.

Vi studerar först grundformerna EPSbasic ¦ EpsPJM, och går sedan på huvudmålet EPSonBesML.

EPSBasic ¦ 1980:

PLANPROJEKTIONERNA

Grundsamband — cirkelns planprojektion med omskriven kvadrat

ELLIPSAXLARNA Sd/Md=E KÄNDA:

————————————————

Md Sd M :

Sd/Md=E ;

————————————————

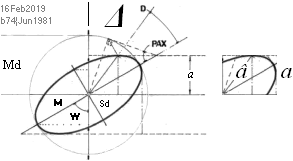
a = Md√ 1 – sin²M(1– E²) ; sambandet beror av efterföljande utvecklingar:

————————————————

tanΔ = (1 – E²)/(TanM + E²/TanM) ;

tanD = E/tanPAX = E²/tanM ; tanPAX = tanM/E

â = Md√ [1 + (E²/tanM)²]/[1 + (E/tanM)²]

sinΔ = a/â ;

Md Sd M :

————————————————

Vi bestämmer vinkelvärdena:

————————————————

EPS—PJM:

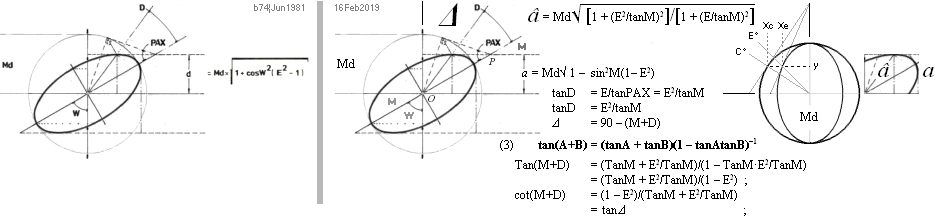
UTVECKLINGARNA för beräkningen av a:

—————————————————

E = Sd/Md = Xe/Xc ;

Xc/y = tanC° ;

Xe/y = tanE° ;

y = Xc/tanC° = Xe/tanE° ;

Xe/Xc = tanE°/tanC° = E ;

= tanM/tanPAX

= tanDtanPAX ;

tanD = E/tanPAX ;

tanM = E·tanPAX ;

tanPAX = E/tanD = tanM/E ; = 1/(tanW·E)

tanM·tanD = E² ;

tanD = E²/tanM ;

Δ = 90 – (M+D)

Tan(M+D) = (TanM + E²/TanM)/(1 – TanM·E²/TanM)

= (TanM + E²/TanM)/(1 – E²) ;

cot(M+D) = (1 – E²)/(TanM + E²/TanM)

= tanΔ ;

tanΔ = (1 – E²)/(TanM + E²/TanM) ;

GrundKonversioner

sinΔ = 1/√ 1 + tan²Δ

= 1/√ 1 + [(1 – E²)/(TanM + E²/TanM)]² ;

a/â = sinΔ ;

aFlex1:

â = a√ 1 + [(1 – E²)/(TanM + E²/TanM)]² ; OK ¦ Tab2 ¦ EllipsPMT.ods

= (Md√ 1 – sin²M(1– E²)) · (√ 1 + [(1 – E²)/(TanM + E²/TanM)]²) ; OK

= Md√(1 – sin²M(1– E²)) · (1 + [(1 – E²)/(TanM + E²/TanM)]²) ; OK

â = Md√(1 – (1– E²)/[1 + (TanM)²]) · (1 + [(1 – E²)/(TanM + E²/TanM)]²) ; OK

Sambandet utvecklas på ett alternativt, enklare, sätt i aFlexAlternativet:

— Vi samkör löpande med Kalkylkort för att testa OK på motsvarande geometrisk mängder i noggrant kvantitetsangivna ritningar.

AVSTÅNDET OP = d ;

PREFIXxSIN:

Md/d = cosPAX ;

a/d = sinW = cosM ;

a = d·sinW

= Md·sinW/cosPAX

GrundKonversioner

= Md·sinW√ (1 + 1/tan²PAX = 1 + [tanW·E]²)

= Md·sinW√ (1 + [tanW·E]²)

= Md·√ (sin²W + [sinWtanW·E]²) ; cos/sin=tan: cos=sinTan:

= Md·√ (sin²W + [cosW·E]²) ; sin²W = 1 – cos²W :

= Md·√ (1 – cos²W + cos²W·E²)

= Md·√ (1 + cos²W(1–E²) ; sinM = cosW ;

a = Md·√ (1 + sin²M(1–E²) ;

aFlexAlternativet:

â: ........... alternate a-flex:

PREFIXxSIN:

—————————————————

E = Sd/Md = Xe/Xc ;

Xc/y = tanC° ;

Xe/y = tanE° ;

y = Xc/tanC° = Xe/tanE° ;

Xe/Xc = tanE°/tanC° = E ;

tanC° = tanE°/E ;

y/Md = sinC° ;

y/â = sinE° ;

y = Md·sinC° = â·sinE° ;

â/Md = sinC°/sin(E°=D)

GrundKonversioner

sinC° = 1/√ 1 + tan²C°

= 1/√ 1 + (tanE°/E)²

= 1/√ 1 + (tanD/E)² ;

sinD = 1/√ 1 + tan²D

= 1/√ 1 + (E²/tanM)² ;

â/Md = √ [1 + (E²/tanM)²]/[1 + (tan[E°=D]/E)²]

= √ [1 + (E²/tanM)²]/[1 + ([E²/tanM]/E)²]

= √ [1 + (E²/tanM)²]/[1 + (E/tanM)²] ;

â = Md√ [1 + (E²/tanM)²]/[1 + (E/tanM)²] ............................................................... ; CONCORDANT.

Kalkylkort 1 ¦ Tabell2 — EllipsPMT.ods — 16Feb2019

Med dessa grundformer kan vi nu studera huvudmålet: Hur Cirklarna passas in som Ellipser i linjärperspektiven.

ElliPole:

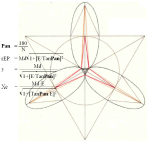
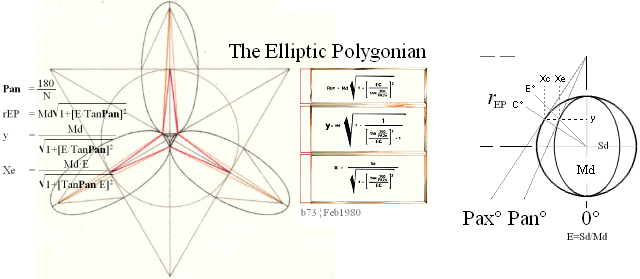
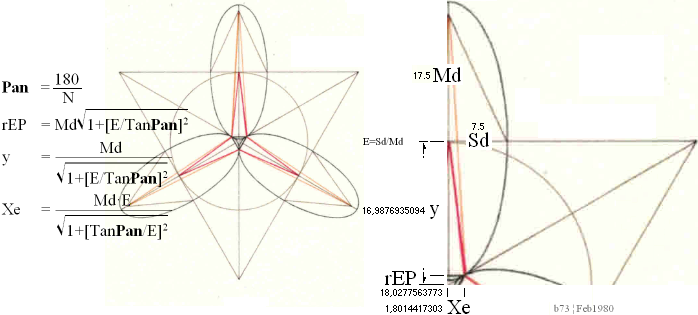
BONUS — The Elliptic Polygonian ¦ Orig.Feb1980 ¦ PREFIXxSIN:

Md Sd N :

—————————————————

E = Sd/Md ; Primary Elliptic Excentricity

Xe/Xc = tanE°/tanC° = E

PAX = Pax ; Polygonian Axel Angle — CIRCLE

Pan = (360/N)/2 ; polygnianAngle — ELLIPSE

= 180/N ; N polygonian number

tanE° = E tanC° ;

TanPan = E TanPax ;

TanPAX = TanPan/E ; cosPax = (1 + [E/TanPan]²)^–1/2 :

CHEOPS RECTANGLE : CR — ab=c² ; RightAngled Triangle

y(rEP–y) = Xc²

= (Xe/E)² ; Xe = E√y(rEP–y) = E√Md²–y² = E√Md²–y²:

cosPax = y/Md ; Xe = E√Md²–y² = E√Md²–(Md·cosPax)² = Md·E√1–(cosPax)² ;

= Md/rEP

GrundKonversioner

= 1/√ 1 + 1/(TanPax)²

= 1/√ 1 + (E/TanPan)²

= 1/√ 1 + (E/Tan[180/N])² ; Summing:

Pan = 180/N ; N number of ellipses:

rEP = Md/cosPax

= Md√ 1 + [E/TanPan]² ;

y = Md·cosPax

= Md/√ 1 + [E/TanPan]² ;

Xe = Md·E√ 1 – (cosPax)² ; = Md·E·sinPax = Sd·sinPax ;

= Md·E√ 1 – (1 + [E/TanPan]²)^–1 :

= Md·E/√ 1 + [TanPan/E]² ;

—————————————————

EXAMPLE in mM — in PREFIXxSIN — Tab2 ¦ EllipsPMT.ods

—————————————————

— Use the Ellipse E=15/35=S/M=3/7=7.5/17.5=Sd/Md=0.428571428.. to construct An Elliptic Polygonian N=3:

— Just show the result — with a numerical account.

Solution:

Pan° = 180/3 = 60 ;

cosPax = (1 + [E/TanPan]²)^–1/2

= 0,9707253434 ;

rEP = Md/cosPax

= 18,0277563773 ;

y = Md·cosPax

= 16,9876935094 ;

Xe = Md·E√ 1 – (cosPax)²

= 1,8014417303 ;

Author’s Note Feb2019: [Brother ColorLaser PRINTER¦SCANNER makes NOT the Worlds Best Performance]:

— We saw better scanning results from Original Papers around 2000 [HP-Scanner]

— BrotherDevice ADDS minor impurities [from not »exact flat white» pappers] — not easliy removed

— »electron microscope version». Use »MacroMode».

Kalkylkort 2 ¦ Tabell2 — EllipsPMT.ods — 17Feb2019

PARC:

BONUS — The Polygonian Arc ¦ Orig.1979 ¦ PREFIXxSIN:

Often very useful in instrumentation ...

How it all began ...

N R r :

—————————————————

Pan = 180/N ; N polygonian number

r/(R+r) = cosPan = r/Q ; PREFIXxSIN

= PARC

= (Rr^–1 + 1)^–1 ;

Rr^–1 = PARC^–1 – 1 ;

R = r(PARC^–1–1) ;

Ø = ø(PARC^–1–1)

R+2r = rPARC^–1 + r

= r(PARC^–1+1)

Ø+2ø = ø(PARC^–1–1)

r = R(PARC^–1 – 1)^–1

= (R+ø)(PARC^–1 – 1)^–1

2r=ø; 2R=Ø

FractPARC: PARC

The FRACTAL Polygonian Arc ¦ Orig. Jul1991 ¦ PREFIXxSIN:

Se PRAKTISKT EXEMPEL.

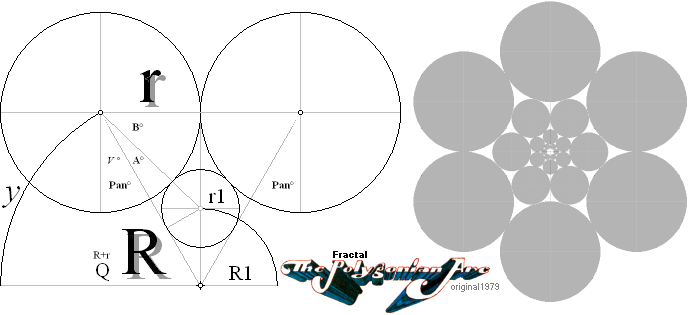
N (R) r :

—————————————————

Pan = 180/N ; N polygonian number

F = r/r1 = Q/R1 = (R+r)/R1 ; FracTALET — upprepas ändlöst mot 0:

1/F¹ ¦ 1/F² ¦ 1/F³ ¦ 1/F⁴ ¦ ... 1/Fⁿ ¦

—————————————————

a = (Q/TanPan + r)/(Q² – r²) ; Mellanräkning:

—————————————————

r1 = (a + √ a – 1/r²)^–1 ;

R1 = Qr1/r ;

Från början användes ett

r1 — ITERATIONSKRITERIUM

asin r/(r+r1) + acos r1/(r+r1) = Pan° ¦ PREFIXxSIN — kan också skrivas:

acos (√ 1 – [r/(r+r1)]²) + acos r1/(r+r1) = Pan° = B + A

för att finna värdet på r1: r1 matas in tills Pan-värdet nås:

— Man låter mittkulans r1-värde växa från 0 tills Pan-vinkelvärdet nås.

— Lösningen gavs (strax) senare via en andragradsekvation.

HÄRLEDNINGEN:

r1/a = tanA; r1/v = tan(V=Pan);

a = r1/tanA ;

v = r1/tanV ;

r1 = a·tanA = v·tanV ;

a + v = Q

= r1(cotA + cotV) ;

cotA = √ 1/cos²A – 1 = √ ([r+r1]/r1)² – 1 = √ [r/r1]² + 2r/r1 ;

Q = r1([√ [r/r1]² + 2r/r1] + cotV) ;

(Q/r1 – cotV)² = [Q/r1]² + [cotV]² – 2QcotV/r1 = [r/r1]² + 2r/r1 ;

– [cotV]² = [Q/r1]² – [r/r1]² – (2QcotV/r1+ 2r/r1) ;

– [cotV]² = (r1^–2)(Q² – r²) – (r1^–1)(2QcotV+ 2r) ;

– [cotV]² = (r1^–2)c – (r1^–1)d

= c(r1^–2) – d(r1^–1)

= c[(r1^–2) – (d/c)(r1^–1)] ;

– [cotV]²/c = r1^–2 – (e) r1^–1 ;

[cotV]²/c = 1/(tanV = r/y)²(Q² – r² = y²) = 1/r² ; förberedande formatering:

– 1/r² = r1^–2 – (e) r1^–1 ; forts. SUBSTITUTIONEN:

e/2 = (d/2c) = 2(QcotV+ r)/2(Q² – r²)

= (Q/tanV + r)/(Q² – r²) ;

SUBSTITUTIONEN:

– 1/r² = (1/r1)² – e/r1 + e/2 – e/2 ; a² — Aa + B = 0

– 1/r² + e/2 = (1/r1)² – e/r1 + e/2

= (1/r1 – e/2)² ; AndraGradsEkvationen:

1/r1 = e/2 ± (e/2)² — 1/r² ; AndraGradsEkvationens Lösning.

SE ANDRAGARADSEKVATIONENS ALLMÄNNA LÖSNING:

— Sambandet

– 1/r² = (1/r1)² – e/r1

– B = a² – Aa

på allmän form (”... = 0”)

a2 – Aa + B = 0

visar av princip ATT ”+B > –Aa” — under alla omständigheter. BEVIS: + > –.

ROTKARTAN anvisar oss då ATT andragradsekvationens lösning består av två (teckenolika) reella rötter:

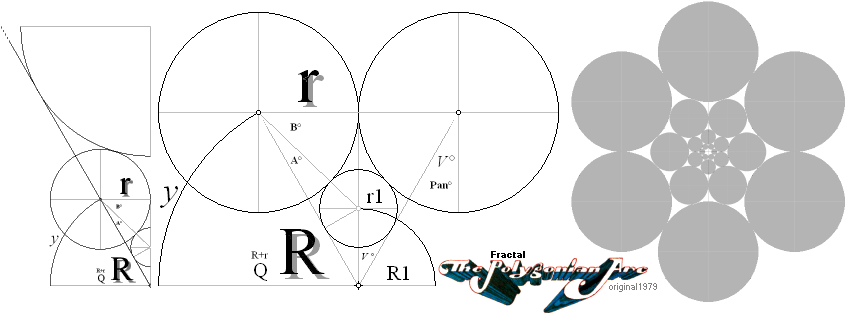
Kalkylkort 3 ¦ Tabell2 — EllipsPMT.ods — 17Feb2019

±-Rotvärdet ger cirkelradierna i närmast undre(r1)-övre(r0) fraktalnivå.

NEGATIVT rotvärde ger FraktalPolygonCirkelRadien över r-nivån (r0), POSITIVT under (r1);

r1 = 1/[e/2 + (e/2)² — 1/r²] ;

e/2 = (Q/tanPan + r)/(Q² – r²) ; y² = Q² – r²;

Q = R + r ;

GIVNA: N (R) r ¦ Pan = 180/N ;

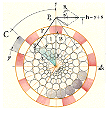
FractPARCex1988:

Praktiskt illustrerat polygonfraktalexempel:

Användes i grundarbetena till TNED-utvecklingarna för prövning på raka enskilda elektriska ledares sammanlagda magnetism:

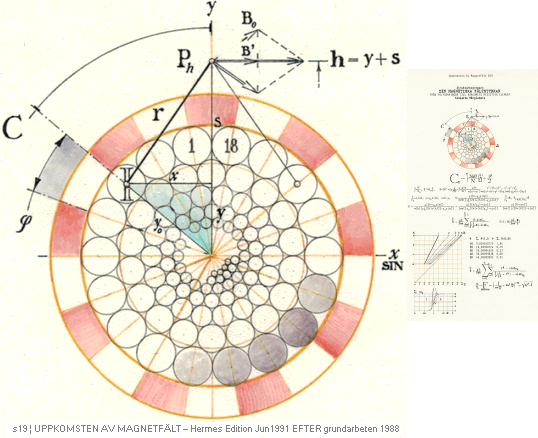
Polygonfraktalexempel från 1988 som användes i en utvärdering i samband med teorin till magnetismens matematiska fysik.

— Cirklarna ritade med en 0,1mM Rotrings nåltuschpenna på nollpassare.

EPSpmtArt:

ELLIPSENS OMKRETS

Sammanställt från utvecklingar Jan1982

Figuren nedan sammanfattar utvecklingarna till sambandsformen för beräkning av ellipsens omkrets.

— Ett kalkylkort finns särskilt som kan användas. se Kalkylkortet Tabell1.

Kalkylkort Tabell1 ¦ EllipsPMT.ods Feb2019

PREFIXxSIN

FärgLaserSkrivaren med Scanner — Brother DCP—9020CDW — har en envis benägenhet att skanna in skarpa tuschoriginal på vitt papper med resultat i delvis märkbart suddiga och diffusa kopior — hur man än bär sig åt. Tyvärr.

Sambandsformen för ELLIPSENS PERIMETER (omkretsen, pmt:n) grundar sig, som vi ser i figuren ovan, på en cirkulär polygonuppdelning i n stycken lika delvinklar.

— Vi går från cirkeln till ellipsen genom en vridningsprojektion (Sd/Md=E=[1–e²]^½) som ger oss en motsvarande elliptiskt transformerad polygonserie enligt

Ellipsens omkrets:

Ellipsens perimeter— ellipsens omkrets

TNED

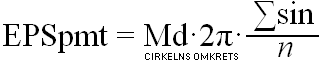
E = Sd/Md = cos EA ; Sd¦Md ellipsens halva Lill¦StorAxel

e = sinEA = 1 – E² ; lilla excentricitetstalet

n = antalet lika delvinklar i kvartscirkelns 90° ;

A(p) = (2p–1)45/n ;

n^–1Σsin = (Σd₀)/(Σd)

= (EPSpmt)/(CRLpmt)

= (EPSpmt)/(2πMd) ;

EPSpmt = 2πMd · n^–1Σsin .......................................... ellipsens omkrets

= 2πMd · (1/n) · p=1→n∑1 – (cos[(2p–1)(45/n)])e² ;

= 2πMd · (1/n) ·

1 – (cos[(1)(45/n)])e²

+ 1 – (cos[(3)(45/n)])e²

+ 1 – (cos[(5)(45/n)])e²

+ 1 – (cos[(7)(45/n)])e²

+ 1 – (cos[(9)(45/n)])e²

+ ...

+ 1 – (cos[(2n–1)(45/n)])e²

Ellipser när cirkelformen kräver bara ett fåtal polygoner (säg n=5) medan allt mer avlånga ellipser kräver högre n-tal.

— Test i kalkylkortet med n=10 visar 9 korrekta decimaler med (i varje fall) E ner till 0,0001 med motsvarande e lika med 0,999999995.

Uppställningarna finns i särskilt Kalkylkort Tabell1.

EPSonBesML:

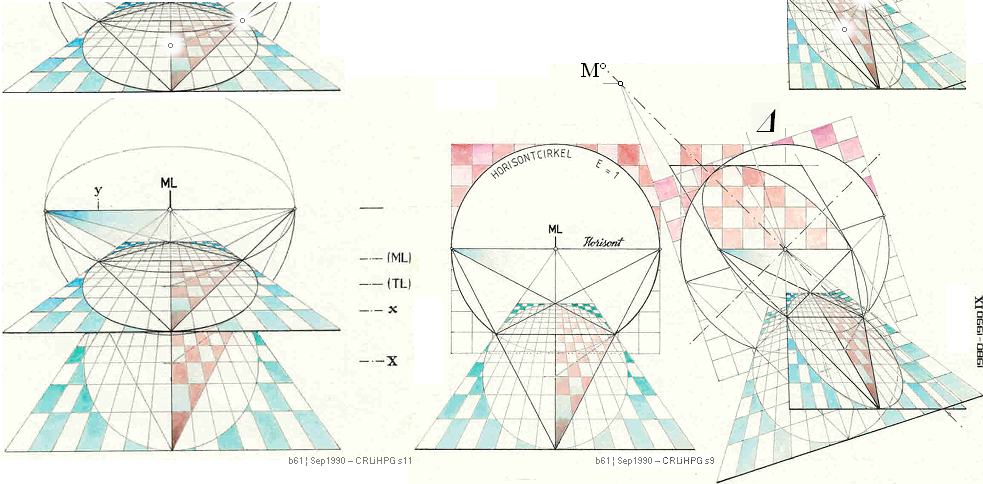
EPSonBesML

ELLIPSER PÅ OCH VID SIDAN AV

VERTIKALA MITTLINJEN

EllipsGrunderna inom den linjära perspektivgeometrin

——————————————————————

GRUNDBEGREPP

Projektionsgrunderna:

Detaljerna nedan som berör Projektionsgrunderna särskilt till Ellipserna i HorisontalPerspektivGeometrin hade tidigare inte, explicit, formulerats i den här härledande historiens ljus. Fram till nu (Feb2019) är det är först i den samlade översiktsbilden av tidigare arbeten som den här mera syntetiserade beskrivningen har funnit en författare. Detaljerna har, genom hela utvecklingshistorien, eftersökts i etablerad litteratur men ännu inte påträffats. Där figurer använts från originalförfattningarna (1978+) anges dessa särskilt med aktuellt illustrations- och författningsdatum för att ge författarens kronologiska referenser.

Se även en sammanfattning i ILLUSTRERAD SUMMERANDE UTVECKLINGSHISTORIA.

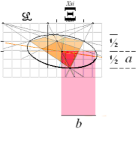
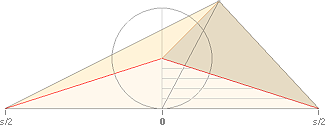
• Alla givna HorisontParallella objektslinjer bevaras längdkonstanta i linjärperspektiven.

BEVIS:

FörskjutningsSatsen — Plana ProjektionsTriangelYtan över närdistansen (z=i=avståndet till projektionsplanet L) av en given Baslängd (b) är lika med a × i dividerat med två. Figuren nedan vänster illustrerar beviset.

— Triangelytan PC.C.D ges som halva skillnaden mellan rektanglarna iD och iC: A =i(D–C)/2=ia/2=bi²/2j.

En given linjärperspektivistisk grundellips behåller sina horisontparallella konstruktionselliptiska basparametrar oberoende av placering i perspektivets sidled.

— Basvärdena kvarstår, men en del av dem transponeras över på alternativa interna ellipsvärden.

Vänsterfiguren (»konceptet sett ovanifrån») illustrerar också BILDEKVATIONEN i linjärperspektivet: a/i=b/j; b=aj/i: Alla punkter i objektsrummet a (=X) på avståndet i (=Z) från perceptionscentrum PC avbildas i bildplanet på dess avstånd j från PC som b: b=aj/i, = x=Xj/Z.

BESKRIVNING — givet projektionsplan L på givet avstånd i från en fast perceptionspunkt PC:

— Med en given baslängd (b) parallell med en given horisont (L) avbildas b på L med samma mått (a) från PC helt oberoende av var b befinner sig i rummet mellan PC och L: a avbildas som en konstant på L.

— Så följer automatiskt omvändningen i den motsvarande linjära perspektivbilden:

• Alla givna HorisontParallella objektslinjer bevaras längdkonstanta i linjärperspektiven.

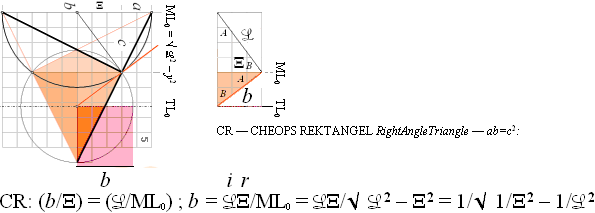
— Speciellt för ELLIPSERNA som perspektivcirklar innebär det att ellipsbestämningen i perspektivet kan återföras på fasta plangeometriska grundmått ur det enkla sambandet för den rätvinkliga triangeln — CHEOPS REKTANGEL ab=c² ;

Med något förenklade beteckningar (L=L=i, Ξ=r):

b/r = i/ML₀ som ger

b = 1/√ r^–2 – i^–2 ;

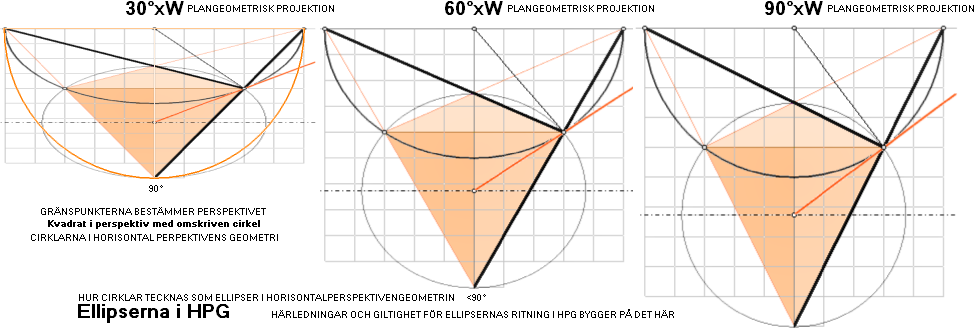
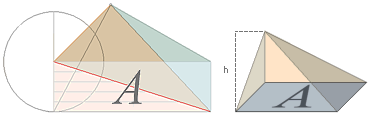
Distanserna r och L blir genom förskjutningssatsen givna fasta basdistanser med givet vertikalavstånd ML till HorisontParallellen b. Enligt förskjutningssatsens enkla men mäktiga geometriska matematik, innebär det tydligen att exakt samma värden rb bevaras konstant med givna vertikalavstånd ML och horisontalindex L. Därmed kan perspektivcirkelns motsvarande plangeometriska ellips bestämmas och därmed placeras exakt i linjärperspektivet som motsvarande objektscirkel.

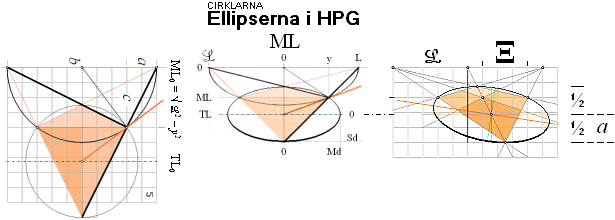
FÖLJDSATS linjära perspektivgeometrin — SPECIELLT FÖR ELLIPSBESTÄMNINGEN:

TL bevaras konstant med givet ML och Ξ:

— Cirkelns planprojektion (vänster ovan) uppvikt som ellips (mitten)

bevarar cirkelhalvans mittlinje projicerad som konstruktionsellipsens mittlinje (TL):

— Med en given perspektivkvadrat med given diagonal på givet vertikalavstånd (ML) från horisontlinjen (L), bevaras SÅ konstruktionsellipsens övre och undre och mittre (TL) gränslinjer oberoende av hur perspektivkvadraten placeras vid sidan av mittvertikallinjen:

GIVEN VERTIKALDISTANS (ML) MELLAN HORISONT med given KVADRATDIAGONAL 2Ξ:

VertikalAvståndet (TL) mellan horisonten (L) och Ellipsens origopunkt som perspektivCirkel bibehålls konstant för

Alla Kvadrater med samma ML och Ξ oberoende av placering vid sidan av vertikala mittlinjen (VML).

Grundbevis: Cheops Rektangel ¦

— BASLINJEN (a, höger ovan) med vertikaldistansen till ellipsorigot är konstant för alla perspektivcirklar med givna ML och Ξ;

— Grundformen bevisas av (vänsterfiguren) med objektsCIRKELN och HorisontCirkeln: Plangeometriska uppvridningen av den grundformen definierar alla möjliga ellipser som perspektivcirklar via ett bestämt ML och Ξ som ger ett bestämt ellipsorigo på vertikala mittlinjen (VML), och därmed alla perspektivcirklar och deras ellipsorigo vid sidan av VML som har samma ML och Ξ; Med andra ord:

— Med givet ML och Ξ är TL konstant för alla möjliga perspektivcirklars ellipser.

Är man inte klar över dessa grundprojektiva (enkla) grundbegrepp, hamnar man förr eller senare i (gruvliga) svårigheter med att (försöka) bevisa (följd-) satser inom (speciellt) perspektivgeometrins motsvarande planprojektiva detaljer — och som i så fall nära nog kan ta knäcken på vem som helst: NÄR grunderna framträder, ger sig resten »lätt som en plätt». Annars, »rena omöjliga gåtor».

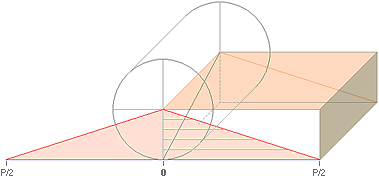
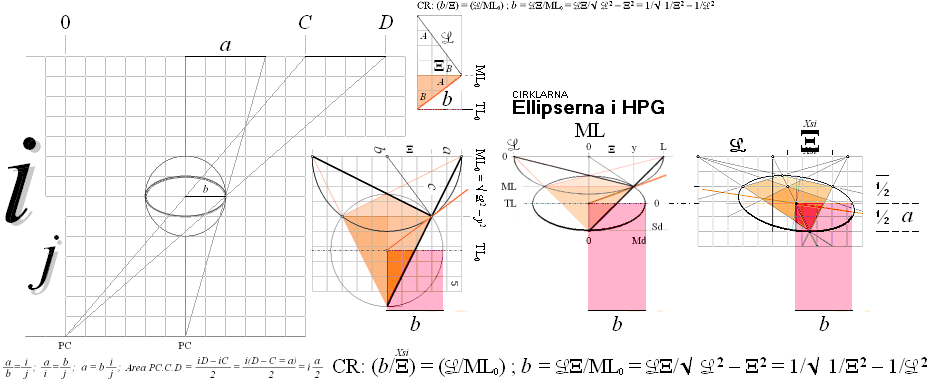
I CRLepsHPG CIRKLARNA I PERSPEKTIVGEOMETRIN visades hur cirklar med origo på vertikallinjen tecknas som ellipser i linjära perspektiv enligt det ytterst enkla beviset från Cheops Rektangel:

EOM:

Kalkylkort 4 ¦ Tabell2 — EllipsPMT.ods — 17Feb2019

Där visades också — men utan härledning — sambanden generellt för objektscirklarnas godtyckliga origopositioner i perspektivbilden, illustrationen nedan:

EBM:

TL-värdet ges ekvivalent från EPSonML-sambanden ovan som

TL = TL₀(E₀=a/b): TL&a = konstanta med givna ML och Ξ=Xsi=ri:

— Se särskilt Härledningen till b, om ej redan bekant.

Kalkylkort 5 ¦ Tabell2 — EllipsPMT.ods — 17Feb2019

Kalkylkortets samband justerade för samtliga EPSonBesML-fall. Se vidare förklaring nedan i ALTERNATIVA SAMBAND.

Vi studerar härledningen här: M-vinkeln särskilt.

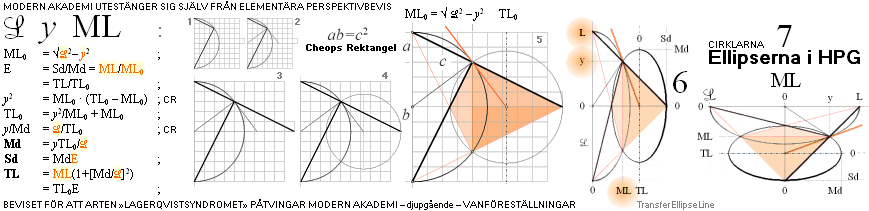
KÄRNAN i komplexet ligger i parameterformerna till ellipsbågens xy-koordinat.

— Grundsambanden finns härledda och utskrivna i och genom figurillustrationen nedan.

Den avgörande faktorn är internvinkeln A som avgör definitionen av ellipsbågens xy-punkt.

Vi ställer samman grunduttrycken och försöker lösa ut A — för det speciella fallet med tanM=x/y.

— Lösningen kräver en (omständlig) trigonometrisk derivering. En alternativ (enklare) lösningsmetod har eftersökts (-Feb2019), men ännu inte upphittats.

Fig11CRLiHPG:

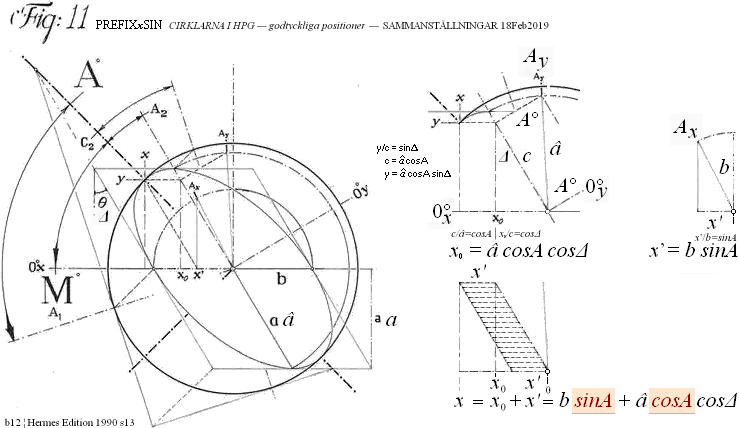
SAMMANSTÄLLNING MED VIDAREUTVECKLING — figuren ovan ger ledning:

TanM = y/x ;

x = b sinA + â cosA cosΔ ;

y = â cosA sinΔ ;

x/y = (b sinA + â cosA cosΔ)/(â cosA sinΔ) = 1/TanM:

= (b sinA)/(â cosA sinΔ) + (â cosA cosΔ)/(â cosA sinΔ) ; cos/sin=y/x=tan:

= (b sinA)/(â cosA sinΔ) + tanΔ

= b/(â tanA sinΔ) + tanΔ ;

TanM = (b/[â tanA sinΔ] + tanΔ)^–1

1

= ———————————— = (â tanA sinΔ)/(b + â tanA cosΔ) ;

b

——————— + tanΔ ;

â tanA sinΔ

Lösningen till A-vinkelvärdet

ELLIPSENS HALVA STORAXEL Md vid M°(xy):

Md(EPS) = x² + y²

= (b sinA + â cosA cosΔ)² + (â cosA sinΔ)²

= (b sinA)²

+ 2b sinA â cosA cosΔ → âb(2sinA cosA = cos2A)cosΔ

+ (â cosA cosΔ)²

+ (â cosA sinΔ)²

= (b sinA)² + âb cos2A cosΔ + (â cosA)²(cos²Δ + sin²Δ)
= (b sinA)² + âb cos2A cosΔ + (â cosA)²(1)

= (â cosA)² + (b sinA)² + âb cosΔ cos2A

= (P)^1/2

Trigonometrisk Derivering:

ETT MAXIMUM FÖRELIGGER FÖR A-vinkeln vid Md(EPS): Vi kan lösa ut den A-vinkeln för det fallet om vi också kan lösa ut nollderivatan (=0 vid MAX) till P-formen (Se GIref11):

Dn (P)^1/2 = ½(P)^–1/2 DnP = 0 ;

DnP = 0 / ½(P)^–1/2 = 0 ;

DnP = Dn [(â cosA)² + (b sinA)² + âb cosΔ cos2A]

= Dn(â cosA)² + ; → + â² cos2A ¦ A(DnB)+B(DnA): 2cos sin ¦GIref15¦

Dn(b sinA)² + ; → – b² cos2A

Dn(âb cosΔ cos2A) ; → + 2âb cosΔ sin2A ¦ cosΔ 2sin2A

= 0 ; derivatalösningen utskriven.

cos2A (b² – â²)

sin2A = ——————————— ;

2âb cosΔ

sin2A = (b² – â²)(1 – sin²2A)/(2âb cosΔ) ;

1/(1/sin²2A – 1) = (b² – â²)/(2âb cosΔ) ;

1/sin²2A – 1 = (2âb cosΔ)/(b² – â²) ;

1/sin²2A – 1 = (2âb cosΔ)²/(b² – â²)² ;

1/sin²2A = (2âb cosΔ)²/(b² – â²)² + 1 ;

1/sin²2A = [(2âb cosΔ)² + (b² – â²)²]/(b² – â²)² ;

sin²2A = (b² – â²)²/[(2âb cosΔ)² + (b² – â²)²] ;

sin2A = (b² – â²)/[(2âb cosΔ)² + (b² – â²)²] ;

(b² – â²)

sin2A = ———————————————— ;

(b² – â²)² + (2âb cosΔ)²

SAMBANDET FÖR sin2A kan skrivas på flera olika sätt — men endast som ovan med automatiskt innefattade KVADRANTVILLKOR;

— Är t.ex. â>b krävs negativt sin2A, vilket ovanstående form garanterar. Inkluderas (b² – â²) i rotformen som

(b² – â²)² försvinner den optionen. Det gäller även för Tan2A — som i så fall måste villkoras typ ”IF A< 0 THEN ..”.

AltSam:

Δ<=0:

ALTERNATIVA SAMBAND EPSonBesML

—————————————————————————————

Speciellt utformad ±-x-matematik för objekten nedanför horisontlinjen

— En del sambandsformer måste FORMatERAS för att eliminera typen N/0:

— Viss aktsamhet med sambandsformerna måste iakttas vid inskrivningen av sambanden i kalkylceller för att undvika kalkylprogrammens otillåtna typ ”DivisonMed0!”

Justerade kalkylceller med AKTUELLA ALTERNATIV som ger genomgående värden utan kalkylfel:

Δ:perspektivcirkelns deplacementvinkel från vertikalläget

Given som tanΔ:

Δ = arctan(Δ); därfrån anges de särskilda cellerna med resp. sinΔ och cosΔ: inga rotekvivalenter

TanM:

TanM = (b/[â tanA sinΔ] + tanΔ)^–1

1

= ———————————— = (â tanA sinΔ)/(b + â tanA cosΔ) ;

b

——————— + tanΔ ;

â tanA sinΔ

1: Vi skriver om sambandet som ovan från

(b/[â tanA sinΔ] + tanΔ)^–1

på den mera omständliga formen

(â tanA sinΔ)/(b + tanΔ â tanA sinΔ)

som ger

(â tanA sinΔ)/(b + â tanA cosΔ)

eftersom i PREFIXxSIN tan=cos/sin: (cos/sin)sin=cos..

2: I fallen med negativa Delta-värden ges fel resultat genom b + â tanA (–cosΔ):

— För korrekt slutresultat måste TanM-ledet tecknas i sv.OpenOfficeKalkyl som

(â tanA sinΔ)/(b +ABS[â tanA cosΔ])(TECKEN[TanΔ]) ;

— Negativa Δ-värden ger nu korrekt samma absolutvärden som positiva.

ML₀:

— Vi lägger till ML₀ så att vi kan beräkna E₀=ML/ML₀ så att vi kan bestämma TL ur grundvillkoret från EPSonML-sambanden via

TL₀ = (y=Ξ)²/ML₀ + ML₀

E:

Justeringen utan kalkylfel då Δ=0 för ellipsens excentricitet (E=Sd/Md) blir

E = (E₀^–1 + tanΔ tanA)

För negativa Δ måste en ytterligare slutjustering göras i kalkylcellen:

E = (E₀^–1 + ABS[tanΔ] tanA)

Md:

Justeringen utan kalkylfel för negativa Δ=θ i originalets Md-form

måste PREFIXxSIN skrivas med absolutvärde för Δ=θ enligt ABS(cosθ).

EndAlternativa.

20Feb2019

ISU:

PERSPEKTIVCIRKLARNA som konstruerade ellipser I LINJÄRA PERSPEKTIVTECKNINGAR

Illustrerad SUMMERANDE UTVECKLINGSHISTORIA

ELLIPSERNA I HPG från ursprungliga arbeten och författning från 1978 med olika efterföljande sammanställningar och vidare utvecklingar — 20Feb2019

————————————

A BellDHARMA production — 1978+

Perspektivlära i etablerad litteratur

— »Observatör som tittar på objekt genom en glasvägg».

Det är ännu 2019 i princip den enda etablerat synbart »enhetliga information» som finns i ämnet perspektivlära — hela ämnesområdet. Dess etablerade synbarhet, enligt här erfaren genomgång, kan sammanfattas på figurformen nedan till höger — med olika versioner och teman beroende på källverk.

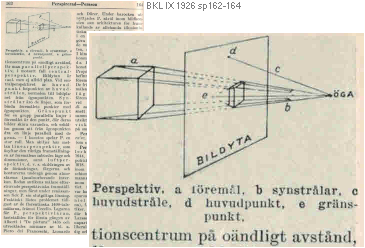
Figuren ovan vänster från BILDEKVATIONEN i 3D-Geometrin.

Ett äldre uppslagsverk ger en viss historisk dokumentär i sättet att presentera ämnet, här BONNIERS KONVERSATIONS LEXIKON Band IX 1926 från spalt162:

Perspektivbegreppet, citat 1926:

Se hela artikeltexten citerad i BKL.Citatet1926.

” Perspekti’v (av lat. perspi’cere, se genom). 1. Inom optiken förstås med P. det intryck, som erhålles av förhållandet mellan dimensionerna hos föremål i olika plan, då en projektion av föremålen på en given yta betraktas. Förhållandet i fråga beror endast på projektionscentrums och den givna ytans läge och på ytans form.”;

” Betraktaren erhåller ett riktigt perspektivistiskt intryck, endast om hans ståndpunkt sammanfaller med projektionscentrum, vilken då även benämnes ögonpunkt. I motsatt fall erhålles ett oriktigt P., som yttrar sig i ett felbedömande av avbildningens djupdimensioner l. av på olika avstånd belägna föremåls relativa storlek.”;

” Ligger projektionscentrum på oändligt avstånd, får man parallellperspektiv, i motsatt fall centralperspektiv.”,

BKL.Citatet1926.

Här framträder — återigen, jämför LagerqvistSyndromet — grunderna i den moderna akademins speciellt storslagna föreställningar om ÅSKÅDLIGHET — som tydligen och bevisligen stänger vägen som leder studenten fram till en formulerad ENHETLIG ämneskunskap.

Ursäkta intrånget:

— Det finns inga ”oriktiga Perspektiv” och inga ”felbedömda Avbildningens Dimensioner”.

— Varför då?

— DÄRFÖR ATT DEN TYPEN AV MENINGSFORM BARA KAN KOMMA FRÅN ÄNNU OUTVECKLADE INTELLEKT SOM ENSIDIGT FAVORISERAR FENOMENVÄRLDENS SYNPUNKTER FRAMFÖR FÖRSTÅNDSVÄRLDENS: ”SES Det Inte från Våra väl inskränkta Värderingar — då är det FEL”.

— En PerspektivBILD utgår från EN central perceptionspunkt: Alla perspektivbilder ÄR också RIKTIGA perspektivbilder OM de utgår från EN perceptionspunkt. Rätta gärna om fel.

— Därför att begreppet BILD inte är uteslutande reserverat för FENOMENVÄRLDEN — fysiken, den lekamliga sinnevärlden — utan FRÄMST för FÖRSTÅNDSVÄRLDEN som garanterat INTE finns i fenomenvärlden. Mest Prominenta Exemplet -Jan2019:

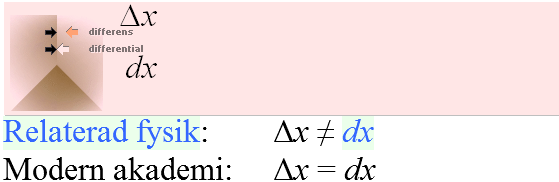Differentialbegreppet i Modern Akademi

— I Modern Akademi har man — tydligen genomgående med vissa spår längre bakåt i historien än 1800 — antagit ett väl ensidigt FENOMENBASERAT naturvetenskapligt beskrivningssätt. Dess främsta — vådliga — konsekvens visar sig, tydligen, i den moderna akademins avgörande oförmåga att skilja noll — 0, punkten, differentialbegreppet som bara existerar i förståndsvärlden: geometrin, matematiken — från ICKE-noll, differensen, intervallet som ÄR fenomenvärlden. Och därmed ett lika ensidigt »TOTALITÄRT» fasthållande vid fenomenvärldens preferenser — samtidigt som förståndsvärldens grunder inte kan undvaras, inte ens för den mest inbitna idiot. Resultat med Fenomenvärldens Preferenser: Förståndsvärldens sammanlänkande och förklarande grunder förnekas, trängs undan, med många tydliga exempel. Exemplet med dx och Δx är ett skolexempel på exceptionell övertydlighet. Perspektivgeometrin ger ytterligare exempel.

Som redan visats i samband med beskrivningen av det här benämnda LAGERQVISTSYNDROMET[‡]

Plangeometrisk Projektion av ett PerspektivGeometriskt grundläggande elementärt Begrepp:

Figuren från CIRKLARNA I LINJÄRPERSPEKTIVEN i 3D-Geometrin.

— ”En sådan avbildning av en kvadrat i linjärt perspektiv är direkt felaktig, under alla förhållanden orimlig”. Inga referenser anges.

— Varför påstås ”orimligt” och ”felaktigt”? Bokkällan[‡] ger ingen upplysning.

— Vad vi däremot SER är att ”orimligt .. felaktigt ..” GRUNDLÄGGER ÄMNESFÖRKLARINGEN.

— Modern Akademi känner inte till Grunderna — på grund av självstyrd självutestängning. Rätta gärna om fel.

— ”Även 90° exakt är felaktigt”. LAGERQVISTSYNDROMET — i arv möjligen från runt år 1300: »ColumbusGruppen Upptäcker Världen på Nytt». Stödcenter.

är man tydligen i moderna kvarter — genom de så LÅSTA RENT FYSISKT KROPPSLIGA föreställningssätten — HELT oförmögen att SYNTETISERA elementära matematiska geometriska perspektivgrunder:

— Ett enhetligt matematisk synsätt finns inte i den moderna akademins lärosystem i ämnet.

I relaterad matematik (och fysik) är — således — PARALLELLA PROJEKTIONER, konv. ”parallellperspektiv”, helt fristående ifrån varje form av begrepp om något ”projektionscentrum” eller ett ”perceptionscentrum”. Ingenting sådant existerar — citatmeningen[‡] till trots:

— ”Projektionscentrum på oändligt avstånd” betyder i relaterad mening samma som

oändligt små objekt, som medför detsamma som HELT osynliga objekt. RELATIVT EN PERCEPTIONSPUNKT.

Plangeometrins begrepp är INTE — interfererar inte med — perspektivgeometrins.

— Plangeometri — s.k. parallellprojektion — och perspektivgeometri är två väsensskilda begrepp, två helt olika begreppsdomäner.

PLANPROJEKTIONER eller parallellprojektioner är I RELATERAD MENING föremålens avbildade mått på plana bildytor utan inblandning av något begrepp om PERSPEKTIV.

— En planprojektion av ett perspektivkoncept är fortfarande en planprojektion — som kan[‡] förklara (sammansatta, komplicerade) detaljer i perspektivmatematiken.

PLANPROJEKTIONERNA ÄR OCH FÖRBLIR MATEMATIKENS absoluta GRUND:

1. Passare, Linjal, Plan rityta — enhetsrutnätet, mönstergrunden:

— Eftersökt i etablerad litteratur, finns möjligen, men inget direkt citerbart upphittat:

Verktygen som krävs för att förstå Fenomenvärldens sammansättning, struktur och innehåll.

2. Matematikens Fem Grundlagar

— syntetiserade av den enda Cheops Rektangel (Nr1):

— Inget etablerat omnämnande.

Verktygen som krävs för att förstå Fenomenvärldens sammansättning, struktur och innehåll.

3. Matematiken i syntes — TANGENSKVADRATEN:

— Inget etablerat omnämnande.

aritmetiken • räknelagarna • perspektivgeometrins elementära grunder

Verktygen som krävs för att förstå Fenomenvärldens sammansättning, struktur och innehåll;

— Delningsprinciper, räknelagar, perspektivgrunder — tydligen. Aritmetik. Behovet att utveckla en motsvarande Algebra: Självservering.

I allt:

— FÖRSTÅNDSVÄRLDENS BEGREPPSGRUNDER — hur fenomenvärldens sammansättning, struktur och innehåll låter sig förklaras. Och som i slutänden leder fram till den enhetliga förklarande — förlösande, befriande — perspektivkroppen: enhetshyperbelns matematik som förklarar, beskriver — och leder vidare:

3D-Geometrin — Linjära — och sfäriska —HORISONTALPERSPEKTIVEN xyzXYZ I RELATERAD MATEMATIK OCH FYSIK

— What?

— Varför (i himmelens) namn ingår inte det här ovan, i grunden otroligt enkla — i ETABLERAD UNDERVISNING? Varför fick vi inte veta det här runt 12 — i femman?

— What’sUp? Utmärkt DEKORATION på skolväggar — stadsmiljö, vad VI Lever av ..

Antal Visade: 0. Det kanske är säkrast att sätta handklovar på befolkningen också.

Utegångsförbud .. Lösenord .. Kameraövervakning .. Jämför HÄVDEN.

Ellipserna i linjärperspektiven. ”FEL”.

— Det är alldeles tydligt i Den Moderna Akademins Naturvetenskapliga Historiska Ljus att någon — något — har missat pårampen.

Inte undra på att mänskligheten har det som den har det i våra tider.

— Utomordentligt väl insatt och kunnig Personal. Jättebra.

Undervisningsmaterialet bara dräller »underbara uppenbarelser». Åå vad jag längtar till skolan. Särskilt högskolan. Fantastiskt kunnig personal.

Så: Hur kom det sig då, med en sådan präktigt Etablerad välmatad mattegrund i bagaget att något alls kom fram i ämnet, som ovan?

STARKT — starkt — MOTIVERAD att undersöka grunderna genomfördes ett ”generalangrepp” på det etablerade s.k. ”trepunktsperspektivet”:

— Med kvadratritningen allt längre under horisonten blir omskrivna ellipsen alltmer cirkulär.

— Så: VAR, exakt, ligger Cirkeln?

Mycket världsomspännande intressant händer och är på gång runt 1980:

• INTEL håller på att slutföra produktionen av den första reguljära Mikroprocessorn 8080:

• Bokhandlarna har nyligen börjat sälja elektroniska räknare med inbyggd trigonometri;

• Delvis banbrytande experiment utförs inom partikelfysiken May 1979 Scientific American: Alan. D. Krisch, The Spin of the Proton (Med en uppföljare i SA Augusti 1987).

Brytningstiden runt 1980: Miniräknarna har redan introducerats. Datorrevolutionen är på stark frammarsch. Och delvis avgörande partikelexperiment tilldrar sig en del intresse från vissa engagerade håll. Bildkollaget ovan fotograferat 24Feb2019 med en Nikon-D90 från bevarat exempel av Scientific American May 1979, samt miniräknaren Casio fx-39 — som följde med den här författaren troget ända fram tills nu 2019 då kontakterna i manövertrycken inte fungerar så bra längre.

Det enda som fanns att ta på i den här historiens ljus omkring (strax före) 1980 var i princip inget annat än det vi redan skummat här i citat och referenser och som vi kan läsa om idag i bibliotekslitteraturen (Se Citaten från Lagerqvist), och f.ö. på Wikipedia i ämnet Perspective (graphics), Mathematics and art, m.fl.: ingen upplysande grundmatematik alls. Noll. Vi »fick börja från början» med (ISU) »Observatör som tittar på föremål genom en glasvägg».

Efter flera (omständliga) försök — och med hjälp av en enklare miniräknare (som började dyka upp i affärerna i slutet på 1970-talet) — infann sig till slut lösningen.

Figuren nedan tecknades upp i samband med arbetsresultatet (Apr1980)

PREFIXxSIN

Problemet med Cirkeln Genom Horisontalindexet löst våren 1980. Har eftersökts i etablerad litteratur, men inte påträffats.

Se mera utförligt här från EPSonBesML.

— men då Apr1980 ännu fortfarande i HELT ovetande om det ytterst enkla underliggande Cheops Rektangel-konceptet[‡] som verkligen djupförklarar hela matematikdelen:

— HorisontCirkelTangenten: Den utpekar direkt CirkelOrigot på MittLinjen. Det kom långt senare (HermesEdition1985+) — med »integrerad dramatik».

Resten »gav sig självt»; Det ena ledde till det andra, som ledde vidare ..

— Med visst fortsatt laborerande med ”triangelperspektivet” uppdagades strax den enkla totalförklarande EnhetsHyperbelns matematik (HorisontalTeoremet) i Horisontalekvationens[‡Eng]¦[‡Orig] försorg.

Med fortsatta utvecklingar, renskrivningar med vidare sammanställningar, utkristalliserade sig ämnet självt till det som finns här nu presenterat idag (21Feb2019).

Vä: Ellipsproblemet löst Apr1980.

Hö: När HP-geometrin blir alltmer bekant, kan illustrativt goda frihandsritningar göras utan direkta stödlinjer, enbart på synintrycket med baskunskaperna.

— Se även ELLIPSOGRAFEN, ritinstrumentet som användes för ellipsritningarna (från slutet av 1970-talet).

— Men hur kom termen eller begreppet ”Cheops Rektangel” med i bilden?

Cheops Rektangel

Alla utvecklingsdetaljer i Universums Historia grundas HELT på den matematiska fysiken från CHEOPS REKTANGEL:

Se även från MEL1 och MEL 2 ¦ SOLFYSIKEN I TNED TESTAS

Upplösningen med Ellipserna i HPG — HorisontalPerspektivGeometrin — innefattar, som vi ser, den rätvinkliga triangelns mäktiga sambandsform ab=c² här benämnd Cheops Rektangel. Men utvecklingsdelarna från 1985 (HermesEdition Sep1900) i det komplexet hade inte Det ytterst enkla figurkonceptet framför ögonen: Cheops Rektangel var vid den tiden ett helt okänt begrepp i den här historiens ljus. Figuren (Fig:10) nedan visar den motsvarande originalillustrationen i samband med härledningarna till sambanden för Ellipserna i HPG — på en (betydligt) mera omständlig väg men med samma slutresultat:

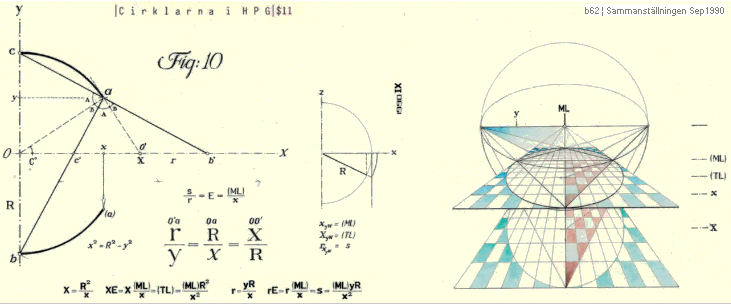
Samma nettoresultat som i den mera syntetiserade CR-illustrationen.

Det var inte förrän ett halvt decennium senare Aug1989 (Historien Bakom) som begreppet ”Cheops Rektangel” tog form i den här historiens ljus. Nämligen främst genom ett fördjupat studium av Galileo Galileis bidrag (1636) där också sambandsformen ab=c² intar en central roll i utvecklingsarbetet.

Den geometriskt framträdande sambandsformen ab=c² som — frekvent — visade sig i visst avgörande utvecklingsarbete tilldrog sig ett visst naturligt fokus: Varifrån kommer det tydligt enkla men mäktiga — och märkvärdigt märkliga, »fascinerande enkla» — sambandet rent historiskt?

Det var en »ytterst intressant fråga» i den spårande och spännande historiens ljus:

— Var det Renässansens pionjärer som upptäckte det?

— Eller var det kanske de antika grekerna som först uppmärksammade den starkt praktiska användbarheten?

Det blev angeläget att göra vissa efterforskningar.

Så ledde spåren bakåt till Cheopspyramiden — genom grekernas (Herodotos 484-424 f.Kr.) egna arkiv.

I MATEMATIKENS FEM GRUNDLAGAR

intar ”Cheops Rektangel” en högst central — tydligt syntetiserande — roll för de (så) fem mest grundläggande och elementära sambanden i matematiken: ALL ÖVRIG matematik beror av och baseras PÅ Nr1-5.

Så rådde (Aug1989) inte längre något tvivel om saken:

— Vare sig Herodotos anvisning till Cheopspyramiden har eller inte har någon koppling till ursprungssambandet ab=c² för ”Cheops Rektangel”, är det alldeles tydligt att Det Sambandet ÄR väldigt mycket CentralStation för hela matematiken som naturvetenskapligt ämnesområde:

— Avgång och Ankomst.

Alltid. Centralen där allt händer, där allt sammanstrålar och sammanknyts — i varje SÅ relaterbar mening.

Ljusets gravitella beroende[‡Härl.]¦[‡Sammanst.Jämf.]

Det avgörande rent FYSISKA inslaget med ”Cheops Rektangel” kom med härledningen till ljusets g-beroende (7Jun1990 — med strax efterföljande atomkärnans härledning Jul1993: N3m20): ljushastighetens toppvärde bevaras oberoende av gravitationens inverkan — garanterat av det centralt avgörande samband v²=c²+w²=cc0 i ”Cheops Rektangel” som, tydligen, hela härledningens geometriska fysik bygger på: kraftvektorledet[‡] Fc = Fc0 — Fg.

— Men, märkligheternas märkligheter: Kopplingen ”Cheops Rektangel” framkom först (strax) EFTER själva härledningsarbetet med ett tillägg (11Feb1992): Lösningen till sambandet för ljusets gravitella beroende har (4) olika kopplingar. Och det var först genom en fördjupad analys av dessa som Cheops Rektangel-geometrin visade sig — via just Cheops Rektangel-geometrins avgörande upplysande cc0=c²+w²: Naturkonstanten c0 bevaras oberoende av gravitationens inverkan via en del cirkel och en del hyperbel: kraftvektorledets upplysande sammanhang.

Hela den vidare genomgången med utvärderingar, citat, beskrivningar och jämförelser mellan dessa resultat (TNED) och de som hävdas från modern akademi (MAC) bildade upptakten till Universums Historia. Se särskilda sammanställningar i Atomkärnans Härledning, LISTAN, EXPERIMENTELLA BEKRÄFTELSER och noMACfysik om ej redan bekant.

Jämför f.ö. TNED (relaterad fysik) och MAC (modern akademi, här via Einstein[‡]):

MAC c/c0 = (1 — w²/c²) — Einstein accepterade inte c=0, ”tidens upphörande” enligt ”ingenting fortare än c”.

TNED c/c0 = (1 — w²/cc0) — Cheops Rektangel: Kraftvektorledet

Alla utvecklingsdetaljer i Universums Historia grundas HELT på den matematiska fysiken från CHEOPS REKTANGEL:

Se även från MEL1 och MEL 2 ¦ SOLFYSIKEN I TNED TESTAS

Det avgörande uppslaget till kopplingen med ”Cheops Rektangel” kom Nov2017 med uppgifterna från Flinders Petrie (1883) på basdata av det som nu återstår av Cheopspyramiden (efter minst 4000 år) kontra de vidare undersökningarna i TNED:

— Med uppgifterna från Flinders Petrie ges fysikbilden generellt i Universums Historia en viss — överraskande, vidare — HISTORISK KONTUR.

Nämligen rJ-cirkeln — med hela den (så) uppdagade Cheopspyramidens mönsterform[‡PetrieIn] — som den tydligen får förstås:

— Cheopspyramiden antyder — starkt — att hela TNED-matematiken har varit känd av folk som konstruerade och bestämde måttsättningarna till Cheopspyramiden:

— »TNED-fysiken är den man finner OM man söker på Naturens Villkor» säger TNED.

— Urgammalt. Cheops Rektangel.

Det räcker med ett minsta ynka lilla motbevis som visar att TNED inte håller för att förpassa hela den avhandlingen till återvinningskrossen. Absolut. Har eftersökts. Inte ännu påträffats.

En motsvarande angelägenhet uppkommer — följdriktigt, asså — att försöka MOTBEVISA ståndpunkten som säger att ”VI VAR HÄR FÖRE DIG, genius, vet du väl”. Främst därför att inga ANDRA direkta arkeologiska/geologiska/geografiska bevis finns — frånsett dimmiga och suddiga historiska konturer från bl.a. Platon (500 f.Kr.) om ett ”Det försvunna Atlantis” — en nu försvunnen kontinent som, förmodligen (kanske 10-50 000 år bakåt), antogs ha förenat nuvarande Europa med Nordamerika, och som påstås ha givit namn åt havet Atlanten.

Kopiösa mängder skrifter (»det mesta opublicerat») finns i ämnet Atlantis i s.k. modern tid. Men så länge mera direkta bevis (utom Cheopspyramiden) saknas, framstår hela det komplexet som »ren mytologi utan bevisbar naturgrund».

Öppettiderna för Speceributiken som saluför Slumpartade Sammanträffanden hade — drastiskt — minskat.

Fördämningarna brister

Det vara bara början.

TNED-kosmologin[‡]¦[‡Basic]

— atomkärnans härledning genom Plancks konstant och därmed ursprungsmaterialet som NEUTRONER[‡] med en garanterad inkompressibel maxtäthet Dmax = 1,82 T17 KG/M³ —

innefattar detaljerade beräkningsgrunder för stjärnorna, i synnerhet Solen;

TNED anvisar ett bestämt fotometriskt effektvärde i Solens fall (Solen som Normstjärna).

Den matematiken är också synnerligen omfattande — tillsammans med TNED-värden som ger Solens/Vintergatans ålder.

Därmed öppnas en möjlighet att kontrollera nu experimentellt NOGA uppmätta fotometriska värden (IAU2015) i Solfallet, kontra det som TNED-fysiken anvisar.

Vad visade jämförelsen?

IAU2015 3,827 500 000 ±0,001 4 T26 W (förenklat: T för 10^+, t för 10—)

TNED2018 3,827 500 101 ±0,000 0 T26 W

Klockren fullträff.

Rakt PÅ.

Finns inte en chans.

Helt uteslutet.

Speceributiken som saluför Slumpartade Sammanträffanden hade — drastiskt — avancerat till ”Butiken stänger inom kort”.

TNED + Experimentalfysiken = Sant. Igen[‡].

IAU-beröringen ledde fram till ytterligare ett avancemang i hela TNED-historien som frammanad av Cheops Rektangel (ab=c²):

Hela TNED-matematiken i Solfallet grundas på ett värde för Solens Nu-massa analogt med det som beräknas ur Keplermomentet (K=vr=J/m) — Jordens periheliepassager runt Solen, det s.k. anomaliska året.

INTE det sideriska (i förhållande till fixstjärnorna) årets längd.

— Skillnaden är liten, men fullt märkbar i slutresultatet.

IAU-beröringen antydde för sin del att Keplermomentets alternativ — verkligen enastående — DOKUMENTERAR ett »Banmoments Ursprung» — så:

— OM TNED-kosmologin håller streck, ska vi kunna HÄRLEDA — förklara, beskriva och relatera i varje djupdetalj — hela Solsystemets uppkomst. Och det NOGA, genom att räkna baklänges på nuvarande Solsystemets omloppskroppars givna impulsmoment J=mvr=mK — inkluderat Vintergatans primära bildning, också NOGA, enligt TNED-anvisningarna i K-cellens värmefysik[‡].

Avsnittet i CheopsRektangelIIbA avhandlar den utvärderingen — med tillhörande bihang:

KOMPLEMENTÄRA DOKUMENT TILL SLUTTESTET med Solsystemen i VINTERGATAN :

RESULTATBILD (Sep2018-Feb2019) — Solsystemen i Vintergatan:

— »Klockren Maskinordning»[‡].

Cheops Rektangel.

BKLcitatet1926:

Perspektivbegreppet, citat 1926

” Perspekti’v (av lat. perspi’cere, se genom). 1. Inom optiken förstås med P. det intryck, som erhålles av förhållandet mellan dimensionerna hos föremål i olika plan, då en projektion av föremålen på en given yta betraktas. Förhållandet i fråga beror endast på projektionscentrums och den givna ytans läge och på ytans form.”;

” Betraktaren erhåller ett riktigt perspektivistiskt intryck, endast om hans ståndpunkt sammanfaller med projektionscentrum, vilken då även benämnes ögonpunkt. I motsatt fall erhålles ett oriktigt P., som yttrar sig i ett felbedömande av avbildningens djupdimensioner l. av på olika avstånd belägna föremåls relativa storlek.”;

” Ligger projektionscentrum på oändligt avstånd, får man parallellperspektiv, i motsatt fall centralperspektiv. Bildytan är vanl. men ej alltid plan.”;

” Vid centralperspektivet är huvudpunkt fotpunkten av huvudstrålen, normalen till bildplanet från ögonpunkten. Synstrålar äro de linjer, som förbinda föremålets punkter med ögonpunkten.”;

” Gränspunkt för en grupp parallella linjer i föremålet är den punkt, där deras bilder skära varandra, och erhålles genom att från ögonpunkten dra en linje parallell med de givna.”;

” — I konsten spelar P. en stor roll. Man skiljer här mellan linearperspektiv som åsyftar den riktiga framställningen av föremålens inbördes läge och dimensioner, samt luftperspektiv, d. v. s. skildringen av de förändringar, färgerna och konturerna undergå genom atmosfärens ljusabsorberande inverkan.”;

” Redan antikens målare eftersträvad perspektivistiska framställningar, men först under renässansen [1300-1600] fick P. sin slutgiltiga lösning.”;

” Praktiskt löstes problemet tidigast av de florentiska 1400-talsmålarna, främst Uccello.”;

” Lagarna för P., perspektivläran, fastställdes för första gången av Alberti i ”De pictura” 1435 och utvecklades närmare av bl. a. Piero dei Franceschi, Lionardo och Dürer.”;

” Under barocken utnyttjades P. såväl inom bildkonsten som arkitekturen för framkallande av allehanda illusionistiska verkningar. Genom att t. ex. i en kolonnad undan för undan göra kolonnerna kortare, stegrade man den perspektivistiska effekten, s. k. skenperspektiv.”;

” I kinesisk och japansk konst förekommer även det s. k. omvända P., som i modern europeisk konst upptagits bl. a. av Cézanne. Projektionscentrum tänkes härvid befinna sig bortom bildplanet och föremålen, från betraktaren sett. De från denne mest avlägsna föremålen bli härvid störst.”;

” — Vid fågelperspektivet ses föremålen rakt l. snett uppifrån, vid grodperspektivet (ital. do sotto in sù, nedifrån upp) snett nedifrån.”;

” — I överförd bet.: sammanhang, överblick, framtidsutsikt. — Adj.: perspekti’visk. — 2. Föråldrad benämning på smärre terrestriska kikare.”,

BKL IX 1926sp162: Perspektiv.

” Luftperspektiv, den blåaktiga ton, som avlägsna föremål få genom luftens ofullkomliga genomskinlighet.”,

BKL VII 1925sp812: Luftperspektiv.

Kalkylkort: EllipsPMT.ods — Tabell3 — Tabell4 — Tabell5 — d-sambandet — Ellipsekvationer:

KALKYLKORTEN TILL ELLIPSGEOMETRIN

KALKYLKORT — EllipsPMT.ods

EllipsPMT.ods från 16-24Feb2019

Kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN EllipsPMT.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/EllipsPMT.ods

Tabell 1 — rad 65-70 — Ellipsens omkrets

En tabellmake finns längre upp i tabellarket rad 1-10 som användes särskilt för test av vårt Solsystems planetdata.

Tabell 2 — Kort1 rad 02-09 .... — Perspektivellipserna, härledningar med kontrollräkningar för sambandens genuinitet

Tabell 2 — Kort2 rad 12-15 .... — Ellipspolygonen, generellt kalkylkort

Tabell 2 — Kort3 rad 18-22 .... — Fraktala polygoncirklarna, generellt kalkylkort

Tabell 2 — Kort4 rad 29-32 .... — Ellipserna i HPG: EPSonML

Tabell 2 — Kort5 rad 34-64 .... — OJUSTERAD — förlagan till 5.1¦2 nedan — EPSonBesML, generellt:

Tabell 2 — Kort5.1 rad 45-52 ....... — Förlaga till 5.2 — alternativa samband som eliminerar typen DivisionMedNoll;

Tabell 3 — ..................................................... — Kontrollräkning: härledningen till ac-sambandet.

Tabell 4 — ..................................................... — Kontrollräkning: eEAfRPs-EPSeq8102 — 90 ellipsekvationer:

PREFIXxSIN

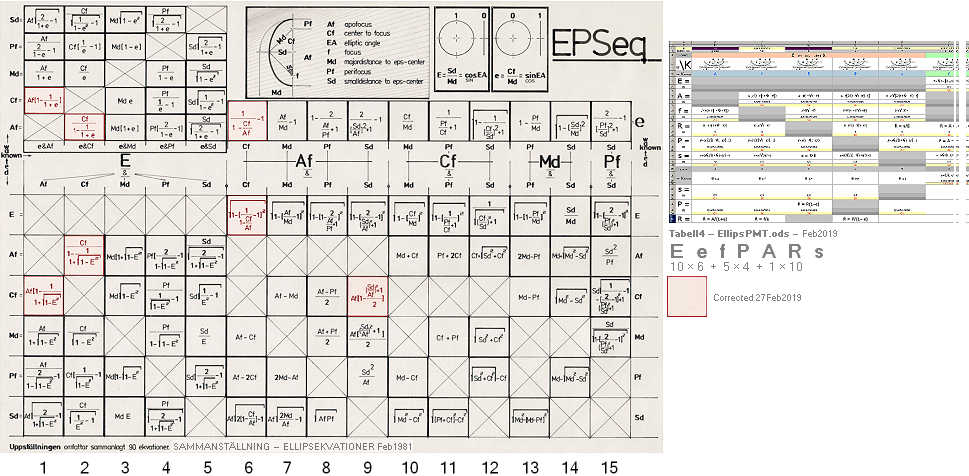
Uppställningen av ekvationskartan ovan är i Tabell4 är utformad med ovanstående övre del underst med förkortningar:

E=cosEA=Sd/Md=s/R A=Af f=Cf R=Md P=Pf s=Sd e=sinEA=1–E²

och en synkroniserad tablåNavigeringsKarta:

Tab4EkvKart: se originalet i Tabell4

PREFIXxSIN

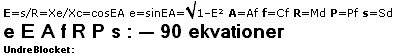
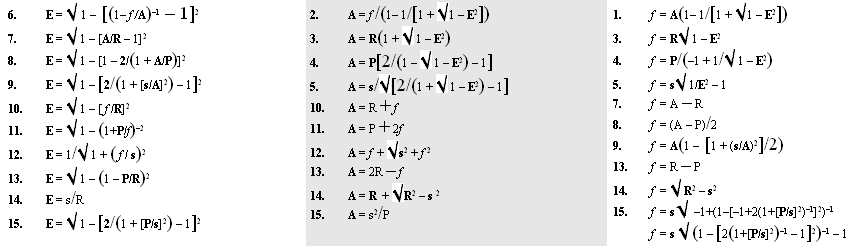
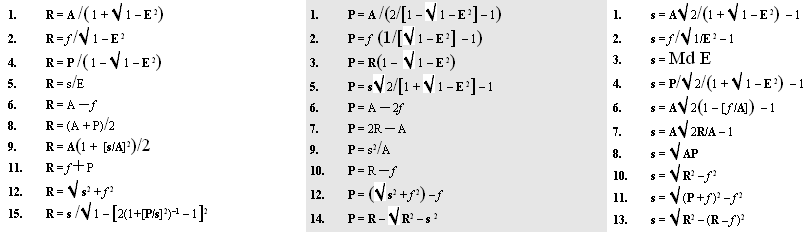
Kalkylkortets testvärden i Tabell4 — utrymmeskrävande —

har utformats mot ett kontrollexempel med numrerade kolumner synkront efter ekvationskartan.

— Varje kalkylcell har försetts med ovanstående blockforms sambandstypografi.

— Testformen säkrar att DE I KALKYLCELLERNA INSKRIVNA SAMBANDSFORMERNA är korrekta. Men ingen annan kontroll än den rent visuella finns på att kalkylformlerna och sambandstypografin också är av typen felsäker — risken för överföringsfel i visuella kontroller finns alltid.

Tabell 5 — ..................................................... — Kontrollräkning: EsRxyT-EPSeq8106 — 36 ellipsekvationer:

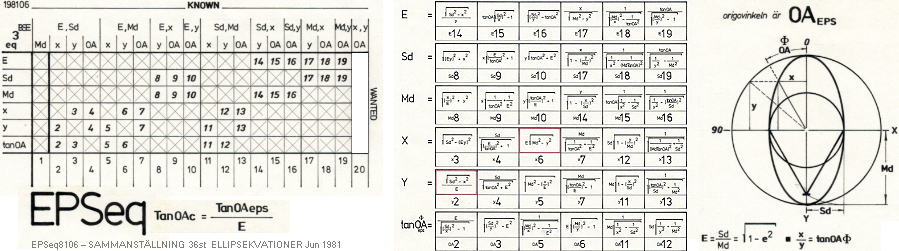
Kalkylkortets testvärden i Tabell5 — mindre utrymmeskrävande —

har utformats som i T4 men enklare enligt

FELSÄKERBILDEN är i bägge fallen, i vilket fall, densamma: Kalkylcellernas inskrivna i OK-kontrollerade — felsäkra — sambandsformer garanterar INTE att författaren också har skrivit ut Den algebraiska formen på korrekt sätt — men felmöjligheten bör vara minimal med dessa (dubbla) kontroller:

Tab5EkvKart: Tabell5

PREFIXxSIN

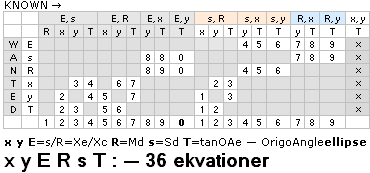
dSambabdet: EPSfört.

SÄRSKILDA ELLIPSUTVECKLINGAR — originalet från Aug1981:

y R E :

PREFIXxSIN

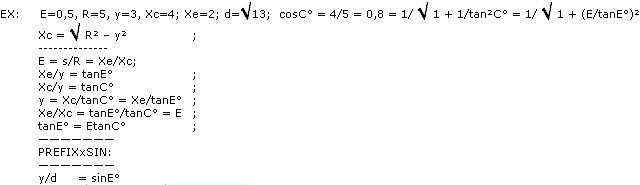
Sambandsformerna som har tagits med här

(ett urval — komplexen inom den geometriska matematiken är synnerligen omfattande)

har använts från och till under hela det förberedande utvecklingsarbetet inom matematiken (och geometrin) som grund för sakinnehållet i Universums Historia (@Internet från Aug2008), främst perioden från runt 1980 till nu (Feb2019).

END.

Elementarytorna

innehåll: SÖK äMNESORD på denna sida Ctrl+F ·

Elementarytorna

ämnesrubriker

innehåll

ELEMENTARYTORNA I MATEMATIKEN

htm-ORIGINALFRAMSTÄLLNINGEN från 2009 med gängse konventionella matematiska särskilda tecken i SYMBOL

———————————————————————————————————————————————————————

Sfärens Yta och Sfärens Volym — i enkla klassiska härledningar

Förteckning till härledningarna

Alla Härledningar — Tabell

Förskjutningssatsen — 2A = bh

Förskjutningssatsen

Tillämpning

Konens Volym

KonVolymen från kubens 6 delpyramider — V(CON) = Ah/3

Exempel: UPPKLIPPNING — cirkulära konen med rektangulär basyta

Cylinderns volym

Cylindervolymen genom UPPKLIPPNING — V(CYL) = 2 pi r²h

Sfärvolymen genom Cylindervolymens uppklippning

— Konanalogi med sfärvolymen V(KON) = AREA h/3 = V(SPH) = 2 pi r · 2r · r/3 = 4 pi r³/3

SFÄRYTAN UR Sfärvolymen genom Cylindervolymens uppklippning — A(SPH) = 2 pi r · 2r = 4 pi r²

Elementarytorna

Elementarytorna

Genomgång av den enkla, klassiska geometrins ytbegrepp

Klassiska geometrins ytbegrepp

Cirkeln — omkrets 2 pi R, yta pi R², sektoryta Rs/2

Konen — cirkelsektorn Rs/2 formar konens mantelyta

Konytan — R pi r

Tyngdlinjen

— Konytan via tyngdlinjen — R·2·pi·(T=r/2)

Konytan

— konytan R2piT, cylinderns yta 2piTR, stympade konens yta 2piTR, cylinderns yta 2pirh, tyngdlinjens rotationsyta 2piTl

Tyngdpunktssatsen

Historia — Guldins Regler, Paul Guldin 1577-1643

Cirkelbågens tyngdpunkt PREFIXxSIN

Sfärytan via tyngdpunktssatsen — 4pir² — godtyckligt från origo (2pir)x

— cirkelbågens tyngdpunkt från origo R=kr/l

— cirkelbågens tyngdpunkt från origo via kordan k och radien r, obs acos i radianer: R=k/2[acos(k/2r)]

— cirkelbågens tyngdpunkt från origo via båglängden s: R=(1/s)2r²cos(s/2r)

— cirkelbågens tyngdpunkt från origo via radianvinkeln a=A°(pi/180): R=a·cos(a/2)·2r

Halvcirkelns tyngdpunkt — R=r(2/pi) = r(0,6366197)

Tyngdpunkten för halvcirkeln

Sfärytan och cylinderytan genom perceptionsanalysen

Sfärytan och Cylinderytan

Beskrivning

Perceptiv analys

SfärytanCylindern — A = (pir/2)2 · 8 · 1/(pi/2) = 4pir²

Sfären och Cylindern genom Förskjutningssatsen

Sfärytan genom förskjutningssatsen

KONENS BASYTA FÖRENAR SFÄREN MED CYLINDERN GENOM FÖRSKJUTNINGSSATSEN

OCH DEFINIERAR SAMTIDIGT SFÄRENS VOLYM FRÅN CYLINDERNS VOLYM

Beskrivning

Sfärytan och Cylinderytan — Sfärvolymen och Cylindervolymen

SfärytanKonenCylindern

Sfärytan Konen Cylindern

SFÄRYTAN ÄR IDENTISK MED OMSKRIVNA CYLINDERYTAN GENOM FÖRSKJUTNINGSSATSEN 2pir · 2r

Bonus — Sfärens Volym

SFÄRENS VOLYM ÄR CYLINDERNS VOLYM MINUS DE BÄGGE KOMPAKTA ÄNDKONERNA V(SPH)=2r(pr2) — 2[V(CON)] .. = 4pir³/3

Sfärvolymerna i illustrerad sammanställning — Sektor, Zon, Segemnt

Sfärvolymerna i sammanställning

Integrala exempel PREFIXxSIN

Integrala exempel

Sfärvolymen via integralkalkylen — dV=piy²dx — V=4pir³/3

SFÄRVOLYMEN VIA INTEGRALKALKYLEN

Exponentialintegralen Ref

Sfärytan via integralkalkylen — = 4pir²

SFÄRYTAN GENOM INTEGRALKALKYLEN

Konen via integralkalkylen

KONEN GENOM INTEGRALKALKYLEN

— = Ah/3

—

Cylinderfelet

DET FATALA CYLINDERFELET

DEN FÖRMODADE SFÄRYTAN GENOM CYLINDRAR

Rotseriens summa

Borlands Pascal DELPHI

Delphi

Borlands Pascal

ARKIMEDES LÖSNING

Arkimedes lösning

Sfärens yta och volym

SFÄRENS YTA OCH VOLYM — grundform

Lunds Universitet — webbreferens

Ellipsen

ELLIPSEN I UNIVERSUMS HISTORIA

Allmänna EllipsBeteckningar

ac-Härledningen

ac-Sambandet, beskrivning

Förteckning ÖVER EllipsArtiklarna i UNIVERSUMS HISTORIA

———————————————————————————————————————————————————————

TILLÄGGSAVSNITT Feb2019 MED GÄNGSE KONVENTIONELLA MATEMATISKA SÄRSKILDA TECKEN i Unicode

— vissa webbläsare accepterar inte det konventionella naturvetenskapliga ENHETLIGA teckensnittet SYMBOL = Grekiska Alfabetet,

utan envisas med att ha ett UNICODE ”sådant” för VARJE teckensnitt — bara med resultatet att ENHETLIGHETEN HAR FÖRLORATS.

Du kan hoppa över det här:

— Varför inte göra slag i saken direkt och börja med YTREWQ-tangentbord — MED enter LÄNGST UPP? Det vore väl KUL.

— Man måste ju förnya sig, sa maken som hade tröttnat på hustruns utseende redan efter första dagen.

— INTERNET är så väldigt innovativt. Pekplattor för tårna är, helt säkert, på väg — för folk som vill solbada ifred, med hörlurar.

WebbINTERNETprogrammakarna, väldigt innovativa typer, sprider ut enhetligheterna på otaliga ställen

— sökträffar med GummiStudsEffekter, m.m. Jättefint. Verkligen högintelligent DatorUtveckling, typ TopGun: ”The best of the best”.

— Och vanliga textproducenter får arbeta (hårt) för att försöka lappa ihop och släta över »så att det ser fint ut» i den egna produktionen.

JätteUtbildad Planetbefolkning. JätteA i matte, och sådär. MIT. Forskningsanslag ges bara till personer med PhD. Jättefint.

———————————————————————————————————————————————————————

PerspektivEllipserna

Härledningarna till PERSPEKTIVELLIPSERNA I HPG

EPSBasic ¦ 1980

EPS—PJM

aFlex1

aFlexAlternativet

The Elliptic Polygonian

Example

The Polygonian Arc — PolygonCirklarna

The FRACTAL Polygonian Arc

Exempel

EPSpmt — ellipsens omkrets

EPSpmt-sambandet

EPSonBesML

EPSonML

EPSbesML

Fig11CRLiHPG

Trigonometrisk Derivering

ALTERNATIVA SAMBAND

Illustrerad SUMMERANDE UTVECKLINGSHISTORIA

Perspektivbegreppet, citat 1926

Plangeometrisk Projektion av ett PerspektivGeometriskt grundläggande elementärt Begrepp

BKLcitatet1926

Kalkylkort

EllipsEkvationer

Tabell 3

Tabell 4 — EPSeq8102

EKVATIONSKARTA Tab4

Tabell 5 — EPSeq8106

EKVATIONSKARTA Tab5

d-sambandet

referenser

[BKL]. BONNIERS KONVERSATIONS LEXIKON Band I-XII med SUPPLEMENT, Alb. Bonniers Boktryckeri, Stockholm 1922-1929

MAC, i Universums Historia ofta använd förkortning för Modern Akademi (eng. Modern ACademy)

TNED — Related PHYSICS And MATHEMATICS — Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

SHORT ENGLISH — TNED in general is not found @INTERNET except under this domain

(Universe[s]History, introduced @INTERNET 2008VII3).

TNED or Toroid Nuclear Electromechanical Dynamics is the dynamically equivalent resulting description following the deductions in THE PLANCK RING, analogous AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, each, details claim to be fully logically explainable and understandable, or not at all. With TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’ Deduction.

Senast uppdaterade version: 2019-03-01

*END.

Stavningskontrollerat 2009-05-26 ¦ 2019-02-24.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ L τ π ρ ħ ε UNICODE — often used charcters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡ ↔↕ ħ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ ϑ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; 25 ↓; 26 →; 27 ←; 22 ▬

23 ↨ — also 18 ↕; 29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

*

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se