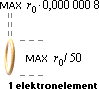ELEKTRONENS BUBBELKAMMARSPÅR | 2006IV23 | 2008VI26 | Senast uppdaterade version: 2017-01-06 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

magnetiska B-vektorn upp genom bildytan

Bubbelkammarfotografi från FOCUS MATERIEN 1975 s139

Elektronens bubbelkammarspår ENLIGT TNED

ELEKTRONENS RÖRELSEBANA I HOMOGENA MAGNETISKA FÄLT MED FÖRSUMBARA INHOMOGENITETER

Se sambandsformerna i sammanställning i Referenser

Notera att webbläsaren Firefox läser INTE teckensnittet Symbol — 64 av 118 htm-dokument 2016 i Universums Historia. I detta htm-fall har delvis ersättningar gjorts i efterhand med Times New Roman Unicode.

Notera att webbläsaren Firefox läser INTE teckensnittet Symbol — 64 av 118 htm-dokument 2016 i Universums Historia. I detta htm-fall har delvis ersättningar gjorts i efterhand med Times New Roman Unicode.

f_CYL = (1–v/c₀) · v(d/R)/k_t ....................... Hz, k_t=1,0817 t15 M

v_c = f_CYL(2p)r_t ................................................................. M/S, r_t=2,74 t17 M

E_c/E_v = (d/R)²/2p² = 2(v_c/v)²

Det här ämnet är nog det mest märkvärdiga i hela den här presentationen — främst därför att det (ännu Juni 2008) verkar snart sagt omöjligt att få någon klarhet i vad som menas med hjälp av tillgängliga källor. Saken är den här — exemplifierat:

I många fotografier av elektronernas bubbelkammarspår kan man se hur det cirkulerande elektronspåret driver tvärs bubbelkammarens magnetfält (B), typ exemplet ovan; B är alltid riktat rakt uppåt från bildytan, se särskild beskrivning. Men en punktformad (idealt sfärisk) elektrisk laddning (konv. elektronen) kan omöjligen uppvisa en sådan banform, se särskild beskrivning i Helix; För en idealt punktformig elektrisk laddning (Q) i ett homogent B-fält ska Q uppvisa en perfekt cirkulär bana kring de uppåtriktade magnetiska fältlinjerna. I praktiken blir rörelsen spiralformad i och med att elektronen förlorar energi kontinuerligt på sin färd genom bubbelkammarens vätska, samt med en möjlig men ytterst liten avvikelse i sidled beroende på anordningens onoggrannhet (max ca 1%, se särskild beskrivning) — men absolut ingenting i den storleksordning som ovanstående exempel uppvisar. Det är helt uteslutet.

Men källorna som finns tillgängliga — traditionella fackböcker, bibliotekslitteratur, webben Juni 2008 — omnämner inte det problemet. I min referens, har ännu inte en enda källa påträffats som ens rör vid själva observationen. Det är ännu mera märkligt eftersom partikelspåren i bubbelkammare har studerats i detalj sedan början av 1950-talet (1952, Donald A. Glaser), och man (då) tycker att just ovanstående detalj borde ha sett åtskilliga avhandlingar (förklaringar, utförliga beskrivningar) under de runt 50 år som bubbelkammaren använts.

När detaljen uppmärksammades i min historia — i ljuset av TNED — blev naturligtvis den spontana reflexionen att fenomenet kanske kunde förklaras genom elektronmassans komponenter. Den undersökningen visade sig också vara fruktbar, och det är vad den här framställningen ska handla om: spåren förklaras galant genom TNED.

Vi börjar först genomgången nedan med grundbegreppen, tillsammans med citat från olika etablerade verk som beskriver själva anordningens olika delar och förutsättningar, samt sedan vidare med konkreta bildexempel med analyser och jämförelser — tillsammans med härledningarna enligt TNED.

Möjligen kan framställningen bidra till att folk i etablerade led mera ingående förklarar sina synpunkter.

Förekomsten av starkt avvikande banformer för elektronmassan i anordningar som INTE förväntas uppvisa motsvarande kraftiga variationer i B-fältet, har HÄR föranlett en ingående granskning av ämnet och som lett fram till en alternativ bild av elektronens geofysik — och som till synes perfekt kan förklara de observerade banformernas geometri.

Ämnet — för jämförande referenser — finns emellertid ypperligt dåligt representerat på webben (@INTERNET 2008). Det finns dock en del värdefulla detaljer som kommer att framvisas genom den här presentationen.

helix

Inledande grundbegrepp

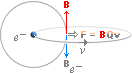
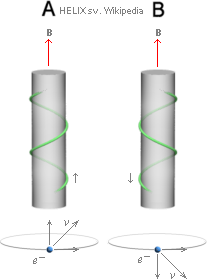
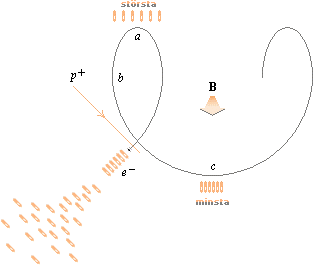
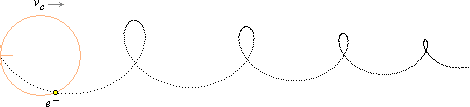
Vänstra figurdelen: En idealt sfärisk punktladdning (e^–) som med hastigheten v inträder ett yttre magnetfält (B) med v vinkelrätt mot B, kommer att böja av kring B-riktningen i en idealt cirkulär bana. Grundriktningarna bestäms enligt Högerhandsregeln.

Högra figurdelen med A och B: A; (e^–) kommer in till det yttre uppåtriktade B med v snett uppåt: e^– beskriver en uppåtgående skruvlinje som sett ovanifrån beskriver en moturs rörelse i en perfekt cirkel. B; (e^–) kommer in till det yttre uppåtriktade B med v snett neråt: e^– beskriver en nedåtgående skruvlinje som sett ovanifrån beskriver en moturs rörelse i en perfekt cirkel.

EN SFÄRISK IDEAL ELEKTRISK PUNKTFORMAD LADDNING (Q=e^–, ovan vänster) som färdas med konstant hastighet (v) i ett yttre lokalt dominant gravitationsfält, utbildar i g-fältets fixa referenspunkter ett magnetisk fält (B_e–) vars fältringar expanderar idealt cirkulärt från Q-centrum.

OM Q är en enskild elektronmassa (e^–) som färdas med v rakt upp från bildplanet mot betraktaren och som inträder ett område av rummet där det finns ett yttre magnetisk fält (B) som har den riktning vertikalt uppåt som antyds i ovanstående illustrationer (röd pil markerad B), kommer växelverkan mellan de bägge B-fälten att resultera i en kraft (F) som drar in Q i en cirkulär bana med radien r enligt högerhandsregeln och magnetiska kraftlagen

F = BQv = m(v²/r) ;

BQ = m(v/r) ;

Br = mv/Q ;

r = mv/BQ

Dessa samband är konventionellt välkända. Se exv. eng. Wikipedia på Magnetic field och Guiding center — men akta referenserna i Wikipedia: vi ska återkomma till en del av dessa, här längre fram — med tydliga exempel från andra källor.

Om B är homogent — vilket betyder att ev. avvikelser i B-fältet är försumbara — och v är konstant — rätvinkligt B — kommer Q att beskriva en perfekt cirkulär bana med konstant radie (r), precis som illustrationen ovan antyder. Nedanstående illustration beskriver de två primärt cirkulära rörelsealternativ som finns att välja på.

beskrivning

Om Q kommer in till B-fältet med v snett mot B-riktningen, kan v-resultanten delas in i en del parallellt med B och en del rätvinkligt B, se ovanstående illustration (högerdelen);

v-delen rätvinkligt B ger den vanliga perfekt cirkulära banan;

v-delen parallellt med B endast förskjuter cirkelbanan nedåt — eller uppåt — beroende på om v är motsvarande riktad nedåt eller uppåt.

I dessa senare fall sägs elektronbanan uppvisa helix, eller en motsvarande tredimensionell skruvformad bana i 3D-rummet.

Illustrationen ovan förtydligar de två möjliga fallen.

Helmholtzspolen

BUBBELKAMMARENS CENTRALA HELMHOLTZSPOLAR — det centrala yttre B-fältet

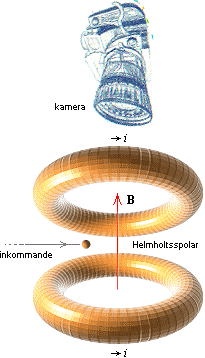
Helmholtzspolarna

En Helmholtzspole består egentligen av två närliggande parallella speciellt lindande elektriska spolar. De bildar den funktionella kärnan i den traditionella (numera pensionerade) bubbelkammaren, den beskrivs vidare nedan. Genom sin speciella konstruktion kan Helmholtzspolen ge ett mycket homogent centralt B-fält. Illustrationerna och bilderna nedan visar hur den traditionella s.k. bubbelkammaren är konstruerad; Den fångar bilden av (t.ex.) spåret efter en elektron då den kommer in i kammarens B-fält; Funktionen liknar den som ges av ett reaplan högt ovanför marken som lämnar en tunn kondenserad vit molnstrimma efter sig. Negativt laddade partiklar böjer av åt ena hållet genom växelverkan med B, och positiva åt andra hållet. Särskilda kameror är lämpligt monterade för att få bästa möjliga bild av det centrala området där B-fältet är som mest likformigt.

Bubbelkammarfotografi från FOCUS MATERIEN 1975 s139
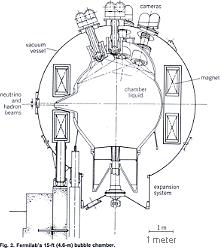
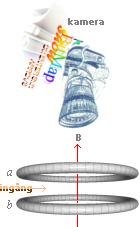
Bubbelkammaren från Fermilab. Källa: ENCYCLOPEDIA OF SCIENCE AND TECHNOLOGY McGraw-Hill 1992 Band 3 Bubble Chamber s91	Principen: B-fältet i mitten ges av tvillingspolarna i Helmholtzspolen, de bägge ringarna med trådlindningar i ringplanen.	Vertikalsnitt genom en Helmholtzspole Magnetfältet i centrum uppvisar en hög grad av likformighet — om avståndet ab mellan spolarna är lika med spolarnas ringradie. Bildkälla: Wikipedia Helmholtz coil

Allmänt, anordningen för bubbelkammarfotografering, se exempelritningen ovan vänster

En sluten behållare (flytande väte) omges av ett par Helmholtzspolar — som ger ett mycket homogent B-fält i öppningen. I behållaren finns upptill i B-riktningen ett antal kameror som fotograferar innanmätet. Från sidan (vänster) finns en speciell öppningsdel som tillåter inkommande partiklar (protoner, em-strålning) att penetrera behållarens material (i behållarens underdel finns en speciell kompressionskolv som sammanhänger med bubbelkammartekniken, men vi berör inte den delen vidare här). Bubbelkammarfotografierna visar i samtliga fall B-fältet med riktning rakt upp genom bilden, med hög noggrannhet över hela bildytan.

Beträffande storleken skriver McGraw-Hill-källan ovan från 1992 på s91sp2ö:

”Size. The first test bubble chamber was only a few iches across. Bubble chambers have steadily become larger and are now built as large as 15 ft (4.6 m) across. The main reason for making such a larger chamber is to be able to study neutrino interactions.”.

Min översättning:

Storlek. De första testbubbelkammarna var vara några få tum tvärs över. Bubbelkammare har stadigt blivit större och byggs nu så stora som 15 fot (4,6 meter) tvärs över. Den huvudsakliga anledningen för att göra en sådan större kammare är för att kunna studera neutrinoväxelverkan.

MAGNETISKA FÄLTSTYRKAN i den centrala Helmholtzspolen som ger det centrala B-fältet har, analogt med utvecklingen av bubbelkammarnas storlek, ökat drastiskt. Typvärden på B-styrkan i samband med bubbelkammare kan hittas på webben (2008) på många olika ställen — med uppgifter allt från runt 0,3 Tesla (30 000 Gauss) till över 10 Tesla (100 000 Gauss).

Med hjälp av sambandet

r = mv/BQ

— och viss information om vilka partikelaccelererande energier som används, se vidare nedan — kan vi få en orienterande uppfattning om storleken på (exv.) r med givet m/Q.

Exempel:

Med

Q = 1,602 t19 C ................................... elektronmassans enhetsladdning

m₀ = 9,11 t31 KG ................................. elektronens vilomassa

m = m₀/[1–(v/c)²]^1/2 ............................. Planckenergins massekvivalent

v = c(1–1/[(UQ/m₀c²)+1]²)^0,5 ............... Q:s hastighet v i vakuum via accelerationsspänningen U

(v/c)² = 1–1/[(UQ/m₀c²)+1]²

1–(v/c)² = 1/[(UQ/m₀c²)+1]²

U = Q^–1m₀c²([1/Ö 1–(u/c)²] – 1) ........... accelerationsspänningen från sluthastigheten u=v

c = 2,99792458 T8 M/S ...................... ljushastigheten i vakuum

kan r beräknas för elektronen som ideal sfärisk punktladdning om vi också vet accelerationsspänningen U.

En av webbkällorna

[http://ieeexplore.ieee.org/Xplore/login.jsp?url=/iel3/3817/11161/00550247.pdf?tp=&isnumber=&arnumber=550247]

anger (2008-06-28) uppgiften max 20 MeV — som motsvarar U = 20 MV — i samband med en bubbelkammare med en central B-styrka på 1,5-2 Tesla.

Vi använder ett mindre U, här U=1MV=1 T6 V och får m₀/[1–(v/c)²]^1/2 = m₀2,9566031 som ger

m = 2,69346 t30 KG

v = 0,9410649c

Med

B = 1,5 T

Q = 1,602 t19 C

ges då initiellt

r = mv/BQ

= (2,69346 t30 KG)(2,82124 T8 M/S)/[(1,5)(1,602 t19 C)]

= 3,16226 t3 M eller drygt tre millimeter

Nära samma r-värde (3,7 mM) ges med U=0,1MV — vilket ger v=0,55c — och B=0,3 T.

Accelerationsspänningen U brukar normalt anges för den partikelstråle som drivs in i bubbelkammaren (som i webbkällan ovan max 20 MV). Motsvarande accelerationsspänning för frigörandet av t.ex. en elektron i bubbelkammaren bör vara något lägre, men här finns för närvarande inga direkta citatkällor som kan uppvisa konkreta praktiska typexempel. Att beräkna MERA EXAKT hur en inkommande proton frigör en stationär elektron från kammarens flytande vätgas är en mera intrikat fråga. Ingen enkel redovisning finns (ännu, här) på den delen. Klart är i vilket fall att energin som åtgår för att frigöra elektronen blir (avsevärt) lägre än den energi som användes för att skicka in primärpartikeln (protonen) i kammaren.

kalkylkort · endast i bild · ingångsdata för den idealt sfäriska laddningens bana i homogena B-fält (bubbelkammarspår)

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik2 Kalkylkort 1 — Ingångsdata — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

OM MAN HAR ETT PASSANDE PROGRAM (här MsWORKS 4.0) kan ett kalkylblad med enskilda kalkylceller för sambanden ovan bekvämt insättas och därmed direkt få fram resultatvärden med helt enkla inmatningar. Tyvärr fungerar inte ett sådant kalkylkort på webben (utan vidare). Ovan visas endast bilden av originalet.

Generellt måste i varje fall jag sätta ihop typ ovanstående kalkylkort om sambandsformerna är flera — för att kontrollera resultat och korrekta samband; min erfarenhet har lärt mig att det är det rätta sättet — skrivfel och överföringsfel är tyvärr alltför vanligt i datorsammanhang, och utan ett sammanhängande kontrollkort är i princip sambanden värdelösa!

noggrannheten

Bubbelkammarprincipen ansluter alltså till samma typ av riktningsbeskrivning som visades i föregående illustrationer.

TYPDATA PÅ HELMHOLTZSPOLENS NOGGRANNHET finns i referens @INTERNET t.ex. på

[http://www.integratedsoft.com/Papers/research/magnetron.pdf];

”The Helmholtz Coil achieves a highly uniform magnetic field in a volume near the center (where the particles will be launched). This field is directed along the axis defining center of the two coils.”.

”Lorentz calculates a flux density at the center of 35.33 G - a difference of 0.2% owing to the thickness of the coils.”.

Min översättning:

Helmholtzspolen får ett högeligen likformigt magnetfält i en volym nära centrum (där partiklarna kommer att sjösättas). Detta fält är riktat utmed axeln som definierar de bägge spolarnas centrum.

Lorents [företagets benämning på ett apparatkoncept] beräknar flödestätheten vid centrum på 35,35 Gauss — en skillnad på 0,2% som beror på spolarnas grovlek.

Se även eng. Wikipedia Helmholtz coil

[http://en.wikipedia.org/wiki/Helmholtz_coil] 2008-06-26;

Källan anger en noggrannhet inom 1% i spolarnas centralområde.

Se även Bildexempel på Helmholtzspolarnas onoggrannhet.

MED ANDRA ORD:

Vi räknar INTE med att den eventuella marginella inhomogenitet som ev. finns i B-fältet från anordningens Helmholtzspole har någon som helst direkt betydelse eller signifikans i det aktuella område som kameran tittar på.

Vi SKULLE TILL OCH MED DIREKT KUNNA KONTROLLERA — via ett bubbelkammarfotografi — eventuella avvikelser i den lokala B-styrkan via sambandsformen som ovan

Br = mv/Q = idealt konstant;

Med mvQ konstanta ändras B och r direkt omvänt proportionellt mot varandra; ökar B-fältet i styrka med 1%, måste r avta med 1%:

B(n)·r(n)^–1 = konstant

Med den angivna (förmodade) noggrannheten på (mindre än) 1% har vi därmed ingen anledning att misstänka några större avvikelser — definitivt inte sådana som t.ex. skulle uppvisa flera hundra procent.

Hastigheten (v) för elektronen vet vi emellertid måste avta på grund av energiförluster då den rusar runt i bubbelkammarens vätska. Den effekten innebär emellertid bara att den idealt perfekta cirkelbanan avtar i radie så att vi istället får en motsvarande ideal spiral. Vi kan därmed (ännu enklare) se om B-fältet lokalt innehåller någon påtaglig olikhet genom att studera jämnheten i spiralvarvens intervall; Finns det någon liten (max 1%) skillnad, kan vi hänföra den till anordningens instrumentella onoggrannhet.

MEN ABSOLUT INTE STÖRRE AVVIKELSER ÄN ca 1%.

Låt oss därmed studera det fotografiska exemplet i FOCUS MATERIEN 1975 s139.

Bubbelkammarfotografiet från FOCUS MATERIEN 1975 s139

Bubbelkammarfotografiet från FOCUS MATERIEN 1975 s139

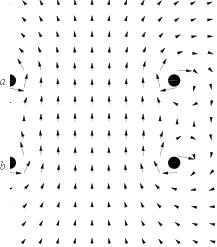
Om vi studerar fotografiet och letar efter områden som uppvisar avvikelser, kan vi se att det finns flera — tydliga — sådana:

Låt oss först titta närmare på den första (bilden nedan uppvriden vertikalt):

den stora

vinkelavvikelsen

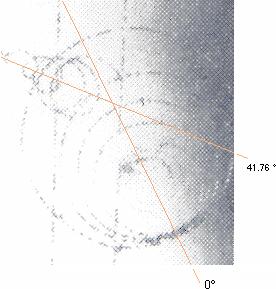
För det första:

Den stora spiralen driver tydligen neråt höger som elektronens v avtar;

Den lilla spiralen driver tydligen — emellertid — åt andra hållet — uppåt vänster som elektronens v avtar;

För det andra:

Skillnaden mellan de olika riktningarna i avvikelse är tydligen — här — exceptionellt stor: mera än 40 grader;

Vi skulle INTE ha skäl att anta SÅ extremt stora avvikelser i B-fältets SPECIELLT LOKALA inhomogenitet; med max onoggrannhet på 1% skulle avvikelsen i de bägge riktningarna här knappt bli märkbar; vi skulle knappast kunna se något sådant som i det ovanstående fallet: de varandra korsande ändringarna i B-riktningarna antyder att det skulle finnas TVÅ B-riktningar, inte en. Men en sådan instrumentordning är med Helmholtzspolens konstruktion utesluten.

OM B-fältet skulle variera, borde det variera enhetligt åt en given riktning. Inte åt två tydligt motsatta riktningar.

Den observerade tydligt stora (mer än 40°) skillnaden i spiraländringens riktning stämmer inte med anordningens förutsättningar — FÖR EN IDEAL PUNKTFORMIG ELEKTRISK LADDNING; En sådan kan inte uppvisa den ovan avbildade banformen.

DESSUTOM ser spiraländringen i bägge fallen ut att vara exceptionellt osymmetrisk — men det finns flera faktorer som kan inverka här varför vi tills vidare lämnar den aspekten.

Slutsats:

· Den observerade onormalt stora avvikelsen i ändringsriktningen mellan de olika spiraldragningarna kan — här veterligt — INTE hänföras till anordningens onoggrannhet;

· En ideal sfärisk punktformad elektrisk laddning har ingen fysikalisk förutsättning för att uppvisa den observerade banformen;

· Den observerade banformens partikelobjekt måste ha en helt annan formgeometri — än den förmodat »klassiska» som konventionellt antas gälla för elektronen.

Om vi som andra objekt betraktar den tredje föregående bilddelen i bubbelkammarfotografiet,

— den högra bilddelen uttagen och inverterad med inlagd cirkel till jämförelse —

ser vi direkt ännu en exceptionell avvikelse som definitivt INTE kan hänföras till Helmholtzspolens onoggrannhet:

Kolla radieskillnaden via föregående samband

Br = mv/Q = idealt konstant;

Frånsett v, som vi redan vet minskar mer eller mindre och som ger den avtagande spiraltypen och som kan studeras ovan i den större avtagande cirkelns radie som den läggs motsvarande på delarna utåt höger, är här skillnaden mellan den större cirkeln och den närliggande mindre definitivt onormal: vi kan direkt mäta i figuren och ser att första stora relativt första mindre är större med ett förhållande grovt 21/3

— en skillnad i Br-magnitud på runt 700%.

Också en sådan stor avvikelse är helt utesluten för anordningens onoggrannhet — denna bör inte vara större än 1%.

SAMBANDEN FÖR ONOGGRANNHETERNAS OLIKA DRIFTBANOR är i konventionell mening välkända.

En (relativt) utförlig beskrivning — med referenser — finns på källan @INTERNET Wikipedia Magnetic field och Guiding center 2008-06-26.

Emellertid;

Wikipediakällan illustrerar dessa sambandsformer med liknande driftkurvor som den ovan avbildade till höger — men kan inte förklara det praktiska resultatet typ ovan då det, här veterligt med ovan angivna referenser, inte finns någon onoggrannhet i anordningen som kan ge upphov till den bantypen

— typ 700% driftfel.

Slutsatsen som måste dras måste därför bli att den partikelgeometri som bär ansvaret för den avbildade bantypen, exemplet ovan till höger, INTE är den i Wikipedia (och andra liknande källverk) antagna ”idealt sfäriskt punktformiga” elektriska elementarladdningen e.

Banformen kan inte förklaras såsom bildad av en ideal sfärisk punktformad elektrisk laddning som färdas i ett B-fält med typ 700% spridning på B-fältets styrka — och inte heller kan banformen förklaras med en anordning som uppvisar en hög instrumentell noggrannhet med max 1% avvikelse i B-fältet med en ideal sfärisk punktformad elektrisk laddning alls överhuvudtaget.

bild av varierande B-fält

Jämför även den här källan @INTERNET (2008-06-28) [måttsrelationen i pixels inlagd av mig till jämförelse];

Bilden nedan bekräftar den ungefärliga maximala avvikelsen i B-fältets styrka på max 1%. Den inlagda måttsrelationen över bilden (här grovt hoftad) visar ett förhållande 1/124 eller 0,8%, vilket (grovt sett) bekräftar föregående givna uppgifter.

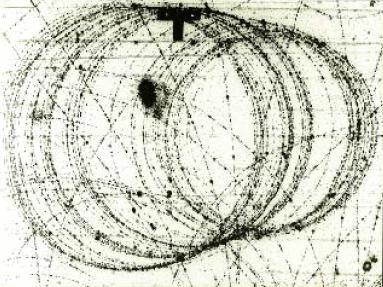
Advanced Aerospace Propulsion, David B. Sereda Copyright 2005 | bilden här inverterad

[http;//americanantigravity.com/documents/Advanced-Aerospace-Prpulsion.pdf] s17ö,

ADVANCED AEROSPACE PROPULSION A New Theoretical and & Experimental Approach By David B. Sereda Copyright 2005

”Photo of free Electron Spiraling

This photo from “The Particle Odyssey,” shows an electron changing its orbital diameter from a larger diameter to a smaller one. From page 37:

Under the influence of a magnetic field, an electron in a cloud chamber spirals around some 36 times, producing a track around 10 m long. The electron starts its life at the left of the picture, where it has been created together with an anti-electron or positron, by an invisible gamma ray. The electron’s spiral moves slowly across the page due to a slight variation in the magnetic field. Notice how the spiral becomes significantly tighter about halfway across the picture. This is because the electron has lost energy by radiating a photon.

”.

Min översättning:

Foto av fritt Spiralerande Elektron

Detta foto från ”The Particle Odyssey,” visar en elektron som ändrar sin bandiameter från en större till en mindre en. Från sidan 37:

Under inverkan av ett magnetiskt fält, spiralerar en elektron i en dimkammare runt en 36 gånger, producerande ett spår kring 10 m långt. Elektronen börjar sitt liv till vänster i bilden, där den har skapats tillsamman med en antielektron eller positron av en osynlig gammastråle. Elektronens spiral rör sig långsamt över sidan beroende på en mindre variation i det magnetiska fältet. Notera hur spiralen blir märkbart tätare ungefär halvvägs över bilden. Det är därför att elektronen förlorar energi genom att utstråla en foton.

SOM REDAN EXEMPLIFIERATS OVAN har vi knappast att förvänta oss större variationer i B-fältet från Helmholtzspolarna är (max) 1%: En jämn v-minskning med max 1% (en hundradel) B-ändring betyder att vi på en cirkel på bildskärmen med diametern 200 pixel (57 mM på en 9 tums WideScreen) inte ska kunna avläsa en större variation än på max en eller två pixel (ca 0,3-0,6 mM). Bilden ovan uppvisar med en direkt mätning i pixels grovt sett ett förhållande på 1/124 vilket ger en avvikelse på 0,8%, vilket bekräftar föregående uppgifter.

Jämför även den här källan @INTERNET (2008-06-28);

Exempelbilden nedan uppvisar däremot betydligt större variationer än 1 á 2 pixel per spiralvarv (snarare runt halvcentimetrar, vilket betyder avvikelser på drygt 15%). Dessutom finns ytterligare asymmetrier i spiralformen (spiralen självskär) som gör att vi (helt) kan avfärda uppfattningen att formexemplet nedan (vilket vi hittar typiskt för många elektron-positronbanor) skulle bero på variationer i anordningens ytterst avancerade instrumentellt bildade B-fält. Den avbildade driften nedan har tydligen helt andra orsaker.

den stora

positronspiralen

Advanced Aerospace Propulsion, David B. Sereda Copyright 2005 | bilden här inverterad

[http;//americanantigravity.com/documents/Advanced-Aerospace-Prpulsion.pdf] s17n,

ADVANCED AEROSPACE PROPULSION A New Theoretical and & Experimental Approach By David B. Sereda Copyright 2005

”Photo of Particle Explosion Page 12 of Particle Odyssey

This photo shows an array of particles in a collision from CERN in Geneva, Switzerland. From page 13 of “The Particle Odyssey,” the description of the explosions shows the same hidden data:

The tracks of many charged particles are made visible in this image from the NA35 experiment at CERN, Geneva. The particles emerge from the collision of an oxygen ion with an atomic nucleus in a lead target at the left of the image. Tiny luminous streamers reveal their tracks as they pass through an electrified gas and curve under the influence of a magnetic field, positive particles bending one way, negative particles the other. Most of the particles are very energetic, so their paths curve only slightly, but at least one particle has a lower energy, and it curls around several times in the detector, mimicking the shell of an ammonite.

”.

Min översättning:

Foto av partikelexplosion Sidan 12 i Particle Odyssey

Detta foto visar ett arrangemang av partiklar i en kollision från CERN i Genève, Schweiz. Från sidan 13 i ”The Particle Odyssey,” visar beskrivningen av explosionen samma gömda data:

Spåren från många partiklar görs synliga i denna bild från NA35 experimentet vid CERN, Genève. Partiklarna utgår från kollisionen mellan en syrejon och en atomkärna i ett blymål i bildens vänstra del. Smala lysande strömlinjer avslöjar deras spår som de passerar genom en elektrifierad gas och kröks under inverkan av ett magnetiskt fält, positiva partiklar avböjande åt ena hållet, negativa partiklar åt det andra. De flesta partiklar är mycket energirika, så deras banor kröks bara marginellt, men åtminstone en partikel har lägre energi, och den kröks runt flera gånger i detektorn, härmande skalet hos en ammonit.

Kommentar:

OM kammarens B-fält är riktat uppåt betraktaren (som det brukligen anges) är spåret ovan (unikt) från en positron.

Spiralen avtar medurs — inte moturs som en elektronbana skulle göra, förutsatt kammarens B-fält är riktat uppåt betraktaren, vilket är det brukliga.

En punktladdning kan inte förklara frigörandet av sekundära elektroner

Men det finns också ytterligare ett speciellt argument som ansluter till föregående slutsats, att partikeln som bär ansvaret för de avbildade banformerna INTE kan vara en idealt sfäriskt punktformad elektriskt laddad dito.

Bilden nedan vänster med uttagna förstoringar höger visar på flera ställen i spiralbanan hur sekundära elektroner tas (dras) ut av primärelektronen.

elektronspår

Bubbelkammarfotografi · ELEKTRON OCH ATOMFYSIK · R. Westöö · ESSELTE STUDIUM 1975 · s71

En fritt framrusande elektron med tillräcklig rörelseenergi kan »vid kollision med en atom» tillföra den tillräckligt mycket jonisationsenergi för att låta den släppa ifrån sig en elektron. Därmed är hela saken förklarad, menar man, och ingen tycks fråga efter hur eller på vilket sätt.

Men en punktformad laddning kan inte åstadkomma en sådan funktion.

Bildspåren visar tydligt att primärelektronen DRAR ut sekundärelektroner

BEVIS:

Om primärelektronen antas kollidera med en atom i primärspårets väg, har vi rätt att förvänta oss att primärelektronbanan samtidigt ändras (kraftigt). Men spiralbilden visar tvärtom att primärelektronens spiralbana i stort sett är obruten. Det verkar alltså som att primärelektronen fungerar oberoende av att den förorsakar sekundärt frigjorda elektronmassor:

Primärelektronen genomgår aldrig någon »atomkollision»;

Sekundärelektronerna dras då tydligen ut — utan nämnvärd ändring i primärelektronens framfart, den delen påverkas tydligen inte.

Men en punktformad (sfäriskt symmetrisk) negativ laddning har ingen möjlighet att dra till sig andra liknande minusladdningar. Istället sker repulsion för varje ansats till närmande.

Slutsats:

Ovanstående banform med sekundärt uttagna elektroner uppvisar alldeles tydligt att den primära elektronpartikel som bär ansvaret för hela funktionen och dess dynamik INTE kan vara en klassiskt föreställd punktformad idealt sfärisk elektrisk laddning.

PROBLEM

Men OM det nu skulle vara så som slutsatserna ovan pekar på:

VARFÖR finns inte detaljerna omskrivna — beskrivna, förklarade, genomlysta?

VARFÖR finns (ännu 2008) ingen beskrivning på webben?

Om vi söker exakt på frasen ”elektronens bubbelkammarspår” på svenska finner vi noll: ämnet är orepresenterat.

Tas citationstecknen bort blir det samma depraverande resultat: fortfarande noll. Ingenting. Inte en enda träff.

Inte en enda sida. Inte ett ord.

Går vi över på engelska delen blir det — ungefär — likadant, men jobbigare:

Det finns en uppsjö av TEXTBASERADE DOKUMENT som TYCKS avhandla ämnet — men de visar inga bilder.

Med reservation för ev. missade delar ser det ut så här:

»electron in homogeneous magnetic field» .... inget

»electron trajectories in magnetic field» ........ inget

”electron drift in magnetic field” ................... inget

Sökning på

”electron in magnetic field”

ger en träff — en animerad beskrivning på webbsidan

[http://www.google.se/search?hl=sv&q=%22electron+in+magnetic+field%22&meta=]

— men den visar bara en halv cirkel: hur elektronen kommer in, vänder och åker ut igen. Alltid något. Men det är fortfarande långt ifrån bubbelkammarfotografiets typiska elektron-positronbana.

DESSUTOM finns MÅNGA träffar som man inte FÅR se: det är typ vetenskapliga dokument som man bara får se om man 1. är medlem eller 2. kan betala runt 30-40 dollar per (jag genomsöker normalt 5-50 olika dokumentexemplar i mina sökningar, vilket skulle betyda ansenliga summor bara för att skumma enstaka omnämnanden i särskilda detaljer; det håller inte). Dessa träffar är (således) värdelösa — även om de skulle innehålla svaret, vilket likväl alltså inte kommer fram här.

Bilder är BEVIS här, och vad vi vill se är en detaljerad bild av hur den motsvarande MATEMATISKT TEORETISKA kurvan ser ut till jämförelse med aktuella verkliga fotografier. Vi ska INTE nöja oss med mindre.

Det finns även ett ”TrackMaker” studentprogram i källan @INTERNET

[http://www.onscreen-sci.com/Reviews.html]

Källan påstår sig beskriva elektronbanor med till synes alla avancerade parametrar som studenten kan ställa in, till och med mitt under pågående banform.

— Men det visas inte mycket som kan användas i någon direkt kritisk utvärdering. Referenser saknas här helt i den här webbkällan.

TrackMaker-källan skriver (till jämförelse med nästföljande citat),

”The basic principle in analyzing particle data is this: a particle sailing through space like a little bullet will show a curved track in a magnetic field.”

Min översättning:

Grundprincipen i analysen av partikeldata är den här: en partikel som seglar genom rymden likt en liten kula kommer att uppvisa ett spår i ett magnetiskt fält.

— Återkom gärna när det finns presenterade detaljer på hur parametrarna är uppbyggda så att man kan se varifrån de kommer. Så omnämns till exempel ingenting alls om elektronens formgeometri i TrackMaker-källan — alla vet redan att den detaljen är ett högeligen känsligt ämne i den moderna teorins kärnfysikaliska korridorer; den klassiska ideala sfären är redan erkänt kasserad som aspirant:

”In addition, each electron has a spin and associated magnetic moment, for which no classical model (such as a spinning sphere) is very useful.”

HANDBOOK OF PHYSICS · McGraw-Hill 1967 · s(4—132)sp2mö

Min översättning:

Tilläggsvis har varje elektron ett spinn och associerat magnetiskt moment för vilken ingen klassisk modell (så som en spinnande sfär) är särskilt användbar.

INTRESSANTA — men för vår fråga ointressanta — LABORATORIEBILDER finns i källan @INTERNET nedan; Bilderna visar elektronvägar i utpräglat olika inhomogena sammanhang, vilket inte är vårt problem:

[http://www.physics.ucla.edu/plasma-exp/beam/]

Engelska Wikipedia ser ut att beröra frågan exakt, men …

På @INTERNET Wikipedia Magnetic field 2008-06-26 visas exakt illustrerat det formämne vi här sysslar med — bangeometrin: själva driften av typen cykloidisk. Mera preciserat beskrivs saken på Wikipediaartikeln Guiding center.

Men den beskrivningen bygger HELT på avvikelser i B-fältet (eller andra anomalier) — och det är enligt föregående referenser inte vår fråga.

Inte heller den till synes utförliga Wikipediaartikeln är till någon hjälp här.

OM någon kan påvisa DEN BANMATEMATIK som GENOM DEN KONVENTIONELLT UNDERFÖRSTÅDDA ELEKTRONEN SOM EN IDEAL SFÄR klart och tydligt beskriver motsvarande teoretiskt-matematiskt erhållna kurvformer för elektronen och som stämmer tydligt och klart överens med de faktiska, typiska bubbelkammarfotografier vi faktiskt kan se, då kan den här framställningen helt och hållet avskrivas.

METAPARTIKLAR — metafysik är HELLER INTE ämnet för den här presentationen

Med referens till citatet ovan från HOP, ligger det i sakens natur att elektronens praktiska banform i yttre B-fält inte kan beskrivas preciserat med mer än man preciserar elektronens laddningsform — och en sådan kan inte härledas av modern vetenskap och akademi.

Under genomletning efter referenser på webben efter noggranna, illustrerade konventionella beskrivningar av elektronbanan i homogena B-fält upphittades en annan, mera, originell, aspekt på hela saken — och som till viss del kan TYCKAS ansluta till TNED, men som inte gör det likväl. Ämnet berör det engelska begreppet ”metaparticle”, metapartikel.

Genom vetenskapshistoriens erkänt svårgenomträngliga problem med elektronens blotta geometri

— elektronen är ett kvantum, en mängd, och har som sådan ingen form, färg eller skepnad alls, allra minst någon ”radie”

— är det givet att det förr eller senare uppkommer ”hybrider” typ »metafysiska förklaringsgrunder».

En sådan (typisk) METAFYSIK finns exemplifierad i källan @INTERNET

[http://www.metaparticles.com/Structure.htm] (2001)

En utförlig beskrivning av vad saken går ut på ges i Toroidal Metamaterial på webbsidan @INTERNET

[http://www.metaparticles.com/Wave-Particle%20Duality.htm]

Grunden till materialet med ”metapartikeln” sägs ha uppstått i slutet på 1970-talet (1978). Metapartikeln baseras på — till synes illustrativt — liknande men inte samma detaljer som ringmomentet i TNED från Planckringen J=mvr — alltså typ ”toroidmatematik”.

METAPARTIKELN har emellertid som det visar sig föga gemensamt med TNED. Källan ovan beskriver ”metapartikeln” i korthet så här:

Elektronen som Metapartikel består av ”en mindre fysikaliskt reell pol” med ”en motstående större osynlig pol” som roterar i en gemensam cirkel; cirkeln gestaltar därmed en slags spinnande ”dynamisk skiva” — som därmed i sin egen spinnform också kan representera en vad författarna benämner ”tredimensionell metapartikel”. Tillsammans med den typbeskrivningen förekommer också en eventuell ”femte naturkraft”

(ref. s31, METAPARTICLES Fifth Edition [http://www.metaparticles.com/MetaparticlesBookCopy/.pdf]).

På den vägen klär författarna också upp motsvarande illustrerade elektriska toroidspolar som bekläs med matematiska formler som beskriver moment med elektriska och magnetiska krafter på integrala grunder.

Hela framställningen om Metapartikeln grundas — dessutom — på samma matematiska och fysikaliska grundbegrepp som i den ordinära moderna akademins lärosystem — och kan därmed — förvisso — ge vidare rent kvantitativa bidrag till atom och kärnfysikens detaljer i ljuset av modern vetenskap — eftersom Metapartikelns teori inbegriper ett ytterligare system av ”intuitivt fattade parametrar” (som modern akademi redan är bekant med för övrigt) som betyder en vidare flora av möjliga lösningar.

Med kännedom om grunderna i TNED — som referensram — är det dessutom klart att blotta idén om en ”partikelgrund” i elektronmassan — som redan föreslogs från 1925 genom Heisenberg och Schrödinger men som förkastades 1927 — betyder ett närmande mot den mera praktiska fysiken. Därmed är det givet att Metapartikelns sublima teori också på sitt sätt ligger närmare naturfysiken är den moderna vetenskapens idéer.

Emellertid är Metapartikelns Teori just också metafysisk: teorin använder MENTALA STRÖMNINGSBEGREPP typ ovan exemplifierade ”polbegrepp” — ”intuitivt fattade naturfunktioner” vars konkreta praktiska fysik mera sammanhänger med tillståndet i en SUPERINTELLIGENT ”dagdrömmares tankevärld” (och som få, om ens några, kan hänga med på) än med den konkreta experimentalfysik som en seriös naturvetenskap kräver — för att underbygga (motsvarande lika vagt framställda) ”fysikaliska beskrivningsgrunder” och vilket GARANTERAT ingen sann naturvetare står ut med. Metapartikelns Teori kan ha sina bidrag, men utan en konkret formgeometri för de föreställda kraftbegreppen är den teorin lika hopplös som den moderna akademins konventionella föreställningsvärld där ”alla föreställningar under en viss nivå” är förbjuden vara. Blotta tanken om en föreställning om atomkärnan som FORM är utesluten i modern akademi. Så än mer beträffande elektronen och dess förmodade element.

Under tiden vi väntar på bidragsgivarna till den avhandlingen, finns det ett annat, mera direkt sätt, och som verkligen ger sådana resultat — men INTE med elektronen som den klassiska punktformiga idealt sfäriska partikeln, utan istället t-ringarna vi erhöll från atomkärnans härledning via PLANCKRINGEN — och som så förnämligt lät oss härleda detaljerna i Spektrum och Kvanttalen.

Låt oss studera den delen (i väntan på huvudentrepenören).

ELEKTRONENS BUBBELKAMMARSPÅR ENLIGT TNED

Fortsättning, elektronens bubbelkammarspår

— Nehej. Vad är det då för någon laddningsform som KAN lösa oss ur frågans grepp och servera en perfekt heltäckande förklaring?

— t-ringen. Helt galant.

Hur t-ringen framgår ur atomkärnans härledning

beskrivs utförligt i ELEKTRONMASSANS KOMPONENTER,

om ej redan bekant. Atomens kraftekvation F_BT + F_eZ = 0 beskriver det allmänna sambandet för t-ringarnas dynamiska samhörighet med moderkärnan genom elektronen som enhetskvantiteten för t-ringarna. Den elektriska komponenten i ledet (F_eZ) sammanhänger speciellt intimt med atomens spektrum och elektronens olika s.k. kvanttal. Se utförligt i Spektrum och Kvanttalen, om ej redan bekant. Observera att t-ringens dimensioner i dessa illustrationer har gjorts starkt överdrivna för tydlighetens ändamål.

Alla föregående uppvisade banformer

— med drivande spiraler, starkt utdragna spiraler, och alla övriga

— kan förklaras av elektronmassan ENLIGT TNED;

En DYNAMISKT FORMBAR lång rak motsvarande elektrisk spole

— de enskilda ringarna som separata t-ringar som utför en dämpad svängning eller »pumpning» i det att hela spolstaven drivs att rotera via en initiell vinkelhastighet

— som det yttre B-fältet bär ansvaret för:

Sekundärelektronerna i exemplet ovan dras ENLIGT TNED ut av den roterande spolens magnetfält. Utan en sådan principiell dynamisk grund blir det uppenbarligen svårt att förklara själva det faktum att sekundärelektroner alls kommer ut via primärelektronens bana.

Vi studerar hur.

Se även i Sekundära elektronemissioner, som förutsätter bekantskapen med elektroncylindern som beskrivs och härleds nedan.

ELEKTRONENS BUBBELKAMMARSPÅR forts. | Elektroncylindern

HUR ELEKTRONMASSAN

AVDELAS FRÅN SIN MODERATOM

– +

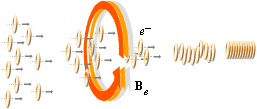
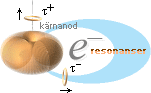
Hur elektronmassan avdelas från sin moderkärna

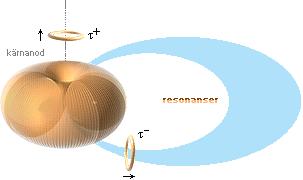
Om — som antyds i ovanstående illustration — en tillräckligt stark elektrisk fältspänning påverkar t-ringarna i en atom — till exempel från en förbipasserande proton (p), den kan t.ex. komma ”nerifrån bildytan till höger” på väg uppåt mot betraktaren (till att börja med på stort avstånd) — dras de negativt laddade t-ringarna ut mot p-kärnan. Med den rörelsen utbildar de också egna B-fält (B_e ); B-fältens växelverkan inbördes mellan t-ringarna (se Högerhandsregeln) tvingar in dem på linje — och därmed bildas den långa motsvarande elektriska spolen med sitt motsvarande samlade centralmagnetiska spolfält.

rotationsmomentet

När spolen dras samman av ringarnas samverkande B-fält, bör detta ske genom en motsvarande elektrisk-mekanisk tyngdpunkt (TP) i spolens centrum.

Då alla ringar strävar att dras mot TP på grund av ringarnas nyligen omnämnda samverkande attraherande B-fält, kommer ena spolhalvans ringar att öka i hastighet mot den attraherande protonen. Den andra spolhalvans ringar kommer att minska något i hastighet då dessa attraheras mot spolhalvan bakom TP. Internt relativt TP sker alltså en inre sammandragning; bakre spolhalvans ringar dras framåt mot TP och främre spolhalvans ringar dras bakåt mot TP.

ursprunget till e-cylinderns rotation

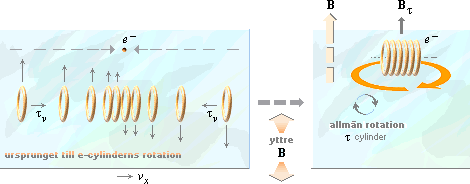
Styrkan i kraften med vilken t-ringarna sammandras motsvarar naturligt styrkan i det vridande moment som bildar e-cylinderns rotation, förutsatt givet yttre B-fält. Snarare än själva den hastighet med vilken elektronmassans t-ringar dras ut från förälderkärnan, blir det alltså själva accelerationen eller häftigheten i den utdragningen som bestämmer magnituden i e-cylinderns rotation — givetvis tillsammans med det yttre B-fältets styrka. Den häftigheten kan vi omöjligen ställa upp någon allmän ekvation för då dess parametrar beror på substansens atombindningar, såväl stationära som tillfälliga lokala. En och samma sluthastighet för elektronmassans tyngdpunkt kan uppvisa vitt skilda e-cylinderrotationer.

Den bakre spolhalvans rörelse mot TP samverkar med det yttre B-fältet (riktat vertikalt uppåt som i föregående illustrationer) så att denna spolhalva dras i riktning som en vridande visare medurs kring TP (illustrationen ovan vänster, vänstra delen). Den främre spolhalvan som dras bakåt mot TP utbildar då relativt den bakre spolhalvans ringkropp en verkan med det yttre B-fältet som också vrider den främre spolhalvan medurs kring TP. Vilket vill säga: Det faktum att de två spolhalvornas ringar närmar sig en gemensam tyngdpunkt, bildar i kraft av det yttre B-fältet en rotation hos spolen kring TP.

Vi ska nu se hur denna rotation tillsammans med förflyttningen av spolkroppens ideala elektriska tyngdpunkt, kan bilda de observerade banformerna. Verkligen intressant ämne.

Elektronelementens elektromagnetism

– +

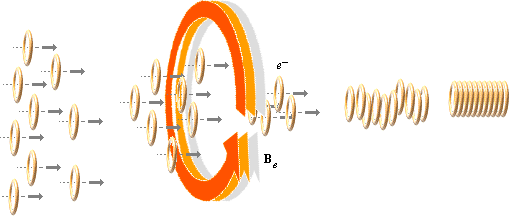
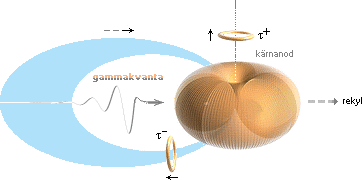
Den snabbt inrusande protonen (p+) drar en elementarladdning e– ut från en närliggande väteatom. Som lika laddningar i samma strömflöde påverkar varandra magnetiskt, blir nettoeffekten att laddningarna radar upp sig på strömlinjen.

— Lika elektriskt laddade ringar (Elektriska fältets geometri) som färdas parallellt jämsides i samma riktning

[↑](– –)

repelleras via ringplanen (Elektriska fältet, dipol- och antidipolbegreppen)

[↑](– –)

men attraheras magnetisk (Summerande B-fält) dels via allmänna magnetiska fältverkan (Högerhandsregeln) och dels speciellt via ringströmmarna (Elektronringens spinn) liknande makroströmmen i ett elektriskt spolvarv

[↑](=):

— Lika elektriskt laddade ringar (Elektronmassans komponenter) som färdas i samma rikting

|

| . . . . → → → → → | | | | | | | | . . . .

|

strävar att ställa in sig efter varandra i rörelseriktningen, samt attraheras inbördes via ringströmmarnas samverkande magnetfält (motsvarande makrofysikens magnetfält i en elektrisk spole, se Exempel Elektrisk Spole om ej redan bekant).

— Den inbördes magnetiska ringattraktionen begränsas av de lika laddade ringarnas elektriska repulsion som gör att ringarna inte kan komma hur nära varandra som helst. Om de lika laddade ringarna plötsligt stoppas upp (se parannihilation), tvingas de med samma kraft kastas tillbaka på grund av den inbördes elektriska repulsionen. Se mera utförligt i Parannihilation.

historia

KORT HISTORIK

Runt 1925 introducerades ett antal ekvationer av Werner Heisenberg och Erwin Schrödinger. Ekvationerna förklarade atomens spektrala beteende — med en hittills oöverträffad precision. 1926 visade Schrödinger att hans och Heisenbergs till synes väsensskilda sambandsformer i själva verket var olika uttryck för samma grundidé. I sina ekvationer hade Heisenberg introducerat en vibrator motsvarande en liten del av elektronmassan liknande molekylerna i en vibrerande massiv cymbal. Attityden till dessa vibratorer är omvittnad av George Gamow i hans bok TRETTIO ÅR SOM SKAKADE FYSIKEN (Prisma 1968). Gamow beskriver (s90mn) hur forskarna ”i flera år grubblade över mysteriet vad det var som vibrerade”. Trots att Heisenbergs matrisekvationer och Schrödingers vågekvationer gav excellenta förutsägelser i atomspektrum, kunde de inte kasta det erforderliga ljuset över frågan: ”Vilken fysikalisk innebörd skulle man tillskriva dessa egendomliga vågor och dessa underliga matriser” (s104ö). 1927 skrev Heisenberg en uppsats där de små vibratorernas grundliga matematik motades bort till förmån för relativitetsteorin. Frågan om vibratorerna besvarades aldrig.

Införs — alltså — istället den struktur för elektronmassan som RENT MATEMATISKT redan var känd runt 1925 men som tydligen i (o)kraft av bättre vetande förkastades på grund av relativitetsteorin, ställer sig saker och ting helt annorlunda. Alla funktioner förklaras till synes galant med t-ringarna — naturligtvis inkluderat detaljerna i Spektrum och Kvanttalen och som modern vetenskap och akademi heller inte kan förklara.

Med resultaten från PLANCKRINGEN och Spektrum består ENLIGT TNED e-massan av (minst) 177 062 enskilda fristående toroidala t-ringar med en maxdiameter på 1/50 av protonradien r₀. Varje ring har en absolut största tjocklek r₀/ 1 250 000. Tillsammans på rad formar de en maximalt packad cylinder med längden r₀/7 (runt 2 t16 M, litet t för

10^–). Dessa värden är emellertid absoluta maxvärden och dimensionerna kan vara (mycket) mindre med (mycket) större antal.

Draget på e^– från p⁺ i det yttre magnetiska fältet (B) introducerar ett adderande rotationsmoment till cylindern — i respekt till dess elektriska och gravitella centrum.

periodiska

svängningen

Noll vinkelrotation (w_CYL) för e-cylindern är uteslutet i ett yttre B-fält så länge Q färdas relativt g-referensen i B.

Genom växelverkan med det yttre B-fältet, kommer därför alltid ett visst minimum vridande moment (rotation) att matas in i e-cylindern. Tas yttre B-fältet bort, upphör matningskraften till e-cylinderns rotation.

Vinkelrotationen w introducerar magnetisk växelverkan genom redan väl kända basregler: e-cylindern genererar ett centralt B-fält likriktat med det yttre B-fältet. Nettoeffekten i respekt till det yttre B-fältets g-referens blir att t-ringarnas sammandragning motverkas och övergår i en cylinderförlängning. Förlängningshastigheten i sig ger ett B-fält som i växelverkan med det yttre B-fältet bromsar rotationen. Lägsta rotationen inträffar i e-banans långsammaste del (längsta cylindern). Genom att så FORMEN på elektronen e ändras uppkommer ett dubbelmoment som beskrivs nedan i Primära och Sekudära ekvivalenterna och som från lägsta e-cylinderns rotation via magnetiska kraftlagens elementära form åstadkommer att e-laddningens tyngdpunkt börjar accelerera mot banans snabbaste punkt — vilket för oss tillbaka till motsvarande initierande protondrag: t-ringarna strävar att dras ihop (igen) vilket på motsvarande sätt ökar e-cylinderns rotation.

e-cylindern drivs alltså in i en periodisk (dämpad) svängning tillsammans med e-cylinderns varierande rotation.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

primära och sekundära

ekvivalenterna

PRIMÄRA OCH SEKUNDÄRA

EKVIVALENTERNA

Impulsmomentets bevarande i den roterande e^–-cylindern är J_CYLe=mwr². När r ökar måste vinkelfrekvensen w minska med m konstant.

I det slutna elektriska systemet, med den emitterade elektronmassan kontra den exempelproton som förorsakar elektronemissionen genom elektrisk attraktion, är massan konstant enligt Planckekvivalenterna; I förhållande till e-cylinderns rotation kontra hela cylinderns distansbana i elektronspåret kan — i allmänhet — varje inbördes massvariation i det systemet helt bortses ifrån då ett varv för cylinderrotationen bara motsvarar en bråkdel av ett helt spårvarv och inom vilken bråkdel massändringar knappast har någon praktisk betydelse. Sambandsmässigt kan detta klargöras enligt leden nedan.

Antalet varv som e-cylindern roterar på ett varv för idealspårets R-cirkel blir (se Matematiska referenser)

T_R = (2pR)/v ....................... tiden för ett varv i R-cirkeln

T₀ = f_CYL^–1 .......................... tiden för ett varv i e-cylinderns rotation

T_R/T₀ = [(2pR)/v]/[f_CYL^–1] = f_CYL(2pR)/v = v(d/Rk_t)(2pR)/v = 2pd/k_t = 2pd/(2pr_t)(2p) = d/(2pr_t) = (5,80857 T15)d

Med d i storleksordningen bråkdelar av R (nästan ingen spiralform) eller större än R (påtagligt utdragen spiralform) med

R från F=BQv=mv²/R enligt R=mv/BQ ges absolut sämsta fallets absolut minsta R-värden med B omkring 1 Tesla och Q=e=1,602 t19 C och idealt max v=c=3 T8 M/S med minimum elektronens vilomassa 9,11 t31 KG enligt R(max)=mc/BQ=1,70599 t3 M. Större B ger mindre R.

För att d i T_R/T₀ = (5,80857 T15)d ska ge T_R=T₀ krävs alltså idealt extremt höga B-värden. Referenskällorna i den här presentationen anger som mest i samband med uppgifter från bubbelkammare inte över 20 Tesla. Det betyder i vilket fall att den rent praktiska sidan av saken i tillgängliga bubbelkammarfotografier uppvisar en motsvarande betydande övervikt åt ett stort antal T₀ inom elektronens spårcirkel T_R. I den meningen kan vi alltså betrakta eventuella massändringar i referens till e-cylinderns roterande varv som helt försumbara då massändringarna istället har betydelse först över större spårlängder, analogt flera T_R.

Elektronmassan som dras ut i spåret kan alltså egentligen inte betraktas isolerat konstant som sådan i och med att den acceleraras av exempelprotonen, men ändringen då elektronen tappar rörelseenergi och går mot sitt normala vilovärde blir försumbar i den praktiska jämförelsen med cylinderrotationens period.

Därmed saktas vinkelrotationen av. Effekten är densamma (nedan vänster) som att införa en expanderande hastighet i elektroncylindern och genom vars utvidgning det yttre B-fältet svarar med en kraft (se Högerhandsregeln) motsatt den som förknippas med vinkelrotationen w. Alltså minskas w.

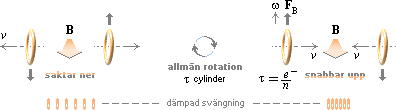
Erinra ringens gravitationsgrunder i analogi till det starkaste planet för elektrisk attraktion som är ringplanet; Rätvinkligt detta är elektriska kraften svag men de magnetiskt ömsesidigt attraherande krafterna mycket starka vid nära avstånd. Ringarna repelleras internt med ringkropp mot ringkropp, men attraheras starkt av den magnetiska ringkraften då ringarna visar varandra sina ringplan. Ju flera ringar som kommer nära tillsammans, desto mera liknar de en ideal elektrisk spole med ett relativt starkt centralfält. Detta centrala spolfält attraherar naturligtvis andra yttre, mera avlägset belägna ringar. På så sätt kan hela cylindern forma en enda kompakt elektronmassa på dess absolut allra minsta möjliga volym. För t-ringens dimensioner, se ELEKTRONMASSANS KOMPONENTER, om ej redan bekant.

e-cylindern kommer alltså att utföra en harmonisk svängning mellan ändlägena kortaste-längsta motsvarande snabbaste-långsammaste banpunkterna. Därmed kan banformen härledas matematiskt i detalj.

ELEKTRONENS BUBBELKAMMARSPÅR forts.

matematiska samband

Elektronbanorna i homogena magnetiska fält enligt TNED får en abstrakt allmän primär ekvivalent och en sekundär ekvivalent. Den senare ger en upplösning i reala komponenter som förklarar de bägge och nära växelverkande impulsmomentsdelarna i detalj.

Den primära ekvivalenten

Den primärt abstrakta ekvivalenten

I respekt till elektriska och gravitella tyngdpunkten i den roterande anordningen, betraktar vi en negativt laddad partikel Q’=e^–_CYLINDER som färdas i B med v och med sådana egenskaper att kunna ändra sin form enligt aktuellt passande ändamål.

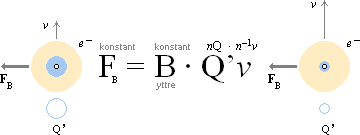
Med en given initiell hastighet v för Q i ett yttre magnetfält B, framkommer den kända kraftens funktion

F = BQv ............................. magnetiska kraftlagen, N

F pekar i riktning rätvinkligt v. En ideal laddning Q i ett idealt vakuum med ett idealt homogent B-fält skulle inträda en cirkulär bana och stanna där för evigt: Det yttre B och det interna Q är konstanter, och så är också v om ingen yttre källa interfererar med Q.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

Parameterformen för den perfekta och klassiska cirkulära banan är given i PREFIXxSIN som

x = R(1–sinx) och

y = R(0–cosx)

som visas illustrerad nedan.

Den ideala Q-cirkeln i PREFIXxSIN

DEN IDEALA Q-CIRKELN v_c = 0 | J_c = 0 | J_e = 0

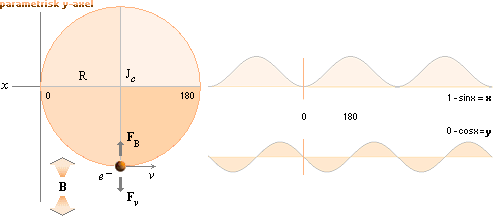
I DETTA KLASSISKA FALL är bägge BQ konstanter, v är initiellt given via e efter draget från den inkommande protonen. v kan dock inte ändras i efterhand (frånsett via energiförluster, men vi frånser dessa här till att börja med) såvida inte e påverkas från någon yttre källa. Denna solida egenskap kan certifieras vidare genom följande korta genomgång av den allmänna mekaniken.

Med J=ET=mvr=FrT, är F konserverad av J. r (eller R) är storcirkeln som omsluter Q. En ändring i r skulle tvinga en invers ändring i T, vilket skulle antyda en identifikation för T med vinkelrotationen w=v/r=2pf₀·r i e_CYL. Men en ändring i r skulle kräva en ändring i F, som emellertid är konstant enligt F=BQv; v kan inte ändras, och BQ är konstanter.

Därmed är F garanterad konstant. Med andra ord garanterar konstanten F att r är konserverad och därmed T intakt i funktion, vilket betyder att den ideala Q-cirkeln kvarstår helt opåverkad.

Den enda möjliga återstående förklaringen till den observerade icke cirkulära banan rätvinkligt B, och förutsatt B hålls konstant, kräver uppenbarligen att Qv ändras exakt och reciprokt — på något sätt med resultat att hela v-referensen ändras, och ändå via ekvivalenter, lämnar v opåverkad i sin klassiska referensram. Det kräver uppenbarligen en sofistikerad konstruktion beträffande Q-fysiken. Som vi ska se, satisfierar t-cylindern den detaljen perfekt.

Den spinnande w_CYL motsätter sig varje icke linjär ändring genom att uppställa ett proportionellt vridmoment med referens till varje centrum som försöker dra w_CYL runt det. Vilket vill säga; Två eller flera individuella spinn inom en eller flera massiva former kan aldrig förenas i en gemensam byggnad — på någon annan typ än en strikt expansion (explosion). Detta är precis fallet med J_CIRKEL-rotationen: w_CYL (tyngdpunkten), som den klassiska Q-punktpartikeln, bildar roterande punkt i J_CIRKEL. Följaktligen strävar g-centrum i w_CYL att brytas ut ur J_CIRKEL — vilket den inte kan. Funktionen blir istället att w_CYL tvingas dra med sig hela J_CIRKEL.

Den fysiska uppkomsten av vridmomentet på den spinnande w_CYL från J_CIRKEL-rotationen tvingas alltså ta tag i den enda slutliga och fysiskt tillgängliga kvarvarande punkten: det rena centrum i J-cirkeln. Därmed tvingas J-cirkeln att följa en konstant hastighet (v_c), proportionell mot högsta momentet från w_CYL.

Den inre Q-rotationen som ändrar Q-formen växelverkar alltså dynamiskt med B via J för att framtvinga en ändring i referensen för v med en faktor n. Genom ekvivalens, måste samma faktor påföras Q för att balansen mot F och J ska stämma. Då gäller sambandet för F nedan där nQ=Q’.

F = B · nQ · n^–1v = konstant

Trögheten i referensändringen för v påverkas mest då n antar sitt lägsta värde. Färdriktningen för e^– vid den punkten definierar en konstant hastighet (v_c) för v-referensen som motsvarar högsta e-cylinderns moment. På så sätt genomförs en uppdelning av de ordinära xy-koordinaterna i ideala Q-cirkeln på två separata faktorled. I gemensam mening visar dessa ett v_min och ett v_max i respekt till rörelseriktningen hos Q-cirkeln genom v_c. Generellt, också tillämpat här, är v_c-riktningen bekvämt vald i samma riktning som horisonten eller x-axeln.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

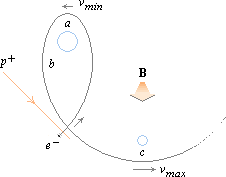
e^– accelererar alltså på Q’ från v_min vid positionen (a) med längsta cylindern och lägsta rotationen med ett maximerat n, och når v_max vid positionen (c) med en maximalt kort cylinder med maximalt hög rotation med ett minimerat n.

Illustrationen nedan visar de matematiska detaljerna med e-cylinderns rotation och den totala banbilden för elektronen i det yttre homogena B-fältet.

DET PRAKTISKA FALLET v_c > 0 | J_c > 0 | J_e > 0 sambanden i PREFIXxSIN

Den sekundära ekvivalenten

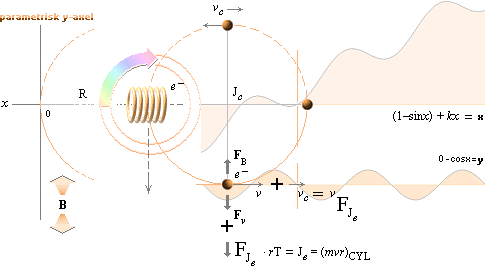
Den sekundära ekvivalenten — förklaringen till TNED-elektronbanfysiken

DEN ALLMÄNNA EKVATIONSEKVIVALENTEN F=BnQn^–1v=konstant

— där v:=v/n och Q:=Qn ändras med ett konstant F (skrivsättet := är ett s.k. tilldelningstecken som kan användas generellt i olika matematiskt beskrivande sammanhang för att eliminera indexeringar i olika termbeteckningar, jmfr. alt., Q_n=Qn)

— upplöses och förklaras i detalj av impulsmomentets två komponenter

J_c+J_e = konstant = (J_c=mvr)_CRL + (J_e=mvr)_CYL

Som konsekvens av J_e-rotationen tillkommer en hastighet v_c som adderas till den allmänna ideala v-banan i J_c.

Mekaniska ursprunget för v_c är kraften (F_Je) i J_e som kommer från och motverkar den överridande rotationsändringen på e_CYL från J_c. Som denna kraft F_Je svarar tröghetsmässigt genom Newtons tredje lag (genom att försöka konservera den linjära vägen hos e-cylinderns tyngdpunkt utmed tangenten till v_e), tvingas den av J_c att göra så med en centrifugal växelverkan. Då är v_c som den tangentiella delen i centrifugalverkan introducerad additivt till den ordinära hastighetsdelen i J_c. Som högsta hastigheten också har en högsta påverkan på effekt och energi, definieras v_c där e-cylindern genomgår sin högsta hastighet och snabbaste rotation. Vilket vill säga i den utdragna spiralens riktning, i mitten av dess bottencirkulära båge motsvarande v_max.

Komplexets totala matematik kan alltså skrivas på den enkla och allmänna ideala stora Q-cirkeln — med enda tillägget att den själv färdas, tvingad att göra så av w_CYL som beror på yttre B-fältet. Vilket vill säga, helt enkelt — frånsett tillkommande (funktionella) konstanter — v_c = (wr)_CYL med r som halva cylinderlängden.

v_c har med andra ord ingen annan reell fysikalisk faktor att återföras på i sin fysikaliska orsaksdynamik än just e-cylinderns allra mest utpräglade rotation: det finns ENLIGT TNED uppenbarligen ingen annan fysikalisk faktor att härleda på. Därmed blir också varje annan typhärledning utesluten: En enda fast formgeometri för elektronen som fysikalisk laddningsmassa räcker inte som grund för att kunna härleda de verkliga elektronbanorna i homogena B-fält.

Elektronen som fysikalisk form måste vara variabel. Annars går det inte.

Nu vet vi, emellertid, att formen (wr)_CYL måste bli ytterst komplicerad med alla parametrar medräknade:

· med e-cylinderns inre periodiska svängning tvingas r som halva cylinderns idealt axiella längd variera: hur definieras r?

· när e-cylindern är som mest sammantryckt, analogt har högsta rotationen, utverkar den också den starkaste egenmagnetiska kraften i sin egen spolaxel genom de samverkande t-ringarna och kan därmed relateras en speciell växelverkan med det yttre B-fältet mot vilken e-cylindern strävar att räta upp sig; vi har i föregående delar helt frånsett den aspekten, men i en mera ingående behandling måste den tas med i beräkningen; föreställningen om ett ”r” får därmed en mera sammansatt innebörd: hur definieras r?

· styrkan i e-cylinderns vinkelrotation beror på energin (kraften) med vilken elektronen frigörs från sin moderkärna [genom t-ringarnas attraktion mot emissionsagenten] och därmed den motsvarande energi som elektroncylindern binder upp genom sin rotation i försorg av det yttre B-fältet; ju snabbare cylindern roterar, inom vissa gränser, dess mera kompakt blir den och därmed olika distansgrader för de periodiska r-variationerna: hur definieras r?

I alla ovannämnda fall krävs speciella parameterväxlar med särskilda funktionsblock, och vi ser härav (enkelt) att en sådan samlad matematisk form (här) skulle bli otymplig. För att söka en första approximation som kan användas i översiktliga grovberäkningar för en mera hanterlig presentation kan vi därför använda t-ringens egenvärde som en approximativ allmän medelform för e-cylinderns halva ideala längsaxel — för samtliga fall, om inget annat anges.

Från ELEKTRONMASSANS KOMPONENTER vet vi att sämsta fallets TNED-värden ger de n=177062 t-ringarnas samlade cylinderlängd som (0,15)r₀ eller grovt r₀/7 med protonradien r₀=1,37 t15 M. Med t-ringens diameter enligt TNED motsvarande sämsta fallets maximala värde enligt r₀/50 finns en marginalfaktor på runt 7 som vi kan utnyttja i ett approximativt uppskattat medelvärdesbildande syfte — som alldeles säkert garanterat ENLIGT TNED representerar absolut sämsta fallets maximala värden.

Antas den nu beskriva approximativa allmänna formen för e-cylindern får vi med diametervärdet r_t = r₀/50 sambanden

v_c = (wr)_CYL

= w_CYLr_t

= 2pf_0CYLr_t

r_t = r₀/50 = (1,37 t15 M)/50

= 2,74 t17 M

Observera att v_c med avseende på grundcirkelns rörelseform (inte på e-cylinderns variabla rotationshastighet) här är härledd som ett konstant toppvärde motsvarande e-cylinderns maximala rotation. Nedan (se från Dämpfaktorerna) visas formellt hur ett avtagande v_c kan approximeras med växande spårlängd som följd av energiförluster.

För att referera ovanstående förenklingar

— som alltså innehåller betydligt mera fördjupade aspekter och som här på grund av deras allmänna komplexitet har förenklats enligt ovanstående redovisning

— kan vi kalla värdegrunderna med ovanstående sambandsbaser för nominella. De nominella värdena baseras främst på sämsta fallets beräkningar enligt TNED med resultaten från Spektrum via t-ringens dimensioner. Se utförligt i ELEKTRONMASSANS KOMPONENTER. Se även vidare sammanställningar nedan i MATEMATISKA REFERENSER.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

dämpfaktorerna

magnetiska B-vektorn upp genom bildytan

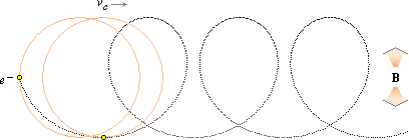
I parameterformen är y-komponenten R(0 – cosj) samma för bägge klassiska ideala och den aktuella banan. Den enda ändringen i den ideala parametriska klassiska Q-banans uttryck refererar till v_c erhållen från w_CYL. Tilläggshastigheten v_c=(wr)_CYL=x_c/T får tilläggsdistansen på x som x_c=v_cT. Som T är proportionell mot vinkeln j i J_c genom relationen T/T₀=j/2p som ger

T=j/(2p/T₀)=j/w med j=wT=(2pf)T,

kan x_c skrivas på formen x_c=v_cj. Elektronbanans parametriska form i PREFIXxSIN blir då

x = R(1 – sinj) + v_cj

y = R(0 – cosj)

DÄMPFAKTORERNA

DÄMPFUNKTIONERNA — dämpfaktorerna

DEN PRAKTISKA BANAN

DE DÄMPANDE KOEFFICIENTERNA — Närmare den praktiska banan

Som magnituden för w_CYL regerar v_c, bestämmer den också spiralens utdragning. Ett litet w med givet R centrerar den cirkulära banan och ger en nära helt tät cirkulär banform medan ett stort w drar ur cirklarna till en lång spiral med korta mellanloopar.

När den färdas i en substans, förlorar e_CYL gradvis rörelsemängd när den attraheras och affekteras elektriskt av omgivande atomer — som också är orsaken till att vätskan i bubbelkammaren »kokar» i partikelspåren. Som sannolikheten för en sådan impulsverkan ökar med tiden, kan en allmän och enkel R-dämpande faktor (a_0R) införas proportionellt mot den växande vinkeln j, analogt växande T; a_0R kan relateras till en energisubtrahend som kommer att växa med tiden på a_0Rj. R reduceras då med växande j på den enklaste formen

a_R = 1–a_0Rj genom R:=a_RR

Spårvägen slutar definitivt när a_0Rj = 1.

På liknande sätt kan också v_c dämpas tillsammans med växande j genom införande av en motsvarande högst enkel

v_R = 1–v_0Rj som ger v_c:=v_Rv_c

När e_CYL påverkas av närliggande atomer, är det naturligt om också dess spinnande w_CYL påverkas — generellt med en minskande effekt om ingen ytterligare acceleration hos cylindern introduceras. En minskande w_CYL avspeglas emellertid inte på R, endast på spiralens förlängning eftersom w_CYL är proportionell mot v_c.

En förmodan med äventyr — kortare linjära inslag i spiralbilden

Eftersom alla effekter och ändringar i J-systemet måste operera genom e_CYL motsvarande den ideala Q, skulle man kunna förmoda att elektriska attraktioner som resulterar i ett avtagande R obönhörligen måste återspeglas direkt också på en ändring i spinnet hos w_CYL. För långdistansiga attraktioner mellan e_CYL och »en förbipasserande» proton, kommer dock e_CYL att synas som en ideal punktladdning. I sådana fall behöver inte cylinderspinnet affekteras alls medan R påverkas desto mera. Alltså är (den till synes positiva) förmodan äventyrlig, och inget direkt eller allmänt samband finns i riktning mellan R-påverkan och w_CYL-påverkan.

Genom en liknande argumentation finns heller ingen direkt eller allmän koppling i riktning mellan w_CYL-påverkan och R-påverkan (alltså i omvändningen). Om e-cylindern periodiskt och händelsevis (vilket borde vara fallet) attraheras approximativt lika på bägge (alla) sidor av det aktuella strömspåret, behöver inte rörelsemängden hos det ideala Q påverkas speciellt mycket medan å andra sidan spinnet w verkligen bör göra det. Under längre eller kortare intervall kan cylinderns tyngdpunkt färdas praktiskt taget linjärt medan w_CYL reduceras, vilket lämnar R praktiskt taget intakt med smärre linjära inslag.

Med andra ord finns inget allmänt samband mellan ändringar i R och w_CYL.

Därmed ska de separata dämpfaktorerna på R och v_c vara en rättvis medelmässig representation för det praktiska fallet — med någon reservation för andra incidenter som kan ändra banan. De fullständiga parametriska ekvationerna i PREFIXxSIN för elektronbanan blir då

x = R(1–a_0Rj)(1 – sinj) + v_cj(1–v_0Rj)

y = R(1–a_0Rj)(0 – cosj)

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

praktiska exempel

Del av bubbelkammarfotografi från CERN ur FOCUS MATERIEN 1975 s139

Genom att justera banformen efter de enkla parametrar som angivits och härletts ur TNED kan vi nu från resultaten söka olika ungefärliga matchningar till givna avsnitt med elektronspår från bubbelkammarfotografier. Den vidstående delen visar en sådan ungefärlig matchning och vilken detalj vi redan studerade inledningsvis som en av flera starka avvikelser i fotografiets elektronbanor. Att döma av den principiella formen, är det tydligt att banformen beskrivs tillfredsställande väl av TNED-matematiken. Inte med mer än motsvarande banform kan uppvisas av den ideala punktformiga klassiska elektriska laddningens alternativ — som förespråkar starkt störda B-värden i starkt störda partier av det fotograferade området — kan en motsvarande hävd grundad på matematisk fysik komma ifråga. Tills dess finns det, uppenbarligen, ingenting att jämföra med. Källorna på webben är (ännu 2008 VI) tysta.

Illustrationen visar i a en del av bubbelkammarfotografiet från FOCUS MATERIEN 1975 s139. Elektronspåret i den markerade röda rektangeln visas förstorat i b med motsvarande resultat till jämförelse i c från den utritade funktionsgrafen i d. Parameterdelarna i d redovisas i Exempel 1 nedan. Sambandsformen för hastigheter och energier visas i sammanställning i matematiska referenser. Där framgår att av hela elektronmassans energi i ovanstående typspår (d/R=1,26) upptar e-cylindern nominella rotationsenergin (mv_CYL²) endast 8%. Spiraler som inte är så extremt utdragna uppvisar en motsvarande mindre procentuell rotationsenergi hos e-cylindern.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

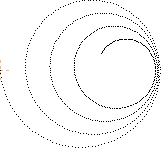
— Visa mig sambandsformerna i ett motsvarande grafritande program som enligt modern akademisk teori grundas på elektronbanan i HOMOGENA B-fält och som kan uppvisa ovanstående typform och som vi vanligtvis finner typisk för många elektronspår på bubbelkammarfotografier, se även Exempel 3 nedan — då, först, men inte förr, ska jag konvertera.

EXEMPEL 1 — elektronbanor i homogena B-fält

Exempel — j (j i Symbol) i grader (cirkulär tidsenhet 360):

Övre, låg w_CYL/R: unit 20, upplösning 150, varv 3.9, R 4, dämpning a_0R 4.5 t4, v_c 3.5 t3, dämpning v_0R 2.1 t5

Undre, hög w_CYL/R: unit 40, upplösning 100, varv 4.3, R 1, dämpning a_0R 4.5 t4, v_c 9.5 t3, dämpning v_0R 1.5 t4

v_c definieras i ovanstående ritprogram (V) genom cirkelns hela gradtal 360 dividerat med ideala cirkelradien R; med V=1/360»0,00278 dras spiralen ut så att dess första vänstra del mot startpunkten bildar distansen d=R.

För att få motsvarande reala praktiska v_c-värde (ideal cirkel, analogt litet d) ur motsvarande praktiska V görs räkningen

v_c = d/(2pR/v) = vd/2pR = v(d/R)(2p)^–1 ..................... M/S

med v lika med elektronens verkliga utgångshastighet i M/S.

Omvandligsenheten (x) för d=R i grafens referenssystem blir då x=360R så att d=R ger d=x/360=(360R)/360=R. d/R=360(V=v_c).

Se även i sammanställningen MATEMATISKA REFERENSER — där finns också en mera fullständig illustration med dR-beteckningar

Därför att dämpfunktionen v_cj(1–v_0Rj) är parabolisk (en upp-och-nervänd) kommer dess fallande del från toppen aldrig att bli aktuell i det praktiska fallet — såvida inte e^– ändras till en e⁺. Nerdelen kommer nämligen att ge en negativ riktning för v_c. För att utesluta denna del från elektroncylindern i matematikleden, måste x_c-delen av x göras matematiskt begränsad till dess paraboliska topp. Den x_c-gränsen, med respekt till vinkeln j, är derivatan (dvs., tangenten) till x_c enligt sambanden

d(x_c)/dj = d(v_cj(1–v_0Rj))/dj = v_cDn j–v_0Rj² = 1–2v_0Rj = 0 ; j_lim = (2v_0R)^–1

Från ögonblicket då j_lim=(2v_0R)^–1, måste värdet x_c=v_cj(1–v_0Rj) konserveras, vilket betyder att den ideala Q-cirkeln står stilla, låst på x_c-positionen i B-fältet; Mera korrekt uttryckt är Q-cirkeln låst på den parametriska y-axeln (x_C=0).

Men en stillastående Q-cirkel är inte fysiskt samstämmigt med en åkande e-cylinder i ett yttre B-fält. Så länge Q_e förflyttas i B, finns det alltid en spinn-w_CYL och alltså en åtföljande rörelse v_c hos den ideala Q-cirkeln — analogt alltid ett växande x_c. Tillbörligt och konsekvent kan v_c aldrig bli exakt noll. Tillämpat på dämpfunktionen betyder det att x_c genom j aldrig når gränsen j_lim=(2v_0R)^–1. Då parabeltoppen nås är elektronspåret följaktligen promptat att upphöra. Den motsvarande dynamiska verkan förväntas då uppvisa ett avslut för spinn-w_CYL.

Men det finns också en teoretisk möjlighet att ett minsta w_CYL kan fortsätta på e-vägen i Q-cirkeln — praktiskt låst på y-parameteraxeln av vinkelgränsen j_lim. Om w_CYL minimeras, kan rörelsen hos Q-cirkelcentrum göras infinitesimalt liten motsvarande ett praktiskt noll. Med ett minimalt w_CYL är elektronen optimalt i stånd att svara på attraktioner och affektioner från närliggande atomer. Förutsatt ideal och homogen sådan hastighetsdämpande effekt på e, blir resultatet att R avtar analogt med ett ordinärt objekt som färdas i luft eller vatten genom friktion. Q-cirkelns centrum närmar sig då den j_lim-låsta parametriska y-axeln (x_C=0). Resultatet blir att vägen för e-cylindern obönhörligt måste sluta när den når x₀=0 — såvida inte föremål för någon yttre tillfällig inverkan.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

EXEMPEL 2 — elektronbanor i homogena B-fält

Exempel — j i grader (cirkulär tidsenhet 360):

låg w_CYL/R: unit 20, upplösning 150, varv (right) 4.3, R 4, dämpning a_0R 4.5 t4, v_c 3.5 t3, dämpning v_0R 5.1 t4

Värden skilda från föregående exempel är markerade i fetstil.

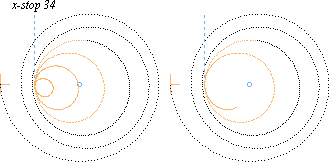
Illustration till vinkelgränsen j_lim

Med samma värden som i föregående exempel på lågformen w_CYL/R, kan vinkelgränsen j_lim illustreras av figuren (vänster) ovan. (Värden skilda från föregående exempel är markerade i fetstil ovan under figurerna)

— Sådana ”konsekventa ihoptryckningar” i en riktning tycks vara typiska (i många fall) för de elektronspår man kan se i olika bubbelkammarfotografier. Se exv. storspiralen i exemplet med den stora vinkelavvikelsen, den stora positronspiralen, samt parbildningsexemplet från Scientific American (m.fl.).

Den orangea delen börjar vid j_lim och spåret fortsätter med avtagande R mot den vertikala streckade linjen markerad x-stop. Teoretiskt kan elektronen aldrig passera den linjen — frånsett direkt stöt. Den blå punkten markerar Q-cirkelns centrum vid j_lim.

ADDERANDE ROTATIONSMOMENT kan enkelt introduceras för sambanden genom attraktiv växelverkan genom att tillåta hela Q-cirkeln rotera i sitt eget plan (perihelierotation), vilket medför att den parametriska y-axelns tangentposition ändras (vrids) kontinuerligt. Nettoeffekten kommer bara att skilja sig mot de givna sambanden i det att x-stopplinjen kan ha en godtycklig orientering och lokation på den ideala Q-cirkelns radie. Vilket vill säga, ”kantCirkling” mot ett x-stopp kan uppträda i vilkensom riktning, självt föremål för rotation eller translation.

EXEMPEL 3 — elektronbanor i homogena B-fält

Exemplet nedan visar precisionen i hur TNED-parametrarna kan fås att matcha elektronspåret från ett bubbelkammarfotografi.

Optimala parametrar som uppvisar sekundära elektronemissioner inte medtagna.

Bilden vänster från ELEKTRON OCH ATOMFYSIK · R. Westöö · ESSELTE STUDIUM 1975 · s71

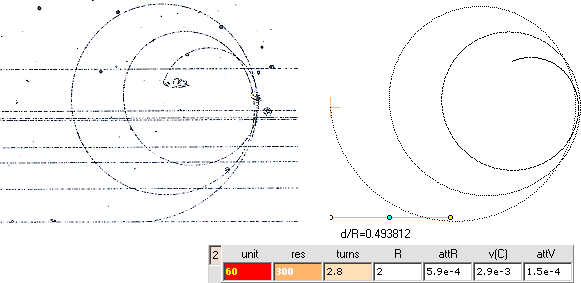
Med grovt d/R=0,5 ges från sammanställningen i MATEMATISKA REFERENSER e-cylinderns rotationsenergi relativt hela elektronenergin

E_c/E_v = (d/R)²/2p²

= 0,0126651 eller grovt 1,27%

allmän energiprövning

I avsnittet längre ner om Sekundära elektronemissioner beskrivs hur vi (enkelt) kan få en uppfattning om förhållandet mellan elektronens totalenergi — motsvarande elektronspårradiens största värde (mv²/2) — och minsta möjliga energi som ENLIGT SPÅRBILDERNA krävs för att frigöra en sekundär elektron och få den att uppvisa ett minsta möjliga individuellt spår — motsvarande en från primärspåret utdragen elektronspårradies minsta värde. Vi behöver bara mäta förhållandet mellan spårdiametrarna. I ovanstående spårbild betyder det ett förhållande (vad som kan ses i källoriginalet) på grovt sett 1/75. För att e-cylinders rotationsenergi (E_c) alls ska ha en chans att dra ut en elektron från en närliggande atom måste E_c-delen av hela elektronenergin (E_v) alltså minst vara 1/75:e del. I exemplet ovan får vi 1/0,0127 = 78,740157 eller avrundat 80 — vilket alltså stämmer bra med det relativa grovvärdet 75. Sambanden från e-cylinderns härledning är alltså, och så långt, approximativt rimliga och kan förklara energibilden i stort för det praktiska fallet.

OBSERVERA att en motsvarande DYNAMIK som enligt modern teori SKULLE kunna frigöra sekundära elektroner ur primärspåret via en klassisk sfärisk ideal punktladdning helt SAKNAR BEGRIPLIG FYSISK GRUND. Se vidare utförligt illustrerat i Sekundära elektronemissioner.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

I föregående En förmodan med äventyr omnämndes möjligheten till kortare linjära inslag i spiralbanan.

Bilden nedan till vänster är ett bubbelkammarfotografi från SCIENTIFIC AMERICAN, August 1991 s45. Det visar hur en elektron (vänstra) och en positron (högra) emitteras från en atomkärna (som själv splittras) då den träffas av en partikel (eller em-strålning) med tillräcklig energi.

parbildning SA

Vänster. Bubbelkammarfotografi från SCIENTIFIC AMERICAN, August 1991 s45.

Höger. Positronelement och elektronelement emitteras diametralt från atomkärnan (väsentligen efter olika sätt). Emellertid påverkas laddningarna olika av kärnans närmagnetiska fält, och initiella totalvinkeln mellan e⁺ och e^– antar därför olika värde beroende på omständigheterna.

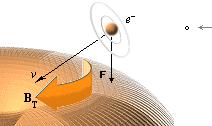
Bilden ovan visar skalenligt (sämsta fallet) en del av protonytans toroidmantel vid kärnkatoden i jämförelse med absolut maximala elektronringens diameter som visas vid den lilla pilen övre höger (1/50 av protonradien). Vektorpilarna B_TvF exemplifierar hur ett förstorat elektronelement (den lilla sfären) motsvarande en ideal (klassisk) punktladdning som är på väg in till atomkärnan men tvingas böja av mot kärnkatodens toroidmagnetiska ytfält (B_T) för att sedan längre fram vända och drivas iväg utåt höger i bilden. Se utförligt från ATOMKÄRNANS HÄRLEDNING, om ej redan bekant.

Flera mindre intervall av tydligt linjär karaktär kan ses i elektronspåret,

här i förstoring från bilden ovan

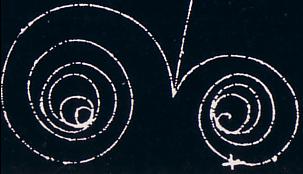
— men också åtminstone ett relativt långt i positronspåret (se avbräcket till höger om krysset).

R-dämpningen mot ett x-bottenstopp är här vidare speciellt tydligt i den inre delen av ovanstående exempels e^–-fall.

Positronemission

FÖRTROGEN MED TNEDGRUNDERNA kan en positron manifesteras endast ur en atomkärna eller från partiklar som uppvisar atomkärnans egenskaper. Vilket vill säga, en TNED-form grundad på toroidaggregatet N3m20. En sådan manifestation kan ske om en atomkärna i utbyte mot positronens (och elektronens) massenergi (E=mc²) erhåller en lika stor mängd Planckenergi (E=hf). Illustrationen nedan visar hur TNED definierar en sådan parbildning (t-ringarna ej utritade, de är inte synliga i denna skala).

Medan ett nuklidaggregat kan emittera positroner såväl som att fånga in elektroner, är positronerna normalt sett inte närvarande utanför atomkärnan. När en positron först manifesteras, måste den komma ifrån ett kärnaggregat. I TNED garanterar den balanserande kraftekvationen F_BT+F_eZ=0 en kontinuerlig kommunikation mellan förälderkärnan och dess elektronmassor genom t-ringarna. Den fria och isolerade positronen har ingen del i denna balans utan är alltid associerad med en ändring (en avfallsprodukt) hos en förälderkärna då den omfördelar sin struktur med att söka balans i sin allmänna impulsekvation J_0K+3J_1K=0. Alla sådana ändringar är alltid associerade med en massdestruktion (m®g); Massdestruktionen tillhandahåller energin för att frigöra elektroner, positroner och eventuellt lättare atomkärnor i återuppbyggnadsproceduren — för att erhålla en kvarvarande och stabil kärna. När en positron kastas ut från en förälderkärna, genomgår den således en helt annan väg än en utkastad elektron. Medan elektronen är bunden till sin förälder, kastas positronen helt enkelt rakt ut (med hänsyn till atomkärnans kärnbrunn, se illustrationen nedan).

helixprincipen

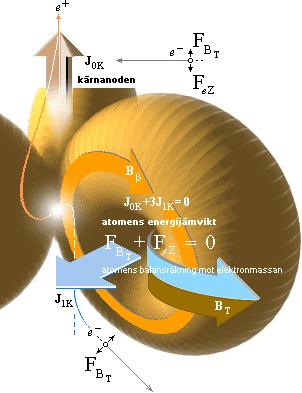
Positronens Helixprincip — varför positronspåret i allmänhet bör uppvisa helix

Atomkärnans egenskaper (se från Atomkärnans härledning om ej redan bekant) garanterar att positronelementet kastats rakt ut utmed kärnaxeln vid kärnanoden, medan elektronen utgår vid motsatta kärnkatoden; Elektronelementet följer först den starka kärnytans magnetfält, sedan gradvis i reträtt från kärnan i riktning vinkelrätt mot kärnans toppspinnande axel. Elektronelementet fortsätter sedan idealt i sin bana runt tills det åter genomgår kärnbrunnen på anodsidan enligt kraftekvationen F_BT+F_eZ=0. Positronelementet däremot har ingen liknande banekvation.

Från dessa enkla TNED-egenskaper ses enkelt varför (och hur) utkastningen av en positron i ett yttre B-fält måste eller bör skilja sig från en motsvarande elektronemission.

Vi studerar hur.

Till viss del, beroende på styrkan i det yttre B-fältet, är väteatomerna i bubbelkammarvätskan (flytande väte) riktade jäms B så som indikeras av illustrationen med B uppåt i bubbelkammaren mellan tvillingspolarna i bubbelkammarens Helmholtzspole.

Om förälderkärnan kastar ut ett positron-elektronpar från kontakt med en (från vänster mot höger i illustrationen ovan) inkommande partikel, eller från växelverkan med em-strålning, vilketsom — vilket betyder att förälderkärnan får en rekyl eller hastighet v_N också från vänster till höger (vid sidan av de redan inneboende molekylära oscillationerna som normalt redan finns i substansen) — se vi enkelt att positronen, men inte elektronen, erhåller en påtaglig djupkomponent uppåt (v_z) i riktningen för B och tillsammans med rekylen v_N; Elektronen däremot får endast den rekylerande komponenten v_N. Följaktligen bör positronspåret uppvisa någon (liten) helix med en relativt liten periferihastighet, vilket betyder ett mindre R, medan elektronen knappast bör uppvisa någon helix alls.

Det föregående exemplet från Scientific American stämmer perfekt med dessa förutsättningar — fastän det här saknas en direkt uppfattning om vad det fotografiska djupet visar. Ju större rekylkomponenten v_N är, desto större cirkelradie R exponeras av positronspåret. Artikeln ger emellertid ingen specifikation annan än ”bubbelkammarfotografi”; artikeln använder bara bilden som en belysande illustration till en allmän beskrivning av olika spårtekniker under 1900-talets utveckling inom partikelfysiken.

Medan elektronens t-ringar uppvisar mindre separation i rekylriktningen (v_N), uppvisar positronens t-ringar mera;

Om vi betraktar v_N i riktningen åt höger ® med kärnanoden riktad uppåt i positronutkastningens riktning, är det tydligt att v_N® enklare separerar positronens vertikalstaplade t-ringar i sidled inbördes då dessa i vilket fall också uppvisar inbördes repellerande elektriska krafter; Elektronens horisontalpackade t-ringar å andra sidan pressas snarare ihop än mera av rekylriktningen ® och uppvisar därmed en (betydligt) mindre separation. Därmed skulle cylindersvängningen, och således magnituden i dess vinkelrotation w_CYL, (möjligen) bli mera uttalad för positronen än för elektronen — vilket betyder att positronspåret knappast borde uppvisa tätt liggande cirkulära spår utom i djupled. Det ska dock här tilläggas att dessa utvikningar inte är direkt enkla att kontrollera utom genom någon form av statistisk kontroll på en större mängd bubbelkammarfotografier. Det finns nämligen också en annan möjlighet.

parbildning GF

Bubbelkammarfotografi av parbildning · GYMNASIETS FYSIK åk3 Liber 1980 s249

Effekten som (möjligen) förklarar varför elektronspåret har den initiellt största cirkeln exponerar bara en sida av två möjliga.

Om elektronens t-ringar i föregående illustration kastas ut momentant motsatt riktningen för rekylhastigheten v_N (inte samriktat med v_N och den oberoende partikeln eller em-strålen) finns möjligheten att elektroncylindern får en initiellt mindre hastighet relativt positronen. Vilket vill säga, rekylhastigheten (v_N) och elektronutkastningen kan i någon mening relateras ta ut varandra med följd i en låg elektronenergi i det yttre B-fältet. Då borde den initiella bredden på elektroncirkeln bli den mindre av de två.

Figuren nedan förtydligar resonemanget. Se även det revolutionerande experimentet som genomfördes (1956) i bevis för att elektronemissioner från atomkärnan (företrädesvis) uppvisas i (den konventionella kärnmagnetiska) spinnriktningen.

Fotografiet ovan (inverterat) visar också ett sådant möjligt fall [GYMNASIETS FYSIK åk3 Liber 1980 s249 Bubbelkammarfotografi av parbildning] — som komplement till föregående typexempel från Scientific American.

Om den ansvariga källan (en gammastråle) för kärnexcitationen som leder till parutkastningen kvarstår även efter händelsen i energi-massautbytet med atomkärnan, växelverkar den med det utkastade paret med ett ytterligare bidrag till rekylkomponenten v_N (se även i Comptoneffekten).

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

Exempelformen nedan verifierar direkt den ovannämnda »positronens helixprincip». Positronspår framträder (möjligen) på flera ställen i nedanstående bild (höger).

Positronspår

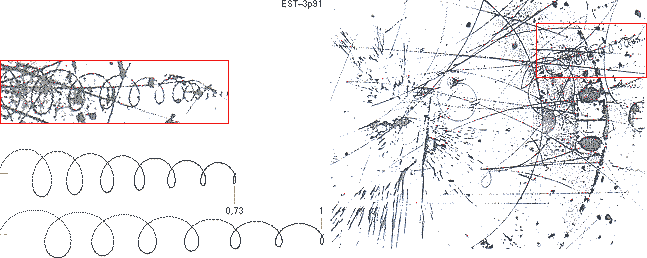
Neutrinoproducerat bubbelkammarfotografi från Fermilab, här inverterat · ENCYCLOPEDIA OF SCIENCE & TECHNOLOGY · McGraw-Hill 1992 · Band 3 s91 ·

Nederst finns infällda delar från e-cylinderns härledning som visar dess resultat till jämförelse. Helixiteten är ca 0,73 mot plancirkelns 1.

I jämförelse med det fotografiska spåret från positronen (som här uppvisar en tydlig helix) med ett motsvarande plant elektronspår (helt utan helix), uppvisar positronspåret en tydlig excentricitet som bör motsvara en djuprörelse (helix) med excentriciteten ca 0,73. Jämförelsen visas i illustrationen ovan nederst vänster via resultaten från härledningarna till elektroncylindern.

Från dessa exempel (och andra) bör det inte längre råda något tvivel i frågan om elektronen och dess grundläggande egenskaper.

Elektronmassans egenskap som bestående av element eller ”vibratorer” avtäcktes redan kring år 1925. Den moderna akademins främsta genier avfärdade dock dessa svängande komponenter, trots deras förmåga att ge en i det närmaste glänsande matematisk förklaring — för tillfället att istället uppfinna »andra fenomendetaljer» i deras ställe; fenomendetaljer som ingen varken då, senare eller nu kan förklara eller begripliggöra. Ingen nämnd. Ingen glömd.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

sekundära

elektronemissioner

SEKUNDÄRA ELEKTRONEMISSIONER

Med en maximalt låg cylindersvängning — vilket betyder en nästan cirkulär bana med en maximalt perifer hastighet med en tillhörande minimal induktiv inverkan från cylindersvängningarna — sammanfattar den åkande TNED-cylindriska elektronen principiellt samma dragande agent som en nära förbipasserande proton, men på en mycket mindre volym och därmed också mera fokuserat. Ett sådan nästan cirkulärt spår skulle möjligen uppvisa sekundära elektronutkastningar, men på låga energier triggade av den roterande huvudcylindern e^–. Ett till synes väl bekräftande exempel visas i en av de föregående presenterade källbilderna, här i repris nedan med infälld principbild (övre höger) för e-cylinderns del.

Bubbelkammarfotografi · ELEKTRON OCH ATOMFYSIK · R. Westöö · ESSELTE STUDIUM 1975 · s71 ·

Signifikanta delar förstorade samt en illustration övre höger tillagd från härledningarna genom e-cylindern.

Hur förklaras de sekundära elektronemissionerna?

Sekundära elektronutkastningar i elektronspåren från låga w_CYL/R

AVGÖRANDE BEVIS FÖR ELEKTRONCYLINDERN

Bildspåren visar tydligt att primärelektronen DRAR ut sekundärelektroner

Den dynamiska orsaken bakom DEN växelverkan elektron-elektron som förorsakar sekundära e-emissioner är i varje fall för bubbelkammarfotografiernas del uppenbar från huvudbyggnaden i e_CYL. Vi studerar hur tillsammans med nedanstående förtydligande illustrationer.

INTE GENOM ELEKTRISK UTAN HUVUDSAKLIGEN GENOM MAGNETISK ATTRAKTION tenderar den lilla men starka e^–-magnetspolen att dra till sig elektronelement eller t-ringar kontinuerligt. Är energin tillräcklig för att frigöra elektronelementen i deras RESONANTA bindning till sin moderatom, dras ringarna ut och bildar en egen fristående e-cylinder med ett tydligt (men litet) spår.

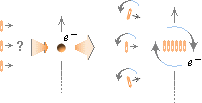
Vänster:

Om den åkande elektronen vore en laddad partikel utan struktur (homogen symmetrisk sfär) som antyds i vänstra figurdelen, har vi ingen agerande kraft på vilken kan hängas en attraktion, en resulterande utdragning. Det finns ingen dynamik.

Höger:

Med e_CYL å andra sidan som en snabbt roterande liten elektromagnetisk spole, ändras situationen dramatiskt.

I ett sådant läge är en komplett fullt tydligt dragande attraherande kraft uppenbar.

Det magnetiskt attraherande förhållandet mellan varje t-ring

och hela e_CYL är minst 1/177062.
Det visar att kraftverkan bör vara välgrundad.

Den dynamiska förklaringen kan alltså ges enligt följande.

Inte genom elektrisk påverkan utan huvudsakligen genom magnetisk attraktion tenderar den lilla men starka e^–-spolemagneten att dra närliggande elektronringar till sig. Strax avkänner moderkärnan störningen genom sin allmänna kraftekvation F_BT+F_eZ=0 då dess skalresonanta vågekvation (F_eZ-delen) ändras för att indikera ett exciterat tillstånd om draget är tillräckligt starkt. Då frikopplar moderkärnan ett helt kvantum elementarladdning e lika med en hel elektronmassa — som nu är fri att forma sin egen lilla men observerbara bana.

BINDNINGSENERGIN för väteatomens enda elektron — bubbelkammarens substans — ligger på minimum 13,6 eV.

I ovanstående bildkälla (bokens original) är förhållandet mellan primära elektronbanans utgångsdiameter (ca 75 mM grovt) och den största sekundärt utdragna elektronbanans diameter (grovt 4 mM) ca 75/4=18,75 eller nära 1 till 19. Det betyder analogt att minsta energin för primärelektronen i det exemplet skulle vara runt (19)(13,6 eV) = 258,4 eller grovt 260 eV.

Vi ska emellertid egentligen ta förhållandet mellan banbildens största och minsta diametrar eftersom olika näravstånd bildar olika förutsättningar och de som uppvisar största variationen också visar den mest relevanta utgångsbilden för energin. Det ger då (efter inspektion) ett motsvarande förhållande (för det man kan se på fotografiet) 75/1, motsvarande (75)(13,6 eV) = 1020 eV för primärelektronens egen utdragning — minimum, i detta exempel.

*TNEDbasics forts. ELEKTRONENS BUBBELKAMMARSPÅR

referenser, matematik

matematiska REFERENSER komprimerat

Från ELECTRON 2004VII12

Hur sambanden framkommit beskrivs utförligt med början från inledningen i Helix

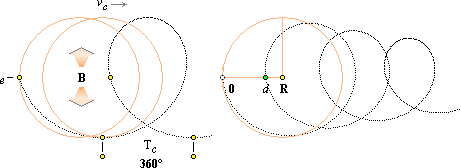
f_CYL = (1–v/c₀) · v(d/R)/k_t ......................... Hz, k_t=1,0817 t15 M

f_CYL(v=c₀) = c₀(d/R)/k_t = (2,77149 T23 Hz)(d/R) · Observera dock att räkningen här till vänster bortser från den reella reduktionsfaktorn (1–v/c₀). Med denna blir resultatet noll.

v_c = f_CYL(2p)r_t ................................................................. M/S, r_t=2,74 t17 M

v_c = v(d/R)/2p .............................................................. M/S

v_c = v(d/R)/2p

E_c/E_v = (d/R)²/2p² = 2(v_c/v)²

E = E_v + E_c = mv²/2 + (mv_c²/r)r = mv²/2 + mv_c² = mv²/2 + m(vd/2pR)² = mv²[1/2 + (d/2pR)²];

E_c/E_v = (mv_c²)/(mv²/2) = 2(v_c/v)² = 2([vd/2pR]/v)² = 2(d/2pR)² = (d/R)²/2p²

Elektroncylindern tar via sin rotation upp olika grad av energi (E_c) relativt cylinderns tyngdpunkt (mv²/2) som den ideala fasta laddningen. Det som bestämmer E_c är accelerationsförloppet (häftigheten) i t-ringarnas utdragning från förälderatomen, tillsammans med det yttre B-fältets styrka. Se från Ursprunget till e-cylinderns rotation.

F=BQv=mv²/R ; BQ=mv/R ; BQ/m=v/R ; R(BQ/m)=v=kR

(v=2pR/T_c)/(v_c=[x_c=d]/T_c)=2pR/d ; v/v_c=2pR/d=v/(w_CYLr_t)=v/(2pf_CYLr_t); r_t=(1,37 t15 M)/50

; (2pr_t)(2p)R/d=v/f_CYL ; r_t ~ (r₀/50_min=2,74 t17 M) ; (2pr_t)(2p)=1,0817 t15 M = k_t ;

; (d/R)/k_t=f_CYL/v = f_CYL/kR ; (k/k_t)d=f_CYL ® (c/c₀)(1–v/c) · (k/k_t)d=f_CYL

; v=(1–v/c)kR ; 1=(1/v–1/c)kR ; 1/kR=1/v–1/c ; 1/kR+1/c=1/v ; v=(1/kR+1/c)^–1

; v=(c/c₀)(1–v/c)kR ; v=(1/c₀)(c–v)kR ; 1=(1/c₀)(c/v–1)kR ; c₀/kR=c/v–1 ; c₀/kR+1=c/v

; v=c(c₀/kR+1)^–1

; c=c₀ ; v=(1/kR+1/c₀)^–1

——————————

(c/c₀)(1–v/c)=(c–v)/c₀

——————————

;

v=kR ® v=c(c₀/kR+1)^–1

Vi måste observera här att konstanten k_t uppvisar ett maxvärde via största — sämsta fallets — r_t toroidparametrar: r_t är med största sannolikhet mindre än maxvärdet ovan vilket innebär att också k_t blir motsvarande mindre — och därmed f_CYL motsvarande högre. De värden för f_CYL som ges av ovanstående samband får alltså ses som de absolut lägsta möjliga.

Se mera utförligt i ELEKTRONMASSANS KOMPONENTER (beräkningen av r_t enligt TNED).

Kolla ovanstående webbtext (2008-07-08): I originalet (WORD/WORKS) är raderna jämna och snygga med perfekt snygg minimal nivåskillnad i det nedsänkta suffixet. Webbläsarnas Programmerare måste emellertid av här ej kända skäl VANDALISERA den möjligheten genom att ta bort fingraderingen i textFormateringsNivån.

Varför då? Vilket är syftet?

1–v/c₀

I ORDINÄRA TEKNISKA APPLIKATIONER är laddningshastigheten i en normal ledare extremt liten — I en kopparledare med diametern Ø1,13 mM som håller strömstyrkan 1 Ampere, är medelhastigheten för laddningarna 0,074 mM per sekund. Det garanterar att en fullständig och ideal proportionalitet råder mellan hastigheten v för laddningen Q och den magnetiska fältstyrka (B) den producerar som funktion av v.

I AVDELNINGEN PARTIKELEXPERIMENT MED HÖGA ENERGIER blir däremot den normala tekniska tillämpningen »en ren dockskåpsteater». Laddningar med höga hastigheter avkänner mindre elektrisk och magnetisk växelverkan som hastigheterna närmar sig den övre gränsen c (mekanisk-elektriska sambandet). Med hänsyn till den gränsen måste en faktor

(c–v)/c=(1–v/c)

associeras med sättet på vilket det fixa yttre B-fältet greppar med sin kraft i Q. Även den lokalt allmänna gravitationen inverkar på ljusets fysik med faktorn (c/c₀). Den har reducerande inverkan på all elektrisk och magnetisk fenomenalitet, speciellt sådana i sammanhang som rör atomkärnan och atomens nivåer. Total ger oss detta en reducerande faktor

(c/c₀)(1–v/c)=(c–v)/c₀

som måste associeras med varje kraftgrundad parameter av universell karaktär i höghastighetsfysikens partikelanalys.

Med antagande av förenklingen c=c₀ reduceras den associerade faktorn till det föregående (1–v/c).

kalkylkort · elektronens bana i homogena B-fält · utvecklade sambandsformer · inkluderat massökningseffekten

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik2 Kalkylkort 2 — Elektronens bana — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

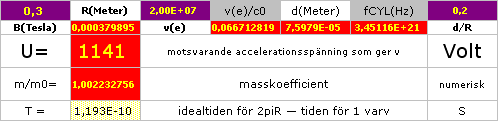
allmänna reduktionen (1–v/c)

inmatningresultatvärden kalkylkortet ovan endast i bild FRÅN ORIGINALETS MsWORKS 4.0.

FÖRE TIDEN FÖR DEN MERA OMFATTANDE TILLGÄNGLIGHETEN VIA WEBBEN (grovt sett före 2000) kunde man säga så här:

TYVÄRR presenteras bara ett minimum av specifikationer tillsammans med bubbelkammarelektroniken i de olika källverk som (ens alls) visar några fotografier. Som en godtycklig läsare av tillgänglig litteratur (här främst vad som står på hyllorna i stadsbiblioteken), är det svårt att få en uppfattning om dimensioner och magnituder helt enkelt därför att sådana inte anges. För att beräkna verkliga värden, måste vi (åtminstone) känna dimensionerna för Q-cirkeln och magnituden för det yttre B-fältet.

FOCUS MATERIEN 1975 s139, till exempel, anger inte en enda ledtråd till dimensionerna hos den bubbelkammare (CERN) som fotografiet kommer från, eller någon motsvarande skala på fotografiet. Här är man helt utlämnad! Inga rådata alls lämnas, t.ex. beträffande B-fältets styrka.

En uppskattning baserad på »vissa indikationer» antyder att B-styrkan ligger i området 0,3 Tesla och den största Q-cirkeln har en diameter 2R på approximativt 1 cM — men dessa värden är högst osäkra. Som den initiella elektronhastigheten i magnetiska termer minskar i B-växelverkan från approximativt c/2 och uppåt, bör också detta vara en gräns för v_e i Q-cirkeln såsom bildad från en inkommande, nära passerande proton.

Vid sådana magnituder arbetar vinkelrotationen f_CYL i spektrumets ordinära gammadel — från runt 2 T22 Hz och uppåt. Men som den e_CYL roterande induktionen inte har någon materiellt grundad kanal att överföra sin vågkaraktär på till atomskalen och deras allmänna vågemitterande uppförande, passerar den lilla elektrongammastrålningen obemärkt för artificiellt elektroniskt avkännande instrument — men är fortfarande aktiv i kommunikationen med en atomkärna med vilken den kan växelverka i påverkan av tröskelvärden i dess energitillstånd — och som på den vägen likväl kan lämna ett spår.

NUMERA (2008) blir ”källorna på webben” allt flera — beroende på att allt flera också upptäcker att webben är det mest bekväma och enkla referensforumet för allt möjligt — till skillnad från ”gamla dammiga muséer” (som naturligtvis också måste få finnas).

En del av de tillgängliga webbkällorna med grunddata på bubbelkammare har angivits (eller antytts) i den här presentationen, tillräckligt för att kunna göra enklare, men mera konkret förankrade beräkningar för vidare jämförelser.

…

När den färdas i den interatomära rymden (grovt mellan 1Å=1 t10 M till 3 Å) har e_CYL rotationen en chans att bilda en svans på 177062 t-ringar om v_e är av storleksordningen c/2 och f_CYL är av storleksordningen T22 Hz (som betyder att B är omkring 0,3 Tesla).

*TNEDbasics ELEKTRONENS BUBBELKAMMARSPÅR

Kurvformerna via OnLine Grafritare:

Kurvformerna via OnLine Grafritare

ELEKTRONENS BUBBELKAMMARSPÅR Tillägg 29Dec2016:

Notera att webbläsaren Firefox läser INTE teckensnittet Symbol — 64 av 118 htm-dokument 2016 i Universums Historia. I detta htm-fall har delvis ersättningar gjorts i efterhand med Times New Roman Unicode.

PREFIXxSIN:

x = R(1–a_0Rφ)(1 – sinφ) + v_cφ(1–v_0Rφ)

y = R(1–a_0Rφ)(0 – cosφ)

PREFIXxCOS — aktuellt på Webben:

x = R(1–a_0Rφ)(1 – cosφ) + v_cφ(1–v_0Rφ)

y = R(1–a_0Rφ)(0 – sinφ)

Notera att webbläsaren Firefox läser INTE teckensnittet Symbol — 64 av 118 htm-dokument 2016 i Universums Historia. I detta htm-fall har delvis ersättningar gjorts i efterhand med Times New Roman Unicode.

För den som själv vill undersöka parameterformerna till elektronens bubbelkammarspår finns på Webben en OnLineParameterGrafRitare (graphsketch.com).

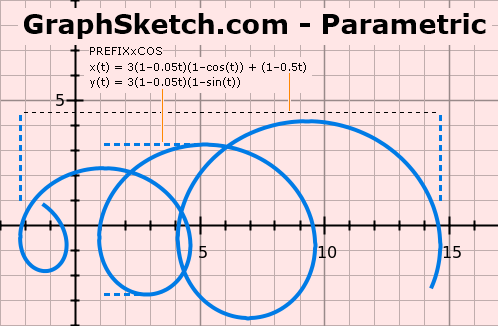
Från GraphSketch.com 29Dec2016 — Den Principiella rörelseformen från Elektronens Bubbelkammarspår -- enligt huvudtextens samband.

Den kan rita upp principiellt motsvarande formen för elektronens bubbelkammarspår, enligt exemplifierade insättningsvärden med konventionella PREFIXxCOS

x(t) = 3(1-0.05t)(1-cos(t)) + (1-0.5t)

y(t) = 3(1-0.05t)(0-sin(t))

Parameterfaktorn (1-0.05t) styr ändringen i R, och parameterfaktorn (1-0.5t) styr spiralens utdragning.

Notera att webbläsaren Firefox läser INTE teckensnittet Symbol — 64 av 118 htm-dokument 2016 i Universums Historia. I detta htm-fall har delvis ersättningar gjorts i efterhand med Times New Roman Unicode.

END.

ELEKTRONENS BUBBELKAMMARSPÅR

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Elektronens bubbelkammarspår

ämnesrubriker

innehåll

ELEKTRONENS BUBBELKAMMARSPÅR

Elektronens bubbelkammarspår enligt TNED

Inledande grundbegrepp

Helix

Bubbelkammarens centrala Helmholtzspolar

Helmholtzspolen

Beräkningsexempel

Kalkylkort · basdata

Bubbelkammarfotografiet från FOCUS MATERIEN

Bild av varierande B-fält

Elektronspår · Westöö

Elektronens bubbelkammarspår enligt TNED

Elektroncylindern

Rotationsmomentet

Elektronelementens Elektromagnetism

Historia

Periodiska svängningen

Primära och sekundära ekvivalenterna

Matematiska samband

Primära ekvivalenten

Sekundära ekvivalenten

Dämpfaktorerna

Den praktiska banan

Förmodan med äventyr

Praktiska exempel

Exempel 1

Exempel 2

Exempel 3

Parbildning

Helixprincipen

Positronspår

Sekundära elektronemissioner

Hur förklaras de sekundära elektronemissionerna?

REFERENSER · MATEMATIK

Magnetiska kompensationen

Kalkylkort · allmänna resultat

Kurvformerna via OnLine Grafritare

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[FM]. FOCUS MATERIEN 1975 — Almqvist & Wiksell Förlag AB Stockholm 1965 — Andra reviderade upplagan 1975:

Det senare 1900-talets i särklass bästa sammanfattande allmänorienterande (svenska) verket i allmän fysik.

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2017-01-06

*END.

Stavningskontrollerat 2008-07-07

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se