SOLFYSIKEN · TEMPERATURFYSIKEN 2008I2 a BellDHARMA production · Stjärnfysikens fundamentala grunder enligt TNED | Senast uppdaterade version: 2022-12-09 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Koronafysiken | Allmänna gaslagen

Värmegraderna · Solens Temperaturfysik

värmegraderna

SOLENS VÄRMEGRADER ENLIGT TNED — Värmegraderna i TNED

SOLENS FYRA VÄRMEGRADER ENLIGT TNED

Se även Solens Femte Värmegrad

Solkoronans blotta förekomst

T, T_W och T_g är okända i modern akademi.

OBS BUGG I WORD 2000:

2008VI20

Verktyg, Alternativ, Spara, Bädda in TrueType …

Hela raden av htm-dokument fram till SolfysikenTemperaturfysiken gick OK att inkludera på det sättet. Men med SolfysikenTemperaturfysiken uppstod WORD-krasch då det alternativet valdes. Kör man utan det alternativet verkar allt fungera OK. Någonstans finns alltså en inbakad spärr, men vi känner inte den här.

Buggen visar sig så: sedan man sparat, och sedan försöker öppna dokumentet igen, fastnar det med en dialog som svamlar något obegripligt som går ut på att det inte går att öppna dokumentet. Då man klickar av, kommer MÅSTE AVSLUTAS-dialogen upp med Skicka till Microsoft, och WORD stängs ner.

Nu måste jag göra om det här dokumentet igen! HELA! Jävlar.

samlingsbeskrivning (scholium) 2007III13

Tg bildas ur strålningstrycket ^gp=ak_PT⁴ från Tg=(^gp/ak_P)^1/4 vars generatris är ^gp = (r/3)^4/3(4p)^1/3Gm₂^2/3 – r²k(Ze/[m_A/4r₀³ – 1]pr₀²)²

som också bildar stjärnornas allmänna tryckekvation, ^gp=p–p_e. T bildas ur ekvivalenterna för strålningstrycket ^gp=ak_PT⁴=4pG(rr/3)²=4pGr^–6(r₀R⁴/3)² enligt

T⁴ = (ak_P)^–1 r^–6 4pG(r₀R⁴/3)² med SOLENS FÖRSTA EKVATION T_a = (4pG/ak_P)^1/4 r^–3/2 (r₀R⁴/3)^1/2.

Vi säger (enklast därmed) att T bildas ur Tg, analogt: T bildas ur ^gp som återfaller på stjärnornas allmänna tryckekvation.

T vid obs gravitella Solytan enligt TNED: 6150 °K

Solradiens variation med den här lokala skaltäthetens variation, r=r_C(R/r)⁴, gör att vi återfinner Solytans skalvärmegrad T enligt den här T-kurvan,

T=(4pG/ak_P)^1/4r^–3/2(r_CR⁴/3)^1/2, se SOLENS FÖRSTA EKVATION. Den variationen upphör vid Solens g-radie och återfinns inte utanför den. T varierar med 1/r^1,5.

[I T-funktionen ska egentligen också ingå formen för e-trycket, r²k(Ze/[m_A/4r₀³ – 1]pr₀²)²; e-trycket är emellertid helt kvantitativt försumbart vid Solytan (11:e decimalen) och har därför bortsetts ifrån i härledningen. Därav den något lägre T-basen i Solkärnan i den grafiska presentationen. Tas e-trycket med jämkas T ihop med basen för Tg i Solkärnan vid städet (R)].

T_P vid obs gravitella Solytan enligt TNED: 6150 °K

LJUS- OCH VÄRMESTRÅLNINGEN FRÅN SOLYTAN ombesörjs istället av en annan T-funktion, effektvärmestrålningen eller Planckstrålningen via T-formen i Stefan-Boltzmanns strålningslag med P®T enligt T_P=(P_{3,84 T26}/aAk_{5,7 t8})^1/4. T_P förutsätter att effekten (P) är given med given kroppsradie och därmed given strålyta (A): effektvärmegraden från Solytans g-radie och utåt obegränsat avtar med kvadratroten ur avståndet. Här, vid Jordbanan, är T_P ca 120 °C (393 °K) med a=1, Wikipediavärdet P=3,84 T26 W och Solens g-radie 6,97 T8 M. T_P varierar med 1/r^0,5.

BARA T_P ÄR KÄND AV MODERN AKADEMI

SOLENS FYRA VÄRMEGRADER ENLIGT TNED

Se även SPEKTROSKOPISKA JonVÄRMEGRADEN

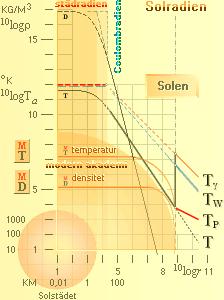
Ovanstående figurdelar i sammanställning visar (återigen) att någon regelrätt jämförelse mellan TNED och MAC (modern akademi) inte kan göras: det är två vitt skilda föreställningsvärldar utan varje matematisk beröringspunkt. Av de fyra avbildade värmegraderna är det bara TP som är känd av modern akademi. Beteckningarna

markerar den moderna akademins motsvarande funktionskurvor för respektive temperatur och täthet [BAs128].

Övergången vid Solranden kan inte härledas av modern akademi

MODERN AKADEMISK TEORI SAKNAR MATEMATISK GRUNDVAL FÖR T_g

Strålningstryckets värmegradsekvivalent (Tg) kopplar till strålningstryckets laddningskänsliga kärninduktiva kraftverkan (FT) enligt sambandet F_T=Tg²Z(8,54859 t22)(c/c₀)^1/2. F_T åstadkommer verkan på atomens och atomkärnans kraftekvation, i TNED enligt F_BT+F_eZ=0 varav f.ö. kvanttalen definieras ur F_eZ. Strålningstryckets lokalt reducerande inverkan på atomens elektromagnetiska fältbild åstadkommer en kraftjonisation som får atomerna i området närmast Solytan med störst F_T att framstå som högeligen energijoniserade (Fe16+ har observerats). Se vidare beskrivande räkneexempel med observationsdata i Joniseringen i Solkoronan.

T_g vid obs gravitella Solytan enligt TNED: 24 miljoner °K

Solradiens variation med den här medeltätheten, r=m₂/V, gör att vi återfinner strålningstryckets värmegrad Tg enligt den här T-kurvan,

Tg=(a[^gp=p–p_e]/k_P)^1/4, och vars temperaturekvivalent (Tg) egentligen börjar från g-radien — eftersom Solmassan m₂ måste ha minst g-radien som definitionsbas, analogt det klot som Solklotet spänns upp på av strålningstrycket i jämvikt med g-trycket. (e-trycket vid Solradien är försumbart [elfte decimalen] och bortses ifrån). Observera dock att strålningstryckets funktion (^gp) som sådan i vilket fall utgår från Solstädet och gäller därifrån enligt stjärnornas allmänna tryckekvation.

Tg varierar med 1/r.

T_W vid obs gravitella Solytan enligt TNED: 5 miljoner °K

T_W är g-energins Wienekvivalenta värmegrad (Wienvärmegraden). Eftersom den bestäms av g-energin (fördelad per fast antal atomkärnor m_A) och därmed via Solens fasta g-massa (m₂), gäller den med början från g-sfären och utåt: T_W = k_{2,898 t3 M°K}m_AGm₂/rhc₀.

T_W varierar med 1/r.

G-energins Wienekvivalent

T_W: g-energins Wienekvivalenta värmegrad

G-energins singulärt medelatom- ekvivalenta Wientemperatur

T = k_{2,898 t3 M°K}l^–1; E=hf=hc₀/l ; l^–1=E/hc₀=([Gm₂²/r]/(m₂/m_A))/hc₀=r^–1(m_AGm₂/hc₀);

T = r^–1(m_AGm₂k_{2,898 t3 M°K}/hc₀)

= k_{2,898 t3 M°K}m_AGm₂/rhc₀

För Solen med Väte-1-bas:

T=r^–1(3,235489608 T15 M°K)

Strålningstryckets värmegrad

T_g (T-gamma): ALLA VÄRMEGRADER OCH DERAS EKVIVALENTER utgår i stjärnornas fall från STRÅLNINGSTRYCKETS FUNKTION OCH DYNAMIK,

^gp = 2ak₀T⁴/c₀ = ak_PT⁴ = p–p_e.

Tg = (^gp/ak_P)^1/4 ..................................... strålningstryckets värmegradsekvivalent

T_ar = (4pG/ak_P)^1/4(rr_r/3)^1/2 ................... Solytans värmegrad, från Solens första ekvation

^gp = p – p_e

= (^gr/3)^4/3[(4p)^1/3Gm₂^2/3] – ^gr²[k(Ze/d)²/(pr₀)² = k(Ze/(m_A/4r₀³ – 1)pr₀²)²]

= (^gr/3)^4/3a_G – ^gr²a_e med k = Rc₀= 1/4pe₀ @ 9 T9 VM/C

r = m₂/V=3m₂/4pr³ ............................ medeltätheten (^gr) för ^gp dikteras direkt från variabeln r

TEMPERATUREN VID SOLYTAN är alltså med Jordiska mått mätt starkt beroende av tätheten (r_r).

Värmeteorin i det allmänna lärosystemet

generellt, MAC

REFERENSERNA I DEN MODERNA AKADEMINS VÄRMETEORI

Se även från VÄRMEBILDNINGENS GRUNDER GENOM STJÄRNFYSIKEN ENLIGT TNED

MODERN AKADEMI HAR INGEN massbaserad

VÄRMETEORI

Jämför även den moderna akademins ”termodynamikens första huvudsats”.

Se även från Materiefysiken och Massfysiken.

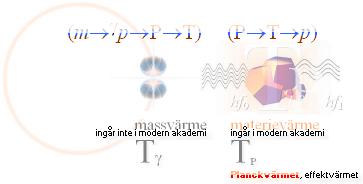
Modern akademi kan inte härleda värmegrunderna från noll, därför att man inte förstår grunderna i Plancks Strålningslag, därför att man inte kan härleda ATOMKÄRNAN ur Plancks konstant. Se från Planckringen. Figurens vänstra ringdel illustrerar Solstädet som fusionerna bakas fram på och som därmed bildar värmegrunden enligt TNED, men som inte kan härledas av modern akademi.

Värmegraderna T_g, T_W och T som bildas ur massdestruktionerna (m®g) genom olika kärnreaktionsprocesser har ingen representation i den moderna akademins lärosystem.

Intrinsiskt RENT.

ALLMÄNNA GASLAGEN kan (nämligen) inte tillämpas på stjärnornas fysik:

· ALLMÄNNA GASLAGEN (pV=kT) kan INTE tillämpas på en kropp som självgenererar energi, analogt vars tryckekvivalenter grundas på elektriska krafter — därför att temperaturen (T, värmet eller rörelseenergin) genereras primärt INDUKTIVT inom fysiken: T till pV är OK, men omvändningen täcks inte av gaslagen.
Strålningstrycket ENLIGT TNED däremot, ^gp = (r_nC/3)^4/3a_G – r_nC²a_e, klarar den saken galant. Men den grundfysiken finns inte upptagen i modern vetenskap. Inte alls överhuvudtaget.

Jämför den moderna vetenskapens allmänna energiuppfattning i ljuset av TNED:

”Termodynamikens huvudsatser

Första huvudsatsen: I ett slutet system är den totala energin (inkluderande massan) konstant.”

BONNIERS ASTRONOMI 1978s481sp1m

TNED SVARAR DIREKT:

Det finns inga slutna system i fysiken i termodynamisk mening.

beskrivning

Det finns slutna mekaniska system (konstant m). Det finns slutna elektriska system (konstant Q). Men några ”slutna” termodynamiska system existerar inte — i full konsekvens av energilagen. Vi studerar detta.

INOM VARJE DELKROPP I K — en stjärna, nebulosa, galax eller annan strålande kropp DK — läcker energin i strålningen (m®g) ut utanför DK, försvinner ur kroppen, och därmed också totalt ur varje K. Eller sagt på annat sätt: den totala energin i ett s.k. ändligt och slutet materiellt system bevaras inte. Den enda möjligheten för energin att bevaras kan bara vara ett materiellt icke ändligt system med den beskaffenheten att den utläckande strålenergin (m®g) i varje del exakt uppvägs av en lika stor obegränsad (lokalt inflödande) tillgång på icke strålande g-massa. I denna, nämligen, kan (m®g) ”gömma sig” och därmed ”bevaras”. Endast under den förutsättningen gäller energilagen: energi kan varken skapas eller förintas utan måste förutsättas. Nämligen i kraft av en obegränsad, oskapad, befintlig g-massa. Då stämmer ekvationerna. Se även från Allmänna Kosmiska Tillståndslagen. Där härleds massans kosmiska ursprung i detalj.

M.a.o.: Modern akademi exponerar, som det får förstås, grundläggande uppfattningsfel rörande fysikens natur.

Ett (ytterligare) exempel nedan i artikeln i MASSA ÄR INTE VÄRME klargör detta (ytterligare).

Massvärmet · annihilationsstrålningens grunder enligt TNED

massvärmet i TNED

MASSDESTRUKTIONEN (m®g) — annihilationsstrålningens grunder

MASSA ÄR INTE VÄRME

Men det är precis vad som hävdas i modern akademi.

(Se exv @INTERNET Wikipedia Binding energy 2007-04-01).

Vi studerar hur.

parannihilation

TNED:

Massan i (m®g) enligt

b– + b+ = 0 ............... laddning

s_b– + s_b+ = 0 .............. spinn (rörelse)

m_b– + m_b+ = 2m_b ......... massa

upphör att existera i exakt samma ögonblick den motsvarande laddningen (Q) gör det genom annihilationen. Det betyder att också den vägande aspekten, gravitationen, går förlorad med strukturen — och vilket är enda sättet för massan att kunna förstöras: det finns inga ”slutna system” i något enda termodynamiskt fall. Strålningen som associeras med massdestruktionen (m®g) kallas generellt också annihilationsstrålning.

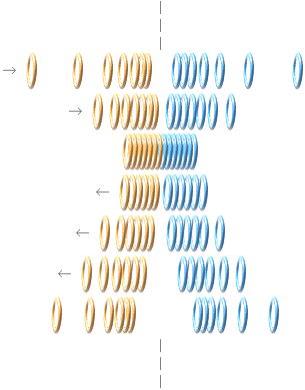
PARANNIHILATION ENLIGT RELATERAD FYSIK. Elektronmassans komponenter i formen av t-ringarna attraheras genom motsatta elektriska flöden (±). Se utförligt i Elektronelementens Elektromagnetism. När fronterna med de motsatta ringarna möts sker kvalitativ massförintelse. Ringar med samma laddning som också möts på grund av frontkollisionen, rekylerar emellertid starkt. Därigenom återkastas ±-cylindrarna diametralt — och sammandras återigen genom den elektriska attraktion som strax tar vid. ±-cylindrarna »pumpar» på så sätt ut varandra genom att annihilera (förinta) ett par ±-ringar per kollisionspuls tills alla ringar har förintats. Resultatet i netto ger en »jetstråle» av elektromagnetisk natur som avbildar annihilationsprocessens induktiva verkan genom cylindrarnas gemensamma axel. Dvs., annihilationsstrålningen (den induktiva huvudvektorn i em-strålningen) bildar en rät 180 graders linje rakt genom t-cylindrarna.

DÄRFÖR ATT om så vore fallet att ”massan bevaras i slutna värmesystem”, våldförs energins bevarande genom induktansens och laddningens proportionalitet E=LQ²/t² (t är en offsetkonstant, se vidare nedan om ej redan bekant), vilket å ena sidan SKULLE FRAMTVINGA en nollenergiekvivalent för ”det slutna systemet” med indikeringen »ingen massa-energi transferering»; Normalt när mQ försvinner, ökar induktansen (L) genom den induktiva effekten från det försvinnande mQ genom dess inre destruktiva pulsning: OM ”massan finns kvar” sedan »även om förintad», skulle den induktiva delen (L) inte vara i stånd att agera och därmed heller inte förmögen att infånga energiöverföringen från den förintade massan och i kraft av den masslösa induktionens fenomenform. Dvs., m måste förintas för att L ska kunna agera och därmed mass-energin från den förintade massan kunna överföras induktivt på andra mQ-system i form av värme och ljus. M.a.o.: Modern akademi motsäger induktionsfysikens fenomengrund med hävden ”värme är massa”.

Massan förstörs alltid genom motsatta spinn med motsatta laddningspolariteter i formen av ringar (J=mvr). Ringarna oscillerar (eg. pumpar →←) axiellt, som indikeras av ovanstående illustration:

— ±Ringblockens inbördes elektriska attraktion skapar en linjär färdriktning och därmed ett magnetfält som rättar in respektive laddningsblocks ringar på rät linje (Se illustrerat i Elektronelementens Elektromagnetism om ej redan bekant). Då ±ringblocken möts tvingas de inbördes ringavstånden i samma laddningsled PLUS och MINUS var för sig i princip bilda oändlig Coulombisk repulsion med följd i att respektive PLUSe och MINUSe tvingas rekylera bort från kollisionsområdet (←→), för att strax åter dras ihop av elektriska attraktionen mellan de två motsatt laddade blocken, och så länge ringar återstår. Denna »±e-pumpning» fortsätter tvunget än tills sista ±e-paret annihilerats.

— Genom kollision efter attraktion, följt av en stark rekyl när Coulombkraften svarar på de sammandragna ringarna, självunderhålls annihilationsprocessen. Den induktivt linjärt pumpande annihilationsstrålningen kan på så sätt förstås bilda en diametral linjär ”180° jet-stråle”.

— Annihilationsstrålarna kan bildas av betaaktiva grundämnen. Verkningssättet används bl.a. inom medicinen (PET Positron Emission Tomography) för att få fram datorsimulerade bilder av detaljer inuti levande organiska kroppar.

För varje sådan puls eller period, försvinner två ringar, eller ett par ±e. mQ-reduktionen lämnar ”systemet” i minus netto på graviterande massa och aktiv elektrisk laddning, och överför en motsvarande ökning i induktans (L) med ljushastigheten och med riktningen hos den inducerade spänningen från massnedbrytningarna.

kommutativa ekvivalenten

Minskande ström betyder ökande induktans om energin är konstant

SÅLEDES

är ”massfrånvaron” garanterad att existera TILLSAMMANS MED varje exciterat tillstånd hos ett oscillerande system, således så att å den andra sidan en dubbel energis existens elimineras i induktans-laddningsbevarandets ekvivalent E=LQ²/t². Dvs., energin skulle tvingas vara dubbel om den moderna akademins företrädare fick bestämma över Universums Praktiska Fysik enligt ”värme är massa”. Vilket vill säga, ”massfrånvaro” och värme samarbetar VERKLIGEN i utbyte genom Planckenergin E=hf=mc²=LQ²/t²=(m®g)c² där (m®g) SÅLUNDA är kvalitativt tvingande irreversibelt — (m®g)c² ¹ (m¬g)c² — MEDAN kvantitativt kommutativt — (m®g)c² = (m¬g)c².

Med andra ord: värme har ingen KVALITET AV MASSA — ingen struktur — bara en kvantitet: energi. Ingen graviterande egenskap. Ingen strukturell egenskap. Bara ljus. E=LQ²/t²=LI²=konstant för varje massivt destruktivt ändamål.

KLARGÖRANDE ATT VÄRME INTE ÄR MASSA OCH MASSA INTE ÄR VÄRME

E=LQ²/t²

massdestruktion [@INTERNET Wikipedia ännu 2007-04-02 ingen artikel på Mass Destruction annan än som behandlar VÄRLDSPOLITIK/VAPEN]

MASSDESTRUKTION m®[(E=hf)c^–2] är uppenbarligen en process.

Under massdestruktionens process, bevaras energin (E) i massan (m) av en intern förintelse av fysisk struktur i m; Spinnet (s) och laddningen (Q) förintas fullständigt tillsammans med kvaliteten massa och dess graviterande egenskap. Se även i Atomkärnans Härledning II:

FRAGMENTERINGSKRAFTEN kan bara upphävas genom en ±bn-struktur: SUMMA NOLLSPINN, SUMMA NOLLADDNING: attraherande massor som upphäver fragmenteringskraften F och därmed nollzonerna (m®g):

· accelerationen överförs på andra massor via induktionen (COEI), således går ingen energi förlorad [se även i COEI]

Analogt med att laddningen (b) och spinnet (s) upphör genom massförintelsen

b– + b+ = 0 ............... laddning

s_b– + s_b+ = 0 .............. spinn (rörelse)

m_b– + m_b+ = 2m_b ......... massa

händer alltså ingenting annat än att induktansen ökar med laddningens avtagande enligt nyssnämnda formella samband E/t²=LQ²=konstant.

Induktansökningen — som tydligen måste associeras med den Q rumsuppfyllande strukturen och inget annat — garanterar (nämligen) att ett reducerande Q bildar ett motsvarande induktivt tryck, motsvarande den grundläggande garantin för att en induktiv puls ska komma fram, och som därmed överför Q-massans energi (accelerationen) masslöst på andra kringliggande massystem så att ingen energi går förlorad (COEI, energins bevarande genom induktionen). Induktionstrycket från induktansökningen får i energiekvivalenter den enkla formen med ekvivalens mellan divergensenergi (mcc) och Planckenergi (hf) enligt

E = mc² = hf

Till denna energi tillkommer respektive elektronmassas kinetiska energi (mv²/2) som resultat av ömsesidig attraktion typ parannihilerande ±e. Den extra energin ger ett motsvarande högre totalt energitryck som totalt kan återföras på en högre frekvens (f), analogt en kortare »stopptid» då ±e kolliderar och den induktiva delpulsen bildas.

I formella ekvivalenter kan vi eftersöka ett (relativt) kvantitativt uttryck för elektroninduktansen (L) i elektronens divergensenergi E=LQ²/t²=mc² enligt

L = mc²t²/e²

om vi också utnyttjar sämsta fallets räkning på t-ringen (Se Elektronmassans komponenter) med diametern 1/50 av protonradien (1,37 t15 M), Ø=r₀/50, och använder toppdivergensen (c=c₀) som absolut referensvärde enligt c=Øp/t=3 T8 M/S som ger ct=Øp med e=1,602 t19 C och därmed

L = m(ct)²/e² = m(Øp/e)² = (9,11 t31 KG)(537,32608 M/C)²

= 2,63023 t25 (H=WS=VS/A=VS²/C)

Ekvivalenta konstanta strömstyrkan i varje t-ring blir då I = [Q=e/n_=177062]/t = ec/Øpn = 3,1532468 A.

Notera att dessa värden är de formellt optimala med utnyttjande av givna naturkonstanter. Eventuellt befintliga koefficienter har här helt bortsetts ifrån.

Förintelsen verkställs således i samma ögonblick rörelsekraften i m=ma=F/a — i E som mc²=hf — överförs masslöst (m®g) till det induktiva grundtrycket (ökningen i L som ersätter Q) och som sedan i induktionens vidare verkan kan bilda värme och ljus (E=mc²=hf) — i garanti av ekvivalenten E=LQ²/t².

Induktionsverkan via LÛQ² överför därigenom massenergin från Q på andra nära eller avlägsna massiva laddningar (mQ) genom ljushastigheten c.

HÄRLEDNINGEN AV MASSDESTRUKTIVA PROCESSEN (T och t för tid nedan):

FRÅN EKVIVALENTEN LQ²/t²=E=(konstant för varje massa)=mc²=hf=k/a med a=t² ges k/E=a+T² DÄR T=0 definierar (massdestruktiva) villkor tillsammans med DEN E_max-OFFSET som energi-massa transfereringens process måste grundas på. Då är E/k=1/(a+T²), och vi har E=k(a+T²)^–1. E-derivatan (varianten) bildar TRANSIENTA EFFEKTEN dE/dt = P = (–)kT(a+T²)^–2. Konstanten a motsvarar en (kort) period med tändning innan den aktuella massa-energi transfereringen inträffar: Från tillfället för kontakt mellan de destruktivt motställda krafterna — mellan de betraktade massiva elektriskt laddade positiva och negativa ytorna hos de kroppar som ska förstöras — framträder en tidrymd innan verkan »tänder». Vilket vill säga, verkan inträffar inte omedelbart från kontakt (nolltid) utan kräver ett litet tidsfönster för att få fram ett ledande ansvar.

Illustration (eng.vers): funktionen för massdestruktion PER enligt härledning i texten

ALLMÄNNA FUNKTIONSFORMEN FÖR TRANSIENTENS EFFEKT

t(a+t²)^–2

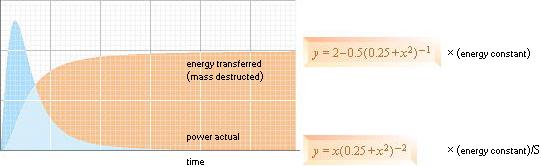
Om koefficienten a sätts lika med noll, tvingas effekttoppen mot oändligt. I praktiken bildar (alltså) a en mera praktiskt balanserad fysik genom en tidskonstant litet större än noll — och som måste härledas i varje särskild tillämpning.

MASSANS KVALITET garanterar alltså en icke koppling eller en icke sammanbindning med värme. Kopplingen massa-värme kan bara ges kvantitativt genom Planckenergins ekvivalent E=hf=mc², vilket betyder: Massdestruktion (m®g) är kvalitativt irreversibel för att kunna realisera värme från massa, OCH kvantitativt kommutativ (likheten gäller åt bägge hållen), E=(m®g)c²= (”m”¬g)c², för att kunna realisera den aktuella destruktiva transfereringsprocessen: DEN kunde inte bli av om ljus kunde bilda eller skapa gravitation = massa.

Koronafysiken · se även från Solens Fyra Värmegrader

förklaringen till Koronajonisationerna

från Strålningstryckets Kraftekvivalent

Koronajonisationens fysik enligt TNED

inledning

Atomkärnan är ENLIGT TNED en strömstyrd komponent.

Grundformen ges från TNED enligt atom- och kärnfysikens två kungsekvationer

J_0K+3J_1K = 0 .............. atomkärnans och elektronmassans gemensamma spinnjämvikt

F_BT+F_eZ = 0 .............. elektronelementets kärnkoppling (ström- och kemiekvationen)

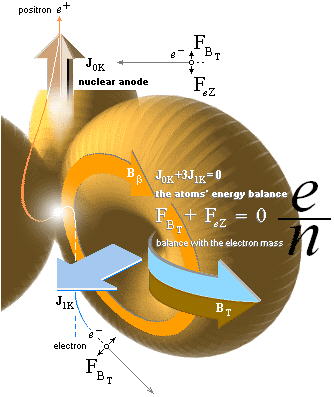
Koronajonisationens

grundfysik

Genom strålningstryckets kraftekvivalent (F_T) utanför Solytan (som också har en motsvarande värmegradsekvivalent) försvagas atomens kraftfält proportionellt mot kärnladdningen genom att elektronmassan av strålningstrycket drivs bort från sin moderkärna. Denna blottas (helt eller delvis) och åstadkommer därmed en obalans i atomens normala resonansfysik (F_BT+F_eZ=0) och som atomkärnans tyngdcirkel — som bygger på att kontinuerligt avkänna elektronmassan — uppfattar som ett motsvarande exciterat tillstånd. Därmed uppför sig atomen som om den vore energijoniserad då den i själva verket »bara är kraftjoniserad». Graden av kraftpåverkan kan beräknas generellt utifrån vissa idealiseringar, och man finner enligt TNED att motsvarande jonisationsnivåer bekräftas. Vi studerar detta.

INLEDANDE BERÄKNINGSEXEMPEL

Se även mera utförligt från Joniseringen i Solkoronan

Koronafysiken verifierad enligt TNED

Om vi använder halva atomens medelradie i fasta ämnen (grovt R/2 ca 1,5 Å med medelavståndet ca 3 Å) som en grov preferens i följande översiktsberäkningar för att fastställa de rimliga gränserna (för vidare prövning) kan vi ur tillgängliga tabelldata för motsvarande laboratoriedata på jonisationsenergier beräkna en medelkraft (F) till jämförelse med strålningstryckets lokala kraft. @INTERNET på Wikipedia i Ionization energies of the elements anger för Järnets jonisation till sextonde elektronnivån (Fe¹⁶⁺) värdet 47206 KJ/mol [‡3] vilket motsvarar 489,24805 eV eller 7,83775 t17 J. Division med R/2=1,5 Å ger då kraften

F = 5,22516 t7 N

Källuppgift Järnets jonisation till nivå 16:

”During a period of about two days in early May, 1998, the ACE spacecraft was immersed in plasma associated with a coronal mass ejection (CME). The SWICS instrument on ACE, which determines unambigously the mass and charge of solar wind ions with high time resolution, has produced a new and very exciting data set from this event. These data carry a wealth of information on the origin and thermal history of the CME ejecta and have the potential of being the missing link between solar observations and in situ plasma observations.

Here, we concentrate on the iron charge state distribution, which has been measured once per hour during the entire CME period. These distributions are imprints of the electron temperature distribution function within a few solar radii from the solar surface where the ejecta were accelerated. During this event the observed charge states range from the very rare Fe3+, during phases of very cold plasma, to Fe16+, when the plasma is extraordinarily hot, indicating an enormous range in electron temperatures from 10⁵ K to several 10⁶ K.”

@INTERNET från Googlesökning på »Fe16+» 2007-03-09

More on Recent Coronal Mass Ejection

[www.windows.ucar.edu/tour/link=/headline_universe/aceme.htm|&edu=high]

Sambandet

F_T = T_g² · Z(8,54859 t22)(c/c₀)^1/2

med T_g=24 T6 °K vid Solytan och Z=1 ger som sämsta fall till jämförelse värdet

F = 4,92398 t7 N

Med Z=16 har strålningstrycket rent teoretiskt en kraftpotential på runt

5 t7 × 16 = 8 t6 Newton vid Solytan.

Förhållandet mellan de olika värdena är 1,0611642, och det visar oss att resultatet från strålningstryckets temperaturekvivalent verkligen ger relevanta värden och väl ligger inom den observerade ordningens magnitud. Om vi däremot till jämförelse skulle använda Solytans Planckvärme, T_P=6000 °K, skulle F-värdet bara bli 3,07749 t14 N, vilket visar att den motsvarande observerade jonisationen (Fe16+) inte på långa vägar kan förklaras med den modellen.

Därmed är den teoretiska förklaringen till koronahettan rent kvalitativt verifierad enligt TNED.

Joniseringen i Solkoronan

från Strålningstryckets Kraftekvivalent

Joniseringen i Solkoronan

JONISATIONEN I SOLKORONAN · Se även från SOLKLOTETS ELEKTRONFRIHET

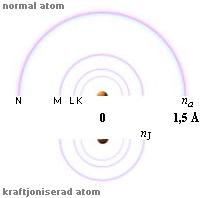
Den av en grundämnesatom — i fasta tillståndets fysik med medelavståndet grovt 3 Å för samtliga atomer***

*** För Väte och Helium gäller sämsta fallets d=r_a=0,529Å som är elektronens ekvivalenta grundradie i Väte-1.

— maximalt inneslutna kraftpotentialen (F_T) som sammanhänger med atomens jonisationsenergi (E_J) kan helt säkert fastställas enligt sambandet

SÄMSTA FALLETS KRAFTPOTENTIAL

E_J 3 Å

F_T = —————— ; r_a = ———

d = r_a n_J² 2n_a²

F_T maximalt inneslutna kraftpotentialen, E_J jonisationsenergin, d distansekvivalent

med grund i härledningen för vätets enkla spektrum (huvudkvanttalet n med sambandet d=r_a n² och som även gäller med god approximation för alla övriga atomer med endast en elektron) och med ledning av en tabell över jonisationsenergierna (E_J) samt med kännedom om atomens elektronkonfiguration (k_K-l_L-m_M-n_N-o_O-…) motsvarande talen n_a och n_J,

n_a grundämnesatomens högst besatta huvudkvanttal

n_J joniserade atomens huvudkvanttal

n_J är det huvudkvanttal som återstår i den joniserade atomens elektronbesättning sedan jonelektronerna reducerats ur na

Uppgiften (F_T) anger då den lägsta (strålande) kraft, jonisationskraften, som HELA atomen måste utsättas för, för att helt säkert åstadkomma den aktuella jonisationen (E_J). Uppgiften är meningsfull bl.a. för kontroll av rimligheten i teorin för Solkoronans temperaturekvivalent (T_g) som framkommit enligt TNED och som ger det laddningsberoende strålningstryckets kraftpotential (F_T) enligt sambandet

F_T = T_g² · Z(8,54859 t22)(NM^–2°K^–4 VMC)^1/2

T_g vid övergången till Solkoronan (6,97 T8 M) är drygt 24 miljoner °K, vilket för sämsta fallet Z=1 ger en absolut lägsta kraftpotential på

F_T1 = 4,92398 t7 Newton. Med Z=16 ges

F_T16 = 7,87836 t6 N.

Enligt uppgift [‡1] har man (hittills som mest) i Solkoronan observerat en jonisation för Järn in till just sextonde jonelektronen (Fe16+). Enligt tabelluppgift [‡2] för jonisationen Fe16+ krävs i Jordiska laboratorier jonisationsenergin

E_J = 47206 KJ/mol [‡3]

vilket motsvarar 489,24805 eV eller

E_J = 7,83775 t17 J.

Järn (₂₆Fe⁵⁶) har elektronkonfigurationen 2_K-8_L-14_M-2_N [‡4] som efter eliminering av 16 yttre elektroner ger 2_K-8_L. Vi får då ur ovanstående förutsättningar

n_a = 4 grundämnesatomens högst besatta huvudkvanttal

n_J = 2 joniserade atomens huvudkvanttal

r_a = 9,375 t12 M

d = 3,75 t11 M

F_T16 = (7,83775 t17 J)/(3,75 t11 M)

= 2,09006 t6 N

Fe¹⁶⁺ i Solkoronan kan alltså enligt TNED förklaras med en rund och god marginal på 3,7694458 ggr: det finns mer, om det behövs

‡[1] @INTERNET från Googlesökning på »Fe16+» More on Recent Coronal Mass Ejection

[www.windows.ucar.edu/tour/link=/headline_universe/aceme.htm|&edu=high]

‡[2] @INTERNET Wikipedia Ionization energies of the elements 2007-03-09

‡[3] I The Periodic Table i Wikipedia (och andra, @INTERNET), används en enhet “kJ/mol” [=1000J×1000/Kmol] som energienhet (E₁) för elektronens bindningsenergi (till atomen eller molekylen). För att få den rena bindningsenergin (E₀) i enheten i Joule (J) förutsatt substansen är atomär, alltså inte molekylär, räknas

E₀ = E₁×1000(u=1,66033 t27 KG)1000/1KG = E₁(1,66033 t21) Joule.

För att få värdet direkt i elektronvolt (eV) räknas

E_eV = E₀/(1,602 t19 C) = E₁(1,66033 t21)/(1,602 t19 [C]) = E₁(0,0103641)/[C] = E₁(1/96,486843)/[C]. Se även i molbegreppet.

‡[4] Se utförligt i GRUNDÄMNENAS PERIODISKA SYSTEM

Solkoronans Jongräns

Från Joniseringen i Solkoronan

SOLKORONANS JONGRÄNS

Solkoronans absoluta största radiella kraftjonbildningsgräns — 11 Solradier

I jonisationstabellen [‡2] innehas den lägsta jonisationsenergin (antalet jonelektroner Z_J) för Z_J=1 av den radioaktiva alkalimetallen Francium med atomnummer 87 och E_J=380 KJ/mol eller 3,9383607 eV. Om vi söker ekvivalenta stråltryckstemperaturen (Tg) där Z_J=1 precis satisfierar strålningstryckets kraftekvivalent för det fallet, alltså Solkoronans absoluta största radiella joniseringsgräns enligt TNED (masstrålningens jongräns),

F_T1=E_J/(d=1,5 Å)=4,20616 t9 N, ges

Tg=Ö F_T1/(8,54859 t22)=2,2181766 T6 °K, samma grundparametrar som i föregående (se från Joniseringen i Solkoronan). Det motsvarar (beräkning i separat kalkylkort) avståndet d=7,65783 T9 M eller nära 11 Solradier (r_G=6,97 T8 M). Det innebär enligt TNED att utanför den gränsen finns inte ens en teoretisk möjlighet för Solen att åstadkomma någon enda atoms jonisation.

Observera dock att Solens energijoniserande kapacitet beror på em-strålningen från Solen generellt och som innefattar den reguljära materiestrålningens alla möjliga frekvenser. Därmed bildar Solstrålningen i vilket fall en reellt joniserande energikälla (E=hf).

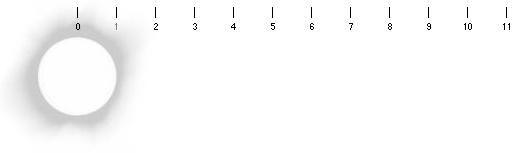
Illustrationen visar Solen med en avståndsskala uttryckt i synliga Solradien (ca 6,96 T8 M) som enhet. Från ca 11 Solradier och vidare utåt finns inte längre någon fysisk förutsättning för en direkt aktiv kraftjonisation från strålningstryckets kraftekvivalent, enligt TNED. Den motsvarande spektroskopiska jonisation som finns i Solvinden bildas alltså enligt TNED innanför 11-radiegränsen.

Vi noterar att dessa resultat blir helt omöjliga enbart med tillgång till ”den konventionella” Planckvärmestrålningen (T_P).

Med Z_J=16 ligger Fe16+-jonisationsgränsen vid nära 2 Solradier från centrum (Tg=12,362 T6 °K) om gränsvärdet är föregående F_T16=2,09006 t6 N från tabelldata och den idealiserade kraftmodellen.

teorin i TNED

Om vi ser till hur STRÅLTRYCKSTEMPERATURENS RADIELLA VARIATION fungerar i stjärnfysiken enligt TNED,

Tg = a^–1/4(^gp/k_P)^1/4 ......................................................... k_P= 3,781904041 t16 NM^–2°K^–4

^gp = (r/3)^4/3a_G – r²a_e ............. från stjärnornas allmänna tryckekvation, N/M² med

a_G = (4p)^1/3Gm₂^2/3

a_e = k(Ze/[m_A/4r₀³ – 1]pr₀²)²

r = m₂/V=3m₂/4pr³ ................. medeltätheten dikteras direkt från variabeln r via den fasta stjärnmassan m₂

ser vi att det är den övervägande g-energin [(r/3)^4/3a_G] som bär ansvaret för värmegraden Tg (r²a_e är helt försumbart vid och utanför Solytan). Men dess teori existerar inte i modern akademi — därför att teorin grundas på massfysik och den är helt orepresenterad i moderna kvarter.

— Vet du varför det är så?

— Ja. Det vet jag. Man har PARTIKULÄRT låst sig vid föreställningen att Plancks konstant (h) INTE är en strukturkonstant [L] utan att den gäller ABSOLUT för elektronnivån i atomen och därmed varje åskådning av atomkärnan som modell utesluten, förbjuden, omöjlig, stendöd massfysik, don’t even think about it. Utklassning. Utan h som en strukturkonstant E=hn^–1fn=hf blir det omöjligt att härleda uppkomsten av värmebildning ur atomkärnan från massdestruktionen (m®g). Se även från Härledningen till Plancks Strålningslag.

Jämför referenserna:

materiefysik, massfysik

MATERIEFYSIK

Materiefysiken beskrivs från temperatur till tryck, T®p, typ allmänna gaslagen (pV=kT). Materiefysiken är utomordentligt väl representerad i modern akademi.

MASSFYSIK

Massfysiken däremot beskrivs från tryck till temperatur, p®T. Men den typen ingår inte i modern akademi — därför att man inte kan härleda atomkärnan där. Massfysiken står helt orepresenterad i modern akademi. Se särskilt från SOLFYSIKEN.

Se även mera utförligt och vidare från Värmegrunderna och Neutrinospektrum.

Spektroskopiska värmegraden · spektrala värmegraden | 2007V09 | 2007XII29

Från SOLENS FYRA VÄRMEGRADER

SPEKTROSKOPISKA JONVÄRMEGRADEN T_SI

Solens femte värmegrad

Rekombinationerna mellan de kraftjoniserade atomerna i Solklotet (se jonisationskraften) och elektronerna i Solskalet bildar grundvalen för en spektroskopisk jonvärmegrad (T_SI). T_SI kopplar direkt till observationella resultat och teorin för T_SI kan därför prövas direkt.

Restenergin från rekombinationen mellan en kraftjoniserad atom (kärna, se Joniseringen i Solkoronan) och dess elektronbesättning definierar en inom lokalens dynamik motsvarande spektral excitation vars observationella ekvivalent visar en motsvarande, konventionell, värmegrad (T_SI).

Eftersom den bildade fiktiva värmegraden (T_SI) genereras av strålningstryckets verkan [se strålningstrycket i relaterad fysik] och därmed enligt TNED i relation till strålningstryckets redan väl kända temperaturekvivalent (Tg), är det enligt TNED möjligt att härleda en relativt noggrann grafisk bild av hur T_SI varierar. Därmed ges direkt konkret grund för jämförande data mellan teori och praktik.

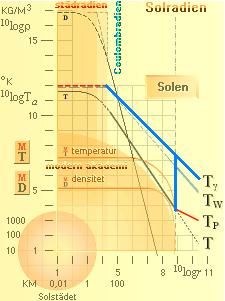
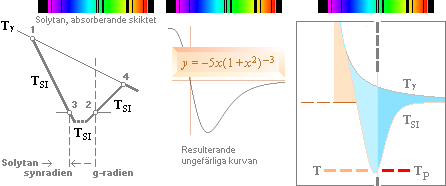
Solfysiken enligt TNED påvisar alldeles tydligt att det är det högtäta elektronskiktet i Solytan som bär ansvaret för att atomerna i det området uppvisar fullständiga (men turbulenta) rekombinationer med sina elektronbesättningar — och på den vägen åstadkommer en motsvarande spektral djupdykning i Solytan mot nolltemperatur från taket för Tg. Den blå heldragna linjen med djupdykningen vid Solytan i figuren ovan visar hela funktionen, här i logaritmiska skalor. Emellertid syns ingenting av detaljerna innanför Solytan, dessa kan inte inspekteras direkt på grund av det skyddande ytskiktet. Den fiktiva spektralkurvan dyker istället upp plötsligt just vid Solytan, sjunker något, för att sedan snabbt klättra uppåt mot taket för Tg igen. En mera synligt relaterad funktionsform beskrivs nedan samt längre fram i slutet av artikeln.

grundteori

GRUNDTEORI spektroskopiska jonvärmegraden · se Solens 4 värmegrader för inledande översikt

Solen är ENLIGT TNED en internt starkt polariserad kropp.

Initiellt (primärt) består Solytan av 100% elektrontäthet — kontra centrum med 100% jontäthet. Se utförligt från Solranden

beskrivning

M

ed en maximalt elektronrippad atom i en lokal med en maximalt packad elektrontäthet finns bara en väg: fullständig rekombination: Atomen återtar hela sin elektronbesättning. Atomen framstår därmed som både termiskt och spektroskopiskt neutral: atomen bildar en absorptionsreferens motsvarande en absolut nollpunkt, och kan på den vägen absorbera energi från omgivande atomer som inte är helt nollställda. Därmed uppvisar atomen ett absorptionsspektrum (mörka spektrallinjer mot det kontinuerliga spektrums bakgrund): relativt omgivningen framstår den spektralt absorberande atomen som »svalare». Se även i Opaciteten.

S

olytan är enligt TNED just en sådan lokal. Atomernas långt gångna kraftjonisation i försorg av strålningstryckets inverkan gör liten skillnad mellan atomer i Solkärnan och atomer vid Solytan. Jonisationspotentialen avtar markant först från 2-3 Solradier och når enligt TNED minimum vid ca 11 Solradier. Se Solkoronans Jongräns.

Rekombinationskraften vid Solytan avtar snabbt inåt eftersom kraftjonisationen dels ökar och elektrontätheten dels avtar. Eftersom TSI har Tg som generatris, utgår vi ifrån att Tg och TSI sammanstrålar i Solstädet.

Det är den första referenspunkten.

Den fullständiga rekombinationen vid Solytans gravitella radie (r_G) ger en principiell nollreferens som framtvingar ett TSI-värde lägre än Solkroppens egen värmegradsfunktion (T) vid Solytan: Rekombinationen som sådan ger (idealt) 0°K vid g-radien, exakt.

Omedelbart utanför r_G utverkar emellertid inte Solkroppen längre något sådant inflytande. Där återgår atomerna till mera normala (enligt Jordlaboratoriets välkända experiment) emitterande beteenden, och vi bör därför (på något ställe) få en med T_SOLYTAN (ca 6000 °K) motsvarande Planckvärmegrad T_P, alldeles precis utanför g-radien.

Det ger den andra referenspunkten.

Rekombinationerna vid Solytan eliminerar den fria elektronförekomsten där, vilket också eliminerar den ursprungliga opaciteten eller synranden, som därmed istället flyttas längre inåt Solklotet där den fria elektronförekomsten är mera markant.

Med växande avstånd, inåt från den så osynliggjorda g-Solytan och TSI, avtar alltså elektrontätheten och ökar kraftjonisationen, vilket leder till att TSI också tvunget ökar och går mot sitt gränsvärde vid Tg. Ett sämsta fallets riktmärke som anger brantheten i TSI-ändringen vid Solytan fås genom att sätta maxvärdet för TSI lika med Solytvärdet för Tg (ca 24 T6 °K). Med en linjär skala på 1000 °K per 100 KM, som med g-Solradien vid rG=6,97 T8 M betyder 6 970 st 1000-gradersintervall ges då lutningen (minus)

(Tg=24 T6 °K)/(6970×1000) = 3,44 avrundat: källan i Källa 4 ger 3,5 vid ingången till Solytan.

Det är den tredje referenspunkten.

TSI-värdena utanför Solkroppen återvänder mot Tg-funktionen, analogt spektralgraderna mellan Solytan och koronan.

Det ger den fjärde referenspunkten.

V

i känner inte det exakt lägsta Solytvärdet (TSI=T–DT). Idealt är det 0°K enligt ovanstående utläggningar, och bildar därmed en idealt absorberande bakgrund på vilken övriga emissioner från Solkroppen kan framträda. Olika mätningar (i olika epoker) rapporterar också (ständigt) nya uppgifter beroende på instrumentteknikens utveckling mot allt högre precision. Se vidare i källredovisningen som följer närmast nedan.

D

ärmed är den grafiska grunden för TSI-funktionen härledd. Kurvformen beskrivs mera matematiskt exakt i Spektrala jonvärmegradens funktion med en mera åskådlig form för det smala området vid Solytan.

jämförande

observationsdata

Jämför konventionellt presenterade observationsdata:

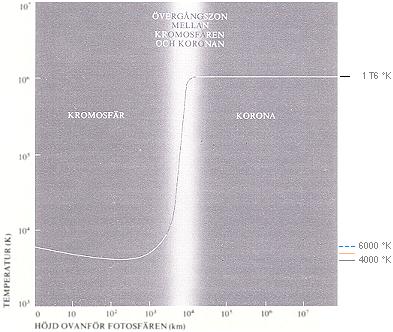
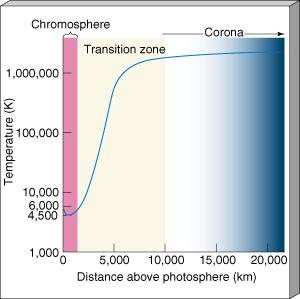
Vänster Källa 1: 1978 BONNIERS ASTRONOMI 1978 s136fig8.11

Konventionellt (spektroskopiskt) uppmätt värmekurva utanför Solytan.

Höger Källa 2: 2001 Figure 16.13 Solar Atmospheric Temperature

@INTERNET [http://138.238.143.191/astronomy/Chaisson/AT416/HTML/AT41603.htm] 2007-05-08

Nedan Källa 3: 1976

@INTERNET [http://www.alfvenlab.kth.se/edu/courses/2A1160/forel2.pdf] 2007-(12-10)

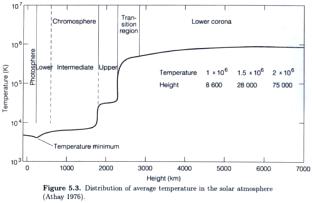
Nedan Källa 4: uppgift om källår saknas Solar Photosphere as a function of Depth

@INTERNET [http://csep10.phys.utk.edu/astr162/lect/sun/photosphere.html] 2007-05-08

Källa: Fraknoi, Morrison, and Wolf, Voyages through the Universe

”

Solar Photosphere as a function of Depth

Depth (km) % Light from this Depth Temperature (K) Pressure (bars)

0 99.5 4465 6.8 × 10^–3

100 97 4780 1.7 × 10^–2

200 89 5180 3.9 × 10^–2

250 80 5455 5.8 × 10^–2

300 64 5840 8.3 × 10^–2

350 37 6420 1.2 × 10^–1

375 18 6910 1.4 × 10^–1

400 4 7610 1.6 × 10^–1

Source: Fraknoi, Morrison, and Wolf, Voyages through the Universe

”

Ovanstående Källa-4-data omsatt till kurvorna nederst

r_G för gravitella Solradien, r_F för fotometriska (skillnaden ca 1000 KM)

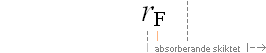
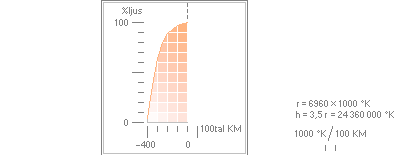
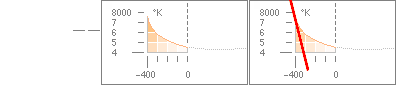
Lutningen i grafen ovan höger motsvarar ca –3,5. Jämför TSI-funktionens värde –3,44.

Nedan Källa 5: 1994 AMERICAN INSTITUTE OF PHYSICS 1994

@INTERNET [http://www.aip.org/pnu/1994/split/pnu160-4.htm] 2007-05-15

[http://www.sciencemag.org/cgi/content/abstract/263/5143/64] 2007-05-15

”

High-resolution infrared observations of carbon monoxide molecules at the limb of the sun provide a new minimum temperature of 3500 K which, furthermore, seems to occur at a higher altitude, 1100 km. Robert Noyes of Harvard Smithsonian says that carbon monoxide clouds may be a transitory phenomenon in the solar atmosphere. (Science, 7 Jan. 1994, Science News, 8 Jan.)

”

GRAFISK SAMMANSTÄLLNING AV

termiska KÄLLDATA |2|4|5| FRÅN SOLYTAN

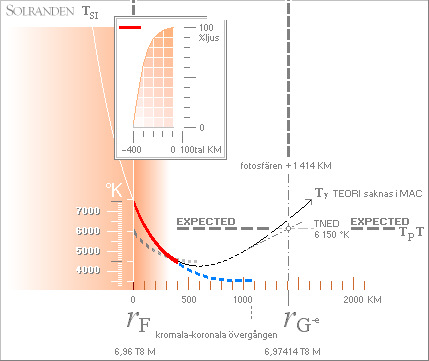
Källa 2 |: Se även separat graf i Källa 2.

Figure 16.13 Solar Atmospheric Temperature

@INTERNET [http://138.238.143.191/astronomy/Chaisson/AT416/HTML/AT41603.htm] 2007-05-08

Källa 4 |: Se även separat graf i Källa 4.

Solar Photosphere as a function of Depth

Source: Fraknoi, Morrison, and Wolf, Voyages through the Universe

@INTERNET [http://csep10.phys.utk.edu/astr162/lect/sun/photosphere.html] 2007-05-08

Källa 5 |: Se även separat citat i Källa 5.

AMERICAN INSTITUTE OF PHYSICS 1994 · [http://www.aip.org/pnu/1994/split/pnu160-4.htm] 2007-05-15

[http://www.sciencemag.org/cgi/content/abstract/263/5143/64] 2007-05-15

Spektrala värmegradens funktion

Från SPEKTRALA VÄRMEGRADEN

SPEKTRALA JONVÄRMEGRADENS FUNKTION I SOLEN

historisk inledning

KORONAFYSIKEN OCH SPEKTROSKOPISKA VÄRMEGRADENS FUNKTION

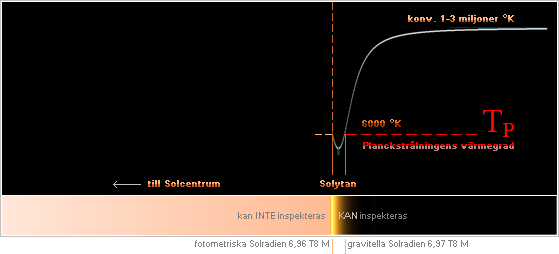
Med början under 1940-talet [ENCARTA 2004 Sun] visade ett mera ingående studium av ljuset strax ovanför Solytan, den s.k. koronan, att det innehåller järnatomer (Fe) som berövats upp till (minst) 13 av sina elektroner (Fe+13). För att förklara en sådan förekomst med Jordlaboratoriets förutsättningar, tvingades man till uppfattningen att temperaturen i området måste vara (minst) flera miljoner grader (den ljusa grafen).

Planckstrålningens värmegrad (streckad röd TP) är den man förväntar sig från Solen som strålande kropp. Ytvärdet runt grovt 6000 °K ges med grund i spektroskopiska observationer, och man skulle därmed förmoda att temperaturen därifrån avtar sakta mot värdet runt drygt 390°K ute vid Jordbanan. I det praktiska fallet visade de första Solmätningarna istället att temperaturen just från Solytan och utåt i själva verket först dyker neråt (observerade värden mindre än 4000 °K finns rapporterade) för att strax klättra brant uppåt igen, men nu till flera miljoner grader in i Solkoronan. Detta resultat beskrivs i ENCARTA 2004 Sun som “one of the classic problems of astrophysics”. Istället för en enda värmegradstyp (Planckvärmegraden) uppvisar Solen klart och tydligt två olika.

Följande illustrativa sammanställning visar olika källdata i området;

Se separat källredovisning

Se separat källredovisning

Anledningen varför den till synes gåtfulla förklaringen aldrig uppmärksammades i moderna kretsar beskrivs ingående i VAD GÖR MODERN AKADEMI FÖR FEL.

I TNED är förklaringen både enkel och naturlig. Vi studerar hur.

STRÅLNINGSTRYCKETS TERMONUKLEÄRA EKVIVALENT (^gp = 2ak₀T⁴/c₀) GARANTERAR genom sin kraftjoniserande verkan (F_T=Tg²Z(8,54859 t22)(c/c₀)^1/2) ATT Solklotet hålls intrinsiskt RENT på elektronmassa. Se även jämförande RÄKNEEXEMPEL i Solkoronans Jonisation.

Undantag: Heliumatomer KAN ha elektronbesättning med början från halva Solradien och vidare utåt. Se Exempel.

De allra tyngsta grundämnena: Ifall de alls förkommer längre in i Solkroppen än Helium (vilket strålningstrycket i sig knappast medger) kan de ha elektronbesättning: allt längre in mot Solkärnan med den allt tyngre grundämnesatomens allt högre jonisationspotential. De tyngre grundämnena är emellertid ytterst ringa representerade i Solen (konv. ca 1%) utöver Väte och Helium och bortses därför ifrån i alla översiktliga beräkningar. Huvudfrågan gäller Väte och Helium.

Med den POLARISATION, som i följd av ovanstående, uppkommer i Solklotet mellan den inre fullständigt joniserade kärnan och det yttre elektronhöljet, en närmast ENORM ELEKTRONTÄTHET (se Elektrontätheten i Solytan). Elektronförekomsten i Solen, som funktion av avståndet r från Solcentrum, kan då ställas på en enkel och helt elementär PULSFORM av typen

f (r_e)= a(b+c[d(r–e)]²)^–1 enligt (illustrationen nedan; a=1=b; c=20; d=2; e=0)

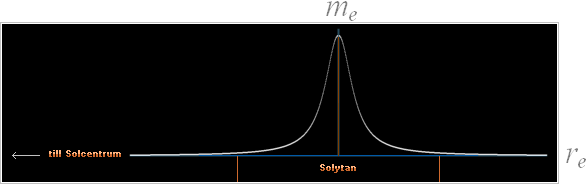
Elektronmassans förekomst i Solkroppen som funktion av avståndet från centrum

grafiskt (1+20[2(x–0)]'2)'–1

STRÅLNINGSTRYCKETS VÄRMEGRADSEKVIVALENT (Tg) i samma område vid Solytan,

Tg = (a^gp/k_P)^1/4

där vi observerar att ^gp = (r/3)^4/3a_G – r²a_e med r = m₂/V=3m₂/4pr³ = r_n (medeltätheten dikteras direkt från variabeln r via den fasta stjärnmassan m₂) ENLIGT TNED ges av stjärnornas allmänna tryckekvation (^gp = p–p_e) och som beräknas separat via g-trycket (p) och Coulombtrycket (p_e) i TNED, och som visar att Tg blir en funktion av 1/r (Tg=k_T/r) och som ger motsvarande grafiska funktionsbild av KRAFTJONISATIONENS VERKAN (F_T),

visar att Tg ligger i området som ett i det närmaste RAKT toppvärdestak med max värmegrad runt 24 miljoner °K vid Solytan; Ute vid Jordbanan är Tg-värdet ca 113 000 °K;

Med den enorma elektrontätheten garanterad just i Solytan,

elektrontätheten i Koppar till jämförelse är max två elektronmassor per Kopparatom som med Kopparens täthet 8930 KG/M³ och masstal runt 64 ger 1,7 T29 elektroner/M³; till jämförelse är elektrontätheten i Solytan runt 6 T32 elektroner/M³, det är mer än 3000 gånger större

är det omöjligt att undvika en FULLSTÄNDIG REKOMBINATION mellan alla atomkärnor som befinner sig där och alla elektronmassor. Allt annat är UTESLUTET. Temperaturbegreppet i det området (som för heta gaser normalt mäts just genom graden av en atoms tillfälliga elektronunderskott eller excitation) förlorar därmed sin normala mening:

ELEKTRONYTAN genom de rekombinerade atomerna som därmed fejkar låga excitationer »ÄTER UPP» Tg-FUNKTIONEN (streckade delen överst nedan),

och bildar därmed just från Solytan och utåt (den inre delen förblir skymd och kan inte observeras direkt) en motsvarande djupdykande SPEKTROSKOPISK (fiktiv) VÄRMEGRAD (T_SI) av den nedanstående illustrerade formen (omvända elektronförekomsten, exakt). Delen utanför Solytan sammanhänger med materialet som läcker ut (se Solvinden); Området uppvisar i det praktiska fallet stora lokala och periodiska variationer (stigflanken innehåller platåer och oscillationer som hela tiden ändras och fluktuerar beroende på den lokala aktiviteten). Området innanför Solytan förblir fördolt och kan inte observeras direkt på grund av den ljusavskärmande elektronmassan.

Se även separat Strålningstryckets temperaturekvivalent · Solytans skalvärmegrad · Planckstrålningens värmegrad · Spektroskopiska värmegraden

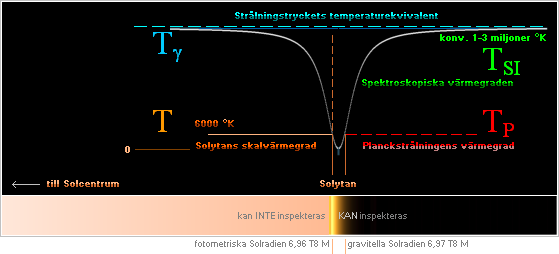
Planckstrålningens värmegrad (streckad röd TP) är den man förväntar sig från Solen som strålande kropp. Ytvärdet runt grovt 6000 °K ges med grund i spektroskopiska observationer, och man skulle därmed förmoda att temperaturen därifrån avtar sakta mot värdet runt drygt 390°K ute vid Jordbanan. I det praktiska fallet visade de första Solmätningarna istället att temperaturen just från Solytan och utåt i själva verket först dyker neråt (observerade värden mindre än 4000 °K finns rapporterade) för att strax klättra brant uppåt igen, men nu till flera miljoner grader in i Solkoronan. Detta resultat beskrivs i ENCARTA 2004 Sun som “one of the classic problems of astrophysics”. Istället för en enda värmegradstyp (Planckvärmegraden) uppvisar Solen klart och tydligt två olika.

Se även separat Strålningstryckets temperaturekvivalent · Solytans skalvärmegrad · Planckstrålningens värmegrad · Spektroskopiska värmegraden

BEROENDE PÅ VILKA SPEKTRALT EXCITERADE GRUNDÄMNESATOMER SOM STUDERAS i området, ges (naturligtvis) olika motsvarande Jordiskt korrelerade spektrala excitationsvärden (konventionellt ges uppgifter mellan 1-3 miljoner grader) — den lokala kampen mellan kraftjonisation (F_T) och elektronrekombination (r_e) bör växelverka på olika sätt för olika atomtyper. Olika källverk (som grundas på olika mätmetoder i olika epoker) redovisar olika spektroskopiska observationsdata (se Jämförande Källverk). Den generella funktionsbilden av dessa är dock densamma som visas ovan i illustrationen, från Solytan och utåt. Den inre delen förblir dold och kan inte inspekteras direkt spektroskopiskt på grund av ytskiktets avskärmande/absorberande inverkan.

Kraftjonisationens (F_T) inverkan i Solkoronan ges enligt TNED per räkneexempel (se från Koronafysiken). Resultaten visar att F_T-värdena är helt rimliga relativt de normalt Jordiska jonisationsvärdena i de observerade (typiska) fallen med Fe+16 (och högre). Det är alltså INTE fråga om någon ordinär joniserande energi som är orsak till den observerade typen (Fe+16), utan istället en kraftpåverkan som separerar — utan att excitera — elektronmassan från atomkärnan i strålningstryckets försorg.

GLAPPET på ca 1000 KM mellan fotometriska Solradien (r_F=6,96 T8 M) och gravitella Solradien (r_G=6,97 T8 M) sammanhänger just med elektronskiktet i Solytan: Från Solhistoriens början packas elektronskiktet mot g-radien (se Solranden). Området måste dock utarmas snabbt i Solhistoriens början av atomer som dels dras dit av den elektriska polarisationen och dels trycks dit av strålningstrycket — och därmed rekombinerar. De så återförenade atomkärnorna med sina elektronmassor framstår som spektroskopiskt svala mot den underliggande betydligt hetare och mindre atomärt elektronbesatta Solytan, och skapar på så sätt det s.k. omvändande skiktet: strålningen från den underliggande Solytan absorberas i »det svala» skiktet ovanför och framträder som ljusa spektrallinjer mot en mörkare (svalare) bakgrund (s.k. Fraunhofers linjer). Se mera utförligt i Solklotets Elektronfrihet och Solranden.

Spektrala värmegradens funktion blir alltså, som ovan (helt enkelt och idealt), sammansättningen med Tg=k_T/r och elektronförekomstens ytpulsform

f (r_e)= a(b+c[d(r–e)]²)^–1. Speciellt cd-koefficienterna blir mycket stora på grund av den snäva öppningen e=(r_G–r_F)/2, eller ca 1/1400 av Solradien. Den sammansatta funktionen för r blir alltså (utan vidare fördjupningar)

T_SI = k_T/r – a(b+c[d(r–e)]²)^–1 ...................... °K

Infällda beteckningar ^MT ^MD anger motsvarande kurvor för temperatur (T) och täthet (D) i Solen enligt modern akademi [från BAs128 fig.8.1—8.2].

Den tjocka blå linjen i figuren ovan markerar den föregående härledda Spektroskopiska Jonvärmegraden i Solen ENLIGT TNED — och som (vi nu vet) omöjligen kan härledas genom den modern akademins lärosystem: man känner ingen annan värmegrad i fysiken än T_P.

I gängse verk (2007) ställer man frågan: hur ska man förklara ENERGIN i Solkoronan? En så hög jonisationsgrad som Fe16⁺ har observerats.

MEN Det finns ingen joniserande energi i Solkoronan — enligt TNED. Jonisationen sker inte per energi utan per kraft genom strålningstryckets inverkan (se Kraftjonisation), och den kan inte härledas i modern akademi (MAC) eftersom man inte förstår funktionen p®T utan envisas med att DIKTERA fysiken på omvända vägen, p¬T . MAC befinner sig i låsning. Se även RÄKNEEXEMPEL i Koronafysiken som visar att TNED håller. Se även Vad gör Modern Akademi för Fel?

Se även de kompletterande värmekurvorna från föregående omnämnda konventionella oberoende källor (särskilt) i Källa 2 och Källa 4 som kvalitativt verifierar T_SI-kurvan — samt även den äldre källan från BONNIERS ASTRONOMI 1978 s136.

Notera att endast EN av de fem värmegraderna T | T_g | T_W | T_P | samt T_SI är känd av modern vetenskap och akademi: Det universella material- och täthetsoberoende Planckvärmet T_P. De övriga finns (här veterligt) inte omnämnda i den tillgängliga litteraturen.

De fyra värmegraderna

| Tg | Tw | T | TP |

beskrivs separat i VÄRMEGRADERNA I TNED.

KORONAJONISATIONEN visar BERÄKNINGSEXEMPEL som bekräftar den kraftjoniserande inverkan av Tg i Solkoronan. Se beskrivning i KORONAJONISATIONENS FYSIK med Joniseringen i Solkoronan.

Koronafysiken · modern akademi

Vad gör MAC fel?

Koronafysiken, spektrala värmegradens grunder

VAD GÖR MODERN AKADEMI FÖR FEL?

STRÅLNINGSTRYCKETS TERMONUKLEÄRA EKVIVALENT, se STRÅLNINGSTRYCKETS TERMONUKLEÄRA EKVIVALENT , ^gp = 2ak₀T⁴/c₀

från Stefan-Boltzmanns strålningslag

P = aAkT⁴ .................. Stefan-Boltzmanns strålningslag, A anger strålytan, W

Med P=E/t=pV/t ges p=Pt/V. Då är p = Pt/V = (aA · k · T⁴)t/Ad = (a · k · T⁴)t/d.

Elektriska verkan av p på Q sker alltid i energizonen med divergensen [Se även från Potentialbarriären]

t^–1d=c₀/2=c_z där laddningspotentialen i Q är maximal. Därmed t/d=2/c₀

vilket ger trycket p som ett

KÄRNINDUKTIVT VÄRMEMOTSTÅND (^gp) enligt

p = 2(a · k)T⁴/c₀

Med (se Konstanten i Stefan-Boltzmanns Strålningslag)

2k/c₀=k_P=2(5,6689315 t8)/(2,99792458 T8)=3,7819 t16 [°K⁴WS/M³=JM^–3°K^–4=NM^–2°K^–4]

ges

p = ak_PT⁴ := ^gp ....................... strålningstrycket, kärninduktiva värmemotståndet, N/M²

k_P = 2k/c₀ = 3,781904041 t16 NM^–2°K^–4

som visar att strålningstrycket p®T är en värmegivare,

kan inte härledas ur den moderna akademins lärosystem.

Varför inte då?

Därför att den moderna akademins lärosystem inte har något utvecklat begrepp för ordningen

p®T®P

KÄRNtrycket p från massdestruktioner (m®g) är temperaturens T absoluta generatris och som leder till effekten P

Den primära värmegivaren är (m®gp®T);

Modern akademi har helt missat fysikens elementära värmegrunder. Alldeles tveklöst helt klart är det så.

Jämför den moderna akademins ”termofysikens första huvudsats”.

Stefan-Boltzmanns strålningslag är välkänd i modern akademi. MEN:

Man tillämpar istället betraktelsesättet (typ dockskåpsteater):

T®p®P

temperaturen genererar trycket som leder till effekten

Den primära värmegivaren är T

och som leder till föreställningen om

1. ett kinetiskt strålningstryck med betydligt mindre magnitud (se JÄMFÖRANDE RÄKNEEXEMPEL) och

2. oförmågan att härleda PLANCKS STRÅLNINGSLAG

med grund i de allra minsta våglängderna som utgår från noll

och som är själva den temperaturgenererande fysikens (Planckstrålningens) absoluta grundval.

Se även i härledningen till Strålningstrycket, med Plancks strukturkonstant som är helt avgörande. Se även Neutrinospektrum.

Modern akademi missar den delen. HELT. E=hf. Se utförligt från Planckringen, där beskrivs hela ämnet — från grunden: atomkärnans härledning. Den existerar inte i den moderna akademins lärosystem. Och den kommer heller aldrig dit. (Lärosystemet i modern akademi är felaktigt grundat, och det kan inte användas för att beskriva eller förklara naturfysiken: det måste förr eller senare överges för vad det är: ett primitivt, ytligt tänkande som [med grund i 1800-talets sensationella omvälvningar] anser att intelligensen är en människoskapelse, inte en föregiven naturlig urgrund som människan hämtar sitt dagliga bröd ur).

Varför då?

Därför att modern akademi inte kan härleda ATOMKÄRNAN,

se från Planckringen, vilket i sig beror på att

modern akademi inte kan härleda DEN ELEKTRISKA LADDNINGEN Q=Ö (m/R)(A/dT),

se Q, med de följande och avgörande PLANCKEKVIVALENTERNA, se PLANCKEKVIVALENTERNA (med vidare), som istället blandas ihop med RELATIVITETSTEORIN, se RELATIVITETSTEORIN. Och varför kan inte moderna akademi härleda elektriska laddningen? Därför att

modern akademi inte skiljer mellan punkt (differential dx) och intervall (differens Dx),

se faktorn dT i Q, utan sätter likhetstecken mellan dessa (se dx=Dx) för att

annars kollapsar den under det berömda 1800-talet uppkomna moderna akademins föreställning om var den rent MATEMATISKA intelligensens främsta företräde har sitt huvudsäte. Nämligen, enligt relaterad fysik och matematik, i naturen. Inte i modern akademi.

Ingen av oss kan vända sig till MAC (Modern Academy) med dessa frågor därför att det inte finns någon där som kan svara — ÄVEN om viljan skulle finnas.

Pröva gärna själv.

Se även från Neutrinospektrum.

Spektrala värmegradens funktion END.

Allmänna gaslagen

Allmänna gaslagen pV=kT — Se även grundformerna i Termodynamikens primära energiekvivalenter.

RÖRELSENS ALLMÄNNA TILLSTÅNDSLAG eller

Allmänna Gaslagen

Inledning

MASSENHETEN u OCH FIXMASSAN M

Med föreställningen att all materia som består av fritt rörliga partiklar kan återföras på en fast absolut minsta massenhet u som kan bygga U större masspartiklar m₁ med massan m₁=uU, kan alla massor m beskrivas m=Nm₁=NuU med N som antalet m₁ i m. Då gäller också m/U=Nu.

Betrakta

m Nm₁ NuU M

—— = ——— = ——— = Nu = ———

U U U U=1

OM M fixeras till en fast preferensmassa M_konstant — som kopplar till enheten U=1 — blir också N en konstant eftersom u är den fasta massenheten. Genom konstanten M blir då alla massor m automatiskt justerade via den numeriska enheten U så att alla möjliga m med alla möjliga U bildar en ekvivalent m/U=konstant=M. Tätheten (r=m/V) för vilken som helst massa med fritt rörliga masselement lyder då m/V=m₁/V₁=M/V₀. Från förutsättningen m=Nm₁ ges N=m/m₁ och därmed N=m/m₁=V/V₁.

Med förutsättningen att fixmassan M i rummet med volymen V befinner sig i gas eller ånga

inte fast eller flytande, ty dessa kan bägge återföras på principiellt samma rörelselöshet eller med samma innebörd inkompressibilitet och betraktas därför i den enkla matematiska fysikens grundform som väsentligen fasta, stela material som beror av interna elektriska bindningskrafter

med tätheten r₀=M/V₀, utan hänsyn till andra krafter än de som lyder under kinetiken (ingen elektricitet alltså), vid en bestämd temperatur (vattnets fryspunkt), samt vid ett bestämt tryck (vid havsnivån, ekvatorn) vilket vi kallar

STP

STP (Standard Temperature and Pressure), kommer alla möjliga sammansättningar m/U att uppvisa exakt samma beteende som M förutsatt att mätningar och observationer görs under STP. Därför, nämligen, att m/U=M.

Oavsett ämne skulle man därmed kunna bestämma en fysisk gaspartikels massa m₁ enligt m₁=uU=m/N förutsatt man visste N, och därmed få grundläggande uppgifter om materiens minsta beståndsdelar.

Under 1800-talet tilldrog sig dessa tankegångar ett stort och intensivt intresse bland vetenskapsfolket.

Med de nämnda förutsättningarna kan materiens allmänna grunder beskrivas generellt genom en allmän matematisk fysik enligt allmänna tillståndets rörelselag eller allmänna gaslagen. I komprimerad syntes framgår kärnan i allmänna gaslagen som följer:

Summering

SUMMERING — Allmänna gaslagen i komprimerad syntes

Vid STP [Standard Temperature and Pressure] med täthetsenheten KG/M³ kan alla gaser (och ångor) återföras på en enda ideal fundamentalgas som följer energiekvivalenten

Fd=E=(F/d²)d³=(F/A)V=pV; p_TRYCKETV_VOLYMEN=k_370,95002T_{KELVINTEMPERATUREN}.

Den består av N=2,6869722 T25 stycken ideala mekaniska sfärer inom volymen V=1 M³, var och en med massan u=1,66033 t27 KG, totalt med en fundamental masstäthet av

r₀= 0,0446126 KG/M³ (mycket nära envärd Vätgas). Med varje sfär sammansatt av U₀=22,415189 stycken u ges en gasekvivalent med en masstäthet r=m/V av 1KG/M³ (nära Neon). Vilket vill säga;

ur₀^–1N = 1M³ = uUr^–1N.

Tätheten för en godtyckligt aktuell gas eller ånga beräknas då

r=Ur₀=(U₁+U₂+U₃+…+U_n)r₀.

Molbegreppet

Begreppet mol (eg. grammol) används traditionellt för antalet

NU₀/1000=(2,6869722 T25)(U₀=22,415189)/1000=6,02289 T23, även benämnt Avogadros tal.

Exempel

Då man i konventionell facklitteratur anger (t.ex.) »… per mol» menas alltså »… per NU₀/1000 stycken enheter (atomer eller molekyler av godtycklig sammansättning)».

— Se en mera utförlig genomgång med exempel och härledningar i Molbegreppet i MKSA-systemet.

Enligt allmänt tillgängliga referensverk formulerades allmänna gaslagen (pV=kT) först på 1600-talet av Robert Boyle. Dess olika delar med termer, begrepp och konstanter bildar på sitt sätt grundvalen i den (s.k.) moderna vetenskapshistorien.

Artikeln nedan beskriver allmänna gaslagen mera i detalj.

Allmänna Gaslagen — Härledning — Se även grundformerna i Termodynamikens primära energiekvivalenter.

Se även från INLEDNING

ALLMÄNNA GASLAGEN — pV=kT

Allmänna gaslagen med absoluta temperaturskalan

Den elementära teoretiska metoden för att finna materiens minsta beståndsdelar

MATERIENS ALLRA ENKLASTE VARIATIONSMODELL utgår från tillståndets princip i formen av en ideal fullständigt stel och orörlig kristall vid 0°K.

Utarbetandet av denna enkla materiemodell hjälper oss bl.a. att finna betydelsefulla svar på frågor som berör materiens minsta beståndsdelar.

Härledning

Vi tänker oss kristallen som en (tunn) jämntjock rektangulär platta P med toppytan A och en fast fixerad massa (M_konstant). Kristallen består av ett visst antal fundamentala masselement (atomer eller molekyler). Över P ligger ett lock L med tyngden (F). Varje temperatur T som skiljer sig från 0°K betyder att kristallens molekyler kommer att börja flytta på sig (i vertikalled) vilket medför att L lyfts en sträcka d. Därmed har den ideala kristallen förvandlats till en ideal gas; av Ad bildas en volym V. Är V noll är också T noll. Vi säger att T>0 åstadkommer ett statiskt tryck p=F/A på L. T betyder alltså detsamma som inre rörelse mellan de ideala kristallatomerna.

Arbetet E=Fd som åtgår för att lyfta L beror enbart på d då F via lockets tyngd är given. d bildar därmed den direkt proportionella ekvivalenten till temperaturen T; Dd/DT=konstant=k=DE/DT. Förhållandet mellan ändringar i T och d (eller E) är alltid exakt proportionella: kT=E. Därmed är allmänna gaslagen formulerad,

E = Fd = pAd = kT = pV

pV = kT ........................................... allmänna gaslagen, Joule

k ..................................................... fundamentala gaskonstanten, J/°K

Med ytan A given ändras alltså volymen (DV) eller trycket (Dp) proportionellt mot temperaturen enligt DV/DT=konstant=Dp/DT.

Praktiskt

Enklaste mätanordningarna för att erhålla relativt goda approximativa grunddata är en kombination av glas (behållare, rör-kärl), luft och kvicksilver.

Vatten kan användas i stället för kvicksilver (numera klassificerat som gift), men då endast i ett begränsat temperaturintervall; vattnets förångning kan ge (våldsamt) stora mätfel eftersom bara minsta lilla vattenmängd ger en stor gasvolym (förhållandet är 1/1250 mellan vattenångans och vattnets täthet);

Höjden 8/1000 mM vatten i en 4×7mM PVC-slang ger i ånga en 10mM hög pelare.

För stora temperaturändringar (0-100°C) är olika plastmaterial som behållare uteslutna vid mätningar då detta material har en påtagligt stor längdutvidgningskoefficient. Glas är det idealiska materialet (helst kvartsglas).

Allmänna Gaslagen — Absoluta temperaturskalan

Absoluta temperaturskalan, Kelvinskalan och Celciusskalan

ABSOLUTA TEMPERATURSKALAN

— så framkommer den

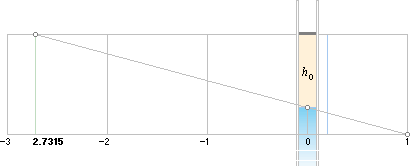
h₀-gaspelaren krymper mot absoluta nollpunkten och expanderar obegränsat åt andra hållet.

Höjden h_K i den inneslutna luftvolymen V avsätts ekvivalent som horisontell enhet 1 vid kokpunkten (enheten 1 i figuren ovan, h_K=h₀). Därefter läggs V i smältande is. Minskningen h_i (den blå delen ner till baslinjen under h₀ i figuren) från h_K avsätts som höjden vid horisontella nollpunkten 0. Då bildar h_i med h_K=1 förhållandet h_i/1=1/3,7315 som är termiska naturkonstanten i den helt linjära absoluta temperaturskalan. Med indelningen i 100 enheter om 1° (en värmegrad) för h_K med nollan vid h_i får man Celsiusskalan, och med absoluta nollpunkten för volymtrycket vid –273,15°C får man Kelvinskalan.

Genom att använda en (av en kvicksilverkula) innesluten mängd vanlig luft som ett substitut för den helt ideala allmänna gasen med dess sammandragning och utvidgning mellan de två fundamentala materietillstånden vattnets fryspunkt och kokpunkt som temperaturgivare motsvarande enheten 1 (is-ånga) för temperaturreferensen — och därmed avläsa motsvarande metriska nivåskillnader i luftvolymens ändring (h_K till h_i, allmänna gaslagen ger då en helt linjär graf) — kan man (med hyfsad noggrannhet) finna den linjära grafens teoretiska utsträckning (absoluta nollpunkten) vid grovt sett –2,70 enheter (mera exakt vid –2,7315). Den ideala gasens volymtryck är då noll.

Den undre gränsen –2,7315 is-ånga-enheter markerar via nollvolymtrycket absoluta nollpunkten och därmed den absoluta temperaturskalan.

1/100 av den naturliga termiska is-ånga enheten kallas en värmegrad. Den benämns 1gradCelsius och skrivs 1°C med nollpunkten vid isfasen. I den absoluta temperaturskalan med nollpunkten vid –273,15°C kallas då Celsiusskalan för Kelvinskalan. Det gäller alltså att

1°K = 1°C

Enda skillnaden mellan skalorna är att nollpunkten ligger på olika ställen.

Allmänna Gaslagen — Fundamentala gaskonstanten

Fundamentala gaskonstanten

k beräknas pV/T genom att sätta V=1M³ och använda ett standardvärde (STP Standard Temperature and Pressure) för trycket p=1atm=1,01325 T5 Pa = 1,01325 T5 N/M² = 1,01325 bar (i äldre standard ca 760mM Hg eller »1 torr») vid havsytan vid

T=0°C=273,15°K. Man får alltså k=pV/T=(1,01325 T5 N/M²)(1M³)/(273,15°K) som ger

k = 370,95002 J/°K ........................ fundamentala gaskonstanten

Allmänna Gaslagen — Allmänna gaskonstanten

Allmänna gaskonstanten

Allmänna gaskonstanten

Eftersom den kinetiska energin (M_konstantv₀²/2=E_k) definierar gasmassans inre rörelse, totalt via M som en enskild fast oföränderlig massekvivalent med hastigheten v₀, kan temperaturen T betraktas som absolut proportionell mot hastigheten (eller kinetiska potentialen) v₀²,

T Û v₀²

T anges absolut från noll enligt Kelvinskalan (0°K=–273,15°C). För att få proportionalitet mellan storheterna för T (°K) och v₀² (M/S)² införs proportionalitetskonstanten R som ger

RT = v₀²

Med ytterligare en justering för rörelseenergin ges i Joule/KG

RT/2 = v₀²/2 = RT = E_k/M

R/2=R;

R = v₀²/2T ................................................... allmänna gaskonstanten, J/(KG°K)

Allmänna Gaslagen — Boltzmanns konstant

Boltzmanns konstant

Boltzmanns konstant

I inledningen fastställdes förutsättningarna för hur fixmassan M kopplar till alla möjliga m via koefficienten U enligt

m/U=konstant=M=Nu. Speciellt framgick att N=m/m₁=V/V₁ (Avogadros lag), varigenom V₁=V/N.

Massenheten u representerar den minsta möjliga massdel som den kinetiska rörelseenergin kan återföras på med hänsyn till alla möjliga m-värden.

Varje gasboll eller molekyl m₁ kan då bestå av ett antal U massenheter,

m₁=Uu ................... gasbollens massa, KG

U ............................. bollvikten, molekylvikten eller atomvikten, anger antalet u i m₁, numerisk koefficient

Totala antalet gasbollar blir således

N = m/m₁ = V/V₁ .......................... antalet gasbollar i m, numerisk koefficient

där V är totalvolymen för m och V₁ den för m₁.

För enhetsvolymen V=1M³ får vi då

NV₁=V=1M³ ................................... konstant

Enda konstanta V₁ som kan finnas är den som associerar till u. Vilket vill säga (®, motsvarar eller bildar); V₁®V₀.

r=m/V=m₁/V₀=uU/V₀=Ur₀ ........... gasens täthet, KG/M³

Med klarläggandet av N som en konstant via M=Nu följer att volymen V i gaslagen pV=kT kan återföras på gaselementets volym (V₁) enligt ovanstående V/N=V₁. Fundamentala gaskonstanten k med ekvivalenten k=pV/T kan därmed skrivas alternativt k/N=pV/T=p(V/N)/T=p(V₁)/T.

Denna k-form kallas konventionellt Boltzmanns konstant

b = k/N ........................................... Boltzmanns konstant, J/°K

Allmänna Gaslagen forts.

Allmänna gaslagen kan därmed också skrivas pV=NbT=E. Vi ska längre fram se hur b också kopplar till allmänna gaskonstanten R.

Med V=enhetskonstant som ger V₁®V₀ får vi alltså även

V₁=N^–1M³ .................................... konstant

u/V₁=r₀ ......................................... konstant

u=V₁r₀ .......................................... konstant

m=m₁N=UuN ;

m/U=Nu=NV₁r₀=1M³r₀ ............ konstant

m/U=1KG/U₀=1M³r₀ .................. konstant

U₀=1M^–3KGr₀^–1=U/m · 1KG .... konstant

Se även i Konstanternas värden längre fram.

Beskrivningen av allmänna gaslagen fortsätter nedan i artikeln om temperaturbildningens uppkomst.

Allmänna Gaslagen — Orsaken till T

Orsaken till T

Orsaken till T inryms inte i allmänna gaslagen.

Ändringar i T resulterar i ändringar i pV — men omvändningen har ingen koppling därför att orsaken till T innefattar strålning (induktion) och den omfattas inte av kinetiken.

[Se DEEP från GRIP samt Ljusets friställning från kinetiken].

Allmänna gaslagen fungerar alltså på sätt och vis som en enkelriktad väg i avseende på de ingående parametrarna och hur de ska tolkas, förstås och användas.

Jämför konstant volym V i pV=kT: enda sättet att ändra pT är att gå från T till p; konstant tryck p: enda sättet att ändra VT är att gå via T.

Värmebildningen, Grunder

TEMPERATURBILDNINGENS INDUKTIVA GRUNDER

Orsaken till T inryms inte i allmänna gaslagen

VÄRMEBILDNINGENS GRUNDER

Eftersom ljusets fysik inte lyder under kinetiken (ljusvägen [divergensen] [tomma rymden] är viktlös, se Ljusfrihetssatsen) kan varken ändring i explict tryck (p) eller ändring i explicit volym (V) förorsaka ändring i T. Allmänna gaslagen innefattar bara ändringar från T till pV, aldrig omvända vägen.

Alla ändringar i pV måste gå genom ett arbete och arbetet återfaller alltid ytterst på en masslös överföring av energi enligt (m®g) genom den primära massförstöraren E=mcc; Alla fysikaliska tillståndsändringar återfaller ytterst på att T ändras masslöst. Därmed är orsaken återförd på massdestruktionen i allmänna kosmiska tillståndsekvationen. På detta sätt kan man säga att allmänna gaslagen, eller rörelsens allmänna tillståndslag är en direkt konsekvens av den allmänna kosmiska tillståndsekvationen, nämligen via (m®g).

Uppkomsten av T ur den termiska energin — hur tryck och volym kopplar till temperaturens bildning

Genom energilagen sker värmeöverföringen — temperaturbildningen T — på omgivande massystem enligt den (kosmiska) primära masslösa överföringen av strålning (g, värme och ljus) från en massdestruktion enligt (m®g) via den primära massförstöraren E=mcc. Denna masslösa överföring lyder alltså INTE under kinetiken (Se även DEEP från GRIP via POM2). Följaktligen gäller heller inte allmänna tillståndets rörelselag eller allmänna gaslagen med ändringar från p eller V till T. Ändringarna kan bara ges från T till pV, aldrig reverserat: Ändringar i tryck eller volym har ingen obetingad koppling till temperaturen i allmänna gaslagen. Därför, nämligen, att sättet på vilket temperaturen kan ändras med arbetet att ändra tryck eller/och volym beror på tiden för ändringen samt material [Se även DEEP]: temperaturdynamiken är (starkt) materialberoende. Det finns alltså ingen enkel koppling.

COEI

COEI — Conservation of Energy by Induction

Värme är (således) i sin grund en masslös överföring av induktiv effekt från en strålkälla (t.ex. från Solen) U_ind på elektriskt laddade målobjekt (elektroner) Q_s. Effekten resulterar i att Q_s påförs en acceleration, alltså en rörelse. Bindningen för Q_s på egna modersystem påverkas, och därmed åstakoms den allmänna mekaniska struktureffekt i hela målsubstansen vi kallar för temperatur. Energin i överföringen kan då beskrivas allmänt på formen

E_e = U_indQ_s

I relaterad fysik kan då den allmänna induktiva överföringen i energi mellan källa-mål (k beror här på materialgeometrin) beskrivas enligt

U_ind=E=^UQ/Q_s=L(di/dt)k=Lk

Ledet beskriver hur energin bevaras genom induktionen och refereras i denna framställning som COEI (energins bevarande genom induktionen).

Med U_ind givet bestäms värmeeffektens magnitud av målobjektets Q_s. Den värmestrålning som är associerad med Q_s (målvärmestrålningen) kan betraktas som en funktion av frekvensen [se utförlig beskrivning i PEFECT, Photoelectric effect, fotoelektriska effekten] enligt

E_e = hf = U_indQ_s

Den rörelseenergi (E_k) i målsubstansen som alstras till följd av v(Q_s) från U_ind beror i hög grad på hur substansen är sammansatt samt under vilka förhållanden den verkar i fysiken. Här har alltså elektriska (och magnetiska) bindningskrafter stor betydelse, medan sådana inte alls förekommer i allmänna gaslagen.

Hur fungerar det?

Allmänna Gaslagen forts.

Hut T bildas ur E

Den relaterade fysikens beskrivning

HUR TEMPERATUREN (rörelsen) BILDAS UR VÄRMET (induktionsenergin)

Kinetiken via g (allmän beteckning för em-strålningen) börjar från divergensen [Se utförligt från LJUSFYSIKEN och DEEP] c_z=c₀/2 i energizonen — ekvivalensen mellan ljusenergin och gravitationsenergin, som definieras från potentialbarriären — stället där Q tas. I den fria rymdens toppdivergens c₀ finns (nämligen) ingen massa att gripa tag i. Där c₀ finns, finns heller ingen massa, analogt nollgravitation.

Den elektriska impulsen dm_ec_e som initierar accelerationen i den kinetiska kraftbildningen, ingriper alltid i en Q-massa i energizonen där divergensen c_z=c₀/2 råder.

Eftersom ingreppet följer det allmänna impulsmoment h=mcd som sammanhänger med massans fundamentalform, se även från Planckringen, och därmed spinnets princip, genomlöps också d i mcd periodiskt via divergensen enligt d=c_zT=c_z/f. d bildar alltså en våglängd l med frekvensen f. Därmed

h=mcd=mcc_z/f varav mc = hfc_z^–1. Med andra beteckningar i differentialer,

dm_ec_e = dh/l = dhfc_z^–1 ; m_ec_e = h/l = hfc_z^–1

Med värmestrålningens energi E_e via divergensen c_e som givare, och rörelseenergin E_k via hastigheten v_k som mottagare,

förhåller sig energierna som hastigheterna,

E_k/E_e=v_k/c_e

Vi studerar detta mera ingående. Se även grundformerna i Termodynamikens primära energiekvivalenter.

MIC

Förhållandet mellan energimängderna är detsamma som förhållandet mellan den mekaniska hastigheten v_k och den elektriska divergensen [Se utförligt från LJUSFYSIKEN och DEEP] c_e som verkar i samband med källstrålningen: Vi ser direkt att överföringen tvunget bygger på att c>v, analogt att E_e>E_k.

Det massinteraktiva sambandet (MIC, mv=hl^–1 fråm h=mvr med r=l) visar hur v_k (här v₀) och c_e (här 2c_z) sammanhänger via strålningsfrekvensen enligt

Mv₀=h/l=hfc_z^–1

Mv₀c_z = hf = U_indQ_s=E_e

I ekvivalenter bildar den elektriska impulsen dm_ec_e — den initierar accelerationen i kraftbildningen — den mekaniska impulsen dm_kv_k så att vi får ekvivalenterna

dm_kv_k=dm_ec_e = dm_kv_k²/v_k=dm_ec_e²/c_e = dE_k/v_k=dE_e/c_e ; E_k/v_k=E_e/c_e

;

E_k/E_e=v_k/c_e

c_e=c₀

v_k=v₀

c_z=c₀/2 .................................................................... energizonens divergens, från potentialbarriären

m_k=M

;

Mv₀ = h/l = hfc_z^–1 = hf(c₀/2)^–1

Mv₀c_z = hf = U_indQ_s = E_e = Mv₀c₀/2 = mc²

;

TemperaturEneregiEkvivalenten

E_k = E_ev₀/c₀ = E_e · v₀/2c_z = Mv₀c_z · v₀/2c_z = Mv₀²/2

ALLMÄNNA GASLAGEN GER då

E_k = Fd = pAd = pV = kT

Arbetet

Arbetet Fd=pAd återfört på den ensamma ideala gasbollen med den endimensionella hastigheten v utmed d för hela den reala gasmassan m utför sitt tryckande arbete endast i kontakten med det tryckande locket L med tyngden F (se allmänna gaslagen från härledningen).

I den linjära gasbollens FRIA vägform d=vT där v är konstant gäller därför

Fd = mad = m · v/T · d = mv · d/T = FT · d/T = p · d/T = pv = mv²

DEN MOTTRYCKANDE GRAVITATIONEN i formen av det tryckande locket L med kraften F möts alltså av

Fd = mv² = Gm²/(d/2) TY

EKVIVALENSEN MELLAN RÖRELSEENERGI OCH GRAVITATIONSENERGI GER speciellt för termodynamiken

mv²/2 = mw² = Gm²/d ; mv² = 2mw² = 2Gm²/d = 2ma(1M) ...................... = Fd = pAd = pV = kT = E_k

Se även grundformerna i Termodynamikens primära energiekvivalenter.

Allmänna Gaslagen — Betydelsen av för identifieringen av u

Mv022

Betydelsen av Mv₀²/2 för identifieringen av universella massenheten u

MED ANDRA ORD:

Vi måste skilja mellan reala fysiska storheterna mv och ideala gasiska ekvivalenterna Mv₀:

E_k = mv² = Mv₀²/2 — Se även grundformerna i Termodynamikens primära energiekvivalenter.

v tillhör den reala gasmassan m medan v₀ bildar formen för den fristående energiekvivalenten till den fundamentala fixmassan M=Nu=m/U som inte existerar i fysiken i någon exakt motsvarighet — men som grundlägger beskrivningen av materiens minsta delar genom införandet av massenheten u, och som beskrivs vidare nedan.

VARFÖR DESSA OLIKHETER?

Därför att ljusfysiken inte kopplar till kinetiken. Det är och förblir en omöjlighet att anställa exakta analogier mellan ljusfysiken och mekaniken; ljusfysiken lyder inte under kinetiken, analogt inte under mekaniken. Men mekanikens begrepp — tillståndets princip genom jämvikt och balans — är de enda logiska arbetsverktyg som finns; Igenom dessa måste således tvunget också ljusfysikens detaljer — induktionsfysiken — relateras. Därav ekvivalenterna.

Rörelseenergins minsta del arbetar på massenheten u enligt E_u=uv₀²/2. Rörelseenergin via u på totala antalet gasbollar N är då

E_N=Nuv₀²/2=Mv₀²/2=E_k.

Som vi ser är det alltså nödvändigt att särskilja den kinetiska v-komponenten — beroende på vilken massform vi rör oss med;

v tillhör den reala gasmassan m medan v₀ bildar den fristående energiekvivalenten till den fundamentala fixmassan M=Nu=m/U.

Vi har därmed, med grund i massenheten u, sambanden

E_k=N · uv₀²/2=Mv₀²/2=MRT Se även grundformerna i Termodynamikens primära energiekvivalenter.

M=Nu=m/U=r₀M³ ...................... konstant. ideala gasmassan, KG

U₀=1/Nu KG .................................. allmänna ideala gasatomvikten via enheten (M)=1KG, numerisk koefficient

N .................................................... konstant=Loschmidts tal, numerisk koefficient

U₀N=u^–1KG .................................. Avogadros tal, numerisk koefficient

r₀ = 1/U₀ M^–3KG = Nu · M^–3 ...... konstant. ideala gasmassans täthet, KG/M³

Se vidare i Konstanternas värden.

Allmänna Gaslagen — Momentekvationen

Momentekvationen

AVSLUTNING

Från föregående M_konstantv₀²/2=E_k med RT/2=v₀²/2=RT har vi därmed sammanbundit temperaturen som orsakad av en allmän termisk strålning med allmänna gaslagen enligt

RT=E_k/M.

E_k=MRT=Mv₀²/2=pV=E

Volymtrycket pV via momentet Fd=pAd utverkar alltså samma arbete som rörelseenergin för M enligt

E=E_k

k=E/T=N · uv₀²/2T=NuR

k=NuR=(m/U)R=r₀1M³R=RM

k ............................ fundamentala gaskonstanten vid STP=pV/T=1,01325 T5·1/273,15=370,95002 J/°K

R=kU₀ .................. allmänna gaskonstanten

b=k/N=uR ............ Boltzmanns konstant

Sambandet — GasbollarnasMedelhastighet

MOMENTEKVATIONEN — gasbollarnas medelhastighet

Arbetet Fd=E i en gas med godtycklig massa m utövar via gashastigheten v ett endimensionellt tryckande momentet över d enligt

Fd=mv²=pV=kT=E ........................ momentekvationen

Totala energin är summan av energierna i alla möjliga riktningar.

För de 1-3 dimensionsriktningarna får man då 1-3 momentsummor som sammantagna ger respektive

Fd_x =mv² =1kT_x v=v_x

Fd_xy =mv² =2kT_xy v=v_xy

Fd_xyz =mv² =3kT_xyz v=v_xyz

Härur kan gasbollarnas totala medelhastighet v beräknas för en given gasmassa m vid absoluta temperaturen T enligt

————————————————————————————————————————

v = Ö 3kT/m ...................... via gasmassa och temperatur, k=370,95002 J/°K

————————————————————————————————————————

Eller, alternativt med de andra konstanterna i föregående samband (för konstanternas värden, se efterföljande artikel).

v = Ö 3RT/U ...................... via atomvikt och temperatur R=8314,9148 J/[KG°K]

v = Ö 3bT/m₁ ..................... via gasbollens (molekylens) massa och temperatur, m₁=m/N_{2,68697 T25}, b=1,3805502 t23 J/°K

För vätgas (m = 0,09, T=273,15) är _VÄTEv_STP=1838 M/S. För luft (m @ 1,293) ges motsvarande 485 M/S, och för syre (m = 1,43) 461 M/S.

Uppgifterna för syre och väte är kontrollerade i Fysik, R Westöö, Esselte 1975 s8, resp. 460 M/S och 1800 M/S.

Genom olika statistiska beräkningar har man ur ovanstående faställt olika maxima och minima för medelvärden i hastigheterna.

Dessa samband beskrivs utförligt i FOCUS MATERIEN 1975 s188.

Allmänna Gaslagen forts.

KONSTANTERNA — konstanterna

KONSTANTERNAS VÄRDEN

I den verkliga fysiken finns inte den ideala gasmassan M. Därmed finns heller strängt taget inga exakta värden på den ideala atomvikten U₀.

Det närmaste vi kan komma i ren algebra är via sambandet

U₀N=u^–1KG .................................. Avogadros tal, numerisk koefficient

Värdet på massenheten u har genom vetenskapshistorien haft olika referenser. Numera (från år 1960) används 1/12 av atomvikten för ₆C¹² [ENCARTA 99 Molecular Weight]

1u ................................................... 1,66033 t27 KG [ENCARTA 99]

Tidigare (före år 1960) användes enheten för 1/16 av syreisotopen ₈O¹⁶.

Boltzmanns konstant b=k/N=uR och därmed allmänna gaskonstanten R beror på Loschmidtska talet N. Fundamentala gaskonstanten k är känd (370,95002 J/°K).

Genom att u är bestämt som ovan får man

U₀N=u^–1KG .................................. 6,02289 T 26, Avogadros tal, numerisk koefficient

I viss litteratur med referens till begreppet grammol brukar Avogadros tal anges på tusendelen av ovan, analogt 6,02289 T23.

Idealt kan N bestämmas singulärt om man känner tätheten i KG/M³ för Vätgas (H₂) vid STP och har en separat uppmätt massa för Väteatomen (₁H¹) enligt

N=r_H2/2m_1H1=(0,0899…)/(2 · 1,0078252u)=2,68627 T25.

Detta N-värde blir emellertid unikt. För andra gaser ges ett något litet annorlunda värde.

Genom M=Nu=m/U=r₀M³ (ideala gasmassan) med U₀=1KG/Nu (ideala atomvikten för M motsvarande 1 KG) kan 1/U₀=Nu=m/U istället beräknas statistiskt genom att ta medelvärden av (högst tvåvärda) gaser via deras täthetsvärden och uppmätta atomvikter. På den vägen får man fram ett mera representativt, praktiskt medelvärde för samtliga fall.

»Det exakta värdet» på Loschmidts tal N kan alltså omöjligen preciseras men kan ges ett relativt noggrant medelvärde.

Tabellen nedan utgör en samling värden på gaser som hämtats från några olika källor och som ger ett mycket bra medelvärde i referens till uppgifter från åter andra faktaverk.

Gaser vid STP

Gaser vid STP

		m			N=m/(m1=uU)	antal m1 i 1 KG
		r=m/M^3	atomvikt	KG	N	Nr^–1 = 1KG/(uU)	KG/M^3
namn	GAS	KG/M^3	U=m1u^–1	m/U=r0M^3	N1KGr	N1KG i KG	r0	källa
Väte	H2	0,09	2,016	0,0446428	2,68879 T25	2,99 T26	0,0446428	KH
Helium	He	0,1785	4,0026	0,0445960	2,68597 T25	1,51 T26	0,0445960	KH
Kväve	N2	1,251	28,0134	0,0446571	2,68965 T25	2,15 T25	0,0446571	KH
Syre	O2	1,43	31,9988	0,0446891	2,69158 T25	1,88 T25	0,0446891	KH
Neon	Ne	0,9	20,183	0,0445919	2,68573 T25	2,98 T25	0,0445919	KH
Koldioxid	CO2	1,977	44,0099	0,0449217	2,70558 T25	1,37 T25	0,0449217	GF
Argon	Ar	1,78	39,948	0,0445579	2,68367 T25	1,51 T25	0,0445579	KH
Krypton	Kr	3,74	83,8	0,0446300	2,68802 T25	7,19 T25	0,0446300	KH
Xenon	Xe	5,85	131,3	0,0445544	2,68346 T25	4,59 T25	0,0445544	KH
Radon	Rn	9,9	222	0,0445945	2,68588 T25	2,71 T24	0,0445945	KH

Källa: GF, GYMNASIETS FYSIK [åk2 1980 s159]; KH, KARLEBO HANDBOK [uppl.12 s95]

u = 1,66033 t27 KG .......... atomära massenheten, 1/12 av mest vanliga kolisotopen, 6C12 [ENCARTA 99]

r-kolumnen (m) motsvarar uppgifter från i stort sett vilken faktabok som helst (senare 1900-talets litteratur) som anger specifika vikter för gaser. U-kolumnen är beräknad från tillgängliga tabelldata över atomvikter. Kolumnerna för m/U, r₀ och N ansluter till beräkningarna från de härledda sambanden.

N_1KG-kolumnen är beräknad N_1KG=1KG/Uu. Multiplicerad med m ges N=N_1KGr-kolumnen. Den högra r₀-kolumnen är beräknad som m/U-kolumnen men anges särskilt rent för att förtydliga sammanhangen.

Frånsett koldioxidgasen (CO₂) som skiljer sig något från de övriga, blir medelvärdet i N-kolumnen

N = 2,6869722 T25 ................................................... Loschmidts tal, antalet gasbollar i 1 M³ ideal gas vid STP

Med N-värdet bestämt kan så de övriga fyllas på med bestämda värden enligt uppställningen nedan där u och k är givna.

Konstanternas värden

u = 1,66033 t27 KG ........................................ atomära massenheten [ENCARTA 99 Molecular Weight]

k = 370,95002 J/°K ........................................ fundamentala gaskonstanten [pVT^–1] vid STP

N = 2,6869722 T25 ......................................... antal idela gasbollar i 1M³ idealgas vid STP, Loschmidts tal

V₀ = 3,7216611 t26 M³= 1M³N^–1 = (2,6869722 T25)^–1 ............................................................. elementvolymen för u

r₀ = 0,0446126 = Nu = 2,6869722 T25 · 1,66033 t27 = (22,415189=U₀)^–1 KG/M³ ................ ideala gasmassans täthet

U₀ = 22,415189 ................................................. allmänna enhetsideala gasatomvikten (nära Neon. Ne[20-22])

R = 8314,9148 J/(°K) KG^–1 ........................... allmänna gaskonstanten. = kN^–1u^–1= kU₀KG

b = 1,3805502 t23 J/°K .................................. Boltzmanns konstant = kN^–1, J/°K

U₀N = u^–1 = 6,0228989 T26 ............................... Avogadros Tal i MKSA-systemet (6,0228989 T23 i grammol)

uU₀N = 1

I gängse litteratur är R specificerad som 8314 eller 8314,4 eller 8315, och Boltzmanns konstant i signifikanden som 1,380 eller 1,381, allt beroende på källa.

Så här kan det se ut:

R = 8,314 J(mol °K)^–1 ......................... [ENCARTA, Gases]

= 8,315 joule/grad kmol .................... [FOCUS MATERIEN 1975 s187sp2ö]

= 8,3144 J/mol · K ........................... [GYMNASIETS FYSIK åk2 1980 s159]

PEFECT

Fotoelektriska effekten

FOTOELEKTRISKA EFFEKTEN

elektronemission från metallytor genom ljusbestrålning — experimentella observationer från 1887

I härledningen till Grundämnenas Periodiska System genom Keplermomentet visas hur elektronmassan är bunden till sin moderatom genom resonanser. Med Planckenergin E=hf kan derssa resonanser också kallas Planckresonanser eller hf-resonanser.

Frekvenserna f (eg. resonanserna) bestäms ekvivalent av det allmänna konstanta impulsmomentet (Keplerresonanserna) J=mK under svängningsperioden (T) enligt J/T=E. Uttryckt i Plancks konstant (från år 1900) således E=J/T=hf=h(f₁–f₂)=E₁–E₂. Den minsta möjliga intensiteten i en sådan aktivitet inbegriper tydligen minsta möjliga antal elektroner, en. Då är intensitetsfaktorn i strålningen från atomen direkt proportionell mot antalet elektroner på samma sätt som strömstyrkan (intensiteten) i en elektrisk ström är proportionell mot antalet laddningar (I=Q/T).

Om frekvensen, alltså rörelseenergin, överstiger gränsen för elektronens atombindning kan den alltså frigöras (kickas ut) från atomen.

Den utkastade elektronens rörelseenergi blir en funktion av skillnaden mellan dess bindningsfrekvens (f₀) och den pålagda strålfrekvensen.

Om elektronens atombindning (eg. materialbindning) bestäms av E₀=hf₀=W blir den utkastade elektronens energi

E = h(f – f₀) = hf – W .......... fotoelektriska effekten, elektronenergin

förutsatt f >f0.

W är f.ö. särskilt låg i gruppen alkalimetallerna (3, 11, 19, 37, 55, 87).

De empiriskt experimentella observationerna från 1877 visade också att det förhåller sig så. Man hade observerat att vissa metaller avger elektroner om metallen bestrålas med lämpligt ljus.

Fenomenet fick namnet fotoelektrisk effekt.

Mätningarna på de frigjorda elektronerna visade (George Gamow TRETTIO ÅR SOM SKAKADE FYSIKEN Prisma 1968 s35)

I. Vid given frekvens men variabel intensitet hos ljuset är elektronenergin konstant medan elektronmängden varierar proportionellt mot intensiteten.

II. Med variabel frekvens emitteras elektronerna — från en viss miniminivå som varierar för olika metaller — med en rörelseenergi som är helt linjärt proportionell mot frekvensen.

…

END.

Editor2008V

Solfysiken Temperaturfysiken

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Temperaturfysiken

ämnesrubriker

innehåll:

TEMPERATURFYSIKEN

Solens temperaturfysik enligt TNED

Värmegraderna

Scolium (samlingsbeskrivning)

T · skalvärmet

Tp · Planckvärmet

Tg · stråltrycksvärmet

Tw · Wienvärmet

Värmeteorin i det allmänna lärosystemet

Massvärmet

Parannihilation — MASSDESTRUKTIONEN (m→γ) — annihilationsstrålningens grunder

E=LQ²/t² klargör: värme inte är massa och massa inte är värme

Allmänna transienteffektens funktion

Koronafysiken

Koronajonisationens fysik enligt TNED

Inledande beräkningsexempel

Joniseringen i Solkoronan

Sämsta fallets kraftpotential

Solkoronans jonisationsgräns

Teorin i TNED

Materiefysik

Massfysik

Spektroskopiska (eller Spektrala) jonvärmegraden — Solens femte värmegrad TSI

Grundteori

Jämförande observationsdata

Grafiska sammanställning · termiska observationsdata från Solytan

Spektrala värmegradens funktion

Koronafysiken i modern akademi

Vad gör modern akademi för fel?

Allmänna gaslagen

Inledning

STP

Summering — allmänna gaslagen i komprimerad syntes

Molbegreppet

Allmänna gaslagens härledning

Absoluta temperaturskalan

Fundamentala gaskonstanten — 370,95002 J/°K

Allmänna gaskonstanten — R = v₀²/2T

Boltzmanns konstant

Orsaken till T · inryms inte i allmänna gaslagen

VÄRMEBILDNINGENS GRUNDER

COEI — energins bevarande genom induktionen

Hur T bildas ur energin

TemperaturEnergiEkvivalenten

Arbetet

Betydelsen av Mv022 för identifieringen av universella massenheten

Momentekvationen

Sambandet

Gasbollarnas medelhastighet

KONSTANTERNA

Tabellvärden för gaser vid STP

KONSTANTERNAS VÄRDEN

PEFECT

Fotoelektriska effekten

innehåll (föregående):

Solfysiken · Värmefysiken

Solens Temperaturfysik · Solens 4 värmegrader · Värmegraderna

G-energins Wienekvivalent

Strålningstryckets värmegrad

Värmeteorin i det allmänna lärosystemet

Massvärmet

Solfysiken · Koronafysiken

Koronafysiken

Joniseringen i Solkoronan

Spektroskopiska värmegraden

Spektrala värmegradens funktion

Fortsättning i Solfysiken …

REGISTER

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[BA]. BONNIERS ASTRONOMI 1978

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad 10-potensbeteckning, t för 10^–, T för 10⁺

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav — liksom nedanstående tusenprefix.

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM.

TNED

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2022-12-09

*END.

Stavningskontrollerat 2008-03-06

rester

OBS BUGG I WORD 2000

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se