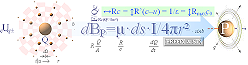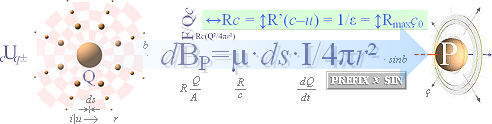MAGNETISMEN | 2007IV15 | Senast uppdaterade version: 2024-09-09 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Induktionen och Magnetismen kan [nära exakt] liknas vid mekanikens hydrodynamik: En vattendroppe som efter träffen mot vattenytan bildar expanderande ringar, magnetism, och fria droppserier via kraftrekylen, induktion. Av ej närmare känd anledning [naturföraktet frånsett] varken omskrivs eller används den analogin i den moderna akademins lärosystem.

Base • Fysikens 7 Principer | DIVERGENSEN | Ljusbrytningen | Ljusfrihetssatsen | Ljusets Gravitella Beroende | Elektriska Kraftlagen | Elektriska Laddningen | Elektriska Fältet |

Main • Kausalsambandet | MAGNETISMEN | Närverkan och Fjärrverkan | Magnetiska Kraftlagen | Expansionsintegralen | Magnetiska Konstanten | Planvektorsumman | Fältformerna | H | B i Q | B-vektorn |

BILDKÄLLA: Författarens arkiv · Ovan: 21Apr2009VattenDropDiskBild3 · NikonD90 · Detalj

Magnetismens specifika ekvationer · Rakledaren · Toroiden · Spolen · Ringen · Konen | Elektromekaniska induktionen | Magnetisk och Elektrisk Polarisation | Järnkärnetransformatorn |

magnetismen

FORTSATT BESKRIVNING AV MAGNETISMEN FRÅN INLEDNINGEN

MAGNETISMEN

MED VIDARE FORTSÄTTNING FRÅN EN INTRODUKTION TILL INDUKTIONEN OCH MAGNETISMEN

— Se även Grundläggande elektriska storheter där elektrofysikens grundbegrepp beskrivs mera utförligt

SAMMA c förenklar

Både induktionen och magnetismen är utvidgande fenomen som utbreder sig genom tomrummet inom det gravitellt reglerade området för ljushastigheten — eller som det heter mera renodlat enligt relaterad fysik: divergensen (c).

I den enklaste behandlingen och studiet av magnetismen och andra elektriska fenomen på nivån elementära samband, är skillnaderna i divergens små och kan bortses ifrån. Med denna bekvämlighet i användningen av en allmän och universell divergens c för samtliga fall, elimineras alla komplexa och komplicerade matematiska uttryck. I de flesta elementära fall måste vi också frånse de praktiska fördröjningar mellan olika delar av rymden och därmed (mycket) förenkla problemen i (den allmänna) beräkningen av magnetism och induktion i tillämpningar som rör de mer näraliggande vardagliga tingen. Ett undantag utgör Solfysikens magnetism där vi helt enkelt måste ta hänsyn till olika skärmingseffekter som normalt sett inte finns i vår vardagsmiljö. Dessa problem kommer dock inte att beröras här, men vi gör nog redan från början klokt i att iaktta en viss respekt för deras existens; Allmänna matematiska uttryck som beaktar dessa detaljer skulle generellt bli så komplicerade att kanske få (om ens några) skulle vara i stånd att hantera dem. Emellertid är det just vad som ändå sker på många håll i världen i dessa tider men då med datorernas hjälp: alltså: animeringsteknik grundat på omfattande numeriska operationer med stora parametermängder och som ingen dödlig kan hantera i någon som helst matematisk mening. Ingenting av dessa delar kommer dock att beröras mera i den följande presentationen.

*cont. MAGNETISM

En grundlig förklaring till uppkomsten av det magnetiska fältet och dess motsvarande divergens ges i

KAUSALSAMBANDET med INLEDNINGEN till induktionen och magnetismen.

Vi förutsätter här bekantskap med grundbegreppen från den inledningen.

Beskrivningen fortsätter i den här sektionen med magnetismen.

För största möjliga bekvämlighet ges länkar frekvent i den följande huvudtexten. Länkformen kopplar till aktuella avsnitt (klicka med höger musknapp på markerad text) generellt med himmelsblå text på havsgrön bakgrund som det här (här utan kopplad länk).

B-VEKTORN

Vektorrepresentationen för magnetiska fältstyrkan och hur elektriska laddningar i rörelse växelverkar

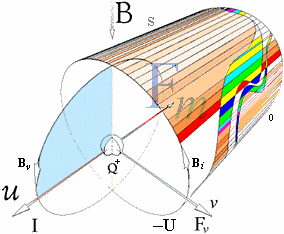
Den magnetiska fältvektorn B

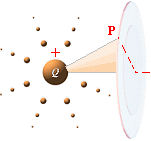
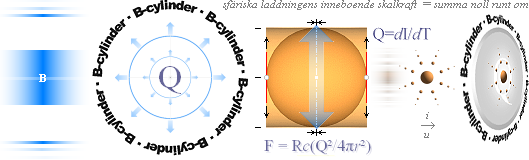
Fältringens expansion från centrallinjen

Av alla rymdpunkter i ett specifikt plan rätvinkligt Q-rörelsen, ger den centrala P den högsta magnituden i reduktionen ç₀. Från den punkten utgår den plana magnetiska fältvågen eller fältringen perfekt cirkulärt — förutsatt en idealt homogen rymd. Med vidare förutsättning i ett idealt sfäriskt Q-system, fortsätter vågen sin cirkulära expansion: den högre resistans som utgör den magnetiska fältvågen, och som börjar från R_max vid ç₀ , bryts ner som vågen expanderar. I bevarandet av elektriska konstanten (Rc) i vågen, närmar sig dess divergens likaledes toppdivergensen c₀ för fri rymd.

sammanfattning, repetition

Magnetiska fältringar utgår från varje punkt (P) i den gravitellt dominanta rymden som omger en elektrisk laddning som färdas med hastigheten v relativt P. De utgår med största magnitud från laddningens centrallinje (kortaste divergensdistansen, se illustrationen ovan t.h.). Fältstyrkan (B) i P som täckas av den magnetiska fältringen i dess expansion rätvinkligt rörelseriktningen v, beror på divergensen ç₀ i utgångsögonblicket. Reduktionen från c till ç₀ via v, formar tillsammans med elektriska konstanten (Rc=1/e) en motsvarande resistiv ökning med dess maximum (R_max) vid ç₀. Denna ökning utgör magnituden i födelsen av den magnetiska fältstyrkan. Reduktionen är punktlokal och dess riktning är i bildningsögonblicket, i den homogena och enhetliga g-rymden, fullständigt cirkulär och rätvinkligt v. Efterhand, tillsammans med de potentiella ändringarna i den omgivande rymden med tillhörande reduktioner via v då Q-systemet sveper över den stationära g-referensen, ackumuleras ringens fältstyrka över alla successiva rymdpunkter den översveper. Figuren nedan antyder hur fältstyrkan finns samlad i en rymdpunkt (P) med alla möjliga bidrag från alla möjliga punkter mellan P och centrallinjen i formen av en ideal ensam fältring som skär P.

	Notera att denna del i modern akademi och vetenskap är helt frånvarande, inte representerad, i beskrivningen av magnetismen som fenomen. Expansionsintegralen innefattas inte i modern akademi, men den förklaras perfekt av relaterad fysik.
Jämför generellt från MODERN VETENSKAP OCH AKADEMI KONTRA RELATERAD FYSIK TRE PRECISA EXEMPEL FÖR EXAKT JÄMFÖRELSE

När vågen når P, innehåller den alla de samlade (differentiellt bidragande) reduktionerna (från alla P utmed den radiella expansionen) som används i fenomenet för att bygga upp den karaktäristiska ringstyrkan med början från centrum. För att beräkna styrkan i P från en momentan lägesändring ds i positionen för Q utmed vägen s, måste alla dessa differentiella bidrag integreras. I beräkningen av en total verkan i P från ett ändligt s, måste sedan denna inre eller expansionsintegral själv integreras över s (den aktuellt kurverade strömlinjens integral).

Från denna översikt kan vi enkelt förstå att flera förenklingar och idealiseringar tvunget måste göras i den matematiska behandlingen av ämnet. Den främsta idealiseringen är att förutsätta små Q-hastigheter relativt den lokala divergensen c för att därmed förenkla den rent matematiska beskrivningen i magnetismens mest elementära hantering. Det visar sig också att laddningshastigheterna i ordinära tekniska strömledare är ypperligt små — och därmed en mer eller mindre ideal matematik som bara gynnar den här understrukna idealiseringens allmänna metod.

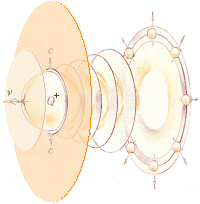
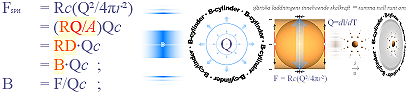
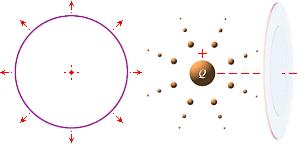
Styrkan i den expanderande ringen ACKUMULERAS därför att ringbågen »samlar» all reduktionsverkan från den växande mängden rymdpunkter i takt med att de skilda och elektriskt c-återkopplande expanderande Q-skalen skär vågplanet. Figuren nedan (vänster) är ett försök att illustrera denna detalj: hur ackumuleringen fungerar i ett idealt sfäriskt laddningssystem (Q) i respekt till ett samlande vågplan sådant det beskrivs enligt den matematiska härledningen.

Expansionsintegralen

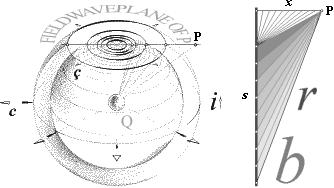
dB_Px/db_y = µ₀(I/4px)sinb·db_x .............. expansionsintegralens differentialekvation i PREFIXxSIN

exkluderad av modern vetenskap och akademi — MEN DIFFERENTIELEKVATIONENS LÖSNING FINNS UPPTAGEN, se vidare i huvudtexten

Vi observerar att skärningarna med det fasta P-planet innefattar fördröjningar mellan de olika c-expanderande Q-skalen och alltså INTE sker omedelbart för olika expanderande Q-skal. Därmed tillkommer (således) ytterligare reduktioner allteftersom i P-planet och som läggs till och synkroniserar en totaleffekt i formen av den aktuella ringexpansionen i P-planet. Erinra här endast den magnetiska fältvågens differentiella aspekt: genom att c och v inte är additiva i fysiken tvingas den magnetiska effekten helt bygga på en resistiv fenomenform rätvinkligt v i elektriska konstantens bevarande. Se även mera utförligt i KAUSALSAMBANDET. Som fältringarnas tätare R från reduktionerna ç₀ strävar att diffundera till den tunnare omgivande rymdens normala R, kan fältringen expandera med en hastighet som allt mera närmar sig normalrymdens c₀.

Hur B-vektorn förstås

DET MAGNETISKA KRAFTFÄLTET

Introduktion

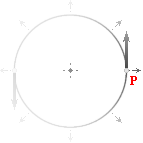
I ERINRAN AV ATT reduktionerna utgör en differentiell elektrisk fältstyrka (X) i expansionens riktning

(¬ P ® ),

kommer alla reduktioner på EXAKT r från P att framstå som helt ekvivalenta — förutsatt ideal homogen rymd. Den kontinuerliga vägformen för ekvivalenta fältstyrkan måste följaktligen följa cirkelbågens kurvatur i den expanderande fältringen: samma fältstyrka på samma r från P; Kurvan med samma reduktioner bildar kurvaturen för den effektiva fysiska och karaktäristiska magnetiska kraftens fältlinje med en motsvarande vektor (B) som representerar fältstyrkan i kurvans tangent

(¯ P ),

analogt i reduktionskurvaturens vägriktning.

Vektorn B »utgår» således — kan man säga — från punkten (P) rätvinkligt v där ekvivalenta reduktioner förenas till en sluten vägform.

Magnetiska fältstyrkans referensvektor (B) blir alltså riktad rätvinkligt expansionsriktningen: B blir den fysiska fältstyrkans momentana arbetsriktning i ekvivalens med omgivande reduktioner på samma r från P — precis som järnspånen lägger sig i ringar kring en strömgenomfluten elektrisk ledare.

Jämför resultatet av en fallande vattendroppe som träffar en lugn vattenyta; de bildade ringarna vid träffen illustrerar tämligen exakt den magnetiska fältverkan i det g-relaterade elektriska P-planet.

Den tangentiella riktningen för B är, verkligen, OCKSÅ en rent matematisk transkription som följer av de inneboende lagarna inom trigonometrin (spegel- och symmetriformer). Denna detalj beskrivs, förklaras och härleds utförligt illustrerat i

Magnetiska fältvektorns matematiska uppkomst. Nedan följer en något komprimerad beskrivning.

Att förstå B-VEKTORN

— Som magnituden för B beror uteslutande på Q-rörelsen, det är på den (effektiva) strömmens styrka, kommer adderande eller medströmmar

I = I₁+ I₂ att motsvara B = B₁+ B₂.

— Som också en minskning i strömstyrkan I minskar B med samma magnitud som I – I₂ = I₁, vilket motsvarar B – B₂ = B₁, »följer magnetismens fysik exakt matematiken».

— Då ”– I” betyder antingen en ström med motsatt Q-polaritet (+ –) relativt I, eller samma typ men i motsatt riktning, följer ur denna enkla matematiska lag att idén om reduktionen som vektor i fallen då olika laddningspolariteter är aktuella måste tolkas omvänt (reverserat).

— Som alla reduktioner i realiteten har samma riktning, alltså expanderande, inser vi att enbart dessa nu beskrivna riktlinjer som grund för magnetismens förklaring måste bli krångliga (men inte helt omöjliga);

En mera ambitiös beskrivning finns [frn.Okt2011] sammanställd i Riktningsbegreppens upphov för magnetismen [magnetismens detaljer i relaterad fysik MED Maxwells Analogier] och Riktningsprincipernas förklaring [riktningsgrunderna]. Tillägget har föranletts, främst, av angelägenheten att belysa den moderna akademins teoretiska grunder i noga jämförelse genom den numera gratis tillgängliga webbens PDF-dokument från pionjären James Clerk Maxwell och hans ledande arbeten [främst 1855-1861] inom magnetismen.

— En bra hjälp för att illustrera de olika aspekterna är att föreställa sig ett rör med ett eller flera mindre inskjutna rör motsvarande olika strömriktningar via individuella strömvägar. Genom att relatera riktningar, med eller mot, negativa eller positiva laddningar, med parallella strömvägar motsvarande rörväggarna om nödvändigt, kan alla möjliga relationer kontempleras som utgår från detta system och enbart grundat på reduktionernas enkla expanderande princip.

— Denna krävande metod för magnetismen förståelse har emellertid en mera elegant och långt enklare syntes i formen av den redan välkända högerhandsregeln. Vi studera denna nedan i HÖGERHANDSREGELN.

HÖGERHANDSREGELN

HÖGERHANDSREGELN

Överföringen av reduktioner till tangenter

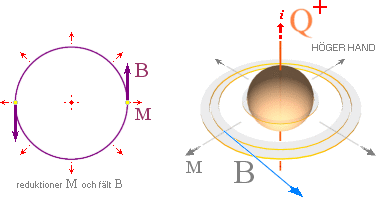
Den enkla och universella tekniken att transformera en reduktionsvektor (M, expanderande) till en motsvarande B-vektor utgörs av den konvention som blivit känd under benämningen högerhandsregeln:

Använd alltid Q⁺ som basreferens med höger hand: Sträck ut tummen att peka i riktningen v eller i för Q⁺-rörelsen. Då sluter sig fingrarna kring iv-riktningen i den magnetiska fältringens vektorriktning B analogt med fingrarnas riktning och med reduktionsvektorerna (M) expanderande radiellt utåt från det inre av handen från motsvarande Q-laddningens elektriska fältsystem:

tummen i strömriktningen, fingrarna utpekar B-riktningen.

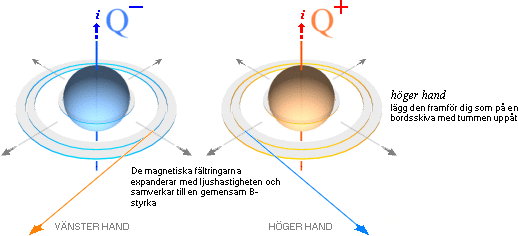
Denna enkla men mycket effektiva referens används (ypperligt) frekvent av alla som sysslar med viktiga magnetiska problem inom elektrofysiken.

För en negativ laddning Q^–, upprepa bara hela proceduren men använd vänster hand — eller se högerhandsregeln i en spegelbild. Vilket vill säga: vänsterhanden motsvarar Q^– med reduktionerna nedvikta medurs.

Högerhandsregeln Fokusera på tummen genom att föra den till pannan, fäll sedan i tanken ner reduktionsvektorerna (M, expanderande) i en moturs rörelse, vilket betyder att de kommer att peka i fingrarnas riktning. Det är vektorriktningen för den magnetiska fältstyrkan B för en positiv elektrisk laddning som lägesändrar i tummens riktning.

reduktionerna finns inte beskrivna i den moderna akademins lärosystem

HANTERING AV B-VEKTORERNA

Medriktade B-vektorer adderar de individuella fältstyrkorna, motriktade B-vektorer antingen tar ut varandra helt eller reducerar styrkan totalt. Vi observerar att denna växelverkan mellan reduktioner i varje specifik rymdpunkt bara upptar en differentiell del i den magnetiska kurvaturen. Det betyder att den (differentiella) vektorsumman för alla olika B-bidrag i P INTE påverkar den magnetiska fältvågen som sådan: den bara summerar sig själv tillsammans med andra i P, går ur, och fortsätter sedan som om inget hänt — precis som vattenvågor gör som växelverkar med summerande amplituder med bevarandet av varje enskild vågs egen individuella amplitud oberoende av de andras. Denna princip känner vi som den tidigare beskrivna superpositionsprincipen. Den är verksam i varje del av fysiken där allmänna fält- och vågfenomen förekommer i växelverkande interferens, och kan därför studeras utomordentligt i vattenbaserade tillämpningar.

PRINCIPEN FÖR DEN CIRKULÄRPOLARISERADE B-VEKTORN

Eftersom B-styrkan — reduktioner med samma magnitud — relateras till riktningen för den resulterande magnetiska fältlinjens kurvatur, inte till riktningen för reduktionerna där vi finner olika B över varje minsta ändliga intervall, blir magnetiska fältstyrkan B också oberoende av reduktionernas orientering i B-normalens plan. Det betyder, tydligen och till exempel, att B-fältet i centrum av en strömgenomfluten ring där alltså reduktionerna möts i mittpunkten från alla möjliga inkommande håll INTE tar ut varandra. I stället bidrar alla de olika reduktionsriktningarna till en gemensam fältstyrka i ringens mitt.

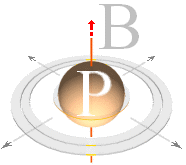
Med andra ord: B-vektorn med dess styrka i P är tydligen en universellt cirkulärpolariserad vektorform. Den gäller överallt, runt om i ett och samma givna vågplan. B-vektorn, med givet fältplan, får alltså förstås som fullständigt oberoende av varifrån magnetiska fältet kommer: alla riktningar gäller.

Magnetiska Q-fönstret

Q-FÄLTETS INRE JÄMVIKT

Att förstå den magnetiska växelverkans natur

from the original 2001-10-22 in Chapter two of Related Physics

Introduktion

Betrakta en laddning Q — med ett idealt sfäriskt laddningssystem — som färdas i fri rymd med hastigheten v relativt rymdpunkterna i ett fast dominant g-system. Om den omgivande rymden är perfekt homogen med noll innehåll av dislokationer eller oregelbundenheter i det ideala Galileiska kraftfältet [inom en och samma g-potential], uppdateras Q-systemet internt av dess eget individuella divergenssystem via c — med en perfekt balans och jämvikt mellan alla dess fältpunkter. Punkten att beskriva i denna artikel är att om, och när, allra minsta dislokation uppträder som har någon möjlig koppling till Q-systemets divergensfält, kommer denna dislokation med tiden att rapporteras till Q-centrum enligt Newtons tredje lag:

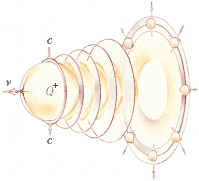
varje ändring i ett givet tillstånd söker alltid utan undantag att motverka sin egen orsak

Som vi vet, finns två sätt att genomföra sådana ändringar för Q-systemet. Det ena sättet är genom elektromotorisk induktion som skapar en direkt elektrisk kraftverkan i strömriktningen. Det andra sättet är genom magnetisk växelverkan som skapar en divergensberoende mekanisk spänningsverkan mellan olika laddningar i rörelse rätvinkligt dessa. Bägge dessa sätt måste ”ta” den aktuella Q-kroppen för att verkställa en ändring. I denna artikel ska vi studera endast delen med »den mekaniska spänningen» eller som vi säger, magnetismens kraftverkan.

I förmodan att Q-fältet inte avkänner någon störning och v är konstant, har rörelsen hos Q ingen känd orsak för att uppvisa ett rörelsemotstånd. Dess eget elektriska fält omsätter ingen energi för att fungera, och Q är dessutom helt oberoende av mekanisk tröghet

— enligt komponenterna Q=Ö (m/R)(A/dT): R finns inte i mekaniken, enbart i elektrofysiken och mekanisk rörelse fungerar därför helt oberoende av Q-massan m, vilket däremot inte är fallet i elektrisk acceleration. Se utförligt från PLANCKEKVIVALENTERNA.

Den avgörande punkten i denna observation är just bara det enkla: som magnituden för v självt inte påverkar rörelsen, så länge ingen variation föreligger, finns heller ingen gräns för kvantiteten v. Med grund i denna observation — ett klassiskt bänkmärke — finns ingen känd fysikalisk faktor som kan motverka rörelsens aspekt:

v kan ha varje möjlig magnitud.

Se även GPS-exemplet och Beviset för multipla c där kopplingen till konventionella uppfattningar klargörs mera ingående exakt.

Men: Vad händer då v går över c? Ingenting. Q förlorar ingenting, och erhåller ingenting, eftersom dess identitet ligger i dess egen centralmassa, inte i dess masslösa fält. Q bevarar alla sina egenskaper oberoende av hastighet. För det yttre fältet betyder detta uppenbarligen bara att fältkopplingen upphör; den dör ut precis som i fallet med ljudet som fysikalisk fenomengrund (Jämför frekvensfunktionen i GPS-exemplet): Laddningen blir helt immun mot varje omgivande elektrisk eller magnetisk fältbild eftersom dess divergenshorisont har reducerats till dess egen massyta. Q kan med andra ord inte svara med någon verksam kraft alls, hur starkt det omgivande fältet än är eftersom den återkopplande verkan är bruten med v högre än c. Med åter andra ord: Q blir »osynlig». Enda möjliga växelverkan med andra kroppar är genom direkt massiv kontakt. Den praktiska hanteringen av magnetiska fältet och dess balanserande och växelverkande aspekter är därmed aktuell endast försåvitt v<c.

Greppande B-vektorn

VÄXELVERKANDE LADDNINGAR I RÖRELSE

Nu när vi — i ovanstående beskrivnings ljus — bör känna till grunderna i hur styrkan i magnetiska fältet arbetar, kan vi genomföra diskussioner för att försöka förstå hur beteendet i varje växelverkan mellan laddningar i rörelse kan förutsägas.

Låt oss återvända till Q-rörelsen och studera dess bildning av B-ringar nära (den idealt sfäriska) Q-kroppen.

Med en ideal Q-sfär, kommer den starkaste B-ringen att bildas av Q-rörelsen rakt framåt från Q-ytans frontpunkt; Vi minns att potentialimpulsen är starkast där genom kortaste avståndet (r) med snabbaste ljusvägen (c) via divergenskraften F=k(Q/r)². I planet som skär den idealt sfäriska Q-kroppen på mitten rätvinkligt v, se även illustrationen nedan, finns ingen magnetisk effekt; Alla Q-potentialer med radiell c-expansion i Q-systemet i detta plan är helt rätvinkliga v, och saknar därmed komponenter i v-riktningen — och kan därför heller inte påverkas av v: ingen magnetisk effekt bildas i just det planet. Omedelbart framför och bakom detta nolleffektsplan däremot kan B-verkan bildas från noll och uppåt mot framsidan-baksidan.

maximala fältverkan

Genom att Q-systemet återkopplar snabbast till Q-centrum genom kortaste ljusvägen, det är via illustrationens markerade storcirkel eller centrala tvärsnittet, ideal sfärisk geometri, »använder» Q sina självbildade frontvågor (B-ringarna som passerar över Q-ytan med hastigheten v) för att SOM MEST reagera eller KOPPLA YTTRE KRAFTVERKAN genom just det centrala tvärsnittets maximala radiella divergens på yttre B-fält: Q använder en optimal centralkraftsverkan. B-ringarna över-under centralplanet bidrar för sina delar genom de divergensprojicerade komponenterna.

Eftersom B-ringarna tillhör det stationära g-fältet som omger Q, måste också varje ring som bildas med början i en punkt omedelbart framför Q svepa över Q med v då Q avancerar genom g-fältets dominans. Finns inget yttre B-fält närvarande, bibehålls den magnetisk-mekaniska spänningsjämvikten i B-ringarna då de sveper över Q-ytan och ingen kraft finns som ”tar i Q” och ändrar dess riktning.

ömsesidig magnetisk växelverkan

Om de Q-svepande B-ringarna däremot växelverkar med ett yttre B-fält, vet vi redan från högerhandsregeln att två diametralt motsatta effekter bildas kring Q; På ena sidan tar fältstyrkorna ut varandra, på den andra sidan summeras de. Därmed är den motsvarande mekaniska spänningsjämvikten bruten, och Q kommer att lägesändra förutsatt v<c.

Om vi tittar i riktningen (v) för ett svepande Q-plan och sett från Q-sfärens yta, betyder det att divergenskomponenten från Q, projicerad i svepplanet, också tar del i de bägge motriktade effekterna: på ena sidan ser vi en tunnare rymd med högre divergens, på andra sidan en tätare rymd med lägre divergens (Se KAUSALSAMBANDET om ej redan bekant). Då »väljer» Q naturligtvis den snabbaste ljusvägen: Q kommer att »dra» mot den tunnare rymden och »skjuta ifrån» mot den tätare rymden. Q kommer alltså att bete sig som attraherad av en kraft på den tunnare sidan, dvs., där de bägge skärande B-fälten är maximalt motriktade — med en motsvarande repellerande kraft på motsatta sidan. Eftersom divergenskomponenten från Q som nyligen noterades är starkast i samma plan som det där ingen B-verkan alls är möjlig (figuren ovan), kommer också den största drag-tryckkraften att uppstå just genom detta plan. Härigenom utbildas helt naturligt en maximalt effektiviserad kraft på Q-centrum från ett yttre B-fält.

En idealt vilande elektrisk laddning Q i ett givet dominant g-fält lämnas ostörd och orubbad av ett existerande B-fält, vare sig styrkan hos detta är konstant eller varierande;

Är Q vilande, vilket betyder att laddningen inte genererar B-vågor i respekt till en stationär referens, har laddningen heller inget verktyg för att notera närvaron av ett B-fält, hur starkt eller intensivt det än är:

Genom att B-vågorna arbetar genom differentiella plan, påverkar de heller inte den normala rymdresistiviteten (R) som är typiskt närvarande i statiska Q-fält. Således lämnas en vilande elektrisk laddning Q orubbad av vilka som helst existerande yttre B-fält.

NOTERA DOCK att i den praktiska fysiken hittar vi omöjligen någon ideal motsvarighet till ovannämnda rent ideala teori, eftersom alla fysikens ämnen befinner sig i oupphörlig rörelse och ingen fast eller vilande punkt alls är möjlig att finna där. Den teoretiska utgångspunkten bör emellertid stå klar enligt föregående beskrivning.

Först från dessa grundläggande inspektioner, kan vi (därför) mera enkelt förstå hur en elektrisk laddning måste reagera på B-fält.

*cont.

Magnetiska Fönstret

I fortsättning från Magnetiska Q-fönstret

BQ-FÖNSTRET

Betrakta ytan eller den nära omgivningen hos ett åkande Q med hastigheten v. B-fältet som bildas nära Q-kroppen och inom utrymmet för dess ideala sfäriska diameter, skapar en omgivande rymd av v-normala R-förtätade plan som utvidgas rätvinkligt v och i respekt till den stationära gravitella referens inom vilken Q befinner sig i rörelse. Med hänsyn till dessa differentiella planvågor med deras partiella eller »planpolariserade» högre R-värden och lägre divergens — således inte i v-riktningen — bildas en magnetisk-mekanisk spänning kring Q. Planens utvidgning och deras bildning inom Q-kroppens fysiska tjocklek — som en rund boll eller kula monterad helt inuti ett ordinärt omgivande plant glas — manifesterar ett karaktäristiskt magnetiskt Q-reaktivt fönster. När et annat B-fält (bildat genom ett parallellt v-stråk av Q-laddningar) äntrar det givna v-bildade BQ-fönstret, bryts den balanserade magnetisk-mekaniska spänningen till två fundamental motsatt riktade delar på var sida om Q. På ena sidan avtar den magnetisk-mekaniska spänningen, på andra sidan ökar den. Bägge effekterna genereras av de interfererande B-fälten. Därmed tvingas Q avvika.

v

¬ Magnetiska Q-fönstret ®

Genom det uppdagade maskineriet är det uppenbart att B-vågorna över och under BQ-fönstret ignoreras helt av Q. Dessa delar har ingen relaterbar inverkan på varken Q eller dess statiska elektriska fält. De är helt enkelt osynliga för föräldern till Q-systemet — men kan fortfarande växelverka med B-fält från andra Q; Endast när, och om, B-vågor utifrån inträder magnetiska Q-fönstret — och om utvidgningen av planen från Q:s egen horisont tillåter en koppling genom divergensen — kan Q-kroppen påverkas.

Den springande ämnespunkten visar att Q inte rörelsemässigt kan påverkas av B-fält på annat sätt än via

1. rätvinkligt dess egen rörelseriktning,

2. bara inom dess eget BQ-fönster.

Den första punkten beror på, så klart vi nu kan se det (och med stöd av punkt 2), att de magnetisk-mekaniska spänningarna (eng. enklare med ordet tension) som bildas kring Q från (som vi här kan kalla den) den tätare planpolariserade rymden helt enkelt är reguljära planspänningar och exakta normaler till Q-rörelsen: Q-ytan kan bara nås i den utvidgande riktningen från dessa.

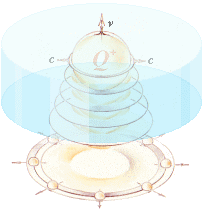
Det magnetiska Q-fönstret

Slutsats: Q självt kan skapa B-vågor på alla möjliga avstånd från Q-centrum. Men Q kan inte påverkas av B-fält utanför dess eget (receptiva) magnetiska fönster.

Området för detta fönster måste (naturligtvis) vara en variabel med respekt till v-magnituden eftersom Q inte kan svara över distans omedelbart utan först genom tid via det ändliga c. Slutsats: magnetiska fönstrets omkrets avtar tvunget med växande v.

*cont.

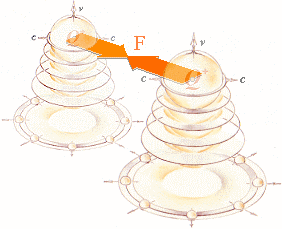
Vi kan enkelt förstå att om Q-rörelsen v är mycket liten relativt c, får också den verkande magnetiska kraften mellan laddningarna en maximalt stark inverkan: magnetisk-mekaniska spänningarnas dislokationer via B-vågornas superpositioner rapporterar nästan omedelbart till den centrala laddningen. Men om v är stort relativt c, kan inte den koppling bli lika enkel och uppenbar.

För det första: när v blir lika med eller mycket nära c, kan magnetiska fönstrets radie knappast vara mycket mera än laddningsradien själv (r=cT; T=r/c; kroppsradien passeras precis på bildningstiden T för c).

För det andra: i det ideala fallet (se Kausalsambandet med ç₀=c–v=0) kommer front-B-ringen aldrig att kunna utvecklas; Framsidan: den ideala Q-ytan ”pressar sig igenom” den motsvarande expansion som den naturligt utbildade B-ringen skulle haft om v vore mindre än c; Baksidan: B-ringen kan inte utbildas där heller eftersom fältåterkopplingen till det framrusande Q-via c är bruten via v=c. I vilket fall kan ingen B-ring bildas.

vc-begränsningen

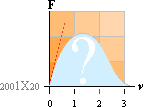
Flera faktorer medverkar alltså (teoretiskt) till att försvaga den magnetiska växelverkan då v närmar sig den fria rymdens toppdivergens (c₀). Med ännu högre v måste som nyligen vidrördes den teoretiska kopplingen försvinna helt. Bara genom denna observation kan vi förvänta oss att den kraftkopplande verkan genom magnetiska fältet som en funktionsgraf (antydd till höger ovan) kommer att nå en nollpunkt då v=c.

Slutsatsen generellt genom dessa observationer, och såvitt relevanta, gör gällande att max magnetisk kraftverkan uppnås med minimum Q-hastighet; Genom att använda stora Q-mängder med lågt gemensamt v istället för få Q med stort v, kommer den mest effektiva magnetiska responsen att uppnås. Den viktiga detaljen att lägga märke till som en generell slutsats från dessa observationer i behandlingen av praktisk elektrodynamik, måste bli att

magnetisk fältstyrka och elektrisk ström är INTE proportionella genom någon fysikalisk princip, utan av omständigheter där Q-rörelserna är försvinnande små vid sidan av den lokala ljushastigheten c.

Utom dessa klargöranden (eller reservationer) kommer vi helt säkert att anlända till verkligt förvirrande slutsatser och rena gåtor i tron att det skulle finnas någon slag fysikalisk princip som säger att laddningar i rörelse attraherar eller repellerar proportionellt mot deras hastighet. De gör uppenbarligen det, verkligen, och det också med närmast enorm precision vilket alla som sysslat något med praktisk elektronik vet helt säkert — men bara där v är försvinnande litet relativt c.

laddningshastighet

Laddningshastigheten i praktiska elektriska ledare av givet material, eller den s.k. drifthastigheten (v) beräknas normalt i ledare med cirkulärt tvärsnitt enligt sambandet (I=Avne)

v = I/(Ane) ............................ CS^–1M^–2M³C^–1 = M/S

I är strömstyrkan, A ledarens tvärsnittsyta (pr²), n elektronmobiliteten (se nedan), e elektriska elementarkvantat 1,602 t19 C, och v den resulterande medelmässiga laddningshastigheten genom ledaren.

För Koppar är elektronmobiliteten n=8,4354 T28 n_e/M³, samma som antalet ledningselektroner per kubikmeter.

För en ström på 1 Ampere i en kopparledare med radien 0,56 mM (1 mM²) blir drifthastigheten 0,074 millimeter per sekund.

[ref. GYMNASIETS FYSIK åk2 Liber 1978/80 s50].

SUMMERING 2001X21

· magnetiska vågor är elektriskt resistivt förtätade plana rymdvågor i den stationära g-referensen som uppkommer ur varje försök att ändra den referensens lokala divergens [se från KAUSALSAMBANDET].

· magnetiska vågor är transparenta för elektriska fält och växelverkar inte med dessa.

· magnetiska vågor växelverkar endast med varandra.

· magnetiska vågor påverkar elektriska laddningar bara om dessa själva genererar magnetiska vågor, och då endast inom det magnetiska fönstret för laddningens egen massiva materieyta.

· B-fält från ett åkande Q bildas inte som ändringar i Q-systemet självt, utan som ansvar från den omgivande stationära g-rymden i det att Q-system i rörelse relativt det fasta g-systemet försöker överföra Q-systemets egendivergens (c) med rörelsen (v) på rymdpunkterna (P), vilket inte går (se Ljusfrihetssatsen). Stationen svarar på närmandet genom att bilda en partiellt tätare rymdresistans rätvinkligt inkräktaren (v) i bevarandet av den elektriska konstanten [se från KAUSALSAMBANDET].

· med uppkomsten av B-vågorna varken förväntar eller besvarar det allmänna Q-systemets elektriska fält närvaro av B-fält: Q-systemets allmänna elektriska fält varken igenkänner eller visar intresse att växelverka med magnetiska fält. Koppling saknas.

· proportionalitet mellan elektrisk ström (I) och magnetisk fältstyrka (B) kan inte relateras som en exakt fysisk egenskap, utan är helt säkert ett praktiskt faktum med hög kvantitativ precision på grund av stora laddningsmängder (Q) med mycket låga laddningshastigheter (v) relativt den lokala toppdivergensen (c₀).

summerande B-fält

Det följande summerande resonemanget beskriver verkningssättet i den magnetiska kraftverkan — resonemanget är giltigt endast i observation av de ovan givna punkterna.

Betrakta situationen som antyds i följande illustration.

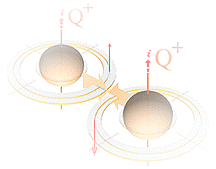
Två lika laddningar Q⁺ färdas parallellt vertikalt uppåt. Genom högerhandsregeln finner vi att B-styrkorna mellan laddningarna är motsatta, och samriktade på motstående utsida. Därmed elimineras fältstyrkan mellan laddningarna helt om bägge B-vektorerna är lika stora. I den summerande superponerade positionspunkten, måste divergensen också bli den normala rymdens toppvärde (c₀) och rymdresistansen likaledes det normala R vilket betyder att magnetiska fältstyrkan är noll. På motsatta sidan gäller motsvarande maximum med ett summerande största R-värde och motsvarande lägsta divergensvärde.

Således kommer Q i dess fältdivergens, i riktningen för B-planet endast, att erfara en tätare, långsammare rymd på utsidan och en tunnare och snabbare på insidan. Reaktion från Q blir naturligt att försöka etablera sitt Q-centrum mot den tunnare och snabbare delen och skjuta sig bort ifrån den tätare och segare delen. Därmed attraheras Q-kropparna mot den tunnaste delen och repellerar från den tätare delen. Den enastående centrala aspekten, om förstådd korrekt, är att den starkasta magnituden med vilken denna effekt visar sig, är i den centrala Q-sektionen — planet som skär (det idealt sfäriska Q-systemet exakt mitt i) men där ingen magnetisk våg kan bildas. Se även föregående figurillustration med beskrivning.

Totaleffekten med lika laddningar som har samma polaritet (++ eller – –) är att bägge laddningarna attraheras mot deras mittpunkt (homogen g-rymd förutsatt). Om laddningarna har motsatta polariteter kommer de att repelleras bort från mittpunkten.

Vilket vill säga: Den magnetiska kraften agerar inte, verkligen, i respekt till ändringarna såsom tillhörande Q-kropparna utan i respekt till g-rymden med dess fixa referenspunkter såsom preferensen för det omgivande dominanta gravitationsfältet.

lika medströmmar i parallella elektriska ledare (via Q⁺ i bägge fallen) strävar att dra ledarna närmare tillsammans medan motsatta strömmar strävar att föra ledarna längre bort från varandra

*cont.

Praktiska magnetiska kretsar

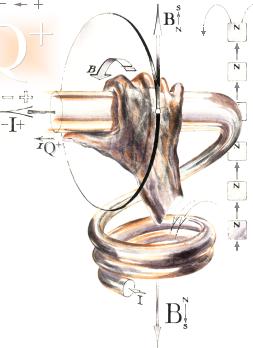
ATT BYGGA STARKA MAGNETISKA FÄLT

Kort allmän översikt

Men insikt i »den hemliga magnetismens lära» enligt ovanstående beskrivningar, kan vi bygga starka och högeligen homogena magnetiska fält med elektriska strömmar genom att använda ytisolerad tråd (vanlig obehandlad koppartråd går inte). Denna typ saluförs i elektronik- och järnvaruhandeln i många olika dimensioner sedan 1800-talet. Illustrationerna nedan antyder den allmänna byggnadsformen.

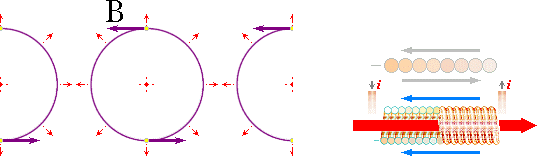
Genom att placera flera strömförande ledare tätt tillsammans kommer de att samarbeta i bildningen av ett gemensamt B-fält om alla strömmar har samma Q-polaritet och färdas i samma riktning. Denna princip byggs enastående praktiskt med hjälp av en enda lång ledare (isolerad koppartråd) som viras med tätt liggande varv i formen av en (cylindrisk) s.k. elektrisk spole (eng. coil). B-fälten utanför och inuti spolen får inbördes samma riktning. Medan det förra blir av den svagare magnituden, blir B-fältet inuti spolen däremot speciellt starkt. Är dessutom spolen lindad på en cylinder av järn kan mycket höga B-fält uppnås vid cylinderns ändar eller de s.k. magnetpolerna.

*cont.

Elektrodynamikens Grundläggande Matematik

ELEKTRODYNAMIKENS MATEMATISKA FYSIK

Introduktion

I den här sektionen ska vi studera en uppsättning matematiska uttryck av exceptionellt både enkel och avgörande natur — med en högst grundläggande betydelse för elektrodynamiken (den elektriska fysiken speciellt med hänsyn till de elektriska krafternas inverkan) på nivån Jordbaserad teknologi.

De är alla relaterade till och beroende av den statiska elementära elektriska kraftlagen F=k(Q/r)².

NÄRVERKAN OCH FJÄRRVERKAN

Near and Far Applications

Både induktionen och magnetismen uppvisar en närverkande [Q till insidan] och fjärrverkande [Q till utsidan] funktion. För att skilja dessa komplex åt i beskrivningen är induktionen i den här presentationen indelad i en primär och en sekundär del, medan magnetismen har behållit terminologin med närverkan och fjärrverkan (eng. near and far application).

Därutöver måste både induktionen och magnetismen högeligen idealiseras (som redan framskymtat i föregående beskrivning) med hänsyn till ljushastighetens fördröjande inverkan mellan olika rymdavsnitt för att få fram en (någotsånär) enhetlig och överskådlig matematisk fysik på elementär bas.

Det betyder att dessa matematiska uttryck med viss nödvändighet MÅSTE få prägeln av att vara

»dockskåpsmatematik».

Vilket vill säga (till exempel): Experiment i den elektriska låghastighetsfysiken som använder ”elementära ekvationer” KAN bli högeligen äventyrliga — om de betraktas som självständiga baser för att verifiera allmänna teorier inom fysiken — därför att förhållandet mellan ström och magnetism bara gäller via kvantitet (in till en viss decimal precision) genom en lägsta möjliga B-genererande mekanisk hastighet (v). Se även föregående i vc-begränsningen.

Ett annat exempel är den tidigare relaterade termen (mikro-noll) ”µ₀” — den är redan garanterat etablerad med en redan väl dokumenterad språkförbistring som få (om ens några) förmår reda ut i ljuset av konventionella begrepp.

Där så är möjligt i denna presentation, kommer mera exakta lösningar att diskuteras.

Grundläggande magnetmatematik

2001-10-17

NOMENKLATUR speciellt i förklaringen till magnetisk fältstyrka, se

Begreppen FÄLTSTYRKA OCH POTENTIAL INOM ELEKTROFYSIKEN

Se även NOMENKLATUREN FÖR B

MAGNETISMEN

Det följande arrangemanget syntetiserar fenomenet magnetism att studeras i denna sektion.

Magnetiskt fält — bildning

1. ett åkande Q som bildar ett stationärt B [Generering av Magnetiska fäl]

NÄRVERKAN

Magnetisk fältstyrka från ytan av elektriska ledare

B på ledarytan

B inuti solid ledare

B inuti ihålig ledare

FJÄRRVERKAN

Magnetisk fältstyrka utanför elektriska ledare

Den magnetiska vågexpansionsintegralen

Den magnetiska linjeintegralen

Magnetiskt fält — växelverkan

2. ett stationärt B som påverkar ett åkande Q [Elektro-mekanisk induktion]

DE FYRA GRUNDLÄGGANDE »dockskåps» LAGARNA I Elektro-MEKANISKA INDUKTIONEN

F = BQv ........................... kraft på fritt rörlig laddning Q som badar i B (magnetiska kraftlagen)

F = BsI ............................. kraft på ledare som håller strömmen I badande i B

U = Bvs ............................ inducerad spänning i fritt rörlig ledare som badar i B

U = dF/dT ........................ allmänna elektro-mekaniska induktionslagen

*cont.

terminologi, allmänt:

Genom relaterad beskrivning används i denna presentation följande terminologi tillsammans med dess fysikaliska storheter

H fältkraft, A/M, också samma som engelskans magnetiserande kraften (magnetizing force), H=I/l

B fältstyrka, VS/M² = Wb/M² = KG/AS², även flödestäthet (eng. flux density)

Se även särskild beskrivning i NOMENKLATUREN FÖR B

I modern vetenskap och akademi är det tydligt att vissa missförstånd och missuppfattningar har etablerats under historien med dessa begrepps uppkomst med början från 1800-talet. En grundlig beskrivning ges via länken ovan med tabeller och exempel som belyser nuvarande begrepp från olika källor — och olika epoker.

skrivsätt

Generellt i den här presentationen används det internationella MKSA-systemet (MeterKiloSekundAmpere)

konsekvent med versaler för fysiska storheter och tusenprefixen större än 1

(Kilo-Mega-Giga-Tera-…), samt små bokstäver för tusenprefixen mindre än 1

(deci-centi-milli-µ(mikro)-nano-pico-femto-…).

Dessutom används här en förenklad exponentiell notation för tiopotenser enligt

T för 10^+ och t för 10^–

exemplifierat som 1,496 T11 M för a 1AU (en astronomisk enhet) och u=1,66033 t27 KG för atomära massenheten.

Matematiska koefficienter skrivs i den här presentationen med prioritet för bästa läsbarhet (utprovat genom många försök och även tester i olika webbmiljöer med olika webbläsare), inte med prioritet för traditionell klass, enligt exempel

aT⁴ att jämföra med aT⁴.

Vilket vill säga; Versaler skrivs (här mestadels) med rak, inte kursiverad, typografi.

Andra typografiska förenklingar i den här presentationen är sådana som medger avancerade matematiska uttryck i rakt skrivsätt. Dessa är av typen integraler och summor med index enligt exemplet

_m=1®n ò

som betyder ”från m=1 TILL n”, och som kan skrivas direkt på samma rader som vanlig text.

Syftet med den typen av förenkling är (naturligtvis) att kunna göra matematisk beskrivning TYDLIG OCH LÄTTLÄST tillsammans med vanlig text utan vidlyftiga konstigheter — med den normala verktygslåda för text som medföljer vanliga ordbehandlingsprogram som har (typiskt) teckensnitten Times New Roman och Symbol.

GRUNDBEGREPPENS INNEBÖRD I MATEMATISK FYSIK — elektrisk och magnetisk fältstyrka

magnetisk fältstyrka B och elektrisk fältpotential U är olika aspekter av samma elektriska fält

Ser vi enbart till den elektriska kraftlagen F=R₀c₀Q²/4pr² i ett statiskt Q-fält sett från dess totala fältstyrka F/Q=R₀c₀Q/4pr² dividerad med divergensen så att vi får F/Qc₀=R₀Q/4pr², har vi endast en kvarvarande rå statisk styrka som pekar i riktningen r. Vi kallar den statiska råformen, F/Qc₀, för den magnetiska fältstyrkan eller den statiska Q-skalmagnetiska fältstyrkan med beteckningen B (det totala B-skalet).

F/Q = X = kQ/A = U/r ..................... elektrisk fältstyrka, A area

X/c = B = RQ/A = (U/r)/c ................ magnetisk fältstyrka, A area

Som vi kan se av den motsvarande differentialformen, pekar den totala B-styrkan

F/Qc₀= B =R₀dQ/4pdr² på varje punkt i änden på r hela det idealt sfäriska Q-skalet igenom. Det talar specifikt om för oss att B-formen är ett alternativt sätt att se det statiska e-fältet: magnetisk fältstyrka och elektrisk fältpotential (över c) är bara olika aspekter på samma principiella elektriska fält.

INTRODUCERANDE EN Q-RÖRELSE

Två olika sätt

För att relatera en dynamisk referens till ett det statiska B-fältet i riktning r, måste vi introducera laddningen Q för en rörelse. Det finns två sätt att relatera effekten av en sådan Q-rörelse:

1. ett åkande Q som genererar ett stationärt B [Generering av Magnetiska fält],

2. ett stationärt B som påverkar ett åkande Q [Elektro-mekanisk induktion]. Vi börjar med det första sättet.

*cont

FÖRSTA SÄTTET

Mobilt Q som genererar ett stationärt B

I relaterandet av B till en rymdpunkt i riktning r för Q-rörelsen från grundformen

F/Qc₀= B = R₀Q/4pr² ...................... V/(M·M/S) = VS/M²

måste vi specificera en allmän och medelmässig divergens (c) för B-effekten att utbreda sig på.

Tidigare i Kausalsambandet studerade vi grunderna till hur B-effekten som B-våg bildas; divergensen c i det fallet tvingas reduceras partiellt i B-vågens utbredningsriktning genom en motsvarande partiellt högre rymdresistans (R) så att bevarandet av elektriska konstanten i elektriska kraftlagen garanteras. B-vågens styrka kommer alltså att bero på magnituden i det reducerade c som kommer att närma sig den fria rymdens c₀ som R närmar sig R₀. Vi finner detta c-beroende för B-uttrycket genom direkt substitution i högra delen med ett allmänt c/c så att vi får den formella kärnformen

B = R₀(c/c)(Q/4pr²)

= (R₀/c)(Q/4pr²) · c

Som den högra delen motsvarar vilkensom distans s under en tid T som ger

= (R₀/c)(Q/4pr²) · s/T ,

kan den användas för att definiera Q-rörelsen som en godtycklig strömstyrka Q/T=I utmed strömvägen s. Då får vi

= (R₀/c)(I/4pr²) · s

= µs · (I/4pr²)

Notera komponenten µs:

Jämför den motsvarande, mera precisa, Rc-transfereringen från artikeln i Kausalsambandet, och som förklarar hur den magnetiska B-vågen uppkommer:

R₀c₀ = ôR’ç = 1/e₀ = ôR_maxç₀ = konstant .......... VM/AS

ôR_max = R₀c₀/ç₀ [= [e₀ç₀]^–1 = [e₀(c₀–v)]^–1 = [e₀c₀ – e₀v]^–1]

ôR_max/ç₀ = R₀c₀/ç₀²

Med små skillnader mellan ç₀ och c₀ gäller det att

ôR_max/ç₀ = R₀c₀/c₀² = R₀/c₀ = µ₀ ....... VS/AM

Således genom generalisering av de föregående termerna R₀/c=µ som µ₀ får vi det mera enkla

B = µ₀s · (I/4pr²)

Komponenten µs —

RYMDMAGNETISERINGEN

Vi noterar att uttrycket med µ₀ taget bokstavligt betyder att ingen B-våg är möjlig: µ₀=R₀/c₀ betyder noll magnetisk effekt[se begreppet reduktion]; µ₀ har, verkligen, ingen anknytning till magnetismen (B). Den centrala delen för magnetismen är istället den elektriska konstanten R₀c₀=R_maxç₀. Var vaksam på (och medveten om) denna formella förenkling, beskriven i ledan närmast ovan. Därför (nämligen) att ”µ₀” kommer att visa sig frekvent i alla sammanhang som berör elektrodynamiken och då speciellt (naturligtvis) i alla knepigare problem; Såvitt här känt (2007-06-18 med vidare), finns i den moderna vetenskapen och akademin ingen teori eller ens ett begrepp om något sådant som en »reduktion». Jämför den speciella introduktionen med expansionsintegralen som exempel (Magnetismen i Modern Vetenskap och Akademi).

Rymdkompaktheten µ i magnetismen relateras rätvinkligt strömvägens utsträckning (s). Således är i magnetismen de bägge faktorerna i µs inte samriktade; Då de är den aktiva delen i uttrycket för B, kan vi (naturligt) kalla dessa faktorer µs för rymdmagnetiseringen (eng. space magnetization).

närverkan och fjärrverkan:

Det finns två grundläggande sätt att relatera Q-rörelsen i denna del.

Det första sättet gäller den magnetiska effekten direkt associerad med Q-ytan (närverkan). Den delen beskriver den motsvarande effekten på ytan av en elektrisk ledare som precis täcker den ideala sfäriska diametern för Q.

Det andra sättet gäller den magnetiska effekten i rymden utanför Q, alltså utanför den aktuella ledaren (fjärrverkan). Denna senare del måste använda differentialer i s-ändringsvägen; Eftersom fjärrverkan ”ser” många olika partier från en given ledare — inte som i närverkansfallet bara ledarens omedelbara tvärsnitt — ger B-differentialen verktyget för fjärrverkans matematik och som tillåter alla möjliga bidrag från alla möjliga kurvaturer eller delar hos s.

Vi börjar med den centrala ledaren.

*cont. Basic Magnetic Mathematics

NÄRVERKAN

® i

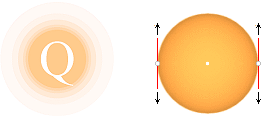
Vi förutsätter som tidigare ideala förhållanden med ett idealt sfäriskt laddningssystem för den elementära elektriska laddningen (Q). Varje Q-rörelse (v) motsvarar en viss strömstyrka I=Q/T.

När vi ser i riktningen (s) för Q-rörelsen (vänster ovan), ser vi en flat Q-skiva som genererar två ytnära B-vågor (höger ovan; den vänstra delen sedd från sidan) och som expanderar rätvinkligt Q-rörelsen genom ds på motsatta Q-sidor. Sett från den ideala Q-sfären är det den dynamiska delen i hela sakfrågan. Men Q-kroppen representerar också en ideal solid ledare. Nämligen den vilkens ytsektion, tvärsnittet A=pr², har Q-ytans täthet Q/A. Detta är den faktiska och motsvarande ideala elektriska ledartvärsnittets yta vi tittar på genom rörelsen hos den ideala Q-sfären.

Men den magnetiska insidan på denna ledare är, för oss, mörk. Den elektriska kraftlagen säger oss ingenting om den, åtminstone inte direkt. För att relatera Q-rörelsen till en solid ledare, måste vi därför utgå i denna sublima magnetiska analys i behandlingen av solida ledare från den punkt där de två motstående B-vågorna exakt når den ideala Q-sfärens diameter och just är på väg att »lämna oss för den yttre rymden». Denna situation blir den motsvarande ”första stöten” i den elektriska historien för en magnetisk fältvåg genererad av Q-ledaren: Den börjar från den projicerade omkretsande Q-cirkeln. Vi observerar att ”Q” i denna bemärkelse måste vara en total (enhetlig) Q-kvantitet representativ för den ideala teoretiska Ensamma Huvud-Q-sfären — som tar sin väg genom ledaren via hela strömmens kvantitet, eftersom det är till den, och endast den, som den nu beskrivna B-formen måste relateras.

DEN MAGNETISERANDE KRAFTEN

Q-skivans princip

Den nyligen beskrivna högeligen idealiserade enda Q-modellen representerar då exakt strömstyrkans definition

I = Q/T;

Strömstyrkan (I) är den laddningsmängd (Q) som passerar en referenspunkt (strömvägens tvärsnitt) per tidsenhet (T).

Med andra ord: Vi ser Q-kvantiteten »passera» ett tvärsnitt (ds) av ledaren vilket sker likaledes under en tidsdifferential (dT). Det är också ämnets centrala punkt: Genom dT-passagen, och därför att det inte finns någon sådan Q-sfär i den verkliga fysiken (åtminstone inte som jag har upplevt det), måste vi komprimera hela Q-sfären till bara en cirkulär plan skiva som passerar dT-ds-punktens referens. Strömstyrkan definieras då differentiellt enligt I=dQ/dT. Illustrationen nedan är tänkt att ge en bild av situationen.

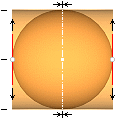
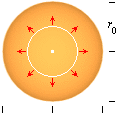
Definition av ström genom utvidgningen för Q

För att relatera den komprimerande fasen, i behållandet av den magnetiska effekten som bildad och ”uppackad” på omkretsen till ledarens tvärsnittscirkel, måste vi innefatta hela Q-sfärens yta som ansvarig för denna initiella B-stöt.

Som vi vet, är sfärytan (4pr²) exakt samma som den omskrivna cylinderytan med diametern 2r. För att innefatta den nyligen omnämnda kompressionen i basuttrycket, måste vi använda s=2r som den representativa rörelsen under den komprimerade ds-passagen. Då får vi direkt från den föregående B-formen µ₀s · (I/4pr²) sambandet

B_YTA = µ₀2r₀ · (I/4pr₀²)

B_YTA = µ₀I/2pr₀

Vi kallar strömförhållandet I/2pr₀ i denna grundläggande första stöt-B-våg på en elektrisk ledare för den magnetiserande kraften med beteckning H (eng. magnetizing force). Då gäller alltså

H_YTA = I/2pr₀ ............................. magnetiserande kraft, A/M

B_YTA = µ₀H ................................ magnetisk fältstyrka, VS/M²

styrkan = motståndet (kompaktheten) · kraften

B-fältet inuti Q

HUR ATT RELATERA B-VÄRDEN INUTI BYGGNADEN FÖR EN SOLID (Q) LEDARE

Med Q-skivan och Q-ytans täthet etablerade, kan B-värdet inuti Q relateras exakt som den initierande rand-vågen expanderar: alltså med början från centralpunkterna (P) på sfärytans motsatta sidor. Vi studerar hur.

Utgående från nollpunkten rakt fram, blir den enda ström I av den totala I₀ som räknas en I-differential. Det är klart för att hela strömmen, som vi tidigare noterade, beror av en enhetlig bestämd ändlig kvantitet; punktformen är differentiell och därmed och ett differentiellt I.

Som ringen expanderar (från P), innesluts en växande kvantitet av det totala I₀ i analogi till ett växande bidrag från Q till B-styrkan. Ytor utanför den aktuella har ännu inte skapats och bortses därför ifrån. Den matematiska delen av denna procedur ansluter till sambanden i artikeln om Strömstyrkan [Se STRÖMTÄTHETEN],

I = I₀(r/r₀)² ....................................... aktuella strömstyrkan inuti ledare, Ampere

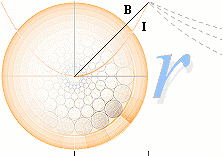
0 r₀

Direkt insättning i föregående B=µ₀I/2pr₀ ger

B = µ₀I/2pr₀ ..................................... ledarytans fältstyrka

B = (µ₀/2p)I₀r/r₀² ........................... efter insättning av sambanden för strömtätheten

m = µ₀/2p ......................................... förenkling, m=1,99997 t7 @ 2 t7 VS/AM

B = m · r · (I₀/r₀²) .......................... VS/M²

Magnetiska fältstyrkan innanför ytan på en cirkulär ledare

Som vi ser är B-värdets funktion helt linjär. Utanför ledaren kommer B-kurvan att bero på ledarens kurvatur och ett (för ljushastigheten) begränsande intervall. Denna del behandlas längre fram i fjärrverkan.

*cont.

Bekräftelse av resultatet, ihåliga ledare

Genom att använda högerhandsregeln kan vi direkt verifiera att centrum i varje cirkulär ledare måste ha noll magnetisk fältstyrka. Illustrationen ovan indikerar hur vi genom teorin kan använda ledare i motstående par med lika strömmar för att genomföra grundtest. Tvärsnittet bildar en (ideal) ring genom de motstående parledarna med totalt N raka parallella ledare som bildar själva den ihåliga ledarens rörvägg. Från den inre B-nollade centralaxeln måste sedan B-värdet i vilket fall växa mot ett maximum ute vid ledarytan.

Resultaten från de enklare rent teoretiska undersökningar som kan genomföras med de föreslagna enkla motstående symmetriska parledarna visar oss direkt enbart via högerhandsregeln (B=0 i centrum, därifrån växer B mot ledarytan) ”en hyfsad överensstämmelse” med den mera utförliga sambandsformen ovan. Sambandet för B ovan bekräftas också genom den redan kända etablerade litteraturen som den elementära ekvationen för B-fältets styrka inuti en kompakt ledare.

En utmärkt konventionell referens som beskriver de grafiska formerna till de allmänt kända sambanden i dessa sammanhang finns på webbsidan

[http://www.ndt-ed.org/EducationResources/CommunityCollege/MagParticle/Physics/CircularFields.htm] 2008-06-06.

[Illustrationerna där är av samma (men inte identiska) typ som nedan].

B

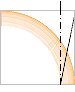r

0 r₀

Om ledaren är ihålig, berättar den nyligen beskrivna Q-skivans princip för oss att den tomma delen måste bortses ifrån. Det skulle antyda att B-styrkan inuti en ihålig ledare är exakt noll överallt. Startpunkten för B-funktionen förskjuts (således, av princip) utmed horisontella axeln till rörets innervägg. Sambandet nedan visar den allra enklaste formen med den förutsättningen:

B = m · (r – r_in) · (I₀/[r₀–r_in]²) ...................... r > r_in , VS/M²

Magnetiska fältstyrkan innanför ytan på en ihålig cirkulär ledare

För att verifiera teoretiskt Q-skivans procedur med förslaget att B inuti ihåliga ledare inte existerar, måste vi känna till hur att beräkna B generellt utanför raka ledare. Därmed kan parallella ledare användas enligt föregående figurs förslag för att beräkna den totala B-resultanten från alla bidragande komponenter. [Resultatet visar överensstämmelse med den enklare Q-skivans modell, vilket här lämnas utan bevis].

Om vi enbart bekymrar oss om matematiskt artisteri, kan den allmänna B-ekvationen för en rakledare härledas direkt från B-ytans ekvation om vi också känner byggnaden för trigonometrin. Den fastslår helt enkelt: med en punkt P utanför en rak ledare som begränsas av ändpunkterna AB, blir sinus för vinklarna A° och B° i PREFIXxSIN lika med 1 om P ligger på ledarens yta. Ekvationen kan då framställas direkt enligt

B = (µ₀/2p)I/r₀ ................................. ledarytans magnetiska fältstyrka

B = (µ₀/4p)(I/r)(sinA+ sinB) ............ rymdfältets magnetiska fältstyrka, rak ledare, PREFIXxSIN

Med sinA = sinB = 1 blir den sista ekvationen ovan den första. Emellertid, hur elektriskt perfekt detta samband än må vara, får en sådan ”härledning” ringa värde för en student som är mera intresserad av elektrisk dynamik än algebraisk gnistbildning. Studenten vill veta hur maskinen arbetar, inte hur tung den är att gå omkring och bära på.

Om någon skulle fråga, hur vet du säkert att detta uttryck har något praktiskt värde?, skulle den enda tillgängliga förklaringen vara

— Helt enkelt på grund av likhetstecknet.

Det stämmer. Matematiken har den kraften. Den mera förklarande härledningen visas (emellertid) i det följande.

Se även från Närverkan

FJÄRRVERKAN

För att relatera Q-rörelsen i fjärrverkan måste vi begränsa hela fältstyrkan F/Q att gälla bara via differentialer — så att godtyckliga bidrag under alla omständigheter kan igenkännas i den aktuella fältpunkten P. Detta tvingar B på differential form så att vi får differentialekvationen

dB = µ₀ds · (I/4pr²)

med Q-rörelsen i riktningen r=s.

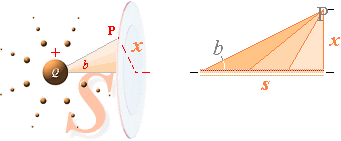
Med vinkeln b mellan r rakt framåt som riktningen för s och varje annan r-riktning från Q-centrum, blir B-effekten i PREFIXxSIN

dB = µ₀ds · (I/4pr²) · sinb ...................... singulära punkteffekten via b

Detta är det enda differentiella bidraget till B från en momentan rörelse hos en enskild laddning Q i respekt till rymdpunkten P (utan fördröjning) på avståndet r från Q via vinkeln b. Som beskrevs noggrant i

Vektorrepresentationen för magnetiska fältstyrkan och hur elektriska laddningar i rörelse växelverkar [B-VEKTORN]

även mera utförligt med referens till den moderna akademins föreställningssätt i EXPANSIONSINTEGRALEN

är detta differentialekvationen för expansionsintegralen:

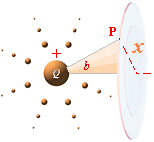dB_P = µ₀(I/4pr²)sinb ds .......... VS/M²

^®s differentialekvation, expansionsintegralen

När vågen når P, innehåller den alla samlade (differentiellt bidragande) reduktioner (från alla P utmed radiella expansionen) som används för att bygga upp den karaktäristiska ringstyrkan med början från centrum. För att beräkna styrkan i P från en momentan ändring ds i läget för Q utmed strömvägen s, måste vi integrera alla dessa differentiella bidrag. I beräkningen av en total effekt i P från en ändlig strömväg s, måste denna inre eller expansionsintegral sedan själv integreras över den speciella kurvaturen för s (strömlinjens integral).

För att integrera dB_P över vinkeln b måste vi först anpassa integrationskonstanten ds till db. Differentialtransformationen i PREFIXxSIN blir

x/s = tanb , s = x/tanb ; med ds/db = Dn s = s’ får vi [för grundderivatorna, se Bastablån]

ds = Dn s db = Dn (x/tanb) db = (–x/cosb²) db; [NOTERA, cosb² här en oegentlig förenkling av det egentliga cos²b=(cosb)²]

Insättning ger

dB_P = µ₀(I/4pr²)sinb (–x/cosb²) db

Med x/r = cosb , x²/r² = cos²b , r²/x² = 1/cos²b får vi

dB_P = µ₀(I/4pr²)sinb·x(r²/x²)·db ;

dB_Px = µ₀(I/4px)sinb·db ............................... fullständiga differentialekvationen, expansionsintegralen

med lösningen

_b®0ò dB_Px = µ₀(I/4px) _b®0ò sinb·db = µ₀ (I/4px)_b®0[cosb] = µ₀(I/4px)cosb

eftersom cos(b=0)=0 enligt PREFIXxSIN. Således

_b®0ò dB_Px = µ₀(I/4px) cosb .............. den magnetiska vågexpansionsintegralen

Q får inte lägesändra under integrationen!

Som omnämndes tidigare, gäller denna integral endast för en momentan lägesändring ds hos Q utmed s. Det betyder att integrandens enhet i vänstra delen egentligen ska skrivas på den mera korrekt indexerade differentialformen

d(dB_Ps/db_s) = dB_Px

där index s refererar till en bestämd utsträckning i Q-rörelsen. Vilket vill säga,

dB_Ps = µ₀(I/4px) cosb db_s ................ magnetiska linjeintegralens differentialekvation, strömvägen

se från fjärrverkan

*cont.

specifika B-ekvationer

MAGNETISMENS SPECIFIKA EKVATIONER

SE ÄVEN FRÅN INTRODUKTIONEN TILL INDUKTIONEN OCH MAGNETISMEN

Den raka ledaren

För en rak ledare [sin90=0 i PREFIXxSIN] blir för magnetiska linjeintegralens differentialekvation lösningen lika med

_b®90ò dB_Ps = µ₀(I/4px) _b®90ò cosb·db_s = µ₀(I/4px)_b®90[–sinb] = –µ₀(I/4px)sinb

B_Ps = –µ₀(I/4px)sinb ........................ VS/M²

magnetiska fältstyrkans linjeintegral, rak ledare, räta vinkeln

För att beräkna delar utanför s kan den enkla subtraktionen nedan användas:

sin b = (sin b_Minsta)_TOTAL – (sin b_{StörstaUTANFÖR})_SUBTRAHEND

FULLSTÄNDIGA SAMBANDET FÖR RAKA LEDARE

Med P godtyckligt utanför s räknas den totala styrkan i P genom summan av de bägge b_L and b_R enligt

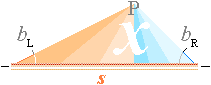
B_Ps = –µ₀(I/4px)(sinb_L+ sinb_R) ...... rak ledare,alla vinklar, 1Tesla=1VS/M²

µ₀ ........................................................ 1,25662 t6 VS/AM

Vinklarna räknas från 0 till 180° med automatiskt ±-tecken inkluderat.

Med ett Halllement kan B mätas i P med hög noggrannhet, vilket bekräftar sambandet.

Exempel 1

Bestäm det teoretiska värdet för den magnetiska fältstyrkan B i en punkt 7,5mM utanför och på mitten av en 0,1 M lång rak ledare som för 30 A elektrisk ström. Använd PREFIXxSIN för att visa relationerna och ge svaret i enheten Tesla (T) motsvarande VS/M².

Lösning

B_Ps = –µ₀(I/4px)(sinb_L+ sinb_R)

sinb_L= sinb_R= sin(atan 7,5/[100/2])= sin atan 0,15 = 0,9889393

B_Ps = –(1,25662 t6)(30/4p[0,0075])2(0,9889393) = –7,91137 t4 T

Svar: Den magnetiska fältstyrkan är 0,8 mT.

Exempel 2

Med samma data som i exempel 1, vad är B-värdet om strömmen halveras och en annan ledare (L2) med samma dimensioner på motsatta P-sidan placeras parallellt med den givna (L1) och på samma avstånd 7,5 mM från P men med motsatt riktat strömflöde?

Lösning

De bägge motriktade strömmarna kommer att bidra med samma magnitud eftersom motriktade strömmar summerar B mellan dem. Resultatet i netto för strömmarna i sambandet blir då 2(30/2)=30. Vilket betyder: ingenting ändras.

Svar: Exakt samma.

Mätning med ett relativt s litet x på mitten av den raka ledarlängden s gör att vinklarna b avviker mycket litet från 0. Då gäller i PREFIXxSIN likheterna

b_L=b_R @ 0 med sin0=1 vilket förenklar uttrycket till

B_Ps = –µ₀(I/2px) ..............................

litet x utanför mittpunkten av en (lång) rak ledare

Som vi ser, är detta samband detsamma som bildade basen i den förenklade härledningen till sambandet för B i rakledare.

Tillämpningar

B-STYRKAN I EN LÅNG RAK SPOLE

En rak ihålig cylindrisk ledare A är indelad i n parallella (tunna) ledare,

B_A = –µ₀nI/2pr

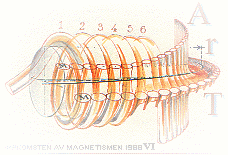
Om vi lindar en toroid T med n varv vilkas insida förenas med A i sektionen M (illustrationen ovan visar principen) får vi

dB_A/n = dB_T/n

Med de n toroidala varven förutsatt idealt cirkulära (tunna trådar), är differentialerna likadana i de motsvarande M-sektionerna i T. Som magnituden för B är likadan över hela den toroidala medelomkretsen 2pr, räknas B för varje del (s) i denna 2pr-båge. Magnetiska fältstyrkan inuti en lång rak spole följer då med god approximation (frånsett fältet i spoländarna) s= 2pr motsvarande spolens längd enligt

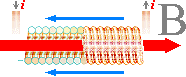
B_C = –µ₀nI/s ..... fältstyrkan inuti lång rak spole i Tesla, VS/M²

n ......................... antal varv

I ......................... strömstyrkan

s ......................... spolens längd

µ₀ ........................ 1,25662 t6 VS/AM

*cont.

Ringen

I tillämpningen av

dB_Ps = µ₀(I/4px) cosb db_s ................ magnetiska linjeintegralens differentialekvation, strömvägen

med magnetiska fältstyrkan i mitten av en ring med radien x är b-vinkeln konstant enligt b=90°. Som cos90=1 i PREFIXxSIN blir differentialekvationen

dB_Ps = µ₀(I/4px)db_s;

Som cirkelbågen i radianer b är b = s/x, får vi differentialtransformationen db=d(s/x)=ds/x. Insättning ger

dB_Ps = µ₀(I/4px²)ds med den integrala lösningen från 0 till s=2px

_0®sò dB_Ps = µ₀(I/4px²) _0®sò ds = µ₀(I/4px²)_0®2pxs = µ₀(I/4px²) 2px = µ₀(I/2x) ;

Vi erinrar de cirkulära grunderna med s A° —— = —— 2pr 360 som ger s p —— = —— · A° = a r 180 med a i radianer

B = µ₀(I/2r) .............. fältstyrkan i mitten av en ring med radien r, VS/M²

µ₀ ............................... 1,25662 t6 VS/AM

Den cirkulära Konen

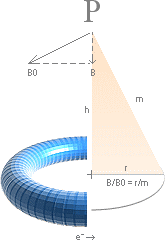
Ligger centralpunkten P i ringen över ringplanet (via h) med radien r — med den giltiga B-vektorn för P pekande som normal (N) till ringplanet genom P, uppåt eller neråt beroende på ringströmmens riktning och dess laddningarnas potential — måste B relateras till hypolinjen

m=Ö r²+h²

(lika med r om h=0). B-styrkan relateras då som projektionen B=B₀(r/m) på normalriktningen N (se ill.), med

dB_0Ps = µ₀(I/4p m) (cos[b=90°]=1) (db=d[s=2pr]/r)_s ...........................

magnetiska linjeintegralens differentialekvation, strömvägen anpassad för en cirkulär kon

= µ₀(I/4p m) (db=d[s=2p])_s

= µ₀r(I/4p m²) (db=d[2p]_s ;

Med B=B₀(r/m) får vi den motsvarande differentialekvationen

dB_Ps = µ₀r(r/m)(I/4p m²) d(2p)_s

= µ₀(r²)(I/4p m³) d(2p)_s

där integrationen för hela konen ska göras över hela basringen 2p. Integrala lösningen blir då

_0®2pò dB_Ps = µ₀(r²)(I/4p m³) _0®2pò d(2p) = µ₀Ir²/2m³ = B_P

Den cirkulära kontoppens magnetiska fältstyrka med ringradien r och höjden h=Ö m²–r² kan alltså beräknas enligt

B = µ₀I(r²/2m³) .............................................................

cirkulära konens magnetiska fältstyrka med höjden h, m=Ö r²+h², VS/M²

[Samma samband finns också i den traditionella lärobokslitteraturen, se exv TEKNISK ELEKTRICITETSLÄRA E. Danielson Gleerups Lund 1965 s47 ].

DEN magnetiska YTSTYRKAN

F = BA ................................. standardenheter, VS

I många tillämpningar inom elektromekanisk induktion [se efterföljande artikel] är det bekvämt att använda en allmän term för en given YTA som håller »en och samma B-styrka». Eftersom B är ett punktvärde, kommer ett motsvarande allmänt ytvärde att vara av den enkla typen B · A. Denna kvantitet kommer alltså att referera till en idealt homogen magnetisk fältstyrka tagen över en ändlig yta — och därmed också definierande B som en magnetisk flödestäthet i ekvivalens med punktstyrkan. Denna kopplande beskrivning mellan de nämnda begreppen förekommer (här veterligt) INTE i gängse litteratur.

Erinra från Q-RÖRELSEN INTRODUCERAS:

För att relatera en dynamisk referens till ett det statiska B-fältet i riktning r, måste vi introducera laddningen Q för en rörelse. Det finns två sätt att relatera effekten av en sådan Q-rörelse:

1. ett åkande Q som genererar ett stationärt B [Generering av Magnetiska fält],

2. ett stationärt B som påverkar ett åkande Q [Elektro-mekanisk induktion]. Vi börjar med det första sättet.

ELEKTROMEKANISKA INDUKTIONEN

Elektromekanisk induktion

DE FYRA GRUNDLÄGGANDE »dockskåps» LAGARNA I Elektro-MEKANISKA INDUKTIONEN

DET ANDRA SÄTTET

Stationärt B som påverkar Mobilt Q

Det andra sättet [Det första sättet var det ovan beskrivna Genereringen av magnetisk fält, se från INTRODUCERANDE EN Q-RÖRELSE] är att relatera den statiska skalmagnetiska fältstyrkan F/Qc₀= B till en yttre källa som helt omger eller »badar» laddningen Q. Därmed kommer på visst sätt också denna del att beskriva en närverkan. Vi studerar hur.

Om riktningen för elektriska fältstyrkan i B (F/Q-delen) tas genom ett tvärsnitt av Q-sfären — cirkulärplanet i figuren ovan — måste det ha en sådan och exakt likformig cylindrisk utvidgning över och under detta tvärsnitt om en motsvarande Q-rörelse ska fortsätta överensstämma med och bevara (satisfiera) den statiska motsvarande riktningen för den elektrisk fältstyrkan i Q-fältet självt i vilkensom r-riktning i tvärsnittsplanet.

Om vi känner grunderna i det magnetiska fältet [Se PRINCIPEN FÖR DEN CIRKULÄRPOLARISERADE B-VEKTORN] ser vi att situationen och villkoren passar perfekt för Q.

Situationen överensstämmer, tydligen, med situationen då Q färdas med hastigheten v i rät linje, vertikalt i figuren ovan och i normal till det illustrerade cirkulära tvärsnittsplanet (P) med dess expanderande fältpilar, och med ett motsvarande bevarande av den elektriska fältstyrkan »i varje P» som Q avancerar; I respekt till denna rörelseriktning (v) kan en ideal projektiv totalbild av alla elektriska fältstyrkors komponenter ses på den givna centrala Q-sfärens tvärsnitt, för att förenkla. Vi ser, då, Q färdas i perfekt balans utan någon ändring i rörelsebanan förutsatt den omgivande rymden är idealt homogen [Se PRINCIPEN FÖR DEN CIRKULÄRPOLARISERADE B-VEKTORN].

Den beskrivande punkten i sammanhanget i denna situation är att det motsvarande statiska magnetfältets styrka F/Qc₀= B med hänsyn till den gemensamma projektionen på P-planet uppvisar reduktioner i vägformen (v) av exakt samma ideala natur som den förtätade rymd som uppträder inom bågen eller kurvan för en reguljär magnetisk fältvågsring (Se från Hur B-vektorn förstås); om Q färdas inom en sådan kurva och utmed dess vägform, uppkommer följaktligen heller ingen magnetisk effekt mellan Q och den givna yttre B-bågen.

*cont.

För att relatera en magnetisk verkan betyder det att Q kan färdas i eller uppvisa hastighetskomponenter i vilkensom riktning rätvinkligt utvidgningen av det omgivande B-fältet (upp-ner i illustrationen) för att en magnetisk växelverkan ska uppträda. Om Q färdas exakt i vertikal riktning, illustrationen, färdas den bara parallellt inom sina egna tangentiella B-styrkor — analogt med den nyligen erinrade djupare liggande förklaringen till magnetismen enligt reduktionerna — och ingenting händer.

För att en verkan ska komma till stånd, kan (således) faktorerna Qc₀ vara av godtycklig komposition laddning-hastighet eftersom den resulterande kraften bara beror på dessa genom magnitud. Då erhåller vi helt enkelt från F/Qc₀= B magnetiska kraftlagen

F = BQv ............................ kraften på en fritt rörlig laddning som badar i ett yttre (homogent) B-fält

För att relatera en verkan kommer varje minsta möjliga avvikelse hos Q-rörelsen från parallellitet med B-kurvaturen — idealt genom varje mekaniskt relaterad hastighet (v) — att introducera magnetisk växelverkan mellan Q och ett yttre magnetiskt fält B. Vilket betyder; Den statiska magnetiska fältstyrkan F/Qc₀= B definierar utanför dess linjära inre kurvaturvillkor en motsvarande dynamisk (yttre) fältstyrka av »den enkla formen»

dynamiska magnetiska fältstyrkan F/Qv= B.

	Magnetiska Kraftlagen — för mera detaljerade jämförelser mellan relaterad fysik och modern akademi EN MERA DETALJERAD HÄRLEDNING ges i efterföljande Magnetiska Kraftlagen.
Magnetiska Kraftlagen

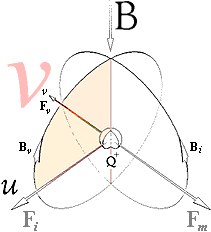
— Högerhandsregeln kan testa och analysera BFv-riktningarna. — Q^+-rörelsen i v uppväcker Bv . Växelverkan B-Bv bildar Fi , och därmed u som bildar Bi. Om Bi existerar (tillåten strömväg), ger B-Bi i växelverkan Fm som försöker motverka (upphäva) Fv. För att behålla u, måste kraften Fi=v=m adderas till systemet. Alltsammans Newton.

En laddning Q med hastigheten v omgiven av ett (homogent) magnetiskt fält med styrkan B kommer att erfara en kraft F som drar Q i en krökt bana. Med vinkelavvikelsen b från en exakt B-rätvinklig rörelse, blir F-formen i PREFIXxSIN

F = BQv · sinb

Med b=90° är kraften noll.

Med v=l/T får vi den motsvarande kraft som avkänns av en ström I inom en strömväg l som badar i ett yttre (homogent) B.

Som Q · l/T=Il får vi

F = BIl ....................... kraften på en ledare med längden l som håller strömmen I som badar i ett yttre B

= µHIl = (µ/2pr)I²l kraft mellan två parallella ledare med samma I , = µ(Hl)²

Strömmen I genom Q^+-rörelsen i u uppväcker Bi . Växelverkan B-Bi skapar Fv . Om ledaren lämnas fritt, färdas den i den riktningen, annars utverkar den bara sin dragkraft. Inuti ledaren tenderar Q i vilket fall att färdas i riktning v genom Fv som bildar Bv . Växelverkan B-Bv ger då Fm som strävar att motverka den strömdrivande kraften Fi . För att bevara den dragande Fv , måste kraften Fi=v=m , eller egentligen strömmen I, adderas till systemet.

*cont.

Det centrala sambandet F=BIl är avgörande för att bygga elektriska mätinstrument (i beräkningen av kraften på visarnålen i ett magnetiskt spolinstrument). Vi ser direkt att kraften är direkt proportionell mot alla faktorer BIl. Vi kan knappast får en bättre hjälp. Vinkelprefixet i x-sinus (se PREFIXxSIN) ger en komponent

F = BIl · sinb.

Som X=F/Q vilket ger F = X · Q får vi också X = Bv = U/l. Då gäller tydligen

U = Bvl ............................. inducerad spänning i fritt rörlig laddning badande i B

En ledare med längden l som färdas med hastigheten v i ett (homogent) B-fält erhåller ett spänningsfall U mellan ändarna.

Notera att v måste vara mycket mindre än c för att sambandet ska gälla

elektromekaniska induktionslagen

Som v=d/T får vi explicit den inducerade potentialen på formen U = B(d/T)l = BA/T. Förutsatt A håller samma punktvärden för B helt igenom , ger oss den nyligen beskrivna magnetiska fältets ytstyrka BA=F

U = F/T ............................. inducerad spänning i l som sveper över d under badande i B; U = BA/T

U = dF/dT ......................... allmänna (universella) elektro-mekaniska induktionslagen

Faradays lag

Se även i resultatredovisning av parallellexperimenten där elektromekaniska induktionslagen beskrivs mera ingående i jämförelse med den moderna akademins uppfattningar (Faradays lag, U = dF/dT).

Exempel 1

En 0,05 M rak tråd roterar kring en av sina ändpunkter i planet för en magnetisk ytfältstyrka F (Grekiskans Fi) med värdet 0,1 Tesla (= 0,1 VS/M²). Rotationshastigheten är ett varv per sekund. Bestäm den inducerade spänningen mellan trådändarna.

Lösning

A = pr²

A/T = pr²/1S

U = B · A/T = 0,1 · p (0,05)²/1S = 7,85398 t4 V.

Svar: Den inducerade spänningen är 0,785 mV.

Exempel 2

Sju likadana entums (l=2,54 cM) kopparcylindrar rullar parallellt med samma konstanta hastighet i och rätvinkligt ett yttre homogent B-fält med styrkan 0,25 T. Varje cylinder passerar ytan 2 kvadrattum på 0,75 sekunder. Bestäm summan inducerad spänning i alla sju cylindrarna samt deras gemensamma hastighet i standardenheter.

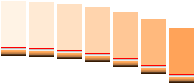
Lösning

Varje cylinder räknar

U = B · A/T = 0,25 · (2 · 0,0254²)/0,75 = 4,30106 t4 V.

Alla sju ger 3,01074 t3 V.

Hastigheten är (A_2×0.02542/l_0.0254)/0,75 = 0,0677333 M/S

Svar: Summan inducerad spänning är 3 Volt och hastigheten är 0,0677 M/S.

*cont. separat tillägg

DEN MAGNETISKA KRAFTEN — Magnetic ForceLaw — Magnetiska Kraftlagen (anges i engelsk litteratur ofta som Lorentz Force)

Magnetic ForceLaw

Magnetiska kraftlagen — härledningens principiella grunder

DEN MAGNETISKA KRAFTEN

Den elektrodynamiska magnetiska kraftens ekvation eller magnetiska kraftlagen

F = BQv .................... kraften på en fritt rörlig laddning badande i B

originalet	magnetiska kraftlagen KF från Kausalsambandet och Elektriska Kraftlagen	magnetiska kraftlagen Q genom Elektriska Laddningen
v i varje riktning av det antydda expansionsplanet med B rätvinkligt till det (uppåt-nedåt)
	Mera utförlig beskrivning för mera detaljerad jämförelse	Mera utförlig beskrivning för mera detaljerad jämförelse

gäller den fysiska dynamiken i den omedelbara närheten av Q: kraftens växelverkan med Q-ytan — vid stället där Q tas elektriskt under dT i v. Vid den tiden, har inget yttre fält från rörelseladdningen (eng. MoveQ) ännu visat sig.

Uttrycket F=BQv är en direkt vidareutveckling av »det inre B-fältets Q-form» F/Qc₀=B=X/c₀=R₀Q/A (se föregående den statiska Q-skalmagnetiska fältstyrkan), som tydligen är en (penetrerande) egenskap hos Q-kroppens yta [notera den ursprungliga reduktionsvektorn M, som ställföreträder B]: Som verkan av kraftdelen, F=BQc₀, uppenbarligen avser en magnitud för hastigheten om BQ är givna, med villkoret att F/Q=X måste skilja sig från (det yttre) B för att förverkliga en verkan på Q skild från B, är den ovannämnda framställda formen (BQv) principiellt klar:

det finns ingen annan grundläggande härledning.

vc-begränsningen

Med avseende på den avtagande B-verkan när v närmar sig gränsen c (se vc-begränsningen), blir det fullständiga sambandet

F=BQv(c–v)/c=BQv(1–v/c). Vilket betyder; F blir helt säkert noll med v=c.

Som redan diskuterats i sektionen om B-bildningen (se från B-VEKTORN), bestäms den växelverkande B-kraften från F=BQv av domänerna i den omgivande g-dominanta rymden med respektive lägsta och högsta koncentration av reduktioner, där Q attraheras mot den lägsta (tunnaste rymden) och repellerar från den högsta (tätaste rymden). Vilket vill säga, analogt: rum med minsta täthet exponerar en snabbare väg för den magnetiska fältvågen att utbreda sig på än rum med högre täthet, vilket med c-kopplingen bringar Q med dem.

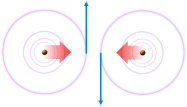
Följaktligen (illustrationen vänster), kommer alltid parallellt färdande och lika laddningar (++ eller – –) att attraheras magnetiskt medan parallellt färdande och olika laddningar (+–) alltid repelleras magnetiskt; Två ledande ringar med samma typ av laddningar och samgående strömmar kommer att attraheras magnetiskt; motsatta ringströmmar kommer att repelleras magnetiskt; två ledande elektriska spolar, liknande en stavmagnet respektive, kommer att attrahera varandra vid sina ändar av en synkroniserande vridkraft (eng. torque).

Med ytterligare liknande detaljer i jämförelse mellan magnetiska ämnen (järn) och elektriska ringströmmar kan, och vad vi hittills vet, det magnetiska beteendet beskrivas genomgående utan undantag på de enklare »ringströmslagarna».

Modern Akademi har ingen FYSIKALISK teori för elektricitet, induktion eller magnetism, utan en MATEMATISK kvantitetsMedelvärdesbildad vektorkalkyl utvecklad under 1800-talet.

Se också i Maxwells Ekvationer.

g-divergens ljushastighetens lokala värde med referens till den lokalt dominanta gravitationens inverkan, från Ljusets gravitella beroende.
— Divergensen är i relaterad fysik alltså det gravitellt punktlokala värdet på ljushastigheten och som INTE bildas över intervall;
— Se utförligt från DEEP och definitionen i DIVERGENSEN.
Ljushastigheten i normal mening däremot bildas över intervall som medelvärdet av ljusvägens g-divergenser.

reduktion divergensens lägre värde i den magnetiska fältbildningen för bevarandet av elektriska konstanten, se reduktionen utförligt i Kausalsambandet om ej redan bekant.

Magnetiska Kraftlagen — utförlig beskrivning i relaterad fysik för mera detaljerade jämförelser | 2011IX28

Magnetiska kraftlagen F=BQu — direkt från Kausalsambandet och Elektriska kraftlagen

Alla analogier I RELATERAD FYSIK som söker FÖRKLARA magnetismens olika verkningssätt bygger, eller återfaller, UTESLUTANDE på resultat från Kausalsambandets enkla form:

— MAGNETISKA effekter i Q-ändringens riktning [u(Q)] förekommer inte på grund av ljusets friställning från kinetiken: all MAGNETISK effektverkan på Q sker rätvinkligt u(Q).

— Följaktligen sker heller ingen vektorsummering, ingen magnetisk växelverkan, mellan kraftfältsriktningen för ett givet fast magnetfält (B) och det magnetfält B(Q) som bildas av en elektrisk laddning (Q) som färdas med en hastighet u i samma riktning som det yttre B-fältets kraftfältsriktning.

Genom att elektriska kraftlagen F=Rc(Q/r)² redan innefattar en motsvarande statisk, fast, form för den fysikaliska storheten magnetisk fältstyrka i elektriska laddningens statiskt elektriska fält som B=F/Qc=R(Q/A)=VS/M², speciellt tydigt med Q idealt vilande, kan tydligen och med kausalsambandets rätvinkelvillkor från ljusfrihetssatsen en magnetisk kraftverkan förstås direkt mellan Q i rörelse via en absolut minsta hastighet u större än noll och rätvinkligt det yttre B-fältets kraftfältsriktning genom en helt enkel omskrivning; Från Q:s egenform B=F/Qc till en allmän form för växelverkan mellan Q och ett yttre B enligt B=F/Qu. Därmed direkt på enklaste sättet magnetiska kraftlagen F=BQu.

Se även i vc-begränsningen för vidare aspekter på begränsningar i u relativt c.

En mera utförlig och detaljerad beskrivning — ursprungligen i UNIVERSUMS HISTORIA från originalet av magnetiska kraftlagen i DEN MAGNETISKA KRAFTEN — ges nedan i Magnetiska kraftlagen genom Q; Den beskrivningen har här utformats, särskilt i efterhand (Sep2011), för att få en mera exakt jämförande grund med motsvarande detaljer i den omfattande magnetismens matematik som utvecklades av James Clerk Maxwell (från 1855), och som format ämnets lärostol i modern akademi.

— Maxwells arbeten finns numera gratis att studera i PDF-format på Internet Archive,

THE SCIENTIFIC PAPERS OF JAMES CLERK MAXWELL, DOVER PUBLICATIONS, INC., NEW YORK [1890]

Finns som gratis PDF-dokument på Internet Archive,

http://www.archive.org/details/scientificpapers01maxw

En (första, Okt2011) sammanställd beskrivning ges i bildlänken nedan — Ampere, Maxwell och B i MAC

Magnetiska kraftlagen genom Q — utförlig beskrivning i relaterad fysik för mera detaljerade jämförelser | 2011IX28

Magnetiska kraftlagen genom Q

Magnetiska kraftlagen i RELATERAD FYSIK — Med särskilt härledande grund direkt från den elektriska laddningens kroppsyta

Magnetiska kraftlagen i Q — F=BQu

Vidare detaljerad beskrivning för jämförelser med Maxwell — Från ursprungsförfattningen i DEN MAGNETISKA KRAFTEN

I fysikaliska storheter definieras magnetisk fältstyrka (i relaterad fysik betecknad B, se vidare i NOMENKLATUR) från den idealt homogent sfäriska elektriska laddningen [Q=√(m/R)(A/dT)] i elektriska kraftlagen (F=ma=RcQ²/4πr²) som (magnetiska laddningsfältspotentialen)

B = F/Qc = RD = RQ/A = RQ/4πr², D anger laddningstätheten D=Q/A;

FSPH = Rc(Q²/4πr²) = (RQ/A)Qc = RD·Qc = B·Qc ; B = F/Qc ;

I NÄRVERKAN (verkan begränsad till Q) ges B direkt från laddningsradien (r) medan B i FJÄRRVERKAN (verkan utanför Q) via PREFIXxSIN beräknas från sinuskomponenten (sin0°=1) till laddningspotentialen på avståndet (r) från Q i rörelseriktningen (u). I vilket fall sker bildningen av den magnetiska effekten enligt kausalsambandet (rätvinkelvillkoret): Alltid rätvinkligt laddningens rörelseriktning (u), garanterat av ljusets friställning från kinetiken (se från ljusets gravitella beroende), och alltid med referens till den lokalt dominanta gravitationens fasta och fixa rymdreferenspunkter (i vårt fall Jordytan och dess föremål).

— Genom att RD avbildar den ideala sfäriska laddningsytan (ASPH=4πr²) också EKVIVALENT på den omskrivna CYLINDERYTAN (ACYL=4πr²), och därmed i (cirkulär) projektion liktydigt med en BILD av Q som en cirkulär SKIVA lika med en idealt cirkulär strömledares cirkulära TVÄRSNITT (ACRC=πr²), ges tydligen ett PERCEPT (en analog sinnebild) som VISAR en strömled i=dQ/dT motsvarande en Q-rörelse (u) INUTI »en riktad magnetisk fältstyrka» (dQ-skivan i Q-cylindern i riktningen u), B=F/Qc=RD. Magnetiska kraftens definition kan då tydligen skrivas på motsvarande samband uttryckt i F=BQc; F gäller med referens till en form för ett laddningens idealt sfäriskt, cylindriskt projicerat eget statiska B-skal (ekvivalenta cylinderytan B=RD), c som Q-skalmassans inneboende lokala g-divergens.

— Denna detalj ansluter således PERFEKT till kausalsambandets grundvillkor: Q-rörelse (u) i samma riktning som B innebär ingen växelverkan mellan B och Q, eftersom B-effekter inte kan bildas i laddningens rörelseriktning, just på grund av ljusets friställning från kinetiken, och därför heller inte har några vektorsummerande komponenter att uppvisa i den riktningen.

— Samtidigt, och således, visar magnetiska kraftformen F=BQc på den avgörande faktor som kan åstadkomma kraftväxelverkan mellan B och Q.

Vi studerar det.

— Med givet BQ varierar F direkt proportionellt mot c. Det är alltså bara en hastighetskomponent som avgör. För den principiella magnetiska kraftverkan kan vi alltså skriva magnetiska kraftlagen enligt F=BQu med u hur litet som helst med början från noll (och upp till max c, se vidare i vc-begränsningen för vidare aspekter på begränsningar i u relativt c).

— Med rätvinkelvillkoret ovan tillsammans med u större än noll (men mindre än c) bör alltså magnetiska kraftverkan mellan B och Q gälla om B tillhör ett yttre magnetfält som uppvisar någon vinklad riktning mot Q:s rörelseriktning (u=v·cosA° i PREFIXxSIN med A=0° för v||B, analogt u=0). Med dessa klargöranden således

MAGNETISKA KRAFTLAGEN i relaterad fysik enligt

F=BQu

med u rätvinkligt B (och u mycket mindre än c).

— Samma beskrivning kan komprimeras på en (med alla detaljer bekanta ytterst) kort form som nedan:

— Om en elektrisk laddning (Q) förflyttas (u) i samma riktning som riktningen hos ett yttre B-fält, flyttas Q endast inom sin egen elektriska [»divergensiska»] längsprojektion [F/Qc=B] och ingen växelverkan med B kan därför ske.

— För att en växelverkan ska kunna ske, måste u [analogt F/Qc=B-divergenserna i Q:s egen strömlängdsprojektion] ha någon komponent riktad rätvinkligt det yttre B.

— Eftersom verkan således endast beror av u rätvinkligt B gäller följaktligen formellt för kraftverkan mellan Q och B magnetiska kraftlagen F=BQu.

DISKUSSION:

— Laddningssfärens yta (4πr²) projicerad som CYLINDER ger BILDEN AV men inte effekten för en utsträckt magnetisk fältvektor (med cylinderhöjden lika med sfärdiametern). Det finns här veterligt ingen, sådan, motsvarande bildanalogi utanför den (idealt sfäriska) elektriska laddningen. Den bildanalogin är helt unik för Q. Magnetiska kraftens definitionsanalogi bygger helt på det unika logoceptet, enligt ovanstående beskrivning. Genom att cylinderytan bara är en annan form för den egentliga sfäriska laddningsytan (Q), blir motsvarande B-form också en STATISK bild av Q-laddningens egenskap (Q-laddningens statiska B-skalkraft), och vilken, som ovan, kan användas i den relaterbara härledning till den egentliga magnetiska kraftverkan, och som bara kan observeras utanför Q (magnetiska laddningsfältspotentialen).

— Hela framställningssättet med härledningen till magnetiska kraftlagen F=BQu bygger alltså på en (avancerad) logoceptisk analogi till de matematisk-fysikaliska egenskaperna i komplexet, så som här beskrivet. Magnetiska fältriktningar avbildas ALLTID (från Kausalsambandet) såsom utgående in i det omgivande rummet rätvinkligt Q (dess potentialbild i en g-punkt), medan »bildningskärnan», g-divergensen där effekten verkställs som orsakspunkt och som ombesörjer motsvarande kausalsambandets komplexa beskrivning av den magnetiska fältformens uppkomst, ligger i Q-ytan. PÅ SÄTT OCH VIS, skulle man (då) kunna säga att det LIKVÄL, sett i Q-kroppsytans historia, finns en B-effekt (verkan) »som följer med Q hela tiden» — fast ändå inte eftersom alla B-bildningar från Q-rörelsen u också LÄMNAR Q rätvinkligt u. Det är (den logoceptiska) sammansattheten. Hur man än ser saken, i alla dess detaljer, finns alltså, och såvitt välrelaterat, ingen möjlighet att missförstånd kan uppkomma. Eller rättare sagt, ska inte kunna uppkomma: alla detaljer är, tydligen, väl avgränsade i sina respektive domäner och inkräktar inte på varandras fysik.

VINJETTSAMBANDET Magnetiska Kraftlagen — hur sambanden hänger ihop

Vinjettsamband — dB = µ·ds·I/4πr² magnetiska laddningsfältspotentialen VS/M²

Elektriska kraftlagen F=RC(Q/r)² innehåller den fysikaliska storheten för magnetisk fältstyrka B=F/Qc=R(Q/A); Då gäller också formellt

R(Q/A)=R(c/c)D=(R/c)(s/t)D=µsQ/tA=µsI/A med A som elektriska laddningens idealt statiskt sfäriska laddningsfält med sfärytan A=4πr². Därmed

B = µsI/4πr² med differentieringen dB = µ·ds·I/4πr² samt, med PREFIXxSIN, gånger sinb med tillägg av komponenter som avviker från strömriktningen.

Magnetiska laddningsfältspotentialen — magnetmatematikens absoluta grundform i relaterad fysik — skrivs också mera renodlat (för utvecklingar) i Universums Historia i grundformen via strömlinjevinkeln (b) genom differentialtransformationen i PREFIXxSIN (även utförligt i Fjärrverkan)

x/s = tanb; s = x/tanb; Med ds/db = Dn s = s’ ges [grundderivator, se Bastablån]

ds = Dn s db = Dn (x/tanb) db = (–x/cos²b) db; Med x/r = cosb , x²/r² = cos²b , r²/x² = 1/cos²b ges ds = (–x/cos²b) db = (–xr²/x²) db = (–r²/x) db; Insättning i ds/4πr² ger

ds/4πr² = (–r²/x) db/4πr² = (–)db/4πx. Frånsett minustecknet således illustrationens sambandsform

dB = µ·ds·I/4πr² = µ·(I/4πx) sinb·db.

Mikrokomponenten (µ) framgår från Kausalsambandet (kort sammanställt nedan), ursprungligen med magnetismen från elektriska konstanten

↔Rc = ↨R’(c–u) = 1/ε = ↨R_maxç₀, med ↨R_max som R i ovanstående B=R(Q/A); Med reduktionssubstitutionen R(ç/ç) ges nämnarreduktionen till bildningen av mikrokoefficienten (µ=R/c), och täljarreduktionen som storhet för omvandlingen till ekvivalenta laddningshastigheten (ç=s/t). Därmed

µ = ↨R_max/ç₀

Eftersom också elektriska konstantens bevarande ansvarar för att

1/ε₀=R₀c₀=↨R_maxç₀, som visar att

ε₀^–1ç₀^–1 = R₀c₀ç₀^–1 = ↨R_max gäller också att

ε₀^–1ç₀^–2 = R₀c₀ç₀^–2 = ↨R_maxç₀^–1 = µ

Därmed — då reduktionen ç i vilket fall är försumbar mot c, och Rmax försumbart mot R0 — kan µ=R₀c₀ç₀^–2 förenklas med ç=c som ger

µ=µ₀=R₀/c₀ = 1,25662 t6 VS/AM

Notera (således) i sträng mening, att ingen magnetism finns i µ0. Se även i Magnetiska Konstanten.

Vinjettsamband — ↔Rc = ↨R’(c–u) = 1/ε = ↨R_maxç₀

Centralledet i Kausalsambandet.

Mekanisk-elektriska sambandet

Mekanisk-Elektriska sambandet

Mekanisk-elektriska sambandet

Från BQ-FÖNSTRET vet vi (nu) att verkan av magnetismen tvingas närma sig noll när den mekaniska laddningshastigheten (v) närmar sig den lokala ljushastigheten (c). Utan att bry oss om någon djupare utläggning än så ( i det här skedet), kan vi anta den föreslagna linjära relationen för att, till att börja med, formulera ett generellt mera praktiskt inriktat uttryck för den magnetiska verkan med varierande v.

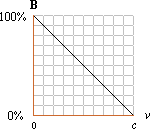
Den enkla linjära relationen, som illustrerad ovan, antyder att det magnetiska sambandet skulle följa ett B-beroende på en allmän reduktion genom förhållandet (c–v)/c enligt

B = B₀(c–v)/c

B₀ är det yttre fixa magnetiska fältet och B är hur B₀ ses av laddningen som färdas med v genom B₀. Vilket vill säga, med v=c ses B₀ som ”0”.

Den mera praktiska magnetiska kraftlagen skulle då ansluta sig till uttrycksformen

F_v=i=m = BQv · (c–v)/c

F_v=i=m = BQv · (1–v/c) ....... räknas upp till v=c endast

På samma sätt får vi spänningsformen (ledarlängden l här ersatt med s)

U = Bvs · (1–v/c) .................. inducerad spänning i fritt rörlig ledare som badar i B

DEN FULLSTÄNDIGA MEKANISK-ELEKTRISKA SAMBANDSFORMEN

Hela den mekaniska-elektriska sambandsformen — mellan ledaren s med hastigheten v i ett yttre magnetfält B₀ och den resulterande magnetiskt producerade laddningshastigheten u på Q i s genom en motsvarande Q-vakuumrelaterad accelerationsspänning [U=Bvs·(1–v/c)] — ges från den tidigare härledda

SAMBANDET FÖR LADDNINGSHASTIGHETEN u GENOM ACCELERATIONSSPÄNNINGEN U

________________________

u = cÖ 1 – 1/[(UQ/m₀c²) + 1]² ........................ laddningshastigheten u från accelerationsspänningen U

U accelerationspotentialen

Q laddningen, 1,602 t19 Coulomb för the elektronmassan (e^–)

m₀ vilomassan för Q; 9,11 t31 KG för e^–

c divergensen i e-fältet, 2,99792458 T8 M/S

u hastigheten för Q via U

Med U=Bvs skulle vi först få

__________________________

u = cÖ 1 – 1/[(BQvs/m₀c²) + 1]² .................... laddningshastigheten u via Bvs

Med förenklingen Qs/m₀c² = K, (CM/VC=M/V) ges

u = cÖ 1 – 1/[(BvK) + 1]²

Insättning av det mera praktiska B = B₀(c–v)/c skulle då ge

u = cÖ 1 – 1/[(B₀[c–v]vK/c) + 1]² ; u = cÖ 1 – 1/[(B₀[1–v/c]vK) + 1]²

K₀ = B₀K ;

u = cÖ 1 – 1/[K₀v(1–v/c) + 1]²

Vänstra delen av illustrationen nedan visar resultatet; med olika värden för K₀ (från noll och uppåt obegränsat) ges olika typkurvor som alla slutar på noll för u då v=c.

*cont. Mechanic-Electric Connection

u enhet u&v T8 M/S

________________________

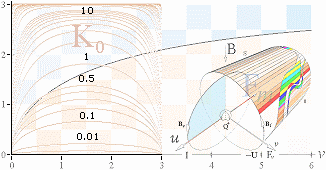
u = cÖ 1 – 1/[K₀v(1–v/c) + 1]² ........................... laddningshastigheten u via v

Mekanisk-elektriska sambandet i vakuum

K₀ B₀Qs/m₀c²

B₀ det yttre B-fältets styrka

Den svarta rotkurvan i grafen ovan är den föregående ”klassiska”

__________________________

u = cÖ 1 – 1/[(BQvs/m₀c²) + 1]² ........................ laddningshastigheten u via Bvs

Den är ”OK” i början, men uppvisar ett växande fel med växande v.

KAUSALSAMBANDET visar att reduktionen är en funktion av v genom

v_u= f (v). Idealiserat som v_u= v ger det en direkt proportionalitet ç=c–v. Oaktat problem i samband med Q-ytan, har vi inte mycket annat att välja på i sökandet efter en orsak till reduktionen ç=c–v. Det finns tydligen ingen annan orsak till magnetismen än Q-rörelsen relativt en fix gravitell referens, och den rörelsen regeras av v.

Detta innebär speciellt att användningen av termen u i den speciella härledningen i kausalkopplingen i kausalsambandet är överflödig: den magnetiska effekten vilar tydligen och enbart och direkt på v.

Magnetisk och Elektrisk polarisation

2002-04-07 [Fasta tillståndets fysik]

Magnetisk och Elektrisk POLARISATION

Magnetisk och Elektrisk POLARISATION

I likhet med de magnetiska egenskaperna hos materien [Se Allmänna teorin för ferromagnetiska material i JÄRNKÄRNETRANSFORMATORN], uppträder motsvarande elektriska parametrar. Den centrala förbindelsen i elektriciteten är fältstyrkan X = Rc · Q/A. Med (Rc)^–1 = e₀ och laddningstätheten D = Q/A gäller det att D = e₀X. Den följande korta översikten förklarar detaljerna och korrespondenserna enligt relaterad fysik. Motsvarande rent formella samband finns också (i trängre beskrivande mening) i den konventionella litteraturen i ämnet, men begreppsgrunderna där har inte den här framställningens referenser.

specifikt allmänt förklaring

B = µ₀H + nµ₀H B = µs I/A relaterar till strömtäthet och magnetisering

^Pm PUNKTSTYRKA.

D = e₀X + ne₀X D = Q/A relaterar till laddningstäthet

^Pe elektrisk PUNKTMÄTTNING.

jämför: p = a m/A tryck (F/A)

mekanisk PUNKTMÄTTNING.

Polarisationen P_m och P_e ansluter bägge till olika material där n är multipliciteten eller konventionellt susceptibiliteten för basparametern. Det är den magnetiserande kraften H för magnetismen och den elektrifierande kraften X för elektriciteten. P_m polariserar magnetiska dipoler, P_e polariserar elektriska dipoler. I gängse litteratur refereras den numeriska faktorn (1+n) som den relativa permeabiliteten för magnetismen och den dielektriska konstanten för elektriciteten.

I relaterade termer beskriver (1+n) den relativa punktstyrkan eller magnetiska punktmättningen för magnetiska fält och den relativa elektriska punktmättningen för elektriska fält. I respekt till fri rymd, beskriver således bägge dessa termer en egenskap av relativ mättning där n spänner från 0 och uppåt obegränsat:

B = (1+n)µ₀H = µ_rµ₀H ............................ magnetiskt, VS/M²

D = (1+n)e₀X = e_re₀X ............................... elektrisk, C/M²

Multiplicitetsfaktorn n kallas allmänt susceptibilitet. För fri rymd (vakuum) är den noll. [Genom att testa olika material kan deras respektive polariserande karaktär bestämmas kvantitativt].

Notera att termen µ₀ är en förenkling från den mera komplexa aktuella rymdkompaktheten. I den kvalitativa magnetiska fysiken är µ₀ aldrig närvarande. Se även i kausalsambandet.

Sammanställd2002VII5 Chapter 2 in Related Physics

Se även i NOMENKLATUREN FÖR B.

Järnkärnetransformatorn

ALLMÄN TILLÄMPNING AV INDUKTION OCH MAGNETISM

JÄRNKÄRNETRANSFORMATORN

ENERGIÖVERFÖRING MELLAN SPOLAR

Allmän beskrivning av transformator med järnkärna

Med föregående klargöranden om induktionen och magnetismen kan vi nu få en perfekt förklaring till den tidigare beskrivna principen i hur en transformator med järnkärna fungerar[Se Transformatorlagen ENERGIÖVERFÖRING MELLAN SPOLAR].

funktion

Betrakta en primär spole P med n varv.

Den växande strömmen i_P i P skapar ett centralt tvärställt magnetiskt fält B.

Polarisationen får materialet att ändra sina dimensioner. Det är känt som Den Magnetostriktiva Effekten (eng. The Magnetostrictive Effect). Järn förlängs (upp till en viss gräns, därefter förkortas), kobolt och nickel förkortas. I bägge fallen sker ändringarna approximativt med bevarande av konstant volym[DANIELSON s74]. Som påpekades i avsnittet om induktionen [RINGENS INRE SEKUNDÄRA INDUKTION] påverkas inte centrum av den induktiva effekten från de överliggande spolarna.

Om B passerar genom järn (Fe), polariseras (riktas) dess redan etablerade men slumpvis orienterade atombundna Fe_iP-strömmar av B. Denna polarisation resulterar tydligen i (makroskopiskt motsvarande) stora kollektiva cirkulerande Fe_iP-strömmar sekventiellt utmed strömändringslederna di/dt — och därigenom också med den påföljden att strömtrögheten överförs från P till varje befintlig sekundär spole.

PRIMARY SECONDARY

En sekundär spole S lindad på samma bärande järnkärna, kommer idealt att ta emot hela den induktiva effekten använd för att bygga upp i_P på di/dt. När laddningarna i S-strömmen i_S börjar accelerera, förorsakar i_S sin egen sekundära induktion u_S. Men denna sekundära induktion u_S från i_S är samriktad med i_P. Eller, med samma innebörd, u_S från i_S är motsatt riktad sekundärinduktionen u_P från i_P; induktionen u_S hindrar inte sin egen ”förälder” i_P, utan matar den [annars skulle effekten strypa sig själv, vilket skulle våldföra fysikens principer].

Således avtar den induktiva resistansen i P med växande i_S: ju mera uttag (output) från S, desto mera tillåter P sådana uttag. P följer S i i. Ingen reglerande anordning typ »volymratt» behövs för att säkerställa denna högeligen sofistikerade automatiska reglering: den är som klippt och skuren för att hjälpa och gynna människans elektrotekniska kultur. Vi får den helt gratis av naturfysiken.

Begränsningar

Ju mera effekt som tas ut från sekundärspolen, desto starkare kommer den att bidra till ett motriktat B-fält. Med höga effekter (uttag) på bägge sidor kommer detta uppenbarligen att leda till en kamp om B-fälten mellan spolarna — och som därigenom skapar stora mängder värmeförluster.

[Bästa (mjukaste) verkningssättet för en järnkärnetransformator är att aldrig använda mer än max halva toppeffekten].

I järnytan (IiS) där sekundärinduktionen från spolarna är starkast, påverkar både de primära och de sekundära spolströmmarna laddningarnas rörelse i järnet och i en tvärställd riktning gentemot de ideala järnströmmarna. I beskrivningen av situationen med bara en ring som en spole som arbetar under ett di/dt, och i användningen av högerhandsregeln, finner vi strax att järnändringarna tvingas avvika från områdena (kontaktytorna) där spolringen finns. Denna sidoeffekt minskar den ideala verkningsgraden (effektiviteten) hos järntransformatorn.

[I avancerade industriella tillämpningar används tunna isolerade järnplåtar för att bygga en motsvarande kompakt fullständig transformator med järnkärna; de inbördes elektriskt isolerade plåtarna tjänar just till att reducera de oönskade cirkulerande järnströmmarna, även benämnda s.k. virvelströmmar].

Allmänna teorin för ferromagnetiska material enligt relaterad fysik

MAGNETISMEN TEORI IN MODERN VETENSKAP OCH AKADEMI är som redan framskymtat i princip obefintlig.

Se Inledande citat.

Se Kärnmagnetiska momentet i modern teori.

Sett i det stora hela betyder det att också förklaringen generellt till alla teknisk-magnetiska tillämpningar innefattar grundliga (svåra) luckor. Den här framställningen är ägnad att försöka belysa dessa detaljer utifrån de helt annorlunda förutsättningarna i den relaterade fysikens horisont med strävan att uppdaga en mera uttömmande förklaring — utan varje form av oklarheter, luckor eller frågetecken.

Den relaterade fysikens teoretiska grund för magnetismens uppkomst i materien finns utförligt beskriven från Kärnmagnetiska momentet.

Eftersom atomkärnans härledning inte ingår i modern akademi, finns följaktligen heller ingen grundteori som kan beröra dess elementära magnetiska egenskaper — och därmed heller ingen teoretisk grund för materialmagnetismen: den framstår fortfarande (efter snart 200 år) som ”mystisk”.

Se Inledande citat.

DIA- PARA OCH FERROMAGNETISMENS EGENSKAPER enligt relaterad fysik, se från Kärnmagnetiska momentet, grundlägger helt naturligt förutsättningen för de mera allmänt redan välkända makroskopiskt observerade s.k. magnetiska domänerna i olika material, speciellt de s.k. ferromagnetiska grundämnena (järn, kobolt, nickel). Utan vidare utläggningar är det från denna grundform uppenbart att, beroende på olika omständigheter, grundämnesatomerna naturligt bildar olika typer av större områden med motsvarande cirkulerande elektronmassor. Den totala effekten av dessa inre cirkulerande strömmar blir naturligtvis en motsvarande påtaglig magnetism. Det är denna fenomengrund man utnyttjar rent tekniskt vid överföringen av elektrisk energi genom den förnämliga anordning som generellt kallas transformator och vars funktion här studeras och beskrivs mera ingående.

periodisk magnetisering

Som varje magnetisk dipol i en materiell substans tillhör ett naturligt tillstånd i substansens kristallina struktur, krävs ett visst arbete i varje ansats att försöka ändra dipolernas orientering. Detta arbete motsvarar ett karaktäristisk vridande moment (eng. torque) för varje individuell B-dipol. Sedan en sådan magnetisering har inträffat, har substansen inträtt ett nytt tillstånd där magnituden för dess totala B-fälts nya tillstånd också kommer att påverka varje vidare försök att ändra dipolernas riktning.

För en spole som är lindad på en viss materialkärna, realiseras den aktiva eller riktande magnetiserande kraften av den tidigare härledda faktorn

H=I/2pr

Eftersom det krävs ett arbete för att reorientera dipolerna i kärnan, kommer B-styrkan emellertid INTE strikt att följa strömmens variationer di/dt. Sedan H har nått sin toppmagnitud, fortsätter den motsvarande B-styrkan att hålla greppet kring kärnan — även sedan H börjat avta. Detta kallas remanens. Med än mera avtagande H, börjar B komma igen blott så småningom. Samma procedur upprepas sedan i andra änden från bottenvärdet för H. Ytan av den så karaktäristiska så kallade hystereskurvan (av viss tradition benämnd ”jungfrukurvan”) beskriver energin som krävs för att ändra dipolernas orientering.

*cont.

Typisk magnetiseringskurva för ett ferromagnetiskt material, idealiserat

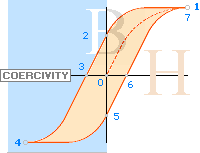
KOERCIV KRAFTYTA

Utgående från noll; Magnetiseringen B följer styrkan i H upp till mättnadspunkten 1. Med avtagande H kvarstår ett remanent B även då H når noll igen i punkt 2. B-nollan nås först i punkt 3. I punkt 4 nås den omvända mättningen för B. Processen upprepas sedan genom punkterna 5-7 och 1-4 som H följer en periodisk di/dt-ändring. Kurvan kallas hysteres och delen av H som krävs för att återställa B till noll kallas den koerciva delen av den magnetiserande kraften.

En bred hysteres betyder större energi för att omrikta materialdipolerna. Mjukt järn har smal hysteres (små förluster) medan stål har en bred hysteres (stora förluster). För permanentmagneter lämpar sig stål bättre än mjukt järn.

Dipolbindningens styrka i kristallen beror på material.

B-styrkan genom kärnan kan beskrivas som en sammansättning av

B=(R₀c₀/ç₀²)H

från en s.k. luftlindad spole (ingen materiell kärna) och

B=(Rc/ç_m²)H

från det magnetiserade materialet där reduktionen ç_m är ett medelvärde. Med (R₀c₀/ç₀²) förenklat som tidigare av ç₀=c₀ och som ger

(R₀c₀/c₀²)=R₀/c₀=µ₀, [se KAUSALSAMBANDET] blir den totala ordningen för magnetiska fältstyrkan det förenklade

B = µ₀H + mµ₀H

B = (1+m)µ₀H

m-faktorn relaterar den relativa multipliciteten för fria rymdens reduktion (förenklad som µ₀). Som m måste relateras 0 för fri rymd, kan vi relatera

(1+m)=(Rc/ç_m²)(R₀/c₀)^–1 i respekt till det aktuella materialet. m-faktorn kallas susceptibilitet (se utförligt i MAGNETISK OCH ELEKTRISK POLARISATION). Den kan vara både positiv (som ger B) och negativ (som tar B) beroende på hur materialet reagerar på ett yttre H.

Tabellen nedan visar m för några substanser (tn for 10^–n).

material m

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯¯¯¯

vakuum ..................................... 0

luft ............................................. +4 t7

vatten (H₂O) ............................. –9 t5

koppar (Cu) ................................ –1 t5

aluminium (Al) ............................ +2,1 t5

järn, kobolt, nickel (Fe, Co, Ni) ..... +(200 - 100 000)

I gängse litteratur refereras stundtals (1+m)-faktorn som den relativa permeabiliteten betecknad µ_r. Det allmänna uttrycket för B blir då

B = µ_rµ₀H ......................... allmänna B-styrkan genom ett medium, VS/M²

µ_r ....................................... (1+m), dimensionslös, 0 till oändligt

*cont.

DIA, PARA OCH FERROMAGNETISKA ELEMENT

[ref. FOCUS M 1975 s235, Encarta 99]

Se även DIA- PARA- OCH FERROMAGNETISMEN ENLIGT RELATERAD FYSIK.

Med hänsyn till m-faktorn och den magnetiserande kraften H, kan alla material (elementärt alla grundämnen) ordnas i tre huvudgrupper. Dessa material uppvisar följande karaktäristiska egenskaper.

magnetisk materialkaraktäristik

GRUPP m förekomst, alla grundämnen med

diamagnetism svag negativ individuella noll atomära B-moment

paramagnetism svag positiv individuella icke-noll atomära B-moment

ferromagnetism stark positiv kollektiva icke-noll atomära B-moment

De mest prominenta (framträdande, utstående) av de ferromagnetiska grundämnena är

järn, kobolt, och nickel (Fe, Co och Ni).

Grundämnenas allmänna magnetiska egenskaper

ÖVERGÅNGSELEMENTEN

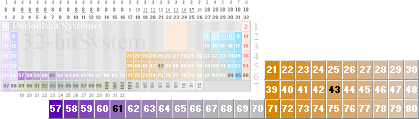
TRE SPECIELLA GRUPPER Grundämnen med atomnumren

21-30 koppargruppen

39-48 silvergruppen

57-80 guldgruppen

uppvisar egenskapen att vara s.k. elektrondonatorer: förmågan att dela på respektive grundämnesatoms yttersta s.k. valenselektroner.

Alla dessa 44 grundämnen har — enligt kärnmatrisiska algoritmen i Periodiska Systemet från Keplerresonanserna — två yttre valenselektroner i sin atoms yttersta skal. [Det är nämligen inte alla (traditionella) tabeller över grundämnenas elektronkonfigurationer som uppvisar analoga konfigurationer: Det skiljer sig (något) mellan olika källverk].

Se utförligt i Periodiska systemet.

ENCARTA99 skriver på artikeln Transition Elements

”The transition elements are commonly defined as the 30 elements with atomic numbers 21 to 30, 39 to 48, and 57 to 80.”.

ENCARTA99 Transition Elements

Min översättning:

Övergångselementen definieras allmänt som de 30 grundämnen med atomnumren 21 till 30, 39 till 48 och 57 till 80.

NOTERING TILL ENCARTACITATET: Antalet 21-30 är 10, 39-48 också 10, 71-80 också 10; därutöver finns 14 från 57-70.

Totalt blir det 30+14=44 grundämnen. Inte 30 som citatet påstår.

Vi kan se anledningen till felet: I 32-bitars systemet (illustrationen ovan) framträder de 44 grundämnena tydligt i övergångselementen — medan bara de tre gånger tio rutorna syns i den traditionella oktala uppställningen.

ÖVERGÅNGSELEMENTEN [2001-11-07]

Den speciella anledningen varför bara vissa grundämnen uppvisa ferromagnetiska egenskaper reflekteras delvis i elektronkonfigurationen för grundämnenas struktur — med elektronmassorna som arvtagarna till en viss partikulärt nukleär strukturell komposition, se från Kärnmagnetiska momentet.

Den avgörande ledtråden till detta beteende ser ut att vara förmågan hos en atomart att dela på elektronmassorna mellan grupper av atomer. Denna egenskap tillåter (nämligen) de fritt rörliga elektronmassorna att färdas i stora kollektiva leder bestämda av den aktuella kopplingen atom-atom (cirkulär, spiral, och andra typer). Varje sådan atomgrupp kan kallas en domän: domänen har en egen karaktäristisk magnetisk dipol grundad på medelvärdet av alla ingående atomindividers bidrag med de cirkulerande elektronmassorna.

I Periodiska systemet finns tre grupper som bildar en sådan speciell mobil s.k. valens av elektroner. Grundämnena i de tre grupperna tillsammans kallas för ÖVERGÅNGSELEMENTEN (eng. transition elements), och alla klassificeras som metaller. Var och en av dessa tre grupper kännetecknas av en berömd representant som vi alla känner: Koppar, Silver och Guld, eller de s.k. myntmetallerna. Grundämnena i de tre grupperna anges i ovanstående illustration från periodiska systemets 32-bitarssystem. Uppställningen nedan anger de 44 grundämnens namn och atomnummer i respektive grupp.

Övergångselementen i de tre grupperna är:

Koppargruppen:

Skandium |Sc 21| · Titan |Ti 22| · Vanadin |V 23| · Krom |Cr 24| · Magnesium |Mn 25| · Järn |Fe 26| · Kobolt |Co 27| · Nickel |Ni 28| · Koppar |Cu 29| · Zink |Zn 30|

Silvergruppen:

Yttrium |Y 39| · Zirkonium |Zr 40| · Niob |Nb 41| · Molybden |Mo 42| · Teknetium |Tc 43| · Rutenium |Ru 44| · Rhodium |Rh 45| · Palladium |Pd 46| · Silver |Ag 47| · Kadmium |Cd 48|

Guldgruppen:

Lantan |La 57| · Cerium |Ce 58| · Praseodym |Pr 59| · Neodym |Nd 60| · Prometium |Pm 61| · Samarium |Sm 62| · Europium |Eu 63| · Gadolinium |Gd 64| · Terbium |Tb 65| · Dysprosium |Dy 66| · Holmium |Ho 67| · Erbium |Er 68| · Tulium |Tu · även Tm 69| · Ytterbium |Yb 70| · Lutetium |Lu 71| · Hafnium |Hf 72| · Tantal |Ta 73| · Volfram |W 74| · Rhenium |Re 75| · Osmium |Os 76| · Iridium |Ir 77| · Platina |Pt 78| · Guld |Au 79| · Kvicksilver |Hg 80|

Grundämnen med inre kollektiva strömmar

Karaktäristiskt för alla goda elektriska ledare (metallerna) är deras allmänna förmåga att dela på så kallade valenselektroner. Dessa kan delas av alla atomer i metallen, vilket formar långa strömled med elektriska laddningar som vi använder i alla möjliga tekniska och praktiska tillämpningar. De förnämsta elektriska ledarmaterialen är (i tur och ordning) Silver (Ag), Koppar (Cu), Guld (Au) och Aluminium (Al).

Men det finns också andra metaller som har den karaktäristiska egenskapen att vara så kallade elektrondonatorer. Dessa material är samlade i det nyligen nämnda block av naturliga grundämnen som kallas övergångselement. De har ett totalt valenstal (elektrontillgänglighetstal) på 0-8.

En av de mest centrala grundämnena av dessa — vid sidan av Kobolt (Co 27) och Nickel (Ni 28) — är Järn (Fe 26). Dess naturliga kristall (kubisk) innefattar små domäner där grupper av atomer delar på samma cirkulerande elektronströmmar, och som enligt relaterad fysik ytterst återfaller på atomkärnans byggnad genom Kärnmagnetiska momentet.

Om inte magnetiserade, pekar de olika magnetiskt orienterade domänerna åt godtyckliga håll. Därmed blir det totala magnetiska fältet från en järnbit relativt svagt. Bara genom att skaka eller stöta försiktigt på järnbiten kan man få dess domäner att rikta in sig efter ett yttre B-fält, t.ex. det naturliga från Jordkroppens egen magnetism. En mera direkt metod är att linda isolerad koppartråd kring järnbiten och sända en kort ström genom den, vilket också ställer in järnbitens magnetiska domäner likformigt och därmed ger ett betydligt starkare B-fält.

Ju flera atomgrupper som på så sätt polariseras (riktas), desto mera kommer materialet att bidra med cirkulerande elektronmassor som ansluter till det kollektiva strömbeteendet. Därigenom kan det totalt genomgående magnetiska fältet hos en magnetiserad järnstav göras ”synligt” genom att förmås uppvisa ett (mycket) starkt B-fält.

Differentialtransformation|Referensbegrepp

DIFFERENTIALTRANSFORMATION: Glöm inte av det enkla d[ · ] = Dn [ · ] dx

En stor del av integralkalkylen handlar STUNDTALS om att transformera differentialer. Alltså motsvarande integrationskonstanter (vanligen dx, denna typterm saknar veterligt explicit benämning i konventionen, erinra f.ö. att ”integrationskonstant” i konventionen betyder något helt annat).

Transformationen av integrationskonstanter görs på det allra enklaste med ovanstående grundform i minnet;

differentialen till[ · ] = Derivatan till[ · ] dx

Eller analogt via den mera rudimentära basformen

y’ = dy/dx = Dn y

Det krävs dock att man har tillgång till en motsvarande Grundtablån i Formlagarna för att kunna lösa transformerna, samt att man förstår deriveringens grunder (se från Nollformsalgebran).

Först med en mera ingående erfarenhet av deriveringstekniken ger sig också de olika typer av differentialtransformationer som kan komma ifråga; Dessa kan (verkligen) ibland vara nog så luriga att lösa. GRUNDLÄGGANDE UTVECKLINGSEXEMPEL som visar hur derivering, och därmed differentiering, fungerar ges i matematikdelen i UTVECKLINGSEXEMPEL. Ett par exempel i detta dokument om magnetismen utnyttjar differentialtransformationer (av enklare typ)

För att integrera dB_P över vinkeln b måste vi först anpassa …

Som cirkelbågen i radianer b är b = s/x, får vi differentialtransformationen db=d(s/x)=ds/x …

och som kan användas som studieexempel, men dessa är här inte explicit framställda i syfte att belysa integralkalkylens metod utan snarare dess resultat.

END magnetismen.

*

Magnetismen

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Induktionen

ämnesrubriker

B-vektorn

Magnetiska Q-fönstret

Praktiska magnetiska kretsar

Elektrodynamikens grundläggande matematik

Grundläggande Magnetmatematik

Järnkärnetransformatorn

REFERENSBEGREPP — Differentialtransformation

innehåll

MAGNETISMEN

inledning

B-vektorn

den magnetiska fältvektorn B

hur B-vektorn förstås

högerhandsregeln

hantering av B-vektorerna

principen för den cirkulärpolariserade b-vektorn

Magnetiska Q-fönstret

att förstå den magnetiska växelverkans natur

växelverkande laddningar i rörelse

maximala fältverkan

ömsesidig magnetisk växelverkan

magnetiska fönstret

BQ-fönstret

vc-begränsningen

laddningshastigheten

SUMMERING

summerande B-fält

Praktiska magnetiska kretsar

att bygga starka magnetiska fält

Elektrodynamikens grundläggande matematik

närverkan och fjärrverkan

»dockskåpsmatematik»

Grundläggande Magnetmatematik

terminologi

magnetiserande kraften I — allmän beteckning

skrivsätt

GRUNDBEGREPPENS INNEBÖRD

statiska Q-skalmagnetiska fältstyrkan

introduktion av Q-rörelsen

Första sättet

rymdmagnetiseringen

närverkan

magnetiserande kraften II — Q-skivans princip

B-fältet inuti Q

förenklad härledning till B för rakledare

fjärrverkan

expansionsintegralens differentialekvation

magnetiska linjeintegralens differentialekvation

specifika B-ekvationer

rakledaren

magnetiska fältstyrkans linjeintegral (B_Ps)

rakledarens fullständiga samband

tillämpningar

B-styrkan i en lång rak spole

ringen

konen

den magnetiska ytstyrkan

elektromekaniska induktionen

Andra sättet

magnetiska kraftlagen F = BQv

Elektromekaniska induktionslagen

Den magnetiska kraften

Magnetiska Kraftlagen från Kausalsambandet

Magnetiska Kraftlagen genom Q

mekanisk-elektriska sambandet

magnetisk och elektrisk polarisation

Järnkärnetransformatorn

funktion

allmänna teorin för ferromagnetiska material

periodisk magnetisering

dia-, para- och ferromagnetiska element

ÖVERGÅNGSELEMENTEN

REFERENSBEGREPP — Differentialtransformation

särskild referens

DANIELSON s74

TEKNISK ELEKTRICITETSLÄRA E. Danielson Gleerups Lund 1965

magnetostriktion (för ev. vidare)

Senast uppdaterade version: 2024-09-09

*END.

Stavningskontrollerat 2008-06-08

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-08-25

åter till portalsidan · portalsidan är www.UniversumsHistoria.se