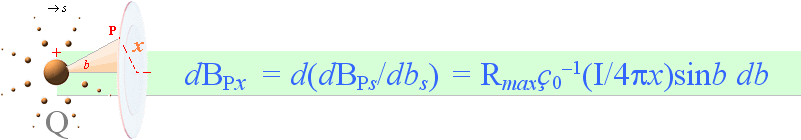INDUKTIONEN&MAGNETISMEN 2008V3 a BellDHARMA production · Efter sammanställningar från 1984  |  Senast uppdaterade version: 2024-09-27 · Universums Historia  ♦   HumanRight is a knowledge domain

 

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

grundfunktioner · översikt · induktionsbegreppet · växelverkansfrihetssatsen

 

utesluten i modern akademi:

men lösningen finns upptagen som Biot-Savarts lag — UTAN något spår av omnämnande VARIFRÅN det kommer —  djupa tvistigheter kantar debatterna  :

 

 

EXPANSIONSINTEGRALEN I MAGNETISMEN finns inte i modern akademi ·  relaterad fysik förklarar

 

Teorin för magnetismen i modern akademi och vetenskap är i princip obefintlig | Se även Tre noggranna exempel

modern akademi har ingen fenomengrundad teori för magnetismen

 

 

induktionen och magnetismen

 

MAGNETISM ENLIGT TNED

är en komprimerad kraftbild i det lokalt dominanta gravitationsfältet av det elektriska fältet från en elektrisk laddning (Q) i rörelse;

Förenklat: magnetism är g-bild av Q-rörelse.

   Magnetfältets riktning (B) ges av högerhandsregeln:

   med Q+-rörelsen i tummens riktning pekar B i fingrarnas riktning, se även illustrationen till vänster.

   Liknas g-fältets lokala dominans av en lugn vattenyta, är ringarna på vattnet kraftbilden i g-fältet från Q-individerna som de genomträngande vattendropparna.

   Magnetismens grundmatematik enligt TNED härleds i KAUSALSAMBANDET.

 

INDUKTION ENLIGT TNED (eg. elektromotorisk induktion)

är motstånd mot rörelseändring för en elektrisk laddning (Q) relativt referenspunkterna i det omgivande lokalt dominanta gravitationsfältet;

Förenklat: induktion är elektrisk tröghet, även matematiskt exakt motsvarande mekanisk tröghet (massans motstånd mot rörelseändring, se integralanalogin).

   Induktionen yttrar sig i en motsvarande inducerad spänning i rymdpunkterna motsatt riktad Q-ändringen och som, genom fältåterkoppling genom den lokala ljushastigheten c, strävar att motverka ändringens orsak (Newtons tredje lag).

   Induktionen som grundbegrepp enligt TNED beskrivs från Induktionsbegreppet.

   Induktionens grundmatematik enligt TNED härleds i INDUKTIONEN.

 

Komplement 2008IV15

Induktionen och Magnetismen

 

Induktionen och magnetismen kräver (rätt) mycket utrymme för att få en rättvis presentation: många illustrationer tävlar med varandra att få synas, och det finns en stor mängd matematik som hör till, dock (som alltid) av den enklare typen ENLIGT RELATERAD FYSIK och MATEMATIK. Med ett (mycket) omfattande material i induktion och magnetism som grund för den här framställningen, ges här till att börja med endast de väsentliga inledningarna i ämnet. Framtiden får sedan utvisa om behov finns — och editerande förmåga — för vidare.

 

 

induktionen och magnetismen

enligt relaterad fysik

kort inledande illustrerad beskrivning

Kurvformen ovan inlagd som illustration till sambandsformerna sammanställda i SYNTES AV INDUKTIONEN OCH MAGNETISMEN

 

Induktionen är motståndet mot ändring i strömflödet.

Magnetismen är förtätningen rätvinkligt induktionen.

 

Induktionen och magnetismen kan tämligen noggrant liknas vid effekten av en vattendroppe som träffar en lugn vattenyta: amplituden i vertikalled, induktionen, sammanhänger med motståndet mot eller genomträngligheten i ändringen av den plana vattenytan (motsv. mekanisk tröghet); utbredningen horisontellt, magnetismen, sammanhänger med ”packningsegenskapen” (»förtätningen») hos vattnet då droppen (föremålet) träffar: förtätningen strävar att uttömma sig i det omgivande lugnare vattet vilket motsvarar den magnetiska fältvågens strävan att uttömma sig i den omgivande, mindre täta elektriska rymden (rymdkompaktheten µ=R/c).

 

I elektrisk mening motsvaras vattenytan av den momentana TILLSTÅNDSBILDEN i det lokalt dominanta g-fältet med sina fasta referenspunkter för elektrisk potential i varje situationsbild (matematiskt i tillståndet dT); då en ändring sker, ”krusas” tillståndbilden genom att potentialen i g-punkterna också ändras — likt droppen som träffar vattenytan.

 

Motsvarande beskrivande/förklarande detaljer i den moderna akademins lärosystem har eftersökts men inte hittats.

 

 

Genereringen av det magnetiska fältets magnitud beror på den momentana hastigheten (v) som elektriska laddningen (Q, motsv, vattendroppen) lägesändrar med. Det betyder att induktionseffekten av princip ENLIGT RELATERAD FYSIK föreligger oberoende av hur Q lägesändrar: den magnetiska effekten bildas i vilket fall ur potentialbildens ändring. Det enda som skiljer beroendet/oberoendet är att då Q lägesändrar med varierande v över ändliga intervall det sker en motsvarande ackumulering av fältpotential relativt de mätande g-punkterna och därmed, enligt »Newtons tredje lag» ett motsvarande intervallbaserat induktivt motstånd och därmed en (med lämplig anordning) kvantitativt mätbar induktionsspänning; Med konstant v blir induktionsvärdet kvantitativt noll med en bibehållen kvalitativ differential (dUÛ0) som grund för magnetismens verkan. Vilket vill säga: av princip blir det i vilket fall ändringen (induktionen) som frambringar magnetismen. Se även i Induktionspotentialens bildning.

   Dessa detaljer diskuteras vidare nedan ENLIGT RELATERAD FYSIK med jämförande korsreferenser till den moderna akademins meningar och uppfattningar för exakt och noggrann jämförelse.

 

ytterligare alternativa kortbeskrivningar

av induktion och magnetism

 

 

 

INDUKTION: Motståndet mot ändring i rörelsen hos en elektrisk laddning med referens till ett omgivande dominant gravitationsfält.

 

MAGNETISM: Den speciella elektriska fältverkan som uppkommer mellan laddningar i rörelse genom en fast, omgivande gemensam gravitell dominans.

 

Magnetismen visar sig som en inbördes attraherande eller repellerande elektrisk kraft som sidledes strävar att dra ihop eller separera laddningar i parallell rörelse.

 

Induktionen visar sig i en attraherande eller repellerande elektrisk (c-bärande) kraft motriktad riktningen för laddningarnas rörelseändringar.

 

 

 

 

induktionsbegreppet

Begreppet induktion inom elektrofysiken har (främst) två  praktiska betydelser, bägge utan hjälp av någon transporterande massa: Den ena betydelsen beskriver elektrostatisk induktion, även benämnd influens, och den andra typen beskriver elektrodynamisk induktion. I den här presentationen om INDUKTIONEN OCH MAGNETISMEN behandlas enbart den dynamiska delen.

elektrodynamiskt

Det finns ENLIGT RELATERAD FYSIK TVÅ typer av elektrodynamisk induktion. Den ena är av typen elektromotorisk och den andra är av typen »magnetomekanisk», men denna senare term finns veterligt inte i någon etablerad litteratur.

 

Den magnetomekaniska induktionen är samma som elektromekanisk induktion, typ strängarna på en elgitarr som svänger i ett fast yttre magnetfält.

   Denna induktionstyp uppkommer genom växelverkan mellan det yttre magnetfältet och magnetfältet som bildas av den mobila laddningen då den förflyttas i sidled genom strängens vibrationer.

 

Den elektromotoriska induktionen, här enklare benämnd induktionen, konventionellt benämnd elektromagnetisk induktion, är den induktion eller masslöst överförda rörelseenergi som enligt relaterad fysik bildas på en sekundär elektrisk laddning genom ändringar i rörelseformerna hos en primär elektrisk laddning (laddningarna »pratar med varandra»).

   Exempel på en sådan överföring ges av Solens energiproduktion som bildar värme och ljus genom elektromotorisk induktion (masslös energiöverföring).

   Modern akademi hävdar den inducerade spänningen i sekundären som förorsakad av magnetiska fältets ändring hos primären enligt Faradays lag (U = dF/dT= B·A/T), medan relaterad fysik innefattar den uppfattningen som PRIMITIV:

   I modern akademi finns, i relaterad mening, ingen fenomengrundad teori för magnetismen (B); denna hänförs istället, i relaterad mening, direkt till den elektromotoriska induktionsfysikens fenomengrund; Den moderna uppfattningen ger ( i trängre mening) en matematiskt kvantitativ syntes av induktionen och magnetismen (Maxwells ekvationer) genom den moderna akademins vektorkalkyl, men till priset av att hela kunskapsbyggnaden för induktionens och magnetismens fenomenmässiga förklaring helt elimineras: ingen kan varken förklara, härleda eller ens begripligt beskriva fenomengrunderna med den moderna akademins begrepp. Ingen förstår ämnet.

   [Studera till exempel @INTERNET Wikipedia Magnetic field på Talkpage: dispyterna har pågår i flera år, stundtals så häftiga att själva artikeln har spärrats av Wikipediaadministrationen].

   En kort beskrivande genomgång visas i Vektorkalkylens regelbrott.

   För att belysa den exakta skillnaden i konkreta resultat mellan modern akademi och relaterad fysik i anledning av dessa diskrepanser, finns uppställda TRE EXAKT JÄMFÖRANDE EXEMPEL där samtliga grundbegrepp exponeras till exakt jämförelse.

 

I relaterad fysik finns ingen växelverkan eller koppling mellan elektromotorisk och elektromekanisk induktion. De existerar helt skilda från varandra. Det praktiska beviset ges i PARALLELLEXPERIMENTET med koppling till ovanstående. Den teoretiska förklaringen beskrivs utförligt i UPPKOMSTEN AV INDUKTION OCH MAGNETISM.

 

En motsvarande »magnetomotorisk» induktion skulle i analogi med ovanstående begreppsformer betyda en roterande, vibrerande eller allmänt mobil magnetkropp som OBS genom sina inre cirkulerande strömmar, inte genom den yttre magnetismen, åstadkommer en elektromotorisk induktion i omgivande fixa ledare.

   Ett exempel på en sådan anordning finns i den elementära skolfysiken: Man använder en fast mångvarvig öppen spole som står uppvänd på ett bord och som är kopplad till en känslig galvanometer. I spolöppningen för man sedan in en stavmagnet vars inre elektriska strömmar påtvingar den fasta spolens laddningar en elektromotorisk induktion och därmed ett utslag på galvanometern. I skolböckerna, däremot, beskriver man INTE funktionen så, utan istället att det är ”det varierande magnetfältet” från stavmagneten då den genomgår någon rörelse som genererar induktionen i den öppna spolen.

 

 

Följande beskrivning redovisar induktionen och magnetismen

ENLIGT RELATERAD FYSIK

— med utförliga korsreferenser till den moderna akademins hävder, samband och uttryck, där sådana är möjliga.

 

 

 

 

 

 

InduktionenOchMagnetismen

 

inledande sammanställning

med allmän genomgång

 

Induktionen och magnetismen framgår genom ändringslagarna, se även nedan, tillämpade på ljusfysiken enligt följande sammanställning:

 

Ändringslagarna (eng. Laws of Change, min beteckning)

 

Hela det totala kosmiska framträdandet kan med excellent tydlighet beskrivas såsom betingat av och grundat på

tre ändringslagar

som är tillämpliga på alla fenomen utan undantag, eller om så INTE skulle vara fallet, inte alls:

 

första ändringslagen  .....................      I           TILLSTÅND råder tills ändrat

andra ändringslagen  .....................       II          ÄNDRINGEN är proportionell mot verkan

tredje ändringslagen  .....................       III         ÄNDRINGENS ANSATS motsvarar tillståndets bevarande

 

Se mera utförlig beskrivning i Ändringslagarna.

OM dessa tre lagar tas för att vara ’fundamentala satser för kropparnas rörelser’ — vilket just hände i det tolkande ljuset av de som läste Isaac Newton med början under 1600-talet — ger de INTE en grundlig och fullständig beskrivning av fysiken;

De så kallade rörelselagarna

 

I           varje kropp förblir i sitt tillstånd av vila eller rätlinjig likformig rörelse om den inte påverkas av en kraft

 

II          påverkas kroppen av en kraft, är tillståndsändringen proportionell mot den tillståndsändrande kraften

 

III         mot varje tillståndsändrande kraft svarar en lika stor motriktad tillståndsbevarande kraft

 

och som med Newtons egna formuleringar från Andrew Mottes översättning av Principia (1687) 1729,

först uppställda av Newton (Principia 1687),

 

I           Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.

II          The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.

III         To every action there is always opposed an equal reaction; or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.

 

ger då »endast» en korrekt beskrivning i respekt till mekaniken utan några aspekter på elektrofysiken, och vilket område vi känner som den klassiska fsyiken. Vilket vill säga: Newtons tre rörelselagar gäller bara för fysiken upp till den moderna akademins födelse under 1800-talet då elektriciteten och magnetismen uppdagades mera på djupet (ref., Örstedts upptäckt/publikation 1820 att elektricitet och magnetism hör ihop). Som vi vet kom dessa upptäckter att ”revidera den gamla uppfattningen”.

   Newton kände naturligtvis inte till den grundläggande matematiska fysiken för ljusets natur, och det var därför helt naturligt för honom att söka formulera ändringslagarna efter mekanikens grundbegrepp som ovan genom att explicit använda ordet ”kropp” (eng. body).

   Emellertid framgår även (direkt) ur Newtons egna formuleringar själva huvudsaken:

 

I mekaniken (gravitationsfysiken, eller g-fysiken) leder ändringslagarna direkt till

den universella kraftlagen,

F=m(dv/dt) = ma

(konv. Newtons andra lag), och vidare till

den universella gravitationslagen,

 

F=ma=m(w2/r)=(w2/rm2)·m2m=(w2/m2)·m2m/r=(w2r/m2)·m2m/r2=G·m2m/r2, G = 6,67 t11 JM/(KG)2  ..............................       g-fysik

 

och sedan vidare genom ljusets grundfysik till

den universella lagen om elektrisk attraktion och repulsion (elektriska kraftlagen),

 

F=ma=m(c/dT)=m(c/dT)(RA/RA)=Rc(m/R)(A/dT)/A=RcQ2/r2, Rc = R0c0/4p = 8,98743 T9 VM/C  ...................................     e-fysik

som innefattar den så härledda definitionen på

den elektriska laddningen enligt

Q=Ö(m/R)(A/dT)  .............................    elektriska laddningen, men vars härledning helt saknas i den moderna akademins lärosystem

För de elektriska storheterna, se vidare ovanstående utvecklingar i Elektromekaniken grundbegrepp

 

I elektrofysiken (e-fysiken) leder ändringslagarna explicit, speciellt den tredje, direkt till

den universella induktionslagen, se de efterföljande leden nedan

û=L(di/dt) = F(r/Q) = E/Q = R’i

från den mekaniska integralen till (mekaniska tröghets-) kraftlagen,

Integralbegreppet på helt elementär bas beskrivs utförligt med utförliga exempel från Atomtriangeln, om ej redan bekant

integrala analogierna

kraftlagen

Mekaniska tröghetseffekten

MEKANIKEN

             m  ......................................        massa (KiloGram)

             F = m · dv/dt .....................       kraft (Newton)  ............................................      universella kraftlagen

             Fv = m · v · dv/dt ...............      effekt (Watt)

             Fvdt = dE = m · v · dv .......      mekaniska rörelseenergin (Joule), differentialekvation, lösningen är

             Fv ò dt = Fvt = òdE = E = m ò v dv  ................................................................     = m · v2/2

 

genom

(mÛL) and (vÛi)

— mekanisk tröghet m motsvarar elektrisk tröghet L i enlighet med tredje ändringslagen från

L=µs=RT

[VARJE ACCELERATION a=dv/dT definierar enligt »Newtons tredje lag» ett motstånd (R) som tillsammans med tiden (T) för accelerationens varaktighet producerar begreppet induktans, L=RT motsvarande massan i mekaniken],

såsom också mekanisk hastighet v motsvarar elektrisk ström i (laddningshastighet q/t),

se mera utförligt och fullständigt i DIVERGENSEN I TREDJE ÄNDRINGSLAGEN,

men dessa InsiderLed saknar representation i modern akademisk litteratur, såvitt här känt

— som ger den motsvarande elektriska integralen

induktionslagen

Elektriska induktionseffekten

ELEKTRICITETEN

             L  ........................................      induktans (Henry), strömtröghet

             û = L · di/dt ........................      inducerad spänning (Volt)  ..........................      universella induktionslagen

             ûI = L · I · di/dt ..................      induktionseffekten (Watt)

             ûIdt = dE = L · I · di ..........      elektriska strömenergin (induktionsenergin, Joule), differentialekvation, lösningen är

             ûI ò dt = ûIt = òdE = E = L ò I di  ....................................................................     = L · I2/2

 

Alltså gäller det att F i mekaniken och U i elektrofysiken (U=û, Alt+0251) håller ekvivalent genom tredje ändringslagen såsom (ekvivalenta) aspekter på kraft (egentligen styrka [kraften är egentligen accelerationen, den bevaras (genom induktionen) medan massan och laddningen förintas som i fallet med Solens energiproduktion], men den delen tillhör en språklig undersökning som INTE DU, INTE JAG, VILL VETA NÅGOT mera OM [därför att den dödar (utplånar) den nuvarande etablerade nomenklaturen, och det vill ingen bidra till: det är allt vi har]; basdefinitionerna per matematisk fysik klarlägger hur som helst den exakta innebörden).

 

 

Att SÅLEDES cementera »Newtons tre lagar» genom att påtvinga dem ordet ”kropp”, dödar effektivt den enorma styrkan som uppdagas i

ändringslagarna själva — och som därmed, korrekt, leder till meningskonsekvensen:

”Newtons lagar gäller inte för fysiken generellt”.

Naturligtvis gör de det

— som framgår tydligt genom den ovan exemplifierade härledningen till

den universella induktionslagen

— men inte som ”Newtons lagar” utan som Ändringslagarna.

Newton bidrog (högeligen) till ämnets klarläggande, men att försöka påstå att han därmed också skulle ha slutfört ämnet är uppenbarligen varken en rättvis eller intelligent beskrivning.

   Först genom en lång vetenskapshistoria med många bidrag som klarlägger de olika detaljernas verkningssätt och som sett i dagens ljus (2008) var långt ifrån kända på Newtons tid, och som kan ge tillräckligt underlag för en vidare bild, finns tydligen förutsättningarna för en mera berikande och grundligt klargörande beskrivning.

 

 

Magnetismen — se även enklare från Illustrerade Grundbegrepp

 

EFTERSOM LJUSHASTIGHETEN c INTE KOPPLAR TILL MEKANIKEN v —  se Ljusets friställning från kinetiken — finns heller ingen motsvarande reguljär vektorrepresentation för resultanten i vektorrektangeln v+ic=Ö v2+c2; c och v kopplar inte i fysiken. Se även i Experimentella observationer. Den ändring i potentialbilden, från den elektriska laddningens eget e-fält, som ges på rymdpunkterna (P) i ett fast gravitellt referenssystem då Q lägesändrar där med hastigheten v, bildar istället genom orsakskomponenterna v+ic en komplex verkan som — i bevarande av elektriska konstanten i riktningen v — påtvingar P en motsvarande rymdförtätning med en tillhörande partiell divergensreduktion (ç=c–v) rätvinkligt v och vilken fenomengrund vi känner som MAGNETISMEN; förtätningen uttömmer sig i det tunnare omgivande rummet som den reducerade divergensen uttömmer sig i den snabbare omgivande normalrymdens högre divergens, dvs., inom/med ljushastigheten c. Effekterna i P som sprids rätvinkligt v från Q-systemets e-fält ges därmed helt oberoende av v-formens typ, om den är konstant eller del i en acceleration vilketsom. Magnetismen som fenomen har alltså ingen direkt koppling till de ovan refererade sambandsformerna.

   Med den här kortfattat givna utläggningen som grund, kan magnetismen därmed sägas vara resultatet av en fältmässig växelverkan: Q-systemets e-fält projiceras på det fasta g-systemets referensrymd, vilket ger magnetismen som en annan form för (det mobila) Q-fältet, nämligen sett i det fasta g-systemets preferens.

Magnetismens grundform med upphovet via v+ic­-formen beskrivs särskilt från KAUSALSAMBANDET.

 

 

 

 

 

 

InduktionenOchMagnetismen

 

översikt

Primära och Sekundärna induktionen med Närverkan och Fjärrverkan i Magnetismen

INDUKTIONENS OCH

MAGNETISMENS MATEMATIK

 

 

Både induktionen och magnetismen uppvisar med nödvändighet en nära [eng. near, Q till insidan] och en fjärran [eng. far, Q till utsidan] verkan på grund av den ändliga fältåterkopplingshastigheten (c).

 

Motsvarande detaljer i den moderna akademins lärosystem har eftersökts men inte hittats.

 

För att särskilja komplexen är induktionen i den här presentationen indelad i en primär och en sekundär del medan magnetismen behåller termoinologin med närverkan och fjärrverkan.

 

 

Sambandsformen ovan med

induktionslagen

û = L · di/dt  ..............................................................      induktionslagen

— den allmänna kvantitetsformen; själva induktionsvärdet, oberoende av hur det kommer till

— är allmän för bägge delarna

primärinduktion

Primärinduktionen berör endast en ledares utsträckning (s) utan hänsyn till dess kurvatur men med hänsyn till ledarens samtliga materialkonstanter och därmed i referens till ledarens specifika induktans (Lc).

och

sekundärinduktion (typ)

dÐ = L(di/dt)(1/4pr2)sinb · ds  ..................................     V/M, induktiva dipolFältstyrkan i P i PREFIXxSIN

och kan inte explicit preciseras på de sistnämndas form, utan ingår där som ämnesbas.

 

 

TILLSAMMANS MED NÄRVERKAN OCH FJÄRRVERKAN ger magnetfysiken ENLIGT RELATERAD FYSIK motsvarande ekvationskomplex uppdelat enligt ordningen

 

1. generering av MAGNETISKA FÄLT — med närverkan och fjärvverkan som underavdelningar

2. växelverkan mellan MAGNETISKA FÄLT — med allmänna kvantitativa samband som ämnesbaser

 

 

Nedanstående delar länkar till de vidare presentationerna om induktionen och magnetismen.

Där så är möjligt ges integrerade korsreferenser till motsvarande etablerade uttryck för exakt och noggrann jämförelse.

 

meny

Snabbgenomgång av

INDUKTIONENS OCH MAGNETISMENS MATEMATISKA FYSIK

enligt relaterad fysik

 

Allmänna samband

En kort översiktlig sammanställning av magnetismens gruppdelar ENLIGT RELATERAD FYSIK visas i Allmänna samband tillsammans med induktionsmatematiken. Där behandlas hela komplexet heltäckande både för närverkan och fjärrverkan, men bara för de mest centrala sambanden — för den korta/snabba översiktens skull.

I NOMENKLATUR visas en del av grunderna till den allmänna språkförbistringen i ämnet magnetism.

 

Induktionen och Magnetismen

En mera fullständig tappning av översikten i Allmänna samband ges med induktionen och magnetismen uppdelade i separata htm-dokument. Se INDUKTIONEN och MAGNETISMEN. Där ges en fullständig beskrivning med noggrann genomgång och härledning av alla de (främsta) samband som brukar förknippas med respektive ämnesområde — tillsammans med exempel och korsreferenser till motsvarande uttryck i modern akademi där sådana är kända.

 

Syntes av induktionen och magnetismen

En fullständigt utförlig härledning ENLIGT RELATERAD FYSIK med induktionens och magnetismens matematiska fysik komplett sammanvävda — som visar hur induktionens och magnetismens matematiska fysik delas upp utifrån en och samma matematiska grundform;

Visas genom nio grundsamband med tillhörande beskrivningar och grundformer i Syntes av induktionen och magnetismen — tonvikten där ligger emellertid ENBART på Den sekundära induktionen och Fjärrverkan i magnetismen.

 

Tre precisa exempel för exakt jämförelse

För att verkligen VISA och konkretisera den relaterade fysikens (rejäla) överlägsenhet relativt den moderna akademins ”tekniskt vetenskapliga system”, ges i TRE PRECISA EXEMPEL FÖR EXAKT JÄMFÖRELSE en noggrann beskrivning av några mycket centrala samband inom induktionen och magnetismen — tagna direkt ur gängse fackböcker och undervisningsmaterial och i direkt matematiskt jämförande konfrontation med resultaten från relaterad fysik (extraherade från härledningarna i INDUKTIONEN och MAGNETISMEN).

 

 

För den som vill studera HUR induktionen och magnetismen härleds i detalj ENLIGT RELATERAD FYSIK, per uppdelade logiska block,

 

Divergensen i tredje Ändringslagen · rymdkompaktheten µ · elektriska konstanten e

 

Universella induktionslagen · induktionen · elektriska analogin till mekaniken · integralanalogin

 

Kausalsambandet · magnetismen

 

ges ovanstående länkbyggnad till hjälp och som ingår integrerat i övriga här omnämnda delar.

 

 

För den som önskar få en direkt begriplig förklaring till den moderna akademins idé om magnetismen,

 

magnetismen i modern akademi · den fullständiga upplösningen av magnetismens fråga

 

— med direkt konkret jämförelse mot relaterad fysik — ges ovanstående länk. Kort och gott.

 

 

För den som vill ha ansatsen till en mera litterärt orienterad beskrivning av induktionen och magnetismen tillsammans med ILLUSTRERADE enkla inledande grundbegrepp som beskriver huvuddelarna i ämnet MED GRUND I DEN RELATERADE FYSIKENS KÄNNEDOM

— som diskuterar korsreferenser och jämförande exempel, även med länkar till ovanstående, och på den vägen ger en mera övergripande författningsbild (på gott och ont eftersom risken KAN vara att författaren tycker han är duktigare än publiken: det kan bli DRYGT)

— finns den följande delen. Där finns den rikast representerade länkbyggnaden då varje detalj MÅSTE förklaras ingående för att inte tappa läsarens grepp.

 

 

 

 

 

 

 

InduktionenOchMagnetismen

 

 

inledningMAC

 

Grundvalen för den här framställningen:

TEORIN FÖR MAGNETISMEN

 I MODERN AKADEMI OCH VETENSKAP

ÄR I PRINCIP OBEFINTLIG:

 

Citaten nedan vittnar om magnetdimmornas dunkla riken:

 

”Magnetism

Trots att utvecklingen av magnetmaterial och användningen av magnetism har ökat våldsamt sedan man upptäckte sambandet mellan magnetism och elektricitet i början av 1800-talet har vi fortfarande svårt att förklara vad magnetism egentligen är.”

[http://www.magnetfabriken.se/Magnetism.htm] 2007-06-14

;

”What a magnetic field actually consists of is somewhat of a mystery, but we do know it is a special property of space.”

[http://www.school-for-champions.com/science/magnetism.htm] 2007-06-14

 

Min översättning:

Vad ett magnetisk fält egentligen består av är något av ett mysterium, men det vi vet är att det är en egenskap hos rymden.

djupgående tvistigheter

Speciellt MAGNETISMEN är (ännu 2008) föremål för (våldsamma) kontroverser inom modern akademi. Se exv Talkpage på Wikipedia Magnetic Field (de häftiga kontroverserna leder bakåt i åratal).

   Här ges den fullständiga förklaringen — det framgår varför denna INTE kan inlemmas i Wikipedia med mer än hela Wikipedia fragmenterar till intet (låt därför Wikipedia bevaras som den moderna akademins samlade referensverk, den samlingen är helt unik — den berikar den här framställningen genom att visa konkreta jämförande praktiska exempel på hur det INTE ska se ut).

 

Se även i NOMENKLATUR — den har (enbart) i Sverige ändrats flera gånger: fram och tillbaka.

Se även i Kärnmagnetiska momentet i modern teori.

 

 

inledning induktionen och magnetismen

 

 

 

 

 

InduktionenOchMagnetismen | Illustrerade Grundbegrepp | Se även den kort inledande illustrativa beskrivningen

 

 

Med utförliga korsreferenser till begreppen i modern akademi och vetenskap — där så är möjligt

INDUKTIONEN OCH MAGNETISMEN

I RELATERAD FYSIK

Korta inledande illustrativa uppsatser — med länkar till vidare — som visar och förklarar grundfunktionerna

 

 

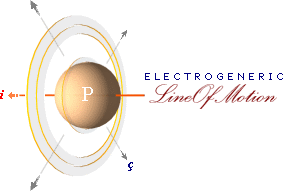
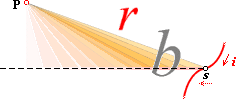
                            Verkan i P

 

Illustrationen visar idealt en (sfärisk) rymdpunkt P som genomträngs av ändringen i elektriska fältet från en elektrisk laddning Q på stort avstånd från P då Q lägesändrar i strömriktningen i. Cirklarna kring P rätvinkligt i markerar den uppkomna effekten i formen av fältringar som expanderar inom ljushastigheten c och som utgår från P, alltid rätvinkligt i eftersom c och v inte växelverkar i fysiken (se ljusfrihetssatsen).

induktionen och magnetismen

DEN LOKALT DOMINANTA GRAVITATIONEN (G) och dess reglerande inverkan på ljushastigheten (c) tillsammans med det elektriska fältets utbredning och återkoppling via c, bildar fasta och fixa referenser för elektrisk fältstyrka i alla rymdpunkter (P) i G. När en elektrisk laddning (Q) lägesändrar (i) relativt P, ändras också (så småningom, fördröjt via c) de tidigare referensvärdena omkring Q i G. Ändringarna i P i rörelseriktningen i bildar induktionen (induktion av lat. indu’cere, leda, föra in; ref. BKL). På grund av att c och v inte kopplar i fysiken bildas dessutom magnetismen rätvinkligt v (magnet av grek. li’tos magne’tes, eg. sten från Magnesia; ref. BKL).

 

 

Illustrationen tydliggör verkan av induktionen motsvarande mekanikens tröghet genom en handhållen stav med en (stor, tunn) plan skiva i änden som ligger på en vattenyta: Varje försök att ändra stavens vertikalläge resulterar i ett märkbart motstånd (induktionen) och därmed en följdverkan med ringar som sprids avtagande utåt, det vi kallar för magnetismen. Vattnets mekaniska tröghet motsvarar rymdens längdkompakthet [L=RT=µs].

 

ANALOGIN TILL INDUKTIONEN OCH MAGNETISMEN kan då liknas vid effekten av en vattendroppe (mQv) som träffar en lugn vattenyta (G) med resultat i en synbar rekyl (induktionen Ð, studsen) med åtföljande ringar (magnetismen B) som sprids expanderande utåt inom den G-lokala ljushastigheten (c). Se även från ljusets g-beroende.

 

 

 

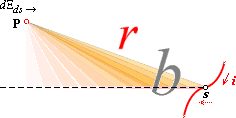
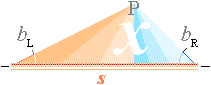
Induktionen i P med hänsyn till lägesändringen ds i strömledaren i bildas av bidragen från alla laddningar Q som lägesändrar utmed samma riktning s. För att kunna formulera saken matematiskt tvingas vi genomföra vissa idealiseringar som frånser ljusvägens tidsfördröjande effekt i godtyckliga kurvaturer för s.

 

INDUKTIONENS MATEMATISKA FYSIK visas i illustrativ syntes ovan; Den accelererade lägesändringen i strömvägen s bildar i en rymdpunkt P från s på avståndet r en induktionsspänning vars värde måste integreras med hänsyn till strömvägens kurvatur och längd. Enklaste fallet antyds av den streckade helt raka, ändliga strömvägen.

 

 

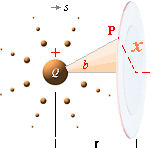
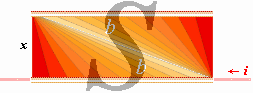
Magnetismen i P summeras rätvinkligt strömriktningen s på bidragen från hela rymden med utgångspunkt från kortaste avståndet r till laddningen utmed s. Även magnetmatematiken måste idealiseras av samma skäl som för induktionsmatematiken. Dessa detaljer garanterar att induktionen och magnetismen bildar det (kanske) i särklass mest komplicerade området av hela den matematiska fysiken.

 

MAGNETISMENS MATEMATISKA FYSIK visas i illustrativ syntes ovan; Ringbildningen utgår, precis som i vattenfallet, från en centralpunkt på avståndet r från Q i rörelseriktningen och summeras rätvinkligt r i P genom x via integration. Även i detta fall har strömlinjens kurvatur och längd betydelse.

 

 

 

 

 

 

InduktionenOchMagnetismen

 

potentialfältet

 

Utförligt förklarande beskrivning

INDUKTIONEN OCH MAGNETISMEN

 

 

DEN ELEKTRISKA LADDNINGEN i formen av den ideala sfäriska formen uppvisar ett potentialfält U=k(Q/r) eller ett radiellt utstrålande elektriskt fält (e-fältet). Dess grund är masskroppens g-fält och den därmed sammanhängande divergensen och dess g-beroende. E-fältet kopplar (uppdaterar) sin potentialbild till centralkroppen genom ljushastigheten (c). Varje kropp bibehåller sitt g-fält, och därmed sitt e-fält, oberoende av samverkan eller interferens med andra kroppar (superpositionsprincipen).

 

Potentialfältet från Q avbildar i det omgivanda dominanta g-fältets referenspunkter (P) fasta referenvärden i P UNDER dT för en viss MOMENTAN potentialbild. Vid en viss tidpunkt råder alltså ett visst tillstånd i P. Varje ändring av potentialbilden i P bildar genom »Newtons tredje lag» en elektrisk induktionsverkan, detsamma som ett motstånd mot tillståndsförändring. Motståndet bildar en elektrisk rymdspänning (U) som verkar i exakt samma riktning som Q lägesändrar endast om ändringen är accelererad. Se mera utförligt i Genereringen av rymdpotentialen i induktionen.

   Med lägesändringen av Q sammanhänger också alltid en magnetisk fältverkan. Den magnetiska fältverkan bildas alltid rätvinkligt Q-ändringen. Den magnetiska verkan gäller emellertid alltid oberoende av hur Q lägesändrar — medan induktionen bara gäller i rörelseändringen, alltså under själva accelerationen. Denna detalj är en ren följd av »Newtons tredje lag» som helt bygger på accelerationen som grund för fysikens olika fenomen. Se även i Ändringslagarna om ej redan bekant.

 

Framställningen nedan ger en (successivt) större detaljrikedom i beskrivningen av funktionssättet.

 

Induktionen och magnetismen — den matematiska fysiken

MATEMATISK FYSIK

 

Följande enkla genomgång är helt avgörande och elementär för förståelsen av grunderna inom induktionen och magnetismen. MEN DEN INGÅR tydligen INTE I DEN MODERNA AKADEMINS LÄROSYSTEM.

 

Motsvarande detaljer i den moderna akademins lärosystem har eftersökts men inte hittats.

 

 

Induktionen och magnetismen forts. | Divergensen tillämpad på III:e ändringslagen ger grundbegreppen för induktionen och magnetismen

uppkomsten av

induktion och magnetism

enligt relaterad fysik

Induktionen och Magnetismen — fenomenens absolut teoretiskt förklarande fundament

DIVERGENSEN I TREDJE ÄNDRINGSLAGEN

Divergensbegreppet (elektricitetens fenomengrund) beskrivs och härleds utförligt i Ljusets fysik, om ej redan bekant.

 

Rymdinduktansen för vakuum, elektrofysikens allmänna grunder

DIVERGENSENS ABSOLUTA ACCELERATION a=c/dT bildar i följd av Newtons tredje lag ett rymdmotstånd (R0). Elektriska enheten för R är Volt/Ampere=W (Ohm). Enligt Newtons tredje lag (ansatsen i varje ändring uppväcker alltid en lika stor motkraft) inbegriper absolutaccelerationen a=c/dT ett motstånd (inertie), en divergensresistans R av rent principiell natur som motverkar inverkan från gravitationens absolutverkan och därmed definierar toppdivergensen c0. Tillsammans med toppdivergensen c0 bildar R0 en absolut minsta rymdkompakthet R0/c0.

Rymdkompaktheten R/c bildar grundvalen för induktionen och magnetismen.

 

             µ = R/c  ..................      rymdkompaktheten, VS/AM

 

Rymdkompaktheten är minst R0/c0. Som också c verkar genom R i rymdpunktens utsträckning ds via en konstant hastighet c = ds(dT)–1, kan effekten av R och c tillsammans beskrivas genom substitutionen R/R=1 i c enligt c=(ds/dT)(R/R). Då gäller

elektriska konstanten

             R · c = R · (ds/dT)  ...   elektriska konstanten, VM/AS ; även tecknad 1/ε,

se även kapacitiviteten i Syntes av magnetismen och induktionen

             RdT = (R/c)ds

             R/c   = µ  ...................    rymdkompaktheten, minst R0/c0=µ0, VS/AM

             RdT = µds  ...............   rymdkompakthetens differentiella längdberoende (strömriktningen), VS/AM · M = VS/A

induktansen

Med konstant c över hela intervallet s får vi en motsvarande rymdlängdskompakthet RT=µs. Med RT=L som den primära elektriska trögheten eller

induktansen

             L = RT ....................     induktansen (motsvarar massan i mekaniken), VS/A

ges rymdkompakthetens ekvivalent enligt

             µ = L/s ....................     rymdkompaktheten, VS/AM

µ (grek. mikro eller my) är den absolut minsta möjliga elektriska tröghet eller primära induktans varje elektrisk strömlinje kan och måste ha för att alls kunna arbeta och fungera i elektrofysiken.

Alla strömlinjer s som arbetar under divergensen c måste utgå från denna BASIC µ rymdPrimära induktans per meter µ=L/s=R/c. Alla. Undantag existerar inte.

 

Rymdlängdskompaktheten L=RT=µs har följande upplösning.

Inom induktionen är rymdkompaktheten µ samriktad med elektriska strömmens riktning s vilket ger

             µs  ..........................      rymdinduktansen

Inom magnetismen är rymdkompaktheten µ tvärriktad (transversell) mot strömriktningen s vilket ger

             µs  ..........................      rymdmagnetiseringen

växelverkansfrihetssatsen

De två riktningsskilda olika aspekterna på Rymdlängdskompaktheten L=RT=µs garanterar således att

magnetism och induktion aldrig växelverkar

 

Se även i KAUSALSAMBANDET där riktningsskillnaden mellan induktion och magnetism ytterligare understryks.

 

 

Induktionen och magnetismen forts.

 

 

ORSAKEN TILL VARFÖR INDUKTIONEN OCH MAGNETISMEN INTE VÄXELVERKAR I FYSIKEN

 

Förklaringen till de bägge skilda riktningarna i µs är speciellt enkel och elementär. Den är den följande — såvitt inte redan bekant.

   Eftersom Rc är begränsad till dT, saknar massa och alltså refererar till en punkt, kan den inte främja eller agera i kinetiken. Dess ekvivalent Rc=konstant=Rxcx kan alltså inte konstrueras vektoriellt i några som helst fria former tillsammans med vektorer som sammanhänger med kinetiken. Då alltså Rc inte kan bidra med någon vektor i den riktning s som försöker påverka Rc, återstår enda möjligheten att Rc kommer att svara tvärs s. Med andra ord i den enda riktning där ansatsen till någon riktning för dess egna komponenter saknar representation. Rc måste alltså reagera så att den inte lämnar några komponenter till kinetiken (den riktning s i vilken Rc förmodas kunna, men inte kan ändras) för att divergensens verkan inte ska kollapsa på energilagen.

   Följaktligen tillhör influensen på Rc magnetismen (tvärs s) och ingenting annat — aldrig induktionen (utmed s).

 

I den vidare utvecklingen av sambanden leder Rc-formen till en motsvarande R/c-form analogt med den nämnda rymdmagnetiseringen µs. Därmed separerar också magnetismens specifika µs från induktionens specifika µs, enligt nyssnämnda grund. Därmed är det klarlagt att magnetism och induktion följdriktigt verkar i två från varandra helt skilda dimensioner: de växelverkar aldrig. Det finns ingen fysikalisk förutsättning för det.

 

De två riktningsskilda, olika, aspekterna på Rymdlängdskompaktheten L=RT=µs garanterar således att:

 

                        magnetism och induktion växelverkar aldrig

 

För att I RELATERAD FYSIK understryka denna viktiga och avgörande skillnad benämns induktionsdelen som elektrodynamisk induktion.

Den konventionella termen elektromagnetisk induktion har absolut ingen som helst representation i relaterad fysik. Vi ska längre fram studera hur denna detalj hänger ihop med den rent tekniska tillämpningen och hur det ser ut i praktiken i jämförelsen mellan modern akademisk matematisk fysik och den som ges av relaterad fysik.

 

I modern akademi tog man ett helt annat grepp på induktionens och magnetismens begrepp då de visade sig i början på 1800-talet: man hänger fortfarande induktionen som fysikaliskt fenomen på magnetismen — därför att strömändringarna (induktionen) i vilket fall OCKSÅ sammanhänger med en magnetisk effekt — och gör därmed ett FÖRENKLAT MATEMATICERAT PAKET av hela komplexet sammanfattat i MAXWELLS EKVATIONER genom begreppet “vektorprodukt” — som också uppfanns av modern akademi under 1800-talet.

 

Nedan följer i PREFIXxSIN en sammanställning som visar vad TYPFORMEN går ut på i skillnaderna mellan modern akademi och relaterad fysik.

Detaljerna beskrivs i separata artiklar, om ej redan bekant.

 

 

PÅ GRUND AV DE HÄR UPPMÄRKSAMMADE OLÄGENHETERNA I DEN MODERNA AKADEMINS LÄROSYSTEM ÄR DEN HÄR PRESENTATIONEN TILLÄGNAD EN OMFATTANDE EXEMPELREDOVISNING I KORSREFERENSER MELLAN MODERN AKADEMI OCH RELATERAD FYSIK SOM UTESLUTANDE, OCH ENDAST SÅ, VISAR ATT DEN MODERNA AKADEMINS FYSIKUPPFATTNING INGÅR I RELATERAD, FÖRKLARANDE, FYSIK SOM EN PRIMITIV UPPFATTNING. Domen i det avseendet faller på dig som läsare.

 

 

Se även i NOMENKLATUREN: (Enbart) I Sverige har nomenklaturen för magnetismen ÄNDRATS FLERA GÅNGER — fram och tillbaka. Begreppen avspeglar alldeles uppenbart varandras (omväxlande) delar, och varje läsare håller säkert med den här författaren på den punkten: det här är rena cirkusen. I relaterad fysik däremot, är begreppen exakt relaterade och kan därför med hög precision jämföras med den moderna akademins (kaotiska) fackuttryck i noggrann korsreferens. Se vidare från Nomenklaturen.

 

jämförande uppställning

Jämför några av resultaten  ..................................................................  DETALJ

 

RELATERAD FYSIK                           MODERN AKADEMI            DETALJ

B          = µ0s · I/A                                 — samma4                                 grundläggande magnetisk fältstyrka, förenklat, VS/M2

            — ingår inte!                           expansionsintegralens differentialform

dBP       = µ0(I/4px)sinb·db                     — ingår inte!                           expansionsintegralens fullständiga differentialekvation i PREFIXxSIN

b                                                                                                                                                                         

ò dBPx   = µ0(I/4px) cosb                        — kan inte relatera                magnetiska expansionsintegralen i PREFIXxSIN

0                                                                                                                                                                         

             = dBPs/dbs                                  — samma4                                 variationen i magnetiska linjeintegralens differentialekvation för strömvägens kurvatur

dBPs      = µ0(I/4pr2) sinb ds                   — samma*                                r-formens differentialekvation av dBPs i PREFIXxCOS

BPs        = –µ0(I/4px)(sinbL+ sinbR)        — samma4                                 B i P på x utanför rak ledare s, lösningen till ovanstående

 

* Biot-Savarts lag, men genom helt annan tolkning

4 men genom helt annan tolkning

RELATERAD FYSIK                           MODERN AKADEMI            DETALJ

µ0s        = L0                                           — kan inte relatera                primära grundläggande rymdinduktansen, VS/A

µL         = K(µ0+µc)                               — kan inte relatera                totala primära ledningsindukt. per meter, VS/AM

µLs       = Lc                                           — kan inte relatera                totala primära induktansen, VS/A

 

µL beror av kristallin struktur, tvärsnitt, temperatur, täthet, magnituden i strömmens ändring och lokal gravitation (c). µL bestämmer den ideala tidsabsoluta verkan i en elektrisk ledare i respekt till varje strömändring di/dt.

 

û           = L(di/dt)                                   — samma4                                 inducerad spänning, allm. samb. (Kirchoffs lagar), V

L          = Lc(di/dt)  ................................................................                  förenklat beteckningssätt, V

dР       = L · A–1sinb · ds                      — kan inte relatera Lc            induktiv dipolfältstyrka i P, fullständig grundform, V

dL         = dU(di/dt)–1                                                                   

             = Lc · (1/A)r ds                         — kan inte relatera Lc            allmänna induktansen, differentialekvation

LT         = Lc + LSCURVE                          — kan inte relatera Lc            totala ledningsinduktansen, VS/A

För rakledare och även rätvinklig ledare är LSCURVE=0.

RELATERAD FYSIK                           MODERN AKADEMI            DETALJ

L           = µLn2 · A/h                               — samma4                                 allmänna ring-spole induktansen, VS/A

L           = ûCOIL(di/dt)–1                                                               

             = d·n2·Ld /1M                            — samma4                                 allmänna ring-spole induktansen, VS/A

L           = –(µL/2p)s[ln(4s/d) – 2s/d]    (µ0/2p)s[ln(4s/d) – 3/4]            allm. självinduktionen på ytan av rakledare

notera skillnaden mellan µL och µ0

4 men genom helt annan tolkning

KVANTITATIVT i praktisk teknisk fysik är skillnaden obetydlig p.g.a. låga strömhastigheter, KVALITATIVT i TEORIN är skillnaden fundamental

Notera µL och µ0. Modern akademi blandar ihop magnetism (e0) med induktion (µ0 — erinra föregående förenkling i magnetismens matematiska fysik för anpassning till den tekniska fysiken) enligt (tätt liggande ledare)

relaterad fysik

(L/4px)(1–0)  = L   (4px)–1   = Ð .................................................. induktion, V/M

 

µ0(I/4px)1       = µ0I (4px)–1   = B .................................................. magnetism, VS/M2

resultat

För alla tekniska applikationer med tätt liggande ledare finns ingen möjlighet att avslöja något fel genom mätning

— om man inte kan skilja på induktion och magnetism.

 

 

För att understryka skillnaden mellan induktionen och magnetismen benämns induktionsdelen I RELATERAD FYSIK som elektrodynamisk induktion.

Den konventionella termen elektromagnetisk induktion har absolut ingen som helst representation i relaterad fysik.

 

 

Dessa detaljer granskas YTTERLIGARE noga till EXAKT PRECIS JÄMFÖRELSE MED RESULTATEN FRÅN RELATERAD FYSIK i särskilt avsnitt.

Innan vi kommer dit måste vi EMELLERTID först ha EXPERIMENTELLA BEVIS för ovanstående rebelliska påstående.

 

Se särskild artikel från PARALLELLEXPERIMENTEN.

För den fortsatta beskrivningens sammanhang förutsätter vi att läsaren är bekant med redovisningen av resultaten i parallellexperimenten.

 

Vi studerar resultatet:

 

 

 

 

 

 

InduktionenOchMagnetismen

 

resultatredovisning

I anledning av resultaten från parallellexperimenten:

U          = Bs · d(d)/dT = B(dF/dT)  .....................................      Faradays lag gäller TYDLIGEN endast elektro-mekanisk induktion

DET FINNS således INGEN »ELEKTROMAGNETISK INDUKTION»

 

ingen emInduktion

SPECIELLT MED REFERENS TILL EXEMPEL 2 I TRE JÄMFÖRANDE EXEMPEL OCH SOM VISAR DEN PRAKTISKA/TEORETISKA GRUNDEN:

Notera den exakta innebörden av den elektroMEKANISKA induktionen U = dF/dT (visuellt exempel: strängarna på en elektrisk gitarr):

 

 

Den inducerade spänningen är tidsändringen OCH INGET ANNAT för den fixa ledarens kurvatur (s) skärande det fixa B-fältet;

             A/T = s · d/T

             U = Bs · d(d)/dT = B(dF/dT)

B och s (eller B och d) måste vara fixa i enlighet med den fysiska referensen som följaktligen OCKSÅ modern akademi våldför sig på

— (Se FUNTOP Fundamental Theorem of Physics, fysikens 2:a princip som modern akademi, tydligen genomgående, våldför sig på):

en ändring kan inte betjäna en mätning utom från ett tillstånd av jämvikt eller likformighet

— FUNTOP: Fysikens lagar gäller FÖR system. Inte i system. »Inertialsystem» existerar inte i fysiken ENLIGT RELATERAD FYSIK.

Genom att kontinuerligt ändra B, ändras också hela referensen kontinuerligt (vilket skulle överflytta referensen till ”B” istället för den lokala g-dominansens laboratorierum: Q-ändringen):

Den inducerade spänningen i g-lokalen kommer följaktligen INTE att bero av B utan av en ren elektrisk sekundär induktion

— VARS FASTA REFERENS ÄR DET OMGIVANDE RUMMETS FIXA G-RELATERADE RYMDPUNKTER.

I BA=F har (den sekundära) induktionen ingen koppling eftersom

Praktiskt: se parallellexperimenten. Teoretiskt: se divergensen i tredje ändringslagen. Jämförelse mellan MODERN AKADEMI och RELATERAD FYSIK: se tre jämförande exempel.

induktion och magnetism inte växelverkar. Relaterad fysik.

DÄRFÖR gäller Faradays Lag (U = dF/dT) enbart elektromekanisk induktion: mobil ledare som rör sig i fixt B-fält (typ strängarna på en elgitarr).

 

 

DET FINNS INGEN »ELEKTROMAGNETISK INDUKTION»

Se jämförande exakta exempel mellan etablerad vetenskap och relaterad fysik i tre exakta exempel.

 

 

Det är alltså INTE magnetismen som förorsakar inducerade strömmar mellan olika ledarkroppar.

Det som förorsakar inducerade strömmar mellan olika ledarkroppar är en primär laddningskropp som lägesändrar accelererat relativt det g-fält som probar den inducerade spänningen: induktionen sker i samma riktning som den primära lägesändringen. Magnetismen har inte ett spår med det att göra. Helt rent. Se parallellexperimenten.

Men den ALGEBRAISKA formen för magnetismen som orsak LIGGER JÄVLIGT NÄRA :

relaterad fysik:

KVANTITATIVT i praktisk teknisk fysik är skillnaden obetydlig p.g.a. låga strömhastigheter, KVALITATIVT i TEORIN är skillnaden fundamental

Notera µL och µ0. Modern akademi blandar ihop magnetism (e0) med induktion (µ0 — erinra föregående förenkling i magnetismens matematiska fysik för anpassning till den tekniska fysiken) enligt (tätt liggande ledare)

 

(L/4px)(1–0)  = L   (4px)–1   = Ð ..................................................             induktion, V/M

 

µ0(I/4px)1       = µ0I (4px)–1   = B ..................................................             magnetism, VS/M2

 

För alla tekniska applikationer med tätt liggande ledare finns ALLTSÅ ingen möjlighet att avslöja något fel genom mätning — om man inte kan skilja på induktion och magnetism.

elektromotoriska

ELEKTROMOTORISKA INDUKTIONENS BEGREPP

För att understryka skillnaden mellan induktionen och magnetismen benämns induktionsdelen I RELATERAD FYSIK som elektrodynamisk* induktion.

Den konventionella termen elektromagnetisk induktion har absolut ingen som helst representation i relaterad fysik.

 

I stället för benämningen elektrodynamisk (induktion) är benämningen elektromotorisk egentligen att föredra (mera förtydligande) — eftersom också den elektromekaniska induktionen är av typen elektrodynamisk.

 

Se även jämförande exempel mellan RELATERAD FYSIK och MODERN AKADEMI.

 

 

referens till induktionen och magnetismen

»InduktionsMagnetismen»

Med det elementära PREFIXxSIN definierar relaterad fysik till jämförelse för raka ledare

             ÐP = (L/4px)(1–cosb)  ..........   V/M induktiva dipolfältstyrkans integral, raka ledare

med L = Lc(di/dt) i Volt och

             BP = –µ0(I/4px)sinb  ..............   VS/M2 magnetiska fältstyrkans linjeintegral, raka ledare

Tätt intill ledaren (modern tekisk standard) finner vi genom relaterad fysik

 

             (L/4px)(1–0)     = L   (4px)–1     = Ð .... induktion, V/M, L = Lc(di/dt) V

             µ0(I/4px)1         = µ0I (4px)–1     = B .... magnetism, VS/M2

            

För Lc=(R0/c0+R’/c0)s= (µ0+µc)s=µLs se även

 

SUMMERING AV PRIMÄRINDUKTANSEN;

Se även den matematiska beskrivningen av termerna Rcµe i

INDUKTIVA R-GRUNDERNA

 

Jämför de upp-och-nervända, redan etablerade termbegreppen, sådana de förklaras i detalj enligt relaterad fysik:

 

             e0          elektriska konstanten                arbetar på magnetismen rätvinkligt Q-rörelsen v

             µ0         magnetiska konstanten              arbetar på induktionen rätt på i Q-rörelsen v

 

Om man inte kan skilja mellan magnetism (e0, epsilon) och induktion (µ0, mikro eller my), kommer dessa samband med ofelbar precision att utföra sina egna uppvisningar — och alla typer av vimsiga begrepp om magnetism kommer att framträda ur ”matematikens lagar” som till exempel i [HOP 4—12 sp2n] ”magnetisk induktion” och liknande, men det exemplet kräver en veritabel avhandling för att utredas på en läsbar och begriplig nivå då dess språk använder högskolematematikens begrepp, och dessa används inte i den här framställningen. Se även motsvarande beskrivning i UPPDAGANDET.

 

 

SammanfattningIndMag:

SAMMANFATTNING — induktionen och magnetismen

 

·        ALLA TROR men misstar sig på ATT något sådant som ELEKTROMAGNETISK INDUKTION existerar;

·        Man TROR att det är variationerna i ett yttre B-fält på en Fix Ledare (FL) som skapar FL-strömmarna — DÄRFÖR att FL-strömmar bildas om FL ändras i fixt B-fält.

·          Alla tror att den ömsesidigheten gäller — den här författaren inkluderat
ända fram till tiden (1994) för parallellexperimenten (efter många, många misslyckade försök att härleda magnetismen).

 

Alla faktaböcker och skolböcker beskriver det så.

Men det är, tydligen, fel — i kraft av parallellexperimentet samt den galant sammanhängande teorin (se även vidare nedan).

B-fältet har ingen sådan koppling.

Det finns ingenting sådant.

 

Elektriska laddningar i vila försätts ALDRIG i rörelse av magnetismen, vare sig denna är fix eller variabel eller på andra sätt. Elektriska laddningar i vila ändras endast av induktionen, och den växelverkar INTE med magnetismen — helt i enlighet med resultaten från parallellexperimenten.

 

PÅ GRUND AV DE HÄR UPPMÄRKSAMMADE OLÄGENHETERNA I DEN MODERNA AKADEMINS LÄROSYSTEM ÄR DEN HÄR PRESENTATIONEN TILLÄGNAD EN OMFATTANDE EXEMPELREDOVISNING I KORSREFERENSER MELLAN MODERN AKADEMI OCH RELATERAD FYSIK SOM UTESLUTANDE, OCH ENDAST SÅ, VISAR ATT DEN MODERNA AKADEMINS FYSIKUPPFATTNING INGÅR I RELATERAD, FÖRKLARANDE, FYSIK SOM EN PRIMITIV UPPFATTNING. Domen i det avseendet faller på dig som läsare.

 

Att elektriska laddningar som IDEALT befinner sig i VILA skulle rubbas det allra minsta på grund av magnetismen är alltså ett påstående som kan klassificeras helt säkert med referens till parallellexperimenten sålunda:

 

Finns inte en fysikalisk chans.

Inte i teorin.

Inte i praktiken.

 

De två riktningsskilda, olika, aspekterna på Rymdlängdskompaktheten L=RT=µs garanterar att magnetism och induktion aldrig växelverkar

 

 

MaxwellsREGEL: SammanfattningINDmag

 

Diskussion, kort:

— Men vad då, modern akademi, det här är ju trivialt;

— Du har ju själv ställt upp »grundreglerna» genom MAXWELLS REGEL och BORDE på den vägen redan ha förstått principen:

Maxwells Regel

Klargörande utvidgad beskrivning 27Sep2024 — med Rättelse från originalförfattningen Maj2008

Se även i Citatblock EMI — associerade elektromagnetiska detaljer i etablerad litteratur

Huvudtexten från Maj2008 är fortfarande bevarad och baserad på teckensnittet Symbol för typen pi och andra,

frånsett tillägget nedan med pilsymboler här i Unicode

 

 

Föregående författning från Maj2008 innehöll inga direkta citat för “Maxwells regel”, enbart en översiktlig (inte helt uttömmande, förtydligat nedan) beskrivning.

   Här ges hela citatdelen från BKL1924 — med tillagda utförliga illustrationer som relaterar de redan väl kända basbegreppen från skolboksfysiken och andra (Högerhandsregeln — också benämnd i Engelsk litteratur “Maxwell’s screw rule”). BKL texten är för övrigt den enda (Sep2024) upphittade elektromagnetiska beskrivning som (numera) finns på termen Maxwells regel. Termen “Maxwell’s rule” finns visserligen omnämnd i den engelska litteraturen. Men då i ett helt annat avseende (byggnadstekniska detaljer). Wikipedia har f.ö. ingen artikel “Maxwell’s rule”.

 

MaxwellsRegelExplain: MR

 

 

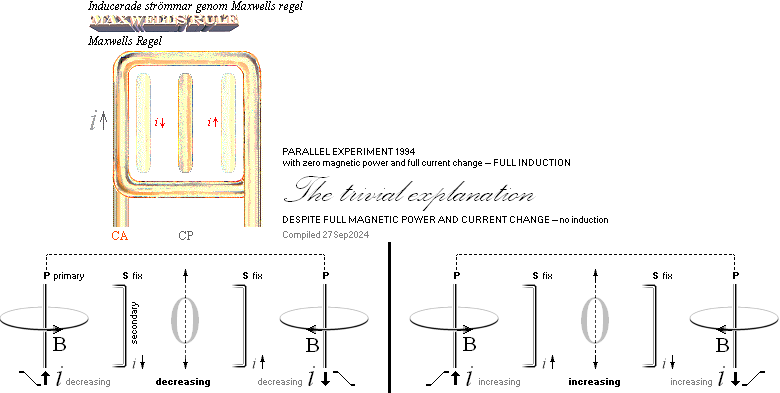
Med avtagande ström i↑ i den fasta spolen (CA) och den mittre mobila spolen (CP) placerad till vänster (orienterad nedåt-inåt vinkelrätt CA), induceras i den en medriktad ström (i↑) — etablerad litteratur har ingen här känd förklaring till varför. Med den mobila spolen CP  placerad till höger, induceras i den en ström med samma riktning som i den fasta spolens vänstra skänkel (i↑). Följaktligen med den mobila spolen i mitten bör ingen ström alls induceras i den — trots att full magnetisk effekt existerar där. Då, i konsekvens — och helt trivialt — borde den inducerade strömmen bero på något ANNAT än magnetismen (Citatblock EMI).

— Förklaring? I det ElektroMekaniska fallet, med mobilen (CP) i mitten och som oscillerar (som en vibrerande sträng: »elgitarr»), är situationen en helt annan: en ström induceras verkligen i CP.

 

Maxwells regel

MAXWELLS REGEL — går generellt ut på att

en given avtagande ström (vänster ovan) genererar en ström motsatt riktad den givna medan en växande ström (höger ovan) genererar en ström medriktad den givna — ref. BONNIERS KONVERSATIONSLEXIKON V 1924 sp1352 Induktion, citatdelen nedan.

— OLIKA KOMBINATIONER med begreppen växande/avtagande kontra fix/mobil (sekundär S) ledare i ett givet (primärt P) magnetiskt fält, ”komplicerar” bilden ytterligare. Ovan visas endast huvuddelen. Komplexet kräver (så) en förhoppningsvis mera uttömmande förklarande illustrerad (och experimentellt relaterat mätande) utläggning.

— Här i UniversumsHistoria genomfördes de första mätningarna i PARALLELLEXPERIMENTEN Från 1994.

Motsvarande klargörande experiment på raka strömledare i etablerad litteratur har eftersökts men inte (ännu) upphittats.

 

MaxwellsREGELcitat:

” Om en elektrisk ledare i form av en sluten strömkrets befinner sig i ett magnetiskt fält och antalet magnetiska kraftlinjer, som skära den av ledaren omslutna ytan, förändras, uppstår (induceras) i strömkretsen en elektrisk spänning, proportionell mot förändringen per sek. av antalet omslutna kraftlinjer. Denna spänning åstadkommer en elektrisk ström,  induktionsström l. sekundärström, som varar under den tid, förändringen försiggår. Bildar ledaren ingen sluten strömkrets, uppstår endast en potentialskillnad mellan ledarens ändar. Fenomenet kallas I. Magnetfältet kan framkallas genom en magnet l. genom en annan strömkrets, som genomlöpes av en elektrisk ström, inducerande, primär- l. huvudström. Nämnda förändringar uppstå, om magneten l. strömkretsen förflyttas l. om primärströmmen slutes, brytes, förstärkes l. försvagas.”,

;

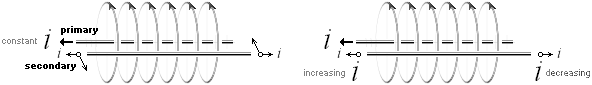
author’s text interpretation Sep2024 — ”.. i kraftlinjernas riktning ..”

;

” Induktionsströmmens riktning framgår a) av Maxwells regel: ökas antalet skärande kraftlinjer, går induktionsströmmens riktning motsols, om strömkretsen betraktas i kraftlinjernas riktning, minskas antalet, går strömmen medsols, b) av höger hand-regeln .. , c) av  Lenz’ lag: induktionsströmmens riktning är sådan, att ledarens förflyttning motverkas av elektromagnetiska krafter ..  Det mekaniska arbete, som fordras för att övervinna dessa krafter, omvandlas genom I. till elektrisk energi, induktionsström.”.

BKL V1924.sp.1352 — Induktio’n  not illustrated

 

 

Hur är det — då — alltså?

— Hur innefattas (då) dessa detaljer i en sammanhängande teori om magnetism och induktion?

   Relaterad fysik och matematik ger svaret genom en teori som tydligen aldrig imponerat på modern akademi.

— Exemplifierat och direkt konkret i detaljer: se EXPANSIONSINTEGRALEN.

MOTSÄTTNINGARNA EXPONERAS MERA I DETALJ — den etablerade litteraturen innehåller en bristande förklaring.

IoMimplikationen: MRE

Renodlat

 IoM-implikationen

DEN KLASSISKA ÖMSESIDIGA FÖRMODAN MELLAN INDUKTION OCH MAGNETISM

 

Om en sekundär (passiv) ledare (CP) förs med hastigheten v skärande B-fältet från en stationär fast aktiv strömledare (CA), produceras en spänning i CP proportionell mot v (magnituderna i v förutsatt mycket mindre än c). Situationen är bekant för alla (lekmän) som spelar elektrisk gitarr. Vi kan kalla fenomenet för elektro-mekanisk induktion.

 

Vi (alla, uteslutande alla, från början även den här författaren) skulle FÖRMODA att samma effekt skulle visa sig med ett varierande B-fält från CA — med bägge ledarna CP och CA fasta: Om B-fältet, passerande över CP, ändras av en ström i CA, kan också en spänning U i CP observeras. Vi skulle, alltså, dra slutsatsen att bildningen av U skulle förorsakas av det varierande B-fältet från CA. Och vi skulle då kalla fenomenet elektro-magnetisk induktion.

 

Så är det också — vad vi vet — man har resonerat genom den moderna vetenskapshistorien.

 

Men ENBART enligt det helt enkla resultaten från den ovan illustrerade CA-CP spolanordningen enligt Maxwells regel, är denna förmodan INTE fallet — faktiskt. Med den passiva CP-mobilen i mitten och huvudaktiva spolen CA som producerar en växande eller avtagande ström, finns i vilket fall ingen inducerad spänning (U=Ri) alls att observera i CP— trots att full magnetisk effekt kan uppmätas där (till exempel genom ett Hallelement ¦ Mätningen 1994). Det är den ovan antydda helt triviala konsekvensen av att CP erhåller inducerad spänning i motsatta riktningar beroende på placering till vänster eller till höger om mittlinjen. I mittlinjen tar de motriktade bidragen ut varandra. Men därmed är OCKSÅ (trivialt, men korrekt logiskt) den underförstådda, förmodade (Citatblock EMI), idén om »ömsesidig induktion» motsagd. Den håller inte. Teorin i etablerade kvarter är uppenbart korrumperad. Klargörande krävs.

 

Parallellexperimenten (från 1994) var ägnade att just studera dessa detaljer noggrant, sedan det (efter många misslyckade försök) stod klart att ingen annan möjlighet fanns att härleda magnetismens elementära fysik. Som redan påpekats i slutsats från den ovan (triviala) illustrerade Maxwells regel, men här i en mera avancerad tappning, kunde också inducerade spänningar observeras via varierande strömmar utan någon närvaro av magnetism. Så väl som omvändningen. Full magnetisk effekt genom varierande strömmar (150 000 A/S) observerades — utan någon som helst observerbar inducerad spänning. Därmed var saken klar.

 

 

 

 

 

 

InduktionenOchMagnetismen | Allmänna samband

 

 

Induktionen och magnetismen

ALLMÄNNA SAMBAND

 

 

 

Allmänna samband i magnetism och induktion I RELATERAD FYSIK enligt den tekniska fysikens tillämpningar

— sambanden förutsätter att laddningshastigheten v << c

Se även relaterad fysik kontra modern akademi

 

NÄRVERKAN OCH FJÄRRVERKAN, PRIMÄRA OCH SEKUNDÄRA

Både induktionen och magnetismen uppvisar en nära [eng. near, Q till insidan] och en fjärran [eng. far, Q till utsidan] verkan. För att särskilja komplexen är induktionen i denna presentation indelad i en primär och en sekundär del medan magnetismen har bevarat termoinologin med närverkan och fjärrverkan. Både induktionen och magnetismen måste högeligen idealiseras i aspekten på ljushastighetens fördröjande verkan för att alls kunna få fram en hanterbar matematisk fysik.

 

PÅ GRUND AV DE HÄR UPPMÄRKSAMMADE OLÄGENHETERNA I DEN MODERNA AKADEMINS LÄROSYSTEM ÄR DEN HÄR PRESENTATIONEN TILLÄGNAD EN OMFATTANDE EXEMPELREDOVISNING I KORSREFERENSER MELLAN MODERN AKADEMI OCH RELATERAD FYSIK SOM UTESLUTANDE, OCH ENDAST SÅ, VISAR ATT DEN MODERNA AKADEMINS FYSIKUPPFATTNING INGÅR I RELATERAD, FÖRKLARANDE, FYSIK SOM EN PRIMITIV UPPFATTNING. Domen i det avseendet faller på dig som läsare.

 

 

Särskilda delar I KORSREFERENS anställer MODERN AKADEMI till jämförelse med RELATERAD FYSIK för klargörande, exakt beskrivning.

Se Tre exakta exempel. Deras matematik ansluter generellt till nedanstående.

 

 

Sambanden beskrivs i härledningar i särskilda avsnitt

MAGNETISMEN — allmänna samband i PREFIXxSIN

1. generering av magnetiska fält

närverkan

             BSURFACE                 = µ0I/2pr0  .........................       fältstyrkan på ledarens yta

             H                      = I/2pr0  .............................       magnetiserande kraften (eng. magnetizing force), A/M

             BSURFACE           = µ0H  ................................      magnetiska fältstyrkan, VS/M2

             B = –µ0/2p · r · (I0/r02)  ..............................       magnetiska fältstyrkan innaför ytan på en ledare med cirkulärt tvärsnitt, VS/M2

             B = –µ0/2p · (r – rin) · (I0/[r0–rin]2)  .........          samma som ovan men med ihålig ledare, r > rin , VS/M2

             µ0 ................................................................       1,25662 t6 VS/AM

 

fjärrverkan

             BPs       = –µ0(I/4px)(sinbL+ sinbR)  ...........       fältstyrkan i P utanför rakledare, 1Tesla=1VS/M2

             B          = µ0(I/2r)  .......................................      fältstyrkan i centrum av en ring med radien r, VS/M2

 

2. växelverkan mellan magnetiska fält

             F          = BQv  .........   magnetiska kraftlagen  ...   kraften på en fritt rörlig laddning med hastigheten v som badar i ett omgivande B-fält

             F          = BIl  ...............................................      kraften på en ledare med längden l som håller strömmen I som badar i B

             U          = Bvs  ..............................................     inducerad spänning i en fritt rörlig ledare med längden s (godtycklig kurvatur) med hastigheten v som badar i B

             U = F/T  .......................................................     inducerad spänning i ledaren s som sveper över distansen d under tiden T badande i B, U=Bsd/T=BA/T=F/T

             U = dF/dT  ...................................................     allmänna elektromekaniska induktionslagen

             F = BA  ........................................................     magnetiska ytstyrkan, VS

 

Sambanden beskrivs i härledningar i särskilda avsnitt

INDUKTIONEN — allmänna samband

allmänt

             L(di/dt) = û  ........................      inducerad spänning, allmänna universella induktionslagen, V

 

primärinduktionen

Primärinduktionen berör endast en ledares utsträckning (s) utan hänsyn till dess kurvatur men med hänsyn till ledarens samtliga materialkonstanter och därmed i referens till ledarens specifika induktans (Lc).

 

 

 

PRIMÄRINDUKTANSEN I SAMMANFATTNING — Se även mera utförligt i INDUKTIONSBEGREPPET I RELATERAD FYSIK

µ0  .......................................      1,25662 t6 VS/AM, fria rymdens primärinduktans per meter

s  .........................................      ledarens längd, M, oberoende av kurvatur

µc  .......................................      ledarens primärinduktans per meter, VS/AM, beror på material, tvärsnittet och uppförandet från den relativa laddningsmobiliteten i ledaren och laddningarnas relativa bindning till materialets struktur vilket framtvingar ett di/dt-beroende av sammansatt typ, för fri rymd är denna faktor noll då den fria rymden inte innehåller någon laddning

K  .......................................      massändringsfaktor för den resistiva delen i ledarens genomsnittsladdning, beror på laddningarna i ledaren och deras relativa bindning till materiestrukturen (induktansens intensitet), lägst 1 (gäller för fri rymd), ingen högsta gräns (uppskattat 2,6 för koppar vid 20°C)

µL = K(µ0+µc)  ..................      totala primära ledningsinduktansen per meter, VS/AM

Lc = µLs  .............................     totala ledningsprimära induktansen, VS/A

 

 

Ovanstående härleds utförligt i separat dokument. Se utförligt i INDUKTIONSBEGREPPET I RELATERAD FYSIK.

 

 

sekundärinduktionen

Sekundärinduktionen berör verkan av strömändringar från en primär ledare till rymden utanför ledarens eget ledningsrum (jämför radiovågor med sändare-mottagare).

                                       sekundära ledaren

                                       primära ledaren

             U          = (L/2p) [ln tan(b/2)  +  1/tanb]  .........................         V

             inducerad spänning i rak sekundärledare parallell med primärledaren via dellängden s med x/s=tanb

             L  ........................................................................................         Lc(di/dt)

OBSERVERA ATT PRIMÄRINDUKTANSEN Lc FÖR s MÅSTE VARA KÄND.

Materialet i sekundärledaren är fullkomligt egalt.

ringen

             ûRING = LK = L · (di/dt) · K  .....................................     ringens induktion

             K  ................................................................................    numerisk koefficient

 

Att beräkna K för ringen är en (fruktansvärt) komplicerad matematisk uppgift

K beror på ringens dimensioner (ringdiametern och dess ringkropp) och den aktuella induktionsvinkeln (normalt 360° för hela varvet).

K blir en högt driven sammansatt koefficient som kräver en helt egen författningsvolym

[ref. CD Kraftlagen 1999 XII, Induktansen.wps 1999XI20].

I strikt mätteknisk synvinkel finns ingen möjlighet att skilja den sekundära induktionen från den primära induktansen i ringen. Med den mera preciserade primärinduktansen Lc=µLs för L där s=2pr, r ringens medelradie, ges EMELLERTID den allmänna ringinduktionen

             ûRING = pµL2r · (di/dt)K  ............................       allmänna ringinduktionen, V

Med förenklat 2r=d som diametern med Ld · 1M–1=pKµL ges det enklare

             ûRING = d·Ld (di/dt)/1M ...............................       allmänna ringinduktionen, V

 

Begreppen som grundlägger induktionen och magnetismen beskrivs ingående från  startInduktionen och magnetismen — med löpande, jämförande exempel i modern akademi.

 

 

 

 

 

 

InduktionenOchMagnetismen | Snabbgenomgång av Induktionen och Magnetismen

 

 

SNABBGENOMGÅNG AV

INDUKTIONENS

OCH MAGNETISMENS MATEMATISKA FYSIK

ENLIGT RELATERAD FYSIK

 

 

 

Matematiken

Både induktionen och magnetismen uppvisar en nära [Q till insidan] och en fjärran [Q till utsidan] verkan. För att särskilja komplexen är induktionen i denna presentation indelad i en primär och en sekundär del medan magnetismen har bevarat termoinologin med närverkan och fjärrverkan. Både induktionen och magnetismen måste högeligen idealiseras i aspekten på ljushastighetens fördröjande verkan för att alls kunna få fram en hanterbar matematisk fysik.

 

MAGNETISMEN

Magnetismens matematik beskrivs särskilt utförligt från MAGNETISMEN.

 

Inom induktionen är rymdkompaktheten µ0 alltid närvarande. Inom magnetismen aldrig.

 

Magnetismens uppkomst förklaras istället från den elektriska konstanten e0–1=R0c0=Rmaxç0 genom kausalsambandet baserat på reduktionen ç=c–v.

Se vidare utförligt från KAUSALSAMBANDET.

 

induktionsmatematiken

INDUKTIONEN

INDUKTIONENS GRUNDMATEMATIK

Induktionen i elektrofysiken motsvarar exakt trögheten i mekaniken.

Den Primära induktionen berör strömändringar inuti elektriska ledare.

Den primära induktionen beror INTE av ledarens kurvatur.

 

Idealt utgår den primära induktionsverkan från vilken som helst homogena strömlinje med längden s

— oberoende av dess kurvatur genom den minsta möjliga rena laddningsfria primära rymdinduktansen,

 

             µ0s    = L0  ................................................      primära rymdinduktansen, VS/A

 

Se den matematiska induktionsfysikens grunder i inledningen från Uppkomsten av induktionen och magnetismen, om ej redan bekant.

Denna grundform är en egenskap genom vilken elektriciteten utbreder sig i tomma rymden genom divergensen (c) från laddningsmassan m via gravitationens ljusreglerande verkan (se från divergensens g-beroende).

Den primära rymdinduktansen är samma som den minsta möjliga elektriska tröghet varje elektrisk flödeslinje kan och måste ha.

Varje strömlinje (s) får sin egen specifika och medelmässiga primära induktans per meter (längdinduktansen)

 

             µL      = K(µ0+µc)  ..................    totala primära ledningsinduktansen per meter, VS/AM

 

             µLs    = Lc  .................................................     totala primära ledningsinduktansen, VS/A

 

µL beror på kristallin struktur, tvärsnitt, temperatur, täthet, magnituden i strömändringar och lokal gravitation (c).

Se även PRIMÄRINDUKTANSEN I SAMMANFATTNING.

µL bestämmer den ideala tidsabsoluta verkan i en ledare i respekt till varje strömändring di/dt.

 

allmänna induktansen

I kvantiteter uttrycker

induktansen (generellt betecknad L)

 

             L = Rt = ûi–1t ; 

             Li = ût ; 

             L(di/dt) = û  ........................      inducerad spänning, allmänna universella induktionslagen, V

 

en resistiv varaktighet, ett (tillfälligt) tillstånd av motverkan (eller medverkan) i produkten av motstånd R=û/i (û, u-flex) och tid t.

   Varje specifik strömväg (eg., byggnaden som strömmen dras igenom) får totalt sett sin egen specifika induktans beroende på strömvägens materiella egenskaper (elektricitetens principiella avskärmande, laddningarnas mobilitet, etc.).

 

BETYDELSE:

Varje momentant (tillfälligt, idealt under nolltid) uppmätt spänningsfall û mellan två punkter i ett godtycklig elektrisk ledningssystem med försumbar resistans, har den totala induktansen

L = û(di/dt)–1. Konstant strömstyrka betyder û=0.

 

 

Den Sekundära induktionen

 

Medan primärinduktionen ingriper (tar) direkt i Q-kroppen som följd av dess lägesändring, vilar den sekundära induktionen på det elektriska fältets utvidgning som följd av divergensen c. Den sekundära induktionen återfaller på en motsvarande men fördröjd ändring i den omgivande rymden av individuella fältpunkter från varje laddning.

 

Den sekundära induktionen ges med andra ord ur Q-rörelsen medan primärinduktionen ges ur divergensen.

Se Potentialbarriären.

 

Som den senare grundlägger den förra, bildar bägge parter en total induktans i varje sluten elektrisk krets såvitt något annat än en rak eller en rätvinklad strömlinje (Se vidare omnämnande nedan).

 

För att relatera en sekundär induktion i vilken som helst g-bestämd rymdpunkt P, ser vi uppkomsten av en separat (sekundär) induktiv resistans R’ i strömriktningen och skild från den fria rymdens resistans R0 vilket innebär att R’ lämnar R0 orörd. Induktionseffekten totalt har ingen inverkan på den lokala divergensen (c) vilket betyder att den elektriska konstanten bevaras.

R’ uppkommer genom varje möjlig strömändring, eller som vi säger, genom strömderivatan di/dt.

 

 

Komprimerad beskrivning — sekundärinduktionens grundmatematik

 

Energi över laddning betyder potential (E/Q=U). Dess mekaniska motsvarighet är den uppvägande kvadrathastigheten som definierar g-skalet eller den sfäriska ekvivpotentialytan (w2=Gm2/r). Potentialens differential i ett sfäriskt Q-system betyder för varje r den elektriska »divergensflashen (a=c/dT)» eller den elektriska potentialen vid ändpunkten på r från Q-massans centrum enligt

 

             dE/Q = dU = Rc · (dQ/A) · r  ............   potentialen, sfäriskt Q-system, V

 

Kraft över laddning motsvarar centrifugalaccelerationens konstant i g-skalet i mekaniken (a=Gm2/r2=F/m). I elektrofysiken är motsvarande benämning (se även elektromekanikens grundbegrepp) elektrisk fältstyrka enligt

 

             dF/Q = dX = Rc · (dQ/A)  ..................  statisk fältstyrka, sfäriskt Q-system, V/M

 

Elektriska fältstyrkans frihetssats. Elektrisk fältstyrka är elektrisk potential dragen över en ändlig distans (X=U/s). Fältstyrkan visar sig alltså först när en mekanisk rörelse hos Q aktualiseras. Men i det elementära statiska Q-systemet finns ingen sådan, mekanisk, rörelse närvarande; det elementära statiska Q-systemet besitter alltså heller ingen elektrisk fältstyrka. Den elektriska fältstyrkans form X=U/r uttrycker MED ANDRA ORD en statisk skalegenskap som katalyserar, uppväcker, en bestämd X först genom en påtriggande Q-rörelse utmed en mekanisk väg s som sammanflyter med den statiska skalflashen X=dU/ds. Den centrala aspekten i en sådan ansats till en Q-rörelse är den momentana hastigheten v i den aktuella Q-accelerationen dv/dT. Som denna acceleration inte har någon koppling till divergensen c, påverkar den heller inte R. Effekten som genereras i en fix rymdpunkt P under Q-accelerationen bildar därmed i P en separat induktionsresistans R’,

 

             dF/Q = dX = R’v · (dQ/A)  ................  induktiv fältstyrka i P, sfäriskt Q-system, V/M

 

R’ blir alltså aktiv bara när Q accelererar.

 

Eller, med samma innebörd: när någon strömderivata di/dt visar sig skild från noll.

Uppkomsten av induktionsresistansen R’ kommer att vara en del av den primära ledningsinduktansen (Lc) eftersom det är primärströmmen som bär ansvaret för sekundärinduktionens kvalitativa effekt, helt vid sidan av andra möjliga rymdegenskaper.

 

 

PÅ VISS SÄTT betydelsefullt: vi tvingas använda (omfattande) generaliseringar och idealiseringar i induktionsmatematiken

§:

Den förenklade induktionsmatematiken. Den ordinära divergensresistansen (R) i divergensfenomenet är rymdberoende (beror av rymdens egenskap). Sekundärinduktionens induktionsmotstånd (R’) är inte det. Sekundärinduktionens induktionsmotstånd uppstår, och försvinner, med variationerna i i. Därmed associerar R’ en egenskap med den primära induktionsströmmen i, dvs., med primärledaren — där R innefattas av den primära induktionens matematiska fysik enligt föregående. Sekundärinduktionen underförstår, eller förutsätter därmed, en total, fullständig -homogenitet över hela det induktiva verkansrummet. Här finns alltså ytterligare detaljer som komplicerar den matematiska formuleringen av induktionsfysikens exakta dynamik och som tvingar oss att använda (omfattande) generaliseringar och idealiseringar.

§.

 

Dipolbegreppet

Utvecklingarna ger då med v=ds/dt fortsättningen

 

             dX        = R’(ds/dt) · (diT/A)  .........      induktiv fältstyrka i P, sfäriskt Q-system

                          = R’T(di/dt) · (1/A) ds

                          = Lc(di/dt) · (1/A) ds = L · (1/A) ds, L Greekiskans Lambda (L), V

             dР       = L · A–1 · ds  ....................      induktiva dipolfältstyrkan i P, V/M

             dU        = L · A–1r · ds  ..................       induktiva dipolspänningen i P, V

 

För att särskilja den vanliga elektriska fältstyrkan (X) från den speciella induktiva dipolfältstyrkan, är den senare i denna presentation representerad av symbolen Ð (Dipol-Elektrisk fältstyrka, Alt+0208). Från Newtons tredje lag följer att en ökning i i uppväcker Ð motriktad i. Avtagande i betyder att Ð är samriktad med primärströmmen. Dessa enkla flödesbegrepp kallas också konventionellt stundom för Maxwells Regel.

   Ð avbildar en spänningskälla som uppkommer i sin mest elementära form i endast en specifik rymdpunkt P i det lokalt dominanta g-systemets mätande referens: P uppvisar inget område, ingen domän, ingen utsträckning, noll. Termen dipol används (här) därför att Ð-källan har (eller kan förstås uppvisa) en distinkt spänningspolaritet som endast överflyttas på P.

 

Induktiva dipolfältstyrkan

Med vinkeln b mellan linjen Q-centrum till P och s-linjens förlängning (i), får sambanden i PREFIXxSIN formen

             dР       = L · A–1sinb · ds  ................    induktiv dipolfältstyrka i P, fullständig grundform

Den praktiska formen för Ð beror både på kurvaturen för den primärt genererande och den sekundärt mottagande ledaren. För att få en användbar slutform för Ð måste vi alltså genomföra ett antal integrationer över angivna intervall.

Med laddningen som en ideal sfärisk yta (A=4pr2) och föregående förenkling L=L(di/dt) ges den mera fullständiga formen

 

             dÐ        = L(di/dt)(1/4pr2)sinb · ds  ...... V/M, praktiska induktiva dipolfältstyrkans grundform i P

 

Den allmänna induktansen (L) från Ð kan skrivas

             dU(di/dt)–1 = dL = Lc · (1/A)r ds  .......  allmänna induktansen, differentialform

Den totala induktansen LT  i en ledare får då sammansättningen

             LT = Lc + LSKURVATUR  ......................   totala ledningsinduktansen, VS/A

där Lc är den totala primära ledningsindukltansen och LSKURVATUR den integrerade komponenten från den ovannämnda allmänna induktansen (L).

   För en rak ledare är LSKURVATUR noll. Detta gäller också för en ledare vars form ansluter till en rät vinkel; ingendera av de motstående sidorna ger något bidrag till sekundär induktion i strömriktningen.

 

Den inducerade spänning som genereras av sekundärinduktionen är en rymdspänning. Rymdspänningen relateras till den g-bestämda rymden (P) i vars rymdpunkter Q-laddningen uppvisar sin ändrade potentialbild i följd av sin accelererade rörelse. Denna rymdspänning är alltså fullständigt oberoende av TYPEN av ledare den tar i. En fin silvertråd kommer att uppvisa exakt samma inducerade spänningsfall per längdenhet som ett fint hårstrå eller en rejält grov kopparstång.

 

INDUKTIONENS OCH MAGNETISMENS MATEMATIK är (extremt) omfattande. Det är naturligt med tanke på att dessa bägge omfattar alla skiftningar och variationer i materiens alla möjliga egenskaper och otaliga formationer.

 

förtydligande

Genereringen av rymdpotentialen i induktionen

 

 

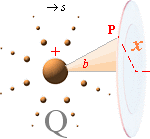
Konstant hastighet. Medan Q lägesändrar med konstant hastighet (v=ds/dT) relativt en given g-referens P, P-exponeras under dT bara en en-till-en-projektion av Q-systemets potential — därför att tid och distans flyter sida vid sida om hastigheten är konstant ds/dT och därmed ingen möjlig ackumulation, analogt noll induktivt (ackumulerande) motstånd.

   Den inducerade rymdspänningen i P stannar då på nivån differentiell, analogt noll. Inget motstånd ackumuleras i P, och därmed heller ingen kvantitativ induktionsspänning.

 

Varierande hastighet. Med Q i en accelererad rörelse däremot (a=dv/dT), upphör den entydiga en-till-en-projektionen av Q-systemets potentialer på P under dT — därför att tid och distans med varierande hastighet nu flyter med olika magnitud och därmed en ackumulering är oundviklig genom  den principiella variation (gradienten för a) som hastighetsändringen innebär, tidsdifferentialen inkluderad, i föreställningen om projicerad potential i P.

   Den inducerade rymdspänningen i P blir därmed tvunget större än noll genom det motsvarande ackumulerade motståndet (induktionsresistansen R’). Den induktiva fältstyrkan (från utvecklingarna längre upp)

dX = d(U/s) = R’v · (dQ/A)

visar sig med andra ord bara då v är konstant under dT, analogt del i en pågående acceleration, varigenom också R’>0.

   Därmed är förklaringen uttömd till hur den rymdrelaterade g-refererade induktionsspänningen uppkommer.

   Genom att potentialbilderna i P ”rapporteras” till andra närliggande Q-system genom deras individuella mQ-fält, kan dessa svara på potentialbilden med motsvarande attraktioner eller repulsioner. Därmed är det elektromotoriska induktionsfenomenet förklarat i princip.

 

Denna förklaring vilar således helt på teorin för differentialens definition — tillsammans med accelerationsfenomenet — vilket I RELATERAD FYSIK måste särskiljas skarpt från intervallets eller differensens definition. De teoretiska grunderna beskrivs utförligt enligt relaterad fysik och matematik från NOLLFORMSALGEBRAN.

 

END.

 

expansionsintegralen

magnetismen i MAC

Utförlig beskrivning av elektrofysikens grunder

UPPKOMSTEN AV INDUKTION OCH MAGNETISM — magnetismen

 

Exakt upplösning i Magnetismen

EXPANSIONSINTEGRALEN

VARFÖR MODERN AKADEMI GARANTERAT INTE KAN HÄRLEDA MAGNETISMEN

 

DEN MAGNETISKA EXPANSIONSINTEGRALEN

Magnetiska fältets differentiella element — jämför dito i modern akademi i citat nedan

Magnetiska laddningsfältspotentialen

Magnetiska fältets differentialelement [dB(Px)] skrivs i relaterad fysik (TNED) — även magnetiska laddningsfältspotentialen från elektriska kraftlagen F=Rc(Q/A) enligt B=F/Qc=RQ/A=(R/c)cQ/A=µ(s/t)Q/A=µsI/A — som expansionsintegralens differentialekvation i PREFIXxSIN;

 

Se Härledningen till dBPx  — Tillägg till Induktionen och Magnetismen 3Okt2011 — Se även separat artikel i Vektorkalkylens sammanbrott inom magnetismen i modern akademi.

 

 

Expansionsintegralens differentialekvation (se utförlig härledning nedan) eller

magnetiska (dB=dF/Qc=RdQ/A=[R/c][s/t]dQ/A) laddningsfältspotentialen

             dBPx = d(dBPs/dbs)=Rmaxç0–1(I/4πx)sinb db

med lösningen (magnetiska expansionsintegralen) = Biot-Savarts lag

 

             dBPs = µ0(I/4πx)cosb dbs

samma som (efter differentialtransformation, utförlig härledning i Fjärrverkan; ds/db=–x/cos²b=–x/(x²/r²)=–r²/x; db=–x/r²ds)

 

             dBPs = µ0(I/4πr2)cosb ds

i etablerad litteratur (PREFIXxCOS) ofta som

             dB = µ0(I/4πr2)sinb ds

 

 

Magnetiska laddningsfältspotentialen, Kausalsambandet, Expansionsintegralen och Planvektorsumman [ekvivalensen mellan expansioner och tangenter] ingår inte i modern akademi. Man börjar istället från expansionsintegralens rätvinkliga [från trigonometrins Planvektorsumma] lösning, konv. benämnd Biot-Savarts lag.

 

Se Härledningen till dBPx  — Tillägg till Induktionen och Magnetismen 3Okt2011 — Se även separat artikel i Vektorkalkylens sammanbrott inom magnetismen i modern akademi.

 

 

Det är differentialekvationen för den grundläggande expansionsmagnetiska integralen eller som vi här enklare ska kalla den, expansionsintegralen (eg. expansionsintegralens differentialekvation för exakt referens) Den finns INTE upptagen i den moderna akademins lärosystem — av skäl som vi här med särskilt tydlig noggrannhet ska studera mera ingående: modern akademi har nämligen garanterat sig själv portförbud. Vänta bara ska du få se.

beskrivning med utförlig härledning

magnetismen

Då den elektriska laddningen Q lägesändrar med v relativt ett givet dominant g-systems fasta rymdpunkter och samtidigt Q:s eget e-fält arbetar återkopplande med c, SKULLE vi förmoda en verkan »c+v» för potentialändringen i en sådan g-relaterad rymdpunkt P. Enligt relaterad fysik, ljusets friställning från kinetiken, finns emellertid ingen fysisk koppling mellan c och v. För att bevara elektriska konstanten (R0c0=1/e0=k) i riktningen v, förklaras därmed verkan i P av ett kausalsamband som leder till en divergensreduktion rätvinkligt v på formen ç=c–v; Det lägre ç medför en motsvarande resistansökning (RN) rätvinkligt v, alltså en högre planresistans i rät vinkel mot v, och som tvunget blir differentiell (helt utan tjocklek) för att k ska bevaras i riktningen v och därmed också c bevaras i v-riktningen. Den så uppkomna förtätningen strävar sedan att uttömma sig i det tunnare R0-rummet med den högre c0-divergensen och bildar därigenom den fenomenform vi kallar för magnetism.

   Motståndet RN i normalplanet till v formar, således, tillsammans med translationen (I=Q/T) en elektriskt fältstyrka (X, Xsi) i P av formen

dU/ds = X = dRNI/ds. Den motsvarande reducerande (MAGNETISKA ç) fältstyrkan (B) i P kan då skrivas

X/ç0      = B i VS/M2 = (V/M)/(M/S)  Tesla

Generellt kan den reduktiva fältstyrkan därmed skrivas

X/ç0      = B = RmaxQ/A = (U/s)/ç0 = Rmaxç0–1ç0Q/A

             = Rmaxç0–1s T–1Q/A = Rmaxç0–1sI/A = µsI/A

Med en försumbar skillnad mellan c0 och ç0 gäller det att

Rmaxç0–1=R0c0–1=µ0 som ger B=µ0sI/A. Med en sfärisk yta för A=4pr2 gäller differentiellt att

dB=µ0(I/4pr2)ds med Q-ändringen i riktning r eller s. Med nollvinkeln b i riktningen s utvidgas sambandet enligt dB=µ0(I/4pr2)sinb ds i PREFIXxSIN. Uttryckt i distansen x mellan P och s via vinkeln b ges då ENLIGT RELATERAD FYSIK expansionsintegralens differentialekvation

expansionsintegralen — Inledning

 

dBPx      = µ0(I/4px)sinb db = d(dBPs/dbs)  ................     magnetiska (reduktiva) expansionens differentialekvation

som har lösningen

dBPs      = µ0(I/4px)cosb dbs  ......................................     expansionsintegralen

Vilket skulle visas.

 

Biot-Savarts lag

DET sambandet finns däremot upptaget i den moderna akademins lärosystem under namnet Biot-Savarts lag. Den skrivs typiskt i läroböcker och facklitteratur på r-form i konventionellt PREFIXxCOS enligt

dB         = µ0(I/4pr2)sinb ds

— eller mera allmänt, speciellt av folk som vill understryka HÖGSKOLEMATEMATIKEN enligt

dB         = (µ0/4p) · I · ds × r/r3

r-formen ansluter till den moderna akademins begrepp vektorprodukt (se vidare efterföljande nedan).

 

Biot-Savarts lag, konventionell beteckning som ansluter till magnetismens grundsamband

Biot-Savarts lag — ref. Sep2011

Biot-Savarts lag

Biot-Savarts lag skrivs i en del etablerad litteratur (PREFIXxCOS)

 

dB = µ0(I/4pr2)sinb ds

 

Se exv.

FOCUS MATERIEN 1975 s223sp2ö

TEKNISK ELEKTRICITETSLÄRA, E. Danielson Gleerups 1965 s44n

HYPERPHYSICS Biot-Savart Law i Webbkällan (2011-09-04)

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/biosav.html

 

Typillustration

 

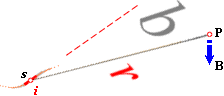
Focus Materien, Danielson, Hyperphysics, m.fl.

Jämför typiskt Biot-Savarts lag i många etablerade fackverk

 

 

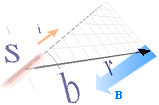
enligt  dB = (I · ds×r/r3)(µ0/4π).

Se även nedan i Differentialelementet i MAC.

 

Se även hur ovanstående samband ingår i och framgår ur utvecklingarna till Magnetiska Expansionsintegralen — från

Kausalsambandet med grund i Uppkomsten av induktion och magnetism, om ej redan bekant.

 

Biot-Savarts lag, konventionell beteckning som ansluter till magnetismens grundsamband

 

Därmed är kalabaliken inom

modern akademi ett faktum.

 

Vi studerar hur.

 

differentialelementet i MAC

I modern vetenskap och teori hävdar man (NÄMLIGEN) att

”if we define a differential element of current Idl then the corresponding differential element of magnetic field is

dB = Km Idl × r/r2 where Km=µ0/4p”,

@INTERNET Wikipedia Biot-Savart law 2007-06-13.

 

Min översättning:

om vi definierar ett differentiellt element av strömmen Idl då är det motsvarande differentialementet av magnetiska fältet

dB = Km Idl × r/r2 där Km=µ0/4p

NOTERING: termen ”r” betyder ”en enhetsvektor r=r/r” .

 

Enligt relaterad fysik är DET differentialelementet ett INTEGRALELEMENT av en mera fundamental differentialekvation som inte kan beskrivas med begreppen från den moderna akademins lärosystem. Nämligen som visats ovan, expansionsintegralens differentialekvation och som inte ingår i modern akademi.

 

Varför kan inte Det — »ENKLA OCH LÄTTA» — beskrivas av modern akademi?

 

Ursprunget kan varken beskrivas eller härledas i modern akademi — eftersom ”vektorprodukten” av denna förvandlas till en ”skalärprodukt” då återderiveringen av vektorn sin|cos ger skalären cos|sin och därmed hela den moderna akademins vektoralgebra i total krasch.

   Ingen kan varken förklara eller härleda någon grund på den vägen — utan att samtidigt totalrasera den moderna akademins egen lärostol: vektoranalysen. Och alltså måste modern akademi börja med magnetismen på Biot-Savarts lag; ”differentialelementets definition”.

   Grundformen, expansionsintegralen, framstår därmed som icke existerande: den kan inte nås. Därmed uppstår (naturligtvis, enorma) motsättningar mellan ”lärde” som ’försöker »förklara» magnetismen’. Alla misslyckas, och motsättningarna blir bara djupare.

 

Jämför @INTERNET Wikipedia Magnetic field på Talkpage: de stundtals häftiga motsättningarna har nu pågått under flera år och ingen lösning är i sikte.

Vilket skulle visas.

teorin saknas i MAC

MAGNETISMEN I MODERN AKADEMI

 

— Men om expansionsintegralen inte finns med i den moderna akademins lärosystem, hur bär man sig då åt i den moderna akademins lärosystem för att förstå själva fenomengrunden i magnetismen? Hur resonerar man för att förstå magnetismens grundfunktion?

 

— Den finns inte med. Man utgår istället från INDUKTIONEN, differentialformen, SOM kvantitativ FENOMENGRUND och hänger sedan hela det magnetiska komplexet på den förutsättningen, enligt den moderna akademins begrepp vektorprodukt. Magnetismen har ingen självständig fenomengrund i termer av den moderna akademins lärosystem. Med den föreställningen försvinner också varje koppling till induktionen som ett begripligt, förklarbart, begrepp inom modern akademi: Man menar, faktaböckerma nämligen, att induktionen förorsakas av magnetismen. Verkligen.

 

 

 

Den svenska delen i Wikipedia @INTERNET skriver på ämnet ”electromagnetisk induktion”:

”Induktion är ett begrepp inom fysiken som innebär att en spänning alstras (induceras) i en ledare om ett magnetfält i dess närhet varierar.”

”Om e är den elektromotoriska spänningen och F är det magnetiska flödet så gäller

e = – dF/dt ”

@INTERNET Wikipedia Elektromagnetisk induktion 2007-06-22

Liknande bidrag bör vara välkända då dessa helt klär upp ytan på planeten Jorden med början från 1800-talet.

 

 

 

— Men herregud, nu blir jag galen. Det betyder alltså att hela den moderna akademin i ämnet magnetism är fullproppad med DJUPGÅENDE OKLARHETER, dispyter, mellan olika s.k. lärde och som inte bidrar med annat än att motsättningarna bara ökar? Hur står folk UT med sånt?

 

— Exakt. Studera till exempel @INTERNET Wikipedia Magnetic field på Talkpage: dispyterna har pågår i flera år, stundtals så häftiga att själva artikeln har spärrats av administrationen.

 

Av dessa skäl kan man gott påstå med eminent bevisbörda att teorin för induktionen och magnetismen i modern akademi i princip är obefintlig.

 

 

Beskrivningen fortsätter på samma tema nedan.

 

 

Vad är Maxwell ekvationer?

Vad är

”Maxwells ekvationer”?

 

MAXWELLS EKVATIONER är en samling matematiska uttryck som beskriver elektriskt kopplade samband (från 1865/1873) baserade på ett artificiellt regelverk av den moderna akademins vektorkalkyl som uppställdes, utvecklades och antogs som det moderna akademiska lärosystemets grund under 1800-talet. Dessa regler exkluderar från dem — onoterat — den grundläggande magnetiska expansionsintegralens differentialekvation, men på vilken så gömda lösning de bygger, inte närvarande eller omnämnd i modern akademisk teori, och därmed behandlande elektromotorisk induktion allmänt som ett framträdande av magnetisk fenomengrund. Vilket vill säga, med en exkluderad — utesluten — magnetisk expansionsintegral. Med detta grepp, ger de så moderniserade ekvationerna en bekväm kvantitativ behandling av alla elektromagnetiska fenomen. Märk den detaljen väl. Därav den breda historiska populariteten hos Maxwells ekvationer i deras rent kvantitativa elektrofysiska tillämpningar.

 

Maxwells ekvationer kan (således) INTE konsulteras för fenomenologisk förklaring till induktionen och magnetismen, utan förorsakar som sådana enbart djupa missuppfattningar med djupgående teoretiska meningsskiljaktigheter. Vilket vill säga, den moderna akademins vektorkalkyl kan inte användas, inte alls över huvud taget, för att diskutera, relatera eller uttrycka matematiskt de teoretiska grunderna till induktionen och magnetismen — utom genom att uppväcka djupa missuppfattningar.

 

Beviset för påståendet i den ovannämnda summerande beskrivningen ges i det följande kortfattat nedan, samt vidare mera utförligt från EXPANSIONSINTEGRALEN.

 

 

uteslutningen i MAC

DEN MODERNA AKADEMINS UTESLUTNING:

 

---------------

Tillägg 2Jul2024: Absolut ytterst gärna rätta om fel. Sakfel får inte förekomma i den här typen av framställning. Inte alls.

 

Det akademiskt etablerade lärosystemets djupgående brister i beskrivningen av magnetismens och induktionens matematiska fysik:

— Etablerad beskrivning relativt verklig fysik kan liknas vid, så beskrivas, och relateras teoretiskt och experimentellt i varje detalj enligt följande: som en dockskåpsteater jämförd med verkligt — precis så som det ser ut för ögat nu på Jordytan efter 200 års modernt akademiskt inrättade härjningar efter den akademiska intelligensens nyordningar 1800+ [MainPurposeIllustrated]: kan inte leva tillsammans med naturligt utfyllande grönska utan att uppvisa vandaliserande exempel. Helt fundamentalt totalt omöjligt. Dödar/hindrar systematiskt — av drift, inte plan — grunden till livets uppkomst och fortlevnad. Efterbliven, lågutbildad, intellektuellt avskärmad. Säg igen.

 

— Modern akademi »primitiviserar» den matematiska fysiken genom att uppfinna — inte härleda — fysikgrunder (Maxwells populära ekvationer [MAXWELL’S ANALOGIES]: modern akademisk vektoralgebra, med tillhörande MIT exempel [MITcoriolisExample] — MaxwellsMagnetiskaFältmekanik). Som mest bidrar det till en ökad festlig stämning och anda i de fortsatta populära Nobelföreläsningarna i Stadshuset — medan planetytan fortsätter att utarmas på LIV i samma proportion. Studenter och elever begriper — rätteligen — inget alls av innehållet — men det är väldigt festligt och populärt. All  verksamhet riktas, tydligen som det får förstås, mot att utnyttja liv och mänsklighet för profit och inflytande, makt och ställning.

 

 

Begreppen ELEKTRO-MAGNETISK INDUKTION kontra ELEKTRO-MEKANISK INDUKTION

PARALLELLEXPERIMENTET Jun1994

PARALLELLEXPERIMENTET

Potentialbarriären: 1994IV16 — F4s28 ¦ DG-PBs2-1995

PARALLELLEXPERIMENTET 1994V4¦7¦26 — Experiment bekräftar teorin — F4s33vä‡s35‡s34 ¦ DG-DEMIs2-1995

 

 

Denna författningsgrund: Genom observation (1984+) av den etablerade akademiska litteraturen och dess referensers ofullständiga grundförklaringar till MAGNETISMEN, genomfördes — efter omfattande utvecklingar, genomgångar och bearbetningar med flera helt komplett totalt misslyckade försök till helhetsförklaringar — PARALLELLEXPERIMENTET Jun1994.

 

Två raka AB 1dM långa parallella elektriska ledare med centrumavståndet 15mM påförs höga strömstyrkor (15A resp. 30A i test). Mellan AB ledarna spänns en fast (fin 0,1 mM) koppartråd C upp för att (via ett oscilloskop) observera och mäta effekten av de pålagda konstant och varierande AB strömmarna. Ett särskilt Hallelement monteras mellan AB (under C) för att mäta den magnetiska fältstyrkan (B).

 

1.  AB strömmarna samriktade — ingen observerbar eller mätbar magnetisk fältstyrka på mitten (C) mellan AB:

— Men det induceras en spänning i C då AB-strömmarna växer från noll till max och sedan åter från max till noll.

2.  AB strömmarna motriktade — full mätbar magnetisk fältstyrka på mitten (C) mellan AB:

— Men ingen — noll — spänning kan observeras eller mätas i C då AB-strömmarna växer från noll till max och sedan åter från max till noll.

3. AB ledarnas material och dimensioner påverkar inte den magnetiska fältstyrkan. C ledarens material och dimensioner påverkar heller inte den i C inducerade spänningen. Men den spänningen påverkas verkligen av material och dimensioner i AB ledarna: tunnare AB ledare ger högre inducerad spänning i C. Förklara: Därför [Newtons tredje] att smalare tråd = högre motstånd motsvarar större tröghet som motsvarar mera induktiv kraft [samma som mekanikens motsvarande större masströghet (omfördelning av g-massa genom induktionsverkan i slutna elektriska system [KRAFTLAG.WPS 1996XI23] ¦ MAFEM), högre inducerad spänning: helt fullkomligt oberoende av magnetismen och helt avstängt från dess inverkan: induktionen bestäms enbart av den elektriska laddningens rörelsebaserade ändring [Newtons tredje] — som naturligtvis också avspeglas i en motsvarande ändring i magnetisk fältstyrka. Och det är den moderna akademins egentliga, primitiva, formuleringsproblem: bekvämligheten att associera strömändring med ändring i magnetisk flöde — utan insikt i det faktum att magnetism [x-led] inte växelverkar med induktion [y-led]: kausalsambandet (KAUSALSAMBANDET) förklarar: ingår inte i den moderna akademins lärosystem.

 

 

SLUTSATS:

Magnetism och induktion växelverkar inte.

 

 

Magnetism

[x-led: här benämnd i ljusutbredning i vakuum som en reduktion (Ljusfrihetssatsen: ljusfysiken kopplar inte kinetiken [särskilt bevis: Solrandsobservationerna från 1919: krökta ljusbanor i g-fält utvecklar ingen centrifugalkraft]: ingår inte i den moderna akademins lärosystem): modern akademi missar hela pårampen till atom- och kärnfysiken, garanterat (komprimerat sammanställt i Fig.1)]

———————————————

AllKeplerMath ¦ TheAtomicNucleus ¦ EXPERIMENTAL CONFIRMATIONS ¦ TheSolarEclipses ¦ MULTIPLEc ¦ TheGPSexample ¦

ThePerihelionPrecessions ¦ LightAndGravitation

 

och induktion [y-led]

(kausalsambandet förklarar den matematiska fysiken: ingår inte i den moderna akademins lärosystem)

 

verkar vektoriellt i två från varandra skilda (rätvinkliga) riktningar.

(Magnetismen: som ringarna på vattnet sedan en sten släppts ner på vattenytan; induktionen: vågrekylen [Newtons tredje lag] i vertikalled: detaljerad matematisk fysik — ingår inte i den moderna akademins lärosystem):

 

EXPANSIONSSAMBANDET (Expansionsintegralens integralmatematik) avtäcker en INRE (tydligen i moderna kvarter helt okänd) PRIMÄR INTEGRAL som föregår den (enda omnämnda) moderna akademins YTTRE integral benämnd Biot-Savarts lag: den moderna akademins beskrivningssätt (modern akademisk vektoralgebra — utförligt från Vektorprodukt [VektorkalkylensSammanbrottMAC, Maxwells detaljer förklaras]) hoppar över [missar, förstår inte — beskrivbart i varje atomär detalj] grunderna, presenterar en ytlig förenklad/förvanskad/missformad bild — som ingen modern PhD eller annan associerad kan begripliggöra, tydligen (undervisningens innehåll utarmas [eleverna flyr den akademiskt dikterande matematiken, eftersom den inte kan förklara grunderna] på kredit av redan akademiskt etablerade växande obegripligheter). Rätta gärna om fel.

BEVISNING, särskilt:

1. TREATISE — tre jämförande exempel — visar hur, och varför, den moderna akademiska så bevisbart PRIMITIVA textbokens matematiska samband i ämnet »elektromagnetisk induktion» ger »tillräckligt noggranna med experimenten överensstämmande resultat» i den rent — övergripande, skolbokstekniska — experimentella behandlingen. Det är, som sagt, som att jämföra en dockskåpsteater med ren verklig fysik. Teatern räcker (utomordentligt) för att konstruera fysiska elektriska maskiner. Men den kopplar inte fysikgrunderna (atom- och kärnfysiken): kan inte förklara sammanhangen (ändstation: modern etablerad akademi missar lösningen till mänsklighetens energiproblem — fullständigt).

2. ATOMKÄRNANS HÄRLEDNING ¦ I ¦ II ¦ III ¦ IV :

   Ljusfysikens gravitella beroende [DGD]; Potentialbarriärens matematiska fysik [PBM]; elektriska laddningens härledning [Q]; Plancks konstant h=mcr: Neutronringen, Neutronkvadraten, Planckekvivalenterna; vic-felet; massökningseffekten inom elektrofysiken [MAFEM]: stället [energizonen, potentialbarriären] där den elektriska laddningen TAS: elektrofysikens elementära Dynamik [HÄRLEDNINGEN TILL GRUNDÄMNENAS PERIODISKA SYSTEM: Keplerresonanserna] [AllKeplerMath]: självförvållat utestängt från den moderna akademins lärosystem: det lärosystemet [»intelligensens självutnämnda högsäte»: relaterbart och detaljerat bevisbart till sista atom: efterblivna, lågutbildade, intellektuellt avskärmade — rätta gärna om fel] bygger istället på motsvarande uppfinningar, förenklingar (vars noll naturkopplingar framdriver motsvarande naturvandaliseringar: av drift, inte plan, rätta gärna om fel), som stänger vägen för den relaterbara härledningen och beskrivningen i naturfysiken; människorätten som kunskapsdomän utesluts; samhällen som degenererar, våldet och otryggheten som tillväxer, undervisningen som urartar i sinnlig krävande, kvävande övervakat individslaveri med krav på konkurrerande nationell servilitet för att bevara den ädelt genomkorkade akademiska elitens idéer om livets ursprung och allmänna syfte: Trafficking. Cookies. Global inlåsning av Tänkande med elektronisk individövervakning (säg att jag har fel, snälla). Allmänt omfattande natur- och miljöförstöring (»råvaruförädling»). Den globala vantrivseln tillväxer. Ingen vill ta tag i den växande problematiken — utom den som statsförvaltningen utesluter ur boendet, på grund av engagemanget: ”Du upprör ju folk!”. ”Upphör ej dessa skrivelser från dig .. kommer din hyresrätt att förverkas”. ”Du kör med det där förbannade människovärdet!”. ”Se till att anpassa dig efter de här människorna!”. Säg igen.

   The will of the people: den egna inneboende värdigheten. Befolkningen förkastar, spottar på, den egna inneboende positiva potentialen.

   Se även i CITATBLOCKET om magnetismen generellt.

---------------

 

 

 

Sambanden nedan i det konventionella PREFIXxCOS:

 

uteslutet ur modern akademi och vetenskap:

dBPx      = Rmaxç0–1(I/4px)cosb db, VS/M2

             = µ0(I/4pr2)cosb ds, förenklat ç0=c0 och Rmax=R0  to µ0=R0/c0. Se vidare från KAUSALSAMBANDET

             = d(dBPs/dbs) differentialekvationen för magnetiska expansionsintegralen enligt RELATERAD FYSIK

 

 

innefattat i modern akademi och vetenskap:

LÖSNINGEN TILL OVAN utan något spår — omnämnande — av den underliggande expansionsintegralen:

dBPs      = µ0(I/4px)sinb dbs , kallad Biot-Savarts lag, modernt tecknad i antagandet av vektorkalkylen (typiskt)

dB        = (µ0/4p) · I · ds × r/r3

 

 

 

Se utförligt från början i EXPANSIONSINTEGRALEN.

 

 

Induktionen och magnetismen forts.

 

 

VEKTORPRODUKTENS BLOTTA BEGREPP ÄR den moderna akademins FEL i försöken att härleda magnetismen — och det som föranleder alla kontroverser, och omöjliga upplösningar av magnetismens elementa inom den moderna akademins olika studentled.

 

Vi studerar det.

 

 

Vektorkalkylens sammanbrott i MAC — Tillägg i Induktionen och Magnetismen 3Okt2011

 

Den moderna akademins Vektoralgebra — i sammanbrott inom magnetismen i modern akademi • BILDKÄLLA: Författarens arkiv · 23Apr2011Excur11Bild25 · NikonD90 · Detalj

 

Anslutning existerar inte I MENINGEN AV ATT DEN MODERNA AKADEMINS VEKTORKALKYL och VEKTORALGEBRA genom begreppet VEKTORPRODUKT [Jämför Biot-Savarts lag] kan beskriva eller överhuvudtaget kopplar MAGNETISMEN i något som helst fenomenmässigt avseende — så som det ändå, på visst sätt men utan direkta formuleringar, förefaller att HA BLIVIT genom läromedlens utveckling under hela 1900-talet;  anvisningar genom de olika fackverkens sätt att beskriva ämnet. I följande genomgång visas HUR den moderna vektoralgebrans begrepp [vektorprodukt, se Biot-Savarts lag] som sådan endast  är ett MATEMATISKT  regelverk utan någon beskrivande koppling till fysikens fenomen, här magnetismen.

— I modern akademi söker man KATEGORISERA alla fysikens s.k. VEKTORFÄLT [här inom magnetismen] via TVÅ egenskaper; DIVERGENS [förk. div] och ROTATION [eng. curl]. Se exv. @INTERNET Wikipedia Magnetic field, Maxwell’s equations [2011-10-08]. Det finns inga andra djupbeskrivande sätt i modern akademi för att »förklara» — beskriva, härleda och relatera — typ magnetismen som fysikalisk fenomenform, än just dessa begrepp, eller EGENSKAPER. Jämför även i Citatblocket: ingen förstår ännu idag magnetismen.

— DÄRMED har [under 1900-talet] en FIKTIV BILD uppkommit — och vars natur vi studerar vidare nedan i huvudtexten — med »Maxwells ekvationer» som [typiskt] »beskriver magnetismen» genom de så antagna, etablerade, vektorkalkylens begrepp. Dessa har, så att säga, blivit självupphöjda under 1900-talet.

— MEN ELEMENTEN I MAXWELLS EKVATIONEN — den moderna akademins div och curl — omfattar INGALUNDA MAGNETISMENS FENOMFYSIK. Beviset ges här i EXPANSIONSINTEGRALEN; den föregår [och kör över hela vektorkalkylen], och leder till, den konventionellt antagna magnetismens grund genom Biot-Savarts lag; Men antagandet av Biot-Savarts lag genom DEN MODERNA AKADEMINS omskrivna Maxwells Ekvationer UTESLUTER magnetismens förklarande FENOMENGRUNDER i relaterad fysik: Kausalsambandet och Planvektorsummans trigonometriska ekvivalens för expansionsvektorer och tangentialvektorer. Medan den relaterade fysiken uppvisar en sammansatt 3D-vektorkropp för magnetismen, ser modern akademi via sin vektorkalkyl bara EN av de tre. Vidare i huvudtexten. Det är poängen i hela historien.

— Det betyder [återigen] att den moderna vektorkalkylens begrepp väl må vara matematiskt användbara i olika mängdbeskrivningar, men att de INTE kopplar fenomenfysiken i någon KVALITATIV mening.

— Men just den KVALITATIVA aspekten på den moderna akademins vektorkalkyl är vad som kommit att utmärka den moderna akademins allmänna beskrivning av, just, MAGNETISMEN. Och utan de begreppen INGENTING.

— Följande »avslöjande» — vektorkalkylens sammanbrott — beskriver detaljerna till HUR den moderna akademins vektorkalkyl SÅ mister den [förment] upphöjda roll den fått [under 1900-talet], samt understryker att MAXWELLS EKVATIONER ingalunda representerar någon slags kunglig promemoria av fysikalisk beskrivning [som många har fått för sig]. Dessa är enbart en MATEMATISK KONVENTION, ett antaget regelverk, och utsäger ingenting om fysikens fenomengrunder. Jämför även i Citatblocket. Maxwells ekvationer bygger i själva verket på att UTESLUTA VÄSENTLIGA PARTIER ur fenomengrunderna, nämligen de två första vektorriktningarna i magnetismens fenomengrundade relaterbara fysik, vilket ska visas i detalj i den efterföljande huvudtexten, för att därigenom NÅ UPP TILL nivån för en »samlad matematisk beskrivning»: modern akademisk vektoralgebra.

— Med andra ord: MAXWELLS EKVATIONER [egenskaperna med div och curl] — eller den moderna akademins vektorkalkyl i ämnet magnetism — besitter varken någon förklarande, beskrivande, eller härledande/relaterbar koppling till fysikens fenomenmässiga grunder, här magnetismen. Det är vad som menas och åsyftas i ovanstående rubrik. Inget annat.

   Vi studerar hur.

 

 

 

Betrakta den illustrerade vektorvinjetten till Magnetiska laddningsfältspotentialen.

Bortse ifrån den relaterade fysikens magnetgrund Magnetiska laddningsfältspotentialen [dB=(Rmax/ç0)(I/4πx)sinb db i PREFIXxSIN] — bry dig inte om den.

       — Finns inte, enligt min bestämda Åsikt.

Strunta också i KAUSALSAMBANDET som förklarar hela magnetismens uppkomst.

Strunta också KVALITATIVT i den efterföljande Magnetiska expansionsintegralen. Betrakta den som icke- existerande, också dess differentialekvation som icke-existerande.

       — Finns inte.                                                                                                               

BÖRJA istället hela magnetismen som fenomenform med expansionsintegralens VINKELRÄTA lösning [dB=µ0(I/4πr²)cosb ds i PREFIXxSIN], den konventionellt benämnda Biot-Savarts lag.

       — Finns.

— Samt ANTA EN UPPFUNNEN VEKTORFORM för den typen (som kan appliceras även generellt på hydro- och aerodynamiken...): SKAPA en vertikalpinne som NORMAL till parallellogrammens yta X×Y=Z, strunta i allt annat. Vidare i RESULTAT nedan.

— Modern akademi har genom antagandet av denna formalism tydligen, grundligt, cementerat summan av en samling vinkelsnillen som i sin egen självinbillade algebraiska ökenkärlek, regelrätt strandsatta som följd av ett exakt lika grundligt och illa dolt naturförakt typ ”Människan har skapat matematiken, därom är alla lärde ense”, trott och fortfarande tror sig förmögna att formulera universums lagar och principer i maximalt abstrakta termer av minimalt uttydbara grafiska tecken med garanterad nollfattning i vanliga trottoarled. Det är, tydligen, devisen att UPPFINNA och HÄRSKA, snarare än att HÄRLEDA och SAMARBETA, att UTESLUTA och BEHÅNA, snarare än att VÄLKOMNA och ARGUMENTERA.

— DET VILL SÄGA; För att TVINGAS vara konsekvent inuti  Strunta-I-Typen: Bortse FÖLJAKTLIGEN också ifrån det [B2=B12+B22 ± 2B1B2sin(A1–A2) i PREFIXxSIN] som FÖRKLARAR föreningen Biot-Savarts lag och Expansionsintegralen genom summerande vektorer, sambandet mellan expansioner och tangenter — samma som beskriver hela elektrogravitationens elementära fältfysik. Dvs., bortse ifrån det trigonometriska sambandet — planvektorsumman — mellan expansioner och tangenter. Se — förstå — den kopplingen som icke-existerande. Radera hela den boken ur kunskapsriket. Killit.

 

RESULTAT:

modern akademi om magnetismen. Se (konventionellt från) Biot-Savarts lag.

 

FEL är uppenbarligen inte ordet. Ordet är PRIMITIV; Ovanstående exempelgenomgång bara visar, understryker och ROPAR: Det går överhuvudtaget inte att DISKUTERA ÄMNET på den moderna akademins vokabulär, dess nyanser, dess Meriter, dess Intyg och Certifikat — eftersom väsentliga, avgörande, kopplingar FATTAS i det moderna akademiska lärosystemets självaste begreppsbas: själva vokabuläret, själva begreppsgrunderna. Vi kan lika gärna försöka uttyda hieroglyfer genom att blunda och peka.

— Vad, exakt, ska du använda typenX×Y=Z till i DEN RELATERADE FYSIKBESKRIVNINGEN av magnetismen som fysikalisk fenomengrund? Visa.

— Det är som att komma med ABC som representativt för hela alfabetet. Trampcykel till F1. Sten för bröd. AGW.

— Genom att vektoralgebran (vektoranalysen under 1900-talet) så starkt har kommit att associeras med begreppet vektorprodukt  som en definition  (Biot-Savarts lag), men som utvikningen ovan visar bara utgör en primitiv del av hela sammanhanget, finns heller ingen möjlighet att »återskapa» det uteslutna genom att söka infoga det i det primitiva.

— Se även vidare illustrerat i Fullständiga magnetiska 3D-vektorkroppen.

— Kort sagt: Medan magnetismens fenomenvärld i relaterad mening, figurkollaget ovan, uppvisar en utpräglad 3D-form (först magnetiska fältpotentialen, sedan expansionsintegralen rätvinkligt denna, och sist magnetiska fältvektorn rätvinkligt bägge [alla kan förstås/sammanfattas med den enkla högerhandsregeln: höger hand med tummen åt höger för Q+ för en positiv elektrisk laddning som färdas i tummens riktning; fingrarna i magnetiska fältexpansionsriktningen, samt nedvikta i resulterande magnetiska fältriktningen]), uppvisas i modern akademi en motsvarande beskrivning med bara EN dimension. En enda. Nämligen den SKAPADE — uppfunna — vektorpinnen från »parallellogrammens yta», en uppfunnen, antagen, fenomenform ingen förstår. Jämför Citatblocket. Den kopplar inte till magnetismen som fenomen — kan inte förklara hur vektorpinnen kommer DIT — ser inte de ORSAKSVEKTORER som de bägge övriga vektorriktningarna i magnetismen i själva verket utpekar. Det finns heller (i detta belysande magnetismens ljus) ingen naturlig koppling mellan modern akademi och relaterad fysik; matematikens begreppsvärld är och förblir en abstraktion för fysiken.

— I relaterad fysik (och matematik) använder vi (således) matematiken som ett verktyg (lagarna som kan utläsas ur det matematiska xy-planet genom flödesbegreppen, Matematiken från början), inte som någon slags härskarmodul, för att formulera fysikens principer, processer och ordningar, samt ur dessa söker utläsa sammansatta fenomen, strukturer och processer. Det är en principfast grund som den moderna akademins eldsjälar tydligen aldrig har känt sig dragna till. Jämför Entropibegreppet, om ej redan bekant.

   Se även mera utförligt från Sanningsbegreppet.

   Se även vidare nedan från Felet i MAC och Uppdagandet.

 

 

Begreppet vektorprodukt — Tillägg i Induktionen och Magnetismen 3Okt2011

 

Begreppet vektorprodukt i den moderna akademins vektoranalys

Referenskälla: BONNIERS KONVERSATIONS LEXIKON XII (1928) sp547. Se även i Webbreferenser

— här i PREFIXxSIN som nedan:

———————————————

SKALÄRPRODUKTEN | eng. dot product

a•b = |a||b|·sin A = x resultatet utmed x-axeln — »skalära värdet»

a×b= |a||b|·cos A = (xy) parallellogrammens yta — »vektoriella  värdet»

VEKTORPRODUKTEN | eng. vector product, cross product

 

Parallellogrammens yta

 

 

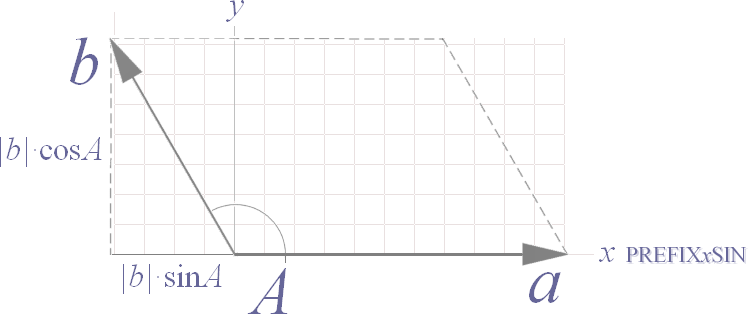
Från FÖRSKJUTNINGSSATSEN i den elementära matematiken [basen·höjden oavsett basens lokal] ges direkt parallellogrammens yta som basen (a) gånger höjden [i PREFIXxSIN] b·cosA.

— Med basen som b gäller kvantitativt ekvivalent b·a·cosA.

 

— NOTERA de ytterligare villkor som uppfunnits i modern akademi för att fullständiga vektoranalysens grundbegrepp vektorprodukt:

— Man använder följande ordning:

Vektorpinnen i MAC

 

— z-resultanten av a×b ska TAS från a TILL b med z-riktningen lika med aTILLb som en högergängad skruv i skruvriktningen (skruven stiger då i riktning z):

— Därmed gäller heller INTE likhet mellan a×b och b×a:

— Dessa blir varandras diametrala motriktningar.

 

— Jämför 3D-logoceptet (i avsnittet om Vektorkalkylens sammanbrott i MAC) i den relaterade fysikbeskrivningen till magnetiska laddningsfältspotentialen [B=F/Qc=RQ/A], och som framträder helt naturligt; Högerhanden med tummen (Q+) i strömriktningen definierar hela 3D-komplexet med en gång: tummen i magnetiska laddningspotentialens riktning (B), fingrarna (rakt ut) i magnetiska expansionsvektorns riktning (M), fingrarna nedvikta i resulterande magnetiska fältkraftens riktning (B[M]); Kopplingen B-M via Kausalsambandet; Kopplingen MB[M] via Planvektorsumman (ekvivalensen mellan expansioner och tangenter). Inga konstigheter.

   Se även Högerhandsregeln explicit.

   Se konventionellt tillämpnngsexempel i Biot-Savarts Lag.

 

 

Webbreferenser, vektorprodukt

 

Webbreferenser för vidare — begreppet vektorprodukt (Sep2011)

 

HYPERPHYSICS

— förklarar bäst (min mening), men är krävande för icke högskoleinsatta — notera dock konventionens PREFIXxCOS

http://hyperphysics.phy-astr.gsu.edu/hbase/vvec.html

 

Hyperphysics-källan ger samtidigt bra orientering till övriga vektoranalytiska begrepp — kort, snabbt, direkt, med exempel — men det kräver förkunskaper i matrisalgebra (den, liksom hela kombinatoriken, står helt orepresenterad i Universums Historia — direkta applikationer saknas), tyvärr.

 

@INTERNET Wikipedia

— förklarar så omständligt (abstrakt) att man inte tror det är sant (Webbens i särklass allra sämsta referensverk i fysik och matematik FÖR VANLIGT FOLK) — garanterat högskoleorienterat till max (alldeles tydligt det moderna globala forumet för folk av härkomst A — som älskar att glänsa över B-folket: Först GUD, sedan A B...).

http://en.wikipedia.org/wiki/Cross_product

 

 

 

Induktionen och magnetismen forts.

 

felet i MAC

vektorkalkylens regelbrott

 

VEKTORPRODUKTENS BEGRÄNSADE TILLÄMPNING I FYSIKEN

eller VARFÖR

EXPANSIONSINTEGRALENS DIFFERENTIALEKVATION

OCH

 

KAUSALSAMBANDET

 

INTE KAN HÄRLEDAS AV MODERN AKADEMI.

Eller:

MODERN VETENSKAP OCH AKADEMI

kontra

RELATERAD FYSIK OCH MATEMATIK

angående

MAGNETISM OCH INDUKTION

 

 

Det finns en alldeles speciell, särskild anledning, varför modern akademi garanterat INTE kan härleda den nyligen ovan beskrivna expansionsintegralens differentialekvation — och därför hamnar i djupgående motsättningar när det gäller att beskriva magnetismens fysik detaljerat: det går inte med den moderna akademins lärosystem. Vi studerar hur.

 

 

Induktionen och magnetismen forts.

 

uppdagandet

 

I fortsättning från Differentialelementet i Modern Akademi

För det FÖRSTA — objektet dB = (µ0/4p) · I · ds × r/r3: Vi studerar det.

 

l × r

 

benämns vektorprodukt (eng. vector product) i modern akademisk preferens. Skrivsättet infördes under det berömda 1800-talet. Vektorprodukten definierar ytan hos en parallellogram med höjden h och sidorna l och r där h/r=cosb i det konventionella PREFIXxCOS. Vilket vill säga,

l × r = | l | · | r | · cosb = | l | · h = lh-parallellogrammens yta

Trigonometriskt Motsvarande, samma prefix, används den så kallade punktprodukten eller skalären (eng. dot product)

l · r = | l | · | r | · sinb = | l | · x = lx-linjeLängden

för att definiera den så kallade skalära produkten.

 

Spårar vi nu den föregående magnetiska härledningen baklänges — expansionsintegralen — i termer av att låta den följa lärosystemet i MAC (Modern ACademy), hamnar vi tvunget enbart i trigonometrins försorg i en magnetisk rotgrund av typen skalär — inte vektor, just på grund av DEN RENT MATEMATISKA NATUREN för (funktionsrangerna) sin|cos och deras deriverande egenskaper: rotkällan, derivatan, blir en sinuskomponent om integralen är en cosinuskomponent, och vice versa; Resultatet I DEN MODERNA AKADEMINS INTELLIGENS- OCH FATTNINGSNIVÅ blir därmed inkonsistent (inbördeskrig uppstår bland begreppsdefinitienterna).

 

I sålunda konsekvens av den verkliga magnetismens härledning enligt expansionsintegralen, skulle vektoralgebran bryta ihop, kollapsa helt, och fullständigt förlora varje sin mening sådan den skapats av modern akademi. Eller sagt på annat sätt:

 

Magnetismens fundamentala fysik kan INTE tillämpas på den moderna akademins begrepp vektorprodukt.

 

Matematiken för den delen — som i termer av vektorproduktens definition skulle kunna »ordna upp saken» — sönderbryter sin egen grund: Härledningen skulle kräva att ”sin=cos”, men alla proffs vet redan att DEN likheten är ett vettlöst begrepp.

   För att härleda magnetismens fysiska grundval, måste man HELT frångå den moderna akademins privata egna uppfinningar om typ ”vektorprodukt”. Det finns helt enkelt ingenting sådant — liknade den moderna akademins vektorprodukt som skulle kunna ersätta fenomenbeskrivningens matematik — i magnetismens grundfysik.

— Se särskilt förtydligande, konkret exempel, i Vektorkalkylens sammanbrott i MAC.

— Begreppet vektorprodukt (den centrala Vektorpinnen med förment naturfysikalisk anknytning) är och förblir en modern akademisk uppfinning, en artificiell skapelse av den akademiska människan, ingen naturgrundad LOGISK härledning.

 

 

Uppdagandet — The Revelation — vektorkalkylens grunder i modern akademi

Under 1800-talet utvecklades också de moderna akademiska idéerna om överhöghet i många matematiska instanser med omfattande generaliserande föreställningar om algebra och formell logik. En sådan gren utvecklades till ett motsvarande hävdområde med universell giltighet i alla typer av ”fält” med en motsvarande algebra nu känd under namnet vektorkalkyl av typen curl, div, grad, a × b (vektor- eller kryssproduct), Ñ(nabla eller del) [och andra liknande]. Samtidigt upplyste de elektriska och magnetiska fenomenen en dramatiskt växande publik som fascinerades av det gnistrande ljuset hos den induktiva kraften.

— Numera (2007) har fascinationen (något) fördunstat och de flesta av oss förstår inte den entusiasm med vilken dessa nya och revolutionerande fenomen sannolikt utforskades under 1800-talet. Emellertid, givande mera kraft till den matematiska uppfinningen än det verkliga fysiska fenomenet, utpekade den institutionaliserade 1900-talsvetenskapen sin egen matematiska beskrivning som fenomenen induktion och magnetism genom de ovan indikerade symbolerna — med en allmän underliggande föreställning om den mänskliga (akademiska) intelligensens universella matematiska suveränitet, f.ö. 1800-talets mest kännetecknande akademiska drag.

— Men som vi nu har sett från det inledande exemplet med den magnetiska expansionsintegralen, särskilt tydligt i Vektorkalkylens sammanbrott, kan magnetismen inte förklaras med sådana moderna akademiska begrepp — FASTÄN en fullt utvecklad kvantitativ magnetism kan det: Genom att ignorera den underliggande dynamiken till induktionen och magnetismen, KAN både induktionen och magnetismen innefattas i en och samma matematiska byggnad känd som modern akademisk vektoralgebra.

— MEN DET HAR OCKSÅ SITT NÄMNDA PRIS: En total destruktion av den högeligen avancerade kunskapsvägen med förklaringen till både induktionen och magnetismen. Modern akademisk vektoralgebra har ingenting gemensamt med de grundläggande rötterna, dynamiken och logiken i induktionen och magnetismen. Modern akademi ger kvantiteterna, men har ingen uppfattning om de underliggande kvaliteterna — och kan heller inte beskriva dem genom sin lärostols termer. Jämför Citablocket.

   PRAKTISKA EXEMPEL PÅ Hur den moderna akademins kvantiteter matchar den relaterade fysikens kvaliteter finns också till noggrant påseende i TRE JÄMFÖRANDE EXEMPEL. Där ges svaren. (Modern akademi är en PRIMITIV inrättning i den mänskliga historiens civilisationer. Min mening). Jämför själv.

 

Se även

De konventionella citaten och Magnetismens Konventionella Djupgående Tvistigheter

 

referens

DÄRFÖR ÄR OCKSÅ DEN HÄR FRAMSTÄLLNINGEN INTRINSISKT REN PÅ HÖGSKOLEMATEMATIK,

typen curl, div, grad, a × b (vektor- eller kryss[eng. cross]product), Ñ(nabla eller del) [och andra liknande].

Det finns ingenting sådant i naturfysiken. Dylika produkter förekommer inte i en elementär naturbeskrivning.

 

Därmed kan man gott säga att modern akademi är »fångad i sin egen uppfinning», vektoralgebran, tvungen att spela med i sin egen »dockskåpsteater» — vektorprodukten — utan att förstå varken varför eller hur. Samt, förbjuden att kunna beskriva något alls i naturgrunden. Kort sagt: begreppet vektorprodukt har INTE den allmängiltighet som den moderna akademin ändå så storvulet förmodat. Naturfysiken funkar inte så, ehuru modern akademi gör det.

   OBSERVERA DOCK att begreppet vektorprodukt (a × b) fortfarande går att använda, men som redan påpekats ovan INTE i någon kvalitativ mening för fysikens fenomengrunder. Det är (nämligen) heller INTE här meningen att eliminera någon metod om nu någon föredrar en viss sådan för att nå något föregivet mål. Men i den här framställningen finns i varje fall ingen som helst användbarhet i begreppet. Det förekommer inte i relaterad fysik.

 

Matematiken i ämnet vektorprodukt blir, trots bästa Högskolenivå, ALLTSÅ bara YTLIG — utan varje möjlighet att penetrera naturfysikens exakta grunder: magnetismens synnerligen ENKLA matematik (när man väl har fattat poängen). Den moderna vetenskapliga förmåga STANNAR med andra ord på nivån med ”Biot-Savarts lag” — ingen kan härleda den på vektoralgebrans logik. Ingen förstår matematiken.

 

 

Induktionen och magnetismen forts.

 

För det ANDRA:

 

µ0

 

betyder rymdkompaktheten R0/c0 vilket, med ett sant [ç0=c0–v]=c0 I termer av den beskrivna relaterade fysiken, skulle ge oss v=0 som betyder noll magnetisk verkan.

Vilket vill säga:

Strikt sagt existerar inte ett µ0=R0/c0 i magnetismen.

 

Magnetismen relaterar till (bevarandet av) elektriska konstanten e0. Inte till µ0. Ett µ0 betyder ingen magnetism alls. En grundlig, elementär matematisk beskrivning av magnetismen skulle alltså INTE använda eller bruka termen µ0 — eller, om så ändå sker, förklara saken. Vad säger MAC (Modern ACademy)?

 

Studera och jämför själv vad som sägs, skrivs, hävdas och framställs i ämnet matematisk fysik beträffande magnetismen i dagens utbud. Nämligen, just det: Modern akademi och vetenskap BYGGER hela magnetismen PÅ µ0 (den s.k. magnetiska konstanten). Man känner inte till något annat.

Kom sedan och tala om dockskåpsteater. Begreppen blandas, ständigt, ihop.

 

Dessa påpekanden eliminerar uppenbarligen den moderna vetenskapens och akademins beskrivningar ifrån scenen för ämnet vetenskap — med referens till redan givna exempel.

 

I SUMMA:

 

Grunderna inom induktionen och magnetismen skyms av den moderna akademins idé om ”vektorprodukt”. Istället för att härleda fenomenet, uppfinner modern akademi ”ett nytt fysikaliskt fenomen” som kallas ”vektorprodukt”, typ l×r. Därav den rent matematiska-logiska naturen i motsättningarna. Den övriga delen beskrivs utomordentligt av PLANCKEKVIVALENTERNA med grund i elektriska laddningen genom ljusets grundläggande natur.

Alla frågetecken uträtade.

 

Magnetismens dynamiskt-matematiska-logiska grund beskrivs mera ingående och uttömmande i KAUSALSAMBANDET, om ej redan bekant.

 

 

Induktionen och magnetismen

kausalsambandet för divergensens reduktion

 

 

                                      KAUSALSAMBANDET

 

 

 

Kausalsambandet — ingår inte i modern akademi

                          ç0 = c – v  ...............................  v << c

Grundvalen för induktionen och magnetismen:

 

 

KAUSALSAMBANDET är den grundform på vars bas magnetismens uppkomst förklaras, härleds och beskrivs rent logiskt.

Men den delen ingår inte i den moderna akademins lärosystem.

Se även från ELEKTRISKA LADDNINGEN: inte heller dess härledning ingår i den moderna akademins lärosystem.

 

 

Från Ljusets grundläggande Fysik (se särskilt Ljusets friställning från Kinetiken).

c och v kopplar inte i fysiken

 

 orsak                  verkan

Förtätad rymdresistans bildar den magnetiska planvågen med tjockleken ds.

Re refererar REella axeln (x-axeln) som komplement till den IMaginära axeln (y-axeln).

Då ingen ändring i c kan ske utmed riktningen för v, finns bara de två återstående dimensionerna kvar: planet rätvinkligt v.

 

 

ANSATSEN att ändra läget för Q genom en hastighet (u=v) påtvingar c-flödet i Q-systemet en ansats att addera u med c. Men u kan inte adderas med c; c bildas inte över intervall; c är en egenskap i rymden (se DEEP från GRIP) som regleras lokalt av gravitationen. Genom Newtons tredje lag bildas, tydligen, istället en komplex motverkan i den gravitellt fixt relaterade rymdpunkten P: Motsatt ansatsen att ändra c i riktning u bildas en ansats –u som bevarar jämvikten med konstant c.

Effekten yttrar sig rätvinkligt u=v som en reduktion ç=c–u som garanterar bevarandet av elektriska konstanten (e) i riktningen v (u överförs komplext till –iu),

 

                          Rc = ôR’ç = 1/e = ôRmaxç0 = elektriska konstanten, VM/AS

 

Elektriska konstanten Rc bevaras i ekvivalens med en reducerad divergens ç och högre resistans ôR’ rätvinkligt v. Omöjligheten med v+c garanterar att planvågen ôR’ç är differentiell, befintlig endast i normalplanet till v. Rymdförtätningen kallas magnetism. Magnetismen bildar därmed en plan fältvåg vars tätare rymd strävar att uttömma sig i den omgivande tunnare Rc-rymden. Fältvågen expanderar därmed (idealt) som en allt tunnare R’ç-ring från incidenspunkten (P).

Expansionsintegralen samlar reduktionerna till den magnetiska totaleffekten i rymdpunkten P.

 

MAGNETISMENS GRUNDMATEMATIK

Från den elektriska konstanten e0–1=R0c0=Rmaxç0 med reduktionen ç=c–v via kausalsambandet ovan ges leden vidare enligt

 

             e0–1ç0–1 = R0c0ç0–1    = Rmax

             e0–1ç0–2 = R0c0ç0–2    = Rmaxç0–1     = µ  ........................  rymdkompaktheten, tvärs v&s

 

             se0–1ç0–2 = sR0c0ç0–2 = sRmaxç0–1s = µs  ......................   rymdmagnetiseringen, tvärs v&s

 

             Bildningen av Magnetiska fält, grundform:

             U                      = k(Q/r)  .......................................        elektriska laddningens potentialimpuls, V

             F/Q = X           = Rmaxç0Q/A = U/s  ......................        elektrisk fältstyrka, A ytan (4pr2)

             X/ç0 = B           = RmaxQ/A = (U/s)/ç0  ..................        magnetisk fältstyrka, VS/M2

                                       = Rmaxç0–1ç0 Q/A

                                       = Rmaxç0–1s T–1Q/A

                                       = Rmaxç0–1s I/A

                                       = µs I/A

 

För att relatera en magnetism=reduktion i vilken som helst g-bestämd rymdpunkt P, ser vi uppkomsten av en partiell förändring i rymdmotståndet R0 från Q-ändringen v. Ändringen i R0 har den egenskapen att ändringens maximala motstånd Rmax är aktivt bara tvärs strömriktningen s, alltså enbart i utvidgningen av plannormalen (N) till strömriktningen s. Detta är en ren konsekvens av att c0 inte kan ändras av v i strömriktningen, och därmed heller inte kan påverka R0 i riktningen s. Därmed bevaras också e0 som

e0–1=R0c0=Rmaxç0. Följaktligen uppkommer en reduktion c0–ç0 i P i N som följd av v. Laddningens fältpotential dU i P från Q ger en elektrisk fältstyrka X=dU/ds som utbreder sig i N på ç0 och som uttömmer Rmax i R0 och därmed ç0 i c0 vilket i P är den magnetiska fältstyrkan B=X/ç0. Utbredningen i N följer superpositionsprincipen.

Med små skillnader mellan en medelform för ç0 och c0 som ger det OBS orimliga men kvantitativt avkortade ç0=c0 fås ur R0c0ç0–2=Rmaxç0–1 den enklare

 

                          Rmax/ç0  Û  R0/c0 = µ0  ...................      rymdkompaktheten, förenklad, VS/AM

                          B = µ0s · I/A  .....................................   grundformen för den magnetiska fältstyrkan, förenklad, VS/M2

 

Notera irrelevansen i att ta µ0 bokstavligt i magnetismen. Många har redan gjort det, utan kunskap, och förvirringen är därefter. Erinra grunderna:

 

                                      R0c0                  = ôR’ç = 1/e0 = ôRmaxç0 = constant  ...........    VM/AS

                                      ôRmax               = R0c0/ç0 [= [e0ç0]–1 = [e0 (c0–v)]–1 = [e0c0 – e0v]–1]

                                      ôRmax/ç0           = R0c0/ç02; Med liten skillnad mellan ç0 och c0 gäller

                                      ôRmax/ç0           = R0c0/c02 = R0/c0 = µ0  .................................    VS/AM

 

 

KAUSALSAMBANDETS ALGEBRAISKA FORM

algebraiskt

Med Q-rörelsen (u=v) på den reella axeln (x-axeln) och divergensen (c) på imaginäraxeln (y-axeln) ges kausalsambandets algebraiska form enligt leden nedan:

 

             v + ic   = 0 + iç0 ;

             ic – iç0 = –v ;

             c – ç0    = –i–1v = iv  ................................................       v-faktorn (orsaken) överflyttad på imaginäraxeln: magnetismen styrs av v;

 

Notering till den komplexa algebran: 1/i=–i=i–1; –1/i=– –i=+i;

 

 

Teckningen v+ic saknar (genom ljusets friställning från kinetiken) en direkt geometrisk motsvarighet:

en ordinär resultant v+ic=Ö v2+c2 finns inte i fysiken.

Enda sättet att teckna v+ic meningsfullt är (således) genom ovanstående led, kausalsambandet i bevarandet av elektriska konstanten, och som leder till magnetismens definition.

 

Se även motsvarande algebraiska utvecklingar i modern akademi enligt v+ic-felet.

 

 

Se även från början i den utförliga inledande exemplifierade beskrivningen med korsreferens i

Magnetismen i Modern Akademi.

 

 

Induktionen och magnetismen forts.

uv-formen

 

Från

KAUSALSAMBANDETS u=v-form med v<<c

I beaktande av magnetismens avtagande verkan då mekaniska laddningshastigheten (v) närmar sig den lokala ljushastigheten (c) ges en mera fullständig sambandsform med utgångspunkt från LADDNINGSHASTIGHETEN u GENOM ACCELERATIONSSPÄNNINGEN U I VAKUUM. Den mera fullständiga sambandsformen och hur den framgår ur och kopplar till nämnda referenser beskrivs utförligt i artikeln MEKANISK-ELEKTRISKA SAMBANDET

 

 

 

 

 

 

InduktionenOchMagnetismen

 

 

NOMENKLATUR — nomenklaturen för B

 

NOMENKLATUREN FÖR MAGNETISK FÄLTSTYRKA

Introduktion

 

I GÄNGSE KVARTER — konventionell litteratur — har olika standarder (frekvent) ersatt varandra — över olika länder också. Så har, till exempel, den svenska magnetiska litterära nomenklaturen ändrats FLERA GÅNGER under 1900-talet. Se Tabell 1 och Tabell 2.. Sådana olyckliga utvecklingar vittnar om en grundläggande brist på insikt i sakernas natur. Det följande är TILL PRÖVNING föremål för certifiering från den relaterade fysikens ståndpunkt: helt exakt klargörande, väl relaterbar begreppsbeskrivning in i minsta detalj.

 

Påstående:

I RELATERAD FYSIK (Naturen) härleds det magnetiska fältet

(F/Qc=B=RQ/4pr2=R(c/c)Q/4pr2=2(R/c)I/4pr=µH) från det elektriska fältet

(F/Q=X=kQ/A=U/r) genom en relaterad hastighet (c) enligt magnetiska fältet

X/c=B=µH (c betyder mera preciserat en reduktion ç=c–v);

µ (=R/c) betyder en (ljushastighetsberoende) resistans (eller omvänt en permitivitet [permittans]):

H=I/l betyder en magnetisk [reducerande] (rätvinkligt induktionen genererande) fältkraft;

B betyder en styrka analogt med den resistivt beroende styrkan i X=R(cQ/A=I/r).

logiskt och språkligt

syntaxargument med förklaring:

OM en LOGISK BESKRIVNING av styrkan X från typen kraft I/l ska hållas konsistent och konsekvent enligt

styrka               = resistans · kraft

X                       = R                  I/d

kommer INTE en tillförd/substituerad (reducerad) divergensfaktor (c–v=ç), som i X/c=B=µH, att överföra eller ändra kraften (H=I/l) till en förmodad idé om »en styrka (H=I/l)»; fältstyrkan X gäller fortfarande;

En tillförd/substituerad (reducerad) divergensfaktor (ç, Alt+0231) kommer heller inte på något sätt att eliminera idén om den redan befintliga FÄLTSTYRKAN eftersom den, fältstyrkan — samma som just reduktionen — enbart förstärks, understöds och accentueras av reduktionens kvantitet i c och som, just enligt relaterad fysik, ÄR och definierar den magnetiska fenomenbasen;

Ändringen ges inte i H=I/l, utan i R=µc, modifierad som en rymdkompakthet [även permeabilitet, genomsläpplighet eller genomtränglighet], analogt

 

R/c=µ med förenklingen µ0 för µ (se R:= ôRmax = R0c0/ç0)

och vilken rymdkompakthet enligt relaterad fysik I DEN MAGNETISKA FÄLTVÅGEN ökar med R — i bevarandet av elektriska konstanten R0c0=Rmaxç0 som tvingar R att öka från R0 till Rmax om (magnetiska fält-) divergensen ç0=c0–v avtar från fria rymdens c0 till magnetismens ç0 — och som, således fortfarande, betyder i princip

 

X                       = R                  I/d

styrka               = resistans · kraft

X/c                    = R/c                I/d

B                       = µ                   I/d

B                       = µ                   H

 

Vilket vill säga; H är inte ett fält utan en kraft; H=I/d självt arbetar inte och fungerar inte som ett fält (egenskap associerad med yta eller rymd) utan en kraft (från den aktuella effekten av en strömlinje [transversellt] komprimerad i formen av omkretsen i en omsluten strömyta analog med en strömledares tvärsnitt, H=I/l; man går alltså i teorin från en ideal strömlinje i till en motsvarande normaliserad planyta med omkretsen l, H=i/l):

En linje kommer inte att kunna (kan inte) förstås som ett fält.

FÄLTASPEKTEN är aktuell FÖRST genom faktorn µ, rymdkompaktheten, ytan eller den 3D-utfyllande faktorn;

Därmed definieras fältet av en styrka (B) tillsammans med en given kraft (H) som underligger fältet, eller språkligt förenklat som »fältets kraft», analogt fältkraften H, inte fältstyrkan H.

 

I relaterad fysik används (således) den följande terminologin EXAKT för enkelhet och logisk preferens, i garantai av noll frekvens missförstånd och oklarheter, enligt ovanstående genomgång:

 

H          fältkraft, A/M, också magnetiserande kraft, eng. magnetizing force

B           fältstyrka, VS/M2 = Wb/M2 = KG/AS2, också flödestäthet, eng. flux density

 

 

TABELLERNA NEDAN ger referenser för den etablerade språkförbistringen.

 

 

H=I/2pr bildar-omsluter en primär magnetisk kraft. H är inget fält. H är [gestaltar] en (magnetisk fält-) kraft.

Det finns knappast något liknande begrepp i fysiken än magnetismen som HAR och fortfarande ÄR föremål för en sådan (enorm) språkförbistring:

 

 

 

Magnetiska fältets nomenklatur

B-NOMENKLATUR | 2007VI10 |

 

Tabell 1 · begreppen för B · se även jämförelsen nedan.

 

 

RELATERAD FYSIK

MODERN AKADEMI

beteckning

fysikalisk enhet

fysikalisk storhet

fysikalisk storhet, eng.

fysikalisk storhet, sv.

B

VS/M2=KG/AS2

magnetisk fältstyrka B=µH,

—

—

magnetisk flödestäthet B=F/A

magnetic flux density

magnetisk flödestäthet

H

A/M

magnetiserande kraft, H=I/2pr

magnetizing force

—

magnetic field strength

H-fält, magnetisk fältstyrka

 

ENDA SÄTTET ATT FÖRSTÅ SAMMANHANGET:

Vi måste härleda magnetismen i detalj, så att vi SÄKERT förstår basfunktionerna. Annars kvarstår språkförbistringen, och vi begriper intet.

DEN SVENSKA STANDARDEN HAR ÄNDRATS FLERA GÅNGER. Se jämför nedan.

 

Tabell 2 · begreppen för B · etablerade referenskällor genom vetenskapshistorien

 

beteckning

VS/M2 = Wb/M2 = KG/AS2

B

språklig specification

 

A/M

H

språklig specification

 

källa

BONNIERS KONVERSATIONSLEXIKON 1925

magnetisk induktion VIIsp1061

fältstyrka

VIIsp1059

intensitet, kraft

TEKNISK ELEKTRICITETSLÄRA E. Danielson 1955

magnetisk fältstyrka s43

magnetiserande fältet

amperevarvstäthet

s53

FOCUS MATERIEN 1975

magnetisk fältstyrka s224vä.m

magnetisk flödestäthet

magnetiserande fältet

s234

@INTERNET Wikipedia 2007-

B-field

magnetic flux density

H-field

magnetic field strength

magnetizing force

 

 

Förklaringar: Enheten Wb står för Weber

 

 

 

styrkan (B) = motståndet (µ) · kraften (H) [organisk fysik]

Jämför: Ju större motståndet är (jämför kroppsbyggarna: skrotlyftning) desto större blir den resulterande styrkan — förutsatt given kraft (näringen, proteiner och vitaminer): samma näringskraft (H) ger olika resultat beroende på motståndet (µ, hur man aktiverar sig).

 

Jämför (tabellkällorna):

 

”1. Magnetisk fältstyrka och flöde.

Det magnetiska fältet karaktäriseras i första hand av den magnetiska fältstyrkan B. Enheten för B är voltsekund per m2 i MKSA-systemet eller med ett annat namn weber per m2 Den tecknas

Vs/m2 eller Wb/m2

Benämningen magnetisk fältstyrka för B är relativt ny. Tidigare har man för samma storhet använt beteckningarna magnetisk flödestäthet eller induktion.”

TEKNISK ELEKTRICITETSLÄRA E. Danielson s43 Gleerups 1955/65

 

”Namnet på H är ännu (1954) ej slutgiltigt bestämt. Tidigare har H kallats magnetisk fältstyrka, men enligt den moderna nomenklaturen är detta felaktigt. I engelsk litteratur är termen ”magnetizing force”.”

TEKNISK ELEKTRICITETSLÄRA E. Danielson s52 Gleerups 1955/65

 

MAN HAR ALLTSÅ I SVERIGE (ej specificerat) NU (2007-) GÅTT TILLBAKA TILL DET TIDIGARE (1954) FASTSTÄLLDA FELAKTIGA BETRAKTELSESÄTTET.

 

Därmed står det klart:

man förstår tydligen inte ämnets inneboende naturligt beskrivande sammanhang

(därför att man blandar ihop fält med kraft och inte förstår väsensskillnaden).

 

Se även:

 

”H-fält (Omdirigerad från Magnetisk fältstyrka)

H-fältet, magnetisk fältstyrka, är ett sätt att betrakta magnetfält. H-fältet mäts i A/m som är ampere per meter, till skillnad från B-fältet som mäts i Tesla, även uttryckt som 1 V·s/m2 (voltsekund per kvadratmeter).”

@INTERNET Wikipedia Magnetisk fältstyrka 2007-06-18

 

 

 

 

 

 

InduktionenOchMagnetismen

 

 

µ0

 

MODERN AKADEMI

orsaken varför  µ0 felaktigt förknippas med magnetismen

 

En magnetisk verkan kräver en divergens lägre än c0 i µ0= R0/c0:  i µ0 existerar ingen rymdmagnetisering.

 

 

I induktansen är den grundläggande rymdkompaktheten µ0 alltid närvarande. I magnetismen förekommer den aldrig.

 

 

Den UNDRE GRÄNSEN för µ som L0/s = µ0 i strömvägen i som genererar magnetismen (B) från

 

den absolut minsta möjliga elektriska tröghet eller primära induktans varje elektrisk strömlinje kan och måste ha för att alls kunna arbeta och fungera i elektrofysiken

             L0 = R0s/c0 = µ0s  .............................    undre gränsen för fria rymdprimära induktansen, VS/A

 

har ingen koppling till magnetismen. Det finns ingen magnetism i R0/c0=µ0. Magnetismen uppkommer först när en högre rymdkompakthet bildas analogt med den magnetiska verkan tvärs strömriktningen. Denna verkan är en differentialform och har en motsvarande divergensreduktion (ç0).

Eftersom magnetismen (här rörelserelaterad enligtô, tvärs induktionens ó) grundas på elektriska konstanten

R0c0 = ôR’ç = 1/e0 = ôRmaxç0 = konstant ges magnetismens motsvarande primärform enligt

 

                          ôRmax              = R0c0/ç0 [= [e0ç0]–1 = [e0(c0–v)]–1 = [e0c0 – e0v]–1]     ;

                          ôRmax/ç0          = R0c0/ç02

 

Med obetydlig skillnad mellan ç0 och c0 — SOM DET OCKSÅ ÄR I DEN ALLMÄNNA TEKNISKA FYSIKEN — gäller

 

                          ôRmax/ç0          = R0c0/ç02 Û R0c0/c02 = R0/c0 = µ0

 

Detta är anledningen varför termen µ0 — FELAKTIGT I MODERN AKADEMI — förknippas med magnetismen.

En förtydligande framställning från modern akademi som påtalar, beskriver och förklarar detta har eftersökts men inte hittats.

Se även i NOMENKLATUR.

 

 

END.

Editor2008V

 

 

 

 

 

 

InduktionenOchMagnetismen

 

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

 

 

 

 

Induktionen och Magnetismen

ämnesrubriker

 

                                      Induktionen och magnetismen

 

                                      Ändringslagarna

 

                                      Induktionen och magnetismen i relaterad fysik | illustrerade grundbegrepp med allmän genomgång

 

                                      Allmänna Samband

 

                                      EXPANSIONSINTEGRALEN

 

                                      Kausalsambandet

 

                                      Nomenklatur

 

                                      µ0

 

 

innehåll

                                      INDUKTIONEN OCH MAGNETISMEN

 

                                      Induktionen och magnetismen

 

                                                         induktionen och magnetismen

 

                                                         induktionsbegreppet

 

                                      Ändringslagarna

 

                                                         integrala analogierna

 

                                                         induktionslagen

 

INDUKTIONENS OCH MAGNETISMENS MATEMATIK

                                                         översikt · rubriker som länkar vidare till beskrivning och härledning av induktionens och magnetismens matematiska fysik ENLIGT RELATERAD FYSIK

 

                                                                            induktionen         utförlig fullständig beskrivning i separat block

 

                                                                            magnetismen     utförlig fullständig beskrivning i separat block

 

                                                         närverkan och fjärrverkan

 

                                                         meny

 

                                                         modern akademi

 

                                      Induktionen och magnetismen i relaterad fysik | illustrerade grundbegrepp med allmän genomgång

 

                                                         potentialfältet

 

                                                         uppkomsten av induktion och magnetism · divergensen i tredje ändringslagen

 

                                                         rymdkompaktheten

 

                                                         elektriska konstanten

 

                                                         induktansen

 

                                                         rymdlängdkompaktheten

 

                                                         induktionen

 

                                                         magnetismen

 

                                                         växelverkansfrihetssatsen

 

                                                         jämförande uppställning · RELATERAD FYSIK kontra MODERN AKADEMI

 

                                                         resultatredovisning för parallellexperimenten

 

                                                         elektromotorisk induktion · begreppsdefinition

 

SammanfattningIndMag

 

                                                         Maxwells Regel

 

MaxwellsRegelExplain

MaxwellsREGELcitat

 

                                                         IoM-implikationen · den klassiska ömsesidiga förmodan mellan induktion och magnetism

 

                                      Allmänna Samband

 

                                                         magnetismen och induktionen

 

                                                         primärinduktansen i sammanfattning

 

                                                         magnetismens matematik            · snabbgenomgång

 

                                                         induktionens matematik                · snabbgenomgång

 

                                                         allmänna induktansen

 

                                                         induktionspotentialens bildning

 

                                      EXPANSIONSINTEGRALEN

 

                                                         magnetismen i modern akademi

 

                                                         Magnetiska laddningsfältspotentialen

 

                                                         magnetismen · kort men utförlig härledning

 

                                                         expansionsintegralen

 

                                                         Biot-Savarts lag

 

                                                         magnetiska fältets differentialelement i modern akademi

 

                                                         modern akademi sakanr teori

 

                                                         Uteslutningen i modern akademi

 

                                                         PARALLELLEXPERIEMENTET 1994

 

                                                         Vektorkalkylens sammanbrott i MAC

 

                                                         Vektorproduktens begrepp i MAC

 

                                                         Webbreferenser — vektorprodukt

 

                                                         felet i modern akademi · vektorkalkylen

 

                                      Kausalsambandet

 

                                                         magnetismens uppkomst

 

                                                         kausalsambandets uv-form

 

                                      Nomenklatur

 

                                                         magnetiska fältets nomenklatur

 

                                      µ0

 

                                                         orsaken varför µ0 felaktigt förknippas med magnetismen

 

 

REGISTER

 

referenser

BONNIERS KONVERSATIONSLEXIKON Band I-XII 1922-1928, etymologiska referenser (vissa ords ursprung)

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

gen. förkortn. generellt

t för 10–, T för 10+, förenklade exponentbeteckningar

 

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

 

Senast uppdaterade version: 2024-09-27

*END.

Stavningskontrollerat 2007-11-21|2008-03-06|2011-10-04 ¦ 27Sep2024

 

rester

*

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG-justerad 2011-08-11

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se