UNIVERSUMS HISTORIA | TRIGONOMETRINS GRUNDBEGREPP I | 2012VIII16 | a BellDHARMA production | Senast uppdaterade version: 2012-08-20 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

TRIGONOMETRINS GRUNDBEGREPP — sinuskurvan i xy-systemet

Kvadrantbegreppet | Sinus | Sinuskurvan | Sinuskurvans ekvation | Sinuskartan basic | Sinuskurvans tangent, förklaring | Sinuskurvans tangent, ekvation | Sambandskartor | Sammanställning |

Sinuskurvan — Vinjett — sinusbegreppets allra mest direkt praktiskt elementära grunder

Se även SINUSKURVAN mera utförligt matematiskt i Kinematiska Trigonometrin [GENOMGÅNG MED HARMONISKA VÅGFUNKTIONERNAS GRUNDER]

TRIGONOMETRINS GRUNDBEGREPP

Efter sammanställningar från 2003III12 i TRIGbasics.wps

Sinuskartan — SINUSKURVAN

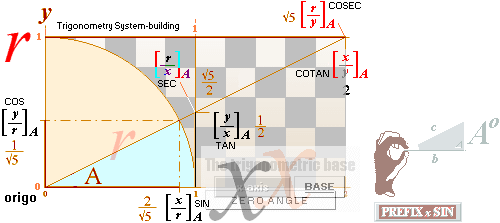
trigonometrins grundkarta

— bilden ovan visar enklaste sättet att få fram en sinuskurva: vi studerar det i det här avsnittet — med samband

Vet du att matematiken — TRIGONOMETRIN — blir mycket enklare att fatta, minnas, förstå och förklara om skyltarna COS byts mot SIN?

— Se utförligt i PREFIXxSIN, om ej redan bekant. Se även här utförligt från ENHETSCIRKELN — SinSec CosCosec TanCotan :

grundform samband invers förkortning samband

sinus x/r secans sec 1/sin = r/x

cosinus y/r cosecans csc, cosec 1/cos = r/y

tangens y/x cotangens cot 1/tan = x/y

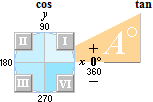
De 4 Kvadranterna — kvadrantbegreppet

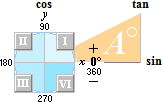
Ovan: DE FYRA KVADRANTERNA I II III IV som markerar det matematiska xy-systemets utsträckning i respektive vinkelintervall via positiv = moturs rotation (0-90)°, (90-180)°, (180-270)°, (270-360)°, tillsammans med projektionsbegreppen sin cos tan — trigonometrins grundkarta enligt PREFIXxSIN.

Innehåll:

En bekräftelse på att modern akademisk matematik MACcitatet och människans naturliga intelligens [VAD VI KAN SE OCH härleda UR DET VI SER] inte är samma sak.

Se Inledning med MATEMATIKEN FRÅN BÖRJAN — om ej redan bekant:

— Matematikens 5 Grundlagar, Räknelagarna [DEN SYMBOLISKA ALGEBRANS GRUNDER].

I Dokumentöversikt MATEMATIKEN listas för övrigt alla htm-dokument i UNIVERSUMS HISTORIA som explicit behandlar matematikens begrepp.

TrigBasics

GRUNDBEGREPPEN INOM

TRIGONOMETRIN

Grundformen använder grundtermen

Sinuskurvan, se även Vinjetten

2003-03-11

TRIGONOMETRIN komplementeringar

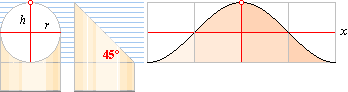
Ta en tom hushållspappersrulle.

Skär av den snett. Sprätta upp den avskurna delen och bred ut den på underlaget. Konturen bildar en kurva som är central och sammanfattande för hela trigonometrins grundkarta av termer, samband och begrepp. Vi ska studera dessa närmare i den följande framställningen.

Sinuskurvans begrepp

En rak cylinder som avskärs snett mot cylindercirkeln avbildar typformen för en sinuskurva om

· cylindern sprättas upp på kortsidan och breds ut, eller om

· cylinderns mantel avrullas

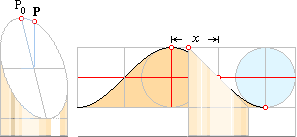
En tom hushållspappersrulle är det perfekta verktyget för att noga och i detalj studera grundbegreppen inom trigonometrin.

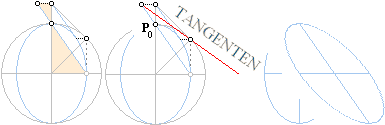
Cylindersnittets figur kallas en ellips. Vi sätter högsta punkten som P₀, och P som föreningen mellan snittet och underlaget. Vartefter snittellipsen rullas av på underlaget, glider P (illustrationens vertikalaxel) upp och ner längs cylinderns mittaxel.

CIRKELNS GRUNDBEGREPP genom särskilt översiktligt i Matematiken från början:

— Den avrullade sträckan x förhåller sig till hela cylindercirkelns omkrets 2πr som delvinkeln A° förhåller sig till hela avrullningscirkelns 360°, x/2πr=A/360.

Genom enhetscirkeln r=1 blir sambandet x/2π=A/360 som ger x/π=A/180. x motsvarar då direkt radianvinkeln så att man får omvandlingen mellan radianer och grader enligt x=A(π/180) och A=x(180/π). Vi studerar hur sinuskurvan är uppbyggd.

P₀

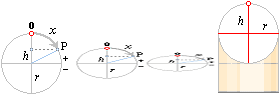
Avrullningscirkeln r, som ligger gömd i vyn ovanifrån, kan vi vika (eller tänka) upp och betrakta som ovanstående figur antyder. Om snittvinkeln är precis 45° sammanfaller den uppvikta cirkeln i vy med den uppvända lutande snittellipsen. Sinuskurvans totala höjd är då lika med avrullningscirkelns eller cylindercirkelns diameter 2r. Avrullningskurvan blir då på motsvarande sätt en enhetskurva. Vi sätter r=1=h_max.

Höjden h (vänstra figurdelen ovan) över eller under sinuskurvans mittlinje definierar tillsammans med r via avrullningen x ett förhållande (F) mellan h och r för varje x enligt en bestämd grundform. Vi kan teckna den h/r=F_h/r eller enklare F_h. Med enhetscirkeln r=1 blir enhetsformen för h

h = F_h

F_h betyder alltså ett numeriskt talvärde lika med h mellan 0 och ±1 med avseende på avrullningen x. Vi ska nu skärpa detta beteckningssätt så att även funktionsvariabeln x kommer med.

Sinus

Positiva x (vänstra figurdelen ovan) åt höger från toppläget noll, precis som vi ser avrullningen, sammanbinder vi nu med ett prefix enligt PREFIXxSIN. Det kommer att stå som en ikon som talar om hur vi har relaterat referenserna. Alltså, enklast tänkbara möjliga från grunden. Det finns ingen som helst möjlighet att missta sig på den grundformen bara man kommer ihåg hela historien med den tomma hushållspappersrullen. Med avrullningen x från nolläget lika med toppläget (P₀), så att r vrider sig medurs med positivt växande x kallar vi grundformen F_h för sinus (ursprungligen dji’va, korda, från Indien; Med arabernas översättning blev det dja’ib vilket transkriberades som dji’ba, vik, som på latin översattes till si’nus).

b/c=sinA

Att F_h i PREFIXxSIN är enkelt av flera skäl visas i illustrationen ovan. Med h och r mot tummen och pekfingret och vinkeln (x) emellan är den elementära sinusformen direktkopplad; kortaste (h, b i bilden ovan) dividerat med längsta (r, c i bilden ovan) är lika med sinus för mellanliggande vinkeln.

Sinuskurvans ekvation

Med PREFIXxSIN kan vi därmed formulera saken sålunda:

Skuggan från r på h-linjen kallas sinusprojektion. Via enhetscirkeln tecknar vi den h=sinx=F_h. Skuggan från r på x-linjen (vi betecknar den här x₀) kallas cosinusprojektion (från ursprungets complimenti sinus) med teckningen x₀=cosx=F_x0. F_h i PREFIXxSIN får alltså innebörden av sinusprojektionen.

Eftersom avrullningskurvan beskrivs med h som en allmän funktion [Funktionsbegreppet DEFINITION] [FUNKTIONSBEGREPPET Allmänt] [FUNKTIONSKLASSERNA] av x enligt h=f(x), där en viss avrullning x ger en viss höjd h enligt

h = sinx = F_h .................................. sinuskurvans ekvation

kallar vi i PREFIXxSIN den avrullade snittellipsens omkrets för en sinuskurva. Den är, som vi strax ska se, en central grundform med vars hjälp vi med häpnadsväckande enkelhet kan memorera (eg. SE) grunderna i hela trigonometrins synnerligen omfattande begreppskarta.

SINUSKURVANS FÖRENING MED DET ALLMÄNNA MATEMATISKA xyPLANET

Sinuskurvans koppling

till xy-matematiken och koordinatcirkeln

Den uppvikta i PREFIXxSIN

cylindercirkeln … bakifrån … nervriden … med aktuella projektioner … det färdiga x(SINUS)y(COSINUS)-konceptet

Sett från avrullningskurvan med sinusprojektionen h i den uppvikta cylindercirkeln, ligger alltså motsvarande cosinusprojektion i det färdiga xy-konceptet ett 90°-steg till vänster om sinusvertikalen (y). I bilden av sinuskurvan motsvarar det en avrullning åt vänster från mittvertikalen h. Eftersom projektionerna för sinus och cosinus är varandras cirkulära komplement — de har alltså exakt samma projektionsvärden men med en inbördes fasförskjutning på 90° som motsvarar de skilda projektionsaxlarna — får cosinuskurvan exakt samma utseende som sinuskurvan. Det är bara referensaxeln som skiljer. På samma sätt blir sinuskurvan en dito –cosinus med referensaxeln plus 90° till höger om h-pinnen, dvs., cosinus omvänd. Med ytterligare ett steg till höger blir sinuskurvan i den referensaxeln helt omvänd ursprunget, alltså en –sinus. Och på samma sätt i andra änden. Avrullningskurvan visar alltså referensaxlarna med tillhörande projektioner i enlighet med en trigonometrisk grundkarta som vi kan kalla för sinuskartan, nedanstående illustration.

Sinuskartan basic

–sinx cosx sinx –cosx –sinx

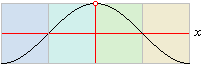
Vinkelkopplingen för sinuskartan med koordinatcirkeln C visar hur motsvarande källtermer är placerade i C.

Flödesekvivalenterna — hur referensaxlarna förhåller sig till motsvarande vinkelförskjutningar — i sinuskartan blir, alltså, på motsvarande sätt allmänna trigonometriska funktionsdefinitioner. Som vi ska se, finns inga som helst konstigheter i ämnet.

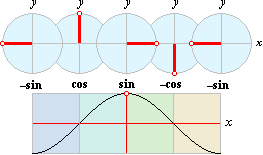
VINKELKOPPLINGEN i prefixxsin

SINUSKARTAN

Vi noterar att vinkelflödet för sinuskurvan med minus åt vänster och plus åt höger motsvarar det allmänna xy-systemets referenser. Referensaxlarnas motsvarande lägen i koordinatcirkeln är flödesomvända relativt den riktningen. Om vi går från höger till vänster (←) i illustrationen, är det kurvans funktionsvariabel x som växer negativt. Denna utsträckning motsvaras i koordinatcirkeln av en positiv vridning, alltså moturs [vi erinrar hur xy-konceptet kopplades ihop med sinuskurvan: aktören bakom cirkelskivorna ovan ser en medurs rotation för vår moturs]. Analogin mellan läget av referensaxlarna relativt mittlinjen sett från sinuskurvan (negativa 90°-steg) och jämfört med motsvarande lägen i koordinatcirkeln (positiva 90°-steg), är alltså inte exakt.

Det är tur för oss det, för den skillnaden i analogi är helt avgörande för hur de olika källfunktionerna ±sin och ±cos beskriver varandras matematiska ekvivalenter med avseende på de olika referensaxlarna. Jämför till exempel cosx=sin(x–90) [testa räknaren! Kom bara ihåg att byta ut skyltarna sin och cos mot varandra!]. Dessa definieras nämligen genom just referensaxlarnas flödesriktning i sinuskartan! Vi ska återkomma till dessa mycket intressanta detaljer senare och studera hur sinuskartan (enkelt!) visar dem alla! Du kommer lätt att bli en trigonometrisk virtuos när du väl kommer in genom »den hemliga dörren»!

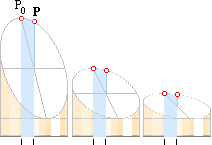
^x0

Oberoende av snittvinkeln bestäms förskjutningen (x₀) mellan P₀ och P i x-led (←→) av avrullningsprojektionen för x. Denna är för varje avrullning eller vinkel x samma som skuggan av r mot x-axeln (Jämför mot föregående utvikta cylindercirkel). Vi kallar den för cosinusprojektionen enligt

x₀/r=cosx

Sinuskurvans tangent — förklaring

Sinuskurvans tangent, ekvation

SINUSKURVANS TANGENT

Tangenten (T) eller beröringen till en krökt form definieras genom en rät linje (eller en plan yta), T. Trigonometriskt definieras tangenten genom lutningen hos T relativt x-axeln. Längden av T är i princip fullständigt oväsentlig eftersom tangenten bara berör en punkt i taget. Om vi sätter en standardlängd för T lika med enhetscirkelns radie r=1 i xy-systemet, definieras T-lutningen som förhållandet mellan r-skuggan på y-axeln och den på x-axeln. Relationen kallas också för tangens med sambandet tanx=y/x. Med lutningsvinkeln T° för tangentlinjen T kan vi skriva tangentens lutning på formen

tanT=y/x.

Grundformen ÄR cirkeltangenten: enklast tänkbara begrepp. När en cirkel ”står” på ett plant underlag T, rör de vid varandra i en och endast en punkt. Finns ingen möjlighet att missa den punkten. T och cirkelradien r bildar med andra ord alltid rät vinkel. Eller som vi också säger, en normal till varandra. Detta gör cirkelns tangent särskild lämplig att använda som analysverktyg då vi därigenom (mestadels lätt) erhåller rätvinkliga trianglar — en förutsättning för att kunna tillämpa trigonometriska begrepp. Utan rätvinkliga trianglar går det inte. Helt kört.

Eftersom tangenten till P i cylinderellipsen härrör från eller kan återföras på cylindercirkelns tangent via dess projektion [hela cylindern är en regelmässig projektionskropp från cirkeln], avbildas motsvarande tangenter för sinuskurvan analogt genom ellipsens avrullning på cylindercirkeln. Vi bör alltså kunna härleda hur. Om vi fixerar P₀ vid cylindercirkelns överdel för samtliga fall får vi direkt den avgörande komprimerade geometrin. Vi studerar hur.

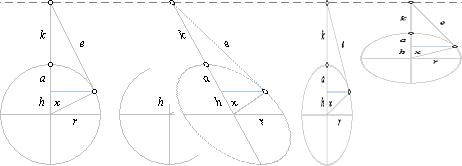
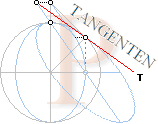
Figuren nedan till höger blir den komprimerade figur ur vilken sinuskurvans tangent, samma som cylinderellipsens tangent, kan härledas. Ellipsen i mitten är en ren förskjutningsekvivalent till cylinderellipsen som egentligen inte behöver finnas i figurformen. Den är dock avgörande ur den rent illustrativa geometriska synvinkel för att få fram själva den aktuella cylinderellipsen (Det har här skett med hjälp av det gamla enkla Paintbrush från Windows 3.1). Behandlingen nedan avser enhetsfunktionen sinx med cylindersnittvinkeln 45° och r=1.

Vi studerar hur tangenten bildas och konstrueras rent geometriskt.

Den utvikta T_P

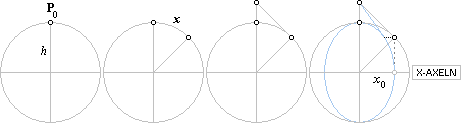
cylindercirkeln … avrullningen x … cirkeltangenten … förskjutningen x₀

Projektionen x₀ av båglängden x på x-axeln ger lillradien i den matematiska grundellipsen till bilden av den aktuella cylinderellipsen.

Alla sträckor parallella med x-axeln förskjuts eller förflyttas linjärt utmed denna via vinkelstaven mellan x₀-P₀ som dras ut från h [förskjutningssatsen, den har en enorm betydelse för hela matematiken]. Därmed puttas också toppunkten (T_P), parallellt med x-axeln, på samma vinkelstav fast i motsatt riktning mot x₀.

T_P’

Eftersom cylinderellipsen alltid möter underlaget i P som alltid glider upp och ner utmed mittlinjen vartefter sinuskurvan rullas av, blir också avståndet mellan h och P samma som förskjutningen x₀. Vinkelstaven x₀-P₀ blir alltså den aktuella bilden av cylinderellipsens mittlinje upp genom P₀ till motsvarande förskjutna T_P som T_P’. Och alltså blir den aktuella tangenten till cylinderellipsen samma som linjen från T_P’ till cirkeltangentens punkt.

Klär vi upp hela saken i beteckningar och tillämpar relationer genom räta vinklar får vi tangentens lösning enligt nedanstående uppställning.

Om du är ovan vid terminologin med sin och cos, erinra bara den enkla handregeln i PREFIXxSIN: sinus för ta-sidorna tumme(basen=kortare)-pekfinger(hyposidan=längre) på den rätvinkliga triangeln avser vinkeln dem emellan. För en cosinusrelation gäller alltså den kvarvarande sidan som basen (är det inte den ena, är det den andra)!

Relationerna sin|cos gäller i vilket fall alltid med den största sidan som nämnaren N i K=T/N så att kvoten alltid blir mindre än eller lika med 1. Jämför ett extrakt från nedanstående figur;

e/(k+r) är enligt den enkla grundregeln i PREFIXxSIN en sinus för vinkeln mellan e och (k+r). Sinus för motsatta vinkeln (x) är i stället r/(k+r). Cosinus (complimenti sinus) för den relationen, r/(k+r), blir då korrekt om vi tar motsatta sidan e i stället för r. Alltså avser e/(k+r) en cosinus om vinkeln som det gäller ska vara x.

d

Sinuskurvans Tangent

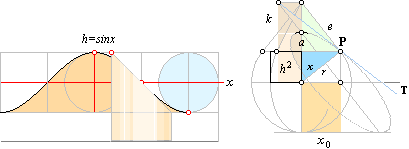
Sinuskurvans tangent, förklaring

Sinus tangent

Cirkeltangentens överföring

SIN

y = sin x .......... sinusfunktionens ekvation · PREFIXxSIN

TANGENT: cos x = [ x₀/r ] = e/(k+r) =

= [ x₀/r ] = d/k = (d+x₀)/(k+r) =

= [ x₀/r ] = (k+a)/(e = d+x₀) = – tan T

tanT = –cosx

Den funktionskurva som likt ovan beskriver tangenterna kan vi kalla för en tangensform.

Som vi ser, FÖREFALLER hela härledningen »förvånansvärt okomplicerad» för »en så pass avancerad konstruktion».

Beteckningen (bildtecken [finns i Symbol som Ð, Alt+0208]) avser en hyporelation [relation som innefattar en triangels snedsida eller hypotenusa], (här också ett bildtecken [finns i Symbol som ¿, Alt+0191]) avser en katetrelation [relation som innefattar rätvinkelsidorna]. Om man inte är van att analysera teckenpåtet, behöver man studera detaljerna en stund innan det (enkla) kopplar. Så framgår till exempel av likheterna att e=d+x₀ först via e/(k+r)=(d+x₀)/(k+r).

Härledningen ovan är särskilt förnämlig därför att konceptet innefattar en relativt stor del av de centrala trigonometriska grundbegreppen. Att härleda sinuskurvan på annat sätt — utifrån någon handhållen motsvarande »instrumentkurva» — kräver ytterst komplicerade arbeten (hjul som roterar med konstant vinkelhastighet, med tillhörande uppritningsverktyg, monteringsdetaljer … en hel verkstad!). Den enkla snedskurna cylindern tar rubbet.

Sinuskartan

SinuskartanBasic, Sinus

Resultat:

sinuskartan

–90° ¬ ® +90° ...................................... källekvivalenter (horisontella)

–sinx cosx sinx –cosx –sinx

sin(x–90) sin(x+90) ............................ källekvivalenter, exempel

De olika trigonometriska enhetsfunktionerna sammanställs av den enkla sinuskartan ovan: den är betydligt mera avancerad än den ser ut. Den indelar sinuskurvan med PREFIXxSIN i fyra delar i steg om 90 grader eller p/2 radianer. Varje typfunktion (F) får därmed sin egen vertikalaxel.

Alla övriga möjliga typfunktioner med F som källfunktion erhålles då som ekvivalenter genom att vinkeladdera i steg om ±90° från källfunktionen F — regelmässigt efter exakt samma flödesordning som gäller allmänt inom xy-systemet! Hur enkelt som helst.

Källekvivalenter — Målekvivalenter

EFTERSOM DET EMELLERTID FINNS TRE OLIKA REFERENSER

· från funktion A till B

· från funktion B till A

· ekvivalenterna

måste vi klargöra ordningarna mera ingående för eliminering av alla möjliga missförstånd.

Nedanstående 25 uttryck sammanfattar sinuskartans ekvivalenter i horisontella och vertikala led enligt

–sin(x–360)	–sin(x–270)	–sin(x–180)	–sin(x–90)	–sinx
–cos(x–270)	–cos(x–180	–cos(x–90)	–cosx	–cos(x+90)
sin(x–180	sin(x–90	sinx	sin(x+90)	sin(x+180)
cos(x–90)	cosx	cos(x+90)	cos(x+180)	cos(x+270)
–sinx	–sin(x+90)	–sin(x+180)	–sin(x+270)	–sin(x+360)
–sin	cos	sin	–cos	–sin

–90° ← → +90° ..................................... källekvivalenter (horisontella)

+90° ← → –90° ..................................... målekvivalenter (vertikala)

–sinx cosx sinx –cosx –sinx

sin(x–90) sin(x+90) ............................ källekvivalenter, exempel

Flödesriktningarna i vår betraktelse är avgörande eftersom hela xy-systemet redan har en fast definierad flödesordning och teckenriktning:

FÖR SINUSKARTAN GÄLLER när vi söker olika ekvivalenter:

· Utgår vi från en känd, söker vi en målekvivalent.

· Utgår vi från en okänd, som dock måste vara känd till källformen, söker vi en källekvivalent.

Betrakta sinX=cosx.

Utgår vi från den kända cosx, söker vi en målekvivalent på formen sinX. Målekvivalenten räknar –90 för varje högersteg. sin ligger ett steg till höger om cos. Lösningen till X blir alltså x–90.

Utgår vi från den okända sinX, som dock är känd till källformen sin, söker vi en källekvivalent för sin. Källekvivalenten räknar +90 för varje högersteg. cos ligger ett steg till vänster om sin. Lösningen till X blir alltså även i detta fall samma x–90.

ÖVNINGAR

Följande övningar är till viss del medvetet utformade för avsikten att ge någon träning i förmågan att fästa uppmärksamhet på implikationerna i vår egen betraktelse. Är vi inte uppmärksamma på vad vi utgår ifrån — ty referenserna källekvivalenter respektive målekvivalenter i uppgifterna kan tolkas från och till beroende på hur vi själva väljer synpunkten! — kan uppgifterna nedan i stort sett bli ”hopplösa fall”. Ta därför god tid på dig, läsare, och njut långsamt av kunskapen.

Uppgift: Hur uttrycks –sinx av funktionen –cos?

Funktionen –sinx ligger tre 90°-vänstersteg eller –270° från funktionen –cos.

Svar: –sinx=–cos(x–270)

Uppgift: Vilken är ekvivalenten till –cosx i funktionen –sin?

Funktionen –cosx ligger tre 90°-högersteg eller +270° från funktionen –sin. Alternativt:

Funktionen –cosx ligger ett 90°-vänstersteg eller –90° från funktionen –sin.

Svar: –cosx=–sin(x+270)=–sin(x–90)

Uppgift: Vilka är målekvivalenterna i sinuskartan till funktionen cosx?

Vi börjar längst till vänster med –sin. Källan cosx ligger ett 90°-steg framåt. Målekvivalenten till cosx i –sin blir alltså –sin(x+90).

Vi fortsätter sedan mata av de övriga: målfunktionen sin ser källan ett steg bakåt, –cos två steg och –sin slutligen tre steg.

Svar: cosx=–sin(x+90)=sin(x–90)=–cos(x–180)=–sin(x–270)

Uppgift: Vilka är källekvivalenterna i sinuskartan till funktionen cos?

Källekvivalenten räknar +90 för varje högersteg.

Vi börjar längst till vänster med –sin. Den ligger ett 90°-steg bakom källan. Källekvivalenten till cos i –sin blir alltså –sinx=cos(x–90).

Vi fortsätter sedan mata av de övriga: källan cos ser ekvivalenten i sin ett steg framåt, –cos två steg och –sin slutligen tre steg.

Svar: Källekvivalenterna i sinuskartan till funktionen cos är

cos(x–90)=–sinx, cosx, cos(x+90)=sinx, cos(x+180)=–cosx, cos(x+270)=–sinx.

Vi får alltså till exempel ekvivalenterna

cosx = sin(x–90) = –cos(x–180) = –sin(x–270) = –sin(x+90)

och så vidare (25 kombinationer totalt). Bara att läsa av. Maken till enkelt regelverk — som beskriver matematikens erkänt svåraste grundbegrepp — finns inte! Men vänta bara, det finns ännu mer att ösa ur denna glänsande, enkla släta källa.

Tangenterna

Tangenten som funktionskurvan tanT=–cosx till sinx ligger tydligen +90° framför grundformen sinx. På samma princip får vi direkt tangensformerna för de övriga funktionsuttrycken genom att helt enkelt läsa av ikonen! I PREFIXxSIN gäller alltså

funktion h= tangensform h’=

sinx –cosx

cosx –sinx

–sinx –cosx

–cosx –sinx

–sinx cosx sinx –cosx –sinx

→ Tangensformen →

Flödesprincipen för tangensformen (den sammanhängande motsvarande kurvan) till grundfunktionerna löper alltså i samma riktning som positiva x. Därmed är sinuskartan utvidgad. Om vi minns den — sinus i mitten och ändarna — blir det relativt enkelt att komma ihåg sinusformens tangensform som h’=–cosx. Resten blir enkelt med den allmänna flödesordningen. Efter följande sammanfattning ska vi titta närmare på hur de trigonometriska funktionerna ser ut i enhetscirkeln — betraktad som ett självständigt och fristående komplex.

–sin
cos
sin
–cos
–sin

TRE olika begreppsreferenser finns logiskt integrerade i sinuskartan [från funktion A till B, från funktion B till A, ekvivalenterna], så det är lätt att fibbla bort sig om man inte känner ordningen. Illustrationen ovan visar de fem källfunktionerna som sinuskartan visar.

Integralerna

SINUSKARTAN INNEFATTAR INTEGRALA SAMBAND

Sinuskartan innefattar begrepp som inte beskrivs explicit i denna framställning. De ska dock här omnämnas för ordningens skull då de redan är kända. Tangensformen, tidigare omnämnd ovan, kallas också för derivata. Derivatans omvändning kallas integral, och endast då. Sinuskartans beskrivning av tangensformernas trigonometriska grundsamband, alltså de trigonometriska derivatorna, beskriver alltså även motsvarande integraler!

sinuskartan

–90° ¬ ® +90° ................................... källekvivalenter (horisontella)

+90° ¬ ® –90° ................................... målekvivalenter (vertikala)

–sinx cosx sinx –cosx –sinx

sin(x–90) sin(x+90) ............................ källekvivalenter, exempel

Jämför sinX=cosx:

· Utgår vi från en känd (cosx), söker vi en målekvivalent.

· Utgår vi från en okänd (sinX), som dock måste vara känd till källformen (sin), söker vi en källekvivalent.

Derivatan eller tangensformen till en källfunktion i sinuskartan ligger alltid ett 90°-steg framåt, alltså från vänster till höger.

Integralen för en källfunktion ligger alltid ett 90°-steg bakåt.

Integralen är också derivatan baklänges i matematiken, och endast då.

Källa –cos

Uppgift: vilken är källintegralen?

Svar: sinx.

NOTERING

FÖRE sinuskartans upptäckt fanns (för min del) veritabla problem att erinra sig ekvivalenterna till grundfunktionerna inom trigonometrin. Även fast man är en van användare, händer det som alltid händer: efterhand som begreppen inte används, sjunker de (sakta) ner i kristalldjupen. Att ”komma ihåg” något så förhållandevis komplicerat som att –sinA=–cos(A–180) är det inte tal om. Med den synnerligen enkla sinuskartan blir problemet nästan pinsamt lätt. Längre fram i den här framställningen ska vi se hur sinuskartan kan syntetiseras än mer om vi lägger till en enkel cirkel med fyrkant i mitten. Dessa detaljer berör de trigonometriska funktionerna speciellt inom koordinatcirkeln och som i sig har i varje fall fyra enkla samband som man direkt kan läsa ut från »kvadratcirkeln». Tillsammans med de övriga inneboende sambandsformerna blir denna förening oerhörd!

Enhetscirkeln

DE TRIGONOMETRISKA FUNKTIONERNA I

ENHETSCIRKELN

I PREFIXxSIN

I enhetscirkeln (r=1) med koordinataxlarna xy betraktas positiv rotation moturs med början från positiva horisontella axeln. Denna kallas x-axeln eller ibland (äldre) abskissan. Vinkeln (A°) räknas alltså nerifrån x-axeln och uppåt. Skuggan eller projektionen av r på x-axeln blir alltså sinus i enlighet med PREFIXxSIN: samma som den utvikta cylindercirkeln från grundformen med cylindersnittet men betraktad från baksidan och med nollan nervriden ett kvarts varv. Med vertikalaxeln som y, motsvarande (äldre) ordinatan, den positiva delen över horisonten, ges därmed motsvarande cosinus som skuggan eller projektionen av r på y-axeln

Illustrationen är given med förhållandet cos/sin=1/2=y/x som ger 2cos=sin=x=2y. Eftersom sin²+cos²=(r=1)=x²+y² får man från x=2y sambanden

x=√1–y², =2y som ger 1–y²=4y² och därmed 1=5y² vilket ger y=1/√5=cos och därmed x=2/√5=sin direkt från sin=x=2y.

I enhetscirkeln är r=1 som alltså ger cos/sin=(y/r)/(x/r)=y/x. Relationen y/x kallas tangens med förkortningen tan. Om vi tittar på handbilden ovan, ser vi att en grundregel för tangensrelationen är att ta andra handen på samma vis som den första (resp. rätvinkelsida kallas katet): med tummen underst blir tangensrelationen förhållandet mellan pekfingerkateten (y) och tumkateten (x) med avseende på centralvinkeln (A) i tummens riktning. Sinus-tangens, symmetriska grepp. Lätt som en plätt (Problemet i längden är att de lätta plättarna blir många).

INVERSERNA till sinus, cosinus och tangens I PREFIXxSIN kallas och betecknas

grundform samband invers förkortning samband

sinus x/r secans sec 1/sin = r/x

cosinus y/r cosecans csc, cosec 1/cos = r/y

tangens y/x cotangens cot 1/tan = x/y

HUR LÄTT SOM HELST ATT KOMMA IHÅG: sinus-secans, cosinus-cosecans, tangens-cotangens. Inga som helst problem. Alltid varandras inverser.

Med PREFIXxSIN i enhetscirkeln får begreppsreferenserna särskilt enkla attribut: xy-systemets x-axel motsvarar direkt sinus axel och y-axeln direkt cosinus axel. PREFIXxSIN relaterar alltså sinus till x i xy-systemet — som i sig alltid är enkelt att minnas. Om någon drar på munnen och tycker att det, väl, är helt självklart, rekommenderas varmt att titta närmare på innehållet i det närmast följande.

Jämför MAC

Jämför modern nomenklatur

PREFIXxCOS

¯¯¯¯¯¯¯¯¯¯¯¯

Det finns vissa personer som har särskilda problem med att förstå matematikens enkelhet. De personerna är mera välrepresenterade INOM MODERN AKADEMI än utom. Garanterat. Om vi ändrar referenserna och sätter x-axeln som COSINUS AXEL och därmed y-axeln som SINUS AXEL och därmed grundformen med cylindersnittets avrullning som en COSINUSFUNKTION — garanterat så omständligt som alls är möjligt — så att vi helt enkelt bara byter ut alla sinus mot alla cosinus (skifta SIN COS mot varandra, inget annat), då får vi följande termschema:

grundform samband invers förkortning samband

sinus y/r secans sec 1/cos = r/x ← kolla

cosinus x/r cosecans csc, cosec 1/sin = r/y ← kolla

tangens y/x cotangens cot 1/tan = x/y

Observera att secans och cosecans behåller sin platsgeometri, samma som föregående illustration. Ingen skillnad för den delen alltså. Enda skillnaden är att termerna sin och cos har bytt plats. Inget annat. För att skriva matematiska samband från det ena till det andra prefixet är det alltså bara att skifta om skyltarna sin och cos mot varandra. Inget annat.

Speciella sambanden

+90° ← målekvivalenterna → –90°

–sinx cosx sinx –cosx –sinx

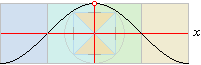
projektionssymmetrierna

SPECIELLA VINKELSAMBAND

I enhetscirkeln, antydd till minne i sinuskartan som ovan, finns speciellt fyra centrala projektionssymmetrier som man ibland kan ha stor nytta av. De två första är

sin A=sin(–A) ; cos(90+A)=cos(90–A) ...... nollvinkelsymmetrierna

Om vi tittar in i xy-cirkeln ser vi direkt att positiva vinklar (A) har samma sinusprojektion som negativa A. På samma sätt ser vi direkt att positiva (A) över 90° har samma cosinusprojektion som negativa A. Tillsammans med den allmänna vinkelformen beskriver dessa bägge speciella vinkelsamband en stor mängd möjliga ekvivalenter. Från föregående typfall

cosx = sin(x–90) = –cos(x–180) = –sin(x+90)

är till exempel

cosx=sin(x–90)=sin(–[90–x])=sin(90–x).

Och på samma sätt direkt

sinx=cos(x+90)=cos(90–x)

Dessa två samband ger oss speciellt bekvämt komplementfunktionerna för vinklarna A+B=90 i den rätvinkliga triangeln: sinA=cos(90–B) och cosA=sin(90–B). De två andra projektionssymmetrierna som framgår ur enhetscirkeln är

cos–A=–cosA ; sin(180–A)=–sinA ............ halvcirkelsymmetrierna

För en given vinkel (A) från cosinusaxeln (y) ser vi direkt (tänk en liten skillnad mellan r och y-axeln) att dess negativa make i cosinusprojektionen ger den förras negation. På samma sätt bildas negationen i sinusprojektionen med den givna vinkeln (A) tagen från andra hållet x-axeln, dvs., med subtraktionen 180–A.

Med ovanstående komplementsatser kan man nu enkelt sammanställa en allmän tablå för de enkla elementära trigonometriska funktionerna speciellt för just den rätvinkliga triangeln — en ovärderlig hjälp vid alla elementära utvärderingar i geometriska problem. Grundtablån nedan förutsätter att vinklarna är kända (känner man en känner man alla: A+B=90°).

Sambandskartor trigonometrin

Allmänna samband

elementära trigonometriska funktioner

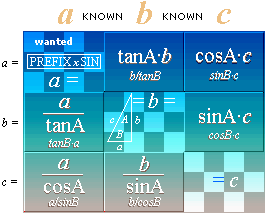
grundtablå

Grundkonversioner

PREFIXxSIN

ALLMÄNNA TRIGONOMETRISKA TRANSFORMATIONER

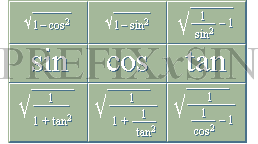
grundkonversioner

Det finns en (ypperligt) stor mängd trigonometriska samband (som lätt kan fylla böcker). Tablån ovan visar en del av grundkonversionerna mellan sinus, cosinus och tangens. Sambanden ovan är relativt lätta (!) att härleda, bara man kommer ihåg grunderna. Vi har i enhetscirkeln Pythagoras sats, sin²+cos²=1, med y/x=tan och den motsvarande cos/sin=tan. Låt oss pröva härledningarna i huvudet med hjälp av ovanstående tablå.

De två första ges direkt från Pythagoras sats. Den tredje är också klar om vi sätter högra rottermen på samma nämnare som den vänstra, dvs., cos/sin=tan.

Nedre vänstra: dela tangenttermen i kvadraten på cos/sin och flytta upp sinustermen; rotbråket blir då denna med summan 1 i botten.

Nedre mittre ger samma resultat men med cosinus. Nedre högra: flytta upp cos², detta ger direkt Ö(cos²/[sin²=1–cos²])=tan.

Arcuskonversioner

arcuskonversioner

EN VINKEL given som sinA=f(x) uttrycks A= arcus sinus f(x), förkortat A=asin f(x).

Knappast i den elementära matematiken har vi någon (större) användning för ovanstående tablå. Den kommer till användning först i den mera avancerade matematiska analysen. Tablån är exakt samma som föregående med alla sin-cos-tan ersatta av variabeln x så att man får (a förkortar arcus)

[sin cos tan]_vilkensom a[cos asin atan]_vilkensom x = [sin cos tan]_vilkensom A

Så är till exempel sin acosx=cos asinx=√1–x².

Sammanställning

Trigonometrins Grundbegrepp

SAMMANSTÄLLNING PREFIXxSIN

TRIGONOMETRINS GRUNDBEGREPP

vinkelbegreppen

Sinuskartan

+90° ← målekvivalenterna → –90°

–sinx cosx sinx –cosx –sinx

→ Tangensformerna →

← integralerna ←

Speciella Sambanden

[sin A= sin(–A)] [cos(90+A)= cos(90–A)] ........ nollvinkelsymmetriska

[cos–A=–cosA ] [sin(180–A)=–sinA ] ........ halvcirkelsymmetriska

Se även mera fördjupat i

DEN KINEMATISKA TRIGONOMETRIN — sinuskurvan från en annan (mera »fysikaliskt formell») aspekt

samt

VINKELSUMMATEOREMET

och

IMAGINÄRTRIGONOMETRISKA FUNKTIONERNA,

samt

SINUS OCH COSINUS SERIER utan i

och

SINUS OCH COSINUS SERIER med i.

END.

TRIGONOMETRINS GRUNDBEGREPP I

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

TRIGONOMETRINS GRUNDBEGREPP I

ämnesrubriker

innehåll

TRIGONOMETRINS GRUNDBEGREPP I

Sinuskurvan — Vinjett

De 4 kvadranterna — KVADRANTBEGREPPET

TRIGONOMETRIN

Sinuskurvan

Sinus

Sinuskurvans ekvation

Sinuskartan basic

Sinuskurvans tangent — förklaring

Sinuskurvans Tangent — ekvation

Sinuskartan

Källekvivalenter — Målekvivalenter

Tangenterna

Integralerna

Enhetscirkeln

Jämför MAC

Speciella sambanden

Sambandskartor trigonometrin

Allmänna samband

Grundkonversioner

Arcuskonversioner

Sammanställning

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

e₀ = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²

BKL BONNERS KONVERSATIONSLEXIKON Band I-XII med Suppement A-Ö 1922-1929, Bonniers Stockholm

[BA]. BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, modern akademi

TNED

(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken

är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.

Senast uppdaterade version: 2012-08-20

*END.

Stavningskontrollerat 2012-08-20.

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

√ τ π ħ ε UNICODE — ofta använda tecken i matematiska-tekniska-naturvetenskapliga beskrivningar

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ

Pilsymboler, direkt via tangentbordet:

Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — även Alt+18 ↕; Alt+29 ↔

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,

■²³¹·¨°¸÷§¶¾‗±

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se