Den Kinematiska Trigonometrin — Universums Historia

UNIVERSUMS HISTORIA | TRIGONOMETRINS GRUNDBEGREPP II | 2012VIII16 | a BellDHARMA production | Senast uppdaterade version: 2012-12-02 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Den Kinematiska Trigonometrin — efter föregående arbeten i sammanställningar från 1999XII

Harmoniska VågFunktionerna Generellt

DEN KINEMATISKA TRIGONOMETRIN

HARMONISKA vågFUNKTIONERNA GENERELLT

Sinuskurvan

Editor1999XII22

DEN KINEMATISK TRIGONOMETRIN

Numeriska och metriska enheter

0 1 2 3 4 5 6 6,2831853 . . .

Sinuskurvan i PREFIXxSIN — toppvärdet med y=r=1 genom y-axeln — genom cirkelns avrullning och punktprojektion mot vertikalaxeln; Varje delposition i figuren motsvarar avrullningen med båglängden lika med en radian — cirkelns radie lagd på cirkelbågen (180/pi=57,295779°). Totalt ges antalet radianer lika med 2π = 6,2831853 …

För grundbegreppen med PI (π) och CIRKELN, se CIRKELNS GRUNDBEGREPP i Matematiken från början.

Se även (mera elementärt för sinusbegreppet) SINUSBEGREPPET GENOM RÖRSNITTET [TrigBasicI].

Om inget annat anges i denna författning, används x för metriska enheter.

COSINUSKURVANS FULLSTÄNDIGA FORM

y = cos(2π[x/L])·r ..........................

2π[x/L] i radianer, x,L,r och y i metriska enheter, L våglängden, r toppamplituden

Vinkelsambanden — grader, radianer

A/360 = x/L

= a/2π ;

A = 360(x/L) ......................... grader

a = 2π(x/L) .............................. radianer

Vinkelfunktionerna

UTFÖRLIG GENOMGÅNG AV SINUSBEGREPPET MED De HARMONISKA VÅGFUNKTIONERNAS GRUNDER

benämningen harmonisk från musikläran; svängningar (toner, stämmor) som avser speciellt multipler av någon viss grundfrekvens

beteckningen v för hastighet från engelskans velocity, hastighet, eller latinets ve'lox, snabb

Vinkelfunktionerna för sinus och cosinus, samt deras tangensformer, kan förstås på ett särskilt enkelt och speciellt sätt. Nämligen genom kinematiken (»läran om rörelse utom kraftens inverkan»).

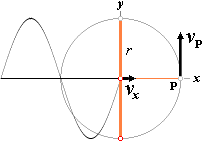
Kurvan y=cosA · r. Våglängden (L) bestäms av storleken på v_x

Låt P rotera moturs (positiv rotation) med konstant hastighet v_P i cirkeln med radien r. Betrakta projektionen av P mot y-axeln som ett utmed y-axeln mobilt pennstift y_P. Om cirkeln står stilla relativt underlaget ritas en rät linje upp av y_P. Om cirkeln färdas med konstant hastighet v_x utmed x-axeln, ritas i stället en periodiskt återkommande kurvform y=cosA·r. Denna kurva kallas i typformen för periodisk (periodisk funktion av tiden). Med PREFIXxSIN kallas den periodiska kurvan i illustrationen för en cosinuskurva (kurvan »ritas» på y-axeln, dvs. på cosinus axel med PREFIXxSIN).

Vinkeln A från noll till 360 grader sluter kurvans period eller våglängd (L). Vinkelvärdet (A) förhåller sig till cirkelns hela 360 grader som värdet av x förhåller sig till våglängden L så att vi får

A/360=x/L=a/2π ; .................. x anger metriska enheter

A = 360(x/L) .......................... A anger vinkeln i grader

a = 2π(x/L) ............................. a anger vinkeln i radianer

Cosinuskurvan kan alltså tecknas på den mera sammansatta formen

y = cos(360[x/L])·r .................. grader

y = cos(2π[x/L])·r .................... radianer

Om L=2πr övergår radianvinkeln a i x/r. För enhetscirkelns r=1 (L=2π) blir a och x identiska vilket ger oss grundformen med enhetscirkeln åter enligt

y = cosa = cosA

P:s hastighet v_P i cirkeln i formen av ett bestämt värde, motsvarar en bestämd geometrisk mängd. Denna längd representerar både P:s hastighet och hastighetens eller rörelsens riktning. Vi kallar en sådan längd för en vektor (av lat. ve'ctor, dragare, bärare).

Tangenten

Tangenten till kurvan y=cosA

Med radiens konstanta rotation v_P och enhetscirkelns konstanta hastighet v_x avbildas genom punkten y_P för cosinusprojektionen en sammanhängande kurva analog med formen y=cosA.

Genom att använda vinkelfunktionen för cosinus genom enhetscirkelns rörelse (v_x) finner man en klargörande, alternativ och förnämlig genväg till bestämningen av tangenterna, analogt med begreppet derivata, för funktionerna sinus och cosinus.

tangenten tanT=v_y /v_x v_y /v_P=sinA

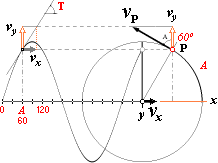
Ändpunkten (P) för r avbildar alltså mängden cosA·r mot y-axeln i formen av en periodiskt upp och nedåtgående rörelse mellan ändpunkterna ±r på y-axeln. Positiva y-värden för vinkeln A i intervallet 0-180, negativa y-värden i intervallet 180-360. I varje del av denna rörelse ges direkt med figurens hjälp via v_y /v_P=sinA·r tangenten T som

v_y = v_PsinA ;

v_y /v_x = tanT = sinA(v_P /v_x) ................... tangenten

På tiden t₀ fullbordar P ett varv i cirkeln så att vi har

v_P=2πr/t₀ .................... M/S

På samma tid ges också kurvas hela period eller våglängd L enligt

v_x=L/t₀

Relationen v_P/v_x ger oss

v_P/v_x= 2πr/L = k

så att vi för ekvationen eller kurvan y=cosA får

tanT = sinA(2πr/L) = sinA·k

Detta mera sammansatta sätt att teckna detaljerna är helt likvärdigt med det enklare

tanT = sinA

för kurvan cosA om r=1 och L=2π vilket ger k=1. Speciellt ser vi att faktorn k via A=0 betyder kurvans maximala branthet tanT_max=2πr/L=k. (Se även vidare i Tangensformens mera sammansatta ekvation).

cosA-kurvan kan alltså förstås som bilden av den sammansatta rörelsen hos två olika hastighetssystem. Dels y-punktens rörelse utmed y-axeln (v_y). Och dels y-punktens konstanta rörelse åt höger utmed x-axeln (v_x). Punktens hastighet och riktning i kurvan följer med andra ord i varje tidpunkt av händelseförloppet av den sammansatta resultanten v till komponenterna v_x och v_y genom Pytagoras sats enligt

v² = (v_x)²+(v_y)² ...................... hastigheten i kurvlinjen

Denna resultant är alltså också analog med den riktning, kurvtangenten, som rörelsen av P har inom varje momentant (”ögonblickligt”=absolut) begrepp om ett tillstånd i händelseförloppet. Denna viktiga riktning, dess form och begrepp, kallar vi för kurvans tangent. Tangensvärdet för vinkeln (T) till denna tangent, kallar vi analogt riktningskoefficienten i en given punkt P på kurvan.

Sammanhanget beskriver med andra ord (trivialt) att P i kurvlinjen alltid rör sig i kurvans tangent (vilket är självklart; varje kropp i rörelse rör sig naturligtvis i sin bana). I motsvarande mening blir kurvans form bilden av hur de momentana tangenterna varierar eller följer på varandra genom intervall i tiden. Därmed blir också begreppet om den räta linjen — tangenten som riktningsbäraren för fysikens alla begrepp — grundat som ett fundamentalbegrepp inom mekaniken (läran om kropparnas rörelser med [kinetik] eller utan [kinematik] kraftens inverkan). Tangentbegreppet, den räta linjen, kan därmed förstås som ett för den matematiska fysiken helt grundläggande och oumbärligt begrepp.

SPECIALARTIKEL

Allmän orientering angående trigonometrins kurvbegrepp

y = cosA

Introduktion till VINKELMULTIPLICITETERNA — Underförståddheterna i vinkelfaktorn [den gömda delen med (x/[r/k])] — PREFIXxSIN

Funktion och kurva gömmer (för lekmannen) sammansattheter som kan leda till frustrationer. Den följande delen beskriver sammansattheterna.

Vi betraktar generellt uttrycket för cosA som en funktion. Mot varje värde för A svarar ett och endast ett enda värde för cosA. Begreppet kurva för cosA finns inte till i någon egentlig mening inom den elementära trigonometrin. Vi talar där i stället om projektionen av enhetscirkelns radie mot koordinataxlarna xy. Som vi emellertid har sett, finns också, verkligen, för uttrycket cosA en motsvarande enhetskurva i xy-planet. Plankurvan har toppvärdet 1 och våglängden 2π motsvarande cirkelns hela 360 grader. Enhetskurvan och funktionsuttrycket är alltså ett och samma, y=cosA. Har man inte riktigt klart för sig vilka faktorer som ligger till grund för enhetskurvans geometri, finns många insteg vars vägar kan leda till depressiva tillstånd, frustration och uppgivenheter på grund av oförmågan att särskilja de väl sammanvävda sammansattheterna. Vi ska belysa denna detalj illustrativt och i all korthet i det följande. Med funktionen cosA har vi inga som helst problem att dividera denna med ett helt tal n enligt (cosA)/n. För enhetskurvans del betyder denna enkla operation detsamma som att kurvan förminskas både i x och y-led enligt samma algebraiska koncept [(cosA)/n]. Illustrationen ovan visar detta med n=1 för den större enhetskurvan och n i heltal från 2 till 6 för de successivt mindre. I den följande framställningen skrivs med grönmarkerad text den motsvarande fullständiga förklaring som den enkla formen i sig explicit inte omtalar. Algebran till den fullständiga förklaringen kommer att behandlas ingående längre fram.

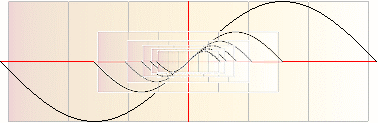
I den följande illustrationen är förminskningarna ovan utsträckta periodiskt över hela den större enhetskurvans våglängd, samt delvis infärgade för att något markera de olika kurvpaketen. Graferna nedan, som »förstås» på den enkla formen

y = [(cosA)/n] .......................................... den elementära teckningen

y = cos(x/[r/n])·r/n ................................... den fullständiga beskrivningen

är alltså för alla n >1 förminskade versioner av cosA och som utsträckts över n perioder. Värdet för enhetscirkelns r=1 är 60 pixels (ca 19mM).

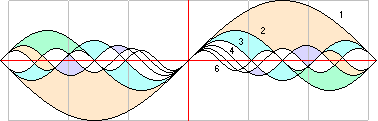
1; (cosA)/1. 2; (cosA)/2. 3; (cosA)/3. 4; (cosA)/4. 5; (cosA)/5. 6; (cosA)/6. r_n=60p/n. L_n=2pr/n.

Eftersom alla cosinuskurvor (A-kurvorna) har samma form och endast är förminskade eller förstorade versioner av varandra, ges tangenskurvorna (T-kurvorna) till alla A-kurvorna som kopior av dessa men förskjutna –90 grader.

[Vi erinrar grundsambanden från trigonometrin enligt cos(A–90)=–sinA].

Någon ändring i T-kurvornas form relativt den givna A-formen ges alltså inte med bibehållen gemensam enhet.

Om nu dessa grafer i konceptet y=[(cosA)/n] förstoras enbart i y-led med beloppet n enligt

y = n · [(cosA)/n] ..................................... konceptet

y = cos(x/[r/n])·r ...................................... den fullständiga beskrivningen

fås naturligtvis toppvärdena för alla A-kurvor med n >1 lika stora; Toppvärdena blir alla desamma som enheten r=1 (60 pixels) för cosA.

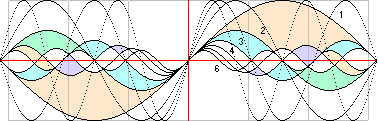
Förhållandet k=2πr/L_n blir för varje kurvpaket n — med L₁=2πr förkortad genom divisionen med n — ekvivalent med faktorn n enligt L₁/(L₁/n). Det gäller alltså att k=n. De motsvarande T-formerna blir, från föregående samband tanT = [sinA]·k, följaktligen av formen

tanT = n[(sinA)/n] · k = n²[(sinA)/n] ..................................... n=k

tanT·E = sin(x/[r/n]) · E · k = sin(x/[r/n]) · r · n ...................... r=E, k=n, fullständigt

Med andra ord: T-kurvorna (ej utritade) blir alltså, relativt A-kurvornas gemensamma toppvärde (E=r) toppvärdesförstorade med faktorn n enligt n·r. Alltså samma kurvpaket som för graferna ovan alla med r=1 men var och en för varje n-individ ytterligare förstorad i y-led med faktorn n.

Det finns ingen möjlighet att »se» dessa sammansattheter enbart genom den elementära trigonometrins algebra — ehuru ekvationsuttrycken är exakt identiska. Exakt.

I »den numeriska algebran» ges (nämligen) exakt samma resultat som i de bägge ovan beskrivna faserna, men på formen

y = cos nA ............................................................... den algebraiska beskrivningen

y = cos(x/[r/n]) = cos(n[x/r]) = cos n[a] ................. den fullständiga beskrivningen

I avsnittet om FORMLAGARNAutförligt visas i TRIG3 hur trigonometriska tangensformernas vinkelmultiplicitet nA härleds ur serierna för sinus och cosinus. Vi ska här längre fram i VINKELMULTIPLICITETEN närmare studera hur vinkelmultipliciteten nA framgår ur samt sammanhänger med de harmoniska kurvformerna (här generaliserad bekväm benämning på [individer och totalbild i] periodiskt samverkande vågfunktioner).

VID LABORERANDET med dessa, och andra liknande, detaljer är det (således) hur lätt som helst att låta sig förvirras. Till exempel av de »till synes motstridiga ekvivalenserna»; det gäller inte att n[(cosA)/n] = cos nA = cosA. Konceptet handlar om inneslutna enhetstransformationer inom relativa [oftast för lekmannen underförstådda, i allmänhet utan klargöranden] preferenssystem. Förklaringarna finns där, men framgår inte enbart ur den rena algebran.

Editor1999XII24

DE HARMONISKA VÅGFUNKTIONERNA [‡Harmonisk vågfunktion]

Allmän beskrivning från grunden

Innan vi berör den mera sammansatta behandlingen av de föregående härledda uttrycken, ska vi först studera den enklare och mera elementära sidan av de harmoniska vågfunktionerna. Vi betraktar enhetscirkeln med radien r=1 och våglängden L=2π. Cosinuskurvan (svart) och dess tangensform (röd) får då utseendet enligt illustrationen nedan. Enheten r=1 utmed y-axeln bestämmer enhetsformen totalt med den motsvarande vinkelenheten i radianer utmed x-axeln.

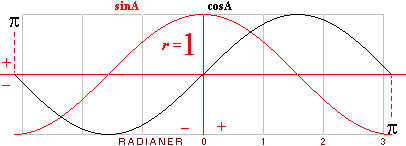
Kurvorna y=cosA (svart) och dess tangensform y=tanT=sinA (röd).

Vid nollgenomgångarna ges maximal branthet k=±1 för bägge kurvorna.

Om vi vill teckna ut dessa kurvor på papper, upptäcker vi emellertid strax att vi i vilket fall måste använda oss av en skala, vanligtvis i centimeter eller millimeter. Detta leder oss åter till den mera sammansatta formalian och som kommer att behandlas längre fram. Vi har emellertid redan angett grundformen i det hela i det föregående enligt sambandet

y = cos(360[x/L])·r .................. 360[x/L]= A grader

Säg att r=1 i figuren motsvarar 15 mM. EnhetsKurvan för cosA med PREFIXxSIN kan då tecknas upp enligt formen nedan med x och y i milliMeter.

y = cos (360[x/(2π·15)]) · 15

Om vi i stället utnyttjar radianformen

y = cos(2π[x/L])·r .................... 2π[x/L]= a radianer

får vi direkt med L=2πr den betydligt enklare sambandsformen

y = cos(x/r)·r ........................... (x/r)= a radianer

Med en godtycklig metrisk enhet (r_M) för r [pixels, millimeter, eller annat] får enhetskurvan för cosA formen

y = cos(x/r_M)·(r_M) .................. (x/r_M)= a radianer

Med exemplet r_M=15mM ovan skulle vi få y=cos(x/15)·(15). Genom omvandlingsformen A/360=a/2π som ger A=a(180/π), eller direkt från sambandet för y längre upp, blir sambandet för enhetskurvan cosA med vinkelenheten i grader enligt

y = cos(x·180/πr_M)·(r_M) .......... (x·180/πr_M)= A grader

Genom att ge olika värden för r_M utmed x-axeln och r utmed y-axeln kan kurvans proportioner ändras. Vi ska återkomma till dessa detaljer längre fram i samband med studium av kurvformernas relativa metrik.

De harmoniska kurvorna och deras tangensformer

De harmoniska kurvorna och deras elementära tangensformer

I huvudavsnittet om Trigonometrin visades under rubriken Komplementvinklarnas ekvivalenter att –sinA=cos(A–90) och sinA=cos(A+90). Detta framgår direkt av projektionerna inom koordinatcirkeln, samt även att cos(A±180)=–cosA. Vi kan utnyttja dessa samband för att få en fullständig bild av de harmoniska kurvorna och deras tangensekvationer. För att finna denna bild behöver vi nämligen endast ändra y-axelns läge i steg om 90 grader för de bägge ovan givna kurvformerna. Figuren nedan illustrerar hur ändringen görs och vilka de motsvarande uttrycken blir. Texten med svart anger huvudkurvan, texten med mörkrött anger motsvarande tangensform.

– sin A cos A sin A – cos A – sin A

– cos A – sin A cos A sin A – cos A

cos A–180 cos A–90 cos A cos A+90 cos A+180

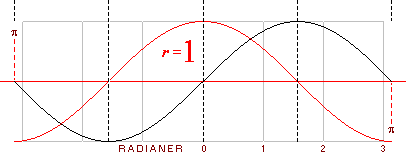
De alternativa uttryckssätten framgår alltså och kan direkt utläsas ur de bägge givna kurvformerna tillsammans med de angivna ekvivalenterna. Eftersom A–90 motsvarar A+270 kan sambanden tecknas alternativt och mera överskådligt med ändringen av y-axelns läge i successiva plus 90-graderssteg. Komplementekvationerna beskrivs då i referens till koordinatcirkelns fyra kvadranter i PREFIXxSIN enligt uppställningen nedan.

KURVANS EKVATION KVADRANT KURVANS TANGENSFORM

cosA I sinA

cos(A+90)= sinA II sin(A+90) = –cosA

cos(A+180) = –cosA III sin(A+180) = –sinA

cos(A+270) = –sinA IV sin(A+270) = cosA

När vi nu fortsättningsvis beskriver en kurvas tangensform tanT måste vi ange vilken grundkurva som avses. Vi kan skriva detta indexerat med cosinuskurvan som exempel tanT_cosA=sinA. Bättre är emellertid att bruka det smidigare skrivsättet

Dn cosA = sinA

som har exakt samma innebörd. Dn synkoperar derivatan och formen Dn cosA utläses ”derivatan (eller tangensformen) till cosinus A”. I gängse litteratur används endast bokstaven D för derivatan. Detta skrivsätt blir emellertid stundtals (avsevärt) mindre överskådligt då mängden variabler (Aa,Bb,Cc,Dd,Ee,…) också i allmänhet är enstaviga varför beteckningssättet Dn blir mera överskådligt. Språkformen är i bestämd singularis (ental) derivatan, i pluralis (flertal) derivator, derivatorna. Beteckningen Dn för derivatan används i denna författning genomgående utan undantag.

Vinkelfrekvensen

Vinkelfrekvensen ω

I det mera utpräglade begrepp som sammanhänger med benämningen harmoniska svängningar med grundkurvorna för sinus och cosinus, betecknas våglängden L analogt med den tid t₀ som vågen bildas på. Från tidigare hade vi att vinkeltalet A förhåller sig till hela cirkelns gradtal 360 som delsträckan x till hela våglängden L, sambanden A/360=x/L=a/2π. Samma relation gäller naturligtvis också för deltiden t och hela perioden t₀ så att vi får

A/360=x/L=a/2π=t/t₀

Om vi använder det mest matematiskt elementära av de bägge föregående uttrycken för cosinus harmoniska vågfunktion

y = cos(360[x/L])·r .................. 360[x/L]= A grader

y = cos(2π[x/L])·r .................... 2π[x/L]= a radianer

får vi med x/L ersatt av ekvivalenten t/t₀

y = cos(2π[t/t₀])·r = cos([2π/t₀]t)·r

Måttet på t₀ och L motsvarar alltså varandra med respektive tiden t och längden x som korresponderande variabler. Inversen till t₀ anger antalet perioder per sekund, detsamma som frekvensen f=1/t₀. Frekvensen anges i storheten Hertz med förkortningen Hz.

f = 1/t₀ ..................................... frekvensen f i Hertz

På detta sätt kan vi alltså teckna konstanten 2π/t₀ med direkt koppling till alla typer av frekvensberoende harmoniska funktioner enligt

ω₀ = 2πf = 2π/t₀ ...................... vinkelfrekvensen, lilla omega för ω

Beteckningen ω₀ kallas för vinkelfrekvensen. Med enhetsformen r=1 ges som tidigare punkthastigheten v_P=2π/t₀ vilket här ger ekvivalens med ω₀.

Från tidigare vet vi att formen 2π/L motsvarar den maximala brantheten k för enhetskurvorna. Eftersom t₀ och L bägge motsvarar ett mått på våglängden blir vinkelfrekvensen ett direkt mått på kurvans maximala branthet. Det gäller alltså att

ω₀ = k/1S ................................ tanT_max

Divisionen med 1Sekund i högerledet är här nödvändig då k är rent numeriskt och vinkelfrekvensen ω₀ har enheten S^–1. Formen för cosinuskurvan kan alltså även tecknas y=cos(ω₀t)·r som i enhetsformen med r=1 ger

y = cos(ω₀t)

Parentesuttrycket (ω₀t) motsvarar vinkeln, vilken kan förstås valfritt i radianer (a) eller grader (A) eftersom (w₀t) har samma innebörd som respektive (2p[x/L]) och (360[x/L]). Eftersom tangensformen (eller derivatan) till cosA är tanT=sinA·k får vi alltså och via ekvivalenten till k ovan ω₀·1S=k att

Dn cos(ω₀t) = sin(ω₀t)·ω₀·1S = sin(ω₀t)·k

Den föregående uppställningen för de fyra kvadranternas harmoniska vågfunktioner och deras derivator kan därmed också tecknas enligt nedanstående uppställning.

KURVANS EKVATION KURVANS TANGENSFORM

y = cos ω₀t tanT = sin ω₀t·ω₀·1S

y = sin ω₀t tanT = –cos ω₀t·ω₀·1S

y = –cos ω₀t tanT = –sin ω₀t·ω₀·1S

y = –sin ω₀t tanT = cos ω₀t·ω₀·1S

där ω₀t är vinkeln (i radianer eller grader) och ω₀ vinkelfrekvensen 2pf .

Funktioner med vinkelfrekvens har många tillämpningsområden inom fysiken. De ovan angivna formerna är vanligt förekommande, och uppställningarna är endast referenser till elementära grundsamband som är betydelsefulla främst vid olika algebraiska utvecklingar inom matematisk fysik. Vi kommer inte att beröra sådana exempel i denna framställning på annat sätt än att använda enhetsformerna för sekund och volt i några av exemplen då de mera sammansatta tillämpningarna för fysikens del förutsätter begrepp som faller utom ramen för denna volym. Vad vi däremot närmare ska studera i detta avsnitt är hur sambandsformerna ovan ligger inneslutna i den rent geometriska och matematiska strukturen för de trigonometriska vågfunktionerna.

Vinkelmultipliciteten

VINKELMULTIPLICITETEN

Dn cosnA = sinnA·n

OM VI RENT TEKNISKT undersöker rotationshastigheten för P i koordinatcirkeln, finner vi att vågformen med exemplet y=cosA, y=cos2A, y=cos3A, … y=cos nA, får motsvarande 2n toppar och dalar i intervallet 0 till 360 grader med n som ett helt tal. Figuren nedan illustrerar dessa vågformer med r=1=2π/L för A, 2A och 3A med kurvtangenter utritade vid 60 grader.

–1 1/2

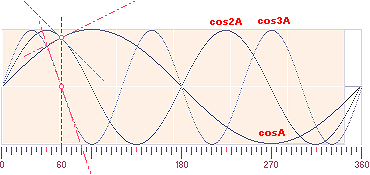
Den motsvarande rotationshastigheten för P blir följaktligen en motsvarande multipel via värdet på n enligt

v_P = n·2πr/t₀

där t₀ anger tiden, eller perioden, för ett varv 0-360º.

Denna detalj följer direkt av föregående samband

y = cos(360[x/L])·r ......................... 360[x/L]= A grader

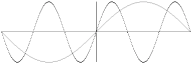
Genom att göra L kortare med 2, 3, 4, … n delningar bildas analogt n kortare våglängder inom enhetsvåglängden. Division med n i nämnarens L för vinkelparentesen ger analogt multiplikation med hela A-vinkeln.

Utvecklar vi sambanden analogt via denna form för v_P får vi

v_y = (sin nA)·v_P ; v_x = L/t₀

v_y /v_x = (sin nA)·(v_P/v_x) = tanT

(v_P/v_x) = (n·2πr/t₀)/(L/t₀) = (n·2πr)/(L) ;

tanT = v_y /v_x = (sin nA)(v_P/v_x) = (sin nA)(n·2πr/L)

Med r=1=2π/L ges den enklare enhetsformen

tanT = (sin nA)·n = Dn cos nA

Med A=60 får vi alltså för A, 2A och 3A de i det illustrerade exemplet motsvarande tangentkoefficienterna 1/2, –1, –3 och vilka figuren framvisar.

För att förtydliga formerna har vi de motsvarande matematiska uttrycken Dn cosA=sinA, Dn cos2A = sin2A·2, Dn cos3A = sin3A·3, och så vidare. Med n som generellt värde för vilka som helst fall har vi alltså den allmänna formen

Dn cosnA = sinnA·n

SOM VI SER är detta alldeles samma uttryck som de föregående tecknade kurvorna på vinkelfrekvensens form. Faktorn n är en konstantterm medan A är den variabla faktorn. Dessa detaljer tillhör, kan man säga, de mera avancerade begreppen inom de trigonometriska funktionerna och deras derivator. Vi har här funnit dem genom att använda kinematikens begrepp med två olika hastighetssystem. Men, som visas i avsnittet om FORMLAGARNAutförligt erhålls sambanden också mera grundligt ur algebran till de sammansatta serierna för sinus och cosinus i TRIG3.

NUMERISKA OCH METRISKA ENHETER (Introduktion)

Branthetskonstanten och tangentens mera fullständiga ekvation

Med figurens hjälp ser vi enklare att k speciellt betyder kurvans maximala lutning via A=0 som ger

tanT=k .................... kurvans maximala lutning vid A=0 grader

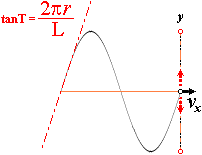
tanT_max = (sin0=1)(v_P /v_x)=2pr/L=k

Med tangentens ekvation tanT= sinA(v_P/v_x) — sinus i PREFIXxSIN — kan vi därmed teckna tangenten mera fullständigt som

NOTERA för konventionella sinus-cosinusbegrepp, att PREFIXxSIN endast betyder att byta ut sin mot cos — inget annat. Tangensbegreppet berörs inte, liksom heller inte något annat. Se mer utförligt i PREFIXxSIN&PREFIXxCOS.

tanT_cosA = sinA(2πr/L) = sinA · k

tanT = sinA(2πr/L)

för ekvationen eller kurvan

y = cosA

Eller, ännu mera fullständigt om vi också tar med den sammansatta formen för A enligt

tanT = sin(360[x/L]) · 2π(r/L)

Eller, enklare på radianformen

tanT = sin(2π[x/2πr]) · 2π(r/L)

tanT = sin(x/r) · 2π(r/L)

Detta mera komplicerade sätt att teckna detaljerna är helt likvärdigt med det enklare tanT=sinA för kurvan cosA om r=1 och L=2π. Vi måste emellertid understryka den mera komplicerade teckningen. Harmoniska vågformer har nämligen alla möjliga förhållanden mellan L och r (inte enbart 2π), och vi blir i vissa fall därför helt beroende av den mera sammansatta formen. (Dess främsta förtjänst är att den förklarar funktionsformerna utifrån en mera fullständig grund som inte direkt framgår ur den enkla enhetsformen).

tanT_cosA = sin(360[x/L]) · 2π(r/L)

Följand exempel y=cosA·r=cos(360[x/1,6])·0,6 belyser sammanhangen.

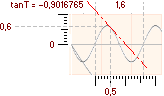
Med r=0,6 och L=1,6 ges tangenten numeriskt vid x=0,5 för kurvan cosA i PREFIXxSIN enligt

tanT = sin(360·0,5/1,6) · 2p(0,6/1,6) = sin(112,5) · 0,75π = –0,9016765

Under alla omständigheter är detta rent numeriska samband det centrala för mätning och beräkning av tangenter hos harmoniska kurvor. Om vinkeln i stället för A räknas i radianer, byt endast ut 360 mot 2π.

tanT = sin(2π·x/L) · 2π(r/L) ................. vinkeln i radianer

tanT = sin(360·x/L) · 2π(r/L) ............... vinkeln i grader

Tangensformens ekvation

Tangensformens ekvation

TANGENSFORMENS MERA SAMMANSATTA FUNKTION

Vi observerar att även om man tillämpar r-värdet från cosinuskurvan på sinusformen för tangensvärdena, erhåller man likväl alltid typformen

y_T · r = sin(x[k/r]) · r · k

Rent numeriskt gäller alltså alltid, i vilket fall för tangensformens lutningsvärden att

y_T = sin(x[k/r]) · k

Numeriska tangensvärdet, här via cosinuskurvan, ges alltid relaterat till enhetsplanet xy där tangentens värde (y/x) bestäms av antalet enheter i y-led dividerat med antalet enheter i x-led. Detta är trigonometrins grundform i plangeometrin. Om vi avancerar på detta och vill teckna upp den motsvarande funktionen, alltså själva kurvan för y_T, kan emellertid vilka som helst enhetsvärden (E) motsvarande y_T_max komma i fråga. För att förtydliga denna detalj kan vi teckna tangensformen med cosinuskurvan som utgångspunkt enligt

y_TE = sin(x[k/r]) · k · E ....................... tangensformens kurva i enheten E

Eller mera allmänt

tanT·E = sinA·E· (2πr/L)

I sambanden för sinus och cosinus i enhetscirkeln är enheten E densamma som enhetscirkelns radie (1) och vi behöver därför aldrig bekymra oss om några enhetstransformationer. Med exemplet ovan via L=2πr skulle tanT helt enkelt bli lika med sin(112,5), analogt tanT=sinA. För metriken hos harmoniska vågfunktioner i allmänhet gäller emellertid vilka som helst våglängder (L) relativt ett givet toppvärde (r), varför E-faktorn kan ges olika värden beroende på förhållanden och omständigheter.

Därmed ställer sig också hela saken annorlunda för den allmänna metriska teckningen av de harmoniska vågfunktionerna. Relationsformernas komplexitet blir speciellt tydlig i olika ytberäkningskomplex. Vi ska diskutera och exemplifiera dessa begrepp vidare i det följande.

Utvecklingsexempel

Sinus och cosinuskurvornas metrik

UTVECKLINGSEXEMPEL

Kurvformernas relativa metrik

Kurvformernas relativa metrik

Kurvorna för sinus och cosinus finner många tillämpningar inom matematiken — främst genom fysiken. Många svängningsförlopp, som rör materiens natur och dess sammansättning, kan återföras på den harmoniska vågformens ekvation. För att kunna hantera kurvorna under alla möjliga förhållanden, måste vi närmare känna till hur dessa kurvor sammanhänger med de rent metriska storheterna. Ingenting hindrar oss nämligen att sätta såväl enheten 1 som våglängden L på godtycklig metrisk bas. Men eftersom därigenom också de trigonometriska proportionerna ändras måste vi närmare känna till hur och på vilket sätt.

Förhållandet mellan omkretsen för vinkelcirkeln 2πr och våglängden L=2πr_M, där r_M anger måttet för 1 vinkelradian utmed x-axeln, ger oss som tidigare förhållandet v_P/v_x=k=2πr/L enligt ekvivalenterna

2πr/2πr_M = 2πr/L = k = r/r_M

Detta ger oss specifikt sambanden

r_M = L/2π

r_M = r/k

Här är alltså r detsamma som toppvärdet för kurvan (sinus eller cosinus) och identiskt med enheten 1 för sinus eller cosinusvärdet i vinkel eller enhetscirkeln. I fallet med enhetskurvan (L=2πr) är k=1 varför det för enhetskurvan också gäller att r_M= r.

Om vi vill uttrycka våglängden L=2πr_M alternativt som en produkt Dr av ett numeriskt värde D (motsvarande cirkelns hela vinkeltal 2p) och vinkelcirkelns radie (r) får vi ur likheten

2π·r_M=L=Dr

sambanden

r_M=L/2π=Dr/2π = r/k

r, vinkelcirkelns radie

D, antalet r

Dr, våglängden

Med användningen av dessa relationer, kan vi nu teckna upp en harmonisk kurva av godtycklig form i förhållandet mellan toppvärde (r) och våglängd (Dr). Grundformen är funktionen för cosinus enligt föregående exempel y=cos(x/r_M)·(r_M). Med bibehållet kurvtoppvärde, ekvivalent med vinkelcirkelns radie r, får vi med r_M=r/k insatt i x/r_M sambandet

y_A = cos(x[k/r]) · r ................. (x[k/r])= a radianer

med tangensformens numeriska samband

y_T = sin(x[k/r]) · k ........... (x[k/r])= a radianer

Genom att ändra k ändras alltså kurvans våglängd med toppvärdet r bibehållet.

Exempel:

Teckna i PREFIXxSIN upp kurvan för cosA och dess tangent med L=6r. Sätt E=r=60 pixels (runt räknat 20 mM).

Lösning:

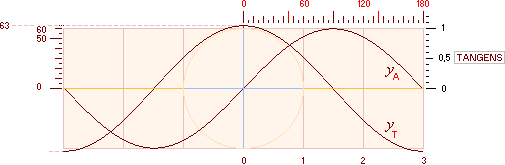
L=Dr=6r, D=6 ; Dr/2π = r/k=6r/2π=3r/π, r=60 ; k=π/3 @ 1,047 ;

r/k=180/π=57,295779=r_M=57 pixels

y_A = cos(x/[57]) · 60 ................................................ kurvan för cosA, (x/[57])= a radianer

y_T60 = sin(x/[57]) · 60k = sin(x/[57]) · 63 ............... kurvan för tangenten till cosA

Exempel:

Teckna i PREFIXxSIN upp kurvan för cosA och dess tangent med L=4r. Sätt E=r=60 pixels.

Lösning:

L=Dr=4r, D=4 ; Dr/2π = r/k=4r/2π=2r/π, r=60 ; k=π/2 @ 1,57 ;

r/k=120/p=38,197186=r_M=38 pixels

y_A = cos(x/[38]) · 60 ........................................... kurvan för cosA, (x/[38])= a radianer

y_T60 = sin(x/[38]) · 60k = sin(x/[38]) · 94 .......... kurvan för tangenten till cosA

Exempel:

I ett dataprogram har man gjort en allmän form där matematikens alla elementära funktioner kan ritas ut; funktionerna för tangenter, rötter, exponenter, logaritmer och trigonometriska funktioner. För trigonometrins del är den goniometriska delen så konstruerad att man anger vilken funktion som gäller genom att ange ”sinx”, ”cosx” eller ”tanx”. Faktorn ”x” kan inte ändras, men man kan ange en enhet (Unit) i pixels gemensam för kurvans vinkelcirkel och radianlängden på x-axeln, samt en eventuell multiplikator a av godtycklig typ med inmatning av formen a(cosx). Internt i programmet ritas kurvan med denna information upp på formen

y = a · cos(x/U)· (U)

(intervallet för ±x har defaultvärdet pU men kan ändras separat).

— Hur ska värdena för U och a väljas för att få samma kurvor som i föregående exempel?

Lösning:

U är givet som r_M. Från sambandet r/k=r_M=U upplöser vi den högra (yttre) U-faktorn r i Uk=r och ersätter enligt

y_A = cos(x/U) · Uk = k · cos(x/U)· (U)

Värdet på a blir alltså detsamma som k-värdet. För tangensformen y_T=sin(x/r_M)·k gäller med enheten r=Uk från cosinuskurvan att y_Tr=sin(x/r_M)·k·r så att vi får

y_Tr = sin(x/U) · k · Uk = k² · sin(x/U)· (U)

Svar :

Kurvorna beräknas internt enligt

y_A = k · cos(x/U)· (U)

y_Tr = k² · sin(x/U)· (U)

med k=a enligt

k=a=2πr/L = 2π/D =r/r_M=r/U

och r som vinkelcirkelns radie i funktionen för cosinus. Användaren anger r_M=U och slår in

y_A = k(cosx)

y_T = k²(sinx)

Exempel:

Vi betraktar ett mera avancerat exempel.

Från en KURVMALL [LINEXKurvmall1104] är givet en cosinuskurva med L=50mM. Toppvärdet vid 90 grader är

r = 1250/(π²[Ö32]) = 22,38903mM

Förhållandet 2πr/L är alltså

k = 2π · 1250/(π²[Ö32]·50) = 2π · 25/(π²[Ö32]) = 50/(π[Ö32]) = 25/(π[Ö8]) = 2,8134884

Med upplösningen 96 pixels per tum (25,4mM), som är standard för bildskärmar [Se NOT.1], vill vi teckna ut denna kurva så att den i grova drag stämmer överens med millimeterskalan som enhet, och sådan den ter sig uppritad på rutat papper. 96/25,4 ger 3,7795275 pixels per mM. Med 5mM rutat papper behöver varje sådan 5mM ruta vara 18,897637 pixels. Vi avrundar till 20 pixels som ger oss 20/5=4 pixels per motsvarande millimeter. Figuren nedan visar resultatet. Den större kurvan (A) är cosinuskurvan, den mindre (T) är kurvan för tangensvärdena till A, bägge med enheter i millimeter. Hur ritas kurvorna?

Lösning :

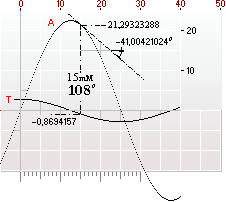
Från föregående r/k=r_M får vi med r i pixels via 4r direkt

r_M = 4r/k = 4 · 22,38903/k = 89,55612/k = 31,830988 = 32 pixels

Grundformen

y_A = cos(x/[r/k]) · r ....................... r/k=r_M

ger oss direkt A-kurvans ekvation med r som 4r=90 pixels och k=2,813 enligt

y_A = cos(x/[90/k]) · 90 .................. kurvan för cosA i pixels

För T-Kurvans motsvarande ekvation skulle vi från föregående samband få tanT·r = sinA · k· r med enheten r (22,4mM) för tangensvärdena. Men detta samband kommer då att vila på r_max-värdet 22,38903mM för A-kurvan. Vårt önskemål här var emellertid att uttrycka T-kurvans tangensvärden i enheten mM, inte i enheten r=22,38903mM. För korrekt resultat måste vi alltså dividera T-formen med r och multiplicera med enheten E=1mM. Eller direkt med utnyttjande av den tidigare relaterade grundformen

y_TE = sin(x/[r/k]) · E · k

med E=1mM. Eller, enklare uttryckt

y_T = sin(x/[r/k]) · k ........................ millimeter

[Med E=4r ges enheten i pixels].

Motsvarande ekvationer för programmet i föregående exempel ges direkt genom substitution enligt

y_A = k · cos(x/[r/k])·[r/k] = 2,81 · cos(x/[32])· (32)

y_T = [k/r] · sin(x/[r/k]) · k[r/k] = [k²/r] · sin(x/[r/k])·[r/k] ..................... i millimeter

Svar: Kurvornas ritas analogt med föregående exempel enligt

y_A = cos(x/[r/k]) · r ....................... r/k=r_M

y_TE = sin(x/[r/k]) · E · k .............. kurvan för tangensformen

med E och r i millimeter.

Exemplet tydliggör att förhållandet mellan toppvärdena för tangenskurvan (r_T) och dess generatris r för cosinuskurvan blir r_T/r = Ek/r så att vi får

r_T = Ek

NOT.1

Skalformen ovan blir tämligen exakt med bildskärmen inställd för upplösningen 1024×768 pixels. [Att ange ”standard för datorer” är en relativ fråga i dessa sammanhang]. Upplösningen är [emellertid] som standard inställd på den lägre 800×600 pixels. Detta gör i x-led att bildskärmen med denna senare standardinställning visar millimeterskalan 1,28 gånger förstorad (15mM visar 19mM, 20 mM visar ganska precis en tum, dvs., nära 25 mM).

Summering

Summering

r_M=r/k=L/2π

Grundformen

y_A = cos(x/[r/k]) · r ................ (x/[r/k])= a radianer

med tangensformen

y_TE = sin(x/[r/k]) · E · k ........ (x/[r/k])= a radianer

och dess toppvärde

r_T = Ek

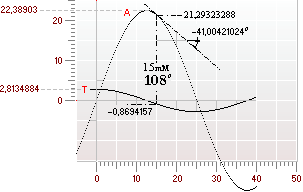
Kurvornas metriska användning vid beräkningar

I figuren ovan har beräkningarna utförts på enheten (E) i millimeter. A-kurvans ekvation används då enligt

y = cosA · r ............................. r = 22,38903mM

med x/L=A/360 som i millimeter för A i grader ger x = A · (L/360), och motsvarande A för x enligt A = x(360/L). För exemplets x=15mM således Aº = 15(360/50)=108º.

Ekvationen metriskt med enheten E i mM för T-kurvan blir motsvarande

tanT·E= sinA · E · k ................ k=2,8134884

Exemplets tangent vid A=108º blir tanT·E=sin108 · E · k = –0,8694157 mM. Avståndet från x-axeln ges av A-kurvans y=cos108 · r = 21,293232 mM.

Kort om ytor

Kort om ytor

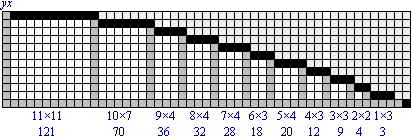
Σ 353/16= 22,0625

Om vi tar oss tid att räkna rutorna i rektanglarna mellan T-kurvan och x-axeln (0 till x=12,5mM) finner vi summan 353. Vi dividerar med omvandlingsfaktorn 4x×4y för att få värdet i millimeter vilket ger oss 22,0625mM². Inte så långt från toppvärdet för y_A_max= 22,38903, skillnaden är mindre än 2%.

Så är det också. Ytan för T-kurvan ges numeriskt av A-kurvan — under förutsättning att bägge är givna på samma metriska enhet.

Dn cosA = dy/dx = sinA = [d(cosA)/dx]

dy = sinA · dx = [d(cosA)/dx]· dx = d(cosA)

∫dy = y = ∫sinA · dx = ∫d(cosA) = cosA

∫ sin(x/[r/k])·E·k dx = cos(x/[r/k]) · r · E

Exempel:

Vidare från föregående exempel. Beräkna skärningspunkterna för ekvationerna

y_A=cosA·r och y_T=sinA·2πrE/L

med E i millimeter (notation mM), L=50mM och r=1250/(π²[Ö32]) = 22,38903mM.

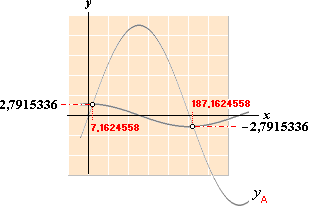
Lösning (Se figuren ovan) :

För skärningspunkterna gäller x=y för bägge ekvationerna. Vi sätter y_A= y_T och får

cosA·r=sinA·2πrE/L ; cosA=sinA·2πE/L ; cosA/sinA = tanA = 2πE/L

Alla tanA och tan(A+180) har samhörande värden (Vi vet detta från separata studier av de trigonometriska projektionerna i enhetscirkeln). Av atan (x=2pE/L) ges därmed två möjliga lösningar:

1. atan x A1= atan 2πE/L = 7,1624558º

2. atan x + 180 A2= atan 2πE/L + 180º = 187,1624558º

För värdena på y-axeln ges de motsvarande värdena (kan lösas från vilkensom av de bägge ekvationerna)

y_A=cosA1·r = 2,7915336 ; y_A=cosA2·r = –2,7915336

SVAR: Skärningspunkterna är respektive (7,1624558º ; 2,7915336) och (187,1624558º ; –2,7915336).

Sammansatta vågfunktioner

Utvecklingsexempel

Sammansatta vågfunktioner

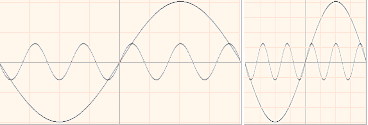
I många olika sammanhang söker man speciella data ur sammansatta vågformer som kan visas ihoptryckta, utdragna, sammanpressade, eller i andra möjliga former. Vad behöver man veta för att ur en sådan, godtyckligt sammansatt, vågform få ut nödvändiga basparametrar och som sedan beräkningar kan göras på? Vad utmärker det signifikanta i en sammansatt harmonisk vågform?

Som illustrationen ovan antyder, kan varje given harmonisk vågform (sinus eller cosinus kurvor) uppfattas som vridna planrojektioner av grundformens våglängd L lika med enhetscirkelns omkrets 2πr — i x eller y-led, eller en sammansättning av bägge.

Inte ens för tangenterna behöver vi bekymra oss (särskilt mycket). Med exemplet y=cosA ges tangenten alltid som tanT=sinA·k med k=2πr/L. Känner vi amplituden (r) och våglängden (L), avsätter vi för L intervallet 0-360 grader eller 2π radianer. Varje distans x förhåller sig då till distansen L som vinkeln A till 360; x/L=A/360 [=a/2π] som ger A=360(x/L) eller i radianer direkt a=2πx/L [Vi underförstår metriska enheter]. Sammansatt uttryckt således

tanT = sin(360x/L) · 2π(r/L) ................... för grader

= sinA · k

tanT = sin(2πx/L) · 2π(r/L) ..................... för radianer

= sin a · k

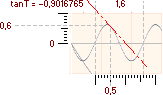
Med r=0,6 och L=1,6 ges tangenten vid x=0,5 för kurvan cosA i PREFIXxSIN enligt

tanT = sin(360·0,5/1,6) · 2π(0,6/1,6) = sin(112,5) · 0,75π = –0,9016765

tanT_cosA = sin(360[x/L]) · 2π(r/L)

Det är alltså xy-skalorna som bestämmer värdena med utgångspunkt från grundformen med enhetssystemet.

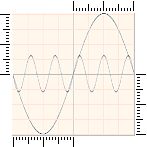
Väsentligt i dessa sammanhang är att enheten som kurvan avmäts på är densamma i bägge led x och y. Det finns många underförståddheter som figurerar i dessa sammanhang, och de flesta (av oss) som sysslar med ämnet, reflekterar knappast över exakt vilka dessa underförståddheter är, eller hur de fungerar eller sammanhänger; man tar dem för givna. Tills, plötsligt en dag, mitt uppe i arbetet, man drabbas av en ”black-out”. Helt rent. Tomt. Inte ett spår av några ”självklara samband”. Varför händer det? Därför att man allt för ensidigt ”tror” att kunskapen är någon privatsak som stundom avgörs och behärskas av vanetänkande. Så är det inte. Kunskap är en »delad resurs» av ansenlig dignitet. Man har den till låns. Och långivaren kräver, om saken inte ska glömmas, att man ständig undersöker grundernas detaljer; att man såvitt möjligt hela tiden söker variera sin insikt med nya synpunkter. Alltså, att man helt enkelt söker relatera sakinnehållet inför sig själv, aldrig ”gå i samma spår”. Detta är emellertid stundom lättare sagt än gjort. Ty vi stödjer oss alla mer eller mindre på olika invandheter och som vi tar för givna (tills eventuellt något ljushuvud upptäcker att det finns fördjupningar, därmed utvecklas vetenskapen).

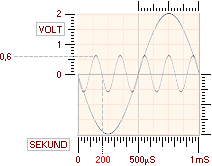
y₁ = cosA ................................ ±2V0, 1mS

y₂ = 0,3·cos5A ........................ ±0V6, 200µS

Låt oss studera ett praktiskt exempel. Figuren närmast ovan illustrerar detaljerna. Man har två harmoniska vågformer av typen cosinus med vardera amplituden ±0V6 och ±2V0. Respektive våglängder är 200µS och 1mS. Vågformerna har en gemensam nollpunkt vid varje 500µS varifrån kurvorna växer i amplitud omväxlande positivt och negativt. Uppgiften är att söka kurvornas skärningspunkter. Var finns dessa?

Utgå från enhetsformen …

Ordna objekten . . . y₁ = cosA y₂ = 0,3·cos5A

Varje cosinuskurva kan återföras på sin enkla grundform y=cosA. För att sammanföra cosinuskurvor med olika amplitud och våglängd, utgår vi (här) från kurvan med största amplituden (index 1 med y₁) och relaterar övriga till den. Vi sätter alltså utgångskurvan (alltid) som

y₁ = cosA·r

med r=1. Med en systematisk uppställning som klargör sambanden i detalj, får vi den andra mindre cosinuskurvan enligt följande uppställning. Vi erinrar här endast från föregående att

Varje distans x förhåller sig till distansen L som vinkeln A till 360; x/L=A/360 [=a/2π] som ger A=360(x/L) eller i radianer direkt a=2πx/L. För kurvor som hänförs till samma enhetskurva (huvudkurvan 1) måste alla x vara lika [Jämför även föregående exempel]. Uppställningarna ger

r₁= 1;

y₁ = cosA₁·r₁ y₂ = cosA₂·r₂

r₁/r₂=2/0,6=1/0,3 r₂= r₁· 0,3 = 0,3 RESULTAT fas I

A₁=360(x₁/L₁) A₂=360(x₂/L₂)

A₁/A₂= (x₁/L₁)/(x₂/L₂), | x₁=x₂ |, = L₂/L₁ = 0,2mS/1mS = 1/5

A₂= 5A₁= 5A RESULTAT fas II

y₂= cos5A· 0,3

Vi tar alltså förhållandena mellan amplituderna hos 1-kurvan och övriga i första fasen, och i den andra förhållandena mellan våglängderna hos 1-kurvan och de övriga.

— De bägge kurvorna har nu blivit sammanställda på gemensam form i den harmoniska enhetskurvans referens:

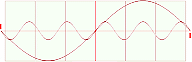
Därmed är de bägge kurvorna återförda på enhetsformen. Och, som vi ser, spelar det nu ingen roll hur man än hanterar denna ”bild”; proportionerna är givna och ändras inte med olika förlängningar och förkortningar.

Vi skulle nu emellertid söka kurvornas skärningspunkter. Detta introducerar oss för en annan aspekt inom matematiken och som delvis ofta är en återkommande detalj i samband med praktiska problem. Skärningspunkterna mellan kurvorna innebär att xy-värdena i dessa punkter är samhörande. Vi har alltså i de sökta fallen ekvivalens mellan y₁ och y₂. Vi får

cosA=(0,3)cos5A

Inte någon direkt inbjudande paroll att veckla ut, eller hur? Att lösa denna ekvation rent algebraiskt är möjligen möjligt. Det finns emellertid (garanterat) ekvationssystem (skärningen mellan många olika kurvor) som definitivt inte kan lösas algebraiskt. För alla möjliga fall måste vi alltså finna någon annan, mera smidig metod såvitt vi vill veta värdena. Vi har redan berört en sådan metod i avsnittet om ITERATIONSTEKNIK. Metoden benämns iterering och är synnerligen kraftfull och effektiv. Men man måste i allmänhet bemöda sig om att undersöka ekvationernas struktur. I det här fallet är formen relativt enkel och okomplicerad och vi finner lösningen direkt genom iteration med startvärdet cosA=1. Vi får för A värdena

17,457603

17,437423

17,435894

17,435776

17,435767

17,435766

Som vi ser är konvergensen i iterationen tämligen snabb. Lösningen med sex korrekta decimaler således A=±17,435766 eftersom också negativt vinkelvärde ger samma goniometriska värde. Cosinusvärdet blir alltså ±0,2996364. Denna lösning motsvarar skärningen symmetriskt på ömse sidor om kurvnollan med amplitudvärdena ±(2V·cosA) = ±0,5992728V.

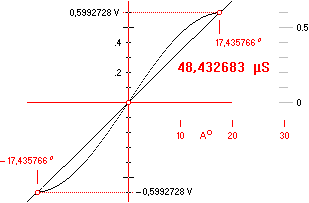
Lösningen gäller emellertid också symmetriskt omkring punkten vid 180 grader. Som vi minns från enhetscirkeln och projektionerna för cosinus, ges ekvivalenta värden för ±A (detsamma som 360±A) och 180±A. Med förhållandet A/360 = t/1mS får vi dessa ställen i tidsvärden enligt

t = (A/360)·(1mS)

Dessa transformationssamband anpassar därmed värdena till det ursprungliga kurvkonceptet i x-led. Värdena blir t = (n0,5 ± 0,0484326)·1mS med n=0,1,2,3,… motsvarande följden av halvperioder från nollpunkten. Anpassningen i y-led ges direkt som kurvans maximala amplitudvärde gånger cosinusvärdena. Därmed har vi genomgått hela lösningen till problemet med att finna skärningspunkterna för de bägge harmoniska cosinusvågorna, samt hur att relatera vågformernas relativa presentation i olika skalor.

I nästföljande exempel använder vi samma kurvor som ovan, men relaterade på ett annat sätt. Exemplet tjänar endast att belysa iterationens roll och användbarhet för mera sammansatta sambandsformer.

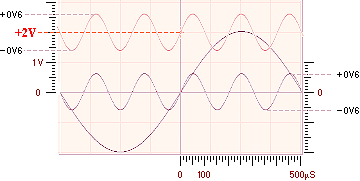
Det enda som skiljer kurvorna i bilden ovan från föregående är att den mindre cosinuskurvan y₂ (övre lilla kurvan) här ligger överlagrad på linjen för 2V. Ekvationen för y₂-kurvan är alltså modifierad med addition +1 enligt

y₂ = 1 + (0,3)cos5A

Vi ska även i detta fall försöka bestämma de periodiskt återkommande skärningspunkterna mellan den övre mindre och den undre större cosinuskurvan.

EXEMPEL

y₁ = cosA ................................ ±2V0, 1mS

y₂ = 1 + 0,3·cos5A .................. ±0V6, 200µS

y₂ ligger överlagrad på y₁ med nollan vid +2V0. Bestäm skärningspunkterna mellan y₁₂.

Lösning:

Samma xy-värden ger ekvivalens mellan ekvationerna för y₁_&₂.

cosA = 1 + 0,3·cos5A

Ekvationen (neutralformen)

0 = 1+ 0,3cos5A – cosA

har två ställen med ±-lösningar i varje, totalt 4 lösningar som upprepas periodiskt. Ena stället ges av

A = acos(1+ 0,3cos5A)

och det andra av

A = (acos[(cosA–1)/0,3] + 360)/5

cosA = 1+ 0,3cos5A

Iterationen ger två noder som slutvärdet ställer in sig togglande på, respektive 44,571393 och 52,74497. Inget av dessa värden är giltigt, det rätta värdet befinner sig (ungefär) mitt emellan.

Iterationen i detta fall är alltså ”noddivergent”; divergensen har en viss ram och kan därför transformeras för konvergens genom att ta medelvärdet av föregående och aktuellt resultatvärde. Genom att således ta aktuellt och föregående, minskas hela tiden skillnaden och iterationen blir därför konvergent. Uppställningen blir

cosA=1+ 0,3cos5A

Metod: A=(A1+A2)/2

Gränspunkten ligger vid 0,3cos5A=0 som ges såväl av A=36 (cos180) som 72 grader (cos360).

Ingångsvärdet blir optimalt medelvärdet (36+72)/2=54.

54 ingångsvärde

44,427004 resultat

49,213502 medelvärde, insätts

46,534838 r

47,87417 m

47,889684 r

47,881927 m

47,880849 r

47,881388 m

47,881463 r

47,881425 m

47,88142 r

47,881422 m

47,881424 r

47,881423 m

47,881423 r 180 – 47,881423

cos5A=(cosA–1)/0,3

Uppställningen för det andra stället blir motsvarande

cos5A=(cosA–1)/0,3

Denna form är direkt iterativt konvergent (vilket jag inte upptäckte förrän samma metod som ovan tillämpats; 48 varv!). Resultatet blir en negativ vinkel. Addition med 360 grader ger den aktuella 5A-vinkeln, A således denna dividerat med 5. Räkningen görs därmed

A = (acos[(cosA–1)/0,3] + 360)/5

Ingångsvärdet blir här 360/5=72 (via 90 grader ges 0, vilket motsvarar 360). Iterationen ger direkt

0=360, 360/5=72

70,122102

69,708954

69,1612364

69,589482

69,584045

69,582752

69,582445

69,582372

69,582354

69,58235

69,582349

69,582348

69,582348 180 – 69,582348

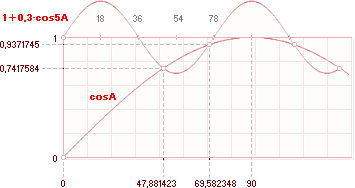
SVAR: Skärningarna ges periodiskt av vinklarna 90±42,118577 [47,881423; 132,11857] med cosA= 0,7417584 och 90±20,417652 [69,582348; 110,41765] med cosA= 0,9371745, analogt

n mS + 250±[116,99604 och ±56,7157]µS med n som heltal 1,2,3,4,5,... n.

END.

Appendix — sin nA

PREFIXxSIN

Sambanden för sinnA och cosnA

från binomialteoremet

Urspr. Sammanställning från Den urgamla kvadraten (Index 12)

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

1 9 36 84 126 126 84 36 9 1

1 10 45 120 210 252 210 120 45 10 1

1 11 55 165 330 462 462 330 165 55 11 1

1 12 66 220 495 792 924 792 495 220 66 12 1

1 13 78 286 715 1287171617161287 715 286 78 13 1

1 14 91 364 1001200230033432300320021001 364 91 14 1

1 15 105 455 13653003500564356435500530031365 455 105 15 1

Som redan tidigare vidrörts utgör matematiken en väv av detaljer som framgår ur en redan given struktur och vars mönsterformer vi finner genom inträngande studium [MATEMATIKEN FRÅN BÖRJAN]. I denna del visas explicit hur sambanden för sinnA och cosnA ligger inneslutna i binomialteoremet. Pyramiden ovan visar en del av den s.k. Pascals triangel och ur vilken (bland annat) framgår koefficienterna till binomialteoremet.

Först en översikt. Detaljerna förklaras mera ingående längre ner.

Binomalteoremet (positiva binomet)

(x+y)ⁿ = xⁿ[1+ _m=_0\n∑(y/x)^m⁺¹(n–m)_m_!/(m+1)!]

Förkortning i skrivsättet: [m_a=(n–m)_m_! ; m₀=(n)₀ ; m₁=(n)₀(n–1)₁ ; m₂=(n)₀(n–1)₁(n–1)₂ ; m₃=(n)₀(n–1)₁(n–1)₂(n–1)₃ ; …]

(x+y)ⁿ = xⁿ[1 + m₀(y/x)¹/1! + m₁(y/x)²/2! + m₂(y/x)³/3! + m₃(y/x)⁴/4! + m₄(y/x)⁵/5! + m₅(y/x)⁶/6! + m₆(y/x)⁷/7! + m₇(y/x)⁸/8! + …

PREFIXxSIN. a=sin nA, b=cos nA ; x=sinA, y=cosA :

(a+b)ⁿ = xⁿ[1 + m₀(y/x)¹/1! – m₁(y/x)²/2! – m₂(y/x)³/3! + m₃(y/x)⁴/4! + m₄(y/x)⁵/5! – m₅(y/x)⁶/6! – m₆(y/x)⁷/7! + m₇(y/x)⁸/8! + …

sin nA = xⁿ[1 – m₁(y/x)²/2! + m₃(y/x)⁴/4! – m₅(y/x)⁶/6! + m₇(y/x)⁸/8! + …

cos nA = xⁿ[ m₀(y/x)¹/1! – m₂(y/x)³/3! + m₄(y/x)⁵/5! – m₆(y/x)⁷/7! + …

sinnA = xⁿ[1+_m=_{1\IntegerOf[n/2]}∑(y/x)²^m(–1)^mn[n–m]_(2m–1)!/(2m)!]

cosnA = xⁿ[_m=_{1\IntegerOf([n+1]/2)}∑(y/x)²^m^–1(–1)^m⁺¹[n–m+1]_(2m–2)!/(2m–1)!]

sin2A = x²–y² cos2A = 2xy

sin3A = x³–3xy² cos3A = 3x²y – y³

sin4A = x⁴–6x²y²+y⁴ cos4A = 4x³y – 4xy³

sin5A = x⁴–10x³y²+5xy⁴ cos5A = 5x⁴y – 10x²y³ + y⁵

→ KOEFFICIENTERNA. Svarta sinus, röda cosinus

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

1 9 36 84 126 126 84 36 9 1

1 10 45 120 210 252 210 120 45 10 1

1 11 55 165 330 462 462 330 165 55 11 1

1 12 66 220 495 792 924 792 495 220 66 12 1

1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1

1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1

1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1

x&y ersatta med sinA&cosA:

sin2A = sin²A–cos²A cos2A = 2sinAcosA

sin3A = sin³A–3sinAcos²A cos3A = 3sin²AcosA – cos³A

sin4A = sin⁴A–6sin²Acos²A+cos⁴A cos4A = 4sin³AcosA – 4sinAcos³A

sin5A = sin⁴A–10sin³Acos²A+5sinAcos⁴A cos5A = 5sin⁴AcosA–10sin²Acos³A+cos⁵A

Sambanden med de rena tan=(y/x)-termerna:

sin2A = (sinA)²[1–(tanA)²] cos2A = (sinA)²[2(tanA)]

sin3A = (sinA)³[1–3(tanA)²] cos3A = (sinA)³[3(tanA) – 1(tanA)³]

sin4A = (sinA)⁴[1–6(tanA)²+(tanA)⁴] cos4A = (sinA)⁴[4(tanA) – 4(tanA)³]

sin5A = (sinA)⁵[1–10(tanA)²+5(tanA)⁴] cos5A = (sinA)⁵[5(tanA) – 10(tanA)³ + (tanA)⁵]

Ekvivalenterna för sinnA och cosnA

ALLA UTVECKLINGAR I PREFIXxSIN — Se även PREFIXxSIN i TRIGONOMETRINS GRUNDBEGREPP

I Vinkelsummateoremet visades härledningen till serierna för sinus och cosinus utan hjälp av i-visaren [SCutan]. De sambandsformernas strukturer ingår också i följande beskrivning.

Av sambanden nedan

sinnA·rⁿ=x_n , cosnA·rⁿ = y_n

framgår att

sinnA=x_n , cosnA=y_n

med r=1. Sambanden för x_n och y_n respektive framgår ur härledningarna enligt sambanden

nedan, vilka här förtydligats på ovanstående förenkling.

x_n= sinnA = xⁿ[1+_m=_1\n∑(y/x)²^m(–1)^mn[n–m]_(2m–1)!/(2m)!]

y_n= cosnA = xⁿ_m=_1\n∑(y/x)²^m^–1(–1)^m⁺¹[n–m+1]_(2m–2)!/(2m–1)!

NOTERING. [Indexeringen m=1\m→∞ för serieleden i nämnda avsnitt [SCutan] får i dessa sammanhang en mera komplicerad innebörd av typen m=1\n då seriens utsträckning är ändlig.

Med r=1 motsvarar termerna x och y respektive sinus och cosinus.

x = sinA, y = cosA ;

Parentesformen för produktsummeringarna har följande innebörd.

n[(n–m)_(2m–1)!] ;

m=1; n[(n(n–m)_1!] = n[(n–1)₁]

m=2; n[(n(n–m)_3!] = n[(n–1)₁(n–2)₂(n–3)₃]

m=3; n[(n(n–m)_5!] = n[(n–1)₁(n–2)₂(n–3)₃(n–4)₄(n–5)₅]

Och så vidare. Då m=n ges en nollfaktor i produktsumman varigenom den aktuella kvoten och efterföljande bortfaller. Med n som 2,3,4,5... ges koefficienterna i produktsumman enligt kvotföljden

n=2: 2(2–1)₁, 2(2–1)₁(2–2)₂(2–3)₃

n=3: 3(3–1)₁, 3(3–1)₁(3–2)₂(3–3)₃, 3(3–1)₁(3–2)₂(3–3)₃(3–4)₄(3–5)₅

n=4: 4(4–1)₁, 4(4–1)₁(4–2)₂(4–3)₃, 4(4–1)₁(4–2)₂(4–3)₃(4–4)₄(4–5)₅, 4(4–1)₁(4–2)₂(4–3)₃(4–4)₄...(4–7)₇

n=5: 5(5–1)₁, 5(5–1)₁(5–2)₂(5–3)₃, 5(5–1)₁(5–2)₂(5–3)₃(5–4)₄(5–5)₅, 5(5–1)₁(5–2)₂(5–3)₃(5–4)₄...(5–9)₉

n=6: 6(6–1)₁, 6(6–1)₁(6–2)₂(6–3)₃, 6(6–1)₁(6–2)₂(6–3)₃(6–4)₄(6–5)₅, 6(6–1)₁(6–2)₂(6–3)₃(6–4)₄...(6–11)₁₁

Uppställningen förtydligar att

(udda n–1)/2 och (jämna n)/2

utvisar formen för seriens indexering, dvs. det antal kvoter som serien ger för givet n. Vi når samma resultat genom att sätta

INT(n/2)

med INT som heltalsdelen av kvoten n/2. Mera förtydligat i det förklarande sammanhanget

IntegerOf(n/2)

Med detta klargörande kan sambandsformen för alla heltaliga n i sinnA tecknas

sinnA = xⁿ[1+_m=_{1\IntegerOf[n/2]}∑(y/x)²^m(–1)^mn[n–m]_(2m–1)!/(2m)!]

EXEMPEL sinus:

n=2 sinus;

sin2A = x²[1+_m=_1\1∑(y/x)²^m(–1)^m2[2–m]_(2m–1)!/(2m)!]

summaledet; –(y/x)²2/2! = –(y/x)²

sin2A = x²[1–(y/x)²] = x²–y² = sin²–cos² = 1–cos²–cos² = 1–2cos²

n=3 sinus;

sin3A = x³[1+_m=_1\1∑(y/x)²^m(–1)^m3[3–m]_(2m–1)!/(2m)!]

summaledet; –(y/x)²3(2)/2! =–3(y/x)²

sin3A = x³[1–3(y/x)²] = x³–3xy² = sin³–3sin·cos²

Genom en mindre utveckling (3sin·cos²=(3sin–3sin³)) fås även

4(sinA)³–3sinA och (4sin·sin²–3sin=4sin(1–cos²)–3sin) sinA–4sinA(cosA)²

n=4 sinus;

sin4A = x⁴[1+_m=_1\2∑(y/x)²^m(–1)^m4[4–m]_(2m–1)!/(2m)!]

summaledet; –(y/x)²4(3)/2! + (y/x)⁴4(3)(2)(1)/24 =–6(y/x)²+(y/x)⁴

sin4A = x⁴[1–6(y/x)²+(y/x)⁴] = x⁴–6x²y²+y⁴ = sin⁴–6sin²cos²+cos⁴

Jämför

1 – 8(sinA)²(cosA)²

enligt (x²+y²)²=1= x⁴+y⁴+2x²y²; 1–2x²y² –6x²y²= x⁴+y⁴–6x²y² = 1–8x²y²

Ur ovanstående fås även

1 – 8(sinA)²+8(sinA)⁴ och 1 – 8(cosA)²+8(cosA)⁴

n=5 sinus;

sin5A = x⁵[1+_m=_1\2∑(y/x)²^m(–1)^m5[5–m]_(2m–1)!/(2m)!]

summaledet; –(y/x)²5(4)/2! + (y/x)⁴5(4)(3)(2)/24 =–10(y/x)²+5(y/x)⁴

sin5A = x⁵[1–10(y/x)²+5(y/x)⁴] = x⁵–10x³y²+5xy⁴ = sin⁵–10sin³cos²+5sin·cos⁴

Vi avslutar här och betraktar motsvarande för cosinus.

y_n= cosnA = xⁿ_m=_1\n∑(y/x)²^m^–1(–1)^m⁺¹[n–m+1]_(2m–2)!/(2m–1)!

[n–m+1]_(2m–2)!

m=1; [n–m+1]_0! = [n]₀

m=2; [n–m+1]_2! = [n]₀[n–1]₁[n–2]₂

m=3; [n–m+1]_4! = [n]₀[n–1]₁[n–2]₂[n–3]₃[n–4]₄

n=2: 2₀, 2₀(2–1)₁(2–2)₂

n=3: 3₀, 3₀(3–1)₁(3–2)₂, 3₀(3–1)₁(3–2)₂(3–3)₃(3–4)₄

n=4: 4₀, 4₀(4–1)₁(4–2)₂, 4₀(4–1)₁(4–2)₂(4–3)₃(4–4)₄, 4₀(4–1)₁(4–2)₂(4–3)₃(4–4)₄(4–5)₅(4–6)₆

n=5: 5₀, 5₀(5–1)₁(5–2)₂, 5₀(5–1)₁(5–2)₂(5–3)₃(5–4)₄, 5₀(5–1)₁(5–2)₂(5–3)₃(5–4)₄(5–5)₅(5–6)₆,... (5–8)₈

n=6: 6₀, 6₀(6–1)₁(6–2)₂, 6₀(6–1)₁(6–2)₂(6–3)₃(6–4)₄, 6₀(6–1)₁(6–2)₂(6–3)₃(6–4)₄(6–5)₅(6–6)₆,... (6–10)₁₀

Uppställningen förtydligar att

1+(udda n–1)/2 och (jämna n)/2

anger det antal kvoter som serien ger för givet n. Vi når samma resultat genom att sätta

INT([n+1]/2)

med INT som heltalsdelen av kvoten (n+1)/2. Mera förtydligat i det förklarande sammanhanget

IntegerOf([n+1]/2)

Med detta klargörande kan sambandsformen för alla heltaliga n i cosnA tecknas

cosnA = xⁿ_m=_{1\IntegerOf([n+1]/2)}∑(y/x)²^m^–1(–1)^m⁺¹[n–m+1]_(2m–2)!/(2m–1)!

EXEMPEL cosinus:

n=2 cosinus;

cos2A = x²_m=_1\1∑(y/x)²^m^–1(–1)^m⁺¹[2–m+1]_(2m–2)!/(2m–1)!

summaledet; (y/x)·2 = 2y/x

cos2A = x²[2y/x] = 2xy = 2sin·cos

n=3 cosinus;

cos3A = x³_m=_1\2∑(y/x)²^m^–1(–1)^m⁺¹[3–m+1]_(2m–2)!/(2m–1)!

summaledet; (y/x)·3 – (y/x)³·3·2·1/3! = 3(y/x) – (y/x)³

cos3A = x³[3(y/x) – (y/x)³] = 3x²y – y³ = 3sin²cos – cos³

3cosA–4(cosA)³

n=4 cosinus;

cos4A = x⁴_m=_1\2∑(y/x)²^m^–1(–1)^m⁺¹[4–m+1]_(2m–2)!/(2m–1)!

summaledet; (y/x)·4 – (y/x)³·4·3·2/3! = 4(y/x) – 4(y/x)³

cos4A = x⁴[4(y/x) – 4(y/x)³] = 4x³y – 4xy³ = 4sin³cos – 4sin·cos³

n=5 cosinus;

cos5A = x⁵_m=_1\3∑(y/x)²^m^–1(–1)^m⁺¹[5–m+1]_(2m–2)!/(2m–1)!

summaledet; (y/x)·5 – (y/x)³·5·4·3/3! + (y/x)⁵·5·4·3·2·1/5! = 5(y/x) – 10(y/x)³ + (y/x)⁵

cos5A = x⁵[5(y/x) – 10(y/x)³ + (y/x)⁵] = 5x⁴y – 10x²y³ + y⁵ = 5sin⁴cos–10sin²cos³+cos⁵

5cosA – 20(cosA)³ + 16(cosA)⁵

Formerna för nA kan också utvecklas alternativt med utgångspunkt från de sammansatta sambanden inom trigonometrin:

sin2A:

sinAsinA – cosAcosA

= (sinA)² – (cosA)²

= 1–(cosA)² – (cosA)²

= 1–2(cosA)²

1–2(cosA)²

sin3A:

sinAsin2A – cosAcos2A

= sinA[1–2(cosA)²] – cosA[2sinAcosA]

= sinA–2sinA(cosA)² – 2sinA(cosA)²

= sinA–4sinA(cosA)²

sinA–4sinA(cosA)²

= sinA–4sinA[1–(sinA)²]

= sinA–4sinA+4sinA(sinA)²

= sinA–4sinA+4(sinA)³

= 4(sinA)³–3sinA

4(sinA)³–3sinA = sin³–3sin·cos²

sin4A:

sinAsin3A – cosAcos3A

= sinA[sinA–4sinA(cosA)²] – cosA[3cosA–4(cosA)³]

= (sinA)²–4(sinA)²(cosA)² – 3(cosA)²+4(cosA)⁴

= 1–(cosA)²–4[1–(cosA)²](cosA)² – 3(cosA)²+4(cosA)⁴

= 1–(cosA)²–[4–4(cosA)²](cosA)² – 3(cosA)²+4(cosA)⁴

= 1–(cosA)²– 4(cosA)²+4(cosA)⁴ – 3(cosA)²+4(cosA)⁴

= 1–4(cosA)²– 4(cosA)²+4(cosA)⁴+4(cosA)⁴

= 1–8(cosA)²+8(cosA)⁴

= 1–8[(cosA)²–(cosA)⁴]

= 1–8(cosA)²[1–(cosA)²]

= 1 – 8(cosA)²(sinA)²

1 – 8(sinA)²(cosA)²

= 1 – 8(sinA)²[1–(sinA)²]

= 1 – (sinA)²[8–8(sinA)²]

= 1 – [8(sinA)²–8(sinA)⁴]

= 1 – 8(sinA)²+8(sinA)⁴

1 – 8(sinA)²+8(sinA)⁴

= 1 – 8[1–(cosA)²](cosA)²

= 1 – [8–8(cosA)²](cosA)²

= 1 – [8(cosA)²–8(cosA)⁴]

= 1 – 8(cosA)²+8(cosA)⁴

1 – 8(cosA)²+8(cosA)⁴

cos2A:

2sinAcosA

cos3A:

sinAcos2A + sin2AcosA

= sinA[2sinAcosA] + [1–2(cosA)²]cosA

= 2(sinA)²cosA + cosA–2(cosA)³

= 2[1–(cosA)²]cosA + cosA–2(cosA)³

= 2cosA–2(cosA)³ + cosA–2(cosA)³

= 3cosA–4(cosA)³

3cosA–4(cosA)³ = 3sin²cos–cos³

cos4A:

sinAcos3A + sin3AcosA

= sinA[3cosA–4(cosA)³] + [sinA–4sinA(cosA)²]cosA

= 3sinAcosA–4sinA(cosA)³ + sinAcosA–4sinA(cosA)³

= 4sinAcosA–8sinA(cosA)³

4sinAcosA–8sinA(cosA)³ = 4sinA[cosA–2(cosA)³]

cos5A:

sinAcos4A + sin4AcosA

= sinA[4sinAcosA–8sinA(cosA)³] + [1 – 8(sinA)²(cosA)²]cosA

= sinA[4sinAcosA–8sinA(cosA)³] + cosA – 8(sinA)²(cosA)³

= 4(sinA)²cosA – 8(sinA)²(cosA)³ + cosA – 8(sinA)²(cosA)³

= 4(sinA)²cosA – 16(sinA)²(cosA)³ + cosA

= 4[1–(cosA)²]cosA – 16(sinA)²(cosA)³ + cosA

= [4–4(cosA)²]cosA – 16(sinA)²(cosA)³ + cosA

= 4cosA – 4(cosA)³ – 16(sinA)²(cosA)³ + cosA

= 5cosA – 4(cosA)³ – 16(sinA)²(cosA)³

= 5cosA – (cosA)³[4 + 16(sinA)²]

= 5cosA – 4(cosA)³[1+ 4(sinA)²]

= 5cosA – 4(cosA)³[1+ 4[1–(cosA)²]]

= 5cosA – 4(cosA)³[1+ 4 – 4(cosA)²]

= 5cosA – 4(cosA)³[5 – 4(cosA)²]

= 5cosA – 20(cosA)³ + 16(cosA)⁵

= 5cosA – 20(cosA)³ + 16(cosA)⁵

…

END.

Sammanställning

De Harmoniska Svängningarna

Sammanställning

Vid A=0º ges tanT=2πr/L=k, som anger kurvans maximala branthet, branthetskonstanten.

(1) t/t₀ = l/L = s/P = s/2πr =a/2π = A/360

(2) tanT = sinA·v_P/v_x = sinA(2πr/L) = sinA·k

Som tangensformen sinA·k till kurvan y=cosA kan uppfattas enbart som en cosA-kurva förskjuten minus 90 grader utmed x-axeln, får k=2πr/L via sinA=1=sin0 innebörden av ett numeriskt toppvärde motsvarande enhetscirkelns r-värde. Förutom k benämner vi här även detta toppvärde som

den numeriska amplituden (r_M)

för tangensformens kurva (omgiven av parentestecken). Med L=2πr fås (r_M)=1. Med (r_M) som numeriskt sammanfallande med amplituden r hos moderkurvan cosA·r, erhålles härigenom (r_M) generellt som antalet r-enheter. Dvs,

(3) (r_M) = 2πr/L = n_r .......................... numeriska värdet (relativt enheten för 1)

Den realt metriska formen för tangensformens kurva (tanT-kurvan) erhålles allmänt genom multiplikation med en godtycklig metrisk enhet E, vilken ger den metriska formen för (r_M) enligt

(4) (r_M)·E = r_M ....................... | (r_M)·r, ENHET = r

| (r_M)[r/(r)], ENHET = ENHETEN FÖR r

Genom att flytta fram y-axeln från vinkelnollindex till de motsvarande tre övriga kvadrantgenomgångarna utmed x-axeln, får man kurvans komplementekvationer. I elementarform med 2πr/L = 1 = v_P/v_x och r som enhet (=1), fås dessa ekvationer enligt nedan.

(5)

KURVANS EKVATION KVADRANT KURVANS TANGENSFORM

cosA I sinA

cos(A+90) = sinA II sin(A+90) =–cosA

cos(A+180) =–cosA III sin(A+180) =–sinA

cos(A+270) =–sinA IV sin(A+270) = cosA

De 4 Kvadranterna — kvadrantbegreppet

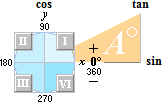
Ovan: DE FYRA KVADRANTERNA I II III IV som markerar det matematiska xy-systemets utsträckning i respektive vinkelintervall via positiv = moturs rotation (0-90)°, (90-180)°, (180-270)°, (270-360)°, tillsammans med projektionsbegreppen sin cos tan — trigonometrins grundkarta enligt PREFIXxSIN.

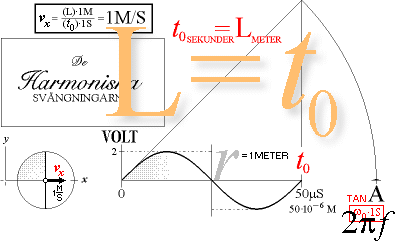
I de tidsperiodiska förloppen, alstras en harmonisk våg under perioden t₀ och med amplituden ±r. Begreppet om vågens längd (L) blir därmed underställt begreppet om utsträckningen av tidsrummet (t₀). Härigenom kan L i princip ges en godtycklig metrik. Formen för L [Se nr(2)] kan därmed tecknas L = (t₀)·1M, där (t₀) är t₀/1S och L/1M = (L). Formellt ges således (L) = (t₀) som via v_x= L/t₀ ger v_x = 1M/S. Branthetskonstanten k kan därmed tecknas

(6) k = 2πr/L = 2πr/[(t₀)·1M] = (2πr/t₀)·1(S/M)

Införs analogt med ovan r = (r)·1M erhålles

(7) k = [2π(r)·1M/t₀]·1(S/M)

k = [2π(r)/t₀]·1S |= 2π(r)/(t₀)

Enhetsdefinitionen för k fås genom att sätta det numeriska (r) som enhet, dvs lika med 1, således med r = 1 METER. Enhetsformen för k via amplitudenheten r lika med en meter blir därmed

(8) k = [2π/t₀]·1S |= (r_M)

Med t₀·f = 1 SEKUND fås antalet f perioder t₀ under en sekund som f = 1/t₀ , där antalet f svarar analogt mot antalet våglängder per sekund. Storheten för f (antal perioder eller våglängder per sekund) anges i enheten

HERTZ ............................... med förkortningen Hz,

och betecknas som frekvensen med enheten 1/S = S^–1. Genom ledet i (1) fås speciellt vinkeln x i radianer a enligt a = t·2π/t₀ där kvoten 2π/t₀ (även lika med v_P/r via v_P = 2πr/t₀) benämns som

VINKELHASTIGHETEN ............... betecknas ω₀

[ω, grekiska bokstaven lilla å(-mega)] och som via 1/t₀ = f även benämns

VINKELFREKVENSEN.

Dessa relationer förtydligat ger

(9) ω₀ = 2π/t₀ = 2πf = v_P/r

Formen för nr(2) via amplitudenheten r = 1 Meter kan därmed och analogt med nr(5) tecknas för de fyra kvadranterna och speciellt för de enkla harmoniska vågorna som funktion av tiden enligt

(10)

KURVANS EKVATION KURVANS TANGENSFORM

y = cos ω₀t tanA = sin ω₀t·ω₀·1S

y = sin ω₀t tanA = –cos ω₀t·ω₀·1S

y = –cos ω₀t tanA = –sin ω₀t·ω₀·1S

y = –sin ω₀t tanA = cos ω₀t·ω₀·1S

där ω₀t är vinkeln (i radianer eller grader) och ω₀ vinkelfrekvensen 2πf .

Terminologi — harmoniska svängningar, harmoniska vågfunktioner

Terminologi — harmoniska vågfunktioner

Termer som används Frekvent i denna Presentation

Periodisk funktion

periodisk funktion, funktion som upprepas periodiskt analogt cyklometriska funktioner: cirkelfunktioner, äv. periodisk vågfunktion

Vågfunktion

vågfunktion, samma som periodisk funktion

Harmonisk vågfunktion

harmonisk vågfunktion, periodiskt samverkande vågfunktioner eller dito funktionskurvor, samma som sammansatta periodiska funktioner; här i beskrivande mening komponenterna såväl som helheten;

— Begreppet ansluter till samma som (grundkomponenten som beskrivs i) HARMONISK SVÄNGNING: sinusvågen; se exv.,

@INTERNET Wikipedia Harmonic oscillator, Simple harmonic oscillator [2012-08-19]

http://en.wikipedia.org/wiki/Harmonic_oscillator

Begreppet HARMONISK FUNKTION generellt i MAC

SPECIELLA EXEMPEL PÅ HARMONISKA VÅGFUNKTIONER:

Harmonic Function — övertonsfunktion: summering av cosinusfunktioner (cosinuskurvor) med harmoniska (heltalsavpassade) frekvenser 2 6 10 14 18 …

y = 0.2[(cos2þx)+(1/4)(cos6þx)+(1/8)(cos10þx)+(1/16)(cos14þx)+(1/32)(cos18þx)]

Unit800 | þ=pi | PREFIXxSIN

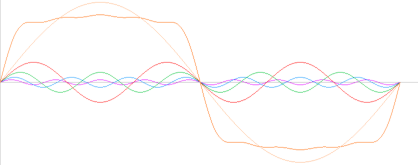
I engelskan används ofta den motsvarande svenska betydelsen ÖVERTON synonymt med engelska ordet harmonic. Dvs., »samma ton men i oktav».

— Sammansättningen av SÅDANA »harmoniska funktioner» finns exemplifierat ovan.

— Se motsvarande i Wikipedia

http://en.wikipedia.org/wiki/Square_wave

— summan av en viss ordnad serie med (harmoniska) cosinusvågor summerar (alltmera noga) en fyrkantvåg.

— Se även illustrerat kurvexempel i WolframMath,

http://mathworld.wolfram.com/FourierSeriesSquareWave.html

y = 0.4[(cos1þx)+(1/3)(cos3þx)+(1/5)(cos5þx)+(1/7)(cos7þx)+(1/9)(cos9þx)]; samma typ som ovan, men med rak topp/botten:

Unit400 | þ=pi | PREFIXxSIN

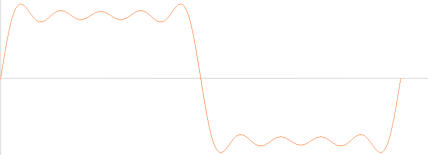
I ÖVERGRIPANDE MATEMATISK MENING är DEN ETABLERADE innebörden av termen eller begreppet »harmonic function», motsvarande svenskans harmonisk funktion, (ypperligt) ABSTRAKT:

— MAC-terminologin ansluter (nämligen) till DEN ANALYTISKA VEKTORALGEBRAN (Se Laplace’s equation i Wikipedia från Harmonic function) [Typ partiella andraderivator d²u/(∂x)² + d²u/(∂y)² = 0, se exv. MATEMATIKLEXIKON W&W 1991, s161]:

— Vi känner den typen redan i MAC-tappning från EXPANSIONSINTEGRALEN (den moderna akademins vektoranalytiska begrepp omöjliggör beskrivningen av magnetismen och induktionen i relaterad mening) — vilket innebär att varje möjlighet att FÖRSTÅ sakinnehållet på den moderna akademins terminologiska villkor redan från ruta ett är dömt till misslyckande (relaterbar koppling saknas — beskrivningarna ansluter till den moderna akademins devis alltsedan 1800-talet att uppfinna olika »regler för fysiken och matematiken», inte att härleda dem); Ingen direkt upphittad webbkälla finns f.ö. som sammanför typkurvorna för sinus-cosinus med begreppet Harmonic Function — medan direkta ord- och termkopplingar finns mellan typen Square Wave och Harmonic (wave) Function — vilket betyder att man behöver vara extra uppmärksam i de olika termförgreningarna.

— Det finns emellertid i den här presentationens referenser (Aug2012) ingen precis genomgång av ämnet, vilket gör att meningen ovan får förstås preliminär (baserad enbart på här nämnda preferenser).

Jämför (som exempel) den relaterbara fysikens begrepp i ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS med Wikipediaartikelns referensexempel till Harmonic Function

http://en.wikipedia.org/wiki/Harmonic_function

@INTERNET Wikipedia Harmonic function, Examples [2012-08-20]

via (det i wikiartikeln anförda) begreppet elektrisk potential:

— Elektriska laddningen har ingen härledande beskrivning i MAC — och därmed heller INTE det elementära elektriska potentialbegreppet [ELEKTRISKA FÄLTET]. I MAC har man (alltså, relativt de härledande beskrivningarna i TNED) gått en »omväg» genom att FÖRST uppfinna hur fysiken ska fungera (harmonic function), innan man ENS vet vad fysiken handlar om, för att SEDAN pressa in fysiken (Harmonic Function) i den så uppfunna moderna matematiska universalintelligensen.

— Det finns ingenting sådant i relaterad fysik.

— Se även motsvarande jämförelser (som ansluter till samma art av exempel) i TREATISE (MAC/TNED i magnetism och induktion generellt); ungefär så (samma typ av allmänt utbrett kaos), generellt.

Med andra ord:

— Det finns (här) ingen ENKEL synonym i termer av RELATERAD (fysik och) matematik till den moderna akademins allmänna begrepp harmonisk funktion (den termen avser [i varje fall] INTE [entydigt någon nu känd allmänt tillgänglig beskrivande webbkälla som kopplar till] harmonisk vågfunktion).

— I engelskan används begreppet harmonic function i vilket fall i flera (olika) betydelser — typ den ovan illustrerade cosinusformen med en övergripande »harmonic wave function» som summan av frekvensavdelade undercosinusfunktioner.

END.

TRIGONOMETRINS GRUNDBEGREPP II

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

TRIGONOMETRINS GRUNDBEGREPP II

ämnesrubriker

innehåll

TRIGONOMETRINS GRUNDBEGREPP II

Den Kinematiska Trigonometrin

Sinuskurvan

Vinkelsambanden — grader, radianer

Vinkelfunktionerna

Tangenten

SPECIALARTIKEL

De harmoniska kurvorna och deras tangensformer

Vinkelfrekvensen

Vinkelmultipliciteten

Tangensformens ekvation

Utvecklingsexempel — Sinus och cosinuskurvornas metrik

Kurvformernas relativa metrik

Summering

Kort om ytor

Sammansatta vågfunktioner

Sammanställning

Kvadranterna

Terminologi — harmoniska vågfunktioner

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

e₀ = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²

BKL BONNERS KONVERSATIONSLEXIKON Band I-XII med Suppement A-Ö 1922-1929, Bonniers Stockholm

[BA]. BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, modern akademi

TNED

(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken

är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.

Senast uppdaterade version: 2012-12-02

*END.

Stavningskontrollerat 2012-08-20.

rester

ORDLISTA till Reg.:

Formlagarna utförligt med härledningar

FYSIKENS VIKTIGASTE BEGREPP lista i jämförelse TNED/MAC

Harmonisk vågfunktion harmoniska vågfunktioner

KVADRANTBEGREPPET matematiska xy-planets utsträckning

NOLLINTEGRALEN utförligt med exempel

Periodisk funktion harmoniska vågfunktioner

Positionspunkter till värdemängder differentialens kontinuitet mot noll (ersättningstecken i Symbol Û [Alt+0219, Û — men vissa webbläsare läser inte den typen])