K-cellens inre | GRB-objektens ursprung

UNIVERSUMS HISTORIA | K-cellens inre — GRB-objektens ursprung i TNED | 2012III1 a BellDHARMA production | Senast uppdaterade version: 2013-06-23 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

GRB-OBJEKTENS URSPRUNG I TNED — Bildkälla, Författarens arkiv, 27Jun2012E10Bild36 NikonD90 Detalj

GRB1—K-CELLENS INRE • GRB1m—MörkaMaterien • GRB1n—Primära v-formen • GRB2—UniversumsSynrand • GRB2a—AkroBreak • GRB3—GRBorigin

Primärtändningarna

Villkoren för GRB

Frekvensen synliga pulsbilder

Prime Energy

Detonationspulsernas reaktionstid

Galaxexpansionerna

^γp

Gravitella ljusavböjningen

Fraktalnivåerna för GRB

Antallet GRB-himmelsfläckar

Primärpulsens energi

Kärnåterkopplingens fördröjning

Osäkerheten i GRB-xyz

GRB-objektens ursprung i TNED — GRB-termen beskrivs i NOMENKLATUR — om ej redan bekant

GRB-objektens ursprung i TNED

— se inledande begrepp från K-cellens detonation om ej redan bekant

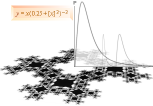
Genom att primärtändningarna (J-kropparnas expansion) i TNED-teorin för himlakropparnas bildning är definitivt associerad med frigörandet av ofantliga (hutlöst enorma) energimängder på ytterst kort tid [GRBenerginMaxTNED], föll det sig naturligt (vid tiden för sakernas uppmärksammande i denna författares referens, förf. nov2007) att (spontant, direkt) associera just primärtändningarnaarna med de rapporterade förekomsterna av GRBs (eng. Gamma Ray Burst’s, sv. här gammastrålskurar eller gammastrålutbrott). Associationen kräver självklart en mera ingående prövning, och denna presentation är tillägnad resultatet.

Vi studerar det.

Referenstabell GRBSNN — topptider-isotropiska (sfäriska) maxenergier för GRB SN N i orienterande grov översikt

typ	topptid	max	energi	energireferens
GRB	sekunder	T47 J	T54 erg	Bloom et al., 2001
Supernova	dagar	T45 J	T52 erg	Ljubljana University 2012, s7mn [1-2 T44 J Wikipedia Supernova 2012-05-15]
Nova	dagar	T37 J	T41 erg	Kasliwal 2011, s337 Figure 1

Referenserna till topptiderna för typen gammastrålskurar (GRB, eng. Gamma Ray Burst) är här ett grovvärde från etablerade rapporter som indelar GRBs i typerna långa (>2S) och korta (<2S). Jämför exemplet GRB 980425. Topptiderna för novor (N) och supernovor (SN) ges generellt i (den optiska) ljusbilden i storleksordningen dagar. Jämför exemplet SN 1998bw. GRB-energierna är angivna idealt isotropiskt (sfärisk utstrålning).

Den observerade allmänna homogena galaxfördelningen i universum [‡HUDF]: finns bara ett sätt i TNED via K-cellens expansion:

— Varje J-moderkropps tyngdpunkt fortsätter i sin ordinära utkastningsriktning från detonationstillfället i K-cellens expansion medan moderkroppen i sin tur och via sin divergenständning avdelar mindre J-kroppar idealt sfäriskt runt om. Men bara de J-kroppar som avdelas inåt K-cellen har förutsättningar för att bilda en slutlig typ »STATISKT UNIVERSUM»: Efterklangen visar en bild med Galaxkropparna inbördes i relativt blygsamma hastigheter, de står i stort sett stilla räknat under långa tidrymder. De observerade rödförskjutningarna blir då istället ett prövande föremål för den lokala gravitella rödförskjutningen (c/c0). Se speciellt exempelräkningen i GRB 061028 z9,7 som klargör den gravitella rödförskjutningens roll i ett praktiskt beräkningsbart exempel. Galaxlokalernas medelmässiga förekomster kan då FÖR VÅR VIDARE PRÖVNING förstås ungefär likafördelade överallt i rymden — så som det också verkar se ut i det praktiska fallet [‡] — i takt med att K-cellen expanderar och avdelar allt flera J-kroppar (speciellt inåt K-centrum). Figuren nedan ger en viss orientering i principen.

Primärtändningarna — GRB-objektens ursprung i TNED — se även mera detaljerat i PRIMÄRTÄNDNINGARNA.

SCHEMATISK ILLUSTRATION — Se mera praktiskt exempel i Referensexempel Vintergatan — hur den primära galaxkroppen utvecklas från sin divergenständning. Grunderna utförligt från Ljusets g-beroende.

Gravitella ljusavböjningen [Se härledningar i Solrandsavböjningarna] Aº = 4Gm₂/rc² · 180/π.

K-cellens primärkroppar expanderar från området markerat A via divergenständning (c>0) från max täthet 1,82 T17 KG/M³ och vidare uppåt — Se Vintergatan som Expansionsexempel. Kropparna i det skedet är alldeles för små för att synas.

Figuren illustrerar TNED-principen bakom galaxbildningarna i K-cellens allmänna expansion. Galaxkropparna (i medeltal) lämnas (i stort vilande) EFTER K-cellens expansion liknande kondensspåret från ett reaplan i den stillastående Jordatmosfären.

— Medan teorin för universums expansion i modern akademi grundas på föreställningen om den observerade rödförskjutningen hos de alltmer avlägsna galaxobjekten — i meningen av att det är DESSA som flyr utåt med motsvarande hastigheter — visar sig teorin i TNED utmynna i att rödförskjutningarna (i huvudsak) beror på gravitationen — syngränsen bakåt är ca 5,5 T9 (miljarder) år vid ca 5,25 T25 M med den inneslutna delmassan 0,1231283 av hela K-cellens totalmassa 4,14 T53 KG. Enligt TNED utgår Galaxbildningarna från universums syngräns genom lokala c=0 och vilken nollzon följer K-cellens expansion (divergensnollzonen). Vartefter nollzonen sveper över de kvarvarande kropparna utanför c=0-zonen från K-cellens detonation, aktiveras deras primärexpansioner analogt med den lokala ljushastigheten c>0, och så länge K-cellens totalmassa medger.

Villkoren för GRB

Uppmätta strålningsenergier hos GRB-objekt i form av gammaenergier har angetts (max) runt 1 T47 J, se Referenstabellen GRBSNN ovan. Men vi måste ha full koll på att de värdena är justerade på bas av observerade rödförskjutningar i etablerad teori [zMAC] — distansparametrar som också sammanhänger med begrepp om luminositet, stråleffektens ändring över avstånd. Gammaenergivärdena från MAC måste därför här, i ljuset av TNED med gravitella rödförskjutningen, förstås med viss försiktighet.

ENLIGT REDOVISAD ÖVERSLAGSRÄKNING kan i våra rymder max 1/10.000 av en stjärnkropps g-energi [Genergin] utges i form av maximalt högenergetiskt strålningsenergi (neutrinostrålning) — från max täthet (1,82 T17 KG/M³, neutronkallplasma) och via kroppens ideala detonation på den g-energin. För att matcha en initiell gravitations(detonations-)energi på E(G)=(10.000)(1 T47 J) = 1 T51 J, motsvarande ett praktiskt grundat objekt för den observerade GRB-energin, och såvitt uppgifterna är tillförlitliga, skulle det alltså krävas en grundmassa på (se samband i [Genergin])

m₂ = [E_G/(6,0932 t5 [KG]^3/5J)]^0,6 ; E(G) = (10.000)(1 T47 J) = 1 T51 J

= 1,34614 T33 KG

~ 647 Solmassor

Gränsmassorna i stjärnfysiken enligt TNED ger stjärnorna max 5-15 Solmassor beroende på sammansättning. Det betyder, tydligen, att GRB-fenomenet INTE har någon möjlig fysisk grund i den redan utbildade galaxfysikens stjärnfält.

— Vänder vi oss — enligt relaterad fysik (TNED) — däremot mot utkanterna av det synliga universumets utsträckning ställer sig sakernas natur annorlunda. Figuren ovan (Primärtändningarna) ger en inledande orientering.

— Gravitella rödförskjutningen (relaterat) sänker effektiviteten ytterligare via divergensenergins c-kvadrat (E=mc²) med en faktor 100 — om vi använder en referenslokal på c/c₀=0,1 som en approximerad medelort för primär detonation av J-kroppar i K-cellens allmänna expansion. Därmed hamnar förhållandet detonationsmassa till möjligt avgiven strålenergi på grovt och runt 1-10 miljoner:

m₂ ~ 1-10 miljoner Solmassor ............ vad som MINST krävs i slutänden vid 0,1c0 för att servera GRB-energierna hit till oss

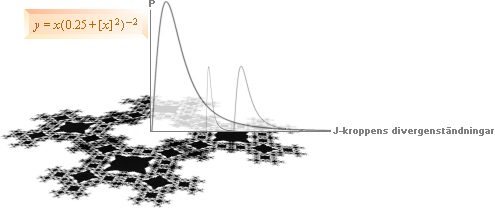
FigurGrundExempel till fraktalnivåerna

Illustration från Fraktaldelningsexemplet Vintergatan/K-cellen.

Med fraktaldelningsexemplet för Vintergatan/Hela K-cellen [ln(1 T11)/ln(6)~14 fraktalnivåer med idealt kubisk=6-sidig 3D-homogen expansionsdelning] betyder det att endast de bägge yttersta fraktalnivåernas pixelrepresentationer gäller i GRB-kandidaturen: Av de 14 nivåerna är bara max 8-9 synliga i bilden.

— Massorna [VILLKOREN FÖR GRB] har då beräknas på följande sätt med hänsyn till förhållandet 1/355 mellan synliga/reella massorna i K-cellen generellt [Mörka materien, allmänt] [MÖRKA MATERIEN ENLIGT TNED]:

Fraktalnivåerna för GRB — GRB-objektens ursprung i TNED

Till FigurGrundExemplet

1. 6×355=2 130 Solmassor: minsta J-moderkroppens massa som ansvarar för Solsystemets avdelning:

2. 6×2130=12 780 ; 6²(355)

3. 6×12780=76 680 ; 6³(355)

4. 6×76680=460 080 ; 6⁴(355)

5. 6×460080=2 760 480 GRB-kandidater, och alla större:

6. 6×2.760.480=16 562 880 ; 6⁶(355)

…

14 6¹⁴(355) = 2,78192 T13 Solmassor Vintergatskroppens primära J-modermassa

Med villkoret [‡VillkorenGRB] att de himlakroppar som ansvarar för GRB-strålenergierna måsta uppvisa minst runt 1-10 miljoner Solmassor för att få fram den aktuellt observerade (isotropiska) GRB-energin (grovt [max] T47 J), kan alltså GRB-energierna komma ifråga FÖRST från fraktalnivå nr5 (uppställningen ovan), räknat nerifrån Solsystemet (14–5=8 räknat uppifrån och neråt, i detonationsordning).

Detonationsenergierna i de fraktalnivåer som ligger högst upp (nr14 ovan) innebär också områden med de allra mest högtäta regionerna — och därmed i princip de lokaler med den allra mest utpräglade strålningsutdämpande/absorberande verkan.

— Men ingenting säkert kan ÄNDÅ sägas om vilka detonationslokaler som »gäller»:

— Möjligheten finns (nämligen) med kombinationer av olika DETONATIONSSTRÅK som kan släppa igenom vissa Planckfrekvenser — och utestänga andra.

— Observera att expansionshastigheten idealt för en J-kropp i TNED (T=7[m_J^1/3/ρ_final]^1/2) med i storleksordningen 1 Solmassa som expanderar från max täthet 1,82 T17 KG/M³ upp till medeltätheten för Jordskorpan (ρ_final=2500 KG/M³, ungefär som sandsten) går på 15.700 S eller drygt 4 timmar — med en kroppsradieändring från nära 1,4 T4 M till nära 6 T8 M, över 4 tiopotenser — medan en rimligt motsvarande aktuell lokal ljushastighet (med exemplet c/c₀=0,1) avverkar distansen 1,4 T4 M på tiden T=d/v~5 t4 S eller 0,5 mS.

— Dvs., Planckstrålningen (E=hf) hinner (precis) rapportera eventuell strålning i samband med den maximalt högtäta kroppen — i samband med dess (relativt) snabba expansion;

Gravitella ljusavböjningen — se även i Illustration och RÄKNEEXEMPEL

— SAMTIDIGT ÄR DET UPPENBART att den strålinformationen också bör (mera av regel än undantag) bli föremål för närliggande J-kroppars ljusgravitella påverkan;

— Från exemplet med Solrandsobservationerna erhölls en allmänt (förenklad) sambandsform [Aº=(4Gm₂/rc²)180/π] för den vinkel som en ljusstråle böjer av då den passerar nära en masskropp; Med m₂ som 1 Solmassa och c=0,1c₀ ges (vi använder här det aktuella sambandet till grovprövning)

Aº = (4Gm₂/rc²)180/π ; Ljusets gravitella avböjning

= (1/r)(4Gm₂/c²)180/π

= (1/r)(33.829.989)

~ (1/r)(3,4 T8) ; m₂ som 1 Solmassa och c=0,1c₀

— Ljus på avståndet ca 3,4 T8 M från m₂:s tyngdpunkt böjs en hel grad (1º) — och än kraftigare med mindre avstånd. Vid minsta näravståndet 1,4 T4 M, m₂ som Solmassan vid max täthet 1,82 T17 KG/M³, ges avböjningsvinkeln avrundat 24286º, eller »67 varv»;

— För att ljuset som passerar m₂ ska gå runt centralkroppen och slippa ut exakt 360º får r-värdet i Solmassaexemplets fall inte vara mindre än max drygt (3,4 T8)/360 ~ 9 T5 M. Större r-värde ger motsvarande mindre utgångsvinkel.

— Exemplet understryker att SIGNALVÄGARNA från dessa TNED-regioner i universums ytterst synliga (c=0) utkanter INTE kommer att följa några »närmast sikträta linjer». Ljusvägarna kommer istället i princip bilda vilka som helst »slutriktningar» i förhållande till ideala siktlinjen observatör(Jorden)-strålkälla(GRB). Med andra ord kommer vi ALDRIG att kunna SE OM två tidsolika signaler kommer från SAMMA INTERNA galaxobjekt. Vi får aldrig veta det per någon exakt signalväg, om nu TNED-teorin beskriver sakens natur riktigt, eftersom signalvägen, tydligen, ändras hela tiden med det aktuella detonationsområdets kroppar och deras positioner (som ändras över timmar [TNED-sambandet J-kropparnas expansion]) samt de längre ut mellanliggande stoftstråken som också kan spela in för ev. absorption och smärre strålriktningsändringar taget över miljarder år.

Signalspridningen — Bildkälla, Författarens arkiv, 27Jun2012E10Bild11 NikonD90 Detalj

Primärpulsernas täta materierum (från 1,82 T17 KG/M³) — från universums absolut yttersta synrand (5,25 T25 M vid c/c₀=0 enligt TNED) — avgränsar utsignalerna och åstadkommer oåterkalleligt bestämda gravitella ljusavböjningar: signalkällan kamoufleras

SIGNALSPRIDNINGEN

Cirka 40 medelgalaxlokaler om vardera 1,8 T22 M ligger mellan universums synrand och galaxexpansionerna efter tidrymden drygt 300 miljoner år — då medelgalaxkroppen expanderat till runt 2/100 av sin normala galaxform (med Vintergatan som referensexempel). Speciellt i början på den perioden (längst till höger ovan) finns de främsta möjligheterna för källsignalen att böjas på största vinkeln av gravitationen via den framförvarande galaxkroppens maximalt täta kropp.

TNED: Mellan universums synrand (5,25 T25 M) och K-centrum finns i grovräkningen drygt 2900 medelgalaxvolymer. Galaxbildningarna börjar från maximalt högtäta J-kroppar (1,82 T17 KG/M³) genom expansion från detonationerna [Se Exemplet Vintergatan] via fusionsfaserna från divergenständningarna då områdena successivt med K-cellens expansion kommer in i lokaler med c>0 (Ljusets g-beroende) [PRIMÄRTÄNDNINGARNA]. Med Vintergatsmassan/kroppen som referensexempel tar det drygt 330 miljoner år [Se Exemplet Vintergatan] (T=7[m_J^1/3/ρ_final]^1/2) för Vintergatan att nå en diametral omfattning på ca 0,8 Kpc ~ 2/100 av nuvarande omfattning (Ø=30 Kpc).

— Figuren ovan illustrerar de ca 40 mellanliggande medelgalaxintervallen i denna period; Drygt 316 miljoner år fördelat på medelnybildningstiden ca 8 miljoner år [‡Randgalaxernas förnyelseperiod] — enligt TNED medeltiden för ett nytt galaxskikt i universums yttersta synrand att komma in i området c>0 via K-cellens totala massexpansion och därmed verkställa sina galaktiska primärbildningar.

— Största chansen för STÖRSTA MÖJLIGA gravitell ljusavböjning av partierna från primärdetonationernas energirika neutrinostötpulser — de superenergier som ansvarar för detonationsenergierna — ligger just i detta parti.

— Då centralkropparna är som mest kompakta, kan ljusstrålarna runt omkring böjas maximalt via maximala näravstånd till randen för den gravitellt ljusbrytande centralmassan. Den möjligheten försvinner sedan, alltmer, ju lägre täthet = större omfång galaxlokalen uppvisar.

I varje fall med ledning av den enkla medelintervallillustrationen ovan — grovt 40 medelgalaxlokaler (medelkubsidan 1,8 T22 M) inom grovt 7,2 T23 M (1/73 av hela sträckan 5,25 T25 M mellan K-centrum och universums synrand i den aktuella epoken) — är det uppenbart ATT gravitella ljusbrytningar bör ske — i 40-intervallet — mer av regel än undantag för VARJE ljusväg som börjar längst till höger (synranden) och avancerar till vänster (in mot K-centrum). I en sfäriskt volymär medeltäthetsanalogi kommer proportionerna (något) att ändras till fördel för en (något) lägre sannolikhet (medelgalaxpositionerna inte exakt på rad). Men det gör å andra sidan saken inte mycket åt sammanhanget, eftersom det är den aktuella ideala siktlinjen mellan K-centrum (vår position) och synranden som räknas i bestämningen av orten för signalkällan [GRBhosts].

— Genom att en nämnvärd ljusavböjning sker, företrädesvis som mest i början av 40-intervallet, blir det lika uppenbart att i stort sett INGEN fenomenmässig fysikalisk koppling finns mellan observerad signal och signalkälla utmed ideala siktlinjen: signalkällan KAN ligga VÄSENTLIGT MYCKET vid sidan av ideala siktlinjen.

Gravitella ljusavböjningen

Bara att det finns NÅGON maximalt tät masskropp mellan signalkällan och K-centrum garanterar att en gravitell ljusavböjning verkställs — obönhörligt. Det går inte att undvika den typen: starka gravitella ljusavböjningar sker med tvärsäker träffsäkerhet mellan signalkälla och K-centrum alldeles i början av signalvägen.

RELATERAD FYSIK:

Gravitell ljusavböjning kamouflerar källan: IDEALA SIKTLINJEN mellan observatör i K-centrum och signalkälla i universums utkanter AVGRÄNSAS primärt via GRAVITELL LJUSAVBÖJNING från universums syngräns: den extrema neutrinostrålningens häftiga primärpulser från galaxernas primärtändningar följer inte ideala siktlinjens väg, utan kamoufleras istället av gravitell ljusavböjning från den primärt närmast liggande galaxlokalen. Beräkningsexempel visas i huvudtexten [RÄKNEEXEMPEL cG].

— Då ljussignalen tränger allt längre in mot K-centrum (åt vänster ovan) och därmed passerar allt mera färdigutvecklade galaxlokaler (lägre täthet betyder svagare g-avböjning), finns inte längre samma möjligheter till gravitell ljusavböjning. Signalvägen kan då anta den mera reguljära ideala siktlinjens utsträckning;

Gravitella rödförskjutningen kamouflerar primära neutrinostrålningen: Speciellt på grund av signalpulsens primära neutrinokaraktär [NEUTRINOSTRÅLNING I RELATERAD FYSIK] [Neutrinostrålningen från Solen enligt TNED] från den utpräglade primärpulsens gravitella rödförskjutning, kommer signalvåglängden att dras ut mot gammaområdet då signalhastighetens lokala ljushastighet går mot toppvärdet c0 i K-centrum [LJUSETS ÄNDLIGA HASTIGHET] [lLJUSETS GRAVITELLA BEROENDE]. Med den förutsättningen av maximalt högfrekvent signal, samma som högsta möjliga genomträngande energi, har ljuset från primärstället också de bästa förutsättningarna för att kunna gå även rakt igenom galaxkärnor [GRBhosts] [OSÄKERHETEN I GRB-OBJEKTENS LOKALER].

När GRB-signalen väl når fram till K-centrum, gör den det obevekligt, undantagslöst, i linje med alla möjliga befintliga mellanliggande galaxlokaler mellan K-centrum och universums yttre delar. Därmed sagt: Det blir, såvitt synliga galaxobjekt alls framträder i närheten av GRB-signaler, hart när omöjligt att INTE hitta en starkare GRB-signal som passerar rakt igenom eller nära en mellanliggande galaxkropp, och en svagare GRB-signal som ses företrädesvis i kanten på synliga galaxobjekt, på grund av att den inte orkar igenom galaxlokalernas tätare centrum.

Figuren ovan antyder resultatet:

— VARJE GALAXLOKAL ger helt tvärsäkert upphov till en SEKTORIELLT sfäriskt UTSPRIDD signalvolym med information om galaxkroppens partikulära primärpulser. Dessa signaler kommer helt säkert att g-avböjas mer eller mindre på närmast längre ut befintliga (mera utvecklade) galaxkroppar.

— Ljustiden i lokaler med c/c₀=0,1 avverkar ett medelgalaxavstånd d=1,8 T22 M på tiden T=d/c=6 T14 S eller drygt 19 miljoner år.

— På samma tid hinner en medelgalax utveckla en medelsfärradie för den inneslutna medelgalaxmassan på 2,24 T18 M [JexpTNED];

— Med bibehållen lokal (c/c₀=0,1) blir avståndsfaktorn för 1° gravitell ljusavböjning lika med d=8,67 T18 M;

— Gravitella ljusavböjningen (Bågsekunder och Distanser) blir i grovräkningen (d=1,8 T22 M) avrundat 3,9 grader;

Gravitella ljusavböjningen, samband

T = 7[m_J^1/3/ρ_final]^1/2 ................... S, J-kropparnas primära expansioner ;

ρ_final = m_J^1/3/(T/7)² ;

= 3m_J/4πr³ ;

T = 7[m_J^1/34πr³/3m_J]^1/2

= 7[m_J^–2/34πr³/3]^1/2 ;

r³ = m_J^2/3(T/7)²3/4π ;

Aº = (4Gm₂/rc²)180/π ............... VinkelGrader, Ljusets gravitella avböjning ;

= (m₂/rc²)(720G/π) ; checkOK

= (m₂/[m_J^2/3(T/7)²3/4π]^1/3c²)(720G/π)

= (m₂/m_J^2/9[(T/7)²3/4π]^1/3c²)(720G/π) ; m₂=m_J ;

= (m_J^7/9[4π/3(T/7)²]^1/3/c²)(720G/π)

= (m_J^7/9/c²)[4π/3(T/7)²]^1/3(720G/π)

= (m_J^7/9/c²)[196πT^–2/3]^1/3(720G/π)

= (m_J^7/9/c²)T^–2/3π^–2/3[196/3]^1/3(720G)

= (m_J^7/9/c²)T^–2/3π^–2/3[2899,8627]G ; checkOK

= (m_J^7/9/c²)T^–2/3[9,017165085 t8 S^2/3KG^–7/9(M/S)^–2]

Avböjningsdistansen (r) lika med idealt omslutna centralmassans medeltäthetssfär.

KalkylkortDirekt KcGRB.ods 3LjusBryt HelpOpen

Kamoflerande g-avböjningsytan

— Genom att var och en av de runt 106 miljoner medelgalaxvolymerna avbildar en upptagande bågvinkel på ca 70 bågsekunder (70’’) på himmelsytan vid synranden — [206265](1,8 T22)/(5,25 T25 M)’’=70,719428’’ — kamouflerar g-avböjningen följaktligen som absolut maximum runt (3,9·3600)/70=200,57142 ~ 200 stycken primära galaxhimmelsfläckar:

— G-avböjningen åstadkommer en spridning av primärsignalens lokal på runt 200 omgivande galaxhimmelsfläckar.

— Med tillgängliga H=106 miljoner möjliga himmelsfläckar (Antalet randgalaxer) som förnyas i perioder om 8 miljoner år (Randgalaxernas förnyelseperiod) och med den maximalt möjliga kamouflerande frekvensen 200 per fläck (Kamouflerande g-avböjningsytan) — som betyder att varje H i medeltal kan avge lika många pulsbilder 200st och få det att se ut som om var och en av dem har 200 olika H-lokaler — ges totalt den apparenta (synbarliga) frekvensen med alla möjliga tillfällen då pulsbilder (P) kan ses från alla tillgängliga himmelsfläckar H enligt

Frekvensen synliga pulsbilder

f(P)_max = (106 T6 H)/(8 T6 år) · (200 P)

= 2650 HP/år

~ 7 HP/dygn

Genom att primärpulserna anställs på en stor mängd maximalt kompakta J-kroppar (figuren nedan illustrerar) som hela tiden befinner sig i snabb rörelse under de snabba detonationsfaserna, finns alltid möjligheten att pulsbilder från samma galaxlokal kan spridas ut på godtyckliga strålvägar från galaxkällan: vissa strålsektorer kan tillfälligt täckas för av J-kroppar (eller mellanliggande högabsorberande stoft från detonationsmassorna [högtäta filament]), som därmed tillfälligt stoppar pulsvägen för en signal som i en tidigare, eller senare, pulsbild kommer fram. Därmed kan också ljusavböjningarna längre fram förstås anta motsvarande olika karaktärer: strålvägar och g-avböjningar varierar med varje enskild pulsbild.

Figuren illustrerar den möjliga källformen bakom GRB-objekten — enligt relaterad fysik. De högtäta kropparna som finns i området, tillsammans med deras maximalt små inbördes medelavstånd och som gäller i primärtändningarna, har de allra bästa förutsättningarna för att effektivt absorbera allt närstrykande ljus. J-kropparna kan alltså i princip effektivt delvis HELT täcka för eller UTSLÄCKA mer eller mindre mängd utträngande signalljus; Endast en FRAGMENTERAD del av det idealt sfäriskt källutstrålade ljuset slipper ut.

— Jämför en ljusstråle som skickas rakt genom New Yorks Avenyer med full biltrafik i alla leder: endast tillfälligtvis slipper en och annan stråle igenom från den långt avlägsna ljuskällan, mer av regel än undantag skyms strålbilden av förbipasserande bilar.

Fraktaldelningsexemplet (bilden ovan) hjälper oss att relatera en del väsentligen metriskt avgörande argument:

— Med Vintergatans primärkropp som exempel, blir som nyligen påpekades de yttersta detonationspulserna i fraktalnivåexemplet numrerad som nr1, de som sammanhänger med typ avdelningen av Solsystemets J-kroppar, alldeles för svaga i energi för att nå upp till de observerade GRB-pulsernas nivåer (isotropiskt runt max T47 J = T54 erg). GRB-kandidaterna bör därför ligga en bit inåt centrum, enligt föregående uppställning [‡Fraktalnivåerna för GRB] i fraktaldetonationsnivå nr8. Därmed garanteras speciellt att det FINNS (stora mängder möjligt) förtäckande J-kroppar (och mellanliggande stoft [filament] från föregående detonationsmassor) som kan alternera valet av sektoriell ljusdivergens.

— Förtäckande J-kroppar, de som ligger längst ut och som ännu inte detonerat, och som därmed i kraft av sin starka gravitation kan ABSORBERA allt närstrykande ljus, har med andra ord de allra bästa förutsättningar för att stänga av eller fragmentera, effektivt, de ursprungligt idealt sfäriska ljusdivergenserna — och därmed frånta dem deras ursprungliga sfäriska stråldivergens;

— Endast de mellanliggande stråk som släpper igenom detonationskällans ljus har förutsättningar att vidarebefordra Plancksignalerna (E=hf) till oss.

Vintergatans totalmassa [LOKALA GALAXGRUPPEN] (synliga×355 enligt TNED), (grovt 2 T41 KG)(355)=7,1 T43 KG har i tillståndet som neutronkallplasma med tätheten 1,82 T17 KG/M³ sfärradien avrundat 4,5 T8 M; Ø=9 T8 M, bilden ovan höger. Den lilla primärkroppen är långt ifrån synlig bakom en framförvarande redan (väsentligen) färdigutvecklad galaxlokal som omspänner (galaxskivan, medeltal) runt 1,9 T20 M. Utsträckningen till synranden (ovan höger) är enligt resultaten i TNED ca 5,25 T25 M.

Med uppgifter i RÄKNEEXEMPEL för Gravitella ljusavböjningarna visades att ytterst små avböjningar behövs för att I PRINCIP åstadkomma (»återkorrigera») en idealt linjeformad (fragmenterad del av idealt sfärisk spridd, se även figuren nedan) ljusriktning.

— Figuren ovan antyder funktionssättet — och begränsningen:

— En fullt utvecklad galaxkropp (i våra regioner med maximal ljushastighet) har bara kapacitet att ge en högst marginell gravitell ljusavböjning, bara en bråkdel av en bågsekund. Däremot då ljus passerar nära galaxkroppen i dess maximalt tidiga utveckling, då kroppen är maximalt tät (T=7[m_J^1/3/ρ_final]^1/2) och därmed maximalt liten, kan ljusvägens g-avböjning bli betydelsefull (Signalspridningen).

Primärpulsernas fördelning på himmelsytan

TNED [Primärtändningarna]:

— VARJE GALAXLOKAL SOM BILDAS PRIMÄRT FRÅN DETONATIONERNA av J-kroppar med början från syngränsen (max 5,25 T25 M) har möjlighet att DISTRIBUERA flera (många) detonationspulser/sekvenser:

— Med hänsyn till de olika fraktalnivåernas inbördes fördröjningstider i stort utspritt över grovt räknat en månad, vidare i Antalet GRB-himmelsfläckar (Randgalaxernas förnyelseperiod) och SIGNALSPRIDNINGEN kan källpulser ses utspridda över vitt skilda himmelsområden via ideala siktlinjer — SOM OM signalerna skulle komma SLUMPARTAT från strängt och godtyckligt olika primära galaxområden.

Vi studerar detaljerna i Antalet GRB-himmelsfläckar och SIGNALSPRIDNINGEN.

Med den tekniskt [2012] observerade GRB-frekvensen på omkring 1 (eller två, vissa anger tre) per dygn [GRB-förekomsterna i MAC] är tydligen resultatet från TNED relevant i Frekvensen synliga pulsbilder (Antalet Max HP): Max 7 per dygn (2560 per år); Inte alla kommer fram hit.

Antalet GRB-himmelsfläckar — Bildkälla, Författarens arkiv, 8Jun2012E7Bild75 NikonD90 Detalj

Antalet himmelsfläckar [‡] som pulserna kan komma ifrån — och hur de ändras med tiden

Medelgalaxerna

— Medelavståndet mellan de (fullt) utbildade galaxlokalerna i synranden (c=0) är enligt TNED ca 1,8 T22 M — baserat på antalet synliga galaxer i hela det synliga universumets grovt 100 miljarder galaxlokaler (1 T11 st, se HUDF) via sfären (c=0 enligt TNED) med radien (R)=5,25 T25 M;

[(4π/3)(5,25 T25 M)³/(1 T11)]^1/3 = 1,82328 T22 M ~ 1,82 T22 M .............. medelgalaxvolymens kubsida

Antalet mellanliggande medelgalaxlokalavstånd blir då (5,25 T25 M)/(1,8 T22 M) = 2916,67~2900

Med den (R)-inneslutna massan (0,1231283)(4,14 T53 KG) fördelat på de 1 T11 medelgalaxerna ges medelgalaxmassan

m_2TOT = 5,09751 T41 KG ............ medelgalaxens totala medelmassa

~ 5,1 T41 KG

m_2VIZ = 1,43591 T39 KG ............ medelgalaxens synliga medelmassa

— Förhållandet mellan synliga och totala massan enligt TNED generellt i K-cellen är 1/355.

— Med Fraktalexemplets grova förebild (Vintergatans primärbildning mera i detalj), finns max 14 detonationsnivåer att välja på; Med vår egen lokala standard, c/c₀=1 tar det runt 14 minuter för neutroner att sönderfalla. I en lokal med c/c₀=0,1 kan vi inte räkna med vår standard; Med en grov hållning på att också neutronsönderfallets tid reduceras tio gånger på den lokalt lägre ljushastighetens kredit, kan vi räkna med att hela medelgalaxens primärdetonation är avklarad inom (inte mindre än) (14×140min)/60min = 32,67 timmar.

— Räknar vi med en hundrafaldig fördröjning blir motsvarande detonationsintervall totalt 327 timmar eller 16,625 dygn.

— Det framkommer dock (nedan i Randgalaxernas förnyelseperiod) ett mera praktiskt (maximalt) medelvärde på runt max 1 månad per galaxlokal som den absoluta gränsen för hela galaxmassans primära detonationsförlopp.

— Det tar ljuset 6 T14 sekunder (drygt 19 miljoner år) att gå vägen (åt sidorna, tangentiellt) 1,8 T22 M med lokala c=0,1c₀.

— Det föreligger därför ingen direkt överhängande anledning att de (idealt) olika galaxlokalernas ursprung kommer att blandas ihop via de olika strålvägarnas möjliga galaxinternt lokala g-avböjningar: när ljuset hinner fram till grannen efter 19 miljoner år har dennas primärbildning redan för länge länge sedan avklarats: max inom en månad.

— Däremot kan de interna processerna i den egna galaxlokalen åstadkomma att (möjligen) en stor del av strålvägarna INTE kommer att få någon exakt riktning in mot K-centrum.

— Med den omskrivna medelgalaktiska kubvolymens kubsida lika med 1,8 T22 M (ca drygt 19 st Vintergatsdiametrar) innehåller hela sfären med radien R=5,25 T25 M

antalet galaxlokaler 4πR³/3(1,8 T22 M)³ = 1,03931 T11;

— Antalet sådana rymdinneslutna galaxlokaler allra längst ut vid synranden mot c=0-kanten blir då

Antalet randgalaxer

(4π/3)[R³ – (R–1,8T22M)³]/(1,8 T22 M)³ = 1,06867 T8 ~ 106 miljoner potentiellt aktiva GRB-aspiranter — med möjlighet att bilda många inre pulser — fördelat jämnt över hela himmelsytan.

— K-cellens expansionshastighet vid R är enligt TNED ca 0,24c₀, vilket med c₀=2,99792458 T8 M/S ger en nybildningstid för hela galaxstocken i genomsnitt (vid den aktuella epoken) på

Randgalaxernas förnyelseperiod

T = d/v = (1,8 T22 M)/0,24c₀ = 2,50173 T14 S = 7,9276846 T6 år ~ 8 miljoner år

— Därmed en nybildningstid i genomsnitt för hur varje galaxlokal ändras med tiden på himmelsytan enligt

(106 T6 st)/(8 T6 år) = 13,25st/år ~ 13st/år — grovt en i månaden.

Se även föregående från Kamouflerande g-avböjningsytan.

Se vidare i huvudbeskrivningen enligt TNED från Hur energin till GRB uppkommer.

RÄKNEEXEMPEL — Gravitella Ljusavböjningen — Se även referensexempel i Vintergatans Primära Expansion — Bildkälla, Författarens arkiv, 8Jun2012E7Bild75 NikonD90 Detalj

RÄKNEEXEMPEL

Gravitella Ljusavböjningen

Aº = (4Gm₂/rc²)180/π ; Ljusets gravitella avböjning

= (1/r)(4Gm₂/c²)180/π

= (1/r)(8,67012 T29 M) ; m₂ som synuniversummassan 0,1231283(4,14 T53 KG) och c=0,1c₀

Är r mindre än 8,67012 T29 M böjs ljusstrålen mer än 1 grad.

— Max tillgänglig r-form begränsas här av 5,25 T25 M;

— MEN: Sambandsformen ovan gäller bara för ljus UTANFÖR en centralkropp, inte inuti.

— Vi kan dock (behjälpligt) från den allmänna optiken (som uppvisas samma riktningsändringsfenomenalitet som i gravitationens utpräglade fall) sluta oss till den övergripande ordning som visar att ljuset även inuti K-cellen och som begränsas av K-cellens synrand utåt, kommer att välja minsta motståndets vägar. Därmed böjer ljusvägen av in mot K-centrum om originalriktningen avviker från radius vektor. Exakt hur avböjningen fungerar inuti K-cellen kommer att bero av den aktuella masslokalens masstäthet.

Aº = (4Gm₂/rc²)180/π ; Ljusets gravitella avböjning

= (1/r)(4Gm₂/c²)180/π

= (1/r)(8,6744 T16 M) ; m₂ som 5,1 T41 KG (Medelgalaxens totalmassa) och c=c₀=2,99792458 T8 M/S

~ (1/r)(2,8 pc)

Största chansen för största möjliga avböjning ges i den allra första utvecklingsepoken av galaxkropparnas expansion: maximal masstäthet ger största gravitella ljusbrytningseffekten via kortaste näravståndet: ljusbrytningen är stor om galaxmassans täthet är hög, och sedan allt mindre ju mera galaxen expanderar till typ Vintergatans form — g-potentialen är alltid störst i skivplanet och då alldeles UTANFÖR galaxskivan (ca 15 Kpc i Vintergatans fall); G-avböjningen i ett sådant läge är ytterst liten ( i princip helt försumbar: 0,24’’).

Aº = (4Gm₂/rc²)180/π ; Ljusets gravitella avböjning

= (1/r)(4Gm₂/c²)180/π

= (1/r)(3,4017 T16 M) ; m₂ som 2 T41 KG (Vintergatans synliga massa) och c=c₀=2,99792458 T8 M/S

~ (1/r)(1 pc)

Antalet mellanliggande galaxlokaler

Mellan syngränsen 5,25 T25 M och K-centrum ligger 2917 medelgalaxvolymer, kubsidan 1,8 T22 M;

— (5,25 T25 M)/(1,8 T22 M) = 2916,6666

— Om ljuset från syngränsen passerar på avståndet 3,4 T16 M från var och en av dessa — vilket betyder strykande nära — kommer ljusstrålen i slutänden relativt källan att ha avböjts nära 3000 grader (ljusstrålen skulle i så fall, i princip, kunna gå »runt, runt i all evighet», och aldrig »hitta hem»).

— För att åstadkomma en ljusspridning på blott 10° krävs alltså i princip bara att källjuset passerar strykande nära 10 stycken galaxkusiner [i lämplig ordning] på vägen in mot K-centrum — ännu mera om vi räknar de lägre ljushastigheterna med början från synranden.

— Men även det blir en STOR siffra i sammanhanget;

— Varje Galaxlokal i universella randsynfärens skal upptar en bågvinkel på himmelsytan lika med

(206265)(1,8 T22 M)/(5,28 T25 M) = 70,719428 bågsekunder = 0,0196442° = 1’ 10,72’’;

— Om en avvikelse på bara 1°=60’ (60 bågminuter) sker — avböjning via endast EN framförvarande galaxmassa — betyder det i princip en osäkerhet i källokal på just och grovt hela 60 möjliga (eg. 51 st) av 1 given — och förutsatt att källsignalen kan avvika så mycket i primärformen innan den böjs tillbaka (vilket det verkar finnas gott om utrymme för, ehuru här endast antytt utan vidare uträkningar).

— Källsignalen, ideala siktlinjen, behöver bara avvika just ½° »rakt ut» för att längre ut, in mot K-centrum, bli avböjningsjusterad tillbaka (1°) enbart med hjälp av EN (1) galaxmassa som ligger i ljusvägen in mot centrum (och det finns alltså rent statistiskt drygt 2900 stycken att välja på vägen centrum-periferi), men via en annan siktlinje (50 galaxlokaler längre bort).

— I så fall finns möjligheten, med stora spridningar, att VARJE galaxlokal kan ge upphov till FLERA primärpulser från samma lokal, men som för en betraktare i K-centrum, Då, SKULLE se ut att komma ifrån (MINST 50 möjliga) OLIKA (när-) belägna (60-70)’’-lokaler.

— Det blir här veterligt omöjligt att utesluta så små avvikelser.

— Flera exempel finns också (även per bild) som visar hur möjliga toleranscirklar för GRB-objekt ansluter nära till eller precis igenom ett tydligt men litet galaxobjekt (som alltså här får förstås ligga framför den längre bakåt liggande egentliga GRB-objektet).

— Speciellt de allra starkaste primärsignalernas högfrekventa primära neutrinonivåer har möjlighet att gå just sådana vägar, rakt genom ett galaxcentrum via neutrinofrekvensens (successiva) förskjutning mot hård gamma via källans höga gravitella rödförskjutning.

— En svagare primärsignal kommer istället att stoppas av den framförvarande galaxens centraldel, och syns därför bara om den signalen får passera i galaxens periferi: Man hittar svagare GRB:s företrädesvis i periferin till synliga galaxkroppar, medan starkare GRBs kan förekomma överallt, även rakt igenom ett galaxcentrum (men mera sannolikt något vid sidan av, om alls).

Se vidare med samband och resulterande basdata i Signalspridningen.

— ‡

UNIVERSITY OF LJUBLJANA Faculty of Mathematics and Physics — THE GAMMA-RAY BURST - SUPERNOVA CONNECTION, March 2012

http://mafija.fmf.uni-lj.si/seminar/files/2011_2012/GRB_Tara.pdf

— ‡

Kan inte (får inte) kopieras

TRANSIENTS IN THE LOCAL UNIVERSE: SYSTEMATICALLY BRIDGING THE GAP BETWEEN NOVAE AND SUPERNOVAE — Mansi M. Kasliwal, Palomar Transient Factory Collaboration, 2011

http://www.ncra.tifr.res.in/~basi/11September/375-Kasliwal.pdf

Gravitationsenergin för K-cellens primärkroppar

E(G) = Gm₂²(1/R – 1/r) ; Idealt utan förluster gå r mot oändligt; med medeltätheten ρ=m/V(SFÄR) ges då

= m₂^5/3G(4πρ/3)^1/3 ; ρMAXprim = 1,82 T17 KG/M³

= m₂^5/3(6,0932 t5 [KG]^3/5J)

Exempel med Solmassan 1,989 T30 KG ger gravitationsenergin E(G[SOL]) = 1,91677 T46 J

;

m₂ = [E_G/(6,0932 t5 [KG]^3/5J)]^0,6

Redovisad överslagsräkning

Största fysiskt möjliga fusionsexotermiska strålenergin

REDOVISAD ÖVERSLAGSRÄKNING

Största fysiskt möjliga fusionsexotermiska strålenergin (Planckenergin E =hf) bestäms i relaterad fysik (TNED) av atomära massdefekten (18e) vid fusion. Järntoppen ligger högst via individen ₂₆Fe⁵⁶ (U=55,9349363);

— På neutronbas ges då ett förhållande mellan totalmassa [g-energi, E(G)=GM²/r_min] och max strålenergi (Planckenergi, E=hf) på

(56n)/(56n–U) = 1/(1–U/56n) = 102,64162;

— Gravitationsenergin för Solmassan från max täthet (1,82 T17 KG/M³) enligt TNED är till jämförelse 1,91677 T46 J [Genergin].

Med Solen som konkret referensexempel, och högsta strålfrekvenserna = maximala strålenergin (E=hf) i form av neutrinostrålning — den strålning som på grund av sin minimala växelverkan med omgivande materia har största chansen att visa sig i detonationen av en maximalt tät kropp — avger Solen endast ca 1% av sin totalt frigjorda Planckenergistrålning från fusionsfasen i formen av neutrinostrålning (Se Neutrinostrålningen från Solen). Totalt med Solmassan som basexempel, och i vår rymd med c/c₀=1, blir alltså maximalt högsta strålfrekvensens bidrag räknat på hela Solmassan lika med max

(1%)(1/102,64162) = 9,74263 t5 eller

en del på drygt 10.000 (eg. 10.264,162)

Ju mera kroppsmassa som neutrinostrålningen måste passera innan den läcker ut, ju mer hinner neutrinostrålningen dämpas (Comptoneffekten), och desto mindre kommer ut i netto. Å andra sidan, sett från gravitationsenergins sida [E(G)=GM²/r_min], ju större detonationsmassan är, desto häftigare frigörs delarna (garanterat av atomkärnans inkompressibilitet), och neutrinostrålningen har delvis större chanser att komma ut på grund av att delarna separerar snabbare. Vi lämnar dock tills vidare den detaljen och använder Solkroppens värden som grov (undersökande) preferens genomgående.

Om GRB-energin (isotropiskt, samma som idealt sfäriskt utgiven) är observerad som (max) 1 T47 J [se Referenstabellen GRBSNN], och det krävs (i vår rymd med c/c₀=1) en kropp med en g-energi på runt 10.000 gånger det värdet för att alls kunna härleda en utlösande detonationsenergi (Supernova) som kan frigöra den observerade GRB-energin, skulle det behövas en kropp med utgångsmassan [Genergin] lika med m₂=1,34614 T33 KG eller, avrundat

647 Solmassor

— Den fysiken är enligt TNED utesluten — i våra regioner.

— Vilken orsaken än är till de i sammanhanget hutlöst stora GRB-energierna, och såvitt uppgifterna om dem är tillförlitliga, står det klart att GRB-fenomenet INTE har någon möjlig fysisk grund i den redan utbildade galaxfysikens stjärnfält. Gränsmassorna enligt TNED ger stjärnorna max 10-15 Solmassor.

Redovisad överslagsräkning [‡Rubr], gravitella rödförskjutningen

— Gravitell rödförskjutning sänker den tillgängliga motsvarande energin ytterligare — vilket ökar den nödvändiga utgångsmässiga ekvivalenta kroppsmassan — via ljushastighetens kvadrat (E=mc²);

— Med en lokal divergens på c/c₀=0,1 kommer strålenergins faktor i förhållande till den maximalt täta kroppsmassans detonationsenergi att vara reducerad med en faktor 100.

— Den återstående effektivt utläckande maximalt högeffektiva strålenergin hamnar då i storleksordningen 100·10.000=1T6;

RESULTAT:

— Enligt TNED i en lokal med c/c₀=0,1 kan endast grovt och runt en miljondel (1/T6) av kroppsmassans ideala sprängenergi (g-energi) läcka ut i formen av observerbar neutrinostrålning, och som tvunget i gravitella rödförskjutningens försorg (med en faktor runt 1/10 enbart via 0,1c₀) kommer att förlängas till området (hård) gammastrålning.

— Med möjliga marginaler (neutrinostrålningens eventuella multiplicitet med växande detonerad basmassa) kanske vi (minst) bör räkna med en del på 1-10 miljoner av kroppsmassan. Detonationsmassor mindre än grovt 1 miljon Solmassor kan alltså (helt) bortses ifrån.

— Se vidare från GRB-objektens ursprung i TNED, GRB-TNED-värdarna och GRB-fraktalerna för GRB-upphoven enligt TNED.

PrimeEnergy — se även initiellt i Fraktalnivåerna för GRB — Bildkälla, Författarens arkiv, 22Maj2012E2Bild28 NikonD90 Detalj

TNEDbasics — hur energin till GRB uppkommer — se även i efterföljande DETONATIONSPULSERNAS REAKTIONSTID

Primärpulsens energi genom radiell packning

Detonationsschema

divergenständning	neutronsönderfall	fusioner	implosion	detonation	expansion	utläckande fusionsstrålningsrester (GRB)	efterglöd i materialet från uppvärmningen
c/c0	c/c0	c/c0	G	G	G	c/c0	c/c0

c/c0 beror av lokala ljushastigheten (som styrs av den lokala gravitationen); G beror och styrs enbart av frigjord gravitationsenergi.

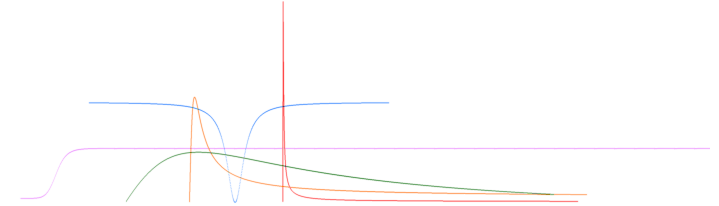
Grafer till kurvbilden y = 0[1–(1+[5x]'–2)'–1]+0[4(100x)(0.25+(100x)'2)'–1]+0.5(x'1.6)'0.5 — kurvbilderna endast illustrativt orienterande utan vidare framställning.

Radiellt idealt summerande detonationseffekten

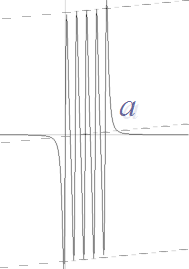
Kort sammanfattande beskrivning: Den mycket snabba fusionsfasen i den primära himlakroppens centrum (maximal divergens c från ljusets g-beroende), som följer efter divergenständning och neutronsönderfall [DIVERGENSTÄNDNINGEN I DETALJ], sammanför flera vätekärnor på enstaka betydligt mindre volymupptagande resulterande tyngre atomkärnor. Volymvakansen i centrum, och förutsatt tillräckligt stort gravitellt tryck, initierar en rörelsemängd (p=mv) för hela den övriga kroppsmassan att söka fylla den lediga centralvolymen. Rörelsemängden (mv) mot centrum tvingas av atomkärnans inkompressibilitet att stoppas upp (figurdelen i a) och detonera [IMPLOSIONSREKYLEN]: de sammanträffande atomkärnorna kastas tillbaka av exakt lika stor kraft (den upplagrade g-energin) som fick dem att sammanföras. Med den explosionsartade expansion som följer på detonationen, kan den tidigare frigjorda exotermiska Planckbaserade fusionsenergin (E=hf) frigöras som observerbar strålning för en yttre observatör — förutsatt expansionen glesar ut kroppstätheten (figurdelen i b) tillräckligt för att den tidsbegränsade primärt bildade Planckstrålningen från fusionsfasen ska kunna läcka ut. Huvudtexten nedan beskriver strålfönstret i detonationsintervallet.

a — Detonation sker alltid på maximalt tätt ytkontakterande atomkärnor via atomkärnans inkompressibilitet: detonationskraften (utan förluster) är exakt lika med den samlade kontraktionsenergin via gravitella energin E(G)=GM²/r.

Genom gravitationens absolutverkan finns i princip ingen annan fördröjningseffekt mellan kontakterande atomkärnor i radiellt metriska utsträckningar än den som anställs av ljushastighetens toppvärde (c₀=2,99792458 T8 M/S) [DETONATIONSPULSERNAS REAKTIONSTID] [ATOMKÄRNANS GRAVITELLA HÄRLEDNING].

Det betyder att reaktionstiden mellan kontakteringstillfället fram till verkställande detonation (expansion) blir av den helt enkla typen [DETONATIONSPULSERNAS REAKTIONSTID]

t = dc₀^–1

— således helt oberoende av gravitationens inverkan [DGD] på den lokala ljushastigheten. Därmed garanteras (idealt) att rekylkraften blir summerande på de enskilda atomkärnornas bidrag: summan av alla enskilda kontraktionsenergier sammanförs i radiella detonationsstråk som EN sammanhängande primärt utlösande effektpuls.

Minsta stigtiden för varje sådan idealt radiell nukleär kärnkontakterande rekyltryckpuls [Kärnåterkopplingens fördröjning] blir då (idealt sfäriskt: ρ=m/V=m/[4πr³/3]=3m/4πr³; r³=3m/4πρ)

t = m_J^1/3[3/4πρ_MAX]^1/3/c₀ ; ρ_MAX=1,82 T17 KG/M³ ; c/c₀=1

t = m_J^1/3(3,65139 t15 KG^–1/3S) ; generell från neutronkallplasma, maximal detonationsfördröjning, S

För en primärkropp av Vintergatans storlek (inkluderat totalmassan; 355 × synliga massan = 355 × 2 T41 KG) blir t = 1,511974 S.

För en primärkropp av Solens storlek (inkluderat totalmassan; 355 × synliga massan ca 355 × 2 T30 KG) blir t = 0,000325744 S = 0,3 mS ca.

För en primärkropp med t = 1 mS är detonationsmassan mJ lika med 2,05411 T34 KG eller runt 10.000 Solmassor.

För en primärkropp med t = 1 mS blir detonationsmassan m(J) tydligen lika med 2,05411 T34 KG eller runt 10.000 Solmassor:

— Det är enligt TNED med andra ord pågående kärnsvängningar [MIC] [PLANCKS STRUKTURKONSTANT] [NEUTRINOSPEKTRUM] som både utlöser och förmedlar den signalbilden via motsvarande Planckstrålningsenergier (E=hf);

GRB-utlösningen i TNED — PrimeEnergy

Förtydligat [DETONATIONEN I DETALJ]:

Fusionerna efter neutronsönderfallen via divergenständning utlöser Planckstrålningsenergierna (E=hf) via massdestruktioner (m→γ). Men dessa strålenergier kan inte tränga ut ur den primärt masskompakta detonationskroppen förrän efter den verkställande detonationen; Detonationen i sig föregås av den IMPLOSIONSREKYL som uppkommer då fusionerna reducerar antalet atomkärnor på allt mera kompakta kärnvolymer; Då vakanserna fylls på av den infallande kroppsmassan via g-trycket, initieras rörelsemängd (mv) för hela masskroppens samlade kärnbesättning, och som därmed obönhörligt och strax stoppas upp då kärnorna kommer i kontakt med varandra; Kärnkontakteringen medför oåterkallelig kärnrekyl via atomkärnans inkompressibilitet, och så inträder den aktuella detonationens expansionsfas; Först från denna punkt har masskroppen möjligheter att släppa ut fusionsstrålningsenergin, nämligen genom detonationsenergins verkställande separation mellan atomkärnorna och därmed snabbt avtagande täthet för den primära detonationskroppen; TIDEN för den (så) utläckande, kvarvarande fusionsenergistrålningen har bara, vad vi vet, EN möjlig preferens; den nämnda atomkärnans genomströmningstid via den redan inneboende toppljushastighetens naturbelopp: t = dc₀^–1; Den utläckande Planckstrålningen avklingar med »öppningen» på detonationskroppens radiella summa av primärt tätt liggande atomkärnor då dessa separeras av den frigjorda g-energin i detonationsfasen; t-värdet kan därmed förstås motsvara det »fönster» som den (starkt) tidsbegränsade Planckenergin (E=hf) har att visa upp sig på för en yttre observatör.

Genom att sedan ingen ytterligare aktivitet finns, frånsett möjligheten med detonationsfasens samtidiga bildning av betaaktiva nuklider [DETONATIONSMASSANS UPPLÖSNING] [BETANUKLIDBILDNINGEN] på kredit av den stora mängden neutronämnen i detonationskroppens yttre delar, samt efterklangen i värmestrålningens avklingande (efterglöden), finns sedan heller ingen mera strålenergi att studera — förrän primärkroppens sekventiella detonationer når fram till slutpunkten: Primärtändningen av galaxlokalens alla primärstjärnor. Men, som vi redan noterat [Fraktalnivåerna för GRB], de detonationsenergierna är — enligt TNED — alldeles för små för att ha någon betydelse i GRB-sammanhang.

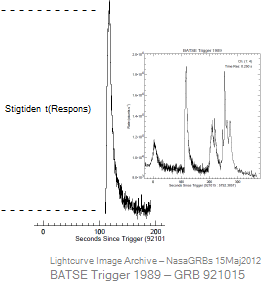
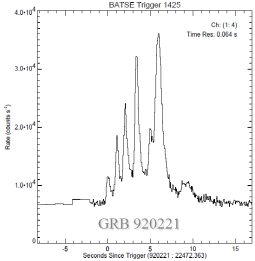
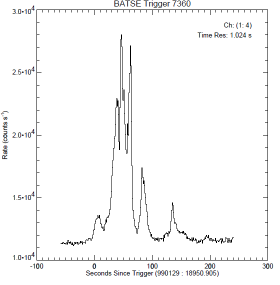
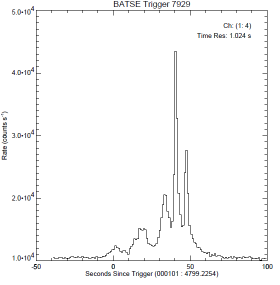
Signalsignaturen ovan från

http://www.batse.msfc.nasa.gov/batse/grb/lightcurve/

BATSE GAMMA RAY BURST LIGHT CURVES

visar hur TNED-tolkningen i GRB-utlösningens pulsfönster MÖJLIGEN kan förstås på det praktiska GRB-fallet.

— BILDEN av den utlösande verksamheten summeras totalt tillsammans med alla (idealt sfäriskt angränsande) sektoriellt spridda motsvarande radialstråk, och sammansätts därmed PER REFERENSPOSITION — inkluderat alla tidsfördröjningar i signalväg mellan de olika sektoriella detaljerna, räknat absolut från en viss metrisk xyz-position vid bestämd tidpunkt — till en totalt summerande pulsbild.

— Speciellt för J-kropparnas detonationer efter divergenständning gäller tydligen symmetriska serier av sammansatta pulser:

Alla J-kroppar (fristående massfärer i figuren ovan) i gemensam ring (eller sfäriskt skal) detonerar (idealt, med försumbar differens) samtidigt:

— Sett för en observatör (ovan höger) med kortaste avståndet källa-mål tillkommer emellertid signalfördröjningar i djupled (korta trigonometriska serier) [PRIMÄRTÄNDNINGARNA] speciellt i försorg av detonationslokalens utpräglade gravitella rödförskjutning (c/c₀=0,1) och på vars tidsbild sedan hela pulsförloppet presenteras i den mätande målstationen.

— I sammanställningen med beräkningsexempel i VÄRDEBEVIS visas att serierna också kan förstås anta rimliga kroppsvärden med inbördes pulsintervall från (bråkdelar av) sekunder till minuter — i det vi genom denna framställning enligt TNED kan förstå som detonationslokalen och dess parametrar. Figuren nedan ger grundbegreppen i avsnittets utdrag [Primär grundtrigonometri för GRB-bildning enligt TNED]:

Pulsbilderna nedan [NasaGRBs 15Maj2012] ger exempel i sekunder till minuter på flera typiska pulsbilder som FÖREFALLER ansluta till ovanstående — med tillhörande möjliga vrängningar, dämpningar och förskjutningar på grund av den långa signalvägen genom hela universum (i TNED ljusvägen runt 5,5 miljarder år), samt detaljer som sammanhänger med den primära lokalens speciella förutsättningar (högtäta [högabsorberande] stoftfilament som möjligen ansvarar för en del av signalbildens karaktär).

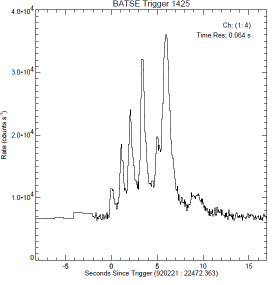
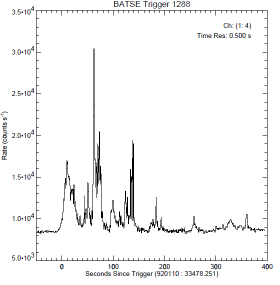
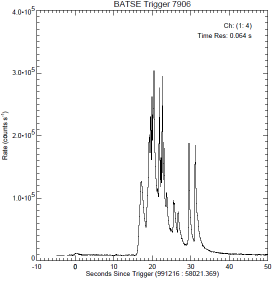
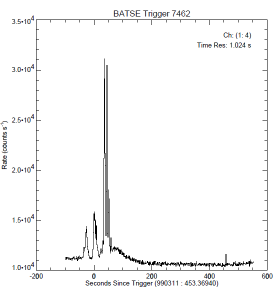
— Bilderna nedan är ett godtyckligt urval av (betydligt) fler av samma typ, och här endast för att illustrera principen: höga, branta stigpulser med tydligt separerade mellanrum som tyder på en utpräglat individuell pulsbildningsfysik.

NASA LightCurves

Lightcurve Image Archive — NASA 2001

http://www.batse.msfc.nasa.gov/batse/grb/lightcurve/

BATSE GAMMA RAY BURST LIGHT CURVES

PRIMÄRPULSENS ENERGI GENOM RADIELL PACKNING

Beskrivning — forts. frn a [Radiellt idealt summerande detonationseffekten]

b — Sedan primärpulsen detonerat masskroppen, sker omgående täthetsminskning på den utkastande kraftens kredit [DETONATIONEN I DETALJ]; Speciellt med hänsyn till redan befintligt vätgasmaterial (Vätekärnor) i detonationskroppen, och förutsatt dennas massa är tillräcklig för att utbilda nolldivergenszon i kroppsytan (här idealt sfärisk), och därmed garanterad neutronförekomst i kroppsytan (se K-cellens återvinning), kan neutroner obehindrat förenas med vätekärnor (och annat). Den möjligheten innebär också att högintensiva, lätta betaaktiva nuklider [DETONATIONSMASSANS UPPLÖSNING] [BETANUKLIDBILDNINGEN] kan bildas lokalt tillsammans med kroppsytans utkastningar i den möjliga blandningen med den inre redan befintliga vätgasen. Genom betasönderfallets utpräglade både neutrinostrålning och gammastrålning, samt med hänsyn till det korta tidsintervall som dessa strålpulser utbildas på, individuellt för varje neutronfusion (med vidare i betasönderfallets ljus, se särskilt Fusionslängden), bryts den radiellt summerande effekten från detonationsögonblicket. Effektpulserna [ENERGIINTEGRAL OCH EFFEKTDERIVATA] från (speciellt) de möjliga enskilda betanuklidbildningarna skulle därmed istället kunna ges möjligheter att bilda enskilt utspridda pulser (sektoriellt med olika vinkelspridning), överlagrade på den primär effektpulsens avtagande amplitud. Då de möjliga betanuklidbildningarnas effektpulser bör vara av dem maximalt kortare typen (FUSIONSGRÄNSTIDEN — max 3 t20 S vid c/c₀=1), finns endast ett motsvarande marginellt (minimalt) utrymme för summerande amplituder. Figuren nedan antyder funktionssättet, med vidare.

FigBNB1

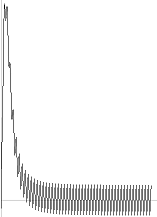
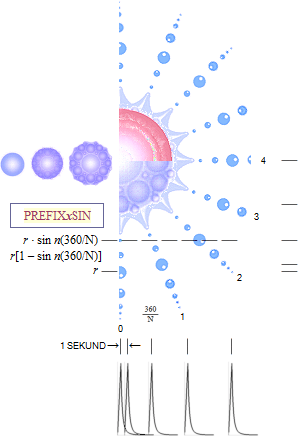
Graf y = [5x(0.25+x'2)'–2]+[(sin10þx)'1]; Unit15pixels i PREFIXxSIN

I AKTUELL LOKAL skulle totalbilden (figuren ovan FigBNB1) av förloppet ab därmed kunna beskrivas som en initierande effektpuls av konventionell typ [ENERGIINTEGRAL OCH EFFEKTDERIVATA] — åtföljd av en snabbt växande aktivitet av småpulser överlagrade på primärpulsen — och i den mån lokalen medger utrymmen för sådana pulsbilder.

— De mindre pulsbilderna (Betanuklidbildningspulserna [BNB-pulser], substituerade av sinusdelen i FigBNB1) kan beskrivas översiktligt med referens till en viss (lägsta) energinivå i den omgivande stationära ljusbilden som det mätande instrumentet (bolometer) ser som grundnivå (beror på ljusbilden från omgivande stjärnlokaler):

— I förhållande till den mätande grundnivån kan BNB-pulserna åstadkomma såväl absorberande (energivärdet avtar) som emitterande (energivärdet ökar) amplituder.

— Med förutsättningen att BNB-pulserna är maximalt korta i tid (FUSIONSGRÄNSTIDEN — max 3 t20 S vid c/c₀=1), singulärt och slumpartat åtskilda (inåt i den lokala djupbilden från en främsta mot oss närmast giltig observationspunkt), samt utspridda med motsvarande tidsfördröjning inbördes, FÖREFALLER möjligheten uppenbar att den summerande totalbilden av alla BNB-pulser tillsammans KAN uppvisa samma fason som i den ideala trigonometriska serieformen [GRB-trigonometrin] för de större J-kropparnas detonationspulser.

— Bilden av de successivt sammanförda BNB-pulsernas ±-transienter omkring den mätande grundnivån skulle därmed kunna beskrivas direkt illustrativt som nedan:

FigBNB2

Unit50pixels; Graf y =

([10x](0.25+[10x]'2)'–2)+([10(x–0.2)](0.25+[10(x–0.2)]'2)'–2)+([10(x–0.4)](0.25+[10(x–0.4)]'2)'–2)+([10(x–0.6)](0.25+[10(x–0.6)]'2)'–2)+([10(x–0.8)](0.25+[10(x–0.8)]'2)'–2)

— FigBNB2: Summerande effektpulser [ENERGIINTEGRAL OCH EFFEKTDERIVATA] bidrar inte med någon amplitudökning om varje puls dels är extremt kortvarig och dels är distinkt skild från grannens: pulståget får en helt linjär utsträckning jäms med horisontalaxeln (x). Finns någon minsta (a) pulsdel som sammanförs med grannens, samt att pulsintervallen är ungefär lika, sker en motsvarande liten, linjär, amplitudökning. Denna ökning visas i figuren ovan med de streckade linjerna. Sinusdelen i FigBNB1 förenklar grafbeskrivningen i effektpulsbildningens summeringar.

— Summeras BNB-pulserna med nära lika tidsintervall — som om pulserna vore utspridda i en ring (eller del av ett sfäriskt skal) — kommer den fallande slutflanken på varje BNB-puls, fotdelen betecknad a i figuren ovan [FigBNB2], att bidra med en liten amplitudsummering. Hela BNB-pulståget kan då liknas vid sinusdelen i FigBNB1 överlagrad på en svagt växande energibas +(0,1x) — samma som den mera reguljära BNB-pulssummeringen i FigBNB2;

FigBNB3

Graf y = [5x(0.25+x'2)'–2]+[(sin10þx)'1]+(0.1x'1); Unit15pixels i PREFIXxSIN

— Är det medelbaserade mellanrummet mellan BNB-pulserna i avtagande med mättiden — pulserna packas tätare — växer amplitudsumman i motsvarande mening, här illustrerat med hjälp av baslinjen som en parabeldel (0,05x²);

FigBNB4

Graf y = [5x(0.25+x'2)'–2]+[(sin10þx)'1]+(0.05x'2); Unit15pixels i PREFIXxSIN

— Växer istället medelavståndet mellan BNB-pulserna ges motsvarande avtagande energinivå för hela BNB-pulståget — in till gränsformen då a-fotdelen i FigBNB2 går mot noll (vilket i så fall för pulståget ut parallellt med x-axelns utsträckning);

FigBNB5

Graf y = [5x(0.25+x'2)'–2]+[(sin10þx)'1]–(0.05x'2); Unit15pixels i PREFIXxSIN

Jämförande praktiska GRB-pulsexempel

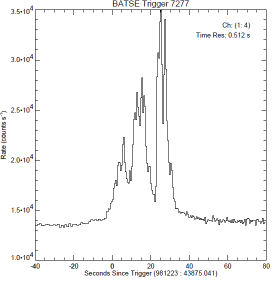
Figuren nedan visar tre praktiska GRB-pulsexempel som MÖJLIGEN ansluter till ovanstående grovt skisserade översikt [från FigBNB1]:

BATSE Trigger 7567—BATSE Trigger 7472—BATSE Trigger 3879;

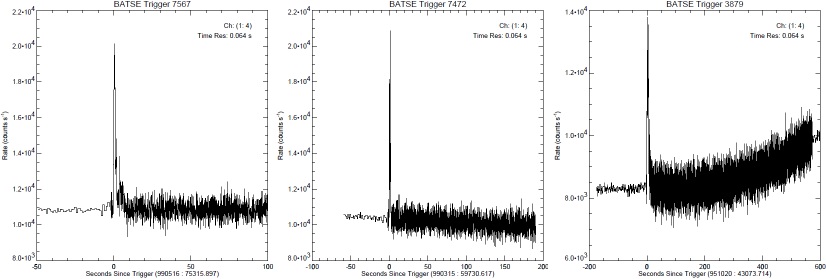
Beskrivning

— Pulsbilderna ovan [Jämförande GRB] framhäver direkt den tidigare påtalade påtriggade aktiviteten efter en initierande primärpuls (motsvarande ovan beskrivna BNB-pulser FigBNB1) efter primärpulsen;

— Speciellt i högra pulsbilden ovan (BATSE Trigger 3879) är trenden tydlig med den i FigBNB4 motsvarande tätare BNB-pulspackning — den beskrivna amplitudhöjningen.

— Speciellt i samma puls (BATSE Trigger 3879) visas också en karaktäristisk AVSLUTNING av motsvarande BNB-aktivitet: Pulsbilningen verkar upphöra tvärt vid en viss tidpunkt. En sådan fason SKULLE MÖJLIGEN kunna sammanhänga med en BNB-pulsbildning som summeras inom ett visst begränsat materialskikt: motsvarande en utsräckning för en del av en detonationsring [GRB-trigonometrin], och därmed en principiellt gemensam sluttid.

BNB-pulsernas mycket lägre energier kan försörja ljusbilden till GRB-pulsens efterglöd

I beskrivningen av ljusbilderna från Supernovor brukar man (främst, i etablerad litteratur) utnyttja supernovautbrottets allmänna tendens att bilda radioaktiva nuklider [Se exemplet SN 1998bw] — typ ₂₈Ni⁵⁶ [Jämna Nuklidserien]; De instabila nukliderna ger ut sönderfallsenergi som, under viss tid, belyser (eventuellt befintligt) omgivande gas- och stoftmassor, och därmed en generell effektform av typ (s.k.) efterglöd.

”Type Ia supernovae follow a characteristic light curve—the graph of luminosity as a function of time—after the explosion. This luminosity is generated by the radioactive decay of nickel-56 through cobalt-56 to iron-56.^[52] ”,

http://en.wikipedia.org/wiki/Supernova

@INTERNET Wikipedia , Supernova [2012-06-21]

;

”A classic example is that of supernova SN 1987A, which emits an "afterglow" of gamma-ray photons from the decay of newly-made radioactive cobalt-56.”,

http://en.wikipedia.org/wiki/Gamma_ray

@INTERNET Wikipedia , Gamma ray [2012-06-21]

Notering:

— De instabila nuklidernas bildningsintervall [BNB-komplexet] utgör ett eget specifikt effektintervall som inte kan initieras förrän expansionen efter detonationen börjar reducera kroppstätheten; Bildningsintervallets längd beror sedan på mängden tillgängliga neutroner och omfattningen av neutronfusionerna.

Primärt utkastade neutronmassor med speciellt höga hastigheter kan leda till ytterligare speciella ljusfenomen

— Utkastningen av material från detonationskroppens yttersta delar KAN om detonationsmassan är stor kvarlämna motsvarande stora mängder höghastighetsneutroner som inte kommer att sönderfalla (eg. koppla Coulombiskt i kraftverkan mellan vätekärna och elektronhölje) förrän centralmassans gravitation bromsat deras hastighet tillräckligt för att neutronhastigheterna ska understiga lokala divergensen (c/c₀), och därmed neutronsönderfall (eg. Colulombisk ordinär kraftkoppling mellan atomkärna och elektronhölje) kan påbörjas.

— Då så sker, och neutronsönderfallet fullbordas, FÖREFALLER MÖJLIGHETEN UPPENBAR ENLIGT TNED att ett NYTT LJUSABSORBERANDE SKIKT har bildats som inte fanns där förut. Om den beskrivningen är riktig, kan det skiktet i sig och på sin strålningsaktiva atombesättning uppvisa speciella ljusfenomen tillsammans med den ordinarie Planckstrålningen från detonationstillfället. Se vidare i AKROMATISKA BRYTNINGSFENOMENET I GRB.

— ‡

Preferensvärdet c/c₀=0,1 är en generaliserad referens som framträder mera tydligt genom ResultatReferensen i framställningen i GRB 061028 z9,7;

— Sammanställningen av alla tillgängliga sambandsformer (från alla möjliga partier) utpekar (nämligen självmant, som det får förstås) en närmast »mest sannolik divergenslokal» för primär himlakroppsbildning som INTE sker idealt i c/c₀=1: omkring c/c₀=0,1. Se exempelredovisningen i Exempel GRB061028.

— Med den referensen kan beskrivningen som helhet ges en mera solid grund med direkt beräkningsbara testvärden för att få fram mera konkret praktiskt prövande kvantitativa värden.

DETONATIONSPULSERNAS REAKTIONSTID — Detonationspulsernas Reaktionstid — Primärpulsens energi — Bildkälla, Författarens arkiv, 22Maj2012E2Bild28 NikonD90 Detalj

DETONATIONSPULSERNAS REAKTIONSTID

GRAVITATIONENS ABSOLUTVERKAN [Se även GcQ-teoremet] garanterar i kraft av LJUSETS GRAVITELLA BEROENDE och därmed speciellt genom ATOMKÄRNANS GRAVITELLA HÄRLEDNING att också ljushastighetens absolut högsta värde (c₀) [DEEP] [Ljusets ändliga hastighet] [c₀ bevaras oberoende av gravitationens inverkan] bevaras av massans fundamentalform: atomkärnan enligt TNED.

— När två atomkärnor klonkar ihop, utan att förenas, enbart i ideal kraft av en motsvarande idealt mekanisk stöt (MIC)

(konv. fullständigt elastisk stöt, all inkommande energi transformeras till exakt lika stor utgående energi: atomkärnan är förlustfri: atomkärnan behöver ingen energipåfyllning för att fungera)

finns genom ATOMKÄRNANS HÄRLEDNING VIA PLANCKRINGEN (massans strukturella fundamentalform [PASTOM] via Planckfraktalerna) och den därmed sammanhängande ATOMKÄRNANS INKOMPRESSIBILITET bara en högst marginell möjlighet för atomkärnan att uppvisa elastisk töjning, se särskilt i Atomkärnans geometri vid deformation.

— Med en metrisk utsträckning på max 1/1000 av kärnradien som maxgränsen för atomkärnans elastiska intervall, och inom den enda tidrymd vi har att relatera den divergens(c₀)bevarande atomkärnans elastiska kopplingstid — alltså via den i atomkärnan nämnda inneboende toppdivergensen c₀ och därmed via tiden t=r/c₀ och följaktligen helt oberoende av gravitationens makroskopiska inverkan på den lokala ljushastigheten — kan tydligen all absolut samtidig kärnkontaktering (sammanstötningens avsaktning MED avstanning och omvänd rekylbildning) återföras på och utbildas med hänsyn till DEN SAMMANTRYCKANDE LINJEN av kontakterande atomkärnor på tiden

t = dc₀^–1

med d som summan av alla samtidigt kontakterande atomkärnor på idealt exakt rät axiell gemensam linje.

— Med hela K-cellens massa (m_K=4,14 T53 KG) från maximala tätheten (ρ_MAX=1,82 T17 KG/M³) betyder det en radiellt linjär reaktionstid, från kontakteringstillfället från föregående kontraktionsfas, till expansionsfasens första del då kroppen detonerar, lika med

Kärnåterkopplingens fördröjning

t = [3m_K/4πρ_MAX]^1/3/(c₀=2,99792458 T8 M/S)

= (r_K=8,15855 T11 M)/(c₀)

= 2721,4022 S

= 45,356704 min ;

t = m_J^1/3[3/4πρ_MAX]^1/3/c₀ ; ρ_MAX=1,82 T17 KG/M³ ;

t = m_J^1/3(3,65139 t15 KG^–1/3S) ; generell från neutronkallplasma, maximal detonationsfördröjning, S

För en primärkropp av Vintergatans storlek (inkluderat totalmassan; 355 × synliga massan = 355 × 2 T41 KG) blir t = 1,511974 S.

Radiella ihopsjunkningen (D) för r_K via max elasticitet [Atomkärnans geometri under axiell deformation] med toleransen max kärnradien (neutronradien)/1000 ger (idealt medelvärde via atomkärnans omskrivna sfär, neutronradien r ~ 1,32 t15 M från Plancks konstant h=mcr, neutronmassan·c₀·r, och utan hänsyn till sektoriella [bredspridande] effekter)

D = [(r_K)/r]_{ANTALET NEUTRONER
PÅ RAD} · r/1000

= r_K/1000

= 8,15855 T8 M ;

r_K := r_K – D

= r_K – r_K/1000 = r_K(1–1/1000) = r_K(0,999)

Atomkärnas inkompressibilitet sett totalt över den kompakt samlade högtäta K-cellsmassan, och med referens till exempelbeskrivningen för Atomkärnans geometri vid deformation, medger dock (i praktiken) INGEN KOMPRESSION ALLS: försöker man komprimera atomkärnan (axiellt), blir resultatet totalt en större ytkärnomspänd volym [Atomkärnans ekvivalenta geometri vid deformation].

— Det betyder, tydligen, att absolut tätt liggande atomkärnor inom en kropp inte kan uppvisa någon ytterligare kroppsförminskning: axiell ihoptryckning resulterar i utvidgning rätvinkligt ihoptryckningen, vilket i princip överför ihoptryckning på en motsvarande utvidgning [Atomkärnans ekvivalenta geometri vid deformation].

— Detonationstillfället som följer på atomkärnornas sammanstötning måste alltså i så fall, och med nämnda orsaksgrund, förstås enbart på det fördröjande intervallets tid (t, Kärnåterkopplingens fördröjning): tiden som förflyter från ögonblicket för sammanstötning eller kärnkontaktering och den efterföljande rekylbildningen då atomkärnorna åter separerar.

— Genom att atomkärnan som massans fundamentalform [PASTOM] är en utpräglad gravitellt fraktalstrukturerad YTFORM — ihåliga toroider, ringar i ringar [Se utförligt från Planckringen om ej redan bekant], vars effektiva masstäthet därmed går mot oändligt med växande fraktaldjup (Se särskilt ATOMKÄRNANS GRAVITELLA HÄRLEDNING) — betyder »kärnkontaktering» i princip samma metriska precision som i fallet mellan två idealt GEOMETRISKA ytkonturer;

Hastigheten som kärnytorna närmar sig varandra med är betydelselös, det är endast tillfället då kontaktering sker — i princip samma som frågan om kontaktering inom ett det geometriska intervallet [Jämför INTERVALLETS OFÖRSTÖRBARHET].

FT1

Detonationen i detalj

Det innebär alltså, också, i princip att ingen icke-utlösande FT-tryckande (p=mv=maT=FT) fysikfenomenform existerar på redan tätt liggande atomkärnor; finns FT-form, leder den »omedelbart» till utlösning:

— Atomkärnor som (av olika anledningar) redan ligger tätt kan inte ’VÄNTA’ på detonationsutlösning genom att inkommande material utifrån »kommer in mjukt och ligger och trycker på under lång tid» tills ’plötsligt’ »barriären överskrids» och detonation inträffar. Händelseförloppet blir följaktligen istället: SÅ SNART kärnkontaktering sker, sker också i exakt samma mening (i t-fördröjning som ovan) en motsvarande detonationsrekyl.

— Den detaljen har (9Maj2012) inte tidigare haft någon tydlig framställning i TNED.

Se även i G-energins FT-ekvivalent — FT-detaljerna generellt i detonationssammanhanget enligt TNED.

Notera att ovanstående sammanhang berör K-cellens primära himlakroppsbildningar:

— När väl stjärnkropparna en gång har bildats, uppkommer en mera intrikat fysik:

— För en utbrunnes stjärna som kan återbilda neutroner (c=0) i den kompakta stjärnrestens sfäriska rand, i TNED som stjärnstädet [GRÄNSMASSORNA], blir motsvarande händelseförlopp små inbördes kärnrörelser (detonationsrekylstötar) mellan neutronerna som stöter emot varandra i stjärnytan i takt med att stjärnstädets kompaktvolym tar emot [Kärnfragmentering bildar neutronkallplasma] infallande material utifrån. Den aktiviteten (stötar, vibrationer) måste, således, variera i styrka med djupet från städytan in mot centrum, och i proportion till städmassan, och som — vilket här endast förmodas — leder till inre svängningsfenomen i stjärnstädet, och därmed en potentiell stjärnrest som kan uppvisa variabla ljusfenomen (utbrott), eller möjligen en pulsar [PULSARMATEMATIKEN]. Den typen av dynamik berör (emellertid) inte vårt område i den här presentationen på annat sätt än i meningen av en samlad, infallande mängd neutroner (»neutronjetstråle») som klonkar ihop gemensamt och därmed åstadkommer en radiell detonationsrekyl på kredit av atomkärnans inkompressibilitet.

Den utlösande faktorn i samband med divergenständningarna i K-cellens expansion — J-kropparnas samlade g-form i neutronkallplasmat från K-cellens detonation — ges av implosionsrekylen från fusionsfasen; Se Divergenständningen i detalj:

0. fusionerna med början i kroppens centrum (max c) åstadkommer volymvakanser (flera atomkärnor förenas på mindre volym):

1. vakanserna i rymd fylls på med inströmmande atomkärnor via g-trycket från kroppsmassan utanför:

2. den igångsatta rörelsemängden kommer obönhörligen att trigga en rekylerande och utlösande primär detonation då

3. instörtningen stoppas upp av de kontakterande atomkärnorna [Atomkärnans inkompressibilitet].

Sammanstötningarna resulterar i kärnsvängningar (av E=hf-typ via Planckfraktalerna); kärnsvängningarna överförs mellan atomkärnorna i rekylbildningen och driver expansionen mellan atomkärnorna vidare på detonationsenergins räkning — neutrinostrålning:

Genom atomkärnornas sammansättning som ±e-strukturer (Planckringen) och därmed deras sammanstötning via atomkärnans struktur av Planckfraktaler (E=[h/n]fn) [Plancks strukturkonstant] med motsvarande fraktalnivåers mekaniska svängningsformer, λ=[h/n]/nmv (MIC), måste tvunget en motsvarande Planckstrålning (E=hf) etableras:

— Svängningar som enligt TNED genomtränger atomkärnans fraktalnivåer är med fraktalnivåernas utsträckning — betingade av obegränsat avtagande mot noll enligt Atomkärnans härledning — samma som neutrinostrålning i TNED. Dessa maximalt högfrekventa svängningsformer kan bara absorberas (Comptoneffekten) genom högtäta massansamlingar av tätt liggande atomkärnor, samt i de fall någon neutrinostrålning alls läcker ut ur de masstäta lokalerna, de höga hf-frekvenserna överföras på längre våglängder (hård gamma strålning) via den gravitella rödförskjutning som de högtäta detonationskropparna uppvisar.

Den utläckande primärstrålningen

Med andra ord:

— OM någon neutrinostrålning ALLS kommer ut ifrån de massiva detonationsmassor som i TNED och i K-cellens expansionshistoria förknippas med galaxerna primära bildningsmassor (galaxernas J-moderkroppar), är det tydligt att

1. neutrinostrålningen sker tidsbegränsat med hänsyn till den inre detonatinslokalens begränsande massa [Kärnåterkopplingens fördröjning], och att

2. neutrinostrålningen via den lokalt utpräglade gravitella rödförskjutningen (c/c₀=0,1) påtvingar en våglängdsförlängning in mot K-centrum (c/c₀=1, vår förmodade position i Vintergatan med Lokala galaxgruppen) och därmed mera utpräglad gammafrekvens med nollförekomst av neutrinostrålning.

Det finns inga primära detonationskroppar i K-cellens historia som genererar (stora kvantiteter) neutrinostrålning på något annat sätt än just momentant vid detonationsögonblicket efter divergenständning.

GRB-objektens ursprung — ingen påvisbar neutrinostrålning

Därmed förefaller hela frågan om GRB-objektens ursprung redan avgjord — enligt relaterad fysik:

— GRBs blir i ljuset av TNED ursprungligen neutrinostrålning vid universums synrand från primära (seriella [Primär grundtrigonometri för GRB-bildning enligt TNED]) detonationspulser av närmast enorma proportioner (tiotusentals till flera hundratals miljoner Solmassor [GRB-energierna i TNED]) i samband med primära galaxbildningar i K-cellens expansiva historia; Då universums syngräns hela tiden utvidgas vid c=0-gränsen [Nolldivergenszonen] [UNIVERSUMS SYNRAND] och nya primärkroppar kommer in i lokalt c>0 [PRIMÄRTÄNDNINGARNA], aktiveras detonationerna därmed genom J‑kropparnas neutronsönderfall, fusionsfas, detonation och primär expansion [Divergenständningen i detalj], och som i slutänden (Se Fraktalexemplet) verkställer primärtändning för alla, samtliga, galaxkroppens stjärnor. Neutrinopulserna ges bara tidsbegränsat via primärdetonationerna, och pulsbredderna (stigtider) markerar detonationsmassornas magnituder [Kärnåterkopplingens fördröjning].

— Som neutrinostrålen ENLIGT TNED tränger in mot K-centrum, avancerar den från lokala c till centrala c₀, och därmed en våglängdsutdragning (Gravitell rödförskjutning) som överför de kortare neutrinofrekvenserna mot de observerade längre våglängderna i formen av gammafrekvenser. Fenomenformen därmed — och som det nu här får förstås enligt TNED — skulle vara densamma som den vilken har fått benämningen GRB (Gamma Ray Burst):

GRBs uppvisar ingen neutrinostrålning [NoGRBneutrino] [Neutrinostrålning fattas].

Man trodde (var helt inställda på) ATT neutrinostrålning skulle kunna påvisas från GRBs — från runt 2007 [GRBNeutrinos2007]). Förvissningen var (kanske) total — ända fram till dess att experimentstationerna (ICEcube m.fl.) började arbeta (2007) och de tomma displayerna radade upp sig. Ännu (veterligt, Jun2012) har bara NOLL framkommit i den delen. Inte ett liv.

— Ingen neutrinostrålning från GRBs.

— I TNED blir, som berörts ovan, den detaljen självskriven från ruta ett: gravitella rödförskjutningen: lokalen där GRB-signalen börjar [PRIMÄRTÄNDNINGARNA] [GRB-objektens ursprung: No Neutrino]: Då GRB-signalen — som börjar från neutrinonivån [NEUTRINOSTRÅLNINGENbasicTNED] [Den utläckande primärstrålningen] — går in mot K-centrum (c/c₀=1 [LJUSETS GRAVITELLA BEROENDE]), får händelseförloppet uppenbarligen förstås som att signalen DELS dras ut mot de längre gammavåglängderna via den successivt högre lokala ljushastigheten (från preferensvärdet c/c₀=0,1 i GRB-bildningslokalen, till c/c₀=1 i K‑centrum), och DELS ytterligare mot längre våglängder via Comptoneffekten i passagen genom speciellt de framförvarande galaxernas centraltäta områden.

Därmed försvinner (nästan helt uteslutande säkert) varje primärt spår av neutrinostrålning [NEUTRINOSTRÅLNINGENbasicTNED] från varje GRB-förekomst: intrinsiskt rent.

— Det som blir kvar är — eller ska vara i den beskrivande konsekvensen: filtrerat av all mellanliggande massa mellan universums yttersta och vår egen — i TNED — förmodade position nära K-centrum — bara gammastrålning (och i vissa fall knappt det) och lägre.

Principen bakom GRB-objekten enligt relaterad fysik — mera utförligt i GRB-trigonometrin

Principen bakom GRB-objekten enligt TNED

Ovan vänster idealiserat ett fraktaldelningsexempel med Vintergatan (eller hela K-cellen) som delningsexempel: J-kropparna avdelas successivt från maximal täthet i neutronkallplasma (1,82 T17 KG/M³) från K-cellens detonation via nolldivergenszonens svep över K-cellen som medför lokal divergenständning (c>0 via ljusets g-beroende): Neutronsönderfall inleds, med obönhörligt efterföljande kroppsdetonation. Detonationerna (ytterst korta, snabba [Divergenständningen i detalj]) frigör enorma energimängder [GRB-energierna i TNED] — och som (lägligt) enligt TNED (möjligen) dykt upp som de s.k. GRB-objekten (mera noggrant lokaliserade från 1991 [BATSE], först från 1967 publ. 1973).

— Bilden ovan höger antyder enligt TNED den möjliga (idealt symmetriska) successionen av detonationer i en given (typisk) galaxkropp.

GRB-exemplet närmast höger [NASA — BATSE GRB Light Curves] exemplifierar den motsvarande möjliga praktiska kopplingen enligt TNED: Ljuskurvan visar den tydliga trigonometriska pulsrepetitionen som många GRB-ljuskurvor har en påtaglig tendens att skylta med — vilket avgör inblandningen av TNED.

— Se även särskilt kalkylkort [VärdebevisTNED-GRB] [Primär grundtrigonometri för GRB-bildning enligt TNED] för undersökning av trigonometriska seriernas eventuella praktiska förankring i tidsbilden — Vissa bestämda grundfysikaliska villkor måste uppfyllas — för att allt ska stämma.

Galaxexpansionerna — Bildkälla, Författarens arkiv, 8Jun2012E7Bild65 NikonD90 Detalj

TNED-sambandet för galaxernas expansion — från primärbildning till fullt utvecklad stjärnlokal

TNED-sambandet J-kropparnas expansion

TNED-sambandet för (J-kropparnas expansion) Himlakropparnas primära expansioner från max täthet 1,82 T17 KG/M³ upp till J‑kroppens slutliga täthet (ρ_final) är i OBS maximal divergenslokal c=c₀ [LJUSETS GRAVITELLA BEROENDE] [PLANCKEKVIVALENTERNA] lika med tiden

T = 7[m_J^1/3/ρ_final]^1/2 ............................ S, J-kropparnas primära expansioner vid c=c0

KalkylkortDirekt KcGRB.ods 2Jexp HelpOpen

Förutsättning: maximal divergenslokal c=c₀

— Exemplet med ett sandkorn (ρ_final=2330 KG/M³) ger runt T=0,017 S, förutsatt idealt »ögonblicklig divergenständning».

— Notera att J-kropparnas detonationsmassa (m_J) i galaxbildningarnas sammanhang (J-kroppar större än 80 Solmassor [1Solmassa=1m(SOL)=grovt(2 T30 KG)], se J80-massan) tvunget inbegriper den allmänna 1/355-masskvoten i K-cellen mellan synliga och verkliga (enligt resultaten från K-cellens värmefysik).

— Med m_J=(1 T6 m[SOL]) och ρ_final upp till vatten (1 KG/dM³), blir till jämförelse expansionstiden (T) lika med

T ~ 0,22m_J^1/6=246941,64 S ~ 2,87 dygn

Ju mer masskompakt J-kroppen är — som betyder att allt större energi frigörs vid detonationen — desto större förmåga besitter också J-kroppen att DÄMPA UT initierande strålning [främst neutrinostrålning och hård gammastrålning]; strålningsläckaget växer i proportion till avtagande täthet.

— Denna detalj kan ha STOR betydelse för tolkningen av uppmätta ljuskurvor, om dessa skulle vara samma som GRB-objektens.

För en hel Vintergata

(mVIN=2,785 T41 KG ~ [1,4 T11][m(SOL)=1,989 T30 KG, se vidare referens nedan BAs313.Tabell.15.2]

med tätheten

ρ_final~VÄTGAS(vid Jordytan)~1KG/M³ [ref. Wikipedia, Density of air ~1,2754 KG/M³ dry air]

blir expansionstiden

T = 7[m_J^1/3/ρ_final]^1/2 ~ 655 dygn .......... till tätheten ungefär som luft 1 KG/M³

Precisionen i expansionssambandet för J-kropparna

via Vintergatan som testobjekt

Se även grundreferensexempel för Vintergatans del i Exempelreferens Vintergatans Expansion.

För hela Vintergatan (som ovan) med (Obs den synliga) tätheten ρ_final ~ 6,77 t20 KG/M³=(mSOL)/(1pc)³

[ref. BAs313.Tabell.15.2 Inventarielista för Vintergatan, Avstånd mellan stjärnorna ca 1 pc, massa i antal Solmassor 1,4 T11;

ρ = (1,4 T11)(1,989 T30 KG)/[(1,4 T11)(3,086 T16 M)³] = (mSOL)/(1pc)³= 6,7696 t20 KG/M³]

ges

T = 7[m_J^1/3/ρ_final]^1/2 ~ 6,89 T9 år ........ till nuv. Vintergatsskivans medeltäthet grovt 6,77 t20 KG/M³

Jämför K-cellens ålder 20,82 T9 år ;

2T:

— T-sambandet stämmer mycket nära för Vintergatans kända metrik via totalmassan m=355×mVINviz om T fördubblas:

T = 14[(355·2,785 T41 KG)^1/3/ρ_final]^1/2 = 20,82 T9 år ;

Ideala Vintergatssfärens medeltäthet ρ_final=3(355·2,785 T41 KG)/4π(~15 Kpc)³ ~ 2 t19 KG/M³ ;

Man får sfärradien mera noga (15,65 Kpc) direkt ur ρ_final från T och m_J enligt

ρ_final = m_J^1/3/(T/14)² = m_J^1/3(14/T)² = 3m_J/4πr³ ;

m_J^1/3(14/T)² = 3m_J/4πr³ ;

m_J^–2/3(14/T)² = 3/4πr³ ;

m_J^–2/3T^–2 = 3/784πr³ ;

r³ = 3m_J^2/3T²/784π ;

r = [3m_J^2/3T²/784π]^1/3 ; checkOK

;

T = 14[m_Jtot^1/3/ρ_final]^1/2 ; m_Jtot=m(VIZ)·355

Justerat samband som visar sig stämma noga med Vintergatan (stavspiralgalax 2×7);

— Sambandet kan alltså användas (med viss försiktighet) för samtliga galaxlokaler — för grov översikt.

— NOTERA EMELLERTID kvoten synliga/totala = 1/355 i TNED:

— Vissa observationer [Mörka Materien BBC 2006] verifierar den värdeformen (i stort).

— Det finns EMELLERTID fortfarande delvis STORA frågetecken inom moderna kvarter i pågående forskning i ämnet (»355» påstås vara endast 10ggr i Vintergatan), varför kvantiteterna här bör användas med viss försiktighet (tills mera bestämda besked framkommer); Vi kan pröva, men ännu inte avgöra.

Jämför modern akademi:

Utvecklingen av »galax per storlek» har (nog) föga mening i MAC:

— Modellerna man använder i modern akademi för galaxbildning [ref. Wikipedia, Milky Way, Formation] utgår ifrån redan samlade gas och stoftmassor över stora områden, och därmed i princip »nuvarande storlek» redan från början.

I TNED är bilden annorlunda:

— Alla himlakroppar börjar från maximalt tätt tillstånd (1,82 T17 KG/M³). Genom divergenständning genomgår varje masskropp en (snabb primär) expansionsfas [enligt den ideala sambandsformen för T].

— För en hel galax betyder det i vilket fall [Se Vintergatans Primära Expansion] en snabb primär utveckling med primärtändning av hela systemets stjärnbesättning — och sedan en mera långsam utveckling med växande expansion i proportion till det växande omfånget. Resultatbilden i denna senare del (Stjärnornas fördelning, indelning och klassificering) beskrivs i TNED mera ingående i STJÄRNFYSIKEN DEL 2.

Hur gäller T-sambandet i lokaler med reducerad divergens?

— Utmärkt:

— I lokaler med väsentligt reducerad divergens (c/c₀=0,1) betyder beräkning av primärmassor (m_J) i storleksordningen (minst 355·J80) en motsvarande reducerad Coulombkraft (elektriska konstanten Rc i elektriska kraftlagen).

— Det är här (ännu Maj2012) inte (riktigt) klarlagt vilken betydelse en reducerad Coulombkraft skulle ha enligt TNED för den idealt förutsatta J-kroppens (i stort sett alltid korta) expansionshistoria. Det främsta argumentet är just en reducerad Coulombkraft i ett makrokosmiskt sammanhang. Genom Atomkärnans gravitella härledning föreligger (nämligen) ALDRIG en motsvarande (direkt) dämpning i atomkärnans formbevarande kraft (se även i K-cellens detonation):

FT2

Detonationskraften hämmas inte.

— Däremot kan TILLFÄLLET FÖR DETONATIONEN göra det; Den reducerade Coulombverkan gör att en detonationsrekyl av princip kan dra ut på tiden (FT=mv) [Vidare klargörande nedan i Förtydligande Resolution], och möjligen på den vägen få J-kropparnas detonationer i området att uppvisa en mera tidsutdragen karaktär: kropparna detonerar med normal kraft, ja, men med inbördes allt längre mellanrum då lokala g-beroende divergensen (ljushastigheten c) går mot 0; vid c=0 föreligger (nämligen) ingen neutronsönderfallande aktivitet alls, och därmed heller ingen detonationsfysik.

Förtydligande Resolution:

— T-sambandet [JexpTNED] T = 7[m_J^1/3/ρ_final]^1/2

är utvecklat från EXPANSIONSSAMBANDET [ρ=3/2πGT²] med ekvivalensen mellan kinetiska och gravitella energierna — tillsammans med den elementära linjära accelerationens T-form a=v/T=2dT^–2 med T=2dv^–1, samt detaljerna från HIMLAKROPPARNAS PRIMÄRMASSOR [iterationsekvationen m_PRIM=m_PRES(1–x^k^/x)^–3/34].

— Alla dessa är utpräglat styrda och betingade enbart av gravitationen, utan hänsyn till andra detaljer.

— Därmed är det tydligt att sambandsformen för T gäller oberoende av divergenslokal.

— Det är endast expansionskraften som räknas. Den är helt oberoende av ljusfysiken.

— Se även i G-energins FT-ekvivalent — FT-detaljerna generellt i detonationssammanhanget enligt TNED.

Editor2012VI11

GRB-objektens lokaler — Bildkälla, Författarens arkiv, 8Jun2012E7Bild63 NikonD90 Detalj

Osäkerheten i GRB-objektets position

Källan nedan redovisar osäkerhetsområdena i samband med GRB 980425 och SN 1998bw,

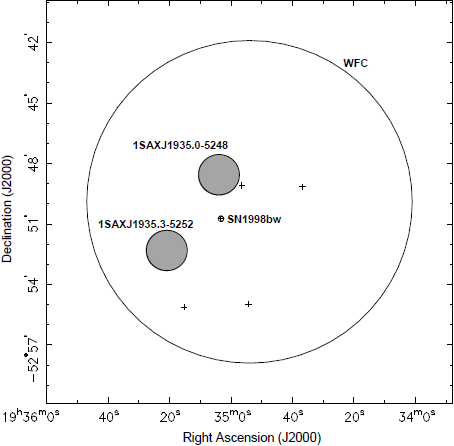
Figure 1 s14

”Figure 1. The position of objects within the 8-arcmin (radius) location error circle of the WFC for GRB 980425 (ref. 13).”,

”The two NFI X-rays sources¹⁸ (the transient 1SAXJ1935.3−5252 and the steady 1SAXJ1935.0−5248) are indicated by hatched [skuggade, svärtade] regions indicating their approximate position uncertainties. Small crosses indicate the positions of radio sources detected by the ATCA. The radio and optical emission from SN 1998bw is given by a circle with a cross.”,

http://arxiv.org/pdf/astro-ph/9807001.pdf

THE γ-RAY BURST OF 980425 AND ITS ASSOCIATION WITH THE EXTRAORDINARY RADIO EMISSION FROM A MOST UNUSUAL SUPERNOVA, Kulkarni et al., 1998

WFC — ofta använd term i PDF-rapporterna, men ännu ingen upphittad som förklarar — står förmodligen för Wide Field Camera, en term som sammanhänger med Isaac Newton Telescope, se utförlig beskrivning [”an optical mosaic camera for use at the prime focus”] i ISAAC NEWTON GROPU OF TELESCOPES 2012

http://www.ing.iac.es/Astronomy/instruments/wfc/

— Vad betyder det med referens till bilden ovan? Menar man att WFC-området markerar själva OSÄKERHETEN, eller att WFC-orådet bara markerar ett speciellt (absolut minsta) avgränsat TELESKOPFOKUS — ?

— Förmodligen så: KVADRATEN är WFC-teleskopets presentabla bildyta; CIRKELN är en i denna angiven domän inom vilken GRB-objektet kan tänkas finnas, ”location error circle of the WFC”. Min tolkning.

— OM det är den stora WFC-cirkeln man menar vara GRB-osäkerheten, kan man just undra vilka signaltomtar som INTE kan komma fram ur samlingen.

Den enda bevisbarhet som verkar finnas i etablerade led för att associera GRB 980425 — med möjlig position inom den stora markerade WFC-cirkeln [‡GRB-objektens lokaler] — med SN 1998bw (den med stor säkerhet utpekade lokalen [‡]) är att ingen annan synbar eller signaltekniskt synlig källa existerar i området.

— En alternativ webbkälla diskuterar samma område på något annorlunda fason:

Fruchter (2003)

PPT-dokument

www.stsci.edu/ts/webcasting/ppt/AndrewFruchter041304.ppt

GAMMA-RAY BURSTS: THINGS THAT REALLY GO BANG IN THE NIGHT, Andy Fruchter datumuppgift saknas (ref.2003)

— I ena fallet ligger SN 1998bw innanför en av cirklarna, i andra fallet utanför bägge.

— Det finns tydligen ingen entydigt säker information.

— Det är i vilket fall tydligt att man medvetet antar de närmast synliga aspiranterna (galaxer, stjärnhopar) för att »haka på GRB-objekt».

Bägge Kulkarni-Fruchter:

— Äventyrligt.

— För min egen del som författare till den här presentationen är det UTESLUTET att utesluta områdena UTANFÖR SN 1998bw som kandidatur för GRB 980425 när man generellt i forskarled redan väl VET att man ännu inte vet vad (GRB) det är man har hittat. Jag skulle för min författande del aldrig ge mig in på en sådan uppenbart tunn is (som att släppa in fåtalet uppenbart stenrika personer — och stänga dörrarna när fattighjonen kommer i mängd) — men det kanske bara beror på att min utgångspunkt (TNED) är helt annorlunda.

Jämför ytterligare en klargörande bildpresentation i jämförelse med ovanstående: en tydligt utvecklad galaxlokal framträder i samband med SN 1998bw (och förutsatt att inga optiska lurifax förkommer som låter lura oss) och som därmed (i TNED) klarlägger preferenserna:

SN 1998bw

FIG. 1 sL92n — här inverterad för jämförelse med närmast ovanstående från Fruchter.

”The arrow marks the position of the SN”, objektet som beskrivs är SN 1998bw,

http://iopscience.iop.org/1538-4357/542/2/L89/pdf/005580.web.pdf

HUBBLE SPACE TELESCOPE SPACE TELESCOPE IMAGING SPECTROGRAPH IMAGING

OF THE HOST GALAXY OF GRB 980425/SN 1998bw, Fynbo et al., 2000

— I TNED är preferensen för nolldivergenszonen (universums absolut yttersta synliga gräns via c/c0=0) 5,25 T25 M med c/c0=0,1 vid 5,19 T25 M; Vintergatans Radiella utsträckning (R=50.000 lå, ca 15 Kpc) upptar på det avståndet bågvinkeln

atan(50000·3T8M/S·1S/3,16888t8)/(5,19T25M)=atan(9,12048t6) = A° = 5,22565t4 = 1,88’’ — hela Vintergatans skivdiameter = 3,76 bågsekunder. Vintergatan anses dessutom tillhöra den större galaxtypen (flertalet galaxer anses bara runt tiondelen så stora [‡]).

— Bilden ovan visar i högra nedre hörnet ett skalintervall på 5 bågsekunder, ca 1cM på bildskärmen. Om galaxen vore av typen Vintergatan i utsträckning och dessutom belägen i universums synliga utkanter, skulle den rymmas inom det angivna skalintervallet på 5’’.

— Hela den avfotograferade galaxens utsträckning ger därför ett helt säkert besked att stavspiralgalaxen ovan verkligen kan förstås befinna sig på ett relativt nära avstånd från vår position — inte alls någon direkt utpräglat avlägsen galax i universums synliga utkanter — där däremot (enligt TNED) GRB-förekomsterna bör vara mera (eg. uteslutande) välrepresenterade.

— Se vidare från GRAVITELLA LJUSAVBÖJNINGEN för TNED-beskrivningen av GRB-upphoven.

— Se även exempel i GRBviz på spridningarna.

PILFOKUS i bilden ovan [‡] (Fynbo2000) visar mera preciserat (liksom författningen generellt — helt tillägnad ämnet) lokalen för SN 1998bw, här i jämförelse med föregående (Fruchter [‡]);

— Fruchters pilvisning [‡] (ref.2003 författarens egna referenser till andra rapporter i dokumentet) visar tydligen ett motsvarande tidigare fotografi där novabildningens ljusfläck syns tydligt, medan Fynbobilden [‡] (infälld nedan höger i successivt anpassad förminskning i jämnhöjd med vänsterbildens pildomän) visar en senare (eller långt tidigare) områdesbild där ingen ljusbildning framträder:

Ytterligare ett bildspel finns (här närmast upphittat) som ansluter till samma pilbild som Fruchter [‡], se (ca 1/3 in i dokumentet ”GRB 980425/SN 1998bw:”)

http://kiaa.pku.edu.cn/Activities/open_symp/Li-li-xin.pdf

The GRB-Supernova Connection — Li-Xin Li (MPA/KIAA), 29 June 2008, KIAA Opening Symposium

”The discovery of GRB 060218 / SN 2006aj has put the GRB-SN connection on a solid foundation”.

Bild på SN-objektets lokal finns i det PDF-dokument som kan nås på webbadressen

http://www.aanda.org/index.php?option=com_article&access=standard&Itemid=129&url=/articles/aa/full/2006/39/aa5530-06/aa5530-06.fig.html

Det verkar dock vara omöjligt [31Maj2012] att hitta en motsvarande astrobild av GRB 060218 med angivna felcirklar — många PDF-dokument beskriver förekomsten, men ingen verkar kunna utpeka den på någon himmelsbild i mått av bågsekunder.

Fynbogruppen [‡] rapporterar att värdgalaxen som sådan verkar vara en tummelplats för många nya stjärnbildningar:

— Utpekandet av SN 1998bw i området ges därför (därmed) extra kredit.

— Se även ExempelSN1998bw.

GRB efter/före SN — Bildkälla, Författarens arkiv, 8Jun2012E7Bild64 NikonD90 Detalj

Den avgörande frågan om dynamiken i hela fenomenkomplexet — TNEDs vara eller icke-vara

Frågan om GRB FÖRE eller EFTER SN

DEN AVGÖRANDE FRÅGAN OM TURORDNINGEN I HELA GRB-n/SN-DYNAMIKEN

GRB Gamma Ray Burst, SN Supernova

”Astronomers have detected one more clue to the origins of gamma-ray bursts, those highly energetic explosions that occur in distant galaxies. The gas cloud radiating from the source of one burst carried with it the telltale by-products of a supernova explosion. The finding, published today in Nature, strengthens the tie between supernovae and gamma-ray bursts and suggests that a burst occurs just a few days after a supernova.”,

http://www.scientificamerican.com/article.cfm?id=supernova-signature-seen

Scientific American —

SUPERNOVA SIGNATURE SEEN IN AFTERGLOW OF GAMMA-RAY BURST, April 4 2002

I MAC han man ingen teori för uppkomsten av (tillräckligt, med observationerna överensstämmande, energirik) gammastrålning FÖRE ett novautbrott (Kulkarni et al., 1998); Man menar att (sådana) gammaförekomster (om alls) måste komma EFTER ett novautbrott. Därför söker man också (inom angivna felområden) efter främst (helst) synliga kandidater som föregivna värdar för ett GRB-objekt (GRB-objektens lokaler, exempel).

Webbkällan

http://arxiv.org/pdf/astro-ph/0609142v1.pdf

THE SUPERNOVA GAMMA-RAY BURST CONNECTION, Woosley et al., 2006

berättar om tidiga teorier (s4m, Colgate, 1968) för gammautbrott föregående ”relativistic shocks”, men hänför styrkan i dessa gammaförekomster som otillräcklig, ”We know now that the transients from breakout itself are too faint to be GRBs at cosmological distances⁶.”.

I TNED är preferenserna helt omvända [GRB-objektens ursprung i TNED]: allt utgår ifrån neutrino-gammastrålning — från massdestruktioner vid all energiomsättning: massa till ljus (m→γ). Det är speciellt elementärt för himlakropparnas primärbildning, men även senare för alla aktiva ljusemitterande himlakroppars fysik: atomkärnans inkompressibilitet (finns inte i MAC, samtidigt som den används i vissa fall …) tillsammans med ett lika centralt detonationsförlopp [Divergenständningarna i detalj] bildar grundvalen för energiomsättningen i alla typer av ljusemissioner.

— Dvs., i TNED kommer GRB-förekomster (med neutrinostrålning) alltid, utan undantag, FÖRST (vilket inte nödvändigtvis betyder att dessa högfrekventa signaler också kan påvisas, vilket som gäller beror på den omgivande masstätheten, med vidare).

— På GRB-objektens bas (kraften bakom centralmassornas primära utkastningar), som det får förstås enligt TNED, utvecklas (följaktligen) sedan alla ljusemitterande fenomen — från pulsarer till novor [PULSARERNA] och alla stadigt lysande stjärnor [SOLFYSIKEN]. Se särskilt utförligt med grunderna i detalj från Solfysiken: Utan de resultat som framkommit ur den genomgången, vore den här författningen noll.

— Initierande, extremt energirika, neutrino-gammapulser [Divergenständningarna i detalj] bildar de allra första möjligt påvisbara em-signalerna som föregår efterföljande massutkastningar med tillhörande mera utpräglade novafenomen: omgivande upplysta stoftområden som expanderar bort från detonationskällan.

Det blir därför, här närmast, särskilt intressant — med det (nu 2012) stora intresse som riktats mot GRB-fysiken och de många nya upptäckterna som strömmar in — att studera förekomster som, speciellt, kan kullkasta TNED-premisserna — och därmed en gång för alla förpassa TNED-teorin till papperskorgen.

— Det finns (nämligen) i TNED ingen här veterligt relaterbar teori som kan förklara uppkomsten av korta, snabba, energirika gammapulser (av den observerade GRB-typen) — EFTER ett novautbrott.

— Den enda glädjande nyheten mellan MAC och TNED är att modellproportionerna i bägge fallen, tydligen, är av samma TYP:

FÖRST detonation (PRIMÄRENERGI) — SEDAN ljusbildning (GRB).

— Jetstråleteorin i MAC [JetMechMAC] kan som sådan inte tillämpas på TNED — på grund av PLANCKEKVIVALENTERNAS innefattade suveränitet över RELATIVITETSTEORIN; atomkärnans härledning från Plancks konstant med speciell resultatreferens till ATOMVIKTERNA. Så är med andra ord, och endast i den resultatreferensens ljus, och därutöver inte alls, fysikens vokabulär i modern akademi tydligen och relaterbarligen otillräckligt i beskrivningen av universums allmänna fysik.

— Det är också anledningen till den (nu Maj2012) etablerade uppfattningen (i överenskommelser) att GRB 980425 25Apr1998 21:49 UTC skulle sammanhänga med SN 1998bw (generellt att GRB sammanhänger med Supernovor).

— SN 1998bw upptäcktes f.ö. 26Apr1998, men enligt den noga passande ljuskurvan (ExempelSN1998bw) påbörjad (senast) CE19Apr1998 13:50:52.8 UTSunday, alltså hela sex dagar före GRB 980425.

— I MAC

— se WFC-felcirkelns omfattning [‡], tillsammans med de synliga kandidaterna, en försvinnande liten del av den möjliga cirkelytan (bilden nedan förminskning av originalet, vänster musklick över bilden leder dit),

samt själva grundteorin (beskriven av Kulkarni et al., 1998)

är den ståndpunkten helt förståelig: enda möjliga existerande energiräkningens lösning. I TNED däremot är den helt utesluten:

— GRB-förekomsten, såvitt associerad med en novaförekomst

och med den energibild som tydligen förknippas med fenomenet (runt max T47 J i princip inom sekunder),

ska under alla omständigheter komma före varje RATIONELLT ASSOCIERBAR nova/supernovaförekomst i ett redan stjärnaktivt kosmiskt sammanhang;

— FÖRST en ljusenergiutlösande GRB [vi frånser här den inledande kroppsdetonationen som frigör den efterföljande GRB-Planckstrålningen via massdestruktion (m→γ) i TNED], en PlanckenergiBank (E=hf) som PER RATIONELL FYSIKALISK LOGIK — TNED — kan försörja efterföljande upplysning av längre ut liggande material.

— SEDAN en resulterande novabildning, själva ljusfenomenet som sammanhänger med det upplysta materialet.

Inte sex dagar efteråt:

— Att en GRB-förekomst skulle komma UR en Supernovabildning sex dagar efter Supernovans uppblossande är i termer av TNED helt uteslutet. Därför är det HELT SÄKERT så — enligt TNED — att sammankopplingen mellan SN 1998bw med GRB 980425 är felaktig, icke fysikaliskt möjlig — men i MAC det uteslutande enda till buds stående teoretiska alternativ som finns.

TNEDnova/Supernova:

0. Utgångspunkten är en primärmassa eller en utbränd stjärnmassa (Stjärnstäd i TNED);

1. Gravitationens sammandragande kraft är större än summan av den frånstötande Coulombkraften + Centrifugalkrafter;

2. Centralmassor större än 10-15 Solmassor (Gränsmassorna) har genom ljusets g-beroende i (1) nolldivergens och kan därmed utbilda neutronåtervinning i massans ytterskikt (konv. neutronstjärna);

3. Infallande material som stoppas upp av den högtäta centralmassan (Stjärnstädet i TNED) rekylerar på det infallande materialets G-energi [E(G)=GM²(1/R – 1/r)], garanterat av atomkärnans inkompressibilitet;

4. Detonationsförloppet (i princip samma faktorfysik som i K-cellens detonation) blir oundvikligt;

5. Centralmassan kastar ut material under samtidigt (primärt) avgivande av neutrinostrålning och gammastrålning från den kärnrekylerande effekten (potentiell GRB-strålning, men alldeles grymt för svag för att matcha de aktuella observationerna), samt vidare genom lokala fusioner och bildning av (starkt) betaaktiva nuklider (via neutroninfall från nyssnämnda neutronbestyckade ytterhölje [neutronkallplasma i TNED]).

I denna process existerar ingen möjlighet för uppkomst av neutrino- och gammaenergier än (i våra regioner med c/c₀=1) i storleksordningen 1/10.000—1/100.000 av den totalt primärt tillgängliga Planckstrålningsenergin [Största fysiskt möjliga fusionsexotermiska strålenergin] — vilket i runda tal med Solen som exempel via dess, enligt TNED, primärt gravitella energi [detonationsreferens] E=GM²/R~2 T46 J [Gravitationsenergin för Solmassan från max täthet 1,82 T17 KG/M³] ger runt (2 T46 J)/10000 = 2 T42 J (=2 T49 erg);

— För att komma upp i storleksordningen T47 J (=T54 erg) skulle det krävas (minst) hundratusen Solmassor för att få fram den observerade GRB-energin.

Det finns ingen sådan verksamhet i universum i redan utbildade stjärnlokaler — enligt TNED.

Enligt TNED finns på sin höjd (Gränsmassorna) stjärnor med max 10-15 Solmassor (i MAC kanske upp till 100 Solmassor) som kan detonera vid slutet av brinntiden, och då dessutom i mera blygsam omfattning.

OM det nu också verkligen är så, att procedurerna i punkterna ovan är minutiöst relaterbara in till minsta praktiska detalj, finns det ingen som helst uppenbart SYNBAR grund för att förstå dynamiken på annat sätt.

— I MAC finns ingen motsvarande beskrivning (SN [supernova] före GRB [gamma-ray burst], se Kulkarni et al., 1998):

— Stjärnfysiken i MAC [JämförelseMAC-TNED] beskriver en innesluten gasmassa med atomkärnor som bildar fusioner på grund av höga kollisionshastigheter. Ett begrepp om ett primärt centralt högtätt stjärnstäd existerar inte i modern akademi — förrän efter »stjärnkollapsen» i formen av de konventionellt benämnda s.k. vita dvärgarna och neutronstjärnorna (med vidare i svarta hål), och då som mer eller mindre passiva (förbrukade) restformer.

— Atomkärnans härledning — rekylerbarhet, och därmed primär uppkomst av gammastrålningseffekter via MIC, λ=h/mv) och de resultat som sammanhänger med den delen — har ingen motsvarighet i den moderna akademins lärosystem. Se Jämförande Atomvikter: Utan den resultatbilden vore den här framställningen helt meningslös. Detaljerna utpekar utklassning.

Det är för denna författning avgörande viktigt att försöka få fram hållbara bevis som kan klarlägga ett säkert kullkastande av ovanstående punkter och i säker astronomisk bevisbarhet. Den frågan gäller, således, huruvida TNED har någon betydelse — generellt.

I MAC beskrivs uppkomsten av GRB enligt följande i citat:

”The cosmological nature of GRBs now frames our basic understanding of the physics of GRB phenomena³. The general energetics are well-constrained: given the observed fluences and redshifts, approximately 10⁵¹–10⁵³ erg in γ-ray radiation is released in a matter of a few seconds in every GRB. The GRB variability timescale suggests that this energy is quickly deposited by a ”central engine” in a small volume of space (radius of ~ 30 km) and is essentially optically thick to γ-ray radiation at early times. This opaque fireball of energy then expands adiabatically and relativistically until the γ-ray radiation can escape; the emitting surface of the GRB is likely to be 10¹⁵–10¹⁷ cm from the explosion site and probably arises from the interaction of internal shocks initiated by the central engine (e.g., Fenimore et al. 1999).”,

s3ö, Bloom2002.

I kraft av de höga GRB-energierna tvingades man anta teorin om Jetstrålar (utan Den utfyllande teorin, kollapsar modern akademi på GRB-kosmologin), som kunde reducera källenergin runt tre tiopotenser,

”When the first redshifts of GRBs were determined (Metzger et al., 1997; Kulkarni et al., 1998), the implied energies were up to ~10³ times larger than 10⁵¹ erg. In fact, the largest inferred γ-ray energy exceeded the rest mass energy of a neutron star (Kulkarni et al., 1999). Later, however, with geometric corrections for beaming (Rhoads, 1997; Halpern et al., 2000), the total energy release in γ-rays came down to around 10⁵¹ erg (Kumar and Piran, 2000; Frail et al., 2001; Freedman and Waxman, 2001; Bloom et al., 2003; Friedman and Bloom, 2005), with a small, but significant number of bursts at lower energies (e.g., Soderberg et al., 2004b). That the actual energy release in long-duration GRBs and SNe is comparable is consistent with an association, but does not require a common origin.”, s4mn,

http://arxiv.org/pdf/astro-ph/0609142v1.pdf

THE SUPERNOVA GAMMA-RAY BURST CONNECTION, Woosley et al., 2006

Källans förkortningar: erg, äldre energienhet: T7 erg = 1 Joule; GRB, Gamma Ray Burst; SN, Super Nova.

MAC:

Bästa (min mening) KORTA sammanfattningen hittills av GRB:

”The Death of Massive Stars is manifest as core collapse supernovae (CCSNe) and gamma-ray bursts (GRBs).”,

”Supernovae (SNe) are a key element in our understanding of stellar evolution, chemical enrichment, and the role they play in triggering star formation. Likewise, since GRBs are the brightest beacons they are strong signposts for determining the star formation rate over large cosmic distances. In a few rare cases, a firm connection between these objects has been established; in all these cases the SN resulted from the explosion of a highly stripped star (Type Ic SN), was very luminous, and exhibited a larger-than-usual kinetic energy (up to one magnitude more than in a normal SN explosion). In contrast, there are clear cases in which no bright SN was found to be associated with a GRB, and vice versa. The quest in understanding SNe and GRBs, and the connection between them, has raised many questions, which will be reviewed at the symposium.”,

http://www.hp.phys.titech.ac.jp/iau279/

IAU Symposium 279 — DEATH OF MASSIVE STARS: SUPERNOVAE AND GAMMA-RAY BURSTS, 2012

I TNED finns å andra sidan ingen anledning att spara på krutet:

— KompaktDetonationerna bakom himlakropparnas primära bildning kan bara frigöra (i grovräkning) 1-10 miljondelar i ren (elektromagnetisk)em-strålningsenergi [Största fysiskt möjliga fusionsexotermiska strålenergin] ur hela energikapitalet från en idealt kompakterad masskropp via dess totala g-energi (1/R=1/[3m/4πρ]^1/3=m^–1/3[4πρ/3]^1/3)

E(G) = Gm₂²(1/R – 1/r) ; Idealt utan förluster går r mot oändligt; med medeltätheten ρ=m/V(SFÄR) ges då

= m₂^5/3G(4πρ/3)^1/3 ; ρMAXprim = 1,82 T17 KG/M³

= m₂^5/3(6,0932 t5 [KG]^3/5J)

Exempel med Solmassan 1,989 T30 KG ger gravitationsenergin E(G)=1,91677 T46 J;

Divergensenergin (mcc) för hela Solmassan E=mcc är till jämförelse 1,78762 T47 KG (9,3262308 ggr E[G]).

Med Solmassan (mSOL=1,989 T30 KG) som exempel [E(G[SOL])=1,91677 T46 J = 1,91677 T53 erg] som den nödvändiga isotropiska (idealt sfäriskt utstrålande) GRB-energin, och förutsatt den primära bildningslokalen med den reducerade divergensen (c/c₀=0,1) som förutsätts i TNED, skulle det — enligt TNED — krävas en KompaktDetonationsmassa på (minst 1-) 10 miljoner Solmassor [GRB-energin i TNED] för att få fram den aktuella GRB-energin ~ 2 T46 J i ren detekterbar Planckenergistrålning (E=hf).

— Enda kandidaturen för den magnituden enligt relaterad fysik är K-cellens primära massbildningar (»primärnovor») — galaxbildningarna — från universums allra ytterst synliga delar: gravitella rödförskjutningen med dess maxområden med c/c₀=0. För vår del i TNED-resultatdelen (täthetsändringsfunktionerna) ger det ett tidsfönster bakåt på i runda tal ca 5,5 T9 (miljarder) år via max distans 5,25 T25 M. Från den distansen och inåt K-centrum växer lokala rymddivergensen (c) mot toppvärdet c/c₀=1; GRB-förekomsterna kan bara finnas i den yttersta synranden (från runt c/c₀=0,1 vid ca 5,19 T25 M). Sedan därifrån och inåt, i takt med att galaxerna har utbildat sin första generationens aktiva stjärnor; Enligt TNED:

— Då sedan de tyngsta av dessa genomgått sin första energicykel [Stjärnornas histogram] bildas pulsarer och novor. Den utvecklingslinjen förlöper sedan hela vägen in till och inkluderat vår egen galax Vintergatan.

— Neutrino- och gammastrålning bildas som redan vidrörts visserligen också initiellt i ett novautbrott, enligt TNED (Pulsarerna), men energin är helt ringa (max 1-10 miljondelar av hela utbrottsenergin [Största fysiskt möjliga fusionsexotermiska strålenergin]) och får därför ingen nämnvärd representation som kan mäta sig med de observerade GRB-energierna.

Notera här (återigen) den avgörande skillnaden mot MAC-teorin:

— GRB-energierna FÖREGÅR i TNED motsvarande (associerade, efterföljande) novafenomen i ljuset av den PRIMÄRA himlakroppsbildningen

(»primär himlakroppsbildning» i modern akademi i ett expanderande universum grundas på uppfattningen om maximalt utspridd materia som sedan sammandras gravitellt, se Jämförelse TNED-MAC)

där enorma materialmängder kastas ut, men då sett ENBART till de mest avlägsna delarna av det synliga universumet [GALAXBILDNINGARNA] [Stjärnhopar och galabildningar Del I].

— Enligt TNED skall ingen GRB-förekomst kunna påvisas omedelbart föregående ett novautbrott I EN UTPRÄGLAT ENTYDIGT synlig NÄRBELÄGEN GALAX (galax som har utvecklats minst under runt en miljon år, så att den säkert kan uppvisa minst en första normal novabildning = stjärna som slocknar och sedan uppvisar ljusflash [STJÄRNORNAS HISTOGRAM]).

— Hittar man något sådant, är GRB-TNED-teorin helt säkert KÖRD.

— I MAC-teorin finns ingen sådan primärteori, varför man istället måste kasta om ordningen och postulera att GRB-objektet kommer EFTER något (super-) novautbrott, tillsammans med ytterligare teoretiska justeringar.

Sexdagarsloppet

Jämför fallet GRB 980425 SN 1998bw; Ljuskurvan för supernovan [‡Exempel] prickar x-axelns tidsskala med början sex dagar FÖRE den efterföljande observerade GRB-förekomsten;

— Inom den STORA WFC-felcirkeln (GRB-objektets lokal) finns en redan aktiverad nova:

— I modern akademi

GRB kommer efter nova [SNföreGRBcitat1]

togs det sammanträffandet som »det första beviset» för samhörigheten SN-GRB.

Totala antalet (via 10 Solmassor super-)novautbrott i hela den aktiva galaxsfären, alltså sett totalt för hela universum och fördelat jämnt över hela himmelsytan, blir enligt TNED (efter en grov överslagsräkning [Antalet SN i Universum]) ca 1 supernova (10 Solmassor) per sekund. Källuppgifter på webben [Podsiadlowski 2012] anger uppmätta förekomsterna av GRBs till ’3 per dygn’ (1 per 28.800 S) och ’1000 gånger mindre vanliga än kärnkollapsande Supernovor’ (1 per 28,8 S).

Om medelgalaxokalen upptar grovt 70’’ på himelssfären och det enligt TNED vid universums synrand ryms 106 miljoner sådana medelgalaxfläckar (H), var och en med en potentiell GRB-förekomst, samt att det skulle finnas i medeltal 1 Supernovautbrott per sekund [Antalet SN i Universum] taget för hela universum och att man får vänta i (upp till) sex dagar [SEXDAGARSLOPPET] för att tillåtas associera en Supernova med en närliggande GRB-förekomst, då hinner det på de sex dagarna uppkomma i medeltal 6×86400=518400 Supernovor med en sannolikhet i himelsfläcksfördelning på (518400 SN)/(106 T6 H)~1/204. Det är ingen helt överväldigande lotterivinst, men å andra sidan heller ingen försvinnande liten sannolikhet att loppet skulle vara kört:

— Det skulle i princip innebära att för varje observerad GRB-förekomst, sannolikheten är 1/204 att det också just där kan finnas en redan exakt centrerad Supernovabild — och med än större sannolikhet om närhetsaspekten (70’’) utvidgas. Omvändningen däremot blir i princip utesluten.

Till den sannolikhetsbilden kommer följande:

— I TNED ligger alla, samtliga utan undantag, Supernovaförekomster framför alla GRB-objekt [PRIMÄRTÄNDNINGARNA] [Gravitella ljusavböjningen]; GRB-objektet från universums ytterst synliga rand måste avverka hela den synliga K-cellens rymd (det synliga universum), och därmed passera drygt 2900 ideala medelgalaxlokaler mellan syngränsen och vår position (5,25 T25 M via 1,8 T22 M medelgalaxlokalavstånd).

— Men de allra svagaste GRB-signalerna löper stor risk att aldrig nå fram till vår position på grund av absorption av mellanliggande galaxlokalers galaxmassor [~ 2900 mellanliggande medelgalaxokaler måste passeras]. De GRB-signaler som har bäst förutsättning för att nå hit till oss, är de med mest energi, och som därmed absorberas minst av mellanliggande galaxcentra; GRB-signaler med störst energi kan tränga igenom även mellanliggande galaxcentrum och få det att se ut som om GRB-signalen kom därifrån.

— I motsvarande mening kan en svagare GRB-signal följaktligen ta sig fram till oss om den passerar mera i utkanten på galaxernas centralmassor, och därmed framstå som att den GRB-signalen kommer ifrån någon lämpligt närliggande galax perifera delar [Bildexempel Genomträngande GRB].

— Sammantaget därmed, och i de fall GRB-signalerna verkligen ligger NÄRA någon galaxlokal (många fall, 25-50%, påstås finnas av s.k. mörka GRB, ref. Petitjean et al., 2011), är det tydligt att så kan förstås ske på grund av att alla andra fall har dämpats ut.

— Sannolikhetsbilden skulle i så fall helt enkelt och grovt sagt fördelas mellan runt 50% GRB-objekt som verkar komma ur ingenting (tomrummet mellan synliga galaxlokaler), inget närliggande galaxobjekt, och de övriga 50% fördelade ungefär lika på 25% GRB-signaler direkt ur något galaxcentrum och 25% från galaxperiferier.

— Med uppgiften om grovt max 50% mörka GRB [Petitjean et al., 2011], och de intygade osäkerheterna i allmänhet i försöken att bestämma GRB-lokalerna, verkar den uppskattningen rimlig. Se även i (osäkerheten i) GRB-objektens lokaler.

Antalet SN i Vintergatan — Bildkälla, Författarens arkiv, 8Jun2012E7Bild66 NikonD90 Detalj

Antalet SUPERnovor per tid i Vintergatan

Konventionellt används för huvudseriens stjärnor (typ Solen) sambandet för livstiden

T = (10 T9 år)(m_SOL/m_STAR)^2,5

http://en.wikipedia.org/wiki/Main_sequence

@INTERNET Wikipedia Main sequence, Lifetime [2012-05-31]

= (10 T9 år)(1/n_SOL)^2,5

= (10 T9 år)/(n_SOL)^2,5

Motsvarande i TNED är (se Tidsekvationen, idealt 100% Väteförbränning)

T = (121 T9 år)/(n_SOL)²

Antalet SUPERnovor per tid i Vintergatan — förutsatt antalet stjärnor med mindre massa än Solmassan är flest

Om SUPERnovabildningens medelstjärnmassa är 10 Solmassor av Vintergatans grovt 1 T11 Solmassor [LOKALA GALAXGRUPPEN], gäller grovt 1 T10 av dessa som (potentiellt massbaserade) SUPERnovakandidater — endast SUPERnovatyper innefattat.

— Räknar vi grovt med att bara 1/100 av de 1 T10 stycken kandidaterna är aktuella SUPERnovakandidater med massan 10 Solmassor, får vi totalt 1 T8 SUPERnovakandidater att räkna med.

— Är brinntiden för varje SUPERnovakandidat i medeltal runt 1,2 T9 år i TNED, sambandet ovan, tar det grovt sett lika lång tid innan stjärnan hinner avstanna och komma in i novastadiet (Stjärnornas histogram);

— Det ger totalt runt 2,4 T9 år för en (sådan medel-) stjärna att brinna, slockna, och sedan uppvisa SUPERnova.

— För hela Vintergatans del ger det:

(1 T8 SUPERnova)/(2,4 T9 år) = 0,04167 SUPERnova/år — eller inverterat:

— 24 år/SUPERnova.

— Bortfaller (minst) 50% på grund av skymmande stoft (vilket möjligen är rimligt för vår del), blir sluträkningen i Vintergatans fall i TNED ca 50 år mellan varje synlig SUPERnova:

”I Vintergatan förekommer supernovor troligtvis med ca 50 års mellanrum.”,

BA1978s65sp2m.

”Although no supernova has been observed in the Milky Way since 1604, supernovae remnants indicate that on average the event occurs about once every 50 years in the Milky Way.^[6]”,

http://en.wikipedia.org/wiki/Supernova

@INTERNET Wikipedia Supernova [2012-05-31]

I MAC skulle motsvarande räkning via livslängden 31.622.776 år för en normalstjärna med 10 Solmassor ge motsvarande

(1 T8 SUPERnova)/(0,032 T9 år) = 3,125 SUPERnova/år eller inverterat 0,32 år/SUPERnova:

— En SUPERnova inträffar en gång per (strax före) var fjärde månad.

— Om den synbara förekomsten gäller enligt 1 Nova per 50 år skulle motsvarande skymmande andel behöva vara ca 99,3%;

0,32/(1–0,993) ~ 45,7. Endast 0,7% av novorna är synliga för oss.

— MAC-jämförelsen visar (här) att man tydligen använder delvis andra referenser för att nå fram till det observerade värdet (runt 1 per 50 år).

Totalt för hela Universum

Enligt bilder från HST (Hubble Space Telescope) innehåller den synliga delen av universum grovt 100 miljarder (T9) galaxer (1 T11), de flesta (grovt sagt [‡] 10ggr) mindre än Vintergatan.

— I TNED (resultatet från täthetsvariationernas funktioner) är syngränsen bakåt grovt 5,5 T9 år. Det motsvarar en innesluten delmassa i K-cellen på 0,1231283mK ~ 5,1 T52 KG. Synliga delen av denna är 1/355 som ger ~ 1,436 T50 KG;

Metriken — från täthetsvariationsfunktionerna i TNED (Maj2012)

Enligt TNED har vi (Jorden med Solsystemet i Vintergatan) ett synfönster på runt 5,5 miljarder [T9] år till randen för universums absoluta nollsynbarhet vid c/c₀=0. Motsvarande avstånd är 5,25 T25 M, med 5,19 T25 M vid c/c₀=0,1 — den föreslagna lokalen för GRB-bildningarna enligt rubrikreferensen [Täthetsvariationsfunktionerna].

— Bilder på himmelsobjekt som refererar test på dessa avstånd finns i Bloom2002 och Fong2009 (Se Tänkbara Galaxvärdar för GRB).

— Medelmassan i TNED för 1 T11 galaxer blir då (1,436 T50 KG)/(1 T11) = 1,436 T39 KG eller grovt 1/140 av Vintergatsmassan (2 T41 KG ~ 1 T11 Solmassor).

— Med bevarad proportionalitet mellan massor och volymer [(r/R)³=m/M] gäller då att medelgalaxens utsträckning relativt Vintergatan i TNED blir ca en femtedel: 1/5,2; (5,2)³~140.

— Med 1/140 av resultatet för Vintergatans SUPERnovaantal skulle vi i TNED få ett grovt medelSUPERnovatal utslaget över hela det synliga universum på

[(1 Nova per 24 år)/140][1 T11] ~ 29 T6 Novor per år

Eller:

Antalet SN i Universum

Från Antalet SN i Vintergatan

FÖR HELA DET SYNLIGA UNIVERSUM:

~ 1 SUPERnova per sekund — jämnt över hela himmelsytan

— I MAC finns uppgifter som säger att SUPERnovor i hela universum är 1000 gånger vanligare än GRBs (3 per dygn; 1 per 8 timmar eller 1 GRB varje 28800 sekunder): 1 SUPERnova per 28,8 sekunder; ref. s22 Philipp Podsiadlowski, SUPERNOVAE AND GAMMA-RAY BURSTS, 2012, ”there are

about 3 GRBs in the Universe per day”, ”core-collapse supernovae are about a factor of 1000 more common.”. Notera dock att referenser saknas.

UPPGIFTERNA VARIERAR på antalet registrerade GRBs per dygn [‡AntalGRBperDygn]. Siffror som anges på webben (Jun2012) ligger i stort mellan 1-2 per dygn, vissa uppgifter finns som anger ca 3 per dygn (Podsiadlowski 2012):

— 3/86400S = 1/28800S;

— Förhållandet mellan förekomsterna skulle i så fall enligt TNED bli (som mest) grovt 28.800 befintliga SUPERnovaförekomster på varje GRB-förekomst;

— Det är (här) frestande att på den siffergrunden spekulera (exekvera) i SANNOLIKHETER. Men jag avböjer:

— Även med den mera försiktiga uppskattningen (Podsiadlowski 2012) med 1 GRB på 1000 SUPERnovor, är det tydligt att det bör finns betydligt flera observerbara SUPERnovaförekomster än registrerade GRB-förekomster.

Bildexempel — genomträngande GRB

Generellt enligt TNED — genom att alla normala SUPERnovaförekomster tvunget ligger FRAMFÖR alla GRB-objekt [PRIMÄRTÄNDNINGARNA] — blir det omöjligt att undvika förekomster där GRB-signalen (om alls) tränger igenom området för en framförvarande galax, och det därmed kommer att se ut som att GRB-objektet skulle härröra från den genomträngda galaxdomänen.

— Se (det möjliga bland flera) exemplet (här utan vidare inblick i detaljerna)

2,0’’ 9 Kpc GRB 990705

Bloom et al., 2002 Fig. 2 s49 Rad3;1 här inverterad

Se även vidare sammanställning i GRBviz — troligt inringande GRB-ursprung i förhållande till befintliga galaxområden med teleskopbilddatabas från Bloom et al., 2002 s48-50 i sammanställd översikt.

GRBviz

GRB-objektens ursprung i möjliga visuella jämförelser

VISUELLT JÄMFÖRANDE STORLEKAR FÖR GRB-OBJEKTENS URSPRUNG

GRB-OBJEKTENS VISUELLA URSPRUNG

— K-cellens inneslutna massa vid c/c0=0 är mK(0,1231283).

Vertikala strecket längst till vänster i varje IMAGE 0,1 bågsekund [0,1’’] med pixellängden (VinPIXEL 0,1’’) motsvarar den aktuella bildvinkelns 0,1’’-del — lika med ca 0,8 Kpc på avståndet 5,19 T25 M eller 1/37 av nuvarande Vintergatans diameter (ca 30 Kpc), se Vintergatans Expansion ; enligt TNED ska alla GRB-ursprung tillhöra galaxobjekt som inte alls är synliga [JexpTNED]: J-kropparna expanderar snabbt från max täthet 1,82 T17 KG/M³ med tillhörande GRB-fenomen enligt TNED, långt innan expansionerna kommer upp i nivå med normalt synliga galaxlokaler [Signalspridningen].

Cirklarna/ellipserna i IMAGE-delarna är originalförfattarnas markeringar av GRB-lokalens osäkerhet.

PDF-dokumentet [‡] i förstoringsgrad 90,7% [IMAGE-delarna nedan höger i originalstorlek med kopierad centraldel];

a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num
s48
1,0’’	3 Kpc	GRB 970228	116	12		1
0,5’’	3 Kpc	GRB 970508	116	23		2
4,0’’	12 Kpc	GRB 970828	111	3		3
a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num
1,0’’	3 Kpc	GRB 971214	116	12		4
1,0’’	-	GRB 980326	57	6		5
1,0’’	-	GRB 980329	58	6		6
a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num
8,0’’	3 Kpc	GRB 980425?	57	1	[‡] supernovaassoc.	7
2,0’’	-	GRB 980519	117	6		8
0,5’’	3 Kpc	GRB 980613	33	7		9
a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num
s49
1,0’’	3 Kpc	GRB 980703	116	12		10
1,0’’	-	GRB 981226	116	12		11
1,0’’	3 Kpc	GRB 990123	116	12		12
a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num
2,0’’	-	GRB 990308	59	3		13
2,0’’	12 Kpc	GRB 990506	58	3		14
0,5’’	3 Kpc	GRB 990510	116	23		15
a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num
2,0’’	9 Kpc	GRB 990705	58	3		16
1,0’’	3 Kpc	GRB 990712	116	12		17
0,5’’	3 Kpc	GRB 991208	60	12		18
a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num
s50
1,0’’	12 Kpc	GRB 991216	57	6		19
1,0’’	9 Kpc	GRB 000301C	61	6		20
1,0’’	4 Kpc	GRB 000418	117	12		21
a	s	GRB	a_PIXEL	Vin_PIXEL 0,1’’	IMAGE 0,1’’	num

Källdata från Bloom et al., 2002 s48-50: THE OBSERVED OFFSET DISTRIBUTION OF GAMMA-RAY BURSTS FROM THEIR HOST GALAXIES.

a källans angivna bågvinkelmått i originalbildens angivna skalintervall (alla till vänster i originalbilden);

s källans angivna metriska värde i originalbildens angivna skalintervall (alla till höger i originalbilden);

GRB källans angivna GRB-beteckning;

a_PIXEL intervallets längd i a uppmätt i antal bildpixel;

Vin_PIXEL 0,1’’ längden i pixels motsvarande 0,1 bågsekund (ca 0,8 Kpc) på referensavståndet 5,19 T25 M i a-intervallets pixellängd;

IMAGE 0,1’’ centraldelen i originalbilden uttagen med vertikalstrecket till vänster lika med Vin_PIXEL 0,1’’;

num ordningstalet för resp. GRB-objekt i tabellen ovan.

— Se även motsvarande i Fong2009.

— Referensavstånd (TNED) för Vintergatskroppens synbarhet är 5,19 T25 M — via gravitell rödförskjutningslokal vid c/c0=0,1 efter expansion [se Vintergatans Expansion] från max täthet (1,82 T17 KG/M³) vid 0,1’’ (0,1 bågsekund), vilket motsvarar en utveckling för Vintergatans del efter ca 300 miljoner år och då med en skivdiameter på ca 1/37 eller ca 0,8 Kpc av nuvarande Vintergatsdiameter ca 30 Kpc,

‡

— GRB-osäkerhetscirklarna i detta fall visas exemplifierat av andra författare i GRB-objektens lokaler.

Supernovaassocierad — webbkällans bild (ovan nr7) ger inte (riktigt) rättvisa åt den aktuella lokalen — en stor och tydlig stavsprialgalax framträder, se jämförande BILD från annan webbkälla.

Vägledande Citatmeningar som anknyter till frågan om GRB-objektens lokala ursprung

ANKNYTANDE CITAT från andra webbdokument

— ‡

s14mö,

”Indeed, most long-duration GRBs do not have a detected associated supernova.”,

http://arxiv.org/pdf/astro-ph/0609142v1.pdf

THE SUPERNOVA GAMMA-RAY BURST CONNECTION, Woosley et al., 2006

s7n,

”This fact serves as a bleak reminder that GRBs which occur at even higher redshifts

may not have their progenitors nor immediate progenitor environments directly observed.”.

— ‡

s10ö,

”For a significant proportion (25%—50%) of all well-localised GRBs, no optical/near-infrared afterglow is detected and/or the optical afterglow emission is lower than that expected from the X-ray afterglow emission (e.g. [17]). These bursts are called "dark GRB". The nature of the dark bursts is still to be understood …”, s10ö, Petitjean et al., 2011

NASA2704GRBskyMap — Bildkälla, Författarens arkiv, 27Jun2012E10Bild41 NikonD90 Detalj

2704 GRB-objekt [perioden 1991-2000 ‡] — NASAwebbSource[Yr|Mo|Da|2012-05-19] — varje fläck mäter ca 6pixels, 15°-intervalletEKV mäter 53pixels, vilket ger fläcken i bågmått lika med ca 1,7°.

http://heasarc.gsfc.nasa.gov/docs/cgro/images/cgro/2704_grbs_fluence.jpg

BATSE ALL-SKY PLOT OF GAMMA-RAY BURST LOCATIONS [2012-05-19]

http://heasarc.gsfc.nasa.gov/docs/cgro/cgro/batse_src.html

”The above figure illustrates the locations of 2704 gamma-ray bursts detected by the BATSE instrument during nine years of observations. Statistical tests confirm that the bursts are isotropically distributed on the sky - no significant quadrupole moment or dipole moment is found. At the same time, a deficiency has been detected in the number of faint bursts, interpreted as an indication that the spatial extent of the burst distribution is limited and that BATSE sees the limit or edge of the distribution. The nature of the sources remains unknown. However, their isotropic distribution on the sky along with the deficiency of faint bursts can be naturally explained if the bursts are located at cosmological distances (far beyond the Milky Way). This interpretation has been confirmed in recent years via distance estimates for optical counterparts to gamma-ray bursts.”

@INTERNET Wikipedia, Gamma ray burst, History [Illustrationen som ovan] [2012-05-19]

http://en.wikipedia.org/wiki/File:BATSE_2704.jpg

använder en icke uppdaterad version av NASA-texten ovan och vilken text anger antalet 2512 tillsammans med med korrekt illustrerad uppgift 2704 , ”The above figure illustrates the locations of 2512 gamma-ray bursts …”. Som vanligt i WikipediaVärlden betyder det också ett antal andra webbkällor som citerar Wikipediaartikelns icke uppdaterade NASA-data. Googlesökning visar noll resultat för citatfrasen med 2704 och 15 träffar med 2512. Sökning på ”locations of 2704” ger 22 träffar, alla med GRB-anknytning (tydligen källor som relaterat GRB-uppgifterna självständigt [NASA2704ill]).

[Texten i Nasas eget originaldokument rättades föredömligt snabbt av NASA-personal efter uppmärksammande och påtalande av BellDharma i dato som ovan].

Multipla GRB — från VISUELLT samma primära signallokal

Multipla GRBs från samma galaxobjekt?

Knappast …

— Det finns en del antydningar i det allmänt tillgängliga webbmaterialet (Apr-Jun2012) som (med motsvarande hög noggrannhet) pekar på en smal bild att flera GRBs möjligen kan komma från samma visuellt bestämda lokal (en bestämd himmelsfläck), eller galaxobjekt. Men utbudet är magert och inget annat verkar finnas än just någon enstaka antydning — som här lämnas för vidare då GRB-osäkerheterna [OSÄKERHETEN I GRB-LOKALERNA] redan i vilket fall är en erkänd problemform.

”We find the data to be consistent with the hypothesis that burst sources do not repeat; however, a repeater fraction of up to about 20% of the bursts cannot be excluded.”,

http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19960002231_1996102231.pdf

DO GAMMA-RAY BURST SOURCES REPEAT? — Meegan et al., 1996

”In addition, there is no evidence for repeated emission. Figure is from BATSE data web page (2001).”,

http://scipp.ucsc.edu/milagro/papers/morales_thesis.pdf

UNIVERSITY of CALIFORNIA — A SEARCH FOR TEV GAMMA-RAY BURST EMISSION WITH THE MILAGRO OBSERVATORY, Miguel. F. Morales, 2002

”In the COMPTEL sample of source locations, two bursts coincide spatially within instrumental uncertainties.⁷ GRB 930704 and GRB 940301 occurred ~8 months apart and are completely consistent with the same position on the sky within the statistical location errors (see FIGURE 1). The probability of such a coincidence occurring by chance in an isotropic distribution has been estimated using Monte Carlo simulations to be < 3% — suggesting the possibility that these two events are related to a single source.⁸ Independent localizations determined by BATSE, EGRET and the Interplanetary Network (using BATSE, Ulysses and Mars Observer arrival time analysis) cannot rule out this possibility.”,

http://www.mpe.mpg.de/~hcs/CBIB/CBIB-articles/Kippen1995d.pdf

COMPTEL OBSERVATIONS OF GAMMA-RAY BURSTS, Kippen et al., (1995)

Webbsökning (Maj2012) på ”DO GAMMA-RAY BURST SOURCES REPEAT” verkar inte ge andra träffar än runt 1993-1994: det finns inga (allmänt tillgängliga) rapporter (senare än 1995) som beskriver ämnet — varken åt det ena eller det andra hållet. En nyare webbkälla (2011) finns som omnämner sammanhanget:

”The precise location of GRBs is a challenge since GRBs are relatively short transient events which do not repeat and that they occur randomly in time and space.”,

Bhat et al., 2011, s472n

2704 lokaler (galaxområden) [NASA SkyMapGRB] finns registrerade som orten för lika många GRB-objekt enligt NASA-källan — enbart sett till GRB-observationerna (1991-2000) från BATSE-instrumentet [Burst and Transient Source Experiment, ett av fyra instrument i CGRO-observatoriet som den satellitburna projektbasen, Compton Gamma Ray Observatory, se @INTERNET Wikipedia Compton Gamma Ray Observatory], perioden 1991-2000 [‡].

— NASAskyMap-bilden visar tydligt att det finns (kanske runt 30%) fria ytor kvar som kan fyllas — med det angivna punktfältets upplösning — vilket skulle ge total runt ca 2704/[1–0,3=0,7]=3863 galaxfläckar för helt fylld himmelsyta [efter ytterligare 2,7 år med samma utrustning]) och med den angivna GRB-fläckytan.

— Det finns emellertid flera olika GRB-registrerande projekt [Bhat2011] (12st t.o.m. 2011), vart och ett med sin specifika upplösning och speciella projektändamål. Tillsammans med den naturligt (snabba) tekniska utvecklingens allt högre noggrannhet — bättre precision för varje ny satellit — ger den summan i netto en (ständigt) mer preciserad bild av GRB-objektens »himmelslokaler» med strävan att få en så noggrann positionsbestämmelse som möjligt.

I TNED bestäms fläcktätheten absolut av antalet medelgalaxlokaler i universums synliga ytterrand till max runt 106 miljoner olika möjliga himmelsfläckar [Medelgalaxerna] [Antalet randgalaxer] [Antalet GRB-himmelsfläckar] som enskilda GRB-utbrott kan komma ifrån — och vilken samling förnyas/genom positionsändring i vågor om de 106 miljonerna galaxlokaler under grovt 8 miljoner år [Randgalaxernas förnyelseperiod] som följd av K-cellens löpande expansion (i medeltal med en ändring i position för en [1] himmelsfläck per månad). Till den TNED-bilden kommer ytterligare en multipel på runt 200 [Signalspridningen] [Kamouflerande g-avböjningsytan] från den möjliga signalens spridning via gravitell avböjning från signalvägens allra första del. Denna del betyder i sig att varje galaxlokal VÄL kan anställa grovt 200 skilda GRB-tillfällen för signalrapport till K-centrum, men att av dessa bara (max)

INGEN kommer att vara direkt associerad med (en minsta möjliga) visuell synlinjes orientering mot en motsvarande ursprungslokal [GRB-objektens ursprung i TNED]: alla ideala synlinjer bryts (kraftigt) via g-brytning [Gravitella ljusavböjningen].

— Det går inte att undvika den statistiken: signalkällan i universums utkant [Gravitella rödförskjutningen] [Ljusets g-beroende] bryts helt tvärsäkert initiellt av ljusvägens kontakt med de allra närmast framförvarande mera expansivt utvecklade galaxlokalerna [JexpTNED], men (inom de första 19 miljonerna åren) fortfarande relativt små kompakta materialokaler och som därmed tvingar ljusvägen att anta g-spridning som i resultaträkning omspänner runt 200 närliggande randgalaxlokaler [Kamouflerande g-avböjningsytan].

— Därmed, kan man säga enligt TNED, att VÄL kan en och samma galaxlokal servera flera olika GRB-förekomster, skilda åt av mellanliggande intervall [VÄRDEBEVIS]. Men de signalerna, i kraft av de stora variationerna i de resulterande strålriktningarna från de högtäta detonationslokalerna [PRIMÄRTÄNDNINGARNA] [Signalspridningen], och dessa strålars närmast kommande g-avböjningar, blir i princip omöjliga att spåra till en och samma lokal som dessutom befinner sig i (våldsam) expansion [JexpTNED] och därmed ändras liktydigt med GRB-signalens innehåll. Knappast således, ska det enligt TNED finnas utrymme för någon större precision i att fastställa »multipla GRB från samma position».

— Att dessutom svårigheterna att bestämma en »precision» för en viss GRB-förekomst är ett svårt företag, understryks av nedanstående bidrag.

EXEMPEL som illustrerar [en del av de enorma] svårigheterna [Figure 1, Fong et al., 2009]:

Fong2009

http://iopscience.iop.org/0004-637X/708/1/9/fulltext/apj330995f1_hr.jpg

The Astrophysical Journal 708 (2010) 9 — HUBBLE SPACE TELESCOPE OBSERVATIONS OF SHORT GAMMA-RAY BURST HOST GALAXIES: MORPHOLOGIES, OFFSETS, AND LOCAL ENVIRONMENTS, Fong et al., 2009

http://iopscience.iop.org/0004-637X/708/1/9/fulltext/

”Figure 1. Left panel: HST/ACS/F814W image of the location of GRB 050509b. The circles mark the X-ray positions of the afterglow from the analysis of Butler (2007; red) and Evans et al. (2009; blue). Center panel: Sérsic model fit from galfit. Right panel: residual image.”.;

”¹¹ For the faint hosts without a known redshift (GRBs 051210, 060121, 060313, and possibly 061201), we assume z = 1 (Berger et al. 2007), and take advantage of the relative flatness of the angular diameter distance as a function of redshift beyond z ~ 0.5.”.

Ovanstående från ett DraftVersion PDF-dokument Dec2009 finns även i (s14)

http://arxiv.org/pdf/0909.1804v2.pdf

Hubble Space Telescope OBSERVATIONS OF SHORT GRB HOST GALAXIES: MORPHOLOGIES, OFFSETS, AND LOCAL ENVIRONMENTS, Fong et al., 2009

Informationen är väl kryptisk — författarna vill INTE ha publik. Jämför: »For Sérsic and Galfit, see endnotes S and G». Utrymme finns.

Vi kan kontrollera storleksordningar i grovräkning:

Gränsen i TNED för metrisk synbarhet (med Vintergatans primärt expansiva utveckling som referensexempel) går vid ca 0,1 bågsekund = 1 pixel i ovanstående typbild, och vilken situation enligt TNED blir aktuell först ca 0,3 T9 år efter primärbildningen från J-kroppens maximala täthet (1,82 T17 KG/M³). SYNBARHETEN FÖRE den tidpunkten kan LIKVÄL komma ifråga på samma sätt som en skarp ljusgnista från en sublimt liten (osynlig) metallspets.

— Den avgörande frågan här är enligt TNED huruvida GRB-objekt ALLS kan associeras med ANDRA himmelsobjekt än just sådana, minimalt SMÅ (pixelstora) galaxkandidater, typ bilden ovan, och som ligger bakom alla större framförvarande objekt. Enligt TNED ska ingen sådan association finnas: endast de maximalt små [eg. helt osynliga, ännu ej fullt expanderade, se Referensexempel Vintergatan] galaxobjekten räknas för sanna GRB-värdar i TNED. Äldre utvecklade galaxer (större, närmare) har redan kört sina GRB-lopp. I MAC finns ingen motsvarande association — man anser [Kulkarni et al., 1998] att en GRB sammanhänger med EN ENSKILD STJÄRNMASSA och via dennas utbrott kommer EFTER ett supernovautbrott [‡SNföreGRB] — alltså generellt i områden med redan sedan länge aktiva stjärnfält, VÄL SYNLIGA.

Bågsekunder och distanser

Avståndet mellan teleskopets kamera och den lilla knappt skönjbara galaxkroppen markerad ca 7 pixels i diameter kan grovberäknas med en uppskattad storlek för den avlägsna galaxen runt [som en första approximerande prövning] 1/5 av Vintergatan [Se HST-djupbilden, ”For example, most of the dozens of galaxies in our Local Group are at least ten times smaller in diameter”]:

(7pixels / [52/5’’])

—————— · π/180 = 3,26316 t6 = δ = d/D ; d=(Vintergatan/5)=30Kpc/5=6Kpc ;

3600

1 pc parsec) = (1AU=1,496 T11 M)·cotan(1°/3600) = 3,08572 T16 M; webben anger 3.08568025 × 10¹⁶ meters

Sambandet ovan för δ (delta) gäller om D (avståndet till objektet) är mycket större än d (objektets största utsträckning), analogt att d motsvarar en båglängd på cirkeln med radien D, vilket direkt ger d/D i radianer. För att få bågvinkeln i grader (A°) multipliceras med 180/[pi=3,1415926...]; Bågvinkeln i bågsekunder (A’’, A dubbelprim) fås genom multiplikation med 3600. Se även den likartade konventionella beskrivningen av dessa sambandsgrunder i Wikipedia Angular diameter [2012-06-01].

δ = d/D · 180/π · 3600 ............. upptagande synvinkeln i bågsekunder (A’’, a-dubbelprim) för diametern d på avståndet D >> d

d = δD / (180/π · 3600) ............ diametern d på avståndet D >> d från upptagande synvinkeln δ i bågsekunder

= δD/(~206265)

;

D = d/δ = (6 Kpc)/(3,26316 t6) = 1.838.703,4 Kpc ~ 5,7 T25 M, 1pc = ”3.08568025 × 10¹⁶ meters” ~ 3,09 T16 M.

— Med galaxobjektets diameter som grovt 1/10 av Vintergatans storlek ges motsvarande

D = d/δ = (3 Kpc)/(3,26316 t6) = 919.351,7 Kpc ~ 2,8 T25 M.

Enligt resultatbilden i TNED för K-cellen (Maj2012, täthetsvariationerna) är max största avståndet till syngränsen vid c/c₀=0 lika med runt 5,25 T25 M (5,19 T25 M vid c/c₀=0,1).

— Är galaxkropparna på bilden mellan 5-10 ggr mindre än Vintergatan (ungefär som våra mindre granngalaxer i Lokala Galaxgruppen), är den resultatbilden alltså helt rimlig (i den grova bilden).

— Notera webbkällans angivna Kpc-värde: (Här anges f.ö. konsekvent prefixen K(kilo)M(mega)G(giga) osv för successiva tusenmultipler); det är av allt att döma ett relativt distansvärde — beroende på någon i källan angiven referens; Bågvinkelmått i sig kopplar inga avstånd, endast den upptagande bildytans eller objektets synvinkel.

— Notera också att avståndsskalan i MAC för maxavståndet till universums synliga gräns är (nära 3ggr) större (ca 1,5 T26 M) på grund av referenserna för rödförskjutningarna tillsammans med den konventionella s.k. Hubblekonstanten, och som inte är direkt tillämpliga avståndsmått i TNED: det är gravitella rödförskjutningen som skiljer och som inte ingår i MAC. Det betyder att det heller inte finns någon enkel »omräkningsfaktor» mellan de olika synsätten (i TNED flyr inte galaxerna med avståndet från oss (Primärtändningarna), de håller sig (av allt att döma) relativt stilla från avdelningsdynamiken i K-cellens expansion som i stort visar en homogen/isotropisk fördelning av galaxer över hela synrummet medan istället gravitella rödförskjutningen ökar med växande avstånd från K-centrum ut mot syngränsen [och vilken rödförskjutning också avtar i takt med K-cellens utveckling], och som i MAC anses bero på bortflyende).

I TNED får vi för fotografiernas del därför helt förlita oss på de relativa (uppskattade) masskropparnas storlek tillsammans med bildkällans specificerade bågvinkelskala.

WikipediaGRB050509B

WIKIPEDIA skriver på sin artikel [2012] om GRB 050509b:

”GRB 050509B was a gamma ray burst (GRB) observed by the NASA Swift satellite on May 9, 2005. It was the first short duration GRB for which an accurate positional measurement was made, accurate enough to locate it near to an elliptical galaxy lying at a redshift of 0.225.

The significance of this finding is that it lends support to the theory that short bursts are formed during the catastrophic merger of two neutron stars, or a neutron star and a black hole. The orbital decay (via gravitational radiation) of stellar binaries consisting of these exotic compact objects is believed to take hundreds of millions of years, hence gamma ray bursts produced this way would be expected to be located in old (misleadingly called "early type") galaxies. In contrast, long-duration gamma ray bursts, which are believed to result from the collapse of a single massive star, are expected to be located preferentially in young galaxies.”,

http://en.wikipedia.org/wiki/GRB_050509B

@INTERNET Wikipedia, GRB 050509b [2012-05-19]

— Det som syns i bakgrunden vid cirklarna, är det galaxkroppar? Webbkällan ger ingen information.

MED VINTERGATAN SOM REFERENSEXEMPEL

Vintergatans skivradie [ref. Wikipedia Milky Way] brukar anges grovt som ca 50.000 ljusår [d=cT=(50.000){(2,99792458 T8 M/S)(1S/3,16888 t8)=9,46051 T15 M}=4,73025 T20 M] eller ca 15.000 pc [(15.000){(1AU=1,496 T11 M)cot(1/3600)=3,08572 T16 M}]=4,62858 T20 M; (4,7 T20 M)/(3,08 T16 M) = 15259,74 pc =ca 15.000 pc = 15 Kpc.

— Syngränsen vid c=0 är enligt täthetsändringsfunktionerna i TNED [Apr2012] för K-cellens delmassa m=0,1231283mK av K-cellens totala mK=4,14 T53 KG lika med ca 5,25 T25 M;

— Motsvarande vid ca 0,1c0 och m=0,12mK är ca 5,19 T25 M — en här helt obetydlig differens (1%).

— Vintergatans skivradie skulle på det avståndet uppvisa bågvinkeln [jämför bilden ovan]

arctan(4,7 T20 M)/(5,25 T25 M) = 5,12933 t4 grader = 1.847 bågsekunder [1,85’’]; För hela skivan ca 3,7’’.

A’’ = (206265)(4,7 T20 M)/(5,19 T25 M) = 1,8679104

— Skalan i bilden för 5’’ [ca 1/3 större än Vintergatsskivan om avståndet är 5,25 T25 M]

är i visuell längd på bildskärmen ca

----------------- ;

— OM de små typfläckarna i och omkring de markerade cirklarna skulle vara »minigalaxer» [i tidigt skede enligt TNED, se J-kropparnas expansion — i MAC utesluter man nog helt säkert den typen] skulle deras diameter vara motsvarande i skalan [grovt]

-- ;

eller ca 1/8 [eller t.o.m. mycket mindre — osynliga för oss sett rent metriskt, men fullt tekniskt möjliga för signal].

— Exakt HUR dessa detaljer förhåller sig till det stora området i bilden ovan kan vara en svårare fråga att reda ut — om det är associerade delar, eller [högra bilden ovan] kanske [pågående] galaxbildningar [enligt TNED från max täthet = osynligt i denna skala och vidare uppåt] i separata områden framför [eller kanske bakom] huvudområdet ...

— Det är [ALLTSÅ] i princip omöjligt att avgöra enbart på den aktuella tidsbilden.

[Cirklarna visar kanske större noggrannhet än vad författarna hade tänkt sig].

— De flesta av oss skulle nog (knappast) kalla ovanstående »identifikation» för någon direkt överväldigande fullträff (om uppgiften gällde att träffa det stora mörka partiet — men vem har bestämt om den uppgiften? Favoriserad Idealism) — cirklarna ligger klart utanför den stora huvudpunkten, vid sidan av det stora (svagt elliptiska) objektet (som Wikipediaartikeln påstår vara GRB-värden av typ »accurate enough», såvitt här korrekt uppfattat). Vi skulle (nog, gärna, helst) se mer solida argument för att fastställa någon koppling: osäkerheten rent visuellt är i vilket fall alldeles tydlig; Vad säger att GRB-värden inte ligger (skymd) inuti cirkelskärningarna i en lokal helt skild från (bakom eller framför) det stora mörka området? Webbkällan ger ingen specifik diskussion, så vi vet här inte närmare vilka argumenten är.

— En ingående detaljerad datalogg för GRB 50509b finns f.ö. i webbkällan

http://gcn.gsfc.nasa.gov/other/050509.gcn3

med meningar av typen ”The XRT imaged the field at 01:47:22.76 (54.8s after the burst), but did not find any bright source in the field.”. Inte speciellt övertygande (min mening); Gamla signalvägar med (som det kanske får förstås) flera miljarder år på nacken behöver nog mera kött på benen för att få en trovärdig källgestalt.

Jämför även kritiska (varnande) röster i konventionella led:

”Abstract. The nearby long GRB 060614 was not accompanied by a supernova, challenging the collapsar model for long GRBs and the traditional classification scheme for GRBs. However, Cobb et al. have argued that the association of GRB 060614 and its host galaxy might be a chance coincidence. In this work we calculate the probability for a GRB to be coincident with a galaxy on the sky using a galaxy luminosity function obtained from SDSS. We find that, up to redshift sim0.7> that can be reached for galaxies in SDSS, the probability is about one percent.”, s68,

”The total probability is a few percent. Although this probability is small, it warns us that identifying a GRB host based only on the superposition of a GRB with a galaxy on the sky is dangerous. So far about 200 GRBs have been detected by Swift. Our results imply that several cases of chance coincidence of a GRB with a galaxy might have already happened. As a result, some GRB hosts that have been found might be superficial, including the case of GRB 060614.”,

http://www.mpa-garching.mpg.de/mpa/publications/preprints/pp2008/MPA2358.pdf

American Institute of Physics 2008 — Max Planck Institute — PROBABILITY FOR A GAMMA-RAY BURST TO BE COINCIDENT WITH A GALAXY ON THE SKY, Maria Angela Campisi (2007)

Det ovannämnda GRB-objektets erkända obekanta signalnatur beskrivs även i Wikipediaartikeln,

”The burst lasted for 102 seconds, placing it soundly in long-burst territory. But the burst lacked the hallmark of a supernova, or star explosion, commonly seen shortly after long bursts. Also, the burst's host galaxy has a low star-formation rate with few massive stars that could produce supernovae and long gamma-ray bursts. "This was close enough to detect a supernova if it existed," said Avishay Gal-Yam of Caltech, Pasadena, Calif., lead author on another Nature report. "Even Hubble didn't see anything."

Certain properties of the burst concerning its brightness and the arrival time of photons of various energies, called the lag-luminosity relationship, suggest that burst behaved more like a short burst (from a merger) than a long burst. Yet no theoretical model of mergers can support a sustained release of gamma-ray energy for 102 seconds. "This is brand new territory; we have no theories to guide us," said Gehrels.”,

http://en.wikipedia.org/wiki/GRB_060614

@INTERNET Wikipedia GRB 060614 [2012-05-28]

Se även en senare analys (2011) av GRB 050509b,

Fig1 s2sp1ö

”Keck LRIS G-band image, zoomed to show the XRT error circle. The larger, blue circle is the revised XRT position from Rol et al. (2005); the smaller, green circle to the west and north of that is the 2σ confidence region of the XRT position computed in Bloom et al. (2006).”,

http://arxiv.org/pdf/1101.5612v5.pdf

Astronomy & Astrophysics — ON THE NATURE OF GRB 050509B: A DISGUISED SHORT GRB,

De Barros et al., 2011

Kommentar:

Bilden ovan i jämförelse med samma objekt i Fong2009 visar den stora svarta fläcken med betydligt större kontrastverkan än i motsvarande Fong2009-bilden. Dessutom är de markerade cirklarna dels betydligt större ovan än i Fong2009-bilden, samt annorlunda inbördes orienterade. Exemplet understryker (delvis tydligt uppenbart olika — om uppgiften gäller — precisa detaljer i) de olika forskningsgruppernas olika resultat — och taget över olika epoker (2009-2011).

NOTERAT är varningarna [Campisi2007] [Petitjean2011] som varnar för att associera närmast TROLIGA med aktuellt detekterade.

Tänkbara galaxvärdar för GRB — Bildkälla, Författarens arkiv, 27Jun2012E10Bild39 NikonD90 Detalj

Gamma-Ray Burst Host Galaxies

Tänkbara galaxvärdar för GRB

GAMMA-RAY BURST HOST GALAXIES

En relativt stor mängd forskarrapporter finns som beskriver ämnet ”GAMMA-RAY BURST HOST GALAXIES”;

Citatdel 1

”Thus, we conclude with high significance that short GRB host galaxies are systematically larger than long GRB hosts, and that this result is not affected by host associations based on XRT positions.”, Fong et al., 2009;

”X-ray (XRT)” [X Ray Telescope], X-ray [ref. Wikipedia, X-ray] motsv. Röntgenområdet (våglängder grovt mellan atomkärnan och elektronhöljet [0,01-10 nM] [gamma (γ), mindre än 0,01nM=10pM]).

”We present a comprehensive study to measure the locations of γ-ray bursts (GRBs) relative to their host galaxies. In total, we find the offsets of 20 long-duration GRBs from their apparent host galaxy centers utilizing ground-based images from Palomar and Keck and space-based images from the Hubble Space Telescope (HST). We discuss in detail how a host galaxy is assigned to an individual GRB and the robustness of the assignment process.”, s1,

”As we will demonstrate, while not all GRBs are well-localized, the overall distribution of GRB offsets proves to be a robust clue to the nature of the progenitors.”, s7n,

”The compilation is complete with well-studied GRBs until May 2000.”, s7n,

”The physical offset is assigned assuming H₀ = 65 km/s Mpc^–1, Λ= 0.7, and Ω_m = 0.3 and assuming the GRB and the presumed host are at the same redshift. Where no redshift has been directly measured a redshift is assigned equal to the median redshift (z = 0.966) of all GRBs with measured redshifts (see text).”, s50 Fig. 3,

Bloom2002

http://astro.berkeley.edu/~jbloom/Papers/offset.pdf

THE OBSERVED OFFSET DISTRIBUTION OF GAMMA-RAY BURSTS FROM THEIR HOST GALAXIES:

A Robust Clue to the Nature of the Progenitors, Bloom et al., (2002)

”It must be noted that it may be very dangerous to derive detailed conclusions from so small samples covering the whole Universe history especially with so few information during the time of highest star formation rate (z > 1; [20]).”,

Petitjean et al., 2011 s4n.

TNEDvärdarna

TNED:

— En starkare GRB-signal som kommer hit till oss (K-centrum [c₀ bevaras oberoende av gravitationen] [UNIVERSUMS FORM]) och som KAN tränga igenom ett eller flera Galaxcentrum har bara möjlighet att göra så om GRB-signalen från början är maximalt energirik:

— All primär Planckstrålning (E=hf [PLANCKENERGIN]) är enligt TNED från början av typen NEUTRINOSTRÅLNING som omvandlas successivt via COMPTONEFFEKTEN till strålning av lägre frekvens.

— Genom att K-cellens fysik betingas av ljusets gravitella beroende, och därmed starka gravitella rödförskjutningar i universums ytterst synliga delar [Exempel GRB061028 z9,7] , kommer analogt alla GRB-signalers primära neutrinofrekvenser att dras ut upp mot gammaområdet, gamma mot röntgen, röntgen mot ultraviolett osv., i takt med att signalen avancerar in mot K-centrum där gravitella rödförskjutningen (i princip) är noll (c/c₀=1).

— Alla GRB-signaler har därför de allra bästa förutsättningar från universums yttersta rand att bevara signalens signatur ÄVEN om det råkar ligga galaktiska centrum i vägen; neutrinostrålningen penetrerar (lätt) ett sådant hinder — samtidigt som det återstående ljus som slipper ut dras vidare mot gammaområdet på Comptoneffektens kredit.

— Genom att synlinjen K-centrum till GRB-bildningslokalen (universums yttersta synliga utkanter enligt TNED max 5,25 T25 M) innehåller drygt 2900 medelgalaxlokaler bör det snarare vara av regel än undantag att en speciellt stark GRB-signal av en (ovetande) observatör kommer att ASSOCIERAS med (centrum i) någon närliggande galaxlokal — men det är heller inte alltid säkert så: Uppgifter finns [Petitjean et al., 2011] som omnämner att 25-50% av alla GRBs är av typen s.k. mörka: ingen direkt närmast närliggande galaxlokal verkar finnas synlig för dessa fall. Den detaljen, således, endast styrker TNED-teorin på den punkten.

— En svagare GRB-signal löper större risk att helt dämpas ut av mellanliggande galaxmassors centraldelar: om GRB-signalen alls kommer igenom, bör den alltså ha gått omvägar kring galaxcentrum (och därmed, som extra bonus, ha bevarat mera av den energirika primärdelen än en starkare GRB-typ som dämpats ut av just en eller flera galaxcentra). Och man finner [Citatdelen ovan GRBhosts] — följdriktigt enligt TNED — också med fördel svagare GRB-objekt i association till galaxobjektens utkanter, om alls.

ShortGRB vs LongGRB

Artikeln på @INTERNET Wikipedia Gamma-ray burst [2012-06-18] ger på underartiklarna (Long gamma-ray bursts, Short gamma-ray bursts) en allmän genomgång av följande komprimerade natur:

ALLMÄN KLASSIFIKATION GRB

typ förekomst varaktighet associerad energi

LongGRB 70% >2 S från kollapasande massiv stjärna, ofta associerad med galax som visar snabb stjärnbildning

ShortGRB 30% <2 S från områden med ringa eller ingen stjärnbildning

Ytterligare etablerade källor som understryker kopplingen LongGRB=HighEnergyGRB—ShortGRB=LowEnergyGRB ges exemplifierat nedan enligt:

”This indicates that the emission mechanism that produces most of the radiation in long GRBs may be present also in short GRBs, but with much lower efficiency.”,

http://arxiv.org/ftp/arxiv/papers/0809/0809.5206.pdf

SPECTRUM-ENERGY CORRELATIONS AND SWIFT GRBS, Lorenzo Amati, (2008) datumuppgift och sidnumrering saknas

”The study of short-duration gamma-ray bursts (GRBs) experienced a complete revolution in recent years thanks to the discovery of the first afterglows and host galaxies starting in May 2005. These observations demonstrated that short GRBs are cosmological in origin, reside in both star forming and elliptical galaxies, are not associated with supernovae, and span a wide isotropic-equivalent energy range of ~ 10⁴⁸ − 10⁵² erg. However, a fundamental question remains unanswered: What are the progenitors of short GRBs?”, s1,

http://arxiv.org/pdf/1005.1068.pdf

Harvard-Smithsonian Center for Astrophysics —

THE ENVIRONMENTS OF SHORT-DURATION GAMMA-RAY BURSTS AND IMPLICATIONS FOR THEIR PROGENITORS, Edo Berger, 2011

Källorna Bloom et al., 2001 (GRB 990712) och Asano et al., 2010 (GRB 090902B) ger maxvärden på drygt T54 erg (T47 J) för typen LongGRBs.

— Den allmänna klassificeringen av GRBs får (följaktligen i ljuset av ovanstående genomgång [TNEDvärdarnaGRB]) speciell inramning (i TNED) genom följande (förnämligt sammanfattande med de ovan berörda underförstådda kopplingarna som göms för MAC av GRB-dynamiken enligt TNED, om alls) bild:

Citatdel 2

”We find that:

(1) the short GRB hosts have systematically larger effective radii than long GRB hosts, in good agreement with their higher luminosities;

(2) the observed short GRB projected physical offset distribution has a median of about 5 kpc, about a factor of 5 times larger than long GRBs, while for the population as a whole >~25% have projected offsets of <~10 kpc, and >~5% have projected offsets of >~20 kpc;

(3) both the observed physical offset distribution and the robust constraints closely match the predicted offset distribution of NS-NS binaries; and

(4) short GRBs uniformly trace the light distribution of their hosts, similar to core-collapse SNe, but distinct from long GRBs.”, Fong et al., 2009.

Frånsett de speciella tolkningsföreträden som förutsätts i MAC via r-teorin och som inte gäller i TNED, kan (alltså) följande motsvarande allmänna (alternativa) översiktliga sammanställning ges:

GRB-värdarna enligt TNED

Korta GRBs:

— I TNED sammanhänger MERA KORTVARIGA J-kroppsdetonationer med lägre energier — motsvarande detonationsmassor av lättare typ [FRAKTALNIVÅERNA FÖR GRB] [GRB-objektens ursprung i TNED]:

längre ut = SENARE i den centrala J-moderkroppens (galaxens) utveckling: mera ljusstark galaxkropp: större omfång.

OM den GRB-signalen når K-centrum, utan att ha dämpats ut på vägen, måste den också tvunget återfinnas i framförvarande galaxlokalers yttre delar, eller generellt i de minst täta delarna av rymden; det är bara en ren konsekvens av »signalens tekniska väglag»

Långa GRBs:

— I TNED sammanhänger MERA LÅNGVARIGA J-kroppsdetonationer med högre energier — motsvarande detonationsmassor av tyngre typ [FRAKTALNIVÅERNA FÖR GRB] [GRB-objektens ursprung i TNED] [VÄRDEBEVIS]:

längre in = TIDIGARE i den centrala J-moderkroppens (galaxens) utveckling: mindre ljusstark galaxkropp: mindre omfång.

OM den GRB-signalen når K-centrum, utan att ha dämpats ut på vägen, bör den också (med fördel kunna) återfinnas i framförvarande galaxlokalers inre delar; det blir bara en ren konsekvens av »signalens tekniska väglag»

Det är, i princip (och med ev. vissa tillägg) tydligen, samma KVALITATIVA resultatbild som den ovan citerade [GRBhostsResults].

— I TNED tillkommer den utpräglade PULSREPETITIONEN [NASA-BATSE-GRB — pulsintervall] [Primär grundtrigonometri för GRB-bildning enligt TNED] [GRB-utlösningen i TNED] som kan ses i många (alla) GRB-ljuskurvor, och som underförstår att alla långa GRBs också av princip innefattar korta GRBs enligt den fraktala delningsformens inneboende detonationsordning [GRB-fraktalerna], ehuru omvändningen INTE gäller.

— Skulle någon direkt KVALITATIVT allvarlig DIFFERENS visa sig i dessa detaljer, är det tydligt att det INTE är TNED som gäller.

SPECIAL — GRB-signalens signatur

GRB-pulsens fullständiga karaktär påvisades inte förrän år 1997 — sex år efter sjösättningen 1991 av BATSE-instrumentets observationer från rymdobservatoriet CGRO (Compton Gamma Ray Observatory):

”Several models for the origin of gamma-ray bursts postulated^[19] that the initial burst of gamma rays should be followed by slowly fading emission at longer wavelengths created by collisions between the burst ejecta and interstellar gas. This fading emission would be called the "afterglow." Early searches for this afterglow were unsuccessful, largely due to the difficulties in observing a burst's position at longer wavelengths immediately after the initial burst. The breakthrough came in February 1997 when the satellite BeppoSAX detected a gamma-ray burst (GRB 970228^{[nb 2]}) and when the X-ray camera was pointed towards the direction from which the burst had originated, it detected fading X-ray emission.”,

http://en.wikipedia.org/wiki/Gamma-ray_burst - Afterglow

@INTERNET Wikipedia, Gamma-ray burst, Afterglow [2012-05-23]

Bhat2011

http://arxiv.org/pdf/1111.4909v2.pdf

AN OVERVIEW OF THE CURRENT UNDERSTANDING OF GAMMA RAY BURSTS IN THE FERMI ERA, Bhat et al., 2011, Table 1, s473

NASA2704ill

Bhat et al., 2011, Table 1, s473, ”List of past and operating space borne instruments that have detected GRBs along with the approximate numbers of GRBs detected by them as of August 2011”.

Petitjean2011

http://arxiv.org/pdf/1104.0844.pdf

GAMMA RAY BURSTS AS PROBES OF THE DISTANT UNIVERSE, Petitjean et al., 2011

”It is possible that such hosts are more common than previously anticipated and that a fraction of dark GRBs explode in regions dusty enough so that their afterglow is very hard to detect in the optical.”, s10mö,

”Unfortunately, as seen previously, galaxies are difficult to detect and study at z > 2 whereas absorption lines are more easily observed at these redshifts. The latter is due to the fact that most of the interesting and useful absorption lines have rest-wavelengths in the UV and are redshifted in the optical for z >= 2.”, s11ö.

Strålningstryckets roll för mörka materiens härledning — Bildkälla, Författarens arkiv, montage, 27Jun2012E10 Bild41 Bild39, NikonD90 Detalj

TNEDbasics Tillägg till Sandkornsanalogin 2012-06-11

MED ANSLUTNING TILL OBSERVATIONERNA AV MÖRKA MATERIEN [New Scientist MW]

Hur Mörka Materiens masskroppar hålls på behörigt avstånd från galaxernas massiva centrum

— Det finns ingen motsvarande teori för det i MAC:

Kärninduktiva Strålningstryckets inverkan

Strålningstryckets termonukleära ekvivalent i TNED

KÄRNINDUKTIVA STRÅLNINGSTRYCKET enligt TNED [Se Jämförande beräkningsexempel i Strålningstrycket i Modern Akademi]

^γp = p – p_e ................................. strålningstrycket, kärninduktiva värmemotståndet, N/M²

med

stjärnyttrycket p = G(m₂/2r²)²/π och

kärnyttrycket p_e = k(Ze/d)²/(πr₀)²

har enligt TNED på stora avstånd från en fusionsproducerade stjärnmassa

(här till exempelräkning idealt hela Vintergatans centrum i formen av alla dess ljusproducerande stjärnor via uppgiften ca 1 T11 Solmassor för hela Vintergatans stjärnpopulation, se Lokala Galaxgruppen)

praktiskt bara stjärnans yttryck som aktiv värdekomponent

[Se Kalkylkort i http://www.universumshistoria.se/AaKort/c0kroppen.ods]

;

STJÄRNYTTRYCKET som representativt för hela kärninduktiva strålningstrycket från den idealt samlade Vintergatans stjärnpopulation på stort avstånd r från Vintergatans centrum kan då grovberäknas i TNED enligt

p = G(m₂/2r²)²/π .............................. N/M² = Pa

För en LITEN materiepartikel m (typ kubiskt sandkorn) med kubsidan R gäller motsvarande GRAVITELLA YTTRYCK på avståndet r enligt

p = F/A

= (Gm₂m/r²)/(A=R²)

= Gm₂m/r²R² ; m=ρR³ ; m/R²=ρR³/R²=ρR

= Gm₂ρR/r²

= G(m₂/2r²)²/π

= Gm₂²/4πr⁴ ;

Gm₂m/r²R² = Gm₂²/4πr⁴ ;

r² = R²m₂/4πm ;

r = R √ m₂/4πm ;

RÄKNEEXEMPEL

Kärninduktiva Strålningstryckets inverkan

Ett kubiskt sandkorn med kubsidan R = 1mM väger (Sandsten, medeltäthet 2323 KG/M³) m=2,323 t6 KG;

— Med synliga Vintergatsmassan 2,785 T41 KG som 1/355 av totalmassan generellt enligt resultaten från K-cellens värmefysik ges jämvikt mellan de bägge krafterna vid

r = R √ m₂/4πm

= (0,001 M) √ (355·2 T41 KG)/4π(2,323 t6 KG)

= 1,8402 T21 M

= 59,64 Kpc ;

R = r √ 4πm/m₂

= r √ 4π(ρR³)/m₂

= R^3/2r√ 4π(ρ)/m₂ ;

R^–1/2 = r√ 4π(ρ)/m₂ ;

R = [r√ 4π(ρ)/m₂]^–2 ;

Sandkornet15mM

För att sandkornet precis ska balansera på Vintergatsskivans omskrivna sfärradie (15 Kpc ~ 4,635 T20 M ) — och inte hamna längre bort från centrum — får R tydligen inte vara mindre än

R = [r√ 4π(ρ)/m₂]^–2

= [(4,635 T20 M)√ 4π(2323 KG/M³)/(355m[VINviz])]^–2

= 0,015763 M

= 15,763 mM

— Det är i sammanhanget en STOR bit materia.

— Med den storleken ges i SANDKORNSANALOGIN för Vintergatan en närmast enorm spridning i medelvolymer — om vi tillåter oss att grovräkna på/PER varje sandkornskub.

— I MAC finns inte TYPEN »kärninduktivt strålningstryck»: Räkningen kan inte genomföras.

57MilsKuben

Kärninduktiva Strålningstryckets inverkan

1 partikel per 1,9 T17 M³

— Man hittar EN sådan på vägen mellan Stockholm-Malmö (619 KM, kubsidan ca).

— Varje sandkornskub med sidan 15,763 mM väger m=ρR³=(2323)(0,015763)³=9,09841 t3 KG;

— Om summan av alla sådana korn är 100 synliga Vintergatsmassor [~2 T(41+2=43) KG] blir totala antalet 2,19818 T45;

— Vintergatans omskrivna sfär har via radien 15 Kpc~4,635 T20 M volymen lika med 4,17097 T62 M³;

— Vintergatssfärens volym fördelat på de 2,19818 T45 kornen ger då 1 korn — en partikel — per 1,89746 T17 M³ — eller en kub med sidan 574,63371 KM.

— Är det alls möjligt att få någon synbarhet för LJUS som affekteras av en sådan enormt låg partikeltäthet? Svaret på den frågan är här inte närmare känd — men ett tidigt Bonnierscitat [‡] antyder att det INTE går att upptäcka den typen.

— Hur kan man förstå att en sådan liten materieklump uppför sig i samband med ljusfenomen generellt i universum?

I det praktiska Vintergatsfallet med strålningstryckets funktion skulle det via strålningstryckets funktion inte finnas korn inom själva Vintergatssfären; strålningstrycket puttar allt stoft utåt. Därmed i analogin krävs allt mindre korn på allt större avstånd för att få ut kornmassan utanför Vintergatssfären.

— Storleken på kornen skulle alltså avta med växande avstånd från Vintergatans centrum; största (sand-)kornen närmast centrum, minsta stoftkornen längst bort från centrum.

Om vi fortsätter grovräkningen på 100 Vintergatsmassor (m=2 T43 KG) med ett 15mM-sandkorn per ~ 1,9 T8 (KM)³;

;

m = ρ(V₁ – V₂) ; massan i skalet med tjockleken d omkring ideala Vintergatssfären

= 4πρ(r₁³ – r₂³)/3

= 4πρ([15 Kpc + d]³ – [15 Kpc]³)/3 ; Vintergatssfärens radie 15 Kpc, medeltäthet ρ efter sandkornets rymdkub

3m/4πρ = [15 Kpc + d]³ – [15 Kpc]³ ;

3m/4πρ + [15 Kpc]³ = [15 Kpc + d]³ ;

(3m/4πρ + [15 Kpc]³)^1/3 = 15 Kpc + d ;

d = (3m/4πρ + [15 Kpc]³)^1/3 – 15 Kpc ; m=2 T43 KG ;

= 3,91 Kpc ; ρ=(9,09841 t3 KG)/(1,89746 T17 M³)=4,8 t20 KG/M³

3m/4πρ är sfärradiens kubikform för 15 Kpc med medeltätheten ρ så att man får ekvivalenten

d = ([15 Kpc]³ + [15 Kpc]³)^1/3 – 15 Kpc

= (2[15 Kpc]³)^1/3 – 15 Kpc

= (2)^1/3[15 Kpc] – 15 Kpc

= [15 Kpc][(2)^1/3 – 1]

= [15 Kpc][0,259921~0,26]

= 3,9 Kpc

Notera att tätheten ρ=4,8 t20 KG/M³ här är framräknad på 15mM-sandkornets massuppfyllande villkor med 100 Vintergatsmassor:

(2 T43 KG)/(9,09841 t3 KG) = 2,20 T45 ;

ρ = m_SAND/(V₂/[m/m_SAND]) = m/V₂ ;

3m/4πρ = 3m/4π(m/V₂) = 3V₂/4π = 3[4πr₂³/3]/4π = r₂³ ;

Nettoresultatet blir att d-värdet 0,26r2 gäller massoberoende;

— HUR hänger det ihop?

— Förutsättningen för att det resulterande d-skalet ska hålla 100m(VIN) = 2 T43 KG med sandkornmassans täthetsvillkor, är att Vintergatsvolymens massfär V(VIN) med sandkornets täthetsbas ska innehålla samma massa som d-skalets m2=100m(VIN)=2 T43 KG; Man får då d-skalets massa m enligt

m(d) = m1 — m2 = m2 = 4 T43 KG – 2 T43 KG = 2 T43 KG ; m1 = 2m2 = 4 T43 KG; Därmed den massoberoende d-formen

m₁ = 2m₂ = 2(4πρR³/3) = 1(4πρ(R+d)³/3) ;

2R³ = (R+d)³ ;

2^1/3 = (R+d)/R = 1+d/R ;

d = R(2^1/3 – 1 ~ 0,26)

Sambandsformen gäller alltså — hur underligt det än kan verka — oberoende av massvärdet;

— Sfärskalet +0,26R innehåller lika stor massa som R-sfären, given medeltäthet förutsatt;

— N massenheter i R-sfären = N massenheter i +0,26R-skalet.

;

Med tillägget av ett extraskal med endast bredden drygt (3,9)/(15)=0,26 ~ 1/4 av Vintergatans omskrivna sfär får vi en grovform vars massinnehåll satisfierar grovräkningen på 100 Vintergatsmassor med hjälp av glest utspridda sandkorn — ett sandkorn (15mM kub) per en rymdkub med sidan drygt 57 mil [57milsKuben].

— Men hur vet vi säkert att kärninduktiva strålningstrycket [Strålningstryckets inverkan] verkligen KAN utverka en sådan påverkan på sandkornet — eller något annat materialelement — ?

Kärninduktiva strålningstrycket (Elektriska verkan på Q i atomkärnans alla delar) är en kärnladdnings(fraktal)baserad tryckform (±e-strukturen i PLANCKRINGEN) [Neutrinostrålningens grunder i TNED] [Planckfraktalerna]: den penetrerar materiens atomkärnemassa, och därmed all övrig laddningsmassa (elektroner) [NEUTRONSÖNDERFALLET]. Enbart med den kraftbaserade förutsättningen — all materia betingas av atomkärnor och elektronhöljen — finns ingen som helst möjlighet för någon atomärt baserad massform att undkomma inverkan. Kraftformen finns, i mer eller mindre utpräglad grad.

Sammansättningen i kosmiskt stoft

”On average, the interstellar matter in our region of the galaxy consists of about one atom of gas per cubic centimeter and 25 to 50 microscopic solid particles per cubic kilometer. In contrast, the air at sea level on Earth contains about 1,019 molecules of gas per cubic centimeter.”,

”In some regions of space, however, the concentration of interstellar matter is thousands of times greater than average. Where there is a large enough concentration of gas and particles (also called cosmic dust), clouds form. Most of the time these clouds are so thin they are invisible. At other times they are dense enough to be seen and are called nebulae”,

http://www.encyclopedia.com/topic/interstellar_matter.aspx

Interstellar Matter — UXL ENCYCLOPEDIA OF SCIENCE | 2002

— 50 partiklar per kubikkilometer 50/[KM]³ = 50/[1000 M]³ = 50/[1 T9 M³] = (5 t8)/M³ motsvarar en partikel per 20 miljoner M³, 1part/(2 T7 M³), eller:

— en partikel per 0,02 [KM]³; 1M³/(5 t8 part) = (0,001 KM)³/(5 t8 part) = 0,02 [KM]³ / 1 part.

TILLGÄNGLIGA BESTRÅLNINGSYTAN för ett material tillväxer naturligt med mängden delar som materialet kan uppdelas på.

— EN kula i ett hörn har sämre möjligheter att avspegla (absorbera/emittera) YTLJUS än om samma kula delas upp i en miljon små delkulor utspridda över en stor yta.

— Förmågan att reflektera är (således) direkt proportionell mot den friliggande rymdytan: endast materialytan som vätter direkt mot den omgivande rymden har förmåga att direkt absorbera eller emittera (reflektera) infallande Planckenergier (E=hf).

Förmågan att absorbera ytljus för en given materialmassa är med andra ord naturligt (direkt) proportionell mot den materialutbredda ytan. Inte massan som sådan.

— Det betyder att en enorm mängd små delfragment av en given massa, och som utspridda besitter STOR ljusabsorberande kapacitet, i princip kan bilda en försvinnande LITEN absorptionsförmåga — om alla delarna göms under ytan av EN central masskropp.

— Och alltså kan bara DEN MÖRKA MATERIEN gynnas av tillfället att få bestå av STÖRRE stoftkorn — typ 15mM-sandkornet — än de som normalt förknippas med allmänt kosmiskt stoft.

Därmed sagt:

— Det är nog INTE så att den mörka materien inte KAN ses;

— Den kan säkert det. Men på grund av den enormt låga partikeltätheten per M³

(enligt räkneövningarna ovan, 57MilsKuben, typ en partikel per T17 M³; en kub med sidan DRYGT 500 kilometer att jämföra med kosmiskt medelstoft: en partikel per en kub med sidan 0,271 kilometer (2 T7 M³; 50 partiklar per kubikkilometer)

är den absorberande/emitterande förmågan taget över stora rymder TYDLIGEN så liten att inga instrument (ännu) kan se glöden.

En partikel per T8 kubikkilometer

Sammansättningen i kosmiskt stoft

1 partikel per 1,9 T17 M³

1 partikel per 1,9 T8 (KM)³

Jämför vanliga kosmiska stoftets partikeltäthet (som mest)

1 partikel på 2 t2 (KM)³ — en partikel per 0,02 kubikkilometer: skillnaden är galet enorm (tio tiopotenser);

— Det finns (ännu 2012, här veterligt) inga instrument som SKULLE KUNNA se en sådan svag ljusemission; Se även samma antydning i Bonnierscitatet från 1978.

Sken från millimeterstora partiklar som återfinns med en partikel en gång per hundra miljoner kubikkilometer rymd — med början från [Strålningstryckets inverkan] den omskrivna Vintergatssfärens radie (15 Kpc) och vidare utåt — tillhör (vad vi vet) inte dagens teknik (än). Jämför (som sagt) Bonnierscitatet från 1978: ”Större stoftpartiklar med storlekar upp till fotbollsformat … förbli omöjliga att upptäcka”.

Om det kommer an på EN RATIONELL FÖRKLARING till mörka materiens existens (upptäckt genom gravitationen) är det tydligt att den ovan beskrivna allmänna sandkornsanalogin är en stark kandidat. Den skulle också vara välbekant i MAC om man bara [Bonnierscitatet från 1978] hade någon teori dels för HUR sådana större stoftkorn skulle ha bildats och dels hur (i himmelens namn) de kan hålla sig borta från oss (Solsystemet) men återfinnas utanför galaxerna. I TNED seglar lösningen i det första fallet in på scenen automatiskt genom DETONATIONSMASSORNA — och därmed samtidigt lösningen till hela frågan om KOSMISKA PARTIKELSTRÅLNINGENS URSPRUNG — och i det andra fallet genom STJÄRNFYSIKEN generellt med resultaten från Solen speciellt; Solradien, Solperioden, Solens magnetism, Koronafysiken.

MMLightMAC

Mörka materien · Detonationsmassorna · Kosmiska partikelstrålningens upphov · GRBs

Mörka materiens ljusemitterande kapacitet

Se inledande exempelräkningar i Strålningstryckets roll för mörka materiens härledning

I TNED [Synliga och totala massan] gäller generellt ett förhållande 1/355 mellan synliga och totala massan [Allmänna resultatbilden från K-cellens värmefysik]. PROBLEMET i det sammanhanget med den övergripande praktiskt överensstämmande beskrivningen av K-cellens inre — vårt praktiska universum — är den tvungna täthetsvariation [Täthetsvariationens funktioner] [tK-faktorn] som K-cellen måste uppvisa i vissa delar mellan inre och yttre massavsnitt för att resultatbilden [K-radien] [K-värdet] från K-cellens värmefysik ska stämma med de angivna praktiskt observerade förutsättningarna [‡De observerade förutsättningarna]. Nämligen på så sätt, och i resultatbilden totalt (Maj2012), att ingen enhetligt generellt idealt sfäriskt HOMOGEN täthetsfördelning existerar på, i och för K-cellens INRE detaljer — ehuru en sådan gäller sett för hela K-cellen utan hänsyn till de inre detaljerna [K-CELLENS ÖVERGÅNG I c0-KROPPEN, HUVUDVY].

— Därmed frågan om Vintergatans PRAKTISKT observerbara VERKLIGA (totala) massa: Den ska, idealt i TNED vara runt 355×(2 T41 KG) — och expansionssambandet för J-kropparna generellt i TNED [Galaxexpansionerna] (för den stavspiralgalax som Vintergatan tros vara byggd på) [J-kropparnas expansion] stämmer också mycket bra in på den basmatematiken för Vintergatans del [med basuppgifter från epoken BA1978; m(VINviz)=2,785 T41 KG = 1,4 T11 m(SOL), Precisionen i J-kropparnas expansion].

— Det beror (nämligen, litet granna) på HUR man bestämmer preferenserna för olika kompenserande gravitella effekter av den (komplicerade) typ (se även bilden nedan från New Scientist) som Vintergatan och andra galaxlokaler uppvisar. Exakt hur dessa detaljer förhåller sig i slutänden till kvoten 1/355 mellan synliga och totala massan i Vintergatans fall finns ännu (Jun2012) här ingen redovisad beskrivning på. Sambandsformen kommer emellertid att fortsätta FÖRMODA en sådan koppling i den vidare beskrivningen i denna presentation — och tills en mera eventuell klarare bild kan presenteras (om alls).

— Vissa forskningsrapporter [Mörka Materien BBC 2006] beskriver nämligen motsvarande kvot synliga/totala på upp till 1/400, men då »i Vintergatans utkanter», ”dwarf galaxies that skirt the edge of our own Milky Way”. Andra uppgifter (mera INOM våra lokaler) talar om ett förhållande synliga totala på 1/10 för Vintergatan [@INTERNET Wikipedia, Milky Way, Size and composition 2012-06-12 anger siffran 1-1,5 T12 m(SOL), samt tillägger: ”Estimates for the mass of the Milky Way vary, depending upon the method and data used.”]. Det finns (således, ännu Jun2012) vissa trixiga omständigheter som visar olika värden efter olika sätt.

NewScientistMW

http://www.newscientist.com/article/dn18344-milky-ways-dark-matter-turned-on-its-side.html

New Scientist — MILKY WAY'S DARK MATTER 'TURNED ON ITS SIDE' — 06 January 2010;

”"I have no idea how you form a disc in that orientation on these kinds of halos," says Law, who presented the results on Monday at a meeting of the American Astronomical Society in Washington DC.”.

TNED:

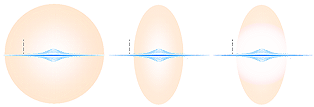
Sfäriska stjärnhopar ger ett homogent fördelat strålningstryck i summan från alla aktiva stjärnor. Omgivande materiestoft kan då förstås drivas ut med en idealt sfärisk rand omkring hopen där balans råder mellan strålningstryck och g-kraft på stoftkornen.

— En spiralgalax har dessutom en aktiv utbredd skiva med stjärnor som kan bilda ett extra BIDRAG, ett extra plattcentralt strålningstrycksbidrag, och som därmed kan tvinga ihop stoftpartiklarna mera in mot centrum. Totalbilden kan därmed förstås bli en ellipsoidisk form (utdragen sfär) snarare än en sfärisk i fallet med en ideal spiralgalax.

— Den streckade markeringen i galaxskivan motsvarar ungefär Solsystemets plats i Vintergatan.

— För att ett stoftkorn av typen sandsten (Kisel) ska befinna sig i balanserande kraftjämvikt med stjärnstrålningstrycket från hela Vintergatans idealt samlade stjärnljusfysik och sandkornets gravitella attraktion in mot centrum på avståndet 15 Kpc — Vintergatans idealt omskrivna sfärradie — får sandkornet som en ideal kubisk form inte ha större kubsida än max 15 mM [Strålningstryckets inverkan] [Sandkornet15mM]: än mindre kornstorlekar drivs motsvarande längre ut. Därmed finns en väl relaterbar kvantitativ analogi till fenomenet — i TNED, men inte i modern akademi. Se räkneexempel i Strålningstryckets roll för mörka materiens härledning.

— I MAC finns ingen motsvarande teori [Strålningstrycket i MAC] för det allmänna kärninduktiva strålningstryck [KÄRNINDUKTIVA STRÅLNINGSTRYCKET] som enligt relaterad fysik [TNED] grundlägger alla stjärnors energiproduktion [Se utförligt med jämförande korsreferenser (SKILDA GRUNDTEORIER) från Solfysiken om ej redan bekant]. Se även jämförande beräkningsexempel i Strålningstrycket i MAC. Därmed omständigheterna i stort till HUR och VARFÖR.

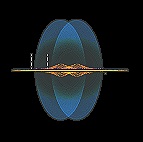
— Om — som det påstås — Vintergatan dessutom är bildad av två (enligt TNED, se STJÄRNHOPAR OCH GALAXBILDNINGAR) idealt fristående primärkroppar som tillsammans format en gemensam stavspiral, kan hela situationen liknas vid två idealt singulära galaxlokaler som ligger inskjutna i varandra och därmed i totalbilden en något »tillplattad ellipsoid» — utdragen i stavriktningen.

— Med den bilden kan en nära KVALITATIV analogi förstås till den resultatbild som visas i New Scientistkällan ovan.

— Jämförande beräkningsexempel [Beräkningsexempel, mörka materien i TNED] från grunderna i TNED som visar hur fenomendetaljerna med mörka materien [Mörka materien i TNED] kan förklaras visas i huvudtexten.

— Se vidare nedan från Sammansättningen Stoft-Gas.

http://en.wikipedia.org/wiki/File:236084main_MilkyWay-full-annotated.jpg

@INTERNET Wikipedia, Milky Way [2012-06-12]

Wikipedias illustration av Vintergatan sett ovanifrån baserat på den samlade datamängden.

Sammansättningen stoft-gas

Sammansättningen generellt av allmänt kosmiskt stoft och gas;

”Cosmic dust is made of various elements, such as carbon, oxygen, iron and other atoms heavier than hydrogen and helium. It is the stuff of which planets and people are made, and it is essential for star formation. Stars like our sun churn out flecks of dust as they age, spawning new generations of stars and their orbiting planets.”,

http://www.jpl.nasa.gov/news/news.cfm?release=2011-204

HERSCHEL HELPS SOLVE MYSTERY OF COSMIC DUST ORIGINS, July 07, 2011

Beräkningsexempel, mörka materien i TNED — Si-kornets ljusskärm

Se även i Si-kornets massbild kring Vintergatan

Exempel:

— Allmänt kosmiskt stoft och gas består av i stort sett alla grundämnen [Cosmic Dust NASA 2011] med största förekomsterna av gaserna Väte (~75%) och Helium (~25%) [Se resultatredovisningen i K-CELLENS VÄRMEFYSIK, konventionella uppgifter anger runt 24% He (Wikipedia Helium [2012-06-12]) och ”roughly 75%” Väte (Wikipedia Hydrogen [2012-06-12]), se även i UXLencyclopedia2002]. Det är alltså fråga om förekomster på nivån enskilda eller par atomer.

— En 15 mM sandkub (Sandsten ρ=m/V=2323 KG/M³, idealt Kiselbaserad [₁₄Si²⁸] atomvikt grovt 28U) innehåller

N = m/Uu = ρV/Uu

= (2323)(0,015 M)³/(28)(1,66033 t27 KG)

= 1,68643 T23

stycken Kiselatomer;

— Med en genomsnittlig fördelning på en sådan stoftpartikel per (som mest) 0,02 [KM]³ [UXLencyclopedia2002], täcks totalvolymen

V = (0,02 [KM]³)(1,68643 T23)

= 3,37286 T21 [KM]³

= 3,37286 T30 M³ ;

r(SPH) = 9,30329 T9 M ; r(SOL) ~ 7 T8 M ;

~ 13,3 r(SOL)

Den volymen fyller lika mycket som en sfär med radien lika med drygt 13 Solradier.

— Men volymen är ju ett stoftmoln, och som sådant kan det anta många olika former och utbredningar;

— Med en jämförande tjocklek på en Jordradie (r[EKV]=6,378 T6 M), i formen av en cirkulär skiva (A=πr²), täcker V ovan en skiva med radien

r(CRC) = √ (V/r[EKV])/π

= √ (3,37286 T30 M³)/[6,378 T6 M]π

= 4,10281 T11 M ; 1AU=1,496 T11 M Medelavståndet Jorden-Solen

= 2,7425235 AU

dubbla medelavståndet Jorden-Solen.

— Ett sådant stoftskikt kan efter omständigheterna (LÄTT) absorbera och emittera ljus, och därmed synas tydligt;

— Men det stoftmolnet kan (också, enkelt) utsträckas ytterligare på bekostnad av en mindre tjocklek;

Är stoftmolnet maximalt utsträckt på tjockleken av ett medelpartikelavstånd (0,02 [KM]³, kubsidan avrundat 270 M) ges maximalt

r(CRC) = √ (V/[270 M])/π

= √ (3,37286 T30 M³)/[270 M]π

= 6,30583 T13 M ; 1AU=1,496 T11 M Medelavståndet Jorden-Solen

= 421,51277 AU

— Den skivan med diametern (2 × 6,3 T13 M ~ 1,26 T14 M) upptar på Krabbnebulosans avstånd (~2Kpc~6,18 T9 M) vinkeln i bågsekunder [Bågsekunder och Distanser]

A’’ = (206265)(1,26 T14 M)/(6,18 T19 M)

= 0,4205402

— Det är i princip tekniskt synligt av Hubble Space Telescope med uppgiften om 0,1’’ upplösning.

— Det kan man kalla ett signifikant kosmologiskt jämförande exempel:

— Hela den stoftskivan med andra ord från ett enda stort sandkorn med kubsidan 15 mM.

Sprids stoftmolnets medelpartikelavstånd istället ut på en partikel per runt en rymdkub med sidan 500 KM, 1 partikel per 1,25 T17 M³ enligt exempelräkningen [STRÅLNINGSTRYCKETS ROLL FÖR MÖRKA MATERIENS HÄRLEDNING] [57MilsKuben] från kärninduktiva strålningstryckets inverkande kraft på möjliga stoftpartiklar

— vilket betyder en minskning av medelmässiga kosmiska partikeltätheten [UXLencyclopedia2002] 1part/(2T7M³) med nära tio tiopotenser [(1,25 T17)/(2 T7)=6,4 T9]

— är det tydligt att det i dagens läge (2012) inte finns instrument som kan se ljusemissioner från ett så hutlöst enormt utspritt materiestoft [En partikel per T8 kubikkilometer] — men att det i stor omfattning kan visa sig i påtagliga gravitella effekter, (Jämför Bonnierscitatet från 1978).

— Men, med den scenbilden spricker också alla kända atom- och massbegrepp i modern akademi:

I grovt vulgäriserad (analog) mening:

— Ingen känner till att det skulle kunna finnas några subatomära partiklar T10 gånger mindre än en Kiselatom.

Ingen i MAC räknar med möjligheten att den mörka materiens partikelelement skulle kunna vara ett sandkorn av storleken 15 mM [Sandkornet15mM], därför att ingen DELS känner till någon härledande fysik [STRÅLNINGSTRYCKETS TERMONUKLEÄRA EKVIVALENT] som kan hålla den typen på behörigt avstånd från galaxernas stjärnljus (i formen av en s.k. halo [New Scientist] omkring), och därför heller ingen har någon chans att associera i sådana banor, och DELS hur i hela himmelens namn sådana »magiska sandkorn», eller materialkorn i allmänhet, skulle ha kunnat bildas ur BigBang-materialets primära galaxstoftbankar [Bonnierscitatet från 1978]. Alla dessa aspekter för så långt ifrån saken i MAC, att inget insteg finns för ett närmande.

Därmed läge för vår nuvarande (2012) tids Nya Aspekter på Ny Fysik — det ena förslaget mera sensationellt enastående än det andra.

— I TNED finns inget sådant.

Mörka materien i modern akademi

MÖRKA MATERIEN I MAC:

1978:

”Man kan också tänka sig mer kondenserad materia. Studiet av fördunkling och färgförändringar i hopens centrum tyder på att det i så fall inte kan röra sig om stoft i stil med det i Vintergatan. Större stoftpartiklar med storlekar upp till fotbollsformat skulle utan svårighet kunna hålla hopen samlad och ändå förbli omöjliga att upptäcka; problemet är bara att vi inte känner till någon enkel process varigenom sådana objekt kan bildas.”

BONNIERS ASTRONOMI 1978 Det internationella standardverket om universum s360sp2n

1999:

”Galaxies are known to have much more matter than telescopes can currently see. Up to 90% of the total mass of the galaxies is simply missing: it has to be there, astronomers know, but it remains undetected. Is this so-called 'dark matter' made up of exotic, virtually undetectable particles, or is it merely ordinary matter hidden to instruments for some reason? A new result obtained by a Dutch team with the European Space Agency's infrared space telescope, ISO, favours the last idea.”,

”However, the team warns that no other alternative dark matter model can be ruled out.”,

http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=12820

esa — ISO DETECTS SIGNAL FROM DARK MATTER IN A GALAXY SIMILAR TO THE MILKY WAY, Aug 1999

esa, European Space Agency

2006:

”Now, the Cambridge team has provided new information with its detailed study of 12 dwarf galaxies that skirt the edge of our own Milky Way.”,

”With the aid of 7,000 separate measurements, the researchers have been able to establish that the galaxies contain about 400 times the amount of dark matter as they do normal matter.”,

http://news.bbc.co.uk/2/hi/science/nature/4679220.stm

DARK MATTER COMES OUT OF THE COLD — By Jonathan Amos, BBC News science reporter, 5 February 2006

Astronomiska observationer (Jan Oort 1932) av de olika himmelsobjektens rörelseformer är orsaken till uppdagandet (Vera Rubin [1975, American Astronomical Society]) att universums galaxlokaler (i allmänhet) måste innehålla betydligt mer massa än den synliga för att få ordning på matematiken i rörelsebanorna.

NOTERA RÖDFÖRSKJUTNINGARNA:

— Enda sättet för direkt bestämning av rörelser av avlägsna objekt i Vintergatan och andra galaxer är med hjälp av (Dopplereffekten) RÖDFÖRSKJUTNINGAR: ljuset från stjärnobjekten ändras i våglängd beroende på stjärnans rörelse.

— I TNED tillkommer GRAVITELL RÖDFÖRSKJUTNING — den ingår inte i modern akademisk kosmologi.

— Det är ännu här INTE känt i detalj HUR forskare i moderna laboratorier beräknar sina data via SPECIFIKA observerade rödförskjutningsvärden (typ avlägsna galaxobjekt), och hur dessa i så fall skulle korreleras för jämförelser med motsvarande värden i TNED. En viss försiktighet måste därför beaktas i användningen av begreppen — tills en mera bestämd beskrivning kommer i dagen.

”Then, in the late 1960s and early 1970s, Vera Rubin, a young astronomer at the Department of Terrestrial Magnetism at the Carnegie Institution of Washington, presented findings based on a new sensitive spectrograph that could measure the velocity curve of edge-on spiral galaxies to a greater degree of accuracy than had ever before been achieved.^[14]”,

http://en.wikipedia.org/wiki/Dark_matter - Galactic_rotation_curves

@INTERNET Wikipedia, Dark matter, Galactic rotation curves [2012-06-11]

Däremot finns ännu (Jun2012 med referens till de mest synbara webbkällorna) ingen konsensus i frågan om exakt vad den felande, graviterande, mörka materien är för något: Den mörka materien syns (ännu) inte i teleskop;

”Dark matter cannot be seen directly with telescopes; evidently it neither emits nor absorbs light or other electromagnetic radiation at any significant level.^[1] Instead, its existence and properties are inferred from its gravitational effects on visible matter, radiation, and the large scale structure of the universe.”,

http://en.wikipedia.org/wiki/Dark_matter

@INTERNET Wikipedia, Dark matter, Galactic rotation curves [2012-06-11]

2012:

’Mörka materiens mysterium tätnar’

”The most accurate study so far of the motions of stars in the Milky Way has found no evidence for dark matter in a large volume around the Sun. According to widely accepted theories, the solar neighbourhood was expected to be filled with dark matter, a mysterious invisible substance that can only be detected indirectly by the gravitational force it exerts.”,

”A new study by a team of astronomers in Chile has found that these theories just do not fit the observational facts. This may mean that attempts to directly detect dark matter particles on Earth are unlikely to be successful. ”,

http://www.dailygalaxy.com/my_weblog/2012/04/milky-way-appears-to-be-void-of-dark-matter-the-mystery-of-dark-matter-deepens-a-new-solution-for-th.html

THE DAILY GALAXY Great Discoveries Channel — April 19 2012

Frånsett mängden ännu oavgjorda exotiska partikelteorier:

— Forskningen på området verkar inte ha kommit mycket längre än i citatet från Bonniers Astronomi 1978: typ (stora) sandkorn, men ingen i MAC vet hur eller på vilket sätt (och därmed finns heller inget mer omnämnt i saken).

— Se vidare jämförande räkneexempel i SANDKORNSANALOGIN och 15mMSandkornet.

EN upphittad — som i varje fall försöker ge en RATIONELL förklaring:

(termoluminiscens — vissa material kan lagra upptagen ljusenergi som släpps ut först sedan materialet upphettas):

”So, the cool dark dust can hide a certain part

of energy of the Universe, not giving us, in fact, any possibility to detect this hidden energy even

at the moment of its release.”,

http://arxiv.org/ftp/astro-ph/papers/0507/0507532.pdf

COOL DARK COSMIC DUST AS A RESERVOIR OF ABSORBED ENERGY — Irakli Simonia (2005)

Sidnummer saknas.

Antalet GRBs per dygn

ANTALET REGISTRERADE GRBs PER DYGN

ref.

— ‡

”BATSE usually detects only about one gamma-ray burst per day”,

http://science.nasa.gov/science-news/science-at-nasa/1996/ast17dec96_1/

NASA SCIENCE — BATSE DISCOVERS UNIQUE GAMMA-RAY BURSTS, 1996

— ‡

”With this link established, two scientists at MIT's Laser Interferometer Gravitational Wave Observatory (LIGO) have just derived an "actual-to-observed" ratio of 450-1. That is, there are roughly 450 GRBs occurring in the observable universe for every one that's detectable by orbiting satellites designed to look for them. This is a figure that not only utilizes the GRB-supernova link but also agrees well with a previous, independently derived ratio that did not use such a link.”,

http://www.ligo.caltech.edu/LIGO_web/gsfc_mit/

NASA — MANY GAMMA-RAY BURSTS GO UNDETECTED, MIT MATHEMATICIAN ESTIMATES, 2003

Notera (här utan annan direkt citatreferens än i Lattimer 2011) att ovanstående uppskattning (förmodligen) baseras på Jetstråleteorin: endast en bråkdel av den idealt sfäriskt utgivna strålningen anses aktuell. Därmed kan (rent statistiskt) motsvarande multipel anställas för »totalt verkliga antalet». Dvs., alla GRBs vars smala Jetstrålar missar Jorden.

— ‡

”Based on almost 30 years of observing gamma-ray bursts, we now think that on average there is one gamma-ray burst per day somewhere in the Universe. However, recent developments in the study of gamma-ray bursts (see below) indicate that the true number of these events may be 100 times larger. This means that we only see one out of every 100 gamma-ray bursts.”,

http://users.obs.carnegiescience.edu/eberger/faq.html

GAMMA-RAY BURSTS FAQ, Edo Berger 2005

— ‡

”More than 1 per day is observed, but due to beaming, the actual rate is perhaps 1 per minute in the universe.”,

http://www.astro.sunysb.edu/lattimer/AST301/lecture_grb.pdf

GAMMA RAY BURSTS LECTURE, J. M. Lattimer Ingen datumuppgift (ref. 2011)

Tekniska begränsningar i GRB-detekteringen enligt citat:

”GRBs with isotropic equivalent energies of ≈10⁴⁸ may be common at z ~> 1 but are undetectable with current instruments.”, sL92sp2n

http://iopscience.iop.org/1538-4357/542/2/L89/pdf/005580.web.pdf

HUBBLE SPACE TELESCOPE SPACE TELESCOPE IMAGING SPECTROGRAPH IMAGING

OF THE HOST GALAXY OF GRB 980425/SN 1998bw, Fynbo et al., 2000

Bara ca 1 GRB per dygn [‡NasaScience1996];

— Konventionellt finns uppgifter som antyder (också under förbehåll att uppskattningarna delvis är omöjliga, men då delvis via andra faktorer än i TNED; främst uppskattade GRB-förekomster baserade på Jetstråleteorin)

450 ggr den registrerade mängden (450 × ~1 per dygn) (NASA2003) ,

100 GRBs per dygn (drygt 4 per timme) (Berger 2005),

1440 GRBs per dygn (1 per minut) (Lattimer 2011),

— I MAC anses GRB-pulserna sammanhänga med JET-strålar; Då bara en smal del, sannolikt, kan träffa vår position per tillfälle, blir motsvarande uppskattning av totala antalet tillfällen en funktion av en sfärisk medelfördelning av jetstrålens koniska öppning på totalt uppskattade antalet GRB-objekt över hela himmelsytan (isotropiskt [lika från alla håll] fördelat). Den medelvärdesbildningen blir alltså helt annorlunda jämfört med förutsättningarna i TNED.

— Genom att sannolikheten för en smal stråle från en avlägsen strålkälla att träffa Jorden är proportionell mot strålkonens del av en hel sfär, kommer motsvarande idealt sfäriska multipel att visa sig i antalet verkliga förekomster om GRB-signalen verkligen skulle vara sfärisk. Alltså MAC-uppskattningens JetMech — gånger jetstrålens del av hela sfären: runt flera tusen (8000 …).

— Den apparaturen skulle därmed ha BEGRÄNSAD kapacitet att följa upp idealt (isotropiskt) sfäriskt detekterande källor: DELS via begränsad upplösning (bara ner till ett visst minimum), och DELS »bara en åt gången» via begränsad teknik, och då, »den som kommer först» (inkluderat de äventyr det innebär i olika ev. blandningar …) (Jämför 132 personer [som aktiverar en tangent i sekunden] med egna tangentbord kopplade till samma dator: datorn accepterar bara ETT tangentbord som signalkälla för den [först] mottagna signalen, övriga utestängs [via snabb grindlogik]).

HUDF — HubbleSpaceTeleskopets DjupUniversumFoto [2009]

”Astronomers think that there are hundreds of billions galaxies in the universe, however the exact number is not known. But astronomers should know how many galaxies we’ve actually seen and discovered, right? Well, not necessarily. “We don’t know,” says Ed Churchwell, professor of astronomy at the University of Wisconsin-Madison. “We know it’s a very large number.” In just one image for example, the Hubble Ultra Deep Field, above, there are about 10,000 galaxies visible.”,

”For the time being, the hundreds of billions in the tally are extrapolated from the Hubble Ultra Deep Field, taken over a time period in 2003 and 2004. Pointed at a single piece of space for several months — a spot covering less than one-tenth of one-millionth of the sky — Hubble returned an image of galaxies 13 billion light years away.”,

http://www.universetoday.com/36610/how-many-galaxies-have-we-discovered/

HOW MANY GALAXIES HAVE WE DISCOVERED? — Nancy Atkinson, August 3, 2009

10.000 × 1/10 × 1/1.000.000 = 1 T11 = 100 miljarder

Se även Hubble Ultra-Deep Field i Wikipedia — bilden på ca 10.000 galaxer, den mest högupplösande bild som någonsin tagits på universums synliga utsträckning med största möjliga upplösning (1/10.000.000 av hela den tillgängliga himmelsytan);

http://en.wikipedia.org/wiki/Hubble_Ultra-Deep_Field

@INTERNET Wikipedia, Hubble Ultra-Deep Field [2012-05-23]

”The Question

(Submitted December 05, 2000)

What is the average size of a galaxy?

The Answer

Thank you for your question. Our Milky Way galaxy is a pretty typical large galaxy. Most of the stars are in a disk that is about 100,000 light years across in diameter and 3000 light years thick. Most of the galaxies in the universe are actually smaller than the Milky Way. For example, most of the dozens of galaxies in our Local Group are at least ten times smaller in diameter.

-- Michael Loewenstein and David Marsden for "Ask an Astrophysicist"”,

http://imagine.gsfc.nasa.gov/docs/ask_astro/answers/001205a.html

ASK AN ASTROPHYSICIST — Dec2000

(4π[5,25T25M]³/3)/(2×9T22M/10)³ = 1,03931 T11

Se även HUDF-bilden ovan.

Maximal teleskopupplösning 2012

Jämför f.ö. potentialen för max upplösning i dagens läge (2012):

”The Hubble Space Telescope represents the greatest clarity of vision ever achieved by a major observatory at visible wavelengths. The 0.1 arcsecond resolution it achieved is only 600 times finer than that experienced with the naked eye. But, the results have been stunning anyway.”,

”Intercontinental baseline radio interferometry has produced images with milli-arcsecond resolution, 100 times finer than that of HST. With these images, astronomers have probed deep into the hearts of quasars and the Milky Way Galaxy.”,

”The MAXIM concept utilizes X-ray interferometry to achieve micro-arcsecond angular resolution. A NASA mission built around this concept could achieve resolution as fine as 300 nano-arcseconds. This resolution is 3,000 times finer than VLBI and 300,000 times finer than HST.”,

http://maxim.gsfc.nasa.gov/docs/vision.html

NASA MAXIM — Micro-Arcsecond X-ray Imaging Mission, The Vision, datum saknas (2010)

Se även angående OBSERVERBARA GRÄNSER:

HubbleSpaceTeleskopets begränsning

”What is Hubble’s range?

The telescope itself has no limit to its range — but the Universe itself does. Hubble is a medium-sized (2.4-metre) telescope with very sharp optics and very good instruments. This enables the telescope to see very faint objects despite its relatively modest size.

According to the theory of the Big Bang, the absolute observational limit to telescopes (as we know them today) is a “sphere” of opaqueness surrounding us and with a “surface” approximately 13–14 billion light-years away. It is called the surface of last scattering, and is also known as the source of the microwave background radiation. Up to 300 000 years after Big Bang, the Universe was totally opaque to light. This means that we know that, when we look out in the Universe and thus back in time, we will never see past, or through, this barrier.”,

http://www.spacetelescope.org/about/faq/

HUBBLE — FAQ - Frequently Asked Questions, datum saknas (2011)

TYVÄRR är NASA-artiklar ofta utan datumpreferenser — samt också generellt utan direkta hänvisningar som grund för olika påståenden. »Vi litar på dig»-typen har LÅG historisk kredit. Please.

Mera allmän beskrivning finns i Astronomical Seeing

http://en.wikipedia.org/wiki/Astronomical_seeing

[GoogleSearch ”maximum visibility universe, resolution arcsecond”]

Exempelreferens Vintergatans primära expansion — Bildkälla, Författarens arkiv, 21Sep2011E17Bild20 NikonD90 Detalj

EXEMPELREFERENS — Vintergatans primära expansion

T = 7[m_J^1/3/ρ_final]^1/2 ............................ S, J-kropparnas primära expansioner vid c/c0=1

R = [3m_J/4πρ_final]^1/3 = m_J^1/3[3/4πρ_final]^1/3

VinExp.PNG: (2,785 T41)^1/3=6,53042 T13

TGrafUnit10 y = 10logT(S); x= n i ρ=1,82·10ⁿ

(0.4343)ln(7[[([6.53(10'13)])([(1.82)10'–x])'–1]'0.5]);

RGrafUnit10 y = 10logR(M); x= n i ρ=1,82·10ⁿ

(0.4343)ln([6.53(10'13)][3/4þ(1.82)10'–x]'1/3);

d = δD / (180/π · 3600) ............ diametern d på avståndet D >> d från upptagande synvinkeln δ i bågsekunder

= δD/(~206265) ;

d = (0,1’’)(5,19 T25 M)/(206265)

= 2,51618 T19 M eller ca d/(9,27 T20 M) ~ 1/37 av Vintergatans nuvarande diameter ca 30Kpc.

Se samband i Bågsekunder och distanser.

Vintergatan metriskt synlig först härifrån via 0,1 bågsekund (~0,8 Kpc)

.................................................................................................................................↓

Vintergatans Expansion från max täthet

Se efterföljande Grafbeskrivning.

Svarta linjen: Utvecklingen av J-kroppen från primär egendetonation (T=0) upp till den normala himlakroppens storlek börjar längst till vänster från max täthet (1,82 T17 KG/M³). Vartefter J-kroppen (Vintergatan i exemplet via ideal sfärisk omfattning) expanderar från sin primära detonation via divergenständning, avtar tätheten (horisontella x-skalan åt höger). GrovTiden (T) anges av vertikala skalans 10log(T). GrafUnit10 y = (1/2.3)ln(7[[([6.53(10'13)])([(1.82)10'–x])'–1]'0.5]).

Orangea linjen: J-kroppens motsvarande synliga storlek under expansionen beskrivs av den orangea linjen: 10log(R) anger J-kroppens ideala sfäriska radie för varje motsvarande täthetsvärde (x-skalans 10log(ρ/1,82), eller om man så vill direkt från vertikalskalans 10log(T)-värde till svarta linjen, därifrån vertikalt till orangea linjen. GrafUnit10 y = (0.4343)ln([6.53(10'13)][3/4þ(1.82)10'–x]'1/3).

Vänstra kompletterande vertikalskalan för 10log(maS): R-värdet taget via distansen 5,19 T25 M (c=0,1c0) enligt resultatbilden från täthetsändringsfunktionerna, ger en motsvarande optisk synbarhet i termer av upptagande synvinkel för J-kroppens diameter. Det värdet i milliARCUSsekunder (maS, ofta förekommande enhet i optiska bilder av galaxområden i samband med GRB-analys) ges av den vänstra vertikalskalan på samma graflinje som R-värdena.

— Med HubbleSpaceTeleskopets angivna upplösning [2012] på 0,1 bågsekund [‡] — 100 maS — skulle ingen synbarhet alls finnas för en primärt expanderande kropp av Vintergatans magnitud förrän vid tiden runt T16 S eller ca T=300 miljoner år;

10log(100maS)=2; –(–9,24 –2)=11,24 i vänstra vertikalskalan räknat från 0 och uppåt; 11,24 motsvarar 10log(R)~19,1 som träffar 10log(T) vid 16; (T16 S)/(1S/3,16888 t8)=3,16888 T8 år ~ 0,3 miljarder år.

— Med teknikens vidare utveckling ökar precisionen: absoluta syngränsen går dock vid exakta c=0.

Vertikalskalan vänster ger 10-logaritmvärdet för synbarheten av galaxskivans diameter i millibågsekunder (maS, milliarcusSekund) med referens till maxavståndet 5,19 T25 M (c=0,1c0) via offsetvärdet –9,25 på grafiska formen för 10logR.

Grafbeskrivning

Graf = y = 10logR(M) Unit10pixels

(0.43429)ln[(3·2.785(10'41)/[4þ(1.82)(10'–x)])'1/3] =

(0.43429)ln[(3.653(10'40)/[(10'–x)])'1/3]

;

Graf = y = 10log(maS) Unit10pixels

(0.43429)ln(2(180/þ)(3600)(1000)atan[[(3.653(10'40)/[(10'–x)])'1/3]/(5.19[10'25])])

(0.43429)ln(2(180/þ)(3600000)atan[[(3.653(10'40)/[(10'–x)])'1/3]/(5.19[10'25])])

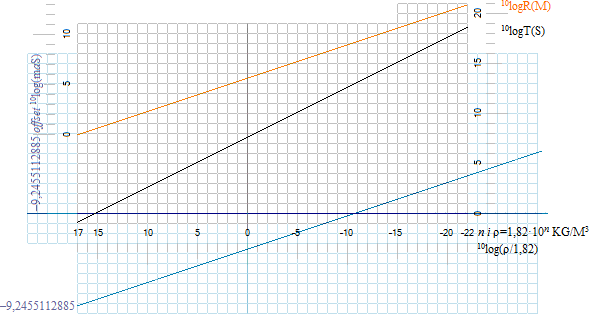
END.

GRB-objektens ursprung i TNED

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

GRB-objektens ursprung i TNED

ämnesrubriker

innehåll

GRB-objektens ursprung i TNED

Referenstabell GRBSNN

Primärtändningarna

Villkoren för GRB

FigurGrundExempel till fraktalnivåerna

Fraktalnivåerna för GRB

Signalspridningen

Gravitella ljusavböjningen, illustration

Gravitella ljusavböjningen, samband

Frekvensen synliga pulsbilder

Antalet GRB-himmelsfläckar

Medelgalaxerna

Antalet randgalaxer

Randgalaxernas förnyelseperiod

RÄKNEEXEMPEL cG

Antalet mellanliggande galaxlokaler

Gravitationsenergin för K-cellens primärkroppar

Redovisad överslagsräkning — Största fysiskt möjliga fusionsexotermiska strålenergin

Redovisad överslagsräkning, gravitella rödförskjutningen

PrimeEnergy

Primärpulsens energi genom radiell packning

Detonationsschema

Radiellt idealt summerande detonationseffekten

GRB-utlösningen i TNED

NASA LightCurves

FigBNB 1 — FigBNB 2 — FigBNB 3 — FigBNB 4 — FigBNB 5

Jämförande praktiska GRB-pulsexempel

DETONATIONSPULSERNAS REAKTIONSTID

Kärnåterkopplingens fördröjning

Den utläckande primärstrålningen

GRB-objektens ursprung — ingen påvisbar neutrinostrålning

Principen bakom GRB-objekten enligt relaterad fysik

Galaxexpansionerna

TNED-sambandet J-kropparnas expansion

Precisionen i expansionssambandet för J-kropparna

GRB-objektens lokaler

Osäkerheten i GRB-objektets position

GRB efter/före SN

Sexdagarsloppet

Antalet SN i Vintergatan

Antalet SN i Universum

Bildexempel — genomträngande GRB

GRBviz

NASA2704GRBskyMap

Multipla GRB — från VISUELLT samma primära signallokal

Fong 2009

Bågsekunder och distanser

WikipediaGRB050509B

Syngränsen TNED ref.

Tänkbara galaxvärdar för GRB

TNEDvärdarna

GRB-värdarna enligt TNED

Strålningstryckets roll för mörka materiens härledning

Kärninduktiva Strålningstryckets inverkan

RÄKNEEXEMPEL

Sandkornet15mM

57MilsKuben

Sammansättningen i kosmiskt stoft

En partikel per T8 kubikkilometer

MMLightMAC

NewScientistMW

Sammansättningen stoft-gas

Beräkningsexempel, mörka materien i TNED — Si-kornets ljusskärm

Mörka materien i modern akademi

Antalet GRBs per dygn

HUDF — HubbleSpaceTeleskopets DjupUniversumFoto [2009]

Maximal teleskopupplösning 2012

HubbleSpaceTeleskopets begränsning

Exempelreferens Vintergatans primära expansion

Grafbeskrivning

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

e₀ = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²

[BA]. BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, modern akademi

TNED

(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken

är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.

Senast uppdaterade version: 2013-06-23

*END.

Stavningskontrollerat 2012-07-03.

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ τ ρ π ε ħ UNICODE — often used characters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω →∞ ≡ ↔↕ ħ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — also Alt+18 ↕; Alt+29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

åter till portalsidan · portalsidan är www.UniversumsHistoria.se