K-cellens inre | Mörka materien — Universums Historia

UNIVERSUMS HISTORIA | K-cellens inre — Mörka Materien | 2012VI16 a BellDHARMA production | Senast uppdaterade version: 2021-12-31 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

GRB1—K-CELLENS INRE • GRB1m—MörkaMaterien • GRB1n—Primära v-formen • GRB2—UniversumsSynrand • GRB2a—AkroBreak • GRB3—GRBorigin

Mörka materien i TNED — Divergenständningarna i detalj — Se HISTORISK BAKGRUND i MörkaMaterienMAC

TNED förklarar mörka materien

Bildkälla: MAGIC NATURE

— Andromedagalaxens observerade Blåförskjutning mot Vintergatan

— Radialhastigheten i Lokala Galaxgruppen motsvarande grovt 300 KM/S, som i en c-homogen rymd indikerar att Andromedagalaxen är på väg att kollidera med Vintergatan [resultatet av den händelsen behöver inte vara så dramatisk som den låter; de stora inbördes avstånden mellan stjärnorna kan göra att galaxkropparna i stort sett bara passerar igenom varandra utan större dramatik]

— behöver i termer av den relaterade fysikens gravitella dopplereffekt/rödförskjutning [Gravitella dopplereffekten] inte alls innebära en sådan resultatbild som utpekar hastighet: Är Andromedagalaxen i K-centrum, och Vintergatan strax utanför, kan gravitella blåförskjutningen få värden JUST i storleksordningen omkring de marginella värdena runt 0,999... c0 — samma som den observerade blåförskjutningen: Andromedagalaxen och Vintergatan skulle i så fall i själva verket befinna sig VILANDE i varandras referenser.

— För att kunna avgöra frågan måste [speciellt ingående] jämförelser genomföras med hänsyn till just Gravitella dopplereffekten. Den undersökningen ligger explicit helt utanför ramen för denna framställning. Gravitell röd/blå-förskjutning mellan stjärnorna ingår f.ö. inte i MAC.

Fraktaldelningsexemplet Vintergatan/K-cellen

K-cellen

SYNLIGA MASSANS FRAKTALER

5,8 T9 Vintergatsmassor

Även grovt hela K-cellen med minsta J-massan som Vintergatan

Delningsexempel

Vintergatans J-moderkropp i fraktalt delningsexempel ända ner till Solsystemets nivå

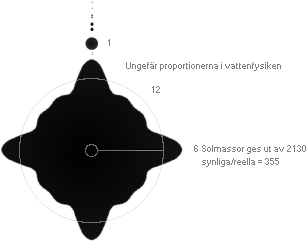
Från K-cellens värmefysik ges ett förhållande 1/355 [Synliga och totala massan] [Innebörden av h-faktorn] mellan synliga och verkliga delar i K-cellens [universums] massa.

— Delningsexemplet i figuren till vänster visar resultatet av en fraktaldelning på den basen med den synliga Vintergatsmassan ca 2 T41 KG eller ca 1 T11 Solmassor [2 T30 KG];

6 enheter i varje fraktalgrupp i 14 fraktalnivåer, varav 4 enheter visas i hela konceptets plansnitt. Pixelbilden kan visa max endast 8-9 nivåer.

Delningen är gjord på enklaste sättet enligt ln[1 T11]/ln[6]=14 fraktalnivåer efter kubens tre diagonalt parsymmetriska ytor, varav 4 av de sex utkastningsriktningarna är synliga i snittplanet, figuren vänster.

Slutfraktalens ändstation är vårt Solsystem eller stjärnbildningar generellt med i genomsnitt 1 Solmassa. Figuren ovan visar den ungefärliga proportionen med 6×355=2130 Solmassor i den J-moderkropp som föder vårt Solsystem — enligt K-cellens värmefysik i TNED.

Detonationsmassorna — mörka materien

Endast slutfraktalernas yttersta massobjekt — stjärnorna och deras eventuella planetsystem — kommer att tillhöra den synliga materien (Se Slutprodukten).

— Alla de centralt belägna stora svarta detonationsmassorna i vänsterfiguren ovan bortfaller som icke synligt material;

— Detta kan enligt TNED (mera utförligt nedan) förstås omvandlas till enorma mängder (Kiselbaserat) damm och stoft (Se Sandkornsanalogin), omöjligt att upptäcka direkt — (möjligen) via tillfälligt högaktiva betalokaler, garanterat av den stora mängden omgivande neutroner i detonationsmassans kallplasmakropp — och vilken STORA massandel successivt tränger in i K-cellen med början från tidpunkten för de allra första divergenständningarna i K-cellens historia (från grovt 10 miljoner år).

— Dessa detonationsmassor skulle i så fall »bara» ha funktionen att DELS få fram ändfraktalernas yttersta finstruktur — stjärnorna — och DELS funktionen att via massavdelningarna inåt K-centrum också öka K-cellens centrala täthet och därigenom garantera en inbromsande verkan på all utanförliggande massa: expansionens avstannande (Se Stoppmoderatorn).

— Det är i stort den övergripande tolkningsbild för K-cellens utveckling som framkommit (Apr2012).

— Vi studerar detonationsmassans (möjliga) upplösning.

Den fraktalbildande detonationsmassans upplösning — från Mörka materien enligt TNED — DETONATIONSMASSANS UPPLÖSNING


a	b	c

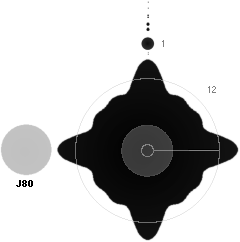
a J80-kroppens storlek, grå, i förhållande till hela den moderkroppens massa som ligger till grund för Solsystemet, enligt fraktalexemplets delning.

b Infallande neutroner från den överviktiga J80-kroppen förvandlar dess inre grundämnesmassa till starkt högenergetiskt betaaktivt material som fragmenterar [explosivt] till molekylärt [Silikatbaserat] stoft.

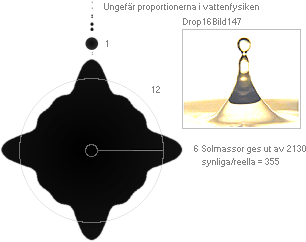
c Proportionaliteten 1/355 visar sig stämma ungefärligt också med storleksrelationerna i vattendroppsexperimenten.

Sambandsformerna är de enklast tänkbara för det illustrerande ändamålets översikt.

Det är bara J80-massan (ca 80 Solmassor, figur a ovan) och större som har möjligheter att avdela fristående J-kroppar med egna nolldivergenser, typ Solsystemets kroppar inkluderat de kroppar som bildar stjärnor i allmänhet.

— Genomgången av matematiken för GRÄNSMASSORNA i stjärnfysiken enligt TNED visar att max 15 Solmassor bildar den övre gränsen för stjärnornas fysik.

En kropp med större massa än 15 Solmassor tvingas expandera bort överskottet genom Atomkärnans inkompressibilitet. Se utförligt i Rekyleringen i Statiska Detonationsgränsmassan.

— För en primär J-kropp med större massa än 80 Solmassor som genomgått divergenständning med åtföljande neutronsönderfall och en påbörjad fusionsfas med inre grundämnesbildning som leder till J-kroppens snabba expansion, finns speciella förutsättningar genom J-kroppens ytterhölje i formen av neutronkallplasma, figurdelen i b ovan:

Betanuklidbildning

FÖLJANDE FRAMGÅR ENLIGT TNED:

— När den ytneutronbestyckade J-kroppen detonerar och en del av dess inre bildade grundämnesmassa tvingas röra sig utåt, tvingas den också på ett eller annat sätt blandas med den yttre neutronmassan (J-kroppen tvingas in i ett svängningsförlopp). Neutroner möter inget hinder att förenas med redan befintliga atomkärnor: TIDEN för föreningen är heller inte kritisk (sker »omedelbart»). Är neutronmängden speciellt stor kan de redan bildade grundämnesnukliderna (längre in mot J-centrum) berika sig i formen av JUMBONEUTRONER, analogt högexciterade betainstabila nuklider. Det finns här veterligt ingen möjlighet att undvika den utvecklingen: Neutronberikningen tvingar nukliderna in i en starkt betaradioaktiv lokal.

— Notera dock J-kroppens yttersta delar:

— Expansionen på den upplagrade g-energins räkning [‡v>c] ger möjligheten för HÖGA (multipla c) utkastningshastigheter i J-kroppens yttersta skikt. I så fall finns också möjligheten för mindre neutronpärlor att avancera genom universum med utkastningshastighetens belopp [KOSMISKA PARTIKELSTRÅLNINGENS URSPRUNG I TNED] [Räkneexempel med den högst observerade partikelenergin] [15mMkuben] [SANDKORNSANALOGIN] — alltså utan att någon fusionsprocess eller kemisk materialbildning ALLS verkställs mellan masselementen förrän deras hastighet (av olika anledningar) bromsats upp till lägre än lokala ljushastigheten. Funktionen i relaterad mening TNED beskrivs översiktligt i Elektrisk och magnetisk verkan mellan atomer och elektroner som färdas fortare än c .

— Är den tillgängliga neutronmängden stor blir energiavgivningen det också, och det finns ingen möjlighet att undvika ett extremläge med en (möjligen starkt) explosiv utveckling av J-kroppen på grundämnesmassans molekylära villkor: J-kroppen kan (här) förstås upplösa sig i (snabbt bortflyende) grundämnesstoft (Silikatdamm eller motsvarande mineraldamm generellt [MINERALGRUNDERNA]) under (underliggande) stark ljusutveckling (högintensiva betasönderfall). I det scenariot finns, här veterligt, ingen förutsättning för kroppsbildning av någon större typ.

— Det är i denna författnings begripande den direkta händelsebild som framgår enligt TNED i förklaringen till de fraktalbildande [FRAKTALEXEMPLET] detonationsmassornas öden — och därmed den veterligt enda primära logiska — rationella (förnuftsmässiga) — förklaringen till den s.k. mörka materien. Jämför inledningscitatet från Bonniers Astronomi 1978.

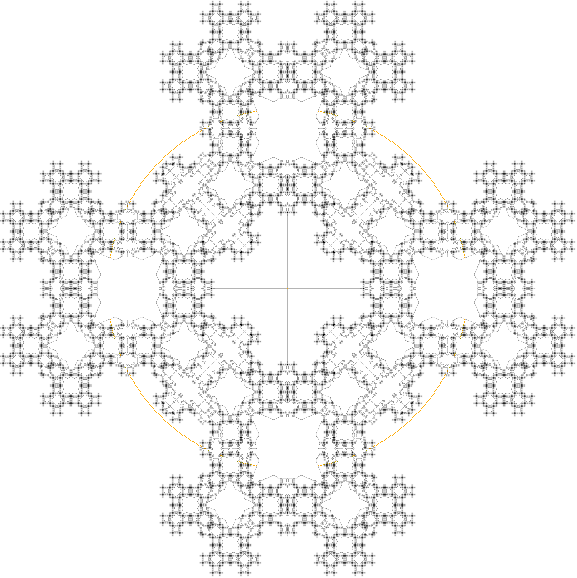
Det som återstår efter divergenständningarna vid slutet [DIVERGENSTÄNDNINGARNA I DETALJ] blir bara FRAKTALPRODUKTEN: alla stjärnor (med tillhörande planetsystem, dessa ingår i stjärnmassorna). Figuren nedan ger en viss orientering (mycket mer mörka områden skulle ha tagits bort här, men då kommer knappt något alls att finnas kvar för illustration).

— Den antydda orangea cirkeln i resultatfiguren nedan markerar nuvarande proportionella distansen för vårt Solsystems avstånd från Vintergatans centrum (ca 30 000 ljusår från centrum med totala radien ca 50 000 ljusår). Lokalen ger (möjligen) en orientering om hur och på vilket sätt vår egen STRUKTURELLA position i Vintergatans kan beskrivas i historisk detalj.

Slutprodukten

Illustrationens underliggande princip visar ett synnerligen GALANT sätt att FÖRKLARA mörka materiens upphov, ursprung, fysik och dynamik.

I praktiken tillkommer — speciellt för K-cellens centrum — även ett komplex med INRE avdelningar från K-cellens innervägg och inåt K-centrum. Dessa delar SKULLE — i K-cellens allmänna beskrivningsform, som det syntes i framställningens början — INTE representera någon större andel i den totalmassa som universums synliga del utvecklas på.

— Den delen är i vilket fall avgörande viktig för förklaringen till Vintergatans uppkomst: Maximal dynamik via max ljushastighet för giltigheten av resultaten från sambanden enligt TNED är avgörande för hela ämnet. Det visade sig, nämligen med en fördjupad matematisk fysik i K-cellens inre, att huvuddelen av det synliga universums utveckling använder bara en LITEN del av K-cellens totalmassa, och då — som det ser ut — mera i orientering mot K-cellens inre än det yttre. Se speciellt i Praktiska GRB-ursprunget som (enligt hittills uppnådda resultat) visar syngränskurvorna till jämförelse i de olika sätten.

Se även vidare om Mörka Materien enligt TNED i Sandkornsanalogin.

————— Bildkälla Mörka materien Magic NATURE

Författarens arkiv · Miljö2012 M3:23Mar2012 Bild62 · Nikon D90 Detalj

Kosmiska partikelstrålningens ursprung

KOSMISKA PARTIKELSTRÅLNINGENS URSPRUNG

Bildkälla, Författarens arkiv, 22Maj2012E2Bild22 NikonD90 Detalj

Kosmiska partikelstrålningens ursprung

Exempelberäkningen som omnämndes i KOSMISKA PARTIKELSTRÅLNINGEN kräver för en enda proton en ekvivalent ideal mekanisk hastighet på strax under en halv miljon c0 (runt 1,5 T14 M/S) för att kunna förklara den observerade rörelseenergin (E_kin=m₀v²/2) i det rapporterade fallet.

— Det finns ännu (Apr2012) ingen (allmänt accepterad) teori i moderna kvarter till hur eller på vilket sätt en sådan enorm partikelenergi skulle ha bildats [‡CitatBerkeleyLabApr2012]. I TNED ställer sig saken annorlunda. Vi studerar detaljerna.

2012IV29

Kosmiska partikelstrålningens ursprung

HUR DE OBSERVERADE HÖGA KOSMISKA PARTIKELENERGIERNA KAN FÖRKLARAS I DETALJ ENLIGT RELATERAD FYSIK

Neutronpärlor som kastas ut med maximal hastighet [multipla c0] från randen av J-kroppar [galaxmassor] efter divergenständning

Gravitationsenergins frigörande vid randen på en J-kropp som efter divergenständning expanderar på den upplagrade gravitationsenergin E(G)=Gm²/r, ger en motsvarande maximal expansionshastighet (flykthastigheten) v=√2Gm/r som med neutronkallplasmats maximala täthet (1,82 T17 KG/M³) ger

v = m^1/3(0,0110392 MS^–1KG^–1/3) [‡Samband]

— För att generera en kinetiskt ekvivalent utkastningshastighet på v=10c₀ vid den kroppsranden från neutronkallplasmats maximala täthet blir den underliggande detonationsmassa (m, sambandet för v ovan) som krävs lika med 2,00285 T34 KG, eller ganska precis 10.000 Solmassor.

— Genom att detonationsmassan bakom J-moderkroppen till Solen minst måste vara drygt 200 Solmassor (J80-massan, plus Solmassans radiella tillskott i J80-massans periferi, utförligt i J-kropparnas hastigheter), samt att förhållandet generellt i K-cellen mellan synlig/verklig massa är (eller alltid måste avspegla kvoten) 1/355, ges i princip en mera praktisk basmassa för bildning av stjärnor generellt (med Solmassan som normal) på MINST runt m(10c0)=200×355=71 000 Solmassor. Därmed är också grundformen med 10.000 Solmassor väl relaterbar.

— m(10c0)-kroppsrandens expansion medför tvunget via detonationsmassans uppenbart stora andel neutronkallplasma också en potentiellt stor möjlighet för den expanderande kroppsranden att bilda inte bara tyngre (starkt lokalt betaaktiva) atomer än Väte, utan även dito mineraliska sammansättningar av alla möjliga typer;

Mineralgrunderna

— MINERALGRUNDERNA ges i TNED utförligt från Udda-Jämna-Nuklidgrupperna [GRUNDÄMNESBILDNINGENS TVÅ BASGRUPPER] — alla nuklider upp till Järntoppen (omkring Järn-Kobolt-Nickel): Med (stor) närvaro av primära neutroner, kan sedan i princip alla övriga möjliga grundämnen bildas;

— Basdiagrammet för GRUNDÄMNESFÖRDELNINGEN via optimala fusionsgränsmassan anvisar hur möjligen J-kropparnas yttre (rika Kisel-Syre-områden) kan bilda typ Silikatmineral i deras goda tillgång på primärneutroner — eller generellt mineralstoft av alla möjliga typer — om v ligger inom lokala c [Elektrisk och magnetisk verkan mellan atomer och elektroner som färdas fortare än c].

— Mot den bakgrunden [PLANCKEKVIVALENTERNA] finns ingenting som hindrar den utkastade materialdelen att bilda högenergetiska partikelfragment på den helt elementära mekaniska kinetiska energiformen

E(kin)=mv²/2=m(10c₀)²/2;

Räkneexempel med den högst observerade partikelenergin

— Ett Kiselkorn med sfärradien 150 nM och specifika vikten 2323 KG/M³ (eller motsvarande mängd neutronkallplasma; en liten neutronpärla som helt obesegrad drar genom nejden med 10c in mot K-centrum [‡v>c]) och därmed massan 3,565 t17 KG skulle då ge rörelseenergin E~160 Joule eller 1 T12 GeV eller ca T21 eV, vilket motsvarar en ekvivalent till den (ännu 2012) högst observerade energin från den kosmiska partikelstrålningen (se citat nedan).

— Även om vi räknar med en lokal divergensdämpning (gravitell rödförskjutning) in till 0,1c₀, som medför en energireduktion på 100 gånger (via mcc), och som därmed kräver en motsvarande hundrafaldigt större detonationsmassa (7.100.000 Solmassor, vilket ändå motsvarar bara en bråkdel av en synlig Vintergatsmassa [T11 Solmassor]) för att nå samma resultat som i ideal c₀-rymd, visar sig just massproportionerna fortfarande HANTERLIGA i resultatänden: det går att diskutera/relatera en möjlig kvalitativ/kvantitativ ursprungsform för den höga kosmiska partikelenergin ÄVEN sett ifrån universums allra yttersta rand [UNIVERSUMS SYNRAND] via motsvarande galaxbildningar — och därmed den gravitella rödförskjutningen inkluderat enligt TNED.

— I modern akademi är en sådan förklaringsgrund helt utesluten.

— Man räknar med att den kosmiska partikelstrålningens energi på sin höjd kan omfatta endast lättare atomkärnor [Sammansättningen i kosmiskt stoft], definitivt inga sandkorn i nanostorlek (eller maximalt tätt packade neutronhopar i picostorlek som färdas med multipla ljushastigheter); det finns ingen teoretisk grund för sådana [PLANCKEKVIVALENTERNA]. Därmed reser sig också de observerade enorma partikelenergierna som i stort sett teoretiskt oövervinneliga barriärer.

Protonen orealistisk som agent för högsta energin

Teorin skulle också (i praktiken) vara omöjlig i TNED om vi enbart vore hänvisade till typen Vätekärnor som den kosmiska partikelenergins agenter. K-cellens ytterradie (detonationsmassan m=4,14 T53 KG) detonerar visserligen initiellt på ekvivalenta runt 27 miljoner (T6) c₀ [‡Samband]. Men det gör ingenting åt den nu LÖPANDE ANDELEN INKOMMANDE PARTIKLAR som måste förklaras: strömmen av partiklar som träffar Jordatmosfären måste tydligen bildas på KORT tid, löpande. Enbart med hänvisning till protonen (1,67 T27 KG) skulle också TNED stå maktlös om uppgiften gällde att få fram praktiskt hållbara resultatvärden på partikelenergier i storleksordningen T21 eV i löpande flöden — runt en halv miljon c₀.

— Detonationsmassan bakom en halv miljon c₀ är med ovanstående v-samband lika med 2,5 T48 KG — lika med 1/165600 av hela K-cellens massa (4,14 T53 KG).

— Den matematiken är utesluten i TNED. Universum innehåller helt säkert mer än runt 165.600 stycken enskilda galaxer. Siffran är snarare i hundratal miljarder — se Hubbleteleskopets djupbild av universum.

Citatdelen nedan ger en grovbild av den etablerade synen på den kosmiska partikelstrålningens förekomster.

Citat Wikipedia om kosmiska partikelstrålningen

”About 89% of cosmic rays are simple protons or hydrogen nuclei, 10% are helium nuclei or alpha particles, and 1% are the nuclei of heavier elements. These nuclei constitute 99% of the cosmic rays. Solitary electrons (much like beta particles, although their ultimate source is unknown) constitute much of the remaining 1%.”,

http://en.wikipedia.org/wiki/Cosmic_ray

@INTERNET Wikipedia, Cosmic ray (2012-04-28)

”Cosmic rays can have energies of over 10²⁰ eV, far higher than the 10¹² to 10¹³ eV that Terrestrial particle accelerators can produce.”

Kosmiska partikelenergins medelvärde

Kosmiska partikelenergins medelvärde

Varken Wikipedia eller andra webbkällor verkar kunna specificera medelpartikelenergin från den kosmiska strålningen.

— MYMESONER eller MYONER, eng. muons, omnämns som de centrala partiklar som bildas ur kosmiska partikelkollisioner i Jordens övre atmosfär [se även i Beviset för multipla c].

— Men inte heller den detaljredovisningen finns med i Wikipediaartikeln, utom i stycket om Detection, för att exemplifiera:

— Det verkar inte finnas någon EXAKT CITERBAR allmän referenskälla till påståendet om något ALLMÄNT MEDELVÄRDE för kosmiska partikelstrålningsenergin.

Den enda [kryptiska] uppgiften som verkar finnas [Apr2012] är av nedanstående typ — runt 6 GeV:

”The mean energy of muons at sea level is still 4 GeV. Therefore the mean energy at creation is probably about 6 GeV.”,

http://cosmic.lbl.gov/SKliewer/Cosmic_Rays/Muons.htm

Muons — The Cosmic Connection, The Berkeley Lab Cosmic Ray Telescope Project, 2012

Citat Berkeley Lab

“A few rare cosmic rays pack an astonishing wallop, however, with energies prodigiously greater than the highest ever attained by human-made accelerators like CERN’s Large Hadron Collider. Their sources are a mystery.”,

http://newscenter.lbl.gov/news-releases/2012/04/18/icecube-grb-cosmic-rays/

BERKELEY LAB News Center — April 18 2012

Where Do the Highest-Energy Cosmic Rays Come From? Probably Not from Gamma-Ray Bursts

Lättare partiklar, ner till enskilda protoner (Vätekärnor) kan obehindrat bildas på samma J-moderkropp [‡v>c] och därmed ge bilden av den allmänna kinetiskt ekvivalenta medelvärdesenergi (mv²/2) som (ofta konventionellt) anges i samband med den kosmiska partikelstrålningen, dvs., runt (1-) 10 GeV [‡Citatreferens];

— För en Vätekärna (eller mera realistiskt en Neutron [‡v>c], grovt m=1,67 T27 KG) som träffar Jordatmosfären med ca 10c₀ ges energin 46,6 GeV=mv²/2/e/T9. Med uppgiften ovan på medelvärdet ca 6 GeV ges motsvarande idealt kinetiska medelvärdet v=3,6c₀ som den mest välbesökta ekvivalenta kinetiska medelhastigheten om partikeln är en vätekärna.

I MODERN AKADEMI finns inte möjligheten med mekaniska utkastningar på en från en föregående kontraktion upplagrad gravitell energi och som frigörs via en maximalt tät massa (K-cellens detonation);

— Atomkärnans inkompressibilitet finns inte i modern akademi — Jämför Svarta Hål. Atomkärnans formbevarande kraft (TNED) sätter effektivt stopp för den moderna akademins »oändlig volymär täthet» (konv. svart hål). Därmed finns heller varken en djupförklaring eller djupbeskrivning i modern akademi till HUR en stjärna kan kasta ut material.

— Kosmiska partikelstrålningens energier, speciellt de allra högsta, är fortfarande (Apr2012) ett olöst fenomen i etablerade led (se citatet Apr2012 från BERKELEY LAB News Center).

Se även vidare om Mörka Materien enligt TNED i Sandkornsanalogin.

———————— ‡

v = Ö 2Gm/r ; r = m/[V=4pr³/3] = 3m/4pr³ ; r = (3m/4pr)^1/3 ; v = Ö 2Gm/(3m/4pr)^1/3 = m^{1/2 – 1/6 = 2/6 = 1/3}Ö 2G(4pr/3)^1/3

r = (1,82 T17 KG/M³) med G= 6,67 t11 JM/(KG)² ger v=m^1/3(0,0110392 MS^–1KG^–1/3)

———————— ‡

Elektrisk och magnetisk verkan mellan atomer och elektroner som färdas fortare än c

— allmän beskrivning från vad som direkt kan utläsas ur TNED

Partiklar som färdas snabbare än eller exakt vid den lokala ljushastigheten (divergensen) har i relaterad fysik ingen direkt förutsättning för att utbilda inbördes mellanliggande elektriska kraftkopplingar: inga kemiska föreningar: inga fusioner.

— I relaterad fysik (TNED):

— Kraftkopplingarna mellan atomkärnor och deras elektroner — för kemiska föreningar i allmänhet och fusioner i synnerhet — bygger på ett deras individuellt naturliga inneboende elektriskt fält. MELLAN de olika partiklarna bestäms referenserna i relaterad fysik för dessa elektriska fält uteslutande entydigt av den lokala gravitationen [LJUSETS GRAVITELLA BEROENDE] som också definierar den lokala ljushastigheten (Divergensen).

— Färdas atomkärnor och elektroner fortare än vad återkopplingshastigheten (c₀) mellan partiklarna hinner med (Magnetiska fönstret), är det tydligt att också kraftåterkopplingarna blir lidande i motsvarande grad.

— Om atomkärnor färdas fortare än c₀ och från början ligger maximalt tätt intill varandra, som fallet är i K-cellens neutronkallplasma, finns på grund av det extrema näravståndet ingenting i princip som hindrar ett pågående neutronsönderfall förutsatt partiklarna för tillfället befinner sig i en g-rymd med c>0. Genom att atomkärnorna redan från början ligger innanför varandras nuklidbarriärer, kan de på normalt sätt också i princip genomgå (originella) fusioner. Men deras associerade yttre elektroner ges då ingen chans att hänga med: elektronmassan som avdelas från atomkärnorna tillhör den yttre rymdens fysik, omkring atomkärnorna, och kommer därför obönhörligt att lämnas efter i proportion till den försvagade kraftkopplingen i det aktuella g-rummet.

— Det ger totalt sett en intrikat bild av de olika möjligheterna, och som här bara har antytts skissartat.

— De atomkärnor som färdas med v>c »lämnar efter sig» de normala elektriska fält som SKULLE utbildas mellan individerna om v vore noll; fusioner är i princip möjliga om atomkärnorna från början ligger tätt (Nuklidbarriären).

SANDKORNSANALOGIN — Mörka materiens upphov i relaterad fysik

SANDKORNSANALOGIN — Bildkälla, Författarens arkiv, 27Jun2012E10montageBild52Bild41 NikonD90 Detalj

En liten utvikning från grundbeskrivningen [2007] i Mörka Materien. Se även särskild artikel här i Mörka Materiens Upphov enligt TNED.

Mörka materiens upphov — sandkornsanalogin

Helt omöjligt att upptäcka 1 sandkorn per 3,85 T13 M³ på stora avstånd från stjärnorna

Kalkylkort för Vintergatans del med uppställda celler i samband för enklare överslagsräkningar finns i KalkylkortDirekt KcGRB.ods 1LokGal HelpOpen

Först proportionerna med kända objekt — Inledande analogi

Hur man kan räkna för att göra en grovkoll:

100 gånger Vintergatsmassan

— SANDSTEN (ungefär Jordskorpans medeltäthet) har tätheten ρ=m/V=2323 KG/M³

[@INTERNET Aqua-Calc; Sandstone, solid; Aug2011];

— ETT sandkorn, grovt en kub med sidan ca 1 mM, väger då

m(1mMKUB)=ρV=(0,001)³(2323 KG/M³) = 2,323 t6 KG=0,002323 Gram; Två tusendels gram.

TREmilsKuben

— Göms ett (1) sådant sandkorn in per en volymkub med sidan 33,78 kilometer

— en kub med sidan drygt 3 mil; ungefär Stockholm-Södertälje, samma som volymen 3,85 T13 M³

— och man tar antalet sådana (33,78KM)³-kuber över hela Vintergatans omskrivna sfärvolym

V(VIN)=4πR³/3 med Vintergatans radie R=4,63 T20 M (nära 50 000 ljusår),

V(VIN)=4,15749 T62 M³,

blir antalet (33,78KM)³-kuber lika med

(4,15749 T62 M³)/(3,85 T13 M³) = 1,07986 T49 stycken (33,78KM)³-kuber;

— Om varje (33,78KM)³-kub innehåller ett sandkorn med massan 2,323 t6 KG blir totalmassan av alla de 1,07986 T49 stycken (33,78KM)³-kub-kubernas sandkorn lika med

m = (1,07986 T49)(2,323 t6 KG) = 2,50853 T43 KG;

Det är (2,50853 T43 KG)/(2,50 T41 KG) = 100ggr Vintergatans egenmassa.

— »Hur lätt som helst».

— Med ledning av det vägledande citatet från Bonniers Astronomi 1978 närmast nedan, finns (ännu) inga tekniska möjligheter att upptäcka den typen. Jämför ;

Mörka materien BA1978

”En självklar kandidat till rollen som den saknade massan är gasen i hopen.”, s360sp2m;

”Man kan också tänka sig mer kondenserad materia. Studiet av fördunkling och färgförändringar i hopens centrum tyder på att det i så fall inte kan röra sig om stoft i stil med det i Vintergatan. Större stoftpartiklar med storlekar upp till fotbollsformat skulle utan svårighet kunna hålla hopen samlad och ändå förbli omöjliga att upptäcka; problemet är bara att vi inte känner till någon enkel process varigenom sådana objekt kan bildas.”, s360sp2n.

BONNIERS ASTRONOMI 1978 Det internationella standardverket om universum

TNED:

— Kärninduktiva Strålningstrycket är den enda tillgängliga kraftkomponent som i termer av relaterad fysik har någon fysisk möjlighet att kunna putta ut (relativt stora, vilket var det väsentliga) materialkorn från de galaktiskt stjärncentrala närområdena — men den kraftkomponenten finns inte med i den moderna akademins lärosystem:

Mörka materien kring Vintergatan i TNED

Mörka materien kring Vintergatan i MAC

MMLightMAC

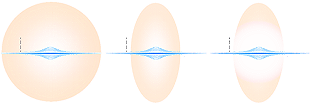
Sfäriska stjärnhopar ger ett homogent fördelat strålningstryck i summan från alla aktiva stjärnor. Omgivande materiestoft kan då förstås drivas ut med en idealt sfärisk rand omkring hopen där balans råder mellan strålningstryck och g-kraft på stoftkornen.

— En spiralgalax har dessutom en aktiv utbredd skiva med stjärnor som bildar ett extra plattcentralt strålningstryck som kan tvinga stoftpartiklarna in mot centrum. Totalbilden blir en ellipsoidisk form snarare än en sfärisk i fallet med spiralgalaxer. Den streckade markeringen i galaxskivan motsvarar ungefär Solsystemets plats i Vintergatan. För illustrationen nedan, se utförligt i GRUNDÄMNESFÖRDELNINGEN.

— Se även mera utförligt beskrivning tillsammans med grunddata från New Scientist i MMLightMAC.

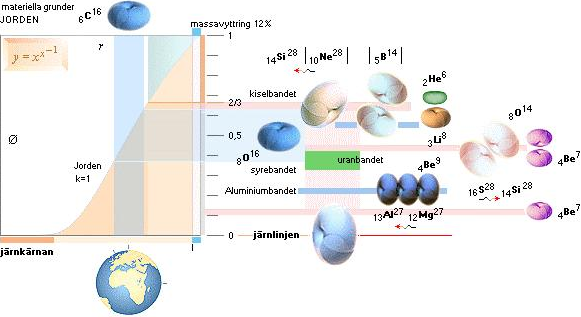
Sandkornens ursprung i K-cellen enligt TNED: Med neutronkvotens maxvärde för grundämnesbildningarna runt 2/3 i sammanfallande ordning med området för KISEL — nära följt av SYRE, figuren ovan i utdrag från GRUNDÄMNESFÖRDELNINGEN — finns ENLIGT TNED speciellt gynnsamma lägen för J-kroppar som INTE kan bilda egna nollzoner [J-massor mindre än 80 Solmassor] att istället sprida ut sitt nuklidbildade material på J-kroppens egen skalmassa [dess yttre skikt]. Det är i varje fall den närmast liggande förklaringen i TNED till HUR stora [enorma] mängder s.k. mörk materia kan bildas — enligt TNED sandkorn — omöjlig att upptäcka på grund av materialkornens litenhet [mycket finare än vanlig sand] och stora avstånd från alla stjärncentra.

— Kiselbandet tillsammans med Syrebandet — om inga fel finns i beskrivningssättet — garanterar tillsammans med den stora mängd J-kroppar med mindre massa än J80-kroppen som avdelas under K-cellens expansion och som genomgår divergenständning — men utan möjlighet för stjärnbildning, se även i GRÄNSMASSORNA I STJÄRNFYSIKEN — att också en stor materiemängd bildas i K-cellens historia av nämnd art: Sand, fint kiseldamm, dessutom [villkorligt] i sådana oerhörda mängder att massan hos den synliga materiens himlakroppar [1/355 av hela K-cellens massa enligt TNED] kan ses som FÖRSUMBAR i varje jämförelse.

— I modern akademi kan visserligen massanalogin utföras med sandkornets bas. Men då det inte finns någon TEORI om varifrån sandkornen skulle komma, hur de bildas, och sprids ut överallt i hela universum [Citat], förloras den rationellt resonerande aspekten: »den mörka materien» framstår i MAC som en ren veritabel gåta.

Om rymden i Vintergatans omskrivna volymsfär innehåller bara ett enda ynka sandkorn (1mM³) per en kub med sidan 33,78 kilometer — i sig ofattbart litet materia per volymenhet — innefattar hela den omskrivna Vintergatssfären med den sandkornsfördelningen 100 gånger mer massa än hela Vintergatan.

— Bara som ett enkelt räkneexempel.

— I det praktiska fallet (se Beräkningsexempel i Strålningstryckets roll för mörka materiens härledning) kommer det inre av galaxvolymen i kärninduktiva strålningstryckets försorg att bli rensat på sand- eller generellt materialkornspärlor: Sandkorn med en viss maximal storlek (grovt runt 15 mM) kommer att parkeras i gravitell jämvikt närmast utanför den omskrivna galaxsfären, med allt mindre sandkorn längre ut, och efter den beskriva exempelräkningen [Sandkornsanalogin] [Strålningstryckets roll för mörka materiens härledning].

— Men »stora mängder glest utspridda (15mM jätte-)sandkorn i rymden» tillhör INTE huvudattraktionen i den moderna akademins kosmologiska teori [Se citatet från Bonniers Astronomi 1978 även i Mörka Materien], ehuru den är självskriven i TNED: primärkropparnas bildning via divergenständning med direkt grundämnesbildning.

— HUR bildningen av sådana materialdelar möjligen kan förklaras enligt TNED beskrivs mera detaljerat i Mineralgrunderna, DETONATIONSMASSORNA och DETONATIONSMASSANS UPPLÖSNING, samt i KOSMISKA PARTIKELSTRÅLNINGENS URSPRUNG.

— I MAC, där bildningsprincipen i relaterad — rationell — mening [MINERALGRUNDERNA] inte ens finns med som ett alternativ, tvingas man istället uppfinna magiska och mystiska nya partiklar — ännu mera Ny Fysik — som ansvariga för fenomenet.

Mörka materien kring Vintergatan i MAC

Mörka materien kring Vintergatan i TNED

Från etablerat håll (via olika simuleringar och beräkningsmodeller kontra basdata via observationer av olika galaktiska och intergalaktiska objekt) räknar man med att »Vintergatans extramassa» är ca 10 ggr egenmassan, se

New Scientist — MILKY WAY'S DARK MATTER 'TURNED ON ITS SIDE', 2010

Det ger med motsvarande sandkornets analogi ett sandkorn per en volymkub med sidan ca Stockholm-Uppsala: 72,77 kilometer (3,85 T14 M³).

— Det är i princip KÖRT för att upptäcka den typen. Se även citatet från Bonniers Astronomi 1978 i Mörka Materien.

— Exempelräkningen tjänar att belysa den centralt avgörande aspekten, att vilken än den sandkornsanaloga extramassan är, det blir omöjligt att påvisa den DIREKT (MörkaMaterienVintergatanTNED) eftersom dess materialstoft (i princip nanopartiklar istället för synliga sandkorn) kan puttas ut (lätt) av stjärnornas (i TNED termonukleära) strålningstryck, och därför inte syns direkt inom »strålzonen» för en aktiv galax.

— Exemplet belyser också att galaxernas egenmassor i princip blir försumbara vid överslagsräkningar (heltalsdelen) som berör lokala masstätheter — om den mörka materien är från 10ggr och större än egenmassan.

J80-kroppens begränsade neutronfysik

J80-KROPPENS BEGRÄNSADE NEUTRONFYSIK — Bildkälla, Författarens arkiv, 27Jun2012E10Bild9 NikonD90 Detalj

J-moderkropparnas praktiska uppdelning

HUR DEN FRAKTALBILDANDE DETONATIONSMASSAN KAN UPPLÖSAS TILL OSYNLIGT MATERIAL MERA I DETALJ

Se grunderna från K-cellens detonation om ej redan bekant.

I praktiken är det inte rimligt att den inre upplysta J80-kroppens kärna ska kunna försörja hur mycket neutronbestyckning som helst av redan bildade grundämnesnuklider.

Från K-cellens detonation, tillfället då neutronerna i det nedsläckta kallplasmat klonkar ihop, finns alltid enligt TNED med hänsyn till atomkärnans formgeometri [Atomkärnans härledning] kraftstråk med mera — och mindre — uttalad koppling.

Som i de övriga naturprocesserna generellt, uppkommer genom de olika kombinationssätten (med olikformade element), tillsammans med olika fördröjningsmekanismer, vågformer med tillhörande strukturbildningar. Och vi bör nog också utgå ifrån att den principen gäller från och med tillfället för K-cellens detonation.

Ett sätt att föreställa sig hur K-cellens detonation utvecklas med början från den innersta J80-massans inre gränsvägg ut mot det nedsläckta neutronkallplasmat, blir med ovan antydda stråkbilder den följande typen:

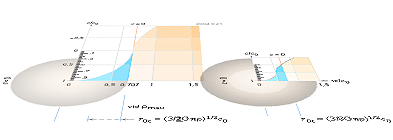
Med en uppdelning i olika radiella kraftstråk av större och mindre omsättning, verkställs detonationen från K-cellens inre J80-kärna genom att de stråk på K-cellens utsida som först visar en formbrytning bildar motsvarande inre svackor som följer utkastningarnas massfördelning. Figurerna nedan i polära koordinater i PREFIXxSIN med funktionen r=1+(Rsin5x)², R i 0,2-intervall 0-1 samt R=1,5.

J-kropparnas primära avdelning från det inre av K-cellen

Se även i Massavyttringens enkla vågfunktion

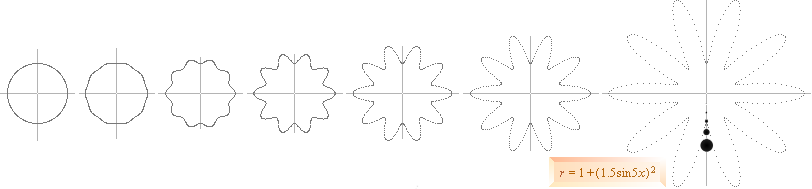
— Med ovanstående uppfattning som förutsätter utbildade kraftvågformer, med början från K-cellens inre, kan en uppdelning ske av J-kroppar internt efter viss tid från den ursprungliga J80-massans innervägg. Avdelningen kan i princip avdela VILANDE J-kroppar relativt K-centrum genom de motsvarande tillbakadragande expansionsfördjupningarna.

— Genom att den ursprungliga J80-massans vätgas och stoft kan samlas på de frilagda J-kropparna (garanterat av deras starka gravitation), kan det inre av K-cellen i princip, och på så sätt, förstås utvecklas på helt massfri grund frånsett de diskret avdelade högtäta J-kropparna. Figuren ovan längst till höger antyder hur J-kroppsavdelningen skulle kunna yttra sig med förebild från den väl observationellt studerade vattenfysiken.

Eftersom DETONATIONSKRAFTEN i den aktuella J-kroppen, vilken den än är, är (maximalt) proportionell mot den g-tryckande massan, analogt den upplagrade g-energin (Gm²/r), kommer ansamlingen av massa utöver J80-massan i en J-kropp också att garantera att J-kroppar med större massa än ca 80 Solmassor eftersträvar en inre uppdelning av typen i proportion till mängden överskjutande neutronkallplasma. Dvs, analogt uppkomsten av motsvarande radiella kraftstråk med tillhörande vågformer.

— Med den grunden säkerställs en optimal uppdelning på ett undersystem av J-kroppar som inte medger hur stora dito som helst i utvecklingen av K-cellens expansion.

— För dessa J-kroppar gäller på vanligt sätt begränsningarna från GRÄNSMASSORNA och som säkerställer att J80-massor med extra neutronkallplasma detonerar med växande kraft i proportion till extramassan. Se utförligt i Rekyleringen i Statiska Detonationsgränsmassan:

— J-kroppar med mer än 15 Solmassor gör sig av med överskottet, hur man än räknar;

— J80-massorna, och in till en viss gräns större som ovan, har via sin proportionellt stora neutronbas i kroppshöljet också stor potential att utveckla högbetaaktiva lokaler genom att neutronerna lätt förenas med de redan internt i J80-massan bildade nukliderna från fusionsfasen efter divergenständningen — och vilken totala J80-kropp därmed kan upplösas i princip i molekylärt (Silikatbaserat) stoft.

— Speciellt stora J80-massExcessKroppar kan, som ovan i grov översikt, utveckla egna inre avdelade mindre J-kroppar som då på vanligt sätt följer J-kropparnas allmänna gränsmassor.

Helhetsbilden med den enklare fraktalindelningens kubiska exempel [Mörka materiens upphov] kan på detta sätt i princip bibehållas bara med skillnaden att den kubiska fragmenteringen på underfraktaler i praktiken bör följa en mera finmaskig struktur — tillsammans med inre uppdelningar (J-kropparnas primära inre avdelningar).

DEN MÖRKA MATERIEN kan tydligen förstås sönderfalla, i vilket fall (i det stora, eller i det lilla), på den beskrivna principen med detonationsmassans upplösning i molekylärt stoft, och i enlighet med resultatbilden från K-cellens värmefysik med fördelningen (sett idealt för hela K-cellens massa) 1/355 mellan synliga och reella massorna.

Se även vidare i Sandkornsanalogin — hur det osynliga materiestoftet kan förstås fördelat i fallet Vintergatan.

Utvecklingen i K-cellens expansion

UTVECKLINGEN I K-CELLENS EXPANSION — Bildkälla, Författarens arkiv, 27Jun2012E10Bild52 NikonD90 Detalj

Utvecklingen i K-cellens expansion

Se även originalförfattningens motsvarande mera allmänna beskrivning i K-cellens expansion — hur K-cellen utvecklas

Med genomgången av och kännedomen om detaljerna i

Mörka materien i TNED

Den fraktalbildande detonationsmassans upplösning

SANDKORNSANALOGIN — Mörka materiens upphov i relaterad fysik

J80-kroppens begränsade neutronfysik

J-kropparnas primära avdelning från det inre av K-cellen

kan vi nu närmare försöka studera detaljerna i K-cellens INRE: den mera internt detaljerade matematiska beskrivningen av K-cellens expansion.

— Det intressanta — och avgörande för helhetsbilden av universums fysik — är här de villkor [CENTRALPARAMETRARNA] som TNED — relaterad fysik — ställer upp med referens till resultaten från K-cellens värmefysik. Frågan är för TNEDs del nämligen om alls en med praktiska observationer sammanhängande totalbild KAN visa sig. Det gäller speciellt beträffande resultatbilden för Vintergatan (vår roll i historien), dess bildning och utveckling med observerade rödförskjutningar tillsammans med dess närmast observerade grannar [Lokala galaxgruppen].

Det blir med andra ord i ljuset av resultatbilden från K-cellens värmefysik faktorerna K-radien och K-värdet 1,5 från resultatredovisningen i grundmatematiken till K-cellens värmefysik (2008) som anvisar formen för HUR, om alls, det inre av K-cellens matematiska fysik ska formuleras. Resultatet av den villkorsformen (2012) finns redovisad från Täthetsändringens funktioner. Resultatbilden totalt för hela K-cellen tillsammans med den övergripande c0-kroppen redovisas i K-cellens övergång i c0-kroppen.

Följande figurdelar och beskrivningar ger allmänna översikter med referenser.

Figuren nedan är till viss del en förenklad sammanställning av detaljerna bakom ovanstående rubricerade avsnitt.

— Det mörka Centralbandet med svackan i mitten, figuren nedan, motsvarar ikoniskt EN PERIOD (672 T9 år från halvperioden 336 T9 år) hos K-cellens utveckling;

— Från detonationstillfället (t0) genom de först avdelade J-kropparna (t1, föremålet för den vidare beskrivningen här) och den efterföljande vidare expansionen fram till avstannandet (efter 336 miljarder år; Se K-cellens halvperiod); Sedan återgången via kontraktionen lika lång tid (K-cellens återvinning).

— Svängningsperioden i början markerad med de avdelade kroppspunkterna (från t0 och fram till effektmaximum vid T=16,32 T9 år, ej markerat i figuren nedan) motsvarar neutronkallplasmats egentliga uppdelning på J-kroppar, och därmed sammanhängande utveckling med de allra första stjänbildningarna:

— Problemet med täthetsändringarna in mot K-centrum

(detonationsmassornas upplösning i molekylärt stoft som successivt sprids ut över hela K-cellen i takt med de fortlöpande divergenständningarna, och som tydligen INTE börjar direkt från t0, och som, successivt, gör att den synliga materiens närvaro (i nutid) blir FÖRSUMBAR [Se Mörka materien kring Vintergatan i MAC] — speciellt angeläget i beskrivningen av den ENLIGT TNED möjliga GRAVITELLA RÖDFÖRSKJUTNINGEN i K-centrum för att, enligt TNED, kunna förklara just förekomsterna där [Lokala galaxgruppen]),

är också föremålet för den vidare beskrivningen här.

UNIVERSUMS HISTORIA — K-cellens vågillustration

— Se även i Grafisk Referens

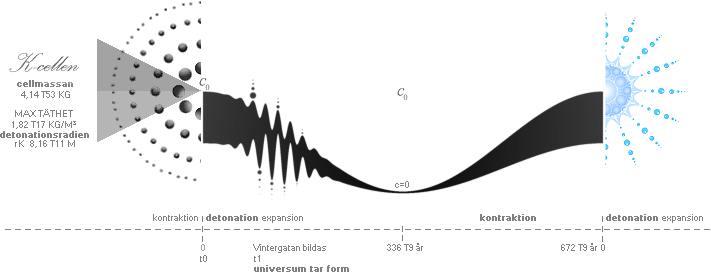
Figurbeskrivning: K-cellens expansion via avstanningsmekanismen — täthetsförskjutningar in mot K-centrum — tvingar expansionen att INTE ske på den maximalt höga ideala flykthastighetens belopp v=[2GM/r]^0,5. Däremot när K-cellens material vänder tillbaka från avstanningsläget, TANGERAS v-formens värden praktiskt om fallsträckan är stor, vilket den är i K-cellens fall. Det medför att perioden från v=0 tillbaka till detonationsläget blir kortare än expansionstiden genom att fria fallets g-fysik ansluter praktiskt till den högre=snabbare flykthastighetens värden. Se explicit i EXPANSIONSSAMBANDETS KOPPLING TILL FRIA FALLETS G-FYSIK. Denna detalj finns inte med i ovanstående illustration.

I ett försök att komma underfund om vilka mera övergripande detaljer det är som ligger till grund för ovanstående möjliga historik, har följande, översiktligt illustrativt, beskrivande genomgång visat sig.

Mörka materiens rationella fysik i TNED

NOTERA SANDKORNSANALOGIN: Detonationsmassorna medger utrymme för närmast hutlöst omfattande neutronkallplasmaområden vilkas utkastade neutronmassor sedan kan forma minimala materiekorn: de redan tätt liggande neutronerna i kallplasmat bildar direkt fusionsringar om och när neutronsönderfallet börjar — och därmed en tvungen bildning av grundämnesatomer som sedan kan förenas materiellt till större korn. SANDKORNET får här illustrera samtliga möjliga typer av sådana massformer. Se även i Sandkornet15mM [Strålningstryckets roll för mörka materiens härledning] [RÄKNEEXEMPEL].

K-cellens värmefysik bygger helt idealt på den expanderande K-cellens ytterrand — och därmed en idealt homogen täthetsfördelning: Medeltätheten tagen över hela K-cellen avtar VIA GRUNDSAMBANDEN med K-cellens expansion enligt Expansionssambandet.

— Men K-cellens expansion I PRAKTIKEN följer INTE en sådan enkel matematik [Behovet av en mera precis översiktsbild]: För att kunna förklara det inre av K-cellen i enlighet med den allmänt uppnådda resultatbilden i K-cellens värmefysik, och i samtidigt bibehållande av K-radien och K-värdet, måste täthetsförskjutningar ske [Täthetsändringsfunktionerna] inåt K-centrum — dessutom från en viss tidpunkt om vår position (Vintergatan med grannar) ska stämma överens med en optimal elektrogravitell dynamik baserad (i det allra närmaste) på ljushastighetens toppvärde. Täthetsförskjutningen medför en liten avsaktning i expansionen på grund av den något tätare samlade centralmassan, och vilken avsaktning (rent kvalitativt) i sig garanterar att K-cellens expansion längre fram kommer att avstanna.

— I originalbeskrivningen till K-cellens värmefysik [Offsetvärdet för T] gjordes förmodan om att täthetsförskjutningen skulle vara »marginell» och därmed kunna bortses ifrån i det allmänna fallet. I denna del däremot måste reduktionen i tidsfaktorn [T] beaktas strängt om vi ska kunna få en sammanhängande matematisk bild av hur det inre av K-cellen utvecklas — vilket INTE grundbeskrivningen i K-cellens värmefysik behandlar.

”Medelavståndet mellan två medelstora galaxer är ca 3 Mpc, dvs. 150 galaxdiametrar.”. BAs324sp2n — 1 pc parsec) = (1AU=1,496 T11 M)·cotan(1°/3600) = 3,08572 T16 M; webben anger 3.08568025 × 10¹⁶ meters

Täthetsförskjutningen in mot K-centrum sammanhänger — vad vi har förstått — med den allmänna detonationsmassans fragmentering. Denna detalj sammanhänger med [den numera Mar2012] välkända s.k. mörka materien i universum och som i moderna kvarter föranlett spekulationer om »nya partiklar». Se även särskilt i MMLightMAC—MörkaMateriens ljusemitterande kapacitet i modern akademi. Anledningen till associationen i modern akademi om »nya partiklar» som de hemliga agenterna för den osynliga materiens mystik är (enligt TNED naturligtvis) självskriven: I modern akademi finns ingen TEORI om grundämnesbildning från maximal täthet, och därmed heller ingen förklaring till en motsvarande Sandkornsanalogi. Enligt TNED verkar hela saken kunna förklaras på (enklast uttryckt) molekylärt stoft [Mörka materiens rationella fysik i TNED]. Se även Inledningscitatet från Bonniers Astronomi 1978.

— För att täthetsförskjutningen ska stämma med den praktiken, måste hänsyn tas till den tidpunkt då det molekylära stoftet börjar tränga in speciellt till K-centrum [vilket här skulle ske med början från de första divergenständningarna, från grovt runt 10 miljoner år efter K-cellens detonation, vidare nedan].

— Den detaljen är VIKTIG i TNED därför att den stora massövervikten från molekylstoftet [typen sandkorn] KAN bidra till en påtaglig gravitell ±-rödförskjutning i K-centrum och som helt klart kan konkurrera med de observerade — förmodade — KONVENTIONELLT FÖRMODAT HASTIGHETSBASERADE rödförskjutningarna [±] från närliggande galaxer — Se räkneexempel i Lokala Galaxgruppen och Andromedagalaxens blåförskjutning.

— Här kan det alltså finnas helt andra förklaringar än de som syns i etablerade led. Gravitell rödförskjutning förekommer som vi vet INTE i modern akademi i samband med galaxerna i vårt närområde [Lokala Galaxgruppen].

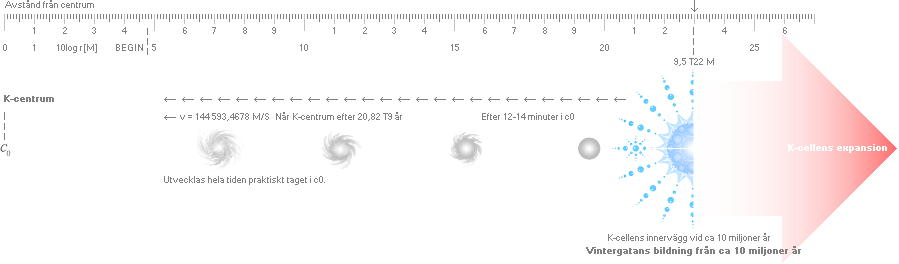
— Den 10-logaritmiska avståndsskalan (nedan) ger en orientering tillsammans med avsatta tidsreferenser.

— Avståndet 9,5 T22 M [Bonniers Astronomi 1978] — grovt medelavståndet mellan medelstora galaxer, Vintergatans möjliga ursprung — är vad K-cellens ideala nolldivergenszon hinner svepa i distans [konstant c0] på ca 10 miljoner år.

K-cellens inre divergensaktiva kärna från detonationsögonblicket är samma som J80-massan med radien ca 60 KM.

— Vid samma tidpunkt sträcker sig den högtäta [1,82 T17 KG/M³] K-cellens massrand med den inneslutna massan 4,14 T53 KG ut till 8,16 T11 M eller nära 5,5 AU [1AU=1,496 T11 M, medelavståndet Jorden-Solen]. När expansionen avtar omspänner K-cellen som mest (frånsett Stoppmoderatorn) en sfär med radien 1,16 T27 M.

— Vattendroppssekvenserna ovan [Författarens arkiv] illustrerar principen hur diskreta J-kroppar avdelas ur K-cellens totalmassa genom K-cellens totalexpansion, dels inåt mot K-centrum [J-kropparnas primära avdelning], och dels utåt reguljärt [Fraktalexemplet] [J-kropparnas expansion] [K-cellens brytning].

Massreduktionen i form av värme och ljus som K-cellen förlorar under sin aktiva period, fylls som tidigare beskrivet på från c0-kroppen genom Allmänna tillståndsekvationen, den del som förklarar den energiräkning som försörjer hela verksamheten. Den massförlusten motsvarar [genom proportionell analogi] Solens massförlust [Solens massdefekt], idealt genom hela väteförbränningens fas, och den uppgår till ca 0,7% av (den synliga delen i) totalmassan.

K-cellens expansion genom FÖRSTA FASEN kommer i ovanstående ljus att innefatta perioden fram till tiden ca 10 miljoner år då divergenständningszonen IDEALT når nuvarande galaxernas (av Vintergatans typ) medelavstånd ca 9,5 T22 M. [d=c0T=3T8·T7år=9,46706 T22 M].

— Anledningen till den tids- och avståndspreferensen i TNED sammanhänger just med det möjliga TIDSGRÄNSVÄRDET för Vintergatans möjliga ålder:

— Nuvarande K-cellens ålder enligt TNED är T = 20,82 T9 år; Hastigheten HÖGST som Vintergatan som mobilt objekt får ha relativt K-centrum för att hinna dit på T är v=d/T=[9,5 T22 M]/[20,82 T9 år] = 144,59346 KM/S. Det är också grovt sett samma värdeform (±300 KM/S) som framgår i den lokala galaxgruppen, se Tabellen.

— Anledning varför Vintergatan MÅSTE komma till K-centrum är LJUSHASTIGHETENS TOPPVÄRDE [Se även i Absoluta Metriken] som hela utvecklingen av UNIVERSUMS HISTORIA i TNED bygger på: Jordens 5 Ekvationer och Solens Tre Ekvationer:

— Maximal dynamik mellan elektriska och gravitella krafter. Vintergatan — Solsystemet — MÅSTE utvecklas i ett område där i det närmaste toppdivergens råder. Annars gäller inte framställningssättet. Alla sambandsformer i denna framställning bygger helt på att vår fysik (Solsystemet, Jorden) har utvecklats i ett område med i det närmaste maximal ljushastighet. Se även i Absoluta Metriken.

Bildlogoceptet till Vintergatans bildningshistorik enligt TNED via K-cellens expansion

UNIVERSUMS HISTORIA — K-cellens vågillustration

— Idealt via K-cellens expansion genom homogen täthet är den inneslutna massan efter tiden ca 10 miljoner år vid avståndet ca 9,5 T22 M från K-centrum lika med ca 2,6 T50 KG

KalkylkortDirekt KcGRB.ods 8KcHome HelpOpen.

— Eftersom K-cellens expansion i vilket fall börjar från idealtillståndet med homogen täthetsfördelning IN TILL EN VISS TID, och att den tidsgränsen BÖR ansluta till den ungefärliga tidpunkt där DIVERGENSTÄNDNING kan börja i det »VintergatsBildningsKritiskska avståndsområdet», dvs., som ovan runt sagt vid ca 9,5 T22 M efter ca 10 T6 år, kan vi använda den referensen som en MARKÖR för K-cellens utveckling då täthetsförskjutningarna påbörjas — analogt med de möjliga divergenständningarna och därigenom detonationsmassornas molekylära fragmentering.

Figuren nedan (extraherad och förtydligad från ovan) visar i syntes hur TNED kan förklara principen bakom Vintergatans bildning (tillsammans med dess grannar [Lokala galaxgruppen] i här ej närmare redovisad ordning).

— Samtidigt klargörs i samma illustrativa bild HUR den — med allmänna observationer överensstämmande [citat i UNIVERSUMS FORM] — allmänna (i stora drag) homogena fördelningen av galaxkroppar kan förstås bildas enligt TNED i samtidigt begrepp om K-cellens (universums) allmänna expansion. Se även i HubbleTeleskopets Djupbild av Universum.

Bildlogocept II till Vintergatans bildningshistorik enligt TNED via K-cellens expansion — från Bildlogocept I

UNIVERSUMS HISTORIA — K-cellens vågillustration

Tolkningsbilden illustrerad ovan kopplar direkt till sektionen om J-kropparnas primära avdelning från det inre av K-cellen: Det inre av K-cellen MÅSTE FÖR TNED:s DEL FÖRSTÅS förbli i stort sett materiefritt FRAM TILL TIDEN FÖR DE FÖRSTA REGULJÄRA DIVERGENSTÄNDNINGARNA — Vintergatans bildning: Den inre stoftmängden ansamlas FRÅN BÖRJAN på K-cellens expanderande innerväggs höggravitellt attraherande kroppsmassor. Därmed kan dynamiken i den delen återföras matematiskt på Ljushastigheten/g-potentialen innanför sfäriska skalet och som garanterar maximal ljushastighet i den aktuella regionen. Utan den förutsättningen kan inte TNED få ihop det med Vintergatans plats i hela historien. Först med den vidare utvecklingen av divergenständningar kan stoftet [MÖRKA MATERIEN KRING VINTERGATAN I MAC][MÖRKA MATERIEN KRING VINTERGATAN I TNED] till DETONATIONSMASSORNA börja spridas i K-cellen, och därmed början till en täthetsförskjutning inåt K-centrum.

Tolkningsbilden illustrerar också en mera handfast grund till den allmänt observerade rödförskjutningen i universum: det är den gravitella rödförskjutningen, inte objektens bortflyende hastigheter, som avgör.

— Snarare än att galaxerna EXPANDERAR bort från vår position, lämnar EXPANSIONEN efter sig ett pärlband av bildade mer eller mindre i stort sett vilande galaxer — likt ett reaplan högt uppe i atmosfären som lämnar efter sig sin strimma av kondenserad vattenånga. Rödförskjutningen, enligt den sinnebilden, beror på att ljushastigheten avtar med avståndet från masscentrum, ljusets gravitella beroende, beroende på att också massmängden ökar räknat från tyngdpunkten. Emellertid ingår inte den föreställningstypen i modern akademi.

— Att de mest avlägset synliga galaxerna uppvisar den största rödförskjutningen skulle då, här enligt TNED, inte bero på någon bortflyende hastighet, utan istället på LJUSETS GRAVITELLA BEROENDE: en naturligt maximalt avtagande ljushastighet med den lokalt verkande g-potentialen i takt med att massan växer med avståndet från K-cellens centrum. Galaxhastigheterna skulle därmed i själva verket vara marginellt utspridda, i stort sett betydelselösa [och därmed en förklaring till deras omvittnade isotropi i universum, se citat i UNIVERSUMS FORM] vid sidan av den allmänna lokala gravitella rödförskjutningen som då skulle vara den fenomenform som den observerade rödförskjutningen huvudsakligen beror på — nettoeffekten är densamma.

— Att så verkligen SER UT ATT VARA DET PRAKTISKA FALLET, visas vidare i sektionen om GRB.

Den mest naturliga förekomsten av avdelade J-kroppar under K-cellens expansion framträder naturligtvis i rum med största möjliga lokala ljushastighet (elektriska konstanten Rc avtar i styrka med avtagande lokalt c, vilket i motsvarande mening ger svagare lyskraft). Det betyder i princip att de kroppar som kan uppvisa mest synbarhet också blir samma som J-kroppar som (via en primär divergenständning från en större J-moderkropp, figuren ovan) avdelas i riktning inåt K-cellens centrum.

— Eftersom de avdelade kropparnas möjliga hastigheter avtar (starkt) med kroppsmassan, bör vi också finna de stora galaxmassorna på de allra lägsta (innersta) hastigheterna.

— Därmed framgår i varje fall principiellt grunden för HUR — trots EXPANSION — K-cellens avdelade masskroppar KAN uppvisa en (i stort sett) homogen fördelning (UNIVERSUMS FORM) i rymden SOM OM det vore fråga om en massrymd med »homogen täthet».

NOTERA att en motsvarande »3D-beskrivning» i modern akademi är omöjlig;

— OM en liknande analogi skulle finnas i MAC, innebure det bara att man samtidigt i beskrivningssättet ERKÄNNER EN SFÄRISK EXPANSIONSGEOMETRI för universums expansion. Men den typen gäller garanterat INTE i modern akademi (Se särskilt citaten i Ballonganalogin). Det finns i själva verket ingen DIREKT visuellt ILLUSTRERBAR analogi ALLS i modern akademi till universums expansion, eftersom, som man säger, »det ser likadant ut överallt» från vilken position man än har — ett framställningssätt som, tydligen och uppenbarligen, helt saknar visuellt illustrerbara exempel (Jämför Ballonganalogin) — samt att ljushastigheten »överallt är samma»: c0 överallt (från r-teorin).

— I LOGISK — visuellt illustrerbar, synlig, observerbar — mening finns bara ett sätt (TNED—Bildlogo2, som ovan).

— Se även i Det ekologiska universumet.

— Se även jämförande visuella intryck i direkt bild av universum i UNIVERSUMS FORM — den faktiska BILD man ser av universum (dess konventionellt intygade isotropi) från vår position visar tydligen EKVIVALENS med en motsvarande SFÄRISKT CENTRERAD POSITION. De facto;

— Med ljusets gravitella beroende via en entydigt bestämd tyngdpunkt, får varje avstånd från masscentrum en egen unik visuell bild av helheten.

— Se även beskrivningen (vidare) i GRB: hur ljusbilderna från de avlägsna objekten kan förstås i harmoni med ovanstående allmänna fördelningsbild.

— Hur Vintergatans bildningshistorik motiveras rent matematiskt i TNED — i bevarande av resultaten från K-cellens värmefysik — beskrivs utförligt i Täthetsändringsfunktionerna.

Den vidare bilden av sammanhanget i K-cellen, ges härifrån i sektionen Täthetsändringsfunktionerna.

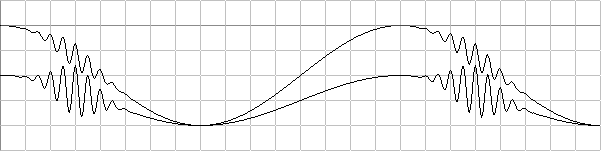
Grafisk Referens till K-cellens vågillustration

Övre:

–0+1(2[(–1–cos2þ[x–4]/16)'1]+0.5(sin2þ[x–3]/0.5)(sin2þ[x–3]/32)'3[(4þ)+sin2þ[x–3]/32])

Undre:

–2+0.5(2[(–1–cos2þ[x–4]/16)'1]+2(sin2þ[x–3]/0.5)(sin2þ[x–3]/32)'3[(4þ)+sin2þ[x–3]/32])

Ljusets g-beroende — sambanden i översikt — [DGD, Divergence’s Gravitational Dependency, Divergensens Gravitella Beroende]

GRUNDFYSIK — elektrogravitationen

Från Sammanställd Resultatredovisning i DGD

ENSAM KROPP — m₂

Statiska tillståndets samband

— Speciellt med absoluta metrikens giltighet f/f₀ = c/c₀ ; c₀/f₀ = c/f = d₀

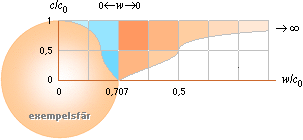
c/c₀ = (1/2)(1 ± Ö | 1 – 4w²/c₀² |) .. ljusets g-beroende enligt relaterad fysik;

brytgränsen vid w=c0/2 ger ROT(0):

c/c₀ = (1/2)(1 + Ö 1 – 4w²/c₀²) från c₀ till c₀/2 cirkeln fi=0

c/c₀ = (1/2)(1 – Ö 4w²/c₀² – 1) från c₀/2 till 0 hyperbeln fi=1

Villkoret mellan <=>c0/2 via faktorn F [fi]: IF 2[w=Gm2/r]/c0 < 1/2 THEN F=0 ELSE F=1;

c/c₀ = (1/2)(1 + (–2F+1)Ö | 1 – (2w/c₀)² | )

F = HELTAL[1 – (ABS[(w/c₀)–1/2] – [(w/c₀)–1/2])/2]

w² = r^–1Gm₂ = r²(4Gpr/3) ......... innanför [upp till] sfärytan,

blå graf, homogen täthet r=3m₂/4pr³.

w² = r^–1Gm₂ ............................... utanför [in till] sfärytan,

orange graf, nollmassa utanför sfären.

Från DIVERGENSENS EXPANSIVA G-BEROENDE

ENSAM KROPP — m₂

Expansiva tillståndets samband

— Linjära accelerationens preferenser:

c/c₀ = ± Ö | 1 – 2(w/c₀)² | .............. divergensens expansiva g-beroende;

brytgränsen vid w=c0/2 ger ROT(0):

c/c₀ = + Ö 1 – 2(w/c₀)² från c₀ till c₀/2 2(w/c₀)² < 1 ; w/c₀=Ö[1–(c/c₀)²]/2

c/c₀ = – Ö 2(w/c₀)² – 1 från c₀/2 till 0 2(w/c₀)² > 1 ; w/c₀=Ö[1+(c/c₀)²]/2

Villkoret mellan <=>c0/2 via faktorn F [fi]: IF 2[w=Gm2/r]/c0 < 1/2 THEN F=0 ELSE F=1;

c/c₀ = (–2F+1)Ö | 1 – 2(w/c₀)² |

F = HELTAL[1 – (ABS[(w/c₀)–1/2] – [(w/c₀)–1/2])/2]

w² = r^–1(G/4)m₂ = r²(Gpr/3) ....... innanför [upp till] sfärytan,

homogen täthet r=3m₂/4pr³.

w² = r^–1(G/4)m₂ .......................... utanför [in till] sfärytan,

nollmassa utanför sfären.

G-potentialen G-potentialens ekvivalent via homogen medeltäthet [r grek. r, rho]:

w² = r^–1Gm₂ ; r=m/V ; m=rV=r(4pr³/3) ; m/r=r(4pr²/3)=r²(4pr/3) ; r^–1=(4pr/3m)^1/3

= r²(4Gpr/3)

= (4pr/3m₂)^1/3Gm₂

= (m₂)^2/3(4pr/3)^1/3G ;

w²/m₂ = (m₂)^–1/3(4pr/3)^1/3G

Centralparametrarna i K-cellens värmefysik

2012IV5

Centralparametrarna i K-cellens värmefysik

UNDER FÖRUTSÄTTNINGEN att de samband som utvecklats här HAR praktisk tillämpbarhet:

K-cellens värmefysik via energiräkningen på synliga massans omsättning Väte-Helium — synliga/totala = 1/355 — innehåller ingen markör för sättet på vilket strålningsenergin omsätts enligt den använda formen i Stefan-Boltzmanns strålningslag.

De PRIMÄRA (icke ändringsbara) parameterbegrepp som ger resultatbilden i K-cellens värmefysik är (förutom synliga materiens medeltäthet, ca 1 Väteatom per 10 M³)

·         K-radien
r_x       = 4,28 T25 M (helt linjärt efter r_x=c₀T_x)
          = c₀T_x = (r_0c/T₀)T_x = r_0cT_x/T₀ .....................               sambanden i sammandrag
r_x²      = [8(3t_2,7)⁴(a_0,67k_5,7t84p)]^–1(27/a)^1/2E_max ........               sambanden i sammandrag

· K-värdet (K=1,5), rödförskjutningens medelvärde

· Tiden vid effektmaximum (16,32 T9 år; T= r_x(2/c₀)Ö[K² + 1] ~ 16,3 T9 år )

· Ljusvägens integral för K-radien (4,52 T9 år, bestämmer universums ålder 20,82 T9 år tillsammans med effektmaximum)

·         Kvoten synliga/totala massan 1/355
(sambanden nedan i härledningar från K-radien)
T       = r (2/c₀)Ö[K² + 1] = 16,29216 T9 år
h        = 3T²/a = 126042, q = 355 = Öh
^qE      = E_max q .........................................................          reella energin
Notera att en viss spridning i värdena förekommer [grovt max 3%] beroende på smärre skillnader i basparametrarnas precision, samt olika resultat i massbestämningen för K-cellen beroende på metod — ändvärdena 4,08 och 4,18 T53 KG med medelvärdet 4,13.

Det finns ingen som helst anvisning i dessa basbegrepp om HUR eller PÅ VILKET SÄTT som det inre av K-cellen uppför sig, visar sig, eller inte visar sig, vilken eventuella REALT inre täthetsfördelning som finns lokalt i någon viss region, eller vilken sådan fördelning det INTE finns. OM sådana ska användas, är det tydligt att resultatbilden, i vilket fall, måste innefatta ovanstående — eller helt nära inom den givna felgränsen (max 3%; [±1,5%]).

De observerade förutsättningarna — i sammanställning för vidare översikt 2012V6

K-CELLENS VÄRMEFYSIK är med grund i TNED en matematisk-fysikalisk grundbeskrivning av universums mest övergripande fysik vars resultatbild baseras på de mest fundamentalt observerade kosmologiska faktorerna (se K-cellens värmefysik). Dessa faktorer är

1. den synliga materiens medeltäthet 1 väteatom per 10 kubikmeter rymd [BAs381sp2mn] inom

2. en synsfär med radien grovt 1000 Mpc [BAs378 Figur 19.1 (Avstånden i Mpc till galaxer ut mot universums synrand)] som innehåller

3. medelvärdet 25% Helium och 75% Väte [BAs124sp2n] med övriga ca 1% i den nu synliga materien tillsammans med

4. medelvärdet av den universella kosmiska Planckstrålningen 2,7 °K [ENCARTA 99 Infrared Astronomy] och

5. det givna (medel-) observationsvärdet för dopplereffekten vid punkt 2 (K=1,5=1/[1–1/(z+1)]; z=2) [BAs375 Figur 18.14 (Rödförskjutning och hastighet), s378 Figur 19.1 (Avstånden i Mpc till galaxer ut mot universums synrand)]

Dessa grunddata beskriver K-cellens utveckling på en helt idealt homogen medeltäthet, utan vidare komplicerade avhandlingar om vilken den rent praktiska täthetsfördelningen är i de olika regionerna av K-cellens inre.

— Detaljerna med K-cellens inre, mera precisa, fysik ges inte explicit ur ovanstående grunddata — men dessa innehåller samtidigt anvisningarna för hur en vidare resultatbild ska framställas, om alls, för att MATCHA ALLA OVAN GIVNA faktorer. Den framställningen, vilken den än är, berör, således, ingen ändring av eller i ovanstående detaljer, eller ska i varje fall inte göra det, och heller ingen ändring av den resultatbild som faktorerna ovan leder till (framkommer sådant är framställningen körd). Dessa bildar i vilket fall grunden till varje vidare framställning.

Resultaten från ovanstående, samt ALLA GRUNDSAMBAND som sammanhänger med ovanstående, används speciellt för att härleda andra grundsamband som sammanhänger med detaljer till olika avsnitt i UNIVERSUMS HISTORIA. Dessa avsnitt/-htm-dokument är speciellt

· UniversumsHistoriaAllmnnaSamband.htm Zonskärningarna, Divergensens expansiva g-beroende

· Nuklidbildningarna.htm Expansionssambandet, Expansionstiden, Offsetvärdet för T, Tidsfären, J-kropparnas expansion, Himlakropparnas bildningstid

· StjrnFysikn2005Del2.htm Gränsmassorna, G-G/4-faktorerna

· UnivHistKcellen.htm Härledningarna till K-cellens värmefysik

· UnivHistPrim.htm K-cellens allmänna data, jämförande situationsbild, Synradien (Ljusintegralen)

· UnivHistStrukt.htm Zonskärningarna

Redan välformulerad inledning som föregick GRB-htm-dokumenten (K-cellens Inre, från 2011):

När nolldivergenszonen passerat K-cellen gäller delvis andra samband eftersom zoncirkeln då expanderar in i den masskropp (c0-kroppen) som omger K-cellen (universum) och därmed omskriver en större massa än enbart K-cellens; Med fortsatt referens till medeltätheten för K-cellen gäller ovanstående idealt.

— MEN: Vad händer då utanför K-cellen, då nolldivergenszonen aktiverar em-fysiken där?

— Ingen framställning finns ännu (Februari 2009) på den delen. Men det är tydligt att OM materia (neutronkallplasma) finns där, den också övergår i vätgas. Täthetspreferensen utanför K-cellen kan inte vara av typen maximal täthet, eftersom den delen (energiräkningen) är reserverad för K-cellen (universum), samt att det kontraktiva inflödet till K-cellen också förutsätter att det omgivande kallplasmats neutronbank uppvisar mellanrum mellan sina individer. Någon annan fas finns veterligt inte att relatera.

UnivHistPrim.htm

Se vidare utförligt från K-cellens inre [GRB1.htm].

Gravitella rödförskjutningen — Se generellt i Gravitella dopplereffekten

GRAVITELLA RÖDFÖRSKJUTNINGEN — Bildkälla, Författarens arkiv, 20Jun2012E9Bild11 NikonD90 Detalj

Kort sammanfattande detaljbeskrivning med illustrerat utdrag från TYPKURVORNA I LJUSETS GRAVITELLA BEROENDE:

Se även K-cellens grundformulering enligt TNED i ALLMÄNNA TILLSTÅNDSLAGEN

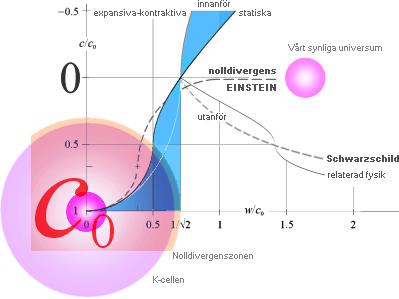
Från LJUSETS GRAVITELLA BEROENDE i relaterad fysik:

— Med växande avstånd från masscentrum [c0] avtar den lokalt punktgravitellt bestämda ljushastigheten [DEEP], samma som divergensen [c] i TNED. Ljus [c] i områden med lägre divergens som intränger områden med högre divergens — ljus som går från det yttre mot det inre med max c/c0=1 i K-centrum — tvingas genomgå en utdragning i våglängd (Gravitell Rödförskjutning):

— Ljus som kommer från områden med lägre c — längre ut från K-centrum — och som observeras från en position i områden med högre c förefaller därför rödförskjutet: ljuset »framhåller» en FÖRESTÄLLNING SOM OM det ljusemitterande föremålet skulle besitta en motsvarande dopplerhastighet [DOPPLEREFFEKTEN] [K-SAMBANDET] [Hubbles Upptäckt] [Universums expansion].

— Fenomenet benämns i TNED gravitell rödförskjutning, och ingår tillsammans med den ordinära dopplereffekten i K-cellens allmänna expansion. Sammanhanget beskrivs ingående nedan från GRAVITELLA DOPPLEREFFEKTEN.

— I modern akademi räknar man INTE med någon allmän gravitell rödförskjutning mellan stjärnorna i universum [DET EKOLOGISKA UNIVERSUMET] — begreppet som fysikalisk företeelse i samband med universums metriska utsträckning [LJUSETS GRAVITELLA BEROENDE — bevarandet av naturkonstanten c0 oberoende av gravitationens inverkan] finns inte ens med i den moderna akademins lärosystem.

Gravitella rödförskjutningen

INNANFÖR GIVEN MASSFÄR VIA HOMOGEN TÄTHET — mellan två godtyckliga sfäriska skal — från rIN till rUT

Med rIN i c0:

v = c₀ – c_ut ......... motsvarar effektiva reduktionen i signalhastighet då våglängden retarderas in till det lägre cUT

= c₀ – c₀(1/2)(1 + (–2F+1)Ö | 1 – (2w/c₀)² |) ;

v/c₀ = 1 – (1/2)(1 + (–2F+1)Ö | 1 – 4w²/c₀² |) ; med homogen täthet:

= 1 – (1/2)(1 + (–2F+1)Ö | 1 – 4[r²(4pGr/3)]/c₀² |) ;

K-cellens idealt homogena medeltäthet via expansionstiden T fås i TNED enligt [EXPANSIONSSAMBANDET] [Se även Kopplingen till Fria fallets G-fysik]

ρ = 3/(2πGT²) ............... expansionssambandet

ρ = T^–2(7,15739 T9 S²KG/M³)

Undersökning av olika v-värden görs lämpligen genom att först bestämma T så att tätheten [rhå, r] kan bestämmas GENERELLT för SMÅ differenser rIN och rUT.

Motsvarande differenser mellan ett rIN och ett rUT:

v = c_in – c_ut

= c₀(1/2)(1 + (–2F+1)Ö | 1 – (2w_in/c₀)² |) – c₀(1/2)(1 + (–2F+1)Ö | 1 – (2w_ut/c₀)² |) ;

2v/c₀ = 1 + (–2F+1)Ö | 1 – (2w_in/c₀)² | – 1 – (–2F+1)Ö | 1 – (2w_ut/c₀)² |)

= (–2F_in+1)Ö | 1 – (2w_in/c₀)² | – (–2F_ut+1)Ö | 1 – (2w_ut/c₀)² |) ;

v/c₀ = 2[((–2F+1)Ö | 1 – (2w/c₀)² |)_in – ((–2F+1)Ö | 1 – (2w/c₀)² |)_ut] ;

För att få v-formen relativt cIN: v/cIN = v/c0 · c0/cIN med

c_in = c₀(1/2)(1 + (–2F_in+1)Ö | 1 – (2w_in/c₀)² |)

Rödförskjutningssambanden — Se även DOPPLEREFFEKTEN

v/c₀ = 1/K ......................... K är lägst 1 vid v=c och max obegränsat vid v=0

= 1 – 1/(z+1) ............. z betecknar det ofta i konventionell litteratur angivna rödförskjutningsvärdet

z = 1/(1–v/c₀) – 1

v/c₀ = 1 – 1/(z+1)

Rödförskjutningssambanden

Allmänna samband — Se även särskilda sammanställningar speciellt i K-sambandet med beskrivning av det konventionella beteckningssättet

z+1 = 1/(1–1/K)

= 1/(1–v/c)

1/(z+1) = (1–1/K)

1/K = v/c

= 1 – 1/(z+1)

Gravitella dopplereffekten — Se även särskilt [ovan] i Gravitella Rödförskjutningen, samt generellt i DOPPLEREFFEKTEN — samband generellt i GraviKinematiska Dopplersambandet

GRAVITELLA DOPPLEREFFEKTEN — Bildkälla, Författarens arkiv, 20Jun2012E9Bild4 NikonD90 Detalj

Gravitella rödförskjutningen och blåförskjutningen

GRAVITELLA DOPPLEREFFEKTEN — Se även i J-kropparnas hastigheter

————————————————————————————————

Se även Ljusets gravitella beroende — motsvarande beskrivningar saknas i MAC

I RELATERAD FYSIK (TNED) medför olika lokalt gravitellt betingande ljushastigheter eller DIVERGENSER

— divergensvärden i TNED [Se även divergensens princip i DEEP]

— motsvarande våglängdsändringar:

Gravitell Rödförskjutning

En given våglängd (l, i ljusemissionen från något känt grundämne) i en given g-lokal med tillhörande lokalt gravitellt (g)-betingad divergens (c), tvingas accelerera i sin signalhastighet upp mot en rymd med högre divergens (c0), vilket MED BIBEHÅLLEN FREKVENS

(Se även mera utförligt i följdsatsen Planckenergins gravitella frekvensnormalisering till Divergensenergins g-beroende — dessa termbegrepp är helt unika för TNED via Ljusets g-beroende, det finns, här veterligt, ingen motsvarande termkropp i MAC)

— antalet källemitterade våglängder per sekund som är en oberoende källparameter, kan endast ändras av källan

— tvingar våglängden som kommer från, emitteras ur, rummet med den lägre divergensen att framstå som förlängd i rummet med den högre divergensen.

Jämför modern teori via @INTERNET Wikipedia Gravitational redshift [2012-04-20]:

PRINCIPEN [nettoresultatet] är densamma — men hänförs i MAC till ”Gravitational dilation”: en frekvensändring, ”reduced in frequency, or redshifted”.

Relaterad fysik [Se PLANCKENERGIN][PLANCKS KONSTANT h = mcr = NEUTRONEN]:

E = hf = konstant = hc/λ oberoende av gravitationen: frekvensen kan bara ändras om energin gör det: tomrummet har ingen sådan förutsättning;

E1 = E2 = hc1/λ1 = hc2/λ2 = hf = E : c1/λ1 = c2/λ2 ; c1/c2 = λ1/λ2;

— Högre divergens [lokalt g-bestämda c-värdet] och lägre våglängd matchar lägre divergens och kortare våglängd: energin är densamma:

— KÄLLJUS, E=hf, som passerar olika g-lokaler, varken erhåller eller förlorar Planckenergi hf:

— Energi kan varken skapas eller förintas [ENERGILAGEN]:

— Våglängderna förhåller sig — således — som divergenserna: c1/c2 = λ1/λ2 ;

Se även i GPS-exemplet — instrumentell synkronisering av g-beroende frekvensändringar.

— Jämför en FLYTT av säg ett radioaktivt preparat mellan två olika g-potentialer: man kan uppmäta en frekvensändring [konv. även MÖSSBAUEREFFEKTEN, resonansabsorption av gammastrålning, FOCUS MATERIEN 1975 s86sp2m]: atomsvängningarna anpassas efter g-nivån;

— Jämför sedan en reguljär UTSÄNDNING MED mekaniskt BESTÄMD RYTM från en viss g-nivå: källfrekvensen ändras inte av g-nivåerna; det finns inga »atomklockor» som styr mekaniken. Men man ANSER det vara fallet i modern akademi — se utförligt med jämförande beskrivningar mot modern akademi från PLANCKEKVIVALENTERNA och Relativitetsteorins Grundmatematik, samt i EXPERIMENTELLA BEKRÄFTELSER.

I relaterad fysik [TNED] finns ingen »tidsdilation», och därmed sker heller inte den frekvensändring i den gravitella dopplereffekten som ändå förespråkas i modern akademi [se @INTERNET-referensen ovan m.fl.], utan istället en acceleration av en källbestämd våglängd över tomma rymden för en variabel gravitationspotential — som bibehåller källfrekvensen: källemissionens position förflyttas inte i g-fältet, endast ljusutbredningen gör det; det finns inga »mellanliggande atomklockor» som kan påverka den fixa källans periodiska vågutskickningar; frånsett växelverkan med mellanliggande massor [Se Comptoneffekten] kan källfrekvensen kan bara ändras av källan, inte mottagaren eller masslösa mellanliggande avsnitt. Se även jämförelser med MAC i GRAVITATIONSENERGIN.

Därmed finns heller, i egentlig mening, ingen samhörande [begriplig] förklaringsgrund i saken mellan TNED och MAC. Se mera utförligt från Relativitetsteorins Grundmatematik, om ej redan bekant.

— Är skillnaden i signalhastighet proportionell mot våglängdsändringen gäller alltså

c/c₀ = (λ f )/( λ f )₀

= (λ f )/ λ₀ f₀

= (λ/λ₀)(f / f₀ = 1) ; källfrekvensen bibehålls

= λ/λ₀ ;

λ = λ₀(c/c₀ = [c₀–v]/c₀ = 1 – v/c₀) ;

λ/λ₀ = 1 – v/c₀

= c/c₀ ;

v/c₀ = 1 – c/c₀ ; kinematiska divergensekvivalenten

GraviKinematiska Dopplersambandet I RELATERAD FYSIK

Totala dopplereffekten för gravitella och kinematiska verkan kan då skrivas på K-formen

v_TOT/c₀ = (1 – c/c₀)_GRAVITELLA + (v/c₀)_KINEMATISKA

= 1/K ; se även K-formen i Rödförskjutningssambanden

K = c₀/v ;

Gravitella-Kinematiska K-formens dopplersamband

K = [1 – c/c₀ + v/c₀]^–1 ;

c/c₀ = 1 + v/c₀ – 1/K ;

Se även Dopplersambanden konventionellt i artikeln om K-sambandet

v/c₀ = c/c₀ – 1 + 1/K

Gravitell Blåförskjutning — exempel

Är källan placerad i rummet med den högre divergensen (c0) och den mottagande stationen i ett rum med lägre divergens (c) blir signalen istället motsvarande blåförskjuten: c0-källans ström av våglängder tvingas retardera (bromsa) in till rummet med den lägre divergensen, vilket resulterar i motsvarande förkortad våglängd, samma samband som ovan.

— För att relatera nettoeffekten av signaler mellan olika c-rum behöver man alltså enbart beräkna motsvarande nettoskillnad i c-värden mellan de olika rummen.

EXEMPEL:

Andromedagalaxen uppvisar mot Vintergatan en blåförskjutning på motsvarande v=300 KM/S.

Uppgift:

— Vilken motsvarande divergens (lokalt g-relaterad ljushastighet) ska observatören i Vintergatan ha för att precis matcha den observerade Andromedagalaxens blåförskjutning?

Lösning:

c = c₀ – v ;

c/c₀ = (c₀ – v)/c₀

= (2,99792458 T8 M/S – 3 T5 M/S)/(2,99792458 T8 M/S)

= 0,9989993

Svar:

c/c₀ = 0,9989993

OM den beskrivningen håller streck — Andromedagalaxen i princip mera nära K-centrum än Vintergatan — betyder INTE den observerade blåförskjutningen att Andromedagalaxen är på väg att KOLLIDERA med Vintergatan, utan ENDAST att Andromedagalxen befinner sig [vilande relativt Vintergatan] i en rymd med MARGINELLT (0,1007%) högre divergens.

Se även exempelbeskrivning i Gravitella rödförskjutningen — vilka samband som gäller INOM en materiesfär i olika partier. Se även i ABSOLUTA METRIKEN som närmare beskriver (eg. förklarar) grunderna för ljushastighetens toppvärde — oberoende av lokal i universum.

EXPANSIONSSAMBANDETS koppling till Fria fallets G-fysik

EXPANSIONSSAMBANDETS KOPPLING TILL FRIA FALLETS G-FYSIK — Bildkälla, Författarens arkiv, 19Jun2012E8Bild29 NikonD90 Detalj

2012IV4

Expansionssambandets koppling till fria fallets g-fysik

NATURLIGA FRIA FALLETS G-FYSIK — fallet med kontinuerligt varierande g-potential

Fritt fall i ett Galileiskt kraftfält — samma accelerationskonstant (a=v/T) överallt — beskrivs av den linjära accelerationens grundbegrepp [Accelerationsbegreppet]. Jordytan med a=9,81 M/S² representerar ett sådant idealt Galileiskt kraftrum inom en viss begränsad fallhöjd (grovt Jordytans atmosfär). En kropp inom atmosfären på avståndet d från Jordytan som släpps mot marken når denna efter tiden T=v/a med v=(a)T=(2d/T²)T=2d/T som ger T=v/a=(2d/T)/a som ger T²=2d/a, förutsatt luftfriktionen bortses ifrån.

En kropp som släpps mot Jordytan på stora avstånd från Jorden däremot — låga a-värden — kommer att innefatta successivt växande a-värden som kroppen avancerar mot Jordytans (standardvärde) a=9,81 M/S².

I serieform via diskreta distanser per sekund i ideala avsnitt av Galileiska kraftrum med successivt växande a-värden, skulle vi få (M, centralmassan)

v(Summa) = T(1S)(a1 + a2 + a3 + … + aN)

= T(1S)(GM/[r1]² + GM/[r2]² + GM/[r3]² + … + GM/[rN]²)

= T(1S)GM(1/[r1]² + 1/[r2]² + 1/[r3]² + … + 1/[rN]²)

De successiva r-värdena fås via d=vT/2 som

[r2] = [r1] – GM/[r1]²(1S)²/2 ;

[r(n+1)] = [r(n)] – GM/[r(n)]²(1S)²/2 ;

Hastigheten — fria G-fallet

Hastigheten-fallsträckan vid naturligt fritt friktionslöst g-fall

Mera elegant med integralkalkylens hjälp [Formlagarna] [Nollformsalgebran] fås hela lösningen enligt differentialekvationerna med integrala lösningarna (bägge direkt bestämda integraler)

v = (T=dr/dv)(a=GM/r²) ;

v dv = GM · dr/r² ;

ò v dv = GM ò dr/r² ;

v²/2 = GM · (–1)/r ;

I absolutvärden med integrationsgränserna [största minus minsta] mellan 1/r(Minsta) och 1/r(Största) ges

v² = 2GM(1/r_MINSTA – 1/r_STÖRSTA) .................. naturliga G-fallets sluthastighet

v = Ö 2GM(1/r_MINSTA – 1/r_STÖRSTA)

Vi ser att sambandsformen ovan är alldeles densamma som för flykthastigheten

(v=√[2GM/r]). Enda skillnaden är att naturliga G-fallet innefattar fallsträckans intervall.

EXEMPEL MED JORDEN (ekvatorialradien 6,378 T6 M):

Flykthastigheten från Jordytan är till jämförelse

v = √ 2GM/r

= Ö 2(6,67 t11 JM/[KG]²)(5,975 T24 KG)/(6,378 T6 M)

= 11 179,042 M/S

~ 11 KM/S

Det är toppgränsvärdet för den teoretiskt högsta hastighet en fritt fallande kropp kan uppnå då den når Jordytan om den släpps från ett obegränsat stort avstånd från Jorden, och frånsett inverkan av alla övriga massor.

— Det är också den hastighet en kropp måste ges i utkastningen från Jordytan om den garanterat aldrig ska dras tillbaka av Jordkroppens g-kraft. Den utkastade kroppen kommer då att avstanna obegränsat mot noll med obegränsat växande avstånd.

Uppgift:

— Vilken sluthastighet får en kropp som släpps från avståndet 2r från Jordens tyngdpunkt (centralmassan M=5,975 T24 KG) då kroppen når Jordytans r=6,378 T6 M? Alla friktionsaspekter bortses ifrån. G=6,67 t11 JM/(KG)².

Lösning:

v = Ö 2GM(1/r_MINSTA – 1/r_STÖRSTA)

= Ö 2GM(1/r – 1/2r)

= Ö (2GM/r)(1 – 1/2)

= Ö GM/r

= 7 904,7768 M/S

Svar:

~ 8 KM/S

Med skillnaden 1 meter mellan största minsta ges v=4,415368 M/S. Jämför fria fallet i ideala Galileiska kraftrummet via fallsträckan 1 meter ovanför Jordytan med a =9,81 M/S² som ger

v=Ö2da = 4,4519658 M/S. Naturliga (friktionslösa) fallet ger alltid något lägre v-värden.

Oavsett varifrån en kropp tillåts falla rakt in mot en isolerad centralmassa, kommer kroppen vid anländandet aldrig att exakt uppnå flykthastigheten, om än obegränsat nära (även för relativt korta utsläppsdistanser i förhållande till det obegränsade). I Jordfallet uppnås till jämförelse sluthastigheten 11,123006 KM/S vid Jordytan om utsläppsavståndet är 100 Jordradier (en mindre bit bortom Månen [ca 60 Jordradier]), vilket redan är ca 99% av flykthastigheten.

Tiden — fria G-fallet

Tiden-fallsträckan vid naturligt fritt friktionslöst g-fall

Från föregående utvecklings differentialled får vi även (ds=dr, dt=dT)

v = (a=GM/r²)T

= ds/dt ;

r² ds = GM · T dt

ò r² ds = GM ò T dt ;

r³/3 = GM · T²/2 ;

r³ = GM(3/2)T² ;

T² = r³(2/3GM) ;

Med integrationsgränserna [största minus minsta] mellan [r(Största)=r]³ och [r(Minsta)=r0]³ ges

r³–r₀³ = GM(3/2)T² ..................... naturliga G-fallets fallsträcka

r³ = GM(3/2)T² + r₀³

T² = (r³–r₀³)(2/3GM)

T = Ö (r³–r₀³)(2/3GM)

EXEMPEL MED JORDEN (ekvatorialradien 6,378 T6 M):

Med föregående exempels utsläppsavstånd 1 meter ovanför Jordytan r₀=6,378 T6 M, Jordmassan M=5,975 T24 KG och gravitationskonstanten G=6,67 t11 JM/(KG)² ges naturliga falltiden

T = Ö (r³–r₀³)(2/3GM)

= 0,4480362 S .................... med enklare teknisk räknare [7 decimalers noggrannhet]

= 0,451822313559 S ........... med kalkylkort [Fria G-fallet] KalkylkortDirekt KcGRB.ods 1LokGal HelpOpen

Fria fallet via d=1 meter ovanför Jordytan med konstant a=9,81 M/S² ger till jämförelse

T = Ö 2d/a

= 0,4515236 S

Accelerationskonstanten vid ekvatorn, r=6,378 T6 M, ska för den mera exakta jämförelsen egentligen mera precist vara a=GM/r²=9,7970362 M/S², vilket via fallsträckan d=1 meter ger det mera korrekta Galileiska kraftrummets T-värde

T = 0,451822278105 S

Accelerationens avtagande med växande r blir (typ exponentiellt avtagande)

a = v/T

= [Ö 2GM(1/r_MINSTA – 1/r_STÖRSTA)]/[Ö (r³–r₀³)(2/3GM)]

= Ö[2(1/r_MINSTA – 1/r_STÖRSTA)]/[(r³–r₀³)(2/3)]

= Ö[3(1/r₀ – 1/r)]/[(r³–r₀³)]

Graf

(3[1–1/x]/[–1+x'3])'0.5

att jämföra med konstant a i det Galileiska kraftrummet.

Expansionssambandet, kopplingen till K-cellen

Expansionssambandets koppling till K-cellen

Om K-cellen i någon enda del, verkligen i praktiken, skulle expandera på flykthastighetens matematik (idealt evig expansion med obegränsat avtagande mot nollhastighet, se från r-sambandets grund), då skulle vi verkligen få Problem att härleda något matematiskt STOPP för expansionens avstannande till noll.

— Genom att K-cellens expansion i UNIVERSUMS HISTORIA använder den idealt linjära accelerationens matematik (v=2d/T, se från r-sambandets grund) är redan expansion satt på en principiellt avstannande formtyp (ehuru fortfarande odefinierad).

— Slutpunkten innebär att K-cellens halvperiod (336 T9 år) fram till avstanningen tvunget blir en annan än kontraktionsperioden; Den senare följer i princip samma praktiska värden som fria G-fallets fysik och som (som vi har sett av ovanstående härledningar) skiljer sig obetydligt från flykthastighetens form för stora fallsträckor: Ett visst uppnått avstånd på den högre flykthastighetens språk — obetydligt skilt från fria G-fallets praktiska värden för stora fallsträckor — betyder en motsvarande snabbare falltid.

— Framställningen nedan redovisar grunden till hur K-cellens STOPPLÄGE kan relateras med de förutsättningar som K-cellens värmefysik grundats på.

Eftersom K-cellens expansion utformats elementärt beskrivande efter den likformiga accelerationens förebild (v=2d/T, se r-sambandets grund) blir den linjära expansionsformens T-form det här benämnda expansionssambandet,

T(E) = Ö 2r³/Gm₂

I jämförelse med fria G-fallets (m2=M)

T(G) = Ö (r³–r₀³)(2/3GM)

som via stora avstånd med försumbart r0 kan skrivas liktydigt

T(G) = Ö 2r³/3GM

blir skillnaden T(G)/T(E)=(1/3)^0,5=0,5773502.

— r-formernas samband är på motsvarande sätt

r(E) = [T²GM/2]^1/3 ;

r(G) = [T²GM(3/2) + r₀³]^1/3

~ [T²GM(3/2)]^1/3

som ger r(G)/r(E)=(3)^1/3=1,4422496 [‡Exp.samb.Koppl.Kcellen].

— Det betyder att K-cellens beskrivna expansion r|T(E) enligt expansionssambandet redan är en i förhållande till det närmast flykthastigheten relaterade fria G-fallets r|T(G)-former AVSAKTAD expansionsform.

— Den har EXPLICIT inte framställts så i tidigare beskrivningar i UNIVERSUMS HISTORIA. Beskrivningen har snarare fokuserat på FLYKTHASTIGHETENS roll och den därmed förknippade idealt oändligt utsträckta expansionen.

— Det är en FÖRDJUPNING i framställningssättet, och som först nu tagit beskrivbar form i samband med studiet av fördjupningarna i K-cellens inre.

Beräkningsexempel K-cellen

EXEMPEL:

— K-cellens expansionsradie vid 336 T9 år (K-cellens halvperiod) är [r-formen] idealt via r|T(E)-sambanden

1,16 T27 M;

— Fria G-fallets motsvarande värde via r|T(G)-sambanden visar (3)^1/3=1,44 gånger större värde [‡Exp.samb.Koppl.Kcellen] med

1,67 T27 M efter en fri falltid på samma 336 T9 år.

— Det BEVISAR bara att r|T(E)-sambanden, det lägre värdet

1,16 T27 M, INTE ansluter till den påstådda flykthastighetens ideala rymd.

Den ska inte heller göra det.

— Det ligger i den avsaktande expansionens natur att INTE, inte på något sätt, ansluta till flykthastighetens idealt eviga expansion med obegränsat avtagande mot en nollpunkt.

Stoppmoderatorn — expansionens avstannande

Expansionssambandets koppling till fria fallets g-fysik

— Utvecklingarna från G-faktorerna — en mera reguljärt DYNAMISKT ORSAKSGRUNDAD formulerad bromsverkan (detonationsmassorna, den mörka materiens ursprung) — visar hur täthetsändringsfunktionen (justering av Tidsformens funktion) kan fås att harmoniera med grundparametervärdena från K-cellens värmefysik: de avgörande två K-radien och K-värdet 1,5.

— Den täthetsändrande justeringen täcker dock inte FORMEN (integral-derivata) för K-cellens hastighet-distansändringar [v|r(E)-sambanden] mot avstanningspunkten.

Det finns NATURLIGTVIS olika sätt att framställa en sådan stoppunkt, och här, i detta skede, finns inga anspråk på att ge någon annan helhetsbild i den resultatredovisningen än den som visar en (inledande) grov översikt:

— Det enkla sättet är att lägga till en »stoppmoderator»;

— För v-formen betyder det en subtraherande linjär acceleration av formen

a=v/T (grovt 6,73 t12 M/S²) med funktionen

v = + (–aT) ;

— För r-formen betyder det den ovannämnda formens integral, lika med en subtraherande distansform enligt

r = + (–aT²/2) ;

— Med dessa tillägg måste också föregående koefficientvärden justeras (dock endast marginellt) för att matcha de avgörande bägge faktorerna från K-cellens värmefysik, K-radien och K-värdet 1,5.

Se beräkningsgrunderna generellt i KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen.

Stoppfunktionens inverkan då den omslutna massan går mot noll — vi betraktar en delsfär allt längre in mot K-centrum — bör också gå mot noll då den inneslutna massan gör det. I annat fall uppkommer underliga BackStab-punkter [hugger minusvärden i galna former] som kremerar precisionen i centrum. För att kompensera för den aspekten behöver man bara multiplicera a-faktorn med m-faktorn: m/mK=0 ger nollverkan — med full pedal vid m/mK=1;

v = + (–a[m/m_K]T) ;

r = + (–a[m/m_K]T²/2) ;

Med slutvärdet för K-cellens radie r = 7,79792 T26 M vid T=336 T9 år visar fria G-fallets samband [‡Tiden, fria G-fallet] att kontraktionsperioden (M=4,14 T53 KG) blir bara en tredjedel av expansionstiden:

T(G) = Ö 2r³/3GM

= 3,38344 T18 S

= 107,217 T9 år

Notera att eftersom flykthastigheten PREFERERAR fria G-fallets praktiska värden, är det också flykthastighetens toppvärde som bestämmer det motsvarande fria G-fallets falltid;

— För ett visst tillryggalagt avstånd blir ALLTID tiden i G-formen den kortare. Därmed samma tid för motsvarande återfall.

— Lägre hastighet upp till ett visst avstånd betyder också längre tid.

I sektionen K-cellens övergång i c0-kroppen visas hur fria G-fallets samband, som ovan, kan användas för att precisera ALLMÄNNA TILLSTÅNDSBILDEN av hur övergången ser ut mellan K-cellen och c0-kroppen mera i detalj.

;

Analysen går vidare för att försöka precisera dessa aspekter — i vidare strävan att finna olika kvantitativa beräkningsjämförelser (helst med grund i observationella grunddata); det kan fortfarande vara FEL (felutrymmet avtar med växande antal tillfällen för noggranna jämförelser).

Ljusvägens integral

LJUSVÄGENS INTEGRAL — Bildkälla, Författarens arkiv, 19Jun2012E8Bild7 NikonD90 Detalj

Ljusvägens integral

K-cellen — MERA ALLMÄN BESKRIVNING Mar2012

Funktionen y = (1–x²)^–1/2

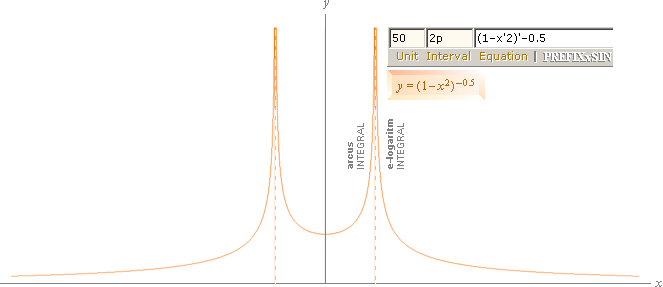
är av samma typ som distansderivatans funktion via hastighetsvarianten v=dr/dt i den relaterade g-fysiken med v som divergensen [DEEP] c enligt (från c0 till c0/2)

(1) c = c₀[1 – 2(w/c₀)²]^1/2

Funktionen uppvisar en funktionell brytgräns (streckat) vid vertikala gränslinjen x²=1, figuren ovan.

— Om vi vill (försöka) lösa integralformen för hur ljustiden kan bestämmas för ett visst avstånd (r=x) från c0 (K-cellens centrum) där en viss lokalt g-bestämd

(w²=Gm/r för statiska och w²=[G/4]m/r för expansiva-kontraktiva [G-faktorerna])

divergens (c) råder, och som går mot maxvärdet c0 som signalen avverkar x in mot centrum, måste vi — för att medge x från obegränsat utåt, där i princip nolldivergens (c=0) finns — utnyttja den motsvarande c-formen

(2) c = c₀[2(w/c₀)² – 1]^1/2

= [2w² – c₀²]^1/2 ;

w² = Gm₂/r ..................... statiska

w² = (G/4)m₂/r ............... expansiva-kontraktiva

Skillnaden mellan dessa ligger i att den förra (1) har en arcusintegral (figuren ovan mitten) medan den senare (2) har en e-logaritmisk integral.

Vi studerar först e-logaritmens lösning.

Om vi vill testa ett alternativt sätt till integrallösningen genom att använda SERIEFORMER, gäller för ovanstående problemtyp

t(SUMMA) = t1 + t2 + t3 + … + tn

= d(ITV)/c1 + d(ITV)/c2 + d(ITV)/c3 + … + d(ITV)/cn

= d(ITV)[1/c1 + 1/c2 + 1/c3 + … + 1/cn]

d(ITV) = x/n

med (x från obegränsat)

1/cn = [2w² – c₀²]^–1/2

Exempel som ansluter till K-cellen finns uppställt i Kalkylkortet KalkylkortDirekt KcGRB.ods 10cTime HelpOpen

Integranden 1/(x²±a)^1/2 har den obestämda logaritmiska integralen [från dy/dx=(P); dy=(P)dx] [NOLLFORMSALGEBRAN] [FORMLAGARNA] [DERIVATA OCH INTEGRAL] [POTENSDERIVATAN]

ò (x² ± a)^–1/2 dx = ln[x + (x² ± a)^1/2] = y

Återderivering ger [se FORMLAGARNA] [R=rotformen] y’ = [P]’/P med [P]’ = 1+x/R = R+x/R; Eftersom R+x=P återstår 1/R, vilket är integranden.

Den bestämda integralformen fås här genom att för x insätta en adderande offsetfaktor x:=x+(a)^1/2 så att integralen visar nollvärde (integralen blir en bestämd integral) för x=0 enligt (i fallet –a)

Q = ln[(x+a^1/2) + [(x+a^1/2)² – a]^1/2]

= ln[(0+a^1/2) + ((0+a^1/2)² – a)^1/2]

= ln[(a^1/2) + ((0)^1/2]

= ln[a^1/2] ..................................................................... integralkonstanten

y = ln[(x+a^1/2) + ((x+a^1/2)² – a)^1/2] – ln[a^1/2] ............. bestämda integralen

= ln[x+a^1/2 + ((x+a^1/2)² – a)^1/2] – ln[a^1/2]

I det statiska fallet [G-faktorerna]

w² = Gm/r ..................... statiska

ges integranden

c = [2w² – c₀²]^1/2

= [2Gm/r – c₀²]^1/2

med m/r via lokala medeltätheten (r=3m/4pr³) från

m = 4pr³r/3 ;

m/r = 4pr²r/3

som ger integranden

c = [2Gm/r – c₀²]^1/2

= [2G4pr²r/3 – c₀²]^1/2

= [(8prG/3)r² – c₀²]^1/2 ;

b = (8prG/3) ;

a = c₀² ;

r = x ;

c = [bx² – a]^1/2

= [b]^1/2[x² – a/b]^1/2

= [b]^1/2[x² – k]^1/2 ;

k = a/b

= c₀²/(8prG/3) ;

Därmed, via logaritmiska lösningen (vi ersätter dess [termkonflikt] a med k), ges t=y

ò [b]^–1/2(x² – k)^–1/2 dx = [b]^–1/2(ln[x+k^1/2 + ((x+k^1/2)² – k)^1/2] – ln[k^1/2]) = t ;

t = [b]^–1/2(ln[x+[a/b]^1/2 + ((x+[a/b]^1/2)² – [a/b])^1/2] – ln[[a/b]^1/2])

Med x=4,28 T25 M [vid T=16,32 T9 år] och (prövningsexempel) lokala tätheten (via max x-sfären) r=1,77 t25 KG/M³ med lokala divergensen c=0,71c0 vid x ges (via kalkylkort) ljustiden (t) för signalvägen x in till K-centrum vid c0 lika med

t = 4,88 T9 år

Om vi använder arcuslösningen, här i PREFIXxSIN,

ò [b]^–1/2(k – x²)^–1/2 dx

= [b]^–1/2(acos[x/k^1/2]) = t ; visa lösningen — Se Cirkelns integral

t = [b]^–1/2(acos[x/k^1/2])

kan också den lösningen ge relevanta resultat OM x<k^1/2.

— Med statiska g-fysikens g-potential (w²=Gm/r) blir [k=a/b]^1/2 max 3,01 T25 M, vilket är mindre än x.

— Den statiska formen kan alltså enbart av det skälet inte användas i arcusfallet.

— Däremot för arcusfallet via expansiva-kontraktiva g-fysikens g-potential [G-faktorerna] (w²=[G/4]m/r) blir gränsdistansen [k=a/b]^1/2 acceptabel: lika med max 1,54 T26 M;

— Med x=4,28 T25 M — b=8prG/4/3=2prG/3 — blir lösningsvärdet i detta fall, som ovan via r=1,77 t25 KG/M³,

t = 5,03 T9 år

Med tätheten för hela K-cellens medeltäthet vid T=16,3 T9 år, r=2,71 t26 KG/M³, ges ljustiden för x lika med t = 4,58 T9 år.

— Notera att resultatdelen ovan INTE tar med i beräkningen K-cellens ÅLDRING [motsvarande divergensökning] under tiden t.

— Tas också den delen med, blir reella t-värdet något mindre [minus grovt ca 0,8 T9 år].

Det är också avrundat samma värde man får genom prövning via (1000st) diskreta serietermer (separat kalkyl) via expansiva g-fysikens samband.

— Expansiva (w²=G[/4]m/r) g-fysikens t-värde blir något större genom den pågående expansionen hos den ljushastighetsstyrande g-massan.

Innefattas också i den serietabellen ytterligare ett särskilt samband

r=3/2pGT², motsvarande integrala lösningen för arccos(a/x) i PREFIXxSIN, den integralen är mera komplicerad

som tar hänsyn till hur divergensen samtidigt går mot c0 (K-cellens åldrande) med ljustidens fortlöpande, blir t-värdet reducerat från 5,03 till 4,95 T9 år — en reduktion med ca 0,8 T9 år (ca15%) i följd av K-cellens åldring under ljusvägen för x.

— Det motsvarar det ursprungligen redovisade resultatet från K-cellens värmefysik med den idealt jämnt fördelade medeltätheten tagen över hela K-cellen i dess expansion tillsammans med ljusvägen över x (4,52 T9 år — omärkligt skilt från ideala statiska ljustiden t=x/c0=[4,28 T25 M]/[3 T8 M/S]=1,42666 T17 S, ×3,16888 t8=4,52093 T år).

J-kropparnas hastigheter

J-KROPPARNAS HASTIGHETER — Bildkälla, Författarens arkiv, 27Jun2012E10Bild41 NikonD90 Detalj

Största utkastningshastigheterna från J-kropparna efter divergenständning

SVÅRIGHETERNA ATT KLASSIFICERA DET INRE AV K-CELLEN

Erinra FÖRST — om ej redan bekant — Planckekvivalenterna tillsammans med Beviset för multipla c för eliminering av varje tänkbart insteg till missförstånd

—J80-kroppen markerar den ungefärliga gränskropp i K-cellens expansion som med lägsta massan har förutsättningar för att avdela andra J-kroppar med nolldivergens. Flykthastigheten i randen på den J-kroppen blir (se sammanställda samband nedan) v=2c0, c0=toppdivergensen 2,99792458 T8 M/S.

— Med approximationen från ALLMÄN DELNINGSKLASSIFICERING skulle Solsystemets J-kroppar haft en J-moderkropp på (minst) ca 200 Solmassor. Flykthastigheten i randen på den J-kroppen blir (se sammanställda samband nedan) v=2,7c0.

v = Ö 2Gm₂/r ........................... flykthastigheten via Ekin=EG=mv²/2=GmM/r=Fr

r = (3m₂/4pr)^1/3

v = [2Gm₂/(3m₂/4pr)^1/3]^1/2 ...... G=6,67 t11 JM/(KG)²

= [2Gm₂^1–1/3=2/3(4pr/3)^1/3]^1/2

= m₂^1/3[2G(4pr/3)^1/3]^1/2 ; r = 1,82 T17 KG/M³

= m₂^1/3[0,0110392] ;

v = 1,9953793c₀ ; m₂ = 80m_SOL = 1,5912 T32 KG

v = 2,7081444c₀ ; m₂ = 200m_SOL = 3,978 T32 KG

Med den sammansättning som utpekas i ALLMÄN DELNINGSKLASSIFICERING finns en stor flora av hastigheter som kan konkurrera med den lokala divergensen — många gånger om.

EXEMPEL

Med en J-kropp på Vintergatans nuvarande massa

m2=1,4 T11 Solmassor [BAs313Tab15.2], Solmassan = 1,989 T30 KG,

m2=2,7846 T41 KG, ges de yttersta delarna hastigheten max

v = m₂^1/3[0,0110392]

= 7,20872 T11 M/S

= 2404,5722 c₀

vid J-kroppens expansion från divergenständningen, maximal c0-dynamik förutsatt.

— J-moderkroppen till Vintergatskroppen via grovräkningen i ALLMÄN DELNINGSKLASSIFICERING, skulle i sin tur vara minst 200ggr större i massa, eller motsvarande

v=14062,024c0.

— Eller mera reguljärt räknat via K-cellens värmefysik med uppgiften att den synliga massan bara är 1/355 av den totala:

— Reala PRIMÄRA Vintergatsmassan skulle då vara (355·2,8T41=9,94T43)KG som skulle ge en maximal flykthastighet i den J-kroppens rand på

v=17057,381c0.

Blåförskjutningar

BLÅFÖRSKJUTNINGAR

Bildkälla, Författarens arkiv, 22Maj2012E2Bild12 NikonD90 Detalj

Varför ser vi ingen större mängd blåförskjutna galaxer (på väg mot oss)?

Förklaring — se Bildlogocept 2 hur J-kropparna avdelas inåt K-centrum enligt K-cellens allmänna expansion, därmed en följdfråga:

— Innebär i så fall inte den typen av ordning att man borde se stora mängder blåförskjutna himmelsobjekt likaväl som rödförskjutna?

— Tydligen inte. Vi studerar det.

centrum

←— →

— J-kroppar som vid en bestämd tidpunkt (T) i K-cellens expansionshistoria divergenständer [DIVERGENSTÄNDNING] [Divergenständningen i detalj] från en J-moderkropp vid ett visst avstånd (d) från K-cellens detonationscentrum (c0) kommer alla att passera K-centrum (efter t=d/v[netto]) om nettohastigheten i J‑utkastningarna är större än eller lika med v=d/T.

EXEMPEL 1

Vid K-cellens effektmaximum [K-cellens värmefysik] T=16,32 T9 år är distansen till medelrödförskjutningen K=1,5 (Se K-värdet 1,5 och K-radien) lika med (ca; något olika beroende på de använda konstanternas precision) d=4,28 T25 M, samma som K-radien.

Uppgift:

— Vilken konstanta nettohastighet relativt K-centrum ska en J-kropp ha vid K-radien för att precis passera K-centrum vid T=16,32 T9 år?

Lösning:

v = d/T

= (4,28 T25 M)/(16,32 T9 ·365,25·24·3600)

= (4,28 T25 M)/(16,32[3,15576 T16])

= (4,28)[3,15576 T8]/(16,32)

= 83 103 563 M/S

= 0,2772036[c0=2,99792458 T8 M/S]

Svar:

Hastigheten måste vara minst konstant (avr.) 0,277c0.

EXEMPEL 2

Uppgift:

Samma förutsättningar som i Exempel 1, men med T=20,82 T9 år; Bestäm v.

Lösning:

v = (4,28)[3,15576 T8]/(20,82)

= 0,2163945c0

Svar:

Hastigheten måste vara minst konstant (avr.) 0,216c0.

RESULTAT:

Räkneexemplen ovan klargör att J-kroppar — ursprungligen från K-radien — på väg in mot centrum med högre nettoutkastningshastighet än 0,216c0 redan har passerat K-centrum och därför inte kan observeras via en Dopplereffektbaserad blåförskjutning (våglängdsförkortning).

DET skulle också enligt TNED vara SVARET PÅ FRÅGAN VARFÖR VI INTE SER NÅGON STÖRRE MÄNGD BLÅFÖRSKJUTNA OBJEKT PÅ VÄG MOT VINTERGATAN:

— De J-kroppar som (UTANFÖR VÅR EGEN GALAX) ursprungligen avdelades vid K-radien (d=4,28 T25 M) in mot K-centrum kan alltså som mest uppvisa en bråkdel av motsvarande v=0,216c0; Exakt 0,216c0 med passagen genom K-centrum (utan hänsyn till divergensändringarna). Men då vi med stor sannolikhet INTE befinner oss EXAKT i K-cellens centrum, om än nära, måste blåförskjutningens gränsvärde 0,216c0 från de aktuella J-kropparna vid K-radien under alla omständigheter vara mindre. Eftersom, således, J-objekten för blåförskjutningen (först och främst) måste ligga utanför Vintergatan, ut mot K-cellens yttre (och dess galaxgrupp), kan vi se att gränsformen 0,216c0 BÖR vara (betydligt) mindre.

— Vi skulle säga i en grovt generaliserad mening — enligt TNED:

— Observerade objekt mellan Vintergatan och K-radien

(d=4,28 T25 M med K=1,5 och z=2=1/[1–1/K]–1)

innehåller knappast någon utpräglad mängd blåförskjutna objekt av någon större magnitud (zMAX=0,28).

— Däremot borde det finnas en mera utpräglad mängd rödförskjutna objekt i samma gränsområde, samt med betydligt högre rödförskjutningsvärden (zMEDEL=2, K=1,5).

Rödförskjutningar

K-CELLENS INRE VID K-RADIEN — tidpunkten för K-cellens effektmaximum vid T=16,3 T9 år

centrum

←— → → →

Frånsett gravitella rödförskjutningen:

— Alla J-kroppar med någon hastighet större än noll bort från K-cellens centrum och som utsänder ljus, kommer också att uppvisa en Dopplereffektbaserad rödförskjutning (våglängdsförlängning) för en viss given våglängd (som baseras på spektrum från något visst känt ämne).

— I K-cellens värmefysik finns ingen EXPLICIT beskrivning av vilken RELATION som gäller för K=1,5-värdet avseende sann rödförskjutning i c0-rymd kontra gravitell rödförskjutning. Kalkylkomplexet för K-cellens värmefysik, helt baserat på en allmän homogen medeltäthet, ger oss i vilket fall endast K-radien (4,28 T25 M) vid K-cellens effektmaximum (T=16,3 T9 år).

— Idealt med homogen c0-rymd motsvaras K=1,5 av v/c0=2/3=0,67.

— Söker vi någon motsvarande PRAKTISK BILD av K=1,5 vid K-radien, alltså tillsammans med en verklig gravitell rödförskjutning som följd av att signalen från K-radien till hit växer i c, blir vi alltså hänvisade till OLIKA MODELLER med olika möjliga fördelningar mellan hastigheter, expansioner, lokala (medel-) tätheter och dito divergenser.

— Det finns (här veterligt) inget som helst föregivet via TNED på den punkten: alla modelldata måste i vilket fall avstämmas mot observationernas värden, och det blir dessa sistnämnda som bestämmer graden av överensstämmelser i modellering och justering.

För slutresultaten generellt till K-cellen (Maj2012), se K-cellens övergång i c0-kroppen.

TRANSITFUNKTIONEN mellan olika funktionsrum — Se även i MODELLERINGSEXEMPEL MED TRANSITFUNKTIONEN — Bildkälla, Författarens arkiv, montage — 27Jun2012E10 Bild52 Bild41 — NikonD90 Detalj

Transitfunktionens rent matematiska-grafiska form beskrivs ingående i MODELLERINGSEXEMPEL MED TRANSITFUNKTIONEN. Här beskrivs tillämpningen för K-cellen.

— Nödvändigheten att förena K-cellens yttre basmatematik [K-cellens värmefysik] (idealt homogen täthet) med den utvecklade inre fysik (praktiskt: inhomogen täthet i vissa partier) som anvisas av K-radien och K-värdet 1,5 [Behovet av en mera precis översiktsbild] framtvingar en matematisk formulering av en övergångsfunktion, en »transitfunktion», mellan två fysikaliskt skilda individuella funktioner: A [K-cellens idealt homogena sfäriska medeltäthet, ρ=3m/4πR³] och B [Täthetsändringsfunktionerna via K-radien och K-värdet].

— Transitfunktionen har ingen annan uppgift än att avsluta A (¯|_) och initiera B (_|¯) inom ett gemensamt tidsintervall (X).

— Transitfunktionen beskrivs nedan i specifik koppling till tillämpningen på K-cellen mellan ideala homogena och (fortfarande till prövning) praktiska inhomogena inre täthetsformerna. För mera allmän matematisk-grafisk beskrivning, se MODELLERINGSEXEMPEL MED TRANSITFUNKTIONEN.

Funktionsprincip

x är huvudfunktionen — [1–(1+[x/1]'100)'–1] är transitfunktionen, den avbildar det konstanta värdet y=1 då x växer obegränsat.

— Huvudfunktionen är i princip avstängd fram till xNämnarKoefficienten i transitfunktionen [lika med 1 i figurexemplet].

— Transitfunktionens exponent bestämmer snävheten i övergången.

GrafUnit50 y = x[1–(1+[x/1.1]'100)'–1] Se vidare utförlig funktionsbeskrivning i MODELLERINGSEXEMPEL MED TRANSITFUNKTIONEN.

Transitfunktionen

HUR K-CELLENS INRE TÄTHETSändrande FUNKTION INITIERAS

Idealsambanden från start — in till viss tid

K-cellens utveckling kan i varje fall i princip sammanställas med K-cellens basmatematik [K-cellens värmefysik] som tillåts gälla från början, in till en viss tidpunkt då övergång sker till täthetsändringsfunktionerna.

— För att genomföra den ordningen kan funktionstypen nedan användas,

y = [1 – (1+[ax]^b)^–1]

Graf: y = [1–(1+[ax]'b)'–1] ; a=1; b=10;

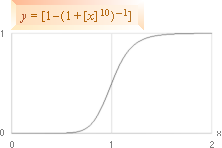
a=1 håller övergången centrerad vid x=1. Högre a-värde drar övergången mot x=0 och gör den samtidigt brantare. 50% av effekten uppnås alltid vid x=1 med a=1.

— Mest gynnsamma symmetriska regleringen [överdelen alltid något längre än underdelen] via exponenten [b]: Större b-värde ger brantare övergång.

t/t0

Exempel:

— Man vill undersöka en 10%-ig effekt vid uppnådda x=t=70% av en viss gränstid t₀=0,01 (motsv. Unit=1); Det motsvarar x=0,7 i grafen ovan, där önskemålet är att y-värdet ska vara 0,1=10%.

Uppgift:

— Hur ska man välja exponenten (n) för detta fall för att få exakt matchning?

Lösning:

y = 1 – (1 + [t/t₀]ⁿ)^–1 ;

[t/t₀]ⁿ = (1 – y)^–1 – 1 ;

n = ln[(1 – y)^–1 – 1]/ln[t/t₀]

y 0,1 = 10% ;

t 0,7t₀ = 70%t₀ ;

t₀ 0,01 ;

t/t₀ = 0,7 ;

Svar:

n = 6,16029977

— Sätts y-formen som exponent till t-formen, gäller [t(k)]^y=⁰=1 in till övergångsområdet vid x=1 som kan göras i princip hur brant som helst via b-exponenten. Därifrån gäller sedan [t(k)]^y=¹=[t(k)] enligt föregående mera avancerade samband.

— Men varför skulle en sådan modifikation vara påkallad?

— Just med referens till hur K-cellens bryts [K-CELLENS BRYTNING]:

K-centrum från början: »utvidgat c0»

Med detonationstillfället från K-centrum dröjer en viss minsta tid innan reguljära sfäriska kroppar börjar uppträda vid K-cellens expanderande innervägg. Genom den starka gravitation som dessa första högtäta sfäriska neutronkallplasmakroppar har, är det rimligt om också K-cellens inre i princip rensas på massa utöver centralkropparna i succession med deras bildning och tillväxt. Bilden med den idealt homogena täthetsfördelningen — [t(k)]^y=⁰=1 — gäller fortfarande in till viss tid när de reguljära divergenständningarna börjar, men nu med olika specifika sfäriska skalcentra som täthetsagenter för den omslutna centralvolymen och som innehåller sin uppsättning sfäriskt formade primärkroppar, i allt specifikt med början i K-cellens inre.

— POÄNGEN med den ordningen är att HELA det inre av K-cellen, ända fram till sfärskalet med de första reguljära sfäriska kropparna, erhåller toppdivergens: c=c₀. Figuren nedan sammanfattar grunden i det påståendet.

— Därmed garanteras maximalt snabb divergenständning för de inre bildade K-cellväggskropparna — och som vi här förmodar, i allt med syftet att få fram den praktiska analogin med Vintergatans bildning och dess moderkroppar.

Räkneexempel Vintergatans J-moderkropp

— En J-kropp på 300 effektiva Vintergatsmassor (synliga 2 T41 KG gånger 355 gånger 300) i neutronkallplasma (r=1,82 T17 KG/M³) har sfärradien r=(3[m=2,13 T46 KG]/4pr)^1/3=3,0344 T9 M; Med svephastigheten v=(1/3)[c₀=2,99792458 T8 M/S] har nollzonen passerat den kroppen efter tiden t=r/v=30,365033 S.

— Med K-cellens basmatematik gäller den matematiken vare sig den inneslutna massan ligger utsprid eller samlad i form av sfäriska större J-kroppar. Om det senare fallet gäller, gäller också motsvarande nedanstående gravitella systemalgoritm som visar att området innanför ett system av g-kroppar i en ring, eller symmetriskt i ett sfäriskt skal alltid uppvisar praktiskt taget ljushastighetens toppvärde. Det är bara i omedelbar närhet till en g-kropp som divergensvärdet avtar drastiskt. Därmed är syftet väl motiverat för att bibehålla basmatematiken speciellt från första stunds början i K-cellens expansion, och blott så småningom släppa in den ordning som följer senare på de aktuella divergenständningarna — [t(k)]^y=¹=[t(k)] enligt föregående mera avancerade samband.

— Svårigheten att innefatta alla praktiska detaljer i denna förenklade och primitiva form är uppenbara (»dockskåpsteater»), men den nödvändiga eftergift som måste göras för att alls få fram någon beskrivande helhet.

Ljushastigheten/g-potentialen innanför sfäriska skalet — G-ringen

KalkylkortDirekt KcGRB.ods 13cgRing HelpOpen D34•TAURING.BMP — från arbetena föregående UNIVERSUMS HISTORIA

Notera att matematiken för N lika g-massor i en RING genom multipla ringar blir identisk med samma antal N homogent fördelade g-kroppar tagna i multipler i en omskriven SFÄR [minus de bägge diametrala ändkropparna för varje ny tillkommen ring om delningen har den typen] — eftersom referenslinjen [h] i vilket fall tecknar PARSYMMETRI för varje par g-kroppar.

Förklarande beskrivning

Om vi anställer en undersökning av vad som gäller för den lokala ljushastighetens variation [LJUSETS G-BEROENDE] via en ljusväg som via olika referenspunkter (h) passerar mellan två kroppar i en ring av N stycken likadana g-kroppar, gäller den ovanstående figurens sammanställda sambandsbild (Ursprungligen i samband med potentialbarriären, från Dynamikens Grunder 1995, författarens privata arkiv).

— Resultatet visar hur det inre av ringens g-kroppar förblir praktiskt taget toppdivergent, som om huvuddelen av det inre tomrummet utverkar ett utvidgat c₀-område. Märkbara reduktioner i ljushastigheten uppkommer bara i den allra närmaste regionen av ringens g-kroppar — emellan dem återigen upp mot c₀ — och sedan i mera långsam takt utanför ringen upp mot c₀ som referensposition (h) går mot oändligt.

— K-cellens motsvarande praktiska form före inflödet av den starkt massövervägande molekylärt fragmenterade detonationsmassan blir ett inre centrum med ett nära (men inte exakt) homogent toppvärde för c₀.

Praktiskt i K-cellen

y = 1 – (1 + [t/t₀]ⁿ)^–1 ;

[t/t₀]ⁿ = (1 – y)^–1 – 1 ;

n = ln[(1 – y)^–1 – 1]/ln[t/t₀]

Med förebild från beskrivningen i J-kropparnas primära avdelning från det inre av K-cellen, kan ovanstående transitfunktionen mellan skilda funktionsrum användas för att — grovt — beskriva den inledande, speciella, utvecklingen i K-cellens expansion från K-centrum.

— Utan en sådan justering skulle det inre av K-cellen, från K-centrum och detonationstillfället, uppvisa en strängt negativt betingad divergens (fortfarande neutronkallplasma), utan möjlighet att se någon öppning för bildning eller avdelning av J-kroppar i positiv divergens — och därmed effektivt stopp för varje möjlighet att härleda Vintergatans (den lokala galaxgruppens) tidiga historia, i allt enligt K-cellens övergripande värmefysik [K-cellens värmefysik].

— Det vi måste garantera — således, som passande kurvkonstruktörer i den observationella beskrivningen, och förklaringen av UNIVERSUMS HISTORIA — är att K-cellens omedelbara innersta delar förblir i princip massfria med den INLEDANDE K-cellens omedelbara expansion.

— Jämför här (återigen, illustrationen ovan Ljushastigheten/g-potentialen innanför ringen) situationen med den fasta K-cellens innervägg (neutronkallplasma) i den centrala, divergensupplysta, J80-kroppens ytterrand från detonationstillfället — i regi av utvecklingstypen illustrerad i J-kropparnas primära avdelning från det inre av K-cellen:

Den centralt inneslutna högtäta Vätgasen tvingas associera sig med cellinnerväggens maximalt täta, starkt gravitellt attraherande kallplasma . . .

Den fasta cellväggen följer, tvunget, delvis med i den initierande expansionen; Cellväggen avdelas/indelas successivt efter/via ett vågmönster, och den centralt inneslutna högtäta vätgasen tvingas associera sig med cellinnerväggens höggravitella, starkt attraherande kallplasma (som medför att vätgasen återgår till neutronläget, se även i Hur K-cellens återvinns).

— I en sfärisk kropp med idealt HOMOGENT FÖRDELAD TÄTHET finns inte den funktionen: inre massdelar som attraheras mot yttre. En homogen täthet garanterar att g-potentialen överallt är likformigt (homogent) fördelad: gravitationen utanför en innesluten massfär påverkar inte delmassor i den inneslutna massan.

— I utvidgningen av K-cellens inre cellvägg gäller emellertid inte den ideala g-fysiken, utan istället den som enklare kan återföras på (g-potentialen i ringen) vad som händer med en delmassa placerad innanför (inte exakt i mitten) av en solid massring, eller dito uppdelad på diskreta centralmassor: Delmassan attraheras mot ringen/skalet.

— Därmed kan det inre av K-cellens centrum förstås utvecklas (idealt) massfritt omkring de successivt framträdande J-kropparna enligt typillustrationerna beskrivna ovan från Ljushastigheten i Ringen. Det garanterar att divergensen, den lokalt gravitellt betingade ljushastigheten i området närmast omkring kallplasmat, också utvecklas med minimal skillnad mot toppvärdet c0. Därmed säkerställs den, enligt TNED nödvändiga, härledningen till (Lokala galaxgruppen) Vintergatans ursprung via optimalt snabb divergenständning.

Övergångstillfället

Med ideal toppdivergens c=c0=2,99792458 T8 M/S

c₀ = 2,99792458 T8 M/S ........... ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

in till nuvarande ungefärliga medelavstånd mellan (de medelstora) galaxerna, ca 3MPc eller grovt 9,5 T22 M, ges expansionstiden T=d/v=3,16885 T14 S eller (×3,16888 t8 1/S) 10 041 733 år ~ 10 miljoner år.

— Om en galaxkropp bildades vid den tidpunkten, och förutsatt lämpligt avdelad, kan den precis hinna fram till K-centrum i våra dagar efter 20,82 T9 år med konstant hastighet om denna är v=d/T=144 593,46 M/S ~ 145 KM/S. Den farten ansluter också grovt till de astronomiskt konventionellt uppskattade hastigheterna i samband med data från Lokala galaxgruppen (grovt inom intervallet ±300 KM/S).

— Det är vad beskrivningen i helhet måste kunna innefatta.

Från ett tidigare jämförande räkneexempel (Räkneexempel Vintergatans J-moderkropp) visades att divergenssvepet med v=c0/3 kräver drygt 30 sekunder för att »tända», alltså översvepa, en J-kropp med massan ca 300 Vintergatsmassor. Det är fortfarande försumbart mot neutronsönderfallets intervall (i rymder med toppdivergens), ca 12-14 minuter.

Praktiska utformningen

— För att anställa en motsvarande relevant tidsgräns (t0) i samband med avdelandet av de allra första J-kropparna från K-cellens innervägg,

från vilken tidsgräns det inre av K-cellens masstäthet bryts från att ha varit praktiskt taget noll från start till ett OMRÅDE, sfäriskt skal, med utpräglat avdelade J-kroppar, och därmed en SKARP ÖVERGÅNG till en markant medelfördelad masstäthet, i princip med negativ divergens (medelbaserat kallplasma),

är det tydligt att ÖVERGÅNGEN i den skarpa brytningen i princip bara ska innefatta tidsavsnittet för »de första reguljära divergenständningarna». Därför att EFTER det tillfället, kommer sedan en vidare STRÖM av divergenständningar att bara fylla på den så framtriggade fysiken med allt växande massinskjutningar (detonationsmassorna) mot K-centrum och deras allmänna fördelning och spridning i hela den tillgängliga K-cellen.

Vi kan alltså sätta tidsgränsen (övergångstillfället) t0=10 miljoner år = 1 T7 år, eller 0,01 T9 år som den övergångspunkt då ÖVERGÅNGEN till den reguljära masstäthetsfördelningen (täthetsändrande funktionen) inträder (tillfället då detonationsmassorna börjar breda ut sig i K-cellen):

— Med i princip ett övergångsintervall på max 1 minut med ovannämnda exempelräkning som jämförande referens (Räkneexempel Vintergatans J-moderkropp), ska i princip nolleffekt råda vid t0–1minut och full effekt vid t0+1minut;

— Bråkdelen med marginalen på 1 minut fram till mitten på divergenständningen, 60S/([1 T 7]/[3,16888 t8 1/S])=1,90132 t13, kan ses, grovt, som en initierande fas där (säg) 1% av toppeffekten uppnåtts. Det ger exponentfaktorn i transitfunktionen som

n = ln[(1 – y)^–1 – 1]/ln[t/t₀]

= ln[(1 – 0,01)^–1 – 1]/ln[(0,01–1,9 t13)/0,01]

E-logaritmen för nämnarvärdet kan i detta fall inte bestämmas, det blir här i princip obegränsat

(0,01–0,00000000000019=0,0099999999998… ~0,01), och därmed även n-värdet i princip obegränsat.

Vi kan emellertid via prövning i kalkylprogrammets celler (här OpenOfficeCalc) få fram i varje fall en känslighet på 1 år med n=1 T8;

— t=0,009 999 999 [varje decimalposition neråt från miljarder år] ger då effekten 0,000045398=0,0045398%.

— Gränsen (OpenOfficeCalc, samma effektvärde 4,5398 t5) går vid n=1 T 16 med t=0,00999999999999999 som motsvarar en känslighet på

1/(1 T8 år) = 0,3155689 S; Se Transitfunktionen i KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen.

— För att matcha ut en känslighet på grovt ca 30 sekunder (31,55689 S) kan alltså n-faktorn 1 T14 användas.

Därmed är slutformen uppnådd.

I PRAKTIKEN kan kalkylprogrammets rutiner (i exemplet ovan, OpenOfficeCalc) inte användas för högre exponentvärden än max (t/0,01)⁶⁸; högre exponentvärde (69) resulterar i MEDDELANDET ”#OGILTIGT!”.

— Det finns ingen extrapolerad matematisk funktion inom konventionell matematik (typ kalkylprogram) som BILDAR typen 1/(n→∞)=0 då flyttalslängden överskrids — vilket skulle vara det rent logiska sättet att få ett användbart resultat genomgående.

— Med andra ord: Konventionella Kalkylprogram är INTE lämpliga för precisionsanalyser i ämnet universums historia. Vi får (frånsett mera avancerade programformer) bara se en grovt översiktlig bild.

MODELLERINGSEXEMPEL MED TRANSITFUNKTIONEN

MODELLERINGSEXEMPEL MED TRANSITFUNKTIONEN — Bildkälla, Författarens arkiv, montage — 25Maj2012E5Bild93 — 27Jun2012E10Bild41 — NikonD90 Detalj

MODELLERINGSEXEMPEL med Transitfunktionen

Se Tillämpningsexempel särskilt för K-cellen.

Med utgångspunkt från en Inaktiv huvudfunktion (X) som ska aktiveras i läge ON — först vid eller från x=a:

Transitfunktionen (on_|¯)

onTransit

y = [1–(1+[x/a]'b)'–1] ; a=1; b=10;

y = [1 – (1+[x/a]^b)^–1]

= T_ON

garanterar med obegränsat stor transitexponent (b) att varje x-funktion X förblir avstängd fram till transitfunktionens övergångsgräns (a) enligt

X-funktionen

y = X[1 – (1+[x/a]^b)^–1]

X kan vara vilken som helst funktion.

— Genom att onTransit-formen i princip kan ställas obegränsat på NOLL fram till x=a kommer också X-funktionen att garanteras likaledes NOLL fram till x=a. Därefter, eftersom onTransit i princip kan fås att övergå i 1 via hög b-exponent, gäller också X från x=a. Vidare exempel följer nedan.

Omvända övergångsformen (off ¯_) ges av motsvarande

offTransit

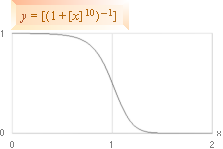
y = [(1+[x/a]'b)'–1] ; a=1; b=10;

y = [(1+[x/a]^b)^–1]

= T_OFF

y = X[(1+[x/a]^b)^–1]

— Genom att offTransit-formen i princip kan ställas obegränsat på NOLL fram till x=a kommer också X-funktionen att garanteras likaledes AKTIV fram till x=a. Därefter, eftersom offTransit i princip kan fås att övergå i 0 via hög b-exponent, gäller också X=0 från x=a. Vidare exempel följer nedan.

Brantheten i övergången

Brantheten i övergången vid x=a visas nedan via onTransit med b-exponenten 1-100.

y = [1–(1+[ax]'b)'–1] ; a=1; b = {1-10 | 10-100 };

Omedelbarheten i övergångsgränsen (a) garanteras av b→∞.

— Övergångens branthet vid a kan alltså styras med b.

EXEMPEL i PREFIXxSIN:

X = 1 + 0,2 sin10px

y = X ;

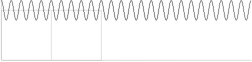
Funktionen inaktiveras mellan x=0 och x=1:

y = X[1 – (1+[x/a]^b)^–1] .................................. X INaktiv 0-1

= XT .......................................................... T verkställer X från x=1 mot oändligt

a=1, b=100:

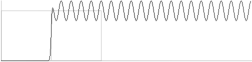
Aktiv huvudfunktion intervallet 0-a

För att låta huvudfunktionen X vara aktiverad i x-intervallet 0-a och sedan avstängd för resten, gäller tydligen

y = X – X[1 – (1+[x/a]^b)^–1]

= X(1 – [1 – (1+[x/a]^b)^–1])

= X(1+[x/a]^b)^–1 ........................................... X aktiv 0-a

Och, vilket vi ser, är samma som offTransitformen:

= X[T] ........................................................ [T] verkställer X från x=0 till a

a=1, b=100:

T-suffixen

För att förenkla suffixen i (den vidare) hanteringen av de olika transitformerna införs här det enkla och bekväma

T ........................... T_ON ₀_¯¹

[T] .......................... T_OFF ¹¯_₀

Exempel på SnabbVäxling (b=100) mellan två olika funktioner genom transitgränsen vid x=a=1

För två olika X-funktioner x och z som ska avlösa varandra genom transitfunktionen (T), eller försvinna mjukt i varandras obegränsade utdämpningar via T, gäller alltså

Sammansatta y-formen

y = x[T(a)] + zT(a)

x är funktionen som gäller direkt från x=0 :

x[T(a)] stänger av ¯_ x från a;

z är funktionen som gäller först från x=a :

zT(a) aktiverar_¯ z från a;

y = x(1+[x/a]^b)^–1 + z[1 – (1+[x/a]^b)^–1]

P = (1+[x/a]^b)^–1 ;

y = xP + z[1 – P]

= xP + z – zP

= xP – zP + z

= P(x – z) + z

= (1+[x/a]^b)^–1(x – z) + z ;

EXEMPEL i PREFIXxSIN:

x = 1 + 0,2 sin10px ............................... x är funktionen som gäller direkt från x=0 :

z = x ..................................................... z är funktionen som gäller först från x=1 :

y = x[T(a)] + zT(a) ; a=1, b=100 :

= (1 + 0,2 sin10px)(1+[x/1]¹⁰⁰)^–1 + x[1 – (1+[x/1]¹⁰⁰)^–1]

= (1+[x/1]¹⁰⁰)^–1[(1 + 0,2 sin10px) – x] + 1 + 0,2 sin10px

Och, vilket vi ser, är samma som i förenklingen direkt från Sammansatta y-formen:

= x + (1+[x/1]¹⁰⁰)^–1[–x + 1 + 0,2 sin10px] :

Praktiska exempel

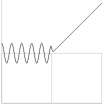
PRAKTISKA EXEMPEL — SN GRB

Verkligt praktiska exempel som direkt visar — och bevisar — TRANSITFUNKTIONEN i dess användbara roll i praktisk fysik framgår av Studieexemplet SN 1998bw

samt i GRB-exempel med jämförande exempel från Zeh 2004 i GRB 970228

och GRB 011121

END.

Bildlänkar till MAGIC NATURE:

K-cellens inre fysik

K-cellens övergång

Formgeometrin

G-potentialer och tätheter i och utanför K-cellen

Mörka materien

Divergenständningarna i detalj

GRB

G-faktorerna

Täthetsändringens funktioner

Divergensenergins gravitella beroende

Mörka materien i TNED

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Mörka materien i TNED

ämnesrubriker

innehåll

MÖRKA MATERIEN I TNED

Mörka materien i TNED

Fraktaldelningsexemplet Vintergatan/K-cellen

Detonationsmassorna

DETONATIONSMASSANS UPPLÖSNING

Betanuklidbildning

Slutprodukten

Kosmiska partikelstrålningens ursprung

Mineralgrunderna

Räkneexempel med den högst observerade partikelenergin

Protonen orealistisk som agent för högsta energin

Citat Wikipedia om kosmiska partikelstrålningen

Kosmiska partikelenergins medelvärde

Citat Berkeley Lab

Elektrisk och magnetisk verkan mellan atomer och elektroner som färdas fortare än c

SANDKORNSANALOGIN — Mörka materiens upphov

TREmilsKuben

Mörka materien BA1978

Mörka materien kring Vintergatan i TNED

Mörka materien kring Vintergatan i MAC

J-moderkropparnas praktiska uppdelning — J80-kroppens begränsade neutronfysik

J-kropparnas primära avdelning från det inre av K-cellen

Utvecklingen i K-cellens expansion

UNIVERSUMS HISTORIA — K-cellens vågillustration

Mörka materiens rationella fysik i TNED

Bildlogoceptet till Vintergatans bildningshistorik enligt TNED

Bildlogocept II till Vintergatans bildningshistorik

Grafisk Referens till K-cellens vågillustration

DGD-samband i översikt

GRUNDFYSIK — elektrogravitationen

G-potentialen

Centralparametrarna i K-cellens värmefysik

De observerade förutsättningarna — i sammanställning för vidare översikt

Gravitella rödförskjutningen

Rödförskjutningssambanden

Gravitella dopplereffekten

Gravitell Rödförskjutning

GraviKinematiska Dopplersambandet I RELATERAD FYSIK

Gravitella-Kinematiska K-formens dopplersamband

Gravitell Blåförskjutning — Andromeda exempel

Expansionssambandets koppling till fria fallets g-fysik

Fria fallets G-fysik

Galileiskt kraftfält

Hastigheten — fria G-fallet

Tiden — fria G-fallet

Expansionssambandet, kopplingen till K-cellen

Beräkningsexempel K-cellen

Stoppmoderatorn — expansionens avstannande

Ljusvägens integral

Ljusvägens integral

J-kropparnas hastigheter

Största utkastningshastigheterna från J-kropparna efter divergenständning

TRANSITFUNKTIONEN

Funktionsprincip

t/t0

K-centrum från början

Räkneexempel Vintergatans J-moderkropp

Ljushastigheten/g-potentialen innanför sfäriska skalet — G-ringen

Övergångstillfället

Praktiska utformningen

MODELLERINGSEXEMPEL med Transitfunktionen

onTRANSIT

X-funktionen

offTRANSIT

Brantheten i övergången

T-suffixen

Sammansatta y-formen

Praktiska exempel

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

e₀ = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²

[BA]. BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, modern akademi

TNED

(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken

är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.

Senast uppdaterade version: 2021-12-31

*END.

Stavningskontrollerat

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ τ π ε ħ UNICODE — often used characters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω →∞ ≡ ↔↕ ħ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — also Alt+18 ↕; Alt+29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

åter till portalsidan · portalsidan är www.UniversumsHistoria.se