Radioaktiva sönderfallets Fysik — enligt TNED | Meteoriterna i UNIVERSUMS HISTORIA | 2012I12 | a BellDHARMA production | Senast uppdaterade version YearMonthDayTime 2017-08-29

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Meteoriternas Ursprung | GRAVITATIONSENERGIN | Jenkinseffekten i relaterad fysik

Mera detaljerade argument i frågan om Jordens och Solsystemets ålder — BILDKÄLLOR nedan WEBBEN montage Jan2012: Örnnebulosan, Google Bilder · Canyon Diablo meteorkratern Arizona, Wikipedia · övrigt författarens arkiv

Jeansteorin — g-kollapsande kosmiska stoftmoln | Om Vätgasmoln i Universum och deras Gravitella sammandragning | Ursprung 92 — De 92 Grundämnenas Jordiska ursprung

Meteoriterna enligt relaterad fysik i Universums Historia

Inledning

Förutsättningar för Meteoritlokalernas ursprung enligt relaterad fysik

Med fortsättning från ALLMÄN DELNINGSKLASSIFICERING — Hur Galaxer och Stjärnsystem avdelas i K-cellens expansion:

— Med J-kropparnas [‡] avdelning enligt SOLSYSTEMETS RESONANSSERIE (Se även som Jordens Tredje Ekvation) inträder strax DIVERGENSTÄNDNING: De maximalt högtäta (1,82 T17 KG/M³) J-kropparnas neutronkallplasma kommer in i positiv divergens (c>0), neutronens sönderfall börjar i lokalen med snabbaste utvecklingen, kortaste tiden, i kropparnas tyngdpunkt (Se från Ljusets gravitella beroende) — där den lokala divergensen (ljushastigheten) är som störst. Därmed inträder strax J-KROPPENS EXPANSION med fusionsfasen (Se från Fusionsbildningen genom exempel) som leder till GRUNDÄMNESBILDNINGEN och den primära GRUNDÄMNESFÖRDELNINGEN: neutronkvoten (Se exempel i Basnuklider med olika neutronkvoter) tillsammans med J-kroppens massa bestämmer hur och på vilket sätt. Se även utförligt från DIAKVADRATEN.

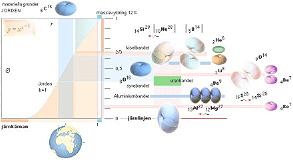
— Illustrationen ovan sammanfattar förloppet i stort från J-kropparnas avdelning i Solserien (Solsystemets Resonansserie) fram till fusionsfasen då kroppen expanderar från sitt maximalt täta tillstånd och blir stjärna, planet, mindre mineralkropp, sandkorn eller molekylärt stoftkorn beroende på samspelet mellan gravitation och elektrisk repulsion. För Solsystemets grundläggande mekanik, se särskilt från PLANETSYSTEMENS GRUNDFORMER och PLANETROTATIONERNAS UPPHOV (undersektion i avsnittet om Galaxbildningen).

— För stjärnorna, se särskilt från STJÄRNFYSIKEN DEL 1.

— Se även i kort illustrerad Översikt av GRUNDÄMNESFÖRDELNING I RELATERAD FYSIK.

Meteoritmaterialens detaljerade ursprung enligt relaterad fysik

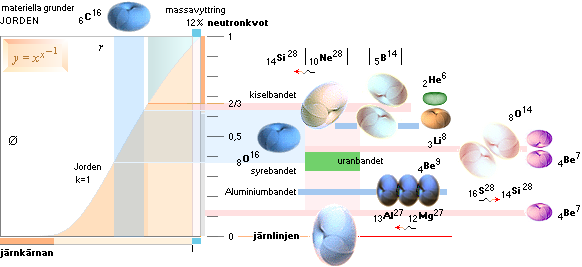
— Grundämnesbildningen i varje avdelad J-kropp beror helt på J-kroppens massa, samt den spridning i neutronkvoten som finns mellan centrum och periferi: neutronkvot NOLL gynnar GRUNDÄMNESBILDNINGENS TVÅ BASGRUPPER som slutar på Järn-Kobolt-Nickel. Neutronkvoter mellan noll och 1 ger alla övriga möjliga grundämnesserier med olika representationer i olika delar.

— Se exempel i Basnuklider med olika neutronkvoter.

— Illustrationerna närmast ovan och nedan associerar till neutronkvoternas olika möjliga mönsterbildningar i form av FUSIONSRINGAR — alltid med Järnet i mitten genom GRUNDÄMNESBILDNINGENS TVÅ BASGRUPPER. Med en stor mängd likartade mönster med givna neutronkvoter i homogena sektioner inom en given J-kropp, kan också förutsättningen bildas för lokalt (isotopiskt) homogena mineralsmältor som senare kan blandas — antingen direkt i det inre av en planet genom senare historia (Se J-kropparnas värmefysik), eller mera dramatiskt kastas ut mellan kropparna om den primära J-kroppens massa inte är tillräckligt stor för att stå emot expansionstrycket från fusionsfasen (J-kroppens expansion). Det senare fallet är tydligen vad vi direkt kan utläsa ur TNED i fallet meteoritmaterialens ursprung: unika, komplicerade, sammansatta mineralstrukturer — som vad vi vet knappast återfinns någon annan stans.

Illustrationen nedan sammanfattar mineralbildningsgrunderna specifikt för meteoriterna — enligt vad som DIREKT kan utläsas KVALITATIVT via TNED.

Mineralbildningsgrunderna specifikt för meteoriterna enligt TNED

	Grundämnesfördelningen
				ARTS & SCIENCES Washington University ETCHED FACE OF THE CANYON DIABLO IRON METEORITE http://eps.wustl.edu/photo-album/canyon_diablo
	Meteoriternas kemi

Figurdelen (a) ovan tydliggör, nedan, meteoritmaterialets speciella ursprungshistoria:

— Alla primära utkastningar från J-kropparna (Se J-KROPPARNAS PRIMÄRMASSOR) bildar mer eller mindre (finfördelat, primärt smält och förångat) mineral som sprids sfärsikt. Genom att alla hastighetsriktningar är representerade finns absolut optimala möjligheter för de utkastade mineralresterna att, i kombination med J-kroppens egenhastighet, bilda resulterande hastighetskomponenter med alla möjliga riktningar.

— Den rent kvalitativa, principiella uppkomsten av omloppskroppar ursprungligen »överallt» i hela Solsystemet i formen av mindre stenkroppar, grus och damm/molekylärt stoft och som uppvisar utpräglade ellipsbanor med hög excentricitet och hög inklination, förklaras därmed principiellt helt utomordentligt via TNED. Från början är det naturligt att föreställa sig att en stor mängd av det korsvis mellan himlakropparna utkastade stoftet och gruset kan tas upp speciellt av de större himlakropparna (Solen, Jupiter och Saturnus); Med tiden utarmas dessa primära stoftområden och en större renhet i strukturen uppkommer naturligt.

J-kroppens expansion i ekliptikan

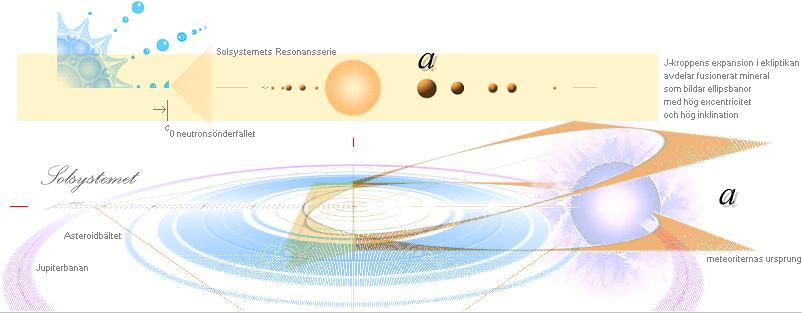
Figuren nedan illustrerar kriterium i största förutsättningarna för MAXIMALT JÄMNT FÖRDELAD OMLOPPSCIRKULÄR materialspridning mellan planetkropparna:

— Materialutkastningar direkt mellan planetkropparna bildar Kollisioner som gynnar minsta möjliga spridning (minskning eller ökning) från den egna J-kroppens idealt cirkulära omloppsbana; Kollisionsmaterialet (mellan himlakropparna) kan därmed bilda motsvarande idealt cirkulära omloppsbanor med lägre (utanför J-kroppens egenbana) eller högre (innanför) banhastighet. Med denna option, tillsammans med de primära utkastningarna som ovan, kan (höger nedan) den ursprungliga stoftkroppen kring Solen förstås bildas; Planeterna och de större asteroidkropparna i mitten tillsammans med det utspridda materialstoftet som en roterande skiva.

Huvudstråken i Ekliptikan

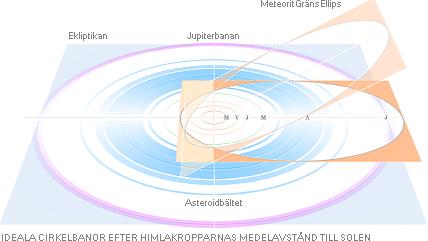
Asteroidbältets ursprung i TNED

Ovan höger i genomskärning genom ekliptikan: Den moderna akademins Primära SolMaterialNebulosa — som ingen kan härleda på den moderna akademins lärostol — därför att den matematiken alltid har varit reserverad för TNED. Det är i varje den närmast framträdande bilden av sammanhanget.

Höga banexcentriciteter

Asteroidkropparnas banmässiga mångfald

— Övriga LOKALER — utkastningar mellan kropparna mera i linje med deras omloppsriktning, figuren ovan vänster (sett ovanifrån ekliptikan) — genererar HÖGA EXCENTRICITETER både framåt och bakåt, både i ekliptikans plan och över/under detta.

— Med TIDENS INFLYTANDE från de största kropparna (Solen-Jupiter) uttunnas systemet, och endast en övergripande resonans återstår: vårt nuvarande Solsystem med de fortfarande många diversifierade mindre materialkropparnas (idealt) elliptiska Solära omlopp. Illustrationen nedan med Solsystemet avgränsat av Jupiterbanan.

— NEDAN: Från Solen och utåt: MVJMAJ: MerkuriusVenusJordenMarsAsteroidernaJupiter.

— Det finns här veterligt inga egentliga frågetecken i ovanstående översiktliga genomgång: alla allmänt kända, observerade och omnämnda kvaliteter beskrivs och förklaras på grundläggande ytterst enkla (elektro-) mekaniska grunder.

De främsta egenskaperna:

· meteoritmineralens RINGA totalmassa (ca 4% av Månmassan [Citat Wikipedia Asteroid belt])

· meteoritmineralens unika mineralogiska sammansättning (Meteoriternas unika kemi)

· meteoritmineralens ursprungligt många olika och diversifierade omloppsbanor kring Solen:
hög excentricitet (påtaglig ovalitet), hög inklination (lutning rel. ekl.), i princip i godtyckliga sfäriska snitt runt Solen [Tabelldata]

———————————— ‡

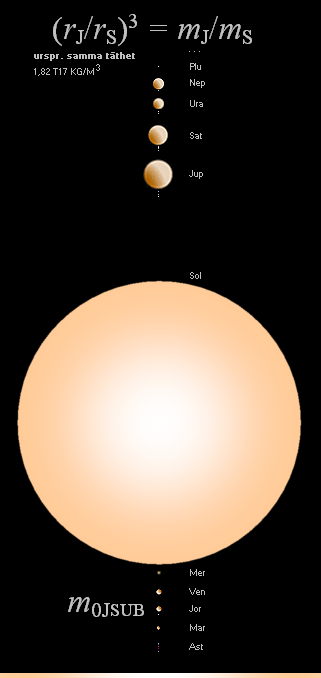
J-kropp: benämningen ursprungligen i UniversumsHistoria dels från himlakropparnas allmänna koppling till impulsmomentet (J=mvr), även i kärnfysikalisk mening (Plancks konstant J=h=mcr), och dels med referens till den totalt sammanfattande matematik som hela K-cellens värmefysik grundas på, se Jordens 5 Ekvationer. En »J-kropp» blir (således) i TNED absolut primära masskroppen baserad på det absolut primärt högtäta neutronkallplasmat med tätheten 1,82 T17 KG/M³.

———————————— ‡

”the belt's low combined mass, which is only about 4% of the mass of the Earth's Moon”, @INTERNET Wikipedia Asteroid belt, Origin [2012-02-06]

———————————— ‡

Allmänna uppgifter på Asteroidbältets spridning i omloppsbanor med olika banexcentricitet (e) och banlutning (i) relativt Jordbanplanet (inklination, relativt ekliptikan) framgår bl.a. i webbkällorna (Wikipedia, Asteroid belt, Origin, Orbits)

@INTERNET Wikipedia Asteroid belt [2012-02-12]

http://en.wikipedia.org/wiki/Asteroid_belt

och, speciellt uppgifter om omloppsbanor med hög inklination (samt med retrograd rotation, motsatt riktad planeternas rotation kring Solen),

@INTERNET Wikipedia List of notable asteroids, Retrograde and highly inclined [2012-02-12]

http://en.wikipedia.org/wiki/List_of_notable_asteroids

Ursprung 92

För planeternas del: Man har i MAC i stora och enkla drag utvecklat en katastrofteori som bygger på kolliderande kroppar som byggs upp till större under inflytande av den centralt sammandragande gravitationen — tillsammans med en central värmekälla som agent för olika primära mineralbildningar.

Meteoriternas ursprung anses vara Solnebulosan — inte »gammalt material från exploderade utbrunna stjärnor».

— Se utförlig MAC-beskrivning av meteoritursprunget i

Meteorites and their properties — II. THE ORIGIN OF METEORITES — David A. Kring, 1998

http://www.lpi.usra.edu/science/kring/epo_web/meteorites/origin.html

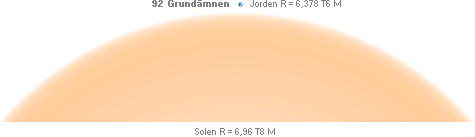
Solen-Jorden: BILDEN ovan som visar proportionerna i det lilla Jordstråket i förhållande till den stora Solkroppen och hur den smala omloppsremsan anställs på en mineralsammansättning med Jordkroppens observerade totalt 92 grundämnen.

— OM 92 grundämnen finns samlade på den smala Jordbanan och dess omlopp kring den ursprungliga Solnebulosans centralkropp [Solen], förefaller det svårt att tänka sig att inte samma fördelning, utomordentliga koncentration och spridning också bör finnas generellt i omloppsbanorna för alla andra bildade planetkroppar.

— Men så är inte fallet. Månytan som närmaste exempel [‡] har delvis helt annorlunda proportioner i mineralsammansättningen än Jordytan. Går vi sedan till meteoriternas ursprung, området mellan Mars och Jupiter, är situationen ännu mera differentierad [‡]. Det är ett av de typiska [omöjliga] problem som visar sig i den moderna akademins teori om Solsystemets uppkomst som grundat på nebularhypotesen och dess svårigheter att förklara nuvarande praktik.

— Jämför Grundämnesbildningen med Grundämnesfördelningen i TNED: direkt kroppslokal mineralkemi — med Järnet i centrum från start.

Grundämnesfördelningen i relaterad fysik, översikt

Se även i Meteoriternas kemi

Grundämnesfördelningen i relaterad fysik, kort översikt

Angående frågan om en likformigt fördelad isotopsammansättning i alla himlakroppar: Det finns ingenting som direkt motsäger det. Men det finns heller ingenting som direkt utsäger det: Varje himlakropp enligt TNED utvecklar Jordlokalens grundämnessammansättning [k=1] med alla ingående isotopa sammansättningar och fördelningar, men i olika proportioner [k≠1]: alla himlakroppar uppvisar samma inbördes isotopa fördelning i de olika grundämnena.

— Vi kan SE det direkt via Diakvadraten [förminskad i utdraget nedan överst] genom att projicera de olika nuklidbildningsstråken, analysen från neutronkvoterna separat, på de olika kropparnas k-värden.

— EMELLERTID: Eftersom det, här [ännu Feb2012] veterligt, inte finns någon direkt algoritm som visat ATT ett visst grundämnes bildning i Jordlokalen som preferens [se utförligt från Fusionsringarna] strängt genomlöper »grundämnets alla möjliga isotoper» finns [ännu] heller inget säkert sätt att framhålla någon »allmän grundämnesfördelningssats» av ovan antydda art. Vi kan misstänka det, enligt TNED, och också räkna med det, men [såvitt här känt] inte bevisa det.

Ovan: Grundämnesfördelningen enligt TNED bestäms av himlakroppens nuklidseparationskoefficient [k], för Jorden lika med 1, tillsammans med neutronkvoterna. Nedan: Olika k-värden resulterar i olika nuklidfördelningar.

Trots att TNED genom den väl relaterbara GRUNDÄMNESFÖRDELNINGEN, specifik för varje individuell materiekropp i kosmos, besitter utomordentliga förutsättningar för att förklara i detalj grundämnesfördelningens principiella karaktär, ända ner till varje enskilt stoftkorn, finns ändå ingen PRIMÄR naturvetenskapligt grundad befogenhet att GENERALISERA istopfördelning eller annan fördelning — inte inom himlakropparna, inte inbördes mellan dem. — Enda undantaget från den regeln är den centrala förekomsten av Järn, garanterat av nuklidbildningens två basgrupper. Men denna del är speciell just för nukliderna omkring Järntoppen (Järn, Kobolt, Nickel) och berör inga andra nuklidintervall. — Den enda tydliga allmänna resultatredovisning som TNED uppvisar, utan vidare djupanalys, är den rent uppenbart kvalitativa, omisskänneliga, individuella mineralkemi som varje himlakropp tvunget får enligt grundämnesbildningen i TNED, vidstående förminskade illustrationer i utdrag. ENBART i kraft av resultatformen i Grundämnesfördelningen — väl relaterbar genom neutronkvoterna och nuklidseparationerna, specifika för varje individuell himlakropp — framgår klart och tydligt i relaterad mening, TNED, att inga som helst antaganden, övergripande approximationer eller andra avgörande förenklingar varken kan eller får göras GENERELLT om isotopfördelningar, inte inom enskilda kroppar, och inte i jämförande mening inbördes mellan olika kroppar. Även om vi kan misstänka att vissa (generaliserade) likheter framträder i grundämnesbildningens olika isotopfördelningar, finns likväl ingen som helst FÖREGIVEN — utan analytiskt berättigad resultatgrund — naturvetenskaplig grund för dylika utsvävningar. — Det som, utan vidare fördjupad analys, enbart i kraft av resultaten i Diakvadraten (nuklidseparationerna vid himlakroppsbildningarna) framgår tydligt och klart via TNED, är ATT varje himlakropp HAR — erhåller — en specifikt utpräglad INDIVIDUELL mineralkemi. — Därmed är varje isotopisk materialgeneralisering utesluten: Det finns i relaterad mening ingen generaliserad primär kosmisk materialrymd, en slags materialgryta ur vars rymd varje himlakropp skulle ha hämtat sin del. Varje himlakropp är bokstavligt talat, relaterad mening, också unik.

Meteoriternas ursprung — Lokalerna som anställer meteoriternas ursprungliga ellipsbanor

Meteoriternas Ursprung

— Viss basinformation om meteoridernas banor finns (Jan2012) på Wikipedia Meteoride,

”From these trajectory measurements, meteoroids have been found to have many different orbits, some clustering in streams (see Meteor showers) often associated with a parent comet, others apparently sporadic.”.

Mera ingående (men inte uttömmande) data på möjliga meteoridbanor finns också i webbkällan NASA’s Cosmos.

— Ellipsbanorna (Se utförlig grundmatematik i Ekvationstablå för Ellipsbanor) blir maximalt smala (lilla excentricitetstalet nära ±1 [minus=lodrätt fall, +=Parabel, återkommer aldrig]) om banobjektet har liten utgångshastighet i banänden, t.ex. räknat från största avståndet från Solen (där meteoriderna antas komma ifrån via asteroidbältet på ca 2,77AU från Solen, 1AstronomicUnit=1AU=1,496 T11 M)

e = 1 – A(v/D)² S²/M, D_SOL = √Gm₂S²/M = 1,1518 T10 M ;

A ApoFocus, som längst bort från Solen

v kroppens hastighet rätvinkligt avståndet A mellan kroppen och Solen:

v = 17,892515 KM/S för exakt cirkulär bana e=0_CRL vid 2,77AU, A(v/D)² S²/M=1; D²/A M/S²=v²

idealt, frånsett inflytande från andra kroppar

— Sambandsformerna ovan innebär att så snart en kropp i Asteroidbältet (genom [katastrofteori] »stöt/kollision med någon annan kropp» eller [mindre elakt] genom lämplig attraktion från någon närliggande planet eller större kropp innanför/utanför bältet, alltså närmast innanför via Mars eller Jupiter utanför) avviker från Asteroidbältets idealt cirkulära gemensamma v ~ 17,9 KM/S, den kroppen också kommer att uppvisa en mer eller mindre utpräglad ellips, allt mera avsmalnad (och därmed allt närmare Solen i PeriFocus) ju häftigare v-formen dämpas.

— Eftersom vi ALDRIG SÄKERT kan veta vilken ellipsbana en viss meteorit haft i sin primära historia [‡], kan vi följaktligen heller ALDRIG SÄKERT VETA huruvida DEN meteoritens historia haft någon del i omloppsbanor NÄRA Merkuriusbanan 0,39AU, och som i sådana fall (från 0,43AU och mindre) skulle betyda temperaturer vid eller högre än blyets smältpunkt, exempelräkningarna i Alternativ 2.

Illustrationen nedan klargör gränserna för vilka ellipsbanor som kan komma i fråga som tilltänkta meteoritobjekt.

Kalkylkort med grundsamband för ellipsbanor [METEORIDELLIPSER] som använts för utvecklingarna i detta dokument finns sammanställt i [[Tabell2KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]].

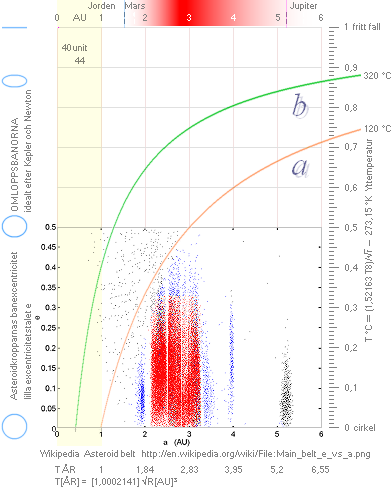
Meteoritgränserna — Gränskurvorna som bestämmer meteoriternas ursprungliga banellipser

Meteoritellipsernas absoluta gräns bestäms av a-kurvan IDEALA ELLIPSBANOR ENLIGT KEPLER OCH NEWTON — Alla banformer under a-kurvan är uteslutna för Jordens del. Vidstående illustration nederst från Wikipedia Asteroid Belt [2012-02-06] visar Asteroidbältets kroppar (prickarna i grått, blått, rött och svart) med horisontalskalan i avståndsenheter AU [a] från Solen (a=0) och vertikalskalan i banans excentricitet (e=√1–[a/b]², ab här ellipsens lill-storaxel, a/b=E). Med kännedom om största avståndet från Solen (Ah, Apohelium) och minsta avståndet (Ph, Perihelium) bestäms omloppsbanans excentricitet (e) idealt från Kepler och Newton som ovan [‡] enligt y(e) = √ 1 – x(Ah)Ph[2/(x(Ah)+Ph)]^2 a-kurvan (yttemperatur 120°C vid Ph) framträder med Ph=1 och b-kurvan (yttemperatur 320°C vid Ph) med Ph=0,43, vilket markerar absolut lägsta gränsformen för blysmälta. Se även ellipsexemplen ovan i NASA-illustrationen. 1AU = medelavståndet Jorden-Solen=1,496 T11 M

a = √AhPh; Vi härleder ellipsformen för a från grundformen [‡] R²=a²+c² med c = R– Ph = √R²–a² ; (R– Ph)² =R²–2RPh+Ph² = R²–a² ; –2RPh+Ph² = –a² ; a² = 2RPh–Ph² = Ph(2R–Ph) = PhAh.

Från ELLIPSEN y=√r²–(x/E)² med y=c och xMAX=a och r=R.

Excentriciteten [e] kan bestämmas enligt

a = √AhPh ;

a/b = (√AhPh)/[(Ah+Ph)/2] = E = √1–e² ;

e = 1 – [2(√AhPh)/(Ah+Ph)]² = [1/(Ah+Ph)]√ [(Ah+Ph)² – AhPh[2]² = Ah²+Ph² + 2AhPh – 4AhPh = Ah²+Ph² – 2AhPh = (Ah–Ph)²] = (Ah–Ph)/(Ah+Ph)

OM speciellt Järnmeteoriterna skulle komma från centraldelen i Asteroidbältet, på ca 2,8 AU från Solen, ser vi direkt att den ideala Keplerska omloppsbanan måste ha relativt hög excentricitet, från allra minst 0,45.

Ovanstående undersökning baseras HELT på ideala ellipsbanor enligt Kepler och Newton — i det praktiska fallet KAN väsentliga avvikelser förekomma beroende på EVENTUELL inverkan från närliggande kroppar, och inget direkt enkelt sätt finns att härleda dessa.

— Med idealformens förbehåll är det — då — tydligt att alla ellipsbanor under a-kurvan är uteslutna: a-kurvan bildar gränsen för att meteoriten överhuvudtaget ska nå fram till Jorden. Meteoritens yttemperatur närmast Solen blir i a-fallets ellipser ca 120 °C. Alla ellipsbanor som ligger över a-kurvan kommer att betyda högre yttemperatur för meteoriten då den befinner sig närmast Solen. b-kurvan ger gränsen för meteoriter på minsta näravståndet 0,43AU från Solen där Placktemperaturen är ca 320 °C.

— Det anmärkningsvärda är som vi ser, i varje fall med referens till Asteroidbältets medelavstånd ca 2,5AU, att alla potentiella meteoritellipser tvunget måsta få HÖGA EXCENTRICITETSVÄRDEN — från 0,5 och uppåt, betydligt större än den begränsade Wikipediagrafen inrymmer.

— Varifrån KOM meteoriterna? OM vi skulle ens FÖRSÖKA »bestämma» vilken eller vilka möjliga ellipsindivider som HAR förekommit ur den MÖJLIGA samlingen banformer ÖVER a-kurvan, finns i varje fall HÄR ingen som helst preferens eller ens en vink om vad som gäller. I princip alla fall kan komma ifråga — speciellt i de regioner som NU är MINST befolkade av omloppskroppar — eftersom områdena I TIDENS LÄNGD utarmas på banindivider i takt med att bankropparna förenas med typ Jorden och andra.

Varifrån kom meteoriterna?

Varifrån kom meteoriterna?

Observera att ingenting här är känt om någon enda meteorits ursprungsbana — inte med någon som helst säkerhet.

— Vi studerar endast de teoretiskt möjliga ursprungen enligt TNED.

EKLIPTIKANS PLAN genomskärs av en skur av meteoridiska omloppsbanor, alla med höga banexcentriciteter och godtyckliga inklinationer.

Kalkylkort med grundsamband för ellipsbanor [METEORIDELLIPSER] som använts för utvecklingarna i detta dokument finns sammanställt i [[Tabell2KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]].

Ett sätt för en tänkt ursprunglig meteoritkropps bana kring Solen att fungera — utan att krascha mot någon annan kropp efter första eller andra varvet i det relativt [mest] tättbefolkade Asteroidbältet — är om ellipsbanan uppvisar någon lutning relativt det övriga nära plana interplanetariska planetekliptiska planet. Därigenom garanteras en optimalt fri väg, motsvarande en maximalt långvarig banform som kan fortsätta ostört tills bankroppen förenas med någon av planeterna. Med tiden försvinner alla sådana ursprung.

— Teorin på området i det allmänt SYNLIGT tillgängliga webbutbudet verkar dock vara i smalaste laget: inget upphittat.

— Inklinationsuppgifter på Asteroidbältets kroppar finns sammanställda i värdegrafiska diagram på @INTERNET Wikipedia Asteroid Belt samt i NASA-länken nedan [‡] — dock utan direkta illustrationer typ ovan: alla möjliga banlutningar [Wikipedia] tycks vara representerade.

— Blotta uppkomsten för en sådan bantyp enligt den moderna akademins planetesimalteori är dock här veterligt [betydligt] mera problematisk än i TNED [se efterföljande illustration].

— En viss orientering i MAC-teorin ges i PDF-dokumentet

Earth Planets Space — ORIGIN OF HIGH ORBITAL ECCENTRICITY AND INCLINATION OF ASTEROIDS, Nagasawa et al., 2001

http://www.terrapub.co.jp/journals/EPS/pdf/2001/5311/53111085.pdf

”The origin of high eccentricity and especially that of inclination have not been well understood yet.”, s1085 [intro],

”Because collisions are a dissipative process, they damp the eccentricities and inclinations rather than excite them, on average.”, s1086sp2m

Termen ’sweeping secular resonances’ används av författarna i koppling till huvudteorin för Solnebulosans utveckling — skivmassans successiva utarmning på massa inifrån och ut med planetbildningarna, vilket skulle kunna bilda tillräckliga moment för att ’pumpa upp excentriciteter och inklinationer’ [s1087sp1ö],

”In order to pump up orbital inclination, the nebula must be depleted non-uniformly, e.g., from inside to outside. We found that random velocities are pumped up high enough to be comparable to the observed magnitude in the entire asteroid belt if the nebula edge migrates from 5 AU to 10 AU on a timescale longer than 5×10⁵ years in the case of the inside-out depletion of nebula.”, 1090sp2mö

Nagasawa-gruppens undersökning och simulering omfattar en stor mängd tidigare teoretisk forskning med många omnämnda bidragsgivare. Författarna beskriver själva hela teorins akilleshäl:

”The deficiency of total mass in the asteroid belt is still unsolved problem in our mechanism of sweeping secular resonances. Although a timing of erosion is not matter in our model, the mass depletion problem must be solved consistently with observed properties of taxonomic asteroidal families.”, s1090sp2n.

— Ett av MAC-Solnebulosateorins stora problem är just Asteroidbältets RINGA totala massa, bara bråkdelar av vår Månmassa, totalt: ”the belt's low combined mass, which is only about 4% of the mass of the Earth's Moon”, @INTERNET Wikipedia Asteroid belt, Origin [2012-02-06].

— Jämför [den nästan oförskämt enkla] lösningen enligt TNED i J-kroppens expansion i Ekliptikan.

NASAs Cosmos Meteorite orbits, webbkällan nedan, ger uppgifter på ”beräknade banor för 5 meteoriter” — inklinationsuppgifter saknas, men ellipserna visas utritade [jämför a-gränskurvan i Meteoritgränserna],

ASTEROIDS AND METEORITES — författarportal och datum saknas [http://ase.tufts.edu/cosmos/ leder till NASA’s Cosmos, R. Lang, 2010]

http://ase.tufts.edu/cosmos/print_images.asp?id=15

MBJ

Kvalitativt allmänna kraftfunktioner med

Värdkroppens potentiella förmåga att generera METEORITISKA BANELLIPSER

[mellan sig själv och Solen, men även andra]

MED HÖG INKLINATION OCH HÖG EXCENTRICITET

MÖJLIGA METEORIDISKA BANELLIPSBILDNINGAR genom J-kropparnas expansion efter fusionsfasen

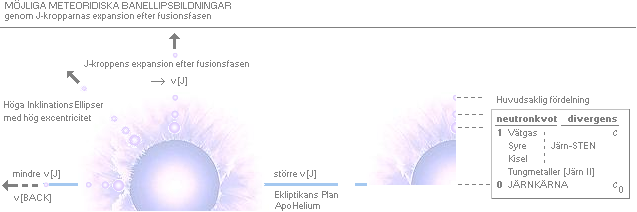
Figuren ovan: J-kropparnas expansion i Ekliptikans plan kan i samband med utloppet vid Resonansserien för Solsystemet och dess kroppar i K-cellens expansion omöjligen undkomma en principiell materialutkastning, speciellt i här beskrivande exempel för frågan om de intrikata asteroid- och meteoridbanornas del i J-kroppens backriktning: banplan som i vissa fall står rätvinkligt ekliptikan (—|—), samt i övrigt alla grader emellan.

— Då J-kroppen initiellt har en nära helt cirkulär banform (e=0) via en bestämd tangentiell omloppshastighet [v(J)], betyder varje reduktion av v(J) en motsvarande banellips med ett e-värde större än noll. Motverkas v(J) helt, blir e=1, motsvarande fritt fall mot Solen. Motverkas v(J) med större belopp än sitt eget, bildas motsvarande retrograda ellipser (kropparna roterar motsatt Värdkroppen kring Solen).

— Genom att också J-kroppens utkastade material avdelas uppåt/neråt, med alla mellanliggande grader, kan på motsvarande sätt ellipser bildas obehindrat med omloppskroppar av nära försumbar massa (in till sandkornet enligt TNED), och vilkas banplan med andra ord avsevärt skiljer sig från Ekliptikans plan.

— Alla ordinära omloppskroppar i ekliptikans plan kan bilda dessa över/under-ellipsplan, befolkade av de mindre massor och mineral som är observerade i Asteroidbältet.

— Grundämnesfördelningen ovan höger är här schematiskt sammanfattad (gäller initiellt för alla sfäriska J-kroppar, men med olika magnituder beroende på J-kroppens primärmassa och placering [g-potentialens inverkan]). Se den mera detaljerade grafbilden som ges från Diakvadraten med neutronkvoterna.

MBG

Idealt LINJÄRA kraftfunktioner med

Värdkroppens potentiella förmåga att BROMSA ANDRA KROPPAR

mellan sig själv och Solen

TILL SIN EGEN OMLOPPSHASTIGHET

MÖJLIGA METEORIDISKA BANELLIPSBILDNINGAR innanför givna Värdkroppar VIA Gravitationen

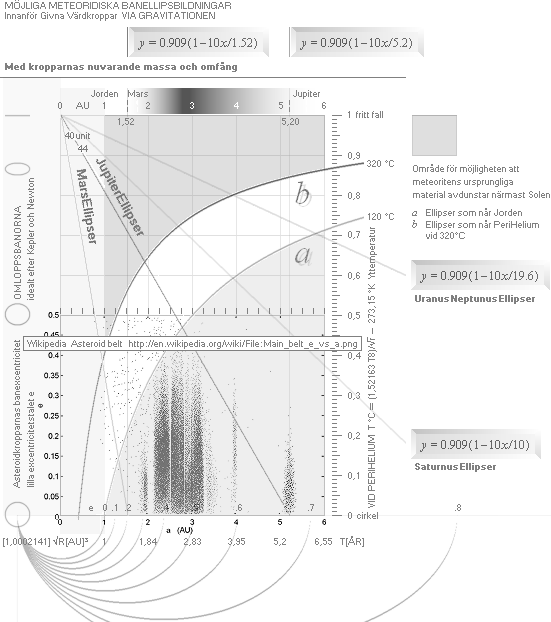
Figurer och grafer ovan med utvidgning från excentricitetsillustrationen i @INTERNET Wikipedia Asteroid belt: Om Värdkroppen (Planeten) idealt på medelavståndet R från Solen (idealt cirkulära omloppsbanor) tillåts utöva sin attraherande gravitationskraft på en godtycklig kropp mellan sig själv och Solen (utan hänsyn till tidsaspekten), kommer den resulterande elliptiska banformens excentricitet (e) att bestämmas av, som mest, Värdkroppens hastighet [v(J)] och största avståndet från Solen (ApoHelium [Ah]), vilket ger den helt enkla funktionen e=1–Ah/R.

— Funktionen avbildar en helt rät linje som slutar på e=0 för samtliga fall. Illustrationen ovan visar e-grafer för respektive Värdkroppar Mars, Jupiter Saturnus och Uranus-Neptunus, här benämnda respektive ellipsgrupper Mars|Jupiter|Saturnus|UranusNeptunus-Ellipser.

— I (nuvarande) praktiska fallet blir kurvorna inte räta linjer, utan böjer av nerifrån höger upp mot vänster: Värdkroppen har bara en begränsad förmåga att bromsa kroppar mellan sig själv och Solen — med en principiellt lika stor potential att accelerera från andra hållet, om vi talar om OBEGRÄNSAD TID till förfogande.

— Funktionsformen är emellertid ändå intressant — speciellt för TNED med avseende på himlakropparnas allra första timmar (och dagar) och därmed en mera accentuerad kraftdynamik (den delen saknar här ännu en mera exakt matematisk redovisning).

— Vertikallinjerna till motsvarande räta lutningslinjer [som utgår uppåt från horisontalaxeln] motsvarar de möjliga excentricitetsbildningarnas mera reguljära »funktionskurvor» enligt föregående illustrations [MBJ] mera primärt aktuella alternativ i TNED.

— I praktiken är det — av materialspridningen att döma — möjligen dessa senare som bär huvudansvaret.

Meteoriternas kemi

Meteoriternas unika kemi

Meteoriternas lokala ursprung

— Meteoriternas mineralsammansättning framstår som helt UNIK [‡].

— Man har (här veterligt) inte hittat meteoriternas specifikt mineralsammansatta material varken i, på, eller inom Jordkroppen.

— Det är också vad TNED visar direkt genom GRUNDÄMNESBILDNINGEN.

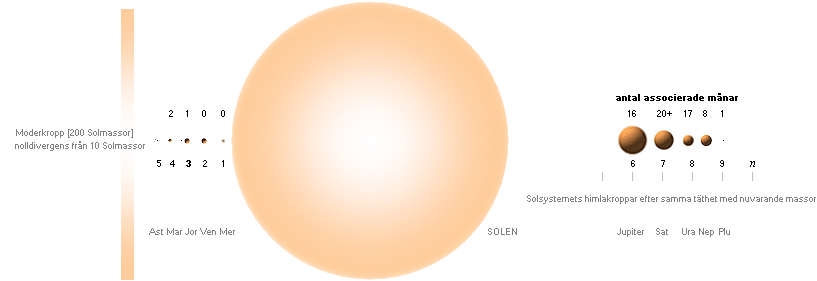
1Merkurius 2Venus 3Jorden/Månen 4Mars 5Asteroidbältet 6Jupiter 7Saturnus 8/9Uranus/Neptunus 9Pluto.

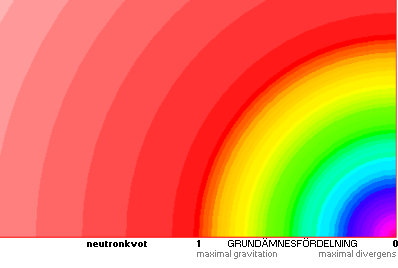
»Spektrumfärgerna» i figuren nedan — Solsystemets kroppar ovan efter samma täthet — illustrerar schematiskt gravitationspotentialens olika kroppszoner. Violett motsvarar områden med lokalt lägsta gravitation, analogt högsta divergens = gravitellt bestämda lokala ljushastigheten. Ett kanske mera enkelt illustrativt sätt är att använda den enkla gråskalan med vitt för toppdivergens.

1Merkurius 2Venus 3Jorden/Månen 4Mars 5Asteroidbältet 6Jupiter 7Saturnus 8.1.2Uranus/Neptunus 9Pluto.

Kropparnas g-fält grovt via färgspektrum — violett svagast g-kraft, störst divergens

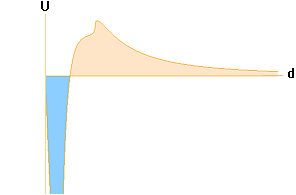
Topparna i de röda gaferna ovan motsvarar ställen där den lokala gravitationen är som lägst, analogt maximal ljushastighet via ljusets gravitella beroende. Mellan himlakropparna (blå grafer) finns analogt också nollgravitationsställen med divergenstoppar. Alla dessa samverkar ENLIGT TNED i den inledande fasen efter divergenständningen — neutronsönderfallet — och som föregår fusionsfasen. Neutronkvoterna avgör fusionsringarnas mönsterbildningar, och därmed den primära grundämnesfördelningen i varje himlakropp, och därmed även mellan himlakropparna.

Varje kropp får genom K-cellens expansion ENLIGT TNED i kraft dels av sin egen massa och dels i samverkan med övriga massor sin alldeles egna speciella unika individuella neutronkvot som föregår fusionsbildning med tillhörande grundämnesbildning enligt TNED i den kroppslokalen. Därmed garanteras att grundämnesbildningen för just den kroppen, eller det området mellan kropparna, blir unik — en specifik kemisk sammansättning för varje specifik lokal:

— Varje Sol, Planet, Måne, Stenblock, Gruskorn, SandKorn och Dammkorn garanteras en alldeles egen, unik KEMISK STRUKTUR: från max materietäthet till färdigbildad material- och mineralkropp inom den tid som divergenständning med efterföljande fusionsfas och primär expansion upptar för varje individuellt lokalt materierum.

Den unika strukturen

”Chondrites are stony meteorites”,

”Prominent among the components present in chondrites are the enigmatic chondrules, millimeter-sized objects that originated as freely floating, molten or partially molten droplets in space”,

Wikipedia Chondrite [2012-01-15]

http://en.wikipedia.org/wiki/Chondrite

”The metals melted in deep space, and were then crystallized in the near absolute-zero, high vacuum void of outer space, resulting in a crystalline structure unlike any found on Earth.”,

”Meteorites often contain minerals not found on Earth.”,

novaspace — METEORITE TYPES AND FACTS

http://www.novaspace.com/METEOR/Types.html

Meteoriternas unika kemi

Meteoriternas kemi

”Today, nearly 300 minerals are found in meteorites with about 40 found exclusively in meteorites.”,

METEORITE MINERALS — James Wittke 2005

http://www4.nau.edu/meteorite/Meteorite/Book-Minerals.html

Ytterligare citatkällor (ett sextiotal Jan2012) finns på webben från exakt sökfras "exclusively in meteorites".

Bly Jordytan-Månytan

—————————————————————————

Pb206/204 Pb207/204 Pb208/204

—————————————————————————

MÅNEN: ~207 ~100 ~226;

JORDEN: ~19,04 ~15,68 ~39,07

—————————————————————————

Datakälla: GoogleBooks, s7

GLOBAL WARMING AND GLOBAL COOLING: EVOLUTION OF CLIMATE ON EARTH — O. G. Sorokhtin, George V. Chilingar, Leonid F. Khilyuk, 2007

Höga Pb206/207 på Månytan (10ggr) jämfört med Jordytan

men svårt att få fram tillförlitliga uppgifter på Bly i Månytan: värdena varierar [kraftigt] med olika lokaler på Månytan

GoogleBooks, s7

GLOBAL WARMING AND GLOBAL COOLING: EVOLUTION OF CLIMATE ON EARTH — O. G. Sorokhtin, George V. Chilingar, Leonid F. Khilyuk, 2007

Översikt i Grundämnesbildningen

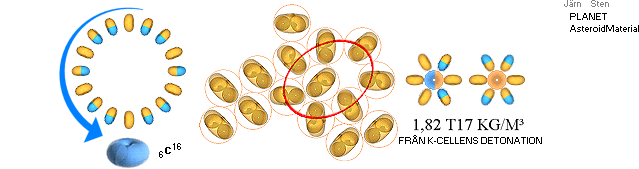
ÖVERSIKT I GRUNDÄMNESBILDNINGEN med Asteroidkropparnas möjliga ursprungliga bildningsplats enligt TNED I VÅRT SOLSYSTEM

— Bilden vänster och bildremsan ovan visar Solsystemets kroppar efter nuvarande massor på samma täthet — i avdelning som neutronkallplasma från en tänkt större [minst 200 Solmassor] moderkropp (underst/till vänster). Illustrationen finns också i huvudillustrationen [längst till höger] i Rekylbilden i avsnittet om Galaxernas ursprung. I TNED initieras grundämnesbildningen tidsanalogt med himlakropparnas avdelning från sin moderkropp i formen av neutronkallplasma [Se utförligt i Allmän delningsklassificering]. — Det sker enligt TNED i analogi med »den enkla vattenfysikens droppbildningsdynamik» [Droppbildningarnas jämförande fysik i närbild]. 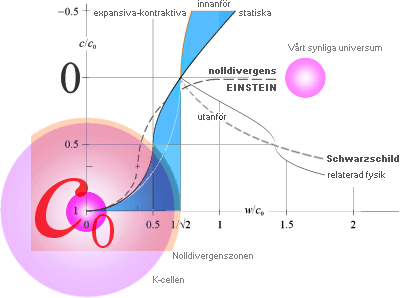Det högtäta neutronkallplasmats detonerande expansion och som uppdelas på mindre småkroppar [Se från Galaxbildningarna] är starkt präglat av ljusets gravitella beroende via en NOLLDIVERGENSZON, stället där c=0. Som expansionerna utvecklas, sveper nolldivergenszonen [med konstant topphastighet c0] över de lokalt avdelade småkropparna och åstadkommer därmed [omedelbar] DIVERGENSTÄNDNING, c större än noll. Därmed inträder NEUTRONENS SÖNDERFALL, som leder till den egentliga grundämnesbildningen i TNED, och därmed GARANTERAT kroppsindividuell mineralkemi — ända ner till sandkornets nivå. — Genom att varje kropps egenmassa tillsammans med omgivande kroppar bestämmer olika gravitationsgradienter, i kropparna och mellan dessa, bildas olika förutsättningar för NEUTRONKVOTERNA föregående fusionerna mellan de tätt liggande neutronerna-vätekärnorna. — Därmed ges också motsvarande spridning i grundämnesfördelningen, inom och mellan de olika kropparna. En allmän, kortare översikt i grundämnesbildningen enligt TNED ges här i Översikt.

GRÄNSMASSAN FÖR NOLLDIVERGENS I YTAN med neutronkallplasmats maximala täthet 1,82 T17 KG/M³ är enligt TNED ca 10 Solmassor [‡]. Moderkroppen till vårt Solsystem skulle enligt ALLMÄN DELNINGSKLASSIFICERING ha varit grovt sett runt [minst] 200 Solmassor. Med den bilden, och den höga utkastningshastighet som den utkastade strängen av J-kroppar Solens resonansserie måste ha, är det tydligt att divergenständningen, tillfället då Solsystemets kroppar kommer in i positiv divergens, analogt aktiv makroskopisk elektromagnetism, i princip blir omedelbar för hela J-serien.

———————— ‡

SAMBANDET FÖR LJUSHASTIGHETENS GRAVITELLA BEROENDE [[Tabell3KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]] [Se även jämförande utvecklingar i SVARTA HÅL FINNS INTE I RELATERAD FYSIK]

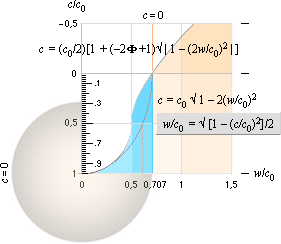
c/c₀ = (1/2)(1 ± √ | 1 – 4w²/c₀² | ) ........................ med w = r√ 4pGρ/3 innanför och w = √ Gm₂/r utanför, ρ tätheten i KG/M³

räknat från den idealt sfäriska kroppsranden ger för r[c=0]

r_c0 = 2Gm₂/c₀² = m₂(1,48427 t27 M/KG)

= c₀/√8πGρ/3

som efter utvecklingarna ger

m₂ = ρ^–1/2(769/90 T39)(KG/M)^3/2 ; Med neutronkallplasmats täthet ρ=1,82 T17 KG/M³ ges

= 2,00284 T31 KG ; Med Solmassan 1,989 T30 KG blir m2 via r[c0] med ρ=1,82 T17 KG/M³ lika med 10,069626 Solmassor.

Utvecklingen för flykthastigheten:

m₂/r_c0 = [ρ^–1/2(769/90 T39)(KG/M)^3/2]/[c₀/√8πGρ/3]

= [ρ^–1/2(c₀/√G)³(√ 3/32π)]/[c₀/√8πGρ/3]

= [(769/90 T39)(KG/M)^3/2][√8πG/3]/c₀ ;

Flykthastigheten för samtliga neutronkallplasmakroppar som uppvisar nolldivergens vid kroppsranden:

v = √ 2Gm₂/r_c0 ; R=(3m₂/4πρ)^1/3 ; m₂/R = m₂(3m₂/4πρ)^–1/3 = m₂^2/3(3/4πρ)^–1/3 ; v = √ 2Gm₂^2/3(3/4πρ)^–1/3 = m₂^1/3√ 2G(3/4πρ)^–1/3 = m₂^1/3(0,0110392), ρ=1,82 T17 KG/M³

= √ 2G[(c₀/√G)³(√ 3/32π)][√8πG/3]/c₀

= √ 2G[c₀³G^–3/2(√ 3/32π)][√8πG/3]/c₀

= √ 2[c₀³(√ 3/32π)][√8π/3]/c₀

= c₀√ 2[(√ 3/32π)][√8π/3]

= c₀√ 2[(√ 8/32)]

= c₀√ 2[(√ 1/4)]

= c₀

Jämför även hastighetsvärdena från K-cellens detonation i DIVERGENSENS EXPANSIVA G-BEROENDE, EXPANSIONSSAMBANDET, Zonskärningarna, Zonbarriärernas hastighet.

— Se även Beviset för Multipla c i DEN KOSMISKA PARTIKELSTRÅLNINGEN — exakt samma samband som det konventionella, men helt annan teori.

Impulsmoment i gravitella system

Impulsmoment i gravitella system

Många

[min högst personliga och bekväma, helt ovetenskapligt grundade omskrivning av de främsta man möter i resultatlistan efter en googlesökning]

webbkällor som beskriver TYP Solsystemets Ursprung brukar börja beskrivningen (ofta illustrerad) med påstående om »impulsmomentets bevarande»:

Wikipedia, urmaterialet

”Because of the conservation of angular momentum, the nebula spun faster as it collapsed. As the material within the nebula condensed, the atoms within it began to collide with increasing frequency, converting their kinetic energy into heat. The centre, where most of the mass collected, became increasingly hotter than the surrounding disc.[10] Over about 100,000 years,[9] the competing forces of gravity, gas pressure, magnetic fields, and rotation caused the contracting nebula to flatten into a spinning protoplanetary disc with a diameter of ~200 AU[10] and form a hot, dense protostar (a star in which hydrogen fusion has not yet begun) at the centre.[20]”,

;

”At this point in its evolution, the Sun is believed to have been a T Tauri star.[21] Studies of T Tauri stars show that they are often accompanied by discs of pre-planetary matter with masses of 0.001–0.1 solar masses.[22] These discs extend to several hundred AU—the Hubble Space Telescope has observed protoplanetary discs of up to 1000 AU in diameter in star-forming regions such as the Orion Nebula[23]—and are rather cool, reaching only one thousand Kelvin at their hottest.[24]”,

Wikipedia, Formation and evolution of the Solar System, Formation [2012-01-19]

http://en.wikipedia.org/wiki/Formation_and_evolution_of_the_Solar_System

”Our theory for the origin of the Solar System is a very old one with some modern innovations called the Nebular Hypothesis. A crucial ingredient in the nebular hypothesis is the conservation of angular momentum.”,

Astronomy 161 The Solar System — CONSERVATION OF ANGULAR MOMENTUM — webbkällan verkar inte ha någon angiven författarreferens eller datum

http://csep10.phys.utk.edu/astr161/lect/solarsys/angmom.html

;

”It is unlikely that such a nebula would be created with no angular momentum, so it is probably initially spinning slowly. Because of conservation of angular momentum, the cloud spins faster as it contracts.”,

Astronomy 161 The Solar System — THE ORIGIN OF THE SOLAR SYSTEM — webbkällan verkar inte ha någon angiven författarreferens eller datum

http://csep10.phys.utk.edu/astr161/lect/solarsys/nebular.html

Se även om Protoplanets i

Nine Planets — APPENDIX 4: THE ORIGIN OF THE SOLAR SYSTEM — F. Crary, CU Boulder, 1994-2011

http://nineplanets.org/origin.html

Se även med en viss självpåtagen självkritik — VI KANSKE HAR FEL:

About.com SPACE ASTRONOMY — THE ORIGIN OF OUR SOLAR SYSTEM — John P. Millis, datumuppgift saknas [som ofta är fallet i amerikanska original]

http://space.about.com/od/solarsystem/a/Origins_of_the_Solar_System.htm

— I korthet: Stoftmolnets rotation ökar inåt via stoftmolnets konstanta massa m via idealt konstant impulsmoment J=mvr allteftersom stoftpartiklarna sammandras av den centrala gravitationen och deras avtagande r ersätts av växande v med konstant J/m — med följd i att den inre centraldelen till slut roterar så snabbt att den börjar plattas ut till en skiva med mindre täthet längre ut och större inåt … och som planeterna har bildats av, med Solen i mitten.

Under förutsättning att det roterande stoftmolnets stoftpartiklar i princip är oändligt små, så att de aldrig någonsin vidrör varandra under stoftmolnets gravitella sammandragning, är beskrivningssättet i (typ) ovanstående webbkällor korrekt: ju mer stoftpartiklarna samlas till en central massform med växande täthet relativt det utspridda stoftets material, desto snabbare roterar centralmassan.

— Men »urmaterialet till Solnebulosan» är verkligen ingalunda någon enkel detalj i MAC:

CREATION—DetAvgörandeMACproblemet

Det STORA problemet i MAC är (nämligen) det här:

— Man har bara EN grundteori om Stjärnornas/Solens/Solsystemets bildning: utspridd vätgas (urmaterialet från Big Bang) som sammandras gravitellt till högtäta maskincentra av fusionspumpande stjärnor (Origin of the Elements, LBL 2000).

Problemet:

— Vart man än tittar i kosmos rymder hittar man bara REDAN FÄRDIGBILDADE stjärncentra; aktiva eller inaktiva stjärnrester med omgivande material i form av gas, stoft, och planeter;

BILDKÄLLA: Samma som i ingressen.

— Heta centra med omgivningar liknande, eller påminnande om, vårt eget (kära) Solsystem: mer eller mindre miniatyriserade Saturnus System, med eller utan Centralbelysning. Speciellt omnämns de s.k. T Tauristjärnorna med ”often accompanied by discs of pre-planetary matter” [Urmaterialet, Wikipedia].

— Men: Det finns ingen bild av sammandragande gas, stoft eller generellt material

utan redan befolkat centrum

— Det är det stora problemet i MAC. Se även i Citat.

— Den gas och det stoft som finns, hålls i schack av omgivande stjärnsystem (speciellt i spiralgalaxerna).

— Det som hela MAC-teorin hänger på, själva sammandragandet utan en REDAN existerande Centralkropp, har med andra ord ingen DIREKT verifierbarhet — och det skulle bara behövas — endast — ETT enda unikt exempel.

— Med uppfattningen att sammandragningsteorin likväl gäller har man heller ingen KLAR bild av HUR det TOMRUMMET skulle kunna förklaras (i väntan på att hitta Exemplet). Nämligen beträffande just DETALJERNA som kopplar BILDNINGEN dels av stjärnkroppen som sådan, och dels det omgivande planetmaterialet.

— Kosmos rymder innehåller bara gas och stoftmoln med redan formerade — tydligt detekterbara — stjärncentra.

I TNED finns inte det problemet.

TNED, med början från maximal nuklidtäthet [K-cellens detonation]:

— Gasmassorna i universum härrör enligt TNED från himlakropparnas primärbildning. Se särskilt i GALAXBILDNINGEN. Gasmassorna fungerar som BIHANG — mellanliggande dimbankar, näringsdepåer — till de omgivande himlakropparna, mestadels stjärnorna, och tjänar i de förekommande fallen som NYTT STJÄRNBRÄNSLE. Den lokala stjärnan »nytankar» när den slocknar genom sitt förlorade strålningstryck; När strålningstrycket avtar, tillåts yttre vätgas att strömma in via gravitell kontraktion [Utförligt i STJÄRNFYSIKEN DEL2, se speciellt Brytpunkten vid 10 Solmassor].

— Genom det sålunda redan upptagna strukturkriteriet (Jämför naturanalogierna: HÖLJE-kärna; FRUKT-frö), redan baserat på gravitell balans, finns inget ytterligare utrymme för typ FRILIGGANDE STOFTMOLN SOM SAMMANDRAS GRAVITELLT.

— Gas/stoftmolnen ligger mellan stjärnorna, och stjärnorna utövar ömsesidiga g-krafter på de mellanliggande gasmolnen som garanterar balansen och stabiliteten;

— Det finns med andra ord ENLIGT RELATERAD FYSIK ingen förutsättning för gravitell sammandragning — ANNAN än den som DIKTERAS av att en stjärna förlorar sitt strålningstryck.

— Föreställningen om friliggande stoftmoln i universum som sammandras gravitellt och som förmodas kunna bilda stjärnlokaler särskilt, saknar därför relaterbar förankring i den praktiska fysiken — enligt TNED.

I mera grundläggande mening förklaras saken i TNED — relaterad fysik — mera i detalj i Impulsmomentets bevarande.

———————— ‡

National Laboratory — ORIGIN OF THE ELEMENTS — Aug 9 2000

http://www.lbl.gov/abc/wallchart/chapters/10/0.html

Impulsmomentets bevarande

— med utgångspunkten att alla stjärnor bildas på NÅGON samtidigt existerande rotation, om än aldrig så liten

Tillfälligt vilande vattendroppe på vattenytan: Praktiken visar hur vattendroppen kan RULLA IVÄG PÅ YTAN och upplösas först då den når kärlkanten.

BILDKÄLLA: Författarens arkiv — Drop16iso3200VilaBild139·22Mar2009 · Nikon D90 EXP 1/4000 S

impulsmomentet — stjärnor som uppvisar ett redan existerande impulsmoment har ingen fysikalisk förutsättning för att bildas ur kosmiskt fridrivande stoftmoln

Impulsmomentets bevarande — J=mvr

I TNED, relaterad fysik — och vad vi vet genom samtliga astronomiska observationer — är det ALLTID så: Där man finner ett kosmologiskt observerbart impulsmoment (massrotation, J=mvr) där finner man också någon centralt roterande massform, en central REST från en gammal utbrunnen stjärna, eller någon annan fast himlakropp;

— Impulsmomentet — från energin E=Fd=mad=m(v/T)d=J/T som ger impulsmomentet ET=mvd=J — kan bara finnas där centralkraftsverkan redan finns: en redan existerande centralmassa. Antingen finns den roterande aspekten redan från början i massformen, oskapad likt energin, eller så kan den bildas inom massformen ur kraftverkan (E=Fd=mad), typ spinnet (v/T) som ges till rekylvattendroppar som bildas av en primärdroppe som träffat vattnet. Se särskilt i Den inducerade rotationens uppkomst.

Tillfälligt vilande vattendroppe på vattenytan: Praktiken visar hur vattendroppen kan RULLA IVÄG PÅ YTAN och upplösas först då den når kärlkanten. Med lämplig anordning kan upprepade avrullningar studeras i detalj.

BILDKÄLLA: Författarens arkiv — Drop16iso3200VilaBild218·22Mar2009 · Nikon D90 EXP 1/4000 S

Föreställningen om att stjärnor skulle kunna bildas från typ fritt utspridda stoftmoln, utan någon redan bestämd centralmassa, skulle därmed, och tydligen med ovannämnda enkla förutsättningar, HELT sakna naturvetenskaplig förankring.

Till viss del stämmer den slutsatsen också med vad man redan, öppet, erkänner inom nutidens astronomi [Lada 2005]: man vet inte HUR stjärnor bildas, men har många övertygande exempel på ATT stjärnbildning sker, även NU inom Vintergatan.

— Med samma förutsättningar kan heller inte gamla utbrunna stjärnor ha ’exploderat’ i meningen ’kvarlämna intet’ i den centrala stjärnkroppens ställe. Inte heller det finns, eller ska inte finnas, enligt relaterad fysik; en fast centralmassa återfinns alltid där det finns impulsmoment. Det finns inga undantag — eller ska i varje fall inte finnas, enligt relaterad fysik [Stjärnbildning enligt TNED].

— En gammal, utbrunnen och förbrukad stjärna, lämnar ALLTID en central gravitell massrest (pulsar, vit dvärg, brun dvärg eller motsvarande [konv. neutronstjärna, eller svart hål]) efter sig, en maximalt tät centralrest som bevaras och som inte kan elimineras. Befinner sig den resten i ett väterikt område (nebulosa) kan — enligt TNED — stjärnan nytända genom att den drar till sig det omgivande vätet som blir nytt stjärnbränsle tillsammans med den högtäta centralmassan [konv. »nya stjärnor skapas»]. Finns ingen sådan omgivande stjärnnäring, slutar också centralresten som en kall, död, kosmologisk himlakropp med viss resterande rotation.

— Av den anledningen är varje föreställning om Solsystemets uppkomst ur typ fritt svävande stoftmoln från gamla stjärnrester — eller ska i varje fall enligt TNED, relaterad fysik, vara det — utan observerbar naturvetenskaplig grund. Stjärnor bildas inte så; Stjärnbildning måste utgå ifrån en redan existerande maximalt tät centralkropp: ett frö. I TNED kallas den stjärngrunden för ett Stjärnstäd (fusionerna verkställs periodiskt på städets mantelyta via höga g-tryck). Se särskilt enligt TNED från Stjärnfysiken Del 1, om ej redan bekant.

Varför MAC aldrig kan nå det beskrivningssättet:

ATOMKÄRNANS HÄRLEDNING — Planckringen h=mcr — som innefattar atomkärnans inkompressibilitet och som redan av princip från grunden garanterar en maximal masstäthet för varje materialsammansättning, ingår inte i den moderna akademins lärostol. Det gör inte PLANCKEKVIVALENTERNA heller som i relaterad fysik ersätter, förklarar, innefattar och klargör relativitetsteorins matematiska formelapparat som en PRIMITIV konstruktion i den mänskliga vetenskapshistoriens bok. Se särskilt i Experimentella bekräftelser.

————————— ‡

Allmän utförlig beskrivning av stjärnbildning

STAR FORMATION IN THE GALAXY, AN OBSERVATIONAL OVERVIEW — Charles J. Lada [2005]

http://www.ifa.hawaii.edu/~reipurth/reviews/lada_yukawa.pdf

;

”Despite its spectacular success in explaining the life histories and deaths of stars,

the theory of stellar evolution is incomplete in a very fundamental aspect. It is not

able to account for the origin of stars.”, s2m,

;

”The inability of the theory of stellar evolution to explain star formation likely

points to the inherent complexity of the physical process itself. Consequently con-

struction of a theory of star formation must require a strong foundation of empirical

data or observation.”, s2mn.

————————— ‡

Grundfysiken på området beror av teorin i kärnfysiken — se Atomvikterna för direkt jämförelse mellan TNED och MAC:

Se Materialutkastningens grundform i PULSARERNA: All novabildning sker enligt TNED via den centraltäta centralmassans YTSKIKT via kärnrekyler [Pulsarmatematikens grundform i TNED, även för vanliga stjärnor, se utförligt enligt TNED från Solfysiken]. Det betyder att det inte finns någon härledningsbar mekanism på vars fysik HELA kärnmassan kan typ »explodera». Det som exploderar, kastas ut, är bara ytterdelen i centralmassan [Jämför Krabbnebulosan]. Den inre kärndelen bevaras, garanterat av den primära gravitation som centralmassan bildades på från K-cellens expansion.

Med den »upplysande grundkursen i elementär mekanik» återstår bara K-cellens värmefysik: TNED.

BILDKÄLLA: Författarens arkiv — Kollage Nikon D90 · Excur13.9Jun2011ÄngsblomBild6·Stjärnfält i fri komposition

— Med utgångspunkt från resultaten i Atomkärnans härledning med allmänt jämförande resultatbild i Atomvikterna, utsäger TNED genom den resulterande Stjärnfysiken att Stjärnor, och alla andra kroppar, bildas från ett primärt TÄTT tillstånd. Se från STJÄRNFYSIKEN DEL 1 samt särskilt från K-cellens detonation om ej redan bekant.

— Det betyder, i princip, i varje fall sett från TNED, att hela MAC-teorin i kosmologisk mening var körd redan från första andetaget.

— Genom den enkla iakttagelsen att DÄRFÖR att det finns stjärnor nu, och att stjärnor onekligen förbrukar sin massa i värme och ljus och därför inte kan lysa i evighet, också en urgrund tvunget måste finnas som, likväl, förser de tindrande ljusen med TID TILL HIT — det förflutnas oändlighet bakåt — är huvudfrågan redan avgjord. Evig puls.

Det har ALDRIG funnits en ANNAN naturfilosofi värd namnet.

Se särskilt från c0-kroppen med Allmänna tillståndslagen, om ej redan bekant.

De olika stjärnbildningsteorierna — med referens till James Jeans teori för de fria vätgasmolnens gravitella sammandragning via kritiska gränsmassor

Stjärnbildning — med utgångspunkten att det finns stjärnor UTAN existerande rotation

De olika stjärnbildningsteorierna

Stjärnbildning — med utgångspunkten att det finns stjärnor UTAN existerande rotation

2012I28

BILDKÄLLA: Författarens arkiv

Skruv&Mutter 4Nov2010Bild11 · Nikon D90

— Få se nu … . Om man tar …

Vid en allmän genomgång av de mest framträdande detaljerna i den moderna akademins stjärnbildningsteori, »gravitationskollapsen» från Jeansteorin (1926), finns enligt TNED (här veterligt) inga direkt uppenbara skäl att avvisa teorin som sådan, gränsmassorna för gravitellt sammandragande vätgasmoln.

— Enligt MAC förklarar Jeans teori från 1926 [Jeansteorin i sammandrag från Bonniers Astronomi] upphovet till stjärnbildning; Friliggande Vätgasmoln i universum sammandras via s.k. kritiska Jeansmassor, delas upp på flera mera högtäta centra som sedan bildar stjärnor.

— Den enda invändningen som finns från TNED i det avseendet är att den typen av stjärnbildning inte existerar i universum — därför att stjärnbildningen redan är upptagen av ett annat sätt:

— Stjärnor bildas från maximalt tätt tillstånd i TNED (Se från K-cellens detonation), med resultat i omgivande vätgasbanker från himlakropparnas primärbildning.

— Det eliminerar Jeansteorins primärbild:

— Gravitell sammandragning är visserligen möjlig, men har ingen praktisk representation i universum: friliggande vätgasmoln i universum utan ett redan etablerat centrum av en eller flera fasta kroppar, finns inte.

Anledningen explicit varför inga direkta argument finns i TNED mot principen för gravitell sammandragning är

1. VETERLIGT att (ingen i modern akademi räknar med att) inga större repulsiva elektriska krafter finns verksamma mellan de fria atomerna i en förmodad ursprunglig vätgas, och

Casimireffekten

2. att denna detalj också ansluter till resultatet i TNED från Casimireffekten — för de större avstånden via F=(4/n)Ake²Z/d^4 med fast genomflödesyta A=πr² associerad med max väteatomens grundradie 0,529Å, n=673026=antalet elektronelement; Alla atomer och material antas utöva (näravstånd upp till max ca 0,2mM) större eller mindre (mer än tiondels millimeter) ömsesidiga attraktioner.

Sinnebilden (illustrerad ovan) med två idealt separerade väteatomer som placeras idealt vilande i ett idealt vakuum och sedan släpps, FÖREFALLER i den ideala meningen med de motvända, idealt täta elektronhöljena, avbilda en inbördes eMINUS-repulsion.

— Experimentella omnämnanden EXPLICIT i denna detalj har eftersökts på webben (Jan2012) men inte hittats.

— Möjligen finns vissa osäkerheter här, men då det nu i vilket fall HELT tycks saknas observationsgrunder i det sammanhanget, finns här heller ingen anledning att spekulera.

— Här förutsätts tills vidare ATT Casimireffektens svaga attraktionskraft AV PRINCIP gäller — även mellan inbördes fria väteatomer. Därmed bortfaller också varje kritisk punkt mot teorin som sådan för Jeansmassorna i MAC.

Undersökning via elementära samband

OM vi vill undersöka vad som gäller allmänt elektrogravitellt — i samtidig giltighet av Jeansteorin — för idealt givna atomära idealt fritt utlämnade vätgasmoln

med avseende på en absolut minsta möjliga elektrisk repulsionskraft (och den blir då väldigt liten) mellan två närliggande fria väteatomer vid randen på en idealt sfärisk vätgasmassa med idealt homogen täthet och vilken repulsion balanseras i exakt jämvikt av den underliggande massfärens attraherande gravitationskraft,

finns helt elementära samband som man kan pröva och laborera med i basexempel från de olika observerade nebulosorna. Se vidare i Kosmiska Vätgasproblemet, räkneexempel ges på Orionnebulosan.

Giltigheten av TNED framför MAC (förklaringarna innefattade) i ämnet stjärnbildning genomgås mera utförligt i detalj från Stjärnfysikens relaterbara grunder.

Stjärnbildningen i MAC

2012I23

Stjärnbildningen i modern akademi — en primitiv uppfattning

Se även i Impulsmomentets bevarande

FRÅN MAXIMAL NUKLIDTÄTHET

RELATERAD FYSIK: Det finns bara en, och endast en enda grundläggande anledning [i resultat av jämförande teorier], orsak, grund och förklaring till varför stjärnor i universum faktiskt INTE varken bildas nu, eller KAN göra det överhuvudtaget genom friliggande vätgasmoln som tillåts sammandras gravitellt:

All himlakroppsbildning i universum, inte bara stjärnorna, utgår tvunget närmast från ett maximalt tätt tillstånd — inte från ett maximalt utspritt tillstånd.

Vi studerar hur.

Absolut komprimerad centralbeskrivning — STJÄRNBILDNINGEN I RELATERAD FYSIK

Absolut komprimerad centralbeskrivning — STJÄRNBILDNINGEN I RELATERAD FYSIK

Illustrationen nedan i utdrag från Ljusets g-beroende i Primära genomgången i Universums Historia.

— PLANCKEKVIVALENTERNA ersätter, beskriver, förklarar och innefattar tydligen Relativitetsteorin som en primitiv företeelse i mänsklighetens kända vetenskapshistoria. Se speciellt resultattolkningen av Galaxernas rödförskjutning genom Dopplereffektens samband i Universums kritiska täthet. — Modern akademi har, tydligen, i favör för en uppenbart primitiv och begränsad teoretisk uppfattning, antagit en grundligt felaktig föreställning om universums fysik. Expansionen är i respekt till giltigheten av Planckekvivalenterna omisskänneligt i entydigt avtagande i referens till observationsvärdena. Från den positionen är det lätt att se huvudsumman: Universum expanderar och kontraherar periodiskt. Grunden är den allmänna c0-kroppen tillsammans med en bevisbar energiräkning som också måste hålla streck: Allmänna tillståndslagen. — K-cellens värmefysik genomgår och innefattar tydligen alla detaljer på Planckekvivalenternas grund — speciellt med klarläggandet av Ljusets gravitella beroende, vidstående illustration för K-cellens del, samt Atomkärnans härledning med Atomkärnans inkompressibilitet via Planckringen eller NEUTRONEN. Neutronmassan, ljusets topphastighet och neutronens tyngdcirkelradie är Plancks konstant h=mcr=6,626 t34 JS, och därigenom den uppdagade NEUTRONKVADRATEN med Atomvikterna som grundlägger K-cellens värmefysik tillsammans med observationerna av Galaxernas rödförskjutning, kosmiska bakgrundsstrålningen, den synliga materiens medeltäthet och den observerade fördelningen mellan Väte och Helium. — K-cellens kontraktion med växande täthet medför avtagande ljushastighet på växande lokal gravitation, vilket via Kärnreaktionslagen garanterar att all föregående grundämnesbildad materia återförs till neutroner genom g-styrd kärnfragmentering, se Hur K-cellen återvinns.

— K-cellens detonation utgår därför alltid från ett maximalt tätt materietillstånd 1,82 T17 KG/M³ med en tillhörande nolldivergenszon — gränsen i K-cellen där ljushastigheten är exakt noll — och som i kraft av ljusets g-beroende också med konstant c0 sveper över K-cellen genom hela K-cellens expansion. Nolldivergenszonens zonsvep TÄNDER följaktligen — aktiverar den yttre rymdens elektromagnetiska fysik — därmed successivt de olika regionerna då zonpassagen medför LOKALT c>0. Därmed börjar NEUTRONENS SÖNDERFALL som medför Coulombrepulsioner enligt Elektriska kraftlagen mellan de frilagda vätekärnorna. Därmed förklaras och beskrivs Stjärnfysiken i allmänhet och Himlakropparnas bildning med Grundämnesbildningen i synnerhet enligt relaterad fysik. Grundmatematiken sammanfattas i Jordens 5 Ekvationer och Solens 3 Ekvationer.

— SPECIELLT framträder Jorden i Fusionsgränsmassan [Jordmassan + 12%]; Solperioderna och Solens magnetism framträder i Solfysiken tillsammans med Solens Allmänna vågfunktion och Koronafysiken — för att nämna de främsta. Den vidare beskrivningen innefattar stjärnfysiken mera generellt genom astronomins allmänna observationer i Stjärnfysiken Del 2 där speciellt Pulsarerna intar en egen särställning — i grunden samma matematik som gäller stjärnorna generellt i TNED:

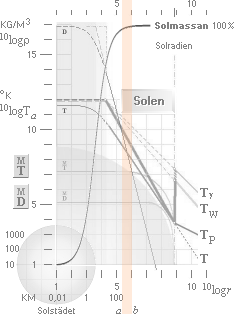
T_P = 4Gρ_MAX(f_D³π²√3)^–1 ..................................... den enkla pulsarmatematiken i TNED

= (1,56072 t11 KG·S^–2M^–3)ρ_MAXf_D^–3 ........... se utförligt från Exempel med Solens Kompaktrotation [Hur Solen kommer att sluta som Pulsar]

— Stjärnbildningen i relaterad fysik grundas på utgångspunkten med maximal neutrontäthet (1,82 T17 KG/M³) — och därmed NOLL rörelse mellan de helt tätt liggande atomkärnorna. Fusionerna Väte-Helium som bildar ljuset och värmen i alla stjärnor bygger på att den ordningen sedan bibehålls:

Genom att atomkärnorna redan från K-cellens detonation tangerar varandras nuklidbarriärer existerar heller inget initiellt motstånd att övervinna för fusion för de frilagda, tätt packade vätekärnorna från neutronsönderfallen. Då kärnorna förenas, först till Deuteroner (1H²), frigörs ett kärninduktivt strålningstryck, samma som den frigjorda fusionsenergin, och som ansvarar för den »maskinsfär» som stjärnan spänns upp på (Se utförligt från Stjärnornas allmänna tryckekvation). Som det lokala strålningstrycket avklingar ur fusionsvågen, tar strax gravitationen återigen överhanden, och en ny fusionsvåg börjar. Förloppet upprepas så länge det finns atomkärnor som kan förenas. Se särskilt Solperioden.

— Gravitationen trycker (ytterst långsamt) in de frilagda vätekärnorna över varandras nuklidbarriärer i ytan på det central stjärnstädet. Den fysiken garanterar samtidigt absolut minimalt yttre extra moment, i princip helt försumbar hastighet mellan atomkärnorna — vilket också exakt är vad Exotermiska kärnreaktionslagen uttrycker.

I modern akademi KAN »oändlig täthet» uppnås »i praktiken» genom att modern akademi inte har någon STRUKTURTEORI för atomkärnan: det finns ingenting som hindrar att atomkärnan kan »komprimeras oändligt» i modern akademi.

— I TNED däremot sätter atomkärnans inkompressibilitet en gräns för varje teori som samtidigt förklarar varför en självutlämnad vätgasmassa aldrig kan bilda maximal täthet: atomkärna mot atomkärna med noll kollisionshastighet via g-tryck. Se särskild beskrivning i Modellbegrepp med hastighet och spinn.

Resultatbild:

— Generellt sett medför TNED-teorin att den uppfattning som finns i MAC om hur Solens energiproduktion fungerar via fusionerna blir en (ytterst) primitiv uppfattning, generellt sett helt utan beröringspunkter med det praktiska fallet. Eller sagt i klartext:

— Modern akademi lever alldeles tydligt i en illusorisk uppfattning om universums allmänna grundfysik:

— I dito monopol på begrepp för utbildning och intelligens — ALLMÄN ÅTLYDNAD under hot av bestraffning — TVINGAS följaktligen, och i den meningens beskrivande ljus, hela mänskligheten leva — verbalt — i stort med början under 1800-talet i en avskild, nermörkad grotta — med MAC som självmeriterad (medaljerad) portvakt.

— Jämför även i Entropibegreppet i modern akademi. Se även i Alla tal om den moderna akademins begrepp oändlighet, gränsvärde och kontinuitet (angående utsagorna från de i modern akademi högt uppsatta 1800-talsgenierna Dedekind, Cantor och Weierstrass).

Sammanfattningarna ovan redovisar, enligt TNED, anledningen varför man i utblicken till universums alla materielokaler ENBART kan se vätgasmoln (generellt gas och stoftmoln) alltid med en eller flera central himlakropp i centrum:

— Det finns (här veterligt) inga exempel på friliggande gasmoln utan redan existerande fasta centralmassor i universum som »håller på att bilda stjärnor genom gravitell sammandragning». Det ska heller inte finnas någon sådan fysik — enligt TNED.

— Allt friliggande väte kan, enligt TNED, återföras på himlakropparnas (i huvudsak de stora stjärnkropparnas) primärutkastningar; Den massan bör följaktligen sedan BINDAS UPP av (och på stort avstånd från) primärkropparna (stjärnhoparnas gemensamma lokala gravitation) efter deras bildning. Friliggande stoft- och vätgasmoln (näring) utan fasta centralkroppar (frön) ska följaktligen inte finnas i universum enligt TNED.

— ATT friliggande vätgasmoln KAN sammandras gravitellt är naturligtvis självklart i sig (Se sammanställda elementära sambandsformer i Kosmiska Vätgasproblemet). Men också den detaljen blir problematisk i teorin i jämförelse med TNED eftersom, som nyligen påpekades, alla gasmoln enligt TNED REDAN är — eller i varje fall ska vara det enligt TNED — associerade med omkringliggande stjärnområden och vilkas gravitationer därmed REDAN har etablerat en viss ordning i den omkringliggande gasen; Vätgasen attraheras av de kringliggande stjärnorna (som håller gasen på avstånd genom stjärnornas aktiva strålningstryck), inte av någon central tyngdpunkt i vätgasmolnet.

— Men ÄVEN om vi frånser den detaljen, och enbart ser till själva det gravitellt sammandragande resultatet, finns ingen möjlighet för gasmolnet NÅGONSIN att nå den avgörande nollrörelse — förutsättningen för stjärnbildningen enligt TNED — som gäller mellan maximalt tätt liggande atomkärnor (Se särskilt från Stjärnfysikens relaterbara grunder) och som är grundvalen för stjärnornas energiproduktion enligt TNED. Se speciellt från Stjärnfysiken Del 1 om ej redan bekant.

— BÖRJAR man med redan separerade atomkärnor, aktiv Coulombkraft mellan vätekärnorna, och på den vägen (via olika kosmologiska teorier) söker pressa samman vätgasen, är det givet — i varje fall med stöd av allmänna gaslagen E=pV=kT — att så länge NÅGON distans finns mellan vätekärnorna det också existerar en rörelseenergi (E) med en tillhörande temperatur (T); För att pressa ihop gasen ytterligare, med ännu mindre avstånd mellan kärnorna, måste E, analogt T, öka. Eftersom ingen (idealt teoretisk) gräns, i princip, existerar för hur mycket Energi som kan läggas in i syftet att öka trycket och därmed minska kärnavståndet ytterligare, finns följaktligen heller ingen egentlig, principiell, gräns för temperaturen (T). Men därmed raseras också det gravitationstekniskt möjliga insteget till den effektiva gravitationsbaserade fusionsfysiken: noll hastighet mellan de fusionerande atomkärnorna; Fusion genom höga tryck under långa tidrymder, inte genom kollision under korta tidrymder. Se särskild resultatredovisning i Solperioden. Se särskilt i jämförande dynamik mellan de olika sätten från Modellbegrepp med hastighet och spinn.

— Denna detalj håller också streck i TNED via atomkärnans inkompressibilitet — omöjligheten i fysiken att åstadkomma typ »oändlig täthet» — atomkärnan står redan på noll garanterat av elektriska kraftlagen tillsammans med atomkärnans härledning (massans fundamentalform) från Planckringen h=mcr — samt den därmed sammanhängande tvunget avtagande fusionseffektiviteten med allt växande temperatur.

— Omöjligheten att via den moderna akademins kollisionsfysik åstadkomma den praktiska fysikens stjärncentra studeras särskilt i Modellbegrepp med hastighet och spinn i sektionen om Stjärnfysikens relaterbara grunder.

Kosmiska Vätgasproblemet

Stjärnorna — oberoende av rotationsbegreppet: Möjliga ursprungliga bildningar

Kosmiska Vätgasproblemet

I princip finns i här känd relaterad mening ingenting som hindrar att fritt utlämnade vätgasmoln i kosmos rymder kan sammandras gravitellt — men då med grund i de vissa premisser som förmår motverka gasens egenexpansion.

OM minimala elektriska repulsioner förekommer mellan atomerna (som fallet är i varje fall vid gasatomernas s.k. kollisioner) KAN (nämligen) gravitationens sammandragande roll HELT spolieras (sammandragning inträffar aldrig). Det är dock här helt okänt vad som gäller i dessa fall för speciellt typen atomär vätgas som sägs utgöra huvuddelen av all interstellär gas.

— Huruvida sådana gravitella sammandragningar, fristående, utan någon redan existerande fast centralkropp, alls existerar, är vad vi vet en hittills obesvarad fråga — enligt TNED ska sådana inte förekomma, inte alls över huvud taget (impulsmomentets bevarande, impulsmoment i gravitella system); Därmed är också vad en sådan förmodad fristående sammandragning skulle kunna åstadkomma, också en historia som här helt saknar observationella grunder.

— Förtätning kräver att gasatomernas strävan att avlägsna sig från varandra måste uppvägas av en motsvarande sammandragande gravitationskraft;

G-kraften ställer upp ett direkt ekvivalent villkor som utpekar ett absolut maxvärde för hur stor en elektrisk repulsionsladdning (Qlim, här läckgränsladdningen) får vara för att exakt balans ska gälla mellan en analogi för elektrisk repulsion och gravitell attraktion.

— Nedanstående exempelblock sammanfattar de högst elementära sambandsgrunder som kan användas för att genomföra enkla, översiktliga prövningar.

Betingelser för gravitell gränsmassasammandragning [[Tabell4-5KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

Betingelser för gravitell gränsmassasammandragning	Grundform	Beskrivning
initiellt vid vätgassfärens rand endast: F(e) = F(G) kQ^2/d^2 = Gm2m/R^2 ; Qlim = (d/R)√(G/k)m2m ; läckgränsladdningen EXEMPEL Orionnebulosan [ref. Wikipedia] m = Väteatommassan; 1,67 t27 K m2 = 2000 Solmassor ca; 3,98 T33 KG d = atommedelavståndet vid sfärranden, 2mM ca R = vätgasens nuvarande sfärradie, 12 LY ca ——————————————————— fullständigt med homogen täthet ρ=m/d^3: Qlim = 3,92 t27 C läckgränsladdningen ρ = m/d^3 vätesfärens homogena medeltäthet = 3m2/4πRlim^3 = 2,09 t19 KG/M³ Rlim = homogena vätesfärens radie = 1,66 T17 M ~ 17,5 LY F = 3,44 t38 N elektrograv. kraftjämv. vid Rlim = F(e) = F(G) · k ................... k=2,13 vRlim = 1790,18 M/S flykthastigheten vid Rlim TRlim = 129,48 °K dito temperatur vid Rlim via gaslagen enligt v^2=3bT/m	Gäller endast två fria väteatomer F(e) = F(G) ; gemensamt d ; kQ^2/d^2 = Gm2m/d^2 ; kQ^2 = Gm^2 ; k/G = (m/Q)^2 ; ~ 1,35 T20 (KG/C)^2 För en väteatom m=1,67 t27 KG får laddningen mellan två lika väteatomer inte överstiga ca 1,44 t37 C om jämvikt ska råda mellan elektrisk och gravitell kraft. G = 6,67 t11 JM/[KG]² k = 9 T9 VM/C b = Boltzmanns konstant 1,38055 t23 J/°K mSOL = 1,989 T30 KG LY = 3600·24·365,25·c0 = 9,46073 T15 M ljusår [eng. LightYear] T | t = förkortningar för 10^±	Gravitella gränsmassasammandrag Vi utnyttjar möjligheten vid gasnebulosans gräns, att gasen läcker ut i rymden utanför. Oavsett orsaken, betyder det i vilket fall att gravitationen i det området tappar greppet om atomerna. Det innebär speciellt att läckgränsen [Rlim] tydligen innefattar den s.k. flykthastigheten [v = √ 2Gm2/R]. — Med grunddata för den aktuella nebulosan som räkne- och prövningsexempel, ges ett bestämt värde för absolut största möjliga läckgränsladdningen [Qlim] vid nebulosagränsen Qlim = (d/R)√(G/k)m2m Vi får Qlim som ovan via uppgiften om medelavståndet [d] mellan gasatomerna vid nebulosagränsen [R], nebulosamassan [m2] och vätgasens väteatommassa [m]. — Därmed kan den idealt ursprungliga vätgassfärens omfång bestämmas [Rlim, direkt ur medeltätheten m/d³], tillsammans med motsvarande ideala värden för flykthastigheten [v] och genom denna, via sambanden i allmänna gaslagen, också gasens temperatur [T] vid flyktgränsen [Rlim]. För sambandens utförliga härledning, se markerade delar i sambanden [länkar till respektive härledande avsnitt]. — Notera att utvecklingen av F[e]/F[G] via medeltätheten [m/d³] framtvingar en konstant [k] som kommer att bero av Qlim enligt k = F(e)/F(G) = m^–5/3m2^–1/3Qlim^2(3/4π)^2/3(k/G) Se särskilt från Medeltätheten från d.
Räkneexempel	Elementära samband	Förklaring

Jämför Jeansmassan [MJ] via T_Rlim: 3953,33 Solmassor mot givna 2000. För att får MJ=m2 krävs ett T_Rlim lika med 82,21 °K.

— Orionnebulosan och andra prövningsexempel innehåller med största sannolikhet även joniserad vätgas — som betyder att vätgasen i nebulosaranden har större benägenhet att läcka ut i rymden utanför än ett mera ursprungligt primärt nebulosaobjekt som helt bör sakna joniserad vätgas [Jonisationskraften kommer från redan existerande stjärnobjekt inbäddade i gasen]. Därmed vrängs prövningsbilden analogt. För att något kompensera den överdriften, måste vi införa en motsvarande jonisationsdämpare, en Temperaturdämpare, för att närmare göra primärformen rättvisa.

— Om sambandet för Jeansmassan är representativt för den översiktligt prövande fysikbilden, kan vi följaktligen få en viss grovt orienterande uppfattning om den valda nu existerande gasnebulosans ekvivalenta jonisationsgrad [via en temperaturanalogi] i nebulosans ytterdel. Temperaturvärdets dämpfaktor [K] kan då bestämmas som nedan:

a=[M_Jlim/(mSOL)] = (3 T4)√(T_J³d³) ; b=[m₂/(mSOL)] = (3 T4)√(T³d³) ; a/b = M_Jlim/m₂ = √(T_J/T)³ ; K = T/T_J = [m₂/M_Jlim]^2/3

I exemplet ovan med Orionnebulosan blir den temperaturdämpande faktorn K=0,63.

Varför självutlämnade vätgasmoln inte kan bilda stjärnor — enligt relaterad fysik

Vi kan genomföra UPPLYSANDE ÖVERSLAGSBERÄKNINGAR som visar huvudsaken:

Stjärnors existens oberoende av egenrotation — se motsvarande för rotationerna i Impulsmomentets bevarande

Jeansteorin

Notera detaljerna i modern akademi:

Se även webbreferens till dokument som härleder den s.k. Jeansmassan per utförlig matematisk teori [dock med matematik på högskolenivå].

— Teorin för stjärnbildning med koppling till »kosmiska vätgasproblemet» i MAC använder resultaten från James Jeans med de så kallade Jeansmassorna [BAs282sp2n, efter James Jeans 1926]; Jeansmassan anses vara den kritiska vätgasmassa vid vilken gasen undergår så kallad gravit[ation]ell kollaps, dvs gravitell sammandragning.

”Ett interstellärt gasmolns utvecklingshistoria bestäms av jämvikten mellan de gravitationskrafter som söker får det att dra ihop sig och det termiska tryck som söker få det att expandera. James Jeans kunde 1926 påvisa att ett moln med given temperatur och densitet kan kollapsa endast om dess massa når över ett visst minimivärde.”,

”Det finns en enkel formel som ger denna kritiska s.k. Jeansmassa (MJ) uttryckt i solmassor:

Jeansmassan

MJ ≥ 3 × 10⁴ √ T³/n solmassor

Molnets täthet (n) uttrycks i antalet väteatomer per kubikmeter, och temperaturen (T) ges i kelvin.”, BAs282sp2n.

Utförlig härledning till Jeansmassan ges i PDF-dokumentet

Astrofysikalisk dynamik, VT 2010 —

GRAVITATIONAL COLLAPSE: JEANS CRITERION AND FREE FALL TIME, Susanne Höfner, Uppsala University (2010)

http://www.astro.uu.se/~hoefner/astro/teach/apd_files/apd_collapse.pdf

Ingenting omnämns i det dokumentet om elektriska krafter. Ordet ”electric” finns inte med. Förutsättningarna beskrivs,

”We consider a homogeneous gas cloud with given density and temperature, and investigate

under which circumstances this configuration is unstable due to self-gravity.”, s2ö.

Jeans teori bygger helt på gasens mekaniska tryckparametrar [inkluderat gasens reaktionshastighet på tryckändringar, analogt ljudhastigheten] och har ingen uttalad koppling till elektrisk kraftverkan. Se länk till utförligt webbdokumentexempel (PDF, Uppsala Universitet ) i Jeansmassan.

Se även från De olika stjärnbildningsteorierna där detaljerna i stjärnbildningens teoretiska problematik beskrivs något vidare.

— Svårigheten att hantera »frilagda vätgasmängder i kosmos» på något begripbart överskådligt sätt är att VARJE teoretisk gasmängd ELEMENTÄRT också är en INNESLUTEN gasmängd och därmed via en eller annan form av TRYCK via en bestämd VOLYM, allmänna gaslagen

E = mad = Fd = Fd·A/A = (F/A)V = pV = kT.

Det finns dock ELEMENTÄRA samband som, på visst sätt, hjälper oss förstå huvudsaken.

Räkneexempel

Jämvikt mellan elektrisk repulsion och gravitell attraktion

Gemensamt separationsavstånd — grundkalkylerna till nedanstående finns sammanställda i [[Tabell5KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]].

d anger avståndet mellan kropparnas tyngdpunkter — gravitationen [den svagare] strävar att förena, Coulombrepulsionen [den starkare] strävar att separera.

Vi studerar sambanden för elektrisk (repulsion, samma Q[e]) och gravitell kraft (attraktion, samma m[H]) för att undersöka villkoren för lika stora men motsatta krafter över gemensamt separationsavstånd (d), från resp. elektriska kraftlagen F(e) och gravitationslagen F(G):

F = k(Q/d)² = G(m/d)² ; G = 6,67 t11 JM/KG² ; F(e/G) = kQ²d²/d²Gm² = (k/G)(Q/m)² ; Q=e, m=m(₁H¹) ;

= F(e) = F(G) ; Tt för 10^±

k/G = (m/Q)²

= (1/4πε₀)/G ; ε₀ = 8,8543 t12 C/VM ; k=1/4πε₀ = 8,98744 T9 VM/C ~ 9 T9 VM/C

= 1,34744 T20 [KG²VM/CJM = KG²V/C(J=VC) = (KG/C)²]

För att jämvikt ska gälla mellan elektrisk repulsion och gravitell attraktion ska förhållandet m/Q tydligen vara

m/Q = √k/G

= 1,16079 T10 KG/C ;

Större m ger gravitell attraktion, mindre m ger elektrisk repulsion.

qMAX

För att en väteatom med massan 1,0078252u INTE ska utöva en elektriskt repellerande kraft på en annan väteatom (som i så fall medför att gravitationen inte orkar hålla emot), får över gemensamt separationsavstånd (d) den effektiva elektriska laddningen från den ena väteatomen till den andra tydligen inte överstiga

qMAX = (1,0078252)(1,66033 t27 KG)/(1,16079 T10 KG/C)

= 1,44153 t37 C

= (8,99833 t19)(e=1,602 t19 C)

— ENDAST om över gemensamt separationsavstånd (d) effektiva inverkan av e=1,602 t19 C är lika med qMAX=1,44153 t37 C (vilken dämpning skulle kunna verkställas genom skärmverkan av olika anledningar) kan gravitationen bromsa elektriska repulsionen. Sedan ytterligare för att åstadkomma gravitell attraktion.

Idealfallet

Vad händer om man, idealt, placerar (håller) två fria Väteatomer på ett fast avstånd, säg 2 mM från varandra (1,28 T8 atomer per M³), i ett rumstempererat laboratorievakuum, och sedan släpper dem: Kommer de att stå kvar på samma ställe, attraheras, eller kanske repelleras?

De yttre motvända elektronhöljena säger oss, i varje fall i den elementära teorin med innebörden att dessa laddningshöljen också är TÄTA, att de kommer att repelleras. Men vad vi vet finns (Jan2012 ännu) inget praktiskt experiment som kan ge besked.

— Casimireffektens samband (adhesions- eller vidhäftningseffekten mellan mycket närliggande materialytor) är (ännu Jan2012) den enda vägledande sambandsform som finns, och den beskriver ENTYDIGT att det föreligger en (med växande avstånd obegränsat) avtagande elektrisk ATTRAKTION mellan alla materials motvända atombesättningar — i princip även mellan två fria väteatomer (tills de kolliderar med följd i elektrisk repulsion).

Short range repulsive, long range attractive

Näravstånd repulsiva, fjärravstånd attraktiva

En del webbkällor (svåra att finna) omnämner också saken explicit:

STATISTICAL MECHANICS IN BIOLOGICAL SYSTEMS, Sean Sun, Fall 2008

http://www.me.jhu.edu/seansun/Sean_Sun/images/statmech.pdf

;

”Altogether, the long range attraction and short range repulsion between neutral atoms is often

modeled as the van der Waals potential”, s8mö.

Det finns inga (här) kända experiment, inte alls över huvudtaget, som försökt studera idealfallet. Väteatomernas kovalenta bindningsform — som på visst uppenbart sätt kontrasterar mot fria vätgasatomer, ger en viss grund för misstanken att en djupare, mera komplicerad ordning gäller. Men ingenting är här känt i den saken.

Initiellt

Genom att vi kan beräkna g-kraften på ett visst avstånd från en viss stjärnhop med en viss massa, kan vi bestämma motsvarande minsta Coulombiska repulsionsladdning som kan finnas för att precis uppväga g-kraften och därmed garantera att vätgasen inte läcker ut från regionen.

F = kQ²/d² = Gm₂m/R² ;

Q² = (G/k)m₂m(d/R)² ; läckgränsladdningen

m₂ = stjärnhopens massa, grovt [öppna stjärnhopar] 100-tals till 1000-tals stjärnindivider, grovt dito Solmassor [BAs46sp2ö] [mSOL=1,989 T30 KG]

m = väteatomens massa, 1,0078252u = 1,67332 t27 KG

d = medelavståndet mellan vätgasatomerna i det omgivande vätgasmolnet — ca 6-2 mM via 5 T6 och 1 T8 stycken atomer per M³ [BAs279sp1ö]

R = avståndet stjärnhopens tyngdpunkt till vätgasmolnets ytterrand — en parsec = 3,0856 T16 M [BAs279sp1ö, ”typiska moln”]

Q = laddningen som atomerna uppvisar mot varandra i exakt jämvikt med g-kraften från stjärnhopen — läckgränsladdningen

= 1,05065 t27 C med m₂mdR respektive 10 Solmassor [10 × 2 T30 KG], Väteatomen, 2mM, 1 pc, ~150 miljoner gånger mindre än e=1,602 t19 C;

= 1,05065 t26 C med m₂mdR respektive 1000 Solmassor [1000 × 2 T30 KG], Väteatomen, 2mM, 1 pc, ~15 miljoner gånger mindre än e=1,602 t19 C;

— OM Väteatomen uppvisar någon STÖRRE elektrisk laddning än Q mot sin granne (i närmast lodled) kommer den väteatomen obönhörligt att avlägsna sig från området.

Utvidgad prövning

Vi testar vidare med en utvidgad modell:

— En hel vätesfärs gravitation utmäts mot en väteatom vid sfärytan och hur gravitationen från den underliggande vätesfärens massa MÖJLIGEN kan bromsa den eventuellt befintliga elektriska repulsionskraften mellan väteatomen och maken närmast under vid sfärytan.

Utvidgad prövning med Vätgas

Vidare:

— Vi använder [här] generellt laddningen Q=e för att representera samtliga fall för Väteatomens del.

Inledande frågeställning som kräver ett bestämt svar:

— Hur stor (idealt atomär) vätgasmassa, homogen täthet förutsatt, måste finnas för att uppväga en viss Coulombrepulsion mellan två närliggande väteatomer?

HÄRLEDNINGEN

Lösning:

HÄRLEDNINGEN:

Medeltätheten från d

För att resultaten ska bli rimliga måste medeltätheten beräknas från det kända d-värdet (här idealt kubiskt rumsuppfyllande), vilket (m/d³) ger

V = Nd³

= (m₂/m)d³ ;

ρ = m₂/V

= m₂/(m₂/m)d³

= m/d³

= 3m₂/4πR³ ;

Notera att d-värdet i kubik inverterat direkt ger antalet atomer per kubikmeter (i interstellära sammanhang ofta i storleksordningen 2-6 mM analogt 1,25 T8 atomer per M³ till 4,62962 T6 atomer per M³, med vidare).

m/d³ = 3m₂/4πR³ ;

R³ = d³3m₂/4πm

= d³(m₂/m)(3/4π) ;

R = d·[(m₂/m)(3/4π)]^1/3 ; .............................. OK kontrollerad verifierad ekvivalent genom separat kalkylprogram

Då gäller också tydligen att

ρ = m₂/V

= m₂/(4πR³/3)

= 3m₂/4πR³ ; R³ = 3m₂/4πρ ;

R³/m₂ = 3/4πρ ;

R²/m₂ = 3/4πρR ; .............................. OK kontrollerad verifierad ekvivalent genom separat kalkylprogram

= 3/4π(ρ=m/d³)

= 3d³/4πm ;

(d/R)³ = (m/m₂)(4π/3) ;

d/R = [(m/m₂)(4π/3)]^1/3 ; Utvecklingarna visar en kraftkoefficient:

Kraftkoefficienten k

F(e) = F(G) ;

ke²/d² = Gm₂m/R² ;

k = F(e)/F(G)

= R²ke²/d²Gm₂m

= (R²/m₂)ke²/d²Gm

= (3/4πρR)ke²/d²Gm

= 3ke²/d²Gm4πρR

= 3ke²/d²Gm4π(m/d³)R

= 3ke²d³/d²Gm²4πR

= 3ke²d/Gm²4πR

= k(d/R)(3/4πG)(e/m)² ;

= (d/R)(e/m)²(3/4π)(k/G) ;

= [(m/m₂)(4π/3)]^1/3(e/m)²(3/4π)(k/G)

= (m/m₂)^1/3(e/m)²(3/4π)^2/3(k/G) ; ................... OK kontrollerad verifierad ekvivalent genom separat kalkylprogram

= m^1/3m₂^–1/3e²m^–2(3/4π)^2/3(k/G)

= m^–5/3m₂^–1/3e²(3/4π)^2/3(k/G) ; ................... OK ; e eg. Qlim.

Därmed

F(e) = F(G) · k ;

k = F(e)/F(G)

= R²ke²/d²Gm₂m ;

R²/m₂ = d²·Gm/ke² · k

= 3/4πρR

= d²m₂^–1/3m^–2/3(3/4π)^2/3

F(e) = F(G) · k

Den (Coulombkraftsdämpande) konstanten k beror av m₂mQ(e) enligt

k = m₂^–1/3m^–5/3e²(3/4π)^2/3(k/G)

NOTERA sammanhanget mot James Jeans ursprungliga teori:

— Teorin för Jeansmassorna (gravitell kollaps för friliggande vätgasmoln) avhandlar bara gasiska tryck (med parametrar för hur snabbt ändringar genom gasmassan bildar återverkningar) och gravitella attraktioner. Det finns tydligen ingen aspekt i Jeansteorin på Coulombrepulsioner (ingen inom MAC räknar med sådana — termen omnämns inte ens [‡]).

Stjärnfysikens relaterbara grunder

Bordet är

Anledningen Varför självutlämnade vätgasmoln INTE bildar stjärnor — enligt relaterad fysik — är att stjärnbildningsprocessen redan är upptagen av ett annat sätt

Varför och Hur ett självutlämnat vätgasmoln i kosmos INTE kan bilda den nödvändiga täthet som krävs för STJÄRNBILDNING ENLIGT TNED, kan klargöras per relaterad fysik genom översiktliga beräkningar av elementär typ. Vi studerar hur från Modellbegreppet nedan.

— Frånsett Impulsmomentets bevarande — som bara gäller stjärnor-himlakroppar som uppvisar rotation — finns inget direkt övergripande sätt att klargöra ämnet generellt (som innefattar även potentiellt icke roterade himlakroppar) »på klassisk bas».

— Enda sättet skulle i så fall vara en allmän utgångspunkt att ALLA — samtliga utan undantag — himlakroppar i universum HAR, eller utgår ifrån att ha, någon rotation.

— Himlakroppsbildning enligt TNED visar att det helt säkert är så (Se från Inducerade rotationens uppkomst).

Standardsolmodellen i MAC

Illustrerat utdrag nedan från Standardsolmodellen i MAC i TNED — hur MAC-Solens fysik är representerad i TNED

SSM i TNED representeras av ett smalt band i Solens inre — med bara 1,6% av totala Solmassan — dessutom med lokala tillägg nära referenspunkten på betydligt högre temperatur och tryck

Området a-b motsvarar det teoretiska området i Solkroppen enligt TNED för den moderna akademins Solmodell (SSM Standard Solar Model). Gränserna går vid b 1,5 T7 °K (0,003 MeV) och approximativt (MAX för kollisionsfusioner) vid a T10 °K (3 MeV). Motsvarande massinneslutningar enligt TNED räknat utifrån och inåt är vid a 2% och vid b 0,4% av Solmassan, totalt för ab-bandets sfäriska skal ca 1,6% av Solmassan. Av rena proportionsskäl är det uteslutet att HELA den uppmätta neutrinostrålningen från Solen skulle komma ENBART ifrån det skiktet. Beträffande den moderna akademins allmänna möjligheter att hävda sig på området stjärnfysik, visar analysen från Neutrinostrålningen i Solen enligt TNED att ÄVEN om vi räknar med att Solen (och stjärnorna) verkställer fusioner genom kollisioner mellan gasatomer, har den delen i Solens fall och enligt TNED endast representation inom ca 1,6% av totala Solmassan, se vidstående utdrag. De 1,6%:en motsvaras av det markerade orangea smala bandet ab i figuren. — Den ringa representationen UTESLUTER — enligt TNED — att Solen och därmed stjärnorna generellt anställer den moderna akademins teoretiska fysik för att underhålla den centrala energiproduktionen. — Anledningen här varför TNED framhålls så favoriserande framför MAC är följande i sammandrag.

Varför TNED inte MAC

Varför stjärnornas fysik stämmer med TNED men inte med MAC

ANLEDNINGEN är blotta möjligheten att härleda följande för Solens del:

· Solens effekt, Solradien (»Solens maskinradie» i TNED, 6,97 T8 M, ca 1000 KM större än fotometriska Solradien 6,96 T8 M),

· Solperioderna (11,44 år från början, nu observerat medelvärde ca 11,1 år),

· Solmagnetismen — hur den flippar, samt de relativa värdena nära Solytan och ute vid Jordbanan, samt i följd därav även

· Solfläckarnas fysik och observationen hur motsvarande praktik ter sig — samt speciellt

· Koronafysiken som i MAC uppvisar en så gäckande utmaning men som i TNED ger en sammanhängande förklarande både kvantitativ och kvalitativ beskrivning:

— Alla dessa bygger på det centrala stjärnstädet som fusionerna anställs på i TNED, dess matematiska fysik och den tillhörande byggnad som återfaller på atomkärnans härledning.

— Inga av dessa ingår i den moderna akademins lärosystem.

— Av den anledningen kan man tydligen med exakt samma säkerhet, och utan den inte alls, påstå att modern akademi aldrig kommer att kunna härleda dessa detaljer — inte kvantitativt, inte kvalitativt. Det går inte med MAC-teorins uppfattning om hur stjärnorna fungerar; det går inte med MAC-teorins idé om kärnfysiken.

— Den följande genomgången kommer (följaktligen) att vara helt vinklad med referens till speciellt TNED (om inga fel uppmärksammas).

Syftet med följande framställning är (således) INTE att omöjligförklara den moderna akademins uppfattning om att kolliderande gasatomer KAN åstadkomma fusioner — man visste redan att det sker (från 1930-talet) genom kosmisk strålning, frånsett den tekniska utvecklingen av partikelacceleratorer. Se även i utvecklingen av Tokamak-tekniken [Wikipedia Tokamak] (försöken att efterhärma Solens energiproduktion på kollisioner mellan gasatomer).

— Syftet med följande framställning är endast att visa att den funktionen INTE ÄR TILLRÄCKLIG i beskrivning och förklaring av Solens och de övriga stjärnornas fysik.

Modellbegrepp med hastighet och spinn

TERMODYNAMISKA FUSIONER

— mot fusioner baserade på Höga Gravitella Tryck

Grundsambanden med kalkylkort finns sammanställt i [[Tabell3KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]].

ARGUMENTEN SOM FAVORISERAR TNED FRAMFÖR MAC

Varför termodynamiska fusioner

[kolliderande protoner]

inte kan tävla med gravitationsbaserade fusioner

[protoner som förenas över barriärgränserna genom lugna, starka TRYCK]

Fusionsgränsen för atomkärnor som befinner sig utanför varandras energi- eller nuklidbarriärer bestäms av den hastighet kärnorna måste ha för att komma över nuklid- eller energibarriären.

Spinnets betydelse

EXPERIMENTELLA BEKRÄFTELSER på spinnets växande betydelse vid växande kollisionsenergier finns väl dokumenterade i Scientific American May 1979 och August 1987 [The Spin of the Proton, Alan D. Krisch, SAMay1979 s58; Collisions between Spinning Protons, Alan D. Krisch, SAAugust1987 s32]. Resultaten har, (avgörande) starkt, bidragit till framkomsten av TNED — Copyrightkulturen tillåter tyvärr inte att resultaten (i bild) finns allmänt tillgängliga (i jämförande, diskuterande analyser) för det allmänna kunskapsintresset.

Sekvensen nedan vänster illustrerar enligt TNED hur fria atomkärnor [här med atomkärnan illustrerad från masstal 2 för den allmänna översiktens skull] ”ser” varandra i förhållande till växande kollisionshastigheter med avseende på kärnans fria och möjliga spinn [Se även motsvarande mera exakt experimentellt grundade fusionskurvor för olika gasämnen i t.ex. Wikipedia Nuclear fusion]. Vid tillräckligt höga kollisionshastigheter »framträder» kärnornas magnetiska moment (motsvarande inre strukturella ekvivalenter). Förutsatt att kärnorna kommer in i varandras nuklidzoner, alltså över Coulombbarriären, är det tydligt att kärnorna också förenas (om kärnstrukturerna stämmer): kärnorna flippar (bilden nedan höger) på varandras kärnmagnetiska fält [på samma sätt som två näraliggande (fritt roterande) tavelmagneter förenas].

Bildsekvenserna ovan höger: Genom Planckringen h_N=m_Nc₀r₀ är protonens periferihastighet (r₀=1,37 t15 M, t för 10^–) i rotationen lika med c₀ (2,99792458 T8 M/S). [c₀=ωr; c₀/r=ω=2,188 T23 S^–1=2π/T₀]. Omkretsen 2πr avverkas då på tiden ca 2,87 t23 sekunder. Inväxlingsfasen enligt TNED med spinnkoppling för fusion i det gemensamma toppspinnet har optimalt 1/3 av 360° att synkronisera vilket ger en toppspinnsynkroniserande tidslokal på 9,567 t24 S. Under denna tid ska den optimalt tillryggalagda protontyngdpunktens väg vara grovt sett lika med protonradien (1,37 t15 M). Detta ger optimala protonhastigheten för absolut idealt mest effektiva fusionssannolikheten, relativt den vilande parten, lika med 1,432 T8 M/S;

v(protonen) = r/T = r/(2πr/c₀/3) = 3c₀/2π = 1,432 T8 M/S = v_F0 = r₀/[(1/3)(2π/ω)].

Hastigheterna, analogier

v_{F 0} = r₀/[(1/3)(2π/ω)]

Ekvationen ska egentligen härledas efter rotationskroppens inväxlingsmässiga tröghetsmoment (tyngre kärnor kräver längre inväxlingsrotation och topptemperaturen för deras optimala fusioner blir därför lägre med växande masstal).

Rotationsanalogin. Termen tröghetsmoment med avseende på inväxlingsaxeln blir emellertid här ett irrelevant begrepp eftersom kärnorna utverkar proportionsvis större sammanlänkande inväxlingskrafter med växande masstal så att motsvarande »tröghetsmoment» framstår [här utan bevis] som konstant genom hela nuklidkartan. Om vi ser inväxlingsaccelerationen i inväxlingsrotationen rätvinkligt spinnaxeln som konstant för alla atomkärnor, ger F=ma att inväxlingskraften växer linjärt med masstalet. För att erhålla motsvarande axelrotation (v_R) i stötarna mellan atomkärnorna krävs ett större arbete för tyngre kärnor vilket med given tvärsnittsenergi sänker v_R med växande masstal, analogt växande kärnradie (kärnradien sammanfattar totalt även tröghetsmomentet rätvinkligt toppspinnet bättre än masstalet eftersom det senare ingår i det förra). Utnyttjar vi referensen ovan med protonens spinnrotation blir dess motsvarande tvärrotation (v_R) 1/4 av ett varv på tiden 9,567 t24 S. Om v_R på detta sätt avtar linjärt med växande kärnradie kan vi därmed i en grov översikt för samtliga atomkärnor sätta

v_F = v_{F 0} (r₀/r)

Våglängdsanalogin. Om vi alternativt utnyttjar föreställningen om en termisk lokal med samma typ av atomkärnor, är det tydligt att deras maximala bidrag via MIC (Mass Interactive Connection, λ=h/mv) begränsas till kärnans diameter. När kärnorna sammanstöter med den impuls som ger våglängder av deras diameter betraktar vi alltså ett termiskt toppvärde för just den nuklidtypen. Härur kan motsvarande maximala temperatur direkt beräknas från Wiens förskjutningslag enligt λ=k_{2,898 t3 M°K}T^–1. Eftersom detta resultat utnyttjar samma princip som i föregående del (proportionalitet mot kärnradien) blir våglängdsanalogin samstämmig med rotationsanalogin (förutsatt korrekt tolkad).

Hastigheterna, samband

Är protonens hastighet högre än v_F0 (inväxlingsprotonen missar inväxlingspunkten) krävs extra moment (för att spinnkoppla och som knappast kan framställas i någon här känd separat process utan att samtidigt också medelhastigheterna tillväxer) och därmed lägre effektivitet för synkroniseringen: fusionssannolikheten avtar. Är protonens hastighet lägre än v_F0 (Coulombrepulsionen i nuklidbarriärerna hinner verka längre, vilket bidrar till att öka inväxlingsprotonens kroppsrotation [frånstötningsprocessen utanför barriärzonen generellt] och därmed minska området för optimal koppling) ser kärnorna varandras inre struktur som alltmera diffus — alt mera likt en spinnande biljardboll — vilket också sänker sannolikheten för optimalt grepp.

Den ovan skisserade optimala fusionssannolikheten motsvarar alltså en genomsnittlig protonhastighet på grovt sett halva ljushastigheten;

— Antingen direkt från Wiens förskjutningslag (λ=k_{2,898 t3 M°K}T^–1, våglängden max protondiametern) eller från allmänna gaslagen [v = Ö 3bT/m₁ = Ö 3(b=1,3805502 t23 J/°K)T/U(u=1,66033 t27 KG)]

v² = (24944,743)T/U °K^–1(M/S)² ; U anger atomvikten

~ T·(25000)/U

ges då den motsvarande optimala (maximala) temperaturen _HT_max som ca 9 T11 °K.

Teoretiska området för kollisionsfusioner enligt TNED

Ovan höger. Graferna ansluter till föregående [vänstra illustration] i Modellbegrepp med hastighet och spinn.

Ovan vänster: Maximala fusionssannolikheten eller fusioneffektiviteten mellan kolliderande vätgaskärnor [protoner] ligger optimalt enligt TNED vid ca 9 T11 °K. På bägge sidor om denna gräns är fusioneffektiviteten lägre: Till vänster [mot noll vid ca T=5 T8 °K [10log T = 8,7] enligt konventionella observationer] därför att kärnrotationerna [snabbare] vinner över kollisionshastigheterna [långsammare] vilket spolierar den nödvändiga kärnspinnkopplingen för fusion; Till höger därför att kollisionshastigheterna vinner över kärnrotationerna; kärnrotationerna tillåts inte få tillräcklig tid för kärnspinnsynkronisering innan kärnorna stöter ihop, vilket missar fusionstillfället av den anledningen; Genom den påföljande kärnkollisionen med atomkärnans inkompressibilitet, tvingas de kolliderande atomkärnorna separera på kollisionsenergin exakt. Då det inte finns någon övre [teoretisk] gräns för ytterligare högre kollisionsenergier med ytterligare motsvarande utkastningar, finns därmed heller ingen egentlig gräns för motsvarande temperaturvärde — enligt TNED. I MAC sätter man topptemperaturgränsen vid runt T32 °K [konv. eng. Planck temperature].

— I praktiken sätter dock universums begränsade massa [vad människan absolut kan komma åt, i varje fall i princip] en motsvarande gräns för max T.

— Webbuppgifterna på max fusionseffektivitet anges också i närheten av ca 9 T11 °K.

Gaslagens v-samband i praktiken

Stöter atomkärnorna ihop godtyckligt (bilden närmast ovan vänster ger en antydan), utan möjlighet att spinnsynkronisera för fusion, är det enligt TNED bara atomkärnans inkompressibilitet som garanterar att komponenterna kastas ut tillbaka med exakt samma kraft som de stötte ihop;

— Som visas i K-cellens värmefysik generellt (Se särskilt i K-cellens detonation), är kärnkrafterna (från Atomkärnans gravitella härledning) elektromagnetiskt oberoende av den yttre (makrokosmiska) rymdens ljushastighet; Atomkärnan avbildar (på närhåll) en idealt mekanisk komponent med (mycket nära) försumbar elasticitet: allt som försöker komprimera eller bara volymändra atomkärnan det allra minsta, åker resolut ut samma väg det kom. Atomkärnan kan inte »dödas» genom någon mekaniskt tryckande, graviterande eller inverkande mekanism, enligt TNED. Se även Atomkärnans geometri under axiell deformation.

— Med den förutsättningen måste också ett motsvarande energikinetiskt samband finnas som KAN beskriva vad som händer om man försöker pressa ihop atomkärnorna ytterligare, med ytterligare tillförande av energi, analogt försöka minska tätheten. Om inget annat gäller, kan vi därför utnyttja gaslagens v-form direkt för alla vidare översiktliga överslagsberäkningar — som ovan via motsvarande obegränsat växande T-värde;

atomkärnans hastighet kan överstiga ljushastigheten med hur stora belopp som helst — därför att energin som används för att komprimera en TYP vätgas i teoretisk princip kan växa obegränsat men inte motsvarande obegränsat växande masstäthet.

— För aspekter på massökningseffekter som funktion av atomkärnornas inbördes accelerationer, kan den aspekten HELT bortses ifrån:

Jämför Ekin = mv²/2:

— Inom slutna elektriska system där en elektriskt laddad m-kropp accelereras av en elektrisk spänning kan v aldrig överstiga ljushastighetens [eller divergens-] toppvärdet c₀=2,99792458 T8 M/S.

— I K-cellens värmefysik däremot där den yttre rymden är elektromagnetiskt inaktiv på grund av att gravitationen definierar c=0, gäller inte elektrofysiken i makroskopisk mening längre. Däremot gäller fortfarande atomkärnans elektromekanik enligt Atomkärnans gravitella härledning: atomkärnans obegränsade fraktala struktur som garanterar att c₀ bevaras av massans fundamentalform = gravitationen av princip. Se även i GRIP och DEEP, om ej redan bekant. Genom att atomkärnan inte kan komprimeras (Se Atomkärnans inkompressibilitet) kommer varje tillförd energi (E=mad=m[v/T]d=pv) som strävar att deformera atomkärnorna i sammanpressande mening att resultera i en lika stor men omvänt utkastande kraft. Genom att inte heller laddningsmassan ändras i den fasta och bestämda massformen (m) totalt, här i exemplet vätgas, återstår bara följaktligen massans hastighet (v), de enskilda vätekärnorna, som parameter för att matcha den tillförda energin (i strävan att öka tätheten). Därmed — i atomkärnornas omedelbara närverkan — har elektrofysiken i makroskopisk mening DELVIS spelat ut sin roll, och det blir, förutsatt korrekt uppfattat, i princip ren elementär klassisk mekanik som gäller;

— OM FUSIONERNA INTE FUNGERAR — det krävs också en spinnkoppling enligt TNED — stöter kärnorna ifrån varandra med samma v som de kolliderade. Därför kan sambandet för rörelseenergin ovan också användas generellt i allmänna gaslagen (i den översiktliga beräkningen);

— Om Energin (E) kan anses obegränsad av princip, så kan Temperaturen (T) det också, och därmed Velociteten (v).

— Men växande E&v kan aldrig eliminera v-formen, sätta den på NOLL, så att ALLA kolliderande atomkärnor (m) inom säg en viss volym, plötsligt upphör att kollidera; växande E&v kan inte verkställa att atomkärnor (genom starkt gravitellt TRYCK) lägger sig MJUKT, tätt tillsammans, utan kollisioner, och börjar FÖRENAS just på grund av att de kommit innanför varandras nuklidbarriärer och just därför kan genomgå SÅDAN fusion som gäller i stjärnornas fall enligt TNED (Se från Stjärnfysiken).

— Anledningen är just den ovan illustrerade principen med att NÄRKONTAKT mellan atomkärnor också kräver SPINNSYNKRONISERING för att fusion ska fungera: inte alla atomkärnor roterar godtyckligt, på EXAKT samma sätt utanför varandras nuklidbarriärer, därmed kan heller inte mer än en viss begränsad (sannolik) mängd förenas åt gången inom en viss begränsad volym och en viss temperatur. Då spinnsynkronisering INTE föreligger, separerar kärnorna på exakt sammanträffande energi: de stöter ifrån varandra.

— Så: ÄVEN om inträngningar sker genom nuklidbarriärerna genom »hur mycket energi som helst», räcker inte det för att också fusioner ska ske: Det måste också finnas en ÖMSESIDIG dynamik som kopplar EXAKT. Fungerar det inte, stöter komponenterna ifrån varandra med lika mycket »hur mycket energi som helst».

— Atomkärnans gravitella härledning:

— Atomkärnans ytbaserade toroida fraktalstruktur GARANTERAR bevarad massa=gravitation genom att MASSTÄTHETEN VÄXER OBEGRÄNSAT MED VÄXANDE FRAKTALDJUP: atomkärnans massa motsvarar praktiskt en YTFORM — och således en form MED OÄNDLIG TÄTHET. Försöker man KOMPRIMERA den formen, svarar den bara med EXAKT SAMMA UTKASTANDE KRAFT — därför att i princip inget töjbart mellanliggande rum existerar att absorbera någon intryckande kraft på. Se utförligt från Atomkärnans inkompressibilitet. Det är också kärnpunkten i TNED: massa = gravitation: atomkärnan är en massans fundamentalform, helt utan inre beståndsdelar.

— Med ökad hastighet (v), från ett visst optimalt läge (se Modellbegreppet ovan), förloras samtidigt förmågan att spinnsynkronisera, och därmed avtar fusionseffektiviteten.

— Därmed kan heller ingen maximal täthet uppnås — atomkärna som gränsar till atomkärna. Universums materiekroppar kan inte byggas så.

Mekanismen som åstadkommer massökningsfenomenet (Se utförligt i TNED från Massa-Kraftutbytesmekanismen [MAFEM]) ligger HELT inom atomkärnornas — den övergripande massformens, här vätemolnets — egen fysik. Den massfysiken garanterar att ingen massa skapas, att ingen massa försvinner, att energiräkningen hålls KONSTANT utan tillägg eller fråndrag.

»Oändlig täthet» — som associerar närmast till ovanstående i ljuset av motsvarande teorier i modern akademi (konv. svarta hål) — existerar INTE i makrofysiken (materiefysiken) enligt TNED: oändlig täthet i TNED är ett begrepp och en fysik HELT reserverat för atomkärnans fraktala struktur, det som definierar atomkärnans inkompressibilitet: massa=gravitation. Se särskilt i Atomkärnans gravitella härledning, om ej redan bekant.

Energigenomströmningsekvivalenten [[Tabell3KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

Genom Energigenomströmningsekvivalenten (1) och och Wiens förskjutningslag (2)

(1) E/h = f = c₀/λ; λ = hc₀/E = hc₀/(E/Q_e eV) =hc₀/([E/e]/[T6] MeV) = hc₀/(T6 e)E_MeV ; h=6,62559 t34 JS, e=1,602 t19 C

(2) λ = k_{2,898 t3 M°K}T^–1

kan — i grov översiktlig mening — motsvarande idealt ekvivalenta °K-temperatur bestämmas, T=k_{2,898 t3 M°K} λ^–1 = E_MeVk_{2,898 t3 M°K} (T6 e)/hc₀ = E_MeV(2,333 T9 °K/J)

v-formen från Hastigheterna får med ovanstående tillägg sammansättningen

v² ~ T(25000)/U °K^–1(M/S)² ;

= E_MeV(2,333 T9 °K/J)(25000)/U °K^–1(M/S)²

= (E_MeV/U)(58325 T9) (M/S)²J^–1

Om energin som försöker komprimera (i vårt allmänna exempel) vätgasen (U=1,007276 räknat enbart för vätekärnan) KAN växa obegränsat, kan kärnornas medelhastighet (v) det också. I annat fall finns ingen begriplig koppling mellan temperatur (T) och mekanisk-kinetisk rörelseenergi (E=pV=kT) mv²/2.

— Det blir också det egentliga svaret på undersökningen:

— En vätgas som utlämnas åt sig själv genom gravitell sammandragning kan ALDRIG komprimeras SÅ mycket att den kan konkurrera med den masstäthet (1,82 T17 KG/M³) för primär vätebaserad stjärnbildning som enligt TNED krävs för att förklara nuvarande observerbara kosmologiska bestånd.

— KOLLISIONSPRINCIPEN SOM SÅDAN för de kolliderande vätekärnorna garanterar (nämligen) ALLTID ETT MEDELAVSTÅND mellan atomkärnorna som är större än noll, och därmed »brakfiasko» (för samtliga konkurrerande teorier). Förutsättningen enligt TNED är noll, så att kärnorna bryter barriärerna TILLSAMMANS — inte enstaka här och där utspritt i massans centraldelar.

— Förutsättningen i modern akademi att stjärnornas HUVUDSAKLIGA energiproduktion kan liknas vid en het innestängd gasmassa (plasma) med termodynamiskt styrda fusioner — fusioner som bygger på kolliderande atomkärnor — har ingen praktisk verifierbar grund i relaterad fysik (TNED).

— Det främsta beviset på att så är fallet, att det också är TNED som förklarar och beskriver sammanhangen, är här speciellt (återigen i erinran) resultaten från Solfysiken:

— Soleffekten, Solradien, Solperioderna, Solmagnetismen och Koronafysiken, alla i (utomordentlig) överensstämmelse med observationerna;

— Soleffekten (råeffekt och fotometrisk effekt), Solradien och Solperioderna, Solmagnetismen (som bygger på Stjärnstädet i TNED), och även Koronafysiken, alla genom TNED — atomkärnans härledning — kan garanterat INTE härledas med hjälp av den moderna akademins lärosystem, ehuru observationerna där är välkända.

Nuklidbarriären

ENERGIN som krävs för att UTIFRÅN, via en kollision, överkomma nuklidbarriären in till en annan (idealt vilande) atomkärna kan bestämmas översiktligt med hjälp av Coulombkraften (Coulombbarriären) i elektriska kraftlagen.

Nuklidbarriären (konv. eng., energy barrier) — översiktliga grovräkningar

Fusionsagenterna av samma typ — t.ex., vätekärnan i Väte 1H1 F = k(Ze/d)^2 , k=Rc0=(R0/4π)c0 ~ 9 T9 VM/C elektriska kraftlagen E(J) = Fd0 = k9 T9 VM/C(Ze)^2/d0 ; energin i Joule E(MeV) = E(J)/e/T6 = E(J)/(1,602 t19 C)(T6) = kZ^2e^2/d0e(T6) = kZ^2e/d0(T6) ; energin i Mega elektronVolt ke/(T6) ~ (9 T9 VM/C)(1,602 t19 C)/(T6) = 1,4418 t15 VM ; E(MeV) = (1,4418 t15 VM)Z^2/d0 ; d0 i t15 M (Fermi): E(MeV) = (1,4418 V)Z^2/d0Fermi För Väteatomens [Z=1] atomkärna är avståndet d0 mellan de bägge atomkärnorna då de vidrör varandra idealt sfäriskt omskrivna nuklidbarriärer lika med d0=2×1,37 Fermi, som ger E[MeV] = 0,5262043 MeV — motsv. [Se Energigenomströmningsekvivalenten] T = 1,228 T9 °K. Atomkärnradien 1,37 Fermi avser emellertid [i TNED] atomkärnans tyngdcirkel: Räknar vi [förenklat] med dubbla kärnradien för reala kärnstorleken, ges halva värdet ovan enligt E[MeV] = 0,2631021 MeV — motsv. T = 6,138 T8 °K ............... 1H1-fusioner Deuterium [1H2] har kärnradier 1/√2 ggr vätekärnans radie enligt TNED [Se Kärnradierna, speciellt i Deuteronens Hemlighet], vilket skulle ge motsvarande T = 4,34 T8 °K ................. 1H2-fusioner Webbkällan HYPERPHYSICS, Coulomb Barrier for Fusion, Temperatures for Fusion http://hyperphysics.phy-astr.gsu.edu/hbase/nucene/coubar.html anger [2012-01-30] ” Deuterium-deuterium fusion: 40 × 10^7 K Deuterium-tritium fusion: 4.5× 10^7 K ”. Deuterium-Deuteriumvärdena 4 T8 °K som särskilt exempel är alltså analoga — vilket understryker experimentalfysikens [elementära] inflytande i TNED. [Tritiummassan är 1,5ggr Deuteriummassan; Den tyngre Tritiumkärnan utövar ett större inflytande i spinnkopplingen på den lättare Deuteriumkärnan, vilket kan förklara varför Deuterium-Tritiumfusionens tröskelvärde ligger lägre. Dock finns f.n. ingen mera detaljerad framställning i TNED på den matematiken].

potentialbarriären nuklidbarriären

Gravitationsenergin TNED-MAC — från c0.doc s85 & UniversumsHistoria.doc Version 2004X10 — Energibegreppet i MAC

KONKRET JÄMFÖRANDE EXEMPEL — relaterad fysik och modern akademi

GRAVITATIONSENERGIN

RELATERAD FYSIK ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ Illustration: Samband: EG = Gm2^2/r ; Beskrivning: Två lika kroppar som befinner sig nära varandra har STÖRRE energi än då samma kroppar befinner sig på stort avstånd från varandra. Exempel: k/2 > k/3 Bevis: matematiken

MODERN AKADEMI ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ Illustration: Samband: uppgift saknas Beskrivning: ”Två materiastycken som ligger nära varandra har mindre energi än när samma materiastycken befinner sig långt bort från varandra” KOSMOS — En kort historik · Stephen Hawking · Prisma Magnum 1994 · s137 st2m Exempel: k/2 < k/3 Bevis: uppgift saknas

Relaterad fysik förklarar Energibegreppet måste relateras till en kvalitativt befintlig instrumentellt påvisbar vägbar och mätbar g-massa. Övrigt tillhör fiktionen och metafysiken, magin och mystiken, skojeri och bedrägeri, och dessa ingår inte i naturvetenskapens matematiska fysik. Föreställningen att masslösa fält besitter energi ingår inte i den förståndsgrundade naturvetenskapen. Energi finns och kan påvisas endast där g-massa finns, och därutöver inte alls. Personer som anser att universum (tiden) har en absolut begynnelse är personer som anser att universums massa är ändlig, att g-fältet är negativ energi och g-massa positiv energi och att summan av dessa är noll. — MEN i den naturvetenskapliga matematiska fysiken finns det ingen förutsättning för att härleda eller påvisa energins kvantiteter där det samtidigt inte finns någon påvisbar och vägbar g-massa. — Mynten till betalningen ska ligga på bordet, inte i någon inrättnings fantasi. Föreställningen att masslösa fält besitter energi ingår därför inte i den förståndsgrundade naturvetenskapen. Vi studerar ett konkret jämförande exempel i vänsterspalterna.

Se även gravitationsenergin mera fördjupat enligt relaterad fysik i Allmänna tillståndslagen.

— K-cellens detonation — universums expansion i relaterad fysik — bygger HELT på ovanstående enkla samband: K-cellen expanderar på exakt samma energi som framträder i K-cellens kontraktion. Inget mer. Inget mindre. Värmeförluster under expansionen gör att g-kraften till slut överväger [Se även i Universums kritiska täthet]: expansionen avstannar, och K-cellen kontraherar [återigen] med den omgivande c0-kroppens påfyllning av neutronkallplasma i exakt proportion till föregående expansionsförlust. Gravitationsenergin i Allmänna tillståndslagen bevisar att verkningssättet är konsistent, motsägelsefritt [är det påståendet felaktigt, är också hela den här framställningen felaktig], och fullkomligt exakt matematiskt-fysikaliskt relaterbart i minsta detalj med förutsättningen av c0-kroppens obegränsade massa och dess eviga kontraktion mot K-cellens centrum för energipåfyllning, analogt energins eviga, oskapade upphov och därmed massan. Utan den förutsättningen gäller inte K-cellens värmefysik — och i så fall inte heller energilagen, och därmed heller inte Fysikens 7 Principer, och därmed heller inte Sanningsbegreppet: tillståndets fysik. Evig puls.

Slutsats

Slutsats:

OM ovanstående citerade är representativt för modern akademi: MODERN AKADEMI UPPFINNER tydligen som det får förstås magiska krafter och fenomen i universum — i enlighet med det allmänt praktiserade VÅLDET PÅ ENERGILAGEN i modern akademi. Se särskilt i Värmeteorin i det Allmänna lärosystemet, samt Energilagen: massa kan förintas för att bilda värme och ljus enligt relaterad fysik därför att den inte kan skapas. Kvantitativt är massa-energi utbytbara, men inte kvalitativt: massa kan inte skapas.

— I modern akademi finns ingen kvalitativ aspekt på fysiken. Därav kalabaliken; Allt behandlas kvantitativt.

Exemplet ovan visar HUR beskrivningssättet i modern akademi [Hawking] har urartat.

Jenkinseffekten enligt Relaterad Fysik

2012II14

JENKINSEFFEKTEN ENLIGT RELATERAD FYSIK

Jenkinseffekten: Observerade ändringar i radioaktivt betasönderfall med variationer i avståndet till Solen [från Jenkins et al., 2006]

[Jenkinseffektens AlfaBetaKomplikation] [Jenkinseffektens omedelbara konsekvenser]:

TNED:

Alla betasönderfallande nuklider påverkas i halveringstider via Solneutrinostrålningens variationer, samt också alla alfaradionuklider OM deras kärnstruktur »igenkänns» av Solneutrinostrålningens (in till 1,1% dämpade) frekvensspektrum

Utförlig beskrivning med LänkReferenser nedan

[Plancks strukturkonstant] [NEUTRINOSPEKTRUM] [Kärnspektrum] [Atomens bildning]:

— En distinkt skillnad föreligger mellan radioaktiva sönderfall av typen som INTE åstadkommer kärndelning, betasönderfall, och de som gör det, nuklidsönderfall [alfa(radio)sönderfall] — enligt TNED.

[Neutrinostrålningen från Solen enligt TNED] [Grovberäkningen i TNED]:

— Frånsett en marginell dämpning (1,1%) är neutrinostrålningen från Solen enligt TNED helt analog med den primära grundämnesbildningens neutrinostrålning, dvs., från de allra högsta neutrinofrekvenserna.

[NEUTRINOINFLUENSEN enligt TNED] [Grundämnesbildningens förutsättningar]:

— Med den förutsättningen ska först och främst alla direkt elektronrelaterade energinivåer kunna omfattas av eventuell neutrinopåverkan från Solen: betasönderfall.

— Men naturligtvis också i princip alfasönderfall, eftersom Solneutrinofrekvenserna (frånsett en liten frekvensdämpning via utträdet från Solkroppen, som ovan ca 1,1%) omfattar hela den FUSIONSBASERADE exotermiskt bildade grundämneskartan — enligt TNED.

— Om det nu, som i vårt fall, gäller ämnesanalysen i förhållandet mellan lokalerna Jorden-Solen, eller från Jordkroppen uttransporterade ämnen (rymdsonder) och deras förhållande till Solen (Coopers Plutonium på Cassini), är det tydligt att den enda SÄKRA växelverkanspremiss som föreligger i ämneskollen TVUNGET måste innefatta BÄGGE kroppslokalerna — och då i förhållande till den fusionsbaserade exotermiska grundämnesbildningens allmänna nuklidkarta, enligt TNED.

— För betasönderfallen är saken redan avgjord genom att elektronsvängningarna gäller gemensamt för alla nuklider, och därmed ingen specifik åtskillnad mellan olika nuklider.

— Däremot för kärnsönderfallande nuklider — neutrinonivåerna är avgörande för varje nuklids egen individuella STRUKTUR — FINNS helt säkra förutsättningar för att nuklider från olika lokaler INTE uppvisar samma växelverkan med Solneutrinostrålningen. Nämligen huruvida OLIKHETER föreligger mellan lokalerna i deras inbördes nuklidsammansättning: allt blir en fråga om STRUKTURELLA RESONANSER på neutrinonivå.

[DIAKVADRATEN]:

— FUSIONSBASERAT PLUTONIUM finns vad vi vet inte i Solen — och TNED ger heller inga förutsättningar för det. SOLKÄRNAN har bara förutsättningar (enligt TNED) att som mest bilda Helium-4 från Väte-1. Inget annat. Övriga förekomster i Solen kommer från primärbildningen, liksom i Jordfallet, men med en annan fördelning.

[Ra226 sönderfallskedjan]:

— Däremot finns, således i Solen, naturligt och ursprungligt bildat både (92)Uran och (90)Thorium — och därmed i sönderfallskedjan också (88)Radium.

— Med den grunden FINNS, tydligen, viss förutsättning också för en alfabaserad händelseseparation i inverkan av Solneutrinos på typ Plutonium (ytterst marginell inverkan; Solneutrinonivåerna känner inte riktigt igen Plutoniumnuklidens neutrinofraktaler) och typ Radium (mera utpräglad inverkan; Solneutrinostrålningen känner igen Radiumnukliderna som kända strukturavsnitt från Uran och Torium [eng. Thorium]).

— Det är den rent kärnstrukturbaserade MÖJLIGHET som, tydligen, utpekas av TNED:

Alla betasönderfallande nuklider påverkas i halveringstider via Solneutrinostrålningens variationer, samt också alla alfaradionuklider OM deras kärnstruktur »igenkänns» av Solneutrinostrålningens (in till 1,1% dämpade) frekvensspektrum.

[Sönderfallstillfället] [Allmän reglering av sönderfallet]:

— Ytterligare en aspekt finns, enligt TNED:

— Neutrinostrålningens inverkan kan antingen verkställa en AVSAKTANDE funktion (hämmande; motsvarande energiupptagning som tillfälligt spärrar normalt sönderfall) eller PÅSKYNDANDE funktion(gynnande; resonansvillkor med energibidrag utifrån som påskyndar förloppet).

— Det finns dock (ännu) i TNED ingen direkt (elementärt) uppmärksammad sambandsform som utpekar HUR det fungerar i de praktiskt avgörande olika specifika nuklidfallen.

DIREKT UPPENBARA KONSEKVENSER AV JENKINSEFFEKTEN

Jenkinseffekten: Observerade ändringar i radioaktivt betasönderfall med variationer i avståndet till Solen [från Jenkins et al., 2006]

Åtskilligt meteoritiskt orienterat material finns (Feb2012) på Webben som intygar SAMSTÄMMIGA RESULTAT [Dalrymple 2006] i radiometriska mätningar [Radiometriska metoder]. Speciellt omnämns dateringar på ca 4,5 miljarder år i resultat av både betabaserade (Rb-Sr) och alfabaserade (U-Pb) radiometriska metoder.

— Om den samstämmigheten verkligen håller streck, och förutsatt att det meteoritiska ursprungsmaterialet haft sådan TID på sig i den ursprungliga Solbanan att väsentliga avvikelser utbildats genom meteoridens varierande Solavstånd enligt Jenkinseffekten,

måste tvunget också alfavariationer existera om betavariationerna gör det.

[Solirradiansens årliga variation]:

— Det betyder i så fall att en eller annan form av övergripande REVISION i ämnet meteoriternas ålder — inom den etablerade forskningens domäner — är oundviklig.

Se vidare i Jenkinseffektens konsekvenser.

Jenkinseffektens konsekvenser

Jenkinseffekten i relaterad fysik — BellDHARMA för UNIVERSUMS HISTORIA 2012-02-15

Jenkinseffektens omedelbara konsekvenser

Jenkinseffekten: Observerade ändringar i radioaktivt betasönderfall med variationer i avståndet till Solen [från Jenkins et al., 2006]

[Solirradiansens årliga variation] [Jenkinseffekten]:

OM, som det ser ut, de observerade Solvariationerna har anställt ändringarna i avståndet Jorden-Solen som den förorsakande agenturen — maxC=1+(1–Ph/Ah)², Ph Perihelium närmast Solen, Ah Apohelium längst bort från Solen — blir variationerna i Jordens fall med banexcentriciteten 0,01671123 [Wikipedia, Earth’s orbit] (ytterst) marginella;

— Med Ph=0,98329134AU och Ah=1,01671388AU ges

C =1+1,08063 t3 =1,00108063, vilket är samma storleksordning som i det rapporterade Jenkinsfallet (max 0,1%).

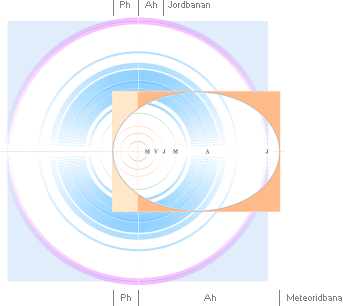
Figuren visar proportionerna mellan de nära idealt cirkulära planetbanorna kring Solen [MerkuriusVenusJordenMarsAsteroidernaJupiter] och en starkt kontrasterande meteoridbana [orange] med Jupiterområdet som största utsträckning. Jenkinseffekten — om inga fel har begåtts — baseras just på variationer i avstånd mellan omloppskropp och Solen. Genom att dessa variationer är nära försumbara i Jordfallet [max 0,1%], men betydande i meteoridfallen [minst från lägst 10% via meteorider från Marsområdet] kommer tidigare förmodat KONSTANTA radiometriska dateringsperioder att påverkas — postumt.

— I meteoriternas fall skulle värdena bli mera (spektakulärt) dramatiska;

— Med Ph max 1AU och Ah som minst (från Marsområdet) 1,52AU ges C=1,117036. Meteoriternas ursprungliga meteoridbanor med ännu större Ah — upp till max ca 5,2AU vid områdena kring Jupiterbanan eller grovt max 6AU — ger dramatiken ännu mera påtaglig kontur: Variationer på mer än 50%.

Räknar vi DESSUTOM med den rent STATISKA konsekvensen — Solens neutrinoinfluens avtar med växande avstånd från Solen — ges följande jämförelse i tabell med Jorden (1) som preferens, sambandet som ovan

maxC(%)=(1–Ph/Ah)² i Solirradiansens årliga variation [[Tabell3KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]:

Solirradiansens grovt översiktliga allmänna inverkan med Jordkroppen [och dess tvärsnitt] som preferens

	Mer	Ven	Jor	Mar	Ast.Ceres	Jup	Sat	Ura	Nep	Plu
AU	0,39	0,72	1	1,52	2,77	5,20	9,54	19,18	30,06	39,44
C[%]	+37	+8	0	–12	–41	–65	–80	–90	–93	–95

1AU = 1,496 T11 M; C(%)=(1–Ph/Ah)², Ph minsta [Perihelium], Ah största [Apohelium]

OM det verkligen är Solneutrinostrålningens irradiativa (bestrålningsmässiga) inflytande som bär ansvaret i Jenkinseffekten, och allt tyder på det (i etablerad mening ännu inte direkt konstaterat Feb2012), innebär det i ljuset av ovanstående olikheter — de aktuella radioaktiva sönderfallens fall — en mer eller mindre fysikrevolution i ämnet kosmologi. Lägg därtill att de olika himlakropparnas egendimensioner också spelar in, enligt TNED, eftersom neutrinostrålningen från Solen enligt TNED kommer från Solstädet (radie 4012,1338 M). I förhållande till Jordkroppen kan Solstädet ses som en ideal punktformig strålkälla. Men inte i förhållande till en meteoridkropp med säg diametern 100 meter. I så fall tillkommer ytterligare effekter, speciellt på nära avstånd till Solen.

Radiometriska metoder

— Mot den bakgrunden är det självskrivet att radiometrisk datering — främst alfabaserade Samarium-Neodymmetoden (106 T9 år) och Uran-Blymetoden (4,5 T9 år); betabaserade Rubidium-Strontiummetoden (50 T9 år) och Kalium-Argonmetoden (1,3 T9 år) [ref. Wikipedia, Radiometric dating, 2012-02-15], som inte tar hänsyn till dessa variationer — blir en ytterst äventyrlig historia.

Dalrymple 2006

Exempel på en tabellerad Rb-Sr dataserie på meteoriter med åldersuppgiften runt 4,5 miljarder år, och som matchar alfabaserade metoder med samma värden, finns i webbkällan

The TALK Origins Archive — SCIENTIFIC AGE OF THE EARTH

How Old is the Earth — A Response to “Scientific” Creationism by G. Brent Dalrymple [2006]

Table 7: Summary of Some Rb-Sr Isochron Ages of Meteorites

http://www.talkorigins.org/faqs/dalrymple/scientific_age_earth.html

Om det gäller radiometrisk datering för material på Jorden finns det alltså inga som helst invändningar: variationer på 0,1% innebär ingen väsentlig ändring i huvudbilden.

— Värre är det med uppvisningarna utanför.

KONSEKVENSER:

— OM resultaten i TID från de olika metoderna i den alfa-betabaserade radiometrin på speciellt METEORITERNAS MATERIAL verkligen är SAMSTÄMMIGA i tidsvärden — vilket påstås [Dalrymple 2006] — och därmed också samstämmiga avseende MINERALOGIN, och i den mån en sådan koppling finns, är det tydligt på BETASÖNDERFALLENS BEKOSTNAD

— Jenkinsgruppens observationer särskilt som ovan [‡],

och förutsatt dessa innefattar SAMTLIGA betanuklider utan åtskillnad —

att Jenkinseffekten TVUNGET även måste innefatta den alfabaserade sönderfallsdynamiken:

— Det skulle i så fall vara ett separat »bevis» för att fenomenet också gäller alfanuklider.

— Dvs., betafallen skulle MEDFÖRA — av rent strukturtekniska skäl — också alfafallen.

— I annat fall SLITS DE PÅSTÅDDA SAMSTÄMMIGA MINERALBASERADE TIDSUPPGIFTERNA ISÄR: samstämmigheten i tidsuppgifter mellan betabaserade och alfabaserade radiometriska uppgifter gäller INTE — vilket vi naturligtvis här (ännu) inte kan utesluta.

— OM vi alltså (rationellt) antar att uppgifterna TID-MINERALOGI hänger ihop (i annat fall blir det, tydligen, mera komplicerat):

— Meteoriternas ursprungliga omloppsbanor kring Solen utgår från lägsta excentriciteten ca e=0,2 (Jordbanans 1Au=Ph, Marsbanans 1,52Au=Ah, e=[Ah–Ph]/[Ah+Ph]). Om Jupiterbanan (5,2AU) sätts som yttersta meteoritgränsen, ges grovt max(Meteorit)e=0,7.

— Om variationerna AhPh ansluter till samma som Jorden-Solen i Jenkinsobservationerna,

C=1+(1–Ph/Ah)² [Solirradiansens årliga variation], ges respektive MinMax-värden för C via de möjliga MarsJupiterMeteoriterna enligt 1,12 (en variation på max 12%) resp. 1,65 (en variation på max 65%).

— Det är något helt annat än Jordlokalens mera blygsamma 1,001 (en variation på max 0,1%).

— I motsvarande mening skulle motsvarande variationer i halveringstider förekomma för ursprungshistorien till meteoriternas del, och därmed en tydligt helt delvis annorlunda tidsbild OM också meteoritbanorna HADE lång historia (miljarder år), vilket vi inte kan utesluta utan mera exakt kännedom på den punkten.

— I vilket fall med Jenkinsobservationerna, såvitt de kan återföras på Solirradiansens årliga variationer, vilket förefaller vara fallet, och de därigenom klarlagda (i varje fall för) betasönderfallens påverkan, står det REDAN klart:

Betabaserade radiometriska metoder (Rb-Sr-metoden [Radiometriska metoder]) har INTE de nu påstådda värdena i de olika meteoritfallen

— Om värdena sedan avviker mer eller mindre är en annan fråga — med hänsyn till den aktuella meteoritens ursprungliga bana kring Solen: Hur lång tid meteoriden hade sin utpräglade elliptiska Solbana bestämmer, enligt Jenkinseffekten, graden av avvikelse mot de idealt konstanta halveringstiderna.

— Meteoridbanorna kring Solen omges ännu (Feb2012) bara av mer eller mindre avancerade spekulationer. Med teknikens vidare utveckling kan (med stor sannolikhet) även meteoriternas ursprungliga banhistoria så småningom fastställas mera precist. Instrument av olika typ blir allt skickligare i att på mikro- och nanometrisk bas genomföra olika spårningar av olika händelsehistorier och som alltid återfaller på olika effekter och avtryck i de olika materialens atomgitter.

Jenkinseffektens AlfaBetaKomplikation

2012-02-14

Mera från Jenkinsgruppen

JENKINSEFFEKTENS ALFA-BETA KOMPLIKATION

Jenkinseffekten: Observerade ändringar i radioaktivt betasönderfall med variationer i avståndet till Solen [från Jenkins et al., 2006]

Jenkinseffektens AlfaBetaKomplikation är här benämning på den direkt observerade avsaknaden i respons mellan alfanuklider och betanuklider i Jenkinseffektens (ursprungliga) uppmärksammande. Vi studerar hur.

— Upptäckten (Jenkinsgruppen 2006) att variationer (ca 0,1%) framträder i betaradioaktiva sönderfall (Magnesium [‡]) som följd av variationer i avståndet Jorden-Solen, tillbakavisades först med hänvisning till att ingen motsvarande variation i alfaradioaktiva sönderfall (Plutonium [‡]) kunde observeras (rymdsonden Cassini), trots mycket större skillnader i avstånd Objekt-Solen än Jordfallet.

— En komplikation i Jenkinsgruppens uppmärksammande är att också det alfaradioaktiva grundämnet (88)Radium(226) uppvisade motsvarande årsvisa variationer: Illustrationen nedan, från Parkhomov 2010, här med tillagda vertikala orangea årslinjer, förtydligar överensstämmelsens periodicitet med en årlig variation på runt ±0,1%;

Parkhomovs redovisade mätdata för Radium-226

RESEARCHES of ALPHA and BETA RADIOACTIVITY at LONG-TERM OBSERVATIONS, A.G.Parkhomov [2010], Fig.8

http://arxiv.org/ftp/arxiv/papers/1004/1004.1761.pdf

— Komplikationen att Radium(226), men inte Plutonium(238) skulle koppla till Jenkinseffektens tydliga betanuklider, kunde nu (Coopers resultat) förklaras med hänvisning till SÖNDERFALLSSERIEN för Radium [‡]; sönderfallsserien innefattar flera betasteg från Bly(214) mot stabila Bly(206). Genom att MÄTANORDNINGEN i Parkhomovs beskrivning ovan inte skiljer mellan alfaenergier och betaenergier (Sturrock et al., 13Jun2011), kunde man (utan egentlig vetskap) favorisera möjligheten med betaförekomsterna, och därmed — behjälpligt — »förklara» Plutoniumresultatet: fenomenet gäller bara för betasönderfall [‡].

— Genom att ännu ingen framställning finns som närmare klargör databildens sammansättning i fallet Radium(226), finns heller ingen riktigt nöjsam allmän förklaring till exakt VAD det är som gäller:

Helhetsbilden i ljuset av Jenkinseffekten för sönderfallstyperna alfa-beta har tydligt medfört direkta svårigheter i tolkningarna, främst beroende på att man ännu (Feb2012) inte har tillräcklig med mätdata för att kunna avgöra vad som gäller.

— Det är (den här benämnda) Jenkinseffektens alfa-beta-komplikation.

— Nedanstående citat i sammanställning ger möjligen en tydligare bild av sammanhanget.

Plaisted 2011

TASC — TRIANGLE ASSOCIATION FOR THE SCIENCE OF CREATION

Radioactive Decay Rates May Change, David Plaisted, December 1st, 2011

http://www.tasc-creationscience.org/content/radioactive-decay-rates-may-change

Källan ovan ger användbara referenser till forskningsrapporter som berör Jenkinseffekten, samt sammanfattar väsentligt innehåll via kortare recitationer av innehållet. På den vägen har, här, ytterligare uppmärksammats — och som (väsentligt) FÖRTYDLIGAR översikten.

Sturrock 13Jun2011

CONCERNING THE PHASES OF ANNUAL VARIATIONS OF NUCLEAR DECAY RATES

P.A. STURROCK, J.B. BUNCHER, E. FISCHBACH, D. JAVORSEK, J.H. JENKINS, AND J.J.MATTES, 13 Jun 2011

http://arxiv.org/pdf/1106.2374v1.pdf

Angående (Z88)Ra(A226):

”The ionization chamber

utilized in the PTB experiment cannot discriminate be-

tween either (alpha or beta) type of decay: the chamber

measures only the total energy deposited by the incident

photons, which have their origins in both types of decay

from several different isotopes.”, s4sp2mö,

CONCERNING THE PHASES OF ANNUAL VARIATIONS OF NUCLEAR DECAY RATES

P.A. STURROCK, J.B. BUNCHER, E. FISCHBACH, D. JAVORSEK, J.H. JENKINS, AND J.J.MATTES, 13 Jun 2011

http://arxiv.org/pdf/1106.2374v1.pdf

Källan ovan (Jun2011) KLARGÖR i sin apparatbeskrivning att RESULTATVÄRDENA från PTB-experimentet (i bild nedan från Parkhomov 2010) inte särskiljer alfaenergier från betaenergier, utan ser dessa som ett och samma; BÅDE alfa och betaenergier ingår i resultatbilden enligt Sturrockgruppens rapport ovan, och ingen kan (ännu) säkert säga vad som tillhör vad.

Parkhomov 2010

Ra226-datat FÖRMODAS (2010) i Parkhomovs apparatbeskrivning avspegla ENDAST betaförekomster:

”For radioactivity measurement 226Ra the ionization chamber was used. It is detector, sensing to β and γ radiations. Usually 226Ra sources are in hermetic ampoules which are not passing α partiсles. In this case registered effect is connected to a β and γ radiation completely. Therefore, the presence in radioactivity measurements 226Ra of variations with 1-year periodicity can be connected with a β radioactivity. For a conclusion about presence such variations in α decays the experiment [11] does not give of any foundations.”, dokumentets sista sida, onumrerat,

RESEARCHES of ALPHA and BETA RADIOACTIVITY at LONG-TERM OBSERVATIONS, A.G.Parkhomov [2010]

http://arxiv.org/ftp/arxiv/papers/1004/1004.1761.pdf

Parkhomovs redovisade mätdata för Radium-226,

RESEARCHES of ALPHA and BETA RADIOACTIVITY at LONG-TERM OBSERVATIONS, A.G.Parkhomov [2010], Fig.8

http://arxiv.org/ftp/arxiv/papers/1004/1004.1761.pdf

Orange vertikala linjer här inlagda vid årsmarkeringarna för att förtydliga samhörigheten.

— Notera att källförfattarna menar [eller rättare sagt MISSTÄNKER] att variationerna INTE kommer från alfasönderfallen i Ra226, utan från betasönderfallen i de dotterprodukter som bildas längre ner i sönderfallskedjan. Se Ra226-sönderfallskedjan längre ner.

— Se dock de senare beskrivningarna från Jenkinsgruppen [Sturrock 2011] som tydliggör att BÄGGE typernas energier registreras i en icke urskiljbar gemensam kompott. I så fall är frågan om alfasönderfallens del i saken ännu oavgjord.

Ovanstående från Parkhomov refereras också till i not.22

22. A.G. Parkhomov, arXiv:1004.1761v1 [physics.gen-ph] , (2010)

i Jenkinsgruppens rapport av 7 Jun 2011

EVIDENCE FOR TIME-VARYING NUCLEAR DECAY DATES: EXPERIMENTAL RESULTS AND THEIR IMPLICATIONS FOR NEW PHYSICS,

E. FISCHBACH, J.H. JENKINS, P.A. STURROCK, 7 Jun 2011

Jämför även Ra226-sönderfallskedjan, med de påstått inbakade betasönderfallsagenterna (Källa @INTERNET Wikipedia, Radon [2012-02-14]): FLERA alfa-steg föregår efterföljande betasönderfall (Från Bly214), här skulle bara betastegen räknas enligt Parkhomov.

Ra226 sönderfallskedjan

http://en.wikipedia.org/wiki/File:Decay_chain(4n%2B2,_Uranium_series).PNG

från

@INTERNET Wikipedia, Radon

http://en.wikipedia.org/wiki/Radon

EMELLERTID framhävs ändå EXPLICIT betanukliderna i samma rapport, Sturrock et al., 13Jun2011, s1sp2n(punkt3), och då för att »förklara» Coopers resultat:

Coopers resultat

Coopers resultat, angående noll observerade variationer i plutoniumets sönderfall (Den plutoniumdrivna rymdsonden Cassini) [resultatet mindre än osäkerheten i den mätande instrumenteringen]:

”However, Jenkins et al. (2010) have shown that

there is in fact no conflict between Cooper’s re-

sults and their results. This is due in part to the

fact that the Cassini RTGs derive their power from

the alpha decay of 238Pu, whereas the periodic ef-

fects observed in various data sets always involve

beta decays.”, s1sp2n(punkt3),

CONCERNING THE PHASES OF ANNUAL VARIATIONS OF NUCLEAR DECAY RATES

P.A. STURROCK, J.B. BUNCHER, E. FISCHBACH, D. JAVORSEK, J.H. JENKINS, AND J.J.MATTES, 13 Jun 2011

http://arxiv.org/pdf/1106.2374v1.pdf

Det föreligger alltså i parentes sagt (Feb2012) ett övergripande AKUT behov inom forskningen att närmare undersöka i stort sett ALLA radioaktiva ämnens sönderfall — i möjligen mer systematiskt samordnad mening mellan alla existerande laboratorium över hela världen för att, säkert, eliminera varje möjlig tänkbar felkälla.

— Inom en period av säg 2-5 år (senast Feb2017) kanske vi får se verkliga resultat av den samlingen — frånsett ev. genombrott av mera radikal natur.

TOTALT framskymtar (således via Sturrock et al. 13Jun2011, citat nedan) en mera NYANSERAD bild som INTE UTESLUTER också alfasönderfallen från fenomenet — MEN med samtidigt understrykande (inte i klartext) att DEN möjligheten KANSKE ändå saknar praktik.

Jenkinsgruppens slutsats, s4sp1n

”different elements have very different

sensitivities to whatever is causing the annual modula-

tion.”,

CONCERNING THE PHASES OF ANNUAL VARIATIONS OF NUCLEAR DECAY RATES

P.A. STURROCK, J.B. BUNCHER, E. FISCHBACH, D. JAVORSEK, J.H. JENKINS, AND J.J.MATTES, 13 Jun 2011

http://arxiv.org/pdf/1106.2374v1.pdf

understryker att variationerna verkligen ÄR (eller, skulle vara) specifika för specifika (beta-) nuklider.

PDF-KATALOG finns som samlar [en del av] Jenkinsgruppens rapporter:

CORNELL UNIVERSITY LIBRARY — ARXIV

http://128.84.158.119/list/physics/10?skip=3325&show=2000

— Om vi går tillbaka i rapporteringen ca 1½ år, är den ÖVERGRIPANDE (dock ännu inte helt klarlagda) bilden av Jenkinseffekten att variationerna bara gäller för betasönderfall:

Betasönderfallen i företräde

”we simply

observe that the data of Ellis [3] and Cooper [11] could be

compatible in a picture in which an external influence predominantly

affects β-decays.”, s5sp1m,

ARXIV 6Jul2010 — POWER SPECTRUM ANALYSES OF NUCLEAR DECAY RATES, Javorsek et al., 6Jul2010

http://arxiv.org/pdf/1007.0924.pdf

— Vi kan förstå svårigheten att navigera i sådana farvatten: Ingen förstår verkningssättet. Än.

Se vidare beskrivning i JENKINSEFFEKTEN ENLIGT RELATERAD FYSIK.

——————— ‡

Betasönderfall är i relaterad fysik mjukt instabila atomer som inte sönderfaller i atomkärnan; betasönderfall berör bara atomens hölje (Kärnladdningen [Z] ändras, masstalet [A] bevaras).

Alfasönderfall, i relaterad fysik även nuklidsönderfall generellt, är instabila atomer som sönderfaller också i atomkärnan; alfasönderfallen medför alltid att atomkärnan delas i minst två delar — ofta en Helium-4-kärna, alfapartikeln, tillsammans med resterande del (Kärnladdning och masstal genomgår uppdelning).

Se utförligt från Allmän Klassifikation — Betainstabila och Nuklidinstabila atomer.

REFERENSER

MAC

modern akademi (här ofta förk. MAC)

TNED

TNED — Related PHYSICS And MATHEMATICS

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Referenser

[VNS]. Van Nostrand’s Scientific Encyclopaedia Fifth Edition 1976

Alla angivna sönderfallstider i denna skrift refererar till ovanstående enligt Table 3, s495-501 om inget annat anges.

[HOP]. Handbook of Physics, E.U. Condon, McGraw-Hill 1956-67

Se de särskilt angivna, och här använda, konstanterna generellt från HOP-källan i HOP-konstanterna.

Alla angivna atomvikter i denna skrift grundas på tabellverket i HOP-källan, 9-65 – 9-86 Table 2.1., Nuclear Masses

Fördelen med HOP-tabellen: Alla NATURLIGT FÖREKOMMANDE ISOTOPER finns angivna [alla kända upp till år 1966] med data för respektive mineralogiska förekomster, samt angivna kända sönderfallstyper, dock utan data på halveringstider;

— VNS-tabellen [från 1975/76] kompletterar [nära heltäckande] HOP-tabellen med specificerade halveringstider, dock endast totala halveringstider för varje nuklidgrupp.

— De senare utvidgade nuklidtabellerna [upp mot år 2000] innefattar en nära enorm mängd artificiellt producerade instabila nuklider som i vissa fall går långt utöver området för HOP-VNS-tabellerna.

[BA]. Bonniers Astronomi 1978, Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

[EST]. Encyclopedia of Science & Technology, McGraw-Hill 1992

[FM]. FOCUS MATERIEN 1975

[GF]. Gymnasiets Fysik 1977-1980, åk 1-3, Liber Läromedel

[BKL]. Bonniers Konversations Lexikon 1922-1929, Band I-XII med Supplement

BILDKÄLLA: Författarens arkiv 21Mar2009 NikonD90 · Drop11 Vila0055 — Tillfälligt vilande vattendroppe på vattenytan.

Synd att JPG-bilder med relativt få färger/färgområden lägger till »smutskanter» — annars skulle den typen vara suverän.

END.

Editor2012II13 |

Meteoriternas ursprung

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Meteoriternas ursprung

ämnesrubriker

innehåll

Meteoriternas ursprung i Universums Historia

Inledning

Förutsättningar för Meteoritlokalernas ursprung enligt relaterad fysik

Meteoritmaterialens detaljerade ursprung enligt relaterad fysik

Mineralbildningsgrunderna specifikt för meteoriterna enligt TNED

J-kroppens expansion i ekliptikan

Huvudstråken i Ekliptikan

Asteroidbältets ursprung i TNED

Asteroidkropparnas banmässiga mångfald

Ursprung 92

Grundämnesfördelningen i relaterad fysik, översikt

Meteoriternas Ursprung

Lokalerna som anställer meteoriternas ursprungliga ellipsbanor

Meteoritgränserna — Gränskurvorna som bestämmer meteoriternas ursprungliga banellipser

Varifrån kom meteoriterna?

Nagasawa 2001

MBJ — Värdkroppens potentiella förmåga att generera METEORITISKA BANELLIPSER MED HÖG INKLINATION OCH HÖG EXCENTRICITET

MBG — Värdkroppens potentiella förmåga att BROMSA/accelerera ANDRA KROPPAR TILL SIN EGEN OMLOPPSHASTIGHET

Meteoriternas kemi

Den unika strukturen

Meteoriternas unika kemi

Bly Jordytan-Månytan

Översikt i Grundämnesbildningen

Impulsmoment i gravitella system

Wikipedia, urmaterialet

Det STORA problemet i MAC

Impulsmomentets bevarande

De olika stjärnbildningsteorierna

Stjärnbildning — med utgångspunkten att det finns stjärnor UTAN existerande rotation

Casimireffekten

Undersökning via elementära samband

Stjärnbildningen i MAC

Absolut komprimerad centralbeskrivning — STJÄRNBILDNINGEN I RELATERAD FYSIK

Resultatbild

Kosmiska Vätgasproblemet

Jeansteorin

Jeansmassan

Räkneexempel — Jämvikt mellan elektrisk repulsion och gravitell attraktion

qMAX

Idealfallet

Initiellt

Utvidgad prövning

HÄRLEDNINGEN

Medeltätheten från d

Kraftkoefficienten k

Stjärnfysikens relaterbara grunder

Standardsolmodellen i MAC

Varför TNED inte MAC

Modellbegrepp med hastighet och spinn

TERMODYNAMISKA FUSIONER — mot fusioner baserade på Höga Gravitella Tryck

Spinnets betydelse

Hastigheterna, analogier

Hastigheterna, samband

Teoretiska området för kollisionsfusioner enligt TNED

Gaslagens v-samband i praktiken

Energigenomströmningsekvivalenten

Nuklidbarriären

GRAVITATIONSENERGIN — KONKRET JÄMFÖRANDE EXEMPEL — relaterad fysik och modern akademi

JENKINSEFFEKTEN ENLIGT RELATERAD FYSIK

Jenkinseffekten i Relaterad Fysik

Jenkinseffektens konsekvenser

Radiometriska metoder

Dalrymple 2006

Jenkinseffektens AlfaBetaKomplikation

Plaisted 2011

Sturrock 13Jun2011

Parkhomov 2010

Ra226 sönderfallskedjan

Coopers resultat

Betasönderfallen i företräde

REFERENSER

MAC

TNED

Referenser

Senast uppdaterade version: 2017-08-29

*END.

Stavningskontrollerat 2012-02-20.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ τ πε ħ UNICODE — often used charcters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω →∞ ≡ ‖ ↔↕ ħ ƛ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓

ϑ ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — also Alt+18 ↕; Alt+29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se