DEN GLOBALA UPPVÄRMNINGEN UNDER 1900-TALET | 2009X10 · a  production |  Senast uppdaterade version: 2014-11-26 · Universums Historia

 

innehåll · denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

Den globala uppvärmningen under 1900-talet · BILDKÄLLA: Författarens arkiv · Gammalt ModerKort · Bild1Aug2010 · NikonD90

 

En mera utförlig beskrivning från Augusti 2010 finns i AGW-beviset — samma som här men fullständigat med kompletterande härledningar för effekt och energi samt jämförande referenser till redan etablerade modeller och begrepp.

 

 

AGW-beviset — illustrerad kortform

 

Jämförande Tabellvärden — jämförande koldioxidhalter (CO2) för kontroll av AGW-bevisets kredibilitet

 

 

 

AGW

eng. Anthropogenic Global Warmning, sv. Antropogen (av människan förorsakad) global uppvärmning

 

Jämför en bland flera eminenta uppfattningar som kan hittas på webben:

”Det är inte koldioxiden som orsakar växthuseffekten utan den globala uppvärmningen som ökar kol”,

 http://www.klimatbalans.info/co2.htm

 

I den här framställningen reder vi ut begreppen.

 

 

 

 

 

 

 

 

 

 

 

 

 

mtEC-kurvorna

 

m

t

E

C

 

 

 

Koldioxid, vatten och atmosfär

 

 

 

 

t från Fossil Carbon

 

 

      Den Globala Uppvärmningen under 1900-talet

 

 

En utförlig och uttömmande beskrivande upplösning av NASA-temperaturkurvans matematiska-klimatologiska sammansättning: du kan själv beräka kurvvärdena — från 1860-SåLångtDuVill med t som funktion av människans (nuvarande fortsatta) kolutsläpp.

 

inledande beskrivning

Det finns en del personer som fått för sig att den uppmätta temperaturökningen (t) under 1900-talet (se NASA-temperaturkurvan) har andra orsaker än människans kolemissioner.

 

Det faktum att t entydigt sammanhänger med kolemissionerna kol-olja-naturgasförbränningen utesluter den möjligheten. Men många personer har (tydligen) inte förstått hur det sammanhanget kan bevisas, förstås eller ens SES i de aktuella (numera berömda) uppmätta kurvformerna. Ett exempel (raka motsatsen till efterföljande):

 

”Titta på en temperaturkurva och fundera en stund på när de stora koldioxidutsläppen började och något omedelbart samband kommer du inte att se. Det stämmer helt enkelt inte”.

http://uppsalainitiativet.blogspot.com/2009/09/behover-klimatskeptikerna-bemotas.html

 

 

Det är precis det det gör.

Vi studerar hur.

 

Finns det ingen enkel matematik som bevisar-avfärdar AGW?

 

AGW, eng. Anthropogenic Global Warming, sv. Antropogen (av människan förorsakad) global uppvärmning

 

Jo. Det finns det. Men det verkar som att inte många känner till den delen (ännu Oktober 2009).

— Kolla:

 

 

 

Kolutsläpp orsakar global temperaturökning — FÖRKLARINGEN TILL DEN UPPMÄTTA GLOBALA TEMPERATURÖKNINGEN UNDER 1900-talet

 

 

   Kolutsläpp

     orsakar global uppvärmning

 

 

                     t från kol-olja-naturgas

t från

Fossil Carbon

 

NASA-kurvans fullständiga upplösning

 

Energihärledningen

 

Koldioxidens integralkurva från den tekniska utvecklingens styrkurva

 

 

 

 

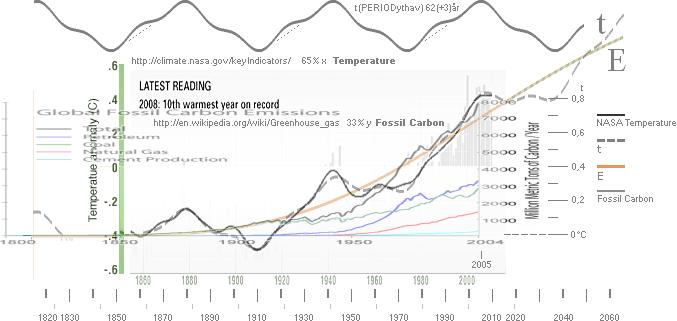
TITTA PÅ NASA-TEMPERATURKURVAN I SAMMANSTÄLLNING MED FOSSIL CARBON EMISSION, NÄR DE STORA KOLDIOXIDUTSLÄPPEN BÖRJADE, OCH DU KOMMER ATT SE ETT OMEDELBART SAMBAND. DET STÄMMER PERFEKT

:

t(NASA) = t(ENERGI) + t(PERIODythav);    

t(NASA) = 6[1-1/(1+[x/10]^4)] + 0.222(0.9[(2cos pi x/1.48) + 0.5(cos 3pi[x-0.1]/1.48)])

— Det är ”plåster” mot NASA-kurvan.

— Du kan räkna ut årsmedeltemperaturen själv, från 1860-såLångtDuVill med nuvarande omsättningstakter och precis så exakt som t(PERIODythav) uppvisar. Det sambandet är (här, ännu) inte optimerat (mera termer krävs), men alldeles tydligt tillräckligt för att ta andan ur varje AGW-ifrågasättande en gång för alla — från 1860-såLångtDuVill.

:

t(NASA):

http://climate.nasa.gov/keyIndicators/

Fossil Carbon Emissions:

http://en.wikipedia.org/wiki/Greenhouse_gas

:

1. Reducera NASA-kurvan till 65% i x-led (horisontellt):

2. Reducera FossilCarbon-kurvan till 33% i y-led (vertikalt):

Placera 1+2 transparent över varandra, samma tidsskala, med 2:ans kurvnolla vid 1:ans y-skalvärde –0,4°C, samma som kurvnollan för t(PERIODythav).

3. Rita ut t(NASA)-kurvan på pixelUnit50 (normal skärmpixelupplösning 96dpi)

4. t(ENERGI)-kurvan stämmer exakt i uppsatsen med Fossil Carbon-kurvan.

5. Eftersom temperatur och energi är proportionella i fysiken, finns bara en matematisk ekvivalent: t(ENERGY) som funktion av Fossil Carbon, analogt t som funktion av ENERGIN: t från Fossil Carbon.

 

förklaringen

till den uppmätta globala temperaturökningen

 

 

 

 

NASA-Temperaturkurvan 2009-10-10

http://climate.nasa.gov/keyIndicators/

 

 

 

Fossil Carbon Emissions:

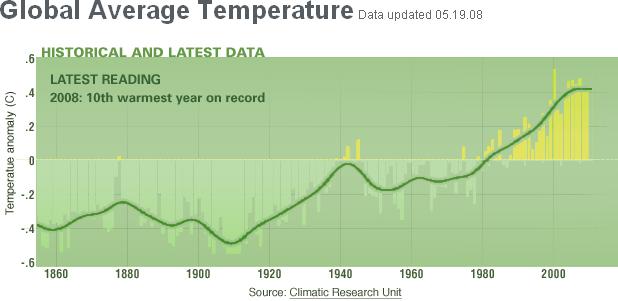
http://en.wikipedia.org/wiki/Greenhouse_gas

 

 

 

t(ENERGI)

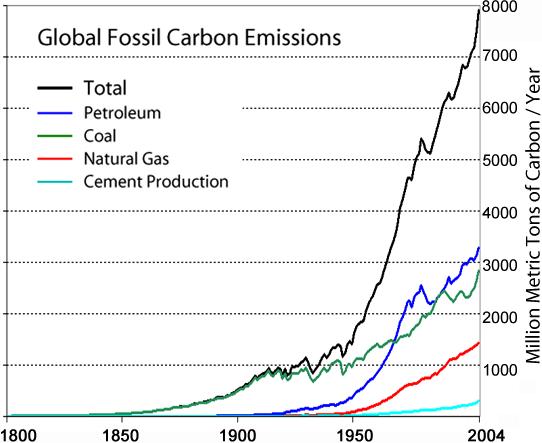
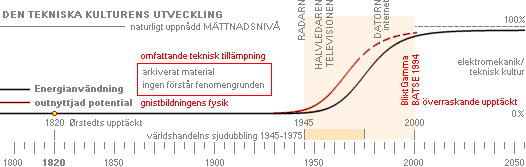
Hela den mänskliga elektro-mekaniska-tekniska utvecklingen (från Ørstedts revolutionerande upptäckt år 1820) sker alldeles tydligt på en elementär styrfunktion,

 

 

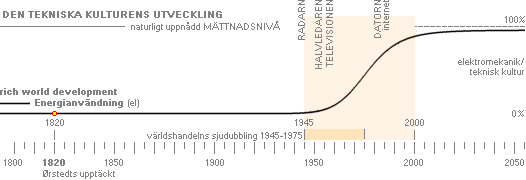
den är av samma form och typ som varje industrilands egen energianvändningsstatistik visar: från nollnivå, snabbt upp med utbyggnad och etablering av det tunga tonnaget i skeppsvarv, verkstäder, pappersbruk, stålverk, sågverk, allmän industri, befolkningens tillgång till typ spis, kyl-frys, dammsugare, etc.

 

mänsklighetens tekniska utveckling:

det finns bara ett lopp att välja på

 

 

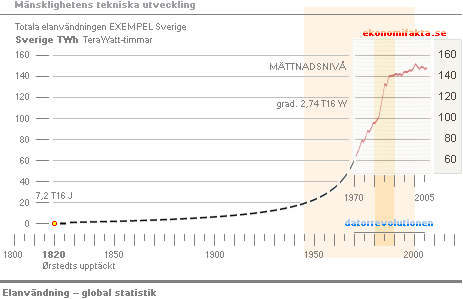
Världsomsättningens motsvarande graf uppvisar (grovt) ca 10 års eftersläpning (här utan specifik redovisning) i jämförelsen mellan de rika industriländerna och den övriga världen, samt motsvarande ”intaxningsbanor” som varje land uppvisar, likt Sverige ovan; När teknikutvecklingen i det landet har mättat befolkningens energibehov (typ allmänna anordningar för ljus och värme, spis, kyl, frys, dammsugare, tvättmaskiner, verkstadsmaskiner, produktionsmotorik, industrimontage, etc.), planar energianvändningsökningen ut och antar endast en svagt växande ökning (främst beroende på naturlig befolkningstillväxt) — om ingen ytterligare teknisk revolution är på gång.

 

 

När den utvecklingen mättas, går processen helt naturligt in i ett lugnare skede (ungefär som personer efter ett kalas blir mätta och slutar att glufsa i sig allt möjligt), men fortfarande i växande men betydligt långsammare. Den funktionen är också en elementär energifunktion,

 

y = a[1–1/(1+[x/b]n)]

 

Är tidsfaktorn (x) linjär gäller den normala energifunktionen med n=2: Är x icke-linjär, vilket tydligen gäller i fallet med t(NASA), sker tillväxten allt snabbare med växande n, i vårt fall tydligen (approximativt) n=4.

 

Källdata

— Energianvändningen i statistik från 1800 verkar (Sep2009) svårt att få fram på webben i någon svensk tappning (jämför ekonomifakta.se). Det finns dock flera engelska webbkällor som beskriver energistatistik från 1800 och som i stort ansluter till den ovanstående streckade grundkurvan, se exv.

 

The Encyclopedia of Earth

[http://www.eoearth.org/article/Energy_transitions], 2008.

Boston University.

 

Energy Intensity and GDP in 2050

[http://www.paulchefurka.ca/WEAP2/Energy_Intensity_GDP_2050.html], 2007.

 

Energy intensity and the challenge that lies ahead

[http://simondonner.blogspot.com/2007/08/energy-instensity-and-challenge-that.html], 2007;

Simon Donner, Geography Department, British Columbia University.

 

 

 

t(PERIODythav)

 

Se från t från Fossil Carbon

 

Alla personer som under någon tid sysslat med PERIODISKA FUNKTIONER och deras matematik, kan (beroende på träning) direkt se mer eller mindre hur en viss periodisk kurvform är sammansatt (läs: kan uppdelas) i separata enskilda komponenter. Det är enklare än du tror när man väl fattat principen.

Studerar man (alltså) NASA-kurvan med FossilCarbon-kurvan transparent överlagrad, framgår ”direkt” inte bara det periodiska mönstret t(PERIODythav) (från 1880) utan även den baskurva t(ENERGI) som havsperioden ligger överlagrad på. Resten består ”bara” i att skriva ut kurvformens matematiska funktion och se till att allt passar in på referenskurvorna.

 

— Men varför har inte folk i Jordens alla forskarkretsar upptäckt det, enkla, redan långt tidigare?

— Fråga dom. För mycket glass och jordgubbar kanske (kombinerat med alldeles för litet sex …).

 

HAVSPERIODEN — ca 62(+max3, växande)år — är här en vald terminologi av det enda enkla tvingande skälet att det inte finns någon annan (veterlig) förklaring till den typen. Det finns också (observerade) DJUPhavsperioder (här utan referens), men dessa är betydligt längre (ca 10ggr minst). Det finns (möjligen) även andra (kortare) land-havs-perioder som kan spela in, men dessa är i så fall (här, ännu) inte kända (och dessutom betydligt mera komplicera att beskriva någon GLOBAL medelform för [en sådan finns strängt taget inte, enbart lokaler] i exakt matematik).

— Se även längre ner i ythavsperiodens grafiska analys.

 

Citat

Citat från FOCUS MATERIEN 1975 s487sp2n, fetstilen min markering:

 

”Mellan vattnet i atmosfären och vattnet i oceanen försiggår ett ständigt utbyte genom systemet avdunstning-nederbörd. Med ledning av koncentrationsfördelningen av vissa radioisotoper i olika delar av oceanen har man funnit att en ocean består av två nästan oberoende cirkulationssystem, nämligen ett mellanskikt i förbindelse med ytvattnet och med polaroceanen samt en djupocean i utbytesförbindelse med polaroceanen. Ytvattnet över 500-metersnivån har enligt denna uppskattning en utbytestid av 5 år, mellanvattnet ca 300 år, djupvattnet ca 800 år samt polaroceanen ca 50 år.”

 

Se även vidare om havsperioderna generellt från D’Aleo.

 

Citat från American Meteorological Society, AMA Journals Online, Journal of Physical Oceanography 1998, Sensitivity of Ventilation Rates and Radiocarbon Uptake to Subgrid-Scale Mixing in Ocean Models, Volume 29, Issue 11 (November 1999),

http://ams.allenpress.com/perlserv/?request=get-document&doi=10.1175%2F1520-0485(1999)029%3C2802%3ASOVRAR%3E2.0.CO%3B2&ct=1

 

”Ocean Deep Water is estimated to be around 1000–1250 years old in the GM cases and the 14C estimates, whereas it is only 200–400 yr in ISO and 300–600 yr in HOR-Z. Overall, it appears that each model case has its own problems in reproducing global ocean ventilation timescales within reasonable levels of accuracy.”,

Min översättning:

Oceaniskt Djupvatten uppskattas vara runt 1000-1250 år gammalt i GM-fallen och 14C-uppskattningarna, medan det är bara 200-400år i ISO och 300-600år i HOR-Z. Totalt, ser det ut som att varje modellfall har sina problem i att reproducera den globala oceaniska ventilationens tidsskala inom rimliga gränser för noggrannhet.

 

Kommentar

Som (också) anges i källan ovan:

— Data på havets olika cykler är (extremt) svåra att få fram, de varierar mellan olika expeditioner och metoder, och uppvisar i slutänden (ännu Oktober 2009) föga mer än ovanstående citatdel från FOCUS MATERIEN 1975.

— Webben innehåller flera (många) liknande rapporter (en del av rapporterna får man inte läsa, kräver särskild behörighet, eller så får man köpa rapporten för dyra pengar), man finner dem på sökfraser (ev. tillsammans med »timescale») typ

»ocean renewal rates»

»rate of ocean ventilation»

 

 

 

 

Ythavsperiodens grafiska analys

Se från t(PERIODythav)

 

För att exemplifiera det redan antydda:

— De approximativa Komponenterna till t(PERIODythav) i t(NASA)-sammansättningen är som nedan enligt

 

 

 

 

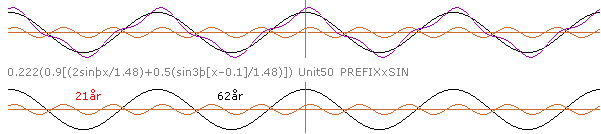
Observera att de angivna trigonometriska sambanden använder PREFIXxSIN, samt en del kryptiska tecken (þ [Alt+0254] för pi) som kommer från det grafritande programmets inmatningsdel.

— Vi ser att matchningen mot NASA-kurvan längst upp visserligen är approximativt OK, men ändå inte så hemskt översvallande.

— Alternativet nedan visar hur en (möjligen, delvis) något bättre överensstämmelse kan anställas på en mera sammansatt trigonometri:

 

 

 

 

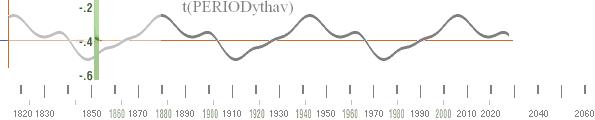
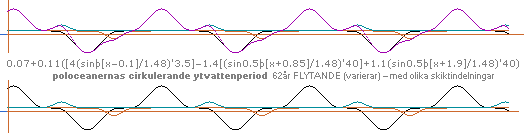
I detta fall framträder bara en enda totalperiod (62 år) — men uppdelad i tre olika »skikt»:

— Huvudformen (svart grafdel) är i princip samma som i föregående alternativ, den är här »bara kvadrerad» (på exponenten 3.5) för att få en hårdare spetsighet för matchningen mot NASA-kurvan.

— Vid sidan av denna finns två mindre och betydligt kortare »ythavstoppar», den ena står för en relativ värmegivare (grön grafdel), den andra för en relativ värmesänkare (orange grafdel), bägge med samma period (62år) som huvudgrafen.

 

Resultatet (ljusviolett grafdel nedan överlagd på NASA-kurvan) [med en liten justering för …+0.11… till …+0.13] blir tillsammans med t-ENERGI-kurvan

 

 

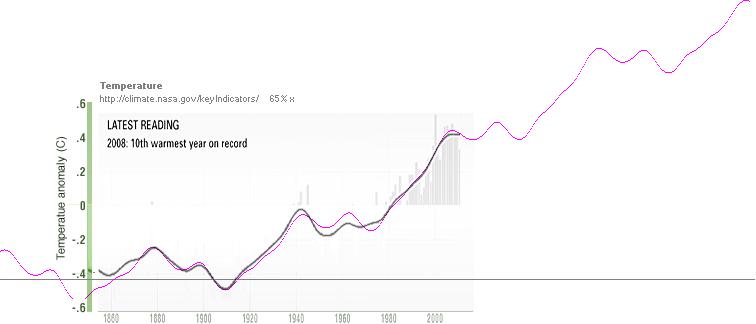
— Det finns (alldeles tydligt) en del detaljer som avslöjas i jämförelsen ovan: tolkningen är i princip korrekt (frånsett perioden före ca 1880, den är mera komplicerad), men det förekommer flera komponenter (djupströmningsdelar med längre perioder men inte så övergripande i styrka), komponenterna varierar dessutom i amplitud på sätt som (garanterat) inte är enkelt att beräkna (men som vi redan kunde förvänta beroende på samverkande faktorer som introducerar oss för ytterligare en mängd klimatparametrar i gruppen växelverkan hav-atmosfär).

— Vi avslutar dock genomgången här då den i vilket fall bara är anställd för syftet att klargöra det mest övergripande, det faktum ATT det (tydligen) förekommer en aktivt verksam ythavsperiod, och att den redan (till viss del) är identifierad och välkänd i form av polaroceanernas vattencirkulation, se föregående citat från FOCUS MATERIEN.

 

Tillägg 2009-10-21|24

 

Ythavsperioderna på webben

Ythavsperioderna på webben

Webbreferenser som förklarar den inre sammansättningen hos t(PERIODythav) finns (bl.a.) på

 

http://icecap.us/docs/change/OceanMultidecadalCyclesTemps.pdf

ICECAP (International Climate and Environmental Change Assessment Project 2007-2008),

Ocean Multi-Decadal Changes and Temperatures, Joseph D'Aleo;

Webbsidans författarreferenser finns på

http://icecap.us/index.php/go/experts

samt

http://www.realclimate.org/index.php/archives/2004/11/atlantic-multidecadal-oscillation-amo/

Climate science from climate scientists — Atlantic Multidecadal Oscillation

 

D’Aleo (2008) beskriver komponentupplösningen i t(PERIODythav) detaljerat via polaroceanernas sammanknutna (Thermohaline-) kopplingar till AMO och PDO [se exv. sv. Wikipedia på Termohalina cirkulationen],

 

AMO (Atlantic Multidecadal Oscillation), Atlantisk multidekadisk svängning resp.

PDO (Pacific Decadal Oscillation), Stillahavsdekadisk svängning.

 

Källorna (Real Climate ovan) anger perioden ungefärligt 50-80 år [medelvärde 65 år].

Nedan följer en kort (ej översatt) genomgång/sammanställning.

 

 

Ythavsperioden på 62år genom AMO och PDO

AMO (Atlantic Multidecadal Oscillation), Atlantisk multidekadisk svängning

PDO (Pacific Decadal Oscillation), Stillahavsdekadisk svängning

Bägge ”ventilerar” (utbyter vatten) genom resp. polaroceaner.

 

Med vidare webbsökning har en del korresponderande material framkommit som just behandlar komponenten t(PERIODythav) i NASA-temperaturkurvan.

 

Ämnet finns relativt noggrant beskrivet i webbkällan

 

http://icecap.us/docs/change/OceanMultidecadalCyclesTemps.pdf

ICECAP (International Climate and Environmental Change Assessment Project 2007-2008),

Ocean Multi-Decadal Changes and Temperatures, Joseph D'Aleo;

Webbsidans författarreferenser finns på

http://icecap.us/index.php/go/experts

 

Uppgifter som korresponderar med NASA-kurvans ythavsperiod finns bl.a. på s10 källan ovan (diagram 1856-2006):

 

— Annual Atlantic MultiDecadal Oscillation (AMO),

s10:

 

”Figure 9: Atlantic Multidecadal Oscillation (NOAA CDC) – the mean ocean temperatures from 0 to 70 degrees north latitude. Note the approximate 70 year cycle.”,

 

 

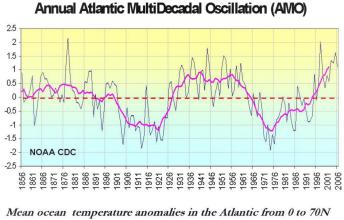
På källsidan 12 finns en sammanställd graf med PDO och AMO tillsammans.

 

Perioden stämmer, fast dess form är inte (helt) fullständig mot ythavsperiodens form i NASA-kurvan eftersom endast en del av norra hemisfären räknats (0-70°Nordlig).

 

s11n:

”Indeed when we plot and add the two indices (after normalizing them) we see a suggestion of global cooling from the 1880s to 1920s, global warming from the late 1920s to early 1950, a global cooling from the late 1950s to late 1970s and then a global warming.”.

s9n:

”Like the Pacific, the Atlantic undergoes decadal scale changes in ocean temperatures with a period that averages 60 -70 years or so. It can be seen to extend back to at least the 1850s in figure 9.”

 

Det är alldeles resultatet för NASA-kurvan.

 

— Därmed är t(PERIODythav) på 62(+3)år i NASA-kurvan helt säkert identifierad.

 

— I DEN MENINGEN kan alltså t(PERIODythav) förstås vara sammansatt av just en del PDO (Pacific Decadal Oscillation) och en del AMO (Atlantic Multidecadal Oscillation). Observera dock att grafen ovan (från D’Aleo 2008) inte direkt kan jämföras med t(PERIODythav) i NASA-kurvan då den senare omfattar mätningar över hela Jorden medan ovanstående endast avser en del av norra hemisfären.

 

Här finns ytterligare uppgifter som ansluter till t(PERIODythav) från NASA-kurvan på 62(+3)år; Webbkällan Real Climate skriver om AMO,

 

http://www.realclimate.org/index.php/archives/2004/11/atlantic-multidecadal-oscillation-amo/

”Atlantic Multidecadal Oscillation (”AMO”)

Filed under: Glossary— group @ 28 November 2004 - ()

 

A multidecadal (50-80 year timescale) pattern of North Atlantic ocean-atmosphere variability whose existence has been argued for based on statistical analyses of observational and proxy climate data, and coupled Atmosphere-Ocean General Circulation Model (”AOGCM”) simulations. This pattern is believed to describe some of the observed early 20th century (1920s-1930s) high-latitude Northern Hemisphere warming and some, but not all, of the high-latitude warming observed in the late 20th century. The term was introduced in a summary by Kerr (2000) of a study by Delworth and Mann (2000).”

 

Proxy Data,

http://www.ncdc.noaa.gov/paleo/globalwarming/proxydata.html

”Proxy Data

Proxy data is data that paleoclimatologists gather from natural recorders of climate variability, e.g., tree rings, ice cores, fossil pollen, ocean sediments, coral and historical data. By analyzing records taken from these and other proxy sources, scientists can extend our understanding of climate far beyond the 140 year instrumental record.”

 

 

 

 

 

räkna ut NASA-kurvan

Observera att kvantiteterna är PRELIMINÄRA enbart för tillfället att bevisa den övergripande överensstämmelsen

— värdena är (ännu Okt2009) inte exakta (mera trigonometriska termer krävs), men nära, se den streckade t-kurvan i sammanställningen

 

t(NASA) = t(ENERGI) + t(PERIODythav);                                                                                

t(NASA) = 6[1–1/(1+[x/10]^4)] + 0,222(0,9[(2cos pi x/1,48)+0,5(cos 3pi[x-0,1]/1,48)])

— Efter mellanräkningar med skalomvandlingar ges t(ENERGI)-kurvan som en medelform för t i

 

                                                t(ENERGI) = (1,765)[1–1/(1+[x/212,7]^4)]

 

— x i antal år tidigast från ca 1815 (havsperioden från lägst 1860) och t i °C från NASA-referensnivån –0,4°C.

 

Motsvarande för t(PERIODythav) blir

t(PERIODythav) = –0,4 + 0,222(0,9[(2cos pi x/1,48)+0,5(cos 3pi[x-0,1]/1,48)])/3,4

t(PERIODythav) = –0,4 + 0,222(0,9[(2cos pi (ÅR–1880)/[21,27·1,48])+0,5(cos 3pi[ÅR–1880-0,1]/[21,27·1,48])])/3,4

— Efter mellanräkningar fås motsvarande för havsperioden

 

                                                t(PERIODythav) = –0,4 + 0,222(0,9[(2cos pi (ÅR–1880)/31,48)+0,5(cos 3pi[ÅR–1880-0,1]/31,48)])/3,4

 

TOTALSAMBANDET

°C på samma skala som NASA-skalan och ÅR tidigast från 1860 för havsperioden

 

— Totalt för t i °C på samma skala som NASA-skalan och ÅR (tidigast från 1860 för havsperioden) i vanlig kronologisk ordning,

 

                                                t = –0,4 + (1,765)[1–1/(1+[(ÅR–1815)/212,7]^4)] + 0,0653(0,9[(2cos pi (ÅR–1880)/31,48)+0,5(cos 3pi[ÅR–1880-0,1]/31,48)])

 

 

noteringar

1. Sambandet har kontrollerats 8Okt2009 i OpenOffice-kalkylblad via stickprov och fungerar i överensstämmelse med graferna.

2. OBS. pi i kalkylblad skrivs pi() för den som vill pröva själv i OpenOffice Kalkylblad.

3. Havsperioden t(PERIODythav) ser ut att vara i avtagande från 1880 bakåt i tiden, ingen analys finns (ännu) här på den formen — samt växande in i framtiden med ca 62(+3) år. Dessa delar är alltså (ännu) helt preliminära i den här mycket förenklade översikten.

 

*END

Editor2009X10

 

 

NASA-kurvans fullständiga upplösning — Grafiskt komprimerad sammanställning

 

16 Oktober 2009

NASA-kurvans fullständiga upplösning

 

 

Det fullständiga grafiska beviset för den globala medeltemperaturens ökning under 1900-talet

*

Den globala medeltemperaturens ökning

som funktion av en elementär styrfunktion (E)

som kopplar direkt till kolemissionerna och (E-integralen) atmosfärens koldioxidhalt

Beviset för ythavsperioden i NASA-kurvan:

 

 

En kortare beskrivning finns med förminskade illustrationer i KORTBESKRIVNING.

 

Vad de allra flesta människor redan tycks ha uppfattat SPONTANT — utan vidare matematiska utläggningar (vilket är ett gott betyg åt människan som sådan: hon fattar vettet i princip utan särskild »utbildning») — är att NASA-temperaturkurvan

fig1

 

 

 

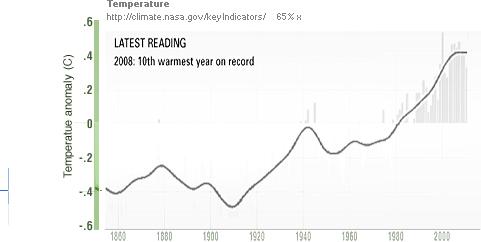
visar en tydligt uppåtgående trend (E)

fig2

 

 

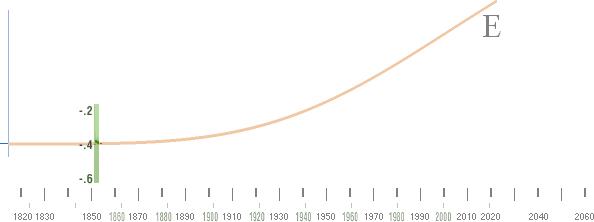
Se härledningen i t(ENERGI)

 

 

— och att det är DEN uppåtgående trenden som hela det uppmärksammade klimatkomplexet handlar om — INTE den naturligt överlagrade periodiska ythavsfunktionen t(PERIODythav) (tidigast från 1860, här approximerad, se vidare sammanställningen nedan mot NASA-kurvan)

fig3

 

 

se även i ythavsperiodens grafiska analys

 

 

som TILLSAMMANS med E-trenden i t(E),

fig4

 

 

 

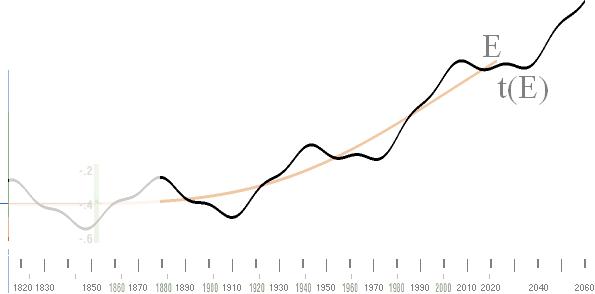
konstituerar — definierar, tydligt, entydigt — NASA-temperaturkurvan enligt sammanställningen (t)

 

fig5

 

 

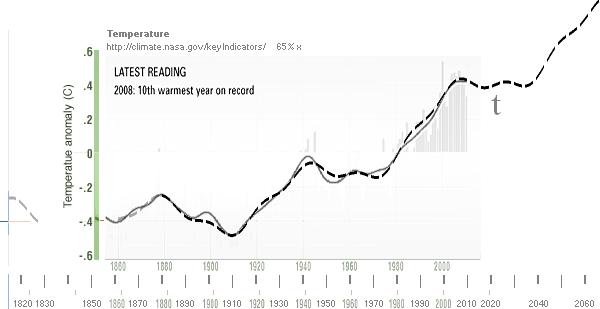
Den observerade temperaturökningen avser naturligtvis INTE explicit de naturliga variationerna i ythavsperioden 62(+3)år från ca 1880 (1880|1942|2004|2066…) utan naturligtvis istället TRENDEN lika med E-kurvan ovan figur 2, den som den naturliga variationen ligger överlagrad PÅ. Se även mera utförligt från t från Fossil Carbon.

— Ythavsperioden med E-kurvan är — tydligen — vad NASA-temperaturkurvan visar.

— Det vore verkligen illa om en majoritet av mänsklighetens enskilda individer INTE uppfattat den delen, spontant — trots att den etablerade litteraturen (av här ännu Oktober 2009 ej känd anledning) inte tycks ha observerat den ENKLA upplösningen med t(PERIODythav).

 

 

 

NASA-kurvans fullständiga upplösning

NASA-kurvans fullständiga upplösning

 

 

Det fullständiga grafiska beviset för den globala medeltemperaturens ökning under 1900-talet

*

Den globala medeltemperaturens ökning

som funktion av en elementär styrfunktion (E fig.2)

som kopplar direkt till kolemissionerna och (E-integralen) atmosfärens koldioxidhalt

Beviset för ythavsperioden i NASA-kurvan:

 

 

Samma beskrivning finns i HUVUDTEXTEN med illustrationerna i originalstorlek.

 

NASA-kurvans fullständiga upplösning

 

 

 

 

 

 

 

 

 

 

 

 

— Det vore verkligen illa om en majoritet av mänsklighetens enskilda individer INTE uppfattat att hela klimatfrågan handlar om den uppåtgående trenden i figur 2. Se utförligt från t från Fossil Carbon.

 

NASA-kurvans fullständiga upplösning

 

VänsterKlicka på bilderna för att se större original.

 

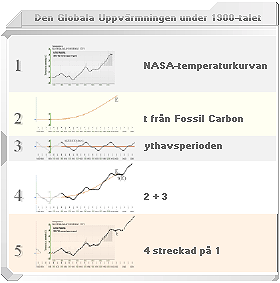
Den etablerade litteraturen tycks inte ha observerat den ENKLA upplösningen (av här ej känd anledning, mig veterligt ännu Oktober 2009). Vi studerar den.

1.

Vad de allra flesta människor redan tycks ha uppfattat SPONTANT — utan vidare matematiska utläggningar (vilket är ett gott betyg åt människan som sådan: hon fattar vettet i princip utan särskild »utbildning») — är att NASA-temperaturkurvan i figur 1 här till vänster

visar en tydligt uppåtgående

2.

trend (E) figur 2

— och att det är DEN uppåtgående trenden som hela det uppmärksammade klimatkomplexet handlar om

— INTE den naturligt överlagrade periodiska ythavsfunktionen

3.

t(PERIODythav) figur 3

period 62(+3)år från ca 1880 (1880|1942|2004|2066…)

 

(tidigast från 1860, här approximerad, se vidare sammanställningen nedan mot NASA-kurvan) som

4.

TILLSAMMANS, figurerna 2 + 3,

figur 4,

tydligen konstituerar — definierar, entydigt — NASA-temperaturkurvan enligt sammanställningen (t, streckad) i

5.

figur 5.

 

Den observerade temperaturökningen avser naturligtvis inte explicit de naturliga variationerna i ythavsperioden, figur 3, 62(+3)år från ca 1880 (1880|1942|2004|2066…); TRENDEN är naturligtvis E-kurvan figur 2, den som den naturliga variationen i figur 3 ligger överlagrad PÅ.

— Se mera utförligt från mtEC-kurvornas härledning i t från Fossil Carbon.

— Ythavsperioden med E-kurvan är — således och tydligen — vad NASA-temperaturkurvan visar.

 

VänsterKlicka på bilderna för att se större original.

 

 

Den uppåtgående trenden (E-kurvan figur 2 ovan) är samma som den allmänna styrfunktionen för mänsklighetens tekniska utveckling (från Ørstedts revolutionerande upptäckt år 1820) — och därmed också mänsklighetens totala energianvändning, vare sig den utvecklas på kol-olja-naturgas eller annat.

 

Olyckan att den utvecklats på kol-olja-naturgas är med andra ord (utförligt från t från Fossil Carbon) anledningen till temperaturökningen (se även från Energihärledningen). Vi återfinner samma typkurva (E) i all energistatistik som presenterar ett industrilands elektro-mekanisk-tekniska utveckling (främst under 1900-talet).

 

— Därmed är den globala medeltemperaturens ökning identifierad enligt E-kurvan. Se vidare från t från Fossil Carbon med Energihärledningen.

 

 

 

Energihärledningen

 

 

                     Energihärledningen

                                                                            med beräkningen av den öppna klimatlokalens luftmassa (M) och höjd (h) över Jordytan

 

 

Uppkomsten av den globala uppvärmningen från kol-olja-naturgasförbränningen

 

I den avgränsade luftgenomströmmade klimatlokalen K med den medelmässiga atmosfäriska genomflödesmassan M på medelhöjden h meter över Jordytan finns en naturlig medelmässig atmosfärisk globalmedeltemperatur Tglobal. Om i M införs ett extra massutflöde m via kolutsläpp Fossil Carbon Emission från en förbränningstemperatur T, ges ett temperaturtillskott t till Tglobal med summan T0 från energiekvivalenterna i den redan välkända allmänna gaslagen E=kT=pV=(F/A)V = (F/A)Ad = Fd enligt

 

m/m = M/M; mv²/2m = Mv²/2M = e/m = E/M = kT0/m = kT/M;

T0/m = T/M;

T0 = T(m/M) = t + Tglobal

 

Temperaturökningen t från normalnivån Tglobal därmed direkt i °C

 

 

                   t = T(m/M)

 

 

M             klimatlokalens medelmässiga atmosfäriska genomflödesmassa, KG

m             kolutsläppet, KG/år

Tglobal      normala naturliga globala medeltemperaturen

T              förbränningstemperaturen vid utsläppet för m, °K

t              temperaturökningen som resultat av T från m, °C från Tglobal

 

Värmeisolationskoefficienten

Med hänsyn till värmeisolationen a eller absorptionskoefficienten (1-a=albedo) i M, högst 1 för noll värmeläckage, lägst 0 för nollatmosfär motsvarande 100% värmeläckage analogt 100% död Jordbiosfär, kan t skrivas mera fullständigt

 

t = T·a·(m/M)

 

Solens inverkan— Solekvivalenta Radiansen (SER)

 

MedelLjusAbsorptionskoefficienten (a) från SolIN-SolUT (1-a=albedo):

Största:    (250 W/M²)/(1336 W/M²) = 0,1871257

Effektiva:   (250 W/M²)/(1000 W/M²) = 0,2500000

ref. @INTERNET Wikipedia 2009-09-30 Insolation

 

Solen kan formellt ersättas med dess energiekvivalent på Jorden. Vi kan kalla den »Solekvivalenta radiansen», SER.

SER kan då förstås som motsvarande markmonterade ”SER-pixelradiatorer” som strålar ut i M;

SER strålar ut i atmosfären från markytan, från havsytan inkluderat, och med medeleffekten samma som solära instrålningens ytjordära effektmedelvärde på ca 250W/M², se grunddata ovan (Wikipedia, Insolation).

 

På samma sätt som föremål uppvisar motstånd mot absolut positionsändring i mekaniken (mv²) och i elektrofysiken uppvisar elektromotorisk induktion med elektriska motströmmar (LI²), tvingas naturligtvis också termofysikens värmemotstånd (t) såsom sammansatt av mekaniska och elektriska krafter uppvisa motsvarande flödesinduktiva fenomen.

 

— Med uppkomsten av t från m i M via T enligt energigrundformen som ovan t/m=T/M bryts tydligen det konstanta värmeflödet i SER;

 

Det högre värmeflödesmotstånd som SER tydligen tvingas möta via t i M måste — tydligen och tvunget — bromsa SER med samma belopp t, i annat fall skulle SER fortsätta stråla ut i M som om t inte funnes. Värmeinduktiva gensvaret i SER från t (via värmeverkan på m i formen av atmosfäriskt koldioxid) blir alltså ett lika stort tillskott t(SER) som i t. Om detta är korrekt formulerat i termer av elementär naturvetenskap blir totala värmegradens tillskott i M därmed via

t = t(SER) tydligen lika med

 

t(AGW)      = t + t(SER) = 2t

               = T·a·(m/M) + T·a·(m/M)

               = 2T·a·(m/M)

 

 

                   t(AGW)  = 2T·a·(m/M)

 

 

AGW, Anthropogenic Global Warming, antropogen (av människan förorsakad) global uppvärmning,

ref. @INTERNET sv.Wikipedia 2009-10-13 Global uppvärmning, Terminologi.

 

— Därmed är — tydligen — temperaturökningen enligt NASA-kurvan entydigt härledd som direkt proportionell mot den fossila kolemissionen (m) och den energi som m förs ut på, samt därmed den extra värmeisolerande verkan som det extra införda kolet i atmosfären tydligen bidrar med i växelverkan med havsytan tillsammans med Solinstrålningen.

— Se även särskild del med mätkurvan (Carbon Dioxide Concentration) som visar atmosfärens koldioxidhalt, tydligt med SPECIELL början från samma uppsats som t(ENERGI)-kurvan från ca år 1860.

 

beräkningen av M

Beräkningen av M

Energihärledningen för den — tydligen i fortsättning från ovanstående resultat — av människan förorsakade globala uppvärmningen t(ENERGI) leder direkt på möjligheten att beräkna den genomströmningsmassa (M) som — tydligen — NASA-temperaturkurvan anställt på den öppna klimatlokalens räkning. Vi studerar det.

 

 

China air pollution — PhotoEverywhere, Shutterstock images

http://www.photoeverywhere.co.uk

 

Eftersom t (NASA-kurvan) och m (Fossil Carbon Emissions) är direkt proportionella kan tydligen M beräknas via m/t om också T och a är kända enligt

 

 

                   M    = 2Ta·m/t(AGW)

 

 

m/t(AGW) fås direkt ungefärligt via skalförhållandet mellan t i NASA-kurvan och m i Fossil Carbon-kurvan enligt

 

7 T12 KG

———————————— = 10,17094 T12 KG/°C

[0,6 + 0,1(1–2/17)]°C

 

 

 

                   m    = t(10,17094 T12 KG/°C)

 

 

(Fossil Carbon-kurvan anger kolemissionen i tusental miljoner metriska ton per år, analogt n·1000·1000 000·1000 KG/år = n T12 KG/år).

 

Gängse fackverk brukar använda albedo 0,3 för (den marknära) Jordatmosfären, analogt a=0,7;

ref. Pierrhumbert s116n Principles of Planetary Climate 2009.

Generellt får vi (emellertid) räkna med att a-värdet fluktuerar tillsammans med det sätt på vilket det utsläppta kolet (som bildar koldioxid i slutänden) associeras med havet/luften i M.

För havets roll, vet man redan att det både kan absorbera och emittera koldioxid,

 

ref.

http://www.mb-soft.com/public3/disaster.html

C Johnson, Chicago University (2007-) 2009;

http://www.atmosphere.mpg.de/enid/basics/1__Oceans_and_climate_1v9.html

The Oceans, 2003-2009;

http://www.aip.org/history/climate/oceans.htm

The Discovery of Global Warming, 2003-2009

Spencer Weart & American Institute of Physics;

http://oceanworld.tamu.edu/resources/oceanography-book/oceansandclimate.htm

Our Ocean Planet, Department of Oceanography, Texas A&M University, Robert R. Stewart 4Aug2009;

m.fl.

 

Men vi behöver explicit inte beakta den delen, vi ser den integrerad i T (och a) eftersom ämnet bara berör den utsläppta kolbasen m i M, inte koldioxidhalten totalt.

 

Uppgifterna för T i kolutsläppet via kol-olja-naturgasförbränningen är

T(Kol) » 2200 °C, T(Olja) » 2150 °C, T(Naturgas) » 2000 °C;

ref. @INTERNET Wikipedia 2009-09-30 Combustion, Temperature.

 

 

China air pollution — PhotoEverywhere, Shutterstock images, undre RGB-omvänd

http://www.photoeverywhere.co.uk

 

M = 3,52138 T16 KG

Med medelvärdet a=0,7 och T=(2200°C + 273°K = 2473°K) blir M via t=1°C lika med

 

M             = 2(2473°K)(0,7)(10,17094 T12 KG/°C)

               = 3,52138 T16 KG.

 

Luftens täthet vid Jordytan (STP, Standard Temperature and Pressure, 0°C vid havsytan och lufttrycket 1 atm)

ref. @INTERNET Wikipedia 2009-10-13 Density of air, Temperature and pressure

är ca D = 1,3 KG/M³ (D avtar med högre temperatur, D=1,225 KG/M³ vid 15°C).

 

h = 53,35 meter

Ett markskikt med höjden 1 meter får då massan via Jordradien (ekvatorn)

R = 6,378 T6 M och D=1,3 KG/M³ som

M(luftJordytan) = D·(4·pi·R²) = 6,6 T14 KG/höjdmeter avrundat

Grovt räknat ges då klimatlokalens höjd i Meter

 

h = M/M(luftJordytan) = 53,35 meter avrundat

 

vilket tydligen blir maxhöjden för genomströmningsmassan M i den öppna klimatlokalen K, NASA-temperaturkurvan. Dvs, NASA-kurvan gäller från och med alla fasta/flytande markområden på Jordytan plus grovt max 50 meter upp och med havsytans klimatdynamik innefattat:

— 50 meter ovanför allt fast och flytande. Det är i varje fall den ekvivalenta klimatlokal som NASA-temperaturkurvan avser i energiekvivalenter mot kolutsläppen enligt ovanstående energihärledning.

 

 

 

Sammanställning av mtEC-kurvorna

 

 

                             Sammanställning av mtEC-kurvorna

 

 

Gemensam nollreferens vid NASA-temperaturkurvans –0,4°C och (lägst) år 1815 (nom. år 1820).

mtE är proportionella, C är E-integralen

 

 

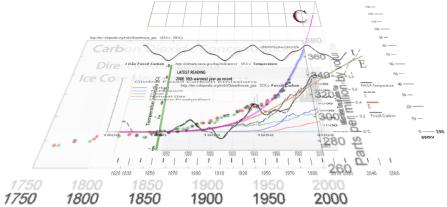
Följande sammanställning visar att alla kurvformer mtEC (nedan) i hela det observerade klimatkomplexet ingår i samma matematiska fysik med grund i en entydig energihärledning som helt baseras på de fossila kolutsläppen. Se även direkt från t från Fossil Carbon.

 

m   årliga kolutsläppet (Global Fossil Carbon-kurvan) (m inte särskilt markerat nedan)

t      globala luftmarina medeltemperaturen vid Jordytan (NASA-temperaturkurvan)

E    energikurvan för t, direkt proportionell mot kolutsläppet m

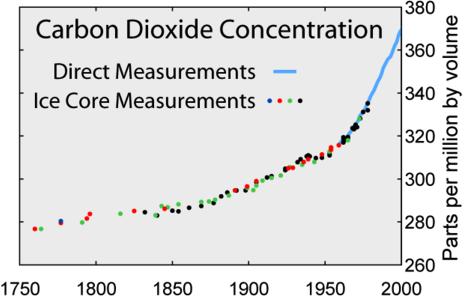
C   motsvarar integralkurvan för E, analogt atmosfärens samlade koldioxidhalt (Carbon Dioxide Concentration-kurvan)

Carbon Dioxide Concentration-kurvan har storleksjusterats så (125% x) att dess brantaste stigning sammanfaller med integralkurvan för E för att därmed bevisa identiteten i den integrala variationens matematiska fysik — och därmed entydigheten i samtliga kurvformer mtEC i hela klimatkomplexet.

— Speciellt den integrala samhörigheten mellan C och E stadfäster därmed den direkta proportionaliteten mellan m (från C) och t (från E), och sammanbinder därmed slutgiltigt och entydigt alla fyra kurvformerna inom ett och samma matematisk fysikaliska naturkomplex: mänsklighetens (den rika världens) klimatpåverkan under 1900-talet framstår därmed som ett obestridligt faktum.

 

 

— Det faktum att koldioxidhalten alls kan ha en integral E-korrelation understryker endast dess otvetydiga samhörighet med t-kurvan analogt med NASA-temperaturkurvans energihärledning. Därmed råder inte längre minsta tvivel om att den observerade globala t-kurvans ökning helt och hållet sammanhänger med de fossila kolutsläppen, tydligen in till sista atomen.

 

totala temperaturen

t(NASA)            = 6[1-1/(1+[x/10]^4)] + 0.222(0.9[(2cos pi x/1.48) + 0.5(cos 3pi[x-0.1]/1.48)])

 

t(NASA)                 = –0.4 + (1.765)[1–1/(1+[(ÅR–1815)/212.7]^4)] + 0.0653(0.9[(2cos pi (ÅR–1880)/31.48)+0.5(cos 3pi[ÅR–1880-0.1]/31.48)])

 

— Totalt för t i °C på samma skala som NASA-skalan och ÅR (tidigast från 1860 för havsperioden) i vanlig kronologisk ordning

medeltemperaturökningen

t(ENERGI)          = 6[1-1/(1+[x/10]^4)]

 

t(ENERGI)              = (1.765)[1–1/(1+[(ÅR–1815)/212.7]^4)]

 

— ÅR i antal år tidigast från ca 1815 (havsperioden från lägst 1860) och t i °C från NASA-referensnivån –0,4°C.

ythavsperioden

t(PERIODythav) = 0.222(0.9[(2cos pi x/1.48) + 0.5(cos 3pi[x-0.1]/1.48)])

 

t(PERIODythav)      = –0.4 + 0.222(0.9[(2cos pi (ÅR–1880)/31.48)+0.5(cos 3pi[ÅR–1880-0.1]/31.48)])/3.4

 

— ÅR i antal år tidigast från ca 1880 och t i °C från NASA-referensnivån –0,4°C.

kolutsläppet

m(ENERGI)         = 6[1-1/(1+[x/10]^4)] = t(ENERGI)(10.17094 T12 KG/°C)

 

m(ENERGI)             = (1.765)[1–1/(1+[(ÅR–1815)/212.7]^4)](10.17094 T12 KG)

 

— ÅR i antal år tidigast från 1815 med m i KG.

koldioxidhalten

C                     = 0.74[(x/5.7)^4.25], atmosfärens koldioxidhalt

 

C                           = (12.7576)[([År-1815]/121.41)^4.25], i ppmv (n t6 = n miljondelar)

 

— ÅR i antal år tidigast från 1815 med C i ppmv av totala atmosfärens volym.

 

m Global Fossil Carbon-kurvan t NASA-temperaturkurvan E energikurvan för t C integralkurvan för E [ref. Carbon Dioxide Concentration]

se även t(PERIODythav)

 

 

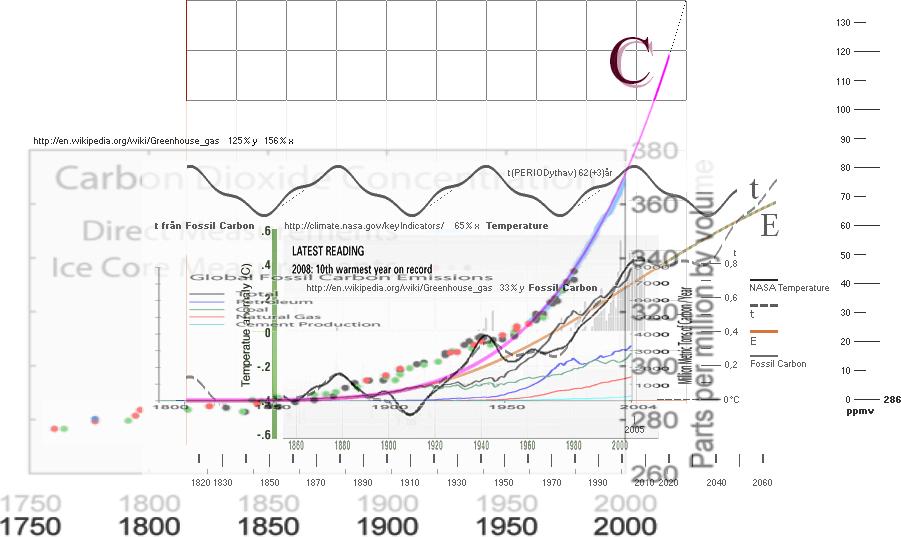
Upptäckt | Rättad felskrivning 2009-12-21: Föregående 125%x 156%y ändrat till 125%y 156%x från originalets Carbon Dioxide Concentration (separat metrisk kontroll i OpenOffice certifierar att ändringen ger identiskt resultat med ovanstående bild — kontrollerat genom överlagda bilder).

 

omvandlingsfaktorer

Tusentalsskalan Million Metric Tons of Carbon/Year i Global Fossil Carbon-kurvan ger motsvarande entalssiffror i T12 KG infört Kol (T för 10^+);

Omvandlingsfaktorn mellan Kol till Koldioxid ges av faktorn 44/12 = 11/3 » 3,67 (atomvikten för CO2 vs Kol):

m(CO2) = m(C)·(3,67)

NOTERING. Kolemissionen ger den årliga kolemissionen, inte den totalt samlade, för den sistnämnda se C.

 

Omvandlingen från ppmm (PartsPerMillionByMass) till ppmv (PartsPerMillionByVolume) ges via 44/28,8 » 1,528, medelatomvikterna för koldioxid (44) och luft (28,8),

CO2(ppmm) = CO2(ppmv)·(1,528)

Källreferens med utförliga räkneexempel: Se PUBLIC SERVICES HOME PAGE [http://www.mb-soft.com/public3/disaster.html]

 

Jordatmosfärens totalmassa grovberäknas [vi frånser alla berg och högre landområden] ur normaltrycket vid havsytan

p=1atm=101325Pa=F/A=Mg/A; g=9,81 M/S², A=4piR², medelRekv.pol=ca637mil=6,37 T6 M, T för 10^+;

M  = pA/g = ca 5,3 T18 KG

 

C-mätkurvan avviker märkbart från ideala C-kurvan (E-kurvans integral) med början från ca 1860 upp till 1940|1960. Först från ca 1960 ges med integralkurvan analoga ppmv-värden.

— Den i princip linjära ökningen 1860-1940|1960, och förutsatt inga systematiska mätfel finns, kan veterligt bara förklaras med inverkan från havet: det finns tydligen ett växelspel mellan hav och atmosfär som uppenbarligen inbegriper både emission och absorption av kolmassa med referens till början av t(ENERGI)-kurvans märkbara uppsats omkring ca 1860. I annat fall kan C-mätkurvans linjära stigning knappast förklaras.

— En linjär stegring från 1860 skulle normalt sett motsvaras av en konstant t(ENERGI)-nivå under samma period, tangens ca 0,5.

— Havsabsorptionen-emissionen (tillsammans med den egentliga kolemissionen, som dock i början är helt försumbar mot havsbidraget från 1860) har tydligen ”parkerat” på en konstant kolemission under perioden 1860-1940|1960, och som tydligen också överlappar den annars förväntade avvikelsen i t-kurvans energibas från ca 1918.

— Eftersom någon motsvarande variation inte går att se i [t(ENERGI)+t(PERIODythav)]-kurvan, som till exempel en plötslig nivåhöjning direkt och abrupt omkring 1860, är det tydligt att hela dynamiken ligger utanför det rent atmosfäriska mät- och observationsområdet — och som därmed orsaksmässigt och tydligen är att finna förklaringen till i havsytans (in till ett visst närdjup) växelverkan med atmosfären.

— Den dynamiken struntar tydligen helt i avbräcket för kolemissionerna från ca 1918: C-gradienten bara fortsätter, rakt upp till 1940|1960, som om inget hänt. Tydligen bara något STORT och TUNGT kan åstadkomma en sådan kraftfysik, knappast något annat än havet, och då tydligen på den uppkomna värmeinduktionens dynamiska bas: havets initiella uppvärmning fram till avbrottet runt 1918.

 

I vilket fall är data för kolemissionerna och koldioxidhalterna DÄRMED samstämmiga: upptakten ges tydligt från ca 1860. Därmed råder heller inte längre något som helst tvivel om att det är de fossila kolemissionerna som bär ansvaret för temperaturökningen. Alla kurvor mtEC följer ur varandra och sammanhänger med grund i energihärledningen.

 

 

Carbon Dioxide Concentration-kurvan

http://en.wikipedia.org/wiki/Greenhouse_gas

 

 

 

 

Integralkurvan för E

 

 

                             INTEGRALKURVAN FÖR E

 

Integralkurvan för det globala kolutsläppet — GLOBALA UPPVÄRMNINGSENERGINS INTEGRALKURVA

Se även INTEGRALKURVAN I PRAKTIKEN.

 

Från sammanställningen av mtEC-kurvorna med C-kurvan explicit som idealformen för atmosfärens koldioxidhalt

 

Sammanfattning

 

 

Integralkurvan till t(ENERGI)

y = 6[1-1/(1+[x/10]^4)]  .................... t(ENERGI)-integranden

kan ersättas approximativt (t.o.m. x=10 motsv. ca år 2028) med

y = 0.85[(x/6)^4.4] | y = 0.74[(x/5.7)'4.25]

 

Det har visat sig nära OMÖJLIGT att få fram t(ENERGI)-integralkurvan med hjälp av OnLineWebbIntegrallösare.

Ingen av de tre referenskällorna (se nedan) ger relevant resultat.

 

— y-formen har utprovats optimalt via separat numerisk lösning av diskreta punktvärden för t(ENERGI)-integranden.

— Felmarginalen i approximationskurvan täcks av Carbon Dioxide Concentration-grafen, tjockleken på presentationsgrafen över C.

 

 

beskrivning

Samband:

6[1–1/(1+[x/10]^4)] = 6[1–(10^4)/(10^4 + x^4)]

6(òdx – a4ò[a4+x4]–1 dx) = 6(x – a4ò[a4+x4]–1 dx)            

— Vi söker först lösningar via allmän bibliotekslitteratur (stadsbibliotek) samt till jämförelse webbens OnLineIntegralLösare [vi söker då enklast på integranden 1/(a^4 + x^4), resten görs manuellt].

 

 

integrand 6[1-1/(1+[x/10]^4)]

 

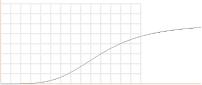
Gråmarkerat fält betyder att ekvationsdelen saknar praktisk grafisk betydelse (ingen skillnad syns med|utan)

 

1. MATHEMATICAL HANDBOOK McGraw-Hill 1968 s936No94

ò (a4+x4)–1 dx    = (4a3Ö2)–1 ln([a2 + axÖ2 + x2]/[a2 – axÖ2 + x2]) + (2a3Ö2)–1 · atan([axÖ2]/[a2 – x2])

(10'4)(0.000177·ln[(100+14x+x'2)/(100–14x+x'2)]+[0.00035atan(14x/[100–x'2])])

; x– ger

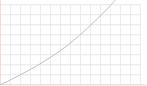
Kurvformen stämmer inte. Något är fel. Ännu värre med 6[.

 

2. WolframMath

http://integrals.wolfram.com/index.jsp

 

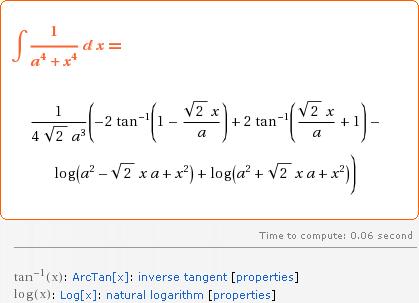
ò (a4+x4)–1 dx    = (4a3Ö2)–1( ln([a2 + axÖ2 + x2]/[a2 – axÖ2 + x2]) + 2atan[1 + a–1xÖ2] – 2atan[1 – a–1xÖ2])

1.77[ln[(100+14x+x'2)/(100–14x+x'2)]+[2atan(1+0.14x)]–[2atan(1–0.14x)]], multiplicerad med 10^4

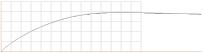
; x– ger

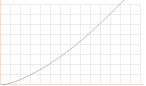
Bättre än MH, men fortfarande (gruvligt) fel. Ännu värre med 6[.

 

3. The Number Empire

http://www.numberempire.com/integralcalculator.php

The Number Empire — © 2006-2008 Vitalii Vanovschi

ò (a4+x4)–1 dx    = (Ö2)[ln([a2 + axÖ2 + x2]/[a2 – axÖ2 + x2]) + 2atan[1 + 2x/aÖ2] – 2atan[–1 + 2x/aÖ2]]/8a3

felformulerad i källan, – 2atan[–1 + 2x/aÖ2] ska vara – 2atan[1 – 2x/aÖ2]

ger då samma resultat som Wolframresultatet ovan,

1.77[ln[(100+14x+x'2)/(100–14x+x'2)]+[2atan(1+x/7)]–[2atan(1-x/7)]], multiplicerad med 10^4

annars helt galet

förminskad skärmdump av källans originalresultat:

 

 

Notera NumberEmpire:s felskrivning, … 2x– i slutet ska vara –2x … OM resultatet ska vara lika WolframMath.

— Generellt (min erfarenhet):

— OnLineIntegralLösare är AVANCERADE verktyg (maskinlösningar som kollas på olika internationella preferensdatorer, samt korsreferenser och i en del fall statistik [och iteration]). Men avancerat är också integralkalkylen som ämnesområde (inte allt som glimmar är guld).

— »I allmänhet» ges korrekta OnLineResultat. Men i särskilda fall, som här, har det tydligen kackat sig rejält: ingen av OnLineLösarna klarar uppgiften (ännu Oktober 2009, om jag själv inte missat någon detalj: gudarna ska veta att det har hänt det också).

— Ursäkta: Var noga med att pröva resultaten på ENKLA grundbegrepp — kolla derivator och ytor först med enkel huvudräkning. På den vägen: Ovanstående stämmer INTE. Lösning, se nedan.

 

Korrekt grafisk form

Korrekt grafisk form är approximationen (till x=10) kring

y = 0.74[(x/5.7)^4.25]

 

 

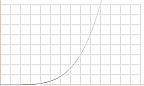
Grovformen fås genom att »gå tillbaka till barnstadiet»: räkna först ytenheterna för integrandkurvan

y = 6[1-1/(1+[x/10]^4)]

antingen genom huvudräkning eller mera exakt med finrutindelning och manuell räkning, pricka in de ungefärliga ytvärdena för varje x-värde, efterkolla kurvan med motsvarande tangensvärden (integrandkurvans y-värde).

(En van kurvlösare grovutför dessa beräkningar direkt i huvudet).

— I efterhand kan olika verktyg för numerisk integrallösning användas, typ Simpsons Formel (eller en mera rudimentär »hyposerie», men det kräver ett masterprogram typ Delphi där man kan skriva egen programkod).

— När tillräckligt antal värdepunkter prickats in, används ett grafritande program (tillsammans med en van person som kan hantera kurvmatematiken) för att söka en närmaste approximation som kan användas.

 

Editor2009X16

Integralkurvan i praktiken

2009-12-21 — INTEGRALKURVAN I PRAKTIKEN

Jämförande tabellvärden från AGW-bevisets teoretiska matematik med uppmätta koldioxidhalter från US South Pole Research

 

EXEMPEL:

År 1970 var totala kolutsläppet (Fossil Carbon Emission) ca

m = 4,18 T12 KG (drygt 4000 billion metric tons) enligt t(ENERGI)-kurvan, vilket motsvarar det statistiskt givna globala utsläppsvärdet (avläsning kan göras direkt på Fossil Carbon-kurvan i Wikipedia, eller se tabellen nedan för år 1970).

Tabelldatat i ppmm från US South Pole Research anger

CO2ppmv(1970) = 324,32; uppmätt värde 1970

CO2-integralvärdet (se sambandet nedan) från AGW-beviset ger

CO2ppmv(1970) = 322,02; beräknat värde 1970 enligt AGW-beviset

Förhållandet AGW-beviset/SouthPoleData ger 0,993.

 

För att beräkna den samlade (ackumulerade) koldioxidmängden (idealt) via uppgifterna från kolutförseln, analogt och idealt via t(ENERGI)-kurvan (original) måste t(ENERGI)-kurvans integral användas. Denna är emellertid (t.o.m.) SÅ besvärlig att även etablerade referenser uppvisar svårigheter att få ihop det med kurvformen (jag har tre källor, alla uppvisar sin version, ingen stämmer, se från Integralkurvan för E). Inom ett begränsat intervall (minst upp till år 2015) kan man (lyckligtvis) använda en starkt förenklad matematisk form — dock utan att tulla på den grafiska precisionen alltför mycket enligt (samma pixelUnit50),

 

y = 0.74[(x/5.7)^4.25]

 

y-formen har utprovats optimalt via separat numerisk lösning av diskreta punktvärden (separat programrutin från integranden 6[1-1/(1+[x/10]^4)], här utan redovisning) för t(ENERGI)-integranden.

(Felmarginalen täcks av Carbon Dioxide Concentration-presentationsgrafens tjocklek — vissa justeringsmarginaler finns beroende på havsytans minsta [marginal-]offset på ca 5 år, se citat från FOCUS MATERIEN med vidare).

Vi behöver dock först skalanpassa sambandsformen;

 

C-integralens anpassning för tidsanaloga värden

Från de första preliminära (grova [125%y]) grafiska jämförelserna (här utan vidare referenser):

(2,9pixels)/ppmv = 377/130; 50/2,9=17,241379ppmv/Unit

x offseträknas från 1815, samma som t(ENERGI)-offset:en, men mera praktiskt/egentligt från 1860, se Carbon Dioxide Concentration-kurvan.

xUnit50 (2,35p/år) 50/2,35 = 21,276595år » 21,3

 

Från referensnivån år 1860 ([grovt] 268ppmv) och y-formen ovan ges

C        = (17.24)(0.74)[([År-1815]/5.7/21.3)^4.25]

        = (12.7576)[([År-1815]/121.41)^4.25] ......................  C-integralens tidsanaloga värde (till max år 2030)

 

Med denna form ges nedanstående tabellvärden till jämförelse med uppmätta CO2-halter, se även efterföljande tabellens förklaringar till respektive kolumner.

 

Tabellvärden med koldioxidhalter (CO2) i jämförelse för kontroll av AGW-bevisets numeriska precision

Värdena i kolumn7 från C-sambandet (ovan) till jämförelse med de uppmätta koldioxidhalterna (US South Pole Research, se länk efter tabellen).

Överensstämmelsen understryker den integrala samhörigheten mellan mätvärden och teoretiskt beräknade dito från AGW-beviset.

 

 

mätvärden

t(AGW)

kol6/kol2

AGW-beviset

kol7/kol3

År

CO2ppmv

T9tonCO2

t°C

num

CO2ppmv

T9tonCO2

num

1

2

3

4

5

6

7

8

1900

296,00

2324

0,04

0,976

288,80

2324,14

1,000

—

 

 

 

 

 

 

 

1958

314,78

2472

0,30

0,990

311,58

2507,42

1,014

1959

315,64

2479

0,31

0,990

312,35

2513,60

1,014

1960

316,45

2485

0,31

0,990

313,13

2519,93

1,014

1961

317,08

2490

0,32

0,990

313,94

2526,40

1,015

1962

317,62

2494

0,33

0,991

314,76

2533,02

1,016

1963

318,35

2500

0,34

0,991

315,60

2539,79

1,016

1964

318,68

2503

0,34

0,993

316,46

2546,70

1,017

1965

319,42

2509

0,35

0,993

317,34

2553,77

1,018

1966

320,72

2519

0,36

0,992

318,24

2561,00

1,017

1967

321,32

2524

0,37

0,993

319,15

2568,38

1,018

1968

321,91

2529

0,37

0,994

320,09

2575,92

1,019

1969

323,12

2538

0,38

0,994

321,05

2583,62

1,018

1970

324,32

2547

0,39

0,993

322,02

2591,48

1,017

1971

325,12

2553

0,40

0,994

323,02

2599,52

1,018

1972

326,00

2560

0,40

0,994

324,04

2607,72

1,019

1973

327,62

2573

0,41

0,992

325,08

2616,09

1,017

1974

328,49

2580

0,42

0,993

326,14

2624,64

1,017

1975

329,50

2588

0,43

0,993

327,23

2633,36

1,018

1976

330,60

2597

0,44

0,993

328,33

2642,27

1,017

1977

332,03

2608

0,44

0,992

329,46

2651,35

1,017

1978

333,69

2621

0,45

0,991

330,62

2660,62

1,015

1979

335,03

2631

0,46

0,990

331,79

2670,07

1,015

1980

336,98

2646

0,47

0,988

332,99

2679,72

1,013

1981

338,26

2656

0,48

0,988

334,21

2689,56

1,013

1982

339,39

2665

0,49

0,988

335,46

2699,59

1,013

1983

341,17

2679

0,49

0,987

336,73

2709,81

1,012

1984

342,58

2690

0,50

0,987

338,02

2720,24

1,011

1985

343,82

2700

0,51

0,987

339,35

2730,87

1,011

1986

345,32

2712

0,52

0,987

340,69

2741,71

1,011

1987

346,99

2725

0,53

0,986

342,06

2752,75

1,010

1988

348,95

2740

0,54

0,984

343,46

2764,01

1,009

1989

350,44

2752

0,55

0,984

344,89

2775,47

1,009

1990

351,77

2762

0,55

0,985

346,34

2787,16

1,009

1991

353,12

2773

0,56

0,985

347,82

2799,06

1,009

1992

354,24

2782

0,57

0,986

349,32

2811,18

1,010

1993

355,16

2789

0,58

0,988

350,86

2823,53

1,012

1994

356,48

2799

0,59

0,989

352,42

2836,11

1,013

1995

358,35

2815

0,60

0,988

354,01

2848,92

1,012

1996

359,99

2828

0,61

0,988

355,63

2861,96

1,012

1997

361,20

2837

0,62

0,989

357,28

2875,23

1,013

1998

363,62

2856

0,62

0,987

358,96

2888,75

1,011

1999

365,56

2871

0,63

0,987

360,67

2902,51

1,011

2000

366,80

2881

0,64

0,988

362,41

2916,51

1,012

2001

368,39

2893

0,65

0,989

364,18

2930,76

1,013

2002

370,49

2910

0,66

0,988

365,99

2945,26

1,012

2003

372,80

2928

0,67

0,987

367,82

2960,02

1,011

2004

374,77

2944

0,68

0,986

369,69

2975,04

1,011

2005

376,51

2957

0,69

0,987

371,58

2990,31

1,011

2006

378,48

2973

0,70

0,987

373,51

3005,85

1,011

2007

381,00

2993

0,70

0,986

375,48

3021,65

1,010

2008

383,00

3008

0,71

0,986

377,48

3037,73

1,010

2009

385,00

3023

0,72

0,986

379,51

3054,07

1,010

1

2

3

4

5

6

7

8

 

tabellförklaringar — CO2 för koldioxid (kem. CO2)

kolumn:                                                                                       

1          År

2          South Pole Concentration, CO2 (ppm)

3          Total Mass of Carbon Dioxide in the Earth's Atmosphere Billions Metric Tons, T9tonCO2, T för 10^+

4          t(AGW), °C

5          kolumn6/kolumn2, numeriskt förhållande

6          AGWberäknat vs kolumn2, CO2ppmv

7          AGW-CO2-beräknat vs kolumn3 enligt (värdet i kolumn 6 = C):
[JordAtmosfärensMassa·C·(t6)(1,528)/(T12)], T9tonCO2, se även EXEMPEL ovan,
= (» 5,27 T18)C(t18)(1,528), T9tonCO2
= C(» 5,27)(1,528), T9tonCO2
» C(8,0475), T9tonCO2, T för 10^+

8          kolumn7/kolumn3, numeriskt förhållande

 

Jämförelsetabell med kolumnerna 2 och 3 från US SOUTH POLE RESEARCH enligt

http://www.mb-soft.com/public3/disaster.html

PUBLIC SERVICES HOME PAGE, se även kolumnförklaringen ovan.

 

Relationsvärdena (frånsett året 1900 som i webbkällan är angivet som en uppskattning; 97,6%) understiger tydligen inte 98% — vilket i princip betyder att överensstämmelsen kan tolkas som en ren fullträff.

 

 

Koldioxid, vatten och atmosfär

 

 

Oktober 2009

Den globala uppvärmningens mekanismer

Koldioxidens vattenlösning

och

Atmosfärens värmebevarande funktion

 

KLIMATKOMPLEXET har uppdagat många olika aspekter som NORMALT SETT ligger (skyhögt) ovanför lekmannens område. Men angelägenheten har tvingat fram frågor från oroliga, vanliga, människor och som kräver verkliga, djupgående, svar. Vi får inte dra oss undan den uppgiften, alla som tror sig kunna ge NÅGOT bidrag. Följande är ett försök till en allmän sammanställning med ett mera samlat grepp på de grundtermer och deras sammanhang som har framkommit och kan utläsas ur mtEC-kurvorna — massa-temperatur-energi-koldioxid-kurvorna — samt med dessa sammanhängande vidare referenser (anges särskilt i den följande huvudtexten).

— Ändamålet: att (någotsånär) förstå — inkludera fattningen på varför det förekommer felformuleringar i — grundmekanismerna i den globala uppvärmningen.

 

 

 

Koldioxidens vattenlösning

2009X18

Koldioxidens vattenlösning

Hur kolutsläppet från fossilförbränningen triggar och överför värmebeloppet till NASA-temperaturkurvans luftmarina lokaler havsyta och atmosfär

 

 

 

Det finns TVÅ sätt:

 

1. koldioxidens egen särskilda KEMISKA lösbarhet i VATTEN

2. koldioxidens särskilda BIOKEMISKA upptagning av HAVSPLANKTON

 

I det första fallet vet man att koldioxidens vattenlösbarhet, alltså vattnets förmåga att ta upp koldioxid ur luften, ökar med LÄGRE temperatur: kallare vatten tar upp mera koldioxid än varmare vatten.

— Speciellt kring Jordens polområden är därför också vattenupptaget av koldioxid särskilt stor. När sedan det vattnet transporteras med oceanströmmarna neråt varmare breddgrader och åter når ytan genom strömningsvägarna, kan koldioxid frigöras vid havsytan. Man har givit den processen namnet ”the physical pump”, »fysikpumpen»,

 

ref.

http://oceanworld.tamu.edu/resources/oceanography-book/oceansandclimate.htm

Department of Oceanography, Texas A&M University, Robert R. Stewart 4Aug2009

Our Ocean Planet

 

I det andra fallet ingår koldioxidupptagningen i havsytan naturligt genom fotosyntesen. Havsalger tar upp koldioxiden ur luften och producerar (det mesta av) det globala syret (pytoplankton ca 50%, se ref. nedan). Hur mycket som tas upp kan bero på (och beror på) flera faktorer såsom temperatur, salthalt och hur planktontillväxten gynnas,

 

ref.

@INTERNET Wikipedia 2009-10-18 Phytoplankton

 

havsytans koldioxidabsorption

50% 33% 25% …

Olika etablerade webbkällor anger olika värden för havsytans koldioxidupptagning (underförstått av havsplankton):

 

25%:

”Of all the carbon dioxide (CO2) emitted into the atmosphere, one quarter is taken up by land plants, another quarter by the oceans.”,

http://harvardmagazine.com/2002/11/the-ocean-carbon-cycle.html

The Ocean Carbon Cycle, 2002

Alla:

”We now know that in that year (2000), human activities CREATED and EMITTED 25.29 billion tons of carbon dioxide. From the table above of the analysis of the South Pole data, we know that 9.66 billion tons of carbon dioxide actually became ADDED TO the atmosphere that year. This might imply that during THAT YEAR 15.63 billion tons of carbon dioxide (the difference) might have gotten absorbed into the oceans. Other years are sometimes very different from that, and it appears that in some years (like 1980 and 1988) the oceans may have RELEASED carbon dioxide. [The measured increase in the atmosphere in those years appeared to be LARGER than the amounts we had created by fossil fuel burning.] However, such differences could also be due to natural variations in the Carbon Cycle if weather patterns caused plants to either flourish or suffer that year. Much more research and study is necessary in those fields.”,

http://www.mb-soft.com/public3/disaster.html

C Johnson, Chicago University (2007-) 2009;

33%:

”Presently, about one third (approximately 2 Gt C y-1)[3][4] of anthropogenic emissions of CO2 are believed to be entering the ocean.”,

@INTERNET Wikipedia 2009-10-03 Biological pump, Anthropogenic changes

50%:

”Almost exactly half of the carbon dioxide put into the air by our burning of fossil fuels is absorbed by the ocean. Carbon dioxide dissolves in cold water near the Arctic and Antarctic. When the cold water sinks deep into the ocean in winter, it carries the carbon dioxide away from the atmosphere. Many years later, the water is gradually pulled closer to the sea surface by mixing in the ocean. When it gets to the surface in warm areas it releases the carbon dioxide back to the air. This process allows the ocean to store great quantities of carbon dioxide for many centuries. We call this the physical pump that takes carbon dioxide out of the air.”,

http://oceanworld.tamu.edu/resources/oceanography-book/oceansandclimate.htm

Department of Oceanography, Texas A&M University, Robert R. Stewart 4Aug2009

Our Ocean Planet

50%:

”Oceans absorb half of all human carbon emissions, but the Southern Ocean is taking up less and less and is reaching its saturation point, reported an international research team in the journal Science.”,

http://ipsnews.net/news.asp?idnews=37774

IPS Inter Press Service NEWS AGENCY — 3 October 2009

ENVIRONMENT — Southern Ocean Nears CO2 Saturation Point, Stephen Leahy

 

 

Flera (många) författare understryker också den (beklämmande) bristen på mera exakt kunskap om växelspelet atmosfär-havsyta: mycket forskning behövs på området, inte mycket är känt (ännu Oktober 2009).

— Observera att temperaturändringarna i NASA-kurvan handlar om små marginaler: några tiondels grader bara.

 

Huvudsaken

Ur ovanstående grunddata framträder alltså (enkelt) grundprincipen:

 

— När kolet från fossilförbränningen kommer ut i atmosfären och bildar koldioxid samlar det sig med fördel nära marken i olika stråk,

 

ref.

Wikipedia Carbon dioxide, In the Earth's atmosphere,

”especially near the ground.”.

 

— Jordytan består till ca 71% av hav och 29% land (se nedanstående referenser); Vindarna för ut koncentrationerna till havet, havet (plankton) absorberar koldioxiden. Värmefaktorn från fossilförbränningen (T) tillsammans med den del som Solinstrålningen åstadkommer (SER) bildar en extra värmefaktor som överförs mer eller mindre direkt till havsytan genom dess koldioxidabsorption.

 

ref.

http://ecology.com/features/mostimportantorganism/

Ecology — Global Network,

”It is estimated that between 70% and 80% of the oxygen in the atmosphere is produced by marine plants.”,

”the oceans cover about 71% of this planet and land is only about 29%”;

http://en.wikipedia.org/wiki/Earth

@INTERNET Wikipedia 2009-10-20 Earth,

”About 71% of the surface is covered with salt-water oceans, the remainder consisting of continents and islands”.

 

 

— Därmed har värmefaktorn spritts också generellt till havsytans vattenbank.

 

— Genom naturlig avdunstning bildar vattnet en naturlig KLIMATFAKTOR: värmetillskottet (t), överfört från den extra koldioxiden till hela atmosfären via havet och vattnets avdunstning genom Solens inverkan, integreras med atmosfären i avdunstning-nederbörd.

 

— Eftersom vatten (vattenånga, 2,080) har en betydligt högre värmekapacitivitet än koldioxid (0,839) [se tabell eng. Wikipedia Specific heat capacity],

bevaras också (därmed) t-delen från T (se energihärledningen) mera effektivt via den så havsöverförda transiteringen.

 

— Den överförda värmefaktorn, från T i fossilförbränningen till havsytan och sedan därifrån till atmosfären via vattnet, kan alltså förstås driva även värmeisolationskoefficienten a (-medelvärdet ytterligare) mot 1.

 

— Den globala temperaturökningen från fossilförbränningen kan då tydligen förstås som att koldioxiden som enskild faktor INTE DIREKT spelar huvudrollen — men verkställer den i läge ON.

 

— Det ser (nämligen) ut som att en del frågeställningar I ETABLERADE KORRIDORER i ämnet tycks ha fastnat på just den detaljen, och som lett till (starkt) polariserade dispyter (med garanterat hopplös utgång: ”inget vet”).

 

— Koldioxiden TRIGGAR hela processen, samt underhåller den till viss del: den värmefaktor som koldioxiden påförs, DELS från fossilförbränningen (T) och DELS från Solinstrålningen, transporteras vidare till havsytan genom havets koldioxidabsorption — och därifrån till atmosfären via vattnets avdunstning.

Bevis:

— Vi kan se det tydligt i mtEC-kurvorna genom att t(PERIODythav) — polaroceanernas ytvattenscykel med en varm och en kall på ca 62 år från ca år 1880 — följer med i t-kurvans energilopp baserad på kolutsläppet (Fossil Carbon): enda möjligheten för t att lyfta (få MED) t(PERIODythav) med resultat i t(NASA)-kurvan är att t(PERIODythav) tydligen ”andas” med t, och den andningen har bara koldioxidens växelverkan med havet — t(PERIODythav), polaroceanerna — att falla tillbaka på.

 

— Huvudrollen spelas då, om allt är korrekt uppfattat, i själva verket av vattnet; havet och Solen genom vattnets avdunstning; havets förmåga att suga upp av människan extra införd värmebaserad (T) koldioxid från fossilförbränningar och därmed värmetransiteringen till havsytan, och sedan därifrån vattnets avdunstning, och därmed en klimatfaktor.

 

— Observera som tidigare att det rör sig om ca 0,7°C på runt 100 år — extremt små förändringar som vi vanligtvis ”helt struntar i”: 0,007°C per år, helt omöjligt att se eller upptäcka utom i ett längre lopp. Nu, runt 2009, kan man säga att Mänskligheten blev tagen på sängen (men det fanns redan röster som varnade för den utvecklingen från ruta ett).

 

— Det är i allt den övergripande förklaring som tydligen framgår i summan av mtEC-kurvorna och deras referenser.

Se även vidare mera utförligt från energihärledningen.

 

 

 

Atmosfärens värmebevarande funktion

2009X18

Atmosfärens värmebevarande funktion

VÄXTHUSEFFEKTEN — ang. att värmestrålning kan kvarstanna hos OCH SLIPPA IGENOM luftmolekyler

 

 

 

Klimatkomplexets innehåll beträffande LJUSETS ELEKTROMAGNETISKA SPEKTRUM distanserar LÄTT lekmannen från experten: spektralfysiken är gruvligt omfattande och innehåller många komplicerade förgreningar som kräver avancerad matematik för att (rätt) begripas. Om lekmannen kan ha överseende med den översiktliga beskrivningen, och med ett minimum av matematisk fysik av den enklare typen, kan hela ämnet (möjligen) beskrivas hyfsat begripligt enligt följande.

 

— När Planckenergin (E=hf) i Solljuset med frekvensen eller ”ljustonen” f enligt redan välkända begrepp tränger ner genom Jordatmosfären, uppdelas, sprids eller fragmenterar f i lägre frekvenser (jämför även Comptoneffekten) motsvarande (utan effektförluster) energiekvivalenten E=hf=n·h(f/n), n antalet uppdelningar.

 

— Atmosfärens luftmolekyler (inte alla) har just en viss förmåga att ABSORBERA låga f och släppa igenom höga f, det som vi kallar för ett materials (en gas) värmeisolation.

— Luftmolekylerna kan göra det genom att de består av flera atomer med motsvarande s.k. frihetsgrader: en molekyl kan rotera, bumpa som en fjäder, vibrera, och kombinera en mängd olika sådana tillstånd, dock inom ett begränsat (lägre) energiintervall. Varje frihetsgrad kräver sin energi. Den energin tas (bl.a.) från värmestrålning.

— Vi säger att atmosfären (med avseende på den och den molekylsammansättningen) har ”filtfunktion”, dvs. är värmeisolerande; den släpper inte så lätt ifrån sig den upptagna energin.

— Med atmosfärens värmeisolerande materialegenskap, blir det med andra ord inte lika lätt för en enskild f/n att komma tillbaka ut i rymden som för en ren f: luftmolekylerna (vissa, inte alla, och dessutom i olika spektrala intervall) absorberar och emitterar med tidsfördröjning, mera med f/n än f, och därmed en motsvarande något högre värmegrad nära Jordytan.

 

— Analogin till att man sveper en filt omkring sig är nära exakt: värmen närmast utanför huden ökar något, inte därför att kroppen producerar mera värme utan för att filten hindrar det normala värmeflödet från att läcka ut så att värmen stannar kvar längre och därmed ”tidspackning”.

 

— Normalt sett bildar atmosfären ett jämviktstillstånd med Solinstrålning (hf) och tillbakareflexion

[n·h(f/n)] med den senare fördröjd genom ”filtfunktionen”.

 

— I DEN NATURLIGA nettoverkan etableras med ovan beskrivna fysik en viss normaliserad global årsmedeltemperatur taget över längre perioder där balansen mellan SolIN och SolUT blir exakt (här används Tglobal=15°C baserat på medelvärden under 1900-talet). Den jämvikten motsvarar alltså den naturliga balansen där biosfärens gasflöden koldioxid-syre återkopplas ömsesidigt genom naturlig återväxt.

— Den utgående delen i den solära instrålnings-reflexionsmekanismen, alltså den som kan ses ekvivalent termiskt från Jordytan och utåt mot rymden, refereras f.ö. till i den här presentationen som »Solekvivalenta radiansen» (SER).

 

Global uppvärmning

— Införs EN SÅDAN extra luftmolekylmassa (TYP kol, som bildar koldioxid) SOM HAR VÄRMEISOLERANDE FUNKTION, läggs naturligtvis den adderande till normalfunktionen, och man finner följdriktigt en (marginellt) högre värmegrad totalt — i verkan tillsammans med HAVET och Solens förmåga att avdunsta havsytan. Se föregående från Koldioxidens vattenlösning.

— Vårt problem just nu (Oktober 2009) är hur balansen ska kunna återställas — vi vill gärna fortsätta leva på Jorden. Det finns starka skäl för att återkomma till den aspekten längre fram.

 

Naturen hjälper oss med termiska fönster

— Flera webbkällor redovisar mera ingående spektrala molekyldata på de olika luftmolekylernas förmåga att absorbera em-strålning med vissa våglängder.

— Den (lekman) som vill försöka sig på att GISSA hur det fungerar, gör sig knappast besväret eftersom vissa absorptioner för vissa molekyler t.o.m. uppvisar SPEKTRALA HÅL (regelrätta strålningssåll) som medger att viss (värmestrålning) kan slinka igenom medan annan absorberas effektivt.

— På den grunden finns (vissa) uppgifter som visar hur naturen ”hjälper människan” genom att servera ett naturligt primärt TERMISKT FÖNSTER;

 

ref.

http://acmg.seas.harvard.edu/people/faculty/djj/book/bookchap7.html

Harvard University, updated October 2009,

”This atmospheric window allows direct escape of radiation from the surface of the Earth to space and is of great importance for defining the temperature of the Earth's surface.”,

Min översättning:

Detta atmosfäriska fönster tillåter direkt utflöde för strålning från Jordytan till rymden och är av stor betydelse i definitionen av Jordytans temperatur.

 

— Typisk värmestrålning av samma art som den som ”läcker ut från köket” — alltså grovt sagt 30-90°C med motsvarande em-våglängder 8-9,6µM — går praktiskt taget rakt ut genom Jordatmosfären, direkt ut i den omgivande kalla rymden utan nämnvärd absorption av Jordatmosfären.

 

— Känner man temperaturen (eller våglängden) kan våglängden beräknas ur Wiens förskjutningslag (samma som Planckstrålningens toppvärde för den kroppen eller materialet, se även Plancks strålningslag),

l = (k=2,898 t3 M°K)/T, l i meter, T i °K (°C + 273).

 

— Fanns inte ett sådant termiskt fönster, skulle Jordytans nuvarande medeltemperatur (grovt 15°C) uppenbarligen sakna ”värmeventilation” och därmed, tydligen, stegras betydligt.

 

— Det betyder också att mänskligheten, i varje fall i princip, tryggt kan fortsätta bygga sina effektiva industrianläggningar och värmeverk så länge de är effektiva nog att uppvisa max atmosfärisk kontaktvärme inom intervallet 30-90°C — vilket också är precis vad de gör. No Problemo.

 

— Det garanterar att industrins värmebidrag till den naturliga biosfärens termodynamik i praktiken blir noll — även fortsättningsvis.

— Att döma av mtEC-kurvorna finns heller ingenting som tyder på ANNAT än att t (se utförligt från energihärledningen) entydigt har grundats på T från kol-olja-naturgasförbränningen. Inget annat. Det måste kännas tryggt att veta det, säkert, för framtiden.

 

— Enda haken i hela slutsumman är att 1. den fossila energiråvaran bakom all kraftproduktion behöver bytas ut, omgående, och 2. en effektiv dammsugning av atmosfären på koldioxid måste ske, också omgående.

 

— Idealet vore naturligtvis om Naturen hade begåvat mänskligheten med något Geni som kunde berätta hur man gör för att kombinera bägge, effektivt via någon mcc-teknik. Noll restprodukter. Ingen m-del att bilda t på. Jag vill tro på det, ända tills jag överbevisats om att det inte går, eller till sista andetaget. Därför att det är vad jag skulle göra om racerbilen vore min. Allt att vinna. Inget att förlora:

 

 

Editor2009X20.

Continued2009X27:

 

Lösningen ligger redan klar i startgroparna, väl förberedd:

 

 

 

 

— Illustrationen ovan kopplar till t(ENERGI) som beskriver styrfunktionskurvan för människans elektro-mekanisk-tekniska utveckling,

 

y = a[1–1/(1+[x/b]n)]

 

— Samtidigt med den tekniska utvecklingen under 1800- och 1900-talet har — tydligen — också utvecklats en POTENTIAL av följande kaliber — redan från ruta ett år 1820, märk väl:

 

 

— ’Vad orsakar blixturladdning?’

— ’Man vet mycket litet om blixturladdning’

— ’Man vet inte hur blixturladdning bildas’

— ’Man vet inte hur g-strålningen bildas’

— ’Det här var något vi absolut inte hade väntat oss’

Se även Tillägg31Aug2010 — Fermisatellit bekräftar TNED

 

 

Citatfraserna ovan i utdrag från Blixturladdningens fysik i modern vetenskap och akademi, från Kort resumé av blixturladdningens fysik.

 

 

Gnistbildningen [källorna nedan är delvis inte helt fullständiga] observerades [troligen] först av Joseph Henry år 1830 [Augusti] — på Henrys uppslag kom Michael Faraday år 1831 att [felaktigt] krediteras för upptäckten av den elektromotoriska induktionen; källor

Joseph Henry Biography,

http://www.madehow.com/inventorbios/75/Joseph-Henry.html;

Joseph Henry — Princeton University 1978,

http://etcweb.princeton.edu/CampusWWW/Companion/henry_joseph.html;

@INTERNET Wikipedia Joseph Henry 2009-10-26,

http://en.wikipedia.org/wiki/Joseph_Henry;

Enheten för induktans [1 Henry] uppkallades dock efter densamme Joseph Henry.

 

 

— Knappast någon fenomenform i mänsklighetens historia är så väldokumenterad, så spridd i tekniska tillämpningar — och så erkänt illa känd som gnistbildningens fysik, generellt blixturladdningens fysik. Citatfraserna ovan i utdrag från Blixturladdningens fysik i modern vetenskap och akademi, från Kort resumé av blixturladdningens fysik.

 

— Anledningen till att modern akademi lyckats hålla sig, väl, borta ifrån ämnet är, tydligen, dess i denna presentation så många gånger redan påtalade och säregna tilltag med att UPPFINNA fysiken, inte HÄRLEDA den (materiefysiken är utomordentligt väl representerad i modern akademi, medan massfysiken står helt orepresenterad). Se ingående från Atomkärnans härledning med utomordentlig tillämpad resultatexempelredovisning i atomvikterna. Resultaten visar att atomkärnan innefattar en sin egen strömfälla, och den energiräkningen innefattar tydligen blixturladdningens fysik tillsammans med svaren på ovanstående citatfraser, samt — tydligen — lösningen på hela energifrågan. Se utförligt från CAT (atomkärnans fullständiga upplösning).

— Vi ska inte säga att modern akademi hade FEL (den är [var] alldeles för YTLIG för det, då den inte ens kunnat närma sig frågeställningarna). Korrekt utsaga är (därför) att modern akademi HAR VISAT SIG VARA (är) PRIMITIV. Den innefattas, beskrivs och förklaras också som sådan i TNED. Ingenting kasseras, allt finns med. Allt förklaras.

 

— Modern akademi missade naturvetenskapens kronjuvel. Helt alldeles säkert.

 

— Middagen är, tydligen som det får förstås, serverad. Det enda som (ännu) fattas är middagsgästerna.

 

 

 

 

Tillägg 31AUG2010

 

31Aug2010

 

Fermisatellit bekräftar TNED — positronförekomster i samband med gammastrålning från blixturladdningar

 

Bekräftelse Nov2009

 

 

 

 

 

DISCLOSE.TV — Lightning’s gamma rays may destroy matter, Irene Klotz Nov2009

http://www.disclose.tv/forum/mystery-terrestrial-gamma-rays-may-destroy-matter-t12272.html

;

MICROSOFT NBC — Lightning’s gamma rays may destroy matter, Irene Klotz Nov2009

http://www.msnbc.msn.com/id/34114891/

;

DISCOVERY NEWS — Lightning Holds Fingerprint of Antimatter, Irene Klotz Nov2009

http://news.discovery.com/space/gamma-rays-lightning-antimatter.html

;

”A satellite dispatched to scout out high-energy gamma rays streaming from the cosmos found that not only were flashes of gamma rays oddly close to home, but they were also powerful enough to annihilate matter.”,

;

”Fermi's observations of terrestrial gamma rays have deepened the mystery. At least one of the flashes contain an unmistakable pattern of positrons — the antimatter counterpart of electrons.”,

;

”"It was a surprise, and now we have to explain it," said Fishman, who is working on a paper about the discovery with colleague Michael Briggs at the University of Alabama in Huntsville.”,

;

Min översättning:

En satellit utsänd för att fånga upp högenergetisk gammastrålning strömmande från kosmos fann att gammaflasharna inte bara återfanns besynnerligt nära hemma, utan också kraftfulla nog att annihilera materia.

Fermis observationer av Jordbaserad (terrestriell) gammastrålning har fördjupat mysteriet. Åtminstone en av flasharna innehåller ett omisskänneligt mönster av positroner — antimateriens motsvarighet till elektroner.

’Det var en överraskning, och nu måste vi förklara det,’ sade Fishman, som arbetar med en uppsats om upptäckten med kollegan Michael Briggs vid Universitetet i Alabama i Huntsville.

 

 

Se utförligt i BLIXTURLADDNINGENS FYSIK (Jun2008) samt ATOMKÄRNANS FULLSTÄNDIGA UPPLÖSNING (ATA/CAT Feb2008).

   [Genom att positronbilden är uppenbar i ämnet finns ingen återvändo; ingen möjlighet att framställningen bygger på missade eller feluppfattade preferenser. Däremot behövs mera preciserad information om RIKTNING och UTBREDNING — så att det säkert framgår att fenomenformen ansluter till just ATA/CAT enligt TNED. Det får inte finnas någon tvekan på den avgörande punkten; Själva fenomenbilden i stort måste stå helt klar innan vidare].

 

 

 

 

mtKorrektion

mt-korrektion

 

Korrektion för vertikalskalan till Global Fossil Carbon Emissions:

 

7 T12 KG

————————— = 10,17094 T12 KG/°C

0,6 + 0,1(1–2/17)]°C

 

— I den preliminära (grova) värdeformen användes omvandlingsfaktorn

m/t = 9,775 T12 KG/°C = (7,82 T12 KG)/(0,8 °C) mellan m(Fossil Carbon) och t(GW).

— Ett med Fossil Carbon-kurvans vertikala masskala (i tusental miljarder metriska ton, eng. billion metric tons) mera noggrant överensstämmande värde har i efterhand visat sig vara som ovan

m/t = 10,17094 T12 KG/°C = (7 T12 KG)/[0,6+0,1(1–2/17)]°C = 1,017094 T13 KG/°C.

Justeringen medför att beräkningen av föregående

M = 3,3843 T16 KG  ...............................         se Beräkningen av M

och

h = 51,3 M  ..............................................          se Beräkningen av h

blir större med

(10,17094)/(9,775) = 1,0405053

motsvarande

M = 3,52138 T16 KG

och

h = 53,35 M

 

Editor2009XII4

 

 

 

AGW-beviset

 2009XII22

AGW-beviset

AGW, från engelskans Anthropogenic Global Warmning, sv. Antropogen (av människan förorsakad) global uppvärmning

 

Se mera utförligt från Den globala uppvärmningen under 1900-talet

 

Enbart med utgångspunkt från den globalt uppmätta NASA-medeltemperaturkurvan och en elementär kännedom om kurvors matematiska/grafiska sammansättning och konstruktion (erfarenhetsgrundat, på samma sätt som böcker/musik per text/noter bara kan läsas/höras av införstådda), framgår grunden för en mera precis energiteknisk härledning: NASA-temperaturkurvan kan uppdelas i två komponenter, en periodisk del som tydligen ansluter till en naturlig (sammansatt) havsperiod (21 år resp. 62[+3] år) [förenklat t(PERIODythav)] och en energi-temperaturkurva [t(ENERGI), t(AGW)] som, tydligen, motsvarar vad det mycket värmetröga havet ser av det globala kolutsläppet (FossilCarbon-kurvan) via förbränningen av kol-olja-naturgas. Att den uppdelningen också stämmer med observationerna verifieras av att

t(AGW)-kurvans integral, motsvarande samma som kolutsläppens samlade summa, sammanfaller med de uppmätta koldioxidhalterna i CarbonDioxideConcentration-kurvan (vidare nedan). Med en sådan generöst överväldigande bevisgrund för samhörande värden — med referens till havets stora värmetröghet och det medelintervall på (minst) 5 år som krävs för havsytvattnets cirkulation taget i globala medelvärden — finns, här veterligt, ingen som helst möjlighet för något som helst minsta tvivel på att det är AGW som gäller. Med den förutsättningen, och endast så, och förutsatt inga felslut förekommer i härledningarna, finns uppenbarligen efter alla konstens regler ingen som helst naturvetenskaplig grund för AGW-skepticism — den är helt ogrundad (och också erkänt behäftad med många meningsfel). Hur bevisets detaljer sammanhänger inbördes beskrivs detaljerat i detta dokument från början. Se även i AGW-beviset komprimerat illustrerat nedan.

 

Varför omnämns inte beviset i etablerad litteratur?

 

Anledningen varför (det, så, förhållandevis enkla) AGW-beviset inte finns representerat i den etablerade litteraturen kan (med flera alternativ) bero på följande (enkla): Energihärledningen i AGW-beviset visar att den massa i den atmosfäriska genomströmningslokal som innefattas av den luftmarint uppmätta NASA-temperaturkurvan (förvånande) inte omfattar mer än grovt ca 50 meter (53,35 M) ovanför allt fast och flytande på Jordytan. Inte mer. Det är långt ifrån det allmänna troposfäriska höjdområde (grovt drygt en mil) som alla s.k. elementära klimatmodeller [1‡] brukar utgå ifrån — med tillhörande, integrerade, luftskiktssummerade värmestrålningskomponenter, komplicerat värre. Att sikta på hela troposfären i ljuset av (det mycket enkla) AGW-beviset blir alltså att sikta alldeles för högt och brett i en elementär energihärledning, samt därmed tillhörande strålningstekniska detaljer som inte alls ens ingår i AGW-beviset — men det enda alternativ som verkar finnas i etablerade kvarter och som diskuteras runt om i världen i de olika webbkällorna. Att, alltså, ens införa diskussioner med argument som behandlar typ »Stefan-Boltzmanns strålningslag» är i det enkla AGW-bevisets strålkastarljus helt ovidkommande, helt irrelevant, för den elementära bevisningen. Uppgiften gäller, tydligen och istället, ett renodlat mark-vattenrelaterat läckfenomen (h=53,35 M). Hur sedan hela troposfären relaterar till den delen via olika värmestrålningsparametrar och skiktbildningar — genom Stefan-Boltzmanns strålningslag — blir en annan fråga; den delen varken behandlas eller ingår i den här presentationen.

 

1[‡]

”All climate models take account of incoming energy as short wave electromagnetic radiation, chiefly visible and short-wave (near) infrared, as well as outgoing energy as long wave (far) infrared electromagnetic radiation from the earth.”,

@INTERNET Wikipedia Climate model 2009-12-21

Min översättning:

Alla klimatmodeller beaktar inkommande energi som kortvågig elektromagnetisk strålning, i huvudsak synligt och kortvågigt (nära) infrarött, så väl som utgående energi såsom långvågig (avlägset) infraröd elektromagnetisk strålning från Jorden.

 

 

 

AGW-beviset komprimerat — Originalbeviset i grafisk sammanställning

 

2009-12-20

AGW-beviset i komprimerat illustrerat förtydligande

Vi studerar sammanställningen av de tre huvudkurvorna i AGW-beviset:

 

 

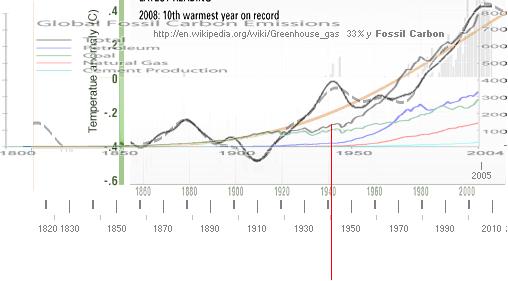
Betrakta FossilCarbon-kurvan, totalt globala utsläppet (svart) som den röda vertikallinjen ovan pekar på; DEN variationens finhet per år SES inte av HAVET beroende på havets stora (enorma) värmetröghet — som att försöka ratta en oceanångare: havet (genom globala medelvärden) jämnar ut alla mindre (årsvisa) variationer. Vad ser då havet av FossilCarbonEmissions?

 

Havet med dess närmast enorma värmetröghet (och som i medelvärdesformerna kräver minst 5 års medelintervall för att bilda begripliga variationer som kan presenteras grafiskt i globalt medelvärde) ser istället FossilCarbon med den ideala t(AGW)-energikurvans jämnhet som den orangea vertikallinjen nedan pekar på:

 

 

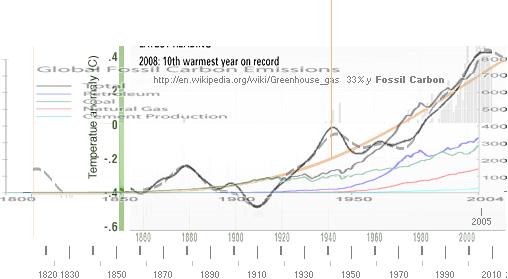
— Men hur kan du säga det? HUR VET man det, att det verkligen ÄR så, säkert? Visa.

Man vet det, helt säkert, och endast så, genom att INTEGRALEN — den samlade summan av alla fossila kolutsläpp i den idealiserade FossilCarbon-kurvan analogt med t(AGW)-kurvan, orange ovan — överensstämmer med den globalt uppmätta Carbon Dioxide Concentration, den svagt blåa kurvdelen nedan från ca 1960 som den blå vertikallinjen nedan höger pekar på, och som tydligen sammanfaller med integralformen [den ljust violetta kurvan nedan] till t(AGW), orange ovan/nedan. Kurvdelarnas matematik korresponderar, kommunicerar, tydligen samstämmighet.

 

 

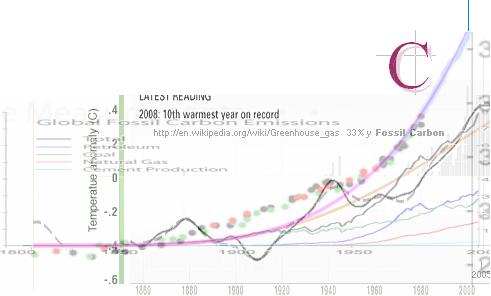
Samhörigheten är, trots vissa uppenbara inre variationer (som alltså, och tydligen, kan återföras på havet), så överväldigande tydlig, att ingen seriös människa, inte under några som helst omständigheter, kan tvivla på att överensstämmelsen också äger en verklig motsvarande naturlig förankring: AGW gäller. Detta är speciellt uppenbart för upptakten i kurvformen, först märkbar runt 1880: själva orsaken, grunden, basen. Det finns inget annat lopp, ingen annan historia, att välja på än den mänskliga kulturens utveckling (den rika världens länder) genom industrialiseringen under de två seklerna 1800-2000: utsläppen av kol genom kol-olja-naturgasförbränningen.

 

t(AGW)-kurvan plus en (enklare) periodisk form t(PERIODythav) (som ansluter till havsperioderna på resp. ca 21 år och ca 62 år), den gråstreckade kurvdelen, visar samma typ av följsamhet mot NASA-temperaturkurvan [originalet] som (i liknelse) ett plåster som läggs an mot huden på ett finger; Ännu bättre precision kan (naturligtvis) fås med flera medtagna parametrar i havsperiodens form, men denna detalj är inte av nöden då huvudsaken redan står klar (se även i summeringen nedan): NASA-temperaturkurvans bevisbarhet med grund i sambandet mellan FossilCarbon och CarbonDioxide med referens till havet. Därmed är det tydligt att t(AGW)-kurvan väl beskriver den i NASA-temperaturkurvan innefattade observerade, uppmätta, globala uppvärmningen.

 

SUMMERING

 

Med ovanstående påvisade resultat — koldioxidmängdens atmosfäriska del som integralen för det globala kolutsläppet — kan man tydligen använda t(AGW)-kurvan tillsammans med NASA-temperaturkurvan för att få fram en mera exakt kunskap om den motsvarande globalt medelbaserade havsperiodens utseende; Kurvan tas ut genom att subtrahera t(AGW)-kurvans amplituder från NASA-temperaturkurvans amplituder (vilket kan ske på pixelbas genom en enklare programrutin i något masterprogram typ Basic eller Delphi, denna del är här ännu Dec2009 inte representerad), motsvarande en mera exakt version av t(PERIODythav).

 

 

Kurvkomponenternas utseende i OpenOffice

 

Bilderna nedan är separerade skärmdumpar (här i JPEG-format) från sammanställningen av de tre komponentkurvorna från importerna (utan transparens) i OpenOffice:s Text/Teckningsdokument (min version 3.0, en nyare version 3.1 finns nu Dec2009).

Syftet är att förtydliga (för den rena bevisbarhetens ändamål) manualen för hur de olika källformerna är sammanställda/kan sammanställas med olika skalanpassningar då rena sifferuppgifter har en tendens att uppvisa olika överföringsfel (som t.ex. nyligen att en storleksändring 125%y 156%x råkade skrivas felaktigt med xy ombytta — rätt resultat, fel uppgift, crash).

Överst NASA-temperaturkurvan justerad horisontellt till 65% av originalmåttet, med den blå referenskvadraten på pixelUnit50 (se grafdelen underst),

mitten FossilCarbon-kurvan reducerad vertikalt till 33%,

underst t(AGW)-kurvan ritad i gratisprogrammet Graph med import till OpenOffice och storleksjusterad efter enheten 1:1 mot den blå pixelkvadraten 50×50 (Graph-programmet har ingen manuell inställning för val av pixelEnhet 1:1, programmet anpassar sig efter programfönstrets storlek från fall till fall, både i Xled och Yled).

 

 

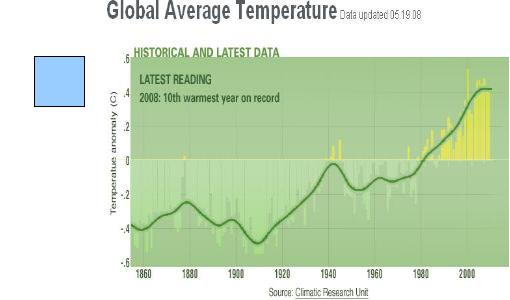
Ovan: Originalet storleksändrat till 65%x

 

 

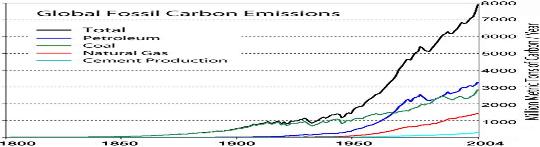
Ovan: Originalet storleksändrat till 33%y

Notera att bildkvalitén efter storleksändring i OpenOffice, beroende på typ av original, inte alltid är optimal jämfört med vissa andra program.

 

 

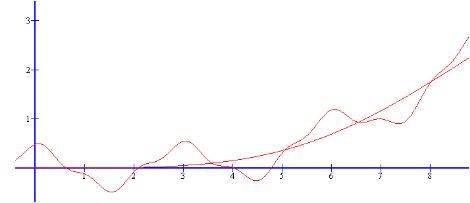
Ovan: Originalet (beror på fönsterstorlek) storleksändrat för passning 1:1 mot den blå 50×50pixelRutan ovan vid NASA-temperaturkurvan

 

 

Nedan: t(AGW)-kurvans motsvarande integralkurva från originalets CarbonDioxideConcentration visas nedan (ej vertikalsynkroniserad med de tre övriga ovan) i skärmdump från OpenOffice-teckningsdokumentet med de anpassade storleksändringarna 125%y och 156%x

(före 21Dec2009 felangivet som 125%x och 156%y):

 

 

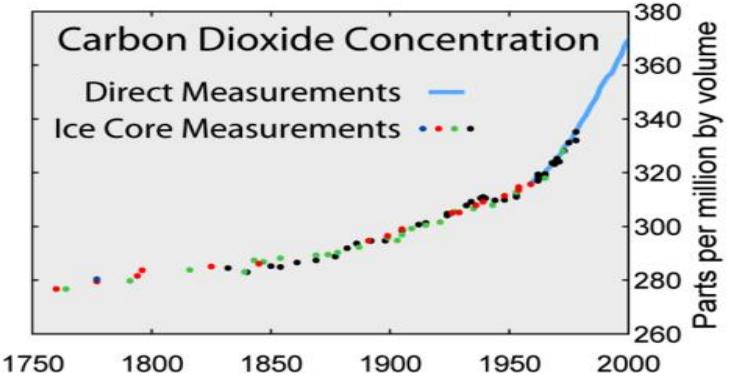
Ovan: Originalet storleksändrat till 125%y och 156%x för passning mot övriga.

 

 

 

Notering

Bilderna generellt i denna presentation använder varken OpenOffice eller Graph, dessa sistnämnda har, här, medtagits och exemplifierats som de (nu Dec2009 enda) kända och kostnadsfria bildbehandlingsprogram som alls finns på webben och som på något enkelt sätt kan verkställa elementära bildsammanställningar med grafritande funktioner inkluderat. (Man tycker att all heder och anständighet kräver att den typen ska finnas, kostnadsfritt, på varje dator från köpet, min mening).

 

 

 

 

Förtydligande inmatningsordning till Graph

Förtydligande till t(NASA)

Inmatningssambandet till Graph måste skrivas med tillagda parenteser enligt

6[1-1/(1+[x/10]^4)] + 0.222(0.9[(2cos (pi x/1.48)) + 0.5(cos (3pi[x-0.1]/1.48))])

till jämförelse med det (enklare) angivna (som ger fel resultat i Graph)

6[1-1/(1+[x/10]^4)] + 0.222(0.9[(2cos  pi x/1.48)  + 0.5(cos  3pi[x-0.1]/1.48)])

— Alltså förtydligat med parentes kring hela den trigonometriska operationsvariabeln, annars blir det inte riktigt.

 

 

 

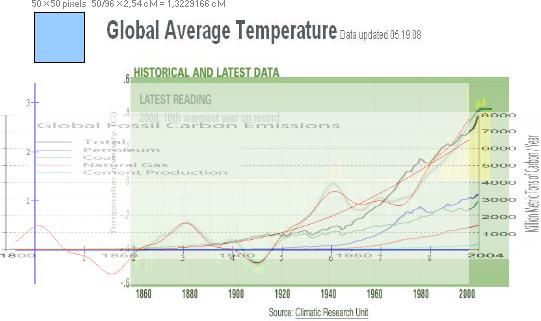
Bilden ovan JPG-kopia från resultatet i OpenOffice text/ritdokument

NASA-kurvans breddvärde gånger 0,65, FossilCarbon-kurvans höjdvärde gånger 0,33 och placerad med sin baslinje (B) vid NASA- kurvans nivå –0,4°C, t(AGW)-graferna (tunn röd) synkroniserade med B samt justerad i sidled med nollan vid ca 1815, optimalt sammanfallande perioder. Se även Kurvkomponenternas utseende i OpenOffice.

 

Bilden ovan JPG-kopia från resultatet i OpenOffice Rit/Textdokument med intagning, storleksändring och inställning med 50% transparens av objekten NASA-kurvan och Fossil Carbon-kurvan, samt på dessa överlagrat transparent 50% energigrafen med ythavsperioden, totalt enligt

6[1-1/(1+[x/10]^4)] + 0.222(0.9[(2cos (pi x/1.48)) + 0.5(cos (3pi[x-0.1]/1.48))])

de bägge sistnämnda med ovanstående samband importerat till och ritade från gratisprogrammet Graph.

Den blå rutan överst vänster är en pixelmall 50×50 pixels (baserat på normal bildskärmsupplösning 96dpi) som ritas in separat (verktygsmallarna nederst i OpenOfficeText/Ritdokumentet, högerklick på bilden ger dialog för inställning av måtten), blåkvadraten används för att justera importgrafen från Graph (de blå koordinataxlarna, den röda tunna grafen) eftersom det programmet inte har någon funktion för manuell (numerisk) inställning av enhet i pixels; Dra i handtagen, och flytta bilden med referens till 1-1-strecken tills dessa sammanfaller med den blå rutans kvadrat.

 

Resultatet i OpenOffice —

DE TRE BILDKOMPONENTERNA NASA-kurvan, Fossil Carbon-kurvan, t(AGW)-kurvan, behandlas, och kvarstår, i OpenOffice-importen som separata, transparent överliggande bildlager. Högerklick på respektive bilddel visar vilka verktyg som bilden kan ändras på, bl.a. bildmåtten (procentuell ändring finns inte i OpenOffice version 3.0 med tidigare, en ny version 3.1 finns nu [Dec2009] där procentuell ändring finns med). Verktyget för transparens 0-100% har ett vinglas som ikon och syns på BildPanelen

(se Menyn: Visa, Verktygsrader, Bild om den inte kommer fram automatiskt då bilden är aktiverad).

 

OpenOffice och Graph är bägge gratisprogram

Graph finns att hämta på

http://padowan.dk/graph/Download.php

Skriv in / importera kurvsamband direkt till inmatningen via INSERT-tangenten, redigera på markerad insättning med ENTER

[Inmatningen är generös, man kan skriva 2cosx direkt, även 2 cos x, och behöver inte skriva typ 2*cos(x)]

 

OpenOffice finns att hämta på

http://sv.openoffice.org/

Importera bilder direkt via Ctrl+V, högerklicka på bilden för att nå verktygen för bildmått, använd Vinglaset för Transparens 0-100% (Visa, Verktyg, Bild), precisionsjustera bildernas inbördes position med Alt+Pilar.

— Ändra bildmåtten (version 3.0) genom att (manuellt, vid sidan om) multiplicera aktuellt värde X|Y med önskad grad av förminskning/förstoring, tex., X(0,65) = X från 100% till 65%, mata sedan in resultatet som det nya värdet.

— I nyare version 3.1 finns ett direkt tillval för procentuell ändring.

 

 

 

*END

Editor2009X27

 

 

 

 

 

 

 

 

 

 

Den Globala Uppvärmningen

 

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

 

 

Den Globala Uppvärmningen

ämnesrubriker

                      

 

innehåll

              DEN GLOBALA UPPVÄRMNINGEN

 

                                                         ”Det är inte koldioxiden som förorsakar växthuseffekten”

 

                       t från Fossil Carbon

 

                                                         NASA-Temperaturkurvan

 

                                                         Fossil Carbon Emissions

 

                                                         t(ENERGI)

 

                                                         t(PERIODythav)

 

                                                                            Ythavsperiodens grafiska analys

 

                                                                            Ythavsperioderna på webben

 

                                                                            Ythavsperioden på 62år genom AMO och PDO

 

                                                         räkna ut NASA-kurvan

 

                       NASA-kurvans fullständiga upplösning

 

                                                         Allmän genomgång som visar och förklarar Nasa-temperaturkurvans olika komponenter

 

                                                         Huvudtext — illustrationer i originalstorlek

 

                                                         Förkortad beskrivning  — förminskade illustrationer

 

                       Energihärledningen

 

                                                         Uppkomsten av den globala uppvärmningen från kol-olja-naturgasförbränningen

 

                                                         Absorptionskoefficienten

 

                                                         Solens inverkan— Solekvivalenta Radiansen (SER)

 

                                                         t(AGW)

 

                                                         beräkningen av M och m

 

                                                         Luftens täthet vid Jordytan

 

                                                         Beräkningen av h

 

                       Sammanställning av mtEC-kurvorna

 

                                                         Grafisk beskrivning av hur kurvorna i klimatkomplexet sammanhänger

 

                                                         totala temperaturen

 

                                                         medeltemperaturökningen

 

                                                         ythavsperioden

 

                                                         kolutsläppet

 

                                                         koldioxidhalten

 

                                                         omvandlingsfaktorer

 

                       INTEGRALKURVAN FÖR E

 

                                                         Beskrivning av kurvan för koldioxidhalten från kolutsläppen

 

                                                         Integralkurvan i praktiken

 

                                                         Tabellvärden med koldioxidhalter

 

                       Koldioxid, vatten och atmosfär

 

                                                         Den globala uppvärmningens mekanismer

 

                                                         Koldioxidens vattenlösning och Atmosfärens värmebevarande funktion

 

                                                         Koldioxidens vattenlösning

 

                                                                            Havsytans koldioxidabsorption

 

                                                                            Huvudsaken

 

                                                         Atmosfärens värmebevarande funktion

 

                                                                            Planckenergin

 

                                                                            Global uppvärmning

 

                       AGW-beviset

 

                                                         Varför omnämns inte beviset i etablerad litteratur?

 

                                                         AGW-beviset komprimerat

 

                                                         Kurvkomponenternas utseende i OpenOffice

 

                                                         Förtydligande inmatningsordning till Graph

 

referenser

t för 10–, T för 10+, förenklade exponentbeteckningar

 

TNED

 

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

 

 

Senast uppdaterade version: 2014-11-26

*END.

Stavningskontrollerat 2009-10-10 | 16 | 20 | 24 | 27 | 2009-12-21.

 

Rester

*

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG-justerad 2011-10-10

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se