UNIVERSUMS HISTORIA | ALLMÄNNA SAMBAND | ref. Kosmos_Sammanställning.wps | version 2004X10 a BellDHARMA production | Senast uppdaterade version: 2013-04-08 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Efter sammanställningar från 2002

Allmänna samband

termiska ekvivalenter

TERMISKA EKVIVALENTER

temperaturekvivalenterna

T=A^–1/3(9 T11 °K) ................ termiska ekvivalenten, optimalfusioner från kallplasmat enligt TNED, A anger masstalet

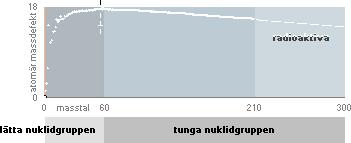
Ekvivalenta Temperaturskalan för nuklidbildningen via max fusionssannolikhet enligt TNED

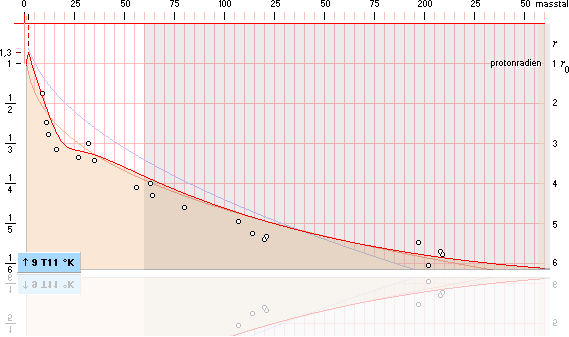
Det mörka fältet från masstal 60 markerar den tunga nuklidgruppen (N60+-gruppen).

De små cirklarna anger19st uppmätta kärnradier med basdata från s387 Table 16-5 i Nuclear Physics (1955) av Irving Kaplan (från prof. Otterlund, Lunds univ. 1996).

OBSERVERA

Temperaturer av ovanstående dignitet kan inte bildas genom fusioner som börjar nerifrån temperaturskalan.

Med en artificiell (eller »sekundär») termodynamik når man »bara» (enligt konventionella begrepp) upp till ca max 5 T9 °K [BAs123sp1m].

Ovanstående skala ligger minst 100 gånger högre.

Bara ett ursprungligt ytterst tätt materietillstånd kan initiera toppen som igångsätter hela den naturliga nuklidbildningen.

EKVIVALENTA kärnhastigheterna i skalans topp — bildade på ytterst kort tid under ytterst starkt repulsiva förhållanden — ligger runt halva topphastigheten för ljuset. Det är också den gräns där magnetiska fältstyrkan i den interatomära rymden (över mycket korta avstånd) har sin maximala verkansdynamik. Högre hastigheter ger lägre magnetisk verkan.

Det finns flera samstämmiga oberoende sätt att härleda termoanalogin på (rotation eller våglängd), och ingen av dem är komplicerad. De bygger på att jämföra kärnans optimala fria spinn med den hastighet kärnan måste ha för att få synkronisering inom nuklidbarriären (kärnans omskrivna sfär). Bägge ändar nämligen i samma enkla direkt proportionella beroende av kärnradien. Sambanden kan återföras på Wiens förskjutningslag med kärndiametern l=k_{2,898 t3 M°K}T^–1. För vätekärnans diameter grovt förenklat som 3 t15 M ges toppvärdet T_max @ 9 T11 °K. Med den förenklade kubgrafen för kärnradierna följer då för varje kärna med masstalet A en optimalfusion med ekvivalenta temperaturen enligt sambandet för T

T=A^–1/3(9 T11 °K) ................ termiska ekvivalenten, optimalfusioner från kallplasmat enligt TNED, A anger masstalet

I illustrationen är kubgrafen representerad av den orangea linjen. Den röda är den mera noggrant beräknade från TNED (massdefekterna oaktade). Den blå kurvan är den som i min historia definierar toroidaggregatet N3m20 genom medelvärdesbildning mot den orangea kubgrafen. Vidare i Kärnradierna.

Allmän beskrivning

Temperaturstrålningens sammansättning (Plancks strålningslag) beror av summan av alla möjliga induktivt verksamma våglängder och frekvenser. Denna summering är alltså oberoende av massformerna och den realiseras endast i fixt givna g-relaterade rymdpunkter enligt superpositionsprincipen. Också neutrinostrålningens spektrum kan därför bidra till temperaturhöjningar därmed att neutrinostrålningens bidrag förskjuter frekvensmaximum allt längre in mot nollvåglängd, detta trots att neutrinovåglängderna explicit ligger långt under vad elektronmassan förmår detektera.

För ett givet temperaturmaximum (T) gäller från Plancks strålningslag ett motsvarande våglängdsmaximum genom Wiens förskjutningslag l=k_{2,898 t3 M°K}T^–1. Men den maximalt materiebaserade temperaturgenererande induktiva frekvenstoppen i Planck-kurvan kan aldrig hängas på kortare våglängd än atomkärnan med minsta diametern. Det är neutron-protonkärnan med diametern (grovt) ca 3 t15 M. Wienstrålningen ger därmed ett absolut temperaturmaximum på 9,6 T11 °K vilket avser en lokal med idel vätekärnor.

Eftersom neutrinostrålningens våglängder är växande med tyngre nuklidbildningar och därmed alltmer närmar sig den maximalt termiska Planck-våglängden (protondiametern), lämnas i vilket fall alltid bidrag från neutrinostrålningen i maximeringen av Planck-toppen — även i bildningen av de tyngre nukliderna som har väsentligt större diametrar än protonkärnan (upp till 600%). Se även i NEUTRINOSPEKTRUM.

Analogt med DEN NATURLIGA bildningen från lättare grundämnen till tyngre, motsvarande från kortare till längre fusionsvåglängder, existerar alltså neutrinostrålningens temperaturmaximerande bidrag också med de tyngre nuklidernas bildning.

Se även allmän beskrivning i VÄRMEBILDNINGENS GRUNDER

Övre temperaturgränsen

I GÄNGSE BESKRIVNINGSSÄTT skiljer man inte på hastigheter genererade av partikelacceleratorer och hastigheter genererade av mekaniska stötar. I den förra är R närvarande i Q=Ö (m/R)(A/dT) medan så inte är fallet i den senare. Eftersom modern akademi inte kan härleda Q och därmed heller inte har något begrepp om innehållet, sammanblandas delarna friskt utan urskiljning. Någon övre gräns för v genererad på termisk väg existerar alltså inte.

Eftersom emellertid den termiska effekten bygger på att generera vågrörelser (MIC MassInteractiveConnection)

MIC

J=m[c=lf]r=E/f=mc²T=mvc/f = mvl;

mv = Jl^–1 också konventionellt känd som de Broglies vågekvation mv=h/l med h som Plancks konstant

som bidrar till att temperaturen växer, framtvingas en viss automatisk övre självreglerande temperaturgräns över vilken ingen fysikalisk aktivitet är möjlig. När nämligen atomkärnornas kollisionshastigheter tangerar eller överskrider c, upphör analogt styrkan i induktionsverkan — eftersom denna återkopplas via c på tid över distans. Därmed stryps en vidare strålningseffekt och därmed sätts gränsen för max temperatur automatiskt.

Gränsformen för elektromagnetisk OPTIMAL verkan genom en kärnhastighet v ligger vid halva toppdivergensen c₀/2 [Se ENERGIZONEN i Potentialbarriären]. Ökas v från denna punkt avtar magnetismen i styrka och den elektriska verkan kräver allt mindre avstånd för att uppvisa effekt. På denna grund bildas ENLIGT TNED en absolut högsta termiskt genererad temperaturtopp som inte kan överskridas därmed att styrkan i kärnornas ömsesidiga repulsioner avtar med växande v och därför inte kan bidra ytterligare till högre v, analogt högre temperaturer.

FRÅN ALLMÄNNA GASLAGEN (Gasbollarnas medelhastighet) gäller

v² = 3b_{1.3805502 t23 J/°K}T/m_{1 GASBOLLENS MASSA} = (3b)T/uU = (24944,743)T/U °K^–1(M/S)²

U anger atomvikten (1,0078252 för Väte), u anger atomära massenheten 1,66033 t27 KG, T anger temperaturen i °K. Med v=c₀ ges för vätgas absoluta temperaturgränsen

_HT_max= 3,63117 T12 °K. Hastigheten c₀ är emellertid orealistisk eftersom den termodynamiska kopplingen i detta läge har upphört. En mera realistisk maximerad topphastighet som medger dynamik är en halvering av v_max till v_max=c₀/2. Då ges för vätgasen

_HT_max= 9,07794 T11 °K ....................................... v_max=c₀/2

Detta resultat är nära alldeles detsamma som enklare fås direkt ur Wiens förskjutningslag (Wienvåglängden) l=k_{2,898 t3 M°K}T^–1. Med neutron-protonkärnans diameter grovt 3 t15 M som l ges T=9,64333 T11 °K.

För en Järnkärna (A=56) ges initiellt ekvivalenta temperaturen T=2,35 T11 °K.

Observera dock att temperaturvärdena i ovanstående analogier är ekvivalenter: kallplasmats tillstånd innehåller i egentlig meningen ingen initiell rörelseenergi och lyder därför heller inte strikt under den konventionella termodynamikens begrepp — i utvecklingens initierande skede.

Energigenomströmningsekvivalent

E/h=f=c₀/l; l = hc₀/E =hc₀/(E/Q_e eV)=hc₀/([E/Q_e]/[T6] MeV)=hc₀/(T6 Q_e)E_MeV ; T=k_{2,893 t3 M°K}l^–1

Genom ovanstående samband får man en grovt approximerad form som uttrycker den motsvarande temperaturen för en viss given energinivå. Nedanstående kalkylkort kan användas för att får fram temperaturvärdena ur givna energivärden.

kalkylkort · energigenomströmningsekvivalenten · kortet endast i bild med exempel · funkar inte aktivt i webbläsare

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik3 — Energigenomströmningsekvivalent — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

Beräknar ekvivalenta temperaturen för given lokal elektromagnetisk genomströmningsenergi E=hf.

Exempel

Energinivån 0,764 MeV beskriver idealt neutrinodifferensen (m®g) i sönderfallet från neutron till väte. Nivån motsvarar 1,78 T9 °K. För att åstadkomma en teoretisk lokal excitation av Helium-4-atomer så att dess nukleoner frigörs i formen av exciterade fristående neutronekvivalenter, krävs alltså en »rå teoretisk» temperatur på 4×1,78=7,12 T9 °K.

MED DEN WIENEKVIVALENTA TEMPERATUR-ENERGI-MODELLEN sätts också den övre fysiska gränsen för en »stjärnas temperatur» till just detta värde, grovt 7 T9 °K. I konventionell kosmologi anger man (följaktligen, med vissa osäkerheter och oavgjorda diskussioner) en stjärnas högsta temperatur till ca 4 T9 °K [BAs123sp1mn].

EN STJÄRNA som uppvisar en sådan temperatur förlorar alltså sin huvudkomponent Helium-4 — som är avgörande för stjärnans exotermiska fusionsenergi varefter Helium-4-agenten har spelat ut sin roll — och därmed sin temperatur.

Denna temperaturmodell är emellertid materiebaserad, och har enligt TNED ingen reell fysikalisk grund i stjärnfysiken som är massbaserad. I TNED får man därför helt andra motsvarande verkliga värmemodeller som helt saknar koppling till den moderna akademins föreställning: massfysiken är i modern akademi helt orepresenterad.

De helt skilda betraktelsesätten ENLIGT TNED redovisas illustrerat nedan. Se även mera utförligt från Solfysiken.

TNED/MAC

SKILLNADEN mellan

TNED (relaterad fysik och matematik) och

MAC (modern akademi)

kan illustreras och beskrivas utomordentligt exakt enligt nedanstående enkla översikt.

	TNED relaterad fysik	konventionell kosmologi MAC modern akademi
	gravitationen bromsar expansion strukturkriterium finns	inre trycket bromsar gravitationen strukturkriterium saknas
ingångsvillkor: begynnelsetillstånd	maximalt HÖG täthet	maximalt LÅG täthet
egenskap:	centrum vill expandera mera men hindras av gravitationen	gravitationen vill komprimera mera men hindras av det inre trycket
initiell temperaturekvivalent:	9 T11 °K max	0 °K min
aktiv primär agent:	inre energi (levande kraft)	gravitation (död kraft)

I relaterad fysik (TNED), föds stjärnor bar en gång; alltså: efter divergenständningens fas i K-cellens expansion efter varje »Big Bang», se K-cellens detonation. Emellertid kan ENLIGT TNED en stjärna existera genom flera (många) energicykler OM den finns till i en region där det finns ”stjärnföda”, det är Väte. Många sådana domäner har observerats, och modern akademi anser att de är bevis för födelsen av helt nya stjärnor direkt från gasmoln till stjärnkropp i enlighet med den traditionella gravitella kontraktionsmodellen (ovan t.h.). TNED erbjuder flera helt nya aspekter på dessa observationer, aldrig (här veterligt) tidigare ens antydda i någon litteratur (inte alls överhuvudtaget mig veterligt, men det kan bero på att min litterära horisont är mindre).

De två modellerna illustrerade ovan, har som vi ser ingenting gemensamt; De kan inte jämföras på någon allmän eller gemensam matematisk basis. Det är helt uteslutet. En av teorierna är primitiv relativt den andra — förutsatt någon av dem är förenlig med naturen — och bör som sådan kunna förklaras i det upplysande ljuset av den andra, enligt de tillkortakommanden som kan förklaras och beskrivas i detalj, vilketsom.

För stjärnornas energiproduktion enligt TNED, se vidare utförligt från Solfysiken.

För himlakropparnas allmänna bildning enligt TNED, se från Himlakropparnas bildningstid.

Allmänna samband | Universums Historia

DIVERGENSENS EXPANSIVA G-BEROENDE

DIVERGENSENS EXPANSIVA G-BEROENDE

Divergensens Expansiva g-beroende (DEG)

G-ekvivalenterna från EXPANSIONSMATEMATIKEN ger i sammanställning

w < c₀/Ö2: positiv divergens

c = c₀ [1 – 2(w/c₀)²]^1/2 .................................... 2(w/c₀)² < 1 ; w/c₀=Ö [1–(c/c₀)²]/2

w > c₀/Ö2: negativ divergens

c = c₀ [2(w/c₀)² – 1]^1/2 .................................... 2(w/c₀)² > 1 ; w/c₀=Ö [1+(c/c₀)²]/2

ZONBARRIÄRENS RADIE — gemensam grundform för hela komplexet

För c=0 vid nollzonen med radien r_0c ser vi direkt att det gäller att

w_0c/c0 = Ö1/2 ; .............................. c=0

Exakt samma resultat gäller i stationära tillståndets fysik [Se DGD].

Det betyder att avståndsskalan från centrum uttryckt i w/c₀ i bägge fallen kontraktiva-expansiva och stationära tillståndets g-fysik är en och densamma enligt

w_0c/c₀ = 1/Ö2 = r_0c/(r_0cÖ2) = nr_0c/n(r_0cÖ2) ; nw_0c/c₀ = nr_0c/(r_0cÖ2) = w/c₀ = r/(r_0cÖ2) ;

så att man alltså får

r/r_0c(Ö2) = w/c₀

eller

r/r_0c = (Ö2)w/c₀ ................................ zonbarriärens allmänna universella koefficient

r = r_0c(Ö2)w/c₀ ................................. godtyckliga radien från g-potentialen (w²) och zonbarriärens radie r_0c

för bägge fallen.

Från ovanstående ekvivalenta w/c0 ges alltså explicit för expansionsmatematiken — med ett explicit tillägg för

zonbarriären r_cz i positiv divergens, den betecknas också stundtals r_0cz i denna presentation beroende på associerande bekvämlighet —

c/c₀ = [1 – (r/r_0c)²]^1/2 ...................... 2(w/c₀)² < 1 ......................... i positiv divergens ;

(r/r_0c)² = 1 – (c/c₀)² ............................................................................ vid c=c_z=c₀/2 med r= r_cz ;

r_cz = r_0cÖ 3/4 .................................................................................... zonbarriären, epansionsfysiken

c/c₀ = [(r/r_0c)² – 1]^1/2 ...................... 2(w/c0)² > 1 ......................... i negativ divergens ;

(r/r_0c)² = 1 + (c/c₀)²

För den vidare presentationen används (här främst, om inget annat anges) uttrycksformen för positiv divergens: Vi går, så att säga, från centrum c₀ och utåt.

Nolldivergenszonens konstanta hastighet

Divergensens Expansiva G-beroende c=c₀Ö 1–2(w/c₀)² ger för c=0 sambandet 1=2(w/c₀)² som ger w=c₀/Ö2.

Allmänna Expansionshastigheten v=wÖ2 ger då v=c₀. Därmed utbreder sig nolldivergenszonen i K-cellen enligt

c₀ = r_0c/T₀ ................. nolldivergenszonens konstanta hastighet, idealt bevarad g-energi

Det betyder att K-cellens nolldivergenszon c=0 expanderar med konstant hastighet v=c₀ — förutsatt ideala förhållanden enligt föregående.

Radien för divergensnollzonen kan då beräknas r_0c=c₀T med T som totala expansionstiden.

Det mera exakta uttrycket för radien innefattar ovannämnda tidsoffset vid r_max [Se Offsetvärdet för T] enligt

r_0c=c₀(T_DET+T) ......................................... expansionen, nolldivergenszonens radie

r_0cMax=c₀(T_DET+T_max)=c₀T_Dm ............. maximala nolldivergensradien då expansionen avstannar

T_Dm ............................................................ T_DET+T_max

T_DET ............................................................ 1,98322 t4 S @ 200µS enligt r_max=1,82 T17 KG/M3, offsetvärdet vid K-cellens detonation

r_0c=c₀(T_Dm–T)=r_0cMax – c₀T ................. kontraktionen, nolldivergenszonens radie, T ® _Tmax

Nolldivergenszonens radie ur tätheten r

r_c=0 ................................................................ r–^1/2(2,53646 T13 M)(KG/M³)^1/2 = c₀T₀= c₀Ö(3/2pGr) = r_0c

Ö 3/2pG ......................................................... universella dagkonstanten = (KG/M³)^1/2 × (84 607,288 S = 23 tim 30 min 7,288 sek)

c₀ .................................................................. 2,99 792 458 M/S, toppdivergensen, (uppmätt år 1970 med referens till Jordytan)

G ................................................................... 6,67 t11 JM/(KG)2, universella gravitationskonstanten (först av Henry Cavendish 1798)

r=r_0c, c=c₀ ;

m_0c ................................................................ 2rc²/G ; från r=(3/2pG)[T₀=r/c]^–2 som ger c²/G=r(2pr²/3) ; 2rc²/G=r(4pr3/3) =rV=m_0c

m_0c ................................................................ den av divergensnollzonen inneslutna massan

ZONBARRIÄRERNAS HASTIGHET OCH DERAS SKÄRNING MED EXPANSIONSSFÄRERNA

Varje r som innesluter centralmassan m₂ enligt tidssfären

r=(T²Gm₂/2)^1/3=m₂G/8c₀²=m2(9,27672 t29 M/KG)

passeras av sfärzonerna

nollzonen r_0c efter tiden

T = m₂(G/2c₀³) ................................. = m₂(1,23775 t36 S/KG) ................. d_r0c=c₀T

vilket inträffar vid distansen

d = c₀T

från K-cellens centrum.

zonbarriären r_0cz efter tiden

T = m₂(4G[c₀³Ö27]^–1) ....................... = m₂(1,90564 t36 S/KG) ................. d_r0cÖ3/4 = d_r0cz = c₀TÖ3/4 [Se ZONBARRIÄRENS RADIE]

vilket inträffar vid distansen

d = c₀TÖ3/4

från K-cellens centrum.

Härledning

Vi har från tidssfären r³=(T²Gm₂/2) och nolldivergenszonens konstanta hastighet r_0c=c₀T ekvivalenterna

(1) r_0c=c₀T=(T²Gm₂/2)^1/3.

Då gäller också via c₀T=(T²Gm₂/2)^1/3 ekvivalensen c₀=(Gm₂/2T)^1/3 som ger c₀³=Gm₂/2T. Alltså gäller

(2) T = m₂(G/2c₀³) = m₂(1,23775 t36 S/KG)

Genom att zonbarriären r_0cz beräknas från r_0c enligt r_0cz=r_0cÖ3/4 [Se ZONBARRIÄRENS RADIE ovan] ges analogt v_r0cz=v_r0cÖ3/4=c₀Ö3/4=T^–1d_r0cÖ3/4 = T^–1d_r0cz.

Dvs., d_r0cÖ3/4 = d_r0cz = c₀TÖ3/4.

Explicit från (1), r=(T²Gm₂/2)^1/3, via resultatet ovan i (2), T = m₂(G/2c₀³), ges med insättning av den senares kvadrat i den förra ekvivalensen

(3) r = (m₂²[G²/4c₀⁶]Gm₂/2)^1/3 = Gm₂/8c₀²

Då barriärzonen r_0cz skär r gäller alltså d_r0cz=r=(T²Gm₂/2)^1/3=c₀TÖ3/4. Ur de två sista leden ges (Gm₂/2T)^1/3=c₀Ö3/4. Tiden blir då

(Gm₂/2T)=c₀³(Ö3/4)³ ;

(4) T = Gm₂/2c₀³(Ö3/4)³

= (4/3)^3/2Gm₂/2c₀³

= (4/3)(4/3)^1/2Gm₂/2c₀³

= (8/3)(1/3)^1/2Gm₂/2c₀³

= (8)(1/27)^1/2Gm₂/2c₀³

= (8/Ö27)Gm₂/2c₀³

= (4/Ö27)Gm₂/c₀³

SOM VI SER av dessa delar, kan det vara på sin plats med en mera termdefinierad härledning (ovanstående är väl kryptiskt).

Följande är en alternativ beskrivning, resultatet är detsamma, men förklaringen är (förhoppningsvis) tydligare.

Zonskärningarna

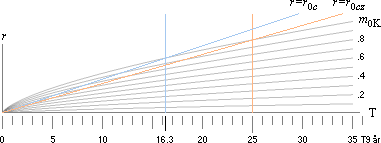
FRÅN sambandet i TIDsfären r = T^2/3(Gm₂/2)^1/3 gäller ovanstående typgrafer.

Kurvskaran visar den tillryggalagda vägen för olika partier av K-cellen beräknade efter dess delmassa och per bevarad genomsnittlig medeltäthet.

Nollzonens hastighet är konstant under K-cellens hela expansion enligt c₀=r_0c/T [Se ovan Nolldivergenszonens konstanta hastighet]. Skärningen mellan nollzonen r_0c och varje expanderande delmassa i K-cellen med radien r via delmassan m_K fås då ur

r_0c =r=T^2/3(Gm_K/2)^1/3_{INTERSECT r0c}=c₀T som ger

T_{INTERSECT r0c} = m_K(G/2c₀³) ................................... nollzonens skärning med K-cellens delmassasfär

Barriärzonens hastighet [Se Zonbarriären ovan] är v_0cz=c0Ö 3/4=r_0cz/T=r_0c(Ö 3/4)/T. Dvs., r_0cz=r_0c(Ö 3/4). Då gäller på samma sätt vid T_{INTERSECT r0cz}

r_0cz = r = r_0c(Ö3/4) ;

r_0c = r_0cz/(Ö 3/4) ;

r_0cz/T =r/T = r_0c(Ö3/4)/T ;

v_0cz = (T2/3(GmK/2)1/3/T)_{INTERSECT r0cz} =c₀Ö 3/4

= (T–1/3(GmK/2)1/3)_{INTERSECT r0cz}

= (Gm_K/2T)1/3_{INTERSECT r0cz} ;

c₀Ö 3/4 = (Gm_K/2T)1/3_{INTERSECT r0cz} ;

T^1/3 = (Ö 3/4)^–1(Gm_K/2c₀3)1/3_{INTERSECT r0cz} ;

T_{INTERSECT r0cz} = (Ö 3/4)–3(Gm_K/2c₀3)

= (Ö 4/3)3(Gm_K/2c₀3)

= (8/Ö27)(Gm_K/2c₀3) ........................ barriärzonens skärning med K-cellens delmassasfär

= (8/Ö27)T_{INTERSECT r0c}

Offsettiden är samma som resultatet i K-cellens allmänna expansionsmatematik

I expansionsmatematiken bestäms nolldivergenszonens radie enligt r_0c=c₀Ö(3/2pGr) och dess inneslutna massa [Se J80-massan] m_0c= (c₀/ÖG)³(6/pr)^1/2.

Lägsta T-värdet för nollzonens skärningar blir då

T_{INTERSECT r0cOFFSET} = m_0c(G/2c₀³)

= (c₀/ÖG)³(6/pr)^1/2(G/2c₀³)

= G^–3/2(6/pr)^1/2(G/2)

= G^–1/2(6/pr)^1/2(1/2)

= (3/2pGr)^1/2

Detta är samma som det tidigare härledda [Se Expansionstiden] via maxtätheten r=1,82 T17 KG/M³

T = 2Ö(3/8pGr) .................... = Ö(3/2pGr) ......................... expansionstiden ur tätheten ;

T_{INTERSECT r0cOFFSET} = T_DET = 1,98322 t4 S @ 200µS

REFERENSVÄRDET för motsvarande tidsoffset för barriärzonen i absolut tidsanalogi med nollzonen blir

T_{INTERSECT r0cOFFSET} = T_DET (8/Ö27)

Expansionshastigheten för delsfären då den skärs av nollzonen

Eftersom r_0c=c₀Ö(3/2pGr) [se Nolldivergenszonens radie ur tätheten] får man expansionshastigheten för sfären ovan via r=r_0c via

v = r · Ö 8pGr/3 [se Expansionshastigheten genom tätheten] som ger

v = c₀Ö(3/2pGr) · Ö 8pGr/3

= 2c₀ ................... momentana expansionshastigheten då delsfären skärs av nollzonen

Notera att MATEMATISKA TECKEN i detta originaldokument använder teckensnittet SYMBOL — som av okänd favorisering INTE accepteras av webbläsarna Firefox, Netscape, Opera, Flock [m.fl].

K-cellens lokala gravitation

Den samlade gravitationen i den lokala rymden behöver ingalunda vara stark för att frammana nolldivergens; det är den samlade massan som räknas

Exempel

Sätt in nuvarande uppskattade medeltäthet för universum r=1,67241 t28 KG/M³ baserat på observationer av den nu synliga materien (en väteatom per tio kubikmeter rymd, synradien grovt 1000 Mpc = 3,0856 T25 M) i sambandet r_0c=r^–1/2(3/2pG)^1/2c₀. Beräkningen ger med förenklat c₀=3 T8 M/S värdet r_0c=1,96271 T27 M.

Tyngdkraftsaccelerationen blir a=r(4Gpr/3)=9,17096 t11 M/S² = 0,000 000 000 0917096… . En sådan liten gravitation finner vi inte ens utanför Jorden, inte ens mellan Jorden-Månen, där ligger all gravitation överlagrad på Solfältet som är betydligt starkare. Räkneexemplet endast understryker att det är den samlade, totala massan som bestämmer.

ref.

J80-MASSAN

Nolldivergenszonens inneslutna massa vid max täthet. Från m_0c=r_maxV=r_max4pr³/3 och r_0c=c₀Ö(3/2pGr_max) ges med beteckningarna mrr

m = r4pr³/3 = r4p c₀³(3/2pGr)^3/2/3 som efter sammanställning ger

= (c₀/ÖG)³(6/pr)^1/2 ;

m_0c= (c₀/ÖG)³(6/pr_max)^1/2 =1,60227 T32 KG @ 80 Solmassor (Solmassan är 1,989 T30 KG).

Se vidare i JORDENS FEMTE EKVATION.

Allmänna samband | Blixturladdningens Fysik — Resumé med vidare

2008VII12

KORT RESUMÉ AV

BLIXTURLADDNINGENS FYSIK

med allmän beskrivning av

Gammastrålningens uppkomst i blixturladdningar

ENLIGT TNED

Se även en senare (Jul2011) mera detaljerad beskrivning i Blixturladdningens Fysik 2011. Framställningen nedan gjordes föregående de (officiellt publicerade) experimentella observationerna av positronförekomster i blixturladdningar. Kortare inlagda stycken beskriver en del av svårigheterna i den allmänna beskrivningen.

Atomkärnan härleds från PLANCKRINGEN genom NEUTRONEN som PLANCKS KONSTANT

h=m_nc₀r_n = 6,62559 t34 JS [HOP s7–155] (t för 10^–, T för 10⁺)

m_n neutronmassan [HOP Table 2.1 s9–65] 1,0086652u = 1,67481 t27 KG med atomära massenheten [ENCARTA 99 Molecular Weight] u=1,66033 t27KG

r_n neutronkärnans tyngdcirkelradie 1,3196611 t15 M [se NEUTRONKVADRATEN]

värdena varierar marginellt beroende på standardiserad epok och institutionell metod

KÄRNRADIERNA ansluter till NEUTRONKVADRATEN med grundindividerna till och med masstal 4 som sedan ger alla övriga grundämnesnuklider med ATOMVIKTERNA genom ATOMÄRA MASSDEFEKTEN. ATOMKÄRNANS FYSIK ENLIGT TNED bygger på ATOMKÄRNANS IMPULS- OCH KRAFTEKVATIONER

J_0K+3J_1K = 0 impulsekvationen

F_BT + F_eZ = 0 kraftekvationen eller kemiekvationen

där elektriska kraftkomponenten F_eZ grundlägger SPEKTRUM OCH KVANTTALEN. Genom ELEKTRONMASSANS KOMPONENTER härleds sedan GRÄNSSPÄNNINGEN FÖR KEMISK FÖRENING (mera utförligt i CAT och gränsspänningen U_G) mellan ett godtyckligt antal atomindivider

(F_BT+F_eZ )₁+(F_BT+F_eZ)₂+(F_BT+F_eZ)₃+…+(F_BT+F_eZ)_n = 0

som delar på samma elektronmassa. Se även i magnetiska kraftekvivalenten.

När spänningen moln-mark överstiger tröskelvärdet U_G bildas sådana makromolekyler i formen av celler eller steg eller trådar som successivt söker sig mot marken tillsammans med en uppåtstigande marktråd. När trådarna möts sker urladdning i den så bildade blixtkanalen enligt ATA.

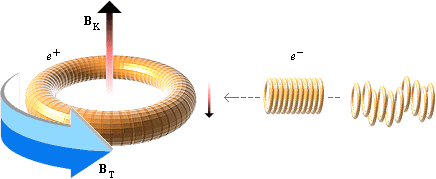
Överstiger den enskilda trådens strömstyrka gränsvärdet för NUKLEÄRA SÖNDERFALLETS GRÄNSSTRÖMSTYRKA har de berörda atomkärnorna inte längre någon elektronmassa att förmedla. Därmed har respektive kärna blottlagts på sin ekvivalenta positronstock i formen av en starkt expanderande kärnring (illustrationen ovan, se vidare i ATA) med positronladdningen A909e.

CAT

Enligt TNED benämns detta tillstånd som kapacitiv transmission (eng. CAT, capacitive transmission), vilket motsvarar atomkärnans fullständiga upplösning.

ENLIGT TNED är det denna mekanism, och endast så, eller så gäller inte TNED, som grundlägger gammastrålning i samband med blixturladdning enligt följande:

Med ideal analogi till EXPERIMENTKOPPLINGENS totalannihilerande positronringar:

Den starkt attraherande positronringen drar till sig omgivande elektronmassor som enligt ELEKTRONMASSANS KOMPONENTER annihileras i upprepade stötar-rekyler mot ringkroppen tills denna är förintad. Gammastrålningens energi med näravstånden (d) för attraktion-rekyl bestäms (formellt, elementärt) av kraftvägen enligt

E = Fd = k_{9 T9 VM/C}(A₁₆918e_{1,602 t19 C})(e_{StarktAVTAGANDE})/d

Med exemplifierat d = 7 t13 M eller ca 200 ggr kärnringens radie (Syrekärna) ges energin ca

E = 30 MeV. Större avstånd ger lägre, mindre högre. De observerade gammanivåerna anges experimentellt uppmätt (RHESSI) till 0,03-10 MeV enligt källan @INTERNET

Measuring x-ray emission from lightning

Joseph R. Dwyer, Department of Physics and Space Sciences, Florida Institute of Technology (2005)

http://www-group.slac.stanford.edu/ais/PublicDocs/presentation68.pdf

Enligt vad som hittills (2008) framkommit ur experimentella mätningar är inte alla blixturladdningar förknippade med gammastrålning. Enligt uppgift från New Scientist (17 Febr 2005 — Earth creates powerful gamma-ray flashes, Maggie McKee) har man hittills registrerat en medelmässig förekomst på runt 50 gammaassocierade blixturladdningar per dygn Jorden runt — man räknar med att det totalt förekommer ca 50 blixturladdningen per sekund Jorden runt året runt. Det ger att bara en på 86 400 är av typen gamma. Enligt TNED krävs också att en blixturladdning måste uppvisa exceptionellt hög strömstyrka för att gammastrålningen ska komma ifråga. Om så sker, ska gammastrålningen dessutom (något) föregå den kommande egentligt observerbara blixturladdningen: positronringen blottläggs från ögonblicket med kopplingen molntråd-marktråd, just då atomstammen förmedlar elektronladdningen till markdelen och som bildar blixtstammens högjoniserade kärnplasma; Gammastrålningen tillhör den delen, först sedan kommer påfyllningen med elektroner utifrån luftdelen in till blixtstammen och därmed den egentliga urladdningsblixten. Se mera utförligt från BLIXTURLADDNINGEN. Observationerna anger också offsettider på runt 1 mS (se bl.a. ovan angivna källa). Så långt är alltså observationerna samstämmiga med TNED.

— Det tar grovt sett ca 1 mS för en ca 1KM lång blixtbanan att utbildas, analogt elektrontömmas uppifrån och ner med funktionen enligt TNED: om g-strålningen börjar först långt upp i toppen vid molnroten (se nedan), tar det ca 1 mS innan markdelen fått tillbaka sin elektrondel och därmed blixtkanalen är beredd att visa den egentliga blixtbilden. Därmed är (så långt) observation och teori samstämmiga, enligt hittills kända mätningar.

Eftersom (sannolikheten för) förekomsten av enskilda atomtrådar bör vara störst uppe vid molnroten (den stegade ledaren börjar därifrån med växande förgreningar nedåt), eller nere vid marktråden, utsäger TNED att gammabildningen också företrädesvis bör utgå från dessa källområden. Emellertid finns ingen strikt bestämd region att peka på eftersom atomtrådarna förekommer överallt utmed hela blixtbanan och gammastrålningen därför i princip kan förekomma var som helst utmed blixtkanalens utsträckning.

Eftersom g-strålningen enligt TNED högeligen beror av kärnringarnas spinnorientering transversellt blixtbanans utsträckning, är det också enligt TNED lika säkert att g-strålningen blir utpräglat »plan»; g-strålningen är INTE rundstrålande utan planriktad, (i huvudsak) analogt parallellt med markytans utsträckning eller egentligen tvärs blixtkanalens utsträckning. Då de flesta (90-95%) av alla blixturladdningar sker mellan moln-mark får därmed också de flesta g-associerade blixturladdningar den nämnda planutsträckningens karaktär.

Tillägg 2011-07-26: Uppgiften/källan från

http://www.nofc.forestry.ca/fire/faq_lightning_e.php

90% är av typen –CG, 10% är av typen +CG.

att ca 90% av alla blixturladdningar skulle vara av typen moln-mark verkar inte längre finnas tillgänglig på webben. Enligt en nyare uppgift (2009) från American Geophysical Union

http://europa.agu.org/?view=article&uri=/journals/jd/98JD01461.xml

är endast ca 23% av typen moln-mark medan resten ca 77% är av typen moln-moln. Vilketsom gör dock, här veterligt, ingenting åt saken i princip. Se även den ursprungliga referensen i MOLNTYP (Blixturladdningens fysik).

Notera den experimentorienterade, begränsade, framställningens ideala grund:

Gammastrålningens teoretiska planform enligt CAT i mera atmosfäriskt utdragen mening diskuteras INTE här. Inverkan av Jordmagnetismen på positronringarnas enskilda positroner (som strävar att sönderdela ringen i dess vidare expansion) bortses helt ifrån. Ringens allmänna fragmentering på grund av parannihilationer bortses också ifrån och som i egentlig mening bör medföra att de längst ut belägna, kvarvarande, positronmassorna knappast uppvisar den här förutsatta, ideala utbredningsriktningen analog med den primära planvågens expansion. I det praktiska fallet är det tydligt att en brytning mot den ideala centrala planformen introduceras, med en ökad grad av motsvarande godtyckliga gammastrålningsriktningar, men att den delen inte diskuteras här explicit.

Därmed är det väsentliga belyst i denna resumé:

· g-strålning från blixturladdning förklaras enligt TNED av de sällsynta fall (en på drygt 80 000) där strömstyrkan i urladdningarna närmar sig eller överstiger NUKLEÄRA SÖNDERFALLETS GRÄNSSTRÖMSTYRKA (78 000 Ampere för Syre): enligt uppgift (allmänt, här utan specifikation, olika källor anger något olika maxgränser) ligger medelblixten på runt 20 000 Ampere, men ända upp till tiofaldiga värden kan förekomma i de mest extrema fallen

· g-strålningen är i de fallen utpräglat planformad — ej rundstrålande — tvärs urladdningskanalens riktning

Genom g-strålningens utpräglade planform blir detekteringen av g-strålning från blixturladdning INTE någon vanlig — enkel — uppgift. Den kan, i princip, INTE spåras direkt från markbaserade mätpunkter. Också den detaljen är (numera) välkänd: g-strålningen från blixturladdningarna upptäcktes först (reguljärt, början av 1990-talet) med satelliter — som var ägnade att mäta på Solen och avlägsna galaxer. Det kom som en överraskning.

Se vidare

Blixturladdningens fysik i modern vetenskap och akademi

genom citat. Se även vidare beskrivning nedan via allmänna citat från webben om gammastrålningen från blixturladdningarna i Möjliga praktiska fall och observationer.

CATannihilationerna

ANNIHILATIONSSTRÅLNINGENS SPECIELLA FYSIK I CAT

Annihilationsstrålningen ±e beskrivs detaljerat enligt TNED från massvärmet. Men den beskrivningen berör idealt endast just annihilationen ±e — vilken är den enda experimentellt kända typen, med eller utan extra rörelseenergi för endera eller bägge komponenterna.

Den nedanstående illustrationen beskriver situationen i kollisionsfronten vid parannihilation, se Parannihilation,

Vid kollisionen med e-maken förintas den främsta t-ringen absolut säkert tillsammans med motsvarande del i maken, varvid de bakomvarande t-ringarnas ihoppressning från kollisionen intvingas i inbördes rekyl — vilket medför att hela cylindern studsar tillbaka — för att återigen accelerera in mot kärnringen, och vilken pumpande process fortlöper tills hela t-cylindern är förbrukad. Cylindern garanteras sin sammanhållning genom den inbördes magnetism som t-ringarna utvecklar genom hastigheten från accelerationen. Se även i Elektronens Bubbelkammarspår.

För varje sådan puls — frånsett inverkan av yttre moment — annihileras (idealt) en t-ring med energins bevarande formellt enligt

E = LQ²/t²

— t en konstant vi igenkänner från samma typ av massförintelse som figurerar i K-cellens värmefysik. Massdestruktionens energi för parannihilationen (frånsett inverkan av yttre moment) beskrivs av Planckenergin E=hf=2mc² med elektronens divergensenergi mc².

Men den typen är uppenbarligen inte den som gäller vid CAT.

gammastrålningens

formfysik

Annihilationerna i CAT är annorlunda, figuren nedan.

3D-modellen mitten ritad med hjälp av det äldre 3D-programmet Simply3D

När kärnringen (mitten, Q=A909e) blottläggs uppkommer en enorm Coulombisk centralattraktion i området. Alla omgivande elektronmassor attraheras dit, med största magnituden mot kärnringens centralplan där Coulombstyrkan är som störst (samma som idealt omskrivna laddningssfärens tvärsnitt).

3D-modellen ritad med hjälp av 3D-programmet Wings 3D

Med en förmodat mycket hög grad av homogenitet kommer — hur vi än ser saken, se vidare illustrerat längre ner i Elektronförintelsen i CAT — ett intermittent mönster av oscillerande resonansringar (figuren ovan, idealiserat) att bildas kring kärnringen — under den tidrymd som annihilationerna fortgår; Elektronmassornas t-ringar accelererar mot den högpositiva kärnringen, och kolliderar med denna via ekvivalenta Planckenergin (idealt, s.k. bromsstrålning, eg. stoppstrålning: kort höginduktiv transient)

E = hf = Fd = k_{9 T9 VM/C}(A₁₆918e_{1,602 t19 C})(e_{StarktAVTAGANDE})/d

= 30 MeV med d_max = 7 t13 M, mindre d ger högre E

strålningen totalt uppvisar i princip hela vågspektrum med största energin i E

Transientens induktiva verkan har sitt maximum i stoppriktningen, analogt i ringplanet.

Att gamma-strålningen enligt TNED också skulle vara ansvarig för de observerade ELVES-ringarna är mindre troligt. Se vidare i ELMEK.

Vilket vill säga: Förintelsen av laddningen (Q) medför I VILKET FALL en ökning av induktansen (L) endast i ringplanets utsträckning (se vidare nedan) så att energin bevaras konstant enligt ENERGILAGEN.

Omvänt, då Q=A909e⁺ blottläggs ur atomkärnan, avtar L lokalt, vilket garanterar underhållet i det häftiga strömdraget. Se vidare mera utförligt i CAT.

eFörintelsen i CAT

Elektronförintelsen i CAT

Den starkt positivt laddade Q=A909e kärnringen utverkar tydligt och tvunget en ytterst dominant elektrisk-magnetisk attraktion på inkommande elektronmassor och deras t-ringar, illustrationen ovan.

Med riktningspreferenserna givna — och välkända — enligt atomkärnans härledning i PLANCKRINGEN, ges uppenbarligen följande närbild i omedelbar anslutning till annihilationsprocessen:

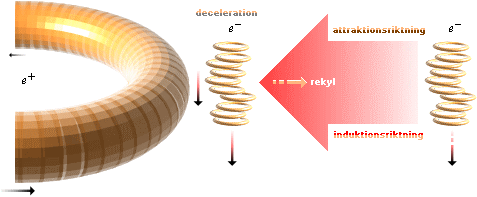
Processen söker mata — vräka — in så mycket elektronmassa som möjligt till kärnringen — Coulombiskt, induktivt. En utpräglad parannihilationsstrålning förekommer inte.

Annihilationerna sker på kärnringens ytterkant.

Med maximal magnetisk-elektrisk attraktion är det tydligt att de elektroncylindrars t-ringar som bildar front mot kärnringen, tiltar in sig med maximal spinnsynkronisering — som därmed »smetar fast» t-ringarna mot kärnringen i deras annihilation som så att säga »rullas av» mot kärnringen i dennas maximalelektriska plan. Därmed sker annihilationerna med maximal Coulombkraft helt transversellt i jämförelse med den konventionella parannihilationen.

Elektronmassorna som ligger bakom fronten och som accelereras in mot kärnringen, tvingas regelrätt till en viss rekyl då de kolliderar med i deras ögon ”elektronfronten” och vilken kollision — med hänsyn till strukturen — måste bli (väsentligen) dämpad: ringarna kan delvis glida in mellan varandra och därmed åstadkomma en närmast enorm elektrontäthet invid kärnringens ytterkant. Därmed är det enkelt att se hur »elektronhavet» kring massringen STÖTER sig fram mot kärnringen i sekvenser med annihilation-attraktion-rekyl-attraktion-annihilation … . Figuren ovan ger en antydan om processen.

Den föregående illustrationen (nedan) tjänar därmed som en tydlig bild av hur de så uppkomna ”ringresonanserna” uppenbarligen formas kring kärnringen: annihilationsstrålningen får bara en och endast en induktiv komponent i lägesändringen: ringplanet. All huvudsaklig em-strålning som sammanhänger med elektronringarnas förintelse initieras (idealt) i ringplanet, radiellt utåt-inåt, och fortplanatas därmed också i den riktningen. Det betyder att CAT-annihilationerna blir ytterst speciella, unika fenomenformer. Idealt utbildas med andra ord ingen strålning alls uppåt-neråt.

Som tidigare noterats i kraft av experimentanordningens ideala fysik: I en utvidgad praktisk atmosfärisk urladdning — luftens täthet minst 1000 ggr lägre än den fasta materiens — finns möjligheten att positronringarnas fragmentering via parannihilationerna, beskrivna ovan, tunnar ut ringen (även tillsammans med inverkan av krafterna från Jordmagnetiska fältet) så att fristående positronmassor kan växelverka med omgivande atomers elektronmassor. Därmed är det inte lika klart — på större avstånd från urladdningsområdet — att gammastrålningen är av den ursprungliga plantypen, utan snarare (alltmer) av den konventionella parannihilationstypen — och därmed tillhörande godtyckligt riktad beroende på orienteringen i komponenternas aktuella färdväg. Denna detalj ingår inte i huvudtextens förutsättningar, utan hela positronringens expansion förutsätts idealt obruten.

Dvs., framställningen i huvudtexten får förstås inom ett relativt begränsat (ej närmare specificerat) närområde sett från urladdningslokalen.

En markbaserad station har då inte ens en minsta chans att registera något alls av den strålningstypen — om den händelsevis inte sker som resultat av blixturladdning horisontellt (moln-moln), precis skärande markstationen dessutom.

Om (som det sägs) de allra flesta blixturladdningarna är av typen moln-mark blir sannolikheten mycket marginell för att kunna påvisa CAT-strålning från markbaserade stationer.

Blixtbanans variation tycks i vilket fall inte göra någon större åtskillnad mellan typerna Moln-Moln och Moln-Mark. Med de olika stråksteg som en blixtbana uppvisar kan i princip alla möjliga riktningsfall återfinnas i vilkensom av de bägge typerna. Den åtskillnad som görs här i huvudtexten, kan av allt att döma bortses ifrån.

Om dessutom, som antyds ovan, elektrontätheten kring kärnringen just i vågutbredningens ringplan är så exceptionellt stor att den helt saknar motsvarande preferenser i hittills kända experimentella observationer, kan vi heller inte tillämpa någon normal materiematematik för beräkning av strålningens radiella dämpning: Strålningsdämpningen per meter bör bli exceptionellt stor, vilket betyder att den omgivande elektronmassan bör absorbera strålningen med hög effektivitet i motsvarande exciterande jonisation på omgivande atomer (motsvarande seismiska cirkulärt expansiva kopplade vibrationer).

Med denna beskrivning framgår det tydligt HUR gammastrålningen (m®g) i ±e-förintelsen tvunget måste gestalta en (ytterst tunn) planform — tvärs blixtkanalens utsträckning — enligt TNED.

praktiska fall

MÖJLIGA PRAKTISKA FALL

— OCH OBSERVATIONER

Vad TNED kräver: Om vi ser till den mest tydligt sannolika blixtkanalens längsriktning relativt lodlinjen med den uppskattade vinkeln ±45°, figuren i a nedan, samt den tillgängliga synhorisont som en satellit på höjden runt 500 KM ser av Jordytan, figurerna b och c nedan, har vi i stort bilden av vilka möjliga fall med gammabildning från blixturladdningar av typen moln-mark som enligt TNED med ovanstående beskrivna riktningspreferenser skulle kunna registreras genom mätning från en (typisk) satellit.

a	b	c
Mest sannolika vinkelområdet ±45 grader relativt lodlinjen	Satellitens synhorisont

Normala satellithöjder är inte så mycket som illustrationens 1000 KM utan ligger (typiskt) runt hälften. Se mera utförlig beskrivning längre ner i Praktiska Satellitbanor.

Vi noterar som tidigare angivits enligt TNED, att inte alla blixturladdningar kan bilda gammastrålning. Se mera utförligt från NUKLEÄRA SÖNDERFALLETS GRÄNSSTRÖMSTYRKA om ej redan bekant.

De små ringarna i figurdelen i c ovan till höger markerar det vinkelområde som [blixturladdningens längsriktning, vars rätvinkliga utsträckning] återstår för infångning av satellitens mätinstrument för att kunna registrera gammaförekomsterna enligt TNED — med samtidig kännedom om det aktuella blixturladdningsområdets vinkelutsträckning om mätningen ska ge exakta besked. Vilket — tydligen — vill säga totalt sett:

ENDAST MED YTTERST AVANCERAD MÄTUTRUSTNING kan man få fram säkra (direkta) data; Flera olika typer av synkroniserade mätanordningar behövs, utspridda (i stor mängd) på olika platser Jorden runt (högt över marken, men lägre än en ordinär satellit).

Det är också fallet numera (Jul2011). Ett global nätverk av sensorer registrerar alla blixturladdningar över hela världen tillsammans med synkronisering via satelliter som kontinuerligt mäter av förekomsterna (Fermisatelliten som exempel). Se vidare notering om Fermisatelliten längre ner.

JÄMFÖR:

I dagens läge (2008VII) har man inte ens koll på varifrån exakt som de blixturladdningar kommer som faktiskt associeras med gammastrålning. Närmaste näravstånd till den mätande anordningen är 30-50 mil. Man känner alltså inte närmare den lokal som gammastrålningen kommer ifrån — om den ens är förknippad med någon ordinär del i blixtstammen.

De rapporter som finns på webben inskränker sig (ännu 2008VII, tyvärr) i stort till skrivningar från 2005. Febril forskning pågår.

I början (slutet på 1990-talet) uttryckte man uppfattningen att gammastrålningen skulle komma från områden högt ovanför blixturladdningen. Senare

(från 2004, ref. [http://www.scienceagogo.com/news/20050403220449data_trunc_sys.shtml]

Terrestrial Gamma Ray Mystery Deepens, by Kate Melville, 4 May 2005, se citat nedan)

har man ”sänkt ribban” till områden inom (eller strax ovanför) det aktuella åskmolnet. Men man har fortfarande ingen preciserad utrustning för att närmare kunna avgöra gammalokalen.

[http://www.scienceagogo.com/news/20050403220449data_trunc_sys.shtml]:

{Terrestrial Gamma Ray Mystery Deepens, by Kate Melville, 4 May 2005}:

”Their report suggested that runaway breakdown at a much lower altitude, created within "strong fields in or just above the thundercloud," could have triggered the TGFs instead. "It still almost certainly has to be runaway breakdown that's creating these," Cummer said. "The only real possibility is that it's much closer to the cloud top, and linked to something else happening inside the cloud."”

Min översättning:

Deras rapport antydde att skenande nedbrytning vid en mycket lägre höjd, bildad inom ”starka fält i eller strax ovanför åskmoln,” kunde ha igångsatt TGFs istället. ”Det måste fortfarande nästan säkert vara skenande nedbrytning som skapar dessa,” sade Cummer. ”Den enda verkliga möjligheten är att det [fenomenet] ligger mycket närmare molntoppen, och kopplat till någonting annat som händer inuti molnet.”

I de första observationer som gjordes från satelliten CGRO (Compton Gamma Ray Observatory, 1991-2000) och dess speciella projekt BATSE (Burst And Transient Source Experiment)

utformades, som nyligen omnämndes, teorierna med uppfattningen att källan till gammastrålningen låg i den övre delen av atmosfären. Webbkällan (1999)

http://www-star.stanford.edu/~vlf/runaway/

ger en pdf-referens från samma år (1999),

http://www-star.stanford.edu/~vlf/runaway/pdf/pap99.pdf

som beskriver grundidén — samt en upptagning (källans ”Figure 9”) från en mätning som indikerar gammasensorns upptagna strålvinkel. Bilden, och texten, ger värdet runt 15° — samt en teckning (Figure 9c, se nedan) som visar hur författarna tänker sig gammastrålningen i dess källning mot satelliten: den utgår högt ovanför åskmolnet med blixten under och genom markerade elektroner som drar iväg uppåt utåt rymden, och som sedan böjer av på utritade Jordmagnetiska fältriktningar.

Gammastrålningens upphov i samband med blixturladdning, Lehtinen et al 1999

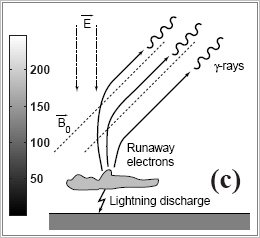
Figure 9c, Monte Carlo simulation of runaway MeV electron breakdown with application to red sprites and terrestrial gamma ray flashes,

N. G. Lehtinen, T. F. Bell, and U. S. Inan, 1999

Författarna skriver:

[http://www-star.stanford.edu/~vlf/runaway/pdf/pap99.pdf] 1999:

{Monte Carlo simulation of runaway MeV electron breakdown with application to red sprites and terrestrial gamma ray flashes, N. G. Lehtinen, T. F. Bell, and U. S. Inan}:

”The prediction is that for midlatitudes the gamma ray emissions are aligned with the geomagnetic field. Unfortunately, the direction of origin of the terrestrial gamma ray flash requires a special analysis of BATSE data and is not in the public domain, so we cannot draw a conclusion about a correlation between it and the geomagnetic field.”

Min översättning:

Förutsägelsen är att för mellanlatituder är gammaemissionerna längsriktade med det geomagnetiska fältet. Tyvärr kräver den ursprungliga riktningen för gammastråleflashen en speciell analys av BATSE data och dessa är inte tillgängliga för allmänheten (is not in the public domain), så vi kan inte dra någon slutsats om justering mellan den och det geomagnetiska fältet.

Min illustration:

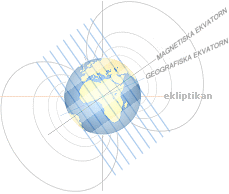
Bilden ovan på Jordmagnetiska fältets riktning är här helt idealiserat som riktningen mellan magnetiska polerna. I praktiken (Se webbdata från CIRES) funger det inte (riktigt) så: Omkring ekvatorialbältet är magnetfältets riktning på Jordytan nära parallellt med Jordkroppens longituder, alltså nära vertikalt i riktning i figuren ovan.

Författarnas teoretiska uppslag med gammastrålningen som förorsakad av elektronrörelser (med mekanism utan känd orsak) uppåt atmosfären och som riktas in av Jordmagnetiska fältet och som genom kollisioner med de atmosfäriska atomerna antas åstadkomma den observerade gammastrålningen, antyder att den så Jordmagnetiskt riktade gammastrålningen eventuellt skulle vara systematiskt längsriktad med Jordmagnetiska fältet ENDAST ”för mellanlatituder”, illustrationens antydda band över-under magnetiska ekvatorn.

Att döma av rapporterna efter 1999 (författarna ovan) fram till nu (2008) finns inget omnämnande om någon systematisk koppling alls i riktningshänseende mellan de observerade gammastrålarna och Jordmagnetiska fältets riktning. Se även källan längre ner RHESSI-observationerna som omnämner sammanhanget i citat. Vi kan därför, och med största sannolikhet, lugnt räkna med att ”magnetteorin” är avskriven — på grund av att man konstaterat att en sådan förmodad riktningspreferens inte har observerats (inte alls över huvud taget) — eller att observationerna i det avseendet (ännu) är så svåra att genomföra att man (ännu) inte kunnat framställa något avgörande alls i saken.

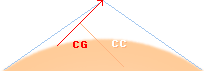
Enligt TNED, figuren ovan, finns också specifika riktningsvillkor, men ingenting som för fallet med gammastrålningen explicit är beroende av Jordmagnetismen (den är alldeles för svag för att ha någon inverkan i dessa sammanhang).

Att Jordmagnetismen skulle koppla någon specifik gammastrålning i samband med blixturladdningar enligt TNED finns här veterligt inga belägg för. Däremot bör Jordmagnetismen som sådan ha betydelse för positronförekomsten som sådan, om en sådan finns på större avstånd från urladdningsområdet. Denna detalj diskuteras dock inte här i huvudtexten (men den kommer med längre fram i och med direkta observationer av positronförekomst utmed Jordmagnetiska fältlinjer — med ursprung i blixturladdningar [Se separat NASA-artikel från Jan2011]). Se mera utförligt från Blixturladdningens Fysik 2011.

Riktningsvillkoren i TNED är emellertid av en helt annan natur jämfört med ovanstående uppslag, TNED-fysiken utesluter på intet sätt någon enda riktning — men skiljer å andra sidan delvis mellan olika möjliga urladdningstyper (CG moln till mark, CC moln till moln). Analysen av mätdata måste alltså i vilket fall (även för TNED:s del) likväl bli synnerligen krävande.

Den röda pilen i illustrationen närmast ovan pekar på satelliten med linjens utsträckning i gammaplanet enligt TNED. Den rätvinkliga orangea linjen anger blixtstammens urladdningsriktning i det aktuella området. För CG-fallen kan alla riktningar 0-90° relativt vertikallinjen i princip komma i fråga (och till och med i mera sällsynta fall uppriktningar) även om de mest troliga fallen bör ligga inom området ±45°. Tas CC-fallen med (horisontella blixturladdningar), blir satellitens uppfångningsområde i princip heltäckande för hela dess synvinkel över Jordkalotten.

Enligt en av de mera namnkunniga huvudkällorna i ämnet gammastrålning från blixturladdningar

RHESSI-observationer i delvis sammanställning från 2005

[http://scipp.ucsc.edu/seminars/experimental/davidsmith11_1_05.pdf] 1 November2005;

{Gamma Rays from Lightning; [SCIPP, U. C. Santa Cruz]: David M. Smith, Brian Grefenstette, Jacob Stanley; [SFSU]: Liliana I. Lopez; [U. British Columbia]: Robert P. Lin, U. C. Berkeley, Christopher P. Barrington-Leigh}:

”The spectrum and intensity* are independent of magnetic latitude and local time: *subject to strong selection effects”.

Min översättning:

Spektrum och intensistet är oberoende av magnetisk latitud och lokal tid.

NOTERING: Föregående arbeten av Lehtinen, Bell och Inan (1999) omnämns i ovanstående referens (som teoretiska premisser i fenomenets allmänna kandidaturer). Emellertid tycks citatet ovan klargöra att inverkan av Jordmagnetismen saknar stöd i RHESSI-observationerna, och därmed att Lehtinen-kollaborationens uppslag inte har fysikaliskt stöd.

Emellertid, meningarna från källan ovan är också preliminära och här på intet sätt definitiva. Vi bör ha den delen i minnet också. Inget är avgjort än.

ligger huvuddelen av de gammaassocierade blixturladdningarna i ett band kring ekvatorn: förekomsten avtar med avståndet från ekvatorn. Eftersom också huvuddelen av satellitens banlängd befinner sig på andra ställen än just över ekvatorn (CGRO-inklinationen var 28,5° och RHESSI-inklinationen är 38° över ekvatorn, se illustrationen nedan) och därmed också tillbringar den mesta mättiden på andra ställen än just över ekvatorn, är indikeringen given: För att satelliten ska kunna se g-strålarna från ekvatorialbandet när den INTE befinner sig där är det tydligt att strålutbredning INTE kan vara direkt uppåtriktad i ekvatorialbandet, utan mera i riktning horisontellt så att strålriktningen når satelliten — typ ovanstående principillustration.

Vilket vill säga: OM g-strålningen vore strängt uppåtriktad, samgående med den normala (vertikala) blixturladdningsriktningen (CG-fallen, de utgör ca 90% av alla fall), skulle satelliten observera de flesta förekomsterna bara just då MÄTÖGAT korsar ekvatorialbältet, och sedan uppvisa helt noll då instrumentögat precis passerar ut ur ekvatorialbandet — och därmed i princip ingenting i resten av satellitbanan. Men heller ingen sådan systematisk observation har rapporterats — och dock bör en sådan, om den föreligger, vara den allra enklaste att konstatera.

Med föregående påpekande om framställningens begränsade gammaplan kontra den mera praktiskt möjliga upplösningen på större avstånd (den utpräglade planriktningen bryts upp med positronringens vidare expansion/fragmentering), kommer riktningsaspekten för gammastrålningen generellt att utjämnas över större avstånd. Det förda resonemanget i huvudtexten får med andra ord allt mindre betydelse ju längre bort från urladdningsområdet som eventuella mätningar genomförs — även sett till höjddelen ovanför urladdningspunkten. Med andra ord: en satellit bör i det praktiska TNED-fallet också kunna infånga gammastrålning från alla riktningar som är synliga sett från satellitens (ljusmässiga) synvinkel.

praktiska satellitbanor

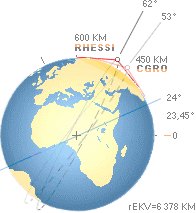
Allmänna SatellitData för CGRO verksam perioden 1991-2000 i cirkulär bana med altitud (höjden över Jordytan) 450 KM, banans lutning mot ekvatorn (inklinationsvinkeln) 28,5° enligt The Earth’s Gamma-ray Albedo as observed by EGRET, Dirk Petry, Joint Center for Astrophysics, University of Maryland Baltimore County, Baltimore, MD 21250 and NASA, Goddard Space Flight Center, Greenbelt, MD 20771, samt

Allmänna SatellitData för RHESSI verksam från 2002- i cirkulär bana med altitud (höjden över Jordytan) 600 KM, banans lutning mot ekvatorn (inklinationsvinkeln) 38° enligt NASA [http://hesperia.gsfc.nasa.gov/hessi/sheet.htm], Se Science Facts på Rhessis Hemsida.

Figuren ovan visar Jorden med ekvatorn i 24° lutning (eg. 23,45°) mot ekliptikan (Jordbanans omloppsplan kring Solen), vilket avrundat illustrativt ger nominella ekliptiska inklinationerna respektive 24+29=53° och 24+38=62° för CGRO och RHESSI.

Enligt TNED bör istället satelliten, just, kunna observera även ekvatorialförekomster under alla delar av satellitbanan (se typillustrationen ovan) — även om frekvensen, runt om mätögat naturligtvis, bör bli större då satelliten kommer närmare ekvatorn som har den högsta frekvensen gammaassocierade blixturladdningar.

— Både CGRO på sin tid, och RHESSI-satelliten nu, torde vara — idealt — totalt rundseende — vi vet det inte här — men resonemanget förutsätter att konstruktörerna haft den föresatsen.

Strålvinkeln på 15° (källans Figure 9b) är en tydlig indikering på att gammaaktiviteten var — i detta speciella fall — ytterligt begränsad, men den uppgiften medger heller ingen mera preciserad bild — typ om den smala strålen är/var av typen generellt radiell förekomst, eller en unik singulär stråle som händelsevis råkade träffa satelliten.

Vi ser redan av den här (lilla) uppgiften att de mättekniska svårigheterna är formidabla: det kommer (uppenbarligen) att krävas decennium innan man kommer fram till något av mera tydlig natur.

Emellertid bevisar källan ovan från 1999 i ljuset av författarnas intresse för strålriktningen av princip en viktig punkt: gammaaktivitetens strålbildning är mycket speciell.

Genom den senare upptäckten [först från 5Nov2009, vidare definitivt klarlagt 14Dec2009, i artikel först Jan2011] av positroner — verkligen — i samband med blixturladdningar som också uppvisar gammastrålning [Se separat NASA-artikel från Jan2011], har frågan om gammastrålningen — hela huvudtexten ovan — delvis spelat ut sin roll. Positronförekomsten delvis förenklar hela frågans svårighet i och med att positronerna löper i Jordmagnetiska fältet — och därmed kan analyseras mera matematiskt på den vägen (även till initiell blixturladdningsriktning [vidare beskrivning under utformning nu Jul2011]).

— Se utförligt från Blixturladdningens Fysik 2011.

Uppfattningen om gammastrålningens smala natur uttrycks också av källan nedan från 2005 (TGF, Terrestrial Gamma ray Flash, JordGammaFlash eller TerraGammaFlash):

[http://currents.ucsc.edu/04-05/02-21/flashes.asp] February 21, 2005:

{New satellite observations of terrestrial gamma-ray flashes reveal surprising features of mysterious blasts from Earth, By Tim Stephens}:

”The authors estimated a global average rate of about 50 TGFs a day, but the rate could be up to 100 times higher if, as some models indicate, TGFs are emitted as narrowly focused beams that would only be detected when the satellite is directly in their path.”

Min översättning:

Författarna uppskattade en global medelförekomst på runt 50 TGFs per dygn, men den förekomsten skulle kunna vara upp till 100 gånger högre om, som en del modeller antyder, TGFs emitteras som smalt fokuserade strålar som bara skulle kunna detekteras när satelliten står direkt i deras väg.

FÖR DET PRAKTISKA FALLET återstår således ännu (2008VII) att avliva TNED: Ingenting har (ännu) framkommit som tyder på att TNED inte gäller. Det behövs mera mätdata.

Uppmärksammat 31Aug2010

Fermisatellit bekräftar TNED — Positronförekomst enligt TNED i TGF bekräftad

Se beskrivning i POSITRONFÖREKOMST I TGF BEKRÄFTAD.

TGF, eng. Terrestrial Gamma ray Flashes, sv. [Terrestriella] Jordbaserade gammastråleflashar.

Fermisatelliten [Fermi Gamma-ray Space Telescope] bekräftar positronförekomst från TGF — Tillkännagivande 5 November 2009 Fermi Symposium, uppmärksammat här först 31Aug2010. Se även i Tillägg31Aug2010 i AGW.

PARANNIHILATIONENS FYSIK

Allmänna grovberäkningar för annihilationsstrålningens energi — för allmän översikt och referens

Idealt, utan yttre kinetisk energi, omsätter varje massförintelse (m®g) av en elektron med massan 9,11 t31 KG divergensenergin (c=3 T8 M/S) E=mc²=8,2 t14 Joule avrundat eller 0,512 MeV (mera noggrant med c=2,99792458 T8 M/S blir värdet 0,51108984 MeV eller avrundat 0,511 MeV).

Med Planckenergin E=hf ges frekvensen

f = (8,2 t14)/h_{6,626 t34 JS} = 1,24 T20 Hz avrundat

— eller räknat i den massförstörande ekvivalenta tiden

T_DESTR = 1/f = 8 t21 Sekunder.

Det är den (ekvivalenta energi-) tid det tar för elektronen-positronen att förinta varandra ömsesidigt med referens till en deras gemensamma (fixa) tyngdpunkt, och förutsatt att inga yttre störande moment finns med.

Med t-ringens dimensioner, sämsta fallets resultat, består varje elektronmassa som minst av n=177062 t-ringar. Massförintelsefrekvensen — och därmed annihilationsstrålningens absolut maximala elektromagnetiskt emitterande vågfrekvens — som överlagras på hf-energin blir då ekvivalent

f = (8,2 t14)/(h/n) ;

= 2,19 T25 Hz

= 4,57 t26 S

För formen h/n, se Plancks Strukturkonstant, om ej redan bekant.

ANNIHILATIONSDISTANSEN — största elektriska attraktionsavståndet mellan tyngdpunkterna elektron-positron under annihilationsförloppet, analogt kraftvägen — beräknas idealt via 2mc² enligt

E = 2mc² = Fd = kQ²/d;

d = ke²/E

= (9 t9 VM/C)(1,602 t19 C)²/2(8,2 t14 J)

= 1,4 t15 M avrundat — nära samma som protonradien (1,37 t15 M)

Vi observerar här preferenserna enligt TNED: divergensenergin mc² gäller med referens till det omgivande lokalt dominanta g-systemets fasta rymdpunkter, vilket normalt sett är Jordytan med dess fasta materiepunkter; Annihilationsmekanismen uttömer sig genom den fasta rymdpunktens referens på beloppet 2mcc.

NOTERING. Ovanstående d-form (dubbla värdet) brukar anges konventionellt med termen elektronens klassiska radie (eng. classical electron radius). Det finns (2008) flera (många) exempel på webben @INTERNET som använder den formen (i samband med beskrivningar av begreppet annihilation).

Enligt TNED finns ingen sådan koppling till elektronen; Elektronen enligt TNED är en kvantitet; den har ingen bestämd form eller utsträckning eller ”radie”, utan består av ett antal individer — t-ringarna som ovan — med de speciella egenskaper som beskrivs ingående i Spektrum och Kvanttalen.

Om vi känner kraftvägen (d) med arbetet (E=Fd) kan vi beräkna kraften (F) och därmed ekvivalenta accelerationen (a=F/m=v/T) och därmed T på en delvis oberoende väg med OBS maximala v=c/2 enligt

T = mv/F = mv/(E/d) = m(c/2)/(E/d) = mcd/2E = mcd/2(2mc²) = d/4c

= (1,4 t15 M)/4(3 t8 M/S)

= 1,167 t24 S

= 8,57 T23 Hz

SOM VI SER är värdena GROVT SETT samstämmiga: Gammafrekvenserna — materiestrålningens allra högsta möjliga frekvenser — ligger i stort maximalt omkring T23 till T25 Hz — hur vi än räknar.

Se även i NEUTRINOSPEKTRUM.

vMAX

vMAX = c/2 är den maximalt ömsesidiga attraktionshastighet som två (lika) elektriskt fritt rörliga laddningar kan utbilda med referens till en deras gemensamma tyngdpunkt. Varje Q-system kan (nämligen) som mest attrahera varje annat Q-system med den i systemet inneboende flödesnaturkonstanten c₀ — oberoende av vilka som helst andra rörelseaspekter som kan finnas. Relativt en gemensam föreningspunkt (kollisionsplatsen) blir därför ekvivalenta attraktionshastigheten endast hälften (förutsatt lika laddningar och massor). MASSÖKNINGSEFFEKTEN i det slutna elektriska systemet är i vilket fall som tidigare härletts i PLANCKEKVIVALENTERNA noll. Därmed är annihilationsämnet uttömt.

ELMEK (eng. ELVES)

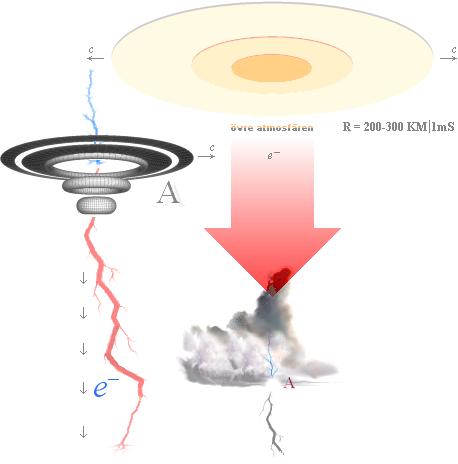
Om urladdningsströmmen överstiger gränsvärdet (78 000 Ampere för Syre) finns ENLIGT TNED förutsättning för atmosfärisk bildning av starkt planformad gammastrålning — men att den delen skulle förorsaka någon speciell återverka på den övre atmosfären i motsvarande observerade snabbt expanderande ring är mindre troligt. Det senare fenomenet har istället sin mera troliga förklaring i den generella transientpuls med sin höga induktiva verkan som aktualiseras just vid randen av själva urladdningsströmmen. Då denna induktionspuls återkopplas uppåt med ljushastigheten och därmed attraherar elektronmassor i den förtunnade atmosfären, kan ljusemission uppkomma i periferin på motsvarande expanderande ring då pulsverkan genomtränger det uttunnade aktuella atmosfäriska skalet.

Under en kort tidrymd (1mS) uppkommer en plötslig positiv STÖT med laddningsökning (med en motsvarande intern induktansminskning enligt E=LQ²/t²). Se utförligt från BLIXTURLADDNINGEN. Den induktiva effekten av den stöten kan bli mycket stark [u=L(di/dt)] om ändringstiden är mycket kort, vilket också är vad som krävs rent tekniskt. Effekten på omgivande materiesystems elektronladdningar sprids rundstrålande (från händelseområdet vid A) med ljushastigheten (c), och genomtränger därmed ett tunt atmosfäriskt ljusemitterande skikt i formen av lokala elektrondrag som svarar på stötströmmen och därmed påverkar den uttunnade atmosfäriska gasen som emitterar en lysande ring med avtagande ljusstyrka som expanderar med c under 1 mS.

På samma sätt som vi kan se att vätgas under lågt tryck (se exv trådstråleröret) blir lysande om man skickar elektroner genom gasen, så kan de övre mycket uttunnade atmosfäriska skikten också uppvisa ett (mycket) svagt sken om det sker ett tillfälligt elektrondrag uppifrån och ner (eller för den delen nerifrån och upp). Ett sådant elektrondrag kan bildas under den korta tid då strömrusningen initieras i blixturladdningen, analogt då blixtstammens atomagenter blottläggs på sina elektronmassor som dras ner till marken genom stamströmmen.

Figuren ovan ansluter till beskrivningen genom att antyda en motsvarande med ljushastigheten expanderande ring i den övre atmosfären, rakt ovanför en blixturladdning (A).

Man har iakttagit (sådana) ringformationer högt upp i atmosfären (med början från 1990-talet, från lägst 80 KM höjd) som sägs expandera med ljushastigheten under ca 1 mS, samt associerade med blixturladdningar — större än 60 KA enligt nedanstående källa @INTERNET:

[http://www-star.stanford.edu/~vlf/publications/theses/cpblThesis.pdf] 2000,

s71:

”… the electric field causing heating, ionization, and optical emissions in elves is that of an electromagnetic wave which is launched by, and occurs in proportion to, changing current moments associated with very impulsive (>60 kA) return stroke currents [e.g., Barrington-Leigh and Inan, 1999]. As a result, elves last no longer than ~1 ms”.

Min översättning

… det elektriska fält som förorsakar uppvärning, jonisation och optisk utstrålning i ELVES är det från en elektromagnetisk våg som sjösätts av, och uppträder i proportion till, ändringar i strömmoment associerade med mycket kraftiga (>60 KA) returstötströmmar

[eg., Barrington-Leigh och Inan, 1999]. Som resulatat av det, varar inte ELVES längre än ungefär 1 millisekund.

NOTERING. ELVES är den engelska akronymen för Emission of Light and Very Low Frequency Perturbations From Electromagnetic Pulse Sources, Emission av Ljus och Mycket Låg Frekvens Störning Från Elektromagnetiska Puls Källor, motsvarande svenskans ELMEK.

Allmänna samband

Sammanställning genom citat

Blixturladdningens fysik i modern vetenskap och akademi

SAMMANHANGET FRAMGÅR GENOM CITAT

’Vad orsakar blixturladdning?’

2008-03-03:

SCIENTIFIC AMERICAN

[http://www.sciam.com/article.cfm?id=experts-do-cosmic-rays-cause-lightning] 24 January 2008:

{Do cosmic rays cause lightning?}:

”Your question lies at the core of one of science's great mysteries: What causes lightning?

Decades of electric field measurements made inside thunderstorms have failed to find large enough electric fields to cause a spark, even when the effects of precipitation are taken into account. Since we know that lightning does occur—in fact, it strikes the earth about four million times a day—we must be missing something in our understanding.”

”So, does all this add up to cosmic rays as the cause of lightning? No one can be sure at present.

Some researchers, including myself, have voiced skepticism about this mechanism, due to a few technical problems. For example, for lightning to propagate it must form a hot, conductive channel. This channel acts like a metal wire, allowing very big electrical currents to flow. It is difficult to understand how a large, diffuse discharge produced by an air shower and runaway breakdown could result in such a hot channel measuring just a few centimeters across. Alternative explanations of lightning initiation have been proposed, including some that involve a conventional breakdown from water and ice particles, as well as others that involve differing forms of runaway breakdown without cosmic rays. Scientists are busy working on models and experiments to test the validity of all these ideas.”.

Min översättning:

Är kosmisk strålning orsaken till blixturladdning?

Din fråga ligger vid kärnan av en av vetenskapens stora mysterium. Vad förorsakar blixturladdning?

Decennium av elektriska fältmätningar som gjorts inuti åskväder har misslyckats att finna tillräckligt stora elektriska fält som kan förorsaka en gnista, även då effekterna av nederbörd tas med i räkningen. Eftersom vi vet att blixturladdning verkligen förekommer — den slår i själva verket Jorden fyra miljoner gånger per dygn — måste vi missa något i vårt begripande.

Så, är då summan av det hela att kosmisk strålning är upphovet till blixturladdning? Ingen kan veta säkert för närvarande.

En del forskare, mig själv inkluderat, har uttalat skepticism beträffande denna mekanism, beroende på en del tekniska problem. Till exempel, för att blixturladdning ska kunna fortplantas måste den bilda en het, ledande kanal. Denna kanal fungerar som en metalltråd, som tillåter mycket stora elektriska strömmar att flyta. Det är svårt att förstå hur en stor, diffus urladdning producerad av en luftdusch och skenande nedbrytning skulle kunna resultera i en sådan het kanal på några få centimeter tvärs över. Alternativa förklaringar till blixurladdningens initiering har föreslagits, inkluderat en del som involverar en konventionell nedbrytning från vatten och ispartiklar, så väl som andra som involverar olika former av skenande nedbrytning utan kosmisk strålning. Vetenskapsmän är upptagna med att arbeta på modeller och experiment för att testa giltigheten för alla dessa uppslag.

’Man vet mycket litet om blixturladdning’

[http://www.space.com/businesstechnology/technology/rocket_lightning_030130.html] 30 January 2003:

{Zap! Rockets Trigger Lightning, Scientists Discover X-rays By Robert Roy Britt}:

”Scientists fired rockets into raging Florida thunderstorms and learned that lightning produces not just bright flashes and a lot of noise, but also intense bursts of radiation believed to be X-rays.

Many theorists had long thought such emissions from lightning impossible.”;

”It also shows how little scientists know about lightning.”;

”Here's what they think is going on: Electrons ambling freely through the air cannot move very fast, because they keep bumping into air molecules. Yet these free electrons, as they are called, behave counterintuitively. Speed them up, and they are impeded less by neighboring molecules. Once some momentum is in place, the electrical field of a lightning storm is then free to accelerate the electrons to nearly the speed of light.

"We're assuming that's what is happening, because nobody has a better idea," Dwyer said.

”.

Min översättning:

Forskare avfyrade raketer in i Floridas härjande åskväder och fick veta att blixturladdning producerar inte bara ljusa blixtar och en massa buller, utan också intensiva skurar av strålning som tros vara röntgenstrålning.

Många teoretiker hade länge trott sådana utstrålningar från blixturladdning omöjligt.

Det visar också hur litet forskarna vet om blixturladdning.

Här är vad de tror pågår: Elektroner som lunkar fritt genom luften kan inte färdas särskilt fort, därför att de hela tiden bumpar emot luftmolekyler. Ändå beter sig dessa fria elektroner, som de kallas, omvänt intuitivt. Snabba upp dem, och de hejdas mindre av närliggande molekyler. När väl ett visst moment föreligger, kan det elektriska fältet hos ett åskväder fritt accelerera elektroner till nära ljushastigheten.

Vi antar att det är vad som händer, därför att ingen annan har någon bättre idé, sade Dwyer.

’Man vet inte hur blixturladdning bildas’

[http://news.nationalgeographic.com/news/2007/10/071011-lightning-rays.html] 11 October 2007:

{Thunderstorm Gamma Rays Linked to Lightning, Brian Handwerk for National Geographic News, October 11, 2007}:

”How thunderclouds produce the rays has not been explained. Neither has the nature of their apparent link to lightning formation, about which many long-standing mysteries remain.”.

”The electric fields in thunderstorms appear to be too weak to form lightning, so scientists have been puzzled by how the bolts form. Cosmic rays have also been suggested as a trigger for the flashes.”

Min översättning:

Hur åskväder producerar strålarna har inte förklarats. Det har inte heller naturen hos deras uppenbara koppling till blixturladdningens bildning, omkring vilken många långvariga mysterium kvarstår.

De elektriska fälten i åskväder verkar vara för svaga att bilda blixturladdning, så forskarna har varit förbryllade över hur blixtarna bildas. Kosmiska strålar har också föreslagits som en igångsättare för flasharna.

’Man vet inte hur g-strålningen bildas’

[http://www.nasa.gov/vision/universe/solarsystem/rhessi_tgf.html] 17 February 2005:

”"The energies we see are as high as those of gamma rays emitted from black holes and neutron stars," said David Smith, an assistant professor of physics at UC Santa Cruz and author of a scientific paper on this topic.”;

”The exact mechanism that accelerates the electron beams to produce TGFs is still uncertain, he said”.

Min översättning:

Energierna vi ser är så höga som de i gammastrålar som utsänds från svarta hål och neutronstjärnor, sade David Smith, en assisterande professor i fysik vis UC Santa Cruz och författare till en vetenskaplig rapport i ämnet.

Den exakta mekanism som accelererar elektronstrålar att producera TGF:s är fortfarande okänd, sade han.

Notering. TGF (Terrestrial Gamma-ray Flashes), Jord(Terra)GammaFlashar.

MED DEN EXCELLENS som TNED beskriver, härleder och förklarar ämnet (min uppfattning), är det tydligt att den moderna vetenskapen och akademin kan hålla på i evigheter med ovanstående problem: de kommer garanterat ALDRIG att kunna begripliggöras — därför att området ligger utanför den moderna akademins lärostol: massfysik. Inte materiefysik. TNED. Inte modern akademi.

Se utförligt från BLIXTURLADDNINGENS FYSIK.

’Det här var något vi absolut inte hade väntat oss’

[http://www.sciencedaily.com/releases/2005/05/050502190314.htm] 2 May 2005:

”Gamma Rays From Thunderstorms? ScienceDaily (May 2, 2005) — DURHAM, N.C. --

Duke University engineers have led the most detailed analyses of links between some lightning events and mysterious gamma ray emissions that emanate from earth's own atmosphere. Their study suggests that this gamma radiation fountains upward from starting points surprisingly low in thunderclouds. Counter-intuitively, these strong gamma outbursts also seem to precede associated lightning discharges by a split second.

"All of this comes as a huge surprise," said Steven Cummer, an assistant professor of electrical and computer engineering at Duke's Pratt School of Engineering. "These are higher energy gamma rays than come from the sun. And yet here they are coming from the kind of terrestrial thunderstorm that we see here all the time."

…

Natural emissions of gamma rays, the most energetic forms of light, are usually triggered only by high-energy events in outer space. Such events include thermonuclear reactions within the sun, interactions between cosmic rays and black-hole-creating star collapses.

But in 1994, scientists using the Compton Gamma Ray Observatory satellite first detected gamma rays seemingly originating near the earth's surface. And researchers quickly found evidence that those emissions were connected to lightning, Cummer said.

Beginning in 2002, the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) satellite -- launched to study x-rays and gamma rays from the sun --also began detecting larger numbers of what scientists began terming terrestrial gamma ray flashes (TGFs).

…

The detailed Duke-led analysis also disclosed that, on average, TGFs occurred 1.24 milliseconds before their associated lightning strokes. "That was something we absolutely were not expecting," Cummer said. "But the coincidence between the lightning and the TGFs we found is too good to be random. So, even if the TGFs precede the lightning, they are in some way connected."”.

Min översättning:

Gammastrålning från åskväder — ScienceDaily, May 2, 2005

Ingenjörer från Duke-universitetet har lett den mest detaljerade analysen av kopplingen mellan en del urladdningshändelser och mystiska gammastrålningsemissioner som utgår från Jordens egen atmosfär. Deras studie antyder att denna gammastrålning fontäniserar uppåt från startpunkter förvånansvärt låga i åskmoln. Motsatt intuitivt, verkar detta gammautbrott också föregå associerade blixturladdningar med en bråkdels sekund.

”Allt det här kommer som en enorm överraskning”, sade Steven Cummer, en assisterande professor i elektrisk och dataorienterad maskinteknik vid Dukes Pratt Skolan för ingenjörsvetenskap. ”Dessa är kraftigare energi-gammastrålar än de som kommer från Solen. Och ändå, här, kommer de från det slag av jordåskväder som vi ser här hela tiden.”

…

Naturlig utsändning av gammastrålar, den mest energirika formen av ljus, uppväcks vanligen bara av högenergitillfällen i yttre rymden. Sådana tillfällen innefattar termonukleära reaktioner inom Solen, växelverkan mellan kosmiska strålar och svartahålskapade stjärnkollapser.

Men år 1994, upptäckte för första gången forskare som använde Compton Gamma Stråle Observatoriets satellit gammastrålar som såg ut att komma nära ifrån Jordytan. Och forskare fann snabbt bevis för att de utstrålningarna var kopplade till blixturladdning, sade Cummer.

Med början 2002, började också Reuven Ramaty Hög Energi Solära Spektroskopiska Imaginären (RHESSI) satelliten — sjösatt för att studera röntgenstrålar och gammastrålar från Solen — registrera större antal av vad forskare började kalla jordiska gamma stråle flashar (TGFs).

…

Den detaljerade Duke-ledda analysen konstaterade också att, i medeltal, TGFs uppträdde 1,24 millisekunder före deras associerade blixturladdningsstöt. ”Det var något vi absolut inte hade väntat,” sade Cummer. ”Men samtidigheten mellan blixturladdningen och de TGF:ar vi fann är för noggrann för att vara slumpartad. Så, även om TGFs föregår blixturladdning, är de på något sätt sammankopplade.”

Ända fram till 2006, under hela arbetet med TNED (speciellt från 1991, ursprungligen från runt 1972), hade jag (författaren) ingen som helst kännedom om ovanstående. Internet som begrepp introducerades för mig först sommaren 2006. Det var därför särskilt tillfredsställande att (där) få läsa om att man — verkligen — upptäckt det som just TNED kräver för sin praktiska fysik på det här området: gammastrålning från blixturladdningar. Jag behövde inte anstränga mig, särskilt, på den punkten.

Återstår: att se om också (verkligen) TNED kan hålla jämna steg med experimentalfysiken. Jämför ATOMVIKTERNA. Det bör fungera lika bra här — annars adjö till TNED.

Allmänna samband | MPcNeutronkvadraten 2004I23 | Nuklidkartans gränsvärde | 2008VIII8

Med fortsatt koppling från Nuklidbildningarna

Nukliderna i den tunga gruppen

MAXIMALA MASSTALET (A) ENLIGT TNED ÄR A = 300

beskrivning

ÄNDRINGEN I ATOMÄRA MASSDEFEKTEN är som störst för basnukliderna. Då dessa bildats har Heliumpreferensen etablerats. Nukliderna över denna referens får en betydligt mindre avtagande massdefektsändring upp till 18-gränsen, Järn-Nickeltoppen. Alla fusioner upp till denna punkt betecknas (konventionellt, med lån från kemins begrepp) som utpräglat EXOTERMISKA. Komponenterna avyttrar energi (atomära massdefekten, antalet avbrända elektronmassor per ekvivalent bildningsneutron) som följd av föreningen.

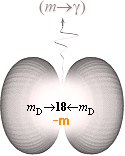Järnsidan — grovt allt till vänster om masstal 60

Exotermiska kärnreaktioner betyder alltså att nukleonindividerna i resultanten (eg. med avseende på resultanten — eftersom atomkärnan enligt TNED inte innehåller några beståndsdelar) tappar g-massa (m®g). 18-värdet (i mitten på illustrationen närmast ovan) kan i själva verket vara vilket som helst legala massdefektsvärde (0-18) som tillåts rent fusionstekniskt. Renodlat exotermiska fusioner kan därmed inte bara sträcka sig in i den tunga nuklidgruppen, utan även helt omfatta denna enligt TNED — förutsatt lämpliga fusionsagenter, se utförligt från Nuklidbildningarna, Den tunga nuklidgruppens certifiering, Maximalringens komponenter. Förutsättningen i fusionen K1+K2=K är att massdefekterna bägge i K1 och K2 är lägre än i resultanten K.

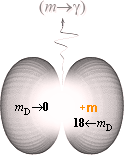Nickelsidan — grovt allt till höger om masstal 60

För att UNDER NORMALA JORDBASERADE LABORATORIEFÖRHÅLLANDEN kunna bilda ännu tyngre kärnor på nickelsidan av 18-gränsen måste nukleonindividerna i resultanten tillföras g-massa (⁺m) i fusionsfasen. Denna DEL i kärnreaktionen kommer då att kallas ENDOTERMISK. En viss del avyttras ALLTID även i dessa fall som arbetsenergi (m®g), den aktuella g-massa som systemet tappar och som omvandlas till värme och ljus. Därmed reduceras massdefekten netto hos nukleonindividerna i mottagaren från 18-gränsen och neråt på bekostnad av givarens växande massdefekt samtidigt som den resulterande kärnan blir tyngre. Om sådana kärnor sönderfaller (eller delas) utvinns den föregående massbindningen i form av värme och ljus. De avdelade primärkomponenterna (vänsterdelen nedan t.h.) återtar därmed en internt högre massdefekt upp mot 18-gränsen relativt moderkärnan samtidigt som en (eller flera) sekundärkomponent bildas med motsatt lägre massdefekt (vanligen neutron, proton eller Heliumkärna).

Detta innebär att hårda sönderfall (med nuklidavyttring) i den tunga nuklidgruppen uppvisar en intern exotermisk process för primärkomponenternas bildning:

Sönderfallet eller fissionen kan bestå av enbart primärkomponenterna (som om sekundärkomponenten redan lämnat moderkärnan), eller enbart av sekundärkomponenten (som om moderkärnan reagerar långsamt med efterföljande primärkomponenter), eller en kombination av bägge.

atomer i den tunga nuklidgruppen, alltså på nickelsidan om 18-gränsen, kan inte ha massdefekter lägre än eller lika med Helium-4

— om det också gäller möjligheten att kunna avyttra en Helium-4-individ i samband med sönderfall eller delning

resultat

En moderkärna på nickelsidan om 18-gränsen med m_D<Helium-4_14,5 kan med dessa förutsättningar genom fission (delning) inte avyttra en Helium-4-individ. En sådan förmodad Helium-4-bildning från en kärna med lägre m_D än Helium-4 kräver en exotermisk process, och den är för Helium-4:s del reserverad för järnsidan om 18-gränsen.

Enbart i kraft av denna ordning är det tydligt att atomer i den tunga nuklidgruppen, alltså på nickelsidan om 18-gränsen, inte kan ha massdefekter lägre än eller lika med Helium-4

— om det också gäller möjligheten att kunna avyttra en Helium-4-individ i samband med sönderfall eller delning.

På den grunden blir det möjligt ENLIGT TNED att fastställa nuklidkartans praktiska utsträckning med hjälp av neutronkvadratens fasta geometri. Dvs.:

Absolut maximala masstalet (för atomkärnor som kan avyttra en heliumkärna) kan bestämmas med referens till Heliumnivån.

Vi studerar hur.

GULDHYPERBELN

Nuklidbildningarna från neutronen och upp mot Järntoppen (A=56) visar i neutronkvadraten att den atomära massdefektsändringen genomgående är strängt avtagande.

Med förutsättningen att ändringen i massdefekt också fortsätter avta från 18-gränsen ut mot nuklidkartans yttersta områden kan vi fastställa vilket typ av funktionskurva ändringen ritas upp på. Vore nämligen ändringen från 18-gränsen helt linjär skulle funktionen ritas på en parabel (konstant ändring). Ändringen skulle emellertid vara som störst just från 18-gränsen och sedan avta. Detta säkerställer att massändringen (elementärt) kommer att ritas upp på en hyperbel. Jämförelse med de experimentellt uppmätta atomvikterna (se resultatkurvan nedan) visar att så också är fallet, enligt TNED.

Neutronkvadraten visar sig innehålla lösningen även på den så Avgörande Viktiga eftersökta ”Guldhyperbeln” (min privata beteckning).

Grundnuklidernas allmänna medelvärdesform på järnsidan från Heliumnivån ritas på den allmänna elliptiska funktionen (grafiskt, se från Neutronkvadraten i Planckringen)

y = offset + E(1/5)Ö 600x+25x² .................... huvudekvationens toppellips

Direkt ur denna form får man en hyperbel genom att eliminera x i 600x samt sätta +E som –E,

y = offset – E(1/5)Ö 600+25x²

där E(1/5) blir enhetshyperbelns ihoptryckning. Med hyperbelnollan som A=60 gäller analogt

y = offset – E(1/5)Ö 600 + (A–60)² ............ aktuella massdefektsekvationens hyperbel

Resterande delar bestäms — som det visar sig i resultatgrafen, nära men inte exakt — av 18-gränsvärdet för Järntoppen (det är 17,759142).

samband

Med Heliumreferensen 6+12/Ö2=14,485281=h-nivå kan vi nu härifrån approximera en hyperbel från ovanstående huvudekvationens grundsamband — genom att använda ett övre grovt skattat övre minimigräns via 1/3-e-massa från 18-taket vid A=60-gränsen enligt

18–1/3 = 18 – kÖ 600 + (A–60)² = 17,666666;

= 18 – De

k = 1/3Ö 600

= De/Ö 600

= 0,0136082 ;

A_max = 60 + Ö [(18–h)/k]²–600;

= 60 + Ö [12(1–1/Ö2)/k]²–600, vi löser ut A i (18–1/3)-sambandet ovan.

= 317,11385

Kalkylkort — max masstal

kalkylkort max masstal

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik3 — Max Masstal — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

m_D=17,643134…

Om värdet avrundas till fem jämna Neutronkvadrater, A=300, kan k justeras enligt

h = 18 – kÖ 600 + (300–60)² = 18 – kÖ 58200

k = (18–h)/Ö 58200 = 12(1–1/Ö2)/Ö 58200

= 0,014568977

A_max = 300 = 5×60

NOTERING i PREFIXxSIN — heltaliga motsvarande grundsamband

k=0,0146 motsvarar (ungefär) (1/5)cos(360/17/5)=0,2cos(360/85)=0,2cos(72/17)=0,0147705

Asymptotvinkeln (0° från x-axeln) från k blir acos 5k = 4,01768366°; eller något närmare

k=0,0146 motsvarar (ungefär) (1/5)cos(360/86)=0,2cos(180/43)=0,014599.

Asymptotvinkeln (0° från x-axeln) från k blir acos 5k = 4,1860465°.

Den resulterande råhyperbeln — grafritad

y = – 0.0146[600 + 25x²]^0,5

— avstämd mot experimentellt uppmätta värden för atomvikterna i [HOP-tabellen Table 2.1 s9-65–9-86] visas nedan i Jämna och Udda-formerna; den tunga nuklidgruppens stabila nuklider uppdelade i respektive jämna och udda nuklider, samt nederst sammantaget för bägge.

Udda nuklider avser udda masstal A (1 3 5 7 9 …), analogt nuklider med udda antal bildningsindivider neutroner+protoner.

Jämna nuklider avser jämna masstal A (0 2 4 6 8 …), analogt nuklider med ett jämt antal bildningsindivider neutroner+protoner.

De

Jämna nuklider i tunga nuklidgruppen — endast stabila nuklider — ringarna markerar HOP-värdena, linjen i svart är råhyperbeln från härledningen ovan

Vertikala skalan: atomär massdefekt i antal elektronmassor per ekvivalent bildningsneutron. Horisontella skalan: masstal, analogt ekvivalenta bildningsantal neutroner och protoner.

Udda nuklider i tunga nuklidgruppen — endast stabila nuklider — ringarna markerar HOP-värdena, linjen i svart är råhyperbeln från härledningen ovan

Vertikala skalan: atomär massdefekt i antal elektronmassor per ekvivalent bildningsneutron. Horisontella skalan: masstal, analogt ekvivalenta bildningsantal neutroner och protoner.

Tunga nuklidgruppen — endast stabila nuklider — ringarna markerar HOP-värdena, linjen i vitt är råhyperbeln från härledningen ovan

Vertikala skalan: atomär massdefekt i antal elektronmassor per ekvivalent bildningsneutron. Horisontella skalan: masstal, analogt ekvivalenta bildningsantal neutroner och protoner.

Råhyperbeln visar sig alltså stämma tämligen väl med den tunga nuklidgruppens stabila nuklider.

— inte långt ifrån motsvarigheten till ett grässtrå som man trätt upp smultron och blåbär på.

m_D = 18 – 0,0146Ö 600 + (A–60)² .........................

aktuella massdefektsekvationens råhyperbel, m_D i antal elektronmassor

Amax = 300 stämmer väl

Om vi i sambandshärledningen till ovanstående Guldhyperbeln istället för det första hoftvärdets 18-subtrahend De=1/3 insätter den som motsvarar den aktuella Järntoppen enligt HOP-tabellens värden — värdet m_D = 17,759142 som ger De=0,24 avrundat — får vi istället en råhyperbel som skär Heliumlinjen — basen vid m_D = 14,5 i ovanstående grafer — vid A=417, illustrationen närmast ovan höger.

Vi ser direkt att OM också resterande nuklidbildningar håller sig till den redan utstakade funktionslinjen fram till runt A=210, blir A-maxvärdet 417 orimligt — helt klart utanför hyperbelns funktionskurva. Men även en så liten utvidgning som 17 nuklidkvanta, från 300 till 317, visar att inte heller den referenspunkten stämmer särskilt väl med den redan givna hyperbellinjen. Med dessa beskrivningar visar analysen sammantaget att A-maxvärdet knappast ligger utanför 300-gränsen.

slutsats

På ovanstående grund, och förutsatt att alla övriga möjliga nuklidbildningar också håller sig till den givna ”guldhyperbeln”, kan vi säkert enligt TNED fastställa att fysiken är helt ren från nuklidbildningar med masstal större än 300.

Allmänna samband

END.

Allmänna samband

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Allmänna samband

ämnesrubriker

innehåll

ALLMÄNNA SAMBAND

Termiska ekvivalenter

Temperaturekvivalenterna

MIC

Energigenomströmningsekvivalenten

Kalkylkort

TNED/MAC — skillnaden mellan relaterad fysik och modern akademi

Divergensens Expansiva G-Beroende

ZONBARRIÄRENS RADIE

Zonbarriären

Nolldivergenszonens konstanta hastighet

Nolldivergenszonens radie ur tätheten

universella dagkonstanten

ZONBARRIÄRERNAS HASTIGHET OCH DERAS SKÄRNING MED EXPANSIONSSFÄRERNA

Zonskärningarna

K-cellens lokala gravitation

J80-massan

Blixturladdningens Fysik — Resumé

Kort resumé av blixturladdningens fysik enligt TNED

CAT · allmän beskrivning

Citatkälla, röntgenstrålning från blixturladdningar

Annihilationsstrålningens speciella fysik i CAT

gammastrålningens formfysik

Elektronförintelsen i CAT

Möjliga praktiska fall

Citatkälla, gammastrålningen samriktad med Jordmagnetiska fältet (Lehtinen et al 1999)

Citatkälla, RHESSI-observationerna t.o.m. 2005

Praktiska Satellilbanor

PARANNIHILATIONENS FYSIK

Annihilationsdistansen

vMAX

ELMEK (motsv. eng. ELVES) — särskilt atmosfäriskt blixfenomen

Blixturladdningens fysik i modern akademi, sammanställningar genom citat

Nuklidkartans gränsvärde

Nukliderna i den tunga gruppen

Guldhyperbeln

Kalkylkort — max masstal

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[BA]. BONNIERS ASTRONOMI 1978

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

et al, allmän förkorting (i engelskan) som används för att ange typ X et al, X med medarbetare, eller X med kolleger

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

KALKYLKORTEN från Microsofts ordbehandlingsprogram (MsWORKS 4.0 | Från WINDOWS 95-eran) fungerar tyvärr inte utan vidare i webbformer (htm/html-filer). I denna presentation visas enbart kalkylkortets bild.

UTVECKLAT (Apr2010):

Samtliga kalkylkort med original från MsWors 4.0 finns nu i UNIVERSUMS HISTORIA. Se särskild beskrivning med förteckning i MANUAL.

Senast uppdaterade version: 2013-04-08

*END.

Stavningskontrollerat 2008-07-12 | 2008-08-08 | 2008-10-19

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-07-24

åter till portalsidan · portalsidan är www.UniversumsHistoria.se