AGW-BEVISET — UNIVERSUMS HISTORIA
| 2010VII13 | 2010VIII18 | en![]() produktion
| Senast uppdaterade version: 2016-01-06 · Universums Historia
produktion
| Senast uppdaterade version: 2016-01-06 · Universums Historia
innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Inledning — allmän
orientering · Kort snabbgenomgång
med Globala Uppvärmningens Historia · De 6 Kurvkomponenterna · NASA-kurvans
ythavsperioder ·
|
Havsytans |
Jämförelse mellan |
Arrhenius |
Sammanställning på
Engelska |
Bildkälla ovan: IMAGE COURTESY OF THE
IMAGE SCIENCE & ANALYSIS LABORATORY — NASA Johnson Space Center — NASA
astronaut photograph ISS022-E-6678
http://earthobservatory.nasa.gov/Features/GlobalWarming/
Energin
till den globala uppvärmningen · HUR den
antropogena globala uppvärmningen FRAMTRÄDER · Havet spelar
huvudrollen · AGW-beviset
FÖRKLARAR NASA-CRU ·
AGW-beviset enligt relaterad fysik — Den
globala uppvärmningens matematik och fysik
|
Utvidgad mera fullständig beskrivning från Originalförfattningen 10Okt2009 |
DEN GLOBALA UPPVÄRMNINGEN — beviset för att orsaken är INDUSTRIN
— från ca 1800 och framåt
|
AGW-beviset |
||||
|
4. t|E—temperatur|Energi-kurvan som 3 7. AGW-effekten 8. AGW-effektens integral som 4 |
|
effekten AGW förbränningen fossilsläppet lokalen |
||
I originalförfattningen från 10Okt2009
finns ingen kvantitativt specificerad härledning till AGW-effekt och AGW-energi
— ytterst trixiga detaljer att komma underfund med, trots deras relativa
enkelhet som det har visat sig; Det har hänt flera gånger under
författningsarbetet: JUST när man tror sig ha gått igenom allt, visar sig
plötsligt en liten detalj, ett förbiseende i matematiken som naturligtvis
raserar hela arbetet, och man får börja om från början igen.
I den här utvidgade
presentationen ges full beskrivning — med ämnets hela möjliga flora av
korsrefererande jämförelser med de mest framträdande etablerade beskrivningarna
för att i möjligaste mån ge soliditet åt helheten [Se från Etablerade
klimatmodeller och Satellitmätningar, Jämförelse
mellan IPCC och t(AGW) och Varför Arrhenius samband inte matchar AGW].
Som det ser ut, är det bara AGW-beviset som kan samla alla seriösa bidrag i
samma övergripande beskrivning. Se även Varför alla andra
orsaker är uteslutna, och sist i AGW-bevisets
slutform.
AGW-beviset Del 1 —
Den globala uppvärmningens matematik och fysik
Ursäkta:
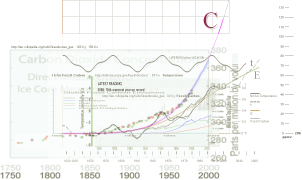
I
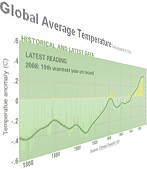
åsynen [‡] av NASA(CRU)-temperaturkurvan,
den uppmätta globala uppvärmningskurvan
från 1850,
http://climate.nasa.gov/keyIndicators/
18Juli2010: Bilden nedan finns
inte längre på URL-adressen ovan; Originalet från CRU finns
dock fortfarande kvar på
http://www.cru.uea.ac.uk/cru/info/warming/
men i något annorlunda skala — ytterligare exempel på hur
SVÅRT det är att hålla sig till Etablerade Referenser — de ändras hela tiden.
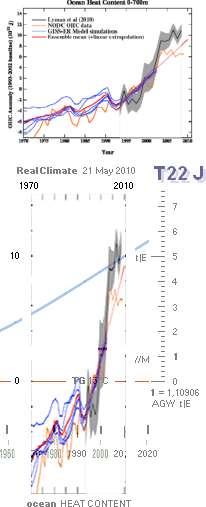
Från NASA-källan som ovan, September 2009 — Bilden finns
inte längre på den adressen 18Juli2010.
ser
en van person direkt att den i princip består av två komponenter:
en
periodisk
Graf pixelUnit50 — PREFIXxCOS:
y = 0.222(0.9[(2cos pi x/1.48) +
0.5(cos 3pi[x-0.1]/1.48)])
NASA-kurvans tidsskala (x) kronologiskt
reducerad till 65% för tidsmatchning med Fossil-Carbon-kurvan
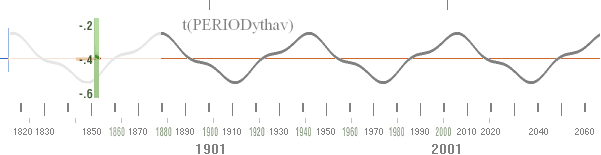
för sammanställd prövning; t(PERIODythav) nedan med de enkla approximerade
naturliga komponenterna (orange 21 år, svart 62 år) som en van person direkt
kan skriva ut,

i den förtydligade sammansättningen
(violett summerar de bägge perioderna på 21 år och 62 år) [vidare i YTHAVSPERIODERNA],
Se även NASA-kurvan
innehåller information om ythavsperioderna;

och
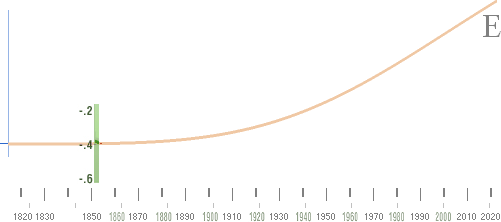
en jämnt uppåtstigande kurvdel — AGW-kurvan
som, också för en van person, direkt
identifieras med en energifunktion
[E];
som
tillsammans (streckad nedan) approximerar NASA-kurvan med — tydligen — god
allmän följsamhet:
Fram till ca 2038 följer en relativt jämn temperaturperiod
från 2005. Därefter stegras temperaturen drastiskt återigen liknande perioden
1972-2005. »Den tickande bomben» är just en utdragen högre global
medeltemperatur: Permafrostens metanlager. Metan (CH4) är en molekyl med fem atomärt bundna
komponenter [5·3=15 frihetsgrader] som därmed vida överglänser alla
andra förekommande atmosfäriska molekylära bindningar; Om metanhalten
ökar, vilket gynnas av globalt högre temperatur, kommer också värmemotståndet i
Jordatmosfären att öka drastiskt, vilket medför ännu mera temperaturökning.
Därmed förefaller en lavineffekt omöjlig att avstyra. Vilka konsekvenser en
sådan utveckling får ligger helt utom ramen för den här presentationens
framställning.
— och som tydligen kan göras mera
noggrann med vidare insikter;
Separat webbsökning [Se Ythavsperioderna
på Webben] visar att
periodkurvan också har motsvarande möjliga experimentellt observerade
ythavsperiod (50-80 år) — Men forskningen på området är komplicerad och är
delvis rent experimentellt dåligt representerad: man vet inte mycket om
detaljerna, det tar lång tid att mäta sig fram till tydliga resultat (jämför
klimatdebatterna: i stort sett konstant grälande).
Den
uppåtstigande kurvan (E) definierar tydligen den råa temperaturökningen i netto
[direkt proportionalitet
mellan t och E]. Om den kurvan kan
visas stämma med industrikurvan
för Fossil-Carbon, samt slutligen dess integral i formen av
motsvarande samhörande värden med uppmätta koldioxidutsläpp [eg. koldioxidhalter
som följd av kolutsläpp via fossil förbränning] (Carbon-Dioxide-kurvan)
är temperaturökningens källa tydligen entydigt identifierad — alla sex komponenter identifierade.
Se vidare från AGW-beviset
i Del 2.
AGW, översikt
2010-08-12
AGW — den antropogena globala
uppvärmningen
DEN
ANTROPOGENA GLOBALA UPPVÄRMNINGEN I ÖVERSIKT — hur den framträder
|
AGW
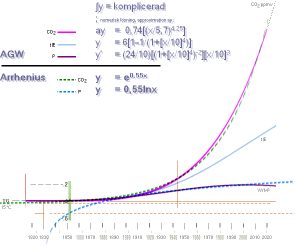
— antropogen global uppvärmning —————————————— Med
utgångspunkt från en formgrafisk kännedom om effekt
och energi i synnerhet (Fig:1)
och periodiska funktioner (sin|cos) i allmänhet (Fig:4), tillsammans
med åsynen av den observationellt grundade globala NASA(CRU)-temperaturkurvan (Fig:2) framgår med tankens omedelbara verkan att den
uppmätta kurvan grundas på summan av två kurvformer: en
elementär energifunktion, t|E-kurvan (Fig:3) — vi finner samma typ i
den allmänna världsstatistikens beskrivning över totala energianvändningen —
och en periodisk funktion (Fig:4). Periodformen (ca 60 år) kan bara ha koppling
till havet (ythavsperioderna) — vilket också är precis
vad som framkommer vid närmare granskning; Se Havet spelar
huvudrollen. —————————————————————— Klicka
på bilderna för original i artikel. |
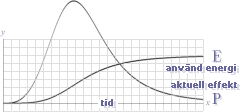
Fig:1 Effekt (P) och energi (E) med tiden som variabel bildar en
integral enhet : Fig:2 Den empiriskt luftmarint uppmätta globala temperaturkurvan : Fig:3 Energikuvan, även temperaturkurva genom E=kT : Fig:4 Två sammansatta — enkla — trigonometriska perioder |
Med industrialismens utveckling under
1900-talet som helt baserad på fossila bränslen (kol, olja, naturgas), blir det
relativt enkelt (efter förarbetets stora möda) att anställa en mera
ingående matematisk prövning av detaljerna. Nämligen på de enda fem (5)
parametrar som alls hela komplexet kan handla om [PtTmM]:
Tillskottet i temperatur (t) som läggs till globala
medelvärdestemperaturen (15°C) från fossilförbränningens temperatur (T) via
fossilförbränningens kolsläpp (m) i marklokalen (M) på Jordytan; Ökningen (nuvärdet 2010) i genomströmningsmaterialets termiska resistans hindrar ca 1/250 av det redan etablerade konstanta
värmeflödet (P=250W/M²) som Solinstrålningen redan har etablerat på Jordytan (SER) att återutstråla
till rymden. Den innestängda delen verkställer en motsvarande uppvärmning av
markskiktet, analogt havsytan på kolsläppets kredit. Ingen extra energi behövs
— utöver fossilförbränningens bidrag. Helt gratis.
Se utförligt från Värmemotståndets
fysik, om ej redan bekant.
Hela slutresultatet för AGW-beviset finns redovisat i Effekt&Energi.
Se även i
Se även i
DEN GLOBALA UPPVÄRMNINGENS
VETENSKAPSHISTORIA.
Upptakten till AGW-beviset
Upptakten till AGW-beviset
Alla
distinkt urskiljbara processer i fysiken följer exakt samma grundläggande
princip:
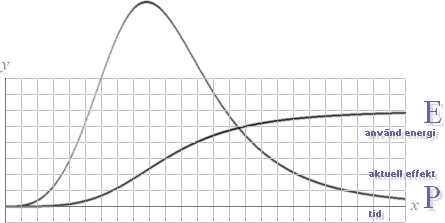
Effekt (P=y’)
och energi (E=y).
Se även DERIVATA (y’) och INTEGRAL (y)
i NOLLFORMSALGEBRAN om ej redan bekant.
Processen har en början, ett förlopp, och
ett slut.
Det finns inga undantag. Jämför även K-cellens Värmefysik.
Principen är densamma som för en
(elementär) s.k. transientfunktion, figuren ovan — liknande en fyrverkeripjäs
som bränns av, lyser upp en stund med maximal effekt, och som sedan falnar av i
lugnare takt. För funktionernas elementära matematik, se Generella energikurvan.
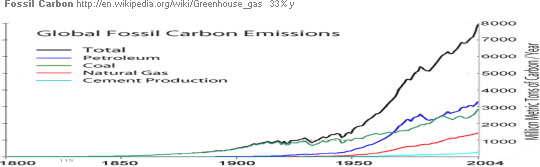
Kurvbilden
ovan från Fossil-Carbon-kurvan [övre svarta] tillsammans med den
motsvarande utjämnade ideala energianvändningskurvan [t|E-kurvan] [ljusorange i bakgrunden].
På
alldeles samma sätt är det med hela mänsklighetens tekniska utveckling
(industrialiseringen);
Fram till elektrofysiken är
utvecklingen relativt ljum (den frånses här helt i sammanhanget);
DEN EGENTLIGA TEKNISKA Historien börjar med
att man upptäcker sambandet mellan magnetism och elektricitet (1820 Ørstedt) —
elektrofysikens framträdande som naturvetenskap — och på vars grund den
egentliga mera omfattande tekniska energianvändning kan börja;
Energianvändningen utvecklas som mest med
största effekten i uppbyggnaden av den övergripande s.k. infrastrukturen:
Skeppstonnage, verkstadsindustri
och kommunikation (1940-1970 världshandelns sjudubbling). När den
delen har byggts ut, går energianvändningstakten in i en lugnare fas med en
mera långsam utveckling med betydligt lägre dageffekter men fortfarande ökad
energianvändning.
Industriländerna planar ut först, och efter
dem kommer de mindre utvecklade länderna (med fördröjningar på runt max 20 år här
utan vidare referenser).
Oavsett vilken energiform som försörjer den
utvecklingen, är den att anse som naturlig i sig (självklart). Summan av
alla bidrag ger hela världsutvecklingens industrialisering, och vi känner igen
kurvformerna från olika statistiska presentationsgrafer, såväl landsvis som
totalt.
Själva grundidentifieringen av den globala uppvärmningens mest enträgna
kandidat blir således en enkel uppgift — till en första prövning:
Industrialismens utveckling under
1900-talet.
Med den uppmätta NASA(CRU)-temperaturkurvan som empirisk bas framgår sedan de resterande delarna
automatiskt.
Se
även kort sammanställning i
HUR DEN
ANTROPOGENA GLOBALA UPPVÄRMNINGEN FRAMTRÄDER.
Se
även kort i
DEN
GLOBALA UPPVÄRMNINGENS VETENSKAPSHISTORIA.
Se
utförligt från AGW-beviset Del 1.

BILDKÄLLA: Författarens arkiv · Bild12Excur6 ·
Jul2010 · NikonD90
Att det är havet, inte atmosfären, som innehar huvudrollen i den
globala uppvärmningskurvan
från NASA(CRU)
framgår direkt ur den sistnämnda via de
tydligt framträdande havsperioderna.
Sammanställningen nedan
visar hur havsperioderna framgår ur det som hittills är känt (D’Aleo 2007 [Se Ythavsperioderna på Webben]).
Den längre perioddelen (62[+3] år) framgår speciellt tydligt från AMO (Atlantic
Multidecadal Oscillation, sv. AtlantMultidekadiska svängningen), nedan endast
representerat av norra hemisfärens bidrag (ekvatorn till 70°N). Sidreferenserna
hänvisar till PDF-dokumentet av Joseph D’Aleo [Se Ythavsperioderna på Webben].
D’Aleos figurer här skalanpassade efter gemensam kronologi för jämförelsens
översikt. PDO refererar till Pacific Decadal Oscillation, sv.
Stillahavsdekadiska svängningen.

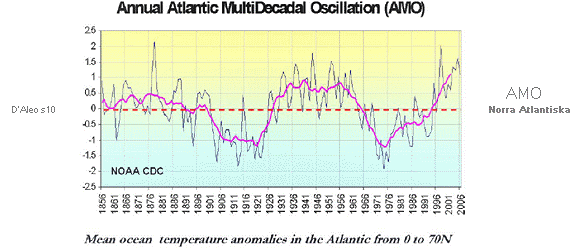
Notera att komponenterna till t(PERIODythav) togs ut (i min referens,
helt utan vetskap om några »ythavsperioder», enbart på ren matematiskt grafisk
formekvivalens) som närmaste matchning till NASA(CRU)-temperaturkurvan
på formen [PREFIXxCOS]
(cos x1)KORT + (cos x2)LÅNG, se utförligt från AGW-beviset
Del 1. Överensstämmelsen KRÄVER sedan (därmed) att det MÅSTE
finnas åtminstone EN tydlig motsvarande praktiskt observerbar motsvarande
havsperiod (på drygt 60 år). Och, som vi själva kan se av ovanstående
sammanställning, är detta också alldeles uppenbart fallet — och så långt
jämförelserna kan antas med nu (ännu 2010) kända observationella stöd.
För källreferenserna till D’Aleos
framställningar, se Ythavsperioderna
på Webben.
AGW:
Med, således, havet som huvudaktör har
vi bara att också konstatera HUR den huvudrollens FYSIKALISKA DYNAMIK, tvunget,
måste fungera — det finns, mig veterligt, ingenting annat att välja på, och som
även styrks via AGW-beviset Del 2
där ekvivalenterna till NASA(CRU)-kurvan
med dess 5 komponenter
identifieras:
Den
globala temperaturökningens fysikaliska dynamik
Fossilförbränningen (T) medför ökad mängd atmosfärisk
koldioxid som via sin större gastyngd transporteras utmed marken [‡]
till kontinentalgränserna på liknande sätt som en uppvällande golvbrunn tvingar
vattnet att breda ut sig på markytan för att till slut tömmas i havet [Mera
utförligt i Koldioxidens
markbundenhet]; Havet absorberar koldioxiden som bildas från
fossilförbränningen.
Den värmegrad som associeras med koldioxidsläppet — samma som den grad
av ökad värmeresistivitet som fossilförbränning anställer — ombesörjs
automatiskt av den redan befintliga värmegenomströmningeseffekten (P=250 W/M²) från Solen; fossilutsläppets
resistiva uppvärmning stjäl (nu 2010) ca 1/250. Se utförligt från Värmemotståndets fysik.
(m)t|E-kurvan
generellt — havsversionen av Fossil-Carbon-kurvan
Från AGW-beviset Del 1
y = 6[1–1/(1+[x/10]^4)] , se t-kurvans elementära energifunktion
Se även utförligt generellt om
energikurvorna i statistiken i t-ENERGI-kurvan.
y’ = Dn 6[1–(1+[x/10]4)–1] = (24/10)(1 + [x/10]4)–2[x/10]3
y’ =
(24/10)[(1+[x/10]'4)'–2][x/10]'3
Allmänna gaslagen E=kt ger
direkt proportionalitet mellan temperatur (t) och energi (E) — med E-kurvans
motsvarande analoga temperaturfunktion [t(AGW)];
t|E-kurvan tillsammans med ythavsperioden uppvisar tydligen det enda direkt grafiska formbeviset som finns
för att NASA-kurvan
verkligen kan ses innehålla en jämnt uppåtstigande temperaturkurva.
m-kurvan
som t|E-kurvan — Fossil-Carbon-utsläppet
Med GRUNDSAMBANDET t/T=a(m/M), se AGW-beviset Del 2, framgår att t och m
är direkt proportionella enligt m/t=(M/T)/a; Uppvärmningen (t) i den OBS
avgränsade atmosfärmassan (M, se Beräkningen av M)
är direkt proportionell mot kolutsläppet (m) i atmosfärmassan (M) via
förbränningen (T).
Havsversionen
av Fossil-Carbon
Det enda som krävs för att få fram den
mera noggranna HAVSUPPLAGAN, kurvan ovan, ur den industriellt mera
variationsrika Fossil-Carbon-kurvan
är att beräkna skalförhållandet m/t med t i NASA-kurvan
och m i Fossil-Carbon-kurvan
— och vilket skalförhållande i sig bestäms av E-typkurvan ovan tillsammans med YTHAVSPERIODERNA.
Med kurvoriginalens skalanpassningar som använts i denna framställning
blir förhållandet
7 T12 KG
—————————— = 10,17094 T12 KG/°C = m/t
[0,6 + 0,1(1–2/17)]°C
Se även i Beräkningen
av M.
Med andra ord: Ordningen är alltså — i
sträng mening — den följande:
Ovanstående m/t-kvot bestäms i princip
DIREKT i och med att NASA-kurvan
identifieras på de bägge komponenterna E-typkurvan ovan plus perioderna som beskrivs utförligt i AGW-beviset Del 1.
Därmed är i princip hela härledningen genomförd.
Den återstående delen består endast i att skalanpassa originalet till Fossil-Carbon-kurvan
i vertikalled så att totalkurvan
uppvisar maximal följsamhet med den så redan formidentifierade E-typkurvan ovan. Med den
anpassningen (33%y) framgår m/t-kvoten ovan genom att (i något bild/ritprogram)
läsa av skalstrecken och utföra divisionen.
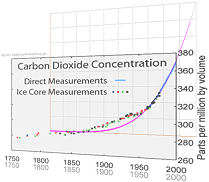
Men därmed är också Fossil-Carbon-kurvans INTEGRAL — koldioxidens
KONCENTRATION eller andel motsvarande någon Carbon-Dioxide-dito
— av princip redan bestämd. OM man också lyckas få ut den integralkurvan i form
och värde återstår bara att skalanpassa någon experimentellt uppmätt
original-Carbon-Dioxide-kurva och se till så att den passar — om alls möjligt,
vilket visats vara vårt fall — kronologin horisontellt och (därmed) integralformen
vertikalt, se De 6 kurvorna.
Allt ska passa som ett pussel.
Kort sagt: Möjligheten att AV PRINCIP hamna FEL i härledningen av
AGW-beviset är UTESLUTEN genom att beviset bygger på en matematisk formekvivalent
som i sig består av FEM FRISTÅENDE
OBEROENDE KOMPONENTER som alla måste passa ihop i samma
matematisk-fysikaliska byggnad: den empiriskt givna NASA-temperaturkurvan.
Tabelljämförelsen
mellan den slutligt uppnådda integralkurvan och Carbon-Dioxide-mätningarna
utgör därmed själva bevisets slutform; Med en överensstämmelse på lägst 98% är
det tydligt att den överensstämmelsen är så exakt man kan önska.
Genom att t|E-kurvan
har samma uppstigande fot och bas som den statistiska industriella Fossil-Carbon-kurvan
är enbart av det skälet AGW-beviset i princip redan stadfäst.
Därmed framstår AGW-beviset
och dess detaljer till skarp åtskillnad från en förhållandevis stor mängd
personer som (möjligen bara för att jävlas på icke naturvetenskapliga grunder)
vill gendriva AGW med meningen att NASA-kurvan
i själva verket skulle avspegla naturliga variationer [‡],
alltså processer som inte har med människans roll att göra.
Därmed
— processens utveckling — bortfaller
också automatiskt samtliga övriga klimatförändrande aspiranter som har föreslagits,
typ variationer i Solens energiproduktion och-eller inverkan från den kosmiska
partikelstrålningen.
Dessa bägge främsta kandidater kan i sig visas [‡1]
sammanhänga med dels alldeles för små bidrag för att alls ha någon signifikant
betydelse i sammanhanget, och som dels helt bortfaller på grund av att de
saknar motsvarighet till den avgörande t|E-kurvans
komponent som tillsammans med ythavsperioderna
beskriver och förklarar NASA(CRU)-kurvans
principiella variation [Se särskilt i De 6 kurvornas
enhetliga sammansättning]; Enbart av det skälet saknar
kandidaterna Solvariationer-kosmisk strålning helt koppling till den
observerade globala uppvärmningens komplex.
ArtikelReferenser
———————————————————————————————————————————————
Solen: Variationen i energin från Solljuset är dels alldeles för liten (0,1%, citatet nedan) för att själv kunna åstadkomma någon systematisk ändring över ett århundrade, och dels alldeles för periodiskt bunden till 11-årscykeln för att kunna åstadkomma något annat än motsvarande periodiska (väl märkbara men mindre) variationer i temperatur på Jordytan.
”Total solar output is now measured to vary (over the last three 11-year sunspot cycles) by approximately 0.1% [2][3][4]”,
@INTERNET Wikipedia Solar variation 2010-07-16.
http://en.wikipedia.org/wiki/Solar_variation
Min översättning:
Totala solära utflödet är nu uppmätt att variera (över de
senaste tre 11-åriga solfläckscyklerna) med approximativt 0,1%.
Dock kan variationer generellt över längre perioder i Solens energiflöde tillsammans med naturliga variationer i avståndet Jorden-Solen åstadkomma motsvarande temperaturvariationer (möjligen också mycket större än de som förknippas med NASA-kurvan) — men som då också tvunget omspänner motsvarande längre tidsperioder (typ från tusentals år till tiotusentals och hundratusentals år). Dessa variationer har alltså, helt säkert, ingen koppling till någon motsvarande kandidatur för Fossil-Carbon-kurvan — den enda vars matematiska fysik kan harmoniera med de övriga fem nödvändiga kurvkomponenterna för att få fram NASA-kurvans variationsbyggnad.
Kosmiska strålningen: Även energin förknippad med den kosmiska strålningen [‡] är (på tok) alldeles för liten för att ensam kunna åstadkomma några större variationer i Jordytskiktets temperatur. Inte heller här finns några källor som kan ställa upp motsvarande kandidatur för Fossil-Carbon-kurvan. Jämför även
”The influence of cosmic rays on cloud cover is about a factor of 100 lower than needed to explain the observed changes in clouds or to be a significant contributor to present-day climate change.[69]”,
@INTERNET Wikipedia Global warming 2010-07-16.
http://en.wikipedia.org/wiki/Global_warming
Min översättning:
Inverkan av kosmisk strålning på molntäcket är omkring en
faktor 100 lägre än den som krävs för att förklara de observerade
molnändringarna eller för att vara en signifikant bidragare till dagens
klimatändring.
De
6 Kurvkomponenterna — INLEDANDE
ALLMÄNT ORIENTERANDE översiktlig BESKRIVNING
se även Snabbgenomgång
AGW-beviset
— beviset för att
NASA-temperaturkurvans förklaring kan anställas på industrins Fossil-Carbon
under 1900-talet: den globala uppvärmningen förorsakad av människan
AGW-beviset Del 1
— den enkla grunden
AGW-beviset Del 2
— den enkla grundens matematik
AGW-beviset Del 3
— effekt och energi i AGW (havets värmelagring)
Globala uppvärmningen
De med den
uppmätta temperaturkurvan
SAMHÖRANDE fem
temperatur-energi-kurvkomponenterna:
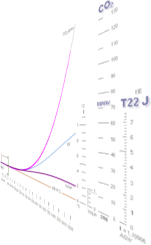
0. NASA-kurvan, 1.
ythavsperioderna, 2. t|E-kurvan, 3. Fossil-Carbon-kurvan, 4. Carbon-Dioxide-kurvan, 5. t|E-integralen (C).
:
Ovanstående 5 komponenter
beskrivs mera ingående genom följande sektions artikelblock.
De 6 komponenterna — Klicka på bilderna för
original i artikel
|
0 |
1 |
2 |
3 |
4,5 |
|
|
|
|
|
|||
Alla sex
komponenter måste kunna visas stämma överens i en och samma matematiska
energibeskrivning för att den uppmätta
temperaturkurvans ekvivalenta kredibilitet ska vara
trovärdig.
Det enda, enkla, sammanknytande grundsambandet som möter det villkoret
är tydligen t/T=m/M.
Sambandet utpekar entydigt den industriella Fossil-Carbon-kurvan som liktydig med
den komponent som havet
ser som orsak till sin
magasinerade förhöjda temperatur och som tydligen styr och reglerar hela
den biologiska klimatsfären — drygt 50 meter över allt
fast och flytande på Jordytan. Inte mer. Utförligt i Beräkningen av M.
Samhörigheten för de sex komponenterna stadfäster därmed och tydligen
bortom varje tvivel AGW-beviset
med Fossil-Carbon-kurvan som orsaken till den globala temperaturökningen på
totalt ca 0,7 °C — som framgår med den naturligt överlagrade ythavsperioden frånräknad.
Många personer tycks helt ha missat
just NASA-kurvans inslag med havsperiodens naturliga
variation (på grovt 65 år, eg. [eller möjligen] två något
olika perioder med olika amplitud), och därmed på olika sätt misstolkat olika
kurvplatåer och nivåer i NASA-kurvan — vilket föranlett högst godtyckliga
inslag av varierande klimattolkningar.
Inget av dessa spekulativa påståenden har — i ljuset av ovannämnda
resultat — någon som helst naturvetenskaplig grund. Se även nedan i Kort Snabbgenomgång, där bl.a. resultat
från IPCC belyses.
Med en verkligt energigrundad orsak som grund för den globala
uppvärmningen, måste förklaringen tvunget innefatta alla de ovan angivna
sex kurvkomponenterna som en enhetlig matematisk-fysikalisk
beskrivning
av en energiutvecklande process.
Med den stränga samhörigheten är det tydligt att alla andra möjligheter
är uteslutna.
Se vidare utförligt från AGW-beviset Del 1, samt vidare i AGW-beviset Del 2.
Snabbgenomgång —
Historien från början
DEN GLOBALA UPPVÄRMNINGENS VETENSKAPSHISTORIA
Kort snabbgenomgång — globala uppvärmningens korta
historia
Globala
uppvärmningens uppmätta temperaturkurva
De första indikationerna på global
uppvärmning uppmärksammandes i slutet på 1700-talet genom paleontologiska
analyser (som innefattar hela Jordhistorien).
Ref. @INTERNET Wikipedia History
of climate change science 2010-07-16.
http://en.wikipedia.org/wiki/History_of_climate_change_science
Wikipediakällan ovan ger en allmän
beskrivning;
1896 Svante Arrhenius genomför de första
reguljära beräkningarna på effekten av ökad koldioxidhalt (från tidigare
arbeten av Arvid Högbom [CO2] och Samuel Langley [värmestrålning])
-1950 Kontroverser, dispyter, osäkerheter
-1965 Städer uppvisar (problem med) smog
-1975 Allt flera forskare ansluter till
uppfattningen om en förestående eller pågående global uppvärmning (som följd av
växande koldioxidhalter från fossila kolutsläpp)
-1990 Forskarvärlden
generellt går alltmer i riktning mot vetenskaplig samstämmighet i uppfattningen
om en pågående global uppvärmning; IPCC etableras 1988
(Intergovernmental Panel on Climate Change, sv. (förenklat) »internationella
klimat[regerings]panelen»)
-2010 Flera internationella konferenser med
vetenskapliga sammanställningar understryker den globala uppvärmningen, olika överenskommelser
undertecknas för att försöka begränsa koldioxidutsläppen (eg. koldioxid
associerad med fossilt kolutsläpp)
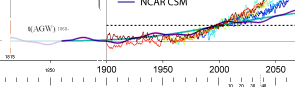
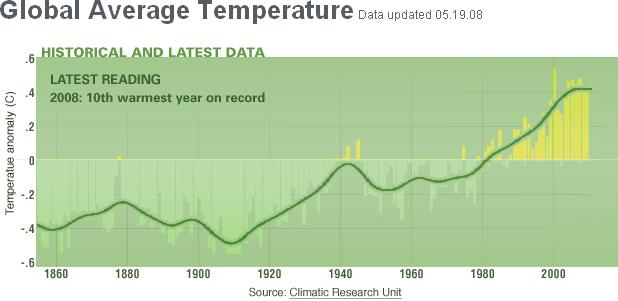
Globala uppvärmningens uppmätta temperaturkurva
NASA-temperaturkurvan sammanfattar
de uppmätta årsmedeltemperaturerna baserade på luftmarina mätningar vid
Jordytan (land-hav) (med början från 1850).
IPCC: Alltmera
avancerade klimatmodeller (2010) tillsammans med utvecklad forskning uppvisar
en tvärvetenskaplig samstämmighet i omdömet att det mesta av den påvisade
globala temperaturökningen tycks bero på mänskliga aktiviteter
(fossilförbränning av kol-olja-naturgas), ref. @INTERNET Wikipedia, Scientific
opinion on climate change 2010-07-16,
http://en.wikipedia.org/wiki/Scientific_opinion_on_climate_change
Relaterad fysik AGW123 [analog med ovanstående, men mera preciserat]:
— LOKALEN FÖR Solstrålningens
globala medeleffekt på Jordytan (250 W/M²)
materialändras med fossilförbränningen vilket medför en termisk resistansökning som leder till
att den normala Solåterstrålningens återinträde till rymden utanför Jorden
hindras av den inträngande värmeagenten (CO2, koldioxid). Den så hindrade
återutstrålningen medför motsvarande uppvärmning i det luftmarina markskiktet
där uppvärmningseffekten i stort sett dumpas direkt i havet genom
CO2-absorption och därmed bidragets överföring till vattnets klimatkretslopp.
Utförligt från AGW2. Se
även från De 6 Komponenterna.
Svårigheten i den rent matematiska
delen i AGW-beviset —
Den
havsupptagande temperatur- energikurvans integral
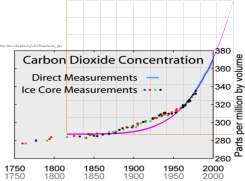
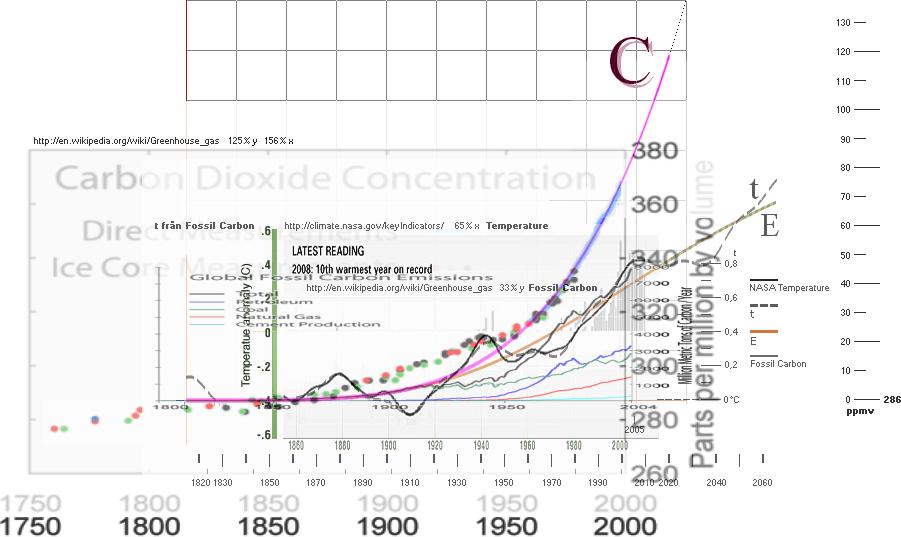
http://en.wikipedia.org/wiki/Greenhouse_gas
http://en.wikipedia.org/wiki/File:Carbon_History_and_Flux_Rev.png
Bilden skalanpassad 125%y 156%x, integralkurvan till
havsversionen av Fossil-Carbon-kurvan ljusviolett
Även om AGW-bevisets
grafiska detaljer verkar förhållandevis enkla att komma på
spåren, finns det en avgörande detalj som nära nog och här veterligt gör att de
flesta droppar av när det kommer till kritan:
För att kunna få fram de slutliga,
avgörande teoretiskt härledda värdena till jämförelse med de uppmätta, måste
INTEGRALKURVAN till havsversionen av Fossil-Carbon-kurvan
— som den uttagna t|E-kurvan
—
y = 6[1–1/(1+[x/10]^4)] , se t-kurvans elementära energifunktion
kunna lösas ut. Vilket vill säga: Man
måste kunna lösa ut den motsvarande (ovan) Carbon-Dioxide-kurvans teoretiska
del för att kunna jämföra den med den praktiskt uppmätta motsvarigheten.
DEN SPECIELLA Svårigheten är den, att
ÄVEN med tillgång till dagens avancerade arkiv och maskinella datorbaserade
integrallösarmetoder, finns — tydligen — ingen direkt algebraisk lösning att
jämföra med [Se sammanställningen i Integralkurvan
för E; flera svar ges, men inget är rätt].
För att finna den korrekt KVANTITATIVA
lösningen måste man då — då tydligen inget annat fungerar — använda numerisk
integrallösning
[Simpsons Formel] — man räknar ut diskreta punktvärden, antingen via den
välkända Simpsons
Formel, eller mera avancerat genom en mera elementär enklare
Hyposerie (som inte kräver någon derivata;
kurvan-integranden intervalldelas [kräver
en snabb dator, intervallen måste vara minst runt hundratusen eller mer], varje intervalls linjära kurvlutning beräknas via
Pythagoras
sats, alla intervallytorna
summeras), samt att man i slutänden — om så är möjligt, vilket i vårt
fall visat sig vara fallet — söker någon enklare kurvfunktions delavsnitt som
kan användas och som uppvisar tillräckligt god approximativ överensstämmelse
[måste ligga inom den grafiskt presenterade mätkurvans tjocklek].
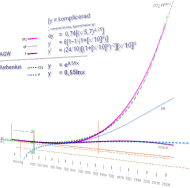
I vårt fall visar sig approximationskurvan relativt enkel: som en
ordinär exponentialkurva (typ x^4) men uträtad i slutet i formen av en (med
begränsad utsträckning) praktiskt taget helt rät linje med viss lutning:
skoklack med lutad rätlinje.
Med hjälp av diskreta punktvärden från den numeriska integrallösningen,
har så approximationskurvan
y = 0.74[(x/5.7)^4.25] ............. approximationen gäller fram till max år 2030
använts i jämförelsen med de uppmätta
tabelldata för Carbon-Dioxide (från 1958 och framåt).
Överensstämmelsen är som lägst 98%. Se särskild
tabellredovisning.
Med den följsamheten är det tydligt att alla de
sex kurvkomponenterna harmonierar.
Därmed är AGW-beviset tydligen stadfäst.
Det
mest anmärkningsvärda — 50 meter
Det mest anmärkningsvärda — och som
tydligen utagerar de etablerade klimatmodellernas blotta utgångspunkt i
meningen av att de skulle vara lösningens
HUVUDSAKLIGA ingrediens — är tydligen följande resultat:
I det enkla grundsambandet
t/T=a(m/M) kan den berörda atmosfärmassan (M) som
ansvarar för NASA-kurvans uppmätta värden via kolutsläppet (m) från
fossilförbränningen (T) beräknas via ett höjdskikt h.
Värdet man, något förvånande, finner är drygt
h ~ 50 meter ................................ se Beräkningen
av h i M
Det är långt ifrån den förmodade totala
atmosfäriska skiktmodell (minst flera kilometer) man vanligtvis brukar hitta i
omnämnande av de etablerade korridorernas klimatmodelldiskussioner (här utan
vidare referenser).
ÄMNETS MATEMATIK pekar alltså precis på ämnesreklamen: en marknära,
havsytupptagande historia.
Utflykter med klimatmodeller som använder typ Stefan-Boltzmanns strålningslag
(strålningspåverkan i atmosfäriska skikt, generellt olika former av radiativ
överföring) har med detta resultat tydligen inte ett spår med ämnets
huvudsakliga fysikaliska matematik att göra — men är i stort sett den enda
matematiska utgångspunkt man ser i de etablerade korridorernas litterära flora.
Artikeln om Climate Models på Wikipedia (Zero-dimensional
models) ger ett exempel på den KONVENTIONELLT allra enklaste
klimatmodellens matematik via Stefan-Boltzmanns strålningslag
[P = aAkT4].
Alltså, i och för sig inte helt fel,
men tydligen ändå långt från målet:
AGW kan inte förenas med normalt
naturliga variationer [‡].
Ett exempel som visar hur tokigt det kan bli om man ändå försöker FÖRENA
typ Stefan-Boltzmanns strålningslag med funktioner som kopplar till
CO2-variationer visas i Stefan-Boltzmann-gasiska
felapproximationen: Jättefina resultat NU — i generell
mening, rena skräpet.
Jag skulle också ingå i det amatörsällskapet om det inte vore för den
avvikande uppfattningen.
Utförligt från AGW-beviset Del 1.
Med t|E-kurvans
integral som analog med Carbon-Dioxide-kurvan
och därmed värdena i Tabelljämförelsen,
är AGW-beviset Del 2 fullständigat.
Se vidare i AGW-beviset Del 3.
Där slutförs AGW-beviset genom härledningen till komplexets allmänna effekt och
energi. Sammanställning i Effekt&Energi.
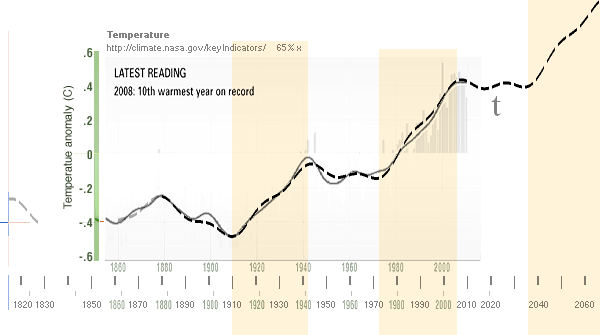
NASA-temperaturkurvan innehåller preciserad
information om ythavsperiodernas form
Webbutbudet av
olika »NASA-temperaturkurvor»; Om det gäller blotta möjligheten att få fram en
mera precis bild av havsperioderna (Jul2010) räcker det med att bara
rekognoscera utbudet på BILDER till »global average temperature» — i stort sett
en hel butik av GENERELLT SAMSTÄMMIGA kurvformer finns — men i detaljerna
uppenbart OLIKA. Det understryker bara den allmänna svårigheten att få ut
»exakta data» på YTHAVSPERIODERNA med tillgång till »etablerade mätdata»:
Temperaturkurvorna måste ha MINST 5 ÅRS MEDELVÄRDEN för att kunna matcha
havsdynamiken med lägst 5 års
ytperioder.
Genom att Fossil-Carbon-kurvan utgör
den enda energibas som finns i det
antropogena energibidraget till Jordytans klimatologi (AGW), och att havet som den huvudsakliga agenten för
den värmeenergins upptagning uppvisar en stor tröghet mot alla mindre och
kortare variationer, blir t-kurvan
den idealt praktiska Fossil-Carbon
som havsmagasinet ser av den antropogena verksamheten.
Inledande
Jämförelse

Alla massor i människans vardag är i
princip försumbara i jämförelse med havet som massform.
Även stora (enorma) industrianläggningar ses av havet som pyttesmå
lokaler med i princip helt försumbar massa.
Vi kan beräkna
totala havsmassan via Jordytan vid ekvatorn med ett djupskikt på runt 4KM;
Volymen blir
V=(4πr²
)(4KM)=2,04474 T18 M³ ~ 2 T18 M³; Varje M³ vatten väger ca 1 ton (1000 KG) som
ger totalmassan 2 T21 KG; ca 70% av Jordytan är hav, så slutsumman hamnar på
1,2 T21 KG.
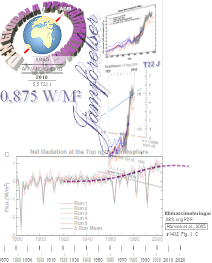
Den samlade världsindustrins kolutsläpp, Fossil-Carbon-kurvan nedan, och den så
bildade koldioxidens extra termiska motstånd
utgör enligt AGW orsaken till att den genomsnittliga
globala och konstanta Soleffekten på 250 W/M²
vid Jordytan numera (2010) reserverar ca 1 W/M² (0,875
W/M²) vid marknivån för global uppvärmning.
Det gör ett temperaturtillskott på ca 0,7 °C på runt 100 år med ett
motsvarande pyttelitet bidrag
(0,7°C)/(365,25d·100) = 1,91649 t5 °C/d
~ 0,000019 °C per dygn som havet genom sin koldioxidupptagande värmetröghet och
genom Solens blotta kraft ser från alla världens bidragande
industrianläggningar tillsammans;
Dag in och dag ut, vecka in och vecka ut, månad in och månad ut, år in
och år ut;
Varje år ges ett fortfarande pyttelitet medelbidrag på bara 0,007 °C som
havsmassan tar upp via det påtriggade värmetillskottet från industrins
atmosfäriska kolutsläpp, Fossil-Carbon-kurvan
nedan.
På hundra år i medelvärden vid havsytan och den närmaste luften blir det
fortfarande det löjligt lilla 0,7 °C.
Det är fortfarande bara litet större än ’nästan pyttelitet’, men hela NASA-temperaturkurvans nivåändring
(från 1860) om man frånräknar de naturliga
ythavsperiodernas variation.
Genom människans metriska litenhet får emellertid det pyttelilla
bidraget vådliga konsekvenser.
Ett direkt konkret exempel är att vattnets täthet avtar med högre
temperatur: vattenvolymen ökar med högre temperatur: havsnivån stiger. Sett för
Jorden som helhet, är ökningen inte mer än mikroskopisk. Men sett till den
lilla ytvarelsen människan, speciellt samhällen i låglänta oceanområden, hamnar
kulturen i en katastrofzon.
Alla
mindre variationer jämnas ut av havets magasinerande
värmekapacitet.
Genom att havets stora värmetröghet
jämnar ut alla mindre variationer, samt så ännu mer taget med ett globalt
medelvärde där alla lokala havsvariationer inte längre syns, framgår den rena
temperaturökningskurvan ur det mera variationsrika industrioriginalet i
Fossil-Carbon-energibasen enligt t|E(AGW) nedan.
Helheten i beskrivningen pekar i princip på en liknelse i metrisk
analogi med människans hud (Jordytan) och mikrober på eller i huden
(fossileldade industrier) som förorsakar irritationer (lokala besvär
[infektioner]) genom onaturliga omsättningar som påtvingar individen sjukdom —
och som ev. kan leda till döden (t.ex. blodförgiftning) om personen inte får
kunnig vård per omgående.
Energibidragskurvan i den industriella statistiken —
Fossil-Carbon (svarta, totalt) :
Originalet på WIKIMEDIA COMMONS:
http://commons.wikimedia.org/wiki/File:Global_Carbon_Emission_by_Type_to_Y2004.png
Även (m.fl.) RENEWABLE ENERGY — Critical Evaluation of the
U.S. Renewable Energy Policy, 2009:
http://www.renewableenergy.typepad.com/
NOTERING. I AGW.htm-dokumentet från Okt2009 är originalet
ovan angivet på URL-adressen
http://en.wikipedia.org/wiki/Greenhouse_gas
Men den typgrafen finns inte där (längre) — eller att den
har flyttats (eller att något överföringsfel inträffade i redigeringen).
Hur
havet ser den industrikurvan
— t|E(AGW):
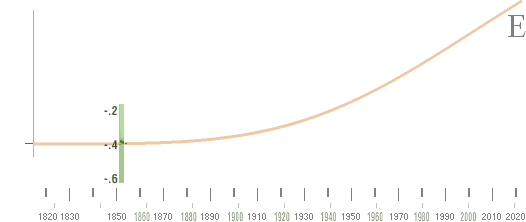
y = 6[1–1/(1+[x/10]^4)] , se t-kurvans elementära energifunktion
Kurvan ovan är genom proportionaliteten mellan temperatur och energi [Se t|E-kurvan generellt] samma som själva
den råa rena temperaturkurva som finns i NASA-kurvan om man tar bort havsperioderna. Vi kan därför också
(här) kalla kurvan ovan för AGW-temperaturkurvan.
Bägge
tillsammans:
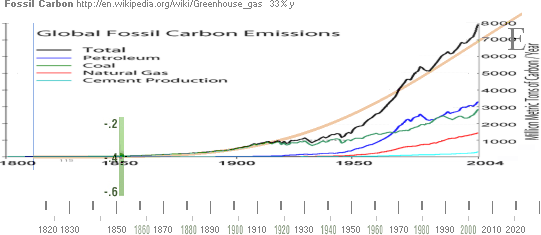
Att
t|E(AGW)-kurvan tillsammans med Fossil-Carbon-originalet hamnar rätt i
vertikalskala kontrolleras genom att sammanställa ythavsperioderna

y = 0.222(0.9[(2cos pi x/1.48) +
0.5(cos 3pi[x-0.1]/1.48)])
ythavsperioden i PREFIXxCOS
— Hur får man fram periodformen?
— På samma fason som en notkunnig
person kan höra musikstycket enbart genom att SE på partituret, medan en
okunnig inte ’hör’ ett skvatt. Det är en ren övningsfråga.
— Enbart genom att SE på NASA-temperaturkurvan SER en
’notkunnig person’ direkt att NASA-temperaturkurvan består av en perioddel
(ovan) och en elementär
energikurva [t|E(AGW)].
— Med kännedom om periodernas
elementära aritmetik, och tillgång till ett grafritande program, kan sedan den
personen skriva in den elementära periodens matematiska funktion
[typiskt, från scratch i PREFIXxCOS: (cos x1)KORT + (cos
x2)LÅNG]
och få fram den direkt på papperet, här
enligt den anpassade formen som ovan, pixelUnit50)
med
t|E(AGW)-kurvan (orange)
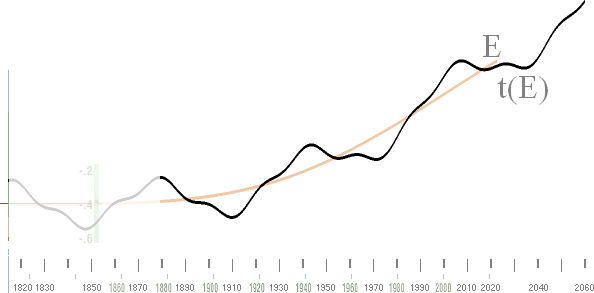
y = 6[1–1/(1+[x/10]^4)] , se t-kurvans elementära energifunktion
+ 0.222(0.9[(2cos pi x/1.48) + 0.5(cos 3pi[x–0.1]/1.48)])
ythavsperioden
i PREFIXxCOS
och
se till att resultatet (streckat nedan) överensstämmer så nära som möjligt med NASA-temperaturkurvan (heldragen
nedan).

— Vilket betyder att med den passningen
finns inte mycket att missa på:
Med
den tydligt plåsteraktiga passningen är det tydligt att SKILLNADEN kan avslöja
information om själva den mera preciserade ythavsformen.
Vi kan gå tillväga rent pixelmässigt,
räkna ut skillnaden pixel för pixel (med linjetjocklekens toleranser) för att
få fram EXAKT havsperioddata. Låt oss emellertid ta ett mera matematiskt
prövande grepp bara för att illustrera helhetsgreppet per matematik.
Alternativet nedan uppvisar en något bättre passning,

y = 0.222(0.8[(2sinþx/1.48)+0.8(sin3þ[x–0.1]/1.48)–0.02–(sin0.5þ[x+0.95]/1.48)'12])
Den grå kurvdelen i bakgrunden föregående till jämförelse,
ovanstående lagd streckad på NASA-kurvan nedan med t(AGW) orange
Sambanden i PREFIXxSIN
NASA(CRU)-kurvans
motsvarande ekvivalent,
se ovan från Inledande jämförelse
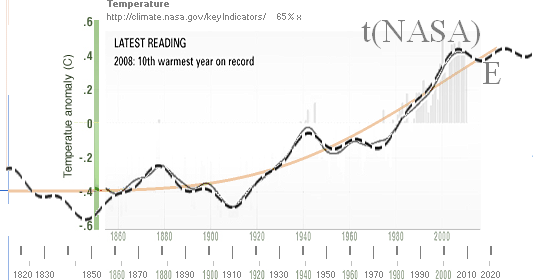
y = 6[1–1/(1+[x/10]^4)] , se t-kurvans elementära energifunktion
+ 0.222(0.8[(2sinþx/1.48)+0.8(sin3þ[x–0.1]/1.48)–0.02–(sin0.5þ[x+0.95]/1.48)'12])
ythavsperioden
i PREFIXxSIN
Se även ytterligare alternativt
matematiskt modulationsexempel i Ythavsperiodens
grafiska analys.
Slutsats:
Med
tämligen säkra belägg — havets stora värmetröghet, och därmed t-kurvans stabila havskopia av
industrins Fossil-Carbon-kurva
— bör alltså NASA-kurvan
minus t-kurvan uppvisa en tämligen noggrann medelform för just havsperioderna.
Man behöver, tydligen, ingen mer
information för att helt säkert kunna se ämnets natur.
Epilog
t|E-kurvan tillsammans
med ythavsperioderna visar SPECIELLT
tydligt och helt säkert att varje KATEGORISK art, typ och form av
AGW-opposition är — och alltid har varit, och så kommer att förbli — helt
ogrundad.
Varje
principiell invändning mot uppfattningen att den globala temperaturökningen som
visas av NASA-kurvan
beror på 1900-talets industriella fossilförbränning är, uppenbarligen, en
naturvetenskapligt helt ogrundad invändning.
Se mera utförligt från De 6 Komponenterna.
NASA(CRU)-kurvans
intervallvärden
18Juli2010
Variationerna
i NASA(CRU)-temperaturkurvan som funktion av olika intervallmedelvärden —
större än den redan exempelvisade precisionen i ythavsperioderna
Om
vi (nu 18Juli2010) jämför graferna på URL-adressen
(NASA, om
den finns kvar …)
http://climate.nasa.gov/keyIndicators/
—
Nej. Ytterligare ett nytt byte har nyligen gjorts, bild 3 nedan (upptäckt här
först 26Aug2010). Den amerikanska tekniken att ange datumformat är, dessutom,
här närmare inte känd: källan ger ingen specifikation, anger ”Data updated
07.21.10”, vilken kryptik möjligen får förstås kronologiskt som (År-Må-Da)
2010-07-21 — men kan möjligen också betyda 2007-10-21 om inget annat anges.
För bild 3, Se Förtydligande
längre ner.
enligt
versionerna
———————————————————————
|
|
|
|
|
NASA September 2009 |
NASA Juli 2010 |
———————————————————————
1. NASA vers 1 från September
2009 och som nu ersatts (man
har alltså helt enkelt fimpat den gamla: finns inte längre) av
2. NASA vers 2 (Juli2010)
här med passande skalanpassningar
[(1)75%hrz; (2)75%vrt] och 50% transparens enligt
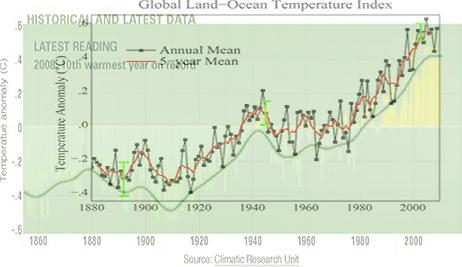
ser
vi strax
att man har ändrat nivån (i bilden ovan
höjt den med 20 pixels vertikalt) för själva den ursprungliga nivåkurvan, samt
infört en annan (tätare) intervallmedelform (angiven som PER 5 år).
CRU-datakällan (NASAvers1)
http://www.cru.uea.ac.uk/cru/info/warming/
”The time series shows the combined global land and marine surface temperature record from 1850 to 2009.”,
Min översättning:
Tidsserien visar den kombinerade globala land och marina
yttemperaturens dokumentering från 1850 till 2009.
redovisar å sin sida inte
dataintervallet explicit (eller hur kurvjämnheten uppnåtts, vilket i sig är en
bedrift som inte borde förekomma i naturvetenskapligt orienterade ämnen). Vi
ser dock tydligt att följsamheten avspeglas inbördes harmoniskt i de bägge
versionerna, vilket är det väsentliga.
Att kurvformen ligger på olika nivåer
har i denna presentations ljus ingen som helst betydelse eftersom
utgångspunkten i vilket fall är kurvans övergripande variation, se från AGW-beviset Del 1.
Vi kan dock (just) se HUR den motsvarande ythavsperiodiciteten tvunget
måste följa i ett praktiskt motsvarande fall via PER-intervallet (5 år i
NASAvers2 ovan) — och därmed direkt (här utan vidare undersökning) med en typform
som helt överrider den föregående exemplifierade jämförelsen med två något
olika ythavsperioder. Se Periodskillnaden.
Denna observation understryker
(tydligen) främst två väsentligt avgörande punkter:
1. De inbördes olika
intervallversionerna uppvisar tydliga om än marginella skillnader;
2. Intervallversionerna inbördes är
(således) MÖJLIGEN större än toleranserna tillåter för en noggrann bestämning
av ythavsperiodernas medelform; intervallversionerna behöver (möjligen)
PRECISERAS (skärpas, betydligt) för att rendera KREDIBILITET i begreppet
precision sett från klimathuvudaktören havets mycket värmetröga synvinkel
(minst 10 års globalt medelintervall);
3. Havsperioderna är möjligen MYCKET
mer sammansatta än vad den enkla versionen i NASAvers1 visar, så att
ythavsexemplen i denna presentation måste förstås av typen MYCKET förenklade.
Speciellt för det 5-åriga
minimiintervallet för havets del, se citatet
från FOCUS MATERIEN.
Tillägg 27Aug2010
Förtydligande
— Klimatwebbsidan
som ständigt byter preferenser
http://climate.nasa.gov/keyIndicators/
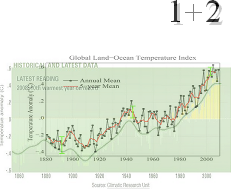

Beteckningarna från Nasaversionerna ovan.
Vi ser att den senaste nykomlingen (3:an) från NASA i stort uppvisar en
utdragen blåsbälg av dragspelet i den föregående modellens (2:an) mera komprimerade design. Man har
i sin senaste modell dessutom lagt till en animerad sondblinkande punkt längst
ut i kronologin på senaste mätvärdet.
3-grafen har här relativt 1-grafen komprimerats till 75% i
horisontalled för gemensam kronologisk passning.
NASA(CRU)-kurvans ekvivalenter
AGW-beviset i Del 1
visar grundanalysen med en periodisk plus en jämnt uppåtstigande kurva;
Med den periodiska kurvan överlagrad på den
jämna ges tydligen en mycket god approximativ överensstämmelse med och
följsamhet mot NASA-kurvan.
AGW-beviset i Del 2
visar hur den jämnt uppåtstigande kurvdelen
motsvarar vad havet ser av industristatistikens
Fossil-Carbon-kurva, samt hur dess integral (C-kurvan) matchar en
motsvarande uppmätt Carbon-Dioxide
med redovisade tabellvärden
till jämförelse från år 1958 till nu.

Tabellvärdena finns
redovisade separat i Kalkylkortet (Tabell3).
OM Fossil-Carbon är orsaken till NASA.kurvan,
DÅ ska också INTEGRALEN
(C) TILL HAVSVERSIONEN av Fossil-Carbon-kurvan
med C som en Carbon-Dioxide-kopia STÄMMA
ÖVERENS MED UPPMÄTTA KOLDIOXIDHALTER enligt
tabell. Det gör den också — med lägst precision på
98%. Se Jämförande Tabell.
Överensstämmelsen mellan
den så härledda havsversionen
av Fossil-Carbon-kurvans INTEGRAL, tydligen
identifierad som Carbon-Dioxide-kurvan
(mätvärdena från 1958), lämnar därmed inte längre något tvivel om att orsaken
till den jämna temperaturstegringskurvan också är industrins Fossil-Carbon: Den
fossila förbränningen av kol-olja-naturgas under runt sagt hela 1900-talet
beskriver tydligen tämligen exakt orsaken bakom till NASA-kurvans
temperaturökning.
Därmed har alla de
sex kurvkomponenterna sammanförts till en och
samma enhetliga matematiska-fysikaliska byggnad.
Därmed kan man också påstå, bortom varje
tvivel, att den globala uppvärmning som framgår i NASA-temperaturkurvan
är antropogent orsakad. Nämligen i anledning av den
industriella Fossil-Carbon-kurvan.
Inledande
beskrivning,
forts.
frn. AGW-beviset Del1&2,
Med t(AGW)-kurvans
C-integral och dess
överensstämmande mätdata står det följaktligen
lika tydligt och klart:
Den antropogena
(människoskapade) fossilförbränningen (kol, olja, naturgas, T
~2200 °C) uttöms enligt AGW-beviset Del 2
i atmosfären i form av ett koldioxidskikt (CO2) med verkningshöjden bara drygt 50
meter över Jordytan.
Tillskottet per år från denna försmädliga, lömska källa
är helt omärkligt: 0,007 °C. Sju tusendelar. Per dygn lika med ca 20 µ°C
(0,000019 °C). Hela 1900-talets industriella statistik: Timme in och timme ut.
Dag in och dag ut. År in och år ut. Solstrålningens naturliga utåtreflexion
täpps långsamt till, molekyl för molekyl. Sakta, men stadigt växer temperaturen
på Jordytan som en osynlig värmande filt som bres ut över allt och alla.
Plötsligt, en dag som alla andra, går det upp för alla (seriösa)
att något är fel.
Med genomförd
sluträkning, se Det enhetliga
resultatet från de 6 komponenterna, blir slutsumman
tydligtvis den visade: den uppmätta NASA-temperaturkurvan.
AGW-beviset — Del 2 | Se även originalförfattningens separata härledning med alternativ formulering i Energihärledningen.

BILDKÄLLA — bakgrund: Författarens arkiv ·
Bild7Un2010|10—Bild129RMaj2009 · NikonD90 · montage · BILDKÄLLA — infälldVä: Fossila bränslen, @INTERNET sv. Wikipedia Fossila bränslen
2009-09-10
BILDTEXTEN i INLEDNING
Den globala uppvärmningens temperaturbild
I följande
utvidgade version från Originalförfattningen (10Okt2009)
ges en mera fullständig beskrivning av den till (en början) synes så
svårfattliga process som tydligen sammanhänger med temperaturbilden i den
observerade globala uppvärmningen. Den i grunden enkla termiska
resistansmatematiken [Se från Värmemotståndets fysik] som tydligen — i koppling till den globala
uppvärmningen — mera ingående förklarar hela dynamiken tillsammans med den
redan uppkopplade konstanta Soleffekten (P) finns [här veterligt (Aug2010)]
inte omnämnt i de mest synliga allmänt tillgängliga webbkällorna. En (ytterst
enkel) liknelse som närmast hör till »vardagsköket» beskrivs kort i Liknelsen med CPU-kylningen.
SOLENS
INVERKAN — energin till AGW — SolEkvivalenta
Radiansen (SER)
2010-08-13
Energin till AGW
MÖJLIGEN
nybörjarens allra största svårighet i bekantskapen med (det förtvivlade)
orsakssökandet till mekanismerna i den observerade globala uppvärmningens stora
dramatik, är Problemet med Energikällan bakom hela föreställningen. Att det är
SOLEN som utför själva huvudnumret är nog de allra flesta redan på det klara
med. Men när det sedan kommer till HUR det huvudnumret utförs blir det tyst i
de allra flesta leden. Har man ingen exakt koll på vilket exakt matematik som
kan förklara sammansättningen, är man också chanslös på helheten. Följande
figurer med text och samband är ett försök att (på enklaste sättet) bringa
klarhet i grundfrågan.

Exakt
naturlig värmebalans på Jordytan: instrålning är lika med utstrålning. Ingen
uppvärmning sker. Balansräkningen
utT = inT – t(AGW) ger
utT
= inT så länge ingen onaturlig [antropogen] införsel av värmemotståndsökande element sker:
t(AGW) = 0.
Om en sådan införsel sker, hindras den naturliga Solåterutstrålningen i
motsvarande grad, och en uppvärmning [t] bildas i den ansvariga
lokalen i samma takt som den antropogena verksamhetens förorenande
energianvänding utvecklas. Eftersom den enda naturliga klimatvariationens agent
är Solen — och Solen anställer, vad vi vet, inga bergborrningar för upphämtande
av fossila bränslen att elda med under Solen — är alla större kortperiodiska [som omspänner enstaka
sekel], systematiska, globala temperaturändringar
uteslutna [‡] enbart med Solen [inkl. den närmast
variabla kosmiska strålningen] som klimatfaktor. Den
sammanhängande matematik som tydligen kan förklara hela komplexet genom
ekvivalenta former som inbegriper alla kända variationer [‡], och därmed den enda, är tydligen den som anställts av det
fossila kolsläppet under 1900-talet. Sambanden beskrivs här utförligt i AGW2.
Normalt sett råder exakt värmebalans på Jordytan: Den Solmedeleffekt per ytkvadratmeter som
(från råvärdet ca 1367 W) håller Jordytan vid globala medeltemperaturen (TG=15°C) är ca 250 W. Den betecknas här som SER, SolEkvivalenta Radiansen
på Jordytan: SolIN=SolUT. Globala medeltemperaturen (T=TG) kan då f.ö. beräknas
direkt ur Stefan-Boltzmanns strålningslag enligt
P = AakT4 ; k ~ 5,7 t8 WM–2°K–4
om
ett globalt medelvärde på ca 0,64 antas på absorptionskoefficienten (a);
T = [(P/A)/ak]1/4
= [(250 W/M²)/(0,64 · 5,7 t8 WM–2°K–4)]1/4
= 287,72082 °K ; närmevärdet –273°C för
0°K (eg. –273,15) ;
~ 15 °C
AGW:
Införs luftföroreningar (värmeledningsändrande element) i ett markskikt
(M) från en fossil förbränning (T)

Termisk
obalans på Jordytan: ett förorenat markskikt (M) spärrar Solens naturliga
återutstrålning. Föroreningsspärren tvingar det kvarhållna Solljuset att värma
upp Jordytan.
Både en enklare överslagsberäkning [‡] och slutresultatet i sig i AGW3 visar att den Soleffekt som
fördelat
på Jordytan hindras att återstråla uppgår till ca 1 W/M² [som mest 0,884 W/M² — här frånsett
alla ev. adderande bieffekter] via den observerade
globala uppvärmningen på ca 0,7 °C — och som därmed bär ansvaret för AGW. Energin absorberas av CO2-molekylen i formen av cirkulära och
linjära extramoment [Se Frihetsgrad].

Den
använda energin i uppvärmningseffekten delas naturligt mellan hav och atmosfär
via havets
CO2-absorption med vidare cirkulation
av R-bidragen. Därmed kommer en del av M-skiktets effektform att ventileras
ut på den överliggande Jordatmosfärens räkning — vilket också reducerar
möjligheten för havet att lagra hela den använda energin som värme. Exakt
vilken proportion som havet bevarar finns här ingen uppställd räkning på.
Sämsta fallets gränsvärde (som därmed aldrig uppnås praktiskt) är att hela den
använda energin återfinns lagrad i havet (enligt AGW3
lika med 5,5 T22 J nu 2010). Se dock separat i Havets
Uppvärmning.
tvingas
[Mera utförligt från Värmemotståndets
fysik] den redan befintliga
Solinstrålningeffekten per Jordytskvadratmeter (P=250 W) att se
varje tillförd CO2-molekyls temperaturtillskott (Δt) från förbränningen (T) som ett
extra värmemotstånd enligt
ΔR
= Δt/P ...................... termiska
motståndet ändras med extra
införd temperatur
Δt från fossilförbränningens
förbränningstemperatur
Men
temperaturtillskottets R-form besitter också [Se Frihetsgrad]
genom själva den införda molekylens massform en alldeles egen, särskild
värmeabsorptionsförmåga som kopplar samma värmemotstånd via samma Δt,
sambandet ovan, enligt
R = Δt/P ....................... ändringen R motsvarar ändringen t med
konstant P
R från materialets molekylmassa — R beror av t
Separat materialinförsel
utan förbränning uppvisar ett annat förlopp via en annan matematik som inte
omfattas av AGW:
Är förbränningen noll, är
också Δt noll, och sambanden ovan gäller inte — i varje fall inte i den
tecknade formen.
Se även AGW-bevisets slutform.
Tillsammans
med CO2-molekylens särskilt materialinförda högre värmemotstånd bildas en
dubbel Δt-kvantitet, analogt ett dubbelt R-tillskott: (R=t/P) = (R=t/P).
Bägge
resistansändringsfaktorerna ΔR + R
—
dels den som sammanhänger med temperaturen från fossilsläppet
[ΔR=Δt/P] och dels den
som sammmanhänger med själva molekylämnets R-faktor [R=t/P]
ΔR
+ R = Δt/P + t/P
— har
tydligen samma arbetsgivare — fossilsläppet från
T — vilket
SÅLEDES ger två lika stora bidrag på samma konstanta effektbas: den redan etablerade
konstanta Soleffekten P.
Resultatet ger alltså ett motsvarande
temperatur-energirelaterat bidrag på 2t —
som obönhörligen kommer att hämma — strypa — Soleffektens möjliga
återutstrålning på JUST det beloppet, i just den lokalen, och endast så.
Den
tunga, markstrykande, CO2-gasen (frånsett vindarnas inverkan) tvingas ut mot
kontinentalgränserna likt vattnet på golvet som sprids från utsläppet och
absorberas av havet [‡]. Därmed har t|R-tillskotten också överförts till
vattnets betydligt högre värmekapacitivitet — och därmed en klimatfaktor i cirkulation mellan hav
och luft.
Fortsättning
i GRUNDSAMBANDET i Värmemotståndets
fysik.
Proportionaliteten mellan temperatur och energi
Eftersom
temperatur och energi är direkt proportionella i den elementära fysiken
(Se Allmänna gaslagen, E=pV=kT) blir alltid varje elementärt temperaturresonemang analogt med
ett motsvarande (underliggande, utan särskild framställning) energiresonemang; temperatur är rörelseenergi. Se utförligt
från Allmänna gaslagen, om ej redan bekant.
Grundillustration med beskrivning i SOLENS INVERKAN.
2010VIII2
Energin till den globala uppvärmningen
Termiska
motståndets fysik — OM EJ REDAN BEKANT:
Det
»enda som behövs» för att påtrigga en global uppvärmning är att det redan
befintliga luftmarina Jordatmosfäriska skiktet genomgår en materialförändring i
det effektflöde (P) som redan är etablerat från Solen — på alldeles precis
samma sätt som då vi inom den elementära elektroniken ersätter en kylare med
given kylyta på moderkortet i datorn till CPU:n (eng. Central Processing
Unit, datorns själva centrala mikroprocessor) med en typ som har högre termisk resistans (samma kropp, annat material):
Bildkälla: FÖRFATTARENS ARKIV


Del av författarens gamla uttjänta moderkort
(CPU:n ovan vänster) — Bild1Aug2010 — efter nära 6 års kontinuerlig drift (1,5
GHz) — kondensatorerna åldras — Till slut vägrar datorn ens att starta.
CPU:n
utvecklar (idealt) precis lika mycket energi som tidigare, men blir varmare
eftersom mindre värme än tidigare leds bort per tidsenhet på grund av den nya
kylarens större termiska tröghet.
Analogin
är precis den som brukar användas med en filt som man sveper omkring sig; Det
både känns och blir varmare närmast huden, inte därför att man tillför
någon extra energi, utan för att den befintliga värmen hindras från att läcka
ut i den tidigare takten; Värme ackumuleras; Värmeventilationen avtar.
VÄRMEMOTSTÅNDETS FYSIK — Grundsambandet i AGW
Värmemotståndets
fysik
Termisk resistans R=t/P
(°K/W) i
ett material med given strålyta kan
ändras på två olika sätt — utan att den givna värmeeffekten (P) påverkas. Dvs.,
sett från konstant effekt (P):
1.
Ett materials termiska resistans (R) kan öka om ett separat temperaturtillskott
(t) införs från någon oberoende källa;
2.
Ett materials termiska resistans (R) kan också öka genom att andelen (antalet)
termiska isolationselement i materialet ökar — eller att de som finns ändrar
egenskaper [större antal frihetsgrader].
I
första fallet är temperaturtillskottet (t) den drivande R-ändringens orsak,
R=t/P.
I
andra fallet kan också samma temperaturtillskott vara orsaken till R-ändringen
(R=R) — om materialinförseln sker som i det fossilförbrännande fallet på
Jordytan. Dvs., i marklokalen (M) från förbränningstemperaturen (T) i den konstanta Solinstrålningseffektens närvaro (P): Kolemissionen
(m) bildar koldioxid (CO2), CO2-molekylen innehåller ett
temperaturtillskott (t) från förbränningstemperaturen (T), samma
som R (=t/P), och som därmed samtidigt introducerar CO2-molekylen som ett nytt
extra isolationselement (R) i M-lokalen — på exakt samma t-tillskottets
räkning;
(t/P=R)1 =
(R=t/P)2.
Fossilförbränningen
kan alltså förstås introducera t i (1) för sig, och kolkomponenten (C) i
molekylbildningen (CO2) introducerar R i (2) för sig. Bägge således med samma t(1/P=R)|R(=t/P)-belopp [Se även
Termiska motståndets
matematik om ej redan bekant]
via den underliggande konstanta Soleffekten (P)
som ändringseffekten kommer att avdelas ifrån. Summan av de bägge ekvivalenta R-bidragen
blir alltså 2R och som sett
från P-källan bidrar med 2t genom termofysikens allmänna samband R=t/P, P konstant lika med Soleffektens
bidrag (250 W/M²) på
Jordytan.
P-källan påtvingas alltså ett högre
strålutflödesmotstånd via det extra införda 2t (eller 2R), och som därmed
hindrar P-källans normala utflöde;
Hindret anställer en separat lokal
uppvärmning i M: AGW.
Resultatet i AGW3 visar att AGW-uppvärmningseffekten (nu 2010) ligger på
Jordytsbaserade 0,875 W/M² med en total
energianvändning på 5,5 T22 J för hela uppvärmningsperioden (från offset år
1815).
t/T = a(m/M)
Se även separat beskrivning för Enheterna i t&T
Den
införda högre termiska
resistansens (R)
temperaturtillskott (t) återfaller på förbränningstemperaturen (T). Hur t
verkar totalt bestäms av det T-styrda R-ändrande fossilsläppet (m) genom
omfattningen av utsläppslokalen (M). Genom att (således) varje ändring i t
med avseende på T kopplar en motsvarande ändring i m med avseende på M,
kan variationerna t/T och m/M förstås inbördes ekvivalenta om man
tillför en optimal koefficient (a, som mest 1, som minst 0) som
får motsvara värmegradens (t) termiska absorptionsförmåga i M. Därmed ges de
helt linjära variationerna (dt/dT)=a(dm/dM)
som ger grundsambandet
t/T = a(m/M)
med
t =Ta(m/M)
Totalt
för hela AGW-bidraget enligt R-bidraget
därmed
t = 2t
= 2Ta(m/M)
= t(AGW)
Se även GRUNDFORMEN till ovanstående.
Beräkningen av M
EKVIVALENTA Markskiktet som fossilemissionerna
uttöms i — Se även Beräkningen av M i originalförfattningen
Med m&t
direkt proportionella kan M beräknas via m/t om T och a är
kända.
m/t fås via de vertikala skalorna genom
skalförhållandet t i NASA-kurvan och m i Fossil-Carbon-kurvan. Horisontalskalorna för dessa mät- och statistikkurvor
är bägge givna genom samma kronologi. Svårigheten ligger alltså i
vertikaldelen.
Eftersom
t-kurvan redan tydligt framgår som en energikurva (effektintegral),
av samma natur som den industriella Fossil-Carbon-kurvan (havsabsorptionerna garanterar utjämningar av alla
kortare tidsvariationer), behöver man endast söka den mest synbarligt
(ungefärligt) mest (bäst) passande matchningen mellan Fossil-Carbon-kurvan och
motsvarande elementära t-energikurva [t|E-kurvan]. Men även t-kurvans
integral i formen av motsvarande
uppmätta koldioxidhalter ur Fossil-Carbon-kurvans energibas måste finnas med
för att tillsammans med de övriga bilda och uppvisa en gemensam enhet. Se
särskilt Bestämningen av
t-kurvans integral.
Men
för att meningsfullt finna t-Fossil-Carbon-matchkurvornas optimala
passning mot den aktuellt vertikala NASA-kurvans skaldel måste t-kurvan först sammanföras med ythavsperioderna (som f.ö. [för ett vant öga] framgår tydligt i
principformen ur NASA-kurvan) så
att man får en garanterat noggrann synbarhet på den bäst optimerade
vertikalskalpassningen.
Man får alltså genomföra grafiska
(matematiska) iterationer tills ett någotsånär gott, samstämmigt, resultat
uppnås, och som sedan kan göras allt finare [eller,
som oftast sker (men inte alltid) för den som redan är van — nära direkt i
krysset på första försöket].
Alla
sex kurvorna måste alltså kunna
visas spela med i samma band: 0. NASA-kurvan, 1. ythavsperioderna, 2. t-kurvan,
3. Fossil-Carbon-kurvan, 4. Carbon-Dioxide-kurvan, 5. t-integralen (C).
t-kurvans elementära
energifunktion
t-kurvans
elementära energifunktion är i fysiken känd genom teckningen
y
= a[1–1/(1+[x/b]n)]
.......................... t-Fossil-Carbon-kurvans
ideala typform
Se
utförligt i t-ENERGI-kurvan. Se även t|E-kurvan
generellt.
Efter
analys och anpassningar blir t-grafen (efter en första mest optimala
passning efter de grafiska förebilder som valts i presentationen, här i det
konventionella PREFIXxCOS),
y =
6[1-1/(1+[x/10]^4)] + 0.222(0.9[(2cos (pi x/1.48)) + 0.5(cos
(3pi[x-0.1]/1.48))])
Se t(NASA) i sammanställning av mtEC-kurvorna
med
7 T12 KG
m/t = —————————— = 10,17094 T12 KG/°C
[0,6 + 0,1(1–2/17)]°C
Därmed
kan M beräknas enligt
M = 2Ta(m/t)
Med
gängse ungefärliga värden för absorptionskoefficienten på eller omkring
Jordytan (0,7) och T (Kol) ca 2200 °C fås M via t =1°C
M = 3,52138 T16 KG
Med
linjära värden nära Jordytan taget efter tätheten vid STP (Standard
Temperature and Pressure¸normalvärdena vid havsytan), ges i den motsvarande
berörda atmosfärmassan M ovan (i den enkla grundräkningen) ett höjdskikt på
h = 53,35 meter ;
Varje
höjdmeter luft på Jordytan
r
= 6,378 T6 M vid ekvatorn, hela
klotet runt,
har
via täthetssambandet
ρ
= m/V
massan
m=ρV
med
m
= M(luftJORDYTAN)
enligt
M(luftJORDYTAN)
= ρ(LUFT)(A·1M) ; ρ(LUFT) = 1,3 KG/M³ ;
= (1,3
KG/M3)(4πr2·1M)
= 6,64541
T14 KG
~ 6,6 T14
KG
Antalet
sådana enmetersskikt i M blir då (förenklat, alla lika stora och homogena) lika
med höjden h enligt
h =
M/M(luftJORDYTAN) · 1M
= (3,52138
T16 KG)/(6,6 T14 KG) · 1M
=
53,354242 M
~ 53,35 M
Med
ett mera noggrant relaterat täthetsvärde för luften ρ(LUFT) = 1,225 KG/M³
vid globala medeltemperaturen 15°C och havsnivån (normaltrycket) ges värdet (56,233861)
h ~
56,23 meter
Se
även särskilt i originalförfattningens Beräkningen
av M.
Med
grovvärdet 1,3 KG/M³ för luftens medeltäthet vid Jordytan får M-skiktet höjden
53,35 meter. Med det mera noggranna värdet 1,225
KG/M³ vid havsytans 15°C — vilket
har använts i denna framställning — blir M-skiktets höjd 56,23 meter (utan
hänsyn till ev. skillnader i höjdled)
Eftersom
lufttätheten i praktiken avtar med höjden, kan vi räkna med att det praktiska
värdet blir något större, här utan vidare specifikation. (På grund av olika
lokala atmosfäriska variationer med temperatur och tryck kommer i vilket fall
minst lokala variationer på [här] uppskattningsvis 10-20 meter att finnas med
[hur man än räknar]).
Slutresultatet med härledningen till t|E-kurvans integral som analog med Carbon-Dioxide-kurvan via Tabelljämförelsen
med en överensstämmelse på lägst 98%
visar sammantaget hur väl de 5 matematiskt samhörande kurvpassningarna matchar huvudgrafen med NASA-temperaturkurvan i sammanställningen för De 6 Kurvorna.
Med
vidare fortsättning i AGW-beviset Del III.
Termisk resistans
(1/M²) Termisk resistans — R = t/P
Termisk resistans eller termiskt motstånd,
även värmemotstånd [ofta R(th) i engelsk litteratur, °C|°K/W] R=t/P, motsvarar i elektrofysiken elektrisk
resistans R=U/I;
TEMPERATUREN
t (vanligtvis i praktisk elektroteknik) anges i °C och
EFFEKTEN P i Watt (P=UI);
I
elektrofysiken motsvaras elektrisk
strömstyrka (I=U/R) av termisk
effekt i termofysiken (effekten P, samma som
värmeflödet);
elektriska spänningen (U,
»strömpotentialen») inom elektrofysiken motsvarar inom termofysiken temperaturen
eller termiska värmegraden (här t);
Temperaturskillnaden i ett materieavsnitt motsvarar en potentialskillnad inom
vars intervall (termofysiken)temperatur-
eller (elektrofysiken)strömflödet sker.
Omvändningen,
W/°K = 1/R, brukar kallas
Konduktansen motsv. värmeledningsförmågan.
Eftersom
effekten (P) också ansluter till Stefan-Boltzmanns strålningslag (P=A[akT4]) — effektens
utstrålningsyta (A) är avgörande — kommer termiska motståndet (Rth)
för en given kylkropp med viss yta (A) också att variera med just
utstrålningsytan A (RthA). Den mera fullständiga
sambandsformen för termisk resistans kan då skrivas
RthA
= (t/P)/A ...................... termiska
resistansens fullständiga samband
= t/PA .......................... °K/M2W, alt. °K/WM2
från
Stefan-Boltzmanns strålningslag
P = A[akT4] =
t/Rth ;
W = °K/(°K/W)
P/A = [akT4] = t/RthA
; W/(°K/W)M2
irradians intensitet
Rth/A = [akT4] = t/PA =
RthA ; (°K/W)/M2
= °K/WM2
Inom
elektrotekniken brukar kylardata vanligen anges med kvadratmeterenheten
underförstådd [Man mäter kylarens yttemperatur, dividerar med effekten och
kylarytan]. Databladen anger typiskt värden i °C|°K/W för olika kylare. Ju
lägre värde, desto mera effektiv kylning.
Se
f.ö. hur de etablerade begreppen beskrivs i webbkällan
@INTERNET
Wikipedia Thermal conductivity, Conductance|Resistance 2010-08-14
http://en.wikipedia.org/wiki/Thermal_conductivity
:
Wikipediaartikeln
beskriver inte typen t/PA från Stefans-Boltzmanns strålningslag. De
typer Wikiartikeln tar upp anges [13Okt2013] enligt
thermal
conductance P/t ; W/°K
thermal
resistance t/P ; °K/W
heat transf. coefficient P/At ; W/M2°K
thermal
insulance At/P ; M2°K/W
På
artikeln Thermal resistance anger Wikipedia [13Okt2013-10-13] sambandsformen
thermal resistance At/P ; M2°K/W
För praktisk (experimentell) orientering i
termofysiken, se f.ö. med fördel
ELFAKATALOGEN — ELFAKATALOGENS FAKTASIDOR,
ref. Temperaturberoende, PDFs25|ELFAs1745sp2mn, 2013-10-13
https://www1.elfa.se/data1/wwwroot/webroot/Z_STATIC/sv/pdf/fakta.pdf
Enheterna i t&T från grundsambandet
Enheterna i t&T är
tydligen »självreglerande» (autonoma):
Termerna i grundsambandet
t/T=m/M har enheterna med innebörderna
M klimatlokalens medelmässiga atmosfäriska
genomflödesmassa, KG
m kolutsläppet, KG/år
T förbränningstemperaturen vid utsläppet för m, °K
t temperaturökningen som resultat av T från m,
°C från TG
med
TG normala naturliga globala
medeltemperaturen (ca 15°C = 288 °K)
TG
+ t aktuella globala
medeltemperaturen i °C
Autonomin i
grundsambandets rent fysiska funktion ombesörjs tydligen automatiskt genom att
t=0°C motsvarar m=0 KG fossilförbränningsutsläpp och därmed ingen inverkan på TG
— vilket också i princip medför noll genomflödesmassa (M) för det obefintliga
utsläppet (m) som primär förorsakande faktor; M=T([m=0]/t)=0. Se även i AGW-bevisets
slutform.
Värmeisolationskoefficienten eller absorptionskoefficienten
Absorptionskoefficienten
(a, = 1–albedo) som fullständigar
grundsambandets praktiska fysik,
t/T = a(m/M) ;
medger utrymme för
värmeläckage baserat på medelvärden för större land-hav-luftområden. Typiskt
a-värde som ofta används i gängse fackverk i klimatbeskrivningar är för
Jordytan ca 0,7 (albedo 0,3 [ref.
Pierrhumbert, s116n Principles of Planetary Climate 2009]). Se även den mera
utförliga originalbeskrivningen för Värmeisolationskoefficienten.
GRUNDFORMEN TILL Grundsambandet
GRUNDFORMEN
——————————————————————————————
Från SVT:s klimatblogg
[Klimatförnekaren, (18) September 2009]
”Björn H” — i princip ALLA som deltar i den här debatten — får
inget grepp om hur påståendet om värmebidraget från den fortsatta
koldioxidökningens ”logaritmiska avtagande” fungerar.
— Här är ett svar:
.
Hej Björn H
.
Man kan använda sambandet
.
t/T = a(m/M)
.
för att (grov-) beräkna hur stor
värmegrad koldioxiden (utan hänsyn till Solstrålningens inverkan) bidrar med
från olja-kol-naturgasförbränningen.
.
Sambandet beskriver, som du själv ser,
en helt linjär proportionalitet mellan värmegrad och gasmassa med 0°C som
basreferens för Jordytans årliga globala medeltemperatur, den gränsen beskriver
en atmosfär som varken innehåller vattenånga eller avdunstning och därmed
heller inte ingår i någon praktisk klimatmodell. Gränsen går alltså vid exakta
0°C. Alla temperaturvärden således i °C och tvunget större än 0°C.
.
t, värmegradens tillskott över Jordens
globala årsmedeltemperatur (grovt 15°C);
T, förbränningstemperaturen hos
fossilbränslet (minst 2000°C, mest 2200°C, gäller
kol-olja-naturgas);
a, absorptionskoefficient, samma som
Jordatmosfärens medelmässiga värmeisolation, max 1 min 0, nominellt ca 0,67
(grovt motsvarande medelreflektiviteten för granit, sand, gräs sammantaget);
m, koldioxidmängden i KG som förs ut
från fossilförbränningen;
M, totala atmosfärens molekylmassa i KG
m/M är ca 3·10^-6 med grovvärdet 1% av
atmosfärens totala koldioxidbank som tillfogas av människan genom
kol-olja-naturgasförbränning.
.
EXEMPEL:
Med ovannämnda värden insatta ges
t = Ta(m/M) = (2000)(0,67)(3·10^-6) =
0,00402°C/år;
På hundra år alltså 0,402°C, men då är
Solens inverkan inte medräknad (gängse mätdata som visas på webben ger
runt drygt 0,7°C på 100 år, men då
baserat på medelvärden som innefattar en låg trend i början, de första 50 åren,
och en häftigare mot slutet, nära dubbelt).
…
Se vidare från Grundsambandet
i AGW-Beviset Del 2.
Se även originalförfattningen i DEN
GLOBALA UPPVÄRMNINGEN UNDER 1900-TALET.
De 6 kurvorna
NASA-temperaturkurvan innehåller
preciserad information om ythavsperiodernas form
AGW-beviset
Beviset för AGW — Den av
människan förorsakade Globala Uppvärmningen (Anthropogenic Global Warming)
De 6 KURVORNAS ENHETLIGA SAMMANSÄTTNING
De 6 KURVORNAS ENHETLIGA SAMMANSÄTTNING
NASA-temperaturkurvan, heldragen nedan, visar de luftmarint uppmätta
temperaturerna på Jordytan från ca år 1860 (1850).

Den
streckade kurvdelen
y = 6[1–1/(1+[x/10]^4)] +
0.222(0.9[(2cos pi x/1.48) + 0.5(cos 3pi[x–0.1]/1.48)])
t(AGW)+ythavsperioden i PREFIXxCOS,
vidare nedan
består
av sammansättningen
1.
naturliga ythavsperioderna approximerade (man känner dem inte exakt [men nära] [‡])
y = 0.222(0.9[(2cos pi x/1.48) +
0.5(cos 3pi[x-0.1]/1.48)])
ythavsperioden i PREFIXxCOS
2.
den utjämnade havsversionen [t|E(AGW)-kurvan]
y = 6[1–1/(1+[x/10]^4)] , se t-kurvans elementära energifunktion
av Fossil-Carbon-kurvan (svarta övre
nedan)
med
integralkurvan (C, approximerad för substitution [ingen
matematisk institution på Jorden verkar kunna ge en algebraisk integral
lösning, se C-Integralen])
—
som f.ö. verifierar den utjämnade havsversionen som C-kurvans derivata
y = 0.74[(x/5.7)^4.25] ............. C-approximationen gäller fram till max år 2030
—
analog med Carbon-Dioxide-kurvan
och
som via C-approximationens C-värden till jämförelse per tabelldata med mätningar från år 1958
till nu, visar lägst 98% överensstämmelse,
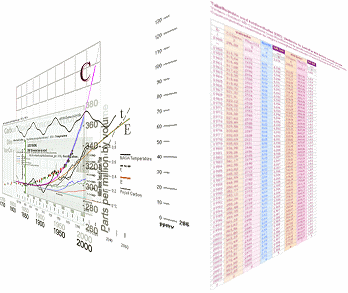
Tabellvärdena finns
redovisade separat i Kalkylkortet (Tabell3).
och
vilken samhörighet därmed bortom varje tvivel bevisar, styrker och certifierar
överensstämmelsens äkthet — boven i dramat, energibasen, är tydligen Fossil-Carbon.
Se även NASA-kurvans
ythavsperioder.
Att Fossil-Carbon-kurvans
havsutjämnande versions integral i formen av C-kurvan skulle ha något med
begreppen ANTAGANDE, TEORI eller HYPOTES att göra är här veterligt helt
uteslutet med samma säkra fysik som den redan notkunnige inte kan anses
framföra ett antagande, teori eller hypotes i det att musikstycket omedelbart
uppfattas analogt med nottecknens framträdande, eller att den redan läskunnige
inte kan anses framföra ett antagande, teori eller hypotes i det att stycket
omedelbart uppfattas analogt med bokstävernas framträdande, ehuru C-kurvan
följer av t|E-kurvan som omedelbart framgår ur NASA(CRU)-kurvan
tillsammans med ythavsperioderna
enligt AGW-beviset Del 1.
Med hänsyn till den
jämna följsamheten, den — med hänsyn till komplexet
nödvändiga mätintervall och globala medelvärdebildning — maximalt höga
överensstämmelsen med lägst 98% i Tabelljämförelsen,
samt de matematiskt samhörande fem
kurvkomponenterna som delar av en och samma fysikaliskt grundade energibas,
framstår tydligt begreppet EKVIVALENT i påvisandet av de
6 olika formdetaljernas komponenter.
C-kurvans
påvisande från t|E-kurvan
som havsversionen av Fossil-Carbon-kurvan
får (således) och tydligen förstås som just en (analog) EKVIVALENT form: NASA-kurvans komponenter.
Alla
de sex kurvorna
0. NASA-kurvan,
1. ythavsperioderna, 2. t|E-kurvan, 3.
Fossil-Carbon-kurvan, 4.
Carbon-Dioxide-kurvan, 5. t|E-integralen (C).
NASA-kurvan
med de fem formekvivalenterna
uppvisar
en tydligt inneboende överensstämmelse
[Se särskild sammanställning i De 6 Kurvorna]
genom
att vara komponenter i samma matematiska-fysikaliska komplex:
Frånsett havsperioderna
som de övriga överlagras på: en UPPTAKT lika
med t|E-kurvan med motsvarande
industribaserad Fossil-Carbon
som energibas och därmed obönhörligen med en tillhörande integral, C-kurvan analog med Carbon-Dioxide-kurvan.
Oberoende
av teori, måste ovillkorligen alla fem angivna komponenter spela med i samma
matematiska orkester — den uppmätta NASA-temperaturkurvan.
Alltsammans förklaras av (det ytterst
enkla) grundsambandet
t/T = a(m/M)
med beskrivning i AGW-beviset Del 2 — med grund i den
uppmätta NASA-temperaturkurvan.
Fortsättning i AGW-beviset
Del 3.
|
|
|
Arrhenius |
Varför inte AGW |
|
|
|
|
|||
|
|
Etablerade
klimatmodeller och |
INLEDNING · Temperaturökningstakten · Värmebidraget
· Vattnets huvudroll · Vattenhalten
i MJ · Samband
· RHSER
· Vattenångans andel · Uppvärmningsgradienten · Soleffekten
vid Jordbanan
2010VII27
AGW-beviset — Del 3 (AGW3)
—————————————————————————
För
att slutföra AGW-beviset fullständigt — hur AGW-bevisets föregående delar (Del 1 och Del 2)
MÖJLIGEN kopplar till de allmänna
klimatmodellerna och deras empiriska
kopplingar till experimentellt uppmätta matchningar — återstår »endast» att
härleda den motsvarande värmeeffekt som krävs av den redan befintliga
Soleffekten på Jordytan i dess uppvärmningsdel för t(AGW) enligt AGW-beviset Del 2.
AGW-beviset Del 3
Den globala uppvärmningens matematik
INLEDANDE BESKRIVNING
|
|
|
|||
|
2t(SOL) |
|
0,85 W/M² |
|
2,79 t10
°C/S |
|
|
|
|

M-skiktet
med massan 3,5 T16 KG är här starkt förstorat för illustrationens tydlighet.
M-skiktets höjd är i själva verket enligt AGW-beviset
Del 2 bara drygt 50 meter över
allt fast och flytande på Jordytan, se Beräkningen
av M. Beräkningen av Solära
uppvärmningseffekten på hela Jordatmosfären från dessa grunddata ger nuvärdet 0,85 W/M²
med en bidragande vattenatmosfärisk luftmarin genomsnittskoncentration på 0,039
(3,9%) i M-delen — Eller 0,87 W/M² med 0,04 (4,0%) vilket visar känsligheten.
Uppmätta värdet (2003) genom oceanernas värmeupptagning är (Hansen et al., 2005) 0,85±0,15 W/M², vidare i huvudtexten.
Medan
SAMMANSÄTTNINGEN i M-skiktet är egalt för AGW12, är den avgörande för AGW3.
— I AGW12 är M-lokalens sammansättning egal. Det är bara t|R-ändringen
som räknas.
— I AGW3 däremot är det avgörande viktigt att den
värmeledande molekylsammansättningen i det fasta medelbaserade ytutstrålande
Jordytsskiktet (A=4πr²) specificeras; För vårt fall (så länge CO2-halten och övriga är relativt liten)
främst avseende halten av vattenånga eftersom just vattnet spelar huvudrollen.
— AGW3-problemet kan då lösas genom att använda det redan
definierade M-skiktets kvantitativa form via en specificerad
M-lokal som vi nu kan kalla MJ-lokalen: MJ-lokalen måste nu betyda det
sammansättningsmässigt ospecificerade M-skiktet
från AGW12 plus hela Jordatmosfärens sammansättning som
en komprimerad ekvivalent i M; MJ-lokalen måste avspegla hela Jordatmosfärens totalt SIGNIFIKANTA
medelsammansättning, alla värmeagenter,
samtliga möjliga termiska fall inbegripna, och vilken sammansättning i sig i M
är egal för AGW12. Se särskild beskrivning
i AGW12.
Vad som redan
framställts i AGW12 äventyras alltså inte
på den mera precisa bekvämligheten i AGW3 — eller ska i varje fall inte göra det (Annars är det
kört).
AGW-beviset Del 3 — genom
utvecklingsexempel
AGW3
beskriver effekt och energi i AGW
Om
den globala temperaturökningen nu (2000-2010) är 0,0882°C/10år, enligt t|E-kurvan (nedan) från AGW-beviset
Del 1 (grafiska) och AGW-beviset Del 2 (matematiska)
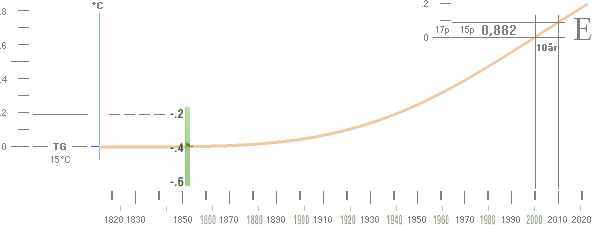
Grafen ovan (t|E-kurvan)
visar på enklaste sättet att temperaturen i intervallet åren 2000-2010 ökar med
15p/17p=0,882 bråkdelar av en tiondels värmegrad, analogt 0,0882°C/10år.
ger det
ett aktuellt värmebidrag (Δt) i standardiserade enheter (per
Sekund) enligt
Δt
= (0,0882
°C)/[10·365,25·24·3600 S]
= 2,79488 t10 °C/S ; ................... nuvarande globala temperaturökningens hastighet
Tillskottet
Δt~2,8 t10 °C/S gäller för hela M-skiktet med höjden h. Dvs., alla värmeagenter i M — varje enskild atom eller
sammansatt medelmolekyl — besitter (som ovan) samma Δt~2,8 t10 °C per
sekund. Men effekten [P(AGW) som avdelas från SER] som åtgår för den
uppvärmningen är inte oberoende av antalet värmeagenter i M utan beror
helt av deras antal (N) och måste därför relateras till en specifik
koncentration av N i M (Därmed MJ). Eftersom också strålningseffekten i SER är bunden till
Jordytan [‡1], måste N återföras på antalet värmeagenter i varje
specifikt Jordytsskikt (A=4πr²) med medelavståndet mellan luftmolekylerna (d~3 nM). Totaleffekten slås alltså ut på summan (n) av
alla sådana skikt i h,
n =
h/d
.................................... antalet
genomstrålningsskikt i h med tjockleken d
Totaleffekten
(P) i SER som avdelas för P(AGW) för att realisera värmeflödet via den termoresistiva
ändringen Δt|R från fossilsläppet m i M via T [Se Grundsambandet i AGW2] således totalt via
(Δt~2,8
t10 °C/S)(n=h/d)(N)
....................... totala
värmebidraget
———————————————————————————
—————————
I
värmeläran (från Stefan-Boltzmanns strålningslag, [SBS]) utgår (som vi minns i härledningen, se dT
nedan) all elementär värmestrålning från en minimal materialyta (A):
volymVärmedifferentialerna
dT(x)=dT(y)=dT(z)
uttrycker värmeflödets (Txyz) 3D-volymdifferential
[dT(x)·dT(y)·dT(z)]
i det ljusutbredande rummets (Divergensens) alla riktningar xyz, vilket för varje fysiskt
strålande källa tvunget också betyder en primär materiell strålyta
[dx·dy·dz
motsv. A·dz] som strålningen utgår ifrån och vars tjocklek [dz]
återfaller på och varierar med materialets atomsammansättning. Förekomsten
av A i grundformen för SBS är alltså »trivial».
Editor2010VIII17
———————————————————————————
Grovt
sett blir n lika med (50 M)/(3 nM)~1,7 T10. Vi ska dock använda mera exakta värden längre
fram i slutresultatet (Se Uppvärmningsgradienten) med hjälp av Kalkylkortet, vidare nedan.
Med ovanstående värmebidrag (Δt)
för varje idealt Jordytskikt (d) blir totala värmebidraget summan av
alla de n bidragande ytskikten,
Δt(TOT) =
(Δt)·(n)
............................ totala
värmebidraget i M
Men,
som nyligen vidrördes, heller inte alla luftmolekyler deltar i uppvärmningen.
Den avgjort största värmeagenten i atmosfären är vatten.
ANLEDNING:
Den avgjort största värmeagenten i atmosfären
är vatten

BILDKÄLLA: Författarens arkiv · Bild130RS ·
17Maj2009 · NikonD90 · Stranddetalj
I
förhållande till andra luftmolekylämnen tar vattnets värmekapacitivitet helt överhanden för alla värmetransporterande funktioner
i kretsloppet
hav-atmosfär — vatten drygt 4000
J/KG°K, vattenånga ca 2000 att jämföra med koldioxid ca 800. Den närmaste
komponent som ens kommer i närheten är metangasens molekyl (CH4),
Tabellkällan
[Wikipedia] i referensen till artikeln om värmekapacitivitetsbegreppet anger 2191 J/KG°K (vid 2°C) för metan. Andelen metan är
emellertid (ÄNNU SÅ LÄNGE 2010) relativt låg (1,7ppm rel. CO2 387ppm [ref.
@INTERNET Wikipedia Greenhouse gas, Natural and anthropogenic sources 2010-07-28]), och kan (ÄNNU 2010) därför helt bortses ifrån i det
övergripande sammanhanget.
eg. värmeagenternas totala andel
Max dynamik bestämmer hur vattenångans andel i MJ ska bestämmas:
— ca 4% anges som ett ungefärligt max vid Jordytan [‡]: Täcker samtliga fall som bidrar till medelglobala temperaturen
TG=15°C
Eftersom
sambanden (empiriskt) redan är (väl) kända [‡] för atmosfärens vattenångtryck vid Jordytan, kan vi
utnyttja dessa för en motsvarande anpassning till hur alternativa
luftfuktigheter varierar relativt det givna 4%-värdet och med globala medeltemperaturen (TG) känd. Som generell koll på gränserna ska (i det
närmaste) 100% vattenhalt tydligen gälla vid (eller nära) kokpunkten 100°C. Vi
studerar lösningen nedan.
— hydrotermiska konstanten
Med
kända maximerade (medelbaserade) toppvärden för lokala temperaturer på Jordytan
framträder ett globalt relevant kriterium för antagande av en (hydrotermisk)
materialkoefficient (c=4%) med känd variationskaraktäristik (dvs., ändringen i
intervallet mellan vattnets fryspunkt och kokpunkt). En motsvarande
(approximativ, generaliserad) maximal luftfuktighet (RH) — i kraft av det nyligen omnämnda vattnet som komplexet huvudrollsinnehavare — kan då härledas/beräknas för samtliga fall inom
Jordytans termofysik via empiriskt kända atmosfäriska ångtryckssamband [‡] enligt följande preferens:
Med
referens till (maximala luftfuktigheten) RH-värdet vid TG=15°C vid havsytan (kalkylkortets mera noggranna värden),
RH =
0,01004 ............... maximala vattenandelen i luft vid
havsytan vid 15°C
= RH15 .................... maximala
vattenhalten för specificerad global medeltemperatur
= RHTG ................... allmänna
maximala vattenhalten för given global medeltemperatur
~ 1% ....................... maximala
vattenandelen i luft vid havsytan vid 15°C
och
det globalt generaliserat maximerade aktuella luftfuktighetsvärdet på 4% vid TG=15°C
RH15M = 4% ....................... globala nominella luftfuktighetsMaxvärdet
vid globala medeltemperaturen 15°C
= RHTGM
med
den allmänna omvandlingsfaktorn (F)
F = RHTGM / RHTG
som
(i vårt nuvarande fall via given globalmedeltemperatur) bestäms via
F = 4% / 1%
= 4
ges
därmed generellt (RHSER = c = RHTGM) sambandet för samtliga globalt relevanta fall (så
länge något levande kan finnas)
RHTGM = F · RHTG ;
RHTGM = RHSER
Den
globalt maximerade luftfuktighetshalt som SolEkvivalenta Radiansen (SER) ser i MJ-lokalen,
kan alltså uttryckas för samtliga fall enligt
RHSER = 4 · RHTG
............... Ekvivalenta
Jordbaserade Solutstrålningskällans koncentration av värmeinduktiva element
(vatten)
RHTG ..................................... allmänna maximala vattenhalten för given
global medeltemperatur
RHTG = (610,78)e17,2694(t/[t+238,3])
med t=TG i °C, se Empiriska
samband för vattenånga.
Med
den matematiken kommer absoluta gränsen för globala medeltemperaturen (TG) att sluta där RHSER=100% vattenhalt. TGmax-värdet för detta blir enligt Kalkylkortet
lika med (74,2525; 4·RHTG=1)
TGmax = 74,3 °C
................ referensgränsen
för absolut globalt högsta möjliga medeltemperaturen
—
max 25% vatten i luften
(Det
går naturligtvis med högre temperatur, men situationen går då tydligen mer och
mer mot en [kokande] bastuvärld).
Andelen
(c [eng. contributing]) värmeupptagande molekyler i varje
molekylärt luftskikt blir alltså (som en första preliminär ansats) i vårt
nuvarande fall med TG=15°C
— där dynamiken är som störst
c =
4% ................................... samma som RHSER
= 0,04 .................................. andelen värmeupptagande molekyler i varje
skikt=1
Med
alla skikt homogena kan det slutgiltigt totala värmebidraget Δt(FIN)
då skrivas
Δt(FIN)
= Δt(TOT)·(c)
.................... slutligt
totala värmebidraget i M
= (Δt)·(n)·(c)
Den
del koldioxid som kommer från Fossil-Carbon-förbränningen kan (som redan omnämnts) i förhållande till c=4%-delen
ses som i stort sett helt försumbar, trots att det är koldixodmolekylen som
ansvarar för AGW-effektens energiöverföring till vattenbanken (att
bankkassören dagligen hanterar stora summor pengar betyder inte att kassören
också blir rik på kuppen): Grovt 400 ppm(v) = 0,04% atmosfärisk andel CO2
betyder bara (förgrovat) 1/100 av vattenångans andel (totalt 0,0404), vilket vi helt kan bortse ifrån.
Uppgifterna för den vidare sammanräkningen
finns sammanställda i Kalkylkortet.
Insättning av kalkylkortets mera noggranna
värden (här avrundat till tre decimaler) från ledet närmast ovan ger oss
effektsatsen
Δt(FIN) = (2,795 t10 °C/S)·(n=1,654 T10)·(0,040)
= 0,185 °C/S ....................... värmebidraget till hela M
Vi
beräknar sedan — och slutligen — vilken ändring i Soleffektens utnyttjande som
Jorden måste uppvisa för servering av ovanstående värmegrad Δt(FIN):
Globaltemperaturen varierar som
Soleffekten
Den [helt »triviala»] satsbilden gäller alltid, under alla
förhållanden, under alla omständigheter, genom alla jämförelser — därför att
det är Solen som försörjer kvantiteterna i hela den termiska effektbilden till
Jordklimatet, oavsett vilka de enskilda problemgrunderna är:
Värmegradens
tillskott Δt(FIN) måste tvunget förhålla sig till aktuella globala
medelvärmegraden (TG=15°C=288°K) som den
till AGW avdelade Soleffekten [per kvadratmeter i SER] (ΔP)
förhåller sig till aktuella maximala Soleffekten (P) [per kvadratmeter vid Jordbanan].
Eftersom Jordytans ändrade sammansättning
avgör hur stor deleffekt av Solära råeffekten vid Jordbanan (P/A=1367 W/M²) som omsätts på Jordytan (250
W/M² i vårt nuvarande
fall) måste också det maxvärdet användas som absolut högsta råvärde för
jämförelsen med den aktuella globala medeltemperatur (TG) som motsvarar den aktuella medelsoleffekten (250 W/M²).
Därmed måste också den globala medeltemperaturen (TG) räknas i absoluta
Kelvingrader (288°K för 15°C med förenklade 0°K=–273°C [eg. –273,15°C]).
Satsbilden således
Δt(FIN) ΔP
———— = ——— ; ([Δt(FIN)/ΔP]ΔR
= [TG/P]R) = (ΔR = R) = globalresistansen 0,21°K/WM²
TG P
;
Δt(FIN)/(TG) = (ΔP)/(P) ; eg. =
(ΔI)/(I0), I = P/A, A=1M² ;
Sambandet för tillskottseffekten (ΔP, den aktuella effektfunktionen i hela AGW3)
bestäms alltså genomgående av funktionen
för Δt(FIN), vidare
nedan. Den avgörande effektkoefficienten [P/TG]
fås med insättning av värdena som ovan. Därmed den eftersökta effektgrafens ekvation enligt
ΔP = Δt(FIN)·(P)/(TG) ;
Funktionen för
Δt(FIN) bestämmer den globala temperaturens variation.
[SolP-värdet
1367
W/M² som används här
hör till gruppen ε=0,612, a=0,7 och P/A=1367 W/M²,
från
@INTERNET
Wikipedia Climate model, Zero-dimensional models 2010-07-24
http://en.wikipedia.org/wiki/Climate_model
Man
får närmevärdet direkt ur Soleffekten 3,846 T26W [ref. Wikipedia [NASA] Sun
(2009-03-23|2010-08-24) 3,846 T26 W] genom medelavståndet Jorden-Solen
1AU enligt
I(J)
= P(SOL)/A(Jordbanan) = (3,846 T26W)/(4π[1AU=1,496 T11 M]2)
= 1367,528 W/M2].
Med
nuvarande värde i exempelutvecklingen från Temperaturökningstakten (2000-2010) som
Δt(FIN)=0,185°C
ges
= (0,185°C)·(1367 W/M²)/(288°K)
=
0,878 W/M²
= 0,878
W/M² ;
ΔP = (Δt)10år·(n)·(c)[(P=1367
W)/(TG=288°K)]
= (Δt)10år·(n)·(c)[4,7465277 W/°K|°C]
= [(0,0878 °C)/(10·365,25·24·3600)SEK]·(n)·(c)·[4,7465277 W/°K|°C]
= (0,0878 °C)[1,50408 t8 W/°K|°C]·(n=1,654 T10)·(c)
= (0,0878 °C)[248,77483 W/°K|°C]·(c)
= (0,0878 °C)[248,77483 W/°K|°C]·(0,04)
~ (0,0878 °C)·(10 W/°K|°C) om atmosfären
inte börjar berikas med mera värmeagenter
De enda egentliga faktorer
(rödmarkerade ovan) som kan påverka resultatet är
1. den molekylära sammansättningen i genomströmningslokalen MJ — som ovan med totalt c=4% värmeaktiva
molekylagenter på
2. en temperaturgradient som i
nuvarande skede visar Δt=0,0878°C/10år, värdena ovan.
— »Skräckscenariot» är att andelen metan (femvärd molekyl, CH4) ska öka
(som på grund av de potentiellt fem [gånger 3, =15] frihetsgraderna också
medför motsvarande mycket höga värmekapacitivitetstal), vilket
drastiskt påtvingar Jordatmosfären en mycket högre värmetröghet; Följden, de
ovan bägge rödmarkerade, betyder att temperaturgradienten, liksom andelen
aktiva värmeagenter totalt ökar (lavinartat), och därmed uppvärmningseffekten;
allt mindre strålning från Solen läcker ut tillbaka till rymden; allt mer
stannar kvar. Mänskligheten har MAX 30 år på sig att avvärja den trenden.
Hur de ovan rödmarkerade värdena ser
ut (i förlängningen från nu och framåt utan avseende på eventuella
sidoeffekter) i förhållande till de allmänna klimatmodellernas olika
scenarion visas i Jämförelse med etablerade klimatmodeller.
Med
det molekylärt uppvärmande bidraget c=0,0388
(fortfarande
utom räckhåll för koldioxidens direkta inverkan, den ligger först i fjärde
decimalen)
ges
till jämförelse mot föregående c=0,040 — för att belysa känsligheten —
värdet
ΔP = 0,85 W/M²

Funktionen för Δt(FINAL)
Sambandet
generellt för effektfunktionen i AGW (ΔP) blir alltså
= Δt(FIN)(1367
W)/(288 °K)
= Δt(FIN)[4,7465277 W/°K|°C]
med
Δt(FIN)
= Δt(TOT)·(c)
.................... slutligt
totala värmebidraget i M
= (Δt)·(n=1,654 T10)·(c=0,040)
och
(Δt) som t-kurvans derivata [Se från Temperaturökningstakten], analogt energiintegralens tangensform lika med
effektgrafens funktion
Δt = (2·459/39/170) [y’= (24/10)(1 + [x/10]4)–2[x/10]3] ............. °C
där koefficientparentesen (2·459/39/170) [5å·459p/195å=459p/39][1°C/170p]
avser utsträckningen ±5 år från x med hänsyn till grafkoefficienterna, hela komplexets grafiska pixelenhet unit50p, samt med
tidsvariabeln x som tidigare lika med
x =
(ÅR – 1815)(2,35/50)
= (ÅR – 1815)(0,047)
= (ÅR – 1815)(1/21,276595), använd i
originalförfattningen
Pixelbasen
gör att de olika kurvoriginalen inte kan passas in med godtycklig precision i
skalanpassningen, en viss mindre tolerans tillåts.
Resultatet av utvecklingsexemplet
;
ΔP = P(AGW) ........................... W, uppvärmningseffekten per M²
Jordyta, gäller vid ÅR±5år
P(AGW) = (n=1,654 T10)·(c=0,040)·(2·459/39/170)·[y’= (24/10)(1 + [x/10]4)–2[x/10]3]
;
För
att få ut effektgrafens Wattskala [Se även Effektkurvan] används det grafiska toppvärdet (tangens = 0,64,
ungefär vid 4Apr2002) tillsammans med resultatvärdet 0,88 W vilket ger
0,64t/0,88W
= 0,727t/W = 1t/(1/1,375)W ;
Med
1t = 50pixel ges 1,375W/50p = 0,0275W/p eller 36p/W. Den motsvarande
generaliserade AGW-effektens funktion kan då skrivas direkt per momentan
(års)tidpunkt
P(AGW) =
(1,375 W)·[y’= (24/10)(1 + [x/10]4)–2[x/10]3] ........ W, per M² Jordyta
x = (ÅR – 1815)(2,35/50)
För
hela Jordytan (via ekvatorialradien rEKV=6,378 t6 M) tillkommer
AJ =
4π(6,378 T6 M)2
= (5,11185 T14 M2)
;
P(AGW) = (5,11185 T14 M2)(1,375
WM–2)·[y’= (24/10)(1 + [x/10]4)–2[x/10]3]
P(AGW) =
(7,0288 T14 W)·[y’= (24/10)(1 + [x/10]4)–2[x/10]3] ........ W, hela Jordytan
x = (ÅR – 1815)(2,35/50)
t|E-kurvan som AGW-energikurvan
Eftersom
tidsskalan för hela kurvkomplexet är årsbaserad, motsvarar ovanstående
AGW-effektfunktion också ett årsbaserat energivärde E=P(1ÅR) med effektenheten
Joule/År.
För att få ut energivärdet i vanliga
standardenheter (MKSA-systemet), dvs., här på sekundbas, måste ytterligare en
koefficient (ÅR till Sekunder) tillfogas till den motsvarande energikurvan (y nedan [Se Energikurvan i Härledningarna]), samma som i Temperaturökningstakten men här i en särskild skalform genom en speciell
koefficient som kopplar energiskalan [allt med grund i proportionaliteten
mellan temperatur och energi];
E(AGW) =
(7,0288 T14 W·ÅR)·[y = 6[1–1/(1+[x/10]4)]]
.................. WattÅr, hela
Jordytan
x = (ÅR – 1815)(2,35/50)
som
ger den sekundbaserade sammanlagt använda AGW-energin i WattSekunder
E(AGW) = (7,0288 T14 W)·ÅR·[y = 6[1–1/(1+[x/10]4)]]
= (7,0288 T14
W)·(365,25·24·3600 S)·[y = 6[1–1/(1+[x/10]4)]]
= (7,0288 T14 W)·(31
557 600 S)·[y = 6[1–1/(1+[x/10]4)]] ;
E(AGW) =
(2,21812 T22 J)·[y = 6[1–1/(1+[x/10]4)]]
........................ J, hela
Jordytan MJ
x = (ÅR – 1815)(2,35/50)
Varje
enhet (50p) i AGW-energikurvans y-skala får alltså värdet 2,21812 T22 J
= 50p, analogt
4,43624
T20 J/p ~ 4,44 T20 J/p;
E(AGW)-värdet
nu (2010) visar 5,51 T22 J.
*
Se
även resultatet för aktuella effekten i sammanställningen för hela
komplexet i EffektEnergiAGW.
RESULTATET
AV UTVECKLINGSEXEMPLET:
Jordkroppen (år 2005) måste kvarhålla ca 0,88 W/M² mera
effekt nere vid marken från Solstrålningen än vad Jorden emitterar tillbaka ut
i rymden för att kunna försörja AGW-bevisets uppvärmning av det drygt 50 meter
höga h-skiktet i M.
Med NASA(CRU)-kurvans
nuvarande [2010] t(AGW)-hastighet gäller den något lägre nivån 0,0875
°C/10år motsvarande ca 0,875 W/M².
Kontrollräkning
2010VIII21
KONTROLLRÄKNING — med utomordentligt resultat
—
med Exempel på dolda fällor · Stefan-Boltzmann-Approximationen · Stefan-Boltzmann-Gasiska
felapproximationen
Vi
kan göra en grov snabbkoll av resultatets rimlighet med hjälp av Stefan-Boltzmanns strålningslag enligt
P/A
= ak(T14 –
T24) = Î ; (Alt+0206, Î, »i-flex», intensiteten eller radiativkraften)
T1 = 288°K + 0,7 °C ;
T2 = 288°K ;
a=1 ger
P/A
= (1)(5,7 t8 WM–2°K–4)(67
130 292 °K4)
= a(3,8264266 WM–2)
Med a=1
åtgår hela radiativkraften Î=P/A (eng. radiative force|forcing)
(~4 W/M²) för uppvärmningen, vilket blir maxvärdet för
tilläggstemperaturen 0,7°C och a=1.
Generellt
(se referensen nedan, albedo α = 1–a) brukar värdet a=0,7
(ungefär medelvärdet av granit, sand, gräs) användas som ett medelvärde
för Jordens absorption av Solljuset; 70% absorberas, 30% reflekteras.
”The
average albedo of the Earth is about 0.3.[7] This is far higher than for the
ocean primarily because of the contribution of clouds.”,
@INTERNET
Wikipedia Albedo 2010-08-19
http://en.wikipedia.org/wiki/Albedo
Min
översättning:
Det genomsnittliga albedovärdet för Jorden är omkring 0,3.
Det är mycket mer än det som gäller för havet, huvudsakligen beroende på bidrag
från moln.
Enligt
BAs481sp2.80
definieras termen albedo (α)
som förhållandet mellan reflekterat (spritt) och infallande ljus. Med
beteckningen I(0) för infallet och I(r) för reflexionen kan albedokoefficienten
då skrivas
α
= Ir/I0
.................... andelen
reflekterat ljus, albedo (här också förenklat â)
Subtraheras
andelen reflekterat från infallet återstår absorberat. Absorptionskoefficienten
(a) kan alltså skrivas
a = (I0
– Ir)/I0
= 1 – Ir/I0
= 1 – α ................... andelen absorberat ljus
Det
finns också en motsvarande s.k. emissionskoefficient (ε)
”It
is a measure of a material's ability to radiate absorbed energy.”,
@INTERNET
Wikipedia Emissivity 2010-07-24
http://en.wikipedia.org/wiki/Emissivity
som
sammanhänger med ett materials uppvärmning (via ljus); Om ingen uppvärmning
sker, återstrålas (genomströmmas) lika mycket som a upptar;
Genomgår kroppen uppvärmning, är a större än ε så länge
uppvärmningen pågår, därefter gäller a=ε.
Generellt på (den engelskspråkiga) webben
(i varje fall i Wikipedia) används knappast (längre, 2010) termen absorptionskoefficient
(a). Man använder istället begreppet albedo (α=1–a)
och emissivitet (ε) i de olika beskrivningarna.
Vi
har alltså
Î = P/A = ak([TG+Δt]4 – [TG]4) ;
Stefan-Boltzmann-Approximationen
Stefan-Boltzmann-Approximationen: I=Îâ
Ovanstående
sambandsform leder till följande användbara linjära approximation för
AGW-effekten:
Jordreflexionskoefficienten 30%
I
fortsättning från Jordytans
medelabsorption:
— Är
reflexionens andel 30%, kan bara max 30% av den totalt tillgängliga radiativkraften
(effektvärmet)
Î = ak(T14
– T24) användas för uppvärmning. Med Jordens tämligen
oföränderliga medelabsorption på ca 70% (a=0,7) — oavsett scenario, så
länge någon grönt finns kvar — finns alltså en motsvarande reflektiv andel på
max
100%–70%
= 30% (â=1–a)
[Alt+0226, â, »a-flex», (â=1–a), reflexionskoefficienten,
även konv. albedo, α], som kan åstadkomma en lokal uppvärmning;
I = Î(1–a)
= Îâ
= a(1–a)k(T14
– T24)
Stefan-Boltzmann-Approximationen
[streckad
blå] till
AGW-effekten [mörkvioletta].
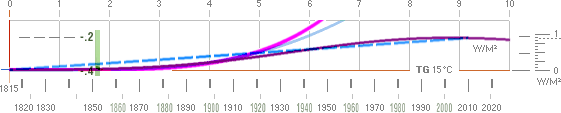
Stefan-Boltzmann-Approximationen
— grafiskt som ovan streckad blå
I = 0,07965[([288+x]4)–(288)4](5,7·10–8)(0,7)(0,3)(1/1,375)
................ W/M2
0.07965[([288+x]'4)–(288)'4](5.7·10'–8)(0.7)(0.3)(1/1.375) ................ GRAFISKA
Koefficienten 0,07965 från år 2010 via Δt=0,73°C
vid ÅR
x=(2010–1815)(0,047)=unit9,165 enligt
0,73°C/9,165u=0,0796508°C/u = 0,0796508°C/50p.
Koefficienten 1,375 från Effektgrafen, se Effektgrafens
Skalfaktor.
Stefan-Boltzmann-Approximationen
— i kalkylkortet, samma som ovan men med
x = (ÅR –
1815)(0,047)
.......................................................................... se Årskoefficienten
I-funktionen
(streckad blå ovan) är praktiskt taget helt linjär ända från startpunkten
(1815), den är helt oberoende av molekylära sammansättningar, och den ger (just
därför) en utomordentlig (överlägsen) approximation till den mera avancerade effektgrafen
(mörkvioletta ovan) — Men, som vi ser, bara upp till maximum, strax under 1 W/M², och vilket maximum inträffar lägligt, just i vår tid
(2002±10år).
Värdet
vid år 2010 blir (streckade blå) I=0,839 W/M²—
att jämföra med AGW3-effektgrafens (mörkvioletta) I=0,875 W/M². En mera utomordentlig approximation lär man nog få leta
länge efter.
Vi studerar nedan hur man kan luras att
förlita sig på jämförande analysvärden med bedrägligt innehåll — från till
synes plausibla och högst förnämliga fysiska grunder.
Det försmädliga BeroendeFelet
Det
försmädliga BeroendeFelet — CO2-variabler demolerar hela
kontrollräkningsmöjligheten:
Har man ingen koll på grafen utan använder den
partikulära värdeöverensstämmelsen i tron om att funktionen verkligen är
signifikant för hela komplexet, hamnar man i ett felberoende beskrivningssätt.
Exemplet nedan visar.
Sätter
man ihop ovanstående med koldioxidhalten (C-formen nedan) blir det som på
Julafton:
UTOMORDENTLIGT
— som bäst just nu 2010-2020. Resten: rena skräpet.
Sambandsformen kopplar inte ämnet.
Stefan-Boltzmann-Gasiska
felapproximationen [streckad röd] till AGW-effekten [mörkvioletta].

Stefan-Boltzmann-Gasiska
felapproximationen — grafiskt som ovan streckad röd
I =
[1–1/(1+0,74[(x/5,7)4,25]/C0)]0,07965[([288+x]4)–(288)4](5,7·10–8)(0,7)(1/1,375)
........................................ W/M2
(1–[1+(0.74[(x/5.7)'4.25])/16.588]'–1)0.07965[([288+x]'4)–(288)'4](5.7·10'–8)(0.7)(1/1.375) ........ GRAFISKA
Koefficienten 16.588:
290p/100ppmv=2,9p/1ppmv; 286ppmv=829,4p=16,588(50p)
Stefan-Boltzmann-Gasiska
felapproximationen — i kalkylkortet, samma som ovan men med
x = (ÅR –
1815)(0,047)
.......................................................................... se Årskoefficienten
;
C0 = 286ppmv(1860)=16,588(50p)
C1 = C0 + C
C = 0,74[(x/5,7)^4,25] .................... Carbon-Dioxide-kurvans AGW-motsvarighet
c = 1 – C0/C1
= 1 – C0/(C0
+ C)
= 1 – 1/(1 + C/C0)
Totalfunktionen
via föregående Î:
Î = P/A = ak([TG+Δt]4 – [TG]4) ;
y = Îc
= ak([TG+Δt]4 – [TG]4)[1 – 1/(1 + C/C0)] ;
Beskrivning
ANVÄNDS
DEN ALLMÄNT POPULÄRA KOLDIOXIDENS ANDEL (C-sambandet ovan) SOM VARIABEL
tillsammans med Stefan-Boltzmann-approximationen hamnar man i situationsbilder som BARA DELVIS och INOM
BEGRÄNSAD TID uppvisar hyfsad överensstämmelse.
— Vi
byter ut föregående Jordreflexionskoefficienten (0,3) mot en generell faktorvariant (1 – C0/C1)
enligt följande:
Med
den normala absorptionskoefficienten på a=0,7 ges alltså ett absolut maxvärde för den absolut maximala
globala uppvärmningseffekt som gäller vid uppnådda +0,7°C global uppvärmning
P/A = (0,7)(3,8264266 WM–2)
= 2,6784986 W/M²
~ 2,7 W/M²
..................... absolut
största AGW-effektens uppvärmande radiativkraft
Används
den tillagda andelen CO2 (koldioxid) från nivån ca C0=285 ppmv (1860) till
nuvarande (2010) ca C1=385 ppmv som en (grovt approximerad)
procentuell värdemätare på hur stor andel av max nivå 2,7 W/M² som uppnåtts (mer CO2 betyder mer energiabsorption i
det luftmarina materialet — mer av Solvärmen stannar kvar där — vilket betyder
motsvarande uppvärmning)
385 –
285
————
= 25,97402% ~ 26% = 1 – C0/C1 ; C1 = C0(1
– %/100)–1
385
vilket
betyder att max nivå 100% kräver obegränsad CO2-halt, och vilken räkning
missgynnar sämsta fallets katastrofscenario så att uppvärmningen dras ut och
segas ut så mycket som möjligt (vilket f.ö. är naturens typiska sätt att hjälpa
till när det går riktigt illa, vilket händer då och då, enligt berikad
erfarenhet)
ges
P/A = (1 – C0/C1)(2,7
WM–2)
= (0,26)(2,7 WM–2)
= 0,702 WM–2
~ 0,7 W/M²
Resultat 2010 (Vi använder här direktvärden från Kalkylkortet):
Se även ovanstående grafresultat här betecknat I(CO2)
ÅR I(CO2), W/M2
I(Stefan-Boltzmann), W/M2 I(AGW3),
W/M2 resultat
——— —————— ——————————— ——————— ————
2010 0,700 0,839 0,875 OK notOK
Att
jämföra med
1960 0,104 0,643 0,708
1900 0,002 0,372 0,201
REDAN
1960 (och vidare bakåt) är I(CO2)-effekten praktiskt taget utnollad;
Jämförelsen på enskilda värden är OK
för 2010, och däromkring (fram till runt 2020).
I vidare mening, inte alls.
Sett till TRENDEN, innebär ovanstående
I(CO2)-resultat en helt motsatt riktning relativt den verkliga enligt effektkurvan.
I(CO2)-RESULTATET GENERELLT betyder att i
VARJE preciserad jämförelse blir värdena i grunden HELT VÄRDELÖSA som
jämförande begrepp; CO2-varianten i kombination med Stefan-Boltzmanns strålningslag demolerar hela funktionskomplexet — därför att en sådan
kombination inte kopplar AGW-komplexets
matematik.
Se
även ARRHENIUS SAMBAND — grafiska formerna som isolerade begrepp ger (delvis,
mycket) goda approximationer, men utan någon direkt sammanhängande matematik.
I
andra ord sagt, och som också påpekas i AGW-bevisets
slutform: AGW-komplexets
matematik är unik med sin variationsbas som energimässigt tidsgrundad
(kronologin med industrins Fossil-Carbon). Komplexet med De
6 Kurvorna uppvisar en
sammanhängande matematik som följer deriveringar i tre rakt nedstigande led —
direkt från Carbon-Dioxide-kurvan: dess derivata som t|E-kurvan, samma som havsversionen av Fossil-Carbon, dess derivata i sin tur som effektkurvan,
och dess derivata i sin tur med toppvärdena. Försöker man blanda in andra varianter typ Stefan-Boltzmanns strålningslag tillsammans med ovannämnda, se Beroendefelet, är det tydligt att komplexet demoleras, och bara vissa
spår återstår.
Kontrollräkningens resultat
I
jämförelse med (det mera noggranna) AGW3-resultatet på 0,87 W/M² kontra ovanstående resultat 0,83 W/M² från Stefan-Boltzmann-approximationen är det tydligt att värdena är (approximativt
utomordentligt) samstämmiga. Resultatet visar samtidigt att det tydligen bara
finns en relevant enklare approximativ funktion, just Stefan-Boltzmann-approximationen, som kan användas generellt i utvärderingen (dock endast
fram till effektmaximum).
Därmed rimligheten generellt i
resultatbilden.
Se även Effektgrafens
skala bekräftas konventionellt.
Resultatet i Stefan-Boltzmann-Approximationen kan användas i prövande jämförelse med
alternativa förklaringsmodeller
Med
AGW-effektens radiativkraft på grovt 1 W/M² i
hela Solbidraget på ca 250 W/M² blir AGW-effektens andel av hela Soleffekten
approximativt
1/250 = 0,004
= 0,4% .................... nuvarande
andel AGW-effekt av hela Soleffekten vs 0,7°C
Den
referenssiffran kan användas i en översiktlig utvärdering av varje annan
tänkbar — och föreslagen — kandidat som vill försöka förklara sig orsak till
den observerade globala uppvärmning som visas i NASA(CRU)-temperaturkurvan.
Jordytans termiska resistans
2010VIII22
Jordytans termiska resistans
GLOBALRESISTANSEN
I en
föregående artikel på UPPVÄRMNINGSGRADIENTEN framkom den allmänna relationsbilden
Δt ΔP
———— = ———
ur
den enkla satsbilden »globaltemperaturen (TG) varierar som Soleffekten (P)»,
Δt här förenklat från Δt(FIN) och P som tidigare
Solära radiativa råeffekten (eg. radiativkraften) 1367 W/M².
Som vi ser, uttrycker omvändningen
Δt TG
———— = ——— = RJth
ΔP P
en termisk resistans R(Jth) som kan förstås liktydig med en Jordytans totala
medeltermiska resistans,
R(Jth)
= TG/P
= (288°K)/(1367 W/M²)
= 0,2106803 °K/WM2 ......... Jordytans
termiska resistans, nominellt referensvärde
Normalt
inom elektrotekniken betraktas en kylare med ett sådant värde som en extremt
bra (effektiv) kylare.
Genom att TG långsamt ökar, i vårt fall
idealiserat med +0,7°C grovt fram till nu (2010),
R(Jth) = (288°K + 0,7°C)/(1367 W/M²)
= 0,2111923 °K/WM2 ......... Jordytans
termiska resistans, aktuella nuvärdet (2010)
blir
resistansändringen av samma storleksordning som temperaturändringen
(288,7°K)/(288°K)
= 1,0024305
Vilket
vill säga, i storleksordningen bråkdelar av procent (0,24305%).
Sagt på annat sätt, kan man alternativt
återföra och beskriva hela den globala uppvärmningen på en motsvarande, ytterst
marginell och långsam ökning i Jordytans termiska resistans.
HÄRLEDNINGAR
AGW3 — allmänna integrala samband
Härledningar — sambanden till AGW3
Som
redan bör ha framskymtat i AGW12, är temperatur-Energikurvan (t|E-kurvan)
y =
6[1–1/(1+[x/10]4)] ................................... temperatur-energikurvan
Se t-kurvans
elementära energifunktion
Se även utförligt generellt
om energikurvorna i statistiken i t-ENERGI-kurvan.
Se även fullständig
matematik i GENERELLA
ENERGIKURVAN.
hela
komplexets grundval via Upptakten till AGW tillsammans med ythavsperioderna. Då vi tydligen söker t|E-kurvans derivata (y’) i formen av den effekt (P=E/tid) som
föranleder energins användning, får vi denna enligt (se Generella energikurvan nedan)
y’ =
(24/10)(1 + [x/10]4)–2[x/10]3 ................... effektkurvan, energikurvans derivata

Med pixelUnit50 motsvarande tangensenheten 1
och toppvärdet tan = 0,64 motsvarande effektvärdet 0,88 ges omvandlingsfaktorn
0,64t/0,88W = 0,727t/W = 1t/(1/1,375)W. Med 1t=50pixel ges 1,375W/50p=0,0275W/p eller
36p/W .
Se utförligt i EFFEKTKURVANS
SKALKOEFFICIENTER. Där beskrivs hur värdena ovan framräknas.
Skalkoefficienterna till effektkurvan
UPPVÄRMNINGSEFFEKTENS
VÄRMEENERGI
Varje
n(W/M2) — intensiteten (I) — avspeglar
medeleffekten (PJ) för hela Jordytan (AJ);
n(W/M2) = PJ/AJ ;
PJ =
n·AJ ;
= n·4π(6,378
T6 M)2 ............ Jordytans
årsbaserade medeleffekt via ekvatorialradien
=
n(5,11185 T14 M2)
.......... n i antal W/M2
UPPVÄRMNINGSENERGIN per WattÅr via
energikurvan fås då (obs
LINJÄRT)***
EJ =
PJ · (365,25·24·3600 S = 31
557 600 S = 1 år)
= n(5,11185 T14
M2)(31 557 600 S)
= n(1,61318 T22
M2S) ; n i W/M2 ; WS=J ;
= n(1,61318 T22
J) ; n
i grafiska enheter
Skalfaktorn
(n) till effektgrafen är som ovan 1,375W/[1tangens=50pixels] och som n-värdet
måste multipliceras med. Därmed
EJ =
n(1,61318 T22 J)(1,375)
= n(2,21812 T22
J) ......................... AGW-energikoefficienten
Slutformen
för den totalt använda energi som åtgår för AGW blir alltså [Se även i Resultatet av
utvecklingsexemplet], EJ = E(AGW);
E(AGW) =
(2,21812 T22 J)·[y = 6[1–1/(1+[x/10]4)]]
........................ J, hela
Jordytan MJ
x = (ÅR – 1815)(2,35/50)
med
motsvarande för AGW-effekten
P(AGW) =
(7,0288 T14 W)·[y’= (24/10)(1 + [x/10]4)–2[x/10]3] .......... W, hela Jordytan
x = (ÅR – 1815)(2,35/50)
där
koefficienten (7,0288 T14 W) är samma
som effektgrafenhetens (1,375 WM–2) gånger Jordytsvärdet (5,11185
T14 M2).
Ovanstående
resultat tillsammans med alla kurvor i AGW-bevisets framställning finns
sammanställda i Effekt&Energi i AGW. Motsvarande beräkningar finns i Kalkylkortet.
————————————————————————————————————————
*** Notera att EFFEKTKURVAN (y’) i princip KAN
göras variabel via RHSER-variationer (om globala medeltemperaturen väsentligen
överstiger nuvarande ca 15 °C) — vilket betyder att viss försiktighet måste iakttas i
uppfattningen av effektkurvan för RHSER
som derivata-kurvan till havsversionens Fossil-Carbon-kurva (t|E-kurvan); Så är det här också — men bara inom just
den angivna medeltemperaturens ramar. Med alternativa värden på RHSER ändras den bilden (dock
så marginellt för små skillnader att det — här — saknar praktisk betydelse i
den översiktliga värdebeskrivningen).
Energiskalan för t|E-kurvan kopplar
till Fossil-Carbon-emissionen, analogt världens totala energianvändning (ref. BP-statistik)
och måste uppfattas strängt skild från integralkurvan till RHSER, trots som nyligen omnämndes, att dessa är identiska i
formen — blott nuvarande globala medeltemperatur kvarstår (med små ändringar,
ca 15 °C).
—————————————————————————————————————————[‡]*
I Effektkurvans toppvärde beräknas högsta tangensvärdet för x lika med
x = 60001/4
................... GRAFISKA
= 8,8011173 ............ unit50p
= 2002,257816 ........ ÅRLIGA
[4 April 2002 kl. 04:00:54,2016]
Därmed
beräknas maxeffekten på effektkurvans funktion [Se Kalkylkortet], och man får
P(max) = 0,8808084 W/M²
~ 0,88
med
tangensvärdet
tan(A) = 0,6391234
~ 0,64
Den
mera noggranna pixelomvandlingsfaktorn blir då
k =
(0,8808084 W/M²)/(0,6391234tan)
= 1,3781508 W/M²tan
att
jämföra med det förenklade värdet från den enklare grafanalysen 1,375.
I KALKYLKORTET finns bägge dessa parameterlinjer representerade i jämförande
celler (Kolumn J).
Värmekapaciteten i AGW
Grafiska
skalförhållandet för t-kurvan är
6(1/3,4
= 0,2941176 °C/50p)=1,7647058 ~ 1,765
som
motsvarar 170p/°C;
Energiskalan
motsvarar som ovan (1,375)(1,61318 T22 J)=2,21812 T22 J per 50p;
t|E-proportionaliteten blir alltså
T/E =
(0,2941176 °C)/(2,21812 T22 J) = 1,32597 t23 °C/J ; [1,32294 t23 via 1,3781508]
med
motsvarande värmekapacitetstal för AGW
E/T =
7,5416 T22 J/°C ..................... värmekapaciteten för antropogena globala
uppvärmningen
[7,55889 T22 via 1,3781508]
Hela
komplexet grundas på proportionaliteten
mellan temperatur och energi:
varje ändring i temperatur motsvaras av en ändring i energi och vice versa:
Hur AGW3 framträder
1 mening — med utförliga
referenser
Värmekapacitetstalet för AGW grundas helt på den centrala effekthärledningen i AGW-beviset Del 3, som helt grundas på energikurvans temperaturanaloga ekvivalent, samma som effektkurvans
integral,
med en maximal bank av värmeinduktivt bidragande luftmarina molekyler [‡] som (i nuvarande skede, om inget annat tillkommer) som mest
består av vattenånga [‡], baserat på maximal luftfuktighet för högsta
möjliga temperaturbidraget (drygt
50°C) till
globala medelvärdet på ca TG=15°C, och vilken beräkningsgrund återfaller
på empiriska samband för atmosfäriska vattenångtrycket [‡], och som leder till den avgörande uppvärmningsgradienten (ca 0,185 °C/S i nuvarande utveckling).
Generaliserad
sammanställning för effekt-och energikurvornas inbördes matematik från generella funktionssambandet, y nedan
GENERELLA ENERGIKURVAN
Energikurvans
allmänna derivata — effektkurvan
y = a[1
– (1+[x/b]n)–1] ;
energikurvan, generella funktionssambandet [‡]
y’ = Dn y
= a · [0 – (–1)(1+[x/b]n)–2(1 + [x/b]n)’]
= a · [0 – (–1)(1+[x/b]n)–2(0 + n[x/b]n–1[x/b]’)]
= a · [0 – (–1)(1+[x/b]n)–2(0 + n[x/b]n–1[1/b])]
= a · [(1+[x/b]n)–2(n[x/b]n–1[1/b])]
= (an/b) · [(1+[x/b]n)–2([x/b]n–1)] ; energikurvans derivata —
effektkurvan
a = 6 ;
vårt aktuella fall:
b = 10 ;
n = 4 ;
y’ =
(24/10)(1 + [x/10]4)–2[x/10]3 ; effektkurvan till t|E-kurvan
;
; effektkurvans integral blir
∫ y’dx =
6[1 – (1+[x/10]4)–1]
= y
Energikurvans integral saknar f.n. algebraiskt
uttryck. Lösningar av denna ges numeriskt.
Se utförligt i INTEGRALKURVAN
FÖR E.
För matematiken ovan, se även FORMLAGARNA om ej redan bekant.
‡
GENERELLA FUNKTIONSSAMBANDET baseras här helt på den elementära effektens
integrala transientfunktion
y = a[1 – (1+[x/b]^2)–1] med generaliserade
koefficienter [vilket betyder: fysikens elementära energifunktion].
Effektkurvans toppvärde — Resultatet
2010VII19
Effektkurvans toppvärde
Vi
utgår från t|E-kurvan som integralkurvan (y):
;
Toppvärdet
till effektgrafen (y’) fås via
effektkurvans derivata — alltså energikurvans andraderivata (y’’):
y’’ = (24/10)[(1 + [x/10]4)–2[x/10]3]’
Vi
frånser tills vidare koefficienten (24/10), och använder den redan välbekanta produktderivatan [(AB)’ = AB’ + A’B] för att lösa ut integralkurvans
andraderivata, analogt effektkurvans förstaderivata; Dn synkoperar Derivatan (Till|För …):
;
Dn(1 + [x/10]4)–2 · [x/10]3
+
(1 + [x/10]4)–2 · Dn[x/10]3
=
(–2)(1 + [x/10]4)–3[0 + 4[x/10]3[1/10]]
· [x/10]3 = (–8/10)(1
+ [x/10]4)–3[x/10]3 · [x/10]3
= (–8/10)(1 + [x/10]4)–3[x/10]6
+
(1 + [x/10]4)–2 · 3[x/10]2
[1/10] = (1 + [x/10]4)–2 · (3/10)[x/10]2
=
–(1 + [x/10]4)–3(8/10)[x/10]6
+(1 + [x/10]4)–2(3/10)[x/10]2
;
Med
koefficienten (24/10) därmed
y’’ = (24/10)[– (1 + [x/10]4)–3(8/10)[x/10]6
+ (1 + [x/10]4)–2(3/10)[x/10]2]
;
Graf unit50
(24/10)(–[[(1+[x/10]'4)'–3](8/10)[x/10]'6]+[[(1+[x/10]'4)'–2](3/10)[x/10]'2])
Grafen förstorad
10ggr i y-led:
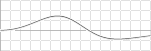
Nollgenomgången
ligger nära x=9
;
Toppvärdet
för förstaderivatan (effektgrafen) y’, betyder nollvärde för
andraderivatan (y’’) ;
0 = (24/10)[– (1 + [x/10]4)–3(8/10)[x/10]6
+ (1 + [x/10]4)–2(3/10)[x/10]2]
0 = [–
(1 + [x/10]4)–3(8/10)[x/10]6 +
(1 + [x/10]4)–2(3/10)[x/10]2] ;
(1 + [x/10]4)–3(8/10)[x/10]6
= (1 + [x/10]4)–2(3/10)[x/10]2
;
(1 + [x/10]4)–1(8/3)[x/10]4
= 1 ;
a = [x/10]
;
termförenkling ;
(1 + a4)–1(8/3)a4
= 1
= (1/a4
+ 1)–1(8/3) ;
8/3 = 1/a4
+ 1 ;
5/3 = 1/a4
= (1/a)4
= (10/x)4
;
(5/3)1/4 = 10/x ;
x =
10/(5/3)1/4
= 10(3/5)1/4
= (6000)1/4
= 8,8011173
;
x =
(ÅR – 1815)(2,35/50);
ÅR = (6000)1/4(50/2,35)+1815
=
2002,257816
= (dag
94,167294)år2002 ;
Jan(31)31;Feb(28)59;Mar(31)90 ;
RESULTAT:
Toppeffektvärdet inträffade alltså (årsmedelbaserat på 365,25 dagar per år baserat på
offset år 1815 00:00:00,0000)
P(AGW)topp = 4 April 2002 04:00:54,2016
*
Bihang till AGW-beviset Del 3
2010VII27
LUFTENS TÄTHET OCH MEDELATOMVIKT
Från Allmänna Gaslagen [SUMMERING
— Allmänna gaslagen i komprimerad syntes] fås tätheten (ρ, grek. rhå, r) för en godtycklig
gas vid STP
via
ρ0 = 1/22,415189
= 0,0446126
med
summan av atomvikterna
U = (U1+U2+U3+…+Un)
enligt
ρ
= Uρ0 .............................. tätheten för en godtycklig gas vid STP
= (U1+U2+U3+…+Un)ρ0
EXEMPEL
— luftens täthet:
Med
tillgång till en sammansättningstabell över luftens beståndsdelar
THE
ENGINEERING TOOLBOX — Molecular Mass of Air, 2005
http://www.engineeringtoolbox.com/molecular-mass-air-d_679.html
ges
uppgiften
U = 28,97(u=1,66033 t27 KG)
.......... luftens
medelatomvikt
= 4,80997 t26 KG
;
ρ
= Uρ0
= (28,97)(0,0446126)
= 1,2924272
KG/M³ ....................... luftens
täthet vi STP (0°C, 101325 Pa, Havsytan)
Det
är f.ö. samma värde (1,2920) som anges i tabellen i
@INTERNET
Wikipedia Density of air, Relationships 2010-07-27
Luftens
variabla täthet vid havsytan (konstant tryck) fås genom
att först ansätta luftkonstanten vid STP enligt
k(L) = p/ρT
= (101325 [Pa=N/M²])/[(1,2924272 KG/M³)(273°K=0°C)]
= 287,17582 J/°K/KG ;
................ luftkonstanten
vid STP
och
sedan utföra beräkningen
ρ = [p/k(L)]T–1
;
= [(101325 [Pa=N/M²=J/M³])/(287,17582
J/KG°K)]T–1
= [352,83262 °K·KG/M³]T–1
Jämför
t.ex. T=15°C=288°K ;
ρ = [352,83262 °K·KG/M³](288°K)
= 1,2251132
KG/M³ ....................... luftens täthet vid havsytan (normaltryck)
och 15 °C
Wikipediatabellen
anger till jämförelse 1,2250.
Notera
att TRYCKET på Jordytan ändras med höjden över havet. För relativt små
höjdavsnitt (tiotals till något hundratal meter) och i generaliserande mening
(här utan referenser) betraktas trycket väsentligen som konstant.
Medelavståndet mellan luftens
molekyler
Medelavståndet
mellan luftmolekylerna kan då beräknas (V=1M³)
N = [m=ρV]/Uu
= [1,2251132 KG]/(4,80997 t26 KG)
= 2,54702 T25 ;
Varje
luftmolekyl tar då upp volymen
V1 =
1M³/N
= 3,92614 t26 M³
med
kubsidan, lika med medelavståndet mellan luftmolekylerna
d =
V 1/3
= [3,92614 t26 M³]1/3
= 3,39877 t9 M
.............................. medelavståndet
mellan luftmolekylerna vid havsytan och 15°C
~ 3 nM
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
Jämförelser med etablerade begrepp
Jämförelse med etablerade klimatmodeller
Jämförelse
mellan IPCC* och t(AGW)
———————————————————————————
*Special Report on Emissions Scenarios (SRES), ref. @INTERNET
Wikipedia Global warming, Climate models, Global Warming Predictions,
2010-07-19
Om vi jämför resultatet i AGW-beviset
med temperaturökningskurvan t(AGW) med de modellbaserade kurvor som framräknats
av olika bidragsgivare t(GWP)
GWP Global Warming Projections, ref. Wikipedia Global
warming 2010-07-19, med bildkällan (högra nedan)
http://en.wikipedia.org/wiki/File:Global_Warming_Predictions.png
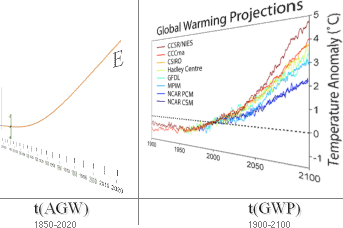
med skalanpassning av t(AGW) så att den får samma passning
som skalorna i t(GWP)
enligt
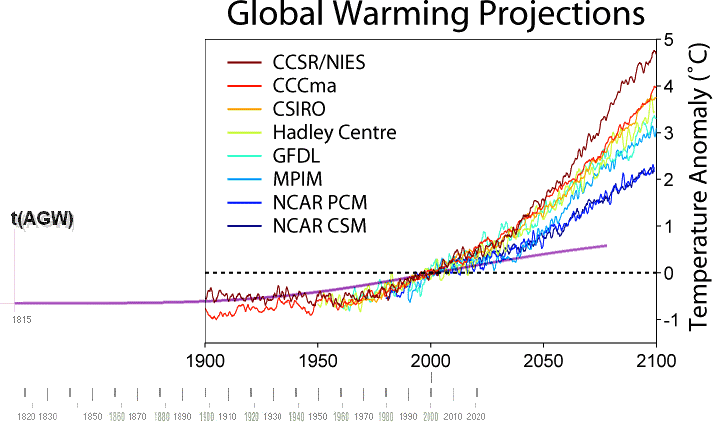
SKALANPASSNING: 96%x[50p]=48pUNIT;
GWP-originalet [280p/6°C]/[170p/°C]=0,2745098 ·1/96% = 0,2859477 = 28,6%y;
GRAFyPREFIXxSIN, mörkvioletta
0.2859[6[1–1/(1+[x/10]'4)]
Nio samhörande globala temperaturkurvor med nominell
preferens vid år 2000 — de övre angivna åtta etablerade innefattar randeffekter
(under sämsta fallets villkor: inga åtgärder vidtas) som inte ingår i den nedre
nionde t(AGW)-kurvan.
Denna sistnämnda kopplar enbart till industrins
Fossil-Carbon. För bildkällan ovan till de åtta olika
bidragen, se bildfilen
http://en.wikipedia.org/wiki/File:Global_Warming_Predictions.png
till huvudartikeln @INTERNET Wikipedia Global Warming,
Climate models 2010-07-20
http://en.wikipedia.org/wiki/Global_warming
framgår att t(AGW)-kurvan
tecknar den allra lägsta temperaturökningen i jämförelsen med alla etablerade
klimatmodeller. Emellertid ingår INTE i t(AGW)-beviset randeffekter typ
metanemissioner (som kan ge närmast våldsamma
extra bidrag med en redan given temperaturökning som påtriggande katalysator,
jämför konv. permafrosten) eller andra bidrag utöver den rent
industriella Fossil-Carbon-emissionen.
Kurvbilden
nedan kompletterad med havsperioderna (violett) överlagrade på t(AGW) ger en mera praktisk jämförelse.
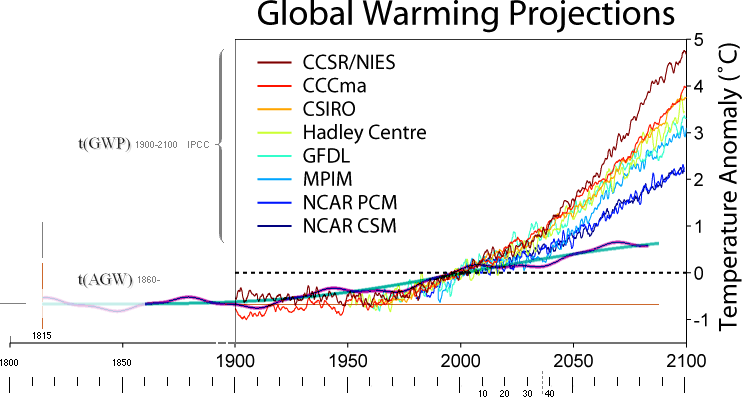
SKALANPASSNING: 96%x[50p]=48pUNIT;
GWP-originalet [280p/6°C]/[170p/°C]=0,2745098 ·1/96% = 0,2859477 = 28,6%y;
GRAFyPREFIXxSIN, mörkvioletta
0.2859[6[1–1/(1+[x/10]'4)]+0.222(0.9[(2sinþx/1.48)+0.5(sin3þ[x–0.1]/1.48)])]
Föregående anpassade
t(AGW)-kurva
här förtydligad tillsammans med de inlagda havsperioderna
i jämförelse med de etablerade klimatmodellernas sämsta fallets scenarion.
AGW-bevisets kurva [mörkvioletta] bortser ifrån alla bieffekter. Se utförligt
från AGW-beviset Del 1.
Huvudlinjerna visar det väsentliga:
Alla (seriöst) bidragande parter uppvisar tydligen inbördes entydigt
överensstämmande temperaturökningskurvor men utifrån olika utgångspunkter i
analys och beräkning.
t(AGW)-kurvan
bevisar explicit NASA(CRU)-kurvans
ekvivalenta samhörighet enligt det
enhetliga resultatet från de 6 komponenterna med den
industriella Fossil-Carbon-emissionen
som t(AGW)-kurvans temperaturkatalyserande energigrund —
och som därmed kategoriskt klassificerar varje invändning mot AGW som helt säkert obefogad.
Arrhenius samband, innebörd
2010VIII2
Arrhenius samband
Logaritmiska koldioxidsambandet (Arrhenius) har ingen praktisk betydelse för AGW-beviset

Man kan inte — inte alls överhuvudtaget — tillämpa specifika materialsammansättningskvantiteter på AGW12. Därför nämligen att AGW12 bara berör energibidraget till värmetröghetens ÄNDRING; AGW12 behandlar den avgränsade M-lokalen — utan hänsyn till dess sammansättning. Det är bara ändringen tidskronologiskt energigrundad i sammansättningen som räknas i AGW12. Arrhenius samband innehåller ingen sådan variationsbas. Därför kan heller inte Arrhenius s.k. växthuslag användas i någon som helst koppling till eller jämförelse med AGW-beviset (i delarna 1-2), eftersom Arrhenius samband just handlar om hela Jordatmosfären och dess sammansättning med Solen som aktivt kraftändrande bas, se även Arrheniussambandets härledning.
För
att få något grepp om Arrheniussambandet i AGW-bevisets ljus, måste vi vända
oss till AGW3:
t|E-kurvans integral — Carbon-Dioxide
— är SNARLIK Arrhenius exponentiellt uttryckta samband (högra nedan, C)
I = I0 ln(C/C0) ; C = C0e^(I/I0) ; Se ursprunget i Arrheniussambandet;
Som en approximation kan Arrhenius samband (alltså, väl)
användas, inom vissa gränser. Men därmed försvinner också kopplingen till
t|E-kurvans derivata , samma som Arrhenius effektiva intensitetsvärde — den kan inte nås
via derivering av naturliga logaritmen (Dn e^x = e^x). Därför kan heller inte
Arrhenius samband tillämpas i någon sträng mening för en mera preciserad
beskrivning av komplexet. Däremot ser vi att t|E-kurvans derivata OCKSÅ kan
approximeras av Arrhenius ursprungsform (se särskild grafisk jämförelse nedan) — till en förvånansvärt betydande del
om vi frånser vissa av historiens intervall och infogar lämpliga koefficienter
(Färgrutorna ovan kopplar till motsvarande kurvdelar nedan):
Arrhenius vs AGW
Från AGW3:
—————————————————————
Se originalstorlek.
—————————————————————
∫y
= komplicerad
;
numerisk lösning,
approximation ay:
![]() CO2 ay = 0,74[(x/5,7)4,25]
CO2 ay = 0,74[(x/5,7)4,25]
![]() t|E y = 6[1–1/(1+[x/10]4)]
t|E y = 6[1–1/(1+[x/10]4)]
AGW ![]() P y’ = (24/10)[(1+[x/10]4)–2][x/10]3
P y’ = (24/10)[(1+[x/10]4)–2][x/10]3
——————————————————————————————————————————————————————————
Arrhenius ![]() CO2 y = e0,55x
CO2 y = e0,55x
![]() P y = 0,55lnx
P y = 0,55lnx
Som framgår av kurvsammanställningen
ovan:
Arrhenius tvågrenade samband — med lämpliga koefficienter —
kan utom den centrala temperatur-energikurvans funktion som inte
ingår
ge hyfsat goda approximationer till hela det komplex som beskrivs mera ingående
av den mera omfattande tripelgruppen derivata-integralgruppen ovan med
Effekt(P)-TemperaturEnergi(t|E)-Koncentration(CO2). Arrhenius
samband innefattar ingen antropogen orsak till koncentrationen
(energiintegralen i AGW), utan beskriver
(förutsätter) endast själva förekomsten som funktion av Solens inverkan:
Från härledningen (nedan) till Arrheniussamband, ser vi (alltså) direkt
orsaken:
Ändringen (värmetröghetens ökning) i Jordatmosfärens koldioxidhalt (dC)
med avseende på Solära radiativkraften (dI);
Ändringen kommer från Solens Naturliga variationer i GW. Inte industrins
gruvdrift (AGW, antropogena GW).
I praktiken gäller värmetröghets ändring INOM DEN
OBSERVERADE GLOBALA UPPVÄRMNINGEN UNDER 1900-TALET inte med
avseende på någon EXPLICIT inverkan från Solen, utan med avseende på inverkan —
katalyserande — av en kraft (industrins
Fossil-Carbon) som — tydligen — ligger helt utanför den
ordinära ekobalansens domäner. Solen har ingen KATALYSERANDE inverkan på den
delen:
Kolemissioner
från fossila bränslen ingår inte i det naturligt ekologiska kretsloppet.
Fossila kolemissioner (med följd i AGW) kan bara
»aktiveras» genom gruvdrift och borrhål i Jordskorpan. Dvs., enbart genom
mänsklig aktivitet.
Däremot KAN Arrhenius samband
(generellt, således) spela in över (betydligt) större tidrymder där Solens
inverkan på längre sikt genom de olika instrålningsintensiteternas variationer
över tusentals, tiotusentals och hundratusentals år förorsakar mera
övergripande variationer i t.ex. atmosfärens koldioxidhalt. Men det är inte
vårt (nuvarande) problem.
I den tillgängliga webblitteraturen ser
vi också att olika författare, med olika förutsättningar och olika
utgångspunkter, använder olika
koefficienter i användningen av Arrhenius samband:
Logaritmiska koldioxidsambandet (Arrhenius) har
ingen praktisk betydelse för AGW-beviset Del1-2
— men kurvkomponenterna, lämpligt
justerade, uppvisar en viss följsamhet, med goda approximationer via
AGW-beviset Del 3
se även INLEDNING från INNEBÖRD
Arrhenius
samband — Arrhenius växthusekvation
I IPCC
räknar man — i ljuset av AGW som ovan — med
koldioxiden som en PASSIV agent — typ Arrhenius tidiga »koldioxidformel», konv.
Arrhenius växthuslag, eng. Arrhenius’
greenhouse law,
[Se sep. härl.],
vidare nedan,
I = I0 ln(C/C0), C
koldioxidhalten (i ppm) från basvärdet C0 (280 ppm
[före 1800]) med intensitetskonstanten
I0=3,75
W/M², även benämnd radiativkraft(ning)en (eng.
radiative forcing), ref. [PHYSICS SOCIENTY
Jan2010],
Andra källverk använder andra
konstanter, t.ex. I0=5,35 W/M²
Exempel från UppsalaInitiativet
ref. (m.fl.)
UPPSALAINITIATIVET — Lin eller Log, 14
DEC 2009
http://uppsalainitiativet.blogspot.com/2009/12/lin-eller-log.html
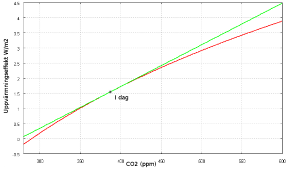
Figuren ovan
(förminskad 50%) från UPPSALAINITIATIVETs klimatblogg som ovan (Dec2009).
Vertikalskalan ( | ) i Uppvärmningseffekt W/M², horisontalskalan ( — ) [variabeln x i
Arrheniussambandet] i CO2 ppm(v).
Sambandets form
anges ΔF = (5,35)ln(C/C0).
— Vilken är den
motsvarande formen i AGW-beviset?
AGW-komplexets
kurvdelar enligt AGW-beviset,
jämförelse med Arrhenius
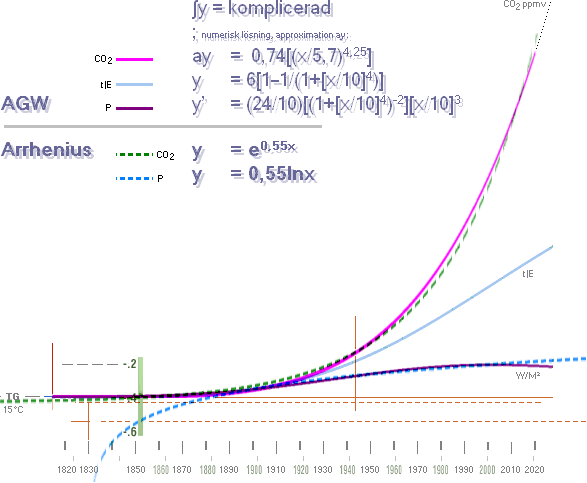
Förklaringar
till kurvbilden och
dess beteckningar ges utförligt från Särskild
Grafisk Jämförelse.
— Vi ser att
Arrhenius formella sambandsgrafik (övre-undre streckade) KAN fås att stämma
nästan utomordentligt väl överens med AGW-grafiken i högst väsentliga partier
(hela perioden 1890-2015) OM Arrheniussambandet
I = I0
ln(C/C0)
i sin strikt
matematiska form
y = e^ax
x = ln ay
delas upp i två
KRONOLOGISKT (den skalan finns inte med i Arrhenius samband) inbördes
beroende kurvor
y = C/C0 = e^0,55t
..... övre streckade gröna
kurvdelen, Arrhenius AGW-CO2-approximation
y = I/I0 =
ln 0,55t ...... undre
streckade blå kurvdelen, Arrhenius AGW-effekt-approximation
med
tilläggskoefficienter för respektive förskjutningar i xy-offset
[ÖVRE: x–303/50,
y–5/50; UNDRE: x–37/50, y–24/50 — enligt illustrationen
ovan, xyUnit50pixels].
— Men det gör å
andra sidan att inte mycket återstår av själva Arrhenius grundsamband:
Arrheniusvariabeln i det övre CO2-kurvfallet är effektvärdet i W/M² (P/A),
medan motsvarande Arrheniusvariabel i det undre P/A-effektfallet är
koldioxidhalten; För att få i hop det med AGW, som ovan i illustrationen, måste
Arrheniusskänklarna (resp. övre och undre kurvarmar) associeras med en
tidsanalog, kronologisk skala, och den ingår, tydligen, inte i Arrhenius’
samband. Arrheniussambandet
kopplar strängt taget inte till AGW.
— Vilket vill
säga: CO2-halten SOM FUNKTION AV effekten (P/A=W/M²), Arrheniussambandets
centrala funktionsform, är ett begrepp som, strängt taget inte omfattas av AGW.
AGW kräver en tidsskala som variabel för
samtliga ingående fysikaliska parametervärden för att få full fysikalisk
matematisk härledningskraft på den viktiga, avgörande och centrala Temperatur-ENERGIKURVAN (t|E ovan).
Arrheniussambandet har ingen sådan.
— Exemplet från UPPSALAINITIATIVET (UI) som
representativt för den etablerade hållningen generellt fungerar alltså OK i
ljuset av AGW-beviset därför att, som vi ser av den grafiska sammanställningen
ovan (AGW-komplexets kurvdelar), avsnitten i
C/C0 resp. I/I0 I VÅR EPOK
(omkring 2000) kan förstås som nära linjära mot den kronologiska skalan. Med
viss försiktighet kan man alltså använda Arrheniussambandets kurvgrafik
för att illustrera den närmaste utvecklingen förgrovat (här uppskattat utan
vidare referens) omkring 2000 (1990-2015) och därutöver med allt större
avvikelse — förutsatt lämpligt koefficientval (mindre än 5,375); vi ser att
olika författare använder olika dito (se referenser från Arrhenius samband).
KurvExemplet från UI, med alla motsvarande
jämförbara exempel, sträcker sig ända från 0 W/M² (förindustrialismen) till
nära 4 W/M², vilket sistnämnda värde ligger långt ovanför AGW-bevisets
grundmatematik; Maxvärdet enligt AGW-beviset Del 3 är 0,884 W/M²,
beräknat utan hänsyn till ev. möjliga adderande bieffekter. UI-exemplet faller
därför helt utom ramen för en generell beskrivning analog med AGW-bevisets
kurvdelar;
Dagsvärdet för
effekten (P) i den pågående globala uppvärmningen (2010, medelvärdet
±5år) enligt AGW3 ligger på 0,875 W/M² med drygt 380
ppmv CO2 och totalt använd energi för hela den globala uppvärmningens
period (från 1815) 5,5 T22 J, Se Kurvsammanställningen. Effekttoppen
nåddes redan i April 2002, men temperaturen och CO2-haltvärdet
fortsätter att öka om inget revolutionerande tekniskt underverk inträffar —
frånsett ev. ytterligare bidragande värden från bieffekter (permafrostens
metan hotar), dessa ingår inte i AGW-bevisets grundräkning. Se vidare full
grafredovisning i Effekt&Energi i AGW.
Med en effektiv insolation på 250 W/M² [‡] betyder dagens koldioxidhalt (2009)
på ca 385 ppm att koldioxidens radiativkraft
(med närmast ovanstående källas intensitetskoefficient 5,35 W/M²) är
I = (5,35)ln(385/280) ~ 1,7 W/M²,
eller 1,7/250 ~ 0,68% av insolationskraften.
Se även resultatet
i KONTROLLRÄKNINGEN samt Effektskalan bekräftas:
Det mera praktiska värdet ligger (således) strax under 1 W/M² — vilket
leder till att Arrheniuskoefficienten I0=3,75 W/M²
ligger närmare till hands (ger 1,19 W/M²).
SOM VI SER finns (förutom
Solinstrålningen) ingen AKTIV energibas i den räkningen:
— Det är inte Solen som borrar efter
olja och gör hål i marken för att bryta stenkol och elda med fyndigheterna.
Därför fungerar inte heller Arrhenius samband i någon sträng mening för AGW.
OM
man använder Arrhenius samband i en alltför strängt bunden mening (och, utan
inblick, inlägger olika innebörder i klimatkomplexet på den delens kredit)
hamnar man, tydligen,
otvetydigt i vissa knepiga problemställningar som det inte är enkelt att se
utvägen ur.
Arrheniussambandets
härledning
————————————————————————————
* dC/dI = C(C0/I0) ;
Ändringen i Jordatmosfärens koldioxidhalt (dC) med avseende på Solära radiativkraften (dI) avspeglar atmosfärens aktuella koldioxidhalt (C) ;
dC/CC0 = dI/I0 ;
∫ dC/CC0 = ∫ dI/I0 ;
ln(C/C0) = I/I0 ; .................... Arrhenius samband (»Arrhenius
växthusekvation» från 1896)
ÅTERDERIVERINGEN GER (Se logaritmderivatan):
Dn ln(P) = DnP/P = [ln(C/C0)]’ = (1/C0)/(C/C0) = 1/C ; Koefficienten (C0) kan alltså läggas till (substitueras) godtyckligt i integranden — om inte annat, alltid lika med 1 (som vi vanligen aldrig skriver ut).
SÅLEDES INTEGRANDEN ÅTER.
;
Vi ser direkt att integralen blir av typen bestämd integral om lägsta I-värdet sätts lika med I0, så att y(x=I0)=0.
Ovanstående led omnämns (här veterligt) inte i den till synes mest tillgängliga webblitteraturen — men bör å andra sidan vara »välbekant huvudräkning» för den som redan känner till grunderna i differential, derivata och integralkalyl, (här NOLLFORMSALGEBRAN) med vidare (här DEN HÖGRE ANALYSEN). Se särskilt i logaritmderivatan, om ej redan bekant.
Jämförelse Hansen AGW
Jämförelse mellan AGW-beviset och
satellitmätningar
PROBLEMBLOCKET
· Etablerade
klimatmodeller och satellitmätningar
|
AGW-energin |
|||
|
Jämförelser, Havsenergins
skala |
|
AGW-effekten förklarar |
|
|
AGW-effekten |
Problem 3 — Effektskalan är OK — men |
PROBLEMBLOCKEN som genomgås ovan innebär i
slutänden — som det ser ut just nu (Aug2010) — mindre problem för alla berörda
parter OM AGW-bevisets sammanhängande presentation verkligen håller streck.
Dvs.: Idel klargöranden.
Jämförande resultat från Hansengruppen 2005
Från
Resultatet av
utvecklingsexemplet, Effektfunktionen i AGW3
Resultatet från
utvecklingsexemplet i AGW3 — 0,88 W/M² perioden 2000-2010 — är också, ganska
precis, den siffra 0,85 W/M² som omnämns (ännu generellt på webben
Aug2010) i referens till genomförda mätningar på HAVETS VÄRMEFYSIK:
’Earth is now absorbing 0.85±0.15 W/m²
more energy’
Notera
dock (ännu, Aug2010) att uppgifterna är sparsamma på grund av de stora
svårigheterna att få fram tillförlitliga mätdata — främst på grund av den
bristande rent tekniska precisionen i mätningarna, samt att uppgifterna är
behäftade med flera (många) frågetecken och orsäkerheter.
Vidare
försök att få fram mera precisa uppgifter på exakt vilka experimentella
observationer man stödjer sig vid stöter också på patrull — man medger öppet
att ingen vet vad som gäller, ref. [‡3] [‡4] [‡5].
RESEARCH
ARTICLES — Earth’s Energy Imbalance: Confirmation and Implications,
James Hansen et al., 2005
http://pubs.giss.nasa.gov/abstracts/2005/Hansen_etal_1.html
;
s1431ö:
”Our
climate model, driven mainly by increasing human-made greenhouse gases and
aerosols among other forcings, calculates that Earth is now absorbing 0.85±0.15 W/m2 more energy from the Sun than it is emitting to space. This imbalance is confirmed by precise
measurements of increasing ocean heat content over the past 10 years.”,
:
s1432sp3mn:
”…
averaged ~ 0.75 W/m2 in the past decade and was ~ 0.85 ± 0.15 W/m2 in 2003 (Fig. 1C).”,
;
s1434sp3ö:
”Continuation
of the ocean temperature and altimetry measurements is needed to confirm that
the energy imbalance is not a fluctuation and to determine the net climate
forcing acting on the planet.”,
Min
översättning:
Vår klimatmodell, styrd i huvudsak av antropogena
växthusgaser och aerosoler bland andra pådrivningar [som påverkar klimatet],
beräknar att Jorden nu absorberar 0,85±0,15 W/M² mera energi från Solen
än den emitterar till rymden. Denna obalans är bekräftad genom precisa
mätningar på ökande oceaniskt värmeinnehåll över de senaste 10 åren.
… medelbaserat ~ 0,75 W/M² i föregående decennium och var ~ 0,85 ± 0,15 W/M² under 2003 (Fig. 1C).
Fortsättning av havstemperatur- och altimetriska
mätningar [små höjdskillnader] behövs för att bekräfta att obalansen i energi inte är
en fluktuation och för att bestämma netto för den klimatpådrivning som påverkar
planeten.
Den
aktuella grafen i Hansengruppens redovisning, nedan i PDF-storlek 85%,
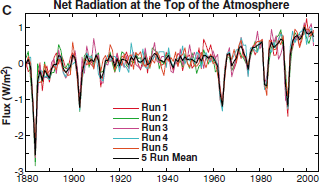
Figuren ovan insatt nedan tillsammans med resultatet i AGW3 för jämförelse:

Grafen nedan höger (Net Radiation) visar resultatet från klimatsimuleringar
från den övre Jordatmosfären
av Hansen et al. 2005.
Den mörkvioletta
kurvan
(vänster nedan, AGW3) tillhör AGW-beviset Del 3
och har lagts in till jämförelse — med samma kronologiska tidsskala och samma
effektskala W/M² som Hansens. I sin framställning, refererar Hansen till värdet 0,85 W/M² som han
påstår (vid år 2003, se vertikalmarkeringen ovan höger med pilen) ska ha
bekräftats av satellitmätningar [IceSat, GRACE, Hansen
s1434sp3ö]. Som vi ser, stämmer också den värdebilden utomordentligt med
resultatet från AGW3 — men
inte genomgående.
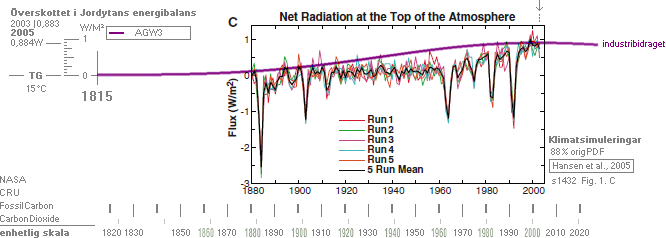
Vi kan dock inte anställa
någon DIREKT jämförelse med Hansengruppens resultat eftersom AGW-bevisets
effektkurva, den jämna mörkvioletta ovan, DELS helt och hållet bortser ifrån
kortperiodiska detaljer (vilket Hansenkurvan inte gör), DELS inte beaktar några
havsperioder (vilket
Hansenkurvan möjligen gör), och DELS att Hansengruppens resultat bygger på en
matematik (växthusgaser) som möjligen inte alls kan jämföras med AGW-bevisets
matematiska domäner enligt exemplet i Stefan-Boltzmann-Gasiska
felapproximationen: Läggs denna ovanpå Hansengruppens resultat
ses en tydlig samhörighet — vilket var syftet med exempelframställningen.
Det kan inte sägas här klart, då inte den
inblicken finns i Hansengruppens resultat; Men jämförelsen tyder på att
Hansengruppen försökt sammanjämka Stefan-Boltzmann-matematik med typ
CO2-koncentrationer, och vilket ofelbart leder till motsvarande Stefan-Boltzmann-Gasiska
felapproximationen. Dvs.: Det går inte att få fram en någorlunda
kronologiskt korrekt form på den matematiska grunden.
Hansengruppens resultat gör f.ö. inte gör
anspråk på annat än en simulering — att jämföra med NASA(CRU)-kurvan
som är en empiriskt grundad mätkurva (dess t-kurva
är ovanstående effektkurvas integral).
Tills vidare kan vi
alltså bara konstatera följande:
Värdena stämmer — runt nutid
(ca 0,9 W/M²).
’Earth is now absorbing 0.85±0.15 W/m²
more energy’
Hansengruppens
klimatmodell
I EN
KLIMATSIMULERAT MODELL förefaller Hansengruppen [Hansen
et al., 2005] påstå (framställningen
är verkligen inte tydligt refererad på den punkten) att simuleringen har bekräftelse via
precisa atmosfäriska mätningar från satellit
året 2003 med uppgiften 0,85±0,15 W/M²;
”Improved
ocean temperature measurements in the past decade, along with high-precision satellite altimetry measurements of the
ocean surface, permit an
indirect but precise quantification of
Earth’s energy imbalance. We compare observed ocean heat storage with simulations of global climate change driven by estimated climate
forcings, thus obtaining a check on the climate model’s ability to simulate the
planetary energy imbalance.”,
s1[1431]sp1n,
;
”Our
climate model, driven mainly by increasing human-made greenhouse gases and
aerosols among other forcings, calculates that Earth is now absorbing 0.85±0.15 W/m2 more energy from the Sun than it is emitting to space. This imbalance is confirmed by precise
measurements of increasing ocean heat content over the past 10 years.”,
:
s1432sp3mn:
”…
averaged ~ 0.75 W/m2 in the past decade and was ~ 0.85 ± 0.15 W/m2 in 2003 (Fig. 1C).”,
;
s1434sp3ö:
”Continuation
of the ocean temperature and altimetry measurements is needed to confirm that
the energy imbalance is not a fluctuation and to determine the net climate
forcing acting on the planet.”,
Webbreferenser i etablerad vetenskap som särskilt
bekräftar/omtalar Hansen et al. 2005
Webbreferenser
som anknyter till Hansens publikation från 2005 angående den påvisade obalansen i den luftmarina
Jordatmosfärens energiräkning
NASA-källan
nedan beskriver också resultaten från Hansen
et al., 2005 (publ. 28
April 2005 i Science),
NASA
— Scientists confirm Earth's Energy is Out of Balance (2005, möjl.
”04.28.05”)
http://www.nasa.gov/vision/earth/environment/earth_energy.html
”Scientists
from NASA, Columbia University, New York, and Lawrence Berkeley National
Laboratory, Berkeley, Calif. used satellites, data from buoys and computer
models to study the Earth's oceans. They confirmed the energy imbalance by using
precise measurements of increasing ocean heat content over the past 10 years.”;
;
”The
study reveals Earth's energy imbalance is large by standards of the planet's
history. The imbalance is
0.85 watts per meter squared. That will
cause an additional warming of 0.6 degrees Celsius (1 degree Fahrenheit) by the
end of this century.”.
Webbkällan
nedan beskriver hur man (från 1950, Murphy 2009) har uppmätt havets växande
energiupptag
SCEPTICAL
SCIENCE — Is global warming still happening? — 2010
http://www.skepticalscience.com/global-cooling.htm
RUBRIKORIENTERINGAR
TILL de följande ProblemEXEMPLEN I Etablerade klimatmodeller och
satellitmätningar
Konventionella PROBLEMEXEMPEL AGW
— med
jämförande beskrivningar
I en
av sina bildillustrerade artiklar [‡1]
påstår WIKIPEDIA Greenhouse effect 2010-07-26 med referens till källan i Problem 1 [Hansen et al., 2005] att den globala uppvärmningseffekten nu (2010) skulle
vara 0,85 W/M² (±0,15; max 1
min 0,7 W/M²) — enligt
genomförda mätningar, ”recent measurements” som artikeln säger.
Uppkollning av wikipediaartikelns
källredovisning visar att originalet också verkar påstå vad referenten säger.
— Men
en vidare uppföljning av det som källan framställer leder till oklarheter,
främst den här: Det ingår aspekter på värmeinnehållet i havsdjupet som DELS
uppdagar påstådda oklarheter (Problem 2) och DELS (Problem 3) uppdagar med AGW3 delvis samstämmiga (effektskalan), delvis inte
samstämmiga (energiskalan) detaljer som berör det möjliga oceanvärmeupptaget.
I
flera nyare artikelkällor (UCAR [‡3],
SCIENCE [‡4], New York Times [‡5]
m.fl.), alla från April 2010, beskrivs vad som i Problem
2 förefaller/påstås vara
mätresultat perioderna 1993|2004(-2008) (men som det verkar hart när omöjligt
att få fram mera precisa referensgrunder för [en väsentlig del av
webbreferenserna kräver särskild behörighet, eller att man betalar per artikel,
vilket väsentligt försvårar en allmänt öppen analys]);
De bägge första ovannämnda artikelkällorna
(UCAR, SCIENCE) refererar till samma illustration [‡4],
samma som i Problem 2; Figur och text berättar att man observerat en hittills
oförklarad skillnad i mätningar mellan havsvärmeeffekt (HP) och atmosfäriskt
(AP) utstrålad värmeeffekt (W/M²).
Differensen beskrivs som ”ett mysterium”:
AP är större än HP — från ca 2003.
I Problem 3
beskrivs ett exempel (från RealClimate) som visar och relaterar den
konventionella uppfattningens oceanlagrade energikvantiteter i jämförelse med AGW-bevisets
energianvändningskurva för hela AGW-komplexet.
Notera också, för de här allmänt beskrivna jämförelserna:
De
konventionellt beskrivna kurvsimuleringarna och dito mätningarna är (vanligen
betydligt) mera korttidsbestämda än den motsvarande NASA(CRU)-temperaturkurvans mera jämna långtidsintervall. Några exakta
kurvjämförelser kan därför (här) inte göras. Det är bara det långa loppet som
(möjligen) framgår.
Dessutom finns
också möjliga förskjutningar och
eftersläpningar på upp till (möjligen) tio år (eller mera, mellan
havsyta och övre Jordatmosfär) som ytterligare kan bidra till att några direkta
(tidsanaloga) jämförelser inte kan göras med någon större exakthet. Emellertid,
ingenting av den mera exakta matematiken bakom dylika övningar är här känd,
bara antydd. AGW-bevisets detaljer (denna framställning) behandlar heller inte
dessa fall.
Etablerade
klimatmodeller och satellitmätningar
OKLARHETER
HAR UPPMÄRKSAMMATS I DEN ALLMÄNNA ENERGIRÄKNINGENS LJUS
Hur väl stämmer AGW3-beviset med
experimentella observationer?
FRÅN
APRIL 2010
Det
ser komplicerat ut. (Men inte omöjligt).
1.— DELVIS samhörande effektvärden
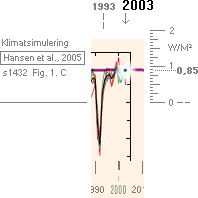
I en simulerad klimatmodell som koncentrerat sig på en delvis modellering av havets
värmeinnehåll tillsammans med påstådda observationer som grundas på
satellitmätningar [Hansen et al., 2005] visas överensstämmelse med AGW3 vid
uppgiftsåret 2003.
Det angivna värdet är 0,85±0,15W/M² som aktuella uppvärmningseffekten i den pågående
observerade globala uppvärmningen.
Eftersom
Hansengruppens klimatsimulering just bara är en simulering, dessutom av detaljer
som inbegriper vad som explicit inte ingår i AGW-bevisets matematik (havsdjupens
värmeinnehåll) samt att detaljerna i sig är av typen kortperiodiska och
inte av AGW-bevisets mera utsträckta (utjämnade) kurvformer, finns heller ingen
direkt grund för någon mera varken exakt eller omfattande jämförelse.
Exemplet
ovan med Hansengruppens resultat är (således) signifikant bara med referens
till att det omnämnda effektvärdet 0,85 W/M²
används som ett — utsträckt över större tidsperiod än just uppgiftsåret 2003 — nuvarande riktmärke för den globala uppvärmningens
effekt av Wikipediaartikeln om Greenhouse effect [‡1].
Effektgrafens
skala bekräftas konventionellt
Det
finns emellertid flera webbkällor [‡2] [‡3] (m.fl. — med vidare) som (med referens till figuren i
nedanstående block [‡2] [‡3] [‡4] [‡5]) också håller sig ikring just det värdet (omkring 1
W/M²) i beskrivningen av en allmän (bekväm, nuvarande 2010) värdeform för
pågående global uppvärmningeffekt.
Därmed, och så långt, en indikering på att AGW-effektkurvan är (någotsånär) överensstämmande med gängse omtalade
värdeproportioner — Eller, omvänt, att man generellt (i det långa loppet) talar
i linje med AGW3.
Ytterligare andra källor som vidrör samma område — mera uttalat
(i större intervall):
Det
finns också (Aug2010) en relativt stor mängd ([minst] flera tiotal)
webbsidor/artiklar/nyhetsmagasin/bloggsajter som refererar till nedanstående:
0,86±0,12 W/M² 1993-2003
s16ö,
Anthropogenic
Warming of the Oceans: Observations and Model Results — David W. Pierce et al., 6 October 2005 (Version 2)
Öppet
PDF-dokument som laddas ner direkt från GoogleSök:
Anthropogenic Warming of the Oceans:
Observations and Model Results
”Willis
et al. (2004), analyzing satellite altimetric height data with observed in-situ
temperature profiles,
estimated
a global ocean warming rate of 0.86 +/- 0.12 watts/m² from 1993 to 2003”.
En
GoogleBok som också (tidigt, 2001) omnämner nivån:
”There
is also a significant uncertainty induced by the largely unknown ocean
outgassing term (QOCEAN). The value 0.3 permeg
year–1 adopted for this term i Table 1 reflects an ocean warming
rate of the order of 1 W
m–2 as inferred from oceanographic
data (Levitus et al., 2000) and from global warming simulations
(Roeckner et al., 1999).”,
GOOGLE
BÖCKER;
GLOBAL
BIOGEOCHEMICAL CYCLES IN THE CLIMATE SYSTEM
— Ernst-Detlef Schulze 2001, s238sp1n
Det
är (alltså) den UNGEFÄRLIGA allmänna uppfattning som finns för närvarande — i
det allmänna webbutbud som finns (Aug2010) om frågan gäller ’vilket är värdet’
— utan anspråk på att vara »det rätta».
Se även i KONTROLLRÄKNING (enklare räkning via Stefan-Boltzmanns strålningslag som ger ungefär samma resultat, 1 W/M²).
(Vidare följer).
Men det är också en hållning som är problematisk — som det
nyligen har visat sig:
Figuren
nedan visar vad som uppmärksammats (April 2010);
2.1 — Forskarkretsar rapporterar underliga
resultat — Effektens variation överlagrad på havsperioden
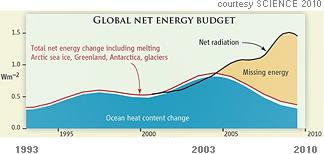
I
flera artiklar ref. [‡2] [‡3] [‡4] [‡5] daterade 15-16 April 2010 refereras ovanstående figur
tillsammans med vad som sägs vara ett uppmärksammande av att man (generellt
inom forskarvärlden) inte riktigt förstår energiräkningen i den
Jordklimatologiska balansen. Vi kan studera det i ljuset av AGW-bevisets
detaljer.
Figuren ovan visar dels ’Total net energy change’, sv. totala
nettoenergiändringen, som på ännu renare svenska betyder effektkurvan.
Effektkurvan som försörjer AGW, samma som energikurvans derivata, (se AGW3) är samma som kurvan nedan i AGW-bevisets ljus, AGW-effektkurvan

Graf pixelUnit50
y =
[(24/10)[(1+[x/10]'4)'–2][x/10]'3]
SCIENCE-figuren visar också en del ’Net radiation’. I
AGW-bevisets ljus motsvarar den delen nettoskillnaden illustrerad nedan
P(AGW)
överlagrad på havsperioderna
(även illustrerad i AGW2)

mellan instrålningen (SOLin) och utstrålningen (SOLut), lika med
t(AGW). I praktiken ligger SolAGW-effektkurvan (t=RP)
[t — vilketsom — följer alla variationer i R
med konstant Soleffekt P]
naturligtvis också PÅ ythavsperiodernas naturliga variation
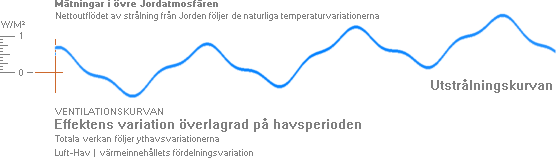
Graf pixelUnit50 —
PREFIXxSIN:
y =
[(24/10)[(1+[x/10]'4)'–2][x/10]'3]+0.222(0.9[(2sinþx/1.48)+0.5(sin3þ[x–0.1]/1.48)])
Med bägge kurvorna till jämförelse,
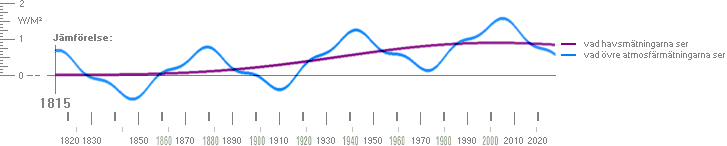
framgår referensform (råeffekten, violett) och verkansform (blå,
AGW-temperaturens energiändringsfunktion [t|E-kurvans derivata] överlagrad på ythavsperioderna) som en harmonisk enhet:
De bägge kurvorna motsäger inte varandra, de förklarar varandra
— samverkar.
De
aktuella artiklarna [‡2] [‡3] [‡4] [‡5], vill emellertid och tydligen, källfiguren
ovan från SCIENCE, göra gällande att SKILLNADEN I PRINCIP mellan Effektkurvan
’Total net energy change’ och Nettoutstrålningskurvan ’Net radiation’ skulle
motsvara en ’Missing energy’. April i all ära, men det är nog inte menat som
ett aprilskämt. Man tar, tydligen, den meningen på fullaste allvar.
SOM
VI SER enligt AGW3-förtydligandet ovan, finns ingen sådan grund. Råeffektkurvan (Totala
nettoenergiändringen, energikurvans derivata) ligger integrerad tillsammans
med den ordinära Solinstrålningseffekten. Eftersom hela temperaturfunktionen i
netto i AGW läggs
till just de naturliga ythavsperioderna, kommer också nettoutstrålningsenergin
ut från Jordkroppen att ses varierande på just ythavsperiodernas rytmik och
amplitud (ev. reaktiva tidsförskjutningar hav-atmosfär här oaktade).
ATT det finns en observerad, tydlig,
skillnad mellan aktuell uppvärmningseffekt (’Total net energy change’,
energikurvans derivata) och observerad nettoutstrålning (’Net radiation’,
energiderivatan plus naturliga havsvariationerna) är alltså helt OK.
— Man
kan då fråga sig varför man i etablerade led vill låta förstå skillnaden mellan
aktuell effekt och den aktuella, praktiskt observerbara, effektutstrålningen
som en felande länk — som inte skulle finnas om ythavsperioderna inte fanns.
—
Svaret på den frågan är tydligen, och som det får förstås, det enkla att man
inte SER några ythavsperioder i sin ’Net radiation’. Sådana omnämns (tydligen)
inte, påtalas aldrig, förekommer inte i framställningarna — utom här.
AGW-bevisets grundsamband finns inte upptaget/uppmärksammat/omnämnt i moderna
korridorer.
Komplikationerna i denna detalj kan MÖJLIGEN förstås mera
grundligt genom följande, kompletterande vy;
2.2 — Effektens variation överlagrad på
havsperioden
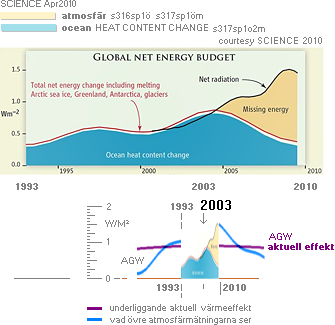
AGW-effektkurvan — den aktuella effekten (heldragen violett)
— ses av Jordatmosfären (heldragen blå) som en överlagrad
temperatur-Energiekvivalent tillsammans med de
naturliga havsvariationerna
(utförligt från Problem 2.1).
Resultatet — som det kan se ut från en
(ideal) atmosfärisk mätning av den globala värmeenergins variation — blir då
den blå AGW-kurvan: vad övre atmosfärmätningarna ser (idealt). Som vi ser,
tycks den nu (2010) sammanfalla (lägligt) med den konventionellt uppfattade
’Net radiation’.
[Notera
att konventionella klimatgrafer vanligen är förknippade med betydligt mera
kortperiodiska variabler än de som visas i AGW-kurvornas jämna lopp]
I AGW-beviset ingår dessutom inga aspekter
på det som sker under havsytan (’Ocean heat content’).
Men vi kan i alla fall betrakta den delen principiellt
till jämförelse med det konventionella betraktelsesättet genom att effektkurvan
(violetta) har ett maximum i AGW-bevisets preferenser vid 4 April 2002.
Efter den toppen ÄNDRAS HAVSVÄRMEUPPTAGETS TAKT (’Ocean Heat Content Change’)
avtagande — ungefär så som SCIENCE-figuren visar ovan (men där möjligen vrängt via kortperiodiska ändringar).
Med
den beskrivningsgrunden försvinner alla eventuella oklarheter — enligt
AGW-beviset (AGW3): Oceanernas värmeupptag avtar från toppunkten
(nominellt) 2002, medan uppvärmningseffekten fortsätter att variera tillsammans
med ythavsperioderna på normalt sätt. Dvs.: Uppvärmningsenergin fortsätter
visserligen att öka, men nu (från 2002) i AVTAGANDE TAKT, men fortfarande med
ökande temperatur SÅ LÄNGE INDUSTRINS BIDRAGANDE FOSSILT GRUNDADE
KOLDIOXIDBIDRAG ÄR AKTUELLT. Inte förrän det fossila CO2-bidraget upphör eller
reduceras kommer AGW att ändra sig.
—
Enligt AGW-beviset skulle alltså hela saken förklaras av att det inte finns
någon ’missing energy’.
—
MÖJLIGEN på den (oturliga) grunden att kurvorna sammanföll (nära,
långperiodiskt) då mätningarna påbörjades
(1993,
ref. TRACKING GLOBAL CLIMATE CHANGE: NASA'S NEW JASON-2 — NASA 2 June 2010
http://solarsystem.nasa.gov/scitech/display.cfm?ST_ID=2218),
samt
fortsatte så under relativt lång tid (till 2003) har man felaktigt invaggats i
föreställningen om att ingen skillnad ska framträda mellan pågående
uppvärmningseffekt och utstrålningseffekt. Det är i så fall en alldeles tydigt
felgrundad uppfattning.
Se även utförligt från Problem 2.
3.— Havsenergins skala
|
I
konventionell analys förekommer mätande/uppskattande AGW-energier på
havsdjupets kredit, figuren vänster med konventionella korttidsvariabler (RealClimate-källan) — här i jämförande insättning med den mycket
utjämnade kurvformen (heldragen ljusblå) enligt AGW3,
energiskalan. Den infällda delen från webbkällan RealClimate
(Maj2010), skalanpassad nedan. AGW-beviset
kan inte tillhandahålla någon DIREKT jämförande matematik på havsinnehållet
eftersom AGW-beviset (AGW3) bara redovisar effekt och energi inom MJ-lokalen. Figuren till vänster visar emellertid och
möjligen en viss (intressant, jämförande) aspekt: OM
värmeupptagningstakten når ett takvärde (4Apr2002 enligt,
effektgrafens topp), BÖR också ett toppvärde för (havsmassans) max
värmeinnehåll uppnås (med någon fördröjning den aktuellt använda energin
…) vid samma tillfälle. I VILKET FALL kan en upptagen värmemängd,
vilkensom i vilket som helst sammanhang, aldrig bli större än den totalt
använda energimängden; I praktiken
bör, för varje material med hänsyn till värmeläckage, en upptagen värmemängd
alltid vara något mindre än en använd värmemängd (är värmeläckaget
litet blir differensen motsvarande liten om tiden också inte är alltför
lång). TANGERINGEN i figuren mot AGW3-bevisets
energikurva skulle möjligen
kunna föreställa en toppindikering, och som sådan en ren bekräftelse — vi ser
att värdemängderna generellt har samma potensordning: T22
Joule. I Havsytans
uppvärmning används
maxvärdet 5,5 T22 J (nu 2010) för beräkning av ett jämförande
uppvärmningsskikt. Toppvärdena, men inte skalreferenserna,
är alltså analoga. Direkt jämförande aspekter med
konventionella djuphavsmätningar ligger emellertid helt utom ramen för
AGW-bevisets domäner. Vidstående är endast en (grafiskt jämförande) reflexion
i ämnet (för vidare). |
———————————————————————————————————
RealClimate
— OCEAN HEAT CONTENT INCREASES UPDATE — 21 May 2010
http://www.realclimate.org/index.php/archives/2010/05/ocean-heat-content-increases-update/
Vertikalskalan
betecknad OHC
Anomaly (1993-2002 baseline) (10²²J)
OHC, förmodl. Ocean Heat Content — webbkällor
är stundtals dåliga på att beskriva använda akronymer
Reflexion
till energiskalan i Problem 3
VÄRDENA STÄMMER INTE — men proportionerna i variationerna gör
det
MAN
KAN I DEN JÄMFÖRANDE artikelns ljus tycka det vore underligt (RealClimateGrafen
ovan) att havets värmelagring skulle vara noll
omkring 1990, och först därifrån skjuta upp med hög pace till sin topplacering på
ca 5,5 T22 J vid nu 2010.
—
Borde inte värmeupptaget ske lugnt och mjukt, utspritt över hela 1900-talets
AGW-upptagande period?
Den infällda Snittbilden från
RealClimate-källan i Problem 3 (motsvarande
original finns i NOAA-databanken
http://www.nodc.noaa.gov/OC5/3M_HEAT_CONTENT/
via RealClimate-länken, men det är inte exakt samma graf,
och RealClimate ger heller ingen ledning till varifrån de har fått sin bild)
omfattar
perioden 1970-2010, tydligt via korttidsvariabler. Vi ser alltså bara en del av
helheten.
— I Levitusgruppens jämförande havsgraf längre ner visas hur den till synes avgränsade
RealClimate-bilden ovan kan ses passa ihop med den vidare historien: trenden passar,
även om skalvärdena inte överensstämmer.
— Ythavsperiodernas t-variationer ligger grovt på nära ±0,2°C topp till topp (max 0,4°C)
med motsvarande fluktuationer i energiinnehåll (med en period på max ca 60 år).
Det motsvarar ca (max) 0,4/0,7=57% av t|E(AGW), eller ca 3 T22 J enligt AGW3 (med
nuvarande år 2010 som referensvärde).
— I
en väldigt förgrovad (elak) mening skulle man alltså kunna säga att Anomalin
kan ’guppa’ upp-ner med »grundmarginalen» på 3 T22 J, beroende på
mätpreferenser, samt med den ytterligare tillagda AGW-delens offset med
referens till början av 1800-talet på också nära ca 3 T22 J, totalt ca 6 T22 J
— i mer eller mindre turbulenta databanker beroende på mätpreferenser.
NOAA-källan
nedan ger för sin del ett PDF-dokument som beskriver hur mätningarna gått till
(Levitus et al., 2009 nedan), perioden 1955-2008|9
GLOBAL
OCEAN HEAT CONTENT 1955–2008 IN LIGHT OF RECENTLY REVEALED INSTRUMENTATION
PROBLEMS
S.
Levitus et al., 2009 — GEOPHYSICAL RESEARCH LETTERS, VOL. 36, L07608,
doi:10.1029/2008GL037155, 2009
ftp://ftp.nodc.noaa.gov/pub/data.nodc/woa/PUBLICATIONS/grlheat08.pdf
Levitusgruppen
använder frekvent ordet estimates, sv. uppskattningar för
resultatpresentationerna (s1sp1ö),
”We
have previously reported
estimates of the variability of the ocean
heat content (OHC) of …”,
”Here
we update these estimates for the upper 700 m of …”
Där visas
så mycket som upp emot 1,2 T23 J som det uppmätta energiinnehållet 0-700 meter
i världsoceanerna året 2009 (Figure 1., s15), och med en (linjärt uppskattad)
nollgenomgång vid ca år 1979.
Nedan
visas hur grafbilden kan göras alldeles klar, se Levitusgruppens jämförande havsgraf.
Levitusgruppens jämförande havsgraf
Levitusgruppens
kurvor i vidare perspektiv
Vi
kan skapa klarhet i saken genom att fälla in (höger nedan) den aktuella
NOAA-figurgrafen (Figure 1., s15 | PDF-34%) från Levitus et al., 2009 i NASA(CRU)-kurvan:
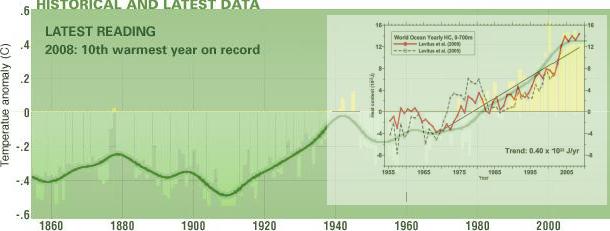
Med
samma kronologiska horisontalskala och (lägligt) samma horisontella nollpreferenslinje
framgår Levitusgruppens resultatgraf (höger, infällda röda, från tidigast 1955)
som grovt sett men tydligt variationsanalog med NASA(CRU)-kurvan. Men vi skulle behöva (minst) 30 år till för att få
någon mera tillförlitlig bekräftelse på det påståendet — en tid mänskligheten
inte har; OM 30 år ska problemet vara ur världen (om det finns något vett och
sans i mänsklighetens möjliga genier).
— OM
nollreferenslinjen håller streck, ska alltså den ythavsperiodiska motsvarande
nolltemperaturreferensen flyttas ner analogt med NASA-kurvans — alldeles vid
kurvfoten år 1860;
— Det
betyder tydligen (separat grafisk analys) ett extra nivåtillägg på ca +12,8 T22
J — med totalsumman (2009) på
(12,8+13)
= 25,8
T22 J ~ 26 T22
J = 2,6
T23 J.
— Det
är nära fem (4,7) gånger så mycket som vad hela E(AGW) = 5,5 T22 J har samlat
till nu (2010) vid nuvarande aktuell uppvärmningseffekt (0,875 W/M², år 2010 AGW3).
—
EMELLERTID: OM vi frånser den använda skalan och mera ser till följsamheten är
det trots allt tydligt att Levitusgruppens oceanvärmeinnehåll alldeles tydligt — korrekt — följer t|E-kurvan.
— Med
det förbehållet ska också energivärdesskalan vara analogt lika med
E-kurvans i AGW3. Alltså max 5,5 T22 J nu (2010).
Det skulle betyda att mätningarna är
variationsmässigt relevanta, medan värdeskalan inte är det.
—
Bara om Levitusgruppens energiskala (1,29 T23 J) halveras två gånger hamnar man
(ungefärligen) rätt.
Maxvärdet är 5,5
T22 J (år 2010).
MÖJLIGA
FELKÄLLOR
Levitusgruppens
jämförande havsvärme
Sätter
vi ihop Levitusgruppens resultat [infällt ovan med NASA(CRU)-kurvan] tillsammans med hela AGW-bevisets kurvsammanställning, (AGW3)
nedan,
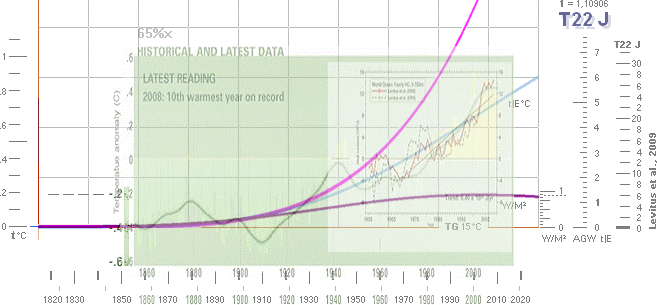
framgår
(mera tydligt), som nyligen påpekades:
Själva följsamheten i Levitusgruppens kurvform kan mycket väl förstås och ses tillhöra den
allmänna kurvsamhörigheten i samstämmig analogi med hela AGW-bevisets komplex
(se De 6 Komponenterna) — MEN att Levitusgruppens energiskalvärde (i så fall) ligger för högt, skalan
ovan längst till höger: Medan Levitusgruppens skalvärde (toppen) vid ca år 2010 visar 26 T22 J visar AGW3 5,5 T22 J.
Genom att effektskalan i bägge fallen är
samstämmig, se Effektgrafens skala
bekräftas konventionellt i Problem 1,
lutar det åt att den konventionellt angivna energiskalan
verkligen också är satt för högt.
JÄMFÖRELSE
ETABLERADE KLIMATMODELLER AGW
Citatreferenser — AGW3 kontra experimentella observationer och den
nyligen uppmärksammande globalt felande energin April 2010
@INTERNET
Wikipedia Greenhouse effect 2010-07-26
http://en.wikipedia.org/wiki/File:Greenhouse_Effect.svg
”However,
recent measurements indicate that the Earth is presently absorbing 0.85 ± 0.15
W/m2 more than it emits into space (Hansen et al. 2005).”,
Min
översättning:
Emellertid, nyare mätningar indikerar att Jorden nu
absorberar 0,85±0,15 W/M² mer än den emitterar till rymden (Hansen et al. 2005).
”…
the amount of energy build-up appears to be
about 1.0 watts per square meter or higher, while ocean instruments indicate a build-up of about 0.5 watts per
square meter. That means about half the total amount of heat is unaccounted for.”,
THE
RESILIENT EARTH — Missing Heat Hides From Climate Scientists, Apr2010
http://www.theresilientearth.com/?q=content/missing-heat-hides-climate-scientists
”BOULDER—Current
observational tools cannot
account for roughly half of the heat that is
believed to have built up on Earth in recent years, according to a “Perspectives” article in this week’s
issue of Science.”,
”Either
the satellite observations are incorrect, says Trenberth, or, more likely, large
amounts of heat are penetrating to regions that are not adequately measured,
such as the deepest parts of the oceans.”,
UCAR
(University Corporation for Atmospherical Research) —
"Missing" heat may affect future climate change, 15Apr2010
http://www2.ucar.edu/news/missing-heat-may-affect-future-climate-change
Min
översättning:
Nuvarande observationella instrument kan inte redovisa
för hälften av det värme som tros ha byggts upp på Jorden från närmast
föregående år, enligt en ”Perspektiv” artikel i denna veckas nummer av Science.
Antingen är satellitobservationerna inkorrekta, säger
Trenberth, eller, mera troligt, är det stora mängder värme som penetrerar
regioner som inte är tillräckligt uppmätta, som typ de djupaste delarna av
oceanerna.
;
Se
även flera liknande artiklar med ungefär samma innehåll,
SCIENCE
DAILY — 'Missing' Heat May Affect Future Climate Change — 15Apr2010
http://www.sciencedaily.com/releases/2010/04/100415141121.htm
;
SCIENCE
AGOGO— Climatologists ponder Earth's missing heat — 16Apr2010
http://www.scienceagogo.com/news/20100316020730data_trunc_sys.shtml
;
THE
DAILY GALAXY — A Central Unsolved Mystery of Climate Change: Where is
Earth's 'Missing' Heat? — 16Apr2010
http://www.dailygalaxy.com/my_weblog/2010/04/missing-heat-may-affect-future-climate-change-.html
;
NEW
YORK TIMES — The Difficulty of Balancing Earth's 'Energy Budget' — 16Apr2010
http://www.nytimes.com/cwire/2010/04/16/16climatewire-the-difficulty-of-balancing-earths-energy-bu-62508.html
…
Alla
dessa (och övriga) använder frasen typiskt ’cannot account for roughly half’, sv. kan inte förklara mer än halva.
”The
difference between the incoming and outgoing energy—the planetary energy
imbalance—at the top of the atmosphere is too small to be measured directly from satellites.”,
”Since
2004, ~3000 Argo floats have provided regular temperature soundings of the
upper 2000 m of the ocean, giving new
confidence in the ocean heat content assessment—yet, ocean temperature
measurements from 2004 to 2008 suggest a
substantial slowing of the increase in global ocean heat content (see
the figure, panel A) ( 10). If the extra energy has not gone into the ocean,
where has it gone?”,
TRACKING
EARTH’S ENERGY [16 APRIL 2010 VOL 328 SCIENCE]
— 16Apr2010
http://www.seas.harvard.edu/climate/seminars/pdfs/Perspectives.pdf
Figuren
som visas i artikeln, här i artikelns PDF-original 100% (JPG),
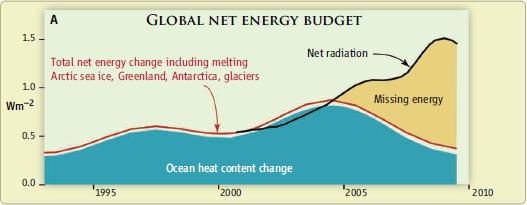
”Greenhouse
gases emitted by human activities help trap more heat in the Earth's
atmosphere, warming the planet. But a new analysis warns that scientists don't fully understand where all that heat is going.”,
”The
planet's oceans absorb about 90 percent of incoming energy in the form of heat,
but measurements collected between 2004 and 2008 show that the rate at which oceans are absorbing
heat is slowing, even as emissions of heat-trapping
gases have risen.”,
NEW
YORK TIMES — The Difficulty of Balancing Earth's 'Energy Budget' — 16Apr2010
http://www.nytimes.com/cwire/2010/04/16/16climatewire-the-difficulty-of-balancing-earths-energy-bu-62508.html

BILDKÄLLA: Övre: Författarens arkiv ·
Månen2Bild119 · 6Apr2009 · NikonD90 · Detalj. Undre: friteckning 2009,
montage
Kosmiska strålningens energi på Jorden
Industrins möjliga effektbidrag till den globala uppvärmningen
Som
vi ser av sammanställningen i Effekt&Energi för AGW-beviset, är industrins
Fossil-Carbon-energianvändning grovt 100 gånger lägre än den energianvändning
som, enligt AGW3, via Soleffekten avdelas för att, på det högre termiska
motståndets kredit [‡], försörja den globala uppvärmningen [‡]. I
siffror, nu 2010, är den samlade AGW-energin ca 5 T22 J medan
den för industrins Fossil-Carbon är ca 5 T20 J. Jämför även siffrorna direkt
från BP-statistiken som för året 2005 anger världens totala energianvändning
till 4,4 T20 J.
Industrins effekt 100ggr mindre
Eftersom
effektskalorna förhåller sig som energiskalorna, kan industrins aktuella effekt
P(FossilCarbon) utläsas som ca 100 gånger mindre än den aktuella AGW-effekten.
AGW-effekten enligt AGW3 visar 0,875 W/M² nu 2010. I KONTROLLRÄKNINGEN visas att ungefär samma resultat uppnås (0,83 W/M²) från en helt oberoende linjär approximation (Stefan-Boltzmann-approximationen) och som visar rimligheten i resultatet från AGW3.
Preferensen för effektvärdet till den globala uppvärmningen nu 2010 kan därmed
förstås som tämligen relevant och välgrundad.
Effektvärdet för den globala uppvärmningen
som omnämns generellt i etablerade kretsar [Se Effektskalan bekräftas] ligger också (1993-2003) omkring 0,9 W/M², vilket ytterligare motiverar den här anförda
användningen till jämförelse.
I jämförelsen (sämsta fallet) nedan används
det mera preciserade grovvärdet 0,8 W/M².
Den kosmiska strålningens roll till jämförelse — har den någon
betydelse?
Kosmiska 5 miljoner ggr mindre
Med
en grov avrundning uppåt till 1 W/M² visar resultatet
(nufallet, 2010) att ca 1/250 eller runt 0,4% av den tillgängliga
Solmedeleffekten 250W/M² på Jordytan åtgår för global uppvärmning [‡] in till
nuvarande uppvärmningsgrad ca 0,7°C. t|E-kurvan (använd energi, t°C [‡]) visar 0,73 °C 2010 [Se Kalkylkortet].
Industrins motsvarande effektandel (1/100 [‡]) via
Fossil-Carbon skulle därmed vara ca 0,004%.
Används industribidragets motsvarande
egeneffekt till jämförelse, får alltså industriandelens 0,004% av Solens radiativkraft
på Jordytan på 250 W/M² innebörden av
den utlösande, och underhållande, faktorn till den pågående globala
uppvärmningen.
Vilket är motsvarande värde för den
kosmiska strålningen?
Till jämförande utlösande faktor utgör den
kosmiska strålningens effektandel (källuppgift nedan) bara motsvarande
0,00000000064% ................. kosmiska strålenergins effektandel av Soleffekten på Jordytan
Det
är bara en andel 6,4 t12 av hela den Jordytstillgängliga Soleffekten på 250 W/M². Eller relativt industrins Fossil-Carbon-TRIGGANDE andel
på 0,004%: (1,6 t9 W/M²)/(0,008 W/M²) = 2 t7; Industribidraget är 5 miljoner gånger större än
den kosmiska strålningens bidrag.
Svaret på frågan om den kosmiska
strålningen har någon betydelse för den globala uppvärmningen blir således, i
varje fall med referens till möjliga effektgrunder, att OM en sådan betydelse
finns, den i så fall är 5 000 000 gånger mindre än vad den samlade världsindustrin
kan bidra med.
Vi studerar räkningen.
KOSMISKA STRÅLNINGENS ANDEL PÅ JORDEN
— Hur
mycket effekt utvecklar den kosmiska strålningen på Jordytan i termer av W/M²
för jämförelse med Solens radiativkraft (P/A) på Jordytan?
;
P/A = 250 W/M²
Den kosmiska strålningen är svår att få fram mera precisa uppgifter på. De
uppgifter som anges i t.ex.
OULU
SPACE PHYSICS TEXTBOOK Cosmic rays (1998-2009)
https://wiki.oulu.fi/display/SpaceWiki/Cosmic+rays
”The
total energy density of CR particles is about 1 eVcm–3.”,
’energitätheten i den kosmiska strålningen är ca 1 eV/cM³’.
visar
att det kosmiska bidraget i stort sett är helt försumbart;
;
Vi
utför en grov överslagsberäkning (V för volymen, E för energin) med
användning av uppgiften från webbkällan ovan på
1
eV/cM³ = (1,602 t19 C
· 1V)/(0,01M)³ ......... kosmiska strålningens volymEnergiTäthet
= E/V ; Samband: E=UQ, U i Volt, Q i
Coulomb; elementarladdningen för Q är 1,602 t19 C;
E/V = (1,602 t19 J)/t6(M)³
= 1,602 t13 J/M³
Om
den energivolymen är representativ för troposfären (grovt ca 10 KM upp, hela intervallet vilket
garanterat inte är det praktiska fallet men som här ändå antas för att göra
marginalerna breda) ges först den troposfäriska volymen (V) via
Jordradien (vid ekvatorn, r~6,38 T6 M) enligt
V =
(4π/3)(rYTTRE³ – rINRE³)
= (4π/3)([6,38 T6 M + 1 T4 M =
6,38 T6 M]³ – [6,38 T6 M]³)
=
(4π/3)(1,22305 T18)
= 5,12309 T18 M³ ;
Kosmiska
Energin räknat på hela Jordens troposfär (10 KM upp) blir alltså
E = V(1,602 t13 J/M³)
=
(1,602 t13 J/M³)(5,12309 T18 M³)
= 8 207 190,1 J
= 8,2071901 T6 J
EFFEKTEN
(P) i Watt är energin (E) i Joule per tidsenhet (storhet T, enhet S),
P = E/T ;
= 8,2071901 T6 J/S
= 8,2071901 T6 W
—
Utslaget per M² på Jordytan (A
via Jordekvatorn r=6,378 T6 M) för jämförelse med Soleffekten ges
A = 4πr²
;
P/A = (8,2071901 T6 W)/(4πr²)
= (8207190,1 W)/(5,11185 T14 M²)
= 1,60551 t9 W/M² ........................... kosmiska strålenergins radiativkraft (W/M²) på Jordytan
~ 1,6nW/M²
I
jämförelse med Solens radiativkraft (P/A) därmed
(1,6nW/M²)/(250 W/M²) = 6,4 t12 = 6,4 t10 %
.......................................................... kosmiska strålningens andel av
Soleffekten på Jordytan
I
jämförelse med industrins
Fossil-Carbon-radiativkraft (P/A)
[sämsta
fallet, från Stefan-Boltzmann-approximationen i resultattabellen från resultatet i KONTROLLRÄKNINGEN]
— 0,8
W/M² och 100 ggr mindre effekt 0,008 W/M²
—
därmed
(1,6nW/M²)/(0,008 W/M²) = 2 t7 = 2 t5 %; industribidraget är 5 000 000
ggr större
.......................................................... kosmiska strålningens andel av hela
världsindustrin på Jordytan
DET
MEST AVGÖRANDE FÖR VARJE FÖRKLARANDE KANDIDAT i hela den globala uppvärmningens
komplex är den tydligt sammanhängande ordning som framgår ur den
uppmätta medelbaserade NASA(CRU)-temperaturkurvan. Kronologin uppvisar en process vars två främsta
komponenter är havsperioderna och t|E-kurvan, helt analog med den motsvarande mera detaljerade
världsindustrins Fossil-Carbon-kurva.
Varje kandidatur till den kurvbildens
förklaring måste kunna härleda en motsvarande energiräkning, samt kunna
beskriva processens övergripande förlopp och utveckling. Med
Fossil-Carbon-kurvan som grund blir den förklaringen given som AGW-bevisets
delar enligt De 6 Komponenterna. Och, följaktligen, är därmed orsaksbilden helt uttömd.
Den kosmiska strålningen utesluts därför
helt naturligt ur komplexet i meningen att ha någon som helst betydelse för det
övergripande resultatet.
Den kosmiska strålningen i sig uppvisar
ingen utvecklande process som följer parallellt med industrins
Fossil-Carbon-kurva; utvecklingen i kosmos följer, vad vi vet, en något vidare
plan än industrins.
Den kosmiska strålningens enda möjliga
variabla faktor är Solen, och dess variationer [‡] är redan tämligen
väl kända och de uppvisar heller ingen koppling till industrins
utvecklingskurvor — och kan därmed heller inte uppvisa någon analog
temperaturökningskurva.
DÄRUTÖVER:
Det förefaller något märkligt (sett enbart till värdet) om man vill försöka
framhäva en komponent (den kosmiska strålningen)
med muskelstyrkan 1,6 nW (0,0000000016 W) framför — överskuggande — en
komponent med muskelstyrkan 0,008 W (världsindustrin) som huvudrollsinnehavaren i förklaringen till det
aktuella fenomenet.
Sifferexercisen leder (således) bara till
att man, tydligtvis, helt kan avfärda den kosmiska strålningens betydelse för
den globala uppvärmningen — så länge världsindustrin uppvisar 5 miljoner gånger
större verkan.
Att den kosmiska strålningen har en viss
effekt är klart, liksom också stjärnljusen generellt har sin del. Men som
räkningen visar, är det kosmiska inslaget tydligen att se som helt försumbart
vid sidan av huvudsaken: industrins Fossil-Carbon.
Se även i Övriga kandidater utesluts.
e = 1,602 t19 C ............................. elektriska elementarladdningen [ref.
FOCUS MATERIEN 1975 s666]

BILDKÄLLA: Författarens arkiv · Bild24Excur6 ·
Jul2010 · NikonD90 · montage
E = [ρV(H1)]CT
Energin som krävs för att värma upp 1
djupmeter ythavsvatten (71% av Jordytan) med värmekapacitiviteten C=4000 J/KG°K och
medeltätheten ρ=1000 KG/M³ till värmegraden T°C med djupmeterskiktets
volym V(H1)=3,62942 T14 M³=(0,71)(4π[r=6,378 T6 M]2)1M kan tecknas på
formen
E = (T °C)(1,45176
T21 J/°K)
Ythavets uppvärmning via AGW

IMAGE COURTESY OF THE IMAGE SCIENCE & ANALYSIS
LABORATORY — NASA Johnson Space Center — NASA astronaut photograph
ISS022-E-6678
http://earthobservatory.nasa.gov/Features/GlobalWarming/
2010-08-11
Ekvivalensräkning för kontroll av det
uppnådda resultatets rim och reson
MED
RESULTATBILDEN FRÅN AGW3
Antalet
(n) djupmeter ythavsvatten (71% av Jordytan [ref @INTERNET Wikipedia
Ocean 2010-07-21]) med en meters höjd SOM med vattnets värmekapacitivitet (C=4000 J/KG°K) har uppvärmts till den nu uppnådda
globala uppvärmningens temperaturnivå (0,7 °C) genom den nu totalt använda
uppvärmningsenergin (5,5 T22 J), kan beräknas som följer:
C = E/mT ;
Varje
djuphavsmeter ythav via vattnets medeltäthet (approximativt) ρ = 1000 KG/M³:
m = ρV
;
V = A·1M
= (4π[r=6,378 T6 M]2)1M
= 5,11185 T14 M³
Med
71% av Jordytan för havsoceanerna ges Jordytshavsvolymen för en meters djup
till ca
V(H1) =
(0,71)(5,11185 T14 M³)
= 3,62942 T14 M³ ;
Energin
som åtgår för att värma upp ett sådant skikt till värmegraden 0,7 °C på
vattnets värmekapacitet 4000 J/KG°K blir
E = mCT
= [ρV(H1)]CT
= [(1000 KG/M³)(3,62942 T14
M³)](4000 J/KG°K)(0,7 °C)
= 1,01623 T21 J
~ 1 T21 J
Antalet
sådana enmetersskikt blir med tillgängliga energin (år 2010 enligt AGW3) 5,5
T22 J lika med
n = (5,5
T22 J)/(1 T21 J)
= 55
RESULTAT (se från Beräkning):
Max idealt 55 meter ythavsvatten kan ha uppvärmts till (år 2010)
t(AGW)=0,7 °C via totalt, under hela AGW-perioden,
tillgängliga 5,5 T22 J med vattnets värmekapacitivitet 4000 J/KG°K.
I det
praktiska fallet avtar temperaturen med havsdjupet (enligt delvis komplicerade
samband) och totalräkningen kommer därför att omfatta betydligt större djup med
hela AGW-intervallet 0-0,7 °C.
Konventionella uppgifter — nära 5 ggr mer
Jämför
konventionella data från Levitusgruppen
2009.
KONVENTIONELLT
påstås att den totalt upplagrade energin i oceanerna skulle ligga på nivån ca
(max) 26
T22 J — räknat från nollnivån
1815 — OM konventionella oceanmätningar verkligen ansluter till de övriga 6 kurvkomponenternas följsamhet. Eller, räknat från den konventionellt
nominella nollnivån (ca år 1980) med motsvarande grafvärde 13 T22 J (nivåoffseten
med nollan vid år 1815 lägger till ca 13 T22 J, se Levitusgruppens jämförande havsvärme).
Det gör totalt max 26/5,5~4,73 ggr högre
värmeinnehåll med motsvarande
4,73×55
~ 260
djuphavsmeter med hela beloppet 0,7 °C.
Hur kan vi kontrollera rimligheten i dessa värden?
Faktum
att säga i sammanhanget — här veterligt:
— Det
finns ingen direkt enkel algoritm för det kontrollerande ändamålet;
GROV ÖVERSIKT — Den
allmänna temperaturändringen i världsoceanerna med växande djup
Världshavens ytmedeltemperatur (ner till flera
tiotal meter) är ca 17 °C

DATAKÄLLA: se webbkällan
WINDOWS TO THE UNIVERSE — Temperature of Ocean
Water — 2001
http://www.windows2universe.org/earth/Water/temp.html
Havsdjupens
variationer är (veterligt) alldeles för komplicerade för att på något enklare
sätt uppvisa någon parallell till en generell kontrollräkning som skulle kunna
utpeka någon plattform till vad som är praktiskt möjligt att kontrollera;
Det gäller »fjuttiga» 0,007 °C per år i
genomsnitt perioden runt 1860-nu; I myllret av alla fluktuationer över hela
världen bara inom en 5-årsperiod är vi i princip chanslösa att få fram några exakt
jämförande globalmedelvärden.
De konventionella havsdjupsuppgifterna brukar anges med
intervallet 0-700 meter (OHC, Ocean Heat Content)
— totalt med alla möjliga
temperaturspridningar och baserat på omfattande beräkningar via volymintegraler
som baseras på tusentals mätceller som grund tillsammans med lika omfattande
statistiska beräkningsgrunder.
Vi
har, veterligt och således, ingen möjlighet att få vetskap i om det är rimligt
att bara 55 djupekvivalenta 0,7°C-metrar stämmer med de mätningarna — sett enbart
till mätningarna som sådana — eller om
det är 255 djupekvivalenta 0,7°C-metrar som gäller.
Den
enda form för kontroll som veterligt finns till jämförelse är den som vi redan
studerat: alla kurvkomponenter tillsammans i hela AGW-komplexet; Energiräkningen i AGW3 kräver
att det är MAX 55 meter som gäller — förutsatt att inga räknefel har begåtts (granskning
nedan);
De konventionella mätvärdena är visserligen
variationsmässigt samhörande med AGW-komplexets alla övriga kurvor (Se Levitusgruppens jämförande graf), men att i så fall den konventionellt antagna
värdeskalan för havsoceanernas värmeinnehåll ligger grovt 5 ggr för högt.
Den återstående möjligheten att
energiskalan i AGW3 skulle vara den felaktiga komponenten kan uteslutas av
närmast två samstämmiga skäl — om inga utvecklingsfel föreligger i den snåriga
skaldjungelns omvandlingskoefficienter:
1.
Effektskalan
(i antal [n] W/M², se Skalkoefficienterna till effektkurvan) baseras på Jordytsvärdet (5,11 T14 M²); Effektgrafen är t|E-kurvans derivata [dess integral ger Carbon-Dioxide-ekvivalenten,
se Tabelljämförelser], vilket ger
PJ =
n(5,11185 T14 M2)
med
omvandligskoefficienten 0,88W/0,64t=1,375W/(1t=50pixels) per M² som ger
PJ =
n(5,11185 T14 M2)(1,375 W/M2)
= n(7,0288 T14
W)
Tidsskalan
är enhetligt årsbaserad, vilket ger motsvarande energivärde från PJ i enheten WattÅr. Energivärdet WattSekunder fås alltså genom
= PJ · (365,25·24·3600 S = 31
557 600 S = 1 år)
= n(2,21812 T22
J)
per
grafisk enhet 50pixels [4,43624 T20 J/p ~ 4,44 T20 J/p]. Se även
sammanställningen i Effekt&Energi, samt utförligt från Härledningarna
till AGW3;
2.
Effektskalans
värdeform (från AGW3) stämmer redan överens med
konventionellt angivna värden (baserade på modellsimuleringar — dock endast i
jämförande avgränsade intervall), typ runt 1 W/M² i
nuvarande utveckling (eg, 0,875 W/M² för 2010), se Effektgrafens skala bekräftas konventionellt.
ENBART
på den senare uppgiftens kredit är det tydligt att banken — utan tvekan —
godtar det allmänt redovisade bokslutet: det bör vara den konventionella
havsenergiskalan som ligger 5 ggr för högt.
[Det är obehagligt, för min del, eftersom
det utpekar en minoritet som mera skickad i korrekturläsningen än hela
forskargruppen, vilket normalt sett är orimligt. Jag måste alltså, likväl
reservera mig för eventuellt ännu oupptäckta fel].
Med denna korrektion stämmer alla (nu sex plus
två = åtta) ingående kurv[skal]komponenter i samma räkning:
0. NASA-kurvan,
1. ythavsperioderna, 2. t|E-kurvan, 3.
Fossil-Carbon-kurvan, 4.
Carbon-Dioxide-kurvan, 5. t|E-integralen (C),
6. AGW-Effekten, 7. AGW-Effektens integral
RESULTAT:
Det är max 55 meters ekvivalent uppvärmningsdjup som gäller. Inte 260.
Koldioxidens markbundenhet — Se även närmast Citatblock nedan
2010VIII26
Koldioxidgasens (CO2) markbundenhet
KLARGÖRANDE
I den
här framställningen används genomgående en liknelse med vatten som breder ut
sig på golvet från en uppvällande golvbrunn eller slang (industrins kolutsläpp)
motsvarande den tunga koldioxidgasens utbredning och transport ut mot
landkontinenternas gränser för att sedan, så småningom, absorberas av havet [Se
Havsytans
Koldioxidabsorption].
Liknelsen
med färgpigment i Vatten
Liknelsen
mellan den tunga markstrykande koldioxidgasen och vattenutbredningen på golvet
är naturligtvis förenklad (och utan hänsyn till vindarnas inverkan) — och
samtidigt inte.

BILDKÄLLA: Författarens arkiv ·
Bild72Färgpigment26Aug2010 · NikonD90 · Avklippt detalj från vattenfärgspenna
nedsläppt i ett glas vatten.
De av
oss som redan (sedan flera decennium tillbaka) har observerat
säsongsvariationerna, speciellt vår/höst av olika gasiska luftstråk som sveper
in över nejderna (med tydlig odör av avgaser), kan enklare förstå den följande,
mera praktiskt underliggande analogin: Om vi häller upp ett vanligt dricksglas
med vatten, och sedan släpper i en droppe bläck (eller annat färgämnespreparat;
koldioxidgasen som sådan då den bildas är betydligt tyngre än den omgivande
luften, likt rökslingorna från ett glödande föremål) ser vi att föroreningen
följer i (långa linjära) stråk som helt beror av vattnets övergripande
strömningsfysik. Så småningom uttunnas färgstråken, och blandningen blir helt
homogen. Det är denna sistnämnda blandning (i hela troposfären från marken
upp till grovt en mil) som avses med Carbon-Dioxide-halterna — vilket betyder att dessa dels bör mätas på MARKNÄRA
ställen [som ansluter till temperaturkurvans luftmarina mätlokaler — människors normala livsrum] och som dels ligger relativt avskilda från större
industrilandskap.
Nedanstående citatsamling understryker faktum att man ännu
(2010) inte har någon uttömmande fullständig bild av hur sammansättningar och
koncentrationer i atmosfären hänger ihop i detalj. Se även citatsamlingen i Havsytans
Koldioxidabsorption.
Utan mera
exakta referenser betraktas det primära utflödet från fossilsläppen i den här
presentationen ungefärligen analogt med den ovannämnda Liknelsen med färgpigment i Vatten; Först i utpräglade markstråk i anslutning till
utsläppslokalerna, sedan allt mer uttunnat i (komplicerad) förening med
havsabsorption och havsemission, se Havsytans Koldioxidabsorption.
Ingenting hindrar naturligtvis att den
avgörande överföringen av t|R-CO2-bidraget till vattnet [Se Vattnets
Huvudroll] sker direkt i
atmosfären — vilketsom, direkt i luften eller via havsytan, går på ett ut för
den övergripande matematiken. Se från AGW3.
Citaten nedan utgör en begränsad samling
där svårigheterna omnämns.
”The
total mass of atmospheric carbon dioxide is 3.16×1015 kg (about
3,000 gigatonnes). Its
concentration varies seasonally (see graph
at right) and also considerably
on a regional basis, especially near the ground.”,
@INTERNET
Wikipedia Carbon dioxide, In the Earth's atmosphere 2010-08-26
http://en.wikipedia.org/wiki/Carbon_dioxide -
In_the_Earth.27s_atmosphere
Se
även ovanstående Liknelsen med
färgpigment i Vatten.
”It's
impossible to give
average atmospheric concentrations for the
less stable compounds in the air. Their
concentrations depend strongly on the chemical conditions in the air at a
particular time.”,
”Its very difficult to give an overview of the concentrations of trace gases in the
troposphere. The same compound can be
present at extremely low concentrations, for example, over the ocean and at
very high concentrations in the urban environment.”,
ENVIRONMENTAL
SCIENCE — Lower atmosphere, 2004
http://www.atmosphere.mpg.de/enid/3tg.html
Se
även ovanstående Liknelsen med
färgpigment i Vatten.
”The
results reported here show that the CO2 mixing ratio is not constant with altitude but rather decreases in the stratosphere, by about 7
p.p.m.v., between the tropopause and 33 km. One conclusion is that recently
increased concentrations of CO2 in the troposphere have not propagated far into
the stratosphere.”,
Artikeln
i sin helhet är inte gratis tillgänglig:
NATURE
— Decrease in CO2 mixing ratio observed in the stratosphere, Bischof et al.,
1980
http://www.nature.com/nature/journal/v288/n5789/abs/288347a0.html
BP-statistik
Enligt statistik från BRITISH PETROLEUM (Jul2010)
http://www.bp.com/sectiongenericarticle.do?categoryId=9023766&contentId=7044197
uppgick världsbefolkningens totala energianvändning år 2005 till
Etot = 10 565,4 T6 [1oe = 42 T9 J] =
4,43746 T20 J.
Sammanställningen
nedan är ett montage med sammanställda skärmdumpar från BP:s olika infosidor,
2010-07-30.

AGW12
snabbsammanfattning
Snabbgenomgång/sammanfattning
av AGW-bevisen Del 1-2

Figuren ovan sammanfattar den AGW-bevisets modellform som
frammanas genom Grundsambandet
[t/T=m/M] och proportionaliteten
mellan temperatur och energi med beräkningen
av M-skiktets höjd.
AGW-beviset,
Del 1-2:
—
Koldioxid(CO2)-molekylen som bildas i M-skiktet via fossilförbränningen når så
småningom havet via den tunga markstrykande koldioxidgasen [‡] då den
trycks ut mot kontinentalgränserna av påfyllningstrycket, vindarnas inverkan
frånsett; När CO2-molekylen absorberas av havsytan, påförs också havet analogt
den värmeinduktiva verkan som följd av det högre värmemotstånd i M-skiktet som
CO2-molekylens bidrag (Δt|R) medför från fossilförbränningen (T);
värmebidraget (Δt) och värmemotståndet (ΔR) ligger bägge överlagrade på den konstanta
Solinstrålningseffekten (P) i M-skiktet [Se Värmemotståndets
fysik], vilket påför M-lokalen
ett nettobidrag av 2Δt, se Grundsambandet i AGW-beviset Del 2.
INTEGRALEN
för havsversionens Fossil-Carbon-kurva (AGW-beviset Del 1) som ger motsvarande Carbon-Dioxide-halten, ger sedan via Jämförande
tabellvärden överensstämmelse
in till lägst 98%, vilket följaktligen
blir det rent kvantitativt konkreta AGW-beviset — in till lägst 98%.
M-lokalens sammansättning är egal för AGW12
NOTERA
(således):
M-lokalens molekylära
sammansättning är egal för AGW-effekten;
Det enda som räknas är bidraget (Δt|R) från fossilförbränningen (T) som ökar
värmemotståndet (genom materialändring) i den konstant påliggande
Solinstrålningseffekten (P) som omsätts genom den givna utstrålningsytan (A),
idealt vid havsytan (r=6,378 T6 M). M-lokalen kan alltså, i princip,
vara helt nerlusad med metan (CH4) eller vattenånga (H2O) — eller andra
komponenter (vilkasom). Det har ingen betydelse. Det enda som räknas är
bidraget (Δt|R) från fossilförbränningen (m) som tas upp av havet
från Fossil-Carbon, och hur det affekterar M-skiktets termodynamik på ändringens
fysik med den givna Soleffekten (P=250 W/M²) vid Jordytan (A). Inget annat. Dvs., bidraget
(Δt|R) — ändringen — STYR effekten. Inget annat.
Allmänna grunddata
JORDENS
ATMOSFÄR
Generellt
för allmänna uppgifter som berör Jordytan och Jordatmosfären i ljuset av
AGW-beviset ges nedanstående värden.
Allmänna
grunddata — JORDENS ATMOSFÄR
M ~ 3,5 T16 KG ....................... genomströmningslokalens
atmosfäriska massa för kolutsläppet m i Fossil-Carbon-förbränningen
JM ~ 5,3 T18 KG ....................... Jordatmosfärens
totala massa
M/JM = 0,00660377
~ 0,7%
= ungefärliga andelen vattenånga
i havsluft (normaltryck) vid 15°C och normal luftfuktighet (grovt 70% RH,
RelativeHumidity)*
= m(W)/m(A) [‡]
Totala
vattenmängden i Jordatmosfären enligt
@INTERNET
Wikipedia Atmosphere of Earth, Composition, Water vapour 2010-07-27
http://en.wikipedia.org/wiki/Atmosphere_of_Earth
anges
~0,4% = 0,4·5,3 T18 KG = 2,12 T16 KG
vilket
är grovt 60% av hela M. Men då är också hela Jordatmosfärens bidrag utspritt på
alla tänkbara tryck och temperaturer från marknivån och uppåt.
RH eng. Relative Humidity, förk. o bet. sv. (relativ) luftfuktighet
* Los
Angeles år 2002, årligt medelvärde RH = 67,25%;
http://www.ncdc.noaa.gov/oa/climate/online/ccd/avgrh.html
http://www.ncdc.noaa.gov/oa/about/ncdccontacts.html
(Uppgiften ovan avser sammanställt
årsmedelvärde för de bägge ”LOS ANGELES C.O., CA” och
”LOS ANGELES AP, CA” — men varken källan ovan eller webben generellt verkar
innehålla någon begriplig information om vad som menas med de tillagda
specificerade apokryferna C.O.[”commanding officer”][»capital offshore» kanske
…] och AP); Tabellen visar att många geografiska platser matchar (grovt)
ungefärligt runt 70% luftfuktighet, morgon/kvällsmedelvärdet [t.ex. Birmingham
med årsmedelvärdet (83+60)/2=71,5%].
Empiriska samband för vattenånga vid de temperaturer som
begränsas av Jordens klimat, se källreferensen nedan (Tim Padfield 1996)
2010-07-28
Vattenånga, samband
Från
EQUATIONS
DESCRIBING THE PHYSICAL PROPERTIES OF MOIST AIR — Tim Padfield 1996
http://www.natmus.dk/cons/tp/atmcalc/atmoclc1.htm
Tim
Padfield’s kalkylator,
http://www.natmus.dk/cons/tp/atmcalc/atmocalc.htm
Webblänken finns inte längre [Mar2014], man kommer bara till danska nationalmuseets portal.
— Upphittad PDF med samma rubrik
EQUATIONS
DESCRIBING THE PHYSICAL PROPERTIES OF MOIST AIR
http://www.conservationphysics.org/atmcalc/atmoclc2.pdf
KALKYLKORTET (AGW-beviset) Tabell 1
MAX
VATTENMÄNGD I LUFT VID HAVSNIVÅN VID GIVEN LUFTMARIN TEMPERATUR — Vattenångtrycksekvationerna — 29Jul2010
ger ungefärliga beräkningsvärden: viktsandel vatten i luft vid olika temperaturer.
— Värdena stämmer ungefärligt med TIS-tabellen i länken nedan.
(TIS)
Transport Information Service — CLIMATE/HUMIDITY TABLE (tysk källa,
datumuppgift saknas)[2014-03-12]
http://www.tis-gdv.de/tis_e/misc/klima.htm
Liknande (med ovan inkluderade) sambandsformer finns — i stort sett alla förekommande sammanställda — i
University
of Colorado — SATURATION VAPOR PRESSURE
FORMULATIONS, Holger Vömel, 2011
http://cires.colorado.edu/~voemel/vp.html
pS = (610,78)e17,2694(t/[t+238,3])
.................. Saturation vapour pressure in pascals | t°C
pS(15°C) =
1698,3316 Pa ................. mättnadsångtrycket vid 15°C
Aktuella
vattenångtrycket (pa) är värdet ovan gånger aktuella relativa
luftfuktigheten
ρa = 0,002166·pa/(t+273,16) .............. Water vapour concentration | KG/M³ | t°C
pa anger
aktuella vattenångtrycket
ρS =
0,0127662 KG/M³ ........... vattenångtätheten
vid 15°C med pS ovan
tDP = 238,3/(–1+17,2694/w) ........................... The Dew Point | °C | Daggpunkten
w =
ln(pa/610,78) = (17,2694)(1+238,3/t)–1
Ω =
(UW/UA)/(pA /pw – 1)
= mW/mA
Anger
luftens vattenVikts(Mass)andel
= (18)/(29) · (pA/pw
– 1)–1
pA anger lokala lufttrycket (101325 Pa vid
havsytan och obs 0°C)
= 0,0100211 vid
15°C och pW=pS
Beräkningen
av Ω finns sammanställd i Kalkylkortet — max vattenmängd i luften vid havsnivån vid olika
globala medeltemperaturer; pS=pW som ovan;
pW = 610,78·e(17,2694)/[1+238,3/t]
pA = (370,95002 J/°K)·(t+273,15)/1M³
Ω = (18)/(29) · (pA/pw
– 1)–1
~ 0,62 · (pA/pw
– 1)–1
......................... anger max
andel vattenmängd i luften vid havsnivån
Absoluta nollpunkten 0°K specificeras genomgående i UNIVERSUMS HISTORIA som
–273,15°C. Källan ovan använder (möjligen, om inte felskrivet) ett mera
avancerat absolutvärde (273,16), se citat nedan (för möjlig felkälla).
Författaren till sambanden ovan redovisar inga referenser, så olikheten kan
möjligen bero på felskrivning. För att bibehålla den fasta standarden i
UNIVERSUMS HISTORIA har värdet
0°K =
–273,15 °C också använts här, fortsättningsvis, i Kalkylkortet
med ovanstående sambandsformer.
Hur de olika värdena förhåller sig framgår
av nedanstående citat,
”By international agreement, the unit kelvin and its scale are defined by two
points: absolute zero, and the triple point of Vienna Standard Mean Ocean Water
(water with a specified blend of hydrogen and oxygen isotopes). Absolute zero, the lowest possible temperature, is defined as being precisely 0 K and
−273.15 °C. The triple point of water
is defined as being precisely 273.16 K and 0.01 °C.”,
@INTERNET
Wikpedia Absolute temperature, Overview 2010-07-29
http://en.wikipedia.org/wiki/Absolute_temperature
Notera
att värdeformen 273,16 grader Kelvin
uttrycker ett positivt Celsiusvärde (+0,01°C): det finns (således)
ingenting sådant som typ
–273,16
°C, analogt »–0,01°K». Absoluta nollpunkten är –273,15 °C = 0°K,
internationellt antaget som ovan.
Kalkylkortet AGW
kalkylkortet nedan DIREKT FRÅN DEN
HÄR WEBBLÄSAREN AGW.ods — se
öppningsmanual
om ej redan bekant — eller kopiera
URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att
SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på
datorn)
http://www.universumshistoria.se/AaKort/AGW.ods

Tabell 1
Tabell
1 innehåller alla motsvarande kurvekvationer och deras resultat i
AGW-komplexets bevisblock: mata in aktuellt år, cellerna beräknar resultaten i
separat angivna resultatrutor.
Tabell 1-bloclet innehåller även en separat
del för den empiriskt
elementära hydroterm(odynam)ikens samband.
Tabell 2
Tabell
2 innehåller den konventionellt tillgängliga grundtabellen från
Carbon-Dioxide-värdena,
Tabellkälla (Okt2009) [ligger nära sist på källans webbsida]:
Atmospheric
CO2 concentrations (ppmv) derived from flask and in situ air samples collected
at the South Pole
http://www.mb-soft.com/public3/disaster.html
Tabell 3
Tabell
3 innehåller AGW-bevisets beräknade Carbon-Dioxide-värden i sammanställd
jämförelse med Tabell 2-data — med en utvidgad AGW-databas (fram till max
år 2030, se C-integralens
anpassning för tidsanaloga värden
i Originalförfattningen).
Tabell 4-6
Tabellerna 4-6 har lagts till (Nov2014) i samband med LavineffektenALARM och BioTermiska
Lavineffekten:
—
Tabell 4-6 innehåller Mauna Loa-kurvorna med koldioxidvärden till
illustrationerna.
Webbkällor
2010-08-11
BASDATA
— Havstemperaturer
Ythav,
termoklin [klin, mellanlutningsskikt],
djuphav
Havsoceanernas
årsglobala medeltemperatur är ca 17°C (–2°C polartrakterna, +36°C Persiska
Viken),
WINDOWS
TO THE UNIVERSE — Temperature of Ocean Water — 2001
http://www.windows2universe.org/earth/Water/temp.html
Flera
sammanställda klimatmätgrafer finns på NOAA:
(Alla finns med där, löpande uppdatering),
CLIMATE
INDICATORS — National Oceanic and Atmospheric Administration — National
Climatic Data Center, 2010
http://www.ncdc.noaa.gov/bams-state-of-the-climate/2009-time-series/?ts=ohc

Frihetsgrad,
eng. degree of freedom.
Termen frihetsgrad
används här i samband med molekylenergin i olika materialrum.
Generellt och konventionellt definieras
antalet (nF) frihetsgrader hos en molekyl som består av N atomer enligt
nF=3N=(xyz)N; Dvs., varje atom i gruppen associeras elementärt med sin egen
specifika rörelsefrihet i tre olika led (xyz) som vart och ett kan utveckla sin
specifika energi — rotation, vibration, och den vanliga translativa energin
(kinetiska energin via impulsen mv).
Se med fördel artikeln i svenska Wikipedia
för vidare beskrivning,
@INTERNET Wikipedia
Frihetsgrad, Molekyler 2010-08-20
http://sv.wikipedia.org/wiki/Frihetsgrad
Motsvarande engelska del finns (bl.a.) i
@INTERNET Wikipedia
Internal energy, Overview 2010-08-20
http://en.wikipedia.org/wiki/Internal_energy
Värmekapacitet, eng. heat capacity.
Enhet J/°K = J°K–1. Även värmekapacitivitetens
massprodukt.
Ett materials förmåga att
lagra värme, eller förmågan hos någon naturprocess att omsätta värme. Se t.ex. Boltzmanns konstant
(1,38 t23 J/°K) och fundamentala gaskonstanten (370,95002 J/°K).
Webbreferens, se bl.a.
@INTERNET Wikipedia Heat capacity 2010-07-21
http://en.wikipedia.org/wiki/Heat_capacity
Värmekapacitivitet, eng. heat capacitivity eller specific
heat capacity.
Enhet (J/°K)/KG = J°K–1KG–1.
Även värmekapaciteten per massenhet.
Ett materials förmåga att
uppvärmas med 1 °C per 1 KG material. Större kapacitetstal betyder större
värmetröghet och därmed också större värmelagringsförmåga per massenhet.
;
KARLEBO HANDBOK uppl12
s76.tab4.5 ger i sin tabell 4.5 för vatten värdena
J/KG°K ämne
1840 vattenånga
4190 vatten vid rumstemperatur
1940 is vid 0°C
;
Den äldre svenska
benämningen är specifikt värme.
Källan nedan (ämnestabell
i Wikipedia Heat capacity) ger till jämförelse för vatten värdena
J/KG°K ämne
2080 vattenånga
4181,3 vatten vid 25°, samma som flytande
vid 100°C
2050 is vid –10°C
att jämföra med
koldioxidens 839 (ingen specifikation utom ”derived by calculation”);
Se ämnestabell bl.a. i
@INTERNET Wikipedia Heat capacity, Table of specific heat capacities 2010-07-21
http://en.wikipedia.org/wiki/Heat_capacity
Se utförlig beskrivning i De 6 Komponenterna.
UnicodeStandard: TYPOGRAFIN I DETTA HTM-DOKUMENT HAR I DE FLESTA (MÖJLIGA)
FALL UTNYTTJAT DEN TILLGÄNGLIGA (men [ännu så länge]krångliga) TECKENSNITTSSTANDARDEN FÖR UNICODE SOM
FINNS KOMPLEMENTÄRT TILL SYMBOL-TECKENSNITTET FÖR DET KLASSISKA GREKISKA
ALFABETET SOM NORMALT ANVÄNDS I NATURVETENSKAPLIG LITTERATUR I OLIKA
MATEMATISKT-FYSIKALISKT BESKRIVANDE SAMMANHANG med typexempel Ω
Φ Σ Π Ξ Λ Θ Δ α β γ δ ε λ θ κ π
ρ τ φ σ ω ∏ √ ∑ ∂ ∆
∫ ≤ ≈ ≥ ← ↑ → ∞ ↓ . VISSA AV DESSA TECKEN UPPVISAR (med
den här presentationens allmänna teckensnitt och storlek Times New Roman 9)
EN NÅGOT SÄMRE REPRESENTATION ( t.ex. ett mindre tydligt pilhuvud, ett mera
otydligt rottecken, m.fl) OCH SOM GÖR ATT UNICODE-ALTERNATIVET (ännu)
INTE UTNYTTJATS FULLT UT. DET ÄR BARA WEBBLÄSARNA INTERNET EXPLORER OCH GOOGLE
CHROME SOM LÄSER SYMBOLTECKENSNITTET (MOZILLA VISAR t.ex. Ö för
rottecknet, etc.).
Effekt&Energi i AGW — sammanställning, alla kurvor —
AGW3 explicit som aktuell effekt nedan
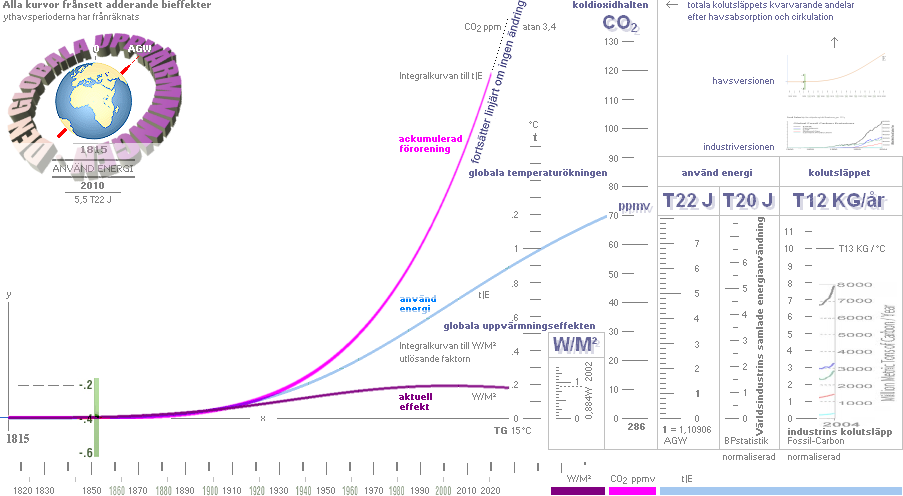
Normaliserade
vertikala | kurvskalor för Världsindustrins
samlade energianvändning och Fossil-Carbon-emissionerna. Normaliseringarna följer den mittre
blå t|E-kurvan, vilket innebär att alla
mindre variationer har frånräknats och ett förgrovat, utjämnat globalt
medelvärde erhållits analogt med Havsversionen av
Fossil-Carbon. Se även motsv. förminskn. i illustrationen
övre höger.
För CO2-kurvan (ackumulerad
förorening), se utförligt från GLOBALA
UPPVÄRMNINGSENERGINS INTEGRALKURVA. Se även från Carbon-Dioxide-kurvan.
För t|E-kurvan (använd
energi), se utförligt från AGW-beviset Del 1
— se även kort sammanfattning i AGW12.
För W/M²-kurvan (aktuell
effekt), se utförligt från AGW-beviset Del 3.
Se även Jämförelse
mellan AGW och Arrhenius samband, Jämförelse mellan IPCC och
AGW, samt Jämförelse mellan AGW
och Hansen 2005.
UnicodeStandard:
TYPOGRAFIN I DETTA HTM-DOKUMENT HAR I DE
FLESTA (MÖJLIGA) FALL UTNYTTJAT DEN TILLGÄNGLIGA (men [ännu så länge]krångliga) TECKENSNITTSSTANDARDEN FÖR UNICODE SOM
FINNS KOMPLEMENTÄRT TILL SYMBOL-TECKENSNITTET FÖR DET KLASSISKA GREKISKA
ALFABETET SOM NORMALT ANVÄNDS I NATURVETENSKAPLIG LITTERATUR I OLIKA
MATEMATISKT-FYSIKALISKT BESKRIVANDE SAMMANHANG med typexempel Ω
Φ Σ Π Ξ Λ Θ Δ α β γ δ ε λ θ κ π
ρ τ φ σ ω ∏ √ ∑ ∂ ∆
∫ ≤ ≈ ≥ ← ↑ → ∞ ↓ . VISSA AV DESSA TECKEN UPPVISAR (med
den här presentationens allmänna teckensnitt och storlek Times New Roman 9)
EN NÅGOT SÄMRE REPRESENTATION ( t.ex. ett mindre tydligt pilhuvud, ett mera
otydligt rottecken, m.fl) OCH SOM GÖR ATT UNICODE-ALTERNATIVET (ännu)
INTE UTNYTTJATS FULLT UT. DET ÄR BARA WEBBLÄSARNA INTERNET EXPLORER OCH GOOGLE CHROME
SOM LÄSER SYMBOLTECKENSNITTET (MOZILLA VISAR t.ex. Ö för rottecknet,
etc.).

BILDKÄLLA: Författarens arkiv · Bild100R ·
24Maj2010 · NikonD90 · Detalj
2010VII19
AGW-BEVISETS
SLUTFORM
NASA(CRU)-Kurvkomplexets ekvivalenter
— saknar naturlig motsvarighet
;
Motsvarigheten
för NASA(CRU)-kurvan via De 6 Kurvkomponenterna är ett helt unikt matematiskt samlingskomplex för AGW — antropogent förorsakad
global uppvärmning. Det finns ingen motsvarande naturlig ordning som kan bilda
ett sådant sammanhängande matematiskt kurvsystem [‡].
;
Den
enda naturliga agent för klimatvariation som vi känner är Solen. Men Solens
redan väl kända, relativt dels ringa, variationer (0,1%)[‡] i
energiflöde med en period på 11 år kan dels inte heller förklara den
observerade systematiska temperaturökningens kurvform och utsträckning, t|E-kurvan,
som tillsammans med de möjliga ythavsperioderna väl överensstämmer med den uppmätta NASA(CRU)-temperaturkurvan. Variationerna på 0,1% räcker inte som någon övergripande
motvikt till den redan koldioxidkända globala temperaturvariabeln (0,4%, se Kontrollräkningens resultat). Den i vissa kretsar omnämnda (Solkontrollerade)
KOSMISKA
STRÅLNINGEN är också i
motsvarande effektform alldeles för liten i sig (0,00000000064%, se Kosmiska strålningens energi), vilket i sig utesluter just den kosmiska strålningens
fenomen som någon övergripande orsak till den globala uppvärmningen.
;
Solens
naturliga variationer bortfaller därmed som möjlig orsak till den observerade
uppvärmningen.
;
Men
Solen anställer heller inte, vad vi vet, bergborrningar för upphämtande av
fossila bränslen att elda med under Solen.
;
Utöver
Solen finns sedan och således ingen ytterligare möjlig variationskälla — utom
människan.
;
BEVISET
för att endast människan så kan åstadkomma den observerade sammansättningen med
De 5 Kurvkomponenter som tydligen matchar den uppmätta sjätte komponenten NASA(CRU)-temperaturkurvan med den konstanta Soleffekten (P) som försörjande energibas på industrins anställda Fossil-Carbon-emissioner, är det enkla faktumet att termiska motståndets bidrag
på R(=t/P) från
fossilsläppets resulterande CO2-komponent kompletteras via ett lika stort
värmetillskott t/P(=R) från själva fossilförbränningen (T) [Se
utförligt från ENERGIN TILL AGW]: bara människan kan åstadkomma den unika
dubbelkopplingen t|R [Se utförligt från GRUNDSAMBANDET] eftersom, som nyligen påpekades, Solen inte anställer,
vad vi vet, bergborrningar för upphämtande av fossila bränslen att (T) elda med
under Solen.
GRUNDSAMBANDET t = Ta(m/M):
Finns
ingen fossil förbränning [T~2200 °C] kan T inte heller bidra med någon
materialinförsel, vilket är liktydigt med att sätta T=0 som leder till t=0;
ingen ändring.
Naturliga CO2-variationer, samt övriga,
avhandlas alltså och tydligen på en helt annan matematisk fysik och som
uppenbarligen helt saknar varje koppling till AGW.
AGW-BEVISETS
SLUTFORM END.
END.
innehåll: SÖK på denna
sida Ctrl+F · sök alla ämnesord
överallt i SAKREGISTER · förteckning över alla webbsidor
AGW-beviset
ämnesrubriker
innehåll
De 6 Kurvkomponenterna
Problem 1 — DELVIS samhörande
effektvärden
Problem 2.1 — Forskarkretsar
rapporterar underliga resultat
Problem 2.2 — Effektens variation
överlagrad på havsperioden
Problem 3 — Havsenergins skala
referenser
250 W/M² Medelvärdet
för Solinstrålningseffekten på Jordytan per kvadratmeter;
@INTERNET Wikipedia Insolation Earth’s insolation 2010-07-17
http://en.wikipedia.org/wiki/Insolation
T(fossil) Uppgifterna
för T i det fossila kolutsläppet via kol-olja-naturgasförbränningen är
T(Kol) ~ 2200 °C, T(Olja) ~ 2150 °C, T(Naturgas) ~ 2000 °C; ref.,
@INTERNET Wikipedia Combustion, Temperature 2009-09-30
http://en.wikipedia.org/wiki/Combustion
TG Jordytans
globala årsmedeltemperatur är enligt uppgift på webben ca 15°C = 288°K.
Ref. 2009-03-17 | 2010-07-25,
NATIONAL OCEANIC AND ATMOSPHERIC ADMINISTRATION — Global Mean Monthly Surface
Temperature Estimates for the Base Period 1901 to 2000;
http://www.ncdc.noaa.gov/oa/climate/research/anomalies/index.php
Källans tabellvärden perioden 1901-2000 ger
medelvärdet 15,016 °C ~ 15°C =
288°K med 0°C=273°K (eg. 273,15);
2010-07-25: URL-adressen
ovan kopplar inte längre, ersatt av
http://www.ncdc.noaa.gov/cmb-faq/anomalies.html
RHTGM Allmän uppgift om globalt
generaliserad maximal vattenhalt i luft (max 4%) vid Jordytan finns i källan
nedan;
@INTERNET Wikipedia Atmosphere of Earth,
Composition, Water vapour 2010-07-27
”typically 1%-4% at surface”,
http://en.wikipedia.org/wiki/Atmosphere_of_Earth
Se även @INTERNET Wikipedia Water vapour 2010-07-27
Ett diagram visar vattenångans mättnadsgrad vid
olika temperaturer (vid havsytan)
Källan
redovisar dock ingen referens till den uppgiften — men den kan kontrolleras genom att studera
statistik över högsta uppmätta temperaturer på Jordytan, se exv.
Part of Family Education Network (2009) — HIGHEST
RECORDED TEMPERATURES
http://www.infoplease.com/ipa/A0001375.html
([Landområde+OceanOmråde]/2=50°C) och därifrån beräkna motsvarande
luftfuktighet (se Kalkylkortet)
via de empiriska sambanden för vattenångtryck [‡]
(45°C med 74% luftfuktighet ger 4,02%). Resultatet visar att uppgiften är
tämligen välgrundad som ett globalt allmänt generaliserat maxvärde vid
nuvarande globalmedeltemperatur TG=15°C.
Radiativ kraft från eng. radiative force|forcing
— i den här framställningen en bekväm term att använda GENERELLT synonymt med
(strål-) intensitet, W/M².
Termen RADIATIVKRAFT(ning) kommer ursprungligen från klimathistoriens IPCC-begrepp, se
@INTERNET Wikipedia Radiative forcing 2010-08-22
http://en.wikipedia.org/wiki/Radiative_forcing
Termen användes ursprungligen INTE för att uttrycka intensiteten
(W/M²) som sådan, utan enligt IPCC
som mått på
”The radiative forcing … is the change in net (down minus up) irradiance (solar plus long-wave; in Wm–2)
at the tropopause AFTER allowing for stratospheric temperatures to readjust to
radiative equilibrium”,
sv. ändringen i netto (ner minus upp) irradians (Solär plus långvåg; i W/M²)
vid tropopausen EFTER medgivet utrymme för stratosfäriska temperaturer att
återställa strålningsjämvikt.
Dvs., som själva intensitetens (påtvingade, eng., forcing) ändring, inte
intensiteten som sådan. Alltså, i syfte att klassificera olika
globaltemperaturändrande agenter.
Termen används generellt i samband med beskrivning av uttryck som kopplar till
typ Arrhenius samband.
Jämför
”ΔF
= α ln(C/C0), where F is radiative forcing, α is 3.75 W/m2, C is atmospheric CO2
concentration, and C0 is the pre-industrial level of 280 ppm.”,
PHYSICS SOCIETY Vol.39No1 January 2010, s7sp1n
http://aps.org/units/fps/newsletters/201001/upload/january2010.pdf
Radiativkraften får en unik svensk
innebörd — alla strålkällor utvecklar radiativ kraft (F=am=aE/c²=ahf/c²=hf/cdT, radiativkraften proportionell mot
strålfrekvensen f)
Genom att strålningsintensiteten (W/M²)
generellt uppvisar en strålningsmässig kraft
— svenskans direkta ord för engelskans force, snarare än påtvingande
(vilket ändå tydligen är det engelska ordvalets ursprungliga syfte) — har vi
fått ett nytt (helsvenskt), mera kraftfullt begrepp (eng, »rayForce»)
som synonym till det mera ljumma strålintensitetsbegreppet.
Jämför SOLÄR RADIATIVKRAFT: vi förstår direkt att det handlar om
Solstrålningens praktiska inverkan — som också innebär en värmetvingande (eng. forcing)
faktor.
Så kan — således — termen radiativkraft (radiativ kraft) användas
i flera bemärkelser, utan någon egentlig risk för sammanblandning;
Radiativkraftning blir den direkta engelska motsvarigheten som radiative
forcing, medan radiativkraft|kraften
som sådan hamnar i synonym med intensitetsbegreppet som sådant, alltså (värme-)
effekt (P) per ytenhet (A). Hela ordformen (termen) radiativkraftning
som sådan används inte explicit i den här framställningen, utom i den här
artikeln.
AGW eng. Anthropogenic
Global Warming, sv. Antropogen [av människan förorsakad] Global
Uppvärmning,
ref. @INTERNET Wikipedia Climate change 2010-07-17,
http://en.wikipedia.org/wiki/Climate_change
BA BONNIERS ASTRONOMI
1978, Albert Bonniers Förlag AB, Stockholm 1978
CRU eng. Climatic
Research Unit, sv. Klimatiska ForskningsEnheten
http://www.cru.uea.ac.uk/
t|T förenklade
exponentbeteckningar; t för 10^–, T för 10^+.
EXEMPEL: t10 = 10–10 = 0,000 000 000 1; T3 = 103 = 1 000.
relaterad
fysik Alla,
samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och
begripliga, eller så inte alls.
Grundpremissen i den relaterbara
fysikbeskrivningen är att varje avgörande detalj ska vara återförbar på den
elementära grundskolefysiken tillsammans med den tillhörande elementära
matematiken, de allra mest elementära grundbegreppen, utan mellanliggande led
som kräver typ universitets- och/eller högskolemeriter för att kunna förstås
eller beskrivas. Nämligen för ändamålet att alla läskunniga människor ska ges
en garanterad chans att förstå och kunna hänga med i det detaljerade
sakinnehållet per grundreferenser som alla garanterat har omedelbart tillgång
till (på Webben) utan särskilda kostnader eller andra besvär.
RELATERAD FYSIK betyder (således)
generellt varje framställning som innefattar (eller eftersträvar att söka
innefatta) en fullständig beskrivning, förklaring och genomgång av ett
naturvetenskapligt ämnes olika sakdetaljer, utan mellanliggande led som saknar
allmänt begripliga kopplingar, eller om sådana är uppmärksammade, strävar att
ge en tydligt begriplig beskrivning av karaktären eller egenskapen hos sådana
ofullbordade argument på grundbegreppens kredit.
UTVIDGAD ORDLISTA — AGWbeviset.htm 2010
AGW (Anthropogenic Global
Warming), antropogent förorsakad global uppvärmning
AGW-beviset enligt
relaterad fysik
AGW-beviset Del 1
AGW-beviset Del 2
AGW-beviset Del 3
Den globala uppvärmningen
Värmekapacitet
Värmekapacitivitet
Havets uppvärmning
Stefan-Boltzmann-Approximationen,
AGW-effektens linjära approximation
Jordytans termiska
resistans
Termisk resistans
Kosmiska strålningen,
energiandelen på Jorden
Senast uppdaterade version: 2016-01-06.
*END.
Stavningskontrollerat 2010-08-25.
*
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se
UPPDATERAD
VERSION FRÅN 2010-05-29 — Totala Soleffekten räknas med kärndelen för sig (26,7
MeV) och skaldelen för sig (2,04 MeV) per bildad Helium4.
UNICODE ofta använda
Symboltecken i naturvetenskapliga sammanhang
σ ρ ν ν π τ γ λ η ≠
Ω Φ Σ Π Ξ Λ Θ Δ α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓
PNG-justerad 2011-06-25
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se