BLIXTURLADDNINGENS FYSIK | 2003IX22 | 2008VI18 |  a BellDHARMA production  |  Senast uppdaterade version: 2018-06-21 · Universums Historia

 

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

Positronbollen | MAC/TNED | BLIXTURLADDNINGENS FYSIK | Stegad ledare | Blixtbanans bildning | Urladdningen | Molnspänningen | B-styrkan | Grundräkning | ATA | Gränsspänningen

 

 

I detta htm-dokument:

 

BLIXTKANALEN ENLIGT TNED

Grunderna i Blixturladdningens Fysik enligt TNED 2008

 

 

JAVKbasic | FlaskExperimentet | FlaskExpeditionen

MOLNBILDNINGENS TEKNISKA FYSIK | Värmeläckningen | ATFT | PDAS

AdiabatBegreppet

 

Blixturladdningen — fördjupad fysik | 2014

 

LADDNINGSBILDENS UPPKOMST

Jordströmmen | Jordfältet | Laddningstransporten | Atmosfäriska Vattenbildningen

Kelvinekvationen

 

 

 

 

 

 

 

 

 

BLIXTURLADDNINGENS FYSIK | ComplATACAT2008 | MPcPb |

 

Kort inledande sammanfattning — blixturladdningen enligt relaterad fysik — mera utförligt från BLIXTBILDNINGEN

 

 

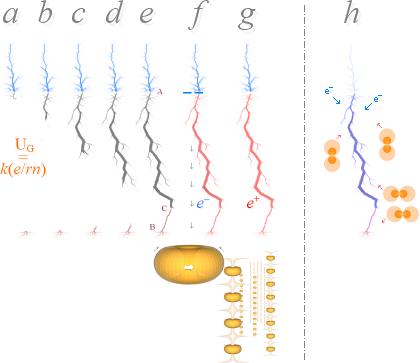
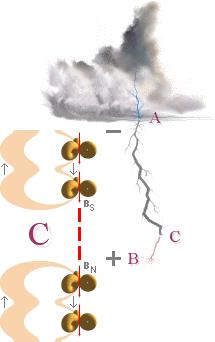
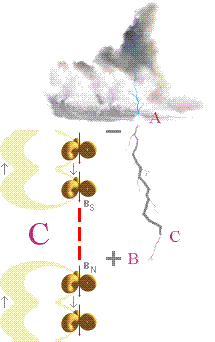
a    Från en negativt elektriskt laddad molndel bildas första tråden till en stegad ledare mot marken om spänningen moln-mark överstiger gränsspänningen (UG).

b    Den stegade ledaren avancerar neråt marken i medelsteg om ca 50 meter genom en lysande spets som flashar ungefär under 1 µS per steg. Förloppet hinner (knappast) uppfattas med ett obeväpnat öga. Stegledarens medelhastighet mot marken ligger i storleksordningen 0,1-1 T6 M/S.

c-d Med luftrummet som det snabbare mediet och markrummet som det trögare, utvecklas ledartråden från molnet i snabbare takt än (flera) motsvarande marktrådar som söker sig upp mot den nedkommande ledaren i strävan att förena sig med denna.

e     När molntråden befinner sig inom ett visst näravstånd till en närliggande marktråd, som varierar i stort mellan 10-50 meter beroende på markföremålets form och därmed elektriska fältstyrka, sker en plötslig (ännu 2008 odokumenterad) koppling mellan trådändarna.

f     ENLIGT TNED har därmed en atomärt kopplad centralstam bildats; stammen består av luftatomer förenade på gemensamma kärnspinn; Stammen bildas av föreningsarbetet UGQ som underhåller ljusflasharna i stegbildningen; En med de neutrala luftatomerna sammanhållande elektronmassorna ekvivalent kraft bildar en samlad magnetisk fältstyrka i trådänden, som gör att ändarna från moln och mark kan dras mot varandra. Centralstammen kännetecknas genom atomens förlustfria natur av nollresistans och nollinduktans;
   Då kopplingen sker i punkten C (se e) dras omedelbart den elektronström ner i marken vid B som anvisas av laddningstryckets initiering i molnladdningen (Q) ovanför startpunkten A i e. Därmed neutraliseras markens positiva del, samtidigt som den nollresistiva ledningen garanterat bränns av mot molnet uppe vid A.

g    Därmed utarmas (e+) blixtstammens atomagenter på sin elektronbesättning (e–); stammen bildar ett plasma (idealt fullständigt joniserade atomkärnor). Effekten blir en enorm aktivitet i luften omkring blixtkanalen;

h    Molnet tömmer sin laddning neråt och vanliga luftatomer dras inåt-uppåt mot blixtstammen för att fylla på det starka elektronunderskottet. Det är själva blixturladdningen vi ser.
   Påfyllning med elektroner från molndel och luftdel kan ske i sekvenser motsvarande påfyllningen av stamagenternas elektronskal (vilket leder till att stammen flashar). Även flera urladdningar kan ske på samma stam om molnområdet uppvisar ytterligare laddning med motsvarande markspänning.

 

 

 

Den ovan beskrivna blixtbildningens teori finns bara delvis i modern vetenskap och akademi.

Följande presentation förklarar varför.

 

 

 

Experimentellt bekräftade Grunddata för stegade ledaren

 

parameter

värde

enhet

 

medelsteglängd 

50

M

Meter

tidsintervall mellan steg

20-50

µS

mikroSekund

stegström

>1000

A

Ampere

stegladdning 

>0,001

C

Coulomb

medelutbredningshastighet

2 T5

M/S

Meter/Sekund

genomgående varaktighet

0,035

S

Sekund

medelström

100-200

A

Ampere

total laddning

5

C

Coulomb

elektrisk potential

~50

MV

MegaVolt

kanaltemperatur

~ 10 000

°K

grader Kelvin

 

Efter boken

LIGHTNING Physics and Effects 2007, Vladimir A. Rakov, Martin A. Uman, s7

Boken finns (i varje fall 2008-06) att läsa på Google Böcker @INTERNET med begränsad åtkomst

 

 

 

TNED/MAC

Huvudlinjer i beskrivningen av och förklaringen till blixtbildningens fysik

HUVUDSKILLNADER MELLAN MAC OCH TNED

MAC förkortar Modern ACademy, modern akademi,

TNED förkortar Toroid Nuclear Electromechanical Dynamics, Toroidnukleära Elektromekaniska Dynamiken och motsvarar relaterad fysik. Grunderna i TNED ges från ELEKTRISKA LADDNINGENS HÄRLEDNING och PLANCKRINGEN, analogt Atomkärnans härledning, samt i Atomtriangeln och Nollformsalgebran. HÄRLEDNINGAR och GRUNDER i och till Atomkärnan, Atomtriangeln och Nollformsalgebran ingår inte i MAC.

 

MAC                            elektroner;
man erkänner öppet (2007) att man inte förstår hur orsaksgrunden är funtad, se referens

 

STEGADE LEDAREN materialbas | orsaksgrund:

 

TNED                           vanliga luftatomer;
stegbildningen initieras om spänningen moln-mark överskriver gränsspänningen för kemisk bindning;
denna är inte känd i MAC på grund av oförmågan att härleda atomkärnan, se utförligt från Planckringen och Elektriska Laddningen, om ej redan bekant

 

MAC                            korta stötströmmar av okänt upphov
under ca 1µS om ca 1000 A hos spetsens medelelektronbesättning 1 mC se grunddata

 

STEGADE LEDAREN energin till ljusflashen i ledarens framände | orsaksgrund:

 

TNED                           arbetet E=UGQ som utförs i induktionseffekten;
Då atomstammens elektroner kopplas upp på gemensamma trådmolekyler genom gränsspänningen UG för de successivt bildade stegen, utförs ett föreningsarbete på varje atoms samtliga ingående elektronmassor, arbetet garanterar elektronmassornas bindningar i det nya tillståndets kemiska koppling;
Exempelräkningen ger för en luftbaserad 10mM grov stam strömstyrkan drygt 700 Ampere som kopplingsflashar under ca 1 µS varje 50 meter

 

MAC                            omnämnande har eftersökts men ännu ej hittats;
induktionen från negativ laddning motsätter sig varje förklaring

 

STEGADE LEDAREN egenskapen att attrahera en motsvarande bildad marktråd för förening | orsaksgrund:

 

TNED                           magnetiska fältkraftens elektriska elektronekvivalent; FBT = –FeZ
den summeras på alla ingående förenade atomer i luftpelarstammens ledarände: föreningskraften är magnetisk, inte elektrisk;
Resultat från grov översiktlig exempelräkning:
Magnetiska kraftekvivalenten i stegledarens nederände attraherar självtyngden av en 5 meter lång luftkanal med grovleken 10mM över distansen 100 meter — om den initierande spänningen moln-mark över typdistansen 7 KM är större än eller lika med 25 MV

 

MAC                            i allmänhet ytterst komplicerade framställningar

 

STEGADE LEDAREN allmän matematisk fysik

 

TNED                           enkla elementära grundsamband

 

 

 

blixturladdningens fysik

 

Med fortsättning från Atomkärnans härledning

Blixturladdningens Fysik — enligt TNED

 

I fortsättning från Atomkärnans härledning

STEGCELLENS BILDNING

GNISTURLADDNINGENS FYSIK ENLIGT TNED

 

 

 

Genom atomens bägge impuls och kraftekvationer

 

J0K+3J1K           = 0  .............     impulsekvationen

FBT+FeZ            = 0  ..............    kraftekvationen (ström- och kemiekvationen)

 

kan i princip hur många atomer som helst förenas (även i fusionsled) i bevarad kraftbalans enligt

 

(FBT+FeZ )1+(FBT+FeZ)2+(FBT+FeZ)3+…+(FBT+FeZ)n               = 0

 

Atomen behöver ingen påfyllning för att fungera: atomen summerar nollmoment och nollkraft med nollresistans och nollinduktans: atomen är fullständigt förlustfri.

 

   Två närliggande atomer förenas via gränsspänningen (UG) genom att gemensamt dela på elektronmassorna. Avkänningen för kraftekvationen per atom överförs analogt på varje atomkärnas enskilda kärnbrunn i gemensam delning med alla övriga ingående kopplade atomers atomkärnor.

 

Atomkärnan enligt TNED

 

 

atomkärnan

kärnan antydd med första underfraktalens spinn

atomkärnans fullständiga kraft och momentbeteckningar

 

 

 

N3m20

J0K+3J1K = 0

grundparametrar enligt TNED

 

 

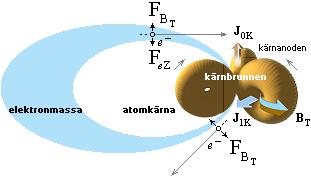
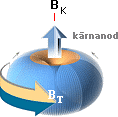
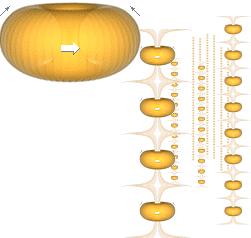
ATOMKÄRNAN ENLIGT TNED ILLUSTRERAS OVAN vänster sådan den ses av en annan atomkärna (på nära håll), i mitten med första underfraktalens tvärställda ringspinn delvis antytt (de tre inre ringdäcken som är avgörande för atomkärnans rent matematiska fysik enligt PLANCKRINGEN), till höger förtydligat med samtliga grundbeteckningar ENLIGT TNED. Notera att flera samtidiga spinn är en omöjlig makroskopisk modellform, märk den delen väl. Se mera utförligt från Atomkärnans härledning.

   Den utfällda ”blå vingen” ovan till höger markerar mycket förenklat atomkärnans omgivande elektronmassa. I verkligheten kan ”vingen” anta högst avancerade formfigurer (s.k. orbitaler) kring sin moderkärna. Kärnan avkänner hela tiden exakt balansräkning via kärnbrunnen genom de bägge ovannämnda atomens två kungsekvationer. De finns inte i modern akademi. Se vidare från PLANCKRINGEN.

   Figurdelen ovan höger visar också riktningsreferenserna för hur en luftatoms atomkärna måste ställa in sig i sin spinnriktning för att ENLIGT TNED matcha kopplingen mot ett negativt laddat moln (överskott på elektroner) som befinner sig överst med den positivt laddade markens motsvarande elektronunderskott underst.

 

 

 .

 

 

 

Elektronmassans bindning till atomkärnan definieras (klassiskt) genom de fem kvanttalen

n q st µt Ft se utförligt i Spektrum och Kvanttalen.

Elektronelementet (t, tau) grundlägger härledningarna till kvanttalen ENLIGT TNED, men t-ringen ingår inte i modern teori (men gjorde det ett tag i form av de ”vibratorer” som Heisenbergs och Schrödingers berömda ekvationer från omkring 1925 byggde på men som förkastades år 1927 efter en uppsats av Heisenberg då de inte ansågs vara förenliga med relativitetsteorin [källa TRETTIO ÅR SOM SKAKADE FYSIKEN George Gamow, Prisma 1968, s104]). Elektronmassan kan anta olika resonanser kring atomkärnan — motsvarande olika mönsterformer, se exemplet med vattenvågorna i härledningen till Periodiska systemet — vilket också betyder att elektronmassan delvis kan skymma och delvis blottlägga den positivt laddade atomkärnan inne i elektronmolnet. Genom den koppling som bildas mellan elektronhölje och moderkärna uppkommer dessutom precession; både atomkärnan och elektronmassan svänger omkring ett gemensamt medelplan på samma sätt som ett snurrande mynt på bordet kränger just när det är på väg att lägga sig. Detta grundlägger dels olika magnetiska kopplingar och dels olika elektriska kopplingar som kännetecknar dels olika atomer för sig och dels deras olika föreningar inbördes. Enkla exempel i Periodiska systemet visar hur olika atomer inbördes strävar att gemensamt fullständiga varandras delvis ofullständigt fyllda elektronresonanser genom s.k. kemisk förening. Därmed introduceras också begreppet dipol som är centralt i alla, samtliga, kemiska, molekylära föreningar; varje atom uppvisar i princip en polaritet, en väl definierad riktning i elektriskt-magnetiskt flöde mellan ena änden och andra änden. Dessa flöden kan anta ett otal mönsterformer eller s.k. resonanser (stående vågmönster) i alla fasta kopplingar.

   För att räkningen för atomkärnans del ska stämma enligt föregående omnämnda grundsamband med atomens två kungsekvationer, måste ovillkorligen kraftbalansen mellan elektronmassans element och atomkärnan stämma exakt mellan magnetismen och elektriciteten,

 

FBT+FeZ = 0

 

Genom neutronens sönderfall avdelar atomkärnan EKVIVALENT elektronmassa (e) som en utvidgning av atomkärnan i formen av atomen. Eftersom e är del i kärnspinnet, måste också det motsvarande e-spinnet bevaras eftersom atomkärnan är förlustfri — vilket innebär att den elektriska attraktionen mellan kärna och ekvivalent frigjord elektronmassa (FeZ) tvunget måste balanseras av en lika stor motriktad magnetisk kraft som associeras med atomkärnans toppspinn (BT). Därmed är balans och jämvikt säkrad.

   I modern vetenskap och akademi finns inte atomkärnans härledning med, och därmed heller inte ovannämnda sambandsgrund. För att försöka förklara kraftverkan i de olika kemiska bindningarna måste man därför i modern akademi tillgripa olika statistiska modeller som alla och i vilket fall måste bygga på de ovan antydda möjliga fältförskjutningarna mellan elektronmassa och atomkärna.

isolator och massledare

 

isolator

massledare

 

 

sluten elektronkrets

öppen elektronkrets

 

 

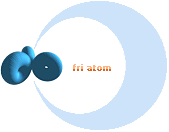
Illustrationen ovan visar de två principiellt möjliga atomformerna:

Vänsterdelen visar den normalt slutna enskilda atomen;

Högerdelen visar hur den enskilda atomens elektronmassa (här) är uppbruten i delning med (en eller) flera andra atomers elektronmassor, enligt kraftekvationen

 

(FBT+FeZ )1+(FBT+FeZ)2+(FBT+FeZ)3+…+(FBT+FeZ)n               = 0

magnetiska kraftekvivalenten

KRAFTEKVIVALENTEN

FBT        = –FeZ

innebär att varje elektrisk atomär koppling — varje molekylär förening — OCKSÅ måste vara balanserad av en motsvarande MAGNETISK koppling — eftersom atomen i netto är förlustfri.

   Enligt TNED bestäms grundvillkoret för kemisk koppling av gränsspänningen UG. Gränsspänningen UG bygger på just t-ringens koppling till atomkärnan, inte hela elektronkvantat. Men, som nyligen påpekades, ingår inte t-ringen (längre) i modern uppfattning — och undgår därför också den modern akademins kvantitativa kännedom — trots dess enkla (elementära) härledning.

   Gränsspänningen är gemensam resurs för alla atomer men beror av deras medelavstånd;

För luft med medelavståndet 3nM mellan luftmolekylerna gäller enligt TNED

UG        =  5,4 µV

ARBETET som utförs på syreatomens åtta elektronmassor genom UG blir

E           = UG(Z=8e=1,602 t19 C) = 6,92064 t24 J

eller direkt i elektronvolt (efter division med e=1,602 t19 C)

E           = 0,0000432 eV

eller i KiloJoule/mol (division av E i Joule med 1,66033 t21 KG som är atomära massenheten u gånger en miljon, termen mol betyder ”per Avogadros tal” som är inverterade värdet av atomära massenheten u dividerat med 1000 vilket görs för att få moltalet i motsvarande gram; mol heter då egentligen gram-mol),

E           = 0,00416823 KJ/mol

 

Till konventionell jämförelse anges de allra svagast verkande bindningskrafterna mellan molekyler (de s.k. Van der Waals krafter) med typiska värden

E           = 0,5-5 KJ/mol;

Källa @INTERNET: DISTANSGYMNASIET KEMI 1,

[http://www.edu.fi/svenska/distansgymnasiet/kemi/kemi1/5.shtml] kronologisk specifikation saknas (tidigast från 1999-2008).

 

FöreningsEnergin från UG är alltså

minst hundra gånger svagare.

 

Det finns en historisk koppling hit också: tiden det tog för de primitiva aminosyrornas bildning att — genom den MYCKET svaga kemikopplingens kraft — blott så småningom kunna bilda den känsliga men avgörande DNA-strukturen, som bygger just på proteiner, som i sin tur bygger på aminosyror. För att det ska kunna ske, krävs extremt långa tidrymder med (på sina ställen) extremt stabila förhållanden (under miljardtals år) där minimala störningar kan garantera en maximalt kemisk-elektrisk-magnetisk dynamik med minsta möjliga kraftverkan. Men det är (ännu så länge) bara min uppfattning.

 

MAXKRAFTEN som KAN utvecklas med grund i UG mellan två syreatomer

— observera detta särskilt för undvikande av missförstånd, eftersom den kraften som nyligen påpekades måste balanseras av en motsvarande magnetisk kraft och som innebär idealt att ingen kraft alls kommer att verka

— fås direkt ur elektriska kraftlagen enligt

F           = k=9 T9 VM/C(Z=8e=1,602 t19 C/d=3 t9 M)2 = 1,64249 t9 N

vilket motsvarar tyngden av 0,0000161129 gram med Jordytans lokala gravitationsacceleration a=9,81 M/S2

eller med multiplikation av d=3nM lika med energin 4,92747 t18 J, eller drygt 30 elektronvolt.

   EKVIVALENTEN för samma magnetiskt balanserande kraft — och som, i jämvikt med den elektriska attraktionen, idealt håller elektronmassorna på plats kring moderkärnan — blir alltså för syreatomen samma 1,64249 t9 N.

 

Vi skulle kunna misstänka att det är samma värdeform som sammanhänger med den s.k. atomära bindningsenergin för syreatomens elektroner. Enligt tabell (Se @INTERNET Wikipedia Ionization energies of the elements 2008-06-22) krävs emellertid runt 840 eV för att frigöra den innersta hårdast bundna elektronen från moderatomen, vilket är nära 30 gånger mera än de 30 eV vi nyligen erhöll för den ekvivalenta elektriska-magnetiska kraftvägen (30 eV räcker bara för att frigöra elektron nummer två i Syret). Vi kan likna den detaljen vid försöket att ”frigöra” en sten från Jordens dragningskraft genom att kasta upp den en bit; Resultatet blir bara att den ramlar ner igen. För att frigöra den (så att den inte längre dras tillbaka alls), krävs betydligt mera energi. Kraftvärdet är alltså bara just en jämviktskraft.

   Vi kan — därför — heller knappast se att F får någon nämnvärd betydelse i de normala sammanhang som berör enskilda (icke joniserade) atomers växelverkan och deras föreningar.

 

 

 

I ekvivalent kvantitet kraft

samverkar alla förenade atomer med sina enskilda bidrag till en samlad verkan.

 

 

Saken ställer sig annorlunda om flera atomer samverkar genom ett yttre pålagt elektriskt fält (>UG) som överskrider gränsspänningen — och som därmed ENLIGT TNED teoretiskt KAN koppla ihop flera atomer på rad i harmoni (synkroniserad koppling) med deras inbördes spinn — och därmed i harmonisk flödessamverkan med de gemensamt delade elektronmassorna — också än vidare i magnetiskt gemensam koppling. Där blir det alltså mera uppenbart att F-formen får en mera signifikant ställning:

  Vi behöver ALLTSÅ här ENDAST söka en ekvivalent kvantitativ form för att undersöka om verkan via F kan vara den förklaring vi söker i naturfenomenet, vilket vi strax ska återkomma till.

   OM F per syreatom samverkar i ett cirkulärt tvärsnitt med diametern 1mM som med medelavståndet 3nM mellan luftmolekylerna innebär runt 1,11 T11 syreatomer, och OM den millimetertråden antas tillhöra en s.k. stegad ledare som vi ska beskriva mera ingående i den löpande texten, då är det tydligt att F i den samlade änden i det gemensamma planet beläget idealt ca 3nM från atomkärnorna, ur den tråden KAN uppvisa en motsvarande magnetisk kraft på

 

F· 1,11 T11 = 182,3175 N

 

Det motsvarar tyngden (182,3175 N)/(9,81 M/S2)=18,58 KP (KiloPond) — grovt sett en back dricka.

Eller — om tvärsnittet ökas till 10mM —

 

F· 1,11 T13 = 18231,75 N

 

som ger tyngden avrundat 1858 KP vilket motsvarar tyngden av en större personbil;

 

Ekvivalenter är ekvivalenter. Och som nyligen påpekades, behöver vi (i det här skedet) inte forska något djupare i den detaljen för att jämföra med motsvarande experimentellt funna värden.

 

Om magnetiska fältstyrkan (B) antas avta som funktion av distansen via 1/d — vilket också är den normala kraftverkansbilden för magnetismen — kan vi skriva en allmän grovform för uppskattning av kraftverkan på avståndet d från referenspunkten 3nM utanför trådändens samlade magnetfält enligt (vi sätter F0=18231,75 N)

 

F = (F0/d)(3nM)

 

Med d=100 meter ges då via Ø10mM-tråden

F = (18232)(3 t9 M)/(100 M) = 5,47 t7 N avrundat.

Uttryckt i grampond [samma som milliPond, mP] (division med 9,81 och sedan multiplikation med 1000) ges

F = 0,0000557594 mP = 5,57594 t5 mP

vilket alltså motsvarar tyngden av 0,0000557594 gram här på Jordytan (a = 9,81 M/S2);

 

Syre har tätheten r = m/V = 1,43 KG/M3;

 

5M luft med tätheten rLUFT=1,43 KG/M3 (här förgrovat med hjälp av värdena för syrgas) med cirkulära tvärsnittet 2×0,05 mM (ungefär som ett hårstrå) innehåller då volymen V=h·pr2 = 3,92699 t8 M3 med atommassan

m = rV = 5,61559 t8 KG eller 0,0000561559 gram

— vilket är nära samma som krafttyngden ovan; (5,47 t7 N)/(9,81 M/S2)=5,57594 t8 KP.

 

Krafttyngden av den grovt hoftade B-verkan på 100 meters avstånd från den aktuella molntrådledaren med diametern 10mM kan teoretiskt (med den här genomförda grovberäkningen) helt säkert få en 5 meter lång motsvarande uppbyggd men med mycket smalare kanal markbildad syretråd att svara på sitt starka B-fält genom att lägesändra för att söka en förening.

 

Resultat:

100 meter magnetiskt attraherande avkänning på egen tyngd för en 5 meter lång markluftkanal med 0,1mM diameter.

 

Med vissa reservationer är det också i stort dessa nu beskrivna storleksrelationer som återkommer i den konventionella beskrivningen av hur den stegade ledaren möter sin markmake — dock utan de teoretiska grunder som givits ovan enligt TNED: ämnet i konventionell teori är erkänt svårt, och ingen kan förklara ämnet ens behjälpligt.

   När den stegade ledaren kommer inom området (något hundratal meter från marken, men den distansen kan variera mycket beroende på fältstyrkan, t.ex. från spetsiga föremål, och därmed ge relativt vida avvikelser), börjar lufttrådar (svagt lysande på grund av jonisationseffekter, se vidare längre fram) sträcka sig uppåt mot ledaren från de markobjekt som uppvisar den största elektriska fältstyrkan mot den annalkande molnledaren.

 

Ett tydligt fotografi på en oavslutad marktråd visas på Discovery Channel i samband med en videopresentation

[http://videos.howstuffworks.com/discovery-channel/...]03:16

Discovery Wonders of Weather: Lightning Phenomena

 

När molnledaren möter en av marktrådarna, sker den egentliga urladdningen.

Det ska emellertid här också framhållas med referens till en av de senare skrivna böckerna i ämnet

 

ref.

LIGHTNING Physics and Effects 2007 Vladimir A. Rakov, Martin A. Uman, s111s137sp2n

 

att den slutliga föreningsprocessen mellan molntråd och marktråd är en av de delar man känner till minst och som är det experimentellt mest fattigt representerade i hela blixtbildningskomplexet.

 

Vad (flertalet) däremot är mera på det klara med är den allmänna kemibildningens dynamik såsom förknippad med dipolbildning. Jämför från @INTERNET 2008-06-21 DISTANSGYMNASIET KEMI 1 (färgmarkeringar belyser nyckelmeningarna):

 

”1. Dipol-dipolbindning

En dipol är en molekyl med en positiv och en negativ delladdning. Om två dipoler kommer i närheten av varandra kommer den positiva ändan i den ena att attraheras av den negativa ändan i den andra molekylen. Denna elektriska attraktionskraft kallas dipol-dipolbindning. Den betecknas med punkter.

 

Ex. Dipol-dipolbindning

 

I de molekyler där en liten väteatom är kovalent bunden till en liten starkt elektronegativ atom som fluor, syre eller kväve är elektronerna i den kovalenta bindningen kraftigt förskjutna mot den mera elektronegativa atomen. Den kraftiga laddningsförskjutningen gör att dessa molekyler är starka dipoler och motsvarande dipol-dipolbindning är speciellt stark. Denna speciella typ av dipol-dipolbindning kallas vätebindning eller vätebrygga. Vätebindningarna kan ha stor betydelse för ett ämnes fysikaliska egenskaper. Vattnets kokpunkt höjs avsevärt på grund av vätebindningarna mellan vattenmolekylerna (se boken sidan 72).

 

Ex. Vätebindningar mellan vatten och ammoniak molekyler.

 

Vätebindningar kan också förekomma mellan olika delar inom samma molekyl. Det är vätebindningar som håller ihop DNA-spiralen. Före arvsanlagen kan kopieras av RNA måste vätebindningarna mellan dubbelspiralerna i DNA brytas av ett enzym.”

[http://www.edu.fi/svenska/distansgymnasiet/kemi/kemi1/5.shtml]

kronologisk specifikation saknas (tidigast från 1999-2008)

 

 

ELEKTRISKA FÄLT som läggs på över (till exempel) gräsfrön får fröskidorna att vrida in sig i det yttre fältets riktning.

Bilder på sådana fröexperiment tycks INTE vara populär vara på @INTERNET (ännu inte en enda träff 2008-06-22). Bilden nedan är från en numera föråldrad lärobok,

GYMNASIETS FYSIK åk2 Liber 1980 s7.

 

 

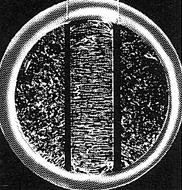
Gräsfrön rättar in sig efter ett yttre pålagt elektriskt fält.

Från GYMNASIETS FYSIK åk2 Liber 1980 s7

 

Det finns författare (på webben) som menar att gräsfrönas inrättning beror på INDUCERAD DIPOLLADDNING: fria elektroner vandrar i gräsfröet och dras mot det yttre fältets positiva elektrod med ett bildat elektronunderskott i andra änden.

Markeringen av textens storlek är min i nedanstående internetcitat (2008-06-22);

 

 

”MAKING AN ELECTRIC FIELD VISIBLE: If long thin grass seeds are placed on a smooth glass plate near a highly charged object, the seeds turn so that they are parallel to the electric field, making a visible pattern.

Why do the seeds turn in this way? (Answer: 54)”.

”54. The field induces a charge distribution in each seed, making it a dipole with one positive end and one negative end. There, electric forces rotate the seed until it is aligned with the field.”.

[http://physnet2.pa.msu.edu/home/modules/pdf_modules/m421.pdf]2002

Min översättning:

VISUALISERING AV ETT ELEKTRISKT FÄLT: Om långa tunna grässtrån placeras på en plan glasskiva nära ett starkt laddat objekt, vrider sig fröna så att de är parallella med de elektriska fältet, bildande ett synligt mönster. Varför vrider sig fröna på detta sätt? (Svar: 54). 54. Fältet inducerar en laddningsfördelning i varje frö, som gör det till en dipol med en positiv ände och en negativ ände. Där, roterar det elektriska fältet fröet tills det är i linje med fältet.

 

 

Stämmer det?

   I organiskt material, t.ex. ett gräsfrö, finns i ljuset av ovannämnda DNA- beskrivning inga direkt fria laddningsbärare; Organiska material är i sig själva isolatorer; All elektronmassa som finns utnyttjas redan för organismens byggnad; Organismen bygger på en välordnad POLSTRUKTUR av förenade molekyler som REDAN UPPVISAR ELEKTRISK DIPOLKARAKTÄR — med referens till det ovan citerade källexemplet med DNA — som också väl ansluter till den ovan beskrivna allmänna kemikopplingens matematiska fysik enligt TNED.

   När ett elektrisk fält läggs på över fröet, vrider det in sig i fältriktningen på samma sätt som en REDAN magnetiserad magnetnål vrider in sig i ett yttre pålagt magnetfält.

   Ovanstående bidragsgivare tycks däremot mena att dipolen bildas i gräsfröet då ett yttre e-fält läggs på. Den uppfattningen är i ljuset av ovannämnda DNA-beskrivning uppenbarligen inte naturgrundad. Källan ger heller ingen relaterad beskrivning. (Webben är full av liknande [ogenomtänkta] bidrag).

 

I t.ex. fritt hängande elektriskt laddade kulor av metall däremot — som har fria ledningselektroner — är det fritt fram för en dipolkaraktär att skapas — med kraftgrund i rummet mellan elektroderna på en spänningskälla. Organismerna däremot har ingen förutsättning för att släppa ifrån sig någon elektronmassa i någon slags separat vandrande inre kanal — utom genom en inre välordnad organisk-kemiska process, eller genom yttre direkt mekanisk friktion (som inte demolerar organismen). Den förklaringen är i varje fall den mest synbarligt logiska.

 

 

 

 

 

 

BLIXTURLADDNINGENS FYSIK | ComplATACAT2008 | MPcPb | Blixtbildningen

stegad ledare

 

Blixtbildningen ENLIGT TNED

 

 

 

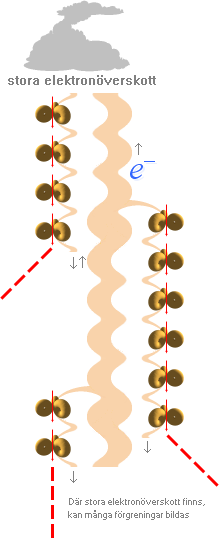
Molnets elektronöverskott mot markens elektronunderskott (ca 90% av alla fall) genererar genom gränsspänningen UG en stegvis bildad kanal (eng. stepped leader, stegad ledare) som dels utgår från den snabbare molnsidan och dels från den trögare marksidan.

   Kanalen bildas genom att flera atomer sammankopplas på gemensam kärnspinnriktning om gränsspänningen atom-atom överstiger gränsvärdet (UG), vad vi här kan kalla för en atomtråd. Dvs., en via atomens kraftekvation sammanhängande linje av atomer som delar på samma elektronmassa, en speciell makromolekyl. Flera sådana trådar kan bildas tillsammans med resultat i en central kanal med varierande grovlek.

 

 

Är elektronöverskottet stort från molnsidan, kan kanalen förgrenas på flera atomtrådar; Trådbildningen via UG utför ett arbete UQ på varje förenad atom som sammantaget ger effekten för en ekvivalent ljusbildning;

arbetet

 

För varje nytillkommen atommedlem utförs i föreningen

0           = (FBT+FeZ )1+(FBT+FeZ )2+(FBT+FeZ )3+…+(FBT+FeZ )n

 

ett arbete

 

E  = UG(Ze)

 

Rent formellt kan E (=hf) omsätta ljusemission enligt skillnaden i energi mellan den fria atomen och den förenade;

 

 

fria atomer

föreningsenergi frigörs

förenade atomer

 

 

högre energi

lägre energi

 

 

Från grundräkningen med atomtrådar från luften inom Ø1mM ges grovt sett en effekt på ca

2 500 Watt under 1µS via medelsteglängden på 50 meter

 

— eller med pulsviddsförhållandet (typiskt) 1/50, medeleffektiva effekten 50 Watt.

Det motsvarar ENLIGT TNED ett typvärde för den stegade ledarens ljusbildning från molndelen.

 

 

Den motsvarande effektbilden från markdelens trådstegning uppvisar ENLIGT TNED en delvis annorlunda karaktär på grund av att dess atomagenter är (eller bör vara delvis) joniserade (underskott på elektronmassa); flashbildningen blir mindre uttalad med en mera kontinuerligt lysande effektform som också här underhålls av arbetet via gränsspänningen UG på atomagentens elektronbesättning — som alltså innebär en mindre effekt på grund av elektronunderskottet.

 

Speciellt från molndelens stegbildning är det tydligt att flasheffektens ljusstyrka KAN öka med antalet möjliga förgreningar.

Referensen nedan antyder ett sådant resultat;

fotografisk observation av stegbildning

Fotografisk observation av stegbildning med växande ljusstyrka

0,2 mS mellan varje bild

 

 

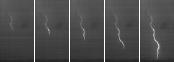
medelhastighet 0,867 T6 M/S, källa Zhang 2006

blixtbanans bildning i syntes

Blixtbanans bildning i sammanfattande (vidare) syntes

BLIXTBANANS BILDNING I SYNTES

 

 

Sammanfattning

BLIXTBANANS CELLBILDNING (det enskilda steget i stegade ledaren).

I a (vänstra bildkolumnen) gäller normala slumpvisa ordningar i luftrummet med alla möjliga riktningar på atomernas/atomkärnornas centralspinn. Men endast likriktade spinn med kärnanoden (+) uppvänd mot molnets negativt laddade del (–) är aspiranter för den kommande strömstammens atomagenter. Av de 100% atomer som finns per (idealt kopplande) längdmeter bortfaller ca 4/5 på grund av spinn och symmetriskäl (se särskild beskrivning). Endast ca 1/5 är egentliga aspiranter (i idealt rakt nedstigande led).

 

I b (högra bildkolumnen) visas idealt förtydligat hur en koppling bildats mellan ett antal luftatomer som via UG för tillfället kommer i synkroniserat spinnläge — med direkt koppling till molnets elektronöverskott och den kritiska spänningen moln-mark som krävs för att kopplingen ska fungera (se särskild beskrivning i gränsspänningen UG). LängdKopplingen kan vi här kalla för en blixtcell eller en stegcell. När första blixtcellen har kopplat har också molnets motsvarande spänningselektrod förflyttats neråt marken analogt med cellens nedre toppunkt. Det cellkopplande arbetet E=UQ utförs på varje ingående atoms samtliga elektronmassor (Q=Ze) enligt grundräkningen,

 

E = UQ = UG(8×1,602 t19) = 6,95729 t24 J » 7 t24 J

 

Enligt Umans bokuppgifter (och andra källverk) är steglängden i medeltal 50 meter (Uman s87). Med grundräkningen betyder det en metereffekt på 50 Watt per 1/5 T11 luftatomer inom en central ledarkanal med diametern 1 mM. Vi observerar att denna kanaldimension både kan vara mindre (lägre ljusstyrka) och större (högre ljusstyrka) och ingen allmän medelvärdesform finns för den delen. Varje blixtbana har sin egen dimension och beteende, allt efter omständigheter — som dessutom kan variera mitt under själva stegbildningen.

   Vi har därmed ett gott referensvärde  — en central kanal på (minst) Ø1mM i normal luft — med grund i experimentellt påstådda dimensioner grundade på experimentella observationer av blixturladdningar (med vissa osäkerheter).

   Se även källan @INTERNET från det äldre materialet med Boys kamera på 26 000 bilder per sekund.

   På 50 meter skulle vi då få en totaleffekt på runt 2,5 KW — som refererande teoretiskt grundvärde enligt TNED.

   Uman beskriver stegbilden vidare; den karaktäriseras av en »ljusflash» på ca 1 µS med en mellanliggande mörktid på ca 50µS. Vi studerar detta enligt TNED.

 

Eftersom stegbildningen ENLIGT TNED tvunget måste bygga på en atomär spinnsynkroniserad tillväxt (se från Stegcellens Bildning), har också arbetet (E) sin fokuserade lyspunkt på stegcellens nedre spets, analogt senaste tillkomna atom. Om vi tänker oss att en stegcell med n atomer kopplas på tiden tC av UG, då bör den aktiva energiomsättningen också genomlöpa hela steget, ända uppifrån och ner, på samma tid (tC) — i formen av en »flash»: själva kopplingstiden bör vara (betydligt) kortare än »söktiden för stegets koppling» och vilken senare del vi måste förutsätta tar en betydligt längre tid för att hitta stegets alla atomärt synkroniserade spinn. Vi identifierar tC med uppgiften (medelvärden) om ca 1µS för stegflashen (Uman s87) och totaltiden 50µS (medelvärde med T6 M/S via medelsteglängden 50 meter, men dessa värden kan variera både uppåt och neråt) för hela stegbildningen; idealt 49µS för att initiera kopplingen för alla stegets atomagenter och 1µS för själva kopplingsögonblicket, ända uppifrån och ner; Stegbildningen (se grundberäkning av ljusflashens effektvärde) »flashar» under 1µS via en lysande spets som avancerar snabbt uppifrån och ner, och är sedan helt mörk under 49µS.

   Den snabba genomrinningen på 1µS bör naturligtvis generera en motsvarande närinduktion i stegbildningens närmaste förlängning — och därmed i princip en motsvarande svag ljusbildning (korona) i närområdet omedelbart framför/nedanför stegcellens spets. En sådan koronaeffekt är också precis vad som beskrivs av Uman (s87st1n).

 

 

 

Enda skillnaden för en ”positivt laddad stegad ledare” är att atomkopplingarna där sker via joner, inte neutrala atomer; Atomer som befinner sig i områden med utpräglat elektronunderskott och som kopplar sina elektronmassor på en motsvarande gemensam stormolekyl via UG, bör naturligtvis också uppvisa en motsvarande ljusflash (tC). Emellertid är då också hela atomlinjen mer eller mindre joniserad, vilket betyder att den (lättare än i det neutrala fallet) kan emittera egenljus under tC-flashen. Det är också den experimentellt gjorda observation som Uman beskriver (s87ö, experimenten genomfördes under 1950- och 1960-talen); positivt laddade stegade ledare emitterar en del ljus mellan stegen, vilket inte är fallet för negativt laddade stegade ledare. I beskrivningen generellt förutsätter vi här referensen med den vanligaste blixtbildningstypen (ca 90% av alla fall) som vi kan kalla »den negativt laddade stegade ledaren» (elektronströmning från molnets minus till markens plus).

 

flashtid  ..................     tC=1 µS (mörktid TC=49 µS)

effekt  .....................     2 500 W via blixtkanal med diametern 1mM

steglängd  ...............     50 M, Uman s87 (medelhastighet T6 M/S ref. Zhang 2006)

korona  .....................   svagt induktivt bildat ljustöcken framför flashspetsen

 

Med ett pulsviddsförhållande på 1/50 och toppeffekten 2500 W blir den effektiva medeleffekten grovt räknat 50 Watt — jämför en konstant lysande 50-Wattslampa på avståndet ental till tiotal kilometer (knappast ens synbar med mörk omgivning i klar luft, men en känslig mätanordning kan se den).

 

 

 

 

 

 

BLIXTURLADDNINGENS FYSIK | ComplATACAT2008 | MPcPb | Urladdningen

 

URLADDNINGEN

 

Uman anger (s62) ett medelvärde t9 C/M3 för den typiska elektrontätheten i åskmoln, men också ett molnmedelvärde per kubikkilometer på 20 C/KM3. Med nedanstående exempelräkning (1-10 C/KM3) ges här en enkel praktisk räkneform till en första grov jämförelse;

 

Med medelavståndet mellan luftmolekylerna (normal luft) ca 3nM räknat på en Syreatom med Z=8 ges laddningstätheten

D » 10 C/KM3 om en syreatom på 4 T15 bidrar med en överskottselektron enligt räkningen (1e=1,602 t19 C)

D = [(8e)/(3 t9 M)3]/(4 T15) = 1,1867 t8 C/M3 » 12 C/KM3

Med fördelningen per T16 (alltså tio gånger mera glest bidrag) ges

D = [(8e)/(3 t9 M)3]/(4 T16) = 1,1867 t9 C/M3 » 1,2 C/KM3

 

För att få fram den typiska laddningstätheten runt 10 C/KM3 i ett typiskt åskmoln och grundat på Syre-Kvävemedelatomen (som vi här använder Syre 16 genomgående för att illustrera) krävs alltså att endast en syreatom på 1015 syreatomer får en extra elektronmassa från marken.

 

Om vi enligt källreferensen nedan, ,

 

”experimental and observational evidence has established the core to be some 2 square millimetres in cross sectional area.”

@INTERNET [http://volcaniclightning.tripod.com/aflashof.htm]

Dr Colin Pounder Copyright 1990

Min översättning:

Experimentella och observationella bevis har fastställt kärnan att vara en 2 kvadratmillimeter i tvärsnittsyta.

 

betraktar halva det ungefärliga tvärsnittet av en rund tandpetare (2mM/2=1mM) som en representativ diameter för en blixtkanal (som kan vara både mindre och större), har vi med medelavståndet 3nM mellan luftmolekylerna drygt T11 (sådana) syreatomer i Ø1mM tvärsnittet med höjden 3nM. Med höjden 1mM för den 1mM-cylindern finns drygt 3 T16 syreatomer. En syreatom som erhåller (drygt) 5 extra elektroner per den mängden motsvarar uppgiften från Uman med medelvärdet för laddningstätheten runt t9 C/M3 (se beräkningsformen nedan). Det visar oss hur ofantligt liten den extra elektronmängd är och som tydligen behövs för att trigga åskvädren; Fem enda ynka extra elektroner per luftcylinder med höjden och bredden ca 1 mM. Varje blixturladdning behöver grovt sett 1 kubikkilometer med en sådan fördelad atomärt bestyckad luftcylinder. Det motsvarar drygt 1 Coulomb, vilket är den ungefärliga undre gränsen för den laddningsmängd (2-100 C) som enligt uppgifterna dras från moln till mark.

   För att i jämförande illustrerande exempel via Syreatomen för vanlig luft beräkna hur många elektroner (N) som bidrar till laddningstätheten per V=Ø1mM×1mM cylinderpelare med en given laddningstäthet (D) gäller sambanden

 

N(eD)M–3          = D/e ger antalet laddningstäthetselektroner per kubikmeter i laddningstätheten D;

N(eD)M–3          =7,40761 T9 med 1,2 C/KM3;

N(V)                   = V/V0 = V/(3 t9 M)3 ger 2,90888 T16 » 3 T16 Syreatomer per cylindern V=Ø1mM×1mM

 

1M3/V               = 1M3/[p(0,5 t3 M)2× 1 t3 M] = 1M3/(7,85398 t10)M3

                          = 1,27323 T9 V-enheter i 1M3

 

Antalet laddningstäthetselektroner per kubikmeter i laddningstätheten D (7,40761 T9 med D=1,2 C/KM3) fördelade på

antalet 1,27323 T9 V-enheter i 1M3 ger

N          = (7,40761 T9)/(1,27323 T9)

             = 5,8179669 laddningstäthetselektroner per V=[p(0,5 t3 M)2× 1 t3 M]

             = N(eD)M–3/(1M3/V) = VN(eD)M–3/1M3 = VN(eD)

             = V·D/e = (7,85398 t10 M3)D/(1,602 t19 C)

 

Med det större värdet D=20 C/KM3 ges N=98, eller ca 1 extra laddningstäthetselektron per hundradels cylindermillimeter i höjd.

 

 blixtbildningens energi

Energin till blixtbildningen

Energin som underhåller Jordens alla åskväder dygnet runt överallt

 

Enligt källan @INTERNET

 

Lars Wåhlin [http://www.colutron.com/download_files/chap4.pdf]

kronologisk specifikation saknas (tyvärr ett alltför ofta observerat fenomen på många webbsidor)

 

pågår dagligen, för hela Jorden runt, 50 000 åskväder med en uppskattad frekvens på ca 100 urladdningar per.

   Med medelurladdningsmängden 20 Coulomb (se nedan) och medelspänningen 12,5 MV (separat från energiräkningens integralt induktiva strömekvivalent E=LI2/2=[U/2]Q, se nedan) som ger energin 2,5 T8 J, får vi

(50 000)(100)(2,5 T8 J)7(86400 S) = 1,44675 T10 W;

   Bindningsenergin för den yttersta av Syreatomens elektroner är enligt uppgift i Wikipedias energibindningstabeller

 

Se @INTERNET Wikipedia Ionization energies of the elements

 

1313,9 KJ/mol eller 2,1815 t18 J. Det ger för produktion av åskväder i medeltal

(1,44675 T10 J/S)/(2,1815 t18 J) = 6,63188 T27 avdelade markelektroner till luften per sekund.

   Om vi räknar på vatten (H2O) som huvudsakligen bestående av Syre (O16) med tätheten runt 1 ton per kubikmeter innehåller varje sådan kubikmeter 1000/(16×1,66033 t27 KG) = 3,76431 T28 Syreatomer;

Det är (3,76431 T28)/(6,63188 T27) = 5,6760856 gånger mer än det antal atomer som behövs för att producera laddningsmängden för åskväder — hela Jorden runt, per sekund, om varje atom bidrar med en elektron. Vilket vill säga: den omsättning som åskvädrens ”materialturbulens” iscensätter är TYDLIGEN nästan löjeväckande liten i förhållande till den överväldigande mängden ytmassa på Jorden; inte ens en kubikmeter vatten i elektronbidrag per sekund med en per atom.

globaldata

 

 

 

Sprids antalet 6,63188 T27 atomer över den Solbelysta delen av Jordytan (4prEKV2)/2 ges per sekund antalet atomer per kvadratmeter som behöver bidra med en elektron per för att försörja laddningsmängden till Jordens alla åskväder

(6,63188 T27)/(2,55592 T14 M2)

= 2,5947 T13 atomer/M2;

 

   Antalet luftmolekyler per kvadratmeter i normal luft är till jämförelse drygt T17 stycken (1/[3nM]2). Av den delen berörs alltså bara delen 1/4282. Vilket vill säga:

 

Om varje luftmolekyl (syreatom) vid den Solbelysta Jordhalvan av havsytan per sekund släpper ifrån sig bara en dryg fyra tusendel av en av sina elektronmassors delmassa, är det precis vad som behövs för att försörja hela Jordens totala kontinuerliga åskväder

 

— eller per ytluftatom

som finns på den Solbelysta Jordhalvan vid havsytan

en hel elektronmassa

per 1 timme och 11,36 minuter.

 

allmänna grunddata

Väsentligt för att få en precis uppfattning om urladdningens strömstyrka (I) är kännedom om den elektriska laddningsmängd (Q) som bildar ansatsen i urladdningsströmmen och därmed ”triggar” denna. Den ansatsen ges med början från punkt C i nedanstående illustration, dvs. då den nedåtgående stegledaren från A kopplas ihop med den uppåtgående motsvarande marktråden från B.

 

Enligt Uman (s62-63) framgår enhetliga grunddata ur en stor mängd experimentella undersökningar under 1900-talet med i stort samstämmiga resultat: den medelmässiga laddningsmängd som dras från moln till mark under en urladdning är ca 20 Coulomb. Den laddningen ligger fördelad med laddningstätheten grovt 1-50 C/M3 eller grovt 20 C/KM3 (2 t8 C/M3) med en medelmässig höjdspridning på 6-9 kilometer i molnmassan.

 

Det betyder att vi INTE kan använda någon enkel elementär elekronikmatematik typ kondensatorlagen för att beräkna t.ex. molnets kapacitans (C=Q/U) eftersom laddningsbilden i molnet tydligen bildar en trädstruktur liknade den som antyds (blått) i vidstående bildillustration.

Ytterligare en detalj finns som också är avgörande för urladdningens (eg. stegbildningens) praktiskt teoretiska beskrivning — men som (här veterligt) inte ingår i referenserna till Umans bok: den allmänt (under 1900-talets facklitteratur) LABORATORIELOKALT experimentellt antagna uppgiften på överslagsspänningen i luft om ca 25-30 KV/cM. Det är den uppgiften (nämligen) man brukar utgå ifrån i alla sammanhang som berör atmosfäriska urladdningsfenomen (uppgiften gäller hemma i ett normalt torrt bostadsrum).

 

Kärnpunkten i sammanhanget här är de mera naturligt storskaligt utförda urladdningsexperiment som redovisas i källan @INTERNET

 

[http://205.243.100.155/frames/longarc.htm] 2005 Man made Sparks;

Courtesy of A. Gaivoronsky and A. Ovsyannikov, the Siberian Institute for Power Engineering

Siberian Research Power Institute (SIBNIIE) high voltage testing facility i Novosibirsk, Siberia

 

Källan rapporterar som mest en 200 meter lång urladdningsblixt genererad av endast 5,2 MV — vilket ger en medelöverslagsspänning per meter på endast 26 000 V. Det är bara 1/100 av det konventionella labbvärdet 2 500 000 V/M. Källan ovan berättar också att de första rapporterna om resultaten möttes med (stark) skepticism.

   Källan är ytterst avancerad och visar flera mycket fina videosekvenser på enorma ljusbågar från olika högströmsanordningar, med vidare

— samt en stor tydlig bild på en 150 meter lång luftblixt från anordningen. Verkligen.

   (Författaren kräver tillstånd för att man ska få visa de mycket fina och tydliga bilderna).

   Vi måste ta hänsyn till den, helt klart väl, experimentellt belagda uppgiften — såvida den inte bygger på felaktiga data!

molnspänningen

Molnspänningen

 

 

Om vi helt enkelt använder det enklaste och mest elementära av elektrofysikens alla samband — elektriska kraftlagen F=k(Q/r)2 — med spänningsformen

U=E/Q=Fr=k(Q/r)

får vi för spänningen 7 kilometer över marken med medelladdningen 20 Coulomb värdet

U=(9 T9)(20/7000) » 25 700 000 Volt.

Uman tycks (klokt nog) vara försiktig i spänningsdata; Han använder (här veterligt, frånsett s12, ”in excess of 107 V” för ledarens spets) inga direkta uppgifter på spänningen moln-mark. Men (flera) andra källor @INTERNET använder (friskt) uppgifter av storleksordningen

20 000 000 000 Volt (enligt 7000×3 T6 = 2,1 T10) — alltså runt 1000 gånger större.

 

 

 

Se exv

[http://www.nofc.forestry.ca/fire/faq_lightning_e.php]

”3-4 kilovolt/cm” The Lightning Flash

 

 

 

Det finns emellertid (nyare) källor bl.a. på Wikipedia som antyder senare rön;

 

”However, lightning leader development is not a simple matter of dielectric breakdown”,

@INTERNET Wikipedia Lightning 2008-06-17

Min översättning:

Emellertid är bildandet av en [stegad] ledare ingen simpel fråga om dielektriska överslag.

 

Ovanstående artikel anger data ”inside a well-developed return-stroke channel” på hundratal volt per meter (men utan att ange källreferensen, vilket [fortfarande 2008, tyvärr] är allt för vanligt på Wikipedia) — vilket är något helt annat än den traditionella ”luftens överslagsspänning på miljoner volt per meter” vi är vana vid.

 

Med hjälp av den ovannämna enkla elektriska kraftlagen får man en efter omständigheterna grov men säker grundbild av vilken grundform som tvunget måste gälla — med referens till en ideal medelpunkt för den elektriska kraftverkan vi HELT SÄKERT VET gäller för elektrofysikalisk spänning i vanlig luft (eller med obetydlig skillnad i vakuum).

 

I EN SENARE VERSION 2007 AV UMANS BOK finns också tillrättalagda uppgifter som mera ansluter till den här enligt TNED anvisade storleksordningen på tiotal megavolt i den stegade ledarens anvisade spänning moln-mark:

 

”The electric potential difference between a downward-moving stepped-leader tip and ground is probably some tens of megavolts (e.g., Bazelyan et al. 1978), which is comparable to or a considerable fraction of that between the cloud charge source and ground.”

LIGHTNING Physics and Effects 2007, Vladimir A. Rakov, Martin A. Uman, s111sp1

Boken finns att läsa på Google Böcker @INTERNET med begränsad åtkomst

Min översättning:

Den elektriska potentialskillnaden mellan en nedåtgående stegad ledarspets och mark är förmodligen något tiotal megavolt (eg., Bazelyan et al. 1978), som är jämförbart med eller en rätt stor del av den mellan molnladdningens källa och marken.

et al. betyder f.ö. med medarbetare

 

 

Enligt föregående grundräkning ENLIGT TNED krävs en minsta elektrisk fältstyrka (UG) mellan ideala luftatomer på (högst) 1 800 V/M, eller på 7000 meter runt 12,5 MV. Alltså runt hälften av värdet från den enkla U-formen via experimentella medelvärden. Under den gränsformen kan inte den stegade ledaren bildas — enligt TNED. Det är också samma U-form som fås via den integrala energiformen för strömstyrkans (induktiva) uppbyggnad,

E = LI2/2 = RTI2/2 = (U/2)TI = (U/2)Q med E = Fr = kQ2/2r = (U/2)Q

   Om ett typiskt åskmoln innehåller ”laddningsceller” som relativt varandra är mobila (de kan glida över varandra) och bara ”i synkront läge” bildar en ”potentialpelare” mot marken som överstiger UG, blir det lätt för oss att förstå hur och under vilka förhållanden som det finns respektive inte finns förutsättningar för en urladdning.

urladdningen

Urladdningen

 

 

När den stegade ledaren från A sammanknyts med marktråden från B i föreningspunkten C har en fullständig nollresistiv nollinduktiv masselektronledande taxibana bildats mellan molnpunkten A och markpunkten B via arbetet UQ från föregående beskrivna gränsspänningen UG och atomens kraftekvation enligt TNED. Molnpunkten A står i ledande kontakt med hela ”elektronladdningsträdet” i den ovanförvarande molnmassan, och bestämmer därmed det LADDNINGSTRYCK som bildar ansatsen för den nu närmast kommande strömrusningen i den utbildade blixtbanans centralstam AB.

 

När nämligen föreningen sker i C, dras omedelbart elektronmassa FRÅN ATOMSTAMMENS AGENTER — inte från molnet — ner i markdelen vid B — med den induktiva ansats som bestäms av Q i molndelen. Genom att elektrontätheten MED atomstammens agenter inberäknade är närmast enorm enligt TNED i jämförelse med varje materiell elektrisk ledning, finns ingen sådan materiell elektrisk ledare som kan hänga med i svängarna: allt bränns av vid ansatspunkten A.

 

 

Den tidigare med centralstammens atomstam associerade elektronmassan börjar alltså dras in genom centralstammen från avbrottspunkten i A, för att via kärnspinnen passera ekvivalent genom kärnbrunnarna neråt markdelen inkluderat från föreningspunkten C. Det betyder att den tidigare befintliga yttre »bark-elektronmassan», från punkten C, försvinner uppåt närmast invid centralstammen (och sedan nedåt igen från A mot marken genom centralstammen via det inre ekvivalenta kärnspinnet); där den gemensamt delade elektronmassan tidigare fanns blottläggs alltså centralstammens positivt laddade atomkärnor vilket område därmed omedelbart kommer att fyllas på med motsvarande kraftigt pågående joniserande-rekombinerande omgivande luftmolekyler och deras atomer. Dessa luftatomers elektroner dras alltså starkt inåt-uppåt till den så successivt blottlagda centralstammens högjoniserade plasmatiska stam och med början från punkten C. Resultatet blir (naturligtvis) en enorm ljusutvecklande pelare som drar iväg uppåt molndelen vid avbrottspunkten A med hög hastighet från C.

 

De instörtande yttre luftatomer som nu vräker sig mot MARKDELENS blottlagda starkt positivt laddade plasmatiska centralstam, avverkar tvunget på liknande sätt en inåt-nedåtgående rörelse längs markdelens tidigare atomtråd då dess yttre elektronbark tunnas ut. Det medför (på sätt och vis) att ett samtidigt, mot marken från C, nedåtströmmande kraftigt ljuscentrum bör visa sig.

 

Experimentella observationer som ansluter till denna typfunktion finns beskrivet i källan @INTERNET

 

[http://adsabs.harvard.edu/abs/2007JGRD..11213113J] Juli 2007

 

”These results suggest that the source of the slow fronts observed in the currents and in the distant radiation fields of natural first strokes is likely to be a pair of microsecond-scale current waves, each having a peak of up to some tens of kiloamperes,

propagating in opposite directions from the junction

of the descending and upward connecting leaders at a speed on the order of 108 m s–1, rather than the upward connecting leader itself,

as is often thought. ”.

Min översättning:

Dessa resultat antyder att källan för de långsamma fronterna observerade i strömmarna och i de avlägsna strålningsfälten hos naturliga första stötar troligen är ett par i skalan mikrosekundersvågor, var och en med en topp upp till någonstans tiotal kiloampere, och som utbreder sig i motsatta riktningar från föreningen för de nedstigande och uppåtgående ledarna med en hastighet i storleksordningen T8 M/S, snarare än [i riktningen för] den uppåt förbindande ledaren själv, som det ofta tros.

 

När centralstammen har tillfört markdelen den laddningsmängd som molndelen ovanför A tidigare igångsatte genom ansatsen, kan nu denna molndel ovanför A börja fylla på blixtstammens starkt positiva plasmakanaler. Därmed strömmar molnets överskottselektronmassa — först nu — nedåt, men inte till marken utan till blixtkanalernas centraltrådar som fylls på.

 

 

Med föregående starka jonströmning in till centralstammen i avstannande skede, kan alltså en andra men nu omvänt riktad strömningsfas inledas då blixtkanalerna fylls på av molnmassans elektronöverskott: en motsvarande ljusemission i den strömningsriktningen betyder att blixtkanalerna nu triggas ljusmässigt uppifrån och ner. OM denna strömningstyp sker i någon sekventiell (vågresonant) ordning, kan även en andra (och tredje och n:te) ytterligare omvänd strömningsfas ske mot blixtträdets centralstam med omväxlande jonströmmar uppåt-inåt och elektronpåfyllning nedåt-inåt så länge centralstammen bibehåller sina starkt elektronrippade atomära centralagenter. Ansamlas dessutom ytterligare laddning i molnet eller i samverkan med andra molndelar under tiden på sådant sätt att blixtkanalen vid A (eller i det närmaste) återigen kan öppnas mot en motsvarande markdel, finns alltså möjlighet för flera urladdningar varvid hela proceduren upprepas — tills molnladdningen är uttömd eller gränsspänningen för UG underskrids.

 

Så beskrivs också fenomenet efter experimentell observation; efter fasen med den stegade ledaren och maktrådens sammanträffande i C sker en retur som är den egentliga blixtbildning vi ser: en starkt uppåtgående ljusbildning från C och som sedan (i de flesta fall) efterträds av en återigen nedåtgående (men inte ljusflashande) ljusströmning (eng. dart leader, »spjutledare»), och därefter ytterligare flera liknande omväxlande parsekvenser med ljusströmning uppåt-neråt.

 

I MODERN TEORI finns inte centralstammens atomära besättning;

 

 

Man räknar i modern teori med att urladdningsströmmen går mellan atomkärnorna — inte rakt igenom. Därmed har man heller ingen teori för den nollresistiva och nollinduktiva taxibana som elektronmassan ALLTID uppvisar inom sin moderatom och inom varje kemiskt sluten förening. Och därmed infinner sig de numera välkända tusen och åter tusen teoretiska svårigheter som garanterat INGEN någonsin kommer att kunna reda ut i fenomenets beskrivning och förklaring: urladdningsfenomenet kan inte förklaras med den moderna akademins begrepp. TNED däremot klarar det galant.

 

 

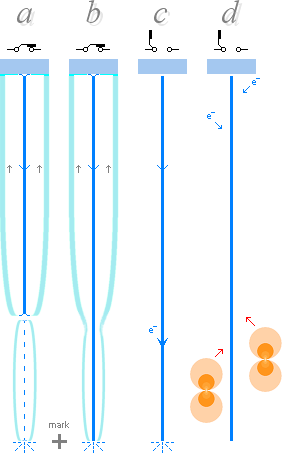
Hela förloppet kan beskrivas illustrerat enligt vidstående delar a-d. I a har molntråden och marktråden precis mötts. I b förenas de med gemensam elektronmassa i samma kemiska makromolekyl, se kraftekvationen. Därmed börjar omedelbart elektroner strömma genom centralstammen till marken i kraft av den ansats som anvisas av molndelen, samt att molntråden också i samma ögonblick omedelbart bränns av uppe vid molnbasen på grund av centralstammens nollresistans som inte molndelen kan hänga med på. Kontakten bryts då i c. Därefter i d kan moln och luft ”i lugn och ro” men under kraftig ljusutveckling fylla på med jonströmning uppåt-inåt centralstammen och elektronströmning neråt-inåt centralstammen för att fylla ut dennas nyligen häftigt (mer eller mindre) blottlagda positiva atomkärnor som genomfördes genom det lika häftiga nollresistiva elektrondraget i massfysiken som modern akademi helt saknar kännedom om. Se vidare utförligt från Atomkärnans härledning. Denna JonUppElektronNer-strömning kan ske i snabba pulser analogt med atomelektronskalens snabba periodiska återfyllningar med molnmassans elektronöverskott och de normala luftatomernas elektroner. Dessutom kan den redan existerande fasta centralstammen återanvändas flera gånger om det finns ytterligare markladdning som behöver fyllas på och en motsvarande molnladdning som kan fylla i.

   För bildningen av marktråd och molntråd, se föregående utförliga beskrivningar från BLIXTBILDNINGEN.

 

 

 

 

 

 

Isolationsspänningen för luft | se även separat sammanställd orienterande tabell

 

2008-06-19

Isolationsspänningen för luft

 

Det här ämnesområdet är ypperligt svårnavigerat — med referens till gängse modern akademisk litteratur.

kort historik

1889 [ref @INTERNET Wikipedia Paschen’s law 2008-06-19] förknippas med året då den tyske fysikern Friedrich Paschen ställde upp en numera

berömd formel för urladdningsspänningen i luft enligt

 

U          = (43,6 T6) · p · d · (ln pd +12,8)–1  ...........................    V

p i enheten atm (1 atmosfär, motsvarande trycket 101325 Pa vid havsytan vid °C [STP, Standard Temperature and Pressure]),

d avståndet i meter mellan två spänningselektroder (U-värdet ändras även med formen på dessa).

Flera källor @INTERNET omtalar att Paschens samband (inom vissa gränser) är ”väl experimentellt bekräftat”.

 

Följande, med hänvisning till experimentella resultat, visar en (delvis) annan ordning.

 

Med d=1cM=0,01M vid STP fås

U          = (43,6 T6) · 1atm · 0,01M · (ln 0,01atmM +12,8)–1

             = 53 204,277 V

 

Olika (oberoende) källor @INTERNET uppvisar liknande (men inte exakta) diagram (t.ex. ”40 KV/cM”). Men uppgifterna är också samtidigt svårtolkade då vissa testlaboratorium delvis använder växelspänningar i olika genomslagsförsök, och dels likspänningar till exempel vid experimentellt påvisande av uppkomsten av ljusbåge ur luft i samband med beskrivningen av Paschens formel, se exv.

[ref. http://www.reynoldsindustries.com/product/1singlepin/other/pdfs/page43.pdf].

   Normalt i växelspänningssammanhang (för sinusformade ström och spänningskurvor) brukar man använda omvanlingsformen med Ö2 för att få motsvarande likspänningsvärde från växelspänningens effektivvärde. Men det hjälper oss ändå inte så mycket i saken då vi här är mindre intresserade av Paschen än naturen på området.

 

Paschens samband visar att U-värdet drastiskt sjunker med lägre atmosfäriskt tryck. Enligt tabell i källan @INTERNET Wikipedia Atmospheric pressure har trycket halverats vid höjden 5 486 m.ö.h. Men det finns flera parametrar som spelar in, och som ingalunda har någon översvallande enhetlig presentationsbild på webben, om man nu söker där.

 

Låt oss som belysande exempel ta d=200 meter vid, säg, STP (p=1atm); Vi får

 

U          = 4,81812 T8 V

             = 480 000 000 Volt

 

Sibiriska exemplet

 

Experimentanordningen i Sibirien använde bara 5,2 MV.

En dryg 93:e del.

 

Vilket vill säga: ett dylikt resultat är INTE bra.

Det finns, tydligen, omständigheter som spelar in här och som INTE är välbekanta — och som i princip gör Paschens formel helt värdelös i en allmän analys av blixturladdningens allmänna fysik — men (oftast) INTE i de förnämas väl bestyckade laboratorium. Vi studerar hur.

 

 

 

Två parallella kopparledare (luft-mark) har mellan ledarna i längsriktningen en och samma teoretiska spänning — som också är densamma om vi förflyttar oss INOM ledarrummen tvärs ledarna utöver avståndet mellan ledarna. Det är densamma spänning vi som elektronikkonstruktörer måste ta hänsyn till på ett kretskort eller annat för att eliminera eventuella överslag om ledarspänningarna är motsvarande relativt höga.

 

Men en sådan analogi — rakt uppåt genom ett elektriskt laddat moln eller luft — kan vi inte använda i beskrivningen av blixturladdningens elgrunder: spänningen VÄXER otvivelaktigt i den riktningen med början från en närmast lägsta molnpunkt; Vilket vill säga: Vi kan INTE framgångsrikt tillämpa en elektrisk ledares elektronfysik på en elektrisk isolerad substans för att därigenom försöka ”luska ut hur det är” — med t.ex, blixtbanans initierande stegbildning och vilka de rent matematiskt-fysikaliska mekanismerna är.

 

ALLTSÅ TYP: när den stegade ledarens nedre spets kommer så nära markdelarna att luftens överslagsspänning uppnås (med vidare …).

 

DÄRFÖR ATT DET INTE FINNS NÅGON SÅDAN ENHETLIG SPÄNNINGSFORSKNING.

Jämför det nyligen omnämnda resultatet från forskningsanläggningen i Sibirien.

 

I modern akademi (NÄMLIGEN) använder man ”luftens överslagsspänning” typ 3MV/M för att ”förklara” uppkomsten av motsvarande marktrådar i deras närmande mot stegledarens molntråd.

Uman skriver på sidan 12, fetstilen min markering:

 

”

As the leader tip nears ground, the electric field at sharp objects on the ground or at irregularities of the ground itself exceeds the breakdown value of air and one or more upward-moving discharges are initiated from those points, thus beginning the attachment process, discussed in Chapter 6.

”.

Min översättning:

Som ledarspetsen närmar sig marken, överskrider elektriska fältet vid spetsiga objekt på marken eller ojämnheter i marken själv överslagsvärdet för luft och en eller flera uppåtgående urladdningar initieras från dessa punkter, således begynnande den anslutande processen, som diskuteras i Kapitel 6.

 

Denna beskrivning från Uman MÅSTE vara teoretisk eftersom, med det Sibiriska exemplet, atmosfäriska blixturladdningar KAN förekomma genom LÅNGT lägre motsvarande ”urladdningsspänningen för luft”; SÅ mycket lägre tydligen (100 gånger) att OM det vore DEN förklaringsgrunden som gäller skulle molnurladdningsprocessen uppenbarligen och vanligtvis vara av en helt annan (100 gånger kraftigare) spänningskaraktär. HUR ska man nämligen kunna förklara uppkomsten av svagt självlysande repliknande trådar som sträcker sig från marken upp i luften mot den annalkande stegade ledaren — om inte genom ”urladdning på grund av spänningsöverslag”?

 

TITTA ÅTERIGEN PÅ KOPPARLEDARNA ovan (här i illustrerad repris):

 

 

 

Med den övre motsvarande ”moln” och den nedre ”mark” ökar elektriska fältstyrkan mellan två fritt rörliga tunna trådelektroder som tas från respektive ledare om de närmas varandra enligt

X = U/d;

Fältstyrkan växer med avtagande distans (d), U givet.

Men som vi nyligen konstaterade (med referens till delvisa indirekta detaljer som dock är uppenbara i molnets laddningskropp), ökar spänningen mark-moln om vi avancerar längre in i molnet från dess lägsta punkt (ända in till molnets elektriska tyngdpunkt) — och borde också analogt MEN INTE I ANALOGI TILL KOPPARLEDARNAS IDEALA HEMMALABB avta (mer eller mindre) om vi går mot marken istället.

 

Med andra ord: Vi kan INTE likna stegledaren — med sin make marktråden — vid två motsvarande probtrådar som avdelas från två motsvarande elektriska »hemmaledare» där vi FÖRVISSO klart och tydligt kan mäta växande elektrisk fältstyrka med minskande avstånd. Molnet-marken fungerar inte så. Därmed sagt kan vi heller inte använda ”överslagsspänningen för luft” — Paschens formel — eftersom den bygger på samma traditionella bekväma »hemmaElektriska Labb». Naturen är utanför labbfönstret. Liksom.

 

Se även referensen

 

[http://www.download.n7tgb.net/Misc/lightning1.pdf] (2000);

 

Den använder rent ut ”induces” enligt (textstorleken min markering):

 

”Below the leader is a region of very high electric field.

As the leader approaches the earth, the high electric field induces objects on the ground to emit leaders of opposite polarity charge.

Since opposite charges attract, the path of the downward leader is influenced by an upward leader of opposite polarity.”.

Min översättning:

Nedanför ledaren finns ett område med mycket hög elektrisk fältstyrka. Som ledaren närmar sig marken, inducerar det starka elektriska fältet markobjekt att emittera ledare av motsatt laddningspolaritet. Som motsatta laddningar attraheras, påverkas vägen för den nedåtgående ledaren av en uppåtgående ledare med motsatt polaritet.

 

 

Det är klart att Umans (och övrigas) ”förklarande beskrivning” med ”det starka elektriska fältet” som anspelar på överslagsspänningen för luft ÄR tilltalande och plausibel — ur hemmalabbets synvinkel sett: alla experimentatorer känner VÄL till de ordningarna. Men som vi nyligen konstaterat, är det tydligt att DEN trevliga hemmabion är mindre aktuell utanför labbfönstret — som en del redan börjat upptäcka, också.

 

— Men hur menar då DU, blixtgubben, hur det ÄR om vi nu inte får använda den bekväma hemmabions labbande elektriska tentakler?

— HUR f-n ska markdelens motsvarande trådstumpar kunna veta VART de ska söka sig om det INTE skulle vara genom ett PÅTAGLIGT KRAFTIGT elektriskt fält? Du menade, ju, att fältstyrkan i själva verket skulle minska, eller hur?

 

— Okej. Låt mig försöka övertyga dig — genom magnetismen.

 

 

En elektrisk laddning (Q) som lägesändrar accelererat åstadkommer ett motsatt riktat rymdelektriskt dipolfält [u=L(di/dt)] som försöker motverka orsaken till Q-ändringen, det vi kallar för (elektromotorisk) induktion.

   Med den förhållandevis starka stötströmstyrka som den stegade ledaren utbildas på (se grundräkningen), i ordningen (minst) runt kiloampere, är det helt klart så att också anmärkningsvärda elektriska fältstyrkor blir följden av stegbildningens UQ-energi — och som alldeles säkert kan uppmätas på känsliga markbaserade stationer i närheten.

 

Men som vi nyligen konstaterade, är denna effekt INGALUNDA den vi söker i förklaringen till stegbildningens KOPPLING med motsvarande markbas.

 

   Och varför är detta klart?

   Det är klart just därför, och som nyligen påpekades, ATT induktionseffekten från stegledarens strömrusningar med motsvarande induktiva effekter på marken och omgivande luft ACCELERERAR MOTSVARANDE NEGATIVA LADDNINGAR mot stegledarens utbildning.

 

Inte medriktat, utan motriktat.

 

Det är och förblir den induktiva nettoeffekten.

   Snarare än att UTBILDA en, via induktionsverkan, komplementerande polmake som försöker förena sig med den nedkommande stegledaren, utbildar denna såsom högeligen negativt elektriskt laddad som det beskrivs i moderna kvarter alltså istället raka motsatsen: den attraherar genom sin induktionsverkan allt befintligt negativt omkring sig — vilket innebär alla omgivande luftens atomneutrala elektronhöljen — och stöter i motsvarande mening bort ifrån sig alla positivt laddade massor.

 

— Hur kan du då mena att det i en sådan uppvisning skulle finnas den allra minsta förutsättning för någon levande betydelse av begreppet elektrisk fältstyrka enligt, som du uttryckte saken, ”HUR f-n ska markdelens motsvarande trådstumpar kunna veta VART de ska söka sig om det INTE skulle vara genom ett PÅTAGLIGT KRAFTIGT elektriskt fält?”. Din mening, som ovan, bygger alltså på en ren förmodan och som nu har visat sig innehålla tydliga motsägelser. Säg gärna ifrån, om du känner för det.

 

   Ett starkt, påtagligt, elektriskt fält finns förvisso associerat med stegledarens utbildning. Ja. Men det är UPPENBARLIGEN inte på det som dynamiken stegledare-markdel hänger.

— Nehej. Vad fan är det då?

— Lugn. Vad jag skulle vilja veta FÖRST är HUR (i h-e) folk i moderna kretsar resonerar i ämnet elektrisk fältstyrka och den FÖRMODADE dynamiska kopplingen till föreningen mellan molntråd och marktråd, föregående urladdningsögonblicket. Som HÄR nyligen konstaterats med grund i de allra enklaste och mest elementära fenomengrunderna i ämnet och som garanterat ingen som känner till ämnets elementära delar har kunnat missa, finns ingen förutsättning för någon förening eftersom stegledarens induktion tydligen motverkar varje sådan typ. Hur kan då folk i moderna kretsar ÄNDÅ mena att själva föreningen verkställs genom att stegledaren ”inducerar uppåtgående markledare”? Det går inte ihop.

 

Man påstår ju:

 

Erinra nyligen ovanstående citat

”the high electric field induces objects on the ground to emit leaders of opposite polarity charge”

”det starka elektriska fältet inducerar markobjekt att emittera ledare av motsatt laddningspolaritet”

 

— Och på samma sätt Uman längre upp

”the electric field at sharp objects on the ground or at irregularities of the ground itself exceeds the breakdown value of air”

”elektriska fältet vid spetsiga objekt på marken eller ojämnheter i marken själv överskrider överslagsvärdet för luft”

 

 

DET FINNS UPPENBARLIGEN INGEN SÅDAN FYSIKALISK FENOMENALITET I NATUREN.

 

Induktionseffekten från den nedstigande förmodat negativt laddade stegledaren försöker tvärtom genom sin induktionsverkan i den flashande stegströmmen MOTA BORT positiva och ATTRAHERA negativa elektriska laddningar — så att VARJE FÖRENING mellan två harmonierande par blir uteslutet: stegledaren betraktas uteslutande (i de här aktuella minst 90% av blixturladdningarna med negativ molndel och positiv markdel) som negativt elektriskt laddad i modernt synsätt — som dessutom enligt samma synpunkt för med sig en laddningsmängd av mellan 1-5 Coulomb, som det anges (grovt sett — vi ska återkomma till den punkten särskilt senare).

 

Se bl.a. källorna

[http://home.earthlink.net/~jimlux/lfacts.htm] 1984/1997; ”0,2 - 6 C”;

[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ligseq.html], ”…some five coulombs …”

 

 

Den dynamiken går uppenbarligen inte ihop.

 

 

Det finns ingen experimentell fysik som kan ge ett enda exempel på typen att ”en växande ström av negativa laddningar drar till sig positiva elektriska laddningar”.

Den negativa strömökningen stöter bort sådana ifrån sig.

   Jag vet själv f.n. INTE hur folket i moderna kretsar resonerat för att komma fram till sin ståndpunkt — absurd som den uppenbarligen är.

   En beskrivande källa har eftersökts på @INTERNET men ännu (2008-06-20) inte hittats.

 

 

— Men HUR kommer då marktråden upp?

— Och hur kan den förena sig (så starkt) med den nedkommande molntråden?

 

— Genom magnetism.

 

 

 

Vi repeterar här helt kort resultatet från räkneexemplet i MAGNETISKA KRAFTEKVIVALENTEN och som visar att räkningen är rimlig:

 

 

 

OM DEN MAGNETISKA KRAFTENS EKVIVALENT F per syreatom samverkar i ett cirkulärt tvärsnitt med diametern 1mM (blixtstammens grovlek) som med medelavståndet 3nM mellan luftmolekylerna innebär runt 1,11 T11 syreatomer, och OM den millimetertråden antas tillhöra en s.k. stegad ledare som vi ska beskriva mera ingående i den löpande texten, då är det tydligt att

 

F i den samlade änden i det gemensamma planet beläget idealt ca 3nM från atomkärnorna, KAN ur den tråden uppvisa en motsvarande magnetisk kraft på

 

             F· 1,11 T11 = 182,3175 N

 

Det motsvarar grovt sett tyngden av en dricksback, eller  drygt

 

             18,58 KP (KiloPond) = (182,3175 N)/(9,81 M/S2).

 

Eller om tvärsnittet ökas till 10mM (vilket brukar anges i viss litteratur som ett typiskt mått på blixtstammens storlek)

 

             F· 1,11 T13 = 18231,75 N

 

vilket motsvarar tyngden av en större personbil (1858 KG);

 

OM I ANDRA ÄNDEN — marken — på 100 meters avstånd från den molntrådens nedermagnetiska öppningsände det finns en utbildad 5 meter lång luftbildad marktråd — men med betydligt smalare tvärsnitt (1/10 mM) — uppvägs dess tyngd HELT av den magnetiska kraftekvivalenten som verkar över de 100 metrarna från molntrådens magnetiska öppningsände; OM den räkningen också är relevant, är det tydligt att den jämförande attraktionens analogi måste anses direkt levande: marktrådens magnetiska överände söker sig (starkt) mot molntrådens magnetiska nederände.

 

På denna beräknings grundval råder inte längre något tvivel om fenomenets orsaksgrund: det är den magnetiska fältkraften, inte den elektriska, som ombesörjer trådändarnas förening moln-mark.

 

 

 

— Stegledarens nederände motsvarar en öppen elektrisk spole — ENLIGT TNED, se kemikopplingen.

— Exakt.

Se räkneexemplet i Magnetiska Kraftekvivalenten i den kvantitativt mera utförliga beskrivningen i den inledande beskrivningen.

 

— Har du sett hur en fjuttigt ynka liten hemmakonstruerad kompassnål, en liten vanlig knappnål bara, med flöte i en tekopp ställer in sig lydigt efter Jordens allmänna magnetfält?

— Eller, för den delen, bara hur den reagerar på andra närvarande B-fält, t.ex. från en avlägset hållen tavelmagnet?

— Magnetfält?

— Jepp.

 

Förhållandet mellan luftens täthet (1,43) och järnets (7 870) motsvarar grovt den lilla tunna magnetnålen med längden ca 2,5 cM och grovleken ca 0,5 mM tagen i form av en motsvarande 140 M lång blixtkanal (0,025×7870/1,43 = 137,58741) i rummet mellan moln-mark.

 

ENLIGT TNED kan bildningen av den stegade ledaren förklaras genom det arbete UGQ som utförs på varje ingående atoms elektronmassor (Ze) då atomerna förenas via UG på samma sätt som sker i ordinära kemiska föreningar fast här i en mycket större skala: framdelen på cellkedjan av atomer bildar en utpräglad magnetisk pol eftersom hela stegbildningen bygger på att föreningen uppvisar symmetriska kärnspinn i atombindningarna. Annars stämmer inte ekvationerna. Det är förutsättningen.

 

Därmed är magnetpolariseringen självskriven, liksom stegbildningens stötström är det. När stegen utbildas med början från molnets lägsta spänningspunkt, uppvisas också en (successivt växande, påtagligt) stark elektrisk fältstyrka. Men det är inte den som det hänger på — men många luras tro det.

 

 

B-styrkan från stegänden

Ledarändens magnetiska fältstyrka

 

 

— Varför sträcker sig inte marktrådar och molntrådar mot varandra med lika belopp så att de möts precis på mitten?

 

LUFT och MOLN utgör relativt MARK det tunnare materierummet och besitter därmed den snabbaste ljusvägen och därmed den kortaste bildningstiden över avstånd. Bildningen av stegade ledare bör alltså även ske från markdelen uppåt molndelen, en s.k. positivt laddad stegledare — men med en annorlunda baskoppling mot marken jämfört med stegbasens infästning i det elektriskt laddade molnet; Luft- och molndelens mera mobila atomer kan snabbt bilda en kopplande kanal nedåt markens positiva del, medan markdelens mera tröga fasta elektronunderskott är hänvisad till mindre mobila redan etablerade toppspänningspunkter i formen av olika fasta föremål;

   MEN inte förrän det finns en påtaglig ”kännedom” om vart en markdel ska skjuta ut någon tentakel till luften kan en uppåtgående marktråd börja bildas. Men då har molntråden redan hunnit nästan ända ner till marken (något hundratal meter ovanför marken). Molntråden avancerar sedan ytterligare neråt innan den träffar på sin marktråd — vilket (enligt Uman s12) sker något tiotal meter ovanför/utanför den berörda markdelens föremål.

 

 

Förklaringen till AVKÄNNINGEN marktråd-molntråd kan ENLIGT TNED — således —bara vara en: magnetfältet mellan trådändarnas motsatta B-poler som söker förening. Slutresultatet blir (enligt observationer) att molntråden sammankopplas med marktråden INOM molntrådens (medelmässiga) steglängd, dvs., inom runt sagt 50 meters radie från molntrådens nederände.

 

 

 

 

Enligt TNED förklaras — således — markdelens uppåtstigande trådar »enbart» ur en magnetisk dynamik;

GRÄNSSPÄNNINGEN UG garanterar att såväl en tråd bildas från moln mot mark som en tråd från mark mot molnets tråd; Den senare delen förklaras ENLIGT TNED av harmonierande B-poler i resp. ände och som styrs av den starka molntrådens primära atomkopplingar (se bestämning av B-fältstyrkan längre ner).

   Via gränsspänningen UG sker — DÄRMED — strävan att förena respektive motställda magnetpoler med avtagande avstånd mellan molntråd och marktråd.

   Marktrådens fotografiskt observerade svagt lysande sken kan återföras på att marktråden kopplas av (svagt) joniserade atomer som tillförs energi genom UGQ-arbetet (se grundräkningen), medan moltrådens mera neutralt kopplande atomer inte omger sig med någon svagt lysande korona alls utan istället uppvisar en kort flash då steget kopplar — samt en motsvarande framåtriktad pulserande »koronastav» som funktion av flashens induktiva verkan — precis så som det också beskrivs funktionellt enligt experimentella observationer (Uman s94).

 

Modern akademi känner inte till massfysiken (TNED) och har därför bara materifysiken att tillgå i varje försök att genomföra någon beskrivning.

 

 

 

 

Hela förloppet börjar med att en överliggande molndel känner av den största spänningsattraktionen mot markens positiva del just i det område som för tillfället bildar största laddningspotentialerna (dessa ändras och fluktuerar kontinuerligt); från molndelen utgår en stegad ledare (med successivt växande tvärsnitt) som söker sig ner mot markdelens positiva område (eller generellt mot motsvarande positiva del som också kan vara ett annat molnområde);

   Först när molnstegledaren närmar sig markområdets utpräglade laddningsspetsar, kan dessa BÖRJA avancera mot molnledaren genom att själva koppla motsvarande steglängder genom bildningen av atomtrådar som sträcker sina starka magnetiska spoländar mot den nedkommande molntråden; bildningen av markdelens atomtrådar förutsätter alltså ett visst minsta näravstånd mot molntråden för att de motstående B-ändarna framgångsrikt ska kunna känna av varandra — och därmed avancera med minskande avstånd.

   När den mest prominenta av dessa uppåtstigande marktrådar kopplar ihop sig med molnledaren sker själva urladdningen.

 

Eftersom marktrådarna bygger på atomtrådar med elektronunderskott, bör (en del av) dessa vara av typen joniserade.

   Om man tittar på en del (avancerade) fotografier från urladdningstillfället, se exv.,

 

[http://videos.howstuffworks.com/discovery-channel/...]03:16

Discovery Wonders of Weather: Lightning Phenomena,

 

kan man se att (en av) de trådar som har byggts upp men som inte hann fram har ett svagt lysande sken omkring sig (korona).

   Detta sken kan (bara) förklaras av en i atomtråden befintlig joniserad linje av sammankopplade atomer som i sina exciterade tillstånd matas av energin i den pågående stegbildningen — och därigenom blivit svagt ljusemitterande. Ljusemissionen från en marktråd som befinner sig nära molntråden bör vara större än ljusemissionen från en marktråd som befinner sig på längre avstånd från molntråden, vilket bör bero på att det är närheten till molntråden som ytterst sett bestämmer energimatningen i marktråden via den lokala fältstyrkan; När urladdningen inträffar, kollapsar de marktrådar som inte nådde fram därmed att energin till stegbildningen upphör; Med gränsspänningens upphörande finns inte längre någon förutsättning för vidare stegbildning.

 

 

 

 

B-styrkan

2008VI16:

B-styrkan

 

Vi kan INTE räkna med att kunna bestämma B-styrkan i något absolutvärde genom kärnspinnet — av flera skäl. Se även i Spektrum och Kvanttalen där inte heller några absolutvärden för atomkärnans spinn kan erhållas enligt TNED. Formen med den långa raka spolens analogi — B = µ0nI/l, se sambandet för magnetiska fältstyrkan i en lång rak spole — kan strängt taget inte användas på atomkärnan enligt TNED: vi har dels en skärmverkan som omöjliggör en normal permeabilitet tvärs genom atomkärnan, och dels en distribuerande laddningstäthet motsvarande atomkärnans Z-laddning fördelad över kärnytan. Vi kan, i princip, skippa den matematiken helt i den här enklare undersökningen. Se dock den inledande beskrivningen som använder ekvivalentformen för atomens kraftekvation, där ges en mera praktiskt orienterande beskrivning med exemplifierade värden som kan kontrolleras.

   Men det finns en annan, mera lämplig matematisk form som kan ge en säker relativ uppfattning om B-fältets inverkan i stegledarens ändpunkt. Nämligen med hjälp av magnetiska fältstyrkan för konen,

 

B          = µ0I(r2/2m3)  ;

cirkulära konens magnetiska fältstyrka med höjden h, m=Ö r2+h2, VS/M2.

 

OM nämligen ett tvärsnitt av blixtkanalen håller (typiskt) diametern 1mM (se grundräkningen) innehåller den samtidigt runt T11 idealt vertikalt nedåtriktade atomtrådar. Vi kan då beräkna på vilket avstånd från konens basring — som är atomkärnan med radien r — som SAMMA B-STYRKA uppnås med multipeln just T11 kärnöppningar. För konens del har vi då sambanden

 

B          = µ0I(r2/2m3)  ;

cirkulära konens magnetiska fältstyrka med höjden h, m=Ö r2+h2, VS/M2.

B0         = µ0I(1/2r)    ;

magnetiska fältstyrkan i ringens centrum med radien r, VS/M2.

B/B0     = (r2/2m3)/(1/2r)

             = 2rr2/2m3

             = (r/m)3             ;

B0/B     = (m/r)3

 

Med kärnradien grovt från kubgrafen r=(1,37 t15 M)A1/3 med A=masstalet (16 för Syre, 15 för Kväve) ges med Syre som preferens

r           = 3,45218 t15 M.

 

Vi sätter avrundat r=3,5 t15 M, och med multipeln B0/B= 1 T11 får vi

 

m          = r(B0/B)1/3

             = 1,62455 t11 M eller drygt 1/185 av medelavståndet mellan luftmolekylerna (3nM).

 

Det BÖR mätt med atomskalornas mått vara en oerhört kraftig lokal magnetisk spolände — förstärkt drygt 4600 gånger från den singulära syrekärnans utgående magnetbrunn, och som söker maken i området.

   Bara med en hundrafaldig ökning — T13 atomtrådar som ger en motsvarande blixtstam med diametern nära 10 mM — bör en sådan »nypa» direkt in i närmaste luftkärna: ingen stegkoppling är nödvändig; överslaget kopplar/sker direkt i ett enda led med atomagenterna på rad.

 

Exemplet visar att det bör finnas ett gränsvärde (runt 10 mM) för den stegade ledarens stamtjocklek som visar dess maximala styrka; mindre stamdiameter ger en svagare (långsammare) stegkoppling, större stamdiameter ger en starkare (snabbare) koppling; Dock inte över gränsformen då denna tydligen i princip innebär ”omedelbar koppling”; Så grova blixtkanaler uppnås aldrig — eller så är det den storleken som gäller minimum!

 

 

 

den mystiska

Coulombtätheten

 

I modern akademi har man inte den ovanstående beskrivna uppfattningen om stegledarens bildning:

 

Det sägs klart ifrån (LIGHTNING Physics and Effects 2007 Vladimir A. Rakov, Martin A. Uman, s111sp1ö) att det inte finns någon vetenskaplig koncensus i den stegade ledarens bildning: inget vet. Teorierna är många, debatterna hårda, meningarna divergenta. Man vet intet om hur den FÖRMODADE HÖGCOULOMBISKA ELEKTRONBESTYCKADE stegledaren bildas.

   Bl.a. finns (numera, mot 1900-talets slut) teorier som hänför orsaken till den kosmiska strålningen: Dess mycket höga energi startar ett förlopp av en handfull höghastighetselektroner som når spänningsområdena moln-mark och som därmed genomgår olika förstärkningsprocesser, s.k. lavineffekter (eng. avalanche effects), och som antas leda till den höga laddningstätheten i den så förmodat bildade stegledaren och som föregår blixturladdningen — dock med stundtals enorma mängder frågetecken som bara tycks växa i antal.

   Men denna detalj är också obskyr: milt sagt dunkel och oklar:

   Laddningstätheten som bär ansvaret för åskvädren Jorden runt, dygnet runt, uppvisar i ett grovt medeltal en laddningstäthet på 20 C/KM3 (Uman s63 ill.). Men med en plötslig scenändring — utan någon som helst förklarande koppling — som förlägger (nära) hela denna laddning (10-20 C, Uman s90) till ett smalt kilometerlångt rep med grovleken runt 1 cM (r=0,005 M = 0,000005 KM), den stegade ledaren moln-mark

— [(1 KM)·p·(0,000005 KM)2=p/(4 T10) KM3=7,85298 t11 KM3; (20C)/([p/(4 T10)] KM3)=2,55 T11 C/KM3 = 255 C/M3]

— och med motsvarande laddningstäthet som är mera än tio miljarder gånger större (flera hundra — 255 — C/M3), landar hela framställningen lika abrupt i en uppenbar totalkrasch rakt framför ögonen på varje seriös läsare. Den matematiken pekar helt enkelt käpprätt åt h-e fel.

 

Av den observerade sensationen med den magiska mystiska täthetsändringen måste vi dra slutsatsen att den moderna akademins beskrivning (Uman och andra liknande) bygger på FÖRMODANDEN som är långt ifrån varken klarlagda eller bevisade, men som ansetts väsentliga för sammanhangets beskrivning — till exempel det faktum att själva blixturladdningen ”tömmer” i storleksordningen just runt 20 C för medelblixtens räkning: ett otvetydigt korrekt experimentellt väl bekräftat faktum. Varifrån kommer den laddningen, då, om den inte förmedlas av den stegade ledaren? Detta är ALLTSÅ ett sådant exempel på ETT »grundbegrepp» som moderna författare tvunget måste använda sig av men som i grunden bara bygger på REN förmodan — som vi dessutom kan se utmynnar i absurda sammanhang utan varje spår av förklarande dynamik: från 0,00000002 C/M3 i molnets laddningsmassa till flera hundra C/M3 i den stegade ledaren — om inga större felräkningar här gjorts.

 

 

I TNED försvinner den absurditeten helt och hållet därmed att det INTE finns någon typ ”1-5 medelCoulomb elektronladdningar” i den stegade ledarens utbildning: Den stegade ledaren består ENLIGT TNED av helt vanliga luftatomer — vars elektronbesättningar längre fram i skedet är de som bär ansvaret för den stygga elektronströmningen till marken — och som sammankopplas via gränsspänningen UG av arbetet UGQ för att bilda den avgörande nollresistiva taxibanan moln-mark; De så kärnbrunnskopplade atomerna uttömmer sina elektronbesättningar i marken efter den anvisning som den ovanförvarande molndelens laddning (på i medeltal 20 C) anvisar; Kontaktpunkten mellan centralstammen och molndelen bränns omedelbart av — vid den induktiva ansatsen till laddningskopplingen — uppe vid molnroten beroende på den nollresistiva taxibanans öppnade masströmskanal på centralstammens kärnkopplingar enligt atomens kraftekvation och som ingen materiell ledare klarar av. Därifrån kommer 20C-potten; 20C-potten kommer från massfysiken. Inte från materiefysiken. Massfysiken ”öppnas” av kemikopplingen (atomens kraftekvation) via gränsspänningen UG vilket gör att materiefysikens samband inte kan användas för att beskriva förloppet; Men i modern akademi är massfysiken helt orepresenterad. Efter centralstammens uttömning kan sedan molnladdningen ovanför »i lugn och ro» fylla på den så elektronrippade blixtstammen med elektronmassa, samt motsvarande från den omgivande luftens vanliga atomära elektronbesättningar, och vilket förlopp (vanligtvis) bör ske med samma återfyllande frekvens som den genom vilken atomskalen återfår sina elektronbesättningar från moln och luft.

   Den förklarande dynamiken är — SÅLEDES — helt orepresenterad i modern akademi eftersom modern akademi inte kan härleda atomkärnan — och i största synnerhet heller inte elektriska laddningen. Därmed framstår blixturladdningens fysik som rena mysteriet. Ingen förstår något.

 

 

I MODERN AKADEMI förutsätter man (traditionellt — men som redan inflikats tidigare finns nyare uppgifter som mera ansluter till TNED)

— genom underförstådda kopplingar till den laboratoriemässiga urladdningsspänningen för luft, runt 3MV/M —

att spänningen mark-moln som igångsätter den stegade ledarens utbildning är (typiskt)

U=Xd=(3MV/M)(säg 1KM) 3 miljarder volt (3 T9 V) — Och ännu mer med större d.

Enligt det Sibiriska exemplet skulle den bara behöva vara U=Xd=(26 KV/M)(säg 1KM) som ger 26 MV. Oavsett vilket värdet är, är det i vilket fall uppenbart att det finns en viss gränsspänning under vilken förutsättningen för blixtbildning HELT elimineras.

 

MOLNMASSANS ELEKTRONÖVERSKOTT är otvetydigt förenat med molnets negativa laddning relativt markens motsvarande positiva del. Men vad säger oss att den stegade blixtledarens trådtentakel, som sträcker sig ner mot marken, OCKSÅ ska uppvisa SAMMA eller någon alls ”negativt joniserade områden”? Är inte också DET en ren traditionell elektrisk FÖRMODAN, så säg.

   ATT den uppvisar en (starkt) varierande elektrisk fältstyrka är alldeles klart (från experimentella mätningar).

   Men; — Än sen då?

   STEGLEDARENS ÄNDE är inte direkt något som någon enda levande varelse eller ens ett ting vidrör med mer än vederbörande strax förångas till i det närmaste atomer:

   Ingen VET något om stegledarens nederände genom något direkt experiment.

 

I boken av Uman (s90) påstås emellertid att mätningar inte bara har genomförts, utan att man även känner den stegade ledarens medelladning som den ”drar ner” till marken; En siffra som varierar från några få till 10 till 20 Coulomb omnämns (med ett medelvärde på 1 C/KM eller t3 C/M) — vilket alltså KAN motsvara hela den medelmässiga laddningsmängden för medelblixtens urladdning, enligt föregående uppgifter från Uman (s62-63).

   Det var också en ny uppgift det. Hela eller i varje fall en betydande del av urladdningsmängden ligger på/i molntråden?

   Hur gick det då med ”laddningsmedeltätheten på t9 C/M3”?

 

Med en stegad ledare med tvärsnittsytan en kvadrattum och längden 5 KM ges volymen V=(2,5 t3 M)2(5KM)=0,03125 M3; Med endast EN Coulomb för den volymen ges en laddningstäthet 1C/V=32 C/M. Saken gällde visst  ”t9 C/M3” enligt Uman sidan 62.

   Det här stämmer verkligen inte.

   Hur ska författaren ha det?

   Är det 1nC/M3 som gäller, eller är det 30C/M3?

 

Hyperphysicskällan (som också använder Uman som referenskälla)

[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ligseq.html]

beskriver saken på liknande sätt: ”När den stegade ledaren närmar sig marken, bärande en sådär 5 Coulomb …”.

   Fem. Inte en. Nu är det plötsligt sisådär en 150C/M3 som gäller.

   Detaljen visar att den moderna akademins teori på detta område blöder ur ett rejält öppet sår — och ingen finns som kan täppa till det.

 

MED OVANSTÅENDE GENOMGÅNG

BÖR DET NU STÅ KLART

att denna ”stegbärande Coulombfrakt” grundar sig på BEGREPP med delvisa resultat i ovannämnda motsägelser — i vad man har slutit sig till, i en begränsad fattning på innehållet och — i kraft av genomförda mätningar på elektriska fältets ändring, och vilka mätningar av allt att döma i sig är helt korrekta, avgörande värdefulla basdata, men vars beskrivningsgrunder (som sagt) lämnar mycket i övrigt att önska.

   Man har uppenbarligen sett det här, teorins uppenbara svårighet — men kan ingenting göra åt den saken då det i vilket fall är lika uppenbart att det krävs en motsvarande elektrisk laddningsmängd för att förklara huvudsaken. Alltså (resonerar man) måste det finnas en sådan förklaring att förmodan om laddningsmängden i stegledaren kommer att bekräftas i framtiden, ehuru ännu ingen känner till någon sådan förklaring nu. Det är i varje fall den förklaring som synes mest logisk till varför »motsägelsen» inte understryks.

 

Eller som det sägs balanserat i källan @INTERNET

 

”Since we are still struggling to understand how lightning works 250 years after Franklin’s kite experiment, perhaps we are missing something important …”.

Measuring x-ray emission from lightning Joseph R. Dwyer, Department of Physics and Space Sciences, Florida Institute of Technology

[http://www-group.slac.stanford.edu/ais/PublicDocs/presentation68,pdf] (2005)

Min översättning:

Eftersom vi fortfarande håller på och kämpar med att förstå hur blixturladdning fungerar 250 år efter Franklins experiment med den flygande draken, kanske vi missar något viktigt …

 

 

 

 

 

 

Isolationsspänningen för luft | tabell

 

elektrisk ledning för olika materierum 2008VI19

allmänt orienterande elektriska data

 

 

rum

typ

ämne

WM; (20°C)

ne/M3

MV/M

 

resistivitet

elektrontäthet*

isolationsspänning

rymd

tomrum

rymd

¥

0

»överslag» i

vakuum beror på

¥

materialen

omkring

luft

gas

luft

beror på

spänningen

mellan

omgivande

(¥)

ledare

med tryck

och

avstånd

beror med

påverkan från

(0)

omgivande

ledare

det lägre värdet

med

effektivvärdet

2-3

för

pålagd

växelspänning

mark

isolator

plexiglas

1 T19

 

(0)

uppgift saknas

lack

5 T13

 

(0)

uppgift saknas

glas (vanligt)

5 T11

 

(0)

uppgift saknas

lera, bränd

5 T9

 

(0)

uppgift saknas

vatten (H2O)

5 T3

 

(0)

uppgift saknas

ledare

silver

1,60 t8

1,59 

1,17 T29 (II)

0

koppar

1,78 t8

1,76

8,46 T28 (I)

0

guld

2,35 t8

 

5,89 T28 (I)

0

aluminium

2,90 t8

2,65

6,02 T28 [I]

0

järn (rent)

10,5 t8

9,70

8,49 T28 [I]

0

 

Teckenförklaringar till tabellen T förenklar 10^+, t förenklar 10^–.

 

uppgifterna om resistivitet från KARLEBO HANDBOK uppl.12 1977 s100-101

värden i orange från sv.Wikipedia Resistivitet 2008-06-19 gäller vid 300°K–273°K=27°C;

till Wikitabellen hör också en motsvarande uppgift om temperaturkoefficient, här ej angiven

 

värden i ljusviolett för elektrontäthet beräknade från tabell över grundämnenas täthet och medelatomvikt

värdena inom parentes refererar till atomens valenselektroner (I eller II) men den parametern ensam räcker inte för en fullständig beskrivning

 

Allmänna tabellData på genomslagsspänning för olika material verkar vara helt omöjligt att få tag på på @INTERNET.

 

 

 

*elektrontäthet används här i samma bemärkelse som elektronmobilitet ne/M3, samma som antalet fria ledningselektroner per kubikmeter

För Koppar är elektronmobiliteten n=8,46466 T28 ne/M3 (=1,35603 T10 C/M3) lika med antalet atomer per kubikmeter (1 valenselektroner per atom) med U=63,54u1,66033 t27 KG och r=8930 KG/M3

 

elektrontätheten för atomkärnan är ENLIGT TNED minst (via N3m20)

8,83775 T46 e/M3 (atomkärnans masstal gånger 909e dividerat med kärnvolymen [topptoroiden p(r/2)22p(r/2)]=p2r3/4]).

 

Laddningstätheten i en atomkärna med radien r0 är (absolut sämsta fallet) ENLIGT TNED med hänsyn till kärnans rätblock r0(2r0)2=4r03 lägst

1818/4r03          = 1,76755 T47 e/M3 med r0=1,37 t15 M

Elektrontätheten (masstalet gånger 909e) är halva det beloppet

909/4r03            = 8,83775 T46 e/M3

För hela topptoroidvolymen V=r3(p/2)2=r3(p/2)2 ges motsvarande för masstalet 1

909/[r3(p/2)2]    = 1,43272 T47 e/M3

Kärnradierna ( från masstal 5) kan beräknas approximativt från kubgrafen r=r0A1/3.

 

 

 

Resistiviteten för fri rymd är oändlig

Resistansen R för en ledare med resistiviteten Rm i WM beräknas

R = RmsA–1 · 1M;

A för fri rymd ansluter till domänen ds för divergensen, analogt noll; därmed motsvarande resistiviteten för fri rymd enligt;

R = Rms(A®0)–1 · 1M = Rms(A–1®¥) = ¥;

Rm(SPACE) = ¥WM; den fria rymden medger ingen elektrisk ledning som sådan.

 

 

 

 

 

Grundräkning | 2008VI14

 

GRUNDRÄKNING

Med

UG        = k(e/rn)  ...........................................    kemiska kopplingens absoluta gränsspänning, från elektriska kraftlagens grundform F=k(Q/r)2

k           = 8,98743 T9 VM/C  .......................     elektriska konstanten » 9 T9 VM/C

e           = 1,602 t19 C  ..................................     elektriska elementarladdningen, elektronens laddning

UG        = (9 T9 VM/C)(1,602 t19 C)/((177062)[r]/2)

ges i sämsta fallets värden (n-faktorn här den absolut minsta möjliga) med r=3nM medelavståndet mellan luftmolekylerna

gränsspänningen

för luft

enligt TNED

UG     = 5,4286 t6 V » 5,4 µV

 

som ger 1800V/M med 3nM mellan luftmolekylerna

Notera att denna form för gränsspänningen avser ”med atomerna vilande”. I den praktiska atmosfären tillkommer förutom luftmolekylernas rörelser också trycket som faktor.

 

(jämför ca 2M5V/M överslagsspänning för luft; U = ke/82r = 7,50937 t3, × 1/3nM = 2 503 124,9 V/M)

 

ARBETET som gränsspänningen utför på varje (medel-) syreatom med Z=8 då den förenas i rakt nedstigande led med tidigare (eller som nummer två enligt kraftekvationen) blir

 

E = UQ

             = UG(8×1,602 t19)

     = 6,95729 t24 J » 7 t24 J

 

Den observerade röntgenstrålningen från stegade ledare

Föreningsenergin per syreatom 7 t24 Joule är alldeles för liten för att som sådan kunna åstadkomma någon mera påtaglig strålningseffekt. Emellertid kan många (flera meter) syreatomer som förenas i samma tråd (dvs., i samma förenande flashmoment) åstadkomma en gemensam induktiv effekt av tillräcklig magnitud för att matcha de observerade röntgenenergierna på ca 0,03-1,3 MeV; varje luftmeter syre med medelavståndet 3nM mellan luftmolekylerna innehåller i medeltal 3,33 T8 atomer; det ger E=(3,33 T8)(7 t24 J) = 2,33 t15 J. På endast tre meter ges då ca 7 t15 J som motsvarar ca 43,7 KeV; på medelsteglängden 50 meter ger det (50/3)(43,7 KeV)=728 KeV eller nära 1MeV. Med spridning på 10-100 meter steglängder täcks därmed det observerade energiområdet 0,03-1,3 MeV in med god marginal, se källreferensen nedan. Planckenergin (E=hf) totalt som åtgår för att bilda röntgenemissionerna beror endast av syreatomernas längdkoppling, alltså meterformen och inte grovleken hos stegkanalen. Därmed kan energin som åtgår för röntgenemissionerna totalt sett hållas helt försvinnande liten (om det är vad saken gäller) vid sidan av huvudenergin som omsätts i de kraftigare ljusflasharna då luftatomerna bildar centralstammen. Se vidare från STEGBILDNINGEN.

 

Uppgiften om röntgenstrålningen från (bl.a.) stegade ledare finns på källan @INTERNET nedan. Där finns flera tydliga (och lättbegripliga) diagram och bilder/illustrationer som visar olika mätresultat, bl.a. med direkta detaljer från en stegad ledare.

 

Measuring x-ray emission from lightning

Joseph R. Dwyer, Department of Physics and Space Sciences, Florida Institute of Technology

[http://www-group.slac.stanford.edu/ais/PublicDocs/presentation68,pdf] (2005)

 

För beskrivningen av den speciella gammastrålning som också observerats från ett begränsat urval av blixturladdningarna (i medeltal strax under 20 per månad året runt för hela Jorden och med energier upp till runt 20 MeV, samma källa som ovan), se vidare i ATA (Atomkärnans Transmissiva Autonomi).

 

Varje cirkulär tvärsnittsyta (A=pr2) i vanlig luft med diametern Ø1mM med medelavståndet 3nM mellan luftmolekylerna, var och en idealt med tvärsnittet

AL    = (p×[3nM/2]2), innehåller då antalet syreatomstvärsnitt lika med

N     = A/(p×[1,5 t9 M]2)

        = (p×[0,5 t3 M]2)/(p×[1,5 t9 M]2)

        = ([0,5 t3]/[1,5 t9])2

        = 1,11 T11

 

Varje tvärsnitt A innehåller per meter med medelavstånden 3nM mellan luftmolekylerna antalet (medelmässiga) syreatomer

 

n=N(1/3nM)= 3,7037 T19

 

 

Görs räkningen istället direkt från Syrets medeltäthet 1,43 KG/M3 med antalet per M3 lika med

n=m/(Uu),

(1,43 KG)/(16×1,66033 t27 KG) = 5,38296 T25

fås för cylindern V=(p[0,5 t3 M]2)(1M)= 7,85398 t7 M3 antalet

 

n(V0)/n(V)         = V0/V = 1M3/V;

n(V)                   = n(V0)V/1M3

                          = n(1M3)(7,85398 t7 M3)/1M3 = 4,22777 T 19

 

 

Energin per meter per cirkulära tvärsnittsytan med diametern 1mM blir då (n=3,7 T19, sämsta värdets fall)

 

E(tot) = nE = 2,57677 t4 J per längdmeter per tvärsnittet A

 

Om varje sådan trådluftmolekylmeter avverkas på i medeltal t6 M/S analogt 1µS, ges effekten

 

E(tot)/1µS = P = 257,67754 Watt

per trådluftsmolekylmeter

 

 

2008-06-20

STRÖMSTYRKAN (I) per tvärsnitt A med N för blixtkanalens (minimala) Ø1mM

om varje längdmeter av den stegade ledaren avverkas nedåt marken på 1 µS per meter,

— varje tvärsnittskärna NA har idealt tjockleken 3nM med den berörda laddningsmängden

Q=8eN=1,42257 t7 Coulomb

— blir då per meter (1µS som ovan)

I = Q/T = (1,42257 t7 C)/(t6 S) = 0,142257 A

— eller om den kontinuerliga strömstyrkan beräknas på den observerade ljusflashen för hela medelsteget 50 meter under 1µS

som bör vara den mera fysikaliskt egentliga värdeformen,

I50 = Q/T = 50(1,42257 t7 C)/(t6 S) = 7,11285 A

 

Räkningen kan göras än mera preciserad — som också innebär en mera komplicerad och krävande sambandsform — om vi räknar på strömstyrkans ändring genom varje medeltjocklek på 3nM som innefattar laddningsmängden Q i varje tvärsnitt av stegkanalen;

Om mängden Q=8eN avverkas på tiden t=(3nM)/(v=T6M/S)=t15 S ges  stötströmstyrkan

I = Q/T = (8e·1,11 T11)/(t15 S) = 1,42257 T8 A

Effektivvärdet för denna stötström reduceras sedan genom att atomtvärsnitten är separerade av atomavstånd, samt att också en viss tid (49µS) förflyter mellan varje medelstegpuls (1µS).

   Eftersom blixtbildningen (tydligen) kan uppvisa en stor flora av olika kanaldimensioner (i exemplet Ø1mM), måste vi räkna med att många olika värden (och möjligheter) kan komma ifråga för det aktuellt praktiska fallet.

   OM pulsviddsförhållandet mellan stötströmmen 1,42257 T8 A och den återkommande perioden för hela stegbildningen antas vara 1/(200 000) — motsvarande ett förhållande på 1S till 10µS — ges samstämmighet med det beräknade effektivvärdet nedan för en stegkanal på Ø10mM med ovanstående basdata.

 

Om centrumkanalen istället sätts som den 10 ggr större Ø10mM — som ger N=1,11 T13 — ges en 100 ggr högre motsvarande

kontinuerlig strömstyrka

I50 = Q/T = 50(8eN C)/(t6 S) = 711,285 A

Energin E=UGQ/2 blir då med UG/2 =12,5 MV (se U-värdets integralform genom strömmens induktiva uppbyggnad E=LI2/2) räknat på en 7000 meter lång luftkanal med grovleken 10mM lika med

E = 50(8e · 1,11 T13 C)(25 T6 V) = 17 782,2 J.

Det motsvarar i ekvivalenter med effekten E/(t=1S)=17,7822 KW likspänningen 25 Volt för likströmmen 711,285 Ampere.

 

Resultat, stegströmmens motsvarande effektiva kontinuerliga strömstyrka:

 

7 Ampere för en stegkanal på Ø1mM eller

700 Ampere för en stegkanal på Ø10mM

Strömstyrkan ökar med kvadraten på stegkanalens diameter.

 

Uppgifterna från undersökningarna under 1900-talet på blixtkanalens grovlek varierar mellan diametrarna grovt 1 mM till några centimeter, se citatkällorna nedan.

Uppgifter om (effektiva) strömstyrkan för stegledarens enskilda steg (som grundas experimentellt på att mäta elektriska fältets styrka och ändring i samband med observerade stegade ledare) anges typiskt — med grund i indirekta slutsatser grundade på mätningar av elektriska fältens ändringar — större än 1000 A , källa LIGHTNING Physics and Effects 2007 Vladimir A. Rakov, Martin A. Uman sidorna 7 (tabell), 111, 134, m.fl. Där anges också en uppskattad medelgrovlek på ”probably less than 1 cm in diameter”,

”troligen mindre än 1cM i diameter” för blixtkanalen (sidan 134 sp2n); Boken finns att läsa på @INTERNET (2008-06-20) med begränsad åtkomst på Google Böcker.

Sett i storleksordningen med ovanstående grovresultat på 0,7 KA (för en kanal med grovleken ca 1 cM), är området för värdena tydligen samstämmigt.

Vi noterar att stegkanalens diameter ENLIGT TNED innefattar den atombundna elektronmassa som sedan försvinner vid den längre fram kommande egentliga blixturladdningen och vars blixtkanal därmed kommer att synas (uppmätas) på (betydligt) mindre diameter — beroende på graden av inverkan från den omgivande jonströmmens yttre delar. Här finns alltså ytterligare parametrar som gynnar marginalerna — i den möjliga jämförelsen med experimentella data.

 

 

UTAN VIDARE UNDERSÖKNINGAR kan vi omöjligen fastställa från fall till fall »vad som gäller» vid blixturladdningens förlopp:

En stegad ledare (eng. stepped leader) KAN ha ett ypperligt litet tvärsnitt, analogt bestå av mycket få luftmolekylstammar, och därmed knappast framstå alls.

Men den kan också ha ett STORT tvärsnitt med många stammar, kanske tiofalt (eller hundrafalt, beräkningsexemplet ovan).

 

Källuppgifterna anger i ett fall en efter experimentella observationer uppskattad blixtkärnyta på två kvadratmillimeter

 

[http://volcaniclightning.tripod.com/aflashof.htm]

från det äldre materialet med Charles Boys (1855-1944) roterande linskamera med upplösningen 26 000 bilder per sekund.

Denna källa anger även

”The diagrams show that the stepped leader advances in a thin channel which has a very luminous tip.”

Min översättning:

Diagrammen visar att den stegade ledaren avancerar i en smal kanal som har en mycket ljusstark spets.

 

Även Uman, se nedan, ansluter till denna beskrivning (s87):

”For several individual steps in dart-stepped leaders (Section 8.2), Orville and Idone (1982) reported a photographed structure consisting of a distinct bright tip at the bottom that fanned out and became more diffuse toward the upper portion of the step.”.

Min översättning

För flera individuella steg i spjutstegade ledare (Sektion 8.2), rapporterade Orville och Idone (1982) en fotografisk struktur bestående av en distinkt ljus spets vid botten som falnade ut och blev mera diffus mot stegets övre del.

 

 

En annan källa anger ”less than one inch in diameter”,

”mindre än en tum [2,5 cM] i diameter”

 

[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ligseq.html]

materialet från Martin Uman, också av den äldre typen (1972/1987).

 

RÄKNEEXEMPLET OVAN

antyder en motsvarande 250 Watts lampa

 

som dras med hastigheten T6 M/S per sekund motsvarande framänden på en stegad ledare som just utbildas.

Zhang 2006

En grupp kinesiska forskare har genomfört en fotografisk dokumentation av en (sådan) motsvarande experimentell observation, se nedan.

 

[http://icae2007.googlepages.com/OS4-4yijunzhang.pdf] från augusti 2006:

Fotografisk observation av stegbildning med växande ljusstyrka

0,2 mS mellan varje bild

 

 

medelhastighet 0,867 T6 M/S, källa Zhang 2006 se nedan

 

 

 

[http://icae2007.googlepages.com/OS4-4yijunzhang.pdf] augusti 2006, från @INTERNET 2008IV14

Yijun Zhang, Jun Li, Weitao Lu, Wangsheng Dong

Laboratory of Lightning Physics and Protection,Chinese Academy of meteorological Sciences

”

The negative natural cloud-to ground lightning occurred at 16:53:23, Aug. 1, 2006.

The CG lightning discharge was 2,1km far from the observation site and includes 13 return strokes.

The luminosity peaks of the 2nd, 3rd, and 8th return strokes are larger than that of the first return stroke.

”.

[CG, förkortn. eng. Cloud to Ground, Moln till Jord].

BILDSEKVENSEN MED DE TIO BILDERNA i intervall om 0,2mS

varav endast de fem sista har medtagits ovan (de fem första är ännu ljussvagare än den första ovan)

har bl.a. texten:

”

The average speed of the leader is 8,67×105m/s.

The luminosity increases with the development of the leader.

”.

Min översättning (sista delen):

Luminositeten ökar med ledarens utveckling.

 

 

 

 

Den observerade stegade ledarens medelhastighet anges till 8,67 T5 M/S — vilket med justering 0,867×257,7W skulle motsvara en dryg 220 Watts lampa med konstant ljusemission om blixttråden håller exakt samma tvärsnitt (se räkneexemplet ovan från GRUNDRÄKNINGEN).

 

Den kinesiska observationen från augusti 2006 (totalt tio bilder i intervall om 200 µS) uppvisar en tydligt luminöst växande blixtbana — från början alls knappt synlig med utrustningens referens. Vartefter tråden växer ner mot marken, tillväxer ljusstyrkan tydligt.

 

Enligt TNED kan orsaken — energin — till den detaljen endast vara en: det växande tvärsnittet i blixtstammen då den avancerar ner mot marken och som därmed innefattar en växande totalmängd stamkopplande luftatomer och därmed en motsvarande induktivt växande flasheffekt. Se vidare från ljusflasharna i stegbildningen.

 

 

 

 

 

 

REFERENSER

 

REFERENSER

antalet atomagenter

Antalet atomagenter

Från MPcPb

   Hur många atomer deltar i strömvägen?

   Luftmolekylernas medelhastighet (vid STP, Standard Temperature and Pressure) är ca 480 M/S.

   Medelavståndet mellan molekylerna är (grovt sett 1/[2,687 T25]1/3 allmänna gaslagens komponenter) 3nM.

   Med hänsyn till att atomernas toppspinn har alla möjliga riktningar vid tillfället för genomslaget kan vi göra en grov skattning på följande sätt.

   Det finns bara två spinnflödesriktningar att välja på. 50% bortfaller alltså direkt. Det är de molekyler vars atomer för tillfället har sin spinnriktning motsatt den som kommer att koppla den aktuella strömstammen. Av de återstående 50%:en kan vi ytterligare eliminera grovt sett 50%. Det är de atomer vars spinnriktningar ligger rätvinkligt strömvägen och upp till 45° mot denna. Ytterligare en del bortfaller av symmetriskäl som sammanhänger med strömlinjens hållfasthet (som idealt kräver atomer av samma sort). Resterade mängd, grovt räknat ca 1/5, blir de potentiella agenter som kommer att konstruera strömstammen.

 

Emellertid, om närliggande atomer tas med runt omkring, kan den bortfallande delen 1/5 kompenseras med sneda atomkopplingar, i princip spiralkopplingar totalt sett och som därmed (likväl) bevarar gränsspänningen (UG) mellan två närliggande atomer. Därmed kan den bortfallande delen på 1/5 hänföras till en motsvarande ekvivalent total trådlängd för de längskopplade atomvägarna (fastän den analogin egentligen borde beskrivas som ”väsentligen spiralformad”). Vi räknar därmed med att varje koppling mellan två närliggande luftatomer med medelavståndet ca 3nM ALLTID kopplar i en blixtstam — men nödvändigtvis inte i rakt nedstigande led.

 

Sedan kan vi alltid diskutera vad som hände med den utelämnade delen på 1/5: de atomer som kopplar bildar en motsvarande stark lokal magnettråd i atomernas gemensamma spinnriktning, och kan därmed påverka utelämnade atomindivider med än större kraft — som därmed kan upptas i atomtråden. Här finns alltså flera möjligheter.

boken av Martin A. Uman

Uman

The Lightning Discharge, Martin A. Uman 1987, GoogleBöcker @INTERNET

med begränsad tillgång, bara ett visst urval sidor är tillgängliga.

De här boken är tydligen något av ”en bibel” på området blixturladdning. Den innefattar ett stort urval av referenser och experimentella rapporter från en stor mängd personer under i stort sett hela 1900-talet.

 

molntyp

Källan nedan anger i medeltal att ca 90% av alla atmosfäriska urladdningar moln-mark (CG) är av typen negativt laddat moln som överför sitt elektronöverskott till markens positiva del. Termen CG används som förkortning för Cloud to Ground, Moln till Jord för att särskilja fallet CC, Cloud to Clound.

 

http://www.nofc.forestry.ca/fire/faq_lightning_e.php

90% är av typen –CG, 10% är av typen +CG.

 

Tillägg 2011-07-26: Uppgiften/källan ovan från

http://www.nofc.forestry.ca/fire/faq_lightning_e.php

90% är av typen –CG, 10% är av typen +CG.

att ca 90% av alla blixturladdningar skulle vara av typen moln-mark verkar inte längre finnas tillgänglig på webben. Enligt en nyare uppgift (2009) från

American Geophysical Union

http://europa.agu.org/?view=article&uri=/journals/jd/98JD01461.xml

är endast ca

23% av typen moln-mark medan resten ca

77% är av typen moln-moln.

Vilketsom gör dock, här veterligt, ingenting åt saken i princip. Det finns i vilket fall ingen framställning i UNIVERSUMS HISTORIA som avhandlar betydelsen av någon skillnad.

 

ATA

GRUNDBESKRIVNING FÖR ATOMKÄRNANS/ATOMENS TRANSMISSIVA AUTONOMI

ATA

Kort inledande grundbeskrivning — ett särskild dokument behandlar ämnet mera utförligt (se från Atomens Totala Energitransferering)

 

Varje atom som ingår i en kopplad atomtråd av den typ som beskrivits i stegledarens bildning har en bestämd gränsströmstyrka (i TNED benämnt nukleära sönderfallets gränsströmstyrka) över vilken den inte längre kan försörja strömpådraget i sin tråd. Gränsströmstyrkan bestäms av de enkla grundparametrarna i TNED enligt

 

IN          = Q/TN = A·(1836/2=918)e/TN, A anger masstalet, e = 1,602 t19 C

 

För atomkärnans centralmassiv 1818e, se atomkärnans härledning från PLANCKRINGEN om ej redan bekant.

Är totala strömstyrkan (ie–Bi) genom kärnbrunnen (idealt och grovt, vi frånser vissa detaljer)

 

IN          = Q/TN = A·918e/TN

 

berövas tydligen kärnan

— enligt ATA-ekvivalenterna

 

 

 

Atomens-Atomkärnans Transmissiva Autonomi

 

 

J0K+3(n)(J1K/n)             = 0  .......................................    toppringarna kan delas obegränsat

3–1J0K+(n)(J1K/n)          = 0  .......................................    momentet kan delas med toppringarnas delning

(3n)–1J0K+(J1K/n2)         = 0  .......................................    ytterligare ekvivalent

J – mwr2                        = 0  .......................................    radien kan växa med avtagande massa, konstant toppspinn

FBT+FeZ                         = 0  .......................................    bägge term. försv. med e-elem. upplösning, balansen bev.

 

Impuls- och kraftekvationerna innefattar ekvivalenter, se ovanstående uppställning, som tillsammans med den teoretiskt beskrivna strömgenomgången i kärnbrunnen kan åstadkomma en REGLERING AV TOPPTOROIDENS RINGFORM: atomkärnans ringform kan svälla.

 

 

 

— fullständigt sin elektrondel (A918e) inom TN och lämnar MINST en resterande frilagd positronkärna på A·918e+, A masstalet.

[Positronen (e+) är benämningen för elektronmassans positiva make (e–), se ±e-strukturerna från Atomkärnans Härledning].

TN (för luft) kan beräknas approximativt med kännedom om parametrar vid ljusbåge:

man får approximativt TN=3 t20 S enligt  = Q1,602 t19 C/I5A — detta värde är också enligt TNED samma som det övre gränsvärdet för atomkärnans ändring vid fusion;

Strömstyrkan I=5A är grovt minsta strömmen för kontinuerlig ljusbåge (enligt gängse referensverk — men vissa källor antyder snarare runt 1 Ampere);

Q=1,602 t19 C är minsta atomladdningen för minsta strömmen. Vi använder här tills vidare grovvärdet

TN         = 3 t20 S; Då är

IN          = A·(1836/2=918)e/ (3 t20 S)

             = A · 4902,12 ........................    A, A anger masstalet

 

För Syre16 som en medelform för luften (75% Kväve15, 25% Syre16) blir gränsströmstyrkan ca 78 434 A, eller grovt ca 80 000 A.

 

Detta värde stämmer också mycket bra med den ungefärliga övre gräns man känner konventionellt för max strömstyrkor i blixturladdningar. Olika källor anger något olika maxgränser, men de brukar sättas till omkring 100 000 A. ”Normalblixten” håller i konventionella termer ca 20 000 Ampere. Observera dock att gränsvärdet med 80 000 Ampere gäller för EN tråd med bara ett enda led av sammanhängande syreatomer — en typisk blixtkanal KAN (i varje fall teoretiskt) innehålla miljardtals sådana på en tunn stam med diametern 1 mM, se vidare från Grundberäkningen. Detta gör en motsvarande experimentell utvärdering mera komplicerad då vi aldrig kan förutsäga blixtkanalens tvärsnitt, bara ange typiska riktvärden.

 

Om en lufttråd bestående av syreatomer påtvingas en kärnbrunnström större än ca 80 000 A inträder en kapacitiv transmission; den/de berörda atomkärnan tvingas sönderfalla enligt ATA-ekvivalenterna (observera att dessa bevarar kärnbalansen) och emitterar därmed enbart av det skälet (starkt koncentrerad) gammastrålning (g). g-strålningen bildas emellertid framför allt då den frilagda starkt Coulombiskt elektronattraherande positronringen drar till sig omgivande elektronmassor; Då elektronerna möter den kompakta positronringen, förintas elektronen och så småningom även den större positrondelen genom s.k. annihilationsstrålning med grundenergin E=mc2=hf=(0,000548598u)(2,99792458 T8 M/S)2 ca 1 MeV: I normala annihilationssammanhang resulterar elektron-positronannihilation alltid i en distinkt diametralpolariserad dubbelriktad (±e) 511 KeV annihilationsstråle — som bl.a. utnyttjas inom medicinen i s.k. PET-kameror (Positron Emission Tomography), vilket klassificeras som g-strålning. I vårt fall motsvarar emellertid den frigjorda positronringen också en närmast enorm attraherare vilket utöver annihilationsenergin som sådan bildar källa för en stor rörelseenergi för elektronernas del; då de kolliderar med positronringen, sker ett abrupt avstannande, och en induktiv transient bildas, en så kallad bromsstrålning (konv. brehmsstrahlung, eng, breaking radiation, eller enklare bara stoppstrålning).

 

OM elektronen enbart på grund av den kraftiga attraktionen mot positronringen utvecklar energin 30 MeV vid kollisionsögonblicket (det finns här ingen exakt räkning på den delen än) — vilket är vad den observerade gammaenergin kräver — motsvarar det en i vakuum pålagd accelerationsspänning på U=30 MV som ger elektronen sluthastigheten 0,998596c enligt (se elektronens massökning)

 

u = c[1 – 1/[(Ue/m0c2) + 1]2]1/2 ..............................       laddningshastigheten u från accelerationsspänningen U

 

Elektronens vilomassa är m0=9,11 t31 KG, dess laddning är r=1,602 t19 C, maxhastigheten i e-fältet är c=2,99792458 T8 M/S.

Det motsvarar grovt sett en idealt mekaniskt accelererad elektron med vilomassan m0 som drivs upp till hastigheten ca 10c (och litet till) med mekaniska rörelseenergin

E = mv2/2 = 4,1 t12 J eller 25,6 MeV.

 

Om vi inte får använda de nu nämnda detaljerna för att SÅ förklara, beskriva och härleda den starka gammastrålningens förekomst i samband med VISSA (långt ifrån alla) blixturladdningar, vill i alla fall jag påstå att det är KÖRT.

 

I MODERN AKADEMI kämpar man med sina elektroner som fenomenets UTESLUTANDE ENDA spöklika vålnader, men som ingen förstår HUR de kan bilda fenomengrunderna. Generellt jobbar man med att försöka använda den kosmiska strålningen som katalyserande, verkställande lysknapp för att ”rulla igång elektronerna” och som är det enda alternativ man känner till för att försöka hitta en initieringspunkt. I TNED finns inte det problemet.

 

Fortsättning följer.

 

gammastrålningen

Den mindre frekvent observerade men mera högenergetiska Gammastrålningen i samband med blixturladdning

GAMMASTRÅLNINGEN

 

Som omnämndes i ATA, kan i vissa mindre vanliga fall mindre kända naturfenomen visa sig i samband med åskväder. Om en syrekärna kan sönderdelas enligt ATA, drar den så frilagda starkt positivt laddade kärnringen till sig motsvarande elektronmassor, och en massförintelse är oundviklig. I följande delartikel ges en grov översiktligt exemplifierad kvantitativ-kvalitativ beskrivning av vilka strålningseffekter och energier som för detta fall kan komma ifråga enligt TNED.

 

Elektron-positronannihilationen är välordnad, (se Parannihilation). Elektronmassans t-ringar (se Elektronmassans komponenter) blir inbördes starkt repellerande då de kommer varandra mycket nära, vilket sker då elektronmassan kolliderar med den frigjorda kärnpositronringen (se ovan från ATA). Därmed kastas den kvarvarande elektronmassan tillbaka ut, för att strax återigen attraheras av den starkt positivt laddade restkärnringen. För varje sådan puls förintas en del av elektronmassan tillsammans med motsvarande positrondel i kärnringen. Under annihilationsprocessen kommer därför den ständigt minskande elektronmassan att avancera mot kärnringen från ett minsta näravstånd som bör vara mycket litet med hänsyn till elektronringarnas små dimensioner (se Elektronmassans komponenter).

 

Med kärnringen i storleksordningen atomkärnan, som för syrekärnan betyder grovt 2,5 gånger protonradien eller ca 3,5 t15 M via (1,37 t15 M)(16)1/3 kan vi sätta maximala oscillationsavståndet mellan den stora kärnringens kroppsyta och elektronmassans cylindriska ringkropp som d; Olika omständigheter kommer att bilda olika förutsättningar med motsvarande magnituder. Vi får då idealt den effektiva energin i arbetet Fd mellan positronringen och elektronen enligt

 

E = Fd =  k9 T9 VM/C(A16918e1,602 t19 C)(eStarktAVTAGANDE)/d

 

EXEMPEL — Resultatvärden, grovt orienterande:

Planckenergin E=hf som utvecklas i elektronannihilationen mot restkärnans positronring blir ekvivalent för olika d-värden:

Värdet i MeV fås genom att dividera energivärdet i Joule med e=1,602 t19 C samt dividera med en miljon;

 

d = 7 t14 M eller ca 20 ggr kärnringens radie ger ca

E = 300 MeV;

 

d = 7 t13 M eller ca 200 ggr kärnringens radie ger ca

E = 30 MeV;

 

d = 7 t12 M eller ca 2 000 ggr kärnringens radie ger ca

E = 3 MeV;

 

d = 7 t11 M eller ca 20 000 ggr kärnringens radie ger ca

E = 0,3 MeV;

 

d = 7 t10 M eller ca 200 000 ggr kärnringens radie ger ca

E = 0,03 MeV;

 

I mera exakta beräkningar måste skärmningseffekten på grund av kärnringens effektiva lokala masstäthet beaktas, vilket reducerar faktorn A918e. Men då måste också elektronmassans starkt avtagande funktion medräknas. Dessa bägge parametrar tar delvis ut varandra. Dessutom måste hänsyn tas till den lokala elektronmasstätheten i kärnringens närhet eftersom också den inbördes repulsionen mellan närliggande elektronmassors elektronringar påverkar förloppet. Ingen av dessa faktorer har tagits hänsyn till i ovanstående grovräkning.

 

Strålriktningen är starkt begränsad

 

Med hänsyn till att kärnringarna bör utvecklas med motsvarande blixtstammens deltråd i centrum, och med hänsyn till elektronmassornas starka attraktion till den frigjorda positronringens ringplan, bör gammastrålningen likaledes vara extremt »planpolariserad» med referens till markytan, alltså INTE typ ”rundstrålande” (den kan i allmänhet INTE detekteras direkt av markbaserade sensorer) utan snarare tangentiell till markytan — vilket av allt att döma är en av anledningarna till varför man (mycket gynnsamt, se illustrationen nedan) upptäckte gammastrålningen från blixturladdningarna (från ett stort område av Jordytan) genom satelliter som egentligen var tänkta att registrera gammastrålning från Solen. Det krävs dock mera ingående källdata för att få den uppgiften säkert bekräftad.

 

 

Källdata på energierna i den observerade och katalogiserade gammastrålningen från blixturladdningar finns bl.a. i källan @INTERNET nedan

 

Measuring x-ray emission from lightning

Joseph R. Dwyer, Department of Physics and Space Sciences, Florida Institute of Technology

[http://www-group.slac.stanford.edu/ais/PublicDocs/presentation68,pdf] (2005)

 

Som vi ser är ovanstående grovvärden analoga med energierna i de observerade gammaskurarna (0,03-10 MeV).

Varaktigheten i gammapulserna ligger i medeltal runt (eller mindre än) 1mS, varav en del uppvisar en inre pulsad finstruktur (pulsgrupper).

Frekvensen i antal tillfällen med de observerade gammaskurarna anges i medeltal per år för hela Jorden till ca 17 (lägst 5, högst 20). Det är alltså tydligt att dessa tillfällen är speciella. Jämför sammanfattningen i ATA.

 

 

positronbollen — utvidgad artikelbeskrivning 2Feb2014-02-02

BILDKÄLLA: Författarens arkiv · 2Okt2010 ·  E9 Bild1 · Nikon D90

 

Den inlagda ljusgloben motsvarar grovt åsynen av »den elektriska ljusbollen» som uppträdde under ett milt sagt kraftigt åskväder enligt vittnesuppgift, se huvudtexten nedan — möjligen en positronboll enligt TNED. Minnesbilden av bollens extrema kantskärpa/konturitet (ungefär som Solranden) är svår att avbilda med enkla medel.

— Många personer under historiens gång har vittnat om liknande fenomenformer. Komplexiteten i samband med de enorma energimängder som omsätts i atmosfäriska blixturladdningar kan här veterligt INTE utesluta att FLERA OLIKA (samverkande) FENOMENFORMER finns beroende på aktuella lokala förutsättningar. Förklaringen nedan berör därför bara just den aktuella vittnesuppgiften, och gör inte anspråk på att vara heltäckande för alla ljusbollsfenomen i samband med åskväder — men kan möjligen vara det.

 

POSITRONBOLLEN

 

 

Fermisatellit bekräftar TNED — Positronförekomst enligt TNED i TGF bekräftad — 31Aug2010

 

 

Under historiens gång har många människor bevittnat det mycket sällsynta fenomenet — alltid i samband med (exceptionellt) häftiga åskväder: På grund av fenomenets sällsynthet, och de teoretiska svårigheterna i den moderna akademins lärosystem har man tidigare (under större delen av 1900-talet) ansett vittnesbörden vara »av typen UFO». På senare tid (Internet) har en viss omsvängning skett. Wikipedia (Ball lightning [http://en.wikipedia.org/wiki/Ball_lightning] 2014-02-02) beskriver fenomenet som »oförklarat naturfenomen», ”Given inconsistencies and lack of reliable data, the true nature of ball lightning is still unknown.[4]”, och ger samtidigt en förteckning över ”föreslagna vetenskapliga förklaringar”: 1. Vaporized silicon hypothesis; 2. Electrically charged solid-core model; 3. Microwave cavity hypothesis; 4. Soliton hypothesis; 5. Hydrodynamic vortex ring antisymmetry; 6. Nanobattery hypothesis; 7. Black hole hypothesis; 8. Buoyant plasma hypothesis; 9. Transcranial magnetic stimulation; 10. Spinning plasma toroid (ring); 11. Rydberg matter concept; 12. Other hypotheses.

   Wikipediaartikeln omnämner inte »Turner-modellen» som omnämns i Encarta99 (Lightning, The Ball Lightning Phenomenon): ”Great Balls of Steam”:

 

”In a thunderstorm, an intense electric field between the positively charged ground and the negatively charged cloud excites air molecules, causing them to lose electrons and become charged ions. A bolt of lightning further energizes the molecules until they become a plasma-a soup of hot, charged molecules and electrons. Perhaps, researchers have suggested, the electric or magnetic field created by a small lump of plasma could trap it in the shape of a ball. Short-lived plasma fireballs have even been created in laboratory experiments, giving the idea some support.”,

”Source: Discover Magazine, July 1993”,

The Ball Lightning Phenomenon, Microsoft Encarta 99

 

Ingen av dessa hör hit.

— En del kallar de lysande kulfenomenen ”eldsklot” eller ”ljusbollar” (»intensivt lysande miniatyrsolar»). Men ännu (2014) finns i etablerade kretsar ingen allmänt erkänd fenomenförklaring. I TNED sätts fenomenet i samband med blixturladdningens fysik generellt: positronbildning vid exceptionellt höga urladdningsströmmar.

— MÖJLIGEN finns olika SÄTT (med olika teorier och hypoteser) till fenomenet, beroende på omständigheter. Den beskrivning-förklaring som ges här gör inte anspråk på att vara den allenarådande — utom för det aktuella vittnesmålet (som möjligen förklarar alla liknande fenomen).

— Källstoffet till beskrivningen nedan grundas på en personlig upplevelse i samband med ett ytterst häftigt åskväder i ett villaområde i Sverige i början på 1960-talet. Den person som sett det ytterst sällsynta fenomenet ser det sedan knappast igen under sin livstid.

 

POSITRONBOLLEN

GRÄNSSTRÖMSTYRKAN FÖR KAPACITIV TRANSMISSION I LUFT är enligt TNED 78 000 Ampere. Strömstyrkorna i medeltal vid atmosfärisk urladdning ligger enligt konventionella uppgifter kring 20 000 Ampere.

 

Praktiskt exempel

 

Plötsligt (efter en kraftig blixtbang) framträdde en basketbollstor (Ø20-30cM) helt stillastående intensivt lysande perfekt rund ljusboll vid pass 2-3 meter utanför fönstret.

 

 

— Själva formen liknade närmast den man kan se vid solnedgång vid direkt betraktelse av Solen, men mera blåaktig: en intensivt starkt lysande perfekt rund skiva med ett karaktäristiskt ”elektriskt sken” i periferin, ungefär som Solkroppens skarpa övergång i den omgivande bildytan: inga ”eldslågor” eller andra ojämnheter. Bollen var helt perfekt rund, ytterst skarpt konturerad.

— Ljusbollen rörde sig inte, stod helt blick stilla, kanske 3-10 sekunder. Sedan lika plötsligt försvann den, utan någon rörelse, utan något ljud.

 

FENOMENET ENLIGT TNED

NERE VID MARKBASEN (anoden) där elektronhastigheten är som störst och därmed strömstammens jonisering som kraftigast, kan i sällsynta fall vid blixtnedslag extremt höga strömstyrkor uppnås. Som framgår av TNED, kan en atomkärna fullständigt berövas sin negativa Q-kropp om strömgenomgångens ekvivalent är

I=Q/T=A·918e1,602 t19/3t20=A·918·5,34 @ 4902A. Detta lämnar en positiv restkärna (se från ATA). A anger masstalet för aktuell nuklidtyp, lika med 16 i fallet Syre.

 

Bara ett ytterst litet område i luften (några hundradels millimeter bara i kub) vars atomkärnor så fullständigt berövas sina negativa Q-massor kan under tio sekunder (lätt) uppvisa en praktiskt taget viktlös basketbollstor perfekt rund elektriskt lysande sfär — med mikrotunt skal dock — med motsvarande ”lampeffekten” 360 Watt. Vi studerar ett praktiskt räkneexempel längre ner.

 

Genom positronbollens skal (med det inre tillfälligt bestående av positiva luftatomjoner) är det naturligt för bollen att uppvisa extraordinära egenskaper — som till exempel att till synes obehindrat ta sig rakt igenom ett glasfönster: positronskalet absoberar-annihilerar glasatomernas elektronmassor och gör därmed lätt som en plätt ett motsvarande materiehål, i princip genom vad som helst. Positronbollens förmåga att följa (negativa) elektriska fältstråk, till exempel via elkablar eller liknande blir också utpräglad, liksom bollens påtagliga lätthet: den kan ses stå helt stilla i luften, i flera (tiotal) sekunder, för att plötsligt och tyst bara försvinna utan ett ljud.

 

Sfäriciteten uppkommer (lätt) OM en lokalt sett större mängd syreatomer genomgår ATA med kärnupplösning gemensamt; genom den lokalt ömsesidiga repulsionen och tillfälliga frånvaron av elektronmassa, kan restkärnringarna expandera bort ifrån varandra sfäriskt homogent för att därmed bilda ett nära perfekt sfäriskt skal mot den omgivande luftens negativa elektroner som nu bollytan strax börjar ”konsumera” — under intensiv ljusemission. Genom utjämningar och luftens homogenitet, sker annihilationerna mellan positroner och luftatomernas elektroner med referens till ett sfäriskt centrum via ytterdelen på sfärens ytterst tunna skal. Då luftatomerna rekombinerar sinsemellan för att återställa elektronbalansen i bollytans närhet bildas intensiv ljusutveckling vilket ger klotet dess karaktäristiska ”elektriska sken”.

 

Den lilla koncentrerade bildningspunkten med positronbollen just efter blixturladdningen kan snabbt växa till ”arbetsstorlek” eftersom den i vilket fall omges av ett relativt stort område av redan starkt joniserade atomer från själva den tidigare strömstammen. Längre ut i kanten är luftjonisationen mindre och bollens växande avtar därför exponentiellt mot denna kant. Under några få sekunder (eller t.o.m. i vissa fall upp till minuter) kan den sedan ha i stort sett konstant radie medan den förbrukar sin vara.

 

Ljusbollen kan stå blickstilla mitt i luften, röra sig längs synliga eller osynliga elektriska ledningsstråk, den kan lätt passera rakt igenom en tjock glasruta, den åstadkommer stor lokal förstörelse vid kontakt med (högspända) elektriska ledningspunkter. Ljusbollens varaktighet (från sekunder till minuter) avtar med växande diameter (vilket här enbart grundas på nödvändigheten med avbränningshastigheten; en stor bollyta bränner snabbare än en mindre).

När positronskalet är förbrukat ”försvinner” ljusbollen bara ”i tomma intet”, helt abrupt och plötsligt, utan minsta ljud.

 

Många har sett det mycket sällsynta fenomenet under historiens gång, men dess mystiska natur har ännu i etablerade kretsar undandragit sig en tillfredsställande förklaring. Det finns dock flera olika teorier och hypoteser som framlagts av olika personer med olika bakgrund. Den beskrivning-förklaring som ges här gör inte anspråk på att vara den allenarådande.

 

RÄKNEEXEMPEL

— betraktelseavstånd ca 2-3 meter för orientering

 

Vi räknar förenklat på ljusbollens diameter 2r=30 cM=0,3 M och använder förenklat syreatomen 8O16 med specifika vikten 1,43 KG/M3 (vid 20°C). Mot varje elektron (b–) i varje syreatom som vidrör bollens yta svarar en positron (b+). Vartefter ±b- annihilationen fortskrider, omvandlas b-massorna till em-strålning. För att beräkna energiflödet kan vi utgå ifrån en given elektrontäthet vid bollens yta och som minst måste uppvägas av en motsvarande positrontäthet. Vi kan beräkna kärmassan hos de syreatomer som ingår i denna yta och därmed få ett första underlag.

   Om vi, grovt, räknar på ett skal ovanför bollytan med tjockleken lika med radien hos en syreatom (vid 20°C), ca 13,5 Å eller d=1,35 t9 M får vi skalvolymen

V = 4p(rut3–rin3)/3 = 4p([r+d]3–r3)/3 @ 4p(1t10 M3)/3 = 4,2 t10 M3

Kärnmassan för denna volym därmed 1,43 · 4,2 t10 = 6,006 t10 KG.

Syrekärnan är 16 ggr tyngre än neutron-protonaggregatet och håller därmed 16×918=14688 positroner, mycket grovt sett 15000. Den syrekärnmassa som via positrondelen definierar ELEKTRONBALANSEN på bollytan, motsvarar alltså 1/15000 av bollskalets beräknade kärnmassa 6,006 t10 KG. Detta ger

(6,006 t10)/15000 = 4,004 t14 KG  .........................      syrekärnans frigjorda positronmassa

Den pyttelilla massan är alltså syrekärnan frigjord som positronmassan i balans med den omgivande elektronmassan.

Totala (positron-) energin blir med c=3 T8 M/S

E=mc2= 4,004 t14 KG · 9 T16 (M/S)2 = 3,6036 KJoule

Eller, med samma innebörd, 360 Watt under tio sekunder.

— Det är som att titta rakt in i en stor stark strålkastare på nära håll.

— Bländande.

 

 

 

 

 

 

 

 

 

END BlixturladdningensFysik.

 

 

 

 

 

 

Blixturladdningens fysik

 

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

 

Blixturladdningens fysik

ämnesrubriker

 

                      

 

innehåll

                                      BLIXTURLADDNINGENS FYSIK

 

                                                         Kort inledande beskrivning

 

                                                         Grunddata för stegade ledaren

 

                                                         Huvudskillnader TNED/MAC

 

                       Blixturladdningens fysik

 

                                                         Stegcellens bildning

 

                                                         Kraftekvationen

 

                                                         Atomkärnan enligt TNED

 

                                                         Isolator och massledare

 

                                                         Magnetiska kraftekvivalenten

 

                                                         Dipolkaraktären i kemiska föreningar

 

 

                       Blixtbildningen

 

                                                         Stegad ledare

 

                                                         Arbetet

 

                                                         Fotografisk observation av stegbildning

 

                                                         Blixtbanans bildning i syntes

 

                                                         Stegflashens bildning

 

 

                       Urladdningen

 

                                                         Blixtbildningens energi

 

                                                         Globaldata

 

                                                         Allmänna grunddata molnladdningen

 

                                                         Molnspänningen

 

                                                         Urladdningsförloppet

 

 

                       Isolationsspänningen för luft

 

                                                         Kort historik

 

                                                         Sibiriska exemplet

 

                                                         Citat e-fältet Uman

 

                                                         B-styrkan från stegänden

 

                                                         B-styrkan

 

                                                         Den mystiska Coulombtätheten

 

                                                         Tabell · allmänna elektriska data för rymd, luft, mark

 

                                                         Elektrontäthet

 

                                                         Resistiviteten för fri rymd

 

 

                       Grundräkning

 

                                                         Gränsspänningen för luft enligt TNED

 

                                                         Föreningsarbetet

 

                                                         Röntgensrålning från stegade ledare

 

                                                         Stegändens strömstyrka

 

                                                         Kinesiska rapporten

 

 

                       REFERENSER

 

                                                         Antalet atomagenter

 

                                                         Boken av Martin A. Uman

 

                                                         Molntyp

 

                                                         ATA

 

                                                         Gammastrålningen

 

                                                         Positronbollen

 

 

referenser

t för 10^–, T för 10^+, förenklade exponentbeteckningar

 

TNED

 

  

 

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

 

Senast uppdaterade version: 2018-06-21. Närmast föregående uppdatering 2008-09-16.

*END.

Stavningskontrollerat 2008-06-23|24; 2014-01-31.

 

rester

*

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG-justerad 2011-08-07

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se