ANALYSEN|EXEMPEL — UNIVERSUMS HISTORIA | a production 2008XII22 | Efter sammanställningar från 1997IX27 | Senast uppdaterade version: 2014-04-03 · Universums Historia

 

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i  SAKREGISTER  ·  förteckning över alla webbsidor

 

 

 

Analysen|EXEMPEL | i sammanställning för Universums Historia

 

FÖRSTA ORDNINGENS VARIANTER | logistiska tillväxtekvationen | fritt fall med luftmotstånd |  | globala vattenflödet | kondensatorn och spolen |

 

ANDRA  ORDNINGENS VARIANTER | svängningsekvationen |

 

 

EXEMPEL

 DEN HÖGRE ANALYSEN

  Se UniVar.wps s75 | M2001_3.wps s146

 

 

 

 

 

Praktiska utvecklingsexempel

KALKYL_02.doc

 

Från Den Högre Analysen, Varianter och Universaler — inledande Praktiska exempel

 

 

— grunderna i matematisk-fysikalisk formulering av naturliga processer

 

 

® GLOBALA VATTENFLÖDETS ALLMÄNNA EKVATION  ................      en första ordningens linjär homogen variant med variabel koefficient

® LJUSETS ÄNDRING GENOM MATERIEN  ........................................      en första ordningens linjär homogen variant med konstant koefficient

® FRITT FALL MED LUFTMOTSTÅND  ...............................................      en första ordningens inhomogen icke linjär variant

® DEN LOGISTISKA TILLVÄXTEKVATIONEN  ....................................     en första ordningens homogen icke linjär variant med variabel koefficient

® ALLMÄNNA SVÄNGNINGSEKVATIONEN  .......................................      en andra ordningens linjär homogen variant med konstanta koefficienter

 

För termen variant, se även varianternas allmänna klassifikation.

 

 

I GLOBALA VATTENFLÖDETS ALLMÄNNA EKVATION innefattas tillämpningar som beskriver och förklarar motsvarande termer inom elektrofysiken genom kondensatorns uppladdning och spolens inkoppling, se från Flödets verkställande egenskap, samt begreppen induktiv och kapacitiv reaktans, se från

GLOBALA VATTENFLÖDETS ALLMÄNNA EKVATION omsatt på elektrofysiken.

 

 

 

 

 

 

 

 

Följande härledda universaler kan betraktas som grund, referens och underlag för vidare studier i integralkalkylens elementa. Vi förutsätter att alla givna varianter också är givna med reella

[ej i-tecknade] koefficienter.

 

 

 

 

 

1:a ordningens varianter

 

 

LJUSETS ÄNDRING ljusintensiteten GENOM MATERIEN

M2001_3.wps s149

 

När LJUS med given intensitet (I, effekt) inträder ett material, förloras en del av intensiteten med ljusets vidare materialgenomgång som följd av växelverkan med materialets masselement (absorption, energiförlust via molekylerna-atomerna och deras konstituenter, se även i Comptoneffekten). När ljuset »färdas» genom tomrummet förloras ingen motsvarande intensitet eftersom det inte finns någon massform (ingen energi) att utbyta växelverkan med i tomrummet. I respekt till det avstånd x som ljuset tillryggalägger i materialets fall får vi då direkt den enkla varianten

 

             dI/dx = –µI

 

µ (mikro) är den motsvarande karaktäristiska proportionalitetskonstant som sammanhänger med ett visst material (inom en viss temperatur).

— Varianten relateras negativ därför att intensiteten avtar, den ses positiv för växande kvantiteter med växande tid.

— Intensiteten (I) har ett visst värde vid en viss avverkad distans (x) och det finns inte mycket annat att välja på i formuleringens matematik.

Uppgift:

Bestäm ekvationen för I som funktion av x.

Lösning:

Varianten dI/dx = –µI = y’ = ay ger differentialekvationen

dI/I = –µdx

som via logaritmderivatan Dn ln(P) = Dn(P)/(P) = d(ln(P))/dx ger fundamentalintegralen (vänstra) tillsammans med enhetsintegralen (högra)

ò dI/I = ln(I) = –µ ò dx = –µx

Eftersom det gäller att ea=(P) ger a=ln(P), se logaritmlagarna, får vi motsvarande

e–µx = I;

 

                y=e–x

 

 

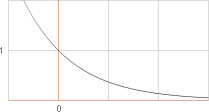
Med x=0 ges ett maxvärde som vi betecknar I0 så att vi kan skriva ekvationen enhetligt enligt

I = I0e–µx

Dvs., I = I0 om x=0, analogt precis då ljuset inträder materialet, och endast då.

Svar:    I = I0e–µx

Konstanten µ (enhet M–1) varierar med material, –µ = (lnI)/x = konstant.

 

 

 

Första Ordningens Varianter — Första Ordningens Inhomogena Variant med En Variabel Koefficient [FOIVEVK]

 

INLEDANDE ALLMÄN ÖVERSIKT

————————————————————————————————————————————

y’ +  f (x)( y – A ) = 0  ......         varianten, allmän form: dy/dx = y’ = f (x)(A – y)

FÖRSTA ORDNINGENS (InHOMOGENA) VARIANTER MED EN VARIABEL KOEFFICIENT

y = A + C e–F(x)  ..............          variantens universal

Härledning

 

I fallen  [ · ] =  f (x)  kan vi optimera varianten  y’ +  f (x) y = [ · ]  enligt

             y’ +  f (x) y = f (x)A

[ · ] betecknar ett godtycklig matematiskt uttryck (den okända).

Varianten skriven på allmän form blir då

             y’ +  f (x) y – f (x)A = 0 = y’ +  f (x)( y – A )

Från  y’ = – f (x)( y – A ) = dy/dx tecknas differentialekvationen

             dy/( y – A ) = – f (x) · dx

med fundamentalintegralerna

             ln ( y – A ) = –F(x) .

speciellt om logaritmintegralen

Vi observerar här att alla relevanta ln(y–A) medför ett absolutvärde | y–A | så att även | A–y | gäller eftersom ln(–x) är irrelevant; formen ln(y–A) för alla y > A får alltså samma värdemängd som formen ln(| A–y |). Saken leder oss till ”det kufiska sambandet” att   

[ dy/( y – A ) = – f (x) ] =  [ dy/( A – y ) =  f (x) ]  som ger  [ – ln (| A – y |) = F(x) ]  med  [ (| A – y |) = e–F(x) = y – A ]  förutsatt y > A . Detaljen sammanhänger med att varianten  [ y’ = – f (x)( y – A ) ]  naturligtvis också kan tecknas  [  y’ =  f (x)( A – y )]. Observerar vi inte dessa detaljer hamnar vi i bryderier då resultatet i det senare fallet relativt resultatet i huvudtexten, strängt, skulle ge  [ y =  A – C e–F(x) ]. Teckningen i e-logaritmens parentes utsäger m.a.o. rent tekniskt att  | y – A | = | A – y | gäller.

 

Generalisering av fundamentalintegralen (högra ledet) ger universalen

             ln ( y – A ) = –F(x)+K

Universalen uttryckt i funktionsvärdet  y  blir därmed

             y – A  = e–F(x)eK = C e–F(x) ;

             y = A + C e–F(x)  ..............................       universalen till varianten  y’ +  f (x)( y – A ) = 0

 

Vid bestämningen av partikulärlösningar till inhomogena (HL¹0) första ordningens varianter är det av viss vikt att först avgöra huruvida (de eventuella) x-funktionerna hos varianten är av samma slag. Alltså, om varianten kan eller inte kan uttryckas på formen

             y’ +  f (x)( y – A ) = 0

Om så är fallet, är dess lösning som ovan av den enklare formen  y = A + C e–F(x).

 

 

 

LOGISTISKA TILLVÄXTEKVATIONEN

 

 

 

 

      utvecklingsexempel

 

 

Logistiska tillväxtekvationen omnämns på flera (många) ställen i lärobokslitteraturen (gymnasiet och högre). Men i varje fall på gymnasienivån tycks benägenheten hos författarna att förbarma sig med en elementär härledning mindre uttalad (en sådan har eftersökts i nämnda men inte hittats). Här följer den.

 

             y’ – ay(M – y) = 0  ............        den logistiska tillväxtekvationen

FÖRSTA ORDNINGENS HOMOGENA IckelinjäraVARIANTER MED EN VARIABEL KOEFFICIENT

             f (x) = ay  ..........................        från  y’ +  f (x)( y – A ) = 0

 

Om  f (x)  i den homogena varianten  [ y’ +  f (x)( y – M ) = 0 ] är av den speciella formen  ay  så att vi får varianten

             y’ + ay(y – M) = 0 , vi kan även teckna den

             y’ – ay(M – y) = 0

om vi vill att | M – y | (M för maximum) ska gälla (se Speciellt om logaritmintegralen), får vi med  y’= dy/dx differentialekvationen

             dy/y(M – y) = a dx .

En nämnare av ovanstående typ i VL är redan faktoriserad i enkla engradiga reala faktorer (se nedanstående härledning) vilket gör den direkt lösbar genom uppdelning i partialbråk; Efter partialbråksuppdelning och generalisering av fundamentalintegralen får vi lösningen

             y = M (C e–Max + 1)–1  ...................        universalen till varianten  y’ – ay(M – y) = 0 .

 

Ovanstående variant på formen  y’ = ay(M – y)  kallas i gängse bruk den logistiska tillväxtekvationen. Den uttrycker att POTENTIALEN FÖR TILLVÄXT inom ett begränsat område  =  produkten av nuvarande individantal  y  och den mängd återstående individer (M–y) det finns plats för innan det blir fullt. a anger magnituden i förhållandet mellan potential och population.

 

Härledningen, vi anger här funktionsvariabeln (x ovan) som t.

Integranden 1/y(M–y) uppdelas först enligt nedan (se partialbråksuppdelning):

 

                   1                 A               B               1/M           1/M                         1               1

             ————  =  ———  +  ——— ;  =  ———  +  ———  =  (1/M)[ ———  +  ——— ] ;

               y(M–y)            y              M–y               y             M–y                        y             M–y

 

             adt = dy/y(M–y) = dy[(1/M)(1/y + 1/[M–y])] = (1/M)[dy/y + dy/(M–y)] ; fundamentalintegralerna ger ;

             at = (1/M)[ln y – ln (M–y)] ; [Vi noterar att  ò dy/(P) = [ln(P)]/Dn(P) om Dn(P) = konstant ].

             at = (1/M) ln[ y/(M–y)] = (1/M) ln[1/(M/y – 1)] ;  generalisering av fundamentalintegralen ;

             at + C’ = (1/M) ln[1/(M/y – 1)] ;

             Mat + MC’ = ln[1/(M/y – 1)] ;

             eMat + MC’ = C eMat = 1/(M/y – 1) ;  C e–Mat = M/y – 1 ;  C e–Mat + 1 = M/y ;  M(C e–Mat + 1)–1 = y ;

Svar:    y = M (C e–Mat + 1)–1  ........................    y individmängd, M max y, C  ekvationskonstant, a populationskonstant, t tid

 

 

 

 

FRITT FALL MED LUFTMOTSTÅND

 

En ytterligare variant på första ordningens inhomogena varianter är den följande. Denna typvariant är av formen icke linjära varianter [motsv. konv. icke linjära differentialekvationer],

 

             y’ + ay2 = b

 

 

 

Efter M2000 1991 [NT]L3 s206 [lösningen varken härleds eller anges i källan]

 

             F = ma – FR = ma – kv2

             F = ma – kv2  ...................................     0 = ma – kv2 ;  kv2 = ma ;  v = Öma/k

             m(dv/dt) = ma – kv2

             dv/dt = a – (k/m)v2

             (k/m) = K

             dv/dt = a – Kv2

             Partialbråksuppdelning med Koefficientbestämning:

             dv/(a – Kv2) = dt ;  faktorisering av VL ;

                     1                                1                                A                      B

             —————  =  ——————————  =  —————  +  —————

                 a – Kv2         (Öa + vÖK)(Öa – vÖK)         Öa + vÖK          Öa – vÖK

 

             1/(a – Kv2) = 1/(Öa + vÖK)(Öa – vÖK) = A/(Öa + vÖK)  +  B/(Öa – vÖK)

             A= 1/(Öa + vÖK)(Öa – vÖK) ;  Öa + vÖK = 0 ; v = –Öa/K

             A= 1/(2Öa) ; 

             B= 1/(Öa + vÖK)(Öa – vÖK) ;  Öa – vÖK = 0 ; v = +Öa/K

             B= 1/(2Öa) ; 

             1/(a – Kv2) = (1/2Öa) [1/(Öa + vÖK)  +  1/(Öa – vÖK)] ;

             differentialekvationen, VL ;

             dv/(a – Kv2) = (1/2Öa) [dv/(Öa + vÖK)  +  dv/(Öa – vÖK)] ;

             fundamentalintegralen VL ;

             òdv/(a – Kv2) = (1/2Öa) [ln(Öa + vÖK)/ÖK  –  ln(Öa – vÖK)/ÖK]

= (1/2ÖKa) [ln(Öa + vÖK)  –  ln(Öa – vÖK)]

= (1/2ÖKa) ln[(Öa + vÖK)/(Öa – vÖK)] ;

             isolering av v-faktorn ;

             A = Öa ;  B = vÖK ;  A/B = (Öa/K)/v

             (A+B)/(A–B) = (A+B –B+B)/(A–B) = (A–B +2B)/(A–B) = 1 + 2B/(A–B) = 1 + 2/(A/B – 1) ;

             bägge fundamentalintegralerna (HL-integralen i  dv/(a – Kv2) = dt  ger rent t ) ;

             (1/2ÖKa) ln[1 + 2/(Ö[a/K ]/v – 1)] = t = òdv/(a – Kv2) ;

             ln[1 + 2/(Ö[a/K ]/v – 1)] = t · 2ÖKa  +  ekvationskonstant ;

             utan vidare generalisering [med generalisering tillkommer en konstant C = eekv.konst. till e-faktorn];

             1 + 2/(Ö[a/K ]/v – 1) = e t 2ÖKa

             v/Ö[a/K ]  = [1+ 2(e t 2ÖKa – 1)–1]–1 ;

             lösningen [ (k/m) = K ] ;

             v  = [Ö a/K ][1+ 2(e t 2ÖKa – 1)–1]–1

             v  = [Ö ma/k ][1+ 2(e t 2Öka/m – 1)–1]–1

                                                            1

             v  = [ma/k ]1/2[ ————————————— ]  .............................        fritt fall med luftmotstånd

                                                                2

                                         1 +  —————————

                                                       C e t 2Öka/m – 1

v = [mak–1 ]1/2 [1 + 2(C e t 2Öka/m – 1)–1]–1

 

Luftmotståndet (FR = kv2) bestäms för varje särskild (fast) kropp av dess tyngd (F=ma=mv/T) och sluthastighet (v, motsvarande t®¥) som ger luftmotståndskonstanten

k = F/v2 = (mv/T)/v2 = m/Tv = m/d  ..........................    KG/M

k beror (alltså) också på hur stor yta som uppvisas mot den förbipasserande luften (särskilda samband).

a anger den lokala tyngdkraftsacceleration (9,81 M/S2 vid Jordytan).

m anger kroppens massa i KG.

 

 

 

 

 

globala vattenflödet

 

 

GLOBALA VATTENFLÖDETS

ALLMÄNNA ELEMENTÄRA EKVATION

Praktiskt Exempel på en första ordningens homogen variant med en variabel koefficient

 

GLOBALA VATTENFLÖDETS ALLMÄNNA ELEMENTÄRA EKVATION — »naturprocessens elementarekvation»

 

 

Utan den här grundformen kan ingen teknisk kultur utvecklas

— den beskriver samma grunder som i elektrofysiken

 

 

 

 

 

I det globala vattenflödet mellan atmosfär och mark, baserat på en konstant mängd vatten, regleras tillflödet till marken proportionellt (»naturligt mjukt» utan hopp eller språng) mot den aktuella vattennivån (U) från den återstående vattenhöjden (U0–U) med toppnivån U0 med en motsvarande mellanliggande atmosfärisk nederbördsdel (molnstocken) — tydligen elementärt enligt varianten (derivataekvationen)

 

dU/dt = K(U0–U)  ............................     varianten [y’ = K(y0–y) = dy/dx]           

varianten KAN också skrivas mera renodlat y’= f (x)(ay);  y’ – ay · f (x) = 0:

en första ordningens homogena variant med variabel koefficient;

Jämför [s153 M2001_3.wps]:

Uppgift:

Bestäm universalen till varianten y’ = f (x) y.

Lösning :

y’ = dy/dx = f (x) y ;  differentialekvationen blir

dy/y = f (x) dx ;  fundamentalintegralen genom logaritmintegralen [Se LOG(5) i Bastablån] för VL,

ò dy/y = ln y

och enhetsintegralen ò f (x) dx som F(x) i HL,

ò f (x) dx= F(x)

ger

ln y = F(x) ;  generalisering av integralen i HL med en ekvationskonstant K ger ; 

ln y = F(x) + K ;  Universalen därmed ;
y = eF(x) + K = eF(x)eK = C eF(x) ;  C  > 0;

Denna integral är emellertid obestämd; integralkonstanten blir

Q = y(0) = C eF(x=0) = C; Därmed den bestämda universalen

y = y – Q = C eF(x) – C = C [1 – eF(x)]

Återderivering ger Dn C eF(x) – C = F’(x)C eF(x) – 0 =  f (x)C eF(x) = y’ = f (x) y.

Således integranden åter.

Svar:    Universalen till varianten y’=f (x) y  är  y=C [1 – eF(x)]  med C  > 0.

Kommentar

Om exponenten F(x) associeras med en optimal koefficient (K) och f(x) återförs (i slutänden) på integrationskonstanten dx som negativ (jämför utvecklingarna längre ner) fås

K ò –dx = –Kx = –KF(x) som ger universalen

y=C [1 – e–Kx]

Jämför slutresultatet i nedanstående utvecklingar.

Ovanstående utläggning motiveras av synpunkten (med ett konkret exempel på) att flera (många) olika sätt finns som en integral lösning kan utvecklas — och beskrivas — på.

 

Förklaring

 

Tillflödets variation bestäms av dU/dt (vattennivån vid en viss given tidpunkt), och verkställigheten uppmäts genom U0–U; det finns inte mycket annat att välja på i grundmatematik.

Faktorn t anger tiden och K är en allmän proportionalitetskonstant som krävs för att garantera balansen i fysikaliska storheter och enheter mellan vänsterdel och högerdel; Genom leddelarnas omflyttning till differentialekvationen

 

dU/(U0–U) = Kdt  ...........................      variantens differentialekvation

 

ser vi direkt att konstanten K måste vara inversen till tiden (T) enligt K=1/T för att få ekvivalens med vänsterledets enhetsform. Ju mindre vattenmängden är i markdelen, desto större är den i molndelen, vilket motsvarar den potentiella nederbörden och därmed tillflödet.

Eftersom Dn ln(P) = Dn(P)/(P), se Bastablån i Formlagarna, som i detta fall skulle ge

Dn(P)/(P) = (0–1)/(U0–U) = Dn ln(U0–U) = –1/(U0–U), får vi fundamentalintegralen

ò dU/(U0–U) = – ln(U0–U);

Integralens bestämda form blir för vänsterdelen i dU/(U0–U) = Kdt lika med

ò dU/(U0–U)      = – ln(U0–U) – – ln(U0) = ln(U0) – ln(U0–U) = ln [U0/(U0–U)] 

                          = – ln [(U0–U)/U0],

och för högerdelen i dU/(U0–U) = Kdt lika med

ò Kdt                  = Kt

Därmed lösningen i de bägge integralernas ekvivalens enligt

ln [(U0–U)/U0] = –Kt

Med ea=P som formellt ger a=ln(P) har vi alltså

e^–Kt = (U0–U)/U0 = 1 – U/U0 = e–Kt

och därmed påfyllningen (nivån UT vid tillflödet) av vatten enligt

 

UT         = U0(1 – e–Kt)  .....................      globala vattenflödets elementära tillflödesekvation

 

Tömningen — avflödet (avdunstningen)

Om vattenminskningen i markdelen besitter samma karaktär över tiden som påfyllningen via nederbörden gäller tydligen

 

U0 – U = U0 – U0(1 – e–Kt) = U0 – U0 + U0e–Kt = UA;

UA        = U0e–Kt  .............................      globala vattenflödets elementära avflödesekvation

 

U anger aktuella vattennivån, U0 anger maximala vattennivån, t anger tiden från U=0 analogt maximalt tömda markvattenområden i fallet UT och i fallet UA från U=U0, K=1/T anger en invers till tidskonstanten T (hur lång tid det tar att fylla på vattennivån tills nära fullt [63%], eller tömma den tills nära tomt) som beror på strömningstrycket i vattentillströmningen (R, motståndet mot omedelbar påfyllning) och vattensystemets lagringskapacitet (C):

U/U0 = 1– e–Kt ; K=1/(T=t) ger  1– 1/e = U/U0 = 0,6321205; U = 0,6321205 U0 » 63% av toppnivån U0.

 

Flödets (strömningens) verkställande egenskap — K = 1/T

Faktorn K — tidskonstantens invers. KONSTRUKTIONEN — som ett fast fysikaliskt materialsystem — som innefattar flödet kan innehålla samtliga parametrar som utmärker de anordningens fysiska mått och egenskaper som sammanhänger med vattenflödet och förmågan att innesluta/uppta vattenmängden; Anordningens verkställande flödesegenskap eller strömningsfaktorn kan bara vara av principiellt två olika typer:

 

konduktiv         R–1T     = C  .............    motsvarande elektrisk kondensator (flöde genom yta), kapacitans

                                                                            flödet (I) föregår ändringar i vattennivån (U)

resistiv              RT        = L  .............     motsvarande elektrisk spole (flöde genom längd), induktans

                                                                            vattennivån (U) föregår ändringar i flödet (I)

Förklaring

 

Med medeltrycket eller motståndet (R) i vattentillförseln i respekt till mängden vatten — eller vattenströmmen (I) — som passerar ytgränsskiktet moln-mark samt aktuell vattennivå (U) ges det vattentillförande medeltrycket relationen U/I=R, analogt U=RI;

Den momentana (differentiella) vattenströmningen (I) kan också beskrivas i termer av vattenvolymen (Q) per tidsenhet (T) enligt I=Q/T.

Kapaciteten i anordningen som innesluter vattenmängden i respekt till ytflödet moln/mark/moln kan på liknade sätt beskrivas som förhållandet mellan vattenvolymen (Q) till vattennivån (U) enligt Q/U=C med C som lagringskapacitansen (eg. förmågan till upptagning); ALTERNATIVT kan C också relateras (enklare) som kvoten av en given tid (T) och ett visst konstant flödesmotstånd (R), C=T/R, så att upptagningsförmågan C växer med avtagande motstånd R på given tid T;

Men motståndet (R) kan också, alternativt mot R–1T, förhålla sig till den givna tiden under vilken själva flödesändringen sker enligt RT — som betyder att totala flödesändringsmotståndet — inte det konstanta motståndet — det som i relaterad fysik kallas för primär induktans (L=RT) — och som motsvaras av mekanikens masströghet (växande massa innebär att större kraft krävs för att ändra läget på given tid) — växer med växande längd på flödesvägen, analogt växande R med växande flödesändringslängd — motsvarande masströgheten i mekaniken som växer med massan. Detta ger flödesinduktansen L=RT. Därmed kan strömningsfaktorn K=1/T skrivas på två olika sätt, och inget annat,

 

C = R–1T           ;            T = RC             ;            K = 1/RC  .................   kapacitiva strömningsfaktorn

L = RT              ;            T = R–1L           ;            K = R/L  ...................    induktiva strömningsfaktorn

 

Om anordningens konstanta flödesmotstånd (R) inte ändras gäller tydligen via U=RI att

UT         = U0(1 – e–Kt) = RI = RI0(1 – e–Kt) och därmed också att

IT          = I0(1 – e–Kt)  .................................        tillflödets momentana styrka

IA          = I0e–Kt  ..........................................        avflödets momentana styrka

 

Speciellt om den induktiva ledningen

I = U/R = TU/RT = TU/L  ................    självinduktionslagen

Förklaring: Under given tid (T) och given vattennivå eller spänning (U) induceras ett motstånd (R) mot flödesändringen på samma sätt som då vi i mekaniken försöker rubba ett föremål (med stor massa) under viss tid, det vi inom elektrofysiken kallar för inducerat motstånd.

Då kan spänningen U också skrivas alternativt via första och sista ledet ovan enligt

U = (L/T)I  ...............    den inducerade spänningen U under tiden T via toppströmmen I med induktansen L

med I som toppströmmen (I0). Dvs., U0 = (L/T)I0 med T som inkopplingstiden och L som induktansen (RT). Se även i Induktion.

 

Vi ser att balansen kräver ekvivalens mellan tillflöde och avflöde — typ litet lokalt avflöde men totalt över en stor yta (Solbelysningen över halva Jordklotet) med motsvarande högt tillflöde men över lokalt små områden och med inbördes långa mellanrum (det regnar bara ibland, lokalt, men avdunstningen pågår kontinuerligt överallt).

 

kondensatorn och spolen

GLOBALA VATTENFLÖDETS ALLMÄNNA EKVATION

— omsatt på elektrofysiken; kondensatorn och spolen

 

Jämför gängse fackverk; sambanden nedan är välkända för alla som studerat grunderna i den allmänna skolboksfysiken

— men förklaringarna i gängse kvarter är inte lika upphetsande (som här …). Se även i ELFA-katalogen, faktasidorna.

 

krets

kondensator

kapacitans

 

induktans

spole

krets

C =

R–1

T

 

L =

R

T

A uppladdning

yta

kapacitans

konduktans

tid

 

induktans

resistans

tid

längd

A inkoppling

B urladdning

K = 1/RC

Farad

Siemens

Sek

 

Henry

Ohm

Sek

K = R/L

B urkoppling

 

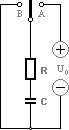
Härledning genom potentialvandringslagen och kondensatorlagen I = C(U/T) = C(dU/dT);

Kondensatorns uppladdning: UC + UR = U0 = UC + RI = UC + R · C(dU/dT) = U0 ;

 

RC · dU/dT = U0 – UC ;  dU/(U0 – UC) = (1/RC)dT ;

ò dU/(U0 – UC)              = ò (1/RC)dT = (1/RC)T = T/RC ;

ò dU/(U0 – UC)              = – ln(U0 – UC) = y ; denna integral är obestämd; integralkonstanten blir Q=–ln(U0 – 0) = –lnU0 ;

y                                     = –ln(U0 – UC) – Q = –ln(U0 – UC) – –lnU0 = lnU0 – ln(U0 – UC) = –ln U0/(U0 – UC) ;  därmed för bägge integralerna

ln U0/(U0 – UC)             = T/RC ;  med ea=P ges a=ln(P) och därmed lösningen

U0/(U0 – UC)                 = eT/RC = 1/(1 – UC/U0) ;  e–T/RC = 1 – UC/U0 ;

UC                                  = U0(1 – e–T/RC)

 

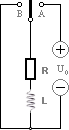
Härledning genom potentialvandringslagen och självinduktionslagen U = L(I/T) = L(dI/dT);

Spolens inkoppling: UL + UR = U0 = UL + RI = L(dI/dT) + RI = U0 ;  (L/R)(dI/dT) + I = U0/R = I0 ; I = IL = IR ;

 

(L/R) · dI/dT = I0 – I ;  dI/(I0 – I) = (R/L)dT ;

ò dI/(I0 – I)                     = ò (R/L)dT = (R/L)T = RT/L ;

ò dI/(I0 – I)                     = – ln(I0 – I) = y ; denna integral är obestämd; integralkonstanten blir Q=–ln(I0 – 0) = –lnI0 ;

y                                     = –ln(I0 – I) – Q = –ln(I0 – I) – –lnI0 = lnI0 – ln(I0 – I) = –ln I0/(I0 – I) ;  därmed för bägge integralerna

ln I0/(I0 – I)                    = RT/L ;  med ea=P ges a=ln(P) och därmed lösningen

I0/(I0 – I)                        = eRT/L = 1/(1 – I/I0) ;  e–RT/L = 1 – I/I0 ;

I                                     = I0(1 – e–RT/L) ;  Med konstant kretsmotstånd R i U=RI ges motsvarande

             U                                   = U0(1 – e–RT/L)

 

KONDENSATORN K=1/RC och SPOLEN K=R/L — Fortsättning från ovanstående beskrivning

 

 

 

                          spänningen                                strömmen

A upp/in            UT        = U0(1 – e–Kt)                IT          = I0(1 – e–Kt)

B ur                  UA        = U0e–Kt                         IA          = I0(1 – e–Kt)

 

 

 

reaktanserna

REAKTANSERNA

Reaktans. Reaktans är benämningen på den resistans (motstånd) som uppstår i kondensatorer och spolar som funktion av varierande strömmar. Tillsammans med den rena ledningsresistansen betecknas reaktansen som impedans (Z), impedansens invers kallas admittans, dvs., det totala s.k. växelströmsmotståndet. Reaktansen är då den s.k. effektiva resistansen medan ledningsresistansen betecknas som förlustresistansen. För periodiska (sinus-) strömmar gäller att reaktansen för kondensatorer är omvänt proportionell mot frekvensen, för spolar är den direkt proportionell mot frekvensen. Kondensatorns reaktans benämns explicit kapacitiv reaktans medan spolens reaktans benämns induktiv reaktans.

 

härledningar till kapacitiva och induktiva reaktanserna

 

KONDENSATORN kondensatorlagen U=T(I/C) — PREFIXxSIN

U/T Û dU/dT = tanA = I/C = U’ se även derivatans definition ; vi betraktar en periodisk sinusström

I = Î sinwT ; Î anger strömmens toppamplitud ; w = 2pf = periodiska vinkelfrekvensen, f anger frekvensen i Hz; varianten blir

dU/dT = I/C = Î/C sinwT = Î/C · 1/w · w · sinwT = Î/wC · w · sinwT ; differentialekvationen blir

dU = Î/wC · w · sinwT dT ;  spänning/ström-integralerna blir

ò dU     = ò Î/wC · w · sinwT dT ;

U          = Î/wC ò w · sinwT dT = Î/wC · coswT ; denna integral är bestämd direkt ;  för coswT = 1 gäller toppvärdet Î/wC = Û;

             = Û coswT

Från ekvivalenten Î/wC = Û ges Î/C = Ûw och därmed

1/wC     = Û/Î = XC  ..........................     den kapacitiva reaktansen, enhet i Ohm eller V/A;

Kapacitiva reaktansen ökar då strömmens variation alltmer liknar likström (reaktansen går mot oändligt då).

 

SPOLEN självinduktionslagen U=T(U/L) — PREFIXxSIN

I/T Û dI/dT = tanA = U/L = I’ se även derivatans definition ; vi betraktar en periodisk sinusspänning

U = Û sinwT ; Û anger spänningens toppamplitud ; w = 2pf = periodiska vinkelfrekvensen, f anger frekvensen i Hz; varianten blir

dI/dT = U/L = Û/L sinwT = Û/L · 1/w · w · sinwT = Û/wL · w · sinwT ; differentialekvationen blir

dI = Û/wL · w · sinwT dT ;  ström/spänning-integralerna blir

ò dI       = ò Û/wL · w · sinwT dT ;

I            = Û/wC ò w · sinwT dT = Û/wL · coswT ; denna integral är bestämd direkt ;  för coswT = 1 gäller toppvärdet Û/wL = Î;

             = Î coswT                                                                                                                                               

Från ekvivalenten Û/wL = Î ges Û/L = Îw och därmed

wL        = Û/Î = XL  ..........................     den induktiva reaktansen, enhet i Ohm eller V/A;

Induktiva reaktansen ökar då strömmens variation ökar (reaktansen går mot kortslutning då).

 

 

 

 

w anger vinkelfrekvensen

 

Vinkelfrekvens — w = 2pf från v=d/t = 2pr/t ; v/r = 2p/t =2pf = w; f anger frekvensn i Hz: w anger vinkelfrekvensen i 2p Hz

 

 

 

 

 

 

 

2:a ordningens varianter

 

 

 

 

                                                                                                                                                                                         

ALLMÄNNA elektromekaniska SVÄNGNINGSEKVATIONEN 

SVÄNGNINGSEKVATIONEN

A(d2y)/(dT)2 + B(dy)/dT + Cy = 0 = y’’ + ay’ + by

 

A förkortas bort via nollekvivalenten, och varianten via dT får allmänformen y’’ + ay’ + by = 0;

 

MEKANIKEN

massa

m

friktionskonstant

R

fjäderkonstant

k

kraftvägen

d

elektrofysiken

induktans

L

resistans

R

kapacitans–1

1/C

spänningen

u

term

A

 

B

 

C

 

y

 

 

 

SVÄNGNINGSEKVATIONEN — mekaniska delen

I mekaniken gäller för tyngdkraften F på en (lodrätt upphängd) fjäder (med en anbringad massa m i änden) sambandet Fk=kd. d anger utdragningen, k anger fjäderkonstanten. Frånsett friktionsförluster gäller att summan av alla verkande krafter inom systemet är noll. Det ger F+Fk=0 som beskriver ett fysikaliskt system utan dämpning.

MEKANISK DÄMPNING betyder att kraften ändras med hastigheten

[F/v=ma/v=m(v/T)/v=m/T=R]. Är dämpfaktorn Rv=FR kan kraftledet kompletteras enligt

F+FR+Fk=0. Med  F=ma  får man  ma+Rv+kd=0. Utbrytning av m ger  a+(R/m)v+(k/m)d = 0. Med singulära koefficienter (s.k. normalform) ges a+Av+Bd = 0. Eftersom accelerationen är  a=d2(d)/(dT)2 samt v=d/T=d(d)/dT ges enhetliga tangensformer (derivator) för d med avseende på T enligt varianten (uttrycket benämns konventionellt svängningsekvationen) 

d’’+ Ad’+ Bd = 0.

                                                                                                                                                                                         

SVÄNGNINGSEKVATIONEN — elektriska delen                                                                                                       

Utbytet av energi mellan massan och fjädern motsvaras inom elektrofysiken av systemet motstånd (R), spole (L) och kondensator (C). Genom

potentialvandringslagen (summan av alla spänningsfallen över alla komponenter är lika med kretsens totala spänningsmatning) i den slutna kretsen ges spänningsekvationen

uL+uR+uC=0. Kondensatorn spärrar för likström och bestämmer genom kondensatorlagen (C=Q/U=IT/U) kretsens till och frånflöde av elektriska laddningar (strömstyrkan I=Q/T) enligt I=CU/T. Momentanformen ger i=Cdu/dT med motsvarande strömdifferential

di=d(Cdu/dT)=Cd2u/dT (vi frånser här indexeringen uC och anger fortsättningsvis endast u). Spolspänningen (uL) ges av självinduktionslagen (L=UT/I) enligt U=LI/T=LQ/T2 med momentanformen uL=Ldi/dt. Med ovanstående för di insatt ges

uL=LCd2u/(dT)2. Spänningen över motståndet (R) ges via Ohms lag (U=RI). Med i=Cdu/dT som kretsens strömstyrka ges då  uR=RCdu/dT. Totalt därmed 

LCd2u/(dT)2 + RCdu/dT + u = 0. Utbrytning av LC ger d2u/(dT)2 + (R/L)du/dT + (1/LC)u = 0. Med A och B för RL och 1/LC ges

d2u/(dT)2 + Adu/dT + Bu = 0. Tangensformerna för u med avseende på T således 

u’’+ Au’+ Bu = 0

och vilket vi ser är samma principform som i resultatet för mekaniska delen.

 

   Se vidare nedan i SVÄNGNINGSEKVATIONENS LÖSNING för lösningen till ovanstående.

 

 

 

SVÄNGNINGSEKVATIONENS LÖSNING

I fortsättning från Praktiskt Utvecklingsexempel

 

Vi hade typformerna

 

d’’+ Ad’+ Bd    = 0  ....................          från mekaniska delen

u’’+ Au’+ Bu    = 0  ....................          från elektriska delen

 

Varianten

 

y’’ + ay’ + by = 0 med transformen

n2 + an + b = 0

 

har lösningen (Se Andra ordningens homogena variant)

 

y = eax(C sinbx + D cosbx)

 

genom transformens lösningsled eller transformens rotkropp

 

n = –(a/2)±Ö[(a/2)2–b]

n = a ± ib  ........................................     transformationens komplexa rötter

 

Rötterna är (n+= a+ib) och (n–= a–ib) med a=–(a/2) och b=Ö |(a/2)2–b|.

a=–(a/2) ger med positiv koefficient a en negativ alfa-koefficient så att vi får

 

             y = e–ax(C sinbx + D cosbx)

 

FJÄDERKONSTANTEN (från särskild del i Mekaniken) b=k=F/d har frekvenskvadraten

T–2 som enhet enligt k=m[a=2d/T2]/d=2mT–2.

Det motsvarar kvadraten på den allmänna vinkelfrekvensen w=2pf.

MEKANISKA DÄMPKOEFFICIENTEN R har formen R=F/v=m/T och vi ser (direkt) att den harmonierar perfekt i rottransformens inre kvadrat tillsammans med fjäderkonstanten. Sätter vi den på dubbla sin form

(2R=a-koefficienten) får vi direkt rotlösningen

n = –R ± Ö[R2 – w2] med rotens inre värde på vinkelFrekvenskoefficientens form

[R2 – w2]=w02.

Rotvärdet blir alltså realt ett b=w0.

Svängningen innebär just imaginära rötter — som betyder att w2 > R2 så att b2 blir negativt;

 

             y = e–Rx(C sinw0x + D cosw0x)

 

Koefficienterna CD. Med C=0 börjar svängningen från y=0, vilket betyder från fjäderns mittläge: den är på väg upp med maximal kraft (största y-lutningen). Övriga lägen (C >0) innebär att vi kommer in på andra ställen i den första perioden (dynamiska trögheten). I den maximala dynamikens beskrivning ska vi alltså (tydligen) utgå (primärt) från just C=0:

 

             y = De–RTcosw0T.

D beror då, tydligen, på energin. Enhetsformen ger alltså slutlösningen

             y = e–RTcosw0T, analogt rent e–x cosx.

 

 

 

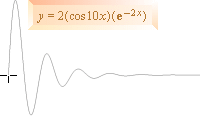
Tillämpning, se Atomkärnans vågnatur.

 

 

 

 

 

 

 

HÖGREDERIVATANS ALLMÄNNA TECKNING

 

y’ = dy/dx ;  d(dy/dx)/dx = d(dy)/dxdx = d2y/(dx)2 = (1/¥)(1/¥ · y)/(dx)2; s128|133 M2001_3.wps

 

 

 

 

 

DIFFERENTIERING AV INTEGRANDER  —  en fråga om ordning

Exempel

I hanteringen av differentiering av en integrand måste vi observera (naturligtvis) — för den allmänna begripligheten och det synnerliga sammanhanget i matematikens uttryck — att exemplifierat

 

 

                  d(x2)

Dn x2  =  ———  =  2x  ;

                   dx

                                          d(x2)

                                    d (———)

                  d  (2x)               dx                   d 2x2

Dn 2x  =  ———  =  ——————  =  ————  =  2 ; 

                    dx                    dx                   (dx)2

 

modern akademi

I MODERN AKADEMI (nämligen) tillämpas den här ordningen (andraderivatan),

 

 d2y

——  ........................     se exv. MATEMATIKLEXIKON W&W 1991 s77sp2ö derivata

 dx2

 

exemplifierat som ovan:

 

 

                  d2 x2                          d x2                     1

Dn 2x  =  ———  =  (2x)’  =  ———  =  d  =  ———  =  2  = kaos i matematiken

                   dx2                           x2                         ¥

               ¯¯¯¯¯¯¯                      ®                  ¯¯¯¯¯¯

Eftersom differentialens definition som formen för noll — varje kvantitets aspekt — inte existerar i den moderna akademins lärosystem, uppkommer, som ovan, logiska brott i den moderna akademins sätt att beskriva matematiken på nivån analys: ingen förstår innehållet i något relaterad mening — därför att de underliggande begreppsformerna inte finns formulerade.

 

Jämför ledet nedan i relaterad matematik:

 

y’                       = dy/dx ; 

d(dy/dx)/dx        = d(dy)/dxdx = d2y/(dx)2 = (1/¥)(1/¥ · y)/(dx)2

 

För att klara av LÄSNING med TOLKNING av den moderna akademins skrivsätt (se ovan) måste man antingen (upplyftande) känna till grunderna relaterat, som i ovanstående beskrivning — eller (deprimerande) ”lära sig härma hur lärarna säger/skriver/använder det”: i detta senare fall finns ingen beskrivning, ingen metod, ingen förklaring; Därmed lämnas också — tydligen — den del av studentledet utanför examineringsrummen som vill verkligen veta grunderna, dvs., huvuddelen. Den återstående delen, nämligen och tydligen, har ännu i denna dag inte bidragit med någon upplysning för sin del.

 

Relaterad matematik — se utförligt från Nollformsalgebran

 

OM en differentialkvot är så skriven att differentialerna ger ¥±1, då är kvoten undantagslöst tvivelslöst alldeles helt säkert felskriven.

 

Som visas ovan, hamnar vi definitivt i ”trubbel” om vi i någon relaterad mening skriver

 

(2x)’ = d2(x2)/dx2  .................     modern akademi, allmän teckning för andraderivatan, med vidare

 

Enda relaterade sättet att förstå denna moderna akademiska specialtyp dx2 för vad den betyder, nämligen (dx)2, är uppenbarligen att inte förstå differentialen dA generellt som en sammansättning mellan en kvantitet A och något annat, vilketsom. Vilket vill säga, genom att cementera idén att ”dA” är ”någonting i sig självt” — vilket dA inte är — och därmed förbjuda  alla sätt som leder till himmelriket. Det är A/¥, som redan beskrivits i nollformsalgebran. Explicit är differentialen dA d · A med d specifikt som den mängdoberoendes invers, 1/¥. Detta är speciellt klart genom den enkla men effektiva demonstrationen

 

ò dA = A

 

Vi använder emellertid (normalt) aldrig den typ av uppdelning med separata d för 1/¥ eftersom det aldrig finns några sådana behov — utom som här i explicit förklaring och djupbeskrivning av grundbegreppen.

                                                                                                                                       

…

 

 

 

 

 

Analysen|EXEMPEL

 

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

 

 

Analysen|EXEMPEL

ämnesrubriker

                                     

 

innehåll

              Analysen|EXEMPEL

 

                                                         Praktiska utvecklingsexempel

 

                       1:a ordningens varianter

 

                                                         ljusintensiteten GENOM MATERIEN

 

                                                         INLEDANDE ALLMÄN ÖVERSIKT

 

                                                                            Speciellt om logaritmintegralen

 

                                                         LOGISTISKA TILLVÄXTEKVATIONEN

 

                                                         FRITT FALL MED LUFTMOTSTÅND

 

                                                         GLOBALA VATTENFLÖDETS allmänna elementära EKVATION

 

                                                                            Flödets verkställande egenskap

 

                                                                            Kondensatorn och Spolen

 

                                                                            Reaktanserna

 

                                                                                               Vinkelfrekvensen

 

                       2:a ordningens varianter

 

                                                         ALLMÄNNA elektromekaniska SVÄNGNINGSEKVATIONEN

 

                       HÖGREDERIVATANS ALLMÄNNA TECKNING

 

                                                         DIFFERENTIERING AV INTEGRANDER

 

referenser

 

 

[M2000].

MATEMATIK 2000, Lärobok 3, Björk · Borg · Brolin · Ljungström, Natur och Kultur 1991

Innehåll och uppgifter är desamma som i den senare läroboken

MATEMATIK 2000, Kurs E, Björk · Brolin, Natur och Kultur 1996

 

t för 10–, T för 10+, förenklade exponentbeteckningar

 

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

 

Senast uppdaterade version: 2014-04-03

*END.

Stavningskontrollerat 2009-01-09.

 

rester

*

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG-justerad 2011-07-18

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se