StjärnFysiken Del II — Universums Historia | 2005IX13 | 2008X20 | Redigering och sammanställning: BellDHARMA 1984-2008 | Senast uppdaterade version: 2021-12-09 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING | 2008X20

Stjärnfysiken DEL II

HR-diagrammets grunder

Stjärnornas fördelning, indelning och klassificering

observationer av stjärnfält

STJÄRNFYSIKEN DEL II

STJÄRNFYSIKEN ENLIGT TNED 2005 IX 13 | 2007I15 | 2008X20

STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

STJÄRNFYSIKEN DEL II

I fortsättning från STJÄRNFYSIKEN DEL I

——————————————————————————————————————————————————————————————

Bilderna ovan: Krabbnebulosan vänster, Örnnebulosan höger — den senare i stark förstoring av detaljerna (här från ENCARTA 99

— men dessa bilder finns numera i överflödande mängd på webben)

Inledning

Den enda säkra metod som finns för att få fram en stjärnas massa bygger på väl iakttagbara dubbelstjärnesystem. Känner man banellipserna och omloppstiderna kan massorna beräknas enligt Keplers tredje lag,

a=F/m= Gm₂/r² =v²/r=(2pr/t)²/r= 4p²r/t² ; Gm₂/4p² = r³/t² ; m₂=(4p²/G)(r³/t²)

BONNIERS ASTRONOMI 1978 ger i tabell [BAs31] exempel på 26 uppmätta individer som visar att

· huvuddelen av de optiskt observerbara stjärnornas mätbara massor ligger mellan
0,34minsta-2,4största Solmassor

Källans kompletterande figurbild av något hundratal uppmätta individer [BAs50] visar en största massa runt

5 Solmassor. Individerna kring 5 Solmassor är emellertid uppmätta som förmörkelsevariabler utan specifikationer om huruvida de också uppvisar klart urskiljbara stjärnkomponenter.

För att finna större massor måste man leta längre ut och därmed i beroende av de mera indirekta metoder som benämns

fotometriska och spektroskopiska. Se även i observationsgränserna.

Stjärnfysikens grunder enligt TNED

— Stjärnfysiken DEL I

— beskrivs utförligt från SOLFYSIKEN.

SKILDA PREFERENSER

Den moderna akademins sorgligt valda

nomenklatur

I härledningen till stjärnornas primära egenrotation som orsak till stjärnornas variabla omfång, kan n stjärnor med samma effekt=luminositet uppvisa n olika yttemperaturer och därmed i kraft av fotometriska och spektroskopiska mätningar n olika ljusstyrkor. Att obetingat sammankoppla begreppet ljusstyrka=magnitud med begreppet luminositet=effekt blir därför ett olyckligt val i beskrivningen av stjärnornas fysik.

————————————————————————————————————————————

”Begreppet absolut magnitud definieras som den ljusstyrka (mätt i magnituder) en stjärna skulle ha om den befann sig på ett visst standardavstånd från oss. Man har enats om att här använda avståndet 10 pc. Den absoluta magnituden är följaktligen ett mått på stjärnans energiproduktion, dess absoluta luminositet.” [BAs29sp2ö].

————————————————————————————————————————————

luminositet · effekt · stjärnmassa · färgindex · magnitud · ljusstyrka · stjärnornas omfång

SKILDA PREFERENSER I TNED OCH MAC

GENERELLT FÖR ALLA STJÄRNOR

TNED:

FÄRGEN AVSPEGLAR STJÄRNANS EFFEKT

— ljusstyrkan avspeglar stjärnans

OMFÅNG = materialmängden i stjärnljuset

liten mängd material som blir belyst av städet stor

rött, låg effekt

blått, hög effekt

Obs:

LJUSETS GRAVITELLA BEROENDE får ENLIGT TNED speciella effekter på stjärnmassor i området 5-15 Solmassor. Strålningstryckets starkt kalljoniserande funktion

(jämför Fe¹³⁺ i Solkoronan) kan överta den ordinära värmegradens område vid (starkt) reducerad divergens (c)

— vilket enligt TNED skulle betyda att stjärnan för detta fall uppvisar starkt förvrängda Planck-kurvor med enorma blåförskjutningar snarare än rödförskjutningar:

— ISTÄLLET för att detektera en mycket sval (dämpad, röd) stjärna, registrerar spektroskopet en enorm hetta (blått, violett) från området. PERIODISKA LJUSVÄXLINGAR av i princip godtycklig form för en sådan divergensdämpad stjärna — den befinner sig då i området för neutronfragmentering enligt kärnreaktionslagen

K+(m®g₌₀) = K1+K2 — kan åstadkomma extremt förvillande »rådata», t.ex. motsvarande förmörkelsevariabler från FÖRMODADE s.k. trånga dubbelstjärnesystem: …

—————_———_———_ …: Neutronfragmenteringen (från gamla Helium-4-stjärnor) producerar nytt väte som gör att stjärnans täthet ändras (periodiskt) med olika möjliga tillhörande förbränningscykler (perioder med godtycklig längd, sammansättning och komplexitet) och därmed variationer i ljusstyrkan.

Se vidare i EXEMPEL.

TNED:

x, luminositet = effekt = stjärnmassa = färgindex

y, omfång = ljusstyrka = magnitud ............................. med hänsyn till de skilda rotationsklasserna

MAC:

y, luminositet = effekt = (stjärnmassa) = magnitud = ljusstyrka

x, färgindex = spektralklass = temperaturklass

”Begreppet absolut magnitud definieras som den ljusstyrka (mätt i magnituder) en stjärna skulle ha om den befann sig på ett visst standardavstånd från oss. Man har enats om att här använda avståndet 10 pc. Den absoluta magnituden är följaktligen ett mått på stjärnans energiproduktion, dess absoluta luminositet.”,

BONNIERS ASTRONOMI 1978 s29sp2ö

Effekt och ljusstyrka kopplar inte för stjärnorna enligt TNED — utom normalstjärnorna. n stjärnor med samma effekt=luminositet kan ha n olika ljusstyrka. Ljusstyrkan eller magnituden bestäms av stjärnans omfång (materialmängden som blir belyst från centrum), inte av stjärnans effekt.

Stjärnornas omfång bestäms enligt TNED av stjärnans primära egenrotation, vilken vi skiljer skarpt från stjärnans egenproducerade rotation under dess brinntid. Den primära egenrotationen är den rotation som varje J-kropp har då den avdelas primärt från sin moderkropp under K-cellens successiva expansion. Endast ytterst små primära egenrotationer krävs för att bilda närmast enorma omfång relativt normalstjärnan. Begreppet normalstjärna ansluter här till Solen som preferens genom dess minimala primära egenrotation som kan anses helt försumbar (Se Solens tre ekvationer). Separata beräkningar visar att effektändringen som följd av de skilda omfången är så liten att den helt kan bortses ifrån. Sambanden för stjärnornas omfång beskriver en ren enkel linjär tillämpning med utnyttjande av resultatet från Jordens femte ekvation (m_E från primärmassorna) enligt

R_out³ = 3Dm/4pr_r + R_Star³

stjärnans absolut minsta ytterradie, konstant r_r från R_Star

Dm = m_EDf /f_LIM = (R_out³ – R_Star³)(4pr_r/3)

tilläggsmassan

m_E .......................................................... maximala tilläggsmassan, se Jordens femte ekvation

Df .......................................................... stjärnans primära egenrotation (max 0,00023 Hz för Solen)

f_LIM = 1135 Hz = Ö Gr_max/3p

gränsfrekvensen för primär egenrotation, massoberoende, med rMAX= 1,82 T17 KG/M³

r_r .......................................................... normalstjärnans reala yttäthet (8,9277145 t5 KG/M³)

se yttäthetskonstanten

Se även särskild grundbeskrivning i STJÄRNRADIERNA.

Här följer en vidare beskrivning med utgångspunkt mera från stjärnans ljusemitterande egenskaper.

INLEDNING TILL HR-DIAGRAMMETS GRUNDER enligt TNED

INLEDNING TILL HR-DIAGRAMMETS GRUNDER enligt TNED

ROTATIONENS INVERKAN PÅ STJÄRNANS FYSIK

— ROTATIONSKLASSERNA

STJÄRNORNAS OMFÅNG — stora ljusmätande anomalier relativt normalstjärnorna kan förekomma enligt TNED

Strålningstryckets (Tg) tvungna inverkan

på tilläggsmassan (Dm) från primära egenrotationen

(P/A)_Q=f ([Dm+m]/m)akT⁴ f (T_g ® T)

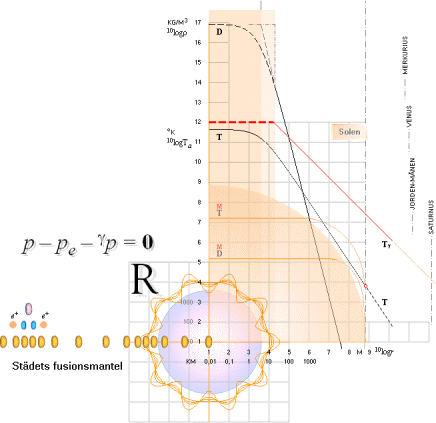
OM STJÄRNAN INOM SIN G-SFÄR innefattar en allt större del av sin normalt utanförstående rymdvolym

— genom ett marginellt tillskott av sin primärmassa som följd av en högre primär egenrotation

— är det klart att strålningstryckets värmegradsbildande effekt också påverkar masstillskottets del: Spektralkartan för stjärnans ekvivalenta värmegrad drivs längre upp mot högre frekvenser; Dm-delen påförs högre T än motsvarande normalstjärnas rymdområde.

funktionssätt

Stjärnans primära egenrotation påtvingar stjärnklotet en större opacitetssfär (Dm) än normalt;

Strålningstryckets kalljoniserande effekt affekterar tvunget det extra materialet i Dm; Resultatet netto kan uppenbarligen INTE vara detsamma som gäller för normalstjärnan eftersom en tilläggsmassa (Dm) tillkommit innanför stjärnans g-sfär och därmed en motsvarande påverkan från strålningstryckets funktion som i normalstjärnans fall ligger utanför dess g-yta.

Om funktionen är linjär med avseende på ytljusstyrkan vid normalstjärnans g-yta, är det tydligt att extramaterialet Dm via Tg ger stjärnklotet ett motsvarande proportionellt tillskott på EXTRA LYSANDE MASSA. Stjärnklotets ljusstyrka kan då liknas vid en lysande boll med ljusemitterande ytpixels av bestämd storlek och effekt vars antal ökar med växande bollyta utan att stjärnans effekt ändras: Stjärnan framstår allt tydligare (ljusare, hetare) med allt större omfång, men utan någon motsvarande effektökning. Verkan är analog med ljusstyrkan från olika mängd material som exponeras i skenet från en strålkastare: ljusstyrkan från materialet kopplar inte till strålkastarens effekt, det är bara materialmängden i skenet som räknas; Eftersom stjärnornas höljen redan i stort är vakuum med våra mått, kan (mycket) stora och dramatiska ljusändringar åstadkommas enbart beroende på stjärnans omfång och materialets täthet, analogt mängden belyst material.

;

Dm-stjärnans ekvivalenta ytvärmegrad (Tg ® T) relativt normalstjärnans, given effekt, växer TVUNGET med växande omfång.

PLANETMATERIAL vanliga Jordiska molekylära föreningar, medelavstånd (d) atom-atom ca 2,5 Å (i luft, 10Å)

STJÄRNMATERIAL vid ytan: vakuum mätt med Jordmaterialens preferenser, d ca 250 Å (1 Å = t10 M)

Alla enatomiga stjärnors absorptionskoefficient står redan på maximala 2/3, och den faktorn kan bara reduceras genom reducerad temperatur, analogt en materierymd med molekylära inslag. Detta är ingalunda fallet i den mera omfångsrika stjärnans större ljusstyrka. För given normalmassa = given effekt framstår DESS PLANETÄRMOLEKYLÄRA MATERIALSTRÅLNINGSEKVIVALENT (Stefan-Boltzmanns strålningslag) som hetare=starkare än samma stjärna oroterad.

thetasambandet

f (T_g ® T) (P/A)_Q=f ([Dm+m]/m)akT⁴

I STEFAN-BOLTZMANNS STRÅLNINGSLAG P=aAkT^4 är ytelementet A kopplat till normala Jordiska föremål typ ytan på strömgenomflutna värmegenererande glödtrådar och andra atomära/molekylära ytelement. Man förutsätter då att massgrunden bakom A bildas ur en ythomogen massfördelning från materialets atomer. I stjärnornas fall är det helt annorlunda. Yttätheten vid Solranden är redan med Jordiska mått mätt ett VAKUUM. För ett Jordiskt material (typ wolframtråd i en glödlampa) är det uteslutet att i A kunna fylla på med mera material. I en stjärna är situationen en helt annan. I en stjärna finns stora möjligheter för utfyllande, extra material. Genom att A i stjärnans fall utsätts för belysning (effekten med upphov i stjärnans centrala städområde) snarare än att A som i de Jordiska föremålens fall utgör en primär värmebildande generatris, kan ytljusstyrkan vid A högeligen tillväxa OM ytterligare material tillfogas — och därmed exponeras för städeffektens »strålkastarljus» — utan att effekten på något sätt ökas. Stjärnan som ljusobjekt HAR INGEN JORDISK MOTSVARIGHET. Det finns ingenting att jämföra med. Stjärnfysiken kan inte beskrivas exakt (kommutativt) av samband som gäller för planetmaterialen.

För PLANETMATERIALEN (icke fusionsproducerande kroppar) OCH NORMALSTJÄRNORNA med Dm=0 skrivs LJUSSTYRKAN som

P/A=akT⁴

a är i normalstjärnans fall (enatomiga tillstånd) redan optimerad på värdet 2/3 och kan inte anta högre värde. Med ett masstillskott (Dm) för given effekt och yta kan stjärnans motsvarande ytljusstyrkeekvation därmed skrivas som en funktion av tilläggsmassan (Dm) enligt

(P/A)_Q=Q(theta)=f ([Dm+m]/m)akT⁴

med m (företrädesvis) som massan i opacitetsskiktet (här okänd) och Dm tilläggsmassan från den primära egenrotationen.

I normalstjärnans fall är Dm=0. Eftersom P inte påverkas av växande Q med växande Dm måste viss försiktighet iakttas. Det gäller alltså INTE att

P= f ([Dm+m]/m)aAkT⁴ OM Dm>0

[I fallen Dm>0 kan vi sätta f (P)_Dm=P_Q ¹ P för att markera skillnaden].

PLANETEKVIVALENTEN innehåller ingen funktion f ([Dm+m]/m) varför enda ekvivalenten till effekten P blir via P_Q genom en motsvarande högre effekt via en högre temperatur enligt

P_Q=aAkT_Q⁴.

Dvs., den högre ljusstyrkans Jordekvivalent (eller planetekvivalent) kan FÖR DEN GRAFISKA SKALÅTERGIVNINGEN återföras på en FIKTIV högre normaleffekt=större normalstjärnmassa, analogt en normalstjärna med högre yttemperatur.

Storleken av Dm relativt stjärnans normalmassa är (blir) i samtliga fall försumbar på grund av den låga yttätheten.

Detta är i vilket fall de »enkla» delar som framgår enligt TNED.

;

f (T_g ® T) (P/A)_Q=f ([Dm+m]/m)akT⁴

Dm-STJÄRNANS VERKLIGA YTTEMPERATUR framgår emellertid INTE ur ovanstående rena ekvivalenter. Som grundpreferens kan vi anta men här inte bevisa att Dm-stjärnans yttemperatur relativt sin normalstjärna är identiskt densamma.

Därmed faller alla PRIMÄRSTJÄRNOR med (väsentligen) samma massa, oavsett omfång och ljusstyrka, inom en och samma temperaturklass, analogt inom ett och samma FÄRGINDEX eller samma spektralklass.

Dm-STJÄRNANS VERKLIGA YTTÄTHET framgår heller INTE ur ovanstående ekvivalenter. Med normalstjärnans yttäthetskonstant (r_r=8,9277145 t5 KG/M³) som preferensvärde, förutsatt tätheten för Dm-stjärnan avtar från r_r i Dm med växande ytterradie, ges en OPTIMAL GRÄNSMASSA för Dm från STJÄRNMASSANS RADIELLA VARIATION

[m_in= k_STAR(1 – R/r) + m_SLIM, k_STAR= (m_STAR – m_SLIM)(1 – R/r_STAR)^–1] enligt

Dm = k_STAR(1 – R/r_out) + m_SLIM – [k_STAR(1 – R/r_STAR) + m_SLIM]

= k_STAR(R/r_STAR)[1 – r_STAR/r_out];

Då r_out®¥ ges limes Dm=k_STAR(R/r_STAR). k_STAR kan approximeras med m_STAR.

För Solen är R=4012 M. Se Solens Städradie.

limes Dm — värdet på tilläggsmassan utöver m_STAR — kommer inte på långa vägar ens i närheten av maximala tilläggsmassan m_E (Jordens femte ekvation, primärmassorna). Vilket vill säga: Sambandet för yttäthetskonstanten (r_r) via volymenergin (MLR) i försorg av strålningstrycket, spärrar stjärnan. Hur mycket stjärnan än roterar, kan den inte eliminera den radiella täthetens funktion, och därmed heller inte gränsvärdet för sin totalmassa.

Ur den givna klassen NORMALSTJÄRNOR blir det därmed MÖJLIGT att, för varje given motsvarande normalstjärnas typeffekt, extrahera motsvarande högre rotationsklass’ magnitud eller LJUSSTYRKA:

ljusstyrkan MED EKVIVALENTA YTTEMPERATUREN OCH FIKTIVA EFFEKTEN, men inte reala effekten, ökar med stjärnor i högre rotationsklasser.

PROBLEMET är emellertid, som antytts i ovanstående genomgång, att vi inte känner några exakta kvantiteter, endast relativa och kvalitativt orienterade sådana med EN den nämnda planetmateriens fasta tillståndets fysik som preferens.

Krävande.

LUMINOSITET = EFFEKT = MASSA = TEMPERATUR = FÄRGINDEX = LJUSSTYRKA = MAGNITUD

kopplar enligt TNED endast för PRIMÄRA stjärnor som ansluter till normalkurvan (alla primärt oroterade stjärnor med Solen som preferensmassa) enligt

T_rSTAR = T_rSUN(m_STAR/m_SUN)^7/12 .............................................................. stjärnytans värmegrad

P_STAR = P_SUN(m_STAR/m_SUN)³ .................................................................. sanna effekten

r_STAR = r_SUN(m_STAR/m_SUN)^1/3 ; r_n= 3m_SUN/4pr_SUN³ = m_STAR/V_STAR ............. g-radien

(P/A)_STAR = P_SUN(m_STAR/m_SUN)^7/3/4pr_SUN² = P_SUN(m_STAR/m_SUN)³/4pr_STAR² ........... ljusstyrkan

FÖR ALLA ÖVRIGA STJÄRNOR gäller enligt TNED

(LUMINOSITET = EFFEKT = MASSA = [TEMPERATUR] = FÄRGINDEX) ¹ (OMFÅNG = LJUSSTYRKA = MAGNITUD)

NORMALYTLJUSSTYRKAN (P/A)_STAR=F kan alltså skrivas skalenligt

F=k(n)^7/3 med k=1 och

n=m_STAR/m_SUN som antalet Solmassor, analogt

F₀=(n)^7/3. Enligt BAs27 motsvarar en magnitudskillnad (M_F) på 1 ett ljusstyrkeförhållande på

10^0,4=2,5118864 » 2,512. Detta ger oss

n_M=1=(F₀=2,512)^3/7=1,4839818=10^6/35.

Magnituderna för 2, 3, 4, … m kan då skrivas på motsvarande antal Solmassor

n=1,4839818^m=10^m(6/35).

Med minsta n=1/165 ges max m=–12,935323. n=1 med m=0 markerar Solen.

PRIMÄRA ÖVERGÅNGEN | normalkurvan

normalkurvan

PRIMÄRA ÖVERGÅNGEN

Stjärnornas fördelning, indelning och klassificering

Nedanstående bashuvudkurva

T_rSTAR = T_rSUN(m_STAR/m_SUN)^7/12

anger den normalkurva på vilken alla primärstjärnor utvecklas enligt TNED.

Bilderna ovan ger några karaktäristiska utdrag. Se även den inledande illustrationens allmänna stjärnklassificering enligt TNED.

Källorna anges infällda (dessa kan numera [2008] hittas på många olika webbsidor, se exv @INTERNET Wikipedia Nebula).

BA förkortar BONNIERS ASTRONOMI 1978.

Kurvan nedan roterad 180° (skalan från höger till vänster) motsvarar »HR-diagrammets baskurva»; Vi kommer här i det närmast att studera dess härledande grund — enligt TNED.

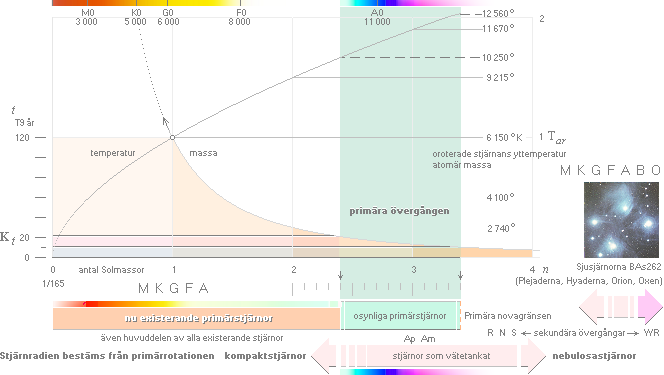
Generaliserad vy över stjärnornas fördelning enligt TNED

I grundbeskrivningen ges skalorna från vänster till höger

— medan HR-diagrammen konventionellt visas och beskrivs från höger till vänster.

Se vidare framställningar i huvudtexten.

—————————————————————————————————————————————————————

ALLA VÄRMEGRADER OCH DERAS EKVIVALENTER utgår i stjärnornas fall från STRÅLNINGSTRYCKETS FUNKTION OCH DYNAMIK,

^gp = 2ak₀T⁴/c₀ = ak_PT⁴ = p–p_e.

Tg = (^gp/ak_P)^1/4 ..................................... strålningstryckets värmegradsekvivalent

T_ar = (4pG/ak_P)^1/4(rr_r/3)^1/2 ................... Solytans värmegrad

^gp = p – p_e ......................................... stjärnornas allmänna tryckekvation

= (^gr/3)^4/3[(4p)+Gm₂^2/3] – ^gr²[k(Ze/d)²/(pr₀)² = k(Ze/(m_A/4r₀³ – 1)pr₀²)²]

= (^gr/3)^4/3a_G – ^gr²a_e med k = Rc₀= 1/4pe₀ @ 9 T9 VM/C

r = m₂/V=3m₂/4pr³ ............................ medeltätheten (^gr) för ^gp dikteras direkt från variabeln r

TEMPERATUREN VID SOLYTAN är alltså med Jordiska mått mätt starkt beroende av tätheten (r_r).

—————————————————————————————————————————————————————

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING | STJÄRNFYSIKEN DEL II

härledning

PRIMÄRA ÖVERGÅNGEN är ett TNED-begrepp.

PRIMÄRA ÖVERGÅNGEN framgår ur ett mycket enkelt HISTOGRAM (vidare nedan) — som samtidigt erbjuder ett enkelt matematiskt verktyg i navigeringen på samtliga förekomster och populationer stjärnindivider — till allmän prövning mot redan genomförda observationer.

Vi studerar hur.

STJÄRNORNAS HISTOGRAM | inledande beskrivning

PRIMÄRA ÖVERGÅNGEN — stjärnornas allmänna histogram

UTVECKLINGEN FÖR EN PRIMÄRT OROTERAD IDEALT ENSAM STJÄRNA kan beskrivas med referens till följande allmänna histogram.

STJÄRNORNAS ALLMÄNNA HISTOGRAM — allmän referens i stjärnfysiken

Uppstart (a, stjärnornas primära födelse och bildning i K-cellens expansion), brinntid (a–b), slockning (b), avstanning (b–c), nova (c, eller a) med vidare.

a b c

b: m_STAR= (t_SUN t_b^–1)^1/2 = 2,4 Solmassor, yttemperatur 10 250 °K [T_ar = T_s=6150(m_STAR/m_s)^7/12]

c: m_STAR= (t_SUN t_c^–1)^1/2 = 3,4 Solmassor, yttemperatur 12 560 °K [T_ar = T_s=6150(m_STAR/m_s)^7/12]

För sambanden ovan, se Tidsekvationen i Stjärnfysiken ;

tSTJÄRNAN = n^–2tSOLEN, n anger stjärnmassan i antalet Solmassor

Histogrammet beskrivs mera utförligt i huvudartikeln för STJÄRNORNAS ALLMÄNNA HISTOGRAM.

Här ges en mera allmän beskrivning som kopplar till stjärnkartans teoretiska härledning generellt — ENLIGT TNED.

Stjärnans egenproducerade impulsmoment (J=mvr) under brinntiden (a–b) kan bara reduceras efter slockningen genom inre friktion eller genom att material tillförs stjärnan utifrån och J på den vägen reduceras. En bekväm referens för den idealt ensamma stjärnan som utlämnas endast åt sin egen inre friktion under avstanningen (b–c) är att sätta perioderna brinntid-avstanning lika långa. I det praktiska fallet kommer novapunkten c att ligga på alla möjliga ställen mellan b och ideala c-punkten.

Primära övergången genom normalstjärnornas allmänna tidsekvation (livslängden) t=t_SUNn², n antalet Solmassor, avdelar alla NU synliga stjärnor genom en gränsmassa på 2,4 Solmassor (b) med optimal marginal (b-c) på 3,4 Solmassor. Primära övergången innebär att alla primära stjärnor större än 2,4 Solmassor har slocknat. Beroende på omgivande vätebanker, har dessa stjärnor inträtt i en andra (och n:te) energicykelfas.

;

Stjärnor > 15 Solmassor finns inte

SE ÄVEN TABELL MED BERÄKNINGSEXEMPEL FÖR OLIKA GRÄNSMASSOR I BASEXEMPEL

Himlakroppar med Väte-1-bas och max täthet erhåller egen yttre nollzon (c=0) vid gränsmassan ca 10 Solmassor (m₁₀),

m_c0=(c₀/ÖG)³(6/64pr)^1/2. Motsvarande gräns för Helium-4-bas går vid ca 5 Solmassor. Alla områden i fysiken som betingas av nollzoner lyder under KÄRNREAKTIONSLAGEN K+(m®g₌₀) = K1+K2 som innebär att alla atomkärnor strävar att sönderdelas tills massdefekten är exakt noll: neutronen. Förutsatt att kroppen befinner sig nära K-cellens centrum (högsta möjliga c-värde) innehåller dess centrum alltid ett motsvarande individuellt c₀-område och därmed alltid en Vätebas från given neutronfragmentering. Därmed bildar kroppen stjärna (kosmiskt egenproducerad fusionsenergi) om massan överstiger stjärngränsmassan (ca 6 Jupitermassor för Väte-1-bas) enligt

stjärnornas allmänna tryckekvation (p – p_e – ^gp = 0), annars planet;

Nollzonens beroende av massan innebär att g-trycket (p) enligt p=F/A tillväxer med avtagande c

— vilket medför att kroppen avyttrar varje massöverskott utöver nollzonsgränsen. Hur avyttringen går till beskrivs utförligt i Statiska Detonationsgränsmassan.

Med hänsyn till en täthetsmarginal som innefattar atomkärnornas inbördes avstånd på deras omskrivna sfärer (r=8,13444 T16 KG/M³), kan därför inga himlakroppar större än ca 15 Solmassor existera statiskt.

Säkra data på stjärnmassor finns bara ”för några få dussin visuella system”, [ref. BAs30sp1ö]. Bilden nedan från

BONNIERS ASTRONOMI 1978 s50 visar 0,16-max5,3 Solmassor.

visuella dubbelstjärnesystem

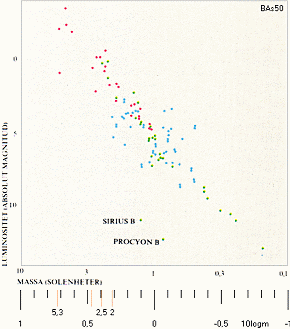
BONNIERS ASTRONOMI 1978 s50 — den förtydligade skalan underst inlagd separat

SÄKRA STJÄRNMASSOR [BAs50] ges bara från visuellt uppmätbara dubbelstjärnesystem med kända omloppstider och banellipser från Keplers III:e lag.

Källan redovisar visuella system:

Gröna punkter (27st), hög noggrannhet

Blå punkter (49st), mindre noggrannhet

Icke-visuella system:

Röda punkter (25st) markerar fotometriska dubbelstjärnor och anges som ”de mest pålitliga” stjärnmassorna.

FOTOMETRISKA DUBBELSTJÄRNOR — i citatkällans epokreferens — FINNS EMELLERTID VETERLIGT INTE ALLS MED SAMTIDIGT VISUELLA STJÄRNKOMPONENTER; Källan klargör INTE det. Avstånden till objekten framgår inte heller.

FÖRUTSÄTTNINGEN för att ett fotometrisk dubbelsystem (stjärnorna skymmer varandra periodvis) MED DE KÄNDA VISUELLA SYSTEMENS DIMENSIONER (!) OCKSÅ ska visa komponenterna SOM VISUELLT SKILDA LJUSPUNKTER är att stjärnbanornas plan måste ligga INOM upptagande synvinkeln för (största) stjärnans diameter. Med andra ord och med hänsyn till de stora avstånden till de närmaste stjärnorna (från 2-3pc och vidare): EXAKT I SYNLINJEN MED ENORM PRECISION.

Vad vi vet, existerar ingen sådan statistik i universum i Solens lokala stjärnfält (inom ca 30pc)

— med referens till en »homogeniserad idealiserad bild» av ”alla typer av himlakroppar”.

STRÄNGT TAGET VET VI DOCK INGENTING I ÄMNET AV FÖLJANDE DELVIS ÄNNU ÖPPNA, OUPPKLARADE FRÅGESTÄLLNING:

Med J-kropparnas avdelning under K-cellens expansion följer som tidigare redovisats i JORDENS TREDJE EKVATION (Solsystemets uppkomst) en resonansmatematik som beskriver de avdelade kropparnas inbördes avstånd — mycket (kvalitativt) liknande det som kan observeras i avdelningen av vattendroppar från en smal stråle eller rekylen från en vattenbaserad ytstuds. Men TNED lämnar ingen DIREKT upplysning om i vilka J-kroppar som vilka storlekar är möjliga; Vilket vill säga: Vi VET inte OM det eventuellt KAN vara så att vissa resonansområden (t.ex. för särskilt stora J-grundmassor) ger »särskilt täta regioner» med typ ”trånga dubbelstjärnesystem”. I så fall skulle anledningen till att vi inte kan se sådana system i Solens närmaste omgivning vara att de helt enkelt tillhör en annan resonansgrupp och av det skälet bara förekommer i speciella regioner — på stora avstånd från Solen.

Jämför (fetstil och övrig textmarkering är min):

”Binary stars that are both visual and spectroscopic binaries are rare, and are a precious source of valuable information when found. Visual binary stars often have large true separations, with periods measured in decades to centuries; consequently, they usually have orbital speeds too small to be measured spectroscopically. Conversely, spectroscopic binary stars move fast in their orbits because they are close together; usually too close to be detected as visual binaries. Binaries that are both visual and spectroscopic thus must be relatively close to Earth.”

@INTERNET Wikipedia Binary star 2007-03-01

Min översättning:

Dubbelstjärnor som är både visuella och spektroskopiska är sällsynta, och är en ovärderlig källa till betydelsefull information då de påträffas. Visuella dubbelstjärnor uppvisar ofta stora sanna separationer, med perioder som mäts i decennium till sekel; följaktligen har de vanligen banhastigheter alldeles för små för att kunna mätas spektroskopiskt. På motsvarande sätt färdas spektroskopiska stjärnor snabbt i sina banor eftersom de ligger nära varandra; vanligen alltför nära varandra för att kunna urskiljas som visuella dubbelstjärnor. Dubbelstjärnor som både är visuella och spektroskopiska måste därför befinna sig relativt nära Jorden.

”Actually, most stars that are classified as binaries are not visual binaries, but instead it has been deduced that they are binaries from the spectrum. Thus, they are spectroscopic binaries.”

@INTERNET 2007III1 [http://csep10.phys.utk.edu/astr162/lect/binaries/spectroscopic.html] från Google Spectroscopic Binaries

Min översättning:

De flesta stjärnor som klassificeras som dubbelstjärnor är egentligen inte visuella dubbelstjärnor, utan det har istället slutsatsdragits från spektrum att de är dubbelstjärnor. Således är de spektroskopiska dubbelstjärnor.

”Only a small portion of binary stars are visual binaries. In order to see a visual binary, the stars must be separated by fairly wide distances, and the orbital periods are usually very long.”

@INTERNET 2007III1 [http://www.astronomical.org/astbook/binary.html] från Google Spectroscopic Binaries

Min översättning:

Bara en liten del av dubbelstjärnorna är visuella dubbelstjärnor. För att kunna se en visuell dubbelstjärna, måste stjärnorna vara separerade av rätt stora avstånd, och banperioderna är vanligen mycket långa.

Diagramredovisningen, röda punkterna, ovan från [BAs50] klargör ingalunda denna detalj, utan FÖRUTSÄTTER tydligen att DE UPPMÄTTA LJUSVÄXLINGARNA bakom de röda punkterna döljer VERKLIGA dubbelsystem.

VI VET INTE DET. Fotometriska data KAN här bli ytterst äventyrliga;

Se EXEMPLEN I PULSARERNA med (främst) PSR 1913+16 som ett grundläggande konkret studieexempel. Vi måste räkna med delen här — så länge inget direkt avgörande finns i frågan.

;

Eftersom ENLIGT TNED LJUSHASTIGHETENS LOKALA REDUKTION MED VÄXANDE STJÄRNMASSA inom intervallet 5-15 Solmassor medför ett instabilitetsområde med starka vrängningar relativt de ideala termodynamiska parametervärdena,

garanteras därmed att stjärnfysiken i förhållande till praktiskt uppmätta fotometriska och spektroskopiska instrumentvärden I MOTSVARANDE GRAD blir ytterst krävande.

Vi studerar ett MÖJLIGT praktiskt exempel enligt TNED.

exempel

STRÅLNINGSTRYCKETS SPEKTAKULÄRA INVERKAN PÅ GRÄNSMASSORNA — enligt TNED

Exempel

En normalstjärna på 10 Solmassor utan hänsyn till ljusets g-beroende (m₁₀) har enligt TNED en ytvärmegrad på

T=23 500 °K. Strålningstryckets starkt kalljoniserande värmegradsekvivalent vid stjärnytan är

Tg=35,8 miljoner grader. Låt oss anta att stjärnan dämpas med en faktor 1000 på grund av reducerad divergens. Detta ger stjärnyttemperaturen

T=23,5 °K och strålningstryckets temperaturekvivalent

Tg= 35 800 °K. Därmed motsvarande SPEKTRALA detaljer. Stjärnljuset kan omöjligen gömma undan den rent spektrala-fotometriska effekten från Tg i detta läge.

Spektralkartan för den stjärnans ekvivalenta värmegrad som närmar sig gränsmassan m₁₀ kan på detta sätt vid en direkt spektral genomgång av allt ljus som stjärnan utsänder förstås uppvisa (våldsamt) högre frekvenser relativt sitt sanna tillstånd; Stjärnans allmänna Planckkurva speglar en betydligt högre temperaturtopp.

OM alltså detta också verkligen håller streck:

KÄNNER MAN INTE DESSA GRUNDER förvillas man dra slutsatsen att stjärnan har betydligt större massa än sin normalekvivalent. I exemplets enkla fall skulle värdet T=35 800 °K motsvara en normal stjärnmassa på

[(35 800)/(6 150)]^12/7=20,5 Solmassor. Inte 10. Felet blir alltså våldsamt.

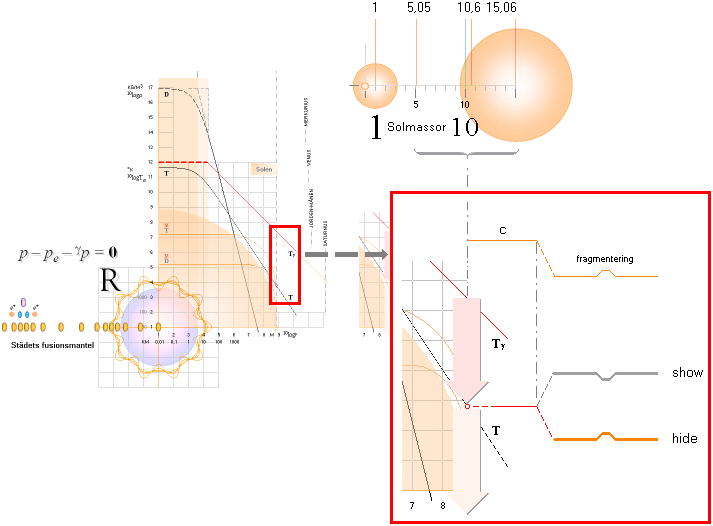
TILLSTÅNDET för en fusionsproducerande exempelstjärna 5-15 Solmassor betingas på detta sätt ENLIGT TNED av en stor flora av möjligheter där strålningstryckets värmegradsekvivalent (Tg) enligt exemplet kan ÖVERTA normalstjärnans motsvarande ljusemitterande roll. PONERA ATT STJÄRNAN NEUTRONFRAGMENTERAR i detta tillstånd;

1. tätheten reduceras med växande antal lättare atomkärnor (neutroner-Väte-1);

2. divergensen (c) ökar därmed, vilket tvingar stjärnans ljusemission mot normalläget (max c) och därmed en REDUKTION i den ljusemitterande funktionen från strålningstrycket;

3. stjärnan uppvisar en fotometrisk ljussvacka motsvarande perioden för fragmentering/förbränning/återgång — med en STOR flora av möjliga sätt och fasoner.

4. STJÄRNANS INRE döljs effektivt av stjärngloben på strålningstryckets funktion, ingenting ses därifrån!

Säg den ljusändringstyp som INTE kan komma ifråga för sådana typexempel kring 5-15 Solmassor!

EXEMPLET KLARGÖR

— om TNED-beskrivningen nu också verkligen ÄR korrekt

— att periodiska ljusändringar RELATIVT EN ÖVERLAGRAD KONSTANT LJUSSTYRKA på intet OBETINGAT tvunget sätt utpekar ett dubbelstjärnesystem. Det är EN stjärna som »jävlas».

Ett praktiskt detaljerat utförligt exempel ges från början i PULSARERNA.

Eftersom modern akademi inte känner till SOLENS FYRA PLUS EN VÄRMEGRADER är det givet att också den allmänna moderna uppfattningen om stjärnornas fysik mera kommer att belysa en dockskåpsteater — en mycket förenklad och schematiserad stjärnfysik

— än det verkliga fallet

— om det nu är TNED som gäller.

HERTZSPRUNG-RUSSEL DIAGRAMMET

HERTZSPRUNG-RUSSEL DIAGRAMMET

HR-DIAGRAMMETS GRUNDER ENLIGT TNED

För att kunna bemöta, illustrera och jämföra TNED med moderna referenser har jag tagit mig friheten att använda Bonniers Astronomi från 1978 och deras illustrationer för att belysa och beskriva hur den konventionella nomenklaturen är uppbygg, samt hur den förhåller sig till TNED

Termen HR förkortar upphovsmännens initialer

— Hertzsprung-Russel

— oberoende av varandra, E. Hertzsprung dansk astronom, H. N. Russel amerikansk astronom, bägge början av 1900-talet, BAs409sp2ö.

Inledning

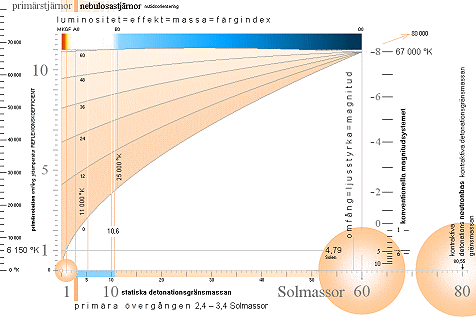
I illustrationen nedan är yttemperaturen-normalkurvan enligt TNED avsatt som funktion av den primärt oroterade stjärnmassan. Kurvorna över denna antyder hur kurvorna för motsvarande primärt roterade stjärnor bör ligga enligt resonemanget.

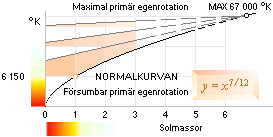
Eftersom hela K-cellens övergripande fysik bygger på primära kroppsavyttringar (Se utförligt från K-cellens detonation) föregående himlakropparnas primära fusionsbildningar enligt olika resonansserier (Jordens tredje ekvation), har vi ingenting annat att förvänta oss än att det bör finnas ett system av rotationer taget gemensamt för samtliga stjärnor. Hur systemet sedan utvecklas beror på egenrotation och expansionspotential i J-moderkropparna: högre värden medför större dynamik och därmed en tydligare struktur. System med liten dynamik (t.ex. klotformiga stjärnhopar) visar också liten rotationsstruktur medan system som utvecklas i galaxernas spiralarmar som bygger på en maximal dynamik också uppvisar maximal rotationsstruktur.

NOTERING

I grundbeskrivningen i TNED ges skalorna från vänster till höger, medan HR-diagrammen konventionellt visas och beskrivs från höger till vänster. Se vidare framställningar i huvudtexten.

HR-diagrammet

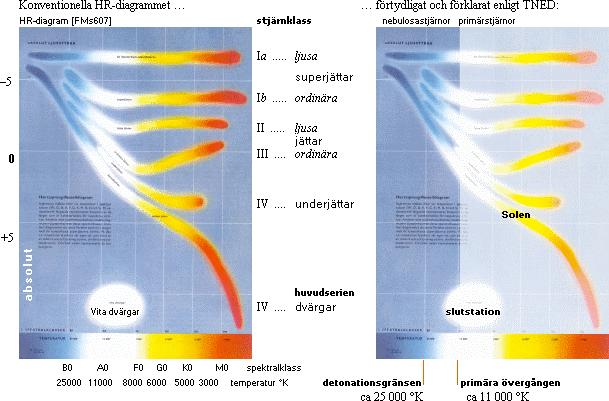
ALLMÄN NOTERING TNED/HR-DIAGRAMMEN I KONVENTIONEN

Bilden oförminskad finns i Stjärnmassorna

1. Skalorna i TNED och HR-diagrammet är vänster-högervända.

2. HELA färgindexskalan (M0röd till B0blå) är i TNED representerad endast av det smala bandet i området 1-10 Solmassor. Konventionella HR-diagrammets delvis krökta delar (undre kurvan angiven som huvudserien) är ett resultat av den förvrängningen. Anpassningen är skalmässigt delvis komplicerad.

Se även i SKILDA PREFERENSER I TNED OCH MAC.

TNED förklarar brytpunkterna i HR-diagrammen

SAMBAND enligt TNED:

———————————————————————————————————

T_STAR = T_SUN(m_STAR/m_SUN)^7/12

m_STAR brytpunkt primära övergången 2,4 Solmassor

m_STAR brytpunkt statiska detonationsgränsmassan 10,6 Solmassor

RESULTAT med T_SUN=6 150 °K: konv. HR-diagram:

—————————————————————— ——————————

T_STAR(primära övergången) = 10 977,513 °K 11 000 °K

T_STAR(detonationsgränsen) = 24 376,435 °K 25 000 °K

TNED förklarar vad brytpunkterna betyder, hur de uppkommer och hur de fungerar.

HR-diagrammets detaljer förklaras vidare i texten längre fram om ej redan bekant.

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

expanssionssambanden

se även från EXPANSIONSSAMBANDET

Bilden oförminskad finns i Stjärnmassorna

Stjärnfysiken enligt TNED grundas på en besättning av primärt avdelade J-massor från K-cellens expansion med lägst 1/165 Solmassor (m_0SLIM, absolut lägsta stjärngränsmassan) och högst 80 Solmassor (J80-massan). Genom massavyttring som sker under J-kroppens expansionsfas efter divergenständning reduceras J80-massan till nätt 60 Solmassor. Alla stjärnor utvecklas och fortbildas sedan på och inom den masstocken. GRÄNSMASSORNA specificeras i TNED enligt sambandsformerna nedan (m-sambanden).

Expansiva-kontraktiva tillståndets g-fysik (se K-CELLENS EXPANSION c=0):

(1) r = (3c₀²/2Gpr)^1/2 = (c₀/ÖG)(3/2pr)^1/2 ; r³ = (c₀/ÖG)³(3/2pr)^3/2 ; m = r³(4pr/3) = (c₀/ÖG)³(6/pr)^1/2

T = 2Ö(3/8pGr) = Ö(3/2pGr) ......................... expansionstiden ur tätheten (se K-CELLENS EXPANSION c=0)

Villkoret med T = r_c=0/c₀ medför (1) ovan, se även i Ty-beskrivningen nedan

Expansiva-Kontraktiva-Statiska tillståndets g-fysik (J-KROPPARNAS EXPANSION c=0):

(2) r = (3c₀²/8Gpr)^1/2 = (c₀/ÖG)(3/8pr)^1/2 ; r³ = (c₀/ÖG)³(3/8pr)^3/2 ; m = r³(4pr/3) = (c₀/ÖG)³(6/64pr)^1/2

förklaring STATISKA [nr(2) ovan] — se explicit i Nolldivergenszonens radie ur tätheten:

r_c=0 = 2Gm₂/c₀² se Ljusets Gravitella beroende med c=0

m = rV = 4prr³/3; r=m/Volymen anger tätheten i KG/M³; sfäriskt ges då;

r = 2G(4prr³/3)/c₀² ;

r² = 3c₀²/8Gpr ;

förtydligande UTVECKLINGSEXEMPEL i (1):

m = r³(4pr/3) ; r³ = (c₀/ÖG)³(3/2pr)^3/2

;

m = r³(4pr/3)

= (c₀/ÖG)³(3/2pr)^3/2(4pr/3)

= (c₀/ÖG)³(3/2pr)^1/2(3/2pr)(4pr/3)

= (c₀/ÖG)³(3/2pr)^1/2(2)

= (c₀/ÖG)³(3/2pr)^1/2(2)

= (c₀/ÖG)³(6/pr)^1/2

OBSERVANDUM

EXPANSIONSSAMBANDEN ENLIGT TNED BESKRIVER DYNAMIKEN I LJUSETS UTBREDNING I SAMBAND MED FRIGÖRANDET AV GRAVITATIONSENERGI

— det är ingen allmän tillståndsbaserad matematisk fysik och den kan inte användas explicit för att härleda grundläggande massformer.

Från Ljusets Gravitella beroende i fasta tillståndets fysik — kroppar som INTE expanderar eller kontraherar — gäller allmänt med särskild beskrivning i Nolldivergenszonens radie ur tätheten att

r_c=0 = 2Gm₂/c₀²

= 1,48427 t27 · m_0c;

Man har ENLIGT RELATERAD FYSIK från hyperbeldelen i Ljusets Gravitella beroende

c=(c₀/2)[1 – Ö (2w/c₀)² – 1 ], som med c=0 ger utvecklingsleden;

1=Ö (2w/c₀)² – 1; 2=(2w/c₀)²; 2=4w²/c₀²; 1=2w²/c₀²=2(Gm₂/r_c=0)/c₀²=2Gm₂/r_c=0c₀²,

varav således

r_c=0 = 2Gm₂/c₀² = 1,48427 t27 · m₂ ........................ massans nolldivergensradie, M ; för varje m finns ett motsvarande r_c=0

m_0c betyder här den massa som innesluts av sfären med radien r_0c då divergensen vid sfärytan är precis noll.

För K-cellens expansion gäller istället — eftersom nolldivergenszonen hela tiden expanderar (och längre fram kontraherar åter) — ett motsvarande

r_0c = Gm_0c/2c₀²

= r_0cSTATISKA/4

För att kunna härleda K-cellens expansion krävdes alltså en särskild avhandling.

;

Härledande beskrivning:

Medan

w² = Gm₂/r gäller för statiska tillståndets g-fysik i K-cellen, analogt g-potentialen, och som leder till ovanstående

r_0c = 2Gm_0c/c₀² — w²=Gm₂/r=c₀²/2; r=2Gm₂/c₀² = (3c₀²/8Gpr)^1/2 —

gäller istället för en K-cellens kropp som uppvisar en utåtriktad eller inåtriktad (elementär) linjär acceleration motsvarande

w² = (G/4)m₂/r

r_0c = Gm_0c/2c₀² — (beskrivningen nedan) — GEXPANSIVA=GSTATISKA/4

»r0cEXPANSIVA / r0cSTATISKA = 1/4».

Ty;

1.

Nolldivergenszonens konstanta hastighet — nolldivergenszonens hastighet

Divergensens Expansiva G-beroende

c=c₀Ö 1–2(w/c₀)² ger för c=0 sambandet

1=2(w/c₀)² som ger

w=c₀/Ö2. Allmänna Expansionshastigheten v=wÖ2

ger då v=c₀. Därmed utbreder sig tydligen nolldivergenszonen i K-cellen enligt

c₀ = r_0c/T₀ ................. nolldivergenszonens konstanta hastighet, idealt bevarad g-energi

Det betyder att K-cellens nolldivergenszon c=0 expanderar med konstant hastighet v=c₀ — förutsatt ideala förhållanden enligt de allmänna premisserna.

Radien för divergensnollzonen kan då beräknas r_0c=c₀T med T som totala expansionstiden;

2.

Från expansionssambandet

T = 2Ö(3/8pGr) .................... expansionstiden ur tätheten — från Keplermomentet, se illustrerat i expansionssambandet

= Ö(3/2pGr) ;

ges via den konstanta topphastigheten c₀ som beskriver nolldivergenszonens konstanta svephastighet i K-cellen

r_c=0 = c₀T₀

= c₀Ö(3/2pGr) = r_0c ;

expansiva:

r_0c = (3c₀²/2Gpr)^1/2 ................ Kontraktiva-Expansiva tillståndets fysik, icke fast kropp

r_0c = (3c₀²/8Gpr)^1/2 ................. jämför statiska, som ovan

och vilket vi ser är samma som i föregående nr(1).

Med enbart isolerade G-termer (absolut PRINCIPIELLA funktionen) EXPAnsiva 2G kontra STATiska 8G gäller tydligen

EXPA(2G)/STAT(8G)=2G/8G=1/4 ; G(EXPA) = G(STAT)/4 ; c₀pr momentant fixa.

— G-faktorernas olika sätt i EXPA[G/4] och STAT[G] är här relaterade till den helt ideala r0c-formen speciellt i K-cellens idealt täthetshomogena massrymd.

— Det är [här, ännu Apr2012] inte känt om någon annan, oberoende, härledningsform finns som leder till samma resultat;

— Tills vidare används generellt ovanstående — den enda ENKELT relaterbara/härledningsbara grundform som f.n. finns.

Editor2012IV19

—————————————————————————————————————————————————————

Se även (mera förenklat) i

GRÄNSMASSORNA GENOM EXPANSIVA-KONTRAKTIVA OCH STATISKA TILLSTÅNDENS MATEMATISKA G-FYSIK.

—————————————————————————————————————————————————————

masskalan

Största neutronbaserade kroppsmassan med egen divergensnollzon från K-cellens expansion blir

80,557044 Solmassor eller 1,602 T32 KG med r=1,82 T17 KG/M³ enligt (1). En sådan primärmassa motsvarar efter primärexpansionen (Jordens femte ekvation) en resulterande massa på 1,16 T32 KG eller 58,4 Solmassor eller avrundat max 60 Solmassor. Jämför (en mer eller mindre direkt observationell bekräftelse):

”Astronomerna har alltid undrat varför det inte existerar några stjärnor med massor som väsentligen överstiger 50 Solmassor.”

BONNIERS ASTRONOMI 1978 s78sp1mö

Samma uppgift anges i [FMs622sp1ö] ”vilket värde tycks vara en övre gräns för verkligen observerade objekt”.

Anledning varför inga större stjärnmassor förekommer än J80-massan är att alla primära massor från den gränspunkten och i försorg av neutronkallplasmats gravitellt egenkontraktiva karaktär besitter kapacitet att avdela mindre delkroppar som i sin tur kan bilda typen stjärna, planet eller mindre mineralkroppar. Primärmassor större än J80-massan betraktas i TNED därför som J-moderkroppar till avdelade J-kroppar med lägre massa. Vilket vill säga: varje J-kropp med massan större eller lika med J-80-kroppens löser upp sig i mindre delkroppar.

GRÄNSMASSORNA insatta i masskala enligt TNED. Bilden oförminskad finns i Stjärnornas masskala

Solmassan 1,989 T30 KG som beräknas ur Keplers tredje lag med känt avståndet Jorden-Solen och tiden för Jordens årliga omlopp, bildar preferensen för stjärnornas matematiska fysik genom Solens tre ekvationer. Dessa samband bildar normalkurvor för alla primärt oroterade primära stjärnmassor med Solen som preferens, och ur den preferensen härleds alla övriga stjärnors matematiska fysik tillsammans med Jordens fem ekvationer.

Högsta Helium-4-baserade tätheten (från neutronradien) är 7,22 T17 KG/M³. Max Coulombtäthet baserad på Väte-1-bas är r_C=8,13444 T16 KG/M³. Med dessa täthetsvärden ges detonationsgränsmassan ett fönster som initieras från 5 Solmassor (Helim-4-bas) och som begränsas av max 15 Solmassor (r_C).

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

MED REFERENS TILL STATISKA DETONATIONSGRÄNSMASSAN:

STATISKA DETONATIONSGRÄNSMASSANS BRYTPUNKT indelar i konventionella beteckningar alla stjärnor i två osvikliga klasser. Till höger om brytpunkten kallas de OB-stjärnor (samt WR-stjärnor), till vänster kallas de AFGKM (RNS)-stjärnor.

ROTATIONSKLASSERNA

HR-DIAGRAMMETS KÄRNVERK — ENLIGT TNED

D

en i strålningstryckets försorg roterade stjärnans högre ytvärmegrad (T) kan återföras på samma T för en normalstjärna med större massa — men med T beläget-förskjutet längre in mot centrum motsvarande verkan av den roterade stjärnans radiella tillskott — och därmed en tillhörande reducerad värmegradient med avseende på normalstjärnans g-yta — analogt en till normalkurvan adderad negativ värmebildare. I annat fall kommer ekvivalenta värmegradens funktion för en och samma rotationsklass att växa över alla gränser. Villkoret innebär att högsta värmegraden (runt 70 000 °K för största möjliga primärstjärnan på 60 Solmassor) sätter en absolut övre gräns för stjärnans största omfång. Gränsradien (r_lim) kan utläsas direkt ur strålningstryckets värmegradsekvivalent som skärningen med toppvärmevärdet (T_max) enligt

^gp = a_2/3k_{P 3,781904041 t16}T_max⁴ = (r/3)^4/3a_G utanför stjärnytan; r=3[(2,52126 t16)T_max⁴/a_G]^3/4

a_G =(4p)^1/3Gm_STAR^2/3 ; r=3m_STAR/4pr_lim³ ; r_lim³=3m_STAR/4pr = (m_STAR/4p)[a_G/(2,52126 t16)T_max⁴]^3/4

I

fallet med 1 Solmassa går gränsen strax bortom Jordbanan — gul stjärna med en ekvivalent Solyttemperatur på 70 000 °K.

S

tjärnornas allmänna temperaturfunktion för enatomiga normalstjärnor är T= (r_STAR/r)^3/2T_S(m_STAR/m_S)^7/12 med r_STAR=r vid stjärnytan, T_S Solens yttemperatur (6150 °K) och m_S Solmassan. Den negativa värmebildaren x/n motsvarar en linje med allt större negativ gradient som garanterar att toppvärdet T_max vid max stjärnmassa inte överskrids för aktuell rotationsgrupp. Offsetvärdet x₀ anger massförskjutningen i antal Solmassor som krävs av villkoret för temperaturekvivalenten.

M

ed referens till största primära stjärnmassan x=60 Solmassor och enhetsvärdet 1=T_S kan vi lösa ut n för varje möjlig rotationsklass relativt offsetvärdet x₀ från T_max=60^7/12=10,895694 T_S enligt

n = x[T_S(x+x₀)^7/12 – T_max]^–1

= 60[(60+x₀)^7/12 – T_max]^–1 ; T_max^12/7= 60 = 60+x₀ ; x_0min= 0 Solmassor

T_max är 6150×60^7/12 = 67 008,518 °K för 60 Solmassor.

För 10 Solmassor ges T_max= 6150×10^7/12 = 23 561,798 °K.

En delning av 60 med 12 ger 5 intervall för illustrationens ändamål,

1/n={0,02038₁₂; 0,03938₂₄; 0,05728₃₆; 0,07427₄₈; 0,09049₆₀}.

Därmed har termen stjärnkarta enligt TNED fått ett mera konkret innehåll.

Bilden nedan visar funktionen för stjärnornas normalkurva (kurvan underst) med de fem markerade rotationsklasserna.

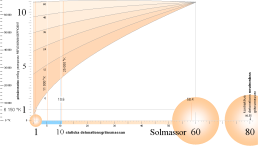Bilden oförminskad finns i Stjärnornas normalkurva

STJÄRNKARTANS KOMPLETTERING MED PRIMÄRA ÖVERGÅNGEN bildar den fullständiga kartbasen.

Primära övergången kopplar till tidsekvationen t=t_S/n². t_S anger Solens livstid med ideal 100% Väteförbränning, n anger antalet Solmassor. Med hänsyn till K-cellens ålder (från K-cellens värmefysik) och tidsekvationens samband (MLR) kan gränsvärdet bestämmas för den primära stjärnmassa som i nutid precis är på väg att slockna. Gränsvärdet är 2,74 Solmassor. För den idealt ensamma stjärnan gäller ett absolut längsta tidsintervall för avsaktningsperioden, idealt lika lång som brinntiden (Stjärnornas allmänna histogram). Med denna preferens bildar primära övergången ett massfönster mellan 2,4-3,4 Solmassor. Alla primära stjärnor med större massa än 2,4 Solmassor har slocknat och alla primära stjärnor med massor större än 3,4 Solmassor har redan genomgått sin första avsaktningsperiod och därmed inträtt en eventuellt andra energicykelfas. Primära övergången indelar på detta sätt alla stjärnor efter nutid i två klasser: primärstjärnor (1:a fasens energicykel) och nebulosastjärnor (n:te fasens energicykler). Gränsen på 2,4 Solmassor är tydligen f.ö. väl omvittnad i de tillgängliga observationerna, se BEKRÄFTELSE.

Vi måste ange detta viktiga fönster i samband med analysen av observationella data eftersom stället innebär en brytpunkt i bilden av alla möjliga förekomster.

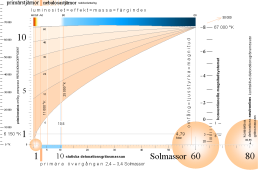Bilden oförminskad finns i Primära övergången med färgindex

STJÄRNKARTANS KOPPLING TILL KONVENTIONELLA OBSERVATIONER

ges genom en färgskala, ett färgindex med en motsvarande redovisad temperaturskala eller luminositetsskalan.

Källreferensen är här FOCUS MATERIEN 1975 s607 som tillsammans med sitt färgindex, temperatur och spektralklass anger en absolut linjär magnitudskala.

Skalorna relativt TNED är emellertid helt annorlunda med delvis logaritmiska förskjutningar av här ej känd art. Skaltolkningarna har gjorts på direkt mätande och jämförande geometrisk bas och får därför ses endast som grovt orienterande (grova preliminära resultat).

Konventionella magnitudskalan omsatt på TNED-kartan visas i färgbandet överst i ovanstående figur.

För skalornas allmänna tolkning i jämförelsen mellan TNED och MAC (modern akademi) observerar vi följande.

Vi är vana vid att en högre ljusstyrka kräver högre effekt, men i stjärnornas fall gäller INTE den analogin enligt TNED eftersom ljusstyrkan inte bestäms av effekten utan av hur mycket material som strålningstrycket påverkar inom stjärnklotet: mer material, större omfång, ger större lyskraft. Effekten kopplar inte dit.

Jämför en person som kastar sand i strålljuset från en strålkastare: några få sandkord ger ingen reflekterande lyseffekt alls, medan ett helt lass reflekterar maximalt. Lampeffekten hör inte hit.

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

luminositet effekt färgindex

Jämför följande enkla förklarande analogi:

TÄNK en strålkastare som riktas rakt ut i tomma rymden. Vi ser ingenting alls. Men om vi kastar fram en näve sand ser vi omedelbart en viss ljusstyrka. Med maximal materialmängd framför strålkastaren framträder också en maximal ljusstyrka. Effekten vi ser kopplar inte till ljuset från det reflekterande materialet utan till mängden material som placeras i strålkastarens ljusväg. En låg strålkastareffekt (en viss färg) ger en låg ljusstyrka även med maximalt reflekterande material, medan en strålkastare med högre effekt (annan färg) ger en motsvarande högre reflekterande ljusstyrka.

På alldeles samma sätt beskrivs termen luminositet = effekt = stjärnmassa = färgindex enligt TNED. Färgen, inte ljusstyrkan, beskriver strålkastareffekten. Ljusstyrkan kopplar istället till mängden material som blir belyst, analogt stjärnans omfång = magnitud = ljusstyrka. I konventionell tolkning sätter man luminositet = absolut magnitud = effekt och betraktar stjärnorna som ordinära laboratoriekonstruerade glödande klot.

”Begreppet absolut magnitud definieras som den ljusstyrka (mätt i magnituder) en stjärna skulle ha om den befann sig på ett visst standardavstånd från oss. Man har enats om att här använda avståndet 10 pc. Den absoluta magnituden är följaktligen ett mått på stjärnans energiproduktion, dess absoluta luminositet.”, BONNIERS ASTRONOMI 1978 s29sp2ö

TNED har ingen sådana analogi. Den absoluta magnituden betyder i TNED endast stjärnans omfång, och har ingenting med stjärnans energiproduktion att göra.

Ett annat förklarande, lika enkelt, sätt att beskriva stjärnornas ljus på enligt TNED är följande.

Varje stjärna liknar en sfärisk boll som emitterar ljus från sin yta via »ytpixels med bestämd färg». Färgen eller luminositeten bestämmer effekten. Röda ytpixels visar låg effekt och liten massa, blått visar hög effekt och stor massa. Ljusstyrkan eller magnituden växer med växande bollyta men INTE effekten. Bollar med samma färg = samma effekt men olika omfång uppvisar olika ljusstyrka. Små bollar syns svaga, stora bollar syns starka.

stjärnkartan

Därmed kan vi nu genomföra en fullständig beskrivning av stjärnornas förekomst och fördelning enligt TNED.

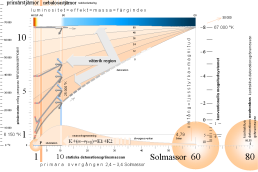
De grå stråken i bilden nedan markerar i grova drag stjärnfördelningen (i Vintergatan) enligt källreferensen och som vi strax ska återkomma till.

Bilden oförminskad finns i Stjärnornas fortbildning

Bilden visar i sammanställning i den högra delen (färgindex blått) hur stjärnor på normalkurvan längst ner, analogt primärstjärnor med maximalt liten primär egenrotation, kan bilda stjärnor med alla typer av omfång enligt föregående resonemang.

Den undre bulkkurvan antyder den ungefärliga praktiska justering som följer av ljushastighetens reduktion då stjärnmassan växer. Idealt frånses denna. Se dock mera utförligt i HR-diagrammets fullständiga TNEDform.

beskrivning

ALLA STJÄRNOR som haft någon minsta möjliga primär egenrotation föregående stjärnans energiproducerande fas bygger upp egenproducerade växande impulsmoment (egenproducerad rotation) under sin brinntid. En stjärna som slocknar och efterlämnar en centraldel för en andra och n:te energifas har därför de allra bästa förutsättningar för att uppvisa en stor flora av motsvarande primära egenrotationer. En slutlig detonation (vid motsvarande brytpunkten 10 Solmassor eller högre beroende på omgivande vätebanker) bildar på så sätt en delare som ger n:te cyklernas lägre stjärnmassor i formen av alla möjliga rotationsklasser och därmed stjärnor med alla möjliga typer av omfång.

STJÄRNOR MED STORA OMFÅNG i sin tur kan inte på samma sätt tända före en total avsaktning efter slockning DÄRFÖR att just det stora omfånget, även i en väterik region, håller vätebankerna på betydligt större avstånd och därmed med längre intankningstider. Det är i varje fall den teoretiska grund som enligt TNED ligger närmast till hands för att kunna förklara de observerade stjärnornas fördelning och spridning. Den svulstiga stjärnans inre normalstjärna (vi erinrar de elementära begreppen) har därför större förutsättningar att i lugn och ro via sin inre friktion göra sig av med sitt impulsmoment under avstanningsfasen, och den kan därför nå sitt maximalt täta tillstånd (vid 10 Solmassor statiskt) och därmed rekylera.

Följaktligen uppvisar stjärnförekomsterna entydigt och klart ett avbrott vid statiska detonationsgränsmassan — för alla rotationsklasser utom normalkurvans, precis så som TNED vill ha det.

· OMFÅNGSRIKA STJÄRNOR kan inte fortbildas över statiska detonationsgränsen ens i de mest väterika områden. De hinner uppnå max täthet innan någon väsentlig nytankning genomförts.

· OMFÅNGSRIKA STJÄRNOR kan endast uppkomma från stjärnor med absolut minsta möjliga primära egenrotation som garanterar en absolut samlad stjärnsfär med absolut optimalt minsta möjliga utsträckning och därmed en optimalt snabb intankning i väterika regioner som därmed garanterar att stjärnan kan passera statiska detonationsgränsmassan innan den når sitt maximalt täta tillstånd under avsaktningsfasen och på den vägen, längre fram i masskalan, bilda de mest omfångsrika stjärnor genom senare brytpunkter.

Med konventionella beteckningar således: OB-stjärnor förekommer inte (numera) i vätefattiga stjärnfält. Intrinsiskt rent.

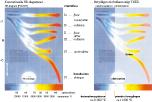Bilden oförminskad finns i Konventionella HR-diagammet

Normalkurvan i TNED motsvarar det undre stråket .

Föregående inscannade och förminskade källreferens (illustrationen ovan) från FOCUS MATERIEN 1975 s607 visar hur konventionella stjärndata (från Vintergatans bestånd) insatts i den traditionella färg-magnitudkartan. Beteckningarna till höger om bilden förtydligar de olika stråkens konventionella beteckningssätt. Bilden till höger är källreferensen omsatt på TNED-kartan med detonationsgränsen (25 000 °K) och primära övergången (11 000 °K) markerad enligt föregående beskrivning.

SPEKTRALKLASSERNA ([W R] O B A F G K M [R N S]) kopplar till den angivna temperaturskalan vilken bildar länken till TNED-kartan.

Siffran 0 efter spektraltermen anger högsta grad av möjliga värden 0-9.

Gränserna med primära övergången och statiska detonationsgränsmassans gränslinje framgår tydligt. Därmed är så långt stjärnornas beskrivningen enligt TNED bekräftad.

Anledningen varför det övre stråket inte visar någon brytpunkt vid detonationsgränsen förklaras ENLIGT TNED av att det är ett tak som ständigt fylls på nerifrån normalkurvans primära agenter enligt föregående resonemang. Därmed överlappas brytpunkten och göms av ständigt nya förekomster så länge regionen tillåter det. Även de övriga stråken fylls naturligtvis på, men då de ligger utspridda kan brytpunkten i deras fall inte lika enkelt döljas.

DEN BRISTFÄLLIGA KONVENTIONELLA KLASSIFICERINGEN AV TYPEN O-STJÄRNOR

DEN BRISTFÄLLIGA KONVENTIONELLA KLASSIFICERINGEN AV TYPEN O-STJÄRNOR

Innan vi går vidare i den allmänna genomgången av den konventionella stjärnkartan till jämförelse med TNED-fysiken är det nödvändigt att ha följande reservation i minnet.

”Hittills har man inte lyckats göra någon tillfredsställande luminositetsklassifikation av O-stjärnorna”.

”Det är emellertid svårt att beräkna deras absoluta ljusstyrka med någon större noggrannhet, eftersom deras antal är litet och inte kan ge underlag för en tillfredsställande statistik”.

”Samtliga ligger dessutom för långt bort, för att man med hjälp av parallaxmetoder skall kunna mäta avståndet till dem”.

”Inga O-stjärnor finns bland de kända stjärnor som är synliga för blotta ögat”.

FOCUS MATERIEN 1975 s604sp2n

Ovanstående innebär att den konventionellt angivna UTSTRÄCKNINGEN ÄR OKLAR för O-stjärnorna i det konventionella stjärndiagrammet. Vi ska här betrakta den delen som ett relativt osäkerhetsområde. Vi ska nämligen längre fram se hur SKALFORMEN i hela stjärnkartan ges en högst dramatisk modifierad innebörd då vi tar med ljushastighetens ändring med stjärnornas växande massa upp mot detonationsgränsen (max 15 Solmassor). I konventionell kosmologi finns inte den aspekten med, inte alls över huvudtaget, eftersom man inte räknar med stjärnfysiken såsom grundad på STJÄRNSTÄDET.

Exempel — se även samma exempel i Strålningstryckets spektakulära inverkan på gränsmassorna

En normalstjärna på 10 Solmassor (m₁₀) har en ytvärmegrad på T=23 500 °K. Strålningstryckets starkt kalljoniserande värmegradsekvivalent vid stjärnytan är Tg=35,8 miljoner grader. Låt oss anta att stjärnan dämpas med en faktor 1000 på grund av reducerad divergens. Detta ger stjärnyttemperaturen T=23,5 °K och strålningstryckets temperaturekvivalent Tg= 35 800 °K. Därmed motsvarande SPEKTRALA detaljer. Stjärnljuset kan omöjligen gömma undan den rent spektrala effekten från Tg i detta läge.

Spektralkartan för den stjärnans ekvivalenta värmegrad som närmar sig gränsmassan m₁₀ kan på detta sätt vid en direkt spektral genomgång av allt ljus som stjärnan utsänder förstås uppvisa (våldsamt) högre frekvenser relativt sitt sanna tillstånd; Stjärnans allmänna Planck-kurva speglar en betydligt högre temperaturtopp.

Eftersom strålningstrycket vid stjärnytan DESSUTOM tvunget befinner sig (långt) utanför det högtäta stjärnstädet

— förhållandet mellan stjärnstädet och ytan är i Solens fall 173 730

— och därmed också långt utanför divergensreduktionens frekvensvrängande zon, föreligger alls ingen nämnvärd rödförskjutning i ljusemissionen.

KÄNNER MAN INTE DESSA GRUNDER förvillas man dra slutsatsen att stjärnan har betydligt större massa än sin normalekvivalent. I exemplets enkla fall skulle värdet T=35 800 °K motsvara en normal stjärnmassa på

[(35 800)/(6 150)]^12/7=20,5 Solmassor. Inte 10. Felet blir alltså våldsamt.

Vi ska (MÖJLIGEN) återkomma mer ingående till dessa aspekter längre fram. För tillfället fortsätter vi på ”den konventionella stjärnkartan”.

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

exempel med observationer av stjärnfält

En vidare djupdykning i konventionellt presenterade stjärndata visar att beskrivningen enligt TNED också fördjupas. Vi studerar detta.

Genom att överföra tillgängliga data från facklitteraturen på TNED-kartan ges en viss (VIDARE) överblick av hur stjärnfördelningen ser ut i de olika fallen. Källreferenserna (här i huvudsak från Bonniers Astronomi 1978) är delvis schematiska och vissa detaljer göms därför av mera övergripande skissartade linjer. Nedanstående bild visar en sammanställning med data hämtade i huvudsak från BONNIERS ASTRONOMI 1978.

observationer av stjärnfält

OBSERVATIONER AV STJÄRNFÄLT

Exempel på Stjärnornas fördelning i olika stjärnfält

1 spiralgalax, 1 klotformig stjärnhop, 5 öppna stjärnhopar (i Vintergatan)

spiralgalax M3 M67 Persei M41 M11 NGC752

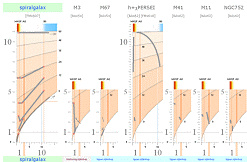Bilden oförminskad finns i STJÄRNORNAS FÖRDELNING I OLIKA STJÄRNFÄLT

I samtliga fall men på olika sätt framgår beroendet av brytpunkterna PRIMÄRA ÖVERGÅNGEN och STATISKA DETONATIONSGRÄNSMASSAN tydligt.

Flera detaljer bekräftar den allmänna dynamiska förklaringen till förekomsterna enligt TNED.

Vi studerar först den till synes udda detaljen i spiralgalaxkartans början på stjärnklassen betecknad IV (underjättarna).

VI KUNDE TRO att stjärnorna i denna lilla nedåtriktade stråkdel tillhör kategorin primära stjärnor ifrån K-cellens allra tidigaste faser, enbart att döma av den låga massan. Ser vi emellertid till det utmärkta (ledande) exemplet med den öppna stjärnhopen med den underliga beteckningen h + c PERSEI (c i symbol för c), har vi i princip samma lilla klutt där. Grovt sett samma lokation. På samma sätt sedan med de övriga exemplen. Vi kan se saken tydligare genom nedanstående heldragna linje tvärs över alla exemplen:

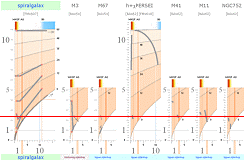Bilden oförminskad finns i STJÄRNORNAS FÖRDELNING I OLIKA STJÄRNFÄLT

Ovanstående kartbesättningar har framarbetats med jämförelse från konventionella färgindex och stjärndata

(BONNIERS ASTRONOMI 1978, FOCUS MATERIEN 1975) för att matcha en motsvarande kartbild enligt TNED

I de första fyra fallen vidrör linjen helt klart samma område på nersidan av gränsen 1 Solmassa. Ser vi, därmed, till exemplet med h + c PERSEI är svaret på frågan klar varifrån dess aktuellt markerade förekomst härrör, enligt föregående förda resonemang. Dvs., från övre böjda stråkets detonationsindivider som även besätter övre vänstra flanken: I en långt avlägsen framtid kan vi (således) förutsäga att den övre böjda grenen så småningom helt försvinner och ersätts av motsvarande vänstra förekomsternas delar med små stjärnmassor i mera vätefattiga områden. Ingenting hindrar att stjärnorna i bågstråket också successivt följer båglinjen i takt med att de brinner ut: den primära egenrotationen avtar med växande fortbildad massa, analogt stjärnor med allt mindre omfång och därmed att bågdelen, i princip, tunnas ut uppifrån och ner. Bågdelen bildades ursprungligen av primärstjärnor med hög massa, analogt relativt låga förekomster av tyngre grundämnen enligt TNED. Att den vänstra övre besättningen INTE är reguljära primärstjärnor avslöjas direkt av att fördelningen i sådana fall borde haft samma jämna representation ända ner till normalkurvan.

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

Klotformiga stjärnhopar (nr2 från vänster ovan med exemplet M3) har liten dynamik och konsumerar snabbt det friliggande primärvätet från K-cellens första faser. Klotformiga stjärnhopar har därför liten representation av den övre klassens omfångsrika stjärnor. Enligt källan [BAs54] är den exemplifierade fördelningen (också) typisk för klotformiga stjärnhopar. Vi kan direkt se att huvuddelen av dess individer bildar en kontinuerlig remsa med alla möjliga rotationsklasser ner till normalkurvan och att dessa stjärnor därmed skulle vara reguljära primärstjärnor som fortfarande befinner sig i den första Väte-Heliumfasen. De spridda klumparna med något högre massa antyder att dessa kan ha haft tyngre föregångare längre upp på normalkurvan, men de kan lika väl tillhöra original från den reguljära primära bildningen för hela hopen.

Öppna stjärnhopar (nr3 från vänster ovan, alla) som omges av väterika områden har de bästa förutsättningar att utveckla en stor flora av stjärnor med de mest skilda omfång. Föregående exempel med h + c PERSEI ger ett tydligt exempel. Mera vätefattiga öppna regioner efterlämnar mera spridda rester i takt med tiden, vilket visas av de återstående exemplen (M67, M41, M11 och NGC752).

O-KLASSENS STJÄRNOR

O-klassens stjärnor

DÄRMED KAN VI SE UPPLÖSNINGEN (fetstilen min markering):

”Wolf‑Rayet‑stjärnorna är enligt många astronomer nästan allesammans trånga dubbelstjärnsystern bestående av en tung, luminös O‑stjärna på huvudserien och en mindre och lättare men än mera lysande följeslagare.”

BONNIERS ASTRONOMI 1978 s103sp1n

”Det är svårt att bestämma deras temperaturer exakt, eftersom energifördelningen i deras kontinuerliga spektra inte tycks motsvara någon bestämd temperatur.”

BONNIERS ASTRONOMI 1978 s43sp1mn

KÄLLAN REDOVISAR INGALUNDA KLART OCH TYDLIGT ATT OBJEKTEN ÄR SPEKTROSKOPISKA — data från EN variabel ljuspunkt. Den delen framkommer först efter jämförande citatdelar ur flera källverk.

Se även föregående citat beträffande just O-stjärnorna i FOCUS MATERIEN 1975.

”Hittills har man inte lyckats göra någon tillfredsställande luminositetsklassifikation av O-stjärnorna”.

”Det är emellertid svårt att beräkna deras absoluta ljusstyrka med någon större noggrannhet, eftersom deras antal är litet och inte kan ge underlag för en tillfredsställande statistik”.

”Samtliga ligger dessutom för långt bort, för att man med hjälp av parallaxmetoder skall kunna mäta avståndet till dem”.

”Inga O-stjärnor finns bland de kända stjärnor som är synliga för blotta ögat”.

FOCUS MATERIEN 1975 s604sp2n

Av allt att döma är de konventionellt benämnda O- och WR-stjärnorna objekt på nersidan mot m₁₅-gränsen, enligt föregående enkla exempel. Strålningstryckets värmegradsekvivalent bildar den spektrala emissionsagenten med växande reduktion av ljushastigheten, och därmed den motsvarande höga spektrala temperaturekvivalenten.

Instabiliteten i området borgar för motsvarande möjliga flora av pulserande egenskaper.

DET AVGJORT STARKASTE ARGUMENTET för att stjärnmassor större än 15 Solmassor INTE EXISTERAR är dock den övergripande matematiken för LJUSETS GRAVITELLA BEROENDE:

;

HR-diagrammets totalkurva i TNED

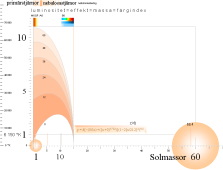Bilden oförminskad finns i TNEDs HR-bas

OMSÄTTS normalkurvans massa(x)-temperatur(T)-funktion (inkluderat rotationsklasserna)

T = T_S(x+x₀)^7/12 – x/n

på LJUSHASTIGHETENS ÄNDRING MED VÄXANDE STJÄRNMASSA enligt EXPANSIVA TILLSTÅNDETS G-FYSIK

c/c₀ = [1–2w²/c₀² ]^1/2 med w² = Gm₂/r = m₂^2/3G(4pr/3)^1/3

med en maximal utsträckning på 15 Solmassor i x-led, som för c=0 medför c₀=15Ö2=21,213203 skalenheter

— totalt grafiska funktionen

y = [(x+x₀)^7/12 – x/n][1–2(x/21,2)² ]^1/2

— får man för hela stjärnkartan den betydligt reducerade kurvskaran enligt vidstående figur.

Eller sagt i summans andra ord:

SPEKTRALEKVATIONEN FÖR STJÄRNOR I OMRÅDET 10-15 Solmassor kan ingen annan PRAKTISK LÖSNING ha än våldsamma förskjutningar mot alla tänkbara spektrums delar med alla tänkbara perioder, alla tänkbara temperaturekvivalenter och alla tänkbara massekvivalenter. Dessa stjärnor tillhör emellertid INTE huvuddelen av universums stjärnbesättning vilken (som tidigare belysts) med största sannolikhet ligger i området 0,3-2,4 Solmassor och som därmed uppvisar mera normala beteenden relativt en försumbar inverkan från ljushastighetens reduktion. I Solens fall är reduktionen som mest ca 5%.

Därmed (och så långt) är den observerade svårfångade klassifikationen av speciellt O-stjärnorna i princip inringad — enligt TNED.

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

Grundämnesfördelningen i stjärnorna

Vi slutar här (så länge, och tills vidare):

DEN ALLMÄNNA ORDNINGEN ENLIGT DIAKVADRATEN (grundämnesfördelningen i himlakropparna) är att de allt tyngre=hetare stjärnorna från sin primärbildning uppvisar en allt mindre andel tyngre grundämnen.

Eftersom de konventionella spektralklasserna (i stort) följer temperaturskalan för normalstjärnorna innebär det att DEN PRIMÄRA halten tyngre grundämnen ENLIGT TNED ska tillväxa uppifrån de hetaste ner mot de svalare enligt spektralbeteckningarna O B A F G K M. Denna ordning med de tyngre grundämnenas förekomst är också den som beskrivs i gängse fackverk [här utan vidare referenser].

…

Därmed är den allmänt presenterade beskrivningen av Universums Historia enligt TNED fullständigt genomförd.

END.

StjärnfysikenDELII | HIMLAKROPPARNAS SYNBARHET OCH ALLMÄNNA FÖRDELNING I VINTERGATAN |

ALLMÄN ÖVERSIKT — observationsgränserna

VINTERGATANS LOKAL

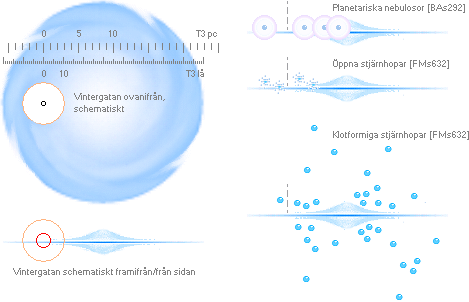
Teckenförklaringar: pc parsec, lå ljusår

basfakta

MEDELAVSTÅNDET MELLAN STJÄRNORNA, ungefärligt inom Solens närmaste grannskap, 2-3 pc [FMs597sp1ö].

Svart cirkel (överst vänster), radien motsvarar ungefär 100pc = max avståndsbestämning genom trigonometrisk parallax [BAs25sp1n].

Röd cirkel, radien motsvarar ca 1000 pc.

Orange cirkel, radien motsvarar ca 3000 pc — ungefär avståndet till de mest avlägset synliga (ej skymda) öppna stjärnhoparna [BAs46sp2ö].

Cirklarnas medelpunkt, strax ovanför skivplanet, markerar Solens läge.

Solens avstånd från Vintegatans centrum, ca 10 Kpc eller grovt 30 000 ljusår [FMs632].

Vintergatans skiva mäter ca 100 000 ljusår tvärs över eller grovt 30 Kpc.

Medelavståndet mellan två medelstora galaxer, ca 3 Mpc [BAs324sp2n]. I skalan ovan ligger närmaste galaxen från ca 6 meter utanför bildskärmen.

1 pc = ——————————————————————————————————— — — | ^a

Bortre sidan (a) mäter avståndet Jorden-Solen = 1 AU = 1,49594 T11 M, vinkeln ska vara 1/3600 grad eller 1 bågsekund. Den längre bassträckan blir då en parsec, 1 pc = 3,0856 T16 meter [BAs9].

1 pc = 3,2614819 lå

HUVUDKÄLLA till ovanstående sammanställda uppgifter: FOCUS MATERIEN 1975 s632

Senare källor kan ha något snävare preferenser (avståndet Solen-Galaxcentrum ca 25 000 lå eller ca 7 000 pc mot ca 30 000 lå och 9 000 pc ovan)

parsec

PARSEC

1 parsec = 1 pc

= 3,08572 T16 M

Är synvinkeln A =1’’ (1 bågsekund) och ändlängden r=1AU=1,496 T11 M (avståndet Jorden-Solen) är distansen d=1pc (en parsec):

1 pc = d = r/(tanA=r/d) = r · cotA = 1,496 T11 M · cot(1’’ = 1/3600)

= 3,08572 T16 M

ljusår

LJUSÅR

1 ljusår = 1 lå

= 9,46073 T15 M

Ett ljusår är antalet sekunder per år (3600·24·365,25) gånger ljushastigheten i vakuum (c₀ = 299 792 458 M/S)

rymdvägen ljuset hinner på ett år

1 pc = 3,2616087 lå

(1pc=3,08572 T16 M)/(1 lå=9,46073 T15 M) = 3,2616087

StjärnfysikenDELII | STJÄRNORNAS ALLMÄNNA HISTOGRAM | 2008IX25 | I sammanställning från 2005II25

STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

STJÄRNORNAS ALLMÄNNA HISTOGRAM

FÖR ALLMÄN ORIENTERING I STJÄRNORNAS SYNBARHET OCH FÖRDELNING, SE VINTERGATANS VISUELLA SYSTEM

Många svåra och utmanande problem har genomkorsat den här analysen i ljuset av TNED. Ibland har delproblemen synts så svåra att man varit benägen att ge upp och tänka, nej, det här klarar jag inte, lösningen på det och det problemet är omöjlig. Men vartefter fördjupningarna inspirerat till nya synpunkter, har frågetecknen rätats ut och ersatts av betraktelsebara — väl relaterbara — matematiska uttryck;

— Att döma av resultaten, håller sig uttrycken väl framme med rapporterade observationer.

Följande allmänna och ytterst enkla utvecklingslinje kan anställas ENLIGT TNED för alla typer av stjärnor — till allmän prövning mot rapporterade observationer.

från 2,4 Solmassor

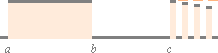
Se även utförligt i Beskrivning längre ner.

b: m_STAR = (t_SUN t_b^–1)^1/2

= 2,4 Solmassor, yttemperatur 10 250 °K, [T_r = T_S=6150(m_STAR/m_S)^7/12]

c: m_STAR = (t_SUN t_c^–1)^1/2

= 3,4 Solmassor, yttemperatur 12 560 °K, [T_r = T_S=6150(m_STAR/m_S)^7/12]

Förklaring:

För en primärstjärna (stjärna som genomgår/är på väg att avsluta sin första Väte-Helium-fas) som precis har nått sitt absoluta avslocknande i vår tid vid fas b (runt 21 T9 år enligt K-cellens värmefysik med tSUN = 120 T9 år med idealt 100% Väteförbränning) betyder dess aktiva energicykelfas a-b halva b-värdet,

analogt runt 10,5 T9 år. Då blir mSTAR som ovan 3,4 Solmassor.

Enligt TNED ska följaktligen den allmänna förekomsten, spridningen och fördelningen av primära stjärnor inte visa sådana med större massa än just max 2,4 Solmassor. Alla tyngre stjärnor ska enligt TNED ha brunnit ut och i förekommande fall ingått i en andra eller n:te energicykelfas. Befintliga stjärnor med större massa än 2,4 Solmassor bör därmed och med histogrammets generaliserande gränser uppvisa ett tomt band mellan 2,4 till 3,4 Solmassor och vilket område alltså bör vara helt tomt på OBS endast primärstjärnor. I TNED benämns detta fönster 2,4-3,4 Solmassor för PRIMÄRA ÖVERGÅNGEN.

BEKRÄFTELSE:

ENDA SÄKRA METODEN för att få fram en stjärnas massa bygger på väl iakttagbara dubbelstjärnesystem. Känner man banellipserna och omloppstiderna kan massorna beräknas enligt Keplers tredje lag,

a=F/m= Gm₂/r² =v²/r=(2pr/t)²/r= 4p²r/t² ; Gm₂/4p² = r³/t² ; m₂=(4p²/G)(r³/t²)

BONNIERS ASTRONOMI 1978 ger i tabell [BAs31] exempel på 26 uppmätta individer som visar att

· huvuddelen av de optiskt observerbara stjärnornas mätbara massor ligger mellan
0,34_minsta-2,4_största Solmassor med väl separerade dubbelkomponenter

Källans kompletterande figurbild av något hundratal uppmätta individer [BAs50] visar en största massa runt 5 Solmassor. MEN då är individerna kring 5 Solmassor uppmätta som förmörkelsevariabler — utan specifikationer om huruvida de också uppvisar klart urskiljbara stjärnkomponenter. Se vidare i Stjärnor > 15 Solmassor.

För att finna större massor måste man leta längre ut (icke urskiljbara komponenter) — och därmed i beroende av de mera indirekta metoder som benämns fotometriska metoder (förmörkelsevariabler) och spektroskopiska metoder (ljusväxlingar genom frekvensändringar dopplerförskjutningar).

beskrivning

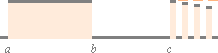
Uppstart (a), brinntid (a–b), slockning (b), avstanning (b–c), nova (c) med eventuell nystart i en andra energifas (med flera).

Alla kompaktstjärnor (stjärnor som slutat producera strålningstryck och därför saknar den normalt fusionsproducerande stjärnans atmosfär) återfinns från c.

Alla stjärnor som finns inom samma ekvipotentialyta i K-cellens expansion (alla hopar och galaxer) är liktidiga med liten spridning.

Anomalierna är växande (varierande ljushastighet) med växande avstånd från K-cellens expansionscentrum.

I den allmänna klassificeringen av stjärnor betraktar vi därför främst förekomsterna i Vintergatan (och närbelägna galaxer).

Alla stjärnors energiproduktion grundas på den tryckande, pressande och stötande periodiska, resonanta verksamheten mot stjärnans centrala STÄD (R-kroppen).

Stjärnor med större massa får längre perioder och uppvisar större variabilitet än stjärnor med mindre massa.

Stjärnor skapas inte fortlöpande.

Stjärnor nybildas ur redan befintliga primärcentra som bildades från K-cellens detonation.

STJÄRNSTÄDET (bibehållen maximal Coulombisk täthet) som grundval för stjärnans termogravitella dynamiska fysik, TNED, garanterar att enda möjliga sättet att bilda SOL (dvs. stjärna) från ”löst existerande partiklar” (typ fria gas, stoft och partikelmoln) genom gravitell sammandragning är reserverat för K-cellen:

stjärnbildning genom kontraktion är reserverat för K-cellens allmänna övergripande pulsfysik.

Brinntidens stjärnor (a–b) representeras av stjärnmassor mellan 1/165 till max 60 stadigvarande klart lysande Solmassor. Stjärnans omfång beror på dess primära egenrotation, inte att beblanda med stjärnans egenproducerade rotation under dess brinntid. Den konventionella benämningen ”jättestjärna” och ”röd jätte” som ett tänkt senarestadium i en stjärnas utveckling, gäller inte här. Jättestjärnor och vanliga stjärnor är ENLIGT TNED olika individer, inte samma individ i olika utvecklingsskeden. En stjärna bibehåller enligt TNED sin typform och kan aldrig utvecklas till en jättestjärna. Vilket som är vad avgörs vid stjärnornas födelse, den primära J-avyttringen i K-cellens allmänna expansion — samt vidare genom stjärnans eventuella fortbildning beroende på omgivande vätenäring.

Slockningen (b) innefattar stjärnklotets successiva reduktion av den jonisation och därmed den polarisation mellan inre och yttre som stjärnan producerat under sin brinntid. Därmed försvinner, dämpas eller uttunnas opacitetsregionen närmast stjärnans g-yta och den framstår som allt mindre i takt med sin allt svagare lyskraft.

Strålningstryckets upphörande innebär att stjärnan förlorar sin termonukleärt alstrade lyskraft. Rekylkraften finns dock fortfarande kvar (men avtar i takt med stjärnans ökande rotation då den sammandras som följd av strålningstryckets reduktion).

Därmed kan stjärnan fortfarande producera ljus, men av en karaktär som mera sammanhänger med kärnrekylerna. Då dessa, i princip, kan generera svängningsformer av alla upptänkliga former kan stjärnan, likväl, fortsätta emittera ljus av alla möjliga våglängder.

Under förutsättning att slockningen sker under perioder av miljoner år finns ingen direkt möjlighet enbart via lyskraften att avgöra huruvida en viss avlägsen stjärna med låg lyskraft också ÄR en stjärna med liten massa, eller om den just är en större stjärnmassa som är inne i sitt avslocknande. Det enda som kan avslöja typen är dess ämnesspektrum — eller om stjärnan ingår i ett dubbeslsystem där man känner bandimensionerna. Men även dessa delar kan vara svåra att avgöra i och med att många stjärnor dels omges av utbredda gasmoln som hindrar eller vränger en direkt inspektion i det inre, och dels inte alltid är enkla att uppmäta i bandimensioner.

En stjärna som genomgått sin primära Väte-Heliumfas bör i stort sett endast ha Helium-4 i sin kropp, tillsammans med en mindre mängd tyngre nuklider. Närvaron av yttre vätebanker vränger starkt den bilden. Emellertid bibehåller alla stjärnor också en viss Väte-1-andel i ytan som följd av ytskiktets elektronöverskott som (främst) binder och rekombinerar det lättare vätet framför tyngre nuklider så länge stjärnan producerar något strålningstryck. Uppgifter på stjärnornas ämnessammansättning kommer emellertid just från spektrala observationer av stjärnornas yta, så, inget bestämt kan sägas om den ovan allmänt givna förklaringen. Stjärnor i stadiet b bör dock finnas som observationsobjekt (i relativt rikliga mängder om avsvalningstiden är miljontals år).

Stjärnans absoluta avslocknande (c). Stjärnans egenproducerade impulsmoment (J=mvr) under brinntiden (a–b) kan bara reduceras efter slockningen genom inre friktion eller genom att material tillförs stjärnan utifrån och J på den vägen reduceras. En bekväm referens för den idealt ensamma stjärnan som utlämnas endast åt sin egen inre friktion under avstanningen (b–c) är att sätta perioderna brinntid-avstanning lika långa. I det praktiska fallet kommer (alltså) novapunkten c att ligga på alla möjliga ställen mellan b och ideala c-punkten.

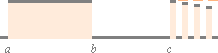
Avstanningen (b–c) inbegriper den tid stjärnan behöver för att reducera sitt under brinntiden egenproducerade impulsmoment. Denna tidrymd bör i fallen normala (fusionsproducerande) stjärnor i en första approximation vara lika lång som brinntidens (idealt ensam stjärna). Impulsmomentet kan endast reduceras genom inre friktion, och-eller tillsammans med yttre primärväte som dras in av stjärnans gravitation (nytankning) och därmed bromsar egenrotationen. I detta senare fall kan stjärnan väteberikas och därmed i princip bilda en andra (och en n:te) generationens stjärna med fast inre termonukleär produktion av fusionsenergi, men då först från punkten c (minimalt impulsmoment).

Är tillgången på omgivande primärväte stor och därmed reduktionen av impulsmomentet snabb, förkortas (eller fragmenteras) positionen för c i motsvarande grad. Vi bör ha denna detalj i bakhuvudet, speciellt i beskrivningen av pulsarerna som kräver maximala impulsmoment (analogt uppkomster strax efter b då strålningstrycket har försvunnit och stjärnan utvecklat maximal rotation genom sin sammandragning). Pulsarerna tillhör emellertid INTE DIREKT typen normalstjärnor (termonukleär exotermisk värmebildare) och intar därför speciella domäner i histogrammet. Vi kan emellertid inte undgå att beröra deras historik och ursprung, varför de likväl måste refereras på något sätt till normalstjärnornas histogram.

Novapunkten (c), kategorin normalstjärnor, inträder då stjärnans g-kraft åstadkommer sitt »kärnrekylerande övertryck»;

Vid denna händelsepunkt har stjärnan tappat det mesta av sitt tidigare egenproducerade impulsmoment (reducerat under lång tid genom friktion mot den insjunkande massdelen) och har därmed bildat grunden för maximal g-tryckande effekt;

Stjärnan har i princip återkommit till sitt primärtillstånd, men med en annan ämnesbas (Helium-4) och kan därför tända mycket snabbt och abrupt — (inom timmar) om den har fått tillräcklig tilläggsmassa (Hur stjärnan energitänder ENLIGT TNED beskrivs utförligt från stjärnornas allmänna tryckekvation);

Beroende på hur stjärnan blivit ämnessammansatt under avstanningsperioden, kan den uppvisa många ansikten vid c. Men alla sätten grundas på en mer eller mindre häftig rekylbildning. Se mera utförligt i statiska detonationsgränsmassan.

StjärnfysikenDELII | STJÄRNORNAS YTTEMPERATUR

STJÄRNORNAS YTTEMPERATUR

OBS GÄLLER ENDAST FÖR PRIMÄRSTJÄRNORNA

— stjärnor som genomgår sin första energicykelfas, se gränsmassan i nutid 2,4 Solmassor

Från Stefan-Boltzmanns strålningslag P = a · A · k · T⁴ i förening med volymenergin (se även MLR) som visar

EE_s^–1= PP_s^–1= (m/m_s)³ med suffixet S för Solen får vi direkt STJÄRNANS YTTEMPERATUR (OBS samma absorptionskoefficient a med samma k) enligt

PP_s^–1= (m/m_s)³=(r/r_s)²(T/T_s)⁴ som ger

T_r = T_s · (m/m_s)^3/4(r_s/r)^1/2

T_r = T_s · (m/m_s)^3/4(r_s/r)^1/2 ................ stjärnans yttemperatur med Solens T_s=6156,575 °K som preferens

i °K. Eftersom r=(m · konstant)^1/3 [Se i ALLMÄNNA STJÄRNKONSTANTEN] ges (r_s/r)=(m_s/m)^1/3 och därmed

(m/m_s)^3/4(r_s/r)^1/2 = (m/m_s)^3/4(m/m_s)^–1/6 = (m/m_s)^7/12 ;

T_r = T_s · (m/m_s)^7/12 .......................... stjärnans yttemperatur med Solens T_s=6157 °K som preferens

Högsta temperaturen för tyngsta stjärnmassan (60 Solmassor, radie ca 2,7 T9 M, Väte-1-bas) blir då

T_max=(6156,6)(60)^7/12 = 67 080 °K.

Lägsta temperaturen för lättaste stjärnan (1/165 av Solmassan, radien ca 1,2 T8 M, Väte-1-bas) blir ca 313 °K (40 °C).

OBSERVERA att dessa värden gäller för endast primärstjärnor, dvs., stjärnor som lyser NORMALT

— enligt MLR primärt oroterade stjärnor med Väte-1-bas under maximal effektförbrukning.

StjärnfysikenDELII | GRÄNSMASSORNA GENOM EXPANSIVA-KONTRAKTIVA OCH STATISKA TILLSTÅNDENS MATEMATISKA G-FYSIK ENLIGT TNED

GRÄNSMASSORNA GENOM EXPANSIVA-KONTRAKTIVA OCH STATISKA TILLSTÅNDENS MATEMATISKA G-FYSIK ENLIGT TNED

I K-cellens övergripande expansionsfysik föreligger ALDRIG tillfället då centralkroppen (den allra innersta kärnan) betingas av nolldivergens c=0. K-cellens centralkropp (c₀-kroppen) bevarar ALLTID naturkonstanten c₀ obetingat och oberoende i centrum: Kärnan lyser alltid. Expansiva-kontraktiva gränsmassan (m_0c) i K-cellen som uppvisar nolldivergens vid randen av sin sfäryta, maximal neutronbaserad täthet (r_max), betingas därför av K-cellens övergripande expansionsmatematik r = 3/(2pGT²) — som baseras på ideal ekvivalens mellan g-energi (gravitell energi) och k-energi (kinetisk energi) — och som beskriver K-cellens varierande medeltäthet från r_max med växande tid. Nolldivergenszonens hastighet då K-cellen expanderar, divergenständzonhastigheten, blir härigenom KONSTANT och lika med c₀ — från första till sista stund. Därmed kan den via expansionsfysiken minsta inneslutna centralmassa m_0c beräknas ur tiden T=r_0c/c₀ enligt (efter utvecklingar)

m_0c = (c₀/ÖG)³(6/pr_max)^1/2

=1,60227 T32 KG

@ 80,55 Solmassor.

AV PRINCIP bildar denna inre K-cellmassa gränsmassan för den individuellt största möjligt förekommande himlakroppen; Dess nolldivergensyta garanterar bildning av separata kroppar då J80-massan divergenständer för sin del.

Nu gäller emellertid INTE samma expansiva betingelser för delkropparna (J-kropparna) i K-cellen. Detta är klart därför, som nyligen påpekades, att endast K-cellens totalkropp KAN ha toppdivergens i sitt centrum. Alla delkroppar betingas därför av ljusets gravitella beroende på formen

c_J=(c_K/c₀) · c₀(P=[f (w)])=c_K(P) där c_K anger den omgivande rymdens övergripande divergens, c_J ansluter till J-kroppens explicita expansionsfysik, och w anger g-potentialens rotvärde (w²=Gm₂/r). IDEALT förutsätter vi för vår del en totalrymd där toppdivergensen c=c₀ råder överallt så att c_K=c₀ och så att vi får det enklare, ideala, c_J=c=c₀(P).

BETINGELSEN för J-kroppens egen explicita divergensberoende g-fysik i fallet då J-kroppen befinner sig UTANFÖR K-cellens divergenszon, c_K=0, blir därför strikt

c_J=c_K(P)=0(P)=0. Därmed hänger den vidare matematiken på (P)=f (w).

I det expansiva fallet (c=0) gäller (P)=Ö 1–2(w/c₀)², som ger 1=2(w/c₀)² med 1/Ö2=w/c₀.

I det statiska fallet (c=0) gäller (P)=(1/2)[1–Ö 1–(2w/c₀)²], som ger 2=4(w/c₀)² med samma 1/Ö2=w/c₀.

GRÄNSMASSAN som motsvarar fallet c=0 blir i bägge fallen

c₀²/2=w²=Gm₂/r=Gm₂^2/3(4pr/3)^1/3 som ger

Gränsmassan med nolldivergens vid stjärnytan

m₂ = [(4pr/3)^–1/3c₀²/2G]^3/2

= 2,00284 T31 KG eller 10,07 Solmassor med r_max=1,82 T17 KG/M³.

Sammanfattat

m₂ = r^–1/2(8,54444 T39) Ö(M³/KG)

@ r^–1/2(769/90) T39 Ö(M³/KG).

Några basexempel med r i KG/M³ ges i BasExempel.

DEN PRIMÄRA HIMLAKROPPSBILDNINGEN i K-cellens expansion betingas sålunda av himlakroppar med massor från max J80-massan och neråt till enskilda atomer.

MINSTA STJÄRNMASSAN (separat analys) är

m_0SLIM = m_A^–2Z³ · e_{1,602 t19}³p^–7/2(288)(k_{8,98743 T9}/G_{6,67 t11})^3/2 = 1,204 T28 KG

eller ca 6 Jupitermassor.

AKTIVA STJÄRNOR begränsas av nolldivergensmassan

m_10STAR = 10 Solmassor som ovan, men den gränsen blir flytande genom stjärnans varierande sammansättning.

Helium-4-bas ger 5 Solmassor. För Väte-1-bas (r=8,13444 T16 KG/M³) blir motsvarande gränsmassa 15,06 Solmassor. Denna blir en absolut gränsmassa därmed att allt tätare stjärnmassor neutronfragmenterar från nolldivergensytan (g₌₀) enligt kärnreaktionslagen

K+(m®g₌₀) = K1+K2

I detta läge bryts den idealt sfäriska stjärnytans förekomster av atomkärnor ner på neutronnivå (se Kärnfragmenteringen) och (delvis) vidare inåt mot centrum; Stjärnmassan omvandlar på det sättet föregående bildat Helium-4 och andra tyngre nuklider tillbaka till Väte-1-bas — som därigenom kan bilda en ny fusionsstock. Stjärnorna kan på så sätt underhålla en unik motsvarande organisk ämnesomsättning. Gränsmassorna m₁₀-m₁₅ framgår f.ö. (särskild analys) i de konventionella HR-diagrammen med utomordentlig — omisskännelig — tydlighet.

StjärnfysikenDELII | STATISKA DETONATIONSGRÄNSMASSAN |

STATISKA DETONATIONSGRÄNSMASSAN

SAMBAND enligt TNED:

———————————————————————————————————

T_STAR = T_SUN(m_STAR/m_SUN)^7/12

m_STAR brytpunkt primära övergången 2,4 Solmassor

m_STAR brytpunkt statiska detonationsgränsmassan 10,6 Solmassor

Ovanstående ger

m_STAR = m_SUN(T_STAR/T_SUN)^12/7

RESULTAT med T_SUN=6 150 °K: konv. HR-diagram:

—————————————————————— ——————————

T_STAR(primära övergången) = 10 977,513 °K 11 000 °K

T_STAR(detonationsgränsen) = 24 376,435 °K 25 000 °K

GRUNDSAMBAND

Expansiva-kontraktiva tillståndets g-fysik (K-CELLENS EXPANSION c=0):

(1) r = (3c₀²/2Gpr)^1/2 = (c₀/ÖG)(3/2pr)^1/2 ; r³ = (c₀/ÖG)³(3/2pr)^3/2 ; m = r³(4pr/3) = (c₀/ÖG)³(6/pr)^1/2

Expansiva-Kontraktiva-Statiska tillståndets g-fysik (J-KROPPARNAS EXPANSION c=0):

(2) r = (3c₀²/8Gpr)^1/2 = (c₀/ÖG)(3/8pr)^1/2 ; r³ = (c₀/ÖG)³(3/8pr)^3/2 ; m = r³(4pr/3) = (c₀/ÖG)³(6/64pr)^1/2

Diagrammet nedan från FOCUS MATERIEN 1975 s607, se vidare beskrivning i HR-diagrammets grunder enligt TNED

Beskrivning

STATISKA DETONATIONSGRÄNSMASSAN — idealt vid 10,6 Solmassor

DETONATIONSGRÄNSMASSAN ENLIGT TNED motsvarar en materialyta där kroppens ytgravitation påtvingar kroppsytan ljushastigheten noll (se ljusets gravitella beroende) — här också benämnt nolldivergens (r=r_c0). Se även begreppet divergens i TNED.

Observera att nolldivergens för en materiell kropp INTE har någon som helst samhörighet med den moderna akademins begrepp typ ”svarta hål”; SVARTA HÅL i modern akademi beskrivs liktydigt med oändlig täthet, analogt noll utsträckning; Några sådana tillstånd existerar inte i fysiken enligt TNED: max täthet baserat på neutronbas är enligt TNED 1,82 T17 KG/M³; I det läget vidrör atomkärnorna varandra och kommer inte längre: atomkärnan ENLIGT TNED står redan på noll enligt den enkla elektriska kraftlagen (se även i atomkärnans inkompressibilitet). Situationen medför att varje ytterligare kraft som strävar att närma (pressa ihop) atomkärnorna, resulterar i en återkastning (rekyl, eller detonation, se även i detonationsfysiken).

I situationen r=r_c0 inträder ENLIGT TNED kärnfragmentering enligt kärnreaktionslagens enkla form

(3) K+(m®g₌₀) = K1+K2

Om vi exemplifierar med en Helium-4-kropp (m_c0STATIC=5 Solmassor) producerar den neutroner från r_c0 och vidare inåt centrum med ytterligare ökande massa. Men den fragmenteringen påbörjas i princip redan under tiden kroppen sammandras (efter stjärnans slockning och under avsaktningsperioden) och det blir därför inte helt enkelt att postulera existensen av något sådant som en reguljär Helium-4-detonationsmassa vid exakta m_c0STATICHe. Vi får snarare tillämpa ett övergångsresonemang som tvunget bara kan sluta på NEUTRONEN (med vidare sönderfall till Väteatomen) som detonationsgränsmassans ideala och ekvivalenta element enligt (1).

För stjärnornas del innebär det att vi kan förvänta oss växande instabiliteter från m_c0STATICHe= 5 Solmassor fram till m_c0STATICH = 10,6 Solmassor, där den senare därmed markerar nominella statiska detonationsgränsmassan.

STATISKA DETONATIONSGRÄNSMASSANS BRYTPUNKT (m10) kan därmed specificeras absolut med början från området 10,07 (neutronbas) till 10,6 Solmassor (Väte-1-bas), avrundat max 11 Solmassor med

T_max = 6150×10,6^7/12

= 24 376,435 °K,

med en absolut yttersta gräns genom Coulombtätheten 8,13444 T16 vid

15 Solmassor

med

T_max = 6150×15^7/12

= 29 848,901 °K.

Jämför konventionella HR-data (färgskalan nederst ovan). Vi kan knappast få ett mera exakt facit.

rekyleringen

Statiska detonationsgränsmassan markerar en fundamental BRYTPUNKT i hela stjärnkartan.

Alla stjärnor som slocknat — och som idealt genom inre friktion och under en lång avsaktningsperiod har reducerat hela impulsmomentet (J=mvr) som byggts upp under brinntiden och därmed i princip nått tillbaka till primärstadiet vid divergenständning — innehar från gränsmassan 10 Solmassor vid atomkärnornas direkta kontaktering en egen nolldivergens (c=0) i den maximalt täta sfärytan. Rörelseenergin från kontraktionen med vilken atomkärnorna idealt klonkar ihop i denna situation, garanterar tillsammans med atomkärnans formbevarande kraft att hela kroppsmassan rekylerar absolut och idealt exakt på kontraktionsrörelseenergins belopp. Därmed bryts kroppsmassan upp i en central (fusionerande och därmed inre ytterligare kontrakterande) del och en yttre (för evigt) expanderande del på liknande men inte samma sätt som sker generellt under K-cellens expansion via divergenständningarna. Denna statiska brytpunkt vid ca 10 Solmassor innebär med andra ord att varje kropp som når dit — efter en föregående kontraktionsfas — sönderbryts och efterlämnar en mindre centralmassa som i sin tur kan bilda en andra och n:te generationens stjärna beroende på tillgången på omgivande primärväte.

forts. STJÄRNORNAS ALLMÄNNA SPRIDNING, FÖREKOMST OCH FORTBILDNING

brytpunkten vid m10

Brytpunkten vid m_c0STATICn= 10,07 Solmassor (eller via Väte-1-bas den något högre m_c0STATICH=10,61)

innebär i princip att

· stjärnan rekylerar tvunget och absolut vid max uppnådd täthet

· stjärnan kräver flera energicykler för att nå detonationsgränsen (för primära stjärnor med mindre än 10 Solmassor) eftersom Helium-4 bildas under varje cykel och som måste neutronfragmentera innan gränsmassan kan uppnås

· den rekylerande stjärnan kan bara fortbildas från brytpunkten som en lättare stjärna, alltså längre till vänster i masstocken

· det inte finns några slocknade (helt em-döda) och helt avstannade stjärnor med större massa än max 15 Solmassor: inte alls överhuvudtaget = noll förekomst

· alla stjärnor slutar som massobjekt mellan 1/165 och 15 Solmassor

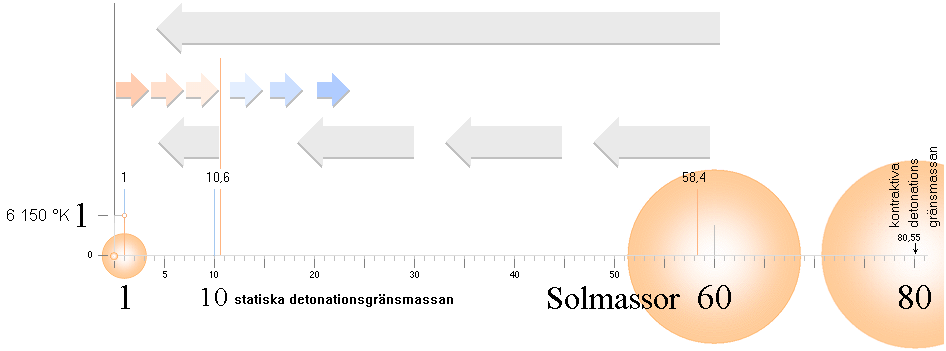Bilden oförminskad finns i Stjärnmassorna enligt TNED

Stjärnmassor <10 Solmassor kan genomgå flera energicykler med successivt växande massa mot brytpunkten och även passera denna på följande sätt OM deras stjärnfält betingas av väterika områden.

När en stjärna slocknar tappar den sitt strålningstryck och blir därmed receptiv för omgivande material som stjärnan nu kan ta emot. Ju väterikare området är, desto snabbare integreras stjärnans massa med den nya vätenäringen. Därmed kan stjärnan nytända i en andra och n:te energicykelfas utan att helt ha nått fram till total avstanning (motsvarande en fullständig reduktion av föregående cykels ackumulerade impulsmoment).

Se även nedanstående (mera precist) i Stjärnkartans allmänna beskrivning enligt TNED.

ALLA STJÄRNOR som haft någon minsta möjliga primär egenrotation föregående stjärnans energiproducerande fas bygger upp egenproducerade växande impulsmoment (egenproducerad rotation) under sin brinntid. En stjärna som slocknar och efterlämnar en centraldel för en andra och n:te energifas har därför de allra bästa förutsättningar för att uppvisa en stor flora av motsvarande »primära egenrotationer». En slutlig detonation (vid motsvarande brytpunkten 10 Solmassor eller högre beroende på omgivande vätebanker) bildar på så sätt en delare som ger n:te cyklernas lägre stjärnmassor i formen av alla möjliga rotationsklasser och därmed stjärnor med alla möjliga typer av omfång.

STJÄRNOR MED STORA OMFÅNG i sin tur kan inte på samma sätt tända före en total avsaktning efter slockning DÄRFÖR att just det stora omfånget, även i en väterik region, håller vätebankerna på betydligt större avstånd och därmed med längre intankningstider. Det är i varje fall den teoretiska grund som enligt TNED ligger närmast till hands för att kunna förklara de observerade stjärnornas fördelning och spridning. Den svulstiga stjärnans inre normalstjärna (vi erinrar de elementära begreppen) har därför större förutsättningar att göra sig av med sitt impulsmoment under avstanningsfasen, och den kan därför nå sitt maximalt täta tillstånd (vid 10 Solmassor statiskt) och därmed rekylera.

Följaktligen uppvisar stjärnförekomsterna entydigt och klart ett AVBROTT VID STATISKA DETONATIONSGRÄNSMASSAN för alla rotationsklasser utom normalkurvans, precis så som TNED vill ha det.

T vid 10 Solmassor är ca 24 000 °K, vilket tämligen precis motsvarar den markerade detonationsgränsen (m10) i HR-diagrammet enligt TNED.

KONVENTIONELL KOSMOLOGI uppvisar (veterligt) ingen motsvarande förklaring till de observerade brytpunkterna. Avgränsningarna omskrivs (veterligt) överhuvudtaget INTE. — TNED verkar alltså (här) helt överlägsen …

Intankningen kan alltså sägas ske snabbare än ideala självutlämnade avstanningen ju mera väterikt området är. Den så fortbildade stjärnan puttas därmed allt högre upp i masstocken, från vänster till höger i masskalan, genom att den för varje ny fas tänder före sitt maximalt avstannade läge och därmed fortbildas i perioder med stadigt växande massa. På den vägen kan alltså stjärnor i speciellt väterika områden likväl passera statiska detonationsgränsmassans brytpunkt.

Med allt växande övermassa relativt brytpunkten blir emellertid stjärnan mera känslig för den detonation som förr eller senare måste inträffa. När stjärnan når denna brytpunkt, vänder dess massreducerade centraldel tillbaka mot masstockens vänstra del och som nu kan bilda grunden för ytterligare energicykler genom fortsatt vätetankning.

StjärnfysikenDELII | DIMENSIONER I ÖVERSIKT FÖR ATOMKÄRNAN ENLIGT TNED |

basexempel med stjärnGränsmassor

Se även grundmatematiken i EXPANSIVA TILLSTÅNDETS G-FYSIK

Basexempel med stjärngränsmassor

Dimensioner med grundytor och volymer i översikt för neutron-protonkärnformen

Neutron(1,32)-protonaggregatet(1,37) N3m20

r₀=1,37 t15 M, m=1,67 t27 KG

A=2p(r₀/2)×2p(r₀/2)=pr₀×pr₀=(pr₀)²

V=p(r₀/2)²×2p(r₀/2)=2p²(r₀/2)³=p²r₀³/4, r=2,63 T17 KG/M³ (2,94 T17 med r_0n=1,32 t15).

A=4(r₀×2r₀)+2(2r₀)²=2(2r₀)²+2(2r₀)²=4(2r₀)²

V=r₀×(2r₀)²=4r₀³, r=1,62 T17 KG/M³ (1,82 T17 med r_0n=1,32 t15)

Med Helium-4 på r_0n-formen med U=4,0026031u (u=1,66033 t27 KG) ges r=7,22362 T17 KG/M².

Används istället protonradien r₀ blir Helium-4täthetens maximala värde 6,46123 T17 KG/M².

Basexempel med olika stjärngränsmassor med nolldivergens i ytan*:

massbas		r Fermi	V=4r^3 M^3	U	r KG/M^3	m2 KG	mS
0n^1	neutron	1,32	9,19987 t45	1,0086652u	1,82036 T 17	2,00264 T31	10,068603
1H^1	Väte-1	1,37	1,02854 t44	1,0078252u	1,62688 T 17	2,11838 T31	10,650502
1H^1	Väte-1	1,37	sfäriskt r = rC	1,0078252u	8,13444 T16	2,99584 T31	15,060880
2He^4	Helium-4	1,37	1,02854 t44	4,0026031u	6,46123 T17	1,06298 T31	5,3443073

Fermi: 1 Fermi = 1 fM = 1 femtoMeter = 1 t15 M ·

1u = 1,66033 t27 KG ·

U: För uppgifterna på U, se HOP ·

1,32: För neutronradien 1,32 Fermi, se

Plancks konstant h=mc₀r=6,62559 t34 JS som med c₀=2,99792458 T8 M/S och neutronmassan som ovan ger avrundat 1,32 Fermi = 1,32 t15 M ·

1,37: Se Neutronkvadraten, samt även HOP ·

m_S = 1,989 T30 KG Solmassan ·

* För divergensbegreppet se divergensbegreppet, ljusets gravitella beroende, om ej redan bekant.

m_2|c=0 = r^–1/2(8,54444 T39) Ö(M³/KG)

Jämför (fetstilen är min markering):

”Expansionshastigheten och linjernas styrka ger oss möjlighet att beräkna hur mycket material som kastas ut. Dessa beräkningar kan jämföras med mätningar av massan hos sådana supernovarester som Krabbnebulosan. I samtliga fall får man en siffra på mellan en och tio solmassor.”

BONNIERS ASTRONOMI 1978 s86sp2mö

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Stjärnfysiken II

ämnesrubriker

innehåll

Stjärnfysiken Del II

Illustrerad inledning

Skilda preferenser i modern akademi och TNED — luminositet · effekt · stjärnmassa · färgindex · magnitud · ljusstyrka · stjärnornas omfång

HR-diagrammets grunder enligt TNED

Funktionssätt

Thetasambandet

Primära Övergången

Normalkurvan · HR.diagrammets absoluta grundval

Härledning

Stjärnornas allmänna histogram

Stjärnmassor > 15 Solmassor finns inte

visuella dubbelstjärnesystem

EXEMPEL — strålningstryckets spektakulära inverkan enligt TNED

Hertzsprung-Russel-diagrammet (HR-diagrammet)

HR-diagrammets grunder enligt TNED

HR-diagrammet — från FOCUS MATERIEN 1975 s607

TNED förklarar brytpunkterna

expansionssambanden · expansiva/kontraktiva och statiska tillståndets g-fysik

masskalan · rotgränsmassan på 80 Solmassor

ROTATIONSKLASSERNA

luminositet · effekt · färgindex

stjärnkartan — HR-diagrammet

O-stjärnorna · den erkänt bristfälliga klassificeringen

Exempel med observationer av stjärnfält

O-klassens stjärnor

HR-diagrammets totalkurva enligt TNED

VINTERGATANS VISUELLA LOKAL

Allmän översikt · observationsgränserna

parsec

ljusår

Stjärnornas Allmänna Histogram

Från 2,4 Solmassor

Bekräftelse

HISTOGRAMMETS ALLMÄNNA BESKRIVNING

Brinntidens Stjärnor

Stjärnans absoluta avslocknande

Avstanningen

Novapunkten

Stjärnornas yttemperatur

GRÄNSMASSORNA

STATISKA DETONATIONSGRÄNSMASSAN

rekyleringen

brytpunkten vid 10 Solmassor

basexempel med stjärngränsmassor

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[BA]. BONNIERS ASTRONOMI 1978

— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.

[FM]. FOCUS MATERIEN 1975

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2021-12-09

*END.

Stavningskontrollerat 2008-10-23.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se