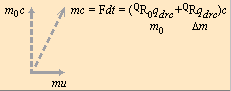PLANCKRINGENS DIMENSIONER 2007XI27 · a  production · Efter sammanställningar från 1993 |  Senast uppdaterade version: 2021-02-19 · Universums Historia

 

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

 

atomkärnans geometri

ATOMKÄRNAN

 

                                                         ATOMKÄRNANS HÄRLEDNING DEL I

 

                                                         ATOMKÄRNANS HÄRLEDNING DEL II

 

                                      Atomkärnans geometri vid axiell deformation

 

Atomkärnan beskrivs, förklaras och härleds utförligt genom PLANCKRINGEN (J=mvr) från fysikens sjunde princip. Härledningen beskriver i Del I atomkärnans formgeometri och i Del II atomkärnan som massans och gravitationens fundamentalform genom kraftens samband. Se även härledningen av atomens yttre egenskaper i PERIODISKA SYSTEMET direkt från Keplermomentet (Km=J).

 

h=mnc0rn

Se härledningen från Planckringen. h är Plancks berömda konstant (6,62559 t34 JS [HOP s7–155]) från år 1900. mn anger neutronmassan, rn ekvivalenta neutronradien och c0 ljushastighetens toppvärde. TNED beskriver Planckringen eller atomkärnan enligt Toroidnukleära Elektromekaniska Dynamiken.

 

atomkärnans dimensioner

ATOMKÄRNAN ENLIGT PLANCKRINGEN

Se härledning från Planckringen.

 

Med ett grundkriterium för antalet underringar N i topptoroiden

(från analysen via kubgrafen, se utförligt från Planckringen, resultatet ger N=3)

kan vi lösa atomkärnans specifika geometri för alla masstal större än A=1

— innan vi ännu vet den exakta geometrin för just A=1.

 

masstal större än 1

A>1:

               

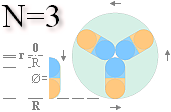
Notera noga: Atomkärnan uppvisar NORMALT ALDRIG sin understruktur i meningen motsvarande en makromodell med underspinn: atomkärnan innehåller inga beståndsdelar enligt TNED. Underfraktalerna är här endast EKVIVALENTER från utvecklingarna i PLANCKRINGEN som för atomkärnans del just kräver TVÅ motsatta spinn för att kunna definiera villkoret med summa nollmoment: J0+3J1=0. Se dock vidare i SPINNRIKTADE KOLLIDERANDE ATOMKÄRNOR. Se även från PLANCKRINGEN.

 

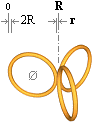
Relationen med ovanstående figurbeteckningar

R/r    = (7/2 – 2Ö3)–1    = 27,856405

 

R/R   = (–3/2 + Ö3)–1   = 4,3094010

 

Ø       = r

 

R/r      = 3 + 2Ö3 = 6,4641016

 

Kärnfysikens grundsatser

INDIVIDKRITERIET FÖR NUKLIDBILDNINGEN ENLIGT TNED

En jämn polygonring med N lika stora cirklar eller sfärer R på en centralring eller sfär r bildas genom sambandet r/R=T–1–1 med T=cos(180/N) i PREFIXxSIN.

Genom derivering av toroidmatematikens grundsamband från PLANCKRINGEN h=mnc0rn ges med ovanstående beteckningar rRØR resultatet R/R = 2(2+T–1–1) = 2(T–1+1) = konstant.

Med N=3 som toroidaggregatets absolut mest optimala spinnbaserade grundform — se prövningarna av resultaten i Planckringen genom jämförelse med kubgrafen — ges då i PREFIXxSIN värdet T=cos60=31/2/2 med

R/R = 2(T–1+1) = (–3/2 + 31/2)–1 = 4,309401 = konstant. Därmed är atomkärnans geometri från masstalet A=2 och uppåt redan fastställd då deriveringen avser alla masstal (A) större än 1.

Förhållandet R/R med givet N är alltså konstant och oberoende av atomkärnans storlek från A=2 och uppåt. Proportionerna för alla aggregat från A=2 och uppåt är därmed garanterade i försorg av de proportioner som gäller i grundformen med A=1 — och som vi explicit alltså inte behöver känna till för att få veta vad som gäller för alla övriga A. Vilket vill säga: Bildningen av A>1 kan bara göras med hjälp av diskreta, enskilda nuklidkvanta A=1 som garanterar att proportionerna i alla A>1 bevaras.

Deriveringen innefattar alltså ett rudimentärt individkriterium för hela kärnfysikens byggnad.

Genom toroidaggregatet N3m20 blir motsvarande (heltalsbaserade) förhållande i grundaggregatet A=1 lika med R/R = 42. Prövningen som leder fram till N3m20-aggregatet redovisas utförligt i KÄRNRADIERNA GENOM PLANCKRINGEN. Leden nedan visar utvecklingarna till föregående samband.

PREFIXxSIN|T=cos 180/N|N=3|T=31/2/2

r/R=1/2 – (T–1+1)–1=7/2 – 2Ö3=a

(T–1+1)–1=1/(2/Ö3)+1=–3+2Ö3; r/R = 3,5–2Ö3 = 7/2 – 2Ö3

a=0,0358983

r=Ra

R  =r(T–1–1)–1

                    r = R(T–1–1)

     =Ra(T–1–1)–1

             =R[1/2 – (T–1+1)–1](T–1–1)–1

             =R[(1/2)(T–1+1) – 1](T–1+1)–1(T–1–1)–1

             =R(1/2)[(T–1+1) – 2](T–1+1)–1(T–1–1)–1

             =R(1/2)[T–1 – 1](T–1+1)–1(T–1–1)–1

             =R(1/2)(T–1+1)–1

             =R(1/2)(T–1+1)–1=R(0,2320508)

R/R=(1/2)(T–1+1)–1 = (–3/2 + Ö3)

 

Ø = R – (4R+r)             ;

R = 2R(T–1+1)              ;

Ø          = 2R(T–1+1) – 4R–r

             = 2RT–1 + 2R – 4R – r

             = 2RT–1 – 2R – r

             = 2R(T–1–1) – r

             = 2R(T–1–1) – R(T–1–1)

             = R(T–1–1)

             = r

Tyngdpunktscirkeln (r) i mitten av Ø räknat från toroidcentrum:

r           = Ø/2 + 2R + r

             = r/2 + 2r(3+2Ö3) + r

             = r(1/2 + 6 + 4Ö3 + 1)

             = r(15/2 + 4Ö3)

             = R(7/2 – 2Ö3)(15/2 + 4Ö3)

             = R(105/4 + (28/2)Ö3 – (30/2)Ö3 – 24)

             = R(105/4 – Ö3 – 24)

             = R(9/4 – Ö3)

             = R · 0,5179491

 

 

 

 

masstalet 1

För A=1, se explicit från KÄRNRADIERNA GENOM PLANCKRINGEN.

A=1 | N3m20

 

Notera noga: Atomkärnan uppvisar NORMALT ALDRIG sin understruktur i meningen motsvarande en makromodell med underspinn: atomkärnan innehåller inga beståndsdelar enligt TNED. Underfraktalerna är här endast EKVIVALENTER från utvecklingarna i PLANCKRINGEN som för atomkärnans del just kräver TVÅ motsatta spinn för att kunna definiera villkoret med summa nollmoment: J0+3J1=0. Se dock vidare i SPINNRIKTADE KOLLIDERANDE ATOMKÄRNOR. Se även från PLANCKRINGEN.

 

R/R    = 42    R/2R = 21 = (m+1) = n

 

R/r     = 42(3+2Ö3) = 271,49226

 

R/r      = 3 + 2Ö3 = 6,4641016

 

Ø/r     = 113 + 76Ö3 = 244,63586

 

r = R(T–1–1) = (R/42)(T–1–1)

r/R = (1/42)(T–1–1) = [42(3+2Ö3)]–1 = 0,00368334

Ø = R – (4R+r) = 42R – 4R–r = 38R – r ;  Ø/r = 38R/r –1 = 38(3+2Ö3) –1 = 114+76Ö3 –1 = 113+76Ö3

Tyngdpunktscirkeln (r) i mitten av Ø räknat från toroidcentrum:

r           = Ø/2 + 2R + r

             = r(113+76Ö3)/2 + 2r(3+2Ö3) + r

             = r([113+76Ö3]/2 + 6+4Ö3 + 1)

             = r(113/2 + 38Ö3 + 7 + 4Ö3)

             = r(127/2 + 42Ö3)

             = R(42[3+2Ö3])–1(127/2 + 42Ö3)

             = R(127/84 + Ö3)[3+2Ö3]–1

             = R · 0,5018416

 

 

 

 

 

 

Planckringens Dimensioner | ÖverflyttatBlockFrånUniversumsHistoriaInledning | 2008VI1B

 

se även atomkärnans geometri

EKVIVALENTA GEOMETRIN VID DEFORMATION

Toroidvolymen fås (konv. se Guldins Regler) idealt ur rotationsytan p(r/2)2 gånger rotationsytans rotationstyngdcirkels omkrets 2p(r/2) med r som yttre toroidradien vilket ger V = p2r3/4

E=a/b

                                                                                   

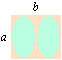
                                4r3                                                         4b3E                                                   4b3E2

                                E=1                                                        E<1                                                     E>1

rätblockets omskrivna volym (a/b=E)

EXEMPEL

volymändring med

konstant perimeter r=1, b=(S)–1                                 VB—E/VC = E(S)–3                                  VB|E/VC = E2(S)–3

Exempel E=1/Ö2:    +11%             –21%

Samband i PREFIXxSIN

                            n       ______________________

(å)    =          å [Ö(1 – [cos[(45°/n)(2p–1)] · e]2)]/n  ...................  polygonserien

                          p=1

E           =          minsta/största = a/b = (a/2)/(b/2) = Sd/Md = cosE°;  sinE° = e = √ 1 – E2 

(å)  ............   alltid mindre än 1 för ellipser

 Exemplet är starkt metriskt överdrivet. I praktiken är ekvivalenten för atomkärnans maximala ihoptryckning så liten (max 1/1000) att den inte ens skulle synas i denna skala.

 

 

 

 

djupbeskrivning

Atomkärnas geometri under axiell deformation

— omkretsen kan inte ändras

dmax=r0n/1000

 

 

 

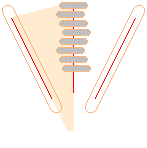
ATOMKÄRNANS FRAKTALA RINGSTRUKTUR (se från Planckringen) har ENLIGT TNED för en given ring ingen som helst möjlighet att ändra de inbördes sektoriella avstånden mellan närliggande underringar — radiellt i ringplanet. Dessa avstånd är fasta och återfaller på de sammanhållande krafterna i underfraktalerna som bevarar atomkärnans totala balansräkning enligt impulsekvationen J0K+3J1K=0. Men varje ring kan genom sin närmaste undernivå av tvärställda ringar »på sätt och vis» ÄNDÅ ändra sektorvinkeln, ehuru (ytterst) marginellt. Hela kärnans reglerande elektromekanik bygger på att ringarna sinsemellan kan justeras både uppåt och neråt. Kärnan använder det ENLIGT TNED (bland annat) för att justera deplacementet och anpassa kärnan till aktuellt kärnmagnetiskt moment. Men dessa ändringar är också (högeligen) verksamma när kärnan blir exciterad. Den utsänder då (normalt) ”vanlig induktiv” em-strålning i exakt proportion till svängningsenergin och fortsätter med det tills den upptagna energi är återlämnad utåt. Svängningarna (allmänna svängningsekvationen) har motsvarande dämpare av kapacitiv art som kopplar till de mycket starka elektriska och magnetiska sammanhållande-frånskjutande ringkrafterna. Eftersom marginalerna bara tillåter precis så små fluktuationer att det positiva deplacementet alltid garanteras (annars havererar hela kärnan), är det bara av den anledningen uppenbart att atomkärnans möjlighet till ordinär formelastisk deformation rent metriskt sett med kärnradien som preferens är YPPERLIGT LITEN.

I neutron-protonaggregatet är diametern för första underfraktalen 1/21 av kärnradien r0. Underringarna till denna nivå är i diameter teoretiskt minst r0/42, men kräver i praktiken minst r0/50, vilket blir ett absolut maximum. Tvärsnittet av dessa, i sin tur, bildar första symmetriska underfraktalen till förstnämnda ringen så att denna kan ses som en förstoring av den mindre sett i vy (vyordningen ges alltid via underfraktala par). Det är i denna region som deplacementet har sin högsta fraktala tvärställda representant (ringen med största diametern) och det är till den vi främst måste hänföra en härledning av den möjliga ringförskjutning som medger kärnans motsvarande (ekvivalenta) elasticitet. Men då befinner vi oss redan i grov uppskattning (42×50=2100) på nivå nära eller omkring ett absolut maximum 1/1000 av kärnradien. För att kärnan ska hålla ihop måste alla fluktuationer ske INOM denna bråkdel. Om vi därför till vidare prövning antar ett hyfsat preferensvärde på N i dmax=r0n/N lika med 1000, är vi i ljuset av TNED inte helt illa ute. Den motsvarande bilden av »atomkärnans hårdhet» blir med denna preferens en ytterst hård fjäder som resolut kastar ut varje yttre kraftorsak som strävar att trycka ihop atomkärnan enligt sambandet

F=kfxf x/(1–x)v med xf=dmax=r0n/N. Termen v = 2–c/c0 anger en divergenskoefficient som sammanhänger med härledningarna till detonationens matematiska fysik.

   Detonationsmatematiken är ytterst detaljerad, är relativt omfattande (sex delar i sex sektioner med bara detaljerad illustrerad matematisk fysik), och utelämnas därför (tills vidare) i den här presentationen.

 

SAMMANFATTNING

Med en given sfär med maximal neutrontäthet 1,82 T17 KG/M3 som påverkas av i princip oändlig sammantryckande gravitation, och med de resultat för atomkärnans fysik som nåtts genom härledningarna i Planckringen, blir varje tendens till en kompression av sfären i det läget en resulterande volymökning i netto: Sfären tvingas expandera på den komprimerande kraftens belopp. Det betyder, speciellt, i klartext: enligt Planckringen finns inga svarta hål i universum (konv. massor vars täthet växer obegränsat)

 

 

 

Atomkärnans formbevarande kraft

 

ATOMKÄRNANS INKOMPRESSIBILITET se även från Planckringen

ATOMKÄRNANS FORMBEVARANDE KRAFT

Atomkärnan står redan på noll

beskrivning

Atomkärnans formbevarande kraft

Atomkärnan kan inte komprimeras — den står redan på NOLL garanterat av kärnans oändliga fraktala ringdelning enligt elektriska kraftlagen

F=k(Q/r)2=k([Q/(n®¥)]/[r/(n®¥)])2=k(Q/r)2. Kärnans omväxlande tvärställda ringstruktur medger emellertid en viss ELASTICITET. Sämsta fallets beräkningar enligt TNED visar att ekvivalent max kompression går vid runt 1/1000 av kärnradien (dmax=r0n/1000). Se utförligt från Atomkärnans Geometri vid Deformation.

 

 

ATOMKÄRNANS STATISKA DEFORMATION — omedelbart föregående detonationsögonblicket i K-cellen — statiska g-trycket

 

 

 

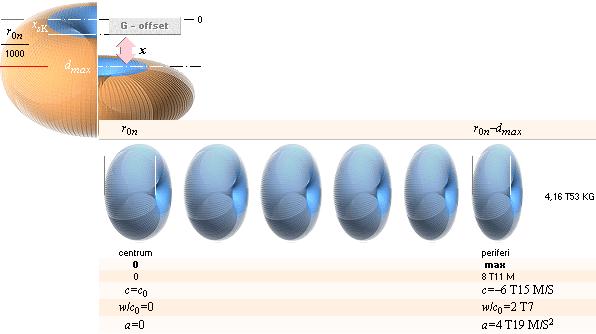
atomkärnans formbevarande kraft

 

Max täthet bestäms av atomkärnans formbevarande kraft, identisk med elektriska kraftlagen enligt

            

                          F = k(Q/d)2=k([Q/(n®¥)]/[d/(n®¥)])2 = k(Q/d)2

 

Atomkärnan står redan på noll garanterat av atomkärnans oändligt fraktala struktur d/(n®¥)] (Se utförligt från Planckringen) och kan därför INTE komprimeras.

ELEKTRISKA KRAFTLAGEN garanterar följaktligen: det finns inga svarta hål, har aldrig funnits, kommer aldrig att finnas.

 

Neutronradien fås från Plancks konstant h=mnc0rn=6,62559 t34 JS enligt rn=h/mnc0 med neutronmassan (empiriskt från 1932 efter James Chadwick)

mn         = 1,67471 t27 KG och toppdivergensen

c0          = 2,99792458 T89 M/S (efter mätningar från 1972) som ger

rn          = 1,31966 t15 M.

Maximala tätheten med neutronbas (se neutronkallplasma) ges enligt atomkärnans geometri som neutronmassan 1,0086652u=1,67471 t27 KG per sitt omskrivna rätblock

V=(2r0n)2r0n=4r0n3=9,19278 t45 M3 som ger maxtätheten

 

rmax= mn/V = 1,82176 T17 KG/M3

Maximal täthet grundad på tätt liggande neutroner

 

I den här framställningen används genomgående det förenklade värdet 1,82 T17 KG/M3 om ingen annat anges.

Se även föregående artikel ATOMKÄRNANS GEOMETRI VID DEFORMATION.

Se även Atomkärnans Inkompressibilitet från Planckringen.

 

Spåras universums expansion baklänges, stannar den tvunget på en maximal täthet (neutronkallplasma): atomkärna vidrör atomkärna. Enligt TNED svarar atomkärnan vid axiellt tryck (EKVIVALENTA GEOMETRIN VID DEFORMATION) med att öka den totala kärnvolymen, vilket för tätt liggande kärnor innebär ett explosionsartat rekylförlopp. Atomkärnan kan inte ”dödas” genom g-tryck, utan svarar med en lika stor motsatt kraft. Därmed grundläggs K-cellens fysik på expansion och kontraktion i den allmänna c0-kroppen.

 

 

 

 

 

ALLMÄNNA RESULTAT

 

atomvikterna

 

kollisioner mellan spinnriktade atomkärnor

 

 

 

 

 

 

Planckringens Dimensioner | 2008IX19 | Bekräftelser på atomkärnan | Nuklidradierna DEL II — Inledning

 

 

BEKRÄFTELSER PÅ ATOMKÄRNAN ENLIGT TNED

Se även kompletterande allmän beskrivning i

Precisionen i Atomvikterna enligt TNED, Jämförelser mellan TNED och Modern Akademi genom Neutronkvadraten.

 

Den helt enastående, överväldigande enhetligheten i atomvikterna genom TNED (se från Atomära Massdefekten) med experimentella resultat (HOP) lämnar inget tvivel om vilken kärnteori som är den korrekta. Här i förtydligande.

 

 

Atomkärnan — som det har visat sig enligt TNED — har visat sig vara betydligt mera komplicerad än vad det finns vokabulär i modern akademi för att uttrycka — det mesta kommer i skymundan. Men EN detalj är central — i ljuset av TNED — och visar på ”den hemliga ingången”: Hofstadters inledande experimentella kärnradiemätningar från 1950-talet. Editor2008XI10.

Ett försök till allmän generalgenomgång av kärnradiebegreppet och atomkärnans storlek ges i KÄRNRADIERNA DEL II.

Nedan följer en kort inledande orientering till huvudsaken i den delen.

Se även KÄRNRADIERNA DEL I i PLANCKRINGEN — ämnets allra mest elementära grunder enligt TNED.

 

 

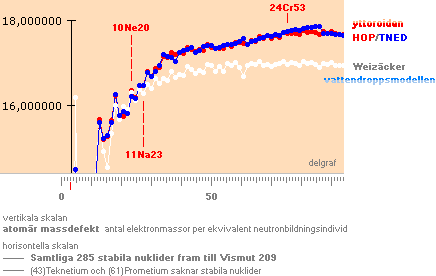
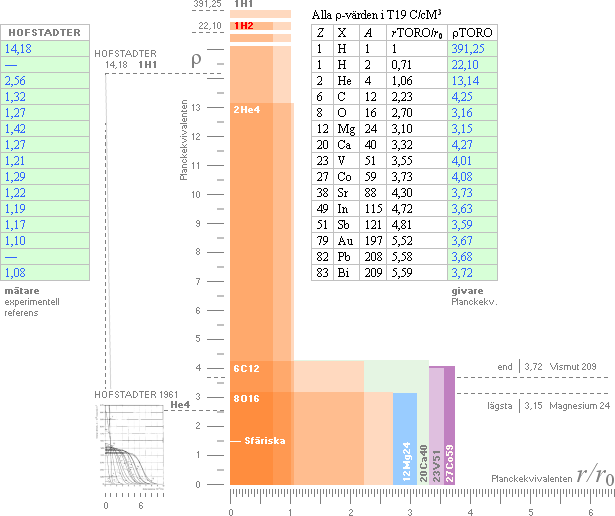
I jämförelsen mellan de olika databankerna för beräkning av atomvikten — illustrationen nedan med Experimentella (HOP, röd), teoretiska (TNED blå, MAC [modern akademi] via Weizäckerekvationen, vit) — ser vi att Weizäckerekvationen bryter sin »uppsats» från 10Neon20. Först från ca 24Krom53 antar Weizäckerekvationen en hyfsad synkronisering i rakhet med HOP/TNED-grafen.

 

Atomära massdefekten i antal elektronmassor per ekvivalent neutronbildningsindivid

 

Diagrammet ritat av MsWORKS 4.0 Kalkylblad med HOP/TNED/MAC-data

 

 

Anledningen varför Weizäckerekvationen inte kan matcha experimentella data — speciellt alldeles särskilt i nuklidkartans början — är att den just bygger på föreställningen om atomkärnan som sfärisk — Den detaljen framträder speciellt tydligt, samt ytterligare till förklaring, med kompletterande jämförande data på laddningstätheten (r) nedan. »MAC», här allmän akronym för ”modern akademi”:

 

Volymära Laddningstätheten i T19 C/cM3

 

TNED

MAC Hofstadter

SFÄR

 

Kärnikonerna ovan vänster visar atomkärnan skalenligt enligt TNED utan det yttre toppspinnet till vänster och med toppspinnet till höger. Atomkärnan ses på olika sätt av den inkommande partikel (elektronkomponenten) som ska avkänna atomkärnans fysik beroende på partikelenergin. Ju högre den är, desto djupare in i strukturen kan den penetrera, och desto högre värden får man på motsvarande laddningstäthet, dvs samma kärnladdning på allt mindre volym: Det är bara TNED som klarar den biten. Se utförligt från atomkärnans härledning i PLANCKRINGEN, om ej redan bekant.

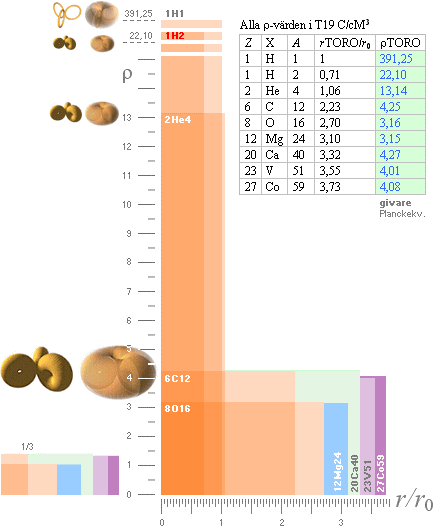
   Ovanstående jämförande stapeldiagram utpekar TNED som basen till de experimentellt funna toppvärdena för laddningstätheten (Hofstadter, se vidare nedan). Dessa bör också vara lägre i experimentet eftersom atomkärnan omger sig med ett kraftfält som stöter bort de avkännande partiklarna innan de når själva formkroppen — och som därmed i vilket statistiska fall tvingas uppvisa en diffus objektsform. Sfären å sin sida, stapeldiagrammet ovan längst ut till höger, är tydligen helt chanslös i värdeformerna: Den befinner sig långt nedanför de experimentellt uppmätta värdena.

   Hur TNED-värdena framräknats beskrivs kortfattat i Beräkningsgrunder. Grundradien r0 refererar till protonradien r0=1,37 Fermi i HOP-tabellen (HOP 7–27) med standardiserade värden från epoken 1967. Samma värde fås enligt TNED från neutronradien (1,32 Fermi) via Neutronkvadratens mönsterform.

   Sfärradierna, ovan höger, har beräknats från kubanalogin (samma som vattendroppsmodellen) med radiefunktionen enligt [r(A1/3)=]r=r0A1/3 med A som masstalet.

   1 Fermi = 1fM = 1 femtoMeter = 1 t15 M.

 

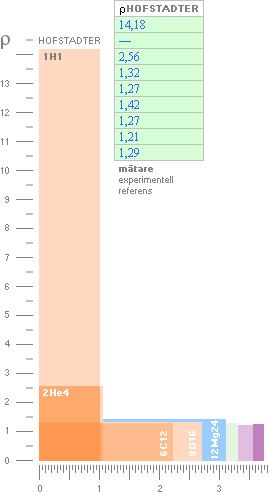
Först från Neon — i den begränsade nukliduppsättningen ovan först från Magnesium — antar värdena en någotsånär homogen sfärisk approximation. Denna del motsvarar den mera utpräglat sfäriska vattendroppsanalogin med i stort sett homogen täthet för atomkärnan. Emellertid garanterar de första nuklidvärdena en helt säker brytning mot den sfäriska formanalogin. Laddningstätheten för Väte 1 (1H1) är närmast våldsamt mycket högre än övriga. Orsaken — ENLIGT TNED — är naturligtvis den skarpa kontrasten i formfaktorer från grundaggregatets N3m20 som gäller för neutronen-protonen till den mera kompakta formen som gäller från masstal 2 (grovt N3m4). Låt oss se hur TNED kan förklara mätvärdena i detta fall enligt mittstapeln ovan (Hofstadters banbrytande experimentella värden från 1950-talet, se vidare längre ner i källredovisningen).

 

 

 

 

            

 

hög laddningstäthet

normal laddningstäthet

statistiskt jämförande experimentella mätkurvor

 

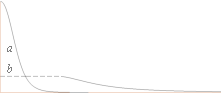
Laddningstätheten (vertikala skalan) i kurvorna ab mot kärnradierna (horisontella skalan).

Kärnfigurerna ovan vänster visar den inre delen av atomkärnan utan det yttre toppspinnet (som kärnan ses av t.ex. en inkommande elektronkomponent).

 

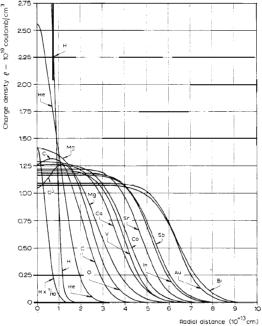
Med den skarpa formkontrast som neutronen-vätekärnan N3m20 uppvisar mot allt övrigt, figurdelen i a ovan vänster, är det tydligt att alla spridningsexperiment kommer att uppvisa en motsvarande mycket hög laddningstäthet i fallet protonkärnan. I Hofstadters fall användes elektroner som fick penetrera atomkärnorna, ”We have used the method of high-energy electron scattering.”, sv. ’Vi har använt metoden med högenergetisk elektronspridning’, Hofstadter s561. Eftersom elektronmassorna i vilket fall kastas tillbaka ut i växelverkan med atomkärnan (här, på grund av atomkärnans starka ytmagnetiska fält) uppvisas ett spridningsmönster med motsvarande skarpa avvikelser på grund av den snäva formgeometrin hos vätekärnan; Vi får en hög och brant typkurva liknande den i a, högra figurdelen. De tyngre atomkärnorna, figurdelen i b ovan mitten, har en bredare inre spinnbas (3J1K-delen i J0K+3J1K=0) med en motsvarande rundare ytform vilket gör att avvikelserna inte blir lika skarpa och därmed ett betydligt lägre statistiskt mätmedelvärde i slutänden. Motsvarande kurvvärden blir betydligt lägre, b högra figurdelen, och de liknar alltmera den sfäriska formens homogena fördelning med allt växande masstal. Kurvskaran nedan visar Hofstadters experimentella resultat och från vilken del har uttagits ovanstående tabells toppvärden. Kärnradierna ovan i Hofstadters toppvärden har för den bekväma jämförelsens skull satts på TNED-formen då Hofstadters motsvarande kärnradiedata i vilket fall saknar experimentell/teoretisk entydighet.

 

 

ROBERT HOFSTADTER

The electron-scattering method and its application to the structure of nuclei and nucleons, Nobel Lecture, December 11 1961

[http://nobelprize.org/nobel_prizes/physics/laureates/1961/hofstadter-lecture.pdf] s570

 

HOFSTADTER Nobel Lecture 1961

Robert Hofstadter (1915-1990), amerikansk fysiker född i New York 1915, Nobelpris i fysik 1961

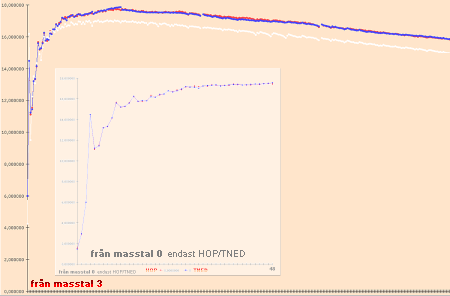
Notera att grafen för Väte-1 försvinner upp långt över illustrationsrutan. I grafens nedre vänstra del finns en förminskad version markerad ’H × 1/10’.

Grafen nedan förtydligar Hofstadters kurvskara i skalan för råvärdena enligt TNED.

 

 

Beträffande den anmärkningsvärda kontrasten mellan Väte-1 och övriga skriver Hofstadter,

 

 

”Note, however, the large disparity between the average central densities of the proton and all other nuclei. The alpha particle (4He) is also a unique case and exhibits a much larger central density than all heavier nuclei.”,

”Except for the extremely light nuclei of hydrogen and helium the constancy of the central nuclear density is clearly represented in the figure.”,

[http://nobelprize.org/nobel_prizes/physics/laureates/1961/hofstadter-lecture.pdf]:

The electron-scattering method and its application to the structure of nuclei and nucleons, s570 Fig. 8

ROBERT HOFSTADTER, Nobel Lecture, December 11, 1961

Min översättning:

Notera emellertid den stora olikheten mellan de genomsnittliga centrala tätheterna hos protonen och alla andra kärnor. Alfapartikeln (4He) är också ett unikt fall och uppvisar en mycket större central täthet än alla tyngre kärnor.

Utom för de extremt lätta kärnorna hos väte och helium, är den centrala kärntäthetens konstans tydligt representerad i figuren.

 

 

Hela den experimentella resultatbilden bygger uppenbarligen på den stora kontrasten hos N3m20-aggregatet mot alla övriga (N3m4). Den garanterar den enastående höga laddningstätheten för Väte-kärnan. Det är med andra ord alldeles tydligt att hela stapeldiagrammets jämförande typform med grund i formbyggnaden för N3m20 uppvisar en tydligt bekräftande generell proportionalitet mot experimentella värden (här Hofstadter). Att värdena också harmonierar generellt med motsvarande experimentellt uppmätta värden för atomvikterna, understryker endast TNED ytterligare.

   Vattendroppsmodellens täthetsfysik har ingen förutsättning för att kunna beskriva den formfysiken. Se explicit i Atomkärnans Gravitella Härledning. Där framgår det närmare.

 

Den helt enastående, överväldigande enhetligheten i atomvikterna mellan TNED och experimentella resultat (HOP) lämnar därmed inte längre något som helst tvivel om vilken kärnteori som är den korrekta.

 

 

 

 

BERÄKNINGSGRUNDER

Till Jämförande Stapeldiagram för Laddningstätheten

 

Atomkärnans grundradie utgår ENLIGT TNED från neutronradien (r = 1,32 Fermi = 1,32 fM = 1,32 t15 M) i Plancks konstant (h) eller med samma innebörd Planckringen h=mcr=6,62559 t34 JS med neutronmassan m=1,0086652u med atomära massenheten 1u=1,66033 t27 KG och c ljushastigheten i vakuum 299 792 458 M/S.

   Atomkärnans Härledning genom Planckringen leder till toroidaggregatet N3m20 motsvarande formen för neutronen-protonen och som ENLIGT TNED bildar alla tyngre atomer från masstal 2 och uppåt genom en mera kompakt toroidform (grovt N3m4). Till denna del hör också en toroidiskt elementär härledning av Kärnradierna.

   På den grunden ges fyra väldefinierade stabila grundnuklider (1H1, 1H2, 2He3, 2He4) som alla andra atomer byggs av.

   Den processen sker formellt enligt kärnreaktionslagen K1+K2–(m®g)=K där (m®g) motsvarar atomära massdefekten (mD).

   Med tillgång till experimentellt uppmätta atomvikter (HOP), tillämpade på atomära massdefekten enligt

mD = (1 – U/AmN)/me  ..........   U atomvikten i u, A masstalet, mN neutronmassan i u, me elektronmassan i u

framkommer neutronkvadraten som en självständig mönsterform med egna interna elliptiska ekvationer för atomära massdefekter och som därmed kan anställas i jämförelse med de experimentellt uppmätta atomvikterna enligt, se föregående basdiagram,

U = AmN(1 – mD·me)

Neutronkvadraten är emellertid avancerad och innehåller flera medelbildningsvägar (ellipser, hyperbel) med vars hjälp atomvikterna kan beskrivas matematiskt mera generellt, alltså inte enbart utifrån masstalet (A) [heltalsbaserade, aritmetiskt »symfoniska harmonier» som innefattar isotopgrupperna, se massdefektsekvationen i sammanställning för exempel].

Toroidmatematiken. GULDINS REGLER (motsvarande matematiken för rotationsytor och rotationsvolymer) ger enkla grundsamband med stöd av N3m20-aggregatets grunddimensioner, se från början i detta dokument i Planckringens Dimensioner. Guldinsambanden är av typen

2pr·2pR  ...................    toroidytan

pr2·2pR  ...................     toroidvolymen

Jämför en (smal) stång (—) med längden R som är fast monterad med änden i centrum av ett mynt  som får rotera: Rotationsytan — toroidytan — som begränsas av myntets omkrets 2pr blir produkten av denna och rotationscirkelns omkrets 2pR. På samma sätt blir rotationsvolymen produkten av myntets tvärsnittsyta pr2 och rotationscirkelns omkrets 2pR;

R anger radien hos den cirkel (Guldins rotationscirkel) som går genom toroidsektionens (ringtvärsnittets) tyngdpunkt — för ringtvärsnittets omkrets 2pr alltså precis i mitten och likaså för ringtvärsnittets yta pr2 också i mitten.

   Laddningstätheten beräknas sedan med kärnladdningen — samma som den atomnuklidens atomnummer (Z) — fördelad över toroidvolymen.

   Enligt TNED — se Atomkärnans Gravitella Härledning — avtar massvolymen med toroidformens fraktaldjup eftersom toroidaggregatet enligt TNED är ihåligt och varje sådan nivås tomrum bortfaller ju djupare ner man tränger. I motsvarande mening tillväxer laddningstätheten, konstant givet Z. För beräkningarna till ovanstående stapeldiagram har endast den första underfraktalen beaktats (kärnikonens vänstra del i stapelillustrationen, alltså, den som ligger närmast under det synliga toppspinnets toroidform) med hänsyn till de ändliga dimensionerna hos de avkännande masselementens dimensioner (se Elektronmassans Komponenter) och deras penetrerande energi.

 

 

En mera utförlig beskrivning av beräkningarna innefattar aspekter som kräver en allmän och ytterst (kopiöst) noggrann generalgenomgång av hela komplexet (se KÄRNRADIERNA DEL II), vilket dock här i denna korta översikt inte är av nöden.

 

 

 

 

 

 

Planckringens Dimensioner | ÖverflyttatBlockFrånUniversumsHistoriaInledning | 2008VI1E | Kolliderande spinnriktade atomkärnor

 

allmänna resultat

 

ALLMÄNNA RESULTAT ENLIGT TNED

SPINNRIKTADE KOLLIDERANDE ATOMKÄRNOR

Impulsmomentets (spinnets) allmänna betydelse i atomfysiken beskrivs ingående från Planckringen.

 

J0K + 3J1K = 0

Summan av alla moment och krafter i atomen är noll eftersom den inte kräver någon påfyllning för att fungera:

OM toppspinnet (J0K) påverkas relativt genom så höga kollisionsenergier att de varandra inträngande kärnorna börjar »spinnkoppla» märkbart, måste i motsvarande grad komplementspinnet (3J1K, som definierar atomkärnans tyngdcirkel och som ger balansen) exponeras i motsvarande grad enligt typformen

J0K–j + 3J1K+j = 0

Det betyder, uppenbarligen, att atomkärnans motsvarande inre toppringar tvingas visa sig i (spektakulär) växelverkan med motsvarande elektriska-magnetiska kopplingar: Atomkärnan visar sitt inre underspinn, mera ju högre kollisionsenergin är:

 

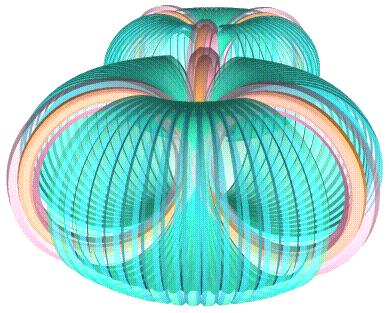
Atomkärnan blottlägger sitt inre underspinn (3J1K-delen i J0K–j + 3J1K+j = 0) mera ju högre kollisionsenergin är.

 

­­­ pilarna representerar spinnriktningen (upp-upp eller ner-ner för parallella spinn)

Om två spinnpolariserade protonaggregat är på väg rakt mot varandra och har lika spinnriktning, s.k. parallella spinn, måste de mötas (optimalt) på motspinnande inre ringar enligt närmast ovanstående/nedanstående illustrationer: motspinnande ringar samverkar inte utan stöter ifrån varandra maximalt: de kolliderande protonerna spinnkopplar en kort stund kring en gemensam rotationstyngdpunkt och stöter sedan ifrån varandra proportionellt med växande kollisionsenergi: parallella spinn uppvisar maximal kollisionsspridning (vilket betyder att kärnorna viker av ±90° från projektilbanan).

 

 

¯

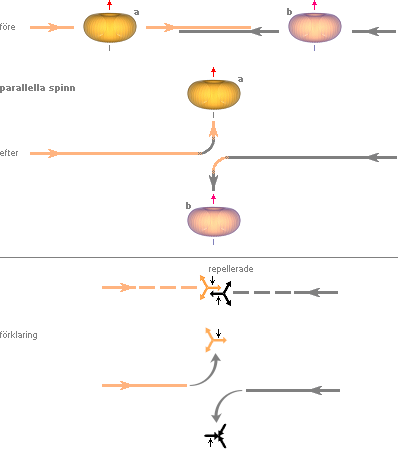
Om däremot två spinnpolariserade protonaggregat är på väg rakt mot varandra och har olika spinnriktning, s.k. antiparallella spinn, måste de mötas (optimalt) på medspinnande inre ringar som i närmast ovanstående/nedanstående illustrationer: medspinnande ringar samverkar. De kolliderande protonerna spinnkopplar också här en kort stund kring en gemensam rotationstyngdpunkt, men då på ett helt annat sätt och släpper sedan taget om varandra med rörelsemängdens styrka då de roterat förbi varandra i förlängningen av sin respektive projektilbana: parallella spinn möter varandra som kuggarna i samverkande kugghjul: som den inre ringgeometrin visar, kan protonaggregatens mittpunkter i princip därmed stryka förbi varandra medan de inre ringarna rullar igenom varandra och det hela ser ut som om kärnorna passerar rakt igenom varandra.

 

 

experimentella bekräftelser

 

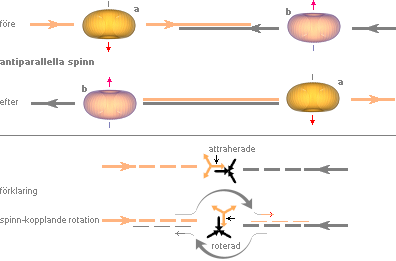
EXPERIMENTELLA BEKRÄFTELSER

QCD-teorin (Quantum Chromo Dynamics) har haft vissa problem med de experimentella resultaten från försöken med kollisioner mellan spinnpolariserade protoner som utfördes 1979 och 1987 enligt artiklar i SCIENTIFIC AMERICAN (May 1979 The Spin of The Proton frn. s.58 och August 1987 Collisions between Spinning Protons frn. s.32). Artikelförfattaren beskriver saken så här (text med färg är min markering):

 

”Most high-energy physicists were quite sure that spin would be unimportant in elementary-particle collisions at billions of electron volts of energy. For years this belief was tested only in a series of difficult experiments done by Owen Chamberlain and Emilio Segré of the University of California at Berkeley, among others. Then in the late 1950's Anatole Abragam of the College de France and Carson D. Jeffries of Berkeley suggested building polarized proton targets. The technique, which has been quite successful, relies on a low temperature and a strong magnetic field to polarize the spins of certain electrons in frozen beads of target material; the magnetic field causes the spins of the electrons to ”line up.” Microwave radiation is then applied to transfer the spin alignment of the electrons to nearby protons, making them spin in one direction. Experiments employing polarized proton targets in the 1960's and early 1970's at Berkeley, CERN (the European laboratory for particle physics) and Argonne revealed small but interesting spin effects in high-energy collisions. Nevertheless, most high-energy physicists still believed spin was not very important and would become even less so at higher energies.

   In 1973 my research group inaugurated a different approach at the Zero Gradient Synchrotron: we polarized the beam as well as the target.”.

SCIENTIFIC AMERICAN August 1987 Collisions between Spinning Protons p32col.2b

 

Spinnets betydelse understryks ytterligare genom ovannämnda artiklar enligt efterföljande sammanställning i citat (text med färg är min markering):

 

”the objects must be spinning very rapidly”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p58col.1b:

The interpretation of these experiments is still uncertain. They seem to imply that inside the proton there are some smaller objects that carry most of the particle’s spin angular momentum. The objects must be spinning very rapidly.

”spin more important with violent collisions”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p58col.1mb:

The influence of spin does not diminish as the energy of a collision increases; on the contrary, spin seems to become more important as the collision becomes more violent.

”it has turned out to be quite wrong”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p58col.1m:

It has long been thought, however, that the influence of spin should decline as the energy of the collision increases. The reasoning behind this assumption is simple: the energy associated with a proton’s spin is constant and so it becomes an ever smaller fraction of the total energy as the collision becomes more violent. At a sufficiently high collision energy it should make no difference whether two colliding protons are spinning the same way or in opposite directions.

   Only in the past few years have experimental techniques been devised for testing this assumption. It has turned out to be quite wrong.

”fact is that the spin directions do make a big difference”

SCIENTIFIC AMERICAN August 1987 Collisions between Spinning Protons p32col.2m:

The energy associated with the spin of a proton is constant, and so the role played by spin should diminish as the energy of the collision increases. At sufficiently high energies it should make little difference whether two colliding protons are spinning in the same direction or in opposite directions. The fact that the spin directions do make a big difference suggests that our understanding of how protons interact with one another is incomplete. The experiments even call into question the currently accepted model of the proton's internal structure, which holds that a proton consists of three smaller constituents known as quarks, held together by the strong nuclear force (the force described by QCD).

 

Mera precist:

 

”objects in the proton spinning very rapidly”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p58t:

When two protons collide, the outcome depends on which way the particles are spinning. The effect seen in violent collisions suggests there are objects in the proton that spin very rapidly

”protons spinning in the same direction rebound”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p58col.1mb:

A recent series of experiments has shown that protons spinning in the same direction are much more likely to rebound violently than protons spinning in opposite directions.

”opposite spins seem to pass through each other”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p58col.1mb:

Protons with opposite spins often seem to pass through each other without interacting at all.

”antiparallel spins seem to pass straight through each other”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p69t.ill:

when the spins are antiparallel, the objects seem to pass straight through each other

”opposite spins often pass through each other as if transparent”

SCIENTIFIC AMERICAN May 1979 The Spin of the Proton p70col.2b:

When two protons spinning in the same direction collide head on, they almost always scatter violently. When the same particles are spinning in opposite directions, they often pass through each other as if they were transparent.

”a surprising dependence on the direction of spin”

SCIENTIFIC AMERICAN August 1987 Collisions between Spinning Protons p32t:

The outcome of a collision between two protons shows a surprising dependence on their directions of spin. The results challenge the prevailing theory that describes the proton’s structure and forces

 

Ovanstående resultat sett generellt endast styrker toroidmodellens ställning: atomkärnans allmänna impulsekvation J0K + 3J1K = 0: det inre spinnet (3J1K) får allt större betydelse om det yttre spinnet (J0K) motverkas — som i fallet med kollisioner mellan atomkärnor med höga partikelenergier, och förutsatt att kärnorna är spinnpolariserade så att de kan synkronisera spinnkopplingen maximalt. Resultatet är (som artikelförfattaren i ovanstående citat också påpekar) emellertid INTE gynnsamt för den förhärskande QCD-teorin: den vill »helst inte se några spinnpolariserade experiment» eftersom dessa (tvivelslöst) sönderbryter QCD-teorins grunder. Ingen kan förklara experimentets resultat, vilket har lett till att »debatten har tystnat».

 

Som redan framgår i den här presentationen från härledningen av den elektriska laddningen med grund i ljusets elementära fysik, har modern akademi redan från början utmärkt sig för att INTE kunna härleda grundläggande fysikbegrepp utan istället försöka uppfinna dem vartefter problemen hopar sig. I den andan bevittnar vi alltså följande vetenskapliga ordning: abstraktionen ökar. Läsekretsen minskar; det blir allt svårare att hänga med i den moderna akademins utläggningar i takt med att allt mer avancerade och sofistikerade ABSTRAKTA LÖSNINGAR ges i följd av problem som uppkommer i följd av att man generellt inte härleder fysiken ur naturintelligensen utan anser att vad intelligensen anbelangar är det den moderna akademin som står för den. Så finns för att exemplifiera med de JÄMFÖRANDE TEORETISKA ATOMVIKTERNA inga partiklar alls i den verkliga atomkärnan ENLIGT TNED, medan atomkärnan enligt modern teori är fullproppad med sådana, allehanda spinnande, objekt.

 

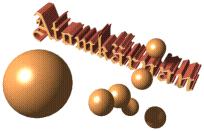
NUKLEÄRT SPINN i modern teori grundas, som vi vet, på föreställningen att atomkärnan är en samling kulor (nukleoner) som snurrar omkring inuti atomkärnan. Vilka rent matematiska aspekter man än kan ha på den typen av fysikalisk dynamik, är det tydligt att den är illa vald i samma rum som det där resultaten från kollisioner mellan spinnpolariserade protoner diskuteras. Se även JÄMFÖRANDE TEORETISKA ATOMVIKTER MELLAN TNED OCH MODERN AKADEMI.

 

Spinnbegreppet i modern akademi är alltså redan på förhand dömt att urarta i total abstraktion eftersom det, uppenbarligen, INTE kopplar till den mera preciserade fysikbeskrivning som visas i ovannämnda exempel. (Det är tydligen utklassning som också fortsättningsvis kommer att gälla).

 

Från denna synvinkel är också den vidare moderna vetenskapshistorien uppenbar: Ytterligare abstraktioner med ännu dyrare partikelacceleratorer med ännu högre kapaciteter för tillfället att få framställa ännu mera avancerade abstrakta teorier på ett ännu mindre begripligt språk och som kan förstås och läsas av en ännu mindre skara människor. Abstraktionsnivån på kärnfysiken idag är påtaglig, det går inte att förstå innehållet utom för de personer som själva utformat innehållet eller som följt med i deras utvecklingshistoria, allt i takt med den växande hopen frågetecken under utvecklingens gång.

 

Med Google-sökning på @INTERNET på »collisions between spin polarized protons» visar sig följande utveckling efter ovannämnda spinnpolariserade kollisionsexperiment (från 1987):

[www.sciencenews.org/pages/pdfs/data/1997/152-10/15210-17.pdf]:

 

”In 1988, however, physicists were shocked to find experimental evidence suggesting that very little—perhaps none—of the proton’s spin comes from the spin of the quarks thought to make up the proton (SN: 4/8/89, p.215). They called this apparent paradox the proton spin crisis.”

 

Omkring 1988 etablerades vad som kallas ”protonens spinnkris” (den kopplar dock veterligt inte till ovannämnda kollisionsexperiment, som generellt inte tycks omnämnas alls i efterhand …): Genom kärnnukleonteorin (QCD) kan man inte få ihop det med det SPINN och dess tillhörande moderna akademiska begrepp som teorin uppvisar, tillsammans med experimentella tolkningar i den allmänna moderna akademins kärnfysikaliska anda. Kort sagt: Det fattas något. Så anställs då (återigen, nu 2007) omfattande projekt för att bygga ännu kraftigare partikelkolliderare. Som vi nu vet, kommer resultatet endast att bli det att abstraktionerna kommer att växa ytterligare. Det finns inget slut på den typen av verksamhet. Den kan fortsätta i evighet, med ständigt mera avancerad utrustning. Det man nu är ute efter är ”gluonerna i atomkärnan” som misstänks vara de partiklar som ansvarar för protonens spinn.

 

1/3-FermiSpökpartikeln

 

Den moderna kärnfysikens 1/3-Fermi-spökpartiklar

 

 

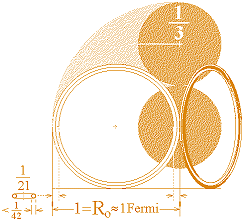
Med geometrin given för atomkärnan från härledningarna i Planckringen ser vi direkt följande: Om en sfär placeras på toppen av den toppspinnande kärntoroiden så att den precis nuddar kärnans omskrivna storsfär i fallet proton-neutron, då är storleken av lillsfären precis 1/3 av den omskrivna protonsfären. Tillämpar man således en sfärisk modell för atomkärnan i olika spridningsförsök där man inte känner till toroidformen som grund, borde man också tycka sig se spår av »1/3-objektet» i olika spridningsförsök. Detta tycks också precis vara det som har inträffat i modern vetenskap. Citaten nedan bekräftar:

 

”The proton and neutron have a radius of roughly one fermi”, s59sp1.

”The sharp break in the cross-section curve was inter­preted as evidence for objects inside the proton with a size of one-third fermi”, s66n-69ö.

”Recent experiments with the Intersecting Storage Rings at CERN support the hypothe­sis of one-third fermi objects”, s69sp1ö.

”The elastic-scattering experiments strongly suggests that the size of these objects is about one-third fermi”, s69sp1n.

”Furthermore, the slope of the large-angle segment, which corresponds to hard-scattering events, gives the same results for the size of the inte­rior objects: one-third fermi”, s70sp1n.

 

Alla citat från SCIENTIFIC AMERICAN May 1979, The Spin of the Proton.

 

 

 

 

 

 

Planckringens Dimensioner | MAFEM 2008VI28 | TNED5 2004I13 | Principles of Physics 2002

 

Från härledningen till Planckekvivalenterna

MASSA-KRAFTUTBYTESMEKANISMEN

MAFEM

mass force exchange mechanism

 

Utförlig beskrivning av elektronens massökning

genom den matematiska fysikens begrepp ENLIGT TNED

 

översikt

Planckenergins massökningsfunktion

 

 

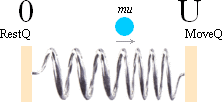
RestQ ViloQ                        MoveQ RörelseQ

 

Ekvivalent till Fig:4 i Planckekvivalenterna

 

 

 

 

 

m=(QR0–QR)qdrc=m0–Dm                      m=(QR0+QR)qdrc=m0+Dm

 

qc         = (Q/c2)  ..............         förkortning

qdrc      = (dQ/T)qc  .........         förkortning

 

m = R=Uökande/iqdrc                              m = R=Uminskande/iqdrc

 

se utförligt i huvudtexten

 

 

Den moderna akademin kan, som tidigare påpekats, inte härleda den elektriska laddningen, inte förklara eller ens beskriva dess ingående element — men gör ändå anspråk på att besitta grundläggande kunskaper. Följdriktigt vantolkas också fysiken därefter. Följande exempel klargör.

beskrivning

UR PLANCKEKVIVALENTERNA framgår bland annat sambandet för hur massan (m0) hos en elektrisk laddning ändras (m) då den genomgår acceleration till sluthastigheten u i ett slutet elektriskt system med gränshastigheten c via en accelerationsspänning (U) enligt Planckenergins massekvivalent eller »Planckimpulsekvationen» (se härledningen i Planckekvivalenterna)

m0/m = Ö 1–(u/c)2

I den härledningen ges ingen direkt förklaring till hur massändringen går till utöver att det är fråga om en omfördelning mellan ett MoveQ och ett RestQ. Följande beskrivning ger den förklaringen.

 

 

Elektriska laddningar som försätts i rörelse (u) av en spänning U följer samma kraftprincip som ändringen av en uppspänd fjäder. Se även ovanstående illustration med sammanfattande samband som beskrivs utförligt nedan.

 

De laddningar (MoveQ) som försätts i rörelse erhåller massa från vilodelarna (RestQ) enligt

 

m          = (QR0±QR)qdrc

             = m0 ± Dm

 

så att systemets massa bevaras konstant. Se Planckekvivalenterna, om ej redan bekant.

Ingen massa skapas, ingen massa försvinner.

 

Genom att låta MoveQ passera i en slinga utanför I-systemet (trådstrålerör) kan man verifiera massökningen i MoveQ genom mätning.

Genom den moderna akademins (synnerligen sensationellt, men ej redovisade) ensidiga intresse för MoveQ-mätningar har särskilt djupgående vanföreställningar etablerats angående fysikens natur — ”med stöd av experimentella bevis”.

Systemet bevarar den elektriska laddningen Q=Ö (m/R)(A/dT) konstant genom att m och R varierar exakt proportionellt.

R ingår inte i mekaniken, massändringseffekten har ingen betydelse utom slutna elektriska system.

Se även i Beviset för multipla c.

MoveQ beskrivs explicit av impulsekvationen eller Planckenergins massekvivalent mc=mu+im0c=Fdt som ger det redan välkända

             m0/m = Ö 1–(u/c)2  ..........................       impulsekvationen

Med E=UQ=Dmc2=(m–m0)c2 får man efter insättning i m0/m och efter utvecklingar

 

             u = c(1–1/[(UQ/m0c2)+1]2)0,5  ........      Q:s hastighet u vid U

 

 

Ändringen u från U framtvingar enligt Newtons tredje lag ett motstånd (QR) i Q där U ”tar” Q. För att Q=Ö (m/R)(A/dT) ska bevaras intakt måste en R exakt motsvarande massa påföras Q vilket garanterar att Q bevaras.

 

Divergensenergin E=mc2=UQ=RIQ visar att m ändras proportionellt mot U med konstant Qc enligt m=U(Q/c2).

För ett strömsystem I i exakta ekvivalenter ges (m/R)=I(Q/c2)=Iqc med förkortningen

qc          = (Q/c2):

systemströmmen I garanterar (m/R)-balansen.

QmoveU

Massändringen kan alltså skrivas m=RIqc.

Förflyttningen av Q via U

Resistansen R i QR blir det aktiva handtag som U griper Q i via ett befintligt Qi: U=QRQi.

U blir med hänsyn till ±Q sammansatt enligt U=Uladdning±Usystem. Ändras inte Q av U gäller U=Uladdning.

Bägge Ri i QRQi tillhör Q, inte systemströmmen I: Usystem = Q(Ri); Qi=dQ/T.

 

U-taget på Q ingriper i Q via dT, alltså differentiellt på QR, varigenom i-formen via QR blir Qi=dQ/T;

m          = Riqc=R(dQ/T)qc= Rqdrc  med förkortningen

qdrc = (dQ/T)qc = (dQ/T)(Q/c2) ;

m          = R(dQ/T)(Q/c2)=Rd(Q2/Tc2) ,  = R · d(Q2/rc)

 

Vi ser att detta stämmer utomordentligt via fältexpansionen c=r/T i Q enligt

(m/R)=d(Q2/rc)=d(Q2T/r2), (m/R)(A/dT)=Q2.

 

Varje Q har en intern R-disposition QR0=QU0/i=QU0/(dQ/T)=QU0T/dQ=UladdningT/dQ.

Så länge Q inte accelereras av U, står denna egenskap fix.

 

När Q accelereras av U griper U tag i Q via

QU0 = Uladdning

vilket ger en ny, additiv (primärinduktiv) resistans QR, så att

R = QR0 + QR.

 

Den gripande U på MoveQ ger en induktion QU i Q; U=QRi=QU.

DÄRMED säkerställer Qi en kraft-massa överföring m=R=U/iqdrc=(QR0i + QRi)qdrc/i där, som ovan,

qdrc=d(Q2/rc) enligt m=U·Q/c2, =QRi·(Q/c2)=QR(dQ/T)·(Q/c2), =QR·d(Q2/rc) ; R=QR0+QR.

 

T-FAKTORN får sin koppling till systemströmmen I (på Q från U) genom

U=QRi=QRdQ/T=QRT · dQ/T2=QL · dQ/T2=QLi/T=QL(di/dT)  .................         i=dQ/T

Därmed gäller energibalansen som krävs för strömmens uppbyggnad enligt det redan välkända

E = QL · I2/2, effektförluster oaktade.

INTEGRATIONEN på systemströmmen I utförs alltså på konstanten Qi som är en Q-egendom, ingen I-kvalitet, väl att märka.

 

EN Q-ACCELERATION VIA U kan alltid tillskrivas ett ömsesidigt förhållande mellan ett par laddningar (Q+ och Q–) åtskilda av en distans (r) med en tillhörande elektrisk fältstyrka U/r=X; U=Xr.

 

Med Q+ fix (RestQ), får Q– (MoveQ) en hastighet (u) genom DU=XDr, (dU=Xdr).

   Det ömsesidiga parförhållandet mellan MoveQ och RestQ är alltså sådant att MoveQ erhåller U relativt 0 (från RestQ), medan RestQ som mottagare relativt MoveQ förlorar samma U. Därmed är U konserverat. Parförhållandet ger alltså

 

             R=(Uladdning+ 0 till U)/i           ...........  MoveQ:            m = R=Uökning/iqdrc  ......................       m ökar

             R=(Uladdning+ U till 0)/i           ...........  RestQ:              m = R=Uminskning/iqdrc  .................      m minskar

 

U-ökningen för MoveQ har därmed transformerats till en massökning i MoveQ, säkerställt av induktionsverkan på Qi, Q bevarad intakt, på bekostnad av en motsvarande massminskning i RestQ.

 

kraftchokning

Accelerationen av Q via U innefattar alltså en intern massomfördelning i det slutna elektriska ledningssystemet;

Ingen massa skapas, ingen massa försvinner. Massändringen återfaller därmed analogt på en kraftchokning — som en inspänd fjäder som ändras från mitten.

Systemet bevarar massan konstant.

 

Summering

 

När MoveQ erhåller massa från I=U/R, förlorar en motsvarande RestQ massa från samma I=U/R. I bägge fallen säkerställer balansen att kvoten m/R hålls konstant: m och R varierar i exakt proportion vilket var villkoret som skulle mötas i Q=Ö (m/R)(A/dT),

(n·m)/(n·R)=m/R=konstant=(R=U/iqdrc)/R=qdrc=Qi(Q/c2)=d(Q2/rc)

Och alltså bevaras Q=Ö (m/R)(A/dT) konstant oberoende av accelerationer eller retardationer i I-systemet,

Q          = Ö(m/R)(A/dT)

             = Öd(Q2/rc)(A/dT)

             = Ö(Q2/rc)(A/T)

             = Ö(Q2r/cT)

             = ÖQ2

 

IMPULSEKVATIONEN

MoveQ i vila har divergensimpulsen m0c i Q via QR0 med m0=QR0qdrc.

MoveQ flyttad av U får den resulterande divergensimpulsen mc i Q av QR med m=(QR0+QR)qdrc=m0+Dm, samma som

mc=Fdt=(QR0qdrc+QRqdrc)c=ma·dt=m(c/dt)dt

MoveQ får den mekaniska impulsen mu med hastigheten u via U.

   Gränsvärdet för u i det elektriskt slutna systemet är c. Med växande U från viloläget m0c där mu=0 vrids då tvunget mc växande från m0c mot den mekaniskt fasta vektorriktningen mu. Därmed beskriver impulserna ett komponentsystem mc=mu+im0c=Fdt

(mc)2 = (mu)2 + (m0c)2,  1 = (u/c)2 + (m0/m)2 ;

             m0/m = Ö 1–(u/c)2  ..........................       impulsekvationen

Med E=UQ=Dmc2=(m–m0)c2 får man efter insättning i m0/m och efter utvecklingar som ovan

             u = c(1–1/[(UQ/m0c2)+1]2)0,5  ........      Q:s hastighet u vid U

 

den sekundära induktionens

friställning

Med särskild tydlighet:

 

I DEN SEKUNDÄRA INDUKTIONEN (laddningar utanför det strömdrivande slutna I-systemet)

noterar vi att

 

             m = R=U/i=KONSTANTqdrc= konstant

 

därför att den induktiva dipolfältstyrkan (Ð) är aktiv i varje rymdpunkt (P) relaterad som fix mot MoveQ:

Uind innefattas direkt i Qi av QR0 så att UindQi–1=konstant:

 

             Uind=Ri ;  Qi = UindR–1 ; 

                    QR0 = R = UindQi–1 = konstant ;  QR = 0.

 

I ett ordinärt U-fält (som mellan plattorna på en plattkondensator) är potentialen U=kQ/r=Xr en statisk egendom i varje rymdpunkt (P). Den induktiva fältdipolen i P däremot håller en dynamisk spänning

U=R’Q/t= Ðs där R’ är den induktiva rymdresistansen som uppkommer tillfälligt i följd av varje laddnings rörelseändring dv/dt. Se även Induktionen.

I modern akademi finns f.ö. inget omnämnande av eller någon beskriven åtskillnad mellan primär (inom I-systemet) och sekundär (utom I-systemet) induktion. Termerna som sådana omnämns inte, antyds inte, diskuteras inte, presenteras inte.

   En vidare introduktion i ämnet ges i Vektorkalkylens grunder i modern akademi.

 

 

Den sekundära induktionens frihet från masseffekter är mera enkelt uppenbar från det faktum att sekundärladdningar inte har någon del i energibalansen som driver primärsystemets laddningar: Det finns ingenting att relatera ett utbyte kraft-massa till.

 

 

Märk alltså noga:

Att elektriska laddningar i sig försätts i rörelse innebär ingalunda någon automatisk koppling till massändringseffekter. Framställningen måste vara noga relaterad för att klargöra vad som är vad.

   Vi vet redan att elektrofysiken är (det i särklass) svåraste området av alla i Naturboken. Att misslyckas eller missuppfatta eller missförstå är ingen skam. Men att vidhålla en felaktig uppfattning utan att släppa in beskrivande argument är det.

 

dimensionsändring

Laddningens dimensioner ändras vid massändring

 

Med grund i Atomkärnans härledning (se även Nukleära spinnkriteriet i Kvanttalen) framgår att begreppet toppspinn är en gemensam egenskap som delas lika av alla atomkärnor — för att garantera att atomen/atomkärnan summerar noll krafter och moment: atomkärnan kräver ingen påfyllning för att fungera. Impulsmomentet J=mvr=mwr2 utsäger — med konstant vinkelrotation (w) och bevarat moment (J) — att radien (r) avtar med växande massa (m).

   Man kunde här inflika att sambandet J=mwr2 likväl medger direkt proportionalitet mellan J och m med konstant wr. Vi måste emellertid ta hänsyn till atomkärnans impulsekvation J0K+3J1K=0 med den avgörande atomkärnans tyngdcirkel; ökar massan, ökar också centrifugalkraftens aspekt och därmed en ökning i tyngdcirkelns radie (r).

   DEN VIDARE FÖRKLARINGEN på den vägen blir emellertid (onödigt) omständlig.

   Betrakta istället följande betydligt mera lättfattliga resonemang.

 

Med lika laddningar som har lika massor är summan av massorna hos MoveQ och RestQ konstant, enligt härledningarna i Planckekvivalenterna. Då ges för motsvarande impulsmoment, för att exemplifiera sambanden, leden

 

J           = mwr2

             = (MOVEm + mREST)wr2

             = MOVEmwr2 + mRESTwr2

;

För att bevara J på given vinkelrotation (w=v/r=2pr/T0/r=2prf0/r=2pf0) måste (kvadraten på) r ändras omvänt proportionellt mot m;

J ändras inte, och därmed heller inte komponenterna i J = moveJ + Jrest. Vilket vill säga: Impulsmomentet bevaras oberoende av ändringarna i m. Därmed återstår endast omvända proportioner i mr2 för att få bibehållet konstant J.

   Notera att ett helt annat fall uppkommer i mekaniken då man plussar på en massa till en given rotationskropp. Där tillväxer J med m — men detta är inte fallet i elektrofysiken eftersom det elektriska systemet bevarar massan konstant — enligt härledningarna i Planckekvivalenterna; I slutna elektriska system där laddningar (Q) accelereras av energin i systemets spänningar (U), ändras (kvadraten på) laddningens ekvivalenta impulsmomenttyngdcirkels radie r omvänt proportionellt mot ändringar i laddningsmassans mass-kraft (m=F/a). Vi kan kalla det för en »masschokning» eller kraftchokning.

   Därmed kan — alltså — INTE Jm-proportionaliteten förutsättas obetingat inom kärnfysiken enligt TNED.

 

 

 

 

 

 

Planckringens Dimensioner | Neutronens nolladdning | 2008VIII13 | Neutronens sönderfall

 

Se även inledande begrepp från Neutronens Sönderfall

NEUTRONENS POSITIVA LADDNINGSDEPLACEMENT —

NEUTRONENS NOLLADDNING

Hur neutronen ENLIGT TNED kan ha ett positivt laddningsdeplacement och ändå framstå utåt som helt elektriskt oladdad

 

LADDNINGSDEPLACEMENTET Förtydligande

Atomkärnans spinnande ringfraktala dynamiska väv bygger på ett i kärnytan befintligt föregivet positivt

 

LADDNINGSDEPLACEMENTET

 

 

Deplacementet förstärks av det inre ringspinnet J1K.

Laddningsdeplacementet ansvarar för den utåt uppvisade kärnans laddning eZ.

Den inre ±b-strukturen (centralmassivet 1818e) framstår som fullständigt neutral utåt.

 

Neutronens sönderfall i illustrerad sammanfattning enligt TNED

 

  

 

frigjord e-massa  

0

25%

50%

75%

100%

tid (12-14 minuter)

0

3

6

9

12

radie t15 M

1,32

 

 

 

1,37

massdefekt

0

 

 

 

1,52e

kärnmagnetiskt moment

negativt

 

0

 

positivt

*

–1,9131

 

 

 

+2,79278

 

*[HOP Table 3.1 s9-93], enhet i s.k. Bohrmagnetoner, se utförligt från Kärnmagnetiskt moment.

 

beskrivning

Protonen börjar inte arbeta som proton förrän neutronen avdelat en hel elektronmassa.

Neutronsönderfallet tar runt 12-14 minuter (äldre källor), en del nyare källor (från ca 2000) kan ange upp till 15 minuter, se t.ex. källan nedan.

När protonen ”tänder” bildas en reaktionspuls (lokal laddningsökning [±] med induktansminskning, konstant bevarad energi) som används för att mäta neutronsönderfallets tidrymd.

Se exv.,

 

[http://physics.nist.gov/Divisions/Div846/Gp3/FunPhys/lifetime.html] 2008-08-12,

NIST Neutron Liftetime Experiment, Physics Laboratory, Ionizing Radiation Division, Neutron Interactions and Dosimetry Group

 

PROTONYTAN med referens till det härledda 1818e-massivet enligt TNED från PLANCKRINGEN, analogt ±909e, bygger på ett i kärnytan utskjutande laddningsadeplacement, figuren överst. Med exakt proportionalitet mellan massa och laddning är deplacementets storlek endast en del på runt 1838. Grovt sett 1/2000.

   Den aktiva verkan av denna effektiva kärnladdning utåt sett är emellertid bunden till just materiefysikens elektronkvanta (exempel på elektronmassans svängningar genom motsvarande endast hela vågtal ges i härledningen till PERIODISKA SYSTEMET genom Keplerresonanserna). Först när atomkärnan etablerat en dynamisk koppling i enheter om en elektronmassa (1,602 t19 C), kan den atomen börja uppvisa sin elektronbaserade svängningsfysik inför detekterande anordningar — inkluderat dynamisk samverkan med andra atomer.

 

Mätningar på neutroner (genom starka magnetiska fält) har visat att neutronen uppvisar ett motsvarande negativt kärnmagnetiskt moment (se Kärnmagnetiskt moment), medan protonen uppvisar ett positivt dito. Denna ändring kan tillsammans med det positiva laddningsdeplacementets roll förklaras enligt TNED på följande dynamiska grund.

   Neutronen börjar från ett litet positivt laddningsdeplacement, precis så litet att det ligger under avkänning för att nå upp till elektronkvantats avkänningsnivå.

 

I den praktiska situationen borde det emellertid finnas ”en ytterst liten obetydlig elektrisk attraktion” mellan neutronens kärnyta och omgivande elektronmassor. En sådan har också påvisats experimentellt. Se vidare nedan i särskild notis NEUTRONKÄRNYTAN UPPVISAR INTE HELT EXAKT NOLLADDNING,

 

   Detta lilla deplacement ansvarar för att neutronen samtidigt får ett negativt kärnmagnetiskt moment (se separat artikelbeskrivning i Neutronens negativa kärnmagnetiska moment).

   Under den tid som neutronen sönderfaller till proton, ändras neutronens laddningsdeplacement dels genom massavbränning (m®g) och dels genom att negativt laddad massa, elektronens komponenter, förs ut från kärnan för att bilda en stabil atom. Men ingenting av den processen syns direkt utåt eftersom materiefysikens minsta mätande enhet just kräver hela elektronkvanta — in till sista prick. Innan den övergången har skett, är processen i princip ”död” för alla mätande sensorer. När protonen så ”tänder” och därmed neutronsönderfallet är avslutat, tillkännages det genom en motsvarande reaktiv puls som utgår med centrum från den nybildade protonen och som genomgår all omgivande atomär materia.

 

Neutronladdningen i termer av elektronkvanta uppvisar alltså ”0” för all mätande utrustning som försöker avkänna laddningen hos komponenten.

   Emellertid finns viss sinnrika experiment som visar att neutronen dels fungerar mycket svagt attraherande mot elektronmassor, se nedan, och dels också har ’ett inre positivt med ett yttre negativt’ så att nettoresultatet likväl utåt framstår som noll (Man bestrålar neutroner med elektronmassor, genom spridningen från kollisionerna får man vissa grunddata på motsvarande laddningsfördelning hos objektet, men de tolkningarna är också äventyrliga då man i vilket fall måste använda någon föregiven modellform — som i de moderna kvarterens laboratorium garanterat INTE är TNED).

 

 

KÄRNBRUNNEN är stället där elektronen frigörs, se ATOMFYSIKENS TVÅ KUNGSEKVATIONER (illustrerat).

Se även CENTRALKONTAKTERNA — dynamiken för elektron- och positronmassans frigörande ur atomkärnan.

 

 

NEUTRONKÄRNYTAN UPPVISAR INTE HELT EXAKT NOLLADDNING

 

Enligt genomförda experiment som redovisas i HOP-källan [HOP s9–210 sp1mn]:

 

”A weak attractive potential exists between the neutron and the electron”,

HANDBOOK OF PHYSICS McGraw-Hill 1967 s9–210 sp1mn

Min översättning:

En svagt attraherande potential finns mellan neutronen och elektronen.

 

Denna detalj enbart bekräftar existensen av det nödvändiga positiva laddningsdeplacementet enligt TNED.

   Den uppmätta elektriska verkan mellan neutronen-elektronen är dock så ytterligt svag att den inte kan ställas i någon direkt koppling till elektronmassans laddning.

   På detta deplacement bygger hela kärnfysiken — och som genom den allmänna c0-kroppen garanterar att begreppet ”antimateria” är förbehållet typen exotiska partikelexperiment i modern vetenskapshistoria.

 

 

 

 

 

 

Planckringens Dimensioner

 

 

 

REGISTER

 

 

 

 

 

Planckringens Dimensioner

 

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

 

 

 

 

Planckringens dimensioner                                                                                                                                          

ämnesrubriker

 

                                     

 

 

innehåll

                                      PLANCKRINGENS DIMENSIONER

 

                       Atomkärnans Dimensioner

 

                                                                            Atomkärnan enligt Planckringen

 

                                                                            Masstal större än 1

 

                                                                                               Kärnfysikens grundsatser

 

                                                                            Masstal lika med 1

 

                       Allmänna resultat enligt TNED

 

                                                                            Atomvikterna

 

                                                                            Kollisioner mellan spinnriktade atomkärnor

 

                       Atomvikterna — bekräftelser på atomkärnan enligt TNED

 

                                                                            Basdiagram massdefekterna HOP/TNED/MAC

 

                                                                            Stapeldiagram laddningstätheten TNED/Hofstadter

 

                                                                            ROBERT HOFSTADTER · några av de första experimentellt uppmätta referenskurvorna från spridningsexperiment med elektroner

 

                                                                            Beräkningsgrunder till stapeldiagrammet

 

                       Spinnriktade Kolliderande Atomkärnor

 

                                                                            Experimentella bekräftelser

 

                                                                            1/3-FermiSpökpartikeln

 

                       MAFEM — MassForceExchangeMechanism MassaKraftUtbytesMekansimen

 

                                                                            Planckenergins massökningsfunktion · illustrerad översikt

 

                                                                            Beskrivning

 

                                                                            Förflyttningen av Q via U

 

                                                                            Summering

 

                                                                            Kraftchokning

 

                                                                            Den sekundära induktionens friställning

 

                                                                            Dimensionsändring

 

                       Neutronens nolladdning

 

                                                                            Neutronens positiva laddningsdeplacement

 

                                                                            Neutronens svaga elektriska fält

 

 

 

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

mn        = 1,0086652u  ......................    neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

me        = 0,000548598u  ..................    elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]

u           = 1,66043 t27 KG  ..............     atomära massenheten [HOP Table 1.4 s7–27, 1967]

u           = 1,66033 t27 KG  ..............     atomära massenheten [ENCARTA 99 Molecular Weight]

u           = 1,66041 t27 KG ...............     atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u           = 1,66053886 t27 KG  ........     atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u           = 1,6605402 t27 KG  ..........     atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u           = 1,660538782 t27 KG  ......     atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c0          = 2,99792458 T8 M/S  ........     ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h           = 6,62559 t34 JS  .................    Plancks konstant [HOP s7–155]

 

t för 10–, T för 10+, förenklade exponentbeteckningar

 

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

 

Senast uppdaterade version: 2021-02-19

*END.

Stavningskontrollerat 2008-03-06 | 06-29 | 2008-10-19

 

rester

*

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG-justerad 2011-10-10

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se