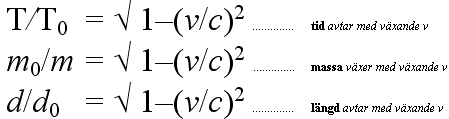NUKLIDBILDNINGARNA eller UNIVERSUMS FÖDELSE ENLIGT TNED 2007XI27 a BellDHARMA production | Senast uppdaterade version: 2023-12-11 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Nuklidbildningarna, förklaring | FUSIONSBILDNINGEN GENOM EXEMPEL | DIVERGENSTÄNDNINGEN | FUSIONSRINGEN | DIAKVADRATEN

— TEORIERNA I MODERN AKADEMI börjar »OK» med BigBang — men missar sedan centralformen genom att INTE utgå ifrån det maximalt täta tillståndet — därför att atomkärnans härledning — TNED — saknas i modern akademi: atomkärnans inkompressibilitet -- max materietäthet är 1,81 T17 KG/M³ ingår inte i modern teori.

— Det gör inte heller PLANCKEKVIVALENTERNA och Ljusets Gravitella Beroende: modern akademi missar avgörande detaljer i naturbeskrivningen. Se även UNIVERSUMS KRITISKA TÄTHET — det avgörande argumentet för Universums Historia enligt relaterad fysik — TNED: universum KAN FÖRSTÅS, BESKRIVAS, FÖRKLARAS OCH HÄRLEDAS I DETALJ SOM en evigt pulserande kosmisk central cell enligt K-cellens värmefysik.

— SE UTFÖRLIGT FRÅN Den allmänna kosmiska masskroppen — med K-cellens allmänna tillståndslag: beviset för att energiräkningen håller.

Se även GcQ-teoremet: modern akademi kan inte härleda elektriska laddningen: Q.

Efter sammanställningar från 2002

Grundformerna, om ej redan bekant:

Planckekvivalenterna — ^Qm betecknar elektronmassan generellt, se även i elektronens massökning

f₀/f = Ö 1–(u/c)² ............. PLANCKENERGINS FREKVENSEKVIVALENT i ^Qm ändras med växande u

m₀/m = Ö 1–(u/c)² .............. PLANCKENERGINS MASSEKVIVALENT i ^Qm ändras med växande u

l/l₀ = Ö 1–(u/c)² ............. PLANCKENERGINS VÅGLÄNGDSEKVIVALENT i ^Qm ändras med växande u

INTE

relativitetsteorin

T/T₀ = Ö 1–(v/c)² .............. tid avtar med växande v

m₀/m = Ö 1–(v/c)² .............. massa växer med växande v

d/d₀ = Ö 1–(v/c)² .............. längd avtar med växande v

förklarar fysiken.

Med fortsättning från resultaten i K-cellens Värmefysik

UNIVERSUMS FÖDELSE

Det som avgör den här framställningen ligger helt på PLANCKEKVIVALENTERNAs vågskål: tidsdilationens matematiska fysik enligt relativitetsteorin har ingen fysikalisk grund: DOPPLEREFFEKTENs matematiska fysik för galaxernas rödförskjutning visar i realiteten märkbart mindre värden än de man får via relativitetsteorins samband (se v+ic-felet). Därmed kan direkta beräkningar göras med utgångspunkt från observationella grunddata. Se vidare i resultatredovisningen i K-cellens Värmefysik med tillhörande grundreferenser, denna framställning bygger på dessa.

K-cellens expansion

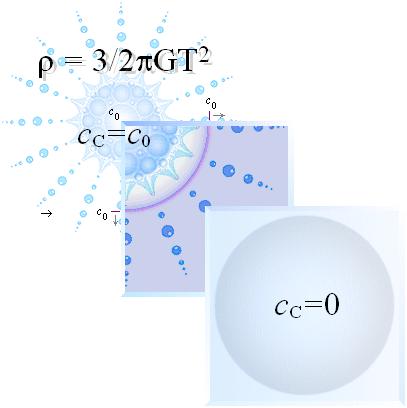
Efter K-cellens detonation expanderar K-cellen idealt mot avtagande täthet enligt EXPANSIONSSAMBANDET r=3/(2pGT²) med initiell hög hastighet som snabbt avtar på grund av den starka g-kraftens inverkan. Expansionsfysikens matematik beskrivs utförligt från K-CELLENS EXPANSIONSFYSIK.

Nolldivergenszonen ([c=0]|®) sveper i följd av K-cellens expansiva g-fysik via ljusets g-beroende utåt K-cellen med konstant hastighet (c₀). Därmed påtriggas successivt K-cellen regioner med positiv divergens:

Divergenständning (tON) betyder att lokalerna återinträder sin normala elektromagnetiskt aktiva dynamik som följd av att nolldivergenszonen med sin (c=0)-zon sveper över området i K-cellens expansion (se illustrationen nedan): universum “tänder”.

Utöver den här berörda rent expansiva aspekten, har förloppet i K-cellens expansiva fas ingen koppling till beskrivningar av typen “universums skapelse” i konventionell kosmologisk teori. Förhållandena enligt TNED är helt annorlunda — samt exakt beskrivbara i detalj, för noggrann jämförelse.

Spåren efter divergenständningarna ger starka gammaskurar med likformig fördelning relativt vår förhållandevis centrala position, som det får förstås. Se vidare bekräftelse i CGRO.

J-kropp — se även Hur J-kroppen identifieras

K-cellens detonation avdelar, genom expansionens avtagande täthet, neutronkroppar (J-kroppar) i negativ divergens

— ideala kroppssfärer med maximal täthet 1,82 T17 KG/M³ bestående av maximalt tätt liggande neutroner i lokaler med motsvarande noll ljushastighet c=0.

— J-kropparnas övergång i positiva divergenslokaler (c>0) genom divergenständningen påverkar varje J-kropp liknande K-cellens detonation, men i miniatyr och med mindre dynamik. J-kropparnas moderkropp är ytterst hela K-cellen vid detonationsögonblicket, och som sedan avdelas i allt mindre delkroppar (J-moderkroppar som avdelar mindre J-kroppar).

Massexakt orienterande delningsbild med beaktande av resultaten från K-CELLENS VÄRMEFYSIK:

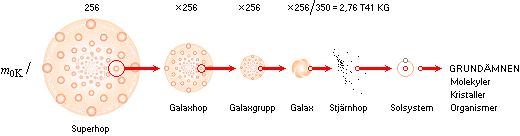
Med en avrundad delning på 1/350 mellan totalmassan bakom värmeeffektens utveckling och den synliga taget som ett medelvärde för hela K-cellen, kan en delningsform med 16×16 kroppar i varje idealt likadan successivt mindre delkropp ner till galaxnivån beskriva hela K-cellens uppdelning med basen 256 enligt

4,16 T53 KG / (256 × 256 × 256 × 256) / 350 = 2,76735 T41 KG

Vintergatans synliga massa är ca 1,4 T11 Solmassor [BAs313 Tab.15.2] eller 2,7846 T41 KG vilket stämmer ungefärligt med ovanstående enklare delningsform. Man får då en grovt generaliserande bild som indelar K-cellens uppdelning i fyra fraktalgrupper: Superhopar med drygt 16 miljoner Vintergatsgalaxer i varje, Galaxhopar med drygt 65 000 Vintergatsgalaxer i varje, Galaxgrupper med ca 250 Vintergatsgalaxer i varje, och slutligen Vintergatsgalaxen som masspreferens. Eftersom galaxbildningarna ingalunda är likartade varken till massa eller typ, och dessutom galaxerna i allmänhet utspridda över stora områden med mindre gruppbildningar från par till flera, blir denna indelning inte helt rättvis mot den verkliga fördelningsbilden — men ger ändå en relativ orientering.

Det är också, ungefärligen, efter denna modell den konventionella kosmologin beskriver den allmänna kosmiska massfördelningen — inkluderat vissa inbördes meningsskiljaktigheter beträffande superhoparnas vara eller icke vara [ref. EST-7s536sp2n Galaxy, Clustering].

Solsystemets Uppkomst enligt TNED

Solsystemets uppkomst

J-kropparna avdelas genom divergenständning (detonation [hydrodynamik]) från sina moderkroppar efter ett RESONANSVILLKOR (resonansserie) av formen (gäller för Solsystemet)

Jordens Tredje Ekvation

d = F3a₀2^n–1+d₀

J

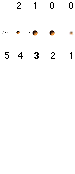
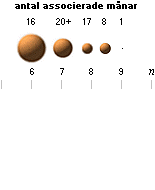
Storleken av Solsystemets kroppar på gemensam täthet.

1 Merkurius, 2 Venus, 3 Jorden-Månen, 4 Mars, 5 Asteroiderna, 6 Jupiter, 7 Saturnus, 8 Uranus-Neptunus, 9 Pluto, …

Serien grundlägger SOLSYSTEMET med referens till en optimal fusionsgränsmassa m_0JSUB som enhetsbildare. Serien är av samma grundform som den redan empiriskt kända TITIUS TALSERIE.

Solsystemets uppkomst · härledning

SOLSYSTEMETS UPPKOMST GENOM K-CELLENS EXPANSION

HÄRLEDNING

inledande beskrivning

Som en direkt konsekvens av Jordens första ekvation, termogravitella jämviktstrycket, följer definitionen av den gränsmassa

[m_JSUB=r_max^–2(3/4p)^–1(k_J/d)³] som i försorg av atomkärnans allmänna fysik ENLIGT TNED bildar exakt balans mellan expansionstryck och g-tryck i momentet som följer alldeles strax efter J-kroppens divergenständning. Denna gränsmassa 6,8 T24 KG utpekar entydigt, utan konkurrens, Jordlokalen. Med denna preferens klarlagd — i ljuset av K-cellens formfysik — kan så härledningen ges till Jordens tredje ekvation, d=F(3/4)a₁2^n–2+d₀ som beskriver en resonansserie i det på hydrodynamikens elementära beskrivna grunder baserade Solsystemets bildning. Jorden och dess koppling till den tunga centralkroppen Solen bildar här en universell enhetspreferens (1). Vi studerar hur.

PROPORTIONERNA mellan Solsystemets kroppar visas i illustrationen nedan, alla omräknade på samma täthet med nuvarande massor:

En moderkropp med impulsmoment mvr avyttrar via divergenständningsexpansion en sträng av J-kroppar. Dessa sprids relativt v med skilda hastigheter i en spiralarm. Det finns alltid en största J-kropp i strängen, och det blir denna som genom sin lokalt dominanta gravitation kommer att samla de mindre J-kropparna i strängen till sig. Vi kan enkelt kontrollera momentens riktningar för givet v, och vi finner att vårt Solsystem uppvisar samma principform. Alla planeter roterar åt samma håll kring Solen.

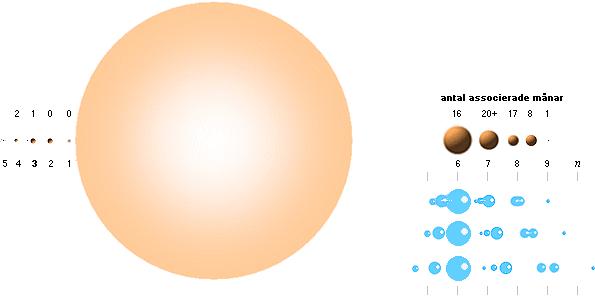
Jordens tredje ekvation beskriver RESONANSSERIEN i Expansionsdistanserna (d) mellan kallplasmakropparna vid avyttringen från moderkroppen

(urspr. Vintergatans centrum, J_V, i sin tur avdelad)

med referens till den tunga centralkropp (Solen, J_s) som innehar tyngdpunkten för hela seriens delkroppar

d = F3a₀2^n–1 + d₀ ..................................... Jordens tredje ekvation

Planeternas medelavstånd från Solen — d anger Titius talserie

n	1	2	3	4	5	6	7	8	9	…
d	0,4	0,7	1	1,6	2,8	5,2	10	19,6	38,8	…
	Mer	Ven	Jor	Mar	Ast CERES	Jup	Sat	U-N	Plu	…
AU	0,39	0,72	1	1,52	2,77	5,20	9,54	19,18URA	39,44	…
								30,06NEP

Noteringar till tabellen:

d enligt Titius talserie, a₀=5/100 ; d₀=4/10

AU, empiriskt observerade värden (1AU = 1,496 T11 M, i viss litteratur stundtals 1,495 T11 M)

Sambandet för d innefattar inte (heltaliga) n-värden för sammansatta J-kroppar som enligt gränsvillkor delas i efterhand — som i fallet Uranus-Neptunus. Vi studerar detta.

Härledningen

Härledningen

Vi betraktar strängen av J-kroppar som avges i ett avsnitt från en större moderkropp under K-cellens expansion.

STÖRSTA J-KROPPEN (J_s) utövar genom sin dominanta gravitation inflytande över närliggande J-kroppar.

Avdelas enhetsvolymen V successivt i 2ⁿ J-kroppar (enklaste elementära harmoniska [fraktala] serieformen) med referens till J_s, förhåller sig V till 2ⁿ som expansionens magnitud (a) förhåller sig till expansionsdistanserna (s) — om och endast då gravitationen separerar kropparna absolut. Det vill säga; de mindre kropparna (stort n) distansexpanderar snabbare än de större (litet n). Gränsfall (Jämför Uranus-Neptunus, n=8) med närliggande kroppar som (av olika skäl) har separeringskraft men först så småningom separerar ges initiellt samma n. Titius talserie blir på detta sätt ingen direkt slutlig planetdatabeskrivning utan istället en primär form som föregår ett senare skede.

Titius talserie är tydligen en primärform som föregår ett senare skede i planetbildningen

TITIUS TALSERIE — dess fysikaliska grund

Expansionens magnitud a kan i varje tidpunkt återföras på enhetssfärens cirkulära omfång genom en expansionskonstant a₀ enligt a=a₀2p; För att åstadkomma expansion med växande r måste också expansionskonstanten växa. a₀ bestäms alltså av förhållandena i den moderkropp som bär ansvaret för avyttringarna

(större omkrets = större muskelmassa = större expansionskraft). Expansionen s med början från d₀ utanför J_s-origo (n=1 är reserverad för d₀) bildar expansionsdistansen

s+d₀=d. Med r=1 för enhetsvolymens homogena materialsfär V ges

r=1 ; V=4p/3 ; V/2ⁿ=1/(s/a)=a/s ; s+d₀=d ; s=d–d₀=a2ⁿ/V ; d = a2ⁿ/V + d₀ ; a = a₀2p ;

d = a₀2p2ⁿ/(4p/3) + d₀ = 3a₀2^n–1 + d₀

Med d₀ som första distansexpansionen måste faktorn 3a₀ nollställas i fallet n=1. Vi insätter F som sekvensdelande heltalsselektor

(funktionen är samma som IF n<1 THEN d:=d₀) enligt

REF = 2

P = (absn+n)/2/2–1

F = INT[1–(absP – P)/2] ................... n|F= … ,₅1,₄1,₃1,₂1,₁0,₀0,_–10,…,_–n0 ;

Resultat:

JORDENS TREDJE EKVATION

d = F3a₀2^n–1 + d₀ = F(3/4)a₁2^n–2+d₀ ....... allmänna sambandet för Solsystemens planetdistanser

DISTANSBILDNINGEN för vårt planetkomplex satisfieras då enligt observationer i heltalsform av

a₀ = 1/20 = 0,05

d₀ = 2/5 = 0,4

Serieformen blir identisk med Titius talserie (från 1770).

Sambandet för d innefattar inte (heltaliga) n-värden för sammansatta J-kroppar som enligt gränsvillkor delas i efterhand (som i fallet Uranus-Neptunus).

Med a₀=5/100 och d₀=4/10 ges talserien

(4 + {0, 3, 6, 12, 24, 48, 96, 192, 384, …})/10 . Talserien anges nedan i tabellkolumnen d_TIT.

Historia

SERIEFORMEN (3·2^n–2+4)/10 i koppling till planeterna (men inte kopplingen till fysiken) är känd från historien som TITIUS TALSERIE (från 1770, BAs162sp1m).

Titius analogi gavs spridning från 1772 genom astronomen Johann Bode, serien refereras numera som Titius-Bodes lag. Den anges vanligen i populärlitteraturen som

talserien 0, 3, 6, 12, 24, 48, 96, 192 och 384. En successiv fördubbling från 3 alltså. Med +4 till summan och efter division med 10 ges tabellvärdena nedan angivna d_TIT med avståndet Jorden-Solen som enhet.

Titius överraskande noggranna talserie SOM FÖREGIVNA — EXAKTA — DATA PÅ SOLSYSTEMET är ofullständig: Neptunus fattas.

Gängse faktaverk redovisar Titius talserie — men avfärdar den som ”en ren slump” (!).

d nedan i AU (Astronomiska Enheter) anger nuvarande avstånden till Solen, 1 AU (Astronomical Unit) = 1,495 T11 M (mera korrekt avrundat 1,496 T11 M).

Himlakropparnas omloppshastigheter och medelavstånd från Solen

	himlakropp	siderisk omloppstid	medelhastighet	rot	d	(F2n–2·3+4)/10
		dygn omloppstid	KM/S banhast.	**	AU	dTIT	n ***
	Merkurius	87,969	47,89		0,3871	0,4	1
	Venus	224,701	35,03		0,7233	0,7	2
	Jorden-Månen	365,256	29,79		1	1	3
	Mars	686,980	24,13		1,5237	1,6	4
..·.	Asteroidbälte	508-2042	24,4-17,1*		1,3-3,2	2,8	5
	Jupiter	4 332,589	13,06		5,2028	5,2	6
	Saturnus	10 759,22	9,64		9,5388	10	7
	Uranus	30 685,4	6,81		19,1819	19,6	8
	Neptunus	60 189	5,43		30,0578	—	—
.	Pluto	90 465	4,74		39,44	38,8	9

Noteringar till tabellen:

* Asteroidbältet, = 2p(1,3-3,2 AU)/1000×24×3600(508-2042), 1AU=1,495 T11 M

** banrotation, sett från JordNordpolen (eg. norra ekliptikan), ENCARTA 99 Solar System

*** se beskrivning nedan

TVILLINGARNA

Varför fattas Neptunus i Titius talserie?

EXPANSIONSFYSIKENS FÖRKLARING TILL VARFÖR NEPTUNUS FATTAS I TALSERIEN

Om det hade varit ett rätt av 10 hade ordet slump helt säkert varit berättigat. Men 9 rätt av 10 är ingen slump, ingen tillfällighet. Det är högsta betyg, definitivt klass A.

Men varför stämmer inte serien med Neptunus?

Därför att Titius talserie tydligen inte beskriver planetsystemet explicit. Planetsystemet är, tydligen, en senare historia. Titius talserie är uppenbarligen bara en variant på ett otal andra möjliga varianter i planetsystemens distansbildningar — beroende på omständigheter. Låt oss se hur.

Titta först på avståndsskalorna:

FÖRST ser man alldeles tydligt att Titius talserie bildar en jämn expansion. Den verkliga ser ”lite kantig” ut och associerar till ”någon historia emellan”.

Alldeles tydligt handlar det avvikande avsnittet om Uranus-Neptunus.

Om vi tittar på kroppskomplexet Uranus-Neptunus, deras verkliga typform

utpekar-kräver Titius talserie snarare typformen

Vilket vill säga, en gemensam kropp efter Saturnus. Plasmahoparnas avdelning från en moderkropp J₀ skulle också regelrätt, frånsett mellanliggande mindre delkroppar som (alltid) följer efter en större, följa typformen

med (strängt) avtagande J-radier med växande expansion från J₀-ytan. I summa sagt och med den extraordinära homogenitet som kallplasmat bör uppvisa som material, finns över huvud taget ingen anledning att förmoda eller postulera andra ordningar än just sådana som strängt följer enkla harmoniska talserier. Typ Titius.

Och alltså?

OM TITIUS TALSERIE ansluter till resonansfysiken, tar den ingen hänsyn till hur J-kropparna formerar sig efter avdelning från moderkroppen.

Det synes inte omöjligt att Uranus-Neptunus (No8), i K-teorins ljus med de avdelade J-kropparna, från början varit en tvillingkropp.

Illustrationen nedan visar principen hur två kroppar, fördröjt efter avyttringen från den större moderkroppen, kan bildas ur en.

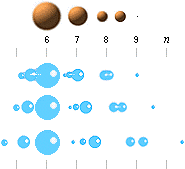
Moderkroppen J₀ befinner sig under expansion. OM expansionen LOKALT bara överväger litet mot den ömsesidiga gravitationen mellan två tänkta J-kroppar, en litet större inåt och en litet mindre utåt, kommer separationen mellan kropparna att ske långsamt och de kan under tiden utjämna varandras masskillnader. När kropparna sedan separerar blir de nära lika stora — precis som Uranus-Neptunus.

LIKHETEN mellan Uranus och Neptunus är också omvittnad. Jämför

”Solsystemet har inga planeter som är helt lika varandra, men Uranus och Neptunus liknar varandra mer än något annat par.”

”Faktiskt är de här båda planeterna så lika varandra att man med fördel kan behandla dem samtidigt”.

BONNIERS ASTRONOMI 1978s224sp1ö

Med samma täthet skiljer sig kroppssfärerna Uranus-Neptunus efter de olika nuvarande massorna med 100:95. Den verkliga radieskillnaden är 100:93.

(Enligt K-teorin betyder det att grundämnessammansättningen i dessa planeter är nära identisk).

En enkel talserie kan inte uttrycka en tvillingkropp (som längre fram kommer att delas i två) vid J-avyttringen och dess ekvivalent på annat sätt än genom att se en J-kropp på ett ställe. Initiellt för ett sådant gränspar gäller alltså samma n. Om kropparna sedan delas gör de det säkert i nära ekvivalenta delar med liten inbördes skillnad eftersom separationen alltså sker långsammare än för övriga J-kroppar.

Med ovanstående resonansform och dess ursprung i Vintergatans moderkroppar bör vi, uppenbarligen, inte se saken på annat sätt än att det finns många system i Vintergatan liknande Solsystemet — och av allt att döma förmodligen också så i närbelägna galaxer. Någon annan ordning vore verkligen underlig eftersom villkoret ovan är ett reguljärt fysikaliskt resonansvillkor i en del av en större kropp: den bör uppvisa många liknande strängar. Vi kan (därför) förmoda att det finns ett bälte kring Vintergatans centrum, liknande vårt eget Solsystem, och på ungefär samma avstånd från centrum som vi själva. Eftersom tidslinjerna är helt analoga (ekvivalenta), i varje fall för Vintergatans del, har vi heller inget annat att förvänta med Jordkroppen som preferens (se Jordens Andra Ekvation) — och därmed förmodan att evolutionen fungerar genomgående efter samma principer — än att de mänskliga civilisationerna där ser ut som de gör här — med endast smärre skillnader. Möjligheten att skapa kontakt mellan dessa olika världar är dock, som vi har förstått, helt utesluten på grund av det stora avståndet. Vi kommer att dö ihjäl många gånger om innan vi ens har hunnit en bråkdel av vägen — även MED ljushastighet.

Exotermiska kärnreaktionslagen

Grundämnesbildningen — från KÄRNREAKTIONSLAGEN

EXOTERMISKA KÄRNREAKTIONSLAGEN

HÄRLEDNINGEN VISAS I SEPARAT DOKUMENT med UTFÖRLIGA EXEMPEL tillsammans med länk till kalkylkort

Tillståndet i varje J-kropp — från tidpunkten för divergenständning — motsvarar de ideala förhållanden som utpekas av (utförlig härledning i) EXOTERMISKA KÄRNREAKTIONSLAGEN

IF m_DK2 + (m_DK1–m_DK)A_K1/A_K2 < m_DK THEN OK ...................... exotermiska fusionslagen

(även exotermiska fusionslagen | fusionsekvationen) som utgår ifrån

maximal täthet — atomkärna mot atomkärna enligt TNED 1,82 T17 KG/M³ för neutron-J-sfärerna —

som GRUNDÄMNESBILDNINGENS GRUNDVAL

— utan yttre störande moment vilket garanterar atomen nollbalans enligt härledningarna från Planckringen.

Efter divergenständning ges en kort initierande period motsvarande neutronens sönderfall där kärnorna formateras och ordnas med hänsyn till begreppet neutronkvot — från J-kroppens centrum (garanterad neutronkvot noll genom lokala tyngdpunkten c₀) till J-kroppens rand (neutronkvot 1 [kemiska randzonen]). Neutronkvoten är samma som motsvarande neutrontal i en given nuklid (A/[A–Z]).

Exempel ENLIGT TNED på beräkningar av olika atombildningar med olika neutronkvoter ges längre ner i beskrivningen.

Se vidare från FUSIONSBILDNINGEN GENOM EXEMPEL.

K-cellens expansionsfysik

2007XII25

Se även J-KROPPARNAS EXPANSION GENOM

K-CELLENS EXPANSIONSFYSIK

I den totala g-energin E_G=Gm²/r som K-cellen utvecklar i ekvivalens med rörelseenergin E_kin=mv²/2 läggs inga som helst aspekter på de sekundära expansioner som utvecklas för J-kropparna då de nås av positiv divergens via zonsvepet r_0c. Som antyds i högra delen av ovanstående förenklade illustration tar (nämligen) de sekundära expansionerna (idealt) ut varandra på gemensam tyngdpunkt. Vilket vill säga: vi förutsätter att en lika stor del som expanderar inåt mot K-cellens centrum och som ger en totalt sett reducerad totalenergi som följd, expanderar utåt med motsvarande högre totalenergi så att skillnaden i netto kvarstår på noll med referens till varje enskild J-kropp. Vi bör ha denna detalj klar för oss i beskrivningen-granskningen av J-kropparnas expansion, så att hela energiräkningen för K-cellen INTE (plötsligt) börjar gäcka oss med misstankar om att Ingenjören bakom hela historien i själva verket har räknat fel på energin! Räkningen stämmer — med J-kropparnas specifika expansion på samma matematiska expansionsfysik inberäknad.

NOTERA VÄL ATT HELA K-CELLENS HÄRLEDANDE MATEMATISKA FYSIK HELT bygger på resultaten från HÄRLEDNINGEN TILL DEN ELEKTRISKA LADDNINGEN och vilken del inte finns med i den moderna akademins lärosystem, varför heller inte K-cellens allmänna värmefysik gör det. Se vidare utförligt från ELEKTRISKA LADDNINGEN med det resulterande GcQ-teoremet och PLANCKEKVIVALENTERNA som klargör, beskriver och förklarar detaljerna i korsreferens mot den moderna akademins föreställningssätt.

Expansionssambandet

Från K-CELLENS EXPANSIONSFYSIK

EXPANSIONSSAMBANDET

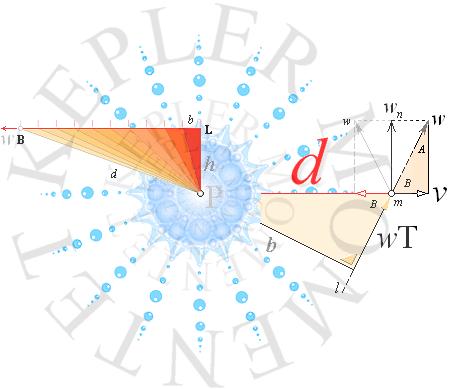
När den radiella accelerationen (a=v₀/T) i en expanderande kropp precis uppvägs av accelerationen (v²/d) i kroppens sammandragande gravitationskraft, råder exakt ideal jämvikt mellan expansion och gravitation. Vi känner denna jämvikt från den elementära matematiska fysiken genom ytmomentet (i viss litteratur benämnd ytlagen) eller Keplermomentet (K, se nedan). Det grundgeometriska konceptet visas i ovanstående kollageillustration med följande beskrivning.

K = A/T

Keplermomentet utsäger:

ORTSVEKTORN d översveper lika stora ytor på lika långa tider — så länge w ändras av krafter verksamma utmed d. Villkoret med tillståndsändringar utmed d benämns generellt centralkraftsverkan. Den är av särskilt grundläggande betydelse för atomfysiken.

K beskriver centralkraftsverkan explicit för centrifugalaccelerationen (v utåt) och centripetalaccelerationen (v inåt) genom räta vinkelns relationer enligt (se även figuren ovan)

v/w=wT/d som ger v/T=w²/d.

Ekvivalenterna definierar explicit jämvikten mellan en linjärt accelererad expansion (a=v/T) och centripetalaccelerationen (a=w²/d) som grundlägger gravitationens definition.

Den cirkulära rotationen på en fast radie beskriver egentligen en centripetalacceleration, men vi kallar (oftast) kraften för en centrifugalkraft och därmed (oegentligt) cirkuläraccelerationen för en centrifugalacceleration.

En mera utförlig beskrivning av Keplermomentet ges i KEPLERS YTMOMENT (appendix till GRUNDÄMNENAS PERIODISKA SYSTEM Genom Keplerresonanserna).

expansionstiden kan utläsas ur kroppens täthet

EXPANSIONSSAMBANDET

r = 3/(2pGT²) ................... expansionssambandet

Härledning

Rörelseenergin m₂v²/2 i ekvivalens med g-energin Gm₂²/r ger ekvivalenterna v²/2=w²=Gm₂/r som ger sambandet för allmänna expansionshastigheten

v = wÖ2 ................................................ allmänna expansionshastigheten

Första och sista leden ger expansionshastigheten genom centralmassan (samma som flykthastigheten)

v = Ö 2Gm₂/r ...................................... momentanvärdet v via sfären med radien r som innesluter massan m₂

[EXPANSIONSHASTIGHETEN för given centralmassa har funktionsformen y=Ök/x. Utan energiförluster, närmar sig kurvskaran obegränsat noll, dvs., K-cellen stannar aldrig helt och vänder. I det praktiska fallet vänder K-cellen tillbaka enligt allmänna tillståndslagen där förlusterna ges av värmebildningen (m®g) samt inre omfördelningar som bromsar den ideala förlustfria expansionen, funktionen blir då snarare y=k cotan (x/a) som ger mera rättvisa åt det praktiska fallet.

Alternativ lösning med Solens hjälp: K-cellens effektcykel Väte®Helium kan återföras på Solens energiproduktion som jämförande exempel. Solens massiva effektförlust (m®g) är ca 0,7% av hela den primära Solmassan under hela Solens ideala brinntid 100% Väte till 100% Helium med övriga ämnen bortsett ifrån. Vi kan alltså säga att K-cellens annars idealt oändliga expansion avstannar på de felande 0,7% Helium, alltså vid 99,3% He. Genom kalkylkortet för K-cellens värmefysik, värdet 99,3% Helium, finner man då att K-cellens halva period blir 20,6294(16,3 T9 år) = 336,25922 T9 år (T för 10⁺). Därefter vänder materialet tillbaka igen med ny påfyllning från den övergripande c0-kroppen].

Expansionstiden. Medeltätheten r=3m₂/4pr³ ger via m₂/r=4pr²r/3 som ger v=rÖ(8pGr/3) med v/r=Ö(8pGr/3). Den linjära accelerationens generella v/T med T=2r/v ger

T = 2Ö(3/8pGr) .................... = Ö(3/2pGr) ......................... expansionstiden ur tätheten

r = 3/(2pGT²) ........................................................................ tätheten ur expansionstiden, expansionssambandet

T = Ö(2r³/Gm₂) ...................................................................... expansionstiden ur radien med given centralmassa

Expansionstiden T kan följaktligen utläsas ur kroppens täthet — förutsatt att expansionen grundas på den med kroppen associerade g-energin, och endast då.

offsetvärdet för T

EXPLICIT FÖR K-CELLENS EXPANSION

Offsetvärdet för T

ges I RELATERAD FYSIK via ett r_max=1,82 T17 KG/M³ som ger T₀=T_DET=1,98322 t4 S @ 200µS. r_max definieras av atomkärnans geometri via TNED.

Expansionshastigheten genom tätheten. EKVIVALENTERNA T=2r/v = T=2Ö(3/8pGr) ger r/v=Ö(3/8pGr) som ger expansionshastigheten

v = rÖ 8pGr/3 ..................... momentanvärdena v via inre radierna r för momentanModerSfären med medeltätheten r

Eftersom [se härledningen längre ner Nolldivergenszonens radie ur tätheten] r_0c=c₀Ö(3/2pGr) får man expansionshastigheten för sfären ovan via r=r_0c som ger

v = c₀Ö(3/2pGr) · Ö 8pGr/3 = 2c₀ ................ momentana expansionshastigheten då delsfären skärs av nollzonen

TIDsfären. Om tätheten för K-sfären med massan m avtar med tiden enligt r=3/(2pGT²)=m₂V=3m₂/4pr³ är det klart att sfärradien efter T fås ur r³=GT²m₂/2 enligt

r = (T²Gm₂/2)^1/3 ................. sfärradien ur tiden med given centralmassa

TIDSFÄREN anger den tillryggalagda distansen (s, radien) för varje given massa (m₂), analogt expanderande partialsfär i K-cellen. Tillsammans med expansionshastigheten genom centralmassan beskriver tidsfären K-cellens expansion fullständigt och i detalj.

Hur tidsfären kopplar till K-cellens specifika zoner beskrivs i DIVERGENSENS EXPANSIVA G-BEROENDE.

Historia — Keplers tredje lag. Genom ovanstående ser vi att r³/T²=Gm₂/2. Samma första del r³/T²=k fast i ett annat sammanhang förknippas med

Keplers tredje lag:

Från kraftlagen F=ma=må=v²/r, med beteckningen å explicit för centrifugalaccelerationen, får man via v=2pr/T=rw sambandet å=v²/r=rw²=r(2p/T)². Eftersom det också gäller att F=må=r^–2Gm₂m [Se gravitationslagen], får man mr(2p/T)²=r^–2Gm₂m varav r³/T²=(2p)^–2Gm₂. Med Solmassan för m₂ ges

(2p)^–2Gm₂@3,36 T18 M³S^–2. Det var f.ö. denna sambandsform r³/T² som Johannes Kepler (1571-1630) upptäckte som grundval för Solsystemets planetrörelser med r för medelavståndet Solen-planeten och T omloppstiden. Relationen r³/T²=k kallas Keplers tredje lag. Se även Keplermomentet (Keplers andra lag).

expansionstiden kan förkortas om kroppens täthet ändras

OM expansionen förlöper på sådant sätt att vissa delar i kroppen skjuts in mot centrum snarare än ut mot periferin, gäller inte balansen exakt. I sådana fall blir expansionsenergin totalt sett mindre än den initiella g-energin (r ökar in mot centrum). Den successiva ökningen i den inre tätheten får därmed en bromsande inverkan på expansionen varigenom T för givet r-medelvärde något förkortas (dvs., kroppens expansionstid avkortas). Om reduktionen i T är marginell (vilket den är i K-cellen) kan den bortses ifrån i det allmänna fallet vilket förenklar beräkningarna.

expansionssambandet alternativt

EXPANSIONSKOPPLINGEN T²=3/2pGr fås ekvivalent genom ett annat, mera uttömmande och genomgripande resonemang som ansluter till den tidigare omnämnda friställningen av ljusets fysik från kinetiken (se ljusets friställning från kinetiken, Ljusfrihetssatsen).

Resonemanget kan inte föras i den moderna akademins lärosystem — därför att man inte beaktar bevarandet av naturkonstanten c₀ oberoende av gravitationens inverkan, se ljusets gravitella beroende — men man bör känna till det, och det är som följer. (Se även vidare i DEEP från GRIP).

Gravitationsenergin E_G=Gm₂²/r=m₂w² — idealt ekvivalent med expansionens rörelseenergi E_kin=m₂v²/2 — kräver en fördubbling av centralmassan för att eliminera kinetikens inverkan på divergensen som inte påverkas av mekanikens tröghet [se Exempel i LJUSETS GRAVITELLA AVBÖJNING]. Det ger

2E_G=2E_kin med 2m₂w²=m₂v² som ger 2w²=v², vilket är samma som i föregående initiering.

v² — INTE w² — är gravitationspotentialens analoga komponent mot divergenspotentialen c² under K-cellens expansion så att man får differentialekvivalenterna enligt

dmv²+dmc²=dmc₀² med potentialerna v²+c²=c₀². Därmed bevaras toppdivergensen (c₀, se divergensen) konstant oberoende av expansionen. Ledet används (här) för att utveckla sambandet för ljushastighetens variation 0 till c₀ genom K-cellens expansion. Elimineringen av trögheten från divergensen ansluter till samma komplex som beskriver divergensvägarna (ljuskrökningarna) under gravitationens inverkan [Exempel i LJUSETS GRAVITELLA AVBÖJNING]. Om man försöker utveckla sambanden alternativt direkt efter modellen w²+c²=c₀² får man (alltså) galna resultat.

NOLLDIVERGENSZONENS RADIE UR TÄTHETEN

Nolldivergenszonens radie ur tätheten r

Vid c=0 gäller från ljusets g-beroende tydligen

0 = (1/2)[c₀ – Ö |–c₀²+4w² | ] ;

0 = c₀ – Ö |–c₀²+4w² | ;

–c₀²+4w² = c₀² ;

4w² = 2c₀² ;

2w² = c₀² = 2Gm₂/r_c0 = 2r_c0²(4pGr/3) = r_c0²(8pGr/3) ;

w/c₀ = Ö1/2 ; .............................. c=0

r_c0² = c₀²(3/8pGr)

GRUNDÄMNESBILDNINGEN —

grundämnesbildningen

Den Primära Grundämnesbildningen i Himlakropparna

GRUNDÄMNESBILDNINGEN

Enligt TNED bildas alla tyngre atomer från neutronen (se från PLANCKRINGEN) med noll atomär massdefekt. Neutronens naturliga sönderfall till Väteatom börjar med divergenständningen för en given J-kropp som avdelas genom K-cellens expansion. Divergenständningen medför att vätekärnorna kan bilda fusionsringar som därmed grundlägger hela grundämnesbildningen enligt TNED. Varje grundämnesatom kan då återföras på ett motsvarande antal primära neutronindivider tillsammans med vätekärnor eller protoner (och därmed en karaktäristisk neutronkvot) motsvarande termen masstal (A). Olika neutronkvoter med samma A kan bilda en och samma grundämnesnuklid på flera olika sätt, alltså med olika kombinationer av vätekärnor och neutroner. Masstalet anger alltså antalet grundindivider (neutroner-protoner) som den aktuella grundämnesatomen är bildad från.

TILLSTÅNDET FÖRE DIVERGENSTÄNDNING

Tillståndet i en J-kropp före divergenständning — tillfället då J-kroppens nås av den expanderande K-cellens nolldivergenszon som från detonationstillfället drar iväg utåt K-cellen med konstant hastighet c₀ och som aktiverar eller “tänder” de olika lokala regionerna elektromagnetiskt — betingas av olika närhetsgrader mellan atomkärnorna beroende på J-kroppens massa, analogt g-trycket, och hur atomkärnorna kommer att formeras med hänsyn till neutronsönderfallet omedelbart efter divergenständningen med hänsyn till den då aktiverade Coulombkraften som strävar att separera atomkärnorna från varandra om de befinner sig utanför varandras nuklidbarriärer.

Eftersom (nämligen) balansräkningen för atomkärnans del blir något olika beroende på om kärnorna betraktas med utgångspunkt från att de ligger innanför varandras nuklidbarriärer (Coulombkraften gäller inte på något enkelt sätt, växelverkan mellan närliggande kärnor [avseende fusionstekniska detaljer] styrs av förhållanden i kärnytorna med hänsyn till kärnbrunnarnas specifika närparametrar), eller om de ligger på eller utanför nuklidbarriären (Coulombrepulsionen kan anses gälla fullt ut), får man två olika klassifikationsgrupper för samtliga himlakroppar — Med en optimal gränsmassa som unik delare, en här benämnd unik fusionsgränsmassa (m_0JSUB). I det första fallet indelas de i stenkroppar (massa mindre än m_0JSUB) och gaskroppar (massa större än m_0JSUB), i det senare fallet i stjärnor (g-trycket större än e-trycket som leder till en fusionsbaserad energiproducent) och planeter (icke aktivt fusionsbaserade himlakroppar).

Fusionsgränsmassan

m_0JSUB definierar substratet för en gränsmassa där g-kraft och Coulombkraft befinner sig i exakt jämvikt.

FUSIONSGRÄNSMASSANS DEFINITION

För utförlig härledning, se Fusionsgränsmassans Härledning

TRE DISTINKTA FALL existerar : motsvarande mJ>m0JSUB, mJ=m0JSUB, och mJ<m0JSUB.

I förenklad typografi betecknas de här [¯GC][GC][GC¯].

C motsvarar kraften från atomkärnans formbevarande styrka i kallplasmat omedelbart föregående divergenständningen och som successivt kommer att ersättas med Coulombkraften då kärnorna kommer in i positiv divergens.

G motsvarar gravitationskraften.

Nuklidseparationen

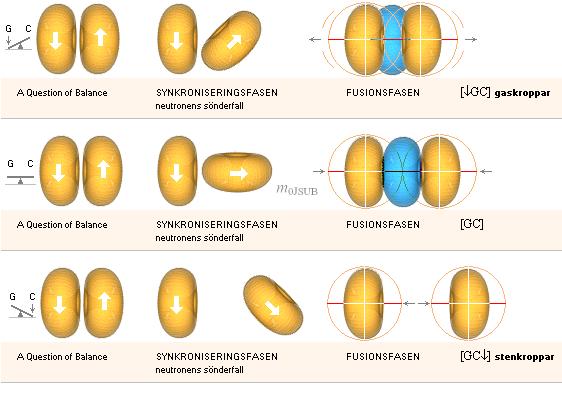
Avståndet mellan atomkärnorna efter divergenständningen avspeglar en motsvarande nuklidseparation (d/r₀) och som grundlägger himlakropparnas allmänna fysik.

Beskrivning

Överst [¯GC]. TUNGA J-KROPPAR har en stark g-kraft som (primärt) överrider Coulombtrycket och därmed reducerar rörelsefriheten fram till tON. En sådan tung J-kropp kan därmed på visst sätt förstås direktkontrahera i följd av deuteriumbildningarna mellan tIGN och tON utan bidrag till ökad rörelsefrihet för närliggande kärnor. Därmed ytterligare en ökning i Coulombkraften, vilket ytterligare kommer att förstärka den J-expansion som utvecklas längre fram i händelseförloppet.

Mitten [GC]. EXAKT BALANSERADE J-KROPPAR definierar substratet för gränsmassan m0JSUB där g-kraft och Coulombkraft befinner sig i exakt jämvikt. Inga extra, yttre moment påförs kärnorna då de vid tON balanserar på varandras nuklidbarriärer, eller redan befinner sig innanför vid ögonblicket omedelbart föregående fusion. Därmed gynnas en optimal fusionsdynamik i enlighet med exotermiska fusionslagen.

Underst [GC¯]. LÄTTARE J-KROPPAR har en svagare g-kraft som inte helt förmår bromsa Coulombtrycket. J-kroppen har i detta fall inte samma möjlighet som i fallen [¯GC][GC] att bevara en maximal täthet. Frånsett deuteriumbildningarna mellan tIGN och tON som även bör förekomma i detta fall, tenderar kärnorna därför att drivas isär av den starkare Coulombkraften. Därmed befinner sig kärnorna utanför varandras nuklidbarriärer vid tON, den optimala synkroniseringen är eliminerad.

Jordens Andra Ekvation -- FUSIONSGRÄNSMASSAN:

Med grund i härledningarna från Planckringen beräknas fusionsgränsmassan enligt TNED helt på kärnfysikalisk bas som

m_0JSUB=r_max^–2(3/4p)^–1(k_J/d)³ = 6,80016 T24 KG

Med en massavyttring på ca 12% från expansionen vid divergenständningen blir det nuvarande Jordmassan 5,975 T24 KG. (Massavyttringen gäller proportionellt för alla himlakroppar genom expansionsfasen direkt efter divergenständning). Närmast alternativa aspirant i Solsystemet skulle vara Venus. Nuvarande Venusmassan är emellertid blott 4,87 T24 KG (82% av Jordmassan), vilket skulle kräva 28% massavyttring. Härav följer: Minsta möjliga massavyttring i samband med himlakroppsbildningen utpekar entydigt Jordkroppen i Solsystemet; Jordkroppen bildar den optimala fysikaliska fusionsgränsmassa som liktydig med den TYPISKA preferenskropp i hela universum som definierar den rent ämnesfysikaliska grundvalen för alla andra himlakroppar. Kort sagt: Jorden gestaltar optimal dynamik.

OBSERVERA DISTANSFELET I NUKLIDSEPARATIONEN d/r₀

Sambanden för gränsmassan m_0JSUB är avpassade för just gränsmassans bestämning — vilket innebär att stora nuklidseparationer (d/r₀) som beskriver allt längre avstånd mellan kärnorna och därmed ger stora d-värden också innehåller ett visst distansfel som växer med avtagande J-massa, analogt växande d-värde. För den överskådliga framställningens del bortses dessa defekter ifrån (men vi bör ha dem i bakhuvudet för att undvika eventuella missförstånd).

Jordens Första Ekvation -- TERMOGRAVITELLA JÄMVIKTSTRYCKET:

Termogravitella jämviktstrycket understryker den ovannämnda fysikaliska (biokemiska) kroppspreferensen för m_0JSUB ytterligare enligt samband och resultat

(1M)2ra=p ..................................... Termogravitella Jämviktstrycket

Uttryckt i absoluta temperaturskalan, T=T₀ · (1M)2rap₀^–1 med T₀=273,15 °K, ges

n°C = (273,15)[(1M)2ra(p₁₀₁₃₂₅)^–1 – 1] med a som tyngdkraftsaccelerationen vid kroppsytan.

Frånsett Solen, finns bara en himlakropp med T över fryspunkten:

Yttemperaturen via termogravitella jämviktstrycket för Solen och planeterna

kroppsyta ±°C från vattnets fryspunkt 273,15 °K

————— —————————————————————————————————————

Solkärnan +532.098,78 ............ r=r_S/4, m=m_S/2, konv. ref.

Solen +1807,89

Merkurius –164,85

Venus –21,94

Jorden +17,26 ..................... den optimerade livskroppen

Månen –243,74

Mars –194,67

Jupiter –108,62

Saturnus –237,45

Uranus –217,52

Neptunus –175,08

Pluto –273,11

r anger kroppens medeltäthet, a anger tyngdkraftsaccelerationen vid ytan. p-ekvivalenten är

p=(3,466 t10 J[M/KG]²)(r⁵m₂)^1/3, litet t för 10^–.

Sambandet kan inte härledas av modern akademi.

Se utförlig härledning i TERMOGRAVITELLA JÄMVIKTSTRYCKET.

RESULTATET utpekar alltså det här — entydigt:

— Jorden.

De facto.

RESONANSSERIEN (den klassiska avståndsskalan kallad Titius Talserie) omnämnd ovan för Solsystemet, understryker ytterligare Jordkroppens fysikaliska ställning som enhetspreferens: avståndet d = F3a₀2^n–1+d₀ ges med referens till avståndet Jorden-Solen som enhet. Se även den teoretiska beräkningen av K-cellens massa ur Solmassan och Neutronmassan.

Jordens Fjärde Ekvation -- GRUNDÄMNESFÖRDELNINGEN:

GRUNDÄMNESFÖRDELNINGEN

DIAKVADRATEN Ø=x^k/x definierar i vilket fall för samtliga himlakroppar genom K-cellens expansion den primära grundämnesfördelningen i alla himlakroppar genom begreppet neutronkvot (Ø). Se TILLSTÅNDET FÖRE DIVERGENSTÄNDNING. Alla atomer byggs upp genom en summa av A (masstalet) NEUTRONER med atomära massdefekter från 0 till max 18 elektronmassor. Se NEUTRONKVADRATEN. Neutronkvoten är för varje atomär nuklid förhållandet mellan den primära neutronmängd och hela masstalet som krävs för att bilda just den nukliden. En och samma nuklid kan ha (många) olika Ø vilket garanterar spridning. Med hänsyn till Ø och hur kropparna uppför sig genom/efter fusionsfasen kan deras primärt givna grundämnesfördelning i princip bestämmas i samtliga fall.

Illustrationerna nedan ger en inledande allmän orientering i begreppen. k-värdet, nuklidseparationskoefficienten, beräknas från kärnfysiken.

Se även DIAKVADRATENS HÄRLEDNING

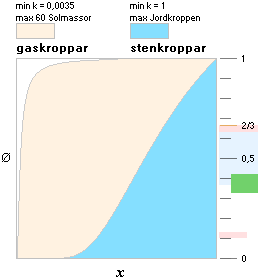
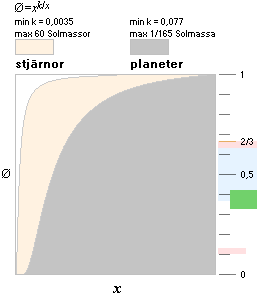
med kärnbrunnens parametrar, primärbildning utan kärnbrunnens parametrar, sekundärbildning

Primärstjärnan

ALLA HIMLAKROPPAR ENLIGT TNED indelas primärt i gaskroppar (k<1) och stenkroppar (k>1) från ett maximalt tätt materietillstånd (se från K-cellens Värmefysik). Gränsen bestäms av en primärt given optimal fusionsgränsmassa (k=1) m0JSUB som reduceras något (12%) genom expansionsfasen som följer efter fusionsfasen. kJ/d innefattar noga avvägda parametrar från atomkärnans fysik ENLIGT TNED. Med denna delning given uppdelas himlakropparna sekundärt beroende på huruvida g-trycket överväger Coulombtrycket. Är g-trycket övervägande, trycks atomkärnorna i g-zonen (stjärnstädet) in över varandras nuklidbarriärer, fusion uppkommer och en stjärna bildas, annars planet. I TNED kallas varje primärt bildad stjärna under K-cellens expansion och genom processen med J-kropparnas primära avdelning för en primärstjärna så länge den förbränner sitt primära innehåll av vätebaserat material; Gränsen för den primära stjärnbildningen med Väte-1-bas går vid ca 6 Jupitermassor eller runt 1/165 Solmassa. Nedan visas baskartan för Jordkroppens grundämnessammansättning enligt diakvadratens grundsamband, och under den en motsvarande allmän ämnesbeskrivning för Solen-Jorden-Månen enligt diakvadratens grunder.

Baskarta

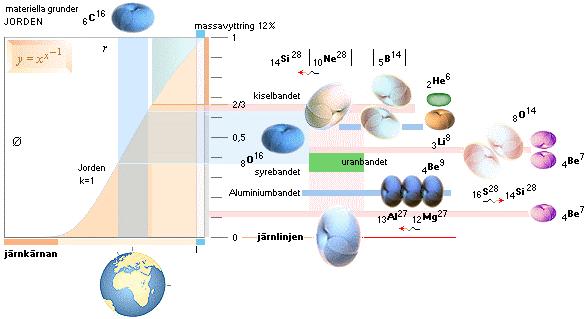
Jordkroppen — baskarta

BASKARTA ÖVER GRUNDÄMNESFÖRDELNINGEN ENLIGT TNED

Fusionerna beskrivs detaljerat längre ner.

Kort beskrivning av Jordens, Månens och Solens materiegrunder, illustrationen nedan i komplement

Järnkärnans utsträckning från centrum för k=1 (Jorden) ligger i stort vid början på den blå grafens bas. De tyngsta grundämnena bildas ungefär i mitten av r. Månen (k=4,388) expanderar under sin optimala fusionsfas och missar därför större delen av sin järnkärna, den blir i stället fragmenterad på en större andel lättare ämnen. Solen å sin sida (k=0,01375) expanderar allt för häftigt för att kunna sluta som annat än en reguljär gaskropp. Inom ett smalt band utvecklar Solen en mycket begränsad uppsättning av den tunga nuklidgruppens grundämnen. Solens g-inflytande på Merkurius (k=2,6712) visar varför Merkurius i sin bildning fick en större järnkärna än den normalt skulle haft på betydligt större avstånd från Solen. Ett liknande (men inte lika starkt) inflytande över Månen från Jorden visar varför Månkroppens mineralsammansättning bör skilja sig på framsidan och baksidan. Enligt ENCARTA (Moon) är det precis också vad som föreligger.

G-skuggning är naturligt mera sannolik där många stora J-kroppar avdelas. Stjärnor nära Vintergatans centrum borde därför exponeras mera för g-skuggning än stjärnor längre ut. Eftersom g-skuggning på en J-kropp till viss del innebär att dess neutronförekomst ökar på bekostnad av en mindre förekomst av vätekärnor, eller bara reducerar en snäv nuklidseparation och därmed gynnar längre fusionsringar (atomkärnor i rad som alla ligger på eller innanför varandras nuklidbarriärer och som därmed kan bilda tyngre atomer i en gemensam s.k. fusionsring, begreppet fusionsring förklaras utförligt i efterföljande artikel), borde stjärnor närmare Vintergatans centrum ha en procentuellt högre (och mera bredbandad) andel nuklider upp mot järntoppen (största massdefektsvärdet: 17,76) än stjärnor längre ut. Det stämmer också med de spektrala observationer som gjorts [BAs124sp2mn]:

Stjärnorna längre ut från Vintergatans centrum är i allmänhet järnfattigare än de längre in.

Himlakropparnas primärmassor

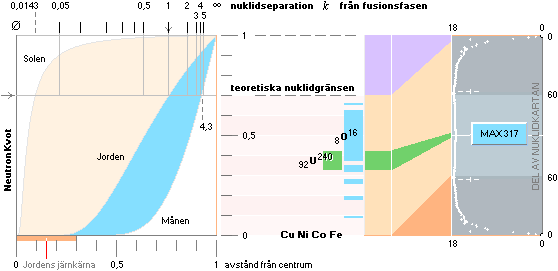
PRIMÄRA MASSAVYTTRINGEN

HIMLAKROPPARNAS PRIMÄRMASSOR

—————————————————————————————————————————————————

En direktberäknande funktion finns nu vidareutvecklad (2018) med kalkylkort — beskrivning i kBestämningen.

—————————————————————————————————————————————————

I de yttre delarna av J-kroppen har ingen nämnvärd täthetsändring inträffat genom den ytterst snabba fusionsfasen, dessa delar betingas generellt av maximal neutronkvot (1). Man kan då betrakta de yttre perifera delarna som den delmassa i J som tillhör den ursprungligt givna ideala g-energin — med tillhörande idealt evig expansion.

De perifera delarna kommer alltså FÖR SIN DEL och TILL VISS DEL att utveckla den ideala g-energins magnitud från tid-täthetssambandet T=Ö(3/2pGr), medan de inre delarna bromsas i försorg av täthetsändringen. De yttre expanderande delarna är i vilket fall beroende enbart av den inre J-massan, vare sig denna expanderar eller inte. Den exakta gränslinjen mellan kvarliggande och avyttrande J-massa bestäms alltså av det smala diffusa området mellan orörd periferidel och täthetsändrad (eller med samma innebörd, tryckändrad) centraldel. Vi studerar hur ett samband kan härledas.

Jordens Femte Ekvation

JORDENS FEMTE EKVATION

m_PRIM=m_PRES(1–x^k/x)^–3/34 ........................ Jordens femte ekvation, x=(1–x^k/x)^1/34 måste itereras

centrum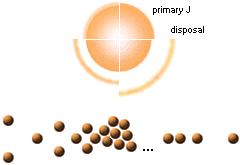periferi

Med given Ø-kvadrat (Ø, dia) och Primärmassan för k=1 som fusionsgränsmassan m_0JSUB=6,8 T24 KG och dess nuvarande — entydiga — motsvarande Jordmassa

m_PRES=5,975 T24 KG, ges en avyttring på runt 12% från den primära till den nuvarande. Den återstående radien från 1 blir då x=0,9578033 @ 0,96 beräknat från r_max.

Med Ø-kvadratens rambegränsning och den enda givna xy-punkten för k=1 vid x_J, förutsatt en likformig fördelning för alla J-kroppar, definieras massavyttringen av potensfunktionen y=Ø_P=1–xⁿ från k=0 och uppåt. k=1 ger Ø_P=Ø=x^k/x=0,9559858.

Lösningen för n blir då n=ln(1–ØP)/lnx=72,44347 @ 72. Förutsatt att massan återförs på en och samma medeltäthet (vi frånser skillnaderna mellan inre och yttre delar), kan primärmassan m_PRIM beräknas via x från den nuvarande massan m_PRES (från V₁/V₂=[x₁/x₂]³=rm₁/rm₂=m₁/m₂ ; x₂=1 ; x₁³=m₁/m₂) enligt sambandet

m_PRES/x³ = m_PRIM ...................................... massavyttringssambandet, x=(1–x^k/x)^1/34 måste itereras

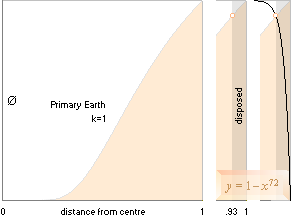
x är skärningen mellan Ø_P=Ø som ger x⁷²=1–x^k/x. k anger kroppens karaktäristiska nuklidseparation vid fusionsfasens början relativt k=1.

Potensfunktionen x^k/x kan inte (enkelt) lösas direkt för x, den måste itereras. Iterationen kan göras direkt på det enkla uttrycket x⁷²=1–x^k/x med början från x=0,5 och vilket gäller för samtliga fall. [Vilket vill säga; Varje nytt x i iterationen beräknas x=(1–x^k/x)^1/72]. Ett slutvärde med runt femton korrekta decimaler uppnås efter runt 20 varv.

Himlakropparnas bildningstid · J-kroppens expansion · HIMLAKROPPARNAS EXPANSIONSHASTIGHET från Primärbildningen

compilation 2007XII27

J-KROPPARNAS EXPANSION

HIMLAKROPPARNAS BILDNINGSTID FRÅN t_ON — Jordens Sjätte Ekvation

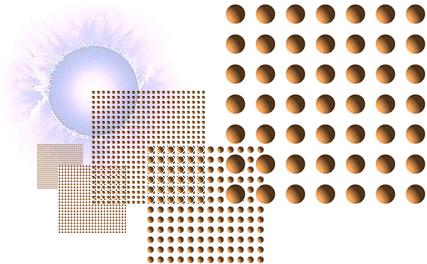
Efter fusionsfasen (se från NUKLIDBILDNINGARNA), som inträder efter divergenständningen för den aktuella J-kroppen genom K-cellens expansion efter detonationen, inträder en snabb expansionfas då J-kroppen utvidgas från sitt maximalt täta tillstånd (r_max=1,87 t17 KG/M³) till sin mera egentliga normaltäthet (rfinal).

Om expansionssambandet för K-cellens expansion T²=3/2pGr tillämpas (se från K-CELLENS EXPANSIONSFYSIK) även på J-kropparnas expansion efter fusionsfasen från divergenständningen (t_ON), ges en bekväm, matematiskt enkelt och överskådlig och heltäckande allmän orientering som generellt och approximativt kan tillämpas på samtliga himlakroppar i deras bildning — ända ner till sandkornets nivå, och ännu finare. För att genomföra detta program, och eftersom T-formen bara gäller för tätheten (r, från max till aktuell), måste vi utvälja en känd kropp som preferens för alla andra som representativ för T-formen — så att även en (relativ) massbestämning kan göras för samtliga fall, inte enbart täthetsparametern (r). Den enda kända preferenskropp vi har är (naturligtvis) fusionsgränsmassan (m_0JSUB=6,80016 T24 KG). Om vi tar med avyttringsmassan — som alla (större) himlakroppar gör sig av med från primärexpansionen (se JORDENS FEMTE EKVATION)

m_PRIM=m_PRES(1–x^k/x)^–3/72

.................................. Jordens femte ekvation; x³ = mPRES/mPRIM; mPRIM = mPRESx^–1/3; x=(1–x^k/x)^1/72 måste itereras

— beskriver också T-sambandets oändliga expansion J-kroppens oändliga expansion just med hänsyn taget till den försvinnande avyttringsmassan (m_E) och vars ständigt växande radie gör att J-kroppens täthet närmar sig noll obegränsat. Använder vi alltså J-kroppens slutgiltiga (nuvarande) täthet som lika med T-formens täthetsvärde (r=r_final), får vi bildningstiden (T) genom hela expansionsfasen — enligt följande: VID T(r_final) befinner sig redan avyttringsmassan (m_E) som ett tunt (gasiskt, lågmineraliskt) expanderande restskal på behörigt av stånd från J-ytan; Den något högre m_0J-massan (m_J+m_E) med den något större sfärradien via m_E definierar via det expanderande m_E-skalet den underliggande fasta m_J-kroppens massa med sin fasta sfärradie på den givna fasta slutkroppens medeltäthet r_final. Faktiskt. Eftersom, vidare, fusionsgränsmassan (m_0JSUB=6,80016 T24 KG) framställer begreppet nuklidseparationskvot k=d/r₀ vid primärbildningen (se från DIAKVADRATEN) och som just sammanhänger med vilka typer av himlakroppar som bildas för olika massor relativt fusionsgränsmassan — som just har k=1 — KAN k-formen användas tillsammans med T-formen T²=3/2pGr enligt T²=k^–13/2pGr för att få motsvarande tidsbildningar för alla typer av himlakroppar.

Vilket vill säga: För J-massor större än m_0JSUB ges k-värden MINDRE än 1: deras starkare gravitation åstadkommer dels en häftigare expansion (genom rekylverkan), men också en proportionsvis större expansionsdämpning genom den möjliga proportionsvis större täthetsändringen mellan inre och yttre och som påverkar expansionshastigheten för allt material utanför. Med samma sluttäthet som m_0JSUB tar det längre tid för en sådan J-kropp att uppnå sin slutform — trots att kroppen gott och väl räknat i meter per sekund kan expandera enormt mycket snabbare än m_0JSUB.

För J-massor mindre än m_0JSUB ges k-värden STÖRRE än 1 (som t.ex. i fallet Månen, k=4,3): deras svagare gravitation hämmar inte Coulombrepulsionerna i expansionsfasen så starkt, och utvecklar heller inte så stor skillnad i täthet mellan inre och yttre delar. De når därför också sin slutform snabbare med samma jämförande täthet som m_0JSUB — trots att de mycket väl kan expandera betydligt långsammare per meter.

Graferna nedan visar resultatet med värdena för Solen (Sol), Jorden (Jor) och Månen (Mån) inlagda, samt högsta J-kroppens bildningsmassa (m₈₀=80 Solmassor) till jämförelse. Tidsbildningen är skärningen mellan respektive k-kurva och J-kroppens slutliga medeltäthetsvärde.

Himlakropparnas bildningstid från t_ON

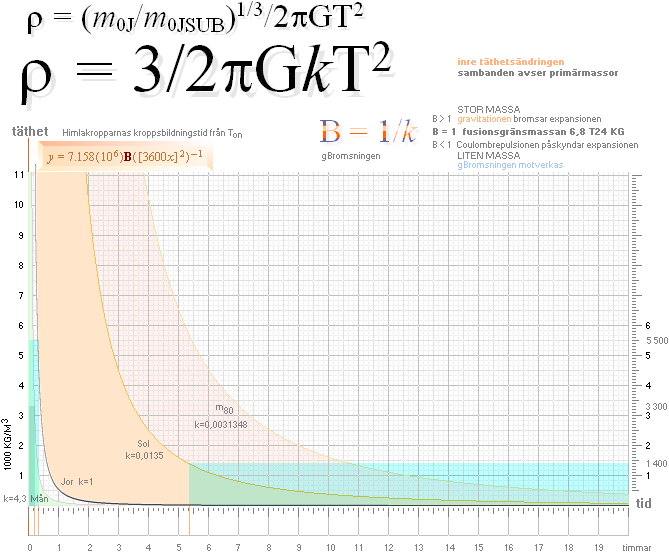
Himlakropparnas bildningstid från t_ON

OBSERVERA PREFERENSERNA: 1. Förutsättningen för massavyttringens fysik vid primärbildningen är identifieringen av m_0JSUB med slutformen Jorden (5,975 T24 KG). Avyttringsmassan fysik hänger HELT på den förutsättningen. m_0JSUB på 6,8 T24 KG har f.ö. ingen annan möjlig planetkropp att återfalla på: Venus ligger närmast Jorden, men massan är för liten med sina 4,87 T24 KG [BAs173], närmast större är Uranus med sina 8,69 T25 KG [BAs206] som är mycket för stor. 2. Förutsättningen för aktiv massavyttring är att avyttringsmassan (m_E) har minst FLYKTHASTIGHETEN v=Ö 2Gm₂/r.

Flykthastigheten härleds ur mekaniken;

E = mv²/2 = Gm₂m/r = Fr ; v² = 2Gm₂/r = 2w² ; v = Ö 2Gm₂/r

Annars dras den tillbaka av den underliggande J-kroppen. OM (alltså) himlakroppsbildningen skulle ske (betydligt) långsammare än ovan, riskerar (likväl) hela teorin ENLIGT TNED att krascha. Det är därför angeläget att finna bevis som KAN kullkasta ovanstående, eftersom i varje fall jag INTE är intresserad av att hålla en dödfödd teori vid liv. Granska. Ifrågasätt. Försök eliminera — seriöst. Därmed kan sanningen bara växa sig starkare. Det finns bara allt att vinna.

ALLMÄNNA SAMBAND

Ett approximativt direktvärde för NUKLIDKVOTEN k (utan vidare uträkningar, se vidare nedan Den exakta k-bestämningen) fås direkt enligt

k = ([6,8 T24 KG]/m_J)^1/3

med

m_J = nuvarande himlakroppsmassan

T-ekvationen kan då skrivas förenklat med avrundade koefficientvärden

T² = (m_J/m_0JSUB)^1/3/2pGr_final

= 12,6m_J^1/3/r_final · KG^2/3S²/M³

Värdena ger ungefär halva T-värdena som fås med korrekt k-bestämning (som kräver iterationer, se vidare nedan Den exakta k-bestämningen).

Därmed det enklare kvantitativa sambandet (till prövning) för allmän orientering, samtliga fall (sandkornet inkluderat!),

T = 7[m_J^1/3/r_final ]^1/2 · KG^1/3S/M^3/2

Det enklare approximativa värdet

EXEMPEL:

Ett sandkorn kan återföras på grundämnet Kisel med medeltätheten (från tabell) r=2330 KG/M³. Kornets omskrivs av (säg) en kub med sidan 1 mM. Vi får kornmassan m=rV=rr³ som ger m=2,33 t6 KG. Med r_final ges då bildningstiden (approximativt orienterande) T=0,0166972 S eller runt 1,7 hundradels sekund från t_ON;

En Järnmeteorid (meteorit blir den först om den kommer in till Jorden) med täthet 7870 KG/M³ och massa 1 KG bildas på motsvarande tid T=0,0789061 S.

OBSERVERA att (i allmänhet) för små J-massor är sannolikheten (i allmänhet) stor att de befinner sig (inte precis mitt) mellan större kroppar och därmed en stor flora av möjliga förskjutningar som vränger varje ideal sfärisk analogi (se G-SKUGGNING). Mindre kroppar blir (alltså, i allmänhet) deformerade och oregelbundna om de primärutvecklas nära större J-kroppar.

Den exakta k-bestämningen

Från HIMLAKROPPARNAS PRIMÄRMASSOR är givet sambandet

m_PRIM = m_PRES/x³ = m_J/x³

[m=r4pr³/3 ; m₁/m₂=(r₁/r₂)³=k ; r₁/r₂=k^1/3=x=(m₁/m₂)^1/3 ; x³m₂=m₁]

med x-värdet

x = (1–x^k/x)^1/72

(För sambandens härledning, se från HIMLAKROPPARNAS PRIMÄRMASSOR).

x-värdet kan inte beräknas direkt med några här kända metoder. Vi kan dock med hjälp av ett kalkylblad, eller ett program-program (typ Delphi) konstruera en numerisk algoritm för att få ut ett värde.

I originalet till den här presentationen används (genomgående) kalkylblad från MsWORKS (vers. 4.0) [och som tyvärr inte fungerar (direkt) i htm-dokument].

Följande metodbeskrivning relaterar dit.

ITERATIONSMETOD: medelvärdesbildning.

Utgångspunkten är ett första approximativt k-värde som beräknas från den givna kända himlakroppsmassan (m_PRES=m_J) enligt

k = k_J/r_max^2/3(3/4p)^1/3m_J^1/3/r₀

Parametrarna k_J, r_max, p och r₀ är kända konstanter (se från Härledningen till fusionsgränsmassan).

Därefter bestäms ett x-värde (x₂) från referensen x₁(k=1)=0,957795796 beroende på om k är större än 1 [x ligger närmare 1, x₂=1–(1–x₁)/2] eller mindre än 1 [x ligger närmare noll, x₂=x₁/2]. Detta x-värde insätts sedan i den allmänna x-ekvationen x=(1–x^k/x)^1/n med givet n(=72,42598474). x-resultatet ger då ett tredje x=x₃. Från denna punkt tas sedan medelvärden x₄=(x₂+x₃)/2 för att bilda nya x och vilket förlopp upprepas tills x inte ändras mera. Det är alltså decimalprecisionen som bestämmer gränsen. I MsWORKS kalkylblad visar sig antalet sådana varv vara typisk 20 för bästa precision. Efter dessa utförs så en ny k-beräkning men nu med m_J ersatt av primärmassan m_PRIM via nyssnämnda m_PRIM = m_PRES/x³ = m_J/x³ enligt

k = k_J/r_max^2/3(3/4p)^1/3(m_J/x³)^1/3/r₀

Därefter dras en ny 20-varvskolumn för att få ett ännu bättre x-värde som sedan återigen används för en ny k-beräkning, osv.

Svaret (med optimal precision), som innebär att k-värdet beräknas i kolumnblock tills det inte ändras mer i decimalformen kräver (med MsWORKS kalkylceller) fem kolumner, totalt runt 100 beräkningar.

MATEMATISK NOTERING. Sambandsformen x=(1–x^k/x)^1/72 är DIREKT itererbar med början från x=0,5 för givet k. Emellertid blir precisionen (mycket) sämre med denna x-metod.

Kalkylkort UTVECKLAD ALTERNATIV x-ITERATION · primärmassan från given nuvarande · nuklidseparationen (d) · nuklidkoefficienten (k=d/r0); dk ingår i kalkylkortet.

Här visas endast bilden av originalets kalkylkort eftersom htm-standarden inte klarar ordbehandlarens standard (kalkylkortet funkar tyvärr inte direktimporterat till webben).

Se originalet i @SourceRef., förf. not.

Ett motsvarande kalkylkort (nära utseendemässigt lika) frinns nu (Apr2010) utformat i gratisprogramvaran OpenOffice. Se

Addition Dec2023:

This PrimStar.ods original Primary Mass Iterative spread sheet version is limited (input values below T18 will be extensively cropped).

A more direct calculable version has been developed (2018) including input present masses down to nano particles.

See further directed from kBestämningen.

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN PrimStar.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/PrimStar.ods

Gränsen ges vid mPRES=4,8 T17 KG med x=0,999999939 mot mPRES=4,7 T17 KG med x=1.

Avyttringen för mPRES=4,8 T17 KG är då 0,00%.

—————————————————————————————————————————————————

En direktberäknande funktion finns nu vidareutvecklad (2018) med kalkylkort — beskrivning i kBestämningen.

—————————————————————————————————————————————————

DATORNS BEGRÄNSADE PRECISION

k-värden större än 241,9687447 (mPRES=4,8 T17 KG) genererar x-värden större än 0,999999939… Därmed befinner vi oss (i denna datorstandard) på gränsen för systemets precision: högre k-värden ger motsvarande x-fel så att beräkningen av nuMassor (m_J) mindre än 4,8 T17 KG blir en meningslös operation. Dvs; vi kan då lika gärna för fallen nuMassor (m_J) mindre än 4,8 T17 KG beräkna k direkt efter nuMassvärdet m_J enligt

k = k_J/r_max^2/3(3/4p)^1/3m_J^1/3/r₀

= (1,89454 T8)/m_J^1/3 = m_0JSUB^1/3/m_J^1/3

= [(6,80016 T24 KG)/m_J]^1/3

där m_J anger himlakroppens nuvarande massvärde. Avyttringsmassan är för dessa fall (typ) försumbar, dvs mindre än 0,00% (läs: från hundratusendelar och mindre).

STORLEKSORDNINGEN T17 KG representeras av kropparna typiskt mindre än eller lika med asteroider

(de största asteroiderna [BAs240, Ceres, Pallas, Vesta] har massor runt T20 KG, månarna har typiskt ca T19-23 KG; Månmassan är 7,35 T22 KG).

Editor2007XII27

G-skuggning | Med exempel från Solen-Merkurius

Från NEUTRONKVOTEN

G-SKUGGNING

G-SKUGGNINGENS MATEMATIK — se grunderna från Grundämnesbildningen

G-skuggning ENLIGT TNED relaterar till J-kropparnas primärbildning och innebär att en mindre J-kropps grundämnessammansättning kan påverkas (i en riktning) i riktning mot tyngre grundämnen genom en närliggande större J-kropps gravitation: den extra gravitationen motverkar att atomkärnorna repelleras under neutronsönderfallets period, och därmed större sannolikhet för större fusionsringar, analogt tyngre grundämnen i den påföljande fusionsfasen. Hur det fungerar beskrivs mera utförligt nedan från G-SKUGGNINGEN GENERELLT. Se även efterföljande Exempel på Fusionsbildningar.

Förutsättningen för att en större primär J-kropp (här Solen till prövning) ska påverka en närliggande mindre J-kropp (här Merkurius till prövning) med någon märkbar effekt för kroppsbildningen vid divergenständning (tON), är att den större J-kroppens accelerationskonstant (a₂=Gm₂/d²) vid den mindres J-kroppens yta (r₁) är lika stor som dennas egenkonstant just vid egenytan (a₁=Gm₁/r²). Därmed kan den större J-kroppens gravitation märkbart affektera den mindre J-kroppens inledande (känsliga) neutronsönderfallsperiod med bildningen av fusionsringarna som grundlägger J-kroppens grundämnessammansättning: Fusionsringarna, väl en gång bildade, låser sig garanterat av nuklidbarriärerna (se Nuklidbarriären), och slutförs således sedan oberoende av kroppsvärd. Gränsdistansen för en sådan aktiv påverkan eller g-skuggning räknat från den större J-kroppens centrum betecknas här d. Verkan blir naturligtvis större ju mindre avståndet är räknat från d-gränsen. Sambanden nedan ger grundformerna med exemplet Solen-Merkurius integrerat.

Exempel Solen-Merkurius

a₂ = Gm₂/d² ......................................... se grundsamband i Gravitationslagen (med vidare länkar till basformerna)

a₁ = Gm/r₁² ;

(a₂=a₁) = (Gm₂/d² = Gm/r₁²) ; r₁²Gm₂/Gm = d² ; r₁²m₂/m = d² ;

d = r₁Ö m₂/m ....................................... ABSOLUTA G-SKUGGDISTANS GRÄNSEN

;

r = 1,82 T17 KG/M³ ; ....................... J-kropparnas primära täthet, alla lika

r1 = (3m/4pr)^1/3

= m^1/3(1,09466 t6)

m_MER = 0,32265 T24 KG

r₁ = 75,079935 M ............................... Merkurius neutronkallplasmaradie

m_SOL = 1,989 T30 KG = m₂

d = 1,8641267 T5 M .......................... Gränsdistansen i fallet Solen-Merkurius

;

m₂/m₁ = rV₂/rV₁ = V₂/V₁ = (r₂/r₁)³ ;

r₁²m₂/m₁ = d² = r₁²r₂³/r₁³ = r₂³/r₁ ;

d = r₁^–1/2 r₂^3/2 ;

r₂ = (3m_SOL/4pr)^1/3

= 1,3766543 T4 M .......................... Solens neutronkallplasmaradie

d/r₂ = 13,540993

Resultat: Endast om Merkurius vid sin fusionsfas befann sig VID eller INNANFÖR d-gränsen _limesd = 1,8641267 T5 M är det möjligt att förklara Merkurius onormalt stora järnkärna (som den bör ha för att förklara sin onormalt höga täthet). I nuläget är avståndet Solen-Merkurius betydligt större (0,39 AU eller ca 5,8344 T10 M). Eftersom hela Solsträngen med planeterna från utkastningen från sin J-moderkropp hade relativt höga egenhastigheter med mycket närliggande avstånd (jämför rekyldropparna från en vattenyta som bryts genom en droppe som träffar), drevs planetavstånden isär successivt och avstannade till slut med Solens gravitella infångning.

Detaljerna ovan kan (således) användas för att göra en (vidare, grov relativ) prövning mot observerade nu gällande avståndsdata.

Notera att gränsdistansen i fallet Solen-Merkurius ligger (låg) väl INOM Solens nuvarande klot som mäter runt 6,96 T8 M att jämföra med gränsdistansens 1,9 T5 M.

Från G-SKUGGNINGENS MATEMATIK

G-SKUGGNINGEN GENERELLT

— hur det fungerar enligt TNED

RELATIVT Extremt små J-kroppar måste enligt TNED förstås bli (ytterst) känsliga för “gravitell skuggning” (g-skuggning) från närliggande större J-kroppar. Det är relativt enkelt att relatera denna procedur då man en gång satt sig in i (den matematiska) principen för gravitell påverkan från divergenständning ENLIGT TNED och den följande perioden med neutronsönderfall. Det finns (nämligen) inte så mycket att välja på. Om en liten J-kropp ligger i g-influens från en större kropp, kan dess normalt stora nuklidseparation minska i åtminstone en riktning, och därigenom härma ett optimalt beteende med maximalt långa fusionsringar i den centrala proceduren (som betyder större fusionsringar, som leder till tyngre grundämnen). I ett sådant fall kommer den påverkade delen av den lilla J-kroppen att sluta som ett block praktiskt taget helt bestående av järn och nickel. Se vidare i Exempel på Fusionsbildningar.

Diamanter i meteoriterna vittnar om processerna

J-kroppens övriga (normala) delar kommer däremot att utveckla mer eller mindre stenmineral på grund av den större nuklidseparationen. En speciell grupp meteoriter (Sideriter) uppvisar också denna typform. Meteoritblock med en andel järn av så mycket som drygt 90% har observerats [FOCUS MATERIEN 1975 s455].

När dessa små kroppar och alla andra också hastigt expanderar efter fusionsfasen, är det naturligt att de bildade grundämnesatomerna ingår kemiska föreningar eftersom utvidgningen sker från max täthet och med liten värmebildning på grund av den låga massan. KOL, till exempel, kommer inte så lätt att ge upp en redan bildad DIAMANTSTRUKTUR från det höga täthetstillståndet under expansionsfasen. Och så har man också funnit i meteoriter av en speciell typ (samma som ovan, Sideriterna): de innehåller just precis — diamanter!

Gravitell skuggning måste också förstås uppträda enligt TNED specifikt mellan den stora centrala J-kroppen i ett mångkroppssystem (typ vårt eget Solsystem) och dess närmaste kroppssvans från den resonanta strängserien från hela systemets avyttring från den ännu större J-moderkroppen. Ett sådant möjligt fall föreligger (möjligen) mellan Solen och Merkurius (se räkneexemplet Solen-Merkurius längre upp). Till att börja med är avståndet Solen-Merkurius litet då kropparna kastas ut från J-moderkroppen. ATT Merkurius har en stor initiell g-affekt från Solkroppen är bara av det skälet redan klart. Men det krävs också att Merkurius J-kropp måste ligga innanför gränsdistansen för g-skuggning (_limesd) NÄR Merkurius passerar neutronsönderfallsperioden, annars kommer ingen påverkan att triggas av Solkroppen gravitation. Om så sker, dras en del av Merkurius massa på Solsidan mot en mindre nuklidseparation med följd i större fusionsringar, analogt tyngre grundämnen, och fråndelen mot en normaliserad större nuklidseparation med motsvarande lättare grundämnen i slutänden. Eftersom fusionsringarna utgår från maximal täthet, och när de väl har kopplat är helt låsta av sina egna nuklidbarriärer, kommer de också att slutföras då de väl en gång har kopplat. Därmed skulle Merkurius, i Solens initiella g-inflytande, kunna få en (betydligt) tyngre centralkärna jämfört med en mera Månliknande stentyp den annars skulle fått på betydligt större avstånd från en närliggande stor J-kropp. Därmed finns i varje fall en teoretisk möjlighet att förklara den observerade onormalt stora tätheten för den lilla Merkuriuskroppen.

Se även om g-skuggningen i Kort beskrivning av Jordens, Månens och Solens materiegrunder.

NUKLIDBILDNINGARNA — hur grundämnesbildningen fungerar enligt TNED i detalj genom Fusionsringar efter Divergenständning

Fusionsbildningen, exempel

FUSIONSBILDNINGEN GENOM EXEMPEL

Exempel

Fusionsbildningen — alla nuklidbildningar sker exotermiskt (Exotermiska kärnreaktionslagen)

Såväl i kemiska föreningar som i fusionsled kan flera atomer sammansättas enligt atomens två impuls och kraftekvationer (fysikens två kungsekvationer) J_0K+3J_1K=0 och F_BT+F_eZ=0. De delar då på samma massuppsättning i gemensamma centralmassiv med gemensamt delad elektronmassa i impulsmomentets bevarande enligt typleden

(J_0K+3J_1K)₁+(J_0K+3J_1K)₂+(J_0K+3J_1K)₃+…+(J_0K+3J_1K)_n = 0

(F_BT+F_eZ )₁+(F_BT+F_eZ )₂+(F_BT+F_eZ )₃+…+(F_BT+F_eZ )_n = 0

En fusionsring är varje möjlig mönsterkoppling av ovanstående art som neutronerna utvecklar från kallplasmat genom nuklidseparation efter divergenständning.

Enda villkoret är att samtliga atomkärnor från start ligger inom eller på varandras nuklidbarriärer. Det betyder enligt TNED på eller inom varandras omskrivna kärnsfärer.

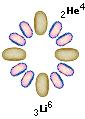
Exempel med neutronkvot 0

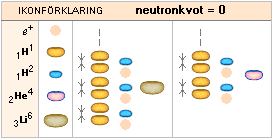
Ringen ovan till vänster innehåller från början bara Väte-1-atomer, analogt protonkärnor. Dessa förenas enligt tabellen ovan i ikonförklaringen till Helium-4, och sedan vidare enligt illustrationen, samma fusionsring.

Fusionslängden

OBSERVERA att

· fusionsringar kan ENDAST bildas teoretiskt-praktiskt så länge inga yttre störande moment eller energier tillkommer: bara i den allra första fasen av kallplasmats tändning, SEDAN ÄR DET KÖRT. Fusionsfasen för samtliga J-kroppar är max 3 t20 sekunder (litet t för 10–) motsvarande en optimal exotermisk nuklidbildning med masstalet 300 (se Fusionstidens beräkning nedan)

· alla atomkärnor inom en fusionsring måste ligga på eller inom varandras nuklidbarriärer, analogt nollmoment för att igångsätta fusionen enligt exotermiska fusionslagen

· elektronräkningen ingår automatiskt för samtliga ingående komponenter eftersom kärnreaktionslagen avser hela atomen

Fusionstidens beräkning. Om toppspinnet relateras idealt till ekvivalenten c₀ blir minsta fusionstiden för två vätekärnor med r=1,37 t15 M lika med 2,8713 t23 S. Införs extra moment som betyder införda extra kärnsvängningar, förlängs denna tid då komponenterna i sådana fall måste tillbringa extra tid för att utjämna de införda svängningsformerna i bildningen av slutprodukten. Med växande kärnradier enligt den approximativa kubgrafen kan fusionstidens lägsta värde för två komponenter beräknas t=(2,8713 t23 S)A^1/3. En uppskattad medelvärdesform för samtliga fall ger t=3×(2,8713 t23 S) @ 9 t23 S eller grovt avrundat 1 t22 S. För maximalt 300 singulära stegfusioner (se utförligt i Nuklidkartans gränsvärde), vilket ENLIGT TNED betecknar fusionsringens absoluta största omfattning, ges maximala tiden 3 t20 S.

FUSIONSRINGEN uttrycker i vilket fall, vare sig fusionsringar förekommer eller inte, en allmän ekvivalent exotermisk fusionsekvation för en grundämnesnuklid.

Med en given fusionsring finns initiellt endast fem olika sätt för komponenterna neutron-proton att fusionera exotermiskt (som ger energi) via de två möjliga sätten binär- eller tripelfusion. Illustrationen nedan sammanfattar dessa fem möjliga exotermiska primärfusioner.

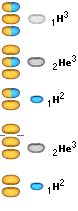
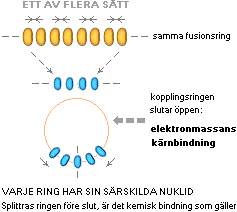
Atomkärnornas nuklidbarriärer sköter automatiskt ringens sammandragning i enlighet med impulsmomentets bevarande. Varje enskild fusion ligger ENLIGT EXOTERMISKA FUSIONSLAGEN tidsmässigt runt ett minimum på grovt t22 sekunder [se Fusionstidens beräkning ovan].

Eftersom fusionsringarna bygger på nollmoment i fusionskopplingarna, är varje experimentell motsvarighet utesluten. Ringens bildning kräver maximal materietäthet, och den kan aldrig realiseras i ett laboratorium utom via två eller möjligen tre kärnor — i våldsamma kollisioner, och därmed extramoment.

FRÅN ATOMKÄRNANS HÄRLEDNING ENLIGT Planckringen

ALLMÄN RESULTATREDOVISNING

Jordkroppen — baskarta

BASKARTA ÖVER GRUNDÄMNESFÖRDELNINGEN ENLIGT TNED

Beskrivning

GRUNDÄMNESBILDNINGEN

neutronkvoten noll — ingen neutronförekomst

GRUNDÄMNESBILDNINGENS TVÅ BASGRUPPER

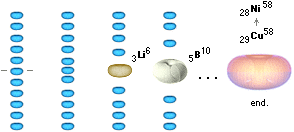
Det finns (främst) två olika grundläggande sätt med neutronkvoten noll: udda nuklidgruppen med neutronkvot noll ovan och jämna nuklidgruppen med neutronkvot noll nedan. Bägge alternativen bildar ändnuklider som innebär att ytterligare fusioner i fusionsringen på exotermisk bas inte kan genomföras på ringens komponenter.

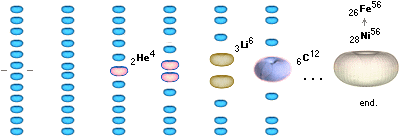
Vi ser redan här varför Järnet (och Nicklet) markerar speciella avsnitt i grundämnesbildningen: Järn-Nickel bildar i allmänhet en inre fusionskärna i en given J-kropp.

BESKRIVNING

_atomnummerX^masstal_{Atomär massdefekt}

Med utgångspunkt i en ekvivalent fusionsring som (efter en första fusionskrevad) består av idel deuteriumkärnor framgår de två följande enda och möjliga FULLSTÄNDIGA ordningarna ur exotermiska fusionslagen. Denna fusionsbildning motsvarar alltså förhållandena i J-kroppens centrum där initiellt, efter divergenständningen, endast vätekärnor finns. För att en ring ska kunna bilda ännu tyngre nuklider krävs agenter med större neutronförekomst. Dessa beskrivs längre fram. Centrumdelens nollförekomst av neutroner är alltså garanterad på följande.

Beteckningen e i tabellen nedan, första raden i fallet ₃Li⁶, anger minimum fusionsenergi i elektronmassor. Beteckningen b+ innefattar även den konventionellt benämnda EC-typen (Electron Capture). Alla normalt betaaktiva nuklider har i den initierande neutrinostrålningens försorg tillfälligt obegränsad varaktighet, fusionsringens optimala dynamik bygger helt på den förutsättningen.

udda nuklider neutronkvot 0 —— fusionsbildningar enligt exotermiska fusionslagen

komponenter produkt typ realt avgiven fusionsenergi per i MeV

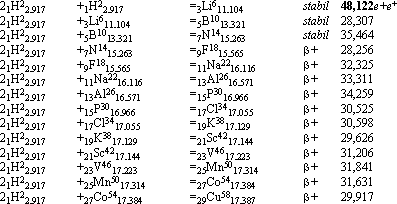
jämna nuklider neutronkvot 0 —— fusionsbildningar enligt exotermiska fusionslagen

komponenter produkt typ realt avgiven fusionsenergi per i MeV

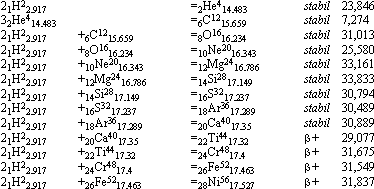
Den tunga nuklidgruppens Certifiering

Certifieringen för de tunga nuklidernas bildning

GRUNDÄMNESBILDNINGENS KÄRNA

Neutrinostrålningen och de betaaktiva nuklidernas bevarande

NEUTRINOSTRÅLNINGENS ALLMÄNNA BETYDELSE för fusionerna beskrivs i separat artikel i samband med beskrivningen av atomkärnans allmänna struktur och Plancks konstant. Se NEUTRINOSPEKTRUM, om ej redan bekant.

För att fusionsbildningen i den tunga nuklidgruppen (från runt A=60 och uppåt) ska fungera genomgående på exotermiska fusioner, krävs ENLIGT TNED en förekomst av tillfälligt varaktiga neutronrika betaaktiva nuklider, Betaagenter. Det är mjukt instabila atomkärnor som bevarar kärnans ursprungliga neutronsammansättning men kan ändra kärnladdningen. Normalt sett sönderfaller betaaktiva nuklider i kärnstrukturen men inte i kärnformen, och tappar därmed delar av utfyllnadsmassan i 18e-stocken som höjer nuklidens massdefekt. Fusionsfasen är visserligen i sig kortvarig (min t22 sekunder) men det är ingen garanti för att normalt sönderfallande betaaktiva nuklider ska hinna fusionera i ringen innan de sönderfaller. Eftersom ENLIGT TNED alla betaaktiva atomkärnor i sina betasönderfall utvecklar exakt samma neutrinobetastrålning (m®g_v) sett till frekvens och våglängd, är det tillräckligt om Betaagenten får »bada» i neutrinobetaEkvivalenten (m®g_v) för neutronens sönderfall enligt energiekvivalenten

(₀N¹)=₁H¹_stabil+(m®g_v). Den betaaktiva nukliden hålls då på en exciterad energinivå och inget betasönderfall sker förrän neutrinobetanivån sjunker under hållvärdet. Att kallplasmatillståndet med fusionsringarna verkligen garanterar Betaagenterna klargörs på följande sätt.

Temperaturekvivalenten till varje energiekvivalent fås genom Planckenergin (E=hf=h_{6,626 t34 JS}c_{0 2,99792458 T8 M/S}/l) och Wiens förskjutningslag

(l=k_{2,898 t3 M°K}T^–1) enligt sambandet T=kl^–1=E(k/hc₀) med T i °K. I neutronens sönderfall till väteatom ges neutrinoenergin i medelvärde som E_eV=0,764 MeV.

Temperaturekvivalenten blir 1,78 T9 °K. I konventionell kosmisk mening finner man bara sådana temperaturer i de allra hetaste av stjärnor. Frånsett de okontrollerade vätebomsexplosioner som kortvarigt kan uppnå temperaturer på runt 10 T9 °K finns alltså och till jämförelse ingen praktisk möjlighet att genomföra experiment ens med de allra lägsta neutrinoenergier för kontroll av den betasönderfallshämmande neutrinoeffekten. Genom analogier som berör atomkärnans frivridande moment i samband med fusionskopplingarna, kan man ENLIGT TNED anställa en jämförande kinematisk analogi som leder till en motsvarande temperaturekvivalent under fusionsfasen från neutronkallplasmat (Se samband och figur i Termiska Ekvivalenter). Resultatet ger en temperaturekvivalent som är omvänt proportionell mot kärnradien. Sambandet kan då i förenklad mening ställas direkt i relation till masstalet A enligt uttrycket T=A^–1/3 T12 °K. Högsta teoretiska masstalet enligt TNED är A=317 (se Nuklidkartans gränsvärde) som ger lägsta T=1,47 T11 °K. Neutrinobetaekvivalenten i fusionsfasen är därmed säkerställd med goda marginaler.

För att neutrinobetaenergins ekvivalent ska ha någon betasönderfallshämmande effekt under den mycket kortvariga fusionsfasen, måste neutrinostrålningen avges i omedelbar närhet till betaagenten. Detta blir också det praktiska fallet genom varje fusionsring genom att atomkärnorna ligger optimalt nära varandra. Ringens sekventiella fusioner garanterar att närliggande eventuella betaagenter bokstavligen kommer att bada i rejält höga neutrinogenererade strålningstryck via massförintelsen (m®g) i fusionerna. Därmed kan fusionsfasen dra fördel av full uppsättning nuklider i hela nuklidkartan utan risk för att några betasönderfall inträffar. Alla, samtliga möjliga nuklider som bildas genom fusionsringarna, blir likaberättigade och certifierade fusionsagenter.

Betaagenterna som krävs för fullständig materiebildning är ₂He⁶, ₃Li⁸ och ₆C¹⁶. Betaaktiva ₁H³ figurerar också, men dess normala sönderfallstid är 12,26 år och är därför inte kritisk i J-kroppens snabba fusionsfas. Samma gäller också egentligen för agenterna ₂He⁶ och ₃Li⁸ som normalt sönderfaller efter respektive 0,82 och 0,86 sekunder [VAN NOSTRAND’s SCIENTIFIC ENCYCLOPEDIA Fifth Edition 1976 s491-515, Table 3].

Vi noterar att lokaler med neutrinostrålningens kvalitativa spektrum INTE kan genereras genom elektronstrålningsekvivalenter därför att sådan strålning gäller lika för samtliga atomer. Neutrinospektrum, betasönderfallen frånsett, är i försorg av — ENLIGT TNED — atomkärnans fraktalstruktur unikt för varje nuklid och kan inte efterhärmas artificiellt. Fusioner vars energier normalt ligger naturligt separerade av neutrinofrekvenserna hindras av artificiellt elektrongenererade energier på samma sätt som privata konversationer i en sal bryts av någon som kräver allas uppmärksamhet. I en naturlig lokal är ett sådant ingrepp uteslutet.

UniversumsHistoria nuklidbildningarna

Basnuklider med olika neutronkvoter

EN STOR MÄNGD MÖJLIGHETER finns som de olika grundnukliderna kan bildas på.

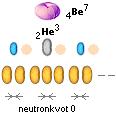
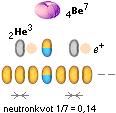
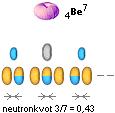
Sekvenserna här visar några möjliga fall med centrala fusionsagenter som kan bildas exotermiskt ur olika neutronkvoter.

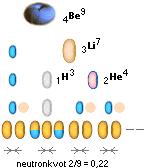
Ovanstående typiska bildningar, tillsammans med en del ytterligare, används delvis som referenser i den fortsatta presentationen.

UniversumsHistoria nuklidbildningarna

Nuklidbildningens fördjupning

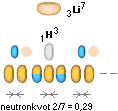
Nuklidbildningen fördjupas avsevärt med bildningen av nuklidagenten ₃Li⁷ (egen neutronkvot 2/7=0,29). Vi är då inne på områden med högre neutronkvot än 0. Enbart med Litium-7 i successiva tripelfusioner från en initierande binärfusion ges optimalt den helt exotermiska ringen

enligt

komponenter produkt typ realt avgiven fusionsenergi per i MeV

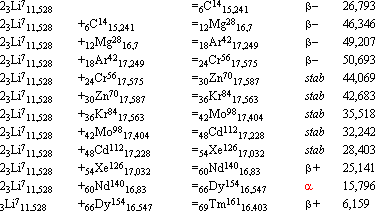
Hela ringens neutronkvot 0,29.

Med 3₃Li⁷=₉F²¹ ges på motsvarande sätt

komponenter produkt typ realt avgiven fusionsenergi per i MeV

UniversumsHistoria nuklidbildningarna

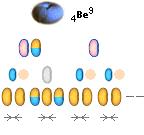
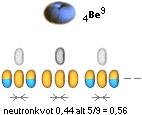
Men redan med en minimal neutronförekomst på endast två neutroner per optimal fusionsring ges en initiell fusionspunkt genom den stabila ₄Be⁹. Då ges nuklidserien via ₁H²-successioner enligt

Neutronkvoten för denna optimala typring blir endast 2/61=0,033. Alla från Argon-37 är jumboprotoner.

Ytterligare ett komplement med endast två neutroner per ring ges av den normalt betaaktiva mycket kortlivade agenten ₂He⁶

Med samma grundsuccessioner på ₁H² ges den optimala ringen

Alla dessa är stabila nuklider utom de två första och de två sista.

Neutronkvoten totalt för hela ringen blir 2/66=0,03. I relativa termer ligger alltså denna ring närmare centrum än föregående ₄Be⁹-ring.

Binärkombinationen ₂He⁶+₄Be⁹ ger substratnukliden ₆C¹⁵ och därmed ytterligare en möjlig optimal ring via ₁H²-successioner med komplementnuklider

På detta sätt utvidgas nuklidbildningen med växande avstånd från J-centrum.

Vi kommer emellertid strax till en punkt när de ovan beskrivna enkla seriefusionerna typiskt på ₁H²-basen tappar representation. Det är naturligt med tanke på att den basen är vätebaserad. Ju längre bort från J-centrum vi kommer, desto kortare måste ₁H²-ringarna bli, med ett växande inslag av allt mer neutronbaserade grundnuklider. Det betyder samtidigt att långa fusionsringar kommer att bli mera komplexa, alltså med inslag av i princip ett flertal olika neutronbaserade nuklidtyper.

UniversumsHistoria nuklidbildningarna

Maximalringens komponenter

Uranbandet

MAXIMALRINGENS KOMPONENTER

BILDNINGEN AV DEN TUNGA NUKLIDGRUPPENS NUKLIDER

Den totala och fullständiga ringtyp som kan omspänna hela nukliddjupet, exotermiskt och i princip ända ner i botten på nuklidkartan (max masstal ENLIGT TNED är 300, se Nuklidkartans gränsvärde) ges av följande typled.

........................ maximalringens komponenter

För fusionsringen som ger sista tabellnukliden i gängse referensverk, ₁₀₃Lw²⁵⁷, blir neutronkvoten i ovanstående komponenter totalt som minst 0,33. Beroende på att samma nuklid kan bildas också via högre neutronkvot, finns en viss spridning för samma ringtyp ₁₀₃Lw²⁵⁷ i varje fall upp till neutronkvoten 0,42.

Uppställningen nedan visar i ikonisk sekvens hur den helt exotermiska nuklidbildningen fungerar successivt i maximalringen. Efterföljande nuklidled visar fusionerna per.

UniversumsHistoria nuklidbildningarna

MAXIMALRINGEN

Hur de tyngre nukliderna bildas enligt TNED

3₄Be⁹ ₃Li⁸

… …

2₁₂Mg²⁷

…

₇N¹⁷ ₆C¹⁶

₂₄Cr⁵⁴

… …

₇N¹⁷ ₆C¹⁶

₃₈Sr⁸⁸

… … ₆C¹⁶ är en ändnuklid, den fusionerar inte med sig själv

₅₀Sn¹²⁰

… … ₆C¹⁶

₆₂Sm¹⁵²

… …

₆₈Er¹⁶⁸

…… ₇₂Hf¹⁸⁰, ₇₆Os¹⁹², ₈₀Hg²⁰⁴, ₈₄Po²¹⁶, ₈₈Ra²²⁸, ₉₂U²⁴⁰

₂He⁶

₉₂U²⁴⁰

…… ₉₆Cm²⁴⁶, ₁₀₀Fm²⁵², ₁₀₂No²⁵⁵, ₁₀₃Lw²⁵⁷ …

₂He³

IKONUPPSTÄLLNINGEN OVAN motsvarar följande fusionsekvivalenter:

UniversumsHistoria nuklidbildningarna

Beteckningar: _AtomnummerNUKLID^Masstal_{AtomärMassdefekt}

Fusionsordning: exotermisk, samtliga i totalsumma från lägre till högre massdefekt

maximalringen 18 steg 1e = 0,51138 MeV

se föregående ikonled komponenter resultant typ ger minimum fusionsenergi per

Ytterligare C¹⁶-fusioner kräver tillförande av energi.

De exotermiska fusionerna realiseras då i närvaro av en agent med lägre massdefekt:

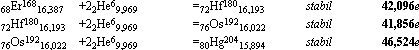
Här slutar i princip den stabila uppbyggnaden av grundämnena. De från Z=84 är i allmänhet alla tungt radioaktiva (a).

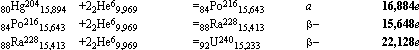
Här slutar för vår del förekomsten av de naturliga grundämnena. Z>92 förekommer inte på Jorden.

Uppbyggnaden i ekvivalenter kan emellertid fortsätta en bit till, men processen kräver då en Heliumagent med lägre masstal.

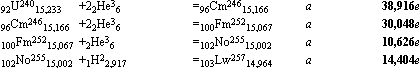
Här slutar gängse tabellreferenser (Handbook of Physics, McGraw-Hill). a anger radioaktiv nuklid.

Uppbyggnaden kan ändå fortsätta en bit till, fram till massdefekten vid Heliumplatån 14,483 som ENLIGT TNED bildar det undre gränsvärdet för den tunga nuklidgruppen (vid max masstalet 317, se Nuklidkartans gränsvärde).

UniversumsHistoria nuklidbildningarna

Samtidigt med de mera komplexa fusionsringarna är det givet att antalet lika ringar minskar. Det betyder att den relativa förekomsten av nuklider som bygger på komplexa fusionsringar också blir proportionsvis mindre (med vissa spridningar).

Neutronkvoten för ovanstående nuklider visar den möjliga spridning som maximalringen kan ha.

nuklid Ø neutronkvot MIN/MAX

—— ———————————

₁H² 0 0,5

₂He³ 0 0,33

₂He⁶ 0,33 0,67

₃Li⁸ 0,375 0,625

₄Be⁹ 0,22 0,44 eller 0,56

Medelvärdet av de 10 värdena ger en neutronkvot (DIA) Ø=0,349 eller 0,3502. Det är tydligt att maximalringens största (mest sannolika) bildningsområde avspeglas av detta medelvärde. Med högre neutronkvot avtar nukliddjupet ut mot J-kroppens yta, och på samma sätt inåt mot J-centrum med avtagande Ø.

Ut mot J-ytan kommer alltså allt mindre (kortare) ringar att prägla nuklidbildningen. Vi kan här till jämförelse även ta med nukliden ₃Li⁷ med neutronkvoten MIN/MAX 0,29/0,57. Det senare värdet visar att den är relativt välrepresenterad utåt.

UniversumsHistoria nuklidbildningarna

nuklidbarriären

inledning

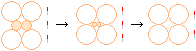
I samband med beskrivningen av fusionerna ENLIGT RELATERAD FYSIK används i förekommande fall enkla ikonformer av närmast ovanstående typ. Tillsammans med dessa används reguljära, skalenliga 3D-modeller av atomkärnan ENLIGT TNED.

Ikonerna — mellan begynnelsefas och slutfas — gör inte anspråk på att beskriva den motsvarande fysikaliskt exakta inre ordning efter vilken atomkärnor förenas (eller delas).

Dessa processer är (nämligen, och veterligen) komplicerade och kan i den motsvarande verkligheten ha andra figurativa förebilder. Exakt vilka dessa är, är här inte känt (och vi behöver heller inte känna dem i detalj, som det har visat sig, då principen för deras verkningssätt redan står klar).

Bakgrund. Ända från första stund då atomkärnan härleddes (i min historia), just genom den matematiska motsvarigheten till grundföreningen mellan två basindivider, har det aldrig funnits något direkt behov av inblick i den mellanliggande, själva den verkställande föreningsproceduren. Atomkärnans härledning på den punkten har bara två matematiska ändlägen: komponenterna före föreningen, produkten efter. Matematiken lägger inga aspekter på mellanläget. För att utrannsaka mellanläget närmare, krävs en särskild matematisk teori. Den är här fullkomligt okänd. Atomkärnans elementära härledning (frånsett massdefekten) ansluter alltså kort och gott till kärnreaktionslagen

K1+K2–(m®g)=K.

NUKLIDBARRIÄREN: inledning

Universums Historia

NUKLIDBARRIÄREN

Se även Potentialbarriären

Potentialbarriären mellan atomkärnorna

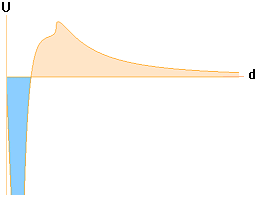
För att förenas, måste kärnorna tränga in över varandras nuklidbarriärer.

NUKLIDBARRIÄREN ansluter på visst sätt till potentialbarriären.

Nuklidbarriären beskriver hur atomkärnan innehåller olika avsnitt och nivåer som innefattar attraherande och repellerande domäner. Dessa styrs av atomkärnan själv i enlighet med dess aktuella struktur och genom impulsekvationen

J_0K+3J_1K = 0

Kärnan kan i samma fraktalnivåer uppvisa både attraherande och repellerande faser, beroende på hur kärnan disponerar sin ekvation för jämvikt.

Fusion

Nuklidbarriären definieras i TNED helt idealt som den sfäriska gränsyta som precis innesluter toroidkärnan [ATOMKÄRNANS HÄRLEDNING].

Två atomkärnor som kan förenas — ingå fusion eller sammanslagning — och som ligger innanför varandras nuklidbarriärer genomgår en mycket stark attraktion. Kärnor som inte kan förenas uppvisar en mycket stark repulsion om de tvingas innanför varandras nuklidbarriärer.

Utanför nuklidbarriären gäller idealt mellan två lika laddade kärnor Coulombkraften [ELEKTRISKA KRAFTLAGEN]

F=k(Q/r)².

Innanför nuklidbarriären gäller inte Coulombkraftens enkla form längre:

· Atomkärnan uppvisar ENLIGT TNED genom sitt centralmassiv ±909e en stor potential att fasväxla, fassynkronisera, fasvrida, faskoppla, och fasändra laddningsbilden i sin ytstruktur;

· Kärnan bestämmer själv från fall till fall genom sin allmänna impulsmomentsekvation J_0K+3J_1K = 0 vad som gäller;

· Kärnan kan justera sig för att ta emot en fusionskomponent, eller justera sig för att kasta ut en — eller bara bestämma sig för att bli exciterad;

· Två Heliumkärnor ₂He⁴ vägrar förening, men tre går utmärkt. Likaså vägrar ₂He⁴ att förena sig med såväl en neutron ₀n¹ som en väteatom ₁H¹

Spinnsynkronisering

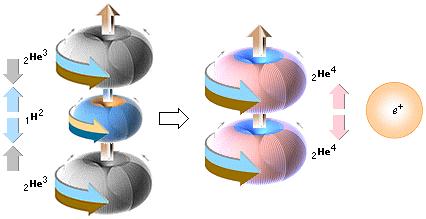
Skalenlig fusionsordning enligt TNED.

Den frigjorda positronmassan (e⁺) här avbildad med den idealt upptagande totala sfäriska volymen för e-massans toppspinnande t-ringar (men elektronmassan visar sig normalt aldrig i den formen).

SPINNSYNKRONISERING

Impulsmomentet J=mvr som grundlägger hela atomkärnans härledning (se från Planckringen) garanterar genom det ytmagnetiska fältet

(B_T, utförligt i B_T-FÄLTETS BETYDELSE FÖR ELEKTRONMASSORNA) att alla atomkärnor som kommer så nära varandra att J-vektorerna börjar växelverka också ställer in sig med samma spinnriktning. Denna självreglerande automatik kallas i TNED för spinnsynkronisering. När spinnsynkroniseringen inträder bildas naturligt också en allt större avkännande dynamik mellan de så motvända toroidytorna och som därmed helt naturligt grundlägger fusionsfysiken.

Innanför kärnsfärerna — mellan de motvända spinnsynkroniserade toroidkärnornas kärnbrunnar, och endast där — blir det alltså istället kärnans aktuella ±e-ytstruktur som bestämmer från fall till fall vad som gäller: om en förening ska ske, eller om kärnorna ska stöta ifrån varandra. Om kärnorna förenas sker det genom en s.k. fusion med en resulterande produkt enligt kärnreaktionslagen

K1+K2–(m®g)=K

om inga yttre moment finns med.

NUKLIDBARRIÄRENS GRAF kan av ovannämnda rent dynamiska skäl således inte beskrivas på någon enkel statisk form.

Det finns dock en ideal riktlinje som kan ges för nuklidbarriärens ideala formgraf och av följande natur:

Om U-grafen i potentialbarriärren relateras till ringfraktalernas underringar i formen av ideala sfärer vars gravitella bidrag summeras på allt växande antal, bildar potentialbarriären en motsvarande potentialbarriärens strukturgraf (uträkningarna redovisas inte här) med formen som ovan. Alltså i princip samma som den redan kända potentialbarriärens U-graf, men förskjuten utåt. U-toppen ligger ”strax utanför kärnytan”. Men enligt vad som nyligen sades beträffande nuklidgrafens principiella dynamik, finns ingen fast, statisk avståndsskala för samtliga fall, eftersom kärnorna som ovan nämnts kan ändra sin ytbild från fall till fall.

Idealbilden beskrivs då enligt TNED på den kärnan omskrivna sfärens gränsform som en fast och bekväm universell referens för nuklidbarriären eller Coulombbarriären.

Nuklidbarriärens funktion får alltså i stora drag samma utseende som den enkla U-grafen från principalpartikelns potentialbarriär, men med den ytterligare karaktären att den mera sammansatta versionen uppvisar negativ divergens före inträdet till ringkroppen. Detta negativa divergensområde har givetvis ingen statisk mening för atomkärnans del, utan tjänar bara som en antydd dynamisk lokal för de fall då atomkärnor kommer mycket nära varandras kärnbrunnar. Vilket vill säga: DET NEGATIVA DIVERGENSOMRÅDET (blått i grafen ovan) illustrerar (alltså främst) en grovt motsvarande orienterande bild av ytkontakter mellan kärnytorna då de befinner sig i TYP fusionsinväxling. Området har (naturligtvis) också en motsvarande positiv del, men det är i slutänden kärnans egen balansräkning som, från fall till fall, bestämmer vad som gäller. På grund av kärnstrukturens ±e-karaktär tillkommer dessutom toppar och dalar av dynamisk karaktär i dessa regioner i följd av nukleär växelverkan som ytterligare komplicerar bilden.

I EKVIVALENTFORMERNA är det MED ANDRA ORD bara konstellationen

som garanterar maximal fusionsdynamik.

Ligger kärnorna närmare varandra finns inte optimalt utrymme för spinnsynkronisering.

Ligger kärnorna längre ifrån varandra ligger de utanför nuklidzonen och extra moment måste tillföras för att få dem i fusionsläge.

En optimal fusionslokal enligt kärnreaktionslagens helt enkla form existerar följaktligen endast utifrån ett optimalt tätt materietillstånd — där kärnorna redan i princip ligger i inväxlingsläge, där inga yttre moment förekommer av någon som helst signifikant vikt, och där ingen yttre affekterande em-strålning existerar.

MED ANDRA ORD HÄR: K-cellen.

GRUNDÄMNESBILDNING I NATURLIG MENING — från ett optimalt tätt materietillstånd — och grundämnesbildning i termonukleär mening (den konventionellt beskrivna processen i stjärnor och solar), samt laboratoriemässiga experiment, uppvisar därför med impulsmomentets bevarande nödvändighet strängt skilda fusionsbeteenden.

Fusionsordningen i TNED medger maximalt tre nuklider per fusionstillfälle. Bara en komponent i taget kan summera balansräkningen mot två omgivande i deras samtidiga kontakt. Detta utesluter inte att flera kärnor än tre kan förenas, men det finns här för dessa fall ingen allmän resultatbild att presentera. Eftersom mellankärnan avskärmar Coulombfältet mellan ändkärnorna, gäller samma Coulombprodukt (cp=Z₁Z_2|3) både för binära fusioner och tripelfusioner.

Diakvadraten: -- Neutronkvoten:

NeutronQuote »dia»

NEUTRONKVOTEN

DIAKVADRATENS HÄRLEDNING

GRUNDÄMNESFÖRDELNINGEN I UNIVERSUMS ALLA HIMLAKROPPAR

Härledningen är helt matematisk

Ø=DIA

Neutronkvoten:

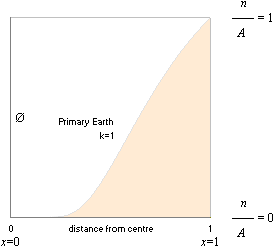
För alla möjliga neutronförekomster n i en godtycklig fusionsring (ekvivalenten som bildar en grundämnesnuklid genom exotermiska fusionslagen) med masstalet A

finns bara en och endast en icke-periodisk funktion (här en kurvskara)

som börjar på n/A=0 vid J-kroppens radievariabel x=0 och som slutar på n/A=1 vid x=r=1

för alla möjliga nuklidseparationer k=d/r₀ efter divergenständningen (från maximala tätheten rmax=1,82 T17 KG/M3 i neutronkallplasmat).

[k definierar J-massan via gränsmassan m_0JSUB med k=1].

Vilken är denna funktion?

Den är

(n/A)^x = x^k = Ø^x

Med x=1=r ges nämligen Ø=1 oberoende av k, så att funktionens enklaste form helt enkelt (trivialt) kan skrivas Ø=n/A;

Ø = n/A

Ø ........... neutronkvoten

n ........... antalet neutroner i en given fusionsring

A ........... masstalet i den nuklid som fusionsringen bildar

Vi benämner neutronkvoten Ø=n/A (o-streck för danska ö Ø, eller »diametertecknet» DIA, Alt+0216).

Synkoperingen från NeutronQuote med N lagt på Q i spegling (eller bakifrån) ger närmaste typografiska akronymen Ø, som också ansluter till grafens form med k=1.

Benämningen (enklast) för Ø blir därmed DIA.

Principfunktionen kan också »enklare» postuleras så:

Det finns bara en och endast en klass av icke-periodiska funktioner som alla utgår från xy=0 och som alla skär en och samma komplexa talpunkt xy=1.

Nämligen klassen potensfunktioner y=x^n/x=xⁿx^1/x som alltså innefattar klassen exponentialfunktioner xⁿ. Se ävern i EULERS EKVIVALENTER.

INVERTERADE klassen potensfunktioner utgår från (0;1), de skär också (1;1), men skrivs y=x^nx. (y=1–x^nx utgår från 0;0 och möts i 1;0).

Klassen logaritmfunktioner (eller exponentfunktioner typ e^x) har också en gemensam skärningspunkt (0;1), men de utgår inte från xy=0.

Klassen trigonometriska funktioner kan både utgå från xy=0 och ha gemensam skärningspunkt, men dessa funktioner är periodiska.

— Vad säger att k-funktionen inte är periodisk?

— Ett värde för hela J-kroppen, analogt hela intervallet r. Det finns bara ett nuklidseparationsvärde för en given J-massa. Detta garanterar att k-formen är helt linjär. Däremot kan J-kroppen uppvisa interna variationer (och gör det också), men dessa ingår inte i den här översikten.

Deriveringen av principfunktionen

[(P)^Q]’ = (P)^Q[Q(P)’/(P) + Q’ln(P)] .............................................................. se allmänna potensderivatan

Termerna PQ gäller för vilka som helst matematiska uttryck.

Q=konstant=n ger ExponentialDerivatan (variabeln i Basen) .................... [(P)ⁿ]’ = (P)ⁿ[Q (P)’/(P)] = n(P)^n–1Dn(P) ExponentialDerivatan

P=konstant=e ger ExponentDerivatan (variabeln i Exponenten) ................. [e^Q]’ = e^QQ’ln(e)] = e^QDn(Q) ExponentDerivatan

Av okänd anledning omnämns inte

allmänna potensderivatan

i den allmänt tillgängliga matematiska litteraturen. Inte ens en antydan.

P=x ; Q=k/x ; [(x)^k/x]’ = (x)^k/x[(k/x)(1)/(x) + (–kx^–2)ln(x)]

= (x)^k/x[kx^–2 – kx^–2 ln x]

= (x)^k/xkx^–2[1 – ln x]

= (x)^{k/x – 2} k[1 – ln x]

= k(x)^{k/x – 2} – (x)^{k/x – 2} ln x^k

;

Tangensformen

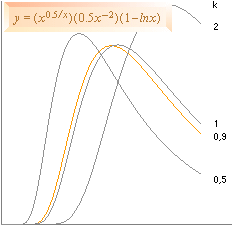
k=1 är INTE den kurva som har minsta variationen. k-värdet för detta fall ligger approximativt vid 0,9.

J-massan för k=0,9 är runt 10 T24 KG. Någon sådan himlakropp finns i varje fall inte i Solsystemet. Närmast större än Jordens 5,975 T24 KG är Uranus med 86,6 T24 KG.

J-massor större än 1,6 T32 KG

För J-kroppar med egen divergensnollzon (från 80 Solmassor och uppåt [J80-massan]) blir k-värdena negativa.

Det innebär att kärnorna utverkar ömsesidigt tryckande moment med den påföljden att J-kroppens expansion blir särskilt häftig.

För dessa fall betraktar vi J-kroppar som har möjligheter att avyttra mindre separata J-kroppar ur sin ytdel och som därmed ansluter till principgrafen med positiva k-värden.

RESULTAT

Ø=x^k/x............................... NEUTRONKVOTEN (DIA)

NEUTRONKVOTEN (Ø) anger antalet neutroner av masstalet (A) i en viss nuklid.

En och samma nuklid kan bildas genom (många) olika alternativ, vilket ger spridningen.

Neutronkvoten noll är speciellt förbehållen Järngruppen, men Järnet kan också bildas på (många) andra sätt. Se utförligt i GRUNDÄMNESBILDNINGENS TVÅ BASGRUPPER.

Hur J-kroppen identifieras — nuklidseparationen

Den aktuella J-kroppen definieras och identifieras genom k-värdet eller nuklidseparationen k=d/r₀

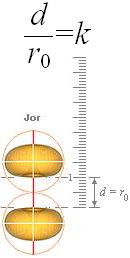
i sambandet för kärngravitella jämvikten [FUSIONSGRÄNSMASSANS DEFINITION]. d är den inbördes nukliddistans som två atomkärnor uppvisar vid den ideala tidpunkt då full divergenständning föreligger och därmed full funktionsdynamik råder. Nuklidseparationen ökar med avtagande J-massa som följd av avtagande g-tryck. Gränsmassan m_0JSUB definieras av k=1 från atomkärnans fysik ENLIGT TNED.

Sambanden är avpassade för gränsmassans bestämning (atomkärnan har på grund av sin geofysik ENLIGT TNED olika barriärer beroende på hur och varifrån den »ses» av en yttre laddning) vilket innebär att k-värden som ger stora nuklidseparationer innehåller ett visst distansfel som växer med avtagande J-massa. För den överskådliga framställningens del bortses dessa defekter ifrån (men vi bör ha dem i bakhuvudet för att undvika eventuella missförstånd).

De mindre J-kropparna

DAMM, SAND, SMÅSTENAR, GRUS och större block

De mindre J-kropparna

Ø-kvadraten (Ø, dia) visar att de små J-kropparna i allmänhet får låga neutronkvoter i större delen av sina kroppar.

Mycket små J-kroppar ”glider” direkt, via expansionen som efterföljer fusionsfasen eller som är integrerad med denna, in i ett kemiskt mineralogisk slutligt fast och kallt tillstånd — i formen av DAMM, SAND, SMÅSTENAR, GRUS och större block. G-skuggningen från stora närliggande moderkroppar blir då speciellt märkbar, med flera (många) olika möjliga resultat.

En liten J-kropp som påverkas litet av g-skuggning har ingen egentlig förutsättning att utveckla fusionsringar i den tyngre nuklidgruppen. Samma J-typ i stark g-skugga däremot, kan attraheras av en stor närliggande moderkropp. Den normalt häftiga nuklidseparationen i den del av J-kroppen som vätter mot g-skuggaren motverkas då, vilket betyder att J-kroppen i denna del kan bilda längre fusionsringar. Optimalt delas därmed J-kroppen i en praktiskt taget 100% tätare Järndel närmast g-skuggaren och en lättare silikatdel på frånsidan.

DIAMANTER — finns i ureiliter

Den snabba expansionen från den höga tätheten i ytskikten på de större J-kropparna medger speciellt att kolrika områden DIREKT kan bilda fasta tillståndets fysik i formen av små diamanter. Det är också precis vad man finner i en viss typ av meteoriter (ureiliter) [BAs247sp2].

Men också en stor mängd primitiva organiska föreningar av typen C—O—H är möjliga genom den snabba avsvalningen för mycket små J-kroppar. Också sådana är välkända i vissa meteoriter (kolhaltiga kondriter).

Mörka materien

DEN MÖRKA MATERIEN — totalt 355 gånger den synliga räknat på hela K-cellens massa

Se härledningen i mk/mVIZ.

Den mörka materien

K-CELLENS ALLMÄNNA MASSFÖRDELNING

Som vi har sett från resultatredovisningen i K-cellens värmefysik utgör stjärnor, solar och lysande gasmoln — den synliga materien i universum — bara en rest (1/355) av den totala massa som bildar värmestrålningen i universum. Sambanden kräver en sådan ordning. TNED förklarar den.

J80-massan

Vi vet att J-kroppar från r_max=1,82 T17 KG/M³ med primärmassa från ca 80 Solmassor (J₈₀, m[SOL]=1,989 T30 KG) och uppåt har egna nolldivergenszoner

c₀²Ö 3/2Gpr=r_0c ; r_0c=59455,6 M ; m_0c=r4pr_0c³/3 ; m_0c=1,60227 T32 KG = 80,556561 m[SOL]

[Från DIVERGENSENS EXPANSIVA G-BEROENDE]; se även i STJÄRNORNAS GRÄNSMASSOR.

Mera kortfattat utförligt i J80massan.

I Ø-analogin (Ø, dia) är massavgivningen för en J-kropp med 80 Solmassor MAX 28% [Se JORDENS FEMTE EKVATION].

Kvantiteten 28% är i sig alldeles för liten för att kunna förklara en matchning med resultaten från K-cellens värmefysik som utpekar att den mörka materien är flera hundra gånger större än den synliga. Det finns emellertid ett mellanläge mellan moderkroppar från J₈₀-gränsen och upp till den massa som kan avge J-strängar typ Solsystemet, men ingen beskrivande eller analyserande framställning finns ännu (2007) på denna punkt.

J-kroppen med större massa än 80-gränsen kan (upp till en viss gräns, av symmetriskäl) inte avyttra egna J-strängar typ Solsystemets kroppar. För den delen är det tydligt att den istället avger mängder av småkroppar. Efter fusionsfasen kommer dessa att sluta i kornstorlekar som DAMM, SAND, STEN, GRUS och STÖRRE BLOCK. Mineralogin för dessa är genom fusionsfasen i Ø-kvadraten alltså given som i stora drag silikatblock och järnklumpar med alla mellanlägen. I nuvarande skede finns emellertid ingen analys på kropparna utanför Ø-kvadraten, alltså från J₈₀-gränsen och uppåt, och dessa meningar är därför bara initierande ansatser.

Att det finns ett mellanläge från J₈₀-gränsen och upp till den massa som kan avge J-strängar typ Solsystemet är uppenbart enligt följande.

Eftersom Solsystemets J-sträng i K-cellens expansion är given som en typisk perifer massavyttring från en större moderkropp, har vi skäl att förvänta att huvuddelen av K-cellens divergenständning sker på J-kroppar med betydligt större massa än Solmassan. Den del som återstår av moderkroppen sedan typsträngar av Solsystemets magnitud avyttrats, kan därmed hänföras till kategorin J₈₀-kroppar över J₈₀-gränsen. Genom deras resterande avyttringar i formen av de nyligen nämnda mindre J-kropparna finns alltså en möjlig ansats till en förklaring varför den avgjort största delen i kallplasmat slutar som icke lysande (osynlig) materia.

Jämför (fetstilen är min markering)

Citat BA1978

”Man kan också tänka sig mer kondenserad materia. Studiet av fördunkling och färgförändringar i hopens centrum tyder på att det i så fall inte kan röra sig om stoft i stil med det i Vintergatan. Större stoftpartiklar med storlekar upp till fotbollsformat skulle utan svårighet kunna hålla hopen samlad och ändå förbli omöjliga att upptäcka; problemet är bara att vi inte känner till någon enkel process varigenom sådana objekt kan bildas.”

BONNIERS ASTRONOMI 1978 Det internationella standardverket om universum s360sp2n

Den moderna akademins befolkning har väl observerat positionerna, men har missat de enkla lösningarna på grund av oviljan att härleda, inte uppfinna, dem. Se utförligt från DEN ELEKTRISKA LADDNINGEN.

Vi har under alla omständigheter all anledning att förmoda att restmassorna bör finnas i stora mängder mellan de egentliga galaktiska hoparna från vilkas J-centra de ursprungligen har expanderat. Någon exakt matematisk formulering på massfördelningen i ämnet finns emellertid inte i detta skede utöver vad resultaten från K-cellens allmänna värmefysik har utpekat.

Nuklidbildningarna

END.

Nuklidbildningarna

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Nuklidbildningarna

ämnesrubriker

K-cellens expansion · Solsystemets uppkomst

Exotermiska kärnreaktionslagen

K-cellens expansionsfysik · Fusionsgränsmassan · Termogravitella jämviktstrycket

Grundämnesbildningen generellt för hela universum

GRUNDÄMNESFÖRDELNINGEN i himlakropparna · BASKARTA ÖVER GRUNDÄMNESFÖRDELNINGEN

HIMLAKROPPARNAS BILDNINGSTID · HIMLAKROPPARNAS PRIMÄRMASSOR · J-kropparnas Expansion

FUSIONSBILDNINGEN GENOM EXEMPEL

Nuklidbarriären

Diakvadraten

Jordens Fem Ekvationer · sammanställning

Jordens Första Ekvation termogravitella jämviktstrycket

Jordens Andra Ekvation optimala fusionsgränsmassan

Jordens Tredje Ekvation Solsystemets uppkomst

Jordens Fjärde Ekvation diakvadraten, grundämnesfördelningen, neutronkvoten

Jordens Femte Ekvation himlakropparnas primärmassor

innehåll

NUKLIDBILDNINGARNA

K-cellens expansion

Nolldivergenszonen

Divergenständning

J-kroppen

Massexakt orienterande delningsbild

Solsystemets uppkomst

Jordens tredje ekvation

Solsystemets uppkomst — Härledning

Härledningen

Titius talserie

Historia

Tabell · Himlakropparnas omloppshastigheter och medelavstånd från Solen

Tvillingarna Uranus-Neptunus

Exotermiska kärnreaktionslagen

Grundämnesbildningen

K-cellens expansionsfysik

Expansionssambandet

Keplermomentet

Expansionstiden

Expansionshastigheten

TIDsfären

Keplers tredje lag

Gravitationsenergin

Nolldivergenszonens radie

Grundämnesbildningen

Tillståndet Före Divergenständning

Fusionsgränsmassan

Jordens andra ekvation

Termogravitella jämviktstrycket

Jordens första ekvation

Grundämnesfördelningen

Jordens fjärde ekvation

Primärstjärnan

DiaKvadraten

BASKARTA ÖVER GRUNDÄMNESFÖRDELNINGEN ENLIGT TNED

G-skuggning, beskrivning

Himlakropparnas primärmassor

Jordens femte ekvation

Himlakropparnas bildningstid

J-kroppens expansion

Flykthastigheten

Allmänna samband

k-bestämningen

G-skuggning, härledning

EXEMPEL Solen-Merkurius

G-skuggningen generellt

Fusionsbildningen genom exempel

Fusionsringen

Fusionslängden

Fusionstidens beräkning

Jordkroppen, baskartan — allmän resultatredovisning

Grundämnesbildningens två basgrupper

Udda nuklider

Jämna nuklider

Den tunga nuklidgruppens certifiering

Basnuklider med olika neutronkvoter

Nuklidbildningens fördjupning

Maximalringens komponenter

Uranbandet

Nuklidbarriären

Potentialbarriären mellan atomkärnorna

Spinnsynkronisering

Diakvadraten

Neutronkvoten

Neutronkvotens ekvation

J-massor större än 80 Solmassor

Hur J-kroppen identifieras

Nuklidseparationen

De mindre J-kropparna

DIAMANTER

Mörka materien

J80-massan

CitatBA1978

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[BA]. BONNIERS ASTRONOMI 1978

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2023-12-11

*END.

Stavningskontrollerat 2008-03-06 | 2017-08-15.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se