SOLFYSIKEN · STJÄRNORNAS OMFÅNG 2008I2 a BellDHARMA production · Stjärnfysikens fundamentala grunder enligt TNED | Senast uppdaterade version: 2018-11-21 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Gränsfrekvensen för primär egenrotation · SolfysikenIIIRadierna

GRÄNSFREKVENSEN FÖR PRIMÄR EGENROTATION — generaliserade samband som gäller alla stjärnor

grundsamband a = w²/r = (2prf)²/r = 4p²r²f ²/r = 4p²rf ² = Gm₂/r²; 4p²f ² = Gm₂/r³ = G4pr/3; pf ² = Gr/3;

f_LIM² = Gr_max/3p

f_LIM = Ö Gr_max/3p ................................... 1135 Hz med r=r_max = 1,82 T17 KG/M²

beskrivning

MAXIMALA ROTATIONEN för en RING där g-kraften vid ringens tyngdcirkel precis uppväger centrifugalkraften ges av sambandet

[w=2p/t₀=2pf, å=v²/r=(2pr/t₀)²/r=w²r]

a=å=Gm/r²=w²r ; w²=Gm/r³=4Gpr/3 ; f = (4Gpr/3)^1/2/2p = (Gr/3p)^1/2 ;

f = (Gr/3p)^1/2 ...................... rotationsfrekvensen i Hertz, massoberoende

För kallplasmats primärkroppar med r=1,82 T17 KG/M³ gäller då tydligen

MAX f =1134,914245 Hz. Tyngre kroppar får större centrifugalkraft vid ytan, men den större massan ger också en större gravitation varför samma f likväl gäller oberoende av massan.

Sambandet gäller alltså strängt taget bara för en RING. I sfärens fall blir sambandet mera komplicerat eftersom delarna närmare polerna påverkas mindre och därför sfärens totala form inte påverkas lika mycket som ringens. Relativt sambandets f-gräns, kvarstår alltså likväl g-kraften som den övervägande i en viss del av en sfär. Vi kan därmed använda sambandsformen som en grov orientering (med säkra marginaler).

Solfysiken · Stjärnornas omfång

stjärnans PRIMÄRA egenrotation

STJÄRNORNAS OMFÅNG

ROTATIONENS INVERKAN PÅ STJÄRNANS FYSIK

Kort Inledning med fortsättning från Stjärnfysiken Del I (Solfysiken)

Med K-CELLENS DETONATION följer i relaterad fysik HIMLAKROPPARNAS AVDELNING OCH EXPANSION genom mindre (sfäriska) massenheter här benämnda J-kroppar [Se J-kroppens definition]. J-kropparnas indelas sedan efter massa i huvudkategorierna stjärnor (termonukleära energiproducenter) och planeter (icke termonukleära energiproducenter). Se även mera utförligt i Den primära himlakroppsbildningen enligt TNED. Se även mera utförligt direkt från GALAXBILDNINGARNA. I detta avsnitt beskrivs den matematiska fysiken för J-kropparnas stjärnmassor med avseende på J-kropparnas (eventuella) primära egenrotation. För rotationens PRINCIPIELLA uppkomst generellt i himlakropparna, se särskilt utförligt i DEN INDUCERADE ROTATIONENS UPPKOMST.

Om J-kroppen har någon primär rotation redan då den avdelas från sin större J-moderkropp, är det tydligt att g-energins omsättning till expanderande J-kropp försvagas genom att kärnkontakterande rekylkrafter, som normalt garanterar g-energins omsättning, oroterad J-kropp, också reduceras på grund av centrifugalkrafterna. Expansionspotentialen reduceras alltså och därmed kvarhålls en allt större del av den primära avyttringsmassa som normalt sett skulle avyttras för en idealt oroterad J-kropp (12% av massan i Jordens fall [Se JORDENS ANDRA EKVATION]). OM primärrotationen kunde utveckla en exakt uppvägande centrifugalkraft (vilket är mindre troligt) mot den g-kraft som normalt skulle utlösa en fullständig expansion genom kärnkontakteringar, skulle J-kroppen alltså inte expandera alls i g-kraftens försorg. En sådan J-kropp skulle därmed behålla hela sin primärmassa. Med ledning av dessa ändlägen och den kända primärmassans avyttring för en oroterad J-kropp (JORDENS FEMTE EKVATION), kan vi beräkna stjärnornas omfång med hänsyn till deras primära rotationer — eller omvänt: primärrotationen från omfånget.

STJÄRNORNAS PRIMÄRA EGENROTATION (w_P), den rotation J-kroppen får via sin avyttring från J-moderkroppen under K-cellens expansion, har dramatisk inverkan på stjärnans slutliga omfång. Relativt små primära impulsmoment, givna vid stjärnans primära maximala täthet, ändrar drastiskt stjärnans slutliga ytterdimensioner. Av det ursprungliga primära impulsmomentet syns knappast något spår alls genom att rotationen i impulsmomentet J=mwr² avtar markant med primärkroppens initiellt snabba expansion på växande r, in till kroppens-stjärnans slutform. Även en ursprunglig relativt stor egenrotation w_P framstår i slutänden som i stort sett obefintlig — fullständigt omöjlig att urskilja i ljuset av den betydligt högre och under långa tidrymder egenproducerade rotationen [Se utförligt i ROTATIONENS INVERKAN] [Se även mera utförligt i DEN INDUCERADE ROTATIONENS UPPKOMST, generaliserad beskrivning för J-kropparnas fysik]. Stjärnans slutform, dess svulstighet, avslöjar dess primära egenrotation. Sirius A är alldeles tydligt vårt närmaste exempel. Se efterföljande EXEMPEL MED SIRIUS.

Stjärnfysiken MED Primär Rotation

Om stjärnornas PRIMÄRA EGENROTATION tas med i bilden — vilket vi skiljer SKARPT från stjärnans egenproducerade rotation under dess brinntid [Se ROTATIONENS INVERKAN] — sker dramatiska förändringar i stjärnans omfång — även med relativt små primärrotationer. I övrigt sker knappast några förändringar.

För att utföra beräkningar (i sammanställning nedan) krävs ett speciellt kalkylkort (se efterföljande exempel) med grund i JORDENS FEMTE EKVATION. En del av sambanden är nämligen en aning knepiga och kräver iterationer [Se allmänt från ITERATIONSTEKNIK (Den beskrivningen är dock ingalunda heltäckande för iterationsmatematiken, men ger en viss orientering)].

STJÄRNORNAS OMFÅNG:

Samband

R_out³ = 3Dm/4pr_r + R_Star³ ....................... stjärnans absolut minsta ytterradie, konstant r_r från R_Star

Dm = m_EDf /f_LIM ................................... tilläggsmassan

= (R_out³ – R_Star³)(4pr_r/3)

m_E ....................................................... maximala tilläggsmassan, se JORDENS FEMTE EKVATION

Df ...................................................... stjärnans primära egenrotation (max 0,00023 Hz för Solen), = f_LIMDm/m_E

f_LIM = 1135 Hz = Ö Gr_max/3p ............... gränsfrekvensen för primär egenrotation, massoberoende

r_r ....................................................... normalstjärnans reala yttäthet

= 8,9277145 t5 KG/M³ .................. gäller primärt oroterade stjärnor

TILLÄGGSMASSAN består i samtliga fall i huvudsak av PRIMÄRVÄTE.

Om stjärnan får tilläggsmassa från primärbildningen via en viss egenrotation, flyttas naturligtvis dess omslutande g-sfär endast ut till ytterranden av tilläggsmassan. Minskningen i strålningstrycket kompenseras av centrifugalkraften så att stjärnan behåller sin grundradie. På denna läggs alltså tilläggsmassan i formen av en extra atmosfär. Tätheten i tilläggsmassan kan bestämmas (grovt) som lika med tätheten vid den oroterade stjärnans yta (med viss möjlig uttunning utåt). BALANSEN mellan g-tryck och strålningstryck kommer därmed, likväl, att ända på stjärnans omslutande g-sfär. Och alltså flyttas endast det negativa jonområdet — stjärnans opacitetsområde — ut till ytterdelen. Därmed kommer det inre av stjärnklotet effektivt att gömmas eller skymmas av den omslutande tunna men ogenomskinliga gasmassan. Primärstjärnan döljs effektivt.

exempel

Räkneexempel som visar känsligheten i stjärnans omfång beroende på stjärnans primära egenrotation

RÄKNEEXEMPEL MED SOLEN SOM OBJEKT

Med kännedom om Solradien, dess synbarhet och precision kan ett absolut minsta gränsvärde bestämmas som gäller för Solens primära rotation vid dess bildning. Värdet blir avrundat 0,00023 Hz (se härledning nedan) som efter Solens primärexpansion till nuvarande storlek ger nuvarande motsvarande period runt 350 000 år. Den syns inte.

härledning, beskrivning

För att Solradien (6,96 T8 M) med eventuellt obetydligt radiellt tillägg ska hålla sig på nersidan inom tredje decimalen 0,00n T8 M får radiekubens faktor 3Dm/4pr_r inte överstiga

(6,965 T8)³=3,3788 T26 M³.

Därmed sätts gränsen för Dm av _limesDm=(6,965 T8)³(4pr_r/3)=1,26354 T23 KG med r_r=8,9277145 t5 KG/M³.

Gränsrelationen ger då med Solens maximala tilläggsmassa (6,24407 T29 KG separat beräkning i JORDENS FEMTE EKVATION)

Dm/m_E=f_LIM^–1Df = 2,02358 t7 som ger Df=(2,02358 t7)(1135) = 2,29676 t4 Hz » 0,00023 Hz. Så känsligt är det. Gränsreferensen blir alltså avrundat neråt 0,00023 Hz för Solens del. Med primärexpansionen via primärimpulsmomentet J₀=mvr avtar vinkelrotationen med växande r enligt

(J=mwR²)₀ = (J=mwr²) som ger (fR²)₀= (fr²) ;

f = f₀(R₀/r)² ............................ R₀=(3m₂/4pr_max)^1/3

Solradien vid r_max=1,82 T17 är R₀=13 767 meter. Gränsfrekvensen f₀=0,00023 Hz blir då vid r=6,96 T8 meter lika med f=9 t14 Hz — eller ett varv på mer än 350 000 år. Att finna spåren efter en sådan typrotation i Solen (lägst 350.000 år, mera troligt flera miljoner år) torde inte tillhöra den allra enklaste uppgiften.

Exemplet ovan är ett grundexempel som används vidare i stjärnfysiken enligt TNED för att referera Solens primärrotation som praktiskt taget noll.

resultat:

Med hänsyn till uppgiften på den fotometriskt observerade Solradien (6,96 T8 M) i förening med den beräknade g-radien 6,97 T8 M samt de övriga detaljer som framgår i SOLENS TRE EKVATIONER finns här veterligt ingen grund för att associera Solen med någon nämnvärd primär egenrotation.

exempel

EXEMPEL MED SIRIUS

EN AV SOLENS NÄRMASTE GRANNAR (f.ö. stjärnhimlens ljusaste objekt) är Sirius A (8,7 ljusår eller 2,7 pc) med massan 2,25 Solmassor [BAs103sp1, ENCARTA 99 Sirius anger 2,4] och den via interferometri uppmätta radien ca dubbla Solens [BAs30sp2ö]. Genom medeltäthetskonstanten r_nom=1408 KG/M³ skulle Sirius som en primärt oroterad J-kropp (typ Solen) fått stjärnradien

r_SIRIUSA = (3m_SIRIUSA/4pr_nom)^1/3 = 9,121 T8 M, eller ca 1,31 gånger Solradien 6,96 T8 meter — att jämföra med den nyligen omnämnda uppmätta ca rSIRIUS=2rSOL. Genom ovanstående resonemang från STJÄRNORNAS OMFÅNG drar vi av detta slutsatsen att Sirius A haft en något högre primär egenrotation än Solen och att den har en liten utbredd atmosfär som ett extraskikt ovanpå sin primära grundradie 1,31 Solradier. Primära egenrotationen (Df) för Sirius A blir 0,000562 Hz för att få slutradien 2 Solradier från oroterade originalet 1,31

[Redovisningen av beräkningen kräver tillgång till kalkylkortet med iterationsresultatet för m_E (se redov. nedan), men kalkylkortet ingår (ännu) inte här på grund av webbläsarnas begränsning (ÅTGÄRDAT 2010-04-21 se nedan)].

Exempelbeskrivning

Med kända Solradien (fotometriska, S_F)

S_F = 6,96 T8 M, samt data för Sirius A

R_out = 2 Solradier .................................. aktuella

R_Star = 1,31 Solradier ............................. normala

beräknas först tilläggsmassan för Sirius A enligt föregående sambandsredovisning

Dm = m_EDf /f_LIM ................................... aktuella tilläggsmassan

= (R_out³ – R_Star³)(4pr_r/3)

= 7,25218 T23 KG med r_r

r_r = 8,9277145 t5 KG/M³ ..................... gäller primärt oroterade stjärnor

Vi använder sedan kalkylkortet (PrimStar.ods i OpenOffice — se Öppningsmanual om ej redan bekant) med inmatningen

m_J = 2,25Solmassor = 4,4753 T30 KG, vilket ger maximala tilläggsmassan

m_E = 1,4624494 T30 KG från kalkylkortet

Vi använder sedan sambandet för aktuella tilläggsmassan Dm enligt

Df = f_LIMDm/m_E och får

= (1135)(4,95892 t7)

= 5,62838 t4 Hz

= 0,000562838 Hz

exempel

RÄKNEEXEMPEL med förenklat r_r = r_Star=1 t4 KG/M³

Hur 1 primär Solmassa kan bli en JÄTTESTOR stjärna

EN STJÄRNA PÅ 1 SOLMASSA 1,989 T30 KG är påförd 18,8% eller ca 1/5 av sin maximalt tillåtna rotation i sin primärbildning som J-kropp vid tätheten 1,82 T17 KG med radien

r_Star =13766,544 M. Det ger en primär rotationsfrekvens på 1135×0,188=213,38 eller avrundat

f_J =214Hz. Vid full stjärnkropp (R_Star) har den minskat [f = f₀(R₀/r)²] till mera blygsamma

f_Star =8,3723 t8 Hz eller ca 138 dygn per varv.

Kalkylkortet nedan endast i bild från originaldokumentet (MsWorks.4.0). Kalkylcellerna fungerar tyvärr inte i htm-dokument, här visas endast bilden.

Ett motsvarande kalkylkort (nära utseendemässigt lika men vidareutvecklat för samtliga himlakroppsmassor) frinns nu (Apr2010) utformat i gratisprogramvaran OpenOffice. Se

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN PrimStar.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/PrimStar.ods

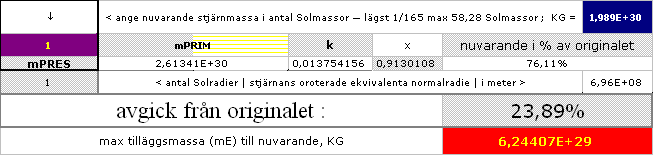
Se även utförlig beskrivning i HIMLAKROPPARNAS PRIMÄRMASSOR.

Maximala tilläggsmassan (m_E) i Solens fall kan beräknas separat genom JORDENS FEMTE EKVATION se bildkopia av resultat från kalkylkort ovan. Vi får den som

m_E = 6,24407 T29 KG

Solkroppen påförs då (linjärt, Dm=m_EDf /f_LIM) en extramassa på ca

Dm = m_E(0,188) = 1,17388 T29 KG =1,2 T29 KG

— vilket är ca 1/5 av maximala tilläggsmassan 6,24407 T29 KG linjärt räknat och som i vanliga fall skulle expandera bort från en oroterad J-kropp genom dess primärbildning.

J-kroppen bildar SOL eftersom massan är större än m_SLIM (lägst 6 Jupitermassor med Väte-1-bas). Radien, med 1 Solmassa som bas, är R_Star=6,97 T8 M. Tätheten vid stjärnytan (oroterad kropp) är avrundat

r_Star=1 t4 KG/M³ (Se yttäthetskonstanten). Med sambandet

m = rV = r(4p/3)(R_out³ – R_Star³)

kan vi därmed beräkna hur långt ut tilläggsmassan sträcker sig om den (med minsta utsträckningen) börjar vid r_Star analogt R_Star och slutar vid R_out och bibehåller

r_Star=1 t4 KG/M³. Vi får då

R_out³ = 3m/4pr + R_Star³ = 3(1,2 T29)/4p(1 t4) + (6,97 T8)³ ;

R_out = 6,59221 T10 M @ 0,44 AU eller 94,6 Solradier

Tilläggsmassan kommer alltså MINST att sträcka sig ut en liten bit utanför motsvarande Merkuriusbanans medelradie som ligger vid ca 0,387AU.

BORTFALLET AV STRÅLNINGSTRYCKET kontra centrifugalkraftens ökning blir (som vi ser) helt försumbar [å=w²r=(2pf_Star)2R_Star=1,92601 t4 M/S²].

;

Stjärnan i exemplet kan likväl lysa med Solens kraft — men kolla omfånget!

EXEMPLET OVAN är ett extremexempel. I de praktiska fallen är f_Star betydligt mindre.

Rotationens inverkan på stjärnans fysik — Stjärnans egenproducerade rotation

EGENPRODUCERADE ROTATIONER ges för alla stjärnor som haft någon minsta PRIMÄR egenrotation [Se utförligt från DEN INDUCERADE ROTATIONENS UPPKOMST]. Den egenproducerade rotationen ingår i stjärnans allmänna tryckekvation (via p) på bekostnad av strålningstryckets reduktion, omfånget konserveras. Detta sker successivt under stjärnans hela energicykel, men skillnaden i effektförbrukning blir ytterst marginell [‡R]. Denna detalj garanterar att

DEN PRIMÄRA Stjärnfysikens parametrar enligt den enkla tryckekvationens ideala form KAN användas för noggranna beräkningar oberoende av stjärnans praktiska egenproducerade rotation.

Vi studerar den matematiska förklaringen.

p – p_e – ^gp = 0 ................................ stjärnans allmänna tryckekvation

DEN OROTERADE STJÄRNANS NORMALFORM, full aktivitet, kan skrivas på referensformen

^gp₀ = p – p_e

OM stjärnan från sin primärbildning har NÅGOT impulsmoment, drivs detta upp successivt [‡] via energiproduktionen med ett bildat (motsvarande) centrifugaltryck p_w. Därmed reduceras samtidigt ^gp₀ eftersom g-trycket avtar (p:=p–p_w) enligt

^gp = ^gp₀–p_w som ger ekvivalenten

^gp₀–p_w = p–p_w – p_e = ^gp ;

^gp = p – (p_w+ p_e) NÄR STJÄRNAN (idealt plötsligt) förbrukat allt bränsle och slocknat gäller alltså, idealt

0 = p – (p_w+ p_e) ;

p_w = p – p_e

Detta är alldeles detsamma som den oroterade normala stjärnans fulla verksamhet enligt nyssnämnda

^gp₀ = p – p_e

Stjärnans egenproducerade rotation

^gp + p_w = konstant = DEN OROTERADE KROPPENS TRYCKEKVIVALENT = ^gp₀

Stjärnradien bibehålls med påförd rotation och lägre strålningstryck

KVANTITETEN p_w är enligt [‡R] emellertid helt ringa och befinner sig långt ifrån varje jämförelse med strålningstryckets kvantitet: centrifugaltrycket p_w ERSÄTTER INTE ^gp₀. Vore så fallet skulle strålningstrycket PARKERA stjärnan på ett impulsmoment som sedan skulle bevaras med konstant kroppsvolym — oberoende av att stjärnan sedan slocknar. I det verkliga fallet har p_w betydelse endast som EN mindre NY OFFSET för g-trycket (p): När stjärnan slocknat (^gp=0) måste g-trycket komma över gränsen p=(p_w+ p_e) för att stjärnan återigen ska kunna producera energi i en andra och n:te energicykelfas. Enda sättet för en IDEALT ENSAM SLOCKNAD STJÄRNA att också reducera den föregående energicykelns p_w är genom INRE FRIKTION. Preferensen (sämsta fallet) för den TID det tar att genomföra den reduktionen är densamma som tiden för uppbyggnaden av p_w. Dvs., stjärnans brinntid.

· IMPULSMOMENTET J=mwr² som stjärnan byggt upp under sin brinntid, och rent kvantitativt frånsett den obetydliga del som ges av p_w, garanterar att stjärnans rotation (w) tillväxer med avtagande radie (r) då ^gp försvinner.

DÅ STRÅLNINGSTRYCKET gamma-p FÖRSVINNER

Se Exempel med Solens Rotationsfrekvens f_D i SolensKompaktRotationEx i PULSARMATEMATIKEN:

— Exemplet visar hur Solen kan sluta som en pulsar med nuvarande rotation om strålningstrycket skulle upphöra.

‡[R]. Vi genomför en sämsta fallets grovberäkning. Periferihastigheten v=2pr/T₀=wr, T₀ omloppstiden för ett varv. I Solens fall är den ca 27 dygn på radien r=6,96 T8 M. Rotationsenergin eller vridmomentet kan skrivas E=mad=m(v²/R)R=mw²R². Med Solmassan m=1,989 T30 KG får vi

E = (1,989 T30)[2p(27 × 86400)^–1(6,96 T8)]² = 6,98969 T36 J, avrundat 7 T36 J. Genom E=Pt ges effekten P=E/t med

t=20,82 T9 år (från resultaten i K-cellens värmefysik) = (20,82 T9)(3,1688087 t8)^–1 sekunder.

Effekten således P_rot=(7 T36)/(6,57029 T17)=1,0654 T19 Watt.

I förhållande till huvudeffekten (runt 4 T26 W) är P_rot alltså helt försumbar.

Skillnaden ligger runt åttonde decimalen och har därmed ingen som helst betydelse för huvudsaken — inte ens om egenrotationen hundrafaldigas!

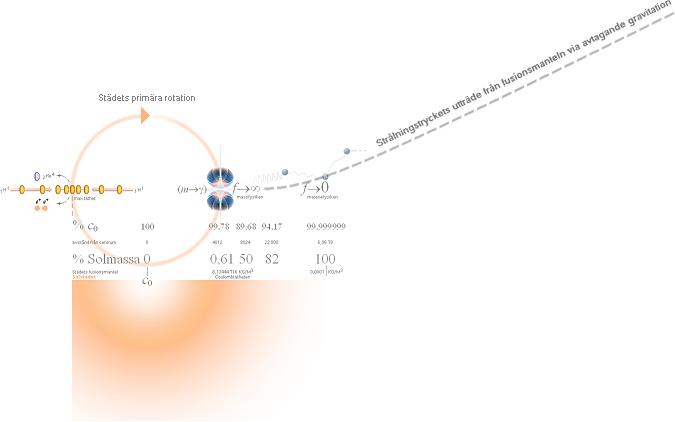
Stjärnans egenproducerade rotation — Tillägg 2012-01-20 i förtydligad illustration — Se separat artikel för Matematiska samband

Stjärnans egenproducerade rotation

Strålningstryckets utträde från stjärnstädets fusionsmantel går via en motsvarande variabel ljushastighet, se särskild illustrerad del (förminskad nedan) från originalförfattningen i Solens energiproduktion.

— Notera att strålningstryckets begrepp här bygger på ett kärninduktivt värmemotstånd. I modern akademi finns inte den typen, endast ett elektrokinetiskt strålningstryck som i dessa sammanhang är helt försumbart.

I RELATERAD FYSIK [TNED] utbreds all elektromagnetisk [em-] strålning relativt det lokalt dominanta gravitationsfältets obönhörligt fasta och absolut fixerade potentialer enligt LJUSETS GRAVITELLA BEROENDE.

— För en icke absolut stel kropp — vad vi vet, likt Solen — som saknar en stel yta överhuvudtaget betyder det i princip att [den gas- eller vätske-] kroppen kan indelas [idealt] i sfäriskt olika separat inbördes [roterande, om kroppen uppvisar rotation] [smala] skikt med en [idealt] bestämd lokalt specifik gravitell ekvipotentialyta för varje skikt. I sektionen om Den Inducerade Rotationen visas generellt hur en primärkropp [Se J-kroppen] i Universums Historia kan erhålla en primär rotation genom den speciella kraftverkan som, i K-cellens allmänna primära expansion, sammanhänger med J-kropparnas avdelning. I det rotationsbegreppet innefattas automatiskt begreppet om s.k. differentiell rotation: delarna längst in i mitten roterar snabbast, de längre ut mera långsamt. Jämför även Bilden av Vattenvirvlar.

Hur strålningstryckets bildning från städytan kan åstadkomma egenproducerad rotation

— Elektromagnetisk strålning som uttränger från ett inre skal eller skikt med högre gravitation till ett yttre skal eller skikt med lägre gravitation — speciellt enligt TNED i fallet med en stjärnas högtäta centralskikt kring Stjärnstädet — måste genomgå en strålväg från lägre divergens [lokalt gravitellt bestämda ljushastigheten] med starkare gravitation till en högre divergens [mot toppvärdet c0 ute vid ytan] med svagare gravitation.

— OM det inre av stjärnan besitter någon primär egenrotation — och då i så fall genom den illustrationstexten ovan nyligen vidrörda differensen i hastighet-gravitation mellan olika g-skikt i stjärnans inre högtäta delar — tvingas följaktligen ljusets väg ut från centrum, genom ljusets g-beroende, böjas av i eftersläpningens riktning inifrån och utåt. Se illustrationen ovan, streckade kurvan.

— Eftersom också ljusemissionerna utövar mekaniska impulser på alla massobjekt [Se Comptoneffekten] — de enskilda atomkärnorna i de berörda g-skikten — överförs tvunget ljusavböjningarna via de olika roterande skikten på motsvarande mekaniskt frånskjutande moment: strålkällans innerst roterande skikt, städmanteln, kan förstås skapa roterande moment mot de yttre delarna. Finns ingen primär rotation, kan stjärnan inte bidra med någon egenproducerad rotation heller under sin livstid.

— Därmed kan en stjärna förstås producera sin egen kärnas centralrotation så länge stjärnstädet producerar fusioner och endast under förutsättning att stjärnan haft en primär egenrotation. I Den Inducerade Rotationen beskrivs hur en kosmisk primärkropp generellt kan erhålla primärrotation i kraft av K-cellens expansion.

— I vårt fall — nuvarande Solrotationen (i skalet) på ca 27 dygn — är det tydligt att Solen från början haft en (liten) primär egenrotation som, tydligen, har byggts upp genom Solens egen energiproduktion [‡R].

Se även i Matematiska samband.

Stjärnans absoluta gränsmassa · teoretiska absoluta gränsvärden för samtliga primärstjärnor

Stjärnans absoluta gränsmassa

med området inkluderat från Stjärnans g-rand och utåt oändligheten

Om stjärnans primärrotation är signifikant (se räkneexempel med Solen) ges stjärnan en tilläggsmassa (Dm) från en maximal expansionsmassa (m_E) som beräknas från JORDENS FEMTE EKVATION.

Med normalstjärnans yttäthetskonstant (r_r=8,9277145 t5 KG/M³) som preferensvärde, förutsatt tätheten för Dm-stjärnan avtar från rr i Dm med växande ytterradie (r_out),

ges UTÖVER Dm, och med matematisk grund i STJÄRNMASSANS RADIELLA VARIATION

[m_in= k_STAR(1 – R/r) + m_SLIM, k_STAR= (m_STAR – m_SLIM)(1 – R/r_STAR)^–1]

m = k_STAR(1 – [1+r/R]^–1) + m_SLIM ................ stjärnmassans radiella variation, r räknas från städradien R

; [1+r/R]^–1 = R/(R+r) = R/r_out för totalmassan och R/r_STAR för stjärnmassan explicit ;

en OPTIMAL GRÄNSMASSA (tillsammans med Dm) enligt

Pm = totala stjärnmassan – normalstjärnmassan = perifera (P, Grek. P) tilläggsmassan

= k_STAR(1 – R/r_out) + m_SLIM — [k_STAR(1 – R/r_STAR) + m_SLIM]

= k_STAR(1 – R/r_out) — k_STAR(1 – R/r_STAR)

= k_STAR[1 – R/r_out — 1 + R/r_STAR]

= k_STAR[R/r_STAR – R/r_out]

= k_STAR(R/r_STAR)[1 – r_STAR/r_out];

Då NÄMLIGEN r_out®¥ ges

_limesPm_E = k_STAR(R/r_STAR) ........................................ maximala tilläggsmassan

(k_STAR kan approximeras med m_STAR). För Solen (Väte-1-bas) är R=4012 M, r_STAR=6,97 T8 M och k_STAR»1,989 T30 KG som ger

_limesPm_E » 1,14 T25 KG; Till jämförelse är i Solens fall maximala tilläggsmassan m_E=6,24 T29 KG (24% av den ursprungliga J-kroppen).

Värdet på den mot ¥ täthetsavtagande _limesPm_E kommer (alltså) inte på långa vägar ens i närheten av den konstant yttäthetsbaserade primära maximala tilläggsmassan m_E.

PERIFERA EXTRAMASSAN (_limesPm_E) kan därmed uppfattas analog med (en approximering av) det material (den s.k. Solvinden) som finns från stjärnans g-rand och som sedan sträcker sig utåt mot oändligheten med avtagande täthet. I Solens fall utgår enligt uppgift [BAs151sp2n] ca 1 T9 KG material per sekund från Solytan i form av Solvinden. För att helt fylla Solens _limesPm_E = 1,14 T25 KG åtgår tiden (1,14 T25)/(T9)= 1,14 T16 S eller avrundat 3,6 T8 år (360 miljoner år). Under hela sin livslängd (idealt 121 T9 år, se Tidsekvationen) förlorar Solkroppen då endast blygsamma (1,14 T25 KG)(121)/(0,36) » 3,83 T27 KG eller 0,0019255907 Solmassor. Knappt 2 promille.

END.

Editor2008V

bihang

SolfysikenRadierna | PULSARENS MATEMATISKA FYSIK ENLIGT TNED | Efter sammanställningar från 2004XI17 |

PULSARMATEMATIKEN ENLIGT TNED

SE ÄVEN inledningsvis BEGREPPET PULSAR I KONVENTIONELL LITTERATUR, BEGREPPET PULSAR ENLIGT TNED

Notera att någon motsvarighet till PULSARMATEMATIKEN sådan den presenteras här INTE finns i modern akademi. Se utförligt i PULSARERNA från Så föddes uppfattningen om den roterande neutronstjärnan.

Noggranna jämförelser följer.

PULSARERNAS GRUNDMATEMATIK ENLIGT TNED

f_D = (4Gr_max/T_Pp²Ö3)^1/3 ....................... rotationsfrekvensen ur pulsfrekvensen

1/T_P = f_D³ · [4Gr_max]^–1p²Ö3 ................... pulsfrekvensen ur rotationsfrekvensen

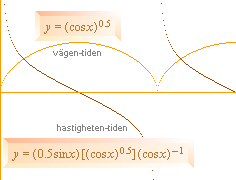
För att undersöka den praktiska, möjliga rimligheten i den bild av pulsarerna som TNED ställer upp, kan vi anställa en grovanalys med enklaste medel utifrån givna grundsamband i expansionsmatematiken. Expansionsmatematikens grundbegrepp i TNED finns också sammanfattade i ovanstående illustration (högerdelen).

Pulsarens grafiska ekvivalent

Alla samband i PREFIXxSIN

DEN PERIODISKT ÅTERKOMMANDE detonationen [Se K-CELLENS DETONATION], expansionen, vändläget och kontraktionen är unikt givna på cykloidens typform. Cykloiden igenkänns på dess fröliknande form om två cykloidbågar läggs tillsammans motvända, se figuren nedan, ändarna uppvisar en något spetsaktig karaktär.

Cykloidens parameterform i PREFIXxSIN

x = a + cosa

y = 1 + sina

Orange ellips, svart cykloid

CYKLOIDEN kan emellertid (veterligt) inte uttryckas på någon ENKEL REKTANGULÄR form: En del illustratörer, typ Encarta 99 Cycloid, bekvämar sig med att använda en ellips för att illustrera en cykloid. Det finns emellertid en typform som MYCKET NÄRA ansluter till cykloiden (inom ovanstående cykloidlinjes tjocklek); på xy-form y=Ö |cosx|. Den benämns här rotcykloiden med förenklingen (fetstil)

cos=|cos|=Ö(cos)²=ABS(cos). Tvärstrecken anger absolutvärdet enligt

|cos|=Ö(cos)²=ABS(cos). Alla samband skrivs här i PREFIXxSIN.

Väg-tidformens derivata ger kurvan för hastighet-tid.

y = Ö cosx ............................................ rotcykloiden

Vägen-tiden

h = r_D + (r₀–r_D)[(cos pT_P^–1t)²]ⁿ ...... höjden

y’ = (0,5sinx)(cosx)^0,5(cosx)^–1 .............. rotcykloidens derivata

Hastigheten-tiden

v = v_max(r₀–r_D)na(cos2at)[(cosat)²]^n–1

ROTCYKLOIDEN beskriver ytterradien hos kompaktstjärnan genom hela förloppet — och därmed motsvarande dopplereffektens ljuskurva för hela kroppsändringen. Rotcykloidens variant, tangensform eller derivata beskriver ytterradiens hastighet genom hela förloppet.

EXPONENTEN n i rotcykloiden från originalets n=0,5 optimerar expansionsformen hos kompaktstjärnan. Låga n-värden motsvarar höga rotationer.

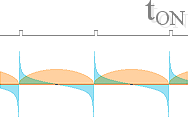
KOMPAKTSTJÄRNANS ENDA MÖJLIGHET att producera LJUS (generellt em-fenomen) ligger vid den omedelbart efterföljande tidrymd som följer på detonationspunkten

— tillfället då stjärnan når sin maximala täthet och atomkärnorna klonkar ihop och bildar rekyl. Den tidrymden är angiven i nedanstående allmänna funktionsgraf genom det exemplifierade idealiserade pulstågets smala ON-intervall markerat tON i figuren nedan. Observera att detta exempel bara är ett av ett otal andra möjligheter.

GRAFEKVATION (0.23þ/5)(cos2þx/5)[(cosþx/5)'2]'0.23–1

När kompaktstjärnan passerat detta skede, måste den invänta nästa stötkontakt för att få fram ytterligare ljusbildning. I mellanläget — och försåvitt begreppet »mellanläge» alls uppvisas — uppvisas ingen aktivitet eftersom kompaktstjärnan är en fusionstekniskt död (läs utbränd) anordning och därför saknar normalstjärnans möjligheter till kontinuerlig ljusemission utan avbrott.

Något om det praktiska fallet från tidpunkten för en stjärnas utslocknande

Om strålningstrycket avtar successivt från den tidpunkt då stjärnans kontinuerliga energiproduktion upphör, och om det medför mellanliggande (små till en början) ljusintensitetsdalar i stjärnans allmänna utstrålning vartefter den går mot sin kompaktform, kan stjärnan likväl uppvisa den normala stjärnans ljuskurva frånsett intensitetsdalarna, dvs. fortfarande över (nästan) hela intervallet (tP). Därmed kan en KOMBINATION ske av ovanstående ideala tON-del med stjärnans (tidigare normala) ljuskurva. Det finns emellertid ytterligare möjligheter i den täta stjärnytan även sedan stjärnans fusionscykel upphört. Kollisionerna mellan atomkärnorna i detonationstillfället KAN, beroende på tillgången på omgivande material, bilda olika ljusemissioner under kortare eller längre tidrymder. Exakt hur, och vilka olika sätt som finns för ljuset att visa sig på totalt sett, finns här av naturliga skäl ingen möjlighet att ge någon som helst ENKEL ekvation för. Vi kan bara ställa upp en allmän form som medger (i stort sett) alla möjligheter, och sedan därifrån undersöka och pröva mot eventuellt befintliga observationer.

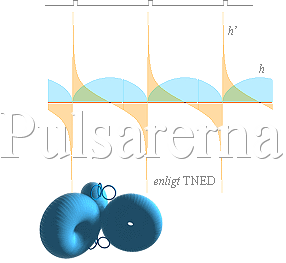
Halvbågformen (orange ovan) är pulstidens motsvarande cykloid (väg-tidformen). Den beskriver hur kompaktstjärnans radie ändras med tiden. Variationen, eller tangensformen (eller derivatan), för detta skeende bildar en hastighet-tid-kurva (blå). Den beskriver vilken hastighet kompaktstjärnans ytterradie har i varje tidpunkt.

Stjärnans rotationsfrekvens vid maximal täthet betecknas här f_D

JU LÄGRE DETONATIONSROTATION (f_D) kompaktstjärnan uppvisar vid stötpunkten, desto mera liknar den en normalstjärna som ännu inte avverkat sin energicykel. Just och nämligen beträffande aspekten rotation.

Alla primärstjärnor som haft minsta lilla egenrotation vid sin bildning (se även Gränsfrekvensen för primär egenrotation, Stjärnornas omfång), producerar en egenrotation under energicykeln.

Rotationen byggs upp ytterst långsamt under miljardtals år som resultat av den differentiella rotationens natur, snabbast längst in på grund av den underhållande fusionsenergin.

När stjärnan sedan slocknar och krymper enbart på grund av att strålningstrycket försvinner, tvingas också stjärnans vinkelhastighet öka (J=mvr). En normalstjärna typ Solen med ett nuvarande ungefärligt omlopp på 27 dygn eller 4,2867 t7 Hz, utverkar vid maximal Coulombtäthet (omkring stötpunkten, när Solen brunnit ut) en rotation med frekvensen (f_D) 642 Hz [‡1]. Den motsvarande hastighet-tid-kurvan (blå) blir för detta fall nästan helt platt på mitten med tvära taggar i stötändarna

‡[1]

Om vi låter Solen krympa totalt till max Coulombtäthet

r₀=8,13444 T16 KG/M³ blir Solen en sfär med radien 18 KM

Solmassan m_S = 1,989 T30 KG

r = (3m/4pr₀)^1/3 = 18008,818 M

Med nuvarande impulsmoment

J = mvr = m(v=2pr/T=[2p/T=2p f ]r=wr)r = mwr² = 2pm·fr²,

får vi med konstant J/2pm=fr2=k=f₀r₀² svaret

f₀ = (r/r₀)²f = 642,12 Hz

På grund av denna egenskap — minsta lilla primärrotation ger en stor egenrotation vid slutet av stjärnans energicykel — har vi en viss rätt att förvänta oss att kompaktstjärnor I ALLMÄNHET bör uppvisa en maximal rotation vid stötpunkten (f_D) i termer av — i runda tal och grovt sett med ovanstående Solens enkla räkneexempel som referensmärke — (minst flera) hundratal Hertz. EMELLERTID måste vi LIKVÄL vara försiktiga i den beskrivningen eftersom varje normalt lysande stjärna i grunden OCKSÅ kan uppfattas som »en pulsar» med extremt lång period (T_P) — i Solens fall runt 11 år med en motsvarande låg rotationsfrekvens (f_D=0,15 Hz). När stjärnan sedan slocknar ökar f_D med motsvarande kortare T_P enligt grundformen (se härledningarna längre ner i Perioden tP)

1 f_D³

—— = —————— · 6,4 T10 · S²M³/KG

T_P r_max

Den cykliska perioden (T_P) beror endast av tätheten (r_max) tillsammans med rotationen (f_D).

Vi noterar att termen f_D inte KAN förekomma i modern akademi (inte i något som helst sammanhang): städstjärnan som begrepp finns inte i modern akademi eftersom man där har en helt annat uppfattning om hur en stjärna producerar sin energi. Se vidare jämförelse i Stjärnstädet.

Stjärnor vars pulser — generellt, stjärnans allmänna ljusvariationer — uppvisar motsvarande lägre rotationer (under 100 Hz — vilket grovt sett motsvarar T_P över 1 sekund) bör därmed i stora och grova drag vara stjärnor som fortfarande befinner sig i sin aktiva energicykel (eller möjligen i slutfasen) och som därmed uppvisar väsentligen annorlunda pulsegenskaper.

Rotcykloidens allmänna ekvation

Vi skriver rotcykloiden mera generellt på formen i PREFIXxSIN

rotcykloidens allmänna ekvation, vägen-tiden:

y = [(cosx)²]ⁿ

rotcykloidens derivata, hastigheten-tiden:

y’ = n[(cosx)²]^n–12(sinx)(cosx)

= n[(cosx)²]^n–1(cos2x) ........... trigonometrisk ekvivalent

Hastighetsfunktionen, y’, definierar en lutning i y=0 som bestämmer grafens typ. Om vi känner x vid y=0 kan typgrafen bestämmas genom hastighetsfunktionens derivata, alltså via [y’]’=y’’. Vi får den enligt

y’’ = [n[(cosx)²]^n–1]’(cos2x) + (cos2x)’[n[(cosx)²]^n–1]

= [n(n–1)[(cosx)²]^n–2(cos2x)](cos2x) + 2(sin2x)[n[(cosx)²]^n–1]

= n(n–1)[(cosx)²]^n–2(cos2x)² + 2n[(cosx)²]^n–1(sin2x) ;

I skärningspunkten gäller rotcykloidens toppvärde, analogt x=90° ;

= 0 + 2n[1]^n–1(–1) ;

= – 2n ;

n = –0,5y’’

Notera att rotcykloidens period är p.

Med vinkelkoefficienten a (a=[p/T_P]=pf) tillsammans med variabeln x ges mera fullständigt

n = –(1/2a²)y’’

Dessa sambandsformer är inte aktuella i detta skede av beskrivningen, men vi kommer att behöva dem längre fram.

Rotcykloidens koppling till pulsaren

Pulsarkopplingen

Betrakta funktionsformen för expansionshastigheten i det evigt utvidgande fallet,

v² = 2Gm₂/r

För varje r finns en innesluten centralmassa m₂ och vilka två variabler ger aktuell expansionshastighet v, förutsatt ekvivalens mellan g-energi (gravitell energi) och k-energi (kinetisk energi).

CENTRIFUGALACCELERATIONEN å=v²/r=Gm₂/r² med v²=Gm₂/r är den komponent som g-kraften (och g-energin) härleds på i grundfysiken.

Eftersom en tilläggsrotation — v_D=wr_D=2pf_D · r_D — reducerar g-kraftens inverkan och därmed sänker v_max i detonationstillfället (D) kan vi för just det tillfället idealt sätta

v_D = wr_D = 2pf_D · r_D ; ................

suffixet D markerar Detonationsläget,

r_D = (3m₂/4pr)^1/3 ;

v_D = f_D(6p²m₂/r_max)^1/3 ; ................

rotationshastigheten via maxtätheten, centralmassan och rotationsfrekvensen

expansionens maxhastighet (v_max), r=r_D:

———————————————

v = (2Gm₂/r)^0,5 – v_D ;

———————————————

v_max betraktas här idealt som en utgångshastighet (under nuklidrekylens intervall) vid r_D.

Om v_D=0, närmar sig v x-axeln obegränsat utan att någonsin tangera denna.

v-DERIVATAN, samma som andra vägderivatan y’’ från rotcykloidens y-funktion, ger då y’’=v’ enligt

v’ = (0,5)(2Gm₂/r₀)^–0,5(–2Gm₂/r₀²) ;

................... lutningen i skärningspunkten vid max r=r₀

= –(Gm₂/2r₀³)^0,5 ;

................... kopplar till föregående y’’ (andra vägderivatan)

Därmed kan föregående omnämnda rotcykloidens formfaktor n=–(1/2a²)y’’ beräknas exakt.

NOTERING. Ur v_D=f_D(6p²m₂/r_max)^1/3 ges även v_D=f_D2pr_D med m₂/r_max=V=4pr_D³/3.

Skärningspunkten med x-axeln definieras via minsta lilla värde på v_D större än noll. Skärningen motsvarar situationen då expansionen helt har avstannat, v=0, vid stjärnradien r=r₀ och expansionsmassan m₂ är på väg att vända tillbaka. Detta ger oss

0 = (2Gm₂/r₀)^0,5 – v_D ;

v_D = (2Gm₂/r₀)^0,5 ;

v_D² = 2Gm₂/r₀ ; (=k_D)

——————————

r₀ = 2Gm₂/v_D²

..................................... v_D>0, stjärnans maximala utsträckning från centrum

——————————

= 2Gm₂/(2pf_D · r_D)² ...................... f_D>0

r_D = (3m₂/4pr_max)^1/3 .......................... stjärnradien vid detonationstillfället

Med r_D avses då rotationen vid tillfället för expansionens första möjliga tidsintervall, dvs., direkt efter detonationen.

Rotationsfrekvensen f_D kan vara hur liten som helst. Oavsett värdet vänder expansionen vid r₀.

Med givet r₀ och huvudmassa (m₂) ges tätheten vid expansionens slutpunkt enligt

r₀ = 3m₂/4pr₀³ = (3m₂/4p)(v_D²/2Gm₂)³

= 3(v_D²)³(32pG³m₂²)^–1

Täthetens variation r

Tätheten idealt med g- och k-ekvivalensen samt utan rotation är via expansionstiden T lika med (allmänna expansionssambandet)

r = (3/2pG)T^–2

TäthetsVarianten med avseende på tiden är

r’ = –2(3/2pG)T^–3 = dr/dT

För att få denna grundvariant att visa nollvärde vid r₀ behöver vi bara addera en motsvarande »enkel» konstant (en täthetshastighetskonstant) enligt

r’(0) = –2(3/2pG)T^–3 + k

SPECIELLT relaterar vi k som konstant med förutsättningen att rotationens dämpande effekt bildas vid själva detonationstillfället (materialkontakten, utan vidare analys) och därmed därefter ger en helt linjär tilläggskomponent. I fall där k är olinjär måst vi i så fall söka orsakerna genom ytterligare, yttre, faktorer.

Cykloidens period T_P, Del I

Vi löser ut k och får

k = (3/pG)T₀^–3

Det är viktigt att markera T här explict (T₀), eftersom den ger cykelns (halva) period. Vi får då

cykloidens period T_P=2T₀.

Differentialekvationen för täthetsfunktionen blir då

dr = –2(3/2pG)T^–3 dT + k dT

med integralen

ò dr = r = (3/2pG)T^–2 + kT = (3/pG)(1/2T²+T/T₀³)

Eller direkt från r:=r+kT.

Vi frånser här tills vidare offsetvärdet för T (i storleksordningen 200µS som gäller för en Vätekropp) vid detonationstillfället och vilken term (av typen a[T+t₀]^–2) måste subtraheras från ovanstående (därmed modifierade, a[0+t₀]^–2-) integral för att denna ska bli fullständigt bestämd.

Cykloidens period T_P, Del II

Med r=(3/2pG)T^–2+(3/pG)T₀^–3T=(3/pG)(1/2T²+T/T₀³) ges med

T_{TOTALA EXPANSIONSTIDEN}=T₀ ekvivalenterna

r₀ = (3/pG)(1/2T₀²+1/T₀²) = (3/pG)(1/2T₀²+2/2T₀²)

= (3/pG)(3/2T₀²)

= 9/2pGT₀² ;

T₀² = 9/2pGr₀ ;

T₀ = 3/Ö 2pGr₀ = TÖ3 med T=Ö (3/2pGr);

T_P = 2T₀

= 3Ö 2/pGr₀ = TÖ12 .......................... cykloidens period

från föregående (suffixet D markerar som tidigare Detonationspunkten):

k_D = v_D²

v_D = (2Gm₂/r₀)^0,5................................... rotationshast. via maxtäth., centralmassan

och rotationsfrekvensen

= 2pf_D · r_D ...................................... allmänna sambandet, v=d/T=2pr/T

r₀ = 2Gm₂/v_D² ..................................... v_D>0, stjärnans maximala utsträckning

från centrum

r_D = (3m₂/4pr_max)^1/3 ......................... stjärnradien vid detonationstillfället

Stjärnradiens största utsträckning r₀

(ideal sfär):

r₀ = 3m₂/4pr₀³ ..................................... allmänna täthetssambandet *

r₀ = 2Gm₂/k_D ...................................... stjärnans maximala utsträckning

från centrum (se ovan)

= 2Gm₂/v_D² .................................... v_D>0

= 2Gm₂/(2pf_D · r_D)² ....................... f_D>0

= Gm₂/2(pf_D · r_D)²

*(r=m/V)

Tätheten vid r₀, r₀

r₀ = 3m₂/4pr₀³ .......................... allmänna täthetssambandet

Efter utvecklingar med ekvivalenten för

r₀ = Gm₂/2(pf_D · r_D)² ................ stjärnans max utsträckn. från centrum (se ovan)

ges

r₀ = (54/16)(pf_D²/G)³r_max^–2 ..... r₀ ändras endast med rotationsfrekvensen

;

Cykloidens period T_P, Del III

T_P = 3Ö 2/pGr₀ ............................... cykloidens period, utvecklingarna i Del II

Efter utvecklingar med ekvivalenten för r₀ ges

= 4Gr_max(3^1/2p²f_D³)^–1 ................. T_P ändras endast med rotationsfrekv.

Rotationsfrekvensen f_D

Rotationsfrekvensen vid detonationen fås ur perioden T_P enligt

f_D = (4Gr_max/T_Pp²Ö3)^1/3 .................... rotationsfrekvensen ur perioden

SLUTFORMEN:

Med r₀ (höjden) och T₀ (halva perioden) kända, och därmed tillämpade på den tidigare härledda allmänna cykliska ekvationen

y = [(cosx)²]ⁿ ......................................

rotcykloidens allmänna ekvation i PREFIXxSIN, vägen-tiden

y’ = n[(cosx)²]^n–1(cos2x) .....................

rotcykloidens derivata, hastigheten-tiden

är matematiken för den dämpade idealt eviga expansionen därmed så långt förklarad — med här angivna förenklingar.

Vi noterar som tidigare att cosinusfunktionens standardperiod om 2p I ROTCYKLOIDENS FALL motsvarar TVÅ T_P — analogt en T_P per p.

Med denna justering ges motsvarande

y = [(cos ax)²]ⁿ

rotcykloidens allmänna ekvation i PREFIXxSIN, vägen-tiden

y’ = na(cos2ax)[(cos ax)²]^n–1

rotcykloidens derivata, hastigheten-tiden

a = [p/T_P] = pf

Rotcykloidens formfaktor n

n = –(1/2a²)y’’ .................................... från föregående utveckligar

= –T_P²(1/2p²)y’’

y’’ = –(Gm₂/2r₀³)^0,5 ............................. från utvecklingarna av v’ ;

n = T_P²(1/2p²) · (Gm₂/2r₀³)^0,5

T_P = 2T₀ = 3Ö 2/pGr₀ = TÖ12 ;

Efter utvecklingar ges

n = 4Gr_max/p⁴f_D³

............................. n (rotcykloidens form) beror enbart på rotationen med given täthet

Pulsarens reduktion med tiden

Om vi ser allmänt till stjärnans impulsmoment J=mvr och förutsätter ett visst inflöde av massa, tillväxer också J likaledes: J och m skulle därmed vara proportionella. Emellertid bestämmer stjärnans maximala täthet vid detonationen r-värdet. Ökar m måste r också öka. Med konstant J (från m) tvingas därför v avta proportionellt med växande r. Därmed reduceras perioden.

På motsvarande sätt kan pulsfrekvensen, analogt rotationen, öka om stjärnan (av olika anledningar) inte tar emot lika stor massa vid en ny puls som den puttade ut i föregående.

· Massa som avges medför alltså högre pulsfrekvens (T_P®0);

· Massa som tillkommer medför lägre pulsfrekvens (T_P®¥).

Analogin är densamma som vi kan iaktta hos ett uppmonterat fritt snurrande hjul. Häller vi på vatten på hjulet (inkommande extramassa) bromsas rotationen.

Till detta måste vi dock observera stjärnans allmänna utveckling under TID: att dess rotation tvunget avtar som funktion av friktionen mellan inre snabbare roterande delar och yttre mera långsamma rotation. Denna detalj gör analysen betydligt mera komplicerad över långa tidsintervall.

Jämför konventionella begrepp (man tittar inte på filmen från biosalongens sida, utan från scenens baksida);

”Vad är det då för energikälla som ger kraft åt dessa starka röntgenkällor? Pulsaren i Krabbnebulosan avger pulserande röntgenstrålning med samma pulsationsperiod på 33 ms som på radiovåglängderna. Den troligaste källan till en så regelbunden pulsation är rotation, och man anser alltså att det är en roterande neutronstjärna som ger upphov till pulserna. Den observerade uppbromsningen av rotationsperioden och den därav följande reduktionen i stjärnans rotationsenergi tyder dessutom på att energikällan måste vara just rotationen, men pulsaren i Krabbnebulosan är i det avseendet unik bland röntgenstjärnorna. Centaurus X‑3 har en mycket längre pulsationsperiod på 4,84 s, vilket innebär att den upplagrade rotationsenergin måste vara i motsvarande grad mindre. Om denna röntgenkälla ”drevs” av rotationsenergin skulle den bromsas upp helt på mindre än tio år. Men så är inte fallet; tvärtom ökar rotationen i stället sitt tempo. Följaktligen kan Centaurus X‑3 och fö. huvudparten av röntgenstjärnorna — till skillnad från radiopulsarerna — inte ha upplagrad rotationsenergi som kraftkälla.”

BONNIERS ASTRONOMI 1978 s118sp1m

Som vi ser är den moderna akademins uppfattande förmåga i ämnet inte (helt) heltäckande i möjligheterna i förhållande till TNED.

pulsar enligt TNED

BEGREPPET PULSAR ENLIGT TNED

För orienterande bekantskap med begreppt stjärna och Stjärnfysikens Grunder enligt TNED, se från Solfysiken.

Pulsarens uppkomst enligt TNED

NÄR VÄTEBRÄNSLET TAR SLUT I EN STJÄRNA tappar stjärnan motsvarande strålningstryck. Det betyder att den stora stjärnglobul (själva den stora enorma lysande stjärnsfären) som utgör den egentliga fysiska stjärnan — och som garanteras av just strålningstrycket — sjunker ihop och kvarlämnar den rena råa städkärnan.

OPACITETSOMRÅDET FÖLJER MED när stjärnan börjar falna ner mot det central stjärnstädet. Detta är klart därför att joniseringen försvinner (utjämnas) successivt med strålningstryckets avtagande. Vartefter strålningstrycket avtar, neutraliseras ytdelarna — och försvinner därmed ur sikte.

LYSGLOBULEN fortsätter (alltså) att sända ut ljus från den allt avtagande opacitetsytan med samma ytljustäthet som gäller för normalstjärnans yta;

Effekten av den slocknande stjärnan blir densamma som att betrakta en glödlampa som lyser med konstant lyseffekt men som avlägsnar sig alltmer tills dess ljus helt försvinner ur vårt synfält.

Därmed framstår stjärnan som allt mindre och mindre, allt svagare och svagare, med bibehållen ytljusstyrka — ända ner till städytan!

Emellertid får vi nog INTE räkna med att ljusemissionen från den falnande stjärnan är så konstant som i det normalt lysande fallet.

När en stjärna når sitt mest kompakta läge och atomkärnorna börjar klonka ihop, finns förutsättningar att bilda kärnrekyl enligt atomkärnans formbevarande kraft. Beroende på omständigheterna kan då stjärnan börja expandera på ett otal möjliga sätt när g-energin från kontraktionen frigörs. Det finns bara en matematik att välja på.

begreppet kompaktstjärna

I den här framställningen kallas en utbränd stjärna av ovanstående beskrivna typ kompaktstjärna. En kompaktstjärna är alltså rätt och slätt den resterande städkärnan hos en stjärna som inte längre producerar energi från fusioner och därför heller inte har något strålningstryck och därför heller inte har någon normal omgivande stor stjärnglobul. Den kallas också i TNED för pulsar — om omständigheterna medger en sådan dynamik.

Pulsar är i TNED en stjärna som producerar ljus i perioder utom fusionsbaserad energiproduktion.

Tillämpningen av elektriska kraftlagen på atomkärnan innefattar automatiskt dess oändliga fraktala ±b-ringstruktur (J=mvr) enligt principformen

F=k(Q/r)²=k([Q/(n®¥)]/[r/(n®¥)])²=k(Q/r)²

Härav följer direkt atomkärnans odeformerbara natur: r står redan i princip på 0. Kärnan är emellertid inte helt stel (men mycket nära). Den besitter en viss (transversell) elasticitet som kan uttryckas via ett axiellt formstopp (x_f, se Atomkärnans geometri under axiell deformation) vid vilket den intryckande och rekylerande deformerande kraften går mot oändligt. Sambanden beskrivs vidare i K-CELLENS DETONATION och bildar grundvalen för K-cellens periodiska fysik — och stjärnornas, enligt TNED.

Sammanfattning

»GAMLA STJÄRNOR» som hunnit igenom sin exotermiska termonukleära energicykel är normalt sett ljusdöda objekt. De strålar inte längre. Stjärnan drar ihop sig mot primärstadiet då strålningstrycket försvinner, vilket i stort sett innebär att endast DET CENTRALA STJÄRNSTÄDET återstår. En sådan stjärna kallas här för en kompaktstjärna. Drivs stjärnans sammandragning så långt att den når sin absolut maximala täthet — tillfället då dess atomkärnor vidrör varandra — måste rörelseenergin från den infallande stjärnmassan omsättas i en motsvarande rekyl då atomkärnorna stöter ihop.

Om stjärnan har egenrotation, motverkas rekylkraften av den dämpande centrifugalkraften. Därmed utvecklas inte den fulla g-energin (gravitationsenergin) i den rekylerande expansionen i ekvivalens med k-energin (kinetiska energin) varför expansionen avstannar och vänder tillbaka. Ju högre rotationen är desto snabbare avstannar expansionen för att bilda ännu en kontraktion med en ny rekyl, osv. Genom att använda en viss förenklad matematisk sambandsform kan pulsningens periodicitet och rotationens frekvens bestämmas ur varandra.

Fortsättning i PULSARMATEMATIKEN ENLIGT TNED.

Citatsamling, pulsar

INLEDANDE CITAT FRÅN KONVENTIONELL LITTERATUR SOM BESKRIVER BEGREPPET OCH TERMEN PULSAR

”Begreppet pulsar är ett annat historiskt misstag — pulsarer roterar, de pulserar inte.”

BONNIERS ASTRONOMI 1978 s68sp2n

Stjärnor som utsänder röntgenstrålning upptäcktes först år 1962 [BAs111sp2ö].

Stjärnor som utsänder pulserande radiostrålning (pulsarer) upptäcktes först år 1967 [BAs111sp2mö].

Fetstilen i styckena är min markering.

”Sedan 1967 har man upptäckt många fler pulsarer (ca 200), med perioder varierande från fyra sekunder till 33 millisekunder — den sistnämnda är perioden för pulsaren i Krabbnebulosan. Denna är särskilt intressant eftersom den gav det slutgiltiga beviset för att

pulsarerna är neutronstjärnor med starka magnetfält; radiopulsernas regelbundenhet åstadkoms genom dessa stjärnors snabba rotation”

BONNIERS ASTRONOMI 1978 s111sp1m

”Krabbnebulosan har redan nämnts; här utgör röntgenstrålningen nästan säkert synkrotronstrålning.”

BONNIERS ASTRONOMI 1978 s298sp2ö

”Eftersom vi har ett så dåligt teoretiskt grepp om orsakerna till strålningen från pulsarerna, säger denna oss ganska lite om neutronstjärnornas natur.”

BONNIERS ASTRONOMI 1978 s114sp1ö

”Begreppet pulsar är ett annat historiskt misstag — pulsarer roterar, de pulserar inte.”

BONNIERS ASTRONOMI 1978 s68sp2n

”De pulserande variablernas ljus ökar och minskar genom att hela stjärnan regelbundet sväller och drar ihop sig.”

BONNIERS ASTRONOMI 1978 s71sp2ö

”År 1968 fann man alltså en pulsar i riktning mot krabbnebulosan, och år 1969 identifierades en stjärna, belägen i supernovaresterna, känd som Baades stjärna och noterad för sitt egendomliga spektrum, som den eftersökta pulsaren.”

BONNIERS ASTRONOMI 1978 s111sp2mn

;

”Tyvärr har hittills inga av de observerade neutronstjärnorna uppvisat några spektrallinjer”

BONNIERS ASTRONOMI 1978 s114sp2ö

”Pulsaren i Krabbnebulosan, den med den kortaste kända perioden, är den enda där man tveklöst upptäcker pulser hela vägen genom det elektromagnetiska spektret, från radiovågor till gammastrålning.”

BONNIERS ASTRONOMI 1978 s113sp2mn

”På något sätt skapas någonstans i den rotande magnetosfären koherent (laserliknande) radiostrålning. Denna koncentreras till en smal stråle och ger liksom blänket från en fyr en radiopuls varje gång denna stråle sveper över jorden. Därutöver emitteras också mycket snabba (relativistiska) partiklar.”

BONNIERS ASTRONOMI 1978 s113sp2mn

”På något sätt matas rotationsenergin från pulsaren ut i den omgivande nebulosan, till en stor del i form av snabba partiklar som vid växelverkan med det omgivande magnetfältet alstrar synkrotronstrålning.”

BONNIERS ASTRONOMI 1978 s113sp2ö

”Krabbnebulosan befinner sig ca 2000 pc från oss och har en diameter på 4 pc. Dess massa är ungefär lika stor som solens. Synkrotronstrålning avges på alla våglängder från radio till röntgen och sannolikt också i gammaområdet”

BONNIERS ASTRONOMI 1978 s297sp2mö

1 pc=3,0856 T16 M = 3,2614819 ljusår; 2 Kpc @ 6 523 ljusår

ENCARTA 99 Crab Nebula anger avståndet till ”about 6,300 light years”.

”En neutronstjärna med samma massa som solen har en radie på bara 15 km.”

BONNIERS ASTRONOMI 1978 s110sp2ö

; r=m/V=3(1,939 T30 KG)/(4pr3)=1,40692 T17 KG/M3

”Vid densiteter kring ca 10¹⁷ kg/m³ har kärnorna dock försvunnit helt (fig. 6.4). Materian består i sådana fall nästan helt av fria neutroner, plus 0,5% protoner och elektroner.”

BONNIERS ASTRONOMI 1978 s110sp1mn

”De korta tidsskalorna tyder på att röntgenemissionen måste komma från relativt små, kompakta objekt.”

BONNIERS ASTRONOMI 1978 s118sp1mö

”Vad är det då för energikälla som ger kraft åt dessa starka röntgenkällor? Pulsaren i Krabbnebulosan avger pulserande röntgenstrålning med samma pulsationsperiod på 33 ms som på radiovåglängderna. Den troligaste källan till en så regelbunden pulsation är rotation, och man anser alltså att det är en roterande neutronstjärna som ger upphov till pulserna. Den observerade uppbromsningen av rotationsperioden och den därav följande reduktionen i stjärnans rotationsenergi tyder dessutom på att energikällan måste vara just rotationen, men pulsaren i Krabbnebulosan är i det avseendet unik bland röntgenstjärnorna. Centaurus X‑3 har en mycket längre pulsationsperiod på 4,84 s, vilket innebär att den upplagrade rotationsenergin måste vara i motsvarande grad mindre. Om denna röntgenkälla ”drevs” av rotationsenergin skulle den bromsas upp helt på mindre än tio år. Men så är inte fallet; tvärtom ökar rotationen i stället sitt tempo. Följaktligen kan Centaurus X‑3 och fö. huvudparten av röntgenstjärnorna — till skillnad från radiopulsarerna — inte ha upplagrad rotationsenergi som kraftkälla.”

BONNIERS ASTRONOMI 1978 s118sp1m

Solfysiken · Stjärnornas omfång | GRÄNSMASSORNAS RADIER ENLIGT TNED | SVARTA HÅL FINNS INTE I FYSIKEN | Jämförelser med MAC

SVARTA HÅL FINNS INTE I FYSIKEN ENLIGT TNED

Jämförande översikt — se utförligt i härledningen till Ljusets Gravitella Beroende

RELATERAD FYSIK (TNED)	MODERN AKADEMI (MAC)
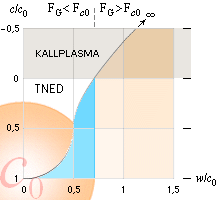
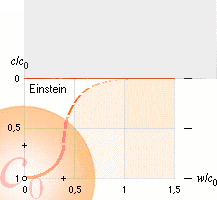
c = c0[1 – w^2/cc0] Korrekt vektorform	c = c0[1 – w^2/cc] Einsteins stympade version
Kraftvektorledet garanterar bevarandet av naturkonstanten c0 — oberoende av gravitationens inverkan	ingen koppling
TNED	MAC/Einstein
Kraftvektorledet, fysikens grund:	får ej förekomma
Fc0 – Fc – FG = 0	får ej förekomma
Vektormodell:	c=0 kan ej existera
	får ej förekomma pga negativa c
rc=0 = 2Gm2/c0^2 = 1,48427 t27 · m2	Benämns Schwarzschildradien
enligt	enligt
Vid c=0 gäller tydligen från ljusets gravitella beroende (1) 0 = (1/2)[c0 – Ö |–c0^2+4w^2 | ] ; (2) 0 = c0 – Ö |–c0^2+4w^2 | ; (3) –c0^2+4w^2 = c0^2 ; (4) 4w^2 = 2c0^2 ; (5) 2w^2 = c0^2 = 2 · Gm2/rc0 (6) = 2rc0^2(4pGr/3) (7) = rc0^2(8pGr/3) ; (8) rc0 = 2Gm2/c0^2 (9) = c0/Ö(8pGr/3) ; ; r = 3m2/4pr^3 anger tätheten i KG/M^3 ; r = (3m2/4pr)^1/3 ; m2/r = m2(4pr/3m2)^1/3 = m2^2/3(4pr/3)^1/3 ; (10) c0^2/2 = w^2 = Gm2/r = Gm2^2/3(4pr/3)^1/3 från (5); (11) c0^2/2 = Gm2^2/3(4pr/3)^1/3 ; (12) m2^2/3 = c0^2/2G(4pr/3)^1/3 ; (13) m2 = c0^3/(2G)^3/2(4pr/3)^1/2 ; (14) = r^–1/2(c0/ÖG)^3Ö 3/32p (15) = r^–1/2(8,54444 T39)(KG/M)^3/2 (16) = r^–1/2(769/90 T39)(KG/M)^3/2	se Deriving the Schwarzschild solution @INTERNET Flera olika källreferenser finns, t.ex. Wikipedia Deriving the Schwarzschild solution 2008-10-04 — dessa avhandlar alla lösningar till Einsteins fältekvationer av Karl Schwarzschild (år 1915): Utvecklingarna går ut på att lösa ut koefficienter för gränsövergångar som innefattar c=0 — vilket i grunden är otillåtet enligt relativitetsteorin, tidens upphörande enligt Einstein

Se vidare i ATOMKÄRNANS GRAVITELLA HÄRLEDNING

Se även i DET EKOLOGISKA UNIVERSUMET och EINSTEINS SAMBAND.

TNED FÖRKLARAR:

Termen svart hål i fysiken kommer från den moderna akademins uppfattning (genom Einsteins relativitetsteori) att atomkärnan KAN (måste kunna) komprimeras oändligt.

För en Helium-4-kropp där atomkärnorna ligger helt tätt mot varandra med tätheten ca r=6,5 T17 KG/M³ uppnås enligt TNED nolldivergens c=0 i kroppsytan då centralmassan (m₂) blir drygt 5 Solmassor (sambandet i nr16 ovan). Alla sådana massor och tyngre som inte utvecklar en aktiv kraft i form av t.ex. fusionsenergi blir enligt modern akademi — obönhörligen och oåterkalleligen — svarta hål. Dämed, som man säger, ”kollapsar massan under nollvolym” — eftersom inget stopp finns i modern tankevärld för den ändliga massans minsta utsträckning: masskroppen förvandlas i princip och enligt MAC (modern akademi) till en helt osynlig ”nollpunkt”.

I TNED DÄREMOT bestäms maximal täthet av atomkärnans formbevarande kraft — som är identisk med den enkla elementära elektriska kraftlagen enligt

F = k(Q/d)²=k([Q/(n®¥)]/[d/(n®¥)])² = k(Q/d)²

Se utförligt från Atomkärnans härledning enligt TNED: Atomkärnan står redan på noll garanterat av atomkärnans oändligt fraktala struktur

[d/(n®¥)]: atomkärnans masstäthet går mot oändligt med växande fraktaldjup [MASSTÄTHETEN I FORMYTAN VÄXER OBEGRÄNSAT med växande n i massekvivalenten m=(n®¥)·m/(n®¥)]: atomkärnans massa ligger i en ytform. Se även utförligt från Planckringen h=mvr. Inte i en volymform. Atomkärnan kan därför INTE komprimeras. ELEKTRISKA KRAFTLAGEN garanterar följaktligen ENLIGT TNED:

det finns inga svarta hål, har aldrig funnits svarta hål, kommer aldrig att finnas svarta hål. Finns inte en chans. Helt rent.

Däremot finns ENLIGT TNED kroppar med nolldivergens (noll ljushastighet) i kroppsytan. Se även utförligt från c₀-kroppen.

Se också i

GRÄNSMASSORNA GENOM EXPANSIVA-KONTRAKTIVA OCH STATISKA TILLSTÅNDENS MATEMATISKA G-FYSIK ENLIGT TNED.

TERMEN ”svart hål” är ett MAC-begrepp som ansluter till den s.k. Schwarzschildradien [Se utförligt i EINSTEINS SAMBAND]

r_c=0 = 2Gm₂/c₀² = 1,48427 t27 (M/KG) · m₂.

Sfäriska radien r_c=0 betyder att ljushastigheten är noll där på grund av den starka gravitationen. Sambandet tillhör TNED, inte MAC, och det är här inte känt varifrån MAC har fått sitt uppslag [Se utförligt i EINSTEINS SAMBAND] på annat sätt än att det bildar en gränsform till TNED (c=0 innebär enligt MAC ’tidens upphörande’).

Obetingat innebär r_c=0 en obegränsat liten kropp vars täthet kan växa obegränsat, en s.k. singularitet enligt MAC.

I TNED gäller r_c=0 — från ljusets gravitella beroende — enligt alternativen

begränsad täthet r r_c=0 = (3c₀²/8pGrmax)^1/2

gäller praktiskt i materiefysiken genom atomkärnans inkompressibilitet

obegränsad täthet r_c=0 gäller i relaterad fysik endast inom atomkärnans ytstruktur, denna ingår inte i MAC, se atomkärnans gravitella härledning

Spåras universums expansion baklänges, stannar den tvunget på en maximal täthet: atomkärna vidrör atomkärna. Enligt TNED svarar atomkärnan vid axiellt tryck med att öka den totala kärnvolymen (se atomkärnans geometri under axiell deformation), vilket för tätt liggande kärnor innebär ett explosionsartat rekylförlopp. Atomkärnan kan inte ”dödas” genom g-tryck, utan svarar med en lika stor motsatt kraft. Därmed grundläggs K-cellens fysik på expansion och kontraktion i centrum av den allmänna c0-kroppen.

Se även vidare från expansionsmatematiken.

novorna i MAC

Den moderna akademins (MACs) uppfattning om hur novorna bildas

— Men om man anser att atomkärnorna inte uppvisar något som helst stopp — frånsett andra uppenbara frågetecken — hur resonerar man då i modern akademi för att försöka förklara uppkomsten av de s.k. novorna, typ Krabbnebulosan? Är det inte uppenbart att en sådan ”explosion” kräver ett motsvarande HÅRT STÄD någonstans?

I modern akademi anser man att massa är högfrekvent ljus [FOCUS MATERIEN 1975 s262sp1mö] och att därför skillnaden mellan ljus och materia inte är skarp och distinkt. Det finns ingen åskådlig modell för atomkärnan. Eller rättare sagt: det får inte finnas någon sådan modell för då bryter det moderna akademiska syndikatet samman. Därmed har man eliminerat den kvalitativa aspekten på massans fysiska natur. Därmed är man också fri att behandla fysiken uteslutande på rent kvantitativ bas — med tillhörande konsekvensmässiga kvalitativa uppfinningar (!). Den mest sevärda är (alltså) den som utsäger att massa kan komprimeras oändligt. Det finns ingen gräns för hur mycket massa som kan komprimeras på hur små volymer som helst, säger modern akademi.

När det sedan gäller att försöka förklara hur en supernova kommer till, finner man LIKVÄL omfattande utläggningar om att atomkärnan visst INTE är kompressibel. Se exv. inline-artikeln i ENCARTA 99 på Novae and Supernovae, How a Supernova Explodes.

Den artikeln kan också nås direkt på @INTERNET (2008-10-04), sök på ”How a Supernova Explodes”.

Fetstilen är min markering:

”Nuclear matter is highly incompressible. Hence once the central part of the core reaches nuclear density there is powerful resistance to further compression. That resistance is the primary source of the shock waves that turn a stellar collapse into a spectacular explosion.”

”The compressibility of nuclear matter is low but not zero, and so momentum carries the collapse beyond the point of equilibrium, compressing the central core to a density even higher than that of an atomic nucleus. We call this point the instant of “maximum scrunch.” Most computer simulations suggest the highest density attained is some 50 percent greater than the equilibrium density of a nucleus. After the maximum scrunch the sphere of nuclear matter bounces back, like a rubber ball that has been compressed.”

ENCARTA 99 Novae and Supernovae, How a Supernova Explodes

Min översättning:

Kärnmaterial är högeligen inkompressibelt. Således när väl den centrala delen hos [stjärn-] kärnan når kärntäthet finns ett kraftfullt motstånd mot ytterligare kompression. Det motståndet är den primära källan till chockvågen som förvandlar en stjärnkollaps till en spektakulär explosion.

Kompressibiliteten hos kärnmateria är liten men inte noll, och så bär rörelsemängden kollapsen bortom jämviktspunkten, komprimerande den centrala [stjärn-] kärnan till en täthet även högre än den hos en atomkärna. Vi kallar denna punkt för tillfället för ’maximal ihopkrasning’. De flesta datorsimuleringar antyder att den högsta täthet som uppnås är sådär en 50 procent större än jämviktstätheten hos en [normal] atomkärna. Efter den maximala ihopkrasningen studsar sfären hos kärnmaterialet tillbaka, som en gummiboll som har pressats ihop.

Frånsett storleksordningen på ihoptryckningen, ’runt 50%’ enligt citatet ovan, är förloppet principiellt detsamma enligt TNED (se särskilt Atomkärnans geometri under axiell deformation). Se även i K-cellens detonation, principen är densamma. [Se även i deplacementets strukturdjup i kärnytan] [Se grundformen i Laddningsdeplacementet]. Artikelförfattaren synes dock ha en högst märklig uppfattning om ’högeligen inkompressibel’ (eng. highly incompressible) i värdeexempel: Om man kan pressa ihop (ovalisera) sitt cykelhjul hela 50% är det en högst betydande kompressionsfaktor. En ENLIGT TNED mera relevant siffra i den praktiska fysiken är själva hjulgummits deformation via det smågrus hjulet möter på sin väg. Inget mer.

Det ska också sägas:

Den moderna akademin är (stundtals) full av kombatterande forskare som försöker övertyga varandra om just SIN ståndpunkt, eller som riktar djupa betänkligheter mot någon viss hypotes eller teori. Frågan om ATOMKÄRNANS MOTSTÅND MOT FORMFÖRÄNDRING tycks vara ett sådant ämne. Söker man på Webben (2008-10-04) hittar man (alltså) inte mycket till upplysning, i själva verket i stort sett ingenting alls — i varje fall i det utbud som är GRATIS.

Fortsättning i Solfysiken …

Länken närmast ovan kopplar till

SOLFYSIKEN DEL I: Solens tre ekvationer med grundmatematiken till stjärnfysiken enligt TNED med jämförande beskrivningar i modern akademi.

I Pulsarerna ges en mera ingående (detaljerad, jämförande) fortsättning på den inledande pulsarmatematiken som genomgåtts ovan (Eller om man så vill, en inledning …).

I STJÄRNFYSIKEN DEL II ges den mera heltäckande beskrivningen ENLIGT TNED för stjärnornas allmänna förekomst och fördelning tillsammans med förklaringen till HR-diagrammen. Där ges också utförliga jämförelser och korsreferenser med den moderna akademins uppfattningar.

SolfysikenRadierna

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Solfysiken Radierna

ämnesrubriker

innehåll:

STJÄRNRADIERNA

Stjärnornas omfång

Gränsfrekvensen för primär egenrotation

Stjärnornas omfång

Stjärnornas primära egenrotation

Rotationens inverkan på stjärnans fysik

Stjärnans egenproducerade rotation — matematik

Stjärnans egenproducerade rotation — illustrerad fysik

Tilläggsmassan

Maximala tilläggsmassan

Solrotationen — räkneexempel med Solen

Rotationerna, transformationssamband

Exempel med Sirius

Räkneexempel — Hur 1 primär Solmassa kan bli en jättestor stjärna

Kalkylkort himlakropparnas primärmassor

Stjärnans absoluta gränsmassa

Pulsarmatematiken

Pulsarmatematiken enligt TNED

Pulsarens grafiska ekvivalent

Rotcykloiden

Stjärnans rotationsfrekvens vid max täthet · fD

Solens kompaktrotation

Rotcykloidens koppling till pulsaren

Täthetens variation

Cykloidens period TP, Del I

Cykloidens period TP, Del II

Stjärnradiens största utsträckning · r0

Tätheten vid r0

Cykloidens period tP

Rotationsfrekvensen fD

Rotcykloidens formfaktor n

Begreppet pulsar enligt TNED

Begreppet kompaktstjärna

Citatsamling pulsarerna

Den moderna akademins svarta hål

Svarta hål finns inte i fysiken enligt TNED

Jämförande översikt

Novorna i modern akademi

REGISTER

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[BA]. BONNIERS ASTRONOMI 1978

— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad 10-potensbeteckning, t för 10^–, T för 10⁺

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav — liksom nedanstående tusenprefix.

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM.

TNED

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2018-11-21

*END.

Stavningskontrollerat 2008-03-06

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se